2015年第十三届走美杯四年级考题及答案
2016年第14届“走美杯”小学数学竞赛试卷(四年级初赛B卷)

2016年第14届“走美杯”小学数学竞赛试卷(四年级初赛B卷)一、填空题Ⅰ(每题8分,共40分)1.(8分)计算:109×92479+6×109×15413=.2.(8分)给定一个除数(不为0)与被除数,总可以找到一个商与一个余数,满足被除数=除数×商+余数,其中,0≤余数<除数.这就是带余数的除法.当余数为0时,也称除数整除被除数,或者称除数是被除数的因数(被除数是除数的倍数).不超过988000并且能够被49整除的大于1的自然数共有个.3.(8分)只能被1与其自身整除的大于1的自然数称为素数或质数,比如2、3、5、7、11、13等.大于1的自然数如果不是素数,则称为合数.除唯一的偶数2之外,相邻的两个素数之间至少间隔一个合数,比如3、5;5、7;7、11等.两个连续的素数之间间隔的合数个数称为这两个连续素数的间隔数,间隔数为1的两个素数称为孪生素数,比如3、5;5、7;而7,11的间隔数为3,那么100以内的连续素数的最大间隔数为.4.(8分)大于0的自然数,如果满足所有因数之和等于它自身的2倍,则这样的数称为完美数或完全数.比如,6的所有因数为1,2,3,6,1+2+3+6=12,6就是最小的完美数,是否有无限多个完美数的问题至今仍然是困扰人类的难题之一.研究完美数可以从计算自然数的所有因数之和开始,567的所有因数之和为.5.(8分)将自然数15的0倍,1倍,2倍,3倍,4倍,5倍,…按照顺序写在下面0、15、30、45、60、75、…这一列数中可以一直写下去,并且后一个总比前一个数大,任何一个自然数要么是这一列数中的某一个,要么介于相邻的两个数之间,我们把这一列数叫做严格递增的无穷数列,从左至右的每一个数分别叫做这个数列的第一项,第二项,第三项,…,即第一项是0,第二项是15,第三项是30,…,依此类推,那么,介于这个数列的第135项与136项之间,并且与这两项中的较小的项的差是6,这个数为.二、填空题Ⅱ(每题10分,共50分)6.(10分)将一个正方形沿对角线剖分为4个直角三角形,然后按照如图所示方法移动4个直角三角形,中间空白处形成的正方形的对角线长为厘米.7.(10分)用一根长为36分米的铁丝做一个长方体框架,并且要求长是宽的2倍,长宽高都是整数分米.如果.不计损耗,可以做成的长方体体积最大为立方分米.8.(10分)在印度河畔的圣庙前,一块黄铜板上立着3根金针,针上穿着很多金盘.据说梵天创世时,在最左边的针上穿了由大到小的64片金盘,他要求人们按照“每次只能移动一片,而且小的金盘必须永远在大的金盘上面”的规则,将所有的64片金盘移动到最右边的金盘上面.他预言,当所有64片金盘都从左边的针移动到右边的时候,宇宙就会湮(yān)灭.现在最左边金针(A)上只有5片金盘,如图(1)所示,要按照规则,移动成图(2)的状态,至少需要移动步.9.(10分)在平面上,用边长为1的单位正方形构成正方形网略,顶点都落在单位正方形的顶点(又称为格点)上的简单多边形叫做格点多边形.而除去三个顶点之外,内部或边上不含格点的格点三角形称为本原格点三角形,如图所示的格点三角形MBN.每一个格点多边形都能很容易地划分为若干个本原格点三角形,那么,图中的格点四边形EBGF可以划分为个本原格点三角形.10.(10分)用2颗红色的珠子,2颗蓝色、2颗紫色、2颗绿色的珠子串成如图所示的手链,要求两颗红色珠子相邻,两颗紫色珠子相邻,那么,可以串成种不同的手链.三、填空题Ⅲ(每题12分,共60分)11.(12分)古罗马的凯撒大帝发明了世界上最早的数学加密方法:按照字母表的顺序,将每一个字母对应到按照某种事先的约定确定的字母.例如,将这个字母对应到他后面的第三个字母,也就是A→D,B→E,C→F,…W→Z,X→A,Y→B,Z→C,于是按照这个加密方法,单词“HELLO”,被加密成“KHOOR”.按照这种加密方法,海亮收到了一个加密后的密文“LORYHBRX”,那么,这个信息的原文是.12.(12分)恰好有12个不同因数的最小的自然数为.13.(12分)两个不全为0的数的公共因数成为它们的公因数.求出26019,826,2065的全体公因数.14.(12分)在一个摆满棋子的正方形棋盘中,甲、乙两人轮流拿取棋子,规则为:在某行或某列中,取走任意连续放置的棋子(即不能跨空格拿取),不允许不取,也不能在多行(多列)中拿取,当棋盘中所有棋子被取尽时游戏结束.取走最后一棵棋子的一方获胜.面对如图所示的棋盘,先手有必胜策略,先手第一步应该取走(写出所有的正确方案),才能确保获胜.15.(12分)在的圆圈中填入从1到14的自然数(每一个数用而且只能用一次),使连接在同一直线上的4个圆圈中的数字之和都相等,这称为一个7阶幻星图,这个相等的数称为7阶幻星图的幻和,那么,7阶幻星图的幻和为,并继续完成以下7阶幻星图.2016年第14届“走美杯”小学数学竞赛试卷(四年级初赛B卷)参考答案与试题解析一、填空题Ⅰ(每题8分,共40分)1.(8分)计算:109×92479+6×109×15413=20160313.【分析】先根据根据乘法的分配律和结合律变形为109×92479+109×92478,然后根据乘法的分配律简算即可.【解答】解:109×92479+6×109×15413=109×92479+109×92478=109×(92479+92478)=109×184957=20160313故答案为:20160313.【点评】此题重点考查了学生对运算定律的掌握与运用情况,要结合数据的特征,灵活选择简算方法.2.(8分)给定一个除数(不为0)与被除数,总可以找到一个商与一个余数,满足被除数=除数×商+余数,其中,0≤余数<除数.这就是带余数的除法.当余数为0时,也称除数整除被除数,或者称除数是被除数的因数(被除数是除数的倍数).不超过988000并且能够被49整除的大于1的自然数共有20163个.【分析】首先看988000除以49的商是多少,商就是小于988000的49的最大倍数,同时也是从1倍开始一共的整数倍个数,问题解决.【解答】解:依题意可知988000÷49=20163…13,故小于988000的49的最大倍数是20163倍.从1倍开始到20163倍共20163个数.故答案为:20163.【点评】本题考查整除的性质,从1倍开始最大的倍数就是能够被49整数的个数.3.(8分)只能被1与其自身整除的大于1的自然数称为素数或质数,比如2、3、5、7、11、13等.大于1的自然数如果不是素数,则称为合数.除唯一的偶数2之外,相邻的两个素数之间至少间隔一个合数,比如3、5;5、7;7、11等.两个连续的素数之间间隔的合数个数称为这两个连续素数的间隔数,间隔数为1的两个素数称为孪生素数,比如3、5;5、7;而7,11的间隔数为3,那么100以内的连续素数的最大间隔数为7.【分析】首先需要知道100以内的质数有2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97.然后观察最大间隔即可.【解答】解:100以内的质数有2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97.共25个.最大的间隔89和97共90,91,92,93,94,95,96共7个.故答案为:7【点评】本题的关键和突破口是数字间隔定义的理解,7和11的间隔是3而不是4,同时牢记100以内的质数观察找出最大间隔即可问题解决.4.(8分)大于0的自然数,如果满足所有因数之和等于它自身的2倍,则这样的数称为完美数或完全数.比如,6的所有因数为1,2,3,6,1+2+3+6=12,6就是最小的完美数,是否有无限多个完美数的问题至今仍然是困扰人类的难题之一.研究完美数可以从计算自然数的所有因数之和开始,567的所有因数之和为968.【分析】要想求出所有的因数和,需要分解质因数算出因数个数然后枚举出来一一相加即可.【解答】解:分解质因数576=32×26,因数共3×7=21个.576=1×576=2×288=3×192=4×144=6×96=8×72=9×64=12×48=18×32=16×36=242.1+576+2+288+3+192+4+144+6+96+8+72+9+64+12+48+18+32+16+36+24=968.故答案为:968.【点评】本题的关键是要计算出因数的个数,然后能够知道自己在枚举过程中是否有遗漏,同时成组写出来避免重复相加问题解决.5.(8分)将自然数15的0倍,1倍,2倍,3倍,4倍,5倍,…按照顺序写在下面0、15、30、45、60、75、…这一列数中可以一直写下去,并且后一个总比前一个数大,任何一个自然数要么是这一列数中的某一个,要么介于相邻的两个数之间,我们把这一列数叫做严格递增的无穷数列,从左至右的每一个数分别叫做这个数列的第一项,第二项,第三项,…,即第一项是0,第二项是15,第三项是30,…,依此类推,那么,介于这个数列的第135项与136项之间,并且与这两项中的较小的项的差是6,这个数为2016.【分析】首先是15倍是0倍开始的,那么第135,136项分别就是134倍和135倍.找出最小的数字加上6即可.【解答】解:数列的第135项即是15的134倍.134×15=2010.数列的第136项即是15的135倍.135×15=2025.与较小的数字2010相差6的数字而且在2010﹣2025之间的数字为2010+6=2016.故答案为:2016.【点评】本题的关键是看好倍数从0倍开始,不是1倍开始,对应的135项就是134倍,找到这两个数最小的加上6问题解决.二、填空题Ⅱ(每题10分,共50分)6.(10分)将一个正方形沿对角线剖分为4个直角三角形,然后按照如图所示方法移动4个直角三角形,中间空白处形成的正方形的对角线长为2厘米.【分析】两图比较可知,空白处是正方形,同时在正方形外每一个大三角形上都多出一个小的三角形.这4个小三角形正好可以拼接成里面空白的正方形.【解答】解:对角线的长度就是2个直角三角形的直角边长即1×2=2(厘米)故答案为:2【点评】本题的关键在于面积不变,多余的4个小三角形正好可以拼接成里面的正方形,边长就是小三角形直角边的2倍.问题解决.7.(10分)用一根长为36分米的铁丝做一个长方体框架,并且要求长是宽的2倍,长宽高都是整数分米.如果.不计损耗,可以做成的长方体体积最大为24立方分米.【分析】可以设长方体框架的宽是a分米,则长是2a分米,铁丝总长是36分米,∴高为(36﹣4a﹣4×2a)÷4,根据长方体的体积公式可以求出体积的关系式,再求体积最大值.【解答】解:根据分析,设长方体框架的宽是a分米,则长是2a分米,∵铁丝总长是36分米,∴高为(36﹣4a﹣4×2a)÷4,根据长方体的体积公式可以求出体积的关系式.V=2a×a×(36﹣4a﹣4×2a)÷4=2a×a×(9﹣3a)当a=2时,体积V取最大值24(平方分米).方法二:因为长、宽、高的和=36÷4=9,而长宽高均为整数分米,而且长是宽的两倍,满足条件的只有:1、2、6和2、4、3两组,①长、宽、高为1、2、6时,体积=1×2×6=12(平方分米);②长、宽、高为2、4、3时,体积=2×4×3=24(平方分米);故答案是:24.【点评】本题考查立体图形的体积,突破点是:根据长方体的体积公式可以求出体积的关系式,再求体积最大值.8.(10分)在印度河畔的圣庙前,一块黄铜板上立着3根金针,针上穿着很多金盘.据说梵天创世时,在最左边的针上穿了由大到小的64片金盘,他要求人们按照“每次只能移动一片,而且小的金盘必须永远在大的金盘上面”的规则,将所有的64片金盘移动到最右边的金盘上面.他预言,当所有64片金盘都从左边的针移动到右边的时候,宇宙就会湮(yān)灭.现在最左边金针(A)上只有5片金盘,如图(1)所示,要按照规则,移动成图(2)的状态,至少需要移动19步.【分析】这是一个汉诺塔的变形问题,根据汉诺塔问题的推理结果,要将n个盘从一个柱全部移到另一个柱上,需要2的n次方﹣1步,根据这个进行推理.【解答】解:为了叙述方便,将五个盘按从小到大编为1~5号第一步:要将5盘移到C柱,先将前4个移到B柱上,所以将5号移到C柱上至少需要2×2×2×2﹣1+1=16步此时3号和4号已经符合要求.第二步:将1号和2号移到C柱上需要2×2﹣1=3步至少需要16+3=19步具体移法如下表【点评】大家做这题的时候记住汉诺塔的问题的基本特征,在此基础上灵活运用.9.(10分)在平面上,用边长为1的单位正方形构成正方形网略,顶点都落在单位正方形的顶点(又称为格点)上的简单多边形叫做格点多边形.而除去三个顶点之外,内部或边上不含格点的格点三角形称为本原格点三角形,如图所示的格点三角形MBN.每一个格点多边形都能很容易地划分为若干个本原格点三角形,那么,图中的格点四边形EBGF可以划分为24个本原格点三角形.【分析】这题根据毕克定理S=2×N+L﹣2即可求出这个图能分成多少个本原格点三角形,其中N表示内部的格点数,L表示边界上的格点数.【解答】解:内部的点是10,边界上的点是6,根据公式列出2×10+6﹣2=24故此题填24.【点评】遇到这种问题时,常运用毕克定理公式直接去求,在求的时候要注意分清是正方形格点问题还是三角形格点问题.10.(10分)用2颗红色的珠子,2颗蓝色、2颗紫色、2颗绿色的珠子串成如图所示的手链,要求两颗红色珠子相邻,两颗紫色珠子相邻,那么,可以串成16种不同的手链.【分析】根据题意,分三种情况:(1)两颗红色珠子和两颗紫色珠子之间有2颗珠子;(2)两颗红色珠子和两颗紫色珠子之间有1颗珠子;(3)两颗红色珠子和两颗紫色珠子相邻;把每种情况下可以串成的手链的数量相加,求出可以串成多数种不同的手链即可.【解答】解:因为是手链,所以旋转、翻转相同的只能算一种,(1)两颗红色珠子和两颗紫色珠子之间有2颗珠子时,与红色珠子相邻的两颗珠子有:蓝蓝、绿绿、蓝绿三种,其中蓝绿有2种可能,一共有4种可能性.(2)两颗红色珠子和两颗紫色珠子之间有1颗珠子时,单独的1颗有2种可能性,另外3颗有3种可能性,一共有:2×3=6(种).(3)两颗红色珠子和两颗紫色珠子相邻时,=6(种)4+6+6=16(种)答:可以串成16种不同的手链.故答案为:16.【点评】此题主要考查了排列组合问题,考查了加法原理和乘法原理的应用,要熟练掌握,注意不能多数、漏数.三、填空题Ⅲ(每题12分,共60分)11.(12分)古罗马的凯撒大帝发明了世界上最早的数学加密方法:按照字母表的顺序,将每一个字母对应到按照某种事先的约定确定的字母.例如,将这个字母对应到他后面的第三个字母,也就是A→D,B→E,C→F,…W→Z,X→A,Y→B,Z→C,于是按照这个加密方法,单词“HELLO”,被加密成“KHOOR”.按照这种加密方法,海亮收到了一个加密后的密文“LORYHBRX”,那么,这个信息的原文是ILOVEYOU.【分析】按照字母表的顺序,将每一个字母对应到按照某种事先的约定确定的字母.例如,将这个字母对应到他后面的第三个字母,也就是A→D,B→E,C→F,…W→Z,X→A,Y→B,Z→C,从以上加密方法可以看出:每个英文字母加密成他后面的第三个字母;解密的时候就把他译成前面的第三个字母.【解答】解:收到了一个加密后的密文是“LORYHBRX”,解密为L→I,O→L,R→O,Y→V,H→E,B→Y,R→O,X→U,于是这个信息的原文是:ILOVEYOU;故答案为:ILOVEYOU.【点评】首先仔细研究等差数列的加密方法,运用逆向推理的方法找到解密的方法.12.(12分)恰好有12个不同因数的最小的自然数为60.【分析】首先把12分成两个数的乘积或3个数的乘积,用因数减1当所求自然数的质因数个数,从最小的质数2开始考虑,使2的个数最多,算出乘积比较得出答案.【解答】解:12=1×12=2×6=3×4=2×2×3,有12个约数的自然数有:①2×2×…×2×2(11个2)=2048,②2×2×…×2(5个2)×3=96,③2×2×2×3×3=72,④2×2×3×5=60;从以上可以看出只有④的乘积最小;所以有12个约数的最小自然数是60.故答案为:60.【点评】此题主要考查一个合数的约数个数的计算公式:a=pα×qβ×rγ(其中a 为合数,p、q、r是质数),则a的约数共有(α+1)(β+1)(γ+1)个约数.13.(12分)两个不全为0的数的公共因数成为它们的公因数.求出26019,826,2065的全体公因数1,7,59,413.【分析】寻找3个因数的公约数的方法叫做辗转相除法.找到最大约数,那么他们的所以因数都是满足条件的.【解答】解:根据辗转相除法三个数做差得出两个数即26019﹣2065=23954,2065﹣826=1239,较大的数除以较小的数.23954÷1239=19…413,再用较小的数除以余数,1239÷413=3整除,说明413就是他们的最大约数,再对413分解质因数=1×413=7×59,即26019,826,2065的全体因数为1,7,59,413.故答案为:1,7,59,413.【点评】本题考查知识点是辗转相除法,就是用大数除以小数,然后再用原来的小数除以余数,再用小的数除以余数最后为0则是整除,为1就是互质问题解决.14.(12分)在一个摆满棋子的正方形棋盘中,甲、乙两人轮流拿取棋子,规则为:在某行或某列中,取走任意连续放置的棋子(即不能跨空格拿取),不允许不取,也不能在多行(多列)中拿取,当棋盘中所有棋子被取尽时游戏结束.取走最后一棵棋子的一方获胜.面对如图所示的棋盘,先手有必胜策略,先手第一步应该取走1、3、5、7、9、258、456(写出所有的正确方案),才能确保获胜.【分析】这个游戏的策略主要是利用图形有对称性(1)先手取5号以及258、456号后,图形完全对称,显然是先手可以取胜.(2)先手取1号,①后手取2、3、4、7中的一个或两个,先手都可以取成正方形获胜;如果后手取3,那先手就取7,后手再取4,那先手就取2,这样就剩下5689这个正方形,在这种情况下,谁先取谁就输.如果后手取23,那先手就取47,剩下5689正方形.②后手取59中的一个,先手可以取另一个形成对称图形而获胜.③后手取3678中的一个或两个,先手一定可以获胜.如果后手取36,先手就可以取8,这时剩下47259,此时后手无论怎样取,先手都可以获胜.如果后手取8,先手就取36,情况同上.如果后手取78,那先手就取6,这时剩下23459,此时后手无论怎样取,先手都可以获胜.7如果后手取6,那先手就取78,情况同上.如果后手取3或7,先手可以参照①的情况获胜.(3)同理,先手取3、7、9也可以确保获胜.(4)除上述情况外,取任意其他一个或相邻两个、三个,后手都可以取成对称图形导致先手失败.(对称图形不包括2×3这样的6个)【解答】解:先手确保获胜只能取1、3、5、7、9、258、456这七种.【点评】这题题目是利用图形的对称知识获胜的,只有在形成对称图形之后才能保证自己获得最后一个棋子.15.(12分)在的圆圈中填入从1到14的自然数(每一个数用而且只能用一次),使连接在同一直线上的4个圆圈中的数字之和都相等,这称为一个7阶幻星图,这个相等的数称为7阶幻星图的幻和,那么,7阶幻星图的幻和为30,并继续完成以下7阶幻星图.【分析】所有的数字和的2倍就是所有的幻和的7倍,那么(1+14)×14=210,那么210就是幻和的7倍,即可求出幻和.再根据数字规律填写7阶幻星图即可.【解答】解:所有的数字和的2倍(1+14)×14=210.幻和为:210÷7=30.7阶幻星图为:故答案为:30【点评】幻方的关键问题就是知道求所有的幻和时把所有的数字加了两遍,同时也考察同学们的数字规律和理解能力,综合分析幻方的能力.问题解决.。
走美杯竞赛真题

11.小美的妈妈有 小美的妈妈有一张手机卡 张手机卡,这张卡里面原有 这张卡里面原有一部分话费 部分话费,而且通信公司 而且通信公司 每月返固定话费。已知如果她每个月花42元,则8个月就能把话费用完; 如果她每个月花38元,则12个月就能把话费花完。如果妈妈想用10个月 把话费花完,那么她每个月应花__________元。 12.如图,若长方形 如图 若长方形APHM、BNHP、CQHN的面积分别为8、4、6,则阴影 则阴影 部分的面积是多少?
13.将写有1,2,3…,9的九张卡片按顺序叠齐,写有1的卡片放在最上面, 然后进行如下操作:把第一张卡片放在最下面,把第二张卡片扔掉; 再把现在的第一张卡片放在最下面,把第二张卡片扔掉……按同样的 方法 反复操作多次 当剩下最后 张卡片时 卡片上写的是______。 方法,反复操作多次,当剩下最后一张卡片时,卡片上写的是
14.有一个14项的等差数列,和为2009,它的每一项都是自然数,那么其中 最大的一项的最大值是_________。
15.甲、乙、丙是三个站,乙站到甲、丙两站的距离相等。小明和小强分别 从甲 丙两站同时出发相向而行 小明过乙站100米后与小强相遇,然 从甲、丙两站同时出发相向而行,小明过乙站 米后与小强相遇 然 后两人又继续前进,小明走到丙站立即返回,经过乙站后300米又追上 小强。问甲、丙两站的距离是_______千米。
1Leabharlann
2015年第十三届走美杯三年级初赛解析

2015年第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛小学三年级试卷注意事项:1.考生要按要求在密封线内填好考生的有关信息.2.不允许使用计算器.3.为方便决赛通知,务必填写联系电话.电话:一、填空题(每小题8分,共40分)1.135797992014++++++-= .【分析】486考点:等差数列计算;原式250201425002014486=-=-=.2.在右图的每个方框中填入一个数字,使得乘法竖式成立.那么,这个算式的乘积是.137⨯【分析】407或777考点:乘法数字谜;由乘积个位是7可知乘数的个位与被乘数的乘积是37,进而得到被乘数即为37,如图所示:371377⨯由于乘数的十位与37相乘所得结果为两位数,因此该位置可能是1或2;①如果乘数的十位填入1,结果如下图所示:②如果乘数的十位填入2,结果如下图所示:3711373747⨯37213774777⨯因此这个算式的乘积是407或777.2015年第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛3.有一堆红球与白球,球的总数不超过50.已知红球个数是白球个数的3倍,那么,红球最多有个.【分析】36个考点:和差倍问题;由于红球个数是白球个数的3倍,因此球的总数应为白球个数的4倍,可得球的总数一定是4的倍数;红球最多的情况即对应了球的总数最多的情况,而不超过50的最大的4的倍数为48;因此球的总数最多有48个,此时红球最多有484336÷⨯=个.4.一袋奶糖分给几位小朋友,如果每人得8颗,还剩4颗;如果每人得11颗,就有一位小朋友拿不到.一共有位小朋友.【分析】5位考点:盈亏问题;如果每人得11颗,就有一位小朋友拿不到,意味着此时奶糖少了11颗,因此此题为“盈亏”型;小朋友人数:()()4111185+÷-=位.5.数一数,图中共有个三角形.【分析】12个考点:图形计数;如果首先去掉三角形右侧内部的斜线,得到如下图形:此时应有()21228+⨯+=个三角形;之后加上被去掉的线,此时会增加4个三角形,如下图所示:因此原图中一共有8412+=个三角形.二、填空题(每小题10分,共50分)6.某小学三年级的部分学生排成一个实心正方形方阵,最外面3层有学生72人,这个方阵共有学生人.【分析】81人考点:间隔与方阵;次外层的人数:72324÷=人;最外层的人数:24832+=人;最外层每边的人数:32419÷+=人;方阵总人数:9981⨯=人.7.把48粒棋子放入9个盒子中,每个盒子至少放1粒,每盒棋子数都不一样,棋子最多的盒子里最多可以放粒棋子.【分析】12粒考点:最值问题;当棋子总数一定时,要使棋子最多的盒子里棋子尽可能的多,另外8个盒子的棋子总数就要尽可能的少;而由于每盒棋子数都不一样,这8个盒子的棋子总数最少为:1234567836+++++++=粒;因此棋子最多的盒子里最多可以放483612-=粒棋子.8.,A B 两地相距1000米,甲从A 地出发,1小时后到达B 地.乙在甲出发后20分钟从B 地出发,40分钟到达A 地.甲、乙二人相遇点距A 地米.【分析】600米考点:行程问题——相遇;由乙40分钟可走1000米,得到乙的速度为10004025÷=米/分钟;甲60分钟可走1000米,而乙60分钟可走25601500⨯=米;由1000与1500的关系不难看出,相同时间内若甲走2份路程,则乙可走3份;现在甲比乙早出发20分钟,即为乙比甲晚出发20分钟;可构造一种情形:乙先向后退20分钟甲再出发,即为乙后退2520500⨯=米;此时甲、乙二人的实际距离为10005001500+=米;甲、乙二人相遇点与A 地的距离即为相遇时甲所走的路程;在二人的路程和1500米当中,甲所走的路程为()1500232600÷+⨯=米;所以甲、乙二人相遇点距A 地600米.9.小明说:“我妈妈比我大24岁,两年前妈妈的年龄是我的4倍.”小明今年岁.【分析】10岁考点:年龄问题;由于2个人年龄差不变,两年前妈妈也比小明大24岁;因此两年前小明的年龄是:()24418÷-=岁;所以小明今年的年龄是:8210+=岁.2015年第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛10.将数字1~9放入图中的小方格中,每格一个数,可得到四条线上三个数的和都相等,请问*应该是.【分析】8考点:数阵图;由于在图中只有1,4,2这三个数字位于其中的两条线上,各被重复计算过一次;因此图中四条线的总和是:12345678914252+++++++++++=;得到每条线上三个数的和应为:52413÷=;由*所在的线可得:*13148=--=.三、填空题(每小题12分,共60分)11.右图是可以一笔画出的,一共有种不同的一笔画法(起点、终点或顺序只要有一样不同,就算不同的画法).【分析】12种考点:一笔画;首先将图中各点命名如下:由于,A B 两点均为奇点,因此画法必定是从A 开始到B 结束,或是从B 开始到A 结束,且不难想到这两种画法的种类数相同;下面以从A 开始到B 结束为例:如果先从A 画到B ,则接下来剩余的正方形只有顺时针和逆时针2种画法,即ABCADB 和ABDACB ;如果先从A 画到C ,那么接下来必定画到B ,之后会有2种选择:一是先直接画到A ,再从D 画到B ,即ACBADB ;二是经过D 画到A ,再从A 画到B ,即ACBDAB ;如果先从A 画到D ,根据图形的对称性其种类数应与先从A 画到C 相同,也是2种;综上所述,从A 开始到B 结束的画法一共有2226++=种,类似的从B 开始到A 结束的画法也有6种;因此该图形一共有6612+=种不同的一笔画法.2015年第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛12.有五个互不相等的非零自然数,最小的一个数是7.如果其中一个减少20,另外四个数都加5,那么得到的仍然是这五个数.这五个数的和是.【分析】85考点:等差数列;由于7不可能是减少20的数,因此这五个数当中一定有7512+=;同理这五个数当中一定还有12517+=和17522+=;如果减少20的数是22,那么这五个数当中一定有22202-=,但27<不满足条件;因此这五个数当中一定还有22527+=,此时27205-=满足条件;即这五个数是7,12,17,22,27,它们的和是71217222785++++=.13.一个正方体的6个面分别标着,,,,,A B C D E F 六个字母,从3个不同角度看正方体如图所示,字母C 的对面是字母.【分析】D考点:图形规律;由图1和图2可得字母D 与字母,,,A B E F 均为邻面,因此其对面为字母C ;另:类似可得字母A 的对面是字母E ,字母B 的对面是字母F .14.24点游戏:用加、减、乘、除、括号等运算符号把4,4,10,10这四个数连起来,使结果等于24,.【分析】()10104424⨯-÷=考点:24点计算;过程略.积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学,积极学习数学的方格表内有四个筹码,这些筹码一面为白色另一面为黑色.每一次操作可以任选一个筹码跳15.在15过一个、二个或三个筹码到空位上,但不可以用走动的.被跳过的筹码都必须翻面,但跳的筹码不翻面.现欲经过六次的操作,将下左图的情况变成下右图的情况.如果依次将跳动的筹码跳动前所在位置的号码记录下来,就可以得到一个六位数.请给出可能完成任务的一个六位数.(填出一个即可).【分析】251425或152415考点:操作性问题;251425操作如下:152415操作如下:。
(word完整版)四年级2015年第十三届走美杯真题和答案与解析(四年级)

第十三届走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学四年级试卷(B 卷)2015年3月8日南京填空题I (每题8分,共40分)1 计算 5X13X31 X73X137= _________________【解析】:本题考查多位数乘法的计算。
直接列式子计算。
2、用1个1、2个2、2个3组成一些4位数,则能够组成的不同 4位数一共有【解析】:本题考查排列组合。
1,2,2,3,3五个数字拿岀 1或2或3。
有①2233②1223③1233这三种组合。
分析第 ①种,当两个 2连在一起, 3223 3322两个2中间隔一个数,2323 3232两个2中间隔两个数 2332.这样第一种小情况有 种。
第②种,同样分析,但是 1和3可以互换一次,所以有6 >2=12种。
第③种,把22和33互换,用换位思考的方法,同第②种。
所以一共有 6+12+12得30种4、一个自然数能够表示成 5个连续的自然数之和,那么将符合以上条件的自然数从小到大排列,前【解析】:平均数和最小公倍数概念。
第一、二句话可以理解这个数可以整除 2.5和3.5因为这是一个自然数,可以理解成这个数可以整除5和7.这样应该是 35、70、105等5、24点游戏”是很多人熟悉的数学游戏,游戏过程如下:任意从 52张扑克牌(不包括大小 王)中抽取 4张,用这4张扑克上的数(A=1、J=11、Q=12、 K=13 )通过加减乘除四则运算得出24,先找到算法者获胜,游戏规定 4张扑克牌都要用到,而且每张只能用1次,比如 2、3、4、Q 则可以有算法(2 X Q ) X (4-3)得到24。
如果在一次游戏中恰好抽到5、5、5、1则你的算法是 ______________________【解析】:24点算法。
5X (5-1越)=24。
这类问题平时训练可以记住集中特殊的算法。
让个。
4个。
相当于 5个拿走一个,只能拿走 223363、整除2015的数称为2015的因数,1和2015显然整除2015,称为2015的平凡因数,除了平 凡因数,2015还有一些非平凡因数,那么【解析】:考查因数概念和分解质因数方法。
小学美术奥林匹克竞赛试题及答案(四年级)

小学美术奥林匹克竞赛试题及答案(四年
级)
试题一
题目描述:
请你绘制一幅你最喜欢的动物的画,并用颜色给它上色。
答案:
以下是一种可能的回答:

试题二
题目描述:
请你用线条勾勒出一个水果篮子,并根据你的想象给它上色。
答案:
以下是一种可能的回答:

试题三
题目描述:
请你用不同的形状拼出一个家的图案,并用彩色填充。
答案:
以下是一种可能的回答:

试题四
题目描述:
请你选择一个喜欢的名人或角色,用线条画出他/她的形象,并尽量用色彩丰富的颜料给他/她上色。
答案:
以下是一种可能的回答:

试题五
题目描述:
请你根据给出的植物图片,尝试用几种不同的颜色绘制出它的样子。
答案:
以下是一种可能的回答:

以上是小学美术奥林匹克竞赛四年级的试题及答案。
希望你能够享受绘画的过程,展示你的创意和想象力!。
四年级走美自测题 教师版

四年级走美杯自测卷填空题Ⅰ(每题8分,共40分)1、2000年后为三个连续自然数乘积的第一个年份是 。
【解析】:11×12×13=1716,12×13×14=2184。
2、将正整数1,2,3,4,5,6,…,10000排成一行。
若一个数不能表示成两个合数的和,则将此数划去。
例如要划去1,但是因为8=4+4,8就不能划去。
根据上面规定划掉所有能划掉的数之后,将剩下的由小到达排列,这时从左数第2016个数是 。
【解析】:从8开始往后的偶数可以拆成两个偶合数的和;从13开始的奇数可以拆成9+2n 的形式(n 大于等于2),而1、2、3、4、5、6、7、9、11要划去,所以剩下的数列为8、10、12、13、14、15……,第2016项即为2025。
3、图中共有 个三角形。
【解析】:①由1个小三角形构成的三角形有24个;②由2个小三角形构成的三角形有20个;③由3个小三角形构成的三角形有8个;④由4个小三角形构成的三角形有8个;⑤由5个小三角形构成的三角形有4个;⑥由6个小三角形构成的三角形有4个;⑦由7个小三角形构成的三角形有4个;所以图中共有三角形24+20+8+8+4+4+4=72个。
4、四位数abcd 与cdab 的和为3636,差为396,那么四位数abcd 为 。
【解析】:100abcd ab cd =+,100cdab cd ab =+。
当ab cd >时: ()1001003636100100396ab cd cd ab ab cd cd ab ⎧+++=⎪⎨+-+=⎪⎩ 整理得36ab cd +=,4ab cd -=,所以20ab =,16cd =,2016abcd =。
同理,ab cd <时,1620abcd =。
5、A、B、C、D四个箱子中分别装有一些小球,现将A箱中的部分小球按如下要求转移到其他三个箱子中:该箱中原有几个小球,就再放入几个小球,此后,按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中,此时,四个箱子都各有16个小球,那么开始时装有小球最多的是______箱,其中装有______小球个。
2015年第13届走美杯上海决赛4年级详解版-2

而目标图形需要用到 2 个索玛立方体,只能是 8 = 4 + 4 ,因此只需要从 2 号至 7 号里面选 2 个。
【第 12 题】给定三个自然数 1,2,3,对这三个数进行一次操作,将其中一个数换成另两个数的和,这样进
行 9 次操作后,所得的三个自然数中,最大数的最大可能的值为
。
考点:杂题
解析:要求操作多次后,所得的三个自然数中,最大数的最大,我们只需要每次将三个数中最小的数换成另
两个数的和即可。
原始数据为:1,2,3
①:1、2、2、3
可以组成
A44 A22
= 12 个不同的四位数
②:1、2、3、3
可以组成 A44 = 12 个不同的四位数 A22
③:2、2、3、3
可以组成
A44 A22 × A22
= 6 个不同的四位数
一共能够组成12 +12 + 6 = 30 个不同的四位数
个。
【第 3 题】 整除 2015 的数称为 2015 的因数,1 和 2015 显然整除 2015,称为 2015 的平凡因数,除了平凡
第十三届“走进美妙的数学花园”上海决赛小学四年级----王洪福老师
第十三届“走进美妙的数学花园”青少年展示交流活动 趣味数学解题技能展示大赛初赛(上海决赛) 小学四年级试卷(B 卷)
2015 年 3 月 8 日 上午 8:15——9:45 满分 150 分
一、填空题(每小题 8 分,共 40 分)
【第 1 题】计算: 5×13× 31× 73×137 =
走美杯四年级试题和答案
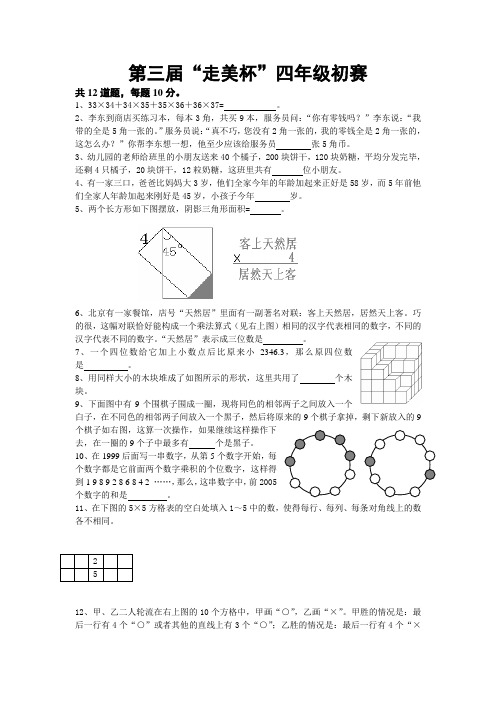
第三届“走美杯”四年级初赛共12道题,每题10分。
1、33×34+34×35+35×36+36×37= 。
2、李东到商店买练习本,每本3角,共买9本,服务员问:“你有零钱吗?”李东说:“我带的全是5角一张的。
”服务员说:“真不巧,您没有2角一张的,我的零钱全是2角一张的,这怎么办?”你帮李东想一想,他至少应该给服务员 张5角币。
3、幼儿园的老师给班里的小朋友送来40个橘子,200块饼干,120块奶糖,平均分发完毕,还剩4只橘子,20块饼干,12粒奶糖,这班里共有 位小朋友。
4、有一家三口,爸爸比妈妈大3岁,他们全家今年的年龄加起来正好是58岁,而5年前他们全家人年龄加起来刚好是45岁,小孩子今年 岁。
5、两个长方形如下图摆放,阴影三角形面积= 。
6、北京有一家餐馆,店号“天然居”里面有一副著名对联:客上天然居,居然天上客。
巧的很,这幅对联恰好能构成一个乘法算式(见右上图)相同的汉字代表相同的数字,不同的汉字代表不同的数字。
“天然居”表示成三位数是 。
7、一个四位数给它加上小数点后比原来小2346.3,那么原四位数是 。
8、用同样大小的木块堆成了如图所示的形状,这里共用了 个木块。
9、下面图中有9个围棋子围成一圈,现将同色的相邻两子之间放入一个白子,在不同色的相邻两子间放入一个黑子,然后将原来的9个棋子拿掉,剩下新放入的9个棋子如右图,这算一次操作,如果继续这样操作下去,在一圈的9个子中最多有 个是黑子。
10、在1999后面写一串数字,从第5个数字开始,每个数字都是它前面两个数字乘积的个位数字,这样得到1 9 8 9 2 8 6 8 4 2 ……,那么,这串数字中,前2005个数字的和是 。
11、在下图的5×5方格表的空白处填入1~5中的数,使得每行、每列、每条对角线上的数各不相同。
12、甲、乙二人轮流在右上图的10个方格中,甲画“○”,乙画“×”。
2015年第十三届走美杯小学四年级试卷初赛上海详解

第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛小学四年级试卷2015年1月11日 上午8:009:30- 满分150分注意事项1.考生要按要求在密封线内填好考生的有关信息。
2.不允许使用计算器。
3.为方便决赛通知,务必填写联系电话。
一、填空题(每小题8分,共40分)【第1题】如果10987654321++⨯÷+-⨯-⨯=□,那么________=□。
【分析与解】109876543218713254691056228++⨯÷+-⨯-⨯=⨯÷=+⨯+⨯---÷==□□□□【第2题】a 、b 、c 都是质数,并且49a b +=,60b c +=,则________c =。
【分析与解】如果两个质数相加等于49,49是奇数; 则两个质数为一奇一偶;所以其中偶数必是2,另一个奇数是49247-=。
⑴当247a b =⎧⎨=⎩时,60604713c b =-=-=是质数,符合题意;⑵当472a b =⎧⎨=⎩时,6060248c b =-=-=是合数,不符题意;综上所述,2a =,47b =,13c =。
第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛上海初赛【第3题】去掉20.15中的小数点,得到的整数比原来的数增加了________倍。
【分析与解】去掉20.15中的小数点,得到的整数为2015; 2015是20.15的100倍;2015比20.15增加了100199-=倍。
【第4题】梯形的上底、高、下底依次构成一个等差数列,其中高是12。
那么梯形的面积是________。
【分析与解】因为梯形的上底、高、下底依次构成一个等差数列; 所以212224+=⨯=⨯=上底下底高;()224122144=+⨯÷=⨯÷=梯形的面积上底下底高。
四年级2015年第十三届走美杯真题和答案与解析(四年级)

第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学四年级试卷(B卷)2015年3月8日南京填空题I(每题8分,共40分)1 计算 5×13×31×73×137=__________________【解析】:本题考查多位数乘法的计算。
直接列式子计算。
2、用 1 个 1、2 个 2、2 个 3 组成一些 4 位数,则能够组成的不同 4 位数一共有__________ 个。
【解析】:本题考查排列组合。
1,2,2,3,3五个数字拿出4个。
相当于5个拿走一个,只能拿走1或2或3。
有①2233②1223③1233这三种组合。
分析第①种,当两个2连在一起,2233 3223 3322 两个2 中间隔一个数,2323 3232 两个2 中间隔两个数2332. 这样第一种小情况有6种。
第②种,同样分析,但是1和3可以互换一次,所以有6×2=12种。
第③种,把22 和 33 互换,用换位思考的方法,同第②种。
所以一共有 6+12+12 得 30 种3、整除 2015 的数称为 2015 的因数,1 和 2015 显然整除 2015,称为 2015 的平凡因数,除了平凡因数,2015还有一些非平凡因数,那么2015的所有非平凡因数之和为______________【解析】:考查因数概念和分解质因数方法。
2015分解质因数2015=5×13×31,每两个因数两两组合,得5+403+13+155+31+65=672。
注明:分解质因数的方法,2015÷50=403,对于403的枚举量很大,很难分解,这里需要知道一个方法,只要试到这个数的开方数以下的质数。
20×20=400,所以只要把403除以20以内的质数就可以试出来。
,如果孩子不明白质因数,可以列举把结果给孩子看。
4、一个自然数能够表示成 5 个连续的自然数之和,也可以表示成 7 个连续的自然数之和,那么将符合以上条件的自然数从小到大排列,前3个数分别为______________【解析】:平均数和最小公倍数概念。
2015年第十三届走美杯四年级考试题及答案

第十三届走美杯四年级1.如果10+9+8*7÷□+6-5*4-3*2=1,那么□=?2.a.b.c 都是质数,并且a+b=49,b+c=60,则c=?3.去掉20.15中的小数点,得到的整数比原来的数增加了?倍4.梯形的上底、高、下底依次构成一个等差数列,其中高是12.那么梯形的面积是?5.两个小胖子一样重,他们决定一起减肥。
三个月后大胖减掉了12千克,二胖减掉7千克。
这时大胖的体重比二胖的体重的2倍少80千克。
原来他们各重?千克6.有两组数,第一组7个数的和是84,第二组的平均数是21,两组中的所有数的平均数是18,则第二组有几个数7.植树节去植树,120米长的路两边每隔3米挖个坑,后来改成5米挖个坑,问最多可以保留多少坑8.ABCD四人进行围棋比赛,每人都要与其他三人各赛一场,比赛在两张棋盘上同时进行,每天每人只赛一盘第一天A与C比赛,第二天C与D比赛,第三天A与谁比赛9.六条铁链,每条四个环,打开一个环要用1分钟,封闭一个环要三分钟,现在要把这24个环连成一条铁链,问至少要几分钟10.一块正放形的钢板,先截去一个宽3厘米的正方形,又截去一个宽5厘米的长方形,面积比原来的正方形减少81平方厘米,原正方形的面积是()平方厘米。
11.王伟从甲地走向乙地,同时张明骑自行车到甲地,半小时后两人在途中相遇,张明到达甲地后,马上返回乙地,在第一次相遇后20分钟又追上王伟。
张敏到乙地后又折回,两人在第二次相遇后的__________分钟第三次相遇。
12.这是一种两人玩的游戏。
两位选手轮流在一条20×1的矩形长带上移动筹码。
每一轮都可将四个筹码的任意一个向右移动任意方格。
但不能放在其他筹码上面或超过其他筹码。
开始时如图中看到的各筹码位置,赢家是最后移动筹码者。
(他移动后,四个筹码恰好占据了长带右端的四个放个,不可能在移动了)。
先移动者应将________向右移动________格,才能保证获胜。
2015走美杯四年级

第十四届“走进美妙的数学花园”初赛四年级一、填空题(每小题8分,共40分)1. 4812162016=__________+++++。
2. 所有自然数如图排列,数300位于字母_____的下面。
3. 右图的两个竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么六位数美妙数学花园=_______________。
4. 如图是一个棋盘,将一个白字和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上,有________种不同的放法。
5. 某校有47个同学参加数学竞赛,将参赛者任意分成五组,必有一组的女生多于2人,参赛者中任意选取12人必有男生,参赛的男生有_______人。
二、填空题(每小题10分,共50分)6. 如图,在一个长、宽分别为22厘米和13厘米的大长方形内放了四个正方形,没有被正方形覆盖的小长方形(图中阴影部分)中最多还可以不重叠地放下______个边长是整数的正方形。
(161514)13121110985674321GF E D C B A 园花学数0116102+-园花学数妙美7. 将1~9九个数字填入下列九个“○”中,使等式成立。
==5568⨯⨯○○○○○○○○○8. 自然数N 有很多个约数,把它的所有约数两两求和得到一组新数,其中最小的为4,最大的为2684,N 等于__________。
9. 甲、乙、丙三个工厂计划购买数量相等的钢材,后来丙厂需要钢材的数量减少了,若干数量的钢材给甲乙两厂,结果甲厂比丙厂多300吨,丙厂比乙厂少240吨,最后丙厂从甲乙两厂收回362880元,每吨钢材的价格是________元。
10. 甲、乙两人沿着同一条100米的跑道赛跑,甲从起跑线起跑,乙的起跑点位于甲的前面15米处,两人同时起跑。
当甲到达终点时,乙离终点还有5米,甲追上乙时距离终点还有_________米。
三、填空题(每小题12分,共60分)11. 由35个边长为1的小正方形拼成一个75⨯的长方形,其中有一格含有“☆”。
05年第三届至13年第十一届走美杯试题答案 (1)

目录第三届“走美杯”答案 (2)第四届“走美杯”答案 (3)第五届“走美杯”答案 (4)第六届走美杯三年级初赛试题参考答案 (6)第六届走美杯三年级决赛试题参考答案 (9)第七届走美杯三年级初赛试题参考答案 (10)第八届走美杯三年级初赛试题参考答案 (11)第九届走美杯三年级A卷初赛试题参考答案 (13)第十届走美杯三年级B卷试题及答案详解 (14)第三届走美杯四年级试题参考答案 (18)第四届走美杯四年级试题参考答案 (19)第六届走美杯四年级初赛试题参考答案 (20)第六届走美杯四年级决赛试题参考答案 (24)第七届走美杯四年级初赛试题参考答案 (24)第八届走美杯四年级初赛试题参考答案 (25)第九届走美杯四年级A卷初赛参考答案 (27)第九届走美杯四年级B卷初赛参考答案 (28)第三届走美杯五年级试题参考答案 (33)第四届走美杯五年级试题参考答案 (34)第五届走美杯五年级初赛试题参考答案 (35)第六届走美杯五年级初赛试题参考答案 (39)第六届走美杯五年级决赛试题参考答案 (42)第七届走美杯五年级初赛试题参考答案 (43)第八届走美杯五年级初赛试题参考答案 (46)第九届走美杯五年级初赛试题参考答案 (48)第九届走美杯五年级B卷初赛试题参考答案 (52)第三届走美杯六年级试题参考答案 (52)第四届走美杯六年级试题参考答案 (53)第五届走美杯六年级试题参考答案 (54)第六届走美杯六年级决赛试题参考答案 (58)第七届走美杯六年级初赛试题参考答案 (59)第八届走美杯六年级初赛试题参考答案 (62)第九届走美杯六年级A卷初赛试题参考答案 (65)第十届2012走美杯六年级试题及答案详 (66)第六届走美杯三年级初赛试题参考答案1.22222.861;574;5733.604.155.4;36.90÷15=34-28=67.10;28.169.22210.3711.略12.361.【答案】100012.【答案】100003.【答案】404.【答案】11705.【答案】MT79366.【答案】2008;87.【答案】38.【答案】49.【答案】灰太狼10.【答案】711.【答案】105 ;312.【答案】7; 213.【答案】55;540 14.【答案】4或315.【答案】1、2 、4 、8 .第八届走美杯三年级初赛试题参考答案第九届走美杯三年级A卷初赛试题参考答案第十届走美杯三年级B卷试题及答案详解1、49042、73、364、35、46、9787、2607或23708、509、810、1203111、12、5,2,6 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2第六届走美杯四年级初赛试题参考答案1.20082.64;15625(64×15625)3.2或54.155.906.200000077.168.1;2;2;39.5610.3011.147张,15块12.2100第七届走美杯四年级初赛试题参考答案1. 100002. 403. 丙;甲4. 3 、1 、25. 156. 2008;87. 灰太狼8. 9009. C.10. 1011. 55;54012. 413. 2614.55 ;259平方厘米15.21、555502、1043、254、445、19;5176、97、388、79、100010、126311、6412、328213、814、415、1176答案:1、2010012 2、19 3、0。
2015年第13届“走美杯”小学数学竞赛试卷(六年级初赛B卷)

2015年第13届“走美杯”小学数学竞赛试卷(六年级初赛B卷)一、填空题(共5小题,每小题8分,满分40分)1.(8分)计算:++=.2.(8分)某商品今年的生产成本比去年增加了5%,扔保持原来的销售价格,则每件产品的利润下降了20%,那么,如果要保持成本在销售价格中所占的百分比,销售价格应该在去年的基础上提高%.3.(8分)用1,2,3,4,5,6,7,8这八个数字给4名男生与4名女生编号,要求是男生用奇数,女生用偶数,那么,一共有种不同的编号方法.4.(8分)用2015减去它的,再减去余下的,再减去余下的,…,以此类推,一直减去余下的,那么最后的得数为.5.(8分)“24点游戏”很多人熟悉的数学游戏,游戏过程如下:任意从52张扑克牌(不包括大小王)中抽取4张,用这4张扑克牌上的数字(A=1,J=11,Q=12,K=13)通过加减乘除四则运算得出24,最先找到算法者获胜.游戏规定4张牌扑克都要用到,而且每张牌只能用1次,比如2,3,4,Q.则可以由算法(2×Q)×(4﹣3)得到24.王亮在一次游戏中抽到了4,4,7,7,经过思考.他发现(4﹣)×7=24.我们将满足(a﹣)×b=24的牌组{a,a,b,b}称为“王亮牌组”,请再写出一组不同的“王亮牌组”.二、填空题(共5小题,每小题10分,满分50分)6.(10分)在荷兰的小镇卡茨林赫弗尔2013年6月建成了一个由三个半圆组成的城市雕塑,三个半圆的直径分别为24.2m,19.3m,4.9m.这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形(Arbelos),即图中的阴影部分所示的图形.那么该城市雕塑中的鞋匠刀形的周长为(圆周率用π表示).7.(10分)“足球”可以近似地看成是由一些五边形与正六边形组成的几何体,每一个顶点处有3条棱,这个几何体是阿基米德立体(Archimedean Solids)中的一个,通常,可以通过如图所示的方法,截正二十面体得到“足球”,那么,一个“足球”的棱数为.8.(10分)如图所示,BD,CE分别是∠ABC的角平分线,如果∠BAC=62°,那么,∠BFC=°.9.(10分)将图中的边染色,要求有共同顶点的两个相邻的边染不同的颜色,则至少需要中颜色.10.(10分)索马里方体是丹麦物理学家皮特•海音(Piet Hein)发明的7个小立方体组块(如图所示),如果假设这些小立方体的边长为1,则利用这7个组块不仅可以组成一个3×3的立方体,还可以组成很多美妙的几何体,那么,要组成下面的几何体,需要用到的3个索玛立方体的编号是.三、填空题(共5小题,每小题12分,满分60分)11.(12分)一个大于0的自然数如果满足所有因数(即约数)之和等于它自身的2倍,则称这个数为完全数(或完美数),比如,最小的完全数是6,因为6的所有因数为1,2,3,6,而1+2+3+6=12.古希腊时代的人们就已经认识完全数,并且找到了前4个6,28,496,8128完全数,那么,8128的全体质因数为.12.(12分)只能被1和自身整除的大于1的自然数叫做质数或素数.比如2,3,5,7,11等,如果将117分拆成10个质数之和,要求其中最大的质数尽可能大,那么,这个最大的质数为.13.(12分)我们可以将全体正整数和正分数按照如图所示的方法,从1开始,一层一层地“生长”出来;是第一层;第二层是,,第三层是,,,,…按照这个规律,在第层.14.(12分)如果两个自然数的积被13除余1,那么我们称这两个自然数互为“模13的倒数”比如,2×7=14,被13除余1,则2和7互为“模13的倒数”;1×1=1,则1的“模13的倒数”是它自身.显然,一个自然数如果存在“模13的倒数”则它的倒数并不是唯一的,比如,14就是1的另一个“模13的倒数”.判断1,2,3,4,5,6,7,8,9,10,11,12是否有“模13的倒数”,并利用所得结论计算1×2×3×4×5×6×7×8×9×10×11×12(记为12!,读作12的阶乘)被13除所得的余数.15.(12分)如果一个正方形能够被分割为若干个边长不等的小正方形,则这个正方形称为完美正方形.下面的正方形是已知包含21个小正方形的完美正方形(称为21阶完美正方形),这是迄今为止知道的最小阶数的完美正方形.分割方法如图所示,其中小正方形中心的数字代表其边长,请计算这个完美正方形的边长,并写在这里.2015年第13届“走美杯”小学数学竞赛试卷(六年级初赛B卷)参考答案与试题解析一、填空题(共5小题,每小题8分,满分40分)1.(8分)计算:++=.【分析】先把算式拆分为×+×+×,再根据乘法的分配律简算即可.【解答】解:++=×+×+×=×(++)=×1=;故答案为:.【点评】此题重点考查了学生对分数的拆项和运算定律的掌握与运用情况,要结合数据的特征,灵活选择简算方法.2.(8分)某商品今年的生产成本比去年增加了5%,扔保持原来的销售价格,则每件产品的利润下降了20%,那么,如果要保持成本在销售价格中所占的百分比,销售价格应该在去年的基础上提高5%.【分析】要使成本在销售价格中所占的百分比不变,设去年的成本为a,销售价格为b,去年成本与销售价格的百分比,即为:,设须提高去年售价的x,则可列关系式,求解即可.【解答】解:根据分析,设去年的成本为a,销售价格为b,去年成本与销售价格的百分比,即为:,销售价格在去年的基础上提高x,则有:,解得:x=5%,即:销售价格应该在去年的基础上提高5%.故答案是:5%.【点评】本题考查了利润利息和纳税的问题,本题突破点是:设成本在销售价格中所占的百分比,列出关系式,求解即可得出.3.(8分)用1,2,3,4,5,6,7,8这八个数字给4名男生与4名女生编号,要求是男生用奇数,女生用偶数,那么,一共有576种不同的编号方法.【分析】按题意,男生用奇数编号,有四个奇数,每个人有四个选择,故将四个奇数与四名男生进行排列,有4×3×2×1=24种编号方法,同理女生的编号方法利用排列的性质也可以求得,故总的编号方法不难求得.【解答】解:根据分析,男生用奇数编号,有四个奇数,每个人有四个选择,故将四个奇数与四名男生进行排列,共有:4×3×2×1=24种编号方法;女生用偶数编号,共有4个偶数编号,故四个偶数与四个女生进行一一排列,共有:4×3×2×1=24种不同的编号方法,一共有:24×24=576种不同编号方法.故答案是:576.【点评】本题考查了排列组合,突破点是:利用排列和组合,以及奇数偶数的个数,求得总的不同的编号方法.4.(8分)用2015减去它的,再减去余下的,再减去余下的,…,以此类推,一直减去余下的,那么最后的得数为65.【分析】把每次减少前的数看作单位“1”,则分别剩下单位“1”的(1﹣)、(1﹣)、(1﹣)、…、(1﹣),然后根据分数乘法的意义,用2015乘这些分率即可解决问题.【解答】解:2015×(1﹣)×(1﹣)×(1﹣)×…×(1﹣)=2015×=2015×=65故答案为:65.【点评】本题关键是确定每次剩余它前面的几分之几,计算中要根据规律约分巧算.5.(8分)“24点游戏”很多人熟悉的数学游戏,游戏过程如下:任意从52张扑克牌(不包括大小王)中抽取4张,用这4张扑克牌上的数字(A=1,J=11,Q=12,K=13)通过加减乘除四则运算得出24,最先找到算法者获胜.游戏规定4张牌扑克都要用到,而且每张牌只能用1次,比如2,3,4,Q.则可以由算法(2×Q)×(4﹣3)得到24.王亮在一次游戏中抽到了4,4,7,7,经过思考.他发现(4﹣)×7=24.我们将满足(a﹣)×b=24的牌组{a,a,b,b}称为“王亮牌组”,请再写出一组不同的“王亮牌组”(2,2,13,13),(3,3,9,9),(6,6,5,5),(8,8,4,4),(12,12,3,3).【分析】先根据“王亮牌组”的特征,得出a,(b﹣1)是24的约数,最后借助扑克牌的特点即可得出结论.【解答】解:依题意可知:根据(a﹣)×b==a(b﹣1)=24;那么a和(b﹣1)就是24的约数;显然(a,b)的数字组合为(2,13),(3,9),(6,5),(8,4),(12,3)(扑克中最大为13)故答案为:(2,2,13,13),(3,3,9,9),(6,6,5,5),(8,8,4,4),(12,12,3,3).【点评】此题是填符号组算式,主要考查了约数,以及理解“王亮牌组”的特点,得出a,(b﹣1)是24的约数是解本题的关键.二、填空题(共5小题,每小题10分,满分50分)6.(10分)在荷兰的小镇卡茨林赫弗尔2013年6月建成了一个由三个半圆组成的城市雕塑,三个半圆的直径分别为24.2m,19.3m,4.9m.这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形(Arbelos),即图中的阴影部分所示的图形.那么该城市雕塑中的鞋匠刀形的周长为24.2π(圆周率用π表示).【分析】显然,阴影部分的周长由三个圆的半圆弧组成的,故图中的阴影部分所示的图形那么该城市雕塑中的鞋匠刀形的周长可以用三个圆的半圆周长公式即可求得.【解答】解:根据分析,阴影部分的周长由三个圆的半圆弧组成的,故图中的阴影部分所示的图形那么该城市雕塑中的鞋匠刀形的周长===24.2π故答案是:24.2π.【点评】本题考查了圆的周长,突破点是:利用圆的周长公式不难求得阴影部分的周长.7.(10分)“足球”可以近似地看成是由一些五边形与正六边形组成的几何体,每一个顶点处有3条棱,这个几何体是阿基米德立体(Archimedean Solids)中的一个,通常,可以通过如图所示的方法,截正二十面体得到“足球”,那么,一个“足球”的棱数为90.【分析】可以根据多面体的顶点V,面数F,棱数E之间关系式V+F﹣E=2,先求出正五边形和正六边形的个数,再求棱数.【解答】解:根据分析,设多面体的顶点V,面数F,棱数E之间关系式为:V+F ﹣E=2;设有正五边形x个,正六边形y个,由题意得:解得:x=12,y=20.则棱的总数为E=(5×12+6×20)=90.故答案是:90.【点评】本题考查了组合图形的计数,突破点是:根据关系式V+F﹣E=2,先求出正五边形和正六边形的个数,再求棱数.8.(10分)如图所示,BD,CE分别是∠ABC的角平分线,如果∠BAC=62°,那么,∠BFC=121°.【分析】根据三角形的内角和,得知:∠A+∠ABC+∠ACB=180°⇒∠A+2∠FBC+2∠FCB=180°⇒∠FBC+∠FCB=(180°﹣∠A)==59°.【解答】解:根据分析,根据三角形的内角和,得知:∠A+∠ABC+∠ACB=180°⇒∠A+2∠FBC+2∠FCB=180°⇒∠FBC+∠FCB=(180°﹣∠A)==59°又∵∠BFC=180°﹣∠FBC﹣∠FCB=180°﹣59°=121°.故答案是:121°.【点评】本题考查了长度和角度,突破点是:根据三角形的内角和以及角平分线的性质,可以求得∠BFC.9.(10分)将图中的边染色,要求有共同顶点的两个相邻的边染不同的颜色,则至少需要3中颜色.【分析】首先分析内五边形的染色最低需要3色,那么只要枚举出3色可以染出来此图即可.【解答】解:依题意可知:首先分析内5点是循环的用数字代表颜色即是至少是12123的情况为3种颜色.如图所示3种颜色可以完成此图的染色.故答案为:3【点评】本题考查对染色问题的理解和运用,关键问题是找到内五边形的最低染色的标准,问题解决.10.(10分)索马里方体是丹麦物理学家皮特•海音(Piet Hein)发明的7个小立方体组块(如图所示),如果假设这些小立方体的边长为1,则利用这7个组块不仅可以组成一个3×3的立方体,还可以组成很多美妙的几何体,那么,要组成下面的几何体,需要用到的3个索玛立方体的编号是1号,3号,5号或1号,3号,6号.【分析】首先确定目标图形需要多少块单位立方体(棱长为1的立方体),由题意可知需要11块,索玛立方体的1号包含3个单位立方体,2号到7号包含4个单位立方体,而目标图形需要11个单位立方体,只能是3+4+4,所以1好必须选择,之后通过观察即可解决问题.【解答】解:首先确定目标图形需要多少块单位立方体(棱长为1的立方体),由题意可知需要11块,索玛立方体的1号包含3个单位立方体,2号到7号包含4个单位立方体,而目标图形需要11个单位立方体,只能是3+4+4,所以1好必须选择,之后通过观察可知,1号,3号,5号或1号,3号,6号是成立的.(3号放在最底层,且保持图中的姿势,1好放在3号上面).故答案为1号,3号,5号或1号,3号,6号.【点评】本题考查剪切拼接、索马里方体,解题的关键是利用数形结合的思想思考问题,学会观察、尝试、动手操作解决问题.三、填空题(共5小题,每小题12分,满分60分)11.(12分)一个大于0的自然数如果满足所有因数(即约数)之和等于它自身的2倍,则称这个数为完全数(或完美数),比如,最小的完全数是6,因为6的所有因数为1,2,3,6,而1+2+3+6=12.古希腊时代的人们就已经认识完全数,并且找到了前4个6,28,496,8128完全数,那么,8128的全体质因数为1,2,4,8,16,32,64,127,254,508,1016,2032,4064,8128.【分析】首先是分解质因数,计算共有多少个约数.同时成组寻找即可.【解答】解:8128=26×127.因数个数(6+1)×(1+1)=14个,8128=1×8128=2×4064=4×2032=8×1016=16×508=32×254=64×127.故答案为:1,2,4,8,16,32,64,127,254,508,1016,2032,4064,8128.【点评】要想找到所以的因数关键在于计算出所有的因数个数然后按照顺序成对写出.12.(12分)只能被1和自身整除的大于1的自然数叫做质数或素数.比如2,3,5,7,11等,如果将117分拆成10个质数之和,要求其中最大的质数尽可能大,那么,这个最大的质数为97.【分析】117分成最小的9个2,第十个数也是小于100的,可以从100以内最大的质数开始枚举.【解答】解:100以内最大的质数是97,117﹣97=20,将20分拆成9的质数的和20=2×7+3×2正好符合题意.故答案为:97.【点评】首先要熟记100以内的25个质数,最大是97,尝试枚举即可,同时要注意本题可以是重复数字.13.(12分)我们可以将全体正整数和正分数按照如图所示的方法,从1开始,一层一层地“生长”出来;是第一层;第二层是,,第三层是,,,,…按照这个规律,在第9层.【分析】首先发现数阵图的规律是数阵图的规律是上边数字的乘积是下方的数字.同时发现的和是8,在相乘的分数中8即是小数3分子又是大数5的分母.枚举即可.【解答】解:依题意可知:根据数阵图规律可知;;;;数阵图的规律是上边数字的乘积是下方的数字.同时发现的和是8,在相乘的分数中8即是小数3分子又是大数5的分母.那么对应相乘的数字就是.那么他们前一个数字就是.×=.可知是第七行.是第八行,和即再第九行.故答案为:9【点评】本题考查对数阵图的理解和运用,关键是找到数字的变化规律.问题解决.14.(12分)如果两个自然数的积被13除余1,那么我们称这两个自然数互为“模13的倒数”比如,2×7=14,被13除余1,则2和7互为“模13的倒数”;1×1=1,则1的“模13的倒数”是它自身.显然,一个自然数如果存在“模13的倒数”则它的倒数并不是唯一的,比如,14就是1的另一个“模13的倒数”.判断1,2,3,4,5,6,7,8,9,10,11,12是否有“模13的倒数”,并利用所得结论计算1×2×3×4×5×6×7×8×9×10×11×12(记为12!,读作12的阶乘)被13除所得的余数12.【分析】判断1,2,3,4,5,6,7,8,9,10,11,12是否有“模13的倒数”只需从定义出发判断即可;计算1×2×3×4×5×6×7×8×9×10×11×12被13除所得的余数需要用同余的性质2来简化运算.【解答】解:观察1,2,3,4,5,6,7,8,9,10,11,12易发现:2×7=14 14÷13=1 (1)3×9=27 27÷13=2 (1)4×10=40 40÷13=3 (1)5×8=40 40÷13=3 (1)6×11=66 66÷13=5 (1)12×12=144 144÷13=11 (1)所以1,2,3,4,5,6,7,8,9,10,11,12都有“模13的倒数”.由同余的性质2可知:对于同一个除数,两个数的乘积与他们的余数的乘积同余,则:1×2×3×4×5×6×7×8×9×10×11×12=1×2×7×3×9×4×10×5×8×6×11×12=14×27×40×40×66×1214×27×40×40×66×12≡12(mod13)所以,1×2×3×4×5×6×7×8×9×10×11×12被13除所得的余数为12.答:1,2,3,4,5,6,7,8,9,10,11,12有“模13的倒数”;1×2×3×4×5×6×7×8×9×10×11×12被13除所得的余数为12.【点评】本题主要考察同余的性质2,但在运用同余性质2时,需要观察并找到2×7,3×9,…,6×11,刚好都是1×2×3×4×5×6×7×8×9×10×11×12的因式这一规律,方可解题.15.(12分)如果一个正方形能够被分割为若干个边长不等的小正方形,则这个正方形称为完美正方形.下面的正方形是已知包含21个小正方形的完美正方形(称为21阶完美正方形),这是迄今为止知道的最小阶数的完美正方形.分割方法如图所示,其中小正方形中心的数字代表其边长,请计算这个完美正方形的边长,并写在这里112.【分析】根据小正方形中心的数字代表其边长,求出变成是50、35、27的三个小正方形的边长的和,即可求出这个完美正方形的边长是多少即可.【解答】解:根据分析,根据小正方形中心的数字代表其边长,求出变成是50、35、27的三个小正方形的边长的和,即:50+35+27=85+27=112.故答案是:112.【点评】本题考查了剪切和拼接,突破点是:根据小正方形中心的数字代表其边长,求出变成是50、35、27的三个小正方形的边长的和.。
(word完整版)四年级2015年第十三届走美杯真题和答案与解析(四年级)

第十三届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学四年级试卷(B卷)2015年3月8日南京填空题I(每题8分,共40分)1 计算 5×13×31×73×137=__________________【解析】:本题考查多位数乘法的计算。
直接列式子计算。
2、用 1 个 1、2 个 2、2 个 3 组成一些 4 位数,则能够组成的不同 4 位数一共有__________ 个。
【解析】:本题考查排列组合。
1,2,2,3,3五个数字拿出4个。
相当于5个拿走一个,只能拿走1或2或3。
有①2233②1223③1233这三种组合。
分析第①种,当两个2连在一起,2233 3223 3322 两个2 中间隔一个数,2323 3232 两个2 中间隔两个数2332. 这样第一种小情况有6种。
第②种,同样分析,但是1和3可以互换一次,所以有6×2=12种。
第③种,把22 和 33 互换,用换位思考的方法,同第②种。
所以一共有 6+12+12 得 30 种3、整除 2015 的数称为 2015 的因数,1 和 2015 显然整除 2015,称为 2015 的平凡因数,除了平凡因数,2015还有一些非平凡因数,那么2015的所有非平凡因数之和为______________【解析】:考查因数概念和分解质因数方法。
2015分解质因数2015=5×13×31,每两个因数两两组合,得5+403+13+155+31+65=672。
注明:分解质因数的方法,2015÷50=403,对于403的枚举量很大,很难分解,这里需要知道一个方法,只要试到这个数的开方数以下的质数。
20×20=400,所以只要把403除以20以内的质数就可以试出来。
,如果孩子不明白质因数,可以列举把结果给孩子看。
4、一个自然数能够表示成 5 个连续的自然数之和,也可以表示成 7 个连续的自然数之和,那么将符合以上条件的自然数从小到大排列,前3个数分别为______________【解析】:平均数和最小公倍数概念。
SH四年级走美杯初赛汇总

第七届走美杯四年级初赛一、填空题Ⅰ(每题8分,共40分)1、 3737263376363⨯+⨯⨯+⨯=______2、 下边的一排方格中,除9、8外,每个方格中的字都表示一个数(不同的字可以表示相同的数字),已知其中任何3个连续的方格中的数相加起来都为22,则“走”+“进”+“数”+“学”+“花”+“园”3、 “走美”商场有下列几种瓶装蜂蜜出售:甲,净重3kg ,售价33.99元;乙,净重2kg ,售价22.99元;丙,净重500g ,售价5.99元,那么,_____种蜂蜜最贵,____种蜂蜜最便宜。
4、 一个数学玩具的包装盒是正方体,其表面展开图如下。
现在每方格内都填上相应的数字。
已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A 、B 、C 内的三个数字依次是________。
5、 某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划:该球拍每只售价为人民币60元,同时购买者可获赠1张奖券,积累3张奖券可兑换1只球拍。
由此可见,1张奖券价值为________元。
二、填空题Ⅱ(第题10分,共50分)6、 A ,B 都是整数,A 大于B ,且2009A B ⨯=,那么A B -的最大值为________,最小值为________。
7、 一天,红太狼和灰太狼同时从“野猪林”出发,到“天堂镇”。
红太狼一半路程溜达,一半路程奔跑。
灰太狼一半时间溜达,一半时间奔跑。
如果它们溜达的速度相同,奔跑的速度也相同,则先到“天堂镇”是___________。
8、 柯南家2008年一年用电10200千瓦时,上半年的月平均用电比下半年的月平均用电少100千瓦时。
柯南家下半年月平均用电为___________千瓦时。
9、 某校A 、B 、C 三名同学参加“走进美妙的数学花园”,其指导教师赛前预测“A 获金牌,B 不会获金牌,C 不会获铜牌”。
结果出来后,三人之中,一人获金牌,一人获银牌,一人获铜牌,指导教师的预测只有一个人与结果相符。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如果10+9+8*7÷□+6-5*4-3*2=1,那么□=?
2.a.b.c 都是质数,并且a+b=49,b+c=60,则c=?
3.去掉20.15中的小数点,得到的整数比原来的数增加了?倍
4.梯形的上底、高、下底依次构成一个等差数列,其中高是12.那么梯形的面积是?
5.两个小胖子一样重,他们决定一起减肥。
三个月后大胖减掉了12千克,二胖减掉7千克。
这时大胖的体重比二胖的体重的2倍少80千克。
原来他们各重?千克
6.有两组数,第一组7个数的和是84,第二组的平均数是21,两组中的所有数的平均数是18,则第二组有几个数
7.植树节去植树,120米长的路两边每隔3米挖个坑,后来改成5米挖个坑,问最多可以保留多少坑
8.ABCD四人进行围棋比赛,每人都要与其他三人各赛一场,比赛在两张棋盘上同时进行,每天每人只赛一盘第一天A与C比赛,第二天C与D比赛,第三天A与谁比赛
9.六条铁链,每条四个环,打开一个环要用1分钟,封闭一个环要三分钟,现在要把这24个环连成一条铁链,问至少要几分钟
10.一块正放形的钢板,先截去一个宽3厘米的正方形,又截去一个宽5厘米的长方形,面积比原来的正方形减少81平方厘米,原正方形的面积是()平方厘米。
11.王伟从甲地走向乙地,同时张明骑自行车到甲地,半小时后两人在途中相遇,张明到达甲地后,马上返回乙地,在第一次相遇后20分钟又追上王伟。
张敏到乙地后又折回,两人在第二次相遇后的__________分钟第三次相遇。
12.这是一种两人玩的游戏。
两位选手轮流在一条20×1的矩形长带上移动筹码。
每一轮都可将四个筹码的任意一个向右移动任意方格。
但不能放在其他筹码上面或超过其他筹码。
开始时如图中看到的各筹码位置,赢家是最后移动筹码者。
(他移动后,四个筹码恰好占据了长带右端的四个放个,不可能在移动了)。
先移动者应将________向右移动________格,才能保证获胜。
13.一个n+3位正整数144…430(n个4),是2015的倍数,正整数n最小是____________。
14.右图的3X3表格已经固定,现将4枚相同的棋子放入格子中,每个格子最多放一枚,如果要求每行,每列都有棋子,那么共有_________种不同方法。
15.右图的9个圆圈间,连有9条直线,每条直线有3个圆圈,甲先乙后轮流将9个圆圈涂上颜色,如果谁先将某条直线上的3个圆圈全涂上自己的颜色,谁就获胜,和局判乙胜,现在,甲先选择了“A”,乙接着选择了“B”,甲要取胜,接下来的一步应填在标号为________的方格中(有几种就填几种)。
答案
1) 28
2) 13
3) 99
4) 144
5) 82
6) 14
7) 17
8) D
9) 12
10) 144
11) 40
12) A,2 或D,2
13) 15, 2015=13*5*31, 144......430=13*5*2*111.......1, 15个1可以被31整除
14) 45
15) 2,3,4。
