初三数学锐角三角函数知识精讲

合集下载

初三数学锐角三角函数知识精讲

初三数学锐角三角函数知识精讲锐角三角函数1. 锐角三角函数的定义直角三角形中有两条直角边和一条斜边，从这三条边中适当取两条边可以得到不同的比，这些比值的大小显然只与直角三角形中锐角的大小有关，这样便定义了直角三角形中锐角的三角函数，常用的有正弦函数sin A a c =余弦函数cos A bc =正切函数tan A ab =余切函数cot A ba=BCAcab2. 互余角的三角函数间的关系sin cos()cos sin()tan cot()cot tan()αααααααα=︒-=︒-=︒-=︒-909090903. 同余角三角函数间的关系（1）倒数关系tan cot αα⋅=1（2）商的关系tan sin cos cot cos sin αααααα==，（3）平方关系sin cos 221αα+=4. 三角函数值角度三角函数0°30°45°60°90°sin α 0 12 22 32 1 cos α1 32 22 120 tan α 0 33 13 不存在 cot α不存在3133 0（2）锐角三角函数值的变化情况 <1>锐角三角函数值都是正数且当090︒<<︒α时，01101<<>>+>sin cos sin cos αααα，，，tan α>0，cot α>0。

<2>当角度在090︒︒~间变化时正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）我们利用以上锐角三角函数的定义及性质，可以解决一些求值、化简以及等式证明等问题。

例（1999某某）已知∆ABC 的两边长a c ==35，，且第三边长b 为关于x 的一元二次方程x x m 240-+=的两个正整数根之一，求sinA 的值。

初三数学解直角三角形(锐角三角函数)知识精讲

初三数学解直角三角形（锐角三角函数）【本讲主要内容】解直角三角形（锐角三角函数）包括锐角三角函数：角的正弦、余弦、正切，解直角三角形等。

【知识掌握】【知识点精析】1. 在直角三角形中，锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA 。

2. 在直角三角形中，锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA 。

3. 在直角三角形中，锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA 。

4. 锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数。

5. 特殊角的三角函数值： 2160cos 30sin =︒=︒，2330cos 60sin =︒=︒；2245cos 45sin =︒=︒；360tan 145tan 3330tan =︒=︒=︒，，21 30° 32 1 145°6. 在直角三角形中，由已知元素求未知元素的过程，就是解直角三角形。

（1）222c b a =+；（2）︒=∠+∠90B A ；（3）ba A tan cb A cosc aA sin ===，，；（4）c ch 21ab 21S ==∆。

BcaA b CDh c8. 应用解直角三角形的知识解一些简单的实际问题。

【解题方法指导】例1. 选择题：在△ABC 中，∠C ＝90°，∠B ＝2∠A ，则tanA 等于（） A.3 B. 33 C. 23 D.21 分析：设法求出∠A 的度数，再求值。

解：Rt △ABC 中，∠A ＋∠B ＝90° 把∠B ＝2∠A 代入，得 3∠A ＝90° ∴∠A ＝30°3330tan A tan =︒=∴ 故选B 。

评析：抓住直角三角形中两锐角互余，求出角的度数。

例 2. （2002年四川）如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，32AB 22AC ==，，设∠BCD ＝α，那么cos α的值是（）A.22 B.23 C.33 D.36分析：由∠ACB ＝90°，CD ⊥AB ，可知∠BCD ＝∠A ＝α，而ABACA cos =，故可解。

九年级锐角三角函数知识点总结

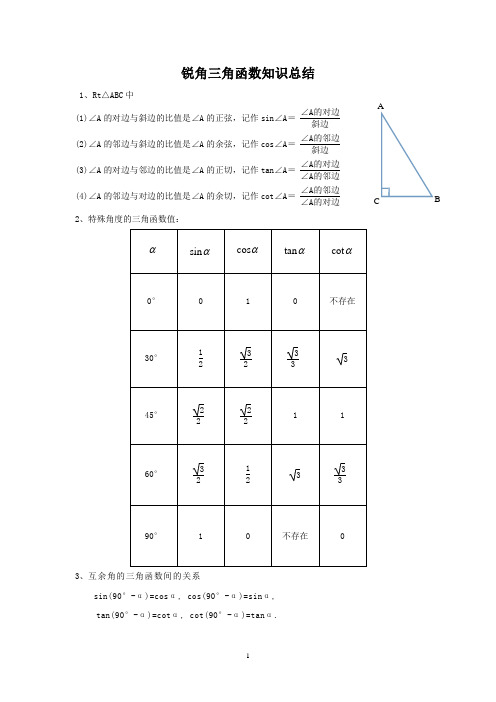
锐角三角函数知识总结 1、Rt△ABC中(1)∠A的对边与斜边的比值是∠A的正弦，记作sin∠A＝∠A的对边斜边(2)∠A的邻边与斜边的比值是∠A的余弦，记作cos∠A＝∠A的邻边斜边(3)∠A的对边与邻边的比值是∠A的正切，记作tan∠A＝∠A的对边∠A的邻边(4)∠A的邻边与对边的比值是∠A的余切，记作cot∠A＝∠A的邻边∠A的对边2、特殊角度的三角函数值：3、互余角的三角函数间的关系sin(90°-α)=cosα, cos(90°-α)=sinα,tan(90°-α)=cotα, cot(90°-α)=tanα.AC B4、同角三角函数间的关系: ，，1cot tan =•αα，1cos sin 22=+αα5、三角函数值（1）特殊角三角函数值（2）0°～90°的任意角的三角函数值，查三角函数表。

（3）锐角三角函数值的变化情况（i ）锐角三角函数值都是正值（ii ）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii ）当角度在0°≤α≤90°间变化时， 0≤sin α≤1, 1≥cos α≥0, 当角度α在0°至90°间变化时，0cot ,0tan >>αα。

6、解直角三角形的基本类型：解直角三角形的基本类型及其解法如下表：7、仰角、俯角当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角．。

中考复习：锐角三角函数

中考复习：锐角三角函数知识梳理一、锐角三角函数（正弦、余弦、正切）1、定义：在Rt △ABC 中，∠C ＝90°，我们把锐角A的对边与斜边的比叫做∠A 的正弦（sinc ），记作sin A ，即sin A aA c∠==的对边斜边。

把∠A 的邻边与斜边的比叫做∠A 的余弦（cosine ），记作cos A ，即；把∠A 的对边与邻边的比叫做∠A 的正切（tangent ），记作tan A ，即。

锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数（trigonometric function of acute angle ）。

当锐角A 的大小确定时，∠A 的对边与斜边的比（正弦）、∠A 的邻边与斜边的比（余弦）、∠A 的对边与邻边的比（正切）分别是确定的。

2、增减性：在0°到90°之间，正弦值、正切值随着角度的增大而增大，余弦随着角度的增大而减小。

3、取值范围：当∠A 为锐角时，三角函数的取值范围是：0＜sin A ＜1，0＜cos A ＜1，tan A ＞0。

4、互余两角的函数关系：如果两角互余，则其中一有的正弦等于另一角的余弦，即：若α是一个锐角，则sin α=cos （90°-α），cos α=sin （90°-α）。

5、正、余弦的平方关系：sin 2α+ cos 2α=1。

二、300、450、600的正弦值、余弦值和正切值如下表：三、解直角三角形bcos c A A ∠==的邻边斜边atan bA A A ∠=∠的对边＝的邻边C ∠A 的邻边b∠A 的对边a在直角三角形中，由已知元素求未知元素的过程就是解直角三角形。

1、在Rt△ABC 中，∠C＝90°，设三个内角A 、B 、C 所对的边分别为a 、b 、c （以下字母同），则解直角三角形的主要依据是：（1）边角之间的关系： sinA ＝cosB ＝a c ， cosA ＝sinB ＝bc，tanA ＝cotB ＝a b ，cotA ＝tanB ＝b a。

锐角三角函数知识点

锐角三角函数知识点锐角三角函数：一、基本概念：1、什么是锐角三角函数：锐角三角函数是一类特殊的函数，涉及到角度和角度对应的三角函数值，用于计算平面向量在多边形中和求解三角形的面积。

2、锐角三角函数的定义：锐角三角函数是基于角度θ，从而定义的三角函数值。

一般情况下，它用半圆线直叙指函数如下所示：sinθ，cosθ，tanθ，cotθ，secθ，cscθ。

3、锐角三角函数的基本关系：cosθ= sin (π/2-θ)；sinθ= cos (π/2-θ)；tanθ=cot (π/2-θ)；cotθ=tan (π/2-θ)；secθ=csc(π/2-θ)；cscθ=sec (π/2-θ)。

二、圆周角：1、什么是圆周角：圆周角是指以圆等分线在a轴上的量度，即由圆心和两个点确定的弧的长度。

圆周角定义在一个圆的周围，与半径的长度有关，可以用角度μ来表示。

2、单位：圆周角的单位是弧度rad，又称为radian，表示当一个圆的半径为1时，圆周角的长度。

三、锐角的余弦定理：1、锐角余弦定理是用弦和角定义的三角形问题，可以求解共有三角形A、B、C三个锐角所对应边长a、b、c满足关系：a²=b²+c²-2bc cosA；b²=a²+c²-2ac cosB；c²=a²+b²-2ab cosC。

2、此外，锐角余弦定理也可以利用三角形所有边长求解A、B、C三个锐角所对应的角度值，记为A=cos-1[(b²+c²-a²)/2bc]；B=cos-1[(a²+c²-b²)/2ac]；C=cos-1[(a²+b²-c²)/2ab]。

四、锐角的正弦定理：1、锐角正弦定理是求解三角形的已知一边和两个对边角的问题，满足条件如下：a=b sinA/sinB；b=a sinB/sinA；c=a sinC/sinA，c=bsinC/sinB。

初三数学锐角三角函数知识归纳解读

初三数学《解直角三角形》知识提纲(孟老师归纳一:锐角三角函数的概念1:在△ABC 中,∠C=90°锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数c a sin =∠=斜边的对边A A c bcos =∠=斜边的邻边A Aba tan =∠∠=的邻边的对边A A A a bcot =∠∠=的对边的邻边A A A2:锐角三角函数的取值范围:0≤sin α≤1,0≤cos α≤1,tan α≥0,cot α≥0. 二:锐角三角函数之间的关系 1:平方关系1cos sin 22=+A A 2:倒数关系tanA ∙cotA=1 3:商关系: tanA=A A cos sin cotA=AA sin cos 4:互余关系 sinA=cos(90°—A =cosB , cosA=sin(90°—A =sinBtanA=cot(90°—A =cotB , cotA=tan(90°—A =tanB 三:特殊角的三角函数值三角函数 0° 30°45°60°90° sinα212223 1cos α 123 2221 0tan α 033 13不存在cot α 不存在31 33 0说明:锐角三角函数的增减性,当角度在0°~90°之间变化时. (1正弦值正切值,随着角度的增大(或减小而增大(或减小 (2余弦值余切值,随着角度的增大(或减小而减小(或增大四:解直角三角形的概念:在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。

实际问题三概念: (1俯、仰角. (2方位角、象限角. (3坡角、坡度.五:补充有关公式(11sin 2S ab C ∆==1sin 2bc A =1sin 2ac B (2Rt △面积公式:1122S ab ch ==(3结论:直角三角形斜边上的高abh c=(4测底部不可到达物体的高度.常见解答方程式:如右图,∵在Rt △ABP 中,BP=xcot α,在Rt △AQB 中,BQ=xcot β,且BQ —BP=a , ∴xcot β-xcot α=a .六:解直角三角形的知识的应用,可以解决: (1测量物体高度.(2有关航行问题. (3计算坝体或边路的坡度等问题西αhli i=h/l=tg αBx。

完整版)锐角三角函数超经典讲义

完整版)锐角三角函数超经典讲义锐角三角函数锐角三角函数是三角函数的一种，包括正弦、余弦和正切。

在一个锐角三角形中，锐角的对边、邻边和斜边之间的比例就是锐角三角函数。

具体来说，对于锐角A，其正弦、余弦和正切分别表示为sinA、cosA和XXX。

其中，XXX表示A的对边与斜边的比，cosA表示A的邻边与斜边的比，XXX表示A的对边与邻边的比。

这些符号都是完整的，单独的“sin”没有意义。

在用大写字母表示角度时，一般省略“∠”符号。

在求解锐角三角函数时，关键在于构造以此锐角所在的直角三角形。

例如，在一个直角三角形ABC中，如果已知∠C=90°，cosB=4/5，则AC：BC：AB=3：4：5.另外，需要注意的是，正弦、余弦和正切是实数，没有单位，它们的大小只与角的大小有关，而与所在直角三角形无关。

例1：在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE。

证明△ABE≌△DFA，并求sin∠EDF的值。

解：首先，连接AC，易得△ABC为等腰直角三角形，∠BAC=45°。

又因为AE=BC，所以△ABE和△ACD相似，即∠ABE=∠ACD，∠XXX∠ADC。

又因为∠ADC=90°，所以∠AEB=90°。

因此，△ABE和△DFA是全等三角形。

接下来，求sin∠EDF的值。

由于∠BAC=45°，所以∠AED=45°。

由于△ABE和△DFA全等，所以∠XXX∠BAE=45°。

因此，sin∠EDF=sin45°=1/√2.例2：在△ABC中，∠A=60°，∠B=45°，AB=8，求△ABC面积（结果可保留根号）。

解：由于∠A=60°，∠B=45°，所以∠C=75°。

根据三角函数的定义，可以得到：sin75°=cos15°=(sin60°cos45°+cos60°sin45°)/2=√6+√2/4cos75°=sin15°=(sin60°cos45°-cos60°sin45°)/2=√6-√2/4因此，△ABC面积为S=(1/2)AB·BC·sin75°=4(√6+√2)。

九年级数学《锐角三角函数》知识点总结归纳

一、三角函数的定义1. 正弦函数sinx：对于任意实数x，将x的终边与x轴正方向的夹角的终点的纵坐标就是sinx。

2. 余弦函数cosx：对于任意实数x，将x的终边与x轴正方向的夹角的终点的横坐标就是cosx。

3. 正切函数tanx：对于任意实数x，将sinx除以cosx就是tanx。

4. 余切函数cotx：对于任意实数x，将cosx除以sinx就是cotx。

5. 正割函数secx：对于任意实数x，将1除以cosx就是secx。

6. 余割函数cscx：对于任意实数x，将1除以sinx就是cscx。

二、三角函数的性质1. 基本关系式：sin^2x + cos^2x = 12. 周期性：sin(x+2kπ) = sinx，cos(x+2kπ) = cosx，其中k为任意整数。

3. 奇偶性：奇函数有sinx、tanx和cotx，偶函数有cosx、secx和cscx。

4. 正函数和负函数：在单位圆上，sinx和cscx为正函数，cosx和secx为负函数。

5. 三角函数的范围：sinx、cosx和tanx的范围是[-1,1]，cotx、secx和cscx的范围是(-∞,∞)。

三、特殊角的三角函数值1.0°、30°、45°、60°和90°的三角函数值。

2.30°、45°、60°和90°的三角函数值的推导。

四、角度的度量转换1.度和弧度之间的转换：π弧度=180°，1°=π/180弧度。

2.角度的换算：1°=60'，1'=60''。

五、倍角、半角和三倍角公式1. 倍角公式：sin2x = 2sinxcosx，cos2x = cos^2x - sin^2x，tan2x = 2tanx / (1 - tan^2x)。

2. 半角公式：sin(x/2) = ±√[(1-cosx)/2]，cos(x/2) =±√[(1+cosx)/2]，tan(x/2) = ±√[(1-cosx) / (1+cosx)]。

(完整word)锐角三角函数讲义

锐角三角函数第一课时：三角函数定义与特殊三角函数值知识点一：锐角三角函数的定义：一、锐角三角函数定义：在Rt △ABC 中，∠C=900, ∠A、∠B、∠C 的对边分别为a 、b 、c ，则∠A 的正弦可表示为：sinA= , ∠A 的余弦可表示为cosA=∠A 的正切：tanA= ，它们弦称为∠A 的锐角三角函数例1．如图所示，在Rt △ABC 中,∠C ＝90°．①斜边)(sin =A ＝______，斜边)(sin =B ＝______； ②斜边)(cos =A ＝______,斜边)(cos =B ＝______; ③的邻边A A ∠=)(tan ＝______, )(tan 的对边B B ∠=＝______．例2. 锐角三角函数求值：在Rt △ABC 中，∠C ＝90°,若a ＝9，b ＝12，则c ＝______,sin A ＝______,cos A ＝______，tan A ＝______, sin B ＝______,cos B ＝______，tan B ＝______．例3．已知:如图，Rt △TNM 中,∠TMN ＝90°，MR ⊥TN 于R 点，TN ＝4，MN ＝3．求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR ．对应练习:1、在Rt△ABC 中,a ＝5，c ＝13，求sinA ，cosA ，tanA ．2、如图,△ABC 中，AB=25,BC=7，CA=24．求sinA 的值．25247C BA3、已知α是锐角，且cos α=34,求sin α、tan α的值．4、在Rt ABC △中，90C ∠=，5AC =,4BC =，则tan A = ．5、在△ABC 中,∠C=90°，sinA=53,那么tanA 的值等于（）。

A ．35B 。

45C. 34D 。

436、在△ABC 中，∠C ＝90°，cosA 3,c ＝4，则a ＝_______．7、如图，P 是∠α的边OA 上一点，且P 点坐标为（2，3），则sinα=_______，cosα=_________,tanα=______ _．αyxP(2,3)OA知识点二：特殊角的三角函数值当时，正弦和正切值随着角度的增大而余弦值随着角度的增大而例1．求下列各式的值．（1）。

九年级数学《锐角三角函数》知识点总结归纳

《锐角三角函数》是九年级数学中的一个重要的章节，它在高中数学中也有重要的应用。

下面是对《锐角三角函数》的知识点进行总结归纳。

一、角度的度和弧度制1.角度的度制：一个圆周分为360等份，每一份称为一度，用符号°表示。

2.角度的弧度制：弧度制通过角对应的弧长与半径的比值来表示。

弧度制度数=角度的度数×π/180二、正弦、余弦、正切关系1. 正弦函数：对于任意锐角A，正弦函数表示为sinA=对边/斜边。

2. 余弦函数：对于任意锐角A，余弦函数表示为cosA=邻边/斜边。

3. 正切函数：对于任意锐角A，正切函数表示为tanA=对边/邻边。

三、特殊角的值1. 30°特殊角的正弦、余弦、正切值：sin30°=1/2，cos30°=√3/2，tan30°=1/√32. 45°特殊角的正弦、余弦、正切值：sin45°=√2/2，cos45°=√2/2，tan45°=13. 60°特殊角的正弦、余弦、正切值：sin60°=√3/2，cos60°=1/2，tan60°=√3四、三角函数的基本性质1. 同角三角函数值的关系：sinA/cosA=tanA，cosA/sinA=1/tanA，sin^2A+cos^2A=12. 三角函数的周期性：sin(A+2π)=sinA，cos(A+2π)=cosA，tan(A+π)=tanA。

3. 正负关系：在第一象限，sinA>0，cosA>0，tanA>0，在第二象限，sinA>0，cosA<0，tanA<0，在第三象限，sinA<0，cosA<0，tanA>0，在第四象限，sinA<0，cosA>0，tanA<0。

五、三角函数的应用1.解三角形：根据已知两边和夹角，用余弦定理和正弦定理求解。

初中数学锐角三角函数知识点

初中数学锐角三角函数知识点锐角三角函数是初中数学中的一个重要知识点。

本文将系统地介绍锐角三角函数的概念、性质和应用。

一、概念1.边长比在直角三角形中，我们可以定义三角函数。

对于锐角三角形，也可以把边长比看作三角函数的定义。

定义如下：- 正弦函数（sin）：指的是对边比斜边的比值，即sinA = 对边AB / 斜边AC。

- 余弦函数（cos）：指的是邻边比斜边的比值，即cosA = 邻边BC / 斜边AC。

- 正切函数（tan）：指的是对边比邻边的比值，即tanA = 对边AB / 邻边BC。

2.三角函数值的取值范围在锐角三角形中，三角函数的取值范围是(0,1)。

具体来说-正弦函数的值在0到1之间变化。

-余弦函数的值在0到1之间变化。

-正切函数的值在0到正无穷之间变化。

二、性质1.互余关系在锐角三角形中，对于同一个角的正弦和余弦函数，它们的数值互为倒数。

即sinA = 1 / cosA，cosA = 1 / sinA。

证明：由定义可知sinA = 对边AB / 斜边AC，cosA = 邻边BC / 斜边AC。

所以sinA / cosA = (对边AB / 斜边AC) / (邻边BC / 斜边AC) = 对边AB / 邻边BC = tanA。

又由于tanA = sinA / cosA，所以sinA = 1 / cosA。

同理可证cosA = 1 / sinA。

2.正切函数的性质在锐角三角形中，正切函数具有以下性质：-任何一个角的正切函数的值是唯一的。

- 对于锐角A和其补角（即90°-A），它们的正切值互为相反数。

（tanA = -tan(90°-A)）。

三、应用锐角三角函数在实际生活和学习中有着广泛的应用，以下是一些常见的应用：1.三角函数在测量中的应用例如，在建筑和工程中，我们经常需要测量高度、角度等，锐角三角函数可以帮助我们计算和测量。

2.角度的计算通过使用正弦函数、余弦函数和正切函数，我们可以根据已知的边长比计算出对应的角度。

锐角三角函数知识点总结

锐角三角函数知识点总结一、引言锐角三角函数是数学中的基础知识点，它在解决与直角三角形相关的问题中扮演着重要角色。

本文将总结锐角三角函数的基本概念、性质和公式，以及它们在实际问题中的应用。

二、基本概念1. 锐角：角度小于90度的角。

2. 直角三角形：一个角为90度的三角形。

3. 边的命名：- 对边（Opposite side）：锐角所对的边。

- 邻边（Adjacent side）：锐角旁边的边，但不包括斜边。

- 斜边（Hypotenuse）：直角三角形中最长的边，对直角的两边进行闭合。

4. 锐角三角函数：- 正弦（Sine, sin）：锐角的对边与斜边的比值。

- 余弦（Cosine, cos）：锐角的邻边与斜边的比值。

- 正切（Tangent, tan）：锐角的对边与邻边的比值。

三、基本公式1. 定义公式：- sin(θ) = 对边 / 斜边- cos(θ) = 邻边 / 斜边- tan(θ) = 对边 / 邻边2. 互余关系：- sin(90° - θ) = cos(θ)- cos(90° - θ) = sin(θ)- tan(90° - θ) = cot(θ)3. 基本恒等式：- sin²(θ) + cos²(θ) = 1- 1 + tan²(θ) = sec²(θ)- 1 + cot²(θ) = csc²(θ)4. 特殊角的三角函数值：- sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = √3/3 - sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1- sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3四、应用1. 解直角三角形问题：- 利用三角函数求解边长。

初中数学锐角三角函数知识点

初中数学锐角三角函数知识点锐角三角函数是一个重要的数学概念，通常在初中数学学习中进行详细讲解。

下面是一个1200字以上的介绍锐角三角函数的知识点：一、角的概念角是由两条射线共同确定的形状。

有三种表示方法：度、弧度和均分。

1.度表示法度是一种角的度量单位，用符号°表示。

一个圆共有360度，一个直角是90度。

当角小于直角时，角的度数为锐角，大于直角角度且小于平角角度的为钝角。

2.弧度表示法弧度是另一种角的度量单位，用符号rad表示。

一个圆的周长等于2π，所以一个圆有2π弧度。

弧度与角度的转化公式为：角度 = 弧度/π * 180，弧度 = 角度* π/180。

3.均分表示法角的均分表示法将圆分为360个等份，每一份都称为一分。

角的度数可以用分数表示。

二、三角函数的定义锐角三角函数包括正弦、余弦和正切。

它们的定义如下：1. 正弦函数（Sine Function）正弦函数是个周期性函数，用sin表示，定义为对于任意锐角A，正弦函数的值为：sin A = 对边/斜边。

2. 余弦函数（Cosine Function）余弦函数也是个周期性函数，用cos表示，定义为对于任意锐角A，余弦函数的值为：cos A = 邻边/斜边。

3. 正切函数（Tangent Function）正切函数也是个周期性函数，用tan表示，定义为对于任意锐角A，正切函数的值为：tan A = 对边/邻边。

三、三角函数的性质锐角三角函数具有一些重要的性质：1.正弦和余弦的平方和为1对于任意锐角A，有sin^2 A + cos^2 A = 1、这一性质又被称为三角恒等式。

2.三角函数的周期性正弦、余弦和正切函数都是周期函数，它们的周期都是2π。

所以，对于任意锐角A，有sin(A+2πn) = sinA，cos(A+2πn) = cosA和tan(A+2πn) = tanA，其中n是任意整数。

3.正弦、余弦和正切的对称性正弦与余弦函数关于y轴对称，即sin(-A) = -sinA，cos(-A) = cosA。

初中九年级数学中考锐角三角函数知识点总结

九年级数学中，锐角三角函数是一个重要的知识点。

锐角三角函数是指对于锐角的正弦、余弦和正切函数。

下面我将对锐角三角函数的基本概念、性质和应用进行总结。

一、基本概念1.弧度和角度：角度是常用的角度度量单位，弧度是角度的另一种度量单位。

1个弧度对应360°/2π≈57.3°。

角度和弧度之间的关系式：弧度=角度×π/180°。

2.锐角：指角度小于90°的角。

3. 三角函数：对于一个锐角A，定义其正弦(sin A)为对边与斜边的比值，余弦(cos A)为邻边与斜边的比值，正切(tan A)为对边与邻边的比值。

二、性质1.正弦函数的性质：（1）对于锐角A，0 < A < 90°，sin A > 0；（2）sin A = sin (180° - A) = sin (A + 360°)；（3）sin (90° - A) = cos A；（4）sin A ≠ 0，当且仅当A是锐角。

2.余弦函数的性质：（1）对于锐角A，0 < A < 90°，cos A > 0；（2）cos A = cos (180° - A) = cos (360° + A)；（3）cos (90° - A) = sin A；（4）cos A ≠ 0，当且仅当A是锐角。

3.正切函数的性质：（1）对于锐角A，0 < A < 90°，tan A > 0；（2）tan A = tan (180° + A)；（3）tan (90° - A) = 1/tan A；（4）tan A ≠ 0，当且仅当A是锐角。

4.三角函数的关系：（1）sin^2 A + cos^2 A = 1；（2）tan A = sin A / cos A。

三、应用1.解三角形：利用已知角的正弦、余弦和正切的值，可以求解未知边长或角度的三角形问题。

九年级人教版数学第二学期第28章锐角三角函数整章知识详解

九年级数学第28章锐角三角函数
【例】求下列各式的值.
(1) cos260°+sin260°
(2) csoins4455

-tan45

【解析】（1）cos²60°+sin²60°
cos²60°表示（cos60°）²，即cos60°的平方.
=（ 12）²+（
3 2
）²
=1；
（2）cos 45 tan 45
九年级数学第28章锐角三角函数
2.（黄冈中考）在△ABC中，∠C＝90°，sinA＝
则tanB＝（ B ）
A. 4
B. 3
C. 3
D. 4
3
4
5
5
3.（丹东中考）如图，小颖利用有一
个锐角是30°的三角板测量一棵树的高度， 30 已知她与树之间的水平距离BE为5m，AB为 °A
B 1.5m（即小颖的眼睛距地面的距离），那
九年级数学第28章锐角三角函数
【例】如图，在Rt△ABC中，∠C=90°，BC=6，sinA= 3 ，
求cosA，tanB的值.
5
B
【解析】 sinA BC ,
AB
6
AB BC 6 5 10，
sinA 3
又 AC AB2 BC2 102 62 8，
A
C
cosA AC 4 , tanB AC 4 .
100
D.不能确定
3.如图 A
B
1
3
，则 sinA=___2___ .
30°
C
7
九年级数学第28章锐角三角函数
1.（温州中考）如图，在△ABC中，∠C=90°, AB=13，

初中数学锐角三角函数知识点

初中数学锐角三角函数知识点锐角三角函数是高中数学的重要内容，它涉及到三角函数的定义、性质以及与三角函数相关的常见解题方法。

以下将详细介绍锐角三角函数的知识点。

一、锐角三角函数的定义1. 正弦函数（sine function）：在锐角ABC中，以角A为自变量，以对边AB与斜边AC的比值作为函数值。

记作sinA = AB/AC。

2. 余弦函数（cosine function）：在锐角ABC中，以角A为自变量，以邻边BC与斜边AC的比值作为函数值。

记作cosA = BC/AC。

3. 正切函数（tangent function）：在锐角ABC中，以角A为自变量，以对边AB与邻边BC的比值作为函数值。

记作tanA = AB/BC。

4. 余切函数（cotangent function）：在锐角ABC中，以角A为自变量，以邻边BC与对边AB的比值作为函数值。

记作cotA = BC/AB。

5. 正割函数（secant function）：在锐角ABC中，以角A为自变量，以斜边AC与邻边BC的比值作为函数值。

记作secA = AC/BC。

6. 余割函数（cosecant function）：在锐角ABC中，以角A为自变量，以斜边AC与对边AB的比值作为函数值。

记作cscA = AC/AB。

二、锐角三角函数的性质1. 正弦函数的定义域为[0, π/2]，值域为[0, 1]，是一个奇函数，即sin(π/2 - A) = cosA。

2. 余弦函数的定义域为[0, π/2]，值域为[0, 1]，是一个偶函数，即cos(π/2 - A) = sinA。

3.正割函数和余割函数的定义域为(0,π/2)∪(π/2,π)，值域为R^+∪R^-。

4.正弦函数和余弦函数的图像是一条周期为2π的曲线，对称于直线x=π/25.正切函数和余切函数的定义域为(0,π/2)∪(π/2,π)，值域为R^+∪R^-。

6.正切函数和余切函数的图像是一条周期为π的曲线，对称于直线x=π/2三、常用的锐角三角函数解题方法1. 利用定义求函数值：根据三角函数的定义，利用已知信息计算出函数值。

锐角三角函数知识点总结

\ 1 /
锐角三角函数知识点总结
一、锐角三角函数的定义：
二、特殊角的三角函数的值：
三、锐角三角函数的性质
\ 2 / 四、解直角三角形
五、解直角三角形中的常见图形:
六、实际应用中的概念：
⑴ 仰角与俯角：在视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角．如图⑴．
⑵ 坡角与坡度：坡面的垂直高度h 和水平宽度l 的比叫做坡度（或叫做坡比），用字母表示为i=h l ，坡面与水平面的夹角记作α，叫做坡角，则i=h l =tan α．坡度越大，坡面就越陡．如图⑵ ⑶ 方位角：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达为北（南）偏东（西）××度．如图⑶．。

初三数学锐角三角函数知识精讲