全等三角形培优竞赛讲义(四)等腰三角形
等腰三角形课件ppt

边与角的相互影响
边长变化对角度的影响
当等边的长度增加或减少时,底角α的大小会发生变化。这是因为角度α与基边的长度成 反比。
角度变化对边长的影响
当底角α的大小发生变化时,基边的长度也会相应地增加或减少。这是因为角度的变化会 影响到三角形的周长,从而影响基边的长度。
Part
03
等腰三角形的判定与证明
04
等腰三角形的面积与周长
面积的计算
1 2
面积公式
等腰三角形的面积可以通过底边长度和对应的高 来计算,公式为 (S = frac{1}{2} times text{底边 长度} times text{高})。
面积与底边和高
等腰三角形的面积与底边长度和高有关,当底边 长度和高发生变化时,面积也会相应地变化。
等腰三角形与勾股定理
总结词
勾股定理是几何学中的重要定理之一 ,它可以应用于等腰三角形,特别是 等腰直角三角形。
详细描述
勾股定理表明在一个直角三角形中, 直角边的平方和等于斜边的平方。对 于等腰直角三角形,两条直角边长度 相等,因此它们的平方和等于斜边的 平方。
详细描述
等腰三角形是两边相等的三角形,根据等腰三角形的性质,两个底角相等,并且 三角形的内角和为180度,因此每个底角的大小为(180度 - 顶角度数)/ 2。
等腰三角形的外角和定理
总结词
等腰三角形的外角和定理表明等腰三角形的一个外角等于它 不相邻的两个内角之和。
详细描述
根据三角形外角定理,一个三角形的外角等于它不相邻的两 个内角之和,对于等腰三角形来说,由于两个底角相等,所 以一个底角的外角等于另一个底角。
等腰三角形课件
• 等腰三角形的定义与性质 • 等腰三角形的边与角 • 等腰三角形的判定与证明 • 等腰三角形的面积与周长 • 等腰三角形的拓展知识
初二等腰三角形培优学案同步讲义

学科教师辅导讲义体系搭建一、知识梳理1、等腰三角形的性质定理(1)两角分别相等且其中一组等角的对边相等的两个三角形全等。
(AAS)(2)等腰三角形的两底角相等。
即等边对等角。
(3)推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。
即三线合一。
(4)等边三角形的三个内角都相等,并且每个角都等于60°。
2、等腰三角形的判定定理(1)有两条边相等的三角形是等腰三角形。
(2)有两个角相等的三角形是等腰三角形。
即等角对等边。
(3)三个角都相等的三角形是等边三角形。
(4)有一个角等于60°的等腰三角形是等边三角形。
3、在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。
4、反证法:先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立。
考点一:等腰三角形的性质例1、一个等腰三角形的两边长分别为4,8,则它的周长为()A.12 B.16C.20 D.16或20例2、如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为()A.15°B.17.5°C.20°D.22.5°例3、一个三角形可被剖成两个等腰三角形,原三角形的一个内角为36度,求原三角形最大内角的所有可能值.例4、如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,∠A n的度数为.例5、如图1,Rt△ABC中AB=AC,点D、E是线段AC上两动点,且AD=EC,AM垂直BD,垂足为M,AM的延长线交BC于点N,直线BD与直线NE相交于点F.试判断△DEF的形状,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程之后,可以从下列①、②中选取一个补充或者更换已知条件,完成你的证明.1、画出将△BAD沿BA方向平移BA长,然后顺时针旋转90°后图形;2、点K在线段BD上,且四边形AKNC为等腰梯形(AC∥KN,如图2).附加题:如图3,若点D、E是直线AC上两动点,其他条件不变,试判断△DEF的形状,并说明理由.考点二:等腰三角形的判定例1、△ABC的三边长a,b,c满足关系式(a﹣b)(b﹣c)(c﹣a)=0,则这个三角形一定是()A.等腰三角形B.等边三角形C.等腰直角三角形 D.无法确定例2、如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有()A.5个B.4个C.3个D.2个例3、如图,△ABC中,BF、CF分别平分∠ABC和∠ACB,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②∠DFB=∠EFC;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的是.(填序号,错选、漏选不得分)例4、如图,以△ABC的边AB、AC为直角边向外作等腰直角△ABE和△ACD,M是BC的中点,请你探究线段DE与AM之间的关系.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.①画出将△ACM绕某一点顺时针旋转180°后的图形;②∠BAC=90°(如图)附加题:如图,若以△ABC的边AB、AC为直角边,向内作等腰直角△ABE和△ACD,其它条件不变,试探究线段DE与AM之间的关系.实战演练➢课堂狙击1、等腰三角形的两边长分别为4cm和8cm,则它的周长为()A.16cm B.17cmC.20cm D.16cm或20cm2、如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为()A.40° B.30°C.70° D.50°3、如图,∠B=∠C,∠1=∠3,则∠1与∠2之间的关系是()A.∠1=2∠2 B.3∠1﹣∠2=180°C.∠1+3∠2=180° D.2∠1+∠2=180°4、如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是()A.①② B.①③ C.③④ D.②③5、如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1= 度,图中有个等腰三角形.6、如图,AD是直角三角形△ABC斜边上的中线,把ADC沿AD对折,点C落在点C′处,连接CC′,则图中共有等腰三角形个.7、如图1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,….,根据上述规律请你写出∠A n+1A n C n= °.(用含n的代数式表示)8、如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.求证:DE=DF.9、如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:△ABC是等腰三角形.➢课后反击1、已知等腰三角形的一个底角的度数为70°,则另外两个内角的度数分别是()A.55°,55° B.70°,40°C.55°,55°或70°,40° D.以上都不对2、等腰三角形顶角是84°,则一腰上的高与底边所成的角的度数是()A.42° B.60°C.36° D.46°3、如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44° B.66°C.88° D.92°4、如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.若α=10°,则β的度数是()A.40° B.50°C.60° D.不能确定5、如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为()A.2个B.3个C.4个D.5个6、如图,△ABC中,AB=AC,AD是∠BAC的平分线,若△ABD的周长为12,△ABC的周长为16,则AD的长为.7、如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):.8、如图,∠BAC=θ(0°<θ<90°),现只用4根等长的小棒将∠BAC固定,从点A1开始依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1,则角θ的取值范围是.9、数学课上,同学们探究下面命题的正确性:顶角为36°的等腰三角形具有一种特性,即经过它某一顶点的一条直线可把它分成两个小等腰三角形.为此,请你解答问题(1).(1)已知:如图①,在△ABC中,AB=AC,∠A=36°,直线BD平分∠ABC交AC于点D.求证:△ABD与△DBC都是等腰三角形;(2)在证明了该命题后,小乔发现:下面两个等腰三角形如图②、③也具有这种特性.请你在图②、图③中分别画出一条直线,把它们分成两个小等腰三角形,并在图中标出所有等腰三角形两个底角的度数;(3)接着,小乔又发现:其它一些非等腰三角形也具有这样的特性,即过它其中一个顶点画一条直线可以将原三角形分成两个小等腰三角形.请你画出两个不同类型且具有这种特性的三角形的示意图,并在图中标出可能的各内角的度数.(说明:要求画出的两个三角形不相似,且不是等腰三角形.)(4)请你写出两个符合(3)中一般规律的非等腰三角形的特征.直击中考1、【2015•长沙】下列条件中,不能判定△ABC是等腰三角形的是()A.a=3,b=3,c=4 B.a:b:c=2:3:4C.∠B=50°,∠C=80° D.∠A:∠B:∠C=1:1:22、【2016•山东】如下图中,将△ABC沿BD对折,使得点C落在AB上的点C′处,且∠C=2∠CBD,已知∠A=36°.(1)求∠BDC的度数;(2)写出图中所有的等腰三角形(不用证明)重点回顾1、等腰三角形的性质定理(1)两角分别相等且其中一组等角的对边相等的两个三角形全等。
培优专题等腰三角形(含答案)

9、等腰三角形【知识精读】(-)等腰三角形的性质1. 有关定理及其推论定理:等腰三角形有两边相等;定理:等腰三角形的两个底角相等(简写成“等边对等角”)。
推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,这就是说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
推论2:等边三角形的各角都相等,并且每一个角都等于60°。
等腰三角形是以底边的垂直平分线为对称轴的轴对称图形;2. 定理及其推论的作用等腰三角形的性质定理揭示了三角形中边相等与角相等之间的关系,由两边相等推出两角相等,是今后证明两角相等常用的依据之一。
等腰三角形底边上的中线、底边上的高、顶角的平分线“三线合一”的性质是今后证明两条线段相等,两个角相等以及两条直线互相垂直的重要依据。
(二)等腰三角形的判定1. 有关的定理及其推论定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”。
)推论1:三个角都相等的三角形是等边三角形。
推论2:有一个角等于60°的等腰三角形是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
2. 定理及其推论的作用。
等腰三角形的判定定理揭示了三角形中角与边的转化关系,它是证明线段相等的重要定理,也是把三角形中角的相等关系转化为边的相等关系的重要依据,是本节的重点。
3. 等腰三角形中常用的辅助线等腰三角形顶角平分线、底边上的高、底边上的中线常常作为解决有关等腰三角形问题的辅助线,由于这条线可以把顶角和底边折半,所以常通过它来证明线段或角的倍分问题,在等腰三角形中,虽然顶角的平分线、底边上的高、底边上的中线互相重合,添加辅助线时,有时作哪条线都可以,有时需要作顶角的平分线,有时则需要作高或中线,这要视具体情况来定。
【分类解读】例1. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
《等腰三角形》培优专题

等腰三角形【分类解析】例1. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
E例2. 如图,已知:AB C ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BAC ∠的度数。
ABCD例3. 已知:如图,AB C ∆中,AB CD AC AB ⊥=,于D 。
求证:DCB 2B AC ∠=∠。
C4、中考题型:1.如图,△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别为∠ABC 与∠ACB 的角平分线,且相交于点F ,则图中的等腰三角形有( )A. 6个B. 7个C. 8个D. 9个A 36° E DFBC 2.)已知:如图,在△ABC 中,AB =AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E 、F 分别是垂足。
求证:AE =AF 。
AE F BDC5、题形展示:例1. 如图,AB C ∆中, 100=∠=A AC AB ,,BD 平分ABC ∠。
求证:B C B D AD =+。
【实战模拟】1. 选择题:等腰三角形底边长为5cm ,一腰上的中线把其周长分为两部分的差为3cm ,则腰长为( ) A. 2cmB. 8cmC. 2cm 或8cmD. 以上都不对2. 如图,AB C ∆是等边三角形,BC BD 90CBD ==∠, ,则1∠的度数是________。
CA 1DB2 33. 求证:等腰三角形两腰中线的交点在底边的垂直平分线上.4. AB C ∆中, 120A AC AB =∠=,,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE =。
【试题答案】(实战模拟) 1. B2. 分析:结合三角形内角和定理,计算图形中角的度数是等边三角形性质的重要应用。
解:因为AB C ∆是等边三角形 所以 60ABC BC AB =∠=, 因为B C B D =,所以B D A B = 所以23∠=∠在AB D ∆中,因为 60ABC 90CBD =∠=∠, 所以 150ABD =∠,所以 152=∠ 所以 75ABC 21=∠+∠=∠3. 分析:首先将文字语言翻译成数学的符号语言和图形语言。
初三特殊的三角形培优同步讲义

初三特殊的三角形培优同步讲义1. 等腰三角形1.1 定义等腰三角形是指具有两边长度相等的三角形。
在等腰三角形中,两边对应的两个角也是相等的。
1.2 性质- 等腰三角形的底角(即两个底边夹角)相等。
- 等腰三角形的顶角(即顶边夹角)也是相等的。
2. 直角三角形2.1 定义直角三角形是指其中一个角度为90度的三角形。
直角三角形的斜边是其他两边之间最长的一边。
2.2 特殊三角形- 30度-60度-90度三角形:其中一个角度为90度,另外两个角度为30度和60度。
这种三角形的边长比例为1:√3:2。
30度-60度-90度三角形:其中一个角度为90度,另外两个角度为30度和60度。
这种三角形的边长比例为1:√3:2。
- 45度-45度-90度三角形:其中一个角度为90度,另外两个角度为45度。
这种三角形的两条直角边的边长相等。
45度-45度-90度三角形:其中一个角度为90度,另外两个角度为45度。
这种三角形的两条直角边的边长相等。
3. 等边三角形3.1 定义等边三角形是指三条边的长度都相等的三角形。
在等边三角形中,每个角的度数都是60度。
3.2 性质- 等边三角形的三个内角都是60度。
- 等边三角形的高、中线、角平分线三者重合,且均通过三角形的重心点。
4. 总结初三特殊的三角形主要包括等腰三角形、直角三角形和等边三角形。
通过对这些三角形的认识和特点的理解,能够更好地解决与三角形相关的问题和题目。
---_注意:以上内容仅供参考,具体知识点和定义请以教材为准。
_。
第四讲培优 全等三角形的性质及判定

第三讲全等三角形的性质及判定【知识要点】1、全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等。
2、三角形全等的判定方法:①SSS ②SAS ③ASA ④AAS ⑤HL(直角三角形)不要自己造三角形全等方法,一般三角形只有SSS、SAS、ASA、AAS、别无他法,特别在运用SAS时,一定记住是两边夹角,而如果是两边及一边对角,则两个三角形不一定全等,更没有“角角角”。
3、HL只适合直角三角形,不适合一般三角形。
【例题解析】例1 已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.(SSS,角平分线的性质,辅助线)例2 .如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE∥BC.1.如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD 与BE相交于点F.(1)求证:△ABE≌△CAD;(SAS)(2)求∠BFD的度数.2.已知:如图Rt△ABC与Rt△DCE都是等腰直角三角形,求证:△ACE≌△BCD变式如上图Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.求证:△ACE≌△BCD(SAS)例3已知:如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.求证:△ABC≌△DEF (ASA)如图,正方形ABCD中,E、F分别为BC、CD上的点,且AE⊥BF,垂足为点G.求证:AE=BF. (ASA)例4.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE ( AAS )同类练习1.如图,AD∥BC,∠A=90°,以点B为圆心,BC长为半径画弧,交射线AD于点E,连接BE,过点C作CF⊥BE,垂足为F,求证:AB=FC.2. 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由(AAS)【拓展训练】1.如图△ABC是等边三角形,点D、E、F分别是线段AB、BC、CA上的点。
第九讲 培优竞赛等腰三角形

第九讲全等三角形培优竞赛——————等腰三角形-、等腰三角形的性质性质1:等腰三角形的对称轴是;性质2:等腰三角形有;性质3:等腰三角形的两个底角相等(简写成“”)。
性质4:等腰三角形①在△ABC中∵AB=AC,AD是BC边上的中线,∴∠ =∠,⊥。
②△ABC中∵AB=AC,AD是∠BAC的平分线,∴⊥, = 。
③在△ABC中∵AB=AC,AD⊥BC,∴∠ =∠, =推论:等边三角形的。
二、等腰三角形的判定1. 定理:如果一个三角形有两个相等,那么这两个角所对的也相等(简写成“”。
)推论1:三个角都相等的三角形是。
推论2:有一个角等于60°的是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
2. 构造等腰三角形解题常用的辅助线做法一般有以下四种方法:(1)依据平行线构造等腰三角形;(2)依据倍角关系构造等腰三角形;(3)依据角平分线+垂线构造等腰三角形;(4)依据120°角或60°角,常补形构造等边三角形。
基础巩固1、等腰三角形的一边长为4cm,另一边长为8cm,则它的周长是2、等腰三角形的周长是20,则它的腰长m的取值范围是________.3、等腰三角形的一个角是30°,其余两个角分别是。
4、等腰三角形一腰上的高与另一腰的夹角是36°,则这个三角形的顶角是。
.5、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的大小是.(烟台市中考题)AFCGBEAB CD6、如图,已知∠A=10°,在∠A两边上分别作点,并连接这些点,使AB=BC=CD=DE……一直作下去,那么图中以这些线段为腰长的等腰三角形最多能找到个。
7、如图,∠C=90°,AD平分∠BAC交BC于D,若BC=5cm,BD=3cm,则点D到AB的距离为()A.5cm B.3cm C、2cm D.不能确定8、如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下三个结论:①AE=BD②CN=CM③MN∥AB(4)△MCN是等边三角形;其中正确结论的个数是()A.1 B.2 C.3 D.4【典型例题】题型一(等角对等边)例1.如图,已知:ABC∆中,ACAB=,D是BC上一点,且CADCDBAD==,,求BAC∠的度数。
八年级数学上册全等三角形(培优篇)(Word版 含解析)

八年级数学上册全等三角形(培优篇)(Word 版 含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在菱形ABCD 中,∠ABC=120°,AB=10cm ,点P 是这个菱形内部或边上的一点.若以P ,B ,C 为顶点的三角形是等腰三角形,则P ,A (P ,A 两点不重合)两点间的最短距离为______cm .【答案】10310-【解析】解:连接BD ,在菱形ABCD 中,∵∠ABC =120°,AB =BC =AD =CD =10,∴∠A =∠C =60°,∴△ABD ,△BCD 都是等边三角形,分三种情况讨论:①若以边BC 为底,则BC 垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”,即当点P 与点D 重合时,PA 最小,最小值PA =10;②若以边PB 为底,∠PCB 为顶角时,以点C 为圆心,BC 长为半径作圆,与AC 相交于一点,则弧BD (除点B 外)上的所有点都满足△PBC 是等腰三角形,当点P 在AC 上时,AP 最小,最小值为10310-;③若以边PC 为底,∠PBC 为顶角,以点B 为圆心,BC 为半径作圆,则弧AC 上的点A 与点D 均满足△PBC 为等腰三角形,当点P 与点A 重合时,PA 最小,显然不满足题意,故此种情况不存在;综上所述,PA 的最小值为10310-(cm ).故答案为:10310-.点睛:本题考查菱形的性质、等边三角形的性质,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.2.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D在第二象限,且ABD与ABC全等,点D的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC全等.故答案为(-4,2)或(-4,3).3.在锐角三角形ABC中.BC=32,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.【答案】4【解析】【分析】过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN 的最小值,再根据32ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.【详解】解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,∵32ABC=45°,BD平分∠ABC,∴△BCE是等腰直角三角形,∴3222=4.∴CM+MN的最小值为4.【点睛】本题考查了轴对称最短路线问题,难度较大,根据题意作出辅助线,构造出等腰直角三角形,利用锐角三角函数的定义求解是解答此题的关键.4.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出下列四个结论:①AE=CF;②△EPF是等腰直角三角形;③EF=AB;④12ABCAEPFS S∆=四边形,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).【答案】①②④【解析】试题分析:∵∠APE、∠CPF都是∠APF的余角,∴∠APE=∠CPF,∵AB=AC,∠BAC=90°,P是BC中点,∴AP=CP,∴∠PAE=∠PCF,在△APE与△CPF中,{?PAE PCFAP CPEPA FPC∠=∠=∠=∠,∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF=12S△ABC,①②④正确;而AP=12BC ,当EF 不是△ABC 的中位线时,则EF 不等于BC 的一半,EF=AP , ∴故③不成立.故始终正确的是①②④.故选D .考点:1.全等三角形的判定与性质;2.等腰直角三角形.5.如图,己知30MON ∠=︒,点1A ,2A ,3A ,…在射线ON 上,点1B ,2B ,3B ,…在射线OM 上,112A B A ∆,223A B A ∆,334A B A ∆,…均为等边三角形,若12OA =,则556A B A ∆的边长为________.【答案】32【解析】【分析】根据底边三角形的性质求出130∠=︒以及平行线的性质得出112233////A B A B A B ,以及22122A B B A =,得出332212244A B A B B A ===,441288A B B A ==,551216A B B A =⋯进而得出答案.【详解】解:△112A B A 是等边三角形,1121A B A B ∴=,341260∠=∠=∠=︒,2120∴∠=︒,30MON ∠=︒,11801203030∴∠=︒-︒-︒=︒,又360∠=︒,5180603090∴∠=︒-︒-︒=︒,130MON ∠=∠=︒,1112OA A B ∴==,212A B ∴=,△223A B A 、△334A B A 是等边三角形,111060∴∠=∠=︒,1360∠=︒,41260∠=∠=︒,112233////A B A B A B ∴,1223//B A B A ,16730∴∠=∠=∠=︒,5890∠=∠=︒,22122242A B B A =∴==,33232B A B A =,33312428A B B A ∴===,同理可得:444128216A B B A ===,⋯∴△1n n n A B A +的边长为2n ,∴△556A B A 的边长为5232=.故答案为:32.【点睛】本题考查了等边三角形的性质以及30°直角三角形的性质,根据已知得出33124A B B A =,44128A B B A =,551216A B B A =进而发现规律是解题关键.6.如图,BD 是ABC 的角平分线,AE BD ⊥,垂足为F ,且交线段BC 于点E ,连结DE ,若50C ∠=︒,设 ABC x CDE y ∠=︒∠=︒,,则y 关于x 的函数表达式为_____________.【答案】80y x =-【解析】【分析】根据题意,由等腰三角形的性质可得BD 是AE 的垂直平分线,进而得到AD =ED ,求出BED ∠的度数即可得到y 关于x 的函数表达式.【详解】∵BD 是ABC ∆的角平分线,AE BD ⊥∴1122ABD EBD ABC x ∠=∠=∠=︒,90AFB EFB ∠=∠=︒ ∴1902BAF BEF x ∠=∠=︒-︒ ∴AB BE =∴AF EF =∴AD ED =∴DAF DEF ∠=∠∵180BAC ABC C ∠=︒-∠-∠,50C ∠=︒∴130BAC x ∠=︒-︒∴130BED BAD x ∠=∠=︒-︒∵CDE BED C ∠=∠-∠∴1305080y x x ︒=-︒-︒=︒-︒∴80y x =-,故答案为:80y x =-.【点睛】本题主要考查了等腰三角形的性质及判定,三角形的内角和定理,三角形外角定理,角的和差倍分等相关知识,熟练运用角的计算是解决本题的关键.7.如图,已知每个小方格的边长为1,A 、B 两点都在小方格的格点(顶点)上,请在图中找一个格点C ,使△ABC 是等腰三角形,这样的格点C 有________个。
等腰三角形培优讲义

求证:AG⊥EF
2.等腰Rt△ABC中,AB=AC,∠BAC=90°,D在BC上,连AD,பைடு நூலகம்E⊥AD且DE=AD,连接EC,求∠BCE得度数
3.△ABC为等腰Rt△ABC,CA=CB,CA⊥CB,∠CDA=45°
求证:AD⊥DB
①如图,若OC=5,求BD长度
②设BD交x轴于F,求证∠OFA=∠DFA
③正△AOB边长为4,点C为x轴一动点,以AC为边在直线AC下方作正△ACD,连ED,求ED最小值
6.△ABC中,AD为BC上中线,E是AD上一点,且AE= BC,BE延长线交AC于F,AF=EF
求证(1)AC=BE (2)∠ADC=60°
7.凸多边形ABCDE中,AB=AC,AD=AE,∠CAD=∠ABE+∠AEB,M为BE中点
求证:CD=2AM
8.△AOB和△ACD均为等边△,其中AB⊥x轴于E点
4.△AOB与△AMN均为等腰Rt△. AO⊥BO,AO=BO,MA⊥MN,MA=MN,P为BN中点,探求并证明PM与PO位置关系与数量关系
5.已知:C点坐标为(4,4),A为y轴负半轴上一动点,连CA、CB,CB⊥CA交x轴于B
①求OB-OA
②E在x轴上,D在y轴上,∠DCE=45°,转动△DCE,求线段BE、DE和AD之间的数量关系
全等三角形培优讲义

全等三角形罕有帮助线作法【常识导图】【导学】全等三角形第一部分:常识点回想罕有帮助线的作法有以下几种:1)碰到等腰三角形,可作底边上的高,运用“三线合一”的性质解题,思维模式是全等变换中的“半数”.2)碰到三角形的中线,倍长中线,使延伸线段与原中线长相等,结构全等三角形,运用的思维模式是全等变换中的“扭转”.3)碰到角等分线,可以自角等分线上的某一点向角的双方作垂线,运用的思维模式是三角形全等变换中的“半数”,所考常识点经常是角等分线的性质定理或逆定理.4)过图形上某一点作特定的等分线,结构全等三角形,运用的思维模式是全等变换中的“平移”或“翻转折叠”5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延伸,是之与特定线段相等,再运用三角形全等的有关性质加以解释.这种作法,合适于证实线段的和.差.倍.分等类的标题.精准诊查概念三边之和大于等于第三边稳定性与三角形有关的线段高中线角平分线与三角形有关的角三角形内角和定理三角形的外角直角三角形性质判定多边形及其内角和三角形ABCBC,CA 的角等分线.例1 AD 为△ABC 的角等分线,直线MN ⊥AD 于A.E 为MN 上一点,△ABC 周长记为A P ,△EBC 周长记为B P .求证B P >A P .例2 如图,在△ABC 的边上取两点D.E,且BD=CE,求证:AB+AC>AD+AE. 四.借助角等分线造全等1.如图,已知在△ABC 中,∠B=60°,△ABC 的角等分线AD,CE 订交于点O,求证:OE=OD2.如图,△ABC 中,AD 等分∠BAC,DG ⊥BC 且等分BC,DE ⊥AB 于E,DF ⊥AC 于F.(1)解释BE=CF 的来由;(2)假如AB=a ,AC=b ,求AE.BE 的长. 五.扭转例1 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF,求∠EAF 的度数.例 2 如图,ABC ∆是边长为3的等边三角形,BDC∆是等腰三角形,且0120BDC ∠=,以D 为极点做一个060角,使其双方分离交AB 于点M,交AC 于点N,衔接MN,则AMN ∆的周长为;例3 设点E.F 分离在正方形ABCD 的边BC.CD 上滑动且保持∠EAF=450, AP ⊥EF 于点P,FED CBAOEDCBABE 与CD 的关系,并解释来由.如图,在△ABC 中,∠ACB =AC =BC ,直线l 经由极点离作l 的垂线AE .BF ,E .F 为垂足.(1)当直线l 不与底边订交时,求证:EF =AE +BF .)如图,将直线顺时针扭转,使l 与底边AB 交于点图11-1图11-2AEAC BBCO于F,BE⊥CD于E.求证:EF=BE—AF5.如图,AD为△ABC的中线,∠ADB和∠ADC的等分线分离交AB.AC于点E.F.求证:BE+CF>EF.。
八年级数学全等三角形综合培优竞赛讲义(38页)

全等三角形培优竞赛讲义(一)知识点全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线. 拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.例题精讲板块一、截长补短【例1】 已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.4321FDOE CB A【解析】BE CD BC +=, 理由是:在BC 上截取BF BE =,连结OF , 利用SAS 证得BEO ∆≌BFO ∆,∴12∠=∠,∵60A ∠=︒,∴1901202BOC A ∠=+∠=,∴120DOE ∠=,∴180A DOE ∠+∠=,∴180AEO ADO ∠+∠=,∴13180∠+∠=, ∵24180∠+∠=,∴12∠=∠,∴34∠=∠,利用AAS 证得CDO ∆≌CFO ∆,∴CD CF =,∴BC BF CF BE CD =+=+.【例2】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?GNEB M A D【解析】 猜测DM MN =.过点M 作MG BD ∥交AD 于点G ,AG AM =,∴GD MB =又∵120ADM DMA +∠=∠,120DMA NMB +=∠∠ ∴ADM NMB =∠∠,而120DGM MBN ==∠∠, ∴DGM MBN ∆∆≌,∴DM MN =.【变式拓展训练】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?NCDEB M A【解析】 猜测DM MN =.在AD 上截取AG AM =,∴DG MB =,∴45AGM =∠∴135DGM MBN ==︒∠∠,∴ADM NMB =∠∠, ∴DGM MBN ∆∆≌,∴DM MN =.【例3】 已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .M F EDCB A【解析】 延长CB 至M ,使得BM =DF ,连接AM .∵AB =AD ,AD ⊥CD ,AB ⊥BM ,BM =DF ∴△ABM ≌△ADF∴∠AFD =∠AMB ,∠DAF =∠BAM ∵AB ∥CD∴∠AFD =∠BAF =∠EAF +∠BAE =∠BAE +∠BAM =∠EAM ∴∠AMB =∠EAM∴AE =EM =BE +BM =BE +DF .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠. 【解析】 因为ABD ∆、ACE ∆是等边三角形,所以AB AD =,AE AC =,CAE ∠=60BAD ∠=,则BAE DAC ∠=∠,所以BAE DAC ∆∆≌,则有ABE ADC ∠=∠,AEB ACD ∠=∠,BE DC =.在DC 上截取DF BO =,连结AF ,容易证得ADF ABO ∆∆≌,ACF AEO ∆∆≌. 进而由AF AO =.得AFO AOF ∠=∠;由AOE AFO ∠=∠可得AOF ∠=AOE ∠,即OA 平分DOE ∠.【例5】 如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.EABC DM N【解析】 如图所示,延长AC 到E 使CE BM =.在BDM ∆与CDE ∆中,因为BD CD =,90MBD ECD ∠=∠=,BM CE =, 所以BDM CDE ∆∆≌,故MD ED =.因为120BDC ∠=,60MDN ∠=,所以60BDM NDC ∠+∠=. 又因为BDM CDE ∠=∠,所以60MDN EDN ∠=∠=.在MND ∆与END ∆中,DN DN =,60MDN EDN ∠=∠=,D M D E =, 所以MND END ∆∆≌,则NE MN =,所以AMN ∆的周长为2.【例6】 五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDEABDEFC【解析】 延长DE 至F ,使得EF =BC ,连接AC .∵∠ABC +∠AED =180°,∠AEF +∠AED =180° ∴∠ABC =∠AEF ∵AB =AE ,BC =EF ∴△ABC ≌△AEF ∴EF =BC ,AC =AF∵BC +DE =CD ∴CD =DE +EF =DF ∴△ADC ≌△ADF ∴∠ADC =∠ADF 即AD 平分∠CDE .板块二、全等与角度【例7】如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.【解析】 如图所示,延长AB 至E 使BE BD =,连接ED 、EC .由AC AB BD =+知AE AC =,而60BAC ∠=,则AEC ∆为等边三角形.注意到EAD CAD ∠=∠,AD AD =,AE AC =, 故AED ACD ∆∆≌.从而有DE DC =,DEC DCE ∠=∠,故2BED BDE DCE DEC DEC ∠=∠=∠+∠=∠.所以20DEC DCE ∠=∠=,602080ABC BEC BCE ∠=∠+∠=+=.【另解】在AC 上取点E ,使得AE AB =,则由题意可知CE BD =.在ABD ∆和AED ∆中,AB AE =,BAD EAD ∠=∠,AD AD =,则ABD AED ∆∆≌,从而BD DE =,进而有DE CE =,ECD EDC ∠=∠,AED ECD EDC ∠=∠+∠=2ECD ∠. 注意到ABD AED ∠=∠,则:1318012022ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=-∠=,故80ABC ∠=︒.【点评】由已知条件可以想到将折线ABD “拉直”成AE ,利用角平分线AD 可以构造全等三角形.同样地,将AC 拆分成两段,之后再利用三角形全等亦可,此思路也是十分自然的.需要说明的是,无论采取哪种方法,都体现出关于角平分线“对称”的思想.上述方法我们分别称之为“补短法”和“截长法”,它们是证明等量关系时优先考 虑的方法.【例8】在等腰ABC ∆中,AB AC =,顶角20A ∠=︒,在边AB 上取点D ,使AD BC =,求BDC ∠.【解析】 以AC 为边向ABC ∆外作正ACE ∆,连接DE .在ABC ∆和EAD ∆中,AD BC =,AB EA =,2060EAD BAC CAE ∠=∠+∠=+= 80ABC =∠,E D CB AED CB AD CBADCB AED CBA则ABC EAD ∆∆≌.由此可得ED EA EC ==,所以EDC ∆是等腰三角形. 由于20AED BAC ∠=∠=,则602040CED AEC AED ∠=∠-∠=-=,从而70DCE ∠=,706010DCA DCE ACE ∠=∠-∠=-=, 则201030BDC DAC DCA ∠=∠+∠=+=.【另解1】以AD 为边在ABC ∆外作等边三角形ADE ∆,连接EC .在ACB ∆和CAE ∆中,6020CAE ACB ︒︒∠=+=∠,AE AD CB ==,AC CA =, 因此ACB CAE ∆∆≌,从而CAB ACE ∠=∠,CE AB AC ==.在CAD ∆和CED ∆中,AD ED =,CE CA =,CD CD =, 故CAD CED ∆∆≌, 从而ACD ECD ∠=∠,2CAB ACE ACD ∠=∠=∠, 故10ACD ︒∠=,因此30BDC ︒∠=. 【另解2】如图所示,以BC 为边向ABC ∆内部作等边BCN ∆,连接NA 、ND .在CDA ∆和ANC ∆中,CN BC AD ==,20CAD ∠=, ACN ACB BCN ∠=∠-∠=806020-=, 故CAD ACN ∠=∠,而AC CA =,进而有CDA ANC ∆∆≌. 则10ACD CAN ∠=∠=,故30BDC DAC DCA ∠=∠+∠=. 【点评】上述三种解法均是向三边作正三角形,然后再由三角形全等得到边长、角度之间的关系.【例9】如图所示,在ABC ∆中,AC BC =,20C ∠=︒,又M 在AC 上,N 在BC 上,且满足50BAN ∠=︒,60ABM ∠=︒,求NMB ∠.【解析】 过M 作AB 的平行线交BC 于K ,连接KA 交MB 于P .连接PN ,易知APB ∆、M KP ∆均为正三角形.因为50BAN ∠=︒,AC BC =,20C ∠=︒,所以50ANB ∠=︒,BN AB BP ==,80BPN BNP ∠=∠=︒,则40PKN ∠=︒,180608040KPN ∠=︒-︒-︒=︒, 故PN KN =.从而MPN MKN ∆∆≌.进而有PMN KMN ∠=∠,1302NMB KMP ∠=∠=︒.【另解】如图所示,在AC 上取点D ,使得20ABD ∠=︒,由20C ∠=︒、AC BC =可知80BAC ∠=︒. 而20ABD ∠=︒,故80ADB ∠=︒,BA BD =. 在ABN ∆中,50BAN ︒∠=,80ABN ∠=︒,故50ANB ∠=︒,从而BA BN =,进而可得BN BD =.E DCBA N DC B APA BCM NK NMCBA D NMCBA而802060DBN ABC ABD ∠=∠-∠=︒-︒=︒, 所以BDN ∆为等边三角形.在ABM ∆中,180180806040AMB ABM BAM ∠=︒-∠-∠=︒-︒-︒=︒, 804040DBM ADB AMB ∠=∠-∠=︒-︒=︒,故DM B DBM ∠=∠,从而D M D B =.我们已经得到DM DN DB ==,故D 是BMN ∆的外心,从而1302NMB NDB ∠=∠=︒.【点评】本题是一道平面几何名题,加拿大滑铁卢大学的几何大师Ross Honsberger 将其喻为“平面几何中的一颗明珠”.本题的大多数解法不是纯几何的,即使利用三角函数也不是那么容易.【例10】在四边形ABCD 中,已知AB AC =,60ABD ︒∠=,76ADB ︒∠=,28BDC ︒∠=,求DBC ∠的度数.【解析】 如图所示,延长BD 至E ,使DE DC =,由已知可得:180********ADE ADB ︒︒︒︒∠=-∠=-=, 7628104ADC ADB BDC ︒︒︒∠=∠+∠=+=,故ADE ADC ∠=∠.又因为AD AD =,DE DC =,故ADE ADC ∆∆≌,因此AE AC =,E ACD ∠=∠,EAD CAD ∠=∠.又因为AB AC =, 故AE AB =,ABC ACB ∠=∠. 而已知60ABD ︒∠=,所以ABE ∆为等边三角形. 于是60ACD E EAB ∠=∠=∠=︒,故18016CAD ADC ACD ∠=︒-∠-∠=︒, 则28CAB EAB CAD EAD ∠=∠-∠-∠=︒,从而1(180)762ABC CAB ∠=︒-∠=︒,所以16DBC ABC ABD ∠=∠-∠=︒.【例11】 如图所示,在四边形ABCD 中,12DAC ︒∠=,36CAB ︒∠=,48ABD ︒∠=,24DBC ︒∠=,求ACD ∠的度数.【解析】 仔细观察,发现已知角的度数都是12︒的倍数,这使我们想到构造60︒角,从而利用正三角形.在四边形ABCD 外取一点P ,使12PAD ︒∠=且AP AC =,连接PB 、PD . 在ADP ∆和ADC ∆中,12PAD CAD ︒∠=∠=,AP AC =,AD AD =,故ADP ADC ∆∆≌. 从而APD ACD ∠=∠.CDB A DC BA EC D B A PDC在ABC ∆中,36CAB ∠=︒,72ABC ∠=︒, 故72ACB ︒∠=,AC AB =, 从而AP AB =.而12123660PAB PAD DAC CAB ∠=∠+∠+∠=︒+︒+︒=︒, 故PAB ∆是正三角形,60APB ︒∠=,PA PB =.在DAB ∆中,123648DAB DAC CAB DBA ︒︒︒∠=∠+∠=+==∠, 故DA DB =.在PD A ∆和PDB ∆中,PA PB =,PD PD =,DA DB =, 故PDA PDB ∆∆≌,从而1302APD BPD APB ︒∠=∠=∠=,则30ACD ︒∠=.【例12】 在正ABC ∆内取一点D ,使DA DB =, 在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.【解析】 如图所示,连接DC .因为AD BD =,AC BC =,CD CD =,则ADC BDC ∆∆≌, 故30BCD ∠=.而DBE DBC ∠=∠,BE AB BC ==,BD BD =, 因此BDE BDC ∆∆≌,故30BED BCD ∠=∠=.【例13】 如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC ∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.D E CB AD E CB A OM B MCAB【解析】 在ABC ∆中,由44BAC BCA ︒∠=∠=可得AB AC =,92ABC ︒∠=.如图所示,作BD AC ⊥于D 点,延长CM 交BD 于O 点,连接OA , 则有30OAC MCA ︒∠=∠=,443014BAO BAC OAC ︒︒︒∠=∠-∠=-=, 301614OAM OAC MAC ︒︒︒∠=∠-∠=-=, 所以BAO MAO ∠=∠.又因为90903060AOD OAD COD ︒︒︒︒∠=-∠=-==∠, 所以120AOM AOB ∠=︒=∠.120BOM ∠=︒ 而AO AO =,因此ABO AMO ∆∆≌, 故OB OM =.由于120BOM ︒∠=,则180302BOMOMB OBM ︒-∠∠=∠==︒,故180150BMC OMB ︒︒∠=-∠=.全等三角形培优竞赛讲义(二)【知识点精读】1. 全等三角形的定义:能够完全重合的两个三角形叫全等三角形;两个全等三角形中,互相重合的顶点叫做对应顶点。
第3课时:等腰三角形和全等三角形的综合应用培优
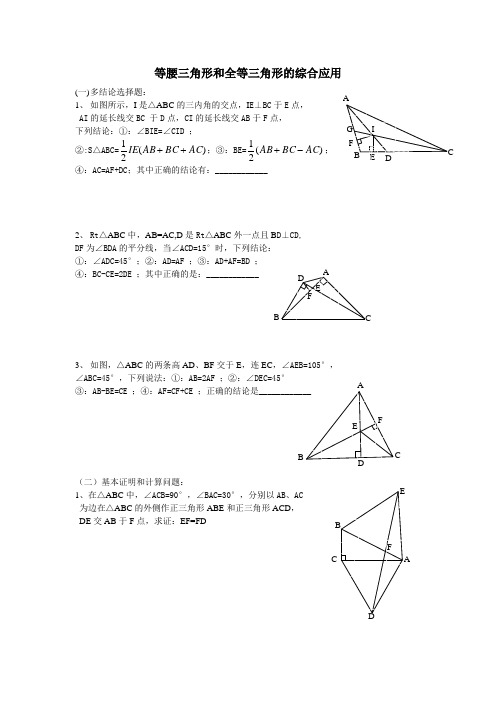
等腰三角形和全等三角形的综合应用(一) 多结论选择题:1、 如图所示,I 是△ABC 的三内角的交点,I E ⊥BC 于E 点, AI 的延长线交BC 于D 点,CI 的延长线交AB 于F 点, 下列结论:①:∠BIE=∠CID ;②:S △ABC=)(21AC BC AB IE ++;③:BE=)(21AC BC AB -+;④:AC=AF+DC ;其中正确的结论有:____________2、 Rt △ABC 中,AB=AC,D 是Rt △ABC 外一点且B D ⊥CD, DF 为∠BDA 的平分线,当∠ACD=15°时,下列结论: ①:∠ADC=45°;②:AD=AF ;③:AD+AF=BD ;④:BC-CE=2DE ;其中正确的是:____________3、 如图,△ABC 的两条高AD 、BF 交于E ,连EC ,∠AEB=105°, ∠ABC=45°,下列说法:①:AB=2AF ;②:∠DEC=45°③:AB-BE=CE ;④:AF=CF+CE ;正确的结论是(二)基本证明和计算问题:1、在△ABC 中,∠ACB=90°,∠BAC=30°,分别以AB 、AC 为边在△ABC 的外侧作正三角形ABE 和正三角形ACD ,DE 交AB 于F 点,求证:EF=FD2、在Rt △ABC 中,∠BAC=90°,AE 平分∠BAC 交BC 于F 点, 交BC 的垂直平分线DE 于E 点,求证:∠DAE=∠DEA3、在△ABC 中,∠B=2∠C,BC=2AB,AD 是中线,求证:△ABD 是等边三角形4、 如图,等边△ABC 中,延长BC 到D ,延长BA 到E , 使AE=BD,连接CE 、DE,求证:CE=DE5、如图,△ABC 中,AB=AC, ∠BAC=80°O 为△ABC 内一点,且∠OBC=10°, ∠OCA=20°,求∠BAO 的度数。
第4讲 等腰三角形

第4讲 等腰三角形考点·方法·破译 1.等腰三角形及其性质有两条边相等的三角形叫做等腰三角形,等腰三角形是轴对称图形,因此它的性质有:⑴等腰三角形的两个底角相等(即等边对等角);⑵等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(即等腰三角形三线合一)2.等腰三角形的判定证明一个三角形是等腰三角形的基本方法是:⑴从定义入手,证明一个三角形有两条边相等;⑵从角入手,证明一个三角形有两个角相等,依据是等腰三角形判定定理;等角对等边.3.构造等腰三角形的常用方法⑴角平分线+平行线=等腰三角形 ⑵角平分线+垂线(或高)=等腰三角形 ⑶线段中垂线构造等腰三角形 ⑷将2倍角转化为相等角构造等腰三角形21321(4)(3)(2)(1)经典·考题·赏析【例1】 等腰三角形一腰上的高与另一腰所成的夹角为400,则这个等腰三角形的底角为________________.【解法指导】 若问题中涉及到三角形的高,则要分别考虑三角形的高是在三角形的外,三角形内的情况.解:如图1,当一腰上的高在三角形内时,∠ACD =400,∴∠A =500 ∴∠B =∠ACB =如图2,当一腰上的高在三角形外时,∠ACD =400,∠DAC =500∴∠DAC =∠B +∠ACB =2∠B ∴∠B =∠ACB =250,故填650或250.C AD BACD B图2图1【变式题组】01.(呼和浩特)在等腰⊿ABC 中,AB =AC ,一边上的中线BD 将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A .7B .11C .7或11D .7或1002.(黄冈)在⊿ABC 中,AB =AC ,AB 的垂直平分线与AC 所在的直线相交所得到锐角为500,则∠B =___________度.03.(襄樊)在⊿ABC 中,AB =AC =12cm ,BC =6cm ,D 为BC 的中点,动点P 从B 点出发,以每秒1cm 的速度沿B →A →C 的方向运动.设运动时间为t ,那么当t =_________秒时,过D 、P 两点的直线将⊿ABC 的周长分成两个部分,使其中一部分是另一部分的2倍.【例2】 如图,在⊿ABC 中,AB =AC ,点D 在AC 上,AD =BD =BC ,求∠A 的度数.【解法指导】 图中的等腰三角形多,可利用等腰三角形的性质,用方程的思想求角的度数.解:设∠A =x ,CABD∵BD=AD,∴∠A=∠ABD=x,∴∠BDC=∠A+∠ABD=2x,∵BD=BC,∴∠C=∠BDC=2x,∵AB=AC,∴∠ C=∠ABC=2x,∵在△ABC中, ∠A+∠ABC+∠ACB=180°∴x+2x+2x=180°,x=36°,∴∠A=36°.【变式题组】01.如图,在⊿ABC中,AB=AC,BD=BC,AD=DE=EB,求∠A的度数.02.如图,在⊿ABC中,AB=AC,BC=BD= ED=EA,求∠A的大小.【例3】已知坐标原点O和点A(2,-2),B是坐标轴上的一点.若⊿AOB是等腰三角形,则这样的点B一共有()个A.4 B.5 C.6 D.8A BCDPE【解法指导】 ⊿AOB 是等腰三角形,但不能确定哪条边是等腰三角形的底,因而要分三种情况进行说明①AO =OB ,②OA =AB ,③BA =BO ,又∵B 是坐标轴上的点.要考虑x 轴与y 轴两种情况.解:①如图1,当OA 是底边时,B 在OA 的中垂线上,又B 在坐标轴上,因而B 是OA 中垂线与坐标轴的交点;②如图2,当OA 为腰时,若O 为顶点,则B 在以O 为圆心,OA 为半径的圆上,又B 在坐标轴上,因而B 是圆与坐标轴的交点;③如图3,当OA 为腰时,若A 为顶点,则B 在以A 为圆心,OA 为半径的圆上,又B 在坐标轴上,因而B 是圆与坐标轴的交点.故选D .【变式题组】01.(海南竞赛试题)在平面直角坐标系xOy 内,已知A (3,-3),点P 是y 轴上一点,则使⊿AOP 为等腰三角形的点P 共有( )A .2个B .3个C .4个D .5个02.如图,在平面直角坐标系中,点A 的坐标是(1,0),点B 的坐标是(0,),点C在坐标平面内.若以A 、B 、C 为顶点构成的三角形是等腰三角形,且底角为30度,则满足条件的点C 有_________个.图3图2图1第2题图第3题图第4题图03.(南昌)如图,已知长方形纸片ABCD ,点E 是AB 的中点,点G 是BC 上一点,∠BEG>600,现沿直线EG 将纸片折叠,使点B 落在纸片中的点H 处,连接AH ,则与∠BEG 相等的角的个数为( )A .4B .3C .2D .104.(济南)如图所示,矩形ABCD 中,AB =4,BC =,点E 是折线段A -D -C 上的一个动点(点E 与点A 不重合),点P 是点A 关于BE 的对称点.在点E 运动的过程中,使△PCB 为等腰三角形的点E 的位置共有( )A .2个B .3个C .4个D .5个【例4】 (枣庄)两个全等的含30°,60°角的三角板ADE 和三角板ABC 如图所示放置,E ,A ,C 三点在一条直线上,连结BD ,取BD 的中点M ,连结ME ,MC .试判断△EMC 的形状,并说明理由.【解法指导】 判断⊿MEC 为等腰直角三角形,M 为直角顶点,即想证∠EMC =900,而⊿ABD 为等腰三角形,M 是BD 的中点,若连接AM 则有∠AMD =900,因而只需证∠DME =∠AMC ,利用全等三角形即可.解:EMC △的形状是等腰直角三角形,理由如下: 连接AM ,由题意得: 90DE AC DAE BAC =+=︒,∠∠. 90DAB ∴=︒∠. 又DM MB =,1452MA DB DM MAD MAB ∴====︒,∠∠.1059M D EM A C D M A ∴==︒=︒,∠∠∠.E D M C A ∴△≌△.DME AMC EM MC ∴==,∠∠.又90DME EMA +=︒∠∠,A CBMDE(例4题90EMA AMC ∴+=︒∠∠. C M E M ∴⊥.所以ECM △的形状是等腰直角三角形. 【变式题组】01.如图,在等腰直角三角形ABC 中,P 是斜边BC 的中点,以P 为直角顶点的两边分别与边AB 、AC 交于点E 、F ,当∠EPF 绕顶点P 旋转时(点E 不与A 、B 重合),⊿PEF 也始终是等腰三角形,请你说明理由.02.如图,在等腰三角形ABC 中,∠ACB =900,D 是BC 的中点,DE ⊥AB 垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF 交AD 于G . ⑴求证:AD ⊥CF ;⑵连接AF ,试判断⊿ACF 的形状,并说明理由.03.如图,⊿ABC 中,∠ACB =900,AC =BC ,CO 为中线.现将一直角三角板顶点放在点O 上并绕点O 旋转,若三角板的两直角边分别交AC 、CB 的延长线于点G 、H .⑴试写出图中除AC =BC ,OA =OB =OC 外其他所有相等的线段;⑵请选一组你写出的相等线段给予证明.【例5】 我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.⑴请写出一个你学过的特殊四边形中是等对边四边形的图形的名称; ⑵如图,在ABC △中,点D E ,分别在AB AC ,上,设CD BE ,相交于点O ,若60A ∠=°,12DCB EBC A ∠=∠=∠.请你写出图中一个与A ∠相等的角,并猜想图中哪个四边形是等对边四边形;⑶在ABC △中,如果A ∠是不等于60°的锐角,点D E ,分别在AB AC ,上,且12DCB EBC A ∠=∠=∠.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.【解法指导】 证明两条线段相等时,若两条线段在同一三角形中,可证明它们所对的角相等.若两条线段在不同的三角形中,则证它们所在的两个三角形全等,若三角形不全等,即可通过构造全等三角形或等腰三角形解决问题.解:⑴如:平行四边形、等腰梯形等⑵答:与∠A 相等的角是∠BOD (或∠COE ),四边形DBCE 是等对边四边形; ⑶答:此时存在等对边四边形,是四边形DBCE .证法一:如图1,作CG ⊥BE 于G 点,作BF ⊥CD 交CD 延长线于∵∠DCB =∠EBC =∠A ,BC 为公共边, ∴△BCF ≌△CBG , ∴BF =CG ,D图1∵∠BDF =∠ABE +∠EBC +∠DCB ,∠BEC =∠ABE +∠A , ∴∠BDF =∠BEC , 可证△BDF ≌△CEG , ∴BD =CE∴四边形DBCE 是等边四边形.证法二:如图2,以C 为顶点作∠FCB =∠DBC ,CF 交BE 于F 点. ∵∠DCB =∠EBC =∠A ,BC 为公共边,∴△BDC ≌△CFB ,∴BD =CF ,∠BDC =∠CFB , ∴∠ADC =∠CFE ,∵∠ADC =∠DCB +∠EBC +∠ABE ,∠FEC =∠A +∠ABE , ∴∠ADC =∠FEC , ∴∠FEC =∠CFE , ∴CF =CE ,∴BD =CE , ∴四边形DBCE 是等边四边形. 【变式题组】01.如图,在ABC 中,∠B =2∠C ,AD 为∠BAC 的平分线.求证:AC =AB +BD .02.(天津初赛试题)如图,在四边形ABCD 中,∠ACB =∠BAD =1050,∠ABC =∠ADC =450,若AB =2,求CD 的长.DEF图203.如图,在ABC中,AB=AC,D在AB上,F在AC延长线上,BD=CF.求证DE=EF.【变式题组】01.(重庆)已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为()A.200B.1200C.200或1200D.360002.(云南)已知等腰三角形的两边分别为6和3,则此等腰三角形周长为()A.9 B.15 C.15 D.12或1503.(云南)如图,等腰ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则BEC的周长为()A.13 B.14 C.15 D.1604.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A =180,则∠GEF的度数是()A.800B.900C.1000D.108005.如图,Rt ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是()A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF06.如图,ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①BDF和CEF都是等腰三角形;②DE=BD+CE;③ADE的周长等于AB与AC的和;④BF=CF.其中正确的有()A .①②③B .①②③④C .①②D .①07.(武汉)如图,已知O 是四边形ABCD 内一点,OA =OB =OC , ∠ABC =∠ADC =700,则∠DAO +∠DCO 的大小是( )A .700B .1100C .1400D .150008.(滨州)已知等腰ABC 的周长为10,若设腰长为x ,则x 的取值范围是__________. 09.如图所示,在ABC 中,已知AB =AC ,∠A =360,BC =2,BD 是ABC 的角平分线,则AD =___________.10.(威海)如图,AB =AC ,BD =BC ,若∠A =400,则∠ABD 的度数是_________. 11.(乌鲁木齐) 在一次数学课上,王老师在黑板上画出图6,并写下了四个等式:①AB DC =,②BE CE =,③B C ∠=∠,④BAE CDE ∠=∠.要求同学从这四个等式中选出两个作为条件,推出AED △是等腰三角形.请你已知:求证:AED△是等腰三角形. 证明:C12.(泰安) 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .⑴请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);⑵证明:DC BE ⊥.13.(包头)如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.⑴如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?⑵若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?图图EQ C14.(临沂)如图1,已知ABC △中,1AB BC ==,90ABC =∠,把一块含30角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转. ⑴在图1中,DE 交AB 于M ,DF 交BC 于N . ①证明DM DN =;②在这一旋转过程中,直角三角板DEF 与ABC △的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;⑵继续旋转至如图2的位置,延长AB 交DE 于M ,延长BC 交DF 于N ,DM DN =是否仍然成立?若成立,请给出证明;若不成立,请说明理由;⑶继续旋转至如图3的位置,延长FD 交BC 于N ,延长ED 交AB 于M ,DM DN =是否仍然成立?请写出结论,不用证明.F1F图2E图3B培优升级·奥赛检测01.如图,∠BAC 与∠CBE 的平分线相交于点P ,BE =BC ,PB 与CE 交于点H ,PG ∥AD 交BC 于F ,交AB 于G ,下列结论:①GA =GP ;②③BP 垂直平分CE ;④FP =FC ;其中正确的判断有( )A .只有①②B .只有③④C .只有①③④D .只有①②③④02.如图,点A 是网格图形中的一个网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A 为其中的一个顶点,面积等于2.5的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是( )A .10个B .12个C .14个D .16个03.如图,在ABC 中,AB =BC ,MN =NA , ∠BAM =∠NAC ,则∠MAC =______. 04.如图,AA ’、BB ’分别是∠EAB 、∠DBC 的平分线,若AA ’=BB ’=AB .则∠BAC 的度数为______________.05.(全国联赛)在等腰Rt ABC 中,AC =BC =1,M 是BC 的中点,CE ⊥AM 于E ,交AB 于F .则 =_____________06.如图,在ABC 中,AB =AC ,EF 为过点A 的任意一条直线,CF ⊥BC ,BE ⊥BC .求证:AE =AF .07.(湖州市竞赛试题)如图,在Rt ABC中,∠ACB=900,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,求证:FK∥AB08.(四川省初二数学联赛试题)有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,求等腰三角形纸片的顶角的度数.09.如图,在ABC中,∠ABC=460,D是边BC上一点,DC=AB, ∠DAB=210,求∠CAD的度数.10.(浙江省杭州市中考试题)如图,在等腰△ABC 中,CH 是底边上的高线,点P 是线段CH 上不与端点重合的任意一点,连接AP 交BC 于点E ,连接BP 交AC 于点F . (1) 证明:CBF CAE ∠=∠; (2) 证明:BF AE =;(3) 以线段BF AE ,和AB 为边构成一个新的三角形ABG (点E 与点F 重合于点G ),记△ABC 和△ABG 的面积分别为ABC S ∆和ABG S ∆,如果存在点P ,能使得ABG ABC S S ∆∆= , 求∠C 的取值范围.11.如图,已知在△ABC 中,AB =AC ,∠BAC =900,AD =AE , AF ⊥BE 交BC 于F ,过F作FG ⊥CD 交BE 的延长线于G .求证:BG =AF +FG。
八年级数学全等三角形(培优篇)(Word版 含解析)

八年级数学全等三角形(培优篇)(Word版含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为______cm.-【答案】10310【解析】解:连接BD,在菱形ABCD中,∵∠ABC=120°,AB=BC=AD=CD=10,∴∠A=∠C=60°,∴△ABD,△BCD都是等边三角形,分三种情况讨论:①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”,即当点P与点D重合时,PA最小,最小值PA=10;②若以边PB为底,∠PCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧BD(除点B外)上的所有点都满足△PBC是等腰三角形,当点P在AC上时,AP-;最小,最小值为10310③若以边PC为底,∠PBC为顶角,以点B为圆心,BC为半径作圆,则弧AC上的点A与点D均满足△PBC为等腰三角形,当点P与点A重合时,PA最小,显然不满足题意,故此种情况不存在;-(cm).综上所述,PA的最小值为10310-.故答案为:10310点睛:本题考查菱形的性质、等边三角形的性质,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.2.如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.【答案】5【解析】【分析】作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN为所求的最小值,再根据AD是∠BAC的平分线可知MH=MN,再由等腰直角三角形的性质即可得出结论.【详解】如图,作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN 为所求的最小值.∵AD是∠BAC的平分线,∴MH=MN,∴BH是点B到直线AC的最短距离(垂线段最短).∵AB=5,∠BAC=45°,∴BH==5.∵BM+MN的最小值是BM+MN=BM+MH=BH=5.故答案为5.【点睛】本题考查了轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.3.如图,已知正六边形 ABCDEF 的边长是 5,点 P 是 AD 上的一动点,则 PE+PF 的最小值是_____.【答案】10【解析】利用正多边形的性质,可得点B 关于AD 对称的点为点E ,连接BE 交AD 于P 点,那么有PB=PF ,PE+PF=BE 最小,根据正六边形的性质可知三角形APB 是等边三角形,因此可知BE 的长为10,即PE+PF 的最小值为10.故答案为10.4.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D (4,2),这时△ABD 与△ABC 全等,分别作点C ,D 关于y 轴的对称点(-4,3)和(-4,2),所得到的△ABD 与△ABC 全等.故答案为(-4,2)或(-4,3).5.如图,ABC 中,ABC=45∠︒,CD AB ⊥于D ,BE 平分ABC ∠,且BE AC ⊥于E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G ,下列结论:BF=AC ①;A=67.5∠︒②;DG=DF ③;ADGE GHCE S S =四边形四边形④,其中正确的有__________(填序号).【答案】①②③【解析】【分析】只要证明△BDF ≌△CDA ,△BAC 是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③正确,作GM ⊥BD 于M ,只要证明GH <DG 即可判断④错误.【详解】解:∵CD ⊥AB ,BE ⊥AC ,∴∠BDC=∠ADC=∠AEB=90°,∴∠A +∠ABE=90°,∠ABE +∠DFB=90°,∴∠A=∠DFB ,∵∠ABC=45°,∠BDC=90°,∴∠DCB=90°−45°=45°=∠DBC ,∴BD=DC ,在△BDF 和△CDA 中,∠BDF=∠CDA ,∠A=∠DFB ,BD=CD ,∴△BDF ≌△CDA (AAS ),∴BF=AC ,故①正确.∵∠ABE=∠EBC=22.5°,BE ⊥AC ,∴∠A=∠BCA=67.5°,故②正确,∵BE 平分∠ABC ,∠ABC=45°,∴∠ABE=∠CBE=22.5°,∵∠BDF=∠BHG=90°,∴∠BGH=∠BFD=67.5°,∴∠DGF=∠DFG=67.5°,∴DG=DF ,故③正确.作GM ⊥AB 于M .如图所示:∵∠GBM=∠GBH ,GH ⊥BC ,∴GH=GM <DG ,∴S △DGB >S △GHB ,∵S △ABE =S △BCE ,∴S 四边形ADGE <S 四边形GHCE .故④错误,故答案为:①②③.【点睛】此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第五个问题难度比较大,添加辅助线是解题关键,属于中考选择题中的压轴题.6.如图,己知30MON ∠=︒,点1A ,2A ,3A ,…在射线ON 上,点1B ,2B ,3B ,…在射线OM 上,112A B A ∆,223A B A ∆,334A B A ∆,…均为等边三角形,若12OA =,则556A B A ∆的边长为________.【答案】32【解析】【分析】根据底边三角形的性质求出130∠=︒以及平行线的性质得出112233////A B A B A B ,以及22122A B B A =,得出332212244A B A B B A ===,441288A B B A ==,551216A B B A =⋯进而得出答案.【详解】解:△112A B A 是等边三角形,1121A B A B ∴=,341260∠=∠=∠=︒,2120∴∠=︒,30MON ∠=︒,11801203030∴∠=︒-︒-︒=︒,又360∠=︒,5180603090∴∠=︒-︒-︒=︒,130MON ∠=∠=︒,1112OA A B ∴==,212A B ∴=,△223A B A 、△334A B A 是等边三角形,111060∴∠=∠=︒,1360∠=︒,41260∠=∠=︒,112233////A B A B A B ∴,1223//B A B A ,16730∴∠=∠=∠=︒,5890∠=∠=︒,22122242A B B A =∴==,33232B A B A =,33312428A B B A ∴===,同理可得:444128216A B B A ===,⋯∴△1n n n A B A +的边长为2n ,∴△556A B A 的边长为5232=.故答案为:32.【点睛】本题考查了等边三角形的性质以及30°直角三角形的性质,根据已知得出33124A B B A =,44128A B B A =,551216A B B A =进而发现规律是解题关键.7.如图,在直角坐标系中,点()8,8B -,点()2,0C -,若动点P 从坐标原点出发,沿y 轴正方向匀速运动,运动速度为1/cm s ,设点P 运动时间为t 秒,当BCP ∆是以BC 为腰的等腰三角形时,直接写出t 的所有值__________________.【答案】2秒或46秒或14秒【解析】【分析】分两种情况:PC 为腰或BP 为腰.分别作出符合条件的图形,计算出OP 的长度,即可求出t 的值.【详解】解:如图所示,过点B 作BD ⊥x 轴于点D ,作BE ⊥y 轴于点E ,分别以点B 和点C 为圆心,以BC 长为半径画弧交y 轴正半轴于点F ,点H 和点G∵点B (-8,8),点C (-2,0),∴DC=6cm ,BD=8cm ,由勾股定理得:BC=10cm∴在直角三角形COG中,OC=2cm,CG=BC=10cm,∴OP=OG= 22-=,10246(cm)当点P运动到点F或点H时,BE=8cm,BH=BF=10cm,∴EF=EH=6cm∴OP=OF=8-6=2(cm)或OP=OH=8+6=14(cm),故答案为:2秒,46秒或14秒.【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用,通过作图找出要求的点的位置,利用勾股定理来求解是本题的关键.8.如图,已知每个小方格的边长为1,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有________个。
《等腰三角形》 讲义

《等腰三角形》讲义一、等腰三角形的定义等腰三角形是指至少有两边相等的三角形。
相等的两条边称为这个三角形的腰,另一边称为底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
例如,在三角形 ABC 中,如果 AB = AC,那么三角形 ABC 就是一个等腰三角形,其中 AB 和 AC 是腰,BC 是底边,∠A 是顶角,∠B 和∠C 是底角。
二、等腰三角形的性质1、两腰相等这是等腰三角形最基本的性质,也是其名称的由来。
2、两底角相等即∠B =∠C。
这一性质可以通过全等三角形的证明方法来得出。
3、三线合一等腰三角形底边上的高、底边上的中线、顶角平分线相互重合。
例如,在等腰三角形 ABC 中,AD 是底边 BC 上的高,那么 AD 也是底边 BC 上的中线和顶角∠A 的平分线。
4、轴对称性等腰三角形是轴对称图形,其对称轴是底边上的高(或顶角平分线、底边上的中线)所在的直线。
三、等腰三角形的判定1、定义法如果一个三角形有两条边相等,那么这个三角形就是等腰三角形。
2、等角对等边如果一个三角形的两个角相等,那么这两个角所对的边也相等。
例如,在三角形 ABC 中,若∠B =∠C,则 AB = AC。
四、等腰三角形中的常见辅助线1、作顶角的平分线利用等腰三角形顶角平分线平分顶角且垂直底边的性质。
2、作底边上的高可以利用“三线合一”的性质解决问题。
3、作底边上的中线同样基于“三线合一”的性质。
五、等腰三角形的周长和面积1、周长等腰三角形的周长等于两腰长度之和加上底边长度。
假设等腰三角形的腰长为 a,底边长为 b,那么周长 C = 2a + b。
2、面积等腰三角形的面积可以用多种方法计算。
常见的方法是先求出底边上的高,假设底边长为 b,底边上的高为h,那么面积 S = 1/2 × b × h。
也可以使用海伦公式,但在等腰三角形中相对较少使用。
六、等腰三角形在实际生活中的应用1、建筑设计许多建筑的结构中会包含等腰三角形的元素,以保证结构的稳定性和美观性。
八年级数学培优竞赛专题16等腰三角形的性质

专题16等腰三角形的性质阅读与思考等腰三角形是一类特殊三角形,具有特殊的性质,这些性质为角度的计算、线段相等、直线位置关系的证明等问题提供了新的理论依据.因此,在解与等腰三角形相关的问题时,除了要运用全等三角形知识方法外,又不能囿于全等三角形,应善于利用等腰三角形的性质探求新的解题途径,应熟悉以下基本图形、基本结论.⑴图1中,1802A B ,01802A B C∠∠∠,22DAC B C ∠∠∠.⑵图2中,只要下述四个条件:①AB AC ;②12∠∠;③CD DB ;④AD BC ⊥中任意两个成立,就可以推出其余两个成立.例题与求解【例1】如图,在△ABC 中,D 在AC 上,E 在AB 上,且AB=AC ,BC=BD ,AD =DE =BE ,则∠A=___________.(五城市联赛试题)解题思路:图中有很多相关的角,用∠A 的代数式表示这些角,建立关于∠A 的等式.【例2】如图,在△ABC 中,已知∠BAC=900,AB=AC ,D 为AC 中点,AE ⊥BD 于E ,延长AE 交BC 于F ,求证:∠ADB =∠CDF .(安徽省竞赛试题)解题思路:∠ADB 与∠CDF 对应的三角形不全等,因此,需构造全等三角形,而在等腰三角形中,作顶角的平分线或底边上的高(中线)是一条常用的辅助线.ABCDE BCAD 图1A D BC1 2图 2【例3】如图,在△ABC 中,AC=BC ,∠ACB=900,D 是AC 上一点,且AE 垂直BD 的延长线于E ,又AE=12BD ,求证:BD 是∠ABC 的角平分线.(北京市竞赛试题)解题思路:∠ABC 的角平分线与AE 边上的高重合,故应作辅助线补全图形,构造全等三角形、等腰三角形.【例4】如图,在△ABC 中,∠BAC=∠BCA=440,M 为△ABC 内一点,使∠MCA=300,∠MAC =160,求∠BMC 度数.(北京市竞赛试题)解题思路:作等腰△ABC 的对称轴(如图1),通过计算,证明全等三角形,又440+160=600;可以AB 为一边,向点C 所在的一侧作等边△ABN ,连结CN ,MN (如图2);或以AC 为一边,向点B 所在的一侧作等边△ACN ,连结BN(如图3).A BCDEF BCMAAEBCDBCMA图1DOBCMA图2N BCMA图3N【例5】如图,△ABC 是边长为1的等边三角形,△BDC 是顶角∠BDC =1200的等腰三角形,以D为顶点作一个600角,角的两边分别交AB 于M ,交AC 于N ,连结MN ,形成一个三角形.求证:△AMN的周长等于2.(天津市竞赛试题)解题思路:欲证△AMN 的周长等于2,只需证明MN=BM +CN ,考虑用补短法证明.【例6】如图,△ABC 中,∠ABC=460,D 是BC 边上一点,DC =AB ,∠DAB=210,试确定∠CAD 的度数.(北京市竞赛试题)解题思路:解本题的关键是利用DC=AB 这一条件.能力训练A 级1.如果等腰三角形一腰上的高另一腰的夹角为450,那么这个等腰三角形的底角为_____________.2.如图,已知∠A=150,AB=BC=CD =DE=EF ,则∠FEM =_____________.3.如图,在等边△ABC 的AC ,BC 边上各取一点P 、Q ,使AP=CQ ,AQ ,BP 相交于点O ,则BD CABACDN M∠BOQ=____________.4.如图,在△ABC 中,∠BCA=900,∠BAC=600,BC=4,在CA 的延长线取点D ,使AD=AB ,则D ,B 两点之间的距离是____________.5.如图,在△ABC 中,AB=AC ,D 为BC 上一点,BF =CD ,CE=BD ,那么∠EDF 等于()A .900-12∠AB .900-∠A C .1800-∠AD .450-12∠A6.如图,在△ABC 中,∠ACB=900,AC=AE ,BC =BF ,则∠ECF =()A .600B .45C .30D .不确定(安徽省竞赛试题)FBCAED第5题图第6题图7.△ABC 的一个内角的大小是400,且∠A=∠B ,那么∠C 的外角的大小是()A .140B .800或100C .1000或140D .800或140(“希望杯”邀请赛试题)8.三角形三边长a ,b ,c 满足1111abca bc,则三角形一定是()A .等边三角形B .以a 为底边的等腰三角形C .以c 为底边的等腰三角形D .等腰三角形(北京市竞赛试题)ACBEF(第2题)BACDE FM NA BC QPO(第3题)ABC D(第4题)9.如图,在△ABC 中,AB=AC ,D ,E 分别是腰AB ,AC 延长线上的点,且BD =CE ,连结DE 交BC 于G ,求证:DG =EG .(湖北省竞赛试题)10.如图,在△ABC 中,∠BAC=900,AB=AC ,BE 平分∠ABC ,CE ⊥BE ,求证:CE=12BD .(江苏省竞赛试题)11.已知Rt △ABC 中,AC=BC ,∠C=900,D 为AB 边中点,∠EDF =900,将∠EDF 绕D 点旋转,它的两边分别交AC ,BC (或它们的延长线)于E 、F ,当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图1),易证:S △DEF +S △CEF =12S △ABC ,当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,S △DEF ,S △CEF ,S △ABC 又有怎样的数量关系?请写出你的猜想,不需证明.(牡丹江市中考试题)ABC D GEABCDE12.如图,在△ABC 中,AB=AC ,∠BAC=800,O 为△ABC 内一点,且∠OBC =100,∠OCA=200,求∠BAO 的度数.(天津市竞赛试题)OABCB 级1.如图,在△ABC 中,∠ABC=1000,AM =AN ,CN=CP ,则∠MNP=_________.2.如图,在△ABC 中,AB=AC ,∠BAC=900,直角∠EPF 的顶点P 是BC 的中点,两边PE ,PF分别交AB ,AC 于点E ,F ,给出以下4个结论:①AE=CF ;②△EPF 是等腰直角三角形;③S 四边形AEPF =12S△ABC;④EF=AP .当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A ,B 重合).上述结论正确的是ABCABCABCEDF EDF DF图1图2图3ABCNMP(第1题)ABC PEF(第2题)AB CN M(第3题)____________.(苏州市中考试题)3.如图,在△ABC 中,AB=BC ,M ,N 为BC 边上两点,并且∠BAM =∠CAN ,MN=AN ,则∠MAC的度数是____________.4.如图,在△ABC 中,AB=AC ,∠BAC 与∠ACB 的平分线相交于D ,∠ADC =1300,那么∠CAB的大小是()A .80B .500C .40D .205.如图,在△ABC 中,∠BAC=1200,AD ⊥BC 于D ,且AB+BD =DC ,则∠C 的大小是()A .20B .25C .30D .456.如图,在△ABC 中,AC=BC ,∠ACB=900,AE 平分∠BAC 交BC 于E ,BD ⊥AE 于D ,DM ⊥AC 交AC 的延长线于M ,连CD ,下列四个结论:①∠ADC=450;②BD =12AE ;③AC+CE=AB ;④AB -BC=2MC .其中正确结论的个数为()A .1个B .2个C .3个D .4个7.如图,已知△ABC 为等边三角形,延长BC 至D ,延长BA 至E ,并且使AE=BD ,连结CE 、DE ,求证:CE=DE .8.如图,△ABC 中,已知∠C=600,AC >BC ,又△ABC ′、△A ′BC 、△AB ′C 都是△ABC 外的等边三角形,而点D 在AC 上,且BC=DC .⑴证明:△C ′BD ≌△B ′DC ;⑵证明:△AC ′D ≌△DB ′A ;⑶对△ABC 、△ABC ′、△A ′BC 、△AB ′C ,从面积大小关系上,你能得出什么结论?(江苏省竞赛试题)A BCDEA(第4题)BCD(第5题)ABCD ABDECM(第6题)9.在△ABC 中,已知AB=AC ,且过△ABC 某一顶点的直线可将△ABC 分成两个等腰三角形,试求△ABC 各内角的度数.(江苏省扬州中学测试题)10.如图,在△ABC 中,∠C=900,∠CAD=300,AC=BC=AD ,求证:CD=BD .11.已知△ABC 中,∠B 为锐角,从顶点A 向边BC 或BC 的延长线引垂线交BC 于H 点,又从顶点C 向边AB 或AB 的延长线引垂线交AB 于K ,试问:当2BH BC,2BK AB是整数时,△ABC 是怎样的三角形?并证明你的结论.(“智能杯”通讯赛试题)ABCDABCDA ′B ′C ′八年级数学培优竞赛专题。
初二数学培优讲义第6章 等腰三角形的性质与判定(尖子)

第六章等腰三角形的性质与判定本章进步目标★★★☆☆☆Level 3通过对本节课的学习,你能够:1.对等腰三角形的性质与判定达到【高级理解】级别;2. 对等腰三角形的分类讨论达到【高级理解】级别VISIBLE PROGRESS SYSTEM进步可视化教学体系69VISIBLE PROGRESS SYSTEM“驴桥定理”(拉丁语:Pons asinorum),即等腰三角形定理,是欧几里得几何中的一个数学定理,指的是等腰三角形两腰对应的两底角相等。
等腰三角形定理也是欧几里得《几何原本》第一卷中命题五的内容。
有关其名称“驴桥定理”的由来有两种说法:一种是《几何原本》中关于该定理的示意图即为一座桥,另外一种更为大家所接受,意指这是《几何原本》中第一个针对读者智力发起的测试,并且是通往后续更难命题的桥梁。
几何学列在中世纪的四术之中,而“驴桥定理”又是《几何原本》出现较为靠前的命题,是考验读者数学能力的一个门槛,也被称为“笨蛋的难关”,指的是任何一门学科中新手入门都会遇到的第一道坎。
一个新手如果能过得去这道坎,后面的学习就不成问题;如果过不去,就没法学习这门学科。
中世纪的欧洲人把这种情况比喻成驴子过桥,因为驴子第一次看到桥都会害怕,不愿过桥,但只要让它过了一次桥,以后就不会再怕。
无论其名称的由来为何,“驴桥定理”一词已经变成一种隐喻,是指对能力或了解程度的关键性测试,可以将对某问题了解及不了解的人区分开来。
70 VISIBLE PROGRESS SYSTEM第一关等腰三角形的性质与判定★★★☆☆☆Level 3本关进步目标★★★☆☆☆Level 3 你会利用等腰三角形的性质和判定解答相关题目;★★★☆☆☆ Level 3你会利用等腰三角形的“三线合一性”解决相关问题。
71VISIBLE PROGRESS SYSTEM72VISIBLE PROGRESS SYSTEM学习重点:理解等腰三角形“等边对等角”“等角对等边”的性质.1. 等腰三角形:(1)定义:有两条边 的三角形叫做等腰三角形.相等的两边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 . (2)性质:两腰 ,两底角 (简称“ ”). 2. 等边三角形:(1)有 相等的三角形叫做等边三角形.(2)性质: 都相等, 都相等,每一个角都等于 度. 3. 等腰三角形的判定:(1)有 的三角形叫做等腰三角形;(2)有 的三角形是等腰三角形(简称“等角对等边”). 4. 等边三角形的判定:(1) 都相等的三角形是等边三角形; (2) 都相等的三角形是等边三角形; (3)有 角是 的等腰三角形是等边三角形.1.如图,在中,点是上一点,,,则______25°_____.判定等腰三角形并掌握其性质【高级理解】理解等腰与等边三角形的定义会判定等腰三角形掌握等腰三角形的性质ABC △D BC 80BAD ∠=°AB AD DC ==C ∠=关卡1-1判定等腰三角形并掌握性质★★★☆☆☆ 高级理解过关指南 Tips笔记例题73VISIBLE PROGRESS SYSTEM2.如图所示,在△ABC 中,∠A =36°,∠C =72°,∠ABC 的平分线交AC 于点D ,则图中共有等腰三角形( D ) A . 0个B . 1个C . 2个D . 3个3.如图,∠DEF =36°,AB =BC =CD =DE =EF ,则∠A =____18°____.如图,直线12//l l ,以直线1l 上的点A 为圆心、适当长为半径画弧,分别交直线1l ,2l 于点B ,C ,连接AC ,BC .若67ABC ∠=︒,则1∠= 46° .如图,在△ABC 中,AB =AC ,点D ,E 在BC 边上,∠ABD =∠DAE =∠EAC =36°,则图中等腰三角形的个数是( C )A .4个B . 5个C . 6个D . 7个FED CB A过关练习 错题记录Exercise 2错题记录Exercise 174VISIBLE PROGRESS SYSTEM如图,,,则等于( D )A .B .C .D .60°如图钢架中,焊上等长的13根钢条来加固钢架,若11223131414AP PP P P P P P A ===⋅⋅⋅==,则A ∠的度数是 12° .15A =o ∠AB BC CD DE EF ====DEF ∠90o 75o 70o 错题记录Exercise 3错题记录Exercise 475VISIBLE PROGRESS SYSTEM 关卡1-2学习重点:会用等腰三角形的“三线合一性”解决相关问题.1.等腰三角形 、 、 互相重合(简称“三线合一”).2.等腰三角形是 图形,其 所在直线是对称轴.1 . 已知:如图,△ABC 中,AB =AC ,CE ⊥AE 于点E ,CE BC =12,点E 在△ABC 外. 求证:∠ACE =∠B . 证明:作AD ⊥BC 于D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形培优竞赛讲义(四)等腰三角形【知识点精读】-、等腰三角形的性质1. 有关定理及其推论定理:等腰三角形有两边相等;定理:等腰三角形的两个底角相等(简写成“等边对等角”)。
推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,这就是说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
推论2:等边三角形的各角都相等,并且每一个角都等于60°。
等腰三角形是以底边的垂直平分线为对称轴的轴对称图形;2. 定理及其推论的作用等腰三角形的性质定理揭示了三角形中边相等与角相等之间的关系,由两边相等推出两角相等,是今后证明两角相等常用的依据之一。
等腰三角形底边上的中线、底边上的高、顶角的平分线“三线合一”的性质是今后证明两条线段相等,两个角相等以及两条直线互相垂直的重要依据。
二、等腰三角形的判定1. 有关的定理及其推论定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”。
)推论1:三个角都相等的三角形是等边三角形。
推论2:有一个角等于60°的等腰三角形是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
2. 定理及其推论的作用。
等腰三角形的判定定理揭示了三角形中角与边的转化关系,它是证明线段相等的重要定理,也是把三角形中角的相等关系转化为边的相等关系的重要依据,是本节的重点。
3. 等腰三角形中常用的辅助线等腰三角形顶角平分线、底边上的高、底边上的中线常常作为解决有关等腰三角形问题的辅助线,由于这条线可以把顶角和底边折半,所以常通过它来证明线段或角的倍分问题,在等腰三角形中,虽然顶角的平分线、底边上的高、底边上的中线互相重合,添加辅助线时,有时作哪条线都可以,有时需要作顶角的平分线,有时则需要作高或中线,这要视具体情况来定。
【分类解析】例1. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
E分析:欲证M 是BE 的中点,已知DM ⊥BC ,所以想到连结BD ,证BD =ED 。
因为△ABC 是等边三角形,∠DBE =21∠ABC ,而由CE =CD ,又可证∠E =21∠ACB ,所以∠1=∠E ,从而问题得证。
证明:因为三角形ABC 是等边三角形,D 是AC 的中点 所以∠1=21∠ABC又因为CE =CD ,所以∠CDE =∠E 所以∠ACB =2∠E 即∠1=∠E所以BD =BE ,又DM ⊥BC ,垂足为M所以M 是BE 的中点 (等腰三角形三线合一定理)例2. 如图,已知:ABC ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BAC ∠的度数。
ABCD分析:题中所要求的BAC ∠在ABC ∆中,但仅靠AC AB =是无法求出来的。
因此需要考虑DB AD =和CA DC =在题目中的作用。
此时图形中三个等腰三角形,构成了内外角的关系。
因此可利用等腰三角形的性质和三角形的内外角关系定理来求。
解:因为AC AB =,所以C B ∠=∠ 因为DB AD =,所以C DAB B ∠=∠=∠;因为CD CA =,所以CDA CAD ∠=∠(等边对等角) 而 DAB B ADC ∠+∠=∠ 所以B DAC B ADC ∠=∠∠=∠22, 所以B 3BAC ∠=∠又因为 180=∠+∠+∠BAC C B即 180B 3C B =∠+∠+∠ 所以 36B =∠ 即求得 108B A C =∠说明:1. 等腰三角形的性质是沟通本题中角之间关系的重要桥梁。
把边的关系转化成角的关系是此等腰三角形性质的本质所在。
本条性质在解题中发挥着重要的作用,这一点在后边的解题中将进一步体现。
2. 注意“等边对等角”是对同一个三角形而言的。
3. 此题是利用方程思想解几何计算题,而边证边算又是解决这类题目的常用方法。
例3. 已知:如图,ABC ∆中,AB CD AC AB ⊥=,于D 。
求证:DCB 2BAC ∠=∠。
C分析:欲证角之间的倍半关系,结合题意,观察图形,BAC ∠是等腰三角形的顶角,于是想到构造它的一半,再证与DCB ∠的关系。
证明:过点A 作BC AE ⊥于E ,AC AB = 所以BAC 2121∠=∠=∠(等腰三角形的三线合一性质)因为90B 1=∠+∠又AB CD ⊥,所以90CDB =∠所以90B 3=∠+∠(直角三角形两锐角互余) 所以31∠=∠(同角的余角相等)即DCB 2BAC ∠=∠说明: 1. 作等腰三角形底边高线的目的是利用等腰三角形的三线合一性质,构造角的倍半关系。
因此添加底边的高是一条常用的辅助线;2. 对线段之间的倍半关系,常采用“截长补短”或“倍长中线”等辅助线的添加方法,对角间的倍半关系也同理,或构造“半”,或构造“倍”。
因此,本题还可以有其它的证法,如构造出DCB ∠的等角等。
4、中考题型:1.如图,△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别为∠ABC 与∠ACB 的角平分线,且相交于点F ,则图中的等腰三角形有( ) A. 6个 B. 7个 C. 8个 D. 9个A 36° E DF分析:由已知条件根据等腰三角形的性质和三角形内角和的度数可求得等腰三角形有8个,故选择C 。
2.)已知:如图,在△ABC 中,AB =AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E 、F 分别是垂足。
求证:AE =AF 。
AE FBDC证明:因为AC AB =,所以C B ∠=∠ 又因为AC DF AB DE ⊥⊥, 所以90CFD B ED =∠=∠ 又D 是BC 的中点,所以DC DB = 所以)A A S (CFD DEB ∆∆≅所以CF BE =,所以AF AE =说明:证法二:连结AD ,通过≅∆AED AFD ∆证明即可 5、题形展示:例1. 如图,ABC ∆中, 100=∠=A AC AB ,,BD 平分ABC ∠。
求证:BC BD AD =+。
E FC分析一:从要证明的结论出发,在BC 上截取BD BF =,只需证明AD CF =,考虑到21∠=∠,想到在BC 上截取BA BE =,连结DE ,易得,则有FD AD =,只需证明CF DE =,这就要从条件出发,通过角度计算可以得出DE DF CF ==。
证明一:在BC 上截取BD BF BA BE ==,,连结DE 、DF 在ABD ∆和EBD ∆中,BD BD 21BE BA =∠=∠=,,80DEF 100A BED DE AD )SAS (EBD ABD =∠∴=∠=∠=∴∆≅∆∴,又 100A A C A B =∠=,40)100180(21C ABC =-=∠=∠∴20402121=⨯=∠=∠∴而BF BD =80)20180(21)2180(21BDF BFD =-=∠-=∠=∠∴ADBD FC BF BC FCDF DE AD FCDF CFDC 404080C DFE FDC 40C 80DFE DFDE 80DFE DEF +=+=∴===∴=∴∠=∠∴=-=∠-∠=∠∴=∠=∠∴=∴=∠=∠∴,即BC BD AD =+分析二:如图,可以考虑延长BD 到E ,使DE =AD ,这样BD +AD=BD+DE=BE ,只需证明BE =BC ,由于202=∠,只需证明80B CE E =∠=∠EFC易证 6020100180A DB EDC =--=∠=∠, 120B DC =∠,故作BDC ∠的角平分线,则有FBD ABD ∆≅∆,进而证明DFC DEC ∆≅∆,从而可证出 80E =∠。
证明二:延长BD 到E ,使DE =AD ,连结CE ,作DF 平分BDC ∠交BC 于F 。
由证明一知: 100A 2021=∠=∠=∠,则有 12060180B DC 603660201001803=-=∠=∠=∠=--=∠,, DF 平分6054B DC=∠=∠∴∠606543=∠=∠=∠=∠∴,在ABD ∆和FBD ∆中 43BD BD 21∠=∠=∠=∠,, )A S A (F BD A BD ∆≅∆∴100A BF D FD A D =∠=∠=∴,,而DE DF DE AD =∴=,在DEC ∆和DFC ∆中,DC DC 65DF DE =∠=∠=,, )S A S (D F C D E C ∆≅∆∴80100180B FD 180DFC E =-=∠-=∠=∠∴在BCE ∆中,803202=∠=∠,B C E E B C E ∠=∠∴=∠∴,80 BC BD AD BE BC =+∴=∴,说明:“一题多证”在几何证明中经常遇到,它是培养思维能力提高解题水平的有效途径,读者在以后的几何学习中要善于从不同角度去思考、去体会,进一步提高自身的解题能力。
【实战模拟】1. 选择题:等腰三角形底边长为5cm ,一腰上的中线把其周长分为两部分的差为3cm ,则腰长为( )A. 2cmB. 8cmC. 2cm 或8cmD. 以上都不对2. 如图,ABC ∆是等边三角形,B C B D 90CB D ==∠, ,则1∠的度数是________。
CA 1DB2 33. 求证:等腰三角形两腰中线的交点在底边的垂直平分线上.4. ABC ∆中, 120A A C A B =∠=,,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE =。
AE DO BC1 2【试题答案】1. B2. 分析:结合三角形内角和定理,计算图形中角的度数是等边三角形性质的重要应用。
解:因为ABC ∆是等边三角形所以60A B C B C A B =∠=,因为BC BD =,所以BD AB = 所以23∠=∠在ABD ∆中,因为 60A B C 90CB D =∠=∠, 所以 150A B D =∠,所以 152=∠ 所以 75A B C 21=∠+∠=∠3. 分析:首先将文字语言翻译成数学的符号语言和图形语言。
已知:如图,在ABC ∆中,AC AB =,D 、E 分别为AC 、AB 边中点,BD 、CE 交于O 点。
求证:点O 在BC 的垂直平分线上。
分析:欲证本题结论,实际上就是证明OC OB =。
而OB 、OC 在ABC ∆中,于是想到利用等腰三角形的判定角等,那么问题就转化为证含有21∠∠、的两个三角形全等。
证明:因为在ABC ∆中,AC AB = 所以ACB ABC ∠=∠(等边对等角)又因为D 、E 分别为AC 、AB 的中点,所以EB DC =(中线定义) 在BCD ∆和 CBE ∆中, ⎪⎩⎪⎨⎧=∠=∠=)(CB BC )(EBC DCB )(EB DC 公共边已证已证 所以)SA S (CB E B CD ∆≅∆所以21∠=∠(全等三角形对应角相等)。
