小学奥数 任意四边形、梯形与相似模型(三).学生版
小学奥数教程:任意四边形、梯形与相似模型_全国通用(含答案)

板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA【考点】相似三角形模型 【难度】2星 【题型】解答 【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD ,所以::4:161:4BF FC BE CD ===,所以410814FC =⨯=+.【答案】8【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?例题精讲任意四边形、梯形与相似模型605040302010EA D C B【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米. 【答案】10【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【考点】相似三角形模型 【难度】2星 【题型】填空 【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=,22:2:54:25ADE ABC S S ==△△, 设4ADE S =△份,则25ABC S =△份,255315BEC S =÷⨯=△份,所以:4:15ADE ECB S S =△△. 【答案】4:15【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【考点】相似三角形模型 【难度】3星 【题型】填空 【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△,因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【答案】1:3:5【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯= 【答案】10【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【考点】相似三角形模型 【难度】3星 【题型】填空 【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【总结】继续拓展,我们得到一个规律:平行线等分线段后,所分出来的图形的面积成等差数列. 【答案】1:3:5:7:9【例 5】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 根据金字塔模型::2:(23)2:5AD AB DE BC ==+=,22:2:54:25ADE ABC S S ==△△,设4ADE S =△份,则25ABC S =△份,25421D B C E S =-=梯形份,D B C E S 梯形比ADE S △大17份,恰好是28.5c m ,所以212.5c m ABC S =△【答案】12.5【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 在沙漏模型中,因为:4:9MPN BCP S S =△△,所以:2:3MN BC =,在金字塔模型中有:::2:3AM AB MN BC ==,因为4cm AM =,4236AB =÷⨯=cm ,所以642cm BM =-=【答案】2【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 由沙漏模型得::3:2BO EO BC DE ==,再由金字塔模型得::2:3AD AB DE BC ==. 【答案】2:3【例 7】 如图,ABC ∆中,14AE AB =,14ADAC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 因为14AE AB =,14AD AC =,ED 与BC 平行,根据相似模型可知:1:4ED BC =,:1:4EO OC =,44COD EOD S S ∆∆==平方厘米, 则415CDE S ∆=+=平方厘米,又因为::1:3AED CDE S S AD DC ∆∆==,所以15533AED S ∆=⨯=(平方厘米).【答案】53【例 8】 如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
4-2-3_任意四边形、梯形与相似模型.题库学生版.doc

板块一 任意四边形模型任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?A【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?B例题精讲任意四边形、梯形与相似模型【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDO【例 3】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDCBA【例 4】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76【例 5】 (2008年清华附中入学测试题)如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BD【巩固】如图,每个小方格的边长都是1,求三角形ABC 的面积.D【例 6】 (2007年人大附中考题)如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG的面积.ABCDEFG【例 7】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF G【例 8】 如图,已知正方形ABCD 的边长为10厘米,E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角形BDG 的面积.AB【例 9】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO ∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是 .NM OCBA【例 10】 (2009年迎春杯初赛六年级)正六边形123456A A A A A A 的面积是2009平方厘米,123456B B B B B B 分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.B 4B A 654A 3A A板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 11】 如图,22S =,34S =,求梯形的面积.【巩固】(2006年南京智力数学冬令营)如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD【例 12】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA B CD【例 13】 (第十届华杯赛)如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 14】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.ODCBA【例 15】 如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH的面积是23,求四边形EGFH 的面积.HG FEDCB A【巩固】(人大附中入学测试题)如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为________.321【例 16】如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.BA【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【例 17】 如图面积为12平方厘米的正方形ABCD 中,,E F 是DC 边上的三等分点,求阴影部分的面积.D【例18】如图,在长方形ABCD中,6AB=厘米,2==,求阴影部分的面积.AD=厘米,AE EF FBD【例19】(2008年”奥数网杯”六年级试题)已知ABCD是平行四边形,:3:2BC CE=,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.B【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.B【巩固】(2008年三帆中学考题)右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.B【例20】如图所示,BD、CF将长方形ABCD分成4块,DEF∆的面积是∆的面积是5平方厘米,CED 10平方厘米.问:四边形ABEF的面积是多少平方厘米?FAB CDE105【巩固】如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是4平方厘米,CED ∆的面积是6平方厘米.问:四边形ABEF 的面积是多少平方厘米?64AB CDEF【巩固】(98迎春杯初赛)如图,ABCD 长方形中,阴影部分是直角三角形且面积为54,OD 的长是16,OB的长是9.那么四边形OECD 的面积是多少?B【例 21】 (2007年”迎春杯”高年级初赛)如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF【例 22】 (98迎春杯初赛)如图,长方形ABCD 中,AOB 是直角三角形且面积为54,OD 的长是16,OB的长是9.那么四边形OECD 的面积是 .ABCDEO【例 23】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?B【例 24】 如图所示,ABCD 是梯形,ADE ∆面积是1.8,ABF ∆的面积是9,BCF ∆的面积是27.那么阴影AEC ∆面积是多少?【例 25】 如图,正六边形面积为6,那么阴影部分面积为多少?【例 26】 如图,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形ABC 由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形ABC 的面积是多少平方厘米?⑥⑤④③②①BFD CA【例 27】 如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为 .【例 28】 如图,在正方形ABCD 中,E 、F 分别在BC 与CD 上,且2CE BE =,2CF DF =,连接BF 、DE ,相交于点G ,过G 作MN 、PQ 得到两个正方形MGQA 和PCNG ,设正方形MGQA 的面积为1S ,正方形PCNG 的面积为2S ,则12:S S =___________.QPNMABCD E FG【例 29】 如下图,在梯形ABCD 中,AB 与CD 平行,且2CD AB =,点E 、F 分别是AD 和BC 的中点,已知阴影四边形EMFN 的面积是54平方厘米,则梯形ABCD 的面积是 平方厘米.D【例 30】 (2006年“迎春杯”高年级组决赛)下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .BEE板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 31】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FEDCBA【例 32】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?605040302010EA D C B【例 33】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【例 34】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD D F FM M P PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【例 35】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 36】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【例 37】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 38】 在图中的正方形中,A ,B ,C 分别是所在边的中点,CDO 的面积是ABO 面积的几倍?ABCDO【例 39】如图,线段AB 与BC 垂直,已知4AD EC ==,6BD BE ==,那么图中阴影部分面积是多少?A BD【例 40】 (2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.G ECBA【例 41】 已知三角形ABC 的面积为a ,:2:1AF FC =,E 是BD 的中点,且EF ∥BC ,交CD 于G ,求阴影部分的面积.【例 42】 已知正方形ABCD ,过C 的直线分别交AB 、AD 的延长线于点E 、F ,且10cm AE =,15cm AF =,求正方形ABCD 的边长.FAEDCB【例 43】 如图,三角形ABC 是一块锐角三角形余料,边120BC =毫米,高80AD =毫米,要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?GNPAD CB【巩固】如图,在ABC △中,有长方形DEFG ,G 、F 在BC 上,D 、E 分别在AB 、AC 上,AH 是ABC △边BC 的高,交DE 于M ,:1:2DG DE =,12BC =厘米,8AH =厘米,求长方形的长和宽.E H GMFAD CB【例 44】 图中ABCD 是边长为12cm 的正方形,从G 到正方形顶点C 、D 连成一个三角形,已知这个三角形在AB 上截得的EF 长度为4cm ,那么三角形GDC 的面积是多少?ABCD E FG【例 45】如图,将一个边长为2的正方形两边长分别延长1和3,割出图中的阴影部分,求阴影部分的面积是多少?【例 46】 (2008年101中学考题)图中的大小正方形的边长均为整数(厘米),它们的面积之和等于52平方厘米,则阴影部分的面积是 .【例 47】 如图,O 是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影部分的一块直角三角形的面积是多少?F DB【例 48】 已知长方形ABCD 的面积为70厘米,E 是AD 的中点,F 、G 是BC 边上的三等分点,求阴影EHO△的面积是多少厘米?DCBA【例49】ABCD是平行四边形,面积为72平方厘米,E、F分别为AB、BC的中点,则图中阴影部分的面积为平方厘米.B【例50】如图,三角形PDM的面积是8平方厘米,长方形ABCD的长是6厘米,宽是4厘米,M是BC 的中点,则三角形APD的面积是平方厘米.AB CDPM【例51】如图,长方形ABCD中,E为AD的中点,AF与BE、BD分别交于G、H,OE垂直AD于E,交AF于O,已知5cmAH=,3cmHF=,求AG.AB CDEFGHO【例52】右图中正方形的面积为1,E、F分别为AB、BD的中点,13GC FC=.求阴影部分的面积.ABE【例 53】 梯形ABCD 的面积为12,2AB CD =,E 为AC 的中点,BE 的延长线与AD 交于F ,四边形CDFE 的面积是 .ABCD EF【例 54】 如图,三角形ABC 的面积为60平方厘米,D 、E 、F 分别为各边的中点,那么阴影部分的面积是 平方厘米.BC【例 55】 如图,ABCD 是直角梯形,4,5,3AB AD DE ===,那么梯形ABCD 的面积是多少?OED CBA【例 56】 边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是多少平方厘米?【例 57】 如右图,长方形ABCD 中,16EF =,9FG =,求AG 的长.DABC EFG【例 58】 (第21届迎春杯试题)如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDCB【例 59】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG ∆的面积.MHGF E D CBA【例 60】 (清华附中入学试题)正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDC BA【例 61】 如图,已知14ABC S =△,点,,D E F 分别在,,AB BC CA 上,且2,5,AD BD AF FC ===,ABE DBEF S S =△四边形则ABE S △是多少?FEDCBA【例 62】 如图,长方形ABCD 中,E 、F 分别为CD 、AB 边上的点,DE EC =,2FB AF =,求::PM MN NQ .PMNQ FEDCBA【例 63】 如下图,D 、E 、F 、G 均为各边的三等分点,线段EG 和DF 把三角形ABC 分成四部分,如果四边形FOGC 的面积是24平方厘米,求三角形ABC 的面积.EDOGCF B A【例 64】 (2008年第十二届香港保良局小学数学世界邀请赛(队际赛))如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少?CA。
(小学奥数)任意四边形、梯形与相似模型(三)

板塊三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所謂的相似三角形,就是形狀相同,大小不同的三角形(只要其形狀不改變,不論大小怎樣改變它們都相似),與相似三角形相關的常用的性質及定理如下:⑴相似三角形的一切對應線段的長度成比例,並且這個比例等於它們的相似比; ⑵相似三角形的面積比等於它們相似比的平方; ⑶連接三角形兩邊中點的線段叫做三角形的中位線.三角形中位線定理:三角形的中位線長等於它所對應的底邊長的一半.相似三角形模型,給我們提供了三角形之間的邊與面積關係相互轉化的工具. 在小學奧數裏,出現最多的情況是因為兩條平行線而出現的相似三角形.【例 1】如圖,已知在平行四邊形ABCD 中,16AB =,10AD =,4BE =,那麼FC 的長度是多少?FEDCBA【考點】相似三角形模型 【難度】2星 【題型】解答 【解析】 圖中有一個沙漏,也有金字塔,但我們用沙漏就能解決問題,因為AB 平行於CD ,所以::4:161:4BF FC BE CD ===,所以410814FC =⨯=+. 例題精講任意四邊形、梯形與相似模型【答案】8【例 2】如圖,測量小玻璃管口徑的量具ABC ,AB 的長為15釐米,AC 被分為60等份.如果小玻璃管口DE 正好對著量具上20等份處(DE 平行AB ),那麼小玻璃管口徑DE 是多大?605040302010EAD C B【考點】相似三角形模型 【難度】3星 【題型】解答 【解析】 有一個金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =釐米. 【答案】10【例 3】如圖,DE 平行BC ,若:2:3AD DB =,那麼:ADE ECB S S =△△________.A ED CB【考點】相似三角形模型 【難度】2星 【題型】填空 【解析】 根據金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=,22:2:54:25ADE ABC S S ==△△,設4ADE S =△份,則25ABC S =△份,255315BEC S =÷⨯=△份,所以:4:15ADE ECB S S =△△.【答案】4:15【例 4】如圖, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==, 則::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【考點】相似三角形模型 【難度】3星 【題型】填空 【解析】 設1ADE S =△份,根據面積比等於相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△,因此4AFG S =△份,9ABC S =△份,進而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【答案】1:3:5【鞏固】如圖,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的長.A ED CB【考點】相似三角形模型 【難度】3星 【題型】解答 【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯= 【答案】10【鞏固】如圖, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,則::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【考點】相似三角形模型 【難度】3星 【題型】填空 【解析】 設1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,進而有3DEGFS =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【總結】繼續拓展,我們得到一個規律:平行線等分線段後,所分出來的圖形的面積成等差數列. 【答案】1:3:5:7:9【例 5】已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △. A ED CB【考點】相似三角形模型 【難度】3星 【題型】解答 【解析】 根據金字塔模型::2:(23)2:5AD AB DE BC ==+=,22:2:54:25ADE ABC S S ==△△,設4ADE S =△份,則25ABC S =△份,25421DBCE S =-=梯形份,DBCE S 梯形比ADE S △大17份,恰好是28.5cm ,所以212.5cm ABC S =△ 【答案】12.5【例 6】如圖:MN 平行BC ,:4:9MPN BCP S S =△△,4cm AM =,求BM 的長度NMPA C B【考點】相似三角形模型 【難度】3星 【題型】解答 【解析】 在沙漏模型中,因為:4:9MPN BCP S S =△△,所以:2:3MN BC =,在金字塔模型中有:::2:3AM AB MN BC ==,因為4cm AM =,4236AB =÷⨯=cm ,所以642cm BM =-= 【答案】2【鞏固】如圖,已知DE 平行BC ,:3:2BO EO =,那麼:AD AB =________.OED C BA【考點】相似三角形模型 【難度】3星 【題型】填空 【解析】 由沙漏模型得::3:2BO EO BC DE ==,再由金字塔模型得::2:3AD AB DE BC ==. 【答案】2:3【例 7】如圖,ABC ∆中,14AE AB =,14AD AC =,ED 與BC 平行,EOD ∆的面積是1平方釐米.那麼AED ∆的面積是 平方釐米.A B CDEO【考點】相似三角形模型 【難度】3星 【題型】填空【解析】 因為14AE AB =,14AD AC =,ED 與BC 平行, 根據相似模型可知:1:4ED BC =,:1:4EO OC =,44COD EOD S S ∆∆==平方釐米,則415CDE S ∆=+=平方釐米,又因為::1:3AED CDE S S AD DC ∆∆==,所以15533AED S ∆=⨯=(平方釐米).【答案】53【例 8】如下圖,正方形ABCD 邊長為l0釐米,BO 長8釐米。
小学奥数 任意四边形、梯形与相似模型(三) 精选练习例题 含答案解析(附知识点拨及考点)

板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA【考点】相似三角形模型 【难度】2星 【题型】解答【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD ,所以::4:161:4B F F C B E C D ===,所以410814FC =⨯=+.【答案】8【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?例题精讲任意四边形、梯形与相似模型605040302010EA D C B【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米. 【答案】10【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【考点】相似三角形模型 【难度】2星 【题型】填空【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=,22:2:54:25ADE ABC S S ==△△,设4ADE S =△份,则25ABC S =△份,255315BEC S =÷⨯=△份,所以:4:15ADE ECB S S =△△.【答案】4:15【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△,因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【答案】1:3:5【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【答案】10【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD D F FM M P PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【总结】继续拓展,我们得到一个规律:平行线等分线段后,所分出来的图形的面积成等差数列.【答案】1:3:5:7:9【例 5】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 根据金字塔模型::2:(23)2:5AD AB DE BC ==+=,22:2:54:25ADE ABC S S ==△△,设4ADE S =△份,则25ABC S =△份,25421D B C E S =-=梯形份,D B C E S 梯形比ADE S △大17份,恰好是28.5c m ,所以212.5c mABC S =△ 【答案】12.5【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 在沙漏模型中,因为:4:9MPN BCP S S =△△,所以:2:3MN BC =,在金字塔模型中有:::2:3AM AB MN BC ==,因为4cm AM =,4236AB =÷⨯=cm ,所以642cm BM =-=【答案】2【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 由沙漏模型得::3:2BO EO BC DE ==,再由金字塔模型得::2:3AD AB DE BC ==. 【答案】2:3【例 7】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 因为14AE AB =,14AD AC =,ED 与BC 平行,根据相似模型可知:1:4ED BC =,:1:4EO OC =,44COD EOD S S ∆∆==平方厘米,则415CDE S ∆=+=平方厘米,又因为::1:3AED CDE S S AD DC ∆∆==,所以15533AED S ∆=⨯=(平方厘米).【答案】53【例 8】 如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
【精品】小学奥数训练专题 任意四边形、梯形与相似模型(二).学生版.doc

1板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 1】 如图,22S =,34S =,求梯形的面积.【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD【巩固】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB =5,CD =3,且梯形ABCD 的面积为4,求三角形OAB 的面积。
例题精讲任意四边形、梯形与相似模型|初一·数学·基础-提高-精英·学生版| 第1讲 第页2 A BCDO【例 2】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA BC D【例 3】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 4】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.3ODCBA【例 5】 在梯形ABCD 中,上底长5厘米,下底长10厘米,20=∆BOC S 平方厘米,则梯形ABCD 的面积是 平方厘米。
4-3-4 任意四边形、梯形与相似模型(二).学生版

板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 1】 如图,22S =,34S =,求梯形的面积.S 4S 3S 2S 1【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD【巩固】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB =5,CD =3,且梯形例题精讲任意四边形、梯形与相似模型ABCD 的面积为4,求三角形OAB 的面积。
A BCDO【例 2】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA B CD【例 3】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 4】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.OD CBA【例 5】在梯形ABCD中,上底长5厘米,下底长10厘米,20=∆BOCS平方厘米,则梯形ABCD的面积是平方厘米。
4-3-4 任意四边形、梯形与相似模型(二).学生用

板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 1】 如图,22S =,34S =,求梯形的面积.S 4S 3S 2S 1【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD例题精讲任意四边形、梯形与相似模型【巩固】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB =5,CD =3,且梯形ABCD 的面积为4,求三角形OAB 的面积。
A BCDO【例 2】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA B D【例 3】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 4】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD中,AOB∆、COD∆的面积分别为1.2和2.7,求梯形ABCD的面积.OD CBA【例 5】在梯形ABCD中,上底长5厘米,下底长10厘米,20=∆BOCS平方厘米,则梯形ABCD的面积是平方厘米。
小学奥数知识点拨 精讲试题 题库 任意四边形、梯形与相似模型(二).学生版

【例 1】 如图, S2 2 , S3 4 ,求梯形的面积.
【巩固】如下图,梯形 ABCD 的 AB 平行于 CD ,对角线 AC , BD 交于 O ,已知 △AOB 与 △BOC 的面积分 别为 25 平方厘米与 35 平方厘米,那么梯形 ABCD 的面积是________平方厘米.
A
B
25
学生版
page 7 of 10
【例 14】 如图所示, ABCD 是梯形, ADE 面积是1.8 , ABF 的面积是 9, BCF 的面积是 27.那么阴影 AEC 面积是多少?
【例 15】 如图,正六边形面积为 6 ,那么阴影部分面积为多少?
【例 16】 如图,已知 D 是 BC 中点, E 是 CD 的中点, F 是 AC 的中点.三角形 ABC 由①~⑥这 6 部分组成, 其中②比⑤多 6 平方厘米.那么三角形 ABC 的面积是多少平方厘米?
.
4-3-4.任意四边形、梯形与相似模型 题库
学生版
page 6 of 10
A
D
A
D
O
O
B
E
C
B
E
C
【例 12】 如图所示,长方形 ABCD 内的阴影部分的面积之和为 70,AB=8,AD=15 四边形 EFGO 的面积为 ______.
A
15
D
O 8
E G
B
C
F
【巩固】如图 5 所示,矩形 ABCD 的面积是 24 平方厘米,、三角形 ADM 与三角形 BCN 的面积之和是 7.8 平
A
D
O
B
C
【巩固】如图,梯形 ABCD 中, AOB 、 COD 的面积分别为1.2 和 2.7 ,求梯形 ABCD 的面积.
小学奥数教程-任意四边形、梯形与相似模型

板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA【考点】相似三角形模型 【难度】2星 【题型】解答【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD ,所以::4:161:4BF FC BE CD ===,所以410814FC =⨯=+.【答案】8【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?例题精讲任意四边形、梯形与相似模型605040302010EA D C B【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米. 【答案】10【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【考点】相似三角形模型 【难度】2星 【题型】填空【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=,22:2:54:25ADE ABC S S ==△△,设4ADE S =△份,则25ABC S =△份,255315BEC S =÷⨯=△份,所以:4:15ADE ECB S S =△△.【答案】4:15【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△,因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【答案】1:3:5【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【答案】10【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【总结】继续拓展,我们得到一个规律:平行线等分线段后,所分出来的图形的面积成等差数列.【答案】1:3:5:7:9【例 5】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 根据金字塔模型::2:(23)2:5AD AB DE BC ==+=,22:2:54:25ADE ABC S S ==△△,设4ADE S =△份,则25ABC S =△份,25421D B C E S =-=梯形份,D B C E S 梯形比ADE S △大17份,恰好是28.5c m ,所以212.5c m ABC S =△【答案】12.5【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 在沙漏模型中,因为:4:9MPN BCP S S =△△,所以:2:3MN BC =,在金字塔模型中有:::2:3AM AB MN BC ==,因为4cm AM =,4236AB =÷⨯=cm ,所以642cm BM =-=【答案】2【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 由沙漏模型得::3:2BO EO BC DE ==,再由金字塔模型得::2:3AD AB DE BC ==. 【答案】2:3【例 7】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【考点】相似三角形模型 【难度】3星 【题型】填空【解析】 因为14AE AB =,14AD AC =,ED 与BC 平行,根据相似模型可知:1:4ED BC =,:1:4EO OC =,44COD EOD S S ∆∆==平方厘米,则415CDE S ∆=+=平方厘米,又因为::1:3AED CDE S S AD DC ∆∆==,所以15533AED S ∆=⨯=(平方厘米).【答案】53【例 8】 如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
4-3-5 任意四边形、梯形与相似模型(三).学生版
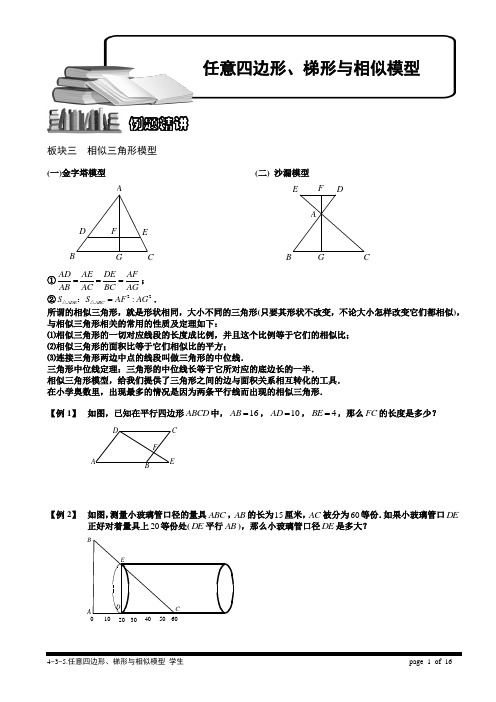
板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?605040302010EA D C B例题精讲任意四边形、梯形与相似模型【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD D F FM M P PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【例 5】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【例 7】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 8】 如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
第三章第八讲:任意四边形、梯形与相似模型.例题精讲

板块一 任意四边形模型任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?A【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABC DO【例 3】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDCBA【例 4】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76【例 5】 (2008年清华附中入学测试题)如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BD【例 6】 (2007年人大附中考题)如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG的面积.ABCDEFG【例 7】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EFG【例 8】 如图,已知正方形ABCD 的边长为10厘米,E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角形BDG 的面积.AB【例 9】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO ∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是 .NM OCBA【例 10】 (2009年迎春杯初赛六年级)正六边形123456A A A A A A 的面积是2009平方厘米,123456B B B B B B 分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.B 4B A 6A 54A 3A A板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 11】 如图,22S =,34S =,求梯形的面积.【例 12】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA BC D【例 13】 (第十届华杯赛)如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 14】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【例 15】 如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG 的面积是11,三角形BCH的面积是23,求四边形EGFH 的面积.HG FEDCB A【例 16】如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.BA【例 17】 如图面积为12平方厘米的正方形ABCD 中,,E F 是DC 边上的三等分点,求阴影部分的面积.DA【例 18】 如图,在长方形ABCD 中,6AB =厘米,2AD =厘米,AE EF FB ==,求阴影部分的面积.D【例 19】 (2008年”奥数网杯”六年级试题)已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.B【例 20】 如图所示,BD 、CF 将长方形ABCD 分成4块,DEF ∆的面积是5平方厘米,CED ∆的面积是10平方厘米.问:四边形ABEF 的面积是多少平方厘米?FAB CDE105【例 21】 (2007年”迎春杯”高年级初赛)如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF【例 22】 (98迎春杯初赛)如图,长方形ABCD 中,AOB 是直角三角形且面积为54,OD 的长是16,OB的长是9.那么四边形OECD 的面积是 .ABCDEO【例 23】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?B【例 24】 如图所示,ABCD 是梯形,ADE ∆面积是1.8,ABF ∆的面积是9,BCF ∆的面积是27.那么阴影AEC ∆面积是多少?【例 25】 如图,正六边形面积为6,那么阴影部分面积为多少?【例 26】 如图,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形ABC 由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形ABC 的面积是多少平方厘米?⑥⑤④③②①BFED CA【例 27】 如图,在一个边长为6的正方形中,放入一个边长为2的正方形,保持与原正方形的边平行,现在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分的面积为 .【例 28】 如图,在正方形ABCD 中,E 、F 分别在BC 与CD 上,且2CE BE =,2CF DF =,连接BF 、DE ,相交于点G ,过G 作MN 、PQ 得到两个正方形MGQA 和PCNG ,设正方形MGQA 的面积为1S ,正方形PCNG 的面积为2S ,则12:S S =___________.QPNMABCD E FG【例 29】 如下图,在梯形ABCD 中,AB 与CD 平行,且2CD AB =,点E 、F 分别是AD 和BC 的中点,已知阴影四边形EMFN 的面积是54平方厘米,则梯形ABCD 的面积是 平方厘米.D【例 30】 (2006年“迎春杯”高年级组决赛)下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .BE板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 31】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FEDCBA【例 32】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?605040302010EA D C B【例 33】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED B【例 34】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【例 35】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 36】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【例 37】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 38】 在图中的正方形中,A ,B ,C 分别是所在边的中点,CDO 的面积是ABO 面积的几倍?ABCDO【例 39】如图,线段AB 与BC 垂直,已知4AD EC ==,6BD BE ==,那么图中阴影部分面积是多少?A BD【例 40】 (2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.G ECBA【例 41】 已知三角形ABC 的面积为a ,:2:1AF FC =,E 是BD 的中点,且EF ∥BC ,交CD 于G ,求阴影部分的面积.【例 42】 已知正方形ABCD ,过C 的直线分别交AB 、AD 的延长线于点E 、F ,且10cm AE =,15cm AF =,求正方形ABCD 的边长.FAEDCB【例 43】 如图,三角形ABC 是一块锐角三角形余料,边120BC =毫米,高80AD =毫米,要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?HGNPAD CB【例 44】 图中ABCD 是边长为12cm 的正方形,从G 到正方形顶点C 、D 连成一个三角形,已知这个三角形在AB 上截得的EF 长度为4cm ,那么三角形GDC 的面积是多少?ABCD E FG【例 45】 如图,将一个边长为2的正方形两边长分别延长1和3,割出图中的阴影部分,求阴影部分的面积是多少?E【例 46】 (2008年101中学考题)图中的大小正方形的边长均为整数(厘米),它们的面积之和等于52平方厘米,则阴影部分的面积是 .H【例 47】 如图,O 是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影部分的一块直角三角形的面积是多少?DB【例 48】 已知长方形ABCD 的面积为70厘米,E 是AD 的中点,F 、G 是BC 边上的三等分点,求阴影EHO △的面积是多少厘米?DC BA【例 49】 ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为AB 、BC 的中点,则图中阴影部分的面积为 平方厘米.B【例 50】 如图,三角形PDM 的面积是8平方厘米,长方形ABCD 的长是6厘米,宽是4厘米,M 是BC的中点,则三角形APD 的面积是 平方厘米.ABCDP M【例 51】 如图,长方形ABCD 中,E 为AD 的中点,AF 与BE 、BD 分别交于G 、H ,OE 垂直AD 于E ,交AF 于O ,已知5cm AH =,3cm HF =,求AG .ABCDEF GHO【例 52】 右图中正方形的面积为1, E 、F 分别为AB 、BD 的中点,13GC FC =.求阴影部分的面积.AB E【例 53】 梯形ABCD 的面积为12,2AB CD =,E 为AC 的中点,BE 的延长线与AD 交于F ,四边形CDFE 的面积是 .ABC D EFGABCD EF【例 54】 如图,三角形ABC 的面积为60平方厘米,D 、E 、F 分别为各边的中点,那么阴影部分的面积是 平方厘米.BC【例 55】 如图,ABCD 是直角梯形,4,5,3AB AD DE ===,那么梯形ABCD 的面积是多少?OEDCBA【例 56】 边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是多少平方厘米?CB【例 57】 如右图,长方形ABCD 中,16EF =,9FG =,求AG 的长.DABC EFG【例 58】 (第21届迎春杯试题)如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDCB【例 59】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG ∆的面积.MHGF E D CBA【例 60】 (清华附中入学试题)正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDC B A【例 61】 如图,已知14ABC S =△,点,,D E F 分别在,,AB BC CA 上,且2,5,AD BD AF FC ===,ABE DBEF S S =△四边形则ABE S △是多少?FEDCBA【例 62】 如图,长方形ABCD 中,E 、F 分别为CD 、AB 边上的点,DE EC =,2FB AF =,求::PM MN NQ .PMNQ FEDCBA【例 63】 如下图,D 、E 、F 、G 均为各边的三等分点,线段EG 和DF 把三角形ABC 分成四部分,如果四边形FOGC 的面积是24平方厘米,求三角形ABC 的面积.EDOGCF B A【例64】(2008年第十二届香港保良局小学数学世界邀请赛(队际赛))如图,ABCD为正方形,1cmAM NB DE FC====且2cmMN=,请问四边形PQRS的面积为多少?C A。
(精品)小学奥数4-3-3任意四边形、梯形与相似模型(一).专项练习及答案解析

例题精讲
板块一 任意四边形模型
任意四边形中的比例关系 ( “蝴蝶定理” ) :
D
A
s1
s2 O
s4
s3
B
C
① S1 : S2 S4 : S3 或者 S1 S3 S2 S4 ② AO : OC S1 S2 : S4 S3
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面 可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面 积对应的对角线的比例关系.
50%,而绿色三角形面积占矩形
面积的 15%,所以黄色三角形面积占矩形面积的 50%- 15%= 35%已知黄色三角
形面积是 21 平方厘米,所以矩形面积等于 21÷35%= 60( 平方厘米 )
【答案】 60
【巩固】如图,四边形被两条对角线分成
4 个三角形,其中三个三角形的面积已知,求:
⑴三角形 BGC 的面积;⑵ AG : GC ?
( AE EB) : (CE DE ) .同理有 ADE , BCE 的面积比为 ( AE DE ) : (BE EC) .所
以有 S ABE × S CDE = S ADE × S BCE ,也就是说在所有凸四边形中,连接顶点得到
2
条对角线,有图形分成上、下、左、右 4 个部分,有:上、下部分的面积之积等于
意比较两种解法, 使学生体会到蝴蝶定理的优势, 从而主观上愿意掌握并使用蝴蝶
定理解决问题.
解法一: ∵ AO : OC S ABD : S BDC 1: 3 ,∴ OC 2 3 6 ,∴ OC : OD 6 : 3 2 :1 .
解法二:作 AH BD 于 H , CG BD 于 G .
小学奥数 任意四边形、梯形与相似模型(三).学生版

板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA例题精讲任意四边形、梯形与相似模型【例 2】如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?605040302010EA D C B【例 3】如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【例 4】如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==, 则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADEDEGFFGNMMNQPPQCBS SS S S =△四边形四边形四边形四边形 . Q E GNMF PA D CB【例 5】已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPC B【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【例 7】如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 8】如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
小学奥数专题-任意四边形、梯形与相似模型(二).学生版

板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO ba S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例 1】 如图,22S =,34S =,求梯形的面积.S 4S 3S 2S 1【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD【巩固】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB =5,CD =3,且梯形ABCD 的例题精讲任意四边形、梯形与相似模型面积为4,求三角形OAB 的面积。
A BCDO【例 2】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA B CD【例 3】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 4】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.OD CBA【例 5】在梯形ABCD中,上底长5厘米,下底长10厘米,20=∆BOCS平方厘米,则梯形ABCD的面积是平方厘米。
任意四边形、梯形与相似模型(三)

【关键词】2008 年,第二届,华杯赛,精英邀请赛
【解析】因为 FGHE 为平行四边形,所以 EC / / AG ,所以 AGCE 为平行四边形.
BG : GC
3 :1 ,那么 GC
: BC
1: 4
,所以 S AGCE
1 4
S
ABCD
1 16 4
4.
又 AE GC ,所以 AE : BG GC : BG 1: 3 ,根据沙漏模型,
【例 4】 如图, △ABC 中, DE , FG , BC 互相平行, AD DF FB ,
则 S△ ADE : S四边形DEGF : S四边形FGCB
.
A
D F
E G
B
C
【考点】相似三角形模型 【难度】3 星 【题型】填空 【解析】设 S△ADE 1 份 , 根 据 面 积 比 等 于 相 似 比 的 平 方 , 所 以 S△ADE : S△AFG AD 2 : AF 2 1: 4 ,
S△ADE : S△ABC AD 2 : AB 2 1: 9 , 因 此 S△AFG 4 份 , S△ABC 9 份 , 进 而 有 S四边形DEGF 3 份 , S四边形FGCB 5 份,所以 S△ADE : S四边形DEGF : S四边形FGCB 1: 3 : 5 【答案】1: 3 : 5
根据梯形蝴蝶定理, SDOE : SDOA : SCOE : SCOA 32 : 3 5 : 3 5 : 52 9 :15 :15 : 25 ,
所以 S阴影
: S梯形ADEC
15 15:
9 15
15 25 15 : 32
,即 S阴影
15 32
S
梯形ADEC
;
又 S梯形ADEC
六年级奥数任意四边形、梯形与相似模型(二)学生版

六年级奥数任意四边形、梯形与相似模型〈二〉学生版梯形中比例关系〈“梯形蝴蝶定理”〉:A BCDO baS 3S 2S 1S 4⒈2213::S S a b =⒉221324::::::S S S S a b ab ab =; 3.S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.〈具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明〉【例 1】 如图,22S =,34S =,求梯形的面积.S 4S 3S 2S 1【巩固】 如下图,梯形ABCD 的AB 平行于CD ,对角线AC ,BD 交于O ,已知AOB △与BOC △的面积分别为25 平方厘米与35平方厘米,那么梯形ABCD 的面积是________平方厘米.3525OABCD例题精讲任意四边形、梯形与相似模型【巩固】 如图所示,在梯形ABCD 中,AB ∥CD ,对角线AC ,BD 相交于点O 。
已知AB =5,CD =3,且梯形ABCD 的面积为4,求三角形OAB 的面积。
A BCDO【例 2】 梯形ABCD 的对角线AC 与BD 交于点O ,已知梯形上底为2,且三角形ABO 的面积等于三角形BOC 面积的23,求三角形AOD 与三角形BOC 的面积之比.OA BC D【例 3】 如下图,四边形ABCD 中,对角线AC 和BD 交于O 点,已知1AO =,并且35ABD CBD =三角形的面积三角形的面积,那么OC 的长是多少?ABCDO【例 4】 梯形的下底是上底的1.5倍,三角形OBC 的面积是29cm ,问三角形AOD 的面积是多少?A BCDO【巩固】如图,梯形ABCD 中,AOB ∆、COD ∆的面积分别为1.2和2.7,求梯形ABCD 的面积.ODCBA【例 5】 在梯形ABCD 中,上底长5厘米,下底长10厘米,20=∆BOC S 平方厘米,则梯形ABCD的面积是 平方厘米。
小学奥数专题-任意四边形、梯形与相似模型(一).学生版

板块一 任意四边形模型任意四边形中的比例关系(“蝴蝶定理”):O DCBA s 4s 3s 2s 1①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDC BA76【例 2】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 3】 一个矩形分成4个不同的三角形(如右图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?黄绿15%例题精讲任意四边形、梯形与相似模型【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC=?B【例 4】四边形ABCD的对角线AC与BD交于点O(如图所示).如果三角形ABD的面积等于三角形BCD的面积的13,且2AO=,3DO=,那么CO的长度是DO的长度的_________倍.OA DCBGHBCDAO【例 5】如图,平行四边形ABCD的对角线交于O点,CEF△、OEF△、ODF△、BOE△的面积依次是2、4、4和6.求:⑴求OCF△的面积;⑵求GCE△的面积.OGF E DCBA【例 6】如图相邻两个格点间的距离是1,则图中阴影三角形的面积为.【巩固】如图,每个小方格的边长都是1,求三角形ABC的面积.D【例 7】 如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG 的面积.ABCDEF GABCDEF G【例 8】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G【例 9】 如图,已知正方形ABCD 的边长为10厘米,E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角形BDG 的面积.【例 10】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO ∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是 .OM NCBA【例 11】 正六边形123456A A A A A A 的面积是2009平方厘米,123456B B B B B B 分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.4B A 543A A4B A 543A A【例 12】 如图,ABCD 是一个四边形,M 、N 分别是AB 、CD 的中点.如果△ASM 、△MTB 与△DSN 的面积分别是6、7和8,且图中所有三角形的面积均为整数,则四边形ABCD 的面积为 .NM STDCBA A DN CTSM B【例 13】 已知ABCD 是平行四边形,:3:2BC CE ,三角形ODE 的面积为6平方厘米。
4 3 5 任意四边形梯形与相似模型(三).学生版

4 35 任意四边形梯形与相似模型(三).学生版4-3-5任意四边形、梯形与相似模型(三).学生版任意四边形、梯形和相似模型例题精讲板三相似三角形模型(一)金字塔模型(二)沙漏模型aeafddb①fgecbgcadaedeaf;???abacbcag②s△ade:s△abc?af2:ag2.所谓的相似三角形是形状相同、大小不同的三角形(只要形状不变,无论大小如何变化,它们都是相似的)。
与相似三角形有关的常见性质和定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;(3)连接三角形两侧中点的线段称为三角形中线三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型为我们提供了一个工具来转换三角形的边和面积之间的关系。
在小学奥林匹克数学竞赛中,最常见的情况是由两条平行线构成的相似三角形【例1】如图,已知在平行四边形abcd中,ab?16,ad?10,be?4,那么fc的长度是多少?dfabec【例2】如图,测量小玻璃管口径的量具abc,ab的长为15厘米,ac被分为60等份.如果小玻璃管口de正好对着量具上20等份处(de平行ab),那么小玻璃管口径de是多大?是a0d10203040c50604-3-5. 任意四边形、梯形和类似模型学生page1of16[例3]如图所示,反平行BC,如果ad:DB?2: 3. 然后是s△ 艾德:是的△ 欧洲央行___adbeC【例4】如图,△abc中,de,fg,bc互相平行,ad?df?fb,然后是s△ ade:s四边形degf:s四边形fgcbadfbegc【合并】如图所示,De与BC平行,ad?2,ab?5,ae?4.找出AC的长度adbe【合并】如图所示,△ ABC,De,FG,Mn,PQ,BC相互平行,ad?df?调频?议员?PB则s△ade:s四边形degf:s四边形fgnm:s四边形mnqp:s四边形pqcb?.c4-3-5。
奥数精编训练-任意四边形、梯形与相似模型(三)

板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?例题精讲任意四边形、梯形与相似模型605040302010EA D C B【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【例 4】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .Q E GNMF PA D CB【例 5】 已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPA C B【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【例 7】 如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 8】 如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
五年级奥数专题 梯形、相似三角形(学生版)

学科培优数学梯形、相似三角形学生姓名授课日期教师姓名授课时长知识定位本讲中的主要知识点有两种基本模型,一个是梯形中的蝴蝶定理,另一个是有关相似三角形的模型。
在这一讲中,相似三角形是重点,它所出现的地方非常多而且拥有很多的变形,用相似三角形的知识也能解决很多平面几何的难题.本讲着重讲解关于怎样判断相似和相似有关的性质和技巧。
掌握好相似,很多难题都能迎刃而解。
相似出现最多的地方是在平行线间,目前的竞赛题中的相似三角形一般离不开平行线。
重点难点1.判别相似三角形2.找准相似三角形的对应角或对应边主要考点:1.梯形的面积公式和蝴蝶定理2.相似的性质3.结合相似三角形的综合型平面几何题目知识梳理知识点:梯形、相似三角形一、模型一:梯形中比例关系(“梯形蝴蝶定理”)②S1︰S3=a2︰b2②S1︰S3︰S2︰S4= a2︰b2︰ab︰ab ;③S的对应份数为(a+b)2二、如何判断相似(1)相似的基本概念:两个三角形对应边城比例,对应角相等。
(2)判断相似的方法:①两个三角形若有两个角对应相等则这两个三角形相似;②两个三角形若有两条边对应成比例,且这两组对应边所夹的角相等则两个三角形相似。
三、模型二:相似三角形性质①a b c hA B C H===;②S1︰S2=a2︰A2例题精讲【试题来源】【题目】如图,在一个梯形内有两个三角形的面积分别为10与12,已知梯形的上底长是下底长的23.那么余下阴影部分的面积是多少?【试题来源】S4S3s2s1bahhHcbaC BAacbH CBA【题目】已知:如图,四边形ABCD 是直角梯形,∠A=∠B=90º,AD=3,BC=4,S=△AOD =1,求四边形ABCD 的面积。
【试题来源】【题目】四边形ABCD 被AC 和DB 分成甲乙丙丁4个三角形,已知BE=80,CE=60,DE=40,AE=30,问:丙、丁两个三角形之和是甲乙两个三角形面积之和的多少倍?【试题来源】【题目】梯形ABCD 的中位线EF 长15厘米(见图),∠ABC=∠AEF=90°,G 是EF 上的一点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长度是多少?FE DCBA例题精讲任意四边形、梯形与相似模型【例 2】如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大?605040302010EA D C B【例 3】如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________.A ED CB【例 4】如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==, 则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADEDEGFFGNMMNQPPQCBS SS S S =△四边形四边形四边形四边形 . Q E GNMF PA D CB【例 5】已知ABC △中,DE 平行BC ,若:2:3AD DB =,且DBCE S 梯形比ADE S △大28.5cm ,求ABC S △.A ED CB【例 6】 如图:MN 平行BC , :4:9MPN BCP S S =△△,4cm AM =,求BM 的长度NMPC B【巩固】如图,已知DE 平行BC ,:3:2BO EO =,那么:AD AB =________.OED C BA【例 7】如图,ABC ∆中,14AE AB =,14AD AC =,ED 与BC 平行,EOD ∆的面积是1平方厘米.那么AED ∆的面积是 平方厘米.A B CDEO【例 8】如下图,正方形ABCD 边长为l0厘米,BO 长8厘米。
AE=____厘米。
EODCBA【例 9】如图,已知正方形ABCD 的边长是12厘米,E 是CD 边上的中点,连接对角线AC ,交BE 于点O ,则三角形AOB 的面积是( )平方厘米。
A 、24B 、36C 、48D 、60【例 10】 在图中的正方形中,A ,B ,C 分别是所在边的中点,CDO 的面积是ABO 面积的几倍?ABCDOEFABCDO【例 11】 图30-10是一个正方形,其中所标数值的单位是厘米.问:阴影部分的面积是多少平方厘米?【例 12】 如图,线段AB 与BC 垂直,已知4AD EC ==,6BD BE ==,那么图中阴影部分面积是多少?A BDA BDA BD【例 13】 如图,四边形ABCD 和EFGH 都是平行四边形,四边形ABCD 的面积是16,:3:1BG GC =,则四边形EFGH 的面积=________.G ECBA【例 14】 已知三角形ABC 的面积为a ,:2:1AF FC =,E 是BD 的中点,且EF ∥BC ,交CD 于G ,求阴影部分的面积.【例 15】 已知正方形ABCD ,过C 的直线分别交AB 、AD 的延长线于点E 、F ,且10cm AE =,15cm AF =,求正方形ABCD 的边长.FAEDCB【例 16】 如图,三角形ABC 是一块锐角三角形余料,边120BC =毫米,高80AD =毫米,要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?HGNPAD CB【巩固】如图,在ABC △中,有长方形DEFG ,G 、F 在BC 上,D 、E 分别在AB 、AC 上,AH 是ABC △ 边BC 的高,交DE 于M ,:1:2DG DE =,12BC =厘米,8AH =厘米,求长方形的长和宽.E H GMFAD CB【例 17】 图中ABCD 是边长为12cm 的正方形,从G 到正方形顶点C 、D 连成一个三角形,已知这个三角形在AB 上截得的EF 长度为4cm ,那么三角形GDC 的面积是多少?ABCD E FGNMABCDE FG【例 18】 如图,将一个边长为2的正方形两边长分别延长1和3,割出图中的阴影部分,求阴影部分的面积是多少?E【例 19】 图中的大小正方形的边长均为整数(厘米),它们的面积之和等于52平方厘米,则阴影部分的面积是 .H【例 20】如图,O是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,那么阴影部分的一块直角三角形的面积是多少?DBDB【例 21】已知长方形ABCD的面积为70厘米,E是AD的中点,F、G是BC边上的三等分点,求阴影EHO△的面积是多少厘米?DCBAAB CD【例 22】 ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为AB 、BC 的中点,则图中阴影部分的面积为 平方厘米.BB【例 23】 如图,三角形PDM 的面积是8平方厘米,长方形ABCD 的长是6厘米,宽是4厘米,M 是BC 的中点,则三角形APD 的面积是 平方厘米.ABCDP MKN ABCDPM【例 24】 如图,长方形ABCD 中,E 为AD 的中点,AF 与BE 、BD 分别交于G 、H ,OE 垂直AD 于E ,交AF 于O ,已知5cm AH =,3cm HF =,求AG .ABCDEF GHO【例 25】 右图中正方形的面积为1, E 、F 分别为AB 、BD 的中点,13GC FC =.求阴影部分的面积.AB EABE【例 26】 梯形ABCD 的面积为12,2AB CD ,E 为AC 的中点,BE 的延长线与AD 交于F ,四边形CDFE 的面积是 .AB CD EFGABCDE F【例 27】 如图,三角形ABC 的面积为60平方厘米,D 、E 、F 分别为各边的中点,那么阴影部分的面积是 平方厘米.B CBCB【例 28】 如图,ABCD 是直角梯形,4,5,3AB AD DE ===,那么梯形ABCD 的面积是多少?OED CBAOED AFCB【例 29】 边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是多少平方厘米?CB【例 30】 如右图,长方形ABCD 中,16EF =,9FG =,求AG 的长.DABC EFG【例 31】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDC BM GFAEDCBGFAEDCB【例 32】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点,BF 交EC 于M ,求BMG 的面积.MHGF E D CBAA【例 33】 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDC BAMH GFEDCBA【例 34】 如图,已知14ABC S =△,点,,D E F分别在,,AB BC CA 上,且2,5,AD BD AF FC ===,ABE DBEF S S =△四边形则ABE S △是多少?FEDCBAFEDCBA【例 35】 如图,长方形ABCD 中,E 、F 分别为CD 、AB 边上的点,DE EC =,2FB AF =,求::PM MN NQ .PMNQ FEDCB AGPMNQ FEDCBA【例 36】 如下图,D 、E 、F 、G 均为各边的三等分点,线段EG 和DF 把三角形ABC 分成四部分,如果四边形FOGC 的面积是24平方厘米,求三角形ABC 的面积.EDOGCF B AED OGCFBA【例 37】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少?CACA【例 38】如图12-6所示,在三角形ABC中,DC=3BD,DE=EA.若三角形ABC的面积是1.则阴影部分的面积是多少?【例 39】一个等腰直角三角形和一个正方形如图摆放,①、②、③这三块的面积比依次为1:4:41.那么,④、⑤这两块的面积比是______.⑤④③②①HKJG IF DCEB A ⑤④③②①【例 40】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的重点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n,那么,m +n 的值等于__________。
EFGHC DBAEFGHCDBA(A )5 (B )7 (C )8 (D )12【例 41】如图所示,三角形AEF,三角形BDF,三角形BCD,都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1.求阴影部分的面积。
【例 42】如图,正方形ABCD中,E、F、G、H分别为各边的中点,J为GD的中点,EJ交CD于I。
已知正方形ABCD边长为10cm,则图中阴影部分的面积是__ ___ cm2.H F CA。
