第六讲MALAB可视化(二)绘三维图
使用matlab绘制三维图形的方法

使用matlab绘制三维图形的方法要使用MATLAB绘制三维图形,首先需要了解MATLAB中的三维绘图函数和绘图选项。
下面将介绍一些常用的绘制三维图形的方法。
1.绘制基本的三维图形要绘制基本的三维图形,可以使用以下函数:- plot3(函数:用于在三维坐标系中绘制线条。
- scatter3(函数:用于在三维坐标系中绘制散点图。
- surf(函数:用于绘制三维曲面图。
- mesh(函数:用于绘制三维网格图。
- bar3(函数:用于绘制三维条形图。
- contour3(函数:用于绘制三维等高线图。
例如,下面的代码演示了如何使用plot3(函数绘制一个三维线条图:```x = linspace(0, 2*pi, 100);y = sin(x);z = cos(x);plot3(x, y, z, 'LineWidth', 2);xlabel('X');ylabel('Y');zlabel('Z');title('3D Line Plot');```2.添加颜色和纹理在绘制三维图形时,可以使用颜色和纹理来增加图形的信息。
MATLAB 提供了一系列函数来处理颜色和纹理,如:- colormap(函数:用于设置颜色映射。
- caxis(函数:用于设置坐标轴范围。
- shading(函数:用于设置颜色插值方法。
- texturemap(函数:用于设置纹理映射方法。
例如,下面的代码展示了如何使用纹理映射来绘制一个球体:```[X, Y, Z] = sphere(50);C = colormap('jet');surface(X, Y, Z, 'FaceColor', 'texturemap', 'CData', C);axis equal;```3.绘制多个数据集要在同一张图中绘制多个数据集,可以使用hold on和hold off命令。
如何使用Matlab进行3D图形绘制

如何使用Matlab进行3D图形绘制1. 引言在科学研究、工程设计和数据可视化的过程中,3D图形绘制是一项非常重要的技能。
Matlab作为一种功能强大且易于上手的工具,在3D图形绘制方面有着很大的优势。
本文将介绍如何使用Matlab进行3D图形绘制,以帮助读者更好地掌握这一技术。
2. 准备工作在开始使用Matlab进行3D图形绘制之前,我们需要先进行一些准备工作。
首先,确保已经安装了Matlab软件,并且具备了一定的基本操作能力。
其次,了解Matlab的数据管理和处理方式,掌握常用的数据结构和操作方法。
最后,对于3D图形绘制的相关概念和技术有一定的了解,包括坐标系、曲线和曲面等基本概念。
3. 坐标系和坐标变换在进行3D图形绘制之前,首先需要了解坐标系的概念以及如何进行坐标变换。
Matlab中使用的3D坐标系是右手坐标系,其中x轴指向右侧,y轴指向前方,z轴指向上方。
在进行坐标变换时,可以使用Matlab提供的函数进行平移、旋转和缩放等操作,以便更好地展示3D图形。
4. 曲线绘制在Matlab中,使用函数plot3可以绘制3D曲线。
该函数的基本用法是plot3(x,y,z),其中x、y、z分别为曲线上各点的x、y、z坐标。
可以通过对坐标点进行适当的变换和调整,绘制出各种形状和曲线。
5. 曲面绘制除了曲线,我们还可以使用Matlab绘制3D曲面。
Matlab提供了函数surf和mesh来实现曲面绘制。
函数surf绘制带有颜色的曲面,而函数mesh绘制网格型的曲面。
这两个函数的基本用法都是类似的,可以通过传入坐标点数据和数据值来绘制出曲面图像。
6. 其他3D图形效果除了曲线和曲面,我们还可以通过Matlab实现其他各种各样的3D图形效果。
例如,绘制3D散点图可以使用函数scatter3,绘制3D柱状图可以使用函数bar3,绘制3D等高线图可以使用函数contour3等。
这些函数都有类似的参数传递方式,通过调整函数参数可以实现各种个性化的效果。
Matlab三维立体画图
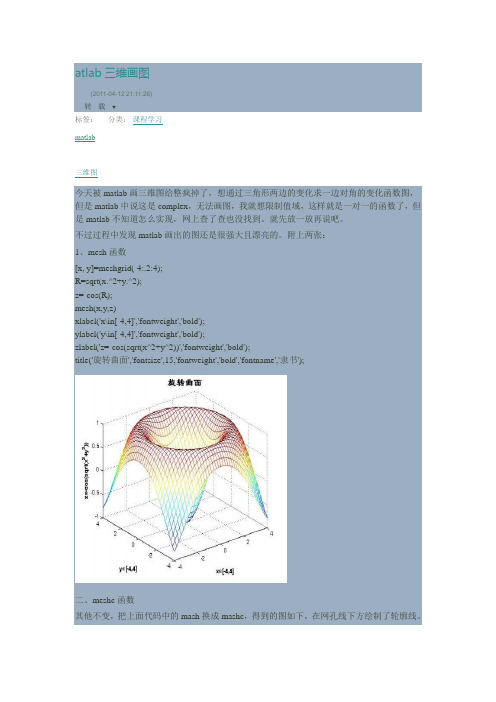
atlab 三维画图(2011-04-12 21:11:26) 转载▼标签: matlab 三维图分类: 课程学习今天被matlab 画三维图给整疯掉了,想通过三角形两边的变化求一边对角的变化函数图,但是matlab 中说这是complex ,无法画图,我就想限制值域,这样就是一对一的函数了,但是matlab 不知道怎么实现,网上查了查也没找到。
就先放一放再说吧。
不过过程中发现matlab 画出的图还是很强大且漂亮的。
附上两张: 1、mesh 函数[x, y]=meshgrid(-4:.2:4); R=sqrt(x.^2+y.^2); z=-cos(R); mesh(x,y,z)xlabel('x\in[-4,4]','fontweight','bold'); ylabel('y\in[-4,4]','fontweight','bold');zlabel('z=-cos(sqrt(x^2+y^2))','fontweight','bold');title('旋转曲面','fontsize',15,'fontweight','bold','fontname','隶书');二、meshc 函数其他不变,把上面代码中的mash 换成mashc ,得到的图如下,在网孔线下方绘制了轮廓线。
三、mashz函数Matlab 三维作图1 画一个可透视的椭球figurea = 15;b = 10;c = 5;k = 5;n = 2^k-1;theta = pi*(-n:2:n)/n;phi = (pi/2)*(-n:2:n)'/n;X = a*cos(phi)*cos(theta);Y = b*cos(phi)*sin(theta);Z = c*sin(phi)*ones(size(theta));surf(X,Y,Z,'FaceColor','interp',...'EdgeColor','none',...'FaceLighting','phong')axis tightcamlight leftalpha(.33) % 产生透视效果这是在7.1.上画的图:....................建立空间等高线[X,Y] = meshgrid([-2:.25:2]); Z = X.*exp(-X.^2-Y.^2);contour3(X,Y,Z,30)h = findobj('Type','patch');set(h,'LineWidth',2)title(' 空间等高线')..................§4.2 三维作图§4.2.1 mesh(Z)语句mesh(Z)语句可以给出矩阵Z元素的三维消隐图,网络表面由Z坐标点定义,与前面叙述的x-y平面的线格相同,图形由邻近的点连接而成.它可用来显示用其它方式难以输出的包含大量数据的大型矩阵,也可用来绘制Z变量函数.显示两变量的函数Z=f(x,y),第一步需产生特定的行和列的x-y矩阵.然后计算函数在各网格点上的值.最后用mesh函数输出.下面我们绘制sin(r)/r函数的图形.建立图形用以下方法:x=-8:.5:8;y=x';x=ones(size(y))*x;y=y*ones(size(y))';R=sqrt(x.^2+y.^2)+eps;z=sin(R)./R;mesh(z) %% 试运行mesh(x,y,z),看看与mesh(z)有什么不同之处?各语句的意义是:首先建立行向量x,列向量y;然后按向量的长度建立1-矩阵;用向量乘以产生的1-矩阵,生成网格矩阵,它们的值对应于x-y坐标平面;接下来计算各网格点的半径;最后计算函数值矩阵Z.用mesh函数即可以得到图形.图4.2.1三维消隐图第一条语句x的赋值为定义域,在其上估计函数;第三条语句建立一个重复行的x矩阵,第四条语句产生y的响应,第五条语句产生矩阵R(其元素为各网格点到原点的距离).用mesh方法结果如上.另外,上述命令系列中的前4行可用以下一条命令替代:[x, y]=meshgrid(-8:0.5:8)§4.2.2与mesh相关的几个函数(1) meshc与函数mesh的调用方式相同,只是该函数在mesh的基础上又增加了绘制相应等高线的功能.下面来看一个meshc的例子:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshc(z) %% 试运行meshc(x,y,z),看看与meshc(z)有什么不同之处?我们可以得到图形:图4.2.2.1 meshc图地面上的圆圈就是上面图形的等高线.(2)函数meshz与mesh的调用方式也相同,不同的是该函数在mesh函数的作用之上增加了屏蔽作用,即增加了边界面屏蔽.例如:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshz(z) %% 试运行meshz(x,y,z),看看与meshz(z)有什么不同之处?我们得到图形:图4.2.2.2 meshz图§4.2.3其它的几个三维绘图函数(1)在Matlab中有一个专门绘制圆球体的函数sphere,其调用格式如下:[x,y,z]=sphere(n)此函数生成三个(n+1)×(n+1)阶的矩阵,再利用函数surf(x,y,z)可生成单位球面.[x,y,z]=sphere 此形式使用了默认值n=20sphere(n) 只绘制球面图,不返回值.运行下面程序:sphere(30);axis square;我们得到球体图形:图4.2.3.1 球面图若只输入sphere画图,则是默认了n=20的情况.(2) surf函数也是Matlab中常用的三维绘图函数.其调用格式如下:surf(x,y,z,c)输入参数的设置与mesh相同,不同的是mesh函数绘制的是一网格图,而surf绘制的是着色的三维表面.Matlab语言对表面进行着色的方法是,在得到相应网格后,对每一网格依据该网格所代表的节点的色值(由变量c控制),来定义这一网格的颜色.若不输入c,则默认为c=z.我们看下面的例子:%绘制地球表面的气温分布示意图.[a,b,c]=sphere(40);t=abs(c); %求绝对值surf(a,b,c,t);axis equalcolormap('hot')我们可以得到图形如下:图4.2.3.2 等温线示意图§4.2.4图形的控制与修饰(1)坐标轴的控制函数axis,调用格式如下:axis([xmin,xmax,ymin,ymax,zmin,zmax])用此命令可以控制坐标轴的范围.与axis相关的几条常用命令还有:axis auto 自动模式,使得图形的坐标范围满足图中一切图元素axis equal 严格控制各坐标的分度使其相等axis square 使绘图区为正方形axis on 恢复对坐标轴的一切设置axis off 取消对坐标轴的一切设置axis manual 以当前的坐标限制图形的绘制(2)grid on 在图形中绘制坐标网格.grid off 取消坐标网格.(3)xlabel, ylabel, zlabel分别为x轴, y轴, z轴添加标注.title为图形添加标题.以上函数的调用格式大同小异,我们以xlabel为例进行介绍:xlabel('标注文本','属性1','属性值1','属性2','属性值2',…)这里的属性是标注文本的属性,包括字体大小、字体名、字体粗细等.例如:[x, y]=meshgrid(-4:.2:4);R=sqrt(x.^2+y.^2);z=-cos(R);mesh(x,y,z)xlabel('x\in[-4,4]','fontweight','bold');ylabel('y\in[-4,4]','fontweight','bold');zlabel('z=-cos(sqrt(x^2+y^2))','fontweight','bold');title('旋转曲面','fontsize',15,'fontweight','bold','fontname','隶书');图4.2.4.1添加标注。
MATLAB中的三维图形绘制与动画制作技巧

MATLAB中的三维图形绘制与动画制作技巧引言MATLAB是一种强大的科学计算软件,广泛应用于工程、物理、数学等各个领域。
其中,三维图形绘制和动画制作是其功能的重要一部分。
本文将深入探讨MATLAB中三维图形绘制与动画制作的技巧,并给出一些实用的示例。
一、三维图形绘制1. 坐标系的设定在绘制三维图形之前,我们需要设定坐标系。
通过使用MATLAB的figure函数和axes函数,我们可以创建一个三维坐标系,并设置其属性,如坐标轴的范围、标签等。
2. 点的绘制在三维图形中,最基本的图元是点。
通过scatter3函数,我们可以绘制出一系列点的三维分布情况。
可以通过设置点的大小、颜色、透明度等属性,增加图像的美观性。
3. 曲线的绘制MATLAB提供了多种绘制曲线的函数,如plot3、line、quiver等。
通过这些函数,我们可以绘制各种样式的曲线,例如直线、曲线、矢量、流线等。
我们可以根据需要设置线条的样式、颜色、宽度等属性。
4. 曲面的绘制除了曲线,我们还可以绘制三维曲面。
通过函数mesh、surf和contour,我们可以绘制出具有平滑外形的曲面。
可以通过设置颜色映射和透明度等属性,使得曲面具有更加细腻的外观。
二、动画制作1. 创建动画对象要制作动画,我们需要先创建一个动画对象。
通过使用MATLAB的videoWriter函数,我们可以创建一个视频文件,并设置其参数,如帧率、分辨率等。
2. 绘制关键帧动画的核心是绘制一系列关键帧,并在每一帧之间进行插值。
通过在每一帧中修改图形对象的属性,我们可以实现对象的平移、旋转和缩放等变换。
通过MATLAB提供的getframe函数,我们可以将当前图像存储为一个帧对象。
3. 帧之间的插值在关键帧之间,我们需要进行插值,以平滑动画的过渡。
通过使用MATLAB 的linspace函数,我们可以生成两个关键帧之间的若干插值。
然后,我们可以在每个插值处更新图形对象的属性,从而实现动画效果。
如何在Matlab中进行二维和三维绘图

如何在Matlab中进行二维和三维绘图在科学研究和工程领域,数据可视化是一项十分重要的任务,而Matlab作为一种功能强大的数值计算和数据分析软件,自然也提供了丰富的绘图功能。
本文将介绍如何在Matlab中进行二维和三维绘图,并探讨一些常见的绘图技巧和应用。
一、二维绘图Matlab中的二维绘图是最常见和基础的绘图任务之一。
在绘制二维图形时,我们通常会用到plot函数。
这个函数可以接受单个向量作为输入,将这个向量的值作为y轴上的数据点,自动生成与该向量长度相同的x轴坐标。
例如,我们可以用以下代码绘制一个简单的二维折线图:```x = 0:0.1:2*pi;y = sin(x);plot(x, y);```上述代码中,x参量取从0到2π的均匀间隔的值,而y则是根据x计算得到的sin函数值。
plot函数会自动根据输入绘制折线图,并添加相应的轴标签和图例。
在实际应用中,我们经常需要绘制多条曲线在同一个坐标系中进行对比分析。
可以通过在plot函数中传入多个x和y向量实现这一功能。
例如,我们可以通过以下代码绘制一个简单的双曲线图:```x = 0:0.1:2*pi;y1 = sin(x);y2 = cos(x);plot(x, y1, x, y2);```这样,就会在同一个坐标系中同时绘制sin曲线和cos曲线。
除了折线图,Matlab还支持其他常见的二维绘图类型,如散点图、柱状图和面积图等。
这些绘图类型可以通过不同的函数实现,例如scatter、bar和area等。
这里不再一一赘述,读者可以通过Matlab的帮助文档或官方网站了解更多的用法和示例。
二、三维绘图除了二维绘图,Matlab也提供了丰富的三维绘图功能,用于可视化更为复杂的数据和模型。
在绘制三维图形时,我们通常会用到surf函数。
这个函数可以接受两个二维矩阵作为输入,将这两个矩阵的值分别作为x、y轴上的坐标,而将第三个二维矩阵的值作为z轴上的数据点。
使用matlab绘制三维图形地方法

使用matlab绘制三维图形地方法使用matlab绘制三维图形的方法三维曲线plot3函数与plot函数用法十分相似,其调用格式为:plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n),其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot 函数相同。
当x,y,z是同维向量时,则x,y,z 对应元素构成一条三维曲线。
当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例绘制三维曲线。
程序如下:t=0:pi/100:20*pi;x=sin(t);y=cos(t);z=t.*sin(t).*cos(t);plot3(x,y,z);gridtitle('Line in 3-D Space');xlabel('X');ylabel('Y');zlabel('Z');如下图:XLine in 3-D SpaceYZ三维曲面1.产生三维数据在MATLAB 中,利用meshgrid 函数产生平面区域内的网格坐标矩阵。
其格式为:x=a:d1:b; y=c:d2:d; [X,Y]=meshgrid(x,y);语句执行后,矩阵X 的每一行都是向量x ,行数等于向量y 的元素的个数,矩阵Y 的每一列都是向量y ,列数等于向量x 的元素的个数。
2.绘制三维曲面的函数surf 函数和mesh 函数的调用格式为:mesh(x,y,z,c):画网格曲面,将数据点在空间中描出,并连成网格。
surf(x,y,z,c):画完整曲面,将数据点所表示曲面画出。
一般情况下,x,y,z 是维数相同的矩阵。
x,y 是网格坐标矩阵,z 是网格点上的高度矩阵,c 用于指定在不同高度下的颜色范围。
例绘制三维曲面图z=sin(x+sin(y))-x/10。
程序如下:[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标 z=sin(x+sin(y))-x/10; mesh(x,y,z);axis([0 4*pi 0 4*pi -2.5 1]); 如下图:-2.5-2-1.5-1-0.500.51此外,还有带等高线的三维网格曲面函数meshc 和带底座的三维网格曲面函数meshz。
matlab三维绘图命令和演示

三维绘图2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2)●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影:contour(peaks, 20);plot3可画出三度空间中的曲线:t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线:t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);三维绘图的主要功能:绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色(一)三维线图plot3 ——基本的三维图形指令调用格式:plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。
MATLAB绘三维图

第六讲M A T L A B可视化(二)绘三维图【目录】一、三维图形绘制步骤 (1)二、三维绘图基本操作 (2)1、三维线图 (2)2、三维网线图 (3)3、三维曲面图 (4)三、透视、镂空和裁切 (5)1、图形的透视 (5)2、图形的镂空 (6)3、图形的裁切 (7)四、三维图形的精细控制 (8)1、视点与旋动 (8)2、色彩控制 (9)3、浓淡处理 (11)五、照明和材质处理 (12)六、简洁绘图指令 (13)【正文】一、三维图形绘制步骤步骤典型指令1三维曲线数据:先取一个参变量采样向量然后计算各坐标数据向量t=p i*(0:100)/100;x=f1(t);y=f2(t);z=f3(t);三维曲面数据:产生自变量采样向量;由自变量向量产生格点矩阵;计算格点矩阵相对应的函数值矩阵x=x1:d x:x2;y=y1:d y:y2;[X,Y]=m e s h g r i d(x,y);Z=f(x,y);2选定图形窗及子窗位置:同二维3调用三维曲线绘图指令:线型、色彩、数据点形p l o t3(x,y,z,'b-')调用三维曲面绘图指令M e s h(X,Y,Z);4设置轴的范围与刻度、坐标分隔线同二维5图形注释:图名、坐标名、图例、文字同二维6着色、明暗、灯光、材质处理c o l o r m a p,s h a d i n g,l i g h t,m a t e r i a l 7视点、三度(横、纵、高)比v i e w,a s p e c t1二、三维绘图基本操作1、三维线图用来画三维曲线,三维曲线与一组(x,y,z)坐标相对应的点连接而成。
绘图格式为:p l o t3(X,Y,Z,'s')p l o t3(X1,Y1,Z1,'s1',X2,Y2,Z2,'s2',...)(1)X、Y、Z是同维向量时,则绘制以X、Y、Z元素为x、y、z坐标的三维曲线;(2)X、Y、Z是同维矩阵时,则以X、Y、Z对应列元素为x、y、z坐标绘制多条曲线,曲线条数等于矩阵的列数;(3)(X1,Y1,Z1,'s1')与(X2,Y2,Z2,'s2')的结构与作用和(X,Y,Z,'s')相同,表示同一指令绘两组以上曲线;(4)s、s1、s2的意义与二维相同。
matlab三维绘图ppt课件

xx
1
三维曲线绘图 三维曲面绘图
2
xx
二、MATLAB三维曲线绘图
plot3——三维曲线绘制指令 plot3的调用格式:
plot3(X,Y,Z) plot3(X,Y,Z,’String’) plot3(X1,Y1,Z1,’ String1’,X2,Y2,Z2,’ String2’,…) plot3与plot的 用法相同
➢ shading faceted
以平面为单位进行着色,在flat用色基础上,在贴片的 四周勾出黑色网线。
23
subplot(131),surf(peaks(40)); subplot(132),surf(peaks(40));shading flat subplot(133),surf(peaks(40));shading interp
subplot(122),h = surf(ones(10,10));rotate(h,[0 0 1],i,[1 0 0]) end
➢ rotate3d
动态旋转命令,可以让用户使用鼠标来旋转视角
19
背景颜色控制命令colordef
➢ colordef white 将图形的背景颜色设置为白色 ➢ colordef black ➢ colordef none 将图形背景和图形窗口的颜色设置
28
对象和句柄
MATLAB把构成图形的各个基本要素称为图形对象, 包括图形窗口、坐标轴、线条、曲面、文本和其它对 象。
每一个对象都有一个数字来标识,叫做句柄。当每次 创建一个对象时,MATLAB就为它建立一个唯一的句 柄。
29
作业ห้องสมุดไป่ตู้P79
5,7,8,9
30
22
MATLAB三维图形绘制

%绘制极坐标图
说明:theta为相角,radius为离原点的距离。
• 【】求传递函数为
G(s) s(0的.51s对1)数幅频特性曲线,
横坐标为w,按对数坐标。
Aw=1./(w.*sqrt((0.5*w).^2+1)); Lw=20*log10(Aw); semilogx(w,Lw) title('对数幅频特性曲线')
• colormap 色图函数—— 色图设定函数
• colormap 色图函数(m)——产生m×3的色图矩阵 缺省64×3。
颜色
Black(黑) White(白) Red(红) Green(绿) Blue(蓝) Yellow(黄) Magenta(品红) Cyan(青) Gray(灰) Dark red(暗红) Copper(铜色) Aquamarine(碧绿)
【上例续】使用消息框显示当阻尼系数大于1时的警告信 息,如下图。
>>msgbox('阻尼系数输入范围出错','警告','warn')
〔2〕其它对话框
【例续】使用警告对话框显示当阻尼系数大于1时的警告 信息。 >>warndlg('阻尼系数输入范围出错','警告')
【例续】使用出错提示框显示当阻尼系数小于0时出错 信息。 >>errordlg('阻尼系数输入出错','出错')
说明:az表示方位角(azimuth),el表示俯仰角(elevation)
°,el=30°
五、色彩的控制
1.色图(colormap)
(1) RGB三元组
RGB三元数组每行表示一种色彩,数组元素R、G、B在 0~1之间取值,分别表示红、绿、蓝基色的相对亮度,如 下表所示。
使用matlab软件进行三维绘图

plot(x,y)其中x和y为长度相同的向量,分别用于 存储x坐标和y坐标数据。
例3-1 在0≤X≤2区间内,绘制曲线y=sin(2πx)。
程序如下: x=0:pi/100:2*pi; y= sin(2*pi*x); plot(x,y); 说明: (1)当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线, 曲线条数等于矩阵的列数。 (2)当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不同色彩的曲 线。曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。 (3)plot函数最简单的调用格式是只包含一个输入参数:plot(x)。
3.MATLAB二维绘图
二维图形的绘制是MATLAB语言图形处理的基础 3.1 plot函数的基本用法 MATLAB最常用的画二维图形的命令是plot ,plot函数的基本调用格 式为:plot(x,y) 看个简单的例子: >> y=[0 0.58 0.70 0.95 0.83 0.25]; >> plot(y) 生成的图形见图。
3.4.绘制图形的辅助操作 1. 图形标注 有关图形标注函数的调用格式为: title(图形名称) xlabel(x轴说明) ylabel(y轴说明) text(x,y,图形说明) legend(图例1,图例2,…)
legend函数的基本用法是 legend(string1,string2,string3, ...) 分别将字符串1、字符串2、字符串3……标注到图中,每 个字符串对应的图标为画图时的图标。 例如: plot(x,sin(x),'.b',x,cos(x),'+r') legend('sin','cos')这样可以把"."标识为'sin',把"+"标识为"cos"
Matlab绘制三维曲线

Matlab绘制三维曲线plot3函数与plot函数用法十分相似,其调用格式为:plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot函数相同。
当x,y,z是同维向量时,则x,y,z 对应元素构成一条三维曲线。
当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例绘制三维曲线。
程序如下:t=0:pi/100:20*pi;x=sin(t);y=cos(t);z=t.*sin(t).*cos(t);plot3(x,y,z);title('Line in 3-D Space');xlabel('X');ylabel('Y');zlabel('Z');三维曲面1.产生三维数据在MATLAB中,利用meshgrid函数产生平面区域内的网格坐标矩阵。
其格式为:x=a:d1:b; y=c:d2:d;[X,Y]=meshgrid(x,y);语句执行后,矩阵X的每一行都是向量x,行数等于向量y的元素的个数,矩阵Y的每一列都是向量y,列数等于向量x的元素的个数。
2.绘制三维曲面的函数surf函数和mesh函数的调用格式为:mesh(x,y,z,c):画网格曲面,将数据点在空间中描出,并连成网格。
surf(x,y,z,c):画完整曲面,将数据点所表示曲面画出。
一般情况下,x,y,z是维数相同的矩阵。
x,y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的颜色范围。
例绘制三维曲面图z=sin(x+sin(y))-x/10。
程序如下:[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标z=sin(x+sin(y))-x/10;mesh(x,y,z);axis([0 4*pi 0 4*pi -2.5 1]);此外,还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。
Matlab中的3D图形绘制方法

Matlab中的3D图形绘制方法Matlab是一种常用于科学计算和数据可视化的高级编程语言和开发环境。
它的强大功能使得它成为工程师、科学家和研究人员的首选工具之一。
其中一个引人注目的特点是它对3D图形的支持。
在本文中,我们将探讨Matlab中的一些3D图形绘制方法。
Matlab提供了多种绘制3D图形的函数和工具。
最基本的方法是使用“plot3”函数绘制三维数据。
这个函数接受x、y和z三个参数,分别表示三维坐标系上的数据点。
通过给定一系列的数据点,我们可以在三维空间中绘制出线条或散点图。
这种方法适用于简单的数据展示和初步的分析。
除了基本的线条和散点图,Matlab还提供了一些更高级的3D图形绘制函数,如“surface”和“mesh”。
这些函数可以用来绘制三维曲面和网格图。
例如,我们可以使用“surface”函数绘制一个三维山丘的图像,其中x和y轴表示地面上的位置,z轴表示地面的高度。
通过调整x、y和z的数值,我们可以创建出各种形状和复杂度的三维表面。
Matlab还在其图形库中提供了许多其他类型的3D图形绘制函数。
例如,“bar3”函数可以用来绘制三维柱状图,其中x和y轴表示不同的类别,z轴表示各类别的数值。
这种图形可以更直观地展示不同类别之间的关系和差异。
类似地,“contour”函数可以用来绘制三维的等值线图,用于可视化函数的等值线和等高面。
另一个值得一提的技术是使用Matlab的“patch”函数绘制复杂的三维图形。
这个函数可以用来创建和修改三维物体的表面,例如绘制球体、立方体和多面体等。
我们可以通过更改物体的属性和位置来构建各种形状和几何体。
这种灵活性使得“patch”函数在计算机图形学和动画领域中得到广泛应用。
除了这些函数和工具,Matlab还允许用户通过编写自定义的脚本和函数来实现更高级的3D图形绘制。
例如,我们可以使用Matlab的3D绘图工具箱中的一些高级函数和方法来创建特定类型的三维图形,如体积渲染、光线追踪和动画效果等。
Matlab中的三维图形绘制技巧

Matlab中的三维图形绘制技巧由于Matlab的强大数据分析和可视化功能,它被广泛应用于许多领域,包括物理学、生物学和工程学。
其中,三维图形绘制是Matlab中一项重要而有趣的技巧。
本文将介绍几种用Matlab绘制三维图形的技巧,并探讨一些常见问题的解决方法。
一、基础知识在开始之前,我们需要了解一些Matlab中三维图形绘制的基础知识。
Matlab 提供了许多函数来绘制三维图形,包括plot3、surf和mesh等函数。
其中,plot3函数用于绘制三维曲线,surf函数用于绘制三维曲面,而mesh函数则可以绘制网格曲面。
此外,Matlab还提供了一些辅助函数来设置坐标轴、标题和标签等。
二、绘制三维曲线首先,我们来学习如何使用plot3函数绘制三维曲线。
该函数接受三个向量作为输入,分别表示曲线上点的x、y和z坐标。
以绘制一个螺旋线为例,我们可以定义一个角度向量theta和对应的x、y和z坐标向量。
然后,使用plot3函数绘制曲线。
```matlabtheta = linspace(0, 10*pi, 1000);x = cos(theta);y = sin(theta);z = linspace(0, 10, 1000);plot3(x, y, z);```通过调整theta的范围和分辨率,我们可以绘制出不同形状和密度的螺旋线。
此外,我们还可以使用颜色、线型和标记等选项来自定义曲线的外观。
三、绘制三维曲面接下来,我们将介绍如何使用surf函数绘制三维曲面。
与绘制曲线类似,surf 函数也接受三个坐标向量作为输入,并将其解释为曲面上的点。
此外,我们还需要定义一个与坐标向量相同维度的矩阵来表示曲面的高度。
以下代码演示了如何绘制一个带有Z轴高度信息的平面曲面。
```matlabx = linspace(-5, 5, 100);y = linspace(-5, 5, 100);[X, Y] = meshgrid(x, y);Z = peaks(X, Y);surf(X, Y, Z);```在此示例中,我们使用meshgrid函数生成X和Y坐标矩阵,并使用peaks函数生成与X和Y相对应的高度矩阵Z。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲M A T L A B可视化(二)绘三维图【目录】一、三维图形绘制步骤 (1)二、三维绘图基本操作 (2)1、三维线图 (2)2、三维网线图 (3)3、三维曲面图 (5)三、透视、镂空和裁切 (5)1、图形的透视 (6)2、图形的镂空 (6)3、图形的裁切 (8)四、三维图形的精细控制 (9)1、视点与旋动 (9)2、色彩控制 (10)3、浓淡处理 (12)五、照明和材质处理 (13)六、简洁绘图指令 (15)【正文】一、三维图形绘制步骤步骤典型指令1三维曲线数据:先取一个参变量采样向量然后计算各坐标数据向量t=p i*(0:100)/100;x=f1(t);y=f2(t);z=f3(t);三维曲面数据:产生自变量采样向量;由自变量向量产生格点矩阵;计算格点矩阵相对应的函数值矩阵x=x1:d x:x2;y=y1:d y:y2;[X,Y]=m e s h g r i d(x,y);Z=f(x,y);2选定图形窗及子窗位置:同二维3调用三维曲线绘图指令:线型、色彩、数据点形p l o t3(x,y,z,'b-')调用三维曲面绘图指令M e s h(X,Y,Z);4设置轴的范围与刻度、坐标分隔线同二维5图形注释:图名、坐标名、图例、文字同二维6着色、明暗、灯光、材质处理c o l o r m a p,s h a d i n g,l i g h t,m a t e r i a l 7视点、三度(横、纵、高)比v i e w,a s p e c t二、三维绘图基本操作1、三维线图用来画三维曲线,三维曲线与一组(x,y,z)坐标相对应的点连接而成。
绘图格式为:p l o t3(X,Y,Z,'s')p l o t3(X1,Y1,Z1,'s1',X2,Y2,Z2,'s2',...)(1)X、Y、Z是同维向量时,则绘制以X、Y、Z元素为x、y、z坐标的三维曲线;(2)X、Y、Z是同维矩阵时,则以X、Y、Z对应列元素为x、y、z坐标绘制多条曲线,曲线条数等于矩阵的列数;(3)(X1,Y1,Z1,'s1')与(X2,Y2,Z2,'s2')的结构与作用和(X,Y, Z,'s')相同,表示同一指令绘两组以上曲线;(4)s、s1、s2的意义与二维相同。
【例】绘单条三维曲线t=(0:0.02:2)*p i;%三维坐标用参数方程表示x=s i n(t);y=c o s(t);z=c o s(2*t);%t为参数,得到三个同维向量p l o t3(x,y,z,'b-',x,y,z,'b d');%绘蓝色线和菱形的点v i e w([-82,58]);%选择观察点b o x o n;%显示坐标框l e g e n d('链','宝石')%图例【例】绘多条三维曲线t=(0:0.02:2)'.*p i;%三维坐标用参数方程表示x=s i n(t);y=c o s(t);z=c o s(2*t);%t为参数,得到三个同维向量r=0.1:0.1:1;%画系数不同的10条曲线x=x*r;y=y*r;z=z*r;p l o t3(x,y,z);v i e w([-82,58]);b o x o n;2、三维网线图以网格的形式显示三维图形。
通常使用方形网格,所以网格上的每一格点必需有一三维坐标(x,y,z)与之相对应。
绘图指令如下:(1)m e s h(Z)-以矩阵Z的列下标为x、行下标为y、矩阵的元素为z组成三维网格数据绘制网线图;(2)m e s h(X,Y,Z)-X、Y、Z是同维矩阵,分别以三个矩阵对应位置的元素x、y、z组成三维网格数据绘制网线图;(3)m e s h(X,Y,Z,C)-C为与其他三个矩阵同维,给出每个格点的用色矩阵。
缺省时C=Z。
(色表说明见后)其中,画z=f(x,y)所代表的网格数据产生如下:(1)x=x1:d x:x2;y=y1:d y:y2;X=o n e s(s i z e(y))*x;Y=y*o n e s(s i z e(x));(2)x=x1:d x:x2;y=y1:d y:y2;[X,Y]=m e s h g r i d(x,y);然后根据函数求出Z矩阵。
【例】用网线图表现函数22yz+=。
xc l f;%清图形窗口x=-4:4;y=x;%x、y的取值范围都是-4到4[X,Y]=m e s h g r i d(x,y);%形成采样点矩阵Z=X.^2+Y.^2;%计算函数值m e s h(X,Y,Z);%绘网格图c o l o r m a p(h o t);%选用色图3、三维曲面图将网线图的网格填色,形成曲面图。
格式为:s u r f(Z)、s u r f(X,Y,Z)、s u r f(X,Y,Z,C)。
含义同网线图。
【例】用曲面图表现函数22y=。
z+xc l f;x=-4:4;y=x;[X,Y]=m e s h g r i d(x,y);Z=X.^2+Y.^2;s u r f(X,Y,Z);c o l o r m a p(h o t);三、透视、镂空和裁切1、图形的透视M a t l a b在绘三维网线图和曲面图时,一般进行消隐处理。
为得到透视效果,用以下命令:h i d d e n o f f-透视被遮挡的图形h i d d e n o n-消隐被遮挡的图形【例】透视效果演示[X0,Y0,Z0]=s p h e r e(30);%产生单位球面的三维坐标X=2*X0;Y=2*Y0;Z=2*Z0;%产生半径为2的球面坐标s u r f(X0,Y0,Z0);%画单位球面s h a d i n g i n t e r p%对球的着色进行浓淡细化处理h o l d o n;%绘图保持m e s h(X,Y,Z)%绘大球c o l o r m a p(h o t);%定义色表h o l d o f f%取消绘图保持h i d d e n o f f%产生透视效果a x i s e q u a l,a x i s o f f%坐标等轴并隐藏2、图形的镂空利用非数(N a N)对图形的剪切处理。
【例】演示利用N a N对图形剪切t=l i n s p a c e(0,2*p i,100);%产生参数r=1-e x p(-t/2).*c o s(4*t);%旋转母线[X,Y,Z]=c y l i n d e r(r,60);%创建圆柱i i=f i n d(X<0&Y<0);%确定x-y平面第四象限的坐标%Z(i i)=N a N;%剪切s u r f(X,Y,Z);c o l o r m a p(s p r i n g),s h a d i n g i n t e r p%l i g h t('p o s i t i o n',[-3,-1,3],'s t y l e','l o c a l')%设置光源%m a t e r i a l([0.5,0.4,0.3,10,0.3])%设置表面反射【例】演示利用N a N对图形镂空P=p e a k s(30);%M a t l a b提供的一个典型三维函数P(18:20,9:15)=N a N;%镂空s u r f c(P);c o l o r m a p(s u m m e r)%加投影等高线的曲面l i g h t('p o s i t i o n',[50,-10,5]),l i g h t i n g f l a tm a t e r i a l([0.9,0.9,0.6,15,0.4])3、图形的裁切镂空处理不能产生切面,为看清图形需要切的表面,把被切部分强制为○。
【例】表现切面c l f;x=[-8:0.05:8];y=x;[X,Y]=m e s h g r i d(x,y);%产生格点数据Z Z=X.^2-Y.^2;%计算函数值i i=f i n d(a b s(X)>6|a b s(Y)>6);%确定超出[-6,6]范围的格点下标Z Z(i i)=z e r o s(s i z e(i i));%强制为0s u r f(X,Y,Z Z),s h a d i n g i n t e r p;c o l o r m a p(c o p p e r)l i g h t('p o s i t i o n',[0,-15,1]);l i g h t i n g p h o n gm a t e r i a l([0.8,0.8,0.5,10,0.5])四、三维图形的精细控制1、视点与旋动(1)视点,即观察点,如下图所示。
M a t l a b控制视点的命令为:v i e w([a z,e l])-通过方位角a z、俯仰角e l来设置视点,单位是度。
(二维图缺省为0、90度。
三维缺省为37.5、30度)v i e w([v x,v y,v z])-通过视点的直角坐标点来设定。
(2)图形的旋动即图形的旋转,命令为:r o t a t e(h,d i r e c t i o n,a l p h a,o r g i n),其中:h-被旋转的对象;d i re c t i o n-方向轴,可用球坐标[t h e t a,p h i]或直角坐标[x,y,z]表示;a l p h a-按右手法则旋转的角度;o r g i n-支点。
【例】旋转指令示例s h g;c l f;%图形窗口置前,清除[X,Y]=m e s h g r i d([-2:.2:2]);%取格点坐标Z=4*X.*e x p(-X.^2-Y.^2);%计算函数值G=g r a d i e n t(Z);%近似梯度s u b p l o t(1,2,1),s u r f(X,Y,Z,G)%子图1画曲面s u b p l o t(1,2,2),h=s u r f(X,Y,Z,G);%子图2画曲面r o t a t e(h,[-2,-2,0],30,[2,2,0]),c o l o r m a p(j e t)%旋转2、色彩控制(1)用色风格函数c o l o rdef C-对屏幕上所有子对象设置缺省值;c o l o rde f(f i g,C)-对图形窗f i g的所有子对象设置缺省h=c o l o r d e f('n e w',C)-对新图形窗设置w h i t e b g-使当前图形窗背景色在黑白间切换w h i t e b g(f i g)-切换指定窗w h i t e b g(C)-使当前图形窗背景色变为C指定的颜色C轴背景色图背景色轴标色色图画线用色次序W h i t e白淡灰黑J e t蓝,深绿,红,青,洋红,黄,黑B l a c k黑黑白j e t黄,洋红,青,红,淡绿,蓝,淡灰(2)色图一种色彩用[R,G,B]基色三元行数组表示。
