回归模型与统计软件1.
统计学中的回归分析

统计学中的回归分析在统计学中,回归分析是一种重要的数据分析方法。
它用于探索自变量与因变量之间的关系,帮助我们理解变量之间的相互作用以及预测未来的趋势。
本文将介绍回归分析的基本概念、原理和应用。
一、回归分析的基本概念回归分析是通过建立数学模型来描述自变量与因变量之间的关系。
自变量是我们在问题中感兴趣的变量,而因变量是我们想要预测或解释的变量。
回归分析可以帮助我们确定自变量如何影响因变量,并找到最佳的拟合曲线或平面来描述这种关系。
回归分析的基本假设是,自变量与因变量之间存在线性关系,并且观测误差服从正态分布。
基于这个假设,我们可以使用最小二乘法来拟合回归模型,使得观测值与预测值之间的残差平方和最小化。
二、回归分析的原理1. 简单线性回归简单线性回归是最基本的回归分析方法,用于研究只包含一个自变量和一个因变量的情况。
我们可以通过绘制散点图来观察两个变量之间的关系,并使用最小二乘法拟合一条直线来描述这种关系。
2. 多元线性回归多元线性回归适用于包含多个自变量和一个因变量的情况。
通过拟合一个多元线性模型,我们可以同时考虑多个自变量对因变量的影响,并研究它们之间的相互作用。
3. 非线性回归非线性回归用于描述自变量与因变量之间的非线性关系。
在这种情况下,我们可以根据问题的特点选择适当的非线性回归模型,并使用最小二乘法进行参数估计。
三、回归分析的应用回归分析在各个领域都有广泛的应用。
以下是一些常见的应用示例:1. 经济学中的回归分析经济学家常常使用回归分析来研究经济现象。
例如,他们可以通过回归分析来研究GDP与各种经济指标之间的关系,以及利率、通胀率等因素对经济增长的影响。
2. 医学研究中的回归分析医学研究中的回归分析可以用于探索治疗方法与患者恢复速度之间的关系。
通过收集患者的相关数据,如年龄、性别、治疗时间等,可以建立多元线性回归模型来预测患者的康复时间。
3. 市场营销中的回归分析市场营销人员可以利用回归分析来确定产品价格与销量之间的关系。
回归线统计学

回归线统计学
回归线统计学是统计学中的一种重要方法,用于建立变量之间的关系模型。
它通过回归分析来探索自变量和因变量之间的关联程度,并通过拟合回归线来预测因变量的值。
在回归线统计学中,我们首先需要收集数据,包括自变量和因变量的观测值。
然后,我们使用统计软件来进行回归分析,通过计算得到回归方程的系数和拟合度量指标。
回归线统计学的核心思想是最小二乘法。
通过最小化观测值与回归线之间的差异,我们可以找到最佳的回归线,使得预测值与观测值之间的差异最小化。
回归线统计学有多种应用场景,例如经济学中的收入预测、市场营销中的销售量预测、医学研究中的药物疗效评估等。
通过回归线统计学,我们可以了解变量之间的关系,并进行预测和决策。
在回归线统计学中,我们还需要注意一些常见的问题。
首先是多重共线性,即自变量之间存在高度相关性,可能导致回归结果不准确。
其次是异方差性,即观测值的方差不恒定,可能需要进行数据转换或使用加权最小二乘法。
此外,还要注意检验回归模型的显著性和残差的正态性。
回归线统计学是一种重要的数据分析方法,通过建立变量之间的关系模型,可以进行预测和决策。
在应用过程中,我们需要注意数据
收集、回归分析和结果解释等方面的问题。
通过合理使用回归线统计学,我们可以更好地理解和利用数据,为决策提供依据。
回归分析及Stata软件应用

阅读感受
在阅读这本书的过程中,我不仅学会了如何进行回归分析,还学会了如何更 有效地使用Stata软件。这些知识和技能将对我的未来学习和职业生涯产生积极 的影响。我相信这本书对于其他读者也会有很大的帮助,无论是初学者还是有一 定经验的统计学者。
目录分析
目录分析
在当今的统计分析领域,回归分析是一种广泛应用的方法,用于探索变量之 间的关系,以及预测和解释数据的变化。而Stata软件则是一款功能强大且易用 的统计软件,被广泛应用于各种数据分析和处理任务中。《回归分析及Stata软 件应用》这本书,以其独特的视角和实用的方法,为读者提供了回归分析和 Stata软件应用方面的深入指导。
目录分析
在这一章中,本书介绍了一些高级的回归分析方法,包括多重共线性处理、 交互效应模型、时间序列回归模型等。还介绍了如何在Stata中实现这些方法。
目录分析
在这一章中,本书详细介绍了Stata编程的基础知识和自定义函数的编写方法。 通过学习这一章,读者可以了解如何编写自己的Stata程序,以实现更复杂的分 析和数据处理任务。
阅读感受
《回归分析及Stata软件应用》是一本理论与实践相结合的好书。它不仅提供 了回归分析的基础知识,还通过Stata软件的应用展示了如何在实际问题中应用 这些知识。这本书的案例和实例非常丰富,使得我可以深入理解回归分析的应用 场景和技巧。书中的软件操作指南也为我提供了极大的帮助,让我可以轻松地使 用Stata软件进行各种统计分析任务。
精彩摘录
Stata软件是一款功能强大的统计分析软件,广泛应用于各种领域。它可以帮 助用户完成从数据管理到高级统计分析的各种任务。Stata软件支持多种回归分 析方法,包括线性回归、逻辑回归、有序回归等。
精彩摘录
回归分析中常用的统计软件介绍(八)

回归分析是一种统计学方法,用来探究两个或多个变量之间的关系。
在回归分析中,常用的统计软件有多种选择,每种软件都有其自身的特点和优势。
本文将介绍几种常用的统计软件,包括SPSS、R、Python和SAS,从不同的角度对它们进行分析和比较,帮助读者选择适合自己需求的统计软件。
SPSS是一款广泛使用的统计软件,它提供了丰富的数据处理和分析功能,尤其擅长做一般线性模型(GLM)和多元线性回归分析。
SPSS的用户界面友好,操作简单,适合初学者使用。
另外,SPSS还具有强大的数据可视化功能,能够生成直观清晰的图表,方便用户进行数据分析和解释。
然而,SPSS也有一些局限,比如它的自定义性不强,不适合进行复杂的编程和模型定制。
R是一款自由开源的统计软件,它拥有庞大的用户群体和丰富的扩展包资源。
R的统计分析功能十分全面,包括回归分析、方差分析、聚类分析等。
R还支持数据可视化和报告生成,用户可以根据自己的需求进行定制化。
另外,R的编程能力强大,用户可以编写自己的函数和算法,满足个性化的统计需求。
但是,R的学习曲线较陡,对于初学者来说可能需要花费更多的时间来掌握。
Python是一种通用编程语言,也可以用来进行统计分析。
Python的数据分析库pandas和统计分析库statsmodels提供了丰富的统计函数和模型,用户可以进行回归分析、时间序列分析等。
另外,Python还有强大的机器学习库scikit-learn,可以进行复杂的预测建模和模型评估。
Python的优势在于其通用性,用户不仅可以进行统计分析,还可以进行数据清洗、数据可视化和模型部署。
SAS是一款专业的统计分析软件,主要应用于企业和学术研究领域。
SAS的统计分析功能非常丰富,覆盖了各种常见的统计方法和模型,包括线性回归、逻辑回归、生存分析等。
SAS的数据管理功能也非常强大,用户可以进行数据清洗、数据转换和数据集合并等操作。
此外,SAS还具有强大的数据挖掘和机器学习能力,能够满足复杂的数据分析需求。
《2024年数据统计分析软件SPSS的应用(五)——相关分析与回归分析》范文

《数据统计分析软件SPSS的应用(五)——相关分析与回归分析》篇一数据统计分析软件SPSS的应用(五)——相关分析与回归分析一、引言在当今的大数据时代,数据统计分析已成为科研、商业决策和日常生活中的重要工具。
SPSS(Statistical Package for the Social Sciences)作为一款广泛使用的数据统计分析软件,其强大的功能为各类数据分析提供了有力支持。
本文将重点介绍SPSS中相关分析与回归分析的应用,探讨其在实际研究中的应用价值。
二、相关分析的应用1. 相关分析的基本概念相关分析是研究两个或多个变量之间关系密切程度的一种统计方法。
SPSS提供了多种相关系数计算方法,如皮尔逊相关系数、斯皮尔曼等级相关系数等,以帮助研究者了解变量间的关系强度和方向。
2. 相关分析在实证研究中的应用以市场营销领域为例,研究者可以通过SPSS计算消费者购买行为与产品价格、广告投入等变量之间的相关系数,从而了解各因素对消费者购买行为的影响程度。
这种分析方法有助于企业制定有效的营销策略。
三、回归分析的应用1. 回归分析的基本概念回归分析是研究一个或多个自变量与因变量之间关系的一种预测性统计方法。
通过建立回归模型,可以分析自变量对因变量的影响程度,并进行预测。
SPSS提供了多种回归分析方法,如简单线性回归、多元线性回归等。
2. 回归分析在实证研究中的应用以医学领域为例,研究者可以通过SPSS建立药物剂量与患者恢复时间之间的回归模型,分析药物剂量对患者恢复时间的影响程度,为临床治疗提供参考依据。
此外,回归分析还可以用于研究其他领域的复杂关系,如教育、经济等。
四、案例分析以某电商平台销售数据为例,通过SPSS进行相关分析与回归分析。
首先,计算商品价格、商品评价数量、商品销量等变量之间的皮尔逊相关系数,了解各因素之间的关联程度。
然后,建立商品价格与商品销量的多元线性回归模型,分析价格对销量的影响程度。
线性回归分析教案

线性回归分析教案一、引言线性回归是一种常用的统计分析方法,用于研究两个连续型变量之间的线性关系。
在实际应用中,线性回归广泛用于经济学、社会学、医学等领域,用于预测和解释变量之间的关系。
本教案将介绍线性回归的基本原理、模型设定和参数估计方法,以帮助学生深入理解线性回归的概念和应用。
二、教学目标1.了解线性回归的基本原理和假设。
2.学习线性回归模型的设定和参数估计方法。
3.能够使用统计软件实现线性回归模型的计算。
4.掌握线性回归模型的解释和预测能力。
5.理解线性回归模型的运用场景和限制条件。
三、教学内容1.线性回归的基本原理1.1 线性关系的定义1.2 线性回归模型的基本假设1.3 线性回归模型的优点和局限性2.线性回归模型的设定2.1 简单线性回归模型及其参数估计2.2 多元线性回归模型及其参数估计2.3 线性回归模型的变量选择方法3.线性回归模型的参数估计3.1 最小二乘法估计3.2 参数估计的性质和假设检验3.3 模型评估和诊断4.线性回归模型的解释和预测4.1 理解回归系数的含义4.2 判断模型对观测数据的拟合程度4.3 利用回归模型进行预测五、教学方法1.理论讲解与示范通过讲解线性回归的基本原理和模型设定,带领学生了解线性回归模型的概念和应用。
同时,通过实例演示和统计软件的使用展示线性回归模型的计算过程。
2.实践操作与练习在课堂上,安排学生利用统计软件进行线性回归模型的实际计算,并结合具体数据集进行模型拟合和预测操作。
通过实际操作提高学生对线性回归模型的应用能力。
3.案例分析与讨论将一些实际问题、经济数据或社会调查数据与线性回归模型结合,引导学生对模型结果进行解读和讨论,提高学生对模型解释和应用的理解。
六、教学评估1.课堂小测验在课程结束前进行一次小测验,考察学生对线性回归的理解程度和应用能力。
2.作业和项目布置线性回归相关的作业和项目,要求学生独立完成线性回归模型的建立和分析,以检验学生对所学知识的掌握程度。
回归分析中常用的统计软件介绍

回归分析是统计学中一种重要的分析方法,用于研究自变量与因变量之间的关系。
在实际的数据分析中,常用的统计软件能够帮助研究人员更轻松地进行回归分析,包括SPSS、R、Python等。
本文将介绍这些常用的统计软件在回归分析中的应用。
SPSS是一款非常经典的统计软件,它提供了丰富的数据分析功能,包括回归分析。
在SPSS中,进行回归分析非常简单,只需要将自变量和因变量输入到软件中,然后选择回归分析模块,即可得到回归方程和相关的统计结果。
此外,SPSS还提供了对结果的可视化展示,包括回归系数的显著性检验、残差分析等,能够帮助研究人员更好地理解回归分析的结果。
R是一种开源的统计软件,它在科研领域中应用非常广泛。
R中有丰富的回归分析包,例如lm、glm等,能够满足不同类型的回归分析需求。
通过R进行回归分析,研究人员可以自定义分析流程,灵活地选择模型和参数,实现个性化的分析。
此外,R还提供了丰富的数据可视化功能,能够帮助研究人员直观地展示回归分析的结果。
Python是一种通用的编程语言,它也有丰富的统计分析库,如pandas、statsmodels等。
通过Python进行回归分析,研究人员可以利用编程的灵活性,构建复杂的回归模型,进行深入的数据处理和分析。
同时,Python还可以与其他领域的数据处理和机器学习工具结合,实现更加复杂的数据分析任务。
除了上述几种常用的统计软件,还有其他一些工具也可以用于回归分析,如Excel、Matlab等。
这些工具各有特点,能够满足不同研究人员的需求。
在选择统计软件时,研究人员需要根据自己的研究目的、数据类型和分析需求进行选择,以便更好地进行回归分析。
在使用统计软件进行回归分析时,研究人员需要注意数据的质量和分析方法的选择。
首先,需要对数据进行清洗和预处理,排除异常值和缺失值,以保证分析的准确性。
其次,需要选择合适的回归模型,根据研究问题和数据特点选择线性回归、Logistic回归等不同类型的模型。
现代统计方法--回归分析1

现代统计方法的种类
三、相关分析方法 1、定性资料分析 2、回归分析 3、典型相关分析 4、主成分分析 5、因子分析 6、对应分析
现代统计方法的种类
四、预测决策方法: 1、回归分析 2、判别分析 3、定性资料分析 4、聚类分析
统计分析方法应用流程
现实经济问题
提炼具体问题 确定欲达目标
分类研究
结构简化 研究
ˆ 1 、 1
1回归分析2判别分析3定性资料分析4聚类分析统计分析方法应用流程现实经济问题提炼具体问题确定欲达目标根据定性理论设计指标变量搜集整理统计数据选择统计方法构造理论模型进行统计计算估计模型参数修改yes应用分类研究结构简化研究相关分析研究预测决策研究教材统计软件简介eview关于spssspssstatisticalpackagesocialscience即社会科学统计软件包是世界著名的统计分析软件
一元线性回归分析
1、一元线性回归模型 2、回归模型的参数估计 3、OLSE估计的性质 4、回归方程的显著性检验 5、回归方程的拟合优度 6、残差分析 7、回归系数的区间估计
一元线性回归分析模型
1、回归模型建模的实践背景 2、一元线性回归模型的数学形式: 1)、理论模型: y 0 1 x
ξ♐♣☯♧
现代统计方法
前言
统计学的几个问题
1、自1969年设立诺贝尔经济学奖以来,已有 42名学者获奖,而其中有2/3的人是统计学家、 计量经济学家、数学家。 2、目前的研究趋势是:从一般的逻辑推理发展 到重视实证研究;从理论论述发展到数量研 究。 3、硕士和博士的学位论文,如果没有数量模型 和分析,其文章的水平会有问题。
关于S-PLUS
另外Auckland大学的Robert Gentleman 和 Ross Ihaka 及其他志愿人员开发了一个R系 统,其语法形式与S语言基本相同,但实现 不同,两种语言的程序有一定的兼容性。R 是一个GPL自由软件,现在的版本是1.00版, 它比S-PLUS 还少许多功能,但已经具有了 很强的实用性
第三讲_多元线性回归模型检验及stata软件应用
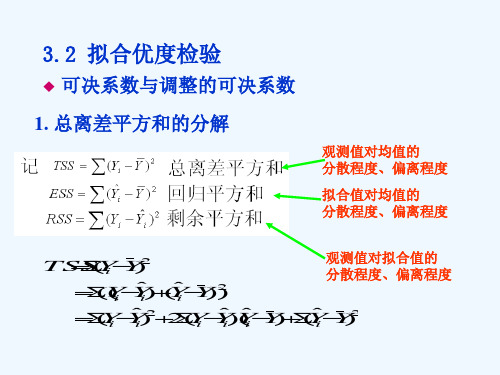
F检验的思想来自于总离差平方和的分解式: TSS=ESS+RSS
2 ˆ ESS y 由 于 回 归 平 方 和 解 释 变 量 X 的 联 合 体 对 被 解 i 是
释 变 量 Y 的 线 性 作 用 的 结 果 , 考 虑 比 值
2 ˆ ESS /RSS y i 2 e i
如果这个比值较大,则X的联合体对Y的解释程度 高,可认为总体存在线性关系,反之总体上可能不存 在线性关系。 因此,可通过该比值的大小对总体线性关系进行推 断。
**关于P值:以t统计量的观测值作为临界值,并计算该检 验的响应显著水平,这就是P值。
P值检验法(p-value test)
p 值的概念: 为了方便,将 t 统计量的值记为
பைடு நூலகம்t0
Se
j j
计算 称为p
p=P{|t|>t 0}
值(p-value )
通常的计量经济学软件都可自动计算出p 值
Excel格式数据的读取
直接拷贝,粘贴到stata中
使用Stat
transfer把其它格式的数据转成 stata格式的数据 读入ASCII格式数据文件:比较麻烦
常见数据格式
格式:dta 文本格式:txt Excel格式:xls 其它格式:sas、spss、gauss等
Stata
检验统计量2250nntn???????当用正态已知时当未知时也可用正态n用分布很小1t变量iiiibtbsb???其中1ixxsbs???12iiiixxbn????2t检验统计量给定显著性水平??可得到临界值t??2nk由样本求出统计量t的数值通过t??t??2nk或t??t??2nk来拒绝或不能拒绝原假设h0从而判定对应的解释变量是否应包括在模型中
统计模型资料

统计模型统计模型是统计学中的重要概念,用于描述和分析数据之间的关系,从而进行推断和预测。
统计模型可以帮助我们理解数据背后的规律和趋势,为决策提供依据。
在统计学中,有各种各样的统计模型,包括线性回归模型、逻辑斯蒂回归模型、时间序列模型等。
线性回归模型线性回归模型是最简单、最常用的统计模型之一。
在线性回归模型中,我们假设自变量和因变量之间存在线性关系,通过最小化残差平方和来估计模型参数。
线性回归模型可以用来预测连续型变量,例如房价、销售额等。
通过线性回归模型,我们可以探索变量之间的相关性,判断变量对因变量的影响程度。
逻辑斯蒂回归模型逻辑斯蒂回归模型是一种广义线性模型,常用于解决二分类问题。
逻辑斯蒂回归模型通过逻辑斯蒂函数将线性回归的输出映射到0和1之间,从而进行分类预测。
逻辑斯蒂回归模型在实际应用中被广泛使用,例如预测客户流失、判断疾病患病风险等。
时间序列模型时间序列模型是用于分析时间序列数据的统计模型。
时间序列数据是按时间顺序排列的数据序列,例如股票价格、气温变化等。
时间序列模型可以帮助我们理解时间序列数据的趋势、季节性和周期性变化,进而进行预测和决策。
常见的时间序列模型包括自回归模型、移动平均模型和ARIMA模型等。
总结统计模型在统计学和数据分析中扮演着重要角色,通过建立合适的统计模型,我们可以深入分析数据,发现数据背后的规律,为决策提供科学依据。
不同的统计模型适用于不同的问题和数据类型,正确选择和应用统计模型可以提升数据分析的效率和准确性。
希望通过本文对统计模型的简要介绍,读者能对统计模型有一个初步的了解,能够在实际应用中灵活运用各种统计模型进行数据分析和决策。
如何利用统计软件进行毕业论文中的回归分析

如何利用统计软件进行毕业论文中的回归分析回归分析是统计学中一种常用的数据分析方法,可以用于探索变量之间的关系、预测未来趋势以及解释现象产生的原因等。
在毕业论文中,回归分析可以帮助研究者验证或拓展研究假设,并提供有效的数据支持。
利用统计软件进行回归分析可以提高分析效率和准确性。
本文将介绍如何利用统计软件进行毕业论文中的回归分析。
一、统计软件的选择在进行回归分析之前,首先需要选择合适的统计软件。
目前市面上有很多优秀的统计软件可供选择,如SPSS、R、Stata等。
针对毕业论文中的回归分析,SPSS是一个常用且易学的统计软件,它提供了丰富的回归分析功能和图形展示工具,适合初学者使用。
本文以SPSS为例进行说明。
二、准备数据在进行回归分析之前,需要准备好研究所需的数据。
一般来说,数据应具备以下特点:1. 数据完整:确保数据没有缺失值,否则可能影响回归分析的准确性。
2. 数据清晰:数据应该具备直观的分类和变量标签,便于后续的数据分析和解读。
3. 数据整理:对于毕业论文中的回归分析,需要对数据进行整理和变量选择,删除不必要的变量,并确保自变量和因变量之间具备一定的相关性。
三、导入数据在SPSS软件中,打开新的数据文件,选择导入数据的方式。
可以是导入外部数据文件,如Excel文件、文本文件等,或者手动输入数据。
在导入数据时,注意设置好数据类型、变量标签和缺失值等。
四、设置回归模型完成数据导入后,可以开始进行回归分析。
在SPSS软件中,选择菜单栏的“回归”选项,然后选择“线性回归”。
在弹出的对话框中,将需要的变量依次加入到自变量和因变量的选项框中。
同时,还可以设置回归模型的类型,如逐步回归、层次回归等。
五、进行回归分析设置好回归模型后,点击运行按钮即可进行回归分析。
SPSS会自动计算回归方程的系数、显著性水平、拟合优度等统计指标,并生成报告和图表展示。
六、解释分析结果在完成回归分析后,需要对结果进行解释和分析。
统计建模与r软件 课后习题答案

统计建模与r软件课后习题答案统计建模与R软件课后习题答案在统计建模与R软件课程中,学生们经常需要完成一系列的习题来巩固所学知识。
这些习题涉及到统计建模的理论和实践,以及如何使用R软件来进行数据分析和建模。
在本文中,我们将给出一些常见的统计建模与R软件课后习题的答案,希望能够帮助学生更好地理解课程内容。
1. 线性回归模型习题:使用R软件对给定数据集进行线性回归分析,并给出回归方程和相关系数。
答案:在R软件中,可以使用lm()函数来进行线性回归分析。
例如,对于数据集data,可以使用以下代码进行线性回归分析:```model <- lm(y ~ x, data=data)summary(model)```其中,y和x分别表示因变量和自变量。
通过summary()函数可以得到回归方程和相关系数等信息。
2. 逻辑回归模型习题:使用R软件对给定数据集进行逻辑回归分析,并给出回归方程和模型拟合度。
答案:逻辑回归分析可以使用glm()函数来进行。
例如,对于数据集data,可以使用以下代码进行逻辑回归分析:```model <- glm(y ~ x, data=data, family=binomial)summary(model)```其中,y和x分别表示因变量和自变量,family=binomial表示使用二项分布进行逻辑回归分析。
通过summary()函数可以得到回归方程和模型拟合度等信息。
3. 方差分析习题:使用R软件对给定数据集进行方差分析,并给出各组之间的差异是否显著。
答案:在R软件中,可以使用aov()函数来进行方差分析。
例如,对于数据集data,可以使用以下代码进行方差分析:```model <- aov(y ~ group, data=data)summary(model)```其中,y和group分别表示因变量和自变量。
通过summary()函数可以得到各组之间的差异是否显著等信息。
毕业论文的数据统计与分析软件推荐

毕业论文的数据统计与分析软件推荐在进行毕业论文的数据统计与分析过程中,选择合适的软件工具具有重要意义。
本文将推荐几款常用的数据统计与分析软件,以供毕业论文写作时参考选择。
一、SPSS软件SPSS(Statistical Package for the Social Sciences)是一款专业的统计软件,被广泛应用于社会科学领域的数据分析。
它提供了强大的统计分析能力和友好的图形界面,能够对数据进行描述性统计、假设检验、回归分析等多种统计分析,并生成可视化的结果展示。
二、Excel软件Excel是微软公司开发的办公软件,也是一款常见的数据统计与分析工具。
它提供了丰富的数据处理函数和分析工具,如排序、筛选、条件格式、数据透视表等,可以进行数据预处理和简单的统计分析。
虽然相较于专业统计软件功能较为有限,但对于一些基础的数据处理和分析需求,Excel仍然是一种常用的选择。
三、R软件R语言及其开源的R软件环境是一种免费的统计分析软件。
由于其强大的数据分析、统计建模和绘图功能,R在学术界和数据科学领域被广泛应用。
与SPSS和Excel相比,R具备更高的灵活性和定制化能力,可以进行更复杂的统计分析和数据可视化。
四、Python软件及相关库Python是一种通用的编程语言,拥有丰富的科学计算库,如Numpy、Pandas和Matplotlib等。
借助这些库,Python可以进行数据处理、分析和可视化。
与R相比,Python具备更广泛的应用领域,不仅可以进行数据统计分析,还可以进行其他领域的编程任务。
五、其他统计软件除了上述几种常见的统计软件,还有许多其他专业领域的统计软件可供选择,如Stata、SAS、JMP等。
这些软件通常针对特定的研究领域,提供了特定领域的统计分析方法和模型。
综上所述,选择合适的数据统计与分析软件对于毕业论文的写作至关重要。
在选择时,可以根据个人的研究领域和分析需求考虑使用SPSS、Excel、R、Python或其他专业领域的统计软件。
回归分析中常用的统计软件介绍(七)

回归分析是统计学中一种重要的分析方法,它被广泛应用于经济学、社会学、生物学等领域。
在回归分析中,我们需要使用统计软件来进行数据处理和模型拟合。
本文将介绍几种常用的统计软件,它们分别是SPSS、Stata和R。
SPSS是一种由IBM公司开发的统计分析软件,它提供了丰富的数据处理和统计分析功能。
在进行回归分析时,我们可以使用SPSS来进行变量筛选、模型拟合和结果解释。
SPSS的界面友好,操作简单,适合初学者使用。
除了回归分析,SPSS还可以进行方差分析、相关分析、聚类分析等多种统计方法。
因此,对于需要进行多种统计分析的用户来说,SPSS是一个不错的选择。
除了SPSS,Stata也是一种常用的统计软件。
与SPSS相比,Stata更加强调数据的面板结构和纵向数据。
在进行回归分析时,Stata可以轻松处理面板数据和纵向数据的模型拟合。
此外,Stata还提供了强大的程序设计功能,用户可以自定义程序来完成复杂的统计分析。
因此,对于需要处理面板数据和进行高级统计分析的用户来说,Stata是一个非常合适的选择。
除了SPSS和Stata,R也是一种非常流行的统计软件。
与SPSS和Stata不同,R是一种开源软件,用户可以免费获取和使用。
在进行回归分析时,R可以使用多种包来进行模型拟合和结果解释。
R的优势在于它有着丰富的统计包和绘图包,用户可以根据自己的需求选择合适的包来完成统计分析和数据可视化。
此外,R还有着强大的编程能力,用户可以使用R语言来编写复杂的统计程序。
因此,对于需要进行定制化统计分析和数据可视化的用户来说,R是一个非常不错的选择。
总之,SPSS、Stata和R是回归分析中常用的统计软件。
它们各有优势,用户可以根据自己的需求和经验选择合适的软件来进行数据处理和模型拟合。
希望本文的介绍能够帮助读者更好地选择合适的统计软件进行回归分析。
回归分析中常用的统计软件介绍(六)

回归分析是一种常用的统计方法,用于研究变量之间的关系。
在进行回归分析时,研究者通常会使用统计软件来处理数据和进行相关的计算。
本文将介绍一些在回归分析中常用的统计软件,以及它们的特点和优势。
SPSS(Statistical Package for the Social Sciences)是一款功能强大的统计软件,广泛应用于社会科学和商业领域。
它具有直观的用户界面和丰富的统计分析功能,可以进行线性回归、多元回归、逻辑回归等多种回归分析。
此外,SPSS还提供了数据可视化和报告生成的功能,便于研究者对分析结果进行展示和解释。
因此,SPSS在回归分析中备受青睐。
除了SPSS,R语言也是一种常用的统计软件,尤其在学术界和数据科学领域广泛应用。
R语言具有强大的数据处理和统计分析能力,可以进行各种回归分析,同时还支持数据可视化和编程扩展。
由于R语言是开源软件,因此可以免费使用,并且有庞大的社区支持和丰富的扩展包,可以满足不同领域的回归分析需求。
另外,SAS(Statistical Analysis System)也是一款知名的统计软件,适用于大规模数据的处理和分析。
SAS具有稳定的性能和丰富的统计函数库,可以进行复杂的回归分析和模型建立。
它还支持数据挖掘和机器学习等高级分析,因此在金融、医疗等领域得到广泛应用。
然而,SAS的学习曲线较陡,使用起来需要一定的技术门槛。
此外,Python也是一种适用于回归分析的统计软件,尤其在数据科学和人工智能领域备受瞩目。
Python具有丰富的数据处理和统计分析库,如NumPy、SciPy、Pandas等,可以进行各种回归分析和模型建立。
而且,Python还支持机器学习和深度学习等先进的分析方法,因此在大数据分析和预测建模方面具有显著优势。
除了上述几种统计软件,还有其他一些较小众但在特定领域有较广泛应用的工具,如Stata(适用于经济学和社会科学)、JMP(适用于质量管理和实验设计)、Minitab(适用于工程和质量控制)等。
回归分析法计算公式

回归分析法计算公式回归分析是一个统计方法,用于建立变量之间的关系模型,并通过该模型预测一个或多个自变量对应的因变量的值。
回归分析方法通常基于最小二乘法,通过寻找使得预测值和实际值之间的误差平方和最小的参数估计。
以下是回归分析中常用的计算公式及其含义:1.简单线性回归模型:简单线性回归模型可以用来分析一个自变量和一个因变量之间的关系。
它的数学形式如下:Y=β₀+β₁X+ε其中,Y是因变量,X是自变量,β₀和β₁是回归系数,ε是误差项。
2.多元线性回归模型:多元线性回归模型可以用来分析多个自变量和一个因变量之间的关系。
它的数学形式如下:Y=β₀+β₁X₁+β₂X₂+...+βₚXₚ+ε其中,Y是因变量,X₁,X₂,...,Xₚ是自变量,β₀,β₁,β₂,...,βₚ是回归系数,ε是误差项。
3.最小二乘法:最小二乘法是一种常用的参数估计方法,用于确定回归系数的值。
它通过最小化残差平方和来估计回归系数,使得预测值和实际值之间的差异最小。
4.残差:残差是实际观测值与回归模型预测值之间的差异。
在最小二乘法中,残差被用来评估模型的拟合程度,残差越小表示模型与实际值越接近。
5.回归系数的估计:回归系数可以通过最小二乘法估计得到。
简单线性回归模型的回归系数β₀和β₁的估计公式如下:β₁=∑((Xi-Xₚ)(Yi-Ȳ))/∑((Xi-Xₚ)²)β₀=Ȳ-β₁Xₚ其中,Xi和Yi是样本数据的自变量和因变量观测值,Xₚ和Ȳ分别是自变量和因变量的样本均值。
6.R²决定系数:R²决定系数用来衡量回归模型对因变量变异程度的解释能力,它的取值范围在0到1之间。
R²的计算公式如下:R²=1-(SSR/SST)其中,SSR是回归平方和,表示模型对因变量的解释能力;SST是总平方和,表示总体变异程度。
以上是回归分析常用的一些计算公式,通过这些公式可以计算回归系数、残差、决定系数等指标,用于评估回归模型的拟合程度和预测能力。
如何使用Stata进行面板数据回归分析

如何使用Stata进行面板数据回归分析Stata是一种流行的统计软件,广泛用于经济学、社会学、医学和其他社会科学领域的数据分析和建模。
面板数据回归分析是一种常用的统计方法,用于研究在时间和横截面上变化的数据。
本文将介绍如何使用Stata进行面板数据回归分析。
一、数据准备在进行面板数据回归分析之前,首先需要准备好面板数据集。
面板数据集包括多个个体在不同时间点上的观测值。
通常,面板数据可分为两种类型:平衡面板数据和非平衡面板数据。
平衡面板数据指的是每个个体在每个时间点上都有观测值,而非平衡面板数据则允许个别个体在某些时间点上缺失观测值。
准备好数据后,可以使用Stata导入数据集。
可以使用命令“use 文件路径/文件名”来加载数据集。
确保数据集的格式正确,并且数据已按照面板数据的要求进行排序。
二、面板数据回归模型面板数据回归模型是通过建立个体和时间的固定效应模型来进行的。
常见的面板数据回归模型包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
1. 固定效应模型固定效应模型是一种控制个体固定特征的面板数据回归模型。
固定效应模型通过添加个体固定效应来控制个体固有特征,假设个体固定效应与解释变量无关。
可以使用命令“xtreg 因变量自变量1 自变量2, fe”来估计固定效应模型。
2. 随机效应模型随机效应模型是一种包含个体和时间随机效应的面板数据回归模型。
随机效应模型允许个体和时间效应与解释变量相关,并且具有更强的灵活性。
可以使用命令“xtreg 因变量自变量1 自变量2, re”来估计随机效应模型。
三、结果解释和分析在进行面板数据回归分析后,可以对结果进行解释和分析。
常见的结果输出包括回归系数、标准误、t值和p值等。
1. 回归系数回归系数表示自变量对因变量的影响程度。
回归系数的符号表示影响方向,正系数表示正向影响,负系数表示负向影响。
回归系数的绝对值大小表示影响程度的强弱。
stata logit回归系数or-概述说明以及解释

stata logit回归系数or-概述说明以及解释1.引言1.1 概述概述部分旨在引导读者了解本篇文章的主要内容和目标。
在本部分,我们将简要介绍logit回归和Stata软件,并强调logit回归系数的重要性和解释。
此外,我们还将讨论logit回归系数的局限性,并提出未来研究的建议。
logit回归是一种广泛应用于社会科学和统计分析领域的回归分析方法。
它适用于具有二元因变量(如成功/失败、发生/未发生)的场景,旨在探索自变量与二元因变量之间的关系。
通过logit回归,我们可以估计自变量对于因变量的影响程度,并从中获得有关变量之间关系的重要信息。
Stata软件是一款功能强大、广泛使用的统计分析软件。
它提供了一系列的经济、社会和卫生领域统计分析方法的工具,其中包括logit回归。
Stata软件的优势在于其简单易用的界面和强大的功能,使得进行logit回归分析变得更加简单和高效。
本文的重点是logit回归系数的解释。
回归系数是logit回归模型中的关键输出,它们表示了自变量对因变量的影响方向和强度。
在本文的后续部分,我们将详细讨论如何解释logit回归系数,包括怎样判断系数的显著性、如何解释正负系数、以及如何比较系数的大小。
然而,虽然logit回归系数具有重要的信息价值,但它们也存在一些局限性。
在本文中,我们将探讨这些局限性,如共线性问题、模型拟合度以及不平衡数据集等,以便读者在使用logit回归系数时能够更全面地评估结果的可靠性和有效性。
最后,本文还将提出一些建议,以引导未来对logit回归系数的进一步研究。
鉴于这个话题的重要性和广泛应用,我们认为有必要深入研究更复杂的回归模型和扩展应用。
这些研究有助于提高logit回归系数的解释能力,进一步拓宽其在实际应用中的适用范围。
通过本文的阅读,读者将能够获得关于logit回归系数的全面理解,并为进一步研究和应用提供有益的指导。
接下来,我们将详细介绍logit 回归的概念和方法。
序数回归模型

序数回归模型(Ordinal Regression Model) 是一种经典的统计模型,用于描述因变量y 为有序类别的情况。
在序数回归模型中,我们假设y 服从一个有序的分布,模型的目的是预测这个有序类别的值或随着自变量X 的增加而有序递增的趋势。
在实际应用中,序数回归模型可以用于各种类型的数据分析,如心理学、医学、教育等领域。
在统计学中,序数回归模型通常被视为Logistic 回归模型的扩展,适用于连续型自变量和有序因变量的情况。
经典的序数回归模型包括Proportional Odds Model (比例几率模型)和Proportional Hazards Model (比例风险模型)等。
其中,比例几率模型是最常见的一种,它假设自变量和因变量之间的关系可以表示为一个通用的Logistic 函数,然后使用最大似然法来估计模型参数。
通常情况下,序数回归模型可以使用各种统计软件和编程语言来实现,如R 语言、Python 和MATLAB 等。
在R 语言中,有许多相关的包可以用来实现序数回归模型,如polr 和ordinal 等。
如果需要在具体应用中使用序数回归模型,可以先了解相关的统计知识和背景,然后选择合适的方法和工具进行实现和分析。
应用回归分析笔记

回归分析是一种统计方法,用于探索自变量(预测变量)和因变量(响应变量)之间的关系。
以下是一份简单的应用回归分析的笔记示例:回归分析笔记1. 简介-回归分析是一种统计技术,用于研究变量之间的关系。
它可以帮助我们理解和预测变量之间的相互作用。
2. 线性回归-线性回归是回归分析中最简单和常用的形式,假设自变量和因变量之间存在线性关系。
-模型表达式:\[ Y = \beta_0 + \beta_1 X + \varepsilon \],其中\( Y \) 是因变量,\( X \) 是自变量,\( \beta_0 \) 和\( \beta_1 \) 是回归系数,\( \varepsilon \) 是误差。
3. 多元回归-多元回归扩展了线性回归模型,允许多个自变量对因变量进行解释。
-模型表达式:\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \varepsilon \]4. 回归分析步骤-数据收集:收集自变量和因变量的观测数据。
-模型拟合:使用统计软件拟合回归模型,估计回归系数。
-模型诊断:检验回归模型的拟合优度,识别异常值和离群点。
-结果解释:解释回归系数的意义和影响,评估模型的预测能力。
5. 应用举例-实例:分析销售额与广告投入之间的关系。
-结论:通过回归分析发现,广告投入与销售额呈正相关关系,每增加一单位的广告投入,销售额平均增加\( \beta_1 \) 单位。
6. 注意事项-回归分析应用需要注意变量选择、模型假设、数据质量等问题,避免产生误导性的结果。
这样的笔记可以帮助记录回归分析的基本概念、步骤、应用举例以及注意事项,对于学习和实际应用回归分析都会有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i 1
n
(4)
下面利用高等数学知识,简单介绍参数 , 的求法.
记
S (a, ) ( yi a xi ) 2
i 1
n
(5)
则
n S 2 ( yi xi ) 0 i 1 n S 2 ( yi xi ) xi 0 i 1
设 ( xi1 , xi 2 , 足:
, xim , yi ) (i 1, 2,
, n)
是 ( x1 , x2 ,
, xm , y )
的 n 个观测值 , 则满
yi 0 1xi1 2 xi 2
m xim i
(i 1,2,
, n)
(10)
其中各 i 相互独立,且 i ~ N (0, 2 ) .
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
166.88 164.07 164.27 164.57 163.89 166.35 165.54 166.75 167.69 162.21 163.54 162.7 164.06 164.66 164.7 164.67 164.69
2.回归分析方法
回归分析,直观地讲,就是对平面上一些散布的点,采 用一条最好的直线去表达.如图 1 是 12 组儿子身高 y 和父亲身 高 x 数据关系的散布点,采用直线拟合的示意图.
图1 平面上散布点的直线拟合示意图
上面的示例中自变量只有一个,属一元回归分析.如果自 变量有多个,则属多元回归分析.如 1 中赛题,自变量是 8 台 发电机组出力 x1 , x2 ,
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
120 120 120 120 120 120 120 120 120 120 120 120 120 120 120 120 120
73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73
118.67 118.75 118.85 119 118.64 119.1 119.09 119.15 119.19 116.03 117.56 116.74 118.24 120.21 120.68 119.68 121.34
134.67 133.75 134.27 134.88 133.28 136.33 135.81 136.55 137.11 135.5 135.44 135.4 135.4 135.28 135.16 135.29 135.12
Y X
(13)
假定矩阵 X 的秩等于 m 1.即列满秩.
则 解得
ˆ X T Y ( X T X ) ˆ ( X T X )1 X T Y
90 90 90 90 90 90 90 90 90 90 90 90 90 104.84 111.22 98.092 120.44
表8.2 各线路的潮流值(各方案与表1相对应,单位:MW) 方案\线路 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 164.78 165.81 165.51 167.93 166.79 164.94 164.8 165.59 165.21 167.43 165.71 166.45 165.23 164.23 163.04 165.54 2 140.87 140.13 140.25 138.71 139.45 141.5 141.13 143.03 142.28 140.82 140.82 140.82 140.85 140.73 140.34 141.1 3 -144.25 -145.14 -144.92 -146.91 -145.92 -143.84 -144.07 -143.16 -143.49 -152.26 -147.08 -149.33 -145.82 -144.18 -144.03 -144.32 4 119.09 118.63 118.7 117.72 118.13 118.43 118.82 117.24 117.96 129.58 122.85 125.75 121.16 119.12 119.31 118.84 5 135.44 135.37 135.33 135.41 135.41 136.72 136.02 139.66 137.98 132.04 134.21 133.28 134.75 135.57 135.97 135.06 6 157.69 160.76 159.98 166.81 163.64 157.22 157.5 156.59 156.96 153.6 156.23 155.09 156.77 157.2 156.31 158.26
159.28 158.83 158.37 158.01 159.12 157.59 157.67 157.59 157.65 154.26 155.93 154.88 156.68 157.65 157.63 157.61 157.64
看到这个问题,我们容易想到该问题就是要找出各线 路上有功潮流与 8 台发电机组出力的函数关系.是数学上一 个函数拟合问题.如果进一步数学化就是:
(7)
另外一个问题就是对 2 的无偏估计问题.可以证明, 2 的无偏 估计为:
ˆ
2
n i 1
ˆx ˆ yi i n2
2
(8)
2.2 多元线性回归模型
模型:
y 0 1 x1 m xm
(9)
~ N (0, 2 ), 0 , 1 , , m , 2 是未知参数.
, x8 ,作回归分析就属多元回归分析.下面
分别概要介绍一元回归分析和多元回归分析的原理和方法.
2.1 一元线性回归
模型:
y x
(2)
其中 ~ N (0, 2 )
对一组观测值 ( xi , yi )(i 1, 2,
yi xi i
, n) ,满足:
180 180 180 180 180 180 180 180 180 180 180 180 180 180 180 180 180
97.824 80 80 80 80 80 80 80 80 80 80 80 80 80 80 80 80
125 150.71 141.58 132.37 156.93 125 125 125 125 125 125 125 125 125 125 125 125
(3)
(i 1, 2, , n)
其中各 i 相互独立且 i ~ N (0, 2 )
找一条最好的直线通过 n 个已知的观测点,实际上就是寻找 满足如下目标的直线参数 , .
目标函数:
ˆx ) ˆ (y a
i 1 i i n 2
min ( yi a xi ) 2
令
(0 , 1, , m )T , (1, 2 , , n )T
Y ( y1 , y2 , , yn )T
(11)
1 1 X 1
x11 x21 xn1
x12 x22 xn 2
x1m x2 m xnm
(12)
则方程组用矩阵表达为
对函数拟合,我们可以采用线性,也可以采用非线性 的函数.非线性有多项式,三角函数,指数函数等,面对如本 问题所示的具体数据,我们当然准备好把这些函数都拿去 尝试的打算.不过那是万不得已,没招的情况下才采用的最后 招数.我们做实际问题,首先想到的还是采用最简单的方法 下手,如果简单的方法都可以完成得很好,当然没必要采 用复杂的方法.况且对该赛题,后面还有四个更难的问题在 等着我们.我们不能把第一个问题都做那么复杂吧?因此, 先采用最简单的方法去尝试,是我们最可能想到的事.最简 单的方法是什么?自然是采用线性的函数去表达.也就是采 用线性回归分析来做! 对本问题,我们采用多元线性回归分析,的确做得很 好.而线性回归分析,在我们多次参赛的经验来看,在许多 的国内国际数学建模型竞赛中,都有可能用到.因此,下面 简单介绍线性回归分析的基本原理,对回归好坏的评价指 标,利用统计软件的实现。
设 6 条线路上有功潮流为 y j ( j 1, 2, 力为 xi (i 1, 2,
,6) , 8
台发电机组出
,8) ,该问题变为寻找函数关系表达式:
y j f j ( x1 , x2 ,
, x8 )
( j 1, 2,
,6)
(1)
想到这里,就算对这个问题 1 的理解入了门,迈进了该 问题的门槛.剩下的问题就是寻找具体的函数表达式.
有:
ˆ ny ˆ nx n n n 2 ˆ ˆ xi xi yi nx i 1 i 1
(6)
1 n 1 n 这里, x xi , y yi n i 1 n i 1
则
ˆx ˆ y n n xi yi nxy ( xi x )( yi y ) ˆ i 1 i 1 n n xi2 nx 2 ( xi x )2 i 1 i 1
125 125 125 125 125 138.88 131.21 141.71 149.29 125 125 125 125 125 125 125 125
81.1 81.1 81.1 81.1 81.1 81.1 81.1 81.1 81.1 60.582 70.962 64.854 75.529 81.1 81.1 81.1 81.1
回归模型与统计软件
1.引言 2004年全国数模竞赛的B题“电力市场的输电阻塞管理” 的第1个问题是这样的: 某电网有8台发电机组,6条主要线路,表1和表2中的方 案0给出了各机组的当前出力和各线路上对应的有功潮流值, 方案1~32给出了围绕方案0的一些实验数据,试用这些数据 确定各线路上有功潮流关于各发电机组出力的近似表达式.
