双星和多星问题 2019年高考物理一轮复习 Word版含解析
高考物理计算题复习《双星问题》(解析版)

《双星问题》一、计算题1.神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律。
天文学家观测河外星系人麦析伦云时,发现了双星系统,它由可见星A和不可见的暗星B构成,两星视为质点,不考虑其它星体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。
引力常量为G,由观测能够得到可见星A的速率v和运行周期T。
可见星A所受暗星B的引力FA可等效为位于O点处质量为的星体可视为质点对它的引力,设A和B的质量分别为,,试求用、表示求暗星B的的质量与可见星A的速率v、运行周期T和质量之间的关系式。
要求等号左边只含有和,,等号右边为其它量2.众多的恒星组成不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,如下图所示,两星各以一定速率绕其连线上某一点匀速转动,这样才不至于因万有引力作用而吸引在一起,已知双星质量分别为、,它们间的距离始终为L,引力常数为G,求:双星旋转的中心O到的距离;双星的转动周期。
3.天文观测中发现宇宙中存在着“双星”,所谓双星,是两颗质量相近,分别为和的恒星,它们的距离为r,而r远远小于它们跟其它天体之间的距离,这样的双星将绕着它们的连线上的某点O作匀速圆周运动.求:这两颗星到O点的距离、各是多大双星的周期.4.现代观测表明,由于引力的作用,恒星有“聚焦”的特点,众多的恒星组成不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星.它们以两者连线上的某点为圆心做匀速圆周运动,这样就不至于由于万有引力的作用而吸引在一起.如图所示,设某双星系统中的两星、的质量分别为m和2m,两星间距为L,在相互间万有引力的作用下,绕它们连线上的某点O转动.已知引力常量G,求:、两星之间的万有引力大小;星到O点的距离;它们运动的周期.5.黑洞是宇宙空间内存在的一种天体。
黑洞的引力很大,使得视界内的逃逸速度大于光速。
黑洞无法直接观测,但可以借由间接方式得知其存在与质量,并且观测到它对其他事物的影响,双星系统中两个星球A、B的质量都是m,A、B相距L,它们正围绕两者连线上某一点做匀速圆周运动。
天体运动的双星和多星问题解析

天体运动的双星和多星问题解析,要求有标题
运动的双星与多星:追随宇宙深处的秘密
任何太阳系里的天体,不管它的外形大小和其他有关特征,总是以我们地球太阳系坐标系为参照,在其中特有的轨道运行的。
这个运动的规律被称为“天体运动规律”。
根据这个规律,一般而言,当天空中有两个特殊的天体出现时,其运行就围绕着某一焦点而进行,这个运动称为双星运动;若有多个天体出现,则它们之间也会相互产生影响,发生“大陆碰撞”,因而形成多星运动。
双星运动首先可分为向心运动和远心运动两种。
当两个天体存在时,它们会围绕着一个活动焦点(例如太阳)进行双星运动,而运动的方向则可分两种。
第一种是双星围绕活动焦点的向心运动,即运动轨迹以活动焦点为中心在一定范围内呈圆形;第二种是双星围绕活动焦点的远心运动,即运动轨迹以活动焦点为中心,运动方向沿正多边形状移动,而不是圆形。
而多星运动则比双星运动更加复杂,从抽象意义上来说,它是宇宙中某一空间属性量度下所有天体运动的组合,在它们间有着良好的关系,它也随着周期性的重现。
只有当人们发现宇宙的深处,构建起既能说明双星和多星间的运动关系、又能预测它们运动情况的科学框架后,人们才能真正洞察到双星与多星的深远奥秘。
因此,我们每个人都应该把握住双星和多星的机会,去研究、去追寻宇宙中深处的秘密,以发掘出更多的天体运动规律。
高考物理专题32双星或多星模型练习含解析

专题32 双星或多星模型1.“双星模型”如图,各自所需的向心力由彼此间的万有引力提供,即Gm 1m 2L 2=m 1ω12r 1,Gm 1m 2L 2=m 2ω22r 2,其中r 1+r 2=L .2.“双星问题”的隐含条件是两者受到的向心力相等,周期相等,角速度相同;双星轨道半径与质量成反比.3.多星问题中,每颗星做圆周运动所需的向心力由它们之间的万有引力的合力提供,即F 合=m v 2r,以此列向心力方程进行求解.1.(多选)如图1所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O 点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L ,质量之比为m 1∶m 2=3∶2,下列说法中正确的是( )图1A .m 1、m 2做圆周运动的线速度之比为2∶3B .m 1、m 2做圆周运动的角速度之比为3∶2C .m 1做圆周运动的半径为25LD .m 2做圆周运动的半径为25L答案 AC解析 设双星m 1、m 2距转动中心O 的距离分别为r 1、r 2,双星绕O 点转动的角速度均为ω,据万有引力定律和牛顿第二定律得Gm 1m 2L2=m 1r 1ω2=m 2r 2ω2,又r 1+r 2=L ,m 1∶m 2=3∶2 所以可解得r 1=25L ,r 2=35Lm 1、m 2运动的线速度分别为v 1=r 1ω,v 2=r 2ω,故v 1∶v 2=r 1∶r 2=2∶3.综上所述,选项A 、C 正确.2.(2020·吉林长春市二模)2019年诺贝尔物理学奖授予了三位天文学家,以表彰他们对人类对宇宙演化方面的了解所做的贡献.其中两位学者的贡献是首次发现地外行星,其主要原理是恒星和其行星在引力作用下构成一个“双星系统”,恒星在周期性运动时,可通过观察其光谱的周期性变化知道其运动周期,从而证实其附近存在行星.若观测到的某恒星运动周期为T ,并测得该恒星与行星的距离为L ,已知引力常量为G ,则由这些物理量可以求得( ) A .行星的质量 B .恒星的质量C .恒星与行星的质量之和D .恒星与行星圆周运动的半径之比 答案 C解析 恒星与行星组成双星,设恒星的质量为M ,行星的质量为m .以恒星为研究对象,行星对它的引力提供了向心力,假设恒星的轨道半径为r 1,由GMm L 2=M (2πT)2r 1得到行星的质量m =4π2L 2r 1GT2,以行星为研究对象,恒星对它的引力提供了向心力,假设行星的轨道半径为r 2,则有GMm L 2=m (2πT )2r 2,得到恒星的质量M =4π2L 2r 2GT 2,则有M +m =4π2L 3GT 2,故A 、B 、D 错误,C正确.3.(多选)(2020·湖北随州市3月调研)2019年12月20日,国防科技大学领衔研制的我国天基网络低轨试验双星在太原卫星发射中心搭载CZ -4B 火箭成功发射,双星顺利进入预定轨道.假设两个质量分别为m 1和m 2(m 1>m 2)的星体A 和B 组成一双星系统,二者中心之间的距离为L ,运动的周期为T ,万有引力常量为G ,下列说法正确的是( )A .因为m 1>m 2,所以星体A 对星体B 的万有引力大于星体B 对星体A 的万有引力 B .星体A 做圆周运动的半径为m 2m 1+m 2LC .星体B 的线速度大小为2πm 2Lm 1+m 2TD .两星体的质量之和为4π2L3GT2答案 BD解析 两者之间的万有引力提供彼此的向心力,此为相互作用力,大小相等,方向相反,故A 错误;对A 、B 两星体,根据牛顿第二定律有Gm 1m 2L 2=m 1r 1(2πT )2和G m 1m 2L 2=m 2r 2(2πT)2,又因为r 1+r 2=L ,联立解得星体A 和星体B 的运动半径分别为r 1=m 2m 1+m 2L ,r 2=m 1m 1+m 2L ,故B 正确;星体B 的线速度大小为v =2πr 2T=2πm 1L m 1+m 2T ,故C 错误;将G m 1m 2L 2=m 1r 1(2πT )2和G m 1m 2L2=m 2r 2(2πT )2简化后相加,结合r 1+r 2=L ,可得m 1+m 2=4π2L3GT2,D 正确.4.(2020·河北保定市调研)把地球和月球看作绕同一圆心做匀速圆周运动的双星系统,质量分别为M 、m ,相距为L ,周期为T ,若有间距也为L 的双星P 、Q ,P 、Q 的质量分别为2M 、2m ,则( )A .地、月运动的轨道半径之比为M mB .地、月运动的加速度之比为M mC .P 运动的速率与地球的相等D .P 、Q 运动的周期均为22T 答案 D解析 对地、月有G Mm L2=M (2πT)2r 地=m (2πT)2r 月,故轨道半径与质量成反比,即r 地r 月=mM,A 错误;加速度a =(2πT)2r ,正比于轨道半径,反比于质量,B 错误;设P 、Q 的周期为T ′,则有G 2M ×2m L 2=2M (2πT ′)2r P=2m (2πT ′)2r Q ,轨道半径与质量成反比且地、月间距跟P 、Q 间距均等于L ,故地球与P 的轨道半径r 相等,于是2T ′2=T 2,解得T ′=22T ,D 正确;由速率v =2πT r 得v P v 地=TT ′=2,C 错误. 5.由三个星体构成的系统,叫作三星系统.有这样一种简单的三星系统,质量刚好都相同的三个星体甲、乙、丙在三者相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同周期的圆周运动.若三个星体的质量均为m ,三角形的边长为a ,万有引力常量为G ,则下列说法正确的是( )A .三个星体做圆周运动的半径均为aB .三个星体做圆周运动的周期均为2πa a3GmC .三个星体做圆周运动的线速度大小均为3GmaD .三个星体做圆周运动的向心加速度大小均为3Gma2 答案 B解析 质量相等的三星系统的位置关系构成一等边三角形,其中心O 即为它们的共同圆心,由几何关系可知三个星体做圆周运动的半径r =33a ,故选项A 错误;每个星体受到的另外两星体的万有引力的合力提供向心力,其大小F =3·Gm 2a 2,则3Gm 2a 2=m 4π2T2r ,得T =2πaa 3Gm ,故选项B 正确;由线速度公式v =2πrT 得v = Gma,故选项C 错误;向心加速度a =F m=3Gma2,故选项D 错误.6.(多选)宇宙中存在一些离其他恒星较远的四颗星组成的四星系统.若某个四星系统中每个星体的质量均为m ,半径均为R ,忽略其他星体对它们的引力作用,忽略星体自转,则可能存在如下运动形式:四颗星分别位于边长为L 的正方形的四个顶点上(L 远大于R ),在相互之间的万有引力作用下,绕某一共同的圆心做角速度相同的圆周运动.已知引力常量为G ,则关于此四星系统,下列说法正确的是( ) A .四颗星做圆周运动的轨道半径均为L2B .四颗星表面的重力加速度均为G m R2C .四颗星做圆周运动的向心力大小为Gm 2L2(22+1)D .四颗星做圆周运动的角速度均为 4+2Gm2L3答案 BD解析 任一颗星体在其他三颗星体的万有引力的作用下,合力方向指向对角线的交点,围绕正方形对角线的交点做匀速圆周运动,轨道半径均为r =22L ,故A 错误;星体表面的物体受到的万有引力等于它受到的重力,即Gmm ′R 2=m ′g ,解得g =GmR 2,故B 正确;由万有引力定律可得四颗星做圆周运动的向心力大小为F n =Gm 22L2+2G m 2L 2cos 45°=Gm 2L 2(12+2),选项C 错误;由牛顿第二定律得F n =Gm 2L 2(12+2)=mω2(22L ),解得ω=4+2Gm2L3,故D正确.。
(完整版)双星三星四星问题

双星模型、三星模型、四星模型一、双星问题1.模型构建:在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。
2.模型条件: (1)两颗星彼此相距较近。
(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。
(3)两颗星绕同一圆心做圆周运动。
3.模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。
(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。
(3)三个反比关系:m1r1=m2r2;m1v1=m2v2;m1a1=m2a2推导:根据两球的向心力大小相等可得,m1ω2r1=m2ω2r2,即m1r1=m2r2;等式m1r1=m2r2两边同乘以角速度ω,得m1r1ω=m2r2ω,即m1v1=m2v2;由m1ω2r1=m2ω2r2直接可得,m1a1=m2a2。
(4)巧妙求质量和:Gm1m2L2=m1ω2r1①Gm1m2L2=m2ω2r2②由①+②得:G m1+m2L2=ω2L ∴m1+m2=ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。
②双星做匀速圆周运动向心力由它们之间的万有引力提供,即它们受到的向心力大小总是相等。
(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点,所以双星做匀速圆周运动的半径与双星间的距离是不相等的,它们的轨道半径之和才等于它们间的距离。
②由m1ω2r1=m2ω2r2知由于m1与m2一般不相等,故r1与r2一般也不相等。
二、多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示).三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律:内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。
高考物理一轮复习学案:双星及多星、天体追及问题

双星及多星、天体追及问题1.双星问题知识点(1)运动模型:远离其他天体的两星在相互间的万有引力作用下绕两星连线上某点O各自做匀速圆周运动。
(2)几个结论:①两星彼此间的万有引力提供向心力,即=m 1r1,=m 2r2。
1②两星绕行方向、周期及角速度都相同,即T1=T2,ω1=ω2。
③两星的轨道半径与它们之间的距离关系为r1+r2=L。
④两星做圆周运动的半径r1、r2与星体质量成反比,即。
⑤两星的运动周期为T=2π。
⑥两星的总质量为m=m1+m2=。
22.多星问题类型三星模型四星模型3结构图2.多星问题类型三星模型四星模型结构图结论:1、每颗星做圆周运动的向心力均由系统内其余星对它万有引力的合力提供42、每颗星做圆周运动转动的方向、周期、角速度、线速度的大小均相同活动一、宇宙双星及多星模型1.宇宙双星模型2017年,人类第一次直接探测到来自双中子星合并的引力波。
根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈。
将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星(BC)A.质量之积B.质量之和C.速率之和D.各自的自转角速度2. 宇宙三星模型三颗质量均为M的星球(可视为质点)位于边长为L的等边三角形的三个顶点上。
如图所示,如果它们中的每一颗都在相互的引力作用下沿等边三角形的外接圆轨道运行,引力常量为G,下列说法正确的是(BD)A.其中一颗星球受到另外两颗星球的万有引力的合力大小为3GM 2 2L2B.其中一颗星球受到另外两颗星球的万有引力的合力指向圆心OC.它们运行的轨道半径为3 2LD.它们运行的速度大小为GML56【习练】宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用。
设四星系统中每个星体的质量均为m ,半径均为R ,四颗星稳定分布在边长为a 的正方形的四个顶点上。
(新课标)高考物理大一轮复习思想方法4“双星”、“多星”问题的处理方法

(2)如右图所示,三颗质量相等的行星位于一正三角形的顶点处,都 绕三角形的中心做圆周运动.每颗行星运行所需向心力都由其余两颗行 星对其万有引力的合力来提供.
Gm2 ×2×cos 30° =ma向,其中L=2rcos 30° . L2 三颗行星转动的方向相同,周期、角速度、线速度的大小相等.
[典例]
Gm m′g,解得g= 2 ,故C正确;由万有引力定律和向心力公式得 R Gm2 2Gm2 4π2 2a =m 2 ,T=2πa 2 2+ a T 2 2a 2a ,故D正确. 4+ 2Gm
2.宇宙三星或多星 (1)如右图所示,三颗质量相等的行星,一颗行星位于中心位 置不动,另外两颗行星围绕它做圆周运动.这三颗行星始终位于 同一直线上,中心行星受力平衡.运转的行星由其余两颗行星的 Gm2 Gm2 引力提供向心力: 2 + =ma向 r 2r2
两行星转动的方向相同,周期、角速度、线速度的大小相等.
2π m T 2RC,可得T=π
a3 Gm.
答案 (4)π
m2 (1)2 3G 2 a a3 Gm
m2 (2) 7G 2 a
7 (3) a 4
[突破训练] 1.2015年4月,科学家通过欧航局天文望远镜在一个河外星 系中,发现了一对相互环绕旋转的超大质量双黑洞系统,如图所 示.这也是天文学家首次在正常星系中发现超大质量双黑洞.这 对验证宇宙学与星系演化模型、广义相对论在极端条件下的适应 性等都具有十分重要的意义.我国今年底也将发射全球功能最强 的暗物质探测卫星.若图中双黑洞的质量分别为M1和M2,它们 以两者连线上的某一点为圆心做匀速圆周运动.根据所学知识, 下列选项正确的是( )
mAmB (2)同上,B星体所受A、C星体引力大小分别为FAB=G r2 2m 2 =G 2 , a m Cm B m2 FCB=G 2 =G 2 ,方向如图所示. r a m2 由FBx=FABcos 60° +FCB=2G 2 ,FBy=FABsin 60° = a
高考物理(热点题型全突破)专题5.5 双星与多星问题(含解析)-人教版高三全册物理试题

专题5.5 双星与多星问题双星模型 1.模型构建在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做周期一样的匀速圆周运动的行星称为双星。
2. 模型条件①两颗星彼此相距较近。
②两颗星靠相互之间的万有引力做匀速圆周运动。
③两颗星绕同一圆心做圆周运动。
3. 模型特点如下列图为质量分别是m 1和m 2的两颗相距较近的恒星。
它们间的距离为L .此双星问题的特点是:(1)两星的运行轨道为同心圆,圆心是它们之间连线上的某一点。
(2)两星的向心力大小相等,由它们间的万有引力提供。
(3)两星的运动周期、角速度一样。
(4)两星的运动半径之和等于它们间的距离,即r 1+r 2=L . 4. 双星问题的处理方法双星间的万有引力提供了它们做圆周运动的向心力,即Gm 1m 2L2=m 1ω2r 1=m 2ω2r 2。
5. 双星问题的两个结论(1)运动半径:m 1r 1=m 2r 2,即某恒星的运动半径与其质量成反比。
(2)质量之和:由于ω=2πT ,r 1+r 2=L ,所以两恒星的质量之和m 1+m 2=4π2L3GT2。
【示例1】2016年2月11日,美国科学家宣布探测到引力波,证实了爱因斯坦100年前的预测,弥补了爱因斯坦广义相对论中最后一块缺失的“拼图〞.双星的运动是产生引力波的来源之一,假设宇宙中有一双星系统由a 、b 两颗星体组成,这两颗星绕它们连线的某一点在万有引力作用下做匀速圆周运动,测得a 星的周期为T ,a 、b 两颗星的距离为l ,a 、b 两颗星的轨道半径之差为Δr (a 星的轨道半径大于b 星的轨道半径),如此() A.b 星的周期为l -Δrl +ΔrT B.a 星的线速度大小为π(l +Δr )TC.a 、b 两颗星的半径之比为ll -ΔrD.a 、b 两颗星的质量之比为l +Δrl -Δr【答案】 B规律总结解答双星问题应注意“两等〞“两不等〞 (1)双星问题的“两等〞: ①它们的角速度相等。
高中物理 双星、多星系统问题

双星、多星系统问题宇宙中不存在孤立的天体,常见的情况是两个或多个天体组成一个相对独立的系统。
高中物理中常常处理一些相对简单的天体系统,其中最简单的是双星系统,相对复杂的有三星、四星系统等。
一、稳定双星系统1、基本模型如图2-14-1所示,质量分别为m 1、m 2的两个天体在万有引力的相互作用下,绕着二者连线上的某个点(公共圆心O )以相同的角速度做圆周运动,构成一个稳定的双星系统。
在这个系统中,两天体的运动存在如下三个基本关系:(1)向心力大小相同:2212n 1n L m m GF F ==;(2)速度大小相同:ωωω==21;(3)轨道半径之和等于两天体的间距:L r r =+21。
2、基本结论(1)轨道半径关系:2211r m r m =由牛顿第二定律,有天体1:121221r m L m Gm ω=,天体2:222221r m Lm Gm ω=;两式联立,有2211r m r m =,即两天体的轨道半径与各自的质量成反比,质量大的天体轨道半径小,质量小的天体轨道半径大;联立L r r =+21,可得L m m m r 2121+=,L m m m r 2112+=。
(2)系统的周期:)(π2213m m G L T +=把L m m m r 2121+=代入121221r m L m m G ω=,可得321)(Lm m G +=ω,则双星系统的周期为)(π2π2213m m G L T +==ω;即两天体间距越小,总质量越大,系统的周期越小,角速度越大。
(3)线速度关系:2211v m v m =,且Lm m G L v v )(2121+==+ω在2211r m r m =式两边乘以共同的角速度ω,得2211r m r m ωω=,也就是2211v m v m =,即两天体的线速度大小与各自的质量成反比,质量大的天体线速度小,质量小的天体线速度大。
联立321)(Lm m G +=ω,2211r v r v ωω==,,L r r =+21,可得两天体的线速度大小之和为:L m m G L v v v )(2121+==+=ω。
高中物理必修二--6.5.2补充双星与多星问题讲解学习

二、双星问题 1、定义:两个质量相当、相对孤立的天体在相互引力 的作用下绕两天体连线上的某点做圆周运动。 2、特点:如图所示
设两天体的质量分别为M1、M2;两天体中心间的距离 为L。试分析两天体做圆周运动的角速度的关系,并求 两天体做圆周运动的周期和半径。 ⑴绕两天体的质心运动,两天体的角速度、周期相同; ⑵半径与质量成反比;
⑵所有天体做圆周运动的角速度、周期都相同。
⑶每个天体受到其它天体引力的矢量和为该天体做圆 周运动的向心力。
3、三星模型 ⑴构成一条直线 ①三个天体质量都相同,一定构成图甲的图形。
②两个天体的质量相同,一个不同,一定构成图乙的 图形。
请大家进行受力分析,列出圆周运动的基本方程。
图甲:Gm 2 r2
Gm 2 4r 2
(1)m/
(m1
m23 m2 )2
(2)
Gm23 (m1 m2 )2
v3T
2
解析:(1)由
得:
r1 r2
m2 m1
Gm1m2 (r1 r2 )2
m1r1 2
m2r2 2
又由:(Gr1m1rm2 )22
Gm1m r12
/
得:
m/
m23 (m1 m2 )2
(2)由
v
2r1 得:
T
r1
vT
2
由 r1 m2
1 T 4 R3 ;2 d 3 12 R
5Gm
5
例题6:由三颗星体构成的系统,忽略其他星体对它们 的作用,存在着一种运动形式:三颗星体在相互之间
的万有引力作用下,分别位于等边三角形的三个顶点 上,绕某一共同的圆心O在三角形所在的平面内做相同 角速度的圆周运动(图示为A、B、C三颗星体质量不相 同时的一般情况).若A星体质量为2m,B、C两星体的 质量均为m,三角形的边长为a,求: (1)A星体所受合力大小FA; (2)B星体所受合力大小FB; (3)C星体的轨道半径RC; (4)三星体做圆周运动的周期T.
高考专题10 双星及多星问题-高考物理一轮复习专题详解 Word版含解析

高考重点难点热点快速突破1.双星模型(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.(2)特点:①各自所需的向心力由彼此间的万有引力相互提供,即Gm 1m 2L 2=m 1ω 21r 1,Gm 1m 2L2=m 2ω 22r 2 ②两颗星的周期及角速度都相同,即T 1=T 2,ω1=ω2③两颗星的半径与它们之间的距离关系为:r 1+r 2=L (3)两颗星到圆心的距离r 1、r 2与星体质量成反比,即m 1m 2=r 2r 1. 2.多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R 的圆形轨道上运行(如图3甲所示).②三颗质量均为m 的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O ,外围三颗星绕O 做匀速圆周运动(如图丁所示).典例分析【例1】 (多选)(2017年昆明模拟)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T ,两星到某一共同圆心的距离分别为R 1和R 2,那么,系统中两颗恒星的质量关系是( )A .这两颗恒星的质量必定相等B .这两颗恒星的质量之和为4π2R 1+R 23GT 2C .这两颗恒星的质量之比为m 1∶m 2=R 2∶R 1D .其中必有一颗恒星的质量为4π2R 1+R 23GT 2【答案】 BC【例2】:2016年2月11日,美国科学家宣布探测到引力波的存在,引力波的发现将为人类探索宇宙提供新视角,这是一个划时代的发现.在如图所示的双星系统中,A、B两个恒星靠着相互之间的引力正在做匀速圆周运动,已知恒星A的质量为太阳质量的29倍,恒星B的质量为太阳质量的36倍,两星之间的距离L=2×105 m,太阳质量M=2×1030 kg,引力常量G=6.67×10-11N·m2/kg2,π2=10.若两星在环绕过程中会辐射出引力波,该引力波的频率与两星做圆周运动的频率具有相同的数量级,则根据题目所给信息估算该引力波频率的数量级是( )A.102 Hz B.104 Hz C.106 Hz D.108 Hz【答案】 A【例3】:.经过用天文望远镜长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识,双星系统由两个星体组成,其中每个星体的线度都远小于两星体之间的距离,一般双星系统距离其他星体很远,可以当成孤立系统来处理.现根据对某一双星系统的测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.(1)计算出该双星系统的运动周期T;(2)若该实验中观测到的运动周期为T 观测,且T 观测∶T =1∶N (N >1).为了理解T 观测与T 的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质.若不考虑其他暗物质的影响,根据这一模型和上述观测结果确定该星系间这种暗物质的密度.【答案】 (1)πL2L GM (2)3N -1M2πL3 【解析】 (1)双星均绕它们连线的中点做圆周运动,万有引力提供向心力,则G M 2L 2=M ⎝⎛⎭⎪⎫2πT 2·L 2,解得T =πL2L GM.【例4】:由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式,三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同角速度的圆周运动(图为A 、B 、C 三颗星体质量不相同时的一般情况).若A 星体质量为2m 、B 、C 两星体的质量均为m ,三角形的边长为a ,求:(1)A 星体所受合力大小F A ; (2)B 星体所受合力大小F B ; (3)C 星体的轨道半径R C ; (4)三星体做圆周运动的周期T .【答案 】 (1)23G m 2a 2 (2)7G m 2a 2 (3)74a (4)πa 3Gm【解析】(1)由万有引力定律,A 星体所受B 、C 星体引力大小为F BA =G m A m B r 2=G 2m 2a2=F CA方向如图所示则合力大小为F A =F BA ·cos 30°+F CA ·cos 30°=23G m 2a2(3)由于m A =2m ,m B =m C =m通过分析可知,圆心O 在BC 的中垂线AD 的中点 则R C =⎝ ⎛⎭⎪⎫34a 2+⎝ ⎛⎭⎪⎫12a 2=74a (4)三星体运动周期相同,对C 星体,由F C =F B =7G m 2a 2=m (2πT)2R C ,可得T =πa 3Gm. 专题练习1:宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m 的星位于等边三角形的三个顶点,三角形边长为R ,忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O 做匀速圆周运动,万有引力常量为G ,则( )A .每颗星做圆周运动的线速度为 Gm RB .每颗星做圆周运动的角速度为 3GmR 3C .每颗星做圆周运动的周期为2πR 33GmD .每颗星做圆周运动的加速度与三星的质量无关 【答案】 ABC【解析】由图可知,每颗星做匀速圆周运动的半径r =R2cos 30°=33R .由牛顿第二定律得Gm 2R 2·2cos 30°=m v 2r =mω2r =m 4π2T2r =ma ,可解得v =GmR,ω= 3GmR 3,T =2πR 33Gm ,a =3GmR2,故A 、B 、C 均正确,D 错误. 2.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m ,半径均为R ,四颗星稳定分布在边长为a 的正方形的四个顶点上.已知引力常量为G.关于宇宙四星系统,下列说法错误的是( )A . 四颗星围绕正方形对角线的交点做匀速圆周运动B . 四颗星的轨道半径均为C . 四颗星表面的重力加速度均为D . 四颗星的周期均为2πa【答案】B3.宇宙中存在一些离其他恒星较远,由质量相等的三个星体组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在的一种形式是三个星体位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图所示.设每个星体的质量均为m,相邻的两个星体之间的距离为L,引力常量为G,则( )A.该圆形轨道的半径为3 2 LB.每个星体的运行周期均为3πL3 2GmC.每个星体做圆周运动的线速度均为Gm LD.每个星体做圆周运动的加速度均与星体的质量无关【答案】:C4.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动,研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化,若某双星系统中两星做圆周运动的周期为T ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时圆周运动的周期为( )A.n 3k 2B.n 3k T C.n 2kT D.n kT 【答案】:B【解析】:设m 1的轨道半径为r 1,m 2的轨道半径为r 2,由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同,两星之间的万有引力提供两星做圆周运动的向心力,即Gm 1m 2r 1+r 22=m 1r 1⎝⎛⎭⎪⎫2πT 2,Gm 1m 2r 1+r 22=m 2r 2⎝ ⎛⎭⎪⎫2πT 2,可得T =2πr 1+r 23G m 1+m 2,故当两恒星总质量变为原来的k倍,两星间距变为原来的n 倍时,圆周运动的周期变为n 3kT ,B 正确. 5.经长期观测,人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的直径远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O 点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L ,质量之比为m 1∶m 2=3∶2.则可知( )A .m 1、m 2做圆周运动的角速度之比为2∶3B .m 1、m 2做圆周运动的线速度之比为3∶2C .m 1做圆周运动的半径为r 1=25LD .m 2做圆周运动的半径为r 2=25L【答案:】C6. (多选)宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统.在浩瀚的银河系中,多数恒星都是双星系统.设某双星系统P、Q绕其连线上的O点做匀速圆周运动,如图所示.若PO>OQ,则( )A.星球P的质量一定大于Q的质量B.星球P的线速度一定大于Q的线速度C.双星间距离一定,双星的质量越大,其转动周期越大D.双星的质量一定,双星之间的距离越大,其转动周期越大【答案】BD7. (多选)宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( ) A.双星相互间的万有引力不变B.双星做圆周运动的角速度均增大C.双星做圆周运动的速度均减小D.双星做圆周运动的半径均增大【答案】CD【解析】双星间的距离在不断缓慢增加,由万有引力定律,F=G,知万有引力减小,A错误;根据万有引力提供向心力得G=m1r1ω2=m2r2ω2,可知m1r1=m2r2,知轨道半径比等于质量之反比,双星间的距离变大,则双星的轨道半径都变大,B 错误,D 正确;根据G=m 1v 1ω=m 2v 2ω,可得线速度减小,C 正确8. (多选)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.若某双星系统中两星做圆周运动的周期为T ,两星总质量为M ,两星之间的距离为r ,两星质量分别为m 1、m 2,做圆周运动的轨道半径分别为r 1、r 2,则下列关系式中正确的是( )A . M =B . r 1=rC . T =2πD . =【答案】AC【解析】由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.由向心力公式可得:对m 1:=m 1ω2r 1① 对m 2:=m 2ω2r 2②;由①②式可得:m 1r 1=m 2r 2 ,即=,D 错误.r 1+r 2=r ,得:r 1=r =r ,B 错误.将ω=,r 1=r 代入①式,可得:=m 1·r,得:T =2π,M =,A 、C 正确.9.宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a 的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T 1;另一种形式是有三颗星位于边长为a 的等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为T 2,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比T 1T 2.【答案】T 1T 2=6+634+2【解析】:对于第一种形式,一个星体在其它三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,其轨道半径为:r1=22a.。
高中物理专题复习---双星与多星问题

微专题25 双星与多星问题【核心要点提示】(1)核心问题是“谁”提供向心力的问题.(2)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同;双星中轨道半径与质量成反比;(3)多星问题中,每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供,即F 合=m v 2r ,以此列向心力方程进行求解.【微专题训练】“双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小于两个星球之间的距离,而且双星系统一般远离其他天体.如图1所示,相距为L 的A 、B 两恒星绕共同的圆心O 做圆周运动,A 、B 的质量分别为m 1、m 2,周期均为T .若有间距也为L 的双星C 、D ,C 、D 的质量分别为A 、B 的两倍,则( )A .A 、B 运动的轨道半径之比为m 1m 2B .A 、B 运动的速率之比为m 1m 2C .C 运动的速率为A 的2倍D .C 、D 运动的周期均为22T 【解析】对于双星A 、B ,有G m 1m 2L 2=m 1(2πT )2r 1=m 2(2πT )2r 2,r 1+r 2=L ,得r 1=m 2m 1+m 2L ,r 2=m 1m 1+m 2L ,T =2πL L G m 1+m 2,A 、B 运动的轨道半径之比为r 1r 2=m 2m 1,A 错误;由v=2πr T 得,A 、B 运动的速率之比为v 1v 2=r 1r 2=m 2m 1,B 错误;C 、D 运动的周期T ′=2πL L G 2m 1+2m 2=22T ,D 正确;C 的轨道半径r 1′=2m 22m 1+2m 2L =r 1,C 运动的速率为v 1′=2πr 1′T ′=2v 1,C 错误.【答案】D(2013·山东理综)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时圆周运动的周期为( ) A.n 3k 2T B.n 3kT C.n 2kT D.n kT 【解析】双星靠彼此的引力提供向心力,则有 G m 1m 2L 2=m 1r 14π2T 2 G m 1m 2L 2=m 2r 24π2T 2 并且r 1+r 2=L 解得T =2πL 3G (m 1+m 2)当两星总质量变为原来的k 倍,两星之间距离变为原来的n 倍时 T ′=2πn 3L 3Gk (m 1+m 2)=n 3k·T 故选项B 正确. 【答案】B(多选)宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m ,半径均为R ,四颗星稳定分布在边长为a 的正方形的四个顶点上.已知引力常量为G .关于四星系统,下列说法正确的是( )A .四颗星围绕正方形对角线的交点做匀速圆周运动B .四颗星的轨道半径均为a2C .四颗星表面的重力加速度均为GmR 2D .四颗星的周期均为2πa2a(4+2)Gm【解析】其中一颗星体在其他三颗星体的万有引力作用下,合力方向指向对角线的交点,围绕正方形对角线的交点做匀速圆周运动,由几何知识可得轨道半径均为22a ,故A 正确,B 错误;在星体表面,根据万有引力等于重力,可得G mm ′R 2=m ′g ,解得g =GmR2,故C 正确;由万有引力定律和向心力公式得Gm 2(2a )2+2Gm 2a 2=m 4π2T 2·2a2,T =2πa2a(4+2)Gm,故D正确. 【答案】ACD(2016·河南省郑州市高三月考)宇宙中有这样一种三星系统,系统由两个质量为m 的小星体和一个质量为M 的大星体组成,两个小星体围绕大星体在同一圆形轨道上运行,轨道半径为r 。
专题10双星及多星问题-2019高考物理一轮复习专题详解(解析版)

1.双星模型(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.(2)特点:①各自所需的向心力由彼此间的万有引力相互提供,即Gm 1m 2L 2=m 1ω21r 1,Gm 1m 2L2=m 2ω22r 2②两颗星的周期及角速度都相同,即T 1=T 2,ω1=ω2③两颗星的半径与它们之间的距离关系为:r 1+r 2=L (3)两颗星到圆心的距离r 1、r 2与星体质量成反比,即m 1m 2=r 2r 1. 2.多星模型(1)定义:所研究星体的万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度或周期相同.(2)三星模型:①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R 的圆形轨道上运行(如图3甲所示).②三颗质量均为m 的星体位于等边三角形的三个顶点上(如图乙所示).(3)四星模型:①其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示).②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动(如图丁所示).典例分析【例1】(多选)(2017年昆明模拟)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T,两星到某一共同圆心的距离分别为R1和R2,那么,系统中两颗恒星的质量关系是() A.这两颗恒星的质量必定相等B.这两颗恒星的质量之和为4π2R1+R23GT2C.这两颗恒星的质量之比为m1∶m2=R2∶R1D.其中必有一颗恒星的质量为4π2R1+R23GT2【答案】BC【例2】:2016年2月11日,美国科学家宣布探测到引力波的存在,引力波的发现将为人类探索宇宙提供新视角,这是一个划时代的发现.在如图所示的双星系统中,A、B两个恒星靠着相互之间的引力正在做匀速圆周运动,已知恒星A的质量为太阳质量的29倍,恒星B的质量为太阳质量的36倍,两星之间的距离L=2×105 m,太阳质量M=2×1030 kg,引力常量G=6.67×10-11 N·m2/kg2,π2=10.若两星在环绕过程中会辐射出引力波,该引力波的频率与两星做圆周运动的频率具有相同的数量级,则根据题目所给信息估算该引力波频率的数量级是()A.102 Hz B.104 Hz C.106 Hz D.108 Hz【答案】 A【例3】:.经过用天文望远镜长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识,双星系统由两个星体组成,其中每个星体的线度都远小于两星体之间的距离,一般双星系统距离其他星体很远,可以当成孤立系统来处理.现根据对某一双星系统的测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.(1)计算出该双星系统的运动周期T;(2)若该实验中观测到的运动周期为T观测,且T观测∶T=1∶N(N>1).为了理解T观测与T的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质.若不考虑其他暗物质的影响,根据这一模型和上述观测结果确定该星系间这种暗物质的密度.【答案】(1)πL2LGM(2)3N-1M2πL3【解析】(1)双星均绕它们连线的中点做圆周运动,万有引力提供向心力,则G M2L2=M2πT2·L2,解得T=πL 2L GM.。
专题31 双星多星问题、张角问题、拉格朗日点和黑洞潮汐现象(解析版)

2023届高三物理一轮复习重点热点难点专题特训专题31 双星多星问题、张角问题、拉格朗日点和黑洞潮汐现象特训目标 特训内容目标1 双星多星问题(1T —4T ) 目标2 张角问题(5T —8T ) 目标3 拉格朗日点(9T —12T ) 目标4黑洞潮汐现象(13T —16T )一、双星多星问题1.宇宙中有很多恒星组成的双星运动系统,两颗恒星仅在彼此的万有引力作用下,绕共同点做匀速圆周运动,如图所示。
假设该双星1、2的质量分别为1m 、2m ,圆周运动的半径分别为1r 、2r ,且1r 小于2r ,共同圆周运动的周期为T ;引力常量为G 。
则下列说法正确的是( )A .恒星1做圆周运动的向心加速度为221m Gr B .恒星1表面的重力加速度一定大于恒星2表面的重力加速度 C .恒星1的动量一定大于恒星2的动量D .某些双星运动晚期,两者间距逐渐减小,一者不断吸食另一者的物质,则它们在未合并前,共同圆周运动的周期不断减小【答案】D【详解】A .对于恒星1m ,其圆周运动方程为()1211212=+n Gm m m a r r 则恒星1m 的向心加速度()21212=+n Gm a r r故A 错误; B .由2GMm mg R =解得2GMg R=由于不能确定两恒星半径R 的大小,故不能确定表面重力加速度的大小,故B 错误;C .对于双星运动有1122m r m r =又因为角速度相同,根据角速度与线速度关系有1122m r m r ωω=即1122m v m v =即动量大小相等,故C 错误;D .设两星球之间距离为L ,对星球1m ,有2121122⎛⎫= ⎪⎝⎭Gm m m r L T π对星球2m ,有2122222⎛⎫= ⎪⎝⎭Gm m m r L T π 上述两式相加得2221122222⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭Gm Gm r r L L T T ππ解得()3122L T G m m =+可以看到当两者间距逐渐减小,总质量不变时,双星运动的共同周期逐渐减小,故D 正确。
高考物理一轮复习第五章微专题32双星和多星问题

双星和多星问题1.考点及要求:(1)万有引力定律的应用(Ⅱ);(2)力的合成与分解(Ⅱ);(3)匀速圆周运动的向心力(Ⅱ).2.方法与技巧:(1)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同;双星中轨道半径与质量成反比;(2)多星问题中,每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供,即F 合=m v 2r,以此列向心力方程进行求解.1.(双星问题)(多选)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T ,两星到某一共同圆心的距离分别为R 1和R 2,那么,系统中两颗恒星的质量关系是( ) A .这两颗恒星的质量必定相等 B .这两颗恒星的质量之和为4π2R 1+R 23GT 2C .这两颗恒星的质量之比为m 1∶m 2=R 2∶R 1D .其中必有一颗恒星的质量为4π2R 1+R 23GT 22.(多星问题)宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图1所示,三颗质量均为m 的星位于等边三角形的三个顶点,三角形边长为L ,忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O 做匀速圆周运动,引力常量为G ,下列说法正确的是( )图1A .每颗星做圆周运动的角速度为3GmL 3B .每颗星做圆周运动的加速度与三星的质量无关C .若距离L 和每颗星的质量m 都变为原来的2倍,则周期变为原来的2倍D .若距离L 和每颗星的质量m 都变为原来的2倍,则线速度变为原来的4倍3.(多选)宇宙间存在一个离其他星体遥远的系统,其中有一种系统如图2所示,四颗质量均为m 的星体位于正方形的顶点,正方形的边长为a ,忽略其他星体对它们的引力作用,每颗都在同一平面内绕正方形对角线的交点O 做匀速圆周运动,引力常量为G ,则( )图2A .每颗星做圆周运动的线速度大小为1+24GmaB .每颗星做圆周运动的角速度大小为Gm 2a3 C .每颗星做圆周运动的周期为2π2a3GmD .每颗星做圆周运动的加速度与质量m 有关4.2002年四月下旬,天空中出现了水星、金星、火星、木星、土星近乎直线排列的“五星连珠”的奇观.假设火星和木星绕太阳做匀速圆周运动,周期分别是T 1和T 2,而且火星离太阳较近,它们绕太阳运动的轨道基本上在同一平面内,若某一时刻火星和木星都在太阳的同一侧,三者在一条直线上排列,那么再经过多长的时间将第二次出现这种现象( ) A.T 1+T 22B.T 1T 2C.T 1T 2T 2-T 1D. T 21+T 2225.宇宙中存在一些离其他恒星较远的两颗星组成的双星系统,通常可忽略其他星体对它们的引力作用.已知双星系统中星体1的质量为m ,星体2的质量为2m ,两星体相距为L ,同时绕它们连线上某点做匀速圆周运动,引力常量为G .求该双星系统运动的周期.6.宇宙中存在质量相等的四颗星组成的四星系统,这些系统一般离其他恒星较远,通常可忽略其他星体对它们的引力作用.四星系统通常有两种构成形式:一是三颗星绕另一颗中心星运动(三绕一),二是四颗星稳定地分布在正方形的四个顶点上运动.若每个星体的质量均为m ,引力常量为G .(1)分析说明三绕一应该具有怎样的空间结构模式.(2)若相邻星球的最小距离为a ,求两种构成形式下天体运动的周期之比.答案解析1.BC [对m 1有:G m 1m 2R 1+R 22=m 1R 14π2T 2,解得m 2=4π2R 1R 1+R 22GT 2,同理可得m 1=4π2R 2R 1+R 22GT 2,故两者质量不相等,故选项A 错误;将两者质量相加得m 1+m 2=4π2R 1+R 23GT 2,故选项B 正确;m 1∶m 2=R 2∶R 1,故选项C 正确;两者质量之和为4π2R 1+R 23GT 2,则不可能其中一个的质量为4π2R 1+R 23GT 2,故选项D 错误.]2.C [任意两星间的万有引力F =G m 2L2,对任一星受力分析,如图所示.由图中几何关系和牛顿第二定律可得:3F =ma =mω2L3,联立可得:ω= 3GmL3,a =ω2L3=3GmL 2,选项A 、B 错误;由周期公式可得:T =2πω=2πL 33Gm ,当L 和m 都变为原来的2倍,则周期T ′=2T ,选项C 正确;由速度公式可得:v =ωL3=GmL,当L 和m 都变为原来的2倍,则线速度v ′=v ,选项D 错误.]3.AD [由星体均围绕正方形对角线的交点做匀速圆周运动可知,星体做匀速圆周运动的轨道半径r =22a ,每颗星体在其他三个星体万有引力的合力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:Gm 22a2+2G m 2a 2cos 45°=m v 222a,解得v =1+24Gm a ,角速度为ω=vr=2+22Gm a 3,周期为T =2πω=2π2a34+2Gm,加速度a =v 2r =22+1Gm 2a 2,故选项A 、D 正确,B 、C 错误.] 4.C [根据万有引力提供向心力得:GMm r 2=m 4π2r T 2,解得T =2π r 3GM,火星离太阳较近,即轨道半径小,所以周期小.设再经过时间t 将第二次出现这种现象,此为两个做匀速圆周运动的物体追及相遇的问题,虽然不在同一轨道上,但是当它们相遇时,运动较快的物体比运动较慢的物体多运行2π弧度.所以2πT 1t -2πT 2t =2π,解得t =T 1T 2T 2-T 1,选项C 正确.]5.2πLL3Gm解析 双星系统围绕两星体间连线上的某点做匀速圆周运动,设该点距星体1为R ,距星体2为r对星体1,有G 2mm L 2=m 4π2T2R对星体2,有G 2mm L2=2m 4π2T2r根据题意有R +r =L ,由以上各式解得T =2πLL 3Gm6.(1)见解析 (2) 4+23-34解析 (1)三颗星绕另一颗中心星运动时,其中任意一个绕行的星球受到的另三个星球的万有引力的合力提供向心力,三个绕行星球的向心力一定指向同一点,且中心星受力平衡,由于星球质量相等,具有对称关系,因此向心力一定指向中心星,绕行星一定分布在以中心星为中心的等边三角形的三个顶点上,如图甲所示.(2)对三绕一模式,三颗星绕行轨道半径均为a ,所受合力等于向心力,因此有2G m 23a 2cos 30°+G m 2a 2=m 4π2T 21a 解得T 21=23-3π2a3Gm对正方形模式,如图乙所示,四星的轨道半径均为22a ,同理有 2G m 2a2cos 45°+G m 22a2=m 4π2T 22·22a 解得T 22=44-2π2a37Gm故T 1T 2= 4+23-34。
模型 双星或多星模型(解析版)
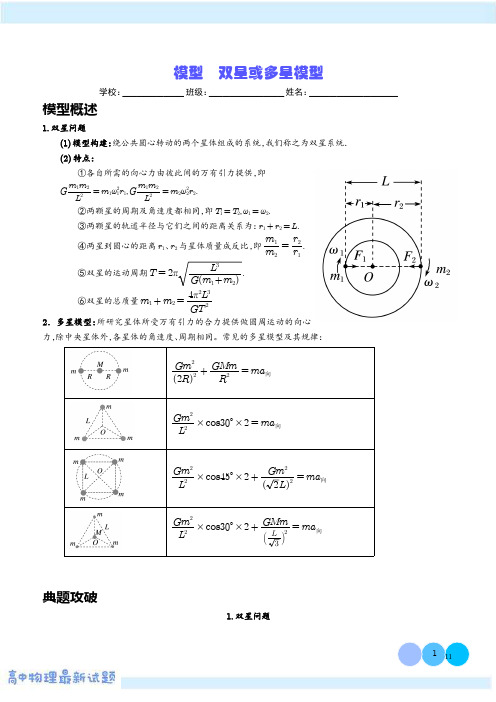
模型双星或多星模型学校:_________班级:___________姓名:_____________模型概述1.双星问题(1)模型构建:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统.(2)特点:①各自所需的向心力由彼此间的万有引力提供,即G m 1m 2L 2=m 1ω21r 1,G m 1m 2L2=m 2ω22r 2.②两颗星的周期及角速度都相同,即T 1=T 2,ω1=ω2.③两颗星的轨道半径与它们之间的距离关系为:r 1+r 2=L .④两星到圆心的距离r 1、r 2与星体质量成反比,即m 1m 2=r 2r 1.⑤双星的运动周期T =2πL 3G (m 1+m 2).⑥双星的总质量m 1+m 2=4π2L 3GT 22.多星模型:所研究星体所受万有引力的合力提供做圆周运动的向心力,除中央星体外,各星体的角速度、周期相同。
常见的多星模型及其规律:Gm 2(2R )2+GMmR2=ma 向Gm 2L2×cos30°×2=ma 向Gm 2L 2×cos45°×2+Gm 2(2L )2=ma 向Gm 2L2×cos30°×2+GMmL 32=ma 向典题攻破1.双星问题1.(2024·重庆·高考真题)在万有引力作用下,太空中的某三个天体可以做相对位置不变的圆周运动,假设a 、b 两个天体的质量均为M ,相距为2r ,其连线的中点为O ,另一天体(图中未画出)质量为m (m <<M ),若c 处于a 、b 连线的垂直平分线上某特殊位置,a 、b 、c 可视为绕O 点做角速度相同的匀速圆周,且相对位置不变,忽略其他天体的影响。
引力常量为G 。
则()A.c 的线速度大小为a 的3倍B.c 的向心加速度大小为b 的一半C.c 在一个周期内的路程为2πrD.c 的角速度大小为GM8r 3【答案】A【详解】D .a 、b 、c 三个天体角速度相同,由于m <<M ,则对a 天体有G MM(2r )2=Mω2r 解得ω=GM4r 3故D 错误;A .设c 与a 、b 的连线与a 、b 连线中垂线的夹角为α,对c 天体有2G Mmrsin α2cos α=mω2rtan α解得α=30°则c 的轨道半径为r c =rtan30°=3r由v =ωr ,可知c 的线速度大小为a 的3倍,故A 正确;B .由a =ω2r ,可知c 的向心加速度大小是b 的3倍,故B 错误;C .c 在一个周期内运动的路程为s =2πr =23πr 故C 错误。
高考物理计算题复习《双星问题》(解析版)

⾼考物理计算题复习《双星问题》(解析版)《双星问题》⼀、计算题1.神奇的⿊洞是近代引⼒理论所预⾔的⼀种特殊天体,探寻⿊洞的⽅案之⼀是观测双星系统的运动规律。
天⽂学家观测河外星系⼈麦析伦云时,发现了双星系统,它由可见星A和不可见的暗星B构成,两星视为质点,不考虑其它星体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所⽰。
引⼒常量为G,由观测能够得到可见星A的速率v和运⾏周期T。
可见星A所受暗星B的引⼒FA可等效为位于O点处质量为的星体可视为质点对它的引⼒,设A和B的质量分别为,,试求⽤、表⽰求暗星B的的质量与可见星A的速率v、运⾏周期T和质量之间的关系式。
要求等号左边只含有和,,等号右边为其它量2.众多的恒星组成不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星,如下图所⽰,两星各以⼀定速率绕其连线上某⼀点匀速转动,这样才不⾄于因万有引⼒作⽤⽽吸引在⼀起,已知双星质量分别为、,它们间的距离始终为L,引⼒常数为G,求:双星旋转的中⼼O到的距离;双星的转动周期。
3.天⽂观测中发现宇宙中存在着“双星”,所谓双星,是两颗质量相近,分别为和的恒星,它们的距离为r,⽽r远远⼩于它们跟其它天体之间的距离,这样的双星将绕着它们的连线上的某点O作匀速圆周运动.求:这两颗星到O点的距离、各是多⼤双星的周期.4.现代观测表明,由于引⼒的作⽤,恒星有“聚焦”的特点,众多的恒星组成不同层次的恒星系统,最简单的恒星系统是两颗互相绕转的双星.它们以两者连线上的某点为圆⼼做匀速圆周运动,这样就不⾄于由于万有引⼒的作⽤⽽吸引在⼀起.如图所⽰,设某双星系统中的两星、的质量分别为m和2m,两星间距为L,在相互间万有引⼒的作⽤下,绕它们连线上的某点O转动.已知引⼒常量G,求:、两星之间的万有引⼒⼤⼩;星到O点的距离;它们运动的周期.5.⿊洞是宇宙空间内存在的⼀种天体。
⿊洞的引⼒很⼤,使得视界内的逃逸速度⼤于光速。
专题四 同步卫星 双星等模型(真题精讲)-2019领军高考物理真题透析一轮复习 Word版含解析

【专题解读】1.本专题是万有引力定律在天体运行中的特殊运用,同步卫星是与地球(中心)相对静止的卫星;而双星或多星模型有可能没有中心天体,近年来常以选择题形式在高考题中出现.2.学好本专题有助于学生加深万有引力定律的灵活应用,加深力和运动关系的理解.3.需要用到的知识:牛顿第二定律、万有引力定律、圆周运动规律等.考向一地球同步卫星1.定义:相对于地面静止且与地球自转具有相同周期的卫星叫地球同步卫星.2.“七个一定”的特点(1)轨道平面一定:轨道平面与赤道平面共面.(2)周期一定:与地球自转周期相同,即T=24 h.(3)角速度一定:与地球自转的角速度相同.(4)高度一定:由GMmR+h2=m4π2T2(R+h)得地球同步卫星离地面的高度h=3.6×107 m.(5)速率一定:v=GMR+h=3.1×103 m/s.(6)向心加速度一定:由GMmR+h2=ma得a=GMR+h2=g h=0.23 m/s2,即同步卫星的向心加速度等于轨道处的重力加速度.(7)绕行方向一定:运行方向与地球自转方向相同.【例1】利用三颗位置适当的地球同步卫星,可使地球赤道上任意两点之间保持无线电通讯.目前,地球同步卫星的轨道半径约为地球半径的6.6倍.假设地球的自转周期变小,若仍仅用三颗同步卫星来实现上述目的,则地球自转周期的最小值约为( )A.1 h B.4 h C.8 h D.16 h【答案】 B卫星的轨道半径为r =Rsin 30°=2R由r 31T 21=r 32T22得 6.6R 3242=2R3T 22.解得T 2≈4 h.解决同步卫星问题的“四点”注意1.基本关系:要抓住:G Mm r 2=ma =m v 2r =mrω2=m 4π2T2r .2.重要手段:构建物理模型,绘制草图辅助分析. 3.物理规律(1)不快不慢:具有特定的运行线速度、角速度和周期. (2)不高不低:具有特定的位置高度和轨道半径.(3)不偏不倚:同步卫星的运行轨道平面必须处于地球赤道平面上,只能静止在赤道上方的特定的点上. 4.重要条件(1)地球的公转周期为1年,其自转周期为1天(24小时),地球的表面半径约为6.4×103km ,表面重力加速度g 约为9.8 m/s 2.(2)月球的公转周期约27.3天,在一般估算中常取27天.(3)人造地球卫星的运行半径最小为r =6.4×103km ,运行周期最小为T =84.8 min ,运行速度最大为v =7.9 km/s .阶梯练习1. 如图,若两颗人造卫星a 和b 均绕地球做匀速圆周运动,a 、b 到地心O 的距离分别为r 1、r 2,线速度大小分别为v 1、v 2,则( )A.v 1v 2=r 2r 1B.v 1v 2=r 1r 2C.v 1v 2=⎝ ⎛⎭⎪⎫r 2r 12D.v 1v 2=⎝ ⎛⎭⎪⎫r 1r22【答案】A.2.(2016·高考四川卷) 国务院批复,自2016年起将4月24日设立为“中国航天日”.1970年4月24日我国首次成功发射的人造卫星东方红一号,目前仍然在椭圆轨道上运行,其轨道近地点高度约为440 km ,远地点高度约为2 060 km ;1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km 的地球同步轨道上.设东方红一号在远地点的加速度为a 1,东方红二号的加速度为a 2,固定在地球赤道上的物体随地球自转的加速度为a 3,则a 1、a 2、a 3的大小关系为( )A .a 2>a 1>a 3B .a 3>a 2>a 1C .a 3>a 1>a 2D .a 1>a 2>a 3【答案】D.【解析】由于东方红二号卫星是同步卫星,则其角速度和赤道上的物体角速度相等,可得:a =ω2r ,由于r 2>r 3,则可以得出:a 2>a 3;又由万有引力定律有:G Mmr2=ma ,且r 1<r 2,则得出a 2<a 1.故选项D 正确.3.假设地球和火星都绕太阳做匀速圆周运动,已知地球到太阳的距离小于火星到太阳的距离,那么( )A .地球公转的周期大于火星公转的周期B .地球公转的线速度小于火星公转的线速度C.地球公转的加速度小于火星公转的加速度D.地球公转的角速度大于火星公转的角速度【答案】D.4.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,地球的其他条件都不变,未来人类发射的地球同步卫星与现在的相比( )A.距地面的高度变大B.向心加速度变大C.线速度变大D.角速度变大【答案】 A【解析】地球的自转周期变大,则地球同步卫星的公转周期变大.由GMmR+h2=m4π2T2(R+h),得h=3GMT24π2-R,T变大,h变大,A正确.由GMmr2=ma,得a=GMr2,r增大,a减小,B错误.由GMmr2=mv2r,得v=GMr,r增大,v减小,C错误.由ω=2πT可知,角速度减小,D错误.5.(多选)地球同步卫星离地心的距离为r,运行速率为v1,加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,地球的第一宇宙速度为v2,半径为R,则下列比例关系中正确的是( )A.a1a2=rRB.a1a2=(rR)2C.v1v2=rRD.v1v2=Rr【答案】AD。
全国通用2019高考物理一轮复习精炼:第四章曲线运动万有引力与航天微专题36双星与多星问题含答案

36 双星与多星问题[方法点拨] (1)核心问题是“谁”提供向心力的问题.(2)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同;双星中轨道半径与质量成反比;(3)多星问题中,每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供,即F 合=m v 2r,以此列向心力方程进行求解.1.(2018·四川泸州一检)“双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小于两个星球之间的距离,而且双星系统一般远离其他天体.如图1所示,相距为L 的A 、B 两恒星绕共同的圆心O 做圆周运动,A 、B 的质量分别为m 1、m 2,周期均为T .若有间距也为L 的双星C 、D ,C 、D 的质量分别为A 、B 的两倍,则( )图1A .A 、B 运动的轨道半径之比为m 1m 2B .A 、B 运动的速率之比为m 1m 2C .C 运动的速率为A 的2倍D .C 、D 运动的周期均为22T 2.(多选)太空中存在一些离其他恒星很远的、由三颗星体组成的三星系统,可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星体始终在一条直线上;另一种是三角形三星系统——三颗星体位于等边三角形的三个顶点上.已知某直线三星系统A 每颗星体的质量均为m ,相邻两颗星中心间的距离都为R ;某三角形三星系统B 的每颗星体的质量恰好也均为m ,且三星系统A 外侧的两颗星体做匀速圆周运动的周期和三星系统B 每颗星体做匀速圆周运动的周期相等.引力常量为G ,则( ) A .三星系统A 外侧两颗星体运动的线速度大小为v =Gm RB .三星系统A 外侧两颗星体运动的角速度大小为ω=12R5GmRC .三星系统B 的运动周期为T =4πRR 5GmD .三星系统B 任意两颗星体中心间的距离为L =3125R3.(多选)(2017·福建龙岩3月质检)冥王星和其附近的星体卡戎的质量分别为M 、m (m <M ),两星相距L ,它们只在相互间的万有引力作用下,绕球心连线的某点O 做匀速圆周运动.冥王星与星体卡戎到O 点的距离分别为R 和r .则下列说法正确的是( )A .可由G Mm R2=MR ω2计算冥王星做圆周运动的角速度B .可由G Mm L 2=M v 2L 计算冥王星做圆周运动的线速度C .可由G Mm L2=mr (2πT)2计算星体卡戎做圆周运动的周期D .冥王星与星体卡戎绕O 点做圆周运动的动量大小相等4.(2017·山东枣庄一模)2015年12月17日我国发射了“悟空”探测卫星,这期间的观测使人类对暗物质的研究又进了一步.宇宙空间中两颗质量相等的星球绕其连线中心转动时,理论计算的周期与实际观测周期不符,且T 理论T 观测=k (k >1);因此,科学家认为,在两星球之间存在暗物质.假设以两星球球心连线为直径的球体空间中均匀分布着暗物质,两星球的质量均为m ,那么,暗物质的质量为( )A.k 2-14mB.k 2-28mC .(k 2-1)mD .(2k 2-1)m5.(2017·广西南宁一模)2016年2月11日,科学家宣布“激光干涉引力波天文台(LIGO)”探测到由两个黑洞合并产生的引力波信号,这是在爱因斯坦提出引力波概念100周年后,引力波被首次直接观测到.在两个黑洞合并过程中,由于彼此间的强大引力作用,会形成短时间的双星系统.如图2所示,黑洞A 、B 可视为质点,它们围绕连线上O 点做匀速圆周运动,且AO 大于BO ,不考虑其他天体的影响.下列说法正确的是( )图2A .黑洞A 的向心力大于B 的向心力 B .黑洞A 的线速度大于B 的线速度C .黑洞A 的质量大于B 的质量D .两黑洞之间的距离越大,A 的周期越小6.(多选)(2018·陕西商洛模拟)宇宙中两颗相距很近的恒星常常组成一个系统,它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知它们的运转周期为T ,两星到某一共同圆心的距离分别为R 1和R 2,那么,系统中两颗恒星的质量关系是( ) A .这两颗恒星的质量必定相等B .这两颗恒星的质量之和为4π2(R 1+R 2)3GT2C .这两颗恒星的质量之比为m 1∶m 2=R 2∶R 1D .其中必有一颗恒星的质量为4π2(R 1+R 2)3GT2答案精析1.D [对于双星A 、B ,有G m 1m 2L 2=m 1(2πT )2r 1=m 2(2πT )2r 2,r 1+r 2=L ,得r 1=m 2m 1+m 2L ,r 2=m 1m 1+m 2L ,T =2πLLG (m 1+m 2),A 、B 运动的轨道半径之比为r 1r 2=m 2m 1,A 错误;由v =2πr T 得,A 、B 运动的速率之比为v 1v 2=r 1r 2=m 2m 1,B 错误;C 、D 运动的周期T ′=2πLLG (2m 1+2m 2)=22T ,D 正确;C 的轨道半径r 1′=2m 22m 1+2m 2L =r 1,C 运动的速率为v 1′=2πr 1′T ′=2v 1,C 错误.]2.BCD [三星系统A 中,三颗星体位于同一直线上,两颗星体围绕中央星体在同一半径为R 的圆轨道上运行.其中外侧的一颗星体由中央星体和另一颗外侧星体的合万有引力提供向心力,有:G m 2R 2+G m 2(2R )2=m v 2R,解得v = 5Gm 4R ,A 错误;三星系统A 中,周期T =2πRv=4πR R 5Gm ,则其角速度为ω=2πT =12R5GmR,B 正确;由于两种系统周期相等,则三星系统B 的运行周期为T =4πRR5Gm,C 正确;三星系统B 中,三颗星体位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图所示,对某颗星体,由万有引力定律和牛顿第二定律得:2Gm 2L 2cos 30°=m L 2cos 30°·4π2T 2,解得L =3125R ,D 正确.]3.CD [冥王星与星体卡戎之间的万有引力提供各自做圆周运动的向心力:可由G Mm(R +r )2=MR ω2计算冥王星做圆周运动的角速度,故A 错误;同理,可由G Mm L 2=M v 2R 计算冥王星做圆周运动的线速度,故B 错误;冥王星与其附近的星体卡戎可视为双星系统.所以冥王星和星体卡戎做圆周运动的周期是相等的,可由G Mm L2=mr (2πT)2计算星体卡戎做圆周运动的周期,故C 正确;因G Mm(R +r )2=MR ω2=mr ω2,由于它们的角速度的大小是相等的,所以:MR ω=mr ω,又:v m =ωr ,v M =ωR ,p m =mv m ,p M =Mv M ,所以冥王星与星体卡戎绕O 点做圆周运动的动量大小相等,故D 正确.]4.A [两星球均绕它们的连线的中点做圆周运动,设它们之间的距离为L ,由万有引力提供向心力得:G m 2L 2=m4π2T 理论2·L2,解得:T 理论=πL2LGm.根据观测结果,星体的运动周期T 理论T 观测=k ,这种差异是由两星球之间均匀分布的暗物质引起的,均匀分布在两星球之间的暗物质对双星系统的作用与一质量等于暗物质的总质量m ′、位于中点O 处的质点的作用相同.则有:G m 2L 2+Gmm ′(L 2)2=m 4π2T 观测2·L2,解得:T 观测=πL2L G (m +4m ′),又T 理论T 观测=k ,所以:m ′=k 2-14m ,故A 正确,B 、C 、D 错误.]5.B [两黑洞靠相互间的万有引力提供向心力,根据牛顿第三定律可知,A 对B 的作用力与B 对A 的作用力大小相等、方向相反,则黑洞A 的向心力等于B 的向心力,故A 错误;两黑洞靠相互间的万有引力提供向心力,具有相同的角速度,由题图可知A 的轨道半径比较大,根据v =ωr 可知,黑洞A 的线速度大于B 的线速度,故B 正确;由于m A ω2r A =m B ω2r B ,由于A 的轨道半径比较大,所以A 的质量小,故C 错误;两黑洞靠相互间的万有引力提供向心力,所以G m A m B L 2=m A 4π2T 2r A =m B 4π2T 2r B ,又:r A +r B =L ,得r A =m B Lm A +m B ,L 为二者之间的距离,所以得:G m A m B L 2=m A 4π2T 2·m B L m A +m B ,即:T 2=4π2L 3G (m A +m B ),则两黑洞之间的距离越小,A 的周期越小,故D 错误.] 6.BC [设两星质量分别为m 1、m 2.对m 1有:G m 1m 2(R 1+R 2)2=m 1R 14π2 T 2,解得m 2=4π2R 1(R 1+R 2)2GT 2,同理可得m 1=4π2R 2(R 1+R 2)2GT 2,故两者质量不相等,故选项A 错误;将两者质量相加得m 1+m 2=4π2(R 1+R 2)3GT2,则不可能其中一个的质量为4π2(R 1+R 2)3GT2,故选项D 错误,选项B 正确;m 1∶m 2=R 2∶R 1,故选项C 正确.]。
2019版高考物理一轮复习备考专题-第四章曲线运动万有引力与航天专题36双星与多星问题2019高考备考

36双星与多星问题
[方法点拨](1)核心问题是“谁”提供向心力的问题. (2) “双星问题”的隐含条件是两者 的向心力相同、周期相同、角速度相同;双星中轨道半径与质量成反比;
(3)多星问题中, 2 每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供,
即F 合=mr ;,以此
列向心力方程进行求解. 1. (2018 •四川泸州一检)“双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小
于两个星球之间的距离,而且双星系统一般远离其他天体•如图 1所示,相距为L 的A 、B 两恒星绕共同的圆心 0做圆周运动,A 、B 的质量分别为 m 、m ,周期均为T.若有间距也为L 的双星C D, C D 的质量分别为 A 、B 的两倍,则( )
图1
m
A. A 、B 运动的轨道半径之比为 一 m
B A B 运动的速率之比为后
C. C 运动的速率为A 的2倍
D.
2. (多选)太空中存在一些离其他恒星很远的、由三颗星体组成的三星系统,可忽略其他星
体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式: 一种是直线三星 系统一一三颗星体始终在一条直线上; 另一种是三角形三星系统一一三颗星体位于等边三角 形的三个顶点上.已知某直线三星系统 A 每颗星体的质量均为 m 相邻两颗星中心间的距离
都为R 某三角形三星系统 B 的每颗星体的质量恰好也均为
m 且三星系统 A 外侧的两颗星 体做匀速圆周运动的周期和三星系统 B 每颗星体做匀速圆周运动的周期相等. 引力常量为G
A. 三星系统A 外侧两颗星体运动的线速度大小为
B. 三星系统A 外侧两颗星体运动的角速度大小为
C D 运动的周期均为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8月23日 双星和多星问题
高考频度:★★☆☆☆
难易程度:★★☆☆☆
(2018·重庆綦江实验中学)2016年2月11日,LIGO 科学合作组织首次探测到了来自宇宙中双黑洞合并所产生的引力波,证实了爱因斯坦100年前所做的预测。
脉冲双星间的距离在减小就已间接地证明了引力波的存在。
如果将该双星系统简化为理想的圆周运动模型,如图所示,两星球在相互的万有引力作用下,绕O 点做匀速圆周运动。
由于双星间的距离减小,则
A .两星的运动角速度均逐渐减小
B .两星的运动速度均逐渐减小
C .两星的向心加速度均逐渐减小
D .两星的运动周期均逐渐减小 【参考答案】D 【试题解析】根据221211222
m m G
m r m r L
ωω==,可得1122m r m r =,知轨道半径比等于质量之反比,双星间的距
离减小,则双星的轨道半径都变小,根据万有引力提供向心力,知角速度变大,周期变小,故A 错误,D 正确。
根据212112
1m m v G
m r L =
,解得:1v =L 平方的减小量比1r 和2r 的减小量大,则线速度增大,故B 错误。
根据121122
m m G m a m a L
==,知,L 变小,则两星的向心加速度增大,故C 错误。
【知识补给】
双星问题的处理方法
双星间的万有引力提供了它们做圆周运动的向心力,即2212
11222
m m G m r m r L
ωω==,由此得出: (1)m 1r 1=m 2r 2,即某恒星的运动半径与其质量成反比;
(2)由于ω=2πT ,r 1+r 2=L ,所以两恒星的质量之和23
122
4πL m m GT
+=。
(2018·百校联盟)2017年三名美国科学家获本年度诺贝尔物理学奖,用以表彰他们在引力波研究方面的贡献。
人类首次发现了引力波来源于距地球之外13亿光年的两个黑洞(质量分别为26个和39个太阳质量)互相绕转最后合并的过程。
设两个黑洞A 、B 绕其连线上的O 点做匀速圆周运动,如图所示。
黑洞A 的轨道半径大于黑洞B 的轨道半径,两个黑洞的总质量为M ,两个黑洞间的距离为L ,其运动周期为T ,则
A .黑洞A 的质量一定大于黑洞
B 的质量 B .黑洞A 的线速度一定大于黑洞B 的线速度
C .两个黑洞间的距离L 一定,M 越大,T 越大
D .两个黑洞的总质量M 一定,L 越大,T 越大
(2018·湖北武汉武昌区模拟)如图所示,双星系统由质量不相等的两颗恒星组成,质量分别是M 、m (M >m ),他们围绕共同的圆心O 做匀速圆周运动。
从地球A 看过去,双星运动的平面与AO 垂直,AO 距离恒为L 。
观测发现质量较大的恒星M 做圆周运动的周期为T ,运动范围的最大张角为Δθ(单位是弧度)。
已知引力常量为G ,Δθ很小,可认为sin Δθ=tan Δθ=Δθ,忽略其他星体对双星系统的作用力。
则
A .恒星m
B .恒星m 的轨道半径大小为Δ2ML m
θ
C .恒星m 的线速度大小为
πΔML mT
θ
D .两颗恒星的质量m 和M 满足关系式
()
()3
23
2
2
πΔ2L m GT m M θ=
+
一点O 为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”,
如图所示。
已知双星的质量为1m 和2m ,它们之间的距离为L 。
求双星运行轨道半径1r 和2r ,以及运行的周期T 。
由三颗星体构成的系统,忽略其他星体对它们的影响,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做角速度相同的圆周运动(图示为A 、B 、C 三颗星体质量不相同时的一般情况)若A 星体的质量为2m ,B 、C 两星体的质量均为m ,三角形的边长为a ,求:
(1)A 星体所受合力的大小F A ; (2)B 星体所受合力的大小F B ; (3)C 星体的轨道半径R C ; (4)三星体做圆周运动的周期T 。
宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用。
已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a 的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T 1;另一种形式是有三颗星位于边长为a 的等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,其运动
周期为T 2,而第四颗星刚好位于三角形的中心不动。
试求两种形式下,星体运动的周期之比1
2
T T 。
【参考答案】
BCD 恒星m 与M 具有相同的角速度,则角速度为2π
T
ω=
,选项A 错误;恒星M 的轨道半径为Δ1tan
Δ22R L L θθ==;对恒星系统:m ω2r =M ω2R ,解得恒星m 的轨道半径大小为Δ2ML r m
θ=,选项B 正确;恒星m 的线速度大小为12πΔπΔ2ML ML v r T m mT
θθω==
⋅=,选项C 正确;对恒星系统:()2Mm G r R +=m ω2r =M ω2
R ,
解得GM =ω2
r (r +R )2
;Gm =ω2
R (r +R )2;相加得:()()
3
2
G M m R r ω
+=+,联立可得:
()
()3
23
2
2
πΔ2L m GT m M θ=
+,
选项D 正确。
2112m L r m m =+ 1212m L r m m =+
设双星中质量为1m 的天体轨道半径为1r ,质量为2m 的天体轨道半径为2r 据万有引力定律和牛顿第二定律,得:2
12112m m G
m r L ω=①212222
m m G m r L
ω=②12r r L +=③ 由①②③联立解得:2112m L r m m =+,1212m L
r m m =+
(1
)F A =
(2)B F = (3
)R C
(4)T = (1)由万有引力定律,A 星受到B 、C 的引力的大小
2
22
2A C BA CA Gm m Gm F F a a ===
方向如图所示,则合力的大小为
F A
=2F BA ·cos 30°=。
