圆切线长定理弦切角定理切割线定理相交弦定理
圆切线长定理弦切角定理切割线定理相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段学习目标1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度;2.切线长定理对于切线长定理,应明确1若已知圆的两条切线相交,则切线长相等;2若已知两条切线平行,则圆上两个切点的连线为直径;3经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;4经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;5圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角;3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角;直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢四个4.弦切角定理:弦切角等于其所夹的弧所对的圆周角;5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角;6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理;7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD. 连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB. 用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T,用两次切割线定理圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||R 为圆半径,因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理;。
切线长定理、弦切角定理、切割线定理、相交弦定理37508

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
(PA长)2.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD. 连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB.(特殊情况)用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB 连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD 过P作PT切⊙O于T,用两次切割线定理(记忆的方法方法)圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
圆的切线、切线长、线切角

CA圆的切线、切线长定理与弦切角定理一、圆的切线: 1.切线的判定:2.切线的性质:【运用举例】例1.如图,已知⊙O 所内接△ABC ,过点B 作直线BD ,∠DBC =∠A ,试说明,BD 与⊙O 相切。
例2.如图,已知CB 是⊙O 的切线,C 是切点,OB 交⊙O 于点D ,∠B =30,BD =6㎝,求BC 。
例3、如图,PA 、PB 切⊙O 于点A 、B ,点C 是⊙O 上一点,且∠ACB =65°,求∠P 的度数.例4、已知:如图AB 是⊙O 的直径,P 是AB 上的一点(与A 、B 不重合),QP ⊥AB ,垂足为P ,直线QA 交⊙O 于点C 点,过C 点作⊙O 的切线交直线QP 于点D ,求证:△CDQ 是等腰三角形.当P 点在AB 的延长线上时,其他条件不变,这个结论还成立吗?试说明.二、切线长定理 1、切线长:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长2、切线长定理:符号语言:∵PA 、PB 是O ⊙的切线,A 、B 是切点,∴,PA=PB 【运用举例】例1.在△ABC 中,AB=5cm BC=7cm AC=8cm, ⊙O 与BC 、AC 、 AB 分别相切于 D 、 E 、F ,则 AF=_____, BD=_______ 、CF=________例2、如图,PA 、PB 是⊙O 的切线,切点分别是A 、B ,直线EF 也是⊙O 的切线,切点为Q ,交PA 、PB 为E 、F 点,已知12PA cm ,求△PEF 的周长.例3、已知:如图,P 为⊙O 外一点,PA ,PB 为⊙O 的切线,A 和B 是切点,BC 是直径. 求证:AC∥OP.例4.如图,AB 、CD 分别与半圆O 切于点A 、D ,BC 切⊙O 于点E ,若AB =4,CD =9,求⊙O 的半径。
OCB AP三、弦切角定理及其推论1、弦切角:________________________________________________________________。
2014年青海教师招聘考试数学专业考点十三:切线长定理、弦切角定理、相交弦定理、切割线定理

中公教育——给人改变未来的力量2014年青海教师招聘考试数学专业考点十三:切线长定理、弦切角定理、相交弦定理、切割线定理
切线性质定理:圆的切线垂直于过其切点的半径;经过半径的非圆心一端,并且垂直于这条半径的直线,就是这个圆的一条切线。
切线判定定理:一直线若与一圆有交点,且连接交点与圆心的直线与该直线垂直,那么这条直线就是圆的切线。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
弦切角概念:顶点在圆上,一边和圆相交、另一边和圆相切的角叫做弦切角。
它是继圆心角、圆周角之后第三种与圆有关的角。
弦切角定理:弦切角等于它所夹的孤对的圆周角。
它是圆中证明角相等的重要定理之一。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到与圆交点的两条线段长的比例中项。
割线定理:从圆外一点引圆的两条割线则有这点到割线与圆交点的两条线段的积相等。
切线长定理、弦切角定理、切割线定理、相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
(PA长)2.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD. 连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB.(特殊情况)用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T,用两次切割线定理(记忆的方法方法)圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
九年级圆的定理总结

九年级圆的定理总结如下:1.圆上三点确定一个圆,且确定一个唯一的圆心,该圆心是三点所连线段垂直平分线的交点。
2.垂径定理:垂直于弦的直径平分该弦,且平分该弦所对的两条弧。
3.切线判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
4.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
5.弦心距定理:弦心距平分弦所对的弧。
6.相交弦定理:弦与直径垂直于弦的直径平分该弦,且平分该弦所对的两条弧。
7.割线定理:从圆外一点引圆的两条割线,这一点和圆心的连线平分两条割线的夹角。
8.直径所对的圆周角等于90度,90度的圆周角所对的弦是直径。
9.同圆或等圆的半径相等,直径等于半径的两倍。
10.圆是中心对称图形,对称中心是圆心。
11.如果两圆相交,那么连接两圆圆心的线段(公共弦)垂直平分两圆的连心线。
12.如果两圆相切,那么两圆的半径之和等于圆心距,或两圆半径之差等于圆心距。
13.两圆的半径之比等于圆心距之比等于两圆周长之比。
14.圆内接四边形的对角互补,内角和等于360度。
15.弧长公式:l=nπr/18016.扇形面积公式:s=1/2lr=1/2nπr²17.圆锥侧面积公式:s=1/2rl=πrl18.点P在圆O内,PA切圆O于A,则OP<PA。
19.点P在圆O上,PA切圆O于A,则OP=PA。
20.点P在圆O外,PA切圆O于A,则OP>PA。
21.从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
22.从圆外一点因圆的两条割线,这一点到割线与圆交点的两条线段长的积等于这一点到圆心的距离与圆的半径的积。
23.直线和圆相交,则有公共点;直线和椭圆相交,则有公共点;直线和双曲线相交,则有公共点;直线和抛物线相交,则有公共点;平面解析几何适用范围要熟记。
【初中数学】圆的相交弦定理、切割线定理和割线定理补充知识点

【初中数学】圆的相交弦定理、切割线定理和割线定理补充知识点一、相交弦定理1、相交弦在圆的内部相交的两条弦,称为相交弦.2、相交弦定理圆内的两条相交弦,被交点分成的两条线段的积相等。
几何语言:弦AB和CD相交于⊙O内一点P,那么PA·PB=PC·PD. 3、相交弦定理的证明证明:连接AC、BD由圆周角定理推论得:∠C=∠B,∠A=∠D∴△ACP∽△DBP∴ PA:PD=PC:PB二、切割线定理1、切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
几何语言:BC是⊙O的一条割线,PA是⊙O的一条切线,切点为A,则:PA²=PB·PC。
2、切割线定理的证明证明:如图,连接AB,AC∵ PA是圆O的切线,由弦切角定理可得∴∠PAC=∠B∵∠APB=∠CPA∴△APC∽△BPA∴ PA:BP=PC:PA三、割线定理1、割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
几何语言:从⊙O一点P引圆的两条割线AB、CD,则:PA·PB=PC·PD.2、割线定理证明证明:如图,连接AD、BC,由圆周角定理推论,得:∠D=∠B∵∠BPC=∠DPA∴△BPC∽△DPA∴ PB:PD=PC:PA∴ PA·PB=PC·PD四、例题例1、如图,在⊙O中,弦AB=CD,AB⊥CD于点E,已知CE·ED=3,BE =1,求⊙O的直径。
解:作OH⊥AB于H,OG⊥CD于G,连接OA由相交弦定理得:CE·ED=AE·EB∴ 3=AE×1∴ AE=3∴ AB=AE+EB=3+1=4∴ AB=CD=4∴ AH=HB=2∴ HE=HB-EB=2-1=1∵ AB=CD,AB⊥CD∴ OH=OG∴四边形OGEH为正方形∴ OH=HE=1由勾股定理得,OA=,∴⊙O的直径为,例2、如题图,⊙O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3, CE:ED=2:1 ,求BE的值。
切线长定理 弦切角和圆有关的比例线段 通用版

切线长定理 弦切角和圆有关的比例线段一. 本周教学内容:切线长定理、弦切角和圆有关的比例线段1. 切线长的概念:在经过圆外一点的切线上这点和切点之间的线段的长,叫做这点到圆的切线长。
2. 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这一点的连线平分这两条切线的夹角。
3. 弦切角的概念:顶点在圆上,一边和圆相交,一边和圆相切的角叫做弦切角。
4. 弦切角定理:弦切角等于它所夹弧所对的圆周角。
5. 弦切角定理的推论:如果两个弦切角所夹的弧相等,那么这两个弦切角相等。
6. 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
7. 相交弦定理的推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
8. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
9. 切割线定理的推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
二. 重点、难点:重点是和圆有关的比例线段,难点是运用和圆有关的比例线段分析问题和解决问题。
易错点分析:1. 要注意切线和切线长,这是两个不同的概念,前者是直线,后者是线段的长。
2. 注意弦切角与圆心角、圆周角的区别与联系,它们的空间位置不同,但在度数上有很密切的联系。
另外弦切角的三个条件缺一不可。
弦切角与切线有着密切的联系,做题时,遇到弦切角找到切点要连结半径,这样就有垂直的关系。
3. 相交弦定理、切割线定理及它们的推论,它们的结论都是线段的等积式,而不是比例式,它们可用来解关于计算和证明的题目。
等积式中的各线段要记牢,不要记混。
【例题分析】例1. 求证:圆外切四边形的两组对边的和相等。
A FB G ED H C已知:四边形ABCD 为⊙O 的外切四边形,E 、F 、G 、H 分别为切点。
求证:AB +CD =AD +BC 证明: AE AF O E F 、为⊙的切线,且切点为、∴====∴+++=++++=+AE AF BF BG DE DH CH CGAF FB DH CH AE BG DE CGAB CD AD BC,同理,,即例2. 如图所示,AB 是⊙O 的直径,AC 、BF 为⊙O 的切线,CF 切⊙O 于D ,DE AB ⊥于E ,交BC 于G ,求证:DG =EGF分析:因为AC//DE//BF ,所以可考虑成比例的线段来证明线段相等。
圆幂定理学生用

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标] 1. 切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线 长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度 量长度。
2. 切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,贝U 切线长相等; (2) 若已知两条切线平行,则圆上两个切点的连线为直径; (3)经过圆外一点引圆的两条 切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切 线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点 向圆引的两条切线所夹的角直线AB 切OO 于P ,PC PD 为弦,图中几个弦切角呢?(四个) 4. 弦切角定理:弦切角等于其所夹的弧所对的圆周角5. 弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6. 遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7. 与圆有关的比例线段 定理OO 中,AB 为直径,PC = PA- PBCDLAB 于 P.已知 结论 OO 中,AB CD 为弦,PA- PB交于 P.PC- PD证法二连结AC 、BD,证: △ APS A DPB用相交弦定理.3.弦切角:顶点在圆上,图形PA- P 吐 PC- PD 过 P 作 PT 切OO 于T , 用两次切割线定理P'C - P'D = r 2—延长 P'O 交OO 于 MOP'2延长OP'交OO 于N,PA- P 吐OP — r 2用相交弦定理证;过P r为OO 的半径 作切线用切割线定理 勾股定理证8.圆幕定理:过一定点P 向OO 作任一直线,交OO 于两点,则自定点P 到两交点的 两条线段之积为常数|1:丁 ( R 为圆半径),因为匕乍■•也叫做点对于OO 的幕,所以将上述定理统称为圆幕定理。
第三课时切割线定理割线定理和切线长定理
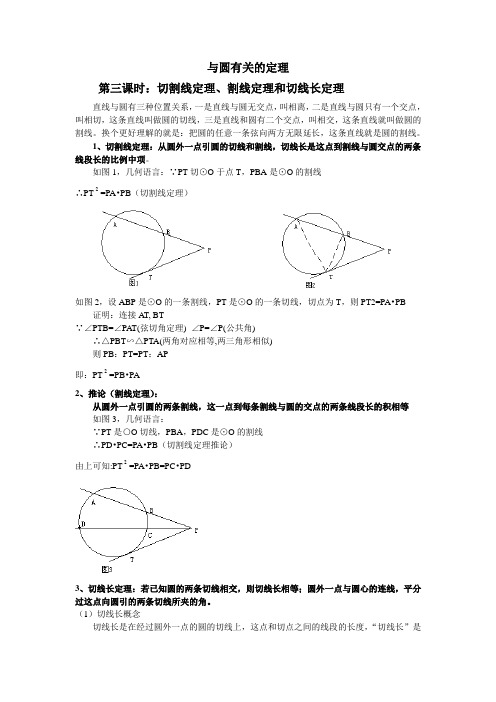
与圆有关的定理第三课时:切割线定理、割线定理和切线长定理直线与圆有三种位置关系,一是直线与圆无交点,叫相离,二是直线与圆只有一个交点,叫相切,这条直线叫做圆的切线,三是直线和圆有二个交点,叫相交,这条直线就叫做圆的割线。
换个更好理解的就是:把圆的任意一条弦向两方无限延长,这条直线就是圆的割线。
1、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
如图1,几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=PA•PB(切割线定理)如图2,设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT2=PA•PB 证明:连接A T, BT∵∠PTB=∠PAT(弦切角定理) ∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT2=PB•PA2、推论(割线定理):从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等如图3,几何语言:∵PT是○O切线,PBA,PDC是⊙O的割线∴PD•PC=PA•PB(切割线定理推论)由上可知:PT2=PA•PB=PC•PD3、切线长定理:若已知圆的两条切线相交,则切线长相等;圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
(1)切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
( 2)几点说明对于切线长定理,应明确(1)若已知两条切线平行,则圆上两个切点的连线为直径;(2)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(3)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补。
(3)推论:圆的外切四边形对边和相等(圆的外切四边形性质定理,逆定理成立);圆的外切等腰梯形的中位线等于腰长.基础知识运用:例1.如图4,正方形ABCD 的边长为1,以BC 为直径。
圆切线长定理、弦切角定理、切割线定理、相交弦定理之欧阳语创编

以及与圆有关的比例线段[学习目标]1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD.连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB.用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T,用两次切割线定理圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
切线长,弦切角,相交弦

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段1.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
2弦切角定理及其推论圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE问:这时∠BAE还是圆周角吗?为什么?像∠BAE这样的角叫做弦切角,请你仿照圆周角的定义,给出弦切角的定义:_____________________________________________________________________________________________问题:以下各图中的角哪个是弦切角?思考:弦切角相对于圆心的位置,分为哪几类?请在右上方画出图。
问题:已知如图,AB是⊙O的一条切线,A为切点,AC是⊙O的一条弦,则∠ADC与∠BAC有什么关系?请给出证明。
(提示:类比圆周角定理的证明方法)弦切角定理:________________________________________________________问题:若两个弦切角所夹的弧相等,,那么这两个弦切角相等吗?为什么?弦切角定理的推论:___________________________________________________例如图,AD是ΔABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB,AC分别相交于E,F. 求证:EF∥BC.一、选择题(共17小题)1、如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?()A、97°B、104°C、116°D、142°2、如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何()A、50°B、60°C、100°D、120°3、如图,CD是⊙O的切线,T为切点,A是上的一点,若∠TAB=100°,则∠BTD的度数为()A、20°B、40°C、60°D、80°4、如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于()A、110°B、115°C、120°D、125°5、如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于()A、30°B、60°C、90°D、120°6、如图,△ABC是⊙O的内接三角形,AD是⊙O的切线,点A为切点,∠ACB=60°,则∠DAB的度数是()A、30°B、45°C、60°D、120°7、已知:如图,E是相交两圆⊙M和⊙N的一个交点,且ME⊥NE,AB为外公切线,切点分别为A,B连接AE,BE,则∠AEB的度数为()8、如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=()A、70°B、50°C、30°D、20°9、如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于()度.A、40B、50C、70D、8010、如图,P为半⊙O直径BA延长线上一点,PC切半⊙O于C,且PA:PC=2:3,则sin∠ACP的值为_______11、如图AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )A、30°B、40°C、50°D、60°12、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于()A、40°B、50°C、60°D、70°13、如图,AB、CD是⊙O的两条平行弦,BE∥AC交CD于E,过A点的切线交DC延长线于P,若AC=则PC•CE的值是()A、18B、6C、D、14、如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有()A、1个B、2个C、3个D、4个则∠ACB等于()A、70°B、55°C、70°或110°D、55°或125°16、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是()A、50°B、55°C、60°D、65°17、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是()A、30°B、45°C、50°D、60°二、填空题(共13小题)18、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=_________度.19、已知⊙O 中,的度数为70°,过点A的直线AC与⊙O相切,则弦切角∠BAC的度数为_________.20、如图,AB切⊙O于C,AO交⊙O于D,AO的延长线交⊙O于E,若∠A=α,则∠ECB=_________(用含α的式子表示).21、如图,△ABC内接于圆⊙O,CT切⊙O于C,∠ABC=100°,∠BCT=40°,则∠AOB=___度.22、如图,割线PAB过圆心O,PD切⊙O于D,C 是上一点,∠PDA=20°,则∠C的度数是______度.23、如图,PA、PB是⊙O的两条切线,A、B为切点,则∠ABO ﹣∠ABP=___.24、如图,四边形ABED内接于⊙O,E是AD延长线上的一点,若∠AOC=122°,则∠B=_________度,25、如图,已知AB是⊙O的弦,AC切⊙O于点A,∠BAC=60°,则∠ADB的度数为_________度.26、如图,AB为⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12cm,∠B=30°,则∠ECB=_________度;CD=_________cm.27、如图,已知AB是圆O的弦,AC是圆O的切线,∠BAC的平分线交圆O于D,连BD并延长交AC于点C,若∠DAC=40°,则∠B=_________度,∠ADC=_________度.28、如图,PA切⊙O于A点,C是弧AB上任意一点,∠PAB=58°,则∠C的度数是_________度.29、如图,EF切△ABC的外接圆于C,∠BAC=80°,那么∠BCE=_________度.30、已知:如图,在⊙O中,AB是直径,四边形ABCD内接于⊙O,∠BCD=130°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为_________.3.与圆有关的比例线段 定理 图形 已知 结论 证法相交弦 定理⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB .相交弦定理的推论⊙O 中,AB 为直径,CD⊥AB 于P.PC 2=PA·PB . 用相交弦定理.切割线 定理⊙O 中,PT 切⊙O 于T ,割线PB 交⊙O 于APT 2=PA·PB 连结TA 、TB ,证:△PTB∽△PAT切割线 定理推论PB 、PD 为⊙O 的两条割线,交⊙O 于A 、CPA·PB=PC·PD 过P 作PT 切⊙O 于T ,用两次切割线定理圆幂定理⊙O 中,割线PB 交⊙O 于A ,CD 为弦 P'C·P'D=r 2-OP'2PA·PB=OP 2-r 2r 为⊙O 的半径延长P'O 交⊙O 于M ,延长OP'交⊙O 于N ,用相交弦定理证;过P 作切线用切割线定理勾股定理证8.圆幂定理:过一定点P 向⊙O 作任一直线,交⊙O 于两点,则自定点P 到两交点的两条线段之积为常数||(R 为圆半径),因为叫做点对于⊙O 的幂,所以将上述定理统称为圆幂定理。
相交弦定理和切割线定理

相交弦定理和切割线定理
相交弦定理也称为割线定理,是圆的性质之一,它表明一个圆上的两个相交弦的长度乘积等于这两个弦所夹的两个弧的长度乘积。
具体地说,设两条相交弦AB和CD在圆O上相交于点E,则有:
\[AE \cdot BE = CE \cdot DE\]
切割线定理,又称为弦切线定理,是圆的性质之一。
它表明如果有一条切割线与一条给定的直径相交于一点E,那么这点E
将把切割线分成两段,其中一段的长度是另一段的长度的平方。
具体地说,如果切线与圆的切点为A,圆的中心为O,则有:\[AE^2 = BE \cdot CE\]
相交弦定理和切割线定理都是在圆的几何性质中应用较广的定理,常用于证明和解决与圆相关的问题。
初中圆的十八个定理

初中圆的十八个定理1、圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
3、垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
4、切线的判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
5、切线长定理:从圆外一点引圆的两条切线,他们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
6、公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
7、相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
8、切割线定理:从圆外一点向圆引一条切线和一条割线,则切线长是这点到割线与圆的两个交点的两条线段长。
9、割线长定理:从圆外一点向圆引两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
10、切线的性质定理:圆的切线垂直于经过切点的半径。
11、弦切角定理:弦切角等于它所夹的弧对的圆周角。
12、定理:相交两圆的连心线垂直平分两圆的公共弦。
13、定理:把圆分成n(n≥3),依次连结各分点所得的多边形是这个圆的内接正n边形;经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。
14、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
15、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
16、定理:正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形17、定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
18、(d是圆心距,R、r是半径)①两圆外离d>R+r;②两圆外切d=R+r;③两圆相交R-r<dr;④两圆内切d=R-r (R>r);⑤两圆内含dr。
圆的十八个定理

圆的十八个定理圆的十八个定理包括:1.圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
3.垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
4.切线之判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
5.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
6.公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
7.相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
8.切割线定理:从圆外一点向圆引一条切线和一条割线,则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。
9.割线长定理:从圆外一点向圆引两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
10.切线的性质定理:圆的切线垂直于经过切点的半径。
11.弦切角定理:弦切角等于它所夹的弧对的圆周角。
12.定理:相交两圆的连心线垂直平分两圆的公共弦。
13.把圆分成n(n≥3)个等分:依次连结各分点所得的多边形是这个圆的内接正n边形;经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形。
14.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
15.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形。
16.圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
17.两圆的半径分别为R、r,圆心距为d:两圆外离d>R+r;两圆外切d=R+r;两圆相交R-r<dr);两圆内切d=R-r(R>r);两圆内含d<R-r(R>r)。
18.圆锥曲线:圆是一种特殊的圆锥曲线,它是由一个固定点(焦点)和一个固定直线(准线)上的所有点的轨迹组成的。
圆的定理大全

圆的定理大全:垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。
切线定理:垂直于过切点的半径;经过半径的外端点,并且垂直于这条半径的直线,是这个圆的切线。
如果从圆外一点引两条切线,它们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
切割线定理:圆的一条切线与一条割线相交于P点,切线交圆于C点,割线交圆于A、B两点,则有pC=pA·pB。
割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
圆有关定理

图1
A. 50°B. 40°C. 60°D. 55°
4.圆内两弦相交,一弦长8cm且被交点平分,另一弦被交点分为1:4,则另一弦长为()
A. 8cm B. 10cm C. 12cm D. 16cm
5.在△ABC中,D是BC边上的点,AD= cm,BD=3cm,DC=4cm,如果E是AD的延长线与△ABC的外接圆的交点,那么DE长等于()
当∠DEF=45°时,求证:点G为线段EF的中点;
图8
【模拟试题】(答题时间:40分钟)
一、选择题
1.已知:PA、PB切⊙O于点A、B,连结AB,若AB=8,弦AB的弦心距3,则PA=()
A.20/3B.25/3C. 5 D. 8
2.下列图形一定有内切圆的是()
A.平行四边形B.矩形
C.菱形D.梯形
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段
定理
图形
已知
结论
证法
相交弦定理
⊙O中,AB、CD为弦,交于P.
PA·PB=PC·PD
连结AC、BD,C=B,A=D,所以△APC∽△DPB
相交弦定理的推论
⊙O中,AB为直径,CD⊥AB于P.
PC2=PA·PB
用相交弦定理.
切割线定理
⊙O中,PT切⊙O于T,割线PB交⊙O于A
PT2=PA·PB
连结TA、TB,则∠PTA=∠B(弦切角等于同弧圆周角)所以△PTA∽△PBT,所以
PT2=PA·PB
切割线定理推论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切线长定理、弦切角定理、切割线定理、相交弦定理
以及与圆有关的比例线段
[学习目标]
1.切线长概念
切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2.切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢(四个)
4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段
定理图形已知结论证法
相交弦定理⊙O中,AB、CD为弦,交
于P.
PA·PB=PC·PD. 连结AC、BD,证:
△APC∽△DPB.
相交弦定理的推论⊙O中,AB为直径,CD⊥AB
于P.
PC2=PA·PB. 用相交弦定理.
切割线定理⊙O中,PT切⊙O于T,
割线PB交⊙O于A
PT2=PA·PB连结TA、TB,证:
△PTB∽△PAT
切割线定理推论PB、PD为⊙O的两条割线,
交⊙O于A、C
PA·PB=PC·PD过P作PT切⊙O于T,用
两次切割线定理
圆幂定理⊙O中,割线PB交⊙O于
A,CD为弦P'C·P'D=r2-
OP'2
PA·PB=OP2-r2
r为⊙O的半径
延长P'O交⊙O于M,延
长OP'交⊙O于N,用相交
弦定理证;过P作切线用
切割线定理勾股定理证
8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数| |(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
