七年级规律探索题答案
新初一规律探索题参考答案

前言:七年级上册数学期中考试,主要考察书本前2章,想要考试取得好的成绩,首先应一般能力:①基本知识、基本技能;②计算能力;其次要想获得高分必须具备高分能力:①观察、猜想、推理、验证的能力;②数形结合思想的建立;③分类讨论思想的建立;④方程思想的建立;对于重点中学学生,尤为重要。
高分能力是今后学习领先的有力保障,需要大量练习、总结、体会,七年级涉及的仅仅是一部分。
一、规律探索类题型规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形等条件,要求学生通过:①读题②观察③分析④猜想⑤验证,来探索对象的规律。
它体现了“特殊到一般”、“数形结合”等数学思想方法,考察学生的分析、解决问题能力。
题型可涉及填空、选择或解答。
【题型分类】【1、数字问题】最好具备数列的有关知识(小学奥数有涉及),实际考察的是:经历探索事物间的数量关系,用字母表示数和代数式表示的过程,建立初步的符号感,发展抽象思维,进一步使学生体会到代数式是刻画现实世界的有效数学模型。
如:1、正整数规律1、2、3、4、5、、、、可以表示为n (其中n 为正整数)2、奇数规律1、3、5、7、9、、、、可以表示为21n -(其中n 为正整数)3、偶数规律2、4、6、8、10、、、、可以表示为2n (其中n 为正整数)4、正、负交替规律变化一组数,不看他们的绝对值,只看其性质,为正负交替(1)、-、+、-、+、-、+、-、+可以表示为(1)n -(2)、+、-、+、-、+、-、+、-可以表示为1(1)n +-5、平方数规律1、4、9、16、、、、可以表示为2n (其中n 为正整数),能看得出:上面的规律数+1、+2、-1、-26、等差数列常识按一定次序排列的一列数就叫数列。
例如:(1)1,2,3,4,5,6,…(2)1,2,4,8,16,32;A 、一个数列中从左至右的第n 个数,称为这个数列的第n 项。
专题06 整式中规律探索的三种考法(解析版)-2024年常考压轴题攻略(7年级上册人教版)

专题06整式中规律探索的三种考法类型一、单项式规律性问题例.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2015次跳后它停的点所对应的数为()A.5B.3C.2D.1【答案】C【分析】先根据题意,求出前几次跳到的点的位置,发现这是一个循环,按照3、5、2、1成一个循环,再用解循环问题的方法求解.【详解】解:按照题意,第一次在1这个点,下一次就跳到3,再下一次跳到5,再下一次跳到2,2是偶数了,就逆时针跳一个点,又回到了1这个点,发现这是一个循环,3、5、2、1是一个循环,÷ ,20154=5033∴最后到2这个点.故选:C.【点睛】本题考查找规律,解题的关键是通过前几个数发现这是一个循环问题,利用解循环问题的方法求解.【变式训练1】按上面数表的规律.得下面的三角形数表:【点睛】本题考查了数字的变化类,找出数字的变化规律是解题的关键.类型三、图形类规律探索例.根小棒,搭2020个这样的小正方形需要小棒()根.A.8080B.6066C.6061D.6060【答案】C【分析】通过归纳与总结得出规律:每增加1个正方形,火柴棒的数量增加3根,由此求出第n个图形时需要火柴的根数的代数式,然后代入求值即可.【详解】解:搭2个正方形需要4+3×1=7根火柴棒;搭3个正方形需要4+3×2=10根火柴棒;搭n个这样的正方形需要4+3(n﹣1)=3n+1根火柴棒;∴搭2020个这样的正方形需要3×2020+1=6061根火柴棒;故选C.【点睛】本题考查了图形规律型:图形的变化.解题的关键是发现各个图形的联系,找出其中的规律,有一定难度,要细心观察总结.【变式训练1】下列每一个图形都是由一些同样大小的三角形按一定的规律排列组成的,其中第①个图形中有5个小三角形,第②个图形中有10个小三角形,第③个图形中有16个小三角形,按此规律,则第⑨个图中小三角形的个数是()A.69B.73C.77D.83【答案】B【分析】根据已知图形得出第⑨个图形中三角形的个数的特点,据此可得答案.【详解】解:∵第①个图形中三角形的个数5=1+2×(1-1),第②个图形中三角形的个数10=5+2×1+3,第③个图形中三角形的个数16=5+2×2+3+4,第④个图形中三角形的个数23=5+2×3+3+4+5,第⑤个图形中三角形的个数31=5+2×4+3+4+5+6,……【答案】57【分析】根据每个图形增加三角形的个数,找到规律即可.【详解】解:第1个图形中一共有1个三角形,第2个图形中一共有1+4=5个三角形,第3个图形中一共有1+4+4=9个三角形,…,第n个图形中三角形的个数是1+4(n﹣1)=(4n﹣3)个,当n=15时,4n﹣3=4×15﹣3=57.故答案为:57.【点睛】本题考查了图形的变化规律,解题关键是通过图形数量的变化发现规律,并应用规律解决问题.课后训练20192020)a a -。
七年级数学人教课标(上册)38规律探索

规律探索一、选择题1.(5分)(2014•毕节地区,第18题5分)观察下列一组数:,,,,,…,它们是按一定规律排列的,那么这一组数的第n个数是.个数是故答案为:2.(2014•武汉,第9题3分)观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第5个图中共有点的个数是()3. (2014•株洲,第8题,3分)在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()二.填空题1. (2014•湘潭,16题,3分)如图,按此规律,第6行最后一个数字是16,第672行最后一个数是2014.2. (2014•扬州,第18题,3分)设a1,a2,…,a2014是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,则a1,a2,…,a2014中为0的个数是165.,得到方程组二.填空题1. (2014•珠海,第10题4分)如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA4的长度为8.OA,=;=2OA2.(2014年四川资阳,第16题3分)如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是(,).考点:规律型:点的坐标;等边三角形的性质.菁优网分析:根据O(0,0)A(2,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去,结合图形求出点P6的坐标.解答:解:由题意可得,每一个正三角形的边长都是上个三角形的边长的,第六个正三角形的边长是,故顶点P6的横坐标是,P5纵坐标是=,P6的纵坐标为,故答案为:(,).点评:本题考查了点的坐标,根据规律解题是解题关键.3.(2014年云南省,第14题3分)观察规律并填空(1﹣)=•=;(1﹣)(1﹣)=•••==(1﹣)(1﹣)(1﹣)=•••••=•=;(1﹣)(1﹣)(1﹣)(1﹣)=•••••••=•=;…(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)=.(用含n的代数式表示,n是正整数,且n≥2)考点:规律型:数字的变化类.分析:由前面算式可以看出:算式的左边利用平方差公式因式分解,中间的数字互为倒数,乘积为1,只剩下两端的(1﹣)和(1+)相乘得出结果.解答:解:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)=••••••…=.故答案为:.点评:此题考查算式的运算规律,找出数字之间的联系,得出运算规律,解决问题.4.(2014•邵阳,第18题3分)如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动28 次后该点到原点的距离不小于41.≥5.(2014•孝感,第18题3分)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是(63,32).6.(2014•滨州,第18题4分)计算下列各式的值:;;;.观察所得结果,总结存在的规律,应用得到的规律可得= 102014.先计算得到,=100=10=1000=10,=1000=10=100=10=1000=10=1000=107.(2014•德州,第17题4分)如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…A n,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…M n,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…A n,….则顶点M2014的坐标为(4027,4027).(((8.(2014•菏泽,第14题3分)下面是一个某种规律排列的数阵:根据数阵的规律,第n(n是整数,且n≥3)行从左到右数第n﹣2个数是(用含n的代数式表示)故答案为:9.(2014年山东泰安,第24题4分)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2014的横坐标为.分析:首先利用勾股定理得出AB的长,进而得出三角形的周长,进而求出B2,B4的横坐标,进而得出变化规律,即可得出答案.解:由题意可得:∵AO=,BO=4,∴AB=,∴OA+AB1+B1C2=++4=6+4=10,∴B2的横坐标为:10,B4的横坐标为:2×10=20,∴点B2014的横坐标为:×10=10070.故答案为:10070.点评:此题主要考查了点的坐标以及图形变化类,根据题意得出B点横坐标变化规律是解题关键.三.解答题1. (2014•安徽省,第16题8分)观察下列关于自然数的等式:32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92﹣4×42=17;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.考点:规律型:数字的变化类;完全平方公式.菁优网分析:由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.解答:解:(1)32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…所以第四个等式:92﹣4×42=17;(2)第n个等式为:(2n+1)2﹣4n2=2(2n+1)﹣1,左边=(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1,右边=2(2n+1)﹣1=4n+2﹣1=4n+1.左边=右边∴(2n+1)2﹣4n2=2(2n+1)﹣1.点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.。
人教版七年级数学上图形的规律和线段及角度的计算专题训练含答案

专题训练(一) 图形的规律探索——教材P70T10的变式与应用教材母题:(教材P70T10)如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n(n>1)个点,每个图形总的点数S是多少?当n=5,7,11时,S是多少?【思路点拨】观察图形,可得到点的总数S与n之间的关系,用含n的式子表示S,便可分别求出当n=5,7,11时,S的值.【解答】观察图形,当n=2时,有两排点,总的点数为1+2=3(个);当n=3时,有三排点,总的点数为1+2+3=6(个);当n=4时,有四排点,总的点数为1+2+2+4=9(个);当n=5时,有五排点,总的点数为1+2+2+2+5=12(个).根据此规律,可知点的总数S=1+2(n-2)+n=3n-3,当n=7时,S=3×7-3=18;当n=11时,S=3×11-3=30.故当n=5,7,11时,S的值分别是12,18,30.【方法归纳】解决图形规律探索问题,首先从简单的基本图形入手,随着“序号”或“编号”增加时,后一个图形与前一个图形相比,在数量上的变化情况或图形变化情况,找出变化规律,从而推出一般性结论.1.如图是用相同长度的小棒摆成的一组有规律的图案,其中图1需要4根小棒,图2需要10根小棒,…,按此规律摆下去,则第11个图案所需小棒的根数为(C)A.70 B.68 C.64 D.582.(荆州中考)如图,用黑白两种颜色的纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2 017个白色纸片,则n的值为(B)A.671 B.672 C.673 D.6743.(益阳中考)小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是13枚.4.如图是用棋子摆成的图案:根据图中棋子的排列规律解决下列问题:(1)第4个图中有22枚棋子,第5个图中有32枚棋子;(2)写出你猜想的第n 个图中棋子的枚数(用含n 的式子表示)是n +2+n 2.5.下面是用棋子摆成的“小房子”.摆第10个这样的“小房子”需要多少枚棋子?摆第n 个这样的“小房子”呢?你是如何得到的?解:第1个“小房子”,下边正方形棋子4×2-4=4(枚),上边1枚,共4+1=5(枚); 第2个“小房子”,下边正方形棋子4×3-4=8(枚),上边3枚,共8+3=11(枚); 第3个“小房子”,下边正方形棋子4×4-4=12(枚),上边5枚,共12+5=17(枚); 第4个“小房子”,下边正方形棋子4×5-4=16(枚),上边7枚,共16+7=23(枚); …第n 个“小房子”,下边正方形棋子4×(n+1)-4=4n(枚),上边(2n -1)枚,共4n +2n -1=(6n -1)(枚).当n =10时,6n -1=6×10-1=59(枚).专题训练(二) 线段的计算——教材P128练习T3的变式与应用教材母题:(教材P 128练习T 3)如图,点D 是线段AB 的中点,C 是线段AD 的中点,若AB =4 cm ,求线段CD 的长度.【解答】 因为点D 是线段AB 的中点,AB =4 cm , 所以AD =12AB =12×4=2(c m ).因为C 是线段AD 的中点, 所以CD =12AD =12×2=1(cm ).【方法归纳】 结合图形,将待求线段长转化为已知线段的和、差形式.若题目中出现线段的中点,常利用线段中点的性质,结合线段的和、差、倍、分关系求解.同时应注意题目中若没有图形,或点的位置关系不确定时,常需要分类讨论,确保答案的完整性.1.如图,线段AB =22 cm ,C 是线段AB 上一点,且AC =14 cm ,O 是AB 的中点,求线段OC 的长度.解:因为点O 是线段AB 的中点,AB =22 cm , 所以AO =12AB =11 cm .所以OC =AC -AO =14-11=3(cm ).2.如图,已知C 是AB 的中点,D 是AC 的中点,E 是BC 的中点.(1)若DE =9 cm ,求AB 的长; (2)若CE =5 cm ,求DB 的长.解:(1)因为D 是AC 的中点,E 是BC 的中点, 所以AC =2CD ,BC =2CE.所以AB =AC +BC =2DE =18 cm . (2)因为E 是BC 的中点, 所以BC =2CE =10 cm .因为C 是AB 的中点,D 是AC 的中点, 所以DC =12AC =12BC =5 cm .所以DB =DC +BC =5+10=15(cm ).3.如图,B ,C 两点把线段AD 分成2∶5∶3三部分,M 为AD 的中点,BM =6 cm ,求CM 和AD 的长.解:设AB =2x cm ,BC =5x cm ,CD =3x cm , 所以AD =AB +BC +CD =10x cm . 因为M 是AD 的中点, 所以AM =MD =12AD =5x cm .所以BM =AM -AB =5x -2x =3x(cm ). 因为BM =6 cm , 所以3x =6,x =2.故CM =MD -CD =5x -3x =2x =2×2=4(cm ), AD =10x =10×2=20(cm ).4.如图,线段AB =1 cm ,延长AB 到C ,使得BC =32AB ,反向延长AB 到D ,使得BD =2BC ,在线段CD 上有一点P ,且AP =2 cm .(1)请按题目要求画出线段CD ,并在图中标出点P 的位置;(2)求出线段CP 的长度.解:(1)线段CD 和点P 的位置如图1、2所示.(2)因为AB =1 cm , 所以BC =32AB =32 cm .所以BD =2BC =3 cm .当点P 在点A 的右边时,CP =AB +BC -AP =12cm ;当点P 在点A 的左边时,点P 与点D 重合,CP =BD +BC =92 cm .专题训练(三) 角的计算类型1 利用角度的和、差关系找出待求的角与已知角的和、差关系,根据角度和、差来计算. 1.如图,已知∠AOC=∠BOD=75°,∠BOC =30°,求∠AOD 的度数.解:因为∠AOC=75°,∠BOC =30°,所以∠AO B =∠AOC-∠BOC=75°-30°=45°. 又因为∠BOD=75°,所以∠AOD=∠AOB+∠BOD=45°+75°=120°. 2.将一副三角板的两个顶点重叠放在一起.(两个三角板中的锐角分别为45°、45°和30°、60°)(1)如图1所示,在此种情形下,当∠DAC=4∠BAD 时,求∠CAE 的度数; (2)如图2所示,在此种情形下,当∠ACE=3∠BCD 时,求∠ACD 的度数.解:(1)因为∠BAD+∠DAC=90°,∠DAC =4∠B AD , 所以5∠BAD=90°,即∠BAD=18°. 所以∠DAC=4×18°=72°. 因为∠DAE =90°,所以∠CAE=∠DAE-∠DAC=18°.(2)因为∠BCE=∠DCE-∠BCD=60°-∠BCD,∠ACE =3∠BCD, 所以∠ACB=∠ACE+∠BCE=3∠BCD+60°-∠BCD=90°. 解得∠BCD=15°.所以∠ACD=∠ACB+∠BCD=90°+15°=105°.类型2 利用角平分线的性质角的平分线将角分成两个相等的角,利用角平分线的这个性质,再结合角的和、差关系进行计算.3.如图,点A ,O ,E 在同一直线上,∠AOB =40°,∠EOD =28°46′,OD 平分∠COE,求∠COB 的度数.解:因为∠EOD=28°46′,OD 平分∠COE, 所以∠COE=2∠EOD=2×28°46′=57°32′. 又因为∠AOB=40°,所以∠COB=180°-∠AOB-∠COE=180°-40°-57°32′=82°28′.4.已知∠AOB=40°,OD 是∠BOC 的平分线.(1)如图1,当∠AOB 与∠BOC 互补时,求∠COD 的度数; (2)如图2,当∠AOB 与∠BOC 互余时,求∠COD 的度数. 解:(1)因为∠AOB 与∠BOC 互补, 所以∠AOB+∠BOC =180°. 又因为∠AOB=40°,所以∠BOC=180°-40°=140°. 因为OD 是∠BOC 的平分线, 所以∠COD=12∠BOC=70°.(2)因为∠AOB 与∠BOC 互余, 所以∠AOB+∠BOC=90°. 又因为∠AOB=40°,所以∠BOC=90°-40°=50°. 因为OD 是∠BOC 的平分线, 所以∠COD=12∠BOC=25°.类型3 利用方程思想求解在解决有关余角、补角,角的比例关系或倍分关系问题时,常利用方程思想来求解,即通过设未知数,建立方程,通过解方程使问题得以解决. 5.一个角的余角比它的补角的23还少40°,求这个角的度数.解:设这个角的度数为x °,根据题意,得 90-x =23(180-x)-40.解得x =30.所以这个角的度数是30°. 6.如图,已知∠AOE 是平角,∠DOE =20°,OB 平分∠AOC,且∠COD∶∠BOC=2∶3,求∠BOC 的度数.解:设∠COD=2x °,则∠BOC=3x °. 因为OB 平分∠AOC, 所以∠AOB=3x °.所以2x +3x +3x +20=180. 解得x =20.所以∠BOC=3×20°=60°.7.如图,已知∠AOB=12∠BOC,∠COD =∠AOD=3∠AOB ,求∠AOB 和∠C OD 的度数.解:设∠AOB=x °,则∠COD=∠AOD=3∠AOB=3x °. 因为∠AOB=12∠BOC,所以∠BOC=2x °.所以3x +3x +2x +x =360. 解得x =40.所以∠AOB=40°,∠COD =120°.类型4 利用分类讨论思想求解在角度计算中,如果题目中无图,或补全图形时,常需分类讨论,确保答案的完整性. 8.已知∠AOB=75°,∠AOC =23∠AOB,OD 平分∠AOC,求∠BOD 的大小.解:因为∠AOB=75°,∠AOC =23∠AOB,所以∠AOC=23×75°=50°.因为O D 平分∠AOC,所以∠AOD=∠COD=25°.如图1,∠BOD =75°+25°=100°; 如图2,∠BOD =75°-25°=50°.9.已知:如图,OC 是∠AOB 的平分线.(1)当∠AOB=60°时,求∠AOC 的度数;(2)在(1)的条件下,∠EOC =90°,请在图中补全图形,并求∠AOE 的度数;(3)当∠AOB=α时,∠EOC =90°,直接写出∠AOE 的度数.(用含α的代数式表示)解:(1)因为OC 是∠AOB 的平分线, 所以∠AOC=12∠AOB.因为∠AOB=60°, 所以∠AOC=30°.(2)如图1,∠AOE =∠EOC+∠AOC=90°+30°=120°;如图2,∠AOE =∠EOC-∠AOC=90°-30°=60°. (3)90°+α2 或90°-α2.。
七年级数学探索规律——图形规律(人教版)(专题)(含答案)

试题难度:三颗星知识点:略
4.有一长条型链子,其外型由边长为1的正六边形排列而成.如图是此链子的任意一段示意图,其中每个黑色六边形与6个白色六边形相邻.若此链子上共有35个黑色六边形,则共有( )个白色六边形.
A.140 B.142
C.210 D.212
答案:B
解题思路:
分析:按照分类的思想来考虑,第1个黑色六边形周围的6个白色六边形可以分成两类,左边的2个白色六边形是一类,剩余的4个白色六边形是一类.黑色六边形每增加1个,白色六边形就增加4个.
第3个图中三角形个数为 ;
将上述规律标序号,如下:
① ;
② ;
③ ;
…
所以第 个图中三角形个数为 ;
当 时, ,
所以第20个图中三角形个数为77.
故选C.
试题难度:三颗星知识点:略
7.下列图形是由同样大小的五角星按一定的规律排列组成,其中第1个图形共有2个五角星,第2个图形共有8个五角星,第3个图形共有18个五角星,…,则第10个图形中五角星的个数为( )
当 时, ,
即此链子上共有35个黑色六边形时,共有142个白色六边形.
故选B.
试题难度:三颗星知识点:略
5.一块瓷砖的图案如图1所示,用这种瓷砖铺设地面,如果铺设成如图2的图案,其中完整的圆一共有5个,如果铺设成如图3的图案,其中完整的圆一共有13个,如果铺设成如图4的图案,其中完整的圆一共有25个,依此规律,第10个图中,完整的圆一共有( )
A.100个B.101个
C.181个D.221个
答案:C
解题思路:
分析:按照分类的思想来考虑,可以分为一块瓷砖自带的圆和多块瓷砖拼成的完整的圆;
第1个图案,自带的圆1个,拼成的圆0个,共 个;
数学找规律题及答案

数学找规律题及答案【篇一:七年级上数学规律发现专题训练习题和答案】.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n)个图案中有白色地砖块。
..??2.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
”如图,在一个边长为1的正方形纸版上,依次贴上面积为1111,n2482第3题的矩形彩色纸片(n为大于1的整数)。
请你用“数形结合”的思想,依数形变化的规律,计算1111?????n。
24823.有一列数:第一个数为x1=1,第二个数为x2=3,第三个数开始依次记为x3,x4,?,xn;从第二个数开始,每个数是它相邻两个数和的一半。
(如:x2=x1?x3) 2(1)求第三、第四、第五个数,并写出计算过程; (2)根据(1)的结果,推测x8= ; (3)探索这一列数的规律,猜想第k个数xk=.(k是大于2的整数)4.将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_ 条折痕 .如果对折n次,可以得到条折痕 .5. 观察下面一列有规律的数123456,,,,,,??,根据这个规律可知第n个数是(n是正整数)38152435486.古希腊数学家把数1,3,6,10,15,21,??,叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为。
7. 按照一定顺序排列的一列数叫数列,一般用a1,a2,a3,?,an 表示一个数列,可简记为2{an}.现有数列{an}满足一个关系式:an+1=an-nan+1,(n=1,2,3,?,n),且a1=2.根据已知条件计算a2,a3,a4的值,然后进行归纳猜想an=_________.(用含n 的代数式表示)8.观察下面一列数:-1,2,-3,4,-5,6,-7,...,将这列数排成下列形式按照上述规律排下去,那么第10行从左边第9个数是 . -1 2-34 -56-7-9 10-1112-1314-15169.观察下列等式9-1=8 (8)16-4=12 25-9=16 36-16=20 ????这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n的等式表示这个规律为10.如图是阳光广告公司为某种商品设计的商标图案,图中阴影部分为红色。
七年级上册数学找规律试题

初一数学找规律:1 .(2013山东滨州,18,4分)观察下列各式的计算过程:5×5=0×1×100+25,15×15=1×2×100+25,25×25=2×3×100+25,35×35=3×4×100+25,…… ……请猜测,第n 个算式(n 为正整数)应表示为____________________________.【答案】 [10(n -1)+5]×[10(n -1)+5]=100n(n -1)+25.2. (2013山东莱芜,17,4分)已知123456789101112…997998999是由连续整数1至999排列组成的一个数,在该数种从左往右数第2013位上的数字为 . 【答案】73.(3分)(2013•青岛)要把一个正方体分割成8个小正方体,至少需要切3刀,因为这8个小正方体都只有三个面是现成的.其他三个面必须用三刀切3次才能切出来.那么,要把一个正方体分割成27个小正方体,至少需用刀切 6 次;分割成64个小正方体,至少需要用刀切 9 次.4.(2013泰安)观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…解答下列问题:3+32+33+34…+32013的末位数字是( )A .0B .1C .3D .7考点:尾数特征.分析:根据数字规律得出3+32+33+34…+32013的末位数字相当于:3+7+9+1+…+3进而得出末尾数字.解答:解:∵31=3,32=9,33=27,34=81,35=243,36=729,37=2187…∴末尾数,每4个一循环,∵2013÷4=503…1,∴3+32+33+34…+32013的末位数字相当于:3+7+9+1+…+3的末尾数为3,故选:C .点评:此题主要考查了数字变化规律,根据已知得出数字变化规律是解题关键.5.对于实数x ,我们规定[]x 表示不大于x 的最大整数,例如[]12.1=,[]33=,[]35.2-=-,若5104=⎥⎦⎤⎢⎣⎡+x ,则x 的取值可以是( ).A.40B.45C.51D.56答案:C .考点:新定义问题.点评:本题需要学生先通过阅读掌握新定义公式,再利用类似方法解决问题.考查了学生观察问题,分析问题,解决问题的能力.6.当白色小正方形个数n 等于1,2,3…时,由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________.(用n 表示,n 是正整数)答案:n 2+4n考点:本题是一道规律探索题,考查了学生分析探索规律的能力.点评:解决此类问题是应先观察图案的变化趋势,然后从第一个图形进行分析,运用从特殊到一般的探索方式,分析归纳找出黑白正方形个数增加的变化规律,最后含有n 的代数式进行表示.7.(3分)(2013•烟台)将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( )A . 502B . 503C . 504D . 505考点: 规律型:图形的变化类.分析: 根据正方形的个数变化得出第n 次得到2013个正方形,则4n+1=2013,求出即可.解答: 解:∵第1次:分别连接各边中点如图2,得到4+1=5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9个正方形…,以此类推,根据以上操作,若第n 次得到2013个正方形,则4n+1=2013,解得:n=503.故选:B .点评: 此题主要考查了图形的变化类,根据已知得出正方形个数的变化规律是解题关键.8、(2013安徽)如图,观察每一个图中黑色正六边形的排列规律,则第10个图中黑色正六边形有 个。
部编数学七年级上册专题05整式中的两种规律探索问题(解析版)(人教版)含答案

专题05 整式中的两种规律探索问题类型一、数字类规律探索例.观察:(x ﹣1)(x +1)=x 2﹣1,(x ﹣1)(x 2+x +1)=x 3﹣1,(x ﹣1)(x 3+x 2+x +1)=x 4﹣1,据此规律,当(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=0时,代数式x 2019﹣1的值为 _____.【答案】0或﹣2【详解】解:根据题意得∶ (x ﹣1)(x +1)=x 2﹣1,(x ﹣1)(x 2+x +1)=x 3﹣1,(x ﹣1)(x 3+x 2+x +1)=x 4﹣1,……∴(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=x 6﹣1∵(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=0,∴x 6﹣1=0,解得:x =1或x =﹣1,则x 2019﹣1=0或﹣2,故答案为:0或﹣2.【变式训练1】a 是不为1的有理数,我们把11-a 称为a 的差倒数,如2的差倒数为1-11-2=,-1的差倒数为111(1)2=--,已知15a =,2a 是1a 差倒数,3a 是2a 差倒数,4a 是3a 差倒数,以此类推……,2021a 的值是()A .5B .14-C .43D .45【答案】B【解析】∵15a = , 2a 是1a 的差倒数,∴211154a ==--,∵3a 是2a 的差倒数,4a 是3a 的差倒数,∴314151-4a ==æö-ç÷èø,∴415415a ==-,根据规律可得n a 以5,1-4,45为周期进行循环,因为2021=673×3…2,所以202114a =-.故选B .【变式训练2】有2021个数排成一行,对于任意相邻的三个数,都有中间数等于前后两数的和,如果第一个数是0,第二个数是1, 那么前6个数的和是______, 这2021个数的和是______.【答案】0 1【解析】由题意得:第3个数是101-=,第4个数是110-=,第5个数是011-=-,第6个数是101--=-,则前6个数的和是()()0110110++++-+-=,第7个数是1(1)0---=,第8个数是0(1)1--=,归纳类推得:这2021个数是按0,1,1,0,1,1--循环往复的,202163365=´+Q ,且前6个数的和是0,\这2021个数的和与前5个数的和相等,即为()011011++++-=,故答案为:0,1.【变式训练3】有一列数11315,,,,228432---,…,那么第n 个数为______.【答案】()12n nn-【详解】解:()11122-=-´,()221221242==-´,()3333182-=-´,()4414414162==-´,()55551322-=-´,……由此发现:第n 个数为()12n n n -.故答案为:()12n nn-【变式训练4】杨辉三角又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:按照前面的规律,则()7a b +的展开式中从左起第三项为______.()1a b a b +=+()2222a b a ab b +=++()3322333a b a a b ab b +=+++()4432234464a b a a b a b ab b +=++++LL【答案】5221a b 【详解】解:根据题意,()7a b +=7652433425677213535217a a b a b a b a b a b ab b +++++++,∴()7a b +的展开式中从左起第三项为5221a b ,故答案为:5221a b .类型二、图形类规律探索例.如图,两条直线相交,有1个交点,三条直线相交最多有3个交点,四条直线相交最多有______个交点,n 条直线相交最多有______个交点.【答案】 6 (1)2n n -【详解】解: 如图,两条直线相交最多有1个交点,即()22112´-=;三条直线相交最多有3个交点,即()33132´-=;四条直线相交最多有6个交点,即()44162´-=,五条直线相交最多有10个交点,即()551102´-=,……∴n 条直线两两相交,最多有(1)2n n -个交点(n 为正整数,且n ≥2).故答案为6;(1)2n n -.【变式训练1】如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第_____个图形共有45个小球.【答案】9【详解】解:第1个图中有1个小球,第2个图中有3个小球,3=1+2,第3个图中有6个小球,6=1+2+3,第4个图中有10个小球,10=1+2+3+4,……n(1+n)个小球,照此规律,第n个图形有1+2+3+4+…+n=12n(1+n)=45,∴12解得n=9或-10(舍去),故答案为:9.【变式训练2】为庆祝“六·一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,则n的值为______.【答案】10【详解】解:由题可知:第n个图形有(6n+2)根火柴棒,第(n+1)个图形有(6n+8)根火柴棒,∵摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,∴6n+2+6n+8=130,解得n=10.故答案为:10.【变式训练3】如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数为___个,第n层含有正三角形个数为___个.n-【答案】114 126【解析】根据题意分析可得:从里向外的第1层包括6个正三角形,第2层包括18个正三角形,此后,每层都比前一层多12个,依此递推,第10层中含有正三角形个数是6+12×9=114个,则第n层中含有正三角形个数是6+12×(n-1)=126n-个,故答案为:114,126n-.【变式训练4】观察下列图形:它们是按一定规律排列的,依照此规律,用6064个五角星摆出的图案应该是第_______个图形.【答案】2021【解析】观察发现,第1个图形五角星的个数是:1+3=4,第2个图形五角星的个数是:1+3×2=7,第3个图形五角星的个数是:1+3×3=10,第4个图形五角星的个数是:1+3×4=13,⋯第n个图形五角星的个数是:1+3•n=1+3n,∵6064120213-=,∴用6064个五角星摆出的图案应该是第2021个图形,故答案为:2021.课后训练1.下列图形都是由同样大小的黑色正方形纸片组成,其中第1个图有3张黑色正方形纸片,第2个图有5张黑色正方形纸片,第3个图有7张黑色正方形纸片,…,按此规律排列下去,若第n个图中有201张黑色正方形纸片,则n的值为( )A.99B.100C.101D.102【答案】B【详解】解:观察图形知:第一个图中有3=1+2×1个正方形,第二个图中有5=1+2×2个正方形,第三个图中有7=1+2×2个正方形,…故第n 个图中有1+2×n =2n +1=201(个)正方形,解得n =100故选B .2.如图,将若干颗棋子按箭头方向依次摆放,记第一颗棋子摆放的位置为第1列第1排,第二颗棋子摆放的位置为第2列第1排,第三颗棋子摆放的位置为第2列第2排……,按此规律摆放在第16列第8排的是第( )颗棋子.A .85B .86C .87D .88【答案】B 【详解】偶数列数与排数表:偶数列数排数22436485……n 12n +∴当n =16时,排数为:192n +=,∴前16列共有棋子:()9102123+-3=2-3=872´+++´…9(颗),∴第16列第8排的棋子位次是:87-1=86.故选B .3.将一正方形按如图方式分成n 个完全相同的长方形,上、下各横排三个,中间两行各竖排若干个,则n 的值为( )A .12B .16C .18D .20【答案】C 【详解】解:设长方形的长为a ,宽为b ,根据题意得,2a +2b =3a , 整理得,a =2b ,∴竖排的一行的长方形的个数为3a ÷b =(3×2b )÷b =6,∴n =3×2+6×2=6+12=18.故选:C .4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则x 与y 的和是( )A .9B .10C .11D .12【详解】解:设如图表所示:根据题意可得:x +6+20=22+z +y ,整理得:x -y =-4+z ,x +22+n =20+z +n ,20+y +m =x +z +m ,整理得:x =-2+z ,y =2z -22,∴x -y =-2+z -(2z -22)=-4+z ,解得:z =12,∴x +y =3z -24=12故选:D .5.如图,按此规律,第6行最后一个数字是_____,第_____行最后一个数是2020.【答案】16 674【详解】Q 每一行的最后一个数字分别是1,4,7,10 ,……,\第n 行的最后一个数字为:1+3(1)32n n -=-,\第6行最后一个数字为:36216´-=;322020n -=,解得:674n =,故答案为:16,674.6.如图,每个图形中的三个数之间均具有相同的规律.根据此规律,若图形中11m =,12n =,则M 的值为________.【详解】解:∵1×(2+1)=3,3×(4+1)=15,5×(6+1)=35,∴右下圆圈内的数=上方圆圈内的数×(左下圆圈内的数+1),∴M =m (n +1),∴M =11×(12+1)=143.故答案为:143.7.为了求220211222+++¼+的值,可令220211222S =+++¼+,则220222222S =++¼+,因此2022221S S -=-,所以220212022122221+++¼+=-.按照以上推理计算出1220211333---+++¼+的值是______.【答案】2021332--【详解】解:令1220211333S ---=+++¼+,则1220212022133333S ----=++¼++,因此20221313S S --=-,则20222313S --=-,得:2021332S --=,所以20211220213313332-----+++¼+=.故答案为:2021332--.8.今年“10.1”黄金周,适逢祖国70大庆,广西柳州赛长桌宴,民族风情浓郁,吸引了大量游客如果长桌宴按下图方式就坐(其中□代表桌子,〇代表座位),则拼接n (n 为正整数)张桌子时,最多可就坐_____人.【答案】(6n +2)【详解】解:根据图示知,拼1张桌子,可以坐(2+6)人.拼2张桌子,可以坐[2+(6×2)]人.拼3张桌子,可以坐[2+(6×3)]人.…拼接n (n 为正整数)张桌子,可以坐(6n +2)人.故答案是:(6n +2).9.在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历.我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交又相乘,再相减,例如:7136147´-´=,172316247´-´=,不难发现,结果都是7.2012年8月日一二三四五六12345678910111213141516171819202122232425262728293031(1)请你再选择两个类似的部分试一试,看看是否符合这个规律;(2)换一个月的月历试一下,是否有同样的规律?(3)请你利用整式的运算对以上的规律加以证明.【答案】(1)111710187´-´=,符合;(2)392107´-´=;(3)见解析【详解】解:(1)由题意得:111710187´-´=,符合;(2)392107´-´=;答:换一个月的月历试一下还是同样的规律;(3)设上边第一个数为x ,则其后的数为(x +1),第二行的两个数分别为(x +7),(x +8),根据题意,得22(1)(7)(8)8787x x x x x x x x ++-+=++--=.10.(1)你知道下面每一个图形中各有多少个小圆圈吗?第5个图形中应该有多少个小圆圈?为什么?(2)完成下表:边上的小圆圈数12345每个图中小圆圈的总数(3)如果用n 表示六边形边上的小圆圈数,m 表示这个六边形中小圆圈的总数,那么m 和n 的关系是什么?【答案】(1)第1个图形:1个;第2个图形:7个;第3个图形:19个;第4个图形:37个;第5个图形:61个,理由见解析;(2)1,7,19,37,61;(3)2331m n n =-+【详解】(1)观察每个图形的特点,就可以算出第1个图形的小圆圈有1个,第2个图形的小圆圈有2+3+2=7个,第3个图形的小圆圈有3+4+5+4+3=19个,第4个图形的小圆圈有4+5+6+7+6+5+4=37个,由此可推知第5个图形的小圆圈有5+6+7+8+9+8+7+6+5=61个;(2)将(1)算出的结果填入下列表格,如下表所示,边上的小圆圈数12345每个图中小圆圈的总数17193761(3)结合(1)(2)可知,m 与n 之间的函数关系为:()()()()()1...212...1m n n n n n n n n n n=+++++-++-++-++++首尾相加得()()21...(2)1m n n n n n n =+++++-++-éùëû()()21322213312n n n n n --=+-=-+2331m n n =-+.11.对任意一个四位正整数m ,如果m 的百位数字等于个位数字与十位数字之和,m 的千位数字等于十位数字的2倍与个位数字之和,那么称这个数m 为“筋斗数”.例如:m =5321,满足1+2=3,2×2+1=5,所以5321是“筋斗数”.例如:m =8523,满足2+3=5,但2×2+3=7≠8,所以8523不是“筋斗数”.(1)判断9633和2642是不是“筋斗数”,并说明理由;(2)若m 是“筋斗数”,且m 与13的和能被11整除,求满足条件的所有“筋斗数”m .【答案】(1)9633是“筋斗数”;2642不是“筋斗数”; 理由见解析(2)m 的值为9909或2110或6422【解析】(1)解:9633是“筋斗数”,2642不是“筋斗数”,理由如下:∵6=3+3,9=2×3+3,∴9633是“筋斗数”;∵6=4+2,28+2¹,∴2642不是“筋斗数”;(2)设m 的个位数为a ,0≤a ≤9,十位数为0<b ≤9,且a 、b 为整数∵m 是“筋斗数”,∴m 的百位数为a +b ,千位数为2b +a ;∴m =1000(2b +a )+100(a +b )+10b +a =1100a +110b +2000b +a∵m 与13的和能被11整除,∴1100a +110b +2000b +a +13能被11整除,∵2b +a ≤9且a 、b 为整数,∴b ≤4.5∵1100a +110b 能被11整除,∴2000b +a +13能被11整除,∴b =0,a =9或b =1,a =0或b =2,a =2或b =3,a =4,或b =4,a =6,∴a +b =9,2b +a =9或a +b =1,2b +a =2或a +b =4,2b +a =6或a +b =7,2b +a =10(舍去)或a +b =10,2b +a =14(舍去),∴m 的值为9909或2110或642212.看图填空:如图,把一个面积为1的正方形等分成两个面积为12的长方形,接着把面积为12的长方形等分成两个面积为14的长方形,再把面积为14的长方形等分成面积为18的长方形,如此进行下去……(1)试利用图形揭示的规律计算:1111111112481632641282562n ++++++++L =_______.并使用代数方法证明你的结论.(2)请给利用图(2),再设计一个能求:2341111122222n +++++L 的值的几何图形.【答案】(1)112n - ,证明见解析;(2)见解析【解析】(1)解:①由题意可知当最后一个小长方形的面积为12n时 ,1111111112481632641282562n ++++++++L 的值为正方形面积减去最后一个小长方形面积,即:112n - ,1111111111124816326412825622n n \++++++++=-L ;②设1111111112481632641282562n s =++++++++L ,111111111212481632641282n s -=++++++++L ,1212n s s \-=-,即112ns =-,1111111111124816326412825622n n \++++++++=-L ;(2)如图所示,将面积为1的正方形等分成两个面积为12的三角形,接着把面积为12的三角形等分成两个面积为14的三角形,再把面积为14的三角形等分成面积为18的三角形,如此进行下去,则2341111122222n +++++L 的值即为正方形面积减去最后一个小三角形面积:112n -。
七年级数学(上)探索规律类-问题及答案

七年级数学(上)探索规律类 问题班级 学号 姓名 成绩一、数字规律类:1、一组按规律排列的数:41,93,167,2513,3621,…… 请你推断第9个数是 .2、(2005年山东日照)已知下列等式: ① 13=12; ② 13+23=32; ③ 13+23+33=62;④ 13+23+33+43=102 ;…………由此规律知,第⑤个等式是 .3、(2005年内蒙古乌兰察布)观察下列各式;①、12+1=1×2 ;②、22+2=2×3; ③、32+3=3×4 ;………请把你猜想到的规律用自然数n 表示出来 。
4、(2005年辽宁锦州)观察下面的几个算式:①、1+2+1=4; ②、1+2+3+2+1=9; ③、1+2+3+4+3+2+1=16;④、1+2+3+4+5+4+3+2+1=25,……根据你所发现的规律,请你直接写出第n 个式子 5、(2005年江苏宿迁)观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( ) A .1 B . 2 C .3 D .4 6、(2005年山东济南市)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________。
第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10(第6题图) 第5行 11 -12 13 -14 15 ……………… (第7题图) 7、(05年江苏省金湖实验区)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成如上所示的形式:按照上述规律排下去,那么第10行从左边数第5个数等于 . 二、图形规律类: 8、(2005年云南玉溪)一质点P 从距原点1个单位的A 点处向原点方向跳动,第一次跳动到OA 的中点1A 处,第二次从1A 点跳动到O 1A 的中点2A 处,第三次从2A 点跳动到1条 2条 3条 图1 图2 图 3 O 2A 的中点3A 处,如此不断跳动下去,则第n 次跳动后,该质点到原点O 的距离为 。
2.1 整式-探索规律问题 人教版数学七年级上册专项练习(含答案)

2023年人教版数学七年级上册《探索规律问题》专项练习一、选择题1.小王利用计算机设计了一个计算程序,输入和输出的数据如表:输入…12345…输出……那么,当输入数据为8时,输出的数据为( )A. B. C. D.2.找出以如图形变化的规律,则第20个图形中黑色正方形的数量是( )A.28B.29C.30D.313.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )A.2998B.3001C.3002D.30054.观察图并寻找规律,x处填上的数字是( )A.﹣136B.﹣150C.﹣158D.﹣1625.将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子12+14+18+…的近似值为()A.0.5B.1C.2D.46.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为22024的末位数字是( )A.2B.4C.6D.87.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n 边形“扩展”而来的多边形的边数为( )A.n(n ﹣1)B.n(n +1)C.(n +1)(n ﹣1)D.n 2+28.观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2…已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a ,用含a 的式子表示这组数的和是( )A.2a 2-2aB.2a 2-2a -2C.2a 2-aD.2a 2+a9.已知一组数a 1,a 2,a 3,…,a n ,…,其中a 1=1,对于任意的正整数n ,满足a n +1a n +a n +1﹣a n =0,通过计算a 2,a 3,a 4的值,猜想a n 可能是( )A.1n B.nC.n 2D.110.把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )A.12B.14C.16D.18二、填空题11.用●表示实心圆,用○表示空心圆,现有若干个实心圆与空心圆,按一定的规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…,在前2029个圆中,有 个实心圆.12.下图是某同学一次旅游时在沙滩上用石子摆成的小房子.观察图形的变化规律,写出第n个小房子用了块石子.13.下面是按照一定规律画出的一列“树型”图:经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.14.有一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,… ,写出第n个 .15.按下列图示的程序计算,若开始输入的值为x=﹣6,则最后输出的结果是 .16.观察下列各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s,按此规律推断出s与n的关系为 .17.如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪裁成四个小正方形,如此继续下去,…,根据以上操作方法,请你填写表:操作次数N 12345…n 正方形的个数47101316…a n则a n = (用含n 的代数式表示).18.如图是用小棒按一定规律摆成的一组图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…,若第n 个图案中有65根小棒,则n 的值为 .三、解答题19.寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:(1)当n 个最小的连续偶数相加时,它们的和S 与n 之间有什么样的关系,用公式表示出来;(2)按此规律计算:①2+4+6+…+200值;②162+164+166+…+400值.20.下面的图形是由边长为l 的正方形按照某种规律排列而组成的.(1)观察图形,填写下表:图形①②③正方形的个数8 图形的周长18 (2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y = .21.用火柴棒摆出下列一组图形:(1)填写下表:图形编号123图形中的火柴棒数 (2)照这样的方式摆下去,写出摆第n个图形中的火柴棒数;(用含n的代数式表示)(3)如果某一图形共有2027根火柴棒,你知道它是第几个图形吗?22.观察下列等式:13+23=3213+23+33=6213+23+33+43=102…(1)根据观察得到规律写出:13+23+33+43+53= .(2)根据观察得到规律写出13+23+33+43+…+1003= .(3)13+23+33+43+53+…+n3= .23.阅读材料:求1+2+22+23+24+…+22023的值.解:设S=1+2+22+23+24+…+22022+22023,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22023+22024将下式减去上式得2S﹣S=22024﹣1即S=22024﹣1即1+2+22+23+24+…+22023=22024﹣1请你仿照此法计算:(1)1+2+22+23+24+…+210(2)1+3+32+33+34+…+3n(其中n为正整数).答案1.C2.C.4.D.5.B.6.C.7.B.8.C9.A10.C11.答案为:1353.12.答案为:(n2+4n).13.答案为:80.14.答案为:(﹣1)n nx n .15.答案为:120.16.答案为:S=4(n﹣1).17.答案为:1+3n.18.答案为:16.19.解:(1))∵1个最小的连续偶数相加时,S=1×(1+1),2个最小的连续偶数相加时,S=2×(2+1),3个最小的连续偶数相加时,S=3×(3+1),…∴n个最小的连续偶数相加时,S=n(n+1);(2)①根据(1)得:2+4+6+…+200=100×(100+1)=10100;②162+164+166+ (400)=(2+4+6+…+400)﹣(2+4+6+…+160),=200×201﹣80×81,=40200﹣6480,=33720.20.解:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.(3)∵y=10n+8,x=5n+3,∴y=2x+2.21.解:(1)第一个图形中火柴棒数=2+5=7,第二个图形中火柴棒数=2+5+5=12,第三个图形中火柴棒数=2+5+5+5=17;故答案为:7;12;17;(2)由(1)的规律可知第n个图形的火柴棒根数=2+5n;(3)由题意可知2027=2+5n,解得n=407,∴是第402个图形.22.解:(1)依题意,得13+23+33+43+53=(1+2+3+4+5)2=152=225;(2)依题意,得13+23+33+…+1003=(1+2+3+…+100)2=50502;(3)一般规律为:13+23+33+…+n3=(1+2+3+…+n)2=[]2.故答案为225;50502;[]2.23.解:(1)设S=1+2+22+23+24+ (210)将等式两边同时乘以2得:2S=2+22+23+24+…+210+211,将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1,则1+2+22+23+24+…+210=211﹣1;(2)设S=1+3+32+33+34+…+3n①,两边同时乘以3得:3S=3+32+33+34+…+3n+3n+1②,②﹣①得:3S﹣S=3n+1﹣1,即S=12(3n+1﹣1),则1+3+32+33+34+…+3n=12(3n+1﹣1).。
北师大版七年级数学上册《探索与表达规律》专项练习(含答案)
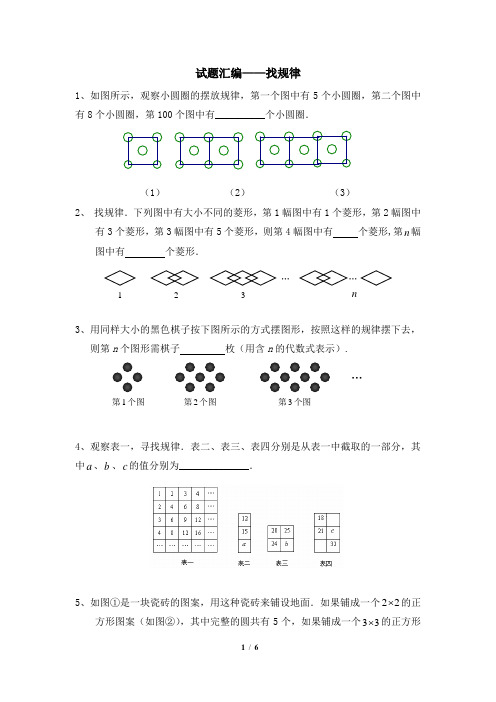
试题汇编——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形1 2 3 n … … 第1个图 第2个图 第3个图…图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子 枚(用含有n 的代数式表示,并写成最简形式).○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形 需 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示实数9,则表示实数17的有序实数对是 .9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是第一排 第二排 第三排 第四排 6 ┅┅ 10 9 87 32 15 410、观察图4的三角形数阵,则第50行的最后一个数是 ( )1-2 3-4 5 -67 -8 9 -10。
(完整版)七年级数学整式的加减探索规律(习题及答案)

探索规律(习题)➢例题示范例1:观察图1至图4中小圆圈的摆放规律,并按这样的规律继续摆放,记第n个图中小圆圈的个数为M,则M=__________(用含n的代数式表示).…图1 图2 图3 图4思路分析做图形规律的题,我们一般从两个方面来研究:(1)观察图形的构成.(2)转化.观察本题的图形,发现后面的图形总比前面的图形多3个小圆圈,可以采用分类的手段进行解决.分成原来的和增加的两类.①2+3×1②2+3×2③2+3×3④2+3×4则第n个:2+3n=3n+2.验证:当n=1时,3n+2=5,成立.故第n个图形中有(3n+2)个小圆圈.(想一想,还有其他观察角度吗?)例2:观察下列球的排列规律(其中●是实心球,○是空心球):…从第1个球起到第2 014个球止,共有实心球________个.思路分析①判断该题是循环规律,查找重复出现的结构,即循环节;②观察图形的变化规律,发现每10个球为一个循环,每个循环节里有3个实心球.故2 014÷10=201…4,201×3=603;③再从某个循环节开始查前4个球,发现有2个实心球,故总数为603+2=605(个).➢巩固练习1.如下数表是由从1开始的连续自然数组成,观察规律并完成下列各题.123456781011121314151617181920212223242526272829303132333435369…(1)表中第8行的最后一个数是_____,它是自然数______ 的平方,第8行共有________个数;(2)用含n 的代数式表示:第n 行的第一个数是_________, 最后一个数是_________,第n 行共有_________个数. 2. 将1,-2,3,-4,5,-6,…按一定规律排成下表:(1)第8行的数是_________________________________; (2)第50行的第一个数是_______.3. 下列图形由边长为1的正方形按某种规律排列而成,依此规律,则第8个图形中正方形有( )…图3图2图1A.38个 B.41个 C.43个D.48个4.如下图所示,摆第1个“小屋子”要5枚棋子,摆第2个要11枚棋子,摆第3个要17枚棋子,则摆第30个要_________枚棋子.…第3个第2个第1个5. 下列图案由边长相等的黑白两色正方形按一定规律拼接而成,依此规律,第n 个图案中白色正方形的个数为_________.…图3图2图16. 观察下列图形,根据图形及相应点的个数的变化规律,第n 个图形中点的个数为__________.图5图4图1图2图3…7. 如图1,一等边三角形的周长为1,将这个等边三角形的每边三等分,在每边上分别以中间的一段为边作等边三角形,然后去掉这一段,得到图2;再将图2中的每一段作类似变形,得到图3;按上述方法继续下去得到图4,则第4个图形的周长为________,第n 个图形的周长为________________.…图1 图2 图38. 一个纸环链,纸环按“红黄绿蓝紫”的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )红 黄 绿 蓝 紫 红 黄 绿 … … 黄 绿 蓝 紫 A .2 012B .2 013C .2 014D .2 0159. 小时候我们就用手指练习过数数,一个小朋友按图中的规则练习数数,数到2 013时对应的手指头是( ) A .大拇指B .食指C .小拇指D .无名指大拇指1234567891011121314151617181910. 如图,平面内有公共端点的八条射线OA ,OB ,OC ,OD ,OE ,OF ,OG ,OH ,从射线OA 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,8,9,….(1)“20”在射线______________上; (2)请任意写出三条射线上的数字排列规律; (3)“2 015”在哪条射线上?➢ 思考小结1. 我们学习了数的规律、式的规律、图形规律、循环规律等,它们都有对应的操作方法.(1)数与式的规律:①_________;②_________;③处理符号;④验证. (2)图形规律:①观察图形的构成:____________________;②转化:________________________________________. (3)循环规律:①________________;②____________________.HD【参考答案】➢巩固练习1.(1)64,8,15;(2)(n-1)2+1(或n2-2n+2),n2,(2n-1).2.(1)29,-30,31,-32,33,-34,35,-36;(2)-1 226.3. C4.1795.5n+36.n2-n+17.6427,143n-⎛⎫⎪⎝⎭8. B9. C10.(1)OD(2)射线OA:8n-7;射线OB:8n-6;射线OC:8n-5;射线OD:8n-4;射线OE:8n-3;射线OF:8n-2;射线OG:8n-1;射线OH:8n.任选三个即可.(3)在射线OG上.➢思考小结1.(1)①标序号;②找结构.(2)①分类,去重,补形;②转化为数的规律或其他图形的规律.(3)①确定起始位置;②找循环节.。
【常考压轴题】专题08 整式中规律性探索的三种考法(解析版)七年级数学上册压轴题攻略

专题08整式中规律探索的三种考法类型一、数字类规律探索问题A .29-,AB .30,DC .29,B 【答案】A 【分析】观察不难发现,每个峰排列5个数,求出5个峰排列的数的个数,中C 位置的数的序数,然后根据排列的奇数为负数,偶数为正数解答;用根据商和余数的情况确定所在峰中的位置即可.【详解】解:由题意得,每个峰排列5个数,排列的奇数为负数,偶数为正数∵每个峰需要5个数,∴5525⨯=,251329++=,∴“峰6”中C 位置的数的是29-,∵202254042÷=⋅⋅⋅⋅⋅⋅,∴2022应排在A 、B 、C 、D 、E 中A 的位置,故选:A .【点睛】本题是对数字变化规律的考查,观察出每个峰有5个数是解题的关键,上的数的排列是从2开始.例2.一组按规律排列的式子:2b a -,52b a ,83b a -,()114,0b ab a ⋯≠A .31n b a--B .()311n n n b a +-C .()311n n n b a --【答案】C【答案】4【分析】由题意知,第一次输出的结果是4,第二次输出的结果是1,第四次输出的结果是4,第五次输出的结果是=⨯+,进而可得第2023次输出的结果.202336741【详解】解:由题意知,第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是2,……,∴可知三次为一个循环,=⨯+,∵202336741∴第2023次输出的结果是4,故答案为:4.【点睛】本题考查了程序流程图与有理数计算,规律探究.解题的关键在于根据推导一般性规律.【变式训练1】按下面的程序计算:若输入n=100,输出结果是501;若输入n=25,输出结果是631,若开始输入的n值为正整数,最后输出的结果为656,则开始输入的n值可能有()A.1种B.2种C.3种D.4种【答案】C【分析】分三种情况讨论,当输入n经过一次运算即可得到输出的结果为656,当输入n经过两次运算即可得到输出的结果为656,当输入n经过三次运算即可得到输出的结果为656,再列方程,解方程即可得到答案.【详解】解:当输入n经过一次运算即可得到输出的结果为656,51556∴+=,n∴=5655,nn∴=131.当输入n经过两次运算即可得到输出的结果为656,()∴++=5511656,n∴+=26.51131,n∴=n当输入n经过三次运算即可得到输出的结果为656,()∴+++=n555111656,⎡⎤⎣⎦()∴++=5126,n5511131,∴+=5n∴=.n综上:开始输入的n值可能是5或26或131.故选:C.【点睛】本题考查的是程序框图的含义,一元一次方程的解法,分类思想的应用,掌握以上知识是解题的关键.课后训练A .31B .49C .62D 【答案】B 【分析】分别计算出前6次“F 运算”的结果即可得到规律,根据规律求解即可.【详解】解:当49n =时,第1次“F 运算”的结果是3495152⨯+=,第2次“F 运算”的结果是3152192=,第3次“F 运算”的结果是193562⨯+=,第4次“F 运算”的结果是62312=,A .13-B .2【答案】CA.73B.81C.91D.109【答案】C【分析】根据图形,将每个图形分为上下两部分,分别数出每个图形两部分中菱形的个数,总结出数量变化的一般规律即可.【详解】解:由图可知:第一个图形:上面由3个菱形,下面有0个菱形,第二个图形:上面有6个菱形,下面有1个菱形,第三个图形:上面有10个菱形,下面有3个菱形,第四个图形:上面有15个菱形,下面有6个菱形,……A .62B .70【答案】B 【分析】观察图形得到第1个五边形数为1,第为14712++=,第4个五边形数为14710+++数都比前面一个数大3的几个数的和,且数的个数等于序号数,则第1471013161970++++++=.【详解】解:∵第1个五边形数为1,第2个五边形数为145+=,第3个五边形数为14712++=,第4个五边形数为1471022+++=,∴第5个五边形数为147101335++++=,第6个五边形数为14710131651+++++=,第7个五边形数为1471013161970++++++=故选:B .【点睛】本题考查了图形的变化规律,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.6.如图是按照一定规律“生长”的“勾股树”.经观察可以发现:图②中共有7个正方形,图③中共有15个正方形,照此规律形的个数是()A .31B .32C .63D .64【答案】C 【分析】根据图形,可以得到正方形个数的变化特点,从而可以得到图⑤中正方形的个数.【详解】解:由图可得,第①个图形中正方形的个数为:212321+==-,第②个图形中正方形的个数为:23122721++==-,第③个图形中正方形的个数为:23412221521+++==-,…则第⑤个图形中正方形的个数为:62164163-=-=,故选:C .【点睛】本题考查图形的变化类,解答本题的关键是明确题意,发现正方形个数的变化特点,求出图⑤中正方形的个数.7.下列图形都是由大小相同的小正方形按一定规律组成的,其中第①个图形中有1个小正方形,第②个图形中有5个小正方形,第③个图形中有11个小正方形,…,按此规律排列下去,第⑦个图形中的小正方形个数为()个A .40B .49C .55D .71【答案】C 【分析】由已知图形中点的分布情况知:横放是图形序号的平方减去1,竖着摆放的数与序号相同,再进行相加即可.【详解】解:根据图形可得第①个图案正方形个数为:21111=-+;第②个图案正方形个数为:2532212=+=-+;第③个图案正方形个数为:21183313=+=-+;第④个图案正方形个数为:219154414=+=-+;所以,第⑦个图形中的小正方形个数为271755-+=(个)故选:C【点睛】本题考查了规律型中的图形变化问题,要求学生首先分析题意,找到规律,并进行推导得出答案.8.如图1,AE 是O 的直径,点B 、C 、D 将半圆分成四等分,把五位同学分别编为序号1、2、3、4、5按顺序站在半圆的五个点上,现把最右边的5号同学调出,站到2号和3号两位同学之间,再把最右边的4号同学调出,站到1号和2号两位同学之间,得到图2,称为“1次换序”.接着按同样的方法,把最右边的3号同学调出,站到4号和2号两位同学之间,再把最右边的5号同学调出,站到1号和4号两位同学之间,得到图3,称为“2次换序”.以此类推……;若从图1开始,经过“n 次换序”后,得到的顺序与图1相同,则n 的值可以是()A .11B .12C .13D .14【答案】B 【分析】先得到前4次换序后的结果,再归纳类推出一般规律,由此即可得.【详解】解:由题意得:1次换序后,得到的顺序为1,4,2,5,3,2次换序后,得到的顺序为1,5,4,3,2,3次换序后,得到的顺序为1,3,5,2,4,4次换序后,得到的顺序为1,2,3,4,5,由此可知,每经过4次换序,得到的顺序与图1相同,即此时4n k =(k 为正整数),观察四个选项可知,只有选项B 符合题意,故选:B .【点睛】本题考查了图形类规律探索,正确归纳类推出一般规律是解题关键.。
七年级数学上册36探索规律试题试题

黄河水利HY 会黄河中学七年级数学上册?3.6 探究规律?试题北师大版对材料信息的加工提炼和运用,对规律归纳和发现能反映出一个人的应用数学、开展数学和进展数学创新的意识和才能。
求解探究规律型试题要求学生有敏锐的观察力,能从特殊的情况出发,经过周密的考虑,全面的分析,去推得一般的结论。
这类试题意在检测解题者驾驭数学的创新意识和才能。
【命题趋势分析】例1日常生活中我们使用的数是十进制数.而计算机使用的数是二进制数,即数的进位方法是“逢二进一〞.二进制数只使用数字0、1,如二进制数1101记为1101)2(,1101)2(通过式子120212123+⨯+⨯+⨯可以转换为十进制数13,仿照上面的转换方法,将二进制数11101)2(转换为十进制数是〔 〕.〔A 〕29 〔B 〕25 〔C 〕4 〔D 〕33 【解答】计算机中的“二进制〞,选A例2观察以下顺序排列的等式:猜测:第n 个等式〔n 为正整数〕应为___________________。
【解答】〔或者〕例3用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成假设干个图案: 〔1〕第四个图案中有白色地砖 块;〔2〕第n 个图案中有白色地砖 块.……第10题图第三个第二个第一个【解答】〔1〕18;〔2〕24+n例4(1)如表,方程1,方程2,.方程3,… ,是按一定规律排列的一列方程, 解方程1,将它的解填在表中的空白处;(2) 假设方程)(11b a bx xa>=--的解是10,621==x x ,求a 、b 的值.该方程是不是(1)中所给出的一列方程中的一个方程?假如是,它是第几个方程? (3) 请写出这列方程的第n 个方程的解,并验证所写的解合适第n 个方程.【分析】比拟、分析、观察、猜测、归纳、概括、验证等思维方法的考察是此题的独到之处. 【解答】(1)1216=--x x,整理,得01272=+-x x . 解得 4,321==x x . 经检验知, 4,321==x x 是原方程的根.(2)将10,621==x x 分别代入11=--bx x a ,得⎪⎪⎩⎪⎪⎨⎧=--=--.110110,1616ba ba 消去a,整理,得060172=+-b b ,解得.12,521==b b 当12,521==b b 时 ;当.12,1222==a b 时∵a>b,∴⎩⎨⎧==.5,12b a 经检验知, ⎩⎨⎧==5,12b a 合适分式方程组. 所得方程为15112=--x x ,它是(1)中所给一列方程中的一个,是第4个. (3)这列方程的第n 个方程为1)1(1)2(2=+--+n x x n (n ≥2,n 为整数). 它的解为).1(2,221+=+=n x n x 检验:当2+=n x 时, 左边=112)1()2(12)2(2=-=+-+-++n n n n = 右边. 当)(12+=n x 时, 左边=11112)1()1(2112)2(2=+-++=+-+-++n n n n n n n )( = 右边 所以).1(2,221+=+=n x n x 是方程1)1(1)2(2=+--+n x x n 的解. 【说明】 ⎪⎪⎩⎪⎪⎨⎧=--=--.110110,1616ba ba应该消去未知数a,而用换元法是徒劳的.验证一个数是否是方程的根方法,只需将这个数作为未知数的值分别代入方程的左右两边,验证左边是否等于右边即可.注意不要直接代入方程.例5探究规律:如图3〔1〕1,直线m ∥n ,A 、B 为直线n 上的两点,C 、P 为直线m 上的两点.〔1〕请写出图中面积相等的各对三角形: .〔2〕假如A 、B 、C 为三个定点,点P 在m 上挪动,那么无论P 点挪动到任何位置 总有: 与△ABC 的面积相等;理由是: .n m第26题图1OBA PC第26题图2EDCBA第26题图3NMEDCBA解决问题:如图3〔2〕,五边形ABCDE 是张大爷十年前承包的一块土地的示意图,经过多年开开荒地,现已变成如图3〔3〕所示的形状,但承包土地与开开荒地的分界小路〔图3〔3〕中折线CDE 〕还保存着,张大爷想过E 点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用有关的几何知识,按张大爷的要求设计出修路方案.〔不计分界小路与直路的占地面积〕〔1〕写出设计方案,并在图3〔3〕中画出相应的图形; 〔2〕说明方案设计理由.【解答】探究规律:〔1〕△ABC 和△ABP, △AOC 和△BOP, △CPA 和△CPB;(2) △ABP.因为平行线间的间隔 相等,所以无论点P 在m 上挪动到任何位置,总有△ABP 与△ABC 同底等高,因此,它们的面积总相等. 解决问题:〔1〕画法如图.连结EC, 过点D 作DF//EC, 交CM 于点F, 连结EF, EF 即为所求直路的位置. 〔2〕设EF 交CD 于点H, 由上面得到的结论,可知: S △ECF =S △ECD , S △HCF =S △EDH .图3〔1〕 图3〔3〕图3〔2〕∴S 五边形ABCDE =S 五边形ABCFE ,S 五边形EDCMN = S 四边形EFMN .【中考试题精选】 一、选择题1.计算机是将信息转换成二进制数进展处理的,二进制即“逢2进1”,如2)1101( 表示二进制数,将它转换成十进制形式是13212021210123=⨯+⨯+⨯+⨯,那么将二进制数2)1111(转换成十进制形式是数〔 〕. A 、8 B 、15 C 、20 D 、30 2.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:那么,当输入数据是8时,输出的数据是〔 〕C A 、618 B 、638 C 、658 D 、678 3.下面一组按规律排列的数:1,2,4,8,16,……,第2021个数应是〔 〕.A 、20022B 、20022-1C 、20012D 、以上答案不对4.小亮从一列火车的第m 节车厢数起,一直数到第n 节车厢〔n >m 〕,他数过的车厢节数是〔 〕.C〔A 〕m +n 〔B 〕n -m 〔C 〕n -m -l 〔D 〕n -m +1CFM5.图〔1〕是一个程度摆放的小正方体木块,图〔2〕、〔3〕是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是〔 〕.C 〔A 〕25 〔B 〕66 〔C 〕 91〔D 〕120二、填空题1.观察以下算式:221= 422= 823= 1624= 3225= 6426=12827= 25628= 通过观察,用你所发现的规律写出98的末位数是 . 22.古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,它有一定的规律性,那么第24个三角形数与第22个三角形数的差为 .3.请你观察考虑以下计算过程:∵211=121,∴121=11;同样:∵2111=12321,∴12321=111;…… 由此猜测76543211234567898= 。
初中数学专题探索规律(一)(含答案)

4.6.1 探索规律(一)想一想●怎样从几个简单的、个别的、特殊的情况出发去研究、探索、归纳出一般的规律和性质?怎样应用一般的规律和性质去解决特殊的问题?做一做1.观察规律,填数:(1)9,11,13,______…,第10个数是________;(2)11,17,27,_____,______,______…,使这列数从第三个数开始,•每个数都是前两个数的和减去1.2.观察右图,填空:由上而下,第n 行,白球有______个,黑球有_______,黑白球的数目共________个.3.给出算式:32-12=8=8*1,52-32=16=8*2,72-52=24=8*3,92-72=32=8*4,…观察上面一系列算式,你能发现什么规律?*表示哪种运算?用代数式表示这一规律.4.观察如图星阵后,推测:1+3=______;1+3+5=______;1+3+5+7=_______;1+3+5+7+9=______;…1+3+5+…+(2n-1)=_______.试一试5.探索规律:(1)计算并观察下列各组算式:88____,79____;⨯=⎧⎨⨯=⎩ 55______,46______;⨯=⎧⎨⨯=⎩ 1212______,1113______;⨯=⎧⎨⨯=⎩(2)已知25×25=625,那么24×26=_________;(3)你能举一个类似的例子吗?(4)从以上的过程中,你发现了什么规律?用语言叙述这个规律,并用代数式表示出来.答案:1.(1)15,27 (2)43,69,111 2.n,2n-1,3n-13.(2n+1)2-(2n-1)2=8n,*表示乘法 4.4;9;16;25;n2 5.(1)略(2)624 (3)略(4)(n-1)(n+1)=n2-1。
探索规律专项练习(含答案)

探索规律练习专题(含答案)1、(2015•山东临沂,第11题3分)观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,….按照上述规律,第2015个单项式是()(A) 2015x2015. (B) 4029x2014. (C) 4029x2015. (D) 4031x2015. 【答案】C【解析】试题分析:根据这组数的系数可知它们都是连续奇数,即系数为(2n -1),而后面因式x的指数是连续自然数,因此关于x的单项式是,所以第2015个单项式的系数为2×2015-1=4029,因此这个单项式为. 故选C考点:探索规律2、(2015•四川省内江市,第16题,5分)如图是由火柴棒搭成的几何图案,则第n个图案中有根火柴棒.(用含n的代数式表示)考点:规律型:图形的变化类.. 专题:压轴题.分析:本题可分别写出n=1,2,3,…,所对应的火柴棒的根数.然后进行归纳即可得出解答:解:依题意得:n=1,根数为:4=2×1×(1+1);n=2,根数为:12=2×2×(2+1);n=3,根数为:24=2×3×(3+1);…n=n时,根数为:2n(n+1).点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.3、(2015·深圳,第15题分)观察下列图形,它们是按一定规律排列的,依照此规律,第5个图形有个太阳。
【答案】21【解析】第一行的规律是1,2,3,4,…,故第五个数是5;第二行的规律是1,2,4,8,…,故第五个数是16;故第五个图中共有21个太阳。
4、(2015·南宁,第18题3分)如图9,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点A N,如果点A N与原点的距离不小于20,那么n的最小值是.考点:规律型:图形的变化类;数轴..分析:序号为奇数的点在点A的左边,各点所表示的数依次减少3,序号为偶数的点在点A的右侧,各点所表示的数依次增加3,于是可得到A13表示的数为﹣17﹣3=﹣20,A12表示的数为16+3=19,则可判断点A n与原点的距离不小于20时,n的最小值是13.解答:解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1﹣3=﹣2﹣2;第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为﹣2+6=4;第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4﹣9=﹣5;第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为﹣5+12=7;第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7﹣15=﹣8;…;则A7表示的数为﹣8﹣3=﹣11,A9表示的数为﹣11﹣3=﹣14,A11表示的数为﹣14﹣3=﹣17,A13表示的数为﹣17﹣3=﹣20,A6表示的数为7+3=10,A8表示的数为10+3=13,A10表示的数为13+3=16,A12表示的数为16+3=19,所以点A n与原点的距离不小于20,那么n的最小值是13.故答案为:13.点评:本题考查了规律型,认真观察、仔细思考,找出点表示的数的变化规律是解决本题的关键.5、(2015·湖北省孝感市,第15题3分)观察下列等式:1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,则1+3+5+…+2015=.考点:规律型:数字的变化类分析:根据1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,可得1+3+5+…+(2n ﹣1)=n2,据此求出1+3+5+…+2015的值是多少即可.解答:解:因为1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,所以1+3+5+…+2015=1+3+5+…+(2×1008﹣1)=10082=1016064 故答案为:1016064.点评:此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:1+3+5+…+(2n﹣1)=n2.6、(2015·湖南省益阳市,第13题5分)如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有有根小棒.考点:规律型:图形的变化类.分析: 由图可知:第1个图案中有5+1=6根小棒,第2个图案中有2×5+2﹣1=11根小棒,第3个图案中有3×5+3﹣2=16根小棒,…由此得出第n 个图案中有5n +n ﹣(n ﹣1)=5n +1根小棒.解答: 解:∵第1个图案中有5+1=6根小棒,第2个图案中有2×5+2﹣1=11根小棒, 第3个图案中有3×5+3﹣2=16根小棒, …∴第n 个图案中有5n +n ﹣(n ﹣1)=5n +1根小棒.故答案为:5n +1.点评: 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.7、(2015·黑龙江绥化,第20题分)填在下面各正方形中的四个数之间都有一定的规律 ,按此规律得出a +b +c =__________考点:规律型:数字的变化类.分析:观察不难发现,左上角+4=左下角,左上角+3=右上角,右下角的数是左下角与右上角两个数的乘积减去1的差,根据此规律列式进行计算即可得解. 解答:解:根据左上角+4=左下角,左上角+3=右上角,右下角的数是左下角与右上角两个数的乘积减去1的差,可得6+4=a ,6+3=c ,ac +1=b ,可得:a =10,c =9,b =91,所以a +b +c =10+9+91=110,故答案为:110点评:本题是对数字变化规律的考查,仔细观察前三个图形,找出四个数之间的变化规律是解题的关键.8、(2015•广东省,第15题,4分)观察下列一组数:13,25,37,49,511,…,根据该组数的排列规律,可推出第10个数是 . 【答案】1221. 【考点】探索规律题(数字的变化类). 【分析】观察得该组数的排列规律为:分母为奇数,分子为自然数,第n 个数为21+n n ,所以,第10个数是1012210121=⨯+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前言:七年级上册数学期中考试,主要考察书本前2章,想要考试取得好的成绩,首先应一般能力:①基本知识、基本技能;②计算能力;其次要想获得高分必须具备高分能力:①观察、猜想、推理、验证的能力;②数形结合思想的建立;③分类讨论思想的建立;④方程思想的建立;对于重点中学学生,尤为重要。
高分能力是今后学习领先的有力保障,需要大量练习、总结、体会,七年级涉及的仅仅是一部分。
一、规律探索类题型规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形等条件,要求学生通过:①读题 ②观察 ③分析 ④猜想 ⑤验证,来探索对象的规律。
它体现了“特殊到一般”、“数形结合”等数学思想方法,考察学生的分析、解决问题能力。
题型可涉及填空、选择或解答。
【题型分类】 【1、数字问题】最好具备数列的有关知识(小学奥数有涉及),实际考察的是:经历探索事物间的数量关系,用字母表示数和代数式表示的过程,建立初步的符号感,发展抽象思维,进一步使学生体会到代数式是刻画现实世界的有效数学模型。
如: 1、正整数规律1、2、3、4、5、、、、可以表示为n (其中n 为正整数) 2、奇数规律1、3、5、7、9、、、、可以表示为21n -(其中n 为正整数) 3、偶数规律2、4、6、8、10、、、、可以表示为2n (其中n 为正整数) 4、正、负交替规律变化一组数,不看他们的绝对值,只看其性质,为正负交替 (1)、-、+、-、+、-、+、-、+可以表示为(1)n- (2)、+、-、+、-、+、-、+、-可以表示为1(1)n +-5、平方数规律1、4、9、16、、、、可以表示为2n (其中n 为正整数),能看得出:上面的规律数+1、+2、-1、-26、等差数列常识按一定次序排列的一列数就叫数列。
例如:(1) 1,2,3,4,5,6,… (2) 1,2,4,8,16,32;A 、一个数列中从左至右的第n 个数,称为这个数列的第n 项。
如,数列(1)的第3项是3,数列(2)的第3项是4。
一般地,我们将数列的第n 项记作a n 。
B 、数列中的数可以是有限多个,如数列(2)(4),也可以是无限多个,如数列(1)(3)(带省略号)。
概念:干个数排成一列称为数列,数列中的每一个数称为一项,其中第一项称为首项(记作:1a ),最后一项称为末项(记作:n a )。
后项与前项之差都相等的数列称为等差数列,后项与前项之差称为公差(记作:d )。
其中:1(1)n a a n d =+-, 11n a a n d-=+,数列的和1()2n n a a nS +⨯= (记得住就记,记不住就推理)方法说明:掌握3个原则:①数据表面上看来排列无序,且形式不一致,那么要进行数据变形,使之形式一致;②一组数中的每个数进行数据分解,有时可快速得出规律;③对数据做一些简单的运算看出规律,如:加一加、减一减,乘一乘、除一除 例1 观察一列数:1,-,3611,259,167,95,43--……根据规律,请你写出第10个数是 。
例2 古希腊数学家把1,3,6,10,15,21,… 叫做三角形数,根据它的规律,则第100个与第98个的差为 ________练习:(1)观察一列数:21,52-,103,174-,265,376-……根据规律,请你写出第10个数是? (2)按一定规律排列的一列数依次为11113102635---11,,,,,,,215按此规律排列下去,这列数中第七个数是(3)某种细胞开始有2个,1小时后分裂成4并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1个,按此规律,5小时后细胞存活数是____,n 小时后细胞存活数是____ 【2、图形规律】根据一组相关图形的变化规律,从中总结图形变化所反映的规律。
解决图形规律问题的方法有两种:一种是数形结合,将图形转化成数字规律,用数字规律的解决问题;一种是通过图形的直观性,观察图形的变化,主要从各图形的形状、方向、数量、大小及各组成部分的相对位置入手,从中找出变化规律。
例3 观察图给出的四个点阵,s 表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n 个点阵中的点的个数s 为( )A 、32n -B 、31n -C 、41n +D 、43n -例4 若按下图方式摆放餐桌和椅子,请探索规律并填表: 餐桌张数 1234…..10n可坐人数练习:(1)观察下列图形,则第n 个图形中三角形的个数是( )A 、22n +B 、44n +C 、44n -D 、4n(2) 如图是一组有规律的图案, 第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……第8个图案由_____个基础图形组成,第n (n 是正整数)个图案中由 ___ 个基础图形组成。
(3)下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .【3、循环排列规律】循环排列规律是运动着的规律,我们只要根据题目的已知部分分析出图案或数据每隔几个就会循环出现,看看最后所求的与循环的第几个一致即可,关键是找出“循环节数”。
其次,就是利用“余数”。
例5 如图所示,数轴被折成90︒,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。
先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴 的正方向滚动,那么数轴上的数2009将与圆周上的数字 重合。
例6 手的示意图,在各个手指间标记字母A 、B 、C 、D .请你按图中箭头所指方向(即A →B →C →D →C →B →A →B →C…的方式)从A 开始数连续的正整数1,2,3,4…,当数到12时,对应的字母是____;当字母C 第 201次出现时,恰好数到的数是____;当字母C 第2n+1次出现时(1)(2) (3)………… ……第1个第2个第3个(1) (2)(3)……9876543123(n 为正整数),恰好数到的数是_______(用含n 的代数式表示). 练习:(1)如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。
先让圆周上数字0所对应的点与数轴上的数1-所对应的点重合,再让数轴按逆时针方向绕在该圆上,那么数轴上的数2006-将与圆周上的数字 重合。
(2)观察下图中正方形四个顶点所标的数字规律,可知数2011应标在( )A 、第502个正方形的左下角B 、第502个正方形的右下角C 、第503个正方形的左上角D 、第503个正方形的右下角(3)观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称) 【4、算式规律】应对的一般原则:①找出等式中的各个部分;②找出等式中的各个部分中不变的部分;③找出等式中的各个部分中变化的部分、并寻找他们的变化规律。
例7 1+2+3+…+100=?经过研究,这个问题的一般性结论是(1)123 (2)n n n +++++=,其中n是正整数。
现在我们来研究一个类似的问题:1223......(n 1)n ⨯+⨯+++=?观察下面三个特殊的等式:将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯ 读完这段材料,请你思考后回答: 例8 观察下列三行数:(1)第①行数按什么规律排列?(2)第②③行数与第①行数分别有什么关系?(3)取每行数的第n 个数,这三个数的和能否等于-1278,如果能,指出是每行的第几个数,并求出这三个数;如果不能,请说明理由。
练习:(1)观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在观察规律之后并用你得到的规律填空:2____________________50⨯+=,第n 个式子呢? ________________________ (2)观察下列各式,你会发现什么规律?3210-5-4-3-2-10-1, 2, -4, 8, -16, 32,…; ① -2, 4, -8, 16, -32, 64,…; ② 0, 6, -6, 18, -30, 66,…; ③3×5=15,而15=241-5×7=35,而35=261-……11×13=143,而143=2121-将你猜想到的规律用只含一个字母的式子表示出来:___________________________。
(3)下列图是由同型号黑白两种颜色的三角形瓷砖按一定规律铺设的图形。
仔细观察图形可知:图①有1块黑色的瓷砖,可表示为21)11(1⋅+=; 图②有3块黑色的瓷砖,可表示为22)21(21⋅+=+;图③有3块黑色的瓷砖,可表示为23)31(321⋅+=++实践探索:(1)请在图④的虚线框内画出第4个图形(只须画出草图)(2)第10个图形有 ________ 块黑色的瓷砖(直接填写结果) (3)第n 个图形有多少块黑色的瓷砖?(用含n 的代数式表示) 【5、数表规律】兼具数字规律和图形规律的特点,难度加大。
例9 将111111,,,,,,23456---按一定规律排列如下:第1行 1 第2行12-13第3行14-15 16-第4行1718-19 110- 第5行 111 112- 113 114- 115…请你写出第20行从左至右第10个数是 。
例10 (1) 在2008年10月的月历中(见图1),任意圈出一竖列上相邻的三个数,设中间的一个为a ,则用含a 的整式表示这三个数(从小到大排列)分别是 ____ 。
图1(2)现将连续自然数1至2008按图中的方式排成一个长方形的数阵,用一个正方形框出9个数(见图2)①图中框出的这9个数的和是 ; ②在图中,能否使一个正方形框出的9个数之和等于2007 ?若不可能,请说明理由;若有可能,请求出该正方形框出的9个数中的最小数和最大数。
(写出详细的解题过程) 练习:(1)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成如下所示的形式:按照上述规律排下去,那么第10行从左边数第5个数等于 . 第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10 第5行 11 -12 13 -14 15 ………………(2)将正偶数排成5列,如下表:第1列 第2列 第3列 第4列 第5列第1行24 6 8第2行1614 12 10第3行 1820 22 24………2826根据上面排列规律,则2000应在( )A 、第25行,第1列B 、第125行,第2列C 、第250行,第1列D 、第250行,第2列 (3)观察一列数表:1 2 3 4 … 第一行 2 3 4 5 … 第二行日一二三 四 五 六1 2 3 4 567891011 12 13 14 15 16 17 18 19 20 21 22 23 242526 27 28 29 30 311 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 …………………1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 20083 4 5 6 … 第三行 4 5 6 7 … 第四行 ┆ ┆ ┆ ┆根据数表所反映的规律,猜想第6行与第6列的交叉点上的数应为多少?第n 行与第n 列交叉点上的数应为多少?(用n 表示) 【5、其它规律】等比数列 如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。
