四川省宜宾县高考数学适应性测试试题(二)文
高三数学适应性考试题(文)

组成曲线 ,其中 ;如图,半椭圆
内切于矩形 ,
且 交 轴于点 ,点 是半圆 上
异于 的任意一点,当点 位于点 时,
的面积最大.
(Ⅰ)求曲线 的方程;
(Ⅱ)连 、 交 分别于点 ,求证: 为定值.
22.(本小题满分14分)
数列 满足 .
(Ⅰ)求 ;
(Ⅱ)求证数列{ }是 以 为公比的等比数列,并求其通项公式;
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
4.所有题目必须在答题卡规定位置上作答,在试题卷上答题无效.
5.考试结束后,将答题卡交回。
参考公式
如果事件 互斥,那么球的表面积公式
; ,
如果事件 相互独立,那么其中 表示球的半径
;球的体积公式
如果事件 在一次试验中发生的概率是 ,那么 ,
6 已知函数 的部分图象如图所示,则 的解析式可能为 ()
(A)
(B)
(C)
(D)
7.已知m是两个正数2,8的等比中 项,则圆锥曲线 的离心率是
(A) 或 (B) (C) (D) 或
8.已知S、A、B、C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC= ,则球O的表面积等于
(A)4 (B)3 (C)2 (D)
所以这2人恰好是研究不同版本教材的男教师的概率是 。……………(4分)
(2)由题意得从15名教师中随机选出4名共 =1365种选法,15名教师有男教师10人,女教师5人;可选1男3女、2男2女、3男1女即 =100、 、 =600
合计:100+4 50+600=1 150 那么既有男教师又有女教师的概率为
宜宾市高中级高考适应性考试题
2020年四川省宜宾市高考数学二诊试卷(文科)
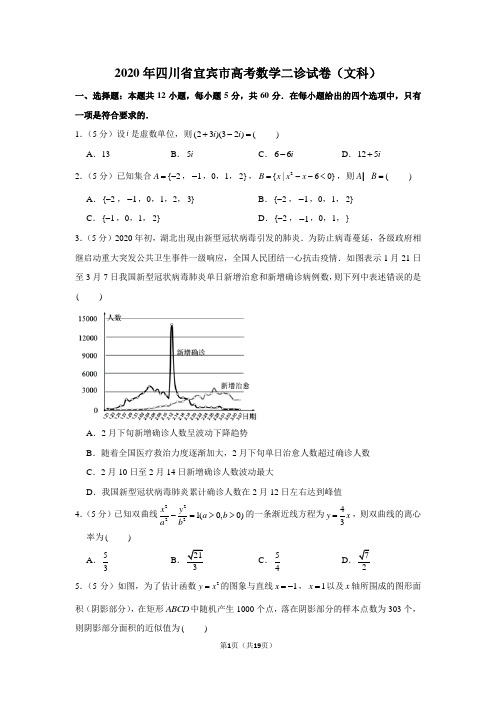
2020年四川省宜宾市高考数学二诊试卷(文科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.1.(5分)设i 是虚数单位,则(23)(32)(i i +-= ) A .13B .5iC .66i -D .125i +2.(5分)已知集合{2A =-,1-,0,1,2},2{|60}B x x x =--<,则(A B =I ) A .{2-,1-,0,1,2,3} B .{2-,1-,0,1,2}C .{1-,0,1,2}D .{2-,1-,0,1,}3.(5分)2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人民团结一心抗击疫情.如图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )A .2月下旬新增确诊人数呈波动下降趋势B .随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数C .2月10日至2月14日新增确诊人数波动最大D .我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值4.(5分)已知双曲线22221(0,0)x y a b a b -=>>的一条渐近线方程为43y x =,则双曲线的离心率为( )A .53B 21C .54D 7 5.(5分)如图,为了估计函数2y x =的图象与直线1x =-,1x =以及x 轴所围成的图形面积(阴影部分),在矩形ABCD 中随机产生1000个点,落在阴影部分的样本点数为303个,则阴影部分面积的近似值为( )A .0.698B .0.606C .0.303D .0.1516.(5分)函数()cos()2f x x x π=-的图象大致为( )A .B .C .D .7.(5分)20世纪产生了著名的“31x +”猜想:任给一个正整数x ,如果x 是偶数,就将它减半;如果x 是奇数,则将它乘3加1,不断重复这样的运算,经过有限步后,一定可以得到1.如图是验证“31x +”猜想的一个程序框图,若输入正整数m 的值为40,则输出的n 的值是( )A .11B .10C .9D .88.(5分)已知1tan()242θπ-=,sin (θ= )ABC .35D .139.(5分)四棱锥P ABCD -所有棱长都相等,M ,N 分别为PA ,CD 的中点,下列说法错误的是( )A .MN 与PD 是异面直线B .//MN 平面PBCC .//MN ACD .MN PB ⊥10.(5分)在ABC ∆中,角A 的平分线交边BC 于D ,4AB =,8AC =,2BD =,则ABD ∆的面积是( ) AB.C .1D .311.(5分)过抛物线212x y =的焦点F 的直线交抛物线于点A ,B ,交抛物线的准线于点C ,若3AF FB =u u u r u u u r,则||(BC = )A .4 B.C .6 D .812.(5分)若定义在R 上的偶函数()f x 满足()(2)0f x f x +-=.当[0x ∈,1],2()1f x x =-,则( )A .1235(log 2)()(log 3)2f f f >>B .1235()(log 2)(log 3)2f f f >>C .1235(log 2)(log 3)()2f f f >>D .2135()(log 3)(log 2)2f f f >>二、填空题:本大题共4个小题,每小题5分,共20分.13.(5分)函数3214()2333f x x x x =+++的零点个数为 .14.(5分)已知()sin f x x x m =++为奇函数,则()2f π= .15.(5分)在ABC ∆中,已知3AB =,2AC =,P 是边BC 的垂直平分线上的一点,则BC AP =u u u r u u u rg .16.(5分)已知圆锥的顶点为S ,过母线SA ,SB 的切面切口为正三角形,SA 与圆锥底面所成角为30︒,若SAB ∆的面积为,则该圆锥的侧面积为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:(1)求y 关于x 的线性回归方程;(2)计算变量x ,y 的相关系数r (计算结果精确到0.01),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若||[0.75r ∈,1],则x ,y 相关性很强;若||[0.3r ∈,0.75),则x ,y 相关性一般;若||[0r∈,0.25],则x ,y 相关性较弱.)5.477≈参考公式:1122211()()ˆ()nnii i ii i nniii i xx y y x ynxybxx xnx ====---==--∑∑∑∑,相关系数()()nii xx y y r --∑.18.(12分)已知数列{}n a 满足123123252525253n n na a a a +++⋯+=----. (1)求数列{}n a 的通项公式; (2)设数列11{}n n a a +的前n 项和为n T ,求n T . 19.(12分)将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体,O 为11A C 的中点. (1)求证://OB 平面1ACD ; (2)求几何体111ACB A D 的体积.20.(12分)已知椭圆2222:1(0)x y C a b a b +=>>的左焦点为(1,0)F -2.(1)求椭圆C 的标准方程;(2)设O 为坐标原点,T 为直线2x =-上一点,过F 作TF 的垂线交椭圆于P ,Q .当四边形OPTQ 是平行四边形时,求四边形OPTQ 的面积.21.(12分)已知函数21()2x f x e x x =-+.证明:(1)函数()f x 在R 上是单调递增函数;(2)对任意实数1x ,2x ,若12()()2f x f x +=,则120x x +<.(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)在极坐标系Ox 中,曲线C 22sin 2sin ρθρθ=-,直线l 的极坐标方程为(cos sin )1ρθθ-=,设l 与C 交于A ,B 两点,AB 中点为M ,AB 的垂直平分线交C 于E ,F .以O 为坐标原点,极轴为x 轴正半轴,建立直角坐标系xOy . (1)求C 的直角坐标方程及点M 的直角坐标; (2)求证:||||||||MA MB ME MF =g g . [选修4-5:不等式选讲]23.已知函数()|1|2|3|f x x x =--+. (1)求不等式()1f x <的解集;(2)若存在实数x ,使不等式23()0m m f x --<成立,求实数m 的取值范围.2020年四川省宜宾市高考数学二诊试卷(文科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.1.(5分)设i 是虚数单位,则(23)(32)(i i +-= ) A .13B .5iC .66i -D .125i +【解答】解:(23)(32)6496125i i i i i +-=-++=+. 故选:D .2.(5分)已知集合{2A =-,1-,0,1,2},2{|60}B x x x =--<,则(A B =I ) A .{2-,1-,0,1,2,3} B .{2-,1-,0,1,2}C .{1-,0,1,2}D .{2-,1-,0,1,}【解答】解:{|23}B x x =-<<Q ,{2A =-,1-,0,1,2}, {1A B ∴=-I ,0,1,2}.故选:C .3.(5分)2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人民团结一心抗击疫情.如图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )A .2月下旬新增确诊人数呈波动下降趋势B .随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数C .2月10日至2月14日新增确诊人数波动最大D .我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值【解答】解:由图可得,2月下旬新增确诊人数呈波动下降趋势,正确,故A 正确,随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数,正确,故B正确,2月10日至2月14日新增确诊人数波动最大,正确,故C正确,我国新型冠状病毒肺炎累计确诊人数,一直在增加,在2月12日左右新增人数达到峰值,故D错误,故选:D.4.(5分)已知双曲线22221(0,0)x ya ba b-=>>的一条渐近线方程为43y x=,则双曲线的离心率为()A.53B.213C.54D.7【解答】解:Q双曲线的中心在原点,焦点在x轴上,∴设双曲线的方程为22221x ya b-=,(0,0)a b>>由此可得双曲线的渐近线方程为by xa=±,结合题意一条渐近线方程为43y x=,得43ba=,设4b t=,3a t=,则225(0)c a b t t=+=>∴该双曲线的离心率是53cea==.故选:A.5.(5分)如图,为了估计函数2y x=的图象与直线1x=-,1x=以及x轴所围成的图形面积(阴影部分),在矩形ABCD中随机产生1000个点,落在阴影部分的样本点数为303个,则阴影部分面积的近似值为()A.0.698B.0.606C.0.303D.0.151【解答】解:设面积区域为x,由概率的几何概型知,则303 10002x=,解之得0.606x=,则该区域面积的近似值为0.606.故选:B .6.(5分)函数()cos()2f x x x π=-的图象大致为( )A .B .C .D .【解答】解:根据题意,()cos()sin 2f x x x x x π=-=,有()()sin()sin ()f x x x x x f x -=--==,即函数()f x 为偶函数,排除B 、D ; 又由在区间(0,)π上,0x >,sin 0x >,有()0f x >,排除C ; 故选:A .7.(5分)20世纪产生了著名的“31x +”猜想:任给一个正整数x ,如果x 是偶数,就将它减半;如果x 是奇数,则将它乘3加1,不断重复这样的运算,经过有限步后,一定可以得到1.如图是验证“31x +”猜想的一个程序框图,若输入正整数m 的值为40,则输出的n 的值是( )A .11B .10C .9D .8【解答】解:根据框图可知:2n =,40m =403,202n m === 204,102n m === 105,52n m === 6n =,35116m =⨯+=167,82n m === 88,42n m === 49,22n m === 10n =,212m ==, 故选:B .8.(5分)已知1tan()242θπ-=,sin (θ= )ABC .35D .13【解答】解:因为1tan()242θπ-=,所以11112tan tan[()]31224412ππθθ+=-+==-, 所以212tan 632sin 119512tan θθθ===++. 故选:C .9.(5分)四棱锥P ABCD -所有棱长都相等,M ,N 分别为PA ,CD 的中点,下列说法错误的是( )A .MN 与PD 是异面直线B .//MN 平面PBCC .//MN ACD .MN PB ⊥【解答】解:由题意可知四棱锥P ABCD -所有棱长都相等,M ,N 分别为PA ,CD 的中点,MN 与PD 是异面直线,正确;取PB 的中点为H ,连接MH ,HC ,可得//MN HC ,所以//MN 平面PBC ,正确;//MN AC ,不正确;MN PB ⊥正确; 故选:C .10.(5分)在ABC ∆中,角A 的平分线交边BC 于D ,4AB =,8AC =,2BD =,则ABD ∆的面积是( ) A .15B .315C .1D .3【解答】解:如图:;因为ABC ∆中,角A 的平分线交边BC 于D ,4AB =,8AC =,2BD =, 所以:4AB BDDC AC DC=⇒=; 6BC ∴=;2222224681cos 22464AB BC AC B AB BC +-+-∴===-⨯⨯g ;2115sin 1()4B ∴=--; 1sin 3152ABC S AB BC B ∆∴==g g 1153ABD ABC S S ∆∆∴=故选:A .11.(5分)过抛物线212x y =的焦点F 的直线交抛物线于点A ,B ,交抛物线的准线于点C ,若3AF FB =u u u r u u u r,则||(BC = )A .4B .43C .6D .8【解答】解:作BM CP ⊥,AN CP ⊥,BH AN ⊥,如图,因为3AF FB =u u u r u u u r,不妨设BF x =,所以33AF BF x ==,4AB x =根据抛物线的定义可得,BM BF HN x ===,3AN AF x ==,6FP p ==,则32AH AN HN x x x =-=-=,所以1sin sin 2AH ABH ACN AB ∠=∠==,则12CF =,2CB x =, 则312CF CB BF x =+==,所以4x =, 则28BC x ==, 故选:D .12.(5分)若定义在R 上的偶函数()f x 满足()(2)0f x f x +-=.当[0x ∈,1],2()1f x x =-,则( )A .1235(log 2)()(log 3)2f f f >>B .1235()(log 2)(log 3)2f f f >>C .1235(log 2)(log 3)()2f f f >>D .2135()(log 3)(log 2)2f f f >>【解答】解:因为定义在R 上的偶函数()f x 满足()(2)0f x f x +-=. 所以(2)()0f x f x ++-=即(2)()()f x f x f x +=--=-, 所以(4)()f x f x +=,即函数的周期为4, 因为当[0x ∈,1],2()1f x x =-单调递减, 因为511()()()0222f f f =--=-<,224(log 3)(log )03f f =-<,1333(2)(log 2)(log 2)0f log f f =-=>,因为2410log 132<<<, 所以241(log )()32f f -<-,所以,12314(2)()(log )23f log f f >->-,即1235(2)()(log 3)2f log f f >>,故选:A .二、填空题:本大题共4个小题,每小题5分,共20分.13.(5分)函数3214()2333f x x x x =+++的零点个数为 2 .【解答】解:Q 函数3214()2333f x x x x =+++,2()43(1)(3)f x x x x x '∴=++=++,令()0f x '=得:3x =-或1-,∴当(,3)x ∈-∞-时,()0f x '>,函数()f x 单调递增;当(3,1)x ∈--时,()0f x '<,函数()f x 单调递减;当(1,)x ∈-+∞时,()0f x '>,函数()f x 单调递增, ∴函数()f x 的极大值为4(3)3f -=,极小值为(1)0f -=, ∴函数()f x 的大致图象如图所示:,由图象可知,函数()f x 有2个零点, 故答案为:2.14.(5分)已知()sin f x x x m =++为奇函数,则()2f π=22π+ .【解答】解:由奇函数的性质可得(0)0f m ==,故()sin f x x x =+,所以11()122f ππ=+.故答案为:112π+.15.(5分)在ABC ∆中,已知3AB =,2AC =,P 是边BC 的垂直平分线上的一点,则BC AP =u u u r u u u rg 52- . 【解答】解:取BC 的中点D ,由条件得:22221115()()()0()(23)2222BC AP BC AD DP BC AD BC DP AC AB AC AB AC AB =+=+=-++=-=-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r g g g g g .故答案为:52-.16.(5分)已知圆锥的顶点为S ,过母线SA ,SB 的切面切口为正三角形,SA 与圆锥底面所成角为30︒,若SAB ∆的面积为43,则该圆锥的侧面积为 83π . 【解答】解:依题意画图,如图:SA SB SC l ===,30SAC ∠=︒,3AC l =,AB l =,SAB ∆Q 的面积为2143sin602l =︒g ,解得4l =,43AC ∴=,23r =,∴该圆锥的侧面积为:83rl ππ=.故答案为:83π.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:(1)求y 关于x 的线性回归方程;(2)计算变量x ,y 的相关系数r (计算结果精确到0.01),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若||[0.75r ∈,1],则x ,y 相关性很强;若||[0.3r ∈,0.75),则x ,y 相关性一般;若||[0r ∈,0.25],则x ,y 相关性较弱.)5.477≈参考公式:1122211()()ˆ()nnii i ii i nniii i xx y y x ynxybxx xnx ====---==--∑∑∑∑,相关系数()()nii xx y y r --∑.【解答】解:(1)由题意得,4,17x y ==,由公式求得51521()()ˆ 3.2()iii ii x x yy bx x ==--==--∑∑,ˆˆ17 3.2429.8ay bx =-=+⨯=, 故y 关于x 的线性回归方程为ˆ 3.229.8yx =-+. (2)()()0.97nii xx y y r --===≈-∑,0r ∴<,∴说明x ,y 负相关,又||[0.75r ∈,1],说明x ,y 相关性很强.∴可以认为该幼儿园去年春期患流感人数与年龄负相关很强.18.(12分)已知数列{}n a 满足123123252525253n n na a a a +++⋯+=----. (1)求数列{}n a 的通项公式;(2)设数列11{}n n a a +的前n 项和为n T ,求n T . 【解答】解:(1)由题意,令25n n nb a =-,设数列{}n b 的前n项和为n S ,则3n nS =. 当1n =时,1113b S ==, 当2n …时,111333n n n n n b S S --=-=-=, ∴数列{}n b 是常数列,即1253n n n b a ==-,故352n n a +=,*n N ∈. (2)由(1)知,114411[](35)[3(1)5]3(35)3(1)5n n a a n n n n +==-++++++,12231111n n n T a a a a a a +∴=++⋯+411411411()()[]331532533253353353(1)5n n =-+-+⋯+-⨯+⨯+⨯+⨯++++ 4111111[]3315325325335353(1)5n n =-+-+⋯+-⨯+⨯+⨯+⨯++++ 411[]33153(1)5n =-⨯+++ 411[]383(1)5n =-++ 146924n =-+ 616nn =+.19.(12分)将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体,O 为11A C 的中点. (1)求证://OB 平面1ACD ; (2)求几何体111ACB A D 的体积.【解答】(1)证明:取AC 中点为1O ,连接1OO ,11B D ,11O D . 在正方形1111A B C D 中,O Q 为11A C 的中点,O ∴为11B D 的中点. 在正方体1111ABCD A B C D -中,11//AA CC Q ,11AA CC =,11//CC BB ,11CC BB =, 11//OO CC ∴,11OO CC =,11//CC BB ,11CC BB =. 11//OO BB ∴,11OO BB =,∴四边形11OO B B 为平行四边形,11//BO B O ∴,11BO B O =,11//BO D O ∴,11BO D O =.∴四边形11O BOD 为平行四边形,则11//BO O D .又BO ⊂/平面1ACD ,11O D ⊂平面1ACD ,//OB ∴平面1ACD ;(2)解:Q 正方体1111ABCD A B C D -的棱长为2, ∴11118ABCD A B C D V -=,1114222323D ACD V -=⨯⨯⨯⨯=. 又11111111111ACB A D ABCC D A B A BCB C B C D V V V V --=--, 且111111111203ABCC D A B ABCD A B C D D ACD V V V --=-=, 而111143A BCBC B CD V V --==, ∴1112042433ACB A D V =-⨯=.20.(12分)已知椭圆2222:1(0)x y C a b a b +=>>的左焦点为(1,0)F -,离心率为22.(1)求椭圆C 的标准方程;(2)设O 为坐标原点,T 为直线2x =-上一点,过F 作TF 的垂线交椭圆于P ,Q .当四边形OPTQ 是平行四边形时,求四边形OPTQ 的面积. 【解答】解:(1)由已知得:21c c a ==,所以2a =;又222a b c =+,解得1b =,所以椭圆的标准方程为:2212x y +=.(2)设T 点的坐标为(2,)m -,则直线TF 的斜率02(1)TF m k m -==----,当0m ≠时,直线PQ 的斜率1PQ k m=,直线PQ 的方程是1x my =-; 当0m =时,直线PQ 的方程也符合1x my =-的形式.由221,21x y x my ⎧+=⎪⎨⎪=-⎩g 得22(2)210m y my +--=.其判别式△2244(2)0m m =++>, 设1(P x ,1)y ,2(Q x ,2)y ,则1221222,212m y y m y y m ⎧+=⎪⎪+⎨-⎪=⎪+⎩g ,121224()22x x m y y m -+=+-=+,因为四边形OPTQ 是平行四边形,所以OP QT =u u u r u u u r,即1(x ,12)(2y x =--,2)m y -, 所以1221222,2422m y y m m x x m ⎧+==⎪⎪+⎨-⎪+==-⎪+⎩g 解得0m =,此时四边形OPTQ的面积11||||222OPTQ S OT PQ ===g 21.(12分)已知函数21()2x f x e x x =-+.证明:(1)函数()f x 在R 上是单调递增函数;(2)对任意实数1x ,2x ,若12()()2f x f x +=,则120x x +<. 【解答】证明:(1)()1x f x e x '=-+,()1x f x e '''=-,令()0f x '''>,得0x >,即函数()f x '在区间(0,)+∞上单调递增; ()0f x ''<,得0x <,函数()f x '在区间(,0)-∞上单调递减;所以()(0)20min f x f '==>,故函数()f x 在R 上是单调递增函数;(4分)(2)因12()()2(0)2f x f x f +==,()f x 在R 上是单调递增函数,不妨设120x x <<, 构造2()()()(0)x x g x f x f x e e x x -=+-=+-<, ()2x x g x e e x -'=--,()20x x g x e e -''=+-…,所以()y g x '=在(,0)-∞上单调递增,所以()(0)0g x g ''<=,所以()y g x =在(,0)-∞上单减,因10x <,11112()()()(0)2()()g x f x f x g f x f x =+->==+,有12()()f x f x ->. 由(1)知,()f x 在R 上是单调递增函数,有12x x ->,即120x x +<.(12分)(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)在极坐标系Ox 中,曲线C2sin ρθ=,直线l 的极坐标方程为(cos sin )1ρθθ-=,设l 与C 交于A ,B 两点,AB 中点为M ,AB 的垂直平分线交C 于E ,F .以O 为坐标原点,极轴为x 轴正半轴,建立直角坐标系xOy . (1)求C 的直角坐标方程及点M 的直角坐标; (2)求证:||||||||MA MB ME MF =g g .【解答】解:(1)曲线C2sin ρθ,转换为直角坐标方程为2222:22,12x C x y y +=+=即.直线l 的极坐标方程为(cos sin )1ρθθ-=转换为直角坐标方程为:1y x =-, 联立C 与l 的方程得;2340x x -=,解得41(0,1),(,)33A B -.由于AB 中点为M , ∴21(,)33M -.证明:(2)由(1)利用两点间的距离公式的应用得:||||MA MB = ∴8||||9MA MB =g . 又设AB的垂直平分线2,3:1,3x EF y ⎧=⎪⎪⎨⎪=-⎪⎩代入C的方程得:2340233t --=,∴483||||||392ME MF -==g .||||||||MA MB ME MF ∴=g g .[选修4-5:不等式选讲]23.已知函数()|1|2|3|f x x x =--+. (1)求不等式()1f x <的解集;(2)若存在实数x ,使不等式23()0m m f x --<成立,求实数m 的取值范围. 【解答】解:(1)7,1()|1|2|3|35,317,3x x f x x x x x x x --⎧⎪=--+=---<<⎨⎪+-⎩…„,当1x …时,71x --<解得1x …; 当31x -<<时,351x --<解得21x -<<; 当3x -„时,71x +<解得6x <-. 综上得6x <-或2x >-.∴不等式的解集为(-∞,6)(2--⋃,)+∞;(2)Q 存在实数x ,不等式23()0m m f x --<成立, ∴存在实数x ,不等式23()m m f x -<成立. ∴存在实数x ,不等式23[()]max m m f x -<成立.又7,1()35,317,3x x f x x x x x --⎧⎪=---<<⎨⎪+-⎩…„,()(3)4max f x f ∴=-=,234m m ∴-<,解得14m -<<. m ∴的范围是(1,4)-.。
四川省宜宾市第四中学校2023届高考适应性考试文科数学试题
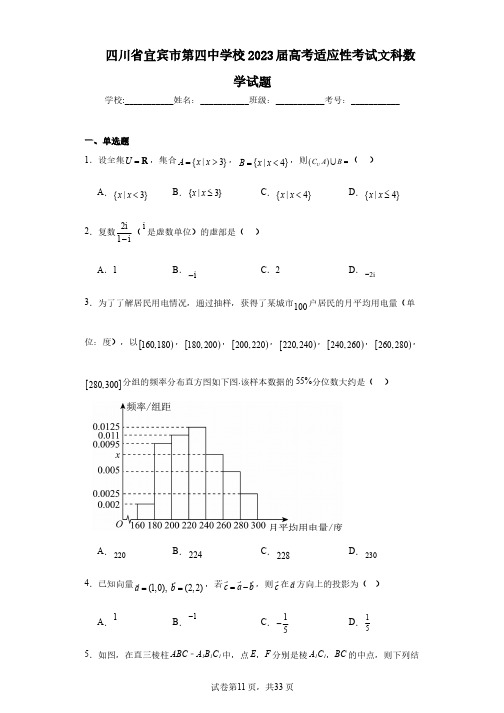
四川省宜宾市第四中学校2023届高考适应性考试文科数学试题学校:___________姓名:___________班级:___________考号:___________二、填空题13.为了迎接春节,小王买了红黄紫三种颜色的花各一盆,准备并排摆放在自家阳、、(2)已知2020年全国居民人均可支配收入为32189元,若从2020年开始,以后每年全国居民人均可支配收入均以6%的速度增长,预计哪一年全国居民每百户家用汽车拥有量可以达到50辆.参考数据:17.(1)2n n a =;(2)22122nnn n T ++=-.【分析】(1)设{}n a 的公比为(2)写出n b ,由分组求和法求【详解】(1)设{}n a 的公比为因为12a =,且2a ,32a +,4a 所以2432(2)a a a +=+,即2q +所以2n n a =;(2)利用等体积法求解点到平面的距离.【详解】(1)延长CD至点F ,且DF =CD ,延长11C D 至点H ,使得111D H C D =,连接FH ,1C F 交1DD 于点Q ,因为四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,24AB CD ==,所以四棱柱111ABCF A B C H -为长方体,11//AB FC ,且Q 为1DD 的中点,取1CC 的中点E ,连接ED ,则1//ED FC ,所以1//AB ED ,故棱1CC 与平面1ADB 的交点E 的位置为1CC 的中点;(2)取AB 的中点M ,连接DM ,因为24AB CD ==,060BAD Ð=,故△ADM 为等边三角形,所以2AM AD ==,因为侧棱1DD ⊥底面ABCD 且112BB DD DC ===,AB Ì平面ABCD ,所以1BB AB ^,。
四川省宜宾市2019-2020学年高考适应性测试卷数学试题(2)含解析

四川省宜宾市2019-2020学年高考适应性测试卷数学试题(2)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若x ,y 满足约束条件40,20,20,x y x x y -+≥⎧⎪-≤⎨⎪+-≥⎩且z ax y =+的最大值为26a +,则a 的取值范围是( )A .[1,)-+∞B .(,1]-∞-C .(1,)-+∞D .(,1)-∞-【答案】A【解析】【分析】画出约束条件的可行域,利用目标函数的最值,判断a 的范围即可.【详解】作出约束条件表示的可行域,如图所示.因为z ax y =+的最大值为26a +,所以z ax y =+在点(2,6)A 处取得最大值,则1a -≤,即1a ≥-.故选:A【点睛】本题主要考查线性规划的应用,利用z 的几何意义,通过数形结合是解决本题的关键.2.设,m n 是两条不同的直线,,αβ是两个不同的平面,则下列命题正确的是( )A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥,则m α⊥C .若m β⊥,n β⊥,n α⊥,则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥【答案】C【解析】【分析】根据空间中直线与平面、平面与平面位置关系相关定理依次判断各个选项可得结果.【详解】对于A ,当m 为α内与n 垂直的直线时,不满足m α⊥,A 错误;对于B ,设l αβ=I ,则当m 为α内与l 平行的直线时,//m β,但m α⊂,B 错误;对于C ,由m β⊥,n β⊥知://m n ,又n α⊥,m α∴⊥,C 正确;对于D ,设l αβ=I ,则当m 为β内与l 平行的直线时,//m α,D 错误.故选:C .【点睛】本题考查立体几何中线面关系、面面关系有关命题的辨析,考查学生对于平行与垂直相关定理的掌握情况,属于基础题.3.51(1)x x -+展开项中的常数项为 A .1B .11C .-19D .51【答案】B【解析】【分析】展开式中的每一项是由每个括号中各出一项组成的,所以可分成三种情况.【详解】展开式中的项为常数项,有3种情况:(1)5个括号都出1,即1T =; (2)两个括号出x ,两个括号出1()x-,一个括号出1,即2222531()130T C x C x =⋅⋅⋅-⋅=;(3)一个括号出x ,一个括号出1()x-,三个括号出1,即11541()120T C x C x =⋅⋅⋅-⋅=-; 所以展开项中的常数项为1302011T =+-=,故选B.【点睛】 本题考查二项式定理知识的生成过程,考查定理的本质,即展开式中每一项是由每个括号各出一项相乘组合而成的.4.设0.50.82a =,sin1b =,lg 3c =,则a ,b ,c 三数的大小关系是A .a c b <<B .a b c <<C .c b a <<D .b c a << 【答案】C【解析】【分析】利用对数函数,指数函数以及正弦函数的性质和计算公式,将a ,b ,c 12比较即可. 【详解】由0.50.50.820.8a =>1334sin1sin 2345b π<=<==<, 11lg3lg 10lg1022c =<==, 所以有c b a <<.选C.【点睛】本题考查对数值,指数值和正弦值大小的比较,是基础题,解题时选择合适的中间值比较是关键,注意合理地进行等价转化.5.已知函数f (x )=e b ﹣x ﹣e x ﹣b +c (b ,c 均为常数)的图象关于点(2,1)对称,则f (5)+f (﹣1)=( )A .﹣2B .﹣1C .2D .4【答案】C【解析】【分析】根据对称性即可求出答案.【详解】解:∵点(5,f (5))与点(﹣1,f (﹣1))满足(5﹣1)÷2=2, 故它们关于点(2,1)对称,所以f (5)+f (﹣1)=2,故选:C .【点睛】本题主要考查函数的对称性的应用,属于中档题.6.若,则( ) A . B . C . D .【答案】B【解析】【分析】由三角函数的诱导公式和倍角公式化简即可.【详解】因为,由诱导公式得,所以 .故选B【点睛】本题考查了三角函数的诱导公式和倍角公式,灵活掌握公式是关键,属于基础题.7.已知12,F F 分别为双曲线()2222:10,0x y C a b a b -=>>的左、右焦点,过1F 的直线l 与双曲线C 的左、右两支分别交于,A B 两点,若22240,5BF AB BF AF ⋅==uu u r u u u u r ,则双曲线C 的离心率为( ) A .13B .4C .2D .3【答案】A【解析】【分析】由已知得2AB BF ⊥,24BF x =,由已知比值得25,3AF x AB x ==,再利用双曲线的定义可用a 表示出1AF ,2AF ,用勾股定理得出,a c 的等式,从而得离心率. 【详解】2220,0,0,90AB BF AB BF ABF ⋅=≠≠∴∠=︒u u u r u u u u r u u u r u u u u r Q .又2245BF AF =Q ,∴可令24BF x =,则25,3AF x AB x ==.设1AF t =,得21122AF AF BF BF a -=-=,即()5342x t x t x a -=+-=,解得3,t a x a ==,∴24BF a =,116BF AB AF a =+=,由2221212BF BF F F +=得222(6)(4)(2)a a c +=,2213c a =,13c a =,∴该双曲线的离心率13c e a ==. 故选:A.【点睛】本题考查求双曲线的离心率,解题关键是由向量数量积为0得出垂直关系,利用双曲线的定义把双曲线上的点,A B 到焦点的距离都用a 表示出来,从而再由勾股定理建立,a c 的关系.8.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 的对边,若ABC ∆的面为S ,且()2243S a b c =+-,则sin 4C π⎛⎫+= ⎪⎝⎭( )A .1B .2C .4D .4【答案】D【解析】【分析】 根据三角形的面积公式以及余弦定理进行化简求出C 的值,然后利用两角和差的正弦公式进行求解即可.【详解】解:由()22a b c =+-,得2221sin 22ab C a b c ab =+-+, ∵ 2222cos a b c ab C +-=,∴ sin 2cos 2C ab C ab =+,cos 1C C -= 即2sin 16C π⎛⎫-= ⎪⎝⎭, 则1sin 62C π⎛⎫-= ⎪⎝⎭, ∵ 0C π<<,∴ 5666C πππ-<-<, ∴ 66C ππ-=,即3C π=,则sin sin sin cos cos sin 4343434C πππππππ⎛⎫⎛⎫+=+=+= ⎪ ⎪⎝⎭⎝⎭12 故选D .【点睛】本题主要考查解三角形的应用,结合三角形的面积公式以及余弦定理求出C 的值以及利用两角和差的正弦公式进行计算是解决本题的关键.9.已知斜率为2的直线l 过抛物线C :22(0)y px p =>的焦点F ,且与抛物线交于A ,B 两点,若线段AB 的中点M 的纵坐标为1,则p =( )A .1B .C .2D .4【答案】C【解析】【分析】设直线l 的方程为x =12y 2p +,与抛物线联立利用韦达定理可得p . 【详解】由已知得F (2p ,0),设直线l 的方程为x =12y 2p +,并与y 2=2px 联立得y 2﹣py ﹣p 2=0, 设A (x 1,y 1),B (x 2,y 2),AB 的中点C (x 0,y 0),∴y 1+y 2=p ,又线段AB 的中点M 的纵坐标为1,则y 012=(y 1+y 2)=12p =,所以p=2, 故选C .【点睛】本题主要考查了直线与抛物线的相交弦问题,利用韦达定理是解题的关键,属中档题. 10.已知0x >,0y >,23x y +=,则23x y xy+的最小值为( ) A.3-B.1 C1 D1【答案】B【解析】 23x y xy+2(2)2111x x y y x y xy y x ++==++≥+=+,选B 11.已知向量(2,4)a =-r ,(,3)b k =r ,且a r 与b r的夹角为135︒,则k =( )A .9-B .1C .9-或1D .1-或9 【答案】C【解析】【分析】由题意利用两个向量的数量积的定义和公式,求k 的值.【详解】解:由题意可得cos1352||||a b a b ︒⋅===-⋅r r r r , 求得9k =-,或1k =,故选:C.【点睛】本题主要考查两个向量的数量积的定义和公式,属于基础题.12.已知函数()()()1sin ,13222,3100x x f x f x x π⎧-≤≤⎪=⎨⎪-<≤⎩,若函数()f x 的极大值点从小到大依次记为12,?··n a a a ,并记相应的极大值为12,,?··n b b b ,则()1n i i i a b =+∑的值为( ) A .5022449+B .5022549+C .4922449+D .4922549+【答案】C【解析】【分析】 对此分段函数的第一部分进行求导分析可知,当2x =时有极大值(2)1f =,而后一部分是前一部分的定义域的循环,而值域则是每一次前面两个单位长度定义域的值域的2倍,故此得到极大值点n a 的通项公式2n a n =,且相应极大值12n nb -=,分组求和即得 【详解】当13x ≤≤时,()cos 22x f x πππ-⎛⎫'= ⎪⎝⎭, 显然当2x =时有,()0f x '=,∴经单调性分析知2x =为()f x 的第一个极值点又∵3100x <≤时,()2(2)f x f x =-∴4x =,6x =,8x =,…,均为其极值点∵函数不能在端点处取得极值∴2n a n =,149n ≤≤,n Z ∈∴对应极值12n nb -=,149n ≤≤,n Z ∈ ∴()4949491(298)491(12)22449212i i i a b =+⨯⨯-+=+=+-∑ 故选:C【点睛】本题考查基本函数极值的求解,从函数表达式中抽离出相应的等差数列和等比数列,最后分组求和,要求学生对数列和函数的熟悉程度高,为中档题二、填空题:本题共4小题,每小题5分,共20分。
宜宾县高中高考适应性考试(二).docx

宜宾县高中2012级高考适应性考试(二)数 学(文史类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
满分150分。
考试时间120分钟。
考试结束后,将本试题卷和答题卡上一并交回。
第Ⅰ卷 (选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛。
由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队,则高三学生队中5班和16班的人数分别为() A.3,5 B.4,5 C.3,4 D.4,3 2.已知集合{}{}2(,)|4,(,)|1A x y y x B x y y x ====+,则AB =( )A. {}(1,2)-B. {}(1,2)C. (1,2)D. (1,2)-3.执行右图所示的程序框图,若输入6x =,则输出y 的值为( )A . 2B . 0C . 1-D .32-4.若0a b <<,则下列选项正确的是( ) A.b a a b < B. 11a b< C .(,2)nna b n N n <∈≥ D. 0c ∀≠,都有ac bc < 5.下列说法正确的是( )A .已知p :2000,10x R x x ∃∈+-=,q :2,10x R x x ∀∈++>,则p q ∧是真命题。
B .命题p :若a b ⊥,则0a b ⋅=的否命题是:若a b ⊥,则0a b ⋅≠。
C .2,10x R x x ∀∈+-<的否定是2000,10x R x x ∃∈+->。
D .3x π=是sin(2)6y x π=-取最大值的充要条件。
2025届四川省宜宾市第四中学高考适应性考试数学试卷含解析

2025届四川省宜宾市第四中学高考适应性考试数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知等比数列{}n a 的各项均为正数,设其前n 项和n S ,若14+=nn n a a (n *∈N ),则5S =( )A .30B .C .D .622.由曲线3,y x y ==)A .512 B .13C .14D .123.在ABC ∆中,30C =︒,2cos 3A =-,2AC =,则AC 边上的高为( )A B .2C D .24.,,a b αβαβ//////,则a 与b 位置关系是 ( ) A .平行 B .异面C .相交D .平行或异面或相交5.已知集合{|{|2,}A x N y B x x n n Z =∈===∈,则A B =( )A .[0,4]B .{0,2,4}C .{2,4}D .[2,4]6.已知双曲线22122:1x y C a b -=与双曲线222:14y C x -=没有公共点,则双曲线1C 的离心率的取值范围是( )A .(B .)+∞C .(D .)+∞7.已知抛物线2:8C y x =的焦点为F ,A B 、是抛物线上两个不同的点,若||||8AF BF +=,则线段AB 的中点到y 轴的距离为( ) A .5B .3C .32D .28.设i 为虚数单位,z 为复数,若z i z+为实数m ,则m =( )A .1-B .0C .1D .29.定义在上的函数满足,且为奇函数,则的图象可能是( )A .B .C .D .10.如果0b a <<,那么下列不等式成立的是( ) A .22log log b a < B .1122b a⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭C .33b a >D .2ab b <11.点M 在曲线:3ln G y x =上,过M 作x 轴垂线l ,设l 与曲线1y x =交于点N ,3OM ON OP +=,且P 点的纵坐标始终为0,则称M 点为曲线G 上的“水平黄金点”,则曲线G 上的“水平黄金点”的个数为( ) A .0B .1C .2D .312.已知直线y =k (x +1)(k >0)与抛物线C 2:4y x =相交于A ,B 两点,F 为C 的焦点,若|FA |=2|FB |,则|FA | =( ) A .1B .2C .3D .4二、填空题:本题共4小题,每小题5分,共20分。
四川省宜宾市宜宾县高考数学适应性试卷(二)文(含解析)

2015年四川省宜宾市宜宾县高考数学适应性试卷(文科)(二)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛.由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队,则高三学生队中5班和16班的人数分别为()A.3,5 B.4,5 C.3,4 D.4,32.已知集合A={(x,y)|y2=4x},B={(x,y)|y=x+1},则A∩B=()A.{(1,﹣2)} B.{(1,2)} C.(1,2) D.(1,﹣2)3.如果执行如图所示的程序框图,输入x=6,则输出的y值为()A.2 B.0 C.﹣1 D.4.若a<b<0,则下列选项正确的是()A.B.C.a n<b n(n∈N,n≥2)D.∀c≠0,都有ac<bc5.下列说法正确的是()A.已知p:∃x0∈R,x02+x0﹣1=0,q:∀x∈R,x2+x+1>0,则p∧q是真命题B.命题p:若,则的否命题是:若,则C.∀x∈R,x2+x﹣1<0的否定是∃x0∈R,x02+x0﹣1>0D.x=是取最大值的充要条件6.如图是某几何体的三视图,其中正视图是斜边长为2的直角三角形,侧视图是半径为1的半圆,则该几何体的表面积是()A. B.C.D.+π7.已知f(x)=x3,若x∈[1,2]时,f(x2﹣ax)+f(1﹣x)≤0,则a的取值范围是()A.a≤1 B.a≥1 C.a≥D.a≤8.数列{a n}满足a n+a n+1=(n∈N,n≥1),若a2=1,S n是{a n}的前n项和,则S21的值为()A.﹣B.1 C.D.﹣9.设椭圆C的两个焦点为F1、F2,过点F1的直线与椭圆C交于点M,N,若|MF2|=|F1F2|,且|MF1|=4,|NF1|=3,则椭圆Г的离心率为()A.B.C.D.10.已知y=f(x)为R上的可导函数,当x≠0时,,则关于x的函数的零点个数为()A.1 B.2 C.0 D.0或2二、填空题:本大题共5小题,每小题5分,共25分.11.已知复数z满足zi=1﹣i,则|z|= .12.已知A,B是y=sin(ωx+φ)的图象与x轴的两个相邻交点,A,B之间的最值点为C.若△ABC 为等腰直角三角形,则ω的值为.13.已知(x,y)满足,若z=2x﹣y的最小值为.14.已知圆C:(x﹣2)2+y2=4.过点的直线与圆C交于A,B两点,若,则当劣弧AB所对的圆心角最小时, = .15.已知命题:①将一组数据中的每个数都变为原来的2倍,则方差也变为原来的2倍;②在△ABC中,若A>B,则sinA<sinB;③在正三棱锥S﹣ABC内任取一点P,使得V P﹣ABC<的概率是;④若对于任意的n∈N*,n2+(a﹣4)n+3+a≥0恒成立,则实数a的取值范围是.以上命题中正确的是(填写所有正确命题的序号).三.解答题16.在△ABC中,角A为锐角,且+cos2A.(1)求f(A)的最大值;(2)若,求△ABC的三个内角和AC边的长.17.教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.(Ⅰ)求x的值,并求一周内阳光体育活动时间在[6,8]小时的人数;(Ⅱ)从阳光体育时间在[6,8]小时的同学中抽取2人,求恰有1人的阳光体育活动时间在[6,7)小时的概率.18.数列{a n}满足na n+1﹣(n+1)a n=0,已知a1=2.(I)求数列{a n}的通项公式;(Ⅱ)若b n=,S n为数列的前n项的和,求证:S n<.19.如图,直三棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=.(1)证明:BC1∥平面A1CD;(2)求异面直线BC1和A1D所成角的大小;(3)当AB=时,求三棱锥C﹣A1DE的体积.20.给定椭圆C: =1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.若椭圆C的一个焦点为,其短轴上的一个端点到F的距离为.(Ⅰ)求椭圆C的方程和其“准圆”方程.(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;②求证:|MN|为定值.21.已知函数f(x)=alnx﹣ax﹣3,a∈R,(Ⅰ)当a=1时,求f(x)的极值;(Ⅱ)求函数f(x)的单调区间.(Ⅲ)若函数f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对任意的t∈[1,2],函数在区间(t,3)上总不是单调函数,求m取值范围.2015年四川省宜宾市宜宾县高考数学适应性试卷(文科)(二)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛.由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队,则高三学生队中5班和16班的人数分别为()A.3,5 B.4,5 C.3,4 D.4,3【考点】分层抽样方法.【专题】概率与统计.【分析】求出抽样比,利用分层抽样求解即可.【解答】解:由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队,可得抽样比为,高三学生队中5班和16班的人数分别为:6×=3; =4;故选:C.【点评】本题考查分层抽样,求解抽样比是解题的关键.2.已知集合A={(x,y)|y2=4x},B={(x,y)|y=x+1},则A∩B=()A.{(1,﹣2)} B.{(1,2)} C.(1,2) D.(1,﹣2)【考点】交集及其运算.【专题】集合.【分析】联立方程组,求得方程组的解集得答案.【解答】解:由A={(x,y)|y2=4x},B={(x,y)|y=x+1},得A∩B={(x,y)|}={(1,2)}.故选:B.【点评】本题考查交集及其运算,考查了方程组的解法,是基础题.3.如果执行如图所示的程序框图,输入x=6,则输出的y值为()A.2 B.0 C.﹣1 D.【考点】程序框图.【专题】算法和程序框图.【分析】执行程序框图,依次写出每次循环得到的x,y的值,当x=﹣1,y=﹣时,满足条件|y﹣x|<1,退出循环,输出y的值为﹣.【解答】解:执行程序框图,可得x=6y=2不满足条件|y﹣x|<1,x=2,y=0不满足条件|y﹣x|<1,x=0,y=﹣1不满足条件|y﹣x|<1,x=﹣1,y=﹣满足条件|y﹣x|<1,退出循环,输出y的值为﹣.故选:D.【点评】本题主要考察了程序框图和算法,根据赋值语句正确得到每次循环x,y的值是解题的关键,属于基础题.4.若a<b<0,则下列选项正确的是()A.B.C.a n<b n(n∈N,n≥2)D.∀c≠0,都有ac<bc【考点】不等式比较大小.【专题】不等式的解法及应用.【分析】A.由a<b<0,可得a2>b2,ab>0,利用不等式的基本性质,即可判断出正误;B.由a<b<0,可得ab>0,利用不等式的基本性质,即可判断出正误;C.由a<b<0,可得a2>b2,即可判断出正误;D.取c<0时,可得ac>bc,即可判断出正误.【解答】解:A.∵a<b<0,∴a2>b2,ab>0,∴,因此正确;B.∵a<b<0,∴ab>0,∴,因此不正确;C.∵a<b<0,∴a2>b2,因此不正确;D.取c<0时,可得ac>bc,因此不正确.故选:A.【点评】本题考查了不等式的基本性质,属于基础题.5.下列说法正确的是()A.已知p:∃x0∈R,x02+x0﹣1=0,q:∀x∈R,x2+x+1>0,则p∧q是真命题B.命题p:若,则的否命题是:若,则C.∀x∈R,x2+x﹣1<0的否定是∃x0∈R,x02+x0﹣1>0D.x=是取最大值的充要条件【考点】命题的真假判断与应用.【专题】简易逻辑.【分析】A.p:由于△>0,因此方程有实数根,p是真命题,q:由x2+x+1=>0,是真命题,即可判断出p∧q的真假;B.利用否命题的定义即可判断出正误;C.利用命题的否定即可判断出正误;D.例如x=+π时函数也可以取得最大值,即可判断出正误.【解答】解:A.p:∃x0∈R,x02+x0﹣1=0,由于△>0,因此方程有实数根,是真命题,q:∀x∈R,x2+x+1=>0,是真命题,因此p∧q是真命题,正确;B.命题p:若,则的否命题是:若与不垂直,则,不正确;C.∀x∈R,x2+x﹣1<0的否定是∃x0∈R,x02+x0﹣1≥0,因此不正确;D.x=是取最大值的充分不必要条件,例如x=+π时也可以取得最大值,因此不正确.故选:A.【点评】本题考查了简易逻辑的判定方法、三角函数的性质、一元二次方程的解与判别式的关系,考查了推理能力与计算能力,属于中档题.6.如图是某几何体的三视图,其中正视图是斜边长为2的直角三角形,侧视图是半径为1的半圆,则该几何体的表面积是()A. B.C.D.+π【考点】由三视图求面积、体积.【专题】计算题;空间位置关系与距离.【分析】根据几何体的三视图,得出该几何体是平放的半圆锥体,根据图中数据求出它的表面积.【解答】解:根据几何体的三视图,得;该几何体是平放的半圆锥体,且半圆锥体的底面圆半径为1,母线长为2,高为;∴该半圆锥体的表面积为π•12+•22•sin60°+π•1•2=+.故选:A.【点评】本题考查了空间几何体的三视图的应用问题,也考查了求几何体的表面积的应用问题,是基础题目.7.已知f(x)=x3,若x∈[1,2]时,f(x2﹣ax)+f(1﹣x)≤0,则a的取值范围是()A.a≤1 B.a≥1 C.a≥D.a≤【考点】函数单调性的性质.【专题】函数的性质及应用;导数的综合应用.【分析】首先看出f(﹣x)=﹣f(x),求f′(x),根据其符号即可判断f(x)为增函数,从而由原不等式可得到x2﹣(a+1)x+1≤0,设g(x)=x2﹣(a+1)x+1,从而必须满足,这样解不等式组即得a的取值范围.【解答】解:f(﹣x)=﹣f(x);f′(x)=3x2>0;∴f(x)在(﹣∞,+∞)上单调递增;∴由f(x2﹣ax)+f(1﹣x)≤0得:f(x2﹣ax)≤f(x﹣1);∴x2﹣ax≤x﹣1,即:x2﹣(a+1)x+1≤0;设g(x)=x2﹣(a+1)x+1,则:;∴.故选C.【点评】考查奇函数的定义及判断方法,根据导数符号判断函数单调性,以及函数单调性定义的运用,要熟练二次函数的图象.8.数列{a n}满足a n+a n+1=(n∈N,n≥1),若a2=1,S n是{a n}的前n项和,则S21的值为()A.﹣B.1 C.D.﹣【考点】数列的求和;数列递推式.【专题】点列、递归数列与数学归纳法.【分析】通过a n+a n+1=及a n+1+a n+2=可得a n+2=a n,利用a2=1可得首项,进而可得结论.【解答】解:∵a n+a n+1=,∴a n+1+a n+2=,∴a n+1+a n+2=a n+a n+1,即a n+2=a n,又∵a2=1,∴a21=a1==﹣,∴S21=(a1+a2)+(a3+a4)+…+(a19+a20)+a21=10×=,故选:C.【点评】本题考查求数列的和,利用已知条件找出规律是解决本题的关键,注意解题方法的积累,属于基础题.9.设椭圆C的两个焦点为F1、F2,过点F1的直线与椭圆C交于点M,N,若|MF2|=|F1F2|,且|MF1|=4,|NF1|=3,则椭圆Г的离心率为()A.B.C.D.【考点】椭圆的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】设椭(a>b>0),运用椭圆的定义,可得|NF2|=2a﹣|NF1|=2a﹣3,|MF2|+|MF1|=2a,即有2c+4=2a,取MF1的中点K,连接KF2,则KF2⊥MN,由勾股定理可得a+c=12,解得a,c,运用离心率公式计算即可得到.【解答】解:设椭圆(a>b>0),F1(﹣c,0),F2(c,0),|MF2|=|F1F2|=2c,由椭圆的定义可得|NF2|=2a﹣|NF1|=2a﹣3,|MF2|+|MF1|=2a,即有2c+4=2a,即a﹣c=2,①取MF1的中点K,连接KF2,则KF2⊥MN,由勾股定理可得|MF2|2﹣|MK|2=|NF2|2﹣|NK|2,即为4c2﹣4=(2a﹣3)2﹣25,化简即为a+c=12,②由①②解得a=7,c=5,则离心率e==.故选:D.【点评】本题考查椭圆的定义、方程和性质,主要考查椭圆的定义的运用和离心率的求法,考查运算能力,属于中档题.10.已知y=f(x)为R上的可导函数,当x≠0时,,则关于x的函数的零点个数为()A.1 B.2 C.0 D.0或2【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】由题意可得,x≠0,因而 g(x)的零点跟 xg(x)的非零零点是完全一样的.当x>0时,利用导数的知识可得xg(x)在(0,+∞)上是递增函数,xg(x)>1恒成立,可得xg(x)在(0,+∞)上无零点.同理可得xg(x)在(﹣∞,0)上也无零点,从而得出结论.【解答】解:由于函数,可得x≠0,因而 g(x)的零点跟 xg(x)的非零零点是完全一样的,故我们考虑 xg(x)=xf(x)+1 的零点.由于当x≠0时,,①当x>0时,(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+)>0,所以,在(0,+∞)上,函数x•g(x)单调递增函数.又∵ [xf(x)+1]=1,∴在(0,+∞)上,函数x•g(x)=xf(x)+1>1恒成立,因此,在(0,+∞)上,函数x•g(x)=xf(x)+1 没有零点.②当x<0时,由于(x•g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+)<0,故函数x•g(x)在(﹣∞,0)上是递减函数,函数x•g(x)=xf(x)+1>1恒成立,故函数x•g(x)在(﹣∞,0)上无零点.综上可得,函在R上的零点个数为0,故选C.【点评】本题考查了根的存在性及根的个数判断,导数与函数的单调性的关系,体现了分类讨论、转化的思想,属于中档题.二、填空题:本大题共5小题,每小题5分,共25分.11.已知复数z满足zi=1﹣i,则|z|= .【考点】复数求模.【专题】平面向量及应用.【分析】直接利用复数的求模的法则求解即可.【解答】解:复数z满足zi=1﹣i,|zi|=|1﹣i|,则|z|=.故答案为:;【点评】本题考查复数的模的求法,基本知识的考查.12.已知A,B是y=sin(ωx+φ)的图象与x轴的两个相邻交点,A,B之间的最值点为C.若△ABC 为等腰直角三角形,则ω的值为.【考点】y=Asin(ωx+φ)中参数的物理意义.【专题】计算题;三角函数的图像与性质.【分析】由图象得到等腰直角三角形斜边AB上的高,则斜边AB可求,即函数y=sin(ωx+φ)的周期可求,由周期公式求得ω的值.【解答】解:由题意可知,点C到边AB的距离为2,即△ABC的AB边上的高为4,∵△ABC是以∠C为直角的等腰三角形,∴AB=2×2=4.即函数y=sin(ωx+φ)的周期T=4.∴ω==.故答案为:.【点评】本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,解答的关键是明确等腰直角三角形斜边上的高等于斜边的一半,是基础题.13.已知(x,y)满足,若z=2x﹣y的最小值为.【考点】简单线性规划.【专题】不等式的解法及应用.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得C(),由z=2x﹣y,得y=2x﹣z,由图可知,当直线y=2x﹣z过点C()时,直线在y轴上的截距最大,z有最小值为.故答案为:.【点评】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.14.已知圆C:(x﹣2)2+y2=4.过点的直线与圆C交于A,B两点,若,则当劣弧AB所对的圆心角最小时, = 3 .【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】由题意,N为AB的中点,当劣弧AB所对的圆心角最小时,M,N重合,并且CM⊥AB,由此得到所求为CM2.【解答】解:由可知N为AB的中点,当劣弧AB所对的圆心角最小时,AB⊥CM,即M,N重合,所以==(1﹣2)2+()2=3;故答案为:3.【点评】本题考查了直线与圆;解答本题的关键是:由题意明确M,N的位置关系,确定所求的实质.15.已知命题:①将一组数据中的每个数都变为原来的2倍,则方差也变为原来的2倍;②在△ABC中,若A>B,则sinA<sinB;③在正三棱锥S﹣ABC内任取一点P,使得V P﹣ABC<的概率是;④若对于任意的n∈N*,n2+(a﹣4)n+3+a≥0恒成立,则实数a的取值范围是.以上命题中正确的是③④(填写所有正确命题的序号).【考点】命题的真假判断与应用.【专题】简易逻辑.【分析】①利用方差的性质可得:方差变为原来的4倍,即可判断出正误;②在△ABC中,若A>B,则a>b,由正弦定理可得sinA>sinB,即可判断出正误;③如图所示,O是正△ABC的中心,分别取棱SA,SB,SC的中点D,E,F,则在△DEF及其内部任取一点P,则V P﹣ABC=,因此使得V P﹣ABC<的概率P=,即可判断出正误;④若对于任意的n∈N*,n2+(a﹣4)n+3+a≥0恒成立,则=﹣,令f(x)=(x≥2),利用导数研究其单调性即可得出.【解答】解:①将一组数据中的每个数都变为原来的2倍,则方差变为原来的4倍,因此①不正确;②在△ABC中,若A>B,则a>b,由正弦定理可得:,∴sinA>sinB,因此②不正确;③如图所示,O是正△ABC的中心,分别取棱SA,SB,SC的中点D,E,F,则在△DEF及其内部任取一点P,则V P﹣ABC=×=,因此使得V P﹣ABC<的概率P==,即③正确;④若对于任意的n∈N*,n2+(a﹣4)n+3+a≥0恒成立,则=﹣,令f(x)=(x≥2),f′(x)=1﹣=,当x≥3时,f′(x)>0,函数f(x)单调递增,∴f(x)≥f(3)==,f(4)=6,当x=2时,f(2)=6,∴a≥﹣(﹣6)=,∴实数a的取值范围是,因此④正确.以上命题中正确的是③④.故答案为:③④.【点评】本题考查了简易逻辑的判定方法、方差的性质、正弦定理、三棱锥的体积、利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.三.解答题16.在△ABC中,角A为锐角,且+cos2A.(1)求f(A)的最大值;(2)若,求△ABC的三个内角和AC边的长.【考点】运用诱导公式化简求值;二倍角的余弦.【分析】(1)先利用诱导公式化简f(A),根据A为锐角,确定f(A)的最大值.(2)利用f(A)=1求出A、B、C三个角,再用正弦定理求出AC边的长.【解答】解:(I)由已知得f(A)=∴取值最大值,其最大值为(II)由 f(A)=1得sin(2A+)=在△ABC中,由正弦定理得:【点评】本题考查诱导公式的化简求值,二倍角的余弦公式等知识,是中档题.17.教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.(Ⅰ)求x的值,并求一周内阳光体育活动时间在[6,8]小时的人数;(Ⅱ)从阳光体育时间在[6,8]小时的同学中抽取2人,求恰有1人的阳光体育活动时间在[6,7)小时的概率.【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图.【专题】概率与统计.【分析】( I)由直方图的性质可得x的方程,解方程可得x值,进而可得在[6,8]小时的人数为;(II)由( I)可得活动时间在[6,7)小时的人数为3,在[7,8]小时的人数为2,分别表示为A1,A2,A3,B1,B2,列举可得总的基本事件共10个,符合题意的有6个,由概率公式可得.【解答】解:( I)∵组距为1,∴由直方图可得[3,4),[4,5),[5,6),[6,7),[7,8]的频率分别为0.1,0.25,0.4,x,0.1,∴0.1+0.25+0.4+x+0.1=1,解方程可得x=0.15∵抽取20个人,∴一周内阳光体育活动时间在[6,8]小时的人数为20×(0.15+0.1)=5,即一周内阳光体育活动时间在[6,8]小时的人数为5;(II)由( I),一周内阳光体育活动时间在[6,7)小时的人数为3,在[7,8]小时的人数为2,分别表示为A1,A2,A3,B1,B2,从这5个人中抽取2个人,有以下基本事件:A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2,A3B1,A3B2,B1B2,共10个,其中恰有一个人的阳光体育活动时间在[6,7)小时的基本事件有6个基本事件.设“恰有1个人的阳光体育活动时间在[6,7)小时”事件M,则【点评】本题考查列举法计算基本事件数以及事件发生的概率,涉及直方图的性质,属基础题.18.数列{a n}满足na n+1﹣(n+1)a n=0,已知a1=2.(I)求数列{a n}的通项公式;(Ⅱ)若b n=,S n为数列的前n项的和,求证:S n<.【考点】数列的求和.【专题】等差数列与等比数列.【分析】(I)通过na n+1=(n+1)a n可得,进而可得结论;(II)通过b n=n、b n+1=n+1分离分母,累加即得结论.【解答】(I)解:∵na n+1=(n+1)a n,∴,∴a n+1=2(n+1),∴a n=2n;(II)证明:由(I)可知,b n=n,∴b n+1=n+1,∴,∴,即(n∈N*);【点评】本题考查求数列的通项、判定数列和的大小范围,注意解题方法的积累,属于中档题.19.如图,直三棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=.(1)证明:BC1∥平面A1CD;(2)求异面直线BC1和A1D所成角的大小;(3)当AB=时,求三棱锥C﹣A1DE的体积.【考点】棱柱、棱锥、棱台的体积;异面直线及其所成的角.【专题】空间位置关系与距离.【分析】(1)连接AC1与A1C相交于点F,连接DF,利用矩形的性质、三角形中位线定理可得:DF∥BC1,再利用线面平行的判定定理即可证明.(2)由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角.不妨取AB=2,在△A1DF中,由余弦定理即可得出.(3)利用面面垂直的性质定理可得:CD⊥平面ABB1A1,利用=﹣S△BDE﹣﹣可得,再利用三棱锥C﹣A1DE的体积V=即可得出.【解答】(1)证明:连接AC1与A1C相交于点F,连接DF,由矩形ACC1A1可得点F是AC1的中点,又D是AB的中点,∴DF∥BC1,∵BC1⊄平面A1CD,DF⊂平面A1CD,∴BC1∥平面A1CD;(2)解:由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角.不妨取AB=2,═==1,A1D===,=1.在△A1DF中,由余弦定理可得:cos∠A1DF==,∠A1DF∈(0,π),∴∠A1DF=,∴异面直线BC1和A1D所成角的大小;(3)解:∵AC=BC,D为AB的中点,∴CD⊥AB,∵平面ABB1A1∩平面ABC=AB,∴CD⊥平面ABB1A1,CD==.=﹣S△BDE﹣﹣=﹣﹣﹣=,∴三棱锥C﹣A1DE的体积V===1.【点评】本题考查了直三棱柱的性质、矩形的性质、三角形中位线定理、线面平行的判定定理、异面直线所成角、余弦定理、勾股定理、线面面面垂直的性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.20.给定椭圆C: =1(a>b>0),称圆心在原点O,半径为的圆是椭圆C的“准圆”.若椭圆C的一个焦点为,其短轴上的一个端点到F的距离为.(Ⅰ)求椭圆C的方程和其“准圆”方程.(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;②求证:|MN|为定值.【考点】直线与圆锥曲线的综合问题.【专题】综合题;压轴题;分类讨论.【分析】(I)由椭圆的方程与准圆的方程关系求得准圆的方程(II)(1)由准圆x2+y2=4与y轴正半轴的交点为P(0,2),设椭圆有一个公共点的直线为y=kx+2,与准圆方程联立,由椭圆与y=kx+2只有一个公共点,求得k.从而得l1,l2方程(2)分两种情况①当l1,l2中有一条无斜率和②当l1,l2都有斜率处理.【解答】解:(I)因为,所以b=1所以椭圆的方程为,准圆的方程为x2+y2=4.(II)(1)因为准圆x2+y2=4与y轴正半轴的交点为P(0,2),设过点P(0,2),且与椭圆有一个公共点的直线为y=kx+2,所以,消去y,得到(1+3k2)x2+12kx+9=0,因为椭圆与y=kx+2只有一个公共点,所以△=144k2﹣4×9(1+3k2)=0,解得k=±1.所以l1,l2方程为y=x+2,y=﹣x+2.(2)①当l1,l2中有一条无斜率时,不妨设l1无斜率,因为l1与椭圆只有一个公共点,则其方程为或,当l1方程为时,此时l1与准圆交于点,此时经过点(或)且与椭圆只有一个公共点的直线是y=1(或y=﹣1),即l2为y=1(或y=﹣1),显然直线l1,l2垂直;同理可证l1方程为时,直线l1,l2垂直.②当l1,l2都有斜率时,设点P(x0,y0),其中x02+y02=4,设经过点P(x0,y0)与椭圆只有一个公共点的直线为y=t(x﹣x0)+y0,则,消去y得到x2+3(tx+(y0﹣tx0))2﹣3=0,即(1+3t2)x2+6t(y0﹣tx0)x+3(y0﹣tx0)2﹣3=0,△=[6t(y0﹣tx0)]2﹣4•(1+3t2)[3(y0﹣tx0)2﹣3]=0,经过化简得到:(3﹣x02)t2+2x0y0t+1﹣y02=0,因为x02+y02=4,所以有(3﹣x02)t2+2x0y0t+(x02﹣3)=0,设l1,l2的斜率分别为t1,t2,因为l1,l2与椭圆都只有一个公共点,所以t1,t2满足上述方程(3﹣x02)t2+2x0y0t+(x02﹣3)=0,所以t1•t2=﹣1,即l1,l2垂直.综合①②知:因为l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直,所以线段MN为准圆x2+y2=4的直径,所以|MN|=4.【点评】本题主要考查直线与曲线的位置关系,通过情境设置,拓展了圆锥曲线的应用范围,同时渗透了其他知识,考查了学生综合运用知识的能力.21.已知函数f(x)=alnx﹣ax﹣3,a∈R,(Ⅰ)当a=1时,求f(x)的极值;(Ⅱ)求函数f(x)的单调区间.(Ⅲ)若函数f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对任意的t∈[1,2],函数在区间(t,3)上总不是单调函数,求m取值范围.【考点】利用导数研究函数的单调性;利用导数研究函数的极值.【专题】导数的综合应用.【分析】(Ⅰ)当a=1时,化简函数的解析式,求出函数的导数,利用函数的单调性求解函数的极值即可.( II)利用函数的导数,当a>0时,当a=0时,当a<0时,求解函数得到单调区间.( III)利用已知条件化简函数g(x),求出函数的导数,通过g′(x)=0有一正一负的两个实数根.利用根的分别列出不等式组求解即可.【解答】解:(Ⅰ)当a=1时,,∴f′(x)<0⇒x>1,f′(x)>0⇒0<x<1所以f(x)在(0,1)上单调递增,在(1,+∞)单调递减,所以f(x)有极大值,极大值为f(1)=﹣4,无极小值.( II)∵,∴当a>0时,f(x)在(0,1)↑,在(1,+∞)↓当a=0时,f(x)=﹣3,无单调区间,当a<0时,f(x)在(0,1)↓,在(1,+∞)↑( III)∵f′(2)═1,∴g(x)=x3+x2(﹣)=x3+()x2﹣2x∴g′(x)=3x2+(m+4)x﹣2,令g′(x)=0,∴3x2+(m+2)x﹣2=0,△=(m+2)2+24>0,∴g′(x)=0有一正一负的两个实数根.又t∈[1,2],x∈(t,3)∵g(x)在(t,3)不单调,∴g′(x)=0在(t,3)上只有一个正实根∴,因为t∈[1,2]恒成立,令,可证⇒.【点评】本题考查函数的导数的应用,函数的单调性以及函数的极值,根的分别,考查分析问题解决问题的能力.。
四川省高考数学适应性试卷文科含答案解析

2021年四川省高考数学适应性试卷〔文科〕一、选择题:本大题共10个小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.集合M,N满足M∪N={1,2,3},M∩N={a},那么〔〕A.a=1B.a=2C.a=3D.a∈M∪N2axb012〕,那么ab的值为〔〕2.假设不等式x++<的解集为〔﹣,A.﹣1B.1C.﹣2D.23z=,那么|z|=〔〕.复数A.1B.C.2D.4.假设“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0〞是假命题,那么实数m的取值范围是〔〕A .〔﹣11B11C1∞D.[01,〕.〔﹣,].[,+〕,]5.=〔2,1〕,=〔3,λ〕.假设〔2〕∥,那么λ的值为〔〕A.B.C.3D.﹣1或36.执行如下图的程序框图,输出的结果是〔〕A.﹣2B.C.D.37sin=,sin〔α+β〕=,那么cos2〕.α、β为锐角,假设αβ的值为〔A.B.C.或D.8.P,Q,R是圆x2+y2﹣2x﹣8=0上不同三点,它们到直线l:x+y+7=0的距离分别为x1,x2,x3,假设x1,x2,x3成等差数列,那么公差的最大值为〔〕A.1B.2C.3D.49.设P 是左、右顶点分别为A,B的双曲线x2﹣y2=1上的点,假设直线PA的倾斜角为,那么直线PB的倾斜角是〔〕A.B.C.D.10.设0<a<1,函数f〔x〕=,假设存在实数b使函数g〔x〕=f〔x〕﹣b有两个零点,那么a的取值范围是〔〕A.B.C.〔0,1〕D.第1页〔共17页〕二、填空题〔每题 5分,总分值 25分,将答案填在答题纸上〕11.假设抛物线 y =ax 2的焦点F 的坐标为〔0,﹣1〕,那么实数 a 的值为_______.12.某几何体的三视图如下图, 其中左视图为半圆, 那么主视图中 α角的正切值为_______.13 f x 〕 =x + 在[ 1 3 2 ,那么正数 k的最大值与最小值之和为.假设函数 〔 ,]上的最小值为 _______.2ax1 214a在区间[16fx=﹣ x++在区间〔,+∞〕上是单调.当实数,]随机取值时,函数〔 〕减函数的概率是_______.15.实数a ,b 满足:5﹣a ≤3b ≤12﹣3a ,e b≤a ,那么 的取值范围为_______.三、解答题〔本大题共 6小题,共 75分.解容许写出文字说明、证明过程或演算步骤.〕 16.为了解学生寒假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表: 本数人数 012345 性别男生 0 1 4 3 2 2女生1331〔I 〕分别计算男生、女生阅读名著本数的平均值 x 1,x 2和方差 ,;II 〕从阅读4本名著的学生中选两名学生在全校交流读后心得,求选出的两名学生恰好是一男一女的概率.17.数列{a n }的前n 项和S n =k?3n﹣m ,且a 1=3,a 3=27.I 〕求证:数列{a n }是等比数列;II 〕假设a n b n =log 3a n+1,求数列{b n }的前n 项和T n .18.在斜三棱柱 A BC ﹣A 1B 1C 1中,底面ABC 是正三角形,E 是AB 中点,A 1E ⊥平面ABC .〔I 〕证明:BC 1∥平面A 1EC ;〔II 〕假设A 1A ⊥A 1B ,且AB=2,求三棱锥B 1﹣ACA 1的体积.第2页〔共17页〕19.如图ABCD 是平面四边形,∠ ADB=∠BCD=90°,AB=4,BD=2.〔Ⅰ〕假设BC=1,求AC 的长;〔Ⅱ〕假设∠ACD=30°,求tan ∠BDC 的值.20.圆锥曲线 E :.〔I 〕求曲线E 的离心率及标准方程;〔II 〕设M 〔x 0,y 0〕是曲线 E 上的任意一点,过原点作⊙M :〔x ﹣x 0〕2+〔y ﹣y 0〕2=8的 两条切线,分别交曲线 E 于点 P 、Q .① 假设直线OPOQ 的斜率存在分别为 k ,k ,求证:kk=﹣; , 1 2 12 ②试问OP 2+OQ 2是否为定值.假设是求出这个定值,假设不是请说明理由. x21.设函数 f 〔x 〕=e ,g 〔x 〕=kx+1. I 〕求函数y=f 〔x 〕﹣〔x+1〕的最小值;II 〕证明:当k >1时,存在x 0>0,使对于任意x ∈〔0,x 0〕都有f 〔x 〕<g 〔x 〕;〔III 〕假设对于任意 x ∈〔0,+∞〕,|f 〔x 〕﹣g 〔x 〕|>x 恒成立,求实数 k 的取值范围.第3页〔共17页〕2021年四川省高考数学适应性试卷〔文科〕参考答案与试题解析一、选择题:本大题共10个小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的. 1.集合M,N满足M∪N={1,2,3},M∩N={a},那么〔〕A.a=1 B.a=2 C.a=3D.a∈M∪N【考点】交集及其运算;并集及其运算.【分析】根据集合关系进行判断即可.【解答】解:∵M∪N={1,2,3},M∩N={a},a=1,或a=2或a=3,即a∈M∪N,应选:D.2.假设不等式x 2+ax+b<0的解集为〔﹣1,2〕,那么ab的值为〔〕A.﹣1B.1C.﹣2D.2【考点】一元二次不等式的解法.【分析】根据一元二次不等式与对应方程之间的关系,利用根与系数的关系求出a、b的值,再计算ab的值.【解答】解:不等式x 2+ax+b<0的解集为〔﹣1,2〕,所以方程x2axb=0的实数根为﹣1和2 ++,所以,解得a=﹣1,b=﹣2,所以ab=﹣1×〔﹣2〕=2.应选:D.3z=,那么|z=〔〕.复数|A.1B.C.2D.【考点】复数代数形式的乘除运算.【分析】根据复数的运算性质化简z,从而求出z的模即可.【解答】解:z===i,那么|z|=1,应选:A.4.假设“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0〞是假命题,那么实数m的取值范围是〔〕A .〔﹣11B11C1∞D.[01,〕.〔﹣,].[,+〕,]【考点】特称命题.【分析】由|x|﹣1>0,解得x>1或x<﹣1.由“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0,可得m>1.利用“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0〞是假命题,即可得出.第4页〔共17页〕【解答】解:由|x|﹣1>0,解得x>1或x<﹣1.∵“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0,∴m>1.∵“?x∈[﹣1,m]〔m>﹣1〕,|x|﹣1>0〞是假命题,∴﹣1<m≤1.应选:B.5.=〔2,1〕,=〔3,λ〕.假设〔2〕∥,那么λ的值为〔〕A.B.C.3D.﹣1或3【考点】平面向量共线〔平行〕的坐标表示.【分析】求出向量2,利用向量共线列出方程,求解即可.【解答】解:=〔2,1〕,=〔3,λ〕.=〔1,2﹣λ〕.〔2〕∥,可得:3〔2﹣λ〕=λ,∴λ=.应选:A.6.执行如下图的程序框图,输出的结果是〔〕A.﹣2 B.C.D.3【考点】程序框图.【分析】根据程序框图,依次计算运行的结果,观察规律可得当a=,k=4时,满足条件k4,退出循环,输出a的值为.【解答】解:模拟执行程序,可得a= ,k=0执行循环体,a=3,k=1不满足条件k≥100,执行循环体,a=﹣2,k=2不满足条件k≥100,执行循环体,a=﹣,k=3第5页〔共17页〕不满足条件k≥100,执行循环体,a=,k=4此时,满足条件k≥4,退出循环,输出a的值为.应选:C.7.α、β为锐角,假设sinα=,sin〔α+β〕=,那么cos2β的值为〔〕A.B.C.或D.【考点】两角和与差的余弦函数.【分析】利用同角三角函数的根本关系求得cosα的值,由题意求得范围π>α+β>,从而可求cosαβcosβcos2β的值.〔+〕的值,进而可求的值,再利用二倍角的余弦公式求得αβsinα=sinαβ=,【解答】解:、都是锐角,且,〔+〕∴cosα==,cos〔α+β〕==±,sin〔α+β〕=sinαcosβ+cosαsinβ=〔2cosβ+sinβ〕=,2cosβ+sinβ=,①∵cosα=,α>,∵>sin〔α+β〕=>,∴π>α+β>,cos〔α+β〕=﹣,cosαcosβ﹣sinαsinβ=﹣,cosβ﹣2sinβ〕=﹣,∴cosβ﹣2sinβ=﹣,②解①②,得cosβ=,cos2β=2cos 2β﹣1=﹣.应选:A.2y22x﹣8=0上不同三点,它们到直线l x+y7=0的距离分别8.P,Q,R是圆x+﹣:+为x1,x2,x3,假设x1,x2,x3成等差数列,那么公差的最大值为〔〕第6页〔共17页〕A .1B .2C .3D .4【考点】直线与圆的位置关系.【分析】求出圆心到直线的距离,判断直线与圆的位置关系,继而得出圆上的点到直线的距离的最大值和最小值,那么距离最值的差的一半为最大公差.【解答】解:圆的圆心为〔 1,0〕,半径r=3,圆心到直线 l 的距离d= = =4,所以直线 l 与圆相离.∴圆上的点到直线 l 的距离的最小值为 d ﹣r=1,最大值为 d+r=7.∴当x 1=1,x 3=7时,等差数列的公差取得最大值 =3.应选C .9.设P 是左、右顶点分别为 A ,B 的双曲线x 2﹣y 2=1上的点,假设直线 PA 的倾斜角为 ,那么直线PB 的倾斜角是〔 〕A .B .C .D .【考点】双曲线的简单性质.【分析】设P 〔m ,n 〕,那么m 2﹣n 2=1,求得A ,B 的坐标,运用两点的直线的斜率公式,计算可得k PA ?k PB =1,再由倾斜角与斜率的关系,即可得到所求.22【解答】解:设P 〔m ,n 〕,那么m ﹣n=1,由题意可得A 〔﹣1,0〕,B 〔1,0〕,即有k PA ?k PB = ? == =1,由直线PA 的倾斜角为 ,可得k PA =tan =﹣, 即有k PB =﹣,可得直线PB 的倾斜角是.应选:C .10.设0<a <1,函数 f 〔x 〕= ,假设存在实数 b 使函数g 〔x 〕=f〔x 〕﹣b 有两个零点,那么 a 的取值范围是〔 〕A .B .C .〔0,1〕D .∴ 【考点】函数零点的判定定理.【分析】由g 〔x 〕=f 〔x 〕﹣b 有两个零点可得 f 〔x 〕=b 有两个零点,即y=f 〔x 〕与y=b的图象有两个交点,那么利用 a= 时,8a 3=1,可求a 的范围.【解答】解:∵g 〔x 〕=f 〔x 〕﹣b 有两个零点f 〔x 〕=b 有两个零点,即y=f 〔x 〕与y=b 的图象有两个交点,由于y=cos πx 在〔0,a]递减,y=8x 3在〔a ,1]递增,第7页〔共17页〕a= 时,8a 3=1.∵存在实数 b 使函数g 〔x 〕=f 〔x 〕﹣b 有两个零点,0<a < 应选:B .二、填空题〔每题 5分,总分值 25分,将答案填在答题纸上〕11.假设抛物线 y =ax 2的焦点F 的坐标为〔0,﹣1〕,那么实数 a 的值为 .【考点】抛物线的简单性质.【分析】先把抛物线方程整理成标准方程,进而根据抛物线的焦点坐标,可得 a 的值.【解答】解:抛物线 y=ax 2的标准方程为 x 2= y , ∵抛物线 y=ax 2的焦点坐标为〔 0,﹣1〕,∴ =﹣1,∴a=故答案为: .12.某几何体的三视图如下图,其中左视图为半圆,那么主视图中α角的正切值为.【考点】由三视图求面积、体积.【分析】由三视图可知:该几何体为圆锥的一半.可得母线长 l=3,底面半径 r=1,圆锥的高h= ,利用直角三角形的边角关系即可得出.【解答】解:由三视图可知:该几何体为圆锥的一半.∵母线长 l=3,底面半径 r=1.∴圆锥的高 h= =2 .∴tan α= = .故答案为:.第8页〔共17页〕13 fx=x 在[ 1 3 上的最小值为 2 ,那么正数 k 的最大值与最小值之和为 10. .假设函数〔〕+ ,] 【考点】根本不等式.【分析】运用根本不等式可得 f x 〕≥ 2 ,由等号成立的条件可得 ∈[ 1 3〔 ,],继而求出k 的最大值与最小值.【解答】解:由题意得:x >0, ∴f 〔x 〕=x+ ≥2 ,∵函数f 〔x 〕=x+ 在[1,3]上的最小值为 2 ,当x=时,函数f 〔x 〕取得最小值2,∴∈[1,3],∴k 的最小值为1,最大值为9.∴正数k 的最大值与最小值之和为 10.故答案为:10.14.当实数a 在区间[1,6]随机取值时,函数f 〔x 〕=﹣x 2+ax+1在区间〔2,+∞〕上是单调减函数的概率是.【考点】几何概型.【分析】由题意,此题属于几何概型的概率求法, 由此只要求出所有事件的区域长度以及满足条件的a 的范围对应的区域长度,利用几何概型概率公式可求.【解答】解:∵函数 f x 〕 = ﹣ x 2ax1 2 ∞〕上是单调减函数,〔 ++在区间〔 ,+∴ ≤2, a ≤4,∵1≤a ≤6,1≤a ≤4,长度为3,∵1≤a ≤6,长度为5∴函数 f 〔x = ﹣ x 2 ax1 在区间〔 2 ∞ 〕 + + ,+ 〕上是单调减函数的概率是.故答案为: .15.实数a ,b 满足:5﹣a ≤3b ≤12 ba的取值范围为[,].﹣3a ,e ≤,那么【考点】不等式的根本性质.【分析】作出不等式组表示的平面区域,那么表示与原点的连线的斜率额取值范围.【解答】解:∵e b≤a , b ≤lna5﹣a ≤3b ≤12﹣3a ,画出如下图的可行域,第9页〔共17页〕由,解得a=,b=,即A〔,〕,=设b=lna,∴b′=,当b=1时,此时斜线的斜率最大,即为=k=,综上所述,的取值范围为,故答案为:[,].三、解答题〔本大题共6小题,共75分.解容许写出文字说明、证明过程或演算步骤.〕16.为了解学生寒假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表:本数人数012345性别男生014322女生001331(〔I〕分别计算男生、女生阅读名著本数的平均值x1,x2和方差,;II〕从阅读4本名著的学生中选两名学生在全校交流读后心得,求选出的两名学生恰好是一男一女的概率.第10页〔共17页〕【考点】极差、方差与标准差;众数、中位数、平均数;列举法计算根本领件数及事件发生的概率.【分析】〔Ⅰ〕利用公式分别求出男生、女生阅读名著本数的平均数与方差即可;〔Ⅱ〕利用列举法计算根本领件数,即可求出对应的概率值.【解答】解:〔Ⅰ〕全班有 12个男生8个女生,∴男生阅读名著本数的平均值 x 1= =3,女生阅读名著本数的平均值x 2=,∴,;〔II 〕阅读4本名著的学生共有 5人,其中两名男生,三名女生,设两名男生分别为A 1,A 2,三名女生分别为B 1,B 2,B 3,从这5人中任选两人的选法有:1A 2,A 1B 1,A 1B 2,A 1B 3,A 2B 1,A 2B 2,A 2B 3,B 1B 2,B 1B 3,B 2B 3共10种,其中一男一女的选法有:1B 1,A 1B 2,A 1B 3,A 2B 1,A 2B 2,A 2B 3共6种,所以从这 5人中选出的两人是一男一女的概率为.17.数列{a n }的前n 项和S n =k?3n﹣m ,且a 1=3,a 3=27.I 〕求证:数列{a n }是等比数列;II 〕假设a n b n =log 3a n+1,求数列{b n }的前n 项和T n . 【考点】数列的求和;等比关系确实定.【分析】〔I 〕利用递推关系与等比数列的定义即可证明. II 〕利用“错位相减法〞、等比数列的求和公式即可得出.【解答】〔I 〕证明:∵ ,∴S 1=a 1=3k ﹣m=3,a 3=S 3﹣S 2=18k=27,解得.那么当n ≥2时,,又a 1=3,∴?n ∈N *,.那么 为常数,故由等比数列的定义可知,数列 {a n }是等比数列.〔II 〕解:∵a n b n =log 3a n+1,∴ . 那么,第11页〔共17页〕∴,那么 ,即〔n ∈N *〕.18.在斜三棱柱A BC ﹣A 1B 1C 1中,底面ABC 是正三角形,E 是AB 中点,A 1E ⊥平面ABC .〔I 〕证明:BC 1∥平面A 1EC ;〔II 〕假设A 1A ⊥A 1B ,且AB=2,求三棱锥B 1﹣ACA 1的体积.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.【分析】〔Ⅰ〕根据线面平行的判定定理进行证明即可. 〔Ⅱ〕根据三棱锥的体积公式求出相应的底面积和高即可.【解答】解:〔I 〕证明:设AC 1与A 1C 交于F 点,连接EF ,∵E ,F 分别是线段 AB ,AC 1的中点,∴ E F ∥BC 1,又EF?平面A 1EC ,BC 1?平面A 1EC 故BC 1∥平面A 1EC〔II 〕由易得BB 1∥平面ACA 1∴点B 到平面ACA 1的距离等于点B 1到平面ACA 1的距离.那么三棱锥B 1﹣ACA 1的体积等于三棱锥 B ﹣ACA 1的体积. 而三棱锥B ﹣ACA 1的体积又等于三棱锥 A 1﹣ABC 的体积,由易得正三角形ABC 的面积为,∵A 1E ⊥平面ABC ,且易得A 1E=1,∴三棱锥A 1﹣ABC 的体积.故三棱锥B 1﹣ACA 1的体积为.第12页〔共17页〕19.如图ABCD是平面四边形,∠ADB=∠BCD=90°,AB=4,BD=2.〔Ⅰ〕假设BC=1,求AC的长;〔Ⅱ〕假设∠ACD=30°,求tan∠BDC的值.【考点】正弦定理;余弦定理.【分析】〔I〕设∠ABD=α,∠CBD=β.在Rt△ABD中,cosα=,可得α.在Rt△CBD 中,cosβ=,可得β.在△ABC中,利用余弦定理即可得出.〔II〕设∠BDC=θ,在△ACD中,由正弦定理可得:=,化为AC=cosθ.同理在△ABC中,利用正弦定理可得:AC=cos〔60°﹣θ〕,化简解出即可得出.【解答】解:〔I〕设∠ABD=α,∠CBD=β.在Rt△ABD中,cosα===,∴α=.在Rt△CBD中,cosβ==,∴β=.αβ=.∴+在△ABC中,AC 2==21.∴AC=.〔II〕设∠BDC=θ,在△ACD中,=,化为AC=cosθ.第13页〔共17页〕在△ABC 中, = ,化为:AC= cos 〔60°﹣θ〕,cos θ═cos 〔60°﹣θ〕,化为:3cos θ=2cos 〔60°﹣θ〕,3cos θ=cos θ+sin θ,tan θ=.20.圆锥曲线 E :.〔I 〕求曲线E 的离心率及标准方程;M :〔x ﹣x 0〕2+〔y ﹣y 0〕2=8的 〔II 〕设M 〔x 0,y 0〕是曲线 E 上的任意一点,过原点作⊙两条切线,分别交曲线 E 于点 P 、Q .①假设直线 OPOQ 的斜率存在分别为 k ,k ,求证:kk=﹣; , 1 2 12②试问OP 2+OQ 2是否为定值.假设是求出这个定值,假设不是请说明理由.【考点】椭圆的简单性质.【分析】〔I 〕由椭圆定义可知,曲线E 是以和为焦点,长轴长为的椭圆,即可得出.〔II 〕〕① 假设过原点与⊙M 相切的直线斜率存在设为k ,那么切线方程为y=kx ,可得,整理得.由题设可知k 1,k 2是以上关于k 的一元二次方程的两个实根,利用根与系数的关系即可得出. ②设P 〔x 1,y 1〕,Q 〔x 2,y 2〕.当直线OP ,OQ 的斜率存在时,由 ①易得 ,,利用两点之间的距离、根与系数的关系即可得出.当直线 OP ,OQ 的斜率不存在时直接验证即可得出.【解答】解:〔I 〕由椭圆定义可知,曲线 E 是以 和 为焦点,长轴 长为 的椭圆,设椭圆的半长轴长、半短轴长、半焦距分别为 a 、b 、c .∴ , ,那么,第14页〔共17页〕∴椭圆的离心率 ,E 的标准方程为 .〔II 〕①证明:假设过原点与⊙ M 相切的直线斜率存在设为 k ,那么切线方程为 y=kx ,∴ ,整理得 . 由题设可知k 1,k 2是以上关于 k 的一元二次方程的两个实根,∴,即 .②设P 〔x 1,y 1〕,Q 〔x 2,y 2〕. 当直线 OP ,OQ 的斜率存在时,由①易得 , ,而== ==当直线 OP 或OQ 的斜率不存在时,圆 M 与y 轴相切,且圆 M 也与x 轴相切 P ,Q 是椭 圆E 的两个顶点,∴OP 2+OQ 2=a 2+b 2=36. 综上所述:OP 2+OQ 2为定值36.21.设函数 f 〔x 〕=e x ,g 〔x 〕=kx+1. I 〕求函数y=f 〔x 〕﹣〔x+1〕的最小值;II 〕证明:当k >1时,存在x 0>0,使对于任意x ∈〔0,x 0〕都有f 〔x 〕<g 〔x 〕;〔III 〕假设对于任意 x ∈〔0,+∞〕,|f 〔x 〕﹣g 〔x 〕|>x 恒成立,求实数 k 的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】〔Ⅰ〕求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可;〔Ⅱ〕设h 〔x 〕=f 〔x 〕﹣g 〔x 〕,求出函数的导数,得到函数的单调性,从而证出结论;〔Ⅲ〕①当k >1时,求出h 〔x 〕的单调区间,得到函数的最小值,证出结论成立; ②当xk1 x1 x 0 k ≤1时,问题等价于f 〔x 〕﹣g 〔x 〕>x ,设φ〔x 〕=e ﹣〔+ 〕﹣ 〔 >〕, 根据函数的单调性证明即可. xx【解答】解:〔I 〕由 y=e ﹣x ﹣1,∴y'=e ﹣1,第15页〔共17页〕∴函数y=e x﹣x ﹣1在〔﹣∞,0〕上递减,在〔0,+∞〕上递增,那么当x=0时,y 有最小值为0证明:〔II 〕设h 〔x 〕=f 〔x 〕﹣g 〔x 〕,即h 〔x 〕=e x﹣kx ﹣1,h'〔x 〕=e x﹣k ,设h'〔x 〕=0,得x=lnk 〔k >1〕,∵k >1,∴当x ∈〔0,lnk 〕时,h'〔x 〕<0,即h 〔x 〕在〔0,lnk 〕上单调递减,而h 〔0〕=0,且h 〔x 〕是R 上的连续函数, h 〔x 〕<0在〔0,lnk 〕上恒成立,即f 〔x 〕<g 〔x 〕在〔0,lnk 〕上恒成立,∴取0<x 0≤lnk ,那么对任意x ∈〔0,x 0〕都有f 〔x 〕<g 〔x 〕解:〔III 〕由〔I 〕知e x ≥x+1即有e x ﹣1≥x ,∴当x >0时有lnx ≤x ﹣1〔仅当x=1时取“=〞〕 〔*〕①当k >1时,设h 〔x 〕=f 〔x 〕﹣g 〔x 〕=e x﹣〔kx+1〕〔x >0〕, h'〔x 〕=e x﹣k令h'〔x 〕>0得x >lnk ,令h'〔x 〕<0得0<x <lnk ,∴h 〔x 〕在〔0,lnk 〕上递减,在〔lnk ,+∞〕上递增,∴h 〔x 〕min =h 〔lnk 〕=k ﹣klnk ﹣1,由〔*〕式知得k ﹣klnk ﹣1<0,又=k 3﹣3klnk ﹣1>k 3﹣3k 〔k ﹣1〕﹣1=k 3﹣ 3k 2 3k 1= k 1 3 0 ,+ ﹣ 〔 ﹣〕>∴函数y=h 〔x 〕在〔lnk ,3lnk 〕上有唯一零点设为x k ,此时h 〔x k 〕=0,显然h 〔x k 〕<x k ,即|f 〔x 〕﹣g 〔x 〕|>x 对任意x ∈〔0,+∞〕不能恒成立,② 当 k ≤ 1 时,对任意数 x0 ∞∈〔,+ 〕,xkx1=e x ﹣〔 x1 〕﹣〔 k 1 x ≥﹣〔 k 1x 0 ,f 〔x 〕﹣g 〔x 〕=e ﹣〔 + 〕+ ﹣ 〕 ﹣〕 ≥ |f 〔x 〕﹣g 〔x 〕|>x 等价于f 〔x 〕﹣g 〔x 〕>x ,即e x﹣〔k+1〕x﹣1>0,设φ〔x 〕=e x ﹣〔k+1〕x ﹣1〔x >0〕,那么φ'〔x 〕=e x﹣〔k+1〕,假设k ≤0,那么k+1≤1,∴e x﹣〔k+1〕>0,那么φ〔x 〕在〔0,+∞〕上递增,注意到φ〔0〕=0,∴φ〔x 〕>φ〔0〕=0,即|f 〔x 〕﹣g 〔x 〕|>x 对任意x ∈〔0,+∞〕恒成立,假设0<k ≤1,令φ'〔x 〕>0得x >ln 〔k+1〕,令φ'〔x 〕<0,得0<x <ln 〔k+1〕,φ〔x 〕在〔0,ln 〔k+1〕〕上递减,在〔ln 〔k+1〕,+∞〕上递增,∴当x ∈〔0,ln 〔k+1〕〕时,φ〔x 〕<φ〔0〕=0,即|f 〔x 〕﹣g 〔x 〕|>x 对于任意x ∈〔0,ln 〔k+1〕〕不成立,那么|f 〔x 〕﹣g 〔x 〕|>x 对任意x ∈〔0,+∞〕不能恒成立,综合①②可得,满足条件的k 的取值范围为〔﹣∞,0]第16页〔共17页〕2021年9月8日第17页〔共17页〕。
四川省宜宾市叙州区第二中学校2023届高三适应性考试数学(文)试题 (2)

一、单选题1. 设函数,则,的大致图象大致是的A.B.C.D.2. 已知函数若关于的方程有三个不同实数根,则的取值范围是( )A.B.C.D.3. 明朝早期,郑和七下西洋过程中,将中国古代天体测量方面所取得的成就创造性地应用于航海,形成了一套先进的航海技术____“过洋牵星术”.简单地说,就是通过观测不同季节、时辰的日月星辰在天空运行的位置和测量星辰在海面以上的高度来判断水位,其采用的主要工具是牵星板,其由12块正方形模板组成,最小的一块高约2厘米(称一指),木板的高度从小到大依次成等差数列,最大的高约24厘米(称十二指),观测时,将木板立起,一手拿着木板,手臂伸直,眼睛到木板的距离大约为72厘米,使牵星板与海平面垂直,让板的下缘与海平面重合,上边缘对着所观测的星辰依高低不同替换、调整木板,当被测星辰落在木板上边缘时牵星板星辰所用的是几指板,观测的星辰离海平面的高度就是几指,然后就可以推算出船在海中的地理纬度,如图所示,若在一次观测中,所用的牵星板为四指板,则约为()A.B.C.D.4. 若,,则A.B.C.D.5. 《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为,弦长为的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为平方米.(其中,)A .15B .16C .17D .186. 某中学有男生600人,女生400人.为了调查学生身高情况,按性别进行分层,用分层随机抽样的方法抽取一个容量为10的样本,样本按比例分配,得到男生、女生的平均身高分别为170cm 和160cm.用样本估计总体,则该校学生的平均身高是( )A .162cmB .164cmC .166cmD .168cm7. 不等式的解集为( )A.B.C.D .或,8. 关于的方程有两个不等的实根,则的取值范围是( )A.B.C.D.四川省宜宾市叙州区第二中学校2023届高三适应性考试数学(文)试题二、多选题三、填空题四、填空题9.设,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10. 某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米,按每立方米3元收费;用水超过10立方米,超过的部分按每立方米5元收费.某职工某月的水费为55元,则该职工这个月实际用水为( )A .13立方米B .14立方米C .15立方米D .16立方米11. 下列命题为真命题的是( )A .若,则B .若,则C .若,且,则D .若,则12. 给定事件A ,B ,C ,且,则下列选项正确的是( )A.B.若,且A ,B 互斥,则A ,B 不可能相互独立C .若,则A ,B 互为对立事件D .若,则A ,B ,C 两两独立13. 已知,且,则下列结论中正确的是( )A.有最小值B .可以取到0C .有最大值D .有最小值214. 已知函数,则( )A.的极大值为B.的极大值为C .曲线在处的切线方程为D .曲线在处的切线方程为15.的展开式中的系数为________.16.如图,正三棱柱各条棱的长度均相等,.D 为的中点,M ,N 分别是线段和线段上的动点(含端点),且满足,当M ,N 运动时,下列结论中正确的是___________(填写序号).①平面平面②在内总存在与平面ABC 平行的线段③三棱锥的体积为定值④可能为直角三角形17.若过点只可以作曲线的一条切线,则的取值范围是__________.五、解答题六、解答题七、解答题18. 若用一个棱长为6的正四面体坯料制作一个正三棱柱模型,使其底面在正四面体一个面上,并且要求削去的材料尽可能少,则所制作的正三棱柱模型的高为___________,体积的最大值为___________.19. 一个盒子中装有5个电子产品,其中有3个一等品,2个二等品,从中每次抽取1个产品.若抽取后不再放回,则抽取三次,第三次才取得一等品的概率为______;若抽取后再放回,共抽取10次,则平均取得一等品______次.20. ChatGPT 是由人工智能研究实验室OpenAI 于2022年11月30日发布的一款全新聊天机器人模型,它能够通过学习和理解人类的语言来进行对话,ChatGPT 的开发主要采用RLHF (人类反馈强化学习)技术.在测试ChatGPT 时,如果输入的问题没有语法错误,则ChatGPT 的回答被采纳的概率为85%,当出现语法错误时,ChatGPT 的回答被采纳的概率为50%.(1)在某次测试中输入了8个问题,ChatGPT 的回答有5个被采纳.现从这8个问题中抽取3个,以表示抽取的问题中回答被采纳的问题个数,求的分布列和数学期望;(2)已知输入的问题出现语法错误的概率为10%,(i )求ChatGPT 的回答被采纳的概率;(ii )若已知ChatGPT 的回答被采纳,求该问题的输入没有语法错误的概率.21. (1)求值:;(2)已知,求的值.22.如图,已知三棱柱中,底面,,,,,,分别为棱,的中点.(1)求异面直线与所成角的大小;(2)若为线段的中点,试在图中作出过,,三点的平面截该棱柱所得的多边形,并求该截面分三棱柱成两部分(较小部分与较大部分)的体积的比值.23.已知函数的最大值为.(1)求的值及的最小正周期;(2)在坐标系上作出在上的图像,要求标出关键点的坐标.八、解答题九、解答题24.如图,为圆的直径,点在圆上,,矩形所在的平面和圆所在的平面互相垂直,且.(1)求证:平面平面;(2)求几何体的体积.25. 在2005年世青赛中,被称作“超白金一代”的中国男足U23代表队打出了中国男足在世界舞台上的最好表现.球队的战术核心,来自沈阳的陈涛入选了奏事最佳阵容.世青赛的赛制分为小组赛、淘汰赛两个阶段.小组赛中,参赛的32支代表队被分为8各小组,每个小组4支球队,按照单循环赛制选出两支球队进入淘汰赛.淘汰赛中16支球队捉对厮杀,败者淘汰胜者晋级,通过4轮比赛决出最后的冠军.(1)已知在小组赛中,每赢一场记3分,打平一场记1分,输一场记0分.小组赛阶段中国队与巴拿马、土耳其、乌克兰三支球队分在同一组.首战中中国队惊险战胜了欧洲亚军土耳其队,在小组赛占据了优势.面对后两场比赛的对手乌克兰队和巴拿马对,根据赛前球探报告分析,中国队都有实力优势,可以近似认为后两场比赛中国的获胜的概率都为0.5,打平的概率都为0.2,输球的概率都为0.3.设中国队三场小组赛之后的总积分为随机变量X ,求出其分布列和期望.(2)10号队员陈涛作为中国队的进攻核心,他的表现对中国队而言举足轻重.过往数据表示,在所有陈涛出场并且有进球或者助攻的比赛中,中国队赢得了其中80%的场次,在所有陈涛没有进球或者助攻的比赛中,中国队赢得了其中20%的场次,陈涛在其代表中国队出场的40场比赛中,有30场比赛完成了进球或者助攻.在本届比赛中,中国队在小组赛中顺利出线,淘汰赛首轮中对阵世界足坛的传统强队德国队.已知在淘汰赛对阵德国队的比赛中,陈涛代表中国队出场比赛,虽然经过全队不懈努力,仍然不敌强大的德国队,遗憾告别世界杯.那么,若以过往的数据估计概率,请估计陈涛在本场比赛贡献进球或者助攻的概率.26. 设,对于项数为的有穷数列,令为中最大值,称数列为数列的“创新数列”.例如数列3,5,4,7的创新数列为3,5,5,7. 考查正整数1,2,…,的所有排列,将每种排列都视为一个有穷数列.(1)若,写出创新数列为3,4,4,4的所有数列;(2)是否存在数列的创新数列为等比数列?若存在,求出符合条件的的创新数列;若不存在,请说明理由.(3)是否存在数列,使它的创新数列为等差数列?若存在,求出满足所有条件的数列的个数;若不存在,请说明理由.。
四川省宜宾市第四中学2022届高考数学第二次适应性考试试题 文

四川省宜宾市第四中学2022届高考数学第二次适应性考试试题 文注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I 卷 选择题(60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合(){}ln 1A x y x ==-,{}240B x x =-≤,则AB =A .{}2x x ≥-B .{}12x x <<C .{}12x x <≤D .{}2x x ≥2.已知复数z 满足()12z i i +=,则z =A .1B .22C .2D .23.某公司生产A ,B ,C 三种不同型号的轿车,产量之比依次为2:3:4,为检验该公司的产品质量,用分层抽样的方法抽取一个容量为n 的样本,若样本中A 种型号的轿车比B 种型号的轿车少8辆,则n = A .96B .72C .48D .364.已知向量a ,b 的夹角为2π,且()2,1a =-,2b =,则2a b +=A .23B .3C .21D .415.为了得到函数sin 26y x π⎛⎫=- ⎪⎝⎭的图象,只需把函数sin 2y x =的图象上所有的点A .向左平移6π个单位长度B .向右平移6π个单位长度C .向左平移12π个单位长度 D .向右平移12π个单位长度6.若实数x ,y 满足条件25024001x y x y x y +-≤⎧⎪+-≤⎪⎨≥⎪⎪≥⎩,目标函数2z x y =-,则z 的最大值为A .52B .1C .2D .07.已知l ,m 为两条不同直线,α,β为两个不同平面,则下列命题中真命题的是 A .若//l m ,m α⊂,则//l α B .若l m ⊥,m α⊂,则l α⊥ C .若//αβ,m α⊂,则//m βD .若αβ⊥,m α⊂,则m β⊥8.已知双曲线C :2221y x b-=的一条渐近线过点(,4)b ,则C 的离心率为A .52 B .32C .5D .39.若不等式210x ax ++≥对于一切10,2x ⎛⎤∈ ⎥⎝⎦恒成立,则a 的最小值是 A .0 B .2-C .52-D .3-10.某简单几何体的三视图如图所示,若该几何体的所有顶点都在球O 的球面上,则球O 的体积是A 82B .43πC .12πD .323π 11.已知ABC 是长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是 A .2-B .32-C .43-D .1-12.函数()()3132xf x x x e x =---在区间[)(]3,22,3-⋃上的零点个数为 A .2 B .3C .4D .5第II 卷 非选择题(90分)二、填空题:本题共4小题,每小题5分,共20分。
高考数学下学期第二次适应性考试试题 文 试题

叙州区第二中学2021届高考数学下学期第二次适应性考试(kǎoshì)试题文考前须知(xūzhī):1.答卷前,所有考生必须将本人的姓名(xìngmíng)和准考证号填写上在答题卡上。
2.答复选择题时,选出每一小题答案后,用铅笔把答题卡对应题目之答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答复非选择题时,将答案写在答题卡上。
写在套本套试卷上无效。
3.在在考试完毕之后(zhīhòu)以后,将本套试卷和答题卡一起交回。
第I卷选择题〔60分〕一、选择题:此题一共12小题,每一小题5分,一共60分。
在每一小题给的四个选项里面,只有一项是哪一项符合题目要求的。
1.设集合,,那么A.B.C.D.2.复数,那么的模为A.B.C.D.3.向量,,假设,那么A.B.C.D.4.随着我国经济实力的不断提升,居民收入也在不断增加.抽样发现某家庭2021年全年的收入与2021年全年的收入相比增加了一倍,实现翻番.同时该家庭的消费构造随之也发生了变化,现统计了该家庭这两年不同品类的消费额占全年总收入的比例,得到了如下折线图:那么(nà me)以下结论中正确的选项是A.该家庭(jiātíng)2021年食品(shípǐn)的消费额是2021年食品(shípǐn)的消费额的一半B.该家庭2021年教育医疗的消费额是2021年教育医疗的消费额的倍C.该家庭2021年休闲旅游的消费额是2021年休闲旅游的消费额的六倍D.该家庭2021年生活用品的消费额与2021年生活用品的消费额相当5.在中,是上一点,且,那么A. B. C. D.6.A.B.C.D.7.,那么A.B.C.D.8.为两条不同的直线,为两个不同的平面,且,,那么以下命题中的假命题是A.假设∥,那么∥B.假设,那么C.假设,a b相交,那么,αβ相交D.假设,αβ相交,那么,a b相交9.抛物线上的点到其焦点的间隔为2,那么M的横坐标是A.B.C.D.10.,那么A. B. C. D.11.假设存在,满足,且,那么的取值范围是A.B. C. D.12.点是椭圆(tuǒyuán)上的动点,过P作圆的两条切线(qiēxiàn)分别为切于点,直线(zhíxiàn)与轴分别(fēnbié)相交于两点,那么〔为坐标原点〕的最小面积为〔〕A.B.C.D.第II卷非选择题〔90分〕二、填空题:此题一共4小题,每一小题5分,一共20分。
四川省宜宾市叙州区第二中学校2023届高三适应性考试数学(文)试题

一、单选题二、多选题1. 已知,是椭圆和双曲线的公共焦点,P是它们一个公共点,设椭圆和双曲线的离心率分别为,,若,则( )A.B.C.D.2.已知,则( )A.B.C.D.3. 设锐角三角形的内角A ,B ,C 所对的边分别为a ,b ,c ,若,,则b 的取值范围为( )A.B.C.D.4.已知数列满足,(),则( )A.B.C .7D .125. 已知是定义在上的奇函数,且在内单调递减,则( )A.B.C.D.6. 在中,是上一点,且,则( )A.B.C.D.7.已知动点的坐标满足方程,则动点的轨迹是( )A .椭圆B .双曲线C .抛物线D .圆8. 设等比数列的公比为q ,若,则( )A .2B .3C .4D .59. 已知正方体的棱长为,点,是棱,的中点,点是侧面内运动(包含边界),且与面所成角的正切值为,下列说法正确的是()A.的最小值为B .存在点,使得C .存在点,使得平面D .所有满足条件的动线段形成的曲面面积为10.设,,,点是线段上的一个动点,,若,则实数的值可以为( )A .1B.C.D.四川省宜宾市叙州区第二中学校2023届高三适应性考试数学(文)试题四川省宜宾市叙州区第二中学校2023届高三适应性考试数学(文)试题三、填空题四、解答题11. 我国小麦育种技术和水平已经达到国际先进水平,研究发现某品种小麦麦穗长度cm 近似服从正态分布.从该品种小麦中任取100株,估计其麦穗长度,则下列说法正确的是( )A .100株小麦麦穗长度的均值约为11.24cmB .100株小麦中约有2株小麦的麦穗长度大于13.5cmC .100株小麦中没有麦穗长度大于14.63cm 的小麦D .若随机变量表示100株小麦中麦穗长度大于13.5cm 的株数,则近似服从二项分布附:,12. 某公司2023年的销售额为1000万元,2023年四个季度的销售额情况统计如图所示.其中第二季度销售额是第一季度销售额的2倍.则下列说法正确的是( )A .该公司四个季度的销售额先增长再下降B .从这四个季度中任选两个,则这两个季度的销售额都大于250万的概率为C .从这四个季度中任选两个,则这两个季度的销售额的和大于500万的概率为D .从这四个季度中任选两个,则这两个季度的销售额差的绝对值小于250万的概率为13. 的值等于_________.14. 某同学设想用“高个子系数k ”来刻画成年男子的高个子的程度,他认为,成年男子身高160及其以下不算高个子,其高个子系数k 应为0;身高190及其以上的是理所当然的高个子,其高个子系数k 应为1,请给出一个符合该同学想法、合理的成年男子高个子系数k 关于身高的函数关系式___________.15. 如图,棱长为2的正方体中,点分别为棱的中点,以为圆心,1为半径,分别在面和面内作弧和,并将两弧各五等分,分点依次为、、、、、以及、、、、、.一只蚂蚁欲从点出发,沿正方体的表面爬行至,则其爬行的最短距离为________.参考数据:;;)16..(Ⅰ)若函数在定义域内有两个极值点,求实数的取值范围;(Ⅱ)若函数有三个不相同的零点,求证:.17. 已知数列的前n项和.(1)求证:数列为等比数列;(2)若数列满足,,求数列的前n项的和.18. 某地政府为推动旅游业高质量发展、加快旅游产业化建设,提出要优化传统业态,创新产品和服务方式,培育新业态新产品、新模式,促进康养旅游快速发展.某景区为了进一步优化旅游服务环境,强化服务意识,全面提升景区服务质量,准备从m个跟团游团队和6个私家游团队中随机抽取几个团队展开满意度调查.若一次抽取2个团队,全是私家游团队的概率为.(1)若一次抽取3个团队,在抽取的3个团队是同类型团队的条件下,求这3个团队全是跟团游团队的概率;(2)若一次抽取4个团队,设这4个团队中私家游团队的个数为,求的分布列和数学期望.19. 已知数列满足,且,,(1)若,求证数列是常数列,并求的通项;(2)若是数列的前n项和,又,且的前项和在时恒成立,求实数t的取值范围.20. 在中,已知,,分别是角,,的对边,,,为的面积,.(1)求;(2)若点在直线上,且,求线段的长度.21. 已知在等比数列中,.(1)求数列的通项公式;(2)设,求数列的前项和.。
四川省高考适应性考试(二)数学(文)试题(解析版)

一、单选题1.集合的真子集的个数为( )(){}*N ln 5A x y x =∈=-A .3 B .7 C .15 D .16【答案】C【分析】由对数函数的定义域结合真子集的知识得出答案.【详解】因为,所以集合A 的真子集的个数(){}{}{}**N ln 5N 501,2,3,4A x y x x x =∈=-=∈->=为. 42115-=故选:C.2.有下列四个命题,其中是真命题的是( ) A .“全等三角形的面积相等”的否命题 B .在中,“”是“”的充分不必要条件 ABC π6A >1sin 2A >C .命题“,”的否定是“,”1x ∀>32x x >1x ∃>32x x <D .已知,其在复平面上对应的点落在第四象限 ()()1i 12i z =+-【答案】D【分析】利用原命题与否命题的关系即可判断A ;利用充分必要条件即可判断B ;利用全称命题的否定的定义即可判断C ;利用复数的几何意义即可判断D .【详解】对于A ,“全等三角形的面积相等”的否命题是“不全等三角形的面积不相等”,这显然是假命题,故A 错误;对于B ,在中,,由,得,所以“”是“”的必要不ABC ()0,πA ∈1sin 2A >π5π66A <<π6A >1sin 2A >充分条件,故B 错误;对于C ,命题“,”的否定是“,”,故C 错误;1x ∀>32x x >1x ∃>32x x ≤对于D ,,所以其对应的点为,在第四象限,故D 正确.()()21i 12i 12i i 2i 3i z =+-=-+-=-()3,1-故选:D .3.某市2022年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入的变化情况,统计了该市招商引资前、后的年经济收入构成比例,得到如下扇形图.下列结论正确的是( )A .招商引资后,工资净收入较前一年减少B .招商引资后,转移净收入是前一年的1.25倍C .招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的 25D .招商引资后,经营净收入较前一年增加了一倍 【答案】D【分析】根据已知条件及扇形图的特点即可求解.【详解】设招商引资前经济收入为M ,则招商引资后经济收入为2M .对于A ,招商引资前工资净收入为,招商引资后的工资净收入为60%0.6M M ⨯=,237%0.74M M ⨯=所以招商引资后,工资净收入增加了,故A 错误;对于B ,招商引资前转移净收入为,招商引资后转移净收入为, 4%0.04M M ⨯=25%0.1M M ⨯=所以招商引资后,转移净收入是前一年的2.5倍,故B 错误; 对于C ,招商引资后,转移净收入与财产净收入的总和为,20.1228%0.6620.85M M M M M +⨯=<⨯=所以招商引资后,转移净收入与财产净收入的总和低于该年经济收入的,故C 错误; 25对于D ,招商引资前经营净收入为,招商引资后经营净收入为, 30%0.3M M ⨯=230%0.6M M ⨯=所以招商引资后,经营净收入较前一年增加了一倍,故D 正确. 故选:D.4.幂函数在区间上单调递减,则下列说法正确的是( )()()233mf x m m x =--()0,∞+A . B .是减函数 4m =()f x C .是奇函数 D .是偶函数()f x ()f x 【答案】C【分析】根据幂函数的定义及单调性可判断AB ,再由奇函数的定义判断CD.【详解】函数为幂函数,则,解得或.()()233mf x m m x =--2331m m --=4m =1m =-当时,在区间上单调递增,不满足条件,排除A ;4m =()4f x x =()0,∞+当时,在区间上单调递减,满足题意.1m =-()1f x x -=()0,∞+函数在和上单调递减,但不是减函数,排除B ;()1f x x -=(),0∞-()0,∞+因为函数定义域关于原点对称,且, 1()()f x f x x-==--所以函数是奇函数,不是偶函数,故C 正确,D 错误. ()f x 故选:C.5.函数图象的对称轴可以是( )()5ππ2sin sin 63f x x x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭A .直线 B .直线5π12x =π3x =C .直线 D .直线 π6x =2π3x =【答案】A【分析】利用诱导公式及二倍角公式将函数化简,再根据正弦函数的性质求出函数的对称轴.【详解】,()πππππ2π2sin sin 2cos sin sin 2323333f x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++=++=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦令,解得, ()2ππ2πZ 32x k k +=+∈()ππZ 122k x k =-+∈所以的对称轴为直线,当时,.()f x ()ππZ 122k x k =-+∈1k =5π12x =故选:A.6.已知m ,n 是两条不同的直线,,是两个不同的平面,则下列命题正确的是( ) αβA .若,,则m α⊥m n ⊥n α∥B .若,,,则 m α m β n αβ= m n ∥C .若,,则,则 αβ⊥n αβ= m n ⊥m β⊥D .若,,则 m n ∥n ⊂αm α 【答案】B【分析】若,,则或,A 错;由线面平行的性质可判断B 正确;由面面垂m α⊥m n ⊥n α∥n ⊂α直的性质定理判断C 错;由线面平行的判定定理即可得出D 错. 【详解】对于A ,若,,则或,故A 错误; m α⊥m n ⊥n α∥n ⊂α对于B ,若,,过m 作平面与,分别交于直线a ,b ,m α m β αβ由线面平行的性质得,,所以, m a m b a b 又,,所以,b β⊂a β⊄a β∥又,,所以,所以,故B 正确; n ⊂αn αβ= a n ∥m n ∥对于C ,由面面垂直的性质定理可得, 当时,,否则不成立,故C 错误;m α⊂m β⊥对于D ,若,,则或,故D 错误. m n ∥n ⊂αm α m α⊂故选:B7.2023年1月底,人工智能研究公司OpenAI 发布的名为“ChatGTP”的人工智能聊天程序进入中国,迅速以其极高的智能化水平引起国内关注.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的,在神经网络优化中,指数衰减的学习率模型为,其中00G GL L D =L 表示每一轮优化时使用的学习率,表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,0L 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.8,衰减速度为12,且当训练0G 迭代轮数为12时,学习率衰减为0.5.则学习率衰减到0.2以下(不含0.2)所需的训练迭代轮数至少为( )(参考数据:) lg 20.3010≈A .36 B .37 C .38 D .39【答案】A【分析】由已知求得衰减系数,然后根据已知模型列不等式求解.D 【详解】由已知,得,所以,12120.80.5D ⨯=58D =则有,即,即, 1250.80.28G ⎛⎫⨯< ⎪⎝⎭125184G ⎛⎫< ⎪⎝⎭51lg lg 1284G <即,因此G 至少为36. 112lg 24lg 2435.4514lg 2lg 8G ->=≈-故选:A.8.目前,全国所有省份已经开始了新高考改革.改革后,考生的高考总成绩由语文、数学、外语3门全国统一考试科目成绩和3门选择性科目成绩组成.已知某班甲、乙同学都选了历史和地理科目,且甲同学的另一科目会从化学、生物、政治这3科中选1科,乙同学的另一科目会从化学、生物这2科中选1科,则甲、乙所选科目不相同的概率是( )A .B .C .D .16133523【答案】D【分析】根据给定条件,利用列举法结合古典概率求解作答.【详解】甲、乙同学所选的科目情况有:(化学,化学),(化学,生物),(生物,化学),(生物,生物),(政治,化学),(政治,生物),共6种,其中甲、乙同学所选的科目不相同的结果有:(化学,生物),(生物,化学),(政治,化学),(政治,生物),共4种, 所以所求概率. 4263P ==故选:D9.已知双曲线的右顶点为A ,左、右焦点分别为,,以为直径()2222:10,0x y C a b a b-=>>1F 2F 12F F 的圆与双曲线C 的渐近线在第一象限的交点为M ,且,则该双曲线的离心率为( ) 13MF MA =A .B .C .D .8797167187【答案】B【分析】先利用渐近线的斜率求得,再利用余弦定理求得,进而求得cos MOA ∠MA b =,从而得到关于的齐次方程,解之即可得解. 1F A =,a c 【详解】设双曲线C 的半焦距为,如图,c由题意可得,直线OM 的方程为,有,即有, by x a =tan b MOA a∠=sin cos b MOA MOA a ∠=∠又,解得, 22sin cos 1MOA MOA ∠+∠=cos aMOA c ∠==在中,, MOA ,OM c OA a ==, b ==因此,即有, 222MA OA OM +=90OAM ∠=︒又,则,,13MF MA =13MF b =1F A =又,于是,1F A a c =+a c +=所以,即,则,()228a c b +=2222288a ac c c a ++=-227290c ac a --=两边同时除以,得,即,解得(舍去)或, 2a 27290e e --=()()1790e e +-=1e =-97e =所以该双曲线的离心率, 97e =故选:B.10.设为等差数列的前n 项和,且,都有,若,则( ) n S {}n a *n ∀∈N 11n n S S n n +<+513S S =A .的最小值是 B .的最小值是 n S 9S n S 10S C .的最大值是 D .的最大值是n S 9S n S 10S 【答案】A 【分析】由结合等差数列的前n 项和公式可知数列为递增的等差数列,由可11n n S S n n +<+{}n a 513S S =得,,即可求出,有最小值,且最小值为. 90a <100a >n S 9S 【详解】由,得,即, 11n n S S n n +<+()()()()1111221n n n a a n a a n n ++++<+1n n a a +<所以数列为递增的等差数列.{}n a 因为,所以,即, 513S S =6789101112130a a a a a a a a +++++++=9100a a +=则,,所以当且时,;90a <100a >9n ≤*n ∈N 0n a <当且时,.因此,有最小值,且最小值为. 10n ≥*n ∈N 0n a >n S 9S 故选:A.11.已知平面上两定点A ,B ,则所有满足(且)的点P 的轨迹是一个圆心在直PA PBλ=0λ>1λ≠线AB 上,半径为的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.21AB λλ⋅-已知动点P 在棱长为6的正方体的一个侧面上运动,且满足,1111ABCD A B C D -11ABB A 2PA PB =则点P 的轨迹长度为( )A .B .C D 8π34π3【答案】B【分析】根据阿氏圆的定义分析得P 点轨迹为球与侧面的交线,计算其弧长即可 【详解】在图1中,以B 为原点建立平面直角坐标系,如图2所示, xBy 设阿氏圆圆心为,半径为r .因为,所以, (),0O a 2PA PB =2PAPB=所以. 22264123r AB =⋅=⨯=-设圆O 与AB 交于点M .由阿氏圆性质,知.2MA MBλ==又,所以.又, 44MB BO a =-=-282MA MB a ==-6MA MB +=所以,解得,所以, 8246a a -+-=2a =()2,0O 所以点P 在空间内的轨迹为以O 为球心,半径为4的球.当点P 在侧面内部时,如图2所示,截面圆与,分别交于点M ,R ,11ABB A AB 1BB 所以点P 在侧面内的轨迹为. 11ABB A MR因为在中,,,所以, Rt RBO △4RO =2BO =π3ROB ∠=所以,所以点P 在侧面内部的轨迹长为. π4π433MR=⨯=11ABB A 4π3故选:B.12.对,不等式恒成立,则实数的取值范围是( )10,2x ⎡⎤∀∈⎢⎥⎣⎦()()e 1ln e 1xa x a -+≥-aA .B .C .D . 12e ⎡⎢⎣[]1,e ⎡⎣1,e 2e ⎡⎤⎢⎥⎣⎦【答案】C【分析】将原不等式化为,令,将问题转化为,()()e 1ln e e 1x xa a -≥-e x t a =,t a ⎡∈⎣,后由单调性结合可得答案.()()e 1ln 10f t t t =--+≥()f t ()()10e f f ==【详解】由有意义可知,.由,得.ln a 0a >()()e 1ln e 1xa x a -+≥-()()e 1ln e e 1x x a a -≥-令,即有.因为,所以. e x t a =()e 1ln 1t t -≥-10,2x ⎡⎤∈⎢⎥⎣⎦e ,xt a a ⎡=∈⎣令,则问题转化为当,恒成立. ()()e 1ln 1f t t t =--+,t a ⎡∈⎣()0f t ≥因为,令,即; ()e 1tf t t--='()0f t '<e 10t --<e 1t ⇒>-令,即,,()0f t '>e 10t -->0e 1t ⇒<<-则在上单调递增,上单调递减.()f t ()0,e 1-()e 1,-+∞注意到,,所以当时,.()10f =()()e e 1ln e e 10f =--+=1e t ≤≤()0f t ≥因为当,恒成立,所以只需且,解得. ,t a ⎡∈⎣()0f t ≥e ≤1a ≥a ⎡∈⎣故选:C.【点睛】关键点睛:本题涉及函数恒成立问题,对于同时含有指数函数和对数函数的函数,常利用指对互化构造出相同结构,从而构造出新函数从而简化问题.二、填空题13.若x ,y 满足约束条件,则的最大值为______.1121y x y y x ≤⎧⎪+≤⎨⎪+≥⎩2z x y =-【答案】2【分析】先作出可行域,再根据目标函数的几何意义分析运算.【详解】作约束条件的可行域,如图所示.1121y x y y x ≤⎧⎪+≤⎨⎪+≥⎩由,解得,令.121x y y x +=⎧⎨+=⎩10x y =⎧⎨=⎩()1,0N 将目标函数变形为,表示斜率为2,纵截距为的直线, 2z x y =-2y x z =-z -根据其几何意义可得,当直线经过点时,其纵截距最小, 2y x z =-()1,0N 即当时,目标函数z 取到最大值,则的最大值为2.10x y =⎧⎨=⎩2z x y =-故答案为:2.14.已知数列满足,,若,,则的值为______.{}n a 221n n n a a a ++=*n ∈N 716a =354a a =2a 【答案】或12-12【分析】由等比的定义结合其性质得出的值.2a 【详解】因为,,所以数列为等比数列,设其公比为q .221n n n a a a ++=*n ∈N {}n a 由,716a =,得,, 23544a a a ==42a =±3748a q a ==±所以.2q =±当时,,则; 2q =42a =212a =当时,,则.综上,的值为或.2q =-42a =-212a =-2a 12-12故答案为:或12-1215.已知函数,若函数有且只有三个零点,则实数的()3223e,1e ,1x x x x f x x x ⎧--+≤⎪=⎨>⎪⎩()()g x f x m =-m 取值范围是______.【答案】{}2e e 4,e 4⎛⎫-⋃ ⎪⎝⎭【分析】利用导数求出函数的单调性与极值,画出函数图象,数形结合即可得解.【详解】当时,,,1x ≤()323e f x x x =--+()()32f x x x '=-+所以当时,当或时,20x -<<()0f x ¢><2x -01x <<()0f x '<所以在上单调递减,在上单调递增,在上单调递减,且()f x (),2-∞-()2,0-()0,1,;()()214e f f -==-+()0e f =当时,,,所以当时,当时, 1x >()2e xf x x=()32e x x f x x -'=2x >()0f x ¢>12x <<()0f x '<所以在上单调递减,在上单调递增,令,则,又.()f x ()1,2()2,+∞()2e x g x x =()1e g =()2e 24f =作出函数的函数图象如下:()f x若有且只有三个零点,即与只有三个交点,()()g x f x m =-()y f x =y m =由图可知需满足.{}2e e 4,e 4m ⎛⎫∈-⋃ ⎪⎝⎭故答案为:{}2e e 4,e 4⎛⎫-⋃ ⎪⎝⎭16.已知A ,B 为抛物线上两点,以A ,B 为切点的抛物线的两条切线交于点P ,过点A ,B 2y x =的直线斜率为,若点P 的横坐标为,则______.AB k 13A B k =【答案】23【分析】设,,,根据导数的几何意义求出以A ,B 为切点的切线方()11,A x y ()22,B x y ()00,P x y 程,可得为方程的两根,根据韦达定理及过两点的斜率公式即可求解. 12,x x 20020x x x y -+=【详解】设,,以A ,B 为切点的抛物线的切线斜率为,, ()11,A x y ()22,B x y A k B k 由,得,故,,2y x =2y x '=12A k x =22B k x =所以切线PA 的方程为,即.()21112y x x x x -=-21120x x x y -+=同理可得,切线的方程为.PB 22220x x x y -+=设点P 的坐标为,()00,x y 所以,,2110020x x x y -+=2220020x x x y -+=所以为方程的两根,故,, 12,x x 20020x x x y -+=1202x x x +=120x x y =则. 1212012223AB y y k x x x x x -==+==-故答案为:.23三、解答题17.某企业为了了解年广告费x (单位:万元)对年销售额y (单位:万元)的影响,统计了近7年的年广告费和年销售额的数据,得到下面的表格: i x ()1,2,3,4,5,6,7i y i =年广告费 x 2345678年销售额 y 25 41 50 58 64 7889由表中数据,可判定变量x ,y 的线性相关关系较强. (1)建立y 关于x 的线性回归方程;(2)已知该企业的年利润z 与x ,y 的关系为,根据(1)的结果,年广告费x 约为何值时z x =(小数点后保留一位),年利润的预报值最大?附:对于一组数据,,…,,其回归直线的斜率和截距的最小二()11,x y ()22,x y (),n n x y y bx a =+$$$乘估计分别为,;参考数据:,()()()1122211n niii i i i nniii i x x y y x y nx ybx x xnx====---==--∑∑∑∑ a y bx =-$$71405i i y ==∑.712305i ii x y==∑【答案】(1)55107y x =+(2)9.2【分析】(1)根据最小二乘法公式计算即可;(2)结合(1)的结果,利用换元法求二次函数最值及取得最值时的自变量值即可.【详解】(1)由表格数据,得,,234567857x ++++++==71140577i i y y ===∑.()()()()7222222221321012328ii x x =-=-+-+-++++=∑由公式,得,,故y 关于x 的7172214057230575710287i ii ii x y x ybxx==--⨯⨯===-∑∑ 4055510577a y bx=-=-⨯=线性回归方程为.55107y x =+(2)由(1)可得,. z x =,则,t =21111014x t =-所以,221111112210141014z t t t t ⎛⎫=--=-++ ⎪⎝⎭故当时,z 取得最大值,此时, 10t =11109.214x =-≈即年广告费约为9.2万元时,年利润的预报值最大.x18.在中,角A ,B ,C 所对的边分别为a ,b ,c ,边BC 上有一动ABC sin sin 2B Ca B +=点D .(1)求角A 的大小;(2)当D 为边BC 中点时,面积的最大值. AD =ABC 【答案】(1) 2π3A =(2)【分析】(1)由三角形内角关系、正弦边角关系及倍角正弦公式可得,进而确定其大sin 2A 小;(2)由,结合向量数量积的运算律、基本不等式可得,最后应用三角形面2AD AB AC =+12bc ≤积公式求最值.【详解】(1, sin sin 2B Ca B +=.πsinsin 2A aB -=cos sin 2Aa B =. cos sin sin 2AB A B ⋅=⋅因为. sin 0B ≠sin 2sin cos 222A A A A ==因为,所以.cos02A ≠sin 2A 又因为,所以,则.π022A <<π23A =2π3A =(2)因为D 为边BC 中点,所以,则.2AD AB AC =+()224AD AB AC =+又,,所以,即,仅当时取等AD =2π3A =222π122cos 3b c bc =++⋅2212b c bc bc =+-≥b c =号,所以面积的最大值为1sin2ABCS bc A=⋅=≤△ABC19.如图,四边形ABCD为菱形,平面ABCD,,.ED⊥FB ED2BD ED FB==(1)求证:平面平面AFC;BDEF⊥(2)记三棱锥的体积为,三棱锥的体积为,求的值.A EFC-1V A BFC-2V12VV【答案】(1)证明见解析(2)123VV=【分析】(1)根据条件先证平面BDEF,再得面面垂直即可;AC⊥(2)根据线段间关系设,表示其它线段,结合三棱锥体积公式及等体积法转化得1BF=,,即可得体积之比.11=22A EOFV V AC-=216F ABCV V AC-==【详解】(1)因为四边形ABCD为菱形,所以.AC BD⊥因为平面ABCD,平面ABCD,所以.ED⊥AC⊂ED AC⊥又,,平面BDEF,所以平面BDEF.ED BD D=ED BD⊂AC⊥又平面AFC,所以平面平面AF C.AC⊂BDEF⊥(2)如图,设BD交AC于点O,连接OE,OF.由(1)可知,平面BDEF,平面BDEF,所以.AC⊥OF⊂AC OF⊥设,则,,所以1BF=1OB OD==2DE=,()12211311212222EOF BOF DOEBDEFS S S S+⨯=--=-⨯⨯-⨯⨯=四边形所以.11131=2=3322A EOF EOFV V S AC AC AC-⋅=⨯=由(1)可知,平面ABCD,BF⊥所以,所以.211113326A BFC F ABC ABCV V V S BF AC OB BF AC--===⋅=⨯⋅⋅=△123VV=20.已知函数.()1ln 1f x x a x ⎛⎫=-- ⎪⎝⎭(1)若,求实数a 的值;()0f x ≥(2)已知且,求证:.*n ∈N 2n ≥111ln 23n n++⋅⋅⋅+<【答案】(1) 1a =(2)证明见解析【分析】(1)注意到,所以是的最小值点也是极小值点,从而可求解;()10f =1x =()f x (2)由(1)得,再取即可证明不等式. ()1ln 11x x x >->111k x=-【详解】(1)因为,所以函数定义域为,.()1ln 1f x x a x ⎛⎫=-- ⎪⎝⎭()f x ()0,∞+()221a x a f x x x x '-=-=因为,且,所以是函数的极小值点,则,所以()10f =()0f x ≥1x =()f x ()10f '=()1101af -'==,得. 1a =当时,, 1a =()21x f x x -'=当时,,当时,, 01x <<()0f x '<1x >()0f x ¢>则函数在上单调递减,在上单调递增, ()f x ()0,1()1,+∞所以,满足条件,故. ()()10f x f ≥=1a =(2)由(1)可得,.令,则,所以,即()1ln 11x x x >->111k x =-1k x k =-1ln1k k k >-,, ()1ln ln 1k k k<--{}2,3,,k n ∈⋅⋅⋅所以.证毕. ()()()111ln 2ln1ln 3ln 2ln ln 1ln 23n n n n ++⋅⋅⋅+<-+-+⋅⋅⋅+--=⎡⎤⎣⎦【点睛】关键点睛:解(2)的关键是由(1)得,然后令,有()1ln 11x x x >->111k x=-,然后累加即可证明. ()1ln ln 1k k k<--21.已知点,,动点满足直线与的斜率之积为.记动点的轨()2,0A -()2,0B (),M x y AM BM 14-M 迹为曲线.C (1)求曲线的方程,并说明是什么曲线;C C (2)设,为曲线上的两动点,直线与直线的斜率乘积为. P Q C BP BQ 128-①求证:直线恒过一定点; PQ ②设的面积为,求的最大值.PQB △S S 【答案】(1);中心在坐标原点,焦点在轴上的椭圆,不含左、右顶点()22124x y x +=≠x (2)①证明见解析;②73【分析】(1)根据斜率公式列式化简从而写出曲线的方程,并根据椭圆的标准方程判断出曲线C 为焦点在轴上的椭圆;(2)①根据题意判断得直线的斜率不为,设直线的方程为C x PQ 0PQ ,与椭圆方程联立方程组,化简得关于的一元二次方程,写出韦达定理,根据()2x ty n n =+≠±y 斜率公式列式得,代入韦达定理化简计算即可求解出的值,从而得所过定点坐281BP BQ k k ⋅=-n 标;②根据①的结果,利用三角形面积公式计算的面积为PQB △,代入韦达定理化简计算,利用二次函数的性质从而计算得的12121372224S y y y y ⎛⎫=⋅-⋅--=- ⎪⎝⎭S 最大值.【详解】(1)由题意,得, ()12224y y x x x ⋅=-≠+-化简得,所以曲线为中心在坐标原点,()22124x y x +=≠C 焦点在轴上的椭圆,不含左、右顶点.x (2)①证明:,.因为若直线的斜率为, ()11,P x y ()22,Q x y PQ 0则点,关于轴对称,必有,不合题意, P Q y 0BP BQ k k ⋅>所以直线的斜率必不为.PQ 0如图,设直线PQ 的方程为.()2x ty n n =+≠±由,得, 2244x y x ty n⎧+=⎨=+⎩()2224240t y tny n +++-=所以,()()222244440t n t n ∆=-+->且.因为,即.因为 12221222444tn y y t n y y t -⎧+=⎪⎪+⎨-⎪=⎪+⎩128BP BQ k k ⋅=-281BP BQ k k ⋅=- ()()()()()()()121212221212121228282828222222BP BQ y y y y y y k k x x ty n ty n t y y t n y y n ⋅===--+-+-+-++- ()()()()()()()()()()22222222222284282282714414224222422244n n n n t n n t n t n t n n t t n n n t t -++++=====----+-+-+--+-++所以,此时,32n =-()()2221644470t n t ∆=+-=+>故直线恒过轴上一定点.PQ x 3,02⎛⎫- ⎪⎝⎭②解:由①可得,,,所以 12234t y y t +=+()122744y y t =-+ 12121372224S y y y y ⎛⎫=⋅-⋅--=-⎪⎝⎭72==, 727233==≤⨯=当且仅当即时等号成立,所以的最大值为. 21249t =+212t =S 73【点睛】(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去 (或)建立一元x y 二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系;(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为或不存在等特殊情形.022.在平面直角坐标系中,曲线的参数方程为(t 为参数),直线l 的方程xOy 1C 4sin cos cos sin k k x t t y t t =⎧⎨=-⎩为.10x y +-=(1)当时,求曲线的直角坐标方程;1k =1C (2)当时,已知点,直线l 与曲线交于A ,B 两点,线段AB 的中点为M ,求的4k =()1,0P 1C PM长.【答案】(1) ()211222y x x =--≤≤【分析】(1)利用完全平方公式与三角函数的基本关系式消去参数即可得解;t (2)先利用三角函数的基本关系式与倍角公式求得曲线的直角坐标方程,再结合题意求得直线1C l 的参数方程,联立两方程得到关于参数的一元二次方程,再利用参数的几何意义即可得解.s s 【详解】(1)当时,曲线的参数方程为(t 为参数),1k =1C 4sin cos cos sin x t ty t t =⎧⎨=-⎩因为,且, 2221cos sin 2cos sin 12y t t t t x =+-=-[]2sin 22,2x t =∈-所以曲线的直角坐标方程为. 1C ()211222y x x =--≤≤(2)当时,曲线的参数方程为(t 为参数), 4k =1C 444sin cos cos sin x t ty t t =⎧⎨=-⎩因为,,()()2222cos sin cos sin cos 2y t t t t t =+-=2sin 2x t =所以曲线的直角坐标方程为,1C 2214x y +=由题意易知在直线,且直线的斜率为,倾斜角为, ()1,0P :10l x y +-=l 1-3π4故设直线l 的参数方程为(为参数),1x y ⎧=⎪⎪⎨⎪=⎪⎩s将直线l 的参数方程代入,得,易得,2214x y +=2560s --=(()24560∆=--⨯⨯->设点A ,B ,M 对应的参数分别为,,,则由韦达定理得, 1s 2s M s 12s s +=又线段AB 的中点为M ,所以 122M s s s +==23.已知函数.()232f x x x x =-++(1)求不等式的解集;()2f x ≥(2)设函数的最小值为m ,正数a ,b ,c 满足.()f x 6a bc m ++=≤【答案】(1) (][),02,-∞⋃+∞(2)证明见解析【分析】(1)分,,三种情况去绝对值解不等式组即可求解; 1x ≤12x <<2x ≥(2)先求出函数的最小值,再用柯西不等式证明.()f x 【详解】(1)解:当时,,所以,解得;1x ≤()222f x x x =-+()2222f x x x =-+≥0x ≤当时,,所以的解集为;12x <<()242f x x x =-+-()2422f x x x =-+-≥∅当时,,所以,解得.2x ≥()222f x x x =-+()2222f x x x =-+≥2x ≥综上,的解集为.()2f x ≥(][),02,-∞⋃+∞(2)证明:由(1)可知,()22222,1,42,12,22, 2.x x x f x x x x x x x ⎧-+≤⎪=-+-<<⎨⎪-+≥⎩当时,,所以. 1x =()1m f x ==66a b c m ++==由柯西不等式可得,,)()()221111211127a b c =+≤++++⨯++=,当且仅当,,时等号成立,原命题得证.≤3a =2b =1c =。
四川省宜宾县高考数学适应性测试试题(二)理

宜宾县高中2012级高考适应性考试(二)数 学(理工类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
满分150分。
考试时间120分钟。
考试结束后,将本试题卷和答题卡上一并交回。
第Ⅰ卷 (选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合{}{}2(,)|4,(,)|1A x y y x B x y y x ====+,则AB =( B )A. {}(1,2)-B. {}(1,2)C. (1,2)D. (1,2)- 2.下列说法正确的是( A )A .已知p :2000,10x R x x ∃∈+-=,q :2,10x R x x ∀∈++>,则p q ∧是真命题。
B .命题p :若a b ⊥,则0a b ⋅=的否命题是:若a b ⊥,则0a b ⋅≠。
C .2,10x R x x ∀∈+-<的否定是2000,10x R x x ∃∈+->。
D .3x π=是sin(2)6y x π=-取最大值的充要条件。
3.若0a b <<,则下列选项正确的是( A )A. b a a b< B. 11a b <C .(,2)nna b n N n <∈≥ D. 0c ∀≠,都有ac bc <4. 如图是某几何体的三视图,其中正视图是斜边长为2的直角三角形,侧视图是半径为1的半圆,则该几何体的表面积是( A )A .32π+.23π+C .6π+D π5.执行右图所示的程序框图,若输入6x =,则输出y 的值为( ) A . 2 B . 0C . 1-D .32-6. 748被7除的余数为(07)a a ≤<,则62()a x x-展开式中3x -的系数为( B ) A.4320 B. 4320- C.20 D. 20-7.已知()sin f x x x =+,若[]1,2x ∈时,2()(1)0f x ax f x -+-≤,则a 的取值范围是( C ) A. 1a ≤ B. 1a ≥ C. 32a ≥D. 32a ≤ 8.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛。
2021届四川省宜宾市高考数学二诊试卷(文科)(解析版)

2021年四川省宜宾市高考数学二诊试卷(文科)一、选择题(共12小题).1.已知集合A={x|x2﹣4<0},B=N,则A∩B=()A.{1}B.{0,1}C.{﹣1,01}D.{x|﹣2<x<2} 2.若复数z满足(2+i)z=4,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知{a n}为等差数列,a4=﹣5,a7=7,则其前10项和S10=()A.40B.20C.10D.84.若l,m是平面α外的两条不同直线,且m∥α,则“l∥m”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.某学校调查了高三1000名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,以下结论不正确的是()D.估计这1000名学生每周的自习时间不小于25小时的人数是3006.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入x=2,n=2,依次输入a的值为1,2,3,则输出的s=()A.10B.11C.16D.177.设a,b=log4,c=log23,则a,b,c的大小关系为()A.a<b<c B.b<c<a C.c<a<b D.b<a<c 8.函数f(x)=的部分图象大致为()A.B.C.D.9.已知直线l:y=x+2与圆O:x2+y2=4相交于A,B两点,则•的值为()A.8B.4C.4D.210.已知数列{a n}的前n项和为S n,且满足2S n+a n=3,则=()A.364B.543C.728D.102211.已知以F为焦点的抛物线y2=4x上的两点A,B满足=3,则点A的横坐标为()A.1B.C.2D.312.已知函数f(x)=﹣1,下列说法正确的是()A.f(x)既不是奇函数也不是偶函数B.f(x)的图象与y=sin x有无数个交点C.f(x)的图象与y=2只有一个交点D.f(﹣2)<f(﹣1)二、填空题:本大题共4个小题,每小题5分,共20分.13.若实数x,y满足约束条件,则z=x+3y的最大值为.14.已知双曲线C:﹣=1(a>0,b>0)的一条渐近线过点(1,3),则C的离心率为.15.将函数y=3cos(2x+)的图象向右平行移动个单位长度得到函数y=f(x)的图象,若f(α)=,则f(2α﹣)=.16.在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB⊥AD,AB=AD=4,∠ACB=,若三棱锥D﹣ABC的四个顶点都在同一个球面上,则该球的表面积为.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.△ABC的内角A,B,C的对边分别为a,b,c,已知b sin A=a cos(B﹣).(1)求B;(2)设a=2,b=,延长AC到点D使AC=2CD,求△BCD的面积.18.某高校筹办大学生运动会,设计两种赛事方案:方案一、方案二、为了了解运动员对活动方案是否支持,对全体运动员进行简单随机抽样,抽取了100名运动员,获得数据如表:方案一方案二支持不支持支持不支持男运动员20人40人40人20人女运动员30人10人20人20人假设所有运动员对活动方案是否支持相互独立.(1)根据所给数据,判断是否有99%的把握认为方案一的支持率与运动员的性别有关?(2)在抽出的100名运动员中,按是否支持方案二分层抽样抽出了5人,从这5人中随机抽取2人,求抽取的2人都支持方案二的概率.附:K2=,n=a+b+c+d.P(K2≥k)k19.已知四边形ABCD是直角梯形,AB∥CD,∠C=45°,AB=2,CD=4,E,F分别为CD,BC的中点(如图1),以AE为折痕把△ADE折起,使点D到达点S的位置且平面SAE⊥平面ABCE(如图2).(1)求证:EF⊥SE;(2)求点C到平面SEF的距离.20.已知A,B分别为椭圆C:+=1(a>b>0)的左、右顶点,F为右焦点,点P 为C上的一点,PF恰好垂直平分线段OB(O为坐标原点),|PF|=.(1)求椭圆C的方程;(2)过F的直线l交C于M,N两点,若点Q满足=+(Q,M,N三点不共线),求四边形OMQN面积的取值范围.21.已知函数f(x)=在x=1处取得极值.(1)求实数a的值,并求函数f(x)的单调区间;(2)证明:f(x)+x+>0.四、(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多做则按所做的第一题计分.[选修44:坐标系与参数方程]22.在平面直角坐标系xOy中,曲线C的参数方程为(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ﹣sinθ)=2.(1)求曲线C的普通方程和直线l的直角坐标方程;(2)已知点P(3,1),直线l与曲线C交于A,B两点,求|PA|+|PB|的值.五、[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣1|+|x﹣5|.(1)解不等式f(x)≤6;(2)若正实数a,b满足a+b=ab,且函数f(x)的最小值为m,求证:a+b≥m.参考答案一、选择题(共12小题).1.已知集合A={x|x2﹣4<0},B=N,则A∩B=()A.{1}B.{0,1}C.{﹣1,01}D.{x|﹣2<x<2}解:∵A={x|﹣2<x<2},B=N,∴A∩B={0,1}.故选:B.2.若复数z满足(2+i)z=4,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解:因为(2+i)z=4,所以,故复数z在复平面内对应的点为,位于第四象限.故选:D.3.已知{a n}为等差数列,a4=﹣5,a7=7,则其前10项和S10=()A.40B.20C.10D.8解:由等差数列的性质可得:a1+a10=a4+a7=﹣5+7=2,则其前10项和S10==5×2=10,故选:C.4.若l,m是平面α外的两条不同直线,且m∥α,则“l∥m”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解:∵l,m是平面α外的两条不同的直线,m∥α,若l∥m,则推出“l∥α”,若l∥α,则l∥m或l与m相交,故若l,m是平面α外的两条不同直线,且m∥α,则“l∥m”是“l∥α”的充分不必要条件.故选:A.5.某学校调查了高三1000名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,以下结论不正确的是()D.估计这1000名学生每周的自习时间不小于25小时的人数是300解:对于A,在频率直方图中,众数即为频率分布直方图中最高矩形的底边中点的横坐标,故估计这1000名学生每周的自习时间的众数是(22.5+25)÷2=23.75,故选项A错误;对于B,在频率直方图中,中位数即为把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标,设中位数为x××2.5+(x﹣22.5)×0.16=0.5,解得x=23.75,所以估计这1000名学生每周的自习时间的中位数是23.75,故选项B正确;对于C,每周的自习时间小于22.5小时的频率为(0.02+0.1)×2.5=0.3,×1000=300,故选项C正确;对于D,每周的自习时间不小于25小时的频率为(0.08+0.04)×2.5=0.3,×1000=300,故选项D正确.故选:A.6.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入x=2,n=2,依次输入a的值为1,2,3,则输出的s=()A.10B.11C.16D.17解:∵输入的x=2,n=2,当输入的a为1时,S=1,k=1,不满足退出循环的条件;当再次输入的a为2时,S=4,k=2,不满足退出循环的条件;当输入的a为3时,S=11,k=3,满足退出循环的条件;故输出的S值为11,故选:B.7.设a,b=log4,c=log23,则a,b,c的大小关系为()A.a<b<c B.b<c<a C.c<a<b D.b<a<c 解:∵y x为减函数,∴0,即0<a<1,∵y=为减函数,∴b=<,即b<0,∵y=为增函数,∴c=>=1,即c>1,∴c>a>b,故选:D.8.函数f(x)=的部分图象大致为()A.B.C.D.解:∵f(﹣x)==﹣f(x),∴函数f(x)为奇函数,排除选项B和C,当x→+∞时,e x比x增长的快,∴f(x)→0,排除选项D,故选:A.9.已知直线l:y=x+2与圆O:x2+y2=4相交于A,B两点,则•的值为()A.8B.4C.4D.2解:设A(x1,y1),B(x2,y2),联立得x2+2x=0,解得x=0,x=﹣2,设A(0,2),则B(﹣2,0),则•=(﹣2,﹣2)•(0,﹣2)=﹣2×0+2×2=4.故选:C.10.已知数列{a n}的前n项和为S n,且满足2S n+a n=3,则=()A.364B.543C.728D.1022解:∵2S n+a n=2S n+(S n﹣S n﹣1)=3,∴S n﹣=(S n﹣1﹣)(n≥2),由2a1+a1=3⇒a1=1⇒a1﹣=﹣,∴数列{S n﹣}是以﹣为首项,为公比的等比数列,∴S n=﹣•,∴S6=﹣.a6=3﹣2S6=,∴==(729﹣1)=364,故选:A.11.已知以F为焦点的抛物线y2=4x上的两点A,B满足=3,则点A的横坐标为()A.1B.C.2D.3解:设直线AB的斜率为k,则直线AB的方程为:y=k(x﹣1),联立方程组,消元得:k2x2﹣(2k2+4)x+k2=0,设A(x1,y1),B(x2,y2),则x1x2=1.∵=3,F(1,0),∴1﹣x1=3(x2﹣1),解方程组,可得x1=3,x2=,故选:D.12.已知函数f(x)=﹣1,下列说法正确的是()A.f(x)既不是奇函数也不是偶函数B.f(x)的图象与y=sin x有无数个交点C.f(x)的图象与y=2只有一个交点D.f(﹣2)<f(﹣1)解:根据题意,依次分析选项:对于A,函数f(x)=﹣1,其定义域为{x|x≠0},则f(﹣x)+f(x)=﹣1+﹣1=﹣﹣2=0,则f(x)为奇函数,A错误;对于B,函数f(x)=﹣1,当x>0时,有f(x)>﹣1=2﹣1=1,又由f(x)为奇函数,则当x<0时,f(x)<﹣1,即f(x)在R上值域为(﹣∞,﹣1)∪(1,+∞),则f(x)的图象与y=sin x没有交点,B错误,对于C,若f(x)=2,则有﹣1=2,即log3(9x+1)=3x,变形可得9x+1=27x,即()x+()x=1,设g(x)=()x+()x,则g(x)为减函数且其值域为(0,+∞),则g(x)=1有且只有1解,即f(x)的图象与y=2只有一个交点,C正确,对于D,f(﹣2)=﹣1=﹣﹣1=﹣()=﹣×log3=﹣log3,f(﹣1)=﹣log3(+1)﹣1=﹣(log3+1)=﹣log3,则有f(﹣2)>f(﹣1),D错误,故选:C.二、填空题:本大题共4个小题,每小题5分,共20分.13.若实数x,y满足约束条件,则z=x+3y的最大值为4.解:由约束条件作出可行域如图,联立,解得A(1,1),由z=x+3y,得y=,由图可知,当直线y=过A时,直线在y轴上的截距最大,z有最大值为4.故答案为:4.14.已知双曲线C:﹣=1(a>0,b>0)的一条渐近线过点(1,3),则C的离心率为.解:双曲线C:﹣=1(a>0,b>0)的一条渐近线过点(1,3),可得双曲线的一条渐近线方程bx﹣ay=0,∴b=3a,∴c==,∴e==.故答案为:.15.将函数y=3cos(2x+)的图象向右平行移动个单位长度得到函数y=f(x)的图象,若f(α)=,则f(2α﹣)=﹣.解:将函数y=3cos(2x+)的图象向右平行移动个单位长度,得到函数y=f(x)=3cos(2x﹣)的图象,若f(α)=3cos(2α﹣)=,∴cos(2α﹣)=,则f(2α﹣)=3cos[2(2α﹣)﹣]=3cos(4α﹣)=3×[2﹣1]=3×(2×﹣1)=﹣,故答案为:﹣.16.在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB⊥AD,AB=AD=4,∠ACB=,若三棱锥D﹣ABC的四个顶点都在同一个球面上,则该球的表面积为80π..解:设△ABC的外心为O1,半径r,三棱锥D﹣ABC的外接球球心O,半径R,过O1作AD的平行线,过D作AO1的平行线,两条直线交于E,因为平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AB⊥AD,所以AD⊥平面ABC,因为OO1⊥平面ABC,所以OO1∥AD,则四边形ADEO1为矩形,易得O为EO1中点,△ABC中,由正弦定理得,2r===8,所以r=4,R2=AO2==16+4=20,故S=4πR2=80π.故答案为:80π.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.△ABC的内角A,B,C的对边分别为a,b,c,已知b sin A=a cos(B﹣).(1)求B;(2)设a=2,b=,延长AC到点D使AC=2CD,求△BCD的面积.解:(1)∵b sin A=a cos(B﹣).由正弦定理,可得b sin A=a sin B,∴可得:a sin B=a cos(B﹣),可得:sin B=cos(B﹣),化简可得:tan B=,∵B∈(0,π),∴B=.(2)由,可得sin A===,可得cos A=,sin C=sin(A+B)=sin A cos B+cos A sin B=,所以S△ABC=2S△BCD=ab sin C=×2××=,可得S△BCD=.18.某高校筹办大学生运动会,设计两种赛事方案:方案一、方案二、为了了解运动员对活动方案是否支持,对全体运动员进行简单随机抽样,抽取了100名运动员,获得数据如表:方案一方案二支持不支持支持不支持男运动员20人40人40人20人女运动员30人10人20人20人假设所有运动员对活动方案是否支持相互独立.(1)根据所给数据,判断是否有99%的把握认为方案一的支持率与运动员的性别有关?(2)在抽出的100名运动员中,按是否支持方案二分层抽样抽出了5人,从这5人中随机抽取2人,求抽取的2人都支持方案二的概率.附:K2=,n=a+b+c+d.P(K2≥k)k解:(1)K2=≈16.667>10.828,∴有99%的把握认为方案一的支持率与运动员的性别有关.(2)由表中数据可得,抽取100人中,支持方案二的有60人,不支持方案二的有40人,所以采用分层抽样抽出的5人中,支持方案二有=3人,不支持方案二有5×=2人,支持方案二的3人记为A,B,C,不支持方案二的2人记为a,b,从这5人中随机抽取2人,所有可能情况有:(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10种,其中抽取的2人都支持方案二的3种,所以所求的概率P=.19.已知四边形ABCD是直角梯形,AB∥CD,∠C=45°,AB=2,CD=4,E,F分别为CD,BC的中点(如图1),以AE为折痕把△ADE折起,使点D到达点S的位置且平面SAE⊥平面ABCE(如图2).(1)求证:EF⊥SE;(2)求点C到平面SEF的距离.【解答】(1)证明:连结BE,因为CD=4,E为CD的中点,所以DE=AB=2,因为四边形ABCD是直角梯形,AB∥CD,所以ABCD是矩形,所以BE⊥CD,又∠C=45°,EC=2,所以AD=BE=EC=2,所以四边形ABED是正方形,△BEC是等腰直角三角形,又F为BC的中点,所以EF⊥BC,又∠C=45°,所以△ADE与△EFC都是等腰直角三角形,所以∠DEA=∠CEF=45°,所以EF⊥AE,因为平面SAE⊥平面ABCE,平面SAE∩平面ABCE=AE,EF⊂平面ABCE,所以EF⊥平面SAE,又SE⊂平面SAE,所以EF⊥SE;(2)解:设AE的中点为O,连结SO,因为平面SAE⊥平面ABCE,所以点S到AE的距离SO=,又S△EFC=1,所以,由(1)可知,EF⊥SE,所以,设点C到平面SEF的距离为h,由等体积法可得,V S﹣EFC=V C﹣SEF,所以,解得h=1,所以点C到平面SEF的距离为1.20.已知A,B分别为椭圆C:+=1(a>b>0)的左、右顶点,F为右焦点,点P 为C上的一点,PF恰好垂直平分线段OB(O为坐标原点),|PF|=.(1)求椭圆C的方程;(2)过F的直线l交C于M,N两点,若点Q满足=+(Q,M,N三点不共线),求四边形OMQN面积的取值范围.解:(1)由题意可知F(c,0),B(a,0),∵PF恰好垂直平分线段OB,∴a=2c,令x=c,代入+=1得:y=,∴,∴,解得,∴椭圆C的方程为:.(2)由题意可知直线l的斜率不为0,设直线l的方程为:x=my+1,设M(x1,y1),N(x2,y2),联立方程,消去x得:(3m2+4)y2+6my﹣9=0,∴△=36m2+36(3m2+4)>0,∴,,设MN的中点为E,则=+=2,∴MN与OQ互相平分,四边形OMQN为平行四边形,∴S平行四边形OMQN=2S△OMN=2×=|y1﹣y2|===,令t=≥1,则S平行四边形OMQN==(t≥1),∵y=3t+=3(t+)在[1,+∞)上单调递增,∴3t+≥4,∴∈(0,3],∴0<S平行四边形OMQN≤3.综上所述,四边形OMQN面积的取值范围为(0,3].21.已知函数f(x)=在x=1处取得极值.(1)求实数a的值,并求函数f(x)的单调区间;(2)证明:f(x)+x+>0.解:(1)∵f(x)=,∴f′(x)=,由题意,f′(1)=﹣1﹣a=0,即a=﹣1,则f′(x)=(x>0),当x∈(0,1)时,f′(x)<0,当x∈(1,+∞)时,f′(x)>0,∴f(x)的减区间为(0,1),增区间为(1,+∞);(2)要证f(x)+x+>0,即证>0,∵x>0,即证>0,令g(x)=x﹣1﹣lnx,则g′(x)=1﹣,当x∈(0,1)时,g′(x)<0,g(x)单调递减,当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,∴g(x)≥g(1)=0,即lnx≤x﹣1,则ln2x≤2x﹣1,得ln2+lnx≤2x﹣1,∴lnx≤2x﹣1﹣ln2,则,令h(x)=,∵ln2>ln=,∴,则h(x)>0,故>0成立,则f(x)+x+>0.四、(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多做则按所做的第一题计分.[选修44:坐标系与参数方程]22.在平面直角坐标系xOy中,曲线C的参数方程为(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ﹣sinθ)=2.(1)求曲线C的普通方程和直线l的直角坐标方程;(2)已知点P(3,1),直线l与曲线C交于A,B两点,求|PA|+|PB|的值.解:(1)曲线C的参数方程为(t为参数),转换为直角坐标方程为,直线l的极坐标方程为ρ(cosθ﹣sinθ)=2,根据,转换为直角坐标方程为x﹣y﹣2=0.(2)直线l的直线坐标方程转换为参数方程为:(t为参数),代入,得到,所以,,所以:|PA|+|PB|=.五、[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣1|+|x﹣5|.(1)解不等式f(x)≤6;(2)若正实数a,b满足a+b=ab,且函数f(x)的最小值为m,求证:a+b≥m.解:(1)因为f(x)=|x﹣1|+|x﹣5|,f(x)≤6,所以当x<1时,不等式即为﹣x+1﹣x+5≤6,解得x≥0,得0≤x<1.当1≤x≤5时,不等式即为x﹣1﹣x+5≤6⇒4≤6,得1≤x≤5.当x>5时,不等式即为x﹣1+x﹣5≤6,解得x≤6,得5<x≤6.综上,不等式f(x)≤6的解集为[0,6].(2)证明:f(x)=|x﹣1|+|x﹣5|≥|(x﹣1)﹣(x﹣5)|=4,所以m=4.正实数a,b,a+b=ab⇒,所以,(当且仅当,即a=b=2时等号成立)所以a+b≥m.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宜宾县高中2012级高考适应性考试(二)数 学(文史类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
满分150分。
考试时间120分钟。
考试结束后,将本试题卷和答题卡上一并交回。
第Ⅰ卷 (选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.高考临近,学校为丰富学生生活,缓解高考压力,特举办一场高三学生队与学校校队的男子篮球比赛。
由于爱好者众多,高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队,则高三学生队中5班和16班的人数分别为() A.3,5 B.4,5 C.3,4 D.4,32.已知集合{}{}2(,)|4,(,)|1A x y y x B x y y x ====+,则AB =( )A. {}(1,2)-B. {}(1,2)C. (1,2)D. (1,2)-3.执行右图所示的程序框图,若输入6x =,则输出y 的值为( )A . 2B . 0C . 1-D .32-4.若0a b <<,则下列选项正确的是( ) A.b a a b< B. 11a b <C .(,2)nna b n N n <∈≥ D. 0c ∀≠,都有ac bc < 5.下列说法正确的是( )A .已知p :2000,10x R x x ∃∈+-=,q :2,10x R x x ∀∈++>,则p q ∧是真命题。
B .命题p :若a b ⊥,则0a b ⋅=的否命题是:若a b ⊥,则0a b ⋅≠。
C .2,10x R x x ∀∈+-<的否定是2000,10x R x x ∃∈+->。
D .3x π=是sin(2)6y x π=-取最大值的充要条件。
6. 如图是某几何体的三视图,其中正视图是斜边长为2的直角三角形, 侧视图是半径为1的半圆,则该几何体的表面积是( )A .32π+.23π+C .6π+D π 7.已知1()f x x x=-,若[]1,2x ∈时,2()(1)0f x ax f x -+-≤,则a 的取值范围是( ) A. 1a ≤ B. 1a ≥ C. 32a ≥ D. 32a ≤8. 数列{a n }满足a n +a n +1=12(n ∈N ,n ≥1),若a 2=1,S n 是{a n }的前n 项和,则S 21的值为( )A .12-B .1C .92D .92- 9.设椭圆C 的两个焦点为1F 、2F ,过点1F 的直线与椭圆C 交于点,M N ,若212MF F F =,且114,3MF NF ==,则椭圆Γ的离心率为( )A .25 B .35C .37 D .5710.已知()y f x =为R 上的可导函数,当0x ≠时, ()'()0f x f x x +>,则函数1()()g x f x x=+的零点个数为 ( )A.1B.2C.0D.0或2第二部分 (非选择题 共100分)注意事项:必须使用0.5毫米黑色签字笔在答题卡上题目所指示的答题区域内作答。
作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚。
答在试题卷上无效。
二 、填空题:本大题共5小题,每小题5分,共25分。
11.已知复数z 满足1zi i =-,则z = 。
12.已知,A B 是sin()y x ωϕ=+的图像与x 轴的两个相邻交点,,A B 之间的最值点为C 。
若ABC ∆为等腰直角三角形,则ω的值为 。
13.已知(,)x y 满足3363y x x y y x ≤+⎧⎪+≤⎨⎪≥+⎩,若2z x y =-的最小值为 。
14.已知圆C :22(2)4x y -+=。
过点(1M 的直线与圆C 交于,A B 两点,若1122CN CA CB =+,则当劣弧AB 所对的圆心角最小时,CN CM ⋅ = 。
15.已知命题:①将一组数据中的每个数都变为原来的2倍,则方差也变为原来的2倍; ②在ABC ∆中,若sin sin A B A B ><,则; ③在正三棱锥S ABC -内任取一点P ,使得12P ABC S ABC V V --<的概率是78; ④若对于任意的()2,430n N n a n a *∈+-++≥恒成立,则实数a 的取值范围是1,3⎡⎫+∞⎪⎢⎣⎭. 16.(本小题满分12分)在△ABC 中,已知角A 为锐角,且[]222cos(2)1sin()sin()22()cos sin ()sin ()22A A A f A A A A πππππ--+-=++--.(I )求()f A 的最大值; (II )若7()1,,2f A A B BC π=+==,求△ABC 的三个内角和AC 边的长.17. (本小题满分12分)教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼。
为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间。
已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图。
(I)求x 的值,并求一周内阳光体育活动时间在[6,8]小时的人数;(II )从阳光体育时间在[6,8]小时的同学中抽取2人,求恰有1人的阳光体育活动时间在[)6,7小时的概率。
18. (本小题满分12分)数列{}n a 满足1(1)0n n na n a +-+=,已知12a =。
(I )求数列{}n a 的通项公式; (II )若12n n b a =,n S 为数列112n n b b +⎧⎫⎨⎬⎩⎭的前n 项的和,求证:12nS <。
19. (本小题满分12分)如图,直三棱柱111ABC A B C -中,,D E 分别是1,AB BB 的中点,1AA AC CB ===. (Ⅰ)证明:1//BC 平面1A CD ;(Ⅱ)求异面直线1BC 和1A D 所成角的余弦值; (III )当AB=1C A DE -的体积. 20.(本小题满分13分)给定椭圆C :22221(0)x y a b a b+=>>,称圆心在原点O ,的圆是椭圆C 的“准圆”。
若椭圆C的一个焦点为F ,其短轴上的一个端点到F(Ⅰ)求椭圆C 的方程和其“准圆”方程.(Ⅱ)点P 是椭圆C 的“准圆”上的一个动点,过动点P 作直线12,l l 使得12,l l 与椭圆C 都只有一个交点,且12,l l 分别交其“准圆”于点,M N .(1)当P 为“准圆”与y 轴正半轴的交点时,求12,l l 的方程. (2)求证:MN 为定值.21.(本小题满分14分)已知函数()ln 3,f x a x ax a R =--∈, (Ⅰ)当1a =时,求()f x 的极值 (II)求函数()f x 的单调区间。
(III )若函数()f x 的图象在点(2,(2)f )处的切线的倾斜角为45,对任意的[]1,2t ∈,函数32()()2m g x x x f x ⎡⎤'=++⎢⎥⎣⎦在区间(,3)t 上总不是单调函数,求m 取值范围宜宾县高中2012级高考适应性考试(二)数 学(文史类)答案一、选择题12. 2π; 13. 154-;14.3; 15.③④ 三、解答题16. (I )222[cos(2)1](sin )cos 22()cos cos sin 22A A A f A A A A ---=+- 222cos sin cos22cos cos A A A AA =+ .21)42sin(22)12cos 2(sin 21cos 2sin 212++=++=+=πA A A A A∵角A 为锐角,50,22444A A ππππ∴<<<+<当242A ππ∴+=时,()f A 最大,此时()f A 12=6分 (II )由()1f A =得:1sin(2)1242A π++=,即sin(2)42A π+=.125.3,127.4,4342ππππππ=∴=∴=+==+∴C B B A A A 又在△ABC 中,由正弦定理得:sin sin sin sin BC AC BC BAC A B A=∴== 12分 17. (I)因为组距为1,所以由直方图,[)[)[)[)[]3,4,4,5,5,6,6,7,7,8的频率分别为0.1,0.25,0.4,x ,0.1,0.10.250.40.11,0.15x x ∴++++=∴=因为抽取20个人,所以一周内阳光体育活动时间在[6,8]小时的人数为20(0.150.1)5⨯+=,即一周内阳光体育活动时间在[6,8]小时的人数为5. 5分(II )由(I),一周内阳光体育活动时间在[)6,7小时的人数为3,在[]7,8小时的人数为2,分别表示为12312,,,,A A A B B ,从这5个人中抽取2个人,有以下基本事件:12131112232122313212,,,,,,,,,A A A A A B A B A A A B A B A B A B B B ,共10个基本事件,其中恰有一个人的阳光体育活动时间在[)6,7小时的基本事件有6个基本事件。
设“恰有1个人的阳光体育活动时间在[)6,7小时”事件M ,则63()105P M ==。
12分 18.(I )由题,1(1)n n na n a +=+,所以11211n n a a an n +===+所以2n a n = 5分 (II )由(I ),11111111,1,()22(1)21n n n n b n b n b b n n n n ++=∴=+∴=⋅=-++,所以11111111111(1)(1)222312122(1)2n S n n n n =-+-++-=-=-<+++ 所以12n S <(*N n ∈) 12分 19.(Ⅰ)连接1AC ,设11AC AC M =,连接DM ,因为直三棱柱的侧面是矩形,故M 是1AC 的中点,在1ABC ∆中,D 是AB 的中点,所以1//DM BC ,因为111,DMACD BC ACD ⊂⊄所以1//BC 平面1A CD 。
(Ⅱ)因为AC CB =,D 是AB 的中点,所以CD AB ⊥,且由题AC BC ⊥,于是可建立以D 为坐标原点的空间直角坐标系,设AB =2,易得11(0,0,0),(1(1,0,0),(0,1D A B C -, 所以11(1,0,2),(1,1DA BC =-=-,113DA BC ⋅=,11||3,||2DABC == 设异面直线1BC 和1A D 所成角为θ,所以1111cos DA BC DA BC θ⋅==因为02πθ<≤,所以异面直线1BC 和1A D 所成角为6π。
