iSIGHT集成Matlab优化Fence实例
Isight教程Basic_03_Fence2

Excel 练习
进入 isightTrn/Fence2 目录 打开 Fence.xls 电子表格 界面中的"加载" 访问 iSIGHT/Excel 界面中的"加载" 映射输入和输出参数 保存描述文件, 保存描述文件 接着用 iSIGHT打开 打开
11
Excel 练习
使用第一个栅栏问题的参数表值 将缺省的优化方法改为一个简单的优化技术, 将缺省的优化方法改为一个简单的优化技术 NLPQL 中打开一个Custom表格 在Solution Monitor 中打开一个 表格 执行该程序
2
访问 iSIGHT/Excel电子表格界面 电子表格界面
两种方法访问界面: 两种方法访问界面
从 Excel软件 软件 从 iSIGHT软件 软件
最简单的方法是从 Excel内部开始 内部开始 工具" 从Excel 的"工具"( "Tools" )菜单中选 取"加载" (Add-In ) 加载"
3
从isight软件最简单的方法是从excel内部开始从excel的工具tools菜单中选取加载addin选择excel的加载addin三个对话框工作手册定义输入参数映射mapping输出参数映射mapping在isight中插入一个excel元件三个可比较的对话框工作手册定义输入参数映射输出参数映射10您完成上述操作之后信息保存在两个文件中
12
�
iSIGHT 基本培训 基本培训 使用 Excel的栅栏问题 的
iSIGHT 与 Excel 电子表格界面
许多工程师和科学家在工程分析中使用微软 公司的 Excel 软件 Excel 软件的应用范围从简单计算到复杂的, 软件的应用范围从简单计算到复杂的, 多表格计算 iSIGHT与 Excel 之间的连接曾被认为是一个高 与 级培训课题—这里是一个简单例子 级培训课题 这里是一个简单例子
Matlab优化算法及应用案例

Matlab优化算法及应用案例一、引言优化算法在科学和工程领域中起着重要的作用。
Matlab作为一款强大的科学计算软件,提供了丰富的优化算法工具箱,为用户提供了广泛的优化应用场景。
本文将介绍Matlab优化算法的基本原理,并通过实际案例来展示其在实际问题中的应用。
二、优化算法的基本原理优化算法的目标是求解一个函数的最优解,通常包括最大化或最小化目标函数。
Matlab中的优化算法主要基于以下两种类型:局部搜索算法和全局优化算法。
1. 局部搜索算法局部搜索算法是在当前解的附近搜索最优解的一类算法。
其中最为常见的是梯度下降法和牛顿法。
梯度下降法是一种迭代方法,通过沿着目标函数的负梯度方向不断调整参数,以逐步接近最优解。
具体步骤如下:(1)计算目标函数在当前解的梯度。
(2)根据梯度方向和步长系数进行参数调整。
(3)重复以上步骤直到满足停止准则。
牛顿法是一种基于二阶导数的优化方法,相比梯度下降法更为高效,但也更为复杂。
其基本思想是通过泰勒展开近似目标函数,然后解析求解导数为零的方程,得到下一次迭代的参数值。
2. 全局优化算法全局优化算法是通过全局搜索空间来找到最优解的方法。
Matlab提供了一些全局优化算法工具箱,其中最常用的是遗传算法和模拟退火算法。
遗传算法是一种模拟自然进化的优化方法,通过不断迭代生成新的解并选择适应度高的个体,并模拟自然选择、交叉和变异等操作来优化目标函数。
遗传算法在搜索空间较大且复杂的问题上有很好的表现。
模拟退火算法是一种以某种概率接受劣解的搜索算法,通过模拟金属退火过程来逐渐降低目标函数的值。
它能够避免局部最优解,并在一定程度上探索全局最优解。
三、Matlab优化算法的应用案例1. 机器学习中的参数调优在机器学习中,模型的性能很大程度上取决于参数的选择。
Matlab提供了优化工具箱,可以帮助用户选择合适的参数以提高模型的性能。
以支持向量机(SVM)为例,通过调整核函数类型、惩罚项系数和软间隔参数等参数,可以提高模型的分类准确度。
ISIGHT里面的优化方法

ISIGHT里面的优化方法大致可分为三类:1 数值优化方法数值优化方法通常假设设计空间是单峰值的,凸性的,连续的。
iSIGHT中有以下几种:(1)外点罚函数法(EP):外点罚函数法被广泛应用于约束优化问题。
此方法非常很可靠,通常能够在有最小值的情况下,相对容易地找到真正的目标值。
外点罚函数法可以通过使罚函数的值达到无穷值,把设计变量从不可行域拉回到可行域里,从而达到目标值。
(2)广义简约梯度法(LSGRG2):通常用广义简约梯度算法来解决非线性约束问题。
此算法同其他有效约束优化一样,可以在某方向微小位移下保持约束的有效性。
(3)广义虎克定律直接搜索法:此方法适用于在初始设计点周围的设计空间进行局部寻优。
它不要求目标函数的连续性。
因为算法不必求导,函数不需要是可微的。
另外,还提供收敛系数(rho),用来预计目标函数方程的数目,从而确保收敛性。
(4)可行方向法(CONMIN):可行方向法是一个直接数值优化方法,它可以直接在非线性的设计空间进行搜索。
它可以在搜索空间的某个方向上不断寻求最优解。
用数学方程描述如下:Design i = Design i-1 + A * Search Direction i方程中,i表示循环变量,A表示在某个空间搜索时决定的常数。
它的优点就是在保持解的可行性下降低了目标函数值。
这种方法可以快速地达到目标值并可以处理不等式约束。
缺点是目前还不能解决包含等式约束的优化问题。
(5)混合整型优化法(MOST):混合整型优化法首先假定优化问题的设计变量是连续的,并用序列二次规划法得到一个初始的优化解。
如果所有的设计变量是实型的,则优化过程停止。
否则,如果一些设计变量为整型或是离散型,那么这个初始优化解不能满足这些限制条件,需要对每一个非实型参数寻找一个设计点,该点满足非实型参数的限制条件。
这些限制条件被作为新的约束条件加入优化过程,重新优化产生一个新的优化解,迭代依次进行。
在优化过程中,非实型变量为重点考虑的对象,直到所有的限制条件都得到满足,优化过程结束,得到最优解。
isight参数优化理论和实例详解

前言●Isight 5.5简介笔者自2000年开始接触并采用Isight软件开展多学科设计优化工作,经过12年的发展,我们欣喜地看到优化技术已经深深扎根到众多行业,帮助越来越多的中国企业提高产品性能和品质、降低成本和能耗,取得了可观的经济效益和社会效益。
作为工程优化技术的优秀代表,Isight 5.5软件由法国Dassault/Simulia公司出品,能够帮助设计人员、仿真人员完成从简单的零部件参数分析到复杂系统多学科设计优化(MDO, Multi-Disciplinary Design Optimization)工作。
Isight将四大数学算法(试验设计、近似建模、探索优化和质量设计)融为有机整体,能够让计算机自动化、智能化地驱动数字样机的设计过程,更快、更好、更省地实现产品设计。
毫无疑问,以Isight为代表的优化技术必将为中国经济从“中国制造”到“中国创造”的转型做出应有的贡献!●本书指南Isight功能强大,内容丰富。
本书力求通过循序渐进,图文并茂的方式使读者能以最快的速度理解和掌握基本概念和操作方法,同时提高工程应用的实践水平。
全书共分十五章,第1章至第7章为入门篇,介绍Isight的界面、集成、试验设计、数值和全局优化算法;第8章至第13章为提高篇,全面介绍近似建模、组合优化策略、多目标优化、蒙特卡洛模拟、田口稳健设计和6Sigma品质设计方法DFSS(Design For 6Sigma)的相关知识。
本书约定在本书中,【AA】表示菜单、按钮、文本框、对话框。
如果没有特殊说明,则“单击”都表示用鼠标左键单击,“双击”表示用鼠标左键双击。
在本书中,有许多“提示”和“试一试”,用于强调重点和给予读者练习的机会,用户最好详细阅读并亲身实践。
本书内容循序渐进,图文并茂,实用性强。
适合于企业和院校从事产品设计、仿真分析和优化的读者使用。
在本书出版过程中,得到了Isight发明人唐兆成(Siu Tong)博士、Dassault/Simulia (中国)公司负责人白锐、陈明伟先生的大力支持,工程师张伟、李保国、崔杏圆、杨浩强、周培筠、侯英华、庞宝强、胡月圆、邹波等参与撰写,李鸽、杨新龙也为本书提供了宝贵的建议和意见,在此向所有关心和支持本书出版的人士表示感谢。
ISIGHT工程优化案例分析
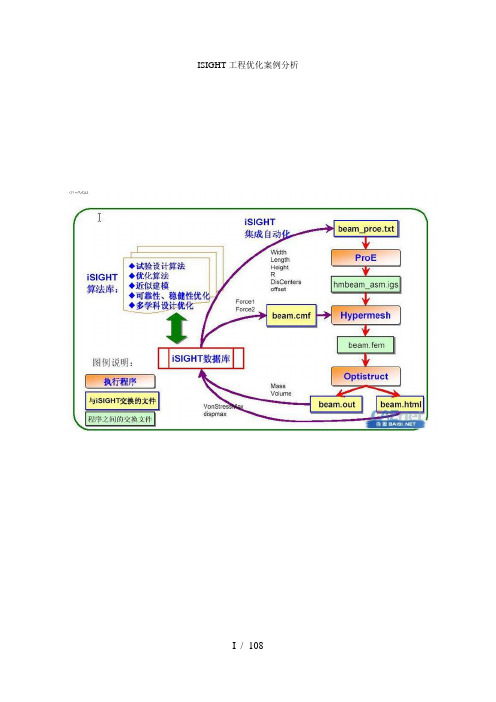
iSIGHT工程优化实例分前言随着设备向大型化、高速化等方向的发展,我们的工业设备(如高速列出、战斗机等)的复杂程度已远超乎平常人的想象,装备设计不单要用到大量的人力,甚至已牵涉到了数十门学科。
例如,高速车辆设计就涉及通信、控制、计算机、电子、电气、液压、多体动力学、空气动力学、结构力学、接触力学、疲劳、可靠性、维修性、保障性、安全性、测试性等若干学科。
随着时代的进步,如今每个学科领域都形成了自己特有研究方法与发展思路,因此在设计中如何增加各学科间的沟通与联系,形成一个统一各学科的综合设计方法(或平台),成为工程和学术界所关注的重点。
多年来,国外已在该领域做了许多著有成效的研究工作,并开始了多学科优化设计方面的研究。
就国外的研究现状而言,目前已经实现了部分学科的综合优化设计,并开发出了如iSIGHT、Optimus等多学科商业优化软件。
iSIGHT是一个通过软件协同驱动产品设计优化的多学科优化平台,它可以将数字技术、推理技术和设计搜索技术有效融合,并把大量需要人工完成的工作由软件实现自动化处理。
iSIGHT软件可以集成仿真代码并提供智能设计支持,对多个设计方案进行评估和研究,从而大大缩短了产品的设计周期,显著地提高了产品质量和可靠性。
目前市面上还没有关于iSIGHT的指导书籍,而查阅软件自带的英文帮助文档,对许多国内用户而言尚有一定的难度。
基于以上现状,作者根据利用iSIGHT做工程项目的经验编写了这本《iSIGHT工程优化实例》。
本书分为优化基础、工程实例和答疑解惑三个部分,其中工程实例中给出了涉及铁路、航空方面多个工程案例,以真实的工程背景使作者在最短的时间内掌握这款优化的软件。
本书在编写的过程中,从互联网上引用了部分资料,在此对原作者表示衷心地感谢!我要真诚地感谢大连交通大学(原大连铁道学院)和王生武教授,是他们给了我学习、接触和使用iSIGHT软件机会!仅以本书献给所有关心我的人!赵怀瑞2007年08月于西南交通大学目录第一章认识iSIGHT (1)1.1 iSIGHT软件简介 (1)1.2 iSIGHT工作原理简介 (5)1.3 iSIGHT结构层次 (6)第二章结构优化设计理论基础 (8)2.1 优化设计与数值分析的关系 (8)2.2 优化设计基本概念 (8)2.3 优化模型分类 (10)2.4 常用优化算法 (11)2.5大型结构优化策略与方法 (25)第三章iSIGHT软件界面与菜单介绍 (32)3.1 iSIGHT软件的启动 (32)3. 2 iSIGHT软件图形界面总论 (32)3.3 任务管理界面 (36)3.4 过程集成界面 (43)3.5 文件分析界面 (46)3.6 过程监控界面 (49)3.4 多学一招—C语言的格式化输入/输出 (53)第四章iSIGHT优化入门 (54)4.1 iSIGHT优化基本问题 (54)4.2 iSIGHT集成优化的一般步骤 (54)4.3 iSIGHT优化入门—水杯优化 (55)第五章模压强化工艺优化 (76)5.1 工程背景与概述 (76)5.2 优化问题描述 (76)5.3 集成软件的选择 (77)5.4有限元计算模型介绍 (77)5.5 模压强化优化模型 (78)5.8 iSIGHT集成优化 (81)5.9优化结果及其分析 (88)5.10 工程优化点评与提高 (89)第六章单梁起重机结构优化设计 (90)6.1 工程与概述 (90)6.2 优化问题描述 (90)6.3 集成软件的选择 (91)6.4起重机主梁校核有限元计算模型介绍 (92)6.5 主梁优化模型 (92)6.8 iSIGHT集成优化 (94)6.9优化结果及其分析 (99)6.10 工程优化点评与提高 (100)6.11 多学一招—ANSYS中结果输出方法 (100)第七章涡轮增压器压气机叶片优化设................................................... 错误!未定义书签。
isight集成matlab例子

【优化】Isight通用集成之Matlab点击图片上方的【思易特】可以快速关注订阅。
1.建立所需文件脚本文件图1.1 Matlab脚本文件Matlab自身作为一款数值计算程序,拥有自己的成熟脚本语言,大部分功能都是基于编写后缀为“.m”的脚本文件来实现的。
使用Matlab本身就是在编写脚本文件,所以这里并不需要对此多做介绍。
批处理文件a. Windows系统下,调用Matlab的批处理命令为:"C:\Program Files\MATLAB\R2012b\bin\win64\MATLAB.exe" /minimize -r test根据所使用电脑中Matlab安装路径修改该命令前面蓝色部分,根据前面所建立的脚本文件调整该命令后面绿色的文件名称。
b.新建txt文本文档,将修改后的命令复制并保存,将该文档的后“.txt”修改为“.bat”,即可得到windows批处理文件,如图1.2所示。
图1.2 Matlab批处理文件输出文件Matlab是一款功能十分强大的分析程序,我们可以利用其脚本语言以多种格式来输出任何信息,该脚本命令为:save 'test.txt' 'z' -ASCII其中“test.txt”为输出文件的格式及名称,“z”为输出变量,“-ASCII”为文本编码格式,该格式为Isight要求,该命令的详细使用方法请参考Matlab相关教程。
图1.3Matlab输出文件2.调整并验证所需文件a.在得到以上三个文件之后,首先需要根据实际情况对脚本文件的内容进行调整,以便于进行Isight集成。
一般需要注意两个方面:(1)在输出结果时,通常是可以指定输出路径的,可以将指定的路径添加至结果文件名称前面,但是为了Isight集成方便,建议去掉输出路径,以保证输出文件默认保存至“当前位置”;------------------以下内容为Isight集成逻辑分析,只在乎结论者可忽略------------------原因在于:Isight在每次迭代优化时,默认情况下,会在其工作路径下建立一个新的文件夹,然后将以上建立的脚本文件及批处理文件由原始位置拷贝至该文件夹,同时修改脚本文件中的设计变量并驱动分析软件的运行,分析结束后,会在该文件中搜索并读取结果文件,然后再次新建一个文件夹,进行下一轮迭代。
isight集成优化简单实例解析

7
of
18
单梁起重机结构优化设计
集成软件
本案例选择大型通用软件ANSYS11.0进行强度校核 分析。 可以在ANSYS 中建立主梁的几何模型, 并对其 划分网格
8
of
18
单梁起重机结构优化设计
主梁优化模型 1、目标函数选择
根据要求质量应该是最终的目标函数,在主梁 跨距一定的情况下截面面积与质量成正比,所以优化 时选取截面面积A 作为目标函数,其与有优化变量如 下关系式成立: A=wl x tl + t2 +w3 x t3
11 of
18
ISIGHT集成优化
1、输入文件分析
输入文件格式及优化变量在其中的位置如6.7所述。由于设计变量定义在 文件的开始,并且每一个设计变量值前面都有“=”,所以通过搜索的方式 让光标移到相应的变量前,再进行替换操作,相关设置如图
12 of
18
2、参数计算
在参数运算之前,首先 需要定义梁截面面积参数 AREA。 点击过程集成界面 工作栏上的参数按钮 , 则弹出如图所示对话框。点 击图中的“Add”按钮,参 数“OBJ”下面的一行被激 活,用户可以在“Task Task1”一栏中输入所添加 变量的名称“AREA”,然后 确认返回过程集成界面。 参数计算设置
18 of
18
THANK YOU 谢谢!
1
of
18
ISIGHT 包含的设计方法
优化设计
设计方法
试验设计 逼近计算 质量工程
2
of
18
ISIGHT
工作原理简介
基于数值分析软件的结构和工作过程,在进行数值分析的时候, 可以通过修改模拟计算模块的输入文件来完成模型的修改,iSIGHT 正是基于这种原理工作的。iSIGHT通过一种搭积木的方式快速集成 和耦合各种仿真软件,将所有设计流程组织到一个统一、有机和逻 辑的框架中,自动运行仿真软件,并自动重启设计流程,使整个设 计流程实现全数字化和全自动化。
Matlab优化算法以及应用案例分析

Matlab优化算法以及应用案例分析引言Matlab是一款功能强大的数学软件,以其丰富的功能和灵活的编程环境而受到广泛的应用。
在数学建模和优化问题中,Matlab优化算法是一个重要的工具。
本文将介绍Matlab优化算法的基本原理和常见应用案例分析。
一、Matlab优化算法的基本原理1.1 最优化问题的定义在开始介绍优化算法之前,我们首先需要了解什么是最优化问题。
最优化问题可以定义为在一定的约束条件下,找到使得目标函数达到最大或者最小的变量取值。
最优化问题可以分为无约束问题和约束问题两种。
1.2 Matlab优化工具箱Matlab提供了丰富的优化工具箱,其中包含了许多优化算法的实现。
这些算法包括无约束优化算法、约束优化算法、全局优化算法等。
这些工具箱提供了简单易用的函数接口和丰富的算法实现,方便用户在优化问题中使用。
1.3 优化算法的分类优化算法可以分为传统优化算法和启发式优化算法两类。
传统优化算法包括梯度下降法、牛顿法、共轭梯度法等,它们利用目标函数的一阶或二阶导数信息进行搜索。
而启发式优化算法则通过模拟生物进化、遗传算法、蚁群算法等方法来进行搜索。
二、Matlab优化算法的应用案例分析2.1 无约束优化问题无约束优化问题是指在没有约束条件的情况下,找到使得目标函数达到最小或最大值的变量取值。
在Matlab中,可以使用fminunc函数来求解无约束优化问题。
下面以一维函数的最小化问题为例进行分析。
首先,我们定义一个一维的目标函数,例如f(x) = 3x^2 - 4x + 2。
然后使用fminunc函数来求解该问题。
代码示例:```matlabfun = @(x)3*x^2 - 4*x + 2;x0 = 0; % 初始点[x, fval] = fminunc(fun, x0);```在上述代码中,fun是目标函数的定义,x0是初始点的取值。
fminunc函数将返回最优解x和目标函数的最小值fval。
iSIGHT-Matlab联合仿真
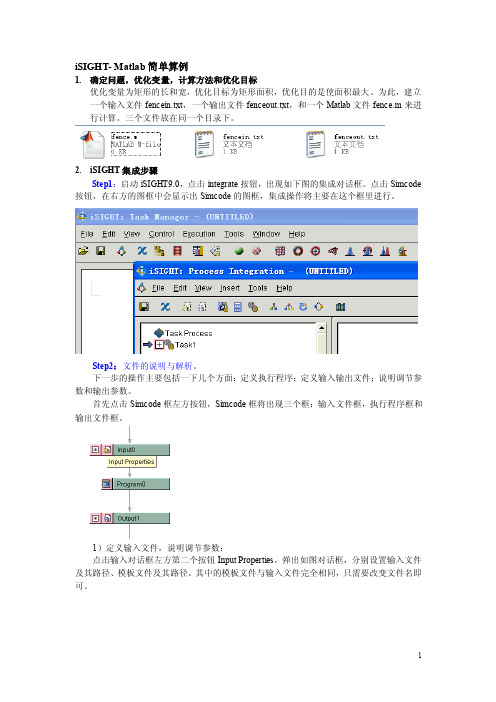
iSIGHT- Matlab简单算例1.确定问题,优化变量,计算方法和优化目标优化变量为矩形的长和宽,优化目标为矩形面积,优化目的是使面积最大。
为此,建立一个输入文件fencein.txt,一个输出文件fenceout.txt,和一个Matlab文件fence.m来进行计算。
三个文件放在同一个目录下。
2.iSIGHT集成步骤Step1:启动iSIGHT9.0,点击integrate按钮,出现如下图的集成对话框。
点击Simcode 按钮,在右方的图框中会显示出Simcode的图框,集成操作将主要在这个框里进行。
Step2:文件的说明与解析。
下一步的操作主要包括一下几个方面:定义执行程序;定义输入输出文件;说明调节参数和输出参数。
首先点击Simcode框左方按钮,Simcode框将出现三个框:输入文件框,执行程序框和输出文件框。
1)定义输入文件,说明调节参数:点击输入对话框左方第二个按钮Input Properties,弹出如图对话框,分别设置输入文件及其路径、模板文件及其路径。
其中的模板文件与输入文件完全相同,只需要改变文件名即可。
模板文件默认生成即可:点击input0图框左方的Input Contents按钮,系统会跳出文件解析对话框。
在文件解析框右边的文本框中,通过鼠标选择第一行的文字:Length= ,注意:选择时要考虑到空格,一定要保证鼠标高亮的位置在10之前,而且要从左往右拖动鼠标。
系统弹出Select Type of Action对话框,点击apply按钮。
在定义变量的对话框中,选中replace next Word标签,并在With对话框中输入Length,点击OK。
对第二行进行类似操作,系统显示结果如图。
在file中保存后关闭。
弹出如下对话框,点击OK即可。
2)定义执行程序:点击Program0左方按钮Program Properties,弹出对话框,设置如下:Simulation code-(path and) name里面选择Matlab安装目录下的MA TLAB.exe文件。
利用iSIGHT实现CFD仿真的全自动化过程
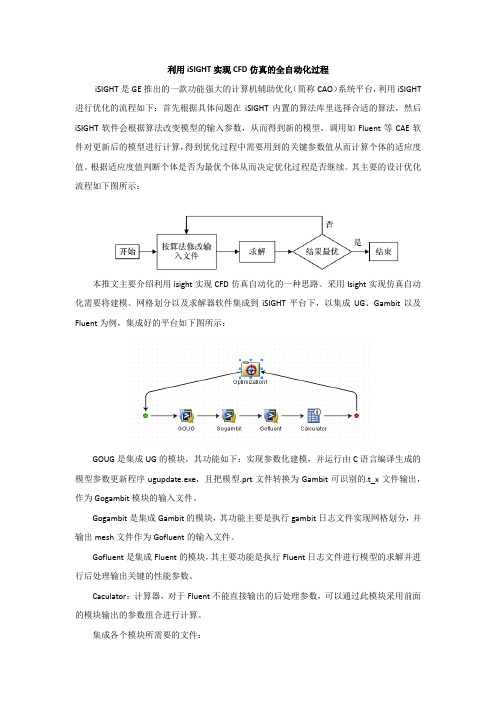
利用iSIGHT实现CFD仿真的全自动化过程iSIGHT是GE推出的一款功能强大的计算机辅助优化(简称CAO)系统平台,利用iSIGHT 进行优化的流程如下:首先根据具体问题在iSIGHT内置的算法库里选择合适的算法,然后iSIGHT软件会根据算法改变模型的输入参数,从而得到新的模型,调用如Fluent等CAE软件对更新后的模型进行计算,得到优化过程中需要用到的关键参数值从而计算个体的适应度值。
根据适应度值判断个体是否为最优个体从而决定优化过程是否继续。
其主要的设计优化流程如下图所示:本推文主要介绍利用isight实现CFD仿真自动化的一种思路。
采用Isight实现仿真自动化需要将建模、网格划分以及求解器软件集成到iSIGHT平台下,以集成UG、Gambit以及Fluent为例,集成好的平台如下图所示:GOUG是集成UG的模块,其功能如下:实现参数化建模,并运行由C语言编译生成的模型参数更新程序ugupdate.exe,且把模型.prt文件转换为Gambit可识别的.t_x文件输出,作为Gogambit模块的输入文件。
Gogambit是集成Gambit的模块,其功能主要是执行gambit日志文件实现网格划分,并输出mesh文件作为Gofluent的输入文件。
Gofluent是集成Fluent的模块,其主要功能是执行Fluent日志文件进行模型的求解并进行后处理输出关键的性能参数。
Caculator:计算器,对于Fluent不能直接输出的后处理参数,可以通过此模块采用前面的模块输出的参数组合进行计算。
集成各个模块所需要的文件:(1)集成UG所需要的文件(在公众号CAE与CAD的集成中介绍了每一个文件的制备方法)如下图所示:①tube.prt,由UG建模完成直接输出;②tube.exp:在UG中直接导出,包含模型关键参数的文件;③qi.exe:由VC6.0编译以下代码生成的可执行程序;④ug_parasolid.bat文件:qi.exe的驱动文件。
matlab优化算法 100例

matlab优化算法 100例Matlab是一种非常强大的数学软件,其中内置了许多实用的优化算法。
本文将围绕“Matlab优化算法100例”这个话题,分享一些基本的优化算法的应用实例。
第一步:优化函数的定义在使用Matlab优化算法之前,我们首先需要定义一个优化函数。
我们可以使用Matlab中的符号计算工具箱来定义优化函数,或者直接在脚本中定义一个函数。
下面是一个函数的例子:```function f = myfun(x)f = 0.26*(x(1)^2+x(2)^2)-0.48*x(1)*x(2);end```其中,这个函数计算了二次函数$f(x_1,x_2)=0.26(x_1^2+x_2^2)-0.48x_1x_2$ 的值。
这个函数的最小值可以通过优化算法来求解。
第二步:使用Matlab中的优化算法Matlab中提供了许多实用的优化算法,包括:梯度下降法、共轭梯度法、拟牛顿法、遗传算法、粒子群算法等等。
这些算法可以通过调用相关的函数来使用。
这里以fminunc函数为例,展示如何使用Matlab中的优化算法来求解前面定义的函数myfun的最小值。
```[x,fval,exitflag,output] = fminunc(@myfun, [0.3 0.3])```其中,@myfun是一个函数句柄,[0.3 0.3]是参数的初始值。
此函数将返回优化的最小值,以及一些其他的输出。
第三步:分析结果并优化我们可以使用Matlab中的 plot 函数来将优化结果可视化,以便更好地理解问题。
通过这个可视化,我们可以分析结果并进行优化。
```[X,Y]=meshgrid(-10:0.1:10,-10:0.1:10);Z=0.26*(X.^2+Y.^2)-0.48*X.*Y;figurecontour(X,Y,Z,50);hold onplot(x(1), x(2), 'ro')hold off```这里,我们使用 meshgrid 函数生成一个平面,并计算出函数的值。
Fence入门培训教材_Emma_排版
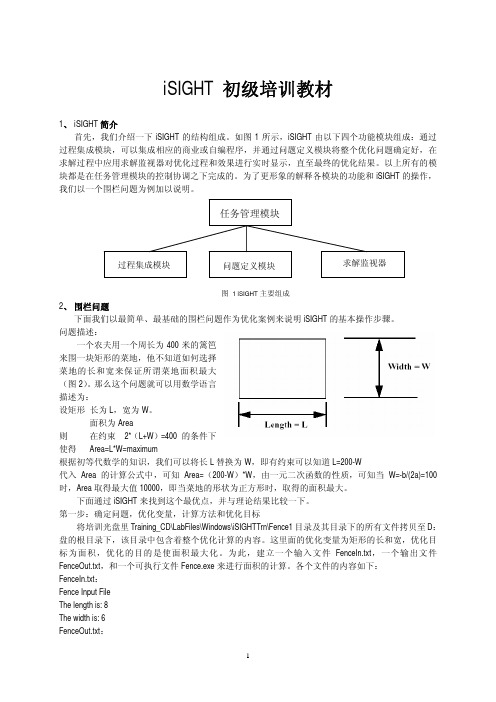
iSIGHT 初级培训教材1、iSIGHT简介首先,我们介绍一下iSIGHT的结构组成。
如图1所示,iSIGHT由以下四个功能模块组成:通过过程集成模块,可以集成相应的商业或自编程序,并通过问题定义模块将整个优化问题确定好,在求解过程中应用求解监视器对优化过程和效果进行实时显示,直至最终的优化结果。
以上所有的模块都是在任务管理模块的控制协调之下完成的。
为了更形象的解释各模块的功能和iSIGHT的操作,我们以一个围栏问题为例加以说明。
图 1 iSIGHT主要组成2、围栏问题下面我们以最简单、最基础的围栏问题作为优化案例来说明iSIGHT的基本操作步骤。
问题描述:一个农夫用一个周长为400米的篱笆来围一块矩形的菜地,他不知道如何选择菜地的长和宽来保证所谓菜地面积最大(图2)。
那么这个问题就可以用数学语言描述为:设矩形长为L,宽为W。
面积为Area则在约束2*(L+W)=400 的条件下使得 Area=L*W=maximum根据初等代数学的知识,我们可以将长L替换为W,即有约束可以知道L=200-W代入 Area的计算公式中,可知 Area=(200-W)*W,由一元二次函数的性质,可知当W=-b/(2a)=100时,Area取得最大值10000,即当菜地的形状为正方形时,取得的面积最大。
下面通过iSIGHT来找到这个最优点,并与理论结果比较一下。
第一步:确定问题,优化变量,计算方法和优化目标将培训光盘里Training_CD\LabFiles\Windows\iSIGHTTrn\Fence1目录及其目录下的所有文件拷贝至D:盘的根目录下,该目录中包含着整个优化计算的内容。
这里面的优化变量为矩形的长和宽,优化目标为面积,优化的目的是使面积最大化。
为此,建立一个输入文件FenceIn.txt,一个输出文件FenceOut.txt,和一个可执行文件Fence.exe来进行面积的计算。
各个文件的内容如下:FenceIn.txt:Fence Input FileThe length is: 8The width is: 6FenceOut.txt:Fence Output FileThe area is: 48.000000The perimeter is: 28.000000Fence.c:fscanf(fp,"Fence Input File\n"); // 数据输入语句fscanf(fp,"The length is: %lf\n", &Length); //读入长度fscanf(fp,"The width is: %lf\n", &Width); //读入宽度Area = Length * Width; //计算面积Perimeter = 2 * Length + 2 * Width; //计算周长fprintf(fp,"Fence Output File\n"); //数据输出语句fprintf(fp,"The area is: %f\n",Area); //输出面积fprintf(fp,"The perimeter is: %f\n",Perimeter); //输出周长程序编译成功后,便可以从输入文件中读取长和宽,计算出周长和面积,并将其输出至输出文件。
MATLAB智能算法30个案例分析(DOC 115页)

MATLAB 智能算法30个案例分析智能算法是我们在学习中经常遇到的算法,主要包括遗传算法,免疫算法,粒子群算法,神经网络等,智能算法对于很多人来说,既爱又恨,爱是因为熟练的掌握几种智能算法,能够很方便的解决我们的论坛问题,恨是因为智能算法感觉比较“玄乎”,很难理解,更难用它来解决问题。
因此,我们组织了王辉,史峰,郁磊,胡斐四名高手共同写作MATLAB智能算法,该书包含了遗传算法,免疫算法,粒子群算法,鱼群算法,多目标pareto算法,模拟退火算法,蚁群算法,神经网络,SVM等,本书最大的特点在于以案例为导向,每个案例针对一个实际问题,给出全部程序和求解思路,并配套相关讲解视频,使读者在读过一个案例之后能够快速掌握这种方法,并且会套用案例程序来编写自己的程序。
本书作者在线,读者和会员可以向作者提问,作者做到有问必答。
本书和目录如下:1 基于遗传算法的TSP算法(王辉)TSP (旅行商问题—Traveling Salesman Problem),是典型的NP完全问题,即其最坏情况下的时间复杂性随着问题规模的增大按指数方式增长,到目前为止不能找到一个多项式时间的有效算法。
遗传算法是一种进化算法,其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则。
遗传算法的做法是把问题参数编码为染色体,再利用迭代的方式进行选择、交叉以及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。
实践证明,遗传算法对于解决TSP问题等组合优化问题具有较好的寻优性能。
2 基于遗传算法和非线性规划的函数寻优算法(史峰)遗传算法提供了求解非线性规划的通用框架,它不依赖于问题的具体领域。
遗传算法的优点是将问题参数编码成染色体后进行优化,而不针对参数本身,从而不受函数约束条件的限制;搜索过程从问题解的一个集合开始,而不是单个个体,具有隐含并行搜索特性,可大大减少陷入局部最小的可能性。
而且优化计算时算法不依赖于梯度信息,且不要求目标函数连续及可导,使其适于求解传统搜索方法难以解决的大规模、非线性组合优化问题。
Matlab的优化工具箱的几个应用函数及例子

optnew = optimget(my_options,'Display','final'); 参见: optimset
如果函数的导数容易求得,一般来说首先考虑使用三次插值法,因为它具有较高
的效率。对于只需要计算函数值的方法中,二次插值法是一个很好的方法,它的 收敛速度较快,尤其在极小点所在区间较小时尤其如此。黄金分割法则是一种十 分稳定的方法,并且计算简单。由于以上原因,Matlab 优化工具箱中使用得较 多的方法是二次插值法、三次插值法、二次、三次混合插值法和黄金分割法。 9.2.1.2 相关函数介绍 fminbnd 功能:找到固定区间内单变量函数的最小值。 语法: x = fminbnd(fun,x1,x2) x = fminbnd(fun,x1,x2,options) x = fminbnd(fun,x1,x2,options,P1,P2,...) [x,fval] = fminbnd(...) [x,fval,exitflag] = fminbnd(...) [x,fval,exitflag,output] = fminbnd(...) 描述: fminbnd 求取固定区间内单变量函数的最小值。 x = fminbnd(fun,x1,x2)返回区间{x1,x2}上 fun 参数描述的标量函数的最小值 x。 x = fminbnd(fun,x1,x2,options)用 options 参数指定的优化参数进行最小化。 x = fminbnd(fun,x1,x2,options,P1,P2,...)提供另外的参数 P1,P2 等,传输给 目标函数 fun。如果没有设置 options 选项,则令 options=[]。 [x,fval] = fminbnd(...)返回解 x 处目标函数的值。 [x,fval,exitflag] = fminbnd(...)返回 exitflag 值描述 fminbnd 函数的退出 条件。 [x,fval,exitflag,output] = fminbnd(...)返回包含优化信息的结构输出。 变量: 函数的输入变量在表 9-7 中进行描述,输出变量在表 9-8 中描述。与 fminbnd 函数相关的细节内容包含在 fun,options,exitflag 和 output 等参数中,如表 9-10 所示。
isight参数优化理论与实例详解

前言●Isight 简介笔者自2000年开始接触并采用Isight软件开展多学科设计优化工作,经过12年的发展,我们欣喜地看到优化技术已经深深扎根到众多行业,帮助越来越多的中国企业提高产品性能和品质、降低成本和能耗,取得了可观的经济效益和社会效益。
作为工程优化技术的优秀代表,Isight 软件由法国Dassault/Simulia公司出品,能够帮助设计人员、仿真人员完成从简单的零部件参数分析到复杂系统多学科设计优化(MDO, Multi-Disciplinary Design Optimization)工作。
Isight将四大数学算法(试验设计、近似建模、探索优化和质量设计)融为有机整体,能够让计算机自动化、智能化地驱动数字样机的设计过程,更快、更好、更省地实现产品设计。
毫无疑问,以Isight为代表的优化技术必将为中国经济从“中国制造”到“中国创造”的转型做出应有的贡献!●本书指南Isight功能强大,内容丰富。
本书力求通过循序渐进,图文并茂的方式使读者能以最快的速度理解和掌握基本概念和操作方法,同时提高工程应用的实践水平。
全书共分十五章,第1章至第7章为入门篇,介绍Isight的界面、集成、试验设计、数值和全局优化算法;第8章至第13章为提高篇,全面介绍近似建模、组合优化策略、多目标优化、蒙特卡洛模拟、田口稳健设计和6Sigma品质设计方法DFSS(Design For 6Sigma)的相关知识。
●本书约定在本书中,【AA】表示菜单、按钮、文本框、对话框。
如果没有特殊说明,则“单击”都表示用鼠标左键单击,“双击”表示用鼠标左键双击。
在本书中,有许多“提示”和“试一试”,用于强调重点和给予读者练习的机会,用户最好详细阅读并亲身实践。
本书内容循序渐进,图文并茂,实用性强。
适合于企业和院校从事产品设计、仿真分析和优化的读者使用。
在本书出版过程中,得到了Isight发明人唐兆成(Siu Tong)博士、Dassault/Simulia(中国)公司负责人白锐、陈明伟先生的大力支持,工程师张伟、李保国、崔杏圆、杨浩强、周培筠、侯英华、庞宝强、胡月圆、邹波等参与撰写,李鸽、杨新龙也为本书提供了宝贵的建议和意见,在此向所有关心和支持本书出版的人士表示感谢。
优化设计Matlab实例解析

优化设计Matlab实例解析MATLAB是一种基于矩阵运算的高级编程语言和环境,被广泛应用于各个领域的科学计算和工程问题。
在实际应用中,我们经常面临优化设计的任务,即在给定的限制条件下,寻找最优的解决方案。
优化设计可以应用于诸如控制系统设计、信号处理、图像处理、机器学习等问题中。
下面我们以一个简单的例子来说明如何使用MATLAB进行优化设计。
假设我们有一个矩形花园,每边有一定的长度,我们希望找到一个长和宽使得花园的面积最大化。
令矩形花园的长和宽分别为x和y,由于边长有限制条件,即x的范围为0到20,y的范围为0到10,同时花园的长度之和不得超过30。
我们的目标是找到一组合适的x和y,使得面积A 最大。
在MATLAB中,我们可以使用优化工具箱中的函数fmincon来求解这个问题。
以下是具体的实现步骤:1.创建目标函数首先,我们需要定义一个目标函数来评估每组x和y的解决方案。
在这个例子中,我们的目标是最大化矩形花园的面积,因此我们的目标函数可以简单地定义为A=x*y。
```matlabfunction A = objective(x)A=-x(1)*x(2);%最大化面积,取负号end```2.设置限制条件接下来,我们需要定义限制条件。
在这个例子中,我们需要考虑两个限制条件,即x和y的范围以及长度之和的限制。
我们可以使用函数fmincon提供的constr函数来定义这些限制条件。
```matlabfunction [c, ceq] = constr(x)c=[x(1)-20;%x的上限x(2)-10;%y的上限x(1)+x(2)-30];%长度之和的限制ceq = []; % 无等式限制end```3.求解问题有了目标函数和限制条件,我们可以使用fmincon函数来求解问题。
```matlabx0=[10,5];%初始猜测lb = [0, 0]; % x和y的下限ub = [20, 10]; % x和y的上限options = optimoptions('fmincon', 'Display', 'iter'); % 设置选项```在这里,我们使用了初始猜测x0、x和y的上下限lb和ub以及其他选项。
iSIGHT集成Matlab优化实例

1
2
3
4
Step 2.2.3 第三步:设置目标函数,fence的面积Area最大。 1. 单击objectives;2. 在Area前打钩;3. directions下面单击选择maximize;
4.Apply。
1 2
3
4
Step 2.2.4 第四步:选择优化算法。 1。单击general;2. 单击optimization technique右侧的下拉箭头, 选择NLPQL; 3. 每个算法下面有些参数可以设置,这里默认就OK了。 4.至此,optimization设置完成,OK返回。
Step 2.1 连接Optimization。具体做法:在driver标签里 面,把Optimization 图标拖到task1上面,松开!
Step 2.2 双击
,设置Optimization ,这下分4步:
Step 2.2.1 第一步:设置优化变量:fence的长Length,宽Width。
1. 单击variables;2. 在变量前打钩;3. 设置每个变量的初始值及取值范围 [lower bound, upper bound] ;4.Apply。
后记
1. 同一个问题,选择不同的算法,得到的结果可能不一样。 So,要做深入研究,必须弄清楚各个算法。
2. 计算程序很核心,要在程序里面把问题描述清楚。但越简单越好, 不容易出错。
3. 刚刚学习,请大家多多指教!
1
2
弹出如下窗口,开始优化。进度显示在1位置。
1
Step 3.2 1.单击history ,进行优化现场直播。 2. 出现经典的黑白格子旗,恭喜你,优化完成了。
2 1
从表中看出,最后一次迭代,Length=100,Width=100时, 满足Perimeter=400的约束条件下,Area达到最大为10000。
excited-isight联合仿真教程(多目标优化)

无iSIGHT整合计算经验者可
快速使用
4
Review
AWS “Connect to iSIGHT”自动完成的工作
建立和管理iSIGHT的数据模型(参数)Creates and manages iSIGHT data
model (parameters)
建立和管理iSIGHT的工作流模型 Creates and manages iSIGHT process flow
8
例一: Generate Results
画出结果曲线(需优化的)
观察扭振峰值,制订优化目标
9
例一: Generate Results
调入优化目标曲线(图中绿线)
优化目标曲线可在原结 果数据基础上制作:
可先将原结果导出为文本
文件
手工编辑调整(或来自其
它计算)
10
例一: Generate Results
24
例二:
例二: Optimization of Damper and Flywheel (2/8)
Step 2: Assign parameters for a speed range
25
例二:
例二: Optimization of Damper and Flywheel (3/8)
Step 3:
31
18
例一: iSIGHT
存盘(缺省名),并执行
n
存盘(缺省名)
o
运行
19
例一: iSIGHT
监控执行
Go to Monitor and Open database *.db-file
n
监控
o
isight和matlab版本

isight和matlab版本iSight和MATLAB版本iSight是一款由苹果公司开发的摄像头,自2006年起被广泛用于苹果的笔记本电脑和显示器上。
它具有高分辨率、高画质和高质量的图像捕捉能力,因此被广泛应用于视频通话、拍摄照片和录制视频等领域。
而MATLAB是一种高级的数学计算和可视化软件,广泛应用于科学、工程和技术领域。
iSight与MATLAB可以结合使用,以实现各种有趣和实用的功能。
下面将介绍一些这方面的应用。
1. 图像处理iSight可以捕捉到的图像可以通过MATLAB进行处理和分析。
例如,可以使用MATLAB的图像处理工具箱进行图像增强、滤波和分割等操作。
通过这种方式,可以改善图像的质量、减少噪声和提取感兴趣的特征。
2. 目标检测和跟踪iSight可以用于目标检测和跟踪。
通过将iSight与MATLAB的计算能力结合起来,可以实现实时的目标检测和跟踪。
例如,可以使用MATLAB的计算机视觉工具箱来检测人脸、车辆或其他感兴趣的目标,并跟踪它们的运动。
3. 视频分析iSight可以捕捉到的视频可以通过MATLAB进行分析。
例如,可以使用MATLAB的视频处理工具箱来提取视频中的运动特征、计算视频的光流、检测视频中的变化等。
这些分析结果可以帮助我们理解视频中发生的事情,并从中获取有用的信息。
4. 三维重建iSight可以用于三维重建。
通过将iSight与MATLAB的图像处理和计算机视觉工具箱结合起来,可以从多个图像中重建出三维场景。
例如,可以使用MATLAB的立体视觉工具箱来计算图像之间的深度信息,然后使用这些深度信息来重建出三维场景。
5. 模式识别iSight可以用于模式识别。
通过将iSight与MATLAB的模式识别工具箱结合起来,可以实现各种模式识别任务。
例如,可以使用MATLAB的机器学习算法来训练一个分类器,然后使用iSight捕捉到的图像来进行分类。
总结而言,iSight和MATLAB的结合可以实现各种图像处理、目标检测和跟踪、视频分析、三维重建和模式识别等应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iSIGHT- Matlab简单算例
1.确定问题,优化变量,计算方法和优化目标
优化变量为矩形的长和宽,优化目标为矩形面积,优化目的是使面积最大。
为此,建立一个输入文件fencein.txt,一个输出文件fenceout.txt,和一个Matlab文件fence.m来进行计算。
三个文件放在同一个目录下。
2.iSIGHT集成步骤
Step1:启动iSIGHT9.0,点击integrate按钮,出现如下图的集成对话框。
点击Simcode 按钮,在右方的图框中会显示出Simcode的图框,集成操作将主要在这个框里进行。
Step2:文件的说明与解析。
下一步的操作主要包括一下几个方面:定义执行程序;定义输入输出文件;说明调节参数和输出参数。
首先点击Simcode框左方按钮,Simcode框将出现三个框:输入文件框,执行程序框和输出文件框。
1)定义输入文件,说明调节参数:
点击输入对话框左方第二个按钮Input Properties,弹出如图对话框,分别设置输入文件及其路径、模板文件及其路径。
其中的模板文件与输入文件完全相同,只需要改变文件名即可。
模板文件默认生成即可:
点击input0图框左方的Input Contents按钮,系统会跳出文件解析对话框。
在文件解析框右边的文本框中,通过鼠标选择第一行的文字:Length= ,
注意:选择时要考虑到空格,一定要保证鼠标高亮的位置在10之前,而且要从左往右拖动鼠标。
系统弹出Select Type of Action对话框,点击apply按钮。
在定义变量的对话框中,选中replace next Word标签,并在With对话框中输入Length,点击OK。
对第二行进行类似操作,系统显示结果如图。
在file中保存后关闭。
弹出如下对话框,点击OK即可。
2)定义执行程序:
点击Program0左方按钮Program Properties,弹出对话框,设置如下:
Simulation code-(path and) name里面选择Matlab安装目录下的MATLAB.exe文件。
Optional command arguments里面填写:automation –r fence ,
注意:有空格,fence后不带后缀。
3)定义输出文件,说明输出参数:
设置输出文件路径:
点击Output1左方第一个按钮,对输出参数进行解析说明。
用鼠标高亮选中80之前的部分,然后在系统弹出Select Type of Action对话框中,点击apply按钮。
在如下图标签下,Store into Parameter中填写Area,Format to Read中填写%f .
对第二行进行类似操作,系统显示结果如图。
在file中保存后关闭。
弹出如下对话框,点击OK即可。
保存描述文件,关闭integrate对话框。
Step3:参数定义与执行:
1)参数设置如下,点击OK.
2)Task Plan,可以选择优化算法:
本算例中选择默认的优化算法,点击OK即可。
3)Monitor,监视器设置。
可以插入图表,选择Length和Width,点击OK.
4)点击执行
结果显示如下:。
