2020年中考数学冲刺专题：几何探究和证明(含答案)

合集下载

2020年中考数学冲刺专题：几何探究与证明(含答案)

2020中考数学冲刺专题：几何探究与证明(含答案)1.如图①，已知在正方形ABCD中，E为对角线BD上一点，过点E作EFLBD交BC于点F,连接DF, G为DF中点，连接EG, CG.图③第1题图(1)求证：EG = CG;(2)将图①中4BEF绕点B逆时针旋转45°,则点F落在对角线BD上，如图②，取DF中点G,连接EG, CG.问EG和CG相等吗？若相等，请给出证明；若不相等，请说明理由；(3)将图①中4BEF绕B点旋转任意角度，如图③，再连接相应的线段，问线段EG 和CG有何关系？(请直接写出答案)(1)证明：:在正方形ABCD 中，・•.zBCD = 90 :VEFXBD,・•.zFED=90 :・.G为DF中点，~ 1 ifL. EG = 2DF , CG = ?DF.. EG = CG;(2)解：EG=CG.证明：如解图①，延长EF交CD于点H,连接GH,第1题解图①;在正方形ABCD中，・•・"BC= 90 , BD 平分/ABC,一1，~ 。

・•.Z EBF=2/ABC=45.VEFXAB,・•.zFEB=90 ,・•.zEFB=90 — /EBF = 45 , ・•.zEBF= /EFB,・•.BE=FE.・zBCD= / ABC= / BEF= 90 , ・•・四边形EBCH是矩形，・•.HC = EB=EF, /FHC = 90 , ・•.zFHD = 180 - ZFHC = 90 : .CD //EB,・•.zHDF = /EBF = 45 ,/.zDFH=90 -ZHDF=45 ,・•.zHDF = /DFH,・•.HD = FH.・.G为DF中点，- 一1 一一。

・•.zDHG = 2ZDHF = 45 ,/. J3HC=180 - ZDHG = 135 .vzEFG= 180 -ZDFH = 135 ,•.zGHC=/EFG,••・在RtDHF中，G为DF中点，1•.GH=5DF= GF,・••/EFG“HG(SAS),•.EG = CG;(3)ft?: EG=CG, EGXCG.【解法提示】如解图③，理由如下:第1题解图②过点F作CD的平行线并延长CG交于点M,连接EM、EC,过点F作FN 垂直于AB于点N,工为FD中点，易证4CDG二△MFG,得到CD=FM,又•.BE=EF, •..zEBF=/EFB,zEFM = 180 —45 — / BFH = 135 — / BFH , /EBC=/EBF+/FBH = 45 +90 —/BFH=135 —/BFH,zEFM = / EBC, 任FM^EBC(SAS),••.zFEM=/BEC, EM = EC, 「zFEC+/ BEC= 90 , / FEC+/FEM = 90°,即/MEC = 90°,「. HEC是等腰直角三角形，为CM中点，.EG = CG, EGXCG.2.如图，在4ABC中，丛CB=90°,过点A作射线API AB,点D是线段AC上一动点(不与点A、C重合)，连接BD,过点D作DELBD,交射线AP于点E.(1)如图①，当/BAC = 45°时，则线段AE与线段CD之间的数量关系为________ ；(2)如图②，当/BAC=300时，猜想线段AE与线段CD之间的数量关系，并说明理由；(3)当/BAC= 0c时，直接写出线段AE与线段CD的数量关系(用含0c的三角函数表示).图①图②图③第2题图解：⑴AE=V2CD；【解法提示】如解图①，在BC上取一点G,使AD = BG,连接DG, v zBAC= 45 , ZACB=90 ,・••/ACB是等腰直角三角形，. AC=BC,. AC—CD=BC—BG,即CD = CG,・••/CDG是等腰直角三角形，. DG = V2CD, /DGC = 45 ,・•.zDGB=135 ；・APXAB,・•.zBAP= 90 ,・•.zDAE=90 +45 = 135 ；・•.zDAE= /DGB,・D EXDB,・•.zEDB= 90 ,・••/EDA+ /BDC = 90 ,vzBDC+ZDBC = 90 ,・•.zEDA= /DBC,/./EAD^zDGB(ASA),. AE=DG,・•AE=/CD；(2)猜想：AE = 2CD,理由是：如解图②，过点D作DF//AB,交BC于点F,___ ____________ 。

2020年中考三轮冲刺复习培优练习证明与计算及答案

2020年中考三轮冲刺复习培优同步练习：《反比例函数》证明与计算（五）1．如图，点A（2，n）和点D是反比例函数y＝（m＞0，x＞0）图象上的两点，一次函数y＝kx+3（k≠０）的图象经过点A，与y轴、x轴分别交于点B和点C，过点D作DE⊥x 轴，垂足为E，连接OA、OD，已知△OAB与△ODE的面积满足S△OAB：S△ODE＝3：4．（1）求S△OAB与反比例函数解析式；（2）已知点P（6，0）在线段OE上，当∠PDE＝∠CBO时，求点D的坐标．2．矩形AOBC中，OB＝4，OA＝3，分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y＝（k＞0）的图象与边AC交于点E．（1）当点F运动到边BC的中点时，点E的坐标为．（2）连接EF，求∠EFC的正切值；（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求BG的长度．3．如图，直线AB经过A（1，0），B（0，1）两点，动点P在双曲线y＝（x＞0）上运动，PM⊥x轴，PN⊥y轴，垂足分别为M，N，PN，PM与线段AB分别交于点F，E．（1）求证：AF?BE＝1；（2）求证：△BOE∽△AFO；（3）设△OEF的外心为G，求证：点G，P关于直线AB对称．4．如图，一次函数y＝﹣x+2的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限作等边△ABC．（1）若点C在反比例函数y＝的图象上，求该反比例函数的解析式；（2）点P（4，m）在第一象限，过点P作x轴的垂线，垂足为D，当△PAD与△OAB 相似且P点在（1）中反比例函数图象上时，求出P点坐标．5．如图，在平面直角坐标系中，直线y＝3x+b经过点A（﹣1，0），与y轴正半轴交于B点，与反比例函数y＝（x＞0）交于点C，且BC＝2AB，BD∥x轴交反比例函数y＝（x＞0）于点D，连接AD．（1）求b、k的值；（2）求△ABD的面积；（3）若E为射线BC上一点，设E的横坐标为m，过点E作EF∥BD，交反比例函数y ＝（x＞0）的图象于点F，且EF＝BD，求m的值．6．已知一次函数y1＝kx﹣（2k+1）的图象与x轴和y轴分别交于A、B两点，A（3，0），一次函数与反比例函数y2＝﹣的图象分别交于C、D两点．（1）求一次函数与反比例函数解析式；（2）求△OCD的面积；（3）直接写出y1＞y2时，x的取值范围．7．实验数据显示，一般成人喝半斤低度白酒后， 1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y＝﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y＝上（k＞0）刻画（如图所示）．（1）根据上述数学模型计算：喝酒后几时血液中的酒精含量达到最大值？最大值为多少？（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．8．如图，在平面直角坐标系中，直线BC与y轴交于点A（0，4），与x轴交于点D，点B，C是反比列函数y＝（x＞0）图象上的点，OB⊥BC于点B，∠BOD＝60°．（1）求直线AB的解析式；（2）求反比例函数的解析式；（3）若△AOB的面积为S1，△BOC的面积为S2，△DOC的面积为S3，直接写出S1，S2，S3的一个数量关系式：9．在平面直角坐标系中，点A，B为反比例函数y＝（k＞0，x＞0）上的两个动点，以A，B为顶点构造菱形ABCD．（1）如图1，点A，B横坐标分别为1，4，对角线BD∥x轴，菱形ABCD面积为，求k的值．（2）如图2，当点A，B在（1）的条件下继续运动至某一时刻，点C，点D恰好落在x 轴和y轴正半轴上，此时∠ABC＝90°，求点A，B的坐标．10．如图，反比例函数y＝与一次函数y＝k2x+b的图象交于点A（﹣1，5），B（m，﹣1）．（1）求k1，k2的值；（2）结合函数图象，写出当k2x+b＞时，x的取值范围；（3）P为y轴上一点，若△ABP的面积是△ABO面积的3倍，请求出点P的坐标．参考答案1．解：（1）由一次函数y＝kx+3知，B（0，3）．又点A的坐标是（2，n），∴S△OAB＝×3×2＝3．∵S△OAB：S△ODE＝3：4．∴S△ODE＝4．∵点D是反比例函数y＝（m＞0，x＞0）图象上的点，∴m＝S△ODE＝4，则m＝8．∴反比例函数解析式为y＝；（2）由（1）知，反比例函数解析式是y＝．∴2n＝8，即n＝4．故A（2，4），将其代入y＝kx+3得到：2k+3＝4．解得k＝．∴直线AC的解析式是：y＝x+3．令y＝0，则x+3＝0，∴x＝﹣6，∴C（﹣6，0）．∴OC＝6．由（1）知，OB＝3．设D（a，b），则DE＝b，PE＝a﹣6．∵∠PDE＝∠CBO，∠COB＝∠PED＝90°，∴△CBO∽△PDE，∴＝，即＝①，又ab＝8 ②．联立①②，得（舍去）或．故D（8，1）．2．解：（1）∵OB＝4，OA＝3，∴点A、B、C的坐标分别为：（0，3）、（4，0）、（4，3），点F运动到边BC的中点时，点F（4，），将点F的坐标代入y＝并解得：k＝6，故反比例函数的表达式为：y＝，当y＝3时，x＝＝2，故E（2，3），故答案为：（2，3）；（2）∵F点的横坐标为4，点F在反比例函数上，∴F（4，），∴CF＝BC﹣BF＝3﹣＝，∵E的纵坐标为3，∴E（，3），∴CE＝AC﹣AE＝4﹣＝，在Rt△CEF中，tan∠EFC＝＝；（3）如图，由（2）知，CF＝，CE＝，＝，过点E作EH⊥OB于H，∴EH＝OA＝3，∠EHG＝∠GBF＝90°，∴∠EGH+∠HEG＝90°，由折叠知，EG＝CE，FG＝CF，∠EGF＝∠C＝90°，∴∠EGH+∠BGF＝90°，∴∠HEG＝∠BGF，∵∠EHG＝∠GBF＝90°，∴△EHG∽△GBF，∴，∴，∴BG＝．3．（1）证明：设P（m，n）．∵A（1，0），B（0，1），∴直线AB的解析式为y＝﹣x+1，∴E（m，﹣m+1），F（1﹣n，n），∴AF＝n，BE＝m，∵m＝，∴mn＝，∴AF?BE＝n?m＝1．（2）证明：∵OA＝OB＝1，∴OA?OB＝AF?BE＝1，∴＝，∵∠OBE＝∠OAF＝45°，∴△BOE∽△AFO．（3）证明：连接GE，GF．∵△BOE∽△AFO，∴∠OEB＝∠FAO，∵∠OEB＝∠EOA+∠OAE，∠FOA＝∠EOF+∠AOE，∴∠EOF＝∠OAE＝45°，∵G是△EOF的外心，∴∠EGF＝2∠EOF＝90°，∴△EGF是等腰直角三角形，∴∠GEF＝∠GFE＝45°，∵∠PEF＝∠PFE＝45°，∴△PEF也是等腰直角三角形，∴设P（m，n）．∴P，G关于AB对称．4．解：（1）对于一次函数y＝﹣x+2，当y＝0，即﹣x+2＝0时，x＝2，当x＝0时，y＝2，则点A的坐标为（2，0），点B的坐标为（0，2），即OA＝2，OB＝2，∴tan∠OAB＝＝＝，∴∠OAB＝30°，∴AB＝2OB＝4，∵△ABC为等边三角形，∴∠BAC＝60°，AC＝AB＝4，∴∠OAC＝90°，∴点C的坐标为：（2，4），∴k＝2×4＝8，∴反比例函数的解析式为：y＝；（2）∵点P（4，m）在第一象限，∴OD＝4，m＞0，∴AD＝OD﹣OA＝2，当△ADP∽△AOB时，＝，即＝，解得，m＝2，此时P点坐标为（4，2）；当△PDA∽△AOB时，＝，即＝，解得，m＝6，此时P点坐标为（4，6）；∵4×2＝8，4×6＝24≠８，∴P点在（1）中反比例函数图象上时，P点坐标为（4，2）．5．解：（1）作CH⊥y轴于点H，∵直线y＝3x+b经过点A（﹣1，0），∴﹣1×3+b＝0，解得，b＝3，对于直线y＝3x+3，当x＝0时，x＝3，∴点B的坐标为（0，3），即OB＝3，∵CH∥OA，∴△AOB∽△CHB，∴＝＝，即＝＝，解得，CH＝2，BH＝6，∴OH＝OB+BH＝9，∴点C的坐标为（2，9），∴k＝2×9＝18；（2）∵BD∥x轴，∴点D的纵坐标为3，∴点D的横坐标为＝6，即BD＝6，∴△ABD的面积＝×6×3＝9；（3）EF＝BD＝×6＝2，设E（m，3m+3），当0＜m＜2时，点F的坐标为（m+2，3m+3），∵点F在反比例函数y＝上，∴（m+2）（3m+3）＝18，解得，m1＝﹣4（舍去），m2＝1，当m＞2时，点F的坐标为（m﹣2，3m+3），∵点F在反比例函数y＝上，∴（m﹣2）（3m+3）＝18，解得，m3＝（舍去），m4＝，综上所述，m的值为1或．6．解：（1）把A（3，0）代入y1＝kx﹣（2k+1）中得，3k﹣（2k+1）＝0，解得：k＝1，∴一次函数的解析式为：y1＝x﹣3，反比例函数解析式为：y2＝﹣；（2）解得，，，∴C（1，﹣2），D（2，﹣1）；∵A（3，0），B（0，﹣3），∴△OCD的面积＝S△AOB﹣S△BOC﹣S△AOD＝﹣﹣＝；（3）∵C（1，﹣2），D（2，﹣1），∴当y1＞y2时，x的取值范围为：0＜x＜1或x＞2．7．解：（1）y＝﹣200x2+400x＝﹣200（x﹣1）2+200，∴x＝1时，血液中的酒精含量达到最大值，最大值为200（毫克/百毫升）；（2）不能驾车上班；理由：∵晚上20：00到第二天早上7：00，一共有11小时，∴将x＝11代入y＝，∵，∴第二天早上7：00不能驾车去上班．8．解：∵A（0，4），∴OA＝4，∵∠BOD＝60°．∴∠AOB＝30°，∵OB⊥BC于点B，∴∠ABO＝90°，∴∠OAD＝60°，∴OD＝OA＝4，∴D（4，0），设直线AB的解析式为y＝kx+b，∴，解得，∴直线AB的解析式为y＝﹣x+4；（2）∵∠AOB＝30°，OA＝4，∴AB＝OA＝2，OB＝OA＝2，∵OA?OD＝AD?OB，∴AD＝＝＝8，∴BD＝AD﹣AB＝6，∵S△AOD＝＝8，∴S△AOB＝×8＝2，S△BOD＝×＝6，设B（m，n），∴S△AOB＝m＝2，S△BOD＝＝6，∴＝2，＝6，解得m＝，n＝3，∴B（，3），∵点B是反比列函数y＝（x＞0）图象上的点，∴k＝＝3，∴反比例函数的解析式为y＝；（3）解得和，∴C（3，1），∴S△COD＝＝＝2，∴S△BOC＝6﹣2＝4，∵S1＝2，S2＝4，S3＝2，∴S1+S3＝S2．故答案为S1+S3＝S2．9．解：（1）连接AC，交BD于点E，∵点A，B横坐标分别为1，4，对角线BD∥x轴，∴BE＝4﹣1＝3，∵四边形ABCD是菱形，∴BD＝2BE＝6，AC⊥DB，∵菱形ABCD面积为，∴×BD×AC＝，∴AC＝，∴AE＝CE＝设点B（4，a），则点A（1，+a）∵点A，B为反比例函数y＝（k＞0，x＞0）上的两个点，∴4a＝1×（+a）∴a＝，∴k＝4a＝；（2）如图，过点A作AE⊥y轴于点E，过点B作BF⊥x轴于点F，∵四边形ABCD是菱形，∠ABC＝90°，∴四边形ABCD是正方形，∴AD＝CD＝BC，∠ADC＝∠DCB＝90°，∴∠ADE+∠EAD＝90°，∠EDA+∠CDO＝90°，∠DCO+∠CDO＝90°，∠BCF+∠DCO ＝90°，∴∠EAD＝∠CDO＝∠BCF，且∠AED＝∠DOC＝90°，AD＝CD，∴△AED≌△DOC（AAS）∴AE＝DO，ED＝OC，同理可得：BF＝OC，CF＝DO，由（1）知，k＝，∴反比例函数的解析式为y＝设点A（m，）∴AE＝DO＝CF＝m，DE＝OC＝BF＝﹣m，∴点B坐标（，﹣m）∴（﹣m）＝，∴m1＝，m2＝﹣（舍去）∴点A（，），点B（，）．10．解：（1）将点A的坐标代入反比例函数表达式得：5＝，解得：k1＝﹣5，将点B的坐标代入反比例函数表达式并解得：m＝5，故点B（5，﹣1），将点A、B坐标代入一次函数表达式得：，解得：，故k1＝﹣5，k2＝﹣1；（2）从函数图象看，当x＜﹣1或0＜x＜5时，k2x+b＞；（3）由（1）知，一次函数的表达式为：y＝﹣x+4，令y＝0，则x＝4，即直线AB与x 轴的交点坐标为（4，0），当△ABP的面积是△ABO面积的3倍时，点P与AB的距离是点O与AB距离的3倍，故点P的坐标为（16，0）或（﹣8，0）．2020年中考三轮冲刺复习培优同步练习：《圆的综合》证明与计算（五）1．如图，AB是⊙O的直径，且AB＝6，点M为⊙O外一点，且MA，MC分别切⊙O于点A、C两点．BC与AM的延长线交于点D．（1）求证：AD＝2CM；（2）填空：①当CM＝时，四边形AOCM是正方形．②当CM＝时，△CDM为等边三角形．2．我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”，三斜即指三角形的三条边长，可以用该方法求三角形面积．若改用现代数学语言表示，其形式为：设a，b，c为三角形三边，S为面积，则S＝①这是中国古代数学的瑰宝之一．而在文明古国古希腊，也有一个数学家海伦给出了求三角形面积的另一个公式，若设p＝（周长的一半），则S＝②（1）尝试验证．这两个公式在表面上形式很不一致，请你用以5，7，8为三边构成的三角形，分别验证它们的面积值；（2）问题探究．经过验证，你发现公式①和②等价吗？若等价，请给出一个一般性推导过程（可以从①?②或者②?①）；（3）问题引申．三角形的面积是数学中非常重要的一个几何度量值，很多数学家给出了不同形式的计算公式．请你证明如下这个公式：如图，△ABC的内切圆半径为r，三角形三边长为a，b，c，仍记p＝，S为三角形面积，则S＝pr．3．如图，AB是⊙O的直径，点C、D是⊙O上的点，且OD∥BC，AC分别与BD、OD相交于点E、F．（1）求证：点D为的中点；（2）若CB＝6，AB＝10，求DF的长；（3）若⊙O的半径为5，∠DOA＝80°，点P是线段AB上任意一点，试求出PC+PD的最小值．4．如图，在△ABC中，∠ABC＝∠ACB，以AC为直径的⊙O，分别交AB、BC 于点M、N，点P在AB的延长线上，且∠OAB＝2∠BCP．（1）求证：直线CP是⊙O的切线；（2）若BC＝2，sin∠BCP＝，求直径AC的长及点B到AC的距离；（3）在第（2）的条件下，求△BCP的周长．5．如图，在Rt△ABC中，∠ACB＝90°，D是AC上一点，过B，C，D三点的⊙O交AB于点E，连接ED，EC，点F是线段AE上的一点，连接FD，其中∠FDE＝∠DCE．（1）求证：DF是⊙O的切线．（2）若D是AC的中点，∠A＝30°，BC＝4，求DF的长．6．如图，△ABC内接于⊙O，AD与BC是⊙O的直径，延长线段AC至点G，使AG＝AD，连接DG交⊙O于点E，EF∥AB交AG于点F．（1）求证：EF与⊙O相切．（2）若EF＝2，AC＝4，求扇形OAC的面积．7．如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，以AD为直径的⊙O 与边BC相切于点E，与边AC相交于点G，且＝，连接GO并延长交⊙O 于点F，连接BF．（1）求证：①AO＝AG．②BF是⊙O的切线．（2）若BD＝6，求图形中阴影部分的面积．8．如图，B是⊙O外一点，连接OB，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．（Ⅰ）求证：AD平分∠BAC；（Ⅱ）若⊙O的半径为4，OB＝7，求AC的长．9．如图，直线y＝﹣2x+6与x轴，y轴分别交A，B两点，点A关于原点O的对称点是点C，动点E从A出发以每秒1个单位的速度运动到点C，点D在线段OB上满足tan∠DEO＝2，过E点作EF⊥AB于点F，点A关于点F的对称点为点G，以DG为直径作⊙M，设点E运动的时间为t秒；（1）当点E在线段OA上运动，t＝时，△AEF与△EDO的相似比为1：；（2）当⊙M与y轴相切时，求t的值；（3）若直线EG与⊙M交于点N，是否存在t使NG＝，若存在，求出t 的值；若不存在，说明理由．40．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连接AC．过上一点E 作EG∥AC交CD的延长线于点G，连接AE交CD于点F，且EG＝FG．（1）求证：EG是⊙O的切线；（2）延长AB交GE的延长线于点M，若AH＝2，CH＝2，求OM的长．参考答案1．证明：（1）如图，连接AC，∵MA，MC分别切⊙O于点A、C两点，∴MC＝MA，AB⊥AD，OC⊥MC，∴∠MCA＝∠MAC，∵AB是直径，∴∠ACB＝90°，∴∠MAC+∠D＝90°，∠MCA+∠MCD＝90°，∴∠D＝∠MCD，∴DM＝CM，∴AD＝2CM，（2）①∵四边形AOCM是正方形，∴OA＝CO＝AM＝CM＝3，∴当CM＝3时，四边形AOCM是正方形，②若△CDM是等边三角形，∴∠D＝60°，且AB⊥AD，AB＝6，∴AD＝2，∵AD＝2CM，∴CM＝，∴当CM＝时，△CDM为等边三角形．2．解：（1）由①得：S＝＝10，由②得：p＝＝10，S＝＝10；（2）公式①和②等价；推导过程如下：∵p＝，∴2p＝a+b+c，①中根号内的式子可化为：（ab+）（ab﹣）＝（2ab+a2+b2﹣c2）（2ab﹣a2﹣b2+c2）＝[（a+b）2﹣c2][c2﹣（a﹣b）2]＝（a+b+c）（a+b﹣c）（c+a﹣b）（c﹣a+b）＝×2p×（2p﹣2c）（2p﹣2b）（2p﹣2a）＝p（p﹣a）（p﹣b）（p﹣c），∴＝；（3）连接OA、OB、OC，如图所示：S＝S△AOB+S△AOC+S△BOC＝rc+rb+ra＝（）r＝pr．3．（1）∵AB是⊙O的直径，∴∠ACB＝90°，∵OD∥BC，∴∠OFA＝90°，∴OF⊥AC，∴＝，即点D为的中点；（2）解：∵OF⊥AC，∴AF＝CF，而OA＝OB，∴OF为△ACB的中位线，∴OF＝BC＝3，∴DF＝OD﹣OF＝5﹣3＝2；（3）解：作C点关于AB的对称点C′，C′D交AB于P，连接OC，如图，∵PC＝PC′，∴PD+PC＝PD+PC′＝DC′，∴此时PC+PD的值最小，∵＝，∴∠COD＝∠AOD＝80°，∴∠BOC＝20°，∵点C和点C′关于AB对称，∴∠C′OB＝20°，∴∠DOC′＝120°，作OH⊥DC′于H，如图，则∠ODH＝30°，则C′H＝DH，在Rt△OHD中，OH＝OD＝，∴DH＝OH＝，∴DC′＝2DH＝5，∴PC+PD的最小值为5．4．（1）证明：（1）∵∠ABC＝∠ACB，∠OAB＝2∠BCP，在△ABC中，∠ABC+∠BAC+∠BCA＝180°∴2∠BCP+2∠BCA＝180°，∴∠BCP+∠BCA＝90°，∴∠ACP＝90°，即AC⊥CP，又C点在圆上，∴直线CP是⊙O的切线．（2）解：如图1，作BE⊥AC于点E，∵PC⊥AC，∴BE∥PC，∴∠PCB＝∠EBC∵BC＝2，sin∠BCP＝，∴sin∠BCP＝sin∠EBC＝，解得：EC＝2，∴BE＝＝＝4，∴点B到AC的距离为4．（3）解：如图2，连接AN，∵AC为直径，∴∠ANC＝90°，∴Rt△ACN中，AC＝．又CE＝2，∴AE＝AC﹣CE＝5﹣2＝3．∵BE∥CP，∴，，∴，在Rt△ACP中，AP＝＝＝，∵，∴AB＝5，∴，∴PB+CP+BC＝＝10+2，∴△BCP的周长为10+2．5．解：（1）∵∠ACB＝90°，点B，D在⊙O上，∴BD是⊙O的直径，∠BCE＝∠BDE，∵∠FDE＝∠DCE，∠BCE+∠DCE＝∠ACB＝90°，∴∠BDE+∠FDE＝90°，即∠BDF＝90°，∴DF⊥BD，又∵BD是⊙O的直径，∴DF是⊙O的切线．（2）如图，∵∠ACB＝90°，∠A＝30°，BC＝4，∴AB＝2BC＝2×4＝8，∴＝4，∵点D是AC的中点，∴，∵BD是⊙O的直径，∴∠DEB＝90°，∴∠DEA＝180°﹣∠DEB＝90°，∴，在Rt△BCD中，＝＝2，在Rt△BED中，BE＝＝＝5，∵∠FDE＝∠DCE，∠DCE＝∠DBE，∴∠FDE＝∠DBE，∵∠DEF＝∠BED＝90°，∴△FDE∽△DBE，∴，即，∴．6．（1）证明：如图1，连接OE，∵OD＝OE，∴∠D＝∠OED，∵AD＝AG，∴∠D＝∠G，∴∠OED＝∠G，∴OE∥AG，∵BC是⊙O的直径，∴∠BAC＝90°，∵EF∥AB，∴∠BAF+∠AFE＝180°，∴∠AFE＝90°，∵OE∥AG，∴∠OEF＝180°﹣∠AFE＝90°，∴OE⊥EF，∴EF与⊙O相切；（2）解：如图2，连接OE，过点O作OH⊥AC于点H，∵AC＝4，∴CH＝，∵∠OHF＝∠HFE＝∠OEF＝90°，∴四边形OEFH是矩形，∴，在Rt△OHC中，OC＝＝＝4，∵OA＝AC＝OC＝4，∴△AOC是等边三角形，∴∠AOC＝60°，∴S扇形OAC＝＝．7．解：（1）证明：①如图1，连接OE，∵⊙O与BC相切于点E，∴∠OEB＝90°，∵∠ACB＝90°，∴∠ACB＝∠OEB，∴AC∥OE，∴∠GOE＝∠AGO，∵，∴∠AOG＝∠GOE，∴∠AOG＝∠AGO，∴AO＝AG；②由①知，AO＝AG，∵AO＝OG，∴∠AO＝OG＝AG，∴△AOG是等边三角形，∴∠AGO＝∠AOG＝∠A＝60°，∴∠BOF＝∠AOG＝60°，由①知，∠GOE＝∠AOG＝60°，∴∠EOB＝180°﹣∠AOG﹣∠GOE＝180°﹣60°﹣60°＝60°，∴∠FOB＝∠EOB，∵OF＝OE，OB＝OB，∴△OFB≌△OEB（SAS），∴∠OFB＝∠OEB＝90°，∴OF⊥BF，∵OF是⊙O的半径，∴BF是⊙O的切线；（2）如图2，连接GE，∵∠A＝60°，∴∠ABC＝90°﹣∠A＝30°，∴OB＝2BE，设⊙O的半径为r，∵OB＝OD+BD，∴6+r＝2r，∴r＝6，∴AG＝OA＝6，AB＝2r+BD＝18，∴AC＝AB＝9，∴CG＝AC﹣AG＝3，由（1）知，∠EOB＝60°，∵OG＝OE，∴△OGE是等边三角形，∴GE＝OE＝6，根据勾股定理得，CE＝＝＝3，∴S阴影＝S梯形GCEO﹣S扇形OGE＝（6+3）×﹣＝．8．（Ⅰ）证明：连OD，如图，∵BD是⊙O的切线，∴OD⊥BD，∵AC⊥BD，∴OD∥AC．∴∠2＝∠3，∵OA＝OD，∴∠1＝∠3．∴∠1＝∠2，即AD平分∠BAC；（Ⅱ）解：∵OD∥AC，∴△BOD∽△BAC，∴，即．解得AC＝．9．解：（1）在y＝﹣2x+6中，令x＝0，得：y＝6，令y＝0，得：﹣2x+6＝0，解得：x＝3，∴A（3，0），B（0，6），C（﹣3，0）∴OA＝3，OB＝6，AB＝3，AE＝t，OE＝3﹣t，∴tan∠BAO＝＝2∵tan∠DEO＝2∴∠BAO＝∠DEO∵EF⊥AB∴∠AFE＝∠DOE＝90°∴△AEF∽△EDO∽△ABO＝，即：＝，∴AF＝t；∵△AEF与△EDO的相似比为1：，∴＝，即OE＝AF∴3﹣t＝×t，解得：t＝；故答案为：t＝；（2）∵⊙M与y轴相切∴DG⊥y轴当0≤t≤３时，G（3﹣t，t），D（0，6﹣2t），∴t＝6﹣2t，解得：t＝；当3＜t≤６时，G（3﹣t，t），D（0，2t﹣6），∴t＝2t﹣6，解得：t＝5综上所述，当⊙M与y轴相切时，t＝或5；（3）存在．当0≤t≤时，G（3﹣t，t），D（0，6﹣2t），∵点A关于点F的对称点为点G，EF⊥AB∴EG＝EA＝t∵∠OEG＝∠OAB+∠EGA＝2∠OAB，∠OED＝∠OAB ∴∠DEG＝∠DEG∵DG为直径∴∠DNG＝∠DOE＝90°，DE＝DE∴△DEN≌△DEO（AAS）∴EN＝OE＝3﹣tNG＝EN﹣EG＝3﹣t﹣t＝3﹣2t∴3﹣2t＝，解得：t＝，当＜t≤３时，NG＝EG﹣EN＝t﹣（3﹣t）＝2t﹣3∴2t﹣3＝，解得：t＝；当3＜t≤６时，如图2，连接DN，过G作GH⊥x轴于H，∵DG是直径，∴∠DNG＝∠DNE＝90°，∵∠DMN＝∠EMO∴△DMN∽△EMO∴∠MDN＝∠OEM∵GH∥y轴∴＝，即OM＝?t＝（t﹣3）∴DM＝OD﹣OM＝2（t﹣3）﹣（t﹣3）＝（t﹣3）∵tan∠OEM＝＝∴EM＝OE＝（t﹣3），∴sin∠OEM＝＝＝sin∠MDN＝∴MN＝×（t﹣3）＝（t﹣3）∴NG＝EG﹣EM﹣MN＝t﹣（t﹣3）﹣（t﹣3）＝﹣t，∴﹣t＝，解得：t＝；综上所述，t＝或或．10．（1）证明：连接OE，如图，∵GE＝GF，∴∠GEF＝∠GFE，而∠GFE＝∠AFH，∴∠GEF＝∠AFH，∵AB⊥CD，∴∠OAF+∠AFH＝90°，∴∠GEA+∠OAF＝90°，∵OA＝OE，∴∠OEA＝∠OAF，∴∠GEA+∠OEA＝90°，即∠GEO＝90°，∴OE⊥GE，∴EG是⊙O的切线；（2）解：连接OC，如图，设⊙O的半径为r，则OC＝r，OH＝r﹣2，在Rt△OCH中，（r﹣2）2+（2）2＝r2，解得r＝3，在Rt△ACH中，AC＝＝2，∵AC∥GE，∴∠M＝∠CAH，∴Rt△OEM∽Rt△CHA，∴＝，即＝，∴OM＝．。

2020年数学中考复习：压轴几何证明题的解法(含答案)

2020年数学中考复习：压轴几何证明题的解法1.(2019.葫芦岛)如图，△ABC 是等腰直角三角形，∠ACB =900，D 是射线CB 上一点（点D 不与点B 重合），以AD 为斜边作等腰直角三角形ADE （点E 和点C 在AB 的同侧），连接CE 。

（1）如图①，当点D 与点C 重合时，直接写出CE 与AB 的位置关系；（2）如图②，当点D 与点C 不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC =150时，请直接写出AB CE 的值。

解析：（1）由∠ECA =∠CAB =450,可得EC ∥AB 。

（2）由22=AB AC =AD AE ,且∠EAC =∠DAB ,可得△EAC ∽△DAB 进而得出∠ECA =∠DBA =450=∠CAB ,所以CE ∥AB .(3)此问分两种情况点D 在BC 上，点D 在CB 延长线上。

①当点D 在BC 上时，如图（2），此时∠CAB =150能得出∠CAD =300，这样就有33=AC CD ,也就是BC -DB =33AC ,BC =AC ,所以BD =333－AC 。

又由△EAC ∽△DAB 得21=BD CE ,因此有BD =2CE ，所以可得CE =6623－AC ，又AB =2AC ，因此ABCE =６３－3.当D 点在CB 延长线上时，∠CDA =300,解三角形得3AC =3CD 。

CD =BC +BD ,由△AEC ∽△ABD ,可得BD =2AC ，就能得到CE =ＡＣ２－１3,AB =2AC ，所以２－１3=AB CE . 2.(2019.沈阳）思维启迪：（1）如图1，A ，B 两点分别位于一个池塘的两端，小亮想用绳子测量A ，B 间的距离，但绳子不够长，聪明的小亮想出一个办法：先在地上取一个可以直接到达B 点的点C ，连接BC ，取BC 的中点P （点P 可以直接到达A 点），利用工具过点C 作CD ∥AB 交AP 的延长线于点D ，此时测得CD =200米，那么A ,B 间的距离是_200_米。

2020年九年级中考数学压轴专题几何探究题(含答案)

2020中考数学压轴专题几何探究题（含答案）1. 我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．第1题图(1)概念理解：请你根据定义举一个“等邻角四边形的”例子；(2)问题探究：如图①，在等邻角四边形ABCD 中，∠DAB ＝∠ABC ，AD 、BC 的中垂线恰好交于AB 边上一点P ，连接AC 、BD ，试探究AC 与BD 的数量关系，并说明理由．(3)应用拓展：如图②，在Rt △ABC 与Rt △ABD 中，∠C ＝∠D ＝90°，BC ＝BD ＝3，AB ＝5，将Rt △ABD 绕着点A 顺时针旋转角α(0°)得到Rt △AB ′D ′(如图③)，当凸四边形AD ′BC 为“等邻角四边形”时，求出它的面积．解：(1)矩形；(答案不唯一)(2)AC ＝BD ；如解图①所示，连接PD 、PC ， ∵PE 是AD 的垂直平分线，PF 是BC 的垂直平分线， ∴P A ＝PD ，PB ＝PC ，∴∠P AD ＝∠PDA ，∠PBC ＝∠PCB ，∴∠DPB ＝180°－∠DP A ＝∠P AD ＋∠PDA ＝2∠P AD ，同理可得∠APC ＝2∠PBC ， ∵∠DAB ＝∠ABC ，即∠P AD ＝∠PBC ，∴∠APC ＝∠DPB ，在△APC 和△DPB 中，⎩⎪⎨⎪⎧PA ＝PD ∠APC ＝∠DPB PB ＝PC，△APC ≌△DPB (SAS)， ∴ AC ＝BD .第1题解图①(3)①当∠AD ′B ＝∠D ′BC 时，如解图②所示，延长AD ′交CB 的延长线于点E ，过点D ′作DF ⊥CE 于点F ， ∠ED ′B ＝∠EBD ′， ∴EB ＝ED ′，∵∠C ＝∠EFD ′，∠EAC ＝∠ED ′F ， ∴△ED ′F ∽△EAC ，则D ′F AC ＝ED ′AE，设EB ＝ED ′＝x ，由勾股定理可知，在Rt △ACB 中，AC ＝AB 2－BC 2＝52－32＝4，则AD ′＝4，CE ＝3＋x ，AE ＝4＋x ，在Rt △ACE 中，AC 2＋CE 2＝AE 2，即42＋(3＋x )2＝(4＋x )2，整理得：2x －9＝0，解得x ＝92，EB ＝ED ′＝92，∴AE ＝172，∴D ′F 4＝92112，∴D ′F ＝3617，S 四边形AD ′BC ＝S △ACE －S △D ′BE ＝12AC ·CE －12D ′F ·BE ＝12×4×(3＋92)－12×92×3617＝15－8117＝17417；第1题解图②②当∠D ′BC ＝90°时，如解图③所示，过点D ′作D ′E ⊥AC ，交AC 于点E ， ∴四边形ECBD ′是矩形，∴ED ′＝BC ＝3，在Rt △AED ′中，根据勾股定理得AE ＝AD′2－ED′2＝42－32＝7，∵S 四边形AD ′BC ＝S △AED ′＋S 矩形ECBD ′＝12AE ·ED ′＋EC ·BC ＝372＋12－37＝12－372.综上所述，当凸四边形AD 为等邻角四边形时，它的面积为17417或12－372.第1题解图③2. (1)发现如图①，点A 为线段BC 外一动点，且BC ＝a ，AB ＝b .填空：当点A 位于________时，线段AC 的长取得最大值，且最大值为________(用含有a ，b 的式子表示)； (2)应用点A 为线段BC 外一动点，且BC ＝3，AB ＝1.如图②所示，分别以AB ，AC 为边作等边三角形ABD 和等边三角形ACE，连接CD，BE.①请找出图中与BE相等的线段，并说明理由；②直接写出线段BE长的最大值；(3)拓展如图③，在平面直角坐标系中，点A的坐标为(2，0)，点B的坐标为(5，0)，点P为线段AB外一动点，且P A＝2，PM＝PB，∠BPM＝90°.请直接写出线段AM长的最大值及此时点P的坐标．第2题图(1)解：CB的延长线上，a＋b；【解法提示】∵点A为线段BC外一动点，且BC＝a，AB＝b，∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC＋AB＝a＋b.(2)解：①DC＝BE，理由如下：∵△ABD和△ACE均为等边三角形，∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°，∴∠BAD＋∠BAC＝∠CAE＋∠BAC，即∠CAD＝∠EAB，∴△CAD≌△EAB(SAS)，∴DC＝BE；②BE长的最大值是4；【解法提示】∵线段BE长的最大值＝线段CD的最大值，由(1)知，当线段CD的长取得最大值时，点D在CB 的延长线上，∴CD长的最大值为BD＋BC＝AB＋BC＝4.(3)解：AM长的最大值是3＋22，点P的坐标是(2－2，2)．【解法提示】如解图①，构造△BNP≌△MAP，则NB＝AM，P A＝PN，∴∠APN＝90°，由(1)得出当点N在BA的延长线上时，NB有最大值(如解图②)，可得AN＝22，∴AM＝NB＝3＋22，过点P作PE⊥x轴于点E，PE＝AE＝2，∴点P的坐标是(2－2，2)．第2题解图3.如图，△ABC是边长为4 cm的等边三角形，边AB在射线OM上，且OA＝6 cm.点D从O点出发，沿OM的方向以1 cm/s的速度运动．当D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE.(1)求证：△CDE是等边三角形；(2)当6<t<10时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由；(3)当点D在射线OM上运动时，是否存在以D、E、B为顶点的三角形是直角三角形？若存在，求出此时t的值；若不存在，请说明理由．第3题图(1)证明：∵△BCE是由△ACD逆时针旋转60°得到的，∴CD＝CE，∠DCE＝60°，∴△CDE是等边三角形；(2)解：存在．理由如下：∵△BCE是由△ACD逆时针旋转60°得到的，∴AD＝BE，又∵△CDE是等边三角形，∴DE＝CD，∴C△BDE＝BD＋BE＋DE＝BD＋AD＋CD＝AB＋CD，∵AB＝4为定值，∴当CD最小，即CD⊥AB时，△BDE的周长最小，∵△ABC是等边三角形，∴当CD最小，即CD⊥AB时，易得CD＝23，∴△BDE的最小周长为23＋4；(3)解：存在．理由如下：如解图，过点C作CF⊥OM于点F，则CF＝23，∴BD＝||t－6，t－10，BE＝AD＝||DE＝CD＝CF2＋DF2＝12＋（t－8）2，①当∠DEB＝90°时，BD2＝BE2＋DE2，即(t－10)2＝(t－6)2＋12＋(t－8)2，第3题解图解得t1＝2，t2＝6(不合题意，舍去)；②当∠EBD＝90°时，DE2＝BD2＋BE2，即12＋(t－8)2＝(t－10)2＋(t－6)2，解得t3＝6，t4＝10(两者均不合题意，舍去)；③当∠BDE＝90°时，BE2＝BD2＋DE2，即(t－6)2＝(t－10)2＋12＋(t－8)2，解得t5＝14，t6＝10(舍去)．综上所述，存在以D、E、B为顶点的三角形是直角三角形，此时t＝2或14.4.如图，将两个全等的直角三角形△ABD、△ACE拼在一起(图①)，△ABD不动．(1)若将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC(图②)，证明：MB＝MC；(2)若将图①中的CE向上平移，∠CAE不变，连接DE，M是DE的中点，连接MB、MC(图③)，判断并直接写出MB、MC的数量关系；(3)在(2)中，若∠CAE的大小改变(图④)，其他条件不变，则(2)中的MB、MC的数量关系还成立吗？说明理由．第4题图（1）证明：如解图①，连接AM，由已知得△ABD≌△ACE，第4题解图①∴ AD ＝AE ， AB ＝AC ， ∠BAD ＝∠CAE ，又∵MD ＝ME ，∴∠MAD ＝∠MAE (三线合一)， ∴∠MAD －∠BAD ＝∠MAE －∠CAE ，即∠BAM ＝∠CAM ，在△ABM 和△ACM 中， ⎩⎪⎨⎪⎧AB ＝AC ∠BAM ＝∠CAM AM ＝AM， ∴△ABM ≌△ACM (SAS )， ∴MB ＝MC ；第4题解图②(2)解：MB ＝MC ；【解法提示】如解图②，延长DB 、AE 相交于点E ′，延长EC 交AD 于点F ， ∴BD ＝BE ′，CE ＝CF ，又∵M 是ED 的中点，B 是DE ′的中点， ∴MB ∥AE ′，∴∠MBC ＝∠CAE ，同理：MC ∥AD ， ∴∠BCM ＝∠BAD ，又∵∠BAD ＝∠CAE ， ∴∠MBC ＝∠BCM ， ∴MB ＝MC .(3)解：MB ＝MC 还成立．理由如下：如解图③，延长BM 交CE 于点F ，第4题解图③∵CE ∥BD ， ∴∠MDB ＝∠MEF ， ∠MBD ＝∠MFE ，又∵M 是DE 的中点， ∴MD ＝ME ，在△MDB 和△MEF 中， ⎩⎪⎨⎪⎧∠MBD ＝∠MFE ∠MDB ＝∠MEF MD ＝ME， ∴△MDB ≌△MEF (AAS)， ∴MB ＝MF ＝12BF ，又∵∠ACE ＝90°，∴∠BCF ＝90°， ∴MC ＝12BF ，∴MB＝MC.5.在正方形ABCD中，点E是对角线AC上的动点(与点A，C不重合)，连接BE.(1)将射线BE绕点B顺时针方向旋转45°，交直线AC于点F.①依题意补全图①；②小研通过观察、实验，发现线段AE，FC，EF存在以下数量关系：AE与FC的平方和等于EF的平方．小研把这个猜想与同学们进行交流，通过讨论，形成证明该猜想的几种想法：想法1：将线段BF绕点B逆时针旋转90°，得到线段BM，要证AE，FC，EF的数量关系，只需证AE，AM，EM的数量关系．想法2：将△ABE沿BE翻折，得到△NBE，要证AE，FC，EF的关系，只需证EN，FN，EF的关系．…请你参考上面的想法，用等式表示线段AE，FC，EF的数量关系并证明；(一种方法即可)(2)如图②，若将直线．．AC于点F.小研完成作图后，发现直线AC上存在三．．BE绕点B顺时针旋转135°，交直线条线段(不添加辅助线)满足：其中两条线段的平方和等于第三条线段的平方，请直接用等式表示这三条线段的数量关系．第5题图解：(1)①补全图形，如解图①；图① 图②第5题解图②AE 2＋FC 2＝EF 2；证明：如解图②，过B 作MB ⊥BF 于点B ，使BM ＝BF ，连接AM 、EM ，∵四边形ABCD 是正方形，∴∠ABC ＝90°，∠1＝∠2＝45°，AB ＝BC ，∵∠3＝45°，∴∠MBE ＝∠3＝45°，在△MBE 和△FBE 中，⎩⎪⎨⎪⎧BM ＝BF ∠MBE ＝∠3BE ＝BE，∴△MBE ≌△FBE (SAS )，∴EM ＝EF ，∵∠4＝90°－∠ABF ，∠5＝90°－∠ABF ，∴∠4＝∠5，在△AMB 和△CFB 中，⎩⎪⎨⎪⎧BM ＝BF ∠4＝∠5AB ＝CB，∴△AMB ≌△CFB (SAS)，∴AM ＝FC ，∠6＝∠2＝45°，∴∠MAE ＝∠6＋∠1＝90°，在Rt △MAE 中，AE 2＋AM 2＝EM 2，∴AE 2＋FC 2＝EF 2；(2)AF 2＋EC 2＝EF 2.【解法提示】如解图③，过B 作MB ⊥BE ，使BM ＝BE ，连接ME 、MF 、AM ，∵直线BE 绕点B 顺时针旋转135°，交直线AC 于点F ，∴∠FBE ＝45°，∴∠MBF ＝90°－45°＝45°，∴∠FBE ＝∠MBF ，在△MBF 和△EBF 中，⎩⎪⎨⎪⎧BM ＝BE ∠MBF ＝∠FBE ，BF ＝BF∴△MBF ≌△EBF (SAS)，∴MF ＝EF ，∵∠MBA ＝90°－∠ABE ，∠EBC ＝90°－∠ABE ，∴∠MBA ＝∠EBC ，在△AMB 和△CBE 中，⎩⎪⎨⎪⎧BM ＝BE ∠MBA ＝∠EBC AB ＝CB，∴△AMB ≌△CEB (SAS )，∴AM ＝EC ，∠BAM ＝∠BCE ＝45°，∴∠MAE ＝∠BAM ＋∠BAC ＝90°，∴∠MAF ＝90°，在Rt △MAF 中，AF 2＋AM 2＝MF 2，∴AF 2＋EC 2＝EF 2.第5题解图③6.在△ABC中，AB＝AC，∠A＝60°，点D是BC边的中点，作射线DE，与边AB交于点E，射线DE绕点D顺时针旋转120°，与直线AC交于点F.(1)依题意补全图形；(2)小华通过观察、实验提出猜想：在点E运动的过程中，始终有DE＝DF.小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：由点D是BC边的中点，通过构造一边的平行线，利用全等三角形，可证DE＝DF；想法2：利用等边三角形的对称性，作点E关于线段AD的对称点P，由∠BAC与∠EDF互补，可得∠AED与∠AFD互补，由等角对等边，可证DE＝DF；想法3：由等腰三角形三线合一，可得AD是∠BAC的平分线，由角平分线定理，构造点D到AB，AC的高，利用全等三角形，可证DE＝DF；…请你参考上面的想法，帮助小华证明DE＝DF(选一种方法即可)；(3)在点E运动的过程中，直接写出BE，CF，AB之间的数量关系．解：(1)补全图形，如解图①；第6题解图(2)想法1：证明：如解图②，过点D作DG∥AB，交AC于点G，∵点D是BC边的中点，∴DG＝12AB，∴△CDG是等边三角形，∴∠EDB＋∠EDG＝120°，∵∠FDG＋∠EDG＝120°，∴∠EDB＝∠FDG，∵BD＝DG，∠B＝∠FGD＝60°，∴△BDE≌△GDF，∴DE＝DF；想法2：证明：如解图③，连接AD，作点E关于线段AD的对称点P，点P在边AC上，∵点D是BC边的中点，AB＝AC，∴直线AD是△ABC的对称轴，∴△ADE≌△ADP，∴DE＝DP，∠AED＝∠APD，∵∠BAC＋∠EDF＝180°，∴∠AED＋∠AFD＝180°，∵∠APD＋∠DPF＝180°，∴∠AFD＝∠DPF，∴DP＝DF，∴DE＝DF；第6题解图想法3：证明：如解图④，连接AD，过D作DM⊥AB于点M，DN⊥AC于点N，∵点D是BC边的中点，∴AD平分∠BAC，∵DM⊥AB于点M，DN⊥AC于点N，∴DM＝DN，∵∠A＝60°，∴∠MDE＋∠EDN＝120°，∵∠FDN＋∠EDN＝120°，∴∠MDE ＝∠FDN ，∴Rt △MDE ≌Rt △NDF ，∴DE ＝DF ；(3)当点F 在AC 边上时，BE ＋CF ＝12AB ；当点F 在AC 的延长线上时，BE －CF ＝12AB . 【解法提示】①当点F 在AC 边上时，如解图⑤，过点D 作DM ⊥AB 于点M ，作DN ⊥AC 于点N ， ∵∠B ＝∠C ＝60°，BD ＝DC ，∠BDM ＝∠CDN ＝30°，∴△BDM ≌△CDN ，∴BM ＝CN ，DM ＝DN ，又∵∠EDF ＝120°＝∠MDN ，∴∠EDM ＝∠NDF ，又∵∠EMD ＝∠FND ＝90°，∴△EDM ≌△FDN ，∴ME ＝NF ，∴BE ＋CF ＝BM ＋EM ＋NC －FN ＝2BM ＝BD ＝12AB ；图⑤ 图⑥第6题解图②当点F 在AC 的延长线上时，如解图⑥，过D 作DM ⊥AB 于点M ，作DN ⊥AC 于点N ，∵∠B ＝∠DCN ＝60°，BD ＝DC ，∠BDM ＝∠CDN ＝30°，∴△BDM ≌△CDN ，∴BM ＝CN ，DM ＝DN ，又∵∠EDF ＝120°＝∠MDN ，∴∠EDM ＝∠NDF ，又∵∠EMD ＝∠FND ＝90°，∴△EDM ≌△FDN ，∴ME ＝NF ，∴BE －CF ＝BM ＋EM －(FN －CN )＝2BM ＝BD ＝12AB ，综上所述，当点F 在AC 边上时，BE ＋CF ＝12AB ；当点F 在AC 的延长线上时，BE －CF ＝12AB . 7. 我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图①，在△ABC 中，AO 是BC 边上的中线，AB 与AC 的“极化值”就等于AO 2－BO 2的值，可记为ABAC ＝AO 2－BO 2.第7题图(1)在图①中，若∠BAC ＝90°，AB ＝8，AC ＝6，AO 是BC 边上的中线，则ABAC＝________，OCOA＝________；(2)如图②，在△ABC中，AB＝AC＝4，∠BAC＝120°，求AB AC、BA BC的值；(3)如图③，在△ABC中，AB＝AC，AO是BC边上的中线，点N在AO上，且ON＝13A A O，已知ABAC＝14，BN BA＝10，求△ABC的面积．解：(1)0 ，7；【解法提示】∵∠BAC＝90°，AB＝8，AC＝6，∴BC＝AB2＋AC2＝10，在Rt△ABC中，AO是BC边上的中线，∴AO＝BO＝5，∴AB AC＝AO2－BO2＝0，如解图①，取AC的中点D ，连接OD ，则OD ∥AB ，OD ＝12AB ＝4，CD ＝12AC ＝3，∴OC OA ＝OD 2－CD 2＝16－9＝7.第7题解图(2)如解图②，作底边BC 上的中线AE ，由题意可知AE 是∠BAC 的平分线、BC 边上的高． ∵AB ＝ΑC ＝4，∠BAC ＝120°，∴在Rt △ABE 中，∠AEB ＝90°，∠ABC ＝30°，∴AE ＝12×4＝2，BE ＝32×4＝23， ∴AB AC ＝AE 2－BE 2＝22－(23)2＝－8.过点B作AC边上中线BM，过点M作MN⊥BC于点N，∴AM＝CM＝1×4＝2.2在Rt△MNC中，∠MNC＝90°，∠C＝30°，×2＝1，CN＝22－12＝ 3.∴MN＝12∵BC＝2BE＝43，∴BN＝BC－CN＝43－3＝33，BM2＝12＋(33)2＝28.∴BA BC＝BM2－AM2＝28－22＝24；(3)如解图③，过点B作△ABN的AN边上中线BM，∵在△ABC中，AB＝AC，AO是BC边上的中线，点N在AO上，且ON＝13AO，第7题解图③∴AM＝MN＝NO，AO⊥BC，即AO＝3NO.∵AB A AC ＝14，BNBA ＝10，∴ AO 2－BO 2＝14，即(3ON )2－BO 2＝9ON 2－BO 2＝14，①∵BM 2－MN 2＝OM 2＋BO 2－MN 2＝(2ON )2＋BO 2－ON 2＝3ON 2＋BO 2＝10，②由①、②得⎩⎪⎨⎪⎧9ON 2－BO 2＝143ON 2＋BO 2＝10， ∴ON 2＝2，即ON ＝2，BO ＝2，∴BC ＝4，AO ＝32，∴S △ABC ＝12BC ·AO ＝12×4×32＝6 2. 8. 问题发现：如图①，在△ABC 中，∠ACB ＝90°，分别以AC 、BC 为边向外侧作正方形ACDE 和正方形BCFG .(1)△ABC和△DCF面积的关系是________；(请在横线上填写“相等”或“不相等”)(2)拓展探究：若∠C≠90°，(1)中的结论还成立吗？若成立，请结合图②给出证明；若不成立，请说明理由；(3)解决问题：如图③，在四边形ABCD中，AC⊥BD，且AC与BD的和为10，分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CD JI、正方形DA LK；运用(2)中的结论，图中阴影部分的面积和是否有最大值？如果有，请求出最大值，如果没有，请说明理由．第8题图解：(1)相等；【解法提示】∵四边形ACDE和四边形BCFG是正方形，∴AC＝DC，BC＝FC，∠ACD＝∠BCF＝90°，∵∠ACB＝90°，∴∠DCF＝90°＝∠ACB.∴12AC·BC＝12DC·CF，∴S△ABC＝S△DFC.(2)成立．理由如下：如解图，延长BC到点P，过点A作AP⊥BP于点P，过点D作DQ⊥FC于点Q，∴∠APC＝∠DQC＝90°.∵四边形ACDE，四边形BCFG均为正方形，∴AC＝CD，BC＝CF，∠ACP＋∠PCD＝90°，∠DCQ＋∠PCD＝90°，∴∠ACP＝∠DCQ.第8题解图在△APC 和△DQC 中，⎩⎪⎨⎪⎧∠APC ＝∠DQC ∠ACP ＝∠DCQ AC ＝DC，∴△APC ≌△DQC (AAS)，∴AP ＝DQ .又∵S △ABC ＝12BC ·AP ，S △DFC ＝12FC ·DQ ， ∴S △ABC ＝S △DFC ；(3)图中阴影部分的面积和有最大值．理由如下：由(2)中的结论可知：S △K D J ＝S △ADC ，S △FBG ＝S △ABC ，S △AE L ＝S △ABD ，S △CH I ＝S △BDC ，∴S 阴影＝S △K DJ ＋S △FBG ＋S △AEL ＋S △CHI ＝S △ADC ＋S △ABC ＋S △ABD ＋S △BDC ＝2S 四边形ABCD .设AC ＝m ，则BD ＝10－m ，∵AC ⊥BD ，∴S 四边形ABCD ＝12AC ·BD ＝12m ·(10－m )＝－12m 2＋5m ＝－12(m －5)2＋252. ∵－12<0，∴S四边形ABCD有最大值，最大值为252.＝25，∴S阴影＝2×252∴阴影部分的面积和有最大值，最大值为25.9.问题背景如图①，在正方形ABCD的内部，作∠DAE＝∠ABF＝∠BCG＝∠CDH，根据三角形全等的条件，易得△DAE ≌△ABF≌△BCG≌△CDH，从而得到四边形EFGH是正方形．类比探究如图②，在正△ABC的内部，作∠BAD＝∠CBE＝∠ACF，AD，BE，CF两两相交于D，E，F三点(D，E，F 三点不重合)．(1)△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；(2)△DEF是否为正三角形？请说明理由；(3)进一步探究发现，△ABD的三边存在一定的等量关系，设BD＝a，AD＝b，AB＝c，请探索a，b，c满足的等量关系．第9题图解：(1)△ABD≌△BCE≌△CAF.证明：如解图①，第9题解图①∵△ABC为正三角形，∴∠CAB＝∠ABC＝∠BCA＝60°，AB＝BC.∵∠ABD＝∠ABC－∠2，∠BCE＝∠ACB－∠3，而∠2＝∠3，∴∠ABD＝∠BCE.又∵∠1＝∠2，∴△ABD≌△BCE(ASA)；(2)△DEF是正三角形．理由如下：∵△ABD≌△BCE≌△CAF，∴∠ADB＝∠BEC＝∠CF A，∴∠FDE＝∠DEF＝∠EFD，∴△DEF是正三角形；(3)如解图②，作AG⊥BD，交BD延长线于点G，第9题解图②由△DEF 是正三角形得到∠ADG ＝60°，(或者∠ADG ＝∠1＋∠ABD ＝∠2＋∠ABD ＝60°.)∴在Rt △ADG 中，DG ＝12b ，AG ＝32b . ∴在Rt △ABG 中，c 2＝(a ＋12b )2＋(32b )2， ∴c 2＝a 2＋ab ＋b 2.10. 在△ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，将△ABC 绕顶点C 顺时针旋转，旋转角为θ(0°＜θ＜180°)，得到△A ′B ′C .(1)设△ACA ′和△BCB ′的面积分别为S 1和S 2.若θ＝40°，请求出S 1S 2的值； (2)如图①，设A ′B ′与CB 相交于点D ，且AB ∥CB ′：①求证：CD ＝B ′D ；②求BD 的长；(3)如图②，设AC 中点为点M ，A ′B ′中点为点N ，连接MN ，MN 是否存在最大值，若存在，求出MN 的值，判断出此时AA ′与BB ′的位置关系；若不存在，请说明理由．第10题图(1)解： ∵△ABC 绕顶点C 顺时针旋转40°，得到△A ′B ′C ， ∴CA ＝CA ′，CB ＝CB ′，∠ACA ′＝∠BCB ′＝θ，∴△ACA ′∽△BCB ′，∴S △ACA ′∶S △BCB ′＝AC 2∶BC 2＝32∶42＝9∶16；∴S 1S 2＝916； (2)①证明：∵AB ∥B ′C ，∴∠ABC ＝∠BCB ′；由旋转的性质得∠ABC ＝∠DB ′C ，即∠BCB ′ ＝∠DB ′C ；∴CD ＝B ′D ；②解：根据勾股定理可得A ′B ′＝AB ＝5，据题意可得∠BCB ′ ＋∠BCA ′ ＝∠DB ′C ＋∠CA ′B ′＝90°，∴∠BCA ′ ＝∠CA ′B ′，∴CD ＝A ′D ＝B ′D ＝12A ′B ′＝52， ∴ BD ＝BC －CD ＝32； (3)解：存在，∵∠A ′CB ′＝90°，点M 为AC 的中点，∴CM ＝12AC ＝32， ∵△A ′B ′C 是由△ABC 绕顶点C 顺时针旋转所得，∴A ′B ′＝AB ＝5，第10题解图如解图，连接CN ，可得MN ≤CM ＋CN ，∴只有当点N 在MC 的延长线上时，MN ＝CM ＋CN ，此时MN 最大，∵点N 为A ′B ′的中点，∴CN ＝12 A ′B ′＝52，MN ＝CM ＋CN ＝4，即MN 的最大值为4.此时AA ′⊥BB ′.。

中考数学-几何证明

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图，正方形ABCD中，对角线AC, BD交于点。

，点E.点OB ,线段AB上，且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点，AE J5,求BF的长：(2)如图2,若AE平分BAC,求证：FG HG;(3)如图3,点E在线段BO (含端点)上运动，连接HE，当线段HE长度取得最大值时，直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图，平行四边形ABCD中，AB=2BC, B 60 . 曲 DC中点，连接AE . F为AD上一点，连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证：EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点，M是BC边上的点.(1)如图1,若点M与点G重合，AH 5, AD 显26 ,求CF的长：2(2)如图2.若AM是BAD的角平分线，连接MH , HMG MAH ,求证：AM 2 .2HM(3)如图3,若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中，E 为边CD 上一点(不与点 C 、D 第4页共34重合)，垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时，若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时，判断线段AN 、MB 、EC 之间的数量关系，并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时，连接 NB,将^ BPN 沿着BN 翻折，点P 落在点P 处，AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中，/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上，且AC=g AF, AF=超时，求CE的长；(2)如图2,当/ AFC = 90°时，求证：E是BC的中点；(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图，在？ABCD中，/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上，且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长；(2)求证：AD+AM= 22DN .(3)如图，连接EF、探究AF、EF、CF之间存在的数量关系，直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图，在平行四边形ABCD中，AC为对角线，过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图，若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图，若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证：DG 立CG22.如图，已知ABCD中，/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证：CD 2DF 版AG .(3)如图，在(2)的条件下，若FG J5,点M、N是线段CF、CD上的动点，DM+MN 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形，CD，AB交AB于M, DBXBC, E是AC上一点，EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图，若EC=-AC , EH=6,求BE 的长. 5(2)如图，连接AF,将AF绕点A顺时针旋转，使F点落在BD边上的G点处，AG交CD 于Q,求证：BG=CF.(3)如图，在(2)的条件下，连接FG,交BE于N,连接MN,若竺勺，4AGF的面QG 3积为49户，求MN的长.3.(万州国本中学初三下期中考试)已知，在0ABCD中，AB BD, AB BD, E为射线BC上一点，连接AE交BD于点F .(1)如图1,若点E与点C重合，且AF 2胫，求AD的长；(2)如图2,当点E在BC边上时，过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证：AF DH FH ；(3)如图3,当点E在射线BC上运动时，过点D作DG AE于G , M为AG的中点，点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .（万州国本中学初三下第一次诊断）【问题背景】如图1所示，在gABC 中，AB= BC, ABC=90，点D 为直线BC 上的一个动点（不与 B 、C 重合），连结AD,将线段AD 绕点D 按顺时针方向旋转90。

2020年九年级数学中考几何探究型问题：线段最值问题——“费马点”问题(含答案)

几何探究型问题(针对第25题)线段最值问题“费马点”问题【问题背景】“费马点”——就是到三角形三个顶点的距离之和最小的点．“费马点”问题在中考考查时主要隐藏在求PA＋PB＋PC的最小值问题，通常将某三角形绕点旋转一定的角度，从而将三条线段转化在同一条直线上，利用两点之间线段最短解决问题．【模型分析】对于一个各角不超过120°的三角形，“费马点”是对各边的张角都是120°的点，对于有一个角超过120°的三角形，费马点就是这个内角的顶点．费马点P使它到△ABC三个顶点的距离之和PA＋PB＋PC最小，这就是所谓的“费马”问题．如图，将△APC绕点A逆时针旋转60°到△AP′C′，则可以构造出等边三角形APP′，从而得到AP＝PP′，CP＝C′P′，所以将PA＋PB＋PC的值转化为PP′＋PB＋P′C′的值，则线段BC′的长即为所求的最小值．例题1．如图，已知点P为等边三角形ABC外接圆的劣弧BC上任意一点，求证：PB＋PC＝PA．证明：如答图，在P A上截取PM＝PC，连接CM.∵△ABC 是等边三角形，∴∠ABC ＝∠ACB ＝60°，BC ＝AC ．∵∠ABC ＝∠APC ，∴∠MPC ＝60°，∴△MPC 是等边三角形，∴∠MCP ＝60°，MC ＝PC ，∴∠ACM ＝∠BCP .在△BPC 和△AMC 中，⎩⎪⎨⎪⎧ BC ＝AC ，∠BCP ＝∠ACM ，PC ＝MC ，∴△BPC ≌△AMC (SAS)，∴BP ＝AM ，∴PB ＋PC ＝AM ＋PM ＝P A ．2．已知三个村庄A ，B ，C 构成了如图所示的△ABC(其中∠A ，∠B ，∠C 均小于120°)，现选取一点P 作为打水井，使水井P 到三个村庄A ，B ，C 所铺设的输水管总长度最小．求输水管总长度的最小值．解：如答图，以BC 为边在△ABC 的外部作等边三角形BCD ，连接AD ．∴AD 的长就是△ABC 的费马距离．易得∠ABD ＝90°，∴AD ＝AB 2＋BD 2＝5(km)．答：输水管总长度的最小值为5 km.练习(2019·陕师大附中六模)问题提出(1)如图1，在△ABC 中，BC ＝2，将△ABC 绕点B 顺时针旋转60°得到△A ′BC ′，则CC ′＝______.【解答】由旋转的性质可知∠CBC ′＝60°，BC ′＝BC ，则∠△BCC ′是等边三角形，故CC ′＝BC ＝2.问题探究(2)如图2，在△ABC中，AB＝BC＝3，∠ABC＝30°，点P为△ABC内一点，连接PA，PB，PC，求PA＋PB＋PC的最小值，并说明理由．解题思路将△ABP绕点B逆时针旋转60°得到△EBF，连接PF，EC．易证PA＋PB＋PC＝EF＋PF＋PC；由PC＋PF＋EF≥EC，推出当点P，F在直线EC上时，PA＋PB＋PC的值最小，即为EC的长，求出EC的长即可解决问题．【解答】如答图1，将△ABP绕点B逆时针旋转60°得到△EBF，连接PF，EC．由旋转的性质可知△PBF是等边三角形，∴PB＝PF.∵P A＝EF，∴P A＋PB＋PC＝EF＋PF＋PC．∵PC＋PF＋EF≥EC，∴当点P，F在直线EC上时，P A＋PB＋PC的值最小，易得BC＝BE＝BA＝3，∠CBE＝90°，∴EC＝2BC＝32，∴P A＋PB＋PC的最小值为3 2.问题解决(3)如图3，在四边形ABCD中，AD∥BC，AB＝6，AD＝4，∠ABC＝∠BCD＝60°.在四边形ABCD内部有一点P，满足∠APD＝120°，连接BP，CP，点Q为△BPC内的任意一点，是否存在一点P和一点Q，使得PQ＋BQ＋CQ有最小值？若存在，请求出这个最小值；若不存在，请说明理由．解题思路将△PBQ绕点B逆时针旋转60°得到△EBG，则PQ＝EG，△BQG是等边三角形，易知PQ＋BQ＋CQ＝EG＋GQ＋QC≥EC，推出当EC取得最小值时，PQ ＋BQ ＋CQ 的值最小．延长BA 交CD 的延长线于点S ，作△ADS 的外接圆⊙O ，将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OB ，OP .易证△BEO ′≌△BPO(SAS)，推出EO ′＝OP ＝433，故点E 在以点O ′为圆心，433为半径的圆上，则当点E 在线段CO ′上时，EC 的值最小，最小值为CO ′－EO ′的长．【解答】如答图2，将△PBQ 绕点B 逆时针旋转60°得到△EBG ，连接GQ ，EC ，则PQ ＝EG ，△BQG 是等边三角形，∴BQ ＝QG ，∴PQ ＋BQ ＋CQ ＝EG ＋GQ ＋QC ≥EC ，∴当EC 取得最小值时，PQ ＋BQ ＋CQ 的值最小．如答图3，延长BA 交CD 的延长线于点S ，作△ADS 的外接圆⊙O ，连接OB ．将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OP.易证△BEO ′≌△BPO (SAS)，∴EO ′＝PO .∵∠APD ＋∠ASD ＝180°，∴A ，P ，D ，S 四点共圆，∴OP ＝433，∴EO ′＝433， ∴点E 在以点O ′为圆心，433为半径的圆上， ∴当点E 在线段CO ′上时，EC 的值最小，最小值为CO ′－EO ′的长，连接OO ′，延长OO ′到点R ，使得O ′R ＝OO ′，连接BR ，则∠OBR ＝90°，作RH ⊥CB 交CB 的延长线于点H ，O ′T ⊥CH 于点T ，OM ⊥BC 于点M .易知在Rt △OBM 中，BM ＝5，OM ＝1133， ∴OB ＝OM 2＋BM 2＝1433， ∴BR ＝3OB ＝14.易知△BHR ∽△OMB ，∴RH BM ＝BR OB，∴RH ＝5 3.∵HR ∥O ′T ∥OM ，OO ′＝RO ′，∴TM ＝TH ，∴O ′T ＝RH ＋OM 2＝1333，∴BT ＝O ′B 2－O ′T 2＝3， ∴CO ′＝CT 2＋O ′T 2＝2633， ∴CE ＝CO ′－EO ′＝2633－433＝2233， ∴PQ ＋BQ ＋CQ 的最小值为2233.类型三 “阿氏圆”问题【问题背景】“PA ＋k ·PB ”型的最值问题是近几年中考考查的热点，更是一个难点．当k 的值为1时，即可转化为“PA ＋PB ”之和最短问题，就可用我们常见的“将军饮马”问题模型来处理，即可以转化为轴对称问题来处理．当k 取任意不为1的正数时，此类问题的处理通常以动点P 的运动轨迹不同来分类，一般分为两类研究，即点P 在直线上运动和点P 在圆上运动．其中点P 在圆周上运动的类型称之为“阿氏圆”问题．【模型分析】如图1，⊙O 的半径为r ，点A ，B 都在⊙O 外，P 为⊙O 上一动点，已知r ＝k ·OB ，连接PA ，PB ，则当PA ＋k ·PB 的值最小时，点P 的位置如何确定？如图2，在线段OB 上截取OC ，使OC ＝k ·r ，则可证明△BPO 与△PCO 相似，即k ·PB ＝PC ．故求PA ＋k ·PB 的最小值可以转化为PA ＋PC 的最小值，其中A ，C 为定点，P 为动点，当点P ，A ，C 共线时，PA ＋PC 的值最小，如图3.“阿氏圆”模型解题策略：第一步：连接动点与圆心O(一般将含有k 的线段两端点分别与圆心O 相连)，即连接OB ，OP ；第二步：计算线段OP 与OB 及OP 与OA 的线段比，找到线段比为k 的情况，如例子中的OP OB ＝k ；第三步：在OB 上取点C ，使得OC OP ＝OP OB ；第四步：连接AC ，与⊙O 的交点即为点P .例题如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝4，CA ＝6，⊙C 的半径为2，P 为圆上一动点，连接AP ，BP ，求AP ＋12BP 的最小值．解：如答图，连接CP ，在CB 上取点D ，使CD ＝1，连接AD ，PD ．∵CD CP ＝CP BC ＝12，∠PCD ＝∠BCD ， ∴△PCD ∽△BCP ，∴PD BP ＝12， ∴PD ＝12BP ，∴AP ＋12BP ＝AP ＋PD ， ∴要使AP ＋12BP 最小，则AP ＋PD 最小，当点A ，P ，D 在同一条直线时，AP ＋PD 最小，即AP ＋12BP 的最小值为AD 的长．在Rt △ACD 中，∵CD ＝1，AC ＝6，∴AD ＝AC 2＋CD 2＝37，∴AP ＋12BP 的最小值为37. 练习问题提出(1)如图1，已知线段AB 和BC ，AB ＝2，BC ＝5，则线段AC 的最小值为______.解题思路当点A 在线段BC 上时，线段AC 有最小值．【解答】∵当点A 在线段BC 上时，线段AC 有最小值，∴线段AC 的最小值为5－2＝3.问题探究(2)如图2，已知在扇形COD 中，∠COD ＝90°，DO ＝CO ＝6，A 是OC的中点，延长OC 到点F ，使CF ＝OC ，P 是CD ︵上的动点，点B 是OD 上的一点，BD ＝1.①求证：△OAP ∽△OPF .解题思路由题意可得OA OP ＝OP OF ＝12，由相似三角形的判定可得△OAP ∽△OPF . 【解答】∵A 是OC 的中点，DO ＝CO ＝6＝OP ，∴OA OP ＝12. ∵CF ＝OC ，∴OF ＝2OC ＝2OP ，∴OP OF ＝12， ∴OA OP ＝OP OF，且∠AOP ＝∠POF ，∴△OAP ∽△OPF .②求BP ＋2AP 的最小值．解题思路由相似三角形的性质可得PF ＝2AP ，可得BP ＋2AP ＝BP ＋PF ，即当F ，P ，B 三点共线时，BP ＋2AP 有最小值，最小值为BF 的长，由勾股定理即可求解．【解答】∵△OAP ∽△OPF ，∴AP PF ＝OP OF ＝12， ∴PF ＝2AP .∵BP ＋2AP ＝BP ＋PF ，∴当F ，P ，B 三点共线时，BP ＋2AP 有最小值，最小值为BF 的长．∵DO ＝CO ＝6，BD ＝1，∴BO ＝5，OF ＝12，∴BF ＝OB 2＋OF 2＝13.问题解决(3)如图3，有一个形状为四边形ABCD 的人工湖，BC ＝9千米，CD ＝4千米，∠BCD ＝150°，现计划在湖中选取一处建造一座假山P ，且BP ＝3千米，为方便游客观光，从C ，D 分别建小桥PD ，PC ．已知建桥PD 每千米的造价是3万元，建桥PC 每千米的造价是1万元，建桥PD 和PC 的总造价是否存在最小值？若存在，请确定点P 的位置，并求出总造价的最小值，若不存在，请说明理由．(桥的宽度忽略不计)解题思路以点B 为圆心，3为半径作圆交AB 于点E ，交BC 于点F ，点P 为EF ︵上一点，连接BP ，PC ，PD ，在BC 上截取BM ＝1，连接MD ，PM ，过点D 作DG ⊥CB ，可证△BPM ∽△BCP ，可得PC ＝3PM ，当点P 在线段MD 上时，建桥PD 和PC 的总造价有最小值，由勾股定理可求MD 的值，即可求出建桥PD 和PC 的总造价的最小值．【解答】存在．如答图，以点B 为圆心，3为半径作圆交AB 于点E ，交BC 于点F ，P 为EF ︵上一点，连接BP ，PC ，PD ，在BC 上截取BM ＝1，连接MD ，PM ，过点D 作DG ⊥BC 交BC 的延长线于点G .∵BM BP ＝13＝BP BC，且∠PBM ＝∠CBP ， ∴△BPM ∽△BCP ，∴PM CP ＝BM BP ＝13，∴PC ＝3PM . ∵建桥PD 和PC 的总造价为3PD ＋PC ＝3PD ＋3PM ＝3(PD ＋PM )，∴当点P 在线段MD 上时，建桥PD 和PC 的总造价有最小值．∵∠BCD ＝150°，∴∠DCG ＝30°.∵DG ⊥BC ，∴DG ＝12DC ＝23(千米)，CG ＝3DG ＝6(千米)， ∴MG ＝BC ＋CG －BM ＝9＋6－1＝14(千米)，∴MD ＝DG 2＋MG 2＝413(千米)，∴建桥PD 和PC 的总造价的最小值为3×413＝1213万元．作业5．(2019·交大附中三模)问题提出(1)如图1，点M ，N 是直线l 外两点，在直线l 上找一点K ，使得MK ＋NK 最小．问题探究(2)如图2，在等边三角形ABC 内有一点P ，且P A ＝3，PB ＝4，PC ＝5，求∠APB 的度数．问题解决(3)如图3，矩形ABCD是某公园的平面图，AB＝30 3 米，BC＝60米，现需要在对角线BD上修一凉亭E，使得到公园出口A，B，C的距离之和最小．问：是否存在这样的点E？若存在，请画出点E的位置，并求出EA＋EB＋EC的最小值；若不存在，请说明理由．解：(1)如答图1，连接MN，与直线l交于点K，点K即为所求．(2)如答图2，把△APB绕点A逆时针旋转60°得到△AP′C，连接PP′.由旋转的性质，得P′A＝P A＝3，P′C＝PB＝4，∠P AP′＝60°，∠AP′C＝∠APB，∴△APP′是等边三角形，∴PP′＝P A＝3，∠AP′P＝60°.∵PP′2＋P′C2＝32＋42＝25，PC2＝52＝25，∴PP′2＋P′C2＝PC2，∴△PP′C为直角三角形，且∠PP′C＝90°，∴∠AP′C＝∠AP′P＋∠PP′C＝60°＋90°＝150°，∴∠APB＝∠AP′C＝150°.(3)存在．如答图3，把△ABE绕点B逆时针旋转60°得到△A′BE′，连接EE′.答图由旋转的性质，得A′B＝AB＝30 3 米，BE′＝BE，A′E′＝AE，∠E′BE＝60°，∠A′BA＝60°，∴△E′BE是等边三角形，∴BE＝EE′，∴EA ＋EB ＋EC ＝A ′E ′＋EE ′＋EC ．根据两点之间线段最短，可知当EA ＋EB ＋EC ＝A ′C 时最短，连接A ′C ，与BD 的交点E 2即为所求，此时EA ＋EB ＋EC 最短，最短距离为A ′C 的长度．过点A ′作A ′G ⊥CB 交CB 的延长线于点G . ∵∠A ′BG ＝90°－∠A ′BA ＝90°－60°＝30°， A ′G ＝12A ′B ＝12AB ＝12×303＝153(米)，∴GB ＝3A ′G ＝3×153＝45(米)， ∴GC ＝GB ＋BC ＝45＋60＝105(米)．在Rt △A ′GC 中，A ′C ＝A ′G 2＋GC 2＝(153)2＋1052＝3013(米)，因此EA ＋EB ＋EC 的最小值为3013 米． 6．问题提出(1)如图1，已知△OAB 中，OB ＝3，将△OAB 绕点O 逆时针旋转90°得△OA ′B ′，连接BB ′，则BB ′＝问题探究(2)如图2，已知△ABC 是边长为43的等边三角形，以BC 为边向外作等边三角形BCD ，P 为△ABC 内一点，将线段CP 绕点C 逆时针旋转60°，点P 的对应点为点Q .①求证：△DCQ ≌△BCP . ②求P A ＋PB ＋PC 的最小值．问题解决(3)如图3，某货运场为一个矩形场地ABCD ，其中AB ＝500米，AD ＝800米，顶点A ，D 为两个出口，现在想在货运广场内建一个货物堆放平台P ，在BC 边上(含B ，C 两点)开一个货物入口M ，并修建三条专用车道P A ，PD ，PM .若修建每米专用车道的费用为10 000元，当M ，P 建在何处时，修建专用车道的费用最少？最少费用为多少？(结果保留根号)解：(1)由旋转的性质，得∠BOB ′＝90°，OB ＝OB ′＝3，根据勾股定理，得BB ′＝3 2. (2)①证明：∵△BDC 是等边三角形， ∴CD ＝CB ，∠DCB ＝60°.由旋转的性质，得∠PCQ ＝60°，PC ＝QC ， ∴∠DCQ ＝∠BCP .在△DCQ 和△BCP 中，⎩⎪⎨⎪⎧CD ＝CB ，∠DCQ ＝∠BCP ，CQ ＝CP ，∴△DCQ ≌△BCP (SAS)． ②如答图1，连接AD ，PQ . ∵PC ＝CQ ，∠PCQ ＝60°，∴△CPQ 是等边三角形，∴PQ ＝PC ，由①知DQ ＝PB ，∴P A ＋PB ＋PC ＝P A ＋QD ＋PQ ，由两点之间线段最短，得P A ＋QD ＋PQ ≥AD ， ∴P A ＋PB ＋PC ≥AD ，∴当点A ，P ，Q ，D 在同一条直线上时，P A ＋PB ＋PC 取得最小值，即为AD 的长，过点D 作DE ⊥AC ，交AC 的延长线于点E . ∵△ABC 是边长为43的等边三角形， ∴CB ＝AC ＝43，∠BCA ＝60°， ∴CD ＝CB ＝43，∠DCE ＝60°， ∴DE ＝6，∠DAE ＝∠ADC ＝30°， ∴AD ＝12，即P A ＋PB ＋PC 的最小值为12.答图(3)如答图2，将△ADP 绕点A 逆时针旋转60°，得△AD ′P ′.由(2)知，当点M ，P ，P ′，D ′在同一条直线上时，P A ＋PM ＋PD 最小，最小值为D ′M 的长．∵M 在BC 上，∴当D ′M ⊥BC 时，D ′M 取得最小值．设D ′M 交AD 于点E ，连接DD ′，AM ，DM . 易知△ADD ′是等边三角形，∴EM ＝AB ＝500米， ∴BM ＝400米，PM ＝EM －PE ＝(500－40033)米，∴D ′E ＝32AD ＝4003(米)，∴D ′M ＝(4003＋500)米， ∴最少费用为10 000×(4003＋500)＝ 1 000 000(43＋5)元．∴当M 建在BC 的中点(BM ＝400米)处，点P 在过M 且垂直于BC 的直线上，且在M上方(500－40033)米处时，修建专用车道的费用最少，最少费用为1 000 000(43＋5)元．类型三 “阿氏圆”问题7．(2018·西工大附中三模) 问题提出(1)如图1，在△ABC 中，AB ＝AC ，BD 是AC 边的中线，请用尺规作图作出AB 边的中线CE ，并证明BD ＝CE ；问题探究(2)如图2，已知点P 是边长为6的正方形ABCD 内部一动点，P A ＝3，求PC ＋12PD 的最小值；问题解决(3)如图3，在矩形ABCD 中，AB ＝18，BC ＝25，点M 是矩形内部一动点，MA ＝15，当MC ＋35MD 最小时，画出点M 的位置，并求出MC ＋35MD 的最小值．解：(1)如答图1，线段EC 即为所求．证明：∵AB ＝AC ，AE ＝EB ，AD ＝CD ，∴AE ＝AD ，在△BAD 和△CAE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠A ＝∠A ，AD ＝AE ，答图1∴△BAD ≌△CAE (SAS)，∴BD ＝CE . (2)如答图2，在AD 上截取AE ，使得AE ＝32.∵P A 2＝9，AE ·AD ＝32×6＝9，∴P A 2＝AE ·AD ，∴P A AD ＝AEP A.∵∠P AE ＝∠DAP ，∴△P AE ∽△DAP ， ∴PE DP ＝P A DA ＝12，∴PE ＝12PD ， ∴PC ＋12PD ＝PC ＋PE .∵PC ＋PE ≥EC ，∴PC ＋12PD 的最小值即为EC 的长，在Rt △CDE 中，∵∠CDE ＝90°，CD ＝6，DE ＝92，∴EC ＝62＋(92)2＝152，∴PC ＋12PD 的最小值为152.答图(3)如答图3，在AD 上截取AE ，使得AE ＝9. ∵MA 2＝225，AE ·AD ＝9×25＝225，∴MA 2＝AE ·AD ，∴MA AD ＝AEMA.∵∠MAE ＝∠DAM ，∴△MAE ∽△DAM ， ∴EM MD ＝MA DA ＝1525＝35，∴ME ＝35MD ， ∴MC ＋35MD ＝MC ＋ME .∵MC ＋ME ≥EC ，∴MC ＋35MD 的最小值即为EC 的长．如答图3，以点A 为圆心，AM 长为半径画弧，交EC 于点M ′，点M ′即为所求．在Rt △CDE 中，∵∠CDE ＝90°，CD ＝18，DE ＝16， ∴EC ＝162＋182＝2145， ∴MC ＋35MD 的最小值为2145.8．(1)如图1，已知正方形ABCD 的边长为4，⊙B 的半径为2，P 是⊙B 上的一个动点，求PD ＋12PC 的最小值和PD －12PC 的最大值；(2)如图2，已知正方形ABCD 的边长为9，⊙B 的半径为6，P 是⊙B 上的一个动点，那么PD ＋23PC 的最小值为，PD －23PC 的最大值为(3)如图3，已知菱形ABCD 的边长为4，∠B ＝60°，⊙B 的半径为2，P 是⊙B 上的一个动点，那么PD ＋12PC 的最小值为，PD －12PC 的最大值为解：(1)如答图1，在BC 上取一点G ，使得BG ＝1，连接PB ，PG ，DG .∵PB BG ＝CBPB＝2，∠PBG ＝∠CBP ， ∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝12，∴PG ＝12PC ， ∴PD ＋12PC ＝PD ＋PG .∵PD ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋12PC 的值最小，最小值为DG ＝42＋32＝5.∵PD －12PC ＝PD －PG ≤DG ，∴如答图2，当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为5.答图(2)106，106.【解法提示】如答图3，在BC 上取一点G ，使BG ＝4，连接PG ，PB ，DG . ∵PB BG ＝64＝32，CB PB ＝96＝32，∴PB BG ＝CB BP. ∵∠PBG ＝∠CBP ，∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝23， ∴PG ＝23PC ，∴PD ＋23PC ＝DP ＋PG .∵DP ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋23PC 的值最小，最小值为DG ＝52＋92＝106.∵PD －23PC ＝PD －PG ≤DG ，∴当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为106.答图(3)37，37.【解法提示】如答图4，在BC 上取一点G ，使得BG ＝1，连接PB ，PG ，DG ，作DF ⊥BC 交BC 的延长线于点F .∵PB BG ＝21＝2，BC PB ＝42＝2，∴PB BG ＝CB BP. ∵∠PBG ＝∠CBP ，∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝12， ∴PG ＝12PC ，∴PD ＋12PC ＝DP ＋PG .∵DP ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋12PC 的值最小，最小值为DG 的长．在Rt △CDF 中，∵∠DCF ＝60°，CD ＝4， ∴DF ＝CD ·sin60°＝23，CF ＝2，∴在Rt △GDF 中，DG ＝(23)2＋52＝37. ∴PD ＋12PC 的最小值为37.∵PD －12PC ＝PD －PG ≤DG ，∴当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为37.。

2020年中考数学复习(通用)专题：几何压轴题型含答案

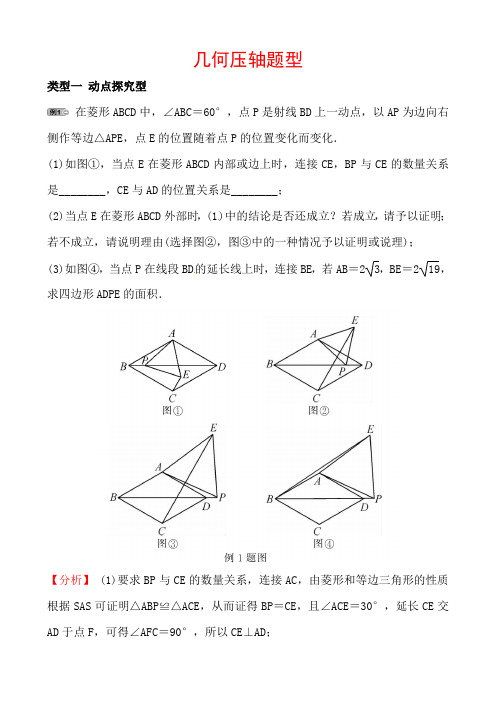
几何压轴题型类型一动点探究型在菱形ABCD中，∠ABC＝60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．(1)如图①，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是________，CE与AD的位置关系是________；(2)当点E在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由(选择图②，图③中的一种情况予以证明或说理)；(3)如图④，当点P在线段BD的延长线上时，连接BE，若AB＝23，BE＝219，求四边形ADPE的面积．【分析】 (1)要求BP与CE的数量关系，连接AC，由菱形和等边三角形的性质根据SAS可证明△ABP≌△ACE，从而证得BP＝CE，且∠ACE＝30°，延长CE交AD于点F，可得∠AFC＝90°，所以CE⊥AD；(2)无论选择图②还是图③，结论不变，思路和方法与(1)一致；(3)要求四边形ADPE的面积，观察发现不是特殊四边形，想到割补法，分成钝角△ADP和正△APE，分别求三角形的面积，相加即可．【自主解答】解：(1)BP＝CE；CE⊥AD；(2)选图②，仍然成立，证明如下：如解图①，连接AC交BD于点O，设CE交AD于点H.在菱形ABCD中，∠ABC＝60°，BA＝BC，例1题解图①∴△ABC为等边三角形，∴BA＝CA.∵△APE为等边三角形，∴AP＝AE，∠PAE＝∠BAC＝60°，∴∠BAP＝∠CAE.在△BAP和△CAE中，例1题解图②∴△BAP≌△CAE(SAS)，∴BP＝CE，∠ACE＝∠ABP＝30°.∵AC和BD为菱形的对角线，∴∠CA D＝60°，∴∠AHC＝90°，即CE⊥AD.选图③，仍然成立，证明如下：如解图②，连接AC交BD于点O，设CE交AD于点H，同理得△BAP≌△CAE(SAS)，BP＝CE，CE⊥AD.(3)如解图③，连接AC交BD于点O，连接CE交AD于点H，由(2)可知，CE⊥AD，CE＝BP.在菱形ABCD中，AD∥BC，∴EC⊥BC.∵BC＝AB＝23，BE＝219，∴在Rt△BCE中，CE＝（219）2－（23）2＝8，例1题解图③∴BP＝CE ＝8.∵AC 与BD 是菱形的对角线， ∴∠ABD＝12∠ABC＝30°，AC⊥BD，∴BD＝2BO ＝2AB·cos 30°＝6， AO ＝12AB ＝3，∴DP＝BP －BD ＝8－6＝2， ∴OP＝OD ＋DP ＝5.在Rt△AOP 中，AP ＝AO 2＋OP 2＝27， ∴S 四边形ADPE ＝S △ADP ＋S △APE ＝12DP·AO＋34·AP 2 ＝12×2×3＋34×(27)2 ＝8 3.【难点突破】本题的难点：一是如何找到全等的三角形，根据含60°内角菱形的特点，连接AC 是解决问题的关键；二是点P 是动点，当它运动到菱形的外部时，在其运动过程中由“手拉手”模型找全等三角形；三是求不规则四边形的面积，要想到运用割补法，将四边形分解成两个三角形求解．点拔几何压轴题中的“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目．解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题．在变化中找到不变的性质是解决数学“动点”探究题的基本思路，这也是动态几何数学问题中最核心的数学本质．1．已知，△ABC是等腰三角形，CA＝CB，0°＜∠ACB≤90°，点M在边AC上，点N在边BC上(点M、点N不与所在线段端点重合)，BN＝AM，连接AN，BM.射线AG∥BC，延长BM交射线AG于点D，点E在直线AN上，且AE＝DE.(1)如图，当∠ACB＝90°时：①求证：△BCM≌△ACN；②求∠BDE的度数；(2)当∠ACB＝α，其他条件不变时，∠BDE的度数是____________________；(用含α的代数式表示)(3)若△ABC是等边三角形，AB＝33，点N是BC边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．2．在Rt△ABC中，∠ACB＝90°，AC＝12.点D在直线CB上，以CA，CD为边作矩形ACDE，直线AB与直线CE，DE的交点分别为F，G.(1)如图，点D在线段CB上，四边形ACDE是正方形．①若点G为DE中点，求FG的长；第2题图②若DG＝GF，求BC的长；(2)已知BC＝9，是否存在点D，使得△DFG是等腰三角形？若存在，求该三角形的腰长；若不存在，试说明理由．类型二新定义型我们定义：如图①，在△ABC中，把AB绕点A顺时针旋转α(0°＜α＜180°)得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′.当α＋β＝180°时，我们称△AB′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．特例感知(1)在图②，图③中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．①如图②，当△ABC 为等边三角形时，AD 与BC 的数量关系为AD ＝________BC ； ②如图③，当∠BAC＝90°，BC ＝8时，则AD 长为________．猜想论证(2)在图①中，当△ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用(3)如图④，在四边形ABCD 中，∠C＝90°，∠D＝150°，BC ＝12，CD ＝23，DA ＝6.在四边形内部是否存在点P ，使△PDC 是△PAB 的“旋补三角形”？若存在，给予证明，并求△PAB 的“旋补中线”长；若不存在，说明理由．【分析】 (1)①证明△ADB′是含有30°角的直角三角形，则可得AD ＝12AB′＝12BC ；②先证明△BAC≌△B′AC′，根据直角三角形斜边上的中线等于斜边的一半即可；(2)结论：AD ＝12BC.如解图①中，延长AD 到点M ，使得AD ＝DM ，连接B′M ，C′M，先证明四边形AC′MB′是平行四边形，再证明△BAC≌△AB′M ，即可解决问题； (3)存在．如解图②中，延长AD 交BC 的延长线于点M ，作BE⊥AD 于点E ，作线段BC 的垂直平分线交BE 于点P ，交BC 于点F ，连接PA ，PD ，PC ，作△PCD 的中线PN ，连接DF 交PC 于点O.先证明PA ＝PD ，PB ＝PC ，再证明∠APD＋∠BPC ＝180°即可．【自主解答】解：(1)①12；【解法提示】 ∵△ABC 是等边三角形， ∴AB ＝BC ＝AB ＝AB′＝AC′. ∵DB′＝DC′， ∴AD⊥B′C′.∵α＋β＝180°，∴∠BAC＋∠B′AC′＝180°， ∵∠BAC＝60°， ∴∠B′AC′＝120°， ∴∠B′＝∠C′＝30°， ∴AD＝12AB′＝12BC.②4；【解法提示】 ∵α＋β＝180°， ∴∠BAC＋∠B′AC′＝180°. ∵∠BAC＝90°，∴∠B′AC′＝∠BAC＝90°.∵AB＝AB′，AC ＝AC′， ∴△BAC≌△B′AC′(SAS)， ∴BC＝B′C′. ∵B′D＝DC′， ∴AD＝12B′C′＝12BC ＝4.(2)结论：AD ＝12BC.证明：如解图①中，延长AD 到点M ，使得AD ＝DM ，连接B′M，C′M.例2题解图①∵B′D＝DC′，AD ＝DM ，∴四边形AC′MB′是平行四边形， ∴AC′＝B′M＝AC. ∵α＋β＝180°，∴∠BAC＋∠B′AC′＝180°. ∵∠B′AC′＋∠AB′M＝180°， ∴∠BAC＝∠MB′A. ∵AB＝AB′，∴△BAC≌△AB′M(SAS)， ∴BC＝AM ，∴AD＝12BC.(3)存在．证明：如解图②中，延长AD 交BC 的延长线于点M ，作BE⊥AD 于点E ，作线段BC 的垂直平分线交BE 于点P ，交BC 于点F ，连接PA ，PD ，PC ，作△PCD 的中线PN ，连接DF 交PC 于点O.例2题解图②∵∠ADC＝150°， ∴∠MDC＝30°，在Rt△DCM 中，∵CD＝23，∠DCM＝90°，∠MDC＝30°， ∴CM＝2，DM ＝4，∠M＝60°. 在Rt△BEM 中，∵∠BEM＝90°，BM ＝14，∠MBE＝30°， ∴EM＝12BM ＝7，∴DE＝EM －DM ＝3. ∵AD＝6，∴AE＝DE. ∵BE⊥AD， ∴PA＝PD. ∵PF 垂直平分BC ，∴PB＝PC.在Rt△CDF中，∵CD＝23，CF＝6，∴tan∠CDF＝3，∴∠CDF＝60°＝∠CPF.易证△FCP≌△CFD，∴CD＝PF.∵CD∥PF，∴四边形CDPF是平行四边形．∵∠DCF＝90°.∴四边形CDPF是矩形，∴∠CDP＝90°，∴∠ADP＝∠ADC－∠CDP＝60°，∴△ADP是等边三角形．∵∠BPF＝∠CPF＝60°，∴∠BPC＝120°，∴∠APD＋∠BPC＝180°，∴△PDC是△PAB的“旋补三角形”．在Rt△PDN中，∵∠PDN＝90°，PD＝AD＝6，DN＝3，∴PN＝DN2＋PD2＝（3）2＋62＝39.【难点突破】第(3)问根据新定义判断点P的存在性是本题难点，但运用“直角三角形中30°的角所对的直角边是斜边的一半”的性质以及三角形全等添加合适辅助线即可求解．点拔解决这类问题，首先要理解新定义的含义及实质；其次要注意，在证明线段、角度相等或某个特殊图形时，主要应用全等，在计算线段的长或图形的周长、面积时，常注意运用相似、勾股定理及图形面积公式等．1．联想三角形外心的概念，我们可引入如下概念．定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心．举例：如图①，若PA ＝PB ，则点P 为△ABC 的准外心．求解：(1)如图②，CD 为等边△ABC 的高，准外心P 在高CD 上，且PD ＝12AB ，求∠APB 的度数；(2)已知△ABC 为直角三角形，斜边BC ＝5，AB ＝3，准外心P 在AC 边上，求PA 的长．2．如图①，在△ABC中，过顶点A作直线与对边BC相交于点D，两交点之间的线段把这个三角形分成两个图形．若其中有一个图形与原三角形相似，则把这条线段叫做这个三角形的“顶似线”．(1)等腰直角三角形的“顶似线”的条数为______；(2)如图②，在△ABC中，AB＝AC，∠A＝36°，BD是∠ABC的角平分线，求证：BD是△ABC的“顶似线”；(3)如图③，在△ABC中，AB＝4，AC＝3，BC＝6，求△ABC的“顶似线”的长．3．如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为这条边上的“奇特三角形”，这条边称为“奇特边”．(1)如图①，已知△ABC是“奇特三角形”，AC＞BC，且∠C＝90°.①△ABC的“奇特边”是________；②设BC＝a，AC＝b，AB＝c，求a∶b∶c；(2)如图②，AM是△ABC的中线，若△ABC是BC边上的“奇特三角形”，找出BC2与AB2＋AC2之间的关系；(3)如图③，在四边形ABCD中，∠B＝90°(AB＜BC)，BC＝27，对角线AC把它分成了两个“奇特三角形”，且△ACD是以AC为腰的等腰三角形，求等腰△ACD 的底边长．4．如果三角形的两个内角α与β满足2α＋β＝90°，那么我们称这样的三角形为“准互余三角形”．(1)若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，则∠B＝__________；(2)如图①，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝5.若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E(异于点D)，使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．(3)如图②，在四边形ABCD中，AB＝7，CD＝12，BD⊥CD，∠ABD＝2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．类型三操作探究型【操作发现】如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．(1)请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；(2)在(1)所画图形中，∠AB′B＝__________．【问题解决】如图②，在等边三角形ABC中，AC＝7，点P在△ABC内，且∠APC＝90°，∠BPC ＝120°，求△APC的面积．小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．请参考小明同学的想法，完成该问题的解答过程．(一种方法即可)【灵活运用】如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD ＝5，AD＝kAB(k为常数)，求BD的长(用含k的式子表示)．【分析】【操作发现】(1)先找到点B，C的对应点B′，C′，再连接构成三角形即可；(2)求∠AB′B的度数可先判断△AB′B是等腰直角三角形，再求角度；【问题解决】根据两种不同的想法，选择其中一个进行证明；【灵活运用】需将△ABD绕点A旋转得到△ACG，再证明∠CDG＝90°即可．【自主解答】解：【操作发现】(1)如解图①所示，△AB′C′即为所求；(2)45°.【解法提示】连接BB′.∵△AB′C′是由△ABC绕点A按顺时针方向旋转90°得到的，∴AB＝AB′，∠B′AB＝90°，∴∠AB′B＝45°.【问题解决】如解图②，∵将△APB绕点A按逆时针方向旋转60°，得到△AP′C，∴△APP′是等边三角形，∠AP′C＝∠APB＝360°－90°－120°＝150°，∴PP′＝AP ，∠AP′P＝∠APP′＝60°，∴∠PP′C＝90°，∠P′PC＝30°， ∴PP′＝32PC ，即AP ＝32PC.∵∠APC＝90°，∴AP 2＋PC 2＝AC 2，即(32PC)2＋PC 2＝72，∴PC＝27，∴AP＝21，∴S △APC ＝12AP·PC＝73；【灵活运用】如解图③，连接AC.∵AE⊥BC，BE ＝EC ，∴AB＝AC ，将△ABD 绕点A 逆时针旋转使得AB 与AC 重合，点D 的对应点为G ，连接DG.则BD ＝CG.例3题解图③∵∠BAD＝∠CAG，∴∠BAC＝∠DAG.∵AB＝AC ，AD ＝AG ，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG.∴DG＝kBC＝4k.∵∠BAE＋∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG＋∠ADC＝90°，∴∠GDC＝90°，∴CG＝DG2＋CD2＝16k2＋25.∴BD＝CG＝16k2＋25.【难点突破】在【灵活运用】一问中，要确定BD与k的数量关系，关键在于旋转△ABD，使得AB与AC重合，从而证明∠CDG＝90°，构造直角三角形是解决本题的难点，也是解决问题的突破口．点拔对于操作探究问题，首先掌握图形变换的性质，如图形的折叠：折痕为对称轴，有折痕就有角平分线，有折痕就有垂直平分等；图形的平移：有平移就有平行；图形的旋转：旋转前后图形全等，对应边相等，对应角相等；对应点与旋转中心的连线所成的角为旋转角，有旋转就有等腰三角形；其次注意运用全等证明线段相等，利用勾股定理或相似求线段的长．1．在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB.(1)若四边形ABCD为正方形．①如图①，请直接写出AE与DF的数量关系______________；②将△EBF绕点B逆时针旋转到图②所示的位置，连接AE，DF，猜想AE与DF 的数量关系，并说明理由．(2)若四边形ABCD为矩形，BC＝mAB，其他条件都不变．①如图③，猜想AE与DF的数量关系，并说明理由；②将△EBF绕点B逆时针旋转α(0°＜α＜90°)得到△E′BF′，连接AE′，DF′，请在图④中画出草图，并直接写出AE′和DF′的数量关系．2．(1)操作发现：如图①，小明画了一个等腰三角形ABC，其中AB＝AC，在△ABC 的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN.小明发现了：线段GM与GN的数量关系是______________；位置关系是______________．(2)类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其他条件不变，小明发现的上述结论还成立吗？请说明理由．(3)深入研究：如图③，小明在(2)的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其他条件不变，试判断△GMN的形状，并给予证明．3．如图，AM是△ABC的中线，D是线段AM上一点(不与点A重合)，DE∥AB交AC于点F，CE∥AM，连接AE.(1)如图①，当点D与点M重合时，求证：四边形ABDE是平行四边形；(2)如图②，当点D不与点M重合时，(1)中的结论还成立吗？请说明理由．(3)如图③，延长BD交AC于点H，若BH⊥AC，且BH＝AM.①求∠CAM的度数；②当FH＝3，DM＝4时，求DH的长．参考答案类型一1．解：(1)①∵CA＝CB，BN＝AM，∴CB－BN＝CA－AM，∴CN＝CM，∵∠ACB＝∠ACB，BC＝CA，∴△BCM≌△ACN.②解：∵△BCM≌△ACN，∴∠MBC＝∠NAC.∵EA＝ED，∴∠EAD＝∠EDA.∵AG∥BC，∴∠GAC＝∠ACB＝90°，∠ADB＝∠DBC，∴∠ADB＝∠NAC，∴∠ADB＋∠EDA＝∠NAC＋∠EAD，∵∠ADB＋∠EDA＝180°－90°＝90°；∴∠BDE＝90°.(2)α或180°－α；(3)43或3 2.2．解：(1)①在正方形ACDE中，DG＝GE＝6，在Rt△AEG中，AG＝AE2＋EG2＝6 5.∵EG∥AC，∴△ACF∽△GEF，∴FGAF＝EGAC＝12，∴FG＝13AG＝2 5.第2题解图①②如解图①，在正方形ACDE中，AE＝ED，∠AEF＝∠DEF＝45°.∵EF＝EF，∴△AEF≌△DEF，∴∠1＝∠2，设∠1＝∠2＝x.∵AE∥BC，∴∠B＝∠1＝x.∵GF＝GD，∴∠3＝∠2＝x，在△DBF中，∠3＋∠FDB＋∠B＝180°，∴x＋(x＋90°)＋x＝180°，解得x＝30°，∴∠B＝30°，∴在Rt△ABC中，BC＝ACtan 30°＝12 3.(2)在Rt△ABC中，AB＝AC2＋BC2＝122＋92＝15，如解图②，当点D在线段BC上时，此时只有GF＝GD.第2题解图②∵DG∥AC，∴△BDG∽△BCA，∴BDDG＝BCAC＝34，∴设BD＝3x，则DG＝4x，BG＝5x，AE＝CD＝9－3x，∴GF＝GD＝4x，则AF＝15－9x.∵AE∥CB，∴△AEF∽△BCF，∴AEBC＝AFBF，∴9－3x9＝15－9x9x，整理得x2－6x＋5＝0，解得x＝1或5(舍去)，∴腰长GD为4.如解图③，当点D在线段BC的延长线上，且直线AB，CE的交点在AE上方时，此时只有GF＝DG，设AE＝3x，则EG＝4x，AG＝5x，第2题解图③∴FG＝DG ＝12＋4x.∵AE∥BC，∴△AEF∽△BCF， ∴AE BC ＝AF BF ， ∴3x 9＝9x ＋129x ＋27，解得x ＝2或－2(舍去)， ∴腰长DG 为20.如解图④，当点D 在线段BC 的延长线上，且直线AB ，EC 的交点在BD 下方时，此时只有DF ＝DG ，过点D 作DH⊥FG 于点H.第2题解图④设AE ＝3x ，则EG ＝4x ，AG ＝5x ，DG ＝4x ＋12， ∴FH＝GH ＝DG·cos∠DGB＝(4x ＋12)×45＝16x ＋485，∴GF＝2GH ＝32x ＋965，∴AF＝GF －AG ＝7x ＋965.∵AC∥DG，∴△ACF∽△GEF， ∴AC EG ＝AF FG ，∴124x ＝7x ＋96532x ＋965，解得x ＝12147或－12147(舍去)，∴腰长GD 为84＋48147，如解图⑤，当点D 在线段CB 的延长线上时，此时只有DF ＝DG ，过点D 作DH⊥AG 于点H.设AE ＝3x ，则EG ＝4x ，AG ＝5x ，DG ＝4x －12， ∴FH＝GH ＝DG·cos∠DGB＝16x －485，第2题解图⑤∴FG＝2FH ＝32x －965，∴AF＝AG －FG ＝96－7x5.∵AC∥EG，∴△ACF∽△GEF， ∴AC EG ＝AF FG ，∴124x ＝96－7x 532x －965，解得x ＝12147或－12147(舍去)，∴腰长DG 为－84＋48147.综上所述，等腰三角形△DFG 的腰长为4或20或84＋48147或－84＋48147.类型二1．解：(1)①如解图①，若PB ＝PC ，连接PB ，则∠PCB＝∠PBC. ∵CD 为等边三角形的高，∴AD＝BD ，∠PCB＝30°， ∴∠PBD＝∠PBC＝30°，∴PD＝33DB ＝36AB ，与已知PD ＝12AB 矛盾，∴PB≠PC；②若PA ＝PC ，连接PA ，同理可得PA≠PC； ③若PA ＝PB ，由PD ＝12AB ，得PD ＝AD ，∴∠APD＝45°，故∠APB＝90°. (2)∵BC＝5，AB ＝3，∠BAC＝90°， ∴AC＝BC 2－AB 2＝52－32＝4.①若PB ＝PC ，设PA ＝x ，则PC ＝PB ＝4－x ， ∴x 2＋32＝(4－x)2，∴x＝78，即PA ＝78；②若PA ＝PC ，则PA ＝2；③若PA ＝PB ，由解图②知，在Rt△PAB 中，不可能存在．综上所述，PA 的长为2或78.2．(1)解：1.(2)证明： ∵AB＝AC ，∠A＝36°，∴∠ABC＝∠ACB＝72°. ∵BD 是∠ABC 的角平分线，∴∠ABD＝∠DBC＝36°，∴∠A＝∠CBD. 又∵∠C＝∠C，∴△ABC∽△BDC， ∴BD 是△ABC 的“顶似线”．(3)解：①如解图①，当△ADC∽△BAC 时，AD 为△ABC 的“顶似线”，则AD AB ＝AC BC ，即AD 4＝36，∴AD＝2； ②如解图②，当△ADC∽△ACB 时，CD 为△ABC 的“顶似线”，则CD CB ＝AC AB ，即CD 6＝34，∴CD＝92； ③过顶点B 的“顶似线”不存在．综上所述，△ABC 的“顶似线”的长为2或92.3．解：(1)①AC；②如解图①，过点B 作AC 边上的中线BE ，则BE ＝AC ＝b ，CE ＝AE ＝12b.在Rt△ABC 中，a 2＋b 2＝c 2，在Rt△BCE 中，a 2＋(12b)2＝b 2.解得a ＝32b ，c ＝72b.∴a∶b∶c＝3∶2∶7.(2)如解图②，过点A 作AF⊥BC 于点F ，则∠AFB＝∠AFC＝90°. 设AM ＝BC ＝a ，AF ＝h ，MF ＝x ，则BM ＝CM ＝12a.在Rt△ABF 中，AB 2＝BF 2＋AF 2＝(a2＋x)2＋h 2，在Rt△ACF 中，AC 2＝CF 2＋AF 2＝(a2－x)2＋h 2，∴AB 2＋AC 2＝a22＋2x 2＋2h 2.在Rt△AMF 中，AM 2＝MF 2＋AF 2，即a 2＝x 2＋h 2.∴AB 2＋AC 2＝5a 22＝52BC 2.(3)∵∠B＝90°，BC ＞AB ，∴BC 为△ABC 的“奇特边”． ∵BC＝27，∴由(1)②知AB ＝32BC ＝21，AC ＝72BC ＝7.设等腰△ACD 的底边长为y ，由(2)中结论知：①当腰为“奇特边”时，有72＋y 2＝52×72，解得y ＝726(负值已舍去)．②当底边为“奇特边”时，有72＋72＝52×y 2，解得y ＝1455(负值已舍去)．∴等腰△ACD 的底边长为726或145 5.4．解：(1)∵∠C＞90°，∠A＝60°， ∴β＝60°，α＝15°，∴∠B＝15°.(2)若存在一点E ，使得△ABE 也是“准互余三角形”，则2∠EBA＋∠EAB＝90°.如解图①，作射线BF ，使得∠FBE＝∠ABE ，延长AE 交BF 于点F ，则∠BFE＝90°.即BE 为∠FBA 的角平分线，过点E 作EG⊥AB 于点G ，则EG ＝EF ，可得△BEF≌△BEG. 又∵△BEG∽△BAC，∴△BEF∽△BAC， ∴BF BC ＝EF AC ，∴BF 5＝EF4①. 又∵△BEF∽△AEC，∴EF CE ＝BF AC ，∴EF 5－BE ＝BF 4②，由①②可得，BE ＝1.8.(3)如解图②，将△BCD 沿BC 翻折得△BCE，则CE ＝CD ＝12，∠ABD＝2∠BC D ＝∠DCE，∠DCE＋∠DBE＝180°，即∠ABD＋∠DBE＝180°，∴点A ，B ，E 共线，易知2∠ACB＋∠BAC＝90°不成立，存在2∠BAC＋∠ACB＝90°，易证得△ECB∽△EAC，∴EC AE ＝BE EC ，即127＋BE ＝BE 12，解得BE ＝9(负值已舍去)，∴AE＝16，在Rt△AEC 中，利用勾股定理得，AC ＝AE 2＋CE 2＝20.类型三1．解：(1)①DF＝2AE ； ②DF＝2AE ；理由：∵∠EBF＝∠ABD＝45°，∴∠ABE ＝∠FBD.∵BE BF ＝AB BD ，∴△ABE∽△DBF，∴AE DF ＝AB BD ＝22，∴DF＝2AE.(2)①如解图①，过点F 作FG⊥AD 于点G ，则四边形AEFG 是矩形，∴GF＝AE. ∵tan∠FDG＝BAAD ＝GFDG ，AD ＝BC ＝mAB ，∴DG＝mGF ，在Rt△DGF 中，由勾股定理得DF ＝GF 2＋DG 2＝1＋m 2GF ，∴DF＝1＋m 2AE.②画出草图如解图②，DF′＝1＋m2AE′.2．解：(1)GM＝GN；GM⊥GN.【解法提示】如解图①，连接BE，CD相交于点H.∵△ABD和△ACE都是等腰直角三角形，∴AB＝AD，AC＝AE，∠BAD＝∠CAE＝90°∴∠CAD＝∠BAE，∴△ACD≌△AEB(SAS)，∴CD＝BE，∠ADC＝∠ABE，∴∠BDC＋∠DBH＝∠BDC＋∠ABD＋∠ABE＝∠BDC＋∠ABD＋∠ADC＝∠ADB＋∠ABD＝90°，∴∠BHD＝90°，∴CD⊥BE.∵点M，G分别是BD，BC的中点，∴MG 12 CD.同理：NG 12BE，∴MG＝NG，MG⊥NG.(2)小明发现的上述结论成立．理由：如解图②，连接CD ，BE 相交于点H. ∵∠DAB＝∠CAE＝90°，∴∠DAC＝∠BAE.∵DA＝BA ，CA ＝EA ，∴△DAC≌△BAE(SAS)，∴∠FBH＝∠ADF，DC ＝BE.∵M 是BD 的中点，G 是BC 的中点，∴MG＝12DC ，同理NG ＝12BE ，∴MG＝NG. 设CD 交AB 于点F ，则∠FHB＝180°－(∠FBH＋∠BFH)＝180°－(∠ADF＋∠AFD)＝90°，∴CD⊥BE，∴MG⊥NG；(3)△GMN 为等腰直角三角形．证明：如解图③，连接EB ，DC ，延长线相交于点H ，同(1)的方法得，MG ＝NG ，同(1)的方法得，△ABE≌△ADC，∴∠AEB＝∠ACD，∴∠CEH ＋∠ECH ＝∠AEH －∠AEC ＋180°－∠ACD －∠ACE ＝∠ACD －45°＋180°－∠ACD－45°＝90°，∴∠DHE＝90°，同(1)的方法得，MG⊥NG.3．(1)证明： ∵DE∥AB，∴∠EDC＝∠ABM.∵CE∥AM，∴∠ECD＝∠ADB.∵AM 是△A BC 的中线，且点D 与点M 重合，∴BD＝DC ，∴△ABD≌△EDC(ASA)，∴AB＝ED.∵AB∥ED，∴四边形ABDE 是平行四边形．(2)解：结论成立．理由如下：第3题解图①如解图①，过点M作MG∥DE交CE于点G.∵CE∥AM，∴四边形DMGE是平行四边形，∴ED＝GM，且ED∥GM.∵AB∥DE，∴AB∥GM，∴∠ABM＝∠GMC.∵AM∥CE，∴∠AMB＝∠GCM.∵AM为△ABC的中线，∴BM＝MC.∴△ABM≌△GMC(ASA)，∴AB＝GM，∴AB＝DE.∵AB∥DE，∴四边形ABDE是平行四边形．(3)解：①如解图②，取线段HC的中点I，连接MI，第3题解图②∵BM＝MC，∴MI 是△BHC 的中位线，∴MI∥BH，MI ＝12BH. ∵BH⊥AC，且BH ＝AM.∴MI＝12AM ，MI⊥AC， ∴∠CAM＝30°.②设DH ＝x ，则AH ＝3x ，AD ＝2x ， ∴AM＝4＋2x ，∴BH＝4＋2x.∵四边形ABDE 是平行四边形，∴DF∥AB， ∴HF HA ＝HD HB ，∴33x ＝x 4＋2x ，解得x ＝1＋5或x ＝1－5(舍去)， ∴DH＝1＋ 5.。

2020中考数学压轴冲刺专题圆的几何证明与计算(含答案)

2020中考数学压轴冲刺专题圆的几何证明与计算（含答案）1.如图，已知AB为⊙O的直径，F为⊙O上一点，AC平分∠BAF且交⊙O于点C，过点C作CD⊥AF于点D，延长AB、DC交于点E，连接BC、CF.(1)求证：CD是⊙O的切线；(2)若AD＝6，DE＝8，求BE的长；(3)求证：AF＋2DF＝AB.第1题图（1）证明：如解图，连接OC.第1题解图∵AC平分∠BAD,∴∠OAC=∠CAD，又∠OAC=∠OCA,∴∠OCA=∠CAD，∴CO∥AD.又CD⊥AD，∴CD⊥OC，又∵OC是⊙O的半径，∴CD 是⊙O 的切线；（2）解：在Rt △ADE 中，∵AD =6，DE =8，根据勾股定理得：AE =10，∵CO ∥AD ，∴△EOC ∽△EAD ,∴ADOC EA EO =. 设⊙O 的半径为r ，∴OE =10-r . ∴61010r r -=， ∴r =415， ∴BE =10-2r =25；（3）证明：如解图，过点C 作CG ⊥AB 于点G .∵∠OAC =∠CAD ，AD ⊥CD ，∴CG =CD ，在Rt △AGC 和Rt △ADC 中，∵CG =CD ，AC =AC ，∴Rt △AGC ≌Rt △ADC （HL ），∴AG =AD .又∵∠BAC =∠CAD ，∴BC =CF ，在Rt △CGB 和Rt △CDF 中，∵BC =FC ，CG =CD ，∴Rt △CGB ≌Rt △CDF （HL ），∴GB =DF .∵AG +GB =AB ，∴AD +DF =AB ，即AF +2DF =AB .2. 如图，在Rt △ABC 中，∠ACB ＝90°，以BC 为直径的⊙O 交AB 于点D ，E 是AC 的中点，OE 交CD 于点F .(1)若∠BCD ＝36°，BC ＝10，求BD ︵的长；(2)判断直线DE 与⊙O 的位置关系，并说明理由；(3)求证：2CE 2＝AB ·EF .第2题图（1）解：如解图，连接OD ，第2题解图 ∵∠BCD ＝36°，∴∠BOD ＝2∠BCD ＝2×36°＝72°，∵BC 是⊙O 的直径，BC ＝10，∴OB ＝5，∴l BD ︵＝72π×5180＝2π；(2)解：DE 是⊙O 的切线；理由如下：∵BC 是⊙O 的直径，∴∠ADC ＝180°－∠BDC ＝90°，又∵点E 是线段AC 中点，∴DE ＝12AC ＝EC ，在△DOE 与△COE 中，⎩⎪⎨⎪⎧OD ＝OCOE ＝OE DE ＝CE，∴△DOE ≌△COE (SSS)．∵∠ACB ＝90°，∴∠ODE ＝∠OCE ＝90°，∵OD 是⊙O 的半径，∴DE 是⊙O 的切线；(3)证明：由(2)知，△DOE ≌△COE ，∴OE 是线段CD 的垂直平分线，∴点F 是线段CD 中点，∵点E 是线段AC 中点，则EF ＝12AD ， ∵∠BAC ＝∠CAD ，∠ADC ＝∠ACB ，∴△ACD ∽△ABC ，则AC AB ＝AD AC ，即AC 2＝AB ·AD ，而AC ＝2CE ，AD ＝2EF ，∴(2CE )2＝AB ·2EF ，即4CE 2＝AB ·2EF ，∴2CE 2＝AB ·EF .3. 如图，PB 为⊙O 的切线，B 为切点，直线PO 交⊙O 于点E 、F ，过点B 作PO 的垂线BA ，垂足为点D ，交⊙O 于点A ，延长AO 与⊙O 交于点C ，连接BC ，AF .(1)求证：直线P A 为⊙O 的切线；(2)求证：EF 2＝4OD ·OP ；(3)若BC ＝6，tan F ＝12，求AC 的长.第3题图（1）证明：如解图，连接OB ，第3题解图∵PB 是⊙O 的切线，∴∠PBO ＝90°，∵OA ＝OB ，BA ⊥PO 于点D ，∴AD ＝BD ，∴点D 为AB 的中点，即OP 垂直平分AB ，∴∠APO ＝∠BPO ，∵∠ADP ＝∠BDP ＝90°，∴△APD ≌△BPD ，∴AP ＝BP ，在△P AO 和△PBO 中，⎩⎪⎨⎪⎧P A ＝PB ∠APO ＝∠BPO OP ＝OP，∴△P AO ≌△PBO （SAS ），∴∠P AO ＝∠PBO ＝90°，∵OA 为⊙O 的半径，∴直线P A 为⊙O 的切线；(2)证明：∵∠P AO ＝∠PDA ＝90°，∴∠OAD ＋∠AOD ＝90°，∠OP A ＋∠AOP ＝90°，∴∠OAD ＝∠OP A ，∴△OAD ∽△OP A ，∴OA OP ＝OD OA，即OA 2＝OD ·OP ，又∵EF ＝2OA ，∴EF 2＝4OD ·OP ；(3)解：∵OA ＝OC ，AD ＝BD ，BC ＝6，∴OD ＝12BC ＝3，设AD ＝x ，∴tan F ＝AD DF ＝x DF ＝12， ∴DF ＝2x ，∴OA ＝OF ＝2x －3，在Rt △AOD 中，由勾股定理得(2x－3)2＝x2＋32，解得x1＝4或x2＝0(不合题意，舍去)，∴OA＝2x－3＝5，∵AC为⊙O的直径，∴AC＝2OA＝10.4.如图，AB是⊙O的直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交直径AB于点F，连接BE.(1)求证：AC平分∠DAB；(2)求证：PC=PF；(3)若tan∠PCB＝34，BE＝52，求PF的长．第4题图（1）证明：如解图，连接OC，第4题解图∵OA＝OC，∴∠OAC＝∠OCA，∵PC是⊙O的切线，且AD⊥CD，∴∠OCP＝∠D＝90°，∴OC∥AD，∴∠CAD＝∠OCA＝∠OAC，即AC平分∠DAB；(2)证明：∵AB是⊙O的直径，∴∠ACB＝90°，∴∠PCB＋∠ACD＝90°，又∵∠CAD＋∠ACD＝90°，∴∠CAB＝∠CAD＝∠PCB.∵CE 平分∠ACB ，∴∠ACE ＝∠BCE ，∵∠PFC ＝∠CAB ＋∠ACE ，∠PCF ＝∠PCB ＋∠BCE ， ∴∠PFC ＝∠PCF ，∴PC ＝PF ；(3)解：如解图，连接AE ，∵∠ACE ＝∠BCE ，∴AE ︵＝BE ︵，∴AE ＝BE ，又∵AB 是直径，∴∠AEB ＝90°，AB ＝2BE ＝10，∴OB ＝OC ＝5，∵∠PCB ＝∠P AC ，∠P ＝∠P ，∴△PCB ∽△P AC ，∴PB PC ＝BC CA ， ∵tan ∠PCB ＝tan ∠CAB ＝34，∴PB PC ＝BC CA ＝34，设PB ＝3x ，则PC ＝4x ，在Rt △POC 中，根据勾股定理得，(3x ＋5)2＝(4x )2＋52，解得x 1＝0，x 2＝307. ∵x ＞0，∴x ＝307，∴PF ＝PC ＝1207. 5. 如图，AB 是⊙O 的直径，C 、G 是⊙O 上两点，且点C 是劣弧»AG 的中点，过点C 的直线CD ⊥BG 的延长线于点D ，交BA 的延长线于点E ，连接BC ，交OD 于点F .(1)求证：CD 是⊙O 的切线；(2)若ED ＝3DB ，求证：3OF ＝2DF ；(3)在(2)的条件下，连接AD ，若CD ＝3，求AD 的长．第5题图(1)证明：如解图①，连接OC 、AC 、CG ，∵AC ︵＝CG ︵，∴AC ＝CG ， ∴∠ABC ＝∠CBG ，∵OC ＝OB ，∴∠OCB ＝∠OBC ， ∴∠OCB ＝∠CBG ，∴OC ∥BG ，∵CD ⊥BG ，∴OC ⊥CD ，∵OC是⊙O的半径，∴CD是⊙O的切线；第5题解图○1(2)证明：∵O C∥BD，∠CFO＝∠DFB，∴∠OCB＝∠CBD，∠EOC＝∠EBD，∴△OCF ∽△DBF，△EOC ∽△EBD，∴OCBD＝OFDF，OCBD＝OEBE，∴OFDF＝OEBE，∵ED＝3DB，∠EDB＝90°，∴∠E＝30°，∴OC＝12OE，∵OA＝OC，∴AE＝OA＝OC＝OB，∴OFDF＝OEBE＝2OA3OA＝23，即3OF＝2DF；(3)解：如解图②，过A作AH⊥DE，交DE于点H，∵∠E ＝30°，∴∠EBD ＝60°，∵∠ABC ＝∠CBD ，∴∠CBD ＝12∠EBD ＝30°， ∵CD＝3，∴BD ＝CD tan30°＝33， ∴BE ＝33sin30°＝63，DE ＝3BD ＝9， ∵AE ＝13BE ，AH ∥BD ， ∴AH ＝13BD ＝3，DH ＝23DE ＝6， ∴AD ＝（3）2＋62＝39.第5题解图○26. 如图，在Rt △ABC 中，∠ACB ＝90°，AO 是△ABC 的角平分线.以O 为圆心，OC 长为半径作⊙O ，连接AO 交⊙O 于点E ，延长AO 交⊙O 于点D.(1)求证：AB 是⊙O 的切线；(2)若tan D ＝12，求AE AC的值； (3)设⊙O 的半径为3，求AB 的长．第6题图(1)证明：如解图，过O作OF⊥AB交AB于F，∵∠ACB＝90°，∴AC⊥BC，∵AO是△ABC的角平分线，OF⊥AB，∴CO＝FO，∴FO为⊙O的半径，∴AB是⊙O的切线；第6题解图(2)解：如解图，连接CE，∵ED是⊙O的直径，∴∠ECD＝90°，∴∠ECO＋∠OCD＝90°，∵∠ACB＝90°，∴∠ACE＋∠ECO＝90°，∴∠ACE＝∠OCD，∵OC＝OD，∴∠OCD＝∠ODC，∴∠ACE＝∠ODC，∵∠CAE＝∠CAE，∴△ACE∽△ADC，∴AEAC＝CEDC，∵tan D＝CECD＝12，∴AEAC＝12；(3)解：由(2)知AEAC＝12，设AE＝c，则AC=2c，在Rt△ACO中，∴(2c)2＋32＝(c＋3)2，解得c＝2或c=0（舍去），∴AF＝AC＝2c＝4，∵在△BFO和△BCA中，∠B＝∠B，∠BFO＝∠BCA＝90°，∴△BFO∽△BCA，∴BFBC＝FOCA＝BOAB，设BF＝x，BO＝y，∴x3＋y＝34＝y4＋x，解得x＝727，y＝757，∴AB＝AF＋BF＝4＋727＝1007.7.如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD，CD.过点D作BC的平行线，与AB的延长线相交于点P.(1)求证：PD是⊙O的切线；(2)求证：△PBD∽△DCA；(3)当AB＝6，AC＝8时，求线段PB的长．第7题图(1)证明：∵圆心O在BC上，∴BC是⊙O的直径，∴∠BAC＝90°.如解图，连接OD.第7题解图∵AD平分∠BAC，∴∠BAC＝2∠DAC.∵∠DOC＝2∠DAC，∴∠DOC＝∠BAC＝90°.即OD⊥BC.∵PD∥BC，∴OD⊥PD.又OD是⊙O的半径，∴PD是⊙O的切线；(2)证明：∵PD∥BC，∴∠P＝∠ABC.又∠ABC＝∠ADC，∴∠P＝∠ADC.∵∠PBD＋∠ABD＝180°，∠ACD＋∠ABD＝180°，∴∠PBD＝∠ACD.∴△PBD∽△DCA；(3)解：∵△ABC是直角三角形，∴BC2＝AB2＋AC2＝62＋82＝100.∴BC＝10.∵OD垂直平分BC，∴DB＝DC.∵BC是⊙O的直径，∴∠BDC＝90°.在等腰直角三角形BDC中．DC＝DB＝5 2.∵△PBD∽△DCA，∴PBDC＝BDCA，即PB＝DC·BDCA＝52×528＝254.8.如图，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点D，连接OE，AC，且∠P＝∠E，∠POE＝2∠CAB.(1)求证：CE⊥AB；(2)求证：PC是⊙O的切线；(3)若BD＝2OD，且PB＝9，求tan P的值．第8题图（1）证明：如解图，连接OC，第8题解图∴∠COB＝2∠CAB，又∵∠POE＝2∠CAB，∴∠COD＝∠EOD，又∵OC＝OE，∴CE⊥AB;(2)证明：∵CE⊥AB，∠P＝∠E，∴∠P＋∠PCD＝∠E＋∠PCD＝90°，又∠OCD＝∠E，∴∠OCD＋∠PCD＝∠PCO＝90°，∵OC是⊙O的半径，∴PC是⊙O的切线；(3)解：设⊙O的半径为r，OD＝x，则BD＝2x，r＝3x，∵CD⊥OP，OC⊥PC，∴Rt△OCD∽Rt△OPC，∴OC2＝OD·OP，即(3x)2＝x(3x＋9)，解得x＝32或x=0（舍去），∴⊙O的半径r为9 2，同理可得PC2＝PD·PO＝(PB＋BD) ·(PB＋OB)＝162，∴PC＝92，在Rt△OCP中，tan P＝OCPC＝24.9.如图，AC是⊙O的直径，弦BE⊥AC于H，F为⊙O上的一点，过点F的直线与AC的延长线交于点D，与BE的延长线交于点M，连接AF交BM于G，且MF＝MG.(1)求证：MD为⊙O的切线；(2)求证：当MD∥AB时，FG2＝MF·EG；(3)在(2)的条件下，若cos M＝45，FD＝6，求AG的长．第9题图(1)证明：∵MF＝MG，∴∠MFG＝∠MGF＝∠AGB，如解图，连接FO，∵OF＝AO，∴∠OF A=∠OAF，∵BE⊥AC，∴∠AGH+∠OAF=∠MFG+∠OF A=90°，即∠MFO＝90°，∵OF为⊙O的半径，∴MD为⊙O的切线；(2) 证明：∵MD∥AB，∴∠M＝∠ABM，如解图，连接EF，∵∠EFG＝∠ABM，∴∠M＝∠EFG，∵∠MGF＝∠FGE，∴△MGF∽△FGE，∴FGMG＝EGFG，又∵MG=MF，∴FG2＝MF·EG；第9题解图（3）∵∠M＝∠ABM，cos M＝45，∴设AH＝3k，AB＝5k，HB＝4k，如解图，连接OB，∵∠FOD＝∠M，FD＝6，∴FO＝8＝OB＝OA，∴OH＝8－3k，∴OH 2＋HB 2＝OB2，∴(4k)2＋(8－3k)2＝82，解得k＝4825或k=0（舍去），∵MD∥AB，∴∠MFG＝∠BAF，∴∠BGA＝∠BAG，∴AB＝GB＝5k，∴GH＝k，∴AG＝10k，∴AG＝48 2510.10.如图①，AB是⊙O的直径，C是圆上一点，∠BAC的平分线交⊙O于点D，过D作DE⊥AC交AC的延长线于点E.(1)求证：DE是⊙O的切线;(2)若AB＝10，AC＝6，求BD的长；(3)如图②，若F是OA的中点，FG⊥OA交直线DE于点G，若FG＝194，tan∠BAD＝34，求⊙O的半径．图①图②第10题图（1）证明：如解图①，连接OD，第10题解图①∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠OAD＝∠DAE，∴∠ODA＝∠DAE，∴OD∥AE，∴∠ODE＋∠AED＝180°，∵∠AED＝90°，∴∠ODE＝90°，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线；(2)解：如解图①，连接BC，交OD于点N，∵AB是⊙O的直径，∴∠BCA＝90°，∵OD∥AE，O是AB的中点，∴ON∥AC，且ON＝12AC，∴∠ONB＝90°，且ON＝3，OB=5，则BN＝4，ND＝2，∴BD＝42＋22＝25；（3）解：如解图②，设FG与AD交于点H，第10题解图②根据题意，设AB＝5x，AD＝4x，则AF＝54x，FH＝AF·tan∠BAD＝54x·34＝1516x，AH＝AFcos∠BAD＝54x45＝2516x，HD＝AD－AH＝4x－2516x＝3916x，由（1）可知，∠HDG＋∠ODA＝90°，在Rt△HF A中，∠F AH＋∠FHA＝90°，∵∠OAD＝∠ODA，∠FHA＝∠DHG，∴∠DHG＝∠HDG，∴GH＝GD，过点G作GM⊥HD，交HD于点M，∴MH＝MD，∴HM＝12HD＝12×3916x＝3932x，∵∠F AH＋∠AHF＝90°，∠MHG＋∠HGM＝90°，∴∠F AH＝∠HGM，在Rt △HGM 中，HG ＝HM sin ∠HGM ＝3932x 35＝6532x ， ∵FH ＋GH ＝194， ∴1516x ＋6532x ＝194，解得x ＝85， ∴此⊙O 的半径为52×85＝4.。

2020年九年级数学中考几何探究型问题：线段最值问题——“费马点”问题(包含答案)

几何探究型问题(针对第25题)线段最值问题“费马点”问题【问题背景】“费马点”——就是到三角形三个顶点的距离之和最小的点．“费马点”问题在中考考查时主要隐藏在求PA＋PB＋PC的最小值问题，通常将某三角形绕点旋转一定的角度，从而将三条线段转化在同一条直线上，利用两点之间线段最短解决问题．【模型分析】对于一个各角不超过120°的三角形，“费马点”是对各边的张角都是120°的点，对于有一个角超过120°的三角形，费马点就是这个内角的顶点．费马点P使它到△ABC三个顶点的距离之和PA＋PB＋PC最小，这就是所谓的“费马”问题．如图，将△APC绕点A逆时针旋转60°到△AP′C′，则可以构造出等边三角形APP′，从而得到AP＝PP′，CP＝C′P′，所以将PA＋PB＋PC的值转化为PP′＋PB＋P′C′的值，则线段BC′的长即为所求的最小值．例题1．如图，已知点P为等边三角形ABC外接圆的劣弧BC上任意一点，求证：PB＋PC＝PA．证明：如答图，在P A上截取PM＝PC，连接CM.∵△ABC 是等边三角形，∴∠ABC ＝∠ACB ＝60°，BC ＝AC ．∵∠ABC ＝∠APC ，∴∠MPC ＝60°，∴△MPC 是等边三角形，∴∠MCP ＝60°，MC ＝PC ，∴∠ACM ＝∠BCP .在△BPC 和△AMC 中，⎩⎪⎨⎪⎧BC ＝AC ，∠BCP ＝∠ACM ，PC ＝MC ，∴△BPC ≌△AMC (SAS)，∴BP ＝AM ，∴PB ＋PC ＝AM ＋PM ＝P A ．2．已知三个村庄A ，B ，C 构成了如图所示的△ABC(其中∠A ，∠B ，∠C 均小于120°)，现选取一点P 作为打水井，使水井P 到三个村庄A ，B ，C 所铺设的输水管总长度最小．求输水管总长度的最小值．解：如答图，以BC 为边在△ABC 的外部作等边三角形BCD ，连接AD ．∴AD 的长就是△ABC 的费马距离．易得∠ABD ＝90°，∴AD ＝AB 2＋BD 2＝5(km)．答：输水管总长度的最小值为5 km.练习(2019·陕师大附中六模)问题提出(1)如图1，在△ABC 中，BC ＝2，将△ABC 绕点B 顺时针旋转60°得到△A ′BC ′，则CC ′＝______.【解答】由旋转的性质可知∠CBC ′＝60°，BC ′＝BC ，则∠△BCC ′是等边三角形，故CC ′＝BC ＝2.问题探究(2)如图2，在△ABC中，AB＝BC＝3，∠ABC＝30°，点P为△ABC内一点，连接PA，PB，PC，求PA＋PB＋PC的最小值，并说明理由．解题思路将△ABP绕点B逆时针旋转60°得到△EBF，连接PF，EC．易证PA＋PB＋PC＝EF＋PF＋PC；由PC＋PF＋EF≥EC，推出当点P，F在直线EC上时，PA＋PB＋PC的值最小，即为EC的长，求出EC的长即可解决问题．【解答】如答图1，将△ABP绕点B逆时针旋转60°得到△EBF，连接PF，EC．由旋转的性质可知△PBF是等边三角形，∴PB＝PF.∵P A＝EF，∴P A＋PB＋PC＝EF＋PF＋PC．∵PC＋PF＋EF≥EC，∴当点P，F在直线EC上时，P A＋PB＋PC的值最小，易得BC＝BE＝BA＝3，∠CBE＝90°，∴EC＝2BC＝32，∴P A＋PB＋PC的最小值为3 2.问题解决(3)如图3，在四边形ABCD中，AD∥BC，AB＝6，AD＝4，∠ABC＝∠BCD＝60°.在四边形ABCD内部有一点P，满足∠APD＝120°，连接BP，CP，点Q为△BPC内的任意一点，是否存在一点P和一点Q，使得PQ＋BQ＋CQ有最小值？若存在，请求出这个最小值；若不存在，请说明理由．解题思路将△PBQ绕点B逆时针旋转60°得到△EBG，则PQ＝EG，△BQG是等边三角形，易知PQ＋BQ＋CQ＝EG＋GQ＋QC≥EC，推出当EC取得最小值时，PQ ＋BQ ＋CQ 的值最小．延长BA 交CD 的延长线于点S ，作△ADS 的外接圆⊙O ，将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OB ，OP .易证△BEO ′≌△BPO(SAS)，推出EO ′＝OP ＝433，故点E 在以点O ′为圆心，433为半径的圆上，则当点E 在线段CO ′上时，EC 的值最小，最小值为CO ′－EO ′的长．【解答】如答图2，将△PBQ 绕点B 逆时针旋转60°得到△EBG ，连接GQ ，EC ，则PQ ＝EG ，△BQG 是等边三角形，∴BQ ＝QG ，∴PQ ＋BQ ＋CQ ＝EG ＋GQ ＋QC ≥EC ，∴当EC 取得最小值时，PQ ＋BQ ＋CQ 的值最小．如答图3，延长BA 交CD 的延长线于点S ，作△ADS 的外接圆⊙O ，连接OB ．将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OP.易证△BEO ′≌△BPO (SAS)，∴EO ′＝PO .∵∠APD ＋∠ASD ＝180°，∴A ，P ，D ，S 四点共圆，∴OP ＝433，∴EO ′＝433， ∴点E 在以点O ′为圆心，433为半径的圆上， ∴当点E 在线段CO ′上时，EC 的值最小，最小值为CO ′－EO ′的长，连接OO ′，延长OO ′到点R ，使得O ′R ＝OO ′，连接BR ，则∠OBR ＝90°，作RH ⊥CB 交CB 的延长线于点H ，O ′T ⊥CH 于点T ，OM ⊥BC 于点M .易知在Rt △OBM 中，BM ＝5，OM ＝1133， ∴OB ＝OM 2＋BM 2＝1433， ∴BR ＝3OB ＝14.易知△BHR ∽△OMB ，∴RH BM ＝BR OB，∴RH ＝5 3.∵HR ∥O ′T ∥OM ，OO ′＝RO ′，∴TM ＝TH ，∴O ′T ＝RH ＋OM 2＝1333，∴BT ＝O ′B 2－O ′T 2＝3， ∴CO ′＝CT 2＋O ′T 2＝2633， ∴CE ＝CO ′－EO ′＝2633－433＝2233， ∴PQ ＋BQ ＋CQ 的最小值为2233.类型三 “阿氏圆”问题【问题背景】“PA ＋k ·PB ”型的最值问题是近几年中考考查的热点，更是一个难点．当k 的值为1时，即可转化为“PA ＋PB ”之和最短问题，就可用我们常见的“将军饮马”问题模型来处理，即可以转化为轴对称问题来处理．当k 取任意不为1的正数时，此类问题的处理通常以动点P 的运动轨迹不同来分类，一般分为两类研究，即点P 在直线上运动和点P 在圆上运动．其中点P 在圆周上运动的类型称之为“阿氏圆”问题．【模型分析】如图1，⊙O 的半径为r ，点A ，B 都在⊙O 外，P 为⊙O 上一动点，已知r ＝k ·OB ，连接PA ，PB ，则当PA ＋k ·PB 的值最小时，点P 的位置如何确定？如图2，在线段OB 上截取OC ，使OC ＝k ·r ，则可证明△BPO 与△PCO 相似，即k ·PB ＝PC ．故求PA ＋k ·PB 的最小值可以转化为PA ＋PC 的最小值，其中A ，C 为定点，P 为动点，当点P ，A ，C 共线时，PA ＋PC 的值最小，如图3.“阿氏圆”模型解题策略：第一步：连接动点与圆心O(一般将含有k 的线段两端点分别与圆心O 相连)，即连接OB ，OP ；第二步：计算线段OP 与OB 及OP 与OA 的线段比，找到线段比为k 的情况，如例子中的OP OB ＝k ；第三步：在OB 上取点C ，使得OC OP ＝OP OB ；第四步：连接AC ，与⊙O 的交点即为点P .例题如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝4，CA ＝6，⊙C 的半径为2，P 为圆上一动点，连接AP ，BP ，求AP ＋12BP 的最小值．解：如答图，连接CP ，在CB 上取点D ，使CD ＝1，连接AD ，PD ．∵CD CP ＝CP BC ＝12，∠PCD ＝∠BCD ， ∴△PCD ∽△BCP ，∴PD BP ＝12， ∴PD ＝12BP ，∴AP ＋12BP ＝AP ＋PD ， ∴要使AP ＋12BP 最小，则AP ＋PD 最小，当点A ，P ，D 在同一条直线时，AP ＋PD 最小，即AP ＋12BP 的最小值为AD 的长．在Rt △ACD 中，∵CD ＝1，AC ＝6，∴AD ＝AC 2＋CD 2＝37，∴AP ＋12BP 的最小值为37. 练习问题提出(1)如图1，已知线段AB 和BC ，AB ＝2，BC ＝5，则线段AC 的最小值为______.解题思路当点A 在线段BC 上时，线段AC 有最小值．【解答】∵当点A 在线段BC 上时，线段AC 有最小值，∴线段AC 的最小值为5－2＝3.问题探究(2)如图2，已知在扇形COD 中，∠COD ＝90°，DO ＝CO ＝6，A 是OC的中点，延长OC 到点F ，使CF ＝OC ，P 是CD ︵上的动点，点B 是OD 上的一点，BD ＝1.①求证：△OAP ∽△OPF .解题思路由题意可得OA OP ＝OP OF ＝12，由相似三角形的判定可得△OAP ∽△OPF . 【解答】∵A 是OC 的中点，DO ＝CO ＝6＝OP ，∴OA OP ＝12. ∵CF ＝OC ，∴OF ＝2OC ＝2OP ，∴OP OF ＝12， ∴OA OP ＝OP OF，且∠AOP ＝∠POF ，∴△OAP ∽△OPF .②求BP ＋2AP 的最小值．解题思路由相似三角形的性质可得PF ＝2AP ，可得BP ＋2AP ＝BP ＋PF ，即当F ，P ，B 三点共线时，BP ＋2AP 有最小值，最小值为BF 的长，由勾股定理即可求解．【解答】∵△OAP ∽△OPF ，∴AP PF ＝OP OF ＝12， ∴PF ＝2AP .∵BP ＋2AP ＝BP ＋PF ，∴当F ，P ，B 三点共线时，BP ＋2AP 有最小值，最小值为BF 的长．∵DO ＝CO ＝6，BD ＝1，∴BO ＝5，OF ＝12，∴BF ＝OB 2＋OF 2＝13.问题解决(3)如图3，有一个形状为四边形ABCD 的人工湖，BC ＝9千米，CD ＝4千米，∠BCD ＝150°，现计划在湖中选取一处建造一座假山P ，且BP ＝3千米，为方便游客观光，从C ，D 分别建小桥PD ，PC ．已知建桥PD 每千米的造价是3万元，建桥PC 每千米的造价是1万元，建桥PD 和PC 的总造价是否存在最小值？若存在，请确定点P 的位置，并求出总造价的最小值，若不存在，请说明理由．(桥的宽度忽略不计)解题思路以点B 为圆心，3为半径作圆交AB 于点E ，交BC 于点F ，点P 为EF ︵上一点，连接BP ，PC ，PD ，在BC 上截取BM ＝1，连接MD ，PM ，过点D 作DG ⊥CB ，可证△BPM ∽△BCP ，可得PC ＝3PM ，当点P 在线段MD 上时，建桥PD 和PC 的总造价有最小值，由勾股定理可求MD 的值，即可求出建桥PD 和PC 的总造价的最小值．【解答】存在．如答图，以点B 为圆心，3为半径作圆交AB 于点E ，交BC 于点F ，P 为EF ︵上一点，连接BP ，PC ，PD ，在BC 上截取BM ＝1，连接MD ，PM ，过点D 作DG ⊥BC 交BC 的延长线于点G .∵BM BP ＝13＝BP BC，且∠PBM ＝∠CBP ， ∴△BPM ∽△BCP ，∴PM CP ＝BM BP ＝13，∴PC ＝3PM . ∵建桥PD 和PC 的总造价为3PD ＋PC ＝3PD ＋3PM ＝3(PD ＋PM )，∴当点P 在线段MD 上时，建桥PD 和PC 的总造价有最小值．∵∠BCD ＝150°，∴∠DCG ＝30°.∵DG ⊥BC ，∴DG ＝12DC ＝23(千米)，CG ＝3DG ＝6(千米)， ∴MG ＝BC ＋CG －BM ＝9＋6－1＝14(千米)，∴MD ＝DG 2＋MG 2＝413(千米)，∴建桥PD 和PC 的总造价的最小值为3×413＝1213万元．作业5．(2019·交大附中三模)问题提出(1)如图1，点M ，N 是直线l 外两点，在直线l 上找一点K ，使得MK ＋NK 最小．问题探究(2)如图2，在等边三角形ABC 内有一点P ，且P A ＝3，PB ＝4，PC ＝5，求∠APB 的度数．问题解决(3)如图3，矩形ABCD是某公园的平面图，AB＝30 3 米，BC＝60米，现需要在对角线BD上修一凉亭E，使得到公园出口A，B，C的距离之和最小．问：是否存在这样的点E？若存在，请画出点E的位置，并求出EA＋EB＋EC的最小值；若不存在，请说明理由．解：(1)如答图1，连接MN，与直线l交于点K，点K即为所求．(2)如答图2，把△APB绕点A逆时针旋转60°得到△AP′C，连接PP′.由旋转的性质，得P′A＝P A＝3，P′C＝PB＝4，∠P AP′＝60°，∠AP′C＝∠APB，∴△APP′是等边三角形，∴PP′＝P A＝3，∠AP′P＝60°.∵PP′2＋P′C2＝32＋42＝25，PC2＝52＝25，∴PP′2＋P′C2＝PC2，∴△PP′C为直角三角形，且∠PP′C＝90°，∴∠AP′C＝∠AP′P＋∠PP′C＝60°＋90°＝150°，∴∠APB＝∠AP′C＝150°.(3)存在．如答图3，把△ABE绕点B逆时针旋转60°得到△A′BE′，连接EE′.答图由旋转的性质，得A′B＝AB＝30 3 米，BE′＝BE，A′E′＝AE，∠E′BE＝60°，∠A′BA＝60°，∴△E′BE是等边三角形，∴BE＝EE′，∴EA ＋EB ＋EC ＝A ′E ′＋EE ′＋EC ．根据两点之间线段最短，可知当EA ＋EB ＋EC ＝A ′C 时最短，连接A ′C ，与BD 的交点E 2即为所求，此时EA ＋EB ＋EC 最短，最短距离为A ′C 的长度．过点A ′作A ′G ⊥CB 交CB 的延长线于点G . ∵∠A ′BG ＝90°－∠A ′BA ＝90°－60°＝30°， A ′G ＝12A ′B ＝12AB ＝12×303＝153(米)，∴GB ＝3A ′G ＝3×153＝45(米)， ∴GC ＝GB ＋BC ＝45＋60＝105(米)．在Rt △A ′GC 中，A ′C ＝A ′G 2＋GC 2＝(153)2＋1052＝3013(米)，因此EA ＋EB ＋EC 的最小值为3013 米． 6．问题提出(1)如图1，已知△OAB 中，OB ＝3，将△OAB 绕点O 逆时针旋转90°得△OA ′B ′，连接BB ′，则BB ′＝问题探究(2)如图2，已知△ABC 是边长为43的等边三角形，以BC 为边向外作等边三角形BCD ，P 为△ABC 内一点，将线段CP 绕点C 逆时针旋转60°，点P 的对应点为点Q .①求证：△DCQ ≌△BCP . ②求P A ＋PB ＋PC 的最小值．问题解决(3)如图3，某货运场为一个矩形场地ABCD ，其中AB ＝500米，AD ＝800米，顶点A ，D 为两个出口，现在想在货运广场内建一个货物堆放平台P ，在BC 边上(含B ，C 两点)开一个货物入口M ，并修建三条专用车道P A ，PD ，PM .若修建每米专用车道的费用为10 000元，当M ，P 建在何处时，修建专用车道的费用最少？最少费用为多少？(结果保留根号)解：(1)由旋转的性质，得∠BOB ′＝90°，OB ＝OB ′＝3，根据勾股定理，得BB ′＝3 2. (2)①证明：∵△BDC 是等边三角形， ∴CD ＝CB ，∠DCB ＝60°.由旋转的性质，得∠PCQ ＝60°，PC ＝QC ， ∴∠DCQ ＝∠BCP .在△DCQ 和△BCP 中，⎩⎪⎨⎪⎧CD ＝CB ，∠DCQ ＝∠BCP ，CQ ＝CP ，∴△DCQ ≌△BCP (SAS)． ②如答图1，连接AD ，PQ . ∵PC ＝CQ ，∠PCQ ＝60°，∴△CPQ 是等边三角形，∴PQ ＝PC ，由①知DQ ＝PB ，∴P A ＋PB ＋PC ＝P A ＋QD ＋PQ ，由两点之间线段最短，得P A ＋QD ＋PQ ≥AD ， ∴P A ＋PB ＋PC ≥AD ，∴当点A ，P ，Q ，D 在同一条直线上时，P A ＋PB ＋PC 取得最小值，即为AD 的长，过点D 作DE ⊥AC ，交AC 的延长线于点E . ∵△ABC 是边长为43的等边三角形， ∴CB ＝AC ＝43，∠BCA ＝60°， ∴CD ＝CB ＝43，∠DCE ＝60°， ∴DE ＝6，∠DAE ＝∠ADC ＝30°， ∴AD ＝12，即P A ＋PB ＋PC 的最小值为12.答图(3)如答图2，将△ADP 绕点A 逆时针旋转60°，得△AD ′P ′.由(2)知，当点M ，P ，P ′，D ′在同一条直线上时，P A ＋PM ＋PD 最小，最小值为D ′M 的长．∵M 在BC 上，∴当D ′M ⊥BC 时，D ′M 取得最小值．设D ′M 交AD 于点E ，连接DD ′，AM ，DM . 易知△ADD ′是等边三角形，∴EM ＝AB ＝500米， ∴BM ＝400米，PM ＝EM －PE ＝(500－40033)米，∴D ′E ＝32AD ＝4003(米)，∴D ′M ＝(4003＋500)米， ∴最少费用为10 000×(4003＋500)＝ 1 000 000(43＋5)元．∴当M 建在BC 的中点(BM ＝400米)处，点P 在过M 且垂直于BC 的直线上，且在M上方(500－40033)米处时，修建专用车道的费用最少，最少费用为1 000 000(43＋5)元．类型三 “阿氏圆”问题7．(2018·西工大附中三模) 问题提出(1)如图1，在△ABC 中，AB ＝AC ，BD 是AC 边的中线，请用尺规作图作出AB 边的中线CE ，并证明BD ＝CE ；问题探究(2)如图2，已知点P 是边长为6的正方形ABCD 内部一动点，P A ＝3，求PC ＋12PD 的最小值；问题解决(3)如图3，在矩形ABCD 中，AB ＝18，BC ＝25，点M 是矩形内部一动点，MA ＝15，当MC ＋35MD 最小时，画出点M 的位置，并求出MC ＋35MD 的最小值．解：(1)如答图1，线段EC 即为所求．证明：∵AB ＝AC ，AE ＝EB ，AD ＝CD ，∴AE ＝AD ，在△BAD 和△CAE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠A ＝∠A ，AD ＝AE ，答图1∴△BAD ≌△CAE (SAS)，∴BD ＝CE . (2)如答图2，在AD 上截取AE ，使得AE ＝32.∵P A 2＝9，AE ·AD ＝32×6＝9，∴P A 2＝AE ·AD ，∴P A AD ＝AEP A.∵∠P AE ＝∠DAP ，∴△P AE ∽△DAP ， ∴PE DP ＝P A DA ＝12，∴PE ＝12PD ， ∴PC ＋12PD ＝PC ＋PE .∵PC ＋PE ≥EC ，∴PC ＋12PD 的最小值即为EC 的长，在Rt △CDE 中，∵∠CDE ＝90°，CD ＝6，DE ＝92，∴EC ＝62＋(92)2＝152，∴PC ＋12PD 的最小值为152.答图(3)如答图3，在AD 上截取AE ，使得AE ＝9. ∵MA 2＝225，AE ·AD ＝9×25＝225，∴MA 2＝AE ·AD ，∴MA AD ＝AEMA.∵∠MAE ＝∠DAM ，∴△MAE ∽△DAM ， ∴EM MD ＝MA DA ＝1525＝35，∴ME ＝35MD ， ∴MC ＋35MD ＝MC ＋ME .∵MC ＋ME ≥EC ，∴MC ＋35MD 的最小值即为EC 的长．如答图3，以点A 为圆心，AM 长为半径画弧，交EC 于点M ′，点M ′即为所求．在Rt △CDE 中，∵∠CDE ＝90°，CD ＝18，DE ＝16， ∴EC ＝162＋182＝2145， ∴MC ＋35MD 的最小值为2145.8．(1)如图1，已知正方形ABCD 的边长为4，⊙B 的半径为2，P 是⊙B 上的一个动点，求PD ＋12PC 的最小值和PD －12PC 的最大值；(2)如图2，已知正方形ABCD 的边长为9，⊙B 的半径为6，P 是⊙B 上的一个动点，那么PD ＋23PC 的最小值为，PD －23PC 的最大值为(3)如图3，已知菱形ABCD 的边长为4，∠B ＝60°，⊙B 的半径为2，P 是⊙B 上的一个动点，那么PD ＋12PC 的最小值为，PD －12PC 的最大值为解：(1)如答图1，在BC 上取一点G ，使得BG ＝1，连接PB ，PG ，DG .∵PB BG ＝CBPB＝2，∠PBG ＝∠CBP ， ∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝12，∴PG ＝12PC ， ∴PD ＋12PC ＝PD ＋PG .∵PD ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋12PC 的值最小，最小值为DG ＝42＋32＝5.∵PD －12PC ＝PD －PG ≤DG ，∴如答图2，当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为5.答图(2)106，106.【解法提示】如答图3，在BC 上取一点G ，使BG ＝4，连接PG ，PB ，DG . ∵PB BG ＝64＝32，CB PB ＝96＝32，∴PB BG ＝CB BP. ∵∠PBG ＝∠CBP ，∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝23， ∴PG ＝23PC ，∴PD ＋23PC ＝DP ＋PG .∵DP ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋23PC 的值最小，最小值为DG ＝52＋92＝106.∵PD －23PC ＝PD －PG ≤DG ，∴当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为106.答图(3)37，37.【解法提示】如答图4，在BC 上取一点G ，使得BG ＝1，连接PB ，PG ，DG ，作DF ⊥BC 交BC 的延长线于点F .∵PB BG ＝21＝2，BC PB ＝42＝2，∴PB BG ＝CB BP. ∵∠PBG ＝∠CBP ，∴△PBG ∽△CBP ， ∴PG CP ＝BG BP ＝12， ∴PG ＝12PC ，∴PD ＋12PC ＝DP ＋PG .∵DP ＋PG ≥DG ，∴当D ，P ，G 三点共线时，PD ＋12PC 的值最小，最小值为DG 的长．在Rt △CDF 中，∵∠DCF ＝60°，CD ＝4， ∴DF ＝CD ·sin60°＝23，CF ＝2，∴在Rt △GDF 中，DG ＝(23)2＋52＝37. ∴PD ＋12PC 的最小值为37.∵PD －12PC ＝PD －PG ≤DG ，∴当点P 在DG 的延长线上时，PD －12PC 的值最大，最大值为37.。

2020年九年级中考数学几何压轴之几何探究题(含答案)

∴ △ABD≌△ CAF(AAS)；归纳证明 :∵∠ 1=∠ 2=∠ BAC,∠1=∠BAE＋ ∠ ABE, ∠ BAC=∠ BAE＋∠ CAF,∠2=∠FCA＋∠ CAF, ∴ ∠ABE=∠ CAF,∠BAE=∠FCA, 在 △ABE 和△CAF 中,
8 / 17
知识像烛光，能照亮一个人，也能照亮无数的人。--培根
2. 特例探究 :如图 ①,已知在△ABC 中,AB=BC,
∠ ABC=90°,D 为 AC 边的中点 ,连接 BD,判断△ABD 是什么三角形,并说明理由;
归纳证明 :如图 ②,已知在△ABC 中,AB=BC,∠ ABC=90°,把 Rt△DEF 的直角顶点 D 放在 AC 的
中点上,DE 交 AB 于 M,DF 交 BC 于 N,连接 BD．证明:DM=DN；
拓展应用 :在图 ②中,AC=4,其他条件都不发生变化 ,请直接写出 Rt△DEF 与△ABC 的重叠部分
的面积．
2 / 17
知识像烛光，能照亮一个人，也能照亮无数的人。--培根
第 2 题图
特例探究 :解:△ABD 是等腰直角三角形．
知识像烛光，能照亮一个人，也能照亮无数的人。--培根
2020 中考数学几何压轴之几何探究题（含答案）
1. 两个全等的直角三角形 ABC 和 DEF 重叠在一起,其中∠A=60°,AC=1,固定△ABC 不动,将△DEF 进行如下操作:
(1)操作发现如图①,△DEF 沿线段 AB 向右平移(即 D 点在线段 AB 内移动),连接 DC、CF、FB,四边形 CDBF 的形状在不断变化,但它的面积不变化,请求出其面积； (2)猜想论证如图②,当 D 点移到 AB 的中点时,请你猜想四边形 CDBF 的形状,并说明理由； (3)拓展研究如图③,将△DEF 的 D 点固定在 AB 的中点,然后绕 D 点按顺时针方向旋转△DEF,使 DF 落在 AB 的边上,此时 F 点恰好与 B 点重合,连接 AE,求 sinα 的值.

2020中考数学几何综合探究专题练习（含答案）

2020中考数学几何综合探究专题练习例题1.如图，在等腰梯形仙CD中，AD//BC,AB=DC=5O,AD=75,BC=135,点F从点3出发沿折线段BA-AD-DC以每秒5个单位长度的速度向点C匀速运动，点。

从点。

出发沿线段CB方向以每秒3个单位长度的速度匀速运动，过点Q向上作射线QK±BC,交折线段CD-ZM-AB于点E,点P、。

同时开始运动，当点F与点C重合时停止运动，点。

也随之停止，设点P、。

运动的时间是，秒(r>0)(1)当点P到达终点C时，求I的值，并指出此时3Q的长；(2)当点P运动到AD上时，I为何值能使PQ。

？(3)设射线好扫过梯形ABCD的面积为S,分别求出点E运动到CD,D4上时，S与t的函数关系式；(不必写出f的取值范围)【答案】⑴7=5。

+；+50=35（$）时，点p到达终点。

,此时，QC=35x3=105,所以3Q的长为135—105=30.⑵如图1,PQ//DC,又曷〃8C,则四边形FQC£＞为平行四边形，从而PD=QC,由QC=3t,BA+AP=5ti?5得50+75-5r=3r,解得t=—,8125经检验：当r时，有PQ//DC.⑶①当点E在CD上运动时，如图2,分别过点A、。

作AFXBC于点F,DHLBC于点H,则四边形为矩形，且AABF^ADCH,从而FH=AD=Y5,于是BF=CH=30,..Z)H=*=40.又QC=3t,从而QE=QC tanC=3t—=4t(注：用相似三角形求解亦可)CH19■■S=S AQCE=-QE.QC=6t2.②当点E在ZM上运动时，如图1,过点。

作DH.LBC于点H,由①知DH=40,CH=30,又QC=3t,从而ED=QH=QC-CH=3t-3OS=S梯形“庞=!（网+四）质=120—600•4例题2.如图，E 、F 分别是边长为4的正方形ABCD 的边3C, C£>上的点，CE = 1, CF = 一,直线EF 交 3垂足分别为M , N ,设加的延长线于G,过线段FG 上的一个动点H 作HML4G, HNLAD,HM = x,矩形钢切V 的面积为y (1) 求v 与x 之间的函数关系式；(2) 当x 为何值时，矩形雄HN 的面积最大，最大面积为多少？4 【答案】(1)・.・正方形ABCD 的边长为4, CE = 1, CF = — 3BE = 3CF CF 又 AG//CF, AFEC^AGEB, ——=——，BG = 4BG BE义 HM//BEA AHMG^AEBG, —BG BE4 4:.MG =—x, AM =8——x 3 39y =尤 84 9 / \%2 + 8x （0 <x<4）4 4 9(2)V y = --x 2+8x = --(x-3)+12.•.当x = 3时，矩形面积最大，最大面积为12例题3.如图，在平面直角坐标系中，点A(0,O), B(30,2), C(0, 2),动点Z)以每秒1个单位的速度从点。

2020年中考数学二轮复习题型六：《几何图形的证明及计算》专题训练及答案解析

题型六几何图形的证明及计算类型一与全等三角形有关的证明及计算1.如图，在四边形ABCD中，AC⊥BD于点E，AB＝AC＝BD，点M为BC中点，N为线段AM上的点，且MB ＝MN.(1)求证：BN平分∠ABE；(2)若BD＝1，连接DN，当四边形DNBC为平行四边形时，求线段BC的长；第1题图2.如图①，在等腰三角形ABC中，AB＝AC，在底边BC上取一点D，在边AC上取一点E，使AE＝AD，连接DE，在∠ABD的内部作∠ABF＝2∠EDC，交AD于点F.(1)求证：△ABF是等腰三角形；(2)如图②，BF的延长线交AC于点G.若∠DAC＝∠CBG，延长AC至点M，使GM＝AB，连接BM，点N是BG的中点，连接AN，试判断线段AN、BM之间的数量关系，并证明你的结论．第2题图3.如图①，在△ABC中，∠ACB＝90°，AC＝BC，E为AC 边上的一点，F为AB边上一点，连接CF，交BE于点D，且∠ACF＝∠CBE，CG平分∠ACB交BD于点G.(1)求证：CF＝BG；(2)如图②，延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP＋CF；(3)在(2)问的条件下，当∠GAC＝2∠FCH时，若S△AEG ＝33，BG＝6，求AC的长．图①图②第3题图4.如图①，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D，E分别在AC，BC上，且CD＝CE.(1)求证：∠CAE＝∠CBD；(2)如图②，F是BD的中点，连接CF交AE于点M，求证：AE⊥CF；(3)如图③，F，G分别是BD，AE的中点，连接GF，若AC＝2 2 ，CE＝1，求△CGF的面积．第4题图5.如图①，在正方形ABCD中，O是对角线AC上一点，点E在BC的延长线上，且OE＝OB，OE交CD于点F.(1)求证：△OBC≌△ODC；(2)求证：∠DOE＝∠ABC；(3)把正方形ABCD改为菱形，其他条件不变(如图②)，若∠ABC＝52°，求∠DOE的度数．第5题图6.已知：如图①，等腰直角△ABC和△ECD中，∠ACB＝∠ECD＝90°，AC＝BC，EC＝DC.(1)求证：BE＝AD；(2)如图②，若将△ECD绕点C按逆时针方向旋转一个锐角，①延长BE交AD于点F，交AC于点O.求证：BF⊥AD；②如图③，取BE的中点M，AD的中点N，连接MN，NC，求∠MNC的度数．第6题图类型二与相似三角形有关的证明及计算1.如图①，已知在△ABC中，∠ABC＝90°，AB＝3，BC＝4.点Q是线段AC上的点，过点Q作AC的垂线交线段AB(如图①)或线段AB的延长线(如图②)于点P.(1)当点P在线段AB上时，求证：△AQP∽△ABC；(2)当△PQB为等腰三角形时，求AP的长．第1题图2.如图，在四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，连接DE、CE.(1)求证：AC2＝AB·AD；(2)求证：CE∥AD；(3)若AD＝5，AB＝7，求ACAF的值．第2题图3.如图①，在△ABC中，AB＝AC，点D、E、F分别在BC、AB、AC上，∠EDF＝∠B.(1)求证：DE·CD＝DF·BE；(2)如图②，若D为BC中点，连接EF，A D.①求证：DE平分∠BEF；②若四边形AEDF为菱形，求∠BAC的度数及AEAB的值．第3题图4.如图①，△ABC中，点D在线段AB上，点E在线段CB 延长线上，且BE＝CD，EP∥AC交直线CD的延长线于点P，交直线AB的延长线于点F，∠ADP＝∠AC B.(1)图①中是否存在与AC相等的线段？若存在，请找出，并加以证明，若不存在，说明理由；(2)若将“点D在线段AB上，点E在线段CB延长线上”改为“点D在线段BA延长线上，点E在线段BC延长线上”，其他条件不变(如图②)．当∠ABC＝90°，∠BAC＝60°，AB ＝2时，求线段PE的长．第4题图5.如图①，△ABC中，BC＞AC，CD平分∠ACB交AB于D，E，F分别是AC，BC边上的两点，EF交CD于H.(1)若∠EFC＝∠A，求证：CE·CD＝CH·BC；(2)如图②，若BH平分∠ABC，CE＝CF，BF＝3，AE ＝2，求EF的长；(3)如图③，若CE≠CF，∠CEF＝∠B，∠ACB＝60°，CH＝5，CE＝4 3 ，求ACBC的值．第5题图类型三与全等和相似三角形有关的证明及计算1.如图，等边△ABC边长是8，过点C的直线l∥AB，点D为BC上一点(不与点B，C重合)，将一个60°角的顶点放在D处，它的边始终过点A，另一边与直线l交于点E，DE交AC于点F.(1)若BD＝6，求CF的长；(2)若点D是BC的中点，判定△ADE的形状，并给出证明；(3)若点D不是BC的中点，则(2)中的结论成立吗？如果成立，请给予证明，如果不成立，请说明理由．第1题图2.如图①，在△ABC中，AC＝BC，∠ACB＝90°，点D、P 分别为AC、AB的中点，连接BD、CP，CP交BD于点E，点F在AB上且∠ACF＝∠CB D.(1)求证：CF＝BE；(2)如图②，过点A作AG⊥AB交BD的延长线于点G.①若CF＝6，求DG的长；②设CF交BD于点H，求HECH的值．第2题图3.如图①，已知D是△ABC的边BC上的中点，DE⊥AB 于点E，DF⊥AC于点F，且BE＝CF，点M、N分别是AE、DE上的点，AN⊥FM于点G.(1)若∠BAC＝90°，求证：△ABC为等腰直角三角形；(2)如图②，若∠BAC≠90°，AF＝2DF.①求证：FMAN＝EMDN；②求AN∶FM的值．图①图②第3题图4. (2018六安市模拟)我们知道，三角形三个内角平分线的交点叫做三角形的内心，已知点I为△ABC的内心．(1)如图①，连接AI并延长交BC于点D，若AB＝AC＝3，BC＝2，求ID的长；(2)如图②，过点I作直线交AB于点M，交AC于点N.①若MN⊥AI，求证：MI2＝BM·CN；②如图③，AI的延长线交BC于点D，若∠BAC＝60°，AI＝4，求1AM＋AN1的值．第4题图5.如图①，在△ABC中，∠ACB＝90°，AC＝BC，顶点C 恰好在直线l上，过A、B分别作AD⊥l，BE⊥l，垂足分别为D、E.(1)求证：DE＝AD＋BE；(2)如图②，在△ABC中，当AC＝kBC，其他条件不变，猜想DE与AD、BE的关系，并证明你的结论；(3)如图③，在Rt△ABC中，AC＝4，BC＝12，∠ACB ＝90°，点D是AC的中点，点E在BC上，过点E作EF⊥DE 交AB于点F，若恰好EF＝2DE，求CE的长．图①图②图③第5题图6.如图①，在等腰Rt△ABC中，∠ACB＝90°，AC＝BC, D 为AB的中点，连接CD，将一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E，F，DF与AC交于点M，DE与BC交于点N.(1)若CE＝CF，求证：△DCE≌△DCF；(2)如图②，在∠EDF绕点D旋转的过程中：①探究线段AB与CE、CF之间的数量关系，并证明；42，CE＝2CF，求DN的长．②若AB＝参考答案类型一与全等三角形有关的证明及计算1. (1)证明：∵AB＝AC，点M是BC的中点，∴AM⊥BC，∠BAM＝∠CAM，∴∠CAM＋∠ACM＝90°，∵AC⊥BD，∴∠MBE＋∠ACM＝90°，∴∠BAN＝∠CAM＝∠MBE，∵MB＝MN，∴∠MNB＝∠MBN，∵∠MNB＝∠ABN＋∠BAN，∠MBN＝∠MBE＋∠NBE，∴∠ABN＋∠BAN＝∠MBE＋∠NBE，∴∠ABN＝∠NBE，即BN平分∠ABE；(2)解：连接DN，∵点M为BC中点，MB＝MN，∴MB＝MN＝12BC，∵四边形DNBC为平行四边形，∴BN＝CD，BN∥CD，∴∠DBN＝∠BDC，由(1)知∠ABN＝∠DBN，∴∠ABN＝∠BDC，∵AB＝BD＝1，∴△ABN≌△BDC，∴AN ＝BC ，∴AM ＝AN ＋MN ＝32BC ，由(1)中条件可知AM ⊥BC ，即∠AMB ＝90°，∴AM 2＋MB 2＝AB 2，即(32BC )2＋(12BC )2＝1，解得BC ＝105.第1题解图2. (1)证明：∵等腰三角形ABC 中，AB ＝AC ，∴∠ABD ＝∠ACD ，∵AE ＝AD ，∴∠ADE ＝∠AED ，∵∠BAD ＋∠ABD ＝∠ADE ＋∠EDC ，∠EDC ＋∠ACD ＝∠AED ，∴∠BAD ＝2∠EDC ，∵∠ABF ＝2∠EDC ，∴∠BAD ＝∠ABF ，∴△ABF 是等腰三角形；(2)解：AN ＝12BM .证明：如解图，延长CA 至点H ，使AG ＝AH ，连接BH ， ∵点N 是BG 的中点，点A 是HG 的中点，∴AN ＝12BH ， ∵(1)中已证明∠BAD ＝∠ABF ，且∠DAC ＝∠CBG ， ∴∠CAB ＝∠CBA ，∴CA ＝CB又∵AB ＝AC ，∴△ABC 是等边三角形，∠BAC ＝∠BCA ＝60°，∴∠BAH ＝∠BCM ，∵GM ＝AB ，AB ＝AC ，∴AC ＝GM ，∴CM ＝AG ，∴AH ＝CM ，在△BAH 和△BCM 中，⎩⎪⎨⎪⎧AB ＝BC ∠BAH ＝∠BCM AH ＝CM， ∴△BAH ≌△BCM (SAS)，∴BH ＝BM ，∴AN ＝12BM .第2题解图3. (1)证明：∵∠ACB ＝90°，AC ＝BC ，∴∠A ＝45°，∵CG 平分∠ACB ，∴∠ACG ＝∠BCG ＝45°，∴∠A ＝∠BCG ，在△BCG 和△CAF 中，⎩⎪⎨⎪⎧∠A ＝∠BCG AC ＝BC ∠ACF ＝∠CBE， ∴△BCG ≌△CAF (ASA)，∴CF ＝BG ；(2)证明：∵PC ∥AG ，∴∠PCA ＝∠CAG ，∵AC ＝BC ，∠ACG ＝∠BCG ，CG ＝CG ，∴△ACG ≌△BCG (SAS )，∴∠CAG ＝∠CBE ，∵∠PCG ＝∠PCA ＋∠ACG ＝∠CAG ＋45°＝∠CBE ＋45°，∠PGC ＝∠GCB ＋∠CBE ＝∠CBE ＋45°， ∴∠PCG ＝∠PGC ，∴PC ＝PG ，∵PB ＝BG ＋PG ，BG ＝CF ，∴PB ＝CP ＋CF ；(3)解：如解图，过E 作EM ⊥AG ，交AG 于M ，∵S △AEG ＝12AG ·EM ＝33，由(2)得：△ACG ≌△BCG ，∴BG ＝AG ＝6，∴ 12×6×EM ＝33，解得EM ＝3，设∠FCH ＝x °，则∠GAC ＝2x °，∴∠ACF ＝∠EBC ＝∠GAC ＝2x °，∵∠ACH ＝45°，∴2x ＋x ＝45，解得x ＝15，∴∠ACF ＝∠GAC ＝30°，在Rt △AEM 中，AE ＝2EM ＝23，AM ＝（23）2－（3）2＝3，∴M 是AG 的中点，∴AE ＝EG ＝23，第3题解图∴BE ＝BG ＋EG ＝6＋23，在Rt △ECB 中，∠EBC ＝30°，∴CE ＝12BE ＝3＋3， ∴AC ＝AE ＋EC ＝23＋3＋3＝33＋3.4. (1)证明：在△ACE 和△BCD 中，⎩⎪⎨⎪⎧AC ＝BC ∠ACE ＝∠BCD CE ＝CD， ∴△ACE ≌△BCD ，∴∠CAE ＝∠CBD ；(2)证明：在Rt △BCD 中，点F 是BD 的中点， ∴CF ＝BF ，∴∠BCF ＝∠CBF ，由(1)知，∠CAE ＝∠CBD ，∴∠BCF ＝∠CAE ，∴∠CAE ＋∠ACF ＝∠BCF ＋∠ACF ＝∠BCA ＝90°， ∴∠AMC ＝90°，∴AE ⊥CF ；(3)解：∵AC ＝2 2 ，∴BC ＝AC ＝2 2 ，∵CE ＝1，∴CD ＝CE ＝1，在Rt △BCD 中，根据勾股定理得，BD ＝CD 2＋BC 2＝3 ， ∵点F 是BD 中点， ∴CF ＝DF ＝12BD ＝32，同理：EG ＝12AE ＝32，如解图，连接EF ，过点F 作FH ⊥BC 于点H ，∵∠ACB ＝90°，点F 是BD 的中点，∴FH ＝12CD ＝12， ∴S △CEF ＝12CE ·FH ＝12×1×12＝14，由(2)知，AE ⊥CF ，∴S △CEF ＝12CF ·ME ＝12×32ME ＝34ME ， ∴ 34ME ＝14， ∴ME ＝13， ∴GM ＝EG －ME ＝32－13＝76， ∴S △CFG ＝12CF ·GM ＝12×32×76＝78. 5. (1)证明：∵AC 是正方形ABCD 的对角线，∴BC ＝DC ，∠BCA ＝∠DCA ，第4题解图在△OBC 和△ODC 中，⎩⎪⎨⎪⎧BC ＝DC∠BCO ＝∠DCOCO ＝CO，∴△OBC ≌△ODC (SAS)；(2)证明：由(1)知，△OBC ≌△ODC ，∴∠CBO ＝∠CDO ，∵OE ＝OB ，∴∠CBO ＝∠E ，∴∠CDO ＝∠E ，∵∠DFO ＝∠EFC ，∴180°－∠DFO －∠CDO ＝180°－∠EFC －∠E ，即∠DOE ＝∠DCE ，∵AB ∥CD ，∴∠DCE ＝∠ABC ，∴∠DOE ＝∠ABC ；(3)解：∵AC 是菱形ABCD 的对角线，∴BC ＝DC ，∠BCA ＝∠DCA ，在△BCO 和△DCO 中，⎩⎪⎨⎪⎧BC ＝DC∠BCO ＝∠DCO CO ＝CO， ∴△BCO ≌△DCO (SAS)，∴∠CBO ＝∠CDO ，∵OE ＝OB ，∴∠CBO ＝∠E ，∴∠CDO ＝∠E ，∵∠DFO ＝∠EFC ，∴180°－∠DFO －∠CDO ＝180°－∠EFC －∠E ，即∠DOE ＝∠DCE ，∵AB ∥CD ，∴∠DCE ＝∠ABC ，∴∠DOE ＝∠ABC ＝52°.6. (1)证明：在△BEC 和△ACD 中，⎩⎪⎨⎪⎧BC ＝AC ∠ACB ＝∠ECD EC ＝DC， ∴△BEC ≌△ADC (SAS)，∴BE ＝AD ；(2)①证明：∵∠ACB ＝∠ECD ＝90°，∴∠ACB －∠ACE ＝∠ECD －∠ACE ，即∠BCE ＝∠ACD ，在△BEC 和△ADC 中，⎩⎪⎨⎪⎧BC ＝AC ∠BCE ＝∠ACD EC ＝DC，∴△BEC ≌△ADC (SAS)，∴∠CBE ＝∠CAD ，在△BCO 和△AFO 中，∠CBE ＝∠CAD ，∠BOC ＝∠AOF ，∴∠AFB ＝∠ACB ＝90°，∴BF ⊥AD ；②解：如解图，连接MC ，∵∠ACB ＝∠ECD ＝90°，∴∠BCE ＝∠ACD ，又∵AC ＝BC ，EC ＝DC ，∴△BEC ≌△ADC ，∴∠CBE ＝∠CAD ，AD ＝BE ，∵M 是BE 的中点，N 是AD 的中点，∴BM ＝AN ，在△BMC 和△ANC 中，⎩⎪⎨⎪⎧BM ＝AN ∠CBE ＝∠CAD BC ＝AC， ∴△BMC ≌△ANC (SAS)，∴CM ＝CN ，∠BCM ＝∠ACN ，∴∠ACN ＋∠MCA ＝∠BCM ＋∠MCA ，∴∠MCN ＝∠ACB ＝90°，∴△MCN 是等腰直角三角形，∴∠MNC＝45°.第6题解图类型二与相似三角形有关的证明及计算1. (1)证明：∵PQ⊥AQ，∴∠AQP＝90°＝∠ABC.在△AQP与△ABC中，∵∠AQP＝∠ABC，∠QAP＝∠BAC，∴△AQP∽△ABC；(2)解：在Rt△ABC中，AB＝3，BC＝4，由勾股定理得AC＝5.①当点P在线段AB上时，如题图①所示．∵∠QPB为钝角，∴当△PQB为等腰三角形时，只可能是PB＝PQ，由(1)可知，△AQP∽△ABC，∴P AAC＝PQBC，即3－PB5＝BP4，解得PB＝4 3，∴AP＝AB－PB＝3－43＝53；②当点P在线段AB的延长线上时，如题图②所示．∵∠QBP为钝角，∴当△PQB为等腰三角形时，只可能是PB＝BQ.∴∠BQP＝∠P，∵∠BQP＋∠AQB＝90°，∠A＋∠P＝90°，∴∠AQB＝∠A，∴BQ＝AB，∴AB＝BP，∴AP＝2AB＝2×3＝6.综上所述，当△PQB为等腰三角形时，AP的长为53或6.2. (1)证明：∵AC平分∠DAB，∴∠DAC＝∠CAB.又∵∠ADC＝∠ACB＝90°，∴△ADC∽△ACB，∴ADAC＝ACAB，∴AC2＝AB·AD;(2)证明：∵E为AB的中点，∠ACB＝90°，∴CE＝12AB＝AE，∴∠EAC＝∠ECA，∵∠DAC＝∠CAB，∴AD∥CE；(3)解：∵CE∥AD，∴∠DAF＝∠ECF，又∵∠DF A＝∠EFC，∴△AFD∽△CFE，∴ADCE＝AFCF，∵CE＝12AB，∴CE＝12×7＝72，∵AD＝5，∴5 72＝AF CF，∴CFAF＝710，∴AF＋CFAF＝1＋CFAF＝1710，即ACAF＝1710.3. (1)证明：∵△ABC中，AB＝AC，∴∠B＝∠C，∵∠B＋∠BDE＋∠DEB＝180°，∠BDE＋∠EDF＋∠FDC＝180°，∠EDF＝∠B，∴△CFD∽△BDE，∴DEDF＝BECD，即DE·CD＝DF·BE；(2)①证明：由(1)证得△BDE∽△CFD，∴BECD＝DEDF，∵D为BC中点，∴BD＝CD，∴BEBD＝DEDF，∵∠B＝∠EDF，∴△BDE∽△DFE，∴∠BED＝∠DEF，∴ED平分∠BEF；②解：∵四边形AEDF为菱形，∴∠AEF＝∠DEF，由(2)知，∠BED＝∠DEF，∵∠AEF＋∠DEF＋∠BED＝180°，∴∠AEF＝60°，∵AE＝AF，∴∠BAC＝60°.∵AB＝AC，∴△ABC是等边三角形，∴∠B＝60°，又∵∠BED＝∠AEF＝60°，∴△BED是等边三角形，∴BE＝DE，∵AE＝DE，∴AE＝BE＝12AB，∴AEAB＝12.4.解：(1)AC＝BF.证明如下：∵∠ADP＝∠ACD＋∠A，∠ACB＝∠ACD＋∠BCD，∠ADP＝∠ACB，∴∠BCD＝∠A，又∵∠CBD＝∠ABC，∴△CBD∽△ABC，∴CDAC＝BCBA，①∵FE∥AC，∴∠CAB＝∠EFB，又∵∠ABC＝∠FBE，∴△ABC∽△FBE，∴BCBA＝BEBF，②由①②可得CDAC＝BEBF，∵BE＝CD，∴BF＝AC；(2)∵∠ABC＝90°，∠BAC＝60°，∴∠ACB＝30°＝∠ADP，∴∠BCD＝60°，∠ACD＝60°－30°＝30°，∵PE∥AC，∴∠E＝∠ACB＝30°，∠CPE＝∠ACD＝30°，∴CP＝CE，∵BE＝CD，∴BE－CE＝CD－CP，∴BC＝DP，∵∠ABC＝90°，∠D＝30°，∴BC＝12CD，∴DP＝12CD，即P为CD的中点，又∵PF∥AC，∴F是AD的中点，∴FP是△ADC的中位线，∴FP＝12AC，∵∠ABC＝90°，∠ACB＝30°，∴AB＝12AC，∴FP＝AB＝2，∵DP＝CP＝BC，CP＝CE，∴BC＝CE，即C为BE的中点，又∵EF∥AC，∴A为FB的中点，∴AC是△BEF的中位线，∴EF＝2AC＝4AB＝8，∴PE＝EF－FP＝8－2＝6.5. (1)证明：∵∠EFC＋∠FEC＋∠ECF＝180°，∠A＋∠B＋∠ACB＝180°，又∵∠EFC＝∠A，∠ECF＝∠ACB，∴∠CEF＝∠B，∵∠ECH＝∠DCB，∴△ECH∽△BCD，∴ECBC＝CHCD，∴CE·CD＝CH·BC；(2)解：如解图①，连接AH.∵BH、CH分别是∠ABC和∠ACB的平分线，∴AH是∠BAC的平分线，∴∠BHC＝180°－12(∠ABC＋∠ACB)＝180°－12(180°－∠BAC)＝90°＋12∠BAC＝90°＋∠HAE，∵CE＝CF，∠HCE＝∠HCF，∴CH⊥EF，HF＝HE，∴∠CHF＝90°，∵∠BHC＝∠BHF＋∠CHF＝∠BHF＋90°，∴∠HAE＝∠BHF，∵CE＝CF，∴∠CFE＝∠CEF，∴∠AEH＝∠BFH，∴△AEH∽△HFB，∴AEHF＝EHFB，∴FH·EH＝6，∴HE＝HF＝6，∴EF＝26；第5题解图①(3)解：如解图②，作HM⊥AC于M，HN⊥BC于N.设HF＝x，FN＝y.∵∠HCM＝∠HCN＝30°，HC＝5，∴HM＝HN＝5 2，CM＝CN＝53 2，∵CE＝4 3 ，∴EM＝332，∴EH＝EM2＋HM2＝13 ，∵S△HCF∶S△HCE＝FH∶EH＝FC∶EC，∴x∶13＝(y＋532)∶43，又∵x2＝y2＋(52) 2，解得y＝5314或332，∵当y＝332时，CF＝CN＋NF＝43，又∵CE≠CF，∴y≠332，即FN＝5314，∴CF＝203 7，∵∠CEF＝∠B，∠ECF＝∠ACB，∴△ECF∽△BCA，∴ECBC＝CFAC，∴AC BC＝CFEC＝203743＝57.第5题解图②类型三与全等和相似三角形有关的证明及计算1.解：(1)∵△ABC是等边三角形，∴∠B＝∠FCD＝60°，∵∠BAD＝180°－60°－∠ADB，∠FDC＝180°－∠ADE －∠ADB＝180°－60°－∠ADB，∴∠BAD＝∠FDC，∴△ABD∽△DCF，∴ABDC＝BDCF，∴CF＝DC·BDAB＝（8－6）×68＝32；(2)△ADE是等边三角形．证明：若D点是BC边中点，则AD⊥BC，∴∠CDE＝∠ADC－∠ADE＝90°－60°＝30°，又∵l∥AB，∴∠DCE＝180°－∠ABC＝180°－60°＝120°，∴∠CED ＝180°－∠DCE －∠CDE ＝180°－120°－30°＝30°，即∠CDE ＝∠CED ，∴CE ＝CD .在△ACD 和△ACE 中，⎩⎪⎨⎪⎧AC ＝AC∠ACD ＝∠ACE ＝60°DC ＝EC， ∴△ACD ≌△ACE (SAS)，∴AD ＝AE ，又∵∠ADE ＝60°，∴△ADE 是等边三角形；(3)(2)中结论仍然成立．证明：如解图，过点D 作DG ∥l 交AC 于点G ，则△GDC ∽△ABC ，∴△GDC 是等边三角形，∴DG ＝DC ，∠GDC ＝∠DGC ＝60°，∵∠ADE ＝60°，∴∠ADE ＝∠GDC ，∴∠ADG ＝∠EDC ，又∵∠AGD ＝180°－60°＝120°，∠DCE ＝180°－∠ABC ＝120°，∴∠AGD ＝∠DCE ，在△ADG 和△EDC 中，⎩⎪⎨⎪⎧∠ADG ＝∠EDC DG ＝DC ∠AGD ＝∠DCE， ∴△ADG ≌△EDC (ASA)，∴AD ＝DE ，又∵∠ADE ＝60°，∴△ADE 是等边三角形．2. (1)证明：∵P 为AB 的中点，AC ＝BC ，∠ACB ＝90°，∴∠BCE ＝12∠ACB ＝12×90°＝45°，∠A ＝45°， ∴∠A ＝∠BCE ，在△ACF 和△CBE 中⎩⎪⎨⎪⎧∠A ＝∠BCE AC ＝BC ∠ACF ＝∠CBD， ∴△ACF ≌△CBE (ASA)，∴CF ＝BE ；(2)解：①由(1)得CF ＝BE ，∴BE ＝CF ＝6，∵AC ＝BC ，CE 平分∠ACB ，P 为AB 的中点， ∴CP ⊥AB ，∵AG ⊥AB ，第1题解图∴CE∥AG，∴∠GAD＝∠ECD，又∵∠ADG＝∠CDE，∴△ADG∽△CDE，∵点D是AC的中点，∴AD＝CD，即相似比k＝1，∴△ADG≌△CDE，∴DG＝DE＝12GE，∵CE∥AG且P为AB中点，∴GE＝BE＝6，∴DG＝3；②设EP＝a，由(2)①得EP∥AG，∴AG＝2a，又由上题得△ADG≌△CDE，∴CE＝AG＝2a，∴CP＝CE＋EP＝3a，∵等腰直角△ABC中CP⊥AB，∴BP＝CP＝3a，由题得∠ACP＝∠CBP＝45°，∵∠ACF＝∠CBD，∴∠ACP－∠ACF＝∠CBP－∠CBD，即∠HCE＝∠PBE ，∵∠CEH ＝∠PEB ，∴∠CHE ＝180°－∠CEH －∠HCE ，∠BPE ＝180°－∠PBE －∠PEB ，∴∠CHE ＝∠BPE ＝90°，∴△CHE 是直角三角形，∴△CHE ∽△BPE ，∴HE CH ＝PE BP ＝a3a ＝13.3. (1)证明：∵DE ⊥AB ，DF ⊥AC ，∴∠BED ＝∠CFD ＝90°，∵D 是BC 的中点，∴BD ＝CD ，在Rt △BED 和Rt △CFD 中，⎩⎪⎨⎪⎧BD ＝CD BE ＝CF，∴Rt △BED ≌Rt △CFD (HL)，∴∠B ＝∠C ，∵∠BAC ＝90°，∴△ABC 为等腰直角三角形；(2)①证明：如解图，连接AD 、EF ，相交于点O ， ∵由(1)可得Rt △BED ≌Rt △CFD ，∴∠B ＝∠C ，DE ＝DF ，∴AB ＝AC ，∵BE ＝CF ，∴AE ＝AF ，∴AD ⊥EF ，又∵∠NEM ＝∠MGN ＝90°，∴∠GME ＋∠ENG ＝∠DNG ＋∠ENG ＝180°， ∴∠EMF ＝∠DNA ，又∵∠AEO ＋∠EAO ＝90°，∠EAO ＋∠NDA ＝90°， ∴∠AEO ＝∠NDA ，∴△FME ∽△AND ， ∴FM AN ＝EM DN；第3题解图②解：设AF ＝2k ，DF ＝k ，在Rt △ADF 中，AD ＝（2k ）2＋k 2＝5k ，由①可得∠B ＝∠C ，DE ＝DF ，∴AD 垂直平分EF ，则OF ＝12EF ， ∵DF ⊥AC ， ∴S △ADF ＝12×5k ·OF ＝12×2k ×k ，∴OF ＝255k ，EF ＝455k ，∴AD EF ＝54，又∵△FME ∽△AND ，∴ANFM ＝ADEF ＝54，即AN ∶FM ＝5∶4.4. (1)解：如解图①中，作IE ⊥AB 于E .设ID ＝x ， ∵AB ＝AC ＝3，AI 平分∠BAC ，∴AD ⊥BC ，BD ＝CD ＝1，在Rt △ABD 中，AD ＝AB 2－BD 2＝32－12＝2 2 ，在△BEI 和△BDI 中，⎩⎪⎨⎪⎧∠EBI ＝∠DBI ，∠BEI ＝∠BDI ＝90°，BI ＝BI ，∴△BEI ≌△BDI ，∴ID ＝IE ＝x ，BD ＝BE ＝1，AE ＝2，在Rt △AEI 中，∵AE 2＋EI 2＝AI 2，∴22＋x 2＝(22－x )2 ，∴x ＝22，∴ID ＝22；第4题解图(2)①证明：如解图②，连接BI、CI.∵I是内心，∴∠MAI＝∠NAI，∵AI⊥MN，∴∠AIM＝∠AIN＝90°，又∵AI＝AI，∴△AMI≌△ANI(ASA)，∴∠AMN＝∠ANM，∴∠BMI＝∠CNI，设∠BAI＝∠CAI＝α，∠ACI＝∠BCI＝β，∴∠NIC＝90°－α－β，∵∠ABC＝180°－2α－2β，∴∠MBI＝90°－α－β，∴∠MBI＝∠NIC，∴△BMI∽△INC，∴BMNI＝MINC，∴NI·MI＝BM·CN，∵NI＝MI，∴MI2＝BM·CN；②解：如解图③，过点N作NG∥AD交MA的延长线于G.∵NG∥AD，∴∠ANG＝∠DAN，∠AGN＝∠BAD，∵∠BAC＝60°，∴∠BAD＝∠DAN＝30°，∴∠ANG＝∠AGN＝30°，∴AN＝AG，NG＝3AN，∵AI∥NG，∴∠MIA＝∠MNG，∠MAI＝∠MGN，∴△AMI∽△GMN，∴AMMG＝AING，∴AMAM＋AN＝43AN，∴AM＋ANAM＝3AN4，∴1AM＋1AN＝34.第4题解图③5. (1)证明：∵∠ACB ＝90°，∴∠ACD ＋∠BCE ＝90°，∵AD ⊥DE ，BE ⊥DE ，∴∠DAC ＋∠DCA ＝90°，∠ADC ＝∠BEC ， ∴∠DAC ＝∠ECB ，在△ADC 和△CEB 中，⎩⎪⎨⎪⎧∠ADC ＝∠CEB ∠DAC ＝∠ECB AC ＝CB， ∴△ADC ≌△CEB (AAS)，∴AD ＝CE ，CD ＝BE ，∴DE ＝CE ＋DC ＝AD ＋BE ；(2)解：DE ＝kBE ＋1kAD . 证明：∵∠ACB ＝90°，∴∠ACD ＋∠BCE ＝90°，∵AD ⊥DE ，∴∠DAC ＋∠DCA ＝90°，∴∠DAC ＝∠ECB ，∵AD ⊥DE ，BE ⊥DE ，∴∠ADC ＝∠CEB ＝90°，∴△ADC ∽△CEB ，∴ADCE＝DCBE＝ACBC＝k，∴DC＝kBE，CE＝1k AD，∴DE＝DC＋CE＝kBE＋1k AD；(3)解：如解图，过点F作FG⊥BC于点G，∵AC＝4，D是AC的中点，∴CD＝2，∵EF＝2DE，易证△DCE∽△EGF，FG＝2CE，EG＝2DC ＝4，设CE＝x，则BG＝BC－CG＝12－4－x＝8－x，∵FG⊥BC，AC⊥BC，∴∠ACB＝∠FGB＝90°，∵∠B＝∠B，∴△FGB∽△ACB，∴FGAC＝BGBC，即2x4＝8－x12，解得x＝8 7，即CE的长为8 7.第5题解图6. (1)证明：∵∠ACB ＝90°，AC ＝BC ，D 为AB 的中点，∴∠BCD ＝∠ACD ＝45°，∠BCE ＝∠ACF ＝90°， ∴∠DCE ＝∠DCF ＝135°，在△DCE 与△DCF 中，⎩⎪⎨⎪⎧CE ＝CF ∠DCE ＝∠DCF CD ＝CD， ∴△DCE ≌△DCF (SAS)；(2) ①解：AB 2＝4CE ·CF .证明：∵∠DCF ＝∠DCE ＝135°，∴∠CDF ＋∠F ＝180°－135°＝45°，∵∠CDF ＋∠CDE ＝45°，∴∠F ＝∠CDE ，∴△CDF ∽△CED ，∴CD CE ＝CF CD，即CD 2＝CE ·CF ，∵∠ACB ＝90°，AC ＝BC ，CD 平分∠ACB ，∴CD ＝AD ＝BD ＝12AB ， ∴(12AB )2＝CE ·CF ， ∴AB 2＝4CE ·CF ；②解：如解图，过D 作DG ⊥BC 于G ，由①得AB2＝4CE·CF，∵AB＝42，CE＝2CF，∴CE＝4，CF＝2，∵DG⊥BC于G，由题得∠B＝45°，BD＝12AB＝2 2∴△DGB是等腰直角三角形，∴BG＝DG＝22·sin45°＝2，∵DG⊥BC，AC⊥BC，∴DG∥AC即DG∥CE，∴∠ECN＝∠DGN又∵∠ENC＝∠DNG∴△CEN∽△GDN，∴CEDG＝CNNG＝42＝2，又∵D点为AB中点，DG∥AC，∴CG＝BG＝2，∴NG＝13CG＝23，在Rt△DGN中，DN＝DG2＋NG2＝22＋（23）2＝2103.第6题解图。

2020中考数学临考冲刺与圆相关的证明与计算(含答案)

2020中考数学临考冲刺与圆相关的证明与计算（含答案）一、选择题（本大题共5道小题）1. 下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形，又是中心对称图形;③在同圆中，相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为 ()A.1B.2C.3D.42. 如图，☉O的直径AB垂直于弦CD.垂足是点E，∠CAO=22.5°，OC=6，则CD的长为()A.6√2B.3√2C.6D.123. 如图，将☉O沿弦AB折叠，AB⏜恰好经过圆心O，若☉O的半径为3，则AB⏜的长为()A.1πB.π2C.2πD.3π4. 如图，△ABC内心为I，连接AI并延长交△ABC的外接圆于D，则线段DI与DB的关系是()A.DI=DBB.DI>DBC.DI<DBD.不确定5. 如图，在半径为√13的☉O中，弦AB与CD交于点E，∠DEB=75°，AB=6，AE=1，则CD的长是()A.2√6B.2√10C.2√11D.4√3二、填空题（本大题共4道小题）6. 如图，一下水管道横截面为圆形，直径为100 cm，下雨前水面宽为60 cm，一场大雨过后，水面宽为80 cm，则水位上升了cm.7. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形.若圆锥的底面圆半径r=2 cm，扇形的圆心角θ=120°，则该圆锥的母线长l为cm.8. 如图，在平面直角坐标系中，已知☉D经过原点O，与x轴、y轴分别交于A，B两点，点B坐标为(0，2√3)，OC与☉D交于点C，∠OCA=30°，则图中阴影部分的面积为(结果保留根号和π).9. 在Rt△ABC中，AB=1，∠A=60°，∠ABC=90°，如图所示，将Rt△ABC沿直线l无滑动地转动至Rt△DEF，则点B所经过的路径与直线l所围成的封闭图形的面积为.(结果不取近似值)三、解答题（本大题共5道小题）10. 如图，BD是☉O的直径，弦BC与OA相交于点E，AF与☉O相切于点A，交DB的延长线于点F，∠F=30°，∠BAC=120°，BC=8.(1)求∠ADB的度数;(2)求AC的长度.11. 如图，BC是☉O的直径，CE是☉O的弦，过点E作☉O的切线，交CB的延长线于点G，过点B作BA⊥GE于点F，交CE的延长线于点A.(1)求证:∠ABG=2∠C;(2)若GF=3√3，GB=6，求☉O的半径.12. 如图，在Rt△ABC中，∠ABC=90°，以AB为直径作☉O，点D为☉O上一点，且CD=CB，连接DO并延长交CB的延长线于点E.(1)判断直线CD与☉O的位置关系，并说明理由;(2)若BE=2，DE=4，求☉O的半径及AC的长.13. 如图，在△ABC中，AB=AC，以AB为直径的☉O与边BC，AC分别交于D，E两点，过点D作DH⊥AC于点H.(1)判断DH与☉O的位置关系，并说明理由;(2)求证:点H为CE的中点.14. 如图，AB为☉O的直径，且AB=4√3，点C是AB⏜上的一动点(不与A，B重合)，过点B作☉O的切线交AC的延长线于点D，点E是BD的中点，连接EC.(1)求证:EC是☉O的切线;(2)当∠D=30°时，求图中阴影部分的面积.2020中考数学临考冲刺与圆相关的证明与计算-答案一、选择题（本大题共5道小题）1. 【答案】C2. 【答案】A[解析]∵∠A=22.5°，∴∠COE=45°，∵☉O 的直径AB 垂直于弦CD ， ∴∠CEO=90°，CE=DE. ∵∠COE=45°， ∴CE=OE=√22OC=3√2， ∴CD=2CE=6√2，故选A .3. 【答案】C[解析]连接OA ，OB ，过点O 作OD ⊥AB 交AEB⏜于点E ，由题可知OD=DE=12OE=12OA ，在Rt △AOD 中，sin A=ODOA =12，∴∠A=30°， ∴∠AOD=60°，∠AOB=120°，∴AB⏜的长=n πr 180=2π，故选C .4. 【答案】A[解析]连接BI ，如图，∵△ABC 内心为I ，∴∠1=∠2，∠5=∠6.∵∠3=∠1，∴∠3=∠2.∵∠4=∠2+∠6=∠3+∠5，∴∠4=∠DBI，∴DI=DB.故选A.5. 【答案】C[解析]过点O作OF⊥CD于点F，OG⊥AB于G，连接OB，OD，OE，AB=3，如图所示，则DF=CF，AG=BG=12∴EG=AG-AE=2.在Rt△BOG中，OG=√OB2-BG2=√13-9=2，∴EG=OG，∴△EOG是等腰直角三角形，∴∠OEG=45°，OE=√2OG=2√2.∵∠DEB=75°，∴∠OEF=30°，OE=√2.∴OF=12在Rt△ODF中，DF=√OD2-OF2=√13-2=√11，∴CD=2DF=2√11.故选C.二、填空题（本大题共4道小题）6. 【答案】10或70[解析]作OD⊥AB于C，OD交☉O于点D，连接OB.由垂径定理得:BC=12AB=30 cm .在Rt △OBC 中，OC=√OB 2-BC 2=40(cm). 当水位上升到圆心以下且水面宽80 cm 时，圆心到水面距离=√502-402=30(cm)，水面上升的高度为:40-30=10(cm).当水位上升到圆心以上且水面宽80 cm 时，水面上升的高度为:40+30=70(cm). 综上可得，水面上升的高度为10 cm 或70 cm . 故答案为10或70.7. 【答案】6[解析]2π×2=120π·l 180，∴l=6.8. 【答案】2π-2√3[解析]连接AB ，∵∠AOB=90°， ∴AB 是直径，根据同弧所对的圆周角相等得∠OBA=∠C=30°， ∵OB=2√3，∴OA=OB tan ∠ABO=OB tan30°=2√3×√33=2，AB=AO sin30°=4，即圆的半径为2， ∴S 阴影=S 半圆-S △ABO =π×222−12×2×2√3=2π-2√3.9. 【答案】1912π+√32 [解析]在Rt △ABC 中，AB=1，∠A=60°，∴BC=√3，∠BCB'=150°，∠B'A'E=120°，点B 第一次转动的路径是以点C 为圆心，BC 为半径的BB'⏜，根据扇形面积公式得，S 扇形BCB'=5π4，第二次转动的路径是以A'为圆心，A'B'为半径的B'E ⏜，S 扇形B'A'E =π3. △A'B'C 的面积为12×1×√3=√32，所求面积为5π4+π3+√32=19π12+√32. 三、解答题（本大题共5道小题） 10. 【答案】解:(1)∵AF 与☉O 相切于点A ，∴AF ⊥OA ， ∵BD 是☉O 的直径，∴∠BAD=90°，∵∠BAC=120°，∴∠DAC=30°，∴∠DBC=∠DAC=30°， ∵∠F=30°，∴∠F=∠DBC ，∴AF ∥BC ， ∴OA ⊥BC ，∴∠BOA=90°-30°=60°， ∴∠ADB=12∠AOB=30°.(2)∵OA ⊥BC ，∴BE=CE=12BC=4， ∴AB=AC ，∵∠AOB=60°，OA=OB ，∴△AOB 是等边三角形，∴AB=OB ， ∵∠OBE=30°，∴OE=12OB ，BE=√3OE=4， ∴OE=4√33，∴AC=AB=OB=2OE=8√33. 11. 【答案】解:(1)证明:连接OE ，∵EG是☉O的切线，∴OE⊥EG，∵BF⊥GE，∴OE∥AB，∴∠A=∠OEC，∵OE=OC，∴∠OEC=∠C，∴∠A=∠C，∵∠ABG=∠A+∠C，∴∠ABG=2∠C. (2)∵BF⊥GE，∴∠BFG=90°，∵GF=3√3，GB=6，∴BF=√BG2-GF2=3，∵BF∥OE，∴△BGF∽△OGE，∴BF OE =BGOG，∴3OE=66+OE，∴OE=6，∴☉O的半径为6.12. 【答案】解:(1)直线CD与☉O相切.理由如下:连接CO.∵点D在圆上，∴OD=OB，又∵CD=CB，CO=CO，∴△COD≌△COB(SSS).∵∠ABC=90°，∴∠ODC=∠ABC=90°，∴OD⊥DC，∴直线CD与☉O相切.(2)设☉O的半径为x，∵DE=4，∴OE=4-x.在Rt△OBE中，BE2+BO2=OE2，即22+x2=(4-x)2，解得x=1.5，∴OD=OB=1.5.AB=2OB=3.∵CB，CD是圆的切线，∴CB=CD.则设CB=CD=y，在Rt△CDE中，CD2+DE2=CE2，即y2+42=(y+2)2，解得y=3，∴BC=3.在Rt△ABC中，AC=√AB2+BC2=3√2.13. 【答案】[解析](1)连接OD，AD，先利用圆周角定理得到∠ADB=90°，再根据等腰三角形的性质得BD=CD，再证明OD为△ABC的中位线得到OD∥AC，根据DH⊥AC，所以OD⊥DH，然后根据切线的判定定理可判断DH为☉O的切线. (2)连接DE，由圆内接四边形的性质得∠DEC=∠B，再证明∠DEC=∠C，然后根据等腰三角形的性质得到CH=EH.解:(1)DH与☉O相切.理由如下:连接OD，AD，如图，∵AB为直径，∴∠ADB=90°，即AD⊥BC，∵AB=AC，∴BD=CD，而AO=BO，∴OD为△ABC的中位线，∴OD∥AC，∵DH⊥AC，∴OD⊥DH，∴DH为☉O的切线.(2)证明:连接DE，如图，∵四边形ABDE为☉O的内接四边形，∴∠DEC=∠B，∵AB=AC，∴∠B=∠C，∴∠DEC=∠C，∵DH⊥CE，∴CH=EH，即H为CE的中点.14. 【答案】解:(1)证明:连接OC，BC，OE，∵AB是☉O的直径，∴∠ACB=∠BCD=90°.∵点E是BD的中点，∴CE=BE，∵OB=OC，OE=OE，∴△OBE≌△OCE.∵BD是☉O的切线，∴∠OBE=90°=∠OCE，∵OC是☉O的半径，∴EC是☉O的切线.(2)∵∠D=30°，∠OBD=90°，∴∠A=60°，∴∠BOC=120°，∠EOB=60°. ∵AB=4√3，∴OB=2√3，BE=6， ∴S 阴影=2S △OBE -S 扇形OBC =2×12×6×2√3−120π×(2√3)2360=12√3-4π.。

专题八几何证明之四边形中的三角形全等问题 2020年中考数学冲刺难点突破几何证明问题(解析版)

2020年中考数学冲刺难点突破几何证明问题专题八几何证明之四边形中的三角形全等问题1、如图1，已知正方形ABCD，E是线段BC上一点，N是线段BC延长线上一点，以AE为边在直线BC的上方作正方形AEFG．（1）连接GD，求证DG＝BE；（2）连接FC，求tan∠FCN的值；（3）如图2，将图1中正方形ABCD改为矩形ABCD，AB＝3，BC＝8，E是线段BC上一动点（不含端点B，C），以AE为边在直线BC的上方作矩形AEFG，使顶点G恰好落在射线CD上．当点E由B向C运动时，判断tan∠FCN的值是否为定值？若是，求出该定值；若不是，请说明理由．解：（1）如图1，∵正方形ABCD和正方形AEFG中，∴∠BAD＝∠EAG＝90°，AB＝AD，AE＝AG，∴△BAE≌△GAD（SAS），∴DG＝BE；（2）如图2，过点F作FM⊥BN于M，则∠B＝∠AEF＝∠FME＝90°，∴∠BAE+∠AEB＝∠FEM+∠AEB＝90°，即∠BAE＝∠FEM，又AE＝EF，∴△BAE≌△MEF（ASA），∴FM＝BE，EM＝AB，又BE+EC＝AB，EM＝EC+CM，∴CM＝FM，在Rt△FCM中，tan∠FCN＝＝1；（3）如图2，过点F作FM⊥BN于M，则∠B＝∠AEF＝∠FME＝90°，∴∠BAE+∠AEB＝∠FEM+∠AEB＝90°，同理可证∠GAD＝∠FEM，又AG＝EF，∴△DAG≌△MEF，△BAE∽△MEF，∴EM＝AD＝BC＝8，＝，设BE＝a，则EM＝EC+CM＝BC＝BE+EC，∴CM＝BE＝a，∴＝，∴FM＝，∴tan∠FCN＝＝＝，即tan∠FCN的值为定值．2、【操作发现】如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连结AM、AN、MN．∠MAN＝45°，将△AMD 绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而得DM+BN＝MN．【实践探究】（1）在图①条件下，若CN＝3，CM＝4，则正方形ABCD的边长是．（2）如图②，点M、N分别在边CD、AB上，且BN＝DM．点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由．【拓展】（3）如图③，在矩形ABCD中，AB＝3，AD＝4，点M、N分别在边DC、BC上，连结AM，AN，已知∠MAN＝45°，BN＝1，求DM的长．【实践探究】（1）解：∵四边形ABCD是正方形，∴AB＝CD＝AD，∠BAD＝∠C＝∠D＝90°，由旋转得：△ABE≌△ADM，∴BE＝DM，∠ABE＝∠D＝90°，AE＝AM，∠BAE＝∠DAM，∴∠BAE+∠BAM＝∠DAM+∠BAM＝∠BAD＝90°，即∠EAM＝90°，∵∠MAN＝45°，∴∠EAN＝90°﹣45°＝45°，∴∠MAN＝∠EAN，在△AMN和△EAN中，，∴△AMN≌△EAN（SAS），∴MN＝EN．∵EN＝BE+BN＝DM+BN，∴MN＝BN+DM．在Rt△CMN中，MN＝＝＝5，则BN+DM＝5，设正方形ABCD的边长为x，则BN＝BC﹣CN＝x﹣3，DM＝CD﹣CM＝x﹣4，∴x﹣3+x﹣4＝5，解得：x＝6，即正方形ABCD的边长是6；故答案为：6；（2）EF2＝BE2+DF2，理由如下：如图②，将△AFD绕点A顺时针旋转90°，点D与点B重合，得到△ABH，连结EH，∴∠ADF＝∠ABH，DF＝BH，∠DAF＝∠BAH，AH＝AF，∵∠EAF＝45°，∴∠DAF+∠BAE＝45°＝∠BAH+∠BAE，∴∠HAE＝45°＝∠EAF，又∵AH＝AF，AE＝AE，∴△EAH≌△EAF（SAS），∴HE＝EF，∵BN＝DM，BN∥DM，∴四边形BMDN是平行四边形，∴DN∥BM，∴∠AND＝∠ABM，∵∠ADN+∠AND＝90°，∴∠ABH+∠ABM＝90°＝∠HBM，∴BE2+BH2＝HE2，∴EF2＝BE2+DF2；（3）如图③，延长AB至P，使BP＝BN＝1，过P作BC的平行线交DC的延长线于Q，延长AN交PQ 于E，连接EM，则四边形APQD是正方形，∴PQ＝DQ＝AP＝AB+BP＝4，设DM＝x，则MQ＝4﹣x，∵PQ∥BC，∴△ABN∽△APE，∴，∴PE＝BN＝，∴EQ＝PQ﹣PE＝4﹣＝，由（1）得：EM＝PE+DM＝+x，在Rt△QEM中，由勾股定理得：（）2+（4﹣x）2＝（+x）2，解得：x＝2，即DM的长是2．3、如图，将▱ABCD的边AB延长到点E，使BE＝AB，连接DE，交BC边于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，请探究：当∠BFD与∠A之间满足怎样的数量关系时，能使四边形BECD成为矩形？为什么？（1）证明：∵四边形ABCD是平行四边形，∵AB＝CD，AB∥CD．∵BE＝AB，∴BE＝CD．∵AB∥CD，∴∠BEF＝∠CDF，∠EBF＝∠DCF，在△BEF与△CDF中，，∴△BEF≌△CDF（ASA）；（2）解：∠BFD＝2∠A时，四边形BECD成为矩形．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∠A＝∠DCB，∵AB＝BE，∴CD＝EB，∴四边形BECD是平行四边形，∴BF＝CF，EF＝DF，∵∠BFD＝2∠A，∴∠BFD＝2∠DCF，∴∠DCF＝∠FDC，∴DF＝CF，∴DE＝BC，∴四边形BECD是矩形．4、已知在△ABC中，AB＝AC，点D在BC上，以AD、AE为腰做等腰三角形ADE，且∠ADE＝∠ABC，连接CE，过E作EM∥BC交CA延长线于M，连接BM．（1）求证：△BAD≌△CAE；（2）若∠ABC＝30°，求∠MEC的度数；（3）求证：四边形MBDE是平行四边形．（1）证明：∵AB＝AC，∴∠ABC＝∠ACB，∴∠BAC＝180°﹣2∠ABC，∵以AD、AE为腰做等腰三角形ADE，∴AD＝AE，∴∠ADE＝∠AED，∴∠DAE＝180°﹣2∠ADE，∵∠ADE＝∠ABC，∴∠BAC＝∠DAE，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，∴∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS）；（2）解：∵AB＝AC，∴∠ACB＝∠ABC＝30°，∵△BAD≌△CAE，∴∠ABD＝∠ACE＝30°，∴∠ACB＝∠ACE＝30°，∴∠ECB＝∠ACB+∠ACE＝60°，∵EM∥BC，∴∠MEC+∠ECD＝180°，∴∠MEC＝180°﹣60°＝120°；（3）证明：∵△BAD≌△CAE，∴DB＝CE，∠ABD＝∠ACE，∵AB＝AC，∴∠ABD＝∠ACB，∴∠ACB＝∠ACE，∵EM∥BC，∴∠EMC＝∠ACB，∴∠ACE＝∠EMC，∴ME＝EC，∴DB＝ME，又∵EM∥BD，∴四边形MBDE是平行四边形．5、如图，在四边形ABCD中，∠A＝90°，AD∥BC，BC＝BD，CE⊥BD，垂足为E．（1）求证：△ABD≌△ECB；（2）若AD＝4，CE＝3，求CD的长．证明：（1）∵AD∥BC，∴∠ADB＝∠EBC，∵CE⊥BD，∠A＝90°，∴∠A＝∠BEC＝90°，在△ABD和△ECB中，，∴△ABD≌△ECB（AAS）；（2）∵△ABD≌△ECB，∴AB＝CE＝3，∵AD＝4，∴在Rt△ABD中，由勾股定理可得：BD＝5，∵△BD≌△ECB，∴D＝BE＝4，∴DE＝BD﹣BE＝1，∴在Rt△CDE中，由勾股定理得：CD＝．6、已知：矩形ABCD中，点E、F为对角线AC上两点，AF＝CE．（1）如图1，求证：BE∥DF；（2）如图2，当AB＝BE＝AD时，连接DE、BF，在不添加任何辅助线的情况下，请直接写出四个三角形，使写出的每个三角形的面积都等于矩形ABCD面积的．（1）证明：∵四边形ABCD是矩形，∴AD＝BC，AD∥BC，∴∠DAF＝∠BCE，在△AFD和△CEB中，，∴△AFD≌△CEB（SAS），∴∠AFD＝∠CEB，∴BE∥DF；（2）解：△ABF，△CDE，△ADF，△BCE；理由如下：由（1）得：△AFD≌△CEB，同理：△ABF≌△CDE（SAS），∴△AFD的面积＝△CEB的面积，△ABF的面积＝△CDE的面积，作BG⊥AC于G，如图2所示：∵四边形ABCD是矩形，∴∠ABC＝90°，BC＝AD，∵AB＝BE＝AD，∴AB＝BE＝BC，∴BC＝2AB，AC＝＝AB，AG＝EG，∵△ABC的面积＝AC×BG＝AB×BC，∴BG＝＝＝AB，∴AG＝＝＝AB，∴AE＝2AG＝AB，∵AF＝CE，∴△ABF的面积＝△BCE的面积，CF＝AE＝AB，∴AF＝AC﹣CF＝AB﹣AB＝AB，∴△ABF的面积＝AF×BG＝×AB×AB＝AB2，∵矩形ABCD的面积＝AB×BC＝AB×2AB＝2AB2，∴△ABF的面积＝矩形ABCD面积的，∴△ABF的面积＝△CDE的面积＝△ADF的面积＝△BCE的面积＝矩形ABCD面积的．7、如图，在平行四边形ABCD中，点G在CD上，点H在AB上，且DG＝BH，点E．F在AC上，且AE＝CF．连接GF，FH，HE，EG．（1）求证：△CFG≌△AEH；（2）若AG＝GC，则四边形EHFG是什么特殊四边形？请说明理由．证明：（1）∵在平行四边形ABCD中，AB∥CD，AB＝CD，∴∠GCF＝∠HAE，∵DG＝BH，∴GC＝AH，在△CFG与△AEH中，，∴△CFG≌△AEH（SAS）；（2）∵△CFG≌△AEH，∴GF＝EH，∠AEH＝∠GFC，∴∠FEH＝∠EFG，∴四边形EGFH是平行四边形，∵AG＝GC，∴∠GAE＝∠GCF，在△GAE与△GCF中，∴△GAE≌△GCF（SAS），∴EG＝GF，∴平行四边形EGFH是菱形．8、如图，在△ABC中，AB＝AC，AD是BC边上的中线，点E是AD边上一点，过点B作BF∥EC，交AD的延长线于点F，连接BE，CF．（1）求证：△BDF≌△CDE．（2）若DE＝BC，求证：四边形BECF是正方形．（1）证明：∵AD是BC边上的中线，AB＝AC，∴BD＝CD，∴∠DBF＝∠DCE，∵∠BDF＝∠CDE，∴△BDF≌△CDE（ASA）；（2）证明：∵△BDF≌△CDE，∴BF＝CE，DE＝DF，∵BF∥CE，∴四边形BECF是平行四边形，∵AB＝AC，AD是中线，∴四边形BECF是菱形，∵DE＝BC，DE＝DF＝EF，∴EF＝BC，∴四边形BECF是正方形．9、阅读材料：教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力，要增强学生的创新精神和综合素质．王老师想尝试改变教学方法，将以往教会学生做题改为引导学生会学习．于是她在菱形的学习中，引导同学们解决菱形中的一个问题时，采用了以下过程（请解决王老师提出的问题）：先出示问题（1）：如图1，在等边三角形ABC中，D为BC上一点，E为AC上一点，如果BD＝CE，连接AD、BE，AD、BE相交于点P，求∠APE的度数．学习，王老师请同学们说说自己的收获．小明说发现一个结论：在这个等边三角形ABC中，只要满足BD＝CE，则∠APE的度数就是一个定值，不会发生改变．紧接着王老师出示了问题（2）：如图2，在菱形ABCD中，∠A＝60°，E为BC上一点，F为CD上一点，BE＝CF，连接DE、BF，DE、BF相交于点P，如果DP＝4，BP＝3，求出菱形的边长．问题（3）：通过以上的学习请写出你得到的启示（一条即可）．解：问题（1）∵△ABC是等边三角形，∴∠ABD＝∠C＝60°，AB＝BC，在△ABD和△BCE中，，∴△ABD≌△BCE（SAS），∴∠BAD＝∠EBC，∵∠APE＝∠ABP+∠BAP，∴∠APE＝∠ABP+∠EBC＝∠ABC＝60°；问题（2）过点D作DG⊥BF交BF于点G，如图2所示：∵四边形ABCD是菱形，∴∠C＝∠A＝60°，BC＝CD，∴△BCD是等边三角形，∴BC＝CD＝BD，由（1）可知∠DPG＝60°，在Rt△DPG中，sin60°＝，即＝，解得：DG＝2，cos60°＝，即＝，解得：PG＝2，∴BG＝BP+PG＝3+2＝5，在Rt△BDG中，由勾股定理得：BD2＝BG2+DG2＝52+（2）2＝37，∴BD＝，∴BC＝BD＝，∴菱形的边长为；问题（3）平时应该注意基本图形的积累，在学习过程中做个有心人．10、如图1，在正方形ABCD（正方形四边相等，四个角均为直角）中，AB＝8，P为线段BC上一点，连接AP，过点B作BQ⊥AP，交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交AD于点N．（1）求证：BP＝CQ；（2）若BP＝PC，求AN的长；（3）如图2，延长QN交BA的延长线于点M，若BP＝x（0＜x＜8），△BMC'的面积为S，求S与x之间的函数关系式．解：（1）证明：∵∠ABC＝90°∴∠BAP+∠APB＝90°∵BQ⊥AP∴∠APB+∠QBC＝90°，∴∠QBC＝∠BAP，在△ABP于△BCQ中，，∴△ABP≌△BCQ（ASA），∴BP＝CQ，（2）由翻折可知，AB＝BC'，连接BN，在Rt△ABN和Rt△C'BN中，AB＝BC'，BN＝BN，∴Rt△ABN≌△Rt△C'BN（HL），∴AN＝NC'，∵BP＝PC，AB＝8，∴BP＝2＝CQ，CP＝DQ＝6，设AN＝NC'＝a，则DN＝8﹣a，∴在Rt△NDQ中，（8﹣a）2+62＝（a+2）2解得：a＝4.8，即AN＝4.8．（3）解：过Q点作QG⊥BM于G，由（1）知BP＝CQ＝BG＝x，BM＝MQ．设MQ＝BM＝y，则MG＝y﹣x，∴在Rt△MQG中，y2＝82+（y﹣x）2，∴．∴S△BMC′＝S△BMQ﹣S△BC'Q＝＝，＝．11、已知，在△ABC中，∠BAC＝90°，∠ABC＝45°，点D为直线BC上一动点（点D不与点B、C重合），以AD为边做正方形ADEF，连接CF．（1）如图①，当点D在线段BC上时，直接写出线段CF、BC、CD之间的数量关系．（2）如图②，当点D在线段BC的延长线上时，其他件不变，则（1）中的三条线段之间的数量关系还成立吗？如成立，请予以证明，如不成立，请说明理由；（3）如图③，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC两侧，其他条件不变；若正方形ADEF的边长为4，对角线AE、DF相交于点O，连接OC，请直接写出OC的长度．解：（1）∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠DAC，∠CAF＝90°﹣∠DAC，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS），∴BD＝CF，∵BD+CD＝BC，∴CF+CD＝BC；故答案为：CF+CD＝BC；（2）CF+CD＝BC不成立，存在CF﹣CD＝BC；理由：∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠DAC，∠CAF＝90°﹣∠DAC，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS）∴BD＝CF∴BC+CD＝CF，∴CF﹣CD＝BC；（3）∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠BAF，∠CAF＝90°﹣∠BAF，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS），∴∠ACF＝∠ABD，∵∠ABC＝45°，∴∠ABD＝135°，∴∠ACF＝∠ABD＝135°，∴∠FCD＝135°﹣45°＝90°，∴△FCD是直角三角形．∵正方形ADEF的边长4且对角线AE、DF相交于点O．∴DF＝AD＝4，O为DF中点．∴Rt△CDF中，OC＝DF＝×＝．13、已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．（1）如图1，连接BG、DE．求证：BG＝DE；（2）如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD．①求∠BDE的度数；②若正方形ABCD的边长是，请求出△BCG的面积．（1）证明：∵四边形ABCD和四边形CEFG为正方形，∴BC＝DC，CG＝CE，∠BCD＝∠GCE＝90°．∴∠BCD+∠DCG＝∠GCE+∠DCG，∴∠BCG＝∠DCE．在△BCG和△DCE中，，∴△BCG≌△DCE（SAS）．∴BG＝DE；（2）解：①连接BE，如图2所示：由（1）可知：BG＝DE，∵CG∥BD，∴∠DCG＝∠BDC＝45°，∴∠BCG＝∠BCD+∠DCG＝90°+45°＝135°，∵∠GCE＝90°，∴∠BCE＝360°﹣∠BCG﹣∠GCE＝360°﹣135°﹣90°＝135°，∴∠BCG＝∠BCE，在△BCG和△BCE中，，∴△BCG≌△BCE（SAS），∴BG＝BE，∵BG＝BD＝DE，∴BD＝BE＝DE，∴△BDE为等边三角形，∴∠BDE＝60°；②延长EC交BD于点H，过点G作GN⊥BC于N，如图3所示：在△BCE和△DCE中，，∴△BCE≌△BCG（SSS），∴∠BEC＝∠DEC，∴EH⊥BD，BH＝BD，∵BC＝CD＝，∴BD＝BC＝2，∴BE＝2，BH＝1，∴CH＝1，在Rt△BHE中，由勾股定理得：EH＝＝＝，∴CE＝﹣1，∵∠BCG＝135°，∴∠GCN＝45°，∴△GCN是等腰直角三角形，∴GN＝CG＝（﹣1），∴S△BCG＝BC•GN＝××（﹣1）＝．15、利用“同角的余角相等”可以帮助我们得到相等的角，这个规律在全等三角形的判定中有着广泛的运用．（1）如图①，B，C，D三点共线，AB⊥BD于点B，DE⊥BD于点D，AC⊥CE，且AC＝CE．若AB+DE＝6，求BD的长．（2）如图②，在平面直角坐标系中，△ABC为等腰直角三角形，直角顶点C的坐标为（1，0），点A 的坐标为（﹣2，1）．求直线AB与y轴的交点坐标．（3）如图③，∠ACB＝90°，OC平分∠AOB，若点B坐标为（b，0），点A坐标为（0，a）．则S四边形AOBC＝．（只需写出结果，用含a，b的式子表示）解：（1）∵AB⊥BD，DE⊥BD，AC⊥CE，∴∠ABC＝∠CDE＝∠ACE＝90°，∴∠A+∠ACB＝90°，∠ECD+∠ACB＝180°﹣∠ACE＝90°，∴∠A＝∠ECD，在△ABC和△CDE中，，∴△ABC≌△CDE（AAS），∴AB＝CD，BC＝DE，∴BD＝CD+BC＝AB+DE＝6；（2）过点A作AD⊥x轴于D，过点B作BE⊥x轴于E，如图②所示：∵△ABC为等腰直角三角形∴∠ADC＝∠CEB＝∠ACB＝90°，AC＝CB，∴∠DAC+∠ACD＝90°，∠ECB+∠ACD＝180°﹣∠ACB＝90°，∴∠DAC＝∠ECB，在△ADC和△CEB中，，∴△ADC≌△CEB（AAS），∴AD＝CE，CD＝BE，∵点C的坐标为（1，0），点A的坐标为（﹣2，1），∴CO＝1，AD＝1，DO＝2，∴OE＝OC+CE＝OC+AD＝2，BE＝CD＝CO+DO＝3，∴点B的坐标为（2，3），设直线AB的解析式为y＝kx+b，将A、B两点的坐标代入，得，解得：，∴直线AB的解析式为：y＝x+2，当x＝0时，解得y＝2，∴直线AB与y轴的交点坐标为（0，2）；（3）过点C作CD⊥y轴于D，CE⊥x轴于E，如图③所示：∵OC平分∠AOB，∴CD＝CE∴四边形OECD是正方形∴∠DCE＝90°，OD＝OE，∵∠ACB＝90°，∴∠DCA+∠ACE＝∠ECB+∠ACE＝90°，∴∠DCA＝∠ECB，在△DCA和△ECB中，，∴△DCA≌△ECB（ASA），∴DA＝EB，S△DCA＝S△ECB，∵点B坐标为（b，0），点A坐标为（0，a），∴OB＝b，OA＝a，∵OD＝OE，∴OA+DA＝OB﹣BE，即a+DA＝b﹣DA，∴DA＝，∴OD＝OA+DA＝a+＝，∴S＝S四边形AOEC+S△ECB＝S四边形AOEC+S△DCA＝S正方形DOEC＝OD2＝（）2＝，四边形AOBC故答案为：．16、如图1，将边长为2的正方形OABC如图放置在直角坐标系中．（1）如图2，若将正方形OABC绕点O顺时针旋转30°时，求点A的坐标；（2）如图3，若将正方形OABC绕点O顺时针旋转75°时，求点B的坐标．解：（1）过点A作AD⊥x轴于点D，如图2所示：则∠AOD＝30°，∵正方形OABC的边长为2，∴AO＝2，∴AD＝AO＝1，∴OD＝＝＝，∴点A的坐标为：（，﹣1）；（2）连接OB，过点B作BE⊥x轴于点E，如图3所示：则∠AOE＝75°，∵四边形OABC是正方形，∴∠AOB＝45°，OB＝AO＝2，在Rt△BOE中，∠BOE＝∠AOE﹣∠AOB＝30°，∴BE＝OB＝，OE＝BE＝，∴点B的坐标为（，﹣）．。

2020年中考数学热点冲刺5 操作探究问题(含答案解析)

热点专题5 操作探究问题实践操作性问题以趣味性强、思维含量高为特点，在具体的实践操作中主要有以下类型：（1）裁剪、折叠、拼图等问题，往往与面积与对称性相联系；（2）画图、测量、猜想、证明等探究性问题，往往要求答题者在给定的操作规则下，进行探索研究、大胆猜想、发现结论，进而提高个人的创新能力与实践能力.在2019年的中考中，操作性行问题主要包含几何体的展开与折叠，图案设计、程序框输入，尺规作图、几何图形的探究等题型，分值不一，难度不等.考向1几何体的展开与折叠1.（2019·济宁）如图，一个几何体上半部为正四校锥，下半部为立方体，且有一个面涂有颜色，该几何体的表面展开图是（）A B C D【答案】B【解析】选项A和C带图案的一个面是底面，不能折叠成原几何体的形式；选项B能折叠成原几何体的形式；选项D折叠后下面带三角形的面与原几何体中的位置不同．2．（2019·山西）某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与"点"字所在面相对的面上的汉字是( )A．青B．春C．梦D．想【答案】B【解析】根据正方体的展开与折叠中面的关系，可知与"点"字所在面相对的面上的汉字是春，故选B ．考向2 图案设计与几何变换1．（2019·烟台）小明将一张正方形纸片按如图所示的顺序折叠成纸飞机，当机翼展开在同一平面时（机翼间无缝隙），AOB ∠的度数是．【答案】22.5︒【解析】在解本题的过程中，可以找一张正方形的纸片进行如题操作，通过测量，来得到答案，也可以利用图形的轴对称的性质，直接得到AOB ∠的度数是22.5︒．2.（2019·南充）如图，正方形MNCB 在宽为2的矩形纸片一端，对折正方形MNCB 得到折痕AE ，再翻折纸片，使AB 与AD 重合，以下结论错误的是( )A ．210AB =+B ．CD BC C ．2BC CD EH =g D ．sin AHD ∠【答案】A【解析】在Rt AEB ∆中，AB == //AB DH Q ，//BH AD ，∴四边形ABHD 是平行四边形，AB AD =Q ，∴四边形ABHD 是菱形，AD AB ∴=1CD AD AD ∴===，∴CD BC =，故选项B 正确，24BC =Q ，1)4CD EH ==g ，2BC CD EH ∴=g ，故选项C 正确， Q 四边形ABHD 是菱形，AHD AHB ∴∠=∠，sin sin AE AHD AHB AH ∴∠=∠==D 正确，故选：A ． 3．（2019 · 北京）已知30AOB ∠=︒，H 为射线OA 上一定点，1OH =，P 为射线OB 上一点，M 为线段OH 上一动点，连接PM ，满足OMP ∠为钝角，以点P 为中心，将线段PM 顺时针旋转150︒，得到线段PN ，连接ON ．（1）依题意补全图1；（2）求证：OMP OPN ∠=∠；（3）点M 关于点H 的对称点为Q ，连接QP ．写出一个OP 的值，使得对于任意的点M 总有ON=QP ，并证明．解：（1）见下图（2）证明：∵30AOB ∠=︒，∴在△OPM 中，=180150OMP POM OPM OPM ︒-∠-∠=︒-∠∠，又∵150MPN ∠=︒，∴150OPN MPN OPM OPM ∠=∠-∠=︒-∠，∴OMP OPN ∠=∠. （3）如下图，过点P 作PK ⊥OA 于K ，过点N 作NF ⊥OB 于F∵∠OMP=∠OPN ，∴∠PMK=∠NPF ，在△NPF 和△PMK 中，90NPF PMKNFO PKM PN PM ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴△NPF ≌△PMK （AAS ），∴PF=MK ，∠PNF=∠MPK ，NF=PK ，又∵ON=PQ ，在Rt △NOF 和Rt △PKQ 中，ON PQ NF PK =⎧⎨=⎩，∴Rt △NOF ≌Rt △PKQ （HL ），∴KQ=OF ，备用图图1A设,MK y PK x ==，∵∠POA=30°，PK ⊥OQ ，∴2OP x =，∴,OK OM y ==-，∴2OF OP PF x y =+=+，)1MH OH OM y =-=--，1KH OH OK =-.∵M 与Q 关于H 对称，∴MH=HQ ，∴11y -++=2y -+，又∵KQ=OF ，∴22y x y -+=+，∴(22x =+，∴1x =，即PK=1，又∵30POA ∠=︒，∴OP=2. 考向3 程序输入与规律探究1.（2019·重庆A 卷）按如图所示的运算程序，能使输出y 值为1的是（） A ．m=1，n=1 B ．m=1，n=0 C ．m=1，n=2D ．m=2，n=1【答案】D ．【解析】∵m=1，n=1，∴y=2m ＋1=3；∵m=1，n=0，∴y=2n －1=－1；∵m=1，n=2，∴y=2m ＋1=3；∵m=2，n=1，∴y=2n －1=1．故选D ．18.(2019·东营)如图，在平面直角坐标系中，函数x y 33=和x y 3-=的图象分别为直线1l ，2l ，过1l 上的点A 1（1，33）作x 轴的垂线交2l 于点A 2，过点A 2作y 轴的垂线交1l 于点A 3，过点A 3作x 轴的垂线交2l 于点A 4…，一次进行下去，则点2019A 的横坐标为 .【答案】：-31009【解析】：本题考查坐标里的点规律探究题，观察发现规律：A 1（1，33），A 2（1，3-），A 3（-3，3-），A 4（-3，33），A 5（9，33），A 6（9，39-），A 7（-27，39-），……A 2n+1[(-3)n ，3×(-3)n ]（n 为自然数），2019=1009×2+1，所以A 2019的横坐标为：(-3)1009=-31009. 考向4 尺规作图1．（2019·长沙）如图，Rt △ABC 中，∠C=90°，∠B=30°，分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于M 、N 两点，作直线MN ，交BC 于点D ，连接AD ，则∠CAD 的度数是（）A ．20°B ．30°C ．45°D ．60°【答案】B【解析】在△ABC 中，∵∠B=30°，∠C=90°，∴∠BAC=180°-∠B -∠C=60°，由作图可知MN 为AB 的中垂线，∴DA=DB ，∴∠DAB=∠B=30°，∴∠CAD=∠BAC -∠DAB=30°，故本题选：B ．2．（2019·兰州）如图，矩形ABCD ，∠BAC=60°，以点A 为圆心，以任意长为半径作弧分别交AB ，AC 于点M ，N 两点，再分别以点M ，N 为圆心，以大于21MN 的长作半径作弧交于点P ，作射线AP 交BC 于点E ，若BE=1，则矩形ABCD 的面积等于 .【答案】【解析】在矩形ABCD 中，∠BAC=60°，∴∠B=90°，∠BCA=30°，∵AE 平分∠BAC ，∴∠BAE=∠EAC=30°∵在Rt △ABE 中，BE=1，∴AE=1sin30︒=2，AB=1tan30=︒EAC=∠ECA=30°，∴EC=AE=2，∴S矩形ABCD=AB ⋅BC=3.（2019·济宁）如图，点M 和点N 在∠AOB 内部．（1）请你作出点P ，使点P 到点M 和点N 的距离相等，且到∠AOB 两边的距离也相等（保留作图痕迹，不写作法）；（2）请说明作图理由．解：(1)画出∠AOB 的角平分线，画出线段MN 的垂直平分线，两者的交点就得到P 点．（2）作图的理由：点P 在∠AOB 的角平分线上，又在线段MN 的垂直平分线上，∠AOB 的角平分线和线段MN 的垂直平分线的交点即为所求．4. （2019·长春）图①、图②、图③处均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C、D、E、F均在格点上.在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法.（1）在图①中以线段AB为边画一个△ABM，使其面积为6.（2）在图②中以线段CD为边画一个△CDN，使其面积为6.（3）在图③中以线段EF为边画一个四边形EFGH，使其面积为9，且∠EFG=90°.解：（1）如图所示；（2）如图所示；（3）如图所示.考向5 几何探究1．（2019·武汉）问题背景：如图1，将△ABC绕点A逆时针旋转60°得到△ADE，DE与BC交于点P，可推出结论：PA＋PC=PE．问题解决：如图2，在△MNG中，MN=6，∠M=75°，MG=24．点O是△MNG内一点，则点O到△MNG 三个顶点的距离和的最小值是___________．【答案】【解析】由题构造等边△MFN，△MHO，图中2个彩色三角形全等（△MFH≌△MNO（SAS））∴OM＋ON＋OG=HO＋HF＋OG，∴距离和最小值为（Rt△FQG勾股定理）2．（2019·山西）综合与实践动手操作:第一步:如图1，正方形纸片ABCD沿对角线AC所在的直线折叠，展开铺平，再沿过点C的直线折叠，使点B，点D都落在对角线AC上.此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一条直线上，折痕分别为CE，CF.如图2.第二步:再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3.第三步:在图3的基础上继续折叠，使点C与点F重合，得到图4，展开铺平，连接EF，FG，GM，ME，如图5.图中的虚线为折痕.问题解决:（1）在图5中，∠BEC的度数是_____，AEBE的值是_____;（2）在图5中，请判断四边形EMGF的形状，并说明理由;（3）在不增加字母的条件下，请你以图5中的字母表示的点为顶点，动手画出．．．．一个菱形（正方形除外），并写出这个菱形:_______.【解题过程】（1）∵正方形ABCD，∴∠ACB=45°，由折叠知:∠1=∠2=22.5°，∠BEC=∠CEN，BE=EN，∴∠BEC=90°－∠1=67.5°，∴∠AEN=180°－∠BEC－∠CEN=45°，∴cos45°=ENAE=，AEEN=，AE AEBE EN=（2）四边形EMGF是矩形.理由如下:∵四边形ABCD是正方形，∴∠B=∠BCD=∠D=90°，由折叠可知:∠1=∠2=∠3=∠4，CM=CG，∠BEC=∠NEC=∠NFC=∠DFC，∴∠1=∠2=∠3=∠4=°904=22.5°，∴∠BEC=∠NEC=∠NFC=∠DFC=67.5°，由折叠知:MH，GH分别垂直平分EC，FC，∴MC=ME，GC=GF.∴∠5=∠1=22.5°，∠6=∠4=22.5°，∴∠MEF=∠GFE=90°.∵∠MCG=90°，CM=CG，∴∠CMG=45°，又∵∠BME=4图2F∠1+∠5=45°，∴∠EMG=180°－∠CMG －∠BME=90°，∴四边形EMGF 是矩形; （3）答案不唯一，画出正确的图形（一个即可）.菱形FGCH （或菱形EMCH ）3．（2019·淮安）如图①，在△ABC 中，AB=AC=3，∠BAC=100°，D 是BC 的中点.小明对图①进行了如下探究：在线段AD 上任取一点P ，连接PB ．将线段PB 绕点P 按逆时针方向旋转80°，点B 的对应点是点E ，连接BE ，得到△BPE.小明发现，随着点P 在线段AD 上位置的变化，点E 的位置也在变化，点E 可能在直线AD 的左侧，也可能在直线AD 上，还可能在直线AD 的右侧. 请你帮助小明继续探究，并解答下列问题：(1)当点E 在直线AD 上时，如图②所示.①∠BEP= °； ②连接CE ，直线CE 与直线AB 的位置关系是 .(2)请在图③中画出△BPE ，使点E 在直线AD 的右侧，连接CE.试判断直线CE 与直线AB 的位置关系，并说明理由.(3)当点P 在线段AD 上运动时，求AE 的最小值.【解题过程】（1）①由题意得，PE=PB ，∠BPE=80°，∴∠BEP=︒=︒-︒50280180； ②如图所示，∵AB=AC ，D 是BC 的中点，∠BAC=100°，∴∠ABC=︒=︒-︒402100180，∵∠BEP=50°，∴∠BCE=∠CBE=40°，∴∠ABC=∠BCE ，∴CE ∥AB ．答案：①50°；②平行（2）在DA 延长线上取点F ，使∠BFA=∠CFA=40°，总有△BPE ∽△BFC ．又∵△BPF ∽△BEC ，∴∠BCE=∠BFP=40°，∴∠BCE=∠ABC=40°，∴CE ∥AB ．(3)当点P 在线段AD 上运动时，由题意得PB=PE=PC ， ∴点B 、E 、C 在以P 为圆心、PB 为半径的圆上，如图所示：∴AE 的最小值为AC=3.。

2020年中考数学二轮专项——几何动态探究题(含答案)

2020年中考数学二轮专项——几何动态探究题类型一动点探究题1. 如图，在矩形ABCD中，AB＝4，AD＝6，点E，F分别是AB，BC边上的两动点，且EF＝2，点G 为EF的中点，点H为AD边上一动点，连接CH，GH，则GH＋CH的最小值为________．第1题图2. (2019锦江区二诊)如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点D是线段BC上一动点，连接AD，以AD为边作△ADE，使△ADE∽△ABC，则△ADE的最小面积与最大面积之比等于______．第2题图3. (2019金牛区二诊)如图，矩形ABCD中，AB＝5，BC＝7，点E是对角线AC上的动点，EH⊥AD，垂足为H，以EH为边作正方形EFQH，连接AF，则∠AFE的正弦值为________．第3题图4. 如图，两个全等的三角形△ABC和△DEF(点A、B分别与点D、E对应)，AB＝AC＝5，BC＝6，点E在BC边上从点B向点C移动(点E不与B、C重合)，在运动过程中，DE始终经过点A，EF与AC相交于点M，当△AEM是等腰三角形时，BE的长为__________．第4题图5. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝2，点P是边AB上一动点，过点P作BC的垂线交BC 于点D ，点F 与点B 关于直线PD 对称，连接AF ，当△AFC 是等腰三角形时，BD 的长为________．第5题图6. (2018成都黑白卷)如图，△ABC 内接于半径为2的⊙O ，∠ABC ＝45°，∠ACB ＝60°，点D 为AB ︵的中点，点M 、N 分别是CD 、AC 上的动点，则MA ＋MN 的最小值为________．第6题图7. 如图，在矩形ABCD 中，点E 是对角线AC 上的动点，连接BE ，MN 是BE 的垂直平分线，分别交AB 、BC 于点M 、N ，连接EM 、EN .过点E 作EF ⊥AD 于点F ，已知AB ＝1，BC ＝2.若△AEM 是直角三角形，则EF 的长为________．第7题图8. 如图，在矩形ABCD 中，AC 和BD 交于点O ，点E 是边BC 上的动点，连接EO 并延长交AD 于点F ，连接AE ，已知AB ＝1，BC ＝3，若△AEF 是等腰三角形，则DF 的长为________．第8题图9. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝2，BC ＝3，点M 是直线BC 上一动点，且∠CAM ＋∠CBA ＝45°，则BM 的长为________．第9题图10. (2019锦江区一诊)如图，矩形OABC的边OC在x轴上，边OA在y轴上，A点坐标为(0，2)．点D 是线段OC上的一个动点，连接AD，以AD为边作矩形ADEF，使边EF过点B，连接OF.当点D与点C 重合时，所作矩形ADEF的面积为6.在点D的运动过程中，当线段OF有最小值时，直线OF的解析式为________．第10题图类型二平移探究题1. 如图，矩形ABCD中，点E是BC边上一点，连接AE，将△ABE向右平移得到△DCF，连接AF.若四边形AEFD为菱形，AF＝45，BE∶EC＝3∶2，则AD长为________．第1题图2．如图，在Rt△AOB中，OA＝2，OB＝4，点E在OB上，且∠OAE＝∠OB A.将△AEO沿AO方向向右平移得到△A′E′O′，连接A′B、BE′.当A′B＋BE′取得最小值时，则EE′的长是________．第2题图3. 如图，在Rt△ABC中，AB＝AC＝2，∠A＝90°，D是AB延长线上一点，过点B在AD上方作射线BE，使得∠DBE＝45°.将△ABC沿射线BE平移，得到△A′B′C′，其中点A，B，C的对应点分别是A′，B′，C′，连接A′B，C′B，则A′B＋C′B的最小值是________ .第3题图4. (2018成都黑白卷)如图，在▱ABCD中，AB＝6，∠BAD＝45°，∠ABD＝75°，点E为线段BD边上一动点，连接AE，第一步：将△AED剪下平移到△BGC处；第二步：将△ABE剪下平移到△DCF处；第三步：将△BGC沿BC的中垂线翻转180°后得到△CG′B；第四步：将△CFD沿DC的中垂线翻转180°后得到△DF′C，连接F′G′；当点E在BD上移动时，F′G′的最小值为________．第4题图类型三旋转探究题1. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2，AC＝6，在AC上取一点D，使AD＝4，将线段AD 绕点A按顺时针方向旋转，点D的对应点是点P，连接BP，取BP的中点F，连接CF，在旋转过程中，CF的最大长度是________．第1题图2. 在Rt △ABC 中，∠ACB ＝90°，tan ∠BAC ＝12.点D 在边AC 上(不与A ，C 重合)，连接BD ，F 为BD 中点．若BC ＝6，点D 在边AC 的三等分点处，将线段AD 绕点A 旋转，点F 始终为BD 中点，则线段CF 长度的最大值是________．第2题图3. 如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝4，AC ＝3，点D ，E 分别是AB ，AC 的中点，点G ，F 在BC 边上(均不与端点重合)，DG ∥EF .将△BDG 绕点D 顺时针旋转180°，将△CEF 绕点E 逆时针旋转180°，拼成四边形MGFN ，则四边形MGFN 周长l 的取值范围是________．第3题图4. (2019高新区二诊)如图，△ABC ，△EFG 分别是边长为2和233的等边三角形，D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ，当△EFG 绕点D 旋转一周时，点M 经过的路径长为________．第4题图5. 如图，△ABC 和△CDE 都是等腰直角三角形(∠ACB ＝∠DCE ＝90°)．保持△ABC 固定不动，将△CDE 绕点C 顺时针旋转一周，连接AD 、AE 、BD ，直线AE 与BD 相交于点H ，点P 、M 、N 分别是AD 、AB 、DE 的中点，若AC ＝4，CD ＝2，则在旋转过程中，△PMN 的面积的最大值为________．第5题图类型四折叠探究题1. 如图，在矩形ABCD中，AB＝6，AD＝8，E是AB的中点，点F是BC边上的动点，将△EBF沿EF 所在的直线折叠到△EGF的位置，连接GD，则GD的最小值是______．第1题图2. 如图，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点分别在AB、BC上(含端点)，且AB＝6，BC＝10.设AE＝x，则x的最大值和最小值的和是______．第2题图3. (2019淮安)如图，在矩形ABCD中，AB＝3，BC＝2，H是AB的中点，将△CBH沿CH折叠，点B 落在矩形内点P处，连接AP，则tan∠HAP＝________．第3题图4. (2019金牛区二诊)如图，在等腰直角三角形ABC 中，∠ACB ＝90°，在△ABC 内有一点P ，已知∠1＝∠2＝∠3，将△BCP 以直线PC 为对称轴翻折，使点B 与点D 重合，PD 与AB 交于点E ，连接AD ，将△APD 的面积记为S 1，将△BPE 的面积记为S 2，则S 2S 1的值为________．第4题图5. 如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝6，点D 是边BC 的中点，点E 是边AB 上任意一点(点E 不与点B 重合)，沿DE 翻折△DBE ，使点B 落在点F 处，连接AF ，则线段AF 的长取最小值时，BF 的长为________．第5题图6. (2019都江堰区一诊)如图，已知在△ABC 中，AB ＝AC ，BC ＝8，D 、E 两点分别在边BC 、AB 上，将△ABC 沿着直线DE 翻折，点B 正好落在边AC 上的点M 处，并且AC ＝4AM ，设BD ＝m ，那么∠ACD 的正切值是______．(用含m 的代数式表示)第6题图7. (2019成华区二诊)已知一个矩形纸片ABCD ，AB ＝12，BC ＝6，点E 在BC 边上，将△CDE 沿DE 折叠，点C 落在C ′处，DC ′，EC ′分别交AB 于点F ，G ，若GE ＝GF ，则sin ∠CDE 的值为________．第7题图8. (2019成都黑白卷)如图，在平行四边形ABCD 中，点E 为AD 边的中点，将△ABE 沿BE 翻折，得到△FBE ，连接DF 并延长交BC 于点G ，若BE ＝AD ＝10，平行四边形ABCD 的面积为60，则FG ＝ ________．第8题图9. 如图，四边形ABCD是矩形纸片，AB＝2，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，展开后再过点B折叠矩形纸片，使点A落在EF上的点N处，折痕BM与EF相交于点Q，再次展平，连接BN，MN，延长MN交BC于点G.P为线段BM上一动点，H是BN的中点，则PN＋PH的最小值是______．第9题图10. 如图，四边形纸片ABCD中，AD⊥AB，AB∥DC，AB＝6，AD＝CD＝3，点E，F分别在线段AB，AD上，将△AEF沿EF翻折，点A的落点记为P.当P落在四边形ABCD内部时，PD的最小值为______．第10题图参考答案类型一动点探究题1. 9 【解析】如解图，由题意可知，点G 在以点B 为圆心，1为半径的14圆弧上运动．作点C 关于AD 的对称点C ′，连接C ′B 交AD 于点H ，交以点B 为圆心，1为半径的圆于点G ，由两点之间线段最短，此时C ′B 的值最小，最小值为BC 2＋CC ′2＝62＋82＝10，∵GH ＋CH ＝GH ＋C ′H ＝BC ′－BG ＝9，∴GH ＋CH 的最小值为9.第1题解图2. 925【解析】如解图，∵点D 为BC 边上一动点，∴AD 的最小值为AD 1，最大值为AD 2，∵在Rt △ABC 中，AB ＝3，BC ＝5，∴AC ＝52－32＝4，∵S △ABC ＝AB ·AC 2＝BC ·AD 12，解得AD 1＝125，∵AD 2为最大值4，∴最小面积与最大面积之比＝(125∶4)2＝925.第2题解图3. 513【解析】∵四边形EFQH 是正方形，∴∠EHA ＝90°，设HE ＝HQ ＝x ，AH ＝y ，∵四边形ABCD 是矩形，∴∠D ＝90°，∴HE ∥CD ，AD ∥EF ，∴△AHE ∽△ADC ，∴HE CD ＝AH AD ，即x 5＝y 7，设x ＝5k ，则y ＝7k ，∵四边形EFQH 是正方形，∴HQ ∥EF ，∴∠AFE ＝∠QAF ，在Rt △AQF 中，AF ＝（5k ）2＋（12k ）2＝13k ，∴sin ∠AFE ＝sin ∠QAF ＝QF AF ＝5k 13k ＝513. 4. 1或116【解析】∵∠AEF ＝∠B ＝∠C ，且∠AME ＞∠C ，∴∠AME ＞∠AEF ，∴AE ≠AM ；①当AE ＝EM 时，则△ABE ≌△ECM ，∴CE ＝AB ＝5，∴BE ＝BC －EC ＝6－5＝1；②当AM ＝EM 时，则∠MAE ＝∠MEA ，∴∠MAE ＋∠BAE ＝∠MEA ＋∠CEM ，即∠CAB ＝∠CEA ，又∵∠C ＝∠C ，∴△CAE ∽△CBA ，∴CE CA ＝AC BC ，∴CE ＝AC 2CB ＝256，∴BE ＝BC －EC ＝6－256＝116.综上所述，BE 的长是1或116. 5. 22或2－1 【解析】∵在Rt △ABC 中，AB ＝AC ＝2，∴BC ＝2 2.①当AF ＝CF 时，∠F AC ＝∠C ＝45°，∴∠AFC ＝90°，∴AF ⊥BC ，∴BF ＝CF ＝12BC ＝2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝22；②当CF ＝CA ＝2时，BF ＝BC －CF ＝22－2，∵直线PD 垂直平分BF ，∴BD ＝12BF ＝2－1；③当AF ＝AC 时，点F 与点B 重合(舍去)．综上所述，BD 的长为22或2－1. 6. 6 【解析】如解图，连接OA 、OC ，∵∠ABC ＝45°，OA ＝OC ＝2，∴∠AOC ＝90°，∴AC ＝2OA ＝22，在CB 上取一点A ′，使CA ′＝CA ，∵∠ACB ＝60°，∴△A ′CA 为等边三角形，过点A ′作A ′N ′⊥AC 于点N ′，∵点D 为AB ︵的中点，∴CD 为∠ACB 的平分线，∴点A 与点A ′关于直线CD 对称，连接A ′M ，∴A ′M＝AM ，即AM ＋MN ＝A ′M ＋MN ，根据直线外一点到直线上的所有连线中，垂线段最短，∴A ′N ′的长即为MA ＋MN 的最小值，∵A ′C ＝AC ＝22，∠ACB ＝60°，∴A ′N ′＝A ′C ·sin60°＝22×32＝6，即MA ＋MN 的最小值为 6.第6题解图7. 13或5－255【解析】如解图①，当∠AME ＝90°时，易知四边形AMEF 是矩形，且四边形BMEN 是正方形．∵ME ∥BC ，∴AM ME ＝AB BC ＝12，∴AM ＋BM ＝AM ＋2AM ＝1，则EF ＝AM ＝13；如解图②，当∠AEM ＝90°时，易证△AEM ∽△ABC ，∴AE ME ＝AB CB ＝12，∴ME ＝2AE ，则BM ＝ME ＝2AE ，AM ＝5AE ，∴AB ＝AM ＋BM ＝2AE ＋5AE ＝1，解得AE ＝5－2.又∵EF ∥CD ，∴EF AE ＝CD AC ＝15，∴EF ＝55(5－2)＝5－255.综上，若△AEM 是直角三角形，则EF 的长为13或5－255.图① 图②第7题解图 8. 43或1或1－63 【解析】如解图①，当AE ＝AF 时，设BE ＝DF ＝a ，则AF ＝AE ＝3－a .在Rt △ABE中，由AE 2＝AB 2＋BE 2得(3－a )2＝12＋a 2，解得a ＝43；如解图②，当AE ＝EF 时，设BE ＝DF ＝a ，则AF ＝3－a ，由AF ＝2BE ，得3－a ＝2a ，解得a ＝1；如解图③，当AF ＝EF 时，设BE ＝DF ＝a ，则AF ＝EF ＝3－a .由∠F AE ＝∠FEA ＝∠AEB 可得AB ＝AG ＝1，易知EG ＝BE ＝a ，∴FG ＝3－2a .在Rt △AFG 中，由AF 2＝AG 2＋FG 2得(3－a )2＝12＋(3－2a )2，解得a ＝1－63或a ＝1＋63(不符合题意，舍去)．综上，若△AEF 是等腰三角形，则DF 的长为43或1或1－63.图① 图② 图③第8题解图 9. 135或175【解析】①当M 在线段BC 上时，如解图，过点M 作MH ⊥AB 于点H ，∵∠CAM ＋∠CBA ＝45°，∠ACB ＝90°，∴∠BAM ＝45°.∵AC ＝2，BC ＝3，∴AB ＝13.∵Rt △BHM ∽Rt △BCA ，∴MH AC ＝BH BC＝BM BA .设MH ＝2x ，则2x 2＝BH 3＝BM 13，∴BH ＝3x ，BM ＝13x ，在Rt △AHM 中，AH ＝MH ＝2x ，∵AB ＝BH ＋AH ＝13，∴5x ＝13，x ＝135，BM ＝13x ＝135；②当M 在BC 延长线上时，如解图，则∠CAM ′＋∠CBA ＝45°，又∵∠CAM ＋ ∠CBA ＝45°，∴∠CAM ＝∠CAM ′.又∵AC ⊥BM ′，∴CM ＝CM ′.由①得CM ＝BC －BM ＝25，∴BM ′＝175；③当M 在CB 的延长线上时，不存在∠CAM ＋∠CBA ＝45°.综上所述，BM 的长为135或175.第9题解图10. y ＝113x 【解析】当点D 与点C 重合时，如解图，过F 作FG ⊥y 轴于点G ，连接OF ，∵S △ABC ＝12S 矩形 AOCB ＝12S 矩形ADEF ＝3，∴S 矩形AOCB ＝6，∵A 点坐标为(0，2)，∴OA ＝2，∴OC ＝3，∵∠F AD ＝90°，易得△FGA ∽△AOD ，∴FG AO ＝AG DO ，即FG AG ＝AO DO ＝23，设|FG |＝2a ，|AG |＝3a 由勾股定理得OF ＝OG 2＋FG 2＝（2＋3a ）2＋（2a ）2＝13a 2＋12a ＋4，令t ＝13a 2＋12a ＋4，∴t ＝13a 2＋12a ＋4＝13(a ＋613)2＋4，∴当a ＝－613时，t 有最小值．∴|FG |＝|2×(－613)|＝1213，|AG |＝|3×(－613)|＝1813，点F 的横坐标为1213，纵坐标为1813＋2＝4413，设OF 解析式为y ＝kx (k ≠0)，求得k ＝113，故函数的解析式为y ＝113x .第10题解图类型二平移探究题1. 5 【解析】∵四边形AEFD 为菱形，∴AE ＝EF ，∵将△ABE 向右平移得到△DCF ，∴BE ＝CF ，AB ＝CD ，∵BE ∶EC ＝3∶2，设BE ＝3k ，EC ＝2k ，∴BC ＝EF ＝5k ，∴AE ＝5k ，∵四边形ABCD 是矩形，∴AD ＝BC ，AB ＝CD ，∠B ＝90°，∴AB ＝AE 2－BE 2＝4k ，∴AB 2＋BF 2＝AF 2，即(4k )2＋(8k )2＝(45)2，∴k ＝1，∴AD ＝BC ＝5.2. 67 【解析】∵OA ＝2，OB ＝4，∠OAE ＝∠OBA ，∠EOA ＝∠AOB ＝90°，∴△OAE ∽△OBA ，∴OA OB ＝OE OA ，即24＝OE 2，解得OE ＝1，如解图，过点A 作AB ′⊥OA ，并使AB ′＝BE ＝3.易证△AB ′A ′≌△EBE ′，∴B ′A ′＝BE ′，∴A ′B ＋BE ′＝A ′B ＋B ′A ′.当点B 、A ′、B ′在同一条直线上时，A ′B ＋B ′A ′最小，即此时A ′B ＋BE ′取得最小值．易证△AB ′A ′∽△OBA ′，∴AA ′OA ′＝AB ′OB ＝34，∴AA ′OA ＝37，AO ＝2，∴AA ′＝37×2＝67，∴EE ′＝AA ′＝67.第2题解图3. 25 【解析】如解图，作射线CC ′，AA ′，AA ′交BC ′于点O ，过点C 作CF ∥AB 交AA ′于F ，连接BF ，由平移性质得AA ′∥BE ∥CC ′，∵∠EBD ＝45°，∴∠F AB ＝∠C ′CF ＝45°，∵Rt △ABC 中，AB ＝AC ，∠CAB ＝90°，∴易得四边形ABFC 是正方形，∴∠FCB ＝45°，∴∠C ′CB ＝90°，∵A ′C ′＝BF ，∠A ′OC ′＝∠FOB ，∠C ′A ′O ＝∠BFO ＝45°，∴△A ′OC ′≌△FOB ，∴BO ＝C ′O ，∴CO ＝C ′O ＝BO ，延长FC 到G ，使得CG ＝CF ，连接A ′G ，则CO 是△FGA ′的中位线，∴A ′G ＝2CO ＝BC ′，∴BC ′＋BA ′＝BA ′＋A ′G ，∴当点B 、A ′、G 在同一条直线上时，BG 取得最小值，那A ′B ＋C ′B 取得最小值．∵在Rt △GFB 中，BF ＝AC ＝2，FG ＝2CF ＝4，∴BG ＝25，∴A ′B ＋C ′B 的最小值为2 5.第3题解图 4. 32＋62 【解析】由翻转可得△BG ′C ≌△CGB ≌△DEA ，∴CG ′＝AE ，∠BCG ′＝EAD ，同理可得CF ′＝AE ，∠DCF ′＝∠BAE ，∴∠BCG ′＋∠DCF ′＝∠EAD ＋∠BAE ＝45°，在平行四边形ABCD 中，∠BAD ＝∠BCD ＝45°，∴∠G ′CF ′＝∠G ′CB ＋∠BCD ＋∠DCF ′＝90°.∴△G ′CF ′为等腰直角三角形，由勾股定理可得F ′G ′＝2CG ′＝2AE ，当AE ⊥BD 时，AE 的值最小，即此时F ′G ′的值最小，∵△AED ≌△BGC ，△ABE ≌△DCF ，且∠AED ＝∠AEB ＝90°，∴∠BGC ＝∠AED ＝90°，∠DFC ＝∠AEB ＝90°，∴BG ∥DF ，又∵BG ＝AE ＝DF ，∴四边形BGFD 为矩形，如解图，过点B 作BM ⊥AD 于点M ，在Rt △ABM 中，∵∠BAM ＝∠ABM ＝45°，AB ＝6，∴AM ＝BM ＝6×22＝3，∵∠ABD ＝75°，∴∠DBM ＝∠ABD －∠ABM ＝75°－45°＝30°，∴∠ADB ＝60°，∴在Rt △DBM 中，BD ＝BM sin60°＝2，MD ＝BM tan60°＝1，∴AD ＝AM ＋MD ＝1＋3，∵S △BAD ＝12BD ·AE ＝12AD ·BM ，即2AE ＝(1＋3)×3.∴AE ＝3＋32，∴F ′G ′的最小值为32＋62.第4题解图类型三旋转探究题1. 10＋2 【解析】如解图，取AB 的中点M ，连接MF 和CM ，∵在Rt △ABC 中，∠ACB ＝90°，AC＝6，BC ＝2，∴AB ＝AC 2＋BC 2＝210.∵M 为AB 中点，∴CM ＝12AB ＝10，∵将线段AD 绕点A 按顺时针方向旋转，点D 的对应点是点P ，∴AP ＝AD ＝4，∵M 为AB 中点，F 为BP 中点，∴FM ＝12AP ＝2.当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝10＋2.第1题解图2. 4＋35 【解析】如解图①，当AD ＝13AC 时，取AB 的中点M ，连接MF 和CM ，∵∠ACB ＝90°，tan ∠BAC ＝12，且BC ＝6，∴AC ＝12，AB ＝6 5.∵M 为AB 中点，∴CM ＝35，∵AD ＝13AC ，∴AD ＝4.∵M 为AB 中点，F 为BD 中点，∴FM ＝12AD ＝2，∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大，此时CF ＝CM ＋FM ＝2＋35；如解图②，当AD ＝23AC 时，取AB 的中点M ，连接MF 和CM ，同理可得CF 的最大值为4＋35，综上，线段CF 的长度的最大值为4＋3 5.第2题解图3. 7＜l ＜17 【解析】如解图，过点A 作AH ∥DG ，∵DG ∥EF ，∴DG ∥EF ∥AH ，∵点D 为AB 的中点，将△BDG 绕点D 顺时针旋转180°后到△ADM 的位置，∴BG ＝AM ，MG ∥AH 且MG ＝AH ，同理CF ＝AN ，NF ∥AH 且NF ＝AH ，∴四边形MGFN 是平行四边形，∴MN ＝GF ＝AM ＋AN ＝BG ＋CF .在Rt △ABC 中，∵AB ＝4，AC ＝3，∴由勾股定理得BC ＝5，即MN ＋GF ＝5，在△ABH 中，由三角形的三边关系可得AB －BH ＜AH ＜AB ＋BH ，同理AC －CH ＜AH ＜AC ＋CH ，两式相加得AB ＋AC －(BH ＋CH )＜2AH ＜AB ＋AC ＋(BH ＋CH )，∴4＋3－5＜2AH ＜4＋3＋5，即2＜2AH ＜12，l ＝MG ＋GF ＋NF ＋MN ＝2AH ＋BC ，∵BC ＝5，2＜2AH ＜12，∴7＜l ＜17.第3题解图4. 4π3【解析】如解图，连接AD 、DG .∵△ABC 和△EFG 均是等边三角形，D 分别是BC 和EF 的中点，∴BD ＝CD ，DE ＝DF ，∴AD ⊥BC ，GD ⊥EF ，∴∠ADC ＝∠GDF ＝90°，∴∠ADG ＝∠CDF ，∵AD CD＝DG DF＝tan60°，∴△ADG ∽△CDF ，∴∠DAG ＝∠DCF ，∴∠AMC ＝90°，∴点M 的轨迹是以AC 为直径的圆，且来回共两个三分之一圆，∴点M 运动的路径长为4π3.第4题解图5. 92【解析】∵△ABC 和△CDE 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，∴AC ＝BC ，CE ＝CD ，∠ACB ＋∠BCE ＝∠BCE ＋∠ECD ，∴∠ACE ＝∠BCD ，∴△ACE ≌△BCD ，∴AE ＝BD ，∠CAE ＝∠CBD ，∴∠HBA ＋∠HAB ＝∠HBC ＋∠CBA ＋∠HAB ＝∠CBA ＋∠CAB ＝90°，∴BD ⊥AE .∵P ，M 分别是AD ，AB的中点，∴PM ∥BD ，且PM ＝12BD ，同理，PN ∥AE ，且PN ＝12AE ，∴PM ⊥PN ，PM ＝PN ，∴△PMN 是等腰直角三角形，∴S △PMN ＝12PM 2＝18BD 2，∴当BD 最大时，△PMN 的面积最大，∵△CDE 绕点C 旋转，∴点D 在以C 为圆心，CD 为半径的圆上，∴当点D 在BC 的延长线上时，BD 最大，此时BD ＝AC ＋CD ＝6，∴△PMN 面积的最大值为18×62＝92.第5题解图类型四折叠探究题1. 73－3 【解析】如解图，由EG ＝EB ＝3，可得当点G 在DE 上时，此时GD 的值最小，根据折叠的性质，△EBF ≌△EGF ，∴EG ⊥GF ，EG ＝EB ，∵E 是AB 边的中点，AB ＝6，∴AE ＝EG ＝3，∵AD ＝8，∴Rt △ADE 中，DE ＝82＋32＝73，∴GD ＝73－3.第1题解图2. 8 【解析】设折痕为PQ ，点P 在AB 边上，点Q 在BC 边上．如解图①，当点Q 与点C 重合时，AE 最小，根据翻折对称性可得EC ＝BC ＝10，在Rt △CDE 中，CE 2＝ED 2＋CD 2，即102＝(10－AE )2＋62，解得AE ＝2，即x ＝2；如解图②，当点P 与点A 重合时，AE 最大，根据翻折对称性可得AE ＝AB ＝6，即x ＝6，所以x 的最大值和最小值的和是8.图① 图②第2题解图 3. 43 【解析】如解图，连接PB 交CH 于点E .在Rt △BCH 中，BC ＝2，BH ＝12AB ＝32，∵△PCH 是由△BCH 折叠得到的，∴PB ⊥CH ，BE ＝PE ，PH ＝HB .∴∠HPB ＝∠HBP .∵AH ＝BH ，∴AH ＝PH .∴∠P AH ＝∠APH .∴∠APH ＋∠BPH ＝12(∠P AB ＋∠APB ＋∠ABP )＝90°.∴AP ∥CH ，∴tan ∠HAP ＝tan ∠BHC ＝BC BH ＝43.第3题解图 4. 12 【解析】如解图，连接BD ，延长CP 交BD 于点F ，由翻折可知CF ⊥BD ，BF ＝DF ，∠BPF ＝∠DPF ，∵∠1＝∠2＝∠3，△ABC 是等腰直角三角形，∴∠1＋∠ACP ＝∠2＋∠ACP ＝90°，∠2＋∠PBC ＝∠3＋∠PBC ＝45°，∴∠APC ＝90°，∠DPF ＝45°，DF ＝FB ＝PF ，∴△APC ≌△CFB ，∴AP ＝CF ，CP＝BF ＝PF ，∴AP ＝BD ，∴四边形ADBP 是平行四边形，∴S 2S 1＝12.第4题解图5. 1255【解析】由题意得：DF ＝DB ，∴点F 在以D 为圆心，BD 长为半径的圆上，如解图，连接AD 交⊙D 于点F .此时AF 的值最小，∵点D 是边BC 的中点，∴CD ＝BD ＝3，由勾股定理得：AD 2＝AC 2＋CD 2，∵AC ＝4，∴AD ＝5，∵FD ＝3，∴F A ＝5－3＝2，即线段AF 长的最小值是2，连接BF ，过点F 作FH ⊥BC 于点H ，∵∠ACB ＝90°，∴FH ∥AC ，∴△DFH ∽△DAC ，∴DF DA ＝DH DC ＝HF CA ，即35＝DH 3＝HF 4，∴HF ＝125，DH ＝95，∴BH ＝245，∴BF ＝BH 2＋HF 2＝1255.第5题解图6. 10m －253【解析】如解图，作AH ⊥BC 于点H ，MG ⊥BC 于点G ，连接EM 、MD 、BM ，∵AB ＝AC ，BC ＝8，AH ⊥BC ，∴CH ＝4，∵AC ＝4AM ，∴CM ∶AC ＝3∶4，∵AH ∥MG ，∴CG HC ＝CM AC ＝34，即CG 4＝34，解得CG ＝3，∴BG ＝5，∴DG ＝m －5，由翻折的性质可知MD ＝BD ＝m ，在Rt △MGD 中，依据勾股定理可知：MG ＝MD 2－GD 2＝m 2－（m －5）2＝10m －25，∴tan ∠ACD ＝tan ∠ACG ＝MG CG ＝10m －253.第6题解图 7. 1010 【解析】设CE ＝x ，则BE ＝6－x .根据折叠的对称性可知DC ′＝DC ＝12，C ′E ＝CE ＝x .在△FC ′G 和△EBG 中，⎩⎪⎨⎪⎧∠C ′＝∠B ＝90°∠FGC ′＝∠EGB GF ＝GE，∴△FC ′G ≌△EBG (AAS)．∴FC ′＝BE ＝6－x .∴DF ＝12－(6－x )＝6＋x .连接FE ，在Rt △FC ′E 和Rt △EBF 中，⎩⎪⎨⎪⎧FC ′＝BE EF ＝EF，∴Rt △FC ′E ≌Rt △EBF (HL)．∴FB ＝EC ′＝x .∴AF ＝12－x .在Rt △ADF 中，AD 2＋AF 2＝DF 2，即36＋(12－x )2＝(6＋x )2，解得x ＝4.∴CE ＝4.在Rt △CDE 中，DE 2＝DC 2＋CE 2，则DE ＝410.∴sin ∠CDE ＝CE DE ＝1010. 8. 2 【解析】∵将△ABE 沿BE 翻折，得到△FBE ，∴AE ＝EF ，∠AEB ＝∠FEB ，∴∠AEB ＝12(180°－∠DEF )，∵E 为AD 边的中点，∴AE ＝DE ，∴DE ＝EF ，∴∠EDF ＝∠EFD ，∴∠EDF ＝12(180°－∠DEF )，∴∠AEB ＝∠EDF ，∴BE ∥DG ，∵四边形ABCD 是平行四边形，∴DE ∥BG ，∴四边形BEDG 为平行四边形，∴DE ＝BG ，DG ＝BE ＝10，∵四边形ABCD 是平行四边形，且面积等于60，AE ＝DE ，∴S △ABE ＝14S ▱ABCD ＝15，如解图，连接AF 交BE 于H ，则AH ⊥BE ，AH ＝HF ，∵BE ＝10，∴AH ＝3，∴AF ＝6，∵BE ∥DG ，∴AF ⊥DG ，∴DF ＝AD 2－AF 2＝8，∴FG ＝DG －FD ＝2.第8题解图9. 3 【解析】如解图，连接AN ，∵∠ABM ＝∠MBN ＝30°，∠BNM ＝∠BAM ＝90°，∴∠BMG ＝∠BNM －∠MBN ＝90°－30°＝60°，∴∠MBG ＝∠ABG －∠ABM ＝90°－30°＝60°，∴∠BGM ＝180°－60°－60°＝60°，∴∠MBG ＝∠BMG ＝∠BGM ＝60°，∴△BMG 为等边三角形，∵点N 是MG 的中点，∴BN ⊥MG ，∵BG＝BM ＝AB cos ∠ABM ＝433，∴BN ＝BG ·sin60°＝433×32＝2，根据题意易知E 点和H 点关于BM 对称，∴PH ＝PE ，∴P 与Q 重合时，PN ＋PH 的值最小，此时PN ＋PH ＝PN ＋PE ＝EN ，∵EN ＝BN 2－BE 2＝22－（2÷2）2＝3，∴PN ＋PH ＝3，∴PN ＋PH 的最小值是 3.第9题解图10. 35－6【解析】如解图①，设A的对应点为P1，连接ED，过P1作PP1⊥ED于点P，∴在Rt△P1PD 中，DP1＞DP，∴当点A的对应点P落在线段ED上时，此时PD有最小值，即当EP取最大值时，PD有最小值，而点E在线段AB上，∴当点E与点B重合时，如解图②，即EP最大，从而此时PD取得最小值，在Rt△ADB中，BD＝AB2＋AD2＝35，∵PB＝AB＝6，∴DP＝BD－BP＝35－6.图①图②第10题解图。

专题二几何证明之四边形中的动点综合问题 2020年中考数学冲刺难点突破几何证明问题(解析版)

2020年中考数学冲刺难点突破几何证明问题专题二几何证明之四边形中的动点综合问题1、如图，已知∠MON＝90°，A，B分别是边OM和ON上的点，四边形ACDB和四边形OEFC都是正方形．（1）当OA＝2，OB＝1时，求OC的长．（2）当OB＝1，点A在直线OM上运动时，求OC的最小值．（3）设S△CDF＝y，OA＝x，求y关于x的函数关系式．解：（1）如图1所示，过点C作CG⊥OM于点G，∵四边形ACDB是正方形，∴AB＝AC，∠BAC＝90°，∵∠MON＝90°，∠AGC＝90°，∴∠BAO+∠ABO＝90°，∠BAO+∠CAG＝90°，∴∠ABO＝∠CAG，∴△AOB≌△AGC（AAS）．∵OA＝2，OB＝1，∴CG＝OA＝2，AG＝OB＝1，∴OG＝3，∴在Rt△OGC中，由勾股定理得：OC＝＝．（2）如图2所示，由题意可得点C在直线l：y＝x﹣1上运动，∴OC的最小值为当OC与直线l垂直时，此时OC＝，∴OC的最小值为．（3）如图3所示，延长OC至点H，使CH＝OC，连接AH，过点C作CG⊥OM，∵CD＝CA，CH＝CF，∠DCF＝∠ACH＝90°+∠ACF，∴△DCF≌△ACH（SAS），由（1）知△AOB≌△AGC（AAS），∴CG＝OA，∵C是OH的中点，∴S△ACH＝S△OAC，∵S△CDF＝y，OA＝x，∴y＝S△OAH＝S△OAC＝x2．∴y关于x的函数关系式为y＝x2．2、已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．（1）如图1，连接BG、DE．求证：BG＝DE；（2）如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD．①求∠BDE的度数；②若正方形ABCD的边长是，请求出△BCG的面积．（1）证明：∵四边形ABCD和四边形CEFG为正方形，∴BC＝DC，CG＝CE，∠BCD＝∠GCE＝90°．∴∠BCD+∠DCG＝∠GCE+∠DCG，∴∠BCG＝∠DCE．在△BCG和△DCE中，，∴△BCG≌△DCE（SAS）．∴BG＝DE；（2）解：①连接BE，如图2所示：由（1）可知：BG＝DE，∵CG∥BD，∴∠DCG＝∠BDC＝45°，∴∠BCG＝∠BCD+∠DCG＝90°+45°＝135°，∵∠GCE＝90°，∴∠BCE＝360°﹣∠BCG﹣∠GCE＝360°﹣135°﹣90°＝135°，∴∠BCG＝∠BCE，在△BCG和△BCE中，，∴△BCG≌△BCE（SAS），∴BG＝BE，∵BG＝BD＝DE，∴BD＝BE＝DE，∴△BDE为等边三角形，∴∠BDE＝60°；②延长EC交BD于点H，过点G作GN⊥BC于N，如图3所示：在△BCE和△DCE中，，∴△BCE≌△BCG（SSS），∴∠BEC＝∠DEC，∴EH⊥BD，BH＝BD，∵BC＝CD＝，∴BD＝BC＝2，∴BE＝2，BH＝1，∴CH＝1，在Rt△BHE中，由勾股定理得：EH＝＝＝，∴CE＝﹣1，∵∠BCG＝135°，∴∠GCN＝45°，∴△GCN是等腰直角三角形，∴GN＝CG＝（﹣1），∴S△BCG＝BC•GN＝××（﹣1）＝．3、如图，正方形ABCD的边长为4cm，动点P从A点出发，在正方形的边上沿A→B→C→D运动，设运动的时间为t（s），△APD的面积为S（cm2），S与t的函数图象如图所示，请回答下列问题：（1）点P在AB上运动时间为s，在CD上运动的速度为cm/s，△APD的面积S的最大值为cm2；（2）将S与t之间的函数关系式补充完整S＝；（3）请求出运动时间t为几秒时，△APD的面积为6cm2．解：（1）由函数图象可知，P在AB上运动的时间为4s，在CD上运动的时间为2s，∵CD＝4cm，∴P在CD上的运动速度为4÷2＝2cm/s，P在BC上运动时，△APD的面积最大为8cm2．（2）当0≤t＜4时，P在AB上运动，由函数图象可知，P在AB上的运动速度为4÷4＝1cm/s，∴AP＝t，∴S＝AD•AP＝2t．当4≤t≤8时，P在BC上运动，△APD的面积为定值8，即S＝8．当8＜t≤10时，P在CD上运动，DP＝4﹣2（t﹣8）＝﹣2t+20，S＝AD•DP＝﹣4t+40．（3）当P在AB上时，令2t＝6，解得t＝3s；当P在CD上时，令﹣4t+40＝6，解得t＝．综上所述，当t为3秒或秒时，△APD的面积为6cm2．4、已知，在△ABC中，∠BAC＝90°，∠ABC＝45°，点D为直线BC上一动点（点D不与点B、C重合），以AD为边做正方形ADEF，连接CF．（1）如图①，当点D在线段BC上时，直接写出线段CF、BC、CD之间的数量关系．（2）如图②，当点D在线段BC的延长线上时，其他件不变，则（1）中的三条线段之间的数量关系还成立吗？如成立，请予以证明，如不成立，请说明理由；（3）如图③，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC两侧，其他条件不变；若正方形ADEF的边长为4，对角线AE、DF相交于点O，连接OC，请直接写出OC的长度．解：（1）∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠DAC，∠CAF＝90°﹣∠DAC，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS），∴BD＝CF，∵BD+CD＝BC，∴CF+CD＝BC；故答案为：CF+CD＝BC；（2）CF+CD＝BC不成立，存在CF﹣CD＝BC；理由：∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠DAC，∠CAF＝90°﹣∠DAC，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS）∴BD＝CF∴BC+CD＝CF，∴CF﹣CD＝BC；（3）∵∠BAC＝90°，∠ABC＝45°，∴∠ACB＝∠ABC＝45°，∴AB＝AC，∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°，∵∠BAD＝90°﹣∠BAF，∠CAF＝90°﹣∠BAF，∴∠BAD＝∠CAF，∵在△BAD和△CAF中，，∴△BAD≌△CAF（SAS），∴∠ACF＝∠ABD，∵∠ABC＝45°，∴∠ABD＝135°，∴∠ACF＝∠ABD＝135°，∴∠FCD＝135°﹣45°＝90°，∴△FCD是直角三角形．∵正方形ADEF的边长4且对角线AE、DF相交于点O．∴DF＝AD＝4，O为DF中点．∴Rt△CDF中，OC＝DF＝×＝．5、如图1，已知正方形ABCD，E是线段BC上一点，N是线段BC延长线上一点，以AE为边在直线BC的上方作正方形AEFG．（1）连接GD，求证DG＝BE；（2）连接FC，求tan∠FCN的值；（3）如图2，将图1中正方形ABCD改为矩形ABCD，AB＝3，BC＝8，E是线段BC上一动点（不含端点B，C），以AE为边在直线BC的上方作矩形AEFG，使顶点G恰好落在射线CD上．当点E由B向C运动时，判断tan∠FCN的值是否为定值？若是，求出该定值；若不是，请说明理由．解：（1）如图1，∵正方形ABCD和正方形AEFG中，∴∠BAD＝∠EAG＝90°，AB＝AD，AE＝AG，∴∠BAE＝∠GAD，∴△BAE≌△GAD（SAS），∴DG＝BE；（2）如图2，过点F作FM⊥BN于M，则∠B＝∠AEF＝∠FME＝90°，∴∠BAE+∠AEB＝∠FEM+∠AEB＝90°，即∠BAE＝∠FEM，又AE＝EF，∴△BAE≌△MEF（ASA），∴FM＝BE，EM＝AB，又BE+EC＝AB，EM＝EC+CM，∴CM＝FM，在Rt△FCM中，tan∠FCN＝＝1；（3）如图2，过点F作FM⊥BN于M，则∠B＝∠AEF＝∠FME＝90°，∴∠BAE+∠AEB＝∠FEM+∠AEB＝90°，即∠BAE＝∠FEM，同理可证∠GAD＝∠FEM，又AG＝EF，∴△DAG≌△MEF，△BAE∽△MEF，∴EM＝AD＝BC＝8，＝，设BE＝a，则EM＝EC+CM＝BC＝BE+EC，∴CM＝BE＝a，∴＝，∴FM＝，∴tan∠FCN＝＝＝，即tan∠FCN的值为定值．6、如图，在平面直角坐标系xOy中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动．（1）当∠OAD＝30°时，求点C的坐标；（2）设AD的中点为M，连接OM、MC，当四边形OMCD的面积为时，求OA的长；（3）当点A移动到某一位置时，点C到点O的距离有最大值？若存在，求此时的值；若不存在，请说明理由．解：（1）如图1，过点C作CE⊥y轴于点E，∵矩形ABCD中，CD⊥AD，∴∠CDE+∠ADO＝90°，又∵∠OAD+∠ADO＝90°，∴∠CDE＝∠OAD＝30°，∴在Rt△CED中，CE＝CD＝2，DE＝＝2，在Rt△OAD中，∠OAD＝30°，∴OD＝AD＝3，∴点C的坐标为（2，3+2）；（2）∵M为AD的中点，∴DM＝3，S△DCM＝6，又S四边形OMCD＝，∴S△ODM＝，∴S△OAD＝9，设OA＝x、OD＝y，则x2+y2＝36，xy＝9，∴x2+y2＝2xy，即x＝y，将x＝y代入x2+y2＝36得x2＝18，解得x＝3（负值舍去），∴OA＝3；（3）OC的最大值为8，如图2，M为AD的中点，∴OM＝3，CM＝＝5，∴OC≤OM+CM＝8，当O、M、C三点在同一直线时，OC有最大值8，连接OC，则此时OC与AD的交点为M，过点O作ON⊥AD，垂足为N，∵∠CDM＝∠ONM＝90°，∠CMD＝∠OMN，∴△CMD∽△OMN，∴＝＝，即＝＝，解得MN＝，ON＝，∴AN＝AM﹣MN＝，在Rt△OAN中，OA＝＝，∴cos∠OAD＝＝＝．即＝．7、如图，在长方形ABCD中，AB＝4cm，BE＝5cm，点E是AD边上的一点，AE、DE分别长acm、bcm，满足（a﹣3）2+|2a+b﹣9|＝0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D．设运动时间为ts．（1）a＝cm，b＝cm；（2）t为何值时，EP把四边形BCDE的周长平分？（3）另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．解：（1）∵（a﹣3）2+|2a+b﹣9|＝0，∴a﹣3＝0，2a+b﹣9＝0，∴a＝3，b＝3；故答案为：3，3；（2）∵AE＝3cm，DE＝3cm，∴AD＝6cm＝BC，∴C＝BC+CD+DE+EB＝18cm，四边形BCDE∵EP把四边形BCDE的周长平分，∴BE+BP＝9cm，∴点P在BC上，BP＝4cm，∴t＝＝2s；（3）解：①点P在BC上（0＜t≤3），∵S△BPQ＝×2t×4＝6，∴t＝；②相遇前，点P在CD上（3＜t≤），∵S△BPQ＝×[（4﹣（t﹣3）﹣（2t﹣6）]×6＝6，∴t＝；③相遇后，点P在CD上（＜t≤5），∵S△BPQ＝×[（（t﹣3）+（2t﹣6）﹣4]×6＝6，∴t＝5；∴综上所述，当t＝s或s或5s时，△BPQ的面积等于6cm2．8、如图所示，四边形ABCD为平行四边形，AD＝13，AB＝25，∠DAB＝α，且cosα＝，点E为直线CD上一动点，将线段EA绕点E逆时针旋转α得到线段EF，连接CF．（1）求平行四边形ABCD的面积；（2）当点C、B、F三点共线时，设EF与AB相交于点G，求线段BG的长；（3）求线段CF的长度的最小值．解（1）如图1，作DK⊥AB于点K，∵将线段EA绕点E逆时针旋转α得到线段EF，∴∠AEF＝α，AE＝EF，在Rt△DAK中，∵cos∠DAK＝cosα＝，且AD＝13，∴AK＝5，∴DK＝＝＝12，∴S＝AB×DK＝25×12＝300；平行四边形ABCD（2）如图2，延长CD至H，作∠AHD＝α，∵∠AHD＝∠ADH＝α，∴AH＝AD＝13，过点A作AM⊥DH于点M，由（1）知AM＝12，∴DM＝＝5，∴DH＝10，∵∠FEH＝∠DEA+∠α＝∠F+α，∴∠DEA＝∠F，在△AEH和△EFC中，，∴△AEH≌△EFC（AAS），∴EH＝CF，CE＝AH＝13，∴DE＝CD﹣CE＝12，BF＝CF﹣BC＝22﹣13＝9，∵BG∥CE，∴△FBG∽△FCE，∴，即，∴BG＝；（3）如图3，延长CD至P，使∠P＝∠ADP＝α，过点F作FM∥BC，交CD于点M，过点FN⊥CD，交CD于点N，由（2）可知∠AEP＝∠EFM，在△EAP和△FEM中．，∴△EAP≌△FEM（AAS），∴EM＝AP＝13，FM＝EP，设DE＝x，则FM＝EP＝10+x，CM＝25﹣（13+x）＝12﹣x，∴FN＝FM•sinα＝（10+x），MN＝FM•cosα＝（10+x），∴CN＝CM+MN＝12﹣x+（10+x）＝，在Rt△CFN中，CF2＝CN2+NF2＝（208x2﹣416x+56836），对称轴x＝﹣＝1，∴当x＝1时，CF的值最小，CF的最小值为．9、在平面直角坐标系中，点O为坐标原点，点A（5，0）在x轴的正半轴上，四边形OABC为平行四边形，对角线OB＝OA，BC交y轴于点D，且S▱OABC＝20．（1）如图①，求点B的坐标：（2）如图②，点P在线段OD上，设点P的纵坐标为t，△PAB的面积为S，请用含t的式子表示S；（3）在（2）的条件下，如图③，点Q在x轴上，点R为坐标平面内一点，若∠OCB﹣∠CBP＝45°，且四边形PQBR为菱形，求t的值并直接写出点Q的坐标．解：（1）∵点A（5，0），OB＝OA，∴OA＝OB＝5，∵S▱OABC＝OA×OD＝5OD＝20，∴OD＝4，∵四边形OABC为平行四边形，∴BC∥AO，BC＝AO＝5，∴∠BDO＝90°，∴DB＝＝＝3，∴点B（3，4）；（2）∵点P的纵坐标为t，∴OP＝t，∴DP＝4﹣t，∴S＝×（3+5）×4﹣×3×（4﹣t）﹣×5×t＝﹣t+10；（3）如图，由（1）知，B（3，4），OA＝5，BC∥OA，∴C（﹣2，4），∴CD＝2取OD的中点E，则DE＝OD＝2，∴DE＝CD，∴∠DCE＝45°，∴∠OCB﹣∠OCE＝45°，∵∠OCB﹣∠CBP＝45°，∴∠OCE＝∠CBP，过点E作EF⊥OC于F，∴∠CFE＝90°＝∠BDP，∴△CFE∽△BDP，∴，在Rt△CDE中，CD＝DE＝2，∴CE＝2，在Rt△ODC中，CD＝2，OD＝4，∴OC＝2，∵CE是△OCD的中线，∴S△OCE＝S△CDO＝××2×4＝2∵S△OCE＝OC•EF＝×EF＝2，∴EF＝，在Rt△CFE中，根据勾股定理得，CF＝，∴，∴DP＝1，∴OP＝OD﹣DP＝3，∴t＝3，∴P（0，3），设Q（m，0），∵B（3，4），∴PQ2＝m2+9，BQ2＝（m﹣3）2+16，∵四边形PQBR为菱形，∴PQ＝BQ，∴m2+9＝（m﹣3）2+16，∴m＝，即Q（，0）．10、已知在四边形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝4，BC＝6．（1）如图1，P为AB边上一点，以PD，PC为边作平行四边形PCQD，过点Q作QH⊥BC，交BC的延长线于H．求证：△ADP≌△HCQ；（2）若P为AB边上任意一点，延长PD到E，使DE＝PD，再以PE，PC为边作平行四边形PCQE．请问对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．（3）如图2，若P为DC边上任意一点，延长PA到E，使AE＝nPA（n为常数），以PE，PB为边作平行四边形PBQE．请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．解：（1）∵AD∥BC，∴∠ADC＝∠DCH，∴∠ADP+∠PDC＝∠DCQ+∠QCH，∵四边形PCQD是平行四边形，∴PD∥CQ，PD＝CQ，∴∠PDC＝∠DCQ，∴∠ADP＝∠QCH，在△ADP和△HCQ中，，∴△ADP≌△HCQ（AAS）；（2）存在最小值，最小值为10，如图1，作QH⊥BC，交BC的延长线于H，设PQ与DC相交于点G，∵PE∥CQ，∴△DPG∽△CQG，∴＝＝，由（1）可知，∠ADP＝∠QCH，∴Rt△ADP∽Rt△QCH，∴＝＝，∴CH＝2AD＝4，∴BH＝BC+CH＝6+4＝10，∴当PQ⊥AB时，PQ的长最小，即为10；（3）存在最小值，最小值为（n+4），如图2，作QH∥DC，交CB的延长线于H，作CK⊥CD，交QH的延长线于K，∵PE∥BQ，AE＝nPA，∴＝＝，∵AD∥BC，∴∠ADP+∠DCH＝90°，∵CD∥QK，∴∠QHC+∠DCH＝180°，∴∠QHC＝∠ADQ，∵∠PAD+∠PAG＝∠QBH+∠QBG＝90°，∠PAG＝∠QBG，∴∠PAD＝∠QBH，∴△ADP∽△BHQ，∴＝＝，∴BH＝2n+2，∴CH＝BC+BH＝6+2n+2＝2n+8，过点D作DM⊥BC于M，又∠DAB＝∠ABM＝90°，∴四边形ABMD是矩形，∴BM＝AD＝2，DM＝AB＝4，∴MC＝BC﹣BM＝6﹣2＝4＝DM，∴∠DCM＝45°，∴∠HCK＝45°，∴CK＝CH•cos45°＝（2n+8）＝（n+4），∴当PQ⊥CD时，PQ的长最小，最小值为（n+4）．11、已知：如图①，在Rt△ABC中，∠ACB＝90°，BC＝8，AB＝10，点P，E，F分别是AB，AC，BC上的动点，且AP＝2CE＝2BF，连结PE，PF，以PE，PF为邻边作平行四边形PFQE．（1）当点P是AB的中点时，试求线段PF的长．（2）在运动过程中，设CE＝m，若平行四边形PFQE的面积恰好被线段BC或射线AC分成1：3的两部分，试求m的值．（3）如图②，设直找FQ与直线AC交于点N，在运动过程中，以点Q，N，E为顶点的三角形能否构成直角三角形？若能，请直接写出符合要求的CE的长；若不能，请说明理由．解：（1）如图①，作PH⊥BC于点H，∵∠ACB＝90°，BC＝8，AB＝10，∴AC＝6．∵AP＝2CE＝2BF，∵点P是AB的中点，∴PA＝PB＝5．∴CE＝BF＝，PH＝3，BH＝CH＝4，∴FH＝．∴PF＝＝．（2）如图②，平行四边形PFQE的面积恰好被线段BC分成1：3的两部分时，则EM＝PF．∵PH⊥BC，∴∠PHF＝90°＝∠ACB，∴PH∥AC，∴△CEM∽△HPF，△PBH∽△ABC，∴PH＝2CE＝2m，＝．∴＝，∴m＝．如图③，平行四边形PFQE的面积恰好被线段AC分成1：3的两部分时，则FD＝QD，QN＝PG，∴CF＝PG．∵△APG∽△ABC，∴＝．∴＝，∴m＝．∴m的值为或．（3）如图④，当∠QNE＝90°时，则点N与点C重合，设CE＝x，∵△PBH∽△ABC，∴＝，∴＝，∴x＝．如图⑤，当∠QNE＝90°时，则点P与点B重合，则2x＝10，∴x＝5．如图⑥，当∠QNE＝90°时，∵△FPR∽△PES，∴＝，∴＝，∴x＝．经检验，x值符合题意．综上，CE的长为或5或．12、将一个矩形纸片OABC放置在平面直角坐标系中，点O（0，0），点A（8，0），点C（0，6）．P是边OC上的﹣一点（点P不与点O，C重合），沿着AP折叠该纸片，得点O的对应点O'．（Ⅰ）如图①，当点O'落在边BC上时，求点O'的坐标；（Ⅱ）若点O'落在边BC的上方，O'P，O'A与分别与边BC交于点D，E．①如图②，当∠OAP＝30°时，求点D的坐标；②当CD＝O'D时，求点D的坐标（直接写出结果即可）．解：（Ⅰ）∵点A（8，0），点C（0，6），OABC为矩形，∴AB＝OC＝6，OA＝CB＝8，∠B＝90°．根据题意，由折叠可知△AOP≌△AO'P，∴O'A＝OA＝8．在Rt△AO'B中，BO'＝＝2．∴CO'＝BC﹣BO'＝8﹣2．∴点O'的坐标为（8﹣2，6）．（Ⅱ）①∵∠OAP＝30°，∴∠OPA＝60°，∵∠OPA＝∠O'PA，∴∠CPD＝180°﹣∠OPA﹣∠O'PA＝60°．∵OA＝8，∴OP＝OA•tan30°＝．∴CP＝6﹣OP＝6﹣．∴CD＝CP•tan60°＝6﹣8．∴点D的坐标为（6﹣8，6）．②连接AD，如图：设CD＝x，则BD＝BC﹣CD＝8﹣x，O'D＝CD＝x，根据折叠可知AO'＝AO＝8，∠PO'A＝∠POA＝90°，∴在Rt△ADO'中，AD2＝AO'2+DO'2＝82+x2＝x2+64；在Rt△ABD中，AD2＝BD2+AB2＝（8﹣x）2+62＝x2﹣16x+100；∴x2+64＝x2﹣16x+100，解得：x＝，∴CD＝，∴D（，6）．13、在等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12．（1）梯形ABCD的面积等于．（2）如图1，动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB 以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．当PQ∥AB 时，P点离开D点多少时间？（3）如图2，点K是线段AD上的点，M、N为边BC上的点，BM＝CN＝5，连接AN、DM，分别交BK、CK于点E、F，记△ADG和△BKC重叠部分的面积为S，求S的最大值．解：（1）如图1，作AE⊥BC于E，DF⊥BC于F，则AE∥DF，∵AD∥BC，AE⊥BC，∴四边形ADFE是矩形，∴AE＝DF，AD＝EF＝6，在Rt△ABE和Rt△DCF中，，∴Rt△ABE≌Rt△DCF（HL），∴BE＝CF，∴BE＝CF＝＝3，由勾股定理得，AE＝＝＝4，梯形ABCD的面积＝×（AD+BC）×AE＝×（12+6）×4＝36，故答案为：36；（2）如图3，过D作DE∥AB，交BC于点E，∵AD∥BC，DE∥AB，∴四边形ABED为平行四边形，∴BE＝AD＝6，∴EC＝6，当PQ∥AB时，PQ∥DE，∴△CQP～△CED，∴，即＝，解得，t＝；（3）如图2，过G作GH⊥BC，延长HG交AD于I，过E作EX⊥BC，延长XE交AD于Y，过F作FU⊥BC 于U，延长UF交AD于W，∵BM＝CN＝5，∴MN＝12﹣5﹣5＝2，∴BN＝CM＝7，∵MN∥AD，∴△MGN～△DGA，∴＝，即＝，解得，HG＝1，设AK＝x，∵AD∥BC，∴△BEN～△KEA，∴＝，即＝，解得，EX＝，同理：FU＝，S＝S△BKC﹣S△BEN﹣S△CFM+S△MNG＝×12×4﹣×7×﹣×7×+×2×1 ＝，当x＝3时，S的最大值为25﹣＝5.4．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020中考数学冲刺专题：几何探究与证明（含答案）1.如图①，已知在正方形ABCD中，E为对角线BD上一点，过点E作EF⊥BD 交BC于点F，连接DF，G为DF中点，连接EG，CG.第1题图(1)求证：EG＝CG；(2)将图①中△BEF绕点B逆时针旋转45°，则点F落在对角线BD上，如图②，取DF中点G，连接EG，CG.问EG和CG相等吗？若相等，请给出证明；若不相等，请说明理由；(3)将图①中△BEF绕B点旋转任意角度，如图③，再连接相应的线段，问线段EG和CG有何关系？(请直接写出答案)(1)证明：∵在正方形ABCD中，∴∠BCD＝90°.∵EF⊥BD，∴∠FED＝90°. ∵G为DF中点，∴EG＝12DF，CG＝12DF.∴EG＝CG；(2)解：EG＝CG.证明：如解图①，延长EF交CD于点H，连接GH，第1题解图①∵在正方形ABCD中，∴∠ABC＝90°，BD平分∠ABC，∴∠EBF＝12∠ABC＝45°.∵EF⊥AB，∴∠FEB＝90°，∴∠EFB＝90°－∠EBF＝45°，∴∠EBF＝∠EFB，∴BE＝FE.∵∠BCD＝∠ABC＝∠BEF＝90°，∴四边形EBCH是矩形，∴HC＝EB＝EF，∠FHC＝90°，∴∠FHD＝180°－∠FHC＝90°. ∵CD∥EB，∴∠HDF＝∠EBF＝45°，∴∠DFH＝90°－∠HDF＝45°，∴∠HDF＝∠DFH，∴HD＝FH.∵G为DF中点，∠DHF＝45°，∴∠DHG＝12∴∠GHC＝180°－∠DHG＝135°.∵∠EFG＝180°－∠DFH＝135°，∴∠GHC＝∠EFG，∵在Rt△DHF中，G为DF中点，∴GH＝12DF＝GF，∴△EFG≌△CHG(SAS)，∴EG＝CG；(3)解：EG＝CG，EG⊥CG.【解法提示】如解图③，理由如下：第1题解图②过点F作CD的平行线并延长CG交于点M，连接EM、EC，过点F作FN 垂直于AB于点N，∵G为FD中点，易证△CDG≌△MFG，得到CD＝FM，又∵BE＝EF，∴∠EBF＝∠EFB，∴∠EFM＝180°－45°－∠BFH＝135°－∠BFH，∠EBC＝∠EBF＋∠FBH＝45°＋90°－∠BFH＝135°－∠BFH，∴∠EFM＝∠EBC，∴△EFM≌△EBC(SAS)，∴∠FEM＝∠BEC，EM＝EC，∵∠FEC＋∠BEC＝90°，∴∠FEC＋∠FEM＝90°，即∠MEC＝90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG＝CG，EG⊥CG.2. 如图，在△ABC中，∠ACB＝90°，过点A作射线AP⊥AB，点D是线段AC上一动点(不与点A、C重合)，连接BD，过点D作DE⊥BD，交射线AP于点E.(1)如图①，当∠BAC＝45°时，则线段AE与线段CD之间的数量关系为________；(2)如图②，当∠BAC＝30°时，猜想线段AE与线段CD之间的数量关系，并说明理由；(3)当∠BAC＝α时，直接写出线段AE与线段CD的数量关系(用含α的三角函数表示)．第2题图解：(1)AE＝2CD；【解法提示】如解图①，在BC上取一点G，使AD＝BG，连接DG，∵∠BAC＝45°，∠ACB＝90°，∴△ACB是等腰直角三角形，∴AC＝BC，∴AC－CD＝BC－BG，即CD＝CG，∴△CDG是等腰直角三角形，∴DG＝2CD，∠DGC＝45°，∴∠DGB＝135°，∵AP⊥AB，∴∠BAP＝90°，∴∠DAE ＝90°＋45°＝135°，∴∠DAE ＝∠DGB ，∵DE ⊥DB ，∴∠EDB ＝90°，∴∠EDA ＋∠BDC ＝90°，∵∠BDC ＋∠DBC ＝90°，∴∠EDA ＝∠DBC ，∴△EAD ≌△DGB (ASA)，∴AE ＝DG ，∴AE ＝2CD ；(2)猜想：AE ＝2CD ，理由是：如解图②，过点D 作DF ∥AB ，交BC 于点F ，则∠FDC ＝∠BAC ＝30°，AD CD ＝BF CF ，∴AD BF ＝CD CF ，∵AP ⊥AB ，DE ⊥BD ，∴∠BAP ＝∠BDE ＝90°，∵∠ADE ＋∠BDE ＋∠BDC ＝180°，∴∠ADE ＋∠BDC ＝90°，∵∠ACB ＝90°，∠FDC ＝30°，∴∠DBC ＋∠BDC ＝90°，CF ＝12DF ，∴∠ADE ＝∠DBC ，∵∠DAE ＝∠BAC ＋∠BAP ，∠BFD ＝∠FDC ＋∠ACB ，∴∠DAE ＝∠BFD ，∴△DAE ∽△BFD ，∴AD BF ＝AE FD ，∴CD CF ＝AE FD ，∴DF CF ＝AE CD ，∴AE CD ＝2，即AE ＝2CD ；(3)CD ＝AE ·sin α，【解法提示】如解图③，过点D 作DF ∥AB ，交BC 于点F ，则∠FDC ＝∠BAC＝α，AD CD ＝BF CF ，∴AD BF ＝CD CF ，∵AP ⊥AB ，DE ⊥BD ，∴∠BAP ＝∠BDE ＝90°，∵∠ADE ＋∠BDE ＋∠BDC ＝180°，∴∠ADE ＋∠BDC ＝90°，∵∠ACB ＝90°，∠FDC ＝α，∴∠DBC ＋∠BDC ＝90°，sin ∠FDC ＝sin α＝CF DF ，∴∠ADE ＝∠DBC ，∵∠DAE ＝∠BAC ＋∠BAP ，∠BFD ＝∠FDC ＋∠ACB ，∴∠DAE ＝∠BFD ，∴△DAE ∽△BFD ，∴AD BF ＝AE FD ，∴CD CF ＝AE FD ，∴CD AE ＝CF FD ＝sin α，∴CD ＝AE ·sin α.第2题解图3.已知在正方形ABCD 中，点E 在直线AB 上，点F 在直线BC 上，连接DE 、DF ，∠EDF ＝45°.(1)如图①，点E ，点F 分别在线段AB ，BC 上时，直接写出AE ，CF ，EF 的数量关系；(2)如图②，点E 在AB 的延长线上，点F 在BC 的延长线上，求AE ，CF ，EF 的数量关系；(3)如图③，在(2)的条件下，若AE＝2AB＝8，求EF的长．第3题图解：(1)EF＝AE＋CF.【解法提示】∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠B＝∠C＝∠ADC＝∠DAB＝90°，如解图①：延长BA，使AM＝CF，且AD＝CD，∠C＝∠MAD，∴△AMD≌△CFD(SAS)，∴∠ADM＝∠CDF，DM＝DF，∵∠EDF＝45°，∴∠ADE＋∠FDC＝45°，∴∠ADM＋∠ADE＝45°＝∠MDE，∴∠MDE＝∠FDE，且DM＝DF，DE＝DE，∴△EDF≌△EDM(SAS)，∴EF＝EM，∵EM＝AM＋AE＝AE＋CF，∴EF＝AE＋CF；第3题解图①第3题解图②(2)如解图②：在AB上截取AM＝CF，∵AD＝CD，AM＝CF，∠A＝∠DCF＝90°，∴△ADM≌△CDF(SAS)，∴DM＝DF，∠ADM＝∠CDF，∵∠ADM＋∠MDC＝90°，∴∠CDF＋∠MDC＝90°，即∠MDF＝90°，∵∠EDF＝45°，∴∠EDF＝∠MDE＝45°，且DM＝DF，DE＝DE，∴△MDE≌△FDE(SAS)，∴EF＝EM，∵AE＝AM＋ME，∴AE＝CF＋EF；(3)∵AE＝2AB＝8，∴AB＝BC＝BE＝4，∵AE＝CF＋EF，∴CF＝8－EF，在Rt△BEF中，EF2＝BE2＋BF2，∴EF2＝16＋(4＋8－EF)2，∴EF＝203.4. 在菱形ABCD中，P为直线AD上的点，Q为直线CD上的点，分别连接PC，PQ，且PC＝PQ.(1)若∠B＝60°，点P在线段DA上，点Q在线段CD的延长线上，如图①，证明：DQ＋PD＝AB；(2)若∠B＝60°，点P在线段DA的延长线上，点Q在线段CD上，如图②，猜想线段DQ，PD和AB之间有怎样的数量关系，并给予证明；(3)若∠B＝120°，点P在线段DA上，点Q在线段CD的延长线上，如图③，猜想线段DQ，PD和AB之间有怎样的数量关系？并给予证明．第4题图(1)证明：如解图①，在CD上取CH＝DQ，连接PH，∵PC＝PQ，∴∠PCQ＝∠PQC，∵CH＝DQ，∴△PCH≌△PQD(SAS)，∴PH＝PD，∵四边形ABCD是菱形，∴CD＝AB，∠PDC＝∠B＝60°，∴△PHD是等边三角形，∴PD＝HD，∴PD＋DQ＝DH＋CH＝CD＝AB；(2)解：猜想PD－DQ＝AB.证明：如解图②，延长CA到点M，使得AM＝AP，连接PM. ∵四边形ABCD是菱形，∠B＝60°，∴△ABC，△ACD都是等边三角形，∴∠CAD＝∠P AM＝60°，∴△P AM是等边三角形，∴AM＝PM，∠M＝∠ACD＝60°，∴PM∥CD，∴∠PCD＋∠CPM＝180°，∵PC＝PQ，∴∠PCQ＝∠PQC，∵∠PQC＋∠PQD＝180°，∴∠CPM＝∠PQD，∴△PCM≌△QPD(AAS)，∴CM＝PD，PM＝DQ＝AM，∵CM＝AC＋AM＝AB＋DQ，∴PD－DQ＝AB；(3)解：猜想：DQ－PD＝AB.证明：如解图③，在DQ上截取DM＝DP，连接PM. ∵∠B＝∠ADC＝120°，∴∠PDM＝60°，∴△PDM是等边三角形，∴PD＝PM，∠PMC＝∠PDQ＝60°，∵PC＝PQ，∴∠PCM＝∠Q，∴△PCM≌△PQD(AAS)，∴CM＝DQ，∴CD＋DM＝DQ，∴AB＋PD＝DQ，即DQ－PD＝AB.第4题解图5.在△ABC 中，已知AB ＞AC ，AD 平分∠BAC 交BC 于点D ，点E 在DC 的延长线上，且DE BD ＝k ，过点E 作EF ∥AB 交AC 的延长线于点F .(1)如图①，当k ＝1时，求证：AF ＋EF ＝AB ；(2)如图②，当k ＝2时，直接写出线段AF 、EF 、AB 之间满足的数量关系：________；(3)如图③，当DE BD ＝k 时，请猜想线段AF 、EF 、AB 之间满足的数量关系(含k )，并证明你的结论．第5题图(1)证明：如解图①，延长AD 、EF 交于点G ，当k ＝1时，DE ＝BD ，∵EF ∥AB ，∴∠BAD ＝∠EGD ，在△ABD 与△GED 中，⎩⎪⎨⎪⎧∠BAD ＝∠EGD ∠BDA ＝∠EDG BD ＝ED，∴△ABD ≌GED (AAS)，∴AB ＝GE ，又∵AD 平分∠BAC ，∴∠BAD ＝∠DAC ，∴∠FGD ＝∠DAC ，∴AF ＝GF ，∵GF ＋EF ＝GE ，∴AF ＋EF ＝AB;(2)解：AF＋EF＝2AB.【解法提示】如解图②，延长AD、EF交于点G，当k＝2时，∵EF∥AB，∴∠BAD＝∠EGD，又∵∠BDA＝∠EDG，∴△ABD∽△GED，∴GEAB ＝DEDB＝2，即GE＝2AB，又∵AD平分∠BAC，∴∠BAD＝∠DAC，∵∠FGD＝∠DAC，∴AF＝GF，∵GF＋EF＝GE，∴AF＋EF＝2AB；(3)解：猜想：AF＋EF＝kAB.证明：如解图③，延长AD、EF交于点G，当DEBD＝k时，∵EF∥AB，∴∠BAD＝∠EGD，又∵∠BDA＝∠EDG，∴△ABD∽△GED，∴GE AB ＝DEBD＝k，即GE＝kAB，又∵AD平分∠BAC，∴∠BAD＝∠DAC，∴∠FGD＝∠DAC，∴AF＝GF，∵GF＋EF＝GE，∴AF＋EF＝kAB.第5题解图类型二两条线段之间的数量关系与位置关系证明6. 如图，已知△ACB和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，连接BE，点F为BE的中点，连接CF，DF.(1)如图①，点D在AC上，延长DF，交BC于点G，请判断线段CF，DF 有怎样的数量关系和位置关系？并说明理由；(2)将图①中的△ADE绕点A旋转到图②位置，延长DF至G使GF＝DF，DG与AB交于点O，连接BG，CG，DC，请判断(1)中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．第6题图解：(1)DF＝CF，DF⊥CF；理由：∵∠ADE＝∠ACB＝90°，∴DE∥BC，∴∠DEF＝∠GBF，∠EDF＝∠BGF.∵F为BE中点，∴EF＝BF，∴△DEF≌△GBF(AAS)，∴DE＝GB，DF＝GF.∵AD＝DE，∴AD＝GB，∵AC ＝BC ，∴AC －AD ＝BC －GB ，∴DC ＝GC .∵∠ACB ＝90°，∴△DCG 是等腰直角三角形，∵DF ＝GF ，∴DF ＝CF ，DF ⊥CF ；(2)(1)中的结论仍然成立，理由是：在△FDE 和△FGB 中，⎩⎪⎨⎪⎧DF ＝FG ∠DFE ＝∠GFB EF ＝FB，∴△FDE ≌△FGB (SAS)，∴∠DEF ＝∠GBF ，DE ＝GB ，∴BG ∥DE ，如解图，延长DE 交BC 于点M ，∵DE ∥BG ，∴∠CBG ＝∠DMB ，∵∠ADE ＝∠ACB ＝90°，∴∠DAC ＋∠DMC ＝180°，∴∠DMB ＝∠DAC ＝∠CBG ，在△CAD 和△CBG 中，∵⎩⎪⎨⎪⎧AD ＝BG ∠DAC ＝∠GBC AC ＝BC，∴△CAD ≌△CBG (SAS)，∴CD ＝CG ，∠DCA ＝∠GCB ，∴∠DCG ＝∠BCG ＋∠BCD ＝∠ACD ＋∠BCD ＝∠ACB ＝90°，∵DF ＝GF ，∴DF ＝CF ，DF ⊥CF .第6题解图7. 在正方形ABCD中，BD是一条对角线，点E在直线CD上(与点CD不重合)，连接AE，平移△ADE使点D移动到点C得到△BCF，过点F作FG⊥BD 于点G，连接AG，EG.第7题图(1)如图①，若点E在线段CD上，试猜想AG与EG的数量关系和位置关系；(2)如图②，若点E在线段CD的延长线上其余条件不变时，猜想(1)中的结论是否仍然成立，请你给出证明；(3)若点E 在线段DC 的延长线上且∠AGF ＝120°，正方形ABCD 的边长为2，直接写出DE 的长度．(1)解：AG ＝EG ，AG ⊥EG ，理由如下：由平移得EF ＝CD ＝AD ，∵BD 是正方形ABCD 的对角线，∴∠ADB ＝∠CDB ＝45°，∵FG ⊥BD ，∴∠DGF ＝90°，∴∠GFD ＋∠CDB ＝90°，∴∠DFG ＝45°，∴GD ＝GF ，在△AGD 和△EGF 中，⎩⎪⎨⎪⎧AD ＝EF ∠ADG ＝∠EFG DG ＝FG，∴△AGD ≌△EGF (SAS)，∴AG ＝EG ，∠AGD ＝∠EGF ，∴∠AGE ＝∠AGD ＋∠DGE ＝∠EGF ＋∠DGE ＝90°，∴AG ⊥EG ；(2)解：(1)中结论仍然成立．证明：由平移得EF ＝CD ＝AD ，∵BD 是正方形ABCD 的对角线，∴∠ADB ＝∠CDB ＝45°，∵FG ⊥BD ，∴∠DGF ＝90°，∴∠GFD ＋∠CDB ＝90°，∴∠DFG ＝45°，∴GD ＝GF ，在△AGD 和△EGF 中，⎩⎪⎨⎪⎧AD ＝EF ∠ADG ＝∠EFG DG ＝FG，∴△AGD ≌△EGF (SAS)，∴AG ＝EG ，∠AGD ＝∠EGF ，∴∠AGE＝∠AGD－∠DGE＝∠EGF－∠DGE＝90°，∴AG⊥EG；(3)DE＝2 3.【解法提示】同(1)可得，AG＝EG，AG⊥EG，∴∠GEA＝45°，∵∠AGF＝120°，∴∠AGB＝∠EGF＝30°，又∵∠GFD＝45°，∴∠CEG＝∠EFG＋∠EGF＝75°，∴∠AED＝∠CEG－∠GEA＝30°，在Rt△ADE中，AD＝2，∴DE＝2 3.第7题解图8.在矩形ABCD中，已知AD＞AB.在边AD上取点E，使AE＝AB，连接CE，过点E作EF⊥CE，与直线AB交于点F.猜想：如图①，当点F在边AB上时，线段AF与DE的大小关系为________；探究：如图②，当点F 在边AB 的延长线上时，EF 与边BC 交于点G .判断线段AF 与DE 的大小关系，并加以证明；应用：如图②，若AB ＝2，AD ＝5，利用探究得到的结论，求线段BG 的长．第8题图解：猜想：AF ＝DE ；【解法提示】∵∠CEF ＝90°，∴∠AEF ＋∠CED ＝90°，∵∠AFE ＋∠AEF ＝90°，∴∠AFE ＝∠CED ，∠AEF ＝∠DCE ，∵AE ＝AB ，AB ＝CD ，∴AE ＝CD ，∴在△AEF和△DCE 中，⎩⎪⎨⎪⎧∠AEF ＝∠DCE ∠AFE ＝∠EDC AE ＝CD，∴△AEF ≌△DCE ，∴AF ＝DE ；探究：AF ＝DE ，证明：∵∠A ＝∠FEC ＝∠D ＝90°，∴∠AEF ＝∠DCE ，在△AEF 和△DCE 中，⎩⎪⎨⎪⎧∠A ＝∠D AE ＝CD∠AEF ＝∠DCE， ∴△AEF ≌△DCE (ASA)，∴AF ＝DE .应用：∵△AEF ≌△DCE ，∴AE ＝CD ＝AB ＝2，AF ＝DE ＝3，FB ＝F A －AB ＝1，∵BG ∥AD ，∴BG AE ＝FB F A ，∴BG 2＝13，∴BG ＝23.9 已知△ABC 为等边三角形，点D 为直线BC 上的一动点(点D 不与点B 、C 重合)，以AD 为边作等边△ADE (顶点A 、D 、E 按逆时针方向排列)，连接CE .(1)如图①，当点D在边BC上时，求证：①BD＝CE，②AC＝CE＋CD；第9题图(2)如图②，当点D在边BC的延长线上且其他条件不变时，结论AC＝CE ＋CD是否成立？若不成立请写出AC、CE、CD之间存在的数量关系并说明理由；(3)如图③，当点D在边BC的反向延长线上且其他条件不变时，直接写出AC、CE、CD之间存在的数量关系．(1)证明：①∵△ABC和△ADE都是等边三角形，∴AB＝AC＝BC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAC－∠CAD＝∠DAE－∠CAD，即∠BAD＝∠CAE，在△ABD和△ACE中，⎩⎪⎨⎪⎧AB ＝AC ∠BAD ＝∠CAE AD ＝AE，∴△ABD ≌△ACE (SAS)，∴BD ＝CE ；②∵BC ＝BD ＋CD ，AC ＝BC ，BD ＝CE ， ∴AC ＝CE ＋CD ；(2)解：AC ＝CE ＋CD 不成立，AC 、CE 、CD 之间存在的数量关系是AC ＝CE －CD . 理由：∵△ABC 和△ADE 都是等边三角形，∴AB ＝AC ＝BC ，AD ＝AE ，∠BAC ＝∠DAE ＝60°， ∴∠BAC ＋∠CAD ＝∠DAE ＋∠CAD ，即∠BAD ＝∠CAE ，在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ∠BAD ＝∠CAE AD ＝AE，∴△ABD ≌△ACE (SAS)，∴BD ＝CE ，∵BC ＝BD －CD ，∴BC ＝CE －CD ，∵AC ＝BC ，∴AC ＝CE －CD ；(3)解：AC 、CE 、CD 之间存在的数量关系是AC ＝CD －CE .【解法提示】∵△ABC 和△ADE 是等边三角形，∴AD ＝AE ，AB ＝AC ，∵∠DAE ＝∠BAC ＝60°，∴∠DAB ＝∠EAC ，∴在△ADB 和△AEC 中，⎩⎪⎨⎪⎧AD ＝AE ∠DAB ＝∠EAC AB ＝AC，∴△ADB ≌△AEC ，∵BD ＝CE ，∵CD ＝BD ＋BC ，∴BC ＝CD －CE ，∴AC ＝CD －CE .10. 已知△ABC 为等边三角形，点D 为直线BC 上的一动点(点D 不与B 、C 重合)，以AD 为边作∠DAF ＝60°，在射线AF 上截取点F ，使AF ＝AD ，过点D 作DE ∥AF ，过点F 作EF ∥AD ，DE 、EF 交于点E ，连接CF ，(1)如图①，当点D在边BC上时，求证：①BD＝CF；②AC＝CF＋CD；(2)如图②，当点D在边BC的延长线上且其他条件不变时，结论AC＝CF＋CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；(3)如图③，当点D在边CB的延长线上且其他条件不变时，并直接写出AC、CF、CD之间存在的数量关系．第10题图(1)证明：∵△ABC是等边三角形，∴AB＝AC＝BC，∠BAC＝∠DAF＝60°，∴∠BAC－∠DAC＝∠DAF－∠DAC，∴∠BAD＝∠CAF，∵在△BAD 和△CAF 中⎩⎪⎨⎪⎧AB ＝AC ∠BAD ＝∠CAF AD ＝AF，∴△BAD ≌△CAF (SAS)，∴CF ＝BD ，∴CF ＋CD ＝BD ＋CD ＝BC ＝AC ，即①BD ＝CF ，②AC ＝CF ＋CD ；(2)解：AC ＝CF ＋CD 不成立，AC 、CF 、CD 之间存在的数量关系是AC ＝CF －CD ，理由是：由(1)知：AB ＝AC ＝BC ，AD ＝AF ，∠BAC ＝∠DAF ＝60°， ∴∠BAC ＋∠DAC ＝∠DAF ＋∠DAC ，即∠BAD ＝∠CAF ，∵在△BAD 和△CAF 中，⎩⎪⎨⎪⎧AB ＝AC ∠BAD ＝∠CAF AD ＝AF，∴△BAD ≌△CAF (SAS)，∴BD ＝CF ，∴CF －CD ＝BD －CD ＝BC ＝AC ，即AC ＝CF －CD ；(3)解：AC ＝CD －CF .【解法提示】理由是：∵∠BAC ＝∠DAF ＝60°， ∴∠DAB ＝∠CAF ，∵在△BAD 和△CAF 中， ⎩⎪⎨⎪⎧AB ＝AC∠DAB ＝∠F AC AD ＝AF，∴△BAD ≌△CAF (SAS)，∴CF ＝BD ，∴CD －CF ＝CD －BD ＝BC ＝AC ，即AC ＝CD －CF .。