第4章视图与投影
工程制图 第4章 基本体的三视图

2.圆锥体
S O
●
O1
●
s
⑷ 圆锥面上取点
在图示位置,俯视图为一圆。 另两个视图为等边三角形,三 角形的底边为圆锥底面的投影, 两腰分别为圆锥面不同方向的 两条轮廓素线的投影。 k(n)
●
(n)
k
n● s
如何在圆锥面 过锥顶作一 上作直线? 条素线。 圆的半径?
k
★辅助直线法 ★辅助圆法
Z
a (b) d(c) e
X
b'
c'
D
YH
ห้องสมุดไป่ตู้
正六棱柱的投影图
返回
dc
e
Y
C’’ 例:求棱柱表面上A、B、C三点的三面投影。 C’ (b’)
a
b’’
a
b C
a
2.棱锥
⑴ 棱锥的组成 A 由一个底面和几个侧棱面组成。 侧棱线交于有限远的一点 锥顶。 ⑵ 棱锥的三视图 ⑶ 在棱锥面上取点 棱锥处于图示位置时, 同样采用平面上取点法。 其底面ABC是水平面,在俯 a 视图上反映实形。侧棱面SAC a 为侧垂面,另两个侧棱面为一 般位置平面。 k
本章内容是在研究点、线、面投影 的基础上进一步论述立体的投影作图问 题。 立体表面是由若干面所组成。表面均 为平面的立体称为平面立体;表面为曲面 或平面与曲面的立体称为曲面立体。 在投影图上表示一个立体,就是把 这些平面和曲面表达出来,然后根据可 见性原理判断那些线条是可见的或是不 可见的,分别用实线和虚线来表达,从 而得到立体的投影图。
一、平面基本体的投影
1.棱柱
⑴ 棱柱的组成
由两个底面和几个侧棱面组成。侧 棱面与侧棱面的交线叫侧棱线,侧 棱线相互平行。 ⑵ 棱柱的三视图 ⑶ 棱柱面上取点 a 先画反映底面形状的视图。 由于棱柱的表面都是平 (b ) 点的可见性规定: 面,所以在棱柱的表面上取 若点所在的平面的投影可见, b 点与在平面上取点的方法相 点的投影也可见;若平面的投影 同。 积聚成直线,点的投影也可见。
室内设计制图与识图第第二版教学课件第四章形体投影表达方法

第三节 断面图
(一)移出断面图 画在物体投影轮廓线之外的断面图 称为移出断面图,如图4-18 所示。图 中的1—1、2—2、3—3断面图均为移 出断面图。移出断面图的轮廓线用粗 实线画出,可以画在剖切平面的延长 线上或其他适当的位置,并画出材料 图例。
同一构件如绘制的位置不够时,也可将该构件分成两部分绘制,再用连接符号表示 相连,如图4-26 所示。
思考与练习
1. 问答题
(1)基本视图包括哪六个视图?
(2)绘制半剖面图时应注意哪些事项?
(3)局部剖面图适合哪些情况使用?
(4)剖面图的标注有哪几方面的规定?
(5)断面图与剖面图有哪几方面的区别?
2. 填空题
第一节 视图
第一节 视图
局部视图一般按投影方向配置, 必要时也可配置在其他适当位置,如 图4-4 的局部视图B 所示。局部视图 的范围应以视图的轮廓线和波浪线组 合表示,如图4-4 的局部视图A 所示。 但当表示的局部结构和形状完整,且 轮廓线封闭时,波浪线可省略,如图 4-4 的局部视图B 所示。
第一节 视图
第一节 视图
(三)镜像视图 当从上向下的正投影法所绘图样的虚线过多,尺寸标注不清楚,无法读图时,可以 采用镜像投影的方法投射,如图4-6a 所示,但应在原图名后注写“镜像”两字。绘图 时,把镜面放在形体下方,代替水平投影面,形体在镜面中反射得到的图像称为“平面 图(镜像)”,如图4-6c 所示;或在平面图的旁边画一个如图4-6d 所示的识别符号以 示区别。
第一节 视图
(二)展开视图 为了表达倾斜于基本投影面那部分的真实形状,设置一个与该部分表面平行的辅助 投影面,然后将该部分向辅助投影面作正投影,所得到的视图称为展开视图,又称旋转 视图。 如图4-5 所示的建筑,左侧部分墙面平行于正立投影面,在正面上反映实形,而右 侧墙面与正立投影面倾斜,其投影图不反映实形。
4.3 灯光与影子 (1)

图(1)
图(2)
2:有天晚上,小丽和小刚在灯下玩耍,小 刚突然高兴地对小丽说: “我踩到你的 ‘脑袋’了”。 请在图中画出 小丽在灯光下 的影子(可用线 段表示),并确 定小刚此时所 站的位置。
B A
3:小朋友晚上在路灯下的马 路上列队行进,队长下命令 说:“注意每个人之间的距 离!每两人间隔的距离应该 有一个人影那么长!”你认 为他下达的这个命令合理吗? 若小朋友按照这个命令来执 行,会出现什么样的情况?
3
“才华”显露
当你乘车沿一盘棋平坦的大道向前行驶时,你会发现 : 前方那些高一些的建筑物好像“沉”到了位于它们 前面的那些矮一些的建筑物后面去了.这则为什么?先 想一想,再与同伴进行交流.
当视点与A的距离越来越近时,所能看到 的B的部分就越来越少,直至完全消失.这 一过程给人的感觉就是B逐渐“沉”到A后 面去了. 盲区
小结:手电筒与物体,改变其中的一个位置 和方向,影子都会发生改变 。
如图,在一间黑屋子里用一盏白炽 灯照一个球。 (1)球在地上的阴影是什么形状? 一个圆 (2)当把白炽 灯向远移时,阴 影的大小会怎样 变化? 阴影会变小
总结
探照灯、手电筒、路灯 和台灯的光线可以看成 是从一点出发的,像这 样的光线所形成的投影 称为中心投影。
小结
拓展
中心投影
• 探照灯,手电筒,路灯,和台灯的光线可以看 成是从一点出发的光线,像这样的光线所形 成的投影称为中心投影(central projection). • 皮影是用兽皮或纸板做成的人物剪影来表演 故事的戏曲.用灯光照射在银幕上,艺人在幕 后一边操纵剪影,一边演唱,并配以音乐. • 在灯光的照射下,做不同的手势可以形成各 种各样的手影. • 皮影和手影都是在灯光照射下形成的影子.
第四章图形的相似位似、投影、视图

位似、投影、视图教学目标1、掌握位似的概念及比例、坐标的计算;2、熟悉投影及比例的计算;3、掌握三视图。
重难点分析重点:1、位似与比例计算;2、位似与坐标计算;3、投影与比例计算;4、视图的读取。
难点:1、位似、投影中的相似与计算。
知识点梳理1、相似的进一步学习(1)证明三角形相似;(2)相似性质的应用。
'2、如果两个相似多边形每组对应顶点A、A'的连线都经过同一个点O,且有OA=kAO⋅(0≠k),那么这两个相似多边形叫做位似多边形,点叫做位似中心。
实际上,k就是这两个相似多边形的相似比。
3、画位似图形的步骤:(1)确定位似中心(可以在图形外部、内部、某一边上、某一顶点);(2)连接图形各顶点与位似中心的连线(延长线);(3)按相似比取点;(4)顺次连接个点,所得图形就是所求图形。
4、位似图形的坐标变化规律5、中心投影与平行投影6、物体的视图:主视图、左视图、俯视图知识点1:相似的进一步认识△中,D是AC上一点,联结BD,且∠ABD =∠ACB.【例1】已知:如图,在ABC(1)求证:△ABD∽△ACB;(2)若AD=5,AB= 7,求AC的长.【随堂练习】△中,D是AB上一点, E是AC上一点,1、已知: 如图,在ABC且∠ADE =∠ACB.(1)求证:△AED∽△ABC;(2)若DE: CB=3:5 ,AE=4, 求AB的长.2、已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B.(1)求证:△ABE∽△DEA;的值.(2)若AB=4,求AE DE3、如图,在△ABC中,点D在边AB上,满足且∠ACD =∠ABC,若AC = 2,AD = 1,求DB 的长.影子三角尺灯泡O AA'知识点2:位似图形的识别与画法【例1】如图,D ,E ,F 分别是OA ,OB ,OC 的中点,下面的说法中:①ABC ∆与DEF ∆是位似图形; ②ABC ∆与DEF ∆的相似比为1:2;③ABC ∆与DEF ∆的周长之比为2:1; ④ABC ∆与DEF ∆的面积之比为4:1.正确的是【 】 A .①②③ B .①③④ C .①②④ D .②③④【例2】如图,△ABC 与△DEF 位似,位似中心为点O ,且△ABC 的面积等于△DEF 面积的94,则 AB :DE= .【随堂练习】 1、三角尺在灯泡的照射下在墙上形成的影子如图所示. 若,则这个三角尺的周长与它在墙上形成的影子的周长的比是【 】 A .5:2 B .2:5 C .4:25 D .25:42、如图,在8×8的网格中,每个小正方形的顶点叫做格点,△OAB 的顶点都在格点上,请在网格中画....出.△OAB 的一个位似图形,使两个图形以O 为位似中心,且所画图形与△OAB 的位似比为2︰1.3、如图,五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形,O 为位似中心,OD=OD ′,则A ′B ′:AB 为【 】A.2:3B.3:2C.1:2D.2:14、在平面直角坐标系中,O 为坐标原点,点)0,2(-A ,)2,1(-B ,请以为位似中心,将OAB ∆放大,使放大后的B A O ''∆与的对应线段比为1:2【例3】如图,在平面直角坐标系中,A (-1,1),B (-2,-1).(1)以原点O 为位似中心,把线段AB 放大到原来的2倍,请在图中画出放大后的线段CD ;(2)在(1)的条件下,写出点A 的对应点C 的坐标为 ,点B 的对应点D 的坐标为 .【例4】如图,△ABO 缩小后变为△A ′B ′O ,其中A 、B 的对应点分别为A ′,B ′,A ′,B ′均在图中格点上,若线段AB 上有一点P (m ,n ),则点P 在A ′B ′上的对应点P ′的坐标为【 】 A .(2m ,n ) B .(m ,n ) C .(2m ,2n ) D .(m ,2n)【例5】如图,在平面直角坐标中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为31,点A ,B ,E 在x 轴上,若正方形BEFG 的边长为6,则C 点坐标为【 】 A .(3,2) B .(3,1) C .(2,2) D .(4,2)【随堂练习】1、如图,在直角坐标系中,△OAB 和△OCD 是位似图形,O 为位似中心,若A 点的坐标为(1,1),B 点的坐标为(2,1),C 点的坐标为(3,3),那么点D 的坐标是 .2、如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD .若B (1,0),则点C 的坐标为______________.3、如图,已知矩形OABC 与矩形ODEF 是位似图形, P 是位似中心,若点B 的坐标为(2,4),点E 的坐标为(﹣1,2),则点P 的坐标为【例6】图中两个四边形是位似图形,它们的位似中心是【 】 A .点M B .点N C .点O D .点P【随堂练习】1、如图,ABO ∆与O B A '''∆是位似图形,且顶点都在格点上,则位似中心的坐标是 .2、如图所示的两个三角形是位似图形,它们的位似中心是点 .【例7】如图,在边长为1个单位长度的小正方形网格中.(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.【例8】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).(1)以O为位似中心,作△A′B′C′∽△ABC,相似比为1:2,且保证△A′B′C′在第三象限;(2)点B′的坐标为(,);(3)若线段BC上有一点D,它的坐标为(a,b),那么它的对应点D′的坐标为()【随堂练习】1、已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)B(3,﹣2)C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC向上平移6个单位得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.2、将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;(1)关于y轴对称的四边形A′B′C′D′;(2)以坐标原点O为位似中心,放大到原来的2倍的四边形A″B″C″D″.知识点3:中心投影与平行投影【例1】下图是我国北方某地一棵树在一天不同时刻拍下的五张图片,说出这五张图片所对应时间的先后顺序.【例2】如图,晚上小明由甲处径直走到乙处的过程中,他在路灯M下的影长在地面上的变化情况是【】A、逐渐变短B、先变短后变长C、先变长后变短D、逐渐变长【随堂练习】1、如图所示,在房子外的屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区在【】A.△ACEB.△BFDC.四边形BCEDD.△ABD2、把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是【】A. B. C. D.3、夜晚当你靠近一盏路灯时,你发现自己的影子是【】A.变短 B.变长 C.由短变长 D.由长变短【例3】小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米,则电线杆AB长=_____。
第四章立体的投影

❖ ㈡两平面立体的表面交线
相交形体的表面交线称为相贯线。
两平面立体相贯线的特征:一般情况为空间折线,特殊情况为平面折线,每 段折线是两立体棱面的交线,每个折点是一立体棱线与另一立体的贯穿点。 立体的相贯形式有两种:
一是全贯,即一个立体完全穿过另一个立体,相贯线有两组; 二是互贯,两个立体各有一部分参与相贯,相贯线为一组。 求两平面体相贯线的方法:有两种 (1)交点法——先作出各个平面体的有关棱线与另一立体的交点,再将所有交 点顺次连成折线,即组成相贯线。连点的规则是:只有当两个交点对每个立体 来说,都位于同一个棱面上时才能相连,否则不能相连。 (2)交线法——直接作出两平面立体上两个相应棱面的交线,然后组成相贯线。
(3)投影分析
(二)棱锥体 (1)形体特征: 底面是多边形,棱 线交于一点,侧棱面均为三角形。 (2)安放位置: 底面△ABC平行于H面。 (3)投影分析
【例4-1】 作四棱台的正投影图 解:(1)分析
1)四棱台的上、下底面都与H面平行, 前、后两棱面为侧垂面,左、右两棱面 为正 垂面。 2)上、下两底面与H面平行,其水平投 影反映实形;其正面、侧面投影积聚为 直线。 3)前、后两棱面与W面垂直,其侧面投影积聚为直线;与H、V面倾斜,投 影为缩小的类似形。 4)左、右两个面与V面垂直,其正面投影积聚为直线;与H、W面倾斜,投 影为缩小的类似形。 5)四根斜棱线都是一般位置直线,其投影都不反映实长。
3)连点。 4)判断可见性。
❖ 三、同坡屋面交线的画法
单坡屋面 坡屋面 双坡屋面
四坡屋面 同坡屋面:既屋檐高度相等、各屋面与水平面倾角相等的屋面。 同坡屋面交线的画法,其实 质是求两平面交线的问题。
同坡屋面上各种交线的名称
九年级数学上册第四章视图与投影

九年级数学上册第四章视图与投影『一』.知识归纳:●知识点1 三视图:主视图、俯视图和左视图三视图之间要保持长对正,高平齐,宽相等。
一般地,俯视图要画在主视图的下方,左视图要画在正视图的右边。
主视图:基本可认为从物体正面视得的图象.俯视图:基本可认为从物体上面视得的图象左视图:基本可认为从物体左面视得的图象.注:①视图中每一个闭合的线框都表示物体上一个表面(平面或曲面),而相连的两个闭合线框一定不在一个平面上。
②在一个外形线框内所包括的各个小线框,一定是平面体(或曲面体)上凸出或凹的各个小的平面体(或曲面体)。
③在画视图时,看得见的部分的轮廓线通常画成实线,看不见的部分轮廓线通常画成虚线。
●知识点2 投影太阳光线可以看成平行的光线,像这样的光线所形成的投影称为平行投影。
探照灯、手电筒、路灯的光线可以看成是从一点出发的,像这样的光线所形成的投影称为中心投影。
——区分平行投影和中心投影:①观察光源;②观察影子。
从正面、上面、侧面看到的图形就是常见的正投影,也就是视图,是当光线与投影垂直时的投影。
①点在一个平面上的投影仍是一个点;②线段在一个面上的投影可分为三种情况:1.线段垂直于投影面时,投影为一点;2.线段平行于投影面时,投影长度等于线段的实际长度;3.线段倾斜于投影面时,投影长度小于线段的实际长度。
③平面图形在某一平面上的投影可分为三种情况:1.平面图形和投影面平行的情况下,其投影为实际形状;2.平面图形和投影面垂直的情况下,其投影为一线段;3.平面图形和投影面倾斜的情况下,其投影小于实际的形状。
『二』典型例题解析【视图类】★例题解析1 如图所示的几何体的俯视图是( B ).A B C D★例题解析2 上图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( D )★例题解析 3 下图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 BA.5 B.6 C.7 D.8★例题解析 4 如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为.★例题解析 5 在如图所示的正方体的三个面上,分别画了填充不同的圆,下面的4个图中,是这个正方体展开图的有( A ).★例题解析6 如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是( C ).A. 4B. 6C. 7D.8【投影类】★例题解析7 比例求高“投影”类题如图1,小华为了测量所住楼房的高度,他请来同学帮忙,在阳光下测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为____48____米.变化1 如果物体的投影一部分落在平地上,另一部分落在坡面上:如图2,在斜坡的顶部有一铁塔AB ,B 是CD 的中点,CD 是水平的,在阳光的照射下,塔影DE 留在坡面上.已知铁塔底座宽CD=12 m ,塔影长DE=18 m ,小明和小华的身高都是1.6m ,同一时刻,小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m 和1m ,那么塔高AB 为( )(A)24m (B)22m (C)20 m (D)18 m1 42 5 36第7题图图2变化2 如果物体的投影一部分落在平地上,另一部分落在台阶上:兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图3,若此时落在地面上的影长为4.4米,则树高为()(A)11.5米(B)11.75米(C)11.8米(D)12.25米变化3 如果将上题中的DE改为斜坡,再改变部分已知条件:梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图4,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2 m,α=o.在同一DE=4m ,BD=20m,DE与地面的夹角30时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(结果保留两个有效数字)★例题解析8 三角函数求高“投影”类题如图5,当太阳光与地面成55°角时,直立于地面的玲玲测得自己的影长为 1.16m,则玲玲的身高约为m.(精确到0.01m)变化1如果将太阳光改为照明灯,再适当改变已知条件和问题的形式:如图6所示,点P表示广场上的一盏照明灯.若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).★例题解析9 相似三角形求高“投影”类题如图7,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具。
(完整word版)建筑识图与构造4

图4—13正六棱柱的正等测画法
(二)圆柱:作图:如图4—14。
(a)(b)(c)(d)
图4—14圆柱的正等测
[例4-1]如图4-16所示,已知具有四坡顶的房屋模型的三视图,画出它的正等测。
[解](1)看懂三视图,想象房屋模型形状。
(2)选定坐标轴,画出房屋的屋檐。
(3)作下部的长方体。(4)作四坡屋面的屋脊线.
图4—9绘制组合体草图底稿
图4—10在台阶模型草图中标注尺寸
4.2轴测图
一、内容:
1、轴测图的特点、适用范围;
2、轴测投影的形成;
3、轴测图的类型、绘制方法。
二、要求及重点:
1、掌握轴测图的特点、适用范围、类型;
2、了解轴测投影的形成;
3、了解轴测图的绘制方法、步骤。
三、教学方式:
利用模型、教具、例题,使学生掌握、了解.
断面图的轮廓线用粗实线绘制。
(a)(b)(c)
图4—24剖面图与断面图
3、剖面图画法
(1)用单一的剖切面剖切,如图4-25。
(a)(b)图4-25用单一剖切面剖切
(2)用两个(或两个以上)互相平行的剖切平面剖切,如图4—26所示。
图4-26用两个平行的剖切面剖切
(3)用两个相交的剖切面(交线垂直于某一投影面)进行剖切,该剖面图的图名后应加注“展开”二字。如图4—27所示。
(a)正投影图(b)轴测投影图
图4-11正投影图与轴测投影图比较图4-12轴测图的形成
1、轴测投影面:用于画轴测图的投影面;
2、轴测轴:空间三根坐标轴(投影轴)O1X1、O1Y1、O1Z1、在轴测投影面上的投影OX、OY、OZ;
3、轴间角:两根轴测轴之间的夹角;
第4章 视图与投影
已知某四棱柱的俯视图如下图所示,尝试画出它的主视图和左视图.
视图如下:
归纳提炼
本节课我们学习了如何根据实物画直三棱柱和直四棱柱的三种视图,以及根据三种视图中的,一种画出另外两种视图,充分体现直三棱柱和直四棱柱与其视图之间的相互转化过程,还讨论了在画视图过程中应注意的事项.
课后作业
习题4.2
板书设计
二、范例学习、理解领会
例 确定图4-14中路灯灯泡所在的位置(见课本)。
学生观察屏幕,动手实验,找出灯泡的位置。
三、联系生活、丰富联想
议一议
1.图4-16(见课本)是两棵小树在同一时刻的影子,请在图中画出形成树影的光线,它们是太阳的光线还是灯光的光线?与同伴交流。
学生画图、观察、比较和识别。
继续探索:
做一做
取一些长短不等的小棒和三角形、矩形纸片,用手电筒去照射这些小棒和纸片。
提问:(1)固定手电筒,改变小棒或纸片的摆放位置和方向,它们的影子分别发生了什么变化?
(2)固定小棒和纸片,改变手电筒的摆放位置和方向,它们的影子发生了什么变化?
学生小组合作,实验感悟。
概念:探照灯、手电筒、路灯和台灯的光线可以看成是从一点发出的,像这样的光线所形成的投影称为中心投影。
2.在同一时刻,大树和小树的影子与它们的高度之间有什么关系?与同伴交流。
学生观察、交流。
做一做
某校墙边有甲、乙两根木杆。
(1)某一时刻甲木杆在阳光下的影子如图4-12所示,你能画出此时乙木杆的影子吗?(用线段表示影子)
在图4-12中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图形中有相似三角形吗?为什么?
实践:取若干长短不等的小棒及三角形、矩形纸片,观察它们在太阳光下的影子。
第四章投影和视图单元教案

第四章投影和视图单元教案第一节教学目标。
1. 了解投影和视图的概念和基本原理。
2. 掌握投影和视图的绘制方法。
3. 理解不同视图之间的关系。
4. 能够应用投影和视图的知识解决实际问题。
第二节教学重点和难点。
1. 投影和视图的概念和基本原理。
2. 投影和视图的绘制方法。
3. 不同视图之间的关系。
第三节教学内容。
1. 投影和视图的概念和基本原理。
1.1 投影的概念。
投影是指将三维空间中的物体投射到二维平面上的过程。
在工程制图中,常用投影的方法来表示物体的形状和尺寸。
1.2 视图的概念。
视图是指从不同方向观察物体所得到的投影。
常用的视图有主视图、俯视图和侧视图等。
1.3 投影和视图的基本原理。
投影和视图的绘制是基于投影的原理,通过投影将物体的形状和尺寸投射到平面上,再根据需要绘制不同的视图。
2. 投影和视图的绘制方法。
2.1 正投影和斜投影。
正投影是指投影线垂直于投影面的投影方法,斜投影是指投影线与投影面不垂直的投影方法。
在工程制图中常用正投影来表示物体的形状和尺寸。
2.2 视图的选择和布置。
在进行投影和视图的绘制时,需要根据物体的形状和尺寸选择合适的视图,并合理布置在图纸上。
3. 不同视图之间的关系。
3.1 主视图、俯视图和侧视图的关系。
主视图是指从正面观察物体所得到的视图,俯视图是指从上方观察物体所得到的视图,侧视图是指从侧面观察物体所得到的视图。
这三个视图之间具有一定的关系,可以通过它们来全面地了解物体的形状和尺寸。
第四节教学过程。
1. 投影和视图的概念和基本原理。
1.1 通过实物或图片等形式,让学生了解投影和视图的概念和基本原理。
1.2 讲解投影和视图的基本原理,引导学生理解投影和视图的绘制方法。
2. 投影和视图的绘制方法。
2.1 展示正投影和斜投影的绘制方法,让学生掌握投影的基本技巧。
2.2 给学生提供一些实例,让他们在老师的指导下进行投影和视图的绘制。
3. 不同视图之间的关系。
3.1 通过实例讲解主视图、俯视图和侧视图之间的关系,引导学生理解不同视图之间的联系。
大学工程制图--第4章立体的投影

一、 圆柱体 二、 圆锥体 三、 圆球 四、 圆环 五、 回转体的尺寸 标注
4.2 曲面立体的投影
一、圆柱
1、圆柱的投影分析 一直线(母 从前往后看在VW 从左向右看在 从上往下看在 线)绕与其平行的 面的投影是一个矩形: 轴线⊥H 面,所 面的投影是一个矩形: H 面上的投影为一 轴线 轴线旋转一周,形 上下两条水平线分别 以在H 面上的投影积 上下两条水平线分别 个圆周:它既是圆 成圆柱面。 是顶圆和底圆的投影, 聚为一点,用两条互 是顶圆和底圆的投影, 柱面的顶圆和底圆 长度为圆周的直径。 相垂直的点画线的交 长度为圆周的直径。 的重合投影,反映 左右两条直线为圆柱 点来表示;轴线//V 左右两条直线为圆柱 顶圆和底圆的实形, 面VW面投影的外形线V 面和W 面,所以在 面 面投影的外形线 又是圆柱面的积聚 (最左和最右素线), 面与W 面的投影反映 (最前和最后素线), 素线 投影。 也是前半圆柱面和后 实长。 也是左半圆柱面和右 半圆柱面的分界线。 半圆柱面的分界线。
4.1 平面立体的投影
二、棱锥
Z
s'
(1) 棱锥的投影分析
V
a'
b ' A a
X
H
棱锥的投影特性: 其底面为水平 图示为一正三棱 棱面△SAC为 s” 面,它的水平投影反 锥,它由底面△ABC 侧垂面,因此侧面投 在底面所平行的 S 映实形,正面和侧面 和三个棱面△SAB、 影积聚成一直线,水 W 投影面上的投影轮廓 投影分别积聚成一直 △SBC、 △SAC所组 平投影和正面投影都 为反映棱锥底面实形 线。 成。 是类似形。棱面 C a” 的多边形,其余两投 (c”) △SAB和△SBC为一般 b” 影由三角形线框组成。 B c 位置平面,它的三面 s 投影均为类似形。 Y b
【机械制图】第4章 立体的投影

表面求点只
k”
能用辅助圆 法!
M
m
(3)圆球表面上取点
完成圆球表面指定点的另两投影。
m’ (n’)
注意:圆球
m”
表面求点只
k”
能用辅助圆 法!
M
m
(3)圆球表面上取点
完成圆球表面指定点的另两投影。
m’ k’ (n’)
m”
k” (n ”)
注意:圆球 表面求点只 能用辅助圆
法!
(n) M
m k
4.3 立体的截交线
截交线为平面几边形?
——平面七边形
2、投影分析:
截交线的正面投影?
——落在截平面的积聚性投 影上;
截交线的水平投影?
——其中六条边落在六棱柱 棱面的积聚性投影上,另一 条边为截平面与棱柱顶面相 交的一条正垂线。
3、投影作图:
4、整理图线:
【例题3】求正四棱锥被截切后的水平和侧面投影。
6′5′7′
4′8′
Y 可见;反之为不可见。
棱柱表面上取点和取线
已知正六棱柱表面上点M的正面投影及点N的 水平投影,分别求它们的其余两面投影。
a’ d’ n’ m’
a” n” d” m” 请同学们思考:
b’ c’
如果将已知点
b”
c” 加上括号,会是
什么结果?
a
(b)
n
m
d(c)
2. 棱锥的投影
V
a'
X
Z
s'
s” S
n”
请同学们思考:
m’
m”
如果将已知点
a’ 2’ b’ c’ a”(c”)
加上括号,会是 b” 什么结果?
鲁教版(五四制)九年级数学上册第四章《投影与视图》章末达标检测(含答案)
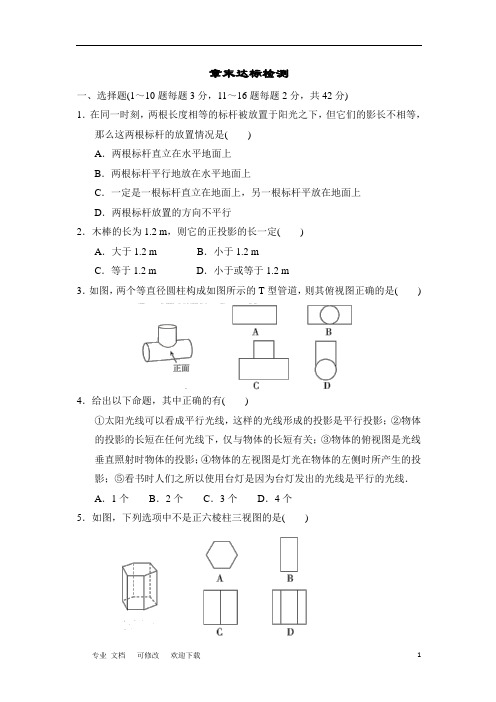
章末达标检测一、选择题(1~10题每题3分,11~16题每题2分,共42分)1.在同一时刻,两根长度相等的标杆被放置于阳光之下,但它们的影长不相等,那么这两根标杆的放置情况是()A.两根标杆直立在水平地面上B.两根标杆平行地放在水平地面上C.一定是一根标杆直立在地面上,另一根标杆平放在地面上D.两根标杆放置的方向不平行2.木棒的长为1.2 m,则它的正投影的长一定()A.大于1.2 m B.小于1.2 mC.等于1.2 m D.小于或等于1.2 m3.如图,两个等直径圆柱构成如图所示的T型管道,则其俯视图正确的是()4.给出以下命题,其中正确的有()①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体的投影的长短在任何光线下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时物体的投影;④物体的左视图是灯光在物体的左侧时所产生的投影;⑤看书时人们之所以使用台灯是因为台灯发出的光线是平行的光线.A.1个B.2个C.3个D.4个5.如图,下列选项中不是正六棱柱三视图的是()6.在同一时刻,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为()A.16 m B.18 m C.20 m D.22 m7.如图是某个几何体的三视图,则该几何体是()A.圆锥C.圆柱B.三棱锥D.三棱柱8.用四个相同的小立方体搭几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是()9.如图是正方体的一种展开图,其中每个面上都标有一个数字.那么在原正方体中,与数字“1”相对的面上的数字是()A.2 B.4 C.5 D.610.已知O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到P时,所经过的最短路径的痕迹如图所示,若沿OM将圆锥侧面剪开并展平,则所得的侧面展开图是()11.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图像刻画出来,大致是()12.如图所示,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=1.5 m,CD=3 m,点P到CD的距离为2.8 m,则点P到AB的距离为()A.2 m B.1.3 m C.1.4 m D.1.5 m13.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置上小正方体的个数,则这个几何体的左视图是()14.如图,是由几个相同的小正方体搭成的几何体的三视图,则这个几何体中小正方体的个数是()A.4 B.5 C.6 D.715.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是()A.5 29B.25C.10 5+5D.3516.如图是某几何体的三视图,根据图中数据,求得该几何体的体积为() A.60π B.70π C.90π D.160π二、填空题(17题4分,18,19题每题3分,共10分)17.工人师傅要制造某一工件,他想知道工件的高,他需要看三视图中的______或______.18.如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为________m.19.如图所示,若一个圆柱的侧面展开图是长、宽分别为4π、2π的矩形,则该圆柱的底面半径为________.三、解答题(20,21题每题8分,22~25题每题10分,26题12分,共68分) 20.如图,分别画出图中立体图形的三视图.21.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.(1)请你在图中画出路灯灯泡所在的位置(用点P表示);(2)画出小华此时在路灯下的影子(用线段EF表示).22.如图,学习小组选一名身高为1.6 m的同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量出该同学的影长为1.2 m,另一部分同学测量出同一时刻旗杆的影长为9 m,你能求出该旗杆的高度是多少米吗?23.如图,有一直径是 2 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.(1)求AB的长;(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.24.如图是一个由若干个同样大小的正方体搭成的几何体的俯视图,正方形中的数字表示在该位置的正方体的个数.(1)请你画出该几何体的主视图和左视图;(2)如果每个正方体的棱长为2 cm,则该几何体的表面积是多少?25.如图①,王华同学在晚上由路灯AC走向路灯BD,当她走到点P时,发现身后她影子的顶部刚好接触到路灯AC的底部,当她向前再走12 m到达Q 点时,发现身前她影子的顶部刚好接触到路灯BD的底部,已知王华同学的身高是1.6 m,两个路灯的高度都是9.6 m.(1)求两个路灯之间的距离;(2)当王华同学走到路灯BD处时,如图②,她在路灯AC下的影子长B F是多少?26.如图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形.现将宽为15 c m的彩色矩形纸带AMCN沿虚线裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.(1)请在图②中,计算∠BAD的度数;(2)计算按图③的方式包贴这个三棱柱包装盒所需的矩形纸带的长度.答案一、1.D 2.D 3.B 4.A 5.B 6.C 7.D 8.D 9.D 10.D 11.C 12.C 13.B 14.B 15.B 16.B 二、17.主视图;左视图 18.1219.1或2 点拨:分两种情况讨论:①若2π是圆柱的底面周长,则r =2π2π=1;②若4π是圆柱的底面周长,则r =4π2π=2,故答案为1或2. 三、20.解:如图.21.解:如图.(1)点P 就是所求的点.(2)EF 就是小华此时在路灯下的影子.22.解:设该旗杆的高度为x m.∵在相同时刻的物高与影长成正比例,∴x 9=1.61.2,即x =9×1.61.2=12.故该旗杆的高度是12 m.23.解:(1)连接BC.∵∠BAC=90°,∴BC为⊙O的直径,即BC= 2 m,∴AB=22BC=1 m.(2)设所得圆锥的底面圆的半径为r m,根据题意得2πr=90·π·1 180,解得r=14.∴所得圆锥的底面圆的半径为14m.24.解:(1)如图所示.(2)该几何体的表面积是(2×2)×(6×2+6×2+5×2+4)=4×38=152(c m2).25.解:(1)由对称性可知AP=BQ,设AP=BQ=x m.∵MP∥BD,∴△APM∽△ABD,∴PMBD=APAB,∴1.69.6=x2x+12,解得x=3,∴AB=2×3+12=18(m).答:两个路灯之间的距离为18 m.(2)设BF=y m.∵BE∥AC,∴△FEB∽△FCA,∴BEAC=BFAF,即1.69.6=yy+18,解得y=3.6.答:当王华同学走到路灯BD处时,她在路灯AC下的影子长BF是3.6 m. 点拨:求两个路灯之间的距离的关键是挖掘题目中的一个隐含条件,即“走到点P时,身后影子的顶部刚好接触到路灯AC的底部;到达Q点时,身前影子的顶部刚好接触到路灯BD的底部”,由此可得AP=BQ.专业 文档 可修改 欢迎下载 1 26.解:(1)AB 的长等于三棱柱的底面周长,为30 cm.∵纸带的宽为15 cm ,∴sin ∠BAD =sin ∠ABM =AM AB =1530=12,∴∠DAB =30°.(2)在题图中,将三棱柱沿过点A 的侧棱剪开,得到如图所示的侧面展开图.将△ABE 向左平移30 cm ,△CDF 向右平移30 cm ,拼成如图所示的平行四边形A ′B ′C ′D ′.此平行四边形即为题图②中的平行四边形ABCD .易得AC ′=2AE =2×AB cos 30°=40 3(cm), ∴在题图②中,BC =40 3cm ,∴所需矩形纸带的长度为MB +BC =30·cos30°+40 3=55 3(cm).。
北师大版九年级数学上册第四章视图与投影(同步+复习)串讲精品课件

第二单元:投影
太阳光
定义:
因为太阳离我们非常遥远,所以太阳光线可以看成平 行光线,像这样的光线所形成的投影称为平行投影.
观察这四幅图片,它们有什么共同特点吗?
观察
一.投影与平行投影
1. 投影现象;物体在阳光的照射下,会在地面 或墙壁上留下它的影子,这就是投影现象。 平行投影:太阳光线可以看成是平行光线, 象这样的平行光线形成的投影称平行投影。 投影的分类
【例2】
1、一天下午,秦老师先参加了校运会200m比赛,然后又参加 400m比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片 (如下图).你认为秦老师参加400m比赛的照片是哪一张?为 什么?
(1) 答案:图(1)
(2)
随堂练 习
1.(2010·珠海中考)一天,小青在校园内发现,旁边一 颗树在阳光下的影子和她本人的影子在同一直线上,树顶 的影子和她头顶的影子恰好落在地面的同一点,同时还发
几何体 主视图 左视图 俯视图
【例2】画出图中各物体的主视图、左视图和俯 视图:
第一幅
第二幅 第三幅
【练习】根据下列主视图和俯视图,找出对应 的物体。
主 视 图 俯 视 图
1
2
3
4
小结
拓展
回味无穷
• 三视图 • 主视图——从正面看到的图 • 左视图——从左面看到的图 • 俯视图——从上面看到的图 • 画物体的三视图时,要符合如下原则: • 位置:主视图 左视图 • 俯视图 • 大小:长对正,高平齐,宽相等. • 挑战“自我”,提高画三视图的能力.
① ② ③ ④ 能较完整地表达物体的结构(用平面图形)。 主视图反映了物体的长和高;(看不到宽) 俯视图反映了物体的长和宽;(看不到高) 左视图反映了物体的宽和高。(看不到长)
04基本体的投影

(1)圆柱面的形成 圆柱面由直线AA1绕与其平行的轴线回转而 成。
(2)投影 当圆柱的轴线垂直于H面时,圆柱的顶面、底面是水平 面,所以水平投影反映圆的实形,其正面投影和侧面投影积聚为直 线,直线的长度等于圆的直径;由于圆柱的轴线垂直于水平面,圆柱 面的所有素线都是铅垂线,故其水平投影积聚为圆,与上下底面圆 的投影重合;在圆柱的正面投影中,前后两半圆柱面的投影重合为 一矩形,矩形的左右两边分别是圆柱面最左、最右素线的投影,这
4.2.2.2 圆锥
圆锥(cone)由圆锥面和底面所围成,如图4-11(a)所示。
(1)圆锥面的形成 圆锥面由直线SA绕与它相交的轴线回转而成, 其上所有素线均交于锥顶S点,且面上任一点与顶点的连线均为属 于圆锥表面的直线。
(2)投影 当圆锥的轴线垂直于H面时,底面为水平面,水平投影反 映实形,其正面投影、侧面投影均积聚成直线;圆锥面在水平面上 的投影为圆内区域,与底面的水平投影重影,另两个投影为等腰三 角形,三角形两腰为锥面的转向轮廓线的投影;最左和最右素线
通常把棱柱、棱锥、圆柱、圆锥、圆球、圆环 等简单立体称为基本几何体,简称基本体(elementary soild)。
4.2.1 平面立体及其表面上的点和线
平面立体的表面都是平面,平面由直线围成,所以绘制平面立 体的投影可归结为绘制各种直线、平面及它们之间相对位 置的投影,再判别可见性,将可见轮廓线的投影画成粗实线,不 可见轮廓线的投影画成细虚线,当粗实线和细虚线重合时画 粗实线,当轮廓线与细点画线重合时画轮廓线。
[例4-2] 已知图4-7所示棱锥外表面上K点的正面投影k'(可见),试 作K点的其他投影。
【作图】
方法一:如图4-7(a)所示。
① 过锥顶S点和K点作一辅助线SD,即在视图上作s'k'延长交b'c'于 点d'。
第4章 视图与投影 2012年单元检测

《第4章视图与投影》2012年单元检测《第4章视图与投影》2012年单元检测一、选择题(共8小题,每小题3分,满分24分))1.(3分)从正面观察下图的两个物体,看到的是(.C D.3.(3分)小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,4.(3分)当你乘车沿一条平坦的大道向前行驶时,你会发现,前方哪些高一些的建筑物好像“沉”到了位于它们前6.(3分)如图是小明一天上学、放学时看到的一根电线杆的影子的俯视图,按时间先后顺序进行排列正确的是()7.(3分)(2006•枣庄)某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是()....8.(3分)(2011•毕节地区)如图所示的Rt △ABC 绕直角边AB 旋转一周,所得几何体的主视图为() .C D .二、填空题(共8小题,每小题3分,满分24分) 9.(3分)小明希望测量出电线杆AB 的高度,于是在阳光明媚的一天,他在电线杆旁的点D 处立一标杆CD ,使标杆的影子DE 与电线杆的影子BE 部分重叠(即点E 、C 、A 在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB 长= _________ 米.10.(3分)如图,是由一些完全相同的小立方体搭成的几何体的三种视图,那么搭成这个几何体所用的小立方体个数是 _________ .11.(3分)矩形在光线下的投影,可能是 _________ 或 _________ 也可能是 _________ .12.(3分)(2006•湖州)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B )8.4米的点E 处,然后沿着直线BE 后退到点D ,这时恰好在镜子里看到树梢顶点A ,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB )的高度为 _________ 米.13.(3分)(2006•防城港)写出一个主视图、左视图、俯视图都相同的几何体: _________ .14.(3分)直角坐标平面内,一点光源位于A(0,5)处,线段CD⊥x轴,D为垂足,C(3,1),则CD在x轴上的影长为_________,点C的影子的坐标为_________.15.(3分)如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:A图象是_________号摄像机所拍,B图象是_________号摄像机所拍,C图象是_________号摄像机所拍,D图象是_________号摄像机所拍.16.(3分)(2004•青岛)观察下列由棱长为1小立方体摆成的图形,寻找规律:如图①中:共有1个小立方体,其中1个看得见,0个看不见;如图②中:共有8个小立方体,其中7个看得见,1个看不见;如图③中:共有27个小立方体,其中19个看得见,8个看不见,…则第⑥个图中,看不见的小立方体有_________个.三、解答题(共6小题,满分52分)17.(6分)画出图中空心圆柱的主视图、左视图、俯视图.18.(6分)如图,F表示一路口交通信号灯的位置,一小汽车停在一货车后面,点C表示小汽车司机头部.问若小汽车司机抬头向正前方望去,他能否看到信号灯F,为什么?19.(10分)(2010•达州)已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.(1)请你在图中画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.20.(10分)如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E 处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?21.(10分)某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成60角,房屋向南的窗户AB高1.6米,现要在窗子外面的上方安装一个水平遮阳蓬AC(如图所示).(1)当遮阳蓬AC的宽度在什么范围时,太阳光线能射入室内?(2)当遮阳蓬AC的宽度在什么范围时,太阳光线不能射入室内?22.(10分)如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的应高为2米,求旗杆的高度.《第4章视图与投影》2012年单元检测参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.(3分)从正面观察下图的两个物体,看到的是().C D.3.(3分)小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,4.(3分)当你乘车沿一条平坦的大道向前行驶时,你会发现,前方哪些高一些的建筑物好像“沉”到了位于它们前6.(3分)如图是小明一天上学、放学时看到的一根电线杆的影子的俯视图,按时间先后顺序进行排列正确的是()7.(3分)(2006•枣庄)某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是()....8.(3分)(2011•毕节地区)如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为().C D.二、填空题(共8小题,每小题3分,满分24分)9.(3分)小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米.则电线杆AB长= 4.5米.10.(3分)如图,是由一些完全相同的小立方体搭成的几何体的三种视图,那么搭成这个几何体所用的小立方体个数是8.11.(3分)矩形在光线下的投影,可能是平行四边形或矩形也可能是线段.12.(3分)(2006•湖州)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 5.6米.∴13.(3分)(2006•防城港)写出一个主视图、左视图、俯视图都相同的几何体:球或正方体.14.(3分)直角坐标平面内,一点光源位于A(0,5)处,线段CD⊥x轴,D为垂足,C(3,1),则CD在x轴上的影长为,点C的影子的坐标为(3.75,0).∴15.(3分)如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:A图象是2号摄像机所拍,B图象是3号摄像机所拍,C图象是4号摄像机所拍,D图象是1号摄像机所拍.16.(3分)(2004•青岛)观察下列由棱长为1小立方体摆成的图形,寻找规律:如图①中:共有1个小立方体,其中1个看得见,0个看不见;如图②中:共有8个小立方体,其中7个看得见,1个看不见;如图③中:共有27个小立方体,其中19个看得见,8个看不见,…则第⑥个图中,看不见的小立方体有125个.三、解答题(共6小题,满分52分)17.(6分)画出图中空心圆柱的主视图、左视图、俯视图.18.(6分)如图,F表示一路口交通信号灯的位置,一小汽车停在一货车后面,点C表示小汽车司机头部.问若小汽车司机抬头向正前方望去,他能否看到信号灯F,为什么?19.(10分)(2010•达州)已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.(1)请你在图中画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.∴∴20.(10分)如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E 处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?解:∵,即=,即=,∴,∴,解得:∵,即,21.(10分)某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成60角,房屋向南的窗户AB高1.6米,现要在窗子外面的上方安装一个水平遮阳蓬AC(如图所示).(1)当遮阳蓬AC的宽度在什么范围时,太阳光线能射入室内?(2)当遮阳蓬AC的宽度在什么范围时,太阳光线不能射入室内?AC=AB=.的宽度小于等于的宽度大于22.(10分)如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的应高为2米,求旗杆的高度.参与本试卷答题和审题的老师有:算术;自由人;CJX;刘超;lanchong;zhqd;玲;hbxglhl;蓝月梦;lbz;如来佛;MMCH;wdxwzk;workholic;zhangCF;438011;lf2-9;csiya;zhjh;zcx(排名不分先后)菁优网2012年9月12日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章视图与投影1.视图第一课时课前预习(该部分要求同学们首先预习本课知识的基础上完成下面的填空)2.3.如图是一个物体的三视图,则该物体的形状是.俯视图左视图主视图第3题图4.圆柱的左视图是,俯视图是;5.主视图、左视图、府视图都相同的几何体为(写出两个)。
典型例题分析例1(06临沂)如图4-1是圆台状的灯罩的示意图,其主视图和俯视图是………()[点拨]1.位置:长对正,高平齐,宽相等.2.实线与虚线:在画视图时,看得见的部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.答案:D例2(2007青岛)一个大长方体是由四个完全一样的长方体拼成的,如果每个小长方体的长、宽、高分别是3,1,1,那么这个大长方体的表面积可能有种不同的值,其中最小值是。
答案:4,32点拨:本题中每个小长方体的六个面的面积分别为3,3,3,3,1,1。
当拼成的长方体表面积最小时,重合起来的面必然最大,因此本题拼成的长方体表面积最小时,长、宽、高分别为2,2,3,最小表面积为32。
例4(2007河南)由一些大小相同的正方体组成的几何体的俯视图如图所示,其中正方形中的数字表示在该位置上的小正方体的个数,那么这几个几何体的左视图是()本题考查的是简单几何体的视图画法,在已知俯视图的情况下,其主视图,左视图的关键是看小正方形中的数字,这就是画主视图、左视图时这一列小正方形的个数,如果已知三视图,让我们确定组成该几何体的小正方体的个数,也应首先在俯视图上操作。
基础训练一、选择题(本大题共3小题,在每小题给出的四个选项中,只有一个符合题目要求,请将此项的标号填在括号内)11232A.B.C.D.图4-11. (06陕西)如图,几何体的左.视图是……………………………………………………………………( )2.主视图可以反映物体的( )(A )长与宽 (B )宽与高 (C )长与高 (D )长、宽和高 3.一个几何体的主视图和左视图都是相同的长方形,俯视图为圆,则这个几何体为( ) A .圆柱 B .圆锥 C .圆台 D .球二、填空题(本大题共3小题,请把正确答案填在题中的横线上) 4.俯视图为圆的几何体是 , 。
5.举两个左视图是三角形的物体例子: , 。
6.如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称 。
三、解答题(本大题共2小题,解答应写出必要的文字说明或演算步骤7.某糖果厂为儿童设计一种新型的装糖果的不倒翁(如图4所示)请你为包装厂设计出它的主视图、左视图和俯视图。
8.如图是一个物体的三视图,请画出物体的形状。
拓展延伸一、选择题(本大题共3小题,在每小题给出的四个选项中,只有一个符合题目要求,请将此项的标号填在括号内)1. (06成都)如图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是…………( )A .5个B .6C .7个D .8个A. B. C. D. 1题图主视图 左视图 俯视图 1题图图4左视图主视图俯视图俯视图左视图主视图6题图2. (06资阳)已知一个物体由x个相同的正方体堆成,它的正视图和左视图如图所示,那么x的最大值是………()A.13 B.12C.11 D.103.圆柱对应的主视图是()。
(A)B)C)D)二、填空题(本大题共3小题,请把正确答案填在题中的横线上)4. 在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是(填上序号即可).5.如图是一个物体的三视图,则该物体的形状是.6. (06济宁)右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是.三、解答题(本大题共2小题,解答应写出必要的文字说明或演算步骤7.用线将下列各物体连同它们相应的视图连结起来.主视图左视图2题图主视图左视图俯视图5题图8、根据下面三视图建造的建筑物是什么样子的?共有几层?一共需要多少个小正方体。
答案与提示基础训练: 一:选择:1B 2C 3A二:填空:4圆柱、圆锥 5圆锥、三棱锥 6圆锥 三:解答:略拓展延伸:一选择:1、D 2、C 3、C 二:填空:4②⑤ 5圆锥 6略 三:解答:略(1) 视图 第二课时课前预习(该部分要求同学们首先预习本课知识的基础上完成下面的填空)主视图 左视图 俯视图1.画视图时,看得见的轮廓线通常画成 ,看不见的部分通常画成 。
2.一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( )3.请将六棱柱的三视图名称填在相应的横线上.4.主视图、左视图、俯视图都是圆的几何体是5.已知某圆柱的俯视图如图所示,尝试画出它的主视图和左视图。
典型例题分析例1(06临沂)如图4-1是圆台状的灯罩的示意图,其主视图和俯视图是…………( ) [点拨]1.位置:长对正,高平齐,宽相等.2.实线与虚线:在画视图时,看得见的部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.答案:D例2(2007山西太原)如图,是一个几何体的主视图与左视图,某班同学在探究它的俯视图时,画出了如图所示的几个图形,其中可能是该几何体俯视图的共有( )A .B .C .D . 图4-1 (A) (B) (C)(D)1题图A .3个 B.4个 C.5个 D.6个[点拨]由于该几何体由两部分组成,因此从图中主视图和左视图,可以猜想几何体的形状由圆柱、三棱柱、正方体三种图形组合而成,这样上、下两部分的几体体的组合方案有9种,如下表:故应选C 。
转化思想是数学常用的思想之一,将未知化为已知,本考题要求从主视图、左视图中通过观察、探究、猜想、实践等学习活动转化为已知的几何体,并考察相应图形的俯视图。
基础训练一、选择题(本大题共3小题,在每小题给出的四个选项中,只有一个符合题目要求,请将此项的标号填在括号内)1. (05常州)如果某物体的三视图是如图所示的三个图形,那么该物体的形状是…………………………………………………………………………………………………………( ) (A )正方体 (B )长方体 (C )三棱柱 (D )圆锥2.如图1是空心圆柱体在指定方向上的视图,正确的是( )图13.某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(A )长方体 (B )圆柱 (C )圆锥 (D )球二、填空题(本大题共3小题,请把正确答案填在题中的横线上)4、如果某物体的三视图是如图所示的三个图形,那么该物体的形状是5、如果一个几何体的主视图、左视图、都是等腰三角形,俯视图为圆,那么我们可以确定这个几何体是(填上一个满足条件的几何体即可)6、在球体、圆椎、正方体、圆柱四个几何体中,同一个几何体的主视图和左视图形状一样的有 三、解答题(本大题共2小题,解答应写出必要的文字说明或演算步骤 7.画出图7中空心圆柱的主视图、左视图、俯视图。
8..根据要求画出下列立体图形的视图。
(画左视图)(画俯视图)(画主视图)拓展延伸一、选择题(本大题共3小题,在每小题给出的四个选项中,只有一个符合题目要求,请将此项的标号填在括号内)1.(2007无锡)下图是由一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )图 7主视图 左视图 俯视图第4题图2.(2007威海)某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是( )3.(2007四川)如右图所示,下列三视图所对应的直观图是:()二、填空题(本大题共3小题,请把正确答案填在题中的横线上)4.(2007浙江)如图所示,是由五个大小相同的正方体搭成的几何体,则关于它的主视图左视图和俯视图的面积的大小关系为:5.(2007吉林)把图(1)的纸片折成一个三棱柱,如图所示放在桌面上,则从左侧看到的面是6.(2007南充)如图所示,立体图形由小正方体组成,这个立体图形中有小正方体个。
三、解答题(本大题共2小题,解答应写出必要的文字说明或演算步骤7.画出下面实物的三视图:8.下列各物体从不同的角度观看,它们的形状可能各不相同,请试着从不同的角度想像它们的形状.⑴试从下列各图中找出上题中各物体的主视图(不考虑大小).⑵从下列各图中找出上题中各物体的左视图(不考虑大小).⑶试从下列各图中找出上题中各物体的俯视图(不考虑大小).答案与提示基础训练:一选择:1C 2C 3B二:填空:4圆柱5三棱椎6球体和正方体三:解答:图略拓展延伸:一选择:1 C 2 A 3C二:填空:4. S主视=S俯视>S左视 5.R 6 .11三:解答:7.8略2 太阳光与影子课前预习(该部分要求同学们首先预习本课知识的基础上完成下面的填空)1.平行投影是由光线形成的。
2.太阳光线可以看成。
3.在我国北方某地上午9点和11点同一颗树的影子 点时树影较长。
4.某一时刻甲木杆高2米,它的影长是1.5米,小颖身高1.6米,那么此时她的影长为 米。
5.在平行投影中,两人的高度和他们的影子 ;典型例题分析例1 (05常州)如图是一天中四个不同时刻两个建筑物的影子,将它们按时间先后顺序进行排列,正确的是………………………………………………………( )A. ③④②①B. ②④③①C. ③④①②D. ③①②④[点拨]从早晨到傍晚,太阳光线下物体影子的指向是:西—西北—北—东北—东 答案:C例2 (05聊城)如图,阳光从教室的窗户射入室内,窗户框AB 在地面上的影长DE =1.8m ,窗户下檐到地面的距离BC =1m ,EC =1.2m ,那么窗户的高AB 为…………………………………………………………( ) A.1.5m B.1.6m C.1.86m D.2.16m [点拨]由于太阳光是平行的,易得△ACD ∽△BCD ,所以AB BCDE EC,即可求得窗户AB 的高.答案:A例3、 (2006柳洲,北海)如下图,一天早上小张正向着教学楼走去,他发现教学楼后面有一水塔DC ,可过了一会儿抬头一看:“怎么不见水塔了?”他心里很是纳闷,经过了解,教学楼、水塔的高分别为20米和30米,它们之间的距离为30米,小张身高为1.6米,小张要想看到水塔,他与教学楼的距离应为多少米?解:当小张看不见水塔时,其视线愉好经过点A ,点D 过其视点M 作CD 的垂线,交CD 、AB图4-2 B例4图A与点F ,由相似得6.130306.120-+=-MF MF 解得MF =55.2m[点拔]本题将“盲区”作为问题的背景,虽然难度不大,但是正确解题要注意运用视点、视线和盲区解决生活中的实际问题。
基础训练一、选择题(本大题共3小题,在每小题给出的四个选项中,只有一个符合题目要求,请将此项的标号填在括号内)1.小明在操场上练习双杠时,在练习的过程中他发现在地上双杠的两横杠的影子( )。
