电子科技大学电磁场数学方法-第9章 二阶常微分方程级数解法
二阶线性常微分方程的级数解法

由 Frobenius & Fuchs 定理,微分方程的两个解可写成 :
y1(x) = xρ1a0 + a1 x + a2 x2 + …, y2(x) = xρ2a0′ + a1′ x + a2′ x2 + …,
因为 ρ2 - ρ1 是非整数 ,故 y2(x) / y1(x) 不可能等于常数 ,y2(x) 和 y1(x) 线性无关 ,其线性组合构成微分方程的通解 。
代入微分方程 (1. 13) 式,将得到以下形如 ck xk = 0 的幂级数形式 ,
k
∞
(k + ρ) (k + ρ - 1) + (k + ρ) g0 + g1 x + g2 x2 + … + h0 + h1 x + h2 x2 + … ak xk+ρ = 0
k=0
因为是解析函数的展开,由唯一性定理,各幂次的系数 ck = 0。 看最低幂次 xρ 项的系数(对应于上式的 k = 0 项):[ρ(ρ - 1) + ρ g0 + h0] a0 = 0 由 Frobenius & Fuchs 定理,形式解的系数 a0 ≠ 0,故可得到一个关于指标的一元二次方程:
x2 y″ + x g(x) y′ + h(x) y = 0, 其中:g(x) 和 h(x) 在 x = 0 点解析
据 Frobenius & Fuchs 定理,该微分方程必定存在一个如下形式的解:
∞
y = xρ ak xk, 其中 a0 ≠ 0 (若为常点 ,则对应于 ρ = 0)
k=0
对级数形式的 y(x) 求导,
二阶线性常微分方程的幂级数解法

二阶线性常微分方程的幂级数解法从微分方程学中知道,在满足某些条件下,可以用幂级数来表示一个函数。
因此,自然想到,能否用幂级数来表示微分方程的解呢? 例1、求方程''0y xy -=的通解解:设2012n n y a a x a x a x =+++++……为方程的解,这里(0,1,2,,,)i a i n =……是待定常系数,将它对x 微分两次,有 将y ,'y 的表达式代入方程,并比较的同次幂的系数,得到x -∞<<∞2210a ⋅=,30320,a a ⋅-= 41430,a a ⋅-= 52540,a a ⋅-=或一般的可推得32356(31)3k a a k k =⋅⋅⋅⋅⋅-⋅,13134673(31)k a a k k +=⋅⋅⋅⋅⋅⋅+,其中1a ,2a 是任意的,因而代入设的解中可得:这个幂级数的收敛半径是无限大的,因而级数的和(其中包括两个任意常数0a 及1a )便是所要求的通解。
例6 求方程'''240y xy y --=的满足初值条件(0)0y =及'(0)1y =的解。
解 设级数2012n n y a a x a x a x =+++++……为方程的解。
首先,利用初值条件,可以得到00a =, 11a =,因而将y ,'y ,''y 的表达式带入原方程,合并x 的各同次幂的项,并令各项系数等于零,得到 因而 最后得21111(1)!!k a k k k +=⋅=- , 20k a =, 对一切正整数k 成立。
将i a (0,1,2,)i =的值代回2012n n y a a x a x a x =+++++……就得到 这就是方程的满足所给初值条件的解。
是否所有方程都能按以上方式求出其幂级数解?或者说究竟方程应该满足什么条件才能保证它的解可用幂级数来表示呢?级数的形式怎样?其收敛区间又如何?这些问题,在微分方程解析理论中有完满的解答,但因讨论时需要涉及解析函数等较专门的知识,在此我们仅叙述有关结果而不加证明,若要了解定理的证明过程,可参考有关书籍。
二阶常微分方程级数解法变换本征值问题.pdf

简化为
T '' = Δv a 2T v
令
T '' a 2T
=
Δv v
= −k 2
T '' a 2T
=
Δv v
= −k 2
分解为 T "+a 2k 2T = 0
Δv + k 2v = 0
称为亥姆霍兹方程
第一个方程的解为
T = C + Dt T = C cos kat + D sin kat
(k = 0) (k ≠ 0)
(m = 0,1,2,3L)
r2
d 2R dr 2
+
2r
dR dr
− l(l
+ 1) R
=
0
R = Crl + Dr−(l+1)
(2)、柱坐标系
Δu
=
∂ 2u
∂ρ 2
+
1
ρ
∂u
∂ρ
+
1
ρ2
∂ 2u
∂ϕ 2
+
∂ 2u ∂z 2
试图将变量变 ρ 与 θ 和 z 分离 代入
u(ρ,ϕ, z) = R(ρ)Φ(ϕ)Z(z)
d (r 2 dR ) = l(l +1)R dr dr
−1
sinθ
∂
∂θ
(sinθ
∂Y
∂θ
)
−
1
sin 2 θ
∂ 2Y
∂ϕ 2
= l(l
+ 1)Y
称为球函 数方程
上边第一式化为
r 2 d 2R + 2r dR − l(l +1)R = 0
数学物理方法第九章二阶常微分方程的劫数解法本征值问题

特殊函数常微分方程
球坐标下拉普拉斯方程的分离变量
一般情况 欧拉方程,球函数方程,连带勒让德方程 轴对称情况 勒让德方程
极坐标下热传导方程的分离变量
一般情况 亥姆霍兹方程,贝塞尔方程 轴对称情况
§9.2常点邻域上的级数解法
常微分方程中点的分类 各点邻域级数解的形式 勒让德方程的级数解 贝塞尔方程的级数解
常微分方程中点的分类
二阶变系数常微分方程的一般形式
w”+p(z)w’+q(z)w=0
方程中点的分类
常点:z0 是 p(z) 和 q(z) 的解析点
正则奇点:z0 是 (z-z0) p 和 (z-z0)2 q 的解析点 非正则奇点:其它情况
各点邻域级数解的形式
•常点z0邻域
sin 1 cos
2 1 2
1 12
2、柱坐标下拉普拉斯方程
2 2 1 u 1 u u 2 ( ) 2 2 0 2 z
0为正则奇点,邻域解为 :y k 0 ak x s k
x y k 0 ak x
2
sk 2
k 2 ak 2 x
sk
k 0 ak 2 x s k
级数解的导数为: y ' k 0 ( s k )ak x s k 1 y" k 0 ( s k )(s k 1)ak x s k 2
1 v 1 2v 2v 2 ( ) 2 k v 0 2 2 z
令
v( , , z ) R( ) ( )Z ( z )
二阶线性常微分方程的级数解法和广义傅里叶级数

接着对常见的变系数线性微分方程进行分类,介绍了如何用 幂级数解法和弗罗贝尼乌斯级数解法求解正则奇点的二阶常微分 方程。
最后对常见的施图姆-刘维尔型微分方程的特征值和特征函 数的性质作了系统的介绍。
sin 9 ))| = sin 2 9 - 2 cos9 = (1 - x2 ) - 2x
这样式(5.1-20)可以写成
(1- x2 ) - 2x + n(n + 1)-
y = 0 (5.1-21)
式(5.1-21)是常见的勒让德方程的一般形式, 称为连带勒让德方程。
17
5.1.2
令m = 0 ,得到
(2) 若p(x)和q(x)中至少有一个不满足(x _ x0 )p(x), (x _ x0 )2 q(x)在
x0点解析, 则x0称为方程(5.3-1)的本性奇点。在本性奇点附近, 方
x 程至少有一解在x0 有本性奇点,
而另一解可能是y =
w
an
(x
_
)n+p
x0
,
n=0
但它往往是发散的, 这种情况在数理方程中不多见, 这里不讨论它。
上式代入式(5.1-7),得到
(5.1-8)
p p + R,, 2
R,+ 入p2
= - = O,, 山
RR
O
式中山为常数。上式是两个常微分方程,分别是
p2 + p + (入p2 - 山)R = 0
(5.1-9)
O,,+ 山O = 0
8
5.1.1
由于V(p,9)是单值函数,所以内(9)应满足周期性边界条件,因而有
第九章 二阶常微分方程的级数解法

∞
(k l )(k + l + 1) a , (3) (k + 1)(k + 2 ) k (l + 1)(l + 3) (l + 2k 1)( l )(2 l ) (2k 2 l ) a a2 k = 0 (2k )! (l + 2 )(l + 4 ) (l + 2k )(1 l )(3 l ) (2k 1 l ) a a2 k +1 = 1 (2k + 1)!
[(
)
]
9.2 二阶常微分方程的级数解法
二阶常微分方程的形式
W
''
(z ) + p (z )W ' + q (z )W (z ) = 0 .(1) W ( z 0 ) = c1 , W ' ( z 0 ) = c 2 .
当z0是p(z)与q(z)的解析点时, z0称为方程(1)的常点,若 z0为p(z)与q(z)的奇点时, z0称为方程(1)的奇点. (一)常点邻域上的级数解法 令:
W(z) = ∑ak (z z0 ) , p(z) = ∑pk (z z0 ) , q(z) = ∑qk (z z0 ) .(2)
k k k k=0 k=0 k=0
∞
∞
∞
代入(1)式可确定系数ak,得出方程的解.
例题1 在x0=0的邻域上用级数解法求解常微分方程
y '' + ω
∞ k
2
y = 0
得出 : Φ '' + λΦ = 0, (3) 对周期性的自然边界条件 : Φ( + 2πn ) = Φ( )(4) .
9-二阶常微分方程级数解法_本征值问题

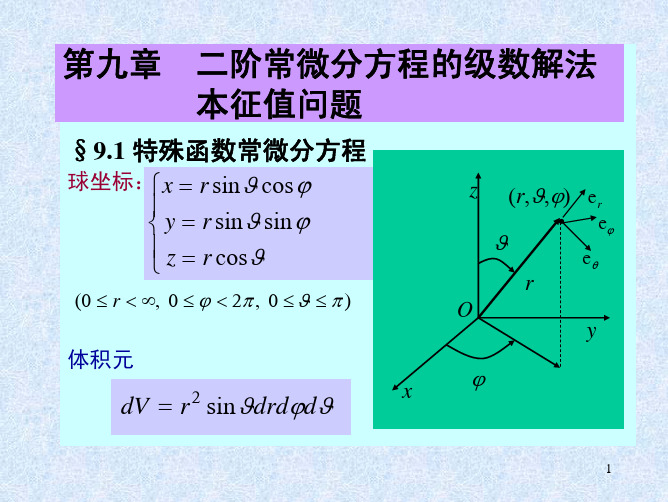
第九章二阶常微分方程级数解法本征值问题§9.1 特殊函数常微分方程(球坐标系、柱坐标系中的分离变量法)球坐标系:⎪⎩⎪⎨⎧===θϕθϕθcos sin sin cos sin r z r y r x 体积元)0,20,0(πθπϕ≤≤<≤∞<≤r ϕθθd drd r dV sin 2=yzOθϕr•(r ,θ,ϕ)e ϕe r e θP⎪⎩⎪⎨⎧===z z y x ρρϕρsin cos ),20 ,0(∞<<∞-<≤∞<≤z πϕρzdV d d d ρϕρ=体积元柱坐标:(一)Laplace 方程(9.1.1) .0sin 1sin sin 112222222=∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂ϕθθθθθur u r r u r r r (1)球坐标系2=∇u •xyz O(ρ, ϕ, z )ϕρze ρe z e ϕP.0sin sin sin d d d d 2222222=∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛ϕθθθθθYr R Y r R r R r r r Y RYr /2⨯代入(9.1.1)得到),()(),,(ϕθϕθY r R r u =分离变量解:2222sin 11sin sin 11d d d d 1ϕθθθθθ∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂-=⎪⎭⎫ ⎝⎛Y Y Y Y r R r r R )1(+≡l l ——Euler 方程0)1(d d d d 2=+-⎪⎭⎫⎝⎛R l l r R r r i )径向方程(9.1.2)0)1(2222=+-+R l l dR r R d r 即:)1()(+-+=l l DrCr r R 该方程的解为:(9.1.4)0)1(2222=+-+R l l drdR r dr R d r ter =dtdR edr dR t -=222222dtR d e dt dR e dr R d t t --+-=0)1()(2)(22222=+-++----R l l dtdR e e dt R d e dt dR ee t t t tt0)1(22=+-+R l l dtdR dt R d )1()1(+-+-+=+=l l tl lt DrCr DeCe Rii )单位球面上方程:0)1(sin 1sin sin 1222=++∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂Y l l YY ϕθθθθθ——球函数方程222d d 1sin )1(d d sin d d sin ϕθθθθθΦΦ-=++⎪⎭⎫ ⎝⎛ΘΘl l )()(ϕθΦΘ=Y 可以进一步分离变量:(9.1.3)λ≡)()2( ,0''ϕπϕλΦ=+Φ=Φ+Φ[]sin )1(d d sin d d sin 2=Θ-++⎪⎭⎫ ⎝⎛Θλθθθθθl l φ方向:(9.1.6)(9.1.5)).0,1,2,3,(,sin cos )(2+=Φm m m B m A λϕϕϕ(9.1.8)),()( ,cos x x Θ=Θ=θθ令:,d dsin d d d d d d xx x θθθ-==,d d sin d d )sin (sin 1d d sin d d sin 12⎪⎭⎫ ⎝⎛Θ--⋅=⎪⎭⎫ ⎝⎛Θx x θθθθθθθ[]0sin )1(d d sin d d sin 22=Θ-++⎪⎭⎫ ⎝⎛Θm l l θθθθθ(9.1.6)’θ2sin /1⨯0sin )1(sin sin 122=Θ⎥⎦⎤⎢⎣⎡-++⎪⎭⎫ ⎝⎛Θθθθθθm l l d d d d (9.1.9)()01)1(d d 1d d 222=Θ⎥⎦⎤⎢⎣⎡--++⎥⎦⎤⎢⎣⎡Θ-x m l l x x x ——称为l 阶连带Legendre 方程(9.1.10)0)1(2)1(22222=Θ⎥⎤⎢⎡-++Θ-Θ-m l l d x d x (9.1.11)即:当m =0 时,称为Legendre 方程:()0)1(d d 1d d 2=Θ++⎥⎦⎤⎢⎣⎡Θ-l l x x x ()0)1(d d 2d d 1222=Θ++Θ-Θ-l l xx x x 注意:因x =cos θ, 而θ的变化范围是[0, π], 所以x 的变化范围是[-1,+1]。
二阶常微分方程级数解法

( d ) E ( d )[( d ) d dz]
( d ) ( ) [E ( d ) ( d ) E ( ) ] d dz
( E ) d d dz ( E ) d d dz ( E ) dV
同理
( d ) ( ) 1 E d d dz 1 E dV
2u
2u
2
1
u
1
2
2u
2
2u z 2
推导
空间中某一点电场的散 度代表该点附近单位体 积
中电通量的净流出量 .
E
1
(E )
1
E
E z z
E
u
eˆ
u
eˆ
1
u
eˆz
u z
(I) (推导见下页 ) (II)
(II)代入(I)式得
u
u
1
( u ) 1
(1
u
)
2u z 2
1
(
u )
(r2 Er ) sin dr d d
r
1 r2
(r2 Er ) r
r 2sin
dr d
d
1 r2
(r2 Er ) r
dV
5
同理
( d ) ( ) 1 E r2 sin dr d d r sin
1 E dV
r sin
( d ) ( ) 1 (E sin ) r2 sin dr d d r sin
0
D2 D l(l 1) 0
[D (l 1)][D l] 0
R(r) C el t D e(l1)t
C el ln r D e(l1) ln r
C rl D r(l1)
14
ii)球函 数方程:
二阶常微分方程级数解法_本证值问题
2 Y ∂ 1 1 ⎞ . ⎟− 2 2 ⎠ Y sin θ ∂ϕ
1 d ⎛ 2 dR ⎞ 1 1 ∂ ⎛ ∂Y ⎞ 1 1 ∂ 2Y = μ. ⎟− ⎜r ⎟=− ⎜ sin θ 2 2 R dr ⎝ dr ⎠ Y sin θ ∂θ ⎝ ∂θ ⎠ Y sin θ ∂ϕ
i)径向方程
d ⎛ 2 dR ⎞ ⎜r ⎟ − μR = 0, dr ⎝ dr ⎠ 后面解出 μ = l (l + 1)
——该方程称为连带 Legendre 方程。
6
当 m=0 时,称为 Legendre 方程:
d ⎡ 2 dy ⎤ ( 1 − x ) ⎥ + μy = 0 ⎢ dx ⎦ dx ⎣
即:
d y dy (1 − x ) dx 2 − 2 x dx + μy = 0
2 2
注意: 因 x=cosϑ, 而 ϑ 的变化范围是 [0, π], 所以 x 的变化范围是 [-1,+1] 。
Φ ' ' + λΦ = 0 Φ (ϕ + 2π ) = Φ (ϕ )
d2R dR r + 2r + k 2 r 2 − l (l + 1) R = 0 R: 2 dr dr 齐次边值
[
]
Z: R:
Z ' '− μZ = 0 齐次边值
k 2v = 0
Θ:
⎡ m2 ⎤ d ⎡ 2 dy ⎤ ( ) − x y =0 + − 1 μ ⎢ dx ⎢ dx ⎥ 1 − x2 ⎥ ⎣ ⎦ ⎣ ⎦ | x |≤ 1 解有界
⎧ J m ( x) ⎪ ⎨N m ( x) ⎪H ( x) ⎩ m
19
分离变量结果
二阶常微分方程的级数解法及本征值问题

m 0,1, 2, ; ( ) A cos m B sin m
记常数 k 2 2 ,即 k 2 2 ,(3)式可改写为:
d 2 R 1 dR m2 R 0 ,相应地作变量代换: x ,可以化为: 2 d2 d
本章习题
P237:1,3 题
10
E F ln (1) 0 , Z ( z ) C ; R m m E F
m0 m 1, 2,3,
(2) 0 , Z ( z ) Ce
z
De
z
d 2R dR 令 ,则方程(4)可化为 2 m 2 R 0 ,称为 m 阶贝塞 2 d d
2
塞尔方程,具体求解后面将具体介绍。 (b)柱坐标系中亥姆霍兹方程的分离变量
1 u 1 2u 2u 2 2 2 k 2v2 0 z
柱坐标系与球坐标系中的讨论类似,令 v( , , z ) R( ) ( ) Z ( z ) ,引入两个常数
d 2 R 1 dR m 2 y ' m2 , m 阶贝塞尔方程。 ( R y 1 0 " 1 2 R 0 ) dx 2 x dx x2 x x
7
第(2)式是偏微分方程,称为亥姆霍兹方程。 同样地,对于输运方程 ut a 2 u 0 同样作分离变量代换,可以得到:
d 2 R 1 dR m 2 1 R 0 d2 d 2
即: 2
d 2R dR 2 m 2 R 0 ,称为 m 阶贝塞尔方程。 2 d d
2
连带勒让德方程隐含 1 ( 0, )的自然边界条件构成本征值问题, 决定 l 只 能取整数值。 第(2)式即 r 2
第九章二阶线性常微分方程级数解法

a1
得到l 阶勒让德方程解:
y
a2k x2k
a x2k1 2k 1
a0y0 ( x) Nhomakorabeaa1 y1( x)
y0
(x)
1
(l)(l 1) 2!
x2
(2
l)(l)(l 1)(l 4!
3)
x4
...
(2k 2 l)(2k 4 l)
(l)(l 1)(l 3) (2k )!
程在点 z0的邻域 z z0 R 内的解可以表示成泰勒级数的
形式:
w(z) an (z z0 )n,
n0
a0 , a1 , …ak , … 待定系数
级数展开式中的待定系数由边界条件或初始条件确定。
初始条件: w(z0 ) C0, w '(z0 ) C1.(C0 , C1为任意复常数)
d
d
d 2
得到两个常微分方程:
d 2
d 2
0
sin d (sin d) [l(l 1)sin2 ] 0
d
d
解常微分方程:
d 2
d 2
0
自然周期边界条件: ( 2 ) ()
得其通解为: () Am cos m Bm sin m
sin
sin2 2
球函数方程
径向函数所满足的方程为欧拉形方程:
d (r2 dR ) l(l 1)R 0, dr dr
r2
d 2R dr2
2r
dR dr
l(l
1) R
9. 二阶常微分方程级数解法

第九章二阶常微分方程级数解法•§9.1 特殊函数常微分方程•§9.2 常点邻域上的级数解法•§9.3 正则奇点邻域上的级数解法•§9.4 施图姆-刘维尔本征值问题•前面讨论的都是两个自变量的偏微分方程,涉及到的本征函数都是三角函数,除了圆形泊松问题外,大多是反射对称的问题;•从现在开始,我们要讨论三维的定解问题。
实际的边界问题可能具有其它对称性,比如球或柱对称边界,这时的本征函数采用三角函数就不方便了,我们将发现新的本征函数和本征值,并且用它们做级数展开来求解偏微分方程。
•本章主要讨论拉普拉斯方程、亥姆霍兹方程等在球坐标系、柱坐标系满足的常微分方程及其定解。
我们依然采用分离变量法。
§9.2 常点邻域上的级数解法•前面我们通过分离变量法得到了一些特殊的二阶常微分方程,本节讨论这些方程在特定的边界条件下的定解问题。
•这些二阶常微分方程大多不能用通常的方法,比如直接积分的方法求解;•通常采用幂级数解法,即在某一选定的点的邻域上将待求的解表示成系数待定的级数,得到系数之间的递推关系,然后利用边界条件确定所有系数的值。
•级数求解问题的关键在于收敛性。
•考虑一般的复变函数w(z)的线性二阶常微分方程:w’’+p(z)w’+q(z)w=0, w(z 0)=C 0, w’(z 0)=C 1. 其中z 为复变数,z 0为选定的点。
•(一)方程的常点和奇点:在z 0邻域,如果p(z)和q(z)是解析的,则z 0称作方程的常点;如果p(z)和q(z)是奇异的,则z 0称作方程的奇点。
•(二)常点邻域上的级数解:如果线性二阶常微分方程的系数p(z)和q(z)在点z 0的邻域|z-z 0|<R 是解析函数,则方程在这个圆中存在满足初值条件的唯一解析解。
•因此可以把解表示成此邻域上的泰勒级数形式:•后面的任务就是确定这些级数解的系数a k ,通常会得到它们之间的一些递推关系。
第九章二阶微分方程的解法

y(x) an (x x0 )n n0
a0 , a1 , …ak , … 待定系数
数学物理方程与特殊函数
第九章
系数的确定
➢ 将解的级数形式代入方程,合并同幂次项; ➢ 令合并后的各系数分别找零,找出系数之间的递推关系; ➢ 用已知的初始调试条件确定系数,从而求得级数解
以l 阶勒让德方程为例进行分析
a1
a7
(5l7)(6l 6)
a5
(5l )(3l() 1l )(l 2)(l 4)(l 6) 7!
a1
………
a2k 1
(2(k2k11l))((l2k2)k )
a2k 1
(2k 1l )(1l )(l 2)(l 2k ) (2k 1)!
a1
数学物理方程与特殊函数
得到l 阶勒让德方程解:
第九章
y
定理
如果方程 y'' p(x) y' q(x) y 0
的系数 p (x) , q (x) 在点 x0的邻域 x x0 R 内解析,则
方程在这圆内存在唯一的解析的解 y (x),满足初始条件
y(x0 ) C0 , y(x0 ) C1. (C0 , C1为任意复常数)
表示成泰勒级数的形式
数学物理方程与特殊函数
第九章
第九章 二阶常微分方程的级数解法
• 概述 • 常点邻域上的级数解法 • 正则奇点邻域上的级数解法 • 本章小结
数学物理方程与特殊函数
第九章
一、概述
分离变量法
直角坐标系、平面极坐标 本征函数是三角函数
实际 正交曲面坐标系 (球坐标系和柱坐标系) 拉普拉斯方程的分离变量
数学物理方程与特殊函数
a2k x2k
数学物理方法课件:二阶常微分方程级数解法

)R
0
( k2 2)
当: 0 (欧拉型常微分方程)
2
d2R
d 2
dR
d
m2R
0
R()
E F ln E m F m
(m 0) (m 0)
当: 0
(m 阶贝塞尔方程)(x )
x2
d2R dx 2
x
dR dx
(x 2
m 2)R
0
§9·2 常点邻域上的级数解法
讨论用级数解法求解带初始条件的
d2Z dz 2
Z
0
d2R
d 2
1
dR
d
(
m2
2
)R
0
Z(z) Ce z De z
对R()作变量代换:x dR dR dx dR
dx d
d dx d
dx
d 2R
d 2
d( dR )
d d
d( dx
dR )dx
dx d
d 2R dx2
m
阶贝塞尔方程:
x
2
d2R dx 2
x
dR dx
(x 2
0
同乘 2 移项:
RZ
2
R
d2R
d 2
R
dR
d
2
Z
d2Z dz 2
k2 2
1
d 2
d 2
分解成两个方程:
d 2
d 2
0
构成本征值问题
( 2) ()(自然周期条件)
本征值: m2 (m 0,1,2,3,)
本征函数:() Acos m B sinm
2
R
d2R
d 2
R
dR
d
第九章第二节 常点邻域上的级数解法

解: (9.2.4)即
y
1
2
x x
2
y
ll 1
1 x2
y
0
与 y pxy qxy 0 比较,方程的系数
p
x
1
2x x2
,
q
x
l l 1
1 x2
p(z)和q(z)在x0=0解析,因此x0=0是方程的常点。根据常点邻域上的解的定理, 解具有泰勒级数形式:
d 2R dx2
1 x
dR dx
1
m2 x2
R
0...9.1.22
即x2
d 2R dx2
x
dR dx
x2
m2
R0
m阶贝塞尔方程。
这就提出一个问题:如何求线性二阶常微分方程
y pxy qxy 0 yx0 C0 , yx0 C1
这些线性二阶常微分方程往往不能用通常的方法解 出,但可用级数解法解出。
3、 x 1 是函数 (9.2.4)的齐点。可以证明 (附录四), y0(x)和y1(x)在 x 1 不可能都是有限的。也就是 说,l 阶勒让德方程没有形如 yx D0 y0 x D1 y1x
而在 x 1 均为有限的无穷级数解。
❖ 当 l =2n 时(n是正整数) , y0(x)是2n次多项式,不是无
……
37
a5
5!
a1
xk项系数:
k 2k 1 ak2 2kak 1ak 0
由此得到一般项系数递推公式
ak 2
2k 1
k 2k
1
ak
一般解中包含有两个任意常数a0与a1,这正是二阶线性常微分方 程的通解中必然出现的两个积分常数。特解y0和y1是线性无关的。
二阶微分方程求解步骤

二阶微分方程求解步骤
嘿,咱今儿就来说说二阶微分方程求解步骤这事儿。
你想想啊,这
二阶微分方程就像是一道有点复杂的谜题,得一步步解开它。
首先呢,咱得确定方程的类型,就好比先认清这是个啥样的“小怪兽”。
然后呢,根据不同的类型,咱就可以选择合适的方法啦。
比如说,要是遇到那种常系数线性的二阶微分方程,咱就可以用特
征方程这一法宝。
这特征方程就像是一把钥匙,能帮咱打开求解的大门。
通过求解特征方程的根,咱就能得到一些关键信息。
这就好像是
找到了打开宝藏的线索一样,多有意思呀!
要是遇到一些特殊形式的二阶微分方程,那咱就得开动脑筋,想想
有没有什么特别的技巧和方法。
这就跟咱解决生活中的难题一样,有
时候得变通一下,不能死脑筋呀。
在求解的过程中,可不能马虎哦。
每一步都得仔细认真,就像走在
钢丝上一样,得稳稳当当的。
不然一个不小心,就可能前功尽弃啦。
而且哦,这求解二阶微分方程可不像吃豆腐那么容易,得有耐心。
有时候可能会遇到一些困难,算着算着就卡住了。
但咱可不能放弃呀,得咬咬牙坚持下去。
想想看,要是咱解开了这个难题,那得多有成就
感呀!
咱还可以通过做一些例题来加深对求解步骤的理解和掌握。
这就好比是练功,得不断地练习,才能越来越厉害。
总之呢,求解二阶微分方程虽然有点挑战性,但只要咱掌握了正确的步骤和方法,再加上那么一点点耐心和细心,就一定能把它拿下!你说是不是呢?咱可不能被这小小的二阶微分方程给难住了呀,要勇敢地去挑战它,征服它!让我们一起在这数学的海洋里畅游吧,去发现那些奇妙的知识和乐趣!。
第9章:常微分方程的级数解法

k = −1
∑
∞
pk ( z − z0 ) k ,
q( z ) =
k = −2
∑
∞
qk ( z − z 0 ) k ,
这时方程的二个线性独立解(称为正则解)为
14
w1 ( z ) = ( z − z0 )
s1
∑ a (z − z )
k =0 ∞ k 0 k =0 k 0
∞
k
w2 ( z ) = ( z − z0 ) 或
−l − 1 +2k 2
24
半奇数 阶 Bessel 函数可用初等函数表示
2 ∞ 1 x k J 1 ( x) = ( −1) ∑ 2 πx k =0 ( 2k + 1)! 2 2 J − 1 ( x) = cos x 2 πx
2 k +1
(2)Legendre 方程 d 2 dy (1 − x ) + l (l + 1) y = 0 dx dx 问题关键:变系数方程,求解析解的困难、解 的特性如何?
2
标准形式
d w dw + p( z ) + q( z ) w = 0 2 dz dz
2
z一般是复 的,即在 复平面上 考虑方程
s2
∑b (z − z )
∞
k
′ ( z ) = Aw1 ( z ) ln(z − z0 ) + ∑ bk ( z − z0 ) s2 + k w2
k =0
其中 s1 和 s2 是判定方程的二个根(且s1> s2 )
s( s − 1) + sp−1 + q− 2 = 0
方程的解与 s1和s2的关系为 s1-s2≠整数,解为w1 和 w2 s1-s2=整数(包括 0),解为w1 和
第九章 二阶常微分方程

x = cos θ
2
m [(1 − x 2 )Θ' ]'+[l (l + 1) − 1−x 2 ]Θ = 0
球 坐 标 下 拉 普 拉 斯 方 程
r −2 [ ∂ r ( r 2 ∂ r u ) + ∆ ' u ] = 0 ( r 2 R ' )' / R = − ∆ ' Y / Y = l ( l + 1)
常微分方程中点的分类
• 二阶变系数常微分方程的一般形式
– w”+p(z)w’+q(z)w=0
• 方程中点的分类
– 常点:z0 是 p(z) 和 q(z) 的解析点 – 正则奇点:z0 是 (z-z0) p 和 (z-z0)2 q 的解析点 – 非正则奇点:其它情况
各点邻域级数解的形式
•常点z0邻域
( s + k )( s + k − 1) a k x s + k − 2 ∑ k =0
代入方程得: {[( k + s ) 2 − m 2 ]a k + a k − 2 } x s + k = 0 ∑ k =0
即: [( k + s ) 2 − m 2 ]a k + a k − 2 = 0
贝塞尔方程的级数解
勒让德方程的级数解
递推公式: a k + 2 = 具体递推: a3 =
(1 − l )( l + 2 ) l a1 = (1− l )(!+ 2 ) a1 3⋅2 3 ) ) l a 5 = ( 3 − l5⋅(4l + 4 ) a 3 = ( 3 − l(1− l )(!+ 2 )( l + 4 ) a1 5 ( 5 − l)l + 6 ) ( ( 5 − l )( 3 − l(1 − l )( l + 2 )( l + 4 )( l + 6 ) ) a7 = a5 = 7 ⋅6 7! k ( k +1) − l ( l +1) ( k + 2 )( k +1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y " 2 a 2 3 2 a 3 x 4 3 a 4 x 2 . . . ( k 2 ) ( k 1 ) a k 2 x k . . .
代入l 阶勒让德方程
(1 x 2 )y" 2 x y' l(l 1 )y 0
合并同幂次的项列表……
k 0 [ ( k 1 ) ( k 2 ) a k 2 k ( k 1 ) a k 2 k a k l ( l 1 ) a k ] x k 0
定理
设 x0 是方程 y''p(x)y'q(x)y0的正则奇点
p(x) pk(xx0)k k1
q(x) qk(xx0)k k2
数学物理方程与特殊函数
第九章
则在 x0的邻域 0 xx0 R 内,方程的两个线性独立解为:
y1(x) ak(xx0)s1k k0
y2(x) bk(xx0)s2k k0
将n记为k, 求得l 阶勒让德多项式 的具体表达式为
[l/2]
k (2l2k)!
l2k
P l(x)
k0
(1)
2lk!(lk)!(l2k)!x
数学物理方程与特殊函数
三、正则奇点邻域上的级数解法
第九章
设 x0 是线性二阶常微分方程
y'' p(x)y' q(x)y0
的奇点,则其解也以x0为奇点,在点x0领域上展开为罗朗级 数形式
在 x0 = 0 的邻域上求解l 阶勒让德方程
(1 x 2 )y " 2 x y' l(l 1 )y 0
即
y"(1 2xx2)y'(l1(lx12))y0
方程的系数
2x
l(l1)
p(x)(1x2), q(x)(1x2)
在 x0 = 0: p( x0 ) = 0, q( x0 ) = l (l+1) , 在 x0 = 0解析
数学物理方程与特殊函数
第九章
递推 a k 公 2k( (k k 1 式 2 )) k l( ( l1 ) 1 )a : k (( k k l) 2 ) k ( k ( l 1 1 ))a k
具体递推:
a3
(1l)(l2) 32
a1
(1l)(l2) 3!
a1
a5
(3l5) (4l4)
a3
(3l( ) 1l)(l2)(l4) 5!
a0 , a1 , …ak , … 待定系数
数学物理方程与特殊函数
第九章
系数的确定
➢ 将解的级数形式代入方程,合并同幂次项; ➢ 令合并后的各系数分别找零,找出系数之间的递推关系; ➢ 用已知的初值确定系数,从而求得级数解
以l 阶勒让德方程为例进行分析
数学物理方程与特殊函数
第九章
勒让德方程的级数解
改写为
ak((kkl)2()k( kl11))ak2
可以把其它系数一一推算出来:
数学物理方程与特殊函数
第九章
l(l1)
l(l1)(2l)!
al2 (2)(2l1) al 2(2l1)2ll!l!
(2l)!
1 (2l2)!
2(2l1)2ll(l1)!(l2)! (1) 2l(l1)!(l2)!
(l2)(l3)
数学物理方程与特殊函数
第九章
自然边界条件
解在区间[-1,1]的两端 x = ±1 保持有限
本征值问题
本征值: l (l + 1)
L 为零或正整数
本征函数: l 阶勒让德多项式
数学物理方程与特殊函数
第九章
勒让德多项式
al
( 2 l)! 2l (l !) 2
反用系数递推公式
ak2((kkl)2()k( kl11))ak
s1-s2 整数
或
y2(x)A y 1(x)ln (xx0) b k(xx0)s2 k
k 0
s1-s2=整数
s1、s2 :判定方程 s(s1 )sp 1q 20的根( s1> s2 )
A, ak , bk, 常系数,A可能为0。
数学物理方程与特殊函数
第九章
贝塞尔方程的级数解
(1) 阶 v 整数或半奇数(贝塞尔方程的级数解)
勒让德方程的解在一切方向 0 ,
即在 x 的闭区间[-1, +1]上保持有限
无穷级数解y0和y1均不满足该要求 出路?
无穷级数退化为有限项的多项式形式!无发散性
数学物理方程与特殊函数
第九章
l 的选择: l 为非负整数,则当k = l 时, 级数解退化为 l 次多项式;
l 阶勒让德多项式 P l ( x )
a1
a7
(5l7) (6l6)
a5
(5l)(3l( ) 1l)(l2)(l4)(l6) 7!
a1
………
a 2 k 1 ( 2 ( k 2 k 1 1 l) ) ( ( l 2 k 2 ) k )a 2 k 1 ( 2 k 1 l) ( ( 1 2 k l ) 1 l ) ! ( 2 ) ( l 2 k )a 1
x = cos , 0
x1 0,
已证明:级数解y0和y1各自在 x = ±1 发散(l 不为整数时)
因此:形如 ya0y0(x)a1y1(x)而且在x = ±1 均有限
的无穷级数解并不存在:l 阶勒让德在x = ±1 均为有限的
级数解并不存在!
数学物理方程与特殊函数
第九章
实际定解问题要求:u 在一切方向都需要保持有限
y2(x) bk(xx0)s2k k0
数学物理方程与特殊函数
第九章
先不分 s1,s2
方程的解
y
ax
sk
k0 k
y' k0(sk)akxsk 1
y " k 0 (s k ) (s k 1 )a k x s k 2
l 为偶数:l = 2n (n为整数)
y0(x)1(l)2 (l!1)x2(2l)(l)4 (l!1)(l3)x4... (2n2l)(2n4l)L((2 n l))! (l1)(l3)L(l2n1)x2n...
从 x2n 项起,系数都含有因子(2n – l )从而为0,y0(x)退化为2n次多项式, 且只含偶次幂项; y1(x) 不含(2n - l ),仍为无穷级数; 取任意常数 a1 = 0 即得只含偶次幂的l 次多项式 a0y0(x) ,当选定a0 得到 的特解,称为l 阶勒让德多项式。
( k 1 ) ( k 2 ) a k 2 [ l ( l 1 ) k ( k 1 ) ] a k 0
数学物理方程与特殊函数
第九章
递推 a k 公 2k( (k k 1 式 2 )) k l( ( l1 ) 1 )a : k (( k k l) 2 ) k ( k ( l 1 1 ))a k
(1x2)d22xdl(l1)0 m = 0 dx2 dx
l 阶勒让德方程
数学物理方程与特殊函数
第九章
拉普拉斯方程 u 0 柱坐标(,,z)
1(u)122u2z2u2 0
uR () ()Z (z)
柱坐标系
贝塞尔方程
R"1x R'(1m x22)R0
数学物理方程与特殊函数
第九章
求解线性二阶常微分方程 (带初始条件)
2 (l2)(l3) (2l2)!
al4(4)(2l3)al2(1) 22!(2l3) 2l(l1)!(l2)!
21
(2l2)!
2 (2l4)!
(1) 22!(2l3) 2l(l1)(l2)!(l4)!(1) 2!2l(l2)!(l4)!
…………
数学物理方程与特殊函数
第九章
n (2l2n)! al2n(1) n!2l(ln)!(l2n)!
x0 = 0 是方程的常点
定理
y(x) an xn n0
数学物理方程与特殊函数
第九章
于是 y ( x ) a 0 a 1 x a 2 x 2 a 3 x 3 . . . a k x k . . .
y ' ( x ) a 1 2 a 2 x 3 a 3 x 2 4 a 4 x 3 . . . ( k 1 ) a k 1 x k . . .
第九章
拉普拉斯方程 u 0 球坐标(r, , )
11(r 2 u )1 (s in u )1( 2 u ) 0 r 2 r r r2 s in r2 s in2
uR (r)Y(,)
…….
球坐标系
连带勒让德方程
(1 x2)d d 2 x 2 2 xd d x [l(l 1 ) 1 m x 22] 0
第九章
判定方程
s ( s 1 ) s p 1 q 2 s ( s 1 ) s v 2 s 2 v 2 0
两个根为: s1= v ,s2 =- v
两根之差: s1 - s2 = 2 v 不等于0或正整数
判定方程的两根之差决定了两个线性独立解的形式:
y1(x) ak(xx0)s1k k0
解析, 称 x0 为方程的常点。 奇点 x0是系数 p(x) , q(x) 的孤立奇点,称 x0 为方程的奇点。 正则 x0是 p(x) 不超过一阶的极点 , 又是 q(x) 的不超过二阶 奇点 的孤立奇点; 称 x0 为方程的正则奇点。否则为非正则
奇点。
数学物理方程与特殊函数
第九章
二、常点邻域上的级数解法
数学物理方程与特殊函数
第九章
第九章 二阶常微分方程的级数解法
• 概述 • 常点邻域上的级数解法 • 正则奇点邻域上的级数解法 • 本章小结
数学物理方程与特殊函数
第九章
一、概述
分离变量法
直角坐标系、平面极坐标 本征函数是三角函数
实际 正交曲面坐标系 (球坐标系和柱坐标系) 拉普拉斯方程的分离变量
