2012年第十届小学希望杯数学试题及答案详解(六年级第1试)
新希望杯六年级数学试卷及解析答案.doc

新希望杯六年级数学试卷及解析答案 (满分120分;时间120分钟) 一、填空题(每题5分;共60分) 1、计算:=-+••114154.0625.3________________. 解析:原式=625.3+••54.0-••63.1=625.2+(••54.1-••63.1)=625.2+••90.0=••09715.2或 原式=8823911108291115115829=-=-+ 2、对于任意两个数x 和y ;定义新运算◆和⊗;规则如下:x ◆y =y x y x 22++;x ⊗y =3÷+⨯y x y x ;如 1◆2=221212⨯++⨯;1⊗2=5115632121==+⨯; 由此计算••63.0◆=⊗)2114(__________. 解析:=⊗)2114(345.465.045.14==+⨯;而11463.0=••;所以原式=25173211132112342114341142=++=⨯++⨯3、用4根火柴;在桌面上可以拼成一个正方形;用13根火柴可以拼成四个正方形;…;如图1;拼成的图形中;若最下面一层有15个正方形;则需火柴__________根。
解析:第二个图形比第一个图形多9根火柴;第三个图形比第二个图形多13根火柴;经尝试;第四个图形比第三个图形多17根火柴;而最下面一层有15根火柴的是第8个图形;所以共需要火柴4+(9+13+17+21+25+29+33)=151根。
4、若自然数N 可以表示城3个连续自然数的和;也可以表示成11个连续自然数的和;还可以表示成12个连续自然数的和;则N 的最小值是_________。
(注:最小的自然数是0)解析:因为奇数个连续自然数之和等于中间数乘以数的个数;所以N 能被3和11整除;也就是能被33整除;因为偶数个连续自然数之和等于中间两个数的平均值乘以数的个数;所以N 等于一个整数加上0.5再乘以12;也就是被12除余6;最小为66。
2012希望杯第2试全部试题详解及分析

2012年第十届希望杯六年级二试试题详解 1、原式=33111113331814124533===441684235⨯⨯+++⨯⨯⨯⨯()() 2、原式=(2+3+5+13)+(2222355779911+++⨯⨯⨯⨯)+(3239355779++⨯⨯⨯) =23+(1112211311557577-++++⨯⨯)() =23+8111313355757++-++() =248333、因为1+2+3+.......+n=n ⨯(n+1) ÷2≈2012所以n ⨯(n+1) ≈=4024 则约为631+2+3+.......+63=63⨯64÷2=2016则漏加的数为:2016-2012=44、最大:0.2012041.5(5循环),最小:0.2.012041.5(0120415循环)5、依题意:412132m ⨯⨯=+⨯,⇒ m=2 3*12=431243122423312677⨯⨯⨯⨯==⨯+⨯⨯ 6、第一次变化后周长变为:9⨯3⨯43=36 第二次变化后周长变为:36⨯43=48 第三次变化后周长变为:48⨯43=64 第四次变化后周长变为:64⨯43=2563 7、这是常规题,多次遇到,分类统计,共35个。
8、依据约数个数判定定理:8=2⨯4=(1+1)⨯(3+1), ⇒ N=312540⨯=8=2⨯2⨯2=(1+1)⨯(1+1)⨯(1+1)⇒ N=11123530⨯⨯=所以N 的最小值为309、因为(189,147)=3⨯7=21,所以购买的数量有三种情况 情况一:3个,则单价为:147÷3=49,不合题意,情况二:7个,则单价为:147÷7=21,符合题意,情况三:21个,则单价为:147÷21=7,不合题意。
故实际单价为:21元,共买了7个10、阴影部分面积为大圆面积减去2个小圆面积:3.14⨯(40/2)2-2⨯3.14⨯102=3.14⨯(400-200)=628(平方厘米)11、 44==743v v -甲乙 ∴ 33438=336=÷⨯⨯⨯ 12、甲:13份,乙:12份,丙:122=83⨯份平均每人:(13+12+8)÷3=11(份)丙差:11-8=3(份),每份:9÷3=3(元)支付甲:3⨯(13-11)=6(元) 支付乙:3⨯(12-11)=3(元)13、答案不唯一 ,在此公提供两种:14、甲共行:3+4+4=11(份) 乙共行:4+3+3=10(份) 603==804v v 甲乙 若乙不休息,可行:11÷34=443(份)少行了:443-10=143(份)所以乙的速度为:143÷14=13(份),则第一次相遇时间为:4÷13=12(分)所以AB=(60+80)⨯12=1680(米)15、可能堆成的长方体有如下8种可能:100=1⨯1⨯100 =1⨯2⨯50 =1⨯4⨯25=1⨯5⨯20=1⨯10⨯10=2⨯2⨯25 =2⨯5⨯10=4⨯5⨯5欲使堆成的表面积尽可能小,长、宽、高的差要尽可能小,所以应选择100=1⨯4⨯25=1⨯5⨯20=1⨯10⨯10=2⨯2⨯25=2⨯5⨯10=4⨯5⨯5这6种组合方式,计算的表面积从小到大(从后向前)依次是130、160、208、240、250、258。
新希望杯六年级数学试卷及解析答案.doc

新希望杯六年级数学试卷及解析答案(满分120分;时间120分钟)一、填空题(每题5分;共60分)1、计算:=-+••114154.0625.3________________. 解析:原式=625.3+••54.0-••63.1=625.2+(••54.1-••63.1)=625.2+••90.0=••09715.2或 原式=8823911108291115115829=-=-+ 2、对于任意两个数x 和y ;定义新运算◆和⊗;规则如下:x ◆y =y x y x 22++;x ⊗y =3÷+⨯y x y x ;如 1◆2=221212⨯++⨯;1⊗2=5115632121==+⨯; 由此计算••63.0◆=⊗)2114(__________. 解析:=⊗)2114(345.465.045.14==+⨯;而11463.0=••;所以原式=25173211132112342114341142=++=⨯++⨯3、用4根火柴;在桌面上可以拼成一个正方形;用13根火柴可以拼成四个正方形;…;如图1;拼成的图形中;若最下面一层有15个正方形;则需火柴__________根.解析:第二个图形比第一个图形多9根火柴;第三个图形比第二个图形多13根火柴;经尝试;第四个图形比第三个图形多17根火柴;而最下面一层有15根火柴的是第8个图形;所以共需要火柴4+(9+13+17+21+25+29+33)=151根.4、若自然数N 可以表示城3个连续自然数的和;也可以表示成11个连续自然数的和;还可以表示成12个连续自然数的和;则N 的最小值是_________.(注:最小的自然数是0)解析:因为奇数个连续自然数之和等于中间数乘以数的个数;所以N 能被3和11整除;也就是能被33整除;因为偶数个连续自然数之和等于中间两个数的平均值乘以数的个数;所以N 等于一个整数加上0.5再乘以12;也就是被12除余6;最小为66.(66可以表示成0到11的和)5、十进制计数法;是逢10进1;如141022410⨯+⨯=;15106103365210⨯+⨯+⨯=;计算机使用的是二进制计数法;是逢2进1;如22101111121217=⨯+⨯+⨯=;2231011001020212112=⨯+⨯+⨯+⨯=;如果一个自然数可以写成m 进制数m 45;也可以写成n 进制数n 54;那么最小的m =_______;n =________.(注:4434421an n a a a a a 个⨯⋅⋅⋅⨯⨯⨯=)解析:4m+5=5n+4;也就是说4(m-1)=5(n-1);如果m-1=5;n-1=4;则m=6;n=5;但此时n进制中不能出现数字5;如果m-1=10;n-1=8;则m=11;n=9;符合题意.6、我国除了用公历纪年外;还采用干支纪年;根据图2中的信息回答:公历1949年按干支纪年法是____________年.解析:干支纪年法60年一循环;1949+60=2009;而2009年是己丑年;所以1949年是己丑年7、盒子中装有很多相同的,但分红、黄、蓝三种颜色的玻璃球,每次摸出两个球;为了保证有5次摸出的结果相同;则至少需要摸球__________次.解析:每次摸出的结果可能是两个球颜色相同;有3种可能;或颜色不同;也有3种可能;共6种可能.最不利情况是每种可能各出现4次;则再摸一次就保证有5次相同;6×4+1=258、根据图3中的信息回答;小狗和小猪同时读出的数是___________.解析:相当于分别从1和1002处以2:5的速度比进行相遇问题;(1002-1)÷7×2+1=2879、图4中的阴影部分的面积是__________平方厘米.( 取3)解析:分别连接两个正方形的"\"的对角线;发现它们平行;所以阴影部分的面积就等于一个扇形的面积;为15×15×3÷4=168.7510、甲、乙两人合买了n 个篮球;每个篮球n 元.付钱时;甲先乙后;10元;10元地轮流付钱;当最后要付的钱不足10元时;轮到乙付.付完全款后;为了使两人所付的钱数同样多;则乙应给甲________元.解析:总共价格为2n 元;最后乙付说明2n 的十位数字为奇数;所以个位为6;乙最后一次付了6元;应该给甲2元11、某代表队共有23人参加第16届广州亚运会;他们按身高从高到低排列;前5位队员的平均身高比前8位队员的平均身高多3厘米;后15位队员的平均身高比后18位队员的平均身高少0.5厘米.那么前8位队员的平均身高比后15位队员的平均身高多_______厘米.解析:前5位队员的平均身高比前8位队员的平均身高多3厘米;也就是说;加入第6~8名后;平均身高减少了3厘米;因此第6~8名的平均身高比前5名的平均身高少3÷3×8=8厘米.第9~23位队员的平均身高比第6~23位队员的平均身高少0.5厘米;也就是说;加入第6~8名后;平均身高增加了0.5厘米;因此第6~8名的平均身高比第9~23名的平均身高多0.5÷3×18=3厘米.因此;前8名的平均身高比第9~23名的平均身高多8-3+3=8厘米12、甲、乙、丙三人同时从A 地出发到B 地;他们的速度的比是12:5:4;其中甲、乙两人步行;丙骑自行车;丙可以带一人同行(速度保持不变).为了使三人在最短的时间内同时到达B 地;则甲、乙两人步行的路程之比是___________.解析:根据对称性;丙先带谁没有区别.设先带甲;返回接乙.设乙步行的路程为x ;丙骑车返回的路程为y ;甲步行的路程为z .乙比骑车从A 地到B 地多用时间(5x -12x );甲比骑车从A 地到B 地多用时间(4z -12z );丙比骑车从A 地到B 地多用时间122y .三人同时到达即这三个相等时;5x -12x =4z -12z =122y ;求得x :y :z =10:7:7;所求路程比为7:10二、解答题(每题15分;共60分)13、一辆汽车从甲地开往乙地;若车速提高%20;可提前25分钟到达;若以原速行驶100千米;再将车速提高%25;可提前10分钟到达;求甲乙两地的距离.解析:车速提高20%;也就是变成原来的56;则时间变成原来的65;减少25分钟;原定时间为25×6=150分钟;车速提高25%;也就是变成原来的45;则时间变成原来的54;减少10分钟;则这段路程的原定时间为10÷5=50分钟.因此;原速行驶100千米需要150-50=100分钟;距离为150÷100×100=150千米14、如图5;在一个棱长为20厘米的正方体密闭容器的下底固定了一个实心圆柱体;容器内盛有m 升水时;水面恰好经过圆柱体的上底面.如果将容器倒置;圆柱体有8厘米露出水面.已知圆柱体的底面积是正方体底面积的81;求实心圆柱体的体积. 解析:两次的空白部分体积相等;而第二次的空白部分的横截面积为第一次的87811=-;所以第一次的空白部分的高度为第二次的87;即7厘米.正方体的底面积为20×20=400平方厘米;所以圆柱体的底面积为400÷8=50平方厘米;高度为20-7=13厘米;体积为50×13=650立方厘米15、有8个足球队进行循环赛;胜队得1分;负队得0分;平局的两队各得0.5分.比赛结束后;将各队的得分按从高到低排名后发现:各队得分互不相同;且第二名的得分与最后四名所得的总分一样多.求这次比赛中;取得第二名的队的得分.解析:全胜的队得7分;而最后四队之间赛6场至少共得6分;所以第二名的队得分至少为6分.如果第一名全胜;则第二名只输给第一名;得6分;如果第二名得6.5分;则第二名6胜1负;第一名最好也只能是6胜1负;与题目中得分互不相同不符.所以;第二名得分为6分16、将两个不同的自然数中较大的数换成他们的差;称为一次操作;如此继续下去;直到这两个数相同为止.如对20和26进行这样的操作;过程如下:(20;26)→(20;6)→(14;6)→(8;6)→(2;6)→(2;4)→(2;2)(1)对45和80进行上述操作.(2)若对两个四位数进行上述操作;最后得到的相同数是17.求这两个四位数的和的最大值.解析:(45,80)→(45,35)→(10,35)→(10,25)→(10,15)→(10,5)→(5,5).这就是用辗转相除法求最大公约数的运算;所以两个四位数的最大公约数为17;9999÷17=588……3;所以最大的四位数是9999-3=9996;第二大的四位数是9996-17=9979;和为19975(祝各位同学学习进步!)。
2012第十届六年级希望杯培训题道及答案解析

2012第十届六年级“希望杯”培训题1.计算 129×10 +2210×11 +…+51259×602.计算:1×2×3×4+3×6×9×122×4×6×83.计算4.用简便方法计算3+1949×(158 -12007 )+58×(11949 -12007 )-2007×(11949 +158)5.图l 所示正方体的展开图是 .(填序号)6.一串数字2134…,从第三个数字起,每个数字都是它前面两个数字之和的个位数字,则这串数字的第2012个数字是 .7.一个三位数是3的倍数,去掉它的个位数字后,所得的两位数是17的倍数.这个三位数最大是 .8.将被11除余1,被l5除余12的自然数按从小到大的顺序排成一列,,,,321⋅⋅⋅a a a 则=1a ;若m m a a <<-20111,则m = 。
9.某市人口总数与上年相比的情况是:2007年比2006年增加1%,2008年比2007年又增加1%,2009年比2008年减少1%,2010年比2009年又减少1%,那么2010、年与2006年相比,该市的人口总数 (填“增加”或“减少”)的百分数大约是 .10.用运算符号及括号将1,3,7,8连接成一个算式(每个数只使用一次),试给出一个使用了“÷”且结果等于24的算式.11.将3,4,5,6,7,,8填入下面的方框里,使两个三位数的乘积最大.□□□×□□□12.将2011年的所有日期的数字依次排列在一起,组成一个数串:1234567891011……. 则7月8日中的“8”排在数串的第 位.13.已知1001=a ,1011=b ,则abb a b a --+-1= 。
14.若A ,B ,C 分别代表l ~9的某个自然数,已知等式105881733=++C B A 成立, 则A = ,B = ,C = .15.请选择一个你喜欢的两位数,将它连续写5遍组成一个十位数(如:两位数12连续写5遍成为1212121212),将这个十位数除以这个两位数,所得到的商再除以9,所得的余数是 .16.图2是一个新月形图案,则用两条直线最多可以将该图案分成 部分.17.将一个正三角形的三条边分别2、3、4等分,获得一些相同的小正三角形,如图3所示.如果将正三角形的三条边都10等分,那么.得到的相同的小正三角形有 个.图318.六年级1班有30多人,个子最高的小明发现,放学站队时无论是2人、还是3人或者4人站成一排,他都只能自己单独站在最后,没有人与他站一排.则六年级1班共有 人.19.设a 、b 、c 分别是甲、乙、丙三人独自完成某项工程所需天数.令ba b a A +⨯=,a c c b b a c b a B ⨯+⨯+⨯⨯⨯= 则A 、B 的大小关系是 .20.公交车的线路号是由数字显示器显示的三位数,其中每个数字由横竖放置的七支荧光管显示,如图4,分别显示689,547和234.图4某公交线路号的数字的应显示器的两支应显示的荧光管不能显示,结果线路号的显示成了“234”,则该公交线路号有 种可能.21.甲、乙两人的钱数比是3:2,如果甲给乙8元,则甲、乙两人的钱数比变成2:3,则两人共有钱 元。
小学六年级“希望杯”第1-10届试题及详解(第一试和第二试)

第四届小学“希望杯”全国数学邀请赛六年级第1试以下每题5分,共120分。
1.2006×2008×()=________。
2.900000-9=________×99999。
3.=________。
4.如果a=,b=,c=,那么a,b,c中最大的是________,最小的是________。
5.将某商品涨价25%,如果涨价后的销售金额与涨价前的销售金额相同,则销售量减少了________%。
6.小明和小刚各有玻璃弹球若干个。
小明对小刚说:“我若给你2个,我们的玻璃弹球将一样多。
”小刚说:“我若给你2个,我的弹球数量将是你的弹球数量的三分之一。
”小明和小刚共有玻璃弹球________个。
7.一次测验中,小明答错了10道题,小刚答错了8道题,小强答对的题的数量等于小明与小刚答对题的数量之和,且小强答错了3道题。
这次测验共有________道题。
8.一个两位数,加上它的个位数字的9倍,恰好等于100。
这个两位数的各位数字之和的五分之三是________。
9.将一个数A的小数点向右移动两位,得到数B。
那么B+A是B-A的________倍。
(结果写成分数形式)10.用10根火柴棒首尾顺次连接接成一个三角形,能接成不同的三角形有________个。
11.希望小学举行运动会,全体运动员的编号是从1开始的连续整数,他们按图中实线所示,从第1珩第1列开始,按照编号从小到大的顺序排成一个方阵。
小明的编号是30,他排在第3行第6列,则运动员共有________人。
12.将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为l的小正方体。
则三个面涂漆的小正方体有________块。
13.如图,∠AOB的顶点0在直线l上,已知图中所有小于平角的角之和是400度,则∠AOB=________度。
14.如图,桌面上有A、B、C三个正方形,边长分别为6,8,10。
B的一个顶点在A 的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是________。
2012年第十届小学希望杯全国数学邀请赛六年级第1试及答案

2012年第十届小学“希望杯”全国数学邀请赛六年级第1试1、计算:2、计算:3、在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的_______.4、一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是_______.5、的个位数字是________.(其中,表示n个2相乘)6、图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是_______.(填序号)7、一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多,两车同时从甲乙两地相对开出2小时后,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲乙两地相距______千米.8、对任意两个数x,y,定义新的运算*为:(其中m是一个确定的数).如果,那么m=______,2*6=_______.9、甲、乙两家商店出售同一款兔宝宝玩具,每只原售价都是25元,为了促销,甲店先提价10%,再降价20%;乙店则直接降价10%.那么,调价后对于这款兔宝宝玩具,______店的售价更便宜,便宜_____元。
10、图3中的三角形的个数是_______.11、若算式(□+121×3.125)÷121的值约等于3.38,则□中应填入的自然数是_______.12、认真观察图4中的三幅图,则第三幅图中的阴影部分应填的数字是________.13、图5中每一个圆的面积都是1平方厘米,则六瓣花形阴影部分的面积是_____平方厘米.14、如图6,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形_______.15、早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是_______点______分.16、从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚,可组成不同的邮资______种.17、从1,2,3,4,…,15,16这十六个自然数中,任取出n个数,其中必有这样的两个数:一个是另一个的3倍,则n最小是______.18、某工程队修建一条铁路隧道,当完成任务的时,工程队采用新设备,使修建速度提高了20%,同时为了保养新设备,每天工作时间缩短为原来的,结果,前后共用185天完工,由以上条件可推知,如果不采用新设备,完工共需______天.19、王老师在黑板上写了若干个从1开始的连续自然数:1,2,3,4,…,然后擦去三个数(其中有两个质数),如果剩下的数的平均是,那么王老师在黑板上共写了______个数,擦去的两个质数的和最大是______.20、小强和小林共有邮票400多张,如果小强给小林一些邮票,小强的邮票就比小林的少;如果小林给小强同样多的邮票,则小林的邮票就比小强的少,那么,小强原有_______张邮票,小林原有______张邮票.。
希望杯六年级答案详解

3
11
61 311 3 61 11 61
16. 若一个长方体,长是宽的 2,宽是高的 2 倍,所有棱长之和是 56,则此长方体的体积是________. 【考点】几何,立体几何 【答案】64 【难度】☆ 【分析】长宽高的和是 14,而设高是 1 份,那么宽是 2 份,长是 4 份,和是 7 份,所以 1 份是 2,这 个长方体的长宽高分别为 8、4、2,体积为 64.
【考点】应用题,倒推 【答案】A、33 【难度】☆☆
【分析】倒推,列表如下:
A
B
C
D
最后(第四次后)
16
16
16
16
第三次后
8
8
8
40
第二次后
4
4
36
20
第一次后
2
34
18
10
开始(第一次前)
33
17
9
5
17. 图 4 中阴影部分的两段圆弧所对应的圆心分别为点 A 和点 C,AE=4m,点 B 是 AE 的中点,那么, 阴影部分的周长是________m,面积是________m2.(圆周率 取 3)
【考点】几何,曲线形
【答案】13、7
【难度】☆☆
【分析】首先容易看出,大小圆半径分别为 4 和 2,而长方形的长和宽分别为 4 和 2,所以周长为
3
3
3
10. 在一个两位数的中间加上小数点,得到一个小数,若这个小数与原来的两位数的和是 86.9,则原
来的两位数是
.
【考点】数字谜
【答案】79
【难度】☆
【分析】列成竖式数字谜,很快可推出原数个位为 9,十位为 7; 或者由于结果中小数部分为 9,则原数个位为 9,而原数加一个小于 10 的数得 80 多,则原数为 79.
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第八-十二届希望杯全国数学邀请赛六年级试题及答案解析
4. 一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是__________.
5. 22012 的个位数字是__________.(其中 2n 表示 n 个 2 相乘)
6. 下图(左)是一个正方体的展开图,图中(右)的四个正方体中只有一个是和这个展开 图对应的,这个正方体是__________.(填序号)
10. 在一个两位数的中间加上小数点,得到一个小数,若这个小数与原来的两位数的和是 86.9 ,则原来的两位数是___________.
11. A、B 两校的男、女生的人数的比分别是 8:7 和 30:31,两校合并后,男、女生人数的比
是 27:26,则 A、B 两校合并前人数的比是___________. 12. 有 2013 名学生参加数学竞赛,共有 20 道竞赛题,每个学生有基础分 25 分,此外,答
b (若a b).
1.1 7 1 0.1
例如: 3.5 2 3.5,1 1.2 1.2, 7 7 1,则
33 4 0.8
___________.
5
7. 有一口无水的井,用一根绳子测井的深度,将绳子对折后垂到井底,绳子的一端高出井 口 9m;将绳子三折后垂到井底,绳子的一端高出井口 2m,则绳子长___________m, 井深___________m.
①
②
③
④
7. 一列快车从甲地开往乙地需要 5 小时,一列慢车从乙地开往甲地所需时间比快车多 1 , 5
两车同时从甲乙两地相对开出 2 小时后,慢车停止前进,快车继续行驶 40 千米后恰与 慢车相遇,则甲乙两地相距__________千米.
8. 对任意两个数 x,y,定义新的运算“*”为: x y x y
1 1
2012年第十届小学“希望杯”全国数学邀请赛(六年级第1试)

第十届小学“希望杯”全国数学邀请赛六年级第1试2012年3月11日上午8:30至10:00 得分______ 以下每题6分,共120分。
1. 计算:21111.2511125%=9943⨯+⨯-⨯______.2. 计算:251251= 2008200920092010+⨯⨯______.3. 在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的______.4. 一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是______.5. 20122的个位数字是______.(其中,2n表示n个2相乘)6. 图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是______.(填序号)7. 一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多15,两车同时从甲、乙两地相对开出2小时后,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲、乙两地相距______千米.8. 对任意两个数x ,y ,定义新的运算“*”为:2x yx y m x y⨯*=⨯+⨯(其中m 是一个确定的数).如果1*2=25,那么m=______,2*6=______. 9. 甲、乙两家商店出售同一款兔宝宝玩具,每只原售价都是25元,为了促销,甲店先提价10%,再降价20%;乙店则直接降价10%.那么,调价后对于这款兔宝宝玩具,______店的售价更便宜,便宜______元。
10. 图3中的三角形的个数是______.11. 若算式(□+121×3.125)÷121的值约等于3.38,则□中应填入的自然数是______.12. 认真观察图4中的三幅图,则第三幅图中的阴影部分应填的数字是______.13. 图5中每一个圆的面积都是1平方厘米,则六瓣花形阴影部分的面积是______平方厘米.14. 如图6,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的是正方形______.15. 早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是______点______分.16. 从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚,可组成不同的邮资______种.17. 从1,2,3,4,…,15,16这十六个自然数中,任取出n个数,其中必有这样的两个数:一个是另一个的3倍,则n最小是______.18. 某工程队修建一条铁路隧道,当完成任务的13时,工程队采用新设备,使修建速度提高了20%,同时为了保养新设备,每天工作时间缩短为原来的45,结果,前后共用185天完工.由以上条件可推知,如果不采用新设备,完工共需______天.19. 王老师在黑板上写了若干个从1开始的连续自然数:1,2,3,4,…,然后擦去三个数(其中有两个质数),如果剩下的数的平均数是8199,那么王老师在黑板上共写了______个数,擦去的两个质数的和最大是______.20. 小强和小林共有邮票400多张,如果小强给小林一些邮票,小强的邮票就比小林的少619;如果小林给小强同样多的邮票,则小林的邮票就比小强的少617.那么,小强原有______张邮票,小林原有______张邮票.。
2012年第10届希望杯六年级一试试题详解】

2012年希望杯六年级第1试试题1、计算:21111.2511125%9943⨯+⨯-⨯=______.【答案】1.25 【解析】2111.251 1.25993⎛⎫=⨯+-= ⎪⎝⎭原式2、计算:2512512008200920092010+=⨯⨯______. 【答案】18040 【解析】11111112512512008200920092010200820108040⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-=⨯-=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦原式 3、在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的是______.【答案】3.1415926∙∙【解析】略4、一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是______.【答案】90【解析】最小的两位数是10,所以被除数最大是10990⨯=5、20122的个位数字是______.(其中,2n 表示n 个2相乘)【答案】6【解析】2的次方的个位数字的规律是2、4、8、6、2、4、8、6、……,它是4个数为一个周期的,而20124503÷=,则20122的个位数字是66、图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是_______.(填序号)图1 图2【答案】【解析】略7、一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多1/5,两车同时从甲乙两地相对开出2小时候,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲乙两地相距______千米.【答案】150千米【解析】快车需要5小时,慢车需要6小时,设快车速度为6份,则慢车速度为5份,则全长为30份,两车相对开出2小时后,两车行驶的路程和为22份,则8份的距离对应40千米,则甲乙两相距40830150÷⨯=千米。
8、对任意两个数x ,y ,定义新的运算*为:*2x y x y m x y ⨯=⨯+⨯ (其中m 是一个确定的数).如果21*25=,那么m =______,2*6=_______. 【答案】1m =,62*67= 【解析】1221*21225m ⨯==⨯+⨯,则1m =,2662*612267⨯==⨯+⨯9、甲、乙两家商店出售同一款兔宝宝玩具,每只原售价都是25元,为了促销,甲店先提价10%,再降价20%;乙店则直接降价10%.那么,调价后对于这款兔宝宝玩具,______店的售价更便宜,便宜_____元。
第十届(2012)小学“希望杯”全国数学邀请赛(初试、复试、答案)

第十届(2012)小学“希望杯”全国数学邀请赛(第1试)四年级第一试1.小惠从开始站立的A点向西走了15米,到达B点,接着从B点向东走了23米,到达C点,那么从C点到A点的距离是米2.长方形MNPQ中,MN=3,MQ=4,过它的中心O(对角线MP和NQ的交点)画一条直线。
长方形MNPQ被分成了两个相同的图形,它们的形状是3.如果a表示一个三位数,b表示一个两位数,那么,a + b最小是,a + b 最大是,a – b最小是,a – b最大是。
4.一次乐器比赛的规则规定:初赛分四轮以此进行,四轮得分的平均分不低于96分的才能进入决赛,小光前三轮的得分依次是 95, 97, 94,那么,他要进入决赛,第四轮的得分至少是分。
5.如果今天是星期五,那么从今天算起,57天后的第一天是星期。
6.如图1所示,5个相同的两位数AB想加得两位数MB,其中相同的字母表示相同的数字,不同的字母表示不同的数字,则AB =。
7.一个口袋有5枚面值1元的硬币和6枚面值5角的硬币。
小明随意从口袋中摸出6枚,那么6枚硬币的面值和有种。
8.某个学习小组有男生和女生共八位同学,其中女生比男生多,那么男生的人数可能是。
9.只能被1和他本身整除的自然数叫做质数, 如:2,3,5,7等,那么,比40大并且比50小的质数是,小于100的最大的质数是。
10.如图2,以小正方形的边向小正方形外作四个正方形,再依次连接几个顶点,若图中阴影部分的面积是S,则面积为2S的三角形有个,面积为8S的正方形有个。
11.在一个长方形内,任意画一条直线,长方形被分成两部分(如图3),如果画三条互不重合的直线,那么长方形至少被分成部分,最多被分成部分。
12.甲,乙二人先后从一个包裹中轮流取糖果。
甲先取1块,乙接着取2块,然后甲再取4块,乙接着取8块,…,如此继续,当包裹中的糖果少于应取的块数时,则取走包裹中所有的糖果,若甲共取了90块糖果,则最初包裹中有块糖果。
希望杯近五年真题汇总+详解(六年级)

图 1
10 6. 已知三个分数的和是 ,并且它们的分母相同,分子的比是 2 : 3 : 4 , 11 那么,这三个分数中最大的是__________.
9
1 2 1 2 3 6
7. 从12点整开始,至少经过__________分钟,时针和分针都与12点整时所 在位置的夹角相等 .(如图2中的 1 2 ) 8. 若三个不同的质数的和是53,则这样的三个质数有__________组. 9. 被11除余7, 被7除余5, 并且不大于200的所有自然数的和是__________.
B
图2
A P O C
1 3 10. 在救灾捐款中, 某公司有 的人各捐款200 元, 有 的人各捐款100 元, 10 4 其余人各捐款50 元,则该公司人均捐款__________元.
图3
11.如图3,圆 P 的直径 OA 是圆O的半径,OA⊥ BC , OA 10 ,则阴影部 分的面积是__________.( π 取3) 12.如图4,一个直径为1厘米的圆绕边长为2厘米的正方形滚动一周后回到原 来的位置,在这个过程中,圆面覆盖过的区域(阴影部分)的面积是
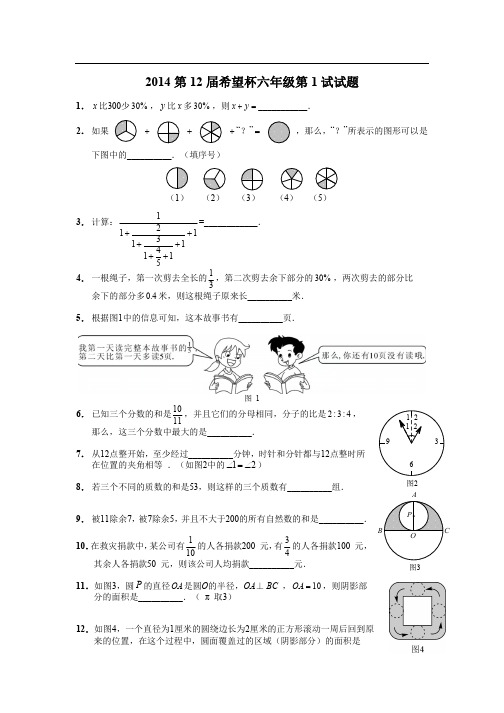
2014 第 12 届希望杯六年级第 1 试试题
1. x 比300少 30% , y 比 x 多 30% ,则 x y ___________. 2. 如果
“ ?”
,那么,“ ?”所表示的图形可以是
下图中的__________.(填序号)
(1)
3. 计算:
(2)
(3)
(4)
(5)
3. 在小数 3.1415926 的两个数字上方加 2 个循环点,得到循环小数,这样的循环小数中, 最小的是__________. 4. 一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是__________. 5.
2020年第十届小学数学“梦想杯”全国数学邀请赛试卷(六年级第1试)

2012年第十届小学“希望杯”全国数学邀请赛试卷(六年级第1试)一、填空题(共20小题,每小题3分,满分60分)1.(3分)计算:1.25×+1×﹣125%×=.2.(3分)计算:+=.3.(3分)在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的.4.(3分)一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是.5.(3分)22012的个位数字是.(其中,2n表示n个2相乘)6.(3分)如图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是.(填序号)7.(3分)一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多,两车同时从甲乙两地相对开出2小时后,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲乙两地相距千米.8.(3分)对任意两个数x,y,定义新的运算*为:(其中m是一个确定的数).如果,那么m=,2*6=.9.(3分)甲、乙两家商店出售同一款兔宝宝玩具,每只原售价都是25元,为了促销,甲店先提价10%,再降价20%;乙店则直接降价10%.那么,调价后对于这款兔宝宝玩具,店的售价更便宜,便宜元.10.(3分)图中的三角形的个数是.11.(3分)若算式(□+121×3.125)÷121的值约等于3.38,则□中应填入的自然数是.12.(3分)认真观察图4中的三幅图,则第三幅图中的阴影部分应填的数字是.13.(3分)图中每一个圆的面积都是1平方厘米,则六瓣花形阴影部分的面积是平方厘米.14.(3分)如图,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的正方形是.15.(3分)早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是点分.16.(3分)从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚,可组成不同的邮资种.17.(3分)从1,2,3,4,…,15,16这十六个自然数中,任取出n个数,其中必有这样的两个数:一个是另一个的3倍,则n最小是.18.(3分)某工程队修建一条铁路隧道,当完成任务的时,工程队采用新设备,使修建速度提高了20%,同时为了保养新设备,每天工作时间缩短为原来的,结果,前后共用185天完工,由以上条件可推知,如果不采用新设备,完工共需天.19.(3分)王老师在黑板上写了若干个从1开始的连续自然数:1,2,3,4,…,然后擦去三个数(其中有两个质数),如果剩下的数的平均数是19,那么王老师在黑板上共写了个数,擦去的两个质数的和最大是.20.(3分)小强和小林共有邮票400多张,如果小强给小林一些邮票,小强的邮票就比小林的少;如果小林给小强同样多的邮票,则小林的邮票就比小强的少,那么,小强原有张邮票,小林原有张邮票.2012年第十届小学“希望杯”全国数学邀请赛试卷(六年级第1试)参考答案与试题解析一、填空题(共20小题,每小题3分,满分60分)1.(3分)计算:1.25×+1×﹣125%×=.【解答】解:1.25×+1×﹣125%×=×+×﹣×,=×(+﹣),=×1,=.故答案为:2.(3分)计算:+=.【解答】解:+,=251×(+),=251×(﹣+﹣),=251×,=;故答案为:.3.(3分)在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的 3.41592.【解答】解:在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的是3.41592;故答案为:3.41592.4.(3分)一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是98.【解答】解:商是10,除数最大是9,余数最大是8,9×10+8=98;被除数最大是98.故答案为:98.5.(3分)22012的个位数字是6.(其中,2n表示n个2相乘)【解答】解:2012÷4=503;没有余数,说明22012的个位数字是6.故答案为:6.6.(3分)如图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是①.(填序号)【解答】解:如图.图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是图2①;故答案为:①7.(3分)一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多,两车同时从甲乙两地相对开出2小时后,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲乙两地相距150千米.【解答】解:慢车行完全程需要:5×(1+),=5×,=6(小时);科技新闻网:##科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料,我们是国内外最新的科技新闻网。
第十届希望杯复赛试题及答案(六年级)

第十届小学“希望杯”全国数学邀请赛六年级 第2试2012年4月8日 上午9:00至11:00得分一、填空题(每小题5分,共60分。
)1. 计算:=⨯⨯⨯⨯+⨯⨯⨯52322153432351413121 2. 计算: =+++++++15535256311992135323. 王涛将连续的自然数1,2,3,…逐个相加,一直加到某个自然数为止,由于计算时漏加了一个自然数而得到错误的结果2012。
那么,他漏加的自然数是 。
4. 在数0.20120415中的小数后面的数字上方加上循环点,得到循环小数,这些循环小数中,最大的是 ,最小的是 。
5. 对任意两个数x ,y 规定运算“*”的含义是:yx m yx y x ⨯+⨯⨯⨯=*34(其中m是一个确定的数),如果1*2 = 1,那么m = ,3*12 = 。
6.对于一个多边形,定义一种“生长”操作:如图1,将其一学习奥数的优点1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心, 以及战胜难题的勇气。
可以养成坚韧不拔的毅力4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
图 1边AB 变成向外凸的折线ACDEB ,其中C 和E 是AB 的三等分点,C ,D ,E 三点可构成等边三角形,那么,一个边长是9的等边三角形,经过两次“生长”操作(如图2),得到的图形的周长是 ;经过四次“生长”操作,得到的图形的周长是 。
7. 如图3所示的“鱼”形图案中共有 个三角形。
8. 已知自然数N 的个位数字是0,且有8个约数,则N 最小是 。
9. 李华在买某一商品的时候,将单价中的某一数字“7”错看成了“1”,准备付款489元,实际应付147元,已知商品的单价及购买的数量都是整数,则这种商品的实际单价是 元,李华共买了 件。
历届希望杯试题

第四届小学“希望杯”全国数学邀请赛六年级第1试以下每题5分,共120分。
1.2006×2008×()=________。
2.900000-9=________×99999。
3.=________。
4.如果a=,b=,c=,那么a,b,c中最大的是________,最小的是________。
5.将某商品涨价25%,如果涨价后的销售金额与涨价前的销售金额相同,则销售量减少了________%。
6.小明和小刚各有玻璃弹球若干个。
小明对小刚说:“我若给你2个,我们的玻璃弹球将一样多。
”小刚说:“我若给你2个,我的弹球数量将是你的弹球数量的三分之一。
”小明和小刚共有玻璃弹球________个。
7.一次测验中,小明答错了10道题,小刚答错了8道题,小强答对的题的数量等于小明与小刚答对题的数量之和,且小强答错了3道题。
这次测验共有________道题。
8.一个两位数,加上它的个位数字的9倍,恰好等于100。
这个两位数的各位数字之和的五分之三是________。
9.将一个数A的小数点向右移动两位,得到数B。
那么B+A是B-A的________倍。
(结果写成分数形式)10.用10根火柴棒首尾顺次连接接成一个三角形,能接成不同的三角形有________个。
11.希望小学举行运动会,全体运动员的编号是从1开始的连续整数,他们按图中实线所示,从第1珩第1列开始,按照编号从小到大的顺序排成一个方阵。
小明的编号是30,他排在第3行第6列,则运动员共有________人。
12.将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为l的小正方体。
则三个面涂漆的小正方体有________块。
13.如图,∠AOB的顶点0在直线l上,已知图中所有小于平角的角之和是400度,则∠AOB=________度。
14.如图,桌面上有A、B、C三个正方形,边长分别为6,8,10。
B的一个顶点在A 的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是________。
2012年第10届小学“希望杯”全国数学邀请赛试卷(五年级第1试)

2012年第10届小学“希望杯”全国数学邀请赛试卷(五年级第1试)一、填空题(共20小题,满分0分)1.计算:1.2×67+6.7×88=_________.2.计算:21.49+52.37﹣0.4+5.51﹣11.37﹣6.6=_________.3.用1,2,3,4,5和+,﹣,×,÷组合成一个算式(不使用括号),计算结果最大是_________.4.一件商品,对原价打八折和打六折的售价相差4.8元,那么这件商品的原价是_________元.5.将252块巧克力,294盒饼干,336袋牛奶分成相同的份数,并且都没有余数,那么最多可以分成_________份.6.若8只羊一星期要吃168千克饲料,一头牛的食量是一只羊的食量的2.8倍,那么,200只羊和180头牛一个月(按30天计)要吃_________千克饲料.7.如图中,阴影面积最大的图形是_________,阴影面积最小的图形是_________.(填序号)、8.一个两位数,将它的十位数字和个位数字对调,得到的数比原来的数大18,这样的两位数有_________个.9.如图,如果小树的愿望能够实现,那么它的身高平均每年要增长到上一年的_________倍.10.两个不同的三位数被13除,若得到相同的余数,那么,这两个三位数的和最大是_________,它们的差最大是_________.11.如图,从左到右,在每列各选出一个框,组成算式(如:5×2+3),则有_________种不同的结果.12.A、B两地间有一条公路.甲车从A驶到B,需60分钟;乙车从B驶到A,需120分钟.若甲、乙两车分别从A、B两地同时出发,则在出发后_________分钟相遇.13.学校购买了数量相同的课桌和椅子,用小货车装运,每车装17张课桌和13把椅子.装了若干车后,课桌剩9张,椅子剩77把.那么,此时已经装了_________车;按1桌1椅为1套,那么学校购买了_________套课桌和椅子.14.如图,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯.现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是_________杯.15.要搭建如图所示的立体,需要_________个相同的小正方体.16.用60个相同的正方体,可以堆积成形状不同的长方体_________个.17.(2012•东城区模拟)恰好有两位数字相同的三位数共有_________个.18.小王为一个16人的旅游团购买飞机票,座位有经济舱和商务舱可选择,其中经济舱的票价是720元/人,商务舱的票价是1500元/人.这次购票共花费13080元,则小王购买了_________张经济舱机票.19.如图,在由9个相同的小正方形拼成的3×3网格中,标出9个角.则它们的度数和是_________.20.在一个海岛上居住者2012人,其中一些人总是说假话,其余的人总是说真话.岛上的每一位居民都崇拜太阳神、月亮神和地球神这三个神中的一个.一位外来的采访者向岛上的每一位居民提出三个问题:(1)你崇拜太阳神吗?(2)你崇拜月亮神吗?(3)你崇拜地球神吗?对第一个问题,有804人回答:“是”;对第二个问题,有1004人回答:“是”;对第三个问题,有1204人回答:“是”.那么,他们中有_________人说的是真话.2012年第10届小学“希望杯”全国数学邀请赛试卷(五年级第1试)参考答案与试题解析一、填空题(共20小题,满分0分)1.计算:1.2×67+6.7×88=670.2.计算:21.49+52.37﹣0.4+5.51﹣11.37﹣6.6=61.3.用1,2,3,4,5和+,﹣,×,÷组合成一个算式(不使用括号),计算结果最大是22.5.4.一件商品,对原价打八折和打六折的售价相差4.8元,那么这件商品的原价是24元.5.将252块巧克力,294盒饼干,336袋牛奶分成相同的份数,并且都没有余数,那么最多可以分成42份.6.若8只羊一星期要吃168千克饲料,一头牛的食量是一只羊的食量的2.8倍,那么,200只羊和180头牛一个月(按30天计)要吃63360千克饲料.7.如图中,阴影面积最大的图形是①,阴影面积最小的图形是③.(填序号)、8.一个两位数,将它的十位数字和个位数字对调,得到的数比原来的数大18,这样的两位数有7个.9.如图,如果小树的愿望能够实现,那么它的身高平均每年要增长到上一年的2倍.10.两个不同的三位数被13除,若得到相同的余数,那么,这两个三位数的和最大是1985,它们的差最大是897.11.如图,从左到右,在每列各选出一个框,组成算式(如:5×2+3),则有13种不同的结果.12.A、B两地间有一条公路.甲车从A驶到B,需60分钟;乙车从B驶到A,需120分钟.若甲、乙两车分别从A、B两地同时出发,则在出发后40分钟相遇.甲车的速度是,()÷,13.学校购买了数量相同的课桌和椅子,用小货车装运,每车装17张课桌和13把椅子.装了若干车后,课桌剩9张,椅子剩77把.那么,此时已经装了17车;按1桌1椅为1套,那么学校购买了298套课桌和椅子.14.如图,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯.现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是乙杯.15.要搭建如图所示的立体,需要95个相同的小正方体.16.用60个相同的正方体,可以堆积成形状不同的长方体10个.17.(2012•东城区模拟)恰好有两位数字相同的三位数共有243个.18.小王为一个16人的旅游团购买飞机票,座位有经济舱和商务舱可选择,其中经济舱的票价是720元/人,商务舱的票价是1500元/人.这次购票共花费13080元,则小王购买了14张经济舱机票.19.如图,在由9个相同的小正方形拼成的3×3网格中,标出9个角.则它们的度数和是405°.20.在一个海岛上居住者2012人,其中一些人总是说假话,其余的人总是说真话.岛上的每一位居民都崇拜太阳神、月亮神和地球神这三个神中的一个.一位外来的采访者向岛上的每一位居民提出三个问题:(1)你崇拜太阳神吗?(2)你崇拜月亮神吗?(3)你崇拜地球神吗?对第一个问题,有804人回答:“是”;对第二个问题,有1004人回答:“是”;对第三个问题,有1204人回答:“是”.那么,他们中有1012人说的是真话.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十届小学"希望杯”全国数学邀请赛
六年级第1试
2012年3月11日上午8:30至10:00
亲爱的小朋友,欢迎你参加第十届小学”希望杯”全国数学邀请赛!
你将进入一个新颖、有趣、有挑战性的数学天地,将会留下一个难忘的经历……以下每题6分,共120分。
1.计算:
2.计算:
3.在小数3.1415926的两个数字上方加2个循环点,得到循环小数,这样的循环小数中,最小的_______.
4.一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是_______.
5.的个位数字是________.(其中, 表示n个2相乘)
6.图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是_______.(填序号)
7.一列快车从甲地开往乙地需要5小时,一列慢车从乙地开往甲地所需时间比快车多,两车同时从甲乙两地相对开出2小时后,慢车停止前进,快车继续行驶40千米后恰与慢车相遇,则甲乙两地相距______千米.
8.对任意两个数x,y,定义新的运算“*”为:(其中m是一个确定的数).如果1*2=2/5,那么m=_____,2*6=_______.
9.甲、乙两家商店出售同一款兔宝宝玩具,每只原售价都是25元,为了促销,甲店先提价10%,再降价20%;乙店则直接降价10%.那么,调价后对于这款兔宝宝玩具,______店的售价更便宜,便宜_____元。
10.图3中的三角形的个数是_______.
11.若算式(□+121×3.125)÷121的值约等于3.38,则□中应填入的自然数是_______.
12.认真观察图4中的三幅图,则第三幅图中的阴影部分应填的数字是________.
13.图5中每一个圆的面积都是1平方厘米,则六瓣花形阴影部分的面积是_____
平方厘米.
14.如图6,正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两
个矩形,小正方形的面积的值已标在图中,分别为20和10,18和12,则正方形ABCD和EFGH中,面积较大的是正方形_______.
15.早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没
有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是_______点______分.
16.从五枚面值为1元的邮票和四枚面值为1.60元的邮票中任取一枚或若干枚,
可组成不同的邮资______种.
17.从1,2,3,4,…,15,16这十六个自然数中,任取出n个数,其中必有这样的
两个数:一个是另一个的3倍,则n最小是______.
18.某工程队修建一条铁路隧道,当完成任务的时,工程队采用新设
备,使修建速度提高了20%,同时为了保养新设备,每天工作时间缩短为原
来的,结果,前后共用185天完工,由以上条件可推知,如果不采用新设备,完工共需______天.
19.王老师在黑板上写了若干个从1开始的连续自然数:1,2,3,4,…,然后擦
去三个数(其中有两个质数),如果剩下的数的平均数是,那么王老师在黑板上共写了______个数,擦去的两个质数的和最大是______.
20.小强和小林共有邮票400多张,如果小强给小林一些邮票,小强的邮票就比
小林的少;如果小林给小强同样多的邮票,则小林的邮票就比小强的少,那么,小强原有_______张邮票,小林原有______张邮票.。
