托勒密定理圆的其它定理
第十一讲托勒密定理和西姆松定理
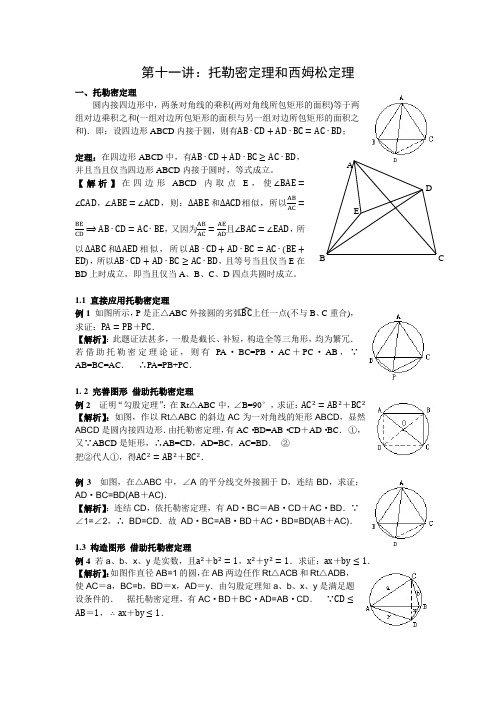
第十一讲:托勒密定理和西姆松定理一、托勒密定理圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).即:设四边形ABCD 内接于圆,则有AB ∙CD +AD ∙BC =AC ∙BD ;定理:在四边形ABCD 中,有AB ∙CD +AD ∙BC ≥AC ∙BD ,并且当且仅当四边形ABCD 内接于圆时,等式成立。
【解析】在四边形ABCD 内取点E ,使∠BAE =∠CAD ,∠ABE =∠ACD ,则:∆ABE 和∆ACD 相似,所以AB AC =BE CD ⟹AB ∙CD =AC ∙BE ,又因为AB AC =AE AD 且∠BAC =∠EAD ,所以∆ABC 和∆AED 相似,所以AB ∙CD +AD ∙BC =AC ∙(BE +ED),所以AB ∙CD +AD ∙BC ≥AC ∙BD ,且等号当且仅当E 在BD 上时成立,即当且仅当A 、B 、C 、D四点共圆时成立。
1.1 直接应用托勒密定理例1 如图所示,P 是正△ABC 外接圆的劣弧BC 上任一点(不与B 、C 重合),求证:PA =PB +PC .【解析】:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗. 若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,∵AB=BC=AC . ∴PA=PB+PC .1. 2 完善图形 借助托勒密定理例2 证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2【解析】:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.由托勒密定理,有AC ·BD=AB ·CD +AD ·BC . ①,又∵ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD . ②把②代人①,得AC 2=AB 2+BC 2.例3 如图,在△ABC 中,∠A 的平分线交外接圆于D ,连结BD ,求证:AD ·BC=BD(AB +AC).【解析】:连结CD ,依托勒密定理,有AD ·BC =AB ·CD +AC ·BD .∵∠1=∠2,∴ BD=CD .故 AD ·BC=AB ·BD +AC ·BD=BD(AB +AC).1.3 构造图形 借助托勒密定理例4 若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.【解析】:如图作直径AB=1的圆,在AB 两边任作Rt △ACB 和Rt △ADB ,使AC =a ,BC=b ,BD =x ,AD =y .由勾股定理知a 、b 、x 、y 是满足题设条件的. 据托勒密定理,有AC ·BD +BC ·AD=AB ·CD . ∵CD ≤AB =1,∴ax +by ≤1.1.4 巧变原式 妙构图形,借助托勒密定理例5 已知a 、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .分析:将a 2=b(b +c)变形为a ·a=b ·b +bc ,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b ,两对角线为a ,一底边为c .【解析】:如图 ,作△ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D ,连结BD 、DC 、DA .∵AD=BC ,∴ACD=BDC ∴∠ABD=∠BAC .又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.于是BD=AC ,则BD =AC =b 依托勒密定理,有BC ·AD=AB ·CD +BD ·AC . ①,而已知a 2=b(b +c),即a ·a =b ·c +b 2. ②,比较○1○2得CD =b =BD ,CD =BD ,∠3=∠1=∠2,∴∠BAC=2∠ABC .1.5 巧变形 妙引线 借肋托勒密定理例6 在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,求证:1AB +1AC =1BC 。
托勒密定理、婆氏定理——圆中基本模型专题(二)(1)

托勒密定理、婆氏定理——圆中基本模型专题(二)【教学重难点】1.圆中托勒密定理;对角互补模型:旋转视角、托勒密视角2.婆罗摩笈多定理3.例题探究【模块一圆中托勒密定理】古希腊最伟大的天文学家,数学家、天文学家伊巴谷(约公元前190年-公元前125年),最早提出了,圆内接四边形两对对边乘积的和等于两条对角线的乘积,后称托勒密定理.古罗马著名的天文学家、光学家克罗狄斯·托勒密(约90年-168年),从伊巴谷的书中将其摘出并完善.托勒密定理实质上是关于共圆性的基本性质,故从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式.1.基本图形与结论:如图1,当A、B、C、D四点共圆,则AC×BD=AB×DC+AD×BC.2.简单证明:在线段BD上取一点E,连AE,使∠AEB=∠ADC,易得△AEB∽△ADC,AC CD=⇒⨯=⨯①AC BE AB CDAB BE旋转一拖二得△ABC∽△AED,AC BC=⇒⨯=⨯②AC DE BC ADAD DE由①+②得:AC×(BE+DE)=AC×BD=AB×DC+AD×BC.3.模型识别:具体情境中出现四点共圆,且四点构成的四边形边长、对角线长信息较多,可以尝试用托勒密定理进行计算.※4.广义托勒密定理:对于任意凸四边形ABCD,则有AC×BD ≤AB×DC+AD×BC.证明从略···【模块二对角互补模型→旋转视角】1.基本图形与模型识别:如图2,对角互补且一组邻边相等...........的四边形,可通过旋转变换将四边形转化为等腰三角形(等腰思旋转).2.四类常见对角互补模型:①模型一:等边60°对120°型条件:如图3,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°结论:(1)CA平分∠BCD;(2)BC+CD=AC.证明:证明:如图,将△ACD绕点A逆时针旋转60°至△AMB,使AD,AB重合,则△ACD≌△AMB,∴∠ADC=∠ABM,AC=AM,CD=BM,∠ACD=∠M,∵∠BAD=60°,∠BCD=120°,∴∠ABC+∠ADC=180°,∴∠ABC +∠ABM =180°, ∴M ,B ,C 三点共线, ∵∠MAC =∠BAD =60°,∴△MAC 为等边三角形,∴MC =AC ,∠M =∠ACD ,∴MB +BC =AC ,∠ACB =∠ACD ,∴CA 平分∠DCB ,CB +CD =AC .②模型二:等腰直角对直角型条件:如图4,在四边形ABCD 中,AB =AD ,∠BAD =∠BCD =90°.结论:(1)CA 平分∠DCB ;(2)CB +CD =2AC .证明:略···③模型三:等腰顶角120°对60°型条件:如图5,在四边形ABCD 中,AB =AD ,∠BAD =120°,∠BCD =60°.结论:(1)CA 平分∠BCD ;(2)CB +CD =3AC .证明:略···※④模型四:同侧双直角型条件:如图6,在四边形ABCD 中,AB =AD ,∠BAD =90°,∠BCD =90°.结论:CB -CD =2AC .证明:略···【模块三 对角互补模型→托密视角】1.等腰△三角函数计算:如图7,2cos 2cos BC AB m αα=⋅=⋅2.托勒密定理应用:①如图8,对角互补型:2cos 2cos ma mb c m a b c αα+=⋅⋅⇒+=⋅结论:当α=60°时,a +b =c当α=45°时,a +b =2c当α=30°时,a +b =3c※利用角平分线性质也可直接得2cos a b c α+=⋅②如图9,同侧等角型:2cos 2cos a m mb mc c b a αα⋅⋅+=⇒-=⋅结论:当α=45°时,c -b =2a···【模块四婆罗摩笈多定理】婆罗摩笈多(约公元598-约660年)是一位印度数学家和天文学家,他出身于古印度的婆罗门种姓,婆罗门掌管着解释和预言天象的权力,掌握着天文学知识,以及测量和计算天体运行的工具——数学.婆罗摩笈多著有两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术,而他的负数乘除法法则在全世界都是领先的.婆罗摩笈多还提出了著名的婆罗摩笈多定理,简称“婆氏定理”.若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.1.简单证明:已知:如图,四边形ABCD内接于圆O,对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD 于点F,求证:F是AD中点.证明:∵AC⊥BD,ME⊥BC∴∠CBD=∠CME∵∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF∵∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,∴AF=DF即F是AD中点.2.婆罗摩笈多逆定理请你阅读婆罗摩笈多定理的证明过程,试证明婆罗摩笈多逆定理:(1)如图1,四边形ABCD内接于圆O,对角线AC⊥BD于点M,F为AD中点,连接FM并延长交BC 于点E,求证:ME⊥BC.(2)如图2,△ABC内接于圆O,∠B=30°,∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,连接并延长NP交AB于点M,求证PM⊥BA,并求PN的长.3.共顶等腰直模型(婆罗摩笈多模型)已知:如图,两个等腰直角三角形Rt△ABO和Rt△CDO,顶点重合,连接AC,BD.结论:①如果F是AC中点,那么一定有EF⊥BD;②如果EF⊥BD,那么一定有F是AC中点;③S△BOD=S△AOC;④2FO=BD.证明:(1)法一:(外)弦图构造法,如图1(2)法二:导角构造→全等构造法,如图2【例1】如图3所示,试证明:上述共顶等腰直模型中①②结论.【例2】如图,向△ABC的外侧作正方形ABDE、ACFG:(1)过A作AH⊥BC于H,AH与EG交于M,求证:①EM = MG,②BC = 2AM.(2)若M为EG的中点,求证:AH⊥BC.【模块四真题探究】【例3】(改编)如图1,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并说明理由;(2)试探究线段P A,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于AB的什么位置时,四边形APBC的面积最大? 求出最大面积.【例4】(2013·成都中考改编)如图2,A,B,C为⊙O上相邻的三个n等分点,AB BC=,点E在BC上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A'重合,点B与B'重合,连接EB',EC,EA'.设EB'=b,EC=c,EA'=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c;请继续探究b,c,p三者的数量关系:当n=4时,p=__________;当n=8时,p=__________;当n=12时,p=__________.(参考数据:62sin15=cos75=4-︒︒,62cos15=sin75=4+︒︒)本讲反思:。
圆(圆幂定理、根轴,托勒密定理、帕斯卡定理、牛顿定理Ⅰ、Ⅱ)

圆(圆幂定理、根轴,托勒密定理、帕斯卡定理、牛顿定理
Ⅰ、Ⅱ)
一、圆幂定理、根轴
1. 圆幂定理:
圆幂定理为以下三个定理的统称,即
相交弦定理(Ⅰ:AP·PB=CP·PD)
割线定理(Ⅱ:PA·PB=PC·PD)
切割线定理(Ⅲ:PA2=PC·PD)
2. 根轴:
到两圆幂相等的点的集合为一条垂直于两圆圆心连线的直线且:若两圆相交则根轴为公共弦所在直线
若两圆相切则根轴为公切线
同心圆无根轴
二、几条重要的定理
1. 托勒密定理
凸四边形 ABCD 中有
AC · BD ≥ AB · CD + AD · BC
等号当且仅当四边形 ABCD 是圆内接四边形时成立
2. 帕斯卡定理
圆内接六边形三组对边所在直线交点共线
3. 牛顿定理Ⅰ
圆外切四边形的对角线交点和以切点为顶点的四边形对角线交点重
合
4. 牛顿定理Ⅱ
圆外切四边形两条对角线中点和该圆圆心,三点共线
本文素材来源网络!。
初等几何五大ZB定理
初等几何五大ZB定理某日,燕尾模型讲毕,一六年级学霸级学生说,其可用燕尾模型证梅涅劳斯定理,大惊,问其如何得之,其说:一老师讲的。
六年级学生学梅涅劳斯定理,ZB大于实用。
既然学生感兴趣,咱就一装到底。
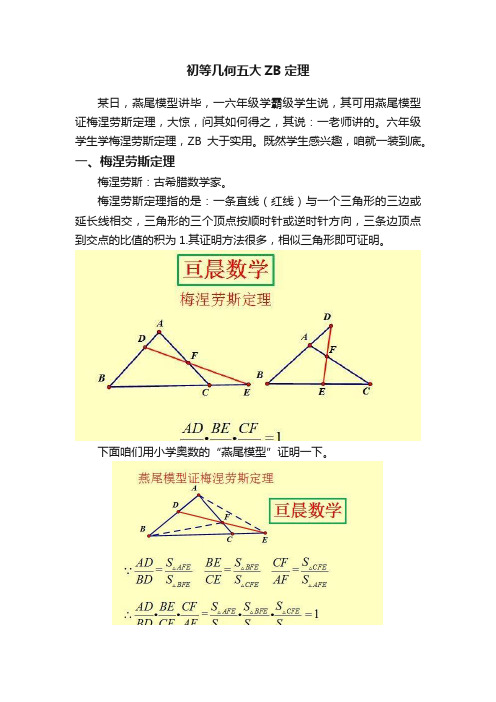
一、梅涅劳斯定理梅涅劳斯:古希腊数学家。
梅涅劳斯定理指的是:一条直线(红线)与一个三角形的三边或延长线相交,三角形的三个顶点按顺时针或逆时针方向,三条边顶点到交点的比值的积为1.其证明方法很多,相似三角形即可证明。
下面咱们用小学奥数的“燕尾模型”证明一下。
二、塞瓦定理塞瓦:意大利数学家、水利工程师,该定理于1678年发表于《直线论》一书。
塞瓦定理:可以简单记为三线共点的充要条件是:顺时针或逆时针的分线段的比值积为1.该定理可以用上面的梅涅劳斯定理证明。
三、斯坦纳定理斯坦纳:瑞士几何学家斯坦纳定理:两内角平分线相等的三角形必为等腰三角形。
早在2000多年前,《几何原本》就有定理:等腰三角形的两底角平分线的长相等。
可是它的逆定理书上却只字未提,估计作者也不会,呵呵。
直到1840年,莱默斯请求斯图姆给予纯几何证明,可斯图姆也不会,最后斯坦纳给出了证明,因此该定理也称作:斯坦纳——莱默斯定理。
现在很多高中生也能证明。
大家可以试试有没有难度。
四、托勒密定理托勒密定理:圆内接凸四边形的对边积的和等于对角线的积。
用相似可以证明五、西姆松定理西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边所在直线垂线,则三垂足在一点直线上,这条直线我们称作西姆松线。
这些定理一般的中考都不考,一和四和中学的相似联系比较紧密,尽量掌握,培优课上可能会有,感兴趣的同学可以看看。
平面几何3--托勒密定理及应用

平面几何(3)----托勒密定理及应用托勒密定理:圆内接四边形的两组对边乘积之和等于两对角线的乘积推论1(三弦定理) 如果A 是圆上任意一点,AB ,AC ,AD 是该圆上顺次的三条弦,则sin sin sin AC BAD AB CAD AD CAB ⋅∠=⋅∠+⋅∠推论2(四角定理) 四边形ABCD 内接于O ,则sin sin sin sin sin sin ADC BAD ABD BDC ADB DBC ∠⋅∠=∠⋅∠+∠⋅∠直线上的托勒密定理(或欧拉定理) 若A ,B ,C ,D 为一直线上依次排序的四点,则AB CD BC AD AC BD ⋅+⋅=⋅四边形中的托勒密定理:设ABCD 为任意凸四边形,则,AB CD BC AD AC BD ⋅+⋅≥⋅当且仅当A ,B ,C ,D 四点共圆时取等号托勒密定理的逆定理: 在凸四边形ABCD 中,若AB CD BC AD AC BD ⋅+⋅=⋅,则A ,B ,C ,D 四点共圆例1:在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若角A ,B ,C 的大小成等比数列,且22b a ac -=,则角B 的弧度数等于多少?例2:凸四边形ABCD 中,60,90o o ABC BAD BCD ∠=∠=∠=,AB=2,CD=1,对角线AC ,BD 交于点O ,如图,求sin AOB ∠例3:如图,在锐角ABC 的BC 边上有两点E ,F ,满足,BAE CAF ∠=∠作FM AB ⊥于M ,FN AC ⊥于N ,延长AE 交ABC 的外接圆于点D ,证明:四边形AMDN 与ABC 的面积相等.例4:如图,在ABC 中,60o A ∠=,,AB AC >点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM=CN ,求MH NH OH+的值例5:若有四个圆都与第五个圆内切,第一个与第二个圆的外公切线长用12l 表示,其他前四个圆中的两两的外公切线也用同样的方法来标记,且前四个圆以顺时针的顺序排列,试证明依次以12233441,,,l l l l 为边长,以1324,l l 为对角线所构成的凸四边的四个顶点共圆.例6:经过XOY ∠的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P,Q ,求证:11OP OQ+为定值例7:圆内接六边形ABCDEF 的对角线共点的充要条件是1AB CD EF BC DE FA ⋅⋅=。
托勒密定理、婆氏定理、圆中基本模型专题(二)

托勒密定理、婆氏定理——圆中基本模型专题(二)【教学重难点】1.圆中托勒密定理;对角互补模型:旋转视角、托勒密视角2.婆罗摩笈多定理3.例题探究【模块一圆中托勒密定理】古希腊最伟大的天文学家,数学家、天文学家伊巴谷(约公元前190年-公元前125年),最早提出了,圆内接四边形两对对边乘积的和等于两条对角线的乘积,后称托勒密定理.古罗马著名的天文学家、光学家克罗狄斯·托勒密(约90年-168年),从伊巴谷的书中将其摘出并完善.托勒密定理实质上是关于共圆性的基本性质,故从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式.1.基本图形与结论:如图1,当A、B、C、D四点共圆,则AC×BD=AB×DC+AD×BC.2.简单证明:在线段BD上取一点E,连AE,使∠AEB=∠ADC,易得△AEB∽△ADC,AC CD=⇒⨯=⨯①AC BE AB CDAB BE旋转一拖二得△ABC∽△AED,AC BC=⇒⨯=⨯②AC DE BC ADAD DE由①+②得:AC×(BE+DE)=AC×BD=AB×DC+AD×BC.3.模型识别:具体情境中出现四点共圆,且四点构成的四边形边长、对角线长信息较多,可以尝试用托勒密定理进行计算.※4.广义托勒密定理:对于任意凸四边形ABCD,则有AC×BD ≤AB×DC+AD×BC.证明从略···【模块二对角互补模型→旋转视角】1.基本图形与模型识别:如图2,对角互补且一组邻边相等...........的四边形,可通过旋转变换将四边形转化为等腰三角形(等腰思旋转).2.四类常见对角互补模型:①模型一:等边60°对120°型条件:如图3,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°结论:(1)CA平分∠BCD;(2)BC+CD=AC.证明:证明:如图,将△ACD绕点A逆时针旋转60°至△AMB,使AD,AB重合,则△ACD≌△AMB,∴∠ADC=∠ABM,AC=AM,CD=BM,∠ACD=∠M,∵∠BAD=60°,∠BCD=120°,∴∠ABC+∠ADC=180°,∴∠ABC +∠ABM =180°, ∴M ,B ,C 三点共线, ∵∠MAC =∠BAD =60°,∴△MAC 为等边三角形,∴MC =AC ,∠M =∠ACD ,∴MB +BC =AC ,∠ACB =∠ACD ,∴CA 平分∠DCB ,CB +CD =AC .②模型二:等腰直角对直角型条件:如图4,在四边形ABCD 中,AB =AD ,∠BAD =∠BCD =90°.结论:(1)CA 平分∠DCB ;(2)CB +CD =2AC .证明:略···③模型三:等腰顶角120°对60°型条件:如图5,在四边形ABCD 中,AB =AD ,∠BAD =120°,∠BCD =60°.结论:(1)CA 平分∠BCD ;(2)CB +CD =3AC .证明:略···※④模型四:同侧双直角型条件:如图6,在四边形ABCD 中,AB =AD ,∠BAD =90°,∠BCD =90°.结论:CB -CD =2AC .证明:略···【模块三 对角互补模型→托密视角】1.等腰△三角函数计算:如图7,2cos 2cos BC AB m αα=⋅=⋅2.托勒密定理应用:①如图8,对角互补型:2cos 2cos ma mb c m a b c αα+=⋅⋅⇒+=⋅结论:当α=60°时,a +b =c当α=45°时,a +b =2c当α=30°时,a +b =3c※利用角平分线性质也可直接得2cos a b c α+=⋅②如图9,同侧等角型:2cos 2cos a m mb mc c b a αα⋅⋅+=⇒-=⋅结论:当α=45°时,c -b =2a···【模块四婆罗摩笈多定理】婆罗摩笈多(约公元598-约660年)是一位印度数学家和天文学家,他出身于古印度的婆罗门种姓,婆罗门掌管着解释和预言天象的权力,掌握着天文学知识,以及测量和计算天体运行的工具——数学.婆罗摩笈多著有两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术,而他的负数乘除法法则在全世界都是领先的.婆罗摩笈多还提出了著名的婆罗摩笈多定理,简称“婆氏定理”.若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.1.简单证明:已知:如图,四边形ABCD内接于圆O,对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD 于点F,求证:F是AD中点.证明:∵AC⊥BD,ME⊥BC∴∠CBD=∠CME∵∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF∵∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,∴AF=DF即F是AD中点.2.婆罗摩笈多逆定理请你阅读婆罗摩笈多定理的证明过程,试证明婆罗摩笈多逆定理:(1)如图1,四边形ABCD内接于圆O,对角线AC⊥BD于点M,F为AD中点,连接FM并延长交BC 于点E,求证:ME⊥BC.(2)如图2,△ABC内接于圆O,∠B=30°,∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,连接并延长NP交AB于点M,求证PM⊥BA,并求PN的长.3.共顶等腰直模型(婆罗摩笈多模型)已知:如图,两个等腰直角三角形Rt△ABO和Rt△CDO,顶点重合,连接AC,BD.结论:①如果F是AC中点,那么一定有EF⊥BD;②如果EF⊥BD,那么一定有F是AC中点;③S△BOD=S△AOC;④2FO=BD.证明:(1)法一:(外)弦图构造法,如图1(2)法二:导角构造→全等构造法,如图2【例1】如图3所示,试证明:上述共顶等腰直模型中①②结论.【例2】如图,向△ABC的外侧作正方形ABDE、ACFG:(1)过A作AH⊥BC于H,AH与EG交于M,求证:①EM = MG,②BC = 2AM.(2)若M为EG的中点,求证:AH⊥BC.【模块四真题探究】【例3】(改编)如图1,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并说明理由;(2)试探究线段P A,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于AB的什么位置时,四边形APBC的面积最大? 求出最大面积.【例4】(2013·成都中考改编)如图2,A,B,C为⊙O上相邻的三个n等分点,AB BC=,点E在BC上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A'重合,点B与B'重合,连接EB',EC,EA'.设EB'=b,EC=c,EA'=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c;请继续探究b,c,p三者的数量关系:当n=4时,p=__________;当n=8时,p=__________;当n=12时,p=__________.(参考数据:62sin15=cos75=4-︒︒,62cos15=sin75=4+︒︒)本讲反思:。
平面几何中几个重要定理在中考中的应用

A
B C F
E
D
E
F
D
C B A
P
A
B
C
D
E F
A
B
C
D
P E
F
P A
B C
F
E
D C
B
A
P
A B
C
D
E F
【例2】等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.
已知:在梯形ABCD中,AD=BC ,AB//CD.求证:2
2
BD BC AB C D =+⋅.
【例3】已知1a b =.求证:2
1A F B D C E F B
D C
E A
⋅⋅=,那么D、E、F三点共线.
梅涅劳斯(Menelaus定理(简称梅氏定理是由古希腊数学家梅涅劳斯首先证明的
三、塞瓦定理:若△ABC的三个顶点与一点P的连线AP、BP、CP交对边或其延长线于D、E、F ,则
1BD CE AF D C
EA
FB
⋅
⋅
=.通常称点P为△ABC的塞瓦点.
交BC于G.求证:AG、BF、EH三线共点.
斯特瓦尔特定理
O
A
F
E
D C
B
M
B
D
E
F
A
N
【例10】
(1990全国初中联赛△ABC中,
AB=,
,P为BC上任一点,则( . A.2PA PB PC <⋅ B.2
P A P B P C =⋅
C. 2
P A P B P C >⋅ D. 2PA PB PC ⋅与的大小关系不能确定
平面几何中的几个重要定理在中考中的应用
各种圆定理总结包括托勒密定理塞瓦定理西姆松定理梅涅劳斯定理圆幂定理和四点共圆

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的“定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE,,∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、C D、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到:(a? b)(c? d) + (a? d)(b? c) = (a? c)(b?d) ,两边取,运用得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一。
平面上,托勒密不等式是三角不等式的形式。
二、设ABCD是。
在BC上,∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD,所以∠CBK = ∠ABD。
圆与相似综合题的有关定理

圆和相似综合题有关定理1、圆幂定理(在证明比例式、求线段长度时将发挥重要作用。
)2、托勒密定理:圆内接四边形两组对边乘积之和,等于两条对角线的乘积。
已知:四边形ABCD 内接于圆,如图,求证:AB·CD + BC·AD = AC·BD证明:在∠BAD 内作∠BAE=∠CAD ,交BD 于E 。
因∠ABE=∠ACD ,所以△ABE ∽△ACD ,从而AB BE ACCD =得 AB·CD = AC·BE ①; … 易证△ADE ∽△ACB ,从而BC AC DE AD = 得BC·AD = AC·DE ②; ①+② 得AB·CD + BC·AD = AC (BE+DE )= AC·BD定理 图形已知 结论 证法 相交*弦定理⊙O 中,AB 、CD 为弦,交于点P 。
PA·PB =PC·PD 连结AC 、BD , 证:△APC ∽△DPB 切 、割线定理 ⊙O 中,PT 切⊙O 于点T ,割线PB 交⊙O 于点A 。
PT 2=PA·PB连结TA 、TB , 证:△PTB ∽△PAT }割线定理PB 、PD 为⊙O 的两条割线,交⊙O 于A 、C 两点。
PA·PB =PC·PD ~ 过P 作PT 切⊙O 于T ,用两次切割线定理 C E3、弦切角定理:顶点在圆上,一边和圆相交,另一边和圆相切的角称为弦切角。
弦切角等于弦与切线所夹弧所对的圆周角。
}弦切角定理的证明:已知:AP切⊙O于P,PQ是弦,则∠APQ是弦切角,∠APQ夹的弧是弧PQ,弧PQ所对的圆周角记为∠PCQ证明:∠APQ=∠PCQ (弦切角的位置分以下三种情况)】1°圆心O在∠APQ外部过P作直径BP,联结BC则BP⊥AP,∠APB=90°,且∠BCP是直径BP所对的圆周角,∠BCP=90°#则有∠APB=∠BCP,即∠APQ+∠BPQ=∠BCQ+∠PCQ由于∠BPQ,∠BCQ都是弧BQ所对的圆周角,所以∠BPQ=∠BCQ所以∠APQ=∠PCQ2°圆心O在∠APQ的一边,PQ上此时PQ是直径,则PQ⊥AP,∠APQ=90°而且∠PCQ是直径PQ所对的圆周角,∠PCQ=90°所以∠APQ=∠PCQ3°圆心O在∠APQ内部过P作直径BP,联结BC则BP⊥AP,∠APB=90°,且∠BCP是直径BP所对的圆周角,∠BCP=90°则有∠APB=∠BCP由于∠BPQ,∠BCQ都是弧BQ所对的圆周角,所以∠BPQ=∠BCQ所以∠APB+∠BPQ=∠BCP+∠BCQ即∠APQ=∠PCQ。
圆中几个著名的定理

中《 天文 学大成 》又称 《 ( 大综 合论》 3卷) 1
主要论述 了他所创 立 的地 心说 ,认 为地
球 是宇宙 的中心 , 且静止不 动 , 月 、 日、 行 星和恒 星均围绕地球运动. 是世界上第 他
一
个系统研究 日月星辰 的构成和运 动方
式并做出成就 的科学家. 此书被尊为天文
4 . 本章知识概 念多且 非常重要 , 圆又是学生熟 而 理的得 出, 、 、 弧 弦 圆心角 的关 系的证 明 , 圆的相关计 悉 的 、 活 中常见 的几何 图形 , 生 因此可 以多让学生举
算公式 的推导 等 , 均充分利用 圆的对称性 , 让学生通 出一 些生 活 中的圆形物 体 , 多用计 算机 模拟 圆形 的 过观察 、 实验 、 探究 出性质 , 再运 用几何 变换 进行 证 运动 等 , 学生在 感受 圆的几 何性 质 的同时体 会其 使
则这个 四边形 的四个 顶点共 圆. 逆定 理的证 明可 由托 从 圆周 上一点 引出三条 弦 的几何 题 ,利用三 弦定 理 勒密定理推广 的证 明得 到.
求解往往很奏效 .
托勒 密定理 的推广 :凸 四边形两 组对边 乘积 之 和不小 于两条对 角线 的乘 积 ,等 号成立 当且仅 当凸
可 以很方 便地制作 图形 , 图形 动起来 , 让 有利 于我们 2 . 圆有很多重要性质 , 但最 主要 的是圆的对称性 在 图形 的运动变 化过程 中发现 其 中的位 置关系 和数 ( 轴对称 和旋转不变性 ) 在研究 圆的有关性质时 , . 充 量关 系 , 现 图形 的性 质 , 进学 生对数 学 的理解 . 发 增 分利用 圆的对称性是本 章编写的一个特点 . 如垂径定
B , P 同时也 得到 B = 这说 明 A AC
圆中的定理

托勒密定理托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.推论1.任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号。
2.托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆、推广托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线。
简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,得不等式AC·BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB·CD+BC·AD注意:1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
2.四点不限于同一平面。
欧拉定理:在一条线段上AD上,顺次标有B、C两点,则AD·BC+AB·CD=AC·BD塞瓦定理塞瓦(Giovanni Ceva,1648~1734)意大利水利工程师,数学家。
塞瓦定理载于塞瓦于1678年发表的《直线论》一书,也有书中说塞瓦定理是塞瓦重新发现。
具体内容塞瓦定理在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1塞瓦定理推论.设E是△ABD内任意一点,AE、BE、DE分别交对边于C、G、F,则(B D/B C)*(C E/A E)*(G A/D G)=1因为(B C/C D)*(D G/G A)*(A F/F B)=1,(塞瓦定理)所以(B D/C D)*(C E/A E)*(A F/F B)=K(K为未知参数)且(B D/B C)*(C E/A E)*(G A/D G)=K(K为未知参数)又由梅涅劳斯定理得:(B D/C D)*(C E/A E)*(A F/F B)=1所以(B D/B C)*(C E/A E)*(G A/D G)=12.塞瓦定理角元形式A D,B E,C F交于一点的充分必要条件是:(s i n∠B A D/s i n∠D A C)*(s i n∠A C F/s i n∠F C B)*(s i n∠C B E/s i n∠E B A)=1由正弦定理及三角形面积公式易证3.如图,对于圆周上顺次6点A,B,C,D,E,F,直线A D,B E,C F交于一点的充分必要条件是:(A B/B C)*(C D/D E)*(E F/F A)=1由塞瓦定理的角元形式,正弦定理及圆弦长与所对圆周角关系易证。
各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆).

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE,,∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式:(a − b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ,两边取模,运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一平面。
平面上,托勒密不等式是三角不等式的反演形式。
二、设ABCD是圆内接四边形。
在弦BC上,圆周角∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK =∠ABC = ∠CBD + ∠ABD,所以∠CBK = ∠ABD。
托勒密定理及西姆松定理

§4托勒密定理与西姆松定理托勒密(∕Vo∕e/切定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).即:定理:在四边形ABCZ)中,有:AB CD + AD BC≥AC BD 证:在四边^ABCD内取点E, ^ZBAE = ZCAD, ZABE = ZACD4 R RF贝Ij: AABE和AACD相似 A-一 =——=>AB∙CD = AC BEAC CDΛD ΛJ7乂•••——=-一HZBΛC = ZEAD :. SABC和ΔAED相似AC ADBC ED——=——GADBC = ACEDAC ADAB CD +AD BC = AC (BE+ ED)・・・AB∙CD + ADBC≥ACBD且等号当且仅当E在BD上时成立,即当且仅当久B、G D四点共圆时成立; 并且当且仅当四边形ABCM接于圆时,等式成立;一、直接应用托勒密定理例1、如图2, P是正AABC外接圆的劣弧EC上任一点(不与B、C重合),求证:PA二PB+ PC.分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.B若借助托勒密定理论证,则有PA ∙ BC二PB ∙ AC + PC ∙AB, T AB=BC=AC..∙.PA=PB+PC.二、完善图形借助托勒密定理例2、证明“勾股定理”:在RtΔABC中,ZB=900 ,求证:AC2=AB2+BC2证明:如图,作以RtΔABC的斜边AC为一对角线的矩形ABCD,显然ABCD是圆内接四边形.由托勒密定理有AC ∙ BD=AB ∙ CD+ AD ∙ BC.①又-/ABCD 是矩形,.∙.AB二CD, AD=BC J AC=BD. ②把②代人①,得AC2=AB2+BC2.例3、如图,在AABC中,上A的平分线交外接圆于D,连结BD, 求证:AD ∙ BC=BD(AB+ AC).证明:连结CD5依托勒密定理有AD ・BC = AB ∙ CD+ AC ∙ BD.•/Z 1 = Z2, .∙. BD=CD.FC故AD ∙ BC=AB ・BD + AC ∙ BD=BD(AB + AC).三、构造图形借助托勒密定理例 4 若 o 、b 、x 、y 是实数,且 α2 + b 2=l, x 2 + y 2=l.求证:ax + by≤ 1. 证明:如图作直径AB 二1的圆,在AB 两边任作RtΔACB 和RtAADB,使AC = O,BC 二b,BD = x, AD = y.由勾股定理知。
托勒密定理、婆氏定理、圆中基本模型专题(二)

第1 页托勒密定理、婆氏定理——圆中基本模型专题(二)【教学重难点】1.圆中托勒密定理;对角互补模型:旋转视角、托勒密视角2.婆罗摩笈多定理3.例题探究【模块一圆中托勒密定理】古希腊最伟大的天文学家,数学家、天文学家伊巴谷伊巴谷(约公元前(约公元前190年-公元前125年),最早提出了,圆内接四边形两对对边乘积的和等于两条对角线的乘积,后称圆内接四边形两对对边乘积的和等于两条对角线的乘积,后称托勒密定理托勒密定理.古罗马著名的天文学家、光学家光学家克罗狄斯·托勒密(约克罗狄斯·托勒密(约90年-168年),从伊巴谷的书中将其摘出并完善.托勒密定理实质上是关于共圆性的基本性质,故从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式.1.基本图形与结论:如图1,当A 、B 、C 、D 四点共圆,则AC ×BD =AB ×DC +AD ×BC .2.简单证明:在线段BD 上取一点E ,连AE ,使∠AEB =∠ADC ,易得△AEB ∽△ADC ,AC CD AC BE AB CD AB BE =Þ´=´①旋转一拖二得△ABC ∽△AED ,AC BC AC DE BC AD AD DE =Þ´=´②由①+②得:AC ×(BE +DE )=AC ×BD =AB ×DC +AD ×BC .3.模型识别:具体情境中出现四点共圆,且四点构成的四边形边长、对角线长信息较多,可以尝试用托勒密定理进行计算.※4.广义托勒密定理:对于对于任意凸四边形任意凸四边形ABCD ,则有AC ×BD ≤AB ×DC +AD ×BC .证明从略···【模块二对角互补模型→旋转视角】1.基本图形与模型识别:如图2,对角互补且一组邻边相等...........的四边形,可通过旋转变换将四边形转化为等腰三角形(等腰思旋转).2.四类常见对角互补模型:①模型一:等边60°对120°型条件:如图3,在四边形ABCD 中,AB =AD ,∠BAD =60°,∠BCD =120°结论:(1)CA 平分∠BCD ;(2)BC +CD =AC .证明:证明:证明:证明:如图,如图,将将△ACD 绕点A 逆时针旋转60°至△AMB ,使AD ,AB 重合,则△ACD ≌△AMB ,∴∠ADC =∠ABM ,AC =AM ,CD =BM ,∠ACD =∠M ,∵∠BAD =60°,∠BCD =120°,∴∠ABC +∠ADC =180°,第 2 页 ∴∠ABC +∠ABM =180°,∴M ,B ,C 三点共线,三点共线,∵∠MAC =∠BAD =60°,∴△MAC 为等边三角形,为等边三角形,∴MC =AC ,∠M =∠ACD ,∴MB +BC =AC ,∠ACB =∠ACD ,∴CA 平分∠DCB ,CB +CD =AC .②模型二:等腰直角对直角型②模型二:等腰直角对直角型条件:如图4,在四边形ABCD 中,AB =AD ,∠BAD =∠BCD =90°.结论:(1)CA 平分∠DCB ;(2)CB +CD =2AC .证明:略···③模型三:等腰顶角120°对60°型条件:如图5,在四边形ABCD 中,AB =AD ,∠BAD =120°,∠BCD =60°.结论:(1)CA 平分∠BCD ;(2)CB +CD =3AC .证明:略···证明:略···※④模型四:同侧双直角型※④模型四:同侧双直角型条件:如图6,在四边形ABCD 中,AB =AD ,∠BAD =90°,∠BCD =90°.结论:CB -CD =2AC .证明:略···证明:略···【模块三 对角互补模型→托密视角】1.等腰△三角函数计算:如图7,2cos 2cos BC AB m a a =×=×2.托勒密定理应用:①如图8,对角互补型:,对角互补型:2cos 2cos ma mb c m a b c a a +=××Þ+=×结论:结论:当α=60°时,a +b =c当α=45°时,a +b =2c当α=30°时,a +b =3c※利用角平分线性质也可直接得2cos a b c a +=×②如图9,同侧等角型:,同侧等角型:2cos 2cos a m mb mc c b a a a ××+=Þ-=×结论:结论:当α=45°时,c -b =2a······【模块四婆罗摩笈多定理】婆罗摩笈多(约公元598-约660年)是一位印度数学家和天文学家,他出身于古印度的婆罗门种姓,婆罗门掌管着解释和预言天象的权力,掌握着天文学知识,以及测量和计算天体运行的工具——数学.婆罗摩笈多著有两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术,而他的负数乘除法法则在全世界都是领先的.婆罗摩笈多还提出了著名的婆罗摩笈多定理,简称“婆氏定理”.若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.1.简单证明:已知:如图,四边形ABCD内接于圆O,对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD 于点F,求证:F是AD中点.证明:∵AC⊥BD,ME⊥BC∴∠CBD=∠CME∵∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF∵∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,∴AF=DF即F是AD中点.2.婆罗摩笈多逆定理请你阅读婆罗摩笈多定理的证明过程,试证明婆罗摩笈多逆定理:(1)如图1,四边形ABCD内接于圆O,对角线AC⊥BD于点M,F为AD中点,连接FM并延长交BC 于点E,求证:ME⊥BC.(2)如图2,△ABC内接于圆O,∠B=30°,∠ACB=45°,AB=2,点D在圆O上,∠BCD=60°,连接AD 交BC于点P,作ON⊥CD于点N,连接并延长NP交AB于点M,求证PM⊥BA,并求PN的长.第3 页第 4 页 3.共顶等腰直模型(婆罗摩笈多模型)已知:如图,两个等腰直角三角形Rt △ABO 和Rt △CDO ,顶点重合,连接AC ,BD . 结论:结论:①如果F 是AC 中点,那么一定有EF ⊥BD ;②如果EF ⊥BD ,那么一定有F 是AC 中点中点;;③S △BOD =S△AOC ; ④2FO =BD .证明:(1)法一:(外)弦图构造法,如图1 (2)法二:导角构造→全等构造法,如图2【例1】如图3所示所示,,试证明:上述共顶等腰直模型中①②结论试证明:上述共顶等腰直模型中①②结论..【例2】如图,向△ABC 的外侧作正方形 ABDE 、ACFG :(1)过A 作 AH ⊥BC 于H ,AH 与EG 交于M ,求证:①EM = M G MG ,②BC = 2A M AM . (2)若M 为EG 的中点,求证:AH ⊥BC .【模块四真题探究】【例3】(改编)如图1,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并说明理由;的形状,并说明理由;(2)试探究线段P A,PB,PC之间的数量关系,并证明你的结论;之间的数量关系,并证明你的结论;(3)当点P位于AB的什么位置时,四边形APBC的面积最大? 求出最大面积.求出最大面积.【例4】(2013·成都中考改编)成都中考改编)如图如图2,A,B,C为⊙O上相邻的三个n等分点,AB BC=,点E在BC上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A'重合,点B与B'重合,连接EB',EC,EA'.设EB'=b,EC=c,EA'=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c;请继续探究b,c,p三者的数量关系:当n=4时,p=__________;当n=8时,p=__________;当n=12时,p=__________.(参考数据:62sin15=cos75=4-°°,62cos15=sin75=4+°°)第5 页本讲反思:第6 页。
托勒密定理及圆的其它定理

托勒密定理及圆的其它定理托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理提出定理的内容。
摘出并完善后的托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
定理表述:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理内容指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.则△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,所以△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式: (a−b)(c−d) + (a−d)(b−c) = (a−c)(b −d) ,两边取模,运用三角不等式得。
托勒密定理的证明及应用

托勒密定理的证明及应用
托勒密定理:圆的内接四边形中,两条对角线的积等于两组对边乘积之和!
证明过程如下,先作辅助线如下:
具体过程如下:
下面,我们看看使用托勒密定理证明两个重要其他定理:勾股定理和余弦定理
(1)利用托勒密定理证明勾股定理如下:
具体过程为:
(2)利用托勒密定理证明余弦定理
具体过程如下:
是不是感觉很强大呢?
下面我们再来看看使用托勒密定理的其他应用,用题目说话吧:题目一:
添加辅助线如下:
具体证明过程如下:
题目二:
本题直接使用托勒密定理,甚是简洁!
题目三:
附辅助线如下:。
著名圆定理、公式

著名圆定理、公式(总19页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理的提出一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD因为△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE,,∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、C D、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式: (ab)(cd) + (ad)(bc) = (ac)(bd) ,两边取模,运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b -c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一平面。
平面上,托勒密不等式是三角不等式的反演形式。
二、设ABCD是圆内接四边形。
在弦BC上,圆周角∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
平面几何重要定理1

平面几何重要定理(一)(高一数学417)托勒密(Ptolemy)定理圆内接四边形ABCD的两组对边乘积的和等于它两条对角线乘积,即AB·CD+BC·DA=AC·BD,其逆定理也成立。
说明:(1)其逆定理为:若四边形两对边乘积之和等于它的对角线乘积,则该四边形内接于圆。
即:若AB•DC+AD•BC=AC•BD,则A、B、C、D四点共圆。
(2)推广(托勒密不等式):对于任意凸四边形ABCD,恒有两对边乘积之和大于或等于它的对角线乘积。
即AB·CD+BC·DA≥AC·BD、已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
2、已知正七边形A 1A 2A 3A 4A 5A 6A 7。
求证:。
3、由圆O 的⋂AB 的中点C 作弦CD 、CE 分别与AB 相交于F 、G 。
求证:DG ·EF=FD ·GE+DE ·FG4、已知ABC ∆中,最大角A 是最小角C 的2倍,夹角两边b=5,c=4,求第三边a 的长和三角形的面积。
(求三角形面积的海伦公式:c b a cb a pc p b p a p p S ,,,2,))()((++=---=分别是三角形的三边长。
)西姆松定理过三角形外接圆上任意一点作三边的垂线,则三垂足共线(称为西姆松线)。
即:从△ABC 的外接圆上任意一点P 向BC 、CA 、AB 或它们的延长线引垂线,垂足分别为D 、E 、F ,则D 、E 、F 三点共线。
(直线DEF 叫做△ABC 的关于P 点的西姆松线。
)说明:(1)其逆定理为:若一点到三角形三边所在直线的垂足共线,则该点在三角形的外接圆上。
(2)推广(卡诺定理):通过△ABC 外接圆上的一点P 引与三边BC 、CA 、AB 分别成同向等角的直线PD 、PE 、PF ,分别与三边交于D 、E 、F ,则D 、E 、F 三点共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理提出定理的内容。
摘出并完善后的托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
定理表述:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理内容指圆内接两对对边乘积的和等于两条对角线的乘积。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.则△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,所以△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到: (a−b)(c−d) + (a−d)(b−c) = (a−c)(b−d) ,两边取,运用得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一。
平面上,托勒密不等式是三角不等式的形式。
二、设ABCD是。
在BC上,∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD,所以∠CBK = ∠ABD。
因此△ABK与△DBC,同理也有△ABD ~ △KBC。
因此AK/AB = CD/BD,且CK/BC = DA/BD;因此AK·BD = AB·CD,且CK·BD = BC·DA;两式相加,得(AK+CK)·BD = AB·CD + BC·DA;但AK+CK = AC,因此AC·BD = AB·CD + BC·DA。
证毕。
三、托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).已知:圆内接四边形ABCD,求证:AC·BD=AB·CD+AD·BC.证明:如图1,过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.得AC:BC=AD:BP,AC·BP=AD·BC ①。
又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP.得AC:CD=AB:DP,AC·DP=AB·CD ②。
①+②得AC(BP+DP)=AB·CD+AD·BC.即AC·BD=AB·CD+AD·BC.四、广义托勒密定理:设四边形ABCD四边长分别为a,b,c,d,两条对角线长分别为m,n,则有:m^2*n^2=a^2*c^2+b^2*d^2-2abcd*cos(A+C)推论1.任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD 时取等号。
2.托勒密定理的同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆、推广托勒密不等式:凸四边形的两组对边乘积和不小于其对角线的乘积,取等号当且仅当共圆或共线。
简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,得不等式AC·BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB·CD+BC·AD运用要点1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
2.四点不限于同一平面。
:在一条线段上AD上,顺次标有B、C两点,则AD·BC+AB·CD=AC·BD弦切角定理弦切角定义顶点在圆上,一边和圆相交,另图示一边和圆相切的角叫做。
(弦切角就是与弦所夹的角)如右图所示,直线PT切圆O于点C,BC、AC为圆O的弦,∠TCB,∠TCA,∠PCA,∠PCB都为弦切角。
弦切角定理弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 弦切角定理证明:证明一:设圆心为O,连接OC,OB,。
∵∠TCB=90-∠OCB∵∠BOC=180-2∠OCB∴,∠BOC=2∠TCB(定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半)∵∠BOC=2∠CAB(圆心角等于圆周角的两倍)∴∠TCB=∠CAB(定理:弦切角的度数等于它所夹的弧的圆周角)证明已知:AC是⊙O的弦,AB是⊙O的切线,A为切点,弧是弦切角∠BAC 所夹的弧.求证:(弦切角定理)证明:分三种情况:(1)圆心O在∠BAC的一边AC上∵AC为直径,AB切⊙O于A,∴弧CmA=弧CA∵为半圆,∴∠CAB=90=弦CA所对的圆周角B点应在A点左侧(2)圆心O在∠BAC的内部.过A作直径AD交⊙O于D,若在优弧m所对的劣弧上有一点E那么,连接EC、ED、EA则有:∠CED=∠CAD、∠DEA=∠DAB∴∠CEA=∠CAB∴(弦切角定理)(3)圆心O在∠BAC的外部,过A作直径AD交⊙O于D那么∠CDA+∠CAD=∠CAB+∠CAD=90 ∴∠CDA=∠CAB∴(弦切角定理)弦切角推论推论内容若两弦切角所夹的弧相等,则这两个弦切角也相等应用举例例1:如图,在Rt△ABC中,∠C=90,以AB为弦的⊙O与AC相切于点A,∠CBA=60° , AB=a 求BC长.解:连结OA,OB.∵在Rt△ABC中, ∠C=90∴∠BAC=30°∴BC=1/2a(RT△中30°角所对边等于斜边的一半)例2:如图,AD是ΔABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB,AC分别相交于E,F.求证:EF∥BC.证明:连DF.AD是∠BAC的平分线∠BAD=∠DAC∠EFD=∠BAD∠EFD=∠DAC⊙O切BC于D ∠FDC=∠DAC∠EFD=∠FDCEF∥BC例3:如图,ΔABC内接于⊙O,AB是⊙O直径,CD⊥AB于D,MN切⊙O于C,求证:AC平分∠MCD,BC平分∠NCD.证明:∵AB是⊙O直径∴∠ACB=90∵CD⊥AB∴∠ACD=∠B,∵MN切⊙O于C∴∠MCA=∠B,∴∠MCA=∠ACD,即AC平分∠MCD,同理:BC平分∠NCD.相交弦定理概念相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等。
(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等)相交弦说明几何语言:若弦AB、CD交于点P则PA·PB=PC·PD(相交弦定理)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的几何语言:若AB是直径,CD垂直AB于点P,则PC^2=PA·PB(相交弦定理推论)如何证明证明:连结AC,BD,由的推论,得∠A=∠D,∠C=∠B。
(推论2: 同(等)弧所对圆周角相等.)∴△PAC∽△PDB,∴PA∶PD=PC∶PB,PA·PB=PC·PD 注:其可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性。
其逆定理也可用于证明四点共圆。
比较相交弦定理、及(切割线定理推论)以及他们的推论统称为。
一般用于求线段长度。
切割线定理定理切割线定理:从圆外一点引圆的和,切线长是这点到割线与圆交点的两条线段长的。
是的一种。
切割线定理示意图几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT的平方=PA·PB(切割线定理)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PBA,PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)()由上可知:PT的平方=PA·PB=PC·PD证明切割线定理证明:设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT^2=PA·PB证明:连接AT, BT∵∠PTB=∠PAT()切割线定理的证明∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT^2=PB·PA比较相交弦定理、及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。
一般用于求直线段长度。
圆幂定理百科名片圆幂定理圆幂定理是对、及(切割线定理推论)以及它们推论统一归纳的结果。
定义=PO^2-R^2(该结论为)所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切定理:从圆外一点引圆的和割线,是这点到割线与圆交点的两条线段长的。
割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D,则有PA·PB=PC·PD。
统一归纳:过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合),则有PA·PB=PC·PD。
证明圆幂定理(相交弦定理、切割线定理及其推论(割线定理)统一归纳为圆幂定理)问题1相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明:连结AC,BD,由的推论,得∠A=∠D,∠C=∠B。
∴△PAC∽△PDB∴PA/PD=PC/PB∴PA·PB=PC·PD问题2割线定理:从圆外一点P引两条割线与圆分别交于A.B.C.D 则有PA·PB=PC·PD,当PA=PB,即直线AB重合,即PA切线时得到切线定理PA^2=PC·PD 证明:(令A在P、B之间,C在P、D之间)∵ABCD为∴∠CAB+∠CDB=180°又∠CAB+∠PAC=180°∴∠PAC=∠CDB∵∠APC公共∴△APC∽△DPB∴PA/PD=PC/PB∴PA·PB=PC·PD切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT^2=PA·PB(切割线定理)推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PBA、PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)问题3过点P任作直线交定圆于两点A、B,证明PA·PB为定值(圆幂定理)。
