北师大版八年级数学上册一次函数的图像画法
合集下载
数学北师大版八年级上册3.1一次函数的图像
4.3 一次函数的图象(第一课时)
1.了解画函数图像的一般步骤 2.会画正比例函数图像并探究正比例函数图像特点. 3.理解正比例函数表达式与图像之间一一对应的关系.
一、情景引入 摩天轮上一点的高度h与旋转时间t之间有一定的关 系,右图就反映了时间t(分)与摩天轮上一点的高度h (米)之间的关系.
四、自主学习活动二
作出正比例函数y=-2x的图象. x 列表:
y
请同学们以小组为单位,讨论下面的问题,把得出的结论写出来. (1)满足关系式y= -2x的x,y所对应的点(3,-6)________(填 “在”“不在”)正比例函数y= -2x的图象上。所有满足关系 式y= -2x的x,y所对应的点(x,y)都在正比例函数y= -2x的 图象上吗?答:_____________ (2)正比例函数y=- 2x的图象上的点(-2,4)_______(填“满 足”“不满足”)满足关系式y= -2x。正比例函数y= -2x的图 象上的点(x,y)都满足关系式y= -2x吗? 答:_____________
六、小结归纳:
正比例函数图像特点: 1、当k>0时,图象在 象限,图像从左到右呈 趋势,y的值随着x值的增大而______ 2、当k<0时,图象在 象限,图像从左到右呈 趋势,y的值随着x值的增大而________ 3、当 越大,直线越靠近y轴,增大(减小)得 也就越快,直线越“陡 ”。
七、巩固练习
1.(2014· 铜仁)正比例函数y=2x的大致图象是( )
3.已知函数y=kx的函数值随x的增大而增大, 则函数的图象经过( ) A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
4 减小,则k可以取( ) A.-2 B.2 C.4 D.6
内描出相应的点.
1.了解画函数图像的一般步骤 2.会画正比例函数图像并探究正比例函数图像特点. 3.理解正比例函数表达式与图像之间一一对应的关系.
一、情景引入 摩天轮上一点的高度h与旋转时间t之间有一定的关 系,右图就反映了时间t(分)与摩天轮上一点的高度h (米)之间的关系.
四、自主学习活动二
作出正比例函数y=-2x的图象. x 列表:
y
请同学们以小组为单位,讨论下面的问题,把得出的结论写出来. (1)满足关系式y= -2x的x,y所对应的点(3,-6)________(填 “在”“不在”)正比例函数y= -2x的图象上。所有满足关系 式y= -2x的x,y所对应的点(x,y)都在正比例函数y= -2x的 图象上吗?答:_____________ (2)正比例函数y=- 2x的图象上的点(-2,4)_______(填“满 足”“不满足”)满足关系式y= -2x。正比例函数y= -2x的图 象上的点(x,y)都满足关系式y= -2x吗? 答:_____________
六、小结归纳:
正比例函数图像特点: 1、当k>0时,图象在 象限,图像从左到右呈 趋势,y的值随着x值的增大而______ 2、当k<0时,图象在 象限,图像从左到右呈 趋势,y的值随着x值的增大而________ 3、当 越大,直线越靠近y轴,增大(减小)得 也就越快,直线越“陡 ”。
七、巩固练习
1.(2014· 铜仁)正比例函数y=2x的大致图象是( )
3.已知函数y=kx的函数值随x的增大而增大, 则函数的图象经过( ) A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
4 减小,则k可以取( ) A.-2 B.2 C.4 D.6
内描出相应的点.
北师大版八年级数学上册第4章 一次函数 一次函数的图象和性质

①列表 ②描点 ③连线 那么你能用同样的方法画出一
次函数的图象吗?
例1 画出一次函数 y = -2x+1 的图象
x y = –2x+1
–2
–1
5
3
y = –2x+1
0
1
1 –1 y
5
01 23 4 5
4
2 列表
–3
一次函数的图 象是什么?
01 23 4 5 01 23 4 5
01 23 4 5 01 23 4 5
思考:观察它们的图象有什么特点?
y y=x+2
.
.
..
.O.
.
.
.
y
.
2
=
x
-
2
x
探究归纳
观察三个函数图象的平移情况:
y y=x+2 y=x
2●
y=x-2
O2
x
●
把一次函数y = x+2,y = x-2的图象与y = x比较,发现: 1. 这三个函数的图象形状都是 直线 ,并且倾斜程度
_相__同___. 2. 函数 y = x 的图象经过原点,函数 y = x + 2 的图象与
y 随 x 的增大而增大. ① b>0 时,直线经过第一、二、三象限;
② b<0 时,直线经过第一、三、四象限. 当 k<0 时,直线 y = kx+b 从左到右逐渐下降,
y 随 x 的增大而减小. ① b>0 时,直线经过第一、二、四象限;
② b<0 时,直线经过第二、三、四象限.
练一练 两个一次函数 y1 = ax+b 与 y2 = bx+a,它们在
要点归纳
思考:与 x 轴的 交点坐标是什么?
b k
次函数的图象吗?
例1 画出一次函数 y = -2x+1 的图象
x y = –2x+1
–2
–1
5
3
y = –2x+1
0
1
1 –1 y
5
01 23 4 5
4
2 列表
–3
一次函数的图 象是什么?
01 23 4 5 01 23 4 5
01 23 4 5 01 23 4 5
思考:观察它们的图象有什么特点?
y y=x+2
.
.
..
.O.
.
.
.
y
.
2
=
x
-
2
x
探究归纳
观察三个函数图象的平移情况:
y y=x+2 y=x
2●
y=x-2
O2
x
●
把一次函数y = x+2,y = x-2的图象与y = x比较,发现: 1. 这三个函数的图象形状都是 直线 ,并且倾斜程度
_相__同___. 2. 函数 y = x 的图象经过原点,函数 y = x + 2 的图象与
y 随 x 的增大而增大. ① b>0 时,直线经过第一、二、三象限;
② b<0 时,直线经过第一、三、四象限. 当 k<0 时,直线 y = kx+b 从左到右逐渐下降,
y 随 x 的增大而减小. ① b>0 时,直线经过第一、二、四象限;
② b<0 时,直线经过第二、三、四象限.
练一练 两个一次函数 y1 = ax+b 与 y2 = bx+a,它们在
要点归纳
思考:与 x 轴的 交点坐标是什么?
b k
北师大版八年级上册数学第4章一次函数 第3节一次函数的图象

的点,所有这些点组成的图形叫做该函数的图象 .
感悟新知
特别提醒 1.函数图象上的任意点P(x,y)中的x,y都满足函数
关系式 . 2.满足函数关系式的任意一对有序实数对 (x,y)所
对应的点一定在函数的图象上. 3.函数图象上的所有点与函数关系式中的两个变量
一一对应.它们是函数两个变量间的关系的两种不 同 (一种是“数”,一种是“形”)呈现方式.
第二、四象限
增减性 y 随 x 的增大而增大 y 随 x 的增大而减小
感悟新知
知3-讲
特别提醒 对于正比例函数y=kx(k≠0),k的符号、图象所
经过的象限、函数的增减性这三者,知其一,则可知 其他两者.
感悟新知
知3-练
例3 [ 中考·珠海 ]已知函数 y=3x 的图象经过点 A(-1, y1),点 B(-2, y2),则 y1_______y2(填“>”“<”或 “=” ) .
在平面直角坐标系中,将直线 l1: y=-3x-2 向左
平移1 个单位长度,再向上平移 3 个单位长度得到直线
l2,则直线 l2对应的函数表达式为(
)
A.y=-3x-9 B.y=-3x-2
C.y=-3x+2
D.y=-3x+9
解题秘方:紧扣“平移规律:上加下减、左加右
减”进行求解 .
感悟新知
知4-练
感悟新知
知识点 4 一次函数的图象
知4-讲
1.一次函数的图象 一次函数 y=kx+b( k, b 是常数,k ≠ 0) 的图象是一条直线,我们称它为直线 y=kx+b.
感悟新知
知4-讲
2. 一次函数的图象与正比例函数的图象的关系 一次函数 y=kx+b(k ≠ 0)的图象可以由直线 y=kx( k ≠ 0)
北师大版八年级数学上册教学课件《一次函数的图像 》

2. 正比例函数y=k1x和y=k2x的图象如图,则k1和
k2的大小关系是(A ) A.k1>k2 B.k1=k2
y y=k1x y=k2x
C.k1<k2 D.不能确定
o
x
例3:已知正比例函数y=mx的图象经过点(m,4), 且y的值随着x值的增大而减小,求m的值。
解:因为正比例函数y=mx的图象经过点(m,4), 所以4=m·m,解得m=±2 又y的值随着x值的增大而减小, 所以m<0,故m=-2。
想一想:下列函数中,随着x的增大,y的值分别如何变化?
当k>0时,
x增大时,y的值也增大
y随x的增大而增大
y y = 2x
当k<0时,
x增大时,y的值反而减小
y随x的增大而减小
y=- 2 3 x y
4
4
2
2
0 12 x
- -3 0 x 6
总结归纳
在正比例函数y=kx中, 当k>0时,y的值随着x值的增大而增大 当k<0时,y的值随着x值的增大而减小
解:(1)由题意得1-2m>0,解 m 1
得
2
(2)由题意得1-2m≠0且m-1<0,m
1且m
1
2
即 (3)由题意得1-2m<0且m-1<0,
1 m 1 2
解得
三、当堂练习
1. 一次函数y=x-2的大致图象为( C )
y
y
y
y
x
x
x
x
A
B
C
D
2.下列函数中,y的值随x值的增大而增大的
4.已知正比例函数y=(2m+4)x。 (1)当m >-2 ,函数图象经过第一、三象限; (2)当m <-2 ,y随x 的增大而减小; (3)当m =0.5 ,函数图象经过点(2,10)。
北师大版数学八年级上册《一次函数的图象》一次函数2
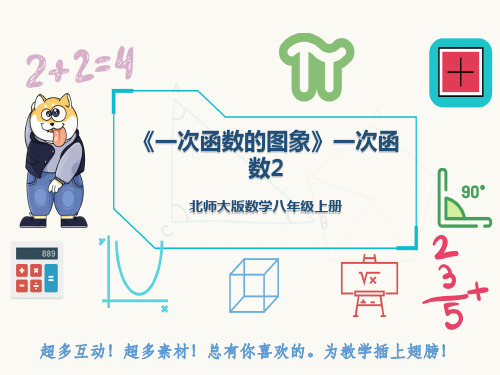
s (千米 )
5
s (千米 )
5
s (千米 )
5
O
( A)
15 t (分)O
(B) 15 t (分)O
15 t (分)
(C )
知识小结
一次函数 y kx b(k 0)
k0
k0
b0 b0 b0 b0 b0
图y
y
y
y
y
象
ox
ox
ox o x o x
b0
y
ox
性 k>0时y随x的增大而增大,图象必经过一、三象限 质 k<0时y随x的增大而减小,图象必经过二、四象限
y
10 y 5 x
8 6
y x2
在哪些象限?
4
2
8 4 o 2 4 6 8 10 x
4
(2)观察每组三个函数图象,随着x
8
值的变化,y的值在怎样变化?
(2)y x 6 、y 2x 、y 1 x 3
y
2
y1x3 2
8 4
10 8 6 4 2
o 2 4 6 8 10 x
(3)从以上观察中,你发现了什么 规律?
直线
y 1x 2
、y 2和x
成的锐角最大?
y 5哪x个与 轴x正方向所
y y 5x
从中k你的发值现决了与定x了轴直正线方向与所成的
10
x 轴锐正角的方大向小所由成什锐么角决的定大?小.
8 6
y 2x
当 k 0 时,k 值越大, 直线与 轴正x方向所成的
4 2
3
2
1
y1x 2
锐角越大.
8 4 o 2 4 6 8 10 x
o
4.3 一次函数的图象(第2课时) 八年级上册北师大版
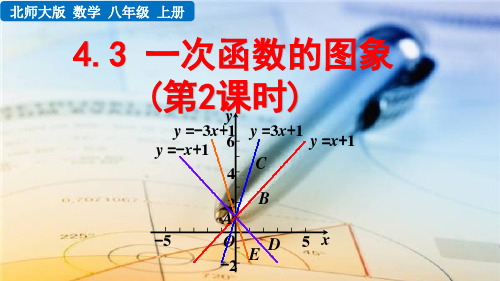
解: 列表
描点
连线
y
12
10
8
x
... -1 0 ...
y=-6x ... 6 0 ...
y=-6x+5 ... 11 5 ...
6 4
2
-2 -1 O 1 2 3 x
探究新知
观察与比较:
比较上面两个函数图象的相同点与不同点.填出你的观
察结果并与同伴交流.
这两个函数的图象形状都 是一条直线,并且倾斜程度相同 .函 数y=-6x的图象经过原点,函数 y=-6x+5的图象与y轴交于点(0,5), 即它可以看作由直线y=-6x向 上 平 移 5 个单位长度得到.
-2
-3
y=-2x+1
探究新知 归纳小结
一次函数y=kx+b的图象也称为直线y=kx+b.
与x轴的交点 坐标
y=kx+b
y
(
-
b k
, 0)
(0, b)
O
x
与y轴的交点 坐标
由于两点确定一条直线,画一次函数图象时
我们只需描点(0,b)和点
b k
,
0
或
(1,k+b),连线即可.
探究新知 探究一 画出函数y=-6x与y=-6x+5的图象.
的两点,下列判断中,正确的是( D )
A.y1>y2 B. y1<y2
C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
提示:反过来也成立:y越大,x就越小.
巩固练习
变式训练
1.在直线y=3x+6上,对于点A(x1,y1)和B(x2,y2)若x1>x2,
则y1 > y2.(填写大小关系)
北师大版八年级上册数学《一次函数的图象》一次函数PPT教学课件

即
y
3 4
x
x
0
.
y/元
(2)列表 x 0 4
6
描点 y 0 3
5 4
连线
3
2
(3)当x=220时,
1
y 3 220 165(元).
O 1 2 34 5 67
x/k m
4
答:该汽车行驶220 km所需油费是165元.
正比例函 数的图象 和性质
课堂小结
画正比例函数图象的一般 步骤:列表、描点、连线
__2__个单位长度而得到.
比较三个函数的解析式, 自变量系数k 相同,
它们的图象的位置关系是 平行
.
要点归纳
思考:与x轴的交 点坐标是什么?
b k
,
0
一次函数y=kx+b(k≠0)的图象经过点(0,b),
可以由正比例函数y=kx的图象平移 b 个单位长度得到
(当b>0时,向 上 平移;当b<0时,向 下 平移).
当k<0时,直线y=kx+b由左到右逐渐下降,y 随x的增大而减小.
① b>0时,直线经过 一、二、四象限; ② b<0时,直线经过二、三、四象限.
练一练
两个一次函数y1=ax+b与y2=bx+a,它们在同
一坐标系中的图象可能是( C )
例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的 m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限; 解:(1)由题意得1-2m>0,解得 m 1
导入新课
复习引入
(1)什么叫一次函数?从解析式上看,一次函数 与正比例函数有什么关系?
北师大版八年级数学上册课件:4.3.1一次函数图象(24张PPT)

只要将点的横纵坐标分别代入关系式 中,看是否满足关系式,若满足关系式, 则该点在直线上,否则不在直线上。
当堂检测
1.下列哪些点在一次函数y=2x-3的图像 上?(2,3),(2,1),(0,3),(3,0)
(2,1)
2.做出 一次函数
y=2x+1 的图象。
当堂检测
3.若一次函数y=-x+b的图象经过 点(0,-3),求b的值. 4.若函数y=-2mx-(m2-9)的图象 经过原点,求m的值.
正比例函数的图象是一条经过原点的直线,一次函数y=kx+b的图象是一条经过(0,b),( ,0)的直线。
只要将点的横纵坐标分别代入关系式中,看是否满足关系式,若满足关系式,则该点在直线上,否则不在直线上。
所有的一次函数的图象都是一条直线。
3、理解一次函数的表达式与图象之间的对应关系。
每日一练
1.已知直线y= (k+1)x+1-2k,若直线与y
小组合作
2.既然我们得出一次函数y=kx+b的 图象是一条直线.那么在画一次函 数图象时有没有什么简单的方法呢?
两点法
小组合作
3.作出y=-x+2的图像(两点法)
描点,连线
教师精讲
1.画函数图像的一般步骤 (1)列表,(2)描点,(3)连线 2.一次函数的图象及画法注意事 项: (1).所有一次函数的图象都是 一条直线,通常我们把一次函数 y=kx+b的图象叫做直线y=kx+b
教师精讲
3、理解一次函数的表达式与图象之间的对应关系。 列表法,图像法,解析式法
(2).一次函数图象的简单画法: 如果正比例函数y=kx的图象经过点(-1,3),那么k=_____
1、满足关系式y= -2x+5的x,y所对应的点(x,y)都在一次函数的图象上吗? (0,b)和(- ,0)。
当堂检测
1.下列哪些点在一次函数y=2x-3的图像 上?(2,3),(2,1),(0,3),(3,0)
(2,1)
2.做出 一次函数
y=2x+1 的图象。
当堂检测
3.若一次函数y=-x+b的图象经过 点(0,-3),求b的值. 4.若函数y=-2mx-(m2-9)的图象 经过原点,求m的值.
正比例函数的图象是一条经过原点的直线,一次函数y=kx+b的图象是一条经过(0,b),( ,0)的直线。
只要将点的横纵坐标分别代入关系式中,看是否满足关系式,若满足关系式,则该点在直线上,否则不在直线上。
所有的一次函数的图象都是一条直线。
3、理解一次函数的表达式与图象之间的对应关系。
每日一练
1.已知直线y= (k+1)x+1-2k,若直线与y
小组合作
2.既然我们得出一次函数y=kx+b的 图象是一条直线.那么在画一次函 数图象时有没有什么简单的方法呢?
两点法
小组合作
3.作出y=-x+2的图像(两点法)
描点,连线
教师精讲
1.画函数图像的一般步骤 (1)列表,(2)描点,(3)连线 2.一次函数的图象及画法注意事 项: (1).所有一次函数的图象都是 一条直线,通常我们把一次函数 y=kx+b的图象叫做直线y=kx+b
教师精讲
3、理解一次函数的表达式与图象之间的对应关系。 列表法,图像法,解析式法
(2).一次函数图象的简单画法: 如果正比例函数y=kx的图象经过点(-1,3),那么k=_____
1、满足关系式y= -2x+5的x,y所对应的点(x,y)都在一次函数的图象上吗? (0,b)和(- ,0)。
北师大八上 6.3一次函数的图象和性质

画一画
在同一坐标系中,画出下列四个一次 函数的 图 象:
(1)y=2x, (2) y=2x+3 , (3) y=一2x, (4) y=一2x+3 。
小结与回顾:
两点法画一次函数图象:
1、正比例函数y=kx(k≠0)的图象是过点(_____),(____0_,_0)的 __1_,__k____。 一条直线
⑵当k<0时,图象过______象二限、。四
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
k_>__0,b_>__0 b___0
k>___0,b<___0
<k___0,>b___0 < k___0<,
两条直线的位置关系:y = k1 x+b1 yk=2 bx2+
1) k1k2 2) k1= k2 b1 b2
④ ③
2 – 、函数y=(m 1)x+1是一次函数,且y随自变量x增大而减小,那么
m的取值为__________
m<1
3、已知一次函数y=2x+4的图象上有两点A(3,a),B(4,b),
则a与b的大小关系为_________
a<b
4、一次函数y=(m2+3)x-2,y随x的增大而_________ 增大
丙:当x<2时,y随x的增大而减小;
丁:当x<2时,y>0.
已知这四位同学的叙述都正确,请构造出满足上述所有性 质的一个函数。
如图,正方形2A、BCD的边长是4,将此正方形置于 直角坐标系中,使AB在x轴的正半轴上,点A的坐
(1)过点C的直线
y= x– 与x轴交于点E,4
在同一坐标系中,画出下列四个一次 函数的 图 象:
(1)y=2x, (2) y=2x+3 , (3) y=一2x, (4) y=一2x+3 。
小结与回顾:
两点法画一次函数图象:
1、正比例函数y=kx(k≠0)的图象是过点(_____),(____0_,_0)的 __1_,__k____。 一条直线
⑵当k<0时,图象过______象二限、。四
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
k_>__0,b_>__0 b___0
k>___0,b<___0
<k___0,>b___0 < k___0<,
两条直线的位置关系:y = k1 x+b1 yk=2 bx2+
1) k1k2 2) k1= k2 b1 b2
④ ③
2 – 、函数y=(m 1)x+1是一次函数,且y随自变量x增大而减小,那么
m的取值为__________
m<1
3、已知一次函数y=2x+4的图象上有两点A(3,a),B(4,b),
则a与b的大小关系为_________
a<b
4、一次函数y=(m2+3)x-2,y随x的增大而_________ 增大
丙:当x<2时,y随x的增大而减小;
丁:当x<2时,y>0.
已知这四位同学的叙述都正确,请构造出满足上述所有性 质的一个函数。
如图,正方形2A、BCD的边长是4,将此正方形置于 直角坐标系中,使AB在x轴的正半轴上,点A的坐
(1)过点C的直线
y= x– 与x轴交于点E,4
北师大版八年级数学上册一次函数的图像课件

_降__落__趋势。
学习内容
一次函数的图象 ——借助描点法画出一次函数的图象
一次函数的性质
——借助图象特点归纳一次函数的性质
第二环节:问题引导,活动探究
(1)探究一次函数的画法
请用描点法画出y=2x+1的图象
x… y=2x+1 …
-2 -1 0 -3 -1 1
12… 35 …
列表
描点
连线
几何画板
-2
y=2x+3
y=5x-2
( , 0) 12 x
(0,-2)
② y=-x, y=-x+3
x
…0 1…
x
…3
y=-x … 0 -1 … y=-x+3 … 0
0… 3…
y=-x+3 y 5
y=-x
4
3
2
1
-4 -3 -2 -1 0 -1
-2 -3 -4
12 3 4 x
合作探究:
y
问题2:
y=2x+3 3
四象限,则有( D )。 =mx-mn
y
A、m>0,n>0
B、m<0、n>0
C、m>0、n<0
D、m<0、n<0
0x
m<0, mn>0 n<0
第五环节:畅谈收获,自我反思 谈谈自己在本节课的收获,学习了哪
些数学方法?有哪些方面的提升?
第六环节:作业布置,巩固提升 1、数学书87页习题4.4:1题、2题、3题、4题 2、在同一直角坐标系中分别画出y=2x+1,
4、正比例函数性质:
y=kx(k≠0)
k>0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
… -2 -1 0 1 2 …
y
… -4 -2 0 2 4 …
y 描点: 5
4 3 连线: 2 1
-4 -3 -2 -1O-1
-2
-3 -4
12345 x
说一说正比例函数的图象形状
正比例函数y=kx (k≠0)的图象是经过 原点(0、0)的一条直线。
画正比例函数y=kx (k≠0)的图象时,只要 确定2个点的位置,这两个点尽量找两个 坐标都是整数的点。
y=2x+1 … -3 -1 1 3 5 …
y 描点: 5
4 3 连线: 2
1
-4 -3 -2 -1O-1
-2 -3 -4
12345 x
一次函数、正比例函数图象的特征:
一次函数y=kx+b(k≠0)的图象是一条 直线。而且正比例函数y=kx (k≠0)的图 象是经过原点(0,0)(1,k)的一条 直线。
y=x
01
y=x+2 2 0
5
4
x
02
3
y=x-2 -2 0
2
2、观察与比较
1
议一议:正比例函数y=x与一 次函数y=x+2 、y=x-2图象
有什么异同点.
-3 -2 -1 0 1 -1
-2
-3
直线的平行及平移
-4
y=x+2 y=x
y=x-2
23 x
1、请大家在同一坐标系内作出下列函数
y=x, y=x+2,y=x-2的图象。
y
直线的平行规律
K相等
直线的平移规律
左加右减,上加下减
5 4 3 2 1
-3 -2 -1 0 1 -1 -2 -3 -4
y=x+2 y=x
y=x-2
23 x
1.直线 y=2x向上平移3个单位得到直线______
2.正比例函数的图象与直线y=-1.5x+4平行,则 该正比例函数的关系式为______
因为图像经过点(-2,0),(0,-2),
y
所以0,=-把2k(+b-2,0),(0,-2)代入y=kx+b可得3
-2=b
2
解之得, k=-1 b=-2
1
所以,该一次函数的解析式 为y=-x-2。
-3 -2 -1 0 1 2 3 x -1
-2
-3
课堂练习
课堂练习
1、已知函数y=-8x+16,求该函数图象与y轴的交点是 (0 , 16) , 与x轴的交点是 (2 , 0) ;
1.什么是一次函数?什么是正比例函数?
如果y=kx+b(k,b是常数,k≠0),那么y 叫做x的函数。特别的,当b=0时, y=kx+b就成为y=kx,这时,y叫做x 的正比例函数。
2、画函数图象的一般步骤:
(1)列表 (2)描点 (3)连线
例1 如何作出y=2x的图象?
解:列表:
(-2,-4) (-1,-2) (0,0) (1,2) (2,4)
y 5
y=3x
y y=-3x+2 5
4
4
3
3 (1,3)
2 (0, 2)
2
1
1
-4 -3 -2 -1O-1
12345
-4 x
-3
-2
-1O-1
-2
12345 (2/3, 0)
x
-2
-3
-3
-4
-4
课堂练习
作出一次函数y=-2x+5的图象。
x
… 0 5/2 …
列: y=-2x+5 … 5 0 …
y=-2x+5
一次函数、正比例图象的画法:
只要在图象上找到两点的坐标,在 坐标系中描出这两点,再经过这两点画 直线即可。一次函数是(0,b)(-b/k,0)
一次函数、正比例例2图分象别的画作法出:一次函数y=3x与
只要在图象y上=-找3到x两+2点的的图坐象标,,并在求坐出标它系们中描与
出这两点,再经坐过标这轴两交点画点直的线坐即标可. 。
y
(0, 5) (5/2,0)
A 6
5 4 3 2 1
B 0 1 2 3 4
x
课堂练习
1.下列各点中,哪些点在函数y=4x+1的图象上? 哪些点不在函数y=4x+1的图象上?为什么? (2,9) (5,1) (-1,-3) (-0.5,-1)
2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)
3.直线y=3x+5平行的直线y=kx+b,则要求( )
A.k=3,b=5 C.k=3,b≠5
B. k=3 D. b=5
请在直角坐标系中作出函数 y 1 x的图像。 3
解: y 1 x
3
x
… 0 3…
y1x … 0 1 …
3
(0,0) (3,1)
y
3
y1x 3
2
1
0 1234
x
例2 如何作出y=2x+1的图象? 解:列表:
(-2,-3) (-1,-1) (0,1) (1,3) (2,5)
x
… -2 -1 0 1 2 …
2、已知函数 y=-2x+6,则它的图象形状是 一条直线 , 图象与坐标轴围成的三角形面积是 9 .
3、已知函数y=kx-2过点(1,1),则k= 3 . 4、已知点(a,4)在直线y=x-2上,则a= 6 .
1、请大家在同一坐标系内作出下列函数
y=x, y=x+2,y=x-2的图象。
y
x
01
x
0 -2
两点, 则a=
b=
3.点已知M(-3, 4)在一次函数y=ax+1的图象上, 则a的值是
4.若一次函数的图像经过点(0,1),(1,2), 则此函数关系式是______________
5、已知一次函数的图像在平面直角坐标系中 如图所示,求该一次函数的解析式。
解:设该一次函数的解析式为:y=kx+b
