高中数学必修综合测试题人教版

合集下载

新课标人教版必修5高中数学_综合检测试卷附答案解析

新课标人教版必修5高中数学综合检测试卷1．如果33log log 4m n +=，那么n m +的最小值是（）A ．4B ．34C ．9D ．18 2、数列{}n a 的通项为n a =12-n ，*N n ∈，其前n 项和为n S ，则使n S >48成立的n 的最小值为（）A ．7B ．8C ．9D ．103、若不等式897x +<和不等式022>-+bx ax 的解集相同，则a 、b 的值为（） A ．a =﹣8 b =﹣10 B ．a =﹣4 b =﹣9 C ．a =﹣1 b =9D ．a =﹣1 b =2 4、△ABC 中，若2cos c a B =，则△ABC 的形状为（） A ．直角三角形 B ．等腰三角形 C ．等边三角形 D ．锐角三角形5、在首项为21，公比为12的等比数列中，最接近1的项是（）A ．第三项B ．第四项C ．第五项D ．第六项6、在等比数列{}n a 中，117a a ⋅=6，144a a +=5，则1020a a等于（）A ．32 B ．23C ．23或32D ．﹣32或﹣237、△ABC 中，已知()()a b c b c a bc +++-=，则A 的度数等于（）A ．120B ．60C ．150D ．30 8、数列{}n a 中，1a =15，2331-=+n n a a （*N n ∈），则该数列中相邻两项的乘积是负数的是（）A ．2221a aB ．2322a aC ．2423a aD ．2524a a9、某厂去年的产值记为1，计划在今后五年内每年的产值比上年增长10%，则从今年起到第五年，这个厂的总产值为（）A ．41.1B ．51.1C ．610(1.11)⨯-D ． 511(1.11)⨯- 10、已知钝角△ABC 的最长边为2，其余两边的长为a 、b ，则集合{}b y a x y x P ===,|),(所表示的平面图形面积等于（） A ．2 B ．2-π C ．4 D ．24-π 11、在△ABC 中，已知BC=12，A=60°，B=45°，则AC= 12．函数2lg(12)y x x =+-的定义域是13．数列{}n a 的前n 项和*23()n n s a n N =-∈，则5a =14、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ，则y x z 32+=的最大值为15、《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。

人教版高中数学必修第二册第九章~第十章综合测试卷 (含答案)

人教版高中数学必修第二册第九章~第十章综合测试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.第Ⅰ卷(选择题共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.现要完成下列两项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查;②东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是()A.①抽签法,②比例分配的分层随机抽样B.①随机数法,②比例分配的分层随机抽样C.①随机数法,②抽签法D.①抽签法,②随机数法2.若A,B为对立事件,则下列式子中成立的是()A.P(A)+P(B)<1B.P(A)+P(B)>1C.P(A)+P(B)=0D.P(A)+P(B)=13.从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的产品不是一等品”的概率为()A.0.2B.0.35C.0.3D.0.44.某宠物商店对30只宠物狗的体重(单位:千克)作了测量,并根据所得数据画出了频率分布直方图如图C6-1所示,则这30只宠物狗体重的平均值大约为()图C6-1A.15.5千克B.15.6千克C.15.7千克D.16千克5.以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是()A.90分B.91.5分C.91分D.90.5分6.一组样本数据a,3,4,5,6的平均数是b,且不等式x2-6x+c<0的解集为(a,b),则这组样本数据的标准差是()A.1B.2C.3D.27.我国历史上有田忌与齐王赛马的故事:“田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.”若双方各自拥有上、中、下等马各1匹,双方各随机选1匹马进行1场比赛,则齐王的马获胜的概率为()A.23B.13C.12D.568.在发生某公共卫生事件期间,有专业机构认为在一段时间内没有发生规模群体感染的标志为“连续10天,每天新增疑似病例数量不超过7”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体的平均数为3,中位数为4B.乙地:总体的平均数为1,总体方差大于0C.丙地:中位数为2,众数为3D.丁地:总体的平均数为2,总体方差为3二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)9.给出下列四个说法,其中正确的说法有()A.做100次抛硬币的试验,结果有51次出现正面朝上,因此,出现正面朝上的概率是51100B.随机事件发生的频率就是这个随机事件发生的概率C.抛掷骰子100次,得点数是1的结果有18次,则出现1点的频率是950D.随机事件发生的频率不一定是这个随机事件发生的概率10.在某次高中学科竞赛中,4000名考生的参赛成绩统计如图C6-2所示,60分以下视为不及格,若同一组中的数据用该组区间的中点值为代表,则下列说法中正确的是()图C6-2A.成绩在[70,80)内的考生人数最多B.不及格的考生人数为1000C.考生竞赛成绩的平均数约为70.5分D.考生竞赛成绩的中位数为75分11.某健身房为了解运动健身减肥的效果,调查了20名肥胖者健身前(如直方图C6-3(1)所示)后(如直方图(2)所示)的体重(单位:kg)变化情况:图C6-3对比数据,关于这20名肥胖者,下面结论正确的是()A.健身后,体重在区间[90,100)内的人数较健身前增加了2B.健身后,体重原在区间[100,110)内的人员一定无变化C.健身后,20人的平均体重大约减少了8kgD.健身后,原来体重在区间(110,120]内的肥胖者体重都有减少12.从甲袋中摸出一个红球的概率是13,从乙袋中摸出一个红球的概率是12,从两袋中各摸出一个球,下列结论正确的是()A.2个球都是红球的概率为16B.2个球不都是红球的概率为13C.至少有1个红球的概率为23D.2个球中恰有1个红球的概率为12请将选择题答案填入下表:题号12345678总分答案题号9101112答案第Ⅱ卷(非选择题共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.从甲、乙两个厂家生产的同一种产品中各抽取8件产品,对其使用寿命(单位:年)跟踪调查的结果如下:甲:3,4,5,6,8,8,8,10;乙:3,3,4,7,9,10,11,12.两个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别采用了平均数、众数、中位数中的哪一个特征数:甲:,乙:.14.如图C6-4是容量为100的样本数据的频率分布直方图,则样本数据落在区间[6,18)内的频数为.图C6-415.已知甲、乙、丙3名运动员射击一次击中目标的概率分别为0.7,0.8,0.85,若这3人向目标各射击一次,则目标没有被击中的概率为.16.甲、乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为a,再由乙猜甲刚才想的数字,把乙猜的数字记为b,且a,b∈{0,1,2,…,9}.若|a-b|≤1,则称甲、乙两人“心有灵犀”.现任意找两人玩这个游戏,则这两人“心有灵犀”的概率为.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)某班选派5人,参加学校举行的数学竞赛,获奖的人数及其概率如下:获奖人数012345概率0.10.16x y0.2z(1)若获奖人数不超过2的概率为0.56,求x的值;(2)若获奖人数最多为4的概率为0.96,获奖人数最少为3的概率为0.44,求y,z的值.18.(12分)甲、乙两台机床同时加工直径为100cm的零件,为检验质量,各从中抽取6个零件测量其直径,所得数据如下.甲:99,100,98,100,100,103;乙:99,100,102,99,100,100.(1)分别计算两组数据的平均数及方差;(2)根据计算结果判断哪台机床加工零件的质量更稳定.19.(12分)某校高一年级举行了一次数学竞赛,为了了解参加本次竞赛的学生的成绩情况,从中抽取了部分学生的成绩(取正整数,单位:分)作为样本(样本量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图C6-5所示,已知成绩在[50,60),[90,100]内的频数分别为8,2.(1)求样本量n和频率分布直方图中的x,y的值;(2)估计参加本次竞赛的学生成绩的众数、中位数、平均数.图C6-520.(12分)生产同一种产品,甲机床的废品率为0.04,乙机床的废品率为0.05,从甲、乙机床生产的产品中各任取1件,求:(1)至少有1件废品的概率;(2)恰有1件废品的概率.21.(12分)某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图C6-6所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.(1)求小亮获得玩具的概率;(2)请比较小亮获得水杯的概率与获得饮料的概率的大小,并说明理由.图C6-622.(12分)2020年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分100分).根据调查数据制成如下表格和如图C6-7所示的频率分布直方图.已知评分在[80,100]内的居民有600人.满意度评分[40,60)[60,80)[80,90)[90,100]满意度等级不满意基本满意满意非常满意(1)求频率分布直方图中a的值及参与评分的总人数.(2)定义满意度指数η=(满意程度的平均分)/100,若η<0.8,则防疫工作需要进行大的调整,否则不需要进行大调整.根据所学知识判断该区防疫工作是否需要进行大调整.(3)为了解部分居民不满意的原因,从不满意的居民(评分在[40,50),[50,60)内)中用比例分配的分层随机抽样的方法抽取6位居民,倾听他们的意见,并从6人中抽取2人担任防疫工作的监督员,求这2人中仅有1人对防疫工作的评分在[40,50)内的概率.图C6-7参考答案与解析1.A[解析]①总体较少,宜用抽签法;②各层间差异明显,宜用分层随机抽样.故选A.2.D[解析]若事件A与事件B是对立事件,则P(A)+P(B)=1.故选D.3.B[解析]∵事件A={抽到一等品},且P(A)=0.65,∴事件“抽到的产品不是一等品”的概率P=1-P(A)=1-0.65=0.35.4.B[解析]由频率分布直方图可以计算出各组的频率分别为0.1,0.2,0.3,0.2,0.1,0.1,故各组的频数分别为3,6,9,6,3,3,则这30只宠物狗体重的平均值为11×3+13×6+15×9+17×6+19×3+21×330=15.6(千克),故选B.5.D[解析]将这15人的成绩(单位:分)由小到大依次排列为56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,因为15×80%=12,第12,13个数据分别为90分、91分,所以这15人成绩的第80百分位数是90.5分.故选D.6.B[解析]由题意得a+3+4+5+6=5b,a+b=6,解得a=2,b=4,所以样本数据的方差s2=15×[(2-4)2+(3-4)2+(4-4)2+(5-4)2+(6-4)2]=2,所以标准差s=2.故答案为B.7.A[解析]依题意,记田忌的上等马、中等马、下等马分别为a,b,c,齐王的上等马、中等马、下等马分别为A,B,C.由题意可知,样本空间Ω={aA,bA,cA,aB,bB,cB,aC,bC,cC},共有9个样本点,其中事件“田忌可以获胜”包含的样本点为aB,aC,bC,共3个,则齐王的马获胜的概率P=1-39=23.故选A.8.D[解析]由于甲地总体数据的平均数为3,中位数为4,即按从小到大排序后,中间两个数据的平均数为4,因此后面的数据可以大于7,故甲地不一定符合.乙地总体数据的平均数为1,因此这10天的新增疑似病例总数为10,又由于方差大于0,故这10天中新增疑似病例数量不可能每天都是1,可以有一天大于7,故乙地不一定符合.丙地总体数据的中位数为2,众数为3,故数据中可以出现8,故丙地不一定符合.丁地总体数据的平均数为2,方差为3,故丁地一定符合.9.CD[解析]对于A,混淆了频率与概率的区别,故A错误;对于B,混淆了频率与概率的区别,故B 错误;对于C,抛掷骰子100次,得点数是1的结果有18次,则出现1点的频率是950,符合频率定义,故C正确;对于D,频率是概率的估计值,故D正确.故选CD.10.ABC [解析]由频率分布直方图可得,成绩在[70,80)内的频率最高,考生人数最多,故A 正确;由频率分布直方图可得,成绩在[40,60)内的频率为0.25,则不及格的考生人数为4000×0.25=1000,故B 正确;由频率分布直方图可得,平均数为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5(分),故C 正确;因为成绩在[40,70)内的频率为0.45,在[70,80)内的频率为0.3,所以中位数为70+10×0.050.3≈71.67(分),故D 错误.故选ABC .11.AD[解析]体重在区间[90,100)内的肥胖者由健身前的6人增加到健身后的8人,增加了2人,故A 正确;健身后,体重在区间[100,110)内的频率没有变,但人员组成可能改变,故B 错误;健身后,20人的平均体重大约减少了(0.3×95+0.5×105+0.2×115)-(0.1×85+0.4×95+0.5×105)=5(kg),故C 错误;因为图(2)中没有体重在区间(110,120]内的人员,所以原来体重在区间(110,120]内的肥胖者体重都有减少,故D 正确.故选AD .12.ACD[解析]设“从甲袋中摸出一个红球”为事件A 1,“从乙袋中摸出一个红球”为事件A 2,则P (A 1)=13,P (A 2)=12,且A 1,A 2独立;在A 中,“2个球都是红球”为事件A 1A 2,其概率为13×12=16,A 正确;在B中,“2个球不都是红球”是“2个球都是红球”的对立事件,其概率为56,B 错误;在C 中,“2个球中至少有1个红球”的概率为1-P ( )P ( )=1-23×12=23,C 正确;在D 中,2个球中恰有1个红球的概率为13×12+23×12=12,D 正确.故选ACD .13.众数中位数[解析]对甲厂的数据进行分析:该组数据中8年出现的次数最多,故广告中采用了众数;对乙厂的数据进行分析:该组数据最中间的是7年与9年,故中位数是7+92=8(年),故广告中采用了中位数.14.80[解析]由题图知,样本数据落在区间[6,18)内的频数为100×0.8=80.15.0.009[解析]由相互独立事件的概率计算公式知,3人向目标各射击一次,目标没有被击中的概率P=(1-0.7)×(1-0.8)×(1-0.85)=0.3×0.2×0.15=0.009.16.725[解析]从{0,1,2,…,9}中任意取两个数(可重复),该试验共有100个样本点,事件“|a-b|≤1”包含的样本点为(0,0),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(7,7),(8,8),(9,9),(0,1),(1,0),(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4),(5,6),(6,5),(6,7),(7,6),(7,8),(8,7),(8,9),(9,8),共有28个,所以所求概率P=28100=725.17.解:记事件“在竞赛中,有k 人获奖”为A k (k ∈N,k ≤5),则事件A k 彼此互斥.(1)∵获奖人数不超过2的概率为0.56,∴P (A 0)+P (A 1)+P (A 2)=0.1+0.16+x=0.56,解得x=0.3.(2)由获奖人数最多为4的概率为0.96,得P (A 5)=1-0.96=0.04,即z=0.04.由获奖人数最少为3的概率为0.44,得P (A 3)+P (A 4)+P (A 5)=0.44,即y+0.2+0.04=0.44,解得y=0.2.18.解:(1)由题中数据可得甲=16×(99+100+98+100+100+103)=100(cm); 乙=16×(99+100+102+99+100+100)=100(cm).甲2=16×(1+0+4+0+0+9)=73, 乙2=16×(1+0+4+1+0+0)=1.(2)由(1)知两台机床所加工零件的直径的平均数相同,又甲2> 乙2,所以乙机床加工零件的质量更稳定.19.解:(1)由题意可知,样本量n=80.016×10=50,y=250×10=0.004,x=0.1-0.016-0.04-0.01-0.004=0.03.(2)由频率分布直方图可估计,参加本次竞赛的学生成绩的众数为75分.设样本数据的中位数为m ,因为(0.016+0.03)×10<0.5<(0.016+0.03+0.04)×10,所以m ∈[70,80),所以(0.016+0.03)×10+(m-70)×0.04=0.5,解得m=71,故估计参加本次竞赛的学生成绩的中位数为71分.由频率分布直方图可估计,参加本次竞赛的学生成绩的平均数为55×0.16+65×0.3+75×0.4+85×0.1+95×0.04=70.6(分).20.解:记从甲、乙机床生产的产品中取1件是废品分别为事件A ,B ,则事件A ,B 相互独立,且P (A )=0.04,P (B )=0.05.(1)设“至少有1件废品”为事件C ,则P (C )=1-P ( )=1-P ( )P ( )=1-(1-0.04)×(1-0.05)=0.088.(2)设“恰有1件废品”为事件D ,则P (D )=P (A )+P ( B )=0.04×(1-0.05)+(1-0.04)×0.05=0.086.21.解:(1)试验的所有样本点为(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),( 4,3),(4,4),共16个.事件“xy≤3”包含的样本点有(1,1),(1,2),(1,3),(2,1),(3,1),共5个,所以小亮获得玩具的概率为516.(2)事件“xy≥8”包含的样本点有(2,4),(3,3),(3,4),(4,2),(4,3),(4,4),共6个,所以小亮获得水杯的概率为38,小亮获得饮料的概率为1-516-38=516,所以小亮获得水杯的概率大于获得饮料的概率.22.解:(1)由频率分布直方图知(0.002+0.004+0.014+0.02+0.035+a)×10=1,即10×(0.075+a)=1,解得a=0.025,设共有n人参与评分,则600 =(0.035+0.025)×10,解得n=1000,即参与评分的总人数为1000.(2)由频率分布直方图知各组的频率分别为0.02,0.04,0.14,0.2,0.35,0.25,所以η=45×0.02+55×0.04+65×0.14+75×0.2+85×0.35+95×0.25100=0.807>0.8,所以该区防疫工作不需要进行大调整.(3)因为0.002×10×1000=20,0.004×10×1000=40,所以评分在[40,50),[50,60)内的居民人数分别为20,40,所以所抽取的评分在[40,50)内的居民人数为20×660=2,将这2人分别记为a,b,所抽取的评分在[50,60)内的居民人数为40×660=4,将这4人分别记为A,B,C,D.从这6人中抽取2人,试验的样本点有ab,aA,aB,aC,aD,bA,bB,bC,bD,AB,AC,AD,BC,BD,CD,共15个.而“仅有1人对防疫工作的评分在[40,50)内”包含的样本点有aA,aB,aC,aD,bA,bB,bC,bD,共8个,则所求事件的概率为815.。

人教版高中数学必修一综合测试题与答案

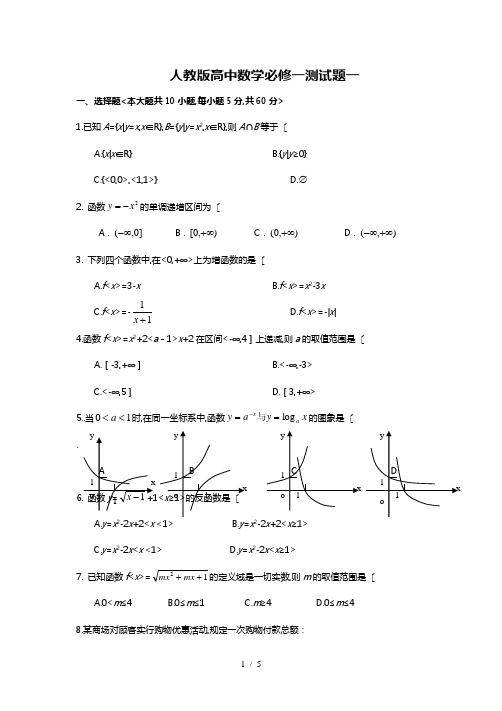
人教版高中数学必修一测试题一一、选择题<本大题共10小题,每小题5分,共60分> 1.已知A ={x |y =x ,x ∈R },B ={y |y =x 2,x ∈R },则A ∩B 等于〔A.{x |x ∈R }B.{y |y ≥0}C.{<0,0>,<1,1>}D.∅2. 函数2x y -=的单调递增区间为〔A ．]0,(-∞B ．),0[+∞C ．),0(+∞D ．),(+∞-∞ 3. 下列四个函数中,在<0,+∞>上为增函数的是〔A.f <x >=3-xB.f <x >=x 2-3xC.f <x >=-11+xD.f <x >=-|x |4.函数f <x >=x 2+2<a －1>x +2在区间<-∞,4］上递减,则a 的取值范围是〔A.［-3,+∞］B.<-∞,-3>C.<-∞,5］D.［3,+∞>5..当10<<a 时,在同一坐标系中,函数x y a y a xlog ==-与的图象是〔.A.y =x 2-2x +2<x x 2-2x +2<x ≥1> C.y =x 2-2x <x ＜1> D.y =x 2-2x <x ≥1>7. 已知函数f <x >=12++mx mx 的定义域是一切实数,则m 的取值范围是〔A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤4 8.某商场对顾客实行购物优惠活动,规定一次购物付款总额：<1>如果不超过200元,则不给予优惠；<2>如果超过200元但不超过500元,则按标价给予9折优惠；<3>如果超过500元,其500元内的按第<2>条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款是〔A.413.7元B.513.7元C.546.6元D.548.7元9. 二次函数y =ax 2+bx 与指数函数y =<ab >x的图象只可能是〔 10. 已知函数f <n >=⎩⎨⎧<+≥-),10)](5([),10(3n n f f n n 其中n ∈N ,则f <8>等于〔A.2B.4C.6D.711、如图,设a,b,c,d>0,且不等于1,y=ax , y=bx , y=cx ,y=dx 在同一坐标系中的图象如图, 则a,b,c,d 的大小顺序〔 A 、a<b<c<d B 、a<b<d<c C 、b<a<d<c D 、b<a<c<d12.已知0<a<1,b<-1,函数f<x>=a x +bA.第一象限;B.第二象限;C.第三象限;D.第四象限二、填空题<本大题共4小题,每小题5分,共20分> 13.已知f <x >=x 2－1<x <0>,则f －1<3>=_______. 14．函数)23(log 32-=x y 的定义域为______________15.某工厂8年来某产品产量y 与时间t 年的函数关系如下图,则：①前3年总产量增长速度增长速度越来越快； ②前3年中总产量增长速度越来越慢； ③第3年后,这种产品停止生产； ④第3年后,这种产品年产量保持不变. 以上说法中正确的是_______.16. 函数y =⎪⎩⎪⎨⎧>+≤<+≤+1)( 5-1),(030),(32x x x x x x 的最大值是_______. 三、解答题。

高中数学人教A版必修第一册综合检测试题

综合检测试题选题明细表一、单项选择题:本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合A={x|2x-1≥1}，B={y|y=log3x，x∈A}，则∁B A等于( B )A.(0，1)B.[0，1)C.(0，1]D.[0，1]解析:由题得A={x|2x-1≥20}={x|x≥1}，B={y|y≥0}，所以∁B A={x|0≤x<1}.故选B.2.若a=0.60.7，b=0.70.6，c=lg 3，则下列结论正确的是( D )A.b>c>aB.c>a>bC.a>b>cD.b>a>c解析:因为y=x0.6为增函数，y=0.6x为减函数，所以0.70.6>0.60.6>0.60.7>0.61，c=lg 3<lg √10=0.5，所以b>a>c.故选D.3.已知正实数x ，y 满足x+2y=2xy ，则x+y 的最小值为( D ) A.4 B.√2 C.√3 D.√2+32解析:因为正实数x ，y 满足x+2y=2xy ，所以x+2y xy=2，即1y +2x =2，所以x+y=(x+y 2)·(1y +2x )=x 2y +1+12+y x ≥32+2√x 2y ·y x =32+√2，当且仅当x 2=2y 2时，等号成立. 故选D.4.已知函数f(x)为奇函数，当x>0时，f(x)=log 2(x+1)+ax ，且f(-3)=a ，则f(7)等于( B ) A.12B.-12C.log 23D.2解析:因为函数f(x)为奇函数，当x>0时，f(x)=log 2(x+1)+ax ，且f(-3)=-f(3)=a ，所以f(3)=-a ，即2+3a=-a ，所以a=-12，则f(7)=log 28+7a=3-72=-12.故选B.5.已知2sin 2α=1+cos 2α，则tan 2α等于( D ) A.-43 B.43C.-43或0 D.43或0解析:因为{2sin2α=1+cos2α,sin 22α+cos 22α=1,所以{sin2α=0,cos2α=-1或{sin2α=45,cos2α=35.所以tan 2α=0或tan 2α=43.故选D.6.将函数f(x)=sin(2x+π6)的图象分别向左、向右平移ϕ(ϕ>0)个单位长度后，所得的图象都关于y 轴对称，则ϕ的最小值分别为( A ) A.π6，π3B.π3，π6C.2π3，5π6D.π6，π12解析:函数f(x)的图象向左平移ϕ个单位长度得到函数g(x)= sin(2x+2ϕ+π6)的图象，因为g(x)图象关于y 轴对称，则2ϕ+π6=π2+k π，k ∈Z ，即ϕ=π6+kπ2，k∈Z ，而ϕ>0，则ϕmin =π6;函数f(x)的图象向右平移ϕ个单位长度得函数h(x)=sin(2x-2ϕ+π6)的图象，因为函数h(x)关于y 轴对称，则有-2ϕ+π6=π2+k π，k ∈Z ，即ϕ=-π6-kπ2，k ∈Z ，而ϕ>0，则ϕmin =π3，所以ϕ的最小值分别为π6，π3.故选A.7.如图所示，其对应的函数解析式可能是( B )A.f(x)=1|x -1|B.f(x)=1||x |-1|C.f(x)=11-x2D.f(x)=11+x 2解析:函数的定义域为{x|x ≠±1}，排除选项A 和D ，当x ∈(1，+∞)时，f(x)>0，可排除选项C.故选B. 8.已知函数f(x)=ln(1+x 2)-11+|x |，若实数a 满足f(log 3a)+f(lo g 13a)≤2f(1)，则a 的取值范围是( D ) A.[1，3] B.(0，13)C.(0，3]D.[13，3]解析:函数f(x)=ln(1+x 2)-11+|x |，故函数f(x)在(0，+∞)上单调递增，且f(x)为偶函数，若实数a 满足f(log 3a)+f(lo g 13a)≤2f(1)，即f(log 3a)+f(-log 3a)≤2f(1)，f(log 3a)≤f(1)，所以|log 3a|≤1，即-1≤log 3a ≤1，故13≤a ≤3.故选D.二、多项选择题:本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.9.已知f(x)={log 3x ,x >0,2x ,x ≤0,角α的终边经过点(1，2√2)，则下列结论正确的是( AC )A.f(cos α)=-1B.f(sin α)=1C.f(f(cos α))=12D.f(f(sin α))=2解析:因为角α的终边经过点(1，2√2)，所以sin α=2√23，cos α=13，所以f(cos α)=f(13)=log 313=-1， f(sin α)=f(2√23)=log 32√23<0，所以f(f(cos α))=f(-1)=2-1=12， f(f(sin α))=2log 32√23.故选AC.10.下列命题正确的是( ABD ) A.函数f(x)=x+1x (x>0)的最小值为2B.函数y=2-x-4x(x>0)的最大值为-2C.函数f(x)=2x+1x的最小值为2√2D.函数f(x)=2√x 2+1的最小值为3解析:因为x>0，所以f(x)=x+1x≥2√1=2，当且仅当x=1x，即x=1时，取等号，所以函数的最小值为2，所以A 正确;因为x>0，所以f(x)=x+4x≥2√4=4，当且仅当x=4x，即x=2时，取等号，所以函数f(x)的最小值为4，所以函数y 的最大值为-2，所以B 正确;当x=-1时，f(-1)=-3，所以C 错误; 设√x 2+1=t(t ≥1)，则x 2=t 2-1，则f(t)=2t 2+1t=2t+1t，在[1，+∞)上任取t 1，t 2.令t 1<t 2，则f(t 1)-f(t 2)=2(t 1-t 2)+(1t 1-1t 2)=(t 1-t 2)·(2-1t 1t 2).因为1≤t 1<t 2，所以t 1-t 2<0，2-1t 1t 2>0，所以f(t 1)<f(t 2).则f(t)=2t+1t在[1，+∞)上为增函数，所以当t=1时，f(t)的最小值为f(1)=3，所以D 正确.故选ABD.11.已知直线x=π8是函数f(x)=sin(2x+ϕ)(0<ϕ<π)的一条对称轴，则( ACD ) A.f(x+π8)是偶函数B.x=3π8是f(x)的一条对称轴C.f(x)在[π8，π2]上单调递减D.y=f(x)与g(x)=sin(2x-π4)的图象关于直线x=π4对称解析:直线x=π8是函数f(x)=sin(2x+ϕ)(0<ϕ<π)的一条对称轴，所以2×π8+ϕ=k π+π2，k ∈Z ，所以ϕ=π4，所以f(x+π8)=sin(2x+π2)=cos 2x ，是偶函数，故A 正确;由2x+π4=k π+π2(k ∈Z)，解得x=kπ2+π8(k ∈Z)，所以f(x)的对称轴方程为x=kπ2+π8(k ∈Z)，而x=3π8不能满足上式，故B 错误;当x ∈[π8，π2]，2x+π4∈[π2，5π4]，此时函数f(x)单调递减，故C 正确;显然，f(x)=sin(2x+π4)与g(x)=sin(2x-π4)的图象关于直线x=π4对称，故D 正确.故选ACD.12.高斯是德国著名的数学家，用其名字命名的“高斯函数”为设 x ∈R ，用[x]表示不超过x 的最大整数，则y=[x]称为高斯函数，例如:[-1.5]=-2，[2.1]=2.已知函数f(x)=2x -11+2x，则关于函数g(x)=[f(x)]的叙述正确的是( BCD ) A.g(x)是奇函数 B.f(x)是奇函数 C.f(x)在R 上是增函数 D.g(x)的值域是{-1，0}解析:因为函数g(x)=[f(x)]，且f(x)=2x -11+2x ，所以g(1)=[f(1)]=0， g(-1)=[f(-1)]=-1，所以g(-1)≠-g(1)，则g(x)不是奇函数，故选项A 错误; 因为f(x)=2x -11+2x，则f(-x)=2-x -11+2-x =1-2x2x +1=-f(x)，所以f(x)为奇函数，故选项B 正确; 因为f(x)=2x -11+2x=1+-22x +1，又y=2x +1在R 上为单调递增函数，则y=-22x +1在R 上为单调递增函数，所以f(x)在R 上为单调递增函数，故选项C 正确; 因为2x >0，则-1<1+-22x +1<1，所以-1<f(x)<1，当-1<f(x)<0时，则g(x)=[f(x)]=-1;当0≤f(x)<1时，则g(x)=[f(x)]=0，所以g(x)∈{-1，0}，则g(x)的值域为{-1，0}，故选项D正确.故选BCD.三、填空题:本题共4小题，每小题5分，共20分.13.已知函数f(x)=(m2+m-1)x m+1是幂函数，且该函数在第一象限是增函数，则m的值是.解析:由函数f(x)=(m2+m-1)x m+1是幂函数，则m2+m-1=1，解得m=-2或m=1;当m=-2时，f(x)=x-1在第一象限内不是增函数，不符合题意;当m=1时，f(x)=x2在第一象限内是增函数，满足题意.所以m的值是1.答案:114.已知函数y=2x，当x>0时，函数值的取值范围构成集合A，函数y=x k，在x∈A时，函数值的取值范围构成集合B，则A∩B=∅的充要条件是.解析:已知函数y=2x，当x>0时，函数值的取值范围构成集合A=(1，+∞)，当x∈(1，+∞)时，函数y=x k∈(0，+∞)，由于A∩B=∅，故x k≤1=x0，故k≤0.故A ∩B= 的充要条件是k ≤0. 答案:k ≤015.已知函数y=f(x)满足f(2)>5，且以(1，1)点为对称中心，写出一个符合条件的函数y= . 解析:因为函数的对称中心为(1，1)，所以不妨设为分式函数f(x)=a x -1+1，因为f(2)>5，所以f(2)=a+1>5，解得a>4，不妨取a=5，即y=5x -1+1.答案:y=5x -1+1(答案不唯一)16.已知f(x)=2sin(2x+π3)，若∃x 1，x 2，x 3∈[0，3π2]，且x 1<x 2<x 3，使得f(x 1)=f(x 2)=f(x 3)，则x 1+x 2+x 3的最小值为，最大值为 .解析:作出f(x)图象如图所示，当f(x)图象与y=√3图象相交时，前三个交点横坐标依次为x 1，x 2，x 3，此时x 1+x 2+x 3最小;x 1+x 2=π12×2=π6，f(π)=2sin(2π+π3)=√3，x 3=π，所以最小值为π6+π=7π6;当f(x)图象与y=-√3图象相交时，交点横坐标依次为x 1，x 2，x 3，此时x 1+x 2+x 3最大，x 1+x 2=7π12×2=7π6，f(3π2)=2sin(3π+π3)=-√3，x 3=3π2，最大值为7π6+3π2=8π3.答案:7π68π3四、解答题:本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)若函数y=lg(√3-2sin x)+√1-x 2的定义域为A. (1)求集合A;(2)当x ∈A 时，求函数y=cos 2x+sin x 的最大值. 解:(1)由题意可得{√3-2sinx >0,1-x 2≥0, 解得-1≤x ≤1，即集合A=[-1，1].(2)y=cos 2x+sin x=-sin 2x+sin x+1，x ∈[-1，1]，令t=sin x ∈[-sin 1，sin 1]，则y=-t 2+t+1=-(t -12)2+54，故当t=12时，函数取得最大值为54.18.(本小题满分12分)某企业欲做一个介绍企业发展史的铭牌，铭牌的截面形状是如图所示的扇形环面(由扇形OAD 挖去扇形OBC 后构成的).已知OA=10，OB= x(0<x<10)，线段BA ，CD 与BC ⏜，AD ⏜的长度之和为30，圆心角为θ弧度.(1)求θ关于x 的函数表达式;(2)记铭牌的截面面积为y ，试问:x 取何值时，y 的值最大?并求出最大值.解:根据题意，可得BC ⏜=x ·θ，AD ⏜=10θ. 又BA+CD+BC⏜+AD ⏜=30，所以10-x+10-x+x ·θ+10θ=30，所以θ=2x+10x+10(0<x<10).(2)y=S 扇形OAD -S 扇形OBC =12θ×102-12θx 2=12θ×(102-x 2)=12θ×(10+x) (10-x)，化简得y=-x 2+5x+50=-(x -52)2+2254.于是，当x=52(满足条件0<x<10)时，y max =2254.所以当x=52时，铭牌的截面面积最大，且最大面积为2254.19.(本小题满分12分) 已知函数f(x)=log 3(3x+1)-12x.若不等式f(x)-12x-a ≥0对x ∈(-∞，0]恒成立，求实数a 的取值范围.解:因为不等式f(x)-12x-a ≥0在区间(-∞，0]上恒成立，即a ≤log 3(3x +1)-x 在区间(-∞，0]上恒成立，令g(x)=log 3(3x +1)-x=log 3(1+13x )，因为x ∈(-∞，0]，所以1+13x ≥2，所以g(x)=log 3(1+13x )≥log 32，所以a ≤log 32，所以a 的取值范围是(-∞，log 32]. 20.(本小题满分12分)已知α∈(0，π2)，β∈(π2，π)，cos β=-13，sin(α+β)=79.(1)求tan β2的值;(2)求sin α的值.解:(1)因为cos β=cos 2β2-sin 2β2=cos 2β2-sin 2β2cos 2β2+sin 2β2=1-tan 2β21+tan 2β2，且cos β=-13，所以1-tan 2β21+tan 2β2=-13，解得tan 2β2=2，因为β∈(π2，π)，所以β2∈(π4，π2)，所以tan β2>0，所以tan β2=√2.(2)因为β∈(π2，π)，cos β=-13，所以sin β=√1-cos 2β=√1-(-13) 2=2√23，又α∈(0，π2)，故α+β∈(π2，3π2)，又sin(α+β)=79，所以cos(α+β)=-√1-sin 2(α+β)=-√1-(79)2=-4√29.所以sin α=sin[(α+β)-β] =sin(α+β)cos β-cos(α+β)sin β =79×(-13)-(-4√29)×2√23=13.21.(本小题满分12分)在①f(x)的图象关于直线x=5π6对称，②f(x)的图象关于点(5π18，0)对称，③f(x)在[-π4，π4]上单调递增，这三个条件中任选一个，补充在下面的问题中，若问题中的正实数a 存在，求出a 的值;若a 不存在，说明理由.已知函数f(x)=4sin(ωx+π6)+a(ω∈N *)的最小正周期不小于π3，且，是否存在正实数a ，使得函数f(x)在[0，π12]上有最大值3?解:由于函数f(x)的最小正周期不小于π3，所以2πω≥π3，所以1≤ω≤6，ω∈N *，若选择①，即f(x)的图象关于直线x=5π6对称，有5π6ω+π6=k π+π2(k ∈Z)，解得ω=65k+25(k ∈Z)，由于1≤ω≤6，ω∈N *，k ∈Z ，所以k=3，ω=4，此时，f(x)=4sin(4x+π6)+a ，由x ∈[0，π12]，得4x+π6∈[π6，π2]，因此当4x+π6=π2，即x=π12时，f(x)取得最大值4+a ，令4+a=3，解得a=-1<0，不符合题意.故不存在正实数a ，使得函数f(x)在[0，π12]上有最大值3.若选择②，即f(x)的图象关于点(5π18，0)对称，则有5π18ω+π6=k π(k ∈Z)，解得ω=185k-35(k ∈Z)，由于1≤ω≤6，ω∈N *，k ∈Z ，所以k=1，ω=3. 此时，f(x)=4sin(3x+π6)+a.由x ∈[0，π12]，得3x+π6∈[π6，5π12]，因此当3x+π6=5π12，即x=π12时，f(x)取得最大值4sin 5π12+a=√6+√2+a ，令√6+√2+a=3，解得a=3-√6-√2<0，不符合题意. 故不存在正实数a ，使得函数f(x)在[0，π12]上有最大值3.若选择③，即f(x)在[-π4，π4]上单调递增，则有{-ωπ4+π6≥2kπ-π2,ωπ4+π6≤2kπ+π2(k ∈Z)，解得{ω≤-8k +83,ω≤8k +43(k ∈Z)，由于1≤ω≤6，ω∈N *，k ∈Z ，所以k=0，ω=1. 此时，f(x)=4sin(x+π6)+a.由x ∈[0，π12]，得x+π6∈[π6，π4]，因此，当x+π6=π4，即x=π12时，f(x)取得最大值2√2+a ，令2√2+a=3，解得a=3-2√2，符合题意.故存在正实数a=3-2√2，使得函数f(x)在[0，π12]上有最大值3.22.(本小题满分12分)设函数f(x)=ka x -a -x (a>0，且a ≠1)是定义域为R 上的奇函数. (1)求k 的值;(2)若f(1)>0，试求不等式f(x 2+2x)+f(x-4)>0的解集;(3)若f(1)=32，且g(x)=a 2x +a -2x -2mf(x)在[1，+∞)上的最小值为-2，求m 的值.解:(1)因为f(x)是定义域为R 上的奇函数，所以f(0)=0，所以k-1=0，所以k=1，经检验k=1符合题意. (2)因为f(1)>0，所以a-1a >0，又a>0，且a ≠1，所以a>1，易知f(x)在R 上单调递增，原不等式化为f(x 2+2x)>f(4-x)，所以x 2+2x>4-x ，即x 2+3x-4>0，所以x>1或x<-4，所以不等式的解集为{x|x>1或x<-4}. (3)因为f(1)=32，所以a-1a =32，即2a 2-3a-2=0，解得a=2或a=-12(舍去)，所以g(x)=22x +2-2x -2m(2x -2-x )=(2x -2-x )2-2m(2x -2-x )+2.令t=f(x)=2x -2-x ，因为x ≥1，所以t ≥f(1)=32，所以g(t)=t 2-2mt+2=(t-m)2+2-m 2，当m ≥32时，当t=m 时，g(t)min =2-m 2=-2，所以m=2，符合题意; 当m<32时，当t=32时，g(t)min =174-3m=-2，解得m=2512>32，舍去.综上可知，m=2.。

人教版高中数学必修4综合测试试题含答案(原创,难度适中)

人教版高中数学必修4综合测试试题含答案(原创,难度适中)高中数学必修4综合测试满分：150分时间：120分钟注意事项：客观题请在答题卡上用2B铅笔填涂，主观题请用黑色水笔书写在答题卡上。

一、选择题：（共12小题，每小题5分，共60分。

）1.sin300°的值为A。

-31 B。

3 C。

22 D。

1/22.角α的终边过点P(4,-3)，则cosα的值为A。

4 B。

-3 C。

2/5 D。

-4/53.cos25°cos35°-sin25°sin35°的值等于A。

3/11 B。

3/4 C。

2/11 D。

-2/114.对于非零向量AB，BC，AC，下列等式中一定不成立的是A。

AB+BC=AC B。

AB-AC=BCC。

AB-BC=BC D。

AB+BC=AC5.下列区间中，使函数y=sinx为增函数的是A。

[0,π] B。

[π,2π] C。

[-π/2,π/2] D。

[-π,0]6.已知tan(α-π/3)=1/√3，则tanα的值为A。

4/3 B。

-3/5 C。

-5/3 D。

-3/47.将函数y=sinx图象上所有的点向左平移π/3个单位长度，再将图象上所有的点的横坐标伸长到原来的2倍（纵坐标不变），则所得图象的函数解析式为A。

y=sin(2x+π/3) B。

y=sin(2x+2π/3)C。

y=sin(2x-π/3) D。

y=sin(2x-2π/3)8.在函数y=sinx、y=sin(2x+π/2)、y=cos(2x+π)中，最小正周期为π的函数的个数为（）A。

1个 B。

2个 C。

3个 D。

4个9.下列命题中，正确的是A。

|a|=|b|→a=b B。

|a|>|b|→a>bC。

|a|=0→a=0 D。

a=b→a∥b10.函数y=Asin(ωx+φ)在一个周期内的图象如右图所示，此函数的解析式为y=2sin(2x-π/3)11.方程sin(πx)=x的解的个数是()A。

(人教版A版2017课标)高中数学必修第一册全册综合测试卷三(附答案)

（人教版A 版2017课标）高中数学必修第一册全册综合测试卷三（附答案）第一章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}21,0,1,2A =--，，{}|1B y y x x A ==-∈，，则下列关系正确的是（）A .AB =B .A B ⊆C .B A ⊆D .A B =∅∩2.已知集合{}2|320A x ax x =-+=中有且只有一个元素，那么实数a 的取值集合是（）A .98⎧⎫⎨⎬⎩⎭B .908⎧⎫⎨⎬⎩⎭，C .{}0D .203⎧⎫⎨⎬⎩⎭， 3.已知函数()()12232x x x f x f x x +⎧⎪-=⎨⎪+⎩，＞，，≤，则()2f 的值等于（）A .4B .3C .2D .无意义4.已知函数()f x 的定义域为R ，则实数k 的取值范围是（）A .()()00-∞+∞，∪，B .[]04，C .[)04，D .()04，5.已知两个函数()f x 和()g x 的定义域和值域都是集合{}123，，，其定义如表所示，则()()f g x 对应的三个值依次为（）A .2，1，3B .1，2，3C .3，2，1D .1，3，26.已知函数()221x f x x =+，则()()()()1111234234f f f f f f f ⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（） A .3B .4C .72D .927.设全集为R ，函数()01x f x +=定义域为M ，则M =R ð（）A .{}|2x x ≥B .{}|21x x x -＜且≠C .{}|21x x x -≥或=D .{}|21x x x -＞或=8.若函数()()221341x x x f x a x a x ⎧-+⎪=⎨-+⎪⎩，＜，，≥满足对任意实数12x x ≠，都有()()12120f x f x x x --＞成立，则实数a 的取值范围是（）A .()1+∞，B .[)13，C .233⎡⎫-⎪⎢⎣⎭， D .()3-∞，9.已知()f x 是奇函数，()g x 是偶函数，且()()112f g -+=，()()114f g +-=，则()1g 等于（） A .4B .3C .2D .110.已知()22f x x ax =-+与()ag x x=在区间[]12，上都是减函数，则a 的取值范围为（）A .()01，B .(]01，C .()()1001-，∪， D .[)(]1001-，∪， 11.已知(){}2min 26f x x x x x =--，，，则()f x 的值域是（）A .(]2-∞，B .(]3-∞，C .[]02，D .[)2+∞，12.已知定义域为R 的函数()f x 在区间()4+∞，上为减函数，且函数()4y f x =+为偶函数，则（） A .()()23f f ＞B .()()25f f ＞C .()()35f f ＞D .()()36f f ＞二、填空题：本大题共4小题，每小题5分，共20分.13.设集合{}24A t =-，，集合{}591B t t =--，，，若9A B ∈∩，则实数t =________.14.)13fx =+，则()f x =________.15.若函数y =的定义域为R ，则a 的取值范围为________. 16.已知函数()y f x =在()()00-∞+∞，∪，上为奇函数，且在()0+∞，上为增函数，()20f -=，则不等式()x f x ⋅＜0的解集为________.三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分10分）已知函数()mf x x x=+，且()13f =. （1）求m ；（2）判断函数()f x 的奇偶性.18.（本小题满分12分）设全集U =R ，{}|13A x x =≤≤，{}|23B x a x a =+＜＜. （1）当1a =时，求()U A B ∩ð；（2）若()U A B B =∩ð，求实数a 的取值范围.19.（本小题满分12分）设函数()()21f x ax bx a b =++，为实数，()()()00.f x x F x f x x ⎧⎪=⎨-⎪⎩，＞，，＜（1）若()10f -=，且对任意实数x 均有()0f x ≥成立，求()F x 的表达式；（2）在（1）的条件下，当[]22x ∈-，时，()()g x f x kx =-是单调函数，求实数k 的取值范围.20.（本小题满分12分）“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度v （单位：千克/年）是养殖密度x （单位：尾/立方米）的函数.当04x ＜≤时，v 的值为2千克/年；当420x ＜≤时，v 是x 的一次函数；当20x ＞时，因缺氧等原因，v 的值为0千克/年. （1）当020x ＜≤时，求v 关于x 的函数表达式.（2）当养殖密度x 为多少时，鱼的年生长量（单位：千克/立方米）可以达到最大？并求出最大值.21.（本小题满分12分）定义在()11-，上的函数()f x 满足()()f x f x -=-，且()()1120f a f a -+-＜.若()f x 是()11-，上的减函数，求实数a 的取值范围.22.（本小题满分12分）已知()f x 是二次函数，()()050f f ==，且()112f -=. （1）求()f x 的解析式；（2）求()f x 在[]0m ，上的最小值()g m ；（3）对（2）中的()g m ，求不等式()()21g t g t -＜的解集.第一章综合测试答案解析一、 1.【答案】C【解析】由集合{}21,0,1,2A =--，，{}|1B y y x x A ==-∈，，得{}101B =-，，.又因为集合{}21,0,1,2A =--，，所以B A ⊆，故选C .2.【答案】B【解析】Q 集合{}2|320A x ax x =-+=中有且只有一个元素，0a ∴=或0980a a ⎧⎨∆=-=⎩≠，，解得0a =或98a =，∴实数a 的取值集合是908⎧⎫⎨⎬⎩⎭，. 3.【答案】C【解析】()()12232x x x f x f x x +⎧⎪-=⎨⎪+⎩Q ，＞，，≤，()()5125252f f +∴===-.故选C .4.【答案】B【解析】()f x Q 的定义域为R ，∴不等式210kx kx ++≥的解集为R .①当0k =时，10≥恒成立，满足题意；②当0k ≠时，2040k k k ⎧⎨∆=-⎩＞，≤，解得04k ＜≤.综上，04k ≤≤.故选B . 5.【答案】A【解析】当1x =时，()11g =，()()()112f g f ==；当2x =时，()23g =，()()()231f g f ==；当3x =时，()32g =，()()()323f g f ==，故选A . 6.【答案】C【解析】因为()221x f x x =+，所以222111111x f x x x ⎛⎫⎪⎛⎫⎝⎭== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭，所以()11f x f x ⎛⎫+= ⎪⎝⎭，故()()()()1111712343234112f f f f f f f ⎛⎫⎛⎫⎛⎫++++++=+= ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭.故选C . 7.【答案】C【解析】要使函数有意义，则120x x +⎧⎨-⎩≠0，＞，得2x ＜且1x -≠，所以{}|21M x x x =＜且≠-，所以{}|2M x x x ==R ≥或-1ð.故选C . 8.【答案】C【解析】Q 对任意实数12x x ≠，都有()()12120f x f x x x --＞成立，()f x ∴在R 上是增函数，()230314121a a a -⎧⎪∴⎨-⨯+-+⨯⎪⎩＞，≥，解得233a -≤＜.故选C . 9.【答案】B【解析】()f x Q 是奇函数，()()11f f -=-. 又()g x Q 是偶函数，()()11g g ∴-=.()()()()112112f g g f -+=∴-=Q ，.① ()()()()114114f g f g +-=∴+=Q ，.②由①②，得()13g =. 10.【答案】B【解析】()()2222f x x ax x a a =-+=--+，其单调递减区间为()a ∞，+，()f x 在区间[]12，上是减函数，则1a ≤.又()ag x x=在区间[]12，上是减函数，则0a ＞.01a ∴＜≤.11.【答案】B【解析】(){}2min 26f x x x x x =--Q ，，，的同一平面直角坐标系中分别作出22y x x =-，6y x =-，y x =的图像，并取其函数值较小的部分，如图所示.则由图像可知函数(){}2min 26f x x x x x =--，，的值域为(]3-∞，，故选B . 12.【答案】D【解析】()4y f x =+Q 为偶函数，()()44f x f x ∴-+=+.令2x =，得()()()()224246f f f f =-+=+=，同理，()()35f f =.又知()f x 在()4+∞，上为减函数，56Q ＜，()()56f f ∴＞.()()23f f ∴＜，()()()265f f f =＜，()()()356f f f =＞.故选D . 二、13.【答案】3-【解析】{}24A t =-Q ，，{}591B t t =--，，，且9A B ∈∩，29t ∴=，解得3t =或3t =-，当3t =时，根据集合元素互异性知不符合题意，舍去；当3t =-时，符合题意.14.【答案】()()2131x x -+≥【解析】由题设1t =，()21x t ∴=-，1t ≥，()()213f t t ∴=-+，()()()2131f x x x ∴=-+≥. 15.【答案】[]19，【解析】Q函数y =的定义域为R ，()()2221101a x a x a ∴-+-++≥恒成立. 当210a -=时，1a =±，当1a =时，不等式恒成立，当1a =-时，无意义；当210a -≠时，()()22210214101a a a a ⎧-⎪⎨∆=---⋅⎪+⎩＞，≤，解得19a ＜≤.综上所述，a 的取值范围为[]19，. 16.【答案】()()2002-，∪，【解析】根据题意画出()f x 的大致图像，如图所示.由图像可知当20x -＜＜或02x ＜＜时，()0x f x ⋅＜. 三、17.【答案】解（1）()13f =Q ，13m ∴+=，2m ∴=. （2）由（1）知，()2f x x x=+，其定义域是{}|0x x x ∈R ≠，，关于原点对称. 又()()22f x x x f x x x ⎛⎫-=--=-+=- ⎪⎝⎭Q ，∴函数()f x 是奇函数. 18.【答案】解（1）当1a =时，{}|24B x x =＜＜.{}|13A x x =Q ≤≤，{}|13U A xx x ∴=＜或＞ð，(){}|34U A B x x ∴=∩＜＜ð.（2）若()U A B B =∩ð，则U B A ⊆ð. ①B =∅时，23a a +≥，则3a ≥；②B ∅≠时，2331a a a +⎧⎨+⎩＜，≤或2323a a a +⎧⎨⎩＜，≥，则2a -≤或332a ≤＜.综上，实数a 的取值范围是(]322⎡⎫-∞-+∞⎪⎢⎣⎭，∪，. 19.【答案】解（1）()10f -=Q ，1b a ∴=+，由()0f x ≥恒成立，知0a ＞且()()22241410b a a a a ∆=-=+-=-≤，1a ∴=，从而()221f x x x =++，()()()221010.x x F x x x ⎧+⎪∴=⎨-+⎪⎩，＞，，＜（2）由（1）可知()221f x x x =++，()()()221g x f x kx x k x ∴=-=+-+. ()g x Q 在[]22-，上是单调函数， 222k -∴--≤或222k--≥，解得2k -≤或6k ≥. 即实数k 的取值范围是(][)26-∞-+∞，∪，. 20.【答案】解（1）由题意得当04x ＜≤时，2v =. 设当420x ＜≤时，v ax b =+，由已知得20042a b a b +=⎧⎨+=⎩，，解得1852a b ⎧=-⎪⎪⎨⎪=⎪⎩，，所以1582v x =-+.故函数20415420.82x v x x ⎧⎪=⎨-+⎪⎩，＜≤，，＜≤ （2）设鱼的年生长量为()f x 千克/立方米，依题意，由（1）可得()220415420.82x x f x x x x ⎧⎪=⎨-+⎪⎩，＜≤，，＜≤当04x ＜≤时，()f x 为增函数，故()()max 4428f x f ==⨯=；当420x ＜≤时，()()2215125108282f x x x x =-+=--+，()()max 1012.5f x f ==.所以当020x ＜≤时，()f x 的最大值为12.5，即当养殖密度x 为10尾/立方米时，鱼的年生长量可以达到最大，最大值为12.5千克/立方米. 21.【答案】解：由()()1120f a f a -+-＜，得()()112f a f a ---＜.()()f x f x -=-Q ，()11x ∈-，， ()()121f a f a ∴--＜. 又()f x Q 是()11-，上的减函数， 1111211121,a a a a --⎧⎪∴--⎨⎪--⎩＜＜，＜＜，＞解得203a ＜＜. 故实数a 的取值范围是203⎛⎫⎪⎝⎭，.22.【答案】解（1）因为()f x 是二次函数，且()()050f f ==，所以设()()()50f x ax x a =-≠. 又因为()1612f a -==，所以2a =，所以()()225210f x x x x x =-=-.（2）由（1）知()f x 的对称轴为52x =，当502m ＜≤时，()f x 在区间[]0m ，上单调递减，所以()f x 的最小值为()2210f m m m =-；当52m ＞时，()f x 在区间502⎡⎤⎢⎥⎣⎦，上单调递减，在区间52m ⎡⎤⎢⎥⎣⎦，上单调递增，所以()f x 的最小值为52522f ⎛⎫=- ⎪⎝⎭.综上所述，()()2min521002255.22m m m f x g m m ⎧-⎪⎪==⎨⎪-⎪⎩，＜≤，，＞（3）因为()()21g t g t -＜，所以210215212t t t t ⎧⎪-⎪-⎨⎪⎪-⎩＞，＜，＜，解得112t ＜＜，即不等式()()21g t g t -＜的解集为1|12t t ⎧⎫⎨⎬⎩⎭＜＜.第二章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列等式一定正确的是（） A .()lg lg lg xy x y =+B .222m n m n ++=C .222m n m n +⋅=D .2ln 2ln x x =2.若函数()12122m y m m x -=+-是幂函数，则m =（）A .1B .3-C .3-或1D .23.下列函数既是增函数，图像又关于原点对称的是（） A .y x x =B .x y e =C .1y x=-D .2log y x =4.函数()ln 3y x =- ）A .[)23，B .[)2+∞，C .()3-∞，D .()23，5.下列各函数中，值域为()0∞，+的是（） A .22xy -= B.y C .21y x x =++D .113x y +=6.已知()x f x a =，()()log 01a g x x a a =＞，且≠，若()()330f g ＜，那么()f x 与()g x 在同一坐标系内的图像可能是（）ABCD7.已知0.2log 2.1a =， 2.10.2b =，0.22.1c =则（） A .c b a ＜＜B .c a b ＜＜C .a b c ＜＜D .a c b ＜＜8.已知()()221122x a x x f x x ⎧-⎪=⎨⎛⎫-⎪ ⎪⎝⎭⎩，≥，，＜是R 上的减函数，则实数a 的取值范围是（）A .()2-∞，B .138⎛⎤-∞ ⎥⎝⎦，C .()02，D .1328⎡⎫⎪⎢⎣⎭， 9.已知函数()y f x =是定义在R 上的偶函数，当0x ≥时，()2x f x e x =+，则()ln 2f -=（） A .12ln 22- B .12ln 22+ C .22ln2-D .22ln2+10.已知函数()()()x xf x x e ae x -=+∈R ，若()f x 是偶函数，记a m =；若()f x 是奇函数，记a n =.则2m n +的值为（） A .0B .1C .2D .1-11.已知实数a ，b 满足等式20172018a b =，则下列关系式不可能成立的是（） A .0a b ＜＜ B .0a b ＜＜ C .0b a ＜＜D .a b =12.已知函数()221222log x mx m x m f x x x m ⎧-++⎪=⎨⎪⎩，≤，，＞，其中01m ＜＜，若存在实数a ，使得关于x 的方程()f x a =恰有三个互异的实数解，则实数m 的取值范围是（）A .104⎛⎫ ⎪⎝⎭，B .102⎛⎫ ⎪⎝⎭，C .114⎛⎫ ⎪⎝⎭，D .112⎛⎫ ⎪⎝⎭，二、填空题：本大题共4小题，每小题5分，共20分.13.满足31164x -⎛⎫⎪⎝⎭＞的x 的取值范围是________.14.若函数()212log 35y x ax =-+在[)1-+∞，上是减函数，则实数a 的取值范围是________.15.如图，矩形ABCD 的三个顶点A ，B ，C分别在函数y x =，12y x =，xy =⎝⎭的图像上，且矩形的边分别平行于两坐标轴.若点A 的纵坐标为2，则点D 的坐标为________.16.定义新运算⊗：当m n ≥时，m n m ⊗=；当m n ＜时，m n n ⊗=.设函数()()()2221log 2xx f x x ⎡⎤⊗-⊗⋅⎣⎦，则函数()f x 在()02，上的值域为________. 三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分10分）计算下列各式的值：（1）7015log 243210.06470.250.58--⎛⎫--++⨯ ⎪⎝⎭；（2）()2235lg5lg2lg5lg20log 25log 4log 9+⨯++⨯⨯.18.（本小题满分12分）已知定义域为R 的单调函数()f x 是奇函数，当0x ＞时，()23x xf x =-. （1）求()f x 的解析式；（2）若对任意的t ∈R ，不等式()()22220f t t f t k -+-＜恒成立，求实数k 的取值范围.19.（本小题满分12分）已知实数x 满足9123270x x -⋅+≤，函数()2log 2xf x =⋅. （1）求实数x 的取值范围；（2）求函数()f x 的最值，并求此时x 的值.20.（本小题满分12分）已知函数()x f x a =，()2x g x a m =+，其中0m ＞，0a ＞且1a ≠.当[]11x ∈-，时，()y f x =的最大值与最小值之和为52. （1）求a 的值；（2）若1a ＞，记函数()()()2h x g x mf x =-，求当[]0x ∈，1时，()h x 的最小值()H m .21.（本小题满分12分）以德国数学家狄利克雷（l805-1859）命名的狄利克雷函数定义如下：对任意的x ∈R ，()10.x D x x ⎧=⎨⎩，为有理数，，为无理数研究这个函数，并回答如下问题：（1）写出函数()D x 的值域；（2）讨论函数()D x 的奇偶性；（3）若()()()212xx D x x f x D x x ⎧-⎪=⎨⎪⎩+，为有理数，+，为无理数，，求()f x 的值域.22.（本小题满分12分）若函数()f x 满足()()21log 011a a f x x a a a x ⎛⎫=⋅- ⎪-⎝⎭＞，且≠. （1）求函数()f x 的解析式，并判断其奇偶性和单调性；（2）当()2x ∈-∞，时，()4f x -的值恒为负数，求a 的取值范围.第二章综合测试答案解析一、 1.【答案】C【解析】对于A ，D ，若x ，y 为非正数，则不正确；对于B ，C ，根据指数幂的运算性质知C 正确，B 错误.故选C . 2.【答案】B【解析】因为函数()12122m y m n x -=+-是幂函数，所以22211m m m +-=且≠，解得3m =-. 3.【答案】A【解析】2200x x y x x x x ⎧⎪==⎨-⎪⎩，≥，，＜为奇函数且是R 上的增函数，图像关于原点对称；x y e =是R上的增函数，无奇偶性；1y x=-为奇函数且在()0-∞，和()0+∞，上单调递增，图像关于原点对称，但是函数在整个定义域上不是增函数；2log y x =在()0+∞，上为增函数，无奇偶性.故选A . 4.【答案】A【解析】函数()ln 3y x =-x 满足条件30240x x -⎧⎨-⎩＞，≥，解得32x x ⎧⎨⎩＜，≥，即23x ≤＜，所以函数的定义域为[)23，，故选A . 5.【答案】A【解析】对于A，222xxy -⎛== ⎝⎭的值域为()0+∞，；对于B ，因为120x -≥，所以21x ≤，0x ≤，y (]0-∞，，所以021x ＜≤，所以0121x -≤＜，所以y 的值域是[)01，；对于C ，2213124y x x x ⎛⎫=++=++ ⎪⎝⎭的值域是34⎡⎫+∞⎪⎢⎣⎭，；对于D ，因为()()1001x ∈-∞+∞+，∪，，所以113x y +=的值域是()()011+∞，∪，. 6.【答案】C【解析】由指数函数和对数函数的单调性知，函数()x f x a =与()()log 01a g x x a a =＞，且≠在()0+∞，上的单调性相同，可排除B ，D .再由关系式()()330f g ⋅＜可排除A ，故选C . 7.【答案】C【解析】 2.100.200.20.2log 2.1log 1000.20.21 2.1 2.1 1.a b c a b c ======∴Q ＜，＜＜，＞＜＜.故选C . 8.【答案】B【解析】由题意得，函数()()221122x a x x f x x ⎧-⎪=⎨⎛⎫-⎪ ⎪⎝⎭⎩，≥，，＜是R 上的减函数，则()2201122,2a a -⎧⎪⎨⎛⎫--⨯⎪⎪⎝⎭⎩＜，≥解得138a ≤，故选B .9.【答案】D【解析】Q 函数()y f x =是定义在R 上的偶函数，且当0x ≥时，()2x f x e x =+，()()ln 2ln 2ln 22ln 222ln 2f f e ∴-==+=+.故选D .10.【答案】B【解析】当()f x 是偶函数时，()()f x f x =-，即()()x x x x x e ae x e ae --+=-⋅+，即()()10x x a e e x -++=.因为上式对任意实数x 都成立，所以1a =-，即1m =-.当()f x 是奇函数时，()()f x f x =--，即()()x x x xx e ae x e ae --+=+，即()()10x x a e e x ---=.因为上式对任意实数x 都成立，所以1a =，即1n =.所以21m n +=.11.【答案】A【解析】分别画出2017x y =，2018x y =的图像如图所示，实数a ，b 满足等式20172018a b =，由图可得0a b ＞＞或0a b ＜＜或0a b ==，而0a b ＜＜不成立.故选A .12.【答案】A【解析】当01m ＜＜时，函数()221222log x mx m x m f x x x m ⎧-++⎪=≤⎨⎪⎩，≤，，＞，的大致图像如图所示.Q 当x m ≤时，()()2222222f x x mx m x m =-++=-+≥，∴要使得关于x 的方程()f x a =有三个不同的根，则12log 2m ＞.又01m ＜＜，解得104m ＜＜.故选A .二、13.【答案】()1-∞，【解析】由题可得，321144x --⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭＞，则32x --＜，解得1x ＜.14.【答案】(]86--，【解析】令()235g x x ax =-+，其图像的对称轴为直线6a x =.依题意，有()1610ag ⎧-⎪⎨⎪-⎩≤，＞，即68.a a -⎧⎨-⎩≤，＞故(]86a ∈--，. 15.【答案】1124⎛⎫ ⎪⎝⎭，【解析】由图像可知，点()2A A x ，在函数y x =的图像上，所以2A x =，2122A x ⎛== ⎝⎭.点()2B B x ，在函数12y x =的图像上，所以122B x =，4B x =.点()4,C C y在函数2x y ⎛= ⎝⎭的图像上，所以4124C y ==⎝⎭.又因为12D A x x ==，14D C y y ==，所以点D 的坐标为1124⎛⎫ ⎪⎝⎭，. 16.【答案】()112，【解析】根据题意，当22x ≥，即1x ≥时，222x x ⊗=；当22x ＜，即1x ＜时，222x ⊗=.当2log 1x ≤，即02x ＜≤时，21log 1x ⊗=；当21log x ＜，即2x ＞时，221log log x x ⊗=. ()()2220122122log 2 2.x x x x xx f x x x x ⎧⎪⎪∴=-⎨⎪-⋅⎪⎩，＜＜，，≤≤，，＞ ∴①当01x ＜＜时，()2x f x =是增函数，()12f x ∴＜＜； ②当12x ≤＜，()221122224xxx f x ⎛⎫=-=-- ⎪⎝⎭，1222 4.x x ∴Q ≤＜，≤＜()221111242424f x ⎛⎫⎛⎫∴---- ⎪ ⎪⎝⎭⎝⎭≤＜，即()212f x ≤＜.综上，()f x 在()02，上的值域为()112，. 三、17.【答案】解（1）70515log 244321510.06470.250.51224822--⎛⎫⎛⎫--++⨯=-++⨯= ⎪ ⎪⎝⎭⎝⎭.（2）()()22352lg52lg 22lg3lg5lg 2lg5lg 20log 25log 4log 9lg5lg5lg 2lg 21lg 2lg3lg5+⨯++⨯⨯=++++⨯⨯11810=++=.18.【答案】解（1）Q 定义域为R 的函数()f x 是奇函数，()00f ∴=.Q 当0x ＜时，0x -＞，()23x xf x --∴-=-. 又Q 函数()f x 是奇函数，()()f x f x ∴-=-，()23x xf x -∴=+. 综上所述，()2030020.3xx x x f x x xx -⎧-⎪⎪==⎨⎪⎪+⎩，＞，，，，＜（2）()()51003f f -==Q ＞，且()f x 为R 上的单调函数，()f x ∴在R 上单调递减.由()()22220f t t f t k -+-＜得()()2222f t t f t k ---＜. ()f x Q 是奇函数，()()2222f t t f k t ∴--＜.又()f x Q 是减函数，2222t t k t ∴--＞，即2320t t k --＞对任意t ∈R 恒成立，4120k ∴∆=+＜，解得13k -＜，即实数k 的取值范围为13⎛⎫-∞- ⎪⎝⎭，. 19.【答案】解（1）由9123270x x -⋅+≤，得()23123270xx -⋅+≤，即()()33390x x --≤，所以339x ≤≤，所以12x ≤≤，满足02x＞0.所以实数x 的取值范围为[]12，.（2）()()()()2222222231log log 1log 2log 3log 2log 224x f x x x x x x ⎛⎫=⋅=--=-+=-- ⎪⎝⎭.因为12x ≤≤，所以20log 1x ≤≤.所以2log 1x =，即2x =时，()min 0f x =；当2log 0x =，即1x =时，()max 2f x =.故函数()f x 的最小值为0，此时2x =，最大值为2，此时1x =.20.【答案】解（1）()f x Q 在[]11-，上为单调函数，()f x ∴的最大值与最小值之和为152a a -+=，2a ∴=或12a =. （2）1a Q ＞，2a ∴=.()2222x x h x m m =+-⋅，即()()2222xx h x m m =-⋅+.令2x t =，则()h x 可转化为()22k t t mt m =-+，其图像对称轴为直线t m =. []01x ∈Q ，，[]12t ∴∈，，∴当01m ＜＜时，()()11H m k m ==-+；当12m ≤≤时，()()2H m k m m m ==-+；当2m ＞时，()()234H m k m ==-+.综上所述，()21011234 2.m m H m m m m m m -+⎧⎪=-+⎨⎪-+⎩，＜＜，，≤≤，，＞21.【答案】解（1）函数()D x 的值域为{}01，.（2）当x 为有理数时，则x -为无理数，则()()1D x D x -==；当x 为无理数时，则为x -为无理数，则()()0D x D x -==. 故当x ∈R 时，()()D x D x -=，所以函数()D x 为偶函数.（3）由()D x 的定义知，()22xx x f x x ⎧⎪=⎨⎪⎩，为有理数，，为无理数.即当x ∈R 时，()2x f x =.故()f x 的值域为()0+∞，.22.【答案】解（1）令log a x t =，则t x a =，()()21t t af t a a a -∴=--. ()()()21x x af x a a x a -∴=-∈-R .()()()()2211x x x x a af x a a a a f x a a ---=-=--=---Q ，()f x ∴为奇函数.当1a ＞时，xy a =为增函数，xy a -=-为增函数，且2201a a -＞，()f x ∴为增函数.当01a ＜＜时，x y a =为减函数，xy a -=-为减函数，且2201a a -＜，()f x ∴为增函数.()f x ∴在R 上为增函数.（2）()f x Q 是R 上的增函数，()4y f x ∴=-也是R 上的增函数.由2x ＜，得()()2f x f ＜，要使()4f x -在()2-∞，上恒为负数，只需()240f -≤，即()22241a a a a ---≤. 422141a a a a-∴⋅-≤，214a a ∴+≤，2410a a ∴-+≤，22a ∴≤.又1a Q ≠，a ∴的取值范围为)(21,2⎡⎣.第三章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.某同学用二分法求方程338=0x x +-在()12x ∈，内近似解的过程中，设()=338x f x x +-，且计算()10f ＜，()20f ＞，()1.50f ＞，则该同学在第二次应计算的函数值为（） A .()0.5fB .()1.125fC .()1.25fD .()1.75f2.函数()22=log f x x x +的零点所在的区间为（）A .1142⎛⎫ ⎪⎝⎭，B .112⎛⎫ ⎪⎝⎭，C .(D .)3.有一组实验数据如表所示：下列所给函数模型较适合的是（） A .()=log 1a y x a ＞B .()=1y ax b a +＞C .()2=0y ax b a +＞D .()=log 1a y x b a +＞4.根据表中的数据，可以判定方程x 的一个根所在的区间为（）A .()10-，B .()01，C .()12，D .()23，5.某家具的标价为132元，若降价以九折出售（即优惠10％），仍可获利10％（相对进货价），则该家具的进货价是（） A .108元B .105元C .106元D .118元6.有一个盛水的容器，由悬在它上空的一根水管匀速向容器内注水，直至把容器注满.在注水过程中，时刻t 与水面高度y 的函数关系如图所示，图中PQ 为一线段，则与之对应的容器的形状是图中的（）AB CD7.已知()()()=2f x x a x b ---，并且α，β是函数()f x 的两个零点，则实数a ，b ，α，β的大小关系可能是（）A .a b αβ＜＜＜B .a b αβ＜＜＜C .a b αβ＜＜＜D .a b αβ＜＜＜8.函数()2230=2ln 0x x x f x x x ⎧+-⎨-+⎩，≤，，＞的零点个数为（）A .0B .1C .2D .39.已知函数()231=24log f x x x x-+++，若()113x ∈，，()23x ∈+∞，，则（） A.()10f x ＞，()20f x ＜ B.()10f x ＜，()20f x ＞ C.()10f x ＜，()20f x ＜D.()10f x ＞，()20f x ＞10.如图所示，ABC △为等腰直角三角形，直线l 与AB 相交且l AB ⊥，直线l 截这个三角形所得的位于直线右方的图形面积为y ，点A 到直线l 的距离为x ，则()=y f x 的图像大致为四个选项中的（）AB CD11.设某公司原有员工100人从事产品A 的生产，平均每人每年创造产值t 万元（t 为正常数）.公司决定从原有员工中分流()0100x x ＜＜人去进行新开发的产品B 的生产.分流后，继续从事产品A 生产的员工平均每人每年创造产值在原有的基础上增长了1.2x ％.若要保证产品A 的年产值不减少，则最多能分流的人数是（）A .15 B .16 C .17 D .18 12.已知函数()2=e x xf x --（e 为自然对数的底数），则方程()21=0f x -的实数根的个数为（） A .1B .2C .3D .4二、填空题：本大题共4小题，每小题5分，共20分.13.用二分法求图像连续不断的函数()f x 在区间[]15，上的近似解，验证()()150f f ⋅＜，给定精确度=0.01ε，取区间()15，的中点115==32x +，计算得()()110f f x ⋅＜，()()150f x f ⋅＞，则此时零点0x ∈________.（填区间）14.已知函数()2=log 2x f x x m +-有唯一的零点，若它的零点在区间()12，内，则实数m 的取值范围是________.15.已知关于x 的方程210=x a -有两个不同的实根1x ，2x ，且21=2x x ，则实数=a ________. 16.某市出租车收费标准如下：起步价为8元，起步里程为3km （不超过3km 按起步价付费）；超过3km 但不超过8km 时，超过部分按每千米2.15元收费；超过8km 时，超过部分按每千米2.85元收费.另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元，则此次出租车行驶的路程为________km .三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分10分）某公司制定了一个激励销售人员的奖励方案：当销售利润不超过10万元时，按销售利润的16％进行奖励；当销售利润超过10万元时，若超出A 万元，则超出部分按()52log 1A +万元进行奖励.记奖金为y （单位：万元），销售利润为x （单位：万元）.（1）写出该公司激励销售人员的奖励方案的函数模型.（2）如果业务员老张获得5.6万元的奖金，那么他的销售利润是多少万元？18.（本小题满分12分）已知函数()=211f x x x --+. （1）请在所给的平面直角坐标系中画出函数()f x 的图像.（2）根据函数()f x 的图像回答下列问题：（回答下述3个小题都只需直接写出结果，不需给出演算步骤）①求函数()f x 的单调区间；②求函数()f x 的值域；③求关于x 的方程()=2f x 在区间[]02，上解的个数.19.（本小题满分12分）已知函数()=e 1x f x -，()3=1exg x +.（1）求函数()g x 的值域；（2）求满足方程()()=0f x g x -的x 的值.20.（本小题满分12分）《污水综合排放标准》规定：污水排放企业进排污口的污水pH 值正常范围为[)69，.某化工企业对本单位污水出水口的pH 值进行全天24小时检测，根据统计资料发现pH 值的大小y 与检测时间点x 之间的函数图像如图所示，AB ，CD 为两条直线段，曲线BC 为函数y b 图像的一部分，其中()08A ，，()46B ，，()2010C ，，()248D ，.（1）请写出pH 值的大小y 与检测时间点x 之间的函数解析式；（2）试求该化工企业在一天内排放pH 值超标污水的时长.21.（本小题满分12分）已知函数()2=283f x x x m -++为R 上的连续函数.（1）若=4m -，试判断()=0f x 在()11-，上是否有根存在.若没有，请说明理由；若有，请在精确度为0.2（即根所在区间长度小于0.2）的条件下，用二分法求出使这个根0x 存在的区间.（2）若函数()f x 在区间[]11-，上存在零点，求实数m 的取值范围.22.（本小题满分12分）已知函数()()2=log 421x x f x a a +⋅++，x ∈R . （1）若=1a ，求方程()=3f x 的解集；（2）若方程()=f x x 有两个不同的实数根，求实数a 的取值范围.第三章综合测试答案解析一、 1.【答案】C【解析】()10f Q ＜，()20f ＞，()1.50f ＞，∴在区间()11.5，内函数()=338x f x x +-存在一个零点，因此在第二次应计算的函数值所对应的x 值为1 1.5=1.252+，故选C . 2.【答案】B【解析】Q 函数()22=log f x x x +在0x ＞时是连续单调递增函数，且()21=1log 1=10f +＞，21113=log =02424f ⎛⎫+- ⎪⎝⎭＜，()1102ff ⎛⎫∴⋅ ⎪⎝⎭＜.∴函数()22=log f x x x +的零点所的在区间是112⎛⎫ ⎪⎝⎭，. 3.【答案】C【解析】由所给数据可知y 随x 的增大而增大，且增长速度越来越快，而A ，D 中的函数增长速度越来越慢，B 中的函数增长速度保持不变，故选C . 4.【答案】C【解析】设()()=2xf x e x -+，则由题设知()1=0.280f -＜，()2=3.390f ＞，故方程2=0x e x --的一个根在区间()12，内.故选C . 5.【答案】A【解析】由题意，132元打9折，售价为()1320.9=118.8⨯元.因为这个价格相对进货价，获利10％，也就是说它是进货价的110％，所以进货价为()110118.8=108÷％元，故选A . 6.【答案】B【解析】由题中函数图像知，水面高度y 上升的速度先是由慢到快，后来速度保持不变，结合容器形状知选B . 7.【答案】C【解析】αQ ，β是函数()f x 的两个零点，()()==0f f αβ∴.又()()==20f a f b -Q ＜，结合二次函数的图像（如图所示）可知a ，b 必在α，β之间.故选C .8.【答案】C【解析】当0x ≤时，令223=0x x +-，得=3x -；当0x ＞时，令2ln =0x -+，得2=e x .所以函数有2个零点.故选C . 9.【答案】A【解析】()()23=15log f x x x --+-Q 在()1+∞，上单调递减，且()3=0f ，()10f x ∴＞，()20f x ＜，故选A .10.【答案】C【解析】设=AB a ，则22221111==2222y a x x a --+，其图像为抛物线的一段，开口向下，顶点在y 轴上方.故选C . 11.【答案】B【解析】由题意，分流前产品A 的年产值为100t 万元，分流x 人后，产品A 的年产值为()()1001 1.2x x t -+％万元.由题意，得()()01001001 1.2100x x x x t t ∈⎧⎪⎨-+⎪⎩N ＜＜，≥，，％解得5003x ＜≤，x ∈N ，所以x 的最大值为16.故选B . 12.【答案】B【解析】由函数()2=ex xf x --，可知方程()21=0f x -，即()1=2f x ，即21e =2x x --，整理可得2=ln2x x ---，即2ln 2=0x x -+或2ln 2=0x x --.在方程2ln 2=0x x -+中，1=14ln 20∆-＜，方程无实数解；在方程2ln 2=0x x --中，2=14ln 20∆+＞，方程有2个不等的实数解.综上可得，方程()21=0f x -的实数根的个数为2.故选B .二、13.【答案】()13，【解析】由()()150f f ⋅＜，()()110f f x ⋅＜及()()150f x f ⋅＞可知()1f 与()1f x 异号，()1f x 与()5f 同号，则()011x x ∈，即()013x ∈，. 14.【答案】()25，【解析】由题意得()f x 在()0+∞，上单调递增，且()()120f f ⋅＜，即()()250m m --＜，解得25m ＜＜. 15.【答案】6【解析】由210=x a -得2=10x a ±，由题设知12=10x a -，22=10x a +.因为21=2x x ，所以()211222=2=2x x x ，所以()210=10a a -+，解得=15a 或=6a .因为100a -＞，所以=15a 不合题意，舍去，所以=6a . 16.【答案】9【解析】设乘客每次乘坐出租车需付费用为()f x 元，则由题意得()(]()(]()()8103=93 2.153895 2.158 2.858.x f x x x x x ⎧+∈⎪+-∈⎨⎪++-∈+∞⎩⨯⨯⨯，，，，，，，，令()=22.6f x ，显然()()95 2.158 2.85=22.68x x ⨯⨯++-＞，解得=9x . 三、17.【答案】（1）由题意得()50.16010=1.62log 910.x x y x x ⎧⎪⎨+-⎪⎩，＜≤，，＞（2）由(]010x ∈，，0.16 1.6x ≤，而=5.6y 可知，10x ＞. ()51.62log 9=5.6x ∴+-，解得=34x .∴老张的销售利润是34万元.18.【答案】（1）当10x -≥，即1x ≥时，()()=211=1f x x x x --+-；当10x -＜，即1x ＜时，()()=211=33f x x x x --+-.()f x 的图像如图所示.（2）①函数()f x 的单调递增区间为[)1+∞，；函数()f x 的单调递减区间为(]1-∞，. ②函数()f x 的值域为[)0+∞，. ③方程()=2f x 在区间[]02，上解的个数为1. 19.【答案】（1）()31=1=31e e x x g x ⎛⎫++ ⎪⎝⎭，因为0x ≥，e 1x≥，所以101e x⎛⎫ ⎪⎝⎭＜≤，1033e x⎛⎫⎪⎝⎭＜≤，即()14g x ＜≤，故()g x 的值域是(]14，. （2）由()()=0f x g x -，得3e 2=0ex x--.当0x ≤时，方程无解；当0x ＞时，3e 2=0ex x--，整理得()2e 2e 3=0x x --，即()()e 1e 3=0x x+-.因为e 0x ＞，所以e =3x ，即=ln3x . 故满足方程()()=0f x g x -的x 的值为ln3.20.【答案】（1）()08A Q ，，()46B ，，∴线段AB 的方程是()1=8042y x x -+≤≤.将()46B ，，()2010C ，的坐标代入y b ，得b b ⎧⎪⎨⎪⎩，，解得=4=6.a b -⎧⎨⎩，故()6420y x +≤≤.()2010C Q ，，()248D ，，∴线段CD 的方程是()1=2020242y x x -+≤≤.综上，y 与x之间的函数解析式为18042=642012020242.x x y x x x ⎧-+⎪⎪-+⎪⎩，≤≤，，≤≤，，≤≤（2）由()08A ，，()46B ，知在AB 段排放污水的pH 值不超标；在BC6=9，解得=13x ，故[)1320x ∈，时排放污水的pH 值超标，时长是()2013=7-小时；在CD 段，令120=92x -+，解得=22x ，故[]2022x ∈，时排放污水的pH 值超标，时长是()2220=2-小时.因此该化工企业在一天内排放pH 值超标污水9小时.21.【答案】（1）当=4m -时，()=0f x ，即()2=281=0f x x x --. 可以求出()1=9f -，()1=7f -，则()()110f f -⋅＜.又()f x 为R 上的连续函数，()=0f x ∴在()11-，上必有根存在.取中点0，计算得()0=10f -＜，()()100f f -⋅＜，∴根()010x ∈-，，取其中点12-，计算得17=022f ⎛⎫- ⎪⎝⎭＞，∴根0102x ⎛⎫∈- ⎪⎝⎭，，取其中点14-，计算得19=048f ⎛⎫- ⎪⎝⎭＞， ∴根0104x ⎛⎫∈- ⎪⎝⎭，，取其中点18-，计算得11=0832f ⎛⎫- ⎪⎝⎭＞， ∴根0108x ⎛⎫∈- ⎪⎝⎭，，区间长度11=0.285＜，符合要求.故符合要求的根0x 存在的区间为108⎛⎫- ⎪⎝⎭，.（2）()2=283f x x x m -++为开口向上的抛物线，对称轴为8==222x ⨯--， ∴在区间[]11-，上，函数()f x 单调递减.又()f x 在区间[]11-，上存在零点，只可能()()1010f f ⎧-⎪⎨⎪⎩≥，≤，即 28302830m m +++⎧⎨-++⎩≥，≤，解得133m -≤≤. 故所求实数m 的取值范围是133m -≤≤.22.【答案】（1）当=1a 时，()()2=log 422x xf x ++.由()=3f x ，得3422=2x x ++，所以426=0x x +-，因此()()2322=0x x +-，解得=1x .所以方程()=3f x 的解集为{}1.（2）方程()2log 421=x xa a x +⋅++有两个不同的实数根，即421=2x x x a a +⋅++有两个不同的实数根.设=2x t ，则()211=0t a t a +-++在()0+∞，上有两个不同的解.令()()2=11g t t a t a +-++，由已知可得()()()200102=1410g a a a ⎧⎪-⎪-⎨⎪⎪∆--+⎩＞，＞，＞，解得13a --＜＜故实数a 的取值范围为(13--，.第四章综合测试一、单项选择题1.式子）ABC .D .2.函数()lg 3f x x x =+-的零点所在区间为（） A .(2,3)B .(3,4)C .(1,2)D .(0,1)3.设lg 2a =，lg3b =，则12log 5=（） A .12aa b -+ B .12aa b-+ C .12aa b++ D .12aa b++ 4. 已知2log 0.1a =，0.12b =，110.2c =，则a ，b ，c 的大小关系是（） A .a b c ＜＜B .b c a ＜＜C .c a b ＜＜D .a cb ＜＜5.函数1()(0,1)x f x a a a a=-≠＞的图象可能是（）A .B .C .D .6.已知函数2,0()21,0x a x f x x x ⎧-≤=⎨->⎩，a R ∈，若函数()f x 在R 上有两个零点，则a 的取值范围是（） A .(,1)-∞-B .(,1]-∞-C .[1,0)-D .(0,1]7.若()2()lg 21f x x ax a =-++在区间(,1]-∞上单调递减，则a 的取值范围为（）A .[1,2)B .[1,2]C .[1,)+∞D .[2,)+∞8.已知函数()|lg |f x x =。

人教版高中数学选择性必修第一册-综合检测卷(含解析)

人教版高中数学选择性必修第一册综合检测卷（原卷版）[时间：120分钟满分：150分]一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若直线过点(1，3)，(4，3＋3)，则此直线的倾斜角是()A.π6B.π4C.π3D.2π32．(2019·北京，理)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，则()A ．a 2＝2b 2B ．3a 2＝4b 2C ．a ＝2bD ．3a ＝4b3.如图，在三棱锥O －ABC 中，D 是棱AC 的中点，若OA →＝a ，OB →＝b ，OC →＝c ，则BD →＝()A.12a －b ＋12c B ．a ＋b －c C ．a －b ＋cD ．－12a ＋b －12c4．直线y ＝x －1被抛物线y 2＝4x 截得的线段AB 的中点坐标是()A ．(2，6)B ．(3，2)C ．(6，4)D ．(4，6)5．已知正四面体ABCD 的棱长为a ，点E ，F 分别是BC ，AD 的中点，则AE →·AF →的值为()A ．a 2 B.14a 2C.12a 2 D.34a 26．已知圆C 的半径为2，圆心在x 轴的正半轴上，直线3x ＋4y ＋4＝0与圆C 相切，则圆C 的方程为()A ．x 2＋y 2－2x －3＝0B ．x 2＋y 2＋4x ＝0C ．x 2＋y 2＋2x －3＝0D ．x 2＋y 2－4x ＝07.四棱锥P －ABCD 中，底面ABCD 为直角梯形，AB ⊥AD ，BC ∥AD ，且AB ＝BC ＝2，AD ＝3，PA ⊥平面ABCD 且PA ＝2，则PB 与平面PCD 所成角的正弦值为()A.427B.77C.33D.638．(2019·课标全国Ⅱ)设F 为双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2＋y 2＝a 2交于P ，Q 两点．若|PQ |＝|OF |，则C 的离心率为()A.2B.3C ．2 D.5二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项是符合题目要求的，全部选对的得5分，部分选对的得3分，有选错的得0分)9．下列说法正确的是()A ．在两坐标轴上截距相等的直线可以用方程x a ＋ya＝1表示B ．存在实数m ，使得方程x ＋my －2＝0能表示平行于y 轴的直线C ．经过点P (1，1)，倾斜角为θ的直线方程为y －1＝tan θ(x －1)D ．点(0，2)关于直线y ＝x ＋1的对称点为(1，1)10．在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是A 1D 1和C 1D 1的中点，则下列结论正确的是()A ．A 1C 1∥平面CEFB ．B 1D ⊥平面CEF C.CE →＝12DA →＋DD 1→－DC→D ．若正方体ABCD －A 1B 1C 1D 1边长为2，点B 1到平面CEF 的距离为111．已知P 是椭圆C ：x 26＋y 2＝1上的动点，Q 是圆D ：(x ＋1)2＋y 2＝15上的动点，则()A ．C 的焦距为5B ．C 的离心率为306C ．圆D 在C 的内部D ．|PQ |的最小值为25512．已知动点P 到两定点M (－2，0)，N (2，0)的距离乘积为常数16，其轨迹为C ，则()A ．C 一定经过原点B ．C 关于x 轴、y 轴对称C ．△MPN 的面积的最大值为43D ．C 在一个面积为64的矩形内三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中的横线上)13．在四棱锥P －ABCD 中，ABCD 为平行四边形，AC 与BD 交于O ，G 为BD 上一点，BG ＝2GD ，PA →＝a ，PB →＝b ，PC →＝c ，试用基底{a ，b ，c }表示向量PG →＝________．14．已知点P 是圆C ：x 2＋y 2＝4上的动点，点A (4，2)，则线段AP 中点M 的轨迹方程是________________；点M 的轨迹与圆C 相交，则过交点的直线方程是________．(本题第一空2分，第二空3分)15．已知点F2为双曲线C：x2a2－y2b2＝1(a>0，b>0)的右焦点，直线y＝kx交双曲线C于A，B两点，若∠AF2B＝2π3，S△AF2B＝23，则双曲线C的虚轴长为________．16．已知椭圆x2a2＋y2b2＝1(a>b>0)的右焦点为F1(1，0)，离心率为e.设A，B为椭圆上关于原点对称的两点，AF1的中点为M，BF1的中点为N，原点O在以线段MN为直径的圆上．设直线AB的斜率为k，若0<k≤3，则e的取值范围为________．四、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤) 17．(10分)已知三角形的顶点A(2，3)，B(0，－1)，C(－2，1)．(1)求直线AC的方程；(2)从①，②这两个问题中选择一个作答．①求点B关于直线AC的对称点D的坐标．②若直线l过点B且与直线AC交于点E，|BE|＝3，求直线l的方程．18．(12分)已知圆C经过三点O(0，0)，A(1，3)，B(4，0)．(1)求圆C的方程；(2)求过点P(3，6)且被圆C截得弦长为4的直线的方程．19．(12分)(2019·课标全国Ⅱ，文)已知F1，F2是椭圆C：x2a2＋y2b2＝1(a>0，b>0)的两个焦点，P为C上的点，O为坐标原点．(1)若△POF2为等边三角形，求C的离心率；(2)如果存在点P，使得PF1⊥PF2，且△F1PF2的面积等于16，求b的值和a的取值范围．20.(12分)如图，在四棱锥P－ABCD中，平面PCD⊥平面ABCD，且△PCD是边长为2的等边三角形，四边形ABCD是矩形，BC＝22，M为BC的中点．(1)求证：AM⊥PM；(2)求二面角P－AM－D的大小；(3)求点D到平面AMP的距离．21．(12分)如图，三棱柱ABC－A1B1C1中，AB＝AC＝AA1＝BC1＝2，∠AA1C1＝60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D.(1)求证：BD⊥平面AA1C1；(2)设点E是直线B1C1上一点，且DE∥平面AA1B1B，求平面EBD与平面ABC1夹角的余弦值．22．(12分)已知定点F(1，0)，动点P在y轴上运动，过点P作PM交x轴于点M，并延长MP 到点N ，且PM →·PF →＝0，|PM →|＝|PN →|.(1)求动点N 的轨迹方程；(2)直线l 与动点N 的轨迹交于A ，B 两点，若OA →·OB →＝－4，且46≤|AB →|≤430，求直线l 的斜率k 的取值范围．1．若椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，则双曲线x 2a 2－y 2b 2＝1的离心率为()A.54B.52C.32D.542．已知四面体顶点A (2，3，1)，B (4，1，－2)，C (6，3，7)和D (－5，－4，8)，则顶点D 到平面ABC 的距离为()A ．8B ．9C ．10D ．113.如图，在四棱锥S －ABCD 中，底面ABCD 是边长为1的正方形，SA ＝SB ＝SC ＝SD ＝2.下列结论中正确的是()A.SA →＋SB →＋SC →＋SD →＝0B.SA →－SB →＋SC →－SD →＝0C.SA →·SB →＋SC →·SD →＝0D.SA →·SC →＝04．已知A 是双曲线E ：x 2a 2－y 2b 2＝1(a >0，b >0)的左顶点，F 是抛物线C ：y 2＝－8ax 的焦点．若在双曲线的渐近线上存在点P ，使得AP →⊥FP →，则E 的离心率的取值范围是()A ．(1，2)，324D ．(2，＋∞)5.如图，在正四棱锥P －ABCD 中，PA ＝AB ，点M 为PA 的中点，BD →＝λBN →.若MN ⊥AD ，则实数λ为()A ．2B ．3C ．4D ．56．已知椭圆C ：x 24＋y 23＝1，M ，N 是坐标平面内的两点，且M 与椭圆C 的焦点不重合．若M 关于椭圆C 的左、右焦点的对称点分别为A ，B ，线段MN 的中点在椭圆C 上，则|AN |＋|BN |＝()A ．4B ．8C ．12D ．167．在平面直角坐标系xOy 中，已知点A (0，－2)，点B (1，－1)，P 为圆x 2＋y 2＝2上一动点(异于点B )，则|PB ||PA |的最大值是()A ．2B ．4C.2D ．228．【多选题】若{a ，b ，c }为空间的一个基底，则()A ．b ＋c ，b －c ，a 共面B ．b ＋c ，b －c ，2b 共面C ．b ＋c ，a ，a ＋b ＋c 共面D ．a ＋c ，a －2c ，c 共面9.【多选题】如图，在长方体ABCD －A 1B 1C 1D 中，AB ＝3AD ＝3AA 1＝3，点P 为线段A 1C 上的动点，则下列结论正确的是()A ．当A 1C →＝2A 1P →时，B 1，P ，D 三点共线B ．当AP →⊥A 1C →时，AP →⊥D 1P→C ．当A 1C →＝3A 1P →时，D 1P ∥平面BDC 1D ．当A 1C →＝5A 1P →时，A 1C ⊥平面D 1AP10．【多选题】已知抛物线E ：y 2＝4x 的焦点为F ，准线为l ，过F 的直线与E 交于A ，B 两点，分别过A ，B 作l 的垂线，垂足为C ，D ，且|AF |＝3|BF |，M 为AB 中点，则下列结论正确的是()A ．∠CFD ＝90°B ．△CMD 为等腰直角三角形C ．直线AB 的斜率为±3D ．△AOB 的面积为411．【多选题】a ，b 为空间两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以AC 为旋转轴旋转，则下列结论正确的是()A ．直线AB 与a 所成角的最小值为π4B ．直线AB 与a 所成角的最大值为π3C ．当直线AB 与a 所成的角为π3时，AB 与b 所成的角为π6D ．当直线AB 与a 所成的角为π3时，AB 与b 所成的角为π312．【多选题】古希腊著名数学家阿波罗尼奥斯发现：平面内到两个定点A，B的距离之比为定值λ(λ≠1)的点的轨迹是圆，此圆被称为“阿波罗尼斯圆”．在平面直角坐标系xOy中，A(－2，0)，B(4，0)，点P满足|PA||PB|＝12.设点P的轨迹为C，下列结论正确的是()A．轨迹C的方程为(x＋4)2＋y2＝9B．在x轴上存在异于A，B的两点D，E使得|PD||PE|＝1 2C．当A，B，P三点不共线时，射线PO是∠APB的平分线D．在C上存在点M，使得|MO|＝2|MA|13．已知直线l：mx－y＝1，若直线l与直线x－my－1＝0平行，则实数m的值为________，动直线l被圆C：x2＋y2＋2x－24＝0截得弦长的最小值为________．14．已知M(－2，0)，N(2，0)，点P(x，y)为坐标平面内的动点，满足|MN→|·|MP→|＋MN→·NP→＝0，则动点P的轨迹方程为________．15．已知直线l：4x－3y＋6＝0，抛物线C：y2＝4x上一动点P到直线l与到y轴距离之和的最小值为________，P到直线l距离的最小值为________．16．已知直线l：y＝－x＋1与椭圆x2a2＋y2b2＝1(a>b>0)相交于A，B两点，且线段AB的中点为(1)求此椭圆的离心率；(2)若椭圆的右焦点关于直线l的对称点在圆x2＋y2＝5上，求此椭圆的方程．17.如图所示，该几何体是由一个直三棱柱ADE－BCF和一个正四棱锥P－ABCD组合而成的，AD⊥AF，AE＝AD＝2.(1)证明：平面PAD⊥平面ABFE；(2)求正四棱锥P－ABCD的高h，使得二面角C－AF－P的余弦值是22318.如图，在直三棱柱ABC－A1B1C1中，AB＝1，AC＝AA1＝3，∠ABC＝60°.(1)证明：AB⊥A1C；(2)求二面角A－A1C－B的正切值大小．19.如图，直四棱柱ABCD－A1B1C1D1的高为3，底面是边长为4且∠DAB＝60°的菱形，AC ∩BD＝O，A1C1∩B1D1＝O1，E是O1A的中点．(1)求二面角O1－BC－D的大小；(2)求点E到平面O1BC的距离．20．已知圆C：x2＋y2＋2x－4y＋3＝0.(1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程；(2)从圆C外一点P(x1，y1)向该圆引一条切线，切点为M，O为坐标原点，若|PM|＝|PO|，求|PM|的最小值及使得|PM|取得最小值的点P的坐标．21．已知过点A(0，1)且斜率为k的直线l与圆C：(x－2)2＋(y－3)2＝1交于M，N两点．(1)求k的取值范围；(2)若OM→·ON→＝12，其中O为坐标原点，求△OMN的面积．22.如图，在平面直角坐标系xOy中，椭圆C：x2a2＋y2b2＝1(a>b>0)的短轴长为2，椭圆C上的点到右焦点距离的最大值为2＋ 3.过点P(m，0)作斜率为k的直线l交椭圆C于A，B两点，其中m>0，k>0，D是线段AB的中点，直线OD交椭圆C于M，N两点．(1)求椭圆C的标准方程；(2)若m＝1，OM→＋3OD→＝0，求k的值；(3)若存在直线l，使得四边形OANB为平行四边形，求m的取值范围．人教版高中数学选择性必修第一册综合检测卷（解析版）[时间：120分钟满分：150分]一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若直线过点(1，3)，(4，3＋3)，则此直线的倾斜角是()A.π6B.π4C.π3D.2π3答案A解析设直线的倾斜角为α，则tan α＝3＋3－34－1＝33，∴α＝π6.故选A.2．(2019·北京，理)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，则()A ．a 2＝2b 2B ．3a 2＝4b 2C ．a ＝2bD ．3a ＝4b答案B 解析椭圆的离心率e ＝c a ＝12，c 2＝a 2－b 2，化简得3a 2＝4b 2.故选B.3.如图，在三棱锥O －ABC 中，D 是棱AC 的中点，若OA →＝a ，OB →＝b ，OC →＝c ，则BD →＝()A.12a －b ＋12c B ．a ＋b －c C ．a －b ＋c D ．－12a ＋b －12c答案A解析OD →＝OA →＋AD →＝OA →＋12AC →＝OA →＋12(OC →－OA →)＝12OA →＋12OC →，因此BD →＝OD →－OB →＝12OA→－OB →＋12OC →＝12a －b ＋12c .4．直线y ＝x －1被抛物线y 2＝4x 截得的线段AB 的中点坐标是()A ．(2，6)B ．(3，2)C ．(6，4)D ．(4，6)答案B解析设点A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)．将y ＝x －1代入y 2＝4x ，整理得x 2－6x ＋1＝0.由根与系数的关系得x 1＋x 2＝6，则x 1＋x 22＝3，y 1＋y 22＝x 1＋x 2－22＝6－22＝2，所以所求点的坐标为(3，2)．故选B.5．已知正四面体ABCD 的棱长为a ，点E ，F 分别是BC ，AD 的中点，则AE →·AF →的值为()A ．a 2 B.14a 2C.12a 2 D.34a 2答案B解析在正四面体ABCD 中，点E ，F 分别是BC ，AD 的中点，AE →＝AB →＋BE →，AF →＝12AD →，所以AE →·AF →＝(AB →＋BE →)·12→＝12AB →·AD →＋12BE →·AD →.因为ABCD 是正四面体，所以BE ⊥AD ，∠BAD ＝π3，即BE →·AD →＝0，AB →·AD →＝|AB →|·|AD →|cos π3＝12a 2，所以AE →·AF →＝14a 2.故选B.6．已知圆C 的半径为2，圆心在x 轴的正半轴上，直线3x ＋4y ＋4＝0与圆C 相切，则圆C 的方程为()A ．x 2＋y 2－2x －3＝0B ．x 2＋y 2＋4x ＝0C ．x 2＋y 2＋2x －3＝0D ．x 2＋y 2－4x ＝0答案D解析由题意设圆心坐标为C (a ，0)(a >0)，∵圆C 与直线3x ＋4y ＋4＝0相切，∴|3a ＋0＋4|9＋16＝2，解得a ＝2.∴圆心为C (2，0)，∴圆C 的方程为(x －2)2＋y 2＝4，即x 2＋y 2－4x ＝0.故选D.7.四棱锥P －ABCD 中，底面ABCD 为直角梯形，AB ⊥AD ，BC ∥AD ，且AB ＝BC ＝2，AD ＝3，PA ⊥平面ABCD 且PA ＝2，则PB 与平面PCD 所成角的正弦值为()A.427 B.77C.33D.63答案B解析建立如图所示的空间直角坐标系，则P (0，0，2)，B (2，0，0)，C (2，2，0)，D (0，3，0)．PB →＝(2，0，－2)，CD →＝(－2，1，0)，PD →＝(0，3，－2)．设平面PCD 的一个法向量为n ＝(x ，y ，z )，2x ＋y ＝0，y －2z ＝0.取x ＝1得n ＝(1，2，3)．cos 〈PB →，n 〉＝PB →·n |PB →||n |＝－422×14＝－77，可得PB 与平面PCD 所成角的正弦值为77.故选B.8．(2019·课标全国Ⅱ)设F 为双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2＋y 2＝a 2交于P ，Q 两点．若|PQ |＝|OF |，则C 的离心率为()A.2B.3C ．2 D.5答案A解析如图，由题意知以OF ＋y 2＝c 24①，将x 2＋y 2＝a 2记为②式，①－②得x ＝a 2c ，则以OF 为直径的圆与圆x 2＋y 2＝a 2的相交弦所在直线的方程为x ＝a 2c，所以|PQ |＝由|PQ |＝|OF |，得c ，整理得c 4－4a 2c 2＋4a 4＝0，即e 4－4e 2＋4＝0，解得e ＝ 2.故选A.二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项是符合题目要求的，全部选对的得5分，部分选对的得3分，有选错的得0分)9．下列说法正确的是()A ．在两坐标轴上截距相等的直线可以用方程x a ＋ya ＝1表示B ．存在实数m ，使得方程x ＋my －2＝0能表示平行于y 轴的直线C ．经过点P (1，1)，倾斜角为θ的直线方程为y －1＝tan θ(x －1)D ．点(0，2)关于直线y ＝x ＋1的对称点为(1，1)答案BD 解析对于A ，若直线过原点，则在两坐标轴上的截距都为零，故不能用方程x a ＋ya＝1表示，所以A 错误；对于B ，当m ＝0时，平行于y 轴的直线方程为x ＝2，所以B 正确；对于C ，若直线的倾斜角为90°，则该直线的斜率不存在，故不能用y －1＝tan θ(x －1)表示，所以C 错误；对于D y ＝x ＋1上，且(0，2)，(1，1)连线的斜率为－1，所以D 正确．故选BD.10．在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是A 1D 1和C 1D 1的中点，则下列结论正确的是()A ．A 1C 1∥平面CEFB ．B 1D ⊥平面CEF C.CE →＝12DA →＋DD 1→－DC→D ．若正方体ABCD －A 1B 1C 1D 1边长为2，点B 1到平面CEF 的距离为1答案AC解析对于A ，因为E ，F 分别是A 1D 1和C 1D 1的中点，所以EF ∥A 1C 1，且EF ⊂平面CEF ，故A 1C 1∥平面CEF 成立，A 正确；对于B ，以点D 为坐标原点，DA →，DC →，DD 1→的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系(如图)，设正方形ABCD －A 1B 1C 1D 1的棱长为2，则D (0，0，0)，C (0，2，0)，A (2，0，0，)，B 1(2，2，2)，D 1(0，0，2)，E (1，0，2)，F (0，1，2)，B 1D →＝(－2，－2，－2)，FC →＝(0，1，－2)，因为B 1D →·FC →＝0－2＋4＝2≠0，所以B 1D →与FC →不垂直，又CF ⊂平面CEF ，所以B 1D 与平面CEF 不垂直，B 错误；对于C ，12DA →＋DD 1→－DC →＝12(2，0，0)＋(0，0，2)－(0，2，0)＝(1，－2，2)，又CE →＝(1，－2，2)，所以CE →＝12DA→＋DD 1→－DC →成立，C 正确；对于D ，连接B 1E ，EF →＝(－1，1，0)，EC →＝(－1，2，－2)，设平面EFC 的法向量为n ＝(x ，y ，z )·n ＝0，·n ＝0，x ＋y ＝0，x ＋2y －2z ＝0，令x ＝2，得n ＝(2，2，1)，又B 1E →＝(－1，－2，0)，所以点B 1到平面CEF 的距离d ＝|B 1E →·n ||n |＝63＝2，D 错误．故选AC.11．已知P 是椭圆C ：x 26＋y 2＝1上的动点，Q 是圆D ：(x ＋1)2＋y 2＝15上的动点，则()A ．C 的焦距为5B ．C 的离心率为306C ．圆D 在C 的内部D ．|PQ |的最小值为255答案BC解析∵x 26＋y 2＝1，∴a ＝6，b ＝1，∴c ＝a 2－b 2＝6－1＝5，则C 的焦距为25，e ＝ca＝56＝306.设P (x ，y )(－6≤x ≤6)，则|PD |2＝(x ＋1)2＋y 2＝(x ＋1)2＋1－x 26＝＋45≥45>15，可知圆D 在C 的内部，且|PQ |的最小值为45－15＝55.故选BC.12．已知动点P 到两定点M (－2，0)，N (2，0)的距离乘积为常数16，其轨迹为C ，则()A ．C 一定经过原点B ．C 关于x 轴、y 轴对称C ．△MPN 的面积的最大值为43D ．C 在一个面积为64的矩形内答案BCD解析设点P 的坐标为(x ，y )，由题意可得（x ＋2）2＋y 2·（x －2）2＋y 2＝16.对于A ，将原点坐标(0，0)代入方程得2×2＝4≠16，故A 错误；对于B ，设点P 关于x 轴、y 轴的对称点分别为P 1(x ，－y )，P 2(－x ，y )，因为（x ＋2）2＋（－y ）2·（x －2）2＋（－y ）2＝（x ＋2）2＋y 2·（x －2）2＋y 2＝16，（－x ＋2）2＋y 2·（－x －2）2＋y 2＝（x －2）2＋y 2·（x ＋2）2＋y 2＝16，所以点P 1，P 2都在曲线C 上，所以曲线C 关于x 轴、y 轴对称，故B 正确；对于C ，设|PM |＝a ，|PN |＝b ，∠MPN ＝θ(0<θ<π)，则ab ＝16，由余弦定理得cos θ＝a 2＋b 2－162ab ＝a 2＋b 2－1632≥2ab －1632＝12，当且仅当a ＝b ＝4时等号成立，则θ，π3，所以sin θ≤32，则△MPN 的面积S △MPN ＝12ab sin θ≤12×16×32＝43，故C正确；对于D ，由16＝（x ＋2）2＋y 2·（x －2）2＋y 2≥（x ＋2）2·（x －2）2＝|x 2－4|，可得－16≤x 2－4≤16，得0≤x 2≤20，解得－25≤x ≤25，由C 知，S △MPN ＝12|MN |·|y |＝12×4×|y |≤43，得|y |≤23，因为45×43＝1615<64，所以曲线C 在一个面积为64的矩形内，故D 正确．故选BCD.三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中的横线上)13．在四棱锥P －ABCD 中，ABCD 为平行四边形，AC 与BD 交于O ，G 为BD 上一点，BG ＝2GD ，PA →＝a ，PB →＝b ，PC →＝c ，试用基底{a ，b ，c }表示向量PG →＝________．答案23a －13b ＋23c 解析PG →＝PB →＋BG→＝PB →＋23BD→＝PB →＋23(BA →＋BC →)＝PB →＋23[(PA →－PB →)＋(PC →－PB →)]＝PB →＋23(PA →－2PB →＋PC →)＝23PA →－13PB →＋23PC →＝23a －13b ＋23c .14．已知点P 是圆C ：x 2＋y 2＝4上的动点，点A (4，2)，则线段AP 中点M 的轨迹方程是________________；点M 的轨迹与圆C 相交，则过交点的直线方程是________．(本题第一空2分，第二空3分)答案(x －2)2＋(y －1)2＝12x ＋y －4＝0解析设M (x ，y )，P (x 1，y 1)，＝x 1＋42，＝y 1＋22，1＝2x －4，1＝2y －2.因为x 12＋y 12＝4，所以(2x －4)2＋(2y －2)2＝4.整理得(x －2)2＋(y －1)2＝1.①又圆C ：x 2＋y 2＝4，②由①－②得2x ＋y －4＝0，即为所求直线方程．15．已知点F 2为双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点，直线y ＝kx 交双曲线C 于A ，B两点，若∠AF 2B ＝2π3，S △AF 2B ＝23，则双曲线C 的虚轴长为________．答案22解析由题意知点B 与点A 关于原点对称，设双曲线的左焦点为F 1，连接AF 1，BF 1，由对称性可知四边形AF 1BF 2是平行四边形，所以∠F 1AF 2＝π3，设|AF 2|＝m ，不妨设点A 在点B 右侧，则|AF 1|＝2a ＋m .在△AF 1F 2中，由余弦定理可得4c 2＝m 2＋(m ＋2a )2－m (m ＋2a )，化简得4c 2－4a 2＝m 2＋2ma ，即4b 2＝m (m ＋2a )．又S △AF 2B ＝12m (m ＋2a )·32＝23，所以b 2＝2，所以2b ＝2 2.16．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的右焦点为F 1(1，0)，离心率为e .设A ，B 为椭圆上关于原点对称的两点，AF 1的中点为M ，BF 1的中点为N ，原点O 在以线段MN 为直径的圆上．设直线AB 的斜率为k ，若0<k ≤3，则e 的取值范围为________．答案[3－1，1)解析设A (m ，n )，则B (－m ，－n )，则k ＝nm，因为原点O 在以线段MN 为直径的圆上，所以OM ⊥ON ，又因为M 为AF 1的中点，所以OM ∥BF 1，同理ON ∥AF 1，所以四边形OMF 1N 是矩形，即AF 1⊥BF 1，而AF 1→＝(1－m ，－n )，BF 1→＝(1＋m ，n )，所以(1－m )(1＋m )－n 2＝0，即m 2＋n 2＝1，又m 2a 2＋n 2b 2＝1，于是有m 2a 2＋n 2b 2＝m 2＋n 2，从而1a 2－11－1b 2＝n 2m 2＝k 2≤3，即1a 2＋3b2≥4，将b 2＝a 2－1代入上式，整理得4a 4－8a 2＋1≤0，解得2－32≤a 2≤2＋32，又a >c ＝1，所以4－23≤1a2<1，即3－1≤e <1.四、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(10分)已知三角形的顶点A (2，3)，B (0，－1)，C (－2，1)．(1)求直线AC 的方程；(2)从①，②这两个问题中选择一个作答．①求点B 关于直线AC 的对称点D 的坐标．②若直线l 过点B 且与直线AC 交于点E ，|BE |＝3，求直线l 的方程．思路分析(1)由A (2，3)，C (－2，1)，可求出直线AC 的斜率，由点斜式即可写出直线的方程；(2)选①由对称点的性质即可求出；选②设出E ，12t ＋t 的值，根据B ，E 两点的坐标即可求出直线的方程．解析(1)因为直线AC 的斜率为k AC ＝12，所以直线AC 的方程为y －3＝12(x －2)，即直线AC 的方程为x －2y ＋4＝0.(2)选择问题①：设D 的坐标为(m ，n )，·12＝－1，2·n －12＋4＝0，＝－125，＝195.所以点D －125，选择问题②：设E，12t ＋|BE |＝33，解得t ＝0或t ＝－125.所以E 的坐标为(0，2)－125，所以直线l 的方程为x ＝0或3x ＋4y ＋4＝0.18．(12分)已知圆C 经过三点O (0，0)，A (1，3)，B (4，0)．(1)求圆C 的方程；(2)求过点P (3，6)且被圆C 截得弦长为4的直线的方程．解析(1)由题意，设圆C 的方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0，＝0，＋9＋D ＋3E ＋F ＝0＋4D ＋F ＝0，＝－4，＝－2，＝0.所以圆C 的方程为x 2＋y 2－4x －2y ＝0，即(x －2)2＋(y －1)2＝5.(2)由(1)知圆心坐标为C (2，1)，半径为5，弦长为4时，圆心C 到直线的距离为1.①若直线斜率不存在，则直线方程为x ＝3，经检验符合题意；②若直线斜率存在，设直线斜率为k ，则直线方程为y －6＝k (x －3)，即kx －y －3k ＋6＝0，则|5－k |1＋k 2＝1，解得k ＝125，所以直线方程为y －6＝125(x －3)，即12x －5y －6＝0.综上可知，直线方程为x ＝3或12x －5y －6＝0.19．(12分)(2019·课标全国Ⅱ，文)已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a >0，b >0)的两个焦点，P 为C 上的点，O 为坐标原点．(1)若△POF 2为等边三角形，求C 的离心率；(2)如果存在点P ，使得PF 1⊥PF 2，且△F 1PF 2的面积等于16，求b 的值和a 的取值范围．解析(1)若△POF 2为等边三角形，则P ，±32c ，代入方程x 2a 2＋y 2b 2＝1，可得c 24a2＋3c 24b2＝1，解得e 2＝4±23，所以e ＝3－1(3＋1已舍去)．(2)由题意可得|PF 1→|＋|PF 2→|＝2a ，因为PF 1⊥PF 2，所以|PF 1→|2＋|PF 2→|2＝4c 2，所以(|PF 1→|＋|PF 2→|)2－2|PF 1→|·|PF 2→|＝4c 2，所以2|PF 1→|·|PF 2→|＝4a 2－4c 2＝4b 2，所以|PF 1→|·|PF 2→|＝2b 2，所以S △PF 1F 2＝12|PF 1→|·|PF 2→|＝b 2＝16，解得b ＝4.因为(|PF 1→|＋|PF 2→|)2≥4|PF 1→|·|PF 2→|，即(2a )2≥4|PF 1→|·|PF 2→|，即a 2≥|PF 1→|·|PF 2→|，所以a 2≥32，所以a ≥42，即a 的取值范围为[42，＋∞)．20.(12分)如图，在四棱锥P －ABCD 中，平面PCD ⊥平面ABCD ，且△PCD 是边长为2的等边三角形，四边形ABCD 是矩形，BC ＝22，M 为BC 的中点．(1)求证：AM ⊥PM ；(2)求二面角P －AM －D 的大小；(3)求点D 到平面AMP 的距离．解析以点D 为原点，分别以直线DA ，DC 为x 轴、y 轴，建立如图所示的空间直角坐标系，依题意，可得D (0，0，0)，P (0，1，3)，A (22，0，0)，M (2，2，0)，PM →＝(2，1，－3)，AM →＝(－2，2，0)．(1)证明：∵PM →·AM →＝(2，1，－3)·(－2，2，0)＝0，即PM →⊥AM →，∴AM ⊥PM .(2)设n ＝(x ，y ，z )为平面PAM 的法向量，·PM →＝0，·AM →＝0，y －3z ＝0，＋2y ＝0，取y ＝1，得n ＝(2，1，3)．取p ＝(0，0，1)，显然p 为平面ABCD 的一个法向量，∵cos 〈n ，p 〉＝n ·p |n ||p |＝36＝22，∴二面角P －AM －D 的大小为45°.(3)设点D 到平面AMP 的距离为d ，由(2)可知n ＝(2，1，3)为平面AMP 的一个法向量，∴d ＝|DA →·n ||n |＝|22×2|2＋1＋3＝263，即点D 到平面AMP 的距离为263.21．(12分)如图，三棱柱ABC －A 1B 1C 1中，AB ＝AC ＝AA 1＝BC 1＝2，∠AA 1C 1＝60°，平面ABC 1⊥平面AA 1C 1C ，AC 1与A 1C 相交于点D .(1)求证：BD ⊥平面AA 1C 1；(2)设点E 是直线B 1C 1上一点，且DE ∥平面AA 1B 1B ，求平面EBD 与平面ABC 1夹角的余弦值．解析(1)证明：由已知得侧面AA 1C 1C 是菱形，D 是AC 1的中点．∵BA ＝BC 1，∴BD ⊥AC 1.∵平面ABC 1⊥平面AA 1C 1C ，且BD ⊂平面ABC 1，平面ABC 1∩平面AA 1C 1C ＝AC 1，∴BD ⊥平面AA 1C 1C .(2)设点F 是A 1C 1的中点，连接DF ，EF ，∵点D 是AC 1的中点，∴DF ∥平面AA 1B 1B .又∵DE ∥平面AA 1B 1B ，∴平面DEF ∥平面AA 1B 1B .又∵平面DEF ∩平面A 1B 1C 1＝EF ，平面AA 1B 1B ∩平面A 1B 1C 1＝A 1B 1，∴EF ∥A 1B 1.∴点E 是B 1C 1的中点．如图，以D 为原点，以DA 1，DA ，DB 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系．由已知可得AC 1＝2，AD ＝1，BD ＝A 1D ＝DC ＝3，BC ＝6，∴D (0，0，0)，A (0，1，0)，A 1(3，0，0)，B (0，0，3)，C 1(0，－1，0)．设平面EBD 的法向量是m ＝(x ，y ，z )，由m ⊥DB →，得3z ＝0⇒z ＝0.又DE →＝12(DC 1→＋DB 1→)＝12(DC 1→＋DB →＋AA 1→)1由m ⊥DE →，得(x ，y ，z10⇒32x －y ＝0.令x ＝1，得y ＝32，∴m ，32，∵平面ABC 1⊥平面AA 1C 1C ，DA 1⊥AC 1，∴DA 1⊥平面ABC 1.∴DA 1→是平面ABC 1的一个法向量，DA 1→＝(3，0，0)．∴cos 〈m ，DA 1→〉＝31＋34×3＝277，∴平面EBD 与平面ABC 1夹角的余弦值是277.22．(12分)已知定点F (1，0)，动点P 在y 轴上运动，过点P 作PM 交x 轴于点M ，并延长MP 到点N ，且PM →·PF →＝0，|PM →|＝|PN →|.(1)求动点N 的轨迹方程；(2)直线l 与动点N 的轨迹交于A ，B 两点，若OA →·OB →＝－4，且46≤|AB →|≤430，求直线l 的斜率k 的取值范围．解析(1)由题意知P 为线段MN 的中点，设N (x ，y )，则M (－x ，0)，由PM →·PF →＝0x，∴(－x )·10，∴y 2＝4x (x ＞0)，∴点N 的轨迹方程为y 2＝4x (x >0)．(2)设l 与抛物线交于点A (x 1，y 1)，B (x 2，y 2)．当l 与x 轴垂直时，则由OA →·OB →＝－4，得y 1＝22，y 2＝－22，|AB |＝42<46，不合题意．故l 与x 轴不垂直．可设直线l 的方程为y ＝kx ＋b (k ≠0)，则由OA →·OB →＝－4，得x 1x 2＋y 1y 2＝－4.由点A ，B 在抛物线y 2＝4x (x >0)上有y 12＝4x 1，y 22＝4x 2，故y 1y 2＝－8.又2＝4x ，＝kx ＋b ，联立消x ，得ky 2－4y ＋4b ＝0.∴4bk ＝－8，b ＝－2k.∴Δ＝16(1＋2k 2)，|AB |2y1－y 2)2∵46≤|AB |≤430，∴96480.解得直线l的斜率取值范围为－1，－12∪12，1.1．若椭圆x2a2＋y2b2＝1(a>b>0)的离心率为32，则双曲线x2a2－y2b2＝1的离心率为()A.54B.52C.32D.54答案B2．已知四面体顶点A(2，3，1)，B(4，1，－2)，C(6，3，7)和D(－5，－4，8)，则顶点D 到平面ABC的距离为()A．8B．9C．10D．11答案D解析设平面ABC的一个法向量为n＝(x，y，z)，则·AB→＝0，·AC→＝0，x，y，z）·（2，－2，－3）＝0，x，y，z）·（4，0，6）＝0.x－2y－3z＝0，x＋6z＝0＝2x，＝－23x，令x＝1，则n，2AD→＝(－7，－7，7)，故所求距离为|AD→·n||n|＝|－7－14－143|1＋4＋49＝11.3.如图，在四棱锥S－ABCD中，底面ABCD是边长为1的正方形，SA＝SB＝SC＝SD＝2.下列结论中正确的是()A.SA→＋SB→＋SC→＋SD→＝0B.SA→－SB→＋SC→－SD→＝0C.SA→·SB→＋SC→·SD→＝0D.SA→·SC→＝0答案B解析本题考查空间向量的加减运算和数量积．由题意易知A错误；因为SA→－SB→＋SC→－SD→＝BA→＋DC→＝0，所以B正确；因为底面ABCD是边长为1的正方形，SA＝SB＝SC＝SD＝2，所以SA →·SB →＝2×2×cos ∠ASB ，SC →·SD →＝2×2×cos ∠CSD ，而∠ASB ＝∠CSD ，于是SA →·SB →＝SC →·SD →≠0，所以C 错误；连接AC ，在△SAC 中，SA ＝SC ＝2，AC ＝2，所以∠ASC ≠90°，所以cos ∠ASC ≠0，又SA →·SC →＝2×2×cos ∠ASC ，所以SA →·SC →≠0，所以D 错误．故选B.4．已知A 是双曲线E ：x 2a 2－y 2b 2＝1(a >0，b >0)的左顶点，F 是抛物线C ：y 2＝－8ax 的焦点．若在双曲线的渐近线上存在点P ，使得AP →⊥FP →，则E 的离心率的取值范围是()A ．(1，2)，324D ．(2，＋∞)答案B解析由题意得，A (－a ，0)，F (－2a ，0)，不妨设0，ba x AP →⊥FP →，得AP →·FP →＝0⇒0＋a ，b a x 0＋2a ，ba x 0⇒c 2a 2x 02＋3ax 0＋2a 2＝0.因为在双曲线E 的渐近线上存在点P ，所以Δ≥0，即9a 2－4×2a 2×c 2a 2≥0，9a 2≥8c 2⇒e 2≤98⇒－324≤e ≤324，又因为E 为双曲线，所以1<e ≤324.故选B.5.如图，在正四棱锥P －ABCD 中，PA ＝AB ，点M 为PA 的中点，BD →＝λBN →.若MN ⊥AD ，则实数λ为()A ．2B ．3C ．4D ．5答案C解析连接AC 交BD 于点O ，以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴，建立如图所示的空间直角坐标系．设PA ＝AB ＝2，则A (2，0，0)，D (0，－2，0)，P (0，0，2)，0B (0，2，0)，∴BD →＝(0，－22，0)，设N (0，b ，0)，则BN →＝(0，b －2，0)．∵BD＝λBN →，∴－22＝λ(b －2)，∴b ＝2λ－22λ，∴N，2λ－22λ，，→－22，2λ－22λ，－AD →＝(－2，－2，0)，∵AD ⊥MN ，∴AD →·MN →＝1－2λ－4λ＝0，解得λ＝4.故选C.6．已知椭圆C ：x 24＋y 23＝1，M ，N 是坐标平面内的两点，且M 与椭圆C 的焦点不重合．若M 关于椭圆C 的左、右焦点的对称点分别为A ，B ，线段MN 的中点在椭圆C 上，则|AN |＋|BN |＝()A ．4B ．8C ．12D ．16答案B解析设MN 的中点为D ，椭圆C 的左、右焦点分别为F 1，F 2，如图，连接DF 1，DF 2.∵F 1是MA 的中点，D 是MN 的中点，∴F 1D 是△MAN 的中位线，∴|DF 1|＝12|AN |，同理|DF 2|＝12|BN |，∴|AN |＋|BN |＝2(|DF 1|＋|DF 2|)．∵点D 在椭圆上，根据椭圆的标准方程及椭圆的定义知，|DF 1|＋|DF 2|＝4，∴|AN |＋|BN |＝8.故选B.7．在平面直角坐标系xOy 中，已知点A (0，－2)，点B (1，－1)，P 为圆x 2＋y 2＝2上一动点(异于点B )，则|PB ||PA |的最大值是()A ．2B ．4C.2D ．22答案A解析设点P (x 0，y 0)，则x 02＋y 02＝2，所以|PB |2|PA |2＝（x 0－1）2＋（y 0＋1）2x 02＋（y 0＋2）2＝x 02＋y 02－2x 0＋2y 0＋2x 02＋y 02＋4y 0＋4＝－2x 0＋2y 0＋44y 0＋6＝－x 0＋y 0＋22y 0＋3，令λ＝－x 0＋y 0＋22y 0＋3，则λ≠0，x 0＋(2λ－1)y 0＋3λ－2＝0，由题意，知直线x ＋(2λ－1)y ＋3λ－2＝0与圆x 2＋y 2＝2有公共点，所以|3λ－2|1＋（2λ－1）2≤2，得λ2－4λ≤0，得0<λ≤4，所以|PB ||PA |的最大值为2.8．【多选题】若{a ，b ，c }为空间的一个基底，则()A ．b ＋c ，b －c ，a 共面B ．b ＋c ，b －c ，2b 共面C ．b ＋c ，a ，a ＋b ＋c 共面D ．a ＋c ，a －2c ，c 共面答案BCD解析易知b ＋c ，b －c ，a 不共面；因为2b ＝(b ＋c )＋(b －c )，所以b ＋c ，b －c ，2b 共面；因为a ＋b ＋c ＝(b ＋c )＋a ，所以b ＋c ，a ，a ＋b ＋c 共面；因为a ＋c ＝(a －2c )＋3c ，所以a ＋c ，a －2c ，c 共面．故选BCD.9.【多选题】如图，在长方体ABCD －A 1B 1C 1D 中，AB ＝3AD ＝3AA 1＝3，点P 为线段A 1C 上的动点，则下列结论正确的是()A ．当A 1C →＝2A 1P →时，B 1，P ，D 三点共线B ．当AP →⊥A 1C →时，AP →⊥D 1P→C ．当A 1C →＝3A 1P →时，D 1P ∥平面BDC 1D ．当A 1C →＝5A 1P →时，A 1C ⊥平面D 1AP答案ACD解析在长方体ABCD －A 1B 1C 1D 1中，连接AC ，以点D 为坐标原点，建立如图所示的空间直角坐标系，因为AB ＝3AD ＝3AA 1＝3，所以AD ＝AA 1＝1，则A (1，0，0)，A 1(1，0，1)，C (0，3，0)，C 1(0，3，1)，D 1(0，0，1)，D (0，0，0)，B (1，3，0)，则A 1C →＝(－1，3，－1)，D 1A →＝(1，0，－1)，DC 1→＝(0，3，1)，DB →＝(1，3，0)，A 1D 1→＝(－1，0，0)．当A 1C →＝2A 1P →时，P 为A 1C 的中点，根据长方体结构特征，可知P 为体对角线的中点，因此P 也为B 1D 的中点，所以B 1，P ，D 三点共线，故A 正确；当AP →⊥A 1C →时，AP ⊥A 1C ，由题意可得A 1C ＝1＋1＋3＝5，AC ＝1＋3＝2，因为S △A 1AC ＝12AA 1·AC ＝12A 1C ·AP ，所以AP ＝255，所以A 1P ＝55，即点P 为靠近点A 1的五等分点，所以，35，D 1P →，35，－AP →＝－15，35，D 1P →·AP →＝－425＋325－425＝－15≠0，所以AP →与D 1P →不垂直，故B 错误；当A 1C →＝3A 1P →时，A 1P →＝13A 1C →－13，33，－BDC 1的一个法向量为n ＝(x ，y ，z )，·DC 1→＝0，·DB →＝0，＋z ＝0，＋3y ＝0，令y ＝1，可得n ＝(－3，1，－3)，又D 1P →＝A 1P →－A 1D 1→＝，33，－D 1P →·n ＝0，因此D 1P →⊥n ，所以D 1P →∥平面BDC 1，故C 正确；当A 1C →＝5A 1P →时，A 1P →＝15A 1C →－15，35，－所以D 1P →＝A 1P →－A 1D 1→，35，－所以A 1C →·D 1P →＝0，A 1C →·D 1A →＝0，因此A 1C ⊥D 1P ，A 1C ⊥D 1A ，又D 1P ∩D 1A ＝D 1，所以A 1C ⊥平面D 1AP ，故D 正确．故选ACD.10．【多选题】已知抛物线E ：y 2＝4x 的焦点为F ，准线为l ，过F 的直线与E 交于A ，B 两点，分别过A ，B 作l 的垂线，垂足为C ，D ，且|AF |＝3|BF |，M 为AB 中点，则下列结论正确的是()A ．∠CFD ＝90°B ．△CMD 为等腰直角三角形C ．直线AB 的斜率为±3D ．△AOB 的面积为4答案AC解析如图，过点M 向准线l 作垂线，垂足为N ，F (1，0)，设A (x 1，y 1)，B (x 2，y 2)，因为|AF |＝|AC |，所以∠AFC ＝∠ACF ，又因为∠OFC ＝∠ACF ，所以∠OFC ＝∠AFC ，所以FC 平分∠OFA ，同理可知FD 平分∠OFB ，所以∠CFD ＝90°，故A 正确；假设△CMD 为等腰直角三角形，则∠CFD ＝∠CMD ＝90°，则C ，D ，F ，M 四点共圆且圆的半径为12|CD |＝|MN |，又因为|AF |＝3|BF |，所以|AB |＝|AF |＋|BF |＝|AC |＋|BD |＝2|MN |＝4|BF |，所以|MN |＝2|BF |，所以|CD |＝2|MN |＝4|BF |，所以|CD |＝|AB |，显然不成立，故B 错误；设直线AB的方程为x ＝my ＋12＝4x ，＋1，所以y 2－4my －4＝01＋y 2＝4m ，1y 2＝－4，又因为|AF |＝3|BF |，所以y 1＝－3y 22y 2＝4m ，3y 22＝－4，所以m 2＝13，所以1m ＝±3，所以直线AB 的斜率为±3，故C 正确；取m ＝331＋y 2＝433，1y 2＝－4，所以|y 1－y 2|＝833，所以S △AOB ＝12·|OF |·|y 1－y 2|＝12×1×833＝433D 错误．故选AC.11．【多选题】a ，b 为空间两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以AC 为旋转轴旋转，则下列结论正确的是()A ．直线AB 与a 所成角的最小值为π4B ．直线AB 与a 所成角的最大值为π3C ．当直线AB 与a 所成的角为π3时，AB 与b 所成的角为π6D ．当直线AB 与a 所成的角为π3时，AB 与b 所成的角为π3答案AD解析由题意知，a ，b ，AC 三条直线两两相互垂直，画出图形如图．不妨设图中所示正方体的棱长为1，则AC ＝1，AB ＝2，斜边AB 以直线AC 为旋转轴旋转，则A 点保持不变，B 点的运动轨迹是以C 为圆心，BC 长为半径的圆，设CB 旋转到直线a 上时为CE ，旋转到直线b 上时为CD ，以C 为坐标原点，以CD 所在直线为x 轴，CE 所在直线为y 轴，CA 所在直线为z 轴，建立空间直角坐标系，则D (1，0，0)，A (0，0，1)，设B 点在运动过程中的坐标为(cos θ，sin θ，0)，其中θ为射线CD 绕端点C 旋转到CB 形成的角，θ∈[0，2π)，∴AB 在运动过程中对应的向量AB →＝(cos θ，sin θ，－1)，|AB →|＝2，设AB 与a 所成的角为α，α∈0，π2，则cos α＝22|sin θ|∈0，22，∴α∈π4，π2，故A 正确，B错误；设AB 与b 所成的角为β，β∈0，π2，则cos β＝22|cos θ|，当AB 与a 所成的角为π3，即α＝π3时，|sin θ|＝2cos α＝2cos π3＝22，∵cos 2θ＋sin 2θ＝1，∴cos β＝22|cos θ|＝12，∵β∈0，π2，∴β＝π3，此时AB 与b所成的角为π3，故D 正确，C 错误．故选AD.12．【多选题】古希腊著名数学家阿波罗尼奥斯发现：平面内到两个定点A ，B 的距离之比为定值λ(λ≠1)的点的轨迹是圆，此圆被称为“阿波罗尼斯圆”．在平面直角坐标系xOy 中，A (－2，0)，B (4，0)，点P 满足|PA ||PB |＝12.设点P 的轨迹为C ，下列结论正确的是()A ．轨迹C 的方程为(x ＋4)2＋y 2＝9B ．在x 轴上存在异于A ，B 的两点D ，E 使得|PD ||PE |＝12C ．当A ，B ，P 三点不共线时，射线PO 是∠APB 的平分线D ．在C 上存在点M ，使得|MO |＝2|MA |答案BC解析设P (x ，y )，则（x ＋2）2＋y 2（x －4）2＋y 2＝12，化简得(x ＋4)2＋y 2＝16，所以A 错误；假设在x轴上存在异于A ，B 的两点D ，E 使得|PD ||PE |＝12，设D (m ，0)，E (n ，0)，则（x －n ）2＋y 2＝2（x －m ）2＋y 2，化简得3x 2＋3y 2－(8m －2n )x ＋4m 2－n 2＝0，由轨迹C 的方程为x 2＋y 2＋8x ＝0，可得8m －2n ＝－24，4m 2－n 2＝0，解得m ＝－6，n ＝－12或m ＝－2，n ＝4(舍去)，即在x 轴上存在异于A ，B 的两点D ，E 使|PD ||PE |＝12，所以B 正确；当A ，B ，P 三点不共线时，由|OA ||OB |＝12＝|PA ||PB |，可得射线PO 是∠APB 的平分线，所以C 正确；假设在C 上存在点M ，使得|MO |＝2|MA |，可设M (x ，y )，则有x 2＋y 2＝2（x ＋2）2＋y 2，化简得x 2＋y 2＋163x ＋163＝0，与x 2＋y 2＋8x ＝0联立，得x ＝2，不合题意，故不存在点M ，所以D 错误．故选BC.13．已知直线l ：mx －y ＝1，若直线l 与直线x －my －1＝0平行，则实数m 的值为________，动直线l 被圆C ：x 2＋y 2＋2x －24＝0截得弦长的最小值为________．答案－1223解析由题得m ×(－m )－(－1)×1＝0，所以m ＝±1.当m ＝1时，两直线重合，舍去，故m ＝－1.因为圆C 的方程x 2＋y 2＋2x －24＝0可化为(x ＋1)2＋y 2＝25，所以圆心为C (－1，0)，半径为5.由于直线l ：mx －y －1＝0过定点P (0，－1)，所以过点P 且与PC 垂直的弦的弦长最短，且最短弦长为2×52－（2）2＝223.14．已知M (－2，0)，N (2，0)，点P (x ，y )为坐标平面内的动点，满足|MN →|·|MP →|＋MN →·NP →＝0，则动点P 的轨迹方程为________．答案y 2＝－8x 解析由题意，知MN →＝(4，0)，|MN →|＝4，MP →＝(x ＋2，y )，NP →＝(x －2，y )．由|MN →|·|MP →|＋MN →·NP →＝0，得4（x ＋2）2＋y 2＋4(x －2)＝0，化简整理，得y 2＝－8x .15．已知直线l ：4x －3y ＋6＝0，抛物线C ：y 2＝4x 上一动点P 到直线l 与到y 轴距离之和的最小值为________，P 到直线l 距离的最小值为________．答案134解析设抛物线C ：y 2＝4x 上的点P 到直线4x －3y ＋6＝0的距离为d 1，到准线的距离为d 2，到y 轴的距离为d 3，由抛物线方程可得焦点坐标为F (1，0)，准线方程为x ＝－1，则d 3＝d 2－1，|PF |＝d 2，因此d 1＋d 3＝d 1＋d 2－1＝d 1＋|PF |－1，因为d 1＋|PF |的最小值是焦点F 到直线4x －3y ＋6＝0的距离，即|4＋6|42＋（－3）2＝2，所以d 1＋d 3＝d 1＋|PF |－1的最小值为2－1＝1；设平行于直线l 且与抛物线C ：y 2＝4x 相切的直线方程为4x －3y ＋m ＝0，由x －3y ＋m ＝0，2＝4x ，得y 2－3y ＋m ＝0，因为直线4x －3y ＋m ＝0与抛物线C ：y 2＝4x 相切，所以Δ＝(－3)2－4m ＝0，解得m ＝94，因此该切线方程为4x －3y ＋94＝0，所以两平行线间的距离为6－9442＋（－3）2＝34，即P 到直线l 距离的最小值为34.16．已知直线l ：y ＝－x ＋1与椭圆x 2a 2＋y 2b 2＝1(a >b >0)相交于A ，B 两点，且线段AB 的中点为(1)求此椭圆的离心率；(2)若椭圆的右焦点关于直线l 的对称点在圆x 2＋y 2＝5上，求此椭圆的方程．解析(1)x ＋1，＋y 2b 2＝1，得(b 2＋a 2)x 2－2a 2x ＋a 2－a 2b 2＝0，∴Δ＝4a 4－4(a 2＋b 2)(a 2－a 2b 2)>0⇒a 2＋b 2>1.设A (x 1，y 1)，B (x 2，y 2)，∴x 1＋x 2＝2a 2b 2＋a 2.∵线段AB ，∴2a 2b 2＋a 2＝43，得a 2＝2b 2.又a 2＝b 2＋c 2，∴a 2＝2c 2，∴e ＝22.(2)设椭圆的右焦点为F (c ，0)，则点F 关于直线l ：y ＝－x ＋1的对称点为P (1，1－c )．∵点P 在圆x 2＋y 2＝5上，∴1＋(1－c )2＝5，即c 2－2c －3＝0.∵c >0，∴c ＝3，又a 2＝2c 2且a 2＝b 2＋c 2，∴a ＝32，b ＝3，∴椭圆的方程为x 218＋y 29＝1.17.如图所示，该几何体是由一个直三棱柱ADE －BCF 和一个正四棱锥P －ABCD 组合而成的，AD ⊥AF ，AE ＝AD ＝2.(1)证明：平面PAD ⊥平面ABFE ；(2)求正四棱锥P －ABCD 的高h ，使得二面角C －AF －P 的余弦值是223解析(1)证明：在直三棱柱ADE －BCF 中，AB ⊥平面ADE ，AD ⊂平面ADE ，所以AB ⊥AD .又AD ⊥AF ，AB ∩AF ＝A ，AB ⊂平面ABFE ，AF ⊂平面ABFE ，所以AD ⊥平面ABFE .因为AD ⊂平面PAD ，所以平面PAD ⊥平面ABFE .(2)由(1)知AD ⊥平面ABFE ，以A 为原点，AB ，AE ，AD 所在直线分别为x ，y ，z 轴建立空间直角坐标系，如图，则A (0，0，0)，F (2，2，0)，C (2，0，2)，P (1，－h ，1)，AF →＝(2，2，0)，AC →＝(2，0，2)，AP →＝(1，－h ，1)．设平面AFC 的一个法向量为m ＝(x 1，y 1，z 1)，·AF →＝2x 1＋2y 1＝0，·AC →＝2x 1＋2z 1＝0，取x 1＝1，则y 1＝z 1＝－1，所以m ＝(1，－1，－1)．设平面AFP 的一个法向量为n ＝(x 2，y 2，z 2)，·AF →＝2x 2＋2y 2＝0，·AP →＝x 2－hy 2＋z 2＝0，取x 2＝1，则y 2＝－1，z 2＝－1－h ，所以n ＝(1，－1，－1－h )．因为二面角C －AF －P 的余弦值为223，所以|cos 〈m ·n 〉|＝|m ·n ||m |·|n |＝|1＋1＋1＋h |3×2＋（h ＋1）2＝223，解得h ＝1或h ＝－35(舍)，所以正四棱锥P －ABCD 的高h ＝1.18.如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝1，AC ＝AA 1＝3，∠ABC ＝60°.。

人教版数学必修一综合测试(含答案)

人教版数学必修一一、单选题1．已知集合A ={x |x =2sin nπ3，n ∈N ∗}，B ={x |x 2―2x ―3<0}，则A ∩B =（）A ．{―3，0，3}B ．{0，3}C ．{―3，0}D ．{―1，0，3}2．函数f (x )=log 2(3―x )+1x ―1的定义域为（）A ．[1，3]B ．[1，3)C ．[1，+∞)D ．(1，3)3．函数 y =2x ―1的定义域为 (―∞,1)∪[2,5) ，则其值域是（） A ．(0,+∞)B ．(―∞,2]C ．(―∞,12)∪[2,+∞)D ．(―∞,0)∪(12,2]4．函数f （x ）＝|x －2|·（x －4）的单调递减区间是（）A ．[2，4]B ．[2，3]C ．[2，＋∞）D ．[3，＋∞）5．已知函数f (x )=cos(ωx +φ)（ω>0，|φ|<π）的部分图象如图所示，且存在0≤x 1<x 2≤π，满足f(x 1)=f (x 2)=―45，则cos(x 2―x 1)=（）A ．―35B ．35C ．45D ．―456．函数 f (x )=3―x 2+4x +3 的单调递增区间为（）A ．(―∞，2)B ．(2，+∞)C ．(―3，2)D ．(2，7)7．已知函数f (x )={x 2+2x ，x⩽0，ln 1x ，x >0.若函数g (x )=f (x )―a |x |恰有三个零点，则实数a 的取值范围是（）A ．(―2，―1e )∪[0，+∞)B ．[―2，―1e ]∪(0，+∞)C ．(―e ，0)∪[2，+∞)D ．{―1e}∪[0，+∞)8．已知a =5log 56―log 29×lo g 32，b =log 56+log 3025，5b +12b =13c ，则（）A．c<b<a B．b<c<a C．a<c<b D．a<b<c二、多选题9．图中阴影部分用集合符号可以表示为（）A．∁U B∩(A∪C)B．∁U((A∩B)∪(B∩C))C．A∪(C∩∁U B)D．(A∩∁U B)∪(C∩∁U B)10．下列命题中正确的是（）A．函数y=1―sin2x的周期是πB．函数y=1―co s2x的图像关于直线x=π4对称C．函数y=2―sinx―cosx在[π4，π]上是减函数D．函数y=cos(2022x―π3)+3sin(2022x+π6)的最大值为1+311．已知抛物线C1：y=x2与抛物线C2：y=a x2+1―a(0<a<13)在第一象限交于M点，过M点的直线l 分别与C1，C2交于P，Q两点，且M为线段PQ的中点，O为坐标原点，则（）A．|PQ|>2|OP|B．|PQ|<|OQ|C．tan∠POQ+2>0D．tan∠POQ+1<012．定义在（―1，1）上的函数f（x）满足f（x）―f（y）=f（x―y1―xy），且当x∈（―1，0）时，f（x）<0，则有（）A．f（x）为奇函数B．存在非零实数a，b，使得f（a）+f（b）=f（12）C．f（x）为增函数D．f（12）+f（13）>f（56）三、填空题13．（lg5）2+lg2×lg50= ．14．不等式ax2+4x+a＞1﹣2x2对一切x∈R恒成立，则实数a的取值范围是．15．已知函数f(x)=3sinωx+cosωx(ω>0)，若函数f(x)在区间(π3，π2)内没有零点，则实数ω的最大值是 .16．设正数x，y满足a≥x+yx+y恒成立，则a的最小值是 .四、解答题17．计算下列各式的值：（1）(14)―1+log23；（2）2723+(5)2―1614+(e―1)0.18．已知方程ax2+x+b=0．（1）若方程的解集为{1}，求实数a，b的值；（2）若方程的解集为{1，3}，求实数a，b的值．19．如图，在直角坐标系xOy中，角α的顶点是原点，始边与轴正半轴重合，终边交单位圆于点A，且α∈(π6，π2)，将角α的终边按照逆时针方向旋转π3，交单位圆于点B，记A(x1，y1)，B(x2，y2)（1）若x1=13，求x2；（2）分别过A、B做x轴的垂线，垂足依次为C、D，记ΔAOC的面积为S1，ΔBOD的面积为S2，若S1=2S2，求角α的值.20．已知函数f(x)满足2f(x)+f(―x)=x+2x(x≠0).（1）求y=f(x)的解析式；（2）若对∀x1、x2∈(2，4)且x1≠x2，都有f(x2)―f(x1)x2―x1>kx2⋅x1(k∈R)成立，求实数k的取值范围.21．已知定义在R上的函数f(x)满足：①对任意x，y∈R，有f(x+y)=f(x)+f(y).②当x <0时，f(x)>0且f(1)=―3.（1）求证：f(x)是奇函数；（2）解不等式f(2x―2)―f(x)≥―12.22．已知函数f(x)=2x+ab⋅2x+1是定义域为R的奇函数．（1）求函数f(x)的解析式；（2）若存在x∈[―2,2]使不等式f(m⋅4x)+f(1―2x+1)≥0成立，求m的最小值．答案解析部分1．【答案】B2．【答案】D3．【答案】D4．【答案】B5．【答案】C6．【答案】A7．【答案】D8．【答案】C9．【答案】A,D10．【答案】A,D11．【答案】A,D12．【答案】A,B,C13．【答案】114．【答案】（2，+∞）15．【答案】17316．【答案】217．【答案】（1）解：原式=(14)―1⋅(2―2)log23=4×3―2=49.（2）解：原式=33×23+5―24×14+1=32+5―2+1=13. 18．【答案】（1）解：若方程的解集为{1}，则①若a=0，则1+b=0，解得a=0，b=﹣1；②若a≠0，则a+1+b=0且1﹣4ab=0，解得a=b=﹣12．综上所述，a=0，b=﹣1或a=b=﹣12（2）解：依题意得：1+3=﹣1a ，1×3= ba，解得a=﹣14，b=﹣3419．【答案】（1）解：由三角函数定义，得x1=cosα，x2=cos(α+π3)．因为 α∈(π6，π2) ， cos α=13 ，所以 sin α=1―cos 2α=223．所以 x 2=cos(α+π3)=12cos α―32sin α=1―266 ．（2）解：依题意得 y 1=sin α ， y 2=sin(α+π3) ．所以 S 1=12x 1y 1=12cos α·sin α=14sin2α ，S 2=12|x 2|y 2=12[―cos(α+π3)]·sin(α+π3)=―14sin(2α+2π3) ．依题意 S 1=2S 2 得 sin2α=―2sin(2α+2π3) ，即 sin2α=―2[sin2αcos 2π3+cos2αsin 2π3]=sin2α―3cos2α ，整理得 cos2α=0 ．因为 π6<α<π2 ，所以 π3<2α<π ，所以 2α=π2 ，即 α=π4 ．20．【答案】（1）解：由条件2f (x )+f (―x )=x +2x，可知函数f (x )的定义域为{x |x ≠0}，所以，2f (―x )+f (x )=―x ―2x，可得{2f (x )+f (―x )=x +2x2f (―x )+f (x )=―x ―2x，解得f (x )=x +2x(x ≠0).（2）解：对∀x 1、x 2∈(2，4)，x 1≠x 2，都有f (x 2)―f (x 1)x 2―x 1>k x 2⋅x 1(k ∈R )，不妨设2<x 1<x 2<4，由f (x 2)―f (x 1)x 2―x 1>k x 2⋅x 1，则f (x 2)―f (x 1)>k (x 2―x 1)x 2⋅x 1=k x 1―k x 2，可得f (x 2)+k x 2>f (x 1)+k x 1，也即可得函数g (x )=f (x )+k x =x +k +2x 在区间(2，4)上递增；g ′(x )=1―k +2x2≥0对任意的x ∈(2，4)恒成立，即k +2≤x 2，当x ∈(2，4)时，4<x 2<16，故k +2≤4，解得k ≤2.因此，实数k 的取值范围是(―∞，2].21．【答案】（1）证明：令 x =y =0 ， f (0)=f (0)+f (0) ，∴ f (0)=0 ，令 y =―x ， ∴ f (0)=f (―x )+f (x )=0∴f(x)=―f(―x).∴函数f(x)是奇函数.（2）解：设x1<x2，则x1―x2<0，∴f(x1)―f(x2)=f(x1)+f(―x2)=f(x1―x2)>0∴f(x)为R上减函数.∵f(2x―2)―f(x)=f(2x―2)+f(―x)=f(x―2)≥―12，―12=4f(1)=f(4).∴x―2≤4即x≤6.∴不等式f(2x―2)―f(x)≥―12的解集为{x|x≤6}.22．【答案】（1）解：因为函数f(x)是定义域为R的奇函数，可知f（0）=0, ∴a=-1,又f(―x)=―f(x)，则2―x―1b⋅2―x+1=- 2x―1b⋅2x+1，∴1―2x b+2x =- 2x―1b⋅2x+1，∴b=1，∴f(x)=2x―12x+1（2）解：∵f(x)=2x―12x+1=1- 22x+1，所以f(x)在[―2,2]上单调递增；由f(m⋅4x)≥―f(1―2x+1)=f(2x+1―1)可得m⋅4x≥2x+1―1在[―2,2]有解分参得m≥2x+1―14x =2⋅12x―14x，设t=12x ,t∈[14,4], m≥―t2+2t=―(t―1)2+1，所以m≥―8,则m的最小值为―8。

人教版高中数学选择性必修第二册全册模块综合检测1(含解析)

人教版高中数学选择性必修第二册全册模块综合检测1(原卷版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．数列{a n}满足a n＋1＝3a n＋1，a1＝1，则此数列的第3项是()A．13B．10C．7D．42．{a n}为等差数列，且a7－2a4＝－1，a3＝0，则公差d＝()A．－2B．－12D．2C．123．已知函数f(x)＝3x2＋2，则f′(5)＝()A．15B．30C．32D．774．设等比数列{a n}满足a1＋a2＝－1，a1－a3＝－3，则S6＝()A．－63B．－21C．21D．635．函数f(x)＝xx2＋1的单调递增区间是()A．(－∞，－1)B．(－1,1)C．(1，＋∞)D．(－∞，－1)和(1，＋∞)6．数列{a n}满足a1＝1，log2a n＋1＝log2a n＋1(n∈N*)，它的前n项和为S n，则满足S n>1025的最小n值是()A．9B．10C．11D．127．函数f(x)＝ln xx＋1的图象大致是()8．函数f (x )＝ln x ＋ax 有小于1的极值点，则实数a 的取值范围是()A ．(0,1)B ．(－∞，－1)C ．(－1,0)D ．(－∞，－1)∪(0，＋∞)二、多项选择题(本题共4小题，每小题5分，共20分)9．过点P (2，－6)作曲线f (x )＝x 3－3x 的切线，则切线方程可能是()A ．3x ＋y ＝0B ．24x －y －54＝0C ．9x －y －24＝0D ．12x －y －24＝010．记S n 为等差数列{a n }的前n 项和．若a 1＋3a 5＝S 7，则以下结论一定正确的是()A ．a 4＝0B ．S n 的最大值为S 3C ．S 1＝S 6D ．|a 3|<|a 5|11．在数列{a n }中，若a 2n －a 2n －1＝p (n ≥2，n ∈N *，p 为常数)，则{a n }称为“等方差数列”．下列对“等方差数列”的判断，其中正确的为()A ．若{a n }是等方差数列，则{a 2n }是等差数列B ．若{a n }是等方差数列，则{a 2n }是等方差数列C ．{(－1)n }是等方差数列D ．若{a n }是等方差数列，则{a kn }(k ∈N *，k 为常数)也是等方差数列12．设f (x )＝x a ·cos x ，x ∈π6，π3的最大值为M ，则()A ．当a ＝－1时，M <3B ．当a ＝2时，M <33C ．当a ＝1时，M >32D ．当a ＝3时，M <12三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n }的前n 项和为S n ，a 1＝9，S 99－S 55＝－4，则a n ＝________.14.设函数f (x )＝x 3＋ax 2，若曲线y ＝f (x )在点P (1，f (1))处的切线方程为x ＋y ＝0，则实数a ＝________.15.已知等差数列{a n }的前n 项和为S n ＝pn 2－2n ＋q (p ，q ∈R ，n ∈N *)，则q ＝______；若a 1与a 5的等差中项为8，则p ＋q ＝________.16.设a ，b ∈R ，若x ≥0时恒有0≤x 4－x 3＋ax ＋b ≤(x 2－1)2，则ab 等于________．四、解答题(本题共6小题，共70分)17.(10分)在等差数列{a n}中，已知a1＋a2＋a3＝21，a1a2a3＝231.(1)求该数列中a2的值；(2)求该数列的通项公式a n.18.(12分)(1)求曲线y＝1x在点(－1，－1)处的切线方程；(2)求经过点(4,0)且与曲线y＝1x相切的直线方程．19.(12分)设f(x)＝a ln x＋12x－32x＋1，曲线y＝f(x)在点(1，f(1))处取得极值．(1)求a的值；(2)求函数f(x)的单调区间和极值．20.(12分)设数列{a n}满足：a1＝1，且2a n＝a n＋1＋a n－1(n≥2)，a3＋a4＝12.(1)求{a n}的通项公式；(2)n项和．21.(12分)已知数列{a n}的前n项和为S n，a1＝1，a2＝13，a na n＋1＝2a n＋1(n∈N*且n≥2)．(1)(2)n项和T n.22.(12分)已知a∈R，函数f(x)＝(－x2＋ax)e x(x∈R)．(1)当a＝2时，求函数f(x)的单调区间；(2)若函数f(x)在(－1,1)上单调递增，求a的取值范围．人教版高中数学选择性必修第二册全册模块综合检测1(解析版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．数列{a n }满足a n ＋1＝3a n ＋1，a 1＝1，则此数列的第3项是()A ．13B ．10C ．7D ．4A解析：因为a n ＋1＝3a n ＋1，a 1＝1，所以a 2＝3a 1＋1＝3×1＋1＝4，所以a 3＝3a 2＋1＝3×4＋1＝13.故选A ．2．{a n }为等差数列，且a 7－2a 4＝－1，a 3＝0，则公差d ＝()A ．－2B ．－12C ．12D ．2B解析：∵a 7－2a 4＝－1，∴a 3＋4d －2(a 3＋d )＝－1，∴4d －2d ＝－1，∴d ＝－12.3．已知函数f (x )＝3x 2＋2，则f ′(5)＝()A ．15B ．30C ．32D ．77B解析：依题意f ′(x )＝6x ，所以f ′(5)＝30.故选B ．4．设等比数列{a n }满足a 1＋a 2＝－1，a 1－a 3＝－3，则S 6＝()A ．－63B ．－21C ．21D ．63B解析：设数列{a n }的公比为q ，∵a 1＋a 2＝－1，a 1－a 3＝－3，1＋a 1q ＝－1，1－a 1q 2＝－3，1＝1，＝－2，∴S 6＝a 1(1－q 6)1－q ＝1－643＝－21.故选B ．5．函数f (x )＝xx 2＋1的单调递增区间是()A ．(－∞，－1)B ．(－1,1)C ．(1，＋∞)D ．(－∞，－1)和(1，＋∞)B解析：f (x )的定义域为R ，且f ′(x )＝x 2＋1－2x ·x (x 2＋1)2＝1－x 2(x 2＋1)2＝(1＋x )(1－x )(x 2＋1)2，所以当－1<x <1时，f ′(x )>0，f (x )单调递增，所以f (x )的单调递增区间为(－1,1)．故选B ．6．数列{a n }满足a 1＝1，log 2a n ＋1＝log 2a n ＋1(n ∈N *)，它的前n 项和为S n ，则满足S n >1025的最小n 值是()A ．9B ．10C ．11D ．12C 解析：数列{log 2a n }是以0为首项，公差为1的等差数列，log 2a n ＝0＋(n －1)×1＝n －1，a n＝2n －1，Sn＝1＋2＋22＋23＋…＋2n －1＝1－2n1－2＝2n －1>1025，2n >1026.因为210＝1024,211＝2048，所以，最小n 值是11.选C ．7．函数f (x )＝ln xx ＋1的图象大致是()C解析：由f (x )＝ln xx ＋1，得f ′(x )＝1＋1x －ln x(x ＋1)2(x >0)．令g (x )＝1＋1x－ln x ，则g ′(x )＝－1x 2－1x ＝－1＋x x 2<0，所以g (x )在(0，＋∞)上单调递减．又g (e)＝1e >0，g (e 2)＝1＋1e 2－ln e 2＝1e 2－1<0，所以存在x 0∈(e ，e 2)，使得g (x 0)＝0，所以当x ∈(0，x 0)时，g (x )＞0，f ′(x )＞0；当x ∈(x 0，＋∞)时，g (x )＜0，f ′(x )＜0.所以f (x )在(0，x 0)上单调递增，在(x 0，＋∞)上单调递减．故选C ．8．函数f (x )＝ln x ＋ax 有小于1的极值点，则实数a 的取值范围是()A ．(0,1)B ．(－∞，－1)C ．(－1,0)D ．(－∞，－1)∪(0，＋∞)B解析：因为f(x)＝ln x＋ax，所以函数定义域为{x|x>0}．由f′(x)＝1x＋a＝0，得a≠0，x＝－1a.又函数f(x)＝ln x＋ax有小于1的极值点，所以－1a<1且a<0，所以a<－1.故选B．二、多项选择题(本题共4小题，每小题5分，共20分)9．过点P(2，－6)作曲线f(x)＝x3－3x的切线，则切线方程可能是()A．3x＋y＝0B．24x－y－54＝0C．9x－y－24＝0D．12x－y－24＝0AB解析：∵y′＝3x2－3.设曲线的切点为(x0，y0)，则k＝3x20－3，y0＝x30－3x0.∴切线方程为y－(x30－3x0)＝(3x20－3)(x－x0)．又切线经过点P(2，－6)，则－6－(x30－3x0)＝(3x20－3)(2－x0)，解得x0＝0或x0＝3，∴切点为(0,0)时，切线方程为3x＋y＝0；切点为(3,18)时，切线方程为24x－y－54＝0.10．记S n为等差数列{a n}的前n项和．若a1＋3a5＝S7，则以下结论一定正确的是() A．a4＝0B．S n的最大值为S3C．S1＝S6D．|a3|<|a5|AC解析：设等差数列{a n}的公差为d，则a1＋3(a1＋4d)＝7a1＋21d，解得a1＝－3d，所以a n＝a1＋(n－1)d＝(n－4)d，所以a4＝0，故A正确；因为S6－S1＝5a4＝0，所以S1＝S6，故C正确；由于无法确定d的正负，故S3可能为最大值，也可能为最小值，故B不正确；因为a3＋a5＝2a4＝0，所以a3＝－a5，即|a3|＝|a5|，故D不正确．故选AC．11．在数列{a n}中，若a2n－a2n－1＝p(n≥2，n∈N*，p为常数)，则{a n}称为“等方差数列”．下列对“等方差数列”的判断，其中正确的为()A．若{a n}是等方差数列，则{a2n}是等差数列B．若{a n}是等方差数列，则{a2n}是等方差数列C．{(－1)n}是等方差数列D．若{a n}是等方差数列，则{a kn}(k∈N*，k为常数)也是等方差数列ACD解析：对于A，{a n}是等方差数列，可得a2n－a2n－1＝p(n≥2，n∈N*，p为常数)，即有{a2n}是首项为a21，公差为d的等差数列，故正确；对于B，例如：数列{n}是等方差数列，但是数列{n}不是等方差数列，所以B不正确；对于C，数列{(－1)n}中，a2n－a2n－1＝[(－1)n]2－[(－1)n－1]2＝0(n≥2，n∈N)，所以数列{(－1)n}是等方差数列，故C正确；对于D,数列{a n}中的项列举出来是：a1，a2，…，a k…，a2k，…，数列{a kn}中的项列举出来是：a k，a2k，a3k，….∵a2kn＋k－a2kn＋k－1＝a2kn＋k－1－a2kn＋k－2＝…＝a2kn＋1－a2kn＝p，∴a2kn＋k－a2kn＝(a2kn＋k－a2kn＋k－1)＋(a2kn＋k－1－a2kn＋k－2)＋…＋(a2kn＋1－a2kn)＝kp，∴a2k(n＋1)－a2kn＝kp,所以，数列{a kn}是等方差数列，故D 正确．故选ACD．12．设f(x)＝x a·cos x，x∈π6，π3的最大值为M，则()A．当a＝－1时，M<3B．当a＝2时，M<33C．当a＝1时，M>32D．当a＝3时，M<12AB解析：对于选项A，当a＝－1时，f(x)＝cos xx在区间π6，π3上递减，所以M＝cosπ6π6＝33π<3，故选项A正确．对于选项B，当a＝2时，f(x)＝x2·cos x，则f′(x)＝x cos x(2－xtanx)>0，∴f(x)在区间π6，π3上递增，即M＝π218<33，故选项B正确．对于选项C，当a＝1时，x<tan x恒成立，所以f(x)＝x cos x<tan x cos x＝sin x≤32，所以M<32，故选项C 错误．对于选项D，当a＝3时，f(x)＝x3·cos x，则f′(x)＝x2cos x(3－xtan x)>0，∴f(x)在区间π6，π3上递增，∴M＝12·>12，故选项D错误．故选AB．三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n}的前n项和为S n，a1＝9，S99－S55＝－4，则a n＝________.－2n＋11解析：设公差为d，因为S99－S55＝－4，所以4d－2d＝－4，即d＝－2.所以a n＝a1＋(n－1)d＝9－2(n－1)＝－2n＋11.14.设函数f(x)＝x3＋ax2，若曲线y＝f(x)在点P(1，f(1))处的切线方程为x＋y＝0，则实数a＝________.－2解析：因为点P(1，f(1))在该切线上，所以f(1)＝－1，则f(1)＝1＋a＝－1，解得a＝－2.15.已知等差数列{a n}的前n项和为S n＝pn2－2n＋q(p，q∈R，n∈N*)，则q＝______；若a1与a5的等差中项为8，则p＋q＝________.02解析：由等差数列的性质可得q＝0.又a1与a5的等差中项为8，所以a1＋a5＝16，即S5＝(a1＋a5)×52＝40，所以25p－10＝40，解得p＝2，即p＋q＝2＋0＝2.16.设a ，b ∈R ，若x ≥0时恒有0≤x 4－x 3＋ax ＋b ≤(x 2－1)2，则ab 等于________．－1解析：验证发现，当x ＝1时，将1代入不等式有0≤a ＋b ≤0，所以a ＋b ＝0，当x ＝0时，可得0≤b ≤1，结合a ＋b ＝0可得－1≤a ≤0.令f (x )＝x 4－x 3＋ax ＋b ，即f (1)＝a ＋b ＝0.又f ′(x )＝4x 3－3x 2＋a ，f ′′(x )＝12x 2－6x ，令f ′′(x )＞0，可得x ＞12，则f ′(x )＝4x 3－3x 2＋a 在0，12上递减，在12，＋∞上递增．又－1≤a ≤0，所以f ′(0)＝a ＜0，f ′(1)＝1＋a ≥0.又x ≥0时恒有0≤x 4－x 3＋ax ＋b ，结合f (1)＝a ＋b ＝0知，1必为函数f (x )＝x 4－x 3＋ax ＋b 的极小值点，也是最小值点．故有f ′(1)＝1＋a ＝0，由此得a ＝－1，b ＝1.所以ab ＝－1.四、解答题(本题共6小题，共70分)17.(10分)在等差数列{a n }中，已知a 1＋a 2＋a 3＝21，a 1a 2a 3＝231.(1)求该数列中a 2的值；(2)求该数列的通项公式a n .解：(1)由等差数列性质得a 1＋a 2＋a 3＝3a 2＝21，∴a 2＝7.(2)设等差数列公差为d ，∴a 1a 2a 3＝(a 2－d )a 2·(a 2＋d )＝7(7－d )(7＋d )＝7(49－d 2)＝231.解得d ＝±4，∴a n ＝a 2＋(n －2)d ，即a n ＝4n －1或a n ＝－4n ＋15.18.(12分)(1)求曲线y ＝1x在点(－1，－1)处的切线方程；(2)求经过点(4,0)且与曲线y ＝1x 相切的直线方程．解：∵y ＝1x ，∴y ′＝－1x2.(1)当x ＝－1时，得在点(－1，－1)处的切线的斜率为－1，∴切线方程为y ＋1＝－(x ＋1)，即x ＋y ＋2＝0.(2)设切点为x 0，1x 0，则切线的斜率为－1x 20，∴切线方程为y －1x 0＝－1x 20(x －x 0)，∵切线过点(4,0)，∴－1x 0＝－1x 20(4－x 0)，解得x 0＝2，∴所求切线方程为y －12＝－14(x －2)，即x ＋4y －4＝0.19.(12分)设f (x )＝a ln x ＋12x －32x ＋1，曲线y ＝f (x )在点(1，f (1))处取得极值．(1)求a 的值；(2)求函数f (x )的单调区间和极值．解：(1)因为f (x )＝a ln x ＋12x －32x ＋1，所以f ′(x )＝a x －12x 2－32.由f ′(1)＝0，可得a －2＝0，解得a ＝2.(2)由(1)可知，f (x )＝2ln x ＋12x －32x ＋1，f ′(x )＝－(3x －1)(x －1)2x 2.令f ′(x )＝0，解得x 1＝13，x 2＝1，又因为函数f (x )定义域为(0，＋∞)，所以f (x )(1，＋∞)故f (x )的极大值为f (1)＝0，f (x )的极小值为2－2ln 3.20.(12分)设数列{a n }满足：a 1＝1，且2a n ＝a n ＋1＋a n －1(n ≥2)，a 3＋a 4＝12.(1)求{a n }的通项公式；(2)n 项和．解：(1)由2a n ＝a n ＋1＋a n －1(n ≥2)可知数列{a n }是等差数列，设公差为d ，因为a 1＝1，所以a 3＋a 4＝a 1＋2d ＋a 1＋3d ＝12，解得d ＝2，所以{a n }的通项公式为a n ＝2n －1(n ∈N *)．(2)由(1)知1a n a n ＋2＝1(2n －1)(2n ＋3)＝n 项和S n …＋＋13－12n ＋1－＝13－n ＋1(2n ＋1)(2n ＋3).21.(12分)已知数列{a n }的前n 项和为S n ，a 1＝1，a 2＝13，a na n ＋1＝2a n ＋1(n ∈N *且n ≥2)．(1)(2)n 项和T n .(1)证明：因为a na n ＋1＝2a n ＋1，所以a n ＝a n ＋1＋2a n a n ＋1，即a n －a n ＋1＝2a n a n ＋1，等式两边同时除以a n a n ＋1，得1a n ＋1－1a n＝2(n ≥2)，且1a 2－1a 1＝2，1，公差为2的等差数列．(2)解：由(1)得1a n ＝2n －1，3na n ＝(2n －1)3n ，则T n ＝1×3＋3×32＋…＋(2n －1)3n ①，3T n ＝1×32＋…＋(2n －3)3n ＋(2n －1)3n ＋1②，①－②得－2T n ＝3＋2(32＋…＋3n )－(2n －1)3n ＋1＝3＋2×9×(1－3n －1)1－3－(2n －1)3n ＋1＝2(1－n )3n ＋1－6，故T n ＝(n －1)3n ＋1＋3.22.(12分)已知a ∈R ，函数f (x )＝(－x 2＋ax )e x (x ∈R )．(1)当a ＝2时，求函数f (x )的单调区间；(2)若函数f (x )在(－1,1)上单调递增，求a 的取值范围．解：(1)a ＝2时，f (x )＝(－x 2＋2x )·e x 的导数为f ′(x )＝e x (2－x 2)．由f′(x)＞0，解得－2<x<2，由f′(x)＜0，解得x＜－2或x> 2.即有函数f(x)的单调递减区间为(－∞，－2)，(2，＋∞)，单调递增区间为(－2，2)．(2)函数f(x)＝(－x2＋ax)·e x的导数为f′(x)＝e x[a－x2＋(a－2)x]．由函数f(x)在(－1,1)上单调递增，则有f′(x)≥0在(－1,1)上恒成立，即为a－x2＋(a－2)x≥0，即有x2－(a－2)x－a≤0，则有1＋(a－2)－a≤0且1－(a－2)－a≤0，解得a≥3 2，则a的取值范围为3 2，＋。

人教A版高中数学必修一综合检测试卷(含解析)

人教A版高中数学必修一综合检测试卷（含解析）综合检测时间：120分钟满分：150分一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1．设全集I＝{x|－3<x<3，x∈Z}，A＝{1,2}，B＝{－2，－1,2}，则A∪∁IB等于( ) A．{1}B．{1,2} C．{2} D．{0,1,2} 解析：∵x∈Z，∴I＝{－2，－1,0,1,2} ∴∁IB＝{0,1} ∴A∪∁IB＝{0,1,2}．答案：D 2．函数y＝1x＋log2(x ＋3)的定义域是( ) A．R B．(－3，＋∞) C．(－∞，－3) D．(－3,0)∪(0，＋∞) 解析：函数定义域x≠0x＋3>0∴－3<x<0或x>0. 答案：D 3．下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是( ) A．y＝1x B．y＝e－x C．y＝－x2＋1 D．y＝lg |x| 解析：偶函数的有C、D两项，当x>0时，y＝lg |x|单调递增，故选C. 答案：C 4．设x0是方程ln x＋x＝4的解，则x0属于区间( ) A．(0,1) B．(1,2) C．(2,3) D．(3,4) 解析：设f(x)＝ln x＋x－4，则有f(1)＝ln 1＋1－4＝－3<0.f(2)＝ln 2＋2－4＝ ln 2－2<1－2＝－1<0，f(3)＝ln 3＋3－4＝ln 3－1>1－1＝0. ∴x0∈(2,3)．答案：C 5．3log34－27 －lg 0.01＋ln e3＝( ) A．14 B．0 C．1 D．6 解析：原式＝4－3272－lg 0.01＋3＝7－－lg 10－2＝9－9＝0. 答案：B 6．若y＝log3x的反函数是y＝g(x)，则g(－1)＝( ) A．3 B．－3 C.13 D．－13 解析：由题设可知g(x)＝3x，∴g(－1)＝3－1＝13. 答案：C 7．若实数x，y满足|x|－ln1y＝0，则y关于x的函数的图象大致是( ) 解析：由|x|＝ln1y，则y＝1ex，x≥0ex，x＜0. 答案：B 8．已知f(x)＝log x，g(x)＝2x－1，则函数y＝f(x)－g(x)的零点个数为( ) A．0 B．1 C．2 D．不确定解析：在同一坐标系中作函数f(x)，g(x)的图象(图略)，从而判断两函数交点个数．答案：B 9．函数f(x)＝－－的零点的个数为( ) A．0 B．1 C．2 D．3 解析：函数的定义域为{x|x≠1}，当x>1时f(x)<0，当x<1时f(x)>0，所以函数没有零点，故选A. 答案：A 10．某新品牌电视投放市场后第1个月销售100台，第2个月销售200台，第3个月销售400台，第4个月销售700台，则下列函数模型中能较好地反映销量y与投放市场月数x之间的关系的是( ) A．y＝100x B．y＝50x2－50x＋100 C．y＝50×2x D．y＝100log2x＋100 解析：代入验证即可．答案：B 11．若f(x)＝ax3＋ax＋2(a≠0)在[－6,6]上满足f(－6)>1，f(6)<1，则方程f(x)＝1在[－6,6]内的解的个数为( ) A．1 B．2 C．3 D．4 解析：设g(x)＝f(x)－1，则由f(－6)>1，f(6)<1得[f(－6)－1][f(6)－1]<0，即g(－6)g(6)<0. 因此g(x)＝f(x)－1在(－6,6)有一个零点．由于g(x)＝ax3＋ax＋1(a≠0)，易知当a>0时g(x)单调递增；当a<0时，g(x)单调递减，即函数g(x)为单调函数，故g(x)仅有一个零点．因此方程f(x)＝1仅有一个根．故选A. 答案：A 12．某公司在甲、乙两地销售一种品牌车，利润(单价：万元)分别为L1＝5.06x －0.15x2和L2＝2x，其中x为销售量(单位：辆)，若该公司在两地共销售15辆车，则能获得的最大利润为( ) A．45.666万元 B．45.6万元 C．45.56万元 D．45.51万元解析：设在甲地销售x辆，在乙地则销售(15－x)辆，∴总利润S＝5.06x－0.15x2＋2(15－x) ＝－0.15x2＋3.06x＋30(0≤x≤15) ∴当x＝10时，S有最大值45.6万元．答案：B 二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中的横线上) 13．已知f(x)是定义在R上的偶函数，且当x>0时，f(x)＝2x－3，则f(－2)＝________. 解析：∵f(x)为定义在R上的偶函数，∴f(－x)＝f(x)，∴f(－2)＝f(2)＝22－3＝1. 答案：1 14．已知集合A＝{x|ax2－3x＋2＝0}至多有一个元素，则a的取值范围为________．解析：集合A有为∅和A中只有一个元素两种情况， a＝0时，A＝{23}满足题意，a≠0时，则由Δ＝9－8a≤0得a≥98. 答案：a≥98或a＝0 15．用二分法求方程ln x＝1x在[1,2]上的近似解时，取中点c＝1.5，则下一个有根区间为________．解析：令f(x)＝ln x－1x，则f(1)＝－1<0，f(2)＝ln 2－12＝ln 2－ln e12>0， f(1.5)＝f(32)＝ln32－23＝ln32－ln e23 e23＝3e2>32，∴ln e23>ln32，即f(1.5)<0. ∴下一个有根区间为(1.5,2)．答案：(1.5,2) 16. 给出下列四个命题：①a>0且a≠1时函数y＝logaax与函数y＝alogax表示同一个函数．②奇函数的图象一定通过直角坐标系的原点．③函数y＝3(x－1)2的图象可由y＝3x2的图象向右平移1个单位得到．④若函数f(x)的定义域为[0,2]，则函数f(2x)定义域为[0,4]．其中正确命题的序号是________(填上所有正确命题的序号) 解析：①两函数定义域不同，y ＝logaax定义域为R，y＝alogax定义域(0，＋∞)．②如果函数在x＝0处没有定义，图象就不过原点，如y＝1x. ③正确．④f(x)定义域[0,2]∴f(2x)定义域0≤2x≤2即0≤x≤1，∴f(2x)定义域为[0,1]．答案：③ 三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分12分)已知A＝{x|x2＋2x－8＝0}， B＝{x|log2(x2－5x＋8)＝1}， C＝{x|x2－ax＋a2－19＝0}．若A∩C＝∅，B∩C≠∅，求a的值．解析：A＝{2，－4}，B＝{2,3}，由A∩C＝∅知2∉C，－4∉C，又由B∩C≠∅知3∈C，∴32－3a＋a2－19＝0解得a＝－2或a＝5，当a＝－2时，C＝{3，－5}，满足A∩C＝∅，当a＝5时，C＝{3,2}，A∩C＝{2}≠∅，(舍去)，∴a＝－2. 18．(本小题满分12分)已知函数f(x)＝ax2＋bx＋1(a，b为实数，a≠0，x∈R) (1)当函数f(x)的图象过点(－1,0)，且方程f(x)＝0有且只有一个根，求f(x)的表达式． (2)在(1)的条件下，当x∈[－2,2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围．解析：(1)因为f(－1)＝0，所以a－b＋1＝0 因为方程f(x)＝0有且只有一个根，∴Δ＝b2－4a＝0，∴b2－4(b－1)＝0，即b＝2，a＝1，∴f(x)＝(x＋1)2. (2)∵g(x)＝f(x)－kx＝x2＋2x＋1－kx ＝x2－(k－2)x＋1 ＝(x－k－22)2＋1－－当k－22≥2或k－22≤－2时即k≥6或k≤－2时，g(x)是单调函数． 19．(本小题满分12分)已知f(x)是定义在(0，＋∞)上的增函数，且对任意x，y∈(0，＋∞)，都有f(xy)＝f(x)－f(y)． (1)求f(1)的值； (2)若f(6)＝1，解不等式f(x＋3)＋f1x≤2. 解析：(1)∵f(x)是(0，＋∞)上的增函数，且对任意x，y∈(0，＋∞)，都有f xy＝f(x)－f(y)，∴f(1)＝f(11)＝f(1)－f(1)＝0. (2)若f(6)＝1，则f(x＋3)＋f 1x≤2＝1＋1＝f(6)＋f(6)，∴f(x＋3)－f(6)≤f (6)－f 1x，即f x＋36≤f(6x)，∴0＜x＋36≤6x，解得x≥335. ∴原不等式的解集为{x|x≥335}． 20．(本小题满分12分)已知函数f(x)＝mx＋n1＋x2是定义在(－1,1)上的奇函数，且f(12)＝25. (1)求实数m，n的值； (2)用定义证明f(x)在(－1,1)上为增函数； (3)解关于t的不等式f(t－1)＋f(t)<0. 解析：(1)∵f(x)为奇函数，∴f(－x)＝－f(x)，即－＋n1＋－＝－mx＋n1＋x2. ∴n＝0. 又∵f12＝12m1＋122＝25，∴m＝1.(2)由(1)得，f(x)＝x1＋x2. 设－1<x1<x2<1，则f(x1)－f(x2) ＝x11＋x21－x21＋x22＝＋－＋＋＋＝－－＋＋－1<x1<x2<1，∴x1－x2<0,1－x1x2>0,1＋x21>0,1＋x22>0，∴f(x1)－f(x2)<0. ∴f(x)在(－1,1)上为增函数．(3)∵f(x)是定义在(－1,1)上的奇函数，由f(t－1)＋f(t)<0，得f(t)<－f(t－1)＝f(1－t)．又∵f(x)在(－1,1)上为增函数，∴－1<t<1，－1<1－t<1，t<1－t，解得0<t<12. 21．(本小题满分13分)某医疗研究所开发了一种新药，如果成人按规定的剂量服用，则服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线． (1)写出服药后y 与t之间的函数关系式； (2)据测定，每毫升血液中含药量不少于4μg时治疗痢疾有效．假设某病人一天中第一次服药时间为上午7：00，问一天中怎样安排服药时间(共4次)效果更佳？解析：(1)依题意，得y＝6t，0≤t≤1，－23t＋203，1<t≤10. (2)设第二次服药在第一次服药后t1小时，则－23t1＋203＝4. 解得t1＝4，因而第二次服药应在11：00. 设第三次服药在第一次服药后t2小时，则此时血液中含药量应为前两次服药后的含药量的和，即－23t2＋203－23(t2－4)＋203＝4. 解得t2＝9小时，故第三次服药应在16：00. 设第四次服药在第一次服药后t3小时(t3>10)，则此时第一次服进的药已吸收完，血液中含药量为第二、三次的和，即－23(t3－4)＋203－23(t3－9)＋203＝4. 解得t3＝13.5小时，故第四次服药应在20：30. 22．(本小题满分13分)已知函数f(x)定义域为[－1,1]，若对于任意的x，y∈[－1,1]，都有f(x＋y)＝f(x)＋f(y)，且x>0时，有f(x)>0， (1)证明： f(x)为奇函数； (2)证明：f(x)在[－1,1]上是增加的． (3)设f(1)＝1，若f(x)<m－2am＋2，对所有x∈[－1,1]，a∈[－1,1]恒成立，求实数m的取值范围．解析：(1)令x＝y＝0，∴f(0)＝0 令y＝－x，f(x)＋f(－x)＝0 ∴f(－x)＝－f(x)，∴f(x)为奇函数．(2)∵f(x)是定义在[－1,1]上的奇函数，令－1≤x1<x2≤1，则f(x2)－f(x1)＝f(x2－x1)>0，∴f(x)在[－1,1]上是增加的． (3)f(x)在[－1,1]上是增加的，f(x)max＝f(1)＝1，使f(x)<m－2am＋2对所有x∈[－1,1]恒成立，只要m－2am＋2>1，即m－2am＋1>0，令g(a)＝m－2am＋1＝－2am＋m＋1，要使g(a)>0时，a∈[－1,1]恒成立，则－，，即1＋3m>0，1－m>0，∴－13<m<1. ∴实数m的取值范围是(－13，1)．。

人教版高中数学新教材必修第一册综合测试题(基础,含多选题)

人教版高中数学新教材必修第一册综合测试题第一部分选择题（共60分）一、单项选择题:(共8小题，每题5分，共40分. 在每个小题给出的四个选项中，只有一项是符合题目要求的 )1.设集合{}1,2,3,4,5U =，,{1,3,5}A =，{2,3,5}B =，则()U C A B 等于（）A ．{3, 5}B ．{ 4 }C ．{1,2,4}D ．∅2.设x∈R，则“05x <<” 是“02x <<”的 ( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3．在下列四组函数中，()f x 与()g x 表示同一函数的是( )A ．,0(),(),0x x f x x g x x x ≥⎧==⎨-<⎩B ．2(),()x f x x g x x==C ．()1(),()1()f x x x g x x x =+∈=+∈R ZD ．2(),()f x x g x ==4. 若c b a >>，则下列不等式成立的是（）A ．22a b >B ．a c b c +>+C ．bc ac >D ．bc ac <5. 函数(){}1,1,1,2f x x x =+∈-的值域是 ( ).A ( 0,2,3 ) .B 03y ≤≤ .C {}0,2,3 .D []0,36．若不等式x 2＋kx ＋1＜0的解集为空集，则k 的取值范围是( )A ．[－2，2]B ．(－∞，－2]∪[2，＋∞)C ．(－2，2)D ．(－∞，－2)∪(2，＋∞)7. 若0,0>>y x ，且28x y +=，则xy 的最大值是（）A ．2B ．4C ．8D ．16 8．甲、乙两同学同时从寝室到教室，甲一半路程步行，一半路程跑步，乙一半时间步行，一半时间跑步，如果两人步行速度、跑步速度均分别相同，则（）A ．甲先到教室B ．乙先到教室C ．两人同时到教室D ．谁先到教室不确定二、多项选择题: (共4题，每题5分，共20分. 在每个小题给出的四个选项中，有多个项符合题目要求. 全部选对的得5分，选对但不全的得3分，未选或有选错的得0分)9．已知集合}01|{2=-=x x A ，则下列式子表述正确的有（）A ．A ∈1B ．A ∈-}1{C ．A ⊆φD ．A ⊆-}1,1{ 10．下列命题为真命题的是（）A ．2,x R x x ∀∈≥B ．0,0a b a ==若则C ．0,0a a b ==若则D ．菱形的对角线互相平分 11. 以下四个不等式, 其中是a 1<b1成立的充分条件的是（） A ．a<0<b B ．b<a<0 C ．b<0<a D ．0<b<a ，12．下列结论正确的是（） A. 1+2x x ≥ B. 11+3-1x x x >时，的最小值是 C. +y=4x 时，y x 的最大值4 D. 0 a ≠时，2212a a ≥+第二部分非选择题（90分）三．填空题: (本题共4个小题,每小题5分,共20分)13. 函数11y x =-的定义域是__________. 14. 满足{}{}1,21,2,3B =的集合B 的个数为15. 不等式225413x x x -+<-+的解集是__________.16. 已知函数()32,f x x =+若()8,f a = 则实数a 的值是_________.四、解答题（共70分，解答必须写出必要的文字说明、证明过程或演算步骤）(){}{}17. 10 121,25P x a x a Q x x =+≤≤+=-≤<分若(1)当a =3时，求(C R P) ∩Q ;(2)0,a P Q a >⊆若，求的取值范围18．(12分) 已知命题P: 2,2,x R x x m ∀∈≠-+命题q: 2,210x R x x m ∃∈+--=(1) 写出命题P ⌝（2）若命题P 为假命题，命题q 为真命题，求实数m 的取值范围19．(12分) 已知集合{}{}2A 22,-8+15=0x a x a B x x x =-≤≤+=（1）当3a =时，A B 判断集合与的关系；（2）x B ∈若“”是x A ∈“”的充分不必要条件，求实数a 的取值范围20．(12分) 已知两个正实数,x y 满足141x y+= (1) 求4y x +的最小值； (2) 若不等式234y x m m +≥-恒成立，求实数m 的取值范围21.（12分）已知函数2()4f x x ax =-++，()5g x x =-+．（1）当1a =时，比较()()f x g x 与的大小；（2）若不等式()()f x g x ≥的解集包含[1，2]，求a 的取值范围。

(人教版A版)高中数学必修第一册第二章综合测试试卷03及答案

第二章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列等式一定正确的是（）A .()lg lg lg xy x y=+B .222m n m n++=C .222m n m n+×=D .2ln 2ln x x=2.若函数()12122m y m m x -=+-是幂函数，则m =（）A .1B .3-C .3-或1D .23.下列函数既是增函数，图像又关于原点对称的是（）A .y x x=B .xy e =C .1y x=-D .2log y x=4.函数()ln 3y x =- ）A .[)23，B .[)2+¥，C .()3-¥，D .()23，5.下列各函数中，值域为()0¥，+的是（）A .22xy -=B.y =C .21y x x =++D .113x y +=6.已知()x f x a =，()()log 01a g x x a a =＞，且≠，若()()330f g ＜，那么()f x 与()g x 在同一坐标系内的图像可能是（）A BC D7.已知0.2log 2.1a =， 2.10.2b =，0.22.1c =则（）A .c b a＜＜B .c a b＜＜C .a b c＜＜D .a c b＜＜8.已知()()221122x a x x f x x ì-ï=íæö-ïç÷èøî，≥，，＜是R 上的减函数，则实数a 的取值范围是（）A .()2-¥，B .138æù-¥çúèû，C .()02，D .1328éö÷êëø，9.已知函数()y f x =是定义在R 上的偶函数，当0x ≥时，()2x f x e x =+，则()ln 2f -=（）A .12ln 22-B .12ln 22+C .22ln 2-D .22ln 2+10.已知函数()()()x xf x x e ae x -=+ÎR ，若()f x 是偶函数，记a m =；若()f x 是奇函数，记a n =.则2m n +的值为（）A .0B .1C .2D .1-11.已知实数a ，b 满足等式20172018a b =，则下列关系式不可能成立的是（）A .0a b ＜＜B .0a b ＜＜C .0b a＜＜D .a b=12.已知函数()221222log x mx m x m f x x x m ì-++ï=íïî，≤，，＞，其中01m ＜＜，若存在实数a ，使得关于x 的方程()f x a=恰有三个互异的实数解，则实数m 的取值范围是（）A .104æöç÷èø，B .102æöç÷èø，C .114æöç÷èøD .112æöç÷èø，二、填空题：本大题共4小题，每小题5分，共20分.13.满足31164x -æöç÷èø＞的x 的取值范围是________.14.若函数()212log 35y x ax =-+在[)1-+¥，上是减函数，则实数a 的取值范围是________.15.如图，矩形ABCD 的三个顶点A ，B ，C分别在函数y x =，12y x =，xy =的图像上，且矩形的边分别平行于两坐标轴.若点A 的纵坐标为2，则点D 的坐标为________.16.定义新运算Ä：当m n ≥时，m n m Ä=；当m n ＜时，m n n Ä=.设函数()()()2221log 2xx f x x éùÄ-Ä×ëû，则函数()f x 在()02，上的值域为________.三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.17.（本小题满分10分）计算下列各式的值：（1）7015log 243210.06470.250.58--æö--++´ç÷èø；（2）()2235lg5lg 2lg5lg 20log 25log 4log 9+´++´´.18.（本小题满分12分）已知定义域为R 的单调函数()f x 是奇函数，当0x ＞时，()23x xf x =-.（1）求()f x 的解析式；（2）若对任意的t ÎR ，不等式()()22220f t t f t k -+-＜恒成立，求实数k 的取值范围.19.（本小题满分12分）已知实数x 满足9123270x x -×+≤，函数()2log 2xf x =×（1）求实数x 的取值范围；（2）求函数()f x 的最值，并求此时x 的值.20.（本小题满分12分）已知函数()x f x a =，()2x g x a m =+，其中0m ＞，0a ＞且1a ≠.当[]11x Î-，时，()y f x =的最大值与最小值之和为52.（1）求a 的值；（2）若1a ＞，记函数()()()2h x g x mf x =-，求当[]0x Î，1时，()h x 的最小值()H m .21.（本小题满分12分）以德国数学家狄利克雷（l805-1859）命名的狄利克雷函数定义如下：对任意的x ÎR ，()10.x D x x ì=íî，为有理数，，为无理数研究这个函数，并回答如下问题：（1）写出函数()D x 的值域；（2）讨论函数()D x 的奇偶性；（3）若()()()212x x D x x f x D x x ì-ï=íïî+，为有理数，+，为无理数，，求()f x 的值域.22.（本小题满分12分）若函数()f x 满足()()21log 011a a f x x a a a x æö=×-ç÷-èø＞，且≠.（1）求函数()f x 的解析式，并判断其奇偶性和单调性；（2）当()2x Î-¥，时，()4f x -的值恒为负数，求a 的取值范围.第二章综合测试答案解析一、1.【答案】C【解析】对于A ，D ，若x ，y 为非正数，则不正确；对于B ，C ，根据指数幂的运算性质知C 正确，B 错误.故选C .2.【答案】B【解析】因为函数()12122m y m n x -=+-是幂函数，所以22211m m m +-=且≠，解得3m =-.3.【答案】A【解析】2200x x y x x x x ìï==í-ïî，≥，，＜为奇函数且是R 上的增函数，图像关于原点对称；x y e =是R 上的增函数，无奇偶性；1y x=-为奇函数且在()0-¥，和()0+¥，上单调递增，图像关于原点对称，但是函数在整个定义域上不是增函数；2log y x =在()0+¥，上为增函数，无奇偶性.故选A .4.【答案】A【解析】函数()ln 3y x =-+x 满足条件30240xx -ìí-î＞，≥，解得32x x ìíî＜，≥，即23x ≤＜，所以函数的定义域为[)23，，故选A .5.【答案】A【解析】对于A，22xxy -==的值域为()0+¥，；对于B ，因为120x -≥，所以21x ≤，0x ≤，y =(]0-¥，，所以021x ＜≤，所以0121x -≤＜，所以y =[)01，；对于C ，2213124y x x x æö=++=++ç÷èø的值域是34éö+¥÷êëø，；对于D ，因为()()1001x Î-¥+¥+，∪，，所以113x y +=的值域是()()011+¥，∪，.6.【答案】C【解析】由指数函数和对数函数的单调性知，函数()x f x a =与()()log 01a g x x a a =＞，且≠在()0+¥，上的单调性相同，可排除B ，D .再由关系式()()330f g ×＜可排除A ，故选C .7.【答案】C【解析】 2.100.200.20.2log 2.1log 1000.20.21 2.1 2.1 1.a b c a b c ======\Q ＜，＜＜，＞＜＜.故选C .8.【答案】B【解析】由题意得，函数()()221122x a x x f x x ì-ï=íæö-ïç÷èøî，≥，，＜是R 上的减函数，则()2201122,2a a -ìïíæö--´ïç÷èøî＜，≥解得138a ≤，故选B .9.【答案】D【解析】Q 函数()y f x =是定义在R 上的偶函数，且当0x ≥时，()2x f x e x =+，()()ln 2ln 2ln 22ln 222ln 2f f e \-==+=+.故选D .10.【答案】B【解析】当()f x 是偶函数时，()()f x f x =-，即()()x x x x x e ae x e ae --+=-×+，即()()10x x a e e x -++=.因为上式对任意实数x 都成立，所以1a =-，即1m =-.当()f x 是奇函数时，()()f x f x =--，即()()x x x x x e ae x e ae --+=+，即()()10x x a e e x ---=.因为上式对任意实数x 都成立，所以1a =，即1n =.所以21m n +=.11.【答案】A【解析】分别画出2017x y =，2018x y =的图像如图所示，实数a ，b 满足等式20172018a b =，由图可得0a b ＞＞或0a b ＜＜或0a b ==，而0a b ＜＜不成立.故选A .12.【答案】A【解析】当01m ＜＜时，函数()221222log x mx m x m f x x x m ì-++ï=£íïî，≤，，＞，的大致图像如图所示.Q 当x m ≤时，()()2222222f x x mx m x m =-++=-+≥，\要使得关于x 的方程()f x a =有三个不同的根，则12log 2m ＞.又01m ＜＜，解得104m ＜＜.故选A .二、13.【答案】()1-¥，【解析】由题可得，321144x --æöæöç÷ç÷èøèø＞，则32x --＜，解得1x ＜.14.【答案】(]86--，【解析】令()235g x x ax =-+，其图像的对称轴为直线6a x =.依题意，有()1610ag ì-ïíï-î，＞，即68.a a -ìí-î≤，＞故(]86a Î--，.15.【答案】1124æöç÷èø，【解析】由图像可知，点()2A A x ，在函数y x =的图像上，所以2A x =，212A x ==.点()2B B x ，在函数12y x =的图像上，所以122B x =，4x =.点()4,C C y 在函数x y =的图像上，所以414C y ==.又因为12D A xx ==，14D C y y ==，所以点D 的坐标为1124æöç÷èø，.16.【答案】()112，【解析】根据题意，当22x ≥，即1x ≥时，222x x Ä=；当22x ＜，即1x ＜时，222x Ä=.当2log 1x ≤，即02x ＜≤时，21log 1x Ä=；当21log x ＜，即2x ＞时，221log log x x Ä=.()()2220122122log 2 2.x x x x xx f x x x x ìïï\=-íï-×ïî，＜＜，，≤≤，，＞\①当01x ＜＜时，()2x f x =是增函数，()12f x \＜＜；②当12x ≤＜，()221122224xxx f x æö=-=--ç÷èø，1222 4.x x \Q ≤＜，≤＜()221111242424f x æöæö\----ç÷ç÷èøèø＜，即()212f x ≤＜.综上，()f x 在()02，上的值域为()112，.三、17.【答案】解（1）70515log 244321510.06470.250.51224822--æöæö--++´=-++´=ç÷ç÷èøèø.（2）()()22352lg52lg 22lg3lg5lg 2lg5lg 20log 25log 4log 9lg5lg5lg 2lg 21lg 2lg3lg5+´++´´=++++´´11810=++=.18.【答案】解（1）Q 定义域为R 的函数()f x 是奇函数，()00f \=.Q 当0x ＜时，0x -＞，()23x xf x --\-=-.又Q 函数()f x 是奇函数，()()f x f x \-=-，()23x xf x -\=+.综上所述，()2030020.3xx x x f x x xx -ì-ïï==íïï+î，＞，，，，＜（2）()()51003f f -==Q ＞，且()f x 为R 上的单调函数，()f x \在R 上单调递减.由()()22220f t t f t k -+-＜得()()2222f t t f t k ---＜.()f x Q 是奇函数，()()2222f t t f k t \--＜.又()f x Q 是减函数，2222t t k t \--＞，即2320t t k --＞对任意t ÎR 恒成立，4120k \D =+＜，解得13k -＜，即实数k 的取值范围为13æö-¥-ç÷èø，.19.【答案】解（1）由9123270x x -×+≤，得()23123270xx -×+≤，即()()33390x x --≤，所以339x ≤≤，所以12x ≤≤，满足02x 0.所以实数x 的取值范围为[]12，.（2）()()()()2222222231log log 1log 2log 3log 2log 224xf x x x x x x æö=×=--=-+=--ç÷èø.因为12x ≤≤，所以20log 1x ≤≤.所以2log 1x =，即2x =时，()min 0f x =；当2log 0x =，即1x =时，()max 2f x =.故函数()f x 的最小值为0，此时2x =，最大值为2，此时1x =.20.【答案】解（1）()f x Q 在[]11-，上为单调函数，()f x \的最大值与最小值之和为152a a -+=，2a \=或12a =.（2）1a Q ＞，2a \=.()2222x x h x m m =+-×，即()()2222xx h x m m =-×+.令2x t =，则()h x 可转化为()22k t t mt m =-+，其图像对称轴为直线t m =.[]01x ÎQ ，，[]12t \Î，，\当01m ＜＜时，()()11H m k m ==-+；当12m ≤≤时，()()2H m k m m m ==-+；当2m ＞时，()()234H m k m ==-+.综上所述，()21011234 2.m m H m m m m m m -+ìï=-+íï-+î，＜＜，，≤≤，，＞21.【答案】解（1）函数()D x 的值域为{}01，.（2）当x 为有理数时，则x -为无理数，则()()1D x D x -==；当x 为无理数时，则为x -为无理数，则()()0D x D x -==.故当x ÎR 时，()()D x D x -=，所以函数()D x 为偶函数.（3）由()D x 的定义知，()22x x x f x x ìï=íïî，为有理数，，为无理数.即当x ÎR 时，()2x f x =.故()f x 的值域为()0+¥，.22.【答案】解（1）令log a x t =，则t x a =，()()21t t a f t a a a -\=--.()()()21x x a f x a a x a -\=-Î-R .()()()()2211x x x x a a f x a a a a f x a a ---=-=--=---Q ，()f x \为奇函数.当1a ＞时，x y a =为增函数，xy a -=-为增函数，且2201a a -，()f x \为增函数.当01a ＜＜时，x y a =为减函数，x y a -=-为减函数，且2201a a -＜，()f x \为增函数.()f x \在R 上为增函数.（2）()f x Q 是R 上的增函数，()4y f x \=-也是R 上的增函数.由2x ＜，得()()2f x f ＜，要使()4f x -在()2-¥，上恒为负数，只需()240f -≤，即()22241a a a a ---≤.422141a a a a-\×-≤，214a a \+≤，2410a a \-+≤，22a \-+≤.又1a Q ≠，a \的取值范围为)(21,2éë.。

人教版高一数学必修一期末综合练习题(含答案)

人教版高一数学必修一期末综合练习题(含答案)人教版高一数学必修一期末综合练题（含答案）一、单选题1.已知实数a，b，c满足lga=10=b，则下列关系式中不可能成立的是（）A。

a>b>cB。

a>c>bC。

c>a>bD。

c>b>a2.已知函数f（x）=x（e^x+a），若函数f（x）是偶函数，记a=m，若函数f（x）为奇函数，记a=n，则m+2n的值为（）A。

0B。

1C。

2D。

-13.命题：“对于任意实数x，x^2+x>0” 的否定是( )A。

存在实数x，使得x^2+x≤0B。

对于任意实数x，x^2+x≤0C。

存在实数x，使得x^2+x＜0D。

对于任意实数x，x^2+x≥04.已知sin2α=-1/2，则cos(α+π/3)=（）A。

-1/3B。

-2/3C。

1/3D。

2/35.已知ω＞0，函数f(x)=cos(ωx+π/2)，则ω的取值范围是（）A。

(0,π/12]B。

(0,π/6]C。

(0,π/4]D。

(0,π/2]6.为了得到函数y=cos2x的图象，只需将函数y=sin(2x-π/2)的图象上所有点A。

向右平移π个单位B。

向左平移π个单位C。

向右平移π/2个单位D。

向左平移π/2个单位7.下列函数中，与函数y=x相同的是（）A。

y=1/xB。

y=x^2C。

y=√xD。

y=|x|8.若2sinx-cos(π/2+x)=1，则cos2x=（）A。

-8/9B。

-7/9C。

7/9D。

8/99.设A={x|x^2-4x+3≥0}，B={x|x^2-6x+5≤0}，则“A包含于B”是“B包含于A”的（）A。

充分必要条件B。

必要不充分条件C。

充分不必要条件D。

既不充分也不必要条件10.已知集合A={x|y=ln(x+1)}，集合B={x|x≤2}，则A∩B等于（）A。

(-1,2]B。

[0,2]C。

(0,∞)D。

(5,6]11.已知集合P={x|x-3≤2，x∈R}，Q={3,5,6}，则P∩Q=（）A。

新课标人教版必修5高中数学综合检测试卷附答案解析

解题技巧
认真审题，理解题意
运用所学知识，分析问题
结合实际，联系生活
细心计算，确保答案准确
易错点提醒
计算错误：学生可能因为粗心或计算能力不足而犯错
概念混淆：学生对相关概念理解不清晰，导致填空题答案错误
逻辑推理错误：学生在解题过程中，可能因为逻辑推理不严密而导致答案错误
审题不清：学生可能因为审题不仔细，导致理解题意出现偏差，从而影响答案的准确性
难度分布：试卷难度适中，注重基础知识的考查，同时也有一定的难度和区分度。
题型设计：本试卷包括选择题、填空题、解答题等多种题型，考查学生的不同能力。
考查重点：本试卷重点考查学生的数学基础知识和应用能力，以及学生的数学思维和解题技巧。
难度分析
基础题占比： 40%
中档题占比： 40%
难题占比：20%
题目设计注重考查学生的数学析
题目类型：单项选择题
题目数量：10道
题目难度：中等
解析：对每道题目进行详细的解析，包括解题思路、方法、答案等
解题技巧
掌握基础知识：选择题通常考察基础知识点，应熟练掌握相关概念和公式。仔细审题：读懂题目要求，找出关键信息，避免因误解而选错答案。
排除法：对于一些难以确定答案的选择题，可以采用排除法，排除明显错误的选项。
善于利用选项：有些选择题的答案可以通过代入选项进行验证，从而快速找到正确答案。
易错点提醒
选项中涉及到的知识点是否准确掌握选项中的陷阱和迷惑性词语是否能够识别计算和分析过程中是否有遗漏或错误解题思路和方法是否正确且符合题意
题目类型及解析
题目类型：填空题题目难度：中等题目数量：10道解析：针对每道题目给出详细的解题思路和答案解析

(人教版B版2017课标)高中数学必修第一册全册综合测试卷一(附答案)

（人教版B 版2017课标）高中数学必修第一册全册综合测试卷一（附答案）第一章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知全集{0,1,2,3,4,5}U =，集合{1,2,3,5}A =，{2,4}B =，则()uA B =U ð（） A .{0,2,4}B .{4}C .{1,2,4}D .{0,2,3,4}2.已知集合{0,2,3}A =，{|,,}B x x a b a b A ==⋅∈，则集合B 的子集的个数是（） A .4B .8C .15D .163.如果甲是乙的必要不充分条件，乙是丙的充要条件，丙是丁的必要不充分条件，则丁是甲的（） A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件4.设a ，b ∈R ，集合{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭，则b a -=（）A .1B .1-C .2D .2-5.若集合{0,1,2}M =，{(,)|210210,,}N x y x y x y x y M =-+--∈且厔，则N 中元素的个数为（） A .9B .6C .4D .26.命题:q x ∀∈R ，3210x x -+„的否定是（） A .32,10x x x ∃∈-+R „B .32,10x x x ∃∈-+R …C .32,10x x x ∃∈-+R ＞D .32,10x x x ∀∈-+R ＞7.已知p 是r 的充分条件，q 是r 的充分条件，s 是r 的必要条件，q 是s 的必要条件.现有下列命题：①s 是q 的充要条件；②p 是q 的充分条件；③r 是q 的必要条件；④p ⌝是s ⌝的必要条件；⑤r 是s 的充分条件.则正确命题的序号是（） A .①④⑤B .①②④C .②③⑤D .②④⑤8.已知集合{}2|0M x x x =->，{|1}N x x =…，则M N =I （） A .[1,)+∞B .(1,)+∞C .∅D .(,0)(1,)-∞+∞U9.设集合{|0}M x x m =-„，{}2|(1)1,N y y x x ==--∈R .若M N =∅I ，则实数m 的取值范围是（） A .[1,)-+∞B .(1,)-+∞C .(,1]-∞-D .(,1)-∞-10.已知全集U R =，集合{|(2)0}A x x x =+<，{|||1}B x x =≤，则如图所示的阴影部分表示的集合是（）A .(2,1)-B .[1,0)[1,2)-UC .(2,1)[0,1]--UD .[0,1]11.设条件p ：关于x 的方程()221210m x mx -+-=的两根一个小于0，一个大于1，若p 是q 的必要不充分条件，则条件q 可设为（）A .(1,1)m ∈-B .(0,1)m ∈C .(1,0)m ∈-D .(2,1)m ∈-12.关于x 的方程2210ax x ++=至少有一个负根的充要条件是（） A .01a 剟B .1a ＜C .1a „D .01a ＜„或0a ＜二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上） 13.已知非空集合M 满足：{1,2,3,4,5}M ⊆，且若x M ∈，则6x M -∈.则满足条件的集合M 有__________个.14.设全集S 有两个子集A ，B ，若sA x x B ∈⇒∈ð，则x A ∈是x sB ∈ð的条件是__________. 15.关于x 的不等式2043x ax x +++＞的解集为(3,1)(2,)--+∞U 的充要条件是__________. 16.已知集合{|||1}A x x a =-„，{}2|540B x x x =-+…，若A B =∅I ，则实数a 的取值范围是__________.三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明、证明过程或演算步骤）17.（本小题满分10分）已知集合{|(2)[(31)]0}A x x x a =--+＜，()22|01x a B x x a ⎧⎫-⎪⎪=⎨⎬-+⎪⎪⎩⎭＜. （1）当2a =时，求A B ⋂；（2）求使B A ⊆的实数a 的取值范围.18.（本小题满分12分）若{|68,,}A x x a b a b ==+∈Z ，{|2,}B x x m m ==∈Z ，求证：A B =.19.（本小题满分12分）已知命题p ：方程2220a x ax +-=在区间[1,1]-上有解；命题q ：只有一个实数x 满足不等式2220x ax a ++≤.若命题“p 或q ”是假命题，求实数a 的取值范围.20.（本小题满分12分）已知{}2|320A x x x =++≥，{}2|410,B x mx x m m =-+-∈R ＞，若 0A B =I ，且A B A =U ，求实数m 的取值范围.21.（本小题满分12分）已知{}2:|10p A x x ax =++≤，{}2:|320q B x x x =-+≤，若p 是q 的充分不必要条件，求实数a 的取值范围.22.（本小题满分12分）已知集合{}2|8200P x x x =--≤，{||1|}S x x m =-„. （1）若()P S P ⊆U ，求实数m 的取值范围.（2）是否存在实数m ，使“x P ∈”是“x S ∈”的充要条件？若存在，求出m 的取值范围；若不存在，请说明理由.第一单元测试答案解析一、 1.【答案】A【解析】由题意得uA {0,4}=ð，又{2,4}B =，所以(){0,2,4}uA B =U ð，故选A . 2.【答案】D【解析】∵{0,4,6,9}B =，∴B 的子集的个数为4216=. 3.【答案】A【解析】因为丁⇒丙⇔乙⇒甲，故丁⇒甲（传递性）. 4.【答案】C【解析】∵集合{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭，又0a ≠∵，0a b +=∴，即a b =-，1ba=-∴，1b =. 2b a -=∴，故选C .5.【答案】C【解析】N ∵为点集，x M ∈，y M ∈，∴由x ，y 组成的点有(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2).其中满足210x y -+≥且210x y --≤的仅有(0,0)，(0,1)，(1,1)，(2,1)四个元素.6.【答案】C【解析】原命题的否定是“32,10x x x ∃∈-+R ＞”. 7.【答案】B【解析】由已知有p r ⇒，q r ⇒，r s ⇒，s q ⇒，由此得g s ⇒且s q ⇒，r q ⇒且q r ⇒，所以①正确，③不正确. 又p q ⇒，所以②正确.④等价于p s ⇒，正确.r s ⇒且s r ⇒，⑤不正确.故选B .8.【答案】B【解析】由20x x -＞得0x ＜或1x ＞，∵(1,)M N =+∞I .故选B . 9.【答案】D【解析】由已知得(,]M m =-∞，[1,)N =-+∞，∵M N =∅I ，1m ∴-＜，故选D . 10.【答案】C【解析】由已知得{|20}A x x =-＜＜，{|11}B x x =-≤≤，所以(2,1]A B =-U ，[1,0)A B =-I ，所以阴影部分表示的集合为()(2,1)[0,1]A B A B =--⋃U I ð，故选C .11.【答案】C【解析】构造函数()22121y m x mx =-+-，则0x =时，1y =-，函数的图像开口向上，由1x =时21210m m -+-＜得2m ＞或0m ＜，又p 是q 的必要不充分条件，所以p ⇒q ，q p ⇒，故选C .12.【答案】C【解析】若0∆=，则440a -=，1a =，满足条件，当0∆＞时，4401a a -⇒＞＜.所以1a ≤. 二、 13.【答案】7【解析】列举如下：{1,5}M =，{2,4}M =，{3}M =，{1,3,5)M =，{2,3,4}M =，{1,2,4,5}M =，{1,2,3,4,5}M =，共7个.14.【答案】必要不充分【解析】由已知得S A B ⊆ð，两边取补集，有()S S S A B ⊇痧?，即S A B ⊇ð，所以S x B x A ∈⇒∈ð，反之，不一定成立，故x ∈A 是S x B ∈ð的必要不充分条件.15.【答案】2a =-【解析】令2430x x ++=，得3x =-或1x =-，∴可猜想20a +=，即2a =-.代入原不等式得22043x x x -++＞，解得(3,1)(2,)x ∈--+∞U .故2a =-.16.【答案】(2,3)【解析】由题意得{|11}A x a x a =-+≤≤，{|14}B x x x 或剠，A B =∅Q I ，1114a a ->⎧⎨+<⎩∴，23a ∴＜＜.三、17.【答案】（1）∵当2a =时，{|27}A x x =＜＜，{|45}B x x =＜＜，{|45}A B x x =I ∴＜＜（2）由已知得{}2|21B x a x a =+＜＜，当13a ＜时，{|312}A x a x =+＜＜，要使B A ⊆，必须满足2231,12,a a a +⎧⎨+⎩…„此时1a =-；当13a =时，A =∅，使B A ⊆的a 不存在；当13a ＞时，(2,31)A a =+，要使B A ⊆，必须满足2222,131,12,a a a a a ⎧⎪++⎨⎪+≠⎩…„此时13a <„.综上可知，使B A ⊆的实数a 的取值范围为(1,3]{1}-U .18.【答案】证明：①设t A ∈，则存在,a b ∈Ζ，使得682(34)t a b a b =+=+.34a b +∈Z ∵t B ∈∴，t B ∴∈即A B ⊆.②设t B ∈，则存在m ∈Z ，使得26(5)84t m m m ==⨯-+⨯.0a =∴t A ∈∴ 5m -∈Z ∵，4m ∈Z ，，即B A ⊆. 由①②知A B =.19.【答案】由2220a x ax +-=，得(2)(1)0ax ax +-=，显然0a ≠，2x a =-∴或1x a=. [1,1]x ∈-∵，故21a ≤或11a„，||1a ∴…. “只有一个实数x 满足2220x ax a ++≤”即抛物线222y x ax a =++与x 轴只有一个交点，2480a a ∆=-=∴，或2a =，∴命题“p 或q ”为真命题时“||1a ≥或0a =”.∵命题“p 或q ”为假命题，∴实数a 的取值范围为{|10 01}a a a -＜＜或＜＜. 20.【答案】A B A =U ∵，B A ⊆∴，又A B =∅I ，B =∅∴{}2|410,B x mx x m m =-+-∈R ∵＞，∴对一切x ∈R ，使得2410mx x m -+-≤恒成立，于是有0,164(1)0,m m m ⎧⎨--⎩＜≤解得m „∴实数m的取值范围是|m m ⎧⎪⎨⎪⎪⎩⎭„21.【答案】{}2|320{|12}B x x x x x =∈-+=R 剟?，p ∵是q 的充分不必要条件，p q ⇒∴，q ⇒p ，即A 是B 的真子集，可A =∅或方程210x ax ++=的两根在区间[1,2]内，210a ∆=-∴＜或0,12,2110,4210,a a a ∆⎧⎪⎪-⎪⎨⎪++⎪++⎪⎩…剟……解得22a -＜„. 22.【答案】由28200x x --≤，得210x -剟，所以{|210P x x =-≤≤. 由|1|x m -≤，得11m x m -+剟.所以{|11}S x m x m =-+≤≤. （1）要使()P S P ⊆U ，则S P ⊆ ①若S =∅，则0m ＜；②若S ≠∅，则0,12,110,m m m ⎧⎪--⎨⎪+⎩……„解得03m 剟.综合①②可知，实数m 的取值范围为(,3]-∞.（2）由“x P ∈”是“x S ∈”的充要条件，知S P =，则12,110,m m -=-⎧⎨+=⎩此方程组无解，所以这样的实数m 不存在.第二章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.若23A a ab =+，24B ab b =-，则A ，B 的大小关系是（） A .A B „B .A B …C .A B ＜或A B ＞D .A B ＞2.下列结论正确的是（） A .若ac bc ＞，则a b ＞ B .若22a b ＞，则a b ＞C .若a b ＞，0c ＜，则a c b c ++＜D .a b ＜3.下列变形是根据等式的性质的是（） A .由213x -=得24x = B .由2x x =得1x = C .由29x =得x=3 D .由213x x -=得51x =-4.实数a ，b 在数轴上的位置如图所示，以下说法正确的是（）A .0a b +=B .b a ＜C .0ab ＞D .||||b a ＜5.已知||a b a ＜＜，则（）A .11a b＞ B .1ab ＜C .1ab＞ D .22a b ＞6.若41x -＜＜，则222()1x x f x x -+=-（） A .有最小值2B .有最大值2C .有最小值2-D .有最大值2-7.已知0a ＞，0b ＞，2a b +=，则14y a b=+的最小值是（） A .72B .4C .92D .58.已知1x ，2x 是关于x 的方程230x bx +-=的两根，且满足121234x x x x +-=，那么b 的值为（） A .5B .5-C .4D .4-9.不等式22120x ax a --＜（其中0a ＜）的解集为（） A .(3,4)a a -B .(4,3)a a -C .(3,4)-D .(2,6)a a10.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析，每辆客车营运的总利润y （单位：10万元）与营运年数()*x x ∈N 为二次函数的关系（如图），则每辆客车营运_____年，营运的年平均利润最大（）A .3B .4C .5D .611.若正数x ，y 满足35x y xy +=，则34x y +的最小值是（） A .245B .285C .5D .612.已知a b ＞，二次三项式220ax x b ++…对于一切实数x 恒成立，又0x ∃∈R ，使20020ax x b ++=成立，则22a b a b+-的最小值为（）A .1BC .2D .二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13.当1x ＞时，不等式11x a x +-≥恒成立，则实数a 的取值范围为__________. 14.若0a b ＜＜，则1a b -与1a的大小关系为__________.15.若正数a ，b 满足3ab a b =++，则ab 的取值范围是__________.16.已知关于x 的一元二次方程2320x x m -+=有两个不相等的实数根1x 、2x .若1226x x -=，则实数m 的值为__________.三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明、证明过程或演算步骤）17.（本小题满分10分）解下列不等式（组）：（1）2(2)01x x x +⎧⎨⎩＞，＜；（2）262318x x x --＜„.18.（本小题满分12分）已知a ，b ，c 为不全相等的正实数，且1abc =.111a b c++＜.19.（本小题满分12分）已知21()1f x x a x a ⎛⎫=-++ ⎪⎝⎭.（1）当12a =时，解不等式()0f x „；（2）若0a ＞，解关于x 的不等式()0f x „.20.（本小题满分12分）某镇计划建造一个室内面积为2800 m 的矩形蔬菜温室.在温室内，沿左、右两侧与后侧内墙各保留1 m 宽的通道，沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？21.（未小题满分12分）设函数2()3(0)f x ax bx a =++≠. （1）若不等式()0f x ＞的解集为(1,3)-，求a ，b 的值；（2）若(1)4f =，0a ＞，0b ＞，求14a b+的最小值.22.（本小题满分12分）解下列不等式. （1）2560x x --+＜；（2）()(2)0a x a x --＞.第二章综合测试答案解析一、 1.【答案】B【解析】()2222334240b A B a ab ab b a b ⎛⎫-=+--=-+ ⎪⎝⎭∵…，A B ∴….2.【答案】D【解析】当0c ＜时，A 选项不正确；当0a ＜时，B 选项不正确；两边同时加上一个数，不等号方向不改变，故C 选项错误. 3.【答案】A【解析】A .根据等式的性质1，在等式213x -=的左右两边同时加上1，可得24x =，故本选项正确；B .在等式2x x =的左右两边同时除以x ，可得1x =，但是当0x =时，不成立，故本选项错误；C .将等式29x =的左右两边开平方，可得3x =±，故本选项错误；D .根据等式的性质1，在等式213x x -=的左右两边同时加上(31)x +，可得561x x =+，故本选项错误. 4.【答案】D【解析】根据题图可知，21a --＜＜，01b ＜＜，所以||||b a ＜. 5.【答案】D【解析】由||a b a ＜＜，可知0||||b a ＜„，由不等式的性质可知22||||b a ＜，所以22a b ＞. 6.【答案】D【解析】2221()(1)11x x f x x x x -+==-+--.又41x -∴＜＜，10x -∴＜，(1)0x --∴＞ 1()(1)2(1)f x x x ⎡⎤=---+-⎢⎥--⎣⎦∴„当且仅当111x x -=-，即0x =时等号成立.7.【答案】C【解析】2a b +=∵，12a b+=∴∴14142a bab a b +⎛⎫+=+⋅⎪⎝⎭52592222a b b a ⎛⎫=+++= ⎪⎝⎭… （当且仅当22a b b a =，即423b a ==时，等号成立）故14y a b=+的最小值为92.8.【答案】A【解析】12,x x ∵是关于x 的方程230x bx +-=的两根，12x x b +=-∴，123x x =-， 121234x x x x +-=∵，94b -+=∴，解得5b =.9.【答案】B【解析】方程22120x ax a --=的两根为4a ，3a -，且43a a -＜，43a x a <<-∴. 10.【答案】C【解析】求得函数式为2(6)11y x =--+，则营运的年平均利润2512122y x x x ⎛⎫=-+-= ⎪⎝⎭„，当且仅当25x x=时，取“=”号，解得5x =. 11.【答案】C【解析】35x y xy +=∵，13155y x+=∴1334(34)1(34)55x y x y x y y x ⎛⎫+=+⨯=++ ⎪⎝⎭∴3941213555555x y y x =++++=…当且仅当31255x y y x =，即1x =，12y =时等号成立. 12.【答案】D【解析】a b ∵＞，二次三项式220ax x b ++≥对于一切实数x 恒成立， 0a ∴＞，且440ab ∆=-„，1ab ≥∴.再由0x ∃∈R ，使20020ax x b ++=成立，可得0∆…，1ab ∴…，又a b ＞，1a ＞.2224231101a a b a a a b a a a a+++==---∴＞ 2242484243624222211*********a a a a a a a a a a a a a a a a ⎛⎫+++ ⎪⎛⎫+++⎝⎭=== ⎪-+-⎛⎫⎝⎭+-+- ⎪⎝⎭ 22222221124412a a a a a a ⎛⎫⎛⎫+-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫+- ⎪⎝⎭令22112a a +=＞，则24231(2)4(2)44(2)444822a t t t a a t t ⎛⎫+-+-+==-+++= ⎪---⎝⎭…，当且仅当4t =，即a 时取等.故2431a a a ⎛⎫+ ⎪-⎝⎭的最小值为8，故22a b a b +-二、13.【答案】(,3]-∞ 【解析】1x ∵＞，11(1)11311x x x x +=-++=--∴….3a ∴„. 14.【答案】11a b a-＜【解析】110()()a ab ba b a a a b a a b -+-==---∵＜. 11a b a-∴＜ 15.【答案】[9,)+∞【解析】33ab a b =++…，所以1)0…，3，所以9ab ….16.【答案】2-【解析】由题意知123x x +=，1226x x -=∵，即12236x x x +-=， 2336x -=∴，解得21x =-，代入到方程中，得1320m ++=，解得2m =-. 三、17.【答案】（1）原不等式组可化为 2 0,11,x x x -⎧⎨-⎩＜或＞＜＜即01x ＜＜，所以原不等式组的解集为{|01}x x ＜＜. （2）原不等式等价于22623,318,x x x x x ⎧--⎨-⎩≤＜即2260,3180,x x x x ⎧--⎨--⎩＜…因式分解，得(3)(2)0,(6)(3)0,x x x x -+⎧⎨-+⎩＜…所以 2 3,36,x x -⎧⎨-⎩或＜＜剠所以132x --＜≤或36x ＜„.所以不等式的解集为{|3236}x x x --＜≤或≤＜.18.【答案】证明：因为a ，b ，c 都是正实数，且1abc =，所以112a b +…11b c +=…11a c +=…以上三个不等式相加，得1112a b c ⎛⎫++ ⎪⎝⎭…，即111a b c++因为a，b，c不全相等，所以上述三个不等式中的“=”不同时成立.111a b c++＜.19.【答案】（1）当12a=时，有不等式25()102f x x x=-+≤，1(2)02x x⎛⎫--⎪⎝⎭∴„，122x∴剟，即所求不等式的解集为1,22⎡⎤⎢⎥⎣⎦.（2）1()()0f x x x aa⎛⎫=--⎪⎝⎭∵„，0a＞且方程1()0x x aa⎛⎫--=⎪⎝⎭的两根为1x a=，21xa=，∴当1aa＞，即011a＜＜，不等式的解集为1,aa⎡⎤⎢⎥⎣⎦；当1aa＜，即1a＞，不等式的解集为1,aa⎡⎤⎢⎥⎣⎦；当1aa=，即1a=，不等式的解集为{1}.20.【答案】设矩形温室的左侧边长为 ma，后侧边长为 mb，蔬菜的种植面积为2mS，则800ab=.所以(4)(2)4288082(2)808648 S a b ab b a a b=--=--+=-+-„当且仅当2a b=，即40a=，20b=时等号成立，则648S=最大值.故当矩形温室的左侧边长为40 m，后侧边长为20 m时，蔬菜的种植面积最大，最大种植面积为2648 m.21.【答案】（1）因为不等式()0f x＞的解集为(1,3)-，所以1-和3是方程()0f x=的两个实根，从而有(1)30,(3)9330,f a bf a b-=-+=⎧⎨=++=⎩解得1,2,ab=-⎧⎨=⎩（2）由(1)4f=，得1a b+=，又0a＞，0b＞，所以1414()a b a b a b ⎛⎫+=++ ⎪⎝⎭4559b a a b =+++… 当且仅当4b a a b =即1,32,3a b ⎧=⎪⎪⎨⎪=⎪⎩时等号成立，所以14a b+的最小值为9. 22.【答案】（1）2560x x --+<∵，2560x x +->∴， (1)(6)0x x -+∴＞，解得6x -＜或1x ＞，∴不等式2560x x --+＜的解集是{| 6 1}x x x -＜或＞. （2）当0a ＜时，()(2)y a x a x =--的图象开口向下，与x 轴交点的横坐标为x a =，2x =，且2a <，()(2)0a x a a --∴＞的解集为{|2}x a x ＜＜.当0a =时，()(2)0a x a x --=，()(2)0a x a x --∴＞无解.当0a ＞时，抛物线()(2)y a x a x =--的图像开口向上，与x 轴交点的横坐标为x a =，2x =.当2a =时，不等式可化为22(2)0x -＞，解得2x ≠. 当2a ＞时，解得2x ＜或x a ＞. 当2a ＜时，解得x a ＜或2x ＞.综上，当0a ＜时，不等式的解集是{|2}x a x ＜＜；当0a =时，不等式的解集是∅；当02a ＜＜时，不等式的解集是{| 2}x x a x ＜或＞；当2a =时，不等式的解集是{|2}x x ≠；当2a ＞时，不等式的解集是{|2}x x x a ＜或＞.第三章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知2()1f x x =+，则[(1)]f f -的值等于（） A .2B .3C .4D .5 2.已知函数()1f x x =+，其定义域为{1,0,1,2}-，则函数的值域为（） A .[0,3]B .{0,3}C .{0,1,2,3}D .{|0}y y …3.函数0y =的定义域是（）A .{|01}x x 剟B .{| 1 1}x x x --＜或＞C .{|01}x x x ≠-＜且D .{}|1 0x x x ≠-≠且4.已知二次函数()y f x =满足(2)(2)f x f x +=-，且函数图像截x 轴所得的线段长为8，则函数()y f x =的零点为（） A .2，6B .2，6-C .2-，6D .2-，6-5.若函数()y f x =的定义域是{|01}x x ≤≤，则函数()()(2)(01)F x f x a f x a a =+++＜＜的定义域是（）A .1|22a a x x -⎧⎫-⎨⎬⎩⎭≤≤B .|12a x x a ⎧⎫--⎨⎬⎩⎭≤≤C .{|1}x a x a --≤≤D .1|2a x a x -⎧⎫-⎨⎬⎩⎭≤≤6.如图所示，可表示函数()y f x =的图像的只可能是（）ABCD7.已知函数2()1f x ax bx =++为定义在[2,1]a a -上的偶函数，则a b +的值是（） A .1B .1-C .1或1-D .0或18.若()f x 满足()()f x f x -=-，且在(,0)-∞上是增函数，(2)0f -=，则()0xf x ＜的解集是（） A .(2,0)(0,2)-UB .(,2)(0,2)-∞-UC .(,2)(2,)-∞-+∞UD .(2,0)(2,)-+∞U9.设函数()f x 与()g x 的定义域是{|1}x x ∈≠±R ，函数()f x 是一个偶函数，()g x 是一个奇函数，且1()()1f xg x x -=-，则()f x 等于（） A .2221x x -B .211x -C .221x -D .221xx - 10.已知2()21(0)f x ax ax a =++＞，若()0f m ＜，则(2)f m +与1的大小关系式为（） A .(2)1f m +＜B .(2)1f m +=C .(2)1f m +＞D .(2)1f m +…11.函数()f x =（） A .是奇函数但不是偶函数 B .是偶函数但不是奇函数 C .既是奇函数又是偶函数D .既不是奇函数又不是偶函数12.已知2()2f x x x =+，若存在实数t ，使()3f x t x +„对[1,]x m ∈恒成立，则实数m 的最大值是（） A .6B .7C .8D .9二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13.已知1,[0,1],()2,[0,1],x f x x x ∈⎧=⎨-∉⎩，当[()]1f f x =时，x ∈__________.14.关于x 的方程240x x a --=有四个不相等的实数根，则实数a 的取值范围为__________.15.已知函数719()1x f x x +=+，则()f x 的图像的对称中心是__________，集合{}*|()x f x ∈=N __________.16.已知函数()f x 是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则52f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭的值是__________.三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明、证明过程或演算步骤）17.（本小题满分10分）已知函数2()2||1f x x x =--.（1）利用绝对值及分段函数知识，将函数()f x 的解析式写成分段函数；（2）在坐标系中画出()f x 的图像，并根据图像写出函数()f x 的单调区间和值域.18.（本小题满分12分）已知函数()f x 对任意实数x 均有()2(1)f x f x =-+，且()f x 在区间[0]1，上有解析式2()f x x =. （1）求(1)f -和(1.5)f 的值；（2）写出()f x 在区间[2,2]-上的解析式.19.（本小题满分12分）函数2()1ax bf x x +=+是定义在(,)-∞+∞上的奇函数，且1225f ⎛⎫= ⎪⎝⎭. （1）求实数a ，b 的值.（2）用定义证明()f x 在(1,1)-上是增函数；（3）写出()f x 的单调减区间，并判断()f x 有无最大值或最小值.如有，写出最大值或最小值（无需说明理由）.20.（本小题满分12分）已知定义域为R 的单调函数()f x ，且(1)f x -的图像关于点(1,0)对称，当0x ＞时，1()3x f x x=-. （1）求()f x 的解析式；（2）若对任意的t ∈R ，不等式()()22220f t t f t k -+-＜恒成立，求实数k 的取值范围.21.（本小题满分12分）对于定义域为D 的函数()y f x =，若同时满足下列条件：①()f x在D 内单调递增或单调递减；②存在区间[,]a b D ⊆，使()f x 在[,]a b 上的值域为[,]a b ，那么称()()x D y f x =∈为闭函数.（1）求闭函数3y x =-符合条件②的区间[,]a b . （2）判断函数31()(0)4f x x x x=+＞是否为闭函数？并说明理由；（3）判断函数y k =+k 的取值范围.22.（本小题满分12分）设函数()f x 的定义域为R ，当0x ＞时，()1f x ＞，对任意,x y ∈R ，都有()()()f x y f x f y +=g ，且(2)4f =. （1）求(0)f ，(1)f 的值.（2）证明：()f x 在R 上为单调递增函数.（3）若有不等式1()2f x f x x ⎛⎫+ ⎪⎝⎭g ＜成立，求x 的取值范围.第三章测试答案解析一、 1.【答案】D【解析】由条件知(-1)2f =，(2)5f =，故选D . 2.【答案】C【解析】将x 的值依次代入函数表达式可得0，1，2，3，所以函数的值域为{0,1,2,3}，故选C . 3.【答案】C【解析】由条件知10x +≠且0x x -＞，解得0x ＜且1x ≠-.故选C 4.【答案】C【解析】由于函数()y f x =满足(2)(2)f x f x +=-，所以直线2x =为二次函数()y f x =图像的对称轴，根据二次函数图像的性质，图像与x 轴的交点必关于直线2x =对称.又两交点间的距高为8，则必有两交点的横坐标分别为1246x =+=，2242x =-=-.故函数的零点为2-，6.故选C . 5.【答案】A【解析】由条件知01,021,x a x a +⎧⎨+⎩剟剟，又01a ＜＜则122a ax --≤≤，故选A .6.【答案】D【解析】由函数定义可得，任意一个x 有唯一的y 与之对应，故选D . 7.【答案】B【解析】因为函数2()1f x ax bx =++为定义在[2,1]a a -上的偶函数，所以21a a =-，1a =-，0b =，因此1a b +=-，故选B.8.【答案】A【解析】根据题意可知函数是奇函数，且在(,0)-∞，(0,)+∞上是增函数，对()0xf x ＜，分0x ＞，0x ＜进行讨论，可知解集为(2,0)(0,2)-U ，故选A.9.【答案】B【解析】1()()1f x g x x -=-∵，1()()1f x g x x ---=--∴，1()()1f xg x x +=--∴， 21122()111f x x x x =-=-+-∴，21()1f x x =-，故选B . 10.【答案】C【解析】因为2()21(0)f x ax ax a =++＞，所以其图像的对称轴为直线1x =-，所以()(2)0f m f m =--＜，又(0)1f =，所以(2)1f m +＞，故选C .11.【答案】A【解析】由定义城可知x 因此原式化简为()f x =那么根据函数的奇偶性的定义，可知该函数是奇函数不是偶函数，故选A . 12.【答案】C【解析】由题意知，对任意[1,]x m ∈，2()2()3x t x t x +++…恒成立，这个不等式可以理解为()f x t +的图像在直线3y x =的图像的下面时x 的取值范围.要使m 最大，需使两图像交点的横坐标分别为1和m .当1x =时，3y =，代入可求得4t =-（0t =舍去）.进而求得另一个交点为(8,24)，故8m =.故选C. 二、13.【答案】[0,1][2,3]{5}U U【解析】因为1,[0,1],()2,[0,1],x f x x x ∈⎧=⎨-∉⎩所以要满足元[()]1f f x =，需()[0,1]f x ∈，[0,1]x ∈或2[0,1]x -∈或5x =，这样解得x 的取值范围是[0,1][2,3]{5}U U .14.【答案】(0,4)【解析】原方程等价于24x x a -=，在同一坐标系内作出函数24y x x =-与函数y a =的图像，如图所示：平移直线y a =，可得当04a ＜＜时，两图像有4个不同的公共点，相应地方程240x x a --=有4个不相等的实数根，综上所述，可得实数a 的范围为04a ＜＜. 15.(1,7)- {13,7,5,4,3,0,1,2,3,5,11}----- 【解析】因为函数71912()711x f x x x +==+++，则()f x 的图像的对称中心为(1,7)-，集合{|()}{13,7,5,4,3,0,1,2,3,5,11}x f x *∈=-----N 16.【答案】0【解析】因为()f x 是定义在R 上的偶函数，因此令12x =-，可知11112222f f ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，所以102f ⎛⎫= ⎪⎝⎭，分别令32x =-，52x =-，可得302f ⎛⎫= ⎪⎝⎭，502f ⎛⎫= ⎪⎝⎭，令1x =-.得(0)0f =，因此可知502f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭. 三、17.【答案】（1）22321,0()2||121,0x x x f x x x x x x ⎧--=--=⎨+-⎩＜….（2）图像如图所示.单调增区间为(1,0)-，(1,)+∞，单调减区间为(,1)-∞-，(0,1). 值域为[2,)-+∞.18.【答案】（1）由题意知(1)2(11)2(0)0f f f -=--+=-=，1111(1,5)(10.5)(0.5)2248f f f =+=-=-⨯=-. （2）当[0,1]x ∈时，2()f x x =；当(1,2]x ∈时，1(0,1]x -∈，211()(1)(1)22f x f x x =--=--；当[1,0)x ∈-时，1[0,1)x +∈， 2()2(1)2(1)f x f x x =-+=-+；当[2,1)x ∈--时，1[1,0)x +∈-，22()2(1)22(11)4(2)f x f x x x ⎡⎤=-+=-⨯-++=+⎣⎦.所以22224(2),[2,1),2(1),[1,0),(),[0,1],1(1),(1,2].2x x x x f x x x x x ⎧+∈--⎪-+∈-⎪⎪=⎨∈⎪⎪--∈⎪⎩19.【答案】（1）2()1ax bf x x +=+∵是奇函数()()f x f x -=-∴， 2211ax b ax bx x -++=-++∴，0b =∴. 故2()1ax f x x =+，又1225f ⎛⎫= ⎪⎝⎭∵，1a =∴ （2）证明：由（1）知2()1xf x x =+，任取1211x x -＜＜＜，()()()()()()1212121222121211111x x x x x xf x f x x x x x ---=-=++++1211x x -∵＜＜＜，1211x x -∴＜＜，120x x -＜，1210x x -＞，2110x +＞，2210x +＞，()()120f x f x -∴＜，即()()12f x f x ＜，()f x ∴在(1,1)-上是增函数.（3）单调减区间为(,1),(1,)-∞-+∞.当1x =-时，min 1()2f x =-；当1x =时，max 1()2f x =.20.【答案】（1）由题意知()f x 的图像关于点(0,0)对称，是奇函数，∴(0)0f = 当0x ＜时，0x -＞，1()3x f x x--=--∴，又∵函数()f x 是奇函数.∴()()f x f x -=-，1()3x f x x=-∴. 综上所述，1(0),()30(0).x x f x x x ⎧-≠⎪=⎨⎪=⎩（2）2(1)(0)03f f =-=∵＜，且()f x 在R 上单调.∴()f x 在R 上单调递减.由()()22220f t t f t k -+-＜，得()()2222f t t f t k ---＜.∵()f x 是奇函数，∴()()2222f t t f k t --＜，又∵()f x 是减函数， ∴2222t t k t --＞即2320t t k --＞对任意t ∈R 恒成立，∴4120k ∆=+＜，得13k -＜.21.【答案】（1）由题意，3y x =-，在[,]a b 上单调递减，则33,,,b a a b b a ⎧=-⎪=-⎨⎪>⎩解得1,1,a b =-⎧⎨=⎩所以，所求区间为[1,1]-.（2）取11x =，210x =，则()()1273845f x f x ==＜，即()f x 不是(0,)+∞上的减函数.取，1110x -=，21100x =，()()12331010040400f x f x =++=＜，即()f x 不是(0,)+∞上的增函数.所以，函数在定义域内不单调递增或单调递减，从而该函数不是闭函数.（3）若y k =+[,]a b ，在区间[,]a b 上，函数()f x 的值域为[,]a b，即a k b k ⎧=+⎪⎨=⎪⎩∴a ，b为方程x k =的两个实根，即方程22(21)20(2,)x k x k x x k -++-=-厖有两个不等的实根，故两根均大于等于2-，且对称轴在直线2x =-的右边.当2k -„时，有220,(2)2(21)20,212,2k k k ⎧⎪∆⎪-+++-⎨⎪+⎪-⎩＞＞…解得924k --＜„.当2k -＞时，有220,(21)20,21,2k k k k k k ⎧⎪∆⎪-++-⎨⎪+⎪⎩＞＞…无解.综上所述，9,24k ⎛⎤∈-- ⎥⎝⎦.22.【答案】（1）因为(20)(2)(0)f f f +=g ，所以44(0)f =⋅，所以(0)1f =，又因为24(2)(11)(1)f f f ==+=，且当0x ＞时，()1f x ＞，所以(1)2f =.（2）证明：当0x ＜时，0x -＞，所以()1f x -＞，而(0)[()]()()f f x x f x f x =+-=-g ，所以1()()f x f x =-，所以0()1f x ＜＜，对任意的12,x x ∈R ，当12x x ＜时，有()()()]()()()1212222121f x f x f x x x f x f x f x x -=⎡-+-=--⎣，因为120x x ＜＜，所以120x x -＜，所以()1201f x x -＜＜，即()1210f x x --＜，所以()()120f x f x -＜，即()()12f x f x ＜，所以()f x 在R 上是单调递增函数.（3）因为1()12f x f x ⎛⎫+ ⎪⎝⎭g ＜，所以11(1)f x f x ⎛⎫++ ⎪⎝⎭＜，而()f x 在R 上是单调递增函数，所以111x x ++＜，即10x x+＜，所以210x x +＜，所以0x ＜，所以x 的取值范围是(,0)-∞.。

人教版高中数学必修一综合测试题(很基础,很全面)

人教版高中数学必修一综合测试题(考试时间为120分钟，满分150分)一、选择题（本大题共12小题，每小题5分，共60分)1.已知集合{2,1,0,1,2}A =--，{|22,}B x x x N =-<<∈,则AB =（） A. {1,0}- B. {0,1} C. {1,0,1}- D. {0,1,2}2.下列图象中表示函数图象的是（）A. B. C. D.3、下列函数中，在(0,)+∞上为增函数的是（）。

A 、()3f x x =-B 、2()3f x x x =-C 、1()1f x x =-+ D 、()||f x x =-4.4等于（）A. 16aB. 8aC. 4aD. 2a 5.计算：log 916·log 881的值为( )A. 18B. 118C. 83D. 386.已知函数2()3(0)x f x a a -=+≠，则()f x 的图象过定点( )A.(0,4)B.(2,4)C. (0,3)D. (4,3) 7. 若11221272,,log 327a b c --⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系为( ) A. a b c << B. a c b << C.c b a << D. c a b << 8. 函数2()log ()21x f x x g x -==-与与在同一平面直角坐标系下的图象大( )9.函数()f x = ） A. {}0x x > B. {}1x x > C. {}1x x ≥ D. {}01x x <≤ 10.如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减函数，那么实数a 的取值范围是（）A. 3a ≤-B. 3a ≥-C. 5a ≤D. 5a ≥11、已知函数f(x)是R 上的减函数，A （0，1），B （2，-1）是其图象上的两点，那么∣f(x)∣<1的解集的补集是（）A.（-1，2）B.（1，4）C.（-∞，-1）∪[4，+∞）D.（∞，0]∪[2，+∞） 12.12R (),f x x ∈定义在上的偶函数满足：对任意的x (]12,0(),x x -∞≠有12)x x -•（[]21()()0.)f x f x n N *->∈则当时，有（ A.()(1)(1)f n f n f n -<-<+ B. (1)()(1)f n f n f n -<-<+C. (1)()(1)f n f n f n +<-<-D. (1)(1)()f n f n f n +<-<-二、填空题(本大题共4小题，每小题5分，共20分)13、210()20x x f x x x ⎧+≤=⎨->⎩ , , , ,若()10f x = ,则_______x =.14.使不等式31220x -->成立的x 的取值范围是 .15、已知函数3()8f x ax bx =+- ，且f(-2) =10，则f (2 ) =_______. 16.下列命题：①若函数()f x 是一个定义在R 上的函数，则函数h x f x f x 是奇函数； ②函数211x x y x 是偶函数； ②函数12x y -=的图象可由12x y的图象向右平移2个单位得到； ②函数1y x=在区间12，上既有最大值，又有最小值；则上述正确命题的序号是________②.三、解答题(本大题共6小题，共70分)17．（本题满分10分）已知全集为U=R ，A={22|<<-x x } ，B={1,0|≥<x x x 或} 求：（1）A ⋂B ，（2）A ⋃B 。

人教版高一数学必修测试题含答案(参考)

人教版高一数学必修测试题含答案一、挑选题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===，则()U A C B =I （）A 、{}2B 、{}2,3C 、{}3D 、{}1,32、已知集合{}{}0,1,2,2,M N x x a a M ===∈，则集合 M N I （）A 、{}0B 、{}0,1C 、{}1,2D 、{}0,23、函数()21log ,4y x x =+≥的值域是（）A 、[)2,+∞B 、()3,+∞C 、[)3,+∞D 、(),-∞+∞ 4、对于A 到B 的一一映射，下列叙述正确的是（）① 一一映射又叫一一对应② A 中别同元素的像别同③ B 中每个元素都有原像④ 像的集合算是集合BA 、①②B 、①②③C 、②③④D 、①②③④5、在221,2,,y y x y x x y x ===+= （） A 、1个 B 、2个 C 、3个 D 、4个6、已知函数()213f x x x +=-+，这么()1f x -的表达式是（） A 、259x x -+ B 、23x x -- C 、259x x +- D 、21x x -+7、若方程0x a x a --=有两个解，则a 的取值范围是（） A 、()0,+∞ B 、()1,+∞ C 、()0,1 D 、?8、若21025x =，则10x -等于（）A 、15- B 、15 C 、150D 、1625 9、若()2log 1log 20a a a a +A 、01a B 、112a C 、102 a10、设 1.50.90.4814,8,2a b c -??=== ，则,,a b c 的大小顺序为（）A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >>11、已知()()2212f x x a x =+-+在(],4-∞上单调递减，则a 的取值范围是（）A 、3a ≤-B 、3a ≥-C 、3a =-D 、以上答案都别对12、若()lg f x x =，则()3f = （）A 、lg 3B 、3C 、310D 、103二、填空题13.设{}{}12,0A x x B x x a =14函数y =的定义域为；15、若2x16、100lg 20log 25+= 。