8,多元函数的微分学-习题课-文档资料

合集下载

多元函数微分学习题课-14页精品文档

法则的推广——任意多个中间变量，任意多个自变量如何求二阶偏导数
6、全微分形式不变性
无论 z是自变量u 、 v 的函数或中间变量u 、 v
的函数，它的全微分形式是一样的.
dzzduzdv. u v
7、隐函数的求导法则
(1) F(x,y)0
dyFx
dx Fy
(2 )F (x ,y ,z) 0
z Fx,z Fy x Fz y Fz
求隐函数偏导数的方法 ①公式法 ②直接法 ③全微分法
8、多元函数的极值
极值、驻点、必要条件P341 (偏导为0)
充分条件P342 P(x,y )
求函数 z f ( x ,y ) 极值的一般步骤：
最值条件极值，目标函数、约束条件
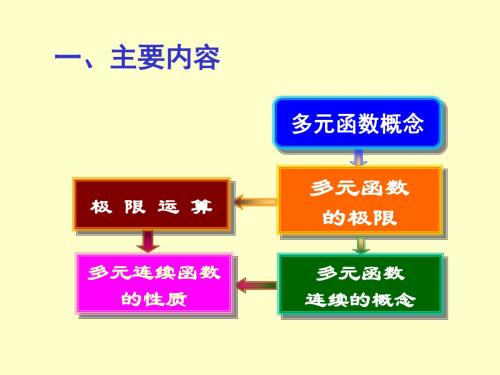
一、主要内容
极限运算多元连续函数
的性质
多元函数概念
多元函数的极限
多元函数连续的概念
复合函数求导法则
全微分形式的不变性
全微分概念
偏导数概念
多元函数的极值
全微分的应用
高阶偏导数
隐函数求导法则微分法在几何上的应用
1、多元函数的极限说明：（1）定义中 PP0的方式是任意的；
（2）二元函数的极限运算法则与一元函数类似．存在性 ——定义，夹逼定理
构造 Lagrange 函数 F ( x ,y ,z ) f ( x ,y ,z ) ( x ,y ,z )
二重积分
1. 二重积分的定义
n

D
f
x, y d
lim
0 i1
f (i ,i ) i
(d dxdy)
2. 二重积分的性质 (与定积分性质相似)

6-8多元函数微分学习题课

x0
x
此极限为函数z f ( x, y)在点( x0 , y0 )处对x 的
偏导数，记为
z x
，f x x0 x
z ，
x x0
x
x x0 y y0
或
f x ( x0 ,
y0 ).
y y0
y y0
同理可定义函数z f ( x, y)在点( x0 , y0 )处对y
的偏导数，为
某邻域存在；
z
（3）
f

x
(
x,
y)x
f

y
(
x
,
y)y
,
(x)2 (y)2
当 (x)2 (y)2 0时是无穷小量.
小结三:
由一个方程确定的隐函数的求导法: 1 公式法:F(x,y,z)确定了z=z(x,y),则 z Fx , z Fy .
x Fz y Fz 2 解方程法:方程两边同时对x或者y求导,由复合函数求导法则解出 z , z .
数，则复合函数 z f [ (t ), (t )] 在对应点t 可
导，且其导数可用下列公式计算：
dz z du z dv ． dt u dt v dt
以上公式中的导数 dz 称为全导数.
dt
如果u ( x, y)及v ( x, y)都在点( x, y)
具有对x 和y 的偏导数，且函数z f (u,v) 在对应
法线方程为 x x0 y y0 z z0 .
Fx ( x0 , y0 , z0 ) Fy ( x0 , y0 , z0 ) Fz ( x0 , y0 , z0 )
15、方向导数
定义函数的增量 f ( x x, y y) f ( x, y) 与

(完整版)多元函数微分法及其应用习题及答案

第八章多元函数微分法及其应用(A)1．填空题(1)若()y x f z ,=在区域D 上的两个混合偏导数y x z ∂∂∂2，xy z∂∂∂2 ，则在D 上，xy zy x z ∂∂∂=∂∂∂22。

(2)函数()y x f z ,=在点()00,y x 处可微的条件是()y x f z ,=在点()00,y x 处的偏导数存在。

(3)函数()y x f z ,=在点()00,y x 可微是()y x f z ,=在点()00,y x 处连续的条件。

2．求下列函数的定义域(1)y x z -=；(2)22arccos yx z u +=3．求下列各极限(1)x xy y x sin lim 00→→； (2)11lim 00-+→→xy xyy x ； (3)22222200)()cos(1lim y x y x y x y x ++-→→4．设()xy x z ln =，求y x z ∂∂∂23及23y x z∂∂∂。

5．求下列函数的偏导数 (1)xyarctgz =；(2)()xy z ln =；(3)32z xy e u =。

6．设u t uv z cos 2+=，t e u =，t v ln =，求全导数dt dz 。

7．设()z y e u x -=，t x =，t y sin =，t z cos =，求dtdu。

8．曲线⎪⎩⎪⎨⎧=+=4422y y x z ，在点(2,4,5)处的切线对于x 轴的倾角是多少？9．求方程1222222=++cz b y a x 所确定的函数z 的偏导数。

10．设y x ye z x 2sin 2+=，求所有二阶偏导数。

11．设()y x f z ,=是由方程y z z x ln =确定的隐函数，求xz∂∂，y z ∂∂。

12．设x y e e xy =+，求dxdy 。

13．设()y x f z ,=是由方程03=+-xy z e z确定的隐函数，求xz∂∂，y z ∂∂，y x z ∂∂∂2。

第八章多元函数微分练习题

5、已知函数 z f (sin x, y 2 ) ，其中 f (u, v) 有二阶连续偏导数，求 z 、 2 z 。 x xy
6、设
z
xf
(x2,
xy)
其中
f
(u, v)
的二阶偏导数存在，求
z y
、
2z yx
。
7、设 z f (2x 3y, xy) 其中 f 具有二阶连续偏导数，求 2 z 。 xy
z x
三、计算题
1、设 z f (x2 , x ) ，其中 f 具有二阶连续偏导数，求 z 、 2 z 。
y
x xy
2、已知 z ln x x2 y 2 ，求 z ， 2 z 。 x xy
3、求函数 z tan x 的全微分。 y
4、设 z f (x y, xy) ，且具有二阶连续的偏导数，求 z 、 2 z 。 x xy
x1 （
y0
)
A、-1
B、 0
C、 1
D、 2
8、函数 z ( x y)2 ，则 dz x1, y0 =（
）
A、 2dx 2dy B、 2dx 2dy
C、 2dx 2dy D、 2dx 2dy
二、填空题
1、函数 z x y 的全微分 dz 2、设 u e xy sin x ，则 u
y
xy
17、设 z f (x2 y, y2 x) ,其中 f 具有二阶连续偏导数,求 2 z 。 xy
18、设
z
z(x,
y)
是由方程
z
ln
z
xy
0
确定的二元函数，求
2z x2
19、设 z yf ( y2, xy) ,其中函数 f 具有二阶连续偏导数，求 2z 。 xy

（完整版）高等数学（同济版）多元函数微分学练习题册.doc

（完整版）高等数学（同济版）多元函数微分学练习题册.doc第八章多元函数微分法及其应用第一作一、填空：1. 函数 z ln(1 2 )y x23x y 的定义域为x12. 函数 f (x, y, z) arccosz的定义域为y 2x 23. 设 f ( x, y) x 2 y 2 , (x) cos x, ( x) sin x, 则f [ (x), (x)].sin xy .4. lim xx 0二、（）： 1. 函数1的所有断点是 :sin x sin y(A) x=y=2n π（ n=1,2,3,?）；(B) x=y=n π (n=1,2,3, ?) ； (C) x=y=m π (m=0, ±1，± 2，? )；(D) x=n π ,y=m π (n=0, ± 1，± 2，?，m=0,± 1,± 2,? )。

答：（）sin 2( x 2 y 2 , x 2y 22. 函数 f (x, y)x 2 y 2在点（ 0， 0）：2 ,x 2 y 2（ A ）无定；（B ）无极限；（ C ）有极限但不；（ D ）。

答：（）三、求 lim2xy 4 .x 0 xyya四、明极限 limx 2 y 22 不存在。

2 2xx y ( x y)y 0第二节作业一、填空题：1 sin( x2 y), xy 01. 设 f ( x, y)xy ,则 f x (0,1) .x 2 ,xy2. 设 f (x, y)x ( y 1) arcsinx, 则 f x ( x,1).y二、选择题（单选）：设 z 2x y 2 , 则 z y 等于 :( A) y 2 x y 2 ln 4; (B) (x y 2 ) 2 y ln 4; (C ) 2 y( x y 2 ) e x y 2 ;(D ) 2 y 4 x y 2 .答：（）三、试解下列各题：1. 设 z ln tan x , 求 z, z .2. 设 z arctan y, 求2z .y x yxx y四、验证 rx 2 y 2 z 2 满足2r2r2r 2 .x 2 y 2 z 2r第三节作业一、填空题：1. 函数 zy 当x 2, y时的全增量z全微分值x 1, x 0.1, y0.2dz.y2. 设z e x , 则dz.二、选择题（单选）：1. 函数 z=f(x,y) 在点 P 0（ x 0,y 0）两偏导数存在是函数在该点全微分存在的：（ A ）充分条件；（ B ）充要条件；（ C ）必要条件；（ D ）无关条件。

(完整版)多元函数微分学复习题及答案

第八章多元函数微分法及其应用复习题及解答一、选择题1. 极限lim x y x yx y→→+00242= （提示：令22y k x =）（ B ） (A) 等于0 (B) 不存在 (C) 等于12 (D) 存在且不等于0或12 2、设函数f x y x y y xxy xy (,)sin sin=+≠=⎧⎨⎪⎩⎪1100，则极限lim (,)x y f x y →→0= （ C ）（提示：有界函数与无穷小的乘积仍为无穷小）(A) 不存在 (B) 等于1 (C) 等于0 (D) 等于23、设函数f x y xy x y x y x y (,)=++≠+=⎧⎨⎪⎩⎪222222000，则(,)f x y （ A ）（提示：①在220x y +≠，(,)f x y 处处连续；②在0,0x y →→ ，令y kx =，200(0,0)x x y f →→→=== ，故在220x y +=，函数亦连续.所以，(,)f x y 在整个定义域内处处连续.）(A) 处处连续 (B) 处处有极限，但不连续 (C) 仅在（0,0）点连续 (D) 除（0,0）点外处处连续4、函数z f x y =(,)在点(,)x y 00处具有偏导数是它在该点存在全微分的（ A ） (A)必要而非充分条件(B)充分而非必要条件(C)充分必要条件 (D)既非充分又非必要条件5、设u y x =arctan ，则∂∂u x = （ B ）(A)xx y 22+(B) -+y x y 22 (C) yx y 22+(D)-+xx y 226、设f x y yx(,)arcsin=，则f x '(,)21= （ A ）（A ）-14（B ）14 （C ）-12 （D ）127、设yxz arctan=，v u x +=，v u y -=，则=+v u z z （ C ）（A ）22v u v u -- （B ）22v u u v -- （C ）22v u v u +- （D ）22v u uv +-8、若f x x x x f x x x x (,),(,)'232612=+=+，则f x x y '(,)2= （ D ） (A) x +32(B) x -32(C) 21x + (D) -+21x 9、设z y x =，则()(,)∂∂∂∂z x zy+=21 （ A ） (A) 2 (B) 1+ln2 (C) 0 (D) 110、设z xye xy =-，则z x x x'(,)-= （ D ） (A)-+2122x x e x () (B)2122x x e x ()- (C)--x x e x ()122 (D)-+x x e x ()12211、曲线x t y t z t ===24sin ,cos ,在点(,,)202π处的法平面方程是（C ）(A) 242x z -=-π (B) 224x z -=-π (C) 42y z -=-π (D) 42y z -=π12、曲线45x y y z ==,,在点(,,)824处的切线方程是（A ）(A)842204x z y --=-= (B)x y z +==+122044 (C) x y z -=-=-85244 (D)x y z -=-=351413、曲面x z y x z cos cos +-=ππ22在点ππ2120,,-⎛⎝ ⎫⎭⎪处的切平面方程为（D ）（A ）x z -=-π1 （B ）x y -=-π1 （C ）x y -=π2 （D ）x z -=π214、曲面x yz xy z 2236-=在点(,,)321处的法线方程为（A ）（A ）x y z +=--=--58531918 （B ）x y z -=-=--3823118（C ）83180x y z --= （D ）831812x y z +-=15、设函数z x y =-+122，则点 (,)00是函数 z 的（ B ）（A ）极大值点但非最大值点（B ）极大值点且是最大值点（C ）极小值点但非最小值点（D ）极小值点且是最小值点 16、设函数z f x y =(,)具有二阶连续偏导数，在P x y 000(,)处，有2)()(,0)()(,0)(,0)(000000======P f P f P f P f P f P f yx xy yy xx y x ，则（ C ）（A ）点P 0是函数z 的极大值点（B ）点P 0是函数z 的极小值点（C ）点P 0非函数z 的极值点（D ）条件不够，无法判定 17、函数f x y z z (,,)=-2在222421x y z ++=条件下的极大值是（ C ）(A) 1 (B) 0 (C)-1 (D) -2 二、填空题 1、极限limsin()x y xy x→→0π= ⎽⎽⎽⎽⎽⎽⎽ .答：π 2、极限limln()x y x y e x y→→++01222=⎽⎽⎽⎽⎽⎽⎽ .答：ln23、函数z x y =+ln()的定义域为 ⎽⎽⎽⎽⎽⎽⎽ .答：x y +≥14、函数z xy=arcsin 的定义域为 ⎽⎽⎽⎽⎽⎽⎽ .答：-≤≤11x ，y ≠0 5、设函数f x y x y xy y x (,)ln =++⎛⎝ ⎫⎭⎪22，则f kx ky (,)= ⎽⎽⎽⎽⎽⎽⎽ .答：k f x y 2⋅(,)6、设函数f x y xy x y (,)=+，则f x y x y (,)+-= ⎽⎽⎽⎽⎽⎽⎽ .答：222x y x-（22()()(,)()()2x y x y x y f x y x y x y x y x+--+-==++-Q ）7、设f x y x y x y A x y (,)ln()//=-⋅+<+≥⎧⎨⎩11212222222，要使f x y (,)处处连续，则A= ⎽⎽⎽⎽⎽⎽⎽ .答：-ln28、设f x y x y x y x y Ax y (,)tan()(,)(,)(,)(,)=++≠=⎧⎨⎪⎩⎪22220000，要使f x y (,)在（0，0）处连续，则A= ⎽⎽⎽⎽⎽⎽⎽ .答：1 9、函数221x y z x +=-的间断点是 .答：直线10x -=上的所有点10、函数f x y x y yx (,)cos =-122的间断点为 ⎽⎽⎽⎽⎽⎽⎽ .答：直线y x =±及x =011、设z x y y =-+sin()3，则∂∂z xx y ===21_________ .答：3cos512、设f x y x y (,)=+22，则f y (,)01= _________ .答：113、设u x y z x y z(,,)=⎛⎝ ⎫⎭⎪，则)3,2,1(d u =_________ .答：38316182d d ln d x y z --14、设u x x y =+22，则在极坐标系下，∂∂ur= _________ .答：0 15、设u xy y x =+，则∂∂22u x = _________.答：23yx16、设u x xy =ln ，则∂∂∂2u x y = ___________ .答：1y17、函数y y x =()由12+=x y e y 所确定，则d d y x = ___________ .答：22xye xy - 18、设函数z z x y =(,)由方程xy z x y z 2=++所确定，则∂∂zy= _______ .答：2112xyz xy --19、由方程xyz x y z +++=2222所确定的函数z z x y =(,)在点（1，0，－1）处的全微分d z = _________ .答：d d x y -220、曲线x t y t z t ===23213,,在点(,,)1213处的切线方程是_________.答：x y z -=-=-12221321、曲线x te y e z t e t t t ===232222,,在对应于 t =-1点处的法平面方程是___________. 答：01132=+--e y x 22、曲面xe y e z e ey z x ++=+223321在点(,,)210-处的法线方程为_________ . 答：e ze y x 22212=-+=- 23、曲面arctan y xz 14+=π在点(,,)-210处的切平面方程是_________.答：y z +=2124、设函数z z x y =(,)由方程123552422x xy y x y e z z +--+++=确定，则函数z的驻点是_________ .答：（－1，2） 27、函数z x y x y =----2346122的驻点是_________.答：（1，1）25、若函数f x y x xy y ax by (,)=+++++22236在点 (,)11-处取得极值，则常数a =_________， b =_________.答：a =0，b =426、函数f x y z x (,,)=-22在x y z 22222--=条件下的极大值是_______答：-4 三、计算题1、求下列二元函数的定义域，并绘出定义域的图形.(1) z = (2)ln()z x y =+ (3)1ln()z x y =+ (4)ln(1)z xy =-解：(1)要使函数z =有意义，必须有2210x y --≥，即有221x y +≤.故所求函数的定义域为22{(,)|1}D x y x y =+≤,图形为图3.1(2)要使函数ln()z x y =+有意义，必须有0x y +>.故所有函数的定义域为{}(,)|0D x y x y =+>，图形为图3.2(3)要使函数1ln()z x y =+有意义，必须有ln()0x y +≠，即0x y +>且1x y +≠.故该函数的定义域为{}(,)|01D x y x y x y =+>+≠，，图形为图3.3(4)要使函数ln(1)z xy =-有意义，必须有10xy ->.故该函数的定义域为{(,)|1}D x y xy =>，图形为图3.4图3.1 图3.2图3.3 图3.42、求极限limsin x y y xxy →→+-0211.解：lim sin x y y xxy →→+-0211=⋅++→→lim sin ()x y y x xy xy 00211= 43、求极限lim sin()x y x y x yxy →→-+0023211. 解：原式=lim ()sin()x y x y x y x y xy →→-++0232211=-++⋅→→limsin()x y x y xy xy 002111=-124、求极限lim x y xxye xy→→-+0416 . 解：lim x y xxye xy→→-+00416=++-→→lim ()x y x xye xy xy 00416= -85、设u x y y x =+sin cos ，求 u u x y ,. 解：u y y x x =-sin sinu x y x y =+cos cos6、设z xe ye y x =+-，求z z x y ,. 解：z e ye x y x =--z xe e y y x =+-7、设函数z z x y =(,)由yz zx xy ++=3所确定，试求∂∂∂∂z x zy,（其中x y +≠0）. 解一：原式两边对x 求导得yz x x zxz y ∂∂∂∂+++=0，则∂∂z x z y y x =-++同理可得：∂∂z y z x y x =-++ 解二：xy xz F F y z xy y z F F x z x y y x ++-=-=++-=-=∂∂∂∂, 8、求函数z x xy y x y =-++-+23243122的极值.解：由z x y z x y x y=-+==-+-=⎧⎨⎩43403430，得驻点(,)-10074334>=--==yy yxxy xx z z z z D z xx =>40，函数z 在点(,)-10处取极小值z (,)-=-101.9、设z e x y =+32，而x t y t ==cos ,2，求d d z t. 解：d d (sin )()zte t e t x y x y =-+++3223232=-++(sin )3432t t e x y10、设z y xy x =ln()，求∂∂∂∂z x z y,. 解：z y y xy xy x x x =⋅+ln ln 1 z xy xy yy y x x =+-11ln() 11、设u a x a x yz a =->+ln ()0，求d u . 解：∂∂u x a a ax x yz =-+-ln 1，∂∂u y a z a x yz =⋅+ln ，∂∂u zya a x yz =+ln d (ln )d ln (d d )u a a ax x a a z y y z x yz x yz =-+++-+112、求函数z x y e xy =++ln()22的全微分.解：∂∂∂∂z x x ye x y e z y y xe x y e xyxyxyxy=+++=+++222222,[]d ()d ()d z x y ex ye x y xe y xyxy xy =+++++12222 四、应用题1、要造一容积为128立方米的长方体敞口水池，已知水池侧壁的单位造价是底部的2倍，问水池的尺寸应如何选择，方能使其造价最低？解：设水池的长、宽、高分别为x y z ,,米.水池底部的单位造价为a .则水池造价()S xy xz yz a =++44 且 xyz =128令 ()L xy xz yz xyz =+++-44128λ由 ⎪⎪⎩⎪⎪⎨⎧=-==++==++==++=01280440404xyz L xy y x L xz z x L yz z y L z y x λλλλ得 x y z ===82由于实际问题必定存在最小值，因此当水池的长、宽、高分别为8米、8米、2米时，其造价最低.2、某工厂生产两种商品的日产量分别为x 和y （件），总成本函数22128),(y xy x y x C +-=（元）.商品的限额为42=+y x ，求最小成本. 解：约束条件为042),(=-+=y x y x ϕ，构造拉格朗日函数22(,,)812(42)F x y x xy y x y λλ=-+++-，解方程组160240420x y F x y F x y F x y λλλ'⎧=-+=⎪'=-++=⎨⎪'=+-=⎩，得唯一驻点)17,25(),(=y x ，由实际情况知，)17,25(),(=y x 就是使总成本最小的点，最小成本为8043)17,25(=C （元）.3、某工厂生产两种产品甲和乙，出售单价分别为10元与9元，生产x 单位的产品甲与生产y 单位的产品乙的总费用是)33(01.03240022y xy x y x +++++元，求取得最大利润时，两种产品的产量各为多少？解：),(y x L 表示获得的总利润，则总利润等于总收益与总费用之差，即有利润目标函数)]33(01.032400[)910(),(22y xy x y x y x y x L +++++-+=)0,0(,400)33(01.06822>>-++-+=y x y xy x y x ，令⎩⎨⎧=+-='=+-='0)6(01.060)6(01.08y x L y x L yx，解得唯一驻点（120，80）.又因06.0,01.0,006.0-=''=-=''=<-=''=yy xy xx L C L B L A ，得0105.332>⨯=--B AC .得极大值320)80,120(=L . 根据实际情况，此极大值就是最大值．故生产120单位产品甲与80单位产品乙时所得利润最大320元. 五、证明题 1、设)11(yx e z +-=, 求证z yz y x z x 222=∂∂+∂∂.证明：因为2)11(1x e xzy x ⋅=∂∂+-, 2)11(1ye y z y x ⋅=∂∂+-, 所以 z e e yz y x z x y x y x 2)11()11(22=+=∂∂+∂∂+-+-2、证明函数nx ey tkn sin 2-=满足关系式22x y k t y ∂∂=∂∂ 证明：因为nx e kn kn nx e ty tkn t kn sin )(sin 2222⋅-=-⋅⋅=∂∂--, nx nex y tkn cos 2-=∂∂, nx e n xy t kn sin 2222--=∂∂, nx e kn xyk t kn sin 2222--=∂∂,所以22x y k t y ∂∂=∂∂.3、设z =xy +xF (u ), 而xyu =, F (u )为可导函数, 证明xy z y z y x z x +=∂∂+∂∂⋅.证明：y z y x z x ∂∂⋅+∂∂⋅])([])()([yu u F x x y x u u F x u F y x ∂∂'+⋅+∂∂'++=)]([)]()([u F x y u F xyu F y x '+⋅+'-+==xy +xF (u )+xy =z +xy .。

第八章_则多元函数微分学_习题课知识课件

求z,
2z ,
2z
.
y y2 xy
解
yzx3(f1xf21x) x4f1 x2f2 ,
y 2z 2x 4(f1 x 1f1 1 x 2)x 2(f2 x 1f2 1 x 2)
x 5 f 1 1 2 x 3 f 1 2x f 2 ,2
x 5 f 1 1 2 x 3 f 1 2x f 2 ,2
x
2
x 2z2a2sia n x(b yc22)
x m m zam sia n xb ( ycm 2)
x m m 1zyam bsian xb ( ycm 2 2)
x m m n y znam bnsian x b ( y c(m 2n ))
例4 设z x3 f(xy, y),( f 具有二阶连续偏)，导数 x
例6 设 xyze (xy z) 求
2z 2z 2z x2 ,xy,y2
解一记 F ( x ,y ,z ) x y z e ( x y z )
则 FxFyFz 1e(xyz)
z z 1 x y
x2z2 x2zyy2z2
0
解二方程两边对 x 求偏导
1ze(xyz)(1z)
x
x
(1z)1 [e(xyz)]0 x
2z 2z xy yx
x(x4f1x2f2)
4x3 f1x4[f11y f12(xy2)]2xf2 x2[f21yf22(xy2)]
4 x 3 f 1 2 x f 2 x 4 y f 1 1 y f 2 .2
例5 设uf(x,y,z),(x2,ey,z)0,ysix n,
(f,具有一阶连 )，且续偏 0,求导 du . 数
称为全导数.
v
设 zfu (x ),v(x ,y),y u x

多元函数微分学习题解知识点与课后习题答案

第8章多元函数微分学§8.1 多元函数的基本概念习题8-1★1.设222(,)xy f x y x y =+，求(1,)y f x。

解：222222(1,)1()yy xy x f y x x y x==++★2. 已知函数(,,)w u v f u v w u w +=+，试求(,,)f x y x y xy +-。

解： 2(,,)()()xy x f x y x y xy x y xy +-=++★★3.设()zx y f x y =++-，且当0y =时，2z x =，求()f x 。

解：将0y =代入原式得： 20(0)x x f x =++- ，故 2()f x x x =-4.求下列函数的定义域： ★（1）2ln(21)zy x =-+解：要使表达式有意义，必须 2210y x -+>∴ 所求定义域为 2{(,)|210}D x y y x =-+>★（2）z=解：要使表达式有意义，必须0x ， ∴{(,)|D x y x =≥★★（3）u =解：要使表达式有意义，必须11-≤≤∴{(,,)|D x y z z =≤★★★（4）z =解：要使表达式有意义，必须 222224010ln(1)0ln1x y x y x y ⎧-≥⎪-->⎨⎪--≠=⎩∴ 222{(,)|01,4}D x y x y y x =<+≤≤★★（5）ln()z y x =-解：要使表达式有意义，必须220010y x x x y ⎧->⎪≥⎨⎪-->⎩∴ 22{(,)|1,0}D x y x y x y =+<≤<5.求下列极限：★（1）10y x y →→知识点：二重极限。

思路：(1,0)为函数定义域内的点，故极限值等于函数值。

解：1ln 2ln 21y x y →→== ★★（2）00x y →→知识点：二重极限。

思路：应用有理化方法去根号。

第八章多元函数的微分法及其应用练习题共7页word资料

第8章多元函数的微分法及其应用§8.1 多元函数的基本概念一、填空题1．已知22),(y x xyy x f -=+ ，则f(x,y)= 。

2．函数)1ln(4222y x y x Z ---=的定义域为。

3．11lim0-+→→xy xy y x = 。

二、判断题1．如果P 沿任何直线y=kx 趋于（0，0）,都有A P f kxy x ==→)(lim 0，则A y x f y x =-→→)(lim 00。

（）2．从0)0,(lim 0=→x f x 和2)2,(lim 0=→x x f x 知),(lim 0y x f y x →→不存在。

（）3．下面定义域的求法正确吗？)ln(11),(y x y x y x f -+-+=解：012)2()1()2(0)1(01>-⇒+⎩⎨⎧>->-+x y x y x 所以定义域为x>1/2的一切实数。

三、选择题1．有且仅有一个间断点的函数是（）（A ）、x y （B ）、)22ln(y x e x +- （C ）、yx x+ （D ）、arctanxy 2.下列极限存在的是（）（A ）、y x x y x +→→00lim（B ）、y x y x +→→1lim 00 （C ）、y x x y x +→→200lim （D ）、y x x y x +→→1sin lim 00四、求下列函数的定义域，并画出定义域的图形。

1．y x y x z --+=112.221)ln(yx x x y z --+-=3．)]1)(9ln[(2222-+--=y x y x z 五、求下列极限，若不存在，说明理由。

1．22101lim y x xy y x +-→→2. 222200cos 1limy x y x y x ++-→→3．y x x y x +→→00lim§8.2 偏导数一、判断题1．如果f(x,y)在(x 0,y 0) 处，xf ∂∂存在，则一元函数f(x,y 0)在（x,y 0）处连续。

吴第8章多元函数微分学-习题课

【解】 lim f(x,y)0f(0,0)所以f 在(0,0)点连续,故否B .
x 0
y 0
f( x ,0 ) f( 0 ,0 ) x 2 s1 ix n 2 ) (
f x ( 0 ,0 ) l x 0 im x
lim 0 x 0 x
fy (0 ,0 ) ly 0 ifm (y ,0 ) yf(0 ,0 ) ly 0 iy m 2 sy i 1y n 2 ) ( 0 偏导数存在, 否A .
第八章习题课
多元函数微分法及其应用
一、关于多元函数极限的题类二、关于多元函数连续、偏导数存在、可微的题类三、关于复合函数求导、隐函数求导，全微分计算题类四、关于多元函数极(最)值的题类
一、关于多元函数极限的题类
【例1】求
lim
x0
xy x2 y2
y0
【解】
xy
lim
x 0
x2

【例8】设x2z2y(fz)其 , f中可微z， . 求
y
y
【解Ⅰ】公式法
抽象函数隐函数求导
令F(x,y,z)x2z2y(fz), y
则
Fz
2zf(z), y
Fyf(zy)zyf(zy),
z y
Fy Fz

yf( z) zf ( z)
y
y
2yz yf(z)
.
y
【例8】设x2z2y(fz)其 , f中可微z， . 求
y
y
抽象函数隐函数求导
【解Ⅱ】（求导直接法） z是x,y的函数
zyz 两边同时对y求导 2zyzf(zy)yf(zy)yy2 ,
yf(z) zf (z)
解得

多元函数微分法习题课

u u f ( x , y , z ), y ( x , t ), t h ( x , z ), 设例30 求 . x
例31 设 y f ( x , t ), t由方程 F ( x , y , t ) 0 确定，
f F f F dy x t t x . 求证 f F F dx t y t
方程由具体函数构成
y dy 例15 设 ln x 2 y 2 arctan , 求 . x dx x z z z ln , . 例16 设求 , z y x y
方程由抽象的简单函数构成例17 设 x x( y, z ), y y( x , z ), z z( x , y ) 由方程F(x,y,z)=0
例34 以u,v作为新的变量，变换 2 z xx z xy z yy z x z y 0,
其中：u x 2 y 2, v x y 1.
(五)杂题
1．变量代换 2．变上限函数
(五)杂题
1．变量代换 2．变上限函数
例35 设 u( x, y ) f (t ) xy t dt , 其中f(t)在[0,1]上连续 0
二、题型练习
（一）多元复合函数求导法（二）隐函数求导法
（三）隐函数组求导法
（四）微分形式不变性（五）杂题
二、题型练习
（一）多元复合函数求导法（二）隐函数求导法
（三）隐函数组求导法
（四）微分形式不变性（五）杂题
（二）隐函数求导法
1．一个方程确定 2．两个方程确定
（二）隐函数求导法
1．一个方程确定 2．两个方程确定
二、题型练习
（一）多元复合函数求导法（二）隐函数求导法

(完整版)多元函数微分学复习习题及答案

欢迎阅读第八章多元函数微分法及其应用复习题及解答一、选择题1.极限lim x y x y x y →→+00242= （ B ） (A)等于0； (B)不存在； (C)等于12； (D)存在且不等于0或122223 0x y →→45、设u x =arctan ，则∂x= （ B ） (A) x x y 22+； (B) -+y x y 22； (C) y x y 22+ ； (D) -+x x y 226、设f x y y x (,)arcsin=，则f x '(,)21= （ A ）（A ）-14；（B ）14；（C ）-12；（D ）127、若)ln(y x z -=，则=∂∂+∂∂yz y x z x（ C ）（A ）y x +；（B ）y x -；（C ）21；（D ）21-． 8、设yx z arctan =，v u x +=，v u y -=，则=+v u z z （ C ）（A ）22v u v u --；（B ）22v u u v --；（C ）22v u v u +-；（D ）22v u u v +-． 9、若f x x x x f x x x x (,),(,)'232612=+=+，则f x x y '(,)2= （ D ）(A)10、设z 11（A （C 12(f x （A （C 1、极限2、极限3、函数z x y =+ln()的定义域为 ??????? 。

答：x y +≥14、函数z x y=arcsin 的定义域为 ??????? 。

答：-≤≤11x ，y ≠0 5、设函数f x y x y xy y x (,)ln =++⎛⎝ ⎫⎭22，则f kx ky (,)= ??????? 。

答：k f x y 2⋅(,)6、设函数f x y xy x y (,)=+，则f x y x y (,)+-= ??????? 。

答：222x y x- （22()()(,)()()2x y x y x y f x y x y x y x y x+--+-==++-Q ） 7、设z x y y =-+sin()3，则∂∂zx x y ===21_________ 。

高等数学题库第08章(多元函数微分学).

- 1 -第八章多元函数微积分习题一一、填空题1. 设f(x,y)=x-3y. ，则f(2,-1)=_______,f(-1,2)=________x2+y2_______. 2. 已知f(x,y)=2x2+y2+1，则f(x,2x)=__________二、求下列函数的定义域并作出定义域的图形 1.z=3. z=y-x 2. z=-x+-y 4-x2-y24. z=log2xy习题二一、是非题1. 设z=x+lny，则2∂z1=2x+ （）∂xy2. 若函数z=f(x,y)在P(x0,y0)处的两个偏导数fx(x0,y0)与fy(x0,y0)均存在，则该函数在P点处一定连续（）3. 函数z=f(x,y)在P(x0,y0)处一定有fxy(x0,y0)=fyx(x0,y0) （）xy⎧,x2+y2≠0⎪4. 函数f(x,y)=⎨x2+y2在点(0,0)处有fx(0,0)=0及⎪0,x2+y2=0⎩fy(0,0)=0 （）5. 函数z=x2+y2在点(0,0)处连续，但该函数在点(0,0)处的两个偏导数zx(0,0),zy(0,0)均不存在。

（）二、填空题- 2 -1. 设z=lnx∂z∂z，则=___________;∂x∂yy2x=2y=1=___________;2. 设f(x,y)在点(a,b)处的偏导数fx(a,b)和fy(a,b)均存在，则limh→0f(a+h,b)-f(a,b-2h)=_________.h2xy+sin(xy);x2+ey三、求下列函数的偏导数：1. z=x3y-y3x+1;2. z=3. z=(1+xy)y;4. z=lntanx; y5. u=xy2+yz2+zx2∂2z∂2z∂2z四、求下列函数的2,和：∂x∂y2∂x∂y3241. z=x+3xy+y+2;2. z=xy五、计算下列各题1. 设f(x,y)=e-sinx(x+2y),求fx(0,1),fy(0,1);∂2z2. 设f(x,y)=xln(x+y)，求2∂x六、设z=ln(x+y)，证明：x1313∂2z,2x=1∂yy=2∂2z,x=1∂x∂yy=2.x=1y=2∂z∂z1+y=. ∂x∂y3习题三一、填空题2xy_____. 1．z=xy+e在点(x,y)处的dz=__________ 2．z=xx+y_____. 在点(0,1)处的dz=__________- 3 -3．设z=f(x,y)在点(x0,y0)处的全增量为∆z，全微分为dz，则f(x,y)在点(x0,y0) 处的全增量与全微分的关系式是__________________.二、选择题1．在点P处函数f(x,y)的全微分df存在的充分条件为（）A、f的全部二阶偏导数均存在B、f连续C、f的全部一阶偏导数均连续D、f连续且fx,fy均存在2．使得df=∆f的函数f为（）A、ax+by+c(a,b,c为常数)B、sin(xy)C、e+eD、x2+y22三、设z=xy，当∆x=0.1,∆y=0.2时，在(1,2)点处，求∆z和dz。

多元函数微分学习题课

2 2
平行的切平面方程为：
.
答案：x + 4 y − z = 0 2
15 二元函数f ( x , y )在点(0, 0)可微的充分条件为[ ]. A. lim [ f ( x , y ) − f (0, 0)] = 0;
( x , y )→ (0,0)
f ( x , 0) − f (0, 0) f (0, y ) − f (0, 0) B .lim = 0, 且 lim = 0; x→0 y→0 x y C.
1 设u = f ( x , y , z ), z = ϕ ( y , t ), t = ψ ( y , x ),
∂u ∂u 其中f , ϕ ,ψ 均可微，求 , . ∂x ∂y
y 2 验证：z = , f ( u)可微， 2 2 f (x − y )
则 1 ∂z 1 ∂z z + = 2. x ∂x y ∂y y
Ans : ( −5, −5, 5),(1,1,1).
27 设z = z ( x , y )是由x 2 − 6 xy + 10 y 2 − 2 yz − z 2 +18=0确定的函数，求z = z ( x , y )的极值点和极值. [2004考研]
x+ y x− y
ψ ( t )dt
其中ϕ 具有二阶导数，ψ 有一阶导数，则必有[ ].
[2005考研]
Ans : B.
22 设f ( x , y ), ϕ ( x , y )均为可微函数，且ϕ y ( x , y ) ≠ 0. 设( x0 , y0 )为f ( x , y )在约束条件ϕ ( x , y )下的一个极值点则必有[ ]. A.若f x ( x0 , y0 ) = 0, 则f y ( x0 , y0 ) = 0; B .若f x ( x0 , y0 ) = 0, 则f y ( x0 , y0 ) ≠ 0; C .若f x ( x0 , y0 ) ≠ 0, 则f y ( x0 , y0 ) = 0; D.若f x ( x0 , y0 ) ≠ 0, 则f y ( x0 , y0 ) ≠ 0. [2006考研]

8,多元函数的微分学-习题课

y x

y x
cos
y x
,
微
zy

y

x sin
y x

cos
y x
,
积
分
曲面在点 M ( x0, y0, z0 ) 处的法向量为
n { sin y0 y0 cos y0 , cos y0 , 1 }
x0 x0 x0
x0
－理学院工科数学教学中心－
n
{ sin
y0 x0
x4
f1 x

( x2 )
f2

x2
f2 x

滨工程

4 x3
f1

x4
[
f1 u

u x

f1 v

v x
]

大
学
u
xy,
v
y x
;

2 xf2

x2
[ f2 u

u x

f 2 v

v x
微
u x

f s

s x

f t

t x
,

v
x

g

x

g

x
.
u x

f1 (u
x
u x
)

f
2

v x
,

v
x

g1

(
u x
1)
g2
2 yv

多元函数微分学(1)

第八章多元函数微分学
5
6、偏导数概念及求法 7、高阶偏导数及求法二阶及二阶以上的偏导数统称为高阶偏导数.
8、全微分概念及求法 9、多元函数连续、偏导存在、可微的关系
微积分Ⅰ
第八章多元函数微分学
6
函数连续
偏导存在
函数可微偏导数连续
微积分Ⅰ
第八章多元函数微分学
7
10、复合函数求导法则
(1) 复合函数的中间变量均为一元函数的情形; (2) 复合函数的中间变量均为多元函数的情形; (3) 复合函数的中间变量既有一元函数, 又有多元函数的情形.
xy et2 dt, 求
0
x y
2 f x2
2 f 2
xy

y x
2 f y2
.
解 f ye x2 y2 , f xe x2 y2 ,
x
y
2 f x 2
2 xy3e x2 y2 ,
2 f y 2
2 x 3 ye x2 y2 ,
2 f ( ye x2 y2 ) xy y

2
1
,

u x

2(1 z
x
( 1)2
)

2
(1

2x 1
( 1)2
)

2(1 2x) ( 1)3
.
微积分Ⅰ
第八章多元函数微分学
23
u f (x, y)
例6
设函数 u (x) 由方程组

g(
x,
y,
x2
x y xy
y2
.
解 x2 y2 2 | xy |,