最新北师大版七年级下册三角形全等的证明测试试题以及答案(SSS、AAS、ASA、SAS)
最新北师大版七年级下册三角形全等的证明试题以及答案(SSS、AAS、ASA、SAS、HL)(各10题)
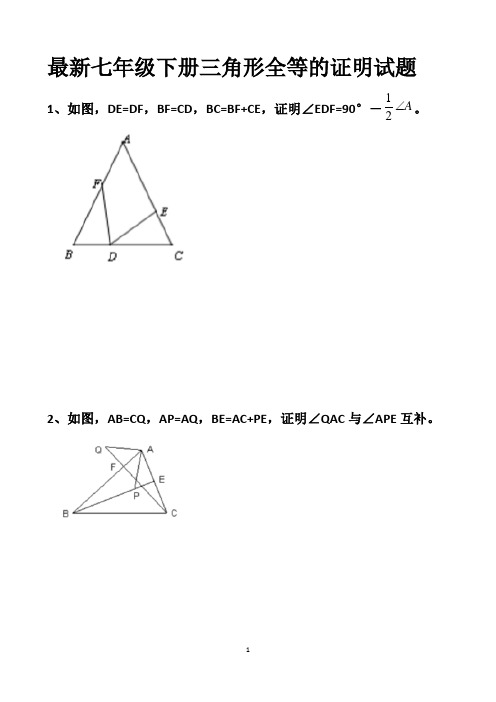
最新七年级下册三角形全等的证明试题1、如图,DE=DF ,BF=CD ,BC=BF+CE ,证明∠EDF=90°-A 21。
2、如图,AB=CQ ,AP=AQ ,BE=AC+PE ,证明∠QAC 与∠APE 互补。
3、如图,AB=CD,AC=BD,BE=CE,证明AE=DE。
4、如图,AE=CF,AD=BC,DF=BE,证明AE∥CF。
5、如图,AB=AD,AC=AE,BD+DC=DE,证明∠1=∠EDC。
6、如图,AB=BD,AC=BE,BC=DE,∠D=90°,证明AC⊥BE。
7、如图,O是BD的中点,OE=OF,DE=BF,证明AD∥BC。
8、如图,O是EF、BD的公共中点,AD=BC,AF=EC,证明AV=CD。
9、如图,AC=BF,AD=DF,BD=DC,证明∠B=∠C。
10、如图DF=DE,AC=BC,AF=BE,证明∠A=∠B。
11、如图,F是CD的中点,A点到C点与A点到D点到距离相等,AB=AE,∠BAF=∠EAF,证明∠B=∠E。
1、如图,AC∥DF,且AC=DF,∠C=∠F,说明BC和EF关系。
2、如图,AB=AC,∠BAC=∠DAE,∠ABD=∠2,证明∠3=∠1+∠2.3、如图,AB=AC,∠BAC=∠DAE,∠ADB=∠AEC,证明∠ADE=∠ACB。
4、如图,E在△ABC的边AC上,且∠AEB=∠ABC.求证:(1)∠ABE=∠C;(2)求∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长。
5、如图,MQ、NR是△PMN的高线,且MQ=NQ,证明PM=HN。
6、如图,BD⊥AC,CE⊥AB,AB=AC,证明∠B=∠C。
7、如图,BC=CD,∠BCE=∠ACD,∠B=∠D,证明AB=ED。
8、如图,AB∥CF,AD=CF,说明E是AC、DF的公共中点。
9、如图,BD⊥DE,CE⊥DE,AB⊥AC,且AB=AC,说明BD、CE和DE 关系。
最新北师大版七年级下册三角形全等证明测试试题以及答案

最新七年级下册数学三角新全等的证明测试试题1. 如图所示,AB=AC,要说明△ADC≌△AEB,需添加的条件不能是()A.∠B=∠C B.AD=AE C.∠ADC=∠AEB D.DC=BE2.下列给出的四组条件中,能判定△ABC≌△DEF的是[]A.∠A=∠D,∠C=∠F,AC=EFB.AB=DE,BC=EF,∠A=∠DC.AB=DE,BC=EF,△ABC的周长等于△DEFD.∠A=∠D,∠B=∠E,AC=EF3. 如图,AC=AD,BC=BD,则图中全等三角形共有______对.4.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带()去和蕴含的道理是().A.①、SASB.②、AASC.③、ASAD.①和②、ASA5.如图,∠1=∠2,∠E=∠A,EC=AD,则△ABD≌△EBC,此时运用的判断依据是()。
A、SSSB、ASAC、AASD、SAS6.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条件,使△AOB≌△DOC,你补充的条件是(填一个即可)7、如图,能用AAS来判断△ACD≌△ABE,需要添加的条件是[] A.∠ACD=∠ABC,∠C=∠B B.∠AEB=∠ADC,CD=BE C.AC=AB,AD=AE D.AC=AB,∠C=∠B8、如图所示,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,则△DBE的周长= cm。
A. 10B. 8C. 6D. 99、如图,已知∠1 =∠2. 则不一定能使△ABD≌△ACD的条件是[]A. AB=ACB. BD= CDC. ∠B=∠CD.∠BDA= ∠CDA10、如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲乙B.甲丙C.乙丙D.乙11、如图,∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件有[ ] A.1个B.2个C.3个D.4个12、如图所示,太阳光线AC与A'C'是平行的,AB表示一棵塔松,A'B'表示一棵小杨树,同一时刻两棵树的影长相等,已知小杨树高3米,则塔松高()A.大于3米B.等于3米C.小于3米D.和影子的长相同13、如图,AB、CD表示两根长度相等的铁条,若O为AB、CD的中点,经测量AC=15cm,则容器内径BD为()A.12cm B.13cm C.14cm D.15cm14、如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是()A.PO B.PQC.MO D.MQ15、如图,将两根钢条、的中点O连在一起,使、可以绕着点0自由转动,就做成了一个测量工件,则AB、的长等于内槽宽AB,那么判定△AOB≌△的理由是()A.边边边B.边角边C.角边角D.角角边16、下面结论:(1)一锐角和斜边对应相等两个直角三角形全等;(2)顶角和底角对应相等的两个等腰三角形全等;(3)顶角和底边对应相等的两个等腰三角形全等;(4)有两个角和一边对应相等的两个三角形全等.其中正确的个数为()A.1个B.2个C.3个D.4个17、如图,已知AB=CD且∠ABD=∠BDC,要证∠A=∠C,判定△ABD ≌△CDB的方法是[]A.AAS B.SAS C.ASA D.SSS17、如图,给出下列四组条件:①AB=ED,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其.其中,能使△ABC≌△DEF的条件共有( )A.1组B.2组C.3组D.4组18、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC19、如图,小华书上的三角形被墨水弄污了一部分,她想在作业本上作一个完全一样的三角形,其根据是()A. SSS B.ASA C.SAS D.AAS21、下列各条件中,不能作出惟一三角形的是()A. 已知两边和夹角B. 已知两角和夹边C. 已知两边和其中一边的对角D. 已知三边22、用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.SAS B.SSS C.ASA D.AAS23、直尺和圆规作一个角的角平分线示意图,说明∠AOC=∠BOC依据。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
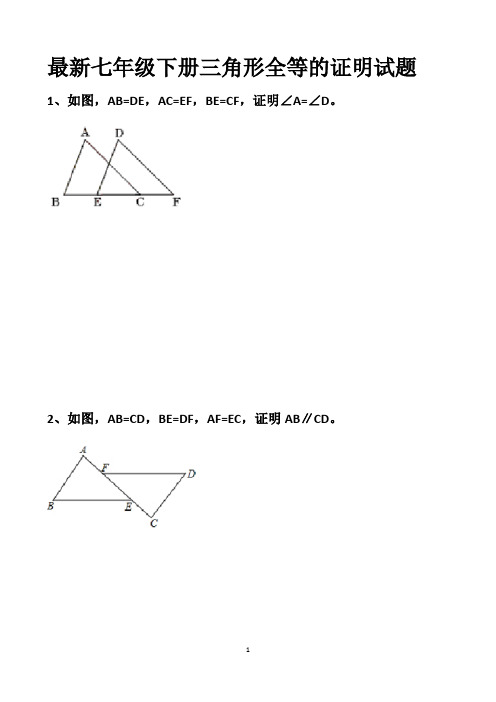
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
最新北师大版七年级下册三角形全等的证明练习题以及答案
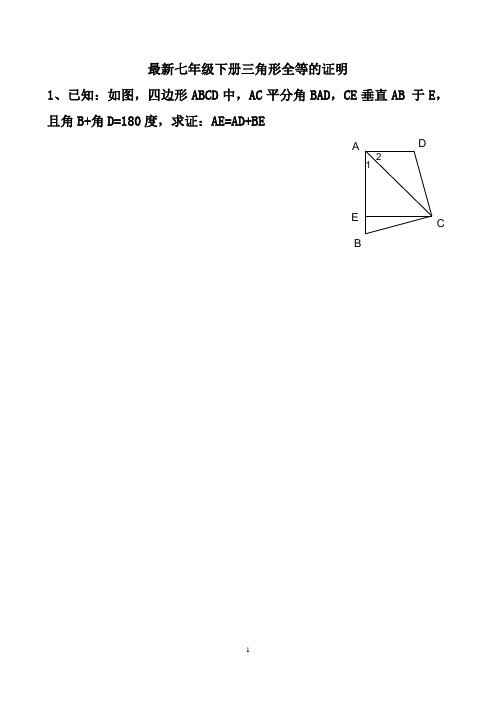
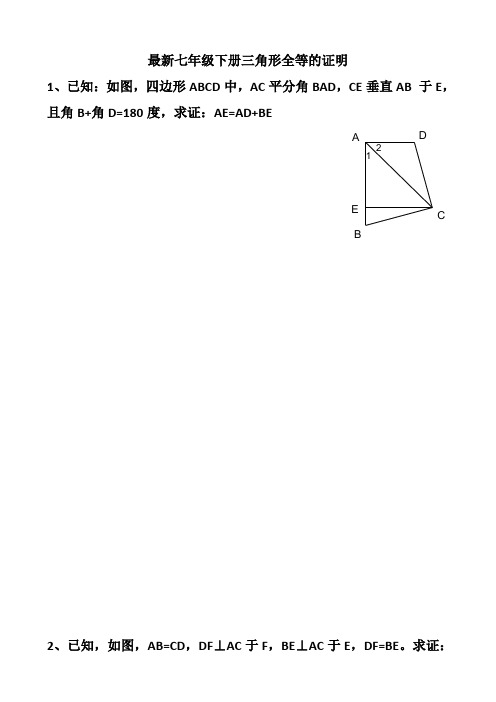
最新七年级下册三角形全等的证明1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB 于E,且角B+角D=180度,求证:AE=AD+BEA B DCE 122、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。
求证:AF=CE。
FE A CDB3、已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
AEDC B4、如图,DE⊥AB,DF⊥AC,垂足分别为E、F,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
①AB=AC ②BD=CD ③BE=CFBD C5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF 交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
E G6、如图,在△ABC中,点D在AB上,点E在BC上,BD=BE。
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明。
你添加的条件是:________ ___(2)根据你添加的条件,再写出图中的一对全等三角形:______________(不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。
求证:EB=ED。
DA E CB8、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
AB CDEFO9、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
AE FDB C10、. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A’B’C’。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

最新七年级下册三角形单元测试试题一、选择题1.一定在△ABC内部的线段是()。
A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线2.下列说法中,正确的是()。
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形B.一个等腰三角形一定是锐角三角形,或直角三角形C.一个直角三角形一定不是等腰三角形,也不是等边三角形D.一个等边三角形一定不是钝角三角形,也不是直角三角形3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有()。
A.4对 B.5对 C.6对 D.7对4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定5.下列各题中给出的三条线段不能组成三角形的是()A.4厘米、5厘米、6厘米B.4厘米、4厘米、4厘米C.5厘米、13厘米、6厘米D.7厘米、9厘米、7厘米6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是()。
A.18 B.15 C.18或15 D.无法确定7.两根木棒分别为6cm和9cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有()种。
A.3 B.4 C.5 D.68.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有()个。
A.4 B.6 C.8 D.109.各边长均为整数的不等边三角形的周长小于13,这样的三角形有()A.1个 B.2个 C.3个 D.4个10.三角形所有外角的和是()A.180° B.360° C.720° D.540°11.锐角三角形中,最大角α的取值范围是( ) A .0°<α<90°; B .60°<α<180°; C .60°<α<90°; D .60°≤α<90°12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为( )A .锐角或直角三角形;B .钝角或锐角三角形C .直角三角形;D .钝角或直角三角形13.已知△ABC 中,∠ABC 与∠ACB 的平分线交于点O ,则∠BOC 一定( )A .小于直角;B .等于直角;C .大于直角;D .大于或等于直角 二、填空题1.如图:(1)AD ⊥BC ,垂足为D ,则AD 是________的高, ∠________=∠________=90°;(2)AE 平分∠BAC ,交BC 于点E ,则AE 叫________,∠________=∠________=∠________,AH叫________;(3)若AF =FC ,则△ABC 的中线是________;(4)若BG =GH =HF ,则AG 是________的中线,AH 是________的中线.212.如图,∠ABC=∠ADC=∠FEC=90°.(1)在△ABC中,BC边上的高是________;(2)在△AEC中,AE边上的高是________;(3)在△FEC中,EC边上的高是________;(4)若AB=CD=3,AE=5,则△AEC的面积为________.3.在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的周长为________.4.五段线段长分别为1cm、2cm、3cm、4cm、5cm,以其中三条线段为边长共可以组成________个三角形.5.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.6.一个等腰三角形的周长为5cm,如果它的三边长都是整数,那么它的腰长为________cm.7.在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则∠A=______;∠B =______;∠C=______.8.如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=________;(2)若∠ABC+∠ACB=120°,则∠BIC=________;(3)若∠A=60°,则∠BIC=________;(4)若∠A=100°,则∠BIC=________;(5)若∠A=n°,则∠BIC=________.三、解答题1.在△ABC中,∠BAC是钝角.画出:(1)∠ABC的平分线;(2)边AC上的中线;(3)边AC上的高.2.△ABC 的周长为16cm ,AB =AC ,BC 边上的中线AD 把△ABC 分成周长相等的两个三角形.若BD =3cm ,求AB 的长.3.如图,AB ∥CD ,BC ⊥AB ,若AB =4cm ,,求△ABD 中AB 边上的高.212cm =∆ABCS4.学校有一块菜地,如下图.现计划从点D 表示的位置(BD ∶DC =2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D 是BC 的中点的话,由此点D 笔直地挖至点A 就可以了.现在D 不是BC 的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么?5.在直角△ABC 中,∠BAC =90°,如下图所示.作BC 边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD 中AB 边上的高,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作、、……、.当作出时,图中共有多少个不同的直角三角形?1DD 21D D 32D D k k D D 1-k k D D 1-6.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.7.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.8.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.9.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.10.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成18cm和9cm两部分,求这个等腰三角形的底边的长.11.如图,已知△ABC中,AB=AC,D在AC的延长线上.求证:BD-BC<AD-AB.12.如图,△ABC 中,D 是AB 上一点.求证:(1)AB +BC +CA >2CD ;(2)AB +2CD >AC +BC .13.如图,AB ∥CD ,∠BMN 与∠DNM 的平分线相交于点G ,(1)完成下面的证明:∵ MG 平分∠BMN ( ),∴ ∠GMN =∠BMN ( ),同理∠GNM =∠DNM .∵ AB ∥CD ( ),∴ ∠BMN +∠DNM =________( ).∴ ∠GMN +∠GNM =________.2121∵∠GMN+∠GNM+∠G=________(),∴∠G= ________.∴ MG与NG的位置关系是________.(2)把上面的题设和结论,用文字语言概括为一个命题:_________________________________________________.14.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.15.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC =60°,求∠BOC的度数.16.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.17.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.18.画出图形,并完成证明:已知:AD是△ABC的外角∠EAC的平分线,且AD∥BC.求证:∠B=∠C.。
最新北师大版七年级下册三角新全等的证明试题以及答案

最新三角形全等的证明练习题1、已知:如图,四边形ABCD中,AB∥CD ∠A=∠C.求证:AD=BC、AB=CD。
A2、已知AD是⊿ABC的中线,BE⊥AD,CF⊥AD,试着说明DE、DF的关系。
FB CDE3、已知CD ∥AB ,DF ∥EB ,AF=CE ,证明AB=CD 。
4、已知∠1=∠2,∠3=∠4,证明AC=AD 。
A DC E F B5、已知∠A =∠B ,∠1=∠2,AB =CD ,说明BF=EC 。
6、已知ED ⊥AB ,EF ⊥BC ,BD =EF ,说明EM 、MD 和BF 的关系;。
A B C DE F 1 27、在⊿ABC 中,高AD 与高BE 相交于点H ,DH=CD ,证明:BH=AC 。
8、已知∠A =∠D ,AC ∥FD ,BF=CE ,问AB 、DE 的关系,并说明理由。
AB CEH AB CEF D9、已知∠AFE=∠BCD ,AF =CD ,AB ⊥BC ,DE ⊥EF ,10、已知AD =AE ,∠BDC =∠CEB ,证明∠B=∠C 。
A B C E D F A D E B C11、已知CE⊥AB,DF⊥AB,AC∥DB,AF=BE,说明CE、FD的关系。
12、已知DE=FE,FC∥AB,证明E是AC的中点。
AD BE FC13、如图,D ,E ,F ,B 在一条直线上,AB =CD ,∠B =∠D ,BF =DE ,问(1)AE =CF(2)AE ∥CF 。
14、已知,E 、F 是AB 上的两点,AE =BF ,又AC ∥DB ,AC =DB ,证明CF=DE 。
CD EFA BBA DFE C15、已知,点C 是AB 的中点,CD ∥BE ,且CD =BE ,证明∠D=∠E 。
16、已知AB =AC ,∠1=∠2,AD =AE ,证明BD=CE 。
A DB EC 1 2D AE C B 1 217、如图,AB =AE ,AC =AD ,证明:BC=DE 。
北师大版七年级下册三角形全等的证明练习题以及答案
5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
最新七年级下册三角形全等的证明
1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB于E,且角B+角D=180度,求证:AE=AD+BE
2、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。求证:AF=CE。
3、已知,如图,AB⊥AC,AB=AC,AD⊥AE,AD=AE。求证:BE=CD。
25、(1)如图,在正方形一边上取中点,并沿虚线剪开,用两块图形拼一拼,能否拼出平行四边形、梯形或三角形画图解释你的判断.
(2)如图(2)E为正方形ABCD边BC的中点,F为DC的中点,BF与AE有何关系请解释你的结论。
26、如图 四点在同一直线上,请你从下面四项中选出三个作为条件,其余一个作为结论,构成一个真命题,并进行证明.
① ,② ,③ ,④
27、已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G。(1)BF=AC(2)CE= BF(3)CE与BC的大小关系如何。
28、如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连结BD,AE,并延长AE交BD于F.求证:
7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。求证:EB=ED。
8、已知:如图,AB、CD交于O点,CE 已知:如图,△ABC和△A'B'C'中,∠BAC=∠B'A'C',∠B=∠B',AD、A'D'分别是∠BAC、∠B'A'C'的平分线,且AD=A'D'。求证:△ABC≌△A’B’C’。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案 (共4套题)

最新七年级下册三角形单元测试试题一、选择题1.一定在△ABC内部的线段是()。
A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线2.下列说法中,正确的是()。
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形B.一个等腰三角形一定是锐角三角形,或直角三角形C.一个直角三角形一定不是等腰三角形,也不是等边三角形D.一个等边三角形一定不是钝角三角形,也不是直角三角形3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有()。
A.4对 B.5对 C.6对 D.7对4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定5.下列各题中给出的三条线段不能组成三角形的是()A.4厘米、5厘米、6厘米B.4厘米、4厘米、4厘米C.5厘米、13厘米、6厘米D.7厘米、9厘米、7厘米6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是()。
A.18 B.15 C.18或15 D.无法确定7.两根木棒分别为6cm和9cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有()种。
A.3 B.4 C.5 D.68.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有()个。
A.4 B.6 C.8 D.109.各边长均为整数的不等边三角形的周长小于13,这样的三角形有()A.1个 B.2个 C.3个 D.4个10.三角形所有外角的和是()A.180° B.360° C.720° D.540°11.锐角三角形中,最大角α的取值范围是( ) A .0°<α<90°; B .60°<α<180°; C .60°<α<90°; D .60°≤α<90°12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为( )A .锐角或直角三角形;B .钝角或锐角三角形C .直角三角形;D .钝角或直角三角形13.已知△ABC 中,∠ABC 与∠ACB 的平分线交于点O ,则∠BOC 一定( )A .小于直角;B .等于直角;C .大于直角;D .大于或等于直角 二、填空题1.如图:(1)AD ⊥BC ,垂足为D ,则AD 是________的高, ∠________=∠________=90°;(2)AE 平分∠BAC ,交BC 于点E ,则AE 叫________,∠________=∠________=∠________,AH叫________;(3)若AF =FC ,则△ABC 的中线是________;(4)若BG =GH =HF ,则AG 是________的中线,AH 是________的中线.212.如图,∠ABC=∠ADC=∠FEC=90°.(1)在△ABC中,BC边上的高是________;(2)在△AEC中,AE边上的高是________;(3)在△FEC中,EC边上的高是________;(4)若AB=CD=3,AE=5,则△AEC的面积为________.3.在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的周长为________.4.五段线段长分别为1cm、2cm、3cm、4cm、5cm,以其中三条线段为边长共可以组成________个三角形.5.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.6.一个等腰三角形的周长为5cm,如果它的三边长都是整数,那么它的腰长为________cm.7.在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则∠A=______;∠B =______;∠C=______.8.如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=________;(2)若∠ABC+∠ACB=120°,则∠BIC=________;(3)若∠A=60°,则∠BIC=________;(4)若∠A=100°,则∠BIC=________;(5)若∠A=n°,则∠BIC=________.三、解答题1.在△ABC中,∠BAC是钝角.画出:(1)∠ABC的平分线;(2)边AC上的中线;(3)边AC上的高.2.△ABC 的周长为16cm ,AB =AC ,BC 边上的中线AD 把△ABC 分成周长相等的两个三角形.若BD =3cm ,求AB 的长.3.如图,AB ∥CD ,BC ⊥AB ,若AB =4cm ,,求△ABD 中AB 边上的高.212cm =∆ABCS4.学校有一块菜地,如下图.现计划从点D 表示的位置(BD ∶DC =2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D 是BC 的中点的话,由此点D 笔直地挖至点A 就可以了.现在D 不是BC 的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么?5.在直角△ABC 中,∠BAC =90°,如下图所示.作BC 边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD 中AB 边上的高,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作、、……、.当作出时,图中共有多少个不同的直角三角形?1DD 21D D 32D D k k D D 1-k k D D 1-6.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.7.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.8.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.9.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.10.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成18cm和9cm两部分,求这个等腰三角形的底边的长.11.如图,已知△ABC中,AB=AC,D在AC的延长线上.求证:BD-BC<AD-AB.12.如图,△ABC 中,D 是AB 上一点.求证:(1)AB +BC +CA >2CD ;(2)AB +2CD >AC +BC .13.如图,AB ∥CD ,∠BMN 与∠DNM 的平分线相交于点G , (1)完成下面的证明:∵ MG 平分∠BMN ( ),∴ ∠GMN =∠BMN ( ),同理∠GNM =∠DNM .∵ AB ∥CD ( ),∴ ∠BMN +∠DNM =________( ). ∴ ∠GMN +∠GNM =________.2121∵∠GMN+∠GNM+∠G=________(),∴∠G= ________.∴ MG与NG的位置关系是________.(2)把上面的题设和结论,用文字语言概括为一个命题:_________________________________________________.14.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.15.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC =60°,求∠BOC的度数.16.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.17.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.18.画出图形,并完成证明:已知:AD是△ABC的外角∠EAC的平分线,且AD∥BC.求证:∠B=∠C.最新七年级下册三角形单元测试试题一、选择题1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为 ( )A.10 B.12 C.14 D.162.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( ) A.a>3 B.2<a<14 C.3<a<13 D.a<133.一个三角形的三个内角中,锐角的个数最少为 ( )A.0 B.1 C.2 D.34.下面说法错误的是 ( )A.三角形的三条角平分线交于一点B.三角形的三条中线交于一点C.三角形的三条高交于一点D.三角形的三条高所在的直线交于一点5.能将一个三角形分成面积相等的两个三角形的一条线段是( )A.中线B.角平分线C.高线D.三角形的角平分线6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )A.∠ 1 B .∠ 2 C .∠ B D .∠ 1、∠ 2和∠ B7.点P 是△ABC 内任意一点,则∠APC 与∠B 的大小关系是 ( )A .∠APC>∠B B .∠APC=∠BC .∠APC<∠BD .不能确定 8.已知:a 、b 、c 是△ABC 三边长,且M =(a +b +c)(a +b -c)(a -b -c),那么 ( )A .M >0B .M =0C .M <0D .不能确定9.周长为P 的三角形中,最长边m 的取值范围是 ( )A .B .C .D .10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )A .5个B .4个C .3个D .2个 二、填空题1.五条线段的长分别为5厘米、6厘米、8厘米、10厘米和13厘米,以其中任意三条线段为边长可以________个三角形.2.在△ABC 中,AB =7,AC =13,那么BC 边的取值范围是________,23Pm P <≤23P m P <<23P m P ≤<23P m P ≤≤周长的取值范围是___________.3.一个三角形的三个内角的度数的比是1:5:6,这个三角形是_________三角形.4.一个等腰三角形两边的长分别是14cm和28cm则它的周长是__________.5.在△ABC中,三边长分别为正整数a、b、c,且c≥b≥a>0,如果b=4,则这样的三角形共有_________个.6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.7.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.8.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是△ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.9.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.10.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.12.等腰三角形的周长为42cm,腰长为xcm,则x的取值范围是________.三、解答题1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形?说明理由.2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.9.已知:如图5—24,P是△ABC内任一点,求证:AB+AC>BP+PC.10.如图5—25,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.最新七年级下册三角形单元测试试题一、选择题。
北师大版七年级数学下册《全等三角形判定的三种类型》专题试题(附答案)

北师大版七年级数学下册专题训练系列(附解析)专训1全等三角形判定的三种类型名师点金:一般三角形全等的判定方法有四种:SSS,SAS,ASA,AAS;直角三角形是一种特殊的三角形,它的判定方法除了上述四种之外,后面还会学到一种特殊的方法,即“HL”.具体到某一道题目时,要根据题目所给出的条件进行观察、分析,选择合适的、简单易行的方法来解题.已知一边一角型应用1一次全等型1.【2016·孝感】如图,BD⊥AC于点D,CE⊥AB于点E,AD =AE.试说明:BE=CD.(第1题)2.如图,在△ABC中,D是BC边上一点,连接AD,过点B 作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.试说明:AD是△ABC的中线.(第2题)应用2两次全等型3.如图,已知AB=AD,∠DAC=∠BAC,若E是AC上一点,试说明:∠CBE=∠CDE.(第3题)4.如图,在△ABC中,∠ABC=∠ACB=45°,AB=AC,D是AC边的中点,AE⊥BD于点F,交BC于点E,连接DE,试说明:∠ADB=∠CDE.(第4题)已知两边型应用1一次全等型5.如图,在△ABC中,AM为BC边上的高,E为AC上的一点,BE交AM于点F,且AM=BM,FM=CM.试说明:BE⊥AC.(第5题)应用2两次全等型6.如图,AB=CB,AD=CD,E是BD上任意一点(不与点B,D重合).试说明:AE=CE.(第6题)7.如图,已知AB∥CD,OA=OD,AE=DF.试说明:EB∥CF.(第7题)已知两角型应用1一次全等型8.如图,已知AC平分∠BAD,∠1=∠2,那么AB与AD有何大小关系?为什么?(第8题)应用2两次全等型9.如图,在△ABC与△DCB中,AC与BD交于点E,且∠BAC =∠CDB,∠ACB=∠DBC,分别延长BA与CD交于点F.试说明:BF=CF.(第9题)答案1.解:因为BD ⊥AC 于点D ,CE ⊥AB 于点E ,所以∠ADB =∠AEC =90°.在△ADB 和△AEC 中,⎩⎪⎨⎪⎧∠ADB =∠AEC ,AD =AE ,∠A =∠A ,所以△ADB ≌△AEC(ASA).所以AB =AC.又因为AD =AE ,所以BE =CD.2.解:因为BE ⊥AD ,CF ⊥AD ,所以∠BED =∠CFD =90°.又因为∠BDE =∠CDF ,BE =CF ,所以△DBE ≌△DCF.所以BD =CD.所以D 是BC 的中点,即AD 是△ABC 的中线.3.解:因为AB =AD ,∠BAE =∠DAE ,AE =AE ,所以△ABE ≌△ADE(SAS).所以BE =DE ,∠AEB =∠AED.所以∠BEC =∠DEC.又因为EC =EC ,所以△BEC ≌△DEC(SAS).所以∠CBE =∠CDE.(第4题)4.解:如图,作CG ⊥AC ,交AE 的延长线于点G ,易得∠BAC =∠DAE +∠BAE =90°,∠ABF +∠BAE =90°, 所以∠DAE =∠ABF.因为CG ⊥AC ,所以∠BAD =∠ACG =90°.在△ABD 和△CAG 中,⎩⎪⎨⎪⎧∠ABD =∠CAG ,AB =CA ,∠BAD =∠ACG ,所以△ABD ≌△CAG(ASA).所以∠ADB =∠G ,AD =CG .因为D 是AC 的中点,所以AD =CD =CG .因为∠ACG =90°,∠ACB =45°,所以∠GCE =∠ACB =45°.在△DEC 和△GEC 中,⎩⎪⎨⎪⎧CD =CG ,∠DCE =∠GCE ,CE =CE ,所以△DEC ≌△GEC(SAS).所以∠CDE =∠G .所以∠ADB =∠CDE.5.解:因为AM ⊥BC ,所以∠BMA =∠AMC =90°.所以∠1+∠2=90°.在△BMF 和△AMC 中,⎩⎪⎨⎪⎧BM =AM ,∠BMF =∠AMC ,FM =CM ,所以△BMF ≌△AMC(SAS).所以∠2=∠C.又因为∠1+∠2=90°,所以∠1+∠C =90°. 在△BEC 中,∠1+∠C =90°,所以∠BEC =180°-90°=90°.所以BE ⊥AC.6.解:在△ABD 和△CBD 中,⎩⎪⎨⎪⎧AB =CB ,AD =CD ,BD =BD ,所以△ABD ≌△CBD(SSS).所以∠ABD =∠CBD.在△ABE 和△CBE 中,⎩⎪⎨⎪⎧AB =CB ,∠ABE =∠CBE ,BE =BE ,所以△ABE ≌△CBE(SAS).所以AE =CE.7.解:方法一:因为AB ∥CD ,所以∠3=∠4.在△ABO 和△DCO 中,⎩⎪⎨⎪⎧∠4=∠3,OA =OD ,∠2=∠1,所以△ABO ≌△DCO(ASA).所以OB =OC. 又因为AE =DF ,OA =OD ,所以OA +AE =OD +DF ,即OE =OF.在△BOE 和△COF 中,⎩⎪⎨⎪⎧OB =OC ,∠2=∠1,OE =OF ,所以△BOE ≌△COF(SAS).所以∠E =∠F. 所以EB ∥CF.方法二:因为AB ∥CD ,所以∠3=∠4.在△ABO 和△DCO 中,⎩⎪⎨⎪⎧∠4=∠3,OA =OD ,∠2=∠1,所以△ABO ≌△DCO(ASA).所以BA =CD.因为∠3=∠4,所以∠CDF =∠BAE.在△CDF 和△BAE 中,⎩⎪⎨⎪⎧CD =BA ,∠CDF =∠BAE ,DF =AE ,所以△CDF ≌△BAE(SAS).所以∠F =∠E. 所以EB ∥CF.8.解:AB =AD.理由如下:因为∠1=∠2,所以∠ABC =∠ADC.又因为AC 平分∠BAD ,所以∠BAC =∠DAC. 又因为AC =AC ,所以△ABC ≌△ADC(AAS). 所以AB =AD.9.解:在△ABC 和△DCB 中,⎩⎪⎨⎪⎧∠BAC =∠CDB ,∠ACB =∠DBC ,BC =CB ,所以△ABC ≌△DCB(AAS).所以AC =DB.又因为∠BAC =∠CDB ,所以∠FAC =∠FDB.在△FAC 和△FDB 中,⎩⎪⎨⎪⎧∠F =∠F ,∠FAC =∠FDB ,AC =DB ,所以△FAC ≌△FDB(AAS).所以BF =CF.。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

七年级下册三角形全等的证明单元测试试题一、选择题。
(共12道选择题,每道选择题只有一个正确答案)1、下列条件中,不能判断△ABC≌△OPQ的是()。
A、AB=OQ,AC=OP,BC=PQB、AB=OP,∠A=∠O,∠C=∠QC、AC=OQ,∠A=∠O,∠C=∠QD、BC=PQ,∠B=∠P,∠A=∠O2、如果△ABD≌△BDE≌△DEC,下列结论中①△ABC是直角三角形;②DE⊥BC;③∠C=60°;④D是线段AC中点;⑤∠ADB=∠BDE=∠EDC,其中错误有()个。
A、1B、2C、3D、43、如图,已知AD=AE,下列再添加一个条件,仍不能证明△ABE≌△ACD是()。
A、∠B=∠CB、∠BDO=∠CEOC、AB=ACD、BE=CD4、如图,将△ABE沿AB折叠得到△ABC,△ACD沿AC折叠得到△ACB,并且∠1:∠2:∠3=25:7:4,则∠a等于()A、30°B、35°C、40°D、50°5、一个等腰三角形的两边长分别是4厘米和8厘米,这个等腰三角形的周长是()。
A、16厘米B、20厘米C、16或20厘米D、18厘米6、锐角三角形中,最大的锐角∠A的范围是()。
A、60°<A<90°B、60°<A<180°C、60°≤A<90°D、0°<A<90°7、如图,在Rt△ABC中,AD是斜边上的高,DF⊥AB,DE⊥AC,下列与∠B相等的角有()个。
A、2B、3C、4D、58、如图,△ACD和△BCE都是等边三角形,下列结论:①AE=BD;②CM=CN;③∠CND=90°;④连接MN,则△MCN是等边三角形;⑤连接MN,MN∥AB。
其中错误的有()个。
A、0B、1C、2D、39、如果一个三角形的三条高交于顶点处,这是()三角形。
A、钝角三角形B、直角三角形C、锐角三角形D、等腰三角形10、如图,一束光经过平面镜CD后反射到AB,在反射到CD,在折射出去。
最新北师大版七年级下册三角形全等(HL)的证明试题以及答案(30道题)

最新七年级下册三角形全等的证明试题1、如图,∠B=∠D=90°,CD=BC,证明AC平分∠BAD。
2、如图,CE⊥AB,DF⊥AB,CE=DF,AC=DB,证明AF=BE。
5、如图,AB⊥BD,AC⊥CD,AC=AB,证明BC⊥AD。
6、如图,AB⊥BD,ED⊥BD,AC=EF,BF=CD,说明AB、DE的关系。
7、如图,CE⊥AB,BD⊥AC,AE=AD,找出图中的全等三角形,并证明其中一个。
8、如图,AD⊥BD,DF=DC,BF=AC,证明BE⊥AC。
9、如图,AD⊥DE,BE⊥DE,AD=CE,AC=BC,证明AD+BE=DE。
10、如图,DF⊥AC,BE⊥AC,AF=EC,DC=AB,证明DF=BE。
11、如图,∠C=90°,MN⊥AB,AM=AC,证明MN=NC。
12、如图,AC⊥CE,DF⊥BD,AF=BE,AC=BD,说明DF和CE的关系。
13、如图,已知AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E、F,证明CE=DF。
14、如图,CF⊥AF,CE⊥AB,BC=DC,CE=CF,证明BE=DF。
15、如图,D是BC的中点,DE⊥AB,DF⊥AC,DE=DF,A、D的连线和BC垂直。
16、如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.(1)若BC在DE的同侧(如图①)且AD=CE,说明:BA⊥AC.(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?若是请予证明,若不是请说明理由.17、如图,DE⊥AB,DF⊥AC,DE=DF,证明D是BC的中点。
18、如图,∠ACF=∠ABD=∠CDF=90°,AB=CD,AC=CF,说明DF、AB、BD的关系。
19、如图,∠B=∠D=90°,AD=AB,∠CAD=∠BAE,证明CF=EF。
20、如图,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.(1)试判断AC与CE的位置关系,并说明理由.(2)如图⑵,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC与BE的位置关系还成立吗?(注意字母的变化)21、如图,AB⊥BD,DF⊥BD,DF=BC,CF=AC。
北师大版数学七年级下册《全等三角形判定》含答案

北师大版数学七年级下册《全等三角形判定》含答案D CB A 全等三角形的判定(SAS)1、如图1,AB ∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A 、3B 、4C 、5D 、62、如图2,AB=AC,AD=AE,欲证△ABD ≌△ACE ,可补充条件( )A 、∠1=∠2B 、∠B=∠C C 、∠D=∠ED 、∠BAE=∠CAD3、如图3,AD=BC ,要得到△ABD 和△CDB 全等,可以添加的条件是( )A 、AB ∥CD B 、AD ∥BC C 、∠A=∠CD 、∠ABC=∠CDA4、如图4,AB 与CD 交于点O,OA=OC ,OD=OB ,∠AOD=________,•根据_________可得到△AOD ≌△COB,从而可以得到AD=_________。
5、如图5,已知△ABC 中,AB=AC,AD 平分∠BAC,请补充完整过程说明△ABD ≌△ACD 的理由。
∵AD 平分∠BAC, ∴∠________=∠_________(角平分线的定义)、在△ABD 和△ACD 中,∵____________________________, ∴△ABD ≌△ACD ( )6、如图6,已知AB=AD ,AC=AE,∠1=∠2,求证∠ADE=∠B 、7、如图,已知AB=AD,若AC 平分∠BAD,问AC 是否平分∠BCD?为什么?8、如图,在△ABC 和△DEF 中,B 、E 、F 、C ,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明、①AB=DE ; ②AC=DF ; ③∠ABC=∠DEF; ④BE=CF 、9、如图⑴,AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且BC=DE ,CD=AB.⑴试判断AC 与CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)答案:1、A2、A3、B 、4、∠COB ,SAS,CB;5、BAD,CAD ,AB=AC,∠BAD=∠CAD ,AD=AD,SAS 、6、证△ABC ≌△ADE 、7、平分,证△ABC ≌△ADC 、8、答案不惟一,有两种选法:⑴由①③④得②;⑵由①②④得③,证明略9、⑴AC ⊥CE ,证△ABC≌△CDE;⑵结论仍成立、。
北师大版数学七年级下册《全等三角形判定》含答案SSS

北师大版数学七年级下册《全等三角形判定》含答案SSS全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )A、120°B、125°C、127°D、104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A、△ABC≌△BADB、∠CAB=∠DBAC、OB=OCD、∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1。
4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS"证明______≌_______得到结论.5、如图,AB=AC,BD=CD,求证:∠1=∠2。
6、如图,已知AB=CD,AC=BD,求证:∠A=∠D.7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF、请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图,A、E、F、C四点共线,BF=DE,AB=CD、⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF、答案1、C;2、C、3、AC=A1C14、CE,△ABF≌△CDE、5、证明△ABE≌△ACE、6、连接BC,证明△ABC≌△DCB、7、⑴证明△ADE≌△CBF;⑵证明∠AEF=∠CFE、8、⑴可添加AE=CF或添加AF=CE,证明△DEC≌△BFA;⑵由⑴得∠BFA=∠DEC,∴DE∥BF、。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案(2套题)

最新七年级下册三角形全等的证明试题1、若a 是正整数,且6x a 2=,则=÷a 62a 5x 4x 2)( 。
2、若4b a 6b a 22==+)-,()(,则ab= 。
3、9b a 22=-,b+a=﹣3,则a -b= 。
4、如图是一台起重机的工作简图,前后两次吊杆位置OP 1、 OP 2与线绳的夹角分别是30°和70°,则吊杆前后两次的夹角∠P 1OP 2=( )°5、如图,扇形OAB 动点P 从点A 出发,沿弧AB ,线段B0、0A 匀速运动到点A ,则0P 的长度y 与运动时间t 之间的函数图象大致是( )A .B .C .D .7、如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于()A.585°B.540°C.270°D.315°8、如图,四边形ABCD是边长为2cm的正方形,动点P在ABCD的边上沿A-B-C-D的路径以1cm/s的速度运动(点P不与A,D重合).在这个运动过程中,△APD的面积S(cm2)随时间t(s)的变化关系用图象表示,正确的为。
A. B.C. D9、如图,用尺规作出∠OBF=∠AOB,作图是()A、以点B为圆心,OD为半径的圆B、以点B为圆心,DC为半径的圆C、以点E为圆心,OD为半径的圆D、以点E为圆心,DC为半径的圆10、利用基本作图,不能作出唯一三角形的是( ) A.已知两边及其夹角 B.已知两角及其夹边C.已知两边及一边的对角 D.已知三边11、已知下列条件,不能作出唯一三角形的是()A.两边及其夹角 B.两角及其夹边C.三边 D.两边及除夹角外的另一个角12、如图所示,小敏做题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,然后粘贴在上面,她作图的依据是( ) A.SSS B.SASC.ASA D.AAS13、用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.SAS B.SSSC.ASA D.AAS14、如图,直尺和圆规作一个角的角平分线示意图,说明∠AOC=∠BOC 依据。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

最新七年级下册三角形单元测试试题一、选择题(每题3分,共30分)1.图中三角形的个数是()A.8 B.9 C.10 D.112.下面四个图形中,线段BE是⊿ABC的高的图是()A B C D3.以下各组线段为边,能组成三角形的是()A.3cm,4cm,7cmB.7cm,6cm,14cmC.12cm,9cm,5cmD.2cm,3cm,6cm4.三角形一个外角小于与它相邻的内角,这个三角形是()A.直角三角形 B.锐角三角形C.钝角三角形 D.属于哪一类不能确定5.如图,在直角三角形ABC 中,AC ≠AB ,AD 是斜边上的高, DE ⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (∠C 除外)相等的角的个数是( ) A 、3个 B 、4个 C 、5个 D 、6个6.下面说法正确的个数有( )①如果三角形三个内角的比是1∶2∶3,那么这个三角形是直角三角形;②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果∠A=∠B=∠C ,那么△ABC 是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在ABC 中,若∠A +∠B=∠C ,则此三角形是直角三角形。
A 、3个B 、4个C 、5个D 、6个7.在ABC 中,的平分线相交于点P ,设用x 的代数式表示的度数,正确的是( ) (A ) (B ) (C ) (D )21∆∆C B ∠∠,,︒=∠x A BPC ∠x 2190+x 2190-x 290+x +908.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A、900B、1200C、1600D、18009.以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是()(A)1个 (B)2个 (C)3个 (D)4个10.给出下列命题:①三条线段组成的图形叫三角形②三角形相邻两边组成的角叫三角形的内角③三角形的角平分线是射线④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外⑤任何一个三角形都有三条高、三条中线、三条角平分线⑥三角形的三条角平分线交于一点,且这点在三角形内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新七年级下册三角形全等的证明试题SSS证明
1、点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,则AB 和DE有怎样的位置关系?请证明
2、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?
3、如图,已知:AB=AD,AC=AE,BC=DE,求证:∠BAE=∠CAD
4、如图,AB=AC,BD=CD,求证:∠1=∠2
5、在△ABC中,∠C=90°,且AD=BD,AE=BC,DE=DC,说明DE⊥AB。
6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF
ASA或AAS证明
1、如图,已知∠A=∠C,AE=CF,DE∥BF,说明AB、CD的关系。
2、如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE交CD于F,且AD=DF,求证:AC=BF
3、如图,已知:BE=CD,∠B=∠C,求证:∠1=∠2。
4、如图,在△ABC中,∠ACB=90,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
5、如图,已知∠1=∠2=∠3,AB=AD.求证:BC=DE
6、在△ABC中,DE⊥AB,DF⊥AC,DA平分∠EDF,说明:(1)∠1=∠2
(2)DE=DF。
7、如图,在△ABC中,∠ACB=90º,D是AC上的一点,且AD=BC,DEAC于D,∠EAB=90º.求证:AB=AE
8、已知:如图,AB⊥BC于B,EF⊥AC于G,DF⊥BC于D, BC=DF.求证:AC=EF
9、如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD
SAS证明
1、如图,AE=AD,AC=AB,∠1=∠2,说明BD=CE。
2、如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED。
3、已知:如图,AB=AD,AC=AE,∠1=∠2,求证:∠B=∠D.
4、如图,△ABC,△BDF为等腰直角三角形。
求证:(1)CF=AD;(2)CE⊥AD
5、已知:如图,△ABC中,AD⊥BC于D,AD=BD,DC=DE,∠C=50°。
求∠EBD的度数。
6、如图⑴,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
⑴试判断AC与CE的位置关系,并说明理由.
⑵如图⑵,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B 重合,此时第⑴问中AC与BE的位置关系还成立吗?(注意字母的变化)
21。
