平衡树模板【C++版本】六

合集下载

平衡树学习总结、LCT练习题

平衡树学习总结、LCT练习题Splay：像BST（⼆叉搜索树）⼀样插⼊查询，可以改变树的形状，可以区间翻转，可以实现动态树，不可持久化。

核⼼代码：1void rotate(int a) // 旋转2{3int b = fa[a], c = fa[b];4int k = son[b][1] == a, w = son[a][!k];56if (no_root(b)) son[c][son[c][1] == b] = a;7 son[a][!k] = b;8 son[b][k] = w;910if (w) fa[w] = b;11 fa[b] = a;12 fa[a] = c;13 pushup(b);14}1516void splay(int x) // 将x移动到splay的根17{18int y = x, z = 0;19 stk[++z] = y;2021while (no_root(y)) stk[++z] = y = fa[y];22while (z) pushdown(stk[z--]);2324while (no_root(x))25 {26 y = fa[x]; z = fa[y];27if (no_root(y)) rotate((son[y][0] == x) ^ (son[z][0] == y) ? x : y);28 rotate(x);29 }30 pushup(x);31 }View CodeTreap：具有堆性质的BST，每个点有两个关键字，⼀个key为原来BST维护的值，⼀个fix值，⼀个节点新建时，给予它⼀个随机的fix值，以fix为关键字构成最⼩根，Treap的期望⾼度为O(log n)。

【模板】普通平衡树（）：1 #include<cstdio>2 #include<cstring>3 #include<iostream>4 #include<algorithm>5using namespace std;67const int N = 2000010, INF = 1e9 + 7;89int root;1011struct Node12{13int l, r, val, size, dat, cnt;14 Node() {}15 Node(int l, int r, int val, int size, int cnt) :l(l), r(r), val(val), size(size), cnt(cnt) {} 16};1718int cnt;19Node tr[N];2021int New(int x)22{23 tr[++cnt] = Node(0, 0, x, 1, 1);24 tr[cnt].dat = rand();25return cnt;26}2728void update(int q)29{30 tr[q].size = tr[tr[q].l].size + tr[q].cnt + tr[tr[q].r].size;31}3233void build()34{35 New(-INF), New(INF);36 root = 1;37 tr[1].r = 2;38 update(root);39}4041void zig(int &q) // 右旋42{43int p = tr[q].l;44 tr[q].l = tr[p].r;45 tr[p].r = q;46 q = p;4748 update(tr[q].r);49 update(q);50}5152void zag(int& q)53{54int p = tr[q].r;55 tr[q].r = tr[p].l;56 tr[p].l = q;57 q = p;5859 update(tr[q].l);60 update(q);61}626364void insert(int& q, int x)65{66if (!q)67 {68 q = New(x);69return;70 }7172if (x == tr[q].val)73 {74 tr[q].cnt++;75 update(q);76return;77 }7879if (x < tr[q].val)80 {81 insert(tr[q].l, x);82if (tr[q].dat < tr[tr[q].l].dat) zig(q);83 }84else85 {86 insert(tr[q].r, x);87if (tr[q].dat < tr[tr[q].r].dat) zag(q);88 }89 update(q);90}9192void Delete(int &q, int x)93{94if (!q) return;95if (x == tr[q].val)96 {97if (tr[q].cnt > 1)98 {99 tr[q].cnt--;100 update(q);101return;102 }103if (tr[q].l || tr[q].r)104 {105if (tr[q].r == 0 || tr[tr[q].l].dat > tr[tr[q].r].dat) zig(q), Delete(tr[q].r, x); 106else zag(q), Delete(tr[q].l, x);107 update(q);108 }109else q = 0;110return;111 }112113if (x < tr[q].val) Delete(tr[q].l, x);114else Delete(tr[q].r, x);115 update(q);116}117118int find_rank(int q, int x)119{120if (!q) return0;121if (x == tr[q].val) return tr[tr[q].l].size + 1;122if (x < tr[q].val) return find_rank(tr[q].l, x);123else return find_rank(tr[q].r, x) + tr[q].cnt + tr[tr[q].l].size;124}125126int find_num(int q, int x)127{128if (!q) return INF;129if (x <= tr[tr[q].l].size) return find_num(tr[q].l, x);130if (x <= tr[tr[q].l].size + tr[q].cnt) return tr[q].val;131return find_num(tr[q].r, x - tr[tr[q].l].size - tr[q].cnt);132}133134int find_befor(int x)135{136int ans = 1, q = root;137while (q)138 {139if (x == tr[q].val)140 {141if (tr[q].l > 0)142 {143 q = tr[q].l;144while (tr[q].r > 0) q = tr[q].r;145 ans = q;146 }147break;148 }149if (tr[q].val<x && tr[q].val>tr[ans].val) ans = q; 150if (x < tr[q].val) q = tr[q].l;151else q = tr[q].r;152 }153return tr[ans].val;154}155156int find_nex(int x)157{158int ans = 2, q = root;159while (q)160 {161if (x == tr[q].val)162 {163if (tr[q].r > 0)164 {165 q = tr[q].r;166while (tr[q].l > 0) q = tr[q].l;167 ans = q;168 }169break;170 }171if (tr[q].val>x && tr[q].val<tr[ans].val) ans = q; 172if (x < tr[q].val) q = tr[q].l;173else q = tr[q].r;174 }175return tr[ans].val;176}177178int main()179{180 build();181182int q;183 scanf("%d", &q);184while (q--)185 {186int op, x;187 scanf("%d%d", &op, &x);188switch (op)189 {190case1:191 {192 insert(root, x);193break;194 }195case2:196 {197 Delete(root, x);198break;199 }200case3:201 {202 printf("%d\n", find_rank(root, x) - 1);203break;204 }205case4:206 {207 printf("%d\n", find_num(root, x + 1));208break;209 }210case5:211 {212 printf("%d\n", find_befor(x));213break;214 }215216case6:217 {218 printf("%d\n", find_nex(x));219break;220 }221 }222 }223 }View Code【模板】⽂艺平衡树（）：1 #include<cstdio>2 #include<cstring>3 #include<vector>4 #include<iostream>5 #include<algorithm>6using namespace std;78const int N = 2000010;910int n;11int w[N];12int lazy[N];13int root;1415 vector<int> ans;1617struct Node18{19int son[2], fa, val, size;20 Node() {}21};2223Node tr[N];2425void update(int q)26{27 tr[q].size = tr[tr[q].son[0]].size + tr[tr[q].son[1]].size + 1; 28}2930int build(int l, int r, int f)31{32int q = (l + r) >> 1;33 tr[q].fa = f;34 tr[q].val = w[q];3536if (l < q) tr[q].son[0] = build(l, q - 1, q);37if (r > q) tr[q].son[1] = build(q + 1, r, q);38 update(q);39return q;40}4142void pushdown(int x)43{44if (!lazy[x]) return;46 lazy[tr[x].son[0]] ^= 1;47 lazy[tr[x].son[1]] ^= 1;48 swap(tr[x].son[0], tr[x].son[1]);49 lazy[x] = 0;50}5152int find1(int x)53{54int q = root;55while (true)56 {57 pushdown(q);58if (tr[q].son[0] && tr[tr[q].son[0]].size >= x) q = tr[q].son[0];59else60 {61int rank = (tr[q].son[0] ? tr[tr[q].son[0]].size : 0) + 1;62if (x <= rank) return q;63 x -= rank;64 q = tr[q].son[1];65 }66 }67}6869void rotate(int x)70{71int y = tr[x].fa, z = tr[y].fa, k = tr[y].son[1] == x, w = tr[x].son[!k]; 7273if (z) tr[z].son[tr[z].son[1] == y] = x;74else root = x;75 tr[y].son[k] = w;76 tr[x].son[!k] = y;7778if (w) tr[w].fa = y;79 tr[x].fa = z;80 tr[y].fa = x;81 update(y);82 update(x);83}8485void splay(int x, int f)86{87while (tr[x].fa != f)88 {89int y = tr[x].fa, z = tr[y].fa;90if (z != f) rotate(((tr[y].son[1] == x) ^ (tr[z].son[1] == y)) ? x : y);91 rotate(x);92 }93}9495void print(int x)96{97 pushdown(x);98if (tr[x].son[0]) print(tr[x].son[0]);99 ans.push_back(tr[x].val);100if (tr[x].son[1]) print(tr[x].son[1]);101}102103int main()104{105int q;106 scanf("%d%d", &n,&q);107108for (int i = 1; i <= n + 2; i++) w[i] = i - 1;109110 root = build(1, n + 2, 0);111112while (q--)114int l, r;115 scanf("%d%d", &l, &r);116 l = find1(l), r = find1(r + 2);117 splay(l, 0), splay(r, l);118 lazy[tr[tr[root].son[1]].son[0]] ^= 1;119 }120121 print(root);122for (int i = 0; i < n; i++) printf("%d ", ans[i + 1]);123 }View Code【模板】⼆逼平衡树（）：1 #include<cstdio>2 #include<cstring>3 #include<iostream>4 #include<algorithm>5using namespace std;67const int N = 2000010, INF = 2147483647;89int n;10int a[N];1112struct Treap13{14struct Node15 {16int l, r, val, size, dat, cnt;17 Node() {}18 Node(int l, int r, int val, int size, int cnt) :l(l), r(r), val(val), size(size), cnt(cnt) {}19 };2021int cnt;22 Node tr[N];2324int New(int x)25 {26 tr[++cnt] = Node(0, 0, x, 1, 1);27 tr[cnt].dat = rand();28return cnt;29 }3031void update(int q)32 {33 tr[q].size = tr[tr[q].l].size + tr[q].cnt + tr[tr[q].r].size;34 }3536void zig(int& q) // 右旋37 {38int p = tr[q].l;39 tr[q].l = tr[p].r;40 tr[p].r = q;41 q = p;4243 update(tr[q].r);44 update(q);45 }4647void zag(int& q)48 {49int p = tr[q].r;50 tr[q].r = tr[p].l;51 tr[p].l = q;52 q = p;5354 update(tr[q].l);55 update(q);56 }5758void insert(int& q, int x)59 {60if (!q)61 {62 q = New(x);63 update(q);64return;65 }6667if (x == tr[q].val)68 {69 tr[q].cnt++;70 update(q);71return;72 }7374if (x < tr[q].val)75 {76 insert(tr[q].l, x);77if (tr[q].dat < tr[tr[q].l].dat) zig(q);78 }79else80 {81 insert(tr[q].r, x);82if (tr[q].dat < tr[tr[q].r].dat) zag(q);83 }84 update(q);85 }8687void Delete(int& q, int x)88 {89if (!q) return;90if (x == tr[q].val)91 {92if (tr[q].cnt > 1)93 {94 tr[q].cnt--;95 update(q);96return;97 }98if (tr[q].l || tr[q].r)99 {100if (tr[q].r == 0 || tr[tr[q].l].dat > tr[tr[q].r].dat) zig(q), Delete(tr[q].r, x); 101else zag(q), Delete(tr[q].l, x);102 update(q);103 }104else q = 0;105return;106 }107else if (x < tr[q].val) Delete(tr[q].l, x);108else Delete(tr[q].r, x);109110if(q) update(q);111 }112113int find_rank(int q, int x)114 {115if (!q) return0;116if (x == tr[q].val) return tr[tr[q].l].size;117else if (x < tr[q].val) return find_rank(tr[q].l, x);118else return find_rank(tr[q].r, x) + tr[q].cnt + tr[tr[q].l].size;119 }120121int find_num(int q, int x)122 {123if (!q) return INF;124if (x <= tr[tr[q].l].size) return find_num(tr[q].l, x);125else if (x <= tr[tr[q].l].size + 1) return tr[q].val;126return find_num(tr[q].r, x - tr[tr[q].l].size - tr[q].cnt);127 }128129int find_pre(int p, int k)130 {131if (!p) return -INF;132if (tr[p].val >= k) return find_pre(tr[p].l, k);133else return max(tr[p].val, find_pre(tr[p].r, k));134 }135136int find_next(int p, int k)137 {138if (!p) return INF;139if (tr[p].val <= k) return find_next(tr[p].r, k);140else return min(tr[p].val, find_next(tr[p].l, k));141 }142};143144Treap treap;145146struct SEG147{148int root[N];149150void build(int q, int l, int r)151 {152for (int i = l; i <= r; i++)153 {154 treap.insert(root[q], a[i]);155 }156157if (l == r) return;158int mid = (l + r) >> 1;159 build(q << 1, l, mid);160 build(q << 1 | 1, mid + 1, r);161 }162163int find_rank(int q, int l, int r, int L, int R, int x)164 {165if (L > r || R < l) return0;166if (L <= l && r <= R) return treap.find_rank(root[q], x);167168int mid = (l + r) >> 1;169return find_rank(q << 1, l, mid, L, R, x) + find_rank(q << 1 | 1, mid + 1, r, L, R, x); 170 }171172int find_num(int L, int R, int k)173 {174int l = 0, r = 1e8;175while (l < r)176 {177int mid = (l + r + 1) >> 1;178if (find_rank(1, 1, n, L, R, mid) < k) l = mid;179else r = mid - 1;180 }181return r;182 }183184void modify(int q, int l, int r, int x, int k)185 {186 treap.Delete(root[q], a[x]);187 treap.insert(root[q], k);188189if (l == r) return;190191int mid = (l + r) >> 1;192if (x <= mid) modify(q << 1, l, mid, x, k);193else modify(q << 1 | 1, mid + 1, r, x, k);194 }195196int find_pre(int q, int l, int r, int L, int R, int x)197 {198if (L > r || l > R) return -INF;199int mid = (l + r) >> 1;200if (L <= l && r <= R) return treap.find_pre(root[q], x);201else return max(find_pre(q << 1, l, mid, L, R, x), find_pre(q << 1 | 1, mid + 1, r, L, R, x)); 202 }203204int find_next(int q, int l, int r, int L, int R, int x)205 {206if (L > r || l > R) return INF;207int mid = (l + r) >> 1;208if (L <= l && r <= R) return treap.find_next(root[q], x);209else return min(find_next(q << 1, l, mid, L, R, x), find_next(q << 1 | 1, mid + 1, r, L, R, x)); 210 }211};212213SEG seg;214215int main()216{217int m;218 scanf("%d%d", &n, &m);219for (int i = 1; i <= n; i++) scanf("%d", &a[i]);220221 seg.build(1, 1, n);222223while (m--)224 {225int op;226 scanf("%d", &op);227if (op == 1)228 {229int l, r, k;230 scanf("%d%d%d", &l, &r, &k);231 printf("%d\n", seg.find_rank(1, 1, n, l, r, k) + 1);232 }233if (op == 2)234 {235int l, r, k;236 scanf("%d%d%d", &l, &r, &k);237 printf("%d\n", seg.find_num(l, r, k));238 }239if (op == 3)240 {241int pos, k;242 scanf("%d%d", &pos, &k);243 seg.modify(1, 1, n, pos, k);244 a[pos] = k;245 }246if (op == 4)247 {248int l, r, k;249 scanf("%d%d%d", &l, &r, &k);250 printf("%d\n", seg.find_pre(1, 1, n, l, r, k));251 }252if (op == 5)253 {254int l, r, k;255 scanf("%d%d%d", &l, &r, &k);256 printf("%d\n", seg.find_next(1, 1, n, l, r, k));257 }258 }259 }View Code这题⽬就离谱【BZOJ1251】序列终结者（）：类似于线段树⼀样传翻转标记与相加标记1 #include<cstdio>2 #include<cstring>3 #include<iostream>4 #include<algorithm>5using namespace std;67const int N = 200010;89int n, m;10int root, cnt;11int num[N];12int fa[N], son[N][2];13int size1[N], v[N], mx[N];14int add[N], rev[N];1516void pushup(int q)17{18 size1[q] = size1[son[q][0]] + size1[son[q][1]] + 1;19 mx[q] = max(v[q], max(mx[son[q][0]], mx[son[q][1]]));20}2122void pushdown(int q)23{24if (rev[q])25 {26 swap(son[q][0], son[q][1]);27 rev[son[q][0]] ^= 1;28 rev[son[q][1]] ^= 1;29 rev[q] = 0;30 }3132if (add[q])33 {34if (son[q][0]) add[son[q][0]] += add[q], v[son[q][0]] += add[q], mx[son[q][0]] += add[q]; 35if (son[q][1]) add[son[q][1]] += add[q], v[son[q][1]] += add[q], mx[son[q][1]] += add[q];36 add[q] = 0;37 }38}3940int build(int l, int r, int pa)41{42if (l > r) return0;43int q = ++cnt;44int mid = (l + r) >> 1;4546 fa[q] = pa;47 v[q] = mx[q] = num[mid];50 pushup(q);51return q;52}5354int find(int x)55{56int q = root;57while (q)58 {59 pushdown(q);60if (x <= size1[son[q][0]]) q = son[q][0];61else62 {63 x -= size1[son[q][0]] + 1;64if (!x) return q;65 q = son[q][1];66 }67 }68return0;69}7071void rotate(int x)72{73int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k];7475 pushdown(x);76 pushdown(y);7778if (z) son[z][son[z][1] == y] = x;79 son[y][k] = w;80 son[x][!k] = y;8182if (w) fa[w] = y;83 fa[y] = x;84 fa[x] = z;8586 pushup(x);87 pushup(y);88}8990void splay(int x, int pa)91{92while (fa[x] != pa)93 {94int y = fa[x], z = fa[y];95if (z != pa) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y);96 rotate(x);97 }98if (!pa) root = x;99}100101void split(int l, int r)102{103 l = find(l), r = find(r + 2);104 splay(l, 0), splay(r, l);105}106107int main()108{109 scanf("%d%d", &n, &m);110111 mx[0] = num[1] = num[n + 2] = -2e9;112 root = build(1, n + 2, 0);113114while (m--)115 {118 split(l, r);119if (k == 1)120 {121 scanf("%d", &s);122 add[son[son[root][1]][0]] += s;123 v[son[son[root][1]][0]] += s;124 mx[son[son[root][1]][0]] += s;125 }126else if (k == 2) rev[son[son[root][1]][0]] ^= 1;127else if (k == 3) printf("%d\n", mx[son[son[root][1]][0]]);128 }129 }View Code【BZOJ3262】陌上花开（）：三维偏序模板，树状数组套平衡树，以b为关键字建树状数组，每个树状数组节点以c为关键字建平衡树，以a 为关键字从⼩到⼤枚举进⾏插⼊操作（a⼀样⼤的要同时插⼊），在树状数组中插⼊b，每次插⼊再在当前节点的平衡树中插⼊c。

【精品】二叉查找树、平衡树和B-树共44页

谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
33、如果惧怕前面跌宕的山岩，生命就永远只能是死水一潭。 34、当你眼泪忍不住要流出来的时候，睁大眼睛，千万别眨眼!你会看到世界由清晰变模糊的全过程，心会在你泪水落下的那一刻变得清澈明晰。盐。注定要融化的，也许是用眼泪的方式。
35、不要以为自己成功一次就可以了，也不要以为过去的光荣可以被永远肯定。
【品】二叉查找树、平衡树和B-树
31、别人笑我太疯癫，我笑他人看不穿。(名言网) 32、我不想听失意者的哭泣，抱怨者的牢骚，这是羊群中的瘟疫，我不能被它传染。我要尽量避免绝望，辛勤耕耘，忍受苦楚。我一试再试，争取每天的成功，避免以失败收常在别人停滞不前时，我继续拼搏。

平衡二叉树（AVLtree）

平衡⼆叉树（AVLtree）⼆叉查找树在极端情况下会演变成⼀棵只有⼀侧⼦孩⼦的树，例如每个⾮叶⼦只有左孩⼦或者右孩⼦，这时候在查找的时候就需要遍历这棵树来找到⽬标值，它的快速搜索价值就体现不出来了，如果这棵搜索树在构建的时候，能够平衡左右⼦树的⾝⾼差，使得左右⼦树⾝⾼差不超过1，那它的搜索效率就是O(lgn)，平衡⼆叉树就是这样的树，它有以下特点：1、左右⼦树的⾼度差不超过12、左右⼦树都是平衡⼆叉树，空节点也视其为⼀棵平衡⼆叉树以上有点递归定义问题的意思，平衡⼆叉树的关键特性是其任何⼀个节点为根的左右⼦树⾼度差不能超过1，因为有这个特性限制，所以在创建平衡⼆叉树的时候如果发现这个平衡被打破了，需要对树进⾏旋转操作，以恢复其平衡的性质，具体的旋转有以下⼏种情况：1、LL类型旋转(单向向右)：这种情况下是某个节点的左孩⼦的左⼦树导致该节点失衡，需要对该节点进⾏向右旋转，如下图：如上图，值为3的节点，当它只有⼀个左孩⼦2时，此时左右孩⼦的⾼度差是1，当再插⼊1时，它的左右孩⼦的⾼度差变成了2，需要对其进⾏右旋：LL_Rotate(node): leftNode=node.left;//待旋转节点的左孩⼦ leftRightNode=leftNode;//待旋转节点的左孩⼦的右孩⼦ leftNode.right=node;//更新左孩⼦节点，将⾃⼰作为作为左孩⼦的右节点，即上图中3变成了2的右孩⼦ node.left=leftRightNode;//更新⾃⼰的左孩⼦， node.height=max(node.left.height,node.right.height)+1;//更新⾼度 leftNode.height=max(leftNode.left.height,leftNode.right.height)+1;//跟新新的根节点⾼度,需要先更新node节点... return leftNode;//返回左孩⼦替代⾃⼰的位置，⽐如上图中，2替代了3的位置2、RR类型旋转(单向向左)：这种情况下是某个节点的右孩⼦的右⼦树导致该节点失衡，需要对该节点进⾏向左旋转，如下图：如上图，因为3的插⼊，根节点1的平衡因⼦变成2，需要对1进⾏左旋，⽅向与LL完全相反：RR_Rotate(node): rightNode=node.right;//获取右孩⼦ rightLeftNode=rightNode.left;//获取右孩⼦的左孩⼦ rightNode.left=node;//更新右孩⼦ node.right=rightLeftNode; node.height=max(node.left.height,node.right.height)+1; rightNode.height=max(rightNode.left.height,right.right.height)+1; return rightNode;//返回3、LR类型旋转(先左后右)：这种情况下是某个节点的左孩⼦的右⼦树导致该节点失衡，需要对该节点的左孩⼦进⾏左旋，然后再对其进⾏右旋，如下图：如上图，节点值为8的节点的左孩⼦，因为6的插⼊，导致8节点失衡，需要先对左孩⼦4进⾏左旋，由6替代4的位置，再对8进⾏右旋，由6替代8：Left_Right_Rotate(node): node.left=LL_Rotate(node.left);//对左孩⼦左旋 return RR_Rotate(node);//对⾃⼰进⾏右旋4、RL类型旋转(先右后左)：这种情况下是某个节点的右孩⼦的左⼦树导致该节点失衡，需要对该节点的右孩⼦进⾏右旋，然后再对其进⾏左旋，如下图：如上图，4的平衡因⼦因为其右孩⼦7新增了⼀个左孩⼦节点6⽽打破，需要对节点7先右旋，再对4进⾏左旋，同LR完全相反，伪代码如下：Right_Left_Rotate(node): node.right=RR_Rotate(node.right);//对右孩⼦进⾏右旋 return LL_Rotate(node);//对⾃⾝进⾏左旋节点的⾼度的获取：Get_Height(node): if node==null: return 0; leftHeight=Get_Height(node.left); rightHeight=Get_Height(node.right); return max(leftHeight,rightHeight)+1;平衡因⼦的获取，某个节点的平衡因⼦是由左右⼦树的⾼度差决定的：Get_Factor(node): return Get_Height(node.left)-Get_Height(node.right);节点的平衡调整，涉及到左旋、右旋、左右旋转、右左旋转：balance(node): if node==null return null; //左⼦树导致不平衡 if getFactor(node)==2 : //左孩⼦的左⼦树导致不平衡 if getFactor(node.left)==1: node=LL_Rotate(node) else: //左孩⼦的右⼦树导致不平衡 node=Left_Right_Rotate(node); //右⼦树导致不平衡 else if getFactor(node)==-2: 右⼦树的右孩⼦导致不平衡 if getFactor(node.right)==-1: node=RR_Rotate(node); else //右孩⼦的左⼦树导致不平衡 node=Right_Left_Rotate(node); //返回旋转后的节点 return node;树的插⼊操作：insert_val(node,val): if node==null: return new Node(val); //这⾥是⼀个递归创建过程 if val<node.val: node.left=insert_val(node.left,val); node.left.parent=node; else node.right=insert_val(node.right,val); node.right.parent=node; //返回调整后的节点 return balance(node);树的删除操作,删除操作有点复杂，需要找到那个替代⾃⼰的节点，其⽅法就是寻找删除节点的左⼦树的最⼤值；如果待删除节点没有左⼦树，则需要寻找右⼦树的最⼩值，如果待删除的节点是叶⼦节点，则直接删除即可：delete_node(node,val): if node==null: return;//没有找到，直接返回 if val < node.val: delete_node(node.left,val); else if val > node.val: delete_node(node.right,val); else: //寻找到了⽬标节点 //⽬标节点是叶⼦节点 if node.left==null && node.right==null: parent=node.parent; //待删除的节点是根节点 if parent==null: root=null; else if parent.left==node: parent.left=null; else: //删除节点 parent.right=null; else if node.left!=null: left=node.left maxNode=left while left!=null: maxNode=right; left=left.right; node.val=maxNode.val delete_node(node.left,node.val); else: //与上⾯node.left!=null中的left相反，将left修改为right balance(node);//调节树的平衡以上AVL树的构建分析完毕，其中关键点为节点的平衡操作，创建和删除节点时使⽤到了递归操作，算是⼀个设计技巧，如下为完整的⽰例代码：package avl;import java.util.ArrayList;import java.util.List;/*** AVL 树的定义*/public class AVLTree {//根节点Node root=null;/*** 插⼊新值* @param val* @return*/public AVLTree insertVal(int val){if(root==null){root=new Node(val);}else{insertVal(root,val);}return this;* 节点的插⼊* @param node* @param val* @return*/private Node insertVal(Node node,int val){if(node==null){node=new Node(val);return node;}if(val<node.val){Node left=insertVal(node.left,val);node.left=left;left.parent=node;}else{Node right=insertVal(node.right,val);node.right=right;right.parent=node;}//调整节点node=balance(node);return node;}/*** 删除节点* @param val*/public void deleteVal(int val){deleteVal(root,val);}private void deleteVal(Node node,int val){//没有找到，直接返回if(node==null){return;}else if(val<node.val){deleteVal(node.left,val);balance(node);}else if(val>node.val){deleteVal(node.right,val);balance(node);}else{//叶⼦节点，直接删除if(node.left==null && node.right==null){Node parent=node.parent;if(parent==null){root=null;}if(parent.left==node){parent.left=null;}else{parent.right=null;}}else{//如果左⼦树不为空，寻找其最⼤的后继节点if(node.left!=null){Node left=node.left;Node maxNode=left;//注意这⾥是怎么找最⼤的后继节点的while(left!=null){maxNode=left;left=left.right;}node.val=maxNode.val;deleteVal(node.left,maxNode.val);balance(node);}else{Node right=node.right;Node maxNode=right;while(right!=null){maxNode=right;right=right.left;}node.val=maxNode.val;deleteVal(node.right,maxNode.val);balance(node);}}}* 平衡节点的操作动作* @param node* @return*/private Node balance(Node node){if(node==null){return null;}if(getFactor(node)==2){if(getFactor(node.left)==1){node= LL_Rotate(node);}else{node= LR_Rotate(node);}}else if(getFactor(node)==-2){if(getFactor(node.right)==-1){node= RR_Rotate(node);}else{node= RL_Rotate(node);}}return node;}/*** 获取节点的⾼度* @param node* @return*/private int getHeight(Node node){if(node==null){return0;}int left=getHeight(node.left);int right=getHeight(node.right);int max=Math.max(left,right);return max+1;}/*** 获取节点的平衡因⼦* @param node* @return*/private int getFactor(Node node){if(node==null){return0;}return getHeight(node.left)-getHeight(node.right); }/*** 先右后左* @param node* @return*/private Node RL_Rotate(Node node){Node right=LL_Rotate(node.right);node.right=right;right.parent=node;return RR_Rotate(node);}/*** 先左后右* @param node* @return*/private Node LR_Rotate(Node node){Node left=RR_Rotate(node.left);node.left=left;left.parent=node;return LL_Rotate(node);}/*** 单向左旋* @param node* @return*/private Node RR_Rotate(Node node){Node right=node.right,parent=node.parent; Node rightLeft=right.left;right.left=node;node.parent=right;node.right=rightLeft;if(rightLeft!=null){rightLeft.parent=node;}right.parent=parent;if(parent!=null){if(parent.left==node){parent.left=right;}else{parent.right=right;}}else{root=right;}return right;}/*** 单向右旋* @param node* @return*/private Node LL_Rotate(Node node){Node left=node.left,parent=node.parent; Node leftRight=left.right;left.right=node;node.parent=left;node.left=leftRight;if(leftRight!=null){leftRight.parent=node;}left.parent=parent;if(parent!=null){if(parent.left==node){parent.left=left;}else{parent.right=left;}}else{root=left;}return left;}/*** 先序遍历* @param node*/public void preOrder(Node node){if(node!=null){System.out.print(node);preOrder(node.left);preOrder(node.right);}}/*** 中序遍历* @param node*/public void inOrder(Node node){if(node!=null){inOrder(node.left);System.out.print(node);inOrder(node.right);}}/*** 后序遍历* @param node*/public void postOrder(Node node){if(node!=null){postOrder(node.left);postOrder(node.right);System.out.print(node);}}/*** 按层遍历树*/public void printByLevel(){System.out.println("=========================");List<Node> temp=new ArrayList<>();if(root!=null){temp.add(root);}while(temp.size()>0){List<Node> nodes=new ArrayList<>();temp.stream().forEach(obj-> {System.out.print(obj);if(obj.left!=null){nodes.add(obj.left);}if(obj.right!=null){nodes.add(obj.right);}});System.out.println();temp.clear();temp.addAll(nodes);}}public static void main(String[] args) {AVLTree tree=new AVLTree();tree.insertVal(1).insertVal(2).insertVal(3).insertVal(4).insertVal(5).insertVal(7).insertVal(6); tree.printByLevel();tree.deleteVal(6);tree.printByLevel();tree.deleteVal(4);tree.printByLevel();}}class Node{public int val;public Node left,right,parent;public Node(int val){this.val=val;}@Overridepublic String toString() {return val+"";}}View Code。

平衡二叉树

Vocabulary

树 tree 子树 subtree 森林 forest 根 root 叶子 leaf 结点 node 深度 depth 层次 level 双亲 parents 孩子 children 兄弟 brother 祖先 ancestor 子孙 descentdant
性质4

具有n个结点的接近完全二叉树的深度为
证明：假设深度为k，则根据性质2和接近完全二叉树的定义有

性质5

如果对一棵有n个结点的接近完全二叉树(其深度为log2n+1,下取整）的结点按层序编号(从第1层到第log2n+1层，每层从左到右)，则对任一结点i(1≤i≤n)，有 (1)如果i＝1，则结点i是二叉树的根，无双亲；如果i＞1，则其双亲PARENT(i)是结点[ i／2]。 (2)如果2i＞n，则结点i无左孩子(结点i为叶子结点)；否则其左孩子LCHILD(i)是结点2i (3)如果2i+l＞n，则结点i无右孩子；否则其右孩子只RCHILD(i) 是结点2i+1
A B C D
E
F Right subtree
Left subtree
Rotate the tree clockwise by 45
A
N
45
B E K
NCBiblioteka FNNDN
G
NN
H M
NN
I
N
J
NN
L
NN
Element Left Right
Left
Right
Several binary trees
depth of ni ::= length of the unique path K from the root to ni. Depth(root) = 0.

C平衡二叉树（AVL）创建和删除

C平衡⼆叉树（AVL）创建和删除 AVL是最先发明的⾃平衡⼆叉查找树算法。

在AVL中任何节点的两个⼉⼦⼦树的⾼度最⼤差别为⼀，所以它也被称为⾼度平衡树，n个结点的AVL树最⼤深度约1.44log2n。

查找、插⼊和删除在平均和最坏情况下都是O（log n）。

增加和删除可能需要通过⼀次或多次树旋转来重新平衡这个树。

定义⽤LH，EH，RH分别表⽰左⼦树⾼，等⾼，右⼦树⾼，即平衡因⼦1、0、-1#include <stdio.h>#include <stdlib.h>#include <stdbool.h>#define LH 1 // 左⾼#define EH 0 // 等⾼#define RH -1 // 右⾼typedef struct TreeNode{int data;int bf;struct TreeNode *left, *right;}TreeNode; 旋转处理左旋和右旋，记住“左逆右顺”就可以/************************************************* 对以*p为根的⼆叉排序树作右旋处理，处理之后p指向新的树根结点，* A B* / / \* B 旋转后变为 C A* / \ /* C D D* 即旋转处理之前的左⼦树的结点。

************************************************/void r_rotate(TreeNode **p){TreeNode *l = (*p)->left;(*p)->left = l->right;l->right = (*p);*p = l;}/************************************************* 对以*p为根的⼆叉排序树作左旋处理，处理之后p指向新的树根结点，* A B* \ / \* B 旋转后变为 A D* / \ \* C D C* 即旋转处理之前的右⼦树的结点。

数据结构第六章平衡树

6.5平衡二叉树平衡二叉树（balanced binary tree）是对二叉搜索树的一种改进。

二叉搜索树有一个缺点，那就是树的结构事先无法预料，随意性很大，它只与结点的值和插入次序有关，往往得到的是一棵很不“平衡”的二叉树。

二叉搜索树与理想平衡树相差越远，树的高度就越高，其运算时间就越长，在最坏的情况log n)下，就是对单链表进行运算的时间，其时间复杂度由O(2变为O(n)，从而部分或全部地丧失了利用二叉搜索树组织数据的优点。

为了克服二叉搜索树的这个缺点，需要在插入和删除结点时对树的结构进行必要的调整，使二叉搜索树始终处于一种平衡的状态，即始终成为一种平衡二叉树(balanced binary tree)，简称平衡树。

当然它不是理想平衡树，因为那将使调整操作更为复杂，使调整带来的好处得不偿失。

本节将首先讨论平衡树的定义和调整操作，然后讨论B_树的定义以及查找、插入和删除等运算。

6.5.1平衡二叉树的定义平衡二叉树简称平衡树是由阿德尔森一维尔斯基和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的，所以又称为AVL树：若一棵二叉树中每个结点的左、右子树的高度至多相差１，则称此树为平衡树。

我们把二叉树中每个结点的左子树高度减去右子树的高度定义为该结点的平衡因子(balance factor)，因此，平衡树中每个结点的平衡因子只能是1,0或-1。

图7-6(a)是一棵平衡树，图7-6(b)和图7-6(c)分别是一棵非平衡树，每个结点的上方所标数字为该结点的平衡因子。

虽然平衡树的平衡性比理想平衡树要差一些，但理论上已经证明：具有n个结点的平衡树的高度在任何情况下决不会比具有相同结点数的理想平衡树高出45%以上。

因此，在平衡树上进行查找运算虽比理想平衡树要慢一些，但通常比任意生成的二叉搜索树快得多，当然，其时间复杂度的数量级表示仍为(a)平衡(b) 非平衡(c)非平衡图7-6 带平衡因子的二叉树当向一棵平衡树插入一个新结点时，若插入后，某些结点的左、右子树的高度不变，则就不会影响这些结点的平衡因子，因而也不会因为这些造成不平衡；若插入后某些结点的左子树高度增加１（右子树高度增加１的情况与之类似），则就影响了这些结点的平衡因子，具体又分为三种情况：(1)若插入前一部分结点的左子树高度为hL与右子树的高度hR相等，即平衡因子为０，则插入后将使平衡因子变为１，但仍符合平衡的条件，不必对它们加以调整；(2)若插入前一部分结点的hL 小于hR，即平衡因子为-1，则插入后将使平衡因子变为０，平衡更加改善，不必对它们进行调整；(3)若插入前一部分结点的hL 大于hR，即平衡因子为１，则插入后将使平衡因子变为２，破坏了平衡树的限制条件，需对它们加以调整，使整个二叉搜索树恢复为平衡树。

课题_一步一步写平衡二叉树(AVL树)

一步一步写平衡二叉树（AVL树）平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。

1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。

平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。

这个方案很好的解决了二叉查找树退化成链表的问题，把插入、查找、删除的时间复杂度最好情况和最坏情况都维持在O(logN)。

但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

平衡二叉树实现的大部分过程和二叉查找树是一样的（学平衡二叉树之前一定要会二叉查找树），区别就在于插入和删除之后要写一个旋转算法去维持平衡，维持平衡需要借助一个节点高度的属性。

我参考了机械工业出版社的《数据结构与算法分析- C语言描述》写了一个C++版的代码。

这本书的AVLTree讲的很好，不过没有很完整的去描述。

我会一步一步的讲解如何写平衡二叉树，重点是平衡二叉树的核心部分，也就是旋转算法。

第一步：节点信息相对于二叉查找树的节点来说，我们需要用一个属性表示二叉树的高度，目的是维护插入和删除过程中的旋转算法。

代码如下：//AVL树节点信息template<class T>class TreeNode{public:TreeNode():lson(NULL),rson(NULL),freq(1),hgt(0){}T data;//值int hgt;//以此节点为根的树的高度unsigned int freq;//频率TreeNode* lson;//指向左儿子的地址TreeNode* rson;//指向右儿子的地址};第二步：平衡二叉树（AVL）类的声明声明中的旋转函数将在后边的步骤中详解。

平衡二叉树操作的演示

平衡二叉树操作的演示#include<stdio.h>#include<malloc.h>typedef int KeyType; //定义关键字类型typedef struct node //记录类型{KeyType key; //关键字项int bf; //平衡因子struct node *lchild,*rchild; //左右孩子指针}BSTNode;void LeftProcess(BSTNode *&p,int &taller) {//对以指针p所指结点为根的二叉树作左平衡旋转处理，本算法结束时，//指针p指向新的根结点BSTNode *p1,*p2;if(p->bf==0) //原本左右子树等高，现因左子树增高而使树增高{p->bf=1;taller=1;}else if(p->bf==-1) //原本右子树比左子树高，现左右子树等高{p->bf=0;taller=0;}else //原本左子树比右子树高，须作左子树的平衡处理{p1=p->lchild; //p指向*p的左子树根节点if(p1->bf==1) //新结点插入在*p的左孩子的左子树上，要做LL调整{p->lchild=p1->rchild;p1->rchild=p;p->bf=p1->bf=0;p=p1;}else if(p1->bf==-1) //新结点插入在*p的左孩子的右子树上，要做LR调整{p2=p1->rchild;p1->rchild=p2->lchild;p2->lchild=p1;p->lchild=p2->rchild;p2->rchild=p;if(p2->bf==0) //新结点插入在*p2处作为叶子结点的情况p->bf=p1->bf=0;else if(p2->bf==1) //新结点插在*p2的左子树上的情况{p1->bf=0;p->bf=-1;}else //新结点插在*p2的右子树上的情况{p1->bf=1;p->bf=0;}p=p2;p->bf=0; //仍将p指向新的根结点，并置其bf值为0}taller=0;}}void RightProcess(BSTNode *&p,int &taller) {//对以指针p所指结点为根的二叉树作右平衡旋转处理，本算法结束时，//指针p指向新的根结点BSTNode *p1,*p2;if(p->bf==0) //原本左右子树等高，现因右子树增高而使树增高{p->bf=-1;taller=1;}else if(p->bf==1) //原本左子树比右子树高，现左右子树等高{p->bf=0;taller=0;}else //原本右子树比左子树高，须作右子树的平衡处理{p1=p->rchild; //p指向*p的右子树根结点if(p1->bf==-1) //新结点插入在*p的右孩子的左子树上，要做RR调整{p->rchild=p1->lchild;p1->lchild=p;p->bf=p1->bf=0;p=p1;}else if(p1->bf==1) //新结点插入在*p的右孩子的左子树上，要做RL调整{p2=p1->lchild;p1->lchild=p2->rchild;p2->rchild=p1;p->rchild=p2->lchild;p2->lchild=p;if(p2->bf==0) //新结点插在*p2处作为叶子结点的情况p->bf=p1->bf=0;else if(p2->bf==-1) //新结点插在*p2的右子树上的情况{p1->bf=0;p->bf=1;}else //新结点插在*p2的左子树上的情况{p1->bf=-1;p->bf=0;}p=p2;p->bf=0; //仍将p指向新的结点，并置其bf值为0}taller=0;}}int InsertA VL(BSTNode*&b,KeyType e,int &taller){//若在平衡二叉排序树b中不存在和e有相同关键字的结点，则插入一个数据元素为e的新结点，//并返回1，否则返回0。

红黑树（洛谷P3369【模板】普通平衡树）

红⿊树（洛⾕P3369【模板】普通平衡树）(以前学习的红⿊树，在今天写算法⼤作业的时候⽤到了，哈哈，即使研究⽣也要继续学习算法呀）红⿊树的五条性质:1) 节点颜⾊为红⾊或⿊⾊2) 根节点为⿊⾊3) 每⼀个叶⼦节点两个NIL节点也为⿊⾊4) 红⾊节点后继为⿊⾊5) 从根节点到叶⼦节点简单路径⿊⾼相同红⿊树是⼀颗⾃平衡的⼆叉查找树, 查询,插⼊,删除的时间复杂度都为O(logn)红⿊树简直就是⼀棵神奇的数据结构~~~~~~~~,我很想知道他们的灵感从哪⾥来的.据说红⿊树是2-3树的变形, RNtree的插⼊操作类⽐2-3树我还可以理解.但BRtree那个删除操作真的好简洁于奇妙~~向这些科学家致敬!!总结⼀下:(1) 插⼊节点z默认时红⾊, 可能违反的性质:1) z的parent节点颜⾊是红⾊2) 根节点是红⾊插⼊时关键要看叔叔节点(2) 删除节点y,并且⽤x节点代替,可能违反的性质1) 经过x的路径,⿊⾼减12) x的为红⾊,x的parent也是红3) x为根节点,颜⾊为红⾊删除时要看兄弟节点代码的逻辑时根据算法导论的逻辑写出, 并且经过洛⾕P3369习题验证(这是我提交过的最长代码.....1 #include <bits/stdc++.h>2using namespace std;3#define RED 14#define BLACK 05#define RBnode node<T> *67 template <class T>8struct node {9 T key;10int sum; //sum⼦树节点数11bool color;12 node *p, *left, *right;13 node() {14 sum = 0; color = BLACK;15 }16 node(T key, int sum, int color, node *p, node *left, node *right) :17 key(key), sum(sum), color(color), p(p), left(left), right(right) {}18void up() {19 sum = 1 + left->sum + right->sum; // nil节点不更新20 }21 };2223 template <class T>24class RBtree {25private:26 RBnode rt;27 RBnode nil;28public:29 RBtree() {30 nil = new node<T>();31 nil->p = nil->left = nil->right = nil;32 rt = nil;33 }38 cout << "key: " << x->key << " color:" << x->color << " sum: " << x->sum << endl;39 mid_print(x->right);40 }4142void my_print() {43 mid_print(rt);44 }4546void insert(T key) {47 RBnode z = new node<T>(key, 1, RED, nil, nil, nil);48 RBnode y = nil; // y: x的parent;49 RBnode x = rt;50while (x != nil) {51 y = x;52if (z->key <= x->key)53 x = x->left;54else55 x = x->right;56 }57 z->p = y; // 特别的根节点⽗节点是nil58if (y == nil)59 rt = z;60else if (z->key <= y->key)61 y->left = z;62else63 y->right = z;64// sum的改变65while (y != nil) {66 y->up();67 y = y->p;68 }69 insert_fixup(z);70 }7172// 可能违反的性质:73// 1)z的parent节点颜⾊是红⾊74// 2)根节点是红⾊75void insert_fixup(RBnode z) { // 插⼊看叔叔节点76while (z->p->color == RED) {77if (z->p == z->p->p->left) {78 RBnode uncle = z->p->p->right;79if (uncle->color == RED) { // case1 叔叔节点是红⾊; 叔叔和⽗亲加⼀层⿊⾊,祖⽗层变⿊(⿊⾊上移)80 z->p->color = BLACK;81 uncle->color = BLACK;82 z->p->p->color = RED;83 z = z->p->p;84 }85else {86if (z->p->right == z) { // case2 叔叔是⿊⾊, 祖孙三代不在⼀条直线, 调整到case387 z = z->p;88 left_rotate(z);89 }90 z->p->color = BLACK; // case3 调整过后,冲突解决91 z->p->p->color = RED;92 right_rotate(z->p->p);93 }94 }95else {96 RBnode uncle = z->p->p->left;97if (uncle->color == RED) { // case198 z->p->color = BLACK;99 uncle->color = BLACK;100 z->p->p->color = RED;101 z=z->p->p;102 }103else {104if (z->p->left == z) { // case 2105 z = z->p;106 right_rotate(z);107 }108 z->p->color = BLACK; // case 3109 z->p->p->color = RED;110 left_rotate(z->p->p);111 }112 }113 }114 rt->color = BLACK;115 }116117// 旋转的性质: 左旋或右旋后,交换两节点的颜⾊不改变⿊⾼(⾃我总结)118void left_rotate(RBnode x) {122 y->left->p = x;123 y->p = x->p;124if (x->p == nil)125 rt = y;126else if (x->p->left == x)127 x->p->left = y;128else129 x->p->right = y;130 y->left = x;131 x->p = y;132if (x!=nil) x->up(); // 先调整x,再调整y133if (y!=nil) y->up();134 }135136void right_rotate(RBnode x) {137 RBnode y = x->left;138 x->left = y->right;139 y->p = x->p;140if (y->right != nil)141 y->right->p = x;142if (x->p == nil)143 rt = y;144else if (x->p->left == x)145 x->p->left = y;146else147 x->p->right = y;148 y->right = x;149 x->p = y;150if (x!=nil) x->up();151if (x!=nil) y->up();152 }153154 RBnode min_mum(RBnode x) {155while (x->left != nil)156 x = x->left;157return x;158 }159160 RBnode max_mum(RBnode x) {161while (x->right != nil)162 x = x->right;163return x;164 }165166 RBnode low_find(int k) { // 寻找⽐k⼩且最⼤的节点167return _low(k,rt);168 }169170 RBnode _low (int k, RBnode x) {171if (x==nil) return x;172if (k<=x->key) return _low(k,x->left);173else {174 RBnode ans=_low(k,x->right);175if (ans!=nil) return ans;176else return x;177 }178 }179180 RBnode upp_find(T k) { // 寻找⽐k⼤且最⼩的节点181return _upp(k,rt);182 }183184 RBnode _upp (T k, RBnode x) {185if (x==nil) return x;186if (k>=x->key) return _upp(k,x->right);187else {188 RBnode ans=_upp(k,x->left);189if (ans!=nil) return ans;190else return x;191 }192 }193194 RBnode rfind(T key) { // 相等元素的最后⼀个节点195 RBnode x = rt;196while (x != nil) {197if (key<x->key)198 x = x->left;199else if (key>x->key)200 x = x->right;201else202return x;204return x;205 }206207 RBnode find(T key) { // 相等元素第⼀个节点208return my_find(key, rt);209 }210211 RBnode my_find(T key, RBnode x) {212if (x == nil) return nil;213if (key<x->key) return my_find(key, x->left);214if (key == x->key) {215 RBnode ans = my_find(key, x->left);216if (ans == nil) return x;217else return ans;218 }219return my_find(key, x->right);220 }221222 RBnode find_kth(int k) { // 排名第k的元素, 相等的元素具有不同的排名223 RBnode x = rt;224if (rt->sum<k) return nil;225while (k != x->left->sum + 1) {226if (k <= x->left->sum)227 x = x->left;228else {229 k -= x->left->sum + 1;230 x = x->right;231 }232 }233return x;234 }235236int get_rank(RBnode x) { // 寻找节点x的排名237 RBnode t=rt; int k=0;238while (t!=x) {239if (x->key<=t->key)240 t=t->left;241else {242 k+=t->left->sum+1;243 t=t->right;244 }245 }246return k+t->left->sum+1;247 }248249void transplate(RBnode y, RBnode x) { // 以节点x代替y,但不对y的⼦节点经⾏替换250if (y->p == nil)251 rt = x;252else if (y->p->left == y)253 y->p->left = x;254else255 y->p->right = x;256 x->p = y->p;257 }258259void remove(RBnode z) { // y: 要删除的节点 x: 代替的节点260 RBnode y = z;261 RBnode x;262int ycolor = y->color;263if (y->left == nil) {264 x = y->right;265 transplate(y, x);266 }267else if (y->right == nil) {268 x = y->left;269 transplate(y, x);270 }271else {272 y = min_mum(y->right);273 ycolor = y->color;274 x = y->right;275if (y->p == z)276 x->p = y; // x可能是nil节点,因此需要记录其⽗亲277else {278 transplate(y, x);279 y->right = z->right;280 z->right->p = y;281 }282 transplate(z,y);283 y->left = z->left;284 z->left->p = y;285 y->color = z->color; // y代替z,但颜⾊不改变286 y = z; // y指向废弃节点288if (ycolor == BLACK)289 remove_fixup(x);290 RBnode t=x->p; // 最后调整sum291while (t!=nil) {292 t->up();293 t=t->p;294 }295delete y;296 }297298// 可能有冲突:299// 1)经过x的路径,⿊⾼减1300// 2)x的为红⾊,x的parent也是红301// 3)x为根节点,颜⾊为红⾊302void remove_fixup(RBnode x) { // 看兄弟节点 // 减少x多的⼀重⿊⾊303while (x != rt&&x->color == BLACK) {304if (x == x->p->left) {305 RBnode bro = x->p->right;306if (bro->color == RED) { // case1 兄弟节点为红⾊,转化为情况234307 bro->color = BLACK;308 bro->p->color = RED;309 left_rotate(x->p);310 bro = x->p->right;311 }312if (bro->left->color == BLACK&&bro->right->color == BLACK) { // case2 兄弟节点及其⼉⼦节点都为⿊⾊313 bro->color = RED;314 x = x->p;315 }316else {317if (bro->right->color == BLACK) { // case3 兄弟右节点不为红⾊318 bro->color = RED;319 bro->left->color = BLACK;320 right_rotate(bro);321 bro = x->p->right;322 }323 bro->right->color = BLACK; //case4 兄弟右孩⼦节点为红⾊,调整之后结束循环324 bro->color = bro->p->color;325 bro->p->color = BLACK;326 left_rotate(x->p);327 x = rt; // 终⽌递归328 }329 }330else {331 RBnode bro = x->p->left;332if (bro->color == RED) { // case 1333 bro->color = BLACK;334 bro->p->color = RED;335 right_rotate(x->p);336 bro = x->p->left;337 }338if (bro->left->color == BLACK&&bro->right->color == BLACK) { // case 2339 bro->color = RED;340 x = x->p;341 }342else {343if (bro->left->color == BLACK) { // case 3344 bro->color = RED;345 bro->right->color = BLACK;346 left_rotate(bro);347 bro = x->p->left;348 }349 bro->left->color = BLACK; // case 4350 bro->color = bro->p->color;351 bro->p->color = BLACK;352 right_rotate(x->p);353 x = rt;354 }355 }356 }357 x->color = BLACK;358 }359360 RBnode successor(RBnode x) { // 后继节点361if (x->right != nil)362return min_mum(x->right);363 RBnode y = x->p;364while (y != nil && y->right == x) {365 x = y;366 y = y->p;367 }368return y;369 }370372if (x->left != nil)373return max_mum(x->left);374 RBnode y = x->p;375while (y != nil && y->left == x) {376 x = y;377 y = y->p;378 }379return y;380 }381382 };383384int main()385 {386387 RBtree<int> tree;388int n; scanf("%d",&n);389while (n--) {390int op,x; scanf("%d %d",&op,&x);391if (op==1) tree.insert(x);392else if(op==2) {393 node<int>* nd=tree.rfind(x);394 tree.remove(nd);395 }396else if(op==3) {397 node<int>* nd=tree.find(x);398 printf("%d\n",tree.get_rank(nd));399 }400else if (op==4) printf("%d\n",tree.find_kth(x)->key); 401else if (op==5) printf("%d\n",tree.low_find(x)->key); 402else printf("%d\n",tree.upp_find(x)->key); 403 }404return0;405 }。

C++pbds库平衡树（tree）

C++pbds 库平衡树（tree ）头⽂件命名空间定义使⽤这个东西和set ⼀样不⽀持重复元素，所以⼀般⽤double ，或者⾃定义结构体变量或者⽤pair 都是可以的，只要记住千万不要插⼊重复元素就好了。

这个东西在⽐赛中是可以⽤的，所以如果嫌打平衡树太⿇烦就可以直接⽤啦。

#include <ext/pb_ds/assoc_container.hpp>#include <ext/pb_ds/tree_policy.hpp>//或者直接⽤#include <bits/extc++.h>using namespace __gnu_pbds;tree<double, null_type, greater<double>, rb_tree_tag, tree_order_statistics_node_update> T;//这个东西有⼀点点长//第⼀个参数是数据类型//第⼆个要填null_type ，低版本编译器填null_mapped_type//第三个填⽐较函数 std::greater<> or std::less<> or cmp//第四个填树的类型，有rb_tree_tag 红⿊树和splay_tree_tag//第五个是为了⽀持查询第k ⼤和排名的⼀个参数//tree_order_statistics_node_update#include <cstdio>#include <ext/pb_ds/tree_policy.hpp>#include <ext/pb_ds/assoc_container.hpp>using namespace std;using namespace __gnu_pbds;tree<double, null_mapped_type, greater<double>, rb_tree_tag, tree_order_statistics_node_update> T;int main(){//freopen("3369.in", "r", stdin);//freopen("3369.out", "w", stdout);int q, opt, x; scanf("%d", &q);for (int i = 1; i <= q; ++ i){ scanf("%d%d", &opt, &x);if(opt == 1)T.insert(x + i * 1e-6); //插⼊⼀个数if(opt == 2)T.erase(T.lower_bound(x));//删除⼀个数if(opt == 3)printf("%d\n", (int)T.order_of_key(x) + 1);//查询⼀个数的排名if(opt == 4)printf("%d\n", (int)*T.find_by_order(x - 1));//查询第k ⼩的数返回的是⼀个迭代器这⾥k 是从0开始算的，意思是最⼩的数是第0⼩的if(opt == 5)printf("%d\n", (int)round(*(-- T.lower_bound(x))));//查询⼀个数的前驱if(opt == 6)printf("%d\n", (int)round(*T.lower_bound(x + 1)));//查询⼀个数的后继}return 0;}Processing math: 0%。

平衡二叉树的实现c语言

平衡二叉树的实现c语言平衡二叉树（AVL树）是一种自平衡的二叉查找树，其中任何节点的两个子树的高度差最多为1。

下面是一个简单的AVL树的C语言实现：```cinclude <>include <>typedef struct AVLNode {int key;int height;struct AVLNode left, right;} AVLNode;typedef struct {AVLNode root;} AVLTree;int getHeight(AVLNode node) {if (node == NULL)return 0;return node->height;}int getBalance(AVLNode node) {if (node == NULL)return 0;return getHeight(node->left) - getHeight(node->right);}AVLNode rotateRight(AVLNode y) {AVLNode x = y->left;AVLNode T2 = x->right;x->right = y;y->left = T2;y->height = max(getHeight(y->left), getHeight(y->right)) + 1; x->height = max(getHeight(x->left), getHeight(x->right)) + 1; return x; // new root is x}AVLNode rotateLeft(AVLNode x) {AVLNode y = x->right;AVLNode T2 = y->left;y->left = x;x->right = T2;x->height = max(getHeight(x->left), getHeight(x->right)) + 1; y->height = max(getHeight(y->left), getHeight(y->right)) + 1; return y; // new root is y}AVLNode insert(AVLTree tree, int key) {AVLNode root = tree->root;if (root == NULL) { // tree is empty, create a new node as root. tree->root = (AVLNode)malloc(sizeof(AVLNode));root = tree->root;root->key = key;root->height = 1;return root;} else if (key < root->key) { // insert into left subtree.root->left = insert(root->left, key);} else if (key > root->key) { // insert into right subtree.root->right = insert(root->right, key);} else { // duplicate keys not allowed.return root; // don't insert duplicate key.}root->height = 1 + max(getHeight(root->left), getHeight(root->right)); // adjust height of current node.int balance = getBalance(root);if (balance > 1 && key < root->left->key) { // left left case.return rotateRight(root); // rotate right.} else if (balance < -1 && key > root->right->key) { // right right case.return rotateLeft(root); // rotate left.} else if (balance > 1 && key > root->left->key) { // left right case. root->left = rotateLeft(root->left); // rotate left first.return rotateRight(root); // then rotate right.} else if (balance < -1 && key < root->right->key) { // right left case.root->right = rotateRight(root->right); // rotate right first.return rotateLeft(root); // then rotate left.} // keep balance.return root; // already balanced.} ```。

15个结点的平衡二叉树

15个结点的平衡二叉树平衡二叉树是一种数据结构，它在处理大量数据时具有很高的效率。

本文将介绍一个15个节点的平衡二叉树，并详细解释其结构和用途。

平衡二叉树是一种特殊的二叉树，它的左子树和右子树的高度差不超过1。

这种结构可以保证在数据插入和删除时，树的高度保持在一个较低的水平，提高了搜索和插入操作的效率。

平衡二叉树的一个重要应用是在数据库中进行快速的搜索和排序。

现在，让我们来构造一个15个节点的平衡二叉树。

为了保证树的平衡性，我们需要按照一定的规则进行节点的插入。

首先，选择第8个节点作为树的根节点，然后将剩下的14个节点分成两组，分别存放在根节点的左子树和右子树中。

在左子树中，我们选择第4个节点作为根节点，并将剩下的3个节点分成两组，分别存放在左子树的左子树和右子树中。

我们继续重复这个过程，直到树的高度达到平衡。

在右子树中，我们选择第12个节点作为根节点，并将剩下的3个节点分成两组，分别存放在右子树的左子树和右子树中。

同样地，在每个子树中进行递归操作，直到树的高度达到平衡。

经过上述步骤，我们成功构造了一个15个节点的平衡二叉树。

每个节点都具有左子树和右子树，且左子树和右子树的高度差都不超过1。

这种平衡性保证了在搜索和插入操作中的高效性。

平衡二叉树在实际应用中有着广泛的用途。

例如，在数据库系统中，平衡二叉树被用来存储索引，以便快速搜索和排序数据。

由于平衡二叉树的高度较低，搜索和插入操作的时间复杂度都为O(log n)，相比于普通的二叉树而言大大提高了效率。

这对于处理大量数据的系统而言尤为重要。

此外，平衡二叉树还可以作为一种动态数据结构，用于处理动态变化的数据集合。

在这种情况下，树的节点可能会频繁地插入和删除。

平衡二叉树的结构可以保证树的高度始终保持在一个较低的水平，从而保证了高效的操作。

总之，平衡二叉树是一种重要的数据结构，用于处理大量数据时具有高效的搜索和插入操作。

本文介绍了一个15个节点的平衡二叉树的构造过程，并讨论了其在实际应用中的用途。

太空人平衡树的技巧-概述说明以及解释

太空人平衡树的技巧-概述说明以及解释1.引言1.1 概述太空人平衡树是一种旨在解决二叉搜索树不平衡的问题的数据结构。

它通过使用节点的"权重"来调整树的结构，使得左子树和右子树的高度差尽量小，从而提供更快速的搜索和插入操作。

太空人平衡树的技巧是一套操作和策略，用于在实际应用中有效地构建和维护平衡的树结构。

这些技巧包括节点的旋转、子树的重建以及权重调整等操作。

通过旋转操作，太空人平衡树可以根据特定情况将节点进行左旋或右旋，从而重新构建树的结构。

这样，较高的子树可以通过旋转操作被转移到较低的位置，使得左子树和右子树的高度差得以减小。

另外，当进行插入或删除操作时，太空人平衡树会通过重建子树的方式来调整整个树的平衡。

这意味着，在插入或删除节点时，可能需要将一部分子树重新构建，以保持整个树的平衡状态。

权重调整是太空人平衡树中的一个重要操作，在插入或删除节点后，树的权重可能会发生变化。

通过适时地增加或减少节点的权重，太空人平衡树可以保持树的整体平衡，避免发生不平衡的情况。

总而言之，太空人平衡树的技巧是一种有效解决二叉搜索树不平衡问题的方法。

通过合理地运用节点旋转、子树重建以及权重调整等操作和策略，可以构建出一个高效、平衡的数据结构，提供更快速的搜索和插入操作。

在接下来的文章中，我们将详细介绍太空人平衡树的基本原理以及实际操作技巧。

1.2文章结构本文包括引言、正文和结论等3个子章节。

引言部分概述了太空人平衡树的技巧，并介绍了本文的目的。

正文部分分为两个部分，即基本原理和技巧讲解。

基本原理部分解释了太空人平衡树的基本原理，包括其数据结构和算法等方面的内容。

技巧讲解部分则介绍了太空人平衡树的实际操作技巧，包括如何构建太空人平衡树和应用中的注意事项等。

结论部分总结了太空人平衡树的技巧和应用，以及展望了其未来的发展方向。

通过本文的阅读，读者可以全面了解太空人平衡树的相关知识和在实际应用中的技巧。

1.3 目的本文的目的是探讨太空人平衡树的技巧及其应用。

平衡树模板【splay的实现】

平衡树模板【splay的实现】【平衡树splay实现】⽆注释代码1 #include<bits/stdc++.h>2using namespace std;3 typedef long long LL;4const int INF=1e9+7,MAXN=1e5+5;5int N;6int key[MAXN],cnt[MAXN],ch[MAXN][2],siz[MAXN],f[MAXN];7int root,sz;8 inline void clear(int x){9 key[x]=cnt[x]=ch[x][0]=ch[x][1]=siz[x]=f[x]=0;10 }11 inline int get(int x){12return x==ch[f[x]][1];13 }14 inline void upd(int x){15if(x){16 siz[x]=cnt[x];17if(ch[x][0]){18 siz[x]+=siz[ch[x][0]];19 }20if(ch[x][1]){21 siz[x]+=siz[ch[x][1]];22 }23 }24 }25 inline void rotate(int x){26int fa=f[x],gf=f[fa],which=get(x);27 ch[fa][which]=ch[x][which^1];28 f[ch[fa][which]]=fa;29 ch[x][which^1]=fa;30 f[fa]=x;31 f[x]=gf;32if(gf){33 ch[gf][ch[gf][1]==fa]=x;34 }35 upd(fa);36 upd(x);37 }38 inline void splay(int x){39for(int fa;(fa=f[x]);rotate(x)){40if(f[fa]){41 rotate(get(x)==get(fa)?fa:x);42 }43 }44 root=x;45 }46 inline void ins(int x){47if(!root){48 sz++;49 clear(sz);50 root=sz;51 cnt[sz]=siz[sz]=1;52 key[sz]=x;53return;54 }55int cur=root,fa=0;56while(1){57if(x==key[cur]){58 cnt[cur]++;59 upd(cur);60 upd(fa);61 splay(cur);62return;63 }64 fa=cur;65 cur=ch[fa][key[fa]<x];66if(!cur){67 clear(++sz);68 f[sz]=fa;69 cnt[sz]=siz[sz]=1;70 ch[fa][key[fa]<x]=sz;71 key[sz]=x;72 upd(fa);73 splay(sz);74return;75 }76 }77 }78 inline int find(int x){79int cur=root,ret=0;80while(1){81if(x<key[cur]){82 cur=ch[cur][0];83 }else{84 ret+=(ch[cur][0]?siz[ch[cur][0]]:0);85if(key[cur]==x){86 splay(cur);87return ret+1;88 }89 ret+=cnt[cur];90 cur=ch[cur][1];91 }92 }93 }94 inline int findx(int x){95int cur=root;96while(1){97if(ch[cur][0]&&x<=siz[ch[cur][0]]){98 cur=ch[cur][0];99 }else{100int tmp=(ch[cur][0]?siz[ch[cur][0]]:0)+cnt[cur]; 101if(x<=tmp){102return key[cur];103 }104 x-=tmp;105 cur=ch[cur][1];106 }107 }108 }109 inline int pre(){110int cur=ch[root][0];111while(ch[cur][1]){112 cur=ch[cur][1];113 }114return cur;115 }116 inline int nxt(){117int cur=ch[root][1];118while(ch[cur][0]){119 cur=ch[cur][0];120 }121return cur;122 }123 inline void del(int x){124 find(x);125if(cnt[root]>1){126 cnt[root]--;127 upd(root);128return;129 }130if(!ch[root][0]&&!ch[root][1]){131 clear(root);132 root=0;133return;134 }135if(!ch[root][0]){136int old=root;137 root=ch[root][1];138 f[root]=0;139 clear(old);140return;141 }142if(!ch[root][1]){143int old=root;144 root=ch[root][0];145 f[root]=0;146 clear(old);147return;148 }149int old=root,p=pre();150 splay(p);151 ch[root][1]=ch[old][1];152 f[ch[old][1]]=root;153 clear(old);154 upd(root);155 }156int main(){157 scanf("%d",&N);158for(int i=1;i<=N;i++){159int ii,jj;160 scanf("%d%d",&ii,&jj);161switch(ii){162case1:{163 ins(jj);164break;165 }166case2:{167 del(jj);168break;169 }170case3:{171 printf("%d\n",find(jj));172break;173 }174case4:{175 printf("%d\n",findx(jj));176break;177 }178case5:{179 ins(jj);180 printf("%d\n",key[pre()]);181 del(jj);182break;183 }184case6:{185 ins(jj);186 printf("%d\n",key[nxt()]);187 del(jj);188break;189 }190 }191 }192return0;193 }View Code变量声明：f[i]表⽰i的⽗结点，ch[i][0]表⽰i的左⼉⼦，ch[i][1]表⽰i的右⼉⼦，key[i]表⽰i的关键字（即结点i代表的那个数字），cnt[i]表⽰i结点的关键字出现的次数（相当于权值），size[i]表⽰包括i的这个⼦树的⼤⼩；sz为整棵树的⼤⼩，root为整棵树的根。

平衡二叉树（C语言）

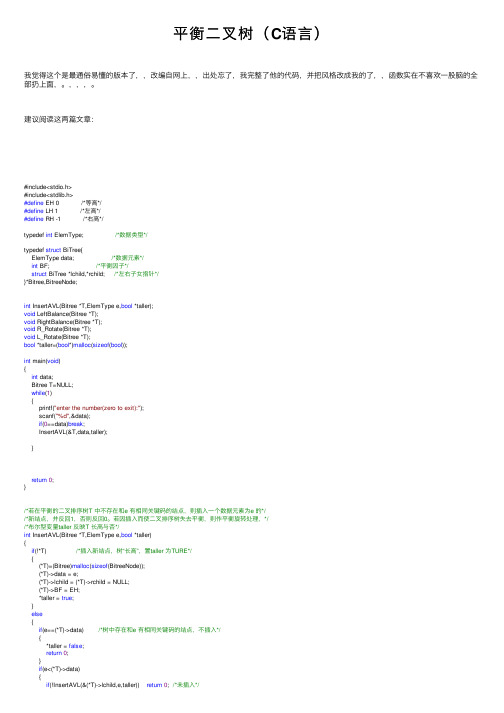
平衡⼆叉树（C语⾔）我觉得这个是最通俗易懂的版本了，，改编⾃⽹上，，出处忘了，我完整了他的代码，并把风格改成我的了，，函数实在不喜欢⼀股脑的全部扔上⾯，。

，，，。

建议阅读这两篇⽂章：#include<stdio.h>#include<stdlib.h>#define EH 0 /*等⾼*/#define LH 1 /*左⾼*/#define RH -1 /*右⾼*/typedef int ElemType; /*数据类型*/typedef struct BiTree{ElemType data; /*数据元素*/int BF; /*平衡因⼦*/struct BiTree *lchild,*rchild; /*左右⼦⼥指针*/}*Bitree,BitreeNode;int InsertAVL(Bitree *T,ElemType e,bool *taller);void LeftBalance(Bitree *T);void RightBalance(Bitree *T);void R_Rotate(Bitree *T);void L_Rotate(Bitree *T);bool *taller=(bool*)malloc(sizeof(bool));int main(void){int data;Bitree T=NULL;while(1){printf("enter the number(zero to exit):");scanf("%d",&data);if(0==data)break;InsertAVL(&T,data,taller);}return0;}/*若在平衡的⼆叉排序树T 中不存在和e 有相同关键码的结点，则插⼊⼀个数据元素为e 的*//*新结点，并反回1，否则反回0。

若因插⼊⽽使⼆叉排序树失去平衡，则作平衡旋转处理，*//*布尔型变量taller 反映T 长⾼与否*/int InsertAVL(Bitree *T,ElemType e,bool *taller){if(!*T) /*插⼊新结点，树“长⾼”，置taller 为TURE*/{(*T)=(Bitree)malloc(sizeof(BitreeNode));(*T)->data = e;(*T)->lchild = (*T)->rchild = NULL;(*T)->BF = EH;*taller = true;}else{if(e==(*T)->data) /*树中存在和e 有相同关键码的结点，不插⼊*/{*taller = false;return0;}if(e<(*T)->data){if(!InsertAVL(&(*T)->lchild,e,taller)) return0; /*未插⼊*/if(*taller)switch((*T)->BF){case EH : /*原本左、右⼦树等⾼，因左⼦树增⾼使树增⾼*/(*T)->BF=LH;*taller=true;break;case LH : /*原本左⼦树⾼，需作左平衡处理*/LeftBalance(T);*taller=false;break;case RH : /*原本右⼦树⾼，使左、右⼦树等⾼*/(*T)->BF=EH;*taller=false;break;}}else{if(!InsertAVL(&(*T)->rchild,e,taller)) return0; /*未插⼊*/if(*taller)switch((*T)->BF){case EH : /*原本左、右⼦树等⾼，因右⼦树增⾼使树增⾼*/(*T)->BF=RH;*taller=true;break;case LH : /*原本左⼦树⾼，使左、右⼦树等⾼*/(*T)->BF=EH;*taller=false;break;case RH : /*原本右⼦树⾼，需作右平衡处理*/RightBalance(T);*taller=false;break;}}}return1;}/*对以*p 指向的结点为根的⼦树，作左平衡旋转处理，处理之后，*p 指向的结点为⼦树的新根*/ void LeftBalance(Bitree *T){Bitree L=(*T)->lchild,Lr; /*L 指向*T左⼦树根结点*/switch(L->BF) /*检查L 平衡度，并作相应处理*/{case LH: /*新结点插在*p 左⼦树的左⼦树上，需作单右旋转处理*/(*T)->BF=L->BF=EH;R_Rotate(T);break;case EH: /*原本左、右⼦树等⾼，因左⼦树增⾼使树增⾼*/(*T)->BF=LH; //这⾥的EH好像没有写的必要*taller=true;break;case RH: /*新结点插在*T 左孩⼦的右⼦树上，需作先左后右双旋处理*/Lr=L->rchild; /*Lr 指向*p 左孩⼦的右⼦树根结点*/switch(Lr->BF) /*修正*T 及其左⼦树的平衡因⼦*/{case LH:(*T)->BF = RH;L->BF = EH;break;case EH:(*T)->BF = L->BF= EH;break;case RH:(*T)->BF = EH;L->BF = LH;break;}Lr->BF = EH;L_Rotate(&L); /*对*T 的左⼦树作左旋转处理*/R_Rotate(T); /*对*T 作右旋转处理*/}}//这⾥和leftbalance⼀个道理，试着⾃⼰写⼀下void RightBalance(Bitree *T){Bitree Lr= (*T)->rchild,L;switch(Lr->BF){case EH:*taller = true;(*T)->BF = RH;break;case RH:(*T)->BF=Lr->BF=EH;L_Rotate(T);break;case LH:L = Lr->lchild;switch(L->BF){case EH:(*T)->BF=Lr->BF= EH;break;case RH:Lr->BF= EH;(*T)->BF = LH;break;case LH:(*T)->BF = LH;Lr->BF = EH;break;}L->BF = EH;R_Rotate(&Lr);L_Rotate(T);}}/*对以*T 指向的结点为根的⼦树，作右单旋转处理，处理之后，*T 指向的结点为⼦树的新根*/ void R_Rotate(Bitree *T){Bitree L=(*T)->lchild; /*L 指向*T 左⼦树根结点*/(*T)->lchild=L->rchild; /*L 的右⼦树挂接*T 的左⼦树*/L->rchild=*T; *T=L; /* *L 指向新的根结点*/}/*对以*p 指向的结点为根的⼦树，作左单旋转处理，处理之后，*p 指向的结点为⼦树的新根*/ void L_Rotate(Bitree *T){Bitree Lr=(*T)->rchild; /*Lr 指向*T 右⼦树根结点*/(*T)->rchild=Lr->lchild; /*L 的左⼦树挂接*p 的右⼦树*/Lr->lchild=*T;*T=Lr; /* *L 指向新的根结点*/}。

平衡二叉树（AVL树）

平衡⼆叉树（AVL树）平衡⼆叉树(AVL树)平衡⼆叉树简介：平衡树(Balance Tree，BT) 指的是，任意节点的⼦树的⾼度差都⼩于等于1。

常见的符合平衡树的有，B树（多路平衡搜索树）、AVL树（⼆叉平衡搜索树）等。

具有以下特点:它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1, 并且左右两个⼦树都是-棵平衡⼆叉树。

平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。

可以保证查询效率⾼。

举例看下下⾯AVL树的特点吧：左右两个⼦树的⾼度差的绝对值不超过1第三棵树的左⼦树⾼度是3，右⼦树⾼度是1,3-1=2,所以第三个不是AVL树AVL树左旋AVL树左旋图解要求: 给你⼀个数列，创建出对应的平衡⼆叉树.数列 {4,3,6,5,7,8}AVL树左旋步骤：1. 创建⼀个新的节点，值为当前节点的值2. 把新节点的的左⼦树设置为原节点的左⼦树：4-->指向33. 把新节点的右⼦树设置为当前节点的右⼦树的左⼦树4. 把当前节点的值：4 换成当前右⼦节点的值：65. 把当前节点的右⼦树设为右⼦树的右⼦树6. 把当前节点的左⼦树设为新的节点：6-->指向4AVL树的⾼度计算核⼼：⾸先要把⼀棵树的⾼度以及左⼦树和右⼦树的⾼度计算出来Node类中添加这三个⽅法：1/**2 * 返回以当前节点为根节点的树的⾼度3 *4 * @return返回树的⾼度5*/6public int heightTree() {7// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

+1是因为树本⾝还要站⼀层8return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;9 }1011/**12 * 返回左⼦树的⾼度13 *14 * @return左⼦树⾼度15*/16public int leftHeight() {17if (left == null) {18return 0;19 }20return left.heightTree();21 }2223/**24 * 返回右⼦树的⾼度25 *26 * @return右⼦树⾼度27*/28public int rightHeight() {29if (right == null) {30return 0;31 }32return right.heightTree();33 }View CodeAVLTree类：直接⽤上个⼆叉排序树的树代码即可！1class AVLTree {2private Node root;34public Node getRoot() {5return root;6 }78/**9 * 查找要删除的节点10 *11 * @param value12 * @return13*/14public Node delSearch(int value) {15if (root == null) {16return null;17 } else {18return root.delSearch(value);19 }20 }2122/**23 * 查找到要删除节点的⽗节点24 *25 * @param value26 * @return27*/28public Node delSearchParent(int value) {29if (root == null) {30return null;31 } else {32return root.delSearchParent(value);33 }34 }3536/**38 *39 * @param node40 * @return返回删除节点的值41*/42public int delRightTreeMin(Node node) {43// 作⼀个辅助节点44 Node target = node;45// 循环往左⼦树进⾏查找，就会找到最⼩值46while (target.left != null) {47 target = target.left;48 }49// 删除最⼩值50 delNode(target.value);51// 返回最⼩值52return target.value;53 }5455/**56 * 删除节点57 *58 * @param value59*/60public void delNode(int value) {61if (root == null) {62return;63 } else {64// 1、找到要删除的节点65 Node targetNode = delSearch(value);66// 没有找到67if (targetNode == null) {68return;69 }70// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)71if (root.left == null && root.right == null) {72 root = null;73return;74 }7576// 2、找到要删除节点的⽗节点77 Node parentNode = delSearchParent(value);78// 表⽰要删除的节点是⼀个叶⼦节点79if (targetNode.left == null && targetNode.right == null) {80// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点81if (parentNode.left != null && parentNode.left.value == value) {82// 将这个叶⼦节点置为空83 parentNode.left = null;84 } else if (parentNode.right != null && parentNode.right.value == value) {85 parentNode.right = null;86 }87 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点 88// 找到最⼩值89int minVal = delRightTreeMin(targetNode.right);90// 重置91 targetNode.value = minVal;92 } else {// 删除只有⼀颗⼦树的节点93if (targetNode.left != null) {// 如果要删除的节点有左⼦节点94if (parentNode != null) {95// 待删除节点是⽗节点的左⼦节点96if (parentNode.left.value == value) {97 parentNode.left = targetNode.left;98 } else {// 待删除节点是⽗节点的右⼦节点99 parentNode.right = targetNode.left;100 }101 } else {102 root = targetNode.left;103 }104 } else {// 如果要删除的节点有右⼦节点105if (parentNode != null) {106// 待删除节点是⽗节点的左⼦节点107if (parentNode.left.value == value) {108 parentNode.left = targetNode.right;109 } else {// 待删除节点是⽗节点的右⼦节点110 parentNode.right = targetNode.right;111 }112 } else {113 root = targetNode.right;114 }115 }116 }117 }118 }119120/**121 * 添加节点的⽅法122 *123 * @param node124*/125public void addNode(Node node) {126// root节点为空，就让root成为根节点127if (root == null) {128 root = node;129 } else {// root节点不为空,就继续向树中添加节点130 root.addNode(node);131 }132 }133134/**135 * 进⾏中序遍历136*/137public void infixOrder() {138if (root != null) {139 root.infixOrder();140 } else {141 System.out.println("⼆叉树为空，⽆法进⾏排序！");142 }143 }144 }View Code测试树的⾼度：public static void main(String[] args) {int[] arr = {4, 3, 6, 5, 7, 8};// 创建AVL树对象AVLTree avlTree = new AVLTree();for (int i = 0; i < arr.length; i++) {// 添加节点avlTree.addNode(new Node(arr[i]));}// 中序遍历System.out.println("======================中序遍历======================");System.out.println("======================没有平衡处理前======================");System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());}附上总体代码实现：1package Demo11_平衡⼆叉树_AVL树;23/**4 * @author zhangzhixi5 * @date 2021/3/12 22:586*/7public class AVLTreeDemo {8public static void main(String[] args) {9int[] arr = {4, 3, 6, 5, 7, 8};1011// 创建AVL树对象12 AVLTree avlTree = new AVLTree();1314for (int i = 0; i < arr.length; i++) {15// 添加节点16 avlTree.addNode(new Node(arr[i]));17 }1819// 中序遍历20 System.out.println("======================中序遍历======================");21 avlTree.infixOrder();22 System.out.println("======================没有平衡处理前======================");23 System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());24 System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());25 System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());26 }27 }2829class AVLTree {30private Node root;3132public Node getRoot() {33return root;34 }3536/**37 * 查找要删除的节点38 *39 * @param value40 * @return41*/42public Node delSearch(int value) {43if (root == null) {44return null;45 } else {46return root.delSearch(value);47 }48 }4950/**51 * 查找到要删除节点的⽗节点52 *53 * @param value54 * @return55*/56public Node delSearchParent(int value) {57if (root == null) {58return null;59 } else {60return root.delSearchParent(value);61 }62 }6364/**65 * 找到最⼩值并删除66 *67 * @param node68 * @return返回删除节点的值69*/70public int delRightTreeMin(Node node) {71// 作⼀个辅助节点72 Node target = node;73// 循环往左⼦树进⾏查找，就会找到最⼩值74while (target.left != null) {75 target = target.left;76 }77// 删除最⼩值78 delNode(target.value);79// 返回最⼩值80return target.value;81 }8283/**84 * 删除节点85 *86 * @param value87*/88public void delNode(int value) {89if (root == null) {90return;91 } else {92// 1、找到要删除的节点93 Node targetNode = delSearch(value);94// 没有找到95if (targetNode == null) {96return;97 }98// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)99if (root.left == null && root.right == null) {100 root = null;101return;102 }103104// 2、找到要删除节点的⽗节点105 Node parentNode = delSearchParent(value);106// 表⽰要删除的节点是⼀个叶⼦节点107if (targetNode.left == null && targetNode.right == null) {108// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点109if (parentNode.left != null && parentNode.left.value == value) {110// 将这个叶⼦节点置为空111 parentNode.left = null;112 } else if (parentNode.right != null && parentNode.right.value == value) {113 parentNode.right = null;114 }115 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点116// 找到最⼩值117int minVal = delRightTreeMin(targetNode.right);118// 重置119 targetNode.value = minVal;120 } else {// 删除只有⼀颗⼦树的节点121if (targetNode.left != null) {// 如果要删除的节点有左⼦节点122if (parentNode != null) {123// 待删除节点是⽗节点的左⼦节点124if (parentNode.left.value == value) {125 parentNode.left = targetNode.left;126 } else {// 待删除节点是⽗节点的右⼦节点127 parentNode.right = targetNode.left;128 }129 } else {130 root = targetNode.left;131 }132 } else {// 如果要删除的节点有右⼦节点133if (parentNode != null) {134// 待删除节点是⽗节点的左⼦节点135if (parentNode.left.value == value) {136 parentNode.left = targetNode.right;137 } else {// 待删除节点是⽗节点的右⼦节点138 parentNode.right = targetNode.right;139 }140 } else {141 root = targetNode.right;142 }143 }144 }145 }146 }147148/**149 * 添加节点的⽅法150 *151 * @param node152*/153public void addNode(Node node) {154// root节点为空，就让root成为根节点155if (root == null) {156 root = node;157 } else {// root节点不为空,就继续向树中添加节点158 root.addNode(node);159 }160 }161162/**163 * 进⾏中序遍历164*/165public void infixOrder() {166if (root != null) {167 root.infixOrder();168 } else {169 System.out.println("⼆叉树为空，⽆法进⾏排序！");170 }171 }172 }173174class Node {175int value;176 Node left;177 Node right;178179public Node(int value) {180this.value = value;181 }182183 @Override184public String toString() {185return "Node{" +186 "value=" + value +187 '}';188 }189190/**191 * 返回以当前节点为根节点的树的⾼度192 *193 * @return返回树的⾼度194*/195public int heightTree() {196// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

平衡树初阶——AVL平衡二叉查找树+三大平衡树（Treap+Splay+SBT）模板【超详解】

平衡树初阶——AVL平衡⼆叉查找树+三⼤平衡树（Treap+Splay+SBT）模板【超详解】平衡树初阶——AVL平衡⼆叉查找树⼀、什么是⼆叉树1. 什么是树。

计算机科学⾥⾯的树本质是⼀个树状图。

树⾸先是⼀个有向⽆环图，由根节点指向⼦结点。

但是不严格的说，我们也研究⽆向树。

所谓⽆向树就是将有向树的所有边看成⽆向边形成的树状图。

树是⼀种递归的数据结构，所以我们研究树也是按照递归的⽅式去研究的。

2.什么是⼆叉树。

我们给出⼆叉树的递归定义如下：（1）空树是⼀个⼆叉树。

（2）单个节点是⼀个⼆叉树。

（3）如果⼀棵树中，以它的左右⼦节点为根形成的⼦树都是⼆叉树，那么这棵树本⾝也是⼆叉树。

⼆、BST1.什么是⼆叉排序树。

⼆叉排序树是⼀种⼆叉树，它满⾜树的中序遍历是有序的。

2.BST（Binary Search Tree）。

⼆叉查找树是⼀种最普通的⼆叉排序树，⼀般称作BST，也称为B-树。

在这棵树中，满⾜在任意⼀个⼦树中，都满⾜左⼦树 < 根节点 < 右⼦树，即该树的中序遍历满⾜从⼩到⼤排序的结果。

3.如何构造⼀个⼆叉排序树？很显然，要想构造⼀个BST，就必须在插⼊节点时，满⾜下⾯的原则：（1）如果节点为空，则直接插⼊到该节点。

（2）如果节点不为空，且要插⼊的值⼩于等于当前节点的值，那么则将该节点插⼊到左⼦树当中。

（3）如果节点不为空，且要插⼊的值⼤于当前节点的值，那么则将该节点插⼊到右⼦树当中。

4.利⽤BST的性质对⼀个数组进⾏剃重。

由于BST有⼆叉排序树的性质，我们可以利⽤这样的性质对⼀个待定数组进⾏剃重。

原理很简单，只需要在插⼊的时候如果已经发现了相等的节点的话，那么则不进⾏插⼊即可。

也就是说，只有该树没有的节点，我们才进⾏相应的插⼊操作。

三、BST的相关操作1.建树（createTree）BST的建⽴是基于⼀个数组进⾏的，本质上是把数组中的数按顺序插⼊的树中。

可以想象，，每插⼊⼀个数，平均时间复杂度为O(logn)，所以建树的平均时间复杂度为O(nlogn)。

详解平衡二叉树

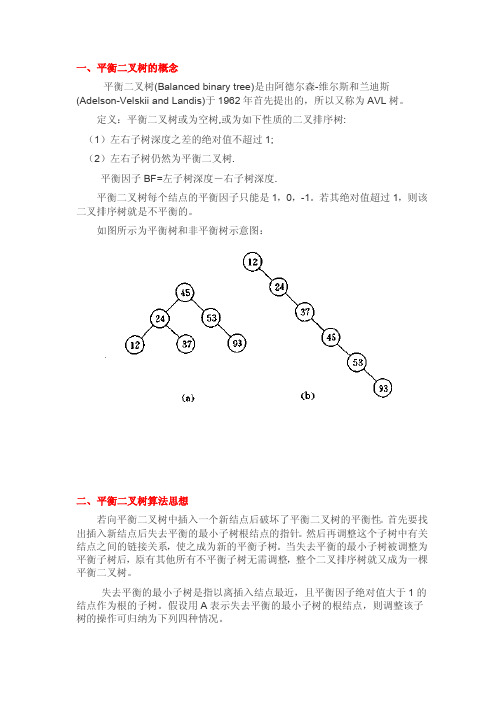
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的，所以又称为AVL树。

定义：平衡二叉树或为空树,或为如下性质的二叉排序树:（1）左右子树深度之差的绝对值不超过1;（2）左右子树仍然为平衡二叉树.平衡因子BF=左子树深度－右子树深度.平衡二叉树每个结点的平衡因子只能是1，0，-1。

若其绝对值超过1，则该二叉排序树就是不平衡的。

如图所示为平衡树和非平衡树示意图：二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。

首先要找出插入新结点后失去平衡的最小子树根结点的指针。

然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。

假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

1）LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。

故需进行一次顺时针旋转操作。

即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。

而原来B的右子树则变成A的左子树。

（2）RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。

故需进行一次逆时针旋转操作。

即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。

而原来C的左子树则变成A的右子树。

（3）LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。

故需进行两次旋转操作（先逆时针，后顺时针）。

即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。

平衡二叉树代码

平衡二叉树代码平衡二叉树是一种特殊的二叉查找树，它的左子树和右子树的高度差不超过1。

平衡二叉树的插入、查找和删除操作的时间复杂度都为O(logn)，比普通二叉查找树更加高效。

以下是平衡二叉树的代码实现：```#include <stdio.h>#include <stdlib.h>typedef struct Node {int data;int height;struct Node *left;struct Node *right;} Node;// 获取节点高度int getHeight(Node *node) {if (node == NULL) {return 0;}return node->height;}// 计算平衡因子int getBalanceFactor(Node *node) {if (node == NULL) {return 0;}return getHeight(node->left) - getHeight(node->right); }// 更新节点高度void updateHeight(Node *node) {node->height = 1 + (getHeight(node->left) > getHeight(node->right) ? getHeight(node->left) : getHeight(node->right));}// 左旋操作Node *leftRotation(Node *node) {Node *temp = node->right;node->right = temp->left;temp->left = node;updateHeight(node);updateHeight(temp);return temp;}// 右旋操作Node *rightRotation(Node *node) {Node *temp = node->left;node->left = temp->right;temp->right = node;updateHeight(node);updateHeight(temp);return temp;}// 插入节点Node *insert(Node *node, int data) {if (node == NULL) {Node *newNode = (Node*)malloc(sizeof(Node)); newNode->data = data;newNode->height = 1;newNode->left = NULL;newNode->right = NULL;return newNode;}if (data < node->data) {node->left = insert(node->left, data);} else {node->right = insert(node->right, data);}// 更新节点高度updateHeight(node);// 计算平衡因子int balanceFactor = getBalanceFactor(node);// 平衡维护if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {// LL情况return rightRotation(node);} else if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {// LR情况node->left = leftRotation(node->left);return rightRotation(node);} else if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {// RR情况return leftRotation(node);} else if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {// RL情况node->right = rightRotation(node->right);return leftRotation(node);}return node;}// 查找节点Node* search(Node *node, int data) {if (node == NULL || node->data == data) {return node;}if (data < node->data) {return search(node->left, data);} else {return search(node->right, data);}}// 删除节点Node* delete(Node *node, int data) {if (node == NULL) {return NULL;}if (data < node->data) {node->left = delete(node->left, data);} else if (data > node->data) {node->right = delete(node->right, data);} else {if (node->left == NULL && node->right == NULL) {node = NULL;} else if (node->left == NULL || node->right == NULL) { node = node->left ? node->left : node->right;} else {Node *temp = node->right;while (temp->left != NULL) {temp = temp->left;}node->data = temp->data;node->right = delete(node->right, temp->data);}}if (node == NULL) {return node;}// 更新节点高度updateHeight(node);// 计算平衡因子int balanceFactor = getBalanceFactor(node);// 平衡维护if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {// LL情况return rightRotation(node);} else if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {// LR情况node->left = leftRotation(node->left);return rightRotation(node);} else if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {// RR情况return leftRotation(node);} else if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {// RL情况node->right = rightRotation(node->right);return leftRotation(node);}return node;}// 中序遍历void inorderTraversal(Node *node) {if (node == NULL) {return;}inorderTraversal(node->left);printf("%d ", node->data);inorderTraversal(node->right);}int main() {Node *root = NULL;int arr[] = {7, 4, 10, 2, 5, 8, 11, 1, 3, 6, 9};int len = sizeof(arr) / sizeof(int);for (int i = 0; i < len; i++) {root = insert(root, arr[i]);}printf("中序遍历结果为：");inorderTraversal(root);printf("\n");int searchVal = 5;Node *searchResult = search(root, searchVal); if (searchResult != NULL) {printf("查找值为%d的节点成功\n", searchVal); } else {printf("查找值为%d的节点失败\n", searchVal); }int deleteVal = 4;root = delete(root, deleteVal);printf("删除值为%d的节点后，中序遍历结果为：", deleteVal); inorderTraversal(root);printf("\n");return 0;}```上述代码实现了平衡二叉树的插入、查找和删除操作，并且在插入和删除节点时进行了平衡维护，保证了平衡二叉树的平衡性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平衡树模板【C++版本】六/////////平衡树//////////////////////////// #define max(x,y) ( (x)>(y)?(x):(y) )#define MAX 2001000#define LEFT 0#define RIGHT 1struct AVL{int data; //数据AVL* child[2]; //左右儿子节点int h; //书高void init(){child[0]=child[1]=NULL;h=1;}};//内存管理================//可以用动态分配内存AVL node[MAX]; //其中node[0]为根节点，空的，int n_end=0; //末尾节点AVL *NewNode(){node[n_end].init();return &node[n_end++];}void ReleaseNode(AVL *p){return;}//内存管理===============int get_height(AVL *rp) //得到子树的高度{if(rp==NULL)return 0;return rp->h;}void rotate(AVL **rp,int dir)//dir=0将左边旋转到右边dir=1反之{//对子树*rp进行旋转AVL *tmp=(*rp)->child[dir];(*rp)->child[dir]=tmp->child[1-dir];(*rp)->h=1+max( get_height( (*rp)->child[0] ),get_height((*rp)->child[1]) );tmp->child[1-dir]=(*rp);tmp->h=1+max( get_height(tmp->child[0]),get_height(tmp->chi ld[1]) );(*rp)=tmp;}void doublerotate(AVL **rp,int dir)//dir=0先对子子树右旋转，再对子树左旋转{rotate( & ( (*rp)->child[dir] ),1-dir);(*rp)->h=1+max( get_height( (*rp)->child[0] ),get_height( (*rp) ->child[1] ) );rotate( rp,dir);}int cmp_child(AVL *rp) //得到相对平衡因子{returnget_height(rp->child[LEFT])<get_height( rp->child[RIGHT]);}void Insert(AVL **rp,int value){if((*rp)==NULL){(*rp)=NewNode();(*rp)->data=value;return;}if((*rp)->data==value)return;int dir=(*rp)->data<value; //得到插入的方向Insert( &( (*rp)->child[dir] ),value);if( get_height( (*rp)->child[dir] )- get_height( (*rp)->child[1-dir] ) >=2){//重新平衡if( cmp_child( (*rp)->child[dir]) ==dir)rotate(rp,dir);elsedoublerotate(rp,dir);}(*rp)->h=1+max( get_height( (*rp)->child[dir] ), get_height( (*rp)->child[1-dir] ) );}bool Delete(AVL **rp,int value){bool ans;int dir;AVL *tmp;if((*rp)==NULL)return false;if((*rp)->data==value){dir=-1;if( (*rp)->child[0]==NULL)dir=0;else if( (*rp)->child[1]==NULL) dir=1;if(dir>=0){tmp=*rp;*rp=(*rp)->child[1- dir]; ReleaseNode(tmp);return true;}else{dir=cmp_child(*rp);rotate(rp,dir);Delete( &(*rp)->child[1-dir],value);}ans=true;}else{dir=(*rp)->data<value; //得到插入的方向ans=Delete( &( (*rp)->child[dir] ),value);}if( get_height( (*rp)->child[1-dir] )- get_height( (*rp)->child[dir] ) >=2){//重新平衡if( cmp_child( (*rp)->child[1-dir]) ==1-dir)rotate(rp,1-dir);elsedoublerotate(rp,1-dir);}(*rp)->h=1+max( get_height( (*rp)->child[dir] ), get_height( (*rp)->child[1-dir] ) );return ans;/////////平衡树///////////////////////////////////debug#include<stdlib.h>void print_child(AVL *rp){if(rp==NULL)printf("NULL");elseprintf("%d",rp->data);}void ShowTheTree(AVL *rp){print_child(rp);if(rp==NULL)return;printf(": h=%d ",rp->h); print_child(rp->child[0]);printf(" ");print_child(rp->child[1]);printf("\n");if(rp->child[0])ShowTheTree(rp->child[0]);if(rp->child[1])ShowTheTree(rp->child[1]);}bool checkthetree(AVL *rp){if(rp==NULL)return true;if(checkthetree(rp->child[0])==false)return false;if(checkthetree(rp->child[1])==false)return false;if( abs(get_height(rp->child[0])-get_height(rp->child[1]) )>=2) return false;return true;}int main(){AVL *pTree=NULL;int i;for( i=0;i<8;i++)Insert(&pTree,i);// for( i=0;i<30;i++)// Insert(&pTree,-1-i);// ShowTheTree(pTree);// Insert(&pTree,11);ShowTheTree(pTree);Delete(&pTree,5);ShowTheTree(pTree);if(checkthetree(pTree)==false)printf("this is not a AVL!\n"); elseprintf("this is a AVL!\n"); return 0;}。