PID and Cascade Controller_ZH
英国欧陆

英国欧陆2116调节器
英国欧陆2116I调节器
英国欧陆2216E/AL/VH/FH/AC/FH/X/X/2X 调节器
英国欧陆2216E/AL/VH/FL/AC/FH/X/X/2X 调节器
英国欧陆2216E/AL调节器
英国欧陆3216/CC/VL/RRXX/R/XXX/S/ENG 调节
英国欧陆3216/CP/VH/LRR调节器
英国欧陆3208/CC 开孔尺寸:45×92 含四个继电器或逻辑输出
英国欧陆3208/CP 带8段程序 其它同3208/CC
英国欧陆3208/CP/VH/DDDR调节器(含485通讯)
英国欧陆4103CA01Z05012 RECORDER
英国欧陆4103CB01Z05022 RECORDER
英国欧陆425A100A240V240V SCR
英国欧陆425A25A120110V POWER CONTROL
英国欧陆425A25A440V110V VOLT REGULATOR
英国欧陆2704VH1XXXXD4XXX CONTROLLER
英国欧陆2704VH321XXTPPVX CONTROLLER
英国欧陆3208LLRR CONTROLLER
英国欧陆3216CCVHLRRXXXGE TEMP CONTROL
英国欧陆3216/CC/VH/LRXX/R/XXX/G/ENG TEMPERATURE CONTROLLER PID
英国欧陆3504CCVH1XX01XXX TEMP CONTROL
英国欧陆3923133303SV0050 RECORDER
Eurotherm 2000系列控制器产品介绍说明书

imagine making theimpossible possible2000Series controllersBuilt on our experience of design and applications knowledge spanning more than 40 years, the Eurotherm®2000 series brings you performance you can rely on and accuracy you can trust.At the same time no other range of controllers makes operation so easy. Menu driven operation provides easy intuitive and consistent access to all the controller functions.Simply imagine process excellence…and with Eurotherm you will achieve it. Our ranges of controllers provide world class control and versatility with clear, user friendly, operator interfaces. Add to this, a strong sales team of qualified engineers who understand your process, an absolute commitment to innovation by continuously re-investing in research and development; we can and do imagine making the impossible possible for our customers.Internal timer– A 5 mode timer suitable for simple time based profiling applications Universal input–9 different thermocouples, PT100, DC linear and a downloadable customcurveFour outputs–up to 4 outputs including 2 modular with many options including DCoutputsCommunication protocols–Modbus RTU, EI-Bisynch, DeviceNet®Three internal alarms–Configurable as High, Low, Deviation and Deviation High or Low alarms Two outputs– 1 relay and 1 logic (can be used as a relay with an external module)Suitable for•Small ovens •Chillers •Sterilisers •Trace heating •Heat sealing •Dwell timer–simple ramp dwell profile applicationsFour internal alarms–configurable as High, Low, Deviation,Deviation High, Deviation Low, Highand Low current alarmsSuitable for•Cold stores •Ovens and furnaces •Plastic extrusion •Packaging machines •Food and brewing applications •Every 2000 Series controller can be tailored to provide thecontrol solution you need. Modular design and easy, on-site configuration matches application requirements andgives you a temperature and process control solution that’sready to run the first time you switch it on.The 2000 Series provides control strategies ranging fromsimple ON/OFF to PID with advanced overshoot protection, providing the best control for the widest range of applications including valve positioning. Within the 2000Series there is also the 2500 Modular Controller and the 2604/2704 Controllers which, with their enhanced functionality and multiloop capability, offer a powerful addition to the range. Please consult Eurotherm sales for more information on these products.requirements Programming –up to 20, 16 segment programs (4 in the 2416) are available with 8 digital event outputs Four internal alarms –configurable as High, Low, Deviation,Deviation High or Low, high and Low Current alarms high and low output,high and low input 2, High and low setpoint and one Rate of change alarmModular –up to 4 outputs of which 3 aremodular with many different optionswithin the different modulesModules –up to 16 different types of moduleare availableCommunication protocols –Modbus RTU, EI-Bisynch, DeviceNet,Profibus DP Suitable for •Single and multi-zone furnaces •Kilns •Environmental chambers •Simple ratio •Humidity •Chemical and pharmaceutical •Applications •Glass furnaces and lehrs •Set p o in t FFOP Flow Meter FTAT Analytical Sensor PID Loo pPV +2400Dosing Pump Setpoint Easy to use controllers for greater flexibilityT im e Te mp e ra t ur e Setpoint Dwell time Switch off Ramp controlDwell Timer FunctionalityTe mp e ra t ur eEnd Type = DwellT im e End Type = Off Holdback atstart of dwellMaster ProgrammerSlave ControllersPDS communications M P gSC mmunic c ations PDS com In 2000 Series controllers it is possible to use the PDS communication link tosend a setpoint from one controller to a network of slave devices - providingthe economical creation of multi-zone temperature control solutions.PDS setpoint retransmissionRatiometric PyrometerThermocouple Output Switchover between two points 4-20mAmocouple Master Output Slave PDS Retransmission with FeedforwardModbus RTU Modbus Master The 2000 Series uses industry standard protocols such as Modbus RTU, DeviceNet or Profibus DPto communicate with supervisory systems andPLCs over EIA232, EIA485 (2 wire) or EIA422 (4wire). This carries the information and overallcontrol into the supervisory system whilemaintaining local access to the local equipmentensuring overall plant integrity in all situations.CommunicationSometimes it is desirable to control a process using two separate inputs toderive the PV (process value). This could be based on a highest wins, lowestwins, some function of the two inputs, or switching between the two inputs atsome pre-determined point in the process.For example, an application could consist of a thermocouple for measuring upto 800°C and a Ratiometric Pyrometer for measuring the range between700°C and 1,400°C.Typically when the temperature is below 740°C the thermocouple providesthe PV and, when between 740°C and 780°C the controller switches gentlyfrom the thermocouple to the Pyrometer which provides the PV up to 1,400°C.Derived inputsUsing Eurotherm setpoint retransmission over PDScommunications it is possible to use two 2400 controllersas a cascade control system with the output of the first (ormaster controller) forming the setpoint of the second (orslave controller).Eurotherm advanced algorithms enable the use of eithersetpoint or PV feedforward to limit the slave setpoint - forexample ±10% of the master setpoint or PV.Cascade control iTools configuration software enables you to store and clone controller configurations, as well as commission your process control system. This facility significantly reduces installation and commissioning time while commissioning timeEurotherm flexible 2000 Series offers a truly versatilesolution to all your requirements.Selection guide Features Panel size (DIN)IP Rating Single LoopDisplay TypeSupply Voltage Input Type PV Accuracy Control Types SP ProgrammerAnalogue IP/OP Digital IP/OPDigital Comms Alarm TypesPC Configuration21161/321/16IP6521002216e 2208e 1/16DIN rail 1/8IP6522002204e 1/4TC, RTD, mV, mA, V 1 x 4 dig LED TC, RTD, mV, mA, Volts 2 x 4 dig LED <0.25%On/Off. PID none In: 1 Out: 0In: 1 Out: 2none none none none none none none none none none none none none List based <0.25%On/Off. PID, VP none none none In: 1 Out: 1In: 3 Out: 4Modbus, DeviceNet List based 24V dc/ac 85-264V ac 85-264V ac 2132Dual input control Hi, Lo, Dev,Sensor break,Event, Heater failHi, Lo, Dev, Sensor break, Event, Heater fail Hi, Lo, Dev, Sensor break, 2416240824041/161/81/4IP652400TC, RTD, mV,mA, Volts 2 x 4 dig LED <0.2%On/Off. PID, VP 20 x 16 segments In: 2 Out: 3In: 11 Out: 11List based 24V dc/ac 85-264V ac Modbus, DeviceNet, Profibus Special FeaturesMaths EquationCombinational LogicTimers/Counters/TotalsReal Time Clock© Copyright Eurotherm Limited 2011Invensys, Eurotherm, the Eurotherm logo, Chessell, EurothermSuite, M ini8, Eycon, Eyris, EPower, nanodac and Wonderware are trademarks ofInvensys plc, its subsidiaries and affiliates. All other brands may be trademarks of their respective owners.All rights are strictly reserved. No part of this document may be reproduced, modified, or transmitted in any form by any means, nor may it be stored in a retrieval system other than for the purpose to act as an aid in operating the equipment to which the document relates, withoutthe prior written permission of Eurotherm limited.Eurotherm Limited pursues a policy of continuous development and product improvement. The specifications in this documentmay therefore be changed without notice. The information in this document is given in good faith, but is intended for guidance only.Eurotherm Limited will accept no responsibility for any losses arising from errors in this document.Bermuda Bolivia Bosnia and Herzegovina Botswana Brazil Brunei Darussalam Bulgaria Cambodia Cameroon Canada Central African Republic Chad Chile Colombia Congo Costa Rica Côte d’Ivoire Croatia Cyprus Czech Republic Denmark Djibouti Ecuador Egypt El Salvador Eritrea Estonia Ethiopia Fiji Finland Georgia Ghana Greece Greenland Guinea Hungary Iceland Indonesia Iraq Israel Jamaica Japan Jordan Kazakhstan Kenya Kuwait Kyrgyzstan Laos MozambiqueMyanmarNamibiaNicaraguaNigerNigeriaNorwayOmanPakistanPalestinian TerritoryPapua New GuineaParaguayPeruPhilippinesPolandQatarRomaniaRussiaRwandaSaudi Arabia Senegal Serbia and Montenegro Sierra LeoneSingapore Slovakia Slovenia Somalia South AfricaSri Lanka SudanSwaziland SyriaTajikistanTanzania Thailand The GambiaTunisia TurkeyTurkmenistanUganda Ukraine United Arab Emirates Uruguay UzbekistanVenezuelaVietnam Yemen Zambia ZimbabweAUSTRALIA Melbourne Invensys Process Systems Australia Pty. Ltd.T (+61 0) 8562 9800F (+61 0) 8562 9801E info.*************************AUSTRIA Vienna Eurotherm GmbH T (+43 1) 7987601F (+43 1) 7987605E info.*************************BELGIUM & LUXEMBOURG Moha Eurotherm S.A/N.V.T (+32) 85 274080F (+32) 85 274081E info.*************************BRAZIL Campinas-SP Eurotherm Ltda.T (+5519) 3707 5333F (+5519) 3707 5345E ******************************CHINA Eurotherm China T (+86 21) 61451188F (+86 21) 61452602E info.*************************Beijing Office T (+86 10) 5909 5700F (+86 10) 5909 5709/5909 5710E info.*************************FRANCE Lyon Eurotherm Automation SA T (+33 478) 664500F (+33 478) 352490E ******************************GERMANY Limburg Eurotherm Deutschland GmbH T (+49 6431) 2980F (+49 6431) 298119E info.*************************INDIA Mumbai Invensys India Pvt. Ltd.T (+91 22) 67579800F (+91 22) 67579999E info.*************************IRELAND Dublin Eurotherm Ireland Limited T (+353 1) 4691800F (+353 1) 4691300E info.*************************ITALY Como Eurotherm S.r.l T (+39 031) 975111F (+39 031) 977512E info.*************************KOREA Seoul Invensys Operations Management Korea T (+82 2) 2090 0900F (+82 2) 2090 0800E info.*************************NETHERLANDS Alphen a/d Rijn Eurotherm B.V.T (+31 172) 411752F (+31 172) 417260E ******************************POLAND Katowice Invensys Eurotherm Sp z o.o.T(+48 32) 7839500F (+48 32) 7843608/7843609E info.*************************SPAIN MadridEurotherm España SA T(+34 91) 6616001F (+34 91) 6619093E info.*************************SWEDEN MalmoEurotherm AB T(+46 40) 384500F (+46 40) 384545E ******************************SWITZERLAND Wollerau Eurotherm Produkte (Schweiz) AG T (+41 44) 7871040F (+41 44) 7871044E info.*************************UNITED KINGDOM Worthing Eurotherm Limited T (+44 1903) 268500F (+44 1903) 265982E info.*************************U.S.A.Ashburn VA Eurotherm Inc.T (+1 703) 724 7300F (+1 703) 724 7301E info.*************************ED63。
pid参数整定方法(PIDparametertuningmethod)

pid参数整定方法(PID parameter tuning method)PID parameter tuning methodIn view of the combined device instrument loop control rate is relatively low, most of the circuit is operated manually, which not only increases the operator's workload, but also have a certain impact on the quality of the products, especially the preparation of a PID parameter tuning method.First, modify the PID parameter must have "SUPPERVISOR" and above permissions, permissions with the keyboard keyHandover permission, the key has been sent to a joint director Chen Sheng hands;Two, open the modified control loop detail screen, turn to the page shown below, modify the PID control backThe three parameters of the path setting are K, T1, T2;Three, the meaning of the PID parameter representsK: proportional gain (amplification), ranging from 0 to 240;T1: integral time, the range is 0 to 1440, the unit is minutes, and the 0 represents no integral action;T2: differential time, the range is 0 to 1440, the unit is minutes, and the 0 represents no differential action.Four, the role of PID parameters(1) the characteristics of proportional adjustment: 1, the adjustment function is quick, the system appears a deviation, the regulator immediately amplifies the deviation K times; and 2, the system has residual.The smaller the K transition process is more stable, but more than the larger difference; the increase of K, residual error will be reduced, but can not completely eliminate the residual error, can only play the role of coarse, but K is too large, the transition process is easy oscillation, K is too large, there may be divergence oscillation.(2) the characteristics of integral regulation: regulation and output change integral input deviation is proportional to the integral and integral function can eliminate the residual error, but reduces the stability of the system, T1 changes from big to small, integral effect from weak to strong, eliminate the residual capacity only from weak to strong, the elimination of bias, the output will stop change.(3) the characteristics of the differential regulation of the output differential regulation is regulated variable rate is proportional to, can improve the quality control in the introduction of differential effect, but the differential effect is too strong, will sometimes open and closed by the control valve, so T2 can not take too much, when T2 increases. Differential effects of capacity lag from weak to strong, has obvious effect, but the effect of no delay.Five. If you want to know how the control loop works, you canenter the detailed picture of the control loop and enter the page shown below:Among them, "CTLACTN" represents the mode of action of the controller, and "REVERSE" means reaction, and "DIRECT" represents the positive function.Six 、 controller selection method(1) the choice of P controller: it is suitable for controlling the system with smaller channel delay, little load change, and allowing the controlled quantity to vary within a certain range;(2) the selection of PI controller: it is suitable for the control system with less delay and little load change, and the controlled quantity is not allowed to be surplus;(3) the choice of PID controller: it is suitable for the control system, such as temperature control system, which has large load change, large capacity delay and high quality control requirements.Seven, PID parameter tuning methodIn engineering applications, empirical test method is adopted.The empirical method is most practical in practice. In setting parameters, the system response must be carefully observed, and the parameters are adjusted according to the response of the system. To observe the response of the system, you can look atthe real-time trend curve in the control loop detail screen, and the decay curve is preferably 4:1, that is, the ratio between the previous peak and the latter peak is 4:1.Experience value: in actual debugging, you can only set an experience value roughly, and then modify it according to the adjustment effect. The P here represents the degree of proportionality, P = 1/K.Parameter rangeControl systemP (1 / K)KT1 / MinT2 / Minlevel20% to 80%1.25 to 5--pressure30% to 70%1.43 to 3.40.4 to 3-flow40% to 100%1 to 2.50.1 to 1-temperature20% to 60%1.7 to 5From 3 to 100.3 to 1In short, in the whole time can not let the system appeardivergent oscillation, such as divergence oscillation, should be immediately cut for the manual, etc. system stability decreases after amplification, increase or decrease the differential integral time time again to switch to automatic control.The smaller the amplification is, the more stable the transition process is, but the larger the residual error is. The larger the amplification is, the easier the oscillation occurs during the transition. The smaller the integration time, the faster the elimination of the residual difference, but the system oscillation will be larger, and the larger the integration time, the slower the system will eliminate the residual error. The differential time is too large, the system oscillation frequency increases, the regulation time increases, the differential is too small, the system regulation is slow.Steps of the method of controller parameter testing:Because the ratio is controlled, so the basic proportion, trying to be good, the transition process has been basically stable, and then add the integral eliminateresidual error finally joined the differential role to further improve the quality control, the basic steps are as follows:(A) for the P controller, the magnification is placed in a smaller position, and the K is gradually increased. The transition process curve of the controlled quantity is observed until the curve is satisfied;(B) the PI controller, the first set of T1=0, according to theproportion of the role of pure tuning amplification to achieve 4:1 attenuation curve; then K reduced (10 ~ 20%), the integral time T1 from large to small gradually added, until the decay process of 4:1;(C) of PID controller, T2 = 0; according to the PI effect of trying setting procedures K, T1 parameters, and then the magnification increases to more than the original large (10 ~ 20%), after T1 also reduced properly to T2 increases gradually, observe the transition curve, until a satisfactory. Through the process of.In a word: when setting parameters, we should carefully observe the system output and the amount of change, and then modify the PID parameters according to the specific conditions. It can be said that as long as process technicians spend more time, most control systems adopt PID regulation to meet the requirements.Eight 、 series pole control loop settingThe setting of the cascade control circuit can be accomplished by two steps, that is, setting the secondary circuit first, then setting the main loop, or adopting a one step method, that is, setting the main and auxiliary circuits simultaneously.(1) when the experience value of the secondary circuit is used as the following value, the general auxiliary circuit only uses proportional control:Secondary variableMagnification factor (K)Degree of proportionality (P)temperature5 to 1.720% to 60%pressure3 to 1.430% to 70%flow2.5 to 1.2540% to 80%level5 to 1.2520% to 80%(2) cascade control loop system is put into operation, and then the parameters of the main controller are adjusted according to the single loop control system parameter tuning method;(3) if there is "resonance" in the tuning process, only the main and auxiliary controller decreases the magnification can be eliminated, if the resonance is too intense, the first switch to manual production, to be stable after re operation, re setting.In conclusion, P is the most basic control function. After adding I, it can control the difference and improve the control accuracy. Adding D can improve the quality of control.Nine, matters needing attention(1) the parameter tuning before calibration of sensors and actuators, ensure the instrument is normal, you can just getDynamic control test, manual state measurement parameters should be stable and reliable.(2) setting the K parameter according to the experience value, turning off the integral adjustment temporarily, and switching to the automatic observation step response,It should be noted that the output of the controller, to determine what is not the negative feedback circuit (wiring design and check whether there are loopholes, when new system debugging will encounter this kind of situation, such as: the need to close the opening of the regulator, it is to enlarge the degree);(3) to ensure the stability of the process when settingparameters, it should be cut immediately when the product quality and process parameters are affectedManual control,When the process is stable, the PID parameter is automatically modified.(4) if it is a cascade and proportional control loop, we must first make a loop, a loop setting, we should also pay attention to the firstThe principle of inner ring, outer back and outer ring.(5) when manually cut to the automatic, make sure that the given value is approximately consistent with the measured value, but for a combinationHoneywell DCS does not have this problem; when manually, the given value automatically tracks the measurements.Ten 、 PID parameter setting shorthandTo find the optimal parameter setting, check the order from small to greatFirst proportion, then integral, and finally add differential additionThe oscillation curve is very frequent, put a small magnificationFloating around the curve magnification to a WAN,The curve deviates slowly and the integration time drops The curve fluctuates long and the integral time is longer The curve oscillates with a frequency that falls off first Moment to slow wave, differential time should be lengthenedThe ideal curve has two waves, the front high and the rear 1, and the lower 4A look at two tones, more analysis, the quality of regulation will not be lowEleven typical control loop1 、 single loop control:(1) control valve action mode selection principle:Control valve in accordance with the role of gas distribution, gas off two. The air opening valve is opened with the increase of the signal pressure, and has no letterNo. when the valve in the fully closed state; on the other hand, with the increase of signal pressure, the valve gradually closed, no signal when the valve is fully open state for gas off valve.The selection principle is mainly from the safety of production, from the guarantee of product quality, from the loss of raw materials and power, from the characteristics of the media to consider these aspects.(2) selection of controller action mode:Selection principle: make the whole single loop constitute negative feedback system.Regulations:Control valve: gas open for "+", "gas off" type -";Controller: the positive action is "+", and the reaction is "" -";Object: when the material or energy increases through the control valve, according to the process mechanism analysis, if the controlled quantity increases with "+", then decreases to "-"";Transmitter: generally considered as a positive link.Then the positive and negative selection discriminant of the controller is:(the controller is "+") (the control valve "+") (object "+") = "-"2 、 cascade loop control:In the single loop control system, it has been pointed out that the principle of selecting the positive and negative modes of the controller is to make the whole control system constitute a negative feedback system, and the discriminant of "product is negative" is given. This criterion is also applicable to the choice of the positive and negative modes of the primary and secondary controllers in the cascade control system.(1) main controller action mode selection:(main controller +) (sub object +) (main object =) = (-)So when the main and auxiliary variables change in the same direction, the main controller should be counterproductive, reversal is the role of Party A.Type.(2) acting mode selection of auxiliary controller:(auxiliary controller +) (control valve +) (secondary object =) = (-)(3) cascade control loop is put into operation:The operation of the utility model is to transfer the master and the auxiliary controllers from the manual operation state to the working state through proper stepsState. Operation method of cascade control system, there are two kinds: one is the first deputy after the main ring ring; the other is the first investment after the main ring ring. Operation method is widely used for the first time, put into operation to ensure the switch without disturbance, because the Honeywell DCS with PV automatic tracking function so basically can switch without disturbance, and the operation is relatively simple.3, split control systemThe split control system is the output signal of a controller to control two or more control valves, each of themThe control valve works only within a signal of the entire range of the output signal.That is, multi valve and sub pass.The implementation method mainly uses two kinds: one is through each control valve positioner, two is through the DCS software realization, in the use of DCS control, we usually through the DCS configuration implementation.In process control system, in accordance with the control valve of the gas switch action and gas can be divided into two categories: one is the same as the action to the valve, the control valve input signal increases or decreases, the valve open or open, the other is different to the valve action, as control valve input signal increases or decreases, the valve is always according to a valve closed and another valve openingdirection of action. The choice of the same or opposite direction of the control valve is determined by the need of the process. As detailed below:4, ratio control loopA ratio control circuit is a system that automatically maintains a certain proportion of two or more of the two materialsThe amount of material from the raw material with the amount of change according to a certain ratio, such as gas waste heat boiler and air intake volume is proportional to the combustion of the boiler to achieve the best effect.。
PID controller

PID controller免费的百科全书Jump to: navigation, search跳转到:导航搜索A block diagram of a PID controller一个PID控制器的框图A proportional比例–integral积分–derivative 微分controller (PID controller) is a generic control loop feedback mechanism (controller) widely used in industrial control systems– a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error by adjusting the process control inputs.The PID controller calculation (algorithm) involves three separate constant parameters, and is accordingly sometimes called three-term control: the proportional, the integral and derivative values, denoted P,I, and D.Heuristically, these values can be interpreted in terms of time: P depends on the present error, I on the accumulation of past errors, and D is a prediction of future errors, based on current rate of change.[1] The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, or the power supplied to a heating element.In the absence of knowledge of the underlying process, a PID controller has historically been considered to be the best controller.[2] By tuning the three parameters in the PID controller algorithm, the controller can provide control action designed for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoots the setpoint and the degree of system oscillation. Note that the use of the PID algorithm for control does not guarantee optimal control of the system or system stability.Some applications may require using only one or two actions to provide the appropriate system control. This is achieved by setting the other parameters to zero. A PID controller will be called a PI, PD, P or Icontroller in the absence of the respective control actions. PI controllers are fairly common, since derivative action is sensitive to measurement noise, whereas the absence of an integral term may prevent the system from reaching its target value due to the control action.Contents[hide]∙ 1 Control loop basics∙ 2 PID controller theoryo 2.1 Proportional term2.1.1 Droopo 2.2 Integral termo 2.3 Derivative term∙ 3 Loop tuningo 3.1 Stabilityo 3.2 Optimum behavioro 3.3 Overview of methodso 3.4 Manual tuningo 3.5 Ziegler–Nichols methodo 3.6 PID tuning software∙ 4 Modifications to the PID algorithm∙ 5 History∙ 6 Limitations of PID controlo 6.1 Linearityo 6.2 Noise in derivative∙7 Improvementso7.1 Feed-forwardo7.2 Other improvements∙8 Cascade control∙9 Physical implementation of PID control∙10 Alternative nomenclature and PID formso10.1 Ideal versus standard PID formo10.2 Basing derivative action on PVo10.3 Basing proportional action on PVo10.4 Laplace form of the PID controllero10.5 PID Pole Zero Cancellationo10.6 Series/interacting formo10.7 Discrete implementationo10.8 Pseudocode∙11 PI controller∙12 See also∙13 References∙14 External linkso14.1 PID tutorialso14.2 Special topics and PID control applications [edit] Control loop basics基本控制回路Further information更多信息: Control system控制系统A familiar example of a control loop is the action taken when adjusting hot and cold faucets (valves) to maintain the water at a desired temperature. This typically involves the mixing of two process streams, the hot and cold water. The person touches the water to sense or measure its temperature. Based on this feedback they perform a control action to adjust the hot and cold water valves until the process temperature stabilizes at the desired value.The sensed water temperature is the process variable or process value (PV). The desired temperature is called the setpoint (SP). The input to the process (the water valve position) is called the manipulated variable (MV). The difference between the temperature measurement and the set point is the error (e) and quantifies whether the water is too hot or too cold and by how much.After measuring the temperature (PV), and then calculating the error, the controller decides when to change the tap position (MV) and by how much. When the controller first turns the valve on, it may turn the hot valve only slightly if warm water is desired, or it may open the valve all the way if very hot water is desired. This is an example of a simple proportional control. In the event that hot water does not arrive quickly, the controller may try to speed-up the process by opening up the hot water valve more-and-more as time goes by. This is an example of an integral control.Making a change that is too large when the error is small is equivalent to a high gain controller and will lead to overshoot. If the controller were to repeatedly make changes that were too large and repeatedly overshoot the target, the output would oscillate around the setpoint in either a constant, growing, or decaying sinusoid. If the oscillations increase with time then the system is unstable, whereas if they decrease the system is stable. If the oscillations remain at a constant magnitude the system is marginally stable.In the interest of achieving a gradual convergence at the desired temperature (SP), the controller may wish to damp the anticipated future oscillations. So in order to compensate for this effect, the controller may elect to temper its adjustments. This can be thought of as a derivative control method.If a controller starts from a stable state at zero error (PV = SP), then further changes by the controller will be in response to changes in other measured or unmeasured inputs to the process that impact on the process, and hence on the PV. Variables that impact on the process other than the MV are known as disturbances. Generally controllers are used to reject disturbances and/or implement setpoint changes. Changes in feedwater temperature constitute a disturbance to the faucet temperature control process.In theory, a controller can be used to control any process which has a measurable output (PV), a known ideal value for that output (SP) and an input to the process (MV) that will affect the relevant PV. Controllers are used in industry to regulate temperature, pressure, flow rate, chemical composition, speed and practically every other variable for which a measurement exists.[edit] PID controller theoryThis section describes the parallel or non-interacting form of the PID controller. For other forms please see the section Alternative nomenclature and PID forms.The PID control scheme is named after its three correcting terms, whose sum constitutes the manipulated variable (MV). The proportional, integral, and derivative terms are summed to calculate the output of the PIDcontroller. Defining as the controller output, the final form of the PID algorithm is:where: Proportional gain, a tuning parameter: Integral gain, a tuning parameter: Derivative gain, a tuning parameter: Error: Time or instantaneous time (the present) [edit] Proportional termPlot of PV vs time, for three values of Kp (Kiand Kdheld constant)The proportional term makes a change to the output that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant K p, called the proportional gain.The proportional term is given by:A high proportional gain results in a large change in the output for a given change in the error. If the proportional gain is too high, the system can become unstable (see the section on loop tuning). In contrast, a small gain results in a small output response to a large input error, and a less responsive or less sensitive controller. If the proportional gain is too low, the control action may be too small when responding to system disturbances. Tuning theory and industrial practice indicate that the proportional term should contribute the bulk of the output change.[citation needed][edit] DroopA pure proportional controller will not always settle at its target value, but may retain a steady-state error. Specifically, drift in the absence of control, such as cooling of a furnace towards room temperature, biases a pure proportional controller. If the drift is downwards, as in cooling, then the bias will be below the set point, hence the term "droop".Droop is proportional to the process gain and inversely proportional to proportional gain. Specifically the steady-state error is given by:Droop is an inherent defect of purely proportional control. Droop may be mitigated by adding a compensating bias term (setting the setpoint above the true desired value), or corrected by adding an integral term.[edit] Integral termPlot of PV vs time, for three values of Ki (Kpand Kdheld constant)The contribution from the integral term is proportional to both the magnitude of the error and the duration of the error. The integral in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously. Theaccumulated error is then multiplied by the integral gain () and added to the controller output.The integral term is given by:The integral term accelerates the movement of the process towards setpoint and eliminates the residual steady-state error that occurs with a pure proportional controller. However, since the integral term responds to accumulated errors from the past, it can cause the present value to overshoot the setpoint value (see the section on loop tuning).[edit] Derivative termPlot of PV vs time, for three values of Kd (Kpand Kiheld constant)The derivative of the process error is calculated by determining the slope of the error over time and multiplying this rate of change by thederivative gain . The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, . The derivative term is given by:The derivative term slows the rate of change of the controller output. Derivative control is used to reduce the magnitude of the overshoot produced by the integral component and improve the combinedcontroller-process stability. However, the derivative term slows thetransient response of the controller. Also, differentiation of a signal amplifies noise and thus this term in the controller is highly sensitive to noise in the error term, and can cause a process to become unstable if the noise and the derivative gain are sufficiently large. Hence an approximation to a differentiator with a limited bandwidth is more commonly used. Such a circuit is known as a phase-lead compensator.[edit] Loop tuningTuning a control loop is the adjustment of its control parameters (proportional band/gain, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response. Stability (bounded oscillation) is a basic requirement, but beyond that, different systems have different behavior, different applications have different requirements, and requirements may conflict with one another.PID tuning is a difficult problem, even though there are only three parameters and in principle is simple to describe, because it must satisfy complex criteria within the limitations of PID control. There are accordingly various methods for loop tuning, and more sophisticated techniques are the subject of patents; this section describes some traditional manual methods for loop tuning.Designing and tuning a PID controller appears to be conceptually intuitive, but can be hard in practice, if multiple (and often conflicting) objectives such as short transient and high stability are to be achieved. Usually, initial designs need to be adjusted repeatedly through computer simulations until the closed-loop system performs or compromises as desired.Some processes have a degree of non-linearity and so parameters that work well at full-load conditions don't work when the process is starting up from no-load; this can be corrected by gain scheduling (using different parameters in different operating regions). PID controllers often provide acceptable control using default tunings, but performance can generally be improved by careful tuning, and performance may be unacceptable with poor tuning.[edit] StabilityIf the PID controller parameters (the gains of the proportional, integral and derivative terms) are chosen incorrectly, the controlled process input can be unstable, i.e., its output diverges, with or withoutoscillation, and is limited only by saturation or mechanical breakage. Instability is caused by excess gain, particularly in the presence of significant lag.Generally, stabilization of response is required and the process must not oscillate for any combination of process conditions and setpoints, though sometimes marginal stability (bounded oscillation) is acceptable or desired.[citation needed][edit] Optimum behaviorThe optimum behavior on a process change or setpoint change varies depending on the application.Two basic requirements are regulation (disturbance rejection – staying at a given setpoint) and command tracking(implementing setpoint changes) –these refer to how well the controlled variable tracks the desired value. Specific criteria for command tracking include rise time and settling time. Some processes must not allow an overshoot of the process variable beyond the setpoint if, for example, this would be unsafe. Other processes must minimize the energy expended in reaching a new setpoint.[edit] Overview of methodsThere are several methods for tuning a PID loop. The most effective methods generally involve the development of some form of process model, then choosing P, I, and D based on the dynamic model parameters. Manual tuning methods can be relatively inefficient, particularly if the loops have response times on the order of minutes or longer.The choice of method will depend largely on whether or not the loop can be taken "offline" for tuning, and the response time of the system. If the system can be taken offline, the best tuning method often involves subjecting the system to a step change in input, measuring the output as a function of time, and using this response to determine the control parameters.Choosing a Tuning MethodMethod Advantages DisadvantagesManual Tuning No math required. Online method. Requires experienced personnel.Ziegler–Nichols Proven Method. Online method. Process upset, sometrial-and-error, veryaggressive tuning.Software Tools Consistent tuning. Online oroffline method. May includevalve and sensor analysis. Allow simulation before downloading. Can support Non-Steady State(NSS) Tuning.Some cost and training involved.Cohen-Coon Good process models. Some math. Offline method. Only good forfirst-order processes.[edit ] Manual tuningIf the system must remain online, one tuning method is to first set and values to zero. Increase the until the output of the loop oscillates, then the should be set to approximately half of that valuefor a "quarter amplitude decay" type response. Then increaseuntil any offset is corrected in sufficient time for the process. However, too muchwill cause instability. Finally, increase , if required, until the loop is acceptably quick to reach its reference after a load disturbance. However, too much will cause excessive response and overshoot. A fast PID loop tuning usually overshoots slightly to reach the setpoint more quickly; however, some systems cannot accept overshoot, in which case an over-damped closed-loop system is required, which will require a setting significantly less than half that of the setting causing oscillation. Effects of increasing a parameter independently Parameter Rise time OvershootSettlingtime Steady-state error Stability [3] Decrease Increase Smallchange DecreaseDegrade Decrease [4] Increase Increase Decrease DegradesignificantlyMinor decrease Minor decrease Minor decrease No effect intheory Improve if small[edit ] Ziegler –Nichols methodFor more details on this topic, see Ziegler –Nichols method .Another heuristic tuning method is formally known asthe Ziegler –Nichols method , introducedbyJohnG.ZieglerandNathaniel B. Nichols in the 1940s. As in the method above, the and gains are first set to zero. TheP gain is increased until it reaches the ultimate gain,, at which the output of the loop starts to oscillate.and the oscillation periodare used to set the gains as shown:Ziegler –Nichols methodControl Type P- - PI-PID These gains apply to the ideal, parallel form of the PID controller. When applied to the standard PID form, the integral and derivative time parameters and are only dependent on the oscillation period . Please see the section "Alternative nomenclature and PID forms ".[edit ] PID tuning softwareMost modern industrial facilities no longer tune loops using the manual calculation methods shown above. Instead, PID tuning and loopoptimization software are used to ensure consistent results. These software packages will gather the data, develop process models, andsuggest optimal tuning. Some software packages can even develop tuning by gathering data from reference changes.Mathematical PID loop tuning induces an impulse in the system, and then uses the controlled system's frequency response to design the PID loop values. In loops with response times of several minutes, mathematical loop tuning is recommended, because trial and error can take days just to find a stable set of loop values. Optimal values are harder to find. Some digital loop controllers offer a self-tuning feature in which very small setpoint changes are sent to the process, allowing the controller itself to calculate optimal tuning values.Other formulas are available to tune the loop according to different performance criteria. Many patented formulas are now embedded within PID tuning software and hardware modules.Advances in automated PID Loop Tuning software also deliver algorithms for tuning PID Loops in a dynamic or Non-Steady State (NSS) scenario. The software will model the dynamics of a process, through a disturbance, and calculate PID control parameters in response.[edit] Modifications to the PID algorithmThe basic PID algorithm presents some challenges in control applications that have been addressed by minor modifications to the PID form.Integral windupFor more details on this topic, see Integral windup.One common problem resulting from the ideal PID implementations is integral windup, where a large change in setpoint occurs (say a positive change) and the integral term accumulates an error larger than the maximal value for the regulation variable (windup), thus the system overshoots and continues to increase as this accumulated error is unwound. This problem can be addressed by:∙Initializing the controller integral to a desired value∙Increasing the setpoint in a suitable ramp∙Disabling the integral function until the PV has entered the controllable region∙Limiting the time period over which the integral error is calculated ∙Preventing the integral term from accumulating above or below pre-determined boundsOvershooting from known disturbancesFor example, a PID loop is used to control the temperature of an electric resistance furnace, the system has stabilized. Now the door is opened and something cold is put into the furnace thetemperature drops below the setpoint. The integral function of the controller tends to compensate this error by introducing another error in the positive direction. This overshoot can be avoided by freezing of the integral function after the opening of the door for the time the control loop typically needs to reheat the furnace. Replacing the integral function by a model based partOften the time-response of the system is approximately known. Then it is an advantage to simulate this time-response with a model and to calculate some unknown parameter from the actual response of the system. If for instance the system is an electrical furnace the response of the difference between furnace temperature and ambient temperature to changes of the electrical power will be similar to that of a simple RC low-pass filter multiplied by an unknownproportional coefficient. The actual electrical power supplied to the furnace is delayed by a low-pass filter to simulate the response of the temperature of the furnace and then the actual temperature minus the ambient temperature is divided by this low-pass filtered electrical power. Then, the result is stabilized by anotherlow-pass filter leading to an estimation of the proportionalcoefficient. With this estimation, it is possible to calculate the required electrical power by dividing the set-point of thetemperature minus the ambient temperature by this coefficient. The result can then be used instead of the integral function. This also achieves a control error of zero in the steady-state, but avoids integral windup and can give a significantly improved controlaction compared to an optimized PID controller. This type ofcontroller does work properly in an open loop situation which causes integral windup with an integral function. This is an advantage if, for example, the heating of a furnace has to be reduced for some time because of the failure of a heating element, or if thecontroller is used as an advisory system to a human operator who may not switch it to closed-loop operation. It may also be useful if the controller is inside a branch of a complex control system that may be temporarily inactive.Many PID loops control a mechanical device (for example, a valve). Mechanical maintenance can be a major cost and wear leads to control degradation in the form of either stiction or a deadband in the mechanical response to an input signal. The rate of mechanical wear is mainly a function of how often a device is activated to make a change. Where wearis a significant concern, the PID loop may have an output deadband to reduce the frequency of activation of the output (valve). This is accomplished by modifying the controller to hold its output steady if the change would be small (within the defined deadband range). The calculated output must leave the deadband before the actual output will change.The proportional and derivative terms can produce excessive movement in the output when a system is subjected to an instantaneous step increase in the error, such as a large setpoint change. In the case of the derivative term, this is due to taking the derivative of the error, which is very large in the case of an instantaneous step change. As a result, some PID algorithms incorporate the following modifications:Derivative of the Process VariableIn this case the PID controller measures the derivative of themeasured process variable (PV), rather than the derivative of the error. This quantity is always continuous (i.e., never has a step change as a result of changed setpoint). For this technique to be effective, the derivative of the PV must have the opposite sign of the derivative of the error, in the case of negative feedbackcontrol.Setpoint rampingIn this modification, the setpoint is gradually moved from its old value to a newly specified value using a linear or first orderdifferential ramp function. This avoids the discontinuity present in a simple step change.Setpoint weightingSetpoint weighting uses different multipliers for the errordepending on which element of the controller it is used in. The error in the integral term must be the true control error to avoidsteady-state control errors. This affects the controller'ssetpoint response. These parameters do not affect the response to load disturbances and measurement noise.[edit] HistoryThis section requires expansion.PID theory developed by observing the action of helmsmen.PID controllers date to 1890s governor design.[2][5] PID controllers were subsequently developed in automatic ship steering. One of the earliest examples of a PID-type controller was developed by Elmer Sperry in 1911,[6] while the first published theoretical analysis of a PID controller was by Russian American engineer Nicolas Minorsky, in (Minorsky 1922). Minorsky was designing automatic steering systems for the US Navy, and based his analysis on observations of a helmsman, observing that the helmsman controlled the ship not only based on the current error, but also on past error and current rate of change;[7]this was then made mathematical by Minorsky. His goal was stability, not general control, which significantly simplified the problem. While proportional control provides stability against small disturbances, it was insufficient for dealing with a steady disturbance, notably a stiff gale (due to droop), which required adding the integral term. Finally, the derivative term was added to improve control.Trials were carried out on the USS New Mexico, with the controller controlling the angular velocity (not angle) of the rudder. PI control yielded sustained yaw (angular error) of ±2°, while adding D yielded yaw of ±1/6°, better than most helmsmen could achieve.[8]The Navy ultimately did not adopt the system, due to resistance by personnel. Similar work was carried out and published by several others in the 1930s.[edit] Limitations of PID controlWhile PID controllers are applicable to many control problems, and often perform satisfactorily without any improvements or even tuning, they can perform poorly in some applications, and do not in general provide optimal control. The fundamental difficulty with PID control is that it is a feed back system, with constant parameters, and no direct knowledge of the process, and thus overall performance is reactive and a compromise –while PID control is the best controller with no model of the process,[2] better performance can be obtained by incorporating a model of the process.The most significant improvement is to incorporate feed-forward control with knowledge about the system, and using the PID only to control error. Alternatively, PIDs can be modified in more minor ways, such as by changing the parameters (either gain scheduling in different use cases or adaptively modifying them based on performance), improving measurement (higher sampling rate, precision, and accuracy, and low-pass filtering if necessary), or cascading multiple PID controllers.PID controllers, when used alone, can give poor performance when the PID loop gains must be reduced so that the control system does not overshoot, oscillate or hunt about the control setpoint value. They also have difficulties in the presence of non-linearities, may trade-off regulation versus response time, do not react to changing process behavior (say, the process changes after it has warmed up), and have lag in responding to large disturbances.[edit] LinearityAnother problem faced with PID controllers is that they are linear, and in particular symmetric. Thus, performance of PID controllers innon-linear systems (such as HVAC systems) is variable. For example, in temperature control, a common use case is active heating (via a heating element) but passive cooling (heating off, but no cooling), so overshoot can only be corrected slowly –it cannot be forced downward. In this case the PID should be tuned to be overdamped, to prevent or reduce overshoot, though this reduces performance (it increases settling time).[edit] Noise in derivativeA problem with the derivative term is that small amounts of measurement or process noise can cause large amounts of change in the output. It is often helpful to filter the measurements with a low-pass filter in order to remove higher-frequency noise components. However, low-pass filtering and derivative control can cancel each other out, so reducing noise by instrumentation is a much better choice. Alternatively, a nonlinear median filter may be used, which improves the filtering efficiency and practical performance.[9]In some case, the differential band can be turned off in many systems with little loss of control. This is equivalent to using the PID controller as a PI controller.。
三菱PLCPID调节手册

Programming ManualMitsubishi Programmable Logic ControllerQCPU(Q Mode)/QnACPU(PID Control Instructions)• SAFETY CAUTIONS •(You must read these cautions before using the product)In connection with the use of this product, in addition to carefully reading both this manual and the related manuals indicated in this manual, it is also essential to pay due attention to safety and handle the product correctly.The safety cautions given here apply to this product in isolation. For information on the safety of the PC system as a whole, refer to the CPU module User's Manual.Store this manual carefully in a place where it is accessible for reference whenever necessary, and forward a copy of the manual to the end user.REVISIONS* The manual number is given on the bottom left of the back cover.Print Date* Manual Number RevisionDec., 1999SH (NA) 080040-A First editionJun., 2001SH (NA) 080040-B Partial additionAbout Manuals, Chapter 1, Chapter 2, Section 2.1, 3.1, 3.2, 3.3, 3.3.1,4.2.3, 4.3.2, 4.3.5, Chapter 5, Section5.1, 5.2, Chapter 6, Chapter 7,Section 8.1, 8.2Japanese Manual Version SH-080022-BThis manual confers no industrial property rights or any rights of any other kind, nor does it confer any patent licenses. Mitsubishi Electric Corporation cannot be held responsible for any problems involving industrial property rights whichmay occur as a result of using the contents noted in this manual.1999 MITSUBISHI ELECTRIC CORPORATIONINTRODUCTIONThank you for choosing the Mitsubishi MELSEC-Q/QnA Series of General Purpose Programmable Controllers. Please read this manual carefully so that the equipment is used to its optimum. A copy of this manual should be forwarded to the end User.CONTENTS1. GENERAL DESCRIPTION 1 – 1 to 1 - 21.1 PID Processing Method...........................................................................................................................1 - 22. SYSTEM CONFIGURATION FOR PID CONTROL 2 - 1 to 2 - 22.1 Applicable PLC CPU................................................................................................................................2 - 13. PID CONTROL SPECIFICATIONS 3 - 1 to 3 - 63.1 Performance Specifications.....................................................................................................................3 - 1 3.2 Operation Expressions.............................................................................................................................3 - 1 3.3 PID Control Instruction List......................................................................................................................3 - 23.3.1 How to read the instruction list..........................................................................................................3 - 33.3.2 PID operation instruction list.............................................................................................................3 - 54. PID CONTROL 4 - 1 to 4 - 124.1 Outline of PID Control..............................................................................................................................4 - 1 4.2 PID Control...............................................................................................................................................4 - 24.2.1 Operation method..............................................................................................................................4 - 24.2.2 Normal operation and reverse operation..........................................................................................4 - 24.2.3 Proportionate operation (P operation)..............................................................................................4 - 44.2.4 Integrating operation (I operation)....................................................................................................4 - 54.2.5 Differentiating operation (D operation).............................................................................................4 - 64.2.6 PID operation.....................................................................................................................................4 - 7 4.3 PID Control Functions..............................................................................................................................4 - 74.3.1 Bumpless changeover function.........................................................................................................4 - 74.3.2 MV higher/lower limit control function...............................................................................................4 - 84.3.3 Monitorning PID control with the AD57(S1) (QnACPU only)...........................................................4 - 94.3.4 Function for transfer to the SV storage device for the PV in manual mode..................................4 - 104.3.5 Changing PID Control Data or input/output Data Setting Range(High Performance model QCPU Only).........................................................................................4 - 11 5. PID CONTROL PROCEDURE 5 - 1 to 5 - 105.1 PID Control Data......................................................................................................................................5 - 35.1.1 Number of loops to be used and the number of loops to be executed in a single scan.................5 - 65.1.2 Sampling cycle..................................................................................................................................5 - 7 5.2 Input/Output Data.....................................................................................................................................5 - 86. PID CONTROL INSTRUCTIONS 6 - 1 to 6 - 27. HOW TO READ EXPLANATIONS FOR INSTRUCTIONS7 - 1 to 7 - 28. PID CONTROL INSTRUCTIONS8 - 1 to 8 - 108.1 PID Control Data Settings.........................................PIDINIT,PIDINITP................................................8 - 2 8.2 PID Control ...............................................................PIDCONT,PIDCONTP.........................................8 - 3 8.3 Monitoring PID Control Status (QnACPU only).......PID57,PID57P......................................................8 - 5 8.4 Operation Stop/Start of Designated Loop No..........PIDSTOP,PIDSTOPP,PIDRUN,PIDRUNP.........8 - 8 8.5 Parameter Change at Designated Loop...................PIDPRMW,PIDPRMWP......................................8 - 99. PID CONTROL PROGRAM EXAMPLES9 - 1 to 9 - 109.1 System Configuration for Program Examples.........................................................................................9 - 1 9.2 Program Example for Automatic Mode PID Control...............................................................................9 - 2 9.3 Program Example for Changing the PID Control Mode between Automatic and Manual....................9 - 6APPENDIX APP - 1APPENDIX 1 PROCESSING TIME LIST................................................................................................APP – 1About ManualsThe following manuals are also related to this product.In necessary, order them by quoting the details in the tables below. Related ManualsManual Name Manual Number (Model Code)High Performance model QCPU (Q mode) User's Manual(Function Explanation/Program Fundamentals)Describes the functions, programming procedures, devices, parameter types and program types necessary in program creation using QCPU (Q mode).(Option)SH-080038 (13JL98)QnACPU Programming Manual (Fundamentals)Describes how to create programs, the names of devices, parameters, and types of program.(Option)IB-66614 (13JF46)QCPU (Q mode) /QnACPU Programming Manual (Common Instructions)Describes how to use sequence instructions, basic instructions, and application instructions.(Option)SH-080039 (13JF58)QnACPU Programming Manual (Special Function)Describes the dedicated instructions for special function modules available when using theQ2ACPU(S1), Q3ACPU, and Q4ACPU.(Option)SH-4013 (13JF56)QnACPU Programming Manual (AD57 Instructions)Describes the dedicated instructions for controlling an AD57(S1) type CRT controller module available when using the Q2ACPU(S1), Q3ACPU, or Q4ACPU.(Option)IB-66617 (13JF49)QCPU (Q mode) / QnACPU Programming Manual (SFC)Describes the system components, performance specifications, and functions, protramming, debugging and error codes of MELSAP-3(Option)SH-080041 (13JF60)Q4ARCPU Programming Manual (Application PID Edition)Describes the programming procedures and device name necessary in program creation to control Applied PID using process control instructions.(Option)IB-66695 (13JF52)Before reading this manual, refer to High Performance model QCPU (Q mode) User'sManual (Function Explanation/Programming Fundamentals) and QnACPUProgramming Manual (Fundamentals) in order to confirm the programs, I/Oprocessing, and devices used with High Performance model QCPU(Q mode)/QnACPU.Describes the instructionsused for Applied PIDcontrol.Generic Names:High Performance model QCPU...Generic names for Q02CPU, Q02HCPU, Q06HCPU, Q12HCPU, Q25HCPU QnACPU ........................................Generic names for Q2ASCPU, Q2ASCPU-S1, Q2ASHCPU, Q2ASHCPU-S1, Q2ACPU, Q3ACPU, Q4ACPU, Q4ARCPUCPU module....................................Generic names for QnACPU, High Performance model QCPU1. GENERAL DESCRIPTION1 This manual describes the sequence program instructions used to execute PID controlwith the High Performance model QCPU/QnACPU.The High Performance model QCPU /QnACPU has the capability to use instructionsfor PID control as a standard feature, so PID control can be executed by loading anA/D conversion module and a D/A conversion module.In addition, the PID control status can be monitored with an AD57(S1).POINTThe Basic model QCPUs (Q00JCPU, Q00CPU, Q01CPU) are not compatible withthe PID control instructions.Use the High Performance model QCPU to use the PID control instructions.REMARKThe High Performance model QCPU is the generic term of the Q02CPU, Q02HCPU,Q06HCPU, Q12HCPU and Q25HCPU.Any of them is abbreviated to the High Performance model QCPU in this manual.1.1 PID Processing MethodThis section describes the processing method for PID control using PID controlinstructions. (For details on PID operations, see Chapter 4.)Execute PID control with PID control instructions by loading an A/D conversion moduleand a D/A conversion module, as shown in Figure 1.1.As shown in Figure 1.1, using the previously set SV (set value) and the digital PV(process value), which is read from the A/D conversion module, PID operation isexecuted to obtain the MV (manipulated value).The calculated MV (manipulated value) is output to the D/A conversion module.The sampling cycle is measured, and the PID operation is performed, when thePIDCONT instruction is executed in the sequence program, as illustrated below.PID operation in accordance with the PIDCONT instruction is executed in presetsampling cycles.MELSEC-Q/QnA2. SYSTEM CONFIGURATION FOR PID CONTROL22. SYSTEM CONFIGURATION FOR PID CONTROLThis section describes the system configuration for PID control using PID control instructions.(For details on the units and modules that can be used when configuring the system, refer to the manual for the CPU module used.)CRTOperation panelD/A conversion moduleA/D conversion moduleMain base unitExtension cableExtension base unitPV (process value) inputFor MV (manipulated value) outputFor PID control monitoring (Only QnACPU)CRT control module AD57 or AD57-S1 onlyQnACPUQCPU High Performance modelPOINT(1) For QnACPU, the reference range for SV, PV, and MV values used in PID operations is 0 to 2000. If the resolution of the A/D conversion module or D/Aconversion module used for input/output in PID control is not 0 to 2000, convert the digital values to 0 to 2000.(2) For High Performance model QCPU, a setting is selectable from fixed values as described in (1) or any appropriate values for the unit used. See Section 4.3.5for details.2.1 Applicable PLC CPUComponent ModuleHigh Performance model QCPU Q02CPU, Q02HCPU, Q06HCPU, Q12HCPU, Q25HCPUQnACPUQ2ASCPU, Q2ASCPU-S1, Q2ASHCPU, Q2ASHCPU-S1Q2ACPU, Q3ACPU, Q4ACPU, Q4ARCPU2. SYSTEM CONFIGURATION FOR PID CONTROLMELSEC-Q/QnA MEMO33. PID CONTROL SPECIFICATIONSThis section gives the specifications PID control using PID control instructions.3.1 Performance SpecificationsThe performance specifications for PID control are tabled below.SpecificationQnACPUItemWith PID Limits for HighPerformance modelQCPU Without PID Limits forHigh Performance modelQCPUNumber of PID control loops—32 loops (maximum)Sampling cycle T S 0.01 to 60.00 sPID operation method—Process value differentiation (normal operation/reverse operation)Proportionate constant K P 0.01 to 100.00Integration constant T I 0.1 to 3000.0 s PID constant setting rangeDifferential constantT D 0.00 to 300.00 sSV (set value) setting range SV 0 to +2000-32768 to +32767PV (process value) setting range PV MV (manipulated value) output range MV-50 to +2050-32768 to +327673.2 Operation ExpressionsThe operation expressions for PID control using PID control instructions are indicated below.NameOperation ExpressionsMeanings of SymbolsNormal operationEV n =PV nf *-SVMV n = MV MV=K p {(EV n -EV n-1)+ EV n - (2PV nf-1-PV nf -PV nf-2)}T S T I T DT SProcess valuedifferentiationReverse operationEV n =SV-PV nf *MV n = MVMV=K p {(EV n -EV n-1)+ EV n + (2PV nf-1-PV nf-PV nf-2)}T ST I T D T S EV n : Deviation in the present sampling cycle EV n-1: Deviation in the preceding sampling cycleSV : Set valuePV nf : Process value of the present sampling cycle (after filtering)PV nf-1: Process value of the preceding samplingcycle (after filtering)PV nf-2: Process value of the sampling cycle two cycles before (after filtering)MV : Output change amount MV n : Present manipulation amount K P : Proportionate constant T S: Sampling cycle T I : Integration constantT D: Differential constant POINT(1) *:PV nf is calculated using the following expression.Therefore, it is the same as the PV (process value) of the input data as long as the filter coefficient is not set for the input data.Process Value after Filtering PV nf = PV n + (PV nf -1-PV n )PV n : Process value of the present sampling: Filter coefficientPV nf-1: Process value of the preceding sampling cycle (after filtering)(2) PV nf is stored in the I/O data area. (See Section 5.2)3.3 PID Control Instruction ListA list of the instructions used to execute PID control is given below.CPU Instruction Name Processing DetailsQ QnAPIDINIT Sets the reference data for PID operation.*1PIDCONT Executes PID operation with the SV (set value) and the PV (process value).*1PID57Used to monitor the results of PID operation at an AD57(S1).×PIDSTOP PIDRUN Stops or starts PID operation for the set loop No.PIDPRMWChanges the operation parameters for the designated loop number to PID control data.*1: For High Performance model QCPU, PID limits can be set to ON or OFF. SeeSections 5.1 and 5.2 for the setting range used in each mode.3.3.1 How to read the instruction listThe instruction list in Section 3.3.2 has the format indicated below:Table 3.1 How to Read the Instruction ListExplanation(1) Classification of instructions according to their application.(2) Instruction names written in a sequence program.(3) Symbols used in the ladder diagram.(4) Processing for each instruction.(5) The execution condition for each instruction. Details are given below.(6) Number of instruction stepsFor details on the number of steps, refer to the QCPU (Q mode) /QnACPU Programming Manual (Common Instructions).(7) A circle indicates that subset processing is possible.For details on subset processing, refer to the QCPU (Q mode) /QnACPU Programming Manual (Common Instructions).(8) Indicates the page number in this manual where a detailed description for theinstruction can be found.3.3.2 PID operation instruction list4.2 PID ControlThe operation methods for PID control with the PID control instructions are the speedmethod and process value differentiation method. The following describes the controlexecuted for both of these methods:4.2.1 Operation method(1) Speed method operationThe speed method operation calculates amounts of changes in the MVs(manipulated values) during PID operation.The actual MV is the accumulatedamount of change of the MV calculated for each sampling cycle.(2) Process value differentiation method operationThe process value differentiation method operation executes PID operations bydifferentiating the PV (process value).Because the deviation is not subject to differentiation, sudden changes in theoutput due to differentiation of the changes in the deviation generated bychanging the set value can be reduced.Either forward operation or reverse operation can be selected to designate thedirection of PID control.4.2.2 Normal operation and reverse operation(1) In normal operation, the MV (manipulated value) increases as the PV (processvalue) increases beyond the SV (set value).(2) In reverse operation, the MV (manipulated value) increases as the PV (processvalue) decreases below the SV (set value).(3) In normal operation and reverse operation, the MV (manipulated value) becomeslarger as the difference between the SV (set value) and the PV (process value)increases.(4) The figure below shows the relationships among normal operation and reverseoperation and the MV (manipulated value), the PV (process value), and the SV(set value):(5) The figure below shows examples of process control with normal operation andreverse operation:4.2.3 Proportionate operation (P operation)The control method for proportionate operation is described below.(1) In proportionate operation, an MV (manipulated value) proportional to thedeviation (the difference between the set value and process value) is obtained.(2) The relationship between E (deviation) and the MV (manipulated value) isexpressed by the following formula:MV=Kp • EKp is a proportional constant and is called the "proportional gain".(3) The proportionate operation in step response with a constant E (deviation) isillustrated in Fig. 4.2.(4) The MV (manipulated value) changes within the range from -50 to 2050 or theuser-defined range (for High Performance model QCPU only).The MV (manipulated value) in response to the same deviation becomes largeras Kp becomes larger, thus the compensating motion is greater.(5) The proportionate operation is always associated with an offset (offset error).4.2.4 Integrating operation (I operation)The control method for integrating operation is described below.(1) In the integrating operation, the MV (manipulated value) changes continuously tozero deviation when it occurs.This operation can eliminate the offset that is unavoidable in proportionateoperation.(2) The time required for the MV in integrating operation to reach the MV forproportionate operation after the generation of deviation is called the integratingtime. Integrating time is expressed as T I.The smaller the setting for T I, the more effective the integrating operation will be.(3) The integrating operation in step response with a constant E (deviation) isillustrated in Fig. 4.3.(4) Integrating operation is always used in combination with proportionate operation(PI operation) or with proportionate and differentiating operations (PID operation).Integrating operation cannot be used independently.4.2.5 Differentiating operation (D operation)The control method for differentiating operation is described below.(1) In differentiating operation, an MV (manipulated value) proportional to thedeviation change rate is added to the system value to zero deviation when itoccurs.This operation prevents significant fluctuation at the control objective due toexternal disturbances.(2) The time required for the MV in the differentiating operation to reach the MV forthe proportionate operation after the generation of deviation is called thedifferentiating time. Differentiating time is expressed as T D.The smaller the setting for T D, the more effective the differentiating operation willbe.(3) The differentiating operation in step response with a constant E (deviation) isillustrated in Fig. 4.4.(4) Differentiating operation is always used in combination with proportionateoperation (PD operation) or with proportionate and integrating operations (PIDoperation).Differentiating operation cannot be used independently.4.2.6 PID operationThe control method when proportionate operation (P operation), integrating operation (Ioperation), and differentiating operation (D operation) are used in combination isdescribed below.(1) During PID operation, the system is controlled by the MV (manipulated value)calculated in the (P + I + D) operation.(2) PID operation in step response with a constant E (deviation) is illustrated in Fig.4.5.4.3 PID Control FunctionsDuring PID control using the PID control instructions, MV upper/lower limit control isautomatically executed by the bumpless changeover function explained below.4.3.1 Bumpless changeover functionThis function controls the MV (manipulated value) continuously when the control modeis changed between manual and automatic.When the control mode is changed between manual and automatic, data is transmittedbetween the MV area for automatic mode and the MV area for manual mode.The control mode is changed in the input/output data area (see Section 5.2).(1) Changing from the manual ...........mode to the automatic mode The MV in the manual mode is transmitted to the MV area for the automatic mode.(2) Changing from the automatic .......mode to the manual mode The MV in the automatic mode is transmitted to the MV area for the manual mode.POINT(1) Manual and automatic modes of PID control:1) Automatic modePID operation is executed with a PID control instruction.The control object is controlled according to the calculated MV.2) Manual modePID operation is not executed. The MV is calculated by the user and thecontrol object is controlled according to the user-calculated MV.(2) The loop set in the manual mode stores the PV (process value) in the set valuearea every sampling cycle.4.3.2 MV higher/lower limit control functionThe MV higher/lower limit control function controls the higher or lower limit of the MVcalculated in the PID operation. This function is only effective in the automatic mode. Itcannot be executed in the manual mode.By setting the MV higher limit (MVHL) and the MV lower limit (MVLL), the MVcalculated in the PID operation can be controlled within the range between the limits.When the MV higher/lower limit control function is used, the MV is controlled asillustrated above.A MVHL (manipulated value higher limit) and MVLL (manipulated value lower limit)takes on a value between -50 and 2050 or a user-defined value (for High Performancemodel QCPU only).The following are the default settings:• Higher limit................2000 (Or user-defined value)• Lower limit................0 (Or user-defined value)The value set for the higher limit must not be smaller than the value set for the lowerlimit.An error will occur if it is.4.3.3 Monitoring PID control with the AD57(S1) (QnACPU only)The PID control operation results can be monitored in a bar graph with an AD57(S1)CRT controller unit.(1) The monitor screen displays the monitored information of eight loops beginningwith the designated loop number.POINTThe SV, PV, and MV present value are displayed as percentages of 2000.1) SV percentage display...............SV2000100 (%)2) PV percentage display...............PV2000100 (%)3) MV percentage display...............MV2000100 (%)(2) Use the PID57 instruction to execute monitoring with an AD57(S1).See Section 8.3 for details on the PID57 instruction.4.3.4 Function for transfer to the SV storage device for the PV in manual modeThe PIDCONT instruction is also executed in manual mode.In the manual mode, it ispossible to select whether or not the PV input from the A/D conversion module onexecution of the PIDCONT instruction is transferred to the SV storage device or not inaccordance with the ON/OFF status of the PID bumpless processing flag (SM774).• When SM774 is OFF : When the PIDCONT instruction is executed, the PV istransferred to the SV storage device.On switching from the manual mode to the automaticmode, the MV output is continued from the value in themanual mode.After switching to the automatic mode, control can beswitched from the MV that was being output to the SV bychanging the SV.• When SM774 is ON : When the PIDCONT instruction is executed, the PV is nottransferred to the SV storage device.On switching from the manual mode to the automaticmode, control can be switched from the MV output in themanual mode to the SV.Before switching to the automatic mode, store a SV in theSV storage device.POINTWhen SM774 is ON or OFF, switching from the manual mode to the automaticmode may cause different control effects as follows.• When SM774 is OFF, the PV is transferred to the SV storage device.When the manual mode is switched to the automatic mode, no difference iscaused between the PV and the SV and the MV does not change rapidly, exceptthat the SV differs from a target value defined in the automatic mode.Use the sequence program to make step-by-step adjustments to the SV so thatthe SV approaches closer to the target value.See sample programs in Section 9.3.• When SM774 is ON, the PV is not transferred to the SV storage device. This maycause a difference between the PV and the SV when the manual mode isswitched to the automatic mode.A greater difference may cause the MV to change rapidly. So this procedure isused for systems in which the manual mode can be switched to the automaticmode only when the PV approaches closer tothe SV.The automatic mode can be effected without using the sequence program tomake step-by-step adjustments to the SV.REMARKThe SV and PV are stored in the devices in the I/O data area designated by thePIDCONT instruction.4.3.5 Changing the PID Control Data or Input/Output Data Setting Range (HighPerformance model QCPU Only)For High Performance model QCPU, setting ranges can be selectable for PID controldata (see Section 5.1) and input/output data (see Section 5.2). To effect the user-defined setting range, designate the loops for which PID limit settings (SD774 and SD775) are defined, and then set these loops' bits to ON before executing the PIDCONTand PIDINT instructions.SD774SD7750 : PID Limit ON (default setting)1 : PID Limit OFF (user-defined setting)A "PID Limit OFF" setting does not effect the limit control over internal data. To effectthe limit control, execute the processing by operating from the user's application side.。
双容液位控制系统的设计

双容液位控制系统的设计摘要在化学工业生产中,液位控制是一项非常重要的环节。
本论文所论述的双容液位控制系统是以过程综合自动化控制系统实验为平台,以仪表控制方法为主要工具,进行液位控制方法设计。
智能控制仪表蕴含大量高科技技术,且具备许多优点,因此越来越广泛的被应用于工业控制领域。
论文也对组态软件MCGS的特点及基本使用方法进行了简单介绍,这样对串级控制实施监控,提供了条件。
在控制算法方面,系统选用PID控制器。
然后根据系统具体的控制要求,主回路选择PI调节器,副回路选择P调节器;并选用适当整定法对调节器参数进行整定。
关键词:双容液位控制系统,智能仪表控制,MCGS组态软件,PID控制?—Dual-tank liquid level control system designAbstractProduction in the chemical industry, liquid level control is a very important part. Discussed in this paper two-tank liquid level control system is based on the process of experiments Integrated Automation Control System as a platform to instrument control as the main instrument designed for liquid level control. Intelligent Control Instrument contains a large number of high technology, and have many advantages, so more and more widely applied in industrial control.Papers also features MCGS configuration software and the basic use a brief introduction, this implementation of the cascade control monitoring, provided the conditions.In the control algorithm, the system adopts PID controller. And specific control requirements according to the system, the main loop select PI regulator, the Deputy loop select P regulator; and an appropriate tuning the parameters of the regulator tuning.\Key words: dual-tank liquid level control system, intelligent instrument control, MCGS configuration software, PID control目录双容液位控制系统的设计 (i)、摘要 (i)Abstract (ii)1 绪论 (1)课题来源,背景及意义 (1)课题研究的内容安排 (2)2 THJ-2型高级过程控制系统 (3)系统简介和组成 (3)系统控制仪表的组成 (3)、检测装置 (3)执行机构 (4)控制器 (4)智能仪表的发展前景、应用领域和优点 (4)系统软件 (5)系统特点 (5)本章小结 (6)3 MCGS组态软件 (7)—什么是MCGS组态软件 (7)MCGS组态软件的系统构成 (7)MCGS组态软件的特点 (7)建立MCGS工程 (8)设计画面流程 (9)整体画面 (13)本章小结 (15)4 液位串级控制系统分析与建模 (16)-串级控制系统的分析 (16)串级控制系统及组成结构 (16)串级控制系统的特点和适用场合 (16)串级控制系统的设计 (16)双容水箱液位串级控制系统的组成 (17)系统建模 (18)系统特性测试 (19)模型最终确定 (21);本章小结 (22)5 系统的PID参数整定 (23)PID概述 (23)控制器参数整定方法 (23)PID参数的确定 (27)系统特性测试. (28)本章小结 (30)6 结论 (31)!参考文献 (32)致谢 (33)?1 绪论课题来源,背景及意义过程控制涉及炼油、化工、发电、冶金、造纸、医药和轻工业等工业部门,对国民经济的发展起着十分重要的作用。
PID控制

Gd ( s )
where the time constant d of the controller is much smaller than the time constants of the process to be controlled and so it may be neglected to be approximated to Gd(s) = KDs. If we set KD = 0 (i.e., no derivative action), then we have the proportional plus integral (PI) controller
R(s)
E ( s)
KP
U c ( s)
Plant
Y ( s)
Fundamentals of Control Engineering - hp.wang@
Three-term(PID) Controllers
Ziegler-Nichols Rules – Second method:
Three-term(PID) Controllers
Ziegler-Nichols Rules – First method:
Table I
Type of Controller
KP
TI
TD
0 0
0.5L
P
T L T 0.9 L T 1.2 L
PI
L 0.3
PID
2L
Fundamentals of Control Engineering - hp.wang@
Hale Waihona Puke Three-term(PID) Controllers
Ziegler-Nichols Rules – Comments:
过程控制装置反应釜液位控制毕业设计

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊安徽工业大学毕业设计(论文)任务书课题名称过程控制装置反应釜液位控制学院电气信息学院专业班级测控技术与仪器081班姓名学号毕业设计(论文)的主要内容及要求:主要内容:1.介绍控制系统的硬件组成,所采用的控制方案;2.利用西门子S7-300可编程逻辑控制器实现反应釜液位PID控制;3.使用组态王对系统组态;4.监控液位PLC 控制系统的运行情况。
要求:1. 以过程控制实验装置中的反应釜液位作为被控对象设计一个控制系统,实现对反应釜液位的恒值控制;2.组态测控界面上,实时设定并显示液位给定值、测量值及控制器输出值;3.实时显示液位给定值实时曲线、液位测量值实时曲线;4.选择合适的整定方法确定PID参数,并能在组态测控界面上实时改变PID参数。
5.设计的反应釜液位控制系统要能够实现反应釜液位的自动控制,控制效果好,运行稳定,操作方便。
指导教师签字:┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊过程控制装置反应釜的液位控制摘要反应釜自1912年发明以来取得迅猛发展,至今全球仍以每年3—5%的速度递增。
全世界反应釜的消费总量达3500万。
我国正处于反应釜生产和消费应用的高速增长期,已广泛应用于石油、化工、轻工、食品、酿酒、制药、家电、水电、机械、建筑、市政和各种民用器具中。
不锈钢反应釜具有加热迅速、耐高温、耐腐蚀、卫生、无环境污染、勿需锅炉自动加温、使用方便等特点。
在相当多的领域里,反应釜的性能优劣决定了产品的质量好坏。
目前反应釜的控制系统大都采用以微处理器为核心的计算机控制技术,既提高设备的自动化程度又提高设备的控制精度。
本次设计的主要任务是利用西门子S7-300PLC和组态王软件设计一个恒液位控制系统,使液位维持在设定值附近。
本文首先介绍了过程控制实验装置和反应釜单元的一些基本资料,包括系统组成和工作原理。
仪表常见专业术语中英文对照表
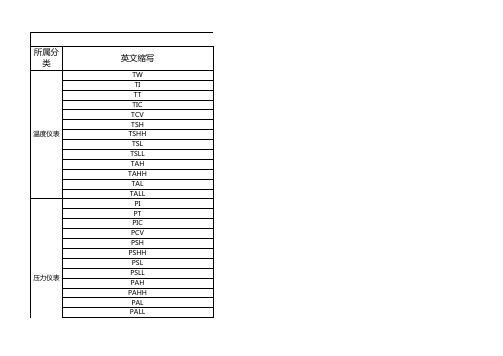
PRAGRAMMABLE LOGIC CONTROLLER EMERGENCY SHUT DOWN FIRE & GAS SYESTEM PROCESS CONTROL SYESTEM DISTRIBUTED CONTROL SYSTEM MAIN SUERACE SAFETY VALVE SURFACE CONTROLLED SUBSURFACE SAFETY VALVE GAS VENT VALVE CONNECTOR UNION ELBOW TEE CROSS PLUG CAP BULKHEAD REDUCING NUT FRONT FERRULE BACK FERRULE MAJOR FLOW LINE PNEUMATIC SIGNAL ELECTRICAL SIGNAL CAPILLARY TUBING HYDRAULIC SIGNAL GATE VALVE BALL VALVE NEEDLE VALVE CHECK VALVE
所属分 类
温度仪表
压力仪表
英文缩写
TW TI TT TIC TCV TSH TSHH TSL TSLL TAH TAHH TAL TALL PI PT PIC PCV PSH PSHH PSL PSLL PAH PAHH PAL PALL
仪表常见专业术语中英文对照表
液位仪表 流量仪表
其他
PDSH PDSL PDAL PDAH
碟阀 放空阀 角阀 节流阀 安全阀 三通阀 四通阀 控制阀 自力式调节阀 手动复位控制阀 电磁阀 就地安装仪表 中控房控制盘上正面安装的仪表 中控房控制盘上背面安装的仪表 就地控制盘正面安装的仪表 就地盘背面安装的仪表 就地控制盘状态灯 中控盘状态灯 电脑显示 质量流量计 到关断系统 来自关断系统 燃气泄漏报警 综合报警 弃平台报警 紫外红外探测器 烟探 可燃气探头 热探
Lecture4_PID Control PID控制

∆U done ∆t
4-2
P control
• Closed-loop dynamics
& + k P y = k P yd + d y
1 kP yd + d y= s + kP s + kP
1 d SS • Steady-state (s = 0) y SS = yd + kP
1 T = 1 / kP
• Causal (low-pass filtered) estimate of the derivative
s 1 1 /τ D &≈ e e= e+ e τ Ds + 1 τD τ Ds + 1
• Modified PD controller:
s u = −k D e − kPe τ Ds + 1
– processing time c[i], period p[i] – CPU utilization: U[i]=c[i]/p[i]
u(t) y(t)
admission rate =
∆U new ∆t
server utilization CPU
-d(t)
Control Engineering
completion rate =
• 2-nd order dynamics • PD control
Example:
• Disk read-write control
& &=u+d y
• Closed-loop dynamics
e = y − yd & − kPe u = −kD e
• Optimal gains (critical damping)
PID Controllers - Theory Design and Tuning 翻译

IntroductionThe PID controller has several important functions: it provides feed¬back; it has the ability to eliminate steady state offsets through in¬tegral action; it can anticipate the future through derivative action.PID controllers are sufficient for many control problems, particularly when process dynamics are benign and the performance requirementsare modest. PID controllers are found in large numbers in all indus¬tries. The controllers come in many different forms. There are stand¬alone systems in boxes for one or a few loops, which are manufac¬tured by the hundred thousands yearly. PID control is an important ingredient of a distributed control system. The controllers are also embedded in many special-purpose control systems. In process con¬trol, more than 95% of the control loops are of PID type, most loopsare actually PI control. Many useful features of PID control have notbeen widely disseminated because they have been considered trade secrets. Typical examples are techniques for mode switches and antiwindup. PID control is often combined with logic, sequential machines, se¬lectors, and simple function blocks to build the complicated automa¬tion systems used for energy production, transportation, and manu¬facturing. Many sophisticated control strategies, such as model pre¬dictive control, are also organized hierarchically. PID control is usedat the lowest level; the multivariable controller gives the setpoints tothe controllers at the lower level. The PID controller can thus be saidto be the "bread and butter" of control engineering. It is an important component in every control engineer's toolbox.PID controllers have survived many changes in technology rang¬ing from pneumatics to microprocessors via electronic tubes, tran¬sistors, integrated circuits. The microprocessor has had a dramatic2 Chapter 1 Introductioninfluence on the PID controller. Practically all PID controllers madetoday are based on microprocessors. This has given opportunities to provide additional features like automatic tuning, gain scheduling,and continuous adaptation. The terminology in these areas is notwell-established. For purposes of this book, auto-tuning means thatthe controller parameters are tuned automatically on demand froman operator or an external signal, and adaptation means that the parameters of a controller are continuously updated. Practically allnew PID controllers that are announced today have some capabilityfor automatic tuning. Tuning and adaptation can be done in many different ways. The simple controller has in fact become a test benchfor many new ideas in control.The emergence of the fieldbus is another important development.This will drastically influence the architecture of future distributed control systems. The PID controller is an important ingredient ofthe fieldbus concept. It may also be standardized as a result of the fieldbus development.A large cadre of instrument and process engineers are familiarwith PID control. There is a well-established practice of installing, tuning, and using the controllers. In spite of this there are substantial potentials for improving PID control. Evidence for this can be found in the control rooms of any industry. Many controllers are put in man¬ual mode, and among those controllers that are in automatic mode, derivative action is frequently switched off for the simple reason that it is difficult to tune properly. The key reasons for poor performance is equipment problems in valves and sensors, and bad tuning practice. The valve problems include wrong sizing, hysteresis, and stiction. The measurement problems include: poor or no anti-aliasing filters; excessive filtering in "smart" sensors, excessive noise and improper calibration. Substantial improvements can be made. The incentive for improvement is emphasized by demands for improved quality, which is manifested by standards such as ISO 9000. Knowledge and un¬derstanding are the key elements for improving performance of the control loop. Specific process knowledge is required as well as knowl¬edge about PID control.Based on our experience, we believe that a new era of PID controlis emerging. This book will take stock of the development, assess its potential, and try to speed up the development by sharing our expe¬riences in this exciting and useful field of automatic control. The goal of the book is to provide the technical background for understanding PID control. Such knowledge can directly contribute to better product quality.Process dynamics is a key for understanding any control problem. Chapter 2 presents different ways to model process dynamics thatare useful for PID control. Methods based on step tests are discussed Chapter 1 Introduction 3together with techniques based on frequency response. It is attempted to provide a good understanding of the relations between the different approaches. Different ways to obtain parameters in simple transfer function models based on the tests are also given. Two dimensionfree parameters are introduced: the normalized dead time and thegain ratio are useful to characterize dynamic properties of systems commonly found in process control. Methods for parameter estimation are also discussed. A brief description of disturbance modeling is also given.An in depth presentation of the PID controller is given in Chap¬ter 3. This includes principles as well as many implementation de¬tails, such as limitation of derivative gain, anti-windup, improvement of set point response, etc. The PID controller can be structured in dif¬ferent ways. Commonly used forms are the series and the parallel forms. The differences between these and the controller parameters used in the different structures are treated in detail. Implementationof PID controllers using digital computers is also discussed. The un¬derlying concepts of sampling, choice of sampling intervals, and anti¬aliasing niters are treated thoroughly. The limitations of PID control are also described. Typical cases where more complex controllers are worthwhile are systems with long dead time and oscillatory systems. Extensions of PID control to deal with such systems are discussed briefly.Chapter 4 describes methods for the design of PID controllers. Specifications are discussed in detail. Particular attention is given to the information required to use the methods. Many different meth¬ods for tuning PID controllers that have been developed over the years are then presented. Their properties are discussed thoroughly.A reasonable design method should consider load disturbances, model uncertainty, measurement noise, and set-point response. A drawback of many of the traditional tuning rules for PID control is that such rules do not consider all these aspects in a balanced way. New tuning techniques that do consider all these criteria are also presented.The authors believe strongly that nothing can replace under¬standing and insight. In view of the large number of controllers used in industry there is a need for simple tuning methods. Such rules will at least be much better than "factory tuning," but they can always be improved by process modeling and control design. In Chapter 5 we present a collection of new tuning rules that give significant improve¬ment over previously used rules.In Chapter 6 we discuss some techniques for adaptation and au¬tomatic tuning of PID controllers. This includes methods based on parametric models and nonparametric techniques. A number of com¬mercial controllers are also described to illustrate the different tech¬niques. The possibilities of incorporating diagnosis and fault detection 4 Chapter 1 Introductionin the primary control loop is also discussed.In Chapter 7 it is shown how complex control problems can be solved by combining simple controllers in different ways. The control paradigms of cascade control, feedforward control, model following, ratio control, split range control, and control with selectors are dis¬cussed. Use of currently popular techniques such as neural networks and fuzzy control are also covered briefly.ReferencesA treatment of PID control with many practical hints is given inShinskey (1988). There is a Japanese text entirely devoted to PID control by Suda et al. (1992). Among the books on tuning of PID controllers, we can mention McMillan (1983) and Corripio (1990), which are published by ISA.There are several studies that indicate the state of the art of in¬dustrial practice of control. The Japan Electric Measuring Instrument Manufacturers'Association conducted a survey of the state of process control systems in 1989, see Yamamoto and Hashimoto (1991). Ac¬cording to the survey more than than 90% of the control loops wereof the PID type.The paper, Bialkowski (1993), which describes audits of papermills in Canada, shows that a typical mill has more than 2000 control loops and that 97% use PI control. Only 20% of the control loops were found to work well and decrease process variability. Reasons for poor performance were poor tuning (30%) and valve problems (30%). The remaining 20% of the controllers functioned poorly for a variety of reasons such as: sensor problems, bad choice of sampling rates, and anti-aliasing filters. Similar observations are given in Ender (1993), where it is claimed that 30% of installed process controllers operatein manual, that 20% of the loops use "factory tuning," i.e., default parameters set by the controller manufacturer, and that 30% of the loops function poorly because of equipment problems in valves and sensors.CHAPTER 2Process Models2.1 IntroductionA block diagram of a simple control loop is shown in Figure 2.1. The system has two major components, the process and the controller, rep¬resented as boxes with arrows denoting the causal relation between inputs and outputs. The process has one input, the manipulated vari¬able, also called the control variable. It is denoted by u. The process output is called process variable (PV) and is denoted by y. This vari¬able is measured by a sensor. The desired value of the process variable is called the setpoint (SP) or the reference value. It is denoted by y sp. The control error e is the difference between the setpoint and the process variable, i.e., e = y sp —y. The controller in Figure 2.1 hasone input, the error, and one output, the control variable. The figure shows that the process and the controller are connected in a closed feedback loop.The purpose of the system is to keep the process variable closeto the desired value in spite of disturbances. This is achieved by thefeedback loop, which works as follows. Assume that the system is in equilibrium and that a disturbance occurs so that the process variable becomes larger than the setpoint. The error is then negative and the controller output decreases which in turn causes the process outputto decrease. This type of feedback is called negative feedback, because the manipulated variable moves in direction opposite to the process variable.The controller has several parameters that can be adjusted. The control loop performs well if the parameters are chosen properly. It performs poorly otherwise, e.g., the system may become unstable. The procedure of finding the controller parameters is called tuning.6 Chapter 2 Process ModelsController! Process- 1 -*Figure 2.1 Block diagram of a simple feedback system.i )This can be done in two different ways. One approach is to choose some controller parameters, to observe the behavior of the feedback system, and to modify the parameters until the desired behavior is obtained. Another approach is to first develop a mathematical model that describes the behavior of the process. The parameters of the controller are then determined using some method for control design. An understanding of techniques for determining process dynamics is a necessary background for both methods for controller tuning. This chapter will present such techniques.Static models are discussed in the next section. Dynamic modelsare discussed in Section 2.3. Transient response methods, which are useful for determining simple dynamic models of the process, are pre¬sented in Section 2.4. Section 2.5 treats methods based on moments. These methods are less sensitive to measurement noise and, further¬more, are not restricted to any specific input signal. The frequency response methods, described in Section 2.6, can be used to obtain both simple models and more detailed descriptions. Methods basedon estimation of parametric models are more complex methods that require more computations but less restrictions on the experiments. These methods are presented in Section 2.7. The models discussed so far describe the relation between the process input and output. It is also important to model the disturbances acting on the system. Thisis discussed in Section 2.8. Section 2.9 treats methods to simplify a complex model and the problem of unmodeled dynamics and mod¬eling errors. Conclusions and references are given in Sections 2.10 and 2.11.2.2 Static ModelsThe static process characteristic is a curve that gives the steady state relation between process input signal u and process output y. See Figure 2.2. Notice that the curve has a physical interpretation onlyfor a stable process.2.2 Static ModelsFigure 2.2 Static process characteristic. Shows process output yas a function of process input u under static conditions.All process investigations should start by a determination of thestatic process model. It can be used to determine the range of control signals required to change the process output over the desired range,to size actuators, and to select sensor resolution. It can also be usedto assess whether static gain variations are so large that they haveto be accounted for in the control design.The static model can be obtained in several ways. It can be de¬termined by an open-loop experiment where the input signal is setto a constant value and the process output is measured when it has reached steady state. This gives one point on the process characteris¬tics. The experiment is then repeated to cover the full range of inputs. An alternative procedure is to make a closed-loop experiment.The setpoint is then given a constant value and the corresponding control variable is measured in steady state. The experiment is then repeated to cover the full range of setpoints.The experiments required to determine the static process modeloften give a good intuitive feel for how easy it is to control the process, if it is stable, and if there are many disturbances.Sometimes process operations do not permit the experiments to be done as described above. Small perturbations are normally permitted, but it may not be possible to move the process over the full operating range. In such a case the experiment must be done over a long period of time.Process NoiseProcess disturbances are easily determined by logging the process output when the control signal is constant. Such a measurement8 Chapter 2 Process Modelswill give a combination of measurement and load disturbances. There are many sophisticated techniques such as time-series analysis and spectral analysis that can be used to determine the characteristicsof the process noise. Crude estimates of the noise characteristicsare obtained simply by measuring the peak-to-peak value and by determining the average time between zero crossings of the error signal. This is discussed further in Section 2.8.2.3 Dynamic ModelsA static process model like the one discussed in the previous sectiontells the steady state relation between the input and the output sig¬nal. A dynamic model should give the relation between the input andthe output signal during transients. It is naturally much more diffi¬cult to capture dynamic behavior. This is, however, very significantwhen discussing control problems.Fortunately there is a restricted class of models that can often beused. This applies to linear time-invariant systems. Such models canoften be used to describe the behavior of control systems when thereare small deviations from an equilibrium. The fact that a system islinear implies that the superposition principle holds. This means thatif the input u\ gives the output yi and the input ui gives the outputj2 it then follows that the input au\ + bui gives the output ay\ + by 2-A system is time-invariant if its behavior does not change with time.A very nice property of linear time-invariant systems is that theirresponse to an arbitrary input can be completely characterized interms of the response to a simple signal. Many different signals can beused to characterize a system. Broadly speaking we can differentiatebetween transient and frequency responses.In a control system we typically have to deal with two signalsonly, the control signal and the measured variable. Process dynamicsas we have discussed here only deals with the relation between thosesignals. The measured variable should ideally be closely related to thephysical process variable that we are interested in. Since it is difficultto construct sensors it happens that there is considerable dynamicsin the relation between the true process variable and the sensor. Forexample, it is very common that there are substantial time constantsin temperature sensors. There may also be measurement noise andother imperfections. There may also be significant dynamics in theactuators. To do a good job of control, it is necessary to be aware ofthe physical origin the process dynamics to judge if a good r绪论PID控制器有几个重要的功能: 它能提供反馈; 它有能力通过积分作用消除稳态补偿; 它通过微分作用可以有预见性。
基于数字PID的双容水箱液位串级控制系统设计

doi :10.3969/j.issn.1009-3230.2019.01.015基于数字PID 的双容水箱液位串级控制系统设计卢春华,王頔,谷瑞邦(安阳工学院电子信息与电气工程学院,河南安阳455000)摘要:液位测量与控制由于受到被测介质的物理化学性质以及工作条件的影响,目前仍然是一个比较薄弱的环节。
文中设计是以双容水箱模拟工业现场高阶对象,以中水箱液位为主参数的液位串级控制系统。
采用西门子S7-200作为控制器,控制规律采用经典的PID ,电容式差压变送器检测水箱液位,对数电动调节阀为执行机构。
通过组态王软件建立组态界面,完成系统的实时监控。
实验结果表明,系统能够实现液位的无静差调节,且抗干扰能力较强,具有良好的动态和稳态性能。
关键词:液位;串级控制;PLC ;组态王中图分类号:TP273文献标志码:B 文章编号:1009-3230(2019)01-0051-03Design of Cascade Control System for Double -tank LiquidLevel Based on Digital PIDLU Chun -hua ,WANG Di ,GU Rui -bang(Anyang Institute of Technology ,Electronic Information and Electrical Engineering College ,Anyang 455000,Henan Province ,China )Abstract :Level measurement and control is still a weak link due to the physical and chemical properties of the medium under test and the influence of working conditions.This design is a liquid level cascade control system ,which simulates the high -order object of industrial field with double -tank and takes the liquid level of intermediate water tank as the main parameter.Siemens S7-200is used as controller ,classical PID is used as control law ,capacitive differential pressure transmitter is used to detect tank level ,and logarithmic electric regulating valve is used as actuator.Configuration interface is established by Kingview software to complete real -time monitoring of the system.The experimental results show that the system can realize the non -static adjustment of liquid level ,and has strong anti -interference ability ,good dynamic and steady -state performance.Key words :Liquid level ;Cascade control ;PLC ;Kingview0引言收稿日期:2018-10-25修订日期:2018-11-28基金项目:2017年河南省科技厅科技攻关项目(17210221-0158)作者简介:卢春华(1982-),男,硕士,讲师,研究方向为工业过程参数检测与控制。
CASCADE CONTROLLER

专利名称:CASCADE CONTROLLER 发明人:HOSHINO UMIHIKO申请号:JP25961790申请日:19900928公开号:JPH04137101A公开日:19920512专利内容由知识产权出版社提供摘要:PURPOSE:To easily change the status of a secondary instrument by providing a supervisory station with a virtual secondary instrument and connecting/ disconnecting a primary instrument and the virtual secondary instrument by a cascade coupling part to realize cascade coupling/non-coupling. CONSTITUTION:With respect to a secondary instrument 64, a virtual secondary instrument 44 follows up a read-back value PV as a manipulated variable MV of a primary instrument 42. Since a communication control station 50 starts the next communication at a time (2), the data change on the side of a supervisory station 40 is discrete. When the status of the secondary instrument 64 is changed to cascade coupling CAS at a time (3), a status LS of the instrument 64 is copied to the status of the instrument 44 at a next communication time (4). A coupling part 54 gives the set value of the instrument 44 to the manipulated variable of a virtual primary instrument 62 in a next communication cycle (5). At this time, cascade coupling between instruments 42 and 64 is established. When the status of the instrument 64 is changed to cascade coupling the inverse of CAS at a time (6), the non-cascade state is set. The status of the instrument 64 is copied to the instrument 44 at a time (7), and independent control of the instrument 64 is started.申请人:YOKOGAWA ELECTRIC CORP更多信息请下载全文后查看。
PlantPAx

PlantPAx™ Distributed Control System Demonstrator Teach PID process control and control strategiesDistributed control systems (DCS) are used across the process industry, from water and wastewater, to chemical, petrochemical, food processing, and more. DCS control various subsystems and control loops in real time to boost operational efficiency and safety of the plant.An in-depth understanding of the such systems, as well as all their instrumentation and equipment, is particularly important for instrumentation and process technicians and engineers, who operate the systems, manage alarms, and install, configure, and trouble -shoot equipment.Designed for training purposes, the PlantPAx™ Distributed Con -trol System Demonstrator repli-cates a DCS showing real-life process applications.A user guide introduces stu-dents to the configuration and use of instruments that control and monitor industrial proces-ses, including temperature, pressure, flow, and level pro -cess variables.An introduction to PlantPAx™ with integrated Endress+Hauser devicesPID controlThe demonstrator is configured to teach different types of PID process control and types of control strategies. It is capable to monitor Pressure, Flow and Temperature process variables. Two level PID control loops work simultaneously to maintain a stable level in each col-umn even when disturbance occurs. The PID level control loop of the large column works in Cascade mode with the flow rate and use a pneumatic control valve as the final element. A pressure control loop maintains a stable pressure at the inlet of the large column. The pressure control loop uses the centrifugal pump with an industrial variable frequency drive to maintain the desired pressure.The system also features a sequencer performing an automatic start-up sequence to facilitate operation. A batch sequencer allows fill-up of the small column with four different amounts of water; running the batches allows students to see the impact on the process stability. For safety purposes and damage prevention, the system includes interlocks similar to the ones in the process industry.Industrial communication protocolsThe demonstrator uses four different communication protocols between smart devices and smart transmitters. The HART® protocol enables communication between devices by superimposing digital signals on top of the existing 4-20 mA outputs. The FOUNDATION™ Fieldbus, Profibus PA and Ethernet I/P protocols work in the same manner as a Local Area Network (LAN) for smart devices.Each smart transmitter has the option to be configured manually or through a computer using either a DCS system or an optional config-uration software. It is also possible to edit the HMI interface and the PLC program to change the control strategies using two optional software such as FactoryTalk Site Edition Studio and RSLogix 5000 Full Edition.Main components of the demonstrator• Instrumentation mounting pipes• Differential-pressure and temperature transmitters• Three-valve manifold• Small- and large-diameter columns• Radar level transmitter with remote display• Electromagnetic flow transmitter• J-type thermocouple• Signal tower• Touchscreen, high-speed computer• Pneumatic control valve• Rotameter, solenoid valve, venturi tube• Disconnect switch and emergency push-button• Two 60-liter (16 gallons) tanks• Two pumps, each coupled to a three-phase motor• Control panel:• Two AC drives• Ethernet I/P to Profibus-PA bridge• Ethernet I/P to FOUNDATION Fieldbus bridge• Programmable logic controller (PLC)• Ethernet managed switchFor more details:Visit our website or contact a sales representative about the PlantPAx™ Distributed Control System Demonstrator, as well as complementary industrial instrumentation and process control training systems.Monitor and control the system using FactoryTalk View SED I D 1257 e n 04/2021 F e s t o D i d a c t i c S EFesto Didactic is part of the Rockwell Automation Machine Builder Partner program and contributes to its University Partnership Program since 2014.01 Main screen overview 02 Batch sequencer 03 Trend recorder 04 + 06 PID control loops 05 Diagnostics010203040605Festo Didactic Inc.607 Industrial Way West Eatontown, NJ 07724y USAPhone +1 732 938-2000 *************************** Festo Didactic Ltd.675, rue du Carbone Quebec City (QC) G1K 8W1CanadaPhone +1 418 849-1000***************************Festo Didactic SERechbergstrasse 373770 Denkendorf GermanyPhone: +49 711 3467-0 *************。
PIDE 增强型PID功能块2

PIDE部分2运行模式选择PIDE 指令允许用户按照所需的功能选择几个不同的选项。
像正向/反向控制动作这样的选项经常使用。
其它的却很少使用。
正向/反向控制动作在正向动作控制器中,当偏差为正值时,输出会增加。
在间接动作控制器中,当偏差为正值时,输出会减少。
控制工程师将根据生产工艺和所使用控制阀的反应来选择动作类型。
提供一个布尔量输入,来选择所需的控制动作。
表 1. –控制动作请求相关/独立增益算法工程师会指定比例增益、积分增益和微分增益如何对生产过程起作用。
通常,如果想要使用传统的回路整定方法时,可以选择使用相关ISA增益算法。
当选择使用独立增益算法时,这三个增益常数会彼此独立运行。
表 2. –相关/独立控制请求控制器增益所选的算法不同,增益的表达式也不同。
比例增益= K p 控制器增益= K c积分增益= K i复位增益= T i微分增益= K d比率增益= T d比例增益(比例带宽)的表达式为:K p = 1/K c表 3. –控制器增益标签另外,在速度算法计算时,有几个标签用于改变比例和微分项。
所使用的算法为:CV n=CV n-1+K p∆E+K i E∆t+K d E n-2E n-1+E n-2图 4 –速度算法表 5 –算法修正标签定时模式PIDE 指令支持三种不同的定时模式。
它们为“周期”、“过采样”和实时采样。
出版物《Process Control and Drives Instruction Manual(过程控制和驱动指令手册)》的附录A对它们的功能和差别作了清除全面的说明。
因为PIDE是根据时间进行计算的,所以选择一种定时模式并正确地填写合适的标签是非常必要的。
周期模式使用PIDE 的最简单模式为周期模式。
PIDE在周期任务中进行编程并且该任务按照控制工程师所选的时间间隔执行。
系统将把任务时间间隔放置到名为DeltaT的输出标签中。
定时模式参数TimingMode被设置为0。
AxeBot机器人:全方位自主移动机器人的机械设计 毕业论文外文翻译

AxeBot Robot: The Mechanical Design for an Autonomous Omni directional Mobile RobotTiago P. do Nascimento, Augusto Loureiro da Costa, Cristiane Correa Paim Post-graduation Program in Electrical EngineeringUniversidade Federal da BahiaSalvador, Bahia, Brasiltiagopn@, augusto.loureiro@ufba.br, cpaim@ufba.brAbstractThe AxeBot robot‟s mechanical design, a fully autonomous mobile robot, for the RoboCup Small Size League, is presented in this paper. The AxeBot robot uses three omnidirectional wheels for movement and is equipped by a shooting device for shooting the ball in different directions. Once the AxeBot robot is a fully autonomous mobile robot all the sensors, engines, servos, batteries, and the computer system, must be embedded on. The project can be separated in four different parts: the chassis design, the wheel design, the shooting device design and the overall assembly which makes a shell design possible to cover the whole robot. The AxeBot mechanical design brings up a new chassis concept for three wheels omnidirectional robot, also present a new shooting device, and finally present AxeBots prototype assembly.1. IntroductionThe RoboCup Initiative is an international research group whose aims are to promote the fields of Robotics and Artificial Intelligence. A standard challenge, a soccer match performed by autonomous robot teams, was proposed in 1996 [1]. Initially with three different leagues 2D: Robot Soccer Simulation league, Small Size Robot league, and Middle Size Robot league. Nowadays these leagues have been increased up to: Four-Legged League, Humanoid League, Middle Size League, RoboCup Junior Soccer, Small Size League, Soccer Simulation, Standard Robot League. Also, another challenge, the RoboCup Rescue was proposed in 1999 to show that the result from the robot soccer research could be directly applied on a real world problem like a disaster rescue made by robots. Through the integration of technology and advanced computer algorithms, the goal of RoboCup is to build a team of humanoid robots that can beat the current World Cup champions by the year 2050. The AxeBot uses three omnidirectional wheels, positioned on a circle with an angle of 120o among each wheel, to move in different directions. Three Maxxon A-22 motors are used to drive the omnidirectional wheels, one motor per wheel. These motors are controlled by two Brainstem Moto 1.0 and a cascade controller made to control the robot trajectory [2] [3]. The AxeBot also holds a shooting device to kick the ball in different directions, a Vision System with a CMUCam Plus and GP202 Infra-red sensor [4], a embedded Computer System based on StrongArm, called StarGate Kit and a IEEE 802.11 wireless network card. This work presents the mechanical project to enclose these equipments into an fully autonomous omnidirectional robot calledAxeBot. The complete AxeBot dynamics and kinematics model can be found in [5], this model was used to specify some mechanical parameter, like the wheel diameter.2. The ChassisThe chassis of the robot is the frame to which all other components can be attached, directly or indirectly. Therefore the chassis must be strong enough to carry the weight of all parts when the robot is in rest o in movement. The chassis has to withstand the forces on it, caused by the acceleration of the robot as well. Another important requirement of the chassis is that it fixes all components in a stiff way, so that there will be small relative displacements of the components within the robot, during acceleration and deceleration. This is particular important for the three driving motors, which are positioned on the ground plane with an angle of 120o between each motor. The performance of the control of the robot is dependent on a precise and stiff placement of the motors [6]. The chassis has to be strong enough also to withstand a collision of the robotagainst the wall or against another robot, with the highest possible impact velocity that can occur. Finally the chassis has to be built with the smallest amount of material. At first to reduce the costs, and to minimize the total weight of the robot. Less weight requires less power to accelerate. So with the same motors, less weight gives you more acceleration. This is of course only true, when all the power generated by the motors can be transferred, via the wheels, to the ground. In other words, the wheels must have enough traction that there will be no slip between the wheels and the ground [7].2.1. MaterialFiberglass was used to build the chassis. This choice is purely financial, because the material is not expensive (although it is strong) and there is no need to hire a professional constructor. The building of all the chassis (six in total) can be done by the team members themselves. Only the moulds have to be built by a professional. The upper and lower chassis can be made using one mould that can be adjusted to produce the different chassis.2.2. DesignThe primary goal of the design is the fixation of the motors in the desired positions. Therefore a ground plate with 3 slots for the motors is modeled. At the front side each motor can be attached to the chassis. At the rim of the ground plate an edge is attached to give the chassis more torsion stiffness. This edge can also be used for attaching other components of the robot, like the covering shell. Also there is a cutout to create space for the shooting device of the robot. In section 5 the design of this device will be discussed. However no final design will be presented and therefore we stick with this assumption that the shooting device needs these cutouts. All edges are rounded, because this will make the construction of the easier part. The final part, the lower chassis, is shown in the figure below. This part is modeled in Solid Edge. To get a stiffer and stronger chassis, a second chassis part, the upper chassis, is modeled. This is almost an exact copy of the first part, only now there are 3 cutouts that provide more space for placing the components of the robot. These cutouts also save some material and therefore weight. The both parts are This sandwich construction gives thewhole chassis more stiffness, and so the total thickness of both the chassis can probably be lower than using one chassis part.Figure 1: Lower chassisFigure 2: Upper and lower chassis attached to each other2.3. Chassis mouldTo build these parts, a mould was made. This is just a negative of the actual robot parts. In figure 3 the mould of the upper chassis. To change this mould in the mould for the lower chassis, where the ground plate does not have holes, the indicated pieces (with white stripes) and the not indicated left piece (symmetric to the most right part) should be lowered 4 mm. For the upper and lower chassis, the basis mould is exactly the same. Only piece one and two are different for the two chassis, the motor piece and the shooting system piece are the same.Figure 3: Chassis mould3. WheelsThe AxeBot robot is equipped with three wheels positioned on a circle with an angle of 120°among attached to each other as shown in the picture below.each wheel. These wheels have to enable the omnidirectionality of the AxeBot robot. This means that the wheels have to be able to let the robot make two translational movements (in x and y-direction, see figure 4) without rotating the robot around its z-axis (the axis perpendicular to the y and x-axis, that is rotation in figure 4). The wheels have also to enable a rotation of the total robot around the z-axis.Figure 4: AxeBot wheels positionsNevertheless, the wheels have to be as small and light as possible to minimize weight and moment of inertia but still remain usable and manageable. The wheels are based on an existing design of an omnidirectional wheel from the Cornell Robot 2003 [8]. Figure 5 shows an exploded view the final version of a wheel. The two shells are connected to each other by screws and hold every part on the right place. The hub is also attached to the shells by screws. The hub is mounted on the output axle of a motor by a screw to transfer the rotational output of a motor to the wheel. The rings of the rollers are in contact with the floor. A roller can rotate around its roller axle.As mentioned above, the wheel has to enable two translations (x and y, see figure 4) without rotating around its z-axis. The whole wheel ensures one translation by rotating around the output shaft of the motors while the rollers ensure the other translation. Combining these translations on a proper way a robot can move anywhere in a plane or make a rotation.3.1. RingThe ring is the only part of the wheel that is in contact with the floor. Note that a wheel can also be in contact with the floor by two rings. To obtain maximum grip (no slip) the Cornell Robot 2003 team first developed rollers without rings. The rollers had sharp edges to cut into the carpet of the football fieldfor maximum grip. This however ruined the carpet and rubber rings were added in the design to obtain maximum grip without ruining the carpet. The rings are circular with a circular profile.Figure 5: Exploded view of the wheelTherefore the rubber rings are also used for the AxeBot 2006. Rubber rings can be bought in several sizes and since they are highly elastic it wasn‟t difficult to find a ring of a right size. Since there are more than one …right sizes‟ and the geometry of the ring is that simple, no technical drawing of the ring was made.3.2. RollerThe geometry of the rollers may not restrict the rotation of the roller and should enable the placement of the rubber ring, without the ring falling off. This can be easily obtained (see drawings). The only problem is friction with their axles and with the shells.The geometry of the rollers can influence the friction with the shells and the friction with its roller axle. To minimize the possibility of wear on the contact area between the roller and the roller axle, this contact area should be as big as possible.When the torque of the motor is transferred through a roller to the ground (driving the robot), the roller that is on the ground is pressed against the shells. It will occur often that, in this situation, the desired driving direction also requires a rotation of the roller (then the summation of the two translational movements will results in the desired driving direction). The rotating roller is, in this situation, pressed against the shells which, in some cases, can result in wear of the roller and or the shells. This depends on the material of the roller, the material of the shell, the magnitude of the force which presses the surfaces on each other (in this case it is the torque of the motor) and the geometry of both contact surfaces. Only the materials and geometry can be chosen in the design process of the wheels.A small contact area results in low friction but possible wear of one of the two surfaces and though materials have to be used to avoid wear. A large contact area will not cause wear but will result in a large friction force. An optimum for the contact area and the materials has to be found. The geometry has to be machinable also. Problems that are mentioned above did not occur with the design of the rollers of the Cornell Robot 2003. Therefore the same geometry for the rollers is used for the AxeBot.The Cornell Robot 2003 team designed a wheel with 15 rollers that worked very well. Therefore also 15 rollers are used in each wheel of the AxeBot 2006.The prototypes of the wheels of the Cornell Robot 2003 first had Delrin rollers to minimize friction and weight. Delrin is a kind of plastic which is used with moving contact surfaces because of its low friction coefficients with other materials. After a few test with the prototype robot it became clear that the Delrin-rollers easily broke with a collision. Therefore the Cornell Robot 2003 was equipped with aluminum rollers. These were strong enough to withstand collisions and aluminum has a low density (compared to other metals).However, during other prototype tests of the Cornell Robot 2003 team some aluminum residue built up on the steel rollers axles. The Cornell Robot 2003 did not encounter problems due to the wearing of the aluminum rollers, but to optimize the design of the AxeBot wheels this problem was solved.To avoid wearing of the aluminum rollers other material for the axles can be used or the rollers can be made of a tougher material. After a few calculations it became clear that roller axles of Delrin (to reduce the friction) are strong enough (see the section about the axles), but it is not possible to produce thin bars of Delrin. Therefore steel axles are used, the same material as the roller axles of the Cornell Robot 2003.So to avoid wear of the rollers a more though material than aluminum has to be used for the rollers. Steel is more though and an easily obtainable and cheap material. Adisadvantage of steel compared to aluminum is its higher density. This will increase the moment of the inertia which …costs‟ more torque of the motor. The total moment of inertia of a wheel with steel rollers is 1.39×10−4kgm2 and the moment of inertia of a wheel with aluminum rollers is 1.30×10−4kgm2. Using steel rollers instead of aluminum rollers would increase the moment of inertia by 7 this increase is neglectable small and steel rollers can be used.Concerning friction, using steel rollers and steel axles is also better than using aluminum rollers and steel axles since the friction-coefficient between steel and steel is lower than that between steel and aluminum. A lubricant can also be used to even more reduce friction.3.3. Roller axleAs mentioned above, the use of Delrin for the roller axles was investigated since it would reduce the wear of the aluminum rollers. In a static situation was calculated whether Delrin axles of 2.4 mm diameter would be strong enough. This was also done in a dynamical situation (dropping the robot on the floor and landing on one roller), but without using a Finite Element Method this did not result in realistic results. When the total weight of 3.5 kg of one AxeBot 2006 would completely be on one roller axle this would result in a shear stress in the axle.In this situation the shear stress can be calculated by dividing the force on the axle (due to the weight of the AxeBot) by the area of the shear plane. The area of the shear plane is of course the area of a circle with a radius similar to the radius of the axles. Note that the weight of the AxeBot has to be divided by two since there are two shear planes in one axle.The magnitude of the shear stress would be 3.8 MPa. Delrin starts to plastically deform in due to shear at around 44 MPa. Statically, Delrin axles would be strong enough.However, this calculation was not necessary it became clear that it is not possible to produce Delrin bars of 2.5 mm (diameter). Therefore steel axles will be used (aluminum axles would result in more friction). To reduce friction, the axles were coated with a lubricant like carbon. Lubricants like carbon are easily available.The Cornell robot team 2003 documentation does not mention problems of wear of their polycarbonate shells due to their steel roller axles. As one can be read further down this section, the shells of the AxeBot wheels will be made of aluminum or polycarbonate. The coefficient of friction between aluminum (shells) and steel (axles) and between polycarbonate (shells) and steel (axles) are of equal sizes (about 0.45 [-]). Also, the geometry of the wheels of the Cornell robot and the AxeBot are almost the same. Therefore it is most likely that wearing due to friction will not be a problem with steel roller axles and polycarbonate or aluminum shells.Production the axles can easily be made out of a steel bar. Depending on the available diameters of steel bars, the diameter of the axles could be adjusted. The edges of the axles are rounded to avoid sharp corners.3.4. HubThe hub connects the wheel to the axle of the motor. A M2-bolt can be used for this purpose, the hole in the hub where this bolt will be placed is dimensioned 1.5 mm indiameter so screw thread can be made to fit in the M2-bolt. The hub is connected to the shells by three M3-screws. Corresponding holes of 2.5 mm will be made in the hub and the shells. The geometry of the hub can be changed to facilitate the production process. The hub can be made out of aluminum or polycarbonate, both light materials. To investigate the option (and price) of injection moulding the hub out of polycarbonate a sketch of a design for a mould has been made.3.5. ShellsAlmost the all geometry of the shells of the Cornell Robot 2003 is used. Only little changes in the slots for the rollers of the axles have been made to facilitate the production process of the shells. In the section about the production of the shells a different design for the slots of the axles is presented to make the production of the shells easily.The shells can be made out of aluminum or a though, light plastic like polycarbonate. The Cornell Robot had shells of polycarbonate. The best machinable material is preferred, and the one used on the AxeBot‟s shell. Wh en using a plastic that can be injection molded, molds have been designed to check the prices of injection moulding.4. Shooting DeviceThis design consists of a vertical arm (the kick arm), that can swing around an axle which is fixed to the robot. This movement will be actuated by one of the two servos, the kicking servo, that is also fixed to the robot. The other servo, the directional servo, is attached to the bottom of the kick arm (the servosocket). A pendulum-like system is formed, so a large mass is concentrated in the lower part of a rotating arm. The kicking servo has a kicking plate attached to it which can rotate and thereby makes it possible to shoot in different directions. The kicking plate can be positioned very accurately since servos are designed for these kinds of tasks. The kicking plate is also connected to the servosocket. Therefore the collision force between the ball and the kicking plate will be guided to and divided by these two connection points. There will be less bending in the kicking platethen with one connection point and smaller reaction forces will act on the connection points.Figure 6: The AxeBot shooting device5. Shell and AxeBot AssemblyThe shell is the cover of the total robot. It will be made from fiberglass as well, for the same reasons as stated in the section about the chassis. In the figure below the design of the shell is shown. There are cutouts to make room for the wheels as well as for the shooting device. The diameter of the shell is 178 mm. Because the maximum allowable diameter is 180 mm, a margin of 2 mm is created.On top of the shell a vision system will be mounted. For the sake of compactness of the robot the height should be as small as possible, with all the parts fitting in. Thismould can be built with the simple milling machine that is available.To assemble the robot the most important demand is to obtain a total centre of gravity that has the lowest possible position in the robot. This will give the robot positive driving abilities. Another demand is of course that all the parts fit in the maximum height of 150 mm.To check this, all the parts of the robot have been modeled in Solid Edge. In figure 7 an exploded view of the total robot assembly is shown.The robot consists of an upper and lower chassis. Three motors with three omnidirectional wheels are attached to it. On the bottom of the robot, the two battery packs are placed, because these parts have the largest mass. The three motor processors are attached to two general processors. Also the overall processor with the data-transfer-unit is assembled. The latter parts are assembled in a way that is most compact. With this assembly it is possible for all parts to fit in a shell with height of 100 mm.A model for the shell of the robot is designed. Also a molt to produce these parts is modeled. It is possible to produce this model by using the milling machine that is available at the university. The assembly of all the parts, except the shooting device, shows that a shell height of 100 mm is possible.Figure 7: Exploded view of the total robot assemblyFigure 8: Total robot assembly6. ConclusionThe AxeBot mechanical design, a fully autonomous mobile robot, for the RoboCup Small Size League, was presented in this paper. This mechanical design brings up a new concept of chassis for three wheels omnidirectional mobile for RoboCup F-180 league, that can be built easily and cheap. Also a new effectuator mobile robot design for RoboCup F-180 league is presented here. This new effectuator allows the mobile robot to shoot the ball in different directions, instead of just shoot a head like the othershooting devices. Finally the mechanical project presented here encloses all part, sensor, actuators, effectuator, computer systems, wheels, chassis and cover shell into the AxeBot prototype. The AxeBot robot was concept for academical proposes, using the robot soccer as a laboratory to research in Autonomous Mobile Robots, Artificial Intelligence and related areas. Looking forward, in a few months, four more AxeBots are expected to be built like the two in figure 9. These robots will form the MecaTeam F-180, and height of 100 mm is possible.will support our research in to multi-robot systems, as it can be seen in figure 9 below.Figure 9: AxeBot photo7. References[1] Kitano, H. “Robocup: The robot world cup initiative”. In: Proc. of The First International Conference on Autonomous Agent (Agents-97)). Marina del Ray, The ACM Press. 1997.[2] Franco, A. C. “Geração e controle de tra jetória de robôs móveis omni-direcionais”, Master‟s thesis, Programa de Pós-Graduação Mecatrônica, UFBA. 2007.[3] PIRES, E. J. S.; MACHADO, J. A. T.; OLIVEIRA, P. B. de M. “Robot trajectory planning using multi-objective genetic algorithm optimization”. In: DEB, K. et al. (Ed.). GECCO (1). [S.l.]: Springer, 2004. (Lecture Notes in Computer Science, v. 3102), p.615-626. ISBN 3-540-22344-4.[4] Oliveira, L. R., Costa, A. L., Schnitman, L. and Souza, J. “An architecture of sensor fusion for spatial locat ion of objects in mobile robotics”, in B. H. Spring-Verlag (ed.), Encontro Português de Inteligência Artificial, EPIA‟2005, Covilhã, 2005. pp. 462–473.[5] Nascimento, T. P., Costa, A. L., Paim, C. C. “Uma abordagem multivariável para modelagem de robôs móveis omnidirecionais”, XVI CBA - Congresso Brasileiro de Automação. 2008.[6] ANGELES, J. “Fundamentals of Robotic Mechanical Systems: Theory, Methods, and Algorithms”. 2. ed. New York: Springer-Verlag New York, Inc., 2003. [7] B. Carter, M. Good, M. Dorohoff, J. Lew, R. L. W. II, and P. Gallina, “Mechanical design and modeling of an omni-directional robocup player,” in Proceedings RoboCup 2001 International Symposium, (Athens, Ohio), pp. 1–10, 2001.[8] Anderson, G., Chang, C., Chung, D., Evansic, L., Law, H., Richardson, S., Robers, J., Sterk, K. and Yim, J. 2003 cornell robocup, mechanical group final documentation, Technical report, /. 2003.翻译:AxeBot机器人:全方位自主移动机器人的机械设计摘要:这篇文章中介绍了一个用来参与机器人世界杯小尺寸等级比赛的完全自主移动AxeBot机器人的机械设计。
基于内模控制的PID在过程控制中的应用研究毕业论文

毕业设计报告(论文)基于内模控制的PID在过程控制中的应用研究所属系化工与制药工程系专业化学工程与工艺学号06110341姓名王大林指导教师陈夕松起讫日期2014.1---2014.5设计地点东南大学四牌楼校区动力楼119东南大学成贤学院毕业设计报告(论文)诚信承诺本人承诺所呈交的毕业设计报告(论文)及取得的成果是在导师指导下完成,引用他人成果的部分均已列出参考文献。
如论文涉及任何知识产权纠纷,本人将承担一切责任。
学生签名:日期:基于内模控制的PID在过程控制中的应用研究摘要内模控制是基于过程数学模型而进行控制器设计的一种新型控制策略。
内模控制具有很多优点,如设计简单,控制性能好,性能分析优越等。
随着工业过程自动化的普及,过程控制越来越受到控制界的广泛关注。
内模控制就是其中之一,它是以控制内部数学模型为基础,通过控制内部模型来达到控制整个系统稳定,进而达到工业过程生产指标的要求。
所以内模控制不仅是一种先进的控制算法,而且是研究预测控制模型的控制策略的重要理论基础!本论文基于东南大学过程控制实验室HGK-1型过程控制实验平台,以该平台中的液位过程为研究对象,设计基于可编程序控制器(PLC)的过程控制系统,采用内模控制(IMC)算法,仿真并实验研究IMC在该过程中的应用效果。
通过本次学习掌握IMC原理及算法,为以后在工作中的工程实际应用打下良好的铺垫!论文在介绍了HGK-1型过程控制实验平台后,阐述了液位过程建模的方法和特点。
在机理建模,试验建模和混合建模中选用试验建模方法建立了被控过程的数学模型。
设计液位过程PLC控制系统,包括液位计、流量计、调节阀、PLC输入/输出模块的接线,以及与PC机间的通讯连接。
仿真比较了IMC-PID控制及IMC的动态与静态性能。
为进一步提高控制系统的动静态性能,设计采用串级IMC控制方案,既提高了系统的动态特性,又保证了系统的稳态精度。
编写基于PLC的IMC应用软件,以及基于PC上位机的应用组态软件,实现液位过程的自动控制和监督管理,仿真和实验证明了该方案的有效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.1 PID 控制:SmartAHU 控制系统中温湿度的控制是根据较为成熟的PID 算法为模型。
01Output()()()tp d i de t K e t e t dt T T dt ⎛⎫=++ ⎪⎝⎭⎰e 代表偏差(输入量-设定值),用这个值进行PID 运算,控制被控对象(制冷系统),再由被控对象的输出量反馈回来重新计算偏差,这样循环反复,直到被控量达到所要求的允差内(死区)。
如下图:.下图显示出了PID 系统的响应曲线:控制输出是由这三个部分组成的,它们对最终的输出结果的作用各有不同:∙ 比例调节作用:是按比例反应系统的偏差,系统一旦出现了偏差,比例环节就立即产生调节作用以减小偏差。
它影响系统反应速度;增大比例作用会加快反应速度并减小稳态误差,但是也会使系统变得更加不稳定(增大了超调量)。
基本参数:比例常数Kp。
∙积分调节作用:消除稳态误差,提高无差度:只要有偏差,积分环节就会进行调节,直至无差,积分调节才会停止,此时积分调节会输出一常值。
但是加入积分调节会使系统稳定性下降,动态反应速度变慢。
积分作用常与另外两种调节规律结合,组成PI调节器或PID调节器。
基本参数:积分常数Ki= Ts / Ti(Ti:积分时间,Ts:采样时间)。
∙微分调节作用:反应系统偏差信号的变化率,具有预见性,能预见偏差变化的趋势,因此能够产生超前的控制作用,在偏差还没有形成之前就已被微分调节作用消除。
因此,可以改善系统的动态性能。
在微分作用选择合适的情况下,可以减少超调,减少调节时间。
但是微分作用对干扰有放大作用,因此加入过强的微分调节会对系统抗干扰不利。
此外,微分反应的是变化率,而当输入没有变化时,微分作用输出为零。
微分作用不能单独使用,需要与另外两种调节规律相结合,组成PD或者PID控制器。
简单的说就是可以抑制快速变化,因此会增加系统稳定性,可以在保持同一稳定性的情况下增大另外两种作用。
基本参数:微分常数Ki=Ti/Ts(Td的:微分时间,Ts:采样时间)。
PID算法的几个重要参数:比例常数Kp,积分常数Ti,微分常数Td,这几个常数的不同组合就会产下图显示了同一超调量下的不同控制方式的响应曲线:通过选择这三种作用的重要参数值,使控制输出得到最优的效果,这个过程称为PID控制的参数整定。
PID的最佳整定参数一般采用现场经验工程整定法。
现场经验工程整定法是人们在长期工作工程实践中,从各种控制规律对系统控制质量的影响的定性分析总结出来的一种行之有效、并得到广泛应用的工程整定方法。
在现场整定过程中,要保持PID参数按先比例,后积分,最后微分的顺序进行,在观察现场过程值过程变量的趋势曲线的同时,慢慢的改变PID参数,进行反复测试,直到控制质量符合要求为止。
下面详细介绍这种整定方法。
工程整定法实行先比例、后积分、再微分的反复调整。
其步骤如下:1)整定比例部分先置PID控制器中的Ti=∞、Td=0,使之成为比例P控制器,再将比例系数由小变大,观察相应的响应,使系统的过渡过程达到4:1的衰减振荡和较小的静差。
如果系统静差已小到允许范围内,并且已达到4:1衰减的响应曲线,那么只需用比例控制器既可,最优比例度就由此确定。
2)加入积分环节如果只用比例控制,系统的静差不能满足要求,则需加入积分环节。
整定时,先将比例系统减小10-20%,以补偿因加入积分作用而引起的系统稳定性下降,然后由大到小调节,在保持系统良好动态性能的情况下消除静差。
这一步可以反复进行,以期得到满意的效果。
3)加入微分环节在整定时,先置Td为零,然后,在第2步整定的基础上再增大T,同时相应地改变比例系数K和积分时间Ti,逐步试凑以获得的控制效果和控制参数。
在进行PID参数整定时可以参考书上的常用口诀:参数整定找最佳,从小到大顺序查;先是比例后积分,最后再把微分加;曲线振荡很频繁,比例度盘要放大;曲线漂浮绕大湾,比例度盘往小扳;曲线偏离回复慢,积分时间往下降;曲线波动周期长,积分时间再加长;曲线振荡频率快,先把微分降下来;动差大来波动慢,微分时间应加长;理想曲线两个波,前高后低4比1;一看二调多分析,调节质量不会低。
1.1.2 基于PID调节的串级控制:为了达到更好的控制性能,SmartAHU控制系统也采用了串级控制作为可选的另一种控制方法。
在这个应用里,主回路用于控制室内温度(湿度) ;副回路用于控制供风温度(湿度)。
串级控制是两个控制回路的相互作用,串级控制利用主回路的输出值来操作副回路的设定点就像它是最终的控制元件一样。
这样它就凭借减小输入源端的扰动来减小系统延迟时间以提高系统的性能。
在串级控制里,主副两个回路都是闭环的。
为了适当的操作,副回路必须比主回路反应快。
而且,如果两个回路控制器(调节器)都有积分作用的话,就可能产生积分饱和(reset windup)现象。
所以在许多串级控制应用中,副回路只用P控制器就足够了。
下图是串级控制与传统PID控制的对比图(对扰动的反应)这样你可以看到串级控制系统的反应速度要比传统PID控制快得多。
单凭增大传统PID控制的参数不一定能够使其反应更快。
串级控制原理方块图如下:简化一下变成如下:在此应用中,主回路由室内温度调节部分(PID1)、室内温度传感器(变送器1) 、室内温度调节器room temperature djuster(执行器1) ,供风温度设定点作为控制器的输出变量和整个房间构成的控制系统。
所以,供风温度作为主回路控制器的操作变量值y 。
为了补偿室内温度的偏离,供风温度设定点是随之变化的,它没有去驱动执行器动作。
副回路由供风温度设定点、供风温度传感器(变送器2)、供风温度控制器(PID2)、热水阀(执行器2) 作为执行器来构成控制系统。
如果P控制器作为主回路控制器而且PI控制器作为副回路控制器的话,整个控制系统则构成一个P+PI 串级控制系统。
串级控制过程如下:•主回路控制器通过传感器获得室内温度。
倘若设定点没有发生偏移,副控制器(PI- 控制器) 使供风温度保持恒定在通过室内温度控制器使用供风温度传感器所指定的设定点keeps the supply air temperature constant at the setpoint specified by the room temperature controller using the supply air temperature sensor。
供风温度扰动被供风温度传感器感知并且被副回路控制器所修正,这样它们就能够影响到室内温度。
Supply air temperature disturbances are detected by the supply air temperature sensor and corrected by the slave controller, independent of the load, before they can affect the room temperature. 实际上,供风温度扰动在未对室内温度产生影响之前已经被抑制了,这样就使主回路控制器的任务变得简单一些,它现在只需要对发生在房间内本身的扰动做补偿即可。
•In case of a deviation of the room temperature from the setpoint,为防止室内温度与设定点偏离,主控制器(P-控制器) 将与控制偏差和设定串级影响成比例地反向改变供风温度设定点shifts the supply air temperature setpoint in the opposite direction in proportion to the control deviation and the set cascade influence.例如,串级影响为20%,则供风温度变化必须比室内温度偏移量地5倍多,With a cascade influence of 20 %, for example, the supply air temperature variation must be five times greater than the room temperature deviation that occurred, 即如果室内温度在设定点之下下降了1℃,供风温度设定点就会被在给定值之上提升5℃。
i.e. if the room temperature falls 1 K below the setpoint, the supply air temperature setpoint is raised 5 K over the set value . •副回路控制器通过传感器获得供风温度,并与新设定点进行比较,调整阀的开度直到重新达到所需的供风温度。
The slave controller acquires the supply air temperature via the sensor, compares it with the new setpoint, and adjusts the valve until the required supply air temperature is reached again•Being a P-controller, 作为一个P-控制器,主回路控制器经常不能完全纠正室内温度的扰动;所以就会有一个成比例的偏移存在。
the master controller cannot usually fully correct a room temperature disturbance; a proportional offset remains. 但是在P+PI 串级控制里,这个成比例的偏移与单P-控制器的要小得多,因为供风温度设定点被副级PI控制器精确地维持着。
cascade control, however, the proportional offset is considerably smaller than with P-control only, because the supply air temperature setpoint is maintained precisely by thePI slave controller. Additionally, since the transfer coefficient KS of room controlled systems is usually < 0.5, the gain of the room temperature controller can be set relatively high. In practice, this means a maximum proportional offset of < 1 K.另外,既然室内控制系统地传递系数Ks经常小于0.5,室内温度控制器地增益可以被设置得相应高些。
