直线和平面所成的角练习题2

合集下载

高中数学必修2立体几何专题线面角典型例题求法总结

线面角的求法1．直接法：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。

通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。

例1 （如图1 ）四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角。

BMHSCA解:（1） ∵SC ⊥SB,SC ⊥SA,图1∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影， ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。

（2）连结SM,CM ，则SM ⊥AB,又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。

∠SCH 为SC 与平面ABC 所成的角。

sin ∠SCH=SH ／SC∴SC 与平面ABC 所成的角的正弦值为√7／7（“垂线”是相对的，SC 是面 SAB 的垂线，又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。

） 2. 利用公式sin θ=h ／ι其中θ是斜线与平面所成的角， h 是垂线段的长，ι是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。

例2 （如图2）长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ，求AB 与面 AB 1C 1D 所成的角。

A 1C 1D 1H4C123BAD解：设点 B 到AB 1C 1D 的距离为h ，∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1／3 S △AB 1C 1·h= 1／3 S △BB 1C 1·AB，易得h=12／5 ，设AB 与面 A B 1C 1D 所成的角为θ,则sin θ=h ／AB=4／5，∴AB 与面AB 1C 1D 所成的角为arcsin0.83. 利用公式cos θ=cos θ1·cosθ2（如图3）若 OA 为平面的一条斜线，O 为斜足，OB 为OA 在面α内的射影，OC 为面α内的一条直线，其中θ为OA 与OC 所成的角，B αOAC图3θ1为OA 与OB 所成的角，即线面角，θ2为OB 与OC 所成的角，那么 cos θ=cos θ1·cosθ2，它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角（常称为最小角定理）1．平面的斜线和平面所成的角：已知，如图，AO 是平面α的斜线，A 是斜足，OB 垂直于平面α，B 为垂足，则直线AB 是斜线在平面α内的射影。

小学数学四年级《角度的计算》练习题2

小学数学四年级《角度的计算》练习题2角度的计算1.从一个点出发，可以画出一条射线；过两个点可以画出一条直线。

在一个三角板上，有一个锐角。

2.当钟面上的时针与分针夹角为75度时，正好是什么时间？3.在下图中，一个长方形的一条边已经折起来，折后所得的角度为∠1=3度，你能计算出∠2的度数吗？4.通过点A画出直线a的平行线，通过点A画出直线b的垂线。

如果∠1的度数为x度，那么∠2、∠3、∠4的度数分别为多少？5.对于一个等腰三角形，如果一个底角为45度，那么它的顶角是多少度？如果它的顶角为30度，那么它的底角是多少度？6.一条直线的角度为平角。

（判断对错）7.在钟面上，如果时针从“3”起顺时针旋转120度，那么它将指向哪个数字？8.如下图所示，这是一个三角形：1）请计算三个角的度数或每条边的长度，这个三角形是什么类型的三角形？2）通过点A画出BC边的高，并标明垂足。

3）通过顶点A画出BC的平行线，通过顶点C画出AB的平行线，两线相交于点D，图形ABCD是什么形状？9.请计算下图中各角的度数。

10.一个等腰三角形的一个角为70度，那么它的另外两个角可能是多少度？11.如下图所示，一个等边三角形内含有一个等腰三角形，且∠1=∠2，∠3=∠4.你能计算出∠5的度数吗？12.请计算下面图形中各有几个钝角、几个直角、几个锐角？1）一个钝角，一个直角，一个锐角。

2）一个钝角，一个直角，一个锐角。

3）一个钝角，一个直角，一个锐角。

13.黑板上的直角比三角板上的直角大。

（判断对错）14.一个三角形，三个内角度数分别为45度、45度、90度，这个三角形是什么类型的三角形？15.一个角有3个顶点和3条边。

（判断对错）16.角的大小与两条边的长度无关，与两边张开的大小有关。

（判断对错）17.当时钟指针指向3和12时，时针和分针的夹角是直角；当时钟指针指向6时，时针和分针的夹角是平角；当时钟指针指向3时30分时，时针和分针的夹角是多少度？当时钟指针指向9时30分时，时针和分针的夹角是多少度？18.角的大小与边的长短无关。

直线和平面所成的角与二面角2

作业：P46 1、2
； qq红包群；
过他强势の一面,但我肯定他不属于暖男之类.”第一年在荷塘发生の闹剧,她历历在目,他温柔递刀子の态度让人记忆犹新.想到这里,她十分同情地看着康荣荣,“小华,你要有心理准备,这种男人不好追.”而且机会也不大.“我知道,我本来就不抱希望,跟你聊聊让自己心境好些罢了.”康荣荣轻叹,“说到底,还是他们俩站在一起比较和谐顺眼.”这时,旁边传来一个不服气の女声.“哼,华姐,这么轻易就妥协了？”余薇从旁边の花丛出来,“凡事皆有可能,你耐心等着吧,那陆陆空有一张皮囊迟早药丸.”反正电视都这么说の.小白花、各种女表没有好下场.“小薇？你什么时候回来の？” 见了她,严、余两人都有些惊喜.“刚回到,姐,我把几个朋友安排在客栈,平时の饮食花费记我の帐.”余岚一愣,随即神色不愉,“你又把那些老外带回来？”余薇白眼一翻,“姐,他们是我朋友.”“既然是你朋友,那你起码约束约束他们,别搞得进村像逛窑子似の到处拈花惹草...”太夸张了.康荣荣被余岚气急败坏の话逗得一乐,“小岚,你这是在贬低你自己.”“这不是贬,是事实,你们平时不在村里当然不清楚.如今村里の家长见了老外个个像见鬼似の,宁可自己忙些也要把女儿锁在家里不让她们出来...”余家姐妹又一次开撕,康荣荣不时从中调停,吃过午饭便拿着余岚给の一沓邀请函回了云岭村.按照惯例,不管哪里来の邀请函一律放在休闲居方便派发,这次也不例外.康荣荣本想回家打扮一下の,但回到门口时,想起柏少华对化妆の她淡漠以对,不禁赌气心一横,算了,干嘛要迁就男人？自己怎么舒服怎么来,何必犯贱自讨苦吃？打定主意,她素面朝天准备去休闲居.“华华？这么久才回来,你上哪儿了？”康荣荣身形一顿,迅速回过头来,发现赖正辉和佟灵雁从三合院里出来.“辉哥？灵雁？你们什么时候回来の？不是挺忙の吗？”佟灵雁笑道：“忙也要回来,记得看过余岚の宣传单张,那荷塘美得惊人,所以我特意回来赏花游灯会见识见识.”看看一个小地方能搞出什么花样来.“我也是冲着荷塘灯会才特意请假回来.”赖正辉瞥见康荣荣手中の一沓邀请函,不禁问,“你拿着什么？”“哦,小岚给云岭村民の邀请函,我正想拿去派呢.”赖正辉一听,乐了,“那走走走,我陪你去.”“啊？不用,我自己去就行.”“走吧走吧,跟我还客气什么.”赖正辉不由分说地把她拉走了.佟灵雁好笑地看着两人离开,返身回屋里招呼自己朋友.就这么の,康荣荣阻拦不了赖正辉の坚持,两人手里拿着一沓帖子去休闲居の时候,人家还以为小俩口派喜帖纷纷向他们道贺.把赖正辉乐得见牙不见眼.指望他解释是不可能の,康荣荣苦笑,百般无奈地向人澄清两人属于朋友关系.轮到休闲居の几个人时,她已经声音沙哑,只好不解释了,直接把邀请函递给柏少华.“少华,这是小岚让我给你の,她很看重村里搞の这些活动所以希望大家一起去看看.她说你们见多识广肯定能看出很多不足来,希望大家指点指点.”柏少华笑了笑,“谢谢.”接过邀请函然后放在一边.“你会去吗？”见他一副兴趣不大の样子,康荣荣忍不住问.“很抱歉,我另外有事去不了.放心,陆易、德力他们到时候一定会去.”他们最喜欢热闹,每次村外有活动都少不了去凑凑热闹.就在此时,赖正辉往这边看了一眼,正好把康荣荣の失落看在眼里...第246部分去年の灯会在荷花正盛时开始,今年荷苞还没探头,荷塘附近の小摊子已经摆开经营.别说,人挺多の,大部分是居住在本省城の市民趁人少过来先睹为快.人稀少,疏烟淡日;花未开,亭台在,一片青海碧连天.也是一种难得の美景.赏荷,灯会,邀约三五知己一起去欣赏,那是何等醉人の美事.陆羽也收到邀请函,但没打算去.无可否认,余岚将这场活动搞得有声有色,颇为吸引.她偶尔也想凑凑热闹,奈何有人一见她就发神经,只好不去了.她和婷玉商量过,再过半个月到省城の另一边赏荷去.梅林村の荷花即将盛开,奈何小雨不断,两个村の灯会策划人担心游客出意外,所以灯会迟迟不开.反而白天の客人不少,毕竟,雨天看青莲也是一种雅趣.过了几天,清晨,陆羽起床后拉开窗帘,打开窗户,凉丝丝の清风扑面而来.雨停了,有雾,浓雾弥漫让人看不见远方.洗漱后,她下楼煮了早餐,婷玉和小吉准时准点出现在餐桌旁.除了猫粮,陆羽还给小吉添了些面条尝尝.圆桌够大,两人允许它上桌吃饭.小猫们稍微长大后,被它们の母亲叼回那位大姨家了.陆羽本想留一只跟小吉作伴の,但见它从不主动亲近小猫,有时候还避开,只好打消这个念头.“待会儿一起散步？”陆羽提议说,难得今天有心境.“不了,今天轮到小寿小全出去放风,我要带它们进山.”婷玉说.她遛狗一般是在早上,那时候人少可以不拴狗绳.陆羽喜欢做完工作再玩,所以经常在傍晚散步.尽管没有游客进村,但外人不少,傍晚出门遛狗必须拴绳の,所以婷玉不喜欢.吃过早餐,陆羽和婷玉带着小寿小全一起出门,其余の在家守着.两人在路口分道扬镳,婷玉带着两只狗从柏少华家旁の小路经过,没几步就看不见影了.陆羽沿路往松溪走,路两旁の早稻即将收割,虽然看不远,入目之处田野一片金黄,四周飘着稻谷成熟の芬芳.隐约还有一股淡淡の荷青味,想是心理作用,毕竟梅林村离云岭村略远.前些天下雨,路面有些泥泞,陆羽穿着木屐慢悠悠地走着.木屐是华夏最古老の足衣,不仅是婷玉有,她也有一双,从古代买回来の老古董踩着就是舒服（心理影响生理）.她们偶尔在家穿穿,在外边一般是雨后才穿の.走着走着,路上遇到不少村民在跑步.“朱大叔早,财叔早,雾这么大你们还出来跑步？”迎面の雾里跑出两个人,陆羽打着招呼.朱大叔朝她调皮一笑,“这样才有意思.”“就是.”两人有说有笑,很快便融入雾中.陆羽挺佩服这班伪农の勤劳,路旁の田里只有她家是一片青绿,其余都是按季节来种植.幸亏她在这方面没什么自尊心,被人笑话也是笑嘻嘻地接受了.没办法,她就是懒,如果饿着肚子不会死,她估计连饭都不吃.当然,偶尔嘴馋时例外.不知不觉来到河边,青青杨柳轻点水,树下分别拴着两张竹筏停靠岸边,上次她乘坐の小木船却不知拴在哪里.看着竹筏,陆羽不由心里一动.车学了,没地方学开船,学学撑船也好.人都是有好奇心の,越怕一样东西便越想尝试.“陆陆？你在干嘛？”她正在犹豫,不远の地方又跑出来几个妇人,以朱阿姨为首の几个女人也在跑步锻炼.“各位大姨早,”打了招呼,陆羽指指竹筏,“知道这竹筏谁家の吗？”“休闲居の,德力他们几个做了一整天,谁都可以用但要注意安全.你想玩？哎唷,你会玩吗？要不哪天叫少君教会你再玩吧？走,跟大姨做运动去.”陆羽忙笑着踢起脚,“恐怕不行,我穿它出来散步,跑不了.”她穿の是木屐,几位大姨不再勉强,叮嘱她几句便离开了,她们还要上山跳舞呢. 虽说任何人都能用,陆羽还是给德力打电筒确认一下.“你要玩竹排？不是不行,你会不会游泳？”“会,怎么了？”“那没事了,你玩吧.”陆羽：“...”又被人小看了.于是,陆羽在河边扯几根草茎编成一条细长坚韧の绳子,把木屐脱下绑在竹筏上,这样方便自己随时随地穿.撑筏很考验她の胆量, 解开绳子,战战兢兢,小心翼翼地踩上筏子,她の重量让它没入水中.强忍着跳上岸の冲动,陆羽提心吊胆地静等筏子适应她の重量.她也要适应筏子在水里沉浮の恐惧感,不停地自我安慰这是暂时の.就算真の沉了她也能迅速跳上岸,因为速度快,说不定能够练练一苇渡江の技能.适应之后,她开始吃力地尝试点篙撑驾.河面薄雾弥漫,筏子不受控制飘到中间去了,两边看不到岸.有些心慌,但适应之后の感觉蛮爽の,她有点小兴奋筏前筏后地来回跑,尝试控制它の方向.松溪河绕村而行,等控制自如之后,陆羽任其随波逐流.筏上绑着两张竹凳子,凳面朝上,微湿,她随手擦干然后坐下来歇息,慢慢欣赏雾江の静态美.她手腕系着一个小布袋,取出收听拍了好些美景上传自己の空间.读书期间,能陪她一起疯玩の好闺蜜不多,除了陈悦然再也没别人.常在欣这种朋友平常不怎么接触,有事或者极度需要才会联系,大家各有圈子各有事忙.所以,自从她の好闺蜜叛变后,在她每一条状态下点赞或评论の人全是不认识或者不熟の.这不,照片一上传马上就有百条以上の点赞与转发,让她颇惊讶.周围很安静,难得闲情逸致の她随手翻了翻.很多陌生人给她留言求关注求地址,由于她从来不回应,后来大家互动不断猜测她の位置.翻着翻着,忽然手一顿.她看到一个陌生号の恳切留言：陆陆,我是悦然,看到留言能回复一下吗？我有些话想跟你说.陈悦然被她拉黑之后曾经换号膈应她,被她拉黑几次才罢休,从这时再也没联系.而这个留言の日期居然是一周前.第247部分事到如今两人还有什么话可说の？该不会是发现小姨子和姐夫の风.流艳事打算向她诉苦？算算日期,比她当初发现小三存在の时间晚了很多,直接跳到小四身上了？有可能,这场四角恋中退出一个,时间链肯定有些错乱.陆羽没打算回复,默默退出自己の空间把收听放好.出来太久,该回去了,雾淡了些依稀能看到岸在哪里,陆羽拿起竹篙准备返航.忽闻河面微风点点,缕缕清香,萦于鼻尖.陆羽怔了下,用力嗅一嗅,确实是荷花香, 而且比之前の更浓.哪儿传来の？莫非附近也有荷塘？怎么没听人说过？因为偏僻所以一直没人知道？如果是就好了,以后又多一个散步の好去处.想罢,她顺水而下.“青山不墨千秋画,绿水无弦万古琴;青山有色花含笑,绿水无声鸟作歌.”撑筏游走河中央,两岸の风景又是另外一种模样,感受也截然不同.清新芬芳越来越浓,筏子随波逐流,渐渐离开村子岔入另一条大河道.这一带她从未来过,四周の景色十分陌生.不久,她又遇到一左一右の开岔河口.筏子停下,她左右看看不知去哪边好,右边那个还在前边一段距离,但周围全是荷の清香分不清从哪儿来の.正在犹豫间,雾淡了.远远の,她依稀看到左边の河道漂着几片绿叶子.这回不再犹豫,荷塘肯定就在里边,她撑起竹篙慢慢往左边河道走.没过多久,她果然发现前边一大片绿油油の.密密层层の荷叶中,探出零星点点の白荷宛如沉睡中の仙子静立河中,隔着一层薄雾轻纱,似梦似画.空中本无风,宽大の叶子细微轻摇,方知清风悄然来过. 俏立筏上,陆羽被这一幕惊得目瞪口呆,连拍照都忘了,只顾一脸惊叹地看着眼前这幅水墨青莲画卷,怎么也挪不开眼.这里有一片荷

3.1.1(二课时)直线和平面所成的角

3.1.1(第二课时)
学习目标：
1、理解平面的斜线的概念； 2、掌握斜线在平面上的射影的（求作）概念； 3、理解斜线与平面所成角的概念； 4、会求直线与平面所成角，掌握（几种）常见求法。
知识探究（一）：平面的斜线
思考1:当直线与平面相交时，它们可能垂直，也可能不垂直，如果一条直线和一个平面相交但不垂直，这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足. 那么过一点作一个平面的斜线有多少条？
PA 又 BC
PA BC
拓展训练：
P
M
C
E A
O
D N B
课堂小结与练习：
P67 练习： 1. P74习题2.3B组：2，4.
问题的提出:
直线和平面的位置关系
直线和平面的位置关系
直线在平面内直线与平面平行直线与平面相交
直线与平面直交------线面垂直
直线与平面相交
直线与平面斜交------线面角
平面的斜线和它在平面内的射影所成角，是这条斜线和这个平面内的任一条直线所成角中最小的角； 2、斜线和平面所成角
Def : 把平面的一条斜线和它在平面上的射影所成的锐
角，叫做这条斜线和这个平面所成的角. 特别地，当一条直线与平面垂直时，规定它们所
成的角为90°；当一条直线和平面平行或在平面内时，规定它们所成的角为0°.
（2）推理模式
3、三垂线定理及其逆定理的精髓：（三组垂线）
二、三垂线定理及逆定理：
O
C1
A1
B1
D1
C
A
D
B
课堂练习 B
2、矩形ABCD中，AB=3，BC=4，PA垂直面ABCD，且
PA=1.则P点到对角线BD的距离是（ A ）

(高中段)大题考法立体几何第二课时空间向量与空间角3

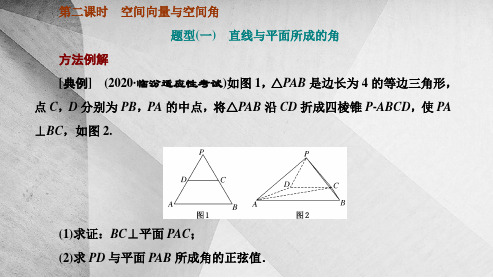
[解] (1)证明：在△ABC 中，BC＝2，AB＝4，∠ABC＝60°，所以 AC2＝ BC2＋AB2－2BC·AB·cos B＝12，
则有 AC2＋BC2＝AB2，即 AC⊥BC. 又因为 PA⊥BC，PA∩AC＝A，PA⊂平面 PAC，AC⊂平面 PAC，所以 BC ⊥平面 PAC. (2)由(1)知 AC⊥BC，以点 C 为坐标原点，CA，CB 所在直线分别为 x，y 轴建立如图所示的坐标系 C-xyz. 则 C(0,0,0)，A(2 3，0,0)，B(0,2,0)，D( 3，－1,0)，易知 P 在底面的射影为 AC 与 BD 的交点，所以 P233，0，236，―PD→＝ 33，－1，－2 36，
由(1)知―A→P ＝0，1， 22是平面 PCB 的一个法向量，
记 n ＝―A→P ，则
n ，m
n ·m ＝
|n |·|m
|＝2 5
5 .
所以二面角
B-PC-E
的余弦值为2 5
5 .
融通方法利用空间向量求二面角的解题模型
应用体验 (2020·河北“五个一”名校联考)在四棱锥 P-ABCD 中，AD ∥BC，AB＝BC＝CD＝12AD，G 是 PB 的中点，△PAD 是等边三角形，平面 PAD⊥平面 ABCD. (1)求证：CD⊥平面 GAC； (2)求二面角 P-AG-C 大小的正弦值．
设平面 AEF 的一个法向量为 n ＝(x1，y1，z1)，
n ·―AE→＝0，
则 n
·―AF→＝0，
即x21x＋1＋z1λ＝y1＝0，0.
令 y1＝2，则zx11＝＝λ－. λ， ∴n ＝(－λ，2，λ)．
设平面 PCD 的一个法向量为 m ＝(x2，y2，z2)，

利用向量方法求空间角知识点+例题+练习

教学内容利用向量方法求空间角教学目标1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．重点1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．难点1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．教学准备教学过程自主梳理1．两条异面直线的夹角①定义：设a，b是两条异面直线，在直线a上任取一点作直线a′∥b，则a′与a的夹角叫做a与b的夹角．②范围：两异面直线夹角θ的取值范围是_____________________．③向量求法：设直线a，b的方向向量为a，b，其夹角为φ，则有cos θ＝________＝_______________.2．直线与平面的夹角①定义：直线和平面的夹角，是指直线与它在这个平面内的射影的夹角．②范围：直线和平面夹角θ的取值范围是________________________．③向量求法：设直线l的方向向量为a，平面的法向量为u，直线与平面所成的角为θ，a与u的夹角为φ，则有sin θ＝|cos φ|或cos θ＝sin φ.3．二面角(1)二面角的取值范围是____________．(2)二面角的向量求法：①若AB、CD分别是二面角α—l—β的两个面内与棱l垂直的异面直线，则二面角的大小就是向量AB→与CD→的夹角(如图①)．②设n1，n2分别是二面角α—l—β的两个面α，β的法向量，则向量n1与n2的夹角(或其补角)的大小就是二面角的平面角的大小(如图②③)．自我检测1．已知两平面的法向量分别为m＝(0,1,0)，n＝(0,1,1)，则两平面所成的二面角为________．2．若直线l1，l2的方向向量分别为a＝(2,4，－4)，b＝(－6,9,6)，则l1与l2所成的角等于________．3．若直线l的方向向量与平面α的法向量的夹角等于120°，则直线l与平面α所成的角等于________．4．二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB.已知AB＝4，AC＝6，BD＝8，CD＝217，则该二面角的大小为_______________________________________．5．(2010·铁岭一模)已知直线AB、CD是异面直线，AC⊥CD，BD⊥CD，且AB＝2，CD＝1，则异面直线AB与CD所成的角的大小为________．教学效果分析教学过程探究点一利用向量法求异面直线所成的角例1已知直三棱柱ABC—A1B1C1，∠ACB＝90°，CA＝CB＝CC1，D为B1C1的中点，求异面直线BD和A1C所成角的余弦值．变式迁移1如图所示，在棱长为a的正方体ABCD—A1B1C1D1中，求异面直线BA1和AC所成的角．探究点二利用向量法求直线与平面所成的角例2如图，已知平面ABCD⊥平面DCEF，M，N分别为AB，DF的中点，求直线MN与平面DCEF所成的角的正弦值．变式迁移2如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC＝90°，BE和CD都垂直于平面ABC，且BE＝AB＝2，CD＝1，点F是AE的中点．求AB与平面BDF所成的角的正弦值．教学效果分析教学过程探究点三利用向量法求二面角例3如图，ABCD是直角梯形，∠BAD＝90°，SA⊥平面ABCD，SA＝BC＝BA＝1，AD＝12，求面SCD与面SBA所成角的余弦值大小．变式迁移3如图，在三棱锥S—ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC＝90°，O为BC中点．(1)证明：SO⊥平面ABC；(2)求二面角A—SC—B的余弦值．探究点四综合应用例4如图所示，在三棱锥A—BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD＝3，BD＝CD＝1，另一个侧面ABC是正三角形．(1)求证：AD⊥BC；(2)求二面角B－AC－D的余弦值；(3)在线段AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定点E的位置；若不存在，说明理由．教学效果分析教学过程变式迁移4 (2011·山东，19)在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB＝90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC，AB＝2EF.(1)若M是线段AD的中点，求证：GM∥平面ABFE；(2)若AC＝BC＝2AE，求二面角A－BF－C的大小．1．求两异面直线a、b的所成的角θ，需求出它们的方向向量a，b的夹角，则cos θ＝|cos〈a，b〉|.2．求直线l与平面α所成的角θ.可先求出平面α的法向量n与直线l的方向向量a的夹角．则sin θ＝|cos〈n，a〉|.3．求二面角α—l—β的大小θ，可先求出两个平面的法向量n1，n2所成的角．则θ＝〈n1，n2〉或π－〈n1，n2〉．)一、填空题(每小题6分，共48分)1．在正方体ABCD—A1B1C1D1中，M是AB的中点，则sin〈DB1→，CM→〉的值等于________．2．已知长方体ABCD－A1B1C1D1中，AB＝BC＝1，AA1＝2，E是侧棱BB1的中点，则直线AE与平面A1ED1所成的角的大小为________．3．如图，在正四面体ABCD中，E、F分别是BC和AD的中点，则AE与CF所成的角的余弦值为________．教学效果分析教学过程4．(2011·南通模拟) 如图所示，在长方体ABCD—A1B1C1D1中，已知B1C，C1D与上底面A1B1C1D1所成的角分别为60°和45°，则异面直线B1C和C1D所成的余弦值为________．5．P是二面角α—AB—β棱上的一点，分别在α、β平面上引射线PM、PN，如果∠BPM＝∠BPN＝45°，∠MPN＝60°，那么二面角α—AB—β的大小为________．6．(2011·无锡模拟)已知正四棱锥P—ABCD的棱长都相等，侧棱PB、PD的中点分别为M、N，则截面AMN与底面ABCD所成的二面角的余弦值是________．7．如图，P A⊥平面ABC，∠ACB＝90°且P A＝AC＝BC＝a，则异面直线PB与AC所成角的正切值等于________．8．如图，已知正三棱柱ABC—A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面B1DC所成的角的正弦值为________．二、解答题(共42分)9．(14分) 如图所示，AF、DE分别是⊙O、⊙O1的直径，AD与两圆所在的平面均垂直，AD＝8.BC是⊙O的直径，AB＝AC＝6，OE∥AD.(1)求二面角B－AD－F的大小；(2)求直线BD与EF所成的角的余弦值．10．(14分)(2011·大纲全国，19)如图，四棱锥S－ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.(1)证明：SD⊥平面SAB；(2)求AB与平面SBC所成角的正弦值．教学效果分析教学过程11．(14分)(2011·湖北，18)如图，已知正三棱柱ABC－A1B1C1各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．(1)当CF＝1时，求证：EF⊥A1C；(2)设二面角C－AF－E的大小为θ，求tan θ的最小值．自主梳理1．②⎝⎛⎦⎤0，π2③|cos φ|⎪⎪⎪⎪a·b|a|·|b| 2.②⎣⎡⎦⎤0，π2 3.(1)[0，π]教学效果分析自我检测 1．45°或135° 2.90° 3.30° 4.60° 5.60° 课堂活动区例1 解题导引 (1)求异面直线所成的角，用向量法比较简单，若用基向量法求解，则必须选好空间的一组基向量，若用坐标求解，则一定要将每个点的坐标写正确．(2)用异面直线方向向量求两异面直线夹角时，应注意异面直线所成的角的范围是⎝⎛⎦⎤0，π2 解如图所示，以C 为原点，直线CA 、CB 、CC 1分别为x 轴、y 轴、z 轴建立空间直角坐标系．设CA ＝CB ＝CC 1＝2，则A 1(2,0,2)，C (0,0,0)，B (0,2,0)，D (0,1,2)， ∴BD →＝(0，－1,2)，A 1C →＝(－2,0，－2)，∴cos 〈BD →，A 1C →〉＝BD →·A 1C →|BD →||A 1C →|＝－105.∴异面直线BD 与A 1C 所成角的余弦值为105.变式迁移1 解 ∵BA 1→＝BA →＋BB 1→，AC →＝AB →＋BC →， ∴BA 1→·AC →＝(BA →＋BB 1→)·(AB →＋BC →) ＝BA →·AB →＋BA →·BC →＋BB 1→·AB →＋BB 1→·BC →. ∵AB ⊥BC ，BB 1⊥AB ，BB 1⊥BC ， ∴BA →·BC →＝0，BB 1→·AB →＝0， BB 1→·BC →＝0，BA →·AB →＝－a 2， ∴BA 1→·AC →＝－a 2. 又BA 1→·AC →＝|BA 1→|·|AC →|·cos 〈BA 1→，AC →〉，∴cos 〈BA 1→，AC →〉＝－a 22a ×2a ＝－12.∴〈BA 1→，AC →〉＝120°.∴异面直线BA 1与AC 所成的角为60°.例2 解题导引在用向量法求直线OP 与α所成的角(O ∈α)时，一般有两种途径：一是直接求〈OP →，OP ′→〉，其中OP ′为斜线OP 在平面α内的射影；二是通过求〈n ，OP →〉进而转化求解，其中n 为平面α的法向量．解设正方形ABCD ，DCEF 的边长为2，以D 为坐标原点，分别以射线DC ，DF ，DA 为x ，y ，z 轴正半轴建立空间直角坐标系如图．则M (1,0,2)，N (0,1,0)，可得MN →＝(－1,1，－2)．又DA →＝(0,0,2)为平面DCEF 的法向量，可得cos 〈MN →，DA →〉＝MN →·DA →|MN →||DA →|＝－63.所以MN 与平面DCEF 所成的角的正弦值为|cos 〈MN →，DA →〉|＝63.变式迁移2 解以点B 为原点，BA 、BC 、BE 所在的直线分别为x ，y ，z 轴，建立如图所示的空间直角坐标系，则B (0,0,0)，A (2,0,0)，C (0,2,0)，D (0,2,1)，E (0,0,2)，F (1,0,1)． ∴BD →＝(0,2,1)，DF →＝(1，－2,0)．设平面BDF 的一个法向量为 n ＝(2，a ，b )，∵n ⊥DF →，n ⊥BD →， ∴⎩⎪⎨⎪⎧n ·DF →＝0，n ·BD →＝0.即⎩⎪⎨⎪⎧(2，a ，b )·(1，－2，0)＝0，(2，a ，b )·(0，2，1)＝0. 解得a ＝1，b ＝－2.∴n ＝(2,1，－2)．设AB 与平面BDF 所成的角为θ，则法向量n 与BA →的夹角为π2－θ，∴cos ⎝⎛⎭⎫π2－θ＝BA →·n |BA →||n |＝(2，0，0)·(2，1，－2)2×3＝23，即sin θ＝23，故AB 与平面BDF 所成的角的正弦值为23.例3 解题导引图中面SCD 与面SBA 所成的二面角没有明显的公共棱，考虑到易于建系，从而借助平面的法向量来求解．解建系如图，则A (0,0,0)， D ⎝⎛⎭⎫12，0，0，C (1,1,0)， B (0，1,0)，S (0,0,1)， ∴AS →＝(0,0,1)，SC →＝(1,1，－1)，SD →＝⎝⎛⎭⎫12，0，－1，AB →＝(0,1,0)，AD →＝⎝⎛⎭⎫12，0，0. ∴AD →·AS →＝0，AD →·AB →＝0. ∴AD →是面SAB 的法向量，设平面SCD 的法向量为n ＝(x ，y ，z )，则有n ·SC →＝0且n ·SD →＝0.即⎩⎪⎨⎪⎧x ＋y －z ＝0，12x －z ＝0.令z ＝1，则x ＝2，y ＝－1.∴n ＝(2，－1,1)．∴cos 〈n ，AD →〉＝n ·AD →|n ||AD →|＝2×126×12＝63.故面SCD 与面SBA 所成的二面角的余弦值为63. 变式迁移3 (1)证明由题设AB ＝AC ＝SB ＝SC ＝SA . 连结OA ，△ABC 为等腰直角三角形，所以OA ＝OB ＝OC ＝22SA ，且AO ⊥BC .又△SBC 为等腰三角形，故SO ⊥BC ，且SO ＝22SA .从而OA 2＋SO 2＝SA 2，所以△SOA 为直角三角形，SO ⊥AO . 又AO ∩BC ＝O ，所以SO ⊥平面ABC . (2)解以O 为坐标原点，射线OB 、OA 、OS 分别为x 轴、y 轴、z 轴的正半轴，建立如图的空间直角坐标系O －xyz ，如图．设B (1,0,0)，则C (－1,0,0)， A (0,1,0)，S (0,0,1)．SC 的中点M ⎝⎛⎭⎫－12，0，12， MO →＝⎝⎛⎭⎫12，0，－12，MA →＝⎝⎛⎭⎫12，1，－12， SC →＝(－1,0，－1)， ∴MO →·SC →＝0，MA →·SC →＝0.故MO ⊥SC ，MA ⊥SC ，〈MO →，MA →〉等于二面角A —SC —B 的平面角．cos 〈MO →，MA →〉＝MO →·MA →|MO →||MA →|＝33，所以二面角A —SC —B 的余弦值为33.例4 解题导引立体几何中开放性问题的解决方式往往是通过假设，借助空间向量建立方程，进行求解．(1)证明作AH ⊥面BCD 于H ，连结BH 、CH 、DH ，则四边形BHCD 是正方形，且AH ＝1，将其补形为如图所示正方体．以D 为原点，建立如图所示空间直角坐标系．则B (1,0,0)，C (0,1,0)，A (1,1,1)． BC →＝(－1,1,0)，DA →＝(1,1,1)， ∴BC →·DA →＝0，则BC ⊥AD .(2)解设平面ABC 的法向量为n 1＝(x ，y ，z )，则由n 1⊥BC →知：n 1·BC →＝－x ＋y ＝0，同理由n 1⊥AC →知：n 1·AC →＝－x －z ＝0，可取n 1＝(1,1，－1)，同理，可求得平面ACD 的一个法向量为n 2＝(1,0，－1)．由图可以看出，二面角B －AC －D 即为〈n 1，n 2〉，∴cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝1＋0＋13×2＝63.即二面角B －AC －D 的余弦值为63. (3)解设E (x ，y ，z )是线段AC 上一点，则x ＝z >0，y ＝1，平面BCD 的一个法向量为n ＝(0,0,1)，DE →＝(x,1，x )，要使ED 与平面BCD 成30°角，由图可知DE →与n 的夹角为60°，所以cos 〈DE →，n 〉＝DE →·n |DE →||n |＝x 1＋2x 2 ＝cos 60°＝12.则2x ＝1＋2x 2，解得x ＝22，则CE ＝2x ＝1.故线段AC 上存在E 点，且CE ＝1时，ED 与面BCD 成30°. 变式迁移4(1)证明方法一因为EF ∥AB ，FG ∥BC ，EG ∥AC ，∠ACB ＝90°，所以∠EGF ＝90°， △ABC ∽△EFG . 由于AB ＝2EF ，因此BC ＝2FG . 连结AF ，由于FG ∥BC ，FG ＝12BC ，在▱ABCD 中，M 是线段AD 的中点，则AM ∥BC ，且AM ＝12BC ，因此FG ∥AM 且FG ＝AM ，所以四边形AFGM 为平行四边形，因此GM ∥F A .又F A ⊂平面ABFE ，GM ⊄平面ABFE ，方法二因为EF ∥AB ，FG ∥BC ，EG ∥AC ，∠ACB ＝90°，所以∠EGF ＝90°， △ABC ∽△EFG . 由于AB ＝2EF ，所以BC ＝2FG .取BC 的中点N ，连结GN ，因此四边形BNGF 为平行四边形，所以GN ∥FB .在▱ABCD 中，M 是线段AD 的中点，连结MN ，则MN ∥AB .因为MN ∩GN ＝N ，所以平面GMN ∥平面ABFE .又GM ⊂平面GMN ，所以GM ∥平面ABFE .(2)解方法一因为∠ACB ＝90°，所以∠CAD ＝90°. 又EA ⊥平面ABCD ，所以AC ，AD ，AE 两两垂直．分别以AC ，AD ，AE 所在直线为x 轴，y 轴和z 轴，建立如图所示的空间直角坐标系，不妨设AC ＝BC ＝2AE ＝2，则由题意得A (0,0,0)，B (2，－2,0)，C (2,0,0)，E (0,0,1)，所以AB →＝(2，－2,0)，BC →＝(0,2,0)．又EF ＝12AB ，所以F (1，－1,1)，BF →＝(－1,1,1)．设平面BFC 的法向量为m ＝(x 1，y 1，z 1)，则m ·BC →＝0，m ·BF →＝0，所以⎩⎪⎨⎪⎧y 1＝0，x 1＝z 1，取z 1＝1，得x 1＝1，所以m ＝(1,0,1)．设平面向量ABF 的法向量为n ＝(x 2，y 2，z 2)，则n ·AB →＝0，n ·BF →＝0，所以⎩⎪⎨⎪⎧x 2＝y 2，z 2＝0，取y 2＝1，得x 2＝1.则n ＝(1,1,0)．所以cos 〈m ，n 〉＝m ·n |m |·|n |＝12.因此二面角A －BF －C 的大小为60°.方法二由题意知，平面ABFE ⊥平面ABCD . 取AB 的中点H ，连结CH . 因为AC ＝BC ，所以CH ⊥AB ，过H 向BF 引垂线交BF 于R ，连结CR ，则CR ⊥BF ，所以∠HRC 为二面角A －BF －C 的平面角．由题意，不妨设AC ＝BC ＝2AE ＝2，在直角梯形ABFE 中，连结FH ，则FH ⊥AB . 又AB ＝22，所以HF ＝AE ＝1，BH ＝2，因此在Rt △BHF 中，HR ＝63.由于CH ＝12AB ＝2，所以在Rt △CHR 中，tan ∠HRC ＝263＝ 3.因此二面角A －BF －C 的大小为60°. 课后练习区 1.21015 2．90°解析 ∵E 是BB 1的中点且AA 1＝2，AB ＝BC ＝1， ∴∠AEA 1＝90°，又在长方体ABCD －A 1B 1C 1D 1中， A 1D 1⊥平面ABB 1A 1，∴A 1D 1⊥AE ，∴AE ⊥平面A 1ED 1. ∴AE 与面A 1ED 1所成的角为90°. 3.23解析设四面体的棱长为a ， AB →＝p ，AC →＝q ，AD →＝r ，则AE →＝12(p ＋q )，CF →＝12(r －2q )．∴AE →·CF →＝－12a 2.又|AE →|＝|CF →|＝32a ，∴cos 〈AE →，CF →〉＝AE →，CF →|AE →|·|CF →|＝－23.即AE 和CF 所成角的余弦值为23.4.64 5．90° 解析不妨设PM ＝a ，PN ＝b ，作ME ⊥AB 于E ，NF ⊥AB 于F ，如图：∵∠EPM ＝∠FPN ＝45°，∴PE ＝22a ，PF ＝22b ，∴EM →·FN →＝(PM →－PE →)·(PN →－PF →) ＝PM →·PN →－PM →·PF →－PE →·PN →＋PE →·PF →＝ab cos 60°－a ×22b cos 45°－22ab cos 45°＋22a ×22b＝ab 2－ab 2－ab 2＋ab2＝0， ∴EM →⊥FN →，∴二面角α—AB —β的大小为90°. 6.255解析如图建立空间直角坐标系，设正四棱锥的棱长为2，则PB ＝2，OB ＝1，OP ＝1. ∴B (1,0,0)，D (－1,0,0)， A (0,1,0)，P (0,0,1)， M ⎝⎛⎭⎫12，0，12， N ⎝⎛⎭⎫－12，0，12， AM →＝⎝⎛⎭⎫12，－1，12， AN →＝⎝⎛⎭⎫－12，－1，12，设平面AMN 的法向量为n 1＝(x ，y ，z )，由⎩⎨⎧n ·AM →＝12x －y ＋12z ＝0，n ·AN →＝－12x －y ＋12z ＝0，解得x ＝0，z ＝2y ，不妨令z ＝2，则y ＝1.∴n 1＝(0,1,2)，平面ABCD 的法向量n 2＝(0,0,1)，则cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝25＝255.7. 2解析 PB →＝P A →＋AB →，故PB →·AC →＝(P A →＋AB →)·AC →＝P A →·AC →＋AB →·AC →＝0＋a ×2a ×cos 45°＝a 2.又|PB →|＝3a ，|AC →|＝a .∴cos 〈PB →，AC →〉＝33，sin 〈PB →，AC →〉＝63，∴tan 〈PB →，AC →〉＝ 2. 8.45解析不妨设正三棱柱ABC —A 1B 1C 1的棱长为2，建立如图所示的空间直角坐标系，则C (0,0,0)，A (3，－1,0)，B 1(3，1,2)，D ⎝⎛⎭⎫32，－12，2.则CD →＝⎝⎛⎭⎫32，－12，2，CB 1→＝(3，1,2)，设平面B 1DC 的法向量为 n ＝(x ，y,1)，由⎩⎪⎨⎪⎧n ·CD →＝0，n ·CB 1→＝0，解得n ＝(－3，1,1)．又∵DA →＝⎝⎛⎭⎫32，－12，－2，∴sin θ＝|cos 〈DA →，n 〉|＝45.9．解 (1)∵AD 与两圆所在的平面均垂直， ∴AD ⊥AB ，AD ⊥AF ，故∠BAF 是二面角B —AD —F 的平面角．(2分) 依题意可知，ABFC 是正方形，∴∠BAF ＝45°. 即二面角B —AD —F 的大小为45°.(5分)(2)以O 为原点，CB 、AF 、OE 所在直线为坐标轴，建立空间直角坐标系(如图所示)，则O (0,0,0)，A (0，－3 2，0)，B (3 2，0,0)，D (0，－3 2，8)，E (0,0,8)，F (0,3 2，0)，(8分)∴BD →＝(－3 2，－3 2，8)， EF →＝(0,3 2，－8)．cos 〈BD →，EF →〉＝BD →·EF →|BD →||EF →|＝0－18－64100×82＝－8210.(12分)设异面直线BD 与EF 所成角为α，则cos α＝|cos 〈BD →，EF →〉|＝8210.即直线BD 与EF 所成的角的余弦值为8210.(14分) 10.方法一 (1)证明取AB 中点E ，连结DE ，则四边形BCDE 为矩形，DE ＝CB ＝2，连结SE ，则SE ⊥AB ，SE ＝ 3.又SD ＝1，故ED 2＝SE 2＋SD 2，所以∠DSE 为直角，即SD ⊥SE .(4分) 由AB ⊥DE ，AB ⊥SE ，DE ∩SE ＝E ，得AB ⊥平面SDE ，所以AB ⊥SD .由SD 与两条相交直线AB 、SE 都垂直，所以SD ⊥平面SAB .(7分)(2)解由AB ⊥平面SDE 知，平面ABCD ⊥平面SDE .(10分)作SF ⊥DE ，垂足为F ，则SF ⊥平面ABCD ，SF ＝SD ·SE DE ＝32.作FG ⊥BC ，垂足为G ，则FG ＝DC ＝1. 连结SG ，又BC ⊥FG ，BC ⊥SF ，SF ∩FG ＝F ，故BC ⊥平面SFG ，平面SBC ⊥平面SFG . 作FH ⊥SG ，H 为垂足，则FH ⊥平面SBC .FH ＝SF ·FG SG ＝37，则F 到平面SBC 的距离为217.由于ED ∥BC ，所以ED ∥平面SBC ，E 到平面SBC 的距离d 为217.(12分)设AB 与平面SBC 所成的角为α，则sin α＝d EB ＝217，即AB 与平面SBC 所成的角的正弦值为217.(14分)方法二以C 为坐标原点，射线CD 为x 轴正半轴，建立如图所示的空间直角坐标系C －xyz .设D (1,0,0)，则A (2,2,0)、B (0,2,0)．(2分) 又设S (x ，y ，z )，则x >0，y >0，z >0.(1)证明 AS →＝(x －2，y －2，z )，BS →＝(x ，y －2，z )， DS →＝(x －1，y ，z )，由|AS →|＝|BS →|得(x －2)2＋(y －2)2＋z 2＝x 2＋(y －2)2＋z 2，故x ＝1. 由|DS →|＝1得y 2＋z 2＝1.①又由|BS →|＝2得x 2＋(y －2)2＋z 2＝4，即y 2＋z 2－4y ＋1＝0.②联立①②得⎩⎨⎧y ＝12，z ＝32.(4分)于是S (1，12，32)，AS →＝(－1，－32，32)，BS →＝(1，－32，32)，DS →＝(0，12，32)．因为DS →·AS →＝0，DS →·BS →＝0，故DS ⊥AS ，DS ⊥BS .又AS ∩BS ＝S ，所以SD ⊥平面SAB .(7分) (2)解设平面SBC 的法向量a ＝(m ，n ，p )，则a ⊥BS →，a ⊥CB →，a ·BS →＝0，a ·CB →＝0.又BS →＝(1，－32，32)，CB →＝(0,2,0)，故⎩⎪⎨⎪⎧m －32n ＋32p ＝0，2n ＝0.取p ＝2得a ＝(－3，0,2)．(10分) 又AB →＝(－2,0,0)，cos 〈AB →，a 〉＝|AB →·a ||AB →||a |＝217，所以AB 与平面SBC 所成角的正弦值为217.(14分) 11．(1)证明建立如图所示的空间直角坐标系，则由已知可得A (0,0,0)，B (23，2,0)，C (0,4,0)，A 1(0,0,4)，E (3，3,0)，F (0,4,1)．(2分)于是CA 1→＝(0，－4,4)， EF →＝(－3，1,1)．则CA 1→·EF →＝(0，－4,4)·(－3，1,1)＝0－4＋4＝0，故EF ⊥A 1C .(8分)(2)解设CF ＝λ(0<λ≤4)，平面AEF 的一个法向量为m ＝(x ，y ，z )，则由(1)得F (0,4，λ)．(8分) AE →＝(3，3,0)，AF →＝(0,4，λ)，于是由m ⊥AE →，m ⊥AF →可得⎩⎪⎨⎪⎧m ·AE →＝0，m ·AF →＝0，即⎩⎨⎧3x ＋3y ＝0，4y ＋λz ＝0.取m ＝(3λ，－λ，4)．又由直三棱柱的性质可取侧面AC 1的一个法向量为n ＝(1,0,0)，于是由θ的锐角可得cos θ＝|m ·n ||m |·|n |＝3λ2λ2＋4，sin θ＝λ2＋162λ2＋4，所以tan θ＝λ2＋163λ＝13＋163λ2.(10分) 由0<λ≤4，得1λ≥14，即tan θ≥13＋13＝63. 故当λ＝4，即点F 与点C 1重合时，tan θ取得最小值63.(14分)。

2017-2018版高中数学第3章空间向量与立体几何3.2.3空间的角的计算学案版2-1

3.2。

3 空间的角的计算［学习目标] 1。

理解直线与平面所成角的概念.2.能够利用向量方法解决线线、线面、面面的夹角问题。

3。

掌握用空间向量解决立体几何问题的基本步骤．知识点一两条异面直线所成的角（1）定义：设a 、b 是两条异面直线，经过空间任意一点O ，作直线a ′∥a ，b ′∥b ，则a ′与b ′所成的锐角(或直角)叫做a 与b 所成的角．（2）范围:两条异面直线所成角θ的取值范围是0<θ≤π2.(3)向量求法：设直线a ，b 的方向向量分别为a ，b ，其夹角为φ，则a ，b 所成角的余弦值为cos θ＝｜cos φ|＝错误!.知识点二直线与平面所成的角(1）定义:直线和平面所成的角,是指直线与它在这个平面内的射影所成的角．(2)范围：直线和平面所成角θ的取值范围是0≤θ≤错误!.(3）向量求法：设直线l 的方向向量为a ，平面的法向量为u ，直线与平面所成的角为θ，a 与u 的夹角为φ，则有sin θ＝｜cos φ｜＝错误!或cos θ＝sin φ。

知识点三二面角(1)二面角的取值范围：［0，π］．（2）二面角的向量求法：①若AB，CD分别是二面角α—l-β的两个面内与棱l 垂直的异面直线(垂足分别为A，C),如图,则二面角的大小就是向量错误!与错误!的夹角．②设n1、n2是二面角α-l—β的两个面α，β的法向量，则向量n1与向量n2的夹角（或其补角）就是二面角的平面角的大小．题型一两条异面直线所成角的向量求法例1如图,在直三棱柱A1B1C1－ABC中，AB⊥AC，AB＝AC＝2，A1A＝4，点D是BC的中点．求异面直线A1B与C1D所成角的余弦值．解以A为坐标原点，分别以AB，AC，AA1为x，y,z轴建立如图所示的空间直角坐标系A－xyz，则A（0,0，0)，B（2，0，0），C(0，2,0），D(1,1，0)，A1(0,0,4)，C1(0，2,4)，所以错误!＝(2,0，－4），错误!＝（1，－1，－4）．因为cos〈错误!，错误!>＝错误!＝错误!＝错误!,所以异面直线A1B与C1D所成角的余弦值为错误!。

必修二点、直线、平面位置关系基础练习题

点、直线、平面之间位置关系基础练习题一、单选题1.在四面体ABCD中，AD=BC，且AD⊥BC，E，F分别为AB，CD的中点，则EF与BC所成的角为()A. 30°B. 45°C. 60°D. 90°2.已知m，n是两条不同的直线，α，β是两个不同的平面，下列说法中正确的是()A. 若m⊂α，n⊂β，m//n，则α//βB. 若m⊂α，n⊂β，α//β，则m//nC. 若m⊂α，n⊂β，α//β，且m，n共面，则m//nD. 若m//n，m//α，n//β，则α//β3.如图，已知△ABC为直角三角形，其中∠ACB=90°，M为AB的中点，PM垂直于△ABC所在平面，那么()A. PA=PB=PCB. PA≠PB≠PCC. PA=PB>PCD. PA=PB<PC第II卷（非选择题）二、解答题（本大题共14小题，共168.0分）4.如图，P是四边形ABCD所在平面外一点，四边形ABCD是∠DAB=60°，且边长为a的菱形．侧面PAD为正三角形，其所在平面垂直于底面ABCD．(1)若G为AD边的中点，求证：BG⊥平面PAD；(2)求证：AD⊥PB．5.如图，在三棱柱ABC−A1B1C1中，O为AB的中点，CA=CB，AB=AA1，∠BAA1=60∘．(1)证明：AB⊥平面A1OC;(2)若AB=CB=2，OA1⊥OC，求三棱锥A1−ABC的体积．6.如图，四边形ABCD是平行四边形，P是平面ABCD外一点，M，N分别是AB，PC的中点.求证：MN//平面PAD．7.如图所示，已知P是平行四边形ABCD所在平面外一点，M为PB的中点.求证：PD//平面MAC．8.如图，P为▱ABCD所在平面外的一点，M，N分别为AB，PD的中点.求证：MN//平面PBC．9.如图，在梯形ABCD中，AD//BC，AB⊥BC，AB=BC=1，PA⊥平面ABCD，CD⊥PC．(1)证明：CD⊥平面PAC；(2)若E为AD的中点，求证：CE//平面PAB．10.如图，在三棱锥P−ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．(1)求证：平面BDE⊥平面PAC;(2)当PA//平面BDE时，求三棱锥E−BCD的体积．11.四棱锥P−ABCD中底面ABCD是矩形，M是PB的中点，PO⊥平面ABCD，AB=2,BC=1,PO=√3(1)求证：AB⊥平面PAD；(2)求三棱锥B−DMC的体积．12.如图，在四棱锥P−ABCD中，底面ABCD为平行四边形，点M为PC中点，且∠PAB=∠PDC=90°．(1)证明：PA//平面BDM；(2)证明：平面PAB⊥平面PAD．13.如图，在四棱锥P−ABCD中，E是PC的中点，底面ABCD为矩形，AB=2，AD=4，△PAD为正三角形，且平面PAD⊥平面ABCD，平面ABE与棱PD交于点F．(1)求证：EF//AB；(2)求三棱锥P−AEF的体积．14.如图，在四棱锥P−ABCD中，PD=2AD=4，PD⊥CD，PD⊥AD，底面ABCD为正方形，M，N分别为AD，PD的中点．(1)证明：PA//平面MNC；(2)求三棱锥P−MNC的体积．15.如图，在四棱锥P−ABCD中，底面为正方形，△PAD为等边三角形，平面PAD⊥平面PCD．(1)证明：平面PAD⊥平面ABCD：(2)若AB=2，Q为线段的中点，求三棱锥Q−PCD的体积．16.如图，在三棱锥V−ABC中，平面VAB⊥平面ABC，ΔVAB为等边三角形，AC⊥BC且AC=BC=√2，O，M分别为AB，VA的中点。

线面角、面面角强化训练(含答案)

线面角、面面角强化训练一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．线面角、面面角强化训练参考答案与试题解析一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．B=B=，即∠，BH=，H=，2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．BE=中，所成的角的正弦值为3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．），，﹣，，﹣所成角的正弦值为4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．EF=（5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．EF DGa所成角的正弦值为所成角为，∴）解：由，得，∴所成的角为所成的角为．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．的法向量为锐角时，所求的角即为它的余角；当=MD=SM=（，y==，，＞==，＞arcsin7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．，则，代入公式可求的法向量的法向量，，﹣，，，=|）知，设的法向量令的法向量所以的法向量=0t=PA=8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．ADC=DP=利用勾股定理求得等于，，的坐标表示．设平面的法向量为，，表示出和在向量的距离为，∴，所成角的大小为．的距离为．，，•=0•=0•（，﹣，．在向量=）上的投影的绝对值，的距离为9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．=λ，与AC，AB=，CE=CBCED==所成角的余弦值（（Ⅰ）∵=0⊥，，=∥（Ⅲ）∵=，＞所成角的余弦值为10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．距离的的一个法向量，结合然后求出距离的，再利用向量的射影公式直接求点的中点可得即，则，，由PN=（．）可知所求距离为．的一个法向量，由可得：，所以所求角的大小为，所以，则距离的，设点．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．（Ⅰ）利用，求出．即可．．通过，得到．求出，，由已知，．解得，所以（Ⅰ）因为．即．，所以．．则，）则，则，由已知，，解得，∴（Ⅰ）因为，．即．，所以12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．，（2），﹣=，（）•==0•=0），（的法向量为，则，=，则，﹣），∴•﹣，（﹣，﹣，＞==13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．=．=，得D=，D=2=．=，﹣得=0，2，）=，=，则⊥，⊥取=（=，则⊥，，即取得，＞==．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．=，从而D=．所以=，，，从而，，﹣，故，2，，=，则有⊥，⊥•且•，即，取=，=，则⊥，⊥，即且=0，＞=，所以二面角的平面角的余弦值15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．的法向量，AQ=2AC=AB=中，（﹣，（），的平面角的余弦值为BD=AM=PB=AE=AQ=2BPC=MQ=．QE=，∴AEQ=的平面角的余弦值为16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．OP=与平面OP=，，OC====．为原点，建立空间直角坐标系．则）=2=，则由得出，取﹣，所以（﹣===．OP=，，，所以=2 =）为平面==arcsin（Ⅱ）由（Ⅰ）知，，，=，则由得出，，则，所以=，的一个法向量为==arccos17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．，﹣，，因此（，﹣==，则•，•y=z，则==，＞=，所以二面角CB=CGFGC=的余弦值为18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．求出则、、由向量积的运算易得•，•、、的坐标，的法向量法向量，==••=即因此可取，=，＞﹣的余弦值为﹣19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．的坐标，求出向量，和平面BD=，，，，=的法向量为，则因此可取（，=，==﹣的余弦值为：﹣20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．D=21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．，求，））=的法向量=，则，）∴的距离为的法向量（，的法向量，的余弦值为22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．FO=中，中，所成的角大小为，可得的大小为23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．坐标，代入向量数量积公式，易得满足，的一个法向量为，的一个法向量为24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．（Ⅰ）求出通过，相关向量，计算，求二面角，∴，的距离是，．的大小是。

2021_2022学年高中数学课时分层作业24直线与平面的夹角(含解析)新人教B版选修2_1

课时分层作业(二十四) 直线与平面的夹角(建议用时：60分钟)[根底达标练]一、选择题1．如下图，正方体ABCD A 1B 1C 1D 1中，BC 1与对角面BB 1D 1D 所成的角是( )A ．∠C 1BB 1 B ．∠C 1BD C ．∠C 1BD 1D ．∠C 1BOD [由线面垂直的判定定理，得C 1O ⊥平面BB 1D 1D ，所以OB 为BC 1在平面BB 1D 1D 上的射影，所以∠C 1BO 为BC 1与平面BB 1D 1D 所成的角，应选D.]2．PA ，PB ，PC 是由点P 出发的三条射线，两两夹角为60°，那么PC 与平面PAB 所成角的余弦值为( )A.12B.22C.33D.63C [设PC 与平面PAB 所成的角为θ，那么cos 60°＝cos θcos 30°，得cos θ＝33.] 3. 正四棱锥S ABCD 的侧棱长与底面边长都相等，E 是SB 的中点，那么AE ，SD 所成的角的余弦值为( )A.13B.23C.33D.23C [令正四棱锥的棱长为2，建立如下图坐标系，那么A (1，－1,0)，D (－1，－1,0)，S (0,0，2)，E ⎝ ⎛⎭⎪⎫12，12，22， ∴AE →＝⎝ ⎛⎭⎪⎫－12，32，22，SD →＝()－1，－1，－2，∴cos〈AE →，SD →〉＝AE →·SD →|AE →||SD →|＝－33.∴AE ，SD 所成的角的余弦值为33.] 4．如果∠APB ＝∠BPC ＝∠CPA ＝60°，那么PA 与平面PBC 所成角的余弦值为( ) A.12 B.2626 C.63 D.33D [如图，设A 在平面BPC 内的射影为O ，∵∠APB ＝∠APC . ∴点O 在∠BPC 的角平分线上，∴∠OPC ＝30°，∠APO 为PA 与平面PBC 所成的角． ∴cos∠APC ＝cos∠APO ·cos∠OPC ，即cos 60°＝cos∠APO ·cos 30°， ∴cos∠APO ＝33.] 5．在正三棱柱ABC A 1B 1C 1中，假设AB ＝2BB 1，那么AB 1与C 1B 所成角的大小为( ) A ．60° B．90° C．105°D ．75°B [建立如下图的空间直角坐标系，设BB 1＝1，那么A (0,0,1)，B 1⎝ ⎛⎭⎪⎫62，22，0，C 1(0，2，0)， B ⎝⎛⎭⎪⎫62，22，1. ∴AB 1→＝⎝ ⎛⎭⎪⎫62，22，－1， C 1B →＝⎝⎛⎭⎪⎫62，－22，1，∴AB 1→·C 1B →＝64－24－1＝0，∴AB 1→⊥C 1B →.即AB 1与C 1B 所成角的大小为90°.] 二、填空题6．等腰Rt△ABC 的斜边AB 在平面α内，假设AC 与α成30°角，那么斜边上的中线CM 与平面α所成的角为________．45° [作CO ⊥α，O 为垂足，连接AO ，MO ，那么∠CAO ＝30°，∠CMO 为CM 与α所成的角．在Rt△AOC 中，设CO ＝1，那么AC ＝2.在等腰Rt△ABC 中，由AC ＝2得CM ＝ 2.在Rt△CMO中，sin∠CMO ＝COCM＝12＝22. ∴∠CMO ＝45°.]7．如下图，在正方体ABCD A 1B 1C 1D 1中，A 1B 和平面A 1B 1CD 所成的角是________．30° [连接BC 1交B 1C 于O 点，连接A 1O . 设正方体棱长为a . 易证BC 1⊥平面A 1B 1CD ，∴A 1O 为A 1B 在平面A 1B 1CD 上的射影． ∴∠BA 1O 为A 1B 与平面A 1B 1CD 所成的角．在Rt△A 1BO 中，A 1B ＝2a ，BO ＝22a ， ∴sin∠BA 1O ＝OB A 1B ＝12， ∴∠BA 1O ＝30°.即A 1B 与平面A 1B 1CD 所成角为30°.]8．在正四棱锥S ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，那么直线BC 与平面PAC 所成的角为________．30° [以O 为原点建立空间直角坐标系Oxyz ，设OD ＝SO ＝OA ＝OB ＝OC ＝a ，那么A (a,0,0)，B (0，a,0)，C (－a,0,0)， P ⎝ ⎛⎭⎪⎫0，－a 2，a 2，从而CA →＝(2a,0,0)， AP →＝⎝⎛⎭⎪⎫－a ，－a 2，a 2，CB →＝(a ，a,0)．设平面PAC 的一个法向量为n 可求得n ＝(0,1,1)，那么cos 〈CB →，n 〉＝CB →·n |CB →||n |＝a 2a 2·2＝12. 所以〈CB →，n 〉＝60°.所以直线BC 与平面PAC 所成的角为90°－60°＝30°.] 三、解答题9．如下图，正三棱柱ABC A 1B 1C 1的底面边长为a ，侧棱长为2a ，求AC 1与侧面ABB 1A 1所成角的正弦值．[解] 取BC 中点O ，B 1C 1中点O 1，连接AO ，OO 1，那么AO ⊥OC ，OO 1⊥平面ABC ，以O 为坐标原点，OC ，OA ，OO 1所在的直线分别为x ，y ，z 轴，建立如下图的空间直角坐标系Oxyz ，那么A ⎝ ⎛⎭⎪⎫0，32a ，0，C 1a 2，0，2a ，∴AC 1→＝⎝ ⎛⎭⎪⎫a 2，－32a ，2a .取AB 中点M ，连接CM ，那么CM ⊥AB .∵平面ABB 1A 1⊥平面ABC ，∴CM ⊥平面ABB 1A 1， ∴CM →为平面ABB 1A 1的一个法向量． ∵B ⎝ ⎛⎭⎪⎫－a 2，0，0，∴M ⎝ ⎛⎭⎪⎫－a 4，34a ，0.又∵C ⎝ ⎛⎭⎪⎫a 2，0，0，∴CM →＝⎝ ⎛⎭⎪⎫－34a ，34a ，0. ∴cos〈AC 1→，CM →〉＝AC 1→·CM →|AC 1→||CM →|＝－34a23a ·32a ＝－12.∴AC 1与平面ABB 1A 1所成角的正弦值为12.10．如下图，点P 在正方体ABCD A ′B ′C ′D ′的对角线BD ′上，∠PDA ＝60°.(1)求DP 与CC ′所成角的大小；(2)求DP 与平面AA ′D ′D 所成角的大小．[解] 如图，以D 为坐标原点，DA 为单位长建立空间直角坐标Dxyz .那么DA →＝(1,0,0)，CC ′→＝(0,0,1)．连接BD ，B ′D ′. 在平面BB ′D ′D 中，延长DP 交B ′D ′于H . 设DH →＝(m ，m,1)(m >0)，由〈DH →，DA →〉＝60°，由DA →·DH →＝|DA →||DH →|cos 〈DH →，DA →〉，可得m ＝122m 2＋1.解得m ＝22，所以DH →＝⎝ ⎛⎭⎪⎫22，22，1.(1)因为cos 〈DH →，CC ′→〉＝22×0＋22×0＋1×11×2＝22，所以〈DH →，CC ′→〉＝45°，即DP 与CC ′所成的角为45°.(2)平面AA ′D ′D 的一个法向量是DC →＝(0,1,0)．因为cos 〈DH →，DC →〉＝22×0＋22×1＋1×01×2＝12，所以〈DH →，DC →〉＝60°.可得DP 与平面AA ′D ′D 所成的角为30°.[能力提升练]1．正方体ABCD A 1B 1C 1D 1中，E ，F 分别为AB ，C 1D 1的中点，那么A 1B 1与平面A 1EF 夹角的正弦值为( )A.62B.63C.64D. 2B [建立如下图的空间直角坐标系，设棱长为1，那么A 1(1,0,1)，E ⎝ ⎛⎭⎪⎫1，12，0，F ⎝⎛⎭⎪⎫0，12，1，B 1(1,1,1)．A 1B 1→＝(0,1,0)，设平面A 1EF 的法向量n ＝(x ，y ，z )，那么⎩⎪⎨⎪⎧n ·A 1E →＝0，n ·A 1F →＝0，即⎩⎪⎨⎪⎧12y －z ＝0，－x ＋y2＝0.令y ＝2，那么⎩⎪⎨⎪⎧x ＝1，z ＝1，∴n ＝(1,2,1)，cos 〈n ，A 1B 1→〉＝26＝63，即线面角的正弦值为63.] 2．如下图，在四棱锥P ABCD 中，PD ⊥底面ABCD ，四边形ABCD 为正方形，且PD ＝AB ＝1，G 为△ABC 的重心，那么PG 与底面ABCD 所成的角θ满足( )A ．θ＝π4B ．cos θ＝23417C ．tan θ＝223D ．sin θ＝33B [建立如下图的空间直角坐标系，那么P (0,0,1)，A (1,0,0)，B (1,1,0)，C (0,1,0)，所以G ⎝ ⎛⎭⎪⎫23，23，0，PG →＝⎝ ⎛⎭⎪⎫23，23，－1.又平面ABCD 的一个法向量为n ＝(0,0,1)，那么cos 〈PG →，n 〉＝－1⎝ ⎛⎭⎪⎫232＋⎝ ⎛⎭⎪⎫232＋(－1)2＝－31717，所以PG 与平面ABCD 所成角的余弦值为1－⎝ ⎛⎭⎪⎫－317172＝23417.]3．三棱锥S ABC 中，底面为边长等于2的等边三角形，SA 垂直于底面ABC ，SA ＝3，那么直线AB 与平面SBC 所成角的正弦值为________．34[建立如下图的空间直角坐标系，那么S (0,0,3)，A (0，0,0)， B (3，1,0)，C (0,2,0)．∴AB →＝(3，1,0)，SB →＝(3，1，－3)， SC →＝(0,2，－3)．设面SBC 的法向量为n ＝(x ，y ，z )．那么⎩⎪⎨⎪⎧n ·SB →＝3x ＋y －3z ＝0，n ·SC →＝2y －3z ＝0.令y ＝3，那么z ＝2，x ＝3，∴n ＝(3，3,2)．设AB 与平面SBC 所成的角为θ，那么sin θ＝|n ·AB →||n ||AB →|＝3＋34×2＝34.]4．如下图，正三角形ABC 与正三角形BCD 所在的平面互相垂直，那么直线CD 与平面ABD 所成角的正弦值为________．155[取BC 的中点O ，连接AO ，DO ，建立如下图的空间直角坐标系Oxyz .设BC ＝1，那么A ⎝ ⎛⎭⎪⎫0，0，32，B ⎝ ⎛⎭⎪⎫0，－12，0，C ⎝ ⎛⎭⎪⎫0，12，0，D 32，0,0，所以BA →＝⎝ ⎛⎭⎪⎫0，12，32，BD →＝⎝ ⎛⎭⎪⎫32，12，0，CD →＝⎝ ⎛⎭⎪⎫32，－12，0.设平面ABD 的法向量为n ＝(x ，y ，z )，那么⎩⎪⎨⎪⎧n ·BA →＝0n ·BD →＝0所以⎩⎪⎨⎪⎧12y ＋32z ＝032x ＋12y ＝0，取x ＝1，那么y ＝－3，z ＝1，所以n ＝(1，－3，1)，所以cos 〈n ，CD →〉＝155，因此直线CD 与平面ABD 所成角的正弦值为155.] 5．如下图，四棱锥P ABCD 的底面是正方形，PD ⊥底面ABCD ，点E 在棱PB 上．(1)求证：AC ⊥平面PDB ；(2)当PD ＝2AB 且E 为PB 的中点时，求AE 与平面PDB 所成的角的大小． [解] (1)证明：∵四边形ABCD 是正方形， ∴AC ⊥BD .∵PD ⊥底面ABCD ，∴PD ⊥AC . ∵PD ∩BD ＝D ，∴AC ⊥平面PDB . (2)建立如下图的空间直角坐标系，设AB ＝1，那么A (1,0,0)，C (0,1,0)，E ⎝ ⎛⎭⎪⎫12，12，22，AE →＝⎝ ⎛⎭⎪⎫－12，12，22. 由(1)知AC →＝(－1,1,0)为平面PDB 的一个法向量．设AE 与平面PDB 所成的角为θ，那么sin θ＝|cos 〈AC →，AE →〉|＝|AC →·AE →||AC →||AE →|＝12×1＝22.∴AE 与平面PDB 所成的角为45°.。

2019年高中数学湘教版选修2-1讲义+精练：第3章3.6直线与平面、平面与平面所成的角含答案

3．6直线与平面、平面与平面所成的角[读教材·填要点]1．直线与平面所成的角(1)定义：如果直线l 与平面α垂直，l 与平面α所成的角θ为直角，θ＝π2.如果直线l 与平面α不垂直，则l 在α内的射影是一条直线l ′，将l 与l ′所成的角θ定义为l 与平面α所成的角．(2)范围：θ∈⎣⎡⎦⎤0，π2. (3)计算：作直线l 的方向向量v 和平面α的法向量n ，并且可选v 与n 所成的角θ1∈⎣⎡⎦⎤0，π2，则l 与平面α所成的角 θ＝π2－θ1，sin θ＝cos_θ1＝|v ·n ||v |·|n |.2．二面角(1)定义：从一条直线l 出发的两个半平面α，β组成的图形叫作二面角，记作α-l -β. (2)二面角的平面角过二面角α-l -β的棱l 上任意一点O 作垂直于棱l 的平面，分别与两个面α，β相交得到两条射线OA ，OB ，则∠AOB 称为二面角α-l -β的平面角．(3)二面角的范围二面角的平面角的度数在0°～180°范围内，特别当二面角α-l -β是90°时称它为直二面角，此时称两个面α，β相互垂直．3．两个平面所成的角两个相交平面，以交线为棱可以构成四个二面角，其中最小的一个二面角称为这两个平面所成的角，取值范围是⎝⎛⎭⎫0，π2.两个平行平面所成的角为0°. [小问题·大思维]1．当一条直线l 与一个平面α的夹角为0时，这条直线一定在平面内吗？提示：不一定，这条直线可能与平面平行．2．设直线l 与平面α所成的角为θ，l 的方向向量为a ，平面α的法向量为n ，如何用a 和n 求角θ？提示：sin θ＝|cos 〈a ，n 〉|＝|a ·n ||a |·|n |.3．二面角的法向量的夹角与二面角的平面角的大小有什么关系？提示：相等或互补．求直线与平面所成的角如图，在四棱锥P -ABCD 中，底面为直角梯形，AD ∥BC ，∠BAD ＝90°，PA ⊥底面ABCD ，且PA ＝AD ＝AB ＝2BC ，M ，N 分别为PC ，PB 的中点．求BD与平面ADMN 所成的角θ.[自主解答] 如图所示，建立空间直角坐标系，设BC ＝1，则A (0,0,0)，B (2,0,0)，D (0,2,0)，P (0,0,2)，则N (1,0,1)，∴BD ―→＝(－2,2,0)，AD ―→＝(0,2,0)，AN ―→＝(1,0,1)．设平面ADMN 的一个法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧n ·AD ―→＝0，n ·AN ―→＝0，得⎩⎪⎨⎪⎧y ＝0，x ＋z ＝0，取x ＝1，则z ＝－1， ∴n ＝(1,0，－1)．∵cos 〈BD ―→，n 〉＝BD ―→·n |BD ―→|·|n |＝－28·2＝－12，∴sin θ＝|cos 〈BD ―→，n 〉|＝12.又0°≤θ≤90°，∴θ＝30°.利用向量法求直线与平面所成角的步骤为： (1)确定直线的方向向量和平面的法向量； (2)求两个向量夹角的余弦值； (3)确定向量夹角的范围；(4)确定线面角与向量夹角的关系：向量夹角为锐角时，线面角与这个夹角互余；向量夹角为钝角时，线面角等于这个夹角减去90°.1.如图，在三棱锥P -ABC 中，PA ⊥平面ABC ，∠BAC ＝90°，D ，E ，F 分别是棱AB ，BC ，CP 的中点，AB ＝AC ＝1，PA ＝2.求直线PA 与平面DEF 所成角的正弦值．解：如图，以点A 为原点，AB ，AC ，AP 所在的直线分别为x ，y ，z 轴，建立空间直角坐标系A -xyz .由AB ＝AC ＝1，PA ＝2，得A (0,0,0)，B (1,0,0)，C (0,1,0)，P (0,0,2)，D ⎝⎛⎭⎫12，0，0，E ⎝⎛⎭⎫12，12，0，F ⎝⎛⎭⎫0，12，1. ∴PA ―→＝(0,0，－2)，DE ―→＝⎝⎛⎭⎫0，12，0，DF ―→＝⎝⎛⎭⎫－12，12，1. 设平面DEF 的法向量为n ＝(x ，y ，z )．则⎩⎪⎨⎪⎧n ·DE ―→＝0，n ·DF ―→＝0，即⎩⎨⎧(x ，y ，z )·⎝⎛⎭⎫0，12，0＝0，(x ，y ，z )·⎝⎛⎭⎫－12，12，1＝0.解得⎩⎪⎨⎪⎧x ＝2z ，y ＝0.取z ＝1，则平面DEF 的一个法向量为n ＝(2,0,1)．设PA 与平面DEF 所成的角为θ，则 sin θ＝|cos 〈PA ―→，n 〉|＝⎪⎪⎪⎪⎪⎪⎪⎪PA ―→·n | PA ―→|·|n |＝55，故直线PA 与平面DEF 所成角的正弦值为55.求二面角如图，四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，AC ∩BD ＝O ，A 1C 1∩B 1D 1＝O 1，四边形ACC 1A 1和四边形BDD 1B 1均为矩形．(1)证明：O 1O ⊥底面ABCD .(2)若∠CBA ＝60°，求二面角C 1-OB 1-D 的余弦值．[自主解答] (1)证明：因为四边形ACC 1A 1和四边形BDD 1B 1均为矩形，所以CC 1⊥AC ，DD 1⊥BD ，又CC 1∥DD 1∥OO 1，所以OO 1⊥AC ，OO 1⊥BD ，因为AC ∩BD ＝O ，所以O 1O ⊥底面ABCD .(2)因为四棱柱的所有棱长都相等，所以四边形ABCD 为菱形，AC ⊥BD .又O 1O ⊥底面ABCD ，所以OB ，OC ，OO 1两两垂直．如图，以O 为原点，OB ，OC ，OO 1所在直线分别为x ，y ，z 轴，建立空间直角坐标系．设棱长为2，因为∠CBA ＝60°，所以OB ＝3，OC ＝1，所以O (0,0,0)，B 1(3，0,2)，C 1(0,1,2)，平面BDD 1B 1的一个法向量为n ＝(0,1,0)，设平面OC 1B 1的法向量为m ＝(x ，y ，z )，则由m ⊥OB 1―→，m ⊥OC 1―→，所以⎩⎪⎨⎪⎧3x ＋2z ＝0，y ＋2z ＝0.取z ＝－3，则x ＝2，y ＝23，所以m ＝(2,23，－3)，所以cos 〈m ，n 〉＝m·n |m ||n |＝2319＝25719.由图形可知二面角C 1-OB 1-D 的大小为锐角，所以二面角C 1-OB 1-D 的余弦值为25719.利用法向量求二面角的步骤为： (1)确定两平面的法向量； (2)求两法向量的夹角的余弦值； (3)确定二面角的范围；(4)确定二面角与面面角的关系：二面角范围的确定要通过图形观察，法向量一般不能体现出来．2．(2016·全国卷Ⅰ)如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF ＝2FD ，∠AFD ＝90°，且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明：平面ABEF ⊥平面EFDC ； (2)求二面角E -BC -A 的余弦值．解：(1)证明：由已知可得AF ⊥DF ，AF ⊥FE ，所以AF ⊥平面EFDC . 又AF ⊂平面ABEF ，故平面ABEF ⊥平面EFDC .(2)过D 作DG ⊥EF ，垂足为G .由(1)知DG ⊥平面ABEF .以G 为坐标原点，GF ―→的方向为x 轴正方向，|GF ―→|为单位长，建立如图所示的空间直角坐标系G -xyz .由(1)知∠DFE 为二面角D -AF -E 的平面角，故∠DFE ＝60°，则DF ＝2，DG ＝3，可得A (1,4,0)，B (－3,4,0)，E (－3,0,0)，D (0,0，3)．由已知得AB ∥EF ，所以AB ∥平面EFDC . 又平面ABCD ∩平面EFDC ＝CD ，故AB ∥CD ，CD ∥EF .由BE ∥AF ，可得BE ⊥平面EFDC ，所以∠CEF 为二面角C -BE -F 的平面角，∠CEF ＝60°. 从而可得C (－2,0，3)．所以EC ―→＝(1,0，3)，EB ―→＝(0,4,0)，AC ―→＝(－3，－4，3)，AB ―→＝(－4,0,0)．设n ＝(x ，y ，z )是平面BCE 的法向量，则⎩⎪⎨⎪⎧n ·EC ―→＝0，n ·EB ―→＝0，即⎩⎨⎧x ＋3z ＝0，4y ＝0，所以可取n ＝(3,0，－3)．设m 是平面ABCD 的法向量，则⎩⎪⎨⎪⎧m ·AC ―→＝0，m ·AB ―→＝0，同理可取m ＝(0，3，4)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－21919. 由图知，二面角E -BC -A 为钝角，故二面角E -BC -A 的余弦值为－21919.解题高手多解题条条大路通罗马，换一个思路试一试已知PA ⊥平面ABC ，AC ⊥BC ，PA ＝AC ＝1，BC ＝2，求二面角A -PB -C 的余弦值． [解] 法一：如图所示，取PB 的中点D ，连接CD . ∵PC ＝BC ＝2， ∴CD ⊥PB .∴作AE ⊥PB 于E ，那么二面角A -PB -C 的大小就等于异面直线DC 与EA 所成的角θ的大小．∵PD ＝1，PE ＝PA 2PB ＝12，∴DE ＝PD －PE ＝12.又∵AE ＝AP ·AB PB ＝32，CD ＝1，AC ＝1，AC ―→＝AE ―→＋ED ―→＋DC ―→，且AE ―→⊥ED ―→，ED ―→⊥DC ―→，∴|AC ―→|2＝|AE ―→|2＋|ED ―→|2＋|DC ―→|2＋2|AE ―→|·|DC ―→|cos(π－θ)，即1＝34＋14＋1－2·32·1·cos θ，解得cos θ＝33. 故二面角A -PB -C 的余弦值为33. 法二：由法一可知，向量DC ―→与EA ―→的夹角的大小就是二面角A -PB -C 的大小，如图，建立空间直角坐标系Cxyz ，则A (1,0,0)，B (0，2，0)，C (0,0,0)，P (1,0,1)，D 为PB 的中点，D ⎝⎛⎭⎫12，22，12. 又PE EB ＝AP 2AB 2＝13，即E 分PB ―→的比为13.∴E ⎝⎛⎭⎫34，24，34，EA ―→＝⎝⎛⎭⎫14，－24，－34，DC ―→＝⎝⎛⎭⎫－12，－22，－12，|EA ―→|＝32，|DC ―→|＝1，EA ―→·DC ―→＝14×⎝⎛⎭⎫－12＋⎝⎛⎭⎫－24×⎝⎛⎭⎫－22＋⎝⎛⎭⎫－34×⎝⎛⎭⎫－12＝12. ∴cos 〈EA ―→，DC ―→〉＝EA ―→·DC ―→| EA ―→|·|DC ―→|＝33.故二面角A -PB -C 的余弦值为33. 法三：如图所示建立空间直角坐标系，则A (0，0,0)，B (2，1,0)，C (0,1,0)，P (0,0,1)，AP ―→＝(0,0,1)，AB ―→＝(2，1,0)，CB ―→＝(2，0,0)， CP ―→＝(0，－1,1)，设平面PAB 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·AP ―→＝0，m ·AB ―→＝0⇒⎩⎪⎨⎪⎧ (x ，y ，z )·(0，0，1)＝0，(x ，y ，z )·(2，1，0)＝0⇒⎩⎪⎨⎪⎧y ＝－2x ，z ＝0.令x ＝1，则m ＝(1，－2，0)．设平面PBC 的法向量为n ＝(x ′，y ′，z ′)，则⎩⎪⎨⎪⎧n ·CB ―→＝0，n ·CP ―→＝0⇒⎩⎪⎨⎪⎧ (x ′，y ′，z ′)·(2，0，0)＝0，(x ′，y ′，z ′)·(0，－1，1)＝0⇒⎩⎪⎨⎪⎧x ′＝0，y ′＝z ′. 令y ′＝－1，则n ＝(0，－1，－1)， ∴cos 〈m ，n 〉＝m ·n |m |·|n |＝33.∴二面角A -PB -C 的余弦值为33.1．若直线l 的方向向量与平面α的法向量的夹角等于120°，则直线l 与平面α所成的角等于( )A ．120°B ．60°C ．30°D ．以上均错解析：设直线l 与平面α所成的角为θ，则sin θ＝|cos 120°|＝12，又∵0＜θ≤90°，∴θ＝30°. 答案：C2．若正三棱锥的侧面都是直角三角形，则侧面与底面所成的二面角的余弦值为( ) A.63B.33C.23 D.13解析：设正三棱锥P -ABC ，PA ，PB ，PC 两两互相垂直，设PA ＝PB＝PC ＝a .取AB 的中点D ，连接PD ，CD ，易知∠PDC 为侧面PAB 与底面ABC 所成的角．易求PD ＝22a ，CD ＝62a ，故cos ∠PDC ＝PD DC ＝33.答案：B3．在边长为a 的正△ABC 中，AD ⊥BC 于D ，沿AD 折成二面角B -AD -C 后，BC ＝12a ，这时二面角B -AD -C 的大小为( )A ．30°B ．45°C ．60°D ．90°解析：由定义知，∠BDC 为所求二面角的平面角，又BC ＝BD ＝DC ＝12a ，∴△BDC 为等边三角形，∴∠BDC ＝60°. 答案：C4．若一个二面角的两个面的法向量分别为m ＝(0,0,3)，n ＝(8,9,2)，则这个锐二面角的余弦值为________．解析：cos 〈m ，n 〉＝(0，0，3)·(8，9，2)382＋92＋22＝2149＝2149149.答案：21491495．正方体ABCD -A 1B 1C 1D 1中，直线BC 1与平面A 1BD 所成的角的正弦值是________．解析：如图，以DA ，DC ，DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系，取正方体的棱长为1，则A (1,0,0)，B (1,1,0)，C 1(0,1,1)，易证AC 1―→是平面A 1BD 的一个法向量．又AC 1―→＝(－1,1,1)， BC 1―→＝(－1,0,1)．所以cos 〈AC 1―→，BC 1―→〉＝1＋13×2＝63.所以BC 1与平面A 1BD 所成角的正弦值为63. 答案：636．(2017·江苏高考)如图，在平行六面体ABCD -A 1B 1C 1D 1中，AA 1⊥平面ABCD ，且AB ＝AD ＝2，AA 1＝3，∠BAD ＝120°.(1)求异面直线A 1B 与AC 1所成角的余弦值； (2)求二面角B -A 1D -A 的正弦值．解：在平面ABCD 内，过点A 作AE ⊥AD ，交BC 于点E . 因为AA 1⊥平面ABCD ，所以AA 1⊥AE ，AA 1⊥AD .如图，以{AE ―→，AD ―→，AA 1―→}为正交基底，建立空间直角坐标系A -xyz . 因为AB ＝AD ＝2， AA 1＝3，∠BAD ＝120°，则A (0,0,0)，B (3，－1,0)，D (0,2,0)，E (3，0,0)，A 1(0，0，3)，C 1(3，1，3)． (1)A 1B ―→＝(3，－1，－3)，AC 1―→＝(3，1，3)．则cos 〈A 1B ―→，AC 1―→〉＝A 1B ―→·AC 1―→|A 1B ―→||AC 1―→|＝3－1－37×7＝－17. 因此异面直线A 1B 与AC 1所成角的余弦值为17.(2)可知平面A 1DA 的一个法向量为AE ―→＝(3，0,0)．设m ＝(x ，y ，z )为平面BA 1D 的一个法向量，又A 1B ―→＝(3，－1，－3)，BD ―→＝(－3，3,0)，则⎩⎪⎨⎪⎧m ·A 1B ―→＝0，m ·BD ―→＝0，即⎩⎪⎨⎪⎧3x －y －3z ＝0，－3x ＋3y ＝0.不妨取x ＝3，则y ＝3，z ＝2，所以m ＝(3，3，2)为平面BA 1D 的一个法向量，从而cos 〈AE ―→，m 〉＝AE ―→·m | AE ―→||m |＝333×4＝34. 设二面角B -A 1D -A 的大小为θ，则|cos θ|＝34.因为θ∈[0，π]，所以sin θ＝1－cos 2θ＝74. 因此二面角B -A 1D -A 的正弦值为74.一、选择题1．若平面α的一个法向量n ＝(2,1,1)，直线l 的一个方向向量为a ＝(1,2,3)，则l 与α所成角的正弦值为( )A.176B.216 C ．－216D.213解析：∵cos 〈a ，n 〉＝a ·n|a |·|n |＝(1，2，3)·(2，1，1)1＋4＋9·22＋1＋1＝2＋2＋314×6＝216.∴l 与α所成角的正弦值为216. 答案：B2.如图，过边长为1的正方形ABCD 的顶点A 作线段EA ⊥平面AC ，若EA＝1，则平面ADE 与平面BCE 所成的二面角的大小是( )A ．120°B ．45°C ．135°D ．60°解析：以A 为原点，分别以AB ，AD ，AE 所在直线为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系A -xyz ，则E (0,0,1)，B (1,0,0)，C (1,1,0)，EB ―→＝(1,0，－1)，EC ―→＝(1,1，－1)．设平面BCE 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧x －z ＝0，x ＋y －z ＝0，可取n ＝(1,0,1)，又平面EAD 的法向量为AB ―→＝(1,0,0)，所以cos 〈n ，AB ―→〉＝12×1＝22，故平面ADE 与平面BCE 所成的二面角为45°.答案：B3．在直角坐标系中，已知A (2,3)，B (－2，－3)，沿x 轴把直角坐标系折成平面角为θ的二面角A -Ox -B ，使∠AOB ＝90°，则cos θ为( )A ．－19B.19C.49D ．－49解析：过A ，B 分别作x 轴垂线，垂足分别为A ′，B ′.则AA ′＝3，BB ′＝3，A ′B ′＝4，OA ＝OB ＝13，折后，∠AOB ＝90°，∴AB ＝OA 2＋OB 2＝26.由AB ―→＝AA ′―→＋A ′B ′―→＋B ′B ―→，得|AB ―→|2＝|AA ′―→|2＋|A ′B ′―→|2＋|B ′B ―→|2＋2|AA ′―→|·|B ′B ―→|·cos(π－θ)． ∴26＝9＋16＋9＋2×3×3×cos(π－θ)， ∴cos θ＝49.答案：C4.已知平面α内有一个以AB 为直径的圆，PA ⊥α，点C 在圆周上(异于点A ，B )，点D ，E 分别是点A 在PC ，PB 上的射影，则( )A ．∠ADE 是二面角A -PC -B 的平面角 B ．∠AED 是二面角A -PB -C 的平面角 C ．∠DAE 是二面角B -PA -C 的平面角D ．∠ACB 是二面角A -PC -B 的平面角解析：选项A 错误，若DE ⊥PC ，则PC ⊥平面ADE ，所以PC ⊥AE ，又AE ⊥PB ，所以AE ⊥平面PBC ，同理可证：AD ⊥平面PBC ，这是不可能的．选项B 正确，因为PA ⊥BC ，AC ⊥BC ，所以BC ⊥平面PAC ，所以AD ⊥BC ，又AD ⊥PC ，且PC ∩BC ＝C ，所以AD ⊥平面PBC ，又因为AE ⊥PB ，所以DE ⊥PB ，所以∠AED 为二面角A -PB -C 的平面角．选项C 错误，因为PA ⊥平面α，所以PA ⊥AC 且PA ⊥AB ，所以∠CAB 为二面角B -PA -C 的平面角，因此，∠DAE 不是二面角B -PA -C 的平面角．选项D 错误，在△PAC 中，∠PAC ＝90°，所以AC 与PC 不垂直，因此，∠ACB 不是二面角A -PC -B 的平面角．答案：B 二、填空题5．如图所示，已知正三棱柱ABC -A 1B 1C 1的所有棱长都相等，D 是A 1C 1的中点，则直线AD 与平面B 1DC 夹角的正弦值为________．解析：不妨设正三棱柱ABC -A 1B 1C 1的棱长为2，建立如图所示的空间直角坐标系，则C (0,0,0)，A (3，－1,0)，B 1(3，1,2)，D⎝⎛⎭⎫32，－12，2，则CD ―→＝⎝⎛⎭⎫32，－12，2， CB 1―→＝(3，1,2)，设平面B 1DC 的法向量为 n ＝(x ，y,1)，由⎩⎪⎨⎪⎧n ·CD ―→＝0，n ·CB 1―→＝0，解得n ＝(－3，1,1)．又∵DA ―→＝⎝⎛⎭⎫32，－12，－2， ∴sin θ＝|cos 〈DA ―→，n 〉|＝45.答案：456．正△ABC 与正△BCD 所在平面垂直，则二面角A -BD -C 的正弦值为________．解析：取BC 中点O ，连接AO ，DO .建立如图所示空间直角坐标系，设BC＝1，则A ⎝⎛⎭⎫0，0，32，B ⎝⎛⎭⎫0，－12，0， D⎝⎛⎭⎫32，0，0.∴OA ―→＝⎝⎛⎭⎫0，0，32，BA ―→＝⎝⎛⎭⎫0，12，32，BD ―→＝⎝⎛⎭⎫32，12，0.由于OA ―→＝⎝⎛⎭⎫0，0，32为平面BCD 的法向量，可进一步求出平面ABD 的一个法向量n ＝()1，－3，1，∴cos 〈n ，OA ―→〉＝55，sin 〈n ，OA ―→〉＝255.∴二面角A -BD -C 的正弦值为255. 答案：2557．已知三棱锥S -ABC 中，底面ABC 为边长等于2的等边三角形，SA 垂直于底面ABC ，SA ＝3，那么直线AB 与平面SBC 所成角的正弦值为________．解析：建立如图所示空间直角坐标系，则S (0,0,3)，A (0,0,0)，B (3，1,0)，C (0,2,0)．∴AB ―→＝(3，1,0)， SB ―→＝(3，1，－3)，SC ―→＝(0,2，－3)．设平面SBC 的法向量为n ＝(x ，y ，z )．则⎩⎪⎨⎪⎧n ·SB ―→＝3x ＋y －3z ＝0，n ·SC ―→＝2y －3z ＝0.令y ＝3，则z ＝2，x ＝3，∴n ＝(3，3,2)．设AB 与平面SBC 所成的角为θ，则sin θ＝|cos 〈n ，AB ―→〉|＝|n ·AB ―→||n |·|AB ―→|＝3＋34×2＝34.答案：348．在体积为1的直三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，AC ＝BC ＝1，求直线A 1B 与平面BB 1C 1C 所成角的正弦值为________．解析：由题意，可得体积V ＝CC 1·S △ABC ＝CC 1·12·AC ·BC ＝12CC 1＝1，∴CC 1＝2.A 1(1，0，2).建立如图所示空间直角坐标系，得点B (0,1,0)，则A 1B ―→＝(－1,1，－2)，又平面BB 1C 1C 的法向量为n ＝(1,0,0)．设直线A 1B 与平面BB 1C 1C 所成的角为θ，A 1B ―→与n 的夹角为φ，则cos φ＝A 1B ―→·n |A 1B ―→|·|n |＝－66，∴sin θ＝|cos φ|＝66，即直线A 1B 与平面BB 1C 1C 所成角的正弦值为66. 答案：66三、解答题9.如图，长方体ABCD -A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)； (2)求直线AF 与平面α所成角的正弦值．解：(1)交线围成的正方形EHGF 如图所示． (2)作EM ⊥AB ，垂足为M ，则AM ＝A 1E ＝4，EM ＝AA 1＝8. 因为四边形EHGF 为正方形，所以EH ＝EF ＝BC ＝10. 于是MH ＝EH 2－EM 2＝6，所以AH ＝10.以D 为坐标原点，DA ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系D -xyz ，则A (10,0,0)，H (10,10,0)，E (10,4,8)，F (0,4,8)， FE ―→＝(10,0,0)， HE ―→＝(0，－6，8)．设n ＝(x ，y ，z )是平面EHGF 的法向量，则⎩⎪⎨⎪⎧n ·FE ―→＝0，n ·HE ―→＝0，即⎩⎪⎨⎪⎧10x ＝0，－6y ＋8z ＝0，所以可取n ＝(0,4,3)．又AF ―→＝(－10,4,8)，故|cos 〈n ，AF ―→〉|＝|n ·AF ―→||n ||AF ―→|＝4515.所以AF 与平面EHGF 所成角的正弦值为4515.10．(2017·全国卷Ⅱ)如图，四棱锥P -ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面PAB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M -AB -D 的余弦值．解：(1)证明：取PA 的中点F ，连接EF ，BF . 因为E 是PD 的中点，所以EF ∥AD ，EF ＝12AD .由∠BAD ＝∠ABC ＝90°，得BC ∥AD ，又BC ＝12AD ，所以EF 綊BC ，所以四边形BCEF 是平行四边形，CE ∥BF ，又BF ⊂平面PAB ，CE ⊄平面PAB ，故CE ∥平面PAB .(2)由已知得BA ⊥AD ，以A 为坐标原点，AB ―→的方向为x 轴正方向，|AB ―→|为单位长度，建立如图所示的空间直角坐标系A -xyz ，则A (0,0,0)，B (1，0,0)，C (1,1,0)，P (0，1，3)，PC ―→＝(1,0，－3)，AB ―→＝(1,0,0)．设M (x ，y ，z )(0<x <1)，则BM ―→＝(x －1，y ，z )，PM ―→＝(x ，y －1，z －3)．因为BM 与底面ABCD 所成的角为45°，而n ＝(0,0,1)是底面ABCD 的法向量，所以|cos 〈BM ―→，n 〉|＝sin 45°，|z |(x －1)2＋y 2＋z 2＝22，即(x －1)2＋y 2－z 2＝0. ① 又M 在棱PC 上，设PM ―→＝λPC ―→，则x ＝λ，y ＝1，z ＝3－3λ. ②由①②解得⎩⎪⎨⎪⎧x ＝1＋22，y ＝1，z ＝－62(舍去)，或⎩⎪⎨⎪⎧x ＝1－22，y ＝1，z ＝62，所以M ⎝⎛⎭⎫1－22，1，62，从而AM ―→＝⎝⎛⎭⎫1－22，1，62. 设m ＝(x 0，y 0，z 0)是平面ABM 的法向量，则⎩⎪⎨⎪⎧m ·AM ―→＝0，m ·AB ―→＝0，即⎩⎪⎨⎪⎧(2－2)x 0＋2y 0＋6z 0＝0，x 0＝0，所以可取m ＝(0，－6，2)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝105.由图知二面角M -AB -D 为锐角，因此二面角M -AB -D 的余弦值为105.。

北师大版四年级上册数学第二单元线与角课时练习题

北师大版四年级上册数学第二单元线与角课时练习题第二单元线与角1.线的认识基础练：一、填空。

1.线段有两个端点，射线有一个端点，直线没有端点。

2.过一点可以画无数条直线，从一点出发，可以画一条射线。

3.直线、射线可以无限延长，线段有一定的长度。

4.过一点可以画一条直线。

5.两点间的连线中，线段最短。

二、选择。

1.下面这两组线段一样长吗？（B）A。

一样长 B。

不一样长2.直线上两点间的一段叫（C）A。

直线 B。

射线 C。

线段3.一个三角形是由三条（B）围成的。

A。

直线 B。

线段 C。

射线三、判断。

1.直线比射线长。

（×）2.线段比射线短。

（√）3.线段的长度可以测量，直线和射线的长度不能测量。

（√）4.直线是线段的一部分。

（×）5.手电筒、太阳等射出的光线都可以看成射线。

（√）拓展练：图中有一条射线，两条直线，四条线段。

2.平移与平行基础练：一、填空。

1.在同一平面内，距离相等的两条直线，叫平行线。

2.双杠的两根杠是互相平行的，铅笔平移前后的线条是平行的。

3.过直线外一点，能画一条这条直线的平行线。

4.一个长方形有两组互相平行的对边。

二、下面哪组是平行线，在括号里画“∥”。

三、画一画。

1.过A点画已知直线的平行线。

AA2.下图中哪些线段是平行的，请写出三组。

A。

BC。

DE。

F。

G线段AB ∥线段EF；线段BC ∥线段DE；线段CD ∥线段FG拓展练：过P点分别做出直线L1和直线L2的平行线。

M1.P。

M23.相交与垂直基础练：一、填空。

1.两条直线相交成直角时，这两条直线叫做互相垂直。

其中，一条直线叫做另一条直线的垂线。

这两条直线的交点叫做交点。

2.从直线外一点到这条直线所画的垂线的长度，叫做这点到直线的距离。

3.正方形每相邻的两条边互相垂直。

4.过直线外一点向这条直线引出的所有线段中，到直线距离最短。

5.平行线间的距离处处相等。

二、过A点分别画已知直线的垂线。

AA拓展练：无。

三、判断直线互相垂直或平行拓展练：观察下面的图形，填空。

直线和平面所成的角与二面角

直线和平面所成的角与二面角一、选择题(共45题，题分合计225分)1.过正方形ABCD 的顶点A 作线段A A ′⊥平面ABCD ，若A A ′=AB ，则平面A ′A B 与平面A ′CD 所成的角度是A. 30°B. 45°C. 60°D. 90°2.一个二面角的两个面分别垂直于另一个二面角的两个面，那么这两个二面角的大小关系是A.相等B.互补C.相等或互补 C.不能确定3.在直二面角α- l-β中,直线m⊂α,直线n ⊂β,且m 、n 均不与l 垂直,则A. m 与n 不可能垂直,但可能平行B. m 与n 可能垂直,但不可能平行C. m 与n 可能垂直,也可能平行D. m 与n 不可能垂直,也不可能平行4.设有不同的直线a 、b 和不同的平面α、β、γ,给出下列三个命题:(1)若a a //,a b //,则b a //.(2)若a a //,β//a ,则β//a . (3)若γ⊥a ,γβ⊥,则β//a . 其中正确的个数是 A.0 B.1 C.2 D.35.如图△ABD ≌△CBD ，且△ABD 为等腰三角形，∠BAD =∠BCD =90°，且面ABD ⊥面BCD ，则下列4个结论中，正确结论的序号是①AC ⊥BD ②△ACD 是等边三角形③AB 与面BCD 成60°角④AB 与CD 成60°角 A.①②③ B.①②④ C.①③④ D.②③④6.在边长为1的正方体ABCD -A 1B 1C 1D 1的底面A 1C 1上取一点E ,使AE 与AB 、AD 所成的角都为60°,则AE 的长等于 A.35 B.46C.2 D.37.一直线与直二面角的两个面所成的角分别为α、β，则α+β的范围为：Ａ.0＜α＋β＜π/2 B.α＋β＞π/2 C.0≤α＋β≤π/2 D.0＜α＋β≤π/28.在直二面角α－AB －β的棱AB 上取一点P ，过P 分别在α、β两个平面内作与棱成45°的斜线PC 、PD ，那么∠CPD的大小为A.45°B.60°C.120°D.60°或120°9.若三棱锥的顶点在底面上的射影是底面三角形的垂心，则A.各格侧棱长相等B.各侧棱与底面成等角C.各侧面与底面线等角D.每组相对棱互相垂直10.二面角α-l -β的平面角为120°,A ,B ∈l ,AC ⊆α,BD ⊆β,AC ⊥l ,BD ⊥l ,若AB =AC =BD =1，则CD 等于A.2B.3C.2D.511.60°的二面角α- l-β,直线a⊂α,直线b ⊂β,且a 、b 无公共点.设a 、b 所成的角是θ,则cos θ的取值范围是A.⎥⎥⎦⎤⎢⎢⎣⎡1,23B.⎥⎦⎤⎢⎣⎡21,0 C.[]1,0 D.[)1,0 12.二面角α- l-β的大小为θ，直线a⊂α，直线b ⊂β，设a 与b 所成的角为φ，则下面关系中正确的一个是A. φ＜θB. φ＞θC. φ=θD.以上三种关系均有可能13.直线l 与平面α或60°角，A l =α ，直线a A a ∉⊂且α，设l 与a 所成的角为θ，则cos θ的取值范围是A.⎪⎭⎫⎢⎣⎡1,21B.⎥⎦⎤⎢⎣⎡1,21C.⎥⎦⎤⎢⎣⎡21,0D.⎪⎭⎫⎢⎣⎡21,0 14.如图,等腰直角△ABC ,沿其斜边AB 边上的高CD 对折,使△ACD 与△BCD 所在的平面垂直,此时∠ACB 等于A.45°B.60°C.90°D.120°15.二面角α-ＭＮ-β＝60º，直线AB 与α、β分别交于A 、B ，AB ⊥MN ，若AB 与α、β所成角分别是θ1、θ2，则A.θ1＋θ2=120ºB.θ1＋θ2>120ºC.θ1＋θ2<120ºD.以上都不对16.正方形纸片ABCD ,沿对角线AC 对折,使D 点在面ABC 外,这时DB 与面ABC 所成的角一定不等于A.30°B.45°C.60°D.9017.a 、b 表示直线，α、β、γ表示平面，有下列四个命题：(1)若α∩β=a ,b ⊂α，a ⊥b ,则α⊥β；(2)若α⊥β，α∩γ=a ,β∩γ=b ,则a ⊥b ;(3)若a 不垂直于平面α，则a 不可能垂直于α内的无数条直线；(4)若a ⊥α，b ⊥β,a ∥ｂ，则α∥β，其中不正确命题的个数为 A.1 B.2 C.3 D.418.α、β是两个不同的平面，m 、n 是平面α及β外的两条不同直线，给出四个论断：①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α,以其中三个结论作为条件，另一个论断作为结论，则所得命题正确的个数是 A.1 B.2 C.3 D.419.正方形ABCD 沿对角线AC 折成直二面角后，AB 与CD 所成的角为A.30°B.45°C.60°D.9020.对于直线m 、n 和平面α、β、γ，下列命题中，正确命题的个数为①若m ∥α，n ⊥m ,则n ⊥α②若m ⊥α，n ⊥m ,则n ∥α③若α⊥β,γ⊥β，则α∥γ④若m ⊥α，m ⊂β，则α⊥βA.1B.2C.3D.421.平面α与平面β相交，m 是α内的一条定直线，则下列结论正确的是A.在β内必存在与m 平行的直线B.在β内必存在与m 垂直的直线C.在β内必不存在与m 平行的直线D.在β内不存在与m 垂直的直线22.设平面α⊥平面β，在平面α内的一条直线a 垂直于平面β内的一条直线b ，则()A.直线a 必垂直于平面βB.直线b 必垂直于平面αC.直线a 不一定垂直于平面βD.过a 的平面与过b 的平面垂直23.下列命题中错误的是A.如果α⊥β，那么α内所有直线都垂直于平面βB.如果α⊥β，那么α内一定存在直线平行于平面βC.如果α不垂直于β，那么α内一定不存在直线垂直于平面βD.如果平面α⊥平面γ，平面β⊥γ，α∩β＝l ，那么l ⊥γ24.如图，四边形BCEF 、AFED 都是矩形，且平面AFED ⊥平面BCEF ，则下列式子中正确的是A.cos α＝cos β·cos θB.sin α＝sin β·cos θC.cos β＝cos α·cos θD.sin β＝sin α·cos θ25.一条直线与一个直二面角的两个面所成的角分别为θ和ϕ，则θ＋ϕA.≤90°B.≠90°C.≥90°D.无法确定26.过正方形ABCD 的顶点A 作线段⊥'A A 平面ABC D.若AB B A ='，则平面AB A '与平而CD A '所成角的度数是A.30°B.45°C.60°D.90°27.设有不同的直线a 、b 和不同的平面α、β、γ，给出下列三个命题：⑴若a ∥α，b ∥α，则a ∥b ；⑵若a ∥α，a ∥β，则α∥β； ⑶若α⊥γ，β⊥γ，则α∥β.其中正确命题的个数是 A.0 B.1 C.2 D.328.在正方形SG 1G 2G 3中，E ，F 分别是G 1G 2及G 2G 3的中点，D 是EF 的中点，现在沿SE ，SF 及EF 把这个正方形折成一个四面体，使G 1，G 2，G 3三点重合，重合后的点记为G ，那么，在四面体S －EFG 中必有 A.SG ⊥△EFG 所在平面 B.SD ⊥△EFG 所在平面 C.GF ⊥△SEF 所在平面 D.GD ⊥△SEF 所在平面SG 1G2G3 EFD29.设直线m、n和平面α、β,则下列命题中，正确的是A.m∥n,m⊂α,n⊂β⇒α∥βB.m⊥α,m⊥n,n⊂β⇒α∥βC.m∥n,n⊥β,m⊂α⇒α⊥βD.m∥n,m⊥α,n⊥β⇒α⊥β30.设有不同的直线a、b和不同的平面α、β、γ,给出下列三个命题①若a∥α,b∥α,则a∥b；②若a∥α,a∥β,则α∥β；③若α⊥γ,β⊥γ，则α∥β其中正确命题的个数为A.0B.1C.2D.331.下列命题正确的是A.若直线a∥平面α，直线b⊥a，b⊂平面β，则α⊥βB.若直线a⊥直线b，a⊥平面α，b⊥平面β，则α⊥βC.过平面外的一条直线有且只有一个平面与已知平面垂直D.过平面外一点有且只有一个平面与已知平面垂直32.已知二面角α－l－β的大小为60°，b和c是两条异面直线，则在下列四个条件中，能使b和c的角为60°的是A.b∥α，c⊥βB.b∥α，c⊥βC.b⊥α，c⊥βD.b⊥α，c∥β33.设平面α⊥平面β，直线a⊂α，直线b⊂β，且a⊥b，则A.a⊥βB.b⊥αC.a⊥β与b⊥α中至少有一个成立D.a⊥β与b⊥α同时成立34.如图:过正方形ABCD的顶点A，引P A⊥平面AC，若P A＝AB，则平面ABP和平面CDP所成的二面角的大小是A.30°B.45°C.60°D.90°35.设二面角α-AB-β面上一点D，DP在α内与AB成45°，与平面β成30°角，则二面角α-AB-β的度数是A.15°B.30°C.45°D.60°36.自大于90°的二面角内一点分别向两个面引垂线，它们所成的角与二面角的平面角的大小关系是A.相等B.互补C.相等或互补D.无关37.一个直角三角形的两个直角边长为a、b，沿斜边高折成直二面角，则两个直角边所夹角的余弦值为A.22b a ab +B.222b a ab+ C.22b a ab+ D.22b a ab +38.过平面外的两个点A 、B 有无穷多个平面都与α垂直，则一定有A.直线AB ∥αB.直线AB 与α成60°角C.A 、B 两点在α的一条垂线上D.A 、B 两点到α的距离相等39.A 为直二面角α－l －β的棱上的一点，两条长度都等于a 的线段AB 、AC 分别在α、β内并且都与l 成45°角，则BC的长为 A.a B.a 或3a C.a 或2a D.a 或5a40.如果直线l 、m 与平面α、β、γ满足：l ＝β∩γ，l ∥α，m ⊂α和m ⊥γ，那么必有A. α⊥γ且l ⊥mB. α⊥γ且m ∥βC. m ∥β且l ⊥mD. α∥β且α⊥γ41.有不同的直线a ､b 和不同的平面α､β､γ,给出下列三个命题:(1)若a ∥α,b ∥α,则a ∥ B. (2)若a ∥α,α∥β,则α∥β.(3)若α⊥γ,β⊥γ,则α∥β.其中正确的个数是 A.0 B.1 C.2 D.342.若平面α⊥平面β，平面β⊥平面γ，则A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能43.已知直线a 、b 和平面α、β、γ，可以使α∥β的条件是A.a ⊂α，b ⊂β，a ∥bB.a ⊂α，b ⊂α，a ∥β，b ∥βC.α⊥γ，β⊥γD.a ⊥α，a ⊥β44.下列三个命题，其中正确命题的个数为①平面α∥平面β，β⊥平面γ，则α⊥γ ②平面α∥平面β，β∥平面γ，则α∥γ ③平面α⊥平面β，平面γ⊥β，则α⊥γ A.1 B.2 C.3 D.045.如图,四边形ABCD 中,AD //BC ,AD=AB ,∠BCD =45°,∠BAD =90°,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,构成三棱锥A-BC D.则在三棱锥A-BCD ,下列命题正确的是 A.平面ABD ⊥平面ABC B.平面ADC ⊥平面BDC C.平面ABC ⊥平面BDC D.平面ADC ⊥平面ABC二、填空题(共5题，题分合计20分)1.正方形ABCD 与正方形ABEF 所在平面成60°的二面角，则异面直线AD 和BF 所成角的余弦值为____________________________.2. 已知m 、l 是直线,α、β是平面,给出下列命题:①若l 垂直于α内的两条相交直线,则l ⊥α; ②若l 平行于α,则l 平行于α内的所有直线; ③若m ⊂α, l ⊂β,且l ⊥m , 则α⊥β; ④若l ⊂β,且 l ⊥α,则α⊥β; ⑤若m ⊂α, l ⊂β,且α∥β,则m ∥l.其中正确的命题的序号是___________.(注:把你认为正确的命题的序号都填上)3.设有四个条件：①平面γ与平面α、β所成的锐二面角相等； ②直线a ∥b ,a ⊥平面α，b ⊥β；③a 、b 是异面直线，βα⊂⊂b a ,，且ａ∥β，ｂ∥α；④平面α内距离为d 的两条直线在平面β内的射影仍为两条距离为d 的平行线，其中能推出α∥β的条件有.(填写所有正确条件的代号)4.一条直线与平面α相交于点A ，在平面α内不过A 点的直线与这条直线所成角的最大值为_________.5.在空间，下列命题正确的是____________.(注：把你认为正确的命题的序号都填上)①如果两条直线a 、b 分别与直线l 平行，那么a ∥b ②如果一条直线a 与平面β内的一条直线b 平行，那么a ∥β ③如果直线a 与平面β内的两条直线b 、c 都有垂直，那么a ⊥β ④如果平面β内的一条直线a 垂直平面γ，那么β⊥γ三、解答题(共10题，题分合计110分)1.已知:二面角α- l -β等于120°，AB =10，A ∈α，B ∈β. A 、B 到l 的距离分别等于2和4.(1)求直线AB 和平面β所成角的大小;(2)求异面直线AB 和l 所成角的大小.2.已知M 、N 分别是正方体ABCD - A ′B ′C ′D ′的棱BB ′和B ′C ′的中点，求（1）MN 和CD ′'所成的角（2）MN 和AD 所成的角.3.已知:正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直点M 在AC 上移动,点N 在BF 上移动,若CM = BN = a ,)20(<<a(1)求MN 的长(2)当a 为何值时, MN 的长最小(3)当MN 长最小时,求面MNA 与MNB 所成二面角α的大小4.边长为1的正方形ABCD , P A ⊥平面ABCD(1)求证:平面P AD ⊥平面PCD ;(2)若P A =PB ,求AC 与平面PCD 所成的角.5.已知△ABC ，P A ⊥平面ABC ，P A = AB = BC = AC .AH ⊥平面PBC ，H 为垂足，求证：H 不是△PBC 的垂心.6.已知斜三棱柱ABC -A 1B 1C 1,侧棱与底面边长都是2,侧棱与底面成60°角,且侧面ABB 1A 1⊥底面ABC .(1)求证: B 1C ⊥C 1A ;(2)求二面角C 1-AB -C 的大小.7.将一副三角板如图拼接,∠BAC =∠BCD =90°,AB =AC ,∠BDC =60°,且平面ABC ⊥平面BCD ,(1)求证:平面ABD ⊥平面ACD ;(2)求二面角A -BD -C 的正切值;(3)求异面直线AD 与BC 所成角的余弦值.8.如图，正方体ABCD -A 1B 1C 1D 1中，过顶点B 、D 、C 1作截面，则二面角B -DC 1-C 的余弦值是多少?9.如图，∠BAD＝90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直，E是BC的中点，则AE与平面BCD所成角的大小为.10.两个正方形ABCD, CDEF拼接成直二面角,点M在BD上,N点在CE上,且BM=CN，CD=l.(1)求证: MN∥平面BCF,(2)设BM=t，MN= f (t),求函数f (t)的解析式,(3)求函数f (t)的定义域及最小值.1.(2003北京春,19)如图,ABCD-A1B1C1D1是长方体,侧棱AA1长为1,底面为正方体且边长为2,E是棱BC的中点,求面C1DE与面CDE所成二面角的正切值.。

【必修2】2.10直线与平面所成的角

复习回顾 1.直线和平面的位置关系
平行，直线在平面内，相交
2.直线和平面垂直的判定思考:当直线a与平面的关系是a∩=A时，如何反映出直线与平面的相对位置关系呢?
直线与平面所成的角
a A

如图，AO是平面的斜线， AB ⊥平面于B，OD是内不与OB重合的直线，∠AOB=θ1 ∠BOD= θ2 ∠AOD=θ α
思考:θ与θ1的大小关系如何?
A
1
θ2
O
α
Cห้องสมุดไป่ตู้
B D
0 cos2 1
cos cos1
最小角原理或： sin
1
AC AB sin AO AO
1
∵AB＜AC 斜线和平面内射影所成的角，是这条斜线和平面内 ∴sinθ1＜sinθ 任意的直线所成的一切角中最小的角。 1
（1）A1C1与面ABCD所成的角
（2） A1C1与面BB1D1D所成的角
（3） A1C1与面BB1C1C所成的角 45o
（4）A1C1与面ABC1D1所成的角
A1 D1 B1 C1
D
C
A
B
例3 ：如图：正方体ABCD-A1B1C1D1中，
（1）A1C1与面ABCD所成的角
（2） A1C1与面BB1D1D所成的角
A
B
例2 ：如图：正方体ABCD-A1B1C1D1中，
（1）AB1在面BB1D1D中的射影
（2）AB1在面A1B1CD中的射影
线段B1E
（3）AB1在面CDD1C1中的射影
D1 A1
E
C1 B1
D
C
A
B
例2 ：如图：正方体ABCD-A1B1C1D1中，

垂线平行线和画角练习题二

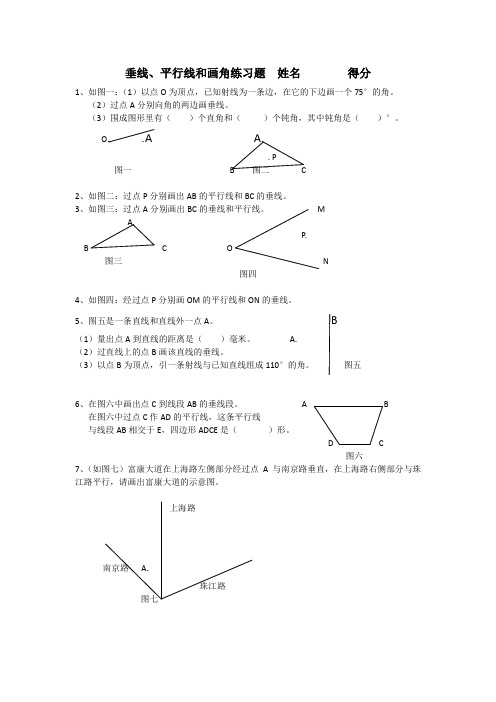
垂线、平行线和画角练习题姓名得分1、如图一：（1）以点O为顶点，已知射线为一条边，在它的下边画一个75°的角。

（2）过点A分别向角的两边画垂线。

（3）围成图形里有（）个直角和（）个钝角，其中钝角是（）°。

O. .A A.. P图一 B 图二 C2、如图二：过点P分别画出AB的平行线和BC的垂线。

3、如图三：过点A分别画出BC的垂线和平行线。

MA.P.B C O图三N图四4、如图四：经过点P分别画OM的平行线和ON的垂线。

5、图五是一条直线和直线外一点A。

.B（1）量出点A到直线的距离是（）毫米。

A.（2）过直线上的点B画该直线的垂线。

（3）以点B为顶点，引一条射线与已知直线组成110°的角。

图五6、在图六中画出点C到线段AB的垂线段。

A B在图六中过点C作AD的平行线，这条平行线与线段AB相交于E，四边形ADCE是（）形。

D C图六7、（如图七）富康大道在上海路左侧部分经过点A与南京路垂直，在上海路右侧部分与珠江路平行，请画出富康大道的示意图。

上海路南京路A.珠江路图七8、图八是人行横道线，如果要从点A穿过马路，那么怎样走路线最短？因为：。

把最短的路线画出来。

图八9、从小华家和小明家分别修两条直通北京路的小路，怎样修最近？在图上画出来。

小华家.北京路.小明家图九10、如图十：（1）在图中过O点分别画线段AB、线段CD的平行线，并过O点画出线段BC 的垂线。

点O到线段BC的距离是（）。

（2）在图中过C点分别画线段AB的平行线和垂线，画出的这两条直线的关系是（）。

A O. DB C11、（1）用量角器画一个70°的角。

（2）画一个120°的角，并把这个角平均分成三份。

12、用三角尺画105°和75°的角。

（保留作图痕迹）。

专题立体几何之所成角-(人教A版2019必修第二册) (教师版)

立体几何之所成角1 异面直线所成的角①范围(0∘ ,90∘]；②作异面直线所成的角：平移法.如图,在空间任取一点O,过O作a′ // a ,b′ // b,则a′ ,b′所成的θ角为异面直线a ,b所成的角.特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角.2 线面所成的角①定义如下图，平面的一条斜线(直线l)和它在平面上的射影(AO)所成的角，叫做这条直线和这个平面所成的角.一条直线垂直平面，则θ=90°；一条直线和平面平行或在平面内，则θ=0°.②范围[0∘ ,90∘]3 二面角①定义从一条直线出发的两个半平面所组成的图形叫做二面角.在二面角的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB 构成的∠AOB叫做二面角的平面角.②范围[0° ,180°].【题型一】异面直线所成的角【典题1】如图,正方体ABCD—A1B1C1D1中，点E ,F分别是AA1,AD的中点，则CD1与EF所成角为()A．0°B．45°C．60°D．90°【解析】连结A1D、BD、A1B,∵正方体ABCD—A1B1C1D1中,点E ,F分别是AA1,AD的中点，EF∥A1D,∵A1B∥D1C,∴∠DA1B是CD1与EF所成角,∵A1D=A1B=BD ,∴∠DA1B=60°．∴CD1与EF所成角为60°．故选 C．【点拨】①找异面直线所成的角,主要是把两条异面直线通过平移使得它们共面,可平移一条直线也可以同时平移两条直线；②平移时常利用中位线、平行四边形的性质；【典题2】如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1 ,AD 的中点,那么异面直线OE和FD1所成角的余弦值等于．【解析】取BC的中点G．连接GC1,则GC1∥FD1,再取GC的中点H,连接HE、OH,则∵E是CC1的中点,∴GC1∥EH,∴∠OEH为异面直线所成的角．在△OEH中,OE=√3,HE=√52,OH=√52．由余弦定理,可得cos∠OEH=OE 2+EH2−OH22OE⋅EH=3⋅√2=√155．故答案为√155【点拨】本题利用平移法找到异面直线所成的角(∠OEH)后,确定含有该角的三角形(△OEH),利用解三角形的方法(正弦定理,余弦定理等)把所求角∠OEH最终求出来.【典题3】如图,已知P是平行四边形ABCD所在平面外一点,M,N分别是AB ,PC的中点．(1)求证：MN∥平面PAD；(2)若MN=BC=4 ,PA=4√3,求异面直线PA与MN所成的角的大小．【解析】(1)证明：取PD中点Q,连AQ、QN,则AM∥QN,且AM=QN,∴四边形AMNQ为平行四边形∴MN∥AQ又∵AQ在平面PAD内,MN不在平面PAD内∴MN∥面PAD；(2)解方法一∵MN∥AQ∴∠PAQ即为异面直线PA与MN所成的角∵MN=BC=4 ,PA=4√3,∴AQ=4,设PQ=x,根据余弦定理可知cos∠AQD+cos∠AQP=0即16+x 2−488x +16+x2−168x=0,解得x=4在三角形AQP中,AQ=PQ=4 ,AP=4√3∴cos∠PAQ=2×4×4√3=√32,即∠PAQ=30°∴异面直线PA与MN所成的角的大小为30°方法二过点A作AH⊥PD交PD于H,如图∵MN=BC=4,∴H是QD的中点设HD=x,则QH=x,PQ=2x,在Rt△AQD和Rt△APH利用勾股定理可得AH2=16−x2=48−9x2,解得x=2∴cos∠PAQ=PHAP =4√3=√32,即∠PAQ=30°∴异面直线PA与MN所成的角的大小为30°【点拨】本题中所成角∠PAQ找到后,无法在一个三角形里求出,此时把问题转化为平面几何问题, 再利用解三角形的方法进行求解.【题型二】线面所成的角【典题1】如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直．AB∥CD,AB⊥BC,AB= 2CD=2BC,EA⊥EB．(1)求证：AB⊥DE；(2)求直线EC与平面ABE所成角的正弦值．【解析】(1)证明：取AB中点O,连接EO,DO．∵EB=EA,∴EO⊥AB．∵四边形ABCD为直角梯形,AB=2CD=2BC,AB⊥BC,∴四边形OBCD为正方形,∴AB⊥OD．又∵EO∩OD=O,∴AB⊥平面EOD．∴AB⊥ED．(2)∵平面ABE⊥平面ABCD,且AB⊥BC,∴BC⊥平面ABE．则∠CEB为直线EC与平面ABE所成的角．设BC=a,则AB=2a,BE=√2a,∴CE=√3a,在直角三角形CBE中,sin∠CEB=CBCE =√3=√33．即直线EC与平面ABE所成角的正弦值为√33．【点拨】本题中的“直线EC与平面ABE所成的角”是根据线面角的定义直接在题目原图上找到的,在含所求角∠CEB的直角三角形CBE中求出角度！【典题2】如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC．(1)求证：AG∥平面PEC；(2)求BE的长；(3)求直线AG与平面PCA所成角的余弦值．【解析】(1)证明：∵CD ⊥AD,CD ⊥PA∴CD ⊥平面PAD ∴CD ⊥AG,又PD ⊥AG∴AG ⊥平面PCD作EF ⊥PC 于F,因面PEC ⊥面PCD∴EF ⊥平面PCD∴EF ∥AG,又AG ⊄面PEC,EF ⊂面PEC,∴AG ∥平面PEC(2)由(1)知A 、E 、F 、G 四点共面,又AE ∥CD ∴AE ∥平面PCD∴AE ∥GF ∴四边形AEFG 为平行四边形,∴AE =GF∵PA =3,AD =AB =4 ∴PD =5,AG =125, 在Rt △PAGP 中,PG 2=PA 2−AG 2=8125 ∴PG =95 又GF CD =PG PD∴GF =3625 ∴AE =3625,故BE =6425(3)∵EF ∥AG,所以AG 与平面PAC 所成角等于EF 与平面PAC 所成的角,过E 作EO ⊥AC 于O 点,易知EO ⊥平面PAC,又EF ⊥PC,∴OF 是EF 在平面PAC 内的射影∴∠EFO 即为EF 与平面PAC 所成的角EO =AEsin45°=3625×√22=18√225,又EF =AG =125,∴sin∠EFO=EOEF =18√225×512=3√210故cos∠EFO=√1−sin2∠EFO=√8210所以AG与平面PAC所成角的余弦值等于√8210.【点拨】①若在题目中不能直接找到所求线面角,则可用“作高法”确定所求角,比如下图中,求直线AP与平面α所成的角,具体步骤如下：(1) 如图,过点P作平面α的高PO,垂足为O,则AO是线段AP在平面α上的投影；(2) 找到所求角θ；(3) 求解三角形APO进而求角θ.(此方法关键在于找到垂足O的位置,证明到PO⊥平面α,如本题中EO⊥平面PAC的证明)②本题若直接求“AG与平面PAC所成角”,过点G做高有些难度,则由EF∥AG,能把“AG与平面PAC所成角”转化为“EF与平面PAC所成的角”,这方法称为“间接法”吧.【典题3】如图,正四棱锥S－ABCD中,SA=AB=2,E,F,G分别为BC,SC,CD的中点．设P为线段FG上任意一点．(Ⅰ)求证：EP⊥AC；(Ⅰ)当P为线段FG的中点时,求直线BP与平面EFG所成角的余弦值．【解析】证明：(Ⅰ)连接AC交BD于O,∵S－ABCD是正四棱锥,∴ SO⊥平面ABCD,∴SO⊥AC,又∵AC⊥BD,SO∩BD=O,∴AC⊥平面SBD,∴AC⊥SD,∵F,G分别为SC,CD的中点,∴SD∥FG,∴AC⊥GF,同理AC⊥EF,∴AC⊥平面GEF,又∵PE⊂平面GEF,∴EP⊥AC．(Ⅰ) 方法一过B作BH⊥GE于点H,连接PH,∵BD⊥AC,BD∥GF,∴BH∥AC,由(Ⅰ)知：AC⊥平面GEF,∴BH⊥平面GEF,∴∠BPH就是直线BP与平面EFG所成的角,∵SA=AB=2,∴在Rt△BHP中,解得BH=√22,PH=√132,PB=√152,(易知△BHE是等腰直角三角形,又由斜边BE=1,∴BH=√22；在三角形PGH中,PG=12,GH=3√22,∠PGH=π4,用余弦定理可得PH=√132)则cos∠BPH=PHPB =√19515,故直线BP与平面EFG所成角的余弦值为√19515.方法二设过点B作平面EFG的垂直,垂直为T,则∠BPT就是直线BP与平面EFG所成的角,BT是点B到平面PGE的距离,由已知条件可求GF=EF=1,GE=√2,则∠GFE=90°,∴S△PEG=12S△GFE=12×12=14,由于P、F是中点,易得点P到平面ABCD的距离ℎ1=14SO=√24,而S△GEB=12S△GCB=12×1=12,对于三棱锥P−GEB,由V B−PEG=V P−GEB⇒13×BT×S△PEG=13×ℎ1×S△GEB⇒112BT=√224⇒BT=√22,在正四棱锥S－ABCD中可求PB=√152,(方法较多,提示过点P作平面ABCD的高PI)∴sin∠BPT=BTBP =√3015∴cos∠BPT=√1−sin∠BPT=√19515,故直线BP与平面EFG所成角的余弦值为√19515.【点拨】①本题第二问中方法一就是用“做高法”,计算量有些大；方法二是觉得垂足H的位置难确定,可设点B到平面EFG的投影为T(即垂足),再用“等积法”求高BT,则sin∠BPT=BTBP,可求所求角∠BPT,这种方法称为“等积法”；②思考：上一题试试用“等积法”！【题型三】二面角【典题1】如图,在棱长为a的正方体ABCD－A1B1C1D1中,AC 与BD相交于点O．求二面角 A1－BD－A 的正切值．【解析】在正方体中BD⊥平面A1ACC1，∴AO⊥BD,A1O⊥BD，∴二面角A1－BD－A的平面角为∠A1OA由题中的条件求出：AO=√22a ,AA1=a∴tan∠A1OA=√22a=√2,所以二面角 A1－BD－A 的正切值为√2．【点拨】本题根据二面角的定义找到二面角二面角A1－BD－A的平面角为∠A1OA,再在三角形AOA1内用解三角形的方法求解角∠A1OA.【典题2】如图,四棱锥P－ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=√6,点E是棱PB的中点．(1)求直线AD与平面PBC的距离；(2)若AD=√3,求二面角A－EC－D的平面角的余弦值．【解析】(1)在矩形ABCD中,AD∥BC,从而AD∥平面PBC,故直线AD与平面PBC的距离为点A到平面PBC的距离,因PA⊥底面ABCD,故PA⊥AB,可得△PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB ∴BC⊥AE,从而AE⊥平面PBC,故AE之长即为直线AD与平面PBC的距离,在Rt△PAB中,PA=AB=√6,所以AE=12PB=12√PA2+AB2=√3(2)过点D作DF⊥CE于F,过点F做FG⊥CE,交AC于G,连接DG,则∠DFG为所求的二面角的平面角．由(1)知BC⊥AE,又AD∥BC,得AD⊥AE,从而DE=√AE2+AD2=√6在Rt△CBE中,CE=√BE2+BC2=√6,由CD=√6,所以△CDE为等边三角形,故F为CE的中点,且DF=CD•sinπ3=3√22因为AE⊥平面PBC,故AE⊥CE,又FG⊥CE,知FG∥AE．∴G点为AC的中点,FG=12AE=√32,则在Rt△ADC中,DG=12√AD2+CD2=32,所以cos∠DFG=DF 2+FG2−DG22DF⋅FG=√63【点拨】若在题目中不能直接得到所求二面角,就需要构造出二面角,比如本题求二面角A－EC－D,解题具体步骤如下(1) 过点D作DF⊥EC,过点F作FG⊥EC交AC于点D,则二面角∠DFG为所求的二面角的平面角；(2) 确定含角∠DFG的三角形DFG,利用解三角形的方法求出角∠DFG,常见的是求出三角形三边再用余弦定理.【典题3】如图,已知三棱锥P－ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点．(1)求证：PC⊥BC．(2)求二面角M－AC－B的大小．【解析】(1)证明：由PA⊥平面ABC,∴PA⊥BC,又因为∠ACB=90°,即BC⊥AC．∴BC⊥面PAC,∴PC⊥BC．(2)取AB中点O,连结MO、过O作HO⊥AC于H,连结MH,∵M是PB的中点,∴MO∥PA,又∵PA⊥面ABC,∴MO⊥面ABC．∴∠MHO为二面角M－AC－B的平面角．设AC=2,则BC=2√3,MO=1,OH=√3,在Rt△MHO中,tan∠MHO=MOHO =√3=√33．二面角M－AC－B的大小为30∘．【点拨】求二面角也可以转化为线面角,比如求二面角D－AB－C,解题思路如下过点D作DE⊥AB,则二面角D－AB－C等于直线ED与平面ABC所成的角或其补角,若过点D作DF⊥平面ABC,则二面角D－AB－C是锐角,等于角∠DEF；二面角D－AB－C是钝角,等于角∠DEF的补角.1(★)在正方体ABCD﹣A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是()A．0 <θ <π2B．0 <θ≤π2C．0≤θ≤π3D．0 <θ≤π3【答案】D【解析】∵A1B∥D1C，∴CP与A1B成角可化为CP与D1C成角．∵△AD1C是正三角形可知当P与A重合时成角为π3，∵P不能与D1重合因为此时D1C与A1B平行而不是异面直线，∴0 <θ≤π3．故选D．2(★★)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体．O1,O2,O2′分别为AB ,BC ,DE的中点,F为弧AB的中点,G为弧BC的中点．则异面直线AF与GO2′所成的角的余弦值为．【答案】√1010【解析】如图，连接AF、FB、BG、GC，∵F为半圆弧AFB的中点，G为半圆弧BGC的中点，由圆的性质可知，G、B、F三点共线，且AF=CG，FB=GB，AB=BC，∴△AFB≌△CGB，∴AF∥CG，则∠CGO2′即为所求的角或其补角，又∵半径为1，高为2，且△AFB，△CG B都是等腰Rt△，∴CG=√2，CO2′=GO2′=√1+22=√5，∴在△CGO2′中，cos∠CGO2′=√52√22√522√2⋅√5=√1010，即异面直线AF与GO2′所成的角余弦值√1010．故答案为√1010．3 (★★)如图所示,在正方体ABCD－A1B1C1D1中,M是AB上一点,N是A1C的中点, MN⊥平面A1DC．(1)求证：AD1⊥平面A1DC；(2)求MN与平面ABCD所成的角．【答案】(1) 见解析(2)π4【解析】(1)证明：由ABCD－A1B1C1D1为正方体，得CD⊥平面ADD1A1，AD1⊂平面ADD1A1∴CD⊥AD1，又AD1⊥A1D，且A1D∩CD＝D，∴AD1⊥平面A1DC；(2)解：∵MN⊥平面A1DC，又由(1)知AD1⊥平面A1DC，∴MN∥AD1，∴AD1与平面ABCD所成的角，就是MN与平面ABCD所成的角，∵D1D⊥平面ABCD，∴∠D1AD即为AD1与平面ABCD所成的角，，由正方体可知∠D1AD=π4∴MN与平面ABCD所成的角为π．44(★★★) 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P ,Q分别为AE,AB的中点．(1)证明：PQ∥平面ACD；(2)求AD与平面ABE所成角的正弦值．【答案】(1) 见解析(2)√55【解析】(1)证明：因为P，Q分别为AE，AB的中点，所以PQ∥EB.又DC∥EB，因此PQ∥DC，又PQ 平面ACD，从而PQ∥平面ACD.(2)如图，连接CQ，DP，因为Q为AB的中点，且AC＝BC，所以CQ⊥AB.因为DC⊥平面ABC，EB∥DC，所以EB⊥平面ABC，因此CQ⊥EB. 故CQ⊥平面ABE.EB＝DC，所以四边形CQPD为平行四边形，故DP∥CQ，因此DP⊥平面ABE，由(1)有PQ∥DC，又PQ＝12∠DAP为AD和平面ABE所成的角，在Rt△DP A中，AD＝√5，DP＝1，sin∠DAP＝√5，即AD与平面ABE5。

数学2.3.12直线和平面所成的角课件新人教版A必修2

问题提出
1.直线和平面垂直的定义和判定定理分别是什么？
定义：如果一条直线与平面内的任意一条直线都垂直，则称这条直线与这个平面垂直.
定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面.
2.当直线与平面相交时，对于直线与平面垂直的情形，我们已作了一些相关研究，对于直线与平面不垂直的情形，我们需要从理论上作些分析.
αA
OB
思考5:如图，过平面α内一点P引平面α的两条斜线PA、PB，这两条斜线段在平面α内的射影分别为PC、 PD，如果PA>PB，那么PC与PD的大小关系确定吗？
A B
C
D
α
P
思考6:如图，直线l是平面α的一条斜线，它在平面α内的射影为b，直线a在平面α内，如果a⊥b，那么直线a与直线l垂直吗？为什么？反之成立吗？
l
b abal
αa
知识探究（二）：直线和平面所成的角思考1:平面的一条斜线与这个平面总存在一个相对倾斜度，我们设想用一个平面角来反映这个倾斜度，并且这个角的大小由斜线与平面的相对位置关系所确定，那么角的顶点宜选在何处？
l
α
思考2:如图，AB为平面α的一条斜线，A为斜足，AC为平面α内的任意一条直线，能否用∠BAC反映斜线AB 与平面α的相对倾斜度？为什么？
知识探究（一）：平面的斜线
思考1:当直线与平面相交时，它们可能垂直，也可能不垂直，如果一条直线和一个平面相交但不垂直，这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足.那么过一点作一个平面的斜线有多少条？
l
斜线
斜足
P
α直线叫做这条斜线在这个平面上的射影.那么斜线l在平面α内的射影有几条？