高考数学原创预测题专题三三角函数平面向量理人教版

合集下载

高考数学压轴专题人教版备战高考《平面向量》真题汇编及解析

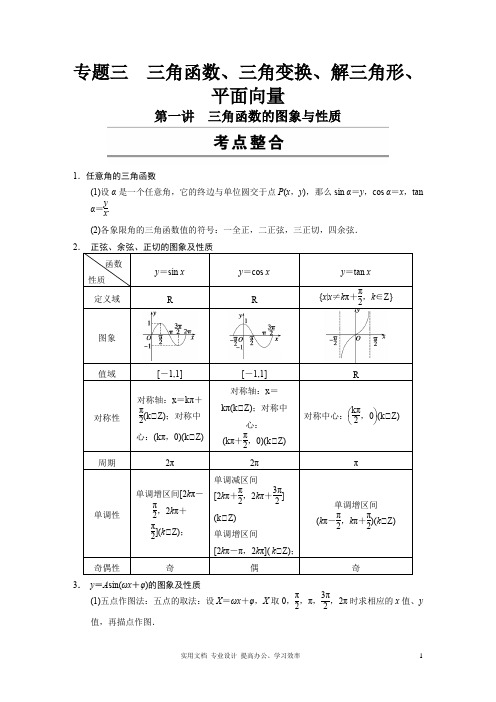
数学《平面向量》高考复习知识点一、选择题1．已知ABC V 为直角三角形，,6,82C BC AC π===，点P 为ABC V 所在平面内一点，则()PC PA PB ⋅+u u u r u u u r u u u r的最小值为（）A ．252-B ．8-C ．172-D ．1758-【答案】A 【解析】【分析】根据,2C π=以C 点建系, 设(,)P x y ,则22325()=2(2)222PC PA PB x y ⎛⎫⋅+-+-- ⎪⎝⎭u u u r u u u r u u u r ,即当3=2=2x y ，时,取得最小值.【详解】如图建系，(0,0), (8,0), (0,6)C A B ,设(,)P x y ，(8,)PA x y =--u u u r ，(,6)PB x y =--u u u r，则22()(,)(82,62)2826PC PA PB x y x y x x y y ⋅+=--⋅--=-+-u u u r u u u r u u u r22325252(2)2222x y ⎛⎫=-+--≥- ⎪⎝⎭.故选:A. 【点睛】本题考查平面向量数量积的坐标表示及其应用,根据所求关系式运用几何意义是解题的关键,属于中档题.2．在ABC ∆中，5,6,7AB BC AC ===，点E 为BC 的中点，过点E 作EF BC ⊥交AC 所在的直线于点F ，则向量AF u u u r在向量BC uuu r 方向上的投影为（）A ．2B ．32C ．1D ．3【答案】A 【解析】【分析】由1()2AF AE EF AB AC EF =+=++u u u r u u u r u u u r u u u r u u u r u u u r ， EF BC ⊥，得12AF BC ⋅=u u u r u u u r，然后套用公式向量AF u u u r 在向量BC uuu r 方向上的投影||AF BCBC ⋅=u u u r u u u ru u u r ，即可得到本题答案. 【详解】因为点E 为BC 的中点，所以1()2AF AE EF AB AC EF =+=++u u u r u u u r u u u r u u u r u u u r u u u r，又因为EF BC ⊥，所以()22111()()()12222AF BC AB AC BC AB AC AC AB AC AB ⋅=+⋅=+⋅-=-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ，所以向量AF u u u r 在向量BC uuu r 方向上的投影为2||AF BCBC ⋅=u u u r u u u ru u u r . 故选：A. 【点睛】本题主要考查向量的综合应用问题，其中涉及平面向量的线性运算及平面向量的数量积，主要考查学生的转化求解能力.3．已知O 是平面上一定点，满足()||cos ||cos AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u ur u u u r ，[0λ∈，)+∞，则P 的轨迹一定通过ABC ∆的（） A ．外心 B ．垂心C ．重心D ．内心【答案】B 【解析】【分析】可先根据数量积为零得出BC uuu r 与()||cos ||cos ABAC AB B AC Cλ+u u u ru u u ru u ur u u u r 垂直，可得点P 在BC 的高线上，从而得到结论．【详解】Q ()||cos ||cos AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u ur u u u r ， ∴()||cos ||cos AB ACOP OA AB B AC C λ-=+u u u r u u u ru u u r u u u r u u ur u u u r ，即()||cos ||cos AB ACAP AB B AC Cλ=+u u u r u u u ru u u r u u ur u u u r ， Q cos BA BC B BA BC ⋅=u u u r u u u r u uu r u u u r ，cos CA CB C CA CB⋅=u u u r u u u r u u u r u u u r ，∴()0||cos ||cos AB ACBC BC BC AB B AC C⋅+=-+=u u u r u u u ru u u r u u u r u u u r u u u r u u u r ， ∴BC uuu r 与()||cos ||cos AB ACAB B AC Cλ+u u u r u u u ru u ur u u u r 垂直，即AP BC ⊥uu u r uu u r，∴点P 在BC 的高线上，即P 的轨迹过ABC ∆的垂心.故选：B ．【点睛】本题重点考查平面向量在几何图形中的应用，熟练掌握平面向量的加减运算法则及其几何意义是解题的关键，考查逻辑思维能力和转化能力，属于常考题.4．如图，在ABC V 中，AD AB ⊥，3BC BD =u u u v u u u v ，1AD =u u u v ，则AC AD ⋅=u u u v u u u v（）A ．3B 3C 3D 3【答案】D 【解析】∵3AC AB BC AB =+=u u u v u u u v u u u v u u u v u u v ，∴(3)3AC AD AB AD AB AD BD AD ⋅=+⋅=⋅⋅u u u v u u u v u u u v u u v u u u v u u u v u u u v u u u v ，又∵AB AD ⊥，∴0AB AD ⋅=uuu r，∴33cos 3cos 33AC AD AD AD ADB BD ADB AD u u u v u u u v u u u v u u u v u u v u u u v u u u v u u u v⋅=⋅=⋅∠=⋅∠==，故选D ．5．在平行四边形OABC 中，2OA =，3OC =6AOC π∠=，动点P 在以点B 为圆心且与AC 相切的圆上，若OP OA OC λμ=+u u u r u u u r u u u r，则43λμ+的最大值为（）A ．223+B ．33+C ．543+D ．723+【答案】D 【解析】【分析】先通过计算证明圆B 与AC 相切于点A ，再求出43OB OA BP OA λμ+=⋅+⋅u u u r u u u r u u u r u u u r，再求出7OB OA ⋅=u u u r u u u r ，BP OA ⋅u u u r u u u r的最大值为23即得解.【详解】如图所示，由2OA =，6AOC π∠=，由余弦定理得234+32231,1AC AC =-⨯⨯⨯=∴=， ∴90OCA BAC ∠=∠=o , ∴圆B 与AC 相切于点A ，又OP OA OC λμ=+u u u r u u u r u u u r ， ∴243OP OA OA OC OA λμλμ⋅=+⋅=+u u u r u u u r u u u r u u u r u u u r；∴()43OP OA OB BP OA OB OA BP OA λμ+=⋅=+⋅=⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r；如图，过点B 作,BD OA ⊥连接,OB 由题得6BAD π∠=,所以22333333,,(2)()1322222AD DB OB =⨯==∴=++=, 所以72cos 13213BOA ∠==, 所以1327213OB OA ⋅=⨯⨯=u u u r u u u r ，因为BP OA ⋅u u u r u u u r的最大值为32cos023⨯⨯=o ，∴43λμ+的最大值是723+. 故选：D.【点睛】本题主要考查三角函数和余弦定理解三角形，考查平面向量的数量积运算和范围的求解，意在考查学生对这些知识的理解掌握水平和分析推理能力.6．已知菱形ABCD 的边长为2，60ABC ∠=︒，则BD CD ⋅=u u u v u u u v（）A ．4B ．6C ．23D ．43【答案】B 【解析】【分析】根据菱形中的边角关系，利用余弦定理和数量积公式，即可求出结果．【详解】如图所示，菱形形ABCD 的边长为2，60ABC ∠=︒，∴120C ∠=︒，∴22222222cos12012BD =+-⨯⨯⨯︒=， ∴23BD =30BDC ∠=︒，∴|||3302|326BD CD BD CD cos =⨯⨯︒==⋅u u u r u u u r u u u r u u u r，故选B ．【点睛】本题主要考查了平面向量的数量积和余弦定理的应用问题，属于基础题.．7．已知在平面直角坐标系xOy 中，O 为坐标原点，()0,2A ，2220OB OA +=，若平面内点P 满足3PB PA =u u u r u u u r，则PO 的最大值为（）A ．7B ．6C ．5D ．4【答案】C 【解析】【分析】设(),P x y ，(),B m n ，根据3PB PA =u u u r u u u r可得262m x n y=-⎧⎨=-⎩，再根据2220OB OA +=可得点P 的轨迹，它一个圆，从而可求PO 的最大值. 【详解】设(),P x y ，(),B m n ，故(),PB m x n y =--u u u r ，(),2PA x y =--u u u r. 由3PB PA =u u u r u u u r可得363m x x n y y-=-⎧⎨-=-⎩，故262m x n y=-⎧⎨=-⎩，因为2220OB OA +=，故()22443420x y +-+=，整理得到()2234x y +-=，故点P 的轨迹为圆，其圆心为()0,3，半径为2，故PO 的最大值为325+=，故选：C. 【点睛】本题考查坐标平面中动点的轨迹以及圆中与距离有关的最值问题，一般地，求轨迹方程，可以动点转移法，也可以用几何法，而圆外定点与圆上动点的连线段长的最值问题，常转化为定点到圆心的距离与半径的和或差，本题属于中档题.8．若向量(1,1)a =r ，(1,3)b =-r ，(2,)c x =r 满足(3)10a b c +⋅=r r r，则x =（）A ．1B ．2C ．3D ．4【答案】A 【解析】【分析】根据向量的坐标运算，求得(3)(2,6)a b +=rr，再根据向量的数量积的坐标运算，即可求解，得到答案. 【详解】由题意，向量(1,1)a =r，(1,3)b =-r ，(2,)c x =r，则向量(3)3(1,1)(1,3)(2,6)a b +=+-=rr ，所以(3)(2,6)(2,)22610a b c x x +⋅=⋅=⨯+=r r r，解得1x =，故选A.【点睛】本题主要考查了向量的坐标运算，及向量的数量积的坐标运算的应用，其中解答中熟记向量的数量积的坐标运算公式，准确运算是解答的关键，着重考查了运算与求解能力，属于基础题.9．已知()4,3a =r ，()5,12b =-r 则向量a r 在b r方向上的投影为( )A ．165-B ．165C ．1613-D ．1613【答案】C 【解析】【分析】先计算出16a b r r⋅=-，再求出b r ，代入向量a r 在b r 方向上的投影a b b⋅r rr 可得【详解】()4,3a =r Q ，()5,12b =-r，4531216a b ⋅=⨯-⨯=-r r，则向量a r 在b r方向上的投影为1613a b b⋅-=r rr ，故选：C. 【点睛】本题考查平面向量的数量积投影的知识点. 若,a b r r的夹角为θ，向量a r 在b r 方向上的投影为cos a θ⋅r 或a b b⋅r rr10．已知向量(1,2)a =v ，(3,4)b =-v ，则a v 在b v方向上的投影为AB．2C ．1 D．5【答案】C 【解析】【分析】根据a v 在b v方向上的投影定义求解.【详解】a v 在b v 方向上的投影为(1,2)(3,4)381(3,4)5a b b⋅⋅--+===-rr r ，选C. 【点睛】本题考查a v在b v方向上的投影定义，考查基本求解能力.11．已知向量(b =r ，向量a r 在b r方向上的投影为6-，若()a b b λ+⊥r r r ，则实数λ的值为（） A ．13B ．13-C ．23D ．3【答案】A 【解析】【分析】设(),a x y =r ，转化条件得362x y +=-，()34x y λ+=-，整体代换即可得解.【详解】设(),a x y =r，Q a r 在b r方向上的投影为6-，∴36a b x y b⋅+==-r rr 即312x y +=-. 又 ()a b b λ+⊥r r r ，∴()0a b b λ+⋅=r r r即1330x y λλ+++=，∴()34x y λ+=-即124λ-=-，解得13λ=. 故选：A. 【点睛】本题考查了向量数量积的应用，属于中档题.12．已知四边形ABCD 是平行四边形，点E 为边CD 的中点，则BE =u u u rA ．12AB AD -+u u ur u u u rB ．12AB AD -u u ur u u u rC ．12AB AD +u u u r u u u rD ．12AB AD -u u u r u u u r【答案】A 【解析】【分析】由平面向量的加法法则运算即可. 【详解】如图，过E 作//,EF BC 由向量加法的平行四边形法则可知1.2BE BF BC AB AD =+=-+u u u v u u u v u u u v u u uv u u u v故选A. 【点睛】本题考查平面向量的加法法则，属基础题.13．已知数列{a n }的前n 项和为S n ，且a n +1=a n +a (n ∈N *，a 为常数)，若平面内的三个不共线的非零向量OAOB OC u u u r u u u r u u u r，，满足10051006OC a OA a OB =+u u u r u u u r u u u r ，A ，B ，C 三点共线且该直线不过O 点，则S 2010等于（）A ．1005B ．1006C ．2010D ．2012【答案】A 【解析】【分析】根据a n +1=a n +a ，可判断数列{a n }为等差数列，而根据10051006OC a OA a OB =+u u u r u u u r u u u r，及三点A ，B ，C 共线即可得出a 1+a 2010=1，从而根据等差数列的前n 项和公式即可求出S 2010的值. 【详解】由a n +1=a n +a ，得，a n +1﹣a n =a ； ∴{a n }为等差数列；由10051006OC a OA a OB =+u u u r u u u r u u u r ，所以A ，B ，C 三点共线； ∴a 1005+a 1006=a 1+a 2010=1， ∴S 2010()12010201020101100522a a +⨯===. 故选：A. 【点睛】本题主要考查等差数列的定义，其前n 项和公式以及共线向量定理，还考查运算求解的能力，属于中档题.14．已知向量(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，则当,1[]2t ∈-时，a tb-r r 的最大值为（）A BC ．2D 【答案】D 【解析】【分析】根据(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，得到1a =r ，1b =r ，0a b ⋅=r r ，再利用a tb -==r r 求解.【详解】因为(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，所以1a =r ，1b =r ，0a b ⋅=r r ，所以a tb -==r r当[]2,1t ∈-时，maxa tb-=r r故选：D 【点睛】本题考查向量的模以及数量积的运算，还考查运算求解能力，属于中档题.15．如图，两个全等的直角边长分别为1,3的直角三角形拼在一起，若AD AB AC λμ=+u u u r u u u r u u u r，则λμ+等于（）A ．333-+ B ．333+ C 31 D 31+【答案】B 【解析】【分析】建立坐标系，求出D 点坐标，从而得出λ，μ的值．【详解】解：1AC =Q ，3AB =30ABC ∴∠=︒，60ACB ∠=︒，以AB ，AC 为坐标轴建立坐标系，则13,12D ⎛+ ⎝⎭． )3,0AB =u u u r，()0,1AC =uu u r ，∴13,12AD ⎛=+ ⎝⎭u u u r ． Q AD AB AC λμ=+u u u r u u u r u u u r ，∴13231λμ⎧=⎪⎪⎨⎪=+⎪⎩，∴3631λμ⎧=⎪⎪⎨⎪=⎪⎩231λμ∴+=+．故选：B ．【点睛】本题考查了平面向量的基本定理，属于中档题．16．如图，在圆O 中，若弦AB ＝3，弦AC ＝5，则AO uuu v ·BC uuu v的值是A ．－8B ．－1C ．1D ．8【答案】D【解析】【分析】【详解】因为AO AC CO AB BO =+=+u u u v u u u v u u u v u u u v u u u v ，所以1()2AO AC BO AB CO =+++u u u v u u u v u u u v u u u v u u u v ，而BC AC AB BO CO =-=-u u u v u u u v u u u v u u u v u u u v ，所以1()2BC AC AB BO CO =-+-u u u v u u u v u u u v u u u v u u u v ，则 1()()4AO BC AC AB CO BO AC AB BO CO ⋅=+++-+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v 1()()()()()()4AC AB AC AB AC AB BO CO CO BO AC AB =+-++-++-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v ()()CO BO BO CO ++-u u u v u u u v u u u v u u u v221(||4AC AB AC BO AC CO AB BO AB CO =-+⋅-⋅+⋅-⋅u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v 22||)CO AC CO AB BO AC BO AB BO CO +⋅-⋅+⋅-⋅+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v2211(||)()42AC AB AC BO AB CO =-+⋅-⋅u u u v u u u v u u u v u u u v u u u v u u u v2211(||)[()]42AC AB AB BC BO AB CO =-++⋅-⋅u u u v u u u v u u u v u u u v u u u v u u u v u u u v 2211(||)()42AC AB AB BC BC BO =-+⋅+⋅u u u v u u u v u u u v u u u v u u u v u u u v 2211(||)42AC AB AO BC =-+⋅u u u v u u u v u u u v u u u v 所以221(||)82AO BC AC AB ⋅=-=u u u v u u u v u u u v u u u v ，故选D17．已知平面直角坐标系xOy 中有一凸四边形ABCD ，且AB 不平行于,CD AD 不平行于BC ．设AD 中点(,),E a b BC 中点(,)F b a -，且222a b +=，求||||AB DC +u u u r u u u r 的取值范围（）A ．(4,)+∞B ．[4,)+∞C ．(0,4)D ．(2,4) 【答案】A【解析】【分析】根据AD 中点(,),E a b BC 中点(,)F b a -，通过向量运算得到2EF AB DC =+u u u r u u u r u u u r ，从而有2AB DC EF +=u u u r u u u r u u u r ，用两点间距离公式得到EF u u u r ，再根据AB 不平行于CD ，由||||AB D AB DC C ++>u u u r u u u r u u u r u u u r 求解. 【详解】因为,EF ED DC CF EF EA AB BF =++=++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ，所以2EF AB DC =+u u u r u u u r u u u r ，又因为2EF ===u u u r ，所以24AB DC EF +==u u u r u u ，因为AB 不平行于CD ，所以||||AB D AB DC C ++>u u u r u u u r u u u r u u u r ，所以||||4AB DC +>u u u r u u u r .故选：A【点睛】本题主要考查平面向量在平面几何中的应用，还考查了数形结合的思想和运算求解的能力，属于中档题.18．下列命题为真命题的个数是（）①{x x x ∀∈是无理数}，2x 是无理数；②若0a b ⋅=r r ，则0a =r r 或0b =r r；③命题“若220x y +=，x ∈R ，y ∈R ，则0x y ==”的逆否命题为真命题； ④函数()x xe ef x x--=是偶函数. A ．1B ．2C ．3D ．4【答案】B【解析】【分析】利用特殊值法可判断①的正误；利用平面向量垂直的等价条件可判断②的正误；判断原命题的真假，利用逆否命题与原命题的真假性一致的原则可判断③的正误；利用函数奇偶性的定义可判断④的正误.综合可得出结论.【详解】对于①中，当x =时，22x =为有理数，故①错误；对于②中，若0a b ⋅=r ，可以有a b ⊥r r ，不一定要0a =r r 或0b =r r ，故②错误；对于③中，命题“若220x y +=，x ∈R ，y ∈R ，则0x y ==”为真命题，其逆否命题为真命题，故③正确；对于④中，()()x x x xe e e ef x f x x x-----===-，且函数的定义域是(,0)(0,)-∞+∞U ，定义域关于原点对称，所以函数()x xe ef x x--=是偶函数，故④正确. 综上，真命题的个数是2.故选：B.【点睛】本题考查命题真假的判断，涉及全称命题的真假的判断、逆否命题真假的判断、向量垂直等价条件的应用以及函数奇偶性的判断，考查推理能力，属于中等题.19．若O 为ABC ∆所在平面内任一点，且满足()()0OB OC OC OA CA AB -⋅-++=u u u r u u u r u u u r u u u r u u r u u u r ，则ABC ∆的形状为（）A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形【答案】A【解析】【分析】利用平面向量加法和减法的三角形法则以及向量数量积的性质即可进行判断.【详解】由()()0OB OC OC OA CA AB -⋅-++=u u u r u u u r u u u r u u u r u u u r u u u r ，即()0CB AC CB CB AB ⋅+=⋅=u u u r u u u r u u u r u u u r u u u r ，所以，CB AB ⊥，即2B π∠=，故ABC ∆为直角三角形.故选：A.【点睛】本题主要考查了平面向量加法和减法的三角形法则以及向量数量积的性质的简单应用，属于基础题.20．已知向量a v ，b v 满足a =v ||1b =v ，且2b a +=v v ，则向量a v 与b v 的夹角的余弦值为（）A ．2B ．3CD ．4【答案】D【解析】【分析】根据平方运算可求得12a b ⋅=r r ，利用cos ,a b a b a b ⋅<>=r r r r r r 求得结果. 【详解】由题意可知：2222324b a b a b a a b +=+⋅+=+⋅=r r r r r r r r ，解得：12a b ⋅=r rcos ,4a b a b a b ⋅∴<>===r r r r r r 本题正确选项：D【点睛】本题考查向量夹角的求解问题，关键是能够通过平方运算求得向量的数量积.。

2020高考数学核心突破《专题3 三角函数、解三角形与平面向量第1讲三角函数的图象与性质》 (2)

专题三第1讲1．函数f (x )＝cos(w x ＋φ)的部分图象如图所示，则f (x )的单调递减区间为( D )A.⎝⎛⎭⎫k π－14，k π＋34，k ∈Z B.⎝⎛⎭⎫2k π－14，2k π＋34，k ∈Z C.⎝⎛⎭⎫k －14，k ＋34，k ∈Z D.⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z 解析由题图可知T 2＝54－14＝1，所以T ＝2.结合题图可知，在⎣⎡⎦⎤－34，54(f (x )的一个周期)内，函数f (x )的单调递减区间为⎝⎛⎭⎫－14，34.由f (x )是以2为周期的周期函数可知，f (x )的单调递减区间为⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z ，故选D. 2．下列函数中，最小正周期为π且图象关于原点对称的函数是( A ) A ．y ＝cos ⎝⎛⎭⎫2x ＋π2 B ．y ＝sin ⎝⎛⎭⎫2x ＋π2 C ．y ＝sin 2x ＋cos 2xD ．y ＝sin x ＋cos x解析 y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x 是奇函数，图象关于原点对称，且最小正周期为π，A 项正确．y ＝sin ⎝⎛⎭⎫2x ＋π2＝cos 2x ，是偶函数，B 项错误．y ＝sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4，非奇非偶，C 项错误．y ＝sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4，非奇非偶，D 项错误．故选A. 3．为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin 2x 的图象上所有的点( A ) A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度解析 ∵y ＝sin(2x ＋1)＝sin 2⎝⎛⎭⎫x ＋12， ∴只需把y ＝sin 2x 图象上所有的点向左平移12个单位长度即得到y ＝sin(2x ＋1)的图象．故选A.4．将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( C )A.3π4 B ．π2C.π4D ．－π4解析 y ＝sin(2x ＋φ)――→左移π8sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8＋φ＝sin ⎝⎛⎭⎫2x ＋π4＋φ是偶函数，即π4＋φ＝k π＋π2(k ∈Z )⇒φ＝k π＋π4(k ∈Z )，当k ＝0时，φ＝π4，故选C.5．如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝⎛⎭⎫π6x ＋φ＋k ，据此函数可知，这段时间水深的最大值为( C )A ．5 mB ．6 mC ．8 mD ．10 m解析由题意可知，当sin ⎝⎛⎭⎫π6x ＋φ＝－1时，函数取得最小值2，即3×(－1)＋k ＝2，∴k ＝5.因此，函数的最大值是8，故水深的最大值为8 m.6．将函数y ＝3cos x ＋sin x (x ∈R )的图象向左平移m (m ＞0)个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是( B )A.π12 B ．π6C.π3D ．5π6解析 y ＝3cos x ＋sin x ＝2sin ⎝⎛⎭⎫x ＋π3，向左平移m 个单位长度后得到y ＝2sin ⎝⎛⎭⎫x ＋π3＋m ，由它关于y 轴对称可得sin ⎝⎛⎭⎫π3＋m ＝±1，∴π3＋m ＝k π＋π2，k ∈Z ，∴m ＝k π＋π6，k ∈Z ，又m >0，∴m 的最小值为π6.7．已知函数f (x )＝A sin(w x ＋φ)(A ，w ，φ均为正的常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( A )A ．f (2)＜f (－2)＜f (0)B ．f (0)＜f (2)＜f (－2)C ．f (－2)＜f (0)＜f (2)D ．f (2)＜f (0)＜f (－2)解析 ∵ω>0，∴T ＝2πω＝π，∴ω＝2.又A >0，∴f ⎝⎛⎭⎫2π3＝－A ，即sin ⎝⎛⎭⎫4π3＋φ＝－1，得φ＋4π3＝2k π＋32π(k ∈Z )，即φ＝2k π＋π6(k ∈Z )．又∵φ>0，∴可取f (x )＝A sin ⎝⎛⎭⎫2x ＋π6， ∴f (2)＝A sin ⎝⎛⎭⎫4＋π6， f (－2)＝A sin ⎝⎛⎭⎫－4＋π6，f (0)＝A sin π6. ∵π<4＋π6<3π2，∴f (2)<0.∵－7π6<－4＋π6<－π，且y ＝sin x 在⎝⎛⎭⎫－7π6，－π上为减函数， ∴sin ⎝⎛⎭⎫－4＋π6<sin ⎝⎛⎭⎫－7π6＝sin π6，且sin ⎝⎛⎭⎫－4＋π6>sin(－π)＝0，从而有0<f (－2)<f (0)．故有f (2)<f (－2)<f (0)．故选A.8．将函数f (x )＝sin 2x 的图象向右平移φ⎝⎛⎭⎫0＜φ＜π2个单位后得到函数g (x )的图象．若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝π3，则φ＝( D )A.5π12 B ．π3C.π4D ．π6解析 g (x )＝sin[2(x －φ)] ＝sin(2x －2φ)． ∵|f (x )|≤1，|g (x )|≤1， ∴|f (x )－g (x )|≤2，当且仅当f (x 1)＝1，g (x 2)＝－1或f (x 1)＝－1，g (x 2)＝1时，满足|f (x 1)－g (x 2)|＝2. 不妨设A (x 1，－1)是函数f (x )图象的一个最低点，B (x 2,1)是函数g (x )图象的一个最高点，于是x 1＝k 1π＋3π4(k 1∈Z )，x 2＝k 2π＋π4＋φ(k 2 ∈Z )．∴|x 1－x 2|≥⎪⎪⎪⎪3π4－⎝⎛⎭⎫π4＋φ＝⎪⎪⎪⎪π2－φ. ∵φ ∈⎝⎛⎭⎫0，π2，|x 1－x 2|min ＝π3， ∴π2－φ＝π3，即φ＝π6，故选D. 9．已知函数f (x )＝2sin x ＋φ2cos x ＋φ2⎝⎛⎭⎫|φ|<π2，且对于任意的x ∈R ，f (x )≤f ⎝⎛⎭⎫π6，则( C ) A ．f (x )＝f (x ＋π) B ．f (x )＝f ⎝⎛⎭⎫x ＋π2 C ．f (x )＝f ⎝⎛⎭⎫π3－xD ．f (x )＝f ⎝⎛⎭⎫π6－x解析 f (x )＝sin(x ＋φ)．由题意，可知f (x )≤f ⎝⎛⎭⎫π6对于任意的x ∈R 恒成立，即sin(x ＋φ)≤sin ⎝⎛⎭⎫π6＋φ.又因为|φ|<π2，所以π6＋φ＝π2，所以φ＝π3，所以f (x )＝sin ⎝⎛⎭⎫x ＋π3.f ⎝⎛⎭⎫π3－x ＝sin ⎝⎛⎭⎫π3－x ＋π3＝sin ⎣⎡⎦⎤－⎝⎛⎭⎫π3＋x ＋π＝sin ⎝⎛⎭⎫x ＋π3＝f (x )．故选C. 10．已知函数f (x )＝3sin w x ＋cos w x (w ＞0)的图象与x 轴的交点的横坐标可构成一个公差为π2的等差数列，把函数f (x )的图象沿x 轴向左平移π6个单位，得到函数g (x )的图象．下列说法正确的是( D )A ．g (x )在⎣⎡⎦⎤π4，π2上是增函数B ．g (x )的图象关于直线x ＝－π4对称C ．函数g (x )是奇函数D ．当x ∈⎣⎡⎦⎤π6，2π3时，函数g (x )的值域是[－2,1]解析 f (x )＝3sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π6，由题意知T 2＝π2，∴T ＝π，∴ω＝2πT ＝2，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6.把函数f (x )的图象沿x 轴向左平移π6个单位，得到g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋π6＝2sin ⎝⎛⎭⎫2x ＋π2＝2cos 2x 的图象，易知g (x )是偶函数且在⎣⎡⎦⎤π4，π2上是减函数，其图象不关于直线x ＝－π4对称，所以A 项，B 项，C 项错误．当x ∈⎣⎡⎦⎤π6，2π3时，2x ∈⎣⎡⎦⎤π3，4π3，则g (x )min ＝2cos π＝－2，g (x )max ＝2cos π3＝1，即函数g (x )的值域为[－2,1]，故选D.11．函数f (x )＝2x －4sin x ，x ∈⎣⎡⎦⎤－π2，π2的图象大致是( D )解析因为函数f (x )是奇函数，所以排除A ，B 项，f ′(x )＝2－4cos x ，令f ′(x )＝2－4cos x ＝0，得x ＝±π3，故选D.12．函数f (x )＝A sin w x (A ＞0，w ＞0)的部分图象如图所示，则f (1)＋f (2)＋f (3)＋…＋f (2 018)的值为( A )A ．2＋ 2B ．32C ．6 2D ．－ 2解析由题图可知，A ＝2，T ＝8，2πω＝8，ω＝π4，∴f (x )＝2sin π4x ，∴f (1)＝2，f (2)＝2，f(3)＝2，f(4)＝0，f(5)＝－2，f(6)＝－2，f(7)＝－2，f(8)＝0，而2 018＝8×252＋2，∴f(1)＋f(2)＋…＋f(2 018)＝f(1)＋f(2)＝2＋ 2.故选A.。

高考数学复习专题三第3讲平面向量课件理

＝ 17－15sin 2β≤4 2. 又(3)当证明β＝－由π4时tan，α等tan号β成＝立16，得所4sc以ions|βbα＋＝c4|s的cion最sαβ大，值为 4 2 所以 a∥b.
归纳拓展向量与三角函数结合是高考命题的一大热点，在解决有关向量的平行、垂直问题时，先利用向量的坐标运算，再利用平行、垂直的充要条件即可简化运算过程．
∴P→A＋3P→B＝52D→A＋(3－4x) D→C，
|P→A＋3P→B|2＝245D→A2＋2×52×(3－4x) D→A·D→C＋(3－4x)2·D→C2
＝25＋(3－4x)2D→C2≥25， ∴|P→A＋3P→B|的最小值为 5.
考点整合
1．向量的概念 (1)零向量模的大小为 0，方向是任意的，它与任意非零向量都共线，记为 0. (2)长度等于 1 个单位长度的向量叫单位向量，a 的单位向量为±|aa|. (3)方向相同或相反的向量叫共线向量(平行向量)． (4)如果直线 l 的斜率为 k，则 a＝(1，k)是直线 l 的一个方向向量．
解
(1)m·n＝
3sin
x 4cos
4x＋cos
2x 4
＝
3 2 sin
2x＋12·cos
2x＋12＝sin(2x＋6π)＋12.
又∵m·n＝1，∴sin(2x＋6π)＝12.
cos(x＋π3)＝1－2sin2(2x＋6π)＝12，
cos(23π－x)＝－cos(x＋π3)＝－12.
(2)∵(2a－c)cos B＝bcos C，
(1)解因为 a 与 b－2c 垂直，所以 a·(b－2c) ＝4cos αsin β－8cos αcos β＋4sin αcos β＋8sin αsin β ＝4sin(α＋β)－8cos(α＋β)＝0. 因此 tan(α＋β)＝2. (2)解由 b＋c＝(sin β＋cos β，4cos β－4sin β)，得|b＋c|＝ (sin β＋cos β)2＋(4cos β－4sin β)2

高考数学考点通关练第三章三角函数、解三角形与平面向量 18 同角三角函数基本关系式与诱导公式名师课件

B．
1 1＋k2
C．－
k 1＋k2
D．－
1 1＋k2
解析因为k＝tan140°＝tan(180°－40°)＝－tan40°，所
以tan40°＝－k，所以k<0，sin40°＝－kcos40°，sin140°＝
sin(180°－40°)＝sin40°，因为sin240°＋cos240°＝1，所以
k2cos240°＋cos240°＝1，所以cos40°＝
－α<π2，所以α－β＝π2－α，所以2α－β＝π2，故选B.
1 16．[2016·四川高考]sin750°＝____2____.
解析 sin750°＝sin(2×360°＋30°)＝sin30°＝12.
三、模拟小题
17．[2017·沈阳育才中学模拟]已知锐角α满足5α的终边
上有一点P(sin(－50°)，cos130°)，则α的值为(
第2步精做大题·练能力
一、高考大题
本考点在近三年高考中未独立命题．
二、模拟大题
1．[2017·甘肃河西月考]已知
tanα tanα－6
＝－1，求下列各
式的值．
(1)23ccoossαα－＋34ssiinnαα； (2)1－3sinαcosα＋3cos2α.
解由tantaαn－ α 6＝－1，得tanα＝3. (1)23ccoossαα－＋34ssiinnαα＝23－＋34ttaannαα＝－175. (2)1－3sinαcosα＋3cos2α
D．sinα－cosα
解析
原式＝sin2α＋cos2
α＋2sinαcosα＋sinα＋cosα 1＋sinα＋cosα
＝sin
α＋cosα2＋sinα＋cosα 1＋sinα＋cosα

高考数学二轮复习专题三三角函数、平面向量 2.3.3 平面向量学案理-人教版高三全册数学学案

2.3.3 平面向量1．(2018·全国卷Ⅱ)已知向量a ，b 满足|a |＝1，a ·b ＝－1，则a ·(2a －b )＝( ) A ．4 B ．3 C ．2 D ．0[解析] 因为|a |＝1，a ·b ＝－1，所以a ·(2a －b )＝2|a |2－a ·b ＝2×12－(－1)＝3.故选B.[答案] B2．(2017·全国卷Ⅲ)在矩形ABCD 中，AB ＝1，AD ＝2，动点P 在以点C 为圆心且与BD相切的圆上．若AP →＝λAB →＋μAD →，则λ＋μ的最大值为( )A ．3B ．2 2 C. 5 D ．2[解析] 分别以CB 、CD 所在的直线为x 轴、y 轴建立直角坐标系，则A (2,1)，B (2,0)，D (0,1)．∵点P 在以C 为圆心且与BD 相切的圆上，∴可设P ⎝ ⎛⎭⎪⎫25cos θ，25sin θ.则AB →＝(0，－1)，AD →＝(－2,0)， AP →＝⎝⎛⎭⎪⎫25cos θ－2，25sin θ－1.又AP →＝λAB →＋μAD →， ∴λ＝－25sin θ＋1，μ＝－15cos θ＋1，∴λ＋μ＝2－25sin θ－15cos θ＝2－sin(θ＋φ)，其中tan φ＝12，∴(λ＋μ)max ＝3.[答案] A3．(2018·全国卷Ⅲ)已知向量a ＝(1,2)，b ＝(2，－2)，c ＝(1，λ)．若c ∥(2a ＋b )，则λ＝________.[解析] 由已知得2a ＋b ＝(4,2)．又c ＝(1，λ)，c ∥(2a ＋b )，所以4λ－2＝0，解得λ＝12.[答案] 124．(2018·上海卷)在平面直角坐标系中，已知点A (－1,0)、B (2,0)，E 、F 是y 轴上的两个动点，且|EF →|＝2，则AE →·BF →的最小值为________．[解析] 设E (0，m )，F (0，n )，又A (－1,0)，B (2,0)， ∴AE →＝(1，m )，BF →＝(－2，n )． ∴AE →·BF →＝－2＋mn ，又知|EF →|＝2，∴|m －n |＝2.①当m ＝n ＋2时，AE →·BF →＝mn －2＝(n ＋2)n －2＝n 2＋2n －2＝(n ＋1)2－3.∴当n ＝－1，即E 的坐标为(0,1)，F 的坐标为(0，－1)时，AE →·BF →取得最小值－3.②当m ＝n －2时，AE →·BF →＝mn －2＝(n －2)n －2＝n 2－2n －2＝(n －1)2－3.∴当n ＝1，即E 的坐标为(0，－1)，F 的坐标为(0,1)时，AE →·BF →取得最小值－3.综上可知，AE →·BF →的最小值为－3. [答案] －35．(2017·天津卷)在△ABC 中，∠A ＝60°，AB ＝3，AC ＝2.若BD →＝2DC →，AE →＝λAC →－AB→(λ∈R )，且AD →·AE →＝－4，则λ的值为________．[解析] 解法一：如图，由BD →＝2DC →得AD →＝13AB →＋23AC →，所以AD →·AE →＝⎝ ⎛⎭⎪⎫13AB →＋23AC →·(λAC →－AB →)＝13λAB →·AC →－13AB →2＋23λAC →2－23AB →·AC →，又AB →·AC →＝3×2×cos60°＝3，AB →2＝9，AC →2＝4，所以AD →·AE →＝λ－3＋83λ－2＝113λ－5＝－4，解得λ＝311.解法二：以A 为原点，AB 所在的直线为x 轴建立平面直角坐标系，如图，因为AB ＝3，AC ＝2，∠A ＝60°，所以B (3,0)，C (1，3)，又BD →＝2DC →，所以D ⎝ ⎛⎭⎪⎫53，233，所以AD →＝⎝ ⎛⎭⎪⎫53，233，而AE →＝λAC →－AB →＝λ(1，3)－(3,0)＝(λ－3，3λ)，因此AD →·AE →＝53(λ－3)＋233×3λ ＝113λ－5＝－4，解得λ＝311.[答案]3111.平面向量是高考必考内容，每年每卷均有一个小题(选择题或填空题)，一般出现在第3～7或第13～15题的位置上，难度较低．主要考查平面向量的模、数量积的运算、线性运算等，数量积是其考查的热点．2．有时也会以平面向量为载体，与三角函数、解析几何等其他知识相交汇综合命题，难度中等．。

高考数学二轮复习专题03 三角函数与平面向量(讲)(含解析)理-人教版高三全册数学试题

专题三三角函数与平面向量考向一三角恒等变形【高考改编☆回顾基础】1．【同角三角函数、二倍角公式】【2017课标3改编】已知4sin cos3αα-=，则sin2α=.A． B．29-C．29D．79【答案】7 9 -【解析】()2sin cos17 sin22sin cos19ααααα--===--.2. 【三角函数的定义、诱导公式】【2017，文9】在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称.若sinα=13，则sinβ=_________．【答案】1 3【解析】3. 【三角函数的同角公式、两角和差的三角函数】【2017课标1，文15】已知π(0)2a∈，，tan α=2，则πcos()4α-=__________．31010【解析】【命题预测☆看准方向】三角部分主要考查三角函数的基本公式、三角恒等变换及解三角形等基本知识.三角函数与解三角形相结合或三角函数与平面向量相结合是考向的主要趋势,试题难度为中低档.三角恒等变换是高考的热点内容,主要考查利用各种三角函数进行求值与化简,其中降幂公式、辅助角公式是考查的重点,切化弦、角的变换是常考的三角变换思想.（1）预计2018年高考仍将在角的变换、角的X围方面对三角恒等变形进行考查，对两角和与差、二倍角公式将重点考查；（2）对三角恒等变换的考查力度可能会加大，对角的变换的考查，使问题更具有综合性，复习时需加强这方面的训练；（3）通过三角恒等变换，化简三角函数式，进一步研究函数的性质、解三角形等是常考题型.【典例分析☆提升能力】【例1】【2018某某省名校联盟第一次段考】已知圆：，点，，记射线与轴正半轴所夹的锐角为，将点绕圆心逆时针旋转角度得到点，则点的坐标为__________．【答案】【解析】设射线OB与轴正半轴的夹角为，有已知有，所以，且，C点坐标为.【趁热打铁】已知角α的X 终边经过点(),22P m ， 22sin 3α=且α为第二象限．（1）求m 的值；（2）若tan 2β=，求()()sin cos 3sin sin 2cos cos 3sin sin παβαβπαβαβ⎛⎫++ ⎪⎝⎭+--的值．【答案】（1）1m =-；（2）211【解析】（1）由三角函数的定义可得22222sin 38m α==+，解得1m =±，又α为第二象限角，所以1m =-。

2020高考数学核心突破《专题三三角函数、解三角形与平面向量》(含往年真题分析)

专题三三角函数、解三角形与平面向量第1讲三角函数的图象与性质题型一三角函数的图象1．(1)要得到函数f (x )＝cos ⎝⎛⎭⎫2x ＋π3的图象，只需将函数g (x )＝sin ⎝⎛⎭⎫2x ＋π3的图象( C ) A ．向左平移π2个单位长度B ．向右平移π2个单位长度C ．向左平移π4个单位长度D ．向右平移π4个单位长度(2) (2017·山西朔州模拟)函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图象如图所示，则函数f (x )在区间⎣⎡⎦⎤0，π2上的最小值为__－1__.突破点拨(1)先利用诱导公式将两函数化为同名三角函数，再利用平移法则求解． (2)先求函数f (x )的解析式，再利用解析式求最值．解析 (1)因为f (x )＝cos ⎝⎛⎭⎫2x ＋π2－π6 ＝sin ⎝⎛⎭⎫π6－2x ＝sin ⎝⎛⎭⎫2x ＋5π6＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π4＋π3，所以要得到函数f (x )＝cos ⎝⎛⎭⎫2x ＋π3的图象，只需将函数g (x )＝sin ⎝⎛⎭⎫2x ＋π3的图象向左平移π4个单位长度．故选C. (2)由函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图象，可得A ＝2，14·2πω＝5π6－7π12，解得ω＝2.再根据图象经过点⎝⎛⎭⎫7π12，0，可得2·7π12＋φ＝π＋2k π，k ∈Z .因为|φ|<π2，所以φ＝－π6，故函数f (x )＝2sin ⎝⎛⎭⎫2x －π6. 因为x ∈⎣⎡⎦⎤0，π2，所以2x －π6∈⎣⎡⎦⎤－π6，5π6，故函数f (x )的最小值为2×⎝⎛⎭⎫－12＝－1. 2. 某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，|φ|＜π2在某一个周期内的图象时，列表并填入了部分数据，如下表：(1)(2)将y ＝f (x )图象上所有点向左平行移动θ(θ＞0)个单位长度，得到y ＝g (x )的图象．若y＝g (x )图象的一个对称中心为⎝⎛⎭⎫5π12，0，求θ的最小值．突破点拨(1)由表中数据先写出A ，ω，φ的值，再由ωx ＋φ＝0，π，2π，求出其余值． (2)写出函数y ＝g (x )的解析式，由y ＝sin x 图象的对称中心为(k π，0)，k ∈Z ，利用整体思想建立关于θ的方程，根据k ∈Z 及θ＞0，求出θ的最小值．解析 (1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6.数据补全如下表.且函数表达式为f (x )＝5sin ⎝⎛⎭⎫2x －π6. (2)由(1)知f (x )＝5sin ⎝⎛⎭⎫2x －π6，得g (x )＝5sin ⎝⎛⎭⎫2x ＋2θ－π6. 因为y ＝sin x 的对称中心为(k π，0)，k ∈Z . 令2x ＋2θ－π6＝k π，解得x ＝k π2＋π12－θ，k ∈Z .由于函数y ＝g (x )的图象关于点⎝⎛⎭⎫5π12，0中心对称，令k π2＋π12－θ＝5π12，解得θ＝k π2－π3，k ∈Z . 由θ>0可知，当k ＝1时，θ取得最小值π6.(1)三角函数图象平移问题需注意三点：一是函数名称是否一致；二是弄清由谁平移得到谁；三是左右的平移是自变量本身的变化．(2)对于由三角函数的图象确定函数解析式的问题，一般由函数的最值可确定A ，由函数的周期可确定ω，由对称轴或对称中心和φ的范围确定φ.题型二三角函数的性质1. 已知函数f (x )＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x . (1)求f (x )的最小正周期和最大值； (2)讨论f (x )在⎣⎡⎦⎤π6，2π3上的单调性．突破点拨(1)先将已知解析式化简，然后求解．(2)根据y ＝A sin(ωx ＋φ)＋k (A ＞0，ω＞0)与y ＝sin x 的关系求解．解析 (1)f (x )＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x ＝cos x sin x －32(1＋cos 2x ) ＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎫2x －π3－32. 因此f (x )的最小正周期为π，最大值为2－32.(2)当x ∈⎣⎡⎦⎤π6，2π3时，0≤2x －π3≤π，从而当0≤2x －π3≤π2，即π6≤x ≤5π12时，f (x )单调递增；当π2<2x －π3≤π，即5π12<x ≤2π3时，f (x )单调递减．综上可知，f (x )在⎣⎡⎦⎤π6，5π12上单调递增；在⎝⎛⎦⎤5π12，2π3上单调递减． 2. 设函数f (x )＝sin ωx ＋sin ⎝⎛⎭⎫ωx －π2，x ∈R . (1)若ω＝12，求f (x )的最大值及相应x 的集合；(2)若x ＝π8是f (x )的一个零点，且0＜ω＜10，求ω的值和f (x )的最小正周期．突破点拨(1)先用公式化简，再利用三角函数的性质求解． (2)将x ＝π8代入，求ω，则周期可求．解析由已知得f (x )＝sin ωx －cos ωx ＝2sin ⎝⎛⎭⎫ωx －π4. (1)若ω＝12，则f (x )＝2sin ⎝⎛⎭⎫12x －π4. 又x ∈R ，则2sin ⎝⎛⎭⎫12x －π4≤2，所以f (x )max ＝2，此时12x －π4＝2k π＋π2，k ∈Z ，即f (x )取最大值时，x 的取值集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝4k π＋3π2，k ∈Z .(2)∵x ＝π8是函数f (x )的一个零点，∴2sin ⎝⎛⎭⎫π8ω－π4＝0，∴π8ω－π4＝k π，k ∈Z . 又0<ω<10，∴ω＝2，∴f (x )＝2sin ⎝⎛⎭⎫2x －π4，其最小正周期为π.求解函数y ＝A sin(ωx ＋φ)的性质的三种意识(1)转化意识：利用三角恒等变换将所求函数转化为f (x )＝A sin(ωx ＋φ)的形式． (2)整体意识：类比y ＝sin x 的性质，只需将y ＝A sin(ωx ＋φ)中的“ωx ＋φ”看成y ＝sin x 中的“x ”，采用整体代入的方法求解．(3)讨论意识：当A 为参数时，求最值应分情况讨论．三角函数的综合应用【预测】已知函数f (x )＝sin ⎝⎛⎭⎫2ωx －π6－4sin 2ωx ＋2(ω＞0)，其图象与x 轴相邻两个交点的距离为π2.(1)求函数f (x )的解析式；(2)若将f (x )的图象向左平移m (m ＞0)个单位长度，得到的函数g (x )的图象恰好经过点⎝⎛⎭⎫－π3，0，求当m 取得最小值时，g (x )在⎣⎡⎦⎤－π6，7π12上的单调递增区间．思维导航(1)解题导引：①先化简函数f (x )的解析式，再利用图象与x 轴相邻两个交点的距离是半个周期求解析式；②先求函数g (x )的解析式，再求在⎣⎡⎦⎤－π6，7π12上的单调递增区间． (2)方法指导：三角函数的综合应用主要是将三角函数的图象和性质与三角变换相结合，通过变换将函数化为y ＝A sin(ωx ＋φ)的形式再研究其性质，解题时注意观察角、名、结构等特征，注意整体思想的应用．规范解答(1)函数f (x )＝sin ⎝⎛⎭⎫2ωx －π6－4sin 2ωx ＋2 ＝32sin 2ωx －12cos 2ωx －4×1－cos 2ωx 2＋2 ＝32sin 2ωx ＋32cos 2ωx ＝3sin ⎝⎛⎭⎫2ωx ＋π3(ω＞0)．根据函数f (x )的图象与x 轴相邻两个交点的距离为π2，可得函数f (x )的最小正周期为2×π2＝2π2ω，得ω＝1. 故函数f (x )＝3sin ⎝⎛⎭⎫2x ＋π3. (2)将f (x )的图象向左平移m (m ＞0)个单位长度得到函数 g (x )＝3sin ⎣⎡⎦⎤2(x ＋m )＋π3＝3sin ⎝⎛⎭⎫2x ＋2m ＋π3的图象．根据g (x )的图象恰好经过点⎝⎛⎭⎫－π3，0，可得3sin ⎝⎛⎭⎫－2π3＋2m ＋π3＝0，即sin ⎝⎛⎭⎫2m －π3＝0，所以2m －π3＝k π(k ∈Z )，m ＝k π2＋π6(k ∈Z )．因为m ＞0，所以当k ＝0时，m 取得最小值，且最小值为π6.此时，g (x )＝3sin ⎝⎛⎭⎫2x ＋2π3. 令2k π－π2≤2x ＋2π3≤2k π＋π2，k ∈Z ，得k π－7π12≤x ≤k π－π12，k ∈Z ，故函数g (x )的单调递增区间为⎣⎡⎦⎤k π－7π12，k π－π12，k ∈Z . 结合x ∈⎣⎡⎦⎤－π6，7π12，可得g (x )在⎣⎡⎦⎤－π6，7π12上的单调递增区间为⎣⎡⎦⎤－π6，－π12和⎣⎡⎦⎤5π12，7π12. 【变式考法】已知向量a ＝(m ，cos 2x )，b ＝(sin 2x ，n )，函数f (x )＝a·b ，且y ＝f (x )的图象过点⎝⎛⎭⎫π12，3和点⎝⎛⎭⎫2π3，－2. (1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ (0＜φ＜π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0,3)的距离的最小值为1，求y ＝g (x )的单调递增区间．解析 (1)由题意，知 f (x )＝a·b ＝m sin 2x ＋n cos 2x .因为y ＝f (x )的图象经过点⎝⎛⎭⎫π12，3和⎝⎛⎭⎫2π3，－2，所以⎩⎨⎧3＝m sin π6＋n cos π6，－2＝m sin 4π3＋n cos 4π3，即⎩⎨⎧3＝12m ＋32n ，－2＝－32m －12n ，解得m ＝3，n ＝1.(2)由(1)知f (x )＝3sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π6. 由题意知g (x )＝f (x ＋φ)＝2sin ⎝⎛⎭⎫2x ＋2φ＋π6. 设y ＝g (x )的图象上符合题意的最高点为(x 0,2)，由题意知x 20＋1＝1，所以x 0＝0，即y ＝g (x )的图象上到点(0,3)的距离为1的最高点为(0,2)．将其代入y ＝g (x )并整理得sin ⎝⎛⎭⎫2φ＋π6＝1，因为0<φ<π，所以φ＝π6.因此g (x )＝2sin ⎝⎛⎭⎫2x ＋π2＝2cos 2x . 由2k π－π≤2x ≤2k π，k ∈Z ，得k π－π2≤x ≤k π，k ∈Z ，所以函数y ＝g (x )的单调递增区间为⎣⎡⎦⎤k π－π2，k π，k ∈Z .1．(教材回归)下列函数中，最小正周期为π且图象关于原点对称的函数是( A ) A ．y ＝cos ⎝⎛⎭⎫2x ＋π2 B ．y ＝sin ⎝⎛⎭⎫2x ＋π2 C ．y ＝sin 2x ＋cos 2xD ．y ＝sin x ＋cos x解析 y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x ，符合题意，故选A. 2．(2017·广西南宁质检)将函数y ＝cos ⎝⎛⎭⎫2x ＋π3的图象向左平移π6个单位长度后，得到f (x )的图象，则( B )A ．f (x )＝－sin 2xB ．f (x )的图象关于直线x ＝－π3对称C ．f ⎝⎛⎭⎫7π3＝12D ．f (x )的图象关于点⎝⎛⎭⎫π12，0对称解析将函数y ＝cos ⎝⎛⎭⎫2x ＋π3的图象向左平移π6个单位长度，得到的图象对应的解析式为f (x )＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋π3＝cos ⎝⎛⎭⎫2x ＋2π3.函数f (x )的图象的对称轴满足2x ＋2π3＝k π(k ∈Z )，即对称轴方程为x ＝k π2－π3(k ∈Z )，所以f (x )的图象关于直线x ＝－π3对称；令2x ＋2π3＝k π＋π2，得x ＝k π2－π12(k ∈Z )，即f (x )的图象关于点⎝⎛⎭⎫－π12，0对称；f ⎝⎛⎭⎫7π3＝－12.故选B. 3．(2017·湖北襄阳模拟)同时具有性质“①最小正周期是4π；②直线x ＝π3是图象的一条对称轴；③在区间⎝⎛⎭⎫2π3，5π6上是减函数”的一个函数是( D )A ．y ＝sin ⎝⎛⎭⎫2x －π6B ．y ＝cos ⎝⎛⎭⎫2x －π6 C ．y ＝cos ⎝⎛⎭⎫x 2＋π3D ．y ＝sin ⎝⎛⎭⎫x 2＋π3解析对于A 项，B 项，∵T ＝2π2＝π，故A 项，B 项不正确．对于C 项，若直线x ＝π3为其图象的一条对称轴，则π3×12＋π3＝k π，k ∈Z ，得π2＝k π，k ∈Z ，k 不存在，不满足题意，故C 项不正确．对于D 项，因为T ＝2π12＝4π，且由x 2＋π3＝k π＋π2，k ∈Z ，解得图象的对称轴方程为x ＝2k π＋π3，k ∈Z ；当k ＝0时，x ＝π3为图象的一条对称轴．由2k π＋π2≤x 2＋π3≤2k π＋3π2，k ∈Z ，解得单调递减区间为⎣⎡⎦⎤4k π＋π3，4k π＋7π3，k ∈Z ，所以函数在区间⎝⎛⎭⎫2π3，5π6上是减函数，故D 项正确．故选D.4．(2017·山西晋中考前测试)已知函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图象如图所示，将函数y ＝f (x )的图象向左平移4π3个单位长度，得到函数y ＝g (x )的图象，则函数y ＝g (x )在区间⎣⎡⎦⎤π2，5π2上的最大值为( C )A ．3B ．332C.322D ．22解析由图象可知函数y ＝f (x )的周期为2⎝⎛⎭⎫7π3－π3＝4π， ∴ω＝12.又点⎝⎛⎭⎫π3，0，⎝⎛⎭⎫0，－32在函数y ＝f (x )的图象上， ∴⎩⎨⎧A sin ⎝⎛⎭⎫π6＋φ＝0，A sin φ＝－32，且|φ|<π2.∴φ＝－π6，A ＝3，则f (x )＝3sin ⎝⎛⎭⎫12x －π6， ∴g (x )＝3sin ⎣⎡⎦⎤12⎝⎛⎭⎫x ＋4π3－π6＝3cos 12x . 由x ∈⎣⎡⎦⎤π2，5π2，可得12x ∈⎣⎡⎦⎤π4，5π4，则3cos 12x ∈⎣⎡⎦⎤－3，322，即g (x )的最大值为322.5．(书中淘金)某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y ＝a ＋A cos ⎣⎡⎦⎤π6(x －6)(x ＝1,2，3，…，12)来表示，已知6月份的月平均气温最高，为28 ℃，12月份的平均气温最低，为18 ℃，则10月份的平均气温为__20.5__℃.解析依题意知，a ＝28＋182＝23，A ＝28－182＝5，所以y ＝23＋5cos ⎣⎡⎦⎤π6(x －6)，当x ＝10时，y ＝23＋5cos ⎝⎛⎭⎫π6×4＝20.5. 答案 20.56．(高考改编)把函数y ＝sin 2x 的图象沿x 轴向左平移π6个单位，纵坐标伸长到原来的2倍(横坐标不变)后得到函数y ＝f (x )的图象，对于函数y ＝f (x )有以下四个判断：①该函数的解析式为y ＝2sin ⎝⎛⎭⎫2x ＋π6；②该函数图象关于点⎝⎛⎭⎫π3，0对称；③该函数在⎣⎡⎦⎤0，π6上是增函数；④若函数y ＝f (x )＋a 在⎣⎡⎦⎤0，π2上的最小值为3，则a ＝2 3. 其中，正确判断的序号是__②④__.解析将函数y ＝sin 2x 的图象向左平移π6个单位得到y ＝sin 2⎝⎛⎭⎫x ＋π6＝sin ⎝⎛⎭⎫2x ＋π3的图象，然后纵坐标伸长到原来的2倍得到y ＝2sin ⎝⎛⎭⎫2x ＋π3的图象，所以①不正确．f ⎝⎛⎭⎫π3＝2sin ⎝⎛⎭⎫2×π3＋π3＝2sin π＝0，所以函数图象关于点⎝⎛⎭⎫π3，0对称，所以②正确．由－π2＋2k π≤2x ＋π3≤π2＋2k π，k ∈Z ，得－5π12＋k π≤x ≤π12＋k π，k ∈Z ，∴函数的单调增区间为⎣⎡⎦⎤－5π12＋k π，π12＋k π，k ∈Z ，而⎣⎡⎦⎤0，π6⃘⎣⎡⎦⎤－512π＋k π，π12＋k π(k ∈Z )，所以③不正确．y ＝f (x )＋a ＝2sin ⎝⎛⎭⎫2x ＋π3＋a ，当0≤x ≤π2时，π3≤2x ＋π3≤4π3，所以当2x ＋π3＝4π3，即x ＝π2时，函数取得最小值，y min ＝2sin 4π3＋a ＝－3＋a ，令－3＋a ＝3，得a ＝23，所以④正确．所以正确的判断为②④.7．(考点聚焦)设函数f (x )＝32－3sin 2ωx －sin ωx ·cos ωx (ω>0)，且y ＝f (x )的图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值；(2)求f (x )在区间⎣⎡⎦⎤π，3π2上的最大值和最小值．解析 (1)f (x )＝32－3sin 2ωx －sin ωx cos ωx ＝32－3·1－cos 2ωx 2－12sin 2ωx ＝32cos 2ωx －12sin 2ωx ＝－sin ⎝⎛⎭⎫2ωx －π3＝sin ⎝⎛⎭⎫2ωx ＋2π3. 因为图象的一个对称中心到最近的对称轴的距离为π4，又ω＞0，所以2π2ω＝4×π4.因此ω＝1.(2)由(1)知f (x )＝－sin ⎝⎛⎭⎫2x －π3. 当π≤x ≤3π2时，5π3≤2x －π3≤8π3，所以－32≤sin ⎝⎛⎭⎫2x －π3≤1. 因此－1≤f (x )≤32.故f (x )在区间⎣⎡⎦⎤π，3π2上的最大值和最小值分别为32，－1. 8．(2018·山东青岛调考)已知函数f (x )＝2sin x sin ⎝⎛⎭⎫x ＋π6. (1)求函数f (x )的最小正周期和单调递增区间； (2)当x ∈⎣⎡⎦⎤0，π2时，求函数f (x )的值域．解析 (1)f (x )＝2sin x ⎝⎛⎭⎫32sin x ＋12cos x＝3×1－cos 2x 2＋12sin 2x＝sin ⎝⎛⎭⎫2x －π3＋32. 函数f (x )的最小正周期为T ＝π. 由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，解得－π12＋k π≤x ≤5π12＋k π，k ∈Z ，所以函数f (x )的单调递增区间是⎣⎡⎦⎤－π12＋k π，5π12＋k π，k ∈Z . (2)当x ∈⎣⎡⎦⎤0，π2时，2x －π3∈⎣⎡⎦⎤－π3，2π3， sin ⎝⎛⎭⎫2x －π3∈⎣⎡⎦⎤－32，1，可得函数f (x )的值域为⎣⎡⎦⎤0，1＋32. 9．(母题营养)已知函数f (x )＝sin x cos x ＋12cos 2x .(1)若tan θ＝2，求f (θ)的值；(2)若函数y ＝g (x )的图象是由函数y ＝f (x )的图象上所有的点向右平移π4个单位长度而得到，且g (x )在区间(0，m )内是单调函数，求实数m 的最大值．解析 (1)因为tan θ＝2，所以sin θ＝2cos θ. 代入sin 2θ＋cos 2θ＝1，得cos 2θ＝15.所以f (θ)＝sin θcos θ＋12cos 2θ＝2cos 2θ＋12(2cos 2θ－1)＝3cos 2θ－12＝110.(2)由已知得f (x )＝12sin 2x ＋12cos 2x ＝22sin ⎝⎛⎭⎫2x ＋π4. 依题意，得g (x )＝22sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4＋π4，即g (x )＝22sin ⎝⎛⎭⎫2x －π4. 因为x ∈(0，m )，所以2x －π4∈⎝⎛⎭⎫－π4，2m －π4. 又因为g (x )在区间(0，m )内是单调函数，所以－π4＜2m －π4≤π2，即0＜m ≤3π8，故实数m的最大值为3π8.10．(母题营养)设函数f (x )＝sin 2ωx ＋23sin ωx ·cos ωx －cos 2ωx ＋λ(x ∈R )的图象关于直线x ＝π对称，其中ω，λ为常数，且ω∈⎝⎛⎭⎫12，1.(1)求函数f (x )的最小正周期；(2)若y ＝f (x )的图象经过点⎝⎛⎭⎫π4，0，求函数f (x )在x ∈⎣⎡⎦⎤0，π2上的值域．解析 (1)因为f (x )＝sin 2ωx ＋23sin ωx ·cos ωx －cos 2ωx ＋λ＝－cos 2ωx ＋3sin 2ωx ＋λ＝2sin ⎝⎛⎭⎫2ωx －π6＋λ，由直线x ＝π是y ＝f (x )图象的一条对称轴，可得sin ⎝⎛⎭⎫2ωπ－π6＝±1，所以2ωπ－π6＝k π＋π2(k ∈Z )，即ω＝k 2＋13(k ∈Z )．又ω∈⎝⎛⎭⎫12，1，k ∈Z ，所以k ＝1，从而ω＝56. 所以f (x )的最小正周期是6π5.(2)由y ＝f (x )的图象过点⎝⎛⎭⎫π4，0，得f ⎝⎛⎭⎫π4＝0，即λ＝－2sin ⎝⎛⎭⎫56×π2－π6＝－2sin π4＝－2，即λ＝－ 2.故f (x )＝2sin ⎝⎛⎭⎫53x －π6－2， ∵x ∈⎣⎡⎦⎤0，π2，∴53x －π6∈⎣⎡⎦⎤－π6，2π3， ∴函数f (x )的值域为[－1－2，2－2]．1．函数f (x )＝cos(w x ＋φ)的部分图象如图所示，则f (x )的单调递减区间为( D )A.⎝⎛⎭⎫k π－14，k π＋34，k ∈Z B.⎝⎛⎭⎫2k π－14，2k π＋34，k ∈Z C.⎝⎛⎭⎫k －14，k ＋34，k ∈Z D.⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z 解析由题图可知T 2＝54－14＝1，所以T ＝2.结合题图可知，在⎣⎡⎦⎤－34，54(f (x )的一个周期)内，函数f (x )的单调递减区间为⎝⎛⎭⎫－14，34.由f (x )是以2为周期的周期函数可知，f (x )的单调递减区间为⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z ，故选D. 2．下列函数中，最小正周期为π且图象关于原点对称的函数是( A ) A ．y ＝cos ⎝⎛⎭⎫2x ＋π2 B ．y ＝sin ⎝⎛⎭⎫2x ＋π2 C ．y ＝sin 2x ＋cos 2xD ．y ＝sin x ＋cos x解析 y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x 是奇函数，图象关于原点对称，且最小正周期为π，A 项正确．y ＝sin ⎝⎛⎭⎫2x ＋π2＝cos 2x ，是偶函数，B 项错误．y ＝sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4，非奇非偶，C 项错误．y ＝sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4，非奇非偶，D 项错误．故选A. 3．为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin 2x 的图象上所有的点( A ) A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度解析 ∵y ＝sin(2x ＋1)＝sin 2⎝⎛⎭⎫x ＋12， ∴只需把y ＝sin 2x 图象上所有的点向左平移12个单位长度即得到y ＝sin(2x ＋1)的图象．故选A.4．将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为( C )A.3π4 B ．π2C.π4D ．－π4解析 y ＝sin(2x ＋φ)――→左移π8sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8＋φ＝sin ⎝⎛⎭⎫2x ＋π4＋φ是偶函数，即π4＋φ＝k π＋π2(k ∈Z )⇒φ＝k π＋π4(k ∈Z )，当k ＝0时，φ＝π4，故选C.5．如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝⎛⎭⎫π6x ＋φ＋k ，据此函数可知，这段时间水深的最大值为( C )A ．5 mB ．6 mC ．8 mD ．10 m解析由题意可知，当sin ⎝⎛⎭⎫π6x ＋φ＝－1时，函数取得最小值2，即3×(－1)＋k ＝2，∴k ＝5.因此，函数的最大值是8，故水深的最大值为8 m.6．将函数y ＝3cos x ＋sin x (x ∈R )的图象向左平移m (m ＞0)个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是( B )A.π12 B ．π6C.π3D ．5π6解析 y ＝3cos x ＋sin x ＝2sin ⎝⎛⎭⎫x ＋π3，向左平移m 个单位长度后得到y ＝2sin ⎝⎛⎭⎫x ＋π3＋m ，由它关于y 轴对称可得sin ⎝⎛⎭⎫π3＋m ＝±1，∴π3＋m ＝k π＋π2，k ∈Z ，∴m ＝k π＋π6，k ∈Z ，又m >0，∴m 的最小值为π6.7．已知函数f (x )＝A sin(w x ＋φ)(A ，w ，φ均为正的常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( A )A ．f (2)＜f (－2)＜f (0)B ．f (0)＜f (2)＜f (－2)C ．f (－2)＜f (0)＜f (2)D ．f (2)＜f (0)＜f (－2)解析 ∵ω>0，∴T ＝2πω＝π，∴ω＝2.又A >0，∴f ⎝⎛⎭⎫2π3＝－A ，即sin ⎝⎛⎭⎫4π3＋φ＝－1，得φ＋4π3＝2k π＋32π(k ∈Z )，即φ＝2k π＋π6(k ∈Z )．又∵φ>0，∴可取f (x )＝A sin ⎝⎛⎭⎫2x ＋π6， ∴f (2)＝A sin ⎝⎛⎭⎫4＋π6， f (－2)＝A sin ⎝⎛⎭⎫－4＋π6，f (0)＝A sin π6. ∵π<4＋π6<3π2，∴f (2)<0.∵－7π6<－4＋π6<－π，且y ＝sin x 在⎝⎛⎭⎫－7π6，－π上为减函数， ∴sin ⎝⎛⎭⎫－4＋π6<sin ⎝⎛⎭⎫－7π6＝sin π6，且sin ⎝⎛⎭⎫－4＋π6>sin(－π)＝0，从而有0<f (－2)<f (0)．故有f (2)<f (－2)<f (0)．故选A.8．将函数f (x )＝sin 2x 的图象向右平移φ⎝⎛⎭⎫0＜φ＜π2个单位后得到函数g (x )的图象．若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝π3，则φ＝( D )A.5π12B ．π3C.π4D ．π6解析 g (x )＝sin[2(x －φ)] ＝sin(2x －2φ)． ∵|f (x )|≤1，|g (x )|≤1， ∴|f (x )－g (x )|≤2，当且仅当f (x 1)＝1，g (x 2)＝－1或f (x 1)＝－1，g (x 2)＝1时，满足|f (x 1)－g (x 2)|＝2. 不妨设A (x 1，－1)是函数f (x )图象的一个最低点，B (x 2,1)是函数g (x )图象的一个最高点，于是x 1＝k 1π＋3π4(k 1∈Z )，x 2＝k 2π＋π4＋φ(k 2 ∈Z )．∴|x 1－x 2|≥⎪⎪⎪⎪3π4－⎝⎛⎭⎫π4＋φ＝⎪⎪⎪⎪π2－φ. ∵φ ∈⎝⎛⎭⎫0，π2，|x 1－x 2|min ＝π3， ∴π2－φ＝π3，即φ＝π6，故选D. 9．已知函数f (x )＝2sin x ＋φ2cos x ＋φ2⎝⎛⎭⎫|φ|<π2，且对于任意的x ∈R ，f (x )≤f ⎝⎛⎭⎫π6，则( C ) A ．f (x )＝f (x ＋π) B ．f (x )＝f ⎝⎛⎭⎫x ＋π2 C ．f (x )＝f ⎝⎛⎭⎫π3－xD ．f (x )＝f ⎝⎛⎭⎫π6－x解析 f (x )＝sin(x ＋φ)．由题意，可知f (x )≤f ⎝⎛⎭⎫π6对于任意的x ∈R 恒成立，即sin(x ＋φ)≤sin ⎝⎛⎭⎫π6＋φ.又因为|φ|<π2，所以π6＋φ＝π2，所以φ＝π3，所以f (x )＝sin ⎝⎛⎭⎫x ＋π3.f ⎝⎛⎭⎫π3－x ＝sin ⎝⎛⎭⎫π3－x ＋π3＝sin ⎣⎡⎦⎤－⎝⎛⎭⎫π3＋x ＋π＝sin ⎝⎛⎭⎫x ＋π3＝f (x )．故选C. 10．已知函数f (x )＝3sin w x ＋cos w x (w ＞0)的图象与x 轴的交点的横坐标可构成一个公差为π2的等差数列，把函数f (x )的图象沿x 轴向左平移π6个单位，得到函数g (x )的图象．下列说法正确的是( D )A ．g (x )在⎣⎡⎦⎤π4，π2上是增函数B ．g (x )的图象关于直线x ＝－π4对称C ．函数g (x )是奇函数D ．当x ∈⎣⎡⎦⎤π6，2π3时，函数g (x )的值域是[－2,1]解析 f (x )＝3sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π6，由题意知T 2＝π2，∴T ＝π，∴ω＝2πT＝2，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6.把函数f (x )的图象沿x 轴向左平移π6个单位，得到g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋π6＝2sin ⎝⎛⎭⎫2x ＋π2＝2cos 2x 的图象，易知g (x )是偶函数且在⎣⎡⎦⎤π4，π2上是减函数，其图象不关于直线x ＝－π4对称，所以A 项，B 项，C 项错误．当x ∈⎣⎡⎦⎤π6，2π3时，2x ∈⎣⎡⎦⎤π3，4π3，则g (x )min ＝2cos π＝－2，g (x )max ＝2cos π3＝1，即函数g (x )的值域为[－2,1]，故选D.11．函数f (x )＝2x －4sin x ，x ∈⎣⎡⎦⎤－π2，π2的图象大致是( D )解析因为函数f (x )是奇函数，所以排除A ，B 项，f ′(x )＝2－4cos x ，令f ′(x )＝2－4cos x ＝0，得x ＝±π3，故选D.12．函数f (x )＝A sin w x (A ＞0，w ＞0)的部分图象如图所示，则f (1)＋f (2)＋f (3)＋…＋f (2 018)的值为( A )A ．2＋2B ．32C ．62D ．－2解析由题图可知，A ＝2，T ＝8，2πω＝8，ω＝π4，∴f (x )＝2sin π4x ，∴f (1)＝2，f (2)＝2，f (3)＝2，f (4)＝0，f (5)＝－2，f (6)＝－2，f (7)＝－2，f (8)＝0，而2 018＝8×252＋2，∴f (1)＋f (2)＋…＋f (2 018)＝f (1)＋f (2)＝2＋ 2.故选A.第2讲三角变换与解三角形题型一三角恒等变换1．(1)(2018·河南郑州模拟)若tan α＝13，tan(α＋β)＝12，则tan β＝( A )A.17 B ．16C ．57D ．56(2) (2017·河北唐山中学模拟)已知α是三角形的内角，sin ⎝⎛⎭⎫α＋π3＝45，则cos ⎝⎛⎭⎫5π12－α＝( D )A.210B ．－210C ．－7210D ．7210突破点拨(1)注意到β＝(α＋β)－α，再结合已知条件求tan β的值． (2)注意到cos ⎝⎛⎭⎫5π12－α＝－cos ⎣⎡⎦⎤⎝⎛⎭⎫α＋π3＋π4，再实施运算．解析 (1)tan β＝tan[(α＋β)－α] ＝tan (α＋β)－tan α1＋tan (α＋β)·tan α＝12－131＋12×13＝17.故选A.(2)∵α是三角形的内角，sin ⎝⎛⎭⎫α＋π3＝45<32， ∴α＋π3是钝角，∴cos ⎝⎛⎭⎫α＋π3＝－35，cos ⎝⎛⎭⎫5π12－α＝－cos ⎣⎡⎦⎤π－⎝⎛⎭⎫5π12－α＝－cos ⎝⎛⎭⎫712π＋α＝－cos ⎣⎡⎦⎤⎝⎛⎭⎫α＋π3＋π4＝－cos ⎝⎛⎭⎫α＋π3·cos π4＋sin ⎝⎛⎭⎫α＋π3sin π4＝7210.故选D. 2. 已知cos ⎝⎛⎭⎫π6＋α·cos ⎝⎛⎭⎫π3－α＝－14，α∈⎝⎛⎭⎫π3，π2. (1)求sin 2α的值； (2)求tan α－1tan α的值．突破点拨(1)利用诱导公式转化为二倍角公式，再利用同角三角函数基本关系式求解． (2)切化弦，转化为二倍角公式，再利用(1)的结论求解．解析 (1)cos ⎝⎛⎭⎫π6＋α·cos ⎝⎛⎭⎫π3－α ＝cos ⎝⎛⎭⎫π6＋α·sin ⎝⎛⎭⎫π6＋α＝12sin ⎝⎛⎭⎫2α＋π3＝－14，即sin ⎝⎛⎭⎫2α＋π3＝－12. ∵α∈⎝⎛⎭⎫π3，π2，∴2α＋π3∈⎝⎛⎭⎫π，4π3， ∴cos ⎝⎛⎭⎫2α＋π3＝－32， ∴sin 2α＝sin ⎣⎡⎦⎤⎝⎛⎭⎫2α＋π3－π3＝sin ⎝⎛⎭⎫2α＋π3cos π3－cos ⎝⎛⎭⎫2α＋π3sin π3＝12. (2)∵α∈⎝⎛⎭⎫π3，π2，∴2α∈⎝⎛⎭⎫2π3，π，又由(1)知sin 2α＝12，∴cos 2α＝－32.∴tan α－1tan α＝sin αcos α－cos αsin α＝sin 2α－cos 2αsin α cos α＝－2cos 2αsin 2α＝－2×－3212＝2 3.利用三角恒等变换公式解题的常用技巧(1)项的分拆与角的配凑：如sin 2α＋2cos 2α＝(sin 2α＋cos 2α)＋cos 2α，α＝(α－β)＋β等． (2)降幂与升幂：通过二倍角公式得到． (3)弦、切互化：一般是切化弦．题型二解三角形1. 已知a ，b ，c 分别为△ABC 内角A ，B ，C 的对边，sin 2B ＝2sin A sin C ． (1)若a ＝b ，求cos B ；(2)设B ＝90°，且a ＝2，求△ABC 的面积．突破点拨(1)根据正弦定理把已知条件转化为边的关系，然后利用余弦定理求解．(2)利用勾股定理得到边的一个方程，结合已知条件解方程组求得边长，然后求面积．解析 (1)由题设及正弦定理可得b 2＝2ac . 又a ＝b ，可得b ＝2c ，a ＝2c . 由余弦定理可得cos B ＝a 2＋c 2－b 22ac ＝14.(2)由(1)知b 2＝2ac . 因为B ＝90°，由勾股定理得a 2＋c 2＝b 2，故a 2＋c 2＝2ac ，进而可得c ＝a ＝ 2. 所以△ABC 的面积为12×2×2＝1.【变式考法】 (1)在本例条件下，求角B 的范围． (2)在本例条件下，若B ＝60°，b ＝2，求a 的值．解析 (1)因为b 2＝2ac ，所以cos B ＝a 2＋c 2－b 22ac ≥2ac －2ac2ac ＝0，又因为0<B <π，所以0<B ≤π2.(2)因为b 2＝2ac ，b ＝2，所以ac ＝1，又因为b 2＝a 2＋c 2－2ac cos B ，所以a 2＋c 2＝3，所以a ＋c ＝5，所以a ＝5＋12或5－12. 2. △ABC 中，D 是BC 上的点，AD 平分∠BAC ，△ABD 面积是△ADC 面积的2倍． (1)求sin ∠B sin ∠C； (2)若AD ＝1，DC ＝22，求BD 和AC 的长．突破点拨(1)利用面积关系得边的关系，再利用正弦定理求解． (2)先利用面积比求BD ，再利用余弦定理求解．解析 (1)S △ABD ＝12AB ·AD sin ∠BAD ，S △ADC ＝12AC ·AD sin ∠CAD .因为S △ABD ＝2S △ADC ，∠BAD ＝∠CAD ，所以AB ＝2AC . 由正弦定理可得sin ∠B sin ∠C ＝AC AB ＝12.(2)因为S △ABD ∶S △ADC ＝BD ∶DC ，所以BD ＝ 2. 在△ABD 和△ADC 中，由余弦定理知 AB 2＝AD 2＋BD 2－2AD ·BD cos ∠ADB ， AC 2＝AD 2＋DC 2－2AD ·DC cos ∠ADC . 故AB 2＋2AC 2＝3AD 2＋BD 2＋2DC 2＝6. 由(1)知AB ＝2AC ，所以AC ＝1.利用正、余弦定理解三角形的技巧解三角形问题一般要利用正、余弦定理和三角形内角和定理，正弦定理可以将角转化为边，也可以将边转化成角，当涉及边的平方关系时，一般利用余弦定理，要根据题目特点和正、余弦定理的结构形式，灵活选用．有关解三角形的综合问题(1)求∠ACP ；(2)若△APB 的面积是332，求sin ∠BAP .思维导航(1)由已知条件选择余弦定理求得AP .(2)由三角形的面积和(1)结论解得PB ，再由余弦定理及正弦定理求得AB 和sin ∠BAP . 规范解答(1)在△APC 中，因为∠P AC ＝60°，PC ＝2，AP ＋AC ＝4，由余弦定理得PC 2＝AP 2＋AC 2－2AP ·AC ·cos ∠P AC ，所以22＝AP 2＋(4－AP )2－2AP ·(4－AP )·cos 60°，整理得AP 2－4AP ＋4＝0，解得AP ＝2，所以AC ＝2.所以△APC 是等边三角形，所以∠ACP ＝60°.(2)因为∠APB 是△APC 的外角，所以∠APB ＝120°.因为△APB 的面积是332，所以12AP ·PB ·sin ∠APB ＝332，所以PB ＝3.在△APB 中，AB 2＝AP 2＋PB 2－2AP ·PB ·cos ∠APB ＝22＋32－2×2×3×cos 120°＝19，所以AB ＝19.在△APB 中，由正弦定理得AB sin ∠APB ＝PBsin ∠BAP，所以sin ∠BAP ＝3sin 120°19＝35738.【变式考法】 (2017·广州模拟)如图，在△ABC 中，∠ABC ＝30°，AB ＝3，AC ＝1，AC <BC ，P 为BC 右上方一点，满足∠BPC ＝90°.(1)若BP ＝2，求AP 的长； (2)求△BPC 周长的最大值．解析由题意知1＝AC 2＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC ＝3＋BC 2－3BC ，解得BC ＝2(BC ＝1舍去，则∠CAB ＝90°.又∠BPC ＝90°，且BP ＝2，所以∠PBC ＝45°，从而∠ABP ＝75°.连接AP ，由余弦定理得AP ＝3＋2－2×3×2×6－24＝6＋22. (2)由(1)可知BC ＝2或BC ＝1，又因为求△BPC 周长的最大值，所以BC ＝2，设BP ＝m ，PC ＝n ，则m 2＋n 2＝4.由于BC 长为定值，因此求△BPC 周长的最大值只需求BP ＋PC ＝m ＋n 的最大值即可．又4＝m 2＋n 2≥(m ＋n )22，则m ＋n ≤22，当且仅当m ＝n ＝2时取等号，此时△BPC 的周长取得最大值，为2＋2 2.1．(教材回归)sin 20°cos 10°－cos 160°sin 10°＝( D ) A ．－32B ．32C ．－12D ．12解析原式＝sin 20°cos 10°＋cos 20°sin 10°＝sin(20°＋10°)＝sin 30°＝12，故选D.2．(2017·“江南十校”模拟)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .若C＝2B ，则sin Bsin A＝( D )A.c 2a 2＋b 2－c 2 B ．b 2a 2＋b 2－c 2C.a 2a 2＋b 2－c2 D ．c 2a 2＋c 2－b2解析由已知，得sin C ＝sin 2B ＝2sin B cos B ，所以sin C sin B ＝2cos B ．由正弦定理及余弦定理，得c b ＝2×a 2＋c 2－b 22ac ，则b a ＝c 2a 2＋c 2－b2. 再由正弦定理，得sin B sin A ＝c 2a 2＋c 2－b 2，故选D.3．已知tan α＝－2，tan(α＋β)＝17，则tan β的值为__3__.解析 tan β＝tan[(α＋β)－α]＝tan (α＋β)－tan α1＋tan (α＋β)tan α＝17－(－2)1＋17×(－2)＝3.4．(2017·河南郑州调考)已知△ABC 中，角C 为直角，D 是边BC 上一点，M 是AD 上一点，且CD ＝1，∠DBM ＝∠DMB ＝∠CAB ，则MA ＝__2__.解析如图，设∠DMB ＝θ，则∠ADC ＝2θ，∠DAC ＝π2－2θ，∠AMB ＝π－θ，∠ABM ＝π2－2θ，在Rt △ABC 中，cos θ＝cos ∠CAB ＝ACAB ；在△CDA 中，由正弦定理得CD sin ⎝⎛⎭⎫π2－2θ＝ACsin 2θ；在△AMB 中，由正弦定理得MA sin ⎝⎛⎭⎫π2－2θ＝ABsin (π－θ)， ∴CD MA ＝AC ·sin θAB ·sin 2θ＝AC ·sin θ2AB ·sin θcos θ＝12，从而MA ＝2. 5．在△ABC 中，a ＝4，b ＝5，c ＝6，则sin 2Asin C＝__1__.解析在△ABC 中，由余弦定理的推论可得cos A ＝b 2＋c 2－a 22bc ＝52＋62－422×5×6＝34，由正弦定理可知sin 2A sin C ＝2sin A cos A sin C ＝2a ·cos Ac ＝2×4×346＝1.6．(书中淘金)如图，一辆汽车在一条水平的公路上向正西行驶，到A 处时测得公路北侧一山顶D 在西偏北30°的方向上，行驶600 m 后到达B 处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD解析依题意有AB ＝600，∠CAB ＝30°，∠CBA ＝180°－75°＝105°，∠DBC ＝30°，DC ⊥CB . ∴∠ACB ＝45°，在△ABC 中，由AB sin ∠ACB ＝CB sin ∠CAB ，得600sin 45°＝CBsin 30°，有CB ＝3002，在Rt △BCD 中，CD ＝CB ·tan 30°＝1006，则此山的高度CD ＝100 6 m.7．(考点聚焦)已知函数f (x )＝2sin ωx ＋m cos ωx (ω＞0，m ＞0)的最小值为－2，且图象上相邻两个最高点的距离为π.(1)求ω和m 的值；(2)若f ⎝⎛⎭⎫θ2＝65，θ∈⎝⎛⎭⎫π4，3π4，求f ⎝⎛⎭⎫θ＋π8的值．解析 (1)易知f (x )＝2＋m 2sin(ωx ＋φ)(φ为辅助角)， ∴f (x )min ＝－2＋m 2＝－2，∴m ＝ 2.由题意知函数f (x )的最小正周期为π，∴2πω＝π，∴ω＝2.(2)由(1)得f (x )＝2sin 2x ＋2cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4， ∴f ⎝⎛⎭⎫θ2＝2sin ⎝⎛⎭⎫θ＋π4＝65， ∴sin ⎝⎛⎭⎫θ＋π4＝35， ∵θ∈⎝⎛⎭⎫π4，3π4，∴θ＋π4∈⎝⎛⎭⎫π2，π，∴cos ⎝⎛⎭⎫θ＋π4＝－1－sin 2⎝⎛⎭⎫θ＋π4＝－45， ∴f ⎝⎛⎭⎫θ＋π8＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫θ＋π8＋π4＝2sin ⎝⎛⎭⎫2θ＋π2 ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫θ＋π4＝4sin ⎝⎛⎭⎫θ＋π4cos ⎝⎛⎭⎫θ＋π4 ＝4×35×⎝⎛⎭⎫－45＝－4825. 8．(教材回归)在△ABC 中，已知AB ＝2，AC ＝3，A ＝60°. (1)求BC 的长； (2)求sin 2C 的值．解析 (1)由余弦定理知，BC 2＝AB 2＋AC 2－2AB ·AC ·cos A ＝4＋9－2×2×3×12＝7，所以BC ＝7.(2)由正弦定理知sin C ＝AB BC ·sin A ＝2sin 60°7＝217.因为AB <BC ，所以C ＜A ，所以C 为锐角，则cos C ＝1－sin 2C ＝1－37＝277. 因此sin 2C ＝2sin C ·cos C ＝2×217×277＝437. 9．(2017·河北唐山二模)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，a 2＋b 2＝λab . (1)若λ＝6，B ＝5π6，求sin A ；(2)若λ＝4，AB 边上的高为3c6，求C . 解析 (1)已知B ＝5π6，a 2＋b 2＝6ab ，结合正弦定理得4sin 2A －26sin A ＋1＝0，解得sin A ＝6±24. 因为0<A <π6，所以sin A <12，所以sin A ＝6－24.(2)由题意可知S △ABC ＝12ab sin C ＝312c 2，得12ab sin C ＝312(a 2＋b 2－2ab cos C )＝312(4ab －2ab cos C )．从而有3sin C ＋cos C ＝2，即sin ⎝⎛⎭⎫C ＋π6＝1. 又π6<C ＋π6<7π6，所以C ＝π3.10．(2017·山东淄博模拟)已知a ，b ，c 分别为△ABC 的内角A ，B ，C 的对边，且a cos C ＋3a sin C －b －c ＝0.(1)求A ；(2)若a ＝2，求△ABC 面积的最大值．解析 (1)由a cos C ＋3a sin C －b －c ＝0及正弦定理，得sin A cos C ＋3sin A sin C －sin B －sin C ＝0. 因为B ＝π－A －C ，所以3sin A sin C －cos A sin C －sin C ＝0. 易知sin C ≠0，所以3sin A －cos A ＝1，所以sin ⎝⎛⎭⎫A －π6＝12.又0<A <π，所以A ＝π3. (2)方法一由(1)得B ＋C ＝2π3⇒C ＝2π3－B ⎝⎛⎭⎫0<B <2π3，因为a sin A ＝2sin π3＝43，所以由正弦定理得b ＝43sin B ，c ＝43sin C . 所以S △ABC ＝12bc sin A ＝12×43sin B ×43sin C ·sin π3＝433sin B ·sin C ＝433·sin B ·sin ⎝⎛⎭⎫2π3－B ＝433⎝⎛⎭⎫32sin B cos B ＋12sin 2B ＝sin 2B －33cos 2B ＋33＝233sin ⎝⎛⎭⎫2B －π6＋33.易知－π6<2B －π6<7π6，故当2B －π6＝π2，即B ＝π3时，S △ABC 取得最大值，最大值为233＋33＝ 3.方法二由(1)知A ＝π3，又a ＝2，由余弦定理得22＝b 2＋c 2－2bc cos π3，即b 2＋c 2－bc ＝4⇒bc ＋4＝b 2＋c 2≥2bc ⇒bc ≤4，当且仅当b ＝c＝2时，等号成立．所以S △ABC ＝12bc sin A ＝12×32bc ≤34×4＝3，即当b ＝c ＝2时，S △ABC 取得最大值，最大值为 3.1．已知函数f (x )＝2cos 2x －sin ⎝⎛⎭⎫2x －7π6. (1)求函数f (x )的最大值，并写出f (x )取最大值时x 的取值集合；(2)已知△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若f (A )＝32，b ＋c ＝2，求实数a的取值范围．解析 (1)f (x )＝(1＋cos 2x )－⎝⎛⎭⎫sin 2x cos 7π6－cos 2x sin 7π6 ＝1＋32sin 2x ＋12cos 2x ＝1＋sin ⎝⎛⎭⎫2x ＋π6， ∴函数f (x )的最大值为2，当且仅当sin ⎝⎛⎭⎫2x ＋π6＝1，即2x ＋π6＝2k π＋π2，k ∈Z ，即x ＝k π＋π6，k ∈Z 时取到．∴函数f (x )取最大值时x 的取值集合为x ⎪⎪⎭⎬⎫x ＝k π＋π6，k ∈Z . (2)由题意，f (A )＝sin ⎝⎛⎭⎫2A ＋π6＋1＝32，化简得sin ⎝⎛⎭⎫2A ＋π6＝12. ∵A ∈(0，π)，∴2A ＋π6∈⎝⎛⎭⎫π6，13π6， ∴2A ＋π6＝5π6，∴A ＝π3.在△ABC 中，a 2＝b 2＋c 2－2bc cos π3＝(b ＋c )2－3bc .由b ＋c ＝2，知bc ≤⎝⎛⎭⎫b ＋c 22＝ 1，即a 2≥1，当b ＝c ＝1时取等号．又由b ＋c >a ，得a <2， ∴a 的取值范围是[1,2)．2．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 所对的边，且c ＝2，C ＝π3.(1)若△ABC 的面积等于3，求a ，b ； (2)若sin C ＋sin(B －A )＝2sin 2A ，求A 的值．解析 (1)∵c ＝2，C ＝π3，∴由余弦定理得4＝a 2＋b 2－2ab cos π3＝a 2＋b 2－ab .∵△ABC 的面积等于3， ∴12ab sin C ＝3，∴ab ＝4，联立⎩⎪⎨⎪⎧ a 2＋b 2－ab ＝4，ab ＝4，解得⎩⎪⎨⎪⎧a ＝2，b ＝2.(2)∵sin C ＋sin(B －A )＝2sin 2A ， ∴sin(B ＋A )＋sin(B －A )＝4sin A cos A ， ∴sin B cos A ＝2sin A cos A . ①当cos A ＝0时，A ＝π2；②当cos A ≠0时，sin B ＝2sin A ，由正弦定理得b ＝2a ，联立⎩⎪⎨⎪⎧a 2＋b 2－ab ＝4，b ＝2a ，解得⎩⎨⎧a ＝233，b ＝433，∴b 2＝a 2＋c 2，∵C ＝π3，∴A ＝π6.综上所述，A ＝π2或A ＝π6.3．(2017·浙江重点中学联考)已知△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c . (1)若C ＝2B ，求证：cos A ＝3cos B －4cos 3B ；(2)若b sin B －c sin C ＝a ，且△ABC 的面积S ＝b 2＋c 2－a 24，求角B .解析 (1)证明：∵C ＝2B ，∴A ＝π－3B ， ∴cos A ＝cos(π－3B )＝－cos(B ＋2B ) ＝－cos B cos 2B ＋sin B sin 2B ＝－cos B (2cos 2B －1)＋2sin 2B cos B＝cos B －2cos 3B ＋2cos B (1－cos 2B )＝3cos B －4cos 3B ， ∴cos A ＝3cos B －4cos 3B .(2)在△ABC 中，∵S ＝b 2＋c 2－a 24，∴S ＝b 2＋c 2－a 24＝12bc sin A .由余弦定理知b 2＋c 2－a 24＝12bc cos A ，∴12bc cos A ＝12bc sin A ，∴tan A ＝1，而A ∈(0，π)，∴A ＝π4.∵b sin B －c sin C ＝a ，由正弦定理，得 sin 2B －sin 2C ＝sin A ＝22， ∴cos 2C －cos 2B ＝ 2.∵2C ＝2π－2A －2B ＝3π2－2B ，∴－sin 2B －cos 2B ＝2，∴sin ⎝⎛⎭⎫2B ＋π4＝－1. ∵B ∈(0，π)，∴2B ＋π4＝3π2，∴B ＝5π8.4．(2017·武汉武昌五月调研)已和函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，0<φ<π2的图象经过点⎝⎛⎭⎫0，12，且相邻两条对称轴的距离为π2.(1)求函数f (x )的解析式及其在[0，π]上的单调递增区间；(2)在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边，若f ⎝⎛⎭⎫A 2－cos A ＝12，bc ＝1，b ＋c ＝3，求a 的值．解析 (1)将⎝⎛⎭⎫0，12代入f (x )的解析式，得sin φ＝12. 又因为0<φ<π2，所以φ＝π6.又因为最小正周期T ＝π2×2＝π，所以ω＝2.所以函数f (x )的解析式为f (x )＝sin ⎝⎛⎭⎫2x ＋π6. 因为x ∈[0，π]，所以π6≤2x ＋π6≤13π6，所以2x ＋π6∈⎣⎡⎦⎤π6，π2或2x ＋π6∈⎣⎡⎦⎤3π2，13π6时，f (x )递增，即x ∈⎣⎡⎦⎤0，π6或x ∈⎣⎡⎦⎤2π3，π时，f (x )递增．所以函数f (x )在[0，π]上的单调递增区间是⎣⎡⎦⎤0，π6，⎣⎡⎦⎤2π3，π. (2)由(1)知f ⎝⎛⎭⎫A 2＝sin ⎝⎛⎭⎫A ＋π6，代入已知等式得 sin ⎝⎛⎭⎫A ＋π6－cos A ＝32sin A ＋12cos A －cos A ＝32sin A －12cos A ＝sin ⎝⎛⎭⎫A －π6＝12，所以A －π6＝π6或5π6，即A ＝π3或A ＝π(舍去)．又因为bc ＝1，b ＋c ＝3，由余弦定理，得a 2＝b 2＋c 2－2bc ·cos A ＝b 2＋c 2－bc ＝(b ＋c )2－3bc ＝6，所以a ＝ 6. 5．(2018·山东青岛模拟)在△ABC 中，边a ，b ，c 的对角分别为A ，B ，C ，且b ＝4，A ＝π3，面积S ＝2 3. (1)求a 的值；(2)设f (x )＝2(cos C sin x －cos A cos x )，将f (x )图象上所有点的横坐标变为原来的12(纵坐标不变)得到g (x )的图象，求g (x )的单调增区间．解析 (1)在△ABC 中，∵S ＝12bc sin A ，∴23＝12×4×c ×32，∴c ＝2.∴a ＝b 2＋c 2－2bc cos A ＝16＋4－2×4×2×12＝2 3.(2)∵a sin A ＝b sin B ，即2332＝4sin B，∴sin B ＝1，又0<B <π，∴B ＝π2，∴C ＝π6，∴f (x )＝2(cos C sin x －cos A cos x )＝2sin ⎝⎛⎭⎫x －π6，将f (x )图象上所有点的横坐标变为原来的12(纵坐标不变)，得到的图象对应的函数解析式为g (x )＝2sin ⎝⎛⎭⎫2x －π6，令2k π－π2≤2x －π6≤2k π＋π2(k ∈Z )，解得k π－π6≤x ≤k π＋π3(k ∈Z )，故g (x )的单调增区间为⎣⎡⎦⎤k π－π6，k π＋π3(k ∈Z )． 6．(2018·辽宁协作体一模)设△ABC 是锐角三角形，三个内角A ，B ，C 所对的边分别为a ，b ，c ，且(sin A －sin B )(sin A ＋sin B )＝sin ⎝⎛⎭⎫π3＋B sin ⎝⎛⎭⎫π3－B . (1)求角A 的值；(2)若AB →·AC →＝12，a ＝27，求b ，c (其中b ＜c )．解析 (1)∵(sin A －sin B )(sin A ＋sin B )＝sin ⎝⎛⎭⎫π3＋B ·sin ⎝⎛⎭⎫π3－B ，∴sin 2A －sin 2B ＝⎝⎛⎭⎫32cos B ＋12sin B⎝⎛⎭⎫32cos B －12sin B ，即sin 2A ＝34cos 2B －14sin 2B ＋sin 2B＝34(cos 2B ＋sin 2B )＝34， ∵角A 为锐角△ABC 的内角，∴sin A >0， ∴sin A ＝32，∴A ＝π3. (2)AB →·AC →＝bc cos A ＝12，∴bc ＝24，又a 2＝b 2＋c 2－2bc cos A ＝(b ＋c )2－3bc ＝(27)2， ∴b ＋c ＝10，又∵b <c ，∴b ＝4，c ＝6.第3讲平面向量题型一向量的概念及线性运算高考中常从以下角度命题：1. (1)平面内给定三个向量a＝(3,2)，b＝(－1,2)，c＝(4,1)．若(a＋k c)∥(2b－a)，则k＝－1613.(2)如图，E为平行四边形ABCD的边DC的中点，F为△ABD的重心，且AB→＝a，AD→＝b，则FE→＝23b＋16a.突破点拨(1)利用向量的坐标运算和向量共线定理求解．(2)利用向量加、减法的几何意义和重心公式求解．解析(1)因为(a＋k c)∥(2b－a)，又a＋k c＝(3＋4k,2＋k)，2b－a＝(－5,2)，所以2×(3＋4k)－(－5)×(2＋k)＝0，所以k＝－1613.(2)由F为△ABD的重心，得AF→＝23×12AC→＝13(a＋b)．又AE→＝AD→＋DE→＝b＋12a，所以FE→＝AE→－AF→＝23b＋16a.2．(1)在△ABC中，点M，N满足AM→＝2MC→，BN→＝NC→.若MN→＝xAB→＋yAC→，则x＝12，y＝－16.(2)已知向量a＝(2,1)，b＝(1，－2)，若m a＋n b＝(9，－8)(m，n∈R)，则m－n的值为__－3__.突破点拨(1)画出图形，利用向量加减法则求解．(2)利用向量的坐标运算求解．。

小题透析-三角函数、解三角形与平面向量-【高考倒计时15天考前过关】2023年高考数学(新高考专用)

2
要点归纳
2.诱导公式的规律
三角函数的诱导公式可概括为“奇变偶不变,符号看象限”.其中“奇变偶不变”
π
的奇、偶分别是指2的奇数倍、偶数倍,变与不变是指函数名称的变化.
要点归纳
3.与三角函数的奇偶性相关的结论
π
(1)若 y=Asin(ωx+φ)为偶函数,则φ=kπ+ (k∈Z);若 y=Asin(ωx+φ)为奇函数,
则 cos θ=
·
| ||b|
=
1 2+ 1 2
2
2
1+ 1
2
2
2+ 2
.
要点归纳
(7)三角形“四心”向量形式的充要条件
设 O 为△ABC 所在平面上一点,角 A,B,C 所对的边长分别为 a,b,c,则
①O 为△ABC 的外心⇔|
|=|
②O 为△ABC 的重心⇔
+
③O 为△ABC 的垂心⇔
·
④O 为△ABC 的内心⇔a
取出来.
要点归纳
7.三角恒等变换的常用结论
1+cos2
1-cos2
2
2
(1)降幂公式:cos2α=
,sin2α=
.
(2)升幂公式:1+cos 2α=2cos2α,1-cos 2α=2sin2α.
(3)公式变形:tan α±tan β=tan(α±β)(1∓tan αtan β).
(4)辅助角公式:asin x+bcos x=
2+ 2
, cos
=
2+ 2
.
2
+
2 sin(x+φ)
其中 sin

高考数学原创预测题专题三三角函数平面向量文人教版

专题三：三角函数、平面向量（老人教文）一、选择题： 1.已知α∈(π2，π)，sin α＝35，则tan(α＋π4)等于( ).17 .7 . －17.－7 2、若A,B 是锐角∆ABC 的两个内角，则点P(cosB －sinA,sinB-cosA) 在（）第一象限第二象限第三象限第四象限3、若(cos ,sin ),a αα= b (cos ,sin )ββ=，则（）a b ⊥a ∥b (a )(a )b b +⊥- (a )b + ∥(a )b -4、设P1(2，－1)，P2(0,5)，且P 在P1P2的延长线上，使|1p p|＝2|2pp |，则点P 为( ).(－2,11) .(34，3) .(23，3) .(2，－7)5、2cos10sin20sin70-的值是（）126 、在ABC 中，若sin cos 1sin 2A B C=，则ABC 的形状一定是（）等腰三角形直角三角形等腰直角三角形等边三角形7、函数f(x)＝sin2x ＋2cosx 在区间[－23π，θ]上的最大值为1，则θ的值是( ).0 .π3 .π2 .－π28、已知函数f(x)＝Acos(ωx ＋φ)的图象如图所示，f(π2)＝－23，则f(0)＝( ).－23 .－12 .23 .129、已知向量a ＝(cos θ，sin θ)，向量b ＝(3，－1)，则|2a －b|的最大、小值分别是 ( ).42，0 .4,2 2 .16,0 .4,0 10、已知f(sinx)=sin3x,则f(cosx)=( )sin3x –cos3x -sin3x 3cos3x 二、填空题11、已知sin α⋅cos α=15,且42ππα<<，则cos α-sin α=________________12、 sin11°，cos10°，sin168°的大小关系为_______________(从小到大排列)13、已知函数f(x)＝2sin(ωx ＋φ)的图象如下图所示，则f(7π12)＝ .14、已知向量a ＝(2，－1)，b ＝(x ，－2)，c ＝(3，y)，若a ∥b ，(a ＋b )⊥(b －c)，M(x ，y)，N(y ，x)，则向量MN的模为 .三解答题15、已知 3cos 2α+2sin2α=1-求（1）tan α的值；(2)3cos2α+4sin2α的值.16、已知函数f(x)＝3sin(12x －π4)，x ∈R.(1)画出函数f(x)在长度为一个周期的闭区间上的简图；(2)将函数y ＝sinx 的图象作怎样的变换可得到f(x)的图象？17、已知AC ＝(cos x 2＋sin x 2，－sin x 2)，BC＝(cos x 2－sin x 2，2cos x2). 且f(x)＝AC ·BC ，（1）求f(x)的最小正周期和单调递减区间；（2）4π)求g(x)的最小值及取得最小值时x 的集合.18、已知函数f(x)＝sin2ωx ＋3sin ωxsin(ωx ＋π2)＋2cos2ωx ，x ∈R(ω>0)，在y 轴右侧的第一个最高点的横坐标为π6.(1)求ω；(2)若将函数f(x)的图象向右平移π6个单位后，再将得到的图象上各点横坐标伸长到原来的4倍，纵坐标不变，得到函数y ＝g(x)的图象，求函数g(x)的最大值及单调递减区间.19、在△ABC 中，设内角A ，B ，C 的对边分别为,,,a b c 向量m ＝(cosA ，sinA)，向量n＝(2－sinA ，cosA)，若|m n +|＝2.(1)求角A 的大小；(2)若b ＝42，且c ＝2a ，求△ABC 的面积.20、已知向量m ＝(3sin x 4，1)，n ＝(cos x 4，cos2x 4).(1)若m n ＝1，求cos(2π3－x)的值；(2)记f(x)＝m n ，在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足(2a －c)cosB ＝bcosC ，求函数f(A)的取值范围.三角函数、平面向量（老人教文）答案解析1解析：选A,由α∈(π2，π)，sin α＝35，得tan α＝－34，tan(α＋π4)＝1＋tan α1－tan α＝17.2解析：选B ， A,B 是锐角三角形的两个内角，∴A+B>90°，∴B>90°－Ａ ∴cosB<sinA,sinB>cosA,故选B.3解析：选C,(a )(a )b b +⋅-=(cos α+cos β)( cos α-cos β)+(sin α+sin β)( sin α-sin β)=cos 2α+sin 2α- cos 2β2-sin β=0，∴选C.4解析：选 A,由题意知122p p p p = ，设P(x ，y)，则(－2,6)＝(x ，y －5)，∴2,56x y =-⎧⎨-=⎩∴2,11x y =-⎧⎨=⎩∴点P 的坐标为(－2,11).5解析：选B,原式=2cos 30-20sin20sin70- （）=2cos30cos202sin30sin20sin20sin70+-=6解析：选A,由原式得2sinAcosB=sin(A+B)+sin(A-B)=sinC因为0A B <+<π, 0C <<π,∴sin(A-B)=0,A=B.故选A.7 解析：选,因为f(x)＝sin2x ＋2cosx ＝－cos2x ＋2cosx ＋1＝－(cosx －1)2＋2，又其在区间[－2π3，θ]上的最大值为1，结合选项可知θ只能取－π2.,故选8解析：选C,由题意可知，此函数的周期T ＝2(1112π－712π)＝2π3，故2πω＝2π3，∴ω＝3，f(x)＝Acos(3x ＋φ). f(π2)＝Acos(3π2＋φ)＝Asin φ＝－23.又由题图可知f(7π12)＝Acos(3×7π12＋φ)＝Acos(φ－14π)＝22(Acos φ＋Asin φ)＝0，∴f(0)＝Acos φ＝23. 9解析：选, 由于|2a －b|2＝4|a|2＋|b|2－4a ·b ＝8－4(3cos θ－sin θ)＝8－8cos(θ＋π6)，最大值为4，最小值为0，故选 10解析：选B,f(cosx)=f(sin(2π-x))=sin(32π-3x)=-cos3x.11解析：cos α-sin α.答案：12解析：∵sin168°＝sin(180°－12°)＝sin12°， cos10°＝sin(90°－10°)＝sin80°.又∵y ＝sinx 在x ∈[0，π2]上是增函数，∴sin11°<sin12°<sin80°，即sin11°<sin168°<cos10°.答案：sin11°<sin168°<cos10°.13解析：由图象知，函数的周期为32×T ＝π，∴T ＝2π3. ∵f(π4)＝0，∴f(7π12)＝f(π4＋π3)＝f(π4＋T 2)＝－f(π4)＝0.答案：014解析：∵a ∥b ，∴x ＝4，∴b ＝(4，－2)，∴a ＋b ＝(6，－3)，b －c ＝(1，－2－y).∵(a ＋b)⊥(b －c)，∴(a ＋b)·(b －c)＝0，即6－3(－2－y)＝0，∴y ＝－4，故向量MN＝(－8,8)， |MN|＝8 2.答案：8 215解析：(1)由已知条件得4cos 2α+4sin αcos α+sin 2α=0,(2cos α+sin α)2=0,∴2cos α=-sin α，∴ tan α=-2.(2) 3cos2α+4sin2α=22223cos sin )8sin cos sin cos αααααα-++（=223tan 8tan 3tan 1ααα-+++=-5.16解析：(1)列表取值：描出五个关键点并用光滑曲线连接，得到一个周期的简图.(2)先把y ＝sinx 的图象向右平移4π个单位，然后纵坐标不变，把所有点的横坐标扩大为原来的2倍，再横坐标不变，把所有点的纵坐标扩大为原来的3倍，得到f(x)的图象.17：解析：(1)由f(x)＝AC ·BC得f(x)＝(cos x 2＋sin x 2)·(cos x 2－sin x 2)＋(－sin x 2)·2cos x 2＝cos2x 2－sin2x 2－2sin x 2cos x2＝cosx －sinx ＝2cos(x ＋π4)，所以f(x)的最小正周期T ＝2π.又由2k π≤x＋π4≤π＋2k π，k ∈Z ，得－π4＋2k π≤x≤3π4＋2k π，k ∈Z.故f(x)的单调递减区间是[－π4＋2k π，3π4＋2k π](k ∈Z).（2）g(x)= 2cos(x ＋π4)+4π)=2cosx ，所以g(x)的最小值为－２，取得最小值时x 的集合为{x| x=2k π+π,k Z ∈} 18解析：(1)f(x)＝32sin2ωx ＋12cos2ωx ＋32＝sin(2ωx ＋π6)＋32. 令2ωx ＋π6＝π2，将x ＝π6代入可得：ω＝1.(2)由(1)得f(x)＝sin(2x ＋π6)＋32.经过题设的变化得到的函数g(x)＝sin(12x －π6)＋32. 当x ＝4k π＋43π，k ∈Z 时，函数取得最大值52. 令2k π＋π2≤12x －π6≤2k π＋32π，即[4k π＋43π，4k π＋103π]，k ∈Z 为函数的单调递减区间.19解析： (1) ∵|m n +|2＝(cosA ＋2－sinA)2＋(sinA ＋cosA)2＝4＋22(cosA －sinA)＝4＋4cos(π4＋A)，∴4＋4cos(π4＋A)＝4，∴cos(π4＋A)＝0，∵A ∈(0，π)，∴π4＋A ＝π2，∴A ＝π4.(2)由余弦定理知：a2＝b2＋c2－2bccosA ，即a2＝(42)2＋(2a)2－2×42×2acos π4，解得a ＝42，∴c ＝8， ∴S △ABC ＝12bcsinA ＝12×42×8×22＝16.20解析：(1)∵m n ＝1，即3sin x 4cos x 4＋cos2x 4＝1，即32sin x 2＋12cos x 2＋12＝1，∴sin(x 2＋π6)＝12.∴cos(2π3－x)＝cos(x －2π3)＝－cos(x ＋π3)＝－[1－2sin2(x 2＋π6)]＝2·(12)2－1＝－12.(2)∵(2a －c)cosB ＝bcosC ，由正弦定理得(2sinA －sinC)cosB ＝sinBcosC.∴2sinAcosB －cosBsinC ＝sinBcosC ，∴2sinAcosB ＝sin(B ＋C)， ∵A ＋B ＋C ＝π，∴sin(B ＋C)＝sinA ，且sinA≠0，∴cosB ＝12，B ＝π3，∴0＜A ＜2π3.∴π6＜A 2＋π6＜π2，12＜sin(A 2＋π6)＜1.又∵f(x)＝m n =sin(x 2＋π6)＋12，∴f(A)＝sin(A 2＋π6)＋12.故函数f(A)的取值范围是(1，32).。

2022年高考数学原创预测题专题三三角函数平面向量文人教版

专题三：三角函数、平面向量（老人教文）一、选择题：1已知α∈错误!，π，inα＝错误!，则tanα＋错误!等于错误! 7 －错误! －72、若A,B 是锐角ABC 的两个内角，则点(cos ,sin ),a αα=b (cos ,sin )ββ=(a )(a )b b +⊥-(a )b +(a )b -2cos10sin20sin70-3222ABC sin cos 1sin 2A B C =ABC 2a2 2 42ππα<<，，N ，，则向量的模为三解答题15、已知 3co2in2=求（1）tan 的值；23co24in2的值16、已知函数f ＝3in 错误!－错误!，∈R1画出函数f 在长度为一个周期的闭区间上的简图；2将函数＝in 的图象作怎样的变换可得到f 的图象17、已知＝co 错误!＋in 错误!，－in 错误!，＝co 错误!－in 错误!，2co 错误! 且f ＝ ·，（1）求f 的最小正周期和单调递减区间；（2）g=fin 求g 的最小值及取得最小值时的集合18、已知函数f ＝in2ω＋错误!inωinω＋错误!＋2co2ω，∈Rω>0，在轴右侧的第一个最高点的横坐标为错误!1求ω；2若将函数f 的图象向右平移错误!个单位后，再将得到的图象上各点横坐标伸长到原来的4倍，纵坐标不变，得到函数＝g 的图象，求函数g 的最大值及单调递减区间19、在△ABC 中，设内角A ，B ，C 的对边分别为向量＝coA ，inA ，向量＝错误!－inA ，coA ，若||＝21求角A 的大小；2若b ＝4错误!，且c ＝错误!a ，求△ABC 的面积20、已知向量＝错误!in 错误!，1，＝co 错误!，co2错误!1若＝1，求co 错误!－的值；2记f ＝，在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足2a －ccoB ＝bcoC ，求函数fA 的取值范围三角函数、平面向量（老人教文）答案解析1解析：选A,由α∈错误!，π，in α＝错误!，得tan α＝－错误!，tan α＋错误!＝错误!＝错误!2解析：选B ，A,B 是锐角三角形的两个内角，AB>90°，B>90°－ＡcoBcoA,故选B3解析：选C, (a )(a )b b +⋅-=coco co-coinin in-in=coin- co 2-sin β=0，选C4解析：选 A,由题意知122p p p p =，设P ，，则－2,6＝，－5，∴2,56x y =-⎧⎨-=⎩∴2,11x y =-⎧⎨=⎩∴点P 的坐标为－2,115解析：选B,原式=2cos 30-20sin20sin70-（）=2cos30cos202sin30sin20sin20sin70+-=3cos20sin70=6解析：选A,由原式得2inAcoB=inABinA-B=inC因为0A B <+<π, 0C <<π,inA-B=0,A=7 解析：选,因为f ＝in2＋2co ＝－co2＋2co ＋1＝－co －12＋2，又其在区间[－错误!，θ]上的最大值为1，结合选项可知θ只能取－错误!,故选8解析：选C,由题意可知，此函数的周期T ＝2错误!π－错误!π＝错误!，故错误!＝错误!，∴ω＝3，f ＝Aco3＋φf 错误!＝Aco 错误!＋φ＝Ain φ＝－错误!又由题图可知f 错误!＝Aco3×错误!＋φ＝Aco φ－错误!π＝错误!Aco φ＋Ain φ＝0，∴f0＝Aco φ＝错误!9解析：选, 由于|2a －b|＝4|a|＋|b|－4a ·b ＝8－4错误!co θ－in θ＝8－8co θ＋错误!，最大值为4，最小值为0，故选10解析：选B,fco=fin-=in-3=-co3 11解析：答案：12解析：∵in168°＝in180°－12°＝in12°， co10°＝in90°－10°＝in80°又∵＝in 在∈[0，错误!]上是增函数，∴in11°<in12°<in80°，即in11°<in168°<co10° 答案：in11°<in168°<co10°13解析：由图象知，函数的周期为错误!×T ＝π，∴T ＝错误! ∵f 错误!＝0，∴f 错误!＝f 错误!＋错误!＝f 错误!＋错误!＝－f 错误!＝0答案：014解析：∵a ∥b ，∴＝4，∴b ＝4，－2，∴a ＋b ＝6，－3，b －c ＝1，－2－∵a ＋b ⊥b －c ， ∴a ＋b ·b －c ＝0，即6－3－2－＝0，∴＝－4，故向量＝－8,8，| |＝8错误!答案：8错误!15解析：1由已知条件得4co4incoin=0,2coin=0,2co=-in ， tan=-22 3co24in2=22223cos sin )8sin cos sin cos αααααα-++（=223tan 8tan 3tan 1ααα-+++=-516解析：1列表取值：π2 3π2 7π2 9π21π24x - 0 π2 3π2f 03 0 -3 0描出五个关键点并用光滑曲线连接，得到一个周期的简图2先把＝in 的图象向右平移4π个单位，然后纵坐标不变，把所有点的横坐标扩大为原来的2倍，再横坐标不变，把所有点的纵坐标扩大为原来的3倍，得到f 的图象 17：解析：1由f ＝·得f ＝co 错误!＋in 错误!·co 错误!－in 错误!＋－in 错误!·2co 错误!＝co2错误!－in2错误!－2in 错误!co 错误!＝co －in ＝错误!co ＋错误!，所以f 的最小正周期T ＝π≤＋错误!≤π＋2π，∈Z ，得－错误!＋2π≤≤错误!＋2π，∈Z故f 的单调递减区间是[－错误!＋2π，错误!＋2π]∈Z（2）g= 错误!co ＋错误!in=2co ，所以g 的最小值为－２，取得最小值时的集合为 {| =2,}18解析：1f ＝错误!in2ω＋错误!co2ω＋错误!＝in2ω＋错误!＋错误!令2ω＋错误!＝错误!，将＝错误!代入可得：ω＝12由1得f ＝in2＋错误!＋错误!经过题设的变化得到的函数g ＝in 错误!－错误!＋错误! 当＝4π＋错误!π，∈Z 时，函数取得最大值错误! 令2π＋错误!≤错误!－错误!≤2π＋错误!π，即[4π＋错误!，4π＋错误!π]，∈Z 为函数的单调递减区间19解析： 1 ∵||2＝coA ＋错误!－inA2＋inA ＋coA2＝4＋2错误!coA －inA ＝4＋4co 错误!＋A ，∴4＋4co 错误!＋A ＝4，∴co 错误!＋A ＝0，∵A ∈0，π，∴错误!＋A ＝错误!，∴A ＝错误! 2由余弦定理知：a2＝b2＋c2－2bccoA ，即a2＝4错误!2＋错误!a2－2×4错误!×错误!aco 错误!，解得a ＝4错误!，∴c ＝8， ∴S △ABC ＝错误!bcinA ＝错误!×4错误!×8×错误!＝1620解析：1∵＝1，即错误!in 错误!co 错误!＋co2错误!＝1，即错误!in 错误!＋错误!co 错误!＋错误!＝1，∴in 错误!＋错误!＝错误!∴co 错误!－＝co －错误!＝－co ＋错误!＝－[1－2in2错误!＋错误!]＝2·错误!2－1＝－错误!2∵2a －ccoB ＝bcoC ，由正弦定理得2inA －inCcoB ＝inBcoC∴2inAcoB －coBinC ＝inBcoC ，∴2inAcoB ＝inB ＋C ，∵A＋B＋C＝π，∴inB＋C＝inA，且inA≠0，∴coB＝错误!，B＝错误!，∴0＜A＜错误!∴错误!＜错误!＋错误!＜错误!，错误!＜in错误!＋错误!＜1 又∵f＝=in错误!＋错误!＋错误!，∴fA＝in错误!＋错误!＋错误!故函数fA的取值范围是1，错误!。

高考数学二轮复习考前专题三三角函数、解三角形与平面向量第3讲平面向量讲学案理-人教版高三全

第3讲平面向量1.考查平面向量的基本定理及基本运算，多以熟知的平面图形为背景进行考查，多为选择题、填空题，难度为中低档．2．考查平面向量的数量积，以选择题、填空题为主，难度为低档；向量作为工具，还常与三角函数、解三角形、不等式、解析几何结合，以解答题形式出现．热点一平面向量的线性运算1．在平面向量的化简或运算中，要根据平面向量基本定理选好基底，变形要有方向不能盲目转化．2．在用三角形加法法则时，要保证“首尾相接”，结果向量是第一个向量的起点指向最后一个向量终点所得的向量；在用三角形减法法则时，要保证“同起点”，结果向量的方向是指向被减向量．例1 (1)(2017届河南息县第一高级中学检测)已知平行四边形ABCD 的对角线分别为AC ，BD ，且AE →＝2EC →，点F 是BD 上靠近D 的四等分点，则( )A.FE →＝－112AB →－512AD →B.FE →＝112AB →－512AD →C.FE →＝512AB →－112AD →D.FE →＝－512AB →－112AD →答案 C解析 AE →＝2EC →，点F 是BD 上靠近D 的四等分点， ∴FO →＝14DB →，OE →＝16AC →，∴FE →＝FO →＋OE →＝14DB →＋16AC →，∵AB →＋AD →＝AC →，AD →－AB →＝BD →，∴FE →＝14(AB →－AD →)＋16(AB →＋AD →)＝512AB →－112AD →.故选C. (2)(2017届湖南师大附中月考)O 为△ABC 内一点，且2OA →＋OB →＋OC →＝0，AD →＝tAC →，若B ，O ，D 三点共线，则t 的值为( )A.13B.14C.12D.23 答案 A解析由AD →＝tAC →，得OD →－OA →＝t (OC →－OA →)，所以OD →＝tOC →＋(1－t )OA →，因为B ，O ，D 三点共线，所以BO →＝λOD →，则2OA →＋OC →＝λt OC →＋(1－t )λOA →，故有⎩⎪⎨⎪⎧2＝(1－t )λ，1＝λt ，t ＝13，故选A.思维升华 (1)对于平面向量的线性运算，要先选择一组基底，同时注意平面向量基本定理的灵活运用．(2)运算过程中重视数形结合，结合图形分析向量间的关系．跟踪演练1 (1)(2017·河北省衡水中学三调)在△ABC 中，AN →＝14NC →，P 是直线BN 上的一点，若AP →＝mAB →＋25AC →，则实数m 的值为( )A ．－4B ．－1C ．1D ．4 答案 B解析因为AP →＝AB →＋BP →＝AB →＋kBN →＝AB →＋k ⎝ ⎛⎭⎪⎫15AC →－AB →＝(1－k )AB →＋k 5AC →，且AP →＝mAB →＋25AC →，所以⎩⎪⎨⎪⎧1－k ＝m ，k 5＝25，解得k ＝2，m ＝－1，故选B.(2)(2017届福建连城县二中期中)已知平面向量a ＝(1,2)，b ＝(－2，m )，且a ∥b ，则2a ＋3b 等于( ) A ．(－5，－10)B ．(－4，－8)C ．(－3，－6)D ．(－2，－4) 答案 B解析因为a ＝(1,2)，b ＝(－2，m )，且a ∥b ，所以m ＋4＝0，m ＝－4,2a ＋3b ＝2(1,2)＋3(－2，－4)＝(－4，－8)，故选B. 热点二平面向量的数量积1．数量积的定义：a ·b ＝|a ||b |cos θ. 2．三个结论(1)若a ＝(x ，y )，则|a |＝a ·a ＝x 2＋y 2.(2)若A (x 1，y 1)，B (x 2，y 2)，则|AB →|＝(x 2－x 1)2＋(y 2－y 1)2.(3)若非零向量a ＝(x 1，y 1)，非零向量b ＝(x 2，y 2)，θ为a 与b 的夹角，则cos θ＝a ·b |a ||b |＝x 1x 2＋y 1y 2x 21＋y 21x 22＋y 22.例2 (1)(2017届湖北省部分重点中学联考)若等边△ABC 的边长为3，平面内一点M 满足CM →＝13CB →＋12CA →，则AM →·MB →的值为( ) A ．2 B ．－152C.152D. －2答案 A解析因为AM →＝CM →－CA →，MB →＝CB →－CM →，则AM →·MB →＝⎝ ⎛⎭⎪⎫13CB →－12CA →⎝ ⎛⎭⎪⎫23CB →－12CA →，即AM →·MB →＝29CB →2－12CA →·CB →＋14CA →2＝2－94＋94＝2，故选A.(2)(2017届河北省衡水中学六调)已知向量a ，b 满足|a |＝1，|b |＝2，a －b ＝(3，2)，则|a ＋2b |等于( ) A ．2 2 B.17 C.15 D ．2 5 答案 B解析向量a ，b 满足|a |＝1，|b |＝2，a －b ＝(3，2)，可得|a －b |2＝5，即|a |2＋|b |2－2a ·b ＝5，解得a ·b ＝0. |a ＋2b |2＝|a |2＋4|b |2＋4a ·b ＝1＋16＝17，所以|a ＋2b |＝17.故选B.思维升华 (1)数量积的计算通常有三种方法：数量积的定义，坐标运算，数量积的几何意义．(2)可以利用数量积求向量的模和夹角，向量要分解成题中模和夹角已知的向量进行计算．跟踪演练2 (1)(2017·全国Ⅱ)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA →·(PB →＋PC →)的最小值是( ) A ．－2 B ．－32 C ．－43 D ．－1答案 B解析方法一 (解析法)建立平面直角坐标系如图①所示，则A ，B ，C 三点的坐标分别为A (0,3)，B (－1,0)，C (1,0)．图①设P 点的坐标为(x ，y )，则PA →＝(－x ，3－y )， PB →＝(－1－x ，－y )， PC →＝(1－x ，－y )，∴PA →·(PB →＋PC →)＝(－x ，3－y )·(－2x ，－2y ) ＝2(x 2＋y 2－3y )＝2⎣⎢⎡⎦⎥⎤x 2＋⎝ ⎛⎭⎪⎫y －322－34≥2×⎝ ⎛⎭⎪⎫－34＝－32.当且仅当x ＝0，y ＝32时，PA →·(PB →＋PC →)取得最小值，最小值为－32.故选B. 方法二 (几何法)如图②所示，PB →＋PC →＝2PD →(D 为BC 的中点)，则PA →·(PB →＋PC →)＝2PA →·PD →.图②要使PA →·PD →最小，则PA →与PD →方向相反，即点P 在线段AD 上，则(2PA →·PD →)min ＝－2|PA →||PD →|，问题转化为求|PA →|·|PD →|的最大值．又|PA →|＋|PD →|＝|AD →|＝2×32＝3，∴|PA →||PD →|≤⎝ ⎛⎭⎪⎫|PA →|＋|PD →|22＝⎝ ⎛⎭⎪⎫322＝34，当且仅当|PA →|＝|PD →|时取等号，∴[PA →·(PB →＋PC →)]min ＝(2PA →·PD →)min ＝－2×34＝－32.故选B.(2)(2017届湖北重点中学联考)已知向量a ，b 满足|a |＝2，|b |＝1，a 与b 的夹角为2π3，则|a ＋2b |＝________. 答案 2解析因为|a |＝2，|b |＝1，〈a ，b 〉＝2π3，故a ·b ＝2cos 〈a ，b 〉＝－1，则(a ＋2b )2＝a 2＋4a ·b ＋4b 2＝4－4＋4＝4，即|a ＋2b |＝2. 热点三平面向量与三角函数平面向量作为解决问题的工具，具有代数形式和几何形式的“双重型”，高考常在平面向量与三角函数的交汇处命题，通过向量运算作为题目条件．例3 (2017·江苏)已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]． (1)若a ∥b ，求x 的值；(2)记f (x )＝a ·b ，求f (x )的最大值和最小值以及对应的x 的值．解 (1)因为a ＝(cos x ，sin x )，b ＝(3，－3)，a ∥b ，所以－3cos x ＝3sin x .若cos x ＝0，则sin x ＝0，与sin 2x ＋cos 2x ＝1矛盾，故cos x ≠0. 于是tan x ＝－33. 又x ∈[0，π]，所以x ＝5π6.(2)f (x )＝a·b ＝(cos x ，sin x )·(3，－3)＝3cos x －3sin x ＝23cos ⎝⎛⎭⎪⎫x ＋π6.因为x ∈[0，π]，所以x ＋π6∈⎣⎢⎡⎦⎥⎤π6，7π6，从而－1≤cos ⎝⎛⎭⎪⎫x ＋π6≤32，于是，当x ＋π6＝π6，即x ＝0时，f (x )取得最大值3；当x ＋π6＝π，即x ＝5π6时，f (x )取得最小值－2 3.思维升华在平面向量与三角函数的综合问题中，一方面用平面向量的语言表述三角函数中的问题，如利用向量平行、垂直的条件表述三角函数式之间的关系，利用向量模表述三角函数之间的关系等；另一方面可以利用三角函数的知识解决平面向量问题，在解决此类问题的过程中，只要根据题目的具体要求，在向量和三角函数之间建立起联系，就可以根据向量或者三角函数的知识解决问题．跟踪演练3 已知平面向量a ＝(sin x ，cos x )，b ＝(sin x ，－cos x )，c ＝(－cos x ，－sin x )，x ∈R ，函数f (x )＝a·(b －c )． (1)求函数f (x )的单调递减区间； (2)若f ⎝ ⎛⎭⎪⎫α2＝22，求sin α的值．解 (1)因为a ＝(sin x ，cos x )，b ＝(sin x ，－cos x )，c ＝(－cos x ，－sin x )，所以b －c ＝(sin x ＋cos x ，sin x －cos x )，f (x )＝a·(b －c )＝sin x (sin x ＋cos x )＋cos x (sin x －cos x )＝sin 2x ＋2sin x cos x －cos 2x ＝sin 2x －cos 2x ＝2sin ⎝⎛⎭⎪⎫2x －π4.当2k π＋π2≤2x －π4≤2k π＋3π2，k ∈Z ，即k π＋3π8≤x ≤k π＋7π8，k ∈Z 时，函数f (x )为减函数．所以函数f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π＋3π8，k π＋7π8，k ∈Z .(2)由(1)知，f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π4，又f ⎝ ⎛⎭⎪⎫α2＝22，则2sin ⎝ ⎛⎭⎪⎫α－π4＝22，sin ⎝ ⎛⎭⎪⎫α－π4＝12. 因为sin 2⎝ ⎛⎭⎪⎫α－π4＋cos 2⎝ ⎛⎭⎪⎫α－π4＝1，所以cos ⎝⎛⎭⎪⎫α－π4＝±32. 又sin α＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π4＋π4＝sin ⎝ ⎛⎭⎪⎫α－π4cos π4＋cos ⎝ ⎛⎭⎪⎫α－π4sin π4，所以当cos ⎝ ⎛⎭⎪⎫α－π4＝32时， sin α＝12×22＋32×22＝2＋64；当cos ⎝⎛⎭⎪⎫α－π4＝－32时， sin α＝12×22－32×22＝2－64.综上，sin α＝2±64.真题体验1．(2017·北京改编)设m ，n 为非零向量，则“存在负数λ，使得m ＝λn ”是“m·n <0”的___________条件．(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”) 答案充分不必要解析方法一由题意知|m |≠0，|n |≠0.设m 与n 的夹角为θ. 若存在负数λ，使得m ＝λn ，则m 与n 反向共线，θ＝180°， ∴m ·n ＝|m ||n |cos θ＝－|m ||n |＜0.当90°＜θ＜180°时，m ·n ＜0，此时不存在负数λ，使得m ＝λn . 故“存在负数λ，使得m ＝λn ”是“m ·n ＜0”的充分不必要条件．方法二 ∵m ＝λn ，∴m ·n ＝λn ·n ＝λ|n |2. ∴当λ＜0，n ≠0时，m ·n ＜0.反之，由m ·n ＝|m ||n |cos 〈m ，n 〉<0⇔cos 〈m ，n 〉＜0⇔〈m ，n 〉∈⎝ ⎛⎦⎥⎤π2，π，当〈m ，n 〉∈⎝⎛⎭⎪⎫π2，π时，m ，n 不共线．故“存在负数λ，使得m ＝λn ”是“m ·n ＜0”的充分不必要条件．2．(2017·山东)已知e 1，e 2是互相垂直的单位向量，若3e 1－e 2与e 1＋λe 2的夹角为60°，则实数λ的值是________．答案33解析由题意知|e 1|＝|e 2|＝1，e 1·e 2＝0，|3e 1－e 2|＝(3e 1－e 2)2＝3e 21－23e 1·e 2＋e 22＝3－0＋1＝2. 同理|e 1＋λe 2|＝1＋λ2.所以cos 60°＝(3e 1－e 2)·(e 1＋λe 2)|3e 1－e 2||e 1＋λe 2|＝3e 21＋(3λ－1)e 1·e 2－λe 2221＋λ2＝3－λ21＋λ2＝12，解得λ＝33. 3．(2017·天津)在△ABC 中，∠A ＝60°，AB ＝3，AC ＝2.若BD →＝2DC →，AE →＝λAC →－AB →(λ∈R )，且AD →·AE →＝－4，则λ的值为________．答案311解析由题意知|AB →|＝3，|AC →|＝2， AB →·AC →＝3×2×cos 60°＝3，AD →＝AB →＋BD →＝AB →＋23BC →＝AB →＋23(AC →－AB →)＝13AB →＋23AC →，∴AD →·AE →＝⎝ ⎛⎭⎪⎫13AB →＋23AC →·(λAC →－AB →)＝λ－23AB →·AC →－13AB →2＋2λ3AC →2＝λ－23×3－13×32＋2λ3×22＝113λ－5＝－4，解得λ＝311. 4．(2017·北京)已知点P 在圆x 2＋y 2＝1上，点A 的坐标为(－2,0)，O 为原点，则AO →·AP →的最大值为________．答案 6解析方法一根据题意作出图象，如图所示，A (－2,0)，P (x ，y )．由点P 向x 轴作垂线交x 轴于点Q ，则点Q 的坐标为(x,0)． AO →·AP →＝|AO →||AP →|cos θ， |AO →|＝2，|AP →|＝(x ＋2)2＋y 2， cos θ＝|AQ →||AP →|＝x ＋2(x ＋2)2＋y 2，所以AO →·AP →＝2(x ＋2)＝2x ＋4.点P 在圆x 2＋y 2＝1上，所以x ∈[－1,1]．所以AO →·AP →的最大值为2＋4＝6.方法二如图所示，因为点P 在圆x 2＋y 2＝1上，所以可设P (cos α，sin α)(0≤α＜2π)，所以AO →＝(2,0)，AP →＝(cos α＋2，sin α)， AO →·AP →＝2cos α＋4≤2＋4＝6，当且仅当cos α＝1，即α＝0，P (1,0)时“＝”号成立．押题预测1．如图，在△ABC 中，AD →＝13AB →，DE ∥BC 交AC 于E ，BC 边上的中线AM 交DE 于N ，设AB →＝a ，AC →＝b ，用a ，b 表示向量AN →，则AN →等于( )A.12(a ＋b )B.13(a ＋b ) C.16(a ＋b ) D.18(a ＋b ) 押题依据平面向量基本定理是向量表示的基本依据，而向量表示(用基底或坐标)是向量应用的基础．答案 C解析因为DE ∥BC ，所以DN ∥BM ，则△AND ∽△AMB ，所以AN AM ＝ADAB.因为AD →＝13AB →，所以AN →＝13AM →.因为M 为BC 的中点，所以AM →＝12(AB →＋AC →)＝12(a ＋b )，所以AN →＝13AM →＝16(a ＋b )．故选C.2．如图，BC ，DE 是半径为1的圆O 的两条直径，BF →＝2FO →，则FD →·FE →等于( )A ．－34B ．－89C ．－14D ．－49押题依据数量积是平面向量最重要的概念，平面向量数量积的运算是高考的必考内容，和平面几何知识的结合是向量考查的常见形式．答案 B解析 ∵BF →＝2FO →，圆O 的半径为1，∴|FO →|＝13，∴FD →·FE →＝(FO →＋OD →)·(FO →＋OE →)＝FO →2＋FO →·(OE →＋OD →)＋OD →·OE →＝⎝ ⎛⎭⎪⎫132＋0－1＝－89.3．在△ABC 中，AB →＝(cos 32°，cos 58°)，BC →＝(sin 60°sin 118°，sin 120°sin 208°)，则△ABC 的面积为( ) A.14 B.38C.32 D.34押题依据平面向量作为数学解题工具，通过向量的运算给出条件解决三角函数问题已成为近几年高考的热点．答案 B解析 |AB →|＝cos 232°＋cos 258°＝cos 232°＋sin 232°＝1， BC →＝⎝⎛⎭⎪⎫32cos 28°，－32sin 28°，所以|BC →|＝⎝ ⎛⎭⎪⎫32cos 28°2＋⎝ ⎛⎭⎪⎫－32sin 28°2＝32. 则AB →·BC →＝cos 32°×32cos 28°－sin 32°×32sin 28°＝32(cos 32°cos 28°－sin 32°sin 28°) ＝32cos(32°＋28°)＝32cos 60°＝34，故cos 〈AB →，BC →〉＝AB →·BC →|AB →||BC →|＝341×32＝12.又〈AB →，BC →〉∈[0°，180°]，所以〈AB →，BC →〉＝60°，故B ＝180°－〈AB →，BC →〉＝180°－60°＝120°. 故△ABC 的面积为S ＝12·|AB →|·|BC →|sin B＝12×1×32×sin 120°＝38.故选B. 4．如图，在半径为1的扇形AOB 中，∠AOB ＝60°，C 为AB 上的动点，AB 与OC 交于点P ，则OP →·BP →的最小值是________．押题依据本题将向量与平面几何、最值问题等有机结合，体现了高考在知识交汇点命题的方向，本题解法灵活，难度适中．答案－116解析因为OP →＝OB →＋BP →，所以OP →·BP →＝(OB →＋BP →)·BP →＝OB →·BP →＋BP →2.又因为∠AOB ＝60°，OA ＝OB ，所以∠OBA ＝60°，OB ＝1.所以OB →·BP →＝|BP →|cos 120°＝－12|BP →|.所以OP →·BP →＝－12|BP →|＋|BP →|2＝⎝⎛⎭⎪⎫|BP →|－142－116≥－116，当且仅当|BP →|＝14时，OP →·BP →取得最小值－116.A 组专题通关1. 设D 为△ABC 所在平面内一点，BC →＝3CD →，则( ) A.AD →＝－13AB →＋43AC →B.AD →＝13AB →－43AC →C.AD →＝43AB →＋13AC →D.AD →＝43AB →－13AC →答案 A解析 ∵BC →＝3CD →，∴AC →－AB →＝3(AD →－AC →)，即4AC →－AB →＝3AD →，∴AD →＝－13AB →＋43AC →.2．(2017届广西省教育质量诊断性联合考试)设向量a ＝(1,2)，b ＝(－3,5)，c ＝(4，x )，若a ＋b ＝λc (λ∈R )，则λ＋x 的值为( ) A ．－112 B.112C ．－292 D.292答案 C解析由已知可得(1,2)＋(－3,5)＝λ(4，x )⇒⎩⎪⎨⎪⎧4λ＝－2，xλ＝7⇒⎩⎪⎨⎪⎧λ＝－12，x ＝－14⇒λ＋x ＝－292，故选C.3．已知向量a ，b ，其中a ＝(－1，3)，且a ⊥(a －3b )，则b 在a 上的投影为( )A.43 B ．－43 C.23 D ．－23 答案 C解析由a ＝(－1，3)，且a ⊥(a －3b )，得a ·(a －3b )＝0＝a 2－3a·b ＝4－3a·b ，a·b ＝43，所以b 在a 上的投影为a·b |a |＝432＝23，故选C.4．如图，在矩形ABCD 中，AB ＝3，BC ＝3，BE →＝2EC →，点F 在边CD 上，若AB →·AF →＝3，则AE →·BF →的值为( )A ．4 B.833C ．0D ．－4 答案 D解析如图所示，BE →＝2EC →⇒BE ＝23BC ＝233，AB →·AF →＝3⇒AF cos ∠BAF ＝1⇒DF ＝1，以点A 为原点建立平面直角坐标系，AD 所在直线为x 轴，AB 所在直线为y 轴，则B (0,3)，F (3，1)，E (233，3)，因此BF →＝(3，－2)，AE →·BF →＝233×3－2×3＝2－6＝－4.5．在△ABC 中，AB ＝5，AC ＝6，若B ＝2C ，则向量BC →在BA →方向上的投影是( )A ．－75B ．－77125C.77125D.75 答案 B解析由正弦定理得ACsin B ＝AB sin C ⇒6sin 2C ＝5sin C ⇒cos C ＝35，由余弦定理得cos C ＝BC 2＋AC 2－AB 22AC ·BC ⇒BC ＝115或5，经检验知BC ＝5不符合，舍去，所以BC ＝115，cos B ＝AB 2＋BC 2－AC 22AB ·BC ＝－725，则|BC →|cos B ＝－77125，故选B.6．(2017届吉林省普通中学调研)在等腰直角△ABC 中，AC ＝BC ，D 在AB 边上且满足CD →＝tCA →＋(1－t )CB →，若∠ACD ＝60°，则t 的值为( ) A.3－12B.3－1C.3－22 D.3＋12答案 A解析因为D 在AB 边上且满足CD →＝tCA →＋(1－t )CB →，所以BD →＝tBA →，不妨设AC ＝BC ＝1，则AB ＝2，AD ＝2(1－t )，在△ACD 中，∠ACD ＝60°，∠CAD ＝45°，则∠ADC ＝75°，由正弦定理，得1sin 75°＝2(1－t )sin 60°，解得t ＝3－12.故选A. 7．(2017届河南南阳一中月考)已知△ABC 的外接圆半径为1，圆心为点O ，且3OA →＋4OB →＋5OC →＝0，则△ABC 的面积为( ) A.85 B.75C.65 D.45答案 C解析如图所示，|OA →|＝|OB →|＝|OC →|＝1，由3OA →＋4OB →＋5OC →＝0，可得3OA →＋4OB →＝－5OC →，两边平方可得9＋24OA →·OB →＋16＝25，所以OA →·OB →＝0，因此OA →⊥OB →.同理3OA →＋5OC →＝－4OB →，4OB →＋5OC →＝－3OA →，两边分别平方可得cos 〈OB →，OC →〉＝－45，cos 〈OA →，OC →〉＝－35，根据同角三角函数基本关系可得sin 〈OB →，OC →〉＝35，sin 〈OA →，OC →〉＝45，所以S △ABC ＝S △AOB ＋S △AOC ＋S △OBC＝12×1×1＋12×1×1×45＋12×1×1×35＝65，故选C. 8．已知向量OA →＝(1,1)，OB →＝(1，a )，其中O 为原点，若向量OA →与OB →的夹角在区间⎣⎢⎡⎦⎥⎤0，π12内变化，则实数a 的取值范围是__________．答案 ⎣⎢⎡⎦⎥⎤33，3 解析因为OA →＝(1,1)，OB →＝(1，a )，所以OA →·OB →＝1＋a .又OA →·OB →＝2·1＋a 2cos θ，故cos θ＝1＋a2(1＋a 2)，因为θ∈⎣⎢⎡⎦⎥⎤0，π12，故cos θ∈⎣⎢⎡⎦⎥⎤6＋24，1，即1＋a2(1＋a 2)∈⎣⎢⎡⎦⎥⎤6＋24，1，解得33≤a ≤ 3. 9．(2017·辽宁省大连市双基测试)已知平面内三个单位向量OA →，OB →，OC →，〈OA →，OB →〉＝60°，若OC →＝mOA →＋nOB →，则m ＋n 的最大值是______．答案233解析由已知条件OC →＝mOA →＋nOB →，两边平方可得1＝m 2＋mn ＋n 2＝(m ＋n )2－mn ，∴(m ＋n )2－1＝mn ，根据向量加法的平行四边形法则，判断出m ，n >0，∴(m ＋n )2－1＝mn ≤14(m ＋n )2，当且仅当m ＝n 时取等号，∴34(m ＋n )2≤1，则m ＋n ≤233，即m ＋n 的最大值为233. 10．(2017届陕西西安铁一中三模)已知向量m ＝(sin x ，－1)，向量n ＝⎝ ⎛⎭⎪⎫3cos x ，－12，函数f (x )＝(m ＋n )·m . (1)求f (x )的单调递减区间；(2)已知a ，b ，c 分别为△ABC 内角A ，B ，C 的对边，A 为锐角，a ＝23，c ＝4，且f (A )恰是f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值，求A ，b 和△ABC 的面积S .解 (1)f (x )＝(m ＋n )·m ＝sin 2x ＋1＋3sin x cos x ＋12＝1－cos 2x 2＋1＋32sin 2x ＋12＝32sin 2x －12cos 2x ＋2 ＝sin ⎝⎛⎭⎪⎫2x －π6＋2.由2k π＋π2≤2x －π6≤2k π＋3π2(k ∈Z )，得k π＋π3≤x ≤k π＋5π6(k ∈Z )．所以f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π＋π3，k π＋5π6(k ∈Z )．(2)由(1)知f (A )＝sin ⎝ ⎛⎭⎪⎫2A －π6＋2，当x ∈⎣⎢⎡⎦⎥⎤0，π2时，－π6≤2x －π6≤5π6，由正弦函数图象可知，当2x －π6＝π2时f (x )取得最大值3.所以2A －π6＝π2，A ＝π3.由余弦定理，a 2＝b 2＋c 2－2bc cos A ，得12＝b 2＋16－2×4b ×12，所以b ＝2.所以S ＝12bc sin A ＝12×2×4sin 60°＝2 3.B 组能力提高11. (2017届江西师大附中、临川一中联考)在Rt △ABC 中，∠BCA ＝90°，CA ＝CB ＝1，P 为AB 边上的点，AP →＝λAB →，若CP →·AB →≥PA →·PB →，则λ的最大值是( ) A.2＋22 B. 2－22C ．1 D. 2 答案 C解析因为CP →＝AP →－AC →＝λAB →－AC →， PB →＝AB →－AP →＝AB →－λAB →，故由CP →·AB →≥PA →·PB →，可得2λ－1≥－2λ(1－λ)，即2λ－1≥－2λ＋2λ2，也即λ2－2λ≤－12，解得1－22≤λ≤1＋22，由于点P ∈AB ，所以1－22≤λ≤1，故选C.12．(2017届荆、荆、襄、宜四地七校联考)如图，三个边长为2的等边三角形有一条边在同一直线上，边B 3C 3上有10个不同的点P 1，P 2，…，P 10, 记m i ＝AB →2·AP →i (i ＝1,2，…，10)，则m 1＋m 2＋…＋m 10的值为( )A ．15 3B ．45C ．60 3D ．180 答案 D解析因为AB 2与B 3C 3垂直，设垂足为C ，所以AP i →在AB 2→上的投影为AC ，m i ＝AB 2→·AP i →＝|AB 2→||AC →|＝23×33＝18，从而m 1＋m 2＋…＋m 10的值为18×10＝180.故选D. 13.(2017届江西上饶一模)已知在Rt △AOB 中，AO ＝1，BO ＝2，如图，动点P 是在以O 点为圆心，OB 为半径的扇形内运动(含边界)且∠BOC ＝90°.设OP →＝xOA →＋yOB →，则x ＋y 的取值范围是__________．答案 [－2,1]解析由已知图形可知OP →，OA →的夹角∠AOP ∈[90°，180°]，所以x ≤0， OP →，OB →的夹角∠BOP ∈[0°，90°]，所以y ≥0，由平行四边形法则可知，当点P 沿着圆弧CB 由C 到B 移动时，负数x 逐渐增大，正数y 逐渐增大，所以当点P 在C 处时x ＋y 取得最小值，因为OC ＝2OA ，OC ⊥OB ，所以x ＝－2，y ＝0，所以x ＋y ＝－2，当点P 在点B 处时x ＋y 取得最大值，因为OA ⊥OB ，所以x ＝0，y ＝1，所以x ＋y ＝1，所以x ＋y 的取值范围为[－2,1]．14．(2017届云南曲靖一中月考)已知向量a ＝(－1,0)，b ＝(cos α，sin α)，c ＝(cos β，sin β)．(1)求|a ＋c |的最大值；(2)若α＝π4，且向量b 与向量(a ＋c )垂直，求cos β的值．解 (1)a ＋c ＝(cos β－1，sin β)，|a ＋c |＝(cos β－1)2＋sin 2β＝2－2cos β，当cos β＝－1时，|a ＋c |＝2，|a ＋c |的最大值为2. (2)若α＝π4，则b ＝⎝ ⎛⎭⎪⎫22，22，a ＋c ＝(cos β－1，sin β)，∵向量b 与向量a ＋c 垂直， ∴22(cos β－1)＋22sin β＝0， ∴sin β＋cos β＝1，故sin 2β＝(1－cos β)2＝1－2cos β＋cos 2β， cos 2β－cos β＝0，∴cos β＝0或1.当cos β＝1时，sin β＝0，a＋c＝(0,0)不符合条件，∴cos β＝0.。

高考数学二轮复习专题2 三角函数、解三角形、平面向量第3讲平面向量练习理-人教版高三全册数学

第3讲平面向量专题复习检测A 卷1．已知向量a ＝(2,6)，b ＝(－1，λ)，若a∥b ，则λ＝( ) A ．3 B ．－3 C ．13 D ．－13【答案】B2．已知向量a ＝(x －1,2)，b ＝(2,1)，则a⊥b 的充要条件是( ) A ．x ＝－12B ．x ＝－1C ．x ＝5D ．x ＝0【答案】D3．在四边形ABCD 中，AC →＝(1,2)，BD →＝(－4,2)，则该四边形的面积为( ) A ． 5 B ．2 5 C ．5 D ．10【答案】C4．(2019年某某模拟)已知|a|＝1，|b|＝2，且a⊥(a －b )，则向量a 在b 方向上的投影为( )A ．1B ． 2C ．12D ．22【答案】D【解析】由a⊥(a －b )，可得a·(a －b )＝a 2－a·b ＝0，所以a·b ＝a 2＝1.所以向量a 在b 方向上的投影为|a |cos 〈a ，b 〉＝a·b |b|＝12＝22.故选D ．5．(2019年某某某某模拟)在△ABC 中，D 为BC 上一点，E 是AD 的中点，若BD →＝λDC →，CE →＝13AB →＋μAC →，则λ＋μ＝() A ．13B ．－13C ．76D ．－76 【答案】B【解析】如图所示，由BD →＝λDC →，可得AD →－AB →＝λ(AC →－AD →)，则AD →＝11＋λAB →＋λ1＋λAC →.又E 是AD 的中点，所以CE →＝CA →＋AE →＝－AC →＋12AD →＝12(1＋λ)AB →＋－λ－22(1＋λ)AC →.又CE →＝13AB →＋μAC →，AB ，AC 不共线，所以12(1＋λ)＝13，－λ－22(1＋λ)＝μ，解得λ＝12，μ＝－56，则λ＋μ＝－13.故选B ．6．(2017年新课标Ⅰ)已知向量a ，b 的夹角为60°，|a|＝2，|b|＝1，则|a ＋2b|＝________.【答案】2 3【解析】|a ＋2b|2＝|a|2＋4a·b ＋4|b|2＝4＋4×2×1×cos 60°＋4＝12，∴|a ＋2b |＝12＝2 3.7．(2019年新课标Ⅲ)已知a ，b 为单位向量，且a·b ＝0，若c ＝2a －5b ，则cos 〈a ，c 〉＝________.【答案】23【解析】a·c ＝a·(2a －5b )＝2a 2－5a·b ＝2，c 2＝(2a －5b )2＝4a 2－45a·b ＋5b 2＝9，则|c|＝3.所以cos 〈a ，c 〉＝a·c |a||c|＝23.8．(2018年某某呼和浩特一模)在△ABC 中，AB ＝3，BC ＝2AC ＝2，满足|BA →－tBC →|≤3|AC →|的实数t 的取值X 围是________．【答案】⎣⎢⎡⎦⎥⎤0，32 【解析】由题意，得AC ＝1，cos 〈BA →，BC →〉＝BA 2＋BC 2－AC 22BA ·BC ＝3＋4－123×2＝32.由|BA →－tBC →|≤3|AC →|，得BA →2－2t |BA →||BC →|cos 〈BA →，BC →〉＋t 2BC →2≤3AC →2，即3－2t ×23×32＋4t 2≤3，解得0≤t ≤32.9．已知|a|＝4，|b|＝8，a 与b 的夹角是120°. (1)求|a ＋b|的值；(2)当(a ＋2b )⊥(k a －b )时，求k 的值．【解析】(1)由已知，得a·b ＝4×8×⎝ ⎛⎭⎪⎫－12＝－16， ∵|a ＋b|2＝a 2＋2a·b ＋b 2＝16＋2×(－16)＋64＝48， ∴|a ＋b|＝4 3.(2)∵(a ＋2b )⊥(k a －b )，∴(a ＋2b )·(k a －b )＝0. ∴k a 2＋(2k －1)a·b －2b 2＝0，即16k －16(2k －1)－2×64＝0，解得k ＝－7.10．已知向量a ＝(cos x,2cos x )，b ＝(2cos x ，sin x )，函数f (x )＝a·b .(1)把函数f (x )的图象向右平移π6个单位长度得到函数g (x )的图象，求g (x )的单调递增区间；(2)当a ≠0，a 与b 共线时，求f (x )的值．【解析】(1)∵f (x )＝a·b ＝2cos 2x ＋2sin x cos x ＝sin 2x ＋cos 2x ＋1＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1， ∴g (x )＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π6＋π4＋1＝2sin ⎝⎛⎭⎪⎫2x －π12＋1.由－π2＋2k π≤2x －π12≤π2＋2k π，k ∈Z ，得－5π24＋k π≤x ≤7π24＋k π，k ∈Z ，∴g (x )的单调递增区间为⎣⎢⎡⎦⎥⎤－5π24＋k π，7π24＋k π，k ∈Z .(2)∵a≠0，a 与b 共线，∴cos x ≠0.∴sin x cos x －4cos 2x ＝0.∴sin x ＝4cos x ，tan x ＝4.则f (x )＝2cos 2x ＋2sin x cos x ＝2cos 2x ＋2sin x cos x sin 2x ＋cos 2x ＝2＋2tan x tan 2x ＋1＝1017. B 卷11．(2017年新课标Ⅱ)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA →·(PB →＋PC →)的最小值是( )A ．－2B ．－32C ．－43D ．－1【答案】B【解析】如图，以BC 所在直线为x 轴，BC 的垂直平分线DA 所在直线为y 轴，D 为坐标原点建立平面直角坐标系，则A (0，3)，B (－1,0)，C (1,0)．设P (x ，y )，则PA →＝(－x ，3－y )，PB →＝(－1－x ，－y )，PC →＝(1－x ，－y )，∴PB →＋PC →＝(－2x ，－2y )，PA →·(PB →＋PC →)＝2x 2－2y (3－y )＝2x 2＋2⎝ ⎛⎭⎪⎫y －322－32≥－32，当x ＝0，y ＝32，即P ⎝⎛⎭⎪⎫0，32时，PA →·(PB →＋PC →)有最小值－32.12．(2018年某某某某模拟)已知A ，B 是圆O ：x 2＋y 2＝4上的两个动点，|AB →|＝2，OC →＝53OA →－23OB →.若M 是线段AB 的中点，则OC →·OM →的值为( )A ．3B ．2 3C ．－2 3D ．－3【答案】A【解析】设A (x 1，y 1)，B (x 2，y 2)，则OA →＝(x 1，y 1)，OB →＝(x 2，y 2)，OM →＝⎝ ⎛⎭⎪⎫x 1＋x 22，y 1＋y 22，AB →＝(x 2－x 1，y 2－y 1)．∴OC →＝53OA →－23OB →＝⎝ ⎛⎭⎪⎫53x 1－23x 2，53y 1－23y 2.由|AB →|＝2，得(x 2－x 1)2＋(y 2－y 1)2＝4.① 又A ，B 在圆O 上，∴x 21＋y 21＝4，x 22＋y 22＝4.② 联立①②得x 1x 2＋y 1y 2＝2，∴OC →·OM →＝⎝ ⎛⎭⎪⎫53x 1－23x 2，53y 1－23y 2·⎝ ⎛⎭⎪⎫x 1＋x 22，y 1＋y 22，化简得56(x 21＋y 21)－13(x 22＋y 22)＋12(x 1x 2＋y 1y 2)＝56×4－13×4＋12×2＝3. 13．(2019年某某)已知正方形ABCD 的边长为1，当每个λi (i ＝1,2,3,4,5,6)取遍±1时，|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|的最小值是________，最大值是________．【答案】0 2 5【解析】由正方形ABCD 的边长为1，可得AB →＋AD →＝AC →，BD →＝AD →－AB →，AB →·AD →＝0， ∴|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|＝|λ1AB →＋λ2AD →－λ3AB →－λ4AD →＋λ5AB →＋λ5AD →＋λ6AD →－λ6AB →|＝|(λ1－λ3＋λ5－λ6)·AB →＋(λ2－λ4＋λ5＋λ6)AD →|.要使|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|最小，只需要|λ1－λ3＋λ5－λ6|＝|λ2－λ4＋λ5＋λ6|＝0，此时只需取λ1＝1，λ2＝－1，λ3＝1，λ4＝1，λ5＝1，λ6＝1，此时所求最小值为0.又|(λ1－λ3＋λ5－λ6)AB →＋(λ2－λ4＋λ5＋λ6)·AD →|2＝(λ1－λ3＋λ5－λ6)2＋(λ2－λ4＋λ5＋λ6)2≤(|λ1|＋|λ3|＋|λ5－λ6|)2＋(|λ2|＋|λ4|＋|λ5＋λ6|)2＝(2＋|λ5－λ6|)2＋(2＋|λ5＋λ6|)2＝8＋4(|λ5－λ6|＋|λ5＋λ6|)＋(λ5－λ6)2＋(λ5＋λ6)2＝8＋4(|λ5－λ6|＋|λ5＋λ6|)2＋2(λ25＋λ26)＝12＋42(λ25＋λ26)＋2|λ25－λ26|＝20，当且仅当λ1－λ3，λ5－λ6均非负或均非正，并且λ2－λ4，λ5＋λ6均非负或均非正，可取λ1＝1，λ2＝1，λ3＝－1，λ4＝－1，λ5＝1，λ6＝1，则所求最大值为20＝2 5.14．(2019年某某眉山模拟)已知△ABC 的角A ，B ，C 所对的边分别是a ，b ，c ，设向量m ＝(a ，b )，n ＝(sin B ，sin A )，p ＝(b －2，a －2)．(1)若m∥n ，求证：△ABC 为等腰三角形；(2)若m⊥p ，边长c ＝2，角C ＝π3，求△ABC 的面积．【解析】(1)证明：因为m ＝(a ，b )，n ＝(sin B ，sin A )，m∥n ，所以a sin A ＝b sin B .结合正弦定理，可得a 2＝b 2，即a ＝b ，所以△ABC 为等腰三角形．(2)因为m ＝(a ，b )，p ＝(b －2，a －2)，m⊥p ，所以m·p ＝a (b －2)＋b (a －2)＝0，则a ＋b ＝ab . 由余弦定理得c 2＝a 2＋b 2－2ab cos C ，其中c ＝2，C ＝π3，所以a 2＋b 2－ab ＝4，则(a ＋b )2－3ab －4＝0. 所以(ab )2－3ab －4＝0，解得ab ＝4(ab ＝－1舍去)．所以S △ABC ＝12ab sin C ＝12×4×sin π3＝ 3.。

高考数学压轴专题人教版备战高考《平面向量》知识点总复习附答案解析

【高中数学】数学《平面向量》试卷含答案一、选择题1．已知向量(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，则当,1[]2t ∈-时，a tb-r r 的最大值为（） A ．2 B ．3C ．2D ．5【答案】D 【解析】【分析】根据(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，得到1a =r ，1b =r ，0a b ⋅=r r ，再利用22()1a tb a tb t -=-=+r r r r 求解.【详解】因为(cos ,sin )a αα=r ，(cos ,sin )b ββ=r ，a b ⊥r r，所以1a =r ，1b =r ，0a b ⋅=r r，所以22()1a tb a tb t -=-=+r r r r ，当[]2,1t ∈-时，max5a tb-=r r. 故选：D 【点睛】本题考查向量的模以及数量积的运算，还考查运算求解能力，属于中档题.2．已知菱形ABCD 的边长为2，60ABC ∠=︒，则BD CD ⋅=u u u v u u u v（）A ．4B ．6C ．23D ．43【答案】B 【解析】【分析】根据菱形中的边角关系，利用余弦定理和数量积公式，即可求出结果．【详解】如图所示，菱形形ABCD 的边长为2，60ABC ∠=︒，∴120C ∠=︒，∴22222222cos12012BD =+-⨯⨯⨯︒=，∴23BD =，且30BDC ∠=︒，∴|||3 302|3262BD CD BD CD cos =⨯⨯︒=⨯⨯=⋅u u u r u u u r u u u r u u u r ，故选B ．【点睛】本题主要考查了平面向量的数量积和余弦定理的应用问题，属于基础题.．3．在△ABC 中，D 是BC 中点，E 是AD 中点，CE 的延长线交AB 于点,F 则（）A ．1162DF AB AC =--u u u r u u u r u u u r B ．1134DF AB AC =--u u u r u u u r u u u rC ．3142DF AB AC =-+u u u r u u u r u u u rD ．1126DF AB AC =--u u u r u u u r u u u r【答案】A 【解析】【分析】设AB AF λ=u u u r u u u r，由平行四边形法则得出144AE AF AC λ=+u u u r u u u r u u u r ，再根据平面向量共线定理得出得出=3λ，由DF AF AD =-u u u r u u u r u u u r，即可得出答案. 【详解】设AB AF λ=u u u r u u u r ，111124444AE AB A A C A AC D F λ==+=+u u u r u u u u u ur u u u r r u u u r u u u r因为C E F 、、三点共线，则1=144λ+，=3λ所以1111132262DF AF AD AB AB AC AB AC =-=--=--u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r故选：A【点睛】本题主要考查了用基底表示向量，属于中档题.4．已知ABC V 中，2,3,60,2,AB BC ABC BD DC AE EC ==∠=︒==，则AD BE ⋅=u u u r u u u r（）A ．1B ．2-C ．12D ．12-【答案】C 【解析】【分析】以,BA BC u u u r u u u r为基底，将,AD BE u u u r u u u r 用基底表示，根据向量数量积的运算律，即可求解.【详解】222,,33BD DC BD BC AD BD BA BC BA ===-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r,11,22AE EC BE BC BA =∴=+u u u r u u u r u u u r,211()()322AD BE BC BA BC BA ⋅=-⋅+u u u r u u u r u u ur u u u r u u u r u u u r22111362BC BC BA BA =-⋅-u u ur u u u r u u u r u u u r 111123622=-⨯⨯⨯=.故选:C. 【点睛】本题考查向量的线性运算以及向量的基本定理，考查向量数量积运算，属于中档题.5．已知向量,a b r r 满足||3a =r ||4=r b ，且()4a b b +⋅=r r r ，则a r 与b r的夹角为（）A ．6π B ．3π C ．23π D ．56π 【答案】D 【解析】【分析】由()4a b b +⋅=r r r ，求得12a b ⋅=-r r ，再结合向量的夹角公式，求得3cos ,2a b 〈〉=-r r ，即可求得向量a r 与b r的夹角．【详解】由题意，向量,a b r r 满足||3a =r||4=r b ，因为()4a b b +⋅=r r r ，可得2164a b b a b ⋅+=⋅+=r r r r r，解得12a b ⋅=-r r ，所以3 cos,||||234a ba ba b⋅〈〉===-⨯r rr rr r，又因ar与br的夹角[0,]π∈，所以ar与br的夹角为56π.故选：D．【点睛】本题主要考查了向量的数量积的应用，其中解答中熟记向量的数量积的计算公式，以及向量的夹角公式，准确计算是解答的关键，着重考查了计算能力．6．在ABC∆中，已知8AB=，4BC=，6CA=，则AB BC⋅u u u v u u u v的值为（）A．22 B．19 C．-19 D．-22【答案】D【解析】由余弦定理可得22211cos216AB BC ACBAB BC+-==⋅，又()11cos482216AB BC AB BC Bπ⎛⎫⋅=⋅⋅-=⨯⨯-=-⎪⎝⎭u u u v u u u v u u u v u u u v，故选D.【思路点睛】本题主要考查平面向量数量积公式以、余弦定理解三角形，属于简单题.对余弦定理一定要熟记两种形式：（1）2222cosa b c bc A=+-；（2）222cos2b c aAbc+-=，同时还要熟练掌握运用两种形式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住30,45,60o o o等特殊角的三角函数值，以便在解题中直接应用.7．如图，在ABCV中，AD AB⊥，3BC BD=u u u v u u u v，1AD=u u u v，则AC AD⋅=u u u v u u u v（）A．3B3C3D3【答案】D【解析】∵3AC AB BC AB=+=u u u v u u u v u u u v u u u v u u v，∴(3)3AC AD AB AD AB AD BD AD⋅=+⋅=⋅⋅u u u v u u u v u u u v u u v u u u v u u u v u u u v u u u v，又∵AB AD⊥，∴0AB AD⋅=uuu r，∴cos cosAC AD AD AD ADB BD ADB ADu u u v u u u v u u v u u u v u u v u u u v u u u v u u u v ⋅=⋅=⋅∠=⋅∠==，故选D．8．已知椭圆2222:1(0)x yT a ba b+=>>的离心率为2，过右焦点F且斜率为()0k k>的直线与T相交于A，B两点，若3AF FB=uu u r uu r，则k=（）A．2 BCD．1【答案】C【解析】【分析】由e=a=，b=，可设椭圆的方程为222334x y c+=，()()1122,,,A x yB x y，并不妨设B在x轴上方，由3AF FB=uu u r uu r得到12123430x x cy y+=⎧⎨+=⎩，再由22211334x y c+=，22222334x y c+=得到A、B两点的坐标，利用两点的斜率公式计算即可.【详解】因为cea===，所以2a b=，所以a=，b=，则椭圆方程22221x ya b+=变为222334x y c+=.设()()1122,,,A x yB x y，不妨设B在x轴上方，则210,0y y><，又3AF FB=uu u r uu r，所以()()1122,3,c x y x c y--=-，所以()121233c x x cy y⎧-=-⎨-=⎩，12123430x x cy y+=⎧⎨+=⎩因为A，B在椭圆上，所以22211334x y c+=，①22222334x y c+=②.由①—9×②，得2121212123(3)(3)3(3)(3)84x x x x y y y y c+-++-=-，所以21234(3)84c x x c⨯-=-，所以12833x x c-=-，所以123x c =，2109x c =，从而13y =-，2y =所以2(,)3A c，10()9B c，故9102393c k c c +==- 故选：C. 【点睛】本题考查直线与椭圆的位置关系，当然本题也可以利用根与系数的关系来解决，考查学生的数学运算求解能力，是一道中档题.9．设双曲线()222210,0x y a b a b -=>>的右焦点为F ，过点F 作x 轴的垂线交两渐近线于,A B 两点，且与双曲线在第一象限的交点为P ，设O 为坐标原点，若(),OP OA OB R λμλμ=+∈u u u v u u u v u u u v ，225+=8λμ，则双曲线的离心率为（）A．BC．2D ．98【答案】A 【解析】【分析】先根据已知求出,u λ，再代入225+=8λμ求出双曲线的离心率. 【详解】由题得双曲线的渐近线方程为b y x a =±，设F(c,0)，则2(,),(,),(,),bc bc b A c B c P c a a a-因为(),OP OA OB R λμλμ=+∈u u u v u u u v u u u v ，所以2(,)((),())b bc c u c u a aλλ=+-.所以,,bu c u cλλ+=-= 解之得,.22b c c bu c cλ+-== 因为225+=8λμ，所以225()(),228b c c b c e c c a +-+=∴=∴= 故答案为A 【点睛】本题主要考查双曲线的几何性质和离心率的求法，意在考查学生对这些基础知识的掌握能力.解答本题的关键是根据(),OP OA OB R λμλμ=+∈u u u v u u u v u u u v求出,u λ.10．已知向量a v ，b v 满足a b a b +=-r rv v ，且||3a =v ，||1b =r ，则向量b v 与a b -v v 的夹角为（） A ．3π B ．23π C ．6π D ．56π 【答案】B 【解析】【分析】对a b a b +=-v v v v 两边平方，求得0a b ⋅=v v ，所以a b ⊥v v .画出图像，根据图像确定b v 与a b-v v 的夹角，并根据它补角的正切值求得对应的角的大小.【详解】因为a b a b +=-v v v v ，所以222222a a b b a a b b +⋅+=-⋅+v v v v v v v v ，即0a b ⋅=v v ，所以a b ⊥v v .如图，设AB a =u u u v v ，AD b =u u u v v，则向量b v 与a b -v v 的夹角为BDE ∠，因为tan 3BDA ∠=，所以3BDA π∠=，23BDE π∠=.故选B.【点睛】本题考查平面向量的模以及夹角问题，考查运算求解能力，考查数形结合的数学思想方法.属于中档题.11．如图，在圆O 中，若弦AB ＝3，弦AC ＝5，则AO uuu v ·BC uuu v的值是A ．－8B ．－1C ．1D ．8【答案】D 【解析】【分析】【详解】因为AO AC CO AB BO =+=+u u u v u u u v u u u v u u u v u u u v，所以1()2AO AC BO AB CO =+++u u u v u u u v u u u v u u u v u u u v ，而BC AC AB BO CO =-=-u u u v u u u v u u u v u u u v u u u v，所以1()2BC AC AB BO CO =-+-u u u v u u u v u u u v u u u v u u u v ，则1()()4AO BC AC AB CO BO AC AB BO CO ⋅=+++-+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v1()()()()()()4AC AB AC AB AC AB BO CO CO BO AC AB =+-++-++-u u uv u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v ()()CO BO BO CO ++-u u u v u u u v u u u v u u u v221(||4AC AB AC BO AC CO AB BO AB CO =-+⋅-⋅+⋅-⋅u u uv u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v 22||)CO AC CO AB BO AC BO AB BO CO +⋅-⋅+⋅-⋅+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v 2211(||)()42AC AB AC BO AB CO =-+⋅-⋅u u uv u u u v u u u v u u u v u u u v u u u v 2211(||)[()]42AC AB AB BC BO AB CO =-++⋅-⋅u u uv u u u v u u u v u u u v u u u v u u u v u u u v 2211(||)()42AC AB AB BC BC BO =-+⋅+⋅u u uv u u u v u u u v u u u v u u u v u u u v 2211(||)42AC AB AO BC =-+⋅u u uv u u u v u u u v u u u v 所以221(||)82AO BC AC AB ⋅=-=u u u v u u u v u u u v u u u v ，故选D12．已知AB 是圆22:(1)1C x y -+=的直径，点P 为直线10x y -+=上任意一点，则PA PB ⋅u u u v u u u v的最小值是（）A ．21-B ．2C ．0D ．1【答案】D 【解析】试题分析：由题意得，设，,,又因为,所以，所以PA PB ⋅u u u r u u u r的最小值为1，故答案选D.考点：1.圆的性质；2.平面向量的数量积的运算.13．已知平面向量,,a b c r r r满足()()2,21a b a b a c b c ==⋅=-⋅-=r r r r r r r r ，则b c -r r 的最小值为（）A ．2B ．2CD ．12【答案】A 【解析】【分析】根据题意，易知a r 与b r的夹角为60︒，设(=1a r ，()20b =，r ，(),c x y =r ，由()()21a c b c -⋅-=r r r r，可得221202x y x +-+=，所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值，利用圆心和点()20，的距离与半径的差，即可求出结果. 【详解】因为2a b a b ==⋅=r r r r ，所以a r 与b r 的夹角为60︒，设(=1a r ，()20b =，r ，(),c x y =r，因为()()21a c b c -⋅-=r r r r ，所以221202x y x +-+=，又b c -=r r所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值，又圆221202x y x +-+=的圆心坐标为1⎛ ⎝⎭，所以点()20，与圆221202x y x +-+=上一动点距离的最小值为22=. 故选：A. 【点睛】本题考查向量的模的最值的求法，考查向量的数量积的坐标表示，考查学生的转换思想和运算能力，属于中档题．14．设()1,a m =r ，()2,2b =r，若()2a mb b +⊥r r r ，则实数m 的值为（）A ．12B ．2C ．13-D ．-3【答案】C【解析】【分析】计算()222,4a mb m m +=+r r，根据向量垂直公式计算得到答案.【详解】()222,4a mb m m +=+r r，∵()2a mb b +⊥r r r ，∴()20a mb b +⋅=r r r ，即()22280m m ⋅++=，解得13m =-.故选：C .【点睛】本题考查了根据向量垂直求参数，意在考查学生的计算能力.15．如图，AB ，CD 是半径为1的圆O 的两条直径，3AE EO =u u u v u u u v ，则•EC ED u u u v u u u v的值是（）A ．45-B ．1516-C ．14-D ．58-【答案】B 【解析】【分析】根据向量表示化简数量积，即得结果. 【详解】()()()()•••EC ED EO OC EO OD EO OC EO OC =++=+-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v2221151416EO OC ⎛⎫=-=-=- ⎪⎝⎭u u u v u u u v ,选B.【点睛】本题考查向量数量积，考查基本分析求解能力，属基础题.16．已知A ，B 是圆224+=O: x y 上的两个动点，||2AB =u u u r，1233OC OA OB =+u u u r u u u r u u u r ，若M 是线段AB 的中点，则OC OM ⋅u u u r u u u u r的值为（）.A 3B ．3C ．2D ．3【答案】D【解析】【分析】判断出OAB ∆是等边三角形，以,OA OB u u u r u u u r 为基底表示出OM u u u u r ，由此求得OC OM ⋅u u u r u u u u r 的值.【详解】圆O 圆心为()0,0，半径为2，而||2AB =u u u r ，所以OAB ∆是等边三角形.由于M 是线段AB 的中点，所以1122OM OA OB =+u u uu r u u u r u u u r .所以OC OM ⋅u u u r u u u u r 12331122OA O O O B A B ⎛⎫=+⋅⎛⎫+ ⎪⎝ ⎪⎭⎝⎭u u u u u u r u u u r r u u u r 22111623OA OA OB OB =+⋅⋅+u u u r u u u r u u u r u u u r 21422cos603323=+⨯⨯⨯+=o . 故选：D【点睛】本小题主要考查用基底表示向量，考查向量的数量积运算，考查数形结合的数学思想方法，属于中档题.17．向量1,tan 3a α⎛⎫= ⎪⎝⎭r ，()cos ,1b α=r ，且//a b r r ，则cos 2πα⎛⎫+= ⎪⎝⎭（） A ．13 B ．223- C ．23- D ．13- 【答案】D【解析】【分析】根据向量平行的坐标运算以及诱导公式，即可得出答案.【详解】//a b ∴r r 1cos tan sin 3ααα∴=⋅= 1cos sin 23παα⎛⎫∴+=-=- ⎪⎝⎭故选：D【点睛】本题主要考查了由向量平行求参数以及诱导公式的应用，属于中档题.18．已知向量a v ，b v 满足a v ||1b =v ，且2b a +=v v ，则向量a v 与b v 的夹角的余弦值为（）A ．2B ．3CD ．4【答案】D【解析】【分析】根据平方运算可求得12a b ⋅=r r ，利用cos ,a b a b a b ⋅<>=r r r r r r 求得结果. 【详解】由题意可知：2222324b a b a b a a b +=+⋅+=+⋅=r r r r r r r r ，解得：12a b ⋅=r rcos ,4a b a b a b ⋅∴<>===r r r r r r 本题正确选项：D【点睛】本题考查向量夹角的求解问题，关键是能够通过平方运算求得向量的数量积.19．已知向量5(,0)2a =r ，(0,5)b =r 的起点均为原点，而终点依次对应点A ，B ，线段AB 边上的点P ，若OP AB ⊥u u u r u u u r ，OP xa yb =+u u u r r r ，则x ，y 的值分别为（）A ．15，45B ．43，13-C ．45，15D ．13-，43【答案】C【解析】【分析】求得向量5(,5)2OP x y =u u u r ，5(,5)2AB b a =-=-u u u r r r ，根据OP AB ⊥u u u r u u u r 和,,A B P 三点共线，列出方程组，即可求解.【详解】由题意，向量5(,0)2a =r ，(0,5)b =r ，所以5(,5)2OP xa yb x y =+=u u u r r r ，又由5(,5)2AB b a =-=-u u u r r r ，因为OP AB ⊥u u u r u u u r ，所以252504OP AB x y ⋅=-+=u u u r u u u r ，可得4x y =，又由,,A B P 三点共线，所以1x y +=，联立方程组41x y x y =⎧⎨+=⎩，解得41,55x y ==. 故选：C .【点睛】本题主要考查了向量的坐标运算，以及向量垂直的坐标运算和向量共线定理的应用，着重考查了运算与求解能力.20．已知1F 、2F 分别为双曲线22146x y -=的左、右焦点，M 为双曲线右支上一点且满足120MF MF ⋅=u u u u v u u u u v ，若直线2MF 与双曲线的另一个交点为N ，则1MF N ∆的面积为（）A ．12B ．C ．24D ．【答案】C【解析】【分析】设1MF m =，2MF n =，根据双曲线的定义和12MFMF ⊥，可求出6m =，2n =，再设2NF t =，则14NF t =+根据勾股定理求出6t =即可求出三角形的面积.【详解】解：设1MF m =，2MF n =， ∵1F 、2F 分别为双曲线22146x y -=的左、右焦点，∴24m n a -==，122F F c ==∵120MF MF ⋅=u u u u v u u u u v，∴12MF MF ⊥，∴222440m n c +==，∴()2222m n m n mn -=+-，即2401624mn =-=，∴12mn =，解得6m =，2n =，设2NF t =，则124NF a t t =+=+，在1Rt NMF ∆中可得()()222426t t +=++，解得6t =，∴628MN =+=，∴1MF N ∆的面积111862422S MN MF =⋅=⨯⨯=. 故选C ．【点睛】本题考查了双曲线的定义和向量的数量积和三角形的面积，考查了运算能力和转化能力，属于中档题．。

2021年高考数学三轮专项模拟试卷理（三角函数解三角形与平面向量）（含解析）新人教A版(1)

三角函数、解三角形与平面向量本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部份，共150分，考试时刻120分钟．第Ⅰ卷一、选择题(本大题共8小题，每题5分，共40分．在每题给出的四个选项中，只有一项为哪一项符合题目要求的)1．已知全集U ＝R ，集合P ＝{x |x 2≤1}，那么∁U P ＝( )A ．(－∞，－1)B ．(1，＋∞)C ．(－1,1)D ．(－∞，－1)∪(1，＋∞) 【解析】 ∵x 2≤1⇔－1≤x ≤1，∴∁U P ＝(－∞，－1)∪(1，＋∞)．【答案】 D2．(2021·江西高考)函数y ＝x ln(1－x )的概念域为( ) A ．(0,1)B ．[0,1)C ．(0,1]D ．[0,1]【解析】由⎩⎪⎨⎪⎧1－x ＞0x ≥0得，函数概念域为[0,1)．【答案】 B3．(2021·重庆高考)已知f (x )是概念在R 上的偶函数，且以2为周期，那么“f (x )为[0,1]上的增函数”是“f (x )为[3,4]上的减函数”的( )A ．既不充分也没必要要的条件B ．充分而没必要要的条件C ．必要而不充分的条件D ．充要条件【解析】 ①∵f (x )在R 上是偶函数，∴f (x )的图象关于y 轴对称．∵f (x )为[0,1]上的增函数，∴f (x )为[－1,0]上的减函数．又∵f (x )的周期为2，∴f (x )为区间[－1＋4,0＋4]＝[3,4]上的减函数．②∵f(x)为[3,4]上的减函数，且f(x)的周期为2，∴f(x)为[－1,0]上的减函数．又∵f (x )在R 上是偶函数，∴f (x )为[0,1]上的增函数．由①②知“f (x )为[0,1]上的增函数”是“f (x )为[3,4]上的减函数”的充要条件．【答案】 D4．已知f (x )＝sin 2⎝ ⎛⎭⎪⎫x ＋π4，假设a ＝f (lg 5)，b ＝f ⎝ ⎛⎭⎪⎫lg 15，那么( ) A ．a ＋b ＝0 B ．a －b ＝0C ．a ＋b ＝1D ．a －b ＝1 【解析】 f (x )＝12⎣⎢⎡⎦⎥⎤1－cos ⎝ ⎛⎭⎪⎫2x ＋π2＝1＋sin 2x 2， ∴a ＝12＋sin 2lg 52， b ＝12＋sin ⎝ ⎛⎭⎪⎫2lg 152＝12－sin 2lg 52.因此，a ＋b ＝1.【答案】 C5．(2021·重庆高考)命题“对任意x ∈R ，都有x 2≥0”的否定为( )A ．对任意x ∈R ，都有x 2<0B ．不存在x ∈R ，使得x 2<0C ．存在x 0∈R ，使得x 20≥0D ．存在x 0∈R ，使得x 20<0【解析】因为“∀x ∈M ，p (x )”的否定是“∃x ∈M ，綈p (x )”，故“对任意x ∈R ，都有x 2≥0”的否定是“存在x 0∈R ，使得x 20<0”．【答案】 D6．在△ABC 中，假设sin 2A ＋sin 2B ＜sin 2C ，那么△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定【解析】由正弦定理，得a 2＋b 2<c 2，∴cos C ＝a 2＋b 2－c 22ab <0，那么C 为钝角，故△ABC 为钝角三角形．【答案】 C7．(2021·福建高考)将函数f (x )＝sin(2x ＋θ)⎝ ⎛⎭⎪⎫－π2＜θ＜π2的图象向右平移φ(φ＞0)个单位长度后取得函数g (x )的图象，假设f (x )，g (x )的图象都通过点P ⎝ ⎛⎭⎪⎪⎫0，32，那么φ的值能够是( )【解析】 ∵P ⎝ ⎛⎭⎪⎪⎫0，32在f (x )的图象上，∴f (0)＝sin θ＝32.∵θ∈⎝ ⎛⎭⎪⎫－π2，π2，∴θ＝π3，∴f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3，∴g (x )＝sin ⎣⎢⎡⎦⎥⎤2x －φ＋π3.∵g (0)＝32，∴sin ⎝ ⎛⎭⎪⎫π3－2φ＝32.验证，φ＝56π时，sin ⎝ ⎛⎭⎪⎫π3－2φ＝sin ⎝ ⎛⎭⎪⎫π3－53π＝sin ⎝ ⎛⎭⎪⎫－43π＝32成立．【答案】 B8．(2021·课标全国卷Ⅱ)已知函数f (x )＝x 3＋ax 2＋bx ＋c ，以下结论中错误的选项是() A ．∃x 0∈R ，f (x 0)＝0B ．函数y ＝f (x )的图象是中心对称图形C ．假设x 0是f (x )的极小值点，那么f (x )在区间(－∞，x 0)上单调递减D ．假设x 0是f (x )的极值点，那么f ′(x 0)＝0【解析】假设c＝0，那么有f(0)＝0，因此A正确．由f(x)＝x3＋ax2＋bx＋c得f(x)－c ＝x3＋ax2＋bx，因为函数f(x)＝x3＋ax2＋bx的对称中心为(0,0)，因此f(x)＝x3＋ax2＋bx＋c 的对称中心为(0，c)，因此B正确．由三次函数的图象可知，假设x0是f(x)的极小值点，那么极大值点在x0的左侧，因此函数在区间(－∞，x0)单调递减是错误的，D正确．【答案】 C第Ⅱ卷二、填空题(本大题共7小题，每题5分，共35分，把答案填在题中横线上)9．(2021·安徽高考改编)设△ABC 的内角A ，B ，C 所对边的长别离为a ，b ，c .假设b ＋c ＝2a,3sin A ＝5sin B ，那么角C ＝________.【解析】由3sin A ＝5sin B ，得3a ＝5b .又因为b ＋c ＝2a ，因此a ＝53b ，c ＝73b ，因此cos C ＝a 2＋b 2－c 22ab ＝⎝ ⎛⎭⎪⎫53b 2＋b 2－⎝ ⎛⎭⎪⎫73b 22×53b ×b ＝－12.因为C ∈(0，π)，因此C ＝2π3. 【答案】 2π310．假设非零向量a ，b 知足|a |＝|b |，(2a ＋b )·b ＝0，那么a 与b 的夹角为________．【解析】 ∵(2a ＋b )·b ＝0，∴2a ·b ＋b 2＝0，∴a ·b ＝－12b 2，设a 与b 的夹角为θ，又|a |＝|b |，∴cos θ＝a ·b |a ||b |＝－12b 2|a ||b |＝－12， ∴θ＝120°.【答案】 120° 11．(2021·天津高考改编)设变量x ，y 知足约束条件⎩⎪⎨⎪⎧ 3x ＋y －6≥0，x －y －2≤0，y －3≤0，那么目标函数z＝y －2x 的最小值为________．【解析】可行域如图阴影部份(含边界)．令z ＝0，得直线l 0：y －2x ＝0，平移直线l 0知，当直线l 过A 点时，z 取得最小值．由⎩⎪⎨⎪⎧y ＝3，x －y －2＝0得A (5,3)． ∴z 最小＝3－2×5＝－7.【答案】－712．(2021·江西高考)设f (x )＝3sin 3x ＋cos 3x ，假设对任意实数x 都有|f (x )|≤a ，那么实数a 的取值范围是________．【解析】由于f (x )＝3sin 3x ＋cos 3x ＝2sin ⎝ ⎛⎭⎪⎫3x ＋π6，那么|f (x )|＝2⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫3x ＋π6≤2，要使|f (x )|≤a 恒成立，那么a ≥2. 【答案】 [2，＋∞)13．设e 1，e 2为单位向量，且e 1，e 2的夹角为π3，假设a ＝e 1＋3e 2，b ＝2e 1，那么向量a 在b 方向上的射影为________．【解析】由于a ＝e 1＋3e 2，b ＝2e 1，因此|b |＝2，a·b ＝(e 1＋3e 2)·2e 1＝2e 21＋6e 1·e 2＝2＋6×12＝5，因此a 在b 方向上的射影为|a |·cos<a ，b >＝a·b |b |＝52. 【答案】 52 14．(2021·北京高考)已知点A (1，－1)，B (3,0)，C (2,1)．假设平面区域D 由所有知足AP→＝λAB →＋μAC →(1≤λ≤2,0≤μ≤1)的点P 组成，那么D 的面积为________．【解析】设P (x ，y )，且AB →＝(2,1)，AC →＝(1,2)．∴OP →＝OA →＋AP →＝(1，－1)＋λ(2,1)＋μ(1,2)，∴⎩⎪⎨⎪⎧ x ＝1＋2λ＋μ，y ＝－1＋λ＋2μ，∴⎩⎪⎨⎪⎧3μ＝2y －x ＋3，3λ＝2x －y －3，又1≤λ≤2,0≤μ≤1， ∴⎩⎪⎨⎪⎧ 0≤x －2y ≤3，6≤2x －y ≤9表示的可行域是平行四边形及内部．如图，点B (3,0)到直线x －2y ＝0的距离d ＝355.又|BN |＝ 5.∴区域D 的面积S ＝355×5＝3.【答案】 3 15．在△ABC 中，∠C ＝90°，M 是BC 的中点．假设sin ∠BAM ＝13，那么sin ∠BAC ＝________.【解析】因为sin ∠BAM ＝13，因此cos ∠BAM ＝223.在△ABM 中，利用正弦定理，得BM sin ∠BAM ＝AM sin B ，因此BM AM＝sin ∠BAMsin B＝13sin B ＝13cos ∠BAC.在Rt △ACM 中，有CM AM＝sin ∠CAM ＝sin(∠BAC －∠BAM )．由题意知BM ＝CM ，因此13cos ∠BAC＝sin(∠BAC －∠BAM )．化简，得22sin ∠BAC cos ∠BAC －cos 2∠BAC ＝1.因此22tan ∠BAC －1tan 2∠BAC ＋1＝1，解得tan ∠BAC ＝2.再结合sin 2∠BAC ＋cos 2∠BAC ＝1，∠BAC为锐角可解得sin ∠BAC ＝63.【答案】63三、解答题(本大题共6小题，共75分，解许诺写出文字说明、证明进程或演算步骤) 16．(本小题总分值12分)函数f (x )＝A sin(ωx －π6)＋1(A >0，ω>0)的最大值为3，其图象相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式；(2)设α∈(0，π2)，f (α2)＝2，求α的值．【解】 (1)∵函数f (x )的最大值为3， ∴A ＋1＝3，即A ＝2.∵函数图象的相邻两条对称轴之间的距离为π2，∴最小正周期T ＝π，∴ω＝2，∴函数f (x )的解析式为y ＝2sin(2x －π6)＋1.(2)∵f (α2)＝2sin(α－π6)＋1＝2，∴sin(α－π6)＝12.∵0<α<π2，∴－π6<α－π6<π3，∴α－π6＝π6，∴α＝π3.17．(本小题总分值12分)(2021·北京高考)在△ABC 中，a ＝3，b ＝26，∠B ＝2∠A ，(1)求cos A 的值； (2)求c 的值．【解】 (1)因为a ＝3，b ＝26，∠B ＝2∠A ，因此在△ABC 中，由正弦定理得3sin A ＝26sin 2A .因此2sin A cos A sin A ＝263.故cos A ＝63.(2)由(1)知cos A ＝63，因此sin A ＝1－cos 2A ＝33. 又因为∠B ＝2∠A ，因此cos B ＝2cos 2A －1＝13. 因此sin B ＝1－cos 2B ＝223.在△ABC 中，sin C ＝sin(A ＋B )＝sin A cos B ＋ cos A sin B ＝539.因此c ＝a sin Csin A＝5.18．(本小题总分值12分)(2021·广东高考)已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫x －π12，x ∈R .(1)求f ⎝ ⎛⎭⎪⎫－π6的值；(2)假设cos θ＝35，θ∈⎝ ⎛⎭⎪⎫3π2，2π，求f ⎝ ⎛⎭⎪⎫2θ＋π3.【解】 (1)因为f (x )＝2cos ⎝ ⎛⎭⎪⎫x －π12，因此f ⎝ ⎛⎭⎪⎫－π6＝2cos ⎝ ⎛⎭⎪⎫－π6－π12＝2cos ⎝ ⎛⎭⎪⎫－π4＝2cos π4＝2×22＝1.(2)因为θ∈⎝ ⎛⎭⎪⎫3π2，2π，cos θ＝35，因此sin θ＝－1－cos 2θ＝－1－⎝ ⎛⎭⎪⎫352＝－45，cos 2θ＝2cos 2θ－1＝2×⎝ ⎛⎭⎪⎫352－1＝－725，sin 2θ＝2sin θcos θ＝2×35×⎝ ⎛⎭⎪⎫－45＝－2425.因此f ⎝ ⎛⎭⎪⎫2θ＋π3＝2cos ⎝⎛⎭⎪⎫2θ＋π3－π12＝2cos ⎝ ⎛⎭⎪⎫2θ＋π4＝2×⎝ ⎛⎭⎪⎪⎫22cos 2θ－22sin 2θ＝cos 2θ－sin 2θ＝－725－⎝ ⎛⎭⎪⎫－2425＝1725.19．(本小题总分值13分)已知向量a ＝(cos 3x 2，sin 3x 2)，b ＝(－sin x 2，－cos x2)，其中x ∈[π2，π]．(1)若|a ＋b |＝3，求x 的值；(2)函数f (x )＝a ·b ＋|a ＋b |2，若c >f (x )恒成立，求实数c 的取值范围．【解】 (1)∵a ＋b ＝(cos 3x 2－sin x 2，sin 3x 2－cos x2)，∴|a ＋b |＝cos 3x 2－sinx22＋sin 3x 2－cosx22＝2－2sin 2x ，由|a ＋b |＝3，得2－2sin 2x ＝3，即sin 2x ＝－12.∵x ∈[π2，π]，∴π≤2x ≤2π.因此2x ＝π＋π6或2x ＝2π－π6，即x ＝7π12或x ＝11π12.(2)∵a·b ＝－cos 3x 2sin x 2－sin 3x 2cos x2＝－sin 2x ，∴f (x )＝a·b ＋|c ＋b |2＝2－3sin 2x ， ∵π≤2x ≤2π，∴－1≤sin 2x ≤0， ∴2≤f (x )＝2－3sin 2x ≤5，∴[f (x )]max ＝5. 又c >f (x )恒成立，因此c >[f (x )]max ，那么c >5.∴实数c的取值范围为(5，＋∞)．20．(本小题总分值13分)(2021·湖北高考)在△ABC中，角A，B，C对应的边别离是a，b，c，已知cos 2A－3cos(B＋C)＝1.(1)求角A的大小；(2)假设△ABC的面积S＝53，b＝5，求sin B sin C的值．【解】 (1)由cos 2A －3cos(B ＋C )＝1，得2cos 2A ＋3cos A －2＝0，即(2cos A －1)(cos A ＋2)＝0. 解得cos A ＝12或cos A ＝－2(舍去)．因为0<A <π，因此A ＝π3.(2)由S ＝12bc sin A ＝12bc ·32＝34bc ＝53，得bc ＝20.又b ＝5，因此c ＝4.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝25＋16－20＝21，故a ＝21.又由正弦定理，得sin B sin C ＝b asin A ·c asin A ＝bc a 2·sin 2A ＝2021×34＝57. 21．(本小题总分值13分)已知函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．假设曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2.(1)求a ，b ，c ，d 的值；(2)假设x ≥－2时，f (x )≤kg (x )，求k 的取值范围．【解】 (1)∵曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)， ∴b ＝d ＝2.∵f ′(x )＝2x ＋a ，故f ′(0)＝a ＝4. ∵g ′(x )＝e x (cx ＋d ＋c )， ∴g ′(0)＝2＋c ＝4，故c ＝2. 从而a ＝4，b ＝2，c ＝2，d ＝2. (2)令F (x )＝kg (x )－f (x )，则F ′(x )＝(k e x －1)(2x ＋4)，由题设可得F (0)≥0，故k ≥1，令F ′(x )＝0得x 1＝－ln k ，x 2＝－2， ①假设1≤k ＜e 2，那么－2＜x 1≤0，从而当x ∈[－2，x 1)时，F ′(x )＜0，当x ∈(x 1＋∞)时，F ′(x )＞0，即F(x)在[－2，＋∞)上最小值为F(x1)＝2x1＋2－x21－4x1－2＝－x1(x1＋2)≥0，现在f(x)≤kg(x)恒成立；②若k＝e2，F′(x)＝(e x＋2－1)(2x＋4)，故F(x)在[－2，＋∞)上单调递增，因为F(－2)＝0，因此f(x)≤kg(x)恒成立；③若k＞e2，那么F(－2)＝－2k e－2＋2＝－2e－2(k－e2)＜0，从而当x∈[－2，＋∞)时，f(x)≤kg(x)不可能恒成立．综上所述k的取值范围为[1，e2]．。

高三数学(理科)押题精练：专题【5】《三角函数、解三角形、平面向量》课件

2.(2014·大纲全国)设a＝sin 33°，b＝cos 55°，
c＝tan 35°，则( )
C
A.a>b>c
B.b>c>a
C.c>b>a
D.c>a>b
解析 ∵a＝sin 33°，b＝cos 55°＝sin 35°，
c＝tan 35°＝ sin 35°， cos 35°
又0<cos 35°<1，∴c>b>a.
x2＋y2>0，那么 sin α＝yr，cos α＝xr，tan α＝xy(x≠0)，三角函数值只与角的大小有关，而与终边上点 P 的位置无关.
3
[问题1] 已知角α的终边经过点P(3，－4)，则sin α
＋cos α的值为___－__15___.
2.同角三角函数的基本关系式及诱导公式 (1)平方关系：sin2α＋cos2α＝1.
6.向量的平行与垂直设a＝(x1，y1)，b＝(x2，y2)，且b≠0，则a∥b⇔b＝ λa⇔x1y2－x2y1＝0. a⊥b (a≠0)⇔a·b＝0⇔x1x2＋y1y2＝0. 0看成与任意向量平行，特别在书写时要注意，否则有质的不同.
[问题6] 下列四个命题：①若|a|＝0，则a＝0； ②若|a|＝|b|，则a＝b或a＝－b；③若a∥b，则 |a|＝|b|；④若a＝0，则－a＝0.其中正确命题是
＋
sin
21π
的值为
3.三角函数的图象与性质 (1)五点法作图； (2)对称轴：y＝sin x，x＝kπ＋π2，k∈Z；y＝cos x，x ＝kπ，k∈Z；对称中心：y＝sin x，(kπ，0)，k∈Z；y＝cos x， kπ＋π2，0，k∈Z；y＝tan x，k2π，0，k∈Z.

高考数学压轴专题人教版备战高考《平面向量》真题汇编及答案解析

数学《平面向量》试卷含答案一、选择题 1．已知向量(sin ,cos )a αα=r ，(1,2)b =r ，则以下说法不正确的是（）A ．若//a b r r ，则1tan 2α=B ．若a b ⊥r r ，则1tan 2α=C ．若()f a b α=⋅r r 取得最大值，则1tan 2α=D ．||a b -r r 1 【答案】B【解析】【分析】根据向量平行、垂直、模以及向量的数量积的坐标运算即可判断.【详解】A 选项，若//a b r r ，则2sin cos αα=，即1tan 2α=，A 正确.B 选项，若a b ⊥r r ，则sin 2cos 0αα+=，则tan 2α=-，B 不正确.C 选项，若()f a b α=⋅r r 取得最大值时，则())f ααϕ=+，取得最大值时，()sin 1αϕ+=，2,2k k Z παϕπ+=+∈，又tan 2ϕ=，则1tan 2α=，则C 正确.D 选项，||a b -==r r 的最大值为1=，选项D 正确.故选：B .【点睛】本题主要考查向量的坐标运算，以及模的求法，掌握向量平行、垂直、数量积的坐标运算是解题的关键，是基础题.2．若向量a b r r ，的夹角为3π，|2|||a b a b -=+r r r r ，若()a ta b ⊥+r r r ，则实数t =（）A ．12-B ．12CD ．【答案】A【解析】【分析】由|2|||a b a b -=+r r r r 两边平方得22b a b =⋅r r r ，结合条件可得b a =r r ，又由()a ta b ⊥+r r r ，可得20t a a b ⋅+⋅=r r r ，即可得出答案.【详解】由|2|||a b a b -=+r r r r 两边平方得2222442a a b b a a b b -⋅+=+⋅+r r r r r r r r . 即22b a b =⋅r r r ，也即22cos 3b a b π=r r r ，所以b a =r r . 又由()a ta b ⊥+r r r ，得()0a ta b ⋅+=r r r ，即20t a a b ⋅+⋅=r r r . 所以2221122b a b t a b⋅=-=-=-r r r r r 故选：A【点睛】本题考查数量积的运算性质和根据向量垂直求参数的值，属于中档题.3．已知O 是平面上一定点，满足()||cos ||cos AB AC OP OA AB B AC Cλ=++u u u r u u u r u u u r u u u r u u u r u u u r ，[0λ∈，)+∞，则P 的轨迹一定通过ABC ∆的（）A ．外心B ．垂心C ．重心D ．内心【答案】B【解析】【分析】可先根据数量积为零得出BC uuu r 与()||cos ||cos AB AC AB B AC C λ+u u u ru u u r u u ur u u u r 垂直，可得点P 在BC 的高线上，从而得到结论．【详解】 Q ()||cos ||cos AB AC OP OA AB B AC Cλ=++u u u r u u u r u u u r u u u r u u u r u u u r ， ∴()||cos ||cos AB AC OP OA AB B AC Cλ-=+u u u r u u u r u u u r u u u r u u u r u u u r ，即()||cos ||cos AB AC AP AB B AC C λ=+u u u r u u u r u u u r u u u r u u u r ， Q cos BA BC B BA BC ⋅=u u u r u u u r u u u r u u u r ，cos CA CB C CA CB⋅=u u u r u u u r u u u r u u u r ， ∴()0||cos ||cos AB AC BC BC BC AB B AC C⋅+=-+=u u u r u u u r u u u r u u u r u u u r u u u r u u u r ， ∴BC uuu r 与()||cos ||cos AB AC AB B AC Cλ+u u u r u u u r u u u r u u u r 垂直，即AP BC ⊥uu u r uu u r， ∴点P 在BC 的高线上，即P 的轨迹过ABC ∆的垂心.故选：B ．【点睛】本题重点考查平面向量在几何图形中的应用，熟练掌握平面向量的加减运算法则及其几何意义是解题的关键，考查逻辑思维能力和转化能力，属于常考题.4．已知菱形ABCD 的边长为2，60ABC ∠=︒，则BD CD ⋅=u u u v u u u v（） A ．4B ．6C ．23D ．43 【答案】B【解析】【分析】根据菱形中的边角关系，利用余弦定理和数量积公式，即可求出结果．【详解】如图所示，菱形形ABCD 的边长为2，60ABC ∠=︒，∴120C ∠=︒，∴22222222cos12012BD =+-⨯⨯⨯︒=， ∴23BD =30BDC ∠=︒，∴|||3 302|326BD CD BD CD cos =⨯⨯︒==⋅u u u r u u u r u u u r u u u r ，故选B ．【点睛】本题主要考查了平面向量的数量积和余弦定理的应用问题，属于基础题.．5．已知,a r b r 是平面向量，满足||4a =r ，||1b ≤r 且|3|2b a -≤r r ，则cos ,a b 〈〉r r 的最小值是（）A ．1116B ．78C ．158D ．31516【答案】B【解析】【分析】设OA a =u u u r r ，3OB b =u u u r r ，利用几何意义知B 既在以O 为圆心，半径为3的圆上及圆的内部，又在以A 为圆心，半径为2的圆上及圆的内部，结合图象即可得到答案.【详解】设OA a =u u u r r ，3OB b =u u u r r，由题意，知B 在以O 为圆心，半径为3的圆上及圆的内部，由|3|2b a -≤r r ，知B 在以A 为圆心，半径为2的圆上及圆的内部，如图所示则B 只能在阴影部分区域，要cos ,a b 〈〉r r 最小，则,a b <>r r 应最大，此时()222222min 4327cos ,cos 22438OA OB AB a b BOA OA OB +-+-〈〉=∠===⋅⨯⨯r r .故选：B.【点睛】本题考查向量夹角的最值问题，本题采用数形结合的办法处理，更直观，是一道中档题.6．在平面直角坐标系中，()1,2A -，(),1B a -，(),0C b -，,a b ∈R ．当,,A B C 三点共线时，AB BC ⋅u u u r u u u r 的最小值是（）A ．0B ．1C 2D ．2【答案】B【解析】【分析】根据向量共线的坐标表示可求得12b a =-，根据数量积的坐标运算可知所求数量积为()211a -+，由二次函数性质可得结果.【详解】由题意得：()1,1AB a =-u u u r ，(),1BC b a =--u u u r ，,,A B C Q 三点共线，()()111a b a ∴⨯-=⨯--，即12b a =-，()1,1BC a ∴=-u u u r ，()2111AB BC a ∴⋅=-+≥u u u r u u u r ，即AB BC ⋅u u u r u u u r 的最小值为1.故选：B .【点睛】本题考查平面向量的坐标运算，涉及到向量共线的坐标表示和数量积的坐标运算形式，属于基础题.7．如图,在梯形ABCD 中, 2DC AB =u u u r u u u r , P 为线段CD 上一点,且12DP PC =，E 为BC 的中点, 若EP AB AD λμ=+u u u r u u u r u u u r （λ， R μ∈）,则λμ+的值为（）A ．13B ．13- C ．0 D ．12 【答案】B【解析】【分析】直接利用向量的线性运算，化简求得1526EP AD AB =-u u u v u u u v u u u v ，求得,λμ的值，即可得到答案. 【详解】由题意，根据向量的运算法则，可得：()1214111232326EP EC CP BC CD AC AB AB AC AB u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v =+=+=--=- ()1111522626AD AB AB AD AB =+-=-u u u v u u u v u u u v u u u v u u u v 又因为EP AB AD λμ=+u u u v u u u v u u u v ，所以51,62λμ=-=，所以511623λμ+=-+=-，故选B. 【点睛】本题主要考查了向量的线性运算及其应用，其中解答中熟记向量的线性运算法则，合理应用向量的三角形法则化简向量EP u u u v是解答的关键，着重考查了运算与求解能力，属于基础题.8．在△ABC 中，D 是BC 中点，E 是AD 中点，CE 的延长线交AB 于点,F 则（）A ．1162DF AB AC =--u u u r u u u r u u u r B ．1134DF AB AC =--u u u r u u u r u u u r C ．3142DF AB AC =-+u u u r u u u r u u u r D ．1126DF AB AC =--u u u r u u u r u u u r 【答案】A【解析】【分析】设AB AF λ=u u u r u u u r ，由平行四边形法则得出144AE AF AC λ=+u u ur u u u r u u u r ，再根据平面向量共线定理得出得出=3λ，由DF AF AD =-u u u r u u u r u u u r ，即可得出答案.【详解】设AB AF λ=u u u r u u u r ，111124444AE AB A A C A AC D F λ==+=+u u u r u u u u u u r u u u r r u u u r u u u r 因为C E F 、、三点共线，则1=144λ+，=3λ 所以1111132262DF AF AD AB AB AC AB AC =-=--=--u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r 故选：A【点睛】本题主要考查了用基底表示向量，属于中档题.9．在ABC ∆中，已知3AB =23AC =D 为BC 的三等分点(靠近C)，则AD BC ⋅u u u v u u u v 的取值范围为（） A ．()3,5B ．(5,53C ．()5,9D ．()5,7【答案】C【解析】【分析】利用向量加法法则把所求数量积转化为向量AB AC u u u r u u u r，的数量积，再利用余弦函数求最值，得解．【详解】如图，()()()13AD BC AC CD AC AB AC CB AC AB ⎛⎫⋅=+⋅-=+⋅- ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r()()11213333AC AB AC AC AB AC AB AC AB u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ⎛⎫⎛⎫=+-⋅-=+⋅- ⎪ ⎪⎝⎭⎝⎭22211333AC AB AB AC =--⋅u u u r u u u r u u u r u u u r＝8﹣113233cos BAC -⨯⨯∠＝7﹣2cos ∠BAC∵∠BAC ∈（0，π），∴cos ∠BAC ∈（﹣1，1），∴7﹣2cos ∠BAC ∈（5，9），故选C ．【点睛】此题考查了数量积，向量加减法法则，三角函数最值等，难度不大．10．已知ABC V 中，2,3,60,2,AB BC ABC BD DC AE EC ==∠=︒==，则AD BE ⋅=u u u r u u u r（）A ．1B ．2-C ．12D ．12- 【答案】C【解析】【分析】以,BA BC u u u r u u u r 为基底，将,AD BE u u u r u u u r 用基底表示，根据向量数量积的运算律，即可求解.【详解】222,,33BD DC BD BC AD BD BA BC BA ===-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r , 11,22AE EC BE BC BA =∴=+u u u r u u u r u u u r , 211()()322AD BE BC BA BC BA ⋅=-⋅+u u u r u u u r u u u r u u u r u u u r u u u r22111362BC BC BA BA =-⋅-u u u r u u u r u u u r u u u r 111123622=-⨯⨯⨯=. 故选:C.【点睛】本题考查向量的线性运算以及向量的基本定理，考查向量数量积运算，属于中档题.11．设x ，y 满足102024x x y x y -≥⎧⎪-≤⎨⎪+≤⎩，向量()2,1a x =r ，()1,b m y =-r ，则满足a b ⊥r r 的实数m的最小值为（）A ．125B ．125-C ．32D ．32- 【答案】B【解析】【分析】先根据平面向量垂直的坐标表示，得2m y x =-，根据约束条件画出可行域，再利用m 的几何意义求最值，只需求出直线2m y x =-过可行域内的点C 时，从而得到m 的最小值即可．【详解】解：不等式组表示的平面区域如图所示：因为()2,1a x =r ，()1,b m y =-r ，由a b ⊥r r 得20x m y +-=，∴当直线经过点C 时，m 有最小值，由242x y x y +=⎧⎨=⎩，得8545x y ⎧=⎪⎪⎨⎪=⎪⎩，∴84,55C ⎛⎫ ⎪⎝⎭， ∴416122555m y x =-=-=-，故选：B. 【点睛】本题主要考查了平面向量共线（平行）的坐标表示，用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属于中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．12．平面向量a →与b →的夹角为π3，()2,0a →=，1b →=，则2a b →→-=（）A ．BC ．0D ．2【答案】D【解析】【分析】根据向量的模的计算和向量的数量积的运算即可求出答案.【详解】()2,0a →=Q ，||2a →∴=22222(2)||4||444421cos 43a b a b a b a b π→→→→∴-=-=+-⋅=+-⨯⨯⨯=r r r r ， |2|2a b ∴-=r r ，故选：D【点睛】本题考查了向量的模的计算和向量的数量积的运算，属于中档题.13．已知ABC V 为直角三角形，,6,82C BC AC π===，点P 为ABC V 所在平面内一点，则()PC PA PB ⋅+u u u r u u u r u u u r 的最小值为（）A ．252-B ．8-C ．172-D ．1758- 【答案】A【解析】【分析】根据,2C π=以C 点建系, 设(,)P x y ,则22325()=2(2)222PC PA PB x y ⎛⎫⋅+-+-- ⎪⎝⎭u u u r u u u r u u u r ,即当3=2=2x y ，时,取得最小值. 【详解】如图建系，(0,0), (8,0), (0,6)C A B ,设(,)P x y ，(8,)PA x y =--u u u r ，(,6)PB x y =--u u u r ，则22()(,)(82,62)2826PC PA PB x y x y x x y y ⋅+=--⋅--=-+-u u u r u u u r u u u r22325252(2)2222x y ⎛⎫=-+--≥- ⎪⎝⎭. 故选:A.【点睛】本题考查平面向量数量积的坐标表示及其应用,根据所求关系式运用几何意义是解题的关键,属于中档题.14．已知数列{a n }的前n 项和为S n ，且a n +1=a n +a (n ∈N *，a 为常数)，若平面内的三个不共线的非零向量OAOB OC u u u r u u u r u u u r ，，满足10051006OC a OA a OB =+u u u r u u u r u u u r ，A ，B ，C 三点共线且该直线不过O 点，则S 2010等于（）A ．1005B ．1006C ．2010D ．2012【答案】A【解析】【分析】根据a n +1=a n +a ，可判断数列{a n }为等差数列，而根据10051006OC a OA a OB =+u u u r u u u r u u u r ，及三点A ，B ，C 共线即可得出a 1+a 2010=1，从而根据等差数列的前n 项和公式即可求出S 2010的值.【详解】由a n +1=a n +a ，得，a n +1﹣a n =a ；∴{a n }为等差数列；由10051006OC a OA a OB =+u u u r u u u r u u u r ，所以A ，B ，C 三点共线；∴a 1005+a 1006=a 1+a 2010=1，∴S 2010()12010201020101100522a a +⨯===. 故选：A.【点睛】本题主要考查等差数列的定义，其前n 项和公式以及共线向量定理，还考查运算求解的能力，属于中档题.15．已知向量m =r (1,cosθ)，(sin ,2)n θ=-r ，且m r ⊥n r ，则sin 2θ+6cos 2θ的值为（）A ．12B ．2C ．22D ．﹣2【答案】B【解析】【分析】根据m r ⊥n r 可得tanθ，而sin 2θ+6cos 2θ22226sin cos cos sin cos θθθθθ+=+，分子分母同除以cos 2θ，代入tanθ可得答案.【详解】因为向量m =r (1，cosθ)，n =r (sinθ，﹣2)，所以sin 2cos m n θθ⋅=-u r r 因为m r ⊥n r ，所以sin 2cos 0θθ-=，即tanθ=2，所以sin 2θ+6cos 2θ22222626226141sin cos cos tan sin cos tan θθθθθθθ++⨯+====+++ 2. 故选：B.【点睛】本题主要考查平面向量的数量积与三角恒等变换，还考查运算求解的能力，属于中档题.16．如图，圆O 是等边三角形ABC 的外接圆，点D 为劣弧AC 的中点，则OD =u u u r（）A ．2133BA AC +u u u r u u u r B ．2133BA AC -u u u r u u u r C ．1233BA AC +u u u r u u u r D ．4233BA AC +u u u r u u u r 【答案】A【解析】【分析】连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，列出相应式子得出结论.【详解】解：连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，则()()221121332333OD BO BE BA BC BA BA AC BA AC ===⨯+=++=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r . 故选：A.【点睛】本题考查向量的表示方法，结合几何特点，考查分析能力，属于中档题.17．已知平面向量,,a b c r r r 满足||||2a b ==r r ，a b ⊥r r ，()()a c b c -⊥-r r r r ，则(a b c ⋅r r r +)的取值范围是( )A ．[0,2]B ．[0,2]C ．[0,4]D ．[0,8] 【答案】D【解析】【分析】以点O 为原点，OA u u u r ，OB uuu r 分别为x 轴，y 轴的正方向建立直角坐标系，根据AC BC ⊥，得到点C 在圆22(1)(1)2x y -+-=，再结合直线与圆的位置关系，即可求解．【详解】设,,OA a OB b OC c ===u u u r r u u u r r u u u r r ，以点O 为原点，OA u u u r ，OB uuu r 分别为x 轴，y 轴的正方向建立直角坐标系，则(2,0),(0,2)A B ，依题意，得AC BC ⊥，所以点C 在以AB 为直径的圆上运动，设点(,)C x y ，则22(1)(1)2x y -+-=，()22a b c x y +⋅=+r r r ，由圆心到直线22x y t +=的距离2222222t d +-=≤+，可得[0,8]t ∈.故选：D ．【点睛】本题主要考查了向量的数量积的坐标运算，以及直线与圆的位置关系的综合应用，着重考查了转化思想，以及推理与运算能力．18．已知A ，B 是圆224+=O: x y 上的两个动点，||2AB =u u u r ，1233OC OA OB =+u u u r u u u r u u u r ，若M 是线段AB 的中点，则OC OM ⋅u u u r u u u u r 的值为（）. A 3B ．3C ．2 D ．3【答案】D【解析】【分析】判断出OAB ∆是等边三角形，以,OA OB u u u r u u u r 为基底表示出OM u u u u r ，由此求得OC OM ⋅u u u r u u u u r 的值.【详解】圆O 圆心为()0,0，半径为2，而||2AB =u u u r ，所以OAB ∆是等边三角形.由于M 是线段AB 的中点，所以1122OM OA OB =+u uu u r u u u r u u u r .所以OC OM ⋅u u u r u u u u r 12331122OA O O O B A B ⎛⎫=+⋅⎛⎫+ ⎪⎝ ⎪⎭⎝⎭u u u u u u r u u u r r u u u r 22111623OA OA OB OB =+⋅⋅+u u u r u u u r u u u r u u u r 21422cos603323=+⨯⨯⨯+=o . 故选：D【点睛】本小题主要考查用基底表示向量，考查向量的数量积运算，考查数形结合的数学思想方法，属于中档题.19．向量1,tan 3a α⎛⎫= ⎪⎝⎭r ，()cos ,1b α=r ，且//a b r r ，则cos 2πα⎛⎫+= ⎪⎝⎭（） A ．13 B ．22 C ．2D ．13- 【答案】D【解析】【分析】根据向量平行的坐标运算以及诱导公式，即可得出答案.【详解】//a b ∴r r1cos tan sin 3ααα∴=⋅= 1cos sin 23παα⎛⎫∴+=-=- ⎪⎝⎭故选：D【点睛】本题主要考查了由向量平行求参数以及诱导公式的应用，属于中档题.20．已知向量(),1a x =-r ， (b =r ，若a b ⊥r r ，则a =r （）AB C ．2 D ．4 【答案】C【解析】由a b r r ⊥，(),1a x =-r ， (b r =，可得：x 0x ，==，即)1a =-r所以2a ==r 故选C。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题三：三角函数、平面向量（老人教理科）一、选择题π3π1 、已知 α ∈ ( 2 ， π) ， sinα ＝ 5 ，则 tan(α ＋ 4 ) 等于().17.7.－17.－72、函数 f(x)＝2sin(2x＋π6 )在[－π2 ，π2 ]上对称轴的条数为().1.2.3.03、若 a (cos,sin), b (cos ,sin ) ，则（）aba∥b(a b) (a b)(a b) ∥ (a b)4、设非零向量 a 、 b, c 满足 a b c ， a b c ，则 sin〈 a,b 〉＝( )1-13.2.1.222cos10 sin 205、 sin 70的值是（）3122322sin Acos B 1 6 、在△ ABC 中，若 sin C 2 ，则△ ABC 的形状一定是（）等腰三角形直角三角形等腰直角三角形等边三角形2 7、函数 f(x)＝sin2x＋2cosx 在区间[－3π，θ]上的最大值为 1，则 θ 的值是( ).0.π3.π2.－π28、已知函数 f(x)＝Acos(ωx＋φ)的图象如图所示，f(π2 )＝－23，则 f(0)＝().－23.－12.23.129、已知向量 a＝(cosθ，sinθ)，向量 b＝( 3，－1)，则|2a－b|的最大值、最小值分别是( ).4 2，0.4,2 2.16,0.4,010、某人在 C 点测得某塔在南偏西 80°，塔顶仰角为 45°，此人沿南偏东 40°方向前进 10 米到 D，测得塔顶的仰角为 30°，则塔高为 ( ).15 米.5 米.10 米D.12 米二、填空题11、在△ABC 中，若 sin2A＋sin2B－sinAsinB＝sin2C，且满足 ab＝4，则该三角形的面积为_______________12 、设△ABC 的内角 A，B，C 所对的边长分别为 a，b，c 且 acosB－bcosA＝35c，则ttaannAB的值为.7π13.已知函数 f(x)＝2sin(ωx＋φ)的图象如下图所示，则 f( 12 )＝.14、已知向量 a ＝(2，－1)，b ＝(x，－2)，c ＝(3，y)，若 a ∥ b ，( a ＋ b )⊥( b － c )，M(x，y)，N(y，x)，则向量 MN 的模为.三、解答题15、已知 3cos 2 +2sin2 = 1 ，求（1）tan 的值；(2)3cos2 +4sin2 的值.16、已知函数 f(x)＝3sin(12x－π4 )，x∈R. (1)画出函数 f(x)在长度为一个周期的闭区间上的简图； (2)将函数 y＝sinx 的图象作怎样的变换可得到 f(x)的图象？17、已知 AC ＝(cosx2＋sinx2，－sinx2)， BC ＝(cosx2－sinx2，2cosx2).(1)设 f(x)＝ AC · BC ，求 f(x)的最小正周期和单调递减区间；(2)设有不相等的两个实数 x1，x2∈－π2 ，π2 ，且 f(x1)＝f(x2)＝1，求 x1＋x2 的值.18、已知函数 f(x)＝sin2ωx＋ 3sinωxsin(ωx＋π2 )＋2cos2ωx，x∈R(ω>0)，在 y 轴右 π侧的第一个最高点的横坐标为 6 .(1)求 ω；(2)若将函数 f(x)的图象向右平移π6 个单位后，再将得到的图象上各点横坐标伸长到原来的 4 倍，纵坐标不变，得到函数 y＝g(x)的图象，求函数 g(x)的最大值及单调递减区间.19、在△ABC 中，设内角 A，B，C 的对边分别为 a,b,c, 向量 m ＝(cosA，sinA)，向量 n ＝( 2 －sinA，cosA)，若| m n |＝2. (1)求角 A 的大小； (2)若 b＝4 2，且 c＝ 2a，求△ABC 的面积. 20、已知向量 m ＝( 3sinx4，1)， n ＝(cosx4，cos2x4). (1)若 m n ＝1，求 cos(2π 3 －x)的值；(2)记 f(x)＝ m n ，在△ABC 中，角 A，B，C 的对边分别是 a，b，c，且满足(2a－c)cosB＝ bcosC，求函数 f(A)的取值范围.三角函数、平面向量（老人教理）答案解析π33π 1＋tanα 11 解析：选 ,由 α∈( 2 ，π)，sinα＝5，得 tanα＝－4，tan(α＋ 4 )＝1－tanα＝7.ππ5ππ7π2 解析：选，∵当－ 2 ≤x≤ 2 ，－ 6 ≤2x＋ 6 ≤6π，∴函数的对称轴为：2x＋ 6 ＝πππ－ 2 ，或 2x＋ 6 ＝ 2 ，ππ∴x＝－ 3 ，或 x＝ 6 .3解析：选C,(a b) • (a b) =(cos +cos )( cos -cos )+(sin +sin )( sin -sin )=cos 2 +sin 2 -cos 2 -sin2 =0，选项 C 正确.224 解析：选,∵ a b c ，∴ c ab2＝a2 2ab b.又abc2，∴ 2ab=-b.21即 2| a || b |cos〈 a ， b 〉＝－ b .∴cos〈 a,b 〉＝ - 23 sin a,b = 2 .5解析：选,原式2co（s 30 -20 ） sin 20 2cos30 cos20 2sin30 sin 20 sin 20 3 cos 20=sin 70=sin 70= sin 70 = 36 解析：选 ,由原式得 2sinAcosB=sin(A+B)+sin(A-B)=sinC，因为 0 A B π, 0 C π,sin(A-B)=0,A=B.故选 . 7 解析：选 ,因为 f(x)＝sin2x＋2cosx＝－cos2x＋2cosx＋1＝－(cosx－1)2＋2，又其在区间[－23π，θ]上的最大值为 1，结合选项可知 θ 只能取－π2 ,故选 .8 解析：选 C,由题意可知，此函数的周期 T＝2(1121π－172π)＝23π，故2ωπ＝23π，∴ω＝3，f(x)＝Acos(3x＋φ).π3π27π7πf( 2 ) ＝ Acos( 2 ＋ φ) ＝ Asinφ ＝－ 3 . 又由题图可知 f( 12 ) ＝ Acos(3× 12 ＋ φ) ＝Acos(φ－14π)22＝ 2 (Acosφ＋Asinφ)＝0，∴f(0)＝Acosφ＝3.9 解析：选 ,由于|2a－b| 2 ＝4|a| 2 ＋|b| 2 －4a·b＝8－4( 3cosθ－sinθ)＝8－8cos(θ＋π6 )，易知 0≤8－8cos(θ＋π6 )≤16，故|2a－b|的最大值为 4，最小值为 0.10 解析：选 C,如图，设塔高为 h，在 Rt△AOC 中，∠ACO＝45°，则 OC＝OA ＝h.在 Rt△AOD 中，∠ADO＝30°，则 OD＝ 3h，在△OCD 中，∠OCD＝120°，CD＝10，由余弦定理得： OD2 ＝ OC2 ＋ CD2 － 2OC·CDcos ∠ OCD ，即 ( 3 h)2 ＝ h2 ＋ 102 － 2h×10×cos120°，∴h2－5h－50＝0，解得 h＝10，或 h＝－5(舍).a2＋b2－c2 11 解析：∵sin2A＋sin2B－sinAsinB＝sin2C， ∴a2＋b2－ab＝c2，∴cosC＝ 2ab ＝1 2，113∴C＝60°.∴S△ABC＝2absinC＝2×4× 2 ＝ 3.答案： 33312 解析：由 acosB－bcosA＝5c 及正弦定理可得 sinAcosB－sinBcosA＝5sinC，即 sinAcosB－sinBcosA＝35sin(A＋B)，即 5(sinAcosB－sinBcosA)＝3(sinAcosB＋sinBcosA)，即 sinAcosB＝4sinBcosA，因此tanA＝4tanB，所以ttaannAB＝4.答案：432ππ13 解析：由图象知，函数的周期为2×T＝π，∴T＝ 3 . ∵f( 4 )＝0，∴f(71π2 )＝f(π4 ＋π3 )＝f(π4 ＋T2)＝－f(π4 )＝0. 答案：0 14 解析：∵a∥b，∴x＝4，∴b＝(4，－2)，∴a＋b＝(6，－3)，b－c＝(1，－2－y).∵(a ＋b)⊥(b－c)，∴(a＋b)·(b－c)＝0，即 6－3(－2－y)＝0，∴y＝－4，故向量 MN ＝(－8,8)，| MN |＝8 2. 答案：8 215 解析：(1)由已知条件得 4cos 2 +4sin cos +sin 2 =0,(2cos +sin ) 2 =0,2cos =-sin ， tan =-2.（3 cos2 sin2 ) 8sin cos 3tan2 8tan 3(2) 3cos2 +4sin2 =sin2 cos2 =tan2 1=-5.16 解析：(1)列表取值：xπ3π 5π 7π 9π2 2 22 21xπ 024f(x) 0π π 3 π 2π2230 -3 0描出五个关键点并用光滑曲线连接，得到一个周期的简图. (2)先把 y＝sinx 的图象向右平移 4 个单位，然后纵坐标不变，把所有点的横坐标扩大为原来的 2 倍，再横坐标不变，把所有点的纵坐标扩大为原来的 3 倍，得到 f(x)的图象.17 解析：(1)由 f(x)＝ AC · BC 得f(x)＝(cosx2＋sinx2)·(cosx2－sinx2)＋(－sinx2)·2cosx2＝cos2x2－sin2x2－2sinx2cosx2＝cosx－sinx＝ 2cos(x＋π4 )，所以 f(x)的最小正周期 T＝2π.又由 2kπ≤x＋π4 ≤π＋2kπ，k∈Z，得－π4 ＋2kπ≤x≤34π＋2kπ，k∈Z.π3π故 f(x)的单调递减区间是[－ 4 ＋2kπ， 4 ＋2kπ](k∈Z).(2)由 f(x)＝1 得π 2cos(x＋ 4 )＝1，故π cos(x＋ 4 )＝2 2 .又x∈－π2 ，π2 ，于是有π x＋ 4∈－π4 ，34π，得 x1＝0，x2＝－π2 ，所以 x1＋x2＝－π2 .18 解析：(1)f(x)＝ 23sin2ωx＋12cos2ωx＋32＝sin(2ωx＋π6 )＋32.令 2ωx＋π6 ＝π2 ，将 x＝π6 代入可得：ω＝1.(2)由(1)得 f(x)＝sin(2x＋π6 )＋32.经过题设的变化得到的函数 g(x)＝sin(12x－π6 )＋32.45π1 π3当 x＝4kπ＋3π，k∈Z 时，函数取得最大值2. 令 2kπ＋ 2 ≤2x－ 6 ≤2kπ＋2π，410即[4kπ＋3π，4kπ＋ 3 π]，k∈Z 为函数的单调递减区间.19 解析： (1)∵| m n |2＝(cosA＋ 2－sinA)2＋(sinA＋cosA)2＝4＋2 2(cosA－sinA)＝4＋4cos(π4 ＋A)，∴4＋4cos(π4 ＋A)＝4，∴cos(π4 ＋A)＝0，∵A∈(0，π)，∴π4 ＋A＝π2 ，∴A＝π4 .(2)由余弦定理知：a2＝b2＋c2－2bccosA，即 a2＝(4 2)2＋( 2a)2－2×4 2× 2acosπ4 ，解得 a＝4 2，∴c＝8， ∴S△ABC＝12bcsinA＝12×4 2×8× 22＝16.20 解析：(1)∵ m n ＝1，即 3sinx4cosx4＋cos2x4＝1，即 23sinx2＋12cosx2＋12＝1，∴sin(x2＋π6 )＝12.∴cos(2π 3 －x)＝cos(x－2π3 )＝－cos(x＋π3 )＝－[1－2sin2(x2＋π6 )]＝2·(12)2－1＝－12.(2)∵(2a－c)cosB＝bcosC，由正弦定理得(2sinA－sinC)cosB＝sinBcosC. ∴2sinAcosB－cosBsinC＝sinBcosC，∴2sinAcosB＝sin(B＋C)，1π ∵A＋B＋C＝π，∴sin(B＋C)＝sinA，且 sinA≠0，∴cosB＝2，B＝ 3 ，2π π A π π 1Aπ∴0＜A＜ 3 .∴ 6 ＜2＋ 6 ＜ 2 ，2＜sin(2＋ 6 )＜1.又∵f(x)＝ m n =sin(x2＋π6 )＋12，∴f(A)＝sin(A2＋π6 )＋12. 故函数 f(A)的取值范围是(1，32).。

高考数学原创预测题 专题三 三角函数 平面向量 理 人教版

高考数学压轴专题人教版备战高考《平面向量》真题汇编及解析

2020高考数学核心突破《专题3 三角函数、解三角形与平面向量 第1讲 三角函数的图象与性质》 (2)

高考数学复习专题三第3讲 平面向量课件 理

高考数学 考点通关练 第三章 三角函数、解三角形与平面向量 18 同角三角函数基本关系式与诱导公式名师课件

高考数学二轮复习 专题三 三角函数、平面向量 2.3.3 平面向量学案 理-人教版高三全册数学学案

高考数学二轮复习 专题03 三角函数与平面向量(讲)(含解析)理-人教版高三全册数学试题

2020高考数学核心突破《专题三 三角函数、解三角形与平面向量》(含往年真题分析)

小题透析-三角函数、解三角形与平面向量-【高考倒计时15天考前过关】2023年高考数学(新高考专用)

高考数学原创预测题 专题三 三角函数 平面向量 文 人教版

2022年高考数学原创预测题 专题三 三角函数 平面向量 文 人教版

高考数学二轮复习 考前专题三 三角函数、解三角形与平面向量 第3讲 平面向量讲学案 理-人教版高三全

最新名师指点 高考数学 考点整合 人教版--专题三 第一讲 三角函数、三角变换、解三角形、平面向量

高考数学二轮复习 专题2 三角函数、解三角形、平面向量 第3讲 平面向量练习 理-人教版高三全册数学