九年级数学平行线分线段成比例
新人教版九年级下册数学课件:平行线分线段成比例

一、相似三角形
相似三角形 相似三角形的判定
平行线分线段成比例
∽ △A′B′C′. 1.记法:△ABC与△A′B′C′相似,记作△ABC 2.判定:在△ABC 与△A′B′C′中,如果∠A= ∠A′ ,∠B= ∠B′ ,∠C= ∠C′ ,且
AB AB
=
BC BC
【导学探究】 1.由DE∥BC可得,△ADE∽
2.由△ADE∽△ABC 可得
△ABC
DE
,△ADG∽
△ABH .
AD = AB
AD = AB BCຫໍສະໝຸດ .由△ADG∽△ABH 可得
AG
AH
.
解:因为 DE∥BC, 所以△ADE∽△ABC,△ADG∽△ABH, 所以 所以
AD DE AD AG = , = , AB BC AB AH DE AG = , BC AH
(A) (C)
AD 1 = AB 2 AD 1 = EC 2
)B
(B) (D)
AE 1 = EC 2 DE 1 = BC 2
2.(2017 临沂)已知 AB∥CD,AD 与 BC 相交于点 O.若
BO 2 = ,AD=10,则 AO= OC 3
4
.
3.(2017长春)如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和D,E,F.若 6. AB∶BC=1∶2,DE=3,则EF的长为
OE 2.由 l1∥l2 得 = OD
解:(2)因为 l1∥l2,所以
OB OA
OE OB = , OD OA
.
因为 OD=30,OE=12,OB=10, 所以 OA=
OB OD 10 30 = =25, OE 12
平行线分线段成比例定理的逆命题正确吗

平行线分线段成比例定理的逆命题在数学中是一个非常重要的定理,它解决了许多与平行线和线段成比例相关的问题。
平行线分线段成比例定理也被称为Thales定理,是希腊数学家泰勒斯提出的一个基本几何定理。
该定理的逆命题是“如果一条直线把两条平行线分成等比的线段,则这条直线与两条平行线平行”。
本文将深入探讨这一主题,并就其正确性进行全面评估和讨论。
1. 定理的主要内容平行线分线段成比例定理是指:如果一条直线与两条平行线相交,那么直线所分两条平行线上的线段对应成比例。
这个定理给出了两个平行线与一条直线的几何关系,是解决成比例问题的一个重要工具。
2. 定理的逆命题根据定理的逆命题,如果一条直线将两条平行线分成等比的线段,那么这条直线与两条平行线必定平行。
这个逆命题是定理的反向推论,其正确性非常重要。
3. 证明与讨论对于平行线分线段成比例定理的逆命题,我们可以通过构造证明来验证其正确性。
假设有两条平行线L1和L2,并且一条直线m相交于它们。
如果直线m将这两条平行线分成等比的线段,即在m上取两点A、B,分别与L1、L2上的点成比例,我们可以通过几何画图或类似三角形的方法证明直线m与L1、L2平行。
这一构造证明可以帮助我们理解逆命题的正确性。
4. 个人观点和理解在我看来,平行线分线段成比例定理的逆命题是正确的。
因为如果一条直线将两条平行线分成等比的线段,它们之间的几何关系会导致直线m与L1、L2必定平行。
这种关系可以用几何图形和数学推理相结合的方式进行理解和证明,因此逆命题的正确性是可以得到验证的。
5. 总结和回顾通过本文的探讨,我们全面评估了平行线分线段成比例定理的逆命题,并得出了结论:逆命题是正确的。
我们还通过几何构造和数学推理分析了逆命题的正确性,得出了对逆命题的深入理解。
我们也提及了定理的主要内容,以便对其进行全面、深刻和灵活的理解。
在知识的文章格式中,我们可以使用以上内容进行排版和展开,从而撰写一篇有价值的关于平行线分线段成比例定理逆命题的文章。
湘教版数学九年级上册3.2《平行线分线段成比例》教学设计1

湘教版数学九年级上册3.2《平行线分线段成比例》教学设计1一. 教材分析《平行线分线段成比例》是湘教版数学九年级上册3.2的内容,本节内容是在学生掌握了平行线的性质,平行线公理及推论的基础上进行学习的。
本节课主要让学生通过观察、操作、探究等活动,发现并证明平行线分线段成比例的定理,培养学生直观推理的能力,提高学生空间想象的能力。
二. 学情分析九年级的学生已经掌握了平行线的性质,平行线公理及推论,对于通过观察、操作、探究等方法获取结论的活动已经比较熟悉。
但是,对于平行线分线段成比例的定理,学生可能还比较陌生,需要通过具体的活动来理解和掌握。
三. 教学目标1.理解平行线分线段成比例的定理。
2.能够运用平行线分线段成比例的定理解决实际问题。
3.培养学生的直观推理能力和空间想象能力。
四. 教学重难点1.重点:平行线分线段成比例的定理的理解和运用。
2.难点:平行线分线段成比例的定理的证明。
五. 教学方法采用观察、操作、探究的教学方法,让学生在活动中发现问题,提出假设,通过推理和证明得出结论。
六. 教学准备1.准备相关的图片和实例,用于导入和巩固环节。
2.准备平行线分线段成比例的定理的证明素材,用于操练和拓展环节。
七. 教学过程1.导入(5分钟)通过展示相关的图片和实例,引导学生观察和思考,提出问题:“你能发现这些图片和实例中的线段有什么特殊的关系吗?”让学生初步感知平行线分线段成比例的现象。
2.呈现(10分钟)通过PPT呈现平行线分线段成比例的定理,并用文字和图形的形式进行解释,让学生理解和记忆定理的内容。
3.操练(10分钟)让学生分组进行实践活动,每组提供一份证明素材,让学生通过推理和证明来验证平行线分线段成比例的定理。
在活动中,教师进行巡回指导,帮助学生解决问题。
4.巩固(10分钟)通过一些相关的例题和练习题,让学生运用平行线分线段成比例的定理来解决问题,巩固所学的内容。
5.拓展(10分钟)让学生思考和探究平行线分线段成比例的定理在实际生活中的应用,提出一些实际问题,让学生运用定理来解决。
平行线分线段成比例结论

平行线分线段成比例结论
平行线分线段成比例的结论可以用以下两个定理来描述:
1. 三角形法则:如果在两条平行线上有两个相交线段,那么这两条线段被平行线切分的部分成比例。
具体表述为:如果AB和CD是两条平行线,并且有两个交叉
线段EF和GH,那么EF/GH = AB/CD。
2. 价恩斯定理:两条平行线被一组相交线段切割所形成的任意两条线段之间的比值,等于这两条线段所在平行线之间的比值。
具体表述为:如果AB和CD是两条平行线,其中EF和GH
是这两条平行线上的两个交叉线段,那么EF/GH = AB/CD。
这些定理指出,在平行线上切割的线段之间存在比例关系,这使得我们可以通过已知线段的比例来推导未知线段的长度。
4.2平行线分线段成比例 课件(共16张PPT) 北师大版数学九年级上册

AF交BC于点D,若BF=3EF,则 =
.
.
( B)
.
.
点拨:过点E作 //交 BC 于点H,则
=
.
∵BE 是 △ 的中线, ∴ = , ∴ = .
∵ //, = , ∴
=
= , ∴
1 2 1 2
3 .计算
与
的值,你有什么发现?
2 3 2 3
如果不通过测量,我们要将一条长为5厘米的细线分成两部
分,使得这两部分之比为2:3.我们如何运用所学知识解决
这个问题呢?
知识讲解
自主探究
1.请同学们阅读课本82-83页内容.
2.思考并完成课本82页导入的内容中的问题可以得出什么结论?
例2:如图,已知AD为△ABC的角平分线,DE//AB交
AC于E,如果
= ,那么BD:BC等于(
D
)
A.3:5 B. 5:3 C.8:5 D. 3:8
点拨: ∵ //, ∴
=
=
,∴
=
.
【题型三】平行线分线段成比例与三角形中位线的综合应用
例3:如图,BE是△BC的中线,点F在BE上,延长
平行的直线,用它们截两条直线,然后测量被截
的每段线段的长度,观察并计算是否满足本节课
所学的基本事实.
清楚哪些线段是对应的,切勿写反.
注意:在应用基本事实和推论时,我们需要注意的是:对应线段成比例,一
《平行线分线段成比例》PPT课件

05
说教法与学法
说教法与学法
1. 讲解法:通过讲解平行线分线段成比例的概念和解题 方法,帮助学生理解知识点。2. 示范法:通过示范具体 的例题解题过程,引导学生掌握解题方法。3. 练习法: 设计一系列练习题,巩固学生对判断线段是否成比例和 求解未知线段长度的能力。4. 启发式教学:引导学生主 动思考和解决问题,培养他们的应用能力。
01
说教材
说教材
本节课的教材来源于初中数学北师大版九年级上 册。教材中包含了平行线分线段成比例的概念、 判断线段是否成比例的方法以及求解未知线段长 度的方法。通过教材中的例题和练习题,学生将 学会运用这些知识解决实际问题。
02
说学情
说学情
学生已经具备了一定的几何图形的认识和应用能力。 他们对平行线和线段的概念有一定的了解,但对平 行线分线段成比例的概念和应用还存在一些困惑。 因此,本节课的教学目标是帮助学生进一步理解和 掌》 说课稿
目录
01. 说教材
02. 说学情
03. 说教学目标 04. 说教学重难点
05. 说教法与学法 06. 说教学过程
07. 说板书设计 08. 说教学反思
敬爱的各位评委老师,下面我将更加 详细地为大家介绍初中数学北师大版 九年级上册第四章图形的相似第2节 《平行线分线段成比例》的说课内容。 下面我将从说教材、说学情、说教学 目标、说教学重难点、说教法与学法、 说教学过程、说板书设计以及说教学 反思这八个方面进行详细的说课。
新课讲解
巩固练习 1. 设计一些练习题,巩固学生对判断线段是否成比例和求解未知线段 长度的能力。 2. 让学生独立或分组完成练习题,并进行讲解和讨论。
新课讲解
知识拓展 1. 设计一些应用题,引导学生将平行线分线段成比 例的知识应用到实际问题中,培养学生的应用能力。 2. 给出一个实际问题,如计算地图上两个城市之间 的距离,让学生运用平行线分线段成比例解决问题。
平行线分线段成比例定理及证明

平行线分线段成比例定理证明简介平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
如图,因为AD∥BE∥CF,所以AB:BC=DE:EF;AB:AC=DE:DF;BC:AC=EF:DF。
也可以说AB:DE=BC:EF;AB:DE=AC:DF;BC:EF=AC:DF。
说明上述图样只是平行线分线段的一种特殊情况。
事实上,直线AC和直线DF 可以在平行线之间相交,同样有定理成立。
推广:过一点的一线束被平行线截得的对应线段成比例。
证明思路该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的知识,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它(用相似三角形可以证明它,在这里要用到平移和设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点法1:过A作平行线的垂线交另两条平行线于M、N过D作平行线的垂线交另两条平行线于P、Q则四边形AMPD、ANQD均为矩形AM=DP,AN=DQAB=AM/cosA,AC=AN/cosA,∴AB/AC=AM/ANDE=DP/cosD,DF=DQ/cosD,∴DE/DF=DP/DQ又∵AM=DP,AN=DQ,∴AB/AC=DE/DF根据比例的性质:AB/(AC-AB)=DE/(DF-DE)∴AB/BC=DE/EF法2:过A点作AN∥DF交BE于M点,交CF于N点,则AM=DE,MN=EF.∵ BE∥CF∴△ABM∽△ACN.∴AB/AC=AM/AN∴AB/(AC-AB)=AM/(AN-AM)∴AB/BC=DE/EF法3:连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE,S△BCE=S△BEF∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF定理推论平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
初三数学第5讲:平行线分线段成比例定理

教学内容一、 知识要点:1、平行线分线段成比例定理:两条直线被三条平行线的直线所截,截得的对应线段成比例。
2、平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段 相等,那么在另一条直线上截得的线段也相等。
FED C B A FEDCBA问题:如果两条直线被三条直线所截,截得的线段成比例,那么这三条线段互相平行吗? 牛刀小试:1、如图AB ∥CD ∥EF ,AC=3,AE=8,BF=10。
求BD 、DF 的长。
A BC DE F2、 如图,1L ∥2L ∥3L ,AB=2,AC=5,DF=10,则DE=_________L 3L 2L 1FEDCBA3、在(1)题中,AB ∥CD ∥EF ,AB=2,CD=3,EF=5,BD=2,AE=8。
求BF 、CE 的长。
第 1 页 共 9 页4、已知如图,AD ∥CF ∥EB ,AB=3,AC=5,DF=9,DA=2,CF=8,求DE 、EF 、BE 的长。
FCED B A二、典型例题:1、如图,已知:AB 、CD 、EF 都垂直于L,AB=12,EF=7,BD :DF=2:3,求CD 的长。
LFCEDBA巩固练习: 1、已知abcx,求作x,则下列作图正确的是( ) Axc ba Bxc b aCxcba Dx c ba2、如图,1L ∥2L ∥3L ,两直线AC 、DF 与1L 、2L 、3L 分别交于A 、B 、C 和D 、E 、F ,下列各式中,不一定成立的是( ) A 、AB DE =BC EF B 、AB DE =AC DF C 、EF BC =FD CA D 、AD BE=BE CF2L 3L 2L 1FED CB A4、如图已知a ∥b ∥c ,AC=2,CG=4,BF=9,DH=10,EM=1,FH=3。
求BE 、AH 、DE 、MH 、AB 的值。
A BC D E M NF G H思维拓展:1、如图,已知:平行四边形ABCD 中,点E 是CD 的中点,点F 在BC 上,21BF FC =,求CO :AO 的值。
北师大版九上数学4.2平行线分线段成比例知识点精讲
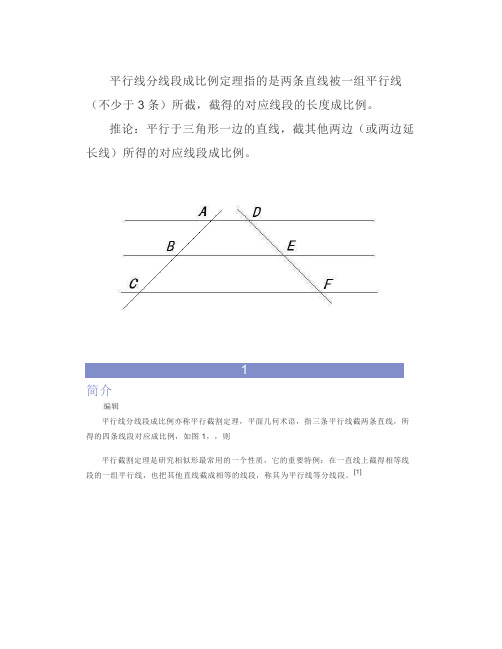
平行线分线段成比例定理指的是两条直线被一组平行线(不少于3条)所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
1简介编辑平行线分线段成比例亦称平行截割定理,平面几何术语,指三条平行线截两条直线,所得的四条线段对应成比例,如图1,,则平行截割定理是研究相似形最常用的一个性质,它的重要特例:在一直线上截得相等线段的一组平行线,也把其他直线截成相等的线段,称其为平行线等分线段。
[1]图12定理证明编辑设三条平行线与直线 m 交于 A、B、C 三点,与直线 n 交于 D、E、F 三点。
连结AE、BD、BF、CE根据平行线的性质可得 S△ABE=S△DBE, S△BCE=S△BEF,∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF。
由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。
3定理推论编辑过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
推广:过一点的一线束被平行线截得的对应线段成比例。
定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
01平行线分线段成比例的基本事实1.基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
2.符号表示:如图02平行线分线段成比例的基本事实的推论1.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例。
2.符号表示:如图【知识梳理】1. 平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
北师大版九年级数学上册第四章图形的相似4.2平行线分线段成比例(教案)

(2)逆向思维的培养:在解决逆向问题,即已知线段比例求平行线问题时,学生往往感到困难。
举例:已知在三角形ABC中,AB/AC = 2/3,点D在BC上,使得AD//BC,求BD/DC的比例。
其次,在新课讲授环节,我采用了理论介绍、案例分析、重点难点解析的方式,逐步引导学生掌握平行线分线段成比例定理。在这个过程中,我发现图示和实际案例的分析对于学生理解这一概念非常有帮助。但在讲解过程中,我应该更加注意语言的简洁明了,避免让学生产生混淆。
在实践活动环节,我安排了分组讨论、实验操作和成果展示。通过这个环节,学生们的动手能力和团队合作能力得到了锻炼。但我也注意到,部分学生在操作过程中还存在一些问题,如对尺度的把握不准确等。因此,在以后的教学中,我可以增加一些关于几何作图的技巧讲解,提高学生们的实践能力。
北师大版九年级数学上册第四章图形的相似4.2平行线分线段成比例(教案)
一、教学内容
本节课选自北师大版九年级数学上册第四章“图形的相似”中的4.2节“平行线分线段成比例”。教学内容主要包括以下两点:
1.探索并掌握平行线分线段成比例定理,即:如果两条直线平行,那么它们所分得的对应线段成比例。
2.学会运用平行线分线段成比例定理解决相关问题,如:求线段比例、相似三角形等。通过对该定理的理解和应用,培养学生空间想象能力和解决问题的能力。
在学生小组讨论环节,我鼓励学生们提出自己的观点和想法,并进行交流。这个环节的效果还不错,学生们积极参与讨论,课堂氛围活跃。但我也注意到,部分学生过于依赖教材,缺乏独立思考的能力。为了培养学生的创新思维,我可以在今后的教学中多设置一些开放性的问题,引导学生进行深度思考。
成比例线段与平行线分线段成比例

初中数学成比例线段与平行线分线段成比例编稿老师董志臣一校杨雪二校黄楠审核郑建彬一、考点突破1. 理解并掌握比例的基本性质,成比例线段的定义。
2. 理解平行线分线段成比例的定理及其证明。
3. 应用相关知识解决问题。
二、重难点提示重点:成比例线段及平行线分线段成比例定理的理解。
难点:应用比例性质及平行线分线段成比例定理解决问题。
1. 成比例线段:在同一单位下,四条线段长度为a、b、c、d,其关系为a:b=c:d,那么,这四条线段叫做成比例线段,简称比例线段。
一般地,如果三个数a,b,c满足比例式a:b=b:c,则b就叫做a,c的比例中项。
【注意顺序问题】A. 当题目给出a、b、c、d为成比例线段时,表示有先后顺序之分:为();B. 当题目问a、b、c、d是否为成比例线段时说明没有先后顺序,只要按照一定的顺序,满足比值相等就行。
2. 常用的比例性质:①基本性质:若则ad=bc,可由ad=bc推出a:b=c:d;a:c=b:d;d:b=c:a和d:c=b:a②合比性质:若则;③反比性质:若则;④等比性质:若=…==k, 则 (b+d+…+n≠0)。
3. 平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
定理推论:①平行于三角形一边的直线截其他两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
例题1(青浦区一模)已知:线段a、b、c,且==。
(1)求的值;(2)如线段a、b、c满足a+b+c=27,求a、b、c的值。
思路分析:(1)根据比例的性质得出=,即可得出的值;(2)首先设===k,则a=2k,b=3k,c=4k,利用a+b+c=27求出k的值即可得出答案。
答案:解:(1)∵=,∴=,∴=;(2)设===k则a=2k,b=3k,c=4k,∵a+b+c=27,∴2k+3k+4k=27,∴k=3,∴a=6,b=9,c=12。
2023-2024学年北师大版九年级数学上册教案:4.2 平行线分线段成比例

2023-2024学年北师大版九年级数学上册教案:4.2 平行线分线段成比例一. 教材分析《2023-2024学年北师大版九年级数学上册》第4.2节“平行线分线段成比例”主要介绍了平行线分线段成比例的性质。
通过这一节的学习,学生能够理解并掌握平行线分线段成比例的定理,并能够运用该定理解决实际问题。
本节内容是初中数学的重要知识点,对于学生来说具有较高的难度,需要通过大量的练习来巩固。
二. 学情分析九年级的学生已经掌握了平行线的性质,对于线段的比例也有一定的理解。
但是,将平行线与线段的比例联系起来,对于他们来说还有一定的难度。
因此,在教学过程中,需要通过具体的实例,引导学生理解并掌握平行线分线段成比例的性质。
三. 教学目标1.了解平行线分线段成比例的定理,并能够运用该定理解决实际问题。
2.培养学生的逻辑思维能力和解决问题的能力。
3.提高学生的数学素养,使他们在数学学习上有所突破。
四. 教学重难点1.平行线分线段成比例的定理的理解和运用。
2.如何将平行线与线段的比例联系起来,形成系统性的认识。
五. 教学方法采用问题驱动的教学方法,通过具体的实例,引导学生发现并总结平行线分线段成比例的定理。
同时,结合小组讨论和练习,巩固所学知识,提高学生的实际应用能力。
六. 教学准备1.准备相关的教学材料,如PPT、实例等。
2.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考平行线与线段的比例之间的关系。
例如,假设有一块土地,被两条平行线和一条横线分成四个部分,如何求出每个部分的面积比例。
2.呈现(10分钟)通过具体的实例,呈现平行线分线段成比例的定理。
引导学生发现并总结定理的内容。
3.操练(10分钟)让学生分组讨论,运用平行线分线段成比例的定理解决实际问题。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)给出一些练习题,让学生独立完成,巩固所学知识。
教师选取部分题目进行讲解,分析解题思路。
平行线分线段成比例定理

3.1 相似形3.1.1.平行线分线段成比例定理在解决几何问题时,我们常涉及到一些线段的长度、长度比的问题。
在数学学习与研究中,我们发现平行线常能产生一些重要的长度比。
在一张方格纸上,我们作平行线123,,l l l (如图3.1-1),直线a 交123,,l l l 于点,,A B C ,2,3AB BC ==,另作直线b 交123,,l l l 于点',','A B C ,不难发现''2.''3A B AB B C BC == 我们将这个结论一般化,归纳出平行线分线段成比例定理: 三条平行线截两条直线,所得的对应线段成比例。
如图3.1-2,123////l l l ,有AB DE BC EF =。
当然,也可以得出AB DEAC DF=。
在运用该定理解决问题的过程中,我们一定要注意线段之间的对应关系,是“对应”线段成比例。
例1 如图3.1-2, 123////l l l ,且2,3,4,AB BCD F ===求,DE EF 。
解:32,//l //l l 321==∴EF DE BC AB , ∴28312,.235235DE DF EF DF ====++ 例2 在ABC ∆中,,D E 为边,AB AC 上的点,//DE BC ,图 3.1-1 图3.1-2求证:AD AE DEAB AC BC==。
证明(1)//,,,DE BC ADE ABC AED ACB ∴∠=∠∠=∠ ADE∆∴∽ABC ∆,.AD AE DEAB AC BC∴== 证明(2)如图3.1-3,过A 作直线//l BC ,////,l DE BC AD AEAB AC∴=。
过E 作//EF AB 交AB 于D ,得□BDEF ,因而.DE BF =//,.AE BF DE EF AB AC BC BC ∴== .AD AE DEAB AC BC∴== 从上例可以得出如下结论:平行于三角形的一边的直线截其它两边(或两边的延长线),所得的对应线段成比例。
平行线分线段成比例八大题型

【变式】如图,已知点 F 在 AB 上,且 AF:BF=1:2,点 D 是 BC 延长线上一点,BC:CD =2:1,连接 FD 与 AC 交于点 M,则 FN:ND= .
解:过点 F 作 FE∥BD,交 AC 于点 E,
∴=,
∵AF:BF=1:2,
∴ = 1,
3
∴ = 1,
3
即 FE= 13BC, ∵BC:CD=2:1,
C l3
【小结】若将所截出的小线段位置靠上的(如 AB )称为上,位置靠下的称为下,两条线段
上上 上上 下下
合成的线段称为全,则可以形象的表示为 下 下 , 全 全 , 全 全 .
【题型1 “井”字型】
【例 1】如图,直线 l1∥l2∥l3,直线 AC 和 DF 被 l1,l2,l3 所截,如果 AB=2,BC=3,EF =2,那么 DE 的长是( )
A.2
B
.4
3
C.1
D.34
【分析】根据平行线分线段成比例定理得出比例式,代入求出即可. 【解答】解:∵直线 l1∥l2∥l3, ∴=,
∵AB=2,BC=3,EF=2,
∴2 = ,
32
∴DE=
4,
3
故选:B.
【变式】如图,a∥b∥c,两条直线与这三条平行线分别交于点 A,B,C 和 D,E,F.已知 AB=3,BC=2,DE=6,则 DF 等于( )
∵ = = 1,
2
∴BG=2DG, ∵BE=4DG, ∴ = 1,
4
故 D 错误,符合题意; 故选:D.
【变式】已知,在△ABC 中,点 D 为 AB 上一点,过点 D 作 DE∥BC,DH∥AC 分别交 AC、 BC 于点 E、H,点 F 是 BC 延长线上一点,连接 FD 交 AC 于点 G,则下列结论中错误的 是( )
平行线分线段成比例判定定理基本模型

平行线分线段成比例判定定理基本模型【摘要】本文将介绍平行线分线段成比例判定定理的基本模型。
在我们将引入该定理的重要性和应用背景。
在首先对定理进行详细说明,然后逐步解释证明步骤,解释相关概念,提供应用举例,并讨论推论拓展。
结论部分将总结归纳所学内容,探讨定理在实际应用中的作用,并展望未来研究方向。
通过本文的阐述,读者将能全面了解平行线分线段成比例判定定理,为进一步的数学学习和应用提供基础。
【关键词】平行线分线段成比例判定定理、引言、定理说明、证明步骤、相关概念解释、应用举例、推论拓展、总结归纳、实际应用、未来研究方向1. 引言1.1 引言平行线分线段成比例判定定理是几何学中的重要定理之一,它解决了平行线与线段之间的关系,为我们在解题过程中提供了便利。
通过这个定理,我们可以轻松判断两条平行线上的线段是否成比例,从而简化问题的复杂度,提高解题效率。
在学习这个定理之前,我们首先需要了解一些基本概念,比如平行线、线段、比例等。
平行线是在同一平面上没有交点的直线,线段是两点之间的连线部分,比例是指两个东西之间的相对大小关系。
这些基本概念是理解平行线分线段成比例判定定理的基础。
在接下来的内容中,我们将详细介绍平行线分线段成比例判定定理的原理和证明步骤,帮助我们更深入地理解这一定理。
我们还将通过相关概念解释、应用举例和推论拓展等部分,进一步探讨这个定理在实际问题中的应用和推广。
通过对平行线分线段成比例判定定理的学习和掌握,我们可以提高解题的效率和准确性,在几何学习中取得更好的成绩。
让我们一起深入探讨这一定理的奥秘,为解决更复杂的几何问题奠定坚实的基础。
2. 正文2.1 定理说明平行线分线段成比例判定定理是初中数学中非常重要的定理之一,它可以帮助我们解决各种与平行线和比例有关的几何问题。
在学习这个定理之前,我们首先要了解什么是平行线和什么是比例。
平行线是在同一个平面内且永远不相交的两条直线,而比例则是指两个量之间的比较关系。
九年级数学上册《平行线分线段成比例》教案、教学设计

2.注重培养学生的几何直观,通过具体实例让学生感受平行线分线段成比例的性质。
3.针对学生个体差异,实施分层教学,使每个学生都能在原有基础上得到提高。
4.加强师生互动,关注学生的心理需求,营造轻松、愉快的学习氛围。
三、教学重难点和教学设想
随后,教师引入平行线分线段成比例的概念,并让学生尝试用自己的语言描述这一概念。通过这种方式,激发学生的好奇心,使他们产生学习的兴趣。
(二)讲授新知
在导入新课的基础上,教师开始讲授平行线分线段成比例的性质。首先,通过几何画板演示平行线分线段成比例的动态过程,让学生直观地感受这一性质。接着,教师引导学生运用几何语言,对这一性质进行严谨的证明。
3.教学评价:
-采用形成性评价,关注学生在学习过程中的表现,如课堂参与度、小组合作、问题解决能力等。
-适时进行总结性评价,通过测试、作业等方式,了解学生对平行线分线段成比例知识的掌握程度。
-鼓励学生进行自我评价和同伴评价,培养他们的反思能力和批判性思维。
4.教学拓展:
-引导学生探索平行线分线段成比例在生活中的应用,如摄影、设计等领域。
在讲授过程中,教师注重讲解与示范相结合,让学生掌握以下知识点:
1.平行线分线段成比例的定义和性质。
2.如何运用比例关系解决几何问题。
3.证明平行线分线段成比例的方法和步骤。
(三)学生小组讨论
讲授新知后,教师组织学生进行小组讨论。每个小组围绕以下问题展开讨论:
1.平行线分线段成比例的性质在现实生活中有哪些应用?
作业要求:
1.学生需独立完成作业,遇到问题可先尝试自行解决,实在解决不了的可请教同学或老师。
平行线分线段成比例定理(通用12篇)

平行线分线段成比例定理(通用12篇)平行线分线段成比例定理篇1教学建议学问结构重难点分析本节的重点是平行线分线段成比例定理.平行线分线段成比例定理是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是平行线分线段成比例定理.平行线分线段成比例定理变式较多,同学在找对应线段时常常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也常常消失错误.教法建议1.平行线分线段成比例定理的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出平行线分线段成比例定理2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到平行线分线段成比例定理,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握平行线分线段成比例定理及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是平行线分线段成比例定理和推论及其应用.2.教学难点:是平行线分线段成比例定理的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤复习提问找同学叙述平行线等分线段定理.讲解新课在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图: ,且 ,∴由于问题:假如 ,那么是否还与相等呢?老师可带领同学阅读教材p211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到 ,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,∴ .其中后两种状况,为下一节学习推论作了预备.例1 已知:如图所示, .求:bc.解:让同学来完成.注:在列比例式求某线段长时,尽可能将要求的线段写成比例的第一项,以削减错误,如例1可列比例式为:例2 已知:如图所示,求证: .有了5.1节例4的教学,同学作此例题不会有困难,建议让同学来完成.小结1.平行线分线段成比例定理正确性的的说明.2.娴熟把握由定理得出的六个比例式.(对比图形,并注意变化)七、布置作业教材p221中3(练习同学克服图形中各线段的干扰).八、板书设计标题复习:平行线等分线段定理问题:……平行线等分线段定理:……4个变式图形(投影仪)板书:形象语言……例1.……例2.……平行线分线段成比例定理篇2教学建议学问结构重难点分析本节的重点是.是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是.变式较多,同学在找对应线段时经常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也经常消失错误.教法建议1.的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是和推论及其应用.2.教学难点:是的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】找同学叙述平行线等分线段定理.【讲解新课】在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图:,且,∴由于问题:假如,那么是否还与相等呢?老师可带领同学阅读教材P211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,∴ .其中后两种状况,为下一节学习推论作了预备.例1 已知:如图所示, .求:BC.解:让同学来完成.注:在列比例式求某线段长时,尽可能将要求的线段写成比例的第一项,以削减错误,如例1可列比例式为:例2 已知:如图所示,求证: .有了5.1节例4的教学,同学作此例题不会有困难,建议让同学来完成.【小结】1.正确性的的说明.2.娴熟把握由定理得出的六个比例式.(对比图形,并留意变化)七、布置作业教材P221中3(训练同学克服图形中各线段的干扰).八、板书设计标题复习:平行线等分线段定理问题:……平行线等分线段定理:……4个变式图形(投影仪)板书:形象语言……例1.……例2.……平行线分线段成比例定理篇3(其次课时)一、教学目标1.使同学在理解的基础上把握平行线分线段成比例定理及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是平行线分线段成比例定理和推论及其应用.2.教学难点:是平行线分线段成比例定理的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】叙述平行线分线段成比例定理(要求:结合图形,做出六个比例式).【讲解新课】在黑板上画出图,观看其特点:与的交点A在直线上,依据平行线分线段成比例定理有:……(六个比例式)然后把图中有关线擦掉,剩下如图所示,这样即可得到:平行于的边BC的直线DE截AB、AC,所得对应线段成比例.在黑板上画出左图,观看其特点:与的交点A在直线上,同样可得出:(六个比例式),然后擦掉图中有关线,得到右图,这样即可证到:平行于的边BC的直线DE截边BA、CA的延长线,所以对应线段成比例.综上所述,可以得到:推论:(三角形一边平行线的性质定理)平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.如图,(六个比例式).此推论是判定三角形相像的基础.注:关于推论中“或两边的延长线”,是指三角形两边在第三边同一侧的延长线,假如已知,DE是截线,这个推论包含了下图的各种状况.这个推论不包含下图的状况.后者,教学中如同学不提起,可不必向同学交待.(考虑改用投影仪或小黑板)例3 已知:如图,,求:AE.教材上采纳了先求CE再求AE的方法,建议在列比例式时,把CE写成比例第一项,即: .让同学思索,是否可直接未出AE(找同学板演).【小结】1.知道推论的探究方法.2.重点是推论的正确运用七、布置作业(1)教材P215中2.(2)选作教材P222中B组1.八、板书设计平行线分线段成比例定理篇4教学建议学问结构重难点分析本节的重点是.是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是.变式较多,同学在找对应线段时经常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也经常消失错误.教法建议1.的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是和推论及其应用.2.教学难点:是的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】找同学叙述平行线等分线段定理.【讲解新课】在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图:,且,∴由于问题:假如,那么是否还与相等呢?老师可带领同学阅读教材P211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,∴ .其中后两种状况,为下一节学习推论作了预备.例1 已知:如图所示, .求:BC.解:让同学来完成.注:在列比例式求某线段长时,尽可能将要求的线段写成比例的第一项,以削减错误,如例1可列比例式为:例2 已知:如图所示,求证: .有了5.1节例4的教学,同学作此例题不会有困难,建议让同学来完成.【小结】1.正确性的的说明.2.娴熟把握由定理得出的六个比例式.(对比图形,并留意变化)七、布置作业教材P221中3(训练同学克服图形中各线段的干扰).八、板书设计标题复习:平行线等分线段定理问题:……平行线等分线段定理:……4个变式图形(投影仪)板书:形象语言……例1.……例2.……平行线分线段成比例定理篇5教学建议学问结构重难点分析本节的重点是.是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是.变式较多,同学在找对应线段时经常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也经常消失错误.教法建议1.的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是和推论及其应用.2.教学难点:是的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】找同学叙述平行线等分线段定理.【讲解新课】在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图:,且,∴由于问题:假如,那么是否还与相等呢?老师可带领同学阅读教材P211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,∴ .其中后两种状况,为下一节学习推论作了预备.例1 已知:如图所示, .求:BC.解:让同学来完成.注:在列比例式求某线段长时,尽可能将要求的线段写成比例的第一项,以削减错误,如例1可列比例式为:例2 已知:如图所示,求证: .有了5.1节例4的教学,同学作此例题不会有困难,建议让同学来完成.【小结】1.正确性的的说明.2.娴熟把握由定理得出的六个比例式.(对比图形,并留意变化)七、布置作业教材P221中3(训练同学克服图形中各线段的干扰).八、板书设计标题复习:平行线等分线段定理问题:……平行线等分线段定理:……4个变式图形(投影仪)板书:形象语言……例1.……例2.……平行线分线段成比例定理篇6教学建议学问结构重难点分析本节的重点是.是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是.变式较多,同学在找对应线段时经常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也经常消失错误.教法建议1.的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是和推论及其应用.2.教学难点:是的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】找同学叙述平行线等分线段定理.【讲解新课】在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图:,且,∴由于问题:假如,那么是否还与相等呢?老师可带领同学阅读教材P211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,∴ .其中后两种状况,为下一节学习推论作了预备.例1 已知:如图所示, .求:BC.解:让同学来完成.注:在列比例式求某线段长时,尽可能将要求的线段写成比例的第一项,以削减错误,如例1可列比例式为:例2 已知:如图所示,求证: .有了5.1节例4的教学,同学作此例题不会有困难,建议让同学来完成.【小结】1.正确性的的说明.2.娴熟把握由定理得出的六个比例式.(对比图形,并留意变化)七、布置作业教材P221中3(训练同学克服图形中各线段的干扰).八、板书设计标题复习:平行线等分线段定理问题:……平行线等分线段定理:……4个变式图形(投影仪)板书:形象语言……例1.……例2.……平行线分线段成比例定理篇7教学建议学问结构重难点分析本节的重点是.是讨论相像形的最重要和最基本的理论,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比.本节的难点也是.变式较多,同学在找对应线段时经常消失错误;另外在讨论平行线分线段成比例时,常用到代数中列方程度方法,利用已知比例式或等式列出关于未知数的方程,求出未知数,这种运用代数方法讨论几何问题,同学接触不多,也经常消失错误.教法建议1.的引入可考虑从旧学问引入,先复习平行线等分线段定理,再转变其中的条件引出2.也可考虑探究式引入,对给定几组图形由同学测量得出各直线与线段的关系,从而得到,并加以证明,较附和同学的认知规律(第一课时)一、教学目标1.使同学在理解的基础上把握及其推论,并会敏捷应用.2.使同学把握三角形一边平行线的判定定理.3.已知线的成已知比的作图问题.4.通过应用,培育识图力量和推理论证力量.5.通过定理的教学,进一步培育同学类比的数学思想.二、教学设计观看、猜想、归纳、讲解三、重点、难点l.教学重点:是和推论及其应用.2.教学难点:是的正确性的说明及推论应用.四、课时支配1课时五、教具学具预备投影仪、胶片、常用画图工具.六、教学步骤【复习提问】找同学叙述平行线等分线段定理.【讲解新课】在四边形一章里,我们学过平行线等分线段定理,今日,在此基础上,我们来讨论平行线平分线段成比例定理.首先复习一下平行线等分线段定理,如图:,且,∴由于问题:假如,那么是否还与相等呢?老师可带领同学阅读教材P211的说明,然后强调:(该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的学问,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它)因此:对于是任何正实数,当时,都可得到:由比例性质,还可得到:为了便于记忆,上述6个比例可使用一些简洁的形象化的语言“ ”.另外,依据比例性质,还可得到,即同一比中的两条线段不在同始终线上,也就是“ ”,这里不要让同学死记硬背,要让同学会看图,达到依据图作出正确的比例即可,可多找几个同学口答练习.:三条平行线截两条直线,所得的对应线段成比例.平行线等分线段定理可看作是这个定理的特例.依据此定理,我们可以写出六个比例,为了便于应用,在以后的论证和计算中,可依据状况选用其中任何一个,参见下图.,。
2023-2024学年北师大版九年级数学上册教学设计:4.2 平行线分线段成比例

2023-2024学年北师大版九年级数学上册教学设计:4.2 平行线分线段成比例一. 教材分析平行线分线段成比例是北师大版九年级数学上册的教学内容,本节课主要通过探究平行线分线段成比例的定理,让学生理解并掌握平行线分线段成比例的性质及应用。
教材通过丰富的例题和练习,引导学生探究并发现平行线分线段成比例的规律,培养学生的逻辑思维能力和解决问题的能力。
二. 学情分析九年级的学生已经掌握了平行线的性质,对图形的变换和推理已经有了初步的认识。
但是,对于平行线分线段成比例的定理,他们可能还比较陌生,需要通过实例和练习来逐步理解和掌握。
因此,在教学过程中,教师需要关注学生的认知基础,通过引导和激励,激发学生的学习兴趣和积极性。
三. 教学目标1.理解平行线分线段成比例的定理及证明过程。
2.能够运用平行线分线段成比例的定理解决实际问题。
3.培养学生的逻辑思维能力和解决问题的能力。
四. 教学重难点1.教学重点:平行线分线段成比例的定理及证明过程。
2.教学难点:理解平行线分线段成比例的证明方法。
五. 教学方法1.引导探究法:通过引导学生观察、思考、讨论,让学生自主发现平行线分线段成比例的规律。
2.实例教学法:通过丰富的例题和练习,让学生理解和掌握平行线分线段成比例的定理。
3.问题解决法:引导学生运用平行线分线段成比例的定理解决实际问题,培养学生的应用能力。
六. 教学准备1.教学课件:制作课件,展示平行线分线段成比例的例题和练习。
2.教学素材:准备相关的例题和练习题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)教师通过展示实际问题,引导学生思考平行线分线段成比例的现象,激发学生的学习兴趣。
2.呈现(10分钟)教师通过课件展示平行线分线段成比例的例题,引导学生观察和分析,让学生自主发现平行线分线段成比例的规律。
3.操练(10分钟)教师给出相关的练习题,让学生独立完成,巩固对平行线分线段成比例的理解。
4.巩固(10分钟)教师通过课件讲解平行线分线段成比例的证明过程,让学生理解和掌握定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;
第三部分(12~20),写胡良不听父亲的劝告在外另开分店,但终究被人品出了味道的不同,生意以失败告终,又回到老胡的身边;第四部分(21~23),写老胡在临终前对胡良在生意上的满意和嘱托。 本阅读第(2)题是阅读的典型题,句子(段落)在文中的作用答题方法:分析某一句话 (一段话)在文章中的作用,一般从结构和内容两方面进行分析。 1、结构方面要看句子在文章中的具体位置.句子(段落)在开头的作用:(1)开篇点题;(2)设置悬念,引起下文;(3)总领全文.句子在文章中间的作用:(1)埋伏笔;(2)承上启下;(3)照应上文;(4)为下文 作铺垫.句子(段落)在结尾的作用:(1)总结全文;(2)照应题目或开头,使文章结构严谨。? 2、句子(段落)在内容上的作用,要紧密联系文章中心分析,看表达了怎样的情感,表现出了人物怎样的精神品质或性格特征.尤其注意结尾的抒情议论句还起到点明中心,深化主旨的作用。 一般分析句子(段落)的作用,要把结构和内容上的作用综合起来分析。 (2017宁夏)(三)(14分) 乡宴 (1)停刀落箸,乡宴至美。 (2)在我的老家,管做乡宴的厨师叫“大师傅”,平日里,他们与土地为伍,与粮食蔬菜相伴,并无异于常人之处。只有在喜事场上,他们才被主家以 “天地君亲师”中的“师”称呼,身份便有了些许特殊。 (3)只见“大师傅”马步扎得稳当,一只炒锅盈握在手,翻炒之间尽显如虹气势,“砧板”和“传菜”臂助左右,不敢怠慢。或许,他们不知“八珍”是何烹饪之术,更叫不出几道“满汉全席”中的菜品名号,不论是批切锲斩,还是 煎炒烹炸,全靠代代传续,耳濡目染,他们用娴熟的烹饪技艺制作出富有地方风味的菜肴,灵趣中透出憨鲁,粗粝中带着精细,一如他们性情的折射。 (4)几乎每个村子里都有一名做乡宴的“大师傅”,我们村也有,是我的伯祖父,也就是我的大爷。二堂哥建春结婚的时候,那十六桌酒席 宴就出自他老人家之手。他是长辈,本应到外村请“大师傅”来伺厨的,他不允,说还是由自己做才放心。家人拗不过他,只好答应。 (5)随着建春哥婚期的临近,我似乎闻到了那股浓浓的菜香。 (6)大爷常说,做宴席讲究五个字:质、色、香、味、器,缺一不可。对于食材的质,大爷 向来很在意。俗话说,一方水土一方人,一方人做一方宴,要想做出亲近唇齿的味道,就不能忽视本地食材,因为它们接了我们脚下的地气,还有渗入我们肌体的水气。 (7)按照本地风俗,不管谁家办喜事,本家族人和左邻右舍都要去帮忙。炉灶锅台,杯碟碗筷,刷得纤尘不染,干货菜蔬, 鸡鸭鱼肉,逐一备齐。大爷并不急于过油、走红,而是先吊了一锅清汤。照他的话说,这叫“唱戏的腔,厨师的汤”。厨师没了清汤,做出的菜肴就没有底味,不论是烧、扒,还是炖、焖、煨、汆、涮、烩、熬,味道再好,终究是浮着的。为人处世亦是如此,没了人味,表面功夫做得再好,
(1)已知如图,在 ABCD中,AB = 6,AD = 2,延长 AD到H,使AH =7,对角线AC、BD相交于点O,
联结HO交CD于F,AB于E,则AE长为___3_._5___。
(2)已知如图, ABCD为正方形,过A的一条直线依次
与BD、DC、BC延长线交于点E、F、G,AE = 5,
EF
=
叶儿,刚秀出的高粱穗儿,很结实的谷子尾巴,都在雾中时隐时现。河堤上的绿草叶儿上挂着亮晶晶的露水珠儿,微微颤抖着,对我打着招呼。 田野里根寂静,爷爷漫不经心地哼起歌子来: 一匹马踏破了铁 甲连环 一杆枪杀败了天下好汉 一碗酒消解了三代的冤情 一文钱难住了盖世的英 雄…… 坦荡荡的旷野上缓慢地爬行着爷爷悲壮苍凉的歌声。听着歌声,我感到陡然间长大了不少,童年似乎就消逝在这条灰白的镶着野草的河堤上。 他带着我善找老茅草,老茅草含水少,干得快,牲口也爱吃。爷爷提着一把大镰刀,我捉着一柄小镰刀,在一片茅草前蹲下来。“看我怎么 割。”爷爷示范给我看。他并不认真教我,比画了几下子就低头割他的草去了。他割草的姿势很美,动作富有节奏。我试着割了几下,很累,厌烦了,扔下镰刀,追鸟捉蚂蚱去了。 【不知何时,天上布满了大块的黑云。 我帮着爷爷把草装上车,小车像座小山包一样。大堤弯弯曲曲,刚走出 里把路,黑云就把太阳完全遮住了。天地之间没有了界限,我竟然感到一种莫名的恐惧。回头看爷爷,爷爷的脸木木的,一点表情也没有。 河堤下的庄稼叶子忽然动了起来,但没有声音。河里也有平滑的波浪涌起,同样没有声音。很高很远的地方似乎传来了世上没有的声音,天地之间变成 紫色,还有扑鼻的干草气息、野蒿子的苦味和野菊花幽幽的香气。 在我们的前方,出现了一个黑色的,顶天立地的圆柱,圆柱飞速旋转着,向我们逼过来,紧接着传来沉闷如雷鸣的呼噜声。 “爷爷,那是什么” “风。” 爷爷淡波地说,“使劲拉车吧,孩子。”说着,他弯下了腰。 我们 钻进了风里,听不到什么声音,只感到有两个大巴掌在使劲扇着耳门子,鼓膜嗡嗡地响。堤下的庄稼像接到命令的士兵,一齐倒伏下去。 爷爷双手攥着车把,脊背绷得像一张弓。他的双腿像钉子一样钉在堤上,腿上的肌肉像树根一样条条棱棱地凸起来。风把车上半干不湿的茅草揪出来,扬 起来,小车在哆嗦。爷爷的双腿开始颤抖了,汗水从他背上流下来。】 夕阳不动声色地露出来,河里通红通红,像流动着冷冷的铁水。庄稼慢慢地直起腰。爷爷像一尊青铜塑像一样保持着用力的姿势。 我高呼着:“爷爷,风过去了。” 他慢慢地放下车子,费劲地直起腰,我看到他的手指 都蜷曲着不能伸直了。 风把我们车上的草全卷走了,不、还有一棵草夹在车粱的榫缝里。我把那棵草举着给爷爷看,一根普通的老茅草,也不知是红色还是绿色。 “爷爷,就剩下一棵草了。”我有点懊丧地说。“天黑了,走吧。”爷爷说着,弯腰推起了小车。 我举着那棵草,跟着爷爷走 了一会儿,就把它随手扔在堤下淡黄色的暮色中了。 (选自《萌芽》,有删改) 15、用一句话概括“【 】”之间文字的主要内容。 16、结合短文,概括说说爷爷是一个怎样的人? 17、结合语境,体会作者写爷爷哼“歌子”的作用。 18、“风把我们车上的草全卷走了,不、还有一棵草夹
在车粱的榫缝里。我把那棵草举着给爷爷看,
3、利用平行线分线段成比例定理作图
(1)任意等分线段 (a)三等分一条线段 (b)将一条线段分成 3 :2两部分 (2)作第四比例项
已知线段a,b,c,作线段x,使 x bc a
a
b
c
4、运用平行线分线段成比例定理
也只不过是浮夸之辈。 (8)炉膛中,松柴毕毕剥剥地燃烧着,酱锅里的汤汁上下翻涌,锅底箅丝上的肉慢慢红润起来。大爷一声令下,大家抖擞起精神,火速“备宴”。搅动鸡蛋的嘚嘚声,切葱姜末发出的唰唰声,“粗斩细剁”肋条肉形成的马蹄声,给鲤鱼、光鸡过油响起的噼里啪啦 声……各种声音融汇在一起,抑扬顿挫,和谐悦耳。小院子的花花草草也被这气氛所感染,欢快地摇曳着。 (9)薄暮时分,“备宴”收尾,建春哥和伯父送来糖茶,表示感谢。大家围坐在八仙桌旁,讲古说今,大爷话不多,深邃的眼神让人捉摸不透。晚九点左右,大家散去,大爷斜躺在连 椅上,不一会儿就响起了沉重混沌的鼾声。 (10)第二天,阳光灿烂,天气晴好。唢呐声声,鞭炮齐鸣。建春哥迎来了堂嫂。他们拜天地,拜高堂,夫妻对拜,空气中弥漫着鞭炮炸开花的呛味,非常好闻。另一头,大爷将两碗宽心面下好了,由本家嫂子用红漆木盘端给两位新人。宽心面, 嫩香腆润,每碗一整根,代表一心一意,蕴含美好的寄托。这时,“传菜”的伙计捎话过来,客人已经遵照安排入座,大爷将手勺一挥,宣布开席! (11)宴席有条不紊地进行着。从天刚破晓到日上中天,大爷在“砧板”的配合下,忙而不乱,一口炒锅在手,或翻或转,动作流畅自然。做 完最后一道“四喜丸子”,他长舒一口气,额头沁出细密的汗珠,脸膛泛红,让人感觉很温暖。 (12)送走宾客,伯父安排大家会餐,再次表示感谢。我又尝到了大爷的手艺。大爷多喝了两盅,他说,他记不清做过多少次乡宴了,但这次喜宴是他做得最满意的一次。大家打趣他,说他之前 故意留了一手。他摆摆手说,每次都很用心,但这次感觉不一样,至于啥感觉,一时半会说不清。 (13)许多年过后,我结婚了,“大师傅”是从外庄请来的,因为大爷再也不能做喜宴了,或者说,我永远没有机会品尝他做的菜了。我陪客人入座,一道道菜端上餐桌,菜品用了很多新式调 料,客人推杯换盏,赞不绝口,我却停了一下筷子,忆起大爷,还有他做的乡宴。 (14)那滋味,那么美,是浓浓的亲情,是家的味道。 (选自《人民日报》,有删改) 19.文章第①段有什么作用?说说你的看法。(2分) 答: 20.与第③段“只见‘大师傅’马步扎得稳当,一只炒锅盈握在手, 翻炒之间尽显如虹气势”相照应的句子是? ?。(2分) 21.理解第⑦段“为人处世亦是如此,没了人味,表面功夫做得再好,也只不过是浮夸之辈”这个句子的含义。(2分) 答:? 22.请从修辞手法的角度赏析第⑧段中画线的句子。(2分) 答:? 23 .简要分析第?段画线句描写人物的方法及作用。 (2分) 答: 24.文章结尾段能否删去?为什么?(2分) 答: 25.文章的题目是“乡宴”,开篇却从做乡宴的“大师傅”写起,这离题吗?请结合全文内容说一说。(2分) 答: 代谢:(三)(14分) 19.(2分)开篇点题,揭示文章的内容;统领全篇;奠定全文感情的基调;吸引读者阅读的兴趣。 20.(2分)一口炒锅在手,或翻或转,动作流畅自然。 21.(2分)为人处世如做乡宴,注重本色底味;做人要有人味,一个人如果只注重做表面功夫,他只能是一个浮夸的人。(意思接近即可) 22.(2分)排比、比喻。赏析点:婚宴“备宴”时的热闹、欢快景象;喜宴菜品的丰盛;厨师精湛、 娴熟的烹饪技艺。 23. (2分)神态、肖像描写;满意、放松的心理;大爷的辛劳。 24.(2分)不能。因为结尾段揭示了文章的主题,突出乡村喜宴的美,照应文章的开头;总结全文,升华主题。(从内容和结构两方面考虑) 25.(2分)不离题。开篇大量的内容写做乡宴的“大师傅”,为下文写大 爷做乡宴做铺垫;使文章内容更充实,突出主题。 (2017四川广安)(14分)记叙文阅读 大 风 莫 言 我家后面有一条弯弯曲曲的胶河、沿着高高的河堤向东北方向走七里左右路,就到了一片方圆数千亩的荒草甸子。每年夏天,爷爷都击那儿割草,我爷爷的镰刀磨得快,割草技术高,割下 来的草干净,不拖泥带水。 最早跟爷爷去荒草甸子剖草,是刚过了七岁生日不久的 一天。堤顶是一条灰白的小路,路的两边长满野草,行人的脚压适迫得它们很瑟缩,但依然是生气勃勃的。爷爷的步子轻悄悄的,走得不紧不慢,听不到脚步声。田野里丝线流苏般的玉米缨儿,刀剑般的玉米
