应用2-利用空间向量证明垂直问题
2利用空间向量证明平行垂直关系(学生版)

利用空间向量证明平行垂直关系(讲案)【教学目标】一、方向向量与法向量概念【知识点】1.直线的方向向量:如果表示非零向量a的有向线段所在直线与直线l平行或重合,则称此向量a为直线l的方向向量。
注:(1)在直线上取有向线段表示的向量,或在与它平行的直线上取有向线段表示的向量,均为直线的方向向量。
(2)在解具体立体几何题时,直线的方向向量一般不再叙述而直接应用,在直线上任取两点,所形成的向量即为该直线的方向向量,可参与向量运算或向量的坐标运算。
(3)直线的方向向量是非零向量且不唯一。
⊥,取直线l的方向向量a,则向量a叫做平面α的法向量。
2.平面的法向量:直线l a(注意:平面的法向量是非零向量且不唯一)3.确定平面的法向量的方法(1)直接法:几何体中有具体的直线与平面垂直,只需证明线面垂直,取该垂线的方向向量即得平面的法向量,即观察是否有垂直于平面的向量,若有,则此向量就是法向量。
(2)待定系数法:几何体中没有具体的直线,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:(i )设出平面的法向量为(,,)n x y z =(ii )找出(求出)平面内的两个不共线的向量的坐标a 111(,,)a b c =,222,,)(b a b c =(iii )根据法向量的定义建立关于,,x y z 的方程0n a n b ⎧⋅=⎪⎨⋅=⎪⎩ ;(iv )解方程组,取其中的一个解,即得法向量.由于一个平面的法向量有无数个,故可在代入方程组的解中取一个最简单的作为平面的法向量. 4. 空间位置关系的向量表示12,n n2l 1212//(n n n kn k R ⇔=∈2l ⊥12120n n n n ⊥⇔⋅=n , 的法向量为m l α0n m n m ⊥⇔⋅=α⊥//()n m n km k R ⇔=∈的法向量分别为,n mβ //()n m n km k R ⇔=∈β⊥0n m n m ⊥⇔⋅=【例题讲解】★☆☆例题1.(2020•和平区)若(1A -,0,1),(1B ,4,7)在直线l 上,则直线l 的一个方向向量为( ) A .(1,2,3) B .(1,3,2) C .(2,1,3) D .(3,2,1)★☆☆练习1.已知直线1l 的方向向量(2,,1)m m =,2l 的方向向量1(1,,2)2n =,且21l l ⊥,则(m = )A .8B .8-C .1D .1-★☆☆练习2.直线1l 、2l 的方向向量分别为(1a =,2,2)-,(2b =-,3,2),则( ) A .12//l l B .1l 与2l 相交,但不垂直C .12l l ⊥D .不能确定★☆☆练习3.若直线l 的方向向量为(2v =,1,3),且直线l 过(0A ,y ,3),(1B -,2-,)z 两点.则y = ,z = .★☆☆练习4.已知点(1A ,2-,0)和向量(3,4,6)a =-,||2||AB a =,且AB 与a 方向相反,则点B 坐标为( )A .(7-,6,12)B .(7,10-,12)-C .(7,6-,12)D .(7-,10,12)★☆☆例题2.已知(2AB =,2,1),(4AC =,5,3),则下列向量中是平面ABC 的法向量的是( ) A .(1,2,6)-B .(2-,1,1)C .(1,2-,2)D .(4,2-,1)★☆☆练习1.(2020•聊城)若直线l 的方向向量为m ,平面α的法向量为n ,则能使//l α的是( ) A .(1m =,2,1),(1n =,0,1) B .(0m =,1,0),(0n =,3,0)C .(1m =,2-,3),(2n =-,2,2)D .(0m =,2,1),(1n =-,0,1)-★☆☆练习2.(2020秋•和平区)如图,在单位正方体1111ABCD A B C D -中,以D 为原点,DA ,DC ,1DD 为坐标向量建立空间直角坐标系,则平面11A BC 的法向量是( )A .(1,1,1)B .(1-,1,1)C .(1,1-,1)D .(1,1,1)-★★☆练习3.(2020•辽宁)已知平面α上三点(3A ,2,1),(1B -,2,0),(4C ,2-,1)-,则平面α的一个法向量为( )A .(4,9-,16)-B .(4,9,16)-C .(16-,9,4)-D .(16,9,4)-★☆☆例题3.直线l 的方向向量(1a =,3-,5),平面α的法向量(1n =-,3,5)-,则有( ) A .//l α B .l α⊥C .l 与α斜交D .l α⊂或//l α★★☆练习1.(2019•杨浦区)空间直角坐标系中,两平面α与β分别以1(2n =,1,1)与2(0n =,2,1)为其法向量,若l αβ=,则直线l 的一个方向向量为 (写出一个方向向量的坐标)★☆☆练习2.若直线l 的方向向量为(4,2,)m ,平面α的法向量为(2,1,1)-,且l α⊥,则m = . ★☆☆练习3.(2020•菏泽)设平面α的法向量为(1,2-,)λ,平面β的法向量为(2,μ,4),若//αβ,则(λμ+= ) A .2 B .4C .2-D .4-二、利用空间向量证明平行关系【知识点】(1)线线平行:若空间不重合两条直线,a b 的方向向量分别为,a b ,则////a b a b ⇔⇔()a b R λλ=∈; (2)线面平行:若直线a 的方向向量为a ,平面α的法向量为n ,且a α⊄,则////a a αα⇔0a n a n ⇔⊥⇔⋅=;(3)面面平行:若空间不重合的两个平面,αβ的法向量分别为a b ,,则////a b αβ⇔⇔a b λ=.【例题讲解】★☆☆例题1.如图,在长方体1111OAEB O A E B -中,||3OA =,||4OB =,1||2OO =,点在棱1AA 上,且12AP PA =,点S 在棱1BB 上,且12SB BS =,点Q 、R 分别是11O B 、AE 的中点,求证://PQ RS .★☆☆例题2.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .建立适当的空间直角坐标系,利用空间向量方法解答以下问题: 求证://PA 平面EDB .★☆☆练习1. 如图,在长方体1111ABCD A B C D -中,12AD AA ==,6AB =,E 、F 分别为11A D 、11D C 的中点.分别以DA 、DC 、1DD 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系D xyz -. (1)求点E 、F 的坐标; (2)求证:1//EF ACD 平面.P★★☆练习2. 如图,在四棱锥P ABCD -中,PB ⊥平面ABCD ,AB AD ⊥,//AB CD ,且1AB =,2AD CD ==,E 在线段PD 上.若E 是PD 的中点,试证明://AE 平面PBC .★☆☆例题3.如图,在正方体1111ABCD A B C D -中,求证:平面11//AB D 平面1BDC .★☆☆练习1. 已知正方体1111ABCD A B C D -的棱长为2,E ,F 分别是1BB ,1DD 的中点,求证: (1)1//FC 平面ADE ; (2)平面//ADE 平面11B C F .★★☆练习2. 如图,已知棱长为4的正方体1111ABCD A B C D -中,M ,N ,E ,F 分别是棱11A D ,11A B ,11D C ,11B C 的中点,求证:平面//AMN 平面EFBD .三、利用空间向量证明垂直关系【知识点】(1)线线垂直:设直线,的方向向量分别为,,则要证明,只需证明,即。
32(二)向量方法证明空间线面垂直关系

学习目标 1.能用向量法判断一些简单线线、线面、面面垂直关系.2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.3.能用向量方法证明空间线面垂直关系的有关定理.知识点一 向量法判断线线垂直思考 若直线l 1的方向向量为μ1=(1,3,2),直线l 2的方向向量为μ2=(1,-1,1),那么两直线是否垂直?用向量法判断两条直线垂直的一般方法是什么?答案 l 1与l 2垂直,因为μ1·μ2=1-3+2=0,所以μ1⊥μ2,又μ1,μ2是两直线的方向向量,所以l 1与l 2垂直.判断两条直线是否垂直的方法:(1)在两直线上分别取两点A 、B 与C 、D ,计算向量AB →与CD →的坐标,若AB →·CD →=0,则两直线垂直,否则不垂直.(2)判断两直线的方向向量的数量积是否为零,若数量积为零,则两直线垂直,否则不垂直. 梳理 设直线l 的方向向量为a =(a 1,a 2,a 3),直线m 的方向向量为b =(b 1,b 2,b 3),则l ⊥m ⇔a·b =0⇔a 1b 1+a 2b 2+a 3b 3=0. 知识点二 向量法判断线面垂直思考 若直线l 的方向向量为μ1=⎝⎛⎭⎫2,43,1,平面α的法向量为μ2=⎝⎛⎭⎫3,2,32,则直线l 与平面α的位置关系是怎样的?如何用向量法判断直线与平面的位置关系?答案 垂直,因为μ1=23μ2,所以μ1∥μ2,即直线的方向向量与平面的法向量平行,所以直线l 与平面α垂直.判断直线与平面的位置关系的方法:(1)直线l 的方向向量与平面α的法向量共线⇒l ⊥α.(2)直线的方向向量与平面的法向量垂直⇒直线与平面平行或直线在平面内. (3)直线l 的方向向量与平面α内的两相交直线的方向向量垂直⇒l ⊥α.梳理 设直线l 的方向向量a =(a 1,b 1,c 1),平面α的法向量μ=(a 2,b 2,c 2),则l ⊥α⇔a ∥μ⇔a =k μ(k ∈R ).知识点三 向量法判断面面垂直思考 平面α,β的法向量分别为μ1=(x 1,y 1,z 1),μ2=(x 2,y 2,z 2),用向量坐标法表示两平面α,β垂直的关系式是什么? 答案 x 1x 2+y 1y 2+z 1z 2=0.梳理 若平面α的法向量为μ=(a 1,b 1,c 1),平面β的法向量为ν=(a 2,b 2,c 2),则α⊥β⇔μ⊥ν⇔μ·ν=0⇔a 1a 2+b 1b 2+c 1c 2=0.类型一 证明线线垂直例1 已知正三棱柱ABC -A 1B 1C 1的各棱长都为1,M 是底面上BC 边的中点,N 是侧棱CC 1上的点,且CN =14CC 1.求证:AB 1⊥MN .证明 设AB 中点为O ,作OO 1∥AA 1.以O 为坐标原点,OB 为x 轴,OC 为y 轴,OO 1为z 轴建立如图所示的空间直角坐标系.由已知得A ⎝⎛⎭⎫-12,0,0,B ⎝⎛⎭⎫12,0,0,C ⎝⎛⎭⎫0,32,0,N ⎝⎛⎭⎫0,32,14,B 1⎝⎛⎭⎫12,0,1, ∵M 为BC 中点, ∴M ⎝⎛⎭⎫14,34,0.∴MN →=⎝⎛⎭⎫-14,34,14,AB 1→=(1,0,1),∴MN →·AB 1→=-14+0+14=0.∴MN →⊥AB 1→, ∴AB 1⊥MN .反思与感悟 证明两直线垂直的基本步骤:建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.跟踪训练1 如图,在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AB =5,AA 1=4,求证:AC ⊥BC 1.证明 ∵直三棱柱ABC -A 1B 1C 1底面三边长AC =3,BC =4,AB =5, ∴AC 、BC 、C 1C 两两垂直.如图,以C 为坐标原点,CA 、CB 、CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系.则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0), ∵AC →=(-3,0,0),BC 1→=(0,-4,4), ∴AC →·BC 1→=0.∴AC ⊥BC 1. 类型二 证明线面垂直例2 如图所示,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .证明 如图所示,取BC 的中点O ,连接AO .因为△ABC 为正三角形,所以AO ⊥BC .因为在正三棱柱ABC -A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1, 所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1,以O 为原点,以OB →,OO 1→,OA →分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则B (1,0,0),D (-1,1,0),A 1(0,2,3),A (0,0,3),B 1(1,2,0). 所以AB 1→=(1,2,-3),BA 1→=(-1,2,3),BD →=(-2,1,0). 因为AB 1→·BA 1→=1×(-1)+2×2+(-3)×3=0. AB 1→·BD →=1×(-2)+2×1+(-3)×0=0.所以AB 1→⊥BA 1→,AB 1→⊥BD →,即AB 1⊥BA 1,AB 1⊥BD . 又因为BA 1∩BD =B ,所以AB 1⊥平面A 1BD . 反思与感悟 用坐标法证明线面垂直的方法及步骤 方法一:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示.(3)找出平面内两条相交直线,并用坐标表示它们的方向向量. (4)分别计算两组向量的数量积,得到数量积为0. 方法二:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示. (3)求出平面的法向量.(4)判断直线的方向向量与平面的法向量平行.跟踪训练2 如图,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,点P 为DD 1的中点.求证:直线PB 1⊥平面P AC .证明 如图建系,C (1,0,0),A (0,1,0),P (0,0,1),B 1(1,1,2),PC →=(1,0,-1),P A →=(0,1,-1),PB 1→=(1,1,1),B 1C →=(0,-1,-2),B 1A →=(-1,0,-2).PB 1→·PC →=(1,1,1)·(1,0,-1)=0, 所以PB 1→⊥PC →,即PB 1⊥PC .又PB 1→·P A →=(1,1,1)·(0,1,-1)=0, 所以PB 1→⊥P A →,即PB 1⊥P A .又P A ∩PC =P ,所以PB 1⊥平面P AC . 类型三 证明面面垂直例3 在三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,AB ⊥BC ,AB =BC =2,AA 1=1,E 为BB 1的中点,求证:平面AEC 1⊥平面AA 1C 1C .证明 由题意知直线AB ,BC ,B 1B 两两垂直,以点B 为原点,分别以BA ,BC ,BB 1所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系,则A (2,0,0),A 1(2,0,1),C (0,2,0),C 1(0,2,1),E (0,0,12),故AA 1→=(0,0,1),AC →=(-2,2,0),AC 1→=(-2,2,1),AE →=(-2,0,12).设平面AA 1C 1C 的法向量为n 1=(x ,y ,z ), 则⎩⎪⎨⎪⎧n 1·AA 1→=0,n 1·AC →=0,即⎩⎪⎨⎪⎧z =0,-2x +2y =0.令x =1,得y =1,故n 1=(1,1,0). 设平面AEC 1的法向量为n 2=(a ,b ,c ), 则⎩⎪⎨⎪⎧ n 2·AC 1→=0,n 2·AE →=0,即⎩⎪⎨⎪⎧-2a +2b +c =0,-2a +12c =0. 令c =4,得a =1,b =-1,故n 2=(1,-1,4). 因为n 1·n 2=1×1+1×(-1)+0×4=0, 所以n 1⊥n 2.所以平面AEC 1⊥平面AA 1C 1C . 反思与感悟 证明面面垂直的两种方法(1)常规法:利用面面垂直的判定定理转化为线面垂直、线线垂直去证明.(2)向量法:证明两个平面的法向量互相垂直.跟踪训练3 在四面体ABCD 中,AB ⊥平面BCD ,BC =CD ,∠BCD =90°,∠ADB =30°,E 、F 分别是AC 、AD 的中点,求证:平面BEF ⊥平面ABC .证明 以B 为原点建立如图所示的空间直角坐标系,设A (0,0,a ),则易得B (0,0,0),C ⎝⎛⎭⎫32a ,32a ,0,D (0,3a ,0),E ⎝⎛⎭⎫34a ,34a ,a 2,F (0,32a ,a 2),故AB →=(0,0,-a ),BC →=⎝⎛⎭⎫32a ,32a ,0.设平面ABC 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·AB →=0,n 1·BC →=0,即⎩⎪⎨⎪⎧-az 1=0,x 1+y 1=0,取x 1=1,∴n 1=(1,-1,0)为平面ABC 的一个法向量. 设n 2=(x 2,y 2,z 2)为平面BEF 的一个法向量, 同理可得n 2=(1,1,-3).∵n 1·n 2=(1,-1,0)·(1,1,-3)=0, ∴平面BEF ⊥平面ABC .1.下列命题中,正确命题的个数为( )①若n 1,n 2分别是平面α,β的法向量,则n 1∥n 2⇔α∥β; ②若n 1,n 2分别是平面α,β的法向量,则α⊥β ⇔ n 1·n 2=0; ③若n 是平面α的法向量,a 与平面α平行,则n ·a =0; ④若两个平面的法向量不垂直,则这两个平面不垂直. A.1 B.2 C.3 D.4 答案 C解析 ①中平面α,β可能平行,也可能重合,结合平面法向量的概念,易知②③④正确. 2.已知两直线的方向向量为a ,b ,则下列选项中能使两直线垂直的为( ) A.a =(1,0,0),b =(-3,0,0) B.a =(0,1,0),b =(1,0,1) C.a =(0,1,-1),b =(0,-1,1)D.a=(1,0,0),b=(-1,0,0)答案 B解析因为a=(0,1,0),b=(1,0,1),所以a·b=0×1+1×0+0×1=0,所以a⊥b,故选B.3.若直线l的方向向量为a=(1,0,2),平面α的法向量为μ=(-2,0,-4),则()A.l∥αB.l⊥αC.l⊂αD.l与α斜交答案 B解析∵a∥μ,∴l⊥α.4.平面α的一个法向量为m=(1,2,0),平面β的一个法向量为n=(2,-1,0),则平面α与平面β的位置关系是()A.平行B.相交但不垂直C.垂直D.不能确定答案 C解析∵(1,2,0)·(2,-1,0)=0,∴两法向量垂直,从而两平面垂直.5.已知平面α与平面β垂直,若平面α与平面β的法向量分别为μ=(-1,0,5),ν=(t,5,1),则t的值为________.答案 5解析∵平面α与平面β垂直,∴平面α的法向量μ与平面β的法向量ν垂直,∴μ·ν=0,即(-1)×t+0×5+5×1=0,解得t=5.空间垂直关系的解决策略40分钟课时作业一、选择题1.设直线l 1,l 2的方向向量分别为a =(-2,2,1),b =(3,-2,m ),若l 1⊥l 2,则m 等于( ) A.-2 B.2 C.6 D.10 答案 D解析 因为a ⊥b ,故a ·b =0,即-2×3+2×(-2)+m =0,解得m =10.2.若平面α,β的法向量分别为a =(-1,2,4),b =(x ,-1,-2),并且α⊥β,则x 的值为( )A.10B.-10C.12D.-12答案 B解析 因为α⊥β,则它们的法向量也互相垂直, 所以a ·b =(-1,2,4)·(x ,-1,-2)=0, 解得x =-10.3.已知点A (0,1,0),B (-1,0,-1),C (2,1,1),P (x ,0,z ),若P A ⊥平面ABC ,则点P 的坐标为( )A.(1,0,-2)B.(1,0,2)C.(-1,0,2)D.(2,0,-1) 答案 C解析 由题意知AB →=(-1,-1,-1),AC →=(2,0,1),AP →=(x ,-1,z ),又P A ⊥平面ABC ,所以有AB →·AP →=(-1,-1,-1)·(x ,-1,z )=0,得-x +1-z =0, ① AC →·AP →=(2,0,1)·(x ,-1,z )=0,得2x +z =0,②联立①②得x =-1,z =2,故点P 的坐标为(-1,0,2).4.在正方体ABCD -A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( ) A.AC B.BD C.A 1D D.A 1A 答案 B解析 建立如图所示的空间直角坐标系.设正方体的棱长为1,则A (0,1,0),B (1,1,0),C (1,0,0),D (0,0,0),A 1(0,1,1),C 1(1,0,1),E ⎝⎛⎭⎫12,12,1,∴CE →=⎝⎛⎭⎫-12,12,1,AC →=(1,-1,0), BD →=(-1,-1,0),A 1D →=(0,-1,-1),A 1A →=(0,0,-1), ∵CE →·BD →=(-1)×(-12)+(-1)×12+0×1=0,∴CE ⊥BD .5.若平面α,β垂直,则下面可以作为这两个平面的法向量的是( ) A.n 1=(1,2,1),n 2=(-3,1,1) B.n 1=(1,1,2),n 2=(-2,1,1) C.n 1=(1,1,1),n 2=(-1,2,1) D.n 1=(1,2,1),n 2=(0,-2,-2) 答案 A解析 ∵1×(-3)+2×1+1×1=0, ∴n 1·n 2=0,故选A.6.两平面α,β的法向量分别为μ=(3,-1,z ),v =(-2,-y ,1),若α⊥β,则y +z 的值是( )A.-3B.6C.-6D.-12 答案 B解析 α⊥β⇒μ·v =0⇒-6+y +z =0,即y +z =6. 二、填空题7.在三棱锥S -ABC 中,∠SAB =∠SAC =∠ACB =90°,AC =2,BC =13,SB =29,则异面直线SC 与BC 是否垂直________.(填“是”或“否”) 答案 是解析 如图,以A 为原点,AB ,AS 分别为y 轴,z 轴建立空间直角坐标系,则由AC =2,BC =13,SB =29, 得B (0,17,0),S (0,0,23),C ⎝ ⎛⎭⎪⎫21317,417,0, SC →=⎝⎛⎭⎪⎫21317,417,-23,CB →=⎝⎛⎭⎪⎫-21317,1317,0. 因为SC →·CB →=0,所以SC ⊥BC .8.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB →=(2,-1,-4),AD →=(4,2,0),AP →=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP →是平面ABCD 的法向量;④AP →∥BD →.其中正确的是________.(填序号) 答案 ①②③解析 ∵AP →·AB →=(-1,2,-1)·(2,-1,-4)=-1×2+2×(-1)+(-1)×(-4)=0,∴AP ⊥AB ,即①正确;∵AP →·AD →=(-1,2,-1)·(4,2,0)=(-1)×4+2×2+(-1)×0=0,∴AP ⊥AD ,即②正确; 又∵AB ∩AD =A , ∴AP ⊥平面ABCD ,即AP →是平面ABCD 的一个法向量,即③正确; ∵AP →是平面ABCD 的法向量, ∴AP →⊥BD →,即④不正确.9.在空间直角坐标系Oxyz 中,已知点P (2cos x +1,2cos 2x +2,0)和点Q (cos x ,-1,3),其中x ∈[0,π].若直线OP 与直线OQ 垂直,则x 的值为________. 答案 π2或π3解析 由题意得OP →⊥OQ →,∴cos x ·(2cos x +1)-(2cos 2x +2)=0. ∴2cos 2x -cos x =0, ∴cos x =0或cos x =12.又x ∈[0,π], ∴x =π2或x =π3.10.在△ABC 中,A (1,-2,-1),B (0,-3,1),C (2,-2,1).若向量n 与平面ABC 垂直,且|n |=21,则n 的坐标为________________. 答案 (-2,4,1)或(2,-4,-1)解析 据题意,得AB →=(-1,-1,2),AC →=(1,0,2).设n =(x ,y ,z ),∵n 与平面ABC 垂直,∴⎩⎪⎨⎪⎧ n ·AB →=0,n ·AC →=0,即⎩⎪⎨⎪⎧ -x -y +2z =0,x +2z =0,可得⎩⎪⎨⎪⎧y =4z ,y =-2x . ∵|n |=21,∴x 2+y 2+z 2=21,解得y =4或y =-4.当y =4时,x =-2,z =1;当y =-4时,x =2,z =-1.三、解答题11.如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,AB =4,BC =3,AD =5,∠DAB =∠ABC =90°,E 是CD 的中点.证明:CD ⊥平面P AE .证明 如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.设P A =h ,则相关各点的坐标为A (0,0,0),B (4,0,0),C (4,3,0),D (0,5,0),E (2,4,0),P (0,0,h ).易知CD →=(-4,2,0),AE →=(2,4,0),AP →=(0,0,h ).因为CD →·AE →=-8+8+0=0,CD →·AP →=0,所以CD ⊥AE ,CD ⊥AP ,而AP ,AE 是平面P AE 内的两条相交直线,所以CD ⊥平面P AE .12.如图,在四棱锥P -ABCD 中,底面ABCD 是矩形,P A ⊥底面ABCD ,P A =AB =1,AD =3,点F 是PB 的中点,点E 在边BC 上移动.求证:无论点E 在BC 边的何处,都有PE ⊥AF .证明 建立如图所示空间直角坐标系,则P (0,0,1),B (0,1,0),F ⎝⎛⎭⎫0,12,12,D ()3,0,0,设BE =x (0≤x ≤3),则E (x ,1,0),PE →·AF →=(x ,1,-1)·⎝⎛⎭⎫0,12,12=0, 所以x ∈[0, 3 ]时都有PE ⊥AF ,即无论点E 在BC 边的何处,都有PE ⊥AF .13.已知正方体ABCDA 1B 1C 1D 1中,E 为棱CC 1上的动点.(1)求证:A 1E ⊥BD ;(2)若平面A 1BD ⊥平面EBD ,试确定E 点的位置.(1)证明 以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.设正方体棱长为a ,则 A (a ,0,0),B (a ,a ,0),C (0,a ,0),A 1(a ,0,a ),C 1(0,a ,a ).设E (0,a ,e ) (0≤e ≤a ),A 1E →=(-a ,a ,e -a ),BD →=(-a ,-a ,0),A 1E →·BD →=a 2-a 2+(e -a )·0=0,∴A 1E →⊥BD →,即A 1E ⊥BD .(2)解 设平面A 1BD ,平面EBD 的法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2). ∵DB →=(a ,a ,0),DA 1→=(a ,0,a ),DE →=(0,a ,e ),∴⎩⎪⎨⎪⎧ ax 1+ay 1=0,ax 1+az 1=0,⎩⎪⎨⎪⎧ ax 2+ay 2=0,ay 2+ez 2=0. 取x 1=x 2=1,得n 1=(1,-1,-1),n 2=(1,-1,a e), 由平面A 1BD ⊥平面EBD 得n 1⊥n 2,∴2-a e =0,即e =a 2. ∴当E 为CC 1的中点时,平面A 1BD ⊥平面EBD .。
空间向量的应用-证明平行与垂直

∴MN⊥n, 又∵MN⊄平面 A1BD,∴MN∥平面 A1BD.
→
1 → 1 → 方法二:∵MN=C1N-C1M=2C1B1-2C1C
→ → → → 1 → 1 → =2(D1A1-D1D)=2DA1,
∴MN∥DA1,又∵MN⊄平面 A1BD. ∴MN∥平面 A1BD.
[点评与警示] 证明线面平行可以用几何法,也可以用向 量法.用向量法的关键在于构造向量并用共线向量定理或共面
→ → → → →
∴DM⊥PB,即DM⊥PB. 又∵PA∩PB=P,∴DM⊥平面PAB, ∵DM⊂ 平面PAD.∴平面PAD⊥平面PAB.
→
[点评与警示] 用向量的方法解决垂直问题即几何问题代
数化,这种方法降低了思维的抽象性,使很多思维量较大的证
明与计算简单化,突出了向量方法的优点.
1.用向量解决立体几何问题时,首先要选择恰当的基 向量,然后将立体几何中的平行、垂直、距离等问题转化为 向量的运算, ①证明线线平行就利用 a∥b(b≠0)⇔a=λb; ② 证明线线垂直,就利用 a⊥b⇔a· b=0;③在求立体几何中线 段的长度时,就利用|a|2=a2 来求;④求角度时就用 cosθ= a· b . |a||b|
所以D1F⊥面AED.
又因为D1F⊂面A1FD1,所以面AED⊥面A1FD1.
[点评与警示 ] 用空间坐标运算证明 “ 面面垂直 ” ,一般
先求出其中一个平面的一个法向量,然后证明它垂直于另一个
平面的法向量.因为本例有(1)、(2)作铺垫,所以直接利用其结 果便可.
在正方形 ABCD - A1B1C1D1 中, E 、 F 分别是 BB1 、 CD 的中
连接EO.
因为底面ABCD是正方形,所以点O是AC的中点.
专题08 利用空间向量证明平行、垂直(解析版)

2020年高考数学立体几何突破性讲练08利用空间向量证明平行、垂直一、考点传真:能用向量语言表述线线、线面、面面的平行和垂直关系二、知识点梳理:证明平行、垂直问题的思路(1)恰当建立空间直角坐标系,准确表示各点与相关向量的坐标,是运用向量法证明平行和垂直的关键.(2)证明直线与平面平行,只需证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,或证直线的方向向量与平面内某直线的方向向量平行,然后说明直线在平面外即可.这样就把几何的证明问题转化为向量运算.3其一证明直线与直线垂直,只需要证明两条直线的方向向量垂直;其二证明线面垂直,只需证明直线的方向向量与平面内不共线的两个向量垂直即可,当然,也可证直线的方向向量与平面的法向量平行;其三证明面面垂直:①证明两平面的法向量互相垂直;②利用面面垂直的判定定理,只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可.三、例题:例1. (2019江苏卷)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.【解析】证明:(1)因为D,E分别为BC,AC的中点,所以ED∥AB.在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A 1B 1∥ED .又因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1, 所以A 1B 1∥平面DEC 1.(2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC . 因为三棱柱ABC-A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC . 又因为BE ⊂平面ABC ,所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C , 所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BE ⊥C 1E .例2.(2016年北京卷) 如图,在四棱锥中,平面PAD ⊥平面,,,,,,(1)求证:平面;(2)求直线与平面所成角的正弦值;(3)在棱上是否存在点,使得平面?若存在,求的值;若不存在,说明理由.【解析】(1)∵面PAD面ABCD AD =,面PAD ⊥面ABCD ,∵AB ⊥AD ,AB ⊂面ABCD ,∴AB ⊥面PAD ,P ABCD -ABCD PA PD ⊥PA PD =AB AD ⊥1AB =2AD =AC CD ==PD ⊥PAB PB PCD PA M //BM PCD AMAP∵PD ⊂面PAD , ∴AB ⊥PD , 又PD ⊥PA ,∴PD ⊥面PAB , (2)取AD 中点为O ,连结CO ,PO ,∵CD AC == ∴CO ⊥AD , ∵PA PD =, ∴PO ⊥AD ,以O 为原点,如图建系易知(001)P ,,,(110)B ,,,(010)D -,,,(200)C ,,,则(111)PB =-,,,(011)PD =--,,,(201)PC =-,,,(210)CD =--,,, 设n 为面PDC 的法向量,令00(,1)n x y =,.011,120n PD n n PC ⎧⋅=⎪⎛⎫⇒=-⎨⎪⎝⎭⋅=⎪⎩,,则PB 与面PCD 夹角θ有,sin cos ,1n PB n PB n PBθ⋅=<>== (3)假设存在M 点使得BM ∥面PCD , 设AMAPλ=,()0,','M y z , 由(2)知()0,1,0A ,()0,0,1P ,()0,1,1AP =-,()1,1,0B ,()0,'1,'AM y z =- 有()0,1,AM AP M λλλ=⇒- ∴()1,,BM λλ=--∵BM ∥面PCD ,n 为PCD 的法向量, ∴0BM n ⋅=,即102λλ-++=,∴1=4λ∴综上,存在M 点,即当14AM AP =时,M 点即为所求. 例3.(2011安徽)如图,ABCDEFG 为多面体,平面ABED 与平面AGFD 垂直,点O 在线段AD 上,1,2,OA OD ==OAB ∆,OAC ∆,ODE ∆,ODF ∆都是正三角形. (Ⅰ)证明直线BC ∥EF ; (Ⅱ)求棱锥F OBED -的体积.【解析】(Ⅰ)(综合法)证明:设G 是线段DA 与EB 延长线的交点. 由于OAB ∆与ODE∆都是正三角形,所以OB ∥DE 21,OG=OD=2, 同理,设G '是线段DA 与线段FC 延长线的交点,有.2=='OD G O 又由于G 和G '都在线段DA 的延长线上,所以G 与G '重合.在GED ∆和GFD 中,由OB ∥DE 21和OC ∥DF 21,可知B 和C 分别是GE 和GF 的中点,所以BC 是GEF ∆的中位线,故BC ∥EF .(向量法)过点F 作AD FQ ⊥,交AD 于点Q ,连QE ,由平面ABED ⊥平面ADFC ,知FQ ⊥平面ABED ,以Q 为坐标原点,QE 为x 轴正向,QD 为y 轴正向,QF 为z 轴正向,建立如图所示空间直角坐标系. 由条件知).23,23,0(),0,23,23(),3,0,0(),0,0,3(--C B F E则有33(,0,),(3,0,BC EF =-=- 所以,2=即得BC ∥EF .(Ⅱ)由OB=1,OE=2,23,60=︒=∠EOB S EOB 知,而O E D ∆是边长为2的正三角形,故.3=OED S 所以.233=+=OED EOB OBED S S S过点F 作FQ ⊥AD ,交AD 于点Q ,由平面ABED ⊥平面ACFD 知,FQ 就是四棱锥F —OBED 的高,且FQ=3,所以.2331=⋅=-OBED OBED F S FQ V 例4.(2011江苏)如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB AD =,BAD ∠=60°,E 、F 分别是AP 、AD 的中点. 求证:(Ⅰ)直线EF ∥平面PCD ;(Ⅱ)平面BEF ⊥平面PAD .【证明】(Ⅰ)在△PAD 中,因为E 、F 分别为AP ,AD 的中点,所以EF//PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD ,所以直线EF//平面PCD .(Ⅱ)连结DB ,因为AB=AD ,∠BAD=60°,所以ABD ∆为正三角形,因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF ⊂平面ABCD ,平面PAD 平面ABCD=AD ,所以BF ⊥平面PAD .又因为BF ⊂平面BEF ,所以平面BEF ⊥平面PAD .例5.(2010广东)如图,¼AEC 是半径为a 的半圆,AC 为直径,点E 为»AC 的中点,点B 和点C 为线段AD 的三等分点,平面AEC 外一点F 满足FB FD ==,EF =.(Ⅰ)证明:EB FD ⊥;(Ⅱ)已知点,Q R 为线段,FE FB 上的点,23FQ FE =,23FR FB =,求平面BED 与平面RQD 所成二面角的正弦值.【证明】:(Ⅰ)连结CF ,因为¼AEC 是半径为a 的半圆,AC 为直径,点E 为»AC 的中点,所以EB AC ⊥.在RT BCE ∆中,EC ===.在BDF ∆中,BF DF ==,BDF ∆为等腰三角形, 且点C 是底边BD 的中点,故CF BD ⊥.在CEF ∆中,222222)(2)6CE CF a a EF +=+==,所以CEF ∆为Rt ∆,且CF EC ⊥.因为CF BD ⊥,CF EC ⊥,且CE BD C =I ,所以CF ⊥平面BED , 而EB ⊂平面BED ,CF EB ∴⊥.因为EB AC ⊥,EB CF ⊥,且AC CF C =I ,所以EB ⊥平面BDF , 而FD ⊂平面BDF ,EB FD ∴⊥.(Ⅱ)设平面BED 与平面RQD 的交线为DG .由23FQ FE =,23FR FB =,知//QR EB . 而EB ⊂平面BDE ,∴//QR 平面BDE , 而平面BDE I 平面RQD = DG , ∴////QR DG EB .由(Ⅰ)知,BE ⊥平面BDF ,∴DG ⊥平面BDF , 而,DR DB ⊂平面BDF ,∴DG DR ⊥,DG DQ ⊥, ∴RDB ∠是平面BED 与平面RQD 所成二面角的平面角. 在Rt BCF ∆中,2CF a ===,sin FC RBD BF ∠===cos RBD ∠==. 在BDR ∆中,由23FR FB =知,133BR FB ==,由余弦定理得,RD== 由正弦定理得,sin sin BR RD RDB RBD=∠∠,即332sin RDB =∠,sin RDB ∠=故平面BED 与平面RQD 所成二面角的正弦值为29.为GC 的中点,FO =3,且FO ⊥平面ABCD .(1)求证:AE ∥平面BCF ; (2)求证:CF ⊥平面AEF .【解析】证明 取BC 中点H ,连接OH ,则OH ∥BD ,又四边形ABCD 为正方形, ∴AC ⊥BD ,∴OH ⊥AC ,故以O 为原点,建立如图所示的直角坐标系,则A (3,0,0),C (-1,0,0),D (1,-2,0),F (0,0,3),B (1,2,0).BC →=(-2,-2,0),CF →=(1,0,3),BF →=(-1,-2,3). (1)设平面BCF 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·BC →=0,n ·CF →=0,即⎩⎨⎧-2x -2y =0,x +3z =0,取z =1,得n =(-3,3,1). 又四边形BDEF 为平行四边形, ∴DE →=BF →=(-1,-2,3), ∴AE →=AD →+DE →=BC →+BF →=(-2,-2,0)+(-1,-2,3)=(-3,-4,3), ∴AE →·n =33-43+3=0,∴AE →⊥n , 又AE ⊄平面BCF ,∴AE ∥平面BCF .(2)AF →=(-3,0,3),∴CF →·AF →=-3+3=0,CF →·AE →=-3+3=0, ∴CF →⊥AF →,CF →⊥AE →, 即CF ⊥AF ,CF ⊥AE , 又AE ∩AF =A , AE ,AF ⊂平面AEF , ∴CF ⊥平面AEF .2.如图所示,在直三棱柱ABC -A 1B 1C 1中,侧面AA 1C 1C 和侧面AA 1B 1B 都是正方形且互相垂直,M 为AA 1的中点,N 为BC 1的中点.求证:(1)MN ∥平面A 1B 1C 1; (2)平面MBC 1⊥平面BB 1C 1C .【解析】证明 由题意知AA 1,AB ,AC 两两垂直,以A 为坐标原点建立如图所示的空间直角坐标系.不妨设正方形AA 1C 1C 的边长为2,则A (0,0,0),A 1(2,0,0),B (0,2,0),B 1(2,2,0),C (0,0,2),C 1(2,0,2),M (1,0,0),N (1,1,1).(1)因为几何体是直三棱柱,所以侧棱AA 1⊥底面A 1B 1C 1.因为AA 1→=(2,0,0),MN →=(0,1,1),所以MN →·AA 1→=0,即MN →⊥AA 1→.MN ⊄平面A 1B 1C 1,故MN ∥平面A 1B 1C 1.(2)设平面MBC 1与平面BB 1C 1C 的法向量分别为 n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2). 因为MB →=(-1,2,0),MC 1→=(1,0,2), 所以⎩⎪⎨⎪⎧n 1·MB →=0,n 1·MC 1→=0,即⎩⎪⎨⎪⎧-x 1+2y 1=0,x 1+2z 1=0,,令x 1=2,则平面MBC 1的一个法向量为n 1=(2,1,-1).同理可得平面BB 1C 1C 的一个法向量为n 2=(0,1,1).因为n 1·n 2=2×0+1×1+(-1)×1=0,所以n 1⊥n 2,所以平面MBC 1⊥平面BB 1C 1C . 3.如图,在多面体ABCDEF 中,底面ABCD 是边长为2的菱形,∠BAD =60°,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,DE =2,M 为线段BF 的中点.(1)求M 到平面DEC 的距离及三棱锥M -CDE 的体积; (2)求证:DM ⊥平面ACE .【解析】(1)设AC ∩BD =O ,以O 为原点,OB 为x 轴,OC 为y 轴,过O 作平面ABCD 的垂线为z 轴,建立空间直角坐标系,则C (0,3,0),D (-1,0,0),E (-1,0,2),M (1,0,1), DE →=(0,0,2),DC →=(1,3,0),DM →=(2,0,1), ∵DE →·DC →=0, ∴DE ⊥DC ,∴S △DEC =12×DE ×DC =12×2×2=2,设平面DEC 的法向量n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·DE →=2z =0,n ·DC →=x +3y =0,取x =3,得n =(3,-1,0),∴M 到平面DEC 的距离h =|DM →·n ||n |=233+1=3,∴三棱锥M -CDE 的体积V =13×S △CDE ×h =13×2×3=233.(2)证明:A (0,-3,0),AC →=(0,23,0),AE →=(-1,3,2), AC →·DM →=0,AE →·DM →=-2+2=0, ∴AC ⊥DM ,AE ⊥DM ,∵AC ∩AE =A ,∴DM ⊥平面ACE .4.如图,在四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形,侧面P AD ⊥底面ABCD ,且P A =PD =22AD ,设E ,F 分别为PC ,BD 的中点.(1)求证:EF ∥平面P AD ; (2)求证:平面P AB ⊥平面PDC .【解析】证明 (1)如图,取AD 的中点O ,连接OP ,OF .因为P A =PD ,所以PO ⊥AD .因为侧面P AD ⊥底面ABCD ,平面P AD ∩平面ABCD =AD ,PO ⊂平面P AD , 所以PO ⊥平面ABCD .又O ,F 分别为AD ,BD 的中点, 所以OF ∥AB .又ABCD 是正方形,所以OF ⊥AD . 因为P A =PD =22AD , 所以P A ⊥PD ,OP =OA =a2.以O 为原点,OA ,OF ,OP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系, 则A ⎝⎛⎭⎫a 2,0,0,F ⎝⎛⎭⎫0,a 2,0,D ⎝⎛⎭⎫-a2,0,0, P ⎝⎛⎭⎫0,0,a 2,B ⎝⎛⎭⎫a 2,a ,0,C ⎝⎛⎭⎫-a2,a ,0. 因为E 为PC 的中点,所以E ⎝⎛⎭⎫-a 4,a 2,a4. 易知平面P AD 的一个法向量为OF →=⎝⎛⎭⎫0,a 2,0, 因为EF →=⎝⎛⎭⎫a 4,0,-a 4,且OF →·EF →=⎝⎛⎭⎫0,a 2,0·⎝⎛⎭⎫a4,0,-a 4=0, 又因为EF ⊄平面P AD , 所以EF ∥平面P AD .(2)因为P A →=⎝⎛⎭⎫a 2,0,-a 2,CD →=(0,-a,0), 所以P A →·CD →=⎝⎛⎭⎫a2,0,-a 2·(0,-a,0)=0, 所以P A →⊥CD →,所以P A ⊥CD . 又P A ⊥PD ,PD ∩CD =D , PD ,CD ⊂平面PDC , 所以P A ⊥平面PDC . 又P A ⊂平面P AB , 所以平面P AB ⊥平面PDC .5.如图,在三棱锥P -ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知BC =8,PO =4,AO =3,OD =2.(1)证明:AP ⊥BC ;(2)若点M 是线段AP 上一点,且AM =3.试证明平面AMC ⊥平面BMC .【解析】证明 如图所示,以O 为坐标原点,以射线OP 为z 轴的正半轴建立空间直角坐标系Oxyz .则O (0,0,0),A (0,-3,0),B (4,2,0),C (-4,2,0),P (0,0,4).(1)∵AP →=(0,3,4),BC →=(-8,0,0),∴AP →·BC →=(0,3,4)·(-8,0,0)=0,AP →⊥BC →,即AP ⊥BC . (2)由(1)知|AP |=5,又|AM |=3,且点M 在线段AP 上, ∴AM →=35AP →=⎝⎛⎭⎫0,95,125. 又AC →=(-4,5,0),BA →=(-4,-5,0), ∴BM →=BA →+AM →=⎝⎛⎭⎫-4,-165,125, 则A P →·BM →=(0,3,4)·⎝⎛⎭⎫-4,-165,125=0, ∴AP →⊥BM →,即AP ⊥BM ,又根据(1)的结论知AP ⊥BC ,BM ∩BC =B , ∴AP ⊥平面BMC ,于是AM ⊥平面BMC . 又AM ⊂平面AMC ,故平面AMC ⊥平面BCM .6. 如图所示,已知四棱锥P -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =PB =PC =2CD ,侧面PBC ⊥底面ABCD .证明:(1)P A ⊥BD ;(2)平面P AD ⊥平面P AB .【解析】证明 (1)取BC 的中点O ,连接PO ,△PBC 为等边三角形,即PO ⊥BC , ∵平面PBC ⊥底面ABCD ,BC 为交线,PO ⊂平面PBC , ∴PO ⊥底面ABCD .以BC 的中点O 为坐标原点,以BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,如图所示.不妨设CD =1,则AB =BC =2,PO = 3.∴A (1,-2,0),B (1,0,0),D (-1,-1,0),P (0,0,3). ∴BD →=(-2,-1,0),P A →=(1,-2,-3). ∵BD →·P A →=(-2)×1+(-1)×(-2)+0×(-3)=0, ∴P A →⊥BD →, ∴P A ⊥BD .(2)取P A 的中点M ,连接DM ,则M ⎝⎛⎭⎫12,-1,32.∵DM →=⎝⎛⎭⎫32,0,32,PB →=(1,0,-3),∴DM →·PB →=32×1+0×0+32×(-3)=0,∴DM →⊥PB →,即DM ⊥PB .∵DM →·P A →=32×1+0×(-2)+32×(-3)=0,∴DM →⊥P A →,即DM ⊥P A .又∵P A ∩PB =P ,P A ,PB ⊂平面P AB , ∴DM ⊥平面P AB . ∵DM ⊂平面P AD , ∴平面P AD ⊥平面P AB .7.如图所示,在四棱柱ABCD -A 1B 1C 1D 1中,A 1D ⊥平面ABCD ,底面ABCD 是边长为1的正方形,侧棱A 1A =2.(1)证明:AC ⊥A 1B ;(2)是否在棱A 1A 上存在一点P ,使得AP →=λP A 1→且面AB 1C 1⊥面PB 1C 1.【解析】 如图所示,以DA ,DC ,DA 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则D (0,0,0),A (1,0,0),C (0,1,0),A 1(0,0,3),B (1,1,0),D 1(-1,0,3),B 1(0,1,3),C 1(-1,1,3).(1)证明:AC →=(-1,1,0),A 1B →=(1,1,-3), ∴AC →·A 1B →=0,∴AC ⊥A 1B . (2)假设存在, ∵AP →=λP A 1→, ∴P ⎝⎛⎭⎪⎫11+λ,0,3λ1+λ. 设平面AB 1C 1的一个法向量为n 1=(x 1,y 1,z 1), ∵AB 1→=(-1,1,3),AC 1→=(-2,1,3), ∴⎩⎪⎨⎪⎧n 1·AB 1→=-x 1+y 1+3z 1=0,n 1·AC 1→=-2x 1+y 1+3z 1=0.令z 1=3,则y 1=-3,x 1=0.∴n 1=(0,-3,3).同理可求面PB 1C 1的一个法向量为n 2=⎝ ⎛⎭⎪⎫0,3λ+1,-1, ∴n 1·n 2=0.∴-331+λ-3=0,即λ=-4.∵P 在棱A 1A 上,∴λ>0,矛盾. ∴这样的点P 不存在.8.如图,棱柱ABCD -A 1B 1C 1D 1的所有棱长都等于2,∠ABC 和∠A 1AC 均为60°,平面AA 1C 1C ⊥平面ABCD .(1)求证:BD ⊥AA 1;(2)在直线CC 1上是否存在点P ,使BP ∥平面DA 1C 1,若存在,求出点P 的位置,若不存在,请说明理由.【解析】(1)证明 设BD 与AC 交于点O ,则BD ⊥AC ,连接A 1O ,在△AA 1O 中,AA 1=2,AO =1,∠A 1AO =60°,∴A 1O 2=AA 21+AO 2-2AA 1·AO cos 60°=3, ∴AO 2+A 1O 2=AA 21, ∴A 1O ⊥AO .由于平面AA 1C 1C ⊥平面ABCD ,且平面AA 1C 1C ∩平面ABCD =AC ,A 1O ⊂平面AA 1C 1C ,∴A 1O ⊥平面ABCD .以OB ,OC ,OA 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则A (0,-1,0),B (3,0,0),C (0,1,0),D (-3,0,0),A 1(0,0,3),C 1(0,2,3).由于BD →=(-23,0,0),AA 1→=(0,1,3), AA 1→·BD →=0×(-23)+1×0+3×0=0, ∴BD →⊥AA 1→,即BD ⊥AA 1.(2)解 假设在直线CC 1上存在点P ,使BP ∥平面DA 1C 1, 设CP →=λCC 1→,P (x ,y ,z ),则(x ,y -1,z )=λ(0,1,3).从而有P (0,1+λ,3λ),BP →=(-3,1+λ,3λ). 设平面DA 1C 1的法向量为n 3=(x 3,y 3,z 3), 则⎩⎪⎨⎪⎧n 3⊥A 1C 1→,n 3⊥DA 1→,又A 1C 1→=(0,2,0),DA 1→=(3,0,3),则⎩⎨⎧2y 3=0,3x 3+3z 3=0,取n 3=(1,0,-1),因为BP ∥平面DA 1C 1, 则n 3⊥BP →,即n 3·BP →=-3-3λ=0,得λ=-1, 即点P 在C 1C 的延长线上,且C 1C =CP .。
3.2.2 利用向量证明空间中的垂直关系

垂直关系
一、基础知识
1、立体几何中如何证明两条直线垂直?
①利用定义:证明两直线所成角为 900; ②利用线面垂直的性质来证明线线垂直.
线面垂直的性质:如果一条直线垂直一个平面,那么这条直线 垂直该平面内的任一直线.
αA
l B
Q C
lα AB α
l
BB1,CD 的中点,求证:D1F⊥平面 ADE.
【解析】如图,以 O 为原点建立空间直角
z
D1
C1 坐标系.设棱长为 2,由题意可得
A1
D(0,0,0),D1(0,0,2),F(0,1,0),A(2,0,0),
B1
E(2,2,1)
D xA
E C
y
D1F (0,1,2),DE (2,2,1),DA (2,0,0)
C.l1⊥l2
D.不能确定
2.设平面α的法向量为a (1,2,2) ,平面β的法向量为
b (2,4,k),若α⊥β,则 k=( B )
A.2
B.-5
C.4
D.-2
3.已知平面α内的两个向量a (2,2,1),b (2,0,0),则平面的一个
法向量是( A )
A.(0,1,2) B.(1,0,2) C.(1, 2, 1) D.(0,0, 2)
(1)l⊥m
(2)l//m
答案: (1)α β
(2)α //β
设两个平面α,β的法向量分别为a ,b ,则
α β ab ab0
二、自我检测
C 1、直线 l1,l2 的方向向量分别为a (1,2,2),b (2,3,2) ,则( )
立体几何中的向量方法2——证明平行和垂直

E
E(0,2,1),F(1,1,0)
A' F (1,1, 2), DB (2, 2,0), DE (0, 2,1) A' F DB (1,1, 2) (2, 2,0) 0
Y
F
A' F DE (1,1, 2) (0, 2,1) 0
X
A' F DB, A' F DE,又DB DE D. A' F 平面BDE
oB
H(0,1-2 a2 ,
E
a)、
2 2
2 2
x
G F
y A
故CGaB,(H01EG)n的-,2法(1 向a量22, 2为a1,0-,
22H(aG0) ,1n,0)H,
,而平面
故
,而 平面CBE
例2.在正方体
D1
C1
ABCD-A1B1C1D1 A1 中,P、Q分别是
P
B1
A1B1和BC上的动 点,且A1P=BQ, M是AB1的中点,N 是PQ的中点. 求证:A MN∥平面AC.
一、 用空间向量处理“平行”问 题
↑n→m
n
m
0
m↑
↑n
n
m
例1.如图:ABCD C
D
与ABEF是正方形,
CB⊥平面ABEF,
H
H、G分别是AC、
M
BF的中点,且
B
A
AH=GF. 求证:
N E
G F
HG∥平面CBE.
C
D
H
B
P
A
E
G
F
证明:分别以BE、BA、
用空间向量证明线线垂直与线面垂直

第二节 用空间向量证明线线垂直与线面垂直一、空间向量及其数量积1、 在空间,既有大小又有方向的量称为空间向量。
用或表示,其中向量的大小称为向量的长度或或a。
正如平面向量可用坐标(x,y.)表示,空间向量也可用坐标(x,y,z)表示。
若已知点A 坐标为(x 1,y 1,z 1),点B 坐标为(x 2,y 2,z 2) 则向量=(x 2 -x 1,y 2- y 1,z 2 -z 1)即是终点坐标减起点坐标。
在空间,知道向量=(x ,y ,z222z y x 2、 空间向量数量积① 已知两个非零向量、,在空间任取一点O ,作=,=,则角∠AOB 叫向量与的夹角,记作<,>规定,若0≤<,>≤ ,若<,>=2,称与垂直,记作⊥b 。
② 已知空间两个向量、COS <,>叫向量、的数量积,记作aCOS<,>若⊥ a=0③ 若已知空间向量=(x 1,y 1,z 1), =(x 2,y 2,z 2) 则•=x 1x 2+y 1y 2+z 1z 2 , COS <,222222212121212121z y x z y x z z y y x x例1 如图,已知直三棱柱ABC-A 1B 1C 1中,∠BCA=900,D 1、E 1分别为A 1B 1、A 1C 1中点,若BC=CA=CC 1,求向量1BD 与1AE 所成角的余弦值。
C 1B 1 A1ACB D 1 E 1练习:已知正方体ABCD —1111D C B A 中,11E B =11F D =411B A ,求向量1BE 与1DF 所成角的余弦值。
二 、利用向量证线线垂直与线面垂直例2 在正方体ABCD —1111D C B A 中,求证A 1C ⊥平面AB 1D 1练习:在正方体ABCD —1111D C B A 中,O 为底面ABCD 的中心,P 为DD 1的中点, 求证:B 1O ⊥平面PAC 。
例3 如图,PA ⊥矩形ABCD 所在平面,M, N 分别是AB ,PC 中点 (1)求证:M N ⊥CDE D A 1FD 1AB 1C BC 1 BA D CB AC D B 1 A 1 D C B A C 1D 1 O P PN(2)若∠PDA=450,求证:MN ⊥平面PCD练习:正方体ABCD —1111D C B A 中,M 是棱D 1D 中点,N 是AD 中点, P 为棱A 1B 1上任一点。
利用向量证明垂直问题

3.利用空间向量的关系来证明相关的垂直问题.
当堂训练
D1
1.正方体ABCD-A1B1C1D1 A1
中,E,F分别是BB1,DC的中
点,求证:平面AD1F⊥平面
D
ADE.
C1 B1EF来自CAB
2.正方体ABCD-A1B1C1D1 D1 中,O是AC与BD的交点,G A1
D
Cy
面VAD是正三角形,平面
VAD⊥底面ABCD.
xA
B
求证:AB⊥平面VAD
证明:以D为坐标原点建立坐标系如图.
设底面边长为1,则A(1,0,0),B(1,1,0),V( 1 ,0, 3 ).
uuur AB
(0,1,
uur 0),VA
(
1
,
0,
3)
22
uuur uur
22
AB VA 0
AB VA,又AB AD,且VA I AD A
AB 平面VAD
题2:在直三棱柱ABC-A1B1C1中,
AB⊥BC,|AB|=|BC|=2,|BB1|=1,
z B1
C1
E为BB1的中点.
求证:平面AEC1⊥平面AA1C1C. A1
E
证明:以B为坐标原点建立坐标系如图,
B
Cy
A(2,0,0), B(0,0,0),C(0, 2,0),
1
A1
(2,
题2:在直三棱柱ABC-A1B1C1中,
z B1
C1
AB⊥BC,|AB|=|BC|=2,|BB1|=1,
E为BB1的中点.
A1
E
求证:平面AEC1⊥平面AA1C1C.
B
Cy
证明平面与平面垂直(空间向量)

1.利用空间向量证明面面垂直通常可以有两个途径:一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,由两个法向量垂直,得面面垂直.2.向量法证明面面垂直的优越性主要体现在不必考虑图形的位置关系,恰当建系或用基向量表示后,只需经过向量运算就可得到要证明的结果,思路方法“公式化”,降低了思维难度..用向量证明垂直的方法(1)线线垂直:证明两直线所在的方向向量互相垂直,即证它们的数量积为零.(2)线面垂直:证明直线的方向向量与平面的法向量共线,或将线面垂直的判定定理用向量表示.(3)面面垂直:证明两个平面的法向量垂直,或将面面垂直的判定定理用向量表示.4.若平面α与β的法向量分别是a=(4,0,-2),b=(1,0,2),则平面α与β的位置关系是( )A.平行 B.垂直C.相交不垂直 D.无法判断解析:∵a·b=4×1+0+(-2)×2=0.∴a⊥b,∴α⊥β.答案:B面面垂直.在正方体ABCD-A1B1C1D1中,E为CC1的中点,证明:平面B1ED⊥平面B1BD.【证明】 以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设正方体的棱长为1,则D (0,0,0),B 1(1,1,1),E (0,1,12),DB 1→=(1,1,1),DE →=(0,1,12),设平面B 1DE 的法向量为n 1=(x ,y ,z ),则x +y +z =0且y +12z =0,令z =-2,∴n 1=(1,1,-2).同理求得平面B 1BD 的法向量为n 2=(1,-1,0),由n 1·n 2=0,知n 1⊥n 2,∴平面B 1DE ⊥平面B 1BD .图3-2-124.在正方体ABCD -A 1B 1C 1D 1中,E 为CC 1的中点,证明:平面B 1ED ⊥平面B 1BD .[证明] 以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系.设正方体的棱长为1,则D (0,0,0),B 1(1,1,1),E ⎝ ⎛⎭⎪⎫0,1,12,DB 1→=(1,1,1),DE →=⎝ ⎛⎭⎪⎫0,1,12,设平面B 1DE 的法向量为n 1=(x ,y ,z ),则x +y +z =0且y +12z =0,令z =-2,则y =1,x =1,∴n 1=(1,1,-2).同理求得平面B 1BD 的法向量为n 2=(1,-1,0),由n 1·n 2=0,知n 1⊥n 2,∴平面B 1DE ⊥平面B 1BD .例3:如图3-2-12,在直三棱柱ABC -A 1B 1C 1中,AB ⊥BC ,AB =BC =2,BB 1=1,E 为BB 1的中点,求证:平面AEC 1⊥平面AA 1C 1C .【解答】 由题意得AB ,BC ,B 1B 两两垂直,以B 为原点,分别以BA ,BC ,BB 1所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系,则A (2,0,0),A 1(2,0,1),C (0,2,0),C 1(0,2,1),E (0,0,12),则AA 1→=(0,0,1),AC →=(-2,2,0),AC 1→=(-2,2,1),AE →=(-2,0,12).设平面AA 1C 1C 的一个法向量为n 1=(x ,y ,z ),则⎩⎪⎨⎪⎧n 1·AA 1→=0n 1·AC →=0⇒⎩⎪⎨⎪⎧z =0,-2x +2y =0.令x =1,得y =1,∴n 1=(1,1,0).设平面AEC 1的一个法向量为n 2=(x ,y ,z ), 则⎩⎪⎨⎪⎧ n 2·AC 1→=0n 2·AE →=0⇒⎩⎪⎨⎪⎧-2x +2y +z =0,-2x +12z =0. 令z =4,得x =1,y =-1.∴n 2=(1,-1,4).∵n 1·n 2=1×1+1×(-1)+0×4=0, ∴n 1⊥n 2.∴平面AEC 1⊥平面AA 1C 1C .如图所示,在直三棱柱ABC -A 1B 1C 1中,AB ⊥BC ,AB =BC =2,BB 1=1,E 为BB 1的中点,证明:平面AEC 1⊥平面AA 1C 1C .思路探究:要证明两个平面垂直,由两个平面垂直的条件,可证明这两个平面的法向量垂直,转化为求两个平面的法向量n 1,n 2,证明n 1·n 2=0.[解] 由题意得AB ,BC ,B 1B 两两垂直.以B 为原点,BA ,BC ,BB 1分别为x ,y ,z 轴,建立如图所示的空间直角坐标系.则A (2,0,0),A 1(2,0,1),C (0,2,0),C 1(0,2,1),E ⎝ ⎛⎭⎪⎫0,0,12,则AA 1→=(0,0,1),AC →=(-2,2,0),AC 1→=(-2,2,1),AE →=(-2,0,12). 设平面AA 1C 1C 的一个法向量为n 1=(x 1,y 1,z 1). 则⎩⎨⎧n 1·AA 1→=0,n 1·AC →=0⇒⎩⎪⎨⎪⎧z 1=0,-2x 1+2y 1=0.令x 1=1,得y 1=1.∴n 1=(1,1,0).设平面AEC 1的一个法向量为n 2=(x 2,y 2,z 2). 则⎩⎨⎧n 2·AC 1→=0,n 2·AE →=0⇒⎩⎨⎧-2x 2+2y 2+z 2=0,-2x 2+12z 2=0, 令z 2=4,得x 2=1,y 2=-1.∴n 2=(1,-1,4). ∵n 1·n 2=1×1+1×(-1)+0×4=0. ∴n 1⊥n 2,∴平面AEC 1⊥平面AA 1C 1C .如图在正方体ABCD -A 1B 1C 1D 1中,E 为BB 1的中点,F 为CD 的中点,G 为AB 的中点.求证:平面ADE ⊥平面A 1FG .证明:连结D 1F ,以D 为原点,DA ,DC ,DD 1所在的直线分别为x ,y ,z 轴建立空间直角坐标系D -xyz ,设正方体棱长为1.∴D (0,0,0),E (1,1,12),A (1,0,0),A 1(1,0,1),G (1,12,0),F (0,12,0).∴AE →=(0,1,12),A 1G →=(0,12,-1),GF →=(-1,0,0).∴AE →·A 1G →=0+12-12=0,AE →·GF →=0+0+0=0. ∴AE →⊥A 1G →,AE →⊥GF →, ∵A 1G ∩GF =G , ∴AE ⊥平面A 1GF . 又AE ⊂平面ADE , ∴平面ADE ⊥平面A 1GF .6.如图, 正四棱柱ABCD -A 1B 1C 1D 1中,底面边长为22,侧棱长为4,E 、F 分别是棱AB 、BC 的中点,EF ∩BD =G .求证:平面B 1EF ⊥平面BDD 1B 1.[证明] 以D 为原点,DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,由题意知:D (0,0,0)、B 1(22,22,4)、E (22,2,0)、F (2,22,0),B 1E →=(0,-2,-4)、EF →=(-2,2,0). 设平面B 1EF 的一个法向量为n =(x ,y ,z ). 则n ·B 1E →=-2y -4z =0,n ·EF →=-2x +2y =0. 解得x =y ,z =-24y ,令y =1得n =(1,1,-24), 又平面BDD 1B 1的一个法向量为AC →=(-22,22,0), 而n ·AC →=1×(-22)+1×22+(-24)×0=0,即n ⊥AC →.∴平面B 1EF ⊥平面BDD 1B 1. 10.如图在正方体ABCD -A 1B 1C 1D 1中,E 为BB 1的中点,F 为CD 的中点,G 为AB 的中点.求证:平面ADE ⊥平面A 1FG .证明:连结D 1F ,以D 为原点,DA ,DC ,DD 1所在的直线分别为x ,y ,z 轴建立空间直角坐标系D -xyz ,设正方体棱长为1.∴D (0,0,0),E (1,1,12),A (1,0,0),A 1(1,0,1),G (1,12,0),F (0,12,0).∴AE →=(0,1,12),A 1G →=(0,12,-1),GF →=(-1,0,0).∴AE →·A 1G →=0+12-12=0,AE →·GF →=0+0+0=0.∴AE →⊥A 1G →,AE →⊥GF →, ∵A 1G ∩GF =G , ∴AE ⊥平面A 1GF . 又AE ⊂平面ADE , ∴平面ADE ⊥平面A 1GF .11.在正四棱柱ABCD -A 1B 1C 1D 1中,底面边长为2,侧棱长为3,E 、F 分别是AB 1、CB 1的中点,求证:平面D 1EF ⊥平面AB 1C .证明:把正四棱柱如图放置在坐标系中,则各点坐标为A (2,0,0),C (0,2,0),B 1(2,2,3),D 1(0,0,3),E (2,22,32),F (22,2,32). 假设平面AB 1C 的法向量为n 1=(1,λ1,u 1),则n 1应垂直于AC →和AB 1→, 而AC →=(-2,2,0),AB 1→=(0,2,3),∴n 1·AC →=-2+2λ1=0, n 1·AB 1→=2λ1+3u 1=0. ∴λ1=1,u 1=-63. ∴n 1=(1,1,-63).再设平面D 1EF 的法向量为n 2=(1,λ2,u 2),则n 2应垂直于D 1E →、D 1F →. 而D 1E →=(2,22,-32),D 1F →=(22,2,-32),n 2·D 1E →=2+22λ2-32u 2=0,∴n 2·D 1F →=22+2λ2-32u 2=0.∴λ2=1,u 2= 6. ∴n 2=(1,1,6). 由于n 1·n 2=1+1-63·6=0, ∴n 1⊥n 2.∴平面D 1EF ⊥平面AB 1C .2.三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为三角形A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC .A 1A =3,AB =AC =2A 1C 1=2,D 为BC 中点.证明:平面A 1AD ⊥平面BCC 1B 1.[证明] 如图,建立空间直角坐标系.则A (0,0,0),B (2,0,0),C (0,2,0), A 1(0,0,3),C 1(0,1,3),因为D为BC的中点,所以D点坐标为(1,1,0),所以BC→=(-2,2,0),AD→=(1,1,0),AA1→=(0,0,3),因为BC→·AD→=-2+2+0=0,BC→·AA1→=0+0+0=0,所以BC→⊥AD→,BC→⊥AA1→,所以BC⊥AD,BC⊥AA1,又AD∩AA1=A,所以BC⊥平面ADA1,而BC⊂平面BCC1B1,所以平面A1AD⊥平面BCC1B1.三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=3,AB=2,AC=2,A1C1=1,BDDC=12.证明:平面A1AD⊥平面BCC1B1.证明:如图,建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,3),C1(0,1,3).∵BD∶DC=1∶2,∴BD→=13BC→,∴D点坐标为(223,23,0),∴AD→=(223,23,0),BC→=(-2,2,0),AA1→=(0,0,3).∵BC→·AA1→=0,BC→·AD→=0,∴BC⊥AA1,BC⊥AD.又A1A∩AD=A,∴BC⊥平面A1AD.又BC⊂平面BCC1B1,∴平面A1AD⊥平面BCC1B1.中等难度建系10.如图3-2-16所示,△ABC 是一个正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD .图3-2-16求证:平面DEA ⊥平面ECA .【答案】建立如图所示的空间直角坐标系Cxyz ,不妨设CA =2, 则CE =2,BD =1,C (0,0,0),A (3,1,0),B (0,2,0),E (0,0,2),D (0,2,1).所以EA →=(3,1,-2),CE →=(0,0,2),ED →=(0,2,-1).分别设平面CEA 与平面DEA 的法向量是n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 1·EA →=0,n 1·CE →=0,即⎩⎨⎧3x 1+y 1-2z 1=0,2z 1=0,解得⎩⎨⎧y 1=-3x 1,z 1=0,⎩⎪⎨⎪⎧n 2·EA →=0,n 2·ED →=0,即⎩⎨⎧3x 2+y 2-2z 2=0,2y 2-z 2=0, 解得⎩⎨⎧x 2=3y 2,z 2=2y 2.不妨取n 1=(1,-3,0), n 2=(3,1,2),因为n 1·n 2=0,所以n 1⊥n 2. 所以平面DEA ⊥平面ECA .2017·开封模拟)如图,已知AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,AD =DE =2AB .图7-7-4求证:平面BCE ⊥平面CDE . 【导学号:97190251】[证明] 设AD =DE =2AB =2a ,建立如图所示的空间直角坐标系Axyz ,则A (0,0,0),C (2a,0,0),B (0,0,a ),D (a ,3a,0),E (a ,3a,2a ).所以BE →=(a ,3a ,a ),BC →=(2a,0,-a ),CD →=(-a ,3a,0),ED →=(0,0,-2a ). 设平面BCE 的法向量为n 1=(x 1,y 1,z 1), 由n 1·BE →=0,n 1·BC →=0可得 ⎩⎪⎨⎪⎧ax 1+3ay 1+az 1=0,2ax 1-az 1=0, 即⎩⎪⎨⎪⎧x 1+3y 1+z 1=0,2x 1-z 1=0.令z 1=2,可得n 1=(1,-3,2). 设平面CDE 的法向量为n 2=(x 2,y 2,z 2), 由n 2·CD →=0,n 2·ED →=0可得 ⎩⎪⎨⎪⎧-ax 2+3ay 2=0,-2az 2=0,即⎩⎪⎨⎪⎧-x 2+3y 2=0,z 2=0.令y 2=1,可得n 2=(3,1,0). 因为n 1·n 2=1×3+1×(-3)=0. 所以n 1⊥n 2,所以平面BCE ⊥平面CDE .底面是梯形如图所示,已知四棱锥P -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =PB =PC =2CD ,侧面PBC ⊥底面ABCD .证明:(1)P A ⊥BD ;(2)平面P AD ⊥平面P AB .证明 (1)取BC 的中点O ,连接PO ,∵平面PBC ⊥底面ABCD ,△PBC 为等边三角形, ∴PO ⊥底面ABCD .以BC 的中点O 为坐标原点,以BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,如图所示.不妨设CD =1,则AB =BC =2,PO = 3.∴A (1,-2,0),B (1,0,0),D (-1,-1,0),P (0,0,3). ∴BD →=(-2,-1,0),P A →=(1,-2,-3). ∵BD →·P A →=(-2)×1+(-1)×(-2)+0×(-3)=0, ∴P A →⊥BD→,∴P A ⊥BD . (2)取P A 的中点M ,连接DM ,则M ⎝ ⎛⎭⎪⎫12,-1,32.∵DM →=⎝ ⎛⎭⎪⎫32,0,32,PB →=(1,0,-3),∴DM →·PB →=32×1+0×0+32×(-3)=0, ∴DM→⊥PB →,即DM ⊥PB . ∵DM →·P A →=32×1+0×(-2)+32×(-3)=0,∴DM →⊥P A →,即DM ⊥P A .又∵P A ∩PB =P ,∴DM ⊥平面P AB .∵DM ⊂平面P AD ,∴平面P AD ⊥平面P AB .9.如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD .证明:平面PQC ⊥平面DCQ .证明 如图,以D 为坐标原点,线段DA 的长为单位长,射线DA ,DP ,DC 分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .依题意有Q (1,1,0),C (0,0,1),P (0,2,0),则DQ→=(1,1,0),DC →=(0,0,1),PQ →=(1,-1,0). ∴PQ →·DQ →=0,PQ →·DC→=0. 即PQ ⊥DQ ,PQ ⊥DC ,又DQ ∩DC =D ,∴PQ ⊥平面DCQ ,又PQ ⊂平面PQC ,∴平面PQC ⊥平面DCQ .[跟踪训练] 如图7-7-5所示,已知四棱锥P -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =PB =PC =2CD ,侧面PBC ⊥底面ABCD .图7-7-5证明:(1)P A ⊥BD ;(2)平面P AD ⊥平面P AB .[证明] (1)取BC 的中点O ,连接PO ,∵平面PBC ⊥底面ABCD ,△PBC 为等边三角形,∴PO ⊥底面ABCD .以BC 的中点O 为坐标原点,以BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,如图所示.不妨设CD =1,则AB =BC =2,PO = 3.∴A (1,-2,0),B (1,0,0),D (-1,-1,0),P (0,0,3).∴BD →=(-2,-1,0),P A →=(1,-2,-3).∵BD →·P A →=(-2)×1+(-1)×(-2)+0×(-3)=0,∴P A →⊥BD →,∴P A ⊥BD .(2)取P A 的中点M ,连接DM ,则M ⎝ ⎛⎭⎪⎫12,-1,32. ∵DM →=⎝ ⎛⎭⎪⎫32,0,32,PB →=(1,0,-3), ∴DM →·PB →=32×1+0×0+32×(-3)=0, ∴DM →⊥PB →,即DM ⊥PB .∵DM →·P A →=32×1+0×(-2)+32×(-3)=0,∴DM →⊥P A →,即DM ⊥P A .又∵P A ∩PB =P ,∴DM ⊥平面P AB .∵DM ⊂平面P AD ,∴平面P AD ⊥平面P AB .4.在正三棱锥P-ABC 中,三条侧棱PA,PB,PC 两两垂直,G 是△PAB 的重心,E,F 分别为BC 、PB 上的点,且BE∶EC=PF∶FB=1∶2.(1)求证:平面GEF ⊥平面PBC.(2)求证:EG ⊥BC,PG ⊥EG.【证明】(1)如图,以三棱锥的顶点P 为原点,以PA 、PB 、PC 所在直线分别作为x 轴、y 轴、z 轴建立空间直角坐标系.设PA=PB=PC=3,则A(3,0,0),B(0,3,0),C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0, 0), 方法一:可得=(3,0, 0),=(1,0,0),故=3,所以PA ∥FG.而PA ⊥平面PBC,所以FG ⊥平面PBC.又FG ⊂平面GEF,所以平面GEF ⊥平面PBC.方法二:可得=(0,-1,-1),=(1,-1,-1).设平面GEF 的法向量是n =(x,y,z), 则有n ⊥,n ⊥,所以{y +z =0,x -y -z =0.令y=1,得z=-1,x=0,即n =(0,1,-1).显然=(3,0,0)是平面PBC的一个法向量.又n·=0,所以n⊥.所以平面GEF⊥平面PBC.(2)因为=(1,-1,-1),=(1,1,0),=(0,-3,3),所以·=1-1=0,·=3-3=0.所以EG⊥PG,EG⊥BC.。
立体几何中不易建系的用空间向量证明垂直问题。

立体几何中不易建系的用空间向量证明垂直问题。
1. 引言1.1 概述立体几何是数学中的一个重要分支,研究空间中的图形和特定关系。
建系问题是立体几何中一个常见的难题,它涉及到如何确定或构建一个合适的坐标系来描述和表示空间中的元素和关系。
在解决建系问题时,传统的方法存在一定局限性和困难,例如难以应对复杂的几何结构、缺乏普适性等。
1.2 文章结构本文将通过引入空间向量理论来探讨解决立体几何中不易建系的问题。
文章分为以下几个部分:- 引言:介绍本文的背景和论文结构。
- 立体几何中的建系问题:阐述建系定义与重要性、传统方法的局限性与困难,以及空间向量在解决建系问题中的优势。
- 空间向量证明垂直问题的基本原理与方法:讨论垂直关系的定义与特征、空间向量表示垂直关系的有效途径,以及应用空间向量证明垂直性质时需要考虑的因素。
- 实例分析:通过一个具体案例来说明使用空间向量证明垂直问题的步骤和推理过程,并对结果进行分析和讨论。
- 结论与展望:总结研究成果并得出结论,同时提出未来研究方向和进一步工作的展望。
1.3 目的本文的目的是介绍空间向量在解决立体几何中不易建系的问题中所起到的作用和优势,并通过实例分析来验证其有效性。
通过本文的研究,读者将能够理解空间向量在解决建系问题中的重要性,并了解使用空间向量证明垂直问题的基本原理与方法。
最终,本文希望为立体几何领域中建系问题的解决提供一种新思路和有价值的参考。
2. 立体几何中的建系问题:2.1 建系的定义与重要性:在立体几何中,建系是指通过选取适当的点或向量作为参照,构建坐标系或基底来描述和表示空间中的几何事物或运动。
建系是解决立体几何问题和进行进一步分析的基础,它可以帮助我们确定方向、测量距离和角度,从而推导出更多关于空间图形、运动和变换的性质。
2.2 建系方法的局限性与困难:传统的建系方法主要包括平行四边形法、角平分线法、垂直线法等。
然而,这些方法在实际应用中存在一定的局限性和困难。
用空间向量解决立体几何中的垂直问题

第2课时用空间向量解决立体几何中的垂直问题学习目标 1.能用向量法判断一些简单线线、线面、面面垂直关系.2.掌握用向量方法证明有关空间线面垂直关系的方法步骤.知识点一向量法判断线线垂直设直线l的方向向量为a=(a1,a2,a3),直线m的方向向量为b=(b1,b2,b3),则l⊥m⇔a·b =0⇔a1b1+a2b2+a3b3=0.知识点二向量法判断线面垂直设直线l的方向向量a=(a1,b1,c1),平面α的法向量μ=(a2,b2,c2),则l⊥α⇔a∥μ⇔a=kμ(k∈R).知识点三向量法判断面面垂直思考平面α,β的法向量分别为μ1=(x1,y1,z1),μ2=(x2,y2,z2),用向量坐标法表示两平面α,β垂直的关系式是什么?答案x1x2+y1y2+z1z2=0.梳理若平面α的法向量为μ=(a1,b1,c1),平面β的法向量为v=(a2,b2,c2),则α⊥β⇔μ⊥v⇔μ·v=0⇔a1a2+b1b2+c1c2=0.(1)平面α的法向量是唯一的,即一个平面不可能存在两个不同的法向量.(×)(2)两直线的方向向量垂直,则两条直线垂直.(√)(3)直线的方向向量与平面的法向量的方向相同或相反时,直线与平面垂直.(√)(4)两个平面的法向量平行,则这两个平面平行;两个平面的法向量垂直,则这两个平面垂直.(√)类型一线线垂直问题例1已知正三棱柱ABC-A1B1C1的各棱长都为1,M是底面上BC边的中点,N 是侧棱CC 1上的点,且CN =14CC 1.求证:AB 1⊥MN .考点 向量法求解直线与直线的位置关系 题点 方向向量与线线垂直证明 设AB 中点为O ,作OO 1∥AA 1.以O 为坐标原点,OB 所在直线为x 轴,OC 所在直线为y 轴,OO 1所在直线为z 轴建立如图所示的空间直角坐标系Oxyz . 由已知得A ⎝⎛⎭⎫-12,0,0, B ⎝⎛⎭⎫12,0,0,C ⎝⎛⎭⎫0,32,0, N ⎝⎛⎭⎫0,32,14,B 1⎝⎛⎭⎫12,0,1, ∵M 为BC 中点, ∴M ⎝⎛⎭⎫14,34,0.∴MN -→=⎝⎛⎭⎫-14,34,14,AB 1-→=(1,0,1),∴MN -→·AB 1-→=-14+0+14=0.∴MN -→⊥AB 1-→,∴AB 1⊥MN .反思与感悟 证明两直线垂直的基本步骤:建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.跟踪训练1 如图,在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AB =5,AA 1=4,求证:AC ⊥BC 1.考点 向量法求解直线与直线的位置关系 题点 方向向量与线线垂直证明 ∵直三棱柱ABC -A 1B 1C 1底面三边长AC =3,BC =4,AB =5,∴AC ,BC ,C 1C 两两垂直.如图,以C 为坐标原点,CA ,CB ,CC 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系Cxyz .则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0), ∵AC →=(-3,0,0),BC 1-→=(0,-4,4), ∴AC →·BC 1-→=0.∴AC ⊥BC 1.类型二 证明线面垂直例2 如图所示,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1的中点. 求证:AB 1⊥平面A 1BD .考点 向量法求解直线与平面的位置关系 题点 向量法解决线面垂直证明 如图所示,取BC 的中点O ,连接AO .因为△ABC 为正三角形,所以AO ⊥BC .因为在正三棱柱ABC -A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1,且平面ABC ∩平面BCC 1B 1=BC ,AO ⊂平面ABC ,所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1,以O 为坐标原点,OB ,OO 1,OA 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Oxyz ,则B (1,0,0),D (-1,1,0),A 1(0,2,3),A (0,0,3), B 1(1,2,0).所以AB 1-→=(1,2,-3),BA 1-→=(-1,2,3), BD -→=(-2,1,0).因为AB 1-→·BA 1-→=1×(-1)+2×2+(-3)×3=0. AB 1-→·BD -→=1×(-2)+2×1+(-3)×0=0.所以AB 1-→⊥BA 1-→,AB 1-→⊥BD -→,即AB 1⊥BA 1,AB 1⊥BD . 又因为BA 1∩BD =B ,所以AB 1⊥平面A 1BD . 反思与感悟 用坐标法证明线面垂直的方法及步骤 方法一:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示.(3)找出平面内两条相交直线,并用坐标表示它们的方向向量. (4)分别计算两组向量的数量积,得到数量积为0. 方法二:(1)建立空间直角坐标系. (2)将直线的方向向量用坐标表示. (3)求出平面的法向量.(4)判断直线的方向向量与平面的法向量平行.跟踪训练2 如图,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,点P 为DD 1的中点.求证:直线PB 1⊥平面P AC .考点 向量法求解直线与平面的位置关系 题点 向量法解决线面垂直证明 如图,以D 为坐标原点,DC ,DA ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Dxyz , C (1,0,0),A (0,1,0),P (0,0,1),B 1(1,1,2), PC →=(1,0,-1),P A →=(0,1,-1), PB 1-→=(1,1,1),B 1C -→=(0,-1,-2), B 1A -→=(-1,0,-2).PB 1-→·PC →=(1,1,1)·(1,0,-1)=0,所以PB 1-→⊥PC →,即PB 1⊥PC . 又PB 1-→·P A →=(1,1,1)·(0,1,-1)=0, 所以PB 1-→⊥P A →,即PB 1⊥P A .又P A ∩PC =P ,所以PB 1⊥平面P AC . 类型三 证明面面垂直问题例3 三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为A 1B 1C 1,∠BAC =90°,A 1A ⊥平面ABC ,A 1A =3,AB =AC =2A 1C 1=2,D 为BC 的中点.证明:平面A 1AD ⊥平面BCC 1B 1. 考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直证明 方法一 如图,以A 为坐标原点,AB ,AC ,AA 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (0,2,0),A 1(0,0,3),C 1(0,1,3). ∵D 为BC 的中点,∴D 点坐标为(1,1,0), ∴AD →=(1,1,0),AA 1-→=(0,0,3),BC →=(-2,2,0), ∴AD →·BC →=1×(-2)+1×2+0×0=0, AA 1-→·BC →=0×(-2)+0×2+3×0=0, ∴AD →⊥BC →,AA 1-→⊥BC →, ∴BC ⊥AD ,BC ⊥AA 1.又A 1A ∩AD =A ,∴BC ⊥平面A 1AD .又BC ⊂平面BCC 1B 1,∴平面A 1AD ⊥平面BCC 1B 1. 方法二 同方法一建系后,得AA 1-→=(0,0,3), AD →=(1,1,0),BC →=(-2,2,0),CC 1-→=(0,-1,3). 设平面A 1AD 的法向量为n 1=(x 1,y 1,z 1), 平面BCC 1B 1的法向量为n 2=(x 2,y 2,z 2).由⎩⎪⎨⎪⎧n 1·AA 1-→=0,n 1·AD →=0,得⎩⎪⎨⎪⎧3z 1=0,x 1+y 1=0,令y 1=-1,则x 1=1,z 1=0, ∴n 1=(1,-1,0).由⎩⎪⎨⎪⎧n 2·BC →=0,n 2·CC 1-→=0,得⎩⎪⎨⎪⎧-2x 2+2y 2=0,-y 2+3z 2=0,令y 2=1,则x 2=1,z 2=33, ∴n 2=⎝⎛⎭⎫1,1,33. ∵n 1·n 2=1-1+0=0,∴n 1⊥n 2, ∴平面A 1AD ⊥平面BCC 1B 1.反思与感悟 证明面面垂直的两种方法(1)常规法:利用面面垂直的判定定理转化为线面垂直、线线垂直去证明. (2)向量法:证明两个平面的法向量互相垂直.跟踪训练3 在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点. (1)求证:平面AED ⊥平面A 1FD 1;(2)在直线AE 上求一点M ,使得A 1M ⊥平面AED . 考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直(1)证明 以D 为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系Dxyz .设正方体的棱长为2,则D (0,0,0),A (2,0,0),E (2,2,1),F (0,1,0),A 1(2,0,2),D 1(0,0,2),∴DA →=D 1A 1-→=(2,0,0),DE →=(2,2,1),D 1F -→=(0,1,-2). 设平面AED 的一个法向量为n 1=(x 1,y 1,z 1).由⎩⎪⎨⎪⎧n 1·DA →=(x 1,y 1,z 1)·(2,0,0)=0,n 1·DE →=(x 1,y 1,z 1)·(2,2,1)=0,得⎩⎪⎨⎪⎧2x 1=0,2x 1+2y 1+z 1=0. 令y 1=1,得n 1=(0,1,-2).同理,平面A 1FD 1的一个法向量为n 2=(0,2,1). ∵n 1·n 2=(0,1,-2)·(0,2,1)=0,∴n 1⊥n 2, ∴平面AED ⊥平面A 1FD 1. (2)解 由于点M 在直线AE 上, 因此可设AM -→=λAE →=λ(0,2,1)=(0,2λ,λ), 则M (2,2λ,λ),∴A 1M -→=(0,2λ,λ-2). 要使A 1M ⊥平面AED ,只需A 1M -→∥n 1, 即2λ1=λ-2-2,解得λ=25. 故当AM =25AE 时,A 1M ⊥平面AED .1.下列命题中,正确命题的个数为( )①若n 1,n 2分别是平面α,β的法向量,则n 1∥n 2⇔α∥β; ②若n 1,n 2分别是平面α,β的法向量,则α⊥β ⇔ n 1·n 2=0;③若n 是平面α的法向量,a 是直线l 的方向向量,若l 与平面α平行,则n ·a =0; ④若两个平面的法向量不垂直,则这两个平面不垂直. A .1 B .2 C .3 D .4考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直 答案 C解析 ①中平面α,β可能平行,也可能重合,结合平面法向量的概念,可知②③④正确.2.已知两直线的方向向量为a,b,则下列选项中能使两直线垂直的为()A.a=(1,0,0),b=(-3,0,0)B.a=(0,1,0),b=(1,0,1)C.a=(0,1,-1),b=(0,-1,1)D.a=(1,0,0),b=(-1,0,0)考点向量法求解直线与直线的位置关系题点向量法解决线线垂直答案 B解析因为a=(0,1,0),b=(1,0,1),所以a·b=0×1+1×0+0×1=0,所以a⊥b,故选B. 3.若直线l的方向向量为a=(1,0,2),平面α的法向量为μ=(-2,0,-4),则()A.l∥αB.l⊥αC.l⊂αD.l与α斜交考点向量法求解直线与平面的位置关系题点向量法解决线面垂直答案 B解析∵a∥μ,∴l⊥α.4.平面α的一个法向量为m=(1,2,0),平面β的一个法向量为n=(2,-1,0),则平面α与平面β的位置关系是()A.平行B.相交但不垂直C.垂直D.不能确定考点向量法求解平面与平面的位置关系题点向量法解决面面垂直答案 C解析∵(1,2,0)·(2,-1,0)=0,∴两法向量垂直,从而两平面垂直.5.在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=13,SB=29,则异面直线SC与BC是否垂直________.(填“是”或“否”)考点向量法求解直线与直线的位置关系题点向量法解决线线垂直答案是解析如图,以A为坐标原点,AB,AS所在直线分别为y轴,z轴建立空间直角坐标系Axyz , 则由AC =2,BC =13, SB =29,得B (0,17,0),S (0,0,23),C ⎝ ⎛⎭⎪⎫21317,417,0, SC →=⎝⎛⎭⎪⎫21317,417,-23, CB →=⎝⎛⎭⎪⎫-21317,1317,0. 因为SC →·CB →=0,所以SC ⊥BC .空间垂直关系的解决策略一、选择题1.设直线l 1,l 2的方向向量分别为a =(-2,2,1),b =(3,-2,m ),若l 1⊥l 2,则m 等于( ) A .-2 B .2 C .6 D .10考点 向量法求解直线与直线的位置关系 题点 方向向量与线线垂直 答案 D解析 因为a ⊥b ,故a ·b =0,即-2×3+2×(-2)+m =0,解得m =10.2.若平面α,β的法向量分别为a =(-1,2,4),b =(x ,-1,-2),并且α⊥β,则x 的值为( ) A .10 B .-10 C.12 D .-12考点 向量法求解平面与平面的位置关系 题点 向量法解决面面垂直 答案 B解析 因为α⊥β,所以它们的法向量也互相垂直, 所以a ·b =(-1,2,4)·(x ,-1,-2)=0, 解得x =-10.3.已知点A (0,1,0),B (-1,0,-1),C (2,1,1),P (x,0,z ),若P A ⊥平面ABC ,则点P 的坐标为( ) A .(1,0,-2) B .(1,0,2) C .(-1,0,2)D .(2,0,-1)考点 向量法求解直线与平面的位置关系 题点 向量法解决线面垂直 答案 C解析 由题意知AB →=(-1,-1,-1),AC →=(2,0,1),AP →=(x ,-1,z ),又P A ⊥平面ABC ,所以有AB →·AP →=(-1,-1,-1)·(x ,-1,z )=0,得-x +1-z =0. ① AC →·AP →=(2,0,1)·(x ,-1,z )=0,得2x +z =0,② 联立①②得x =-1,z =2,故点P 的坐标为(-1,0,2).4.在正方体ABCD-A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( )A .ACB .BDC .A 1D D .A 1A考点 向量法求解直线与直线的位置关系题点 方向向量与线线垂直答案 B解析 以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Dxyz .设正方体的棱长为1.则C (0,1,0),B (1,1,0),A (1,0,0),D (0,0,0),C 1(0,1,1),A 1(1,0,1),E ⎝⎛⎭⎫12,12,1,∴CE →=⎝⎛⎭⎫12,-12,1,AC →=(-1,1,0), BD →=(-1,-1,0),A 1D -→=(-1,0,-1),A 1A -→=(0,0,-1),∵CE →·BD →=(-1)×12+(-1)×⎝⎛⎭⎫-12+0×1=0,∴CE ⊥BD . 5.已知平面α内有一个点A (2,-1,2),α的一个法向量为n =(3,1,2),则下列点P 中,在平面α内的是( )A. (1,-1,1)B.⎝⎛⎭⎫1,3,32C.⎝⎛⎭⎫1,-3,32D.⎝⎛⎭⎫-1,3,-32 考点 直线的方向向量与平面的法向量题点 法向量求解线面垂直答案 B解析 要判断点P 是否在平面α内,只需判断向量P A →与平面α的法向量n 是否垂直,即P A →·n是否为0,因此,要对各个选项进行检验.对于选项A ,P A →=(1,0,1),则P A →·n =(1,0,1)·(3,1,2)=5≠0,故排除A ;对于选项B ,P A →=⎝⎛⎭⎫1,-4,12,则P A →·n =⎝⎛⎭⎫1,-4,12·(3,1,2)=0,故B 正确;同理可排除C ,D.故选B.6.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别在A 1D ,AC 上,且A 1E =23A 1D ,AF =13AC , 则( )A .EF 至多与A 1D ,AC 中的一个垂直B .EF ⊥A 1D ,EF ⊥ACC .EF 与BD 1相交D .EF 与BD 1异面考点 直线的方向向量与平面的法向量题点 求直线的方向向量答案 B解析 以D 为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z轴,建立空间直角坐标系Dxyz ,设正方体的棱长为1,则A 1(1,0,1),D (0,0,0),A (1,0,0),C (0,1,0),E ⎝⎛⎭⎫13,0,13,F ⎝⎛⎭⎫23,13,0,B (1,1,0),D 1(0,0,1),∴A 1D -→=(-1,0,-1),AC →=(-1,1,0),EF →=⎝⎛⎭⎫13,13,-13,BD 1-→=(-1,-1,1),∴EF →=-13BD 1-→,A 1D -→·EF →=0,AC →·EF →=0,从而EF ∥BD 1,EF ⊥A 1D ,EF ⊥AC ,故选B.7.两平面α,β的法向量分别为μ=(3,-1,z ),v =(-2,-y ,1),若α⊥β,则y +z 的值是( )A .-3B .6C .-6D .-12考点 向量法求解平面与平面的位置关系题点 向量法求解面面垂直答案 B解析 ∵α⊥β,∴μ·v =0,即-6+y +z =0,即y +z =6.二、填空题8.如图所示,在三棱锥A -BCD 中,DA ,DB ,DC 两两垂直,且DB =DC ,E 为BC 的中点,则AE →·BC →=_______.考点 向量法求解直线与直线的位置关系题点 方向向量与线线垂直答案 0解析 因为BE =EC ,故AE →=DE →-DA →=12(DB →+DC →)-DA →,在三棱锥A -BCD 中, DA ,DB ,DC 两两垂直,且DB =DC ,故AE →·BC →=⎣⎡⎦⎤12(DB →+DC →)-DA →·(DC →-DB →)=12(DC →2-DB →2)=0. 9.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB →=(2,-1,-4),AD →=(4,2,0),AP →=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP →是平面ABCD 的法向量. 其中正确的是________.(填序号)考点 向量法求解直线与直线的位置关系题点 向量法解决线线垂直答案 ①②③解析 AP →·AB →=(-1,2,-1)·(2,-1,-4)=-1×2+2×(-1)+(-1)×(-4)=0,∴AP ⊥AB ,即①正确.AP →·AD →=(-1,2,-1)·(4,2,0)=-1×4+2×2+(-1)×0=0.∴AP ⊥AD ,即②正确.又∵AB ∩AD =A ,∴AP ⊥平面ABCD ,即AP →是平面ABCD 的一个法向量,③正确.10.在△ABC 中,A (1,-2,-1),B (0,-3,1),C (2,-2,1).若向量n 与平面ABC 垂直,且|n |=21,则n 的坐标为________________.考点 向量法求解线面垂直问题题点 向量法求解线面垂直答案 (-2,4,1)或(2,-4,-1)解析 据题意,得AB →=(-1,-1,2),AC →=(1,0,2).设n =(x ,y ,z ),∵n 与平面ABC 垂直,∴⎩⎪⎨⎪⎧ n ·AB →=0,n ·AC →=0,即⎩⎪⎨⎪⎧ -x -y +2z =0,x +2z =0,可得⎩⎪⎨⎪⎧y =4z ,y =-2x . ∵|n |=21,∴x 2+y 2+z 2=21,解得y =4或y =-4.当y =4时,x =-2,z =1;当y =-4时,x =2,z =-1.三、解答题11.如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,AB =4,BC =3,AD=5,∠DAB =∠ABC =90°,E 是CD 的中点.证明:CD ⊥平面P AE .考点 向量法求解直线与平面的位置关系题点 向量法解决线面垂直证明 如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系Axyz .设P A =h ,则A (0,0,0),B (4,0,0),C (4,3,0),D (0,5,0),E (2,4,0),P (0,0,h ).所以CD →=(-4,2,0),AE →=(2,4,0),AP →=(0,0,h ).因为CD →·AE →=-8+8+0=0,CD →·AP →=0,所以CD ⊥AE ,CD ⊥AP ,而AP ,AE 是平面P AE 内的两条相交直线,所以CD⊥平面P AE.12.如图,在四棱锥P-ABCD中,底面ABCD是矩形,P A⊥底面ABCD,P A=AB=1,AD=3,点F是PB的中点,点E在边BC上移动.求证:无论点E在BC边的何处,都有PE⊥AF.考点向量法求解直线与直线的位置关系题点方向向量与线线垂直证明 以A 为坐标原点,AD ,AB ,AP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示空间直角坐标系Axyz ,则P (0,0,1),B (0,1,0),F ⎝⎛⎭⎫0,12,12,D ()3,0,0, 设BE =x (0≤x ≤3),则E (x,1,0),PE →·AF →=(x,1,-1)·⎝⎛⎭⎫0,12,12=0, 所以x ∈[0, 3 ]时都有PE ⊥AF ,即无论点E 在BC 边的何处,都有PE ⊥AF .13.如图,在底面为平行四边形的四棱锥P -ABCD 中,AB ⊥AC ,P A ⊥平面ABCD ,且P A =AB ,点E 是PD 的中点.求证:(1)AC ⊥PB ;(2)PB ∥平面AEC .考点 向量法求解直线与直线的位置关系题点 方向向量与线线垂直证明 (1)如图,以A 为坐标原点,AC ,AB ,AP 所在直线分别为x 轴,y轴,z 轴,建立空间直角坐标系Axyz ,设AC =a ,P A =b .则有A (0,0,0),B (0,b,0),C (a,0,0),P (0,0,b ),∴AC →=(a,0,0),PB →=(0,b ,-b ).从而AC →·PB →=0,∴AC ⊥PB .(2)由已知得D (a ,-b,0),E ⎝⎛⎭⎫a 2,-b 2,b 2,∴AE →=⎝⎛⎭⎫a 2,-b 2,b 2. 设平面AEC 的一个法向量为n ,则n ⊥AC →且n ⊥AE →,可得n =(0,1,1).∵n ·PB →=0,∴n ⊥PB .又PB ⊄平面AEC ,∴PB ∥平面AEC . 四、探究与拓展14.如图,P A ⊥平面ABCD ,四边形ABCD 为正方形,E 是CD 的中点,F 是AD 上一点,当BF ⊥PE 时,AF ∶FD 的比值为( )A .1∶2B .1∶1C .3∶1D .2∶1 答案 B解析 以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴, 建立如图所示的空间直角坐标系Axyz ,设正方形边长为1,P A =a ,则B (1,0,0),E ⎝⎛⎭⎫12,1,0,P (0,0,a ).设点F 的坐标为(0,y,0),则BF →=(-1,y,0),PE →=⎝⎛⎭⎫12,1,-a .因为BF ⊥PE ,所以BF →·PE →=0,解得y =12,即点F 的坐标为⎝⎛⎭⎫0,12,0,所以F 为AD 的中点,所以AF ∶FD =1∶1.15.如图,已知ABCD -A 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,且AE =FC 1=1.(1)求证:E ,B ,F ,D 1四点共面;(2)若点G 在BC 上,BG =23,点M 在BB 1上,GM ⊥BF ,垂足为H ,求证:ME ⊥平面BCC 1B 1.考点 向量法求解直线与平面的位置关系题点 向量法解决线面垂直证明 (1)以B 为坐标原点,BA ,BC ,BB 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Bxyz ,则BE →=(3,0,1),BF →=(0,3,2),BD 1→=(3,3,3),∴BD 1→=BE →+BF →,故BD 1→,BE →,BF →共面.又它们有公共点B ,∴E ,B ,F ,D 1四点共面.(2)设M (0,0,z ),则GM -→=⎝⎛⎭⎫0,-23,z ,而BF →=(0,3,2), 由题设得GM -→·BF →=-23·3+z ·2=0,得z =1. ∵M (0,0,1),E (3,0,1),∴ME -→=(3,0,0),又BB 1→=(0,0,3),BC →=(0,3,0)∴ME -→·BB 1→=0,ME -→·BC →=0,从而ME ⊥BB 1,ME ⊥BC .又BB 1∩BC =B ,故ME ⊥平面BCC 1B 1.。
利用空间向量解决立体几何中的垂直问题

例2:已知:在空间四边形OABC中,OA⊥BC,OB⊥AC, 求证:OC⊥AB
证明:由已知 OA BC,OB AC
O 所以 OA BC 0 , OB AC 0
OA (OC OB) 0
OB (OC OA) 0
A
C 所以 OA OC OA OB
B
OB OC OB OA
所以 OAOC OB OC 0
l
要证l与g垂直,只需证 l·g = 0
而 m , n 不平行,由共面向量
gl m
n
n
mg
定理知,存在唯一的有序实数 对(x, y), 使得 g =x m + y n
要证 l·g = 0, 只需 l ·g = xl ·m + y l ·n = 0
而 l·m = 0 ,l·n = 0
故 l·g = 0
1.共面向量定理:如果两个向量 a , b不共线,则向量 p 与向量 a , b 共面的充要条件是存在实数对x,y,使
Pp xa yb
2、空间向量的基本定理
如果三个向量 a, b, c不共面,那么对空间任一向量 p ,存
在一个唯一的有序实数对x、y、z,使
p xa yb zc
二、数量积的性质
1)数量积性质 对于非零向量 a , b ,有:
(1) a e=|a|cos a,e
(2) a b a b=0 --证明向量垂直的依据
(3) |a|2 =a a
--求向量的长度(模)的依据
ab
(4) cos a,b =
--求向量夹角的依据
|a||b|
2)数量积满足的运算律
1) (a) b (a b)
所以AC 平面ABD
课堂小结:
专题02 空间向量的坐标表示及用向量法证明平行垂直共面问题(知识梳理+专题过关)(解析版)

专题02空间向量的坐标表示及用向量法证明平行垂直共面问题【知识梳理】1、设()111,,a x y z =,()222,,b x y z =,则(1)()121212,,a b x x y y z z +=+++.(2)()121212,,a b x x y y z z -=---.(3)()111,,a x y z λλλλ=.(4)121212a b x x y y z z ⋅=++.(5)若a ,b 为非零向量,则12121200a b a b x x y y z z ⊥⇔⋅=⇔++=.(6)若0b ≠,则121212//,,a b a b x x y y z z λλλλ⇔=⇔===.(7)a ==.(8)cos ,a b a b a b⋅〈〉==(9)()111x ,y ,z A ,()222x ,y ,z B =,则d AB AB ==.2、在空间中,取一定点O 作为基点,那么空间中任意一点P 的位置可以用向量OP 来表示.向量OP 称为点P 的位置向量.3、空间中任意一条直线l 的位置可以由l 上一个定点A 以及一个定方向确定.点A 是直线l 上一点,向量a 表示直线l 的方向向量,则对于直线l 上的任意一点P ,有ta AP =,这样点A 和向量a 不仅可以确定直线l 的位置,还可以具体表示出直线l 上的任意一点.4、空间中平面α的位置可以由α内的两条相交直线来确定.设这两条相交直线相交于点O ,它们的方向向量分别为a ,b .P 为平面α上任意一点,存在有序实数对()x,y ,使得xa yb OP =+,这样点O 与向量a ,b 就确定了平面α的位置.5、直线的方向向量和平面的法向量(1)直线的方向向量:若A 、B 是直线l 上的任意两点,则AB 为直线l 的一个方向向量;与AB 平行的任意非零向量也是直线l 的方向向量.(2)平面的法向量:若向量n 所在直线垂直于平面α,则称这个向量垂直于平面α,记作n α⊥,如果n α⊥,那么向量n 叫做平面α的法向量.(3)平面的法向量的求法(待定系数法):①建立适当的坐标系.②设平面α的法向量为(,,)n x y z =.③求出平面内两个不共线向量的坐标123123(,,),(,,)a a a a b b b b ==.④根据法向量定义建立方程组00n a n b ⎧⋅=⎪⎨⋅=⎪⎩.⑤解方程组,取其中一组解,即得平面α的法向量.6、用向量方法判定空间中的平行关系(1)线线平行设直线12,l l 的方向向量分别是a b 、,则要证明1l ∥2l ,只需证明a ∥b ,即()a kb k R =∈.即:两直线平行或重合⇔两直线的方向向量共线.(2)线面平行①(法一)设直线l 的方向向量是a ,平面α的法向量是u ,则要证明l ∥α,只需证明a u ⊥,即0a u ⋅=.即:直线与平面平行⇔直线的方向向量与该平面的法向量垂直且直线在平面外②(法二)要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可.(3)面面平行若平面α的法向量为u ,平面β的法向量为v ,要证α∥β,只需证u ∥v ,即证u v λ=.即:两平面平行或重合⇔两平面的法向量共线.7、用向量方法判定空间的垂直关系(1)线线垂直设直线12,l l 的方向向量分别是a b 、,则要证明12l l ⊥,只需证明a b ⊥,即0a b ⋅=.即:两直线垂直⇔两直线的方向向量垂直.(2)线面垂直①(法一)设直线l 的方向向量是a ,平面α的法向量是u ,则要证明l α⊥,只需证明a ∥u ,即a u λ=.②(法二)设直线l 的方向向量是a ,平面α内的两个相交向量分别为m n 、,若,.0a m l a n α⎧⋅=⎪⊥⎨⋅=⎪⎩则即:直线与平面垂直⇔直线的方向向量与平面的法向量共线⇔直线的方向向量与平面内两条不共线直线的方向向量都垂直.(3)面面垂直若平面α的法向量为u ,平面β的法向量为v ,要证αβ⊥,只需证u v ⊥,即证0u v ⋅=.即:两平面垂直⇔两平面的法向量垂直.【专题过关】【考点目录】考点1:空间向量的坐标运算考点2:空间向量模长的坐标运算考点3:空间向量平行的坐标运算考点4:空间向量垂直的坐标运算考点5:空间向量夹角的坐标运算考点6:共面问题考点7:平行问题考点8:垂直问题【典型例题】考点1:空间向量的坐标运算1.(2022·江苏常州·高二期中)平行六面体1111ABCD A B C D -中,()()11,2,3,1,2,4AC C =-,则点1A 的坐标为()A .()0,4,7B .()2,0,1-C .()2,0,1-D .()2,0,1【答案】B【解析】设()1,,A x y z ,∵()()11,2,3,1,2,4AC C =-,又11AC AC =,∴()()1,2,31,2,4x y z =----,解得2,0,1x y z =-==,即()12,0,1A -.故选:B.2.(2021·广东·新会陈经纶中学高二期中)已知向量()3,2,5a =-,()1,5,1b =-,则3a b -=()A .8,11(),14-B .9,3(),15-C .10,1(),16-D .(0,13,2)【答案】C【解析】()3,2,5a =-,()1,5,1b =-,则3(10,1,16)a b -=-故选:C3.(2021·河北省博野中学高二期中)已知()()3,2,5,1,,1a b x =-=-,且2a b ⋅=,则x 的值是()A .5B .6C .3D .4【答案】A【解析】因为3252a b x ⋅=-+-=,所以5x =.故选:A.4.(2021·安徽·高二期中)已知向量()2,3,1a =--,()1,2,4b =,则a b +等于()A .()1,1,5--B .()1,1,5-C .()1,1,5-D .()1,1,5【答案】A【解析】∵向量()2,3,1a =--,()1,2,4b =,∴()()()2,3,11,2,41,1,5a b +=--+=--.故选:A.5.(2022·广西桂林·高二期中(理))已知向量()1,0,1a =r ,()2,1,3b =,则2a b -=()A .()3,2,5-B .()3,2,5--C .()3,2,5--D .()3,2,5---【答案】D【解析】()2,1,3b =()24,2,6b ∴=()23,2,5a b ∴-=---.故选:D.6.(2021·天津天津·高二期中)在空间直角坐标系中,已知点()()1,2,3,3,0,1A B --,则线般AB 的中点坐标是()A .()1,1,2--B .()1,1,2-C .()2,2,4-D .()2,2,4--【答案】A【解析】设线般AB 的中点M 坐标为(),,x y z ,由AM MB =可得()()1,2,33,,1x y z x y z -+-=----,所以13231x x y y z z -=--⎧⎪+=-⎨⎪-=-⎩可得112x y z =-⎧⎪=-⎨⎪=⎩,所以线般AB 的中点坐标是()1,1,2--,故选:A.7.(2021·北京·人大附中高二期中)在空间直角坐标系中,已知()0,1,0A ,()3,2,2B ,点D 满足2AD AB =,则点D 的坐标是()A .()5,4,3B .()3,4,3C .()6,3,4D .()1,2,3【答案】C【解析】设(),,D x y z ,则()(),1,,3,1,2AD x y z AB =-=,由2AD AB =得6124x y z =⎧⎪-=⎨⎪=⎩即()6,3,4D ,故选:C.8.(2021·北京市昌平区实验学校高二期中)已知(1,=-a,(=-b ,则a b ⋅=______【答案】5-【解析】由已知1(2)(315a b ⋅=⨯-+-+⨯=-.故答案为:5-9.(2021·广东·广州市玉岩中学高二期中)空间直角坐标系中,平行四边形ABCD 的顶点()0,1,2A 、()2,1,4B -、()5,0,3C ,则D 点坐标为________.【答案】()3,2,1【解析】设点(),,D x y z ,由题意可得BA CD =,即()()2,2,25,,3x y z --=--,即52232x y z -=-⎧⎪=⎨⎪-=-⎩,解得321x y z =⎧⎪=⎨⎪=⎩,故点D 的坐标为()3,2,1.故答案为:()3,2,1.考点2:空间向量模长的坐标运算10.(2022·江苏徐州·高二期中)已知点()2,1,0A ,()1,3,0B ,()2,1,1C --,()2,3,1D ,则向量AB 在向量CD 上的投影向量的模为______.【答案】22【解析】因为()2,1,0A ,()1,3,0B ,()2,1,1C --,()2,3,1D ,所以()()()1,3,02,1,01,2,0AB =-=-,()()()2,3,12,1,14,4,0CD =---=,所以1424004AB CD ⋅=-⨯+⨯+⨯=,CD ==所以向量AB 在向量CD 上的投影为2AB CD CD⋅==;所以向量AB 在向量CD 上的投影向量为)2114,4,0,0222AB CD CD CDCD⋅⎛⎫== ⎪⎝⎭即向量AB 在向量CD 2=;故答案为:2211.(2022·江苏常州·高二期中)已知正方体ABCD -A 1B 1C 1D 1的棱长为3,112AM MC =,点N 为B 1B 的中点,则||MN =___________.【答案】2【解析】如图所示,以点D 为坐标原点,以DA ,DC ,1DD 所在直线分别为x ,y ,z 轴,建立空间直角坐标系D xyz -,则()()()()113,0,0,0,3,3,3,3,0,3,3,3A CB B ,因为112AM MC =,点N 为1B B 的中点,所以()111,1,13AM AC ==-,所以(2,1,1)M ,3(3,3,)2N ,11,2,2MN ⎛⎫= ⎪⎝⎭故2MN =.故答案为:2.12.(2021·浙江省杭州学军中学高二期中)已知空间向量()1,0,1=a ,()2,1,2b =-,则向量a 在向量b 上的投影向量的坐标是__________.【答案】848(,,)999-【解析】因为空间向量()1,0,1=a ,()2,1,2b =-,所以2024a b ⋅=++=,3b ==,所以向量a 在向量b 上的投影向量为:()418482,1,2(,,)33999a bbb b ⨯=⨯-=-⋅,故答案为:848(,,)999-.13.(2021·湖北武汉·高二期中)已知正四棱柱1111ABCD A B C D -中,2AB =,1AA =若M 是侧面11BCC B 内的动点,且AM MC ⊥,则1A M 的最小值为__________.【解析】如图,以D 为原点建立空间直角坐标系,设点(),2,M m n ,则()()(12,0,0,0,2,0,2,2,A C B,(1A ,()(),0,,2,2,CM m n AM m n ∴==-,又AM MC ⊥得:2220,AM CM m m n ⋅=-+=即()2211m n -+=;又11A B ⊥平面11BCC B ,故11A MB Ð为1A M 与平面11BCC B 所成角,要使1A M 最小,只需1B M 最小,即11tan A MB ∠最大,令[]1cos ,sin ,0,m n θθθπ=+=∈, tan,∴当3πθ=时,11tanA MB ∠最大,则113(2,2,(,2,22A M m n =-=-,所以1||A M ==14.(2022·江苏南通·高二期中)设x 、y ∈R ,向量(),1,1a x =,()1,,1b y =,()3,6,3c =-r且a c ⊥,//bc ,则a b +=()A .B .C .4D .3【答案】D【解析】因为a c ⊥,则3630a c x ⋅=-+=,解得1x =,则()1,1,1a =,因为//b c ,则136y=-,解得2y =-,即()1,2,1b =-,所以,()2,1,2a b +=-,因此,3a b +=.故选:D.15.(2022·福建龙岩·高二期中)已知向量()3,2,4a =-r,()1,2,2b =-,则a b -=()A .B .40C .6D .36【答案】C【解析】由题设(4,4,2)a b -=-,则6a b -=.故选:C考点3:空间向量平行的坐标运算16.(2022·江苏徐州·高二期中)已知向量()2,1,3a =-,(),2,6b x =-,若a b ∥,则实数x 的值为()A .2B .4C .4-D .2-【答案】C【解析】因为向量()2,1,3a =-,(),2,6b x =-,且a b ∥,所以26213x -==-,解得:4x =-.故选:C17.(2022·江苏·响水县第二中学高二期中)已知()2,3,1a =-,则下列向量中与a 平行的是()A .() 1,1,1B .() 4,6,2--C .() 2,3,5-D .()23,5-,-【答案】B【解析】对于A ,因为231111-≠≠,所以A 不正确;对于B ,因为231462-==--,所以B 正确;对于C ,因为231235-=≠-,所以C 不正确;对于D ,因为231235-≠≠--,所以D 不正确.故选:B18.(2022·江苏·淮安市淮安区教师发展中心学科研训处高二期中)已知()2,1,3A ,()1,3,1B ,()4,,C y z ,若AB AC ∥,则2y z -=()A .20-B .17-C .11D .4【答案】B【解析】()1,2,2AB =--,()2,1,3AC y z =--,因为AB AC ∥,所以122213y z --==--,解得3y =-,7z =,故217y z -=-.故选:B19.(2022·安徽省舒城中学高二期中)已知向量(2,1,3),(4,2,)a b x =-=-,若a ∥b ,则x =______.【答案】-6【解析】因为向量(2,1,3),(4,2,)a b x =-=-,且a ∥b ,所以a =b λ,所以42213x-==-,解得:6x =-.故答案为:-6.20.(2021·安徽宣城·高二期中)在空间直角坐标系中,已知()2,2,4A -,()4,4,2B --,()0,0,2C ,若AB AC λ=,则实数λ=______.【答案】3【解析】由题意得()6,6,6AB =--,()2,2,2AC =--,所以()32,2,23AB AC =--=,即3λ=,故答案为:321.(2021·河北·石家庄市第六中学高二期中)已知(,1,3)a x =r ,(1,3,9)b =-r,若a 与b 共线,则x 的值是__________.【答案】13-【解析】因为(,1,3)a x =r ,(1,3,9)b =-r,且a 与b 共线,所以13139x ==-,解得13x =-,故答案为:13-考点4:空间向量垂直的坐标运算22.(2022·新疆·乌鲁木齐市第四中学高二期中(理))已知向量()1,1,0a =r ,()1,0,2b =-r,且ka b +与2a b -互相垂直,则k 的值是()A .-1B .43C .53D .75【答案】D【解析】因为()1,1,0a =r,()1,0,2b =-r ,所以(1,1,0)(1,0,2)(1,,2)ka b k k k +=+-=-,22(1,1,0)(1,0,2)(3,2,2)a b -=--=-,因为ka b +与2a b -互相垂直,所以()()23(1)240ka b a b k k +⋅-=-+-=,解得75k =,故选:D23.(2022·江苏·滨海县五汛中学高二期中)已知向量(1,1,2)a k =,(1,0,1)b =--,(0,2,1)c =,且向量2a b -与c 互相垂直,则k 的值是()A .1B .2-C .4-D .0【答案】B【解析】()23,1,22a b k -=+,因为向量2a b -与c 互相垂直,故3012220k ⨯+⨯++=,故2k =-,故选:B24.(2022·江苏徐州·高二期中)如图,正方体1111ABCD A B C D -的棱长为6,点M 为1CC 的中点,点P 为底面1111D C B A 上的动点,满足BP AM ⊥的点P 的轨迹长度为()A .B .C .D .【答案】B【解析】分别以DA ,DC ,1DD 为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则()6,0,0A ,()6,6,0B ,()0,6,3M ,设(),,6P x y ,[][]0,6,0,6x y ∈∈,则()6,6,3AM =-,()6,6,6BP x y =--,由BP AM ⊥得()()6666360x y --+-+⨯=,即3y x =-,由于[][]0,6,0,6x y ∈∈,所以[]3,6x ∈,[]0,3y ∈,所以点P 的轨迹为面1111D C B A 上的直线:3y x =-,[]3,6x ∈,即图中的线段EF ,由图知:EF =故选:B.25.(2022·江苏徐州·高二期中)已知直线2,l l l 的方向向量分别为()()1,4,2,2,1,a b m =-=-,若12l l ⊥,则m 等于()A .0B .1C .2D .3【答案】B【解析】由于12l l ⊥,所以()()124120,1m m ⨯-+⨯+-⨯==.故选:B26.(2022·江苏省江浦高级中学高二期中)在空间直角坐标系中,(1,2,)A a -,(2,,0)B a ,(1,,2)C a -,若1()2AB AC BC -⊥,则实数a 的值为()A .3B .32C .72D .92【答案】A【解析】由题意(1,2,)AB a a =+-,(0,2,2)AC a a =+--,(1,0,2)BC =--,122(1,,)222a a AB AC +--=,因为1()2AB AC BC -⊥,所以1()1(2)02AB AC BC a -⋅=---=,3a =.故选:A .27.(2022·福建龙岩·高二期中)已知向量()1,3,2a =-,()2,2,1b =--,点()3,1,4-A ,()2,2,2B -.(1)求2a b +;(2)若直线AB 上存在一点E ,使得OE b ⊥,其中O 为原点,求E 点的坐标.【解析】(1)因为()1,3,2a =-,()2,2,1b =--,所以()20,4,3a b +=-,所以25a b +=;(2)设AE AB λ=,由()3,1,4-A ,()2,2,2B -,得()1,1,2AB =-,则(),,2AE AB λλλλ==-,故()()()3,1,4,,23,1,24OE OA AE λλλλλλ=+=-+-=-+-+,因为OE b ⊥,所以0OE b ⋅=,即()()()2321240λλλ--++--+=,解得2λ=-,所以()2,2,4AE =--,设(),,E x y z ,则()()3,1,42,2,4AE x y z =+--=--,所以321244x y z +=-⎧⎪-=-⎨⎪-=⎩,解得518x y z =-⎧⎪=-⎨⎪=⎩,所以()5,1,8E --.考点5:空间向量夹角的坐标运算28.(2022·福建龙岩·高二期中)已知空间中三点(),1,2A m -,()3,1,4B -,()1,,1C n -.(1)若A ,B ,C 三点共线,求m n +的值;(2)若AB ,BC 的夹角是钝角,求m n +的取值范围.【解析】(1)由题设(3,2,6)AB m =--,(2,1,3)CB n =--,又A ,B ,C 三点共线,所以存在R λ∈使AB CB λ=,即322(1)63m n λλλ-=⎧⎪=-⎨⎪-=-⎩,可得210m n λ=⎧⎪=-⎨⎪=⎩,所以1m n +=-.(2)由(2,1,3)BC n =--,由(1)知:当,AB BC π<>=时,有1m n +=-;而cos ,||||AB BC AB BC AB BC ⋅<>==AB ,BC 的夹角是钝角,所以2(3)2(1)182()260m n m n -+--=+-<,可得m n +13<;综上,3m n +<且10m n =-⎧⎨=⎩不同时成立.29.(2022·福建宁德·高二期中)已知空间三点()1,1,1A --,()1,2,2B --,()2,4,1C -,则AB 与AC 的夹角θ的大小是______.【答案】3π【解析】因为()2,1,3AB =--,()1,3,2AC =-,所以2367A AB C ⋅=-++=所以AB =AC ==所以1cos 2AB AB AC ACθ⋅==⋅因为[]0,θπ∈,所以3πθ=故答案为:3π30.(2022·江苏连云港·高二期中)已知空间向量(1,0,1),(1,1,)a b n ==,且3a b ⋅=,则n =_______,向量a 与b 的夹角为_______.【答案】26π【解析】依题意313a b n ⋅==+=,解得2n =,所以(1,0,1),(1,1,2)a b ==,所以cos ,2a b a b a b⋅=⋅,由于[],0,a b π∈,所以向量a 与b 的夹角为6π.故答案为:2;6π.31.(2021·浙江·绍兴一中高二期中)已知动点P 在正方体1111ABCD A B C D -的对角线1BD (不含端点)上.设11D PD Bλ=,若APC ∠为钝角,则实数λ的取值范围为___________.【答案】1(,1)3【解析】如图,建立空间直角坐标系,设正方体棱长为1,则(1,0,0)A ,(0,1,0)C ,1(0,0,1)D ,(1,1,0)B ,1(1,1,1)D B =-,11(,,)D P D B λλλλ==-,所以(,,1)P λλλ-,(1,,1),(,1,1)PA PC λλλλλλ=---=---,APC ∠为钝角,则22(1)(1)(1)3410PA PC λλλλλλλ⋅=----+-=-+<,解得113λ<<.又,,A P C 不可能共线,故答案为:1(,1)3.32.(2022·四川省成都市新都一中高二期中(理))已知()cos ,1,sin a αα=-,()sin ,1,cos b αα=-,则向量a b +与a b -的夹角为()A .90°B .60°C .30°D .0°【解析】因为()cos ,1,sin a αα=-,()sin ,1,cos b αα=-,所以()cos sin ,2,sin cos +=+-+a b αααα,()cos sin ,0,sin cos a b αααα-=--,设向量a b +与a b -的夹角为β,则cos +⨯-+-⨯++-=ααααααααβ2222=0=,因为[]0,βπ∈,所以2πβ=,故向量a b +与a b -的夹角为2π,故选:A.33.(2021·山东·临沭县教育和体育局高二期中)若向量()1,,0a λ=,(2,1,2)b =-且a 与b 的夹角余弦值为23,则实数λ等于()A .0B .-43C .0或-43D .0或43【答案】C【解析】由题知,2cos ,3a b a b a b⋅<>==即2340λλ+=,解得0λ=或43λ=-.故选:C34.(多选题)(2022·江苏·马坝高中高二期中)若(1,,2)a λ=--,(2,1,1)b =-,a 与b 的夹角为120°,则λ的值为()A .17-B .17C .1D .1-【答案】BD【解析】由题意得cos120︒=解得1λ=-或17λ=故选:BD35.(多选题)(2021·湖北省广水市实验高级中学高二期中)若(2,5,4)a x =-r 与(,2,2)b x x =r 的夹角为钝角,则x 的取值可能为()A .5B .3C .4D .2【解析】因为(2,5,4)a x =-r ,(,2,2)b x x =r ,所以221080a b x x ⋅=-+<r r,解得14x <<;当//a b 时,设λa b =,λ无解,即,a b 不能平行;故选:BD考点6:共面问题36.(2021·山东威海·高二期中)如图,在四棱锥P ABCD -中,PA ⊥面ABCD ,,//,2,3AD CD AD BC PA AD CD BC ⊥====.E 为PD 的中点,点F 在PC 上,且13PF PC =.(1)求证:CD ⊥面PAD ;(2)设点G 在PB 上,且PGPBλ=.判断是否存在这样的λ,使得A ,E ,F ,G 四点共面,若存在,求出λ的值;若不存在,说明理由.【解析】(1)由PA ⊥面,ABCD CD ⊂面ABCD ,则PA CD ⊥,又AD CD ⊥且PA AD A ⋂=,可得:CD ⊥面PAD .(2)以A 为原点,面ABCD 内与AD 垂直的直线为x 轴,,AD AP 方向为y 轴,z 轴建立如图所示的空间直角坐标系A xyz -,易知:(0,0,0),(0,0,2),(2,2,0),(0,2,0)A P C D ,存在这样的λ.由PG PB λ=可得:(2,,2)PG λλλ=--,则(2,,22)AG AP PG λλλ=+=--,若A ,E ,F ,G 四点共面,则AG 在面AEF 内,又面AEF 的一个法向量为(1,1,1)m =-,∴0m AG ⋅=,即2220λλλ-+-=,可得23λ=.∴存在这样的23λ=,使得四点共面.37.(2021·广东深圳·高二期中)如图所示,在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别是BC ,11A D 的中点.(1)求证:1B ,E ,D ,F 四点共面;【解析】(1)如图,以1,,AB AD AA 为,,x y z 轴建立空间直角坐标系,又因为E ,F 分别是BC ,11A D 的中点.所以(2,0,0)B ,(2,2,0)C ,(0,2,0)D ,1(2,0,2)B ,1(0,0,2)A ,1(0,2,2)D ,(0,0,0)A ,(2,1,0)E ,(0,1,2)F ,1(2,1,0)B F =-,1(2,1,0)ED B F =-=,所以1//ED B F ,而1E B F ∉,所以1//ED B F ,所以1B ,E ,D ,F 四点共面;38.(2021·广东·广州市第一中学高二期中)已知()2,1,3a =-,()1,4,2b =--,()7,5,c λ=.若a 、b 、c 三向量共面,则实数λ=______.【答案】657【解析】因为,a b 不平行,且a 、b 、c 三向量共面,所以存在实数x ,y ,使c xa yb =+,所以725432x y x y x y λ=-⎧⎪=-+⎨⎪=-⎩,解得337177657x y λ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩,故答案为:65739.(2021·全国·高二期中)已知点A 、B 、C 、D 的坐标分别为(0,1,2),(1,2,3),(1,3,1),(,5,3)x ,且A ,B ,C ,D 四点共面,则x =___________.【答案】3【解析】由题意,A ,B ,C ,D 四点共面故,R λμ∃∈,使得AB AC AD λμ=+又(1,1,1),(1,2,1),(,4,1)AB AC AD x ==-=故12411x λμλμλμ+=⎧⎪+=⎨⎪-+=⎩解得113,,22x λμ==-=故答案为:340.(2021·福建·厦门双十中学高二期中)已知(2,1,3),(1,4,2),(3,5,)a b c λ=-=-=-,若,,a b c 三向量共面,则实数λ=_____.【答案】1-【解析】由题意可知,存在实数,m n 满足:c ma nb =+,据此可得方程组:325432m nm n m nλ-=-⎧⎪=-+⎨⎪=+⎩,求解方程组可得:111m n λ=-⎧⎪=⎨⎪=-⎩.故答案为1-.41.(多选题)(2021·辽宁·建平县实验中学高二期中)在正方体1111ABCD A B C D -中,棱长为2,点P 为线段AB 的中点,Q ,R 分别为线段BC ,1AC 上的动点(含端点),下列结论正确的是()A .存在点Q 使得11A P C Q ⊥B .存在点R 使得11A P D R⊥C .当Q 为BC 中点时,存在点R 使得1A P ,1C Q ,1D R 共面D .当Q 为BC 中点时,存在点R 使得1C ,Q ,1D ,R 四点共面【答案】BD【解析】在正方体1111ABCD A B C D -中,以D为原点,建立如图所示的空间直角坐标系,则()()()()()()1110,0,0,0,2,0,2,0,2,0,0,22,0,0,0,2,2,D D C C A A ,()2,1,0P ,令()01CQ mCB m ≤=≤,()101CR A n nC ≤=≤,则()2,2,0Q m ,()2,22,2R n n n -,因为()10,1,2A P =-,()12,0,2Q m C =-,1140A P C Q ⋅=≠,即1A P 与1C Q 不垂直,A 不正确;而()12,22,22n n D R n =--,1166A P D R n ⋅=-,当1n =时,110A P D R ⋅=,即存在点R 使得11A P D R ⊥,B 正确;当Q 为BC 中点时,()1,2,0Q ,()11,0,2C Q =-,若存在点R 使得1A P ,1C Q ,1D R 共面,则111D R x A P yC Q =+,,R x y ∈,即()()()2,22,220,1,21,0,2n n n x y --=-+-,即2222222y n x n x y n =⎧⎪=-⎨⎪--=-⎩,解得[]10,1n =-∉,C 不正确;当Q 为BC 中点时,若1C ,Q ,1D ,R 四点共面,则1111D R D C D Q λμ=+,,R λμ∈,而()11,2,2D Q =-,()()()2,22,220,2,01,2,2n n n λμ--=+-,即22222222nn n μλμμ=⎧⎪+=-⎨⎪-=-⎩,解得[]10,13n =∈,D 正确.故选:BD42.(2021·云南省泸西县第一中学高二期中)已知空间向量(2,1,),(1,1,0),(1,2,)a m b p t =-=-=-,若,,a b p 共面,则m t +=()A .1-B .0C .1D .12-【答案】B【解析】若a 、b 、p 共面,则a b p λμ=+,即(2-,1,)(m λμ=-,2λμ-+,)t μ,故221t mλμλμμ-=-⎧⎪-+=⎨⎪=⎩,故310t m λμ=-⎧⎪=-⎨⎪+=⎩,故选:B .考点7:平行问题43.(2022·四川成都·高二期中(理))若直线l 的方向向量(1,0,1)a =,平面β的法向量(1,1,1)n =-,则()A .l β⊂B .l β⊥C .l β//D .l β⊂或l β//【答案】D【解析】因为110a n ⋅=-=,所以a n ⊥,所以l β⊂或l β//.故选:D44.(多选题)(2022·江苏·淮安市淮安区教师发展中心学科研训处高二期中)下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是()A .若两条不重合的直线12,l l 的方向向量分别是(2,2,1),(2,2,1)a b =--=--,则12l l //B .若直线l 的方向向量是(1,1,2)a =,平面α的法向量是(2,2,4)n =---,则l α⊥C .若直线l 的方向向量是(0,2,0)a =,平面α的法向量是(2,0,2)n =-,则//l αD .若两个不同的平面,αβ的法向量分别是(3,4,2),(2,0,3)m n =-=-,则αβ⊥【答案】BD【解析】对于A ,因为向量a b ,不平行,所以12l l ,不平行,故A 不正确;对于B ,因为2n a =-,所以//n a ,故B 正确;对于C ,因为()02+20+020a n ⋅=⨯-⨯⨯=,所以a n ⊥,所以//l α或l 在面α内,故C 不正确;对于D ,因为6+060m n ⋅=-+=,所以αβ⊥,故D 正确.故选:BD .45.(2020·广东顺德德胜学校高二期中)设向量,v μ分别是平面,αβ的法向量,向量(1,2,2),(2,4,)v m μ=-=--,若,αβ平行,则实数m =___________【答案】4【解析】∵α∥β∴平面α、β的法向量互相平行,∴(1λ,2,2)(2-=-,4-,)m ,且R λ∈;解得2λ=-,4m =.故答案为:446.(2022·福建宁德·高二期中)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,其中AD BC ∥.,3,2,AD AB AD AB BC PA ⊥===⊥平面ABCD ,且3PA =,点M 在棱PD 上,点N 为BC 中点.(1)若2DM MP =,证明:直线//MN 平面PAB :【解析】(1)如图所示,以点A 为坐标原点,以AB 为x 轴,AD 为y 轴,AP 为z 轴建立空间直角坐标系,则(0,0,3),(2,0,0),(0,3,0),(2,2,0),(2,1,0)P B D C N若2DM MP =,则(0,1,2)M ,(2,0,2)MN =-因为PA ⊥平面ABCD ,所以AD PA⊥又因为,AD AB PA AB A⊥⋂=所以AD ⊥平面PAB平面PAB 的其中一个法向量为(0,3,0)AD =所以0MN AD ⋅=,即AD MN⊥又因为MN ⊄平面PAB所以//MN 平面PAB47.(2021·河北·石家庄市第十二中学高二期中)如图所示,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD AB ⊥,AB ∥DC ,2AD DC AP ===,1AB =.点E 为棱PC 的中点,求证:(1)BE DC ⊥;(2)BE ∥平面PAD ;【解析】(1)因为PA ⊥平面ABCD ,AB Ì平面ABCD ,AD ⊂平面ABCD ,所以,PA AB PA AD ⊥⊥,因为AD AB ⊥,所以,,AB AD AP 两两垂直,所以以A 为原点,,,AB AD AP 所在的直线分别为,,x y z 轴建立空间直角坐标系,如图所示,则(0,0,0),(1,0,0),(2,2,0),(0,2,0),(0,0,2),(1,1,1)A B C D P E ,所以(0,1,1),(2,0,0)BE DC ==,所以0BE DC ⋅=,所以BE DC ⊥,所以BE DC ⊥,(2)平面PAD 的一个法向量为(1,0,0)AB =,因为0AB BE ⋅=,所以AB BE ⊥,因为BE ⊄平面PAD ,所以BE ∥平面PAD ;48.(2021·广东·湛江二十一中高二期中)如图所示,四棱锥S -ABCD 的底面是正方形,每倍,P 为侧棱SD 上的点.(1)若P 为侧棱SD 上的中点,证明SB //平面PAC .(2)若SD ⊥平面PAC ,则侧棱SC 上是否存在一点E ,使得BE //平面PAC ?若存在,求SE ∶EC 的值;若不存在,试说明理由.【解析】(1)证明:如图所示:连接BD 与AC 交于点O ,连接OP ,因为四边形ABCD 是正方形,所以O 为中点,又P 为侧棱SD 上的中点,所以//OP SB ,又OP ⊂平面PAC ,SB ⊄平面PAC ,所以//SB 平面PAC ;(2)建立如图所示空间直角坐标系:设侧棱SC 上存在一点E ,使得BE //平面PAC ,且SE SC λ=,设正方形ABCD 的边长为1,则,,0,,0,0,B C D S ⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以,,0,,,0,SC SB SD ⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则)1BE SE SB SC SB λλ⎛⎫=-=-=--- ⎪ ⎪⎝⎭,因为SD ⊥平面PAC ,所以SD 是平面PAC 的一个法向量,若BE //平面PAC ,则()131022BE SD λ⋅=+-=,解得23λ=,所以侧棱SC 上存在一点E ,使得BE //平面PAC ,且:2:1SE EC =.49.(2021·湖南·怀化五中高二期中)如图所示,在长方体1111ABCD A B C D -中,1AD =,12AB AA ==,N 、M 分别AB 、1C D 的中点.(1)求证://NM 平面11A ADD ;(2)求证:NM ⊥平面11A B M .【解析】(1)以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()1,0,0A 、()0,1,1M 、()1,1,0N 、()11,2,2B 、()11,0,2A ,()1,0,1NM =-,易知平面11A ADD 的一个法向量为()0,1,0m =u r ,1001100NM m ⋅=-⨯+⨯+⨯=,则NM m ⊥,NM ⊄平面11A ADD ,故//NM 平面11A ADD ;(2)设平面11A B M 的法向量为(),,n x y z =,()110,2,0A B =,()11,1,1A M =--,由11100n A B n A M ⎧⋅=⎪⎨⋅=⎪⎩,得200y x y z =⎧⎨-+-=⎩,取1x =-,可得()1,0,1n =-,所以,NM n =,故NM ⊥平面11A B M .考点8:垂直问题50.(多选题)(2021·福建·泉州五中高二期中)已知正三棱柱111ABC A B C -的所有棱长均相等,D ,E 分别是BC ,1CC 的中点,点P 满足()11AP xAB y AC x y AB =++--,下列选项正确的是()A .当12y =时,AP BC ⊥B .当21x y +=时,AP BE⊥C .当x y =时,DEP ∠为锐角D .当12x y -=时,1//A P 平面ADE 【答案】ABD 【解析】建立如图所示空间直角坐标系:设棱长为2,则)()()()()1,0,1,2,0,1,0,0,1,0,0,1,1A B C B E --,所以()()()12,1,0,AB AC AB ==-=,所以()2,2AP y x =-,A.当12y =时,()0,2,0BC =-,420AP BC y ⋅=-=,所以AP BC ⊥,故正确;B.当21x y +=时,()0,2,1BE =-,4220AP BC y x ⋅=-+=,所以AP BE ⊥,故正确;C.当x y =时,()()()0,1,1,0,22,2132ED EP AP AE y x ED EP x y =-=-=--⋅=-+,正负不定,故错误;D.当12x y -=时,()112,22A P AP AA y x =-=--,设平面ADE 的一个法向量为(),,n a b c =,则00DA n ED n ⎧⋅=⎨⋅=⎩,即00b c =-=⎪⎩,令1b =,则()0,1,1n =,所以()1210A P n x y ⋅=--=,又1A P ⊄平面ADE ,所以1//A P 平面ADE ,故正确;故选:ABD51.(2022·四川省成都市新都一中高二期中(理))若直线l 的一个方向向量为()1,2,1a =-,平面a 的一个法向量为()1,2,1b =--,则直线l 与平面α的位置关系是______.【答案】垂直或l α⊥【解析】因为直线l 的一个方向向量为()1,2,1a =-,平面a 的一个法向量为()1,2,1b =--,且a b =-r r ,所以a 与b 共线,,所以直线l 与平面α的位置关系为垂直,故答案为:垂直或l α⊥52.(2022·四川·阆中中学高二期中(理))已知平面,αβ的法向量分别为()11,,4n y =,()2,1,2n x =--,若a β⊥,则x y -的值为___.【答案】8【解析】∵a β⊥,∴平面,αβ的法向量互相垂直,∴120n n ⋅=,即1280n n x y ⋅=--=,解得8x y -=,故答案为:8.53.(2021·福建·泉州五中高二期中)如图,在长方体1111ABCD A B C D -中,1222AB BC CC ===,以D 为坐标原点,向量DA ,DC ,1DD 的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系,点P 在平面1111D C B A 上,若DP ⊥平面1ACD ,则点P 的坐标是___________.【答案】1112⎛⎫ ⎪⎝⎭,,【解析】由题意得:()0,0,0D ,()1,0,0A ,()0,2,0C ,()10,0,1D ,因为点P 在平面1111D C B A 上,所以设点(),,1P m n ,若DP ⊥平面1ACD ,则100DP D C DP AC ⎧⋅=⎨⋅=⎩,即21020n m n -=⎧⎨-+=⎩,解得:121n m ⎧=⎪⎨⎪=⎩,所以点P 的坐标是1112⎛⎫ ⎪⎝⎭,,故答案为:1112⎛⎫ ⎪⎝⎭,,54.(2020·山东省商河县第一中学高二期中)如图,在正四棱柱1111ABCD A B C D -中,已知2AB AD ==,15AA =,E ,F 分别为1DD ,1BB 上的点,且11DE B F ==.(1)求证:BE ⊥平面ACF :【解析】(1)以D 为坐标原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴建立空间直角坐标系,如下图所示:则()()()()()2,0,0,2,2,0,0,2,0,0,0,1,2,2,4A B C E F ,设面ACF 的一个法向量为()=,,n x y z ,()()=2,2,0,0,2,4AC AF -=,可得00n AC n AF ⎧⋅=⎪⎨⋅=⎪⎩,即220240x y y z -+=⎧⎨+=⎩,不妨令1z =则()=2,2,1n BE --=,BE ∴⊥平面ACF .55.(2020·宁夏长庆高级中学高二期中(理))如图,正方体1111ABCD A B C D -中,M 、N 分别为AB 、1B C 的中点.(1)用向量法证明平面1//A BD 平面11B CD ;(2)用向量法证明MN ⊥平面1A BD .【解析】(1)如图建立空间直角坐标系,设正方体的棱长为2,则()12,0,2A ,()2,2,0B ,()12,2,2B ,()0,2,0C ,()0,0,0D ,()10,0,2D ,故()12,0,2DA =,()2,2,0DB =,()12,0,2B C =--uuu r ,()112,2,0B D =--,设平面1A BD 的法向量()1111,,n x y z =,则11100DA n DB n ⎧⋅=⎪⎨⋅=⎪⎩,即1111220220x z x y +=⎧⎨+=⎩,令11x =,则()11,1,1n =--,设平面11B CD 的法向量()2222,,n x y z =,则1211200B C n B D n ⎧⋅=⎪⎨⋅=⎪⎩,即2222220220x z x y --=⎧⎨--=⎩,令21x =,则()21,1,1n =--,所以12n n =,即12//n n ,故平面1//A BD 平面11B CD ;(2)由M ,N 是线段AB ,1B C 中点,则()2,1,0M ,()1,2,1N ,所以()1,1,1MN =-,则1//MN n ,所以MN ⊥平面1A BD.56.(2021·四川凉山·高二期中(理))如图,在正四棱锥P -ABCD边长为2.点E ,F 分别CD ,BC 中点.求证:(1)PA ⊥EF ;(2)平面PAB ⊥平面PCD .【解析】(1)连接AC ,BD 交于点O ,连接PO ,由正四棱锥性质OA ,OB ,OP 两两互相垂直,以OA ,OB ,OP 分别为x ,y ,z轴建系如图.易得2OA 221OP PA OA =-=,∴)2,0,0A ,()0,0,1P ,()2,0B ,()2,0,0C ,()0,2,0D -,22,022E ⎛⎫- ⎪ ⎪⎝⎭,2222F ⎛⎫- ⎪ ⎪⎝⎭,()2,0,1PA =-,()2,0EF =,∵0PA EF ⋅=,∴0PA EF ⊥=,即PA ⊥EF ;(2)设平面PAB ,平面PCD 法向量分别为()111,,m x y z =,()222,,n x y z =,11112020m PA x z m PB y z ⎧⋅=-=⎪⎨⋅=-=⎪⎩,取12z =111x y ==,2)m =,22222020n PD x z n PC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取22z =,则221x y ==,(1,1,2)n =-,1120m n ⋅=+-=,∴m n ⊥,∴平面PAB ⊥平面PCD.57.(2022·江苏·沛县教师发展中心高二期中)如图,在正四棱柱1111ABCD A B C D -中,122AA AB ==,E ,F 分别为棱1AA ,1CC 的中点,G 为棱1DD 上的动点.(1)求证:B ,E ,1D ,F 四点共面;(2)是否存在点G ,使得平面GEF ⊥平面BEF ?若存在,求出DG 的长度;若不存在,说明理由.【解析】(1)证明:如图所示:连接1D E ,1D F ,取1BB 的中点为M ,连接1MC ,ME ,因为E 为1AA 的中点,所以1111////EM A B C D ,且1111EM A B C D ==,所以四边形11EMC D 为平行四边形,所以11//D E MC ,又因为F 为1BB 的中点,所以1//BM C F ,且1BM C F =,所以四边形1BMC F 为平行四边形,所以1//BF MC ,所以1//BF D E ,所以B ,E ,1D ,F 四点共面;(2)以D 为坐标原点,DA ,DC ,1DD 分别为x 轴,y 轴,z 轴建立空间直角坐标系,假设存在满足题意的点G ,设()0,0,G t ,由已知()1,1,0B ,()1,0,1E ,()0,1,1F ,则()1,1,0EF =-,()0,1,1EB =-,()1,0,1EG t =--,设平面BEF 的一个法向量为()1111,,x n y z =,则1100n EF n EB ⎧⋅=⎪⎨⋅=⎪⎩,即111100x y y z -+=⎧⎨-=⎩,取11x =,则()11,1,1n =;设平面GEF 的一个法向量为()2222,,n x y z =,则2200n EF n EG ⎧⋅=⎪⎨⋅=⎪⎩,即()1222010x y x t z -+=⎧⎨-+-=⎩,取21x t =-,则()21,1,1n t t =--;因为平面GEF ⊥平面BEF ,所以120n n ⋅=,所以1110t t -+-+=,所以12t =.所以存在满足题意的点G ,使得平面GEF ⊥平面BEF ,DG 的长度为12.58.(2021·广西·钦州一中高二期中(理))如图,在多面体ABCDEF 中,四边形ADEF 是梯形,四边形ABCD 为矩形,DE ⊥面ABCD ,//AF DE ,112AF AD DE ===,2AB =(1)求证://BF 平面CDE ;(2)点G 为线段CD 的中点,求证AG ⊥面DBE .【解析】(1)证明:如图,建立空间坐标系D xyz -,则(1,0,0)A ,(0,0,2)E ,2,0)B =,(1,0,1)F ,(0,2,1)BF =-uu u r ,DE ⊥面ABCD ,DE AD ∴⊥,且AD DC ⊥,又DE DC D ⋂=,AD ∴⊥面EDC ,(1,0,0)DA ∴=uu u r 为面EDC 的法向量,0DA BF ⋅=uu u r uu u r Q ,DA BF ∴⊥uu u r uu u r ,又BF ⊄平面CDE ,BF ∴∥平面CDE.(2)证明:由(1)可知22G ⎛⎫ ⎪ ⎪⎝⎭,2,02AG ⎛⎫=- ⎪ ⎪⎝⎭uuu r ,(0,0,2)DE =,2,0)DB =uu u r ,0DE AG ∴⋅=uuu r uuu r ,0DB AG ⋅=uu u r uuu r ,DE AG ∴⊥,DB AG⊥又BD DE D ⋂=,AG ∴⊥面DBE .59.(2020·天津·高二期中)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,PA ⊥底面ABCD ,E 是PC 的中点,已知2AB =,2PA =.(Ⅰ)求证:AE PD ⊥;(Ⅱ)求证:平面PBD ⊥平面PAC .【解析】证明:以A 为原点,,,AB AD AP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则(2,0,0)B ,(2,2,0)C ,(0,2,0)D ,(0,0,2)P .(Ⅰ)因为E 是PC 的中点,所以E 的坐标为()1,1,1,所以(1,1,1)AE =,又因为()0,2,2PD =-,所以10121(2)0AE PD ⋅=⨯+⨯+⨯-=,所以AE PD ⊥,即有AE PD ⊥;(Ⅱ)因为底面ABCD 是正方形,所以BD AC ⊥,因为PA ⊥底面ABCD ,BD ⊂平面ABCD ,所以BD AP ⊥,因为AC PA A ⋂=,所以BD ⊥平面PAC ,所以平面PAC 的一个法向量为()2,2,0BD =-,设平面PBD 的一个法向量为(,,)n x y z =,(2,0,2)PB =-,(0,2,2)PD =-uu u r ,由220220n PB x z n PD y z ⎧⋅=-=⎨⋅=-=⎩,取1z =,1x =,1y =,所以平面PBD 的一个法向量为(1,1,1)n =,因为1(2)12000n BD ⋅=⨯-+⨯+⨯=,所以n BD ⊥,所以平面PBD ⊥平面PAC .。
高考数学《利用空间向量证明平行与垂直关系》复习

(4)线面垂直
l a a=kμ a1=ka3,b1=kb3,c=kc3 .
(5)面面平行
v =kv a3=ka4,b3=kb4,c3=kc4.
(6)面面垂直
v ·v=0 a3a4+b3b4+c3c4=0.
解题技巧
利用空间向量证明平行与垂直的方法与步骤 (1) 坐标运算法:一般步骤:①建立空间直角坐标系,建系时, 要尽可能地利用载体中的垂直关系; ②建立空间图形与空间向量之间的关系,用向量表示出问题中所涉及的点、 直线、平面的要素; ③通过空间向量的运算研究平行、垂直关系; ④根据运算结果解释相关问题.
解题技巧
4.利用空间向量求点到平面距离的方法 如图,设 A 为平面 内的一点,B 为平面 外的一点,n 为平面 的法向量,
AB n
则 B 到平面 的距离 d=
.
n
1.如图,某圆锥 SO 的轴截面 SAC 是等边三角形,点 B 是底面圆周上的一点,且 BOC 60 ,
点 M 是 SA 的中点,则异面直线 AB 与 CM 所成角的余弦值是( )
(4)点到平面的距离的向量求法
如图,设 AB 为平面 α 的一条斜线段,n 为平面 α 的法向量,
AB n
则点 B 到平面 α 的距离 d=
.
n
2.模、夹角和距离公式
(1) 设 a=(a1,a2,a3 ),b=(b1,b2,b3 ) ,则 a = a·a a12a22a32 , b = b·b b12b22b32 ,
B.3
ห้องสมุดไป่ตู้
√C.4
D.6
由直棱柱的性质,知直线 A1B1 到平面 ABO 的距离为棱柱的高,不妨设为 t t 0 .以 O 为坐标原
点, OA,OB,OO1 所在的直线分别为 x, y, z 轴,建立如图所示的空间直角坐标系, 则 O(0,0,0), B(0,6,0), A1(2,0,t) , B1(0,6,t) ,则 D(1,3,t) .所以 A1B (2, 6, t),OD (1,3,t) 所以 A1B OD 2 18 t2 0 ,所以 t 4 ,故选 C.
第二节--用空间向量证明线线垂直与线面垂直
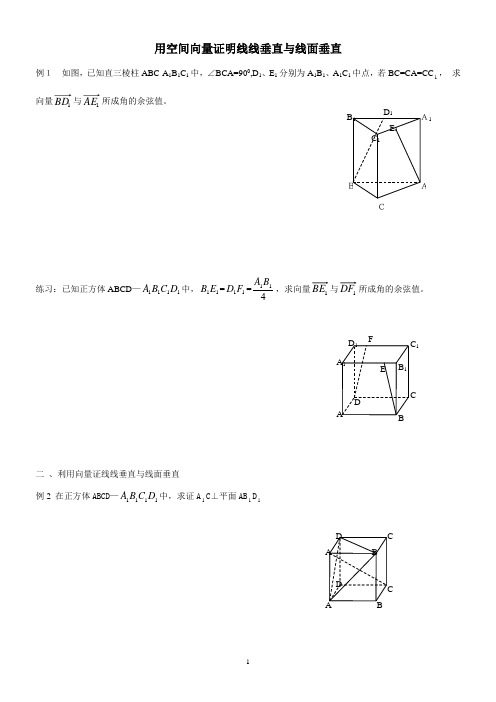
用空间向量证明线线垂直与线面垂直例1 如图,已知直三棱柱ABC-A 1B 1C 1中,∠BCA=900,D 1、E 1分别为A 1B 1、A 1C 1中点,若BC=CA=CC 1,求向量1BD 与1AE 所成角的余弦值。
练习:已知正方体ABCD —1111D C B A 中,11E B =11F D =411B A ,求向量1BE 与1所成角的余弦值。
二 、利用向量证线线垂直与线面垂直例2 在正方体ABCD —1111D C B A 中,求证A 1C ⊥平面AB 1D 1EDA 1 FD 1 AB 1C BC 1BA DCBA CDC 1B 1A1ACBD 1E 1练习:在正方体ABCD —1111D C B A 中,O 为底面ABCD 的中心,P 为DD 1的中点, 求证:B 1O ⊥平面PAC 。
例3 如图,PA ⊥矩形ABCD 所在平面,M, N 分别是AB ,PC 中点 (1)求证:M N ⊥CD(2)若∠PDA=450,求证:MN ⊥平面PCD练习:正方体ABCD —1111D C B A 中,M 是棱D 1D 中点,N 是AD 中点,P 为棱A 1B 1上任一点。
求证:NP ⊥AMB 1A 1 D CB AC 1D 1 OP ABCDPMN B N ACD A 1B 1D 1M P C 1作业:1.如图,正方体ABCD —1111D C B A 中,E 是BB 1中点,O 是底面ABCD 中心,求证:O E ⊥平面D 1AC.2.如图,正方体ABCD —1111D C B A 中,O ,M 分别是BD 1, AA 1中点,求证:OM 是异面直线AA 1和BD 1的公垂线.3、如图,直三棱柱ABC-—A 1B 1C 1中,∠ACB=900,AC=1,CB=2,侧棱AA 1=1,,侧面AA 1B 1B 的两条对角线交点为D ,B 1C 1的中点为M 。
求证:CD ⊥平面BDMCDMA 1AC 1BB 1EOB 1 A 1 DCB AC 1D 1 OMB 1A 1DCBAC 1D 14在棱长为a 的正方体ABCD —1111D C B A 中,E , F 分别为棱AB 和BC 的中点,M 为棱B 1B 上任一点,当MBMB 1值为多少时能使D 1M ⊥平面EFB 15、如图, ABC 为正三角形,AE 和CD 都垂直于平面ABC ,且AE=AB=2a , CD=a ,F 为BE 中点, 求证:A F ⊥BD6、如图,已知直三棱柱ABC-A 1B 1C 1中B 1C 1=A 1C 1,A 1B ⊥AC 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1, 0,
2
1)
2
2
y
A
x
MB
传统思路
uuur
2
DCuuuur(0u,1u,ur0)
MN PD
2 (
1
,
0,
1
)
(1,
0,
1)
0
点积垂直
uuuur uuur MN PD
uuuur MN
uuur DC
2 (
1
2 , 0,
1
)
(0,1,
0)
0
uuuur MN
uuur DC
22
又Q PD I DC D MN 平面PDC
ACB 90,BAC 30, BC 1, A1A 6,
M 是棱 CC1 的中点,
求证:A1B AM
B1
A1
C1
6
M
B
1 90
30 A
C
思路1:uAu1uBr
uuuur AM
uuur uuur A1A AB
uuur uuuur AC CM
B1
A1
C1
6
M
B
1 90
30 A
C
z
证明:分别以 CA,CB,CC1
C1
B1 所在直线为 x 轴,y 轴,z2
A1 3,1, 6
立空间直角坐标系 C xyz
图中相应点的坐标为:
6
x C
1
90 3 30
A
3, 0, 0
2
B 0,1,0
y
所以:
uuur A1B
A1 3,1, 6 , B 0,1, 0
A 3, 0, 0
, M 0, 0,
1
B x
2
2
0
O
0
C
y
uuuur uuur
uuuBur1OguAuuEr
(1,1,
uuuur
2)g(0,
uuur
2,1)
1
0
1
2
2
1
0
B1O AC B1O AE
即B1O⊥AC,B1O⊥AE,又ACI B O⊥平面EAC
AE=A
2. 已 知 PA 垂 直 于 正 方 形 ABCD 所 在 的 平 面 , M 、N 分 别 是 AB 、PC 的 中 点 , 并 且
0,
uuur OE
uuur BD
.
uuur OA1
a 2
,
a 2
,
a
uuur , 则OA1
uuur BD
uuur 0, OA1
uuur BD
, A1OE
为二
面角uuurA1
BD uuur
E
的平面角.
∵ OA1 OE 0 ,则 A1OE 90, 平面A1BD 平面EBD .
作业3:如图,在直三棱柱 ABC- A1B1C1中,
l1
e1 e2
l2
ur ur ur ur l1 l2 e1 e2 e1 e2 0
l
e1
n1
ur uur
l e1∥n1(一般不用)
2 n2
n1
1
1
2
ur uur n1 n2
(线与线)
例1、 如图,在正方体 ABCD A1B1C1D1中,CD1和DC1 相交于点 O ,求证:AO A1B
求证:平面 A1BD ⊥平面 EBD.
1.解:以 DA, DC, DD1 所在直线为 x, y, z 轴,建立空间直角坐
标系,(Ⅰ)
A a, 0,
uuuur
0
,
B
a,
a,
0
,
C
0,
a,
0
,
A1
a,
0,
a
,
C1
0,
a,
a
设
E0,
uuur
a,
e,则
A1
E
a, a, e uuuur
a
uuur
,
BD a,a,0
6 2
3, 0,
6
uuuur , AM
3, 0,
6 2
uuur uuuur
所以: A1B AM 0 即, A1B AM
PA AD ,求证: MN 平面 PDC
证明:
z
P
N
建立如图所示空间直角坐标系 A xyz , 则
D
C
A(0,0,0), B(0,1,0),C(1,1,0), D(1,0,0),
P(0, 0,1) M (0, 1 , 0), N ( 1 , 1 , 1)
uuuur MN
(
1
,
0,
1
2uuur
) PD
作业1:在长方体 ABCD A1B1C1D1 中,AB=5,AD 8,
AA1 4, M为B1C1上的一点,且B1M 2,点N在线段A1D上,
求证:A1D AM .
z
(一)几何法
A1
(二)坐标法
B1 M
A(0, 0, 0), A1(0, 0, 4),D(0,8,0), M (5, 2, 4)
Z
A1
D1
B1
A
C1
O
D y
1.三垂线 2.坐标法
B
C
x
(线与面—与法向量平行?)
1.正方体ABCD-A1B1C1D1的棱长为2,且AC与BD交于点O,E
为棱DD1的中点。求证:B1O⊥平面EAC。 z
解:如图所示,以A为原点建立空间直角坐标系 A-xyz,则A(0,0,0),B(2,0,0),
A1
C(2,2,0),D(0,2,0)E(0,2,1),B1
QB1(O2,是0正,方2)形ABCD的中心, O(1,1,0)A
D1 C1
E
D
uuuur uuBur1O
(1,1,
2)
AC
uuuu(r2u,u2ur, B1OgAC
0) (1,1,
uuur AE (0,2,1)
2)g(2,2,0) 1
2
uuur uuur
,
A1E BD a a a a e a 0 0
,
A1E BD ,即 A1E BD.
(Ⅱ)由题设,
E
0,
a,
a 2
,设
BD的中点为
O,
则O
a 2
,
a 2
,
0
,
uuur OE
a 2
,
a 2
,
a 2
,
uuur BD
a,
a,
0
,
uuur 则OE
uuur BD
uuuur
uuuur
A
AM (5, 2, 4), A1D (0,8, 4),
uuuur uuuur
xB
AM • A1D=0 A1D AM .
D1 C1
Dy
C
作业 2.已知正方体 ABCD— A1B1C1D1 中,E 为棱 CC1上
的动点,
(Ⅰ)求证: A1E ⊥ BD ;
(Ⅱ)当 E 恰为棱 CC1 的中点时,
