2019-2020年中考数学压轴题精选5试题
2019-2020年中考数学二次函数压轴题汇总训练(50题含答案和解析)

解答题(共50题)1.如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.【分析】(1)根据待定系数法即可求得;(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC 的垂直平分线与x轴交于一个点,即可求得点N的坐标;(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=(n+2),然后根据S=S△ABN﹣S△BMN△AMN得出关于n的二次函数,根据函数解析式求得即可.【解答】解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x 轴交于点B、C,点C坐标为(8,0),∴,解得.∴抛物线表达式:y=﹣x2+x+4;(2)△ABC是直角三角形.令y=0,则﹣x2+x+4=0,解得x1=8,x2=﹣2,∴点B的坐标为(﹣2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形.(3)∵A(0,4),C(8,0),∴AC==4,①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).(4)如图,AB==2,BC=8﹣(﹣2)=10,AC==4,∴AB2+AC2=BC2,∴∠BAC=90°.∴AC⊥AB.∵AC∥MN,∴MN⊥AB.设点N的坐标为(n,0),则BN=n+2,∵MN∥AC,△BMN∽△BAC∴=,∴=,BM==,MN==,AM=AB﹣BM=2﹣==AM•MN∵S△AMN=××=﹣(n﹣3)2+5,当n=3时,△AMN面积最大是5,∴N点坐标为(3,0).∴当△AMN面积最大时,N点坐标为(3,0).【点评】本题是二次函数的综合题,解(1)的关键是待定系数法求解析式,解(2)的关键是勾股定理和逆定理,解(3)的关键是等腰三角形的性质,解(4)的关键是三角形相似的判定和性质以及函数的最值等.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t的取值范围.【分析】(1)根据点A、B、C三点的坐标作出△ABC,利用“闭距离”的定义即可得;(2)由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段,再分别求得经过(1,﹣1)和(﹣1,﹣1)时k的值即可得;(3)分⊙T在△ABC的左侧、内部和右侧三种情况,利用“闭距离”的定义逐一判断即可得.【解答】解:(1)如图所示,点O到△ABC的距离的最小值为2,∴d(点O,△ABC)=2;(2)y=kx(k≠0)经过原点,在﹣1≤x≤1范围内,函数图象为线段,当y=kx(﹣1≤x≤1,k≠0)经过(1,﹣1)时,k=﹣1,此时d(G,△ABC)=1;当y=kx(﹣1≤x≤1,k≠0)经过(﹣1,﹣1)时,k=1,此时d(G,△ABC)=1;∴﹣1≤k≤1,∵k≠0,∴﹣1≤k≤1且k≠0;(3)⊙T与△ABC的位置关系分三种情况:①当⊙T在△ABC的左侧时,由d(⊙T,△ABC)=1知此时t=﹣4;②当⊙T在△ABC内部时,当点T与原点重合时,d(⊙T,△ABC)=1,知此时t=0;当点T位于T3位置时,由d(⊙T,△ABC)=1知T3M=2,∵AB=BC=8、∠ABC=90°,∴∠C=∠T3DM=45°,则T3D===2,∴t=4﹣2,故此时0≤t≤4﹣2;③当⊙T在△ABC右边时,由d(⊙T,△ABC)=1知T4N=2,∵∠T4DC=∠C=45°,∴T4D===2,∴t=4+2;综上,t=﹣4或0≤t≤4﹣2或t=4+2.【点评】本题主要考查圆的综合问题,解题的关键是理解并掌握“闭距离”的定义与直线与圆的位置关系和分类讨论思想的运用.3.如图,在平面直角坐标系中,点A在抛物线y=﹣x2+4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当△PBE的面积最大时,求PH+HF+FO的最小值;(3)在(2)中,PH+HF+FO取得最小值时,将△CFH绕点C顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.【分析】(1)求出A、B两点坐标,即可解决问题;(2)如图1中,设P(m,﹣m2+4m),作PN∥y轴交BE于N.构建二次函数利用二次函数的性质求出满足条件的点P坐标,作直线OG交AB于G,使得∠COG=30°,作HK⊥OG于K交OC于F,因为FK=OF,推出PH+HF+FO=PH+FH+Fk=PH+HK,此时PH+HF+OF的值最小,解直角三角形即可解决问题;(3)分两种情形分别求解即可;【解答】解:(1)由题意A(1,3),B(3,3),∴AB=2.(2)如图1中,设P(m,﹣m2+4m),作PN∥y轴J交BE于N.∵直线BE的解析式为y=x,∴N(m,m),=×2×(﹣m2+3m)=﹣m2+3m,∴S△PEB∴当m=时,△PEB的面积最大,此时P(,),H(,3),∴PH=﹣3=,作直线OG交AB于G,使得∠COG=30°,作HK⊥OG于K交OC于F,∵FK=OF,∴PH+HF+FO=PH+FH+FK=PH+HK,此时PH+HF+OF的值最小,。
(完整)中考数学压轴题精选及答案
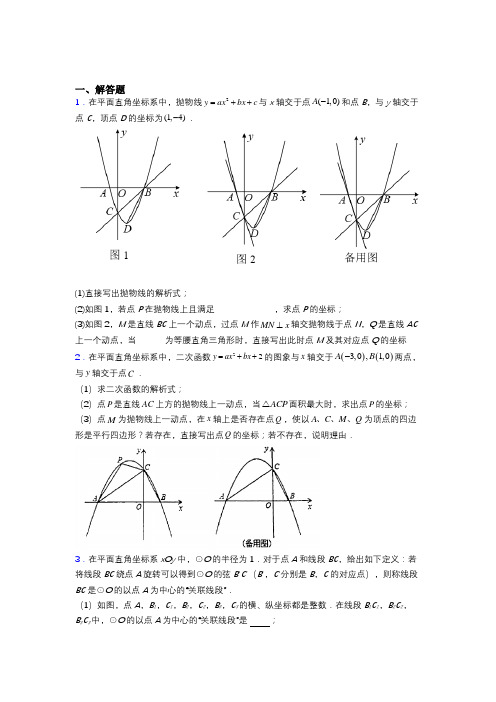
一、解答题1.在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于点(1,0)A -和点B ,与y 轴交于点C ,顶点D 的坐标为(1,4)-.(1)直接写出抛物线的解析式;(2)如图1,若点P 在抛物线上且满足,求点P 的坐标; (3)如图2,M 是直线BC 上一个动点,过点M 作MN x ⊥轴交抛物线于点N ,Q 是直线AC 上一个动点,当为等腰直角三角形时,直接写出此时点M 及其对应点Q 的坐标2.在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △面积最大时,求出点P 的坐标;(3)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A C M Q 、、、为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,说明理由.3.在平面直角坐标系xOy 中,⊙O 的半径为1.对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′(B ′,C ′分别是B ,C 的对应点),则称线段BC 是⊙O 的以点A 为中心的“关联线段”.(1)如图,点A ,B 1,C 1,B 2,C 2,B 3,C 3的横、纵坐标都是整数.在线段B 1C 1,B 2C 2,B 3C 3中,⊙O 的以点A 为中心的“关联线段”是 ;(2)△ABC 是边长为1的等边三角形,点A (0,t ),其中t ≠0.若BC 是⊙O 的以点A 为中心的“关联线段”,求t 的值;(3)在△ABC 中,AB =1,AC =2.若BC 是⊙O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长.4.综合与探究如图,在平面直角坐标系中,点()0,10A ,点B 是x 轴的正半轴上的一个动点,连接AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90°,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(),0t(1)当6t =时,点M 的坐标是 ;(2)用含t 的代数式表示点C 的坐标;(3)是否存在点B ,使四边形AOBD 为矩形?若存在,请求出点B 的坐标;若不存在,请说明理由;(4)在点B 的运动过程中,平面内是否存在一点N ,使得以A 、B 、N 、D 为顶点的四边形是菱形?若存在,请直接写出点N 的纵坐标(不必要写横坐标);若不存在,请说明理由.5.如图(1),在菱形ABCD 中,∠ABC =60°,点E 在边CD 上(不与点C ,D 重合),连结AE ,交BD 于点F .(1)如图(2),若点M 在BC 边上,且DE =CM ,连结AM ,EM .求证:三角形AEM 为等边三角形;(2)设DF x BF=,求tan ∠AFB 的值(用x 的代数式表示); (3)如图(3),若点G 在线段BF 上,且FG =2BG ,连结AG 、CG ,DF x BF =,四边形AGCE 的面积为S 1,ABG 的面积为S 2,求12S S 的最大值.6.如图,在平面直角坐标系中,ABC 的边AB 在x 轴上,且OB OA >,以AB 为直径的圆过点C .若点C 的坐标为()0,4,10AB =,(1)求抛物线的解析式;(2)点P 为该函数在第一象限内的图象上一点(不与BC 重合),过点P 作PQ BC ⊥,垂足为点Q ,连接PC .若以点P 、C 、Q 为顶点的三角形与COA 相似,求点P 的坐标;(3)若ACB ∠平分线所在的直线l 交x 轴与点E ,过点E 任作一直线l '分别交射线CA ,CB (点C 除外)于点M ,N .则11CM CN+的是否为定值?若是,求出该定值;若不是,请说明理由.7.如图1,⊙I 与直线a 相离,过圆心I 作直线a 的垂线,垂足为H ,且交⊙I 于P 、Q 两点(Q 在P 、H 之间).我们把点Q 称为⊙I 关于直线a 的“近点”,点P 称为⊙I 关于直线a 的“远点”把PQ ·QH 的值称为⊙I 关于直线a 的“特征数”.(1)如图2,在平面直角坐标系xOy 中,点E 的坐标为(0,3).半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D .①过点E 画垂直于y 轴的直线m ,则⊙O 关于直线m 的“近点”“远点”分别是点_____和_____(填“A ”、“B ”、“C ”或“D ”),⊙O 关于直线m 的“特征数”为_____;②若直线n 的函数表达式为33y x =-+.求⊙O 关于直线n 的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点M (1,2),点F 是坐标平面内一点,以F 5为半径作⊙F .若⊙F 与直线l 相离,点N (1-,0)是⊙F 关于直线l 的“近点”.且⊙F 关于直线l 的“特征数”是6,求直线l 的函数表达式.8.如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.(1)分别求抛物线和直线AC的解析式;(2)在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.9.已知:如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,以OA,OC为边作矩形ABCO,矩形ABCO的面积是36.(1)求直线AC的解析式.(2)点P为线段AB上一点,点Q为第一象限内一点,连接PO,PQ,∠OPQ=90°,且OP=PQ,设AP的长为t,点Q的横坐标为d,求d与t的函数关系式.(不要求写出自变量t的取值范围)(3)在(2)的条件下,过点Q作QE∥PO交AB的延长线于点E,作∠POC的平分线OF 交PE于点F,交PQ于点K,若KQ=2EF,求点Q的坐标.10.如图,平面直角坐标系中,点O为原点,抛物线交x轴于()2,05,0B两点,交y轴于点C.A-、()(1)求抛物线解析式;(2)点P在第一象限内的抛物线上,过点P作x轴的垂线,垂足为点H,连AP交y轴于点E,设P点横坐标为t,线段EC长为d,求d与t的函数解析式;(3)在(2)条件下,点M在CE上,点Q在第三象限内抛物线上,连接PC、PQ、PM,PQ与y轴交于W,若,,,求点Q的坐标.11.已知:如图1,点A(a,b),AB x⊥轴于点B2++-+=.a b a b24(8)0(1)试判断△AOB的形状,并说明理由;(2)如图2,若点C为线段AB的中点,连OC并作OD OC⊥,且OD OC=,连AD交x轴于点E,试求点E的坐标;(3)如图3,若点M为点B的左边x轴负半轴上一动点,以AM为一边作45∠=︒交MANy轴负半轴于点N,连MN,在点M运动过程中,试猜想式子OM MN ON+-的值是否发生变化?若不变,求这个不变的值;若发生变化,试求它变化的范围.12.直角三角板ABC的斜边AB的两个端点在⊙O上,已知∠BAC=30°,直角边AC与⊙O 相交于点D,且点D是劣弧AB的中点.(1)如图1,判断直角边BC所在直线与⊙O的位置关系,并说明理由;(2)如图2,点P是斜边AB上的一个动点(与A、B不重合),DP的延长线交⊙O于点Q,连接QA、QB.①AD=6,PD=4,则AB= ;PQ= ;②当点P在斜边AB上运动时,求证:QA+QB=3QD.13.如图,已知四边形ABCD内接于⊙O,直径DF交BC于点G.(1)如图1,求证:∠BAD-∠BCF=90°;(2)如图2,连接AC,当∠BAC=∠CFD+∠ACD时,求证:CA=CB;(3)如图3,在(2)的条件下,AC交DF于点H,∠BAC=∠DGB,45CGBG,AC=9,求△CDH的面积.14.同学们学过正方形与等腰三角形发现它们都是轴对称图形,它们之间有很多相似,在正边形ABCD中,E是对角线AC上一点(不与点A、C重合),以AD、AE为邻边作平行四边形AEGD,GE交CD于点M,连接CG.(1)如图1,当12AE AC<时,过点E作EF BE⊥交CD于点F,连接GF并延长交AC于点H.求证:EB EF=;(2)在ABC中,AB AC=,90BAC∠=︒.过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD直线BD交直线AP于点E.如图2,①依题意补全图形;②请用等式表示线段EB,ED,BC之间的数量关系,并予以证明.15.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式.(2)若点P为第三象限内抛物线上一动点,作PD⊥x轴于点D,交AC于点E,过点E作AC 的垂线与抛物线的对称轴和y轴分别交于点F、G,设点P的横坐标为m.①求PE2的最大值;②连接DF、DG,若∠FDG=45°,求m的值.16.【问题提出】如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围.【问题解决】解决此问题可以用如下方法:延长AD 到点E ,使DE =AD ,再连结BE (或将△ACD 绕着点D 逆时针旋转180°得到△EBD ),把AB 、AC ,2AD 集中在△ABE 中,利用三角形三边的关系即可判断.由此得出中线AD 的取值范围是__________【应用】如图②,如图,在△ABC 中,D 为边BC 的中点、已知AB =10,AC =6,AD =4,求BC 的长.【拓展】如图③,在△ABC 中,∠A =90°,点D 是边BC 的中点,点E 在边AB 上,过点D 作D F⊥DE 交边AC 于点F ,连结EF .已知BE =5,CF =6,则EF 的长为__________.17.已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B (1,0)两点,与y 轴交于点()03C -,.(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图象上位于第三象限内的点,若点D 的横坐标为m ,ACD △的面积为S ,求S 与m 之间的函数关系式,并写出ACD △的面积取得最大值时点D 的坐标;(3)M 是二次函数图象对称轴上的点,在二次函数图象上是否存在点N .使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).18.如图,在平面直角坐标系中,已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ,点B 39(2,)16- 是一次函数5119216y x =+上一点.(1)当a =0时,求顶点P 坐标;(2)若a >0,且一次函数2y x b =-+的图象与此抛物线没有交点,请你写出一个符合条件的一次函数关系式(只需写一个,不必写出过程);(3)作直线OC :12y x =与一次函数5119216y x =+交于点C .连结OB ,当抛物线与△OBC 的边有两个交点时,求a 的取值范围.19.已知O 为ABC ∆的外接圆,AC BC =,点D 是劣弧AB 上一点(不与点A ,B 重合),连接DA ,DB ,DC .(1)如图1,若AB 是直径,将ACD ∆绕点C 逆时针旋转得到BCE ∆.若4CD =,求四边形ADBC 的面积;(2)如图2,若AB AC =,半径为2,设线段DC 的长为x .四边形ADBC 的面积为S . ①求S 与x 的函数关系式;②若点M ,N 分别在线段CA ,CB 上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置.DMN ∆的周长有最小值t ,随着点D 的运动,t 的值会发生变化.求所有t 值中的最大值,并求此时四边形ADBC 的面积S .20.如图,在ABCD 中,90ABD ∠=︒,5cm AD =,8cm BD =.点P 从点A 出发,沿折线AB BC -向终点C 运动,点P 在AB 边、BC 边上的运动速度分别为1cm/s 、5cm /s .在点P 的运动过程中,过点P 作AB 所在直线的垂线,交边AD 或边CD 于点Q ,以PQ 为一边作矩形PQMN ,且2QM PQ =,MN 与BD 在PQ 的同侧.设点P 的运动时间为t (秒),矩形PQMN 与ABCD 重叠部分的面积为()2cm S .(1)求边AB 的长.(2)当04t <<时,PQ = ,当48t <<时,PQ = .(用含t 的代数式表示)(3)当点M 落在BD 上时,求t 的值.(4)当矩形PQMN 与ABCD 重叠部分图形为四边形时,求S 与t 的函数关系式.【参考答案】参考答案**科目模拟测试一、解答题1.(1)223y x x =--;(2),; (3),;,;,;,; ,;,. 【解析】【分析】(1)根据顶点的坐标,设抛物线的解析式为y =a (x ﹣1)2﹣4,将点A (﹣1,0)代入,求出a 即可得出答案;(2)利用待定系数法求出直线BD 解析式为y =2x ﹣6,过点C 作CP 1∥BD ,交抛物线于点P 1,再运用待定系数法求出直线CP 1的解析式为y =2x ﹣3,联立方程组即可求出P 1(4,5),过点B 作y 轴平行线,过点C 作x 轴平行线交于点G ,证明△OCE ≌△GCF(ASA),运用待定系数法求出直线CF解析式为y=12x﹣3,即可求出P2(52,﹣74);(3)利用待定系数法求出直线AC解析式为y=﹣3x﹣3,直线BC解析式为y=x﹣3,再分以下三种情况:①当△QMN是以NQ为斜边的等腰直角三角形时,②当△QMN是以MQ为斜边的等腰直角三角形时,③当△QMN是以MN为斜边的等腰直角三角形时,分别画出图形结合图形进行计算即可.(1)解:∵顶点D的坐标为(1,﹣4),∴设抛物线的解析式为y=a(x﹣1)2﹣4,将点A(﹣1,0)代入,得0=a(﹣1﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4=x2﹣2x﹣3,∴该抛物线的解析式为y=x2﹣2x﹣3;(2)解:∵抛物线对称轴为直线x=1,A(﹣1,0),∴B(3,0),设直线BD解析式为y=kx+e,∵B(3,0),D(1,﹣4),∴,解得:,∴直线BD解析式为y=2x﹣6,过点C作CP1∥BD,交抛物线于点P1,设直线CP1的解析式为y=2x+d,将C(0,﹣3)代入,得﹣3=2×0+d,解得:d=﹣3,∴直线CP1的解析式为y=2x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=2x﹣3,解得:x1=0(舍),x2=4,故P1(4,5),过点B作y轴平行线,过点C作x轴平行线交于点G,∵OB=OC,∠BOC=∠OBG=∠OCG=90°,∴四边形OBGC是正方形,设CP1与x轴交于点E,则2x﹣3=0,解得:x=32,∴E(32,0),在x轴下方作∠BCF=∠BCE交BG于点F,∵四边形OBGC是正方形,∴OC=CG=BG=3,∠COE=∠G=90°,∠OCB=∠GCB=45°,∴∠OCB﹣∠BCE=∠GCB﹣∠BCF,即∠OCE=∠GCF,∴△OCE≌△GCF(ASA),∴FG=OE=32,∴BF=BG﹣FG=3﹣32=32,∴F(3,﹣32),设直线CF解析式为y=k1x+e1,∵C(0,﹣3),F(3,﹣32),∴,解得:,∴直线CF解析式为y=12x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=12x﹣3,解得:x1=0(舍),x2=52,∴P2(52,﹣74),综上所述,符合条件的P点坐标为:(4,5)或(52,﹣74);(3)解:(3)设直线AC解析式为y=m1x+n1,直线BC解析式为y=m2x+n2,∵A(﹣1,0),C(0,﹣3),∴,解得:,∴直线AC解析式为y=﹣3x﹣3,∵B(3,0),C(0,﹣3),∴,解得:,∴直线BC解析式为y=x﹣3,设M(t,t﹣3),则N(t,t2﹣2t﹣3),∴MN=|t2﹣2t﹣3﹣(t﹣3)|=|t2﹣3t|,①当△QMN是以NQ为斜边的等腰直角三角形时,此时∠NMQ=90°,MN=MQ,如图2,∵MQ∥x轴,∴Q(﹣13t,t﹣3),∴|t2﹣3t|=|t﹣(﹣13t)|,∴t2﹣3t=±43t,解得:t=0(舍)或t=53或t=133,∴,;,;②当△QMN是以MQ为斜边的等腰直角三角形时,此时∠MNQ=90°,MN=NQ,如图3,∵NQ∥x轴,∴Q(,t2﹣2t﹣3),∴NQ=|t﹣|=13|t2+t|,∴|t2﹣3t|=13|t2+t|,解得:t=0(舍)或t=5或t=2,∴M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);③当△QMN是以MN为斜边的等腰直角三角形时,此时∠MQN=90°,MQ=NQ,如图4,过点Q作QH⊥MN于H,则MH=HN,∴H(t,),∴Q(,),∴QH=|t﹣|=16|t2+5t|,∵MQ=NQ,∴MN=2QH,∴|t2﹣3t|=2×16|t2+5t|,解得:t=7或1,∴M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3);综上所述,点M及其对应点Q的坐标为:,;,;M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3).【点睛】本题是二次函数综合题,主要考查了待定系数法求一次函数和二次函数解析式,求一次函数与二次函数图象交点坐标,全等三角形判定和性质,正方形判定和性质,等腰直角三角形性质等,本题属于中考压轴题,综合性强,难度较大,熟练掌握待定系数法、等腰直角三角形性质等相关知识,运用数形结合思想、分类讨论思想是解题关键.2.(1)224233y x x =--+;(2)35(,)22P -(3)存在,12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【解析】【分析】(1)根据待定系数法求抛物线解析式;(2)设224(,)33P t t --根据(1)的结论求得C 的坐标,进而求得AC 的解析式,过P 作PD ⊥x 轴交AC 于点D ,进而求得PD 的长,根据12APC C A S PD x x =⋅⋅-△求得APC S 的表达式,进而根据二次函数的性质求得取得最大值时,t 的值,进而求得P 点的坐标;(3)分情况讨论,①//CM AQ ,②//AC MQ ,根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标.【详解】(1)二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+ (2)抛物线224233y x x =--+与y 轴交于点C ,令0x =,则2y = (0,2)C ∴设直线AC 的解析式为y kx b =+,由(3,0)A -,(0,2)C ,则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的解析式为223y x =+, 如图,过P 作PD ⊥x 轴交AC 于点D ,设224(,)33P t t --,则2(,2)3D t t +, 2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APC C A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时,APC S 取得最大值,此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P - (3)存在,理由如下抛物线解析式为224233y x x =--+()228133x =-++ ∴抛物线的对称轴为直线1x =①如图,当//CM AQ 时,Q 点在x 轴上,//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称,(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时,如图,设M 的纵坐标为n ,四边形ACQM 是平行四边形,点A ,Q 在x 轴上,则,AQ MC 的交点也在x 轴上, 202n +∴= 解得2n =-设(,2)M m -,2242233x x ∴-=--+ 解得17x =-(17,2)M ∴--A 点到C 点是横坐标加3,纵坐标加2∴M 点到Q 点也是横坐标加3,纵坐标加2 即(173,0)Q -±34(27,0),(27,0)Q Q ∴综上所述,存在点Q ,使得以A C M Q 、、、为顶点的四边形是平行四边形,Q 点的坐标为12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【点睛】本题考查了二次函数综合,待定系数法,二次函数最值,二次函数的图象与性质,平行四边形的性质,综合运用以上知识是解题的关键.3.(1)B 2C 2;(233-3)OA 最小值为1,相应的3BC =OA 最大值为2,相应的6BC =【解析】【分析】(1)结合题意,根据旋转和圆的性质分析,即可得到答案;(2)根据题意,分B C ''在x 轴上方和x 轴上方两种情况;根据等边三角形、勾股定理、全等三角形的性质,得32AD OD ==,从而完成求解; (3)结合题意,得当AC '为⊙O 的直径时,OA 取最小值;当A 、B '、O 三点共线时,OA 取最大值;根据勾股定理、等腰三角形的性质计算,即可得到答案.【详解】(1)线段B 1C 1绕点A 旋转得到的11B C '',均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”;线段B 2C 2绕点A 旋转得到的22B C '',如下图:∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”;线段B 3C 3绕点A 旋转得到的33B C '',均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”;故答案为:B 2C 2;(2)∵△ABC 是边长为1的等边三角形,点A (0,t ),⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况:当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:∵1OB OC ''==∴1122B D B C '''== ∴2232OD OB B D ''=-=∵△ABC 是边长为1的等边三角形,即△AB C ''是边长为1的等边三角形, ∴AC D OC D ''∠=∠,AD B C ''⊥ ∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =;当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:同理,3AO AD OD =+=∴()0,3A -;∴t 3=-;∴3t =或3-;(3)当AC '为⊙O 的直径时,OA 取最小值,如下图:∴OA 最小值为1,90AB C ''∠=︒ ∴223BC B C AC AB ''''==-=;当A 、B '、O 三点共线时,OA 取最大值,2OA AC '== ,如下图:作AE OC '⊥交OC '于点E ,作C F AO '⊥交AO 于点F ,如下图∵2OA AC '==∴1122OE OC '==∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '==∴2214OF OC C F ''=-=∴34B F OB OF ''=-=∴262BC B C C F B F ''''==+=∴OA 最小值为1,相应的3BC =;OA 最大值为2,相应的62BC =. 【点睛】本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识;解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质,从而完成求解.4.(1)(3,5)M ,(2)1(5,)2C t t +;(3)(20,0)B ;(4)154或10. 【解析】 【分析】(1)利用中点坐标公式计算即可.(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .证明()MEB BFC AAS ∆≅∆,利用全等三角形的性质即可解决问题.(3)如图2中,存在.由题意当CF OA =时,可证四边形AOBD 是矩形,构建方程即可解决问题.(4)分三种情形:①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为6.③因为BD AB ≠,所以不存在以AD 为对角线的菱形. 【详解】解:(1)如图1中,(0,10)A ,(6,0)B ,AM BM =, (3,5)M ∴,(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .//ME OA ,AM BM =, 12OE EB t ∴==,152ME OA ==,90MEB CFB CBM ∠=∠=∠=︒,90MBE CBF ∴∠+∠=︒,90MBE BME ∠+∠=︒, BME CBF ∴∠=∠,()MEB BFC AAS ∴∆≅∆,5BF ME ∴==,12CF BE t ==,5OF OB BF t ∴=+=+, 1(5,)2C t t ∴+.(3)存在.如图2中,作ME OB ⊥于E ,CF x ⊥轴于F .理由:由题意当=10CF OA =时,//OA CF , ∴四边形AOFC 是平行四边形,90AOF ∠=︒,∴四边形AOFC 是矩形,90DAO AOB DBO ∴∠=∠=∠=︒,∴四边形AOBD 是矩形,又∵由(2)得12CF BE t ==, 即:1102t =,解得:20t =.(20,0)B ∴.(4)①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.AD BD =, BAD ABD ∴∠=∠,OAB ABD ∴∠=∠,OAB BAD ∴∠=∠. tan tan OAB BAD ∴∠=∠, ∴12OB BC OA BA ==,即1102t =,5t ∴=,5OB ∴=,设AN NB m ==,在Rt OBN △中,则有2225(10)m m =+-, 解得254m =, 25151044ON OA AN ∴=-=-=, ∴点N 的纵坐标为154. ②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为10.③BD AB ≠,∴不存在以AD 为对角线的菱形. 综上所述,满足条件的点N 的纵坐标为154或10. 【点睛】本题属于四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,翻折变换,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.5.(1)证明见解析;(23333xx;(3)194【解析】 【分析】(1)如图,连接,AC 证明,ACB ACD 都为等边三角形,可得,AC AD = 再证明,ACM ADE ≌从而可得答案;(2)如图,记,AC BD 交于点,O 设,,DFa OFb 四边形ABCD 为菱形,60,ABC ∠=︒表示33,33OA OB a b 利用,2DF ax BF a b则2,1a xb x再利用三角函数的定义可得答案;(3)如图,设,DFESn 证明,DFE BFA ∽ 2,BFAnSx 再表示2222,,33ABGAGFn nSS S x x 结合菱形的轴对称的性质可得:2=,3CBG nS x 表示,AFDn S x可得2=,BCD ABDn n S Sxx 可得2212243334,3nn n S x x x x n S x 再利用二次函数的性质可得答案.【详解】证明:(1)如图,连接,AC 菱形ABCD 中,∠ABC =60°,,60,120,60,AB BC CDAD ABC ADC BAD BCD BAC CAD ACB,ACB ACD 都为等边三角形,,AC AD ∴=,60,DE CM ACM ADE,ACM ADE ≌ ,,AMAE MAC EAD 60,MACCAECAEEADAME ∴是等边三角形(2)如图,记,AC BD 交于点,O设,,DF a OF b 四边形ABCD 为菱形,60,ABC ∠=︒,,30,ACBD OB OD a b ABO33,33OAOB a b ,2DF a x BFa b1221,a b bx a a 11,22b ax 则2,1ax bx333tan 13a b OAa AFBOFbb32331,3133xxxx(3)如图,设,DFESn四边形ABCD 是平行四边形,,DFE BFA ∽22=,BFAn DF x S BF2,BFAn SxFG =2BG , 2222,,33ABGAGFn n SS S xx根据菱形的轴对称的性质可得:2=,3CBG n S x ,AFD ABFS DF x SBF2,AFDn n S x x x 2=,BCDABD n n SSxx1222224=333n n n n n nS nn x x x x x x, 2212243334,3n n n S x x x x n S x 30,a所以12S S 有最大值, 当31232x时,最大值为:1119334.424【点睛】本题考查的是菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质,列二次函数关系式,二次函数的性质,锐角三角函数的应用,灵活运用以上知识解题是解本题的关键.6.(1)213442y xx =-++;(2)点P 的坐标为:(6,41,2);(3)11NC MC +=【解析】 【分析】(1)根据题意,先证明AOC ∆∽COB ∆,得到AO OCCO OB=,求出点A 、B 的坐标,然后利用待定系数法,即可求出抛物线解析式;(2)根据题意,可分为两种情况:AOC ∆∽PQC ∆或AOC ∆∽CQP ∆,结合解一元二次方程,相似三角形的判定和性质,分别求出点P 的坐标,即可得到答案;(3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,然后由角平分线的性质定理,得到EI =EJ ,再证明△MEI ∽△MNC ,△NEJ ∽△NMC ,得到111NC MC EI+=,然后求出EI 一个定值,即可进行判断. 【详解】解:(1)∵以AB 为直径的圆过点C , ∴∠ACB =90°, ∵点C 的坐标为()0,4, ∴CO ⊥AB ,∴∠AOC =∠COB =90°,∴∠ACO +∠OCB =∠ACO +∠OAC =90°, ∴∠OCB =∠OAC , ∴AOC ∆∽COB ∆,∴AO OCCO OB=, ∵4CO =,10AO BO AB +==, ∴10AO OB =-, ∴1044OB OB-=, 解得:2OB =或8OB =, 经检验,满足题意, ∵OB OA >, ∴8OB =,∴点A 为(2-,0),点B 为(8,0).设抛物线的解析式为2y ax bx c =++,把点A 、B 、C 三点的坐标代入,有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩,解得:14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式为213442y x x =-++;(2)根据题意,如图:当AOC ∆∽PQC ∆时, ∴ACO PCQ ∠=∠, ∵90ACO OCB ∠+∠=︒, ∴90PCQ OCB ∠+∠=︒, ∴PC ⊥OC , ∴点P 的纵坐标为4,当4y =时,有2134442x x -++=,解得:16x =或20x =(舍去); ∴点P 的坐标为(6,4);当AOC ∆∽CQP ∆时,则此时BC 垂直平分OP ,作PG ⊥y 轴,垂足为G ,如上图, ∴90CQP AOC ∠=∠=︒,∴AC ∥OP , ∴∠ACO =∠POG , ∵90PGO AOC ∠=∠=︒, ∴AOC ∆∽PGO ∆, ∴AO OCPG GO=, 设点P 为(x ,213442x x -++), ∴PG x =,213442GO x x =-++,∴22413442x x x =-++, 解得:171x =±-, ∵点P 在第一象限, ∴171x =-,∴2134217242x x -++=-,∴点P 的坐标为(171-,2172-);综合上述,点P 的坐标为:(6,4)或(171-,2172-); (3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,如图:∵CE 是∠ACB 的角平分线, ∴EI =EJ ,∵EI ∥CN ,EJ ∥CM ,∴△MEI ∽△MNC ,△NEJ ∽△NMC , ∴EI ME NC MN =,EJ NE MC MN =, ∴1EI EJ ME NENC MC MN MN +=+=, ∴1EI EI NC MC +=, ∴111NC MC EI+=, ∵△ACO ∽△AEI ,∴12AI AO EI CO ==,∵AC = ∵AC AI IC AI EI =+=+,12=,解得:EI =∴111NC MC EI +==∴11NC MC+是一个定值. 【点睛】本题考查了二次函数的综合应用,求二次函数的解析式,二次函数的性质,相似三角形的判定和性质,解一元二次方程,角平分线的性质定理等知识,解题的关键是熟练掌握题意,正确的作出辅助线,运用数形结合的思想进行解题.7.(1)①B ;D ;4;②1;(2)1522y x =-+或24y x =-+【解析】 【分析】(1)①根据“近点”、“远点”以及“ 特征数”的定义判断即可;②过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P .先分别求得点E 、F 的坐标,进而可求得EF 的长,再利用等积法求得OH 的长,进而即可解决问题;(2)如图,先求得“近点”N 到直线l 的距离NH AOB AHN △∽△即可求得答案. 【详解】解:(1)①由题意,点B 是O 关于直线m 的“近点”, 点D 是O 关于直线m 的“远点”, ∵点E 的坐标为(0,3).⊙O 的半径为1, ∴OE =3,OB =OD =1,∴BE =OE -OB =2,DB =OB +OD =2,O 关于直线m 的特征数224DB BE =⋅=⨯=, 故答案为:B ;D ;4;②如图,过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P ,设直线33y x =-+交x 轴于点F ,交y 轴于点E , 令y =0,则x =3;令x =0,则y =3, ∴(3F ,0),(0,3)E ,3OE ∴=,3OF =,22223(3)23EF OE OF ∴=+=+=,∵1122EOF S OE OF EF OH =⋅=⋅△, ∴11332322OH ⨯⨯=⨯⋅, 解得:32OH =, 12QH OH OQ ∴=-=, 又∵2PQ OQ OP =+=,O ∴关于直线n 的“特征数” 1212PQ QH =⋅=⨯=;(2)如图,设直线l 交x 轴于点A ,交y 轴于点B ,过点F 作FH ⊥直线l ,垂足为点H ,交⊙F 于N ,G ,∵⊙F 5,∴FN =FG 5,∴GN =FN +FG 5∵⊙F 关于直线l 的“特征数”是6, ∴GN·NH =6,NH =6, 解得:NH设直线l 的解析式是y kx b =+, ∵直线l 经过点M (1,2),∴将(1,2)代入y kx b =+,得:2k b +=, 2b k ∴=-,(2)y kx k ∴=+-,∴当0x =时,2y k =-,∴点B 坐标为(0,2-k ),|2|OB k ∴=-,当0y =时,(2)0kx k +-=, 解得:2k x k-=, ∴点A 坐标为(2k k-,0), 2||k OA k -∴=,22|(1)||1|k k AN k k--=--=+,AB ∴2||k k-= BAO NAH ∠=∠,90AOB AHN ∠=∠=︒, AOB AHN ∴△∽△,∴NH ANOB AB=,∴|2|522|1|||k k k k k-=--+, 整理,得:22520k k ++=,解得:12k =-或2k =-,∴直线l 的解析式为1522y x =-+或24y x =-+.【点睛】本题属于圆综合题,考查了一次函数的性质,相似三角形的判定和性质运用以及勾股定理的运用,远点,近点,特征数等新定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.8.(1)y =-x 2+2x +3,y =-x +3;(2)存在,(-1,0)或(4,-5);(3)存在,(1,2)或(1,-3) 【解析】 【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD AD =,进而判断出ABC 的面积和ACP △的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论. 【详解】(1)把(30)A ,、(10)B -,代入2y x bx c =-++, 解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为(0,3),又(30)A ,,代入1y kx b =+, 得1k =-,13b =, ∴直线AC 的解析式为3y x =-+, (2)如图,连接BC ,∵点D 是抛物线的对称轴与x 轴的交点, ∴AD BD =, ∴2ABCACDSS=,∵2ACP ACD S S =△△,∴ACP ABC S S =△△,此时,点P 与点B 重合, 即:(10)P -,, 过B 点作PB AC ∥交抛物线于点P ,则直线BP 的解析式为1y x =--①, ∵抛物线的解析式为2y x 2x 3=-++②,联立①②解得,10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩,∴P (4,﹣5),∴即点P 的坐标为(﹣1,0)或(4,﹣5); (3)由(1)可知,抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ,如下图所示:22222BM AM ==+,4AB =即222BM AM AB +=则MAB △是等腰直角三角形,符合题意,M 点即为所求Q 点的一种情况,当Q 点在x 轴下方时,设Q 为(1,)m ,0m <, 因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点,则1ADQ QEA ≌ ∴2AD QE ==,1DQ EA m ==- ∴12(1)A m m --,∵点A1恰好落在抛物线2y x 2x 3=-++上, 代入,解得m=-3或2m = (舍去) ∴Q (1,-3)综上,Q 点坐标为(1,2)或(1,-3), 【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,全等三角形的判定与性质,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.9.(1)直线AC 的解析式为y =﹣x +6;(2)d =4-t ;(3)Q (212,1). 【解析】 【分析】(1)先由解析式求出得A 、C 点的坐标,得OA =OC ,得四边形ABCO 为正方形,再根据正方形的面积求得边长,便可得b 的值;(2)过点Q 作QG ⊥AB 交AB 延长沿于点G ,证明Rt △AOP ≌Rt △GPQ (AAS ),得到AP =GQ ,进而求得结论便可;(3)过点P 作PH ⊥OF 于点H ,延长PH 交EQ 的延长线于点R ,EQ 的延长线与x 轴交于点N ,过Q 作QM ⊥x 轴于点M .证明Rt △AOP ≌Rt △GPQ (CCS ),得PK =QR ,∠R=∠OKP,再证明∠R=∠FPR,得EP=ER,再证FE=NR,设FE=NR=k,NQ=m,在Rt△PQE中,由勾股定理列出方程,得到k与m的关系,解Rt△PQE得tan∠PEQ,进而把这个函数值运用到△OAP中,求得t的值,再运用(2)中结论得Q的纵坐标d的值,再运用到△QNM中求得NM,NQ的值,进而求得ON,便可得Q的横坐标的值.【详解】解:(1)∵直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,A b C b,∴(,0),(0,)∴OA=OC=b,∴矩形ABCO为正方形,∵矩形ABCO的面积是36.∴b=6,即直线AC的解析式为y=﹣x+6;(2)如图,过点Q作QG⊥AB交AB延长沿于点G,∵∠OPQ=90°,∴∠APO+∠GPQ=90°,∵∠APO+∠AOP=90°,∴∠AOP=∠GPQ,∵在矩形ABCO,∠OAP=90°,QG⊥AB,∴∠QGP=∠OAP=90°,∵PQ=OP,∴Rt△AOP≌Rt△GPQ(AAS),∴AP=GQ,∵AP=t,∴GQ=t,∴d=4-t;(2)过点P作PH⊥OF于点H,延长PH交EQ的延长线于点R,EQ的延长线与y轴交于点N,过Q作QM⊥y轴于点M.则AP=t,QM=d,且d=6-t.∵OF 平分∠POC , ∴∠POF =∠COF =∠PFO , ∴PF =PO ,∵PH ⊥OF ,∠OPQ =90°, ∴∠OPH =∠FPH ,∠KPH =∠POH , 在△OPK 和△PQR 中, 90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩====, ∴△OPK ≌△PQR (ASA ), ∴PK =QR ,∠R =∠OKP ,∵∠OKP +∠POK =∠POK +∠OPH =90°, ∴∠OKP =∠OPH , ∴∠R =∠OPH , ∵PO =PF ,PH ⊥OF , ∴∠OPH =∠FPH , ∴∠R =∠FPR , ∴EP =ER ,∵PE ∥ON ,OP ∥EN , ∴四边形OPEN 是平行四边形, ∴EN =PO =PF , ∴PE -PF =ER -EN , ∴FE =NR ,设FE =NR =k ,则KQ =2FE =2k , 又设NQ =m ,∴PK=QR=m+k,∴PQ=m+3k,∴PO=EN=PF=m+3k,∴QE=EN-QR=m+3k-m=3k,PE=PF+FE=4k+m,在Rt△PQE中,∵PE2=PQ2+QE2,∴(4k+m)2=(3k+m)2+(3k)2,∴k1=0(舍去),k2=m,∴PQ=4m,QE=3m,∴tan∠PEN=43 PQQE=,∵OP∥EN,∴∠OPA=∠PEN,∴tan∠APO=43,∵AO=6,∴AP=4.5,∴t=4.5,∴QM=d=6-t=1.5,∵PE∥OC,∴∠QNM=∠PEN,∴tan∠QNM=tan∠PEN=43,∴NM=9 tan8QMQNM=∠,∴m=NQ158 =,∴PE=ON=4k+m=5m=758,∴OM=ON+NM=212,∴Q(212,1).【点睛】本题是一次函数与四边形的综合题,主要考查了一次函数的图象与性质,全等三角形的性质与判定,正方形的性质,旋转的性质,解直角三角形的应用,等腰三角形的性质与判定,平行四边形的性质与判定,是一道综合性极强的题目,解决这类问题常用到数形结合、方程和转化等数学思想方法.构造全等三角形是解题的关键,也是问题的突破口.10.(1);(2);(3)【解析】 【分析】(1)由抛物线的二次项系数 再根据交点式可得抛物线为从而可得答案;(2)先画好图形,证明利用相似三角形的性质求解从而可得答案;(3)如图,过P 作轴于,K 过M 作于,N 证明即再求解则,再解方程可得 4,t = 再求解的解析式,再联立解析式解方程可得答案. 【详解】 解:(1) 抛物线交x 轴于()2,0A -、()5,0B 两点,所以可得抛物线为:(2)如图,过P 作于,H 连AP 交OC 于则,x 则令0,(3)如图,过P作轴于,K过M作于,N 由(2)得:,,轴,则轴,,即结合(1)可得:四边形为矩形,。
2020年中考数学压轴题(含答案)
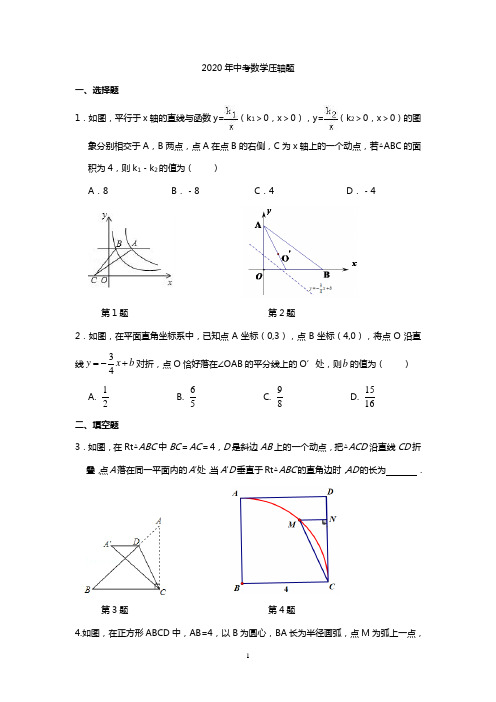
2020年中考数学压轴题一、选择题1.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8 B.﹣8 C.4 D.﹣4第1题第2题2.如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线34y x b=-+对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为()A.12B.65C.98D.1516二、填空题3.如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为.第3题第4题4.如图,在正方形ABCD中,AB=4,以B为圆心,BA长为半径画弧,点M为弧上一点,MN ⊥CD 于N ,连接CM ,则CM -MN 的最大值为 . 三、解答题5.如图,四边形ABCD 是⊙O 的内接四边形,AC 为直径, ⌒ BD = ⌒AD ,DE ⊥BC ,垂足为E . (1)求证:CD 平分∠ACE ;(2)判断直线ED 与⊙O 的位置关系,并说明理由; (3)若CE =2,AC =8,阴影部分的面积为 .6.如图,抛物线y =ax 2+bx +c (a <0,a 、b 、c 为常数)与x 轴交于A 、C 两点,与y 轴交于B 点,A (﹣6,0),C (1,0),B (0,).(1)求该抛物线的函数关系式与直线AB 的函数关系式;(2)已知点M (m ,0)是线段OA 上的一个动点,过点M 作x 轴的垂线l ,分别与直线AB 和抛物线交于D 、E 两点,当m 为何值时,△BDE 恰好是以DE 为底边的等腰三角形?(3)在(2)问条件下,当△BDE 恰妤是以DE 为底边的等腰三角形时,动点M 相应位置记为点M ′,将OM ′绕原点O 顺时针旋转得到ON (旋转角在0°到90°之间);i :探究:线段OB 上是否存在定点P (P 不与O 、B 重合),无论ON 如何旋转,始终保持不变,若存在,试求出P 点坐标:若不存在,请说明理由;ii :试求出此旋转过程中,(NA +NB )的最小值.EO CBA【答案与解析】一、选择题1.A2.D二、填空题3.【分析】由等腰直角三角形的性质和勾股定理得出AB=4,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,根据折叠的性质得到∠A′=∠A=∠A′CB=45°,A′D=AD =x,推出A′C⊥AB,求得BH=BC=2,DH=A′D=x,然后列方程即可得到结果,②如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD =∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=2.【解答】解:Rt△ABC中,BC=AC=4,∴AB=4,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,∴∠A′=∠A=∠A′CB=45°,A′D=AD=x,∵∠B =45°, ∴A ′C ⊥AB , ∴BH =BC =2,DH =A ′D =x ,∴x +x +2=4,∴x =4﹣4, ∴AD =4﹣4;②如图2,当A ′D ∥AC ,∵把△ACD 沿直线CD 折叠,点A 落在同一平面内的A ′处, ∴AD =A ′D ,AC =A ′C ,∠ACD =∠A ′CD , ∵∠A ′DC =∠ACD , ∴∠A ′DC =∠A ′CD , ∴A ′D =A ′C , ∴AD =AC =4, 综上所述:AD 的长为:4﹣4或4.4. 2 三、解答题 5、(1),BD AD BAD ACD =∴=∠∠°+180ABCD O BAD BCD ∴=四边形内接于圆,∠∠°+180BCD DCE =又∠∠,DCE BAD ∴=∠∠ACD DCE ∴=∠∠即CD 平分∠ACE(2)直线ED 与⊙O 相切。
2019年全国中考数学真题精选分类汇编:压轴题+含答案解析

2019年全国中考数学真题精选分类汇编:压轴题含答案解析1.(2019•北京)在△ABC中,D,E分别是△ABC两边的中点,如果上的所有点都在△ABC的内部或边上,则称为△ABC的中内弧.例如,图1中是△ABC的一条中内弧.(1)如图2,在Rt△ABC中,AB=AC=,D,E分别是AB,AC的中点,画出△ABC的最长的中内弧,并直接写出此时的长;(2)在平面直角坐标系中,已知点A(0,2),B(0,0),C(4t,0)(t>0),在△ABC中,D,E 分别是AB,AC的中点.①若t=,求△ABC的中内弧所在圆的圆心P的纵坐标的取值范围;②若在△ABC中存在一条中内弧,使得所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.2.(2019•上海)如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.(1)求证:∠E═∠C;(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出的值.3.(2019•广州)已知抛物线G:y=mx2﹣2mx﹣3有最低点.(1)求二次函数y=mx2﹣2mx﹣3的最小值(用含m的式子表示);(2)将抛物线G向右平移m个单位得到抛物线G1.经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;(3)记(2)所求的函数为H,抛物线G与函数H的图象交于点P,结合图象,求点P的纵坐标的取值范围.4.(2019•深圳)已知在平面直角坐标系中,点A(3,0),B(﹣3,0),C(﹣3,8),以线段BC为直径作圆,圆心为E,直线AC交⊙E于点D,连接OD.(1)求证:直线OD是⊙E的切线;(2)点F为x轴上任意一动点,连接CF交⊙E于点G,连接BG;①当tan∠ACF=时,求所有F点的坐标(直接写出);②求的最大值.5.(2019•武汉)在△ABC中,∠ABC=90°,=n,M是BC上一点,连接AM.(1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN.(2)过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q.①如图2,若n=1,求证:=.②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示)6.(2019•武汉)已知抛物线C1:y=(x﹣1)2﹣4和C2:y=x2(1)如何将抛物线C1平移得到抛物线C2?(2)如图1,抛物线C1与x轴正半轴交于点A,直线y=﹣x+b经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.①若AP=AQ,求点P的横坐标;②若P A=PQ,直接写出点P的横坐标.(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为2,设M、N两点的横坐标分别为m、n,求m与n的数量关系.7.(2019•杭州)如图,已知锐角三角形ABC内接于圆O,OD⊥BC于点D,连接OA.(1)若∠BAC=60°,①求证:OD=OA.②当OA=1时,求△ABC面积的最大值.(2)点E在线段OA上,OE=OD,连接DE,设∠ABC=m∠OED,∠ACB=n∠OED(m,n是正数),若∠ABC<∠ACB,求证:m﹣n+2=0.8.(2019•天津)已知抛物线y=x2﹣bx+c(b,c为常数,b>0)经过点A(﹣1,0),点M(m,0)是x轴正半轴上的动点.(Ⅰ)当b=2时,求抛物线的顶点坐标;(Ⅱ)点D(b,y D)在抛物线上,当AM=AD,m=5时,求b的值;(Ⅲ)点Q(b+,y Q)在抛物线上,当AM+2QM的最小值为时,求b的值.9.(2019•天津)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;②当≤S≤5时,求t的取值范围(直接写出结果即可).10.(2019•成都)如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.(1)求抛物线的函数表达式;(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点C'和点D的坐标;(3)设P是抛物线上位于对称轴右侧的一点,点Q在抛物线的对称轴上,当△CPQ为等边三角形时,求直线BP的函数表达式.11.(2019•安徽)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.(1)求证:△P AB∽△PBC;(2)求证:P A=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2•h3.12.(2019•长沙)如图,抛物线y=ax2+6ax(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.(1)求点A的坐标;(2)过点C作⊙P的切线CE交x轴于点E.①如图1,求证:CE=DE;②如图2,连接AC,BE,BO,当a=,∠CAE=∠OBE时,求﹣的值.13.(2019•苏州)如图①,抛物线y=﹣x2+(a+1)x﹣a与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积是6.(1)求a的值;(2)求△ABC外接圆圆心的坐标;(3)如图②,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,且∠P AQ=∠AQB,求点Q的坐标.14.(2019•青岛)已知:如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD垂直平分A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE ⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t(s)(0<t<5),解答下列问题:(1)当t为何值时,点E在∠BAC的平分线上?(2)设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.15.(2019•枣庄)已知抛物线y=ax2+x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.(1)求抛物线的解析式和A,B两点的坐标;(2)如图1,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M的坐标.16.(2019•陕西)问题提出:(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;问题解决:(3)如图3,有一座塔A,按规定,要以塔A为对称中心,建一个面积尽可能大的形状为平行四边形的景区BCDE.根据实际情况,要求顶点B是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由.(塔A的占地面积忽略不计)17.(2019•恩施州)如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣),与x轴交于A、B两点.(1)求抛物线的解析式.(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.(3)点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.18.(2019•黄冈)如图①,在平面直角坐标系xOy中,已知A(﹣2,2),B(﹣2,0),C(0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合),设运动时间为t(秒).(1)求经过A、C、D三点的抛物线的解析式;(2)点P在(1)中的抛物线上,当M为BC的中点时,若△P AM≌△PBM,求点P的坐标;(3)当M在CD上运动时,如图②.过点M作MF⊥x轴,垂足为F,ME⊥AB,垂足为E.设矩形MEBF与△BCD重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值;(4)点Q为x轴上一点,直线AQ与直线BC交于点H,与y轴交于点K.是否存在点Q,使得△HOK为等腰三角形?若存在,直接写出符合条件的所有Q点的坐标;若不存在,请说明理由.19.(2019•朝阳)如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交点C,抛物线y=﹣2x2+bx+c过A,C两点,与x轴交于另一点B.(1)求抛物线的解析式.(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当EF=BF时,求sin∠EBA的值.(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.20.(2019•连云港)问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.问题探究:在“问题情境”的基础上.(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P 落在点P'处,若正方形ABCD的边长为4,AD的中点为S,求P'S的最小值.问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=,请直接写出FH的长.21.(2019•衢州)如图,在Rt△ABC中,∠C=90°,AC=6,∠BAC=60°,AD平分∠BAC交BC 于点D,过点D作DE∥AC交AB于点E,点M是线段AD上的动点,连结BM并延长分别交DE,AC于点F、G.(1)求CD的长.(2)若点M是线段AD的中点,求的值.(3)请问当DM的长满足什么条件时,在线段DE上恰好只有一点P,使得∠CPG=60°?22.(2019•鞍山)在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.(1)求抛物线的解析式.(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD =2S△APQ时,求点P的坐标.(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.2019年全国中考数学真题精选分类汇编:压轴题含答案解析参考答案与试题解析一.解答题(共22小题)1.(2019•北京)在△ABC中,D,E分别是△ABC两边的中点,如果上的所有点都在△ABC的内部或边上,则称为△ABC的中内弧.例如,图1中是△ABC的一条中内弧.(1)如图2,在Rt△ABC中,AB=AC=,D,E分别是AB,AC的中点,画出△ABC的最长的中内弧,并直接写出此时的长;(2)在平面直角坐标系中,已知点A(0,2),B(0,0),C(4t,0)(t>0),在△ABC中,D,E 分别是AB,AC的中点.①若t=,求△ABC的中内弧所在圆的圆心P的纵坐标的取值范围;②若在△ABC中存在一条中内弧,使得所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.【分析】(1)由三角函数值及等腰直角三角形性质可求得DE=2,最长中内弧即以DE为直径的半圆,的长即以DE为直径的圆周长的一半;(2)根据三角形中内弧定义可知,圆心一定在DE的中垂线上,①当t=时,要注意圆心P在DE 上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;②根据题意,t的最大值即圆心P在AC上时求得的t值.【解答】解:(1)如图2,以DE为直径的半圆弧,就是△ABC的最长的中内弧,连接DE,∵∠A=90°,AB=AC=,D,E分别是AB,AC的中点,∴BC===4,DE=BC=×4=2,∴弧=×2π=π;(2)如图3,由垂径定理可知,圆心一定在线段DE的垂直平分线上,连接DE,作DE垂直平分线FP,作EG⊥AC交FP于G,①当t=时,C(2,0),∴D(0,1),E(1,1),F(,1),设P(,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,∴m≥1,∵OA=OC,∠AOC=90°∴∠ACO=45°,∵DE∥OC∴∠AED=∠ACO=45°作EG⊥AC交直线FP于G,FG=EF=根据三角形中内弧的定义可知,圆心在点G的下方(含点G)直线FP上时也符合要求;∴m≤综上所述,m≤或m≥1.②如图4,设圆心P在AC上,∵P在DE中垂线上,∴P为AE中点,作PM⊥OC于M,则PM=,∴P(t,),∵DE∥BC∴∠ADE=∠AOB=90°∴AE===,∵PD=PE,∴∠AED=∠PDE∵∠AED+∠DAE=∠PDE+∠ADP=90°,∴∠DAE=∠ADP∴AP=PD=PE=AE由三角形中内弧定义知,PD≤PM∴AE≤,AE≤3,即≤3,解得:t≤,∵t>0∴0<t≤.如图5,设圆心P在BC上,则P(t,0)PD=PE==,PC=3t,CE=AC==由三角形中内弧定义知,∠PEC<90°,∴PE2+CE2≥PC2即+≥(3t)2,∵t>0∴0<t≤;综上所述,t的取值范围为:0<t≤.【点评】此题是一道圆的综合题,考查了圆的性质,弧长计算,直角三角形性质等,给出了“三角形中内弧”新定义,要求学生能够正确理解新概念,并应用新概念解题.2.(2019•上海)如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.(1)求证:∠E═∠C;(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出的值.【分析】(1)由题意:∠E=90°﹣∠ADE,证明∠ADE=90°﹣∠C即可解决问题.(2)延长AD交BC于点F.证明AE∥BC,可得∠AFB=∠EAD=90°,=,由BD:DE=2:3,可得cos∠ABC===.(3)因为△ABC与△ADE相似,∠DAE=90°,所以∠ABC中必有一个内角为90°因为∠ABC是锐角,推出∠ABC≠90°.接下来分两种情形分别求解即可.【解答】(1)证明:如图1中,∵AE⊥AD,∴∠DAE=90°,∠E=90°﹣∠ADE,∵AD平分∠BAC,∴∠BAD=∠BAC,同理∠ABD=∠ABC,∵∠ADE=∠BAD+∠DBA,∠BAC+∠ABC=180°﹣∠C,∴∠ADE=(∠ABC+∠BAC)=90°﹣∠C,∴∠E=90°﹣(90°﹣∠C)=∠C.(2)解:延长AD交BC于点F.∵AB=AE,∴∠ABE=∠E,BE平分∠ABC,∴∠ABE=∠EBC,∴∠E=∠CBE,∴AE∥BC,∴∠AFB=∠EAD=90°,=,∵BD:DE=2:3,∴cos∠ABC===.(3)∵△ABC与△ADE相似,∠DAE=90°,∴∠ABC中必有一个内角为90°∵∠ABC是锐角,∴∠ABC≠90°.①当∠BAC=∠DAE=90°时,∵∠E=∠C,∴∠ABC=∠E=∠C,∵∠ABC+∠C=90°,∴∠ABC=30°,此时=2﹣.②当∠C=∠DAE=90°时,∠∠C=45°,∴∠EDA=45°,∵△ABC与△ADE相似,∴∠ABC=45°,此时=2﹣.综上所述,∠ABC=30°或45°,=2﹣或2﹣.【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,平行线的判定和性质,锐角三角函数等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.3.(2019•广州)已知抛物线G:y=mx2﹣2mx﹣3有最低点.(1)求二次函数y=mx2﹣2mx﹣3的最小值(用含m的式子表示);(2)将抛物线G向右平移m个单位得到抛物线G1.经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;(3)记(2)所求的函数为H,抛物线G与函数H的图象交于点P,结合图象,求点P的纵坐标的取值范围.【分析】(1)抛物线有最低点即开口向上,m>0,用配方法或公式法求得对称轴和函数最小值.(2)写出抛物线G的顶点式,根据平移规律即得到抛物线G1的顶点式,进而得到抛物线G1顶点坐标(m+1,﹣m﹣3),即x=m+1,y=﹣m﹣3,x+y=﹣2即消去m,得到y与x的函数关系式.再由m>0,即求得x的取值范围.(3)法一:求出抛物线恒过点B(2,﹣4),函数H图象恒过点A(2,﹣3),由图象可知两图象交点P应在点A、B之间,即点P纵坐标在A、B纵坐标之间.法二:联立函数H解析式与抛物线解析式组成方程组,整理得到用x表示m的式子.由x与m的范围讨论x的具体范围,即求得函数H对应的交点P纵坐标的范围.【解答】解:(1)∵y=mx2﹣2mx﹣3=m(x﹣1)2﹣m﹣3,抛物线有最低点∴二次函数y=mx2﹣2mx﹣3的最小值为﹣m﹣3(2)∵抛物线G:y=m(x﹣1)2﹣m﹣3∴平移后的抛物线G1:y=m(x﹣1﹣m)2﹣m﹣3∴抛物线G1顶点坐标为(m+1,﹣m﹣3)∴x=m+1,y=﹣m﹣3∴x+y=m+1﹣m﹣3=﹣2即x+y=﹣2,变形得y=﹣x﹣2∵m>0,m=x﹣1∴x﹣1>0∴x>1∴y与x的函数关系式为y=﹣x﹣2(x>1)(3)法一:如图,函数H:y=﹣x﹣2(x>1)图象为射线x=1时,y=﹣1﹣2=﹣3;x=2时,y=﹣2﹣2=﹣4∴函数H的图象恒过点B(2,﹣4)∵抛物线G:y=m(x﹣1)2﹣m﹣3x=1时,y=﹣m﹣3;x=2时,y=m﹣m﹣3=﹣3∴抛物线G恒过点A(2,﹣3)由图象可知,若抛物线与函数H的图象有交点P,则y B<y P<y A∴点P纵坐标的取值范围为﹣4<y P<﹣3法二:整理的:m(x2﹣2x)=1﹣x∵x>1,且x=2时,方程为0=﹣1不成立∴x≠2,即x2﹣2x=x(x﹣2)≠0∴m=>0∵x>1∴1﹣x<0∴x(x﹣2)<0∴x﹣2<0∴x<2即1<x<2∵y P=﹣x﹣2∴﹣4<y P<﹣3【点评】本题考查了求二次函数的最值,二次函数的平移,二次函数与一次函数的关系.解题关键是在无图的情况下运用二次函数性质解题,第(3)题结合图象解题体现数形结合的运用.4.(2019•深圳)已知在平面直角坐标系中,点A(3,0),B(﹣3,0),C(﹣3,8),以线段BC为直径作圆,圆心为E,直线AC交⊙E于点D,连接OD.(1)求证:直线OD是⊙E的切线;(2)点F为x轴上任意一动点,连接CF交⊙E于点G,连接BG;①当tan∠ACF=时,求所有F点的坐标,F2(5,0)(直接写出);②求的最大值.【分析】(1)连接ED,证明∠EDO=90°即可,可通过半径相等得到∠EDB=∠EBD,根据直角三角形斜边上中线等于斜边一半得DO=BO=AO,∠ODB=∠OBD,得证;(2)①分两种情况:a)F位于线段AB上,b)F位于BA的延长线上;过F作AC的垂线,构造相似三角形,应用相似三角形性质可求得点F坐标;②应用相似三角形性质和三角函数值表示出=,令y=CG2(64﹣CG2)=﹣(CG2﹣32)2+322,应用二次函数最值可得到结论.【解答】解:(1)证明:如图1,连接DE,∵BC为圆的直径,∴∠BDC=90°,∴∠BDA=90°∵OA=OB∴OD=OB=OA∴∠OBD=∠ODB∵EB=ED∴∠EBD=∠EDB∴EBD+∠OBD=∠EDB+∠ODB即:∠EBO=∠EDO∵CB⊥x轴∴∠EBO=90°∴∠EDO=90°∵点D在⊙E上∴直线OD为⊙E的切线.(2)①如图2,当F位于AB上时,过F作F1N⊥AC于N,∵F1N⊥AC∴∠ANF1=∠ABC=90°∴△ANF∽△ABC∴∵AB=6,BC=8,∴AC===10,即AB:BC:AC=6:8:10=3:4:5∴设AN=3k,则NF1=4k,AF1=5k∴CN=CA﹣AN=10﹣3k∴tan∠ACF===,解得:k=∴即F1(,0)如图3,当F位于BA的延长线上时,过F2作F2M⊥CA于M,∵△AMF2∽△ABC∴设AM=3k,则MF2=4k,AF2=5k∴CM=CA+AM=10+3k∴tan∠ACF=解得:∴AF2=5k=2OF2=3+2=5即F2(5,0)故答案为:F1(,0),F2(5,0).②方法1:如图4,过G作GH⊥BC于H,∵CB为直径∴∠CGB=∠CBF=90°∴△CBG∽△CFB∴∴BC2=CG•CF∴===≤∴当H为BC中点,即GH=BC时,的最大值=.方法2:设∠BCG=α,则sinα=,cosα=,∴sinαcosα=∵(sinα﹣cosα)2≥0,即:sin2α+cos2α≥2sinαcosα∵sin2α+cos2α=1,∴sinαcosα≤,即≤∴的最大值=.【点评】本题是一道难度较大,综合性很强的有关圆的代数几何综合题,主要考查了圆的性质,切线的性质和判定定理,直角三角形性质,相似三角形性质和判定,动点问题,二次函数最值问题等,构造相似三角形和应用求二次函数最值方法是解题关键.5.(2019•武汉)在△ABC中,∠ABC=90°,=n,M是BC上一点,连接AM.(1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN.(2)过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q.①如图2,若n=1,求证:=.②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示)【分析】(1)如图1中,延长AM交CN于点H.想办法证明△ABM≌△CBN(ASA)即可.(2)①如图2中,作CH∥AB交BP的延长线于H.利用全等三角形的性质证明CH=BM,再利用平行线分线段成比例定理解决问题即可.②如图3中,作CH∥AB交BP的延长线于H,作CN⊥BH于N.不妨设BC=2m,则AB=2mn.想办法求出CN,PN(用m,n表示),即可解决问题.【解答】(1)证明:如图1中,延长AM交CN于点H.∵AM⊥CN,∴∠AHC=90°,∵∠ABC=90°,∴∠BAM+∠AMB=90°,∠BCN+∠CMH=90°,∵∠AMB=∠CMH,∴∠BAM=∠BCN,∵BA=BC,∠ABM=∠CBN=90°,∴△ABM≌△CBN(ASA),∴BM=BN.(2)①证明:如图2中,作CH∥AB交BP的延长线于H.∵BP⊥AM,∴∠BPM=∠ABM=90°,∵∠BAM+∠AMB=90°,∠CBH+∠BMP=90°,∴∠BAM=∠CBH,∵CH∥AB,∴∠HCB+∠ABC=180°,∵∠ABC=90°,∴∠ABM=∠BCH=90°,∵AB=BC,∴△ABM≌△BCH(ASA),∴BM=CH,∵CH∥BQ,∴==.②解:如图3中,作CH∥AB交BP的延长线于H,作CN⊥BH于N.不妨设BC=2m,则AB=2mn.则BM=CM=m,CH=,BH=,AM=m,∵•AM•BP=•AB•BM,∴PB=,∵•BH•CN=•CH•BC,∴CN=,∵CN⊥BH,PM⊥BH,∴MP∥CN,∵CM=BM,∴PN=BP=,∵∠BPQ=∠CPN,∴tan∠BPQ=tan∠CPN===.方法二:易证:===,∵PN=PB,tan∠BPQ====.【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.6.(2019•武汉)已知抛物线C1:y=(x﹣1)2﹣4和C2:y=x2(1)如何将抛物线C1平移得到抛物线C2?(2)如图1,抛物线C1与x轴正半轴交于点A,直线y=﹣x+b经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.①若AP=AQ,求点P的横坐标;②若P A=PQ,直接写出点P的横坐标.(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为2,设M、N两点的横坐标分别为m、n,求m与n的数量关系.【分析】(1)y=(x﹣1)2﹣4向左平移1个单位长度,再向上平移4个单位长度即可得到y=x2;(2)①易求点A(3,0),b=4,设D(0,4)关于x轴的对称点为D',则D'(0,﹣4),则可求直线AD'的解析式为y=x﹣4,联立方程,可得P点横坐标为;②同理可得P点横坐标为﹣;(3)设经过M与E的直线解析式为y=k(x﹣m)+m2,∴,则可知△=k2﹣4km+4m2=(k﹣2m)2=0,求得k=2m,得出直线ME的解析式为y=2mx﹣m2,同理:直线NE的解析式为y=2nx﹣n2,则可求E(,mn),再由面积[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣(n2﹣mn)×(﹣n)﹣(m2﹣mn)×(m﹣)=2,可得(m﹣n)3=8,即可求解;【解答】解:(1)y=(x﹣1)2﹣4向左平移1个单位长度,再向上平移4个单位长度即可得到y=x2;(2)如图1,①设抛物线C1与y轴交于C点,直线AB与y轴交于D点,∵C1:y=(x﹣1)2﹣4,∴A(3,0),C(0,﹣3),∵直线y=﹣x+b经过点A,∴b=4,∴D(0,4),∵AP=AQ,PQ∥y轴,∴P、Q两点关于x轴对称,设D(0,4)关于x轴的对称点为D',则D'(0,﹣4),∴直线AD'的解析式为y=x﹣4,由,得x1=3,x2=,∴x Q=,∴x P=x Q=,∴P点横坐标为;②P点横坐标为﹣;(3)设经过M与E的直线解析式为y=k(x﹣m)+m2,∴,则有x2﹣kx+km﹣m2=0,△=k2﹣4km+4m2=(k﹣2m)2=0,∴k=2m,∴直线ME的解析式为y=2mx﹣m2,同理:直线NE的解析式为y=2nx﹣n2,∴E(,mn),∴[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣(n2﹣mn)×(﹣n)﹣(m2﹣mn)×(m﹣)=2,∴(m﹣n)3﹣=4,∴(m﹣n)3=8,∴m﹣n=2;【点评】本题考查二次函数的图象及性质;是二次函数的综合题,熟练掌握直线与二次函数的交点求法,借助三角形面积列出等量关系是解决m与n的关系的关键.7.(2019•杭州)如图,已知锐角三角形ABC内接于圆O,OD⊥BC于点D,连接OA.(1)若∠BAC=60°,①求证:OD=OA.②当OA=1时,求△ABC面积的最大值.(2)点E在线段OA上,OE=OD,连接DE,设∠ABC=m∠OED,∠ACB=n∠OED(m,n是正数),若∠ABC<∠ACB,求证:m﹣n+2=0.【分析】(1)①连接OB、OC,则∠BOD=BOC=∠BAC=60°,即可求解;②BC长度为定值,△ABC面积的最大值,要求BC边上的高最大,即可求解;(2)∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣mx﹣nx=∠BOC=∠DOC,而∠AOD=∠COD+∠AOC=180°﹣mx﹣nx+2mx=180°+mx﹣nx,即可求解.【解答】解:(1)①连接OB、OC,则∠BOD=∠BOC=∠BAC=60°,∴∠OBC=30°,∴OD=OB=OA;②∵BC长度为定值,∴△ABC面积的最大值,要求BC边上的高最大,当AD过点O时,AD最大,即:AD=AO+OD=,△ABC面积的最大值=×BC×AD=×2OB sin60°×=;(2)如图2,连接OC,设:∠OED=x,则∠ABC=mx,∠ACB=nx,则∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣mx﹣nx=∠BOC=∠DOC,∵∠AOC=2∠ABC=2mx,∴∠AOD=∠COD+∠AOC=180°﹣mx﹣nx+2mx=180°+mx﹣nx,∵OE=OD,∴∠AOD=180°﹣2x,即:180°+mx﹣nx=180°﹣2x,化简得:m﹣n+2=0.【点评】本题为圆的综合运用题,涉及到解直角三角形、三角形内角和公式,其中(2),∠AOD=∠COD+∠AOC是本题容易忽视的地方,本题难度适中.8.(2019•天津)已知抛物线y=x2﹣bx+c(b,c为常数,b>0)经过点A(﹣1,0),点M(m,0)是x轴正半轴上的动点.(Ⅰ)当b=2时,求抛物线的顶点坐标;(Ⅱ)点D(b,y D)在抛物线上,当AM=AD,m=5时,求b的值;(Ⅲ)点Q(b+,y Q)在抛物线上,当AM+2QM的最小值为时,求b的值.【分析】(Ⅰ)将点A(﹣1,0)代入y=x2﹣bx+c,求出c关于b的代数式,再将b代入即可求出c 的值,可进一步写出抛物线解析式及顶点坐标;(Ⅱ)将点D(b,y D)代入抛物线y=x2﹣bx﹣b﹣1,求出点D纵坐标为﹣b﹣1,由b>0判断出点D(b,﹣b﹣1)在第四象限,且在抛物线对称轴x=的右侧,过点D作DE⊥x轴,可证△ADE为等腰直角三角形,利用锐角三角函数可求出b的值;(Ⅲ)将点Q(b+,y Q)代入抛物线y=x2﹣bx﹣b﹣1,求出Q纵坐标为﹣﹣,可知点Q(b+,﹣﹣)在第四象限,且在直线x=b的右侧,点N(0,1),过点Q作直线AN的垂线,垂足为G,QG与x轴相交于点M,过点Q作QH⊥x轴于点H,则点H(b+,0),在Rt△MQH中,可知∠QMH=∠MQH=45°,设点M(m,0),则可用含b的代数式表示m,因为AM+2QM=,所以[(﹣)﹣(﹣1)]+2[(b+)﹣(﹣)]=,解方程即可.【解答】解:(Ⅰ)∵抛物线y=x2﹣bx+c经过点A(﹣1,0),∴1+b+c=0,即c=﹣b﹣1,当b=2时,y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的顶点坐标为(1,﹣4);(Ⅱ)由(Ⅰ)知,抛物线的解析式为y=x2﹣bx﹣b﹣1,∵点D(b,y D)在抛物线y=x2﹣bx﹣b﹣1上,∴y D=b2﹣b•b﹣b﹣1=﹣b﹣1,由b>0,得b>>0,﹣b﹣1<0,∴点D(b,﹣b﹣1)在第四象限,且在抛物线对称轴x=的右侧,如图1,过点D作DE⊥x轴,垂足为E,则点E(b,0),∴AE=b+1,DE=b+1,得AE=DE,∴在Rt△ADE中,∠ADE=∠DAE=45°,∴AD=AE,由已知AM=AD,m=5,∴5﹣(﹣1)=(b+1),∴b=3﹣1;(Ⅲ)∵点Q(b+,y Q)在抛物线y=x2﹣bx﹣b﹣1上,∴y Q=(b+)2﹣b(b+)﹣b﹣1=﹣﹣,可知点Q(b+,﹣﹣)在第四象限,且在直线x=b的右侧,∵AM+2QM=2(AM+QM),∴可取点N(0,1),如图2,过点Q作直线AN的垂线,垂足为G,QG与x轴相交于点M,由∠GAM=45°,得AM=GM,则此时点M满足题意,过点Q作QH⊥x轴于点H,则点H(b+,0),在Rt△MQH中,可知∠QMH=∠MQH=45°,∴QH=MH,QM=MH,∵点M(m,0),∴0﹣(﹣﹣)=(b+)﹣m,解得,m=﹣,∵AM+2QM=,∴[(﹣)﹣(﹣1)]+2[(b+)﹣(﹣)]=,∴b=4.【点评】本题考查了待定系数法求解析式,抛物线上的点的坐标满足抛物线方程等,解题关键是能够根据给定参数判断点的位置,从而构造特殊三角形来求解.9.(2019•天津)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;②当≤S≤5时,求t的取值范围(直接写出结果即可).【分析】(Ⅰ)由已知得出AD=OA﹣OD=4,由矩形的性质得出∠AED=∠ABO=30°,在Rt△AED 中,AE=2AD=8,由勾股定理得出ED=4,即可得出答案;(Ⅱ)①由平移的性质得:O′D′=2,E′D′=4,ME′=OO′=t,D′E′∥O′C′∥OB,得出∠E′FM=∠ABO=30°,在Rt△MFE′中,MF=2ME′=2t,FE′===t,求出S△MFE′=ME′•FE′=×t×t=,S矩形C′O′D′E′=O′D′•E′D′=2×4=8,即可得出答案;②当S=时,O'A=OA﹣OO'=6﹣t,由直角三角形的性质得出O'F=O'A=(6﹣t),得出方程,解方程即可;当S=5时,O'A=6﹣t,D'A=6﹣t﹣2=4﹣t,由直角三角形的性质得出O'G=(6﹣t),D'F=(4﹣t),由梯形面积公式得出S=[(6﹣t)+(4﹣t)]×2=5,解方程即可.【解答】解:(Ⅰ)∵点A(6,0),∴OA=6,∵OD=2,∴AD=OA﹣OD=6﹣2=4,∵四边形CODE是矩形,∴DE∥OC,∴∠AED=∠ABO=30°,在Rt△AED中,AE=2AD=8,ED===4,∵OD=2,∴点E的坐标为(2,4);(Ⅱ)①由平移的性质得:O′D′=2,E′D′=4,ME′=OO′=t,D′E′∥O′C′∥OB,∴∠E′FM=∠ABO=30°,∴在Rt△MFE′中,MF=2ME′=2t,FE′===t,∴S△MFE′=ME′•FE′=×t×t=,∵S矩形C′O′D′E′=O′D′•E′D′=2×4=8,∴S=S矩形C′O′D′E′﹣S△MFE′=8﹣,∴S=﹣t2+8,其中t的取值范围是:0<t<2;②当S=时,如图③所示:O'A=OA﹣OO'=6﹣t,∵∠AO'F=90°,∠AFO'=∠ABO=30°,∴O'F=O'A=(6﹣t)∴S=(6﹣t)×(6﹣t)=,解得:t=6﹣,或t=6+(舍去),∴t=6﹣;当S=5时,如图④所示:O'A=6﹣t,D'A=6﹣t﹣2=4﹣t,∴O'G=(6﹣t),D'F=(4﹣t),∴S=[(6﹣t)+(4﹣t)]×2=5,解得:t=,∴当≤S≤5时,t的取值范围为≤t≤6﹣.【点评】本题是四边形综合题目,考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质、梯形面积公式等知识;本题综合性强,有一定难度,熟练掌握含30°角的直角三角形的性质时是解题的关键.10.(2019•成都)如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.(1)求抛物线的函数表达式;(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点C'和点D的坐标;(3)设P是抛物线上位于对称轴右侧的一点,点Q在抛物线的对称轴上,当△CPQ为等边三角形时,求直线BP的函数表达式.【分析】(1)根据待定系数法,把点A(﹣2,5),B(﹣1,0),C(3,0)的坐标代入y=ax2+bx+c 得到方程组求解即可;(2)设抛物线的对称轴与x轴交于点H,则H点的坐标为(1,0),BH=2,由翻折得C′B=CB =4,求出C′H的长,可得∠C′BH=60°,求出DH的长,则D坐标可求;(3)由题意可知△C′CB为等边三角形,分两种情况讨论:①当点P在x轴的上方时,点Q在x 轴上方,连接BQ,C′P.证出△BCQ≌△C′CP,可得BP垂直平分CC′,则D点在直线BP上,可求出直线BP的解析式,②当点P在x轴的下方时,点Q在x轴下方.同理可求出另一直线解析式.【解答】解:(1)由题意得:解得,∴抛物线的函数表达式为y=x2﹣2x﹣3.(2)∵抛物线与x轴交于B(﹣1,0),C(3,0),∴BC=4,抛物线的对称轴为直线x=1,如图,设抛物线的对称轴与x轴交于点H,则H点的坐标为(1,0),BH=2,由翻折得C′B=CB=4,在Rt△BHC′中,由勾股定理,得C′H===2,∴点C′的坐标为(1,2),tan,∴∠C′BH=60°,由翻折得∠DBH=∠C′BH=30°,在Rt△BHD中,DH=BH•tan∠DBH=2•tan30°=,∴点D的坐标为(1,).(3)解:取(2)中的点C′,D,连接CC′,∵BC′=BC,∠C′BC=60°,∴△C′CB为等边三角形.分类讨论如下:①当点P在x轴的上方时,点Q在x轴上方,连接BQ,C′P.∵△PCQ,△C′CB为等边三角形,∴CQ=CP,BC=C′C,∠PCQ=∠C′CB=60°,∴∠BCQ=∠C′CP,∴△BCQ≌△C′CP(SAS),∴BQ=C′P.∵点Q在抛物线的对称轴上,∴BQ=CQ,∴C′P=CQ=CP,又∵BC′=BC,∴BP垂直平分CC′,由翻折可知BD垂直平分CC′,∴点D在直线BP上,设直线BP的函数表达式为y=kx+b,则,解得,∴直线BP的函数表达式为y=.②当点P在x轴的下方时,点Q在x轴下方.。
2020年中考数学压轴题突破专题5 二次函数与线段和角的数量关系问题
2020年中考数学大题狂练之压轴大题突破培优练专题05 二次函数与线段和角的数量关系问题【真题再现】1.(2019年宿迁28题)如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足∠P AB=2∠ACO.求点P的坐标;(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.2.(2019年盐城27题)如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.(1)求A、B两点的横坐标;(2)若△OAB是以OA为腰的等腰三角形,求k的值;(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.3.(2018年常州28题)如图,二次函数y bx+2的图象与x轴交于点A、B,与y 轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是;(2)设直线PB与直线AC相交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.4.(2019年苏州28题)如图①,抛物线y=﹣x2+(a+1)x﹣a与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积是6.(1)求a的值;(2)求△ABC外接圆圆心的坐标;(3)如图②,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,且∠P AQ=∠AQB,求点Q的坐标.5.(2018年无锡28题)已知:如图,一次函数y=kx﹣1的图象经过点A(3,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.(1)求这个一次函数的表达式;(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(,0),求这条抛物线的函数表达式.6.(2017年苏州28题)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1)求b、c的值;(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.【专项突破】【题组一】1.(2020•无锡模拟)如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象交x轴于A、B两点,交y轴于点C.过点A的直线y=kx+2k(k≠0)与这个二次函数的图象的另一个交点为F,与该图象的对称轴交于点E,与y轴交于点D,且DE=EF.(1)求点A的坐标;(2)若△BDF的面积为12,求这个二次函数的关系式;(3)设二次函数的顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此时二次函数的表达式.2.(2020•镇江模拟)如图,在平面直角坐标系中,一次函数y x﹣2的图象分别交x、y轴于点A、B,抛物线y=x2+bx+c经过点A、B,点P为第四象限内抛物线上的一个动点.(1)求此抛物线对应的函数表达式;(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.3.(2020•滨湖区模拟)已知二次函数y=ax2+4amx(m>0)的对称轴与x轴交于点B,与直线l:y交于点C,点A是该二次函数图象与直线l在第二象限的交点,点D是抛物线的顶点,已知AC:CO=1:2,∠DOB=45°,△ACD的面积为2.(1)求抛物线的函数关系式;(2)若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.4.(2020•营口模拟)如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y 轴于点C(0,2).(1)求抛物线的函数表达式;(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.【题组二】5.(2019•梁溪区校级二模)已知,在平面直角坐标系中,直线l与y轴相交于点A(0,m),其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a≠0)经过点B,它与直线l相交于另一点C.(1)若AC:BC=1:3,求a的值(用含m的代数式表示);(2)在(1)的条件下,若抛物线的顶点为F,其对称轴与直线l和x轴分别相交于点D、E,当以F、C、D为顶点的三角形与△BED相似时,求抛物线的函数表达式.6.(2019•邗江区校级二模)如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.(1)求该抛物线的函数解析式.(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC 于点F,当S△COF:S△CDF=4:3时,求点D的坐标.(3)如图2,点E的坐标为(0,﹣2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.7.(2019•靖江市校级一模)如图,抛物线y=mx2﹣16mx+48m(m>0)与x轴交于A,B 两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.(1)若△OAC为等腰直角三角形,求m的值;(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示);(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点.①求m的值;②此时对于该抛物线上任意一点P(x0,y0)总有n4my1250成立,求实数n的最小值.8.(2019•姑苏区校级二模)已知抛物线经过点A(﹣1,0)、点B(3,0)、点C(0,3),点D为抛物线在第一象限内图象上一动点,连接AD,交y轴于点E,将点C关于线段AD作轴对称,对称点为C',连接AC'.(1)求抛物线的解析式;(2)如图1如果点C'落在x轴,求点E坐标;(3)如图2,连接AC、BC,BC与AD交于点F,拖动点D,点C'落在第四象限,作FG∥AC,交x轴于点M,交AC'于点G,若∠AGF=90°,求点M的横坐标.【题组三】9.(2019•宿豫区模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,且抛物线经过点D(2,3).(1)求这条抛物线的表达式;(2)将该抛物线向下平移,使得新抛物线的顶点G在x轴上.原抛物线上一点M平移后的对应点为点N,如果△AMN是以MN为底边的等腰三角形,求点N的坐标;(3)若点P为抛物线上第一象限内的动点,过点B作BE⊥OP,垂足为E,点Q为y轴上的一个动点,连接QE、QD,试求QE+QD的最小值.10.(2019•灌南县二模)如图,在平面直角坐标系中,二次函数y=ax2+bx的图象经过点A(﹣1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;(2)M(s,t)为抛物线对称轴上的一个动点,①若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,直接写出点M的坐标;②连接MA、MB,若∠AMB不小于60°,求t的取值范围.11.(2019•润州区二模)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与直线AB相交,与x轴、y轴交于A(2,0)、B.(1)求点O关于AB的对称点P的坐标;(2)若点P在二次函数y=ax2+bx+c(a≠0)的图象上,求二次函数y=ax2+bx+c(a≠0)的关系式.(3)在(2)的条件下,在△ABP内存在点M,使得MA+MB+MP的值最小,则相应点M的坐标为.12.(2019•洪泽区二模)如图,抛物线y=ax2+bx+5经过A(1,0)和B(5,0),与y轴交于点C点为点D,连接BC,BD.点P是抛物线对称轴上的一个动点(1)a=,b;(2)若∠CPB=90°,求点P的坐标;(3)是否存在点P,使得以P、D、B为顶点的三角形中有两个内角的和等于∠ABC?若存在,求出点P的坐标;若不存在,说明理由.(4)如图②,抛物线对称轴交x轴于点E,设∠BDE的度数为a,点M是线段BC上动点,作射线AM,将AM绕A点逆时针旋转2a度,旋转后的射线交直线BC与点N,请直接写出MN的最小值.(直接写出结果)【题组四】13.(2019•高港区三模)定义:两条长度相等,且它们所在的直线互相垂直,我们称这两条线段互为等垂线段.如图①,直线y=2x+4与x轴交于点A,与y轴交于点B.(1)若线段AB与线段BC互为等垂线段.求A、B、C的坐标.(2)如图②,点D是反比例函数y的图象上任意一点,点E(m,1),线段DE与线段AB互为等垂线段,求m的值;(3)抛物线y=ax2+bx+c(a≠0)经过A、B两点.①用含a的代数式表示b.②点P为平面直角坐标系内的一点,在抛物线上存在点Q,使得线段PQ与线段AB互为等垂线段,且它们互相平分,请直接写出满足上述条件的a值.14.(2019•丹阳市一模)如图(1),二次函数y=ax2﹣bx(a≠0)的图象与x轴、直线y=x的交点分别为点A(4,0)、B(5,5).(1)a=,b=,∠AOB=°;(2)连接AB,点P是抛物线上一点(异于点A),且∠PBO=∠OBA,求点P的坐标;(3)如图(2),点C、D是线段OB上的动点,且CD=2.设点C的横坐标为m.①过点C、D分别作x轴的垂线,与抛物线相交于点F、E,连接EF.当CF+DE取得最大值时,求m的值并判断四边形CDEF的形状;②连接AC、AD,求m为何值时,AC+AD取得最小值,并求出这个最小值.15.(2019•建湖县二模)如图,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y 轴交于点C直线y=﹣x+4经过点B、C.(1)求抛物线的表达式;(2)过点A的直线交抛物线于点M,交直线BC于点N.①点N位于x轴上方时,是否存在这样的点M,使得AM:NM=5:3?若存在,求出点M的坐标;若不存在,请说明理由.②连接AC,当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时,请求出点M的横坐标.16.(2019•无锡二模)已知,如图,二次函数y=ax2+2ax﹣3a(a>0)图象的顶点为C与x 轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx对称.(1)求A、B两点坐标及直线l的解析式;(2)求二次函数解析式;(3)如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l 上的两动点,连接CN,NM、MD,求D的坐标并直接写出CN+NM+MD的最小值.【题组五】17.(2019•兴化市二模)已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x 轴交于点O、A,关于x的一次函数y=﹣ax(a>0).(1)试说明点C在一次函数的图象上;(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足?如果存在,请求出k的值;如果不存在,请说明理由;(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y 轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.18.(2019•清江浦区一模)如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点B(﹣3,0)和C(4,0)与y轴交于点A.(1)a=,b=;(2)点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B 出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t 为何值时,以B、M、N为顶点的三角形是等腰三角形?(3)点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.19.(2019•常州一模)如图,在平面直角坐标系xOy中,直线l:y=kx+m交y轴于点C,与抛物线y=ax2+bx交于点A(4,0)、B(,).(1)直线l的表达式为:,抛物线的表达式为:;(2)若点P是二次函数y=ax2+bx在第四象限内的图象上的一点,且2S△APB=S△AOB,求△AOP的面积;(3)若点Q是二次函数图象上一点,设点Q到直线l的距离为d,到抛物线的对称轴的距离为d1,当|d﹣d1|=2时,请直接写出点Q的坐标.20.(2019•东台市模拟)如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.(1)求抛物线的表达式和顶点D的坐标;(2)在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;(3)将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y x﹣1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.【题组六】21.(2019•昆山市二模)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)交x轴于点A(2,0),B(﹣3,0),交y轴于点C,且经过点D(﹣6,﹣6),连接AD,BD.(1)求该抛物线的函数关系式;(2)若点M为X轴上方的抛物线上一点,能否在点A左侧的x轴上找到另一点N,使得△AMN与△ABD相似?若相似,请求出此时点M、点N的坐标;若不存在,请说明理由;(3)若点P是直线AD上方的抛物线上一动点(不与A,D重合),过点P作PQ∥y轴交直线AD于点Q,以PQ为直径作⊙E,则⊙E在直线AD上所截得的线段长度的最大值等于.(直接写出答案)22.(2019•泰兴市一模)如图1,抛物线l1::y1=a(x﹣2)2与直线l2:y2=﹣am(x﹣2)+b(a,m,b为常数,a≠0,m<0)交于A,B两点,直线l2交x轴交于点C.点A的坐标为(m+2,n).(1)若a=﹣1,m=﹣3,则A的坐标为,b=,点B的坐标为;(2)已知点M(0,﹣4),N(3,﹣4),抛物线l1与线段MN有两个公共点,求a的取值范围;(3)①如图1,求证:AB=3AC;②如图2,设抛物线顶点为F,直线l2交抛物线的对称轴于点D,直线l3:y3=2am(x﹣2)+d(d为常数,d≠0)经过点A,并交抛物线的对称轴于点E,若∠BFD=p∠AED (p为常数),则p的值是否发生变化?若不变,请求出p的值;若变化,请说明理由.23.(2019•铜山区二模)已知,如图,二次函数y=ax2+bx+c图象交x轴于A(﹣1,0),交y轴于点C(0,3),D是抛物线的顶点,对称轴DF经过x轴上的点F(1,0).(1)求二次函数关系式;(2)对称轴DF与BC交于点M,点P为对称轴DF上一动点.①求AP PD的最小值及取得最小值时点P的坐标;②在①的条件下,把△APF沿着x轴向右平移t个单位长度(0≤t≤4)时,设△APF与△MBF重叠部分面积记为S,求S与t之间的函数表达式,并求出S的最大值.24.(2019•靖江市一模)如图1,将抛物线y=ax2(a<0平移到顶点M恰好落在直线y=x+3上,且抛物线过直线与y轴的交点A,设此时抛物线顶点的横坐标为m(m>0).(1)用含m的代数式表示a;(2)如图2,Rt△CBT与抛物线交于C、D、T三点,∠B=90°,BC∥x轴,CD=2.BD =t.BT=2t,△TDC的面积为4.①求抛物线方程;②如图3,P为抛物线AM段上任一点,Q(0,4),连结QP并延长交线段AM于N,求的最大值.参考答案【真题再现】1.(2019年宿迁28题)如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足∠P AB=2∠ACO.求点P的坐标;(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.【分析】(1)把点A、C坐标代入抛物线解析式即求得b、c的值.(2)点P可以在x轴上方或下方,需分类讨论.①若点P在x轴下方,延长AP到H,使AH=AB构造等腰△ABH,作BH中点G,即有∠P AB=2∠BAG=2∠ACO,利用∠ACO 的三角函数值,求BG、BH的长,进而求得H的坐标,求得直线AH的解析式后与抛物线解析式联立,即求出点P坐标.②若点P在x轴上方,根据对称性,AP一定经过点H 关于x轴的对称点H',求得直线AH'的解析式后与抛物线解析式联立,即求出点P坐标.(3)设点Q横坐标为t,用t表示直线AQ、BN的解析式,把x=﹣1分别代入即求得点M、N的纵坐标,再求DM、DN的长,即得到DM+DN为定值.【解析】(1)∵抛物线y=x2+bx+c经过点A(1,0),C(0,﹣3)∴解得:∴抛物线的函数表达式为y=x2+2x﹣3(2)①若点P在x轴下方,如图1,延长AP到H,使AH=AB,过点B作BI⊥x轴,连接BH,作BH中点G,连接并延长AG交BI于点F,过点H作HI⊥BI于点I∵当x2+2x﹣3=0,解得:x1=﹣3,x2=1∴B(﹣3,0)∵A(1,0),C(0,﹣3)∴OA=1,OC=3,AC,AB=4∴Rt△AOC中,sin∠ACO,cos∠ACO∵AB=AH,G为BH中点∴AG⊥BH,BG=GH∴∠BAG=∠HAG,即∠P AB=2∠BAG∵∠P AB=2∠ACO∴∠BAG=∠ACO∴Rt△ABG中,∠AGB=90°,sin∠BAG∴BG AB∴BH=2BG∵∠HBI+∠ABG=∠ABG+∠BAG=90°∴∠HBI=∠BAG=∠ACO∴Rt△BHI中,∠BIH=90°,sin∠HBI,cos∠HBI ∴HI BH,BI BH∴x H=﹣3,y H,即H(,)设直线AH解析式为y=kx+a∴解得:∴直线AH:y x∵解得:(即点A),∴P(,)②若点P在x轴上方,如图2,在AP上截取AH'=AH,则H'与H关于x轴对称∴H'(,)设直线AH'解析式为y=k'x+a'∴解得:∴直线AH':y x∵解得:(即点A),∴P(,)综上所述,点P的坐标为(,)或(,).(3)DM+DN为定值∵抛物线y=x2+2x﹣3的对称轴为:直线x=﹣1∴D(﹣1,0),x M=x N=﹣1设Q(t,t2+2t﹣3)(﹣3<t<1)设直线AQ解析式为y=dx+e∴解得:∴直线AQ:y=(t+3)x﹣t﹣3当x=﹣1时,y M=﹣t﹣3﹣t﹣3=﹣2t﹣6∴DM=0﹣(﹣2t﹣6)=2t+6设直线BQ解析式为y=mx+n∴解得:∴直线BQ:y=(t﹣1)x+3t﹣3当x=﹣1时,y N=﹣t+1+3t﹣3=2t﹣2∴DN=0﹣(2t﹣2)=﹣2t+2∴DM+DN=2t+6+(﹣2t+2)=8,为定值.点睛:本题考查了求二次函数解析式、求一次函数解析式,解一元二次方程、二元一次方程组,等腰三角形的性质,三角函数的应用.第(2)题由于不确定点P位置需分类讨论;(2)(3)计算量较大,应认真理清线段之间的关系再进行计算.2.(2019年盐城27题)如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.(1)求A、B两点的横坐标;(2)若△OAB是以OA为腰的等腰三角形,求k的值;(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.【分析】(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,即可求解;(2)分OA=AB、OA=OB两种情况,求解即可;(3)求出m=﹣k2﹣k,在△AHM中,tanαk tan∠BEC k+2,即可求解.【解析】(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,解得:x=1和2,故点A、B的坐标横坐标分别为1和2;(2)OA,①当OA=AB时,即:1+k2=5,解得:k=±2(舍去2);②当OA=OB时,4+(k+2)2=5,解得:k=﹣1或﹣3;故k的值为:﹣1或﹣2或﹣3;(3)存在,理由:①当点B在x轴上方时,过点B作BH⊥AE于点H,将△AHB的图形放大见右侧图形,过点A作∠HAB的角平分线交BH于点M,过点M作MN⊥AB于点N,过点B作BK⊥x轴于点K,图中:点A(1,2)、点B(2,k+2),则AH=﹣k,HB=1,设:HM=m=MN,则BM=1﹣m,则AN=AH=﹣k,AB,NB=AB﹣AN,由勾股定理得:MB2=NB2+MN2,即:(1﹣m)2=m2+(k)2,解得:m=﹣k2﹣k,在△AHM中,tanαk tan∠BEC k+2,解得:k,此时k+2>0,则﹣2<k<0,故:舍去正值,故k;②当点B在x轴下方时,同理可得:tanαk tan∠BEC(k+2),解得:k或,此时k+2<0,k<﹣2,故舍去,故k的值为:或.点睛:本题为二次函数综合应用题,涉及到一次函数、解直角三角形的知识,其中(3),通过tan2α求出tanα,是此类题目求解的一般方法.3.(2018年常州28题)如图,二次函数y bx+2的图象与x轴交于点A、B,与y 轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是(,0);(2)设直线PB与直线AC相交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.【分析】(1)由点A的坐标,利用二次函数图象上点的坐标特征可求出b的值,代入y =0求出x值,进而可得出点B的坐标;(2)(解法一)代入x=0求出y值,进而可得出点C的坐标,由点A、C的坐标利用待定系数法可求出直线AC的解析式,假设存在,设点M的坐标为(m,m+2),分B、P 在直线AC的同侧和异侧两种情况考虑,由点B、M的坐标结合PM:MB=1:2即可得出点P的坐标,再利用二次函数图象上点的坐标特征可得出关于m的一元二次方程,解之即可得出结论;(解法二)代入x=0求出y值,进而可得出点C的坐标,由点A、C的坐标利用待定系数法可求出直线AC的解析式,过点B作BB′∥y轴交直线AC于点B′,过点P作PP′∥y轴交直线AC于点P′,由点B的坐标可得出BB′的值,结合相似三角形的性质可得出PP′的值,设点P的坐标为(x,x2x+2),则点P′的坐标为(x,x+2),结合PP′的值可得出关于x的含绝对值符号的一元二次方程,解之即可得出结论;(3)(解法一)作∠CBA的角平分线,交y轴于点E,过点E作EF⊥BC于点F,设OE =n,则CE=2﹣n,EF=n,利用面积法可求出n值,进而可得出,结合∠AOC=90°=∠BOE可证出△AOC∽△BOE,根据相似三角形的性质可得出∠CAO=∠EBO,再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB,此题得解;(解法二)将BC沿y轴对折,交x轴于点B′,根据点A、B、C的坐标可得出点B′的坐标,进而可得出AB′=B′C=BC,根据等腰三角形的性质结合三角形的外角性质,可得出∠CBA=2∠CAB.【解析】(1)∵点A(﹣4,0)在二次函数y bx+2的图象上,∴4b+2=0,∴b.当y=0时,有x2x+2=0,解得:x1=﹣4,x2,∴点B的坐标为(,0).故答案为:;(,0).(2)(方法一)当x=0时,y x2x+2=2,∴点C的坐标为(0,2).设直线AC的解析式为y=kx+c(k≠0),将A(﹣4,0)、C(0,2)代入y=kx+c中,得:,解得:,∴直线AC的解析式为y x+2.假设存在,设点M的坐标为(m,m+2).①当点P、B在直线AC的异侧时,点P的坐标为(m,m+3),∵点P在抛物线y x2x+2上,∴m+3(m)2(m)+2,整理,得:12m2+20m+9=0.∵△=202﹣4×12×9=﹣32<0,∴方程无解,即不存在符合题意得点P;②当点P、B在直线AC的同侧时,点P的坐标为(m,m+1),∵点P在抛物线y x2x+2上,∴m+1(m)2(m)+2,整理,得:4m2+44m﹣9=0,解得:m1,m2,∴点P的横坐标为﹣2或﹣2.综上所述:存在点P,使得PM:MB=1:2,点P的横坐标为﹣2或﹣2.(方法二)当x=0时,y x2x+2=2,∴点C的坐标为(0,2).设直线AC的解析式为y=kx+c(k≠0),将A(﹣4,0)、C(0,2)代入y=kx+c中,得:,解得:,∴直线AC的解析式为y x+2.过点B作BB′∥y轴交直线AC于点B′,过点P作PP′∥y轴交直线AC于点P′,如图1﹣1所示.∵点B的坐标为(,0),∴点B′的坐标为(,),∴BB′.∵BB′∥PP′,∴△PP′M∽△BB′M,∴,∴PP′.设点P的坐标为(x,x2x+2),则点P′的坐标为(x,x+2),∴PP′=|x2x+2﹣(x+2)|=|x2x|,解得:x1=﹣2,x2=﹣2,∴存在点P,使得PM:MB=1:2,点P的横坐标为﹣2或﹣2.(3)(解法一)∠CBA=2∠CAB,理由如下:作∠CBA的角平分线,交y轴于点E,过点E作EF⊥BC于点F,如图2所示.∵点B(,0),点C(0,2),∴OB,OC=2,BC.设OE=n,则CE=2﹣n,EF=n,由面积法,可知:OB•CE BC•EF,即(2﹣n)n,解得:n.∵,∠AOC=90°=∠BOE,∴△AOC∽△BOE,∴∠CAO=∠EBO,∴∠CBA=2∠EBO=2∠CAB.(解法二)∠CBA=2∠CAB,理由如下:将BC沿y轴对折,交x轴于点B′,如图3所示.∵点B(,0),点C(0,2),点A(﹣4,0),∴点B′(,0),∴AB′(﹣4),B′C,∴AB′=B′C=BC,∴∠CAB=∠ACB′,∠CBA=∠CB′B.∵∠AB′B=∠CAB+∠ACB′,∴∠CBA=2∠CAB.点睛:题考查了二次函数图象上点的坐标特征、待定系数法求一次函数解析式、三角形的面积、勾股定理、一次函数图象上点的坐标特征以及相似三角形的判定与性质,解题的关键是:(1)由点A的坐标,利用二次函数图象上点的坐标特征求出b的值;(2)(解法一)分B、P在直线AC的同侧和异侧两种情况找出点P的坐标;(解法二)利用相似三角形的性质找出PP′;(3)(解法一)构造相似三角形找出两角的数量关系;(解法二)根据等腰三角形的性质结合三角形的外角性质找出∠CBA=2∠CAB.4.(2019年苏州28题)如图①,抛物线y=﹣x2+(a+1)x﹣a与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积是6.(1)求a的值;(2)求△ABC外接圆圆心的坐标;(3)如图②,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,且∠P AQ=∠AQB,求点Q的坐标.【分析】(1)由y=﹣x2+(a+1)x﹣a,令y=0,即﹣x2+(a+1)x﹣a=0,可求出A、B 坐标结合三角形的面积,解出a=﹣3;(2)三角形外接圆圆心是三边垂直平分线的交点,求出两边垂直平分线,解交点可求出;(3)作PM⊥x轴,则S△BAP AB•PM4d由S△PQB=S△P AB可得A、Q到PB的距离相等,得到AQ∥PB,求出直线PB的解析式,以抛物线解析式联立得出点P坐标,由于△PBQ≌△ABP,可得PQ=AB=4,利用两点间距离公式,解出m值.【解析】(1)∵y=﹣x2+(a+1)x﹣a令y=0,即﹣x2+(a+1)x﹣a=0解得x1=a,x2=1由图象知:a<0∴A(a,0),B(1,0)∵S△ABC=6∴解得:a=﹣3,(a=4舍去)(2)∵A(﹣3,0),C(0,3),∴OA=OC,∴线段AC的垂直平分线过原点,∴线段AC的垂直平分线解析式为:y=﹣x,∵由A(﹣3,0),B(1,0),∴线段AB的垂直平分线为x=﹣1将x=﹣1代入y=﹣x,解得:y=1∴△ABC外接圆圆心的坐标(﹣1,1)(3)作PM⊥x轴交x轴于M,则S△BAP AB•PM4d∵S△PQB=S△P AB∴A、Q到PB的距离相等,∴AQ∥PB设直线PB解析式为:y=x+b∵直线经过点B(1,0)所以:直线PB的解析式为y=x﹣1联立解得:∴点P坐标为(﹣4,﹣5)又∵∠P AQ=∠AQB,∴∠BP A=∠PBQ,∴AP=QB,在△PBQ与△BP A中,,∴△PBQ≌△ABP(SAS),∴PQ=AB=4设Q(m,m+3)由PQ=4得:解得:m=﹣4,m=﹣8(当m=﹣8时,∠P AQ≠∠AQB,故应舍去)∴Q坐标为(﹣4,﹣1)点睛:本题考查二次函数的综合应用,函数和几何图形的综合题目,抛物线和直线“曲直”联立解交点,利用三角形的全等和二次函数的性质把数与形有机的结合在一起,转化线段长求出结果.5.(2018年无锡28题)已知:如图,一次函数y=kx﹣1的图象经过点A(3,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.(1)求这个一次函数的表达式;(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(,0),求这条抛物线的函数表达式.【分析】(1)利用三角形相似和勾股定理构造方程,求AC和m(2)由∠APQ=90°,构造△PQD∽△APE构造方程求点P坐标可求二次函数解析式.【解析】(1)过点A作AF⊥x轴,过点B作BF⊥CD于H,交AF于点F,过点C作CE ⊥AF于点E设AC=n,则CD=n∵点B坐标为(0,﹣1)∴CH=n+1,AF=m+1∵CH∥AF,BC=2AC∴即:整理得:nRt△AEC中,CE2+AE2=AC2∴5+(m﹣n)2=n2把n代入5+(m)2=()2解得m1=5,m2=﹣3(舍去)∴n=3∴把A(3,5)代入y=kx﹣1得k∴y x﹣1(2)如图,过点A作AE⊥CD于点E设点P坐标为(2,n),由已知n>0由已知,PD⊥x轴∴△PQD∽△APE∴∴解得n1=7,n2=﹣2(舍去)设抛物线解析式为y=a(x﹣h)2+k∴y=a(x﹣2)2+7把A(3,5)代入y=a(x﹣2)2+7解得a∴抛物线解析式为:y【点评】本题综合考查二次函数和一次函数性质.在解答过程中,应注意利用三角形相似和勾股定理构造方程,求出未知量.2.(2017年苏州28题)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1)求b、c的值;(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.【分析】(1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线解析式可求得c的值;(2)可设F(0,m),则可表示出F′的坐标,由B、E的坐标可求得直线BE的解析式,把F′坐标代入直线BE解析式可得到关于m的方程,可求得F点的坐标;(3)设点P坐标为(n,0),可表示出P A、PB、PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q、R、N的坐标,在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标,【解析】(1)∵CD∥x轴,CD=2,∴抛物线对称轴为x=1.∴.∵OB=OC,C(0,c),∴B点的坐标为(﹣c,0),∴0=c2+2c+c,解得c=﹣3或c=0(舍去),∴c=﹣3;(2)设点F的坐标为(0,m).∵对称轴为直线x=1,∴点F关于直线l的对称点F的坐标为(2,m).由(1)可知抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,∴E(1,﹣4),∵直线BE经过点B(3,0),E(1,﹣4),∴利用待定系数法可得直线BE的表达式为y=2x﹣6.∵点F在BE上,∴m=2×2﹣6=﹣2,即点F的坐标为(0,﹣2);(3)存在点Q满足题意.设点P坐标为(n,0),则P A=n+1,PB=PM=3﹣n,PN=﹣n2+2n+3.作QR⊥PN,垂足为R,∵S△PQN=S△APM,∴,∴QR=1.①点Q在直线PN的左侧时,Q点的坐标为(n﹣1,n2﹣4n),R点的坐标为(n,n2﹣4n),N点的坐标为(n,n2﹣2n﹣3).∴在Rt△QRN中,NQ2=1+(2n﹣3)2,∴时,NQ取最小值1.此时Q点的坐标为;②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2﹣4).同理,NQ2=1+(2n﹣1)2,∴时,NQ取最小值1.此时Q点的坐标为.综上可知存在满足题意的点Q,其坐标为或.【点评】本题为二次函数的综合应用,涉及待定系数法、轴对称、三角形的面积、勾股定理、二次函数的性质、方程思想及分类讨论思想等知识.在(1)中求得抛物线的对称轴是解题的关键,在(2)中用F点的坐标表示出F′的坐标是解题的关键,在(3)中求得QR的长,用勾股定理得到关于n的二次函数是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,难度很大.【专项突破】【题组一】1.(2020•无锡模拟)如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象交x轴于A、B两点,交y轴于点C.过点A的直线y=kx+2k(k≠0)与这个二次函数的图象的另一个交点为F,与该图象的对称轴交于点E,与y轴交于点D,且DE=EF.(1)求点A的坐标;(2)若△BDF的面积为12,求这个二次函数的关系式;(3)设二次函数的顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此时二次函数的表达式.。
2019-2020年九年级下学期中考数学压轴题汇总

2019-2020年九年级下学期中考数学压轴题汇总如图1,在平面直角坐标系xOy 中,顶点为M 的抛物线y =ax 2+bx (a >0)经过点A 和x 轴正半轴上的点B ,AO =BO =2,∠AOB =120°.(1)求这条抛物线的表达式;(2)连结OM ,求∠AOM 的大小;(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标.例2 2012年苏州市中考第29题如图1,已知抛物线211(1)444b y x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示);(2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.例3 2012年黄冈市中考模拟第25题如图1,已知抛物线的方程C 1:1(2)()y x x m m=-+- (m >0)与x 轴交于点B 、C ,与y 轴交于点E ,且点B 在点C 的左侧.(1)若抛物线C 1过点M (2, 2),求实数m 的值;(2)在(1)的条件下,求△BCE 的面积;(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使得BH +EH 最小,求出点H的坐标;(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.图1例4 2010年义乌市中考第24题如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q 两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2例5 2009年临沂市中考第26题如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1例6 2008年苏州市中考第29题图1因动点产生的梯形问题例1 2012年上海市松江区中考模拟第24题已知直线y=3x-3分别与x轴、y轴交于点A,B,抛物线y=ax2+2x+c经过点A,B.(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,点B 关于直线l 的对称点为C ,若点D 在y 轴的正半轴上,且四边形ABCD 为梯形.①求点D 的坐标;②将此抛物线向右平移,平移后抛物线的顶点为P ,其对称轴与直线y =3x -3交于点E ,若73t a n =∠D P E ,求四边形BDEP 的面积.图1例2 2012年衢州市中考第24题如图1,把两个全等的Rt △AOB 和Rt △COD 方别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点A (1,2),过A 、C 两点的直线分别交x 轴、y 轴于点E 、F .抛物线y=ax 2+bx +c 经过O 、A 、C 三点.(1)求该抛物线的函数解析式;(2)点P 为线段OC 上的一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 为等腰梯形?若存在,求出此时点P 的坐标;若不存在,请说明理由;(3)若△AOB 沿AC 方向平移(点A 始终在线段AC 上,且不与点C 重合),△AOB 在平移的过程中与△COD 重叠部分的面积记为S .试探究S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.图1例 3 2011年义乌市中考第24题已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图2例4 2010年杭州市中考第24题如图1,在平面直角坐标系xOy 中,抛物线的解析式是y =2114x +,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上.(1) 写出点M 的坐标;(2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时.① 求t 关于x 的函数解析式和自变量x 的取值范围;② 当梯形CMQP 的两底的长度之比为1∶2时,求t 的值.图1例5 2009年广州市中考第25题如图1,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45. (1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使以A 、B 、C 、D 为顶点的四边形为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.图1因动点产生的直角三角形问题例1 2013年山西省中考第26题如图1,抛物线213442y x x =--与x 轴交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C ,连结BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m , 0),过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A 、B 、C 的坐标;(2)当点P 在线段OB 上运动时,直线l 分别交BD 、BC 于点M 、N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.图1例2 2012年广州市中考第24题如图1,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求点A 、B 的坐标;(2)设D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求点D 的坐标;(3)若直线l 过点E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有....三个时,求直线l 的解析式.图1例3 2012年杭州市中考第22题在平面直角坐标系中,反比例函数与二次函数y =k (x 2+x -1)的图象交于点A (1,k )和点B(-1,-k ).(1)当k =-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y 随x 增大而增大,求k 应满足的条件以及x 的取值范围;(3)设二次函数的图象的顶点为Q ,当△ABQ 是以AB 为斜边的直角三角形时,求k 的值. 例4 2011年浙江省中考第23题设直线l 1:y =k 1x +b 1与l 2:y =k 2x +b 2,若l 1⊥l 2,垂足为H ,则称直线l 1与l 2是点H的直角线.(1)已知直线①122y x =-+;②2y x =+;③22y x =+;④24y x =+和点C (0,2),则直线_______和_______是点C 的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC 的顶点A (3,0)、B (2,7)、C (0,7),P 为线段OC 上一点,设过B 、P 两点的直线为l 1,过A 、P 两点的直线为l 2,若l 1与l 2是点P 的直角线,求直线l 1与l 2的解析式.图1例5 2010年北京市中考第24题在平面直角坐标系xOy 中,抛物线22153244m m y x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从点O 出发向点A 运动,过点P 作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当点P 运动时,点C 、D 也随之运动).①当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;②若点P 从点O 出发向点A 作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从点A 出发向点O 作匀速运动,速度为每秒2个单位(当点Q 到达点O 时停止运动,点P 也停止运动).过Q 作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当点Q 运动时,点M 、N 也随之运动).若点P 运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t的值.图1例6 2009年嘉兴市中考第24题如图1,已知A 、B 是线段MN 上的两点,4=MN ,1=MA ,1>MB .以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设x AB =.(1)求x 的取值范围;(2)若△ABC 为直角三角形,求x 的值;(3)探究:△ABC 的最大面积?图1例 7 2008年河南省中考第23题如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例8 2008年河南省中考第23题如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1因动点产生的相切问题例 1 2013年上海市杨浦区中考模拟第25题如图1,已知⊙O的半径长为3,点A是⊙O上一定点,点P为⊙O上不同于点A的动点.(1)当1A=时,求AP的长;tan2(2)如果⊙Q过点P、O,且点Q在直线AP上(如图2),设AP=x,QP=y,求y关于x的函数关系式,并写出函数的定义域;(3)在(2)的条件下,当4A=时(如图3),存在⊙M与⊙O相内切,同时与⊙Qtan3相外切,且OM⊥OQ,试求⊙M的半径的长.图1 图2 图3例2 2012年河北省中考第25题如图1,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD//AB,∠CDA =90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1)求点C的坐标;(2)当∠BCP=15°时,求t的值;(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.例3 2012年无锡市中考模拟第28题如图1,菱形ABCD的边长为2厘米,∠DAB=60°.点P从AAC向C作匀速运动;与此同时,点Q也从点A出发,以每秒1厘米的速度沿射线作匀速运动.当点P到达点C时,P、Q都停止运动.设点P运动的时间为t秒.(1)当P异于A、C时,请说明PQ//BC;(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?图一因动点产生的等腰三角形问题例1 2013年上海市虹口区中考模拟第25题如图1,在Rt △ABC 中,∠A =90°,AB =6,AC =8,点D 为边BC 的中点,DE ⊥BC 交边AC 于点E ,点P 为射线AB 上的一动点,点Q 为边AC 上的一动点,且∠PDQ =90°.(1)求ED 、EC 的长;(2)若BP =2,求CQ 的长;(3)记线段PQ 与线段DE 的交点为F ,若△PDF 为等腰三角形,求BP 的长.图1 备用图(1)求点B 的坐标;(2)求经过A 、O 、B 的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P ,使得以点P 、O 、B 为顶点的三角形是等腰三角形?若存在,求点P 的坐标;若不存在,请说明理由.图1例4 2011年盐城市中考第28题如图1,已知一次函数y =-x +7与正比例函数43y x的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l //y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.图1例5 2010年南通市中考第27题如图1,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.(1)求y关于x的函数关系式;(2)若m=8,求x为何值时,y的值最大,最大值是多少?(3)若12ym,要使△DEF为等腰三角形,m的值应为多少?图1例 6 2009年江西省中考第25题如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°.(1)求点E到BC的距离;(2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP=x.①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN 的周长;若改变,请说明理由;②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.图1 图2 图3几何证明及通过几何计算进行说理问题例1 2013年上海市黄浦区中考模拟第24题已知二次函数y=-x2+bx+c的图像经过点P(0, 1)与Q(2, -3).(1)求此二次函数的解析式;(2)若点A是第一象限内该二次函数图像上一点,过点A作x轴的平行线交二次函数图像于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,且所得四边形ABCD恰为正方形.①求正方形的ABCD的面积;②联结PA、PD,PD交AB于点E,求证:△PAD∽△PEA.例2 2013年江西省中考第24题某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:(1)操作发现:在等腰△ABC中,AB=AC,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连结MD和ME,则下列结论正确的是__________(填序号即可).①AF=AG=12AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME.(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连结MD和ME,试判断△MDE的形状.答:_________.图1代数计算及通过代数计算进行说理问题例1 2013年南京市中考第26题已知二次函数y=a(x-m)2-a(x-m)(a、m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图像与x轴总有两个公共点;(2)设该函数的图像的顶点为C,与x轴相交于A、B两点,与y轴交于点D.①当△ABC的面积等于1时,求a的值②当△ABC的面积与△ABD的面积相等时,求m的值.例2 2013年南昌市中考第25题已知抛物线y n=-(x-a n)2+a n(n为正整数,且0<a1<a2<…<a n)与x轴的交点为A n-1(b n-1,0)和A n(b n,0).当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推(1)求a、b的值及抛物线y2的解析式;(2)抛物线y3的顶点坐标为(_____,_____);依此类推第n条抛物线y n的顶点坐标为(_____,_____)(用含n的式子表示);所有抛物线的顶点坐标满足的函数关系式是________________;(3)探究下列结论:①若用A n-1 A n表示第n条抛物线被x轴截得的线段的长,直接写出A0A1的值,并求出A n-1 A n;②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得的线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.备用图(仅供草稿使用)因动点产生的平行四边形问题例1 2013年上海市松江区中考模拟第24题如图1,已知抛物线y=-x2+bx+c经过A(0, 1)、B(4, 3)两点.(1)求抛物线的解析式;(2)求tan∠ABO的值;(3)过点B作BC⊥x轴,垂足为C,在对称轴的左侧且平行于y轴的直线交线段AB于点N,交抛物线于点M,若四边形MNCB为平行四边形,求点M的坐标.图1例2 2012年福州市中考第21题如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C 以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD//BC,交AB于点D,联结PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=_______,PD=_______;(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ的中点M所经过的路径长.图1 图2例3 2012年烟台市中考第26题如图1,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动,同时动点Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)过点E 作EF ⊥AD 于F ,交抛物线于点G ,当t 为何值时,△ACG 的面积最大?最大值为多少?(3)在动点P 、Q 运动的过程中,当t 为何值时,在矩形ABCD 内(包括边界)存在点H ,使以C 、Q 、E 、H 为顶点的四边形为菱形?请直接写出t 的值.图1例4 2011年上海市中考第24题已知平面直角坐标系xOy (如图1),一次函数334y x =+的图象与y 轴交于点A ,点M 在正比例函数32y x =的图象上,且MO =MA .二次函数 y =x 2+bx +c 的图象经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图象上,点D 在一次函数334y x =+的图象上,且四边形ABCD 是菱形,求点C 的坐标.图1例5 2011年江西省中考第24题将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图1所示.(1)请直接写出抛物线c 2的表达式;(2)现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .①当B 、D 是线段AE 的三等分点时,求m 的值;②在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.图1例6 2010年山西省中考第26题在直角梯形OABC 中,CB //OA ,∠COA =90°,CB =3,OA =6,BA =.分别以OA 、OC 边所在直线为x 轴、y 轴建立如图1所示的平面直角坐标系.(1)求点B 的坐标;(2)已知D 、E 分别为线段OC 、OB 上的点,OD =5,OE =2EB ,直线DE 交x 轴于点F .求直线DE 的解析式;(3)点M 是(2)中直线DE 上的一个动点,在x 轴上方的平面内是否存在另一点N ,使以O 、D 、M 、N 为顶点的四边形是菱形?若存在,请求出点N 的坐标;若不存在,请说明理由.图1 图2 例7 2009年江西省中考第24题如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系.图1因动点产生的线段和差问题例1 2013年天津市中考第25题在平面直角坐标系中,已知点A(-2,0),B(0,4),点E在OB上,且∠OAE=∠OBA.(1)如图1,求点E的坐标;(2)如图2,将△AEO沿x轴向右平移得到△AE′O′,连结A′B、BE′.①设AA′=m,其中0<m<2,使用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).图1 图2例2 2012年滨州市中考第24题如图1,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2, -4 )、O(0, 0)、B(2, 0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.图1例3 2012年山西省中考第26题如图1,在平面直角坐标系中,抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,与y 轴交于点C ,点D 是抛物线的顶点.(1)求直线AC 的解析式及B 、D 两点的坐标;(2)点P 是x 轴上的一个动点,过P 作直线l //AC 交抛物线于点Q .试探究:随着点P 的运动,在抛物线上是否存在点Q ,使以A 、P 、Q 、C 为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q 的坐标;若不存在,请说明理由;(3)请在直线AC 上找一点M ,使△BDM 的周长最小,求出点M 的坐标.因动点产生的面积问题例1 2013年苏州市中考第29题如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S .①求S 的取值范围;②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.图1图1例 2 2012年菏泽市中考第21题如图1,在平面直角坐标系中放置一直角三角板,其顶点为A (0, 1)、B (2, 0)、O (0, 0),将此三角板绕原点O 逆时针旋转90°,得到三角形A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是第一象限内抛物线上的一个动点,是否存在点P ,使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,试指出四边形PB ′A ′B 是哪种形状的四边形?并写出它的两条性质.图1例 3 2012年河南省中考第23题如图1,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值;(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图1例 4 2011年南通市中考第28题如图1,直线l 经过点A (1,0),且与双曲线m y x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和m y x=-(x <0)于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.例5 2010年广州市中考第25题如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1).点D 是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x b =-+交折线OAB 于点E . (1)记△ODE 的面积为S ,求S 与b 的函数关系式;(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图1图1例 6 2010年扬州市中考第28题如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB 上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图例7 2009年兰州市中考第29题如图1,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ 能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.图1 图2 由比例线段产生的函数关系问题例1 2013年宁波市中考第26题如图1,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(0,4),点B 的坐标为(4,0),点C 的坐标为(-4,0),点P 在射线AB 上运动,连结CP 与y 轴交于点D ,连结BD .过P 、D 、B 三点作⊙Q ,与y 轴的另一个交点为E ,延长DQ交⊙Q 于F ,连结EF 、BF .(1)求直线AB 的函数解析式;(2)当点P 在线段AB (不包括A 、B 两点)上时.①求证:∠BDE =∠ADP ;②设DE =x ,DF =y ,请求出y 关于x 的函数解析式;(3)请你探究:点P 在运动过程中,是否存在以B 、D 、F 为顶点的直角三角形,满足两条直角边之比为2∶1?如果存在,求出此时点P 的坐标;如果不存在,请说明理由. 图1例2 2012年上海市徐汇区中考模拟第25题在Rt △ABC 中,∠C =90°,AC =6,53sin B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O 是边AB 上的动点.(1)如图1,将⊙B 绕点P 旋转180°得到⊙M ,请判断⊙M 与直线AB 的位置关系;(2)如图2,在(1)的条件下,当△OMP 是等腰三角形时,求OA 的长;(3)如图3,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设NB =y ,OA =x ,求y 关于x 的函数关系式及定义域.。
2019-2020年中考数学压轴题精选(十)与答案 数学中考试题

2019-2020年中考数学压轴题精选(十)与答案 数学中考试题91.(08新疆自治区24题)(10分)某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m ,抛物线拱高为5.6m . (1)在如图所示的平面直角坐标系中,求抛物线的表达式.(2)现需在抛物线AOB 的区域内安装几扇窗户,窗户的底边在AB 上,每扇窗户宽1.5m ,高1.6m ,相邻窗户之间的间距均为0.8m ,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m .请计算最多可安装几扇这样的窗户?(08新疆自治区24题解析)24.(10分)解:(1)设抛物线的表达式为2y ax = 1分点(6 5.6)B -,在抛物线的图象上. ∴ 5.636a -=745a =-····················································· 3分 ∴抛物线的表达式为2745y x =- ·································································· 4分 (2)设窗户上边所在直线交抛物线于C 、D 两点,D 点坐标为(k ,t )已知窗户高1.6m ,∴ 5.6( 1.6)4t =---=- ·················································· 5分27445k --=125.07 5.07k k -≈,≈(舍去) ································································· 6分∴ 5.07210.14CD =⨯≈(m ) ··································································· 7分 又设最多可安装n 扇窗户∴1.50.8(1)10.14n n ++≤ ········································································· 9分4.06n ≤.答:最多可安装4扇窗户. ········································································ 10分 (本题不要求学生画出4个表示窗户的小矩形)图10答案图1 92.(08四川资阳24题)24.(本小题满分12分) 如图10,已知点A 的坐标是(-1,0),点B 的坐标是(9,0),以AB 为直径作⊙O′,交y 轴的负半轴于点C ,连接AC 、BC ,过A 、B 、C 三点作抛物线.(1)求抛物线的解析式;(2)点E 是AC 延长线上一点,∠BCE 的平分线CD 交⊙O′于点D ,连结BD ,求直线BD 的解析式;(3)在(2)的条件下,抛物线上是否存在点P ,使得∠PDB =∠CBD?如果存在,请求出点P 的坐标;如果不存在,请说明理由.(08四川资阳24题解答)(1) ∵以AB 为直径作⊙O′,交y 轴的负半轴于点C ,∴∠OCA+∠OCB=90°, 又∵∠OCB+∠OBC=90°, ∴∠OCA=∠OBC ,又∵∠AOC= ∠COB=90°, ∴ΔAOC ∽ ΔCOB , ··········································································· 1分 ∴OA OC OC OB=. 又∵A(–1,0),B(9,0),∴19OC OC =,解得OC=3(负值舍去). ∴C(0,–3), ····································································································· 3分 设抛物线解析式为y=a(x+1)(x –9),∴–3=a(0+1)(0–9),解得a=13,∴二次函数的解析式为y=13(x+1)(x –9),即y=13x 2–83x –3. ························ 4分(2) ∵AB 为O′的直径,且A(–1,0),B(9,0), ∴OO′=4,O′(4,0), ········································································· 5分 ∵点E 是AC 延长线上一点,∠BCE 的平分线CD 交⊙O′于点D ,∴∠BCD=12∠BCE=12×90°=45°,连结O′D 交BC 于点M ,则∠BO′D =2∠BCD=2×45°=90°,OO′=4,O′D=12AB=5.∴D(4,–5). ··················································································· 6分 ∴设直线BD 的解析式为y=kx+b (k≠0) ∴90,4 5.k b k b +=⎧⎨+=-⎩·················································· 7分解得1,9.k b =⎧⎨=-⎩∴直线BD 的解析式为y=x –9. ······························· 8分 (3) 假设在抛物线上存在点P ,使得∠PDB=∠CBD , 解法一:设射线DP 交⊙O′于点Q ,则BQ CD =. 分两种情况(如答案图1所示):①∵O′(4,0),D(4,–5),B(9,0),C(0,–3).∴把点C 、D 绕点O′逆时针旋转90°,使点D 与点B 重合,则点C 与点Q 1重合,因此,点Q 1(7,–4)符合BQ CD =, ∵D(4,–5),Q 1(7,–4),图10图10答案图2 ∴用待定系数法可求出直线DQ 1解析式为y=13x –193. ····························· 9分解方程组21193318 3.33y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩,得11x y ⎧=⎪⎪⎨⎪=⎪⎩22x y ⎧=⎪⎪⎨⎪=⎪⎩∴点P 1坐标为),[坐标为)不符合题意,舍去]. ····································································································· 10分 ②∵Q 1(7,–4),∴点Q 1关于x 轴对称的点的坐标为Q 2(7,4)也符合BQ CD =. ∵D(4,–5),Q 2(7,4).∴用待定系数法可求出直线DQ 2解析式为y=3x –17. ································ 11分解方程组2317183.33y x y x x =-⎧⎪⎨=--⎪⎩,得1138x y =⎧⎨=-⎩,;221425.x y =⎧⎨=⎩, ∴点P 2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去]. ····································································································· 12分∴符合条件的点P 有两个:P 1,P 2(14,25).解法二:分两种情况(如答案图2所示): ①当DP 1∥CB 时,能使∠PDB=∠CBD . ∵B(9,0),C(0,–3).∴用待定系数法可求出直线BC 解析式为y=13x –3.又∵DP 1∥CB ,∴设直线DP 1的解析式为y=13x+n .把D(4,–5)代入可求n= –193,∴直线DP 1解析式为y=13x –193. ····················· 9分 解方程组21193318 3.33y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩,得11x y ⎧=⎪⎪⎨⎪=⎪⎩22x y ⎧=⎪⎪⎨⎪=⎪⎩ ∴点P 1坐标为),[坐标为)不符合题意,舍去]. ····································································································· 10分②在线段O′B 上取一点N ,使BN=DM 时,得ΔNBD ≌ΔMDB(SAS),∴∠NDB=∠CBD .由①知,直线BC 解析式为y=13x –3.取x=4,得y= –53,∴M(4,–53),∴O′N=O′M=53,∴N(173,0),又∵D(4,–5),∴直线DN 解析式为y=3x –17. ···························································· 11分解方程组2317183.33y x y x x =-⎧⎪⎨=--⎪⎩,得1138x y =⎧⎨=-⎩,;221425.x y =⎧⎨=⎩, ∴点P 2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].图10答案 ····································································································· 12分∴符合条件的点P 有两个:P 1,P 2(14,25).解法三:分两种情况(如答案图3所示): ①求点P 1坐标同解法二. ··································································· 10分 ②过C 点作BD 的平行线,交圆O′于G, 此时,∠GDB=∠GCB=∠CBD . 由(2)题知直线BD 的解析式为y=x –9, 又∵ C (0,–3)∴可求得CG 的解析式为y=x –3, 设G (m,m –3),作GH ⊥x 轴交与x 轴与H ,连结O′G ,在Rt △O′GH 中,利用勾股定理可得,m=7, 由D (4,–5)与G(7,4)可得, DG 的解析式为317y x =-, ································································ 11分 解方程组2317183.33y x y x x =-⎧⎪⎨=--⎪⎩,得1138x y =⎧⎨=-⎩,;221425.x y =⎧⎨=⎩, ∴点P 2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去]. ···················· 12分∴符合条件的点P 有两个:P 1,P 2(14,25).说明:本题解法较多,如有不同的正确解法,请按此步骤给分.93.(08福建南平26题)26.(14分)(1)如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .①如图1,求证:ABE ADC △≌△; ②探究:如图1,BOC ∠= ; 如图2,BOC ∠= ; 如图3,BOC ∠= .(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE CD ,的延长相交于点O .①猜想:如图4,BOC ∠= (用含n 的式子表示); ②根据图4证明你的猜想.(08福建南平26题解答)(1)①证法一:ABD △与ACE △均为等边三角形,AD AB ∴=,AC AE = ··········································································· 2分且60BAD CAE ∠=∠= ········································ 3分BAD BAC CAE BAC ∴∠+∠=∠+∠,即DAC BAE ∠=∠ ················································ 4分ABE ADC ∴△≌△. ··········································· 5分 证法二:ABD △与ACE △均为等边三角形,AD AB ∴=,AC AE = ··········································································· 2分 且60BAD CAE ∠=∠= ··········································································· 3分 ADC ∴△可由ABE △绕着点A 按顺时针方向旋转60得到 ······························ 4分 ABE ADC ∴△≌△. ·············································································· 5分 ②120,90,72. ······························································ 8分(每空1分)(2)①360n·························································································· 10分 ②证法一:依题意,知BAD ∠和CAE ∠都是正n 边形的内角,AB AD =,AE AC =,(2)180n BAD CAEn-∴∠=∠=BAD DAE CAE DAE ∴∠-∠=∠-∠,即BAE DAC ∠=∠. ························· 11分 ABE ADC ∴△≌△. ············································································· 12分 ABE ADC ∴∠=∠,180ADC ODA ∠+∠=,180ABO ODA ∴∠+∠= ······ 13分 360ABO ODA DAB BOC ∠+∠+∠+∠=,180BOC DAB ∴∠+∠= (2)180360180180n BOC DAB n n-∴∠=-∠=-= ··································· 14分证法二:同上可证 A B E A D C △≌△. ···················································· 12分 ABE ADC ∴∠=∠,如图,延长BA 交CO 于F ,180AFD ABE BOC ∠+∠+∠=,180AFD ADC DAF ∠+∠+∠= ···························· 13分 360180BOC DAF BAD n∴∠=∠=-∠=·············· 14分 证法三:同上可证 A B E A D C △≌△. ···················································· 12分 ABE ADC ∴∠=∠.180()BOC ABE ABC ACB ACD ∠=-∠+∠+∠+∠180()BOC ADC ABC ACB ACD ∴∠=-∠+∠+∠+∠180ABC ACB BAC ∠+∠=-∠,180ADC ACD DAC ∠+∠=-∠180(360)BOC BAC DAC ∴∠=--∠-∠ ················································ 13分即360180BOC BAD n∠=-∠=······························································ 14分 证法四:同上可证 A B E A D C △≌△. ···················································· 12分 AEB ACD ∴∠=∠.如图,连接CE ,BEC BOC OCE ∠=∠+∠ AEB AEC BOC ACD ACE ∴∠+∠=∠+∠-∠BOC AEC ACE ∴∠=∠+∠. ······························· 13分 即360180BOC CAEn∠=-∠=··························· 14分 注意:此题还有其它证法,可相应评分.94.(08广东梅州23题)23.本题满分11分.如图11所示,在梯形ABCD 中,已知AB ∥CD , AD ⊥DB ,AD =DC =CB ,AB =4.以AB 所在直线为x 轴,过D 且垂直于AB 的直线为y 轴建立平面直角坐标系.(1)求∠DAB 的度数及A 、D 、C 三点的坐标;(2)求过A 、D 、C 三点的抛物线的解析式及其对称轴L . (3)若P 是抛物线的对称轴L 上的点,那么使∆PDB 为等腰三角形的点P 有几个?(不必求点P 的坐标,只需说明理由)(08广东梅州23题解答)解: (1) DC ∥AB ,AD =DC =CB ,∴ ∠CDB =∠CBD =∠DBA , ···································································· 0.5分 ∠DAB =∠CBA , ∴∠DAB =2∠DBA , ··········· 1分∠DAB +∠DBA =90, ∴∠DAB =60, ········· 1.5分 ∠DBA =30, AB =4, ∴DC =AD =2, ········ 2分 R t ∆AOD ,OA =1,OD =3, ························ 2.5分∴A (-1,0),D (0, 3),C (2, 3). · 4分(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A (-1,0),B (3,0), 故可设所求为 y =a (x +1)( x -3) ····················································· 6分 将点D (0,3)的坐标代入上式得, a =33-.所求抛物线的解析式为 y =).3)(1(33-+-x x ···································· 7分 其对称轴L 为直线x =1. ········································································· 8分 (3) ∆PDB 为等腰三角形,有以下三种情况:①因直线L 与DB 不平行,DB 的垂直平分线与L 仅有一个交点P 1,P 1D =P 1B ,∆P 1DB 为等腰三角形; ······································································ 9分 ②因为以D 为圆心,DB 为半径的圆与直线L 有两个交点P 2、P 3,DB =DP 2,DB =DP 3, ∆P 2DB , ∆P 3DB 为等腰三角形;③与②同理,L 上也有两个点P 4、P 5,使得 BD =BP 4,BD =BP 5. ·················· 10分 由于以上各点互不重合,所以在直线L 上,使∆PDB 为等腰三角形的点P 有5个.95.(08山东聊城25题)25.(本题满分12分)如图,把一张长10cm ,宽8cm 的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).(1)要使长方体盒子的底面积为48cm 2,那么剪去的正方形的边长为多少?(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.(08山东聊城25题解答)(本题满分12分) 解:(1)设正方形的边长为x cm ,则(102)(82)48x x --=. ············································································ 1分 即2980x x -+=.解得18x =(不合题意,舍去),21x =.∴剪去的正方形的边长为1cm . ··································································· 3分(注:通过观察、验证直接写出正确结果给3分) (2)有侧面积最大的情况.设正方形的边长为x cm ,盒子的侧面积为y cm 2, 则y 与x 的函数关系式为:2(102)2(82)y x x x x =-+-.即2836y x x =-+.·················································································· 5分第25题图改写为2981842y x ⎛⎫=--+ ⎪⎝⎭.∴当 2.25x =时,40.5y =最大.即当剪去的正方形的边长为2.25cm 时,长方体盒子的侧面积最大为40.5cm 2. ······ 7分(3)有侧面积最大的情况.设正方形的边长为x cm ,盒子的侧面积为y cm 2.若按图1所示的方法剪折,则y 与x 的函数关系式为:1022(82)22xy x x x -=-+. 即213169666y x ⎛⎫=--+ ⎪⎝⎭.∴当136x =时,1696y =最大. ························· 9分 若按图2所示的方法剪折,则y 与x 的函数关系式为:822(102)22xy x x x -=-+.即2798633y x ⎛⎫=--+ ⎪⎝⎭.∴当73x =时,983y =最大. ······································································ 11分 比较以上两种剪折方法可以看出,按图2所示的方法剪折得到的盒子侧面积最大,即当剪去的正方形的边长为73cm 时,折成的有盖长方体盒子的侧面积最大,最大面积为983cm 2. 说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理,解答正确,均应给出相应分数.96.(08广东佛山25题)25.我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)...........几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究................................. 例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).请你用上面的思想和方法对下面关于圆的问题进行研究:(1) 如图1,在圆O 所在平面上,放置一条..直线m (m 和圆O 分别交于点A 、B ),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?(2) 如图2,在圆O 所在平面上,请你放置与圆O 都相交且不同时经过圆心.......的两条..直线m 和n (m 与圆O 分别交于点A 、B ,n 与圆O 分别交于点C 、D ). 请你根据所构造的图形提出一个结论,并证明之.图1第25题图图2。
2019年中考数学压轴题100题精选(1-15题)

2019年中考数学压轴题100题精选【001】如图,已知抛物线2(1)y a x=-+a≠0)经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB=,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t()s,连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【002】如图16,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).Array(1)当t = 2时,AP = ,点Q到AC的距离是;(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4)当DE经过点C 时,请直接..写出t的值.图16【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。
2019-2020年中考数学压轴题专项训练有答案

训练目标
1. 熟悉题型结构,辨识题目类型,调用解题方法; 2. 书写框架明晰,踩点得分(完整、快速、简洁) 。
题型结构及解题方法
压轴题综合性强,知识高度融合,侧重考查学生对知识的综合运用能力,对问题背景的研究能力 以及对数学模型和套路的调用整合能力。
R
( 2)求 S与 t 的函数关系式,并写出 t 的取值范围.
Q
Q'
( 3) S 能否为 9 ?若能,求出此时 t 的值;
8
C
P
A
C
A
若不能,请说明理由.
4. 如图,在△ ABC中,∠ A=90 °,AB=2cm, AC=4cm,动点 P 从点 A 出发,沿 AB 方向以 1cm/s 的速度向 点 B 运动,动点 Q 从点 B 同时出发,沿 BA 方向以 1cm/s 的速度向点 A 运动.当点 P 到达点 B 时, P,
考查要点 常考类型举例
问题 背景 研究
求坐标或函数 解析式,求角 度或线段长
题型特征
已知点坐标、解析式或几何 图形的部分信息
速度已知,所求关系式和运
求面积、周长 动时间相关
的函 数关 系
模 型 套 路 式,并求最值 坐标系下,所求关系式和坐
调用
标相关
求线段和 (差) 有定点(线)、不变量或不
的最值
变关系
一、图形运动产生的面积问题
一、 知识点睛
1. 研究 _基本 _图形
2. 分析运动状态:
①由 起点、终点 确定 t的范围; ②对 t分段,根据运动趋势画图,找 边与定点 ,通常是 状态转折点 相交时的特殊位置. 3. 分段 画图 ,选择适当方法表达面积.
2019-2020年中考数学压轴题训练

1、(12分)如图,在平面直角坐标系xOy中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点.抛物线y=ax2+bx + c与y轴交于点D,与直线y=x交于点M、N ,且MA、NC分别与圆。
相切于点A和点C.(1)求抛物线的解析式;(2)抛物线的对称轴交x轴于点E ,连结DE,并延长DE交圆O于F ,求EF的长.(3)过点B作圆。
的切线交DC的延长线于点P,在抛物线上找一点Q,使^ BDQ的面积与△ BDP的面积相等,求点Q的坐标.2、如图,已知抛物线y = a(x-1)2+3j3(a #0)经过点A(—2, 0),抛物线的顶点为D ,过O作射线OM // AD .过顶点D平行于x轴的直线交射线OM于点C , B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点。
出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s) .问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC =OB,动点P和动点Q分别从点。
和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t (s),连接PQ ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.x当n=7P 为AB 边中点。
若存在,请求出 m 的值;若不存 a = 土3.如图1,在平面直角坐标系中,抛物线 y=ax^c 与X 轴正半轴交于点 F (16 , 0)、与y 轴 正半轴交于点E (0 , 16),边长为16的正方形ABCD 勺顶点D 与原点O 重合,顶点 A 与点E 重 合,顶点C 与点F 重合;求抛物线的函数表达式;如图2,若正方形 ABC 诳平面内运动,并且边 BC 所在的直线始终与 x 轴垂直,抛线始终与边 AB 交于点P 且同时与边CD^于点Q 运动时,点P 不与A B 两点重合,点Q 不与C D 两点重合)。
2019-2020年中考数学试题分类解析汇编专题20:压轴题

线 l 的距离(即 CD的长)为【
】
A. 4 km B . 2 2 km C . 2 2 km D . 4 2 km
【答案】 B. 【考点】 解直角三角形的应用(方向角问题);矩形的判定和性质;等腰直角三角形的判定 和性质 . 【分析】 如答图,过点 B 作 BE⊥AC交 AC于点 E,过点 E 作 EF⊥ CD交 CD于点 F,
2 故选 B.
10. ( 2015 年江苏淮安 3 分)如图, l 1∥ l 2∥l 3 ,直线 a、b 与 l 1、l 2、l 3 分别相交于点 A、B、
C和点 D、 E、 F,若 AB 2 , DE=4,则 EF的长是【
】
BC 3
A. 8
B.
3
【答案】 C.
20 C. 3
6 D. 10
【考点】 平行线分线段成比例的性质 .
】
A. 2.5 B. 2.8 C. 3 D. 3.2
【答案】 B.
【考点】 圆周角定理;勾股定理;相似三角形的判定和性质
.
【分析】 如答图,连接 BD、 CD,
∵AB为⊙ O的直径,∴∠ ADB=90° .
∴ BD
AB 2 AD 2
62 52
11 .
∵弦 AD平分∠ BAC,∴ CD=BD= 11 . ∴∠ CBD=∠DAB. 在△ ABD和△ BED中,∵∠ BAD=∠ EBD,∠ ADB=∠BDE,
∴△ ABD∽△ BED. ∴ DE
DB
DE
,即
11
11
DE .
DB AD
11 5
5
∴ AE
AB
DE
11 5
2.8 .
5
故选 B.
12. ( 2015 年江苏宿迁 3 分) 在平面直角坐标系中, 点 A,B的坐标分别为 (﹣ 3,0),( 3,
2019-2020年中考数学二次函数压轴题人教新课标版.docx

2019-2020 年中考数学 二次函数压轴题人教新课标版(26) ( 本小题 10 分 )已知二次函数 y = ax 2+bx + c .(Ⅰ)若 a = 2, c =- 3,且二次函数的图象经过点(- 1,- 2),求 b 的值(Ⅱ)若 a = 2, b +c =- 2, b > c ,且二次函数的图象经过点(p ,- 2),求证: b ≥ 0;(Ⅲ)若 a + b +c = 0, a >b > c ,且二次函数的图象经过点( q ,- a ),试问自变量 x = q + 4 时,二次函数y= ax 2+ bx + c 所对应的函数值 y 是否大于 0?并证明你的结论。
26. 本小题满分 10 分 ( 1)当 a2 , c3 时,二次函数为y2x 2bx3∵ 该函数的图象经过点 ( 1 , 2)∴2 2 ( 1) 2 b ( 1) 3解得 b 1 2分( 2)当 a2 , b c2 时,二次函数为y2x 2 bxb 2∵ 该函数的图象经过点 ( p ,2)∴2 2p2bp b 2 ,即 2 p 2bp b 0于是, p 为方程 2x 2 bx b0 的根∴ 判别式 b 28b b(b 8)又 ∵ b c2 , b c∴ b b 2 ,即 b 1 ,有 b 8 0∴b 05 分( 3)∵ 二次函数yax2bxc的图象经过点(q ,a)∴ aq2bq c a 0∴ q为方程 ax 2bx c a 0 的根 于是,判别式b 2 4a(a c) 0又 ∵ a b c 0∴b 2 4ab b(b 4a)b(3a c) 0又 a b c 0 ,且 a b c ,知 a 0 , c 0∴ 3a c 0∴ b0 ∵ q 为方程 ax 2bx ca0 的根qbb 2 4ab qbb 2 4ab2a2a∴或当xq 4时y a(q 4) 2b( q 4) caq 2 8aq 16abq 4b c(aq 2 bqc a) 8aq 15a 4b8aq 15a 4bqbb 2 4ab2a若y8abb 2 4ab 15a 4b 15a4 b 2 4ab则2a∵ ab 0∴ b 24aba 2 4a a 5a 2 ,b 2 4ab 5a4 b24ab4 5a∴y15a4 5a (15 4 5 )aqbb 2 4ab2a若y8a bb 24ab15a 4b 15a4 24ab 02a b 则∴当x q 4时,二次函数y ax2bx c所对应的函数值y大于0 10分2006 年天津市初中毕业生学业考试数学试卷(26) (本小题10分)已知抛物线y= ax 2+ bx+ c 的定点坐标为(2,4).(Ⅰ)试用含 a 的代数式分别表示b, c;(Ⅱ)若直线y= kx + 4( k≠ 0)与 y 轴及该抛物线的交点依次为D、E、F,且SODE=1,其中 O为坐标原点,SOEF3试用含 a 的代数式表示k;(Ⅲ)在(Ⅱ)的条件下,若线段EF 的长 m满足3 2 m 3 5 ,试确定a的取值范围。
2020年江苏中考数学压轴题精选精练5(解析版)

2020年中考数学压轴题精选精练5一、选择题1.若0<m<2,则关于x的一元二次方程﹣(x+m)(x+3m)=3mx+37根的情况是()A.无实数根B.有两个正根C.有两个根,且都大于﹣3mD.有两个根,其中一根大于﹣m2.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP =QO,则的值为()A.B.C.D.3.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为()A.12 B.14 C.24 D.214.如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是()A.4πB.5πC.6πD.8π5.如图,△ABC和△DCE都是边长为8的等边三角形,点B,C,E在同一条直线上接BD,AE,则四边形FGCH的面积为()A.B.C.D.6.如图,△ABC内接于⊙O,∠A=60°,BC=4,当点P在上由B点运动到C点时,弦AP的中点E运动的路径长为()A.πB.πC.πD.2二、填空题1.如图,四边形ABCD中,已知AB=AD,∠BAD=60°,∠BCD=120°,若四边形ABCD 的面积为4,则AC=.第1题第2题2.如图,AB为⊙O的直径,AB=4,C为半圆AB的中点,P为上一动点,延长BP至点Q,使BP•BQ=AB2.若点P由A运动到C,则点Q运动的路径长为.3.如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN 长度的最小值是.第3题第4题4.如图,AB为⊙O的直径,点C、D分别是半圆AB的三等分点,AB=4,点P自A点出发,沿弧ABC向C点运动,T为△P AC的内心.当点P运动到使BT最短时就停止运动,点T运动的路径长为5.如图,在四边形ABCD中,∠ADC=90°,∠BAD=60°,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE、EF、DF,则DF的长为.第3题第4题6.如图,AB为半圆O的直径,点C在半圆O上,AB=8,∠CAB=60°,P是弧上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为.三、解答题1.如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB、直线AC于M、N两点.以点D为中心旋转∠MDN(∠MDN的度数不变),当DM与AB垂直时(如图①所示),易证BM+CN=BD.(1)如图②,当DM与AB不垂直,点M在边AB上,点N在边AC上时,BM+CN=BD是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(2)如图③,当DM与AB不垂直,点M在边AB上,点N在边AC的延长线上时,BM+CN =BD是否仍然成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.2.如图,抛物线23(0)y ax ax c a =-+≠与x 轴交于A ,B 两点,交y 轴于点C ,其中A (-1,0),C (0,3). (1) 求抛物线的解析式(2) 点P 是线段BC 上方抛物线上一动点(不与B ,C 重合),过点P 作PD ⊥x 轴,垂足为D ,交BC 于点E ,作PF ⊥直线BC 于点F ,设点P 的横坐标为x ,△PEF 的周长记为l ,求l 关于x 的函数关系式,并求出l 的最大值及此时点P 的坐标(3) 点H 是直线AC 上一点,该抛物线的对称轴上一动点G ,连接OG ,GH ,则两线段OG ,GH 的长度之和的最小值等于______,此时点G 的坐标为_____(直接写出答案。
2019-2020中考数学分类汇编专题测试——压轴题(含答案)

1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--ab ac a b 44,22)2. 已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经过点T ,折痕TP 与射线AB 交于点P ,设点T 的横坐标为t ,折叠后纸片重叠部分(图中的阴影部分)的面积为S ;(1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式; (2)当纸片重叠部分的图形是四边形时,求t 的取值范围;(3)S 存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由.3. 如图,在Rt ABC △中,90A ∠=,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.4.在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?D图 2B图 1 A BCD ER PH Q图 35、如图1,已知双曲线y=xk(k>0)与直线y=k ′x 交于A ,B 两点,点A 在第一象限.试解答下列问题:(1)若点A 的坐标为(4,2).则点B 的坐标为 ;若点A 的横坐标为m ,则点B 的坐标可表示为 ; (2)如图2,过原点O 作另一条直线l ,交双曲线y=xk(k>0)于P ,Q 两点,点P 在第一象限.①说明四边形APBQ 一定是平行四边形;②设点A.P 的横坐标分别为m ,n ,四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,直接写出mn 应满足的条件;若不可能,请说明理由.6. 如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,连结AP ,并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.(1)求直线AB 的解析式;(2)当点P 运动到点(3,0)时,求此时DP 的长及点D 的坐标;(3)是否存在点P ,使ΔOPD 的面积等于43,若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka, CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k=12,求22BE DG+的值.8. 如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.为s ,s 关于t的函数图象如图2所示, OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.①求梯形上底AB 的长及直角梯形OABC 的面积; ②当42<<t 时,求S 关于t 的函数解析式;(2)在第(1)题的条件下,当直线l 向左或向右平移时(包括l 与直线BC 重合),在直线..AB ..上是否存在点P ,使PDE ∆为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标;若不存在,请说明理由.9.如图,菱形ABCD 的边长为2,BD=2,E 、F 分别是边AD ,CD 上的两个动点,且满足AE+CF=2. (1)求证:△BDE ≌△BCF ;(2)判断△BEF 的形状,并说明理由; (3)设△BEF 的面积为S ,求S 的取值范围.10.如图,抛物线21:23L y x x =--+交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.11.2008淅江宁波)2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A 地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时. (1)求A 地经杭州湾跨海大桥到宁波港的路程.(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A 地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用是多少元?(3)A 地准备开辟宁波方向的外运路线,即货物从A 地经杭州湾跨海大桥到宁波港,再从宁波港运到B 地.若有一批货物(不超过10车)从A 地按外运路线运到B 地的运费需8320元,其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B 地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?12.如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F .(1)求梯形ABCD 的面积; (2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能, 求出正方形MEFN 的面积;若不能,请说明理由.13.如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xky的图象上. (1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A ,B ,M ,N 为顶点的四边形是平行四边形, 试求直线MN 的函数表达式.(3)在平面直角坐标系中,点P 的坐标为(5,0),点Q 的坐标为(0,3),把线段PQ 向右平移4个单位,然后再向上平移2个单位,得到线段P 1Q 1,则点P 1的坐标为 ,点Q 1的坐标为 .C D A BE F NM友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分.14.将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒). (1)用含t 的代数式表示OP OQ ,;(2)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标; (4) 连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.15.如图16,在平面直角坐标系中,直线y =-与x 轴交于点A ,与y 轴交于点C ,抛物线2(0)y ax x c a =-+≠经过A B C ,,三点. (1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理图1(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.16.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =,矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点AE D ,,.(1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.16. 已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?17.如图,在平面直角坐标系xOy 中,△OAB 的顶点A的坐标为(10,0),顶点B 在第一象限内,且AB =3sin ∠. (1)若点C 是点B 关于x 轴的对称点,求经过O 、C 、A 三点的抛物线的函数表达式;(2)在(1)中,抛物线上是否存在一点P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若将点O 、点A 分别变换为点Q ( -2k ,0)、点R (5k ,0)(k>1的常数),设过Q 、R 两点,且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ,其顶点为M ,记△QNM 的面积为QMN S ∆,△QNR 的面积QNR S ∆,求QMN S ∆∶QNR S ∆的值.18.如图①,四边形AEFG 和ABCD 都是正方形,它们的边长分别为a b ,(2b a ≥),且点F 在AD 上(以下问题的结果均可用a b ,的代数式表示). (1)求DBF S △;(2)把正方形AEFG 绕点A 按逆时针方向旋转45°得图②,求图②中的DBF S △;(3)把正方形AEFG 绕点A 旋转一周,在旋转的过程中,DBF S △是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由. . DCBAEFGGF EABCD ①②19. 已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.BADMEC图13 B ADC备用图20.已知:如图①,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:(1)当t为何值时,PQ∥BC?(2)设△AQP的面积为y(2cm),求y与t之间的函数关系式;(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.压轴题答案P图①1. 解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得 c=3,b=2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1对称,所以E(3,0) 设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9(3)相似如图,======所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且AO BO BD BE ==所以AOBDBE ∆∆.2. (1) ∵A ,B 两点的坐标分别是A(10,0)和B(8,32),∴381032OAB tan =-=∠,∴︒=∠60OAB当点A ´在线段AB 上时,∵︒=∠60OAB ,TA=TA ´, ∴△A ´TA 是等边三角形,且A T TP '⊥, ∴)t 10(2360sin )t 10(TP -=︒-=,)t 10(21AT 21AP P A -===',∴2TPA )t 10(83TP P A 21S S -=⋅'=='∆, 当A ´与B 重合时,AT=AB=460sin 32=︒, 所以此时10t 6<≤.(2)当点A ´在线段AB 的延长线,且点P 在线段AB(不与B 重合)上时, 纸片重叠部分的图形是四边形(如图(1),其中E 是TA ´与CB 的交点), 当点P 与B 重合时,AT=2AB=8,点T 的坐标是(2,又由(1)中求得当A ´与B 重合时,T 的坐标是(6,0) 所以当纸片重叠部分的图形是四边形时,6t 2<< (3)S 存在最大值 ○1当10t 6<≤时,2)t 10(83S -=, 在对称轴t=10的左边,S 的值随着t 的增大而减小,∴当t=6时,S 的值最大是32.○2当6t 2<≤时,由图○1,重叠部分的面积EB A TP A S S S '∆'∆-= ∵△A ´EB 的高是︒'60sin B A , ∴23)4t 10(21)t 10(83S 22⨯----=34)2t (83)28t 4t (8322+--=++-=当t=2时,S 的值最大是34;○3当2t 0<<,即当点A ´和点P 都在线段AB 的延长线是(如图○2,其中E 是TA ´与CB 的交点,F 是TP 与CB 的交点),∵ETF FTP EFT ∠=∠=∠,四边形ETAB 是等腰形,∴EF=ET=AB=4,∴3432421OC EF 21S =⨯⨯=⋅=综上所述,S 的最大值是34,此时t 的值是2t 0≤<. 3. 解:(1)Rt A ∠=∠,6AB =,8AC =,10BC ∴=.点D 为AB 中点,132BD AB ∴==.90DHB A ∠=∠=,B B ∠=∠.BHD BAC ∴△∽△, DH BD AC BC ∴=,3128105BD DH AC BC ∴==⨯=. (2)QR AB ∥,90QRC A ∴∠=∠=.xRQ QC AB BC ∴=,10610y x-∴=, 即y 关于x 的函数关系式为:365y x =-+. (3)存在,分三种情况:①当PQ PR =时,过点P 作PM QR ⊥于M ,则QM RM =.1290∠+∠=,290C ∠+∠=,1C ∴∠=∠.84cos 1cos 105C ∴∠===,45QMQP ∴=, 1364251255x ⎛⎫-+ ⎪⎝⎭∴=,185x ∴=. ②当PQ RQ =时,312655x -+=, 6x ∴=.③当PR QR =时,则R 为PQ 中垂线上的点, 于是点R 为EC 的中点,11224CR CE AC ∴===.tan QR BAC CR CA ==,366528x -+∴=,152x ∴=.综上所述,当x 为185或6或152时,PQR △为等腰三角形.4. 解:(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C .∴ △AMN ∽ △ABC .∴ AM AN AB AC=,即43x AN=.∴ AN =43x . ……………2分∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=.(0<x <4) ……………3分 (2)如图2,设直线BC 与⊙O 相切于点D ,连结在Rt △ABC 中,BC =5. 由(1)知 △AMN ∽ △ABC .∴ AM MN =,即x MN=.A BCD ER P H QM 2 1 HA BCD E R PHQB图 1BD 图 2∴ 58OD x =. …………………5分 过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==.在Rt △BMQ 与Rt △BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA . ∴ BM QM BC AC=.∴ 55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线B C 相切.…………………………………7分(3)随点M 的运动,当P 点落在直线BC∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC .∴ △AMO ∽ △ABP .∴ 12AM AO AB AP ==. AM =MB =2.故以下分两种情况讨论: ① 当0<x ≤2时,2Δ83x S y PMN ==. ∴ 当x =2时,2332.82y =⨯=最大 ……………………………………8分 ② 当2<x <4时,设PM ,PN 分别交BC 于E ,F .∵ 四边形AMPN 是矩形, ∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x .∴ ()424PF x x x =--=-. 又△PEF ∽ △ACB .∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭. ∴ ()2322PEF S x ∆=-. ……………………………………………… 9分 MNP PEF y S S ∆∆=-=()222339266828x x x x --=-+-.……………………10分当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭.∴ 当83x =时,满足2<x <4,2y =最大. ……………………11分 综上所述,当83x =时,y 值最大,最大值是2. …………………………12分图 4P 图 3(2) ①由于双曲线是关于原点成中心对称的,所以OP=OQ,OA=OB,所以四边形APBQ 一定是平行四边形②可能是矩形,mn=k 即可不可能是正方形,因为Op 不能与OA 垂直.解:(1)作BE ⊥OA , ∴ΔAOB 是等边三角形∴BE=OB ·sin60o=∴B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =,的以直线AB 的解析式为4y x =+ (2)由旋转知,AP=AD, ∠PAD=60o,∴ΔAPD 是等边三角形,=6. 解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o=B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =,以直线AB 的解析式为4y x =+ (2)由旋转知,AP=AD, ∠PAD=60o,∴ΔAPD 是等边三角形,=如图,作BE ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=+,∴BD=32,OH=OE+HE=OE+BG=37222+=7(3)设OP=x,则由(2)可得D(,2x x +)若ΔOPD 的面积为:13(2)2x x +=解得:x =所以7. 解:(1)①,BG DE BG DE =⊥ ………………………………………………………………2分 ②,BG DE BG DE =⊥仍然成立 ……………………………………………………1分在图(2)中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴ BC CD =,CG CE =, 090BCD ECG ∠=∠=∴BCG DCE ∠=∠…………………………………………………………………1分∴BCG DCE ∆≅∆ (SAS )………………………………………………………1分∴BG DE = CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ …………………………………………………………………………1分(2)BG DE ⊥成立,BG DE =不成立 …………………………………………………2分简要说明如下∵四边形ABCD 、四边形CEFG 都是矩形,且AB a =,BC b =,CG kb =,CE ka =(a b ≠,0k >)∴BCG DCE ∆∆………………………………………………………………………1分∴CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ ……………………………………………………………………………1分(3)∵BG DE ⊥ ∴22222222BE DG OB OE OG OD BD GE +=+++=+ 又∵3a =,2b =,k =12∴ 222222365231()24BD GE +=+++= ………………………………………………1分 ∴22654BE DG +=………………………………………………………………………1分 8. 解:(1)①2AB = ……………………………………………………………………………2分842OA ==,4OC =,S 梯形OABC =12 ……………………………………………2分 ②当42<<t 时, 直角梯形OABC 被直线l扫过的面积=直角梯形OABC 面积-直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分 (2) 存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …(每个点对各得1分)……5分 对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二:① 以点D 为直角顶点,作1PP x ⊥轴Rt ODE ∆在中,2OE OD =∴,设2OD b OE b ==,.1Rt ODE Rt PPD ∆≈∆,(图示阴影) 4b ∴=,28b =,在上面二图中分别可得到P 点的生标为P (-12,4)、P (-4,4) E 点在0点与A 点之间不可能;② 以点E 为直角顶点同理在②二图中分别可得P 点的生标为P (-83,4)、P (8,4)E 点在0点下方不可能.以点P 为直角顶点同理在③二图中分别可得P 点的生标为P (-4,4)(与①情形二重合舍去)、P (4,4), E 点在A 点下方不可能.综上可得P 点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-83,4)、 P (8,4)、P (4,4).下面提供参考解法二:以直角进行分类进行讨论(分三类):第一类如上解法⑴中所示图22P DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b)的中点坐标为b (-,b)2,直线DE 的中垂线方程:1()22b y b x -=-+,令4y =得3(8,4)2bP -.由已知可得DE ==2332640b b -+=解得121883b b P P ==∴=3b,将之代入(-8,4)(4,4)、22(4,4)P -; 第二类如上解法②中所示图22E DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b) ,直线PE 的方程:122y x b =-+,令4y =得(48,4)P b -.由已知可得PE DE =即=化简得22(28)b b =-解之得 ,123443b b P P ==∴=,将之代入(4b-8,4)(8,4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b),直线PD 的方程:1()2y x b =-+,令4y =得(8,4)P b --.由已知可得PD DE ==解得12544b b P P ==-∴=,将之代入(-b-8,4)(-12,4)、 6(4,4)P -(6(4,4)P -与2P 重合舍去).综上可得P 点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-83,4)、 P (8,4)、P (4,4).事实上,我们可以得到更一般的结论: 如果得出AB a OC b ==、、OA h =、设b ak h-=,则P 点的情形如下9.10.11. 解:(1)设A 地经杭州湾跨海大桥到宁波港的路程为x 千米,由题意得1201023x x+=, ··························· 2分 解得180x =.A ∴地经杭州湾跨海大桥到宁波港的路程为180千米.·············· 4分 (2)1.8180282380⨯+⨯=(元),∴该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用为380元. ·······6分 (3)设这批货物有y 车,由题意得[80020(1)]3808320y y y -⨯-+=, ················· 8分 整理得2604160y y -+=,解得18y =,252y =(不合题意,舍去), ·················· 9分∴这批货物有8车.···························· 10分12. 解:(114a ,. ························ 3分 (2. ···· 5分(无“相等”不扣分有“相等”,比值错给1分) (3)设DG x =,在矩形ABCD 中,90B C D ∠=∠=∠=,90HGF ∠=,90DHG CGF DGH ∴∠=∠=-∠,HDG GCF ∴△∽△, 12DG HG CF GF ∴==, 22CF DG x ∴==. ····························6分 同理BEF CFG ∠=∠.EF FG =,FBE GCF ∴△≌△,14BF CG a x ∴==-. ··························· 7分CF BF BC +=,124x a x ∴+-=, ·························· 8分解得x =.即DG =. ····························· 9分 (4)2316a , ······························ 10分2. 12分 13. 解:(1)分别过D ,C 两点作DG ⊥AB 于点G ,CH ⊥AB 于点H . ……………1分 ∵ AB ∥CD ,∴ DG =CH ,DG ∥CH .∴ 四边形DGHC 为矩形,GH =CD =1.∵ DG =CH ,AD =BC ,∠AGD =∠BHC =90°,∴ △AGD ≌△BHC (HL ). ∴ AG =BH =2172-=-GH AB =3. ………2分 ∵ 在Rt △AGD 中,AG =3,AD =5, ∴ DG =4. ∴ ()174162ABCD S +⨯==梯形. ………………………………………………3分(2)∵ MN ∥AB ,ME ⊥AB ,NF ⊥AB , ∴ ME =NF ,ME ∥NF . ∴ 四边形MEFN 为矩形. ∵ AB ∥CD ,AD =BC , ∴ ∠A =∠B .∵ ME =NF ,∠MEA =∠NFB =90°,∴ △MEA ≌△NFB (AAS ).∴ AE =BF . ……………………4分 设AE =x ,则EF =7-2x . ……………5分 ∵ ∠A =∠A ,∠MEA =∠DGA =90°, ∴ △MEA ∽△DGA .∴ DGME AG AE =. ∴ ME =x 34. …………………………………………………………6分∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN 矩形. ……………………8分当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649.……………9分(3)能. ……………………………………………………………………10分A B E FGH A B E F G H由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34.若四边形MEFN 为正方形,则ME =EF .即 =34x 7-2x .解,得 1021=x . ……………………………………………11分∴ EF =21147272105x -=-⨯=<4.∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形. 14. 解:(1)由题意可知,()()()131-+=+m m m m .解,得 m =3. ………………………………3分∴ A (3,4),B (6,2); ∴ k =4×3=12. ……………………………4分(2)存在两种情况,如图: ①当M 点在x 轴的正半轴上,N 点在y 轴的正半轴上时,设M 1点坐标为(x 1,0),N 1点坐标为(0,y 1).∵ 四边形AN 1M 1B 为平行四边形,∴ 线段N 1M 1可看作由线段AB 向左平移3个单位,再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).由(1)知A 点坐标为(3,4),B 点坐标为(6,2), ∴ N 1点坐标为(0,4-2),即N 1(0,2); ………………………………5分 M 1点坐标为(6-3,0),即M 1(3,0). ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ,把x =3,y =0代入,解得321-=k .∴ 直线M 1N 1的函数表达式为232+-=x y . ……………………………………8分②当M 点在x 轴的负半轴上,N 点在y 轴的负半轴上时,设M 2点坐标为(x 2,0),N 2点坐标为(0,y 2). ∵ AB ∥N 1M 1,AB ∥M 2N 2,AB =N 1M 1,AB =M 2N 2, ∴ N 1M 1∥M 2N 2,N 1M 1=M 2N 2.∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称. ∴ M 2点坐标为(-3,0),N 2点坐标为(0,-2). ………………………9分设直线M 2N 2的函数表达式为22-=x k y ,把x =-3,y =0代入,解得322-=k ,∴ 直线M 2N 2的函数表达式为232--=x y .所以,直线MN 的函数表达式为232+-=x y 或232--=x y . ………………11分(3)选做题:(9,2),(4,5). ………………………………………………2分 15. 解:(1)解法1:根据题意可得:A (-1,0),B (3,0);则设抛物线的解析式为)3)(1(-+=x x a y (a ≠0)又点D (0,-3)在抛物线上,∴a (0+1)(0-3)=-3,解之得:a =1∴y =x 2-2x -3 ···························· 3分 自变量范围:-1≤x ≤3 ························ 4分解法2:设抛物线的解析式为c bx ax y ++=2(a ≠0)根据题意可知,A (-1,0),B (3,0),D (0,-3)三点都在抛物线上∴⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a ,解之得:⎪⎩⎪⎨⎧-=-==321c b a∴y =x 2-2x -3 ······················ 3分自变量范围:-1≤x≤3 ·················4分 (2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=3在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4∴点C、E的坐标分别为(0,3),(-3,0) ··············6分∴切线CE分(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ······9分由题意可知方程组⎪⎩⎪⎨⎧--=-=3232xxykxy只有一组解即3232--=-xxkx有两个相等实根,∴k=-2 ············ 11分∴过点D“蛋圆”切线的解析式y=-2x-3 ·············· 12分16.解:(1)6OP t=-,23OQ t=+.,(3)①PQ能与AC平行.若PQ AC∥,如图2,则OP OAOQ OC=,即66233tt-=+,149t∴=,而73t≤≤,149t∴=.图1②PE 不能与AC 垂直.若PE AC ⊥,延长QE 交OA 于F ,如图3,则23335t QF OQ ACOC +==.23QF t ⎫∴=+⎪⎭.EFQF QE QF OQ ∴=-=-2233t t ⎫⎛⎫=+-+⎪ ⎪⎭⎝⎭21)1)3t =-+-.又Rt Rt EPF OCA △∽△,PEOCEF OA∴=, 36=,3.45t ∴≈,而703t ≤≤,t ∴不存在.17. 解:(1)直线y =与x 轴交于点A ,与y 轴交于点C.(10)A ∴-,,(0C ,··························· 1分点A C,都在抛物线上,0a c c ⎧=++⎪∴⎨⎪=⎩ a c ⎧=⎪∴⎨⎪=⎩∴抛物线的解析式为2y x x =················· 3分 ∴顶点1F ⎛- ⎝, ···························· 4分(2)存在 ································· 5分1(0P ,································ 7分 2(2P -, ································ 9分(3)存在 ································ 10分理由: 解法一:延长BC 到点B ',使B C BC '=,连接B F '交直线AC 于点M ,则点M 就是所求的点.························· 11分过点B '作B H AB '⊥于点H .B点在抛物线2y x =上,(30)B ∴, 在Rt BOC △中,tan OBC ∠=, 30OBC ∴∠=,BC =,在Rt BB H '△中,12B H BB ''==6BH H '==,3OH ∴=,(3B '∴--, ·············· 12分设直线B F '的解析式为y kx b =+3k b k b ⎧-=-+⎪∴⎨=+⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y x ∴=-···························· 13分y y x ⎧=-⎪∴⎨=⎪⎩解得37x y ⎧=⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝ ∴在直线AC 上存在点M ,使得MBF △的周长最小,此时37M ⎛ ⎝. ·· 14分 解法二:过点F 作AC 的垂线交y 轴于点H ,则点H 为点F 关于直线AC于点M ,则点M 即为所求.···················· 11分 过点F 作FG y ⊥轴于点G ,则OB FG ∥,BC FH ∥.90BOC FGH ∴∠=∠=,BCO FHG ∠=∠HFG CBO ∴∠=∠同方法一可求得(30)B ,. 在Rt BOC △中,tan OBC ∠=,30OBC ∴∠=,可求得GH GC ==, GF ∴为线段CH 的垂直平分线,可证得CFH △为等边三角形,AC ∴垂直平分FH .即点H 为点F 关于AC的对称点.0H ⎛∴- ⎝, ·············· 12分 设直线BH 的解析式为y kx b =+,由题意得03k b b =+⎧⎪⎨=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y ∴=···························· 13分y y ⎧=⎪∴⎨⎪=⎩解得37x y ⎧=⎪⎪⎨⎪=⎪⎩37M ⎛∴ ⎝, ∴在直线AC 上存在点M ,使得MBF △的周长最小,此时37M ⎛ ⎝. 1 18. 解:(1)点E 在y 轴上 ························· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ····················· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠= ∴在Rt DOM △中,12DM =,OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎭, ·························· 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ··························· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩ ∴所求抛物线表达式为:2829y x x =--+ ················ 9分 (3)存在符合条件的点P ,点Q . ····················· 10分 理由如下:矩形ABOC 的面积3AB BO ==∴以O B P Q ,,,为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边, 又3OB =OB ∴边上的高为2 ···························· 11分依题意设点P 的坐标为(2)m ,点P在抛物线2829y x x =-+上28229m ∴--+=解得,10m =,2m = 1(02)P ∴,,22P ⎛⎫⎪ ⎪⎝⎭以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,PQ OB ==,∴当点1P 的坐标为(02),时, 点Q的坐标分别为1(2)Q,22)Q ; 当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时,点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭,42Q ⎫⎪⎪⎭. ············· 14分 (以上答案仅供参考,如有其它做法,可参照给分) 19. 解:(1)在2334y x =-+中,令0y = 23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B , (1)又点B 在34y x b =-+上302b ∴=-+ 32b =BC ∴的解析式为3342y x =-+························ 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ················ 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =···························· 5分 1994242ABC S ∴=⨯⨯=△ ··························· 6分(3)过点N 作NP MB ⊥于点P EO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△····························· 7分 BN NP BE EO∴= ······························· 8分 由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP ∴=,65NP t ∴= ·························· 9分 16(4)25S t t ∴=-2312(04)55S t t t =-+<< ························· 10分2312(2)55S t =--+ ··························· 11分此抛物线开口向下,∴当2t =时,125S =最大∴当点M 运动2秒时,MNB △的面积达到最大,最大为125.20. 解:(1)如图,过点B 作BD ⊥OA 于点D. 在Rt △ABD 中, ∵∣AB ∣=,sin ∠∴∣BD ∣=∣AB ∣·sin ∠OAB=又由勾股定理,得A D =6==∴∣OD ∣=∣OA ∣-∣AD ∣=10-6=4.∵点B 在第一象限,∴点B 的坐标为(4,3). ……3分 设经过O(0,0)、C (4,-3)、A(10,0)三点的抛物线的函数表达式为y=ax 2+bx(a ≠0).由1,164381001005.4a ab a b b ⎧=⎪+=-⎧⎪⇒⎨⎨+=⎩⎪=-⎪⎩ ∴经过O 、C 、A 三点的抛物线的函数表达式为215.84y x x =- ……2分 (2)假设在(1)中的抛物线上存在点P ,使以P 、O 、C 、A 为顶点的四边形为梯形 ①∵点C (4,-3)不是抛物线21584y x x =-的顶点, ∴过点C 做直线OA 的平行线与抛物线交于点P 1 .则直线CP 1的函数表达式为y=-3. 对于21584y x x =-,令y=-3⇒x=4或x=6. ∴12124,6,3; 3.x x y y ==⎧⎧⎨⎨=-=-⎩⎩ 而点C (4,-3),∴P 1(6,-3).在四边形P 1AOC 中,CP 1∥OA,显然∣CP 1∣≠∣OA ∣.∴点P 1(6,-3)是符合要求的点. ……1分 ②若AP 2∥CO.设直线CO 的函数表达式为1.y k x = 将点C (4,-3)代入,得1134 3..4k k =-∴=- ∴直线CO 的函数表达式为3.4y x =-于是可设直线AP 2的函数表达式为13.4y x b =-+ 将点A (10,0)代入,得315.42x -+ ∴直线AP 2的函数表达式为315.42y x =-+由22315.4246001584y x x x y x x ⎧=-+⎪⎪⇒--=⎨⎪=-⎪⎩,即(x-10)(x+6)=0. ∴121210,60;12;x x y y ==-⎧⎧⎨⎨==⎩⎩ 而点A (10,0),∴P 2(-6,12).过点P 2作P 2E ⊥x 轴于点E ,则∣P 2E ∣=12. 在Rt △AP 2E 中,由勾股定理,得220.AP ==而∣CO ∣=∣OB ∣=5.∴在四边形P 2OCA 中,AP 2∥CO,但∣AP 2∣≠∣CO ∣.∴点P 2(-6,12)是符合要求的点. ……1分 ③若OP 3∥CA,设直线CA 的函数表达式为y=k 2x+b 2 将点A(10,0)、C(4,-3)代入,得2222221100,243 5.k b k k b b ⎧+==⎛⎪⇒⎨+=-⎝⎪=-⎩ ∴直线CA 的函数表达式为15.2y x =- ∴直线OP 3的函数表达式为12y x =由2212140,1584y x x x y x x ⎧=⎪⎪⇒-=⎨⎪=-⎪⎩即x(x-14)=0. ∴12120,14,0;7.x x y y ==⎧⎧⎨⎨==⎩⎩ 而点O(0,0),∴P 3(14,7).过点P 3作P 3E ⊥x 轴于点E ,则∣P 3E ∣=7. 在Rt △OP 3E 中,由勾股定理,得3OP ==而∣CA ∣=∣AB ∣=.∴在四边形P 3OCA 中,OP 3∥CA,但∣OP 3∣≠∣CA ∣.∴点P 3(14,7)是符合要求的点. ……1分 综上可知,在(1)中的抛物线上存在点P 1(6,-3)、P 2(-6,12)、P 3(14,7),。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 3)请探索:是否存在这样的点 F ,使得将 △CEF 沿 EF 对折后, C 点恰好落在 OB 上?若存在,求 出点 F 的坐标;若不存在,请说明理由.
( 08 浙江湖州 24 题解析) 24.(本小题 12 分)
已知:在矩形 AOBC 中, OB 4 , OA 3.分别以 OB, OA 所在直线为 x 轴和 y 轴,建立如图所示的
平面直角坐标系. F 是边 BC 上的一个动点(不与 B,C 重合),过 F 点的反比例函数 y k (k 0) 的图 x
象与 AC 边交于点 E . ( 1)求证: △ AOE 与 △BOF 的面积相等;
8
-
m)
×8-
1 2
(
8-
m
)(
8
-
m
)
= 1( 8- m)( 8- 8+ m)= 1( 8-m) m=- 1m2+ 4m
2
2
2
自变量 m 的取值范围是 0< m< 8 ( 5)存在. 理由:
∵
S=-
1 2
m2+
4m=-
12(
m-
4)
2+
8
∴当 m= 4 时, S 有最大值, S 最大值 = 8
∵ m= 4,∴点 E 的坐标为(- 2, 0)
3
4
1
11
1
S△ ECF
EC CF
4 k 3 k,
2
23
4
S△ EOF
11
S矩形 AOBC
S△ AOE
S△ BOF
S△ ECF
12 k 2
k 2
S△ ECF
12 k S△ ECF
11
1
S S△OEF S△ ECF 12 k 2S△ ECF 12 k 2
4 k3 k
23
4
S
1 k2 k.
12
当k
1
6时, S 有最大值.
∴△ BCE为等腰三角形.
且- 12< 0,
51( 08 重庆市卷)(本题答案暂缺) 28、( 10 分)已知:如图,抛物线 y ax 2 2ax c(a 0) 与 y 轴交
于点 C( 0, 4),与 x 轴交于点 A、 B,点 A 的坐标为( 4,0)。 ( 1)求该抛物线的解析式; ( 2)点 Q是线段 AB上的动点,过点 Q作 QE∥ AC,交 BC于点 E,连接 CQ。当△ CQE的面积最大时,求点 Q 的坐标;
1
2
12
S最大值
1
3.
1
4
12
( 3 )解:设存在这样的点 F ,将 △CEF 沿 EF 对折后, C 点恰好落在 OB 边上的 M 点,过点 E 作
EN OB ,垂足为 N .
由题意得: EN AO 3 , EM
1 EC 4 k , MF
CF
1 3 k,
3
4
EMN FMB FMB MFB 90 , EMN MFB .
接 CE,设 AE 的长为 m,△ CEF 的面积为 S,求 S 与 m 之间的函数关系式,并写出自变量 m 的取值范围;
( 5)在( 4)的基础上试说明 S 是否存在最大值,若存在,请求出 S 的最大值,并求出此时点 E 的坐
标,判断此时△ BCE 的形状;若不存在,请说明理由.
( 08 云南双柏 25 题解析) 25.(本小题 12 分)解:( 1)解方程 x2- 10x+ 16= 0 得 x1= 2, x2= 8
0=36a- 6b+ 8 0= 4a+ 2b+ 8
解得
2 a=- 3
8 b=- 3
∴所求抛物线的表达式为
y=-
23x2-
8 3
x+
8
( 3)∵ AB=8, OC= 8
1 ∴ S△ABC = 2×8×8=32
( 4)依题意, AE =m,则 BE= 8- m,
∵ OA= 6, OC= 8, ∴ AC= 10
∵ EF∥ AC ∴△ BEF ∽△ BAC
∴
EF AC
=
BE AB
即
EF 10
=
8- 8
m
∴EF
=
40- 4
5m
过点 F 作 FG⊥ AB,垂足为 G,则 sin∠ FEG= sin∠ CAB= 4 5
∴
FG EF
=
4 5
∴
FG
=
45·
40- 4
5m =
8-m
∴
S=
S△
BCE-
S△
BFE=
1 2
(
2019-2020 年中考数学压轴题精选 5 试题
50( 08 云南双柏) 25.(本小题( 1)~( 3)问共 12 分;第( 4)、( 5)问为附加题 10 分,每小题 5 分,
附加题得分可以记入总分,若记入总分后超过
120 分,则按 120 分记)
已知:抛物线 y= ax2+ bx+ c 与 x 轴交于 A、 B 两点,与 y 轴交于点 C,其中点 B 在 x 轴的正半轴上,
( 3)若平行于 x 轴的动直线 l 与该抛物线交于点 P,与直线 AC交于点 F,点 D 的坐标为( 2, 0)。问:是 否存在这样的直线 l ,使得△ ODF是等腰三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由。
Y
C
B OQD
AX
28 题图
52( 08 浙江湖州) 24.(本小题 12 分)
∵点 B 在 x 轴的正半轴上,点 C 在 y 轴的正半轴上,且 OB<OC
∴点 B 的坐标为( 2, 0),点 C 的坐标为( 0, 8) 又∵抛物线 y= ax2+bx+ c 的对称轴是直线 x=- 2
∴由抛物线的对称性可得点 A 的坐标为(- 6, 0)
∴ A 、 B、 C 三点的坐标分别是 A(- 6, 0)、 B( 2, 0)、 C(0, 8) ( 2)∵点 C( 0, 8)在抛物线 y= ax2+ bx+ c 的图象上 ∴ c= 8,将 A(- 6, 0)、 B( 2, 0)代入表达式 y= ax2+ bx+ 8,得
( 1)证明:设 E ( x1, y1 ) , F ( x2, y2 ) , △ AOE 与 △ FOB 的面积分别为 S1 , S2 ,
由题意得 y1
k x1 , y2
k
.
x2
1
1
1
1
S1
x1y1
k , S2
x2 y2
k.
2
2
2
2
S1 S2 ,即 △ AOE 与 △FOB 的面积相等.
( 2)由题意知: E, F 两点坐标分别为 E k ,3 , F 4,k ,
点 C 在 y 轴的正半轴上,线段 OB、OC 的长( OB <OC )是方程 x2-10x+ 16=0 的两个根,且抛物线的对
称轴是直线 x=- 2.
( 1)求 A、 B、 C 三 的面积;
( 4)若点 E 是线段 AB 上的一个动点(与点 A、点 B 不重合),过点 E 作 EF ∥ AC 交 BC 于点 F ,连
