铅垂高中考压轴题演练含答案
备战中考物理与浮力类问题有关的压轴题及答案

一、初中物理浮力类问题1.如图甲,将金属球和木球用细绳相连放入某种液体中时,木球露出液面的体积为它自身体积的14,当把细绳剪断后,金属球沉底,木球露出液面的体积是它自身体积的一半,这时金属球受到池底对它的支持力为2N,如图乙,若已知金属球和木球的体积之比是1:8,则A.金属球的重力为2NB.绳子剪断前,木球所受的浮力为8NC.金属球的密度为3×103kg/m3D.绳子剪断前后,两球所受的总浮力相差1N【答案】C【解析】【详解】ABC.把绳子剪断后,木球漂浮,金属球沉底,此时金属球处于平衡状态,受到竖直向上的支持力、浮力和竖直向下的重力作用,由力的平衡条件可得:F支持+F浮金=G金--------①由物体漂浮条件可得:G木=F浮木----------------②绳子剪断前,金属球受到竖直向上绳子的拉力F、浮力和竖直向下的重力作用,木球受到竖直向上的浮力和竖直向下的重力、绳子的拉力F,由力的平衡条件可得:F+F浮金=G金------③,F浮木′=G木+F------④由①③可得:F=F支持=2N-------⑤由②④⑤可得:F浮木′-F浮木=2N,因绳子剪断前木球排开水的体积V排′=(1-14)V木=34V木,绳子剪断后木球排开水的体积V排=(1-12)V木=12V木由阿基米德原理可得绳子剪断前后木球的浮力变化量:ρ水g×34V木 -ρ水g×12V木=2N,解得:ρ水gV 木=8N---------------⑥ 则绳子剪断前,木球所受的浮力:F 浮木′=ρ水g (1-14)V 木=34ρ水gV 木=34×8N=6N , 把G =mg =ρVg 和F 浮金=ρ水gV 金代入①式可得:F 支持+ρ水gV 金=ρ金gV 金,整理可得:(ρ金-ρ水)gV 金=F 支持=2N-------⑦由⑥⑦、金属球和木球的体积之比是1:8可得:ρ金=3ρ水=3×1.0×103kg/m 3=3×103kg/m 3,G 木=F 浮木′-F =6N-2N=4N ,已知V 金:V 木=1:8,则金属球受到的浮力F 金浮=ρ水gV 金=ρ水g ×18V 木=18×8N=1N ; 金属球的重力G 金=F 金浮+F =1N+2N=3N ,故C 符合题意,AB 不符合题意;D .绳子剪断前,木球和金属球整体漂浮,则总浮力F 浮前=G 木+G 金,绳子剪断前后,两物体所受的总浮力之差为:F 浮前-F 浮后=(G 木+G 金)-(G 木+F 金浮)=G 金-F 金浮=F =2N ,故D 不符合题意.2.如图弹簧测力计下悬挂一物体,当物体三分之一的体积浸入水中时,弹簧测力计示数为5N ,当物体二分之一的体积浸入水中时,弹簧测力计示数为 3N ,现将物体从弹簧测力计上取下放入水中,则该物体静止时所受浮力和该物体的密度分别为(ρ 水=1×310kg/3m ,g =10N/kg )( )A .9N ,0.75×103kg/m 3B .9N ,0.8×103kg/m 3C .8N ,0.75×103kg/m 3D .8N ,0.8×103kg/m 3 【答案】A 【解析】 【分析】 【详解】设物体的体积为V ,当物体三分之一的体积浸入水中时,则有F G F '=-浮拉即15N 3g V G ρ⨯=-水 ①当物体二分之一的体积浸入水中时,则有F G F '''=-浮拉即13N 2g V G ρ⨯=-水 ②联立①②解得12N gV ρ=水 ③即物体浸没水中时,所受的浮力为12N F =浮则物体的体积为333312N 12N1.210m 1.010kg m 10N kgV g ρ-===⨯⨯⨯水 将③代入①得9N G =因物体浸没时所受的浮力大于物体的重力,故物体从弹簧测力计上取下放入水中,物体静止时,物体漂浮于水面。
中考物理压轴题专题浮力类问题的经典综合题附答案

一、初中物理浮力类问题1.如图是利用滑轮组匀速提升水中圆柱体M 的示意图,滑轮组固定在钢架上,滑轮组中的两个滑轮质量相等,绕在滑轮组上的绳子能承受的最大拉力为900N ,连接圆柱体M 与动滑轮挂钩的绳子能承受的最大拉力为3000N 。
圆柱体M 高为3m ,底面积为0.02m 2,密度为34.510⨯kg/m 3。
在绳端拉力F 作用下,圆柱体M 从其下表面距水面15m 处匀速上升到其上表面与水面相平的过程中用了3min ,在这个过程中,拉力F 的功率为160W ,滑轮组的机械效率为η,钢架对定滑轮的拉力为T 。
在圆柱体M 被缓慢拉出水的过程中,圆柱体M 的下表面受到水的压强为p 。
不计绳重、轮与轴的摩擦及水的阻力,g 取10N/kg 。
下列选项中正确的是A .压强p 的最小值为15000PaB .拉力T 的大小为2700NC .拉力F 的大小为640ND .滑轮组的机械效率为90% 【答案】A 【解析】 【分析】(1) 对动滑轮和物体做整体受力分析,对定滑轮做受力分析,根据=F gV ρ浮液排,求得M 所受的浮力,再根据重力和浮力之比可求得M 的重力,从而可求得拉力F 大小; (2) 因M 有三段绳子承担,根据平衡条件M 3F F G G +=+浮轮,可求得拉力T 的大小; (3) 根据M M M M ()==+()W W G F h G F W W W G F G h G F G η--==-+-+有有浮浮浮浮总有额动动可求得滑轮组的机械效率;(4)由绕在滑轮组上的绳子能承受的最大拉力为900N 和连接圆柱体M 与动滑轮挂钩的绳子能承受的最大拉力为3000N ,可知圆柱体M 的下表面受到水的压力,再利用Fp S=可求得压强p 的最小值。
【详解】C .圆柱体M 从其下表面距水面15m 处匀速上升到其上表面与水面相平的过程中用了3min ,注意物体上升了12m ,可计算重物上升的速度12m 1m/s 360s 15s v t ===⨯物 动滑轮一共绕了3段绳子,因此绳自由端移动速度为1=3=3m/s 0.2m/s 15v v ⨯=绳物 拉力F 的功率为160W ,根据P Fv =得出拉力160W 800N 0.2m/sP F v === 故C 项错误。
二次函数中面积的最值问题(六大题型)学生版-2024年中考数学压轴题专项训练
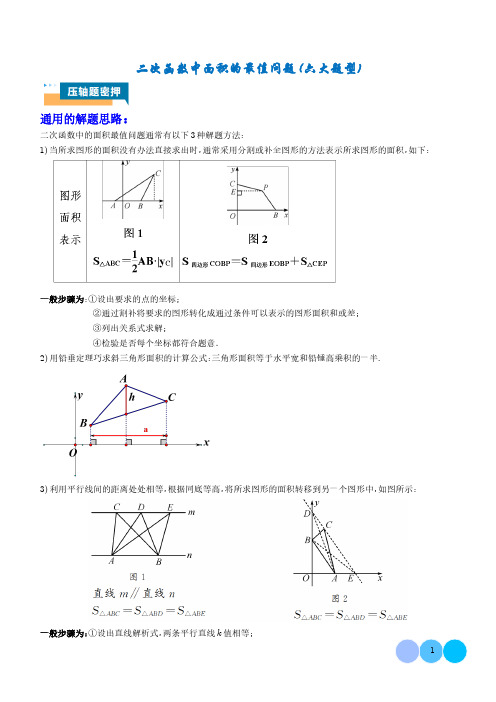
二次函数中面积的最值问题(六大题型)通用的解题思路:二次函数中的面积最值问题通常有以下3种解题方法:1)当所求图形的面积没有办法直接求出时,通常采用分割或补全图形的方法表示所求图形的面积,如下:一般步骤为:①设出要求的点的坐标;②通过割补将要求的图形转化成通过条件可以表示的图形面积和或差;③列出关系式求解;④检验是否每个坐标都符合题意.2)用铅垂定理巧求斜三角形面积的计算公式:三角形面积等于水平宽和铅锤高乘积的一半.3)利用平行线间的距离处处相等,根据同底等高,将所求图形的面积转移到另一个图形中,如图所示:一般步骤为:①设出直线解析式,两条平行直线k值相等;②通过已知点的坐标,求出直线解析式;③求出题意中要求点的坐标;④检验是否每个坐标都符合题意.题型01三角形面积最值问题1(2024·宁夏银川·一模)如图,二次函数y =-x 2+6x 的图象与x 轴的正半轴交于点A ,经过点A 的直线与该函数图象交于点B 1,5 ,与y 轴交于点C .(1)求直线AB 的函数表达式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,且在直线AB 上方,过点P 作直线PE ⊥x 轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①当PD =12OC 时,求m 的值;②设△PAB 的面积为S ,求S 关于m 的函数表达式,并求出S 的最大值.2(2024·新疆克孜勒苏·二模)如图,抛物线y =x ²+bx +c (b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,A 2,0 ,AB =6,点P 为线段AB 上的动点,过P 作PQ ∥BC 交AC 于点Q .(1)求抛物线的解析式;(2)求△CPQ 面积的最大值,并求此时P 点坐标.3(23-24九年级下·湖北武汉·开学考试)如图,抛物线y =ax 2-4ax +3a 交x 轴于A ,B 两点(点A 在点B 的左侧),交y 轴正半轴于点C ,OB =OC ,点P 在抛物线上.(1)求抛物线的解析式;(2)若tan∠ACP=2,求点P的横坐标.(3)平面上有两点M m,-m-3,求△PMN的面积的最小值.,N m+2,-m-54(23-24九年级下·辽宁沈阳·阶段练习)△ABC中,∠BAC=90°,AB=2,AC=4,点P从点C出发,沿射线CA方向运动,速度为每秒1个单位长度,同时点Q以相同的速度从点B出发,沿射线BA方向运动.设运动时间为x(x≠2且x≠4)秒,△APQ的面积为S.(1)当0<x<2时,如图①,求S与x的函数关系式;(2)当2<x<4时,如图②,求S的最大值;(3)若在运动过程中,存在两个时刻x1,x2,对应的点P和点Q分别记为P1,P2和Q1,Q2,对应的△AP1Q1和△AP2Q2的面积分别记为S1和S2,且当CP1=P1P2时,S1=S2,请求出x1的值.5(2023·山东聊城·二模)如图,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),点A 的坐标为-1,0,直线CD:y=2x-3与x轴交于点D.动点M在抛物线上运动, ,与y轴交于点C0,-3过点M作MP⊥x轴,垂足为点P,交直线CD于点N.(1)求抛物线的表达式;(2)当点P在线段OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;(3)点M在运动过程中,能否使以C,N,M为顶点的三角形是以NM为腰的等腰直角三角形?若存在,请直接写出点M的坐标.6(2024·浙江宁波·模拟预测)如图,一次函数y=33x+3的图象与坐标轴交于点A、B,抛物线y=-33x2+bx+c的图象经过A、B两点.(1)求二次函数的表达式;(2)若点P为抛物线上一动点,在直线AB上方是否存在点P使△PAB的面积最大?若存在,请求出△PAB 面积的最大值及点P的坐标,请说明理由.7(2024·甘肃陇南·一模)如图,在平面直角坐标系xOy中,已知直线y=-x-3与x轴交于点A,与y轴交于点C,过A,C两点的抛物线y=ax2+bx+c与x轴交于另一点B1,0,抛物线对称轴为直线l.(1)求抛物线的解析式;(2)点M为直线AC下方抛物线上一点,当△MAC的面积最大时,求点M的坐标;(3)点P是抛物线上一点,过点P作l的垂线,垂足为D,E是l上一点.要使得以P,D,E为顶点的三角形与△BOC全等,请直接写出点P的坐标.8(2024·江苏盐城·模拟预测)已知抛物线y=x2+bx-3与x轴交于A,B(点A在点B的左侧),与y轴交于点C,且OB=OC.(1)求抛物线的解析式和点A的坐标;(2)如图1,点P为直线BC下方抛物线上一点,求△PBC的最大面积;(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x-9上,求证:直线MN必经过一个定点,并求该定点坐标.9(2024·四川广元·二模)如图,在平面直角坐标系中,抛物线y1=-x2+bx+c与x轴交于点B,A(-3, 0),与y轴交于点C(0,3).(1)求直线AC和抛物线的解析式.(2)若点M是抛物线对称轴上的一点,是否存在点M,使得以M,A,C三点为顶点的三角形是以AC为底的等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.(3)若点P是第二象限内抛物线上的一个动点,求△PAC面积的最大值.10(2024·安徽安庆·一模)如图,抛物线y=ax2+bx+3与x轴交于点A1,0两点,与y轴交于、B3,0点C.(1)求此抛物线对应的函数表达式;(2)点E为直线BC上的任意一点,过点E作x轴的垂线与此抛物线交于点F.①若点E在第一象限,连接CF、BF,求△CFB面积的最大值;②此抛物线对称轴与直线BC交于点D,连接DF,若△DEF为直角三角形,请直接写出E点坐标.11(2024·安徽合肥·一模)如图,直线y=x-3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c 经过B、C两点,抛物线与x轴负半轴交于点A.(1)求抛物线的函数表达式;(2)直接写出当x-3>x2+bx+c时,x的取值范围;(3)点P是位于直线BC下方抛物线上的一个动点,过点P作PE⊥BC于点E,连接OE.求△BOE面积的最大值及此时点P的坐标.12(2024·天津西青·一模)已知抛物线y=-x2-4ax-12a(a<0)与x轴交于A,B两点(点A在点B左边),与y轴交于点C.(1)若点D4,12在抛物线上.①求抛物线的解析式及点A的坐标;②连接AD,若点P是直线AD上方的抛物线上一点,连接PA,PD,当△PAD面积最大时,求点P的坐标及△PAD面积的最大值;(2)已知点Q的坐标为-2a,-8a,连接QC,将线段QC绕点Q顺时针旋转90°,点C的对应点M恰好落在抛物线上,求抛物线的解析式.13(2024·山东临沂·二模)如图,抛物线y=ax2+32x+c与x轴交于点A和点B4,0,与y轴交于点C0,2,连接BC,点D在抛物线上.(1)求抛物线的解析式;(2)小明探究点D位置时发现:如图1,点D在第一象限内的抛物线上,连接BD,CD,△BCD面积存在最大值,请帮助小明求出△BCD面积的最大值;(3)小明进一步探究点D位置时发现:如图2,点D在抛物线上移动,连接CD,存在∠DCB=∠ABC,请帮助小明求出∠DCB=∠ABC时点D的坐标.14(2024·广东深圳·二模)如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与轴交于A,B 点,与y轴交于点C0,3,点B的坐标为3,0,点P是抛物线上一个动点.(1)求二次函数解析式;(2)若P点在第一象限运动,当P运动到什么位置时,△BPC的面积最大?请求出点P的坐标和△BPC面积的最大值;(3)连接PO,PC,并把△POC沿CO翻折,那么是否存在点P,使四边形POP C为菱形;若不存在,请说明理由.15(2024·湖北·模拟预测)如图,抛物线y=x-12+k与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C0,-3.设P点在抛物线上运动,横坐标为m.(1)求此抛物线的解析式;(2)当P点位于第四象限时,求△BCP面积的最大值,并求出此时P点坐标;(3)设此抛物线在点C与点P之间部分(含点C和点P)最高点与最低点的纵坐标之差为h.① 求h关于m的函数解析式,并写出自变量m的取值范围;② 根据h的不同取值,试探索点P的个数情况.16(22-23九年级下·重庆·阶段练习)抛物线y=ax²+bx+5经过点A1,0和点B5,0.该抛物线与直线y=12x+5相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.(1)求该抛物线所对应的函数解析式;(2)连接PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;(3)连接PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.17(2024·江苏宿迁·一模)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别相交于A、B两点,与y轴相交于点C,已知点A的坐标为(-1,0),点B的坐标为(3,0).(1)求出这条抛物线的函数表达式;(2)如图2,点D是第一象限内该抛物线上一动点,过点D作直线l∥y轴,直线l与△ABD的外接圆相交于点E.①仅用无刻度直尺找出图2中△ABD外接圆的圆心P.②连接BC、CE,BC与直线DE的交点记为Q,如图3,设△CQE的面积为S,在点D运动的过程中,S是否存在最大值?如果存在,请求出S的最大值;如果不存在,请说明理由.18(2024·新疆乌鲁木齐·一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m 从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C,点P与直线m同时停止运动,设运动时间为t秒t>0.(1)AH=,EF=(用含t的式子表示).(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.19(2024·重庆·模拟预测)如图,在平面直角坐标系中,抛物线y=ax2+bx+c过点(3,-4),交x轴于点A(-1,0),B两点,交y轴于点C(0,2).(1)求抛物线的表达式;(2)连接AC ,BC ,M 为线段AB 上一动点,过点M 作MD ∥BC 交直线AC 于点D ,连接MC ,求△MDC 面积的最大值及此时M 点的坐标;(3)在(2)中△MDC 面积取得最大值的条件下,将该抛物线沿射线BC 方向平移2个单位长度,P 是平移后的抛物线上一动点,连接CP ,当∠PCM 与△OBC 的一个内角相等时,请直接写出所有符合条件的点P 的坐标.20(2024·湖南衡阳·一模)如图,已知抛物线y =ax 2+bx +c 经过A 1,0 ,B -3,0 ,C 0,3 三点.(1)求抛物线的解析式;(2)若点D 为第二象限内抛物线上一动点,求△BCD 面积的最大值;(3)设点P 为抛物线的对称轴上的一个动点,求使△BPC 为直角三角形的点P 的坐标.21(2024·甘肃天水·一模)如图,在平面直角坐标系中,开口向下的抛物线与x 轴交于A ,B 两点,D 是抛物线的顶点.O 为坐标原点.A ,B 两点的横坐标分别是方程x 2-4x -12=0的两根,且cos ∠DAB =22.(1)求抛物线的函数解析式;(2)作AC ⊥AD ,AC 交抛物线于点C ,求点C 的坐标及直线AC 的函数解析式;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在一点P ,使△APC 的面积最大?如果存在,请求出点P 的坐标和△APC 的最大面积;如果不存在,请说明理由.22(2024·山东聊城·一模)在平面直角坐标系中,抛物线y =ax 2+bx -3与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C .(1)求抛物线的解析式及顶点坐标;(2)若点P 为第四象限内抛物线上一点,当△PBC 面积最大时,求点P 的坐标;(3)若点P 为抛物线上一点,点Q 是线段BC 上一点(点Q 不与两端点重合),是否存在以P 、Q 、O 为顶点的三角形是等腰直角三角形,若存在,请直接写出满足条件的点P 的坐标;若不存在,请说明理由.23(2024·吉林长春·一模)如图,在平面直角坐标系中,直线y =x +2分别交x 轴、y 轴于A 、B 两点,过点C 2,2 作x 轴垂线,垂足为D ,连接BC .现有动点P 、Q 同时从A 点出发,分别沿AB 、AD 向终点B 和终点D 运动,若点P 的运动速度为每秒2个单位长度,点Q 的运动速度为每秒2个单位长度.设运动的时间为t 秒.(1)求A、B两点的坐标;(2)当CQ∥AB时,t=;(3)设△CPQ的面积为y,写出y与t的函数关系式,并求△CPQ面积的最大值;(4)当△CPQ为轴对称图形时,直接写出t的值.24(2023·湖南娄底·中考真题)如图,抛物线y=x2+bx+c过点A-1,0,交y轴于点C.、点B5,0(1)求b,c的值.(2)点P x0,y0是抛物线上的动点0<x0<5①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.25(2024·河南安阳·模拟预测)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与抛物线y=-x2+x-1的形状相同,且与x轴交于点-1,0.直线y=kx+2分别与x轴、y轴交于点A,B,和4,0与y=ax2+bx+c于点C,D(点C在点D的左侧).(1)求抛物线的解析式;(2)点P是直线y=kx+2上方抛物线上的任意一点,当k=2时,求△PCD面积的最大值;(3)若抛物线y=ax2+bx+c与线段AB有公共点,结合函数图象请直接写出k的取值范围.26(2024·湖南长沙·一模)如图,抛物线y=x2-bx+c与x轴交于A-1,0两点,与y轴交于,B m,0点C0,-3,顶点为D,直线BD交y轴于点E.(1)求抛物线的解析式.(2)设点P为线段BD上一点(点P不与B,D两点重合),过点P作x轴的垂线与抛物线交于点F,连接DF,BF,求△BDF面积的最大值.(3)连接CD,在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.27(2024·江西萍乡·一模)如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A3,0,连接AC,BC.,C0,3(1)求抛物线的函数解析式;(2)在抛物线的对称轴上找一点P,使得以A、D、P为顶点的三角形与△OBC相似,求出点P的坐标;(3)若点M是抛物线上的一个动点,且位于第一象限内,连接MC,MA.设△ACM的面积为S,试求S的最大值.28(2024·四川广元·二模)如图1,抛物线y=ax²+bx+c与x轴交于A,B两点,且点B的坐标为5,0,与y轴交于点C,该抛物线的顶点坐标为(3,-4).(1)求抛物线和直线BC的解析式.(2)在抛物线上是否存在点M,使得△BCM是以BC为底边的等腰三角形?若存在,求出所有点M的坐标;若不存在,请说明理由.(3)如图2,以点B 为圆心,画半径为2的圆,点P 为⊙B 上的一个动点,连接AC ,求△ACP 面积的最大值.29(2023·山东青岛·中考真题)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,AB =10cm ,BD =45cm .动点P 从点A 出发,沿AB 方向匀速运动,速度为1cm/s ;同时,动点Q 从点A 出发,沿AD 方向匀速运动,速度为2cm/s .以AP ,AQ 为邻边的平行四边形APMQ 的边PM 与AC 交于点E .设运动时间为t s 0<t ≤5 ,解答下列问题:(1)当点M 在BD 上时,求t 的值;(2)连接BE .设△PEB 的面积为S cm 2 ,求S 与t 的函数关系式和S 的最大值;(3)是否存在某一时刻t ,使点B 在∠PEC 的平分线上?若存在,求出t 的值;若不存在,请说明理由.30(2023·湖南怀化·中考真题)如图一所示,在平面直角坐标系中,抛物线y =ax 2+bx -8与x 轴交于A (-4,0)、B (2,0)两点,与y 轴交于点C .(1)求抛物线的函数表达式及顶点坐标;(2)点P 为第三象限内抛物线上一点,作直线AC ,连接PA 、PC ,求△PAC 面积的最大值及此时点P 的坐标;(3)设直线l 1:y =kx +k -354交抛物线于点M 、N ,求证:无论k 为何值,平行于x 轴的直线l 2:y =-374上总存在一点E ,使得∠MEN 为直角.31(2024·海南省直辖县级单位·一模)如图,已知抛物线y =ax 2+2x +c a ≠0 ,与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C ,E 为抛物线的顶点.图1图2(1)求该抛物线的函数表达式;(2)如图1,点P 是第一象限内抛物线上一动点,连接PC 、PB 、BC ,设点P 的横坐标为t .①当t 为何值时,△PBC 的面积最大?并求出最大面积;②当t 为何值时,△PBC 是直角三角形?(3)如图2,过E 作EF ⊥x 轴于F ,若M m ,0 是x 轴上一动点,N 是线段EF 上一点,若∠MNC =90°,请直接写出实数m 的取值范围.32(2024·四川成都·一模)如图,直线y =-x -4分别交x 轴,y 轴于A ,C 两点,点B 在x 轴正半轴上.抛物线y =15x 2+bx +c 过A ,B ,C 三点.(1)求抛物线的解析式;(2)过点B 作BD ∥AC 交y 轴于点D ,交抛物线于点F .若点P 为直线AC 下方抛物线上的一动点,连接PD 交AC 于点E ,连接EB ,求S △PEB 的最大值及最大值时点P 的坐标;(3)如图2,将原抛物线进行平移,使其顶点为原点,进而得到新抛物线,直线y =-2x 与新抛物线交于O ,G 两点,点H 是线段OG 的中点,过H 作直线RQ (不与OG 重合)与新抛物线交于R ,Q 两点,点R 在点Q 左侧.直线GR 与直线OQ 交于点T ,点T 是否在某条定直线上?若是,请求出该定直线的解析式,若不是,请说明理由.33(2024·江苏苏州·一模)如图,在平面直角坐标系中,抛物线y =ax 2-8ax +10a -1a <0 与x 轴的交点分别为A x 1,0 ,B x 2,0 ,其中(0<x 2<x 1),且AB =4,与y 轴的交点为C ,直线CD ∥x 轴,在x 轴上有一动点E t ,0 ,过点E 作直线l ⊥x 轴,与抛物线、直线CD 的交点分别为P 、Q .(1)求抛物线的解析式;(2)当0<t ≤8时,求△APC 面积的最大值;(3)当t >2时,是否存在点P ,使以C 、P 、Q 为顶点的三角形与△OBC 相似?若存在,求出此时t 的值;若不存在,请说明理由.题型02四边形面积最值问题1(2024·安徽阜阳·一模)如图,抛物线y =ax 2+bx +3与x 轴交于A -1,0 ,B 3,0 两点,与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点P ,使△PAC 的周长最小,求△PAC 的周长的最小值及此时点P 的坐标;(3)若M 为抛物线在第一象限内的一动点,求出四边形OCMB 的面积的最大值及此时点M 的坐标.2(2024·山东临沂·一模)如图,在平面直角坐标系中,抛物线y =-14x 2+bx +c 与x 轴交于点A (-2,0)和点B ,与y 轴交于点C (0,4),点P 是直线BC 上方的抛物线上一点(点P 不与点B ,C 重合),过点P 作PD ∥y 轴交直线BC 于点D .(1)求抛物线的函数表达式;(2)求线段PD 长的最大值;(3)连接CP ,BP ,请直接写出四边形ABPC 的面积最大值为.3(2024·山西运城·一模)综合与探究如图,抛物线y=ax2+bx-3a≠0与x轴交于A-1,0、B两点,与y轴交于点C,点D-2,9 2在抛物线上,点P是抛物线在第四象限内的一个动点,过点P作PQ∥y轴交直线BD于点Q,连接PA、PB、QA,设点P的横坐标为m.(1)求抛物线的函数表达式;(2)求四边形PAQB面积的最大值及此时点P的坐标;(3)若点M是抛物线上任意一点,是否存在点M,使得∠MAB=2∠ACO,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.4(2024·安徽合肥·一模)在平面直角坐标系中,点O是坐标原点.抛物线y=ax2+bx-3a≠0与x轴交于A,B两点,直线l:y=kx+2与抛物线交于A,C两点,且A-1,0,B3,0.(1)求a,b,k的值;(2)点M是线段OB上的动点,点N在x轴上,MN=2,且点N在M的左边.过点M作MP⊥x轴,交抛物线于点P.过点N作x轴的垂线,交抛物线于点Q,交直线l于点R.①当以P,Q,R,M为顶点的四边形是平行四边形时,求点M的坐标.②记以P,Q,R,M为顶点的四边形面积为S,求S的最大值.5(2024·安徽蚌埠·一模)如图1,已知直线y=-x+5与坐标轴相交于A、B,点C坐标是-1,0,抛物线经过A、B、C三点.点P是抛物线上的一点,过点P作y轴的平行线,与直线AB交于点D,与x轴相交于点F.(1)求抛物线的解析式;(2)当点P在第一象限时,连接CP交OA于点E,连接EF,如图2所示;①求AE+DF的值;②设四边形AEFB的面积为S,则点P在运动过程中是否存在面积S的最大值,若存在,请求出此时点P的坐标;若不存在,请说明理由.6(2024·安徽马鞍山·一模)如图,过原点的二次函数y=ax2+bx的图象与x轴正半轴交于点A,经过点A的直线与该函数交于B1,-3,与y轴交于点C0,-4.(1)分别求此二次函数与直线AB的解析式.(2)点P是第四象限内二次函数图象上的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为t.①当PD=12OC时,求t的值;②当点P在直线AB下方时,连接OP,过点B作BQ⊥x轴于点Q,BQ与OP交于点F,连接DF,求四边形FQED面积的最大值.7(2024·山东济南·一模)如图,直线y=-12x+3交y轴于点A,交x轴于点C,抛物线y=-14x2+bx+c经过点A,点C,且交x轴于另一点B.(1)求抛物线的解析式;(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;(3)将线段OA绕x轴上的动点P m,0顺时针旋转90°得到线段O A ,若线段O A 与抛物线只有一个公共点,请结合函数图象,求m的取值范围.8(2024·四川广元·二模)如图,二次函数y=ax2+bx+c的图象与x轴交于原点O和点A4,0,经过点A的直线与该函数图象交于另一点B1,3,与y轴交于点C.(1)求直线AB的函数解析式及点C的坐标.(2)点P是抛物线上位于直线AB上方的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,过点B作BF⊥x轴于点F,连接OP,与BF交于点G,连接DG.求四边形GDEF面积的最大值.(3)抛物线上是否存在这样的点Q,使得∠BOQ=45°?若存在,请求出点Q的坐标;若不存在,请说明理由.9(2024·广东珠海·一模)如图,抛物线y=-x2+3x+4和直线y=x+1交于A-1,0点,点B,B3,4在直线x=3上,直线x=3与x轴交于点C.(1)求∠BAC的度数.(2)点P从点A出发,以每秒2个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒t>0.以PQ为边作矩形PQNM,使点N在直线x=3上.①当t为何值时,矩形PQNM的面积最小?并求出最小面积;②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.10(2024·安徽宿州·二模)如图1,抛物线y=ax2+bx-3(a,b是常数且a>0)与x轴交于点A-1,0和点B(点B在点A的右侧),点D是抛物线的顶点,CD是抛物线的对称轴且交x轴于点C1,0.(1)求a,b的值;(2)点P是抛物线上一点且位于点A和点D之间.(i)如图2,连接AP,DP,BD,求四边形ABDP面积的最大值;(ii)如图3,连接AP并延长交CD延长线于点Q,连接BP交CD于点E,求CE+CQ的值.11(2024·安徽·二模)如图1,在平面直角坐标系中,抛物线y=ax2+bx-4交x轴于点A-1,0,B4,0,交y轴于点C,点M在该抛物线上,横坐标为m,将该抛物线M,C两点之间(包括M,C两点)的部分记为图象W.(1)求抛物线的解析式;(2)图象W的最大值与最小值的差为4时,求m的值;(3)如图2,若点M位于BC下方,过点A作AE∥BC交拋物线于点E,点D为直线AE上一动点,连接CM, CD,BM,BD,求四边形CDBM面积的最大值及此时点M的坐标.12(2024·四川广安·二模)如图,抛物线y=-x2+bx+c交x轴于A-4,0.,B两点,交y轴于点C0,4(1)求抛物线的函数解析式.(2)点D在线段OA上运动,过点D作x轴的垂线,与AC交于点Q,与抛物线交于点P,连接AP、CP,求四边形AOCP的面积的最大值.(3)在抛物线的对称轴上是否存在点M,使得以点A、C、M为顶点的三角形是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.13(23-24九年级上·重庆渝北·期末)二次函数y=ax2+bx+4经过点A-1,0,点C,点D,点B4,0分别二次函数与y轴的交点和顶点,点M为二次函数图象上第一象限内的一个动点.(1)求二次函数的解析式;(2)如图1,连接BC ,过点A 作BC 的平行线交二次函数于点E ,连接CM ,BM ,BE ,CE .求四边形CMBE 面积的最大值以及此时点M 的坐标;(3)如图2,过点M 作MN ∥y 轴,交BC 于点N (点M 不与点D 重合),过点D 作DH ∥y 轴,交BC 于点H ,当DM =HN 时,直接写出点M 的坐标.题型03面积比最值问题14(2024·安徽合肥·一模)在平面直角坐标系xOy 中,已知抛物线y =a x +1 x -4 与x 轴交于A 、 B 两点,与y 轴交于点C 0,-2 .(1)求a 的值;(2)点D 为第四象限抛物线上一点①求△BCD 的面积最大值②连接AD ,BC 交于点E ,连接BD ,记△BDE 的面积为S 1,△ABE 的面积为S 2,求S 1S 2的最大值;15(2023·四川遂宁·中考真题)在平面直角坐标系中,O 为坐标原点,抛物线y =14x 2+bx +c 经过点O (0,0),对称轴过点B (2,0),直线l 过点C 2,-2 ,且垂直于y 轴.过点B 的直线l 1交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线l 1下方的抛物线上一动点,连接PQ 、PO ,其中PO 交l 1于点E ,设△OQE 的面积为S 1,△PQE 的面积为S 2.求S2S 1的最大值.16(2024·湖北省直辖县级单位·一模)抛物线y =x 2-4x 与直线y =x 交于原点O 和点B ,与x 轴交于另一点A ,顶点为D .(1)求出点B 和点D 的坐标;(2)如图①,连接OD ,P 为x 轴的负半轴上的一点,当tan ∠PDO =12时,求点P 的坐标;(3)如图②,M 是点B 关于抛物线的对称轴的对称点,Q 是抛物线上的动点,它的横坐标为m 0<m <5 ,连接MQ ,BQ ,MQ 与直线OB 交于点E ,设△BEQ 和△BEM 的面积分别为S 1和S 2,求S1S 2的最大值.17(2023·湖南永州·中考真题)如图1,抛物线y =ax 2+bx +c (a ,b ,c 为常数)经过点F 0,5 ,顶点坐标为2,9 ,点P x 1,y 1 为抛物线上的动点,PH ⊥x 轴于H ,且x 1≥52.(1)求抛物线的表达式;(2)如图1,直线OP :y =y 1x 1x 交BF 于点G ,求S △BPG S △BOG的最大值;(3)如图2,四边形OBMF 为正方形,PA 交y 轴于点E ,BC 交FM 的延长线于C ,且BC ⊥BE ,PH =FC ,求点P 的横坐标.18(2024·四川南充·一模)抛物线y =-38x 2+bx +c b >0 与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C 0,3 ,抛物线对称轴为x =1,点P 是抛物线在第一象限上动点,连接CB ,PB .(1)求抛物线和直线BC 的解析式;(2)如图,连接PA ,交BC 于点M ,设△ABM 的面积为S 1,△PBM 的面积为S 2,求S 1S 2的最小值及此时点P的坐标.19(2024·湖北孝感·一模)如图1,已知抛物线y=ax2+bx+3与x轴交于点A-1,0,B3,0,与y轴交于点C,连接BC.(1)求a,b的值及直线BC的解析式;(2)如图1,点P是抛物线上位于直线BC上方的一点,连接AP交BC于点E,过P作PF⊥x轴于点F,交BC于点G,(ⅰ)若EP=EG,求点P的坐标,(ⅱ)连接CP,CA,记△PCE的面积为S1,△ACE的面积为S2,求S1S2的最大值;(3)如图2,将抛物线位于x轴下方面的部分不变,位于x轴上方面的部分关于x轴对称,得到新的图形,将直线BC向下平移n个单位,得到直线l,若直线l与新的图形有四个不同交点,请直接写出n的取值范围.题型04面积和最值问题1(2024·吉林长春·一模)在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于点A(-1,0)、B(3,0),交y轴于点C,连结AC、BC.点D在该抛物线上,过点D作DE∥AC,交直线BC于点E,连结AD、AE、BD.设点D横坐标为m(m>0),△DAE的面积为S1,△DBE的面积为S2.(1)求a,b的值;(2)设抛物线上D、B两个点和它们之间的部分为图象G,当图象G的最高点的纵坐标与m无关时,求m的取值范围;(3)当点D在第一象限时,求S1+S2的最大值;(4)当S1:S2=2:1时,直接写出m的值.题型05面积差最值问题1(2024·安徽合肥·一模)如图1,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=。
2023年挑战压轴题中考物理强化训练(含解析)

2023年挑战压轴题中考物理强化训练(含解析)介绍在2023年的中考物理试卷中,挑战压轴题一直是考生们的心头之患。
这些题目通常是难度较高,需要对物理知识和解题方法有很高的掌握能力。
本篇文档将为您提供2023年中考物理压轴题的强化训练,包括题目和解析。
题目一: 物体自由落体问题问题描述:一个物体从悬崖上自由下落,下落过程中加速度为重力加速度的一半。
已知物体从悬崖顶部下落到地面用时4秒,求该悬崖的高度。
解析:首先我们需要知道物体在自由落体的情况下,下落过程中的速度会逐渐增加,而加速度则一直等于重力加速度。
根据这个特点,我们可以通过运用物理公式来解决这个问题。
设物体自由落体的加速度为a,重力加速度为g(g约等于9.8 m/s²),物体从悬崖顶部下落的高度为h。
根据物理知识我们知道,物体自由落体的速度满足以下关系式:v = gt,其中v为物体在t时间内的速度。
又因为加速度a等于重力加速度的一半,所以加速度为:a = g/2。
根据题目中的信息,我们可以列出以下方程:1.h = 1/2 * at²(1/2at²为自由落体的位移公式)2.v = gt = 1/2 * g/2 * t = 1/4 * gt(t时间内的速度公式)我们已知t = 4秒,v = 1/4 * gt。
又因为物体从悬崖顶部下落到地面用时4秒,所以物体在t时间内下落的位移就是h。
将已知的信息代入方程1和方程2中,我们可以得到以下两个方程:1.h = 1/2 * g/2 * t² = 1/8 * gt²2.h = v * t = 1/4 * gt * 4 = gt由于两个方程都等于h,所以我们可以将它们相等,得到以下方程:1/8 * gt² = gt将方程中的t消去,我们可以得到以下方程:1/8 * g * t = g将t = 4秒代入方程中,我们可以求解得到答案:1/8 * 9.8 m/s² * 4秒 = 9.8 m所以,该悬崖的高度为9.8米。
中考数学压轴题:二次函数中的面积问题(含答案)

学生/课程年级日期学科时段课型数学授课教师核心内容二次函数中求面积最值,图形平移或折叠面积问题1.会利用函数的图象性质来研究几何图形的面积最值问题;教学目标重、难点2.掌握几种求图形面积的常见解题方法与技巧,如:割补法、平行等积变换法等。
3.掌握图形平移或折叠变换过程中找等量关系列函数解析式求图形面积问题的一般方法.割补法求三角形面积,动态问题一般解题思路。
了解学生的学习情况S△ = a h或S△ = a d (d表示已知点到直线的距离)以动点作垂直(平行)x轴的直线,即铅垂高,再分别过点A,C作PF的高,即和为水平宽。
S△ = ×水平宽×铅垂高如下图:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.如图,AD∥BC中,AC与BD交点O,则S△ABC = S△DBC,S△AOB = S△COD2如图,在平面直角坐标系中,抛物线y=mx -8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x ,10),C(x ,0),且x -x =4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线,直线AD2 2 1的交点分别为P,Q.(1)求抛物线的解析式;(2)当0<t≤8时,求△APC面积的最大值.图形面积的求法常见有三种,分别是:(1)_______________________________(2)_______________________________(3)_______________________________[学有所获答案] (1)直接公式求法 割补法 平行线等积变换法(2)(3) 2 如图,已知抛物线y =x +bx +c 与 轴交于A ,B 两点(点A 在点B 的左侧)与 轴交于点C (0,-3),对称轴是直线x=1,直线BC 与抛物线的对称轴交于点D ,点E 为y 轴上一动点,CE 的垂直平分线交抛物线于P ,Q 两点(点P 在第三象限)(1)求抛物线的函数表达式和直线BC 的函数表达式;(2)当△CDE 是直角三角形,且∠CDE =90°时,求出点P 的坐标;(3)当△PBC 的面积为 时,求点E 的坐标.2 如图,已知抛物线y = x +ax +4a 与x 轴交于点A ,B ,与y 轴负半轴交于点C 且OB =OC ,点P 为抛物线上的一个动点,且点P 位于x 轴下方,点P 与点C 不重合.(1)求该抛物线的解析式;(2)若△PAC 的面积为 ,求点P 的坐标;(3)若以A ,B ,C ,P 为顶点的四边形面积记作S ,则S 取何值时,对应的点P 有且只有2个?将()的图像如何平移到的图像。
中考物理压轴题专题训练(含答案解析)

中考物理中高档压轴题专题训练1、为了将放置在水平地面上、重G=100 N 的重物提升到高处。
小明同学设计了图24(甲)所示的滑轮组装置。
当小明用图24(乙)所示随时间变化的竖直向下拉力F 拉绳时,重物的速度υ和上升的高度h 随时间t 变化的关系图像分别如图24(丙)和(丁)所示。
若重物与地面的接触面积S=5×10-2 m 2,不计摩擦,绳对滑轮的拉力方向均可看成在竖直方向。
求:(1)在2~3s 内,拉力F 的功率P 及滑轮组的机械效率η。
(2)在1~2s 内,拉力F 做的功W 。
(3)在0~1s 内,重物对地面的压强p 。
2、如图甲所示,是某工厂的水平传送带上的产品运输及计数装置示意图。
其中,电源电压为3V ,定值电阻R 0的阻值为200Ω ;S 为激光光源,能发射一条粗细忽略不计的光线;R 为光敏电阻,t /sF /N乙10 5030 20 40 t /sυ/(m/s )丙1.252.50 2.50 t /sh /m丁1.253.75 FG当有光照射时,其阻值较小,无光照射时,其阻值较大。
水平传送带上的产品均是密度ρ=2.5 x 103kg/m3的相同正方体。
当水平传送带上的产品和传送带一起以速度v =0.5m/s匀速通过S与R之间时,射向光敏电阻的光线被产品挡住,光线始终与正方体靠近光源一侧的表面垂直,通过电压表测出光敏电阻R两端电压随时间变化的规律如图乙所示(g = 10N/kg)。
则::①定值电阻Ro消耗的最大功率是多少?②水平传送带对每个产品的支持力为多少?3、家庭室内装修要用到某种液体乙烯材料和三混粉,工人师傅使用加热与搅拌为一体的用电器,下图是该用电器的工作原理图。
先在室温下把液体乙烯材料放入容器中,温控旋转开关接ab开始加热,发光二极管正常发光,当液体温度达到70℃;温控旋转开关自动接cd,发光二极管熄灭,电动机起动,再倒入三混粉在容器中保温搅拌,搅拌均匀后,涂抹到墙壁上使之更加平滑牢固。
初中数学十大经典压轴题

初中数学十大经典压轴题选一、三角形面积等于水平宽与铅垂高乘积的一半如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.(1)求抛物线和直线AB的解析式;(2)点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;(3)在(2)条件下,是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.二.利用相似解决面积问题、等腰三角形的分类讨论已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).(1)求该抛物线的解析式;(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.三、直角三角形分类讨论问题、利用对称求最大值如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).(1)求该抛物线的解析式;(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标P;(3)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标.四、平行四边形的分类讨论如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,﹣4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.(1)求抛物线的解析式;(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F 为顶点的四边形是平行四边形?如果存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.五、重叠部分面积的求解1.已知抛物线y=﹣x2+bx﹣经过点A(7,6),且与x轴交于B、C两点(1)求b值及B、C两点的坐标;(2)若直线x=t与抛物线交于P,与线段AB交于点Q,试问当t为何值时,线段PQ 的长最长?最长是多少?(3)若点D是线段AB上任意一点,过点D作DE∥BC,交AC于点E设ADE的高AF的长为小x,以DE为折痕将△ADE翻折,所得的△A'DE与梯形DBCE重叠部分的面积记为y,当0<x<6时,求y与x的函数关系式;并求y的最大值.六、利用对称和平移变换求最小值的求法如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,﹣3),B(4,﹣1).(1)若P(p,0)是x轴上的一个动点,则当p=_________时,△PAB的周长最短;(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=_________时,四边形ABDC的周长最短;(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=_________,n=_________(不必写解答过程);若不存在,请说明理由.七、利用平行解决面积等相等1.如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.(1)求线段OA所在直线的函数解析式; y=2x(2)设抛物线顶点M的横坐标为m,①用m的代数式表示点P的坐标;②当m为何值时,线段PB最短;(3)当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.八、图形旋转变换,面积转化、平行四边形的分类讨论已知抛物线y=x2﹣2x+a(a<0)与y轴相交于点A,顶点为M.直线y=x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.(1)试用含a的代数式分别表示点M与N的坐标;(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;(3)在抛物线y=x2﹣2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.九、图像运动问题、平移变换和分类讨论如图,已知直线y=﹣x+1交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.(1)请直接写出点C,D的坐标;(2)求抛物线的解析式;(3)若正方形以每秒个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;(4)在(3)的条件下,抛物线与正方形一起平移,同时D停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.十、图形运动、分类讨论问题如图,在平面直角坐标系中,直角梯形ABCO的边OC落在x轴的正半轴上,且AB∥OC,BC⊥OC,AB=4,BC=6,OC=8.正方形ODEF的两边分别落在坐标轴上,且它的面积等于直角梯形ABCO面积.将正方形ODEF沿x轴的正半轴平行移动,设它与直角梯形ABCO的重叠部分面积为S.(1)分析与计算:求正方形ODEF的边长;(2)操作与求解:①正方形ODEF平行移动过程中,通过操作、观察,试判断S(S>0)的变化情况是;A、逐渐增大B、逐渐减少C、先增大后减少D、先减少后增大②当正方形ODEF顶点O移动到点C时,求S的值;(3)探究与归纳:设正方形ODEF的顶点O向右移动的距离为x,求重叠部分面积S与x的函数关系式.。
2020-2021中考物理压轴题专题复习—质量和密度问题的综合含答案解析

一、初中物理质量和密度问题1.体积和质量都相等的铝球、铁球和铅球密度分别是32.7g cm ρ=铝、37.9g cm ρ=铁、311.3g cm ρ=铅,下列说法正确的是()A .若铝球是空心的,则铁球和铅球一定是空心的B .若铁球是实心的,则铝球和铅球一定是空心的C .若铅球是空心的,则铁球和铝球一定是空心的D .三个球都可能是实心的 【答案】A 【解析】 【分析】 【详解】由题意可知,铝、铁、铅的密度关系为ρρρ>>铅铁铝由密度公式的变形式mV ρ=可知,相同质量铝球、铁球和铅球的体积关系为V V V >>铝铅铁又因三球的体积相等,所以,铅球和铁球一定是空心的,铝球可能是实心,也可能是空心的,故BCD 错误;若铝球是空心的,则铁球和铅球一定是空心的,故A 正确。
故选A 。
2.小明利用天平和量杯测量某种液体的密度,得到的数据如下表,根据数据绘出的图象如图所示。
则量杯的质量与液体的密度是 液体与量杯的质量 m /g40 60 80 100 液体的体积V /cm 320406080A .20g, 1.25×103kg/m 3B .20g, 1.0×103kg/m 3C .60g, 1.0×103kg/m 3D .20g, 0.8×103kg/m 3【答案】B 【解析】 【详解】观察图象可知:当体积为0时质量是20g ,所以烧杯质量为20g ;当体积为60cm 3时质量为80g ,液体质量为80g-20g=60g ;即:m V ρ= =360g 60cm=1g/cm 3=1.0×103kg/m 3;故选B 。
3.在“用托盘天平称物体的质量”的实验中,下列操作错误的是( ) A .使用天平时,应将天平放在水平桌面上B .调节横梁平衡时,应先将游码移至标尺左端的零刻度线处C .称量时右盘应放置待称量的物体,左盘放置砝码D .观察到指针在分度盘中线处,表明横梁已平衡 【答案】C 【解析】 【分析】 【详解】A .使用天平时,应将天平放在水平桌面上.故A 说法正确.B .在调节横梁平衡时,首先要将游码移到标尺左端的零刻线处.故B 的说法正确.C .称量物体时,要将物体放在左盘里,用镊子在右盘里加减砝码移动游码.故C 的说法错误.D .横梁平衡的标志有两个:指针指在分度盘的中线处;或者指针偏离分度盘中线的幅度相等.指针在分度盘中线处,表明横梁已平衡,故D 的说法正确. 故选C .4.如图所示,a 、b 是两种物质的质量与体积的关系图像,分别用a 、b 两种物质制成体积相等的甲、乙两实心物体,浸没在水中,松手稳定后( )A .乙漂浮,甲受到的浮力大B .甲漂浮,甲受到的浮力小C .乙下沉,乙的密度大于水D .将甲、乙两物体绑在一起放入水中,将会下沉 【答案】A 【解析】 【分析】 【详解】由图可知:甲物体的密度333a a 3a 3g =1.5g/cm =1.510kg/m 2cmm V ρ==⨯ 乙物体的密度333b b 3b 1.5g =0.5g/cm =0.510kg/m 3cmm V ρ==⨯ 体积相等的甲、乙两实心物体,浸没在水中,由于a b ρρρ水>>,则甲、乙两实心物体在水中稳定后甲下沉,乙漂浮;所以V V 排甲排乙>,根据F gV ρ=浮水排可知:F F 浮甲浮乙>;故A 符合题意,B 、C 不符合题意;当将体积相等的甲、乙捆在一起后,设每一个的体积为V ,则两物体的重力331a b 210kg/m G gV gV gV ρρ=+=⨯⨯两物体所受浮力3312210kg/m F g V gV ρ=⨯=⨯⨯水则11G F =,故将甲、乙两物体绑在一起放入水中,将会悬浮,故D 不符合题意。
中考数学压轴题100题精选[含答案解析]
![中考数学压轴题100题精选[含答案解析]](https://img.taocdn.com/s3/m/26c587a408a1284ac8504370.png)
中考数学压轴题100题精选【含答案】【001】如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【002】如图16,在Rt △ABC 中,∠C=90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB-BC-CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成 为直角梯形?若能,求t 的值.若不能,请说明理由;(4)当DE经过点C 时,请直接写出t的值.【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。
(完整)中考复习专题—二次函数压轴题

(完整)中考复习专题—二次函数压轴题中考复习专题(七)--二次函数压轴题专训题型一:面积问题【例1】(2009湖南益阳)如图2,抛物线顶点坐标为点C (1,4),交x轴于点4(3, 0),交y轴于点8.(1)求抛物线和直线AB的解析式;(2)求ACAB的铅垂高CD及S;△鼐,若存在,求出P点△CAB△CAB【变式练习】1。
(2009广东省深圳市)如图,在直角坐标系中,点A的坐标为(一2, 0),连结OA,将线段OA绕原点。
顺时针旋转120°,得到线段OB.(1)求点8的坐标;(2)求经过A、0、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使^BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么4PAB是否有最大面积?若有,求出此时P点的坐标及4PAB 的最大面积;若没有,请说明理由.2。
(2010绵阳)如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(—4, 0), B (2,0),与y 轴交(完整)中考复习专题一二次函数压轴题于点C,顶点为D. E (1, 2)为线段BC的中点,BC的垂直平分线与X轴、y轴分别交于F、G.3. (2012铜仁)如图,已知:直线y =-x + 3交x轴于点A,交y轴于点8,抛物线y=ax2+bx+c经过A、B、到1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(-1,0),在直线y = -x + 3上有一点「,使AABO与AADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点£,使AADE的面积等于四边形APCE的面积?如果存在,请求出点£的坐标;如果不存在,请说明理由.题型二:构造直角三角形【例2】(2010山东聊城)如图,已知抛物线y=ax2+bx+c (a/0)的对称轴为x = 1,且抛物线经过A (―1, 0)、C (0, -3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x = 1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P为抛物线的对称轴x=1上的一动点,求使NPCB=90 的点P的坐标.第.3题图【变式练习】1.(2012广州)如图,抛物线y二-卫丁-金丁十力与x轴交于A、B两点(点A在点B的左侧),与y轴交于点8 4C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当4ACD的面积等于4ACB的面积时,求点D的坐标;(3)若直线I过点E(4, 0),M为直线I上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时, 求直线I的解析式.2.(2009成都)在平面直角坐标系xOy中,已知抛物线y=〃(x + l)2+c(” > 0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为y = kx-3,与x轴的交点为N,且COSNBCO3<1010(1)求此抛物线的函数表达式;(2)在此抛物线上是否存在异于点C的点P,使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形?若存在,求出点「的坐标:若不存在,请说明理由;⑶过点人作x轴的垂线,交直线MC于点。
二次函数铅垂高演练(答案、解析、总结)教学内容

二次函数铅垂高如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结P A ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆; (3)是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.例1解:(1)设抛物线的解析式为:4)1(21+-=x a y ··········································· 1分把A (3,0)代入解析式求得1-=a所以324)1(221++-=+--=x x x y ············································· 3分设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( ··································· 4分 把)0,3(A ,)3,0(B 代入b kx y +=2中 解得:3,1=-=b k所以32+-=x y ·········································································· 6分 (2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2 所以CD =4-2=2 ········································································· 8分图12-2xC OyABD 1 132321=⨯⨯=∆CAB S (平方单位) ··················································· 10分 (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△P AB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-= ······················ 12分 由S △P AB =89S △CAB 得:389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中, 解得P 点坐标为)415,23( ······························································ 14分总结:求不规则三角形面积时不妨利用铅垂高。
中考数学压轴题突破:铅锤法求二次函数面积

一、引言在中学生的学习生涯中,中考数学一直是备受关注的科目之一。
其中,二次函数是数学教学中的重要内容,而求二次函数面积更是中考数学中的一大难点。
然而,通过铅锤法求二次函数面积,可以帮助学生们更好地掌握这一难题。
本文将从深度和广度两方面展开讨论,帮助读者全面了解铅锤法求二次函数面积,在中考数学中取得突破。
二、铅锤法求解二次函数面积的基本原理铅锤法求解二次函数面积是一种通过几何实例来帮助学生理解二次函数的面积计算方法。
在求解二次函数面积时,首先可以将二次函数图像与x轴围成的图形,分割成若干个几何形状,如梯形、矩形等。
通过对这些几何形状进行面积计算,并进行累加,就可以得到二次函数图像与x轴围成的总面积。
这种方法能够直观地帮助学生理解二次函数的面积计算过程,从而提高他们的数学认知能力。
三、铅锤法求解二次函数面积的实际应用铅锤法求解二次函数面积不仅仅是一种理论计算方法,更适用于实际问题的求解。
当我们需要计算某个二次函数所表示的曲线与x轴围成的面积时,可以通过铅锤法将曲线分割成若干个几何形状,再进行面积计算,并进行累加,最终得到准确的面积结果。
这种方法在实际问题的求解中具有很强的适用性,且可以帮助学生将数学知识与实际问题相结合,提升解题能力。
四、铅锤法求解二次函数面积的个人观点与理解个人认为,铅锤法求解二次函数面积是一种非常有效的教学方法。
通过实际创造性的几何分割和面积累加,学生可以更直观地理解二次函数的面积计算方法,提高数学学习的趣味性和有效性。
在实际教学中,教师可以通过丰富的示例和实际问题,引导学生灵活运用铅锤法求解二次函数面积,从而提高他们的数学学习能力和解题思维。
五、总结与回顾本文从深度和广度两方面介绍了铅锤法求解二次函数面积的基本原理、实际应用和个人观点与理解。
我们可以通过铅锤法,帮助学生更好地理解和掌握二次函数面积的计算方法,提高他们的数学学习能力。
在中考数学的备战中,这一方法能够帮助学生更好地应对二次函数面积题型,取得更好的成绩。
专题 二次函数压轴题-线段周长面积最大值(知识解读)-中考数学(全国通用)

专题01 线段周长面积最大值(知识解读)【专题说明】从近几年的各地中考试卷来看,求线段、周长面积的最大问题在压轴题中比较常见,而且通常与二次函数相结合。
这个专题为同学们介绍解题方法,供同学们参考。
【方法点拨】考点1:线段、周长最大问题考点2 :面积最大问题 (1)铅锤法铅锤高水平宽⨯=21S(2)面积方法如图1,同底等高三角形的面积相等.平行线间的距离处处相等.如图2,同底三角形的面积比等于高的比.如图3,同高三角形的面积比等于底的比.如图1 如图2 如图3(3)利用相似性质利用相似图形,面积比等于相似比的平方。
【典例分析】【考点1 线段最大值问题】【典例1】(盘锦)如图,在平面直角坐标系中,抛物线y=ax2+bx+4交y轴于点C,交x 轴于A、B两点,A(﹣2,0),a+b=,点M是抛物线上的动点,点M在顶点和B点之间运动(不包括顶点和B点),ME∥y轴,交直线BC于点E.(1)求抛物线的解析式;(2)求线段ME的最大值;【变式1-1】(2022春•丰城市校级期末)如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.求线段PM的最大值;【变式1-2】(2021•柳南区校级模拟)如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.(1)求m的值及这个二次函数的关系式;(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为h,点P的横坐标为x.①求h与x之间的函数关系式,并写出自变量x的取值范围;②线段PE的长h是否存在最大值?若存在,求出它的最大值及此时的x值;若不存在,请说明理由?【典例2】(2022•澄海区模拟)如图,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,点A的坐标为(﹣1,0),点C坐标为(0,3),对称轴为x=1.点M为线段OB上的一个动点(不与两端点重合),过点M作PM⊥x轴,交抛物线于点P,交BC 于点Q.(1)求抛物线及直线BC的表达式;(2)过点P作PN⊥BC,垂足为点N.求线段PN的最大值;【变式2】(2022•广元)在平面直角坐标系中,直线y=﹣x﹣2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.(1)求a,b满足的关系式及c的值;(2)当a=1时,若点Q是直线AB下方抛物线上的一个动点,过点Q作QD⊥AB于点D,当QD的值最大时,求此时点Q的坐标及QD的最大值.【考点2 周长最大值问题】【典例3】(2022春•衡阳期中)如图,直线y=﹣x+3与x轴交于点A,与y轴交于点B,抛物线y=ax2+x+c经过A、B两点.(1)求二次函数解析式;(2)如图1,点E在线段AB上方的抛物线上运动(不与A、B重合),过点E作ED⊥AB,交AB于点D,作EF⊥AC,交AC于点F,交AB于点M,求△DEM的周长的最大值;【变式3】(2022春•北碚区校级期中)如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,一次函数y=﹣x﹣1交抛物线于A,D两点,其中点D(3,﹣4).(2)点G为抛物线上一点,且在线段BC上方,过点G作GH∥y轴交BC于H,交x 轴于点N,作GM⊥BC于点M,求△GHM周长的最大值;【考点3 面积最大值问题】【典例4】(2021秋•龙江县校级期末)综合与探究如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式,连接BC,并求出直线BC的解析式;(2)请在抛物线的对称轴上找一点P,使AP+PC的值最小,此时点P的坐标是(,);(3)点Q在第一象限的抛物线上,连接CQ,BQ,求出△BCQ面积的最大值.【变式4-1】(2022春•南岸区月考)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x 轴交于A(﹣1,0),B(3,0),交y轴于点C,且OC=3.(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;【变式4-2】(2022•东方二模)如图,抛物线y=x2+bx+c经过B(3,0)、C(0,﹣3)两点,与x轴的另一个交点为A,顶点为D.(1)求该抛物线的解析式;(2)点E为该抛物线上一动点(与点B、C不重合),当点E在直线BC的下方运动时,求△CBE的面积的最大值;【典例5】(聊城)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),点B(4,0),与y轴交于点C(0,8),连接BC.又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E.(1)求抛物线的表达式;(2)作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.【变式5】(2022•广东)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC 于点Q.(1)求该抛物线的解析式;(2)求△CPQ面积的最大值,并求此时P点坐标.专题01 线段周长面积最大值(知识解读)【专题说明】从近几年的各地中考试卷来看,求线段、周长面积的最大问题在压轴题中比较常见,而且通常与二次函数相结合。
中考数学(二次函数提高练习题)压轴题训练附详细答案

中考数学(二次函数提高练习题)压轴题训练附详细答案一、二次函数1.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=14x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.【答案】(1)抛物线的解析式为y=14x2﹣x+1.(2)点P的坐标为(2813,﹣1).(3)定点F的坐标为(2,1).【解析】分析:(1)由抛物线的顶点坐标为(2,0),可设抛物线的解析式为y=a(x-2)2,由抛物线过点(4,1),利用待定系数法即可求出抛物线的解析式;(2)联立直线AB与抛物线解析式成方程组,通过解方程组可求出点A、B的坐标,作点B关于直线l的对称点B′,连接AB′交直线l于点P,此时PA+PB取得最小值,根据点B的坐标可得出点B′的坐标,根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式,再利用一次函数图象上点的坐标特征即可求出点P的坐标;(3)由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,即可得出(1-12-12y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0,由m的任意性可得出关于x0、y0的方程组,解之即可求出顶点F的坐标.详解:(1)∵抛物线的顶点坐标为(2,0),设抛物线的解析式为y=a(x-2)2.∵该抛物线经过点(4,1),∴1=4a,解得:a=14,∴抛物线的解析式为y=14(x-2)2=14x2-x+1.(2)联立直线AB 与抛物线解析式成方程组,得:214114y x y x x ⎧⎪⎪⎨⎪-+⎪⎩==,解得:11114x y ⎧⎪⎨⎪⎩==,2241x y ⎧⎨⎩==, ∴点A 的坐标为(1,14),点B 的坐标为(4,1). 作点B 关于直线l 的对称点B′,连接AB′交直线l 于点P ,此时PA+PB 取得最小值(如图1所示).∵点B (4,1),直线l 为y=-1,∴点B′的坐标为(4,-3).设直线AB′的解析式为y=kx+b (k≠0),将A (1,14)、B′(4,-3)代入y=kx+b ,得: 1443k b k b ⎧+⎪⎨⎪+-⎩==,解得:131243k b ⎧-⎪⎪⎨⎪⎪⎩==, ∴直线AB′的解析式为y=-1312x+43, 当y=-1时,有-1312x+43=-1, 解得:x=2813, ∴点P 的坐标为(2813,-1). (3)∵点M 到直线l 的距离与点M 到点F 的距离总是相等,∴(m-x 0)2+(n-y 0)2=(n+1)2,∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1.∵M (m ,n )为抛物线上一动点,∴n=14m2-m+1,∴m2-2x0m+x02-2y0(14m2-m+1)+y02=2(14m2-m+1)+1,整理得:(1-12-12y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0.∵m为任意值,∴00220001110222220230yx yx y y⎧--⎪⎪-+⎨⎪+--⎪⎩===,∴021xy⎧⎨⎩==,∴定点F的坐标为(2,1).点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用两点之间线段最短找出点P的位置;(3)根据点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,找出关于x0、y0的方程组.2.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=12DE.①求点P的坐标;②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.【答案】(1)y=﹣x2﹣3x+4;(2)①P(﹣1,6),②存在,M(﹣1,11)或(﹣1,3﹣11)或(﹣1,﹣1)或(﹣1,132). 【解析】【分析】 (1)先根据已知求点A 的坐标,利用待定系数法求二次函数的解析式;(2)①先得AB 的解析式为:y=-2x+2,根据PD ⊥x 轴,设P (x ,-x 2-3x+4),则E (x ,-2x+2),根据PE=12DE ,列方程可得P 的坐标; ②先设点M 的坐标,根据两点距离公式可得AB ,AM ,BM 的长,分三种情况:△ABM 为直角三角形时,分别以A 、B 、M 为直角顶点时,利用勾股定理列方程可得点M 的坐标.【详解】解:(1)∵B (1,0),∴OB=1,∵OC=2OB=2,∴C (﹣2,0),Rt △ABC 中,tan ∠ABC=2,∴AC 2BC =, ∴AC 23=, ∴AC=6, ∴A (﹣2,6), 把A (﹣2,6)和B (1,0)代入y=﹣x 2+bx+c 得:42610b c b c --+=⎧⎨-++=⎩, 解得:34b c =-⎧⎨=⎩, ∴抛物线的解析式为:y=﹣x 2﹣3x+4;(2)①∵A (﹣2,6),B (1,0),∴AB 的解析式为:y=﹣2x+2,设P (x ,﹣x 2﹣3x+4),则E (x ,﹣2x+2),∵PE=12DE , ∴﹣x 2﹣3x+4﹣(﹣2x+2)=12(﹣2x+2), ∴x=-1或1(舍),∴P (﹣1,6);②∵M在直线PD上,且P(﹣1,6),设M(﹣1,y),∵B(1,0),A(﹣2,6)∴AM2=(﹣1+2)2+(y﹣6)2=1+(y﹣6)2,BM2=(1+1)2+y2=4+y2,AB2=(1+2)2+62=45,分三种情况:i)当∠AMB=90°时,有AM2+BM2=AB2,∴1+(y﹣6)2+4+y2=45,解得:y=3,∴M(﹣1,)或(﹣1,3ii)当∠ABM=90°时,有AB2+BM2=AM2,∴45+4+y2=1+(y﹣6)2,∴y=﹣1,∴M(﹣1,﹣1),iii)当∠BAM=90°时,有AM2+AB2=BM2,∴1+(y﹣6)2+45=4+y2,∴y=132,∴M(﹣1,132);综上所述,点M的坐标为:∴M(﹣1,)或(﹣1,3)或(﹣1,﹣1)或(﹣1,132).【点睛】此题是二次函数的综合题,考查了待定系数法求二次函数的解析式,铅直高度和勾股定理的运用,直角三角形的判定等知识.此题难度适中,解题的关键是注意方程思想与分类讨论思想的应用.3.(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=16-x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为172m.(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?【答案】(1)抛物线的函数关系式为y=16-x 2+2x+4,拱顶D 到地面OA 的距离为10 m ;(2)两排灯的水平距离最小是3.【解析】【详解】 试题分析:根据点B 和点C 在函数图象上,利用待定系数法求出b 和c 的值,从而得出函数解析式,根据解析式求出顶点坐标,得出最大值;根据题意得出车最外侧与地面OA 的交点为(2,0)(或(10,0)),然后求出当x=2或x=10时y 的值,与6进行比较大小,比6大就可以通过,比6小就不能通过;将y=8代入函数,得出x 的值,然后进行做差得出最小值.试题解析:(1)由题知点17(0,4),3,2B C ⎛⎫ ⎪⎝⎭在抛物线上 所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩,解得24b c =⎧⎨=⎩,所以21246y x x =-++ 所以,当62b x a =-=时,10t y =≦ 答:21246y x x =-++,拱顶D 到地面OA 的距离为10米 (2)由题知车最外侧与地面OA 的交点为(2,0)(或(10,0)) 当x=2或x=10时,2263y =>,所以可以通过 (3)令8y =,即212486x x -++=,可得212240x x -+=,解得12623,623x x =+=-1243x x -=答:两排灯的水平距离最小是3考点:二次函数的实际应用.4.如图,在平面直角坐标系中有抛物线y =a (x ﹣2)2﹣2和y =a (x ﹣h )2,抛物线y =a (x ﹣2)2﹣2经过原点,与x 轴正半轴交于点A ,与其对称轴交于点B ;点P 是抛物线y =a (x ﹣2)2﹣2上一动点,且点P 在x 轴下方,过点P 作x 轴的垂线交抛物线y =a (x ﹣h )2于点D ,过点D 作PD 的垂线交抛物线y =a (x ﹣h )2于点D ′(不与点D 重合),连接PD ′,设点P 的横坐标为m :(1)①直接写出a 的值;②直接写出抛物线y =a (x ﹣2)2﹣2的函数表达式的一般式;(2)当抛物线y =a (x ﹣h )2经过原点时,设△PDD ′与△OAB 重叠部分图形周长为L : ①求PD DD '的值; ②直接写出L 与m 之间的函数关系式;(3)当h 为何值时,存在点P ,使以点O 、A 、D 、D ′为顶点的四边形是菱形?直接写出h 的值.【答案】(1)①12;②y =212x ﹣2x ; (2)①1; ②L =2(22)(02)21(221)4(24)m m m π⎧+<⎪⎨+++<<⎪⎩…; (3)h =±3 【解析】【分析】(1)①将x =0,y =0代入y =a (x ﹣2)2﹣2中计算即可;②y =212x ﹣2x ; (2)将(0,0)代入y =a (x ﹣h )2中,可求得a =12,y =12x 2,待定系数法求OB 、AB 的解析式,由点P 的横坐标为m ,即可表示出相应线段求解;(3)以点O 、A 、D 、D ′为顶点的四边形是菱形,DD ′=OA ,可知点D 的纵坐标为2,再由AD =OA =4即可求出h 的值.【详解】解:(1)①将x =0,y =0代入y =a (x ﹣2)2﹣2中,得:0=a (0﹣2)2﹣2,解得:a =12; ②y =212x ﹣2x ;. (2)∵抛物线y =a (x ﹣h )2经过原点,a =12; ∴y =12x 2, ∴A (4,0),B (2,﹣2),易得:直线OB 解析式为:y =﹣x ,直线AB 解析式为:y =x ﹣4如图1,222111,2,,,(,0),(,),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ①221122,222PD m m m m DD m '⎛⎫=--== ⎪⎝⎭PD 2m 1DD 2m'∴== ②如图1,当0<m ≤2时,L =OE +EF +OF =2(22)m m m m ++=+,当2<m <4时,如图2,设PD ′交x 轴于G ,交AB 于H ,PD 交x 轴于E ,交AB 于F ,则222111,2,,,(,0),(,4),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,2211(4)23422PF m m m m m ⎛⎫=---=-+- ⎪⎝⎭, 2222322m m 22,PG m 22m FH PH PF ===-+-=-+ ∵DD ′∥EG EG PE DD PD '∴=,即:EG •PD =PE •DD ′,得:EG •(2m )=(2m ﹣12m 2)•2m ∴EG =2m ﹣12m 2,EF =4﹣m ∴L =EG +EF +FH +GH =EG +EF +PG221224222m m m m m ⎛⎫=-+-+-+ ⎪ ⎪⎝⎭221m (221)m 42+=-+++ 2(22)m(0m 2)21m (221)m 4(2m 4)2L ⎧+<⎪∴=⎨+-+++<<⎪⎩…; (3)如图3,∵OADD ′为菱形∴AD =AO =DD ′=4,∴PD =2,23PA =23h ∴=±【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,菱形的性质,抛物线的平移等,解题时要注意考虑分段函数表示方法.5.已知,抛物线y=x 2+2mx(m 为常数且m≠0).(1)判断该抛物线与x 轴的交点个数,并说明理由.(2)若点A (-n+5,0),B(n-1,0)在该抛物线上,点M 为抛物线的顶点,求△ABM 的面积.(3)若点(2,p),(3,g ),(4,r)均在该抛物线上,且p<g<r ,求m 的取值范围.【答案】(1)抛物线与x 轴有2个交点,理由见解析;(2)△ABM 的面积为8;(3)m 的取值范围m>-2.5【解析】【分析】(1)首先算出根的判别式b 2-4ac 的值,根据偶数次幂的非负性,判断该值一定大于0,从而根据抛物线与x 轴交点个数与根的判别式的关系即可得出结论;(2)根据抛物线的对称性及A,B 两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程,求解算出m 的值,进而求出抛物线的解析式,得出A,B,M 三点的坐标,根据三角形的面积计算方法,即可算出答案;(3)方法一(图象法):根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时,显然不符合题目条件;当对称轴在直线x=2的左边时,显然符合题目条件(如图2),从而列出不等式得出m 的取值范围;当对称轴在直线x=2和x=3之间时,满足3-(-m)>-m-2即可(如图3),再列出不等式得出m 的取值范围,综上所述,求出m 的取值范围;方法二(代数法):将三点的横坐标分贝代入抛物线的解析式,用含m 的式子表示出p,g,r ,再代入 p<g<r 即可列出关于m 的不等式组,求解即可。
部编数学九年级上册专题09铅锤线段最值及进阶(解析版)含答案

专题09 铅锤线段最值及进阶类型一求铅锤线段最值1.如图,抛物线y=ax2+bx+6(a≠0)经过A(12,52)和B(4,6)两点,点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;解:(1)∵15,22Aæöç÷èø、()4,6B在抛物线26y ax bx=++上,∴25116 222 61646ba bìæö=++ïç÷íèøï=++î,解得28 ab=ìí=-î,∴抛物线的解析式为2286y x x =-+.(2)设直线AB 的解析式为:y mx n =+,∵15,22A æöç÷èø、()4,6B 在直线y mx n =+上,∴152246m n m n ì+=ïíï+=î,解得12m n =ìí=î,∴直线AB 的解析式为2y x =+,设动点P 得坐标为(),2t t +,则C 点得坐标为()2,286t t t -+,∴()()2229492286294248PC t t t t t t æö=+--+=-+-=--+ç÷èø,∵20-<,∴当94t =时,当P 点坐标为917,44æöç÷èø,线段PC 有最大且为498.2.在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A 、B ,C ,已知A (﹣1,0),C (0,3).(1)求抛物线的解析式;(2)如图,P 为线段BC 上一动点,过点P 作y 轴的平行线,交抛物线于点D ,是否存在这样的P 点,使线段PD 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;【详解】(1)y =﹣x 2+bx +c 经过点C ,则c =3,将点A 的坐标代入抛物线表达式:y =﹣x 2+bx +3,得:0=-1-b +3,解得:b =2,抛物线的表达式为:y =﹣x 2+2x +3;(2)存在,理由:令y =0,得:﹣x 2+2x +3=0,解得:x =﹣1或3,故点B (3,0),设直线BC 为y =kx +b ,将点B 、C的坐标代入得:303k b b +=ìí=î,解得:13k b =-ìí=î.∴直线BC 的表达式为:y =﹣x +3,设点D (x ,﹣x 2+2x +3),则点P (x ,﹣x +3),则PD =(﹣x 2+2x +3)﹣(﹣x +3)=﹣x 2+3x =239()24x --+,当x 32=时,PD 最大值为:94;3.已知抛物线26(0)y ax bx a =++¹交x 轴于点(6,0)A 和点(1,0)B -,交y 轴于点C .(1)求抛物线的解析式和顶点坐标;(2)如图,点P 是抛物线上位于直线AC 上方的动点,过点P 分别作x 轴,y 轴的平行线,交直线AC 于点D ,E ,当PD PE +取最大值时,求点P 的坐标.解:(1)Q 抛物线26y ax bx =++经过点(6,0)A ,(1,0)B -,0603666a b a b =-+ì\í=++î,解得1a =-,5b =,\抛物线的解析式为256y x x =-++.225495624y x x x æö=-++=--+ç÷èøQ ,\抛物线的解析式为256y x x =-++,顶点坐标为549,24æöç÷èø.(2)由(1)知,抛物线的解析式为256y x x =-++,(0,6)C \,6OC \=.(6,0)A Q ,6OA \=,OA OC \=,45OAC \Ð=°.PD Q 平行于x 轴,PE 平行于y 轴,90DPE \Ð=°,45PDE DAO Ð=Ð=°,45PED \Ð=°,PDE PED \Ð=Ð,PD PE \=,2PD PE PE \+=,\当PE 的长度最大时,PE PD +取最大值.设直线AC 的函数关系式为y kx d =+,把(6,0)A ,(0,6)C 代入得066k d d=+ìí=î,解得1k =-,6d =,\直线AC 解析式为6y x =-+.设(,6)(06)E t t t -+<<,则()2,56P t t t -++,22256(6)6(3)9PE t t t t t t \=-++--+=-+=--+.10-<Q ,\当3t =时,PE 最大,此时25612t t -++=,(3,12)P \.【点睛】本题为二次函数综合题,综合性较强,第(1)步根据待定系数法求出函数解析式是解题关键,第(2)步根据函数解析式得到PD=PE ,进而得到当PE 的长度最大时,PE PD +取最大值时解题关键.类型二 求斜锤线段最值4.如图,在平面直角坐标系中,已知点B 的坐标为()1,0-,且4OA OC OB ==,抛物线2y ax bx c =++(0a ¹)图象经过A ,B ,C 三点.(1)求抛物线的解析式;(2)若点P 是直线AC 下方的抛物线上的一个动点,作PD AC ^于点D ,当PD 的值最大时,求此时点P 的坐标及PD 的最大值.解:∵点B 的坐标为()1,0-,∴OB =1,∵4OA OC OB ==,∴OA=OC =4,∴点A 的坐标为(4,0),点C 的坐标为(0,-4),将点A 、B 、C 的坐标代入2y ax bx c =++中,得164004a b c a b c c ++=ìï-+=íï=-î,解得134a b c =ìï=-íï=-î,∴抛物线的解析式为234y x x =--;(2)解:过点P 作PH 平行于y 轴,交AC 于点H ,∵OA=OC ,∴∠OAC =∠OCA =45°,∴∠PHD =∠OCA =45°,设点P (x ,234--x x ),则点H (x ,x -4),∴22sin 434)PD HP PHD x x x x =×Ð=--++=+,∵0<,∴PD有最大值,当x=2时,PD最大值为此时点P(2,-6)..【点睛】此题考查了待定系数法求抛物线解析式,抛物线的对称轴,化一般式为顶点式,最短路径问题,二次函数的性质,锐角三角函数,正确掌握抛物线的各知识点是解题的关键,这是一道二次函数与一次函数的综合题.5.如图,在平面直角坐标系中,已知点B的坐标为(﹣2,0),且OA=OC=4OB,抛物线y=ax2+bx+c (a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P 的坐标及PD的最大值.x2﹣3x﹣8;(3)最大值为【答案】(1)点A、C的坐标分别为(8,0)、(0,﹣8);(2)y=12点P(4,﹣12)【解析】【分析】(1)根据B点坐标及OA=OC=4OB结合图象即可确定A点,C点的坐标;(2)由(1)可将抛物线的表达式写成交点式,然后代入C点坐标即可求出解析式;(3)求出直线CA的解析式,过点P作y轴的平行线交AC于点H,求出∠PHD=∠OCA=45°,设点P a2﹣3a﹣8),则点H(a,a﹣8),写出PD的表达式根据二次函数的性质求最值即可.(a,12【详解】解:(1)∵B的坐标为(﹣2,0),∴OB=2,∴OA=OC=4OB=8,故点A、C的坐标分别为(8,0)、(0,﹣8);(2)由(1)知,抛物线的表达式可写为:y=a(x+2)(x﹣8)=a(x2﹣6x﹣16),把C(0,﹣8)代入得:﹣16a=﹣8,,解得:a=12x2﹣3x﹣8;故抛物线的表达式为:y=12(3)∵直线CA过点C,∴设其函数表达式为:y=kx﹣8,将点A坐标代入上式并解得:k=1,故直线CA的表达式为:y=x﹣8,过点P作y轴的平行线交AC于点H,∵OA =OC =8,∴∠OAC =∠OCA =45°,∵PH ∥y 轴,∴∠PHD =∠OCA =45°,设点P (a ,12a 2﹣3a ﹣8),则点H (a ,a ﹣8),∴PD =HP sin ∠PHD a ﹣8﹣12a 2+3a +8)=2+= 24)a -+,∴当a =4时,其最大值为P (4,﹣12).【点睛】本题主要考查二次函数的综合题,熟练掌握待定系数法求解析式及二次函数的性质结合三角函数是解题的关键.类型三 铅锤斜锤转化求面积周长最值6.如图,已知抛物线y =x 2+bx +c 与x 轴交于点A (2,0),B (﹣4,0),与y 轴交于C (0,﹣3),连接BC .(1)求抛物线的解析式;(2)如图,点P 是直线BC 下方抛物线上一点,过点P 作PD ⊥BC 于点D ,过点P 作PE ∥y 轴交BC 于点E ,求△PDE 周长的最大值及此时点P 的坐标;(1)解:设y =a (x ﹣2)(x +4),把C (0,﹣3)代入得:()243a =´-´-,∴38a =,∴()()2333243884y x x x x =-+=+-;(2)解:如图,延长PE 交x 轴于点F ,设点233,384P x x x æö+-ç÷èø,△PDE 的周长是l ,∵B (﹣4,0),C (0,﹣3),∴OB =4,OC =3,∵BC =5,∴△BOC 的周长是12,设直线BC 的解析式为()0y kx b k =+¹,把B (﹣4,0),C (0,﹣3),代入得:403k b b -+==-ìíî,解得:343k b =-=-ìïíïî,∴直线BC 的解析式是:334y x =--,∴E (x ,﹣34x ﹣3),∴PE =(﹣34x ﹣3)﹣(38x 2+34x ﹣3)=﹣38x 2﹣32x ,∵PD ⊥BC ,∴∠PDE =∠BOC =90°,∵PE ∥y 轴,∴∠PED =∠BEF =∠BCO ,∴△PDE ∽△BOC ,∴12lP E B C=,∴12l =233825x x --,∴l =﹣910(x +2)2+185,∴当x =﹣2时,l 最大=185,即△PDE 周长的最大值为185,当x =﹣2时,y =38×(﹣2+4)×(﹣2﹣2)=﹣3,∴P (﹣2,﹣3);7.如图1,已知抛物线2y ax bx c =++与x 轴交于点()2,0A -、()3,0B ,与y 轴交于点()0,4C ,连接AC 、BC .(1)求抛物线的解析式;(2)如图,点P 是直线BC 上方抛物线上一点,过点P 作//PD x 轴交BC 于点D ,过点P 作PE BC ^于点E ,当PDE △的周长最大时,求出PDE △的周长最大值及此时点P 的坐标;【详解】(1)∵点()2,0A -、()3,0B 、()0,4C 在抛物线的图像上,∴将点A 、B 、C 的坐标代入得:4209304a b c a b c c -+=ìï++=íï=î,解得23234a b c ì=-ïïï=íï=ïïî,∴222433y x x =-++;(2)如图3,过点P 作//PH y 轴交BC 于点H ,图3∵//PD x 轴,∴PDE OBC Ð=Ð,∴4tan tan 3OC PDE OBC OB Ð=Ð==,∴4tan 3PE PDE DE Ð==,∵90PED Ð=°,∴45PE PD =,35DE PD =,∴4312555PDE C PD PE DE PD PD PD PD =++=++=V ,又∵90DPE HPE Ð+Ð=°,∴4tan 3PH PDH PD Ð==,34PD PH =,∴95PDE C PH =V ,∴当PH 取最大值时,PDE C V 取最大值,设222(4)33P t t t -++,,设直线BC 的解析式为:y kx b =+,将点B 、C 的坐标代入得:304k b b +=ìí=î,解得434k b ì=-ïíï=î,∴443y x =-+,∴4(4)3H t t -+,,∴2222424(4)23333PH t t t t t =-++--+=-+,∴2233(322PH t =--+,∴当32t =时,PH 取得最大值,最大值为32,∴PDE C V 的最大值93275210=´=,将32t =代入到222(4)33P t t t -++,中,得22274332t t -++=,∴37(22P ,;8.已知,如图,抛物线2y x bx c =++经过点()2,0A -和()0,2B -.(1)求此抛物线和直线AB 的函数表达式;(2)点P 是直线AB 下方的抛物线上一动点(不与点A 、B 重合),过点P 作x 轴的垂线,垂足为F ,交直线AB 于点E ,作PD AB ^于点D .动点P 在什么位置时,PDE △的面积最大?求出面积的最大值,并求出此时点P 的坐标.【答案】(1)22y x x =+-,2y x =--;(2)PDE △最大面积为14, P 坐标为(-1,-2).【解析】【分析】(1)把(2,0)A -,(0,2)B -,分别代入抛物线与一次函数解析式,可得答案;(2)先证明PDE △是等腰直角三角形,设点P 的坐标为()2,2m m m +-,表示E 的坐标,求解PE 的长度,再表示PDE △的面积,利用二次函数的性质求解面积最大值及点P 的坐标即可.【详解】解:(1)∵抛物线2y x bx c =++经过点(2,0)A -,(0,2)B -,∴4202b c c -+=ìí=-î,解得:12b c =ìí=-î,所求抛物线的解析式为22y x x =+-;设直线AB 的函数表达式为y kx n =+,根据题意得202k n n -+=ìí=-î,解得12k n =-ìí=-î,所求直线AB 的函数表达式为2y x =--;(2)∵(2,0)A -,(0,2)B -,∴2OA OB ==,∴AOB V 是等腰直角三角形,∴45BAO Ð=°,∵PF x ^轴,∴904545AEF PED Ð=°-°=°=Ð,又∵PD AB ^,∴PDE △是等腰直角三角形,222,,PD DE PE PD DE \+==,PD \= ∴PE 越大,PDE △面积越大.设点P 的坐标为()2,2m m m +-,∴点E 坐标为(,2)m m --,∴()222PE m m m =---+-222(1)1(20)m m m m =--=-++-<<,∵10-<,∴抛物线开口向下,∴当1m =-时,PE 有最大值1,此时PDE △的面积为22111222PD DE PD PE ö=·==·÷÷ø 221111444PE ==´=,当1,m =- 则()22112 2.m m +-=+--=-点P 坐标为(-1,-2).【点睛】本题考查的是利用待定系数法求解二次函数与一次函数的解析式,同时考查了利用二次函数的性质解决图形面积的最值问题.类型四 铅锤斜锤综合演练9.如图1,抛物线2()30y ax bx a =++¹与x 轴交于(3,0)A -和(1,0)B 两点,与y 轴交于点C .(1)求该抛物线的函数表达式:(2)P 是抛物线上位于直线AC 上方的一个动点,过点P 作//PD y 轴交AC 于点D ,过点P 作PE AC ^于点E ,过点E 作EF y ^轴于点F ,求出PD EF +的最大值及此时点P 的坐标;【详解】(1)将(3,0)A -和(1,0)B 两点代入解析式得933030a b a b -+=ìí++=î,解得12a b =-ìí=-î,\抛物线得函数表达式为223y x x =--+;(2)由题意,()0,3C ,则OAC V 为等腰直角三角形,45CAO Ð=°,设AC 得解析式为AC y kx b =+,将(3,0)A -与()0,3C 代入求得11k b =ìí=î,则3AC y x =+,Q 点P 在抛物线上,//PD y 轴交AC 于点D ,\设()2,23P m m m --+,则(),3D m m +,23PD m m =--,其中30m -<<,如图,延长FE 交PD 于点G ,则FG BD ^,且由题可知,PDE △为等腰直角三角形,\由“三线合一”知,21322m m EG PD --==,\E 的横坐标为22322m m m m m ----+=,2222m m m m EF --+\==,()2221515253222228m m PD EF m m m m m æö+æö\+=--+=--=-++ç÷ç÷èøèø故由二次函数的性质可得,当52m =-时,PD EF +最大为258,此时57,24P æö-ç÷èø;10.如图1,在平面直角坐标系中,已知点B 的坐标为(1,0),且OA =OC =4OB ,抛物线y =ax 2+bx +c (a ≠0)图象经过A ,B ,C 三点.(1)求抛物线的解析式;(2)若点P 是直线AC 上方的抛物线上的一个动点,作PD ⊥AC 于点D ,当0<PD <时,请直接写出点P 横坐标的取值范围.解:(1)∵点B 的坐标为(1,0),∴OB =1,又∵OA =OC =4OB ,∴OA =OC =4,即点A 坐标为(-4,0);点C 坐标为(0,4);∵抛物线y =ax 2+bx +c (a ≠0)图象经过A ,B ,C 三点.∴401640c a b c a b c =ìï++=íï-+=î,解得:134a b c =-ìï=-íï=î,∴抛物线的解析式为234y x x --+=;(2)∵点A 坐标为(-4,0)点C 坐标为(0,4)∴直线CA 函数表达式为: y =x +4,过点P 作y 轴的平行线交AC 于点Q ,设点P 坐标为2(,34)x x x --+,其中40x -<<,则点Q 坐标为(,4)x x +,∵点P 是直线AC 上方的抛物线上的一个动点,∴22344)()(4P x x Q x x x --+--=+=-,∴2(2)4P x Q -=++,即当x =-2时,P 点坐标为(-2,6),此时PQ 的最大值为4PQ =又∵45CAO OCA Ð=Ð=°,PQ y P 轴,∴45PQD Ð=°,∴PQD △是等腰直角三角形,∴PQ =,又∵0<PD <,∴0<PQ <4,即:2044x x <--<,∴当x =-2时, PQ 的最大值为4PQ =,此时PD =,∴当0<PD <时,P 横坐标的取值范围为:40x -<<且2x ¹-.【点睛】本题考查了二次函数综合运用,涉及到一次函数、等腰直角三角形性质等,其中(3)得出PQ =,并用函数关系表示PQ 是本题解题的关键.11.如图,直线l :112y x =-+ 与x 轴、y 轴分别交于点B 、C ,经过B 、C 两点的抛物线 2y x bx c =++ 与x 轴的另一个交点为A .(1)求该抛物线的解析式;(2)若点P 在直线l 下方的抛物线上,过点P 作//PD x 轴交l 于点D ,//PE y 轴交l 于点E ,求PD PE +的最大值;(1)解:∵直线112y x =-+与x 轴、y 轴分别交于点B 、C ,∴()2,0B 、()0,1C ,∵点B 、C 在抛物线解2y x bx c =++上,∴4201b c c ++=ìí=î,解得:521b c ì=-ïíï=î,∴抛物线的解析式为2512y x x =-+.(2)∵点P 在直线l 下方的抛物线上,设25,12P m m m æö-+ç÷èø,∵//PD x 轴,//PE y 轴,点D ,E 都在直线112y x =-+上,∴1,12E m m æö-+ç÷èø,22525,12D m m m m æö-+-+ç÷èø,∴221511222PE m m m m m æöæö=-+--+=-+ç÷ç÷èøèø,222524PD m m m m m =-+-=-+,∴()22224236PD PE m m m m m m +=-++-+=-+,即:()2236313PD PE m m m +=-+=--+,∴当1m =时,PD PE +的最大值是3.12.如图1,抛物线()20y ax bx c a =++¹与x 轴交于()4,0A -,()10B ,两点,交y 轴于点()0,3C(1)求抛物线的解析式;(2)如图,点P 为直线AC 上方且抛物线对称轴左侧的抛物线上一点,过点P 作х轴的平行线交抛物线于点D ,过点P 作y 轴的平行线交AC 于点H ,求PD PH +的最大值及此时点P 的坐标;(1)解:∵抛物线()20y ax bx c a =++¹与x 轴交于A (-4,0),B (1,0)两点,∴可设抛物线解析式为()()41y a x x =+-.∵该抛物线过点C (0,3),∴将C (0,3)代入()()41y a x x =+-,得:()()30401a =+´-∴34a =-,∴抛物线解析式为()()3414y x x =-+-整理得:239344y x x =--+.(2)解:设经过A 、C 的直线解析式为y kx b =+,∴043k b b=-+ìí=î解得:343k b ì=ïíï=î∴直线AC 的解析式为:334y x =+.∵抛物线解析式为239344y x x =--+,∴对称轴9423324b x a =-=-=---.设点239344P a a a æö--+ç÷èø,,点334H a a æö+ç÷èø,,则2393344D a a a æö----+ç÷èø,.∴[]2393()()(3)(33)444D P P H PD PH x x y y a a a a a +=-+-=---+--+--,即2233101653(4433PD PH a a a +=---=-++∴当103a =-时,PD PH +有最大值为163.将103a =-代入239344a a --+,得:231091013()(343436-´--´-+=.∴此时点101336P æö-ç÷èø,.13.如图,已知二次函数图象的顶点坐标为(1,4)A ,与坐标轴交于B 、C 、D 三点,且B 点的坐标为(1,0)-.(1)求二次函数的解析式;(2)在二次函数图象位于x 轴上方部分有两个动点M 、N ,且点N 在点M 的左侧,过M 、N 作x 轴的垂线交x 轴于点G 、H 两点,当四边形MNHG 为矩形时,求该矩形周长的最大值;【详解】(1)二次函数表达式为:()214y a x =-+,将点B 的坐标代入上式得:044a =+,解得:1a =-,故函数表达式为:223y x x =-++…①;(2)设点M 的坐标为()2,23x x x -++,则点()22,23N x x x --++,则222MN x x x =-+=-,223GM x x =-++,矩形MNHG 的周长()()2222222223282C MN GM x x x x x =+=-+-++=-++,∵20-<,故当22b x a=-=,C 有最大值,最大值为10,此时2x =,点()0,3N 与点D 重合;14.如图,在平面直角坐标系中,抛物线y =ax 2+bx +3(a ≠0)与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,点P 是直线BC 上方抛物线上的动点.(1)求抛物线的解析式;(2)如图,连接BC 与OP ,交于点D ,求当PD OD的值最大时点P 的坐标;解:(1)把A (﹣1,0),B (3,0)分别代入y =ax 2+bx +3(a ≠0)中得:309330a b a b -+=ì\í++=î, 解得:12a b =-ìí=î∴该抛物线的解析式为y =-x 2+2x +3;(2)如图1,作PG ⊥x 轴于点H ,交BC 于点G ,∵抛物线y =-x 2+2x +3与y 轴交于点C ,∴C (0,3),设直线BC 的解析式为y =kx +3,则3k +3=0,解得k =﹣1,∴直线BC 的解析式为:y =﹣x +3;设点P(m,-m2+2m+3),则点G(m,-m+3),∴PG = -m2+2m+3-(-m+3)= -m2+3m∵PG//OC,∴△PDG∽△ODC,∴2239()32433mPD PG m mOD OC--+-+===当32m=时,PDOD有最大值,∴点P(315 ,24).。
初三数学铅垂法练习题

初三数学铅垂法练习题一、填空题1. AB是一根长为12cm的铁丝,当一力中心在A点受到作用时,弯曲成了一条长为8cm的弧线,求弧线的弦长和弧度。
解:弦长 = 2 ×弧的宽度 = 2 × 4 = 8cm弧度 = 弧长 / 半径 = 8 / 6 = 4/3 弧度2. 建筑师在一块长方形的草地上设计了一座波浪形的花坛,波浪形的最高点和最低点分别是距离长方形底边的12m和3m,底边的长度为18m,求波浪形的长度。
解:波浪形的长度 = 两个半圆的周长 + 长方形的底边长度= 2 ×半圆的周长 + 长方形的底边长度= 2 × (圆的周长 ×圆的个数) + 长方形的底边长度= 2 × (2 × π × 3 + 2 × π × 9) + 18= 2 × (6π + 18π) + 18= 72π + 18≈ 227.5m二、选择题1. 在直角三角形ABC中,AC = 6cm,BC = 8cm。
若以BC为底边,作高CD,下列说法正确的是:A. CD > 8cmB. CD = 8cmC. CD < 8cmD. 无法确定解:正确答案是A. CD > 8cm。
由于AC是斜边,所以BC的长度小于AC,故CD的长度必然大于BC。
2. 在一个矩形ABCD中,对角线AC的长度为10cm,若AC = BD,则下列哪个选项是正确的?A. AB = 6cmB. AB = 8cmC. AB = 10cmD. AB = 12cm解:正确答案是B. AB = 8cm。
由于对角线AC的长度为10cm,且AC = BD,根据矩形的性质可知,两条对角线相等,因此BD的长度也为10cm。
而矩形的宽度等于对角线BD的一半,所以AB的长度为8cm。
三、解答题已知直线AB上有两点P和Q,水平线XY与AB相交于P点,垂直线OP与AB的交点为Q点,已知QP = 4cm,而OB = 5cm。
2023年河南省中考物理押题练习试卷B卷附解析

2023年河南省中考物理押题练习试卷B 卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、单选题1.如图所示,一辆小轿车正在平直的公路上加速行驶。
下列关于此车的说法中错误..的是 ............................................................................................................................................ ( )A .在水平方向上受到动力和阻力的作用,动力大于阻力B .驱动轮受到的地面对它的摩擦力充当了轿车前进的动力C .在竖直方向上受重力、支持力和空气对它的升力,三力平衡D .轿车对地面的压强计算:P =F S =G S2.有两瓶失去标签的无色液体,一瓶是饱和氯化钠溶液,一瓶是蒸馏水。
为了把它们区分开,同学们提出了以下方法:①蒸发 ②测密度 ③测导电性 ④测pH ⑤加入氯化钠 ⑥加入食醋。
你认为可行的是 ......................................................................................................... ( )A .①②③⑤B . ①③④⑤C . ②③④⑥D . ②③⑤⑥3.下列数据,符合事实的是 ........................................................................................... ( )A .物理课本中一张纸的厚度约为1mm ;B .光在空气中的传播速度约为340m/s ;C .将一个面积为5cm 2的吸盘从光滑的玻璃面上拉下所用的拉力约为50N ;D .初中学生的体重一般为50N 左右。
二次函数铅垂高演练(答案、解析、总结).doc

二次函数铅垂高演练(答案、解析、总结) 【答案】解:(1)点C的坐标.设抛物线的函数关系式为,则,解得∴所求抛物线的函数关系式为…………①设直线AC的函数关系式为则,解得.∴直线AC的函数关系式为,∴点E的坐标为把x=4代入①式,得,∴此抛物线过E点.(2)(1)中抛物线与x轴的另一个交点为N(8,0),设M(x,y),过M作MG⊥x轴于G,则S△CMN=S△MNG+S梯形MGBC—S△CBN===∴当x=5时,S△CMN有最大值课下练习1.(本题满分12分)已知:如图一次函数y=x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=x2+bx+c的图象与一次函数y=x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)(1)求二次函数的解析式;(2)求四边形BDEC的面积S;(3)在x轴上是否存在点P,使得△PBC是以P 为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.第24题图3.(2010山东临沂)如图,二次函数的图象与轴交于,两点,且与轴交于点.(1)求该抛物线的解析式,并判断的形状;(2)在轴上方的抛物线上有一点,且以四点为顶点的四边形是等腰梯形,请直接写出点的坐标;(3)在此抛物线上是否存在点,使得以四点为顶点的四边形是直角梯形?若存在,求出点的坐标;若不存在,说明理由.第26题图【答案】解:根据题意,将A(,0),B(2,0)代入y=-x2+ax+b 中,得解这个方程,得全品中考网所以抛物线的解析式为y=-x2+x+1.当x=0时,y=1.所以点C的坐标为(0,1)。
所以在△AOC中,AC==.在△BOC中,BC==.AB=OA+OB=.因为AC2+BC2=.所以△ABC是直角三角形。
图1(2)点D的坐标是.(3)存在。
由(1)知,AC⊥BC,若以BC为底边,则BC∥AP,如图(1)所示,可求得直线BC的解析式为.直线AP可以看作是由直线AC平移得到的,所以设直线AP的解析式为,将A(,0)代入直线AP的解析式求得b=,所以直线AP的解析式为.因为点P既在抛物线上,又在直线AP上,所以点P的纵坐标相等,即-x2+x+1=.解得(不合题意,舍去).图2当x=时,y=.所以点P的坐标为(,).②若以AC为底边,则BP∥AC,如图(2)所示,可求得直线AC的解析式为.直线BP可以看作是由直线AC平移得到的,所以设直线BP的解析式为,将B(2,0)代入直线BP的解析式求得b=-4,所以直线BP的解析式为y=2x-4.因为点P既在抛物线上,又在直线BP上,所以点P的纵坐标相等,即-x2+x+1=2x-4解得(不合题意,舍去).当x=-时,y=-9.所以点P的坐标为(-,-9).综上所述,满足题目的点P的坐标为(,)或(-,-9)2(本题10分)如图,已知二次函数y=的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.(1)点A的坐标为_______,点C的坐标为_______;(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?.解:(1)A(0,4),C(8,0). (2)分(2)易得D(3,0),CD=5.设直线AC对应的函数关系式为,则解得∴...........................................3分①当DE=DC 时,∵OA=4,OD=3.∴DA=5,∴(0,4). (4)分②当ED=EC时,可得(,).……………5分③当CD=CE时,如图,过点E作EG⊥CD,则△CEG∽△CAO,∴.即,,∴(,).……………………………………6分综上,符合条件的点E有三个:(0,4),(,),(,).(3)如图,过P作PH⊥OC,垂足为H,交直线AC于点Q.设P(m,),则Q(,).①当时,PQ=()()=,,…………………………7分∴;……………………………………………………………………………8分②当时,PQ=()()=,,∴.………………………………………………………………………………9分故时,相应的点P有且只有两个.…………………………。
中考专项练习之铅垂法

铅垂法一、解答题(共14小题,每小题5分,共70分)1.(2017·毕节市中考真题) 如图,在平面直角坐标系中,二次函数的图象交坐标轴于,,三点,点是直线下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点,使是以为底边的等腰三角形?若存在,求出点坐标;若不存在,请说明理由;(3)动点运动到什么位置时,面积最大,求出此时点坐标和的最大面积.(5分)2.如图,抛物线与轴交与,两点,(1)求该抛物线的解析式;(2)设中的抛物线交轴与点,在该抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.(3)在中的抛物线上的第二象限上是否存在一点,使的面积最大?若存在,求出点的坐标及的面积最大值.若没有,请说明理由.(5分)3.阅读材料:如图,过的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫的“水平宽”,中间的这条直线在内部线段的长度叫的“铅垂高”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图,抛物线顶点坐标为点,交轴于点,交轴于点.(1)求抛物线和直线的解析式;(2)点是抛物线(在第一象限内)上的一个动点,连结,,当点运动到顶点时,求铅垂高及;(3)是否存在一点,使,若存在,求出点的坐标;若不存在,请说明理由.(5分)4.(2015·中山市纪中三鑫双语学校月考)如图,二次函数的图象与轴交于、两点,与轴交于点,已知,且经过点,是第一象限内抛物线上的一个动点,为抛物线的顶点.(1)求抛物线的解析式; (2)求的面积;(3)求的面积的最大值,并求此时点的坐标.(5分)5.(2018·南开实验学校期中考试) 如图所示,抛物线的顶点为,直线与抛物线交于点(1)求抛物线顶点的坐标和点的坐标 (2)求的面积(3)是抛物线上位于直线上方的一点,当点的坐标为多少时,的面积最大?(5分)6.(2015·中山市古镇初级中学期中考试) 如图,在平面直角坐标系中,二次函数的图象与轴交于、两点,点在原点的左侧,点的坐标为,与轴交于点,点是直线下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)当点运动到什么位置时,四边形的面积最大?求出此时点的坐标和四边形的最大面积.(5分)7.(2018·中山市纪中三鑫双语学校中考模拟) 如图,抛物线与轴交于、两点,与轴交于点.(1)求点、、的坐标;(2)在抛物线的对称轴上有一动点,求的值最小时的点的坐标;(3)若点是直线下方抛物线上一动点,求四边形面积的最大值.(5分)8.(2016·中山市期中考试) 如图,二次函数的图象与轴交于、两点,与轴交于点,已知,且经过点,是第一象限内抛物线上的一个动点.(1)求抛物线的解析式;(2)在对称轴上是否存在一点,使得最短?若点存在,求出点的坐标,若点不存在,请说明理由;(3)求面积的最大值,并求出此时点的坐标.(5分)9.抛物线顶点坐标为点,交轴于点,交轴于点.(1)抛物线和直线的解析式;(2)连结、,求的铅垂高及.(5分)10.如图,已知抛物线与轴交于、两点,与轴交于点,为顶点.(1)求;(2)求;(3)若点是第四象限抛物线上一动点,求的最大值.(5分)11.(2016·苏州市昆山市期中考试) 已知抛物线与直线交于点,.(1)求、、的值;(2)直接写出当时,自变量的范围是;(3)已知点是抛物线的顶点,求的面积.(5分)12.(2017·纪雅单元测试) 如图,一次函数的图象与轴交于,与轴交于点,以直线为对称轴的抛物线,经过,两点,与轴正半轴交于点.(1)求一次函数及抛物线的函数表达式;(2)在直线下方的抛物线上,是否存在一点,使得的面积最大,若存在,求出点的坐标,并求出最大面积是多少.(5分)13.如图,抛物线与轴交于、两点,与轴交于点,已知点,点.(1)求抛物线的函数解析式;(2)若点是抛物线位于第一象限上的动点,求面积的最大值及此时点的坐标.(5分)14.(2020·惠州市惠城区月考) 如图,已知二次函数的图象交x 轴于点,交轴于点(1)求这个二次函数的表达式(2)点是直线下方抛物线上的一动点,求面积的最大值(3)直线分别交直线和抛物线于点,当是等腰三角形时,直接写出的值(5分)二、填空题(共1小题,每小题5分,共5分)15.点是抛物线上一个动点,且在直线:上方,当点坐标为时,最大.(5分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考压轴题演练一教学目的理解用“鉛锤高,水平宽”求不规则三角形面积的方法,并用此方法解决二次函数与几何图形的综合题中有关三角形面积计算的问题。
二重点难点1灵活应用铅垂高进行二次函数与几何图形的综合题中有关三角形面积计算的问题。
2铅垂高的寻找方法,以及用坐标表示线段 三.教学方法先让学生阅读理解,自主探究,引导学生掌握方法,讲练结合 四.教学过程 例1阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结P A ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆; (3)是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.例1解:(1)设抛物线的解析式为:4)1(21+-=x a y ··········································· 1分图12-2xC OyABD 1 1铅垂高 水平宽 ha 图12-1A把A (3,0)代入解析式求得1-=a所以324)1(221++-=+--=x x x y ············································· 3分设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( ··································· 4分 把)0,3(A ,)3,0(B 代入b kx y +=2中 解得:3,1=-=b k所以32+-=x y ·········································································· 6分 (2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2 所以CD =4-2=2 ········································································· 8分32321=⨯⨯=∆CAB S (平方单位) ··················································· 10分 (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△P AB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-= ······················ 12分 由S △P AB =89S △CAB 得:389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中, 解得P 点坐标为)415,23( ······························································ 14分总结:求不规则三角形面积时不妨利用铅垂高。
铅垂高的表示方法是解决问题的关键,要学会用坐标表示线段。
例2(2010广东省中考拟)如图10,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),OB =OC ,tan∠ACO=31. (1)求这个二次函数的表达式.(2)经过C 、D 两点的直线,与x 轴交于点E ,在该抛物线上是否存在这样的点F ,使以点A 、C 、E 、F 为顶点的四边形为平行四边形若存在,请求出点F 的坐标;若不存在,请说明理由.(3)若平行于x 轴的直线与该抛物线交于M 、N 两点,且以MN 为直径的圆与x 轴相切,求该圆半径的长度.(4)如图11,若点G (2,y )是该抛物线上一点,点P 是直线AG 下方的抛物线上一动点,当点P 运动到什么位置时,△APG 的面积最大求出此时P 点的坐标和△APG 的最大1)方法一:由已知得:C (0,-3),A (-1,0)将A、B 、C 三点的坐标代入得⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a解得:⎪⎩⎪⎨⎧-=-==321c b a所以这个二次函数的表达式为:322--=x x y方法二:由已知得:C (0,-3),A (-1,0) 设该表达式为:)3)(1(-+=x x a y将C 点的坐标代入得:1=a所以这个二次函数的表达式为:322--=x x y(注:表达式的最终结果用三种形式中的任一种都不扣分) (2)方法一:存在,F 点的坐标为(2,-3) 理由:易得D (1,-4),所以直线CD 的解析式为:3--=x y∴E 点的坐标为(-3,0) 由A 、C 、E 、F 四点的坐标得:AE =CF =2,AE ∥CF ∴以A 、C 、E 、F 为顶点的四边形为平行四边形∴存在点F ,坐标为(2,-3) 方法二:易得D (1,-4),所以直线CD 的解析式为:3--=x y∴E 点的坐标为(-3,0) ∵以A 、C 、E 、F 为顶点的四边形为平行四边形∴F 点的坐标为(2,-3)或(―2,―3)或(-4,3) 代入抛物线的表达式检验,只有(2,-3)符合∴存在点F ,坐标为(2,-3)(3)如图,①当直线MN 在x 轴上方时,设圆的半径为R (R>0)代入抛物线的表达式,解得2171+=R②当直线MN 在x 轴下方时,设圆的半径为r (r>0), 则N (r+1,-r ),代入抛物线的表达式,解得2171+-=r∴圆的半径为2171+或2171+-.(4)过点P 作y 轴的平行线与AG 交于点Q , 易得G (2,-3),直线AG 为1--=x y .设P (x ,322--x x),则Q (x ,-x -1),PQ 22++-=x x .3)2(212⨯++-=+=∆∆∆x x S S S GPQ APQ APG 当21=x时,△APG 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,21,827的最大值为APG S ∆.随堂练习1.(2010江苏无锡)如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=AC与直线x=4交于点E.(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.【答案】解:(1)点C的坐标.设抛物线的函数关系式为2(4)y a x m=-+,则1604ama m+=+=⎧⎨⎩63a m==∴所求抛物线的函数关系式为24)63y x=-+…………①设直线AC的函数关系式为,y kx b=+则402k bk b-+=+=⎧⎨⎩,解得33k b==.∴直线AC的函数关系式为33y=,∴点E的坐标为把x=4代入①式,得24)y=-+=E点.(2)(1)中抛物线与x轴的另一个交点为N(8,0),设M(x,y),过M作MG⊥x轴于G,则S△CMN=S△MNG+S梯形MGBC—S△CBN=111(8)(2)(82)222x y y x-++--⨯-⨯=2233()632y x xx+-=++-=+-=25)22x-+∴当x=5时,S△CMN2课下练习1.(本题满分12分)已知:如图一次函数y=12x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=12x2+bx+c的图象与一次函数y=12x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)(1)求二次函数的解析式;(2)求四边形BDEC的面积S;(3)在x 轴上是否存在点P ,使得△PBC 是以P 为直角顶点的直角三角形若存在,求出所有的点P ,若不存在,请说明理由.3.(2010山东临沂)如图,二次函数2y x ax b =++的图象与x 轴交于1(,0)2A -,(2,0)B 两点,且与y 轴交于点C .(1)求该抛物线的解析式,并判断ABC ∆的形状;(2)在x 轴上方的抛物线上有一点D ,且以A C D B 、、、四点为顶点的四边形是等腰梯形,请直接写出D 点的坐标;(3)在此抛物线上是否存在点P ,使得以A C B P 、、、四点为顶点的四边形是直角梯形若存在,求出P 点的坐标;若不存在,说明理由.【答案】解:根据题意,将A (12-,0),B (2,0)代入y=-x 2+ax+b 中, 得110,42420.a b a b ⎧--+=⎪⎨⎪-++=⎩ 解这个方程,得3,21.a b ⎧=⎪⎨⎪=⎩所以抛物线的解析式为y=-x 2+32x+1. 第26题图第24题图当x=0时,y=1.所以点C 的坐标为(0,1)。
