递归与递推深入32页PPT
递归算法 ppt课件

ppt课件
14
int fib(int n) { if (n==0) return 0; if (n==1) return 1; return (fib(n-1)+fib(n-2)); }
输入 15 输出 fib(15)=610
//满足边界条件,递归返回 //满足边界条件,递归返回 //递归公式,进一步递归
//调用下一层递归
}
int main()
{
int n,k;
cin >> n >> k;
cout << s(n,k);
return 0;
}
ppt课件
19
【例6】数的计数(Noip2001)
【问题描述】
我们要求找出具有下列性质数的个数(包括输入的自然数n)。先输入一 个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:
8
ppt课件
9
假设把第3步,第4步,第7步抽出来就相当于N=2的情况(把上面2片 捆在一起,视为一片):
ppt课件
10
所以可按“N=2”的移动步骤设计:
①如果N=0,则退出,即结束程序;否则继续往下执行;
②用C柱作为协助过渡,将A柱上的(N-1)片移到B柱上,调用过程mov(n-1,
a,b,c);
本题是典型的递归程序设计题。 (1)当N=1 时,只有一个盘子,只需要移动一次:A—>C; (2)当N=2时,则需要移动三次:
A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C. (3)如果N=3,则具体移动步骤为:
算法总结之递推与递归

算法总结之递推与递归递推算法递归算法⼤致包括两⽅⾯的内容:1)递归起点; 2)递归关系递推起点递归起点⼀般由题⽬或者实际情况确定,不由递归关系推出。
如果⽆法确定递归起点,那么递归算法就⽆法实现。
可见,递归起点是递归算法中的重要⼀笔。
递推关系递归关系是递归算法的核⼼。
常见的递归关系有以下⼏项:1)⼀阶递推;2)多阶递推;3)间接递推;4)逆向递推;5)多维递推。
下⾯通过栗⼦来详细介绍⼀下上述类别的递推关系。
1. ⼀阶递推在计算f(i)时,只⽤到前⾯项中的⼀项,如等差数列。
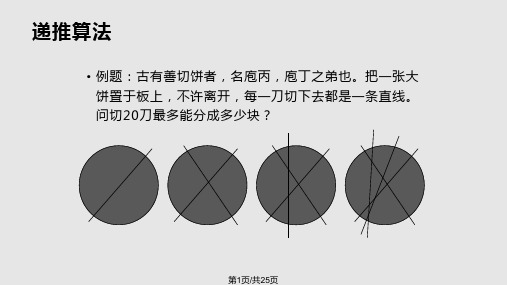
公差为3的等差数列,其递推关系为:f(i)=f(i-1)+3eg. 平⾯上10条直线最多能把平⾯分成⼏部分?分析:以直线数⽬为递推变量,假定i条直线把平⾯最多分成f(i)部分,则f(i-1)表⽰i-1条直线把平⾯分成的最多部分。
在i-1条直线的平⾯上增加直线i,易得i与平⾯上已经存在了的i-1条直线最多各有⼀个交点,即直线i最多被分成i段,⽽这i段将会依次将平⾯⼀分为⼆,即直线i将最多使平⾯多增加i部分。
所以,递推关系可表⽰为:f(i)=f(i-1)+i易得当0条直线时,平⾯为1部分。
所以f(0)=1为递推起点。
上述分析可⽤下⾯代码表⽰(c++):#define MAX 100int f[MAX] //存放f(i)int lines(int n){//输⼊n为直线数⽬//输出最多部分数int i;f(0)=1;for(i=1;i<=n;i++){f[i]=f[i-1]+3;}return f[i];}2. 多阶递推在计算f(i)时,要⽤到前⾯计算过的多项,如Fibonacci数列。
eg.求Fibonacci的第10项。
分析:总所周知,Fibonacci数列中的第n项等于第n-1项加上n-2项。
所以递推关系为f(i)=f(i-1)+f(i-2);且f[0]=f[1]=1。
C++代码如下:#define MAX 100int f[MAX];int fib(int n){//输⼊n为项数//输出第n个fib数int i;f[0]=0;f[1]=1;for(i=2;i<=n;i++){f[i]=f[i-1]+f[i-2];}return f[n]}3. 间接递推在计算f[i]时需要中间量,⽽计算中间量要⽤到之前计算过的项。
离散数学中的递归函数和递推式

离散数学是应用数学的一个重要分支,它研究离散对象和离散结构之间的关系。
递归函数和递推式是离散数学中两个重要的概念,在解决问题和理解数学概念中起到了重要的作用。
递归函数是指定义的函数可以通过对自身的调用来实现计算的过程。
递归函数需要满足两个条件:首先,必须有一个基本情况,这个基本情况是递归函数能够直接计算出结果而不需要再递归调用;其次,递归函数必须能够将问题规模减小,使得递归函数能够趋近于基本情况。
递归函数一般采用递归调用的方式进行计算,通过多次调用最终得到结果。
递归函数的定义通常使用递归方程来表达。
递归函数的应用非常广泛。
比如在计算数列中的斐波那契数列,递归函数可以非常方便地计算当前数列项的值。
斐波那契数列的定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2)。
我们可以通过递归函数来计算出任意一项的值,只需要将问题规模n减小到1时,就可以直接得到结果。
另一个例子是阶乘函数。
阶乘函数的定义是:n!=n×(n-1)!,其中0!=1。
通过递归函数的调用,我们可以直接计算出给定正整数n的阶乘值。
递推式是一种通过前一项推导出后一项的数学表达式。
递推式可以看做递归方程的一种特殊形式。
递推式的求解往往是从已知条件出发,通过逐步推导得到问题的解。
递推式的求解方法一般有两种:一种是直接法,通过简单的代入运算得到递推式的解;另一种是递推法,通过已知条件推导出递推关系式并进行逐步求解。
递推式在离散数学中的应用非常广泛,比如在解决递推关系问题、计算数列中的元素等方面都有重要的作用。
递推式的一个典型应用是求解斐波那契数列的第n项的值。
斐波那契数列的递推式是:F(n)=F(n-1)+F(n-2)(n≥2)。
通过已知条件F(0)=0,F(1)=1,我们可以逐步推导出递推关系式并进行逐步求解,最终得到第n项的值。
递推式还可以用来解决概率问题中的递推关系,比如生存概率、病毒传播概率等。
递推式在离散数学中有着广泛的应用,为解决实际问题提供了重要的数学工具。
C++函数、递推、递归ppt课件

i = 7 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(7) = 2 * (S(8) + 1) // s2 = s1 = S(7)
i = 6 s1 = 2 * (s2 + 1) ; s2 = s1 ;
// S(6) = 2 * (S(7) + 1) // s2 = s1 = S(6)
看一个简单的例子:
1 4
第九讲——函数、递推、递归
递归
有 5 个人坐在一起,问第 5 个人多少岁? 他说比第 4 个人 大两岁。问第 4 个人岁数,他说比第 3 个人大两岁。问第 3 个人,又说比第 2 个人大两岁。问第 2 个人,说比第 1 个人 大两岁。最后问第 1 个人,他说是 10 岁。请问第 5 个人多 大?
3
第九讲——函数、递推、递归
解题思路:
假设用 S(i) 表示第 i 天没吃之前的桃子数目;
则
S(1) 即为第 1 天所摘的桃子数; S(2) = S(1) * 1/2 – 1 第 2 天没吃之前的桃子数
S(3) = S(2) * 1/2 - 1 第 3 天没吃之前的桃子数
…
…
S(9) = S(8) * 1/2 - 1 第 9 天没吃之前的桃子数
= age(2) + 2 + 2 + 2 // c = age(2) + 2
= age(1) + 2 + 2 + 2 + 2;// c = 10;
2 2
计算年龄程序
第九讲——函数、递推、递归
2 3
第九讲——函数、递推、递归
递归算例(2)
用递归方法计算 n! 算法思路:
第五讲递推与递归PPT课件

开始,每1项等于前面3项的和。
f(n)=f(n-1)+f(n-2)+f(n-3)-----递推公式 f(1)=1 , f(2)=2 , f(3)=4 --------递推边界
27
① #include <stdio.h> //上楼问题
② void main( )
③ { int x,n,i,a,b,c;
3)第二只猴子醒来,又把桃子均分成五堆后,还是多了一 个,它也吃掉这个桃子,并拿走了其中一堆。
第三只,第四只,第五只猴子都依次如此分食桃子。 问:五只猴子采得一堆桃子数最少应该有几个呢?
11
例2:猴子分食桃子---逆推法
算法分析:
先要找第N只猴子和其面前桃子数的关系。如 果从第1只开始往第5只找,不好找,但如果思路 一变,从第N到第1去,可得出下面的推导式:
19
例11.2 骨牌问题---顺推法
➢长度为n时的骨牌铺放方案? ➢从最简单的情况开始寻找问题解决的规律?--- 顺推 ➢以 f(i) 表示n=i时的铺放方案数目。 ➢当n=1时,只有1种铺法,即f(1)=1,如下左图所示: ➢当n=2时,只有2种铺法,即f(2)=2,如下右图所示。
20
例11.2 骨牌问题---顺推法
n=1
f(n)=1
n=2
f(n)=2
n=3
f(n)=3
n=4
f(n)=3 + 1 =f[3]+ f[1]=4
n=5
f(n)=f(4)+f(2)
n=6
f(n)=f(5)+f(3)
n=7
f(n)=f(6)+f(4)
规律: f(n)=f(n-1)+f(n-3) (n>=4) 17
PPT-07递推和递归思想

① 定 义 数 组 fish[6], 并 初 始 化 为 1; 定 义 循 环 控 制 变 量 i, 并 初 始 化 为 0。
fish[5]=fish[5]+5; // ② .1
②
for ( i=4; i>=1; i-- ) // ② .2
fish[i+1]% 4 != 0
tru e
false
break; //退 出 for 循 环
为了把这个问题说得再透彻一点。我们画了如下的流 程图:
25
fact(3)
真 3==1
假
调用 fact(2)
计算 3*fact(2)
fact(2)
真 2==1
假
调用 fact(1)
计算 2*fact(1)
fact(1)
真 1==1
假
fact(1) =1
返回
返回
26
为了形象地描述递归过程,将上图改画成下图
B
C
D
A 结点的值最终为 D 的值,但为了求 D 需先求 B 和 C。从图上看, 先求左边的点才能求最右边的点的 值,我们约定最右边 D 点的值就是 A 结点的值。
22
下面我们以 3!为例来画与或结点图,目的是体会 递归的含义。
A
fact(3)
3>1
B fact(2) 2>1
E 3*fact(2)
int i=0;
12
do { fish[5]=fish[5]+5;
for (i=4; i>=1; i=i-1)
{ if ( fish[i+1]%4 !=0 ) break; // 跳出for循环
else fish[i]=fish[i+1]*5/4+1; }
递推算法.完美版PPT

5
7
38
810
2744
45265 【算法分析】
此题解法有多种,从递推的思想出发,设想,当从顶层沿某条路径走到第I 层向第I+1层前进时,我们的选择一定是沿其下两条可行路径中最大数字的方 向前进,为此,我们可以采用倒推的手法,设a[i,j]存放从i,j 出发到达n层的最 大值,则a[i,j]=max{a[i,j]+a[i+1,j],a[i,j]+a[i+1,j+1]},a[1,1] 即为所求的数字总 和的最大值。
1.计算正方形的个数s1 边长为1的正方形个数为n*m 边长为2的正方形个数为(n-1)*(m-1)边长Biblioteka 3的正方形个数为(n-2)*(m-2)
………… 边长为min{n,m}的正方形个数为(m-min{n,m}+1)*(n-min{n,m}+1) 根据加法原理得出
m inm{,n}1
s1= (ni)*(mi) i0
(4)当N=3时:骨牌可以全部竖排,也可以认为在方格中已经有一个竖排 骨牌,则需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排 列两个横排骨牌,则必须在方格中排列一个竖排骨牌。如上右图,再无其他排 列方法,因此铺法总数表示为x3=3. 由此可以看出,当n=3时的排列骨牌的方法数是n=1和n=2排列方法数的和。
第三章 递推算法
递推法是一种重要的数学方法,在数学的各个领域中都 有广泛的运用,也是计算机用于数值计算的一个重要算法。 这种算法特点是:一个问题的求解需一系列的计算,在已知 条件和所求问题之间总存在着某种相互联系的关系,在计算 时,如果可以找到前后过程之间的数量关系(即递推式), 那么,从问题出发逐步推到已知条件,此种方法叫逆推。无 论顺推还是逆推,其关键是要找到递推式。这种处理问题的 方法能使复杂运算化为若干步重复的简单运算,充分发挥出 计算机擅长于重复处理的特点。
《数据结构与算法》PPT课堂课件-第5章-递归

(2) if(n==1)
(3) move(x,z);
(4) else{
(5)
hanoi(n-1,x,z,y);
(6)
move(x,z);
(7)
hanoi(n-1,y,x,z);
(8) }
(9) }
A
B
C
2BAC 8 3ABC 0
1BCA6 2BAC 8 3ABC 0
A
B
C
2BAC 8 3 A B C 0 15
O(n)。对比循环结构的Fib2(n)和递归结构的Fib(n)可发现,循环结构
的Fib2(n)算法在计算第n项的斐波那契数列时保存了当前已经计算得到
的第n-1项和第n-2项的斐波那契数列,因此其时间复杂度为O(n);而递
归结构的Fib(n)算法在计算第n项的斐波那契数列时,必须首先计算第n -1项和第n-2项的斐波那契数列,而某次递归计算得出的斐波那契数列, 如Fib(n-1)、Fib(n-2)等无法保存,下一次要用到时还需要重新递归计
{ printf(“参数错!”);
return -1;
}
if(n == 0) return 1;
else {y = Fact(n - 1); /*递归调用*/
return n * y; }
}
5
为说明该递归算法的执行过程,设计主函数如下
void main(void) {
long int fn;
fn = Fact(3); }
(1) {
(2) if(n= =1)
(3) move(x,z);
(4) else{
(5)
hanoi(n-1,x,z,y);
(6)
move(x,z);
递归及递归算法分析课件

A(1,2)=A(A(0,2),1)=A(1,1)=2,故A(n,2)= 2^n 。
2 222
❖ M=3时,类似的可以推出
n
❖ M=4时,A(n,4)的增长速度非常快,以至于没有适当的数 学式子来表示这一函数。
❖
move(a,b);
❖
hanoi(n-1, c, b, a);
❖
}
❖}
❖ T(n)=2T(n-1)+O(1) n≥1
T(n)=2n-1
0
n=0
4
27
简单递归式的求解
1.T(n)=T(n-1)+c1 n>1
c2
n=1
2. T(n)=2T(n/2)+c1 n ≥2
c2
n<2
3. T(n)=2T(n/2)+Θ(n) n ≥2
O(1)
n<2
28
T( n/2 ) + T( n/2 ) + 1
例1 T(n) =
0
(n = 1)
解 :T(n)=2T(n/2)+1
=22T(n/22)+2+1
=23T(n/23)+22+2+1
令2r=n =2rT(1)+2r-1+。。。+2+1
=(1-2r)/(1-2)=n-1
∴ T( n ) = n - 1
25
递归算法的时间复杂度分析
❖ 递归函数求解
简单递归式求解 master method 递推方程的特征方程求解
递推与递归算法

递推与递归算法递推和递归是编程中常用的基本算法。
在前面的解题中已经用到了这两种方法,下面对这两种算法基本应用进行详细研究讨论。
一、递推递推算法是一种用若干步可重复的简单运算(规律)来描述复杂问题的方法。
[例1] 植树节那天,有五位参加了植树活动,他们完成植树的棵数都不相同。
问第一位同学植了多少棵时,他指着旁边的第二位同学说比他多植了两棵;追问第二位同学,他又说比第三位同学多植了两棵;…如此,都说比另一位同学多植两棵。
最后问到第五位同学时,他说自己植了10棵。
到底第一位同学植了多少棵树?解:设第一位同学植树的棵数为a1,欲求a1,需从第五位同学植树的棵数a5入手,根据“多两棵”这个规律,按照一定顺序逐步进行推算:①a5=10;②a4=a5+2=12;③a3=a4+2=14;④a2=a3+2=16;⑤a1=a2+2=18;Pascal程序:Program Exam1;Var i, a: byte;begina:=10; {以第五位同学的棵数为递推的起始值}for i :=1 to 4 do {还有4人,递推计算4次}a:= a+2; {递推运算规律}writeln(’The Num is’, a);readlnend.本程序的递推运算可用如下图示描述:递推算法以初始{起点}值为基础,用相同的运算规律,逐次重复运算,直至运算结束。
这种从“起点”重复相同的方法直至到达一定“边界”,犹如单向运动,用循环可以实现。
递推的本质是按规律逐次推出(计算)下一步的结果。
二、递归递归算法是把处理问题的方法定义成与原问题处理方法相同的过程,在处理问题的过程中又调用自身定义的函数或过程。
仍用上例的计算植树棵数问题来说明递归算法:解:把原问题求第一位同学在植树棵数a1,转化为a1=a2+2;即求a2;而求a2又转化为a2=a3+2; a3=a4+2; a4=a5+2;逐层转化为求a2,a3,a4,a5且都采用与求a1相同的方法;最后的a5为已知,则用a5=10返回到上一层并代入计算出a4;又用a4的值代入上一层去求a3;...,如此,直到求出a1。
C语言递推与递归PPT课件
• void qsort(int array[], int start, int end) • 把数组下标为start到end的元素进行快速排序第18页/共25页快速排序问题5
7
3
8
1
4
2
6
2
7
3
8
1
4
5
6
2
5
3
8
1
4
7
6
2
4
3
8
1
5
7
6
2
4
3
5
1
8
7
6
2
4
3
1
5
8
7
6
1
4
3
2
第16页/共25页
汉诺塔问题
第17页/共25页
快速排序问题
• 快速排序思路如下
• 将要排序的数据放在数组array中 • 取a[0]变在变量m中,通过分区处理把m排在适当的位置,使
m左边的数都比m小,m右边的数都比m大 • 按照常上面的思路分别处理m左边和右边的数据 • 如果分区长度是1,停止处理
• 思路提示
• m个球取出来的n个,包含两种情况:n在其中和n不在其中
• 编程实现
• 使用递归思想 • 编写递归函数 int cmn(int m, int n)
第12页/共25页
计算组合数
第13页/共25页
汉诺塔问题
• 据说在古代印度bramah神庙中,有个和尚整天把3根 柱子上的金盘倒来倒去。初始在柱子A上有64个盘子串 在一起,每一个盘子都比它下面的盘子小,可以在ABC 三个柱子之间互相移动,最终要全部移动到柱子C上。 移动规则如下:每次只允许移动一个,且较大的盘子永 远不能放在较小的盘子上。
递归及递归算法图解

递归问题的提出
第一步:将问题简化。 – 假设A杆上只有2个圆盘,即汉诺塔有2层,n=2。
A
B
C
递归问题的提出
A
B
C
对于一个有 n(n>1)个圆盘的汉诺塔,将n个圆盘分 为两部分:上面的 n-1 个圆盘和最下面的n号圆盘。将 “上面的n-1个圆盘”看成一个整体。
– 将 n-1个盘子从一根木桩移到另一根木桩上
1
当n 1时
n ! n (n 1)! 当n 1时
long int Fact(int n)
{ long int x;
if (n > 1)
{ x = Fact(n-1);
/*递归调用*/
return n*x; }
else return 1;
/*递归基础*/
}
Fact(n) 开始 传进的参数n N n>1
两种不同的递归函数--递归与迭代
21
(2)递归和迭代有什么差别?
递归和迭代(递推)
迭代(递推):可以自递归基础开始,由前向后依次计算或直
接计算;
递归:可以自递归基础开始,由前向后依次计算或直接计算;
但有些,只能由后向前代入,直到递归基础,寻找一条路径, 然后再由前向后计算。
递归包含了递推(迭代),但递推(迭代)不能覆盖递归。
递归的概念 (5)小结
战德臣 教授
组合 抽象
构造 递归
用递归 定义
用递归 构造
递归计 算/执行
递归 基础
递归 步骤
两种不同的递归函数
递归
迭代
两种不同的递归函数--递归与迭代
20
(1)两种不同的递归函数?
递归和递推:比较下面两个示例
递归与递推深入

一、从斐波那契数列说起
2、递归思想 递归是从问题的目标状态出发,通过自身的递归关系,层层递进,不断把问题的 规模缩小,最终达到问题的边界条件(已知的初始状态)的解题方法。也就是想要求 fib(n)就要先求fib(n-1)和fib(n-2),而想要求fib(n-1)就要先求fib(n-2)和fib(n3),……,想要求fib(3)就要先求fib(2)和fib(1),而fib(2)和fib(1)是已知的。 递归的优点是程序结构清晰,不仅可以用来计数,还可以用来枚举(如汉诺塔问 题)。但通过直接的递归过程和函数实现起来,有时效率很差(有谁试过用直接递归 函数去求fib(1000)要花多少时间吗?)。所以,递归更多的是一种思想、一种分析问 题的手法,有时需要做很多优化和改进工作,甚至还是要转化为递推、动态规划方法 去做。 递归算法一般适用在三个场合: 一是数据的定义形式是递归的,如求Fibonacci数列问题; 二是数据之间的逻辑关系(即数据结构)是递归的,如树、图等的定义和操作; 三是某些问题虽然没有明显的递归关系或结构,但问题的解法是不断重复执行一种 操作,只是问题规模由大化小,直至某个原操作(基本操作)就结束,如汉诺塔问题, 这种问题使用递归思想来求解比其它方法更简单。 下面就举一个递归分析的例子。
begin readln(n,k); writeln(s(n,k)); readln; end.
[测试数据] 输入:23 7 输出:4382641999117305
3、递推、递归、动态规划的关系
他们都是高度概括、高效、能反映问题本质的数学模型。在应用这类算法求解问 题时,需要大家对问题作深入分析和探究,考验大家的数学归纳、概括抽象和逻辑分 析能力。有时基于数据很大或时间限制很紧,还要有追求完美的态度,不仅只满足于 递归公式和表面上的线性关系(O(n))等,要多比较、多变化、多观察、多换角度 去思考,要想方设法去挖掘问题的本质,探究问题的闭公式(通项公式),把算法复 杂度降到O(1)或O(log2n)。 下面,我们会通过多个例子来分别说明。
递归算法和递推算法的原理

递归算法和递推算法的原理-概述说明以及解释1.引言1.1 概述递归算法和递推算法是编程中常用的两种算法思想,它们都是一种问题解决的方法论。
递归算法通过将一个大问题分解为一个或多个相同的小问题来解决,而递推算法则是通过给定初始条件,通过逐步推导出后续结果来解决问题。
递归算法是一种自调用的算法,它将一个问题划分为更小规模的相同子问题,并通过调用自身来解决这些子问题。
每个子问题的解决方案被合并以形成原始问题的解决方案。
递归算法具有简洁的代码结构和易于理解的逻辑。
它在一些问题上能够提供高效的解决方案,例如树的遍历、图的搜索等。
递推算法则是从已知的初始条件开始,通过根据给定的递推公式或规则,逐步计算出后续的结果。
递推算法是一种迭代的过程,每一次迭代都会根据已知条件计算得出下一个结果。
递推算法常应用于数学问题,求解斐波那契数列、阶乘等等。
递归算法和递推算法在解决问题时的思路不同,但也存在一些相似之处。
它们都能够将大问题分解成小问题,并通过解决这些子问题来获得问题的解决方案。
而且递归算法和递推算法都有各自适用的场景和优缺点。
本文将详细介绍递归算法和递推算法的原理、应用场景以及它们的优缺点。
通过比较和分析两者的差异,帮助读者理解和选择合适的算法思想来解决问题。
1.2文章结构文章结构部分的内容可以描述文章的整体框架和各个章节的内容概要。
根据给出的目录,可以编写如下内容:文章结构:本文主要探讨递归算法和递推算法的原理及其应用场景,并对两者进行比较和结论。
文章分为四个部分,下面将对各章节的内容进行概要介绍。
第一部分:引言在引言部分,我们将对递归算法和递推算法进行简要概述,并介绍本文的结构和目的。
进一步,我们将总结递归算法和递推算法在实际问题中的应用和重要性。
第二部分:递归算法的原理在第二部分,我们将详细讨论递归算法的原理。
首先,我们会给出递归的定义和特点,探索递归的本质以及递归算法的基本原理。
其次,我们将展示递归算法在不同的应用场景中的灵活性和效果。
〖2021年整理〗《递归法概述》精品完整教学课件PPT

处,结束回归阶段,完成递归调用。
递归的过程
程序的实现
• 递推公式 • 边界条件 • 定义函数
程序代码
例题:斐波那契数列
• 斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳 多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为 “兔子数列”。 • 指的是这样一个数列:1、1、2、3、5、8、13、21、34、…… • 用递归算法求斐波那契数列第n项的值。
递归算法及其实现
教学内容
◊ 递归的定义 ◊ 递归的要素 ◊ 递归的过程 ◊ 程序的实现
《老和尚给小和尚讲故事》的故事
• 从前有座山,山上有座庙,庙里有个老和尚,老和尚在讲故事给小和 尚听: • 从前有座山,山上有座庙,庙里有个老和尚,老和尚在讲故事给小和 尚听: • 从前座山,山上有座庙,庙里有个老和尚,老和尚在讲故事给小和尚 听:
课堂小结
• 把规模较大的问题变成规模较小的、规模较小的问题又变成规模更小的问题, 当问题小到一定程度时,可以直接得出它的解,从而得到原来问题的解。即 采用“大事化小,小事化了”的基本思想。
• 递推公式→边界条件→定义函数
其它程序举例(课后选做) • 汉诺塔游戏
递归的要素
• 递推公式:
•
通常把一个大型复杂的问题通过“递推公式(也叫递归方程)”层层转化为一个与原问题
相同或相似的但规模更小的问题来求解。
• 边界条件:
•
当通过反复的调用,把问题的规模小到一定程度时,必须能直接给出问题的解,即有明确
的结束递归的边界条件(也叫递归出口)。
计算n!(n的阶乘) • 计算过程:(手动推导)
递归的定义(一)
