2011年数学建模论文-公交车调度问题
全国大学生数学建模竞赛题目B题

B题公交车调度
公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
公交车调度数学建模

公交车调度数学建模公交车调度摘 要本文通过对给定数据进行统计分析,将数据按18个时段、两个行驶方向进行处理,计算出各个时段各个站点以及两个方向的流通量,从而将远问题转化为对流通量的处理。
首先,利用各时段小时断面最高流通量计算出各时段各方向的最小发车次数,进行适当的调整,确定了各时段两个方向的发车次数。
假定采用均匀发车的方式。
继而求出各时段两个方向发车间隔,经部分调整后,列出0A 站和13A 站的发车时刻表,并给出了时刻表的合理性证明,从而制定调度方案。
根据调度方案采用逐步累加各时段新调用的车辆数算法,求出公交车的发配车辆数为57辆。
其次,建立乘客平均待车时间和公交车辆实际利用率与期望利用率的差值这两个量化指标,并用这两个指标来评价调度方案以如何的程度照顾到乘客和公交公司双方利益。
前者为4.2分钟,后者为13.88%。
最后,我们以上述两个指标为优化目标,以乘客的等车时间数学期望值和公交车辆的满载率的数学期望为约束指标,建立了一个双目标的优化模型。
并且给出了具体的求解方法,特别指出的是,给出了计算机模拟的方法求解的进程控制图。
通过了对模型的分析,提出了采集数据的 采集数据方法的建议。
注释:第i 站乘客流通量:∑=ik 1(第k 站的上车的人数与第k 站的下车人数的差值);总的乘客等车时间:∑=m i 1∑=nj 1(第i 时段第j 站等车乘客数)⨯(第I 时段第j 站等待时间);乘客平均等车时间:总的乘客等车时间与总乘客数的比值;实际利用率:总实际乘客流通量与公司车辆总最大客运量的比值;期望利用率:总期望乘客流通量与公司车辆总最大客运量的比值一、问题的提出一条公交线路上行方向共14站,下行方向功13站,给定典型的一个工作日两个运行方向各站上下车的乘客数量统计。
该线路用同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰是一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低与100%,一般也不要地狱50%。
公车调度问题的数学模型

公车调度问题的数学模型班级:信息1102学生:汤韩瑜学号:07111082研究概述•1研究背景•2研究意义•3论文结构•4研究内容•公交车调度问题的背景是某大城市公交部门提出的一个实际科研课题。
该课题要求对一条确定的公交路线,解决三个方面的问题:•第一, 根据历史积累和必要的补充调查数据,提出沿路各站来站与离站的乘客分布规律;•第二, 研制一个模拟该线路公交运行过程的数学模型;•第三, 在前两条的基础上为该线路提出一个配备车辆和司( 机) 售( 票员) 人员数目的方案,以及一个在通常情况下车辆的运行时间表。
•从历史积累和必要的补充调查数据中,提出公交车沿路各站来站与离站的乘客分布规律将实际问题转化为数学模型进行具体化的解答有数学模型解答出的答案制定司售人员的工作安排的正常情况下的车辆时间安排3论文结构•第一部分:论文题目•第二部分:摘要•第三部分:关键词•第三部分:正文•第四部分:结论•第五部分:致谢•第六部分:参考文献4研究内容•首先,选择了该市一条比较典型的公交线路, 沿线上行方向共14 站, 下行方向共13站,根据多年来沿线各站乘客来、离站的人数调查数据,给出了该线一个工作日两个运行方向各站上下车的乘客数量按时间的分布。
•其次,根据上述数据,在尽可能适当考虑公交社会效益和公交公司利益的目标下,为该线路设计一个便于操作的全天( 工作日) 的公交车调度方案,即两个起点站的发车时刻表,并指出实现这个方案至少需要配备多少辆车; 给出这种方案照顾乘客和公交公司双方的利益程度的数量指标,从而将这个调度问题抽象成一个明确、完整的数学模型,并指出求解模型的方法。
研究方法•建立数学模型•具体步骤:•1.建立数学模型•(1)运行模型及其求解•(2)配车模型及其求解•2.得出结论主要结论•根据所给数据中始发站的上车人数, 确定早、晚高峰时段为:早高峰6 ∶40 ~9 ∶40 ;晚高峰15 ∶50 ~18 ∶50 。
2011数学建模优秀论文——交巡警服务平台的设置与调度

交巡警服务平台的设置与调度摘要本文对交巡警服务平台的设置与调度问题,应用Dijstra最短路算法,多目标规划,0-1整数规划,时间步长法,针对不同情况的具体问题,分别建立了相应的数学模型,给出了合理的交巡警服务平台的设置与调度方案。
对A区交巡警服务平台管辖范围的分配问题,首先根据节点坐标计算出节点邻接对称矩阵,然后利用Dijstra算法求解出各节点到每个平台的最短距离,并根据到平台最短距原则分配各节点给相应的平台管辖,最后得到了各平台管辖的范围(见表1),同时给出了各平台管辖范围内3分钟路程外的节点(见表1)。
对封锁A区13条要道节点的交巡警服务平台警力调度问题,考虑到各平台出警时间的同步,出警的平台数量最少以及一个平台警力最多封锁一个路口的约束,运用多目标规划,0-1整数规划建立了一个封锁13条要道节点最长时间最小化模型,并运用Lingo 求解出平台3,4,5,6,7,9,10,11,12,13,14,15,16分别封锁要道节点16,38,62,48,29,30,12,24,22,21,23,28,14,得到了A区13条要道全部封锁完成的最短时间为8分钟。
对确定需要增加交巡警服务平台的个数及位置问题,考虑到各平台工作量的均衡及出警时间,运用各平台工作量(所管辖范围内的发案数和)的标准差来衡量其工作量的均衡,建立了一个对每个节点的出警时间不超过3分钟,且各服务平台工作量的标准差最小(各平台工作量越均衡)的数学模型,并得到可在本区增加4个平台,分别增加在节点28,39,48,87.对评价全市现有交巡警服务平台设置方案的合理性问题,首先根据主城区以及最短距原则将全市各区节点分配给本区现有的平台,然后根据各平台工作量的均衡、出警时间、本区人口密度及发案率对现有平台设置进行了评价,并对明显不合理处进行了调整,给出了新的平台设置方案,同时对新方案各平台工作量,所辖3分钟路程节点数进行了比较,验证了新的平台设置方案明显优于现有平台的设置方案(见表3)。
公交车调度论文分解

关于公交车调度问题摘要随着国民生活水平的提高,公共交通问题也日益重要起来,而公交车调度是制约公共交通的重要因素。
根据题中所给的数据,建立数学模型对公交车调度问题进行分析。
对于问题一:首先,根据城市中某条公交线路各个时段的客流信息,得出了公交车公司的最大客容量,发车车次,发车时间间隔。
运用MATLAB编程,计算出各个时段的最大客容量,在满足公交满载率的情况下得出日最少发车车次为460次,其中上行线230车次,下行线230车次,用LINGO计算出发车时间间隔,并给出公交车发车时刻调整表。
基于公交车从起始站运行到终点站的用时为44分钟,且时间间隔应为整分间隔,可算出早高峰所需最少车辆为58辆。
其次,一个合理的公交车调度方案应该考虑公交公司的最大利益和乘客的满意度两个方面。
故建立了满意度分析模型,在此模型中,运用了层次分析法。
对满意度进行了分析计算。
结合整数规划模型中的结果可求得满意的分析模型中公交公司与乘客双方之间满意度,并且使二者和达到最大,同时双方满意度之差最小,得到上下行的最优满意度(0.8688,0.8688)。
最后,综合了公交车公司的最大客容量、发车车次、公交公司满意度等方面因素,且以公交公司所发的车次最小为目标,乘客的等待时间和公交载客率为约束条件提出了整数规划模型。
此模型是把公交车调度问题抽象成数学模型来表达,从考虑发车车次最小出发,满足各项约束条件,寻求最优解。
运用LINGO编程,可计算出公交公司日发车车次最小值为461次。
因此该解法是在满足乘客的情况下求的最优解。
乘客的等待时间的满意度为100%,但是从舒适度考虑,上行和下行分别有11和9人不满意。
这个结果为满意度模型和整数规划模型的中间情况,故此模型的建立是合理的。
关键词:整数规划满意度MATLAB LINGO一问题的重述公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
一类公交车调度问题的数学模型及其解法

一类公交车调度问题的数学模型及其解法1. 背景介绍公交车作为城市交通的重要组成部分,其运营效率和服务质量直接影响市民出行体验。
而公交车调度问题则是保障公交线路运营效率和准时性的重要环节之一。
在日常运营中,由于路况、乘客量、车辆故障等影响因素,公交车的调度往往面临诸多挑战。
如何利用数学模型解决公交车调度问题成为了一个备受关注的课题。
2. 公交车调度问题的数学建模公交车调度问题的数学建模主要涉及到车辆的合理分配以及路线的优化规划。
在数学建模时,需要考虑的主要因素包括但不限于乘客量、车辆容量、交通状况、站点分布等。
而个体车辆的运行轨迹则需要综合考虑上述因素以及最优化算法对其进行分析。
3. 数学模型的构建针对上述因素,可以将公交车调度问题构建成一个复杂的优化模型。
该模型主要包括以下几个方面的内容:(1)乘客需求预测:通过历史数据和大数据分析,预测不同时段和不同线路的乘客需求,为车辆调度提供依据。
(2)车辆分配优化:根据乘客需求预测和实际路况,采用最优化算法确定每辆车的运行路线和发车间隔。
(3)站点排队优化:结合乘客上下车规律和站点的停靠条件,优化车辆在不同站点的排队顺序,以减少候车时间和提升服务效率。
(4)交通状况仿真:通过交通仿真模型,考虑城市交通状况对公交车运行的影响,提前对可能出现的拥堵情况进行预判,以调整车辆的发车时间和路线。
4. 数学模型的求解在构建好数学模型后,需要采用合适的方法对其进行求解。
常见的求解方法主要包括但不限于线性规划、遗传算法、模拟退火算法等。
在实际求解过程中,需要充分考虑不同方法的适用场景和对模型的拟合程度,以选择最合适的求解方法。
5. 案例分析以某市的公交系统为例,采用上述数学模型对其进行调度优化。
通过收集该市的实际路况数据、站点分布情况以及历史乘客需求数据,建立完整的数学模型。
然后运用遗传算法对其进行求解,得到了最优的车辆运行路线和发车间隔。
在模型求解后,将其应用于实际公交车调度中,并进行了一段时间的实际运行试验。
数学建模中的优化调度问题

数学建模中的优化调度问题在数学建模中,优化调度问题是一个重要的研究领域。
优化调度问题可以通过数学模型和算法来解决,以提高资源利用率、降低成本、提高效率等目标。
本文将介绍数学建模中的优化调度问题,并讨论一些常见的调度算法和应用案例。
一、优化调度问题的定义与形式化描述优化调度问题通常是指在有限的资源和约束条件下,如何合理安排任务和资源的分配,以达到最佳的结果。
优化调度问题可以用数学模型来描述,常见的形式化描述包括:1. 作业调度问题:如何合理安排作业的执行顺序和时间,以最小化总执行时间或最大化作业的完成数量。
2. 机器调度问题:如何安排机器的任务分配和工作时间,以最小化总工作时间或最大化机器的利用率。
3. 运输调度问题:如何合理安排货物的运输路线和车辆的调度,以最小化运输成本或最大化运输效率。
二、常见的调度算法优化调度问题可以借助多种算法来求解,以下是一些常见的调度算法:1. 贪心算法:贪心算法通过每一步的局部最优选择来构建整体最优解。
例如,在作业调度问题中,可以按照作业的执行时间或紧急程度进行排序,然后按顺序进行调度。
2. 动态规划:动态规划通过将问题分解为子问题并记录子问题的最优解,再根据子问题的最优解来求解整体问题的最优解。
例如,在机器调度问题中,可以使用动态规划来确定每个任务在不同机器上的最优执行顺序。
3. 遗传算法:遗传算法是一种模拟进化过程的优化算法,通过模拟自然界的进化过程来寻找问题的最优解。
例如,在运输调度问题中,可以使用遗传算法来优化货物的运输路径和车辆的调度计划。
三、优化调度问题的应用案例优化调度问题广泛应用于生产制造、交通运输、资源分配等领域。
以下是一些优化调度问题的应用案例:1. 生产制造:在工厂生产过程中,如何合理安排设备的使用和任务的执行,以最大化生产效率或最小化成本。
2. 铁路调度:如何安排列车的行动计划和车次的分配,以最大化铁路运输能力和减少列车的延误。
3. 资源分配:如何合理分配有限的资源,如人力、设备和原材料,以最大程度地满足需求和降低成本。
CUMCM优秀论文-公交车调度优化模型【数学建模】(可编辑)

CUMCM优秀论文-公交车调度优化模型【数学建模】维普资讯第19巷建摸专辑工程数学学报Voll9Supp。
月JOURNAL OFENGINEERING MATHEMATICS Feb 2002文章编号:1005―3085(2002)05―0095―06公交车调度优化模型李成功,脱小伟,郭尚彬指导教师:祁忠斌(兰州工业高等专科学校,兰州 730050)鳙者按:本文根据时同和空间客流不均衡变化的情况研究车辆蔼度的规律.在保证一定收益和使顾客满意的情况下给出了调度时刻表。
率文分析问题比较精细,叙连通顺倚练。
本文的不足之址是对原题中50%与 120%的不葡提法考虑不够摘要:车文主要研究了一条公空线路在其每时段内各个车站点的客流坑计数据为已知情况下的车辆运行计埘时刻表的制定问题。
一般情况下.公寰公司在调查研究取得一定数据的基础上帮是按”接连开出的方法安排工作目的车辆行车调度表.使得在运行期内.一组车辆“鱼贯而出.再鱼贯而^ ,而我们主要田F究了-随着时间和空甸上客流不坷街性的变化.车辆应如何调度的规律,建立了目标规j}I模型。
实现了有早出,有晓出.车辆有多青少的调度计划。
在保证一定效益和顾客满意的情况下.使在岗车辆的总运行时间最短。
所有的计算都在计算机上实现,得出了调度时刻表,且最少的车辆散为 42。
顾客与公交公司的满意程度比为:068:046.关麓面:公变车调度;客流量;目标规划分粪号:AMS(2000)90C08 中囤分类号:TB114 1 立标识码:A1 已知数据及问题的提出我们要考虑的是某城市的一条公交线路上的车辆调度问题。
现已知该线路上行的车站总数 N (:14),下行的车站总数 N (=13)。
且在问题中给出了某一个工作日(分为 m 个时间段,第时间段的时问跨度为£.=1小时)中第时间段第站点上行方向上、下车的乘客数量为 Q ( ),Q ( ),第时问段第J站点下行方向上、下车的乘客数量为 Q ( ),Q (,);上、下行站点问的距离分别为 L,,L,。
数学建模论文公交车调问题

2011年数学建模论文——对公交车调度问题的研究摘要:本文根据所给的客流量及运营情况排出公交车调度时刻表,以及反映客运公司和乘客的利益有多个指标,建立了乘客的利益及公司利益两个目标函数的多目标规划数学模型。
基于多目标规划分析法,进行数值计算,从而得到原问题的一个明确、完整的数学模型,并在模型扩展中运用已建的计算机模拟系统对所得的结果和我们对于调度方案的想法进行分析和评价。
首先通过数据的分析,并考虑到方案的可操作性,将一天划为;引入乘客的利益、公司利益作为两个目标函数,建立了两目标优化模型。
通过运客能力与运输需求(实际客运量) 达到最优匹配、满载率高低体现乘客利益;通过总车辆数较少、发车次数最少表示公司利益建立两个目标函数。
应用matlab中的fgoalattain进行多目标规划求出发车数,以及时间步长法估计发车间隔和车辆数。
关键字:公交车调度;多目标规划;数据分析;数学模型;时间步长法,matlab一问题的重述:1、路公交线路上下行方向各24站,总共有L 辆汽车在运行,开始时段线路两端的停车场中各停放汽车m辆,每两车可乘坐S人。
这些汽车将按照发车时刻表及到达次序次发车,循环往返地运行来完成运送乘客的任务。
建立数学模型,根据乘客人数大小,配多少辆车、多长时间发一班车使得公交公司的盈利最高,乘客的抱怨程度最小。
假设公交车在运行过程中是匀速的速度为v。
1路公交车站点客流量见下表从新汽车站出发到市检察院站点名称新汽车站汉庭花园天九湾电信公司天九湾车场西环小区步行街上车人数11 3 1 1 1 2 下车人数1 0 0 0 4 等待时间3.8 5 2 1.5 2站点名称实验小学莆一中后门十字街旧汽车站新街口市农行上车人数5 1 3 4 8 3下车人数1 0 0 1 0 1 等待时间3.8 3 5.3 14.1 3.8站点名称市公交公司中国银行凤凰山八十亩小区石室路口市公交稽证处上车人数3 1 3 3 2 2 下车人数2 3 3 9 2 3 等待时间1.7 1 0.52.5 2.2 5.5 站点名称北磨交通花园三信家园市政府龙桥市场市检察院上车人数2 0 0 0 0 0 下车人数4 2 25 7 10 等待时间4从市检察院出发到新汽车站站点名称市检察院龙桥市场市政府三信家园交通花园北磨上车人数17 3 0 1 2 7 下车人数0 1 1 1 1 4 等待时间3.5 1.2 2.84.8 2.6 4站点名称市公交稽证处石室路口八十亩小区凤凰山中国银行市公交公司上车人数2 3 1 5 8 3 下车人数1 0 12 2 1 等待时间3.3 1.6 5 4 0 9 站点名称市农行新街口旧汽车站十字街莆一中后门实验小学上车人 2 0 2 4 1 0数下车人数2 7 2 5 2 2 等待时间3.4 6 5 1站点名称步行街西环小区天九湾车场天九湾电信公司汉庭花园新汽车站上车人数0 0 1 0 0 0 下车人数3 1 24 3 14 等待时间11 已知数据及问题的提出我们要考虑的是莆田市的一路公交线路上的车辆调度问题。
一种公交调度问题的数学模型及应用

本科生毕业论文(设计)一种公交调度问题的数学模型及应用姓名魏雪燕学号20104150146专业资源环境与城乡规划管理指导教师樊明2014年6月2日摘要本文针对公交车调度问题,在尽量满足乘客和公交车公司双方利益的前提下,建立模型,从一个典型工作日客运人数的一般规律和实际生活中人们的生活规律中采集数据,将所给的数据进行转换处理, 以每个时段发出的公交车将乘客进行重新划分, 分析数据,然后由各时段内站间最大运送乘客数量求出该时段的最少发车次数, 进而求出需要的最少车辆。
文章主要以车辆载客限制、乘客等待时间为约束条件, 以公交公司运营的公交车数最少为目标函数, 建立整数规划模型]1[。
通过具体数据分析, 将公交车运行时段分为早高峰、平峰、晚高峰,进而计算出发车时间间隔。
由于考虑到乘客和公交公司的利益,力求达到社会总效益最大化,对各时段发车时间间隔以及发车次数做出轻微适当调整,尤其是人多人少时段,并计算出公交车的平均满载率,并对所求结果进行评价关键词:整数模型;时段;站间运送乘客数量;平均满载率]8[错误!未找到引用源。
AbstractBus scheduling problem, the author of this paper, to satisfy passengers and bus companies under the premise of the interests of both sides, build a model, on the basis of the general regularity of a typical weekday passenger Numbers and the life of people in actual life rule in collecting data, will give the data conversion process, for each time to the bus passengers from the analysis of the data, and then by the time standing between the maximum number of passengers the least start of the session, and then calculate need minimum of vehicles. Article mainly passenger cars, passenger waiting time as constraint conditions, with the operation of the bus company bus number minimum as objective function, integer programming model is established in [1]. By analyzing specific data, bus operation time can be divided into early peak, peak, peak later, car departure time intervals are calculated. Due to considering the interests of the passengers and bus companies, to achieve social benefit maximization, the number of various departure time intervals of time and start to make a slight adjust, especially people have less time, and calculate the average bus load factors, and to evaluate the result of the petitionsKey Words:Integer model; Period of time; The number of passengers stand between transport; The average load factors目录1.引言……………………………………………………………………(一)研究的背景……………………………………………………………………(二)研究的内容……………………………………………………………………(三)研究的意义……………………………………………………………………2.公交调度数学模型的建立……………………………………………………………………2.1公交问题的提出……………………………………………………………………2.2问题的分析……………………………………………………………………2.3基本假设……………………………………………………………………2.4模型的建立……………………………………………………………………3.模型的实践……………………………………………………………………3.1选取路线的模拟……………………………………………………………………3.2该线路上公交运行概况……………………………………………………………………3.3对采集的数据预处理…………………………………………………………………… 3.4划分时间段及数据计算……………………………………………………………………(一)定义及划分时间段…………………………………………………………(二)各时段最大乘客人数统计及分析…………………………………………………(三)各时段公交车运营次数…………………………………………………………3.5模型计算……………………………………………………………………4.模型的评价……………………………………………………………………4.1乘客的满意程度……………………………………………………………………4.2公交公司的利益评价…………………………………………………………………… 4.3模型中的误差分析……………………………………………………………………4.4本文模型评价综述……………………………………………………………………5.模型的改进与应用……………………………………………………………………5.1模型的改进……………………………………………………………………5.2模型的推广及应用……………………………………………………………………1引言(一)研究的背景随着改革开放和经济的发展,人民的生活水平越来越高,人们的环保和低碳意识也越来越强烈,尤其是这两年雾霾现象越来越困扰着人们的生活,为人们的室外活动造成了很大的影响,因此作为人们出行工具之一的公共交通也备受人们青睐。
公交调度问题的常用算法

公交调度问题是一种优化问题,旨在合理安排公交车辆的发车时间、路线和停靠站点,以提高运输效率、降低成本。
以下是公交调度问题常用的一些算法:1. 遗传算法(Genetic Algorithms):•遗传算法是一种模拟生物进化过程的优化算法。
通过使用交叉、变异等操作,可以生成一组可能的调度方案,并通过适应度函数评估其性能。
优点是可以全局搜索,但可能需要较长的计算时间。
2. 离散事件模拟(Discrete Event Simulation):•使用离散事件模拟来模拟公交系统的运行。
这种方法考虑车辆之间的相互影响,通过模拟车辆在路网上的运动和停留来评估调度方案的性能。
3. 贪婪算法(Greedy Algorithms):•贪婪算法通常用于在每个决策点上做出局部最优的选择。
在公交调度中,可以从某个车站开始,根据某些准则(如最短路径、最早到达时间等)逐步选择下一个站点,构建调度方案。
4. 粒子群算法(Particle Swarm Optimization, PSO):•PSO 模拟鸟群或粒子在搜索空间中的移动,通过合作和信息共享来寻找最优解。
在公交调度中,每个粒子代表一个可能的调度方案,通过更新粒子的位置来搜索更好的解决方案。
5. 模拟退火算法(Simulated Annealing):•模拟退火算法通过模拟金属冶炼时的冷却过程来进行优化。
在公交调度中,可以使用模拟退火来随机选择解决方案,并以一定的概率接受比当前解更差的解,以避免陷入局部最优解。
6. 混合整数规划(Mixed-Integer Programming, MIP):•使用整数规划方法来解决公交调度问题。
这种方法将问题建模为数学规划问题,通过求解整数规划问题得到最优解。
选择算法通常取决于具体问题的性质和规模。
大规模、复杂的公交调度问题可能需要采用启发式算法,而小规模问题可能可以使用精确解法。
公交车调度数学建模

公交车调度摘 要本文通过对给定数据进行统计分析,将数据按18个时段、两个行驶方向进行处理,计算出各个时段各个站点以及两个方向的流通量,从而将远问题转化为对流通量的处理。
首先,利用各时段小时断面最高流通量计算出各时段各方向的最小发车次数,进行适当的调整,确定了各时段两个方向的发车次数。
假定采用均匀发车的方式。
继而求出各时段两个方向发车间隔,经部分调整后,列出0A 站和13A 站的发车时刻表,并给出了时刻表的合理性证明,从而制定调度方案。
根据调度方案采用逐步累加各时段新调用的车辆数算法,求出公交车的发配车辆数为57辆。
其次,建立乘客平均待车时间和公交车辆实际利用率与期望利用率的差值这两个量化指标,并用这两个指标来评价调度方案以如何的程度照顾到乘客和公交公司双方利益。
前者为4.2分钟,后者为13.88%。
最后,我们以上述两个指标为优化目标,以乘客的等车时间数学期望值和公交车辆的满载率的数学期望为约束指标,建立了一个双目标的优化模型。
并且给出了具体的求解方法,特别指出的是,给出了计算机模拟的方法求解的进程控制图。
通过了对模型的分析,提出了采集数据的 采集数据方法的建议。
注释:第i 站乘客流通量:∑=ik 1(第k 站的上车的人数与第k 站的下车人数的差值);总的乘客等车时间:∑=mi 1∑=nj 1(第i 时段第j 站等车乘客数)⨯(第I 时段第j 站等待时间);乘客平均等车时间:总的乘客等车时间与总乘客数的比值;实际利用率:总实际乘客流通量与公司车辆总最大客运量的比值; 期望利用率:总期望乘客流通量与公司车辆总最大客运量的比值一、问题的提出一条公交线路上行方向共14站,下行方向功13站,给定典型的一个工作日两个运行方向各站上下车的乘客数量统计。
该线路用同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰是一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低与100%,一般也不要地狱50%。
数学建模论文校园公交车调度问题大学论文

西南交通大学2012年新秀杯数学建模竞赛题目:A题组别:大二组西南交通大学教务处西南交通大学实验室及设备管理处西南交通大学数学建模创新实践基地校园通行车路线的设计摘要本文主要研究的是校园交通车的站点设置、在固定停车和招手即停两种模式结合下的运载能力、运行路线和时间安排以及相应行驶方案的规划问题。
问题一中,我们对校园通行车现有行车路线网络和常停站点进行了调查和分析。
首先,在数据处理阶段,将站点实体间的线路选择抽象为图论最短路模型,用Matlab软件画出三条主要的行车线路,然后利用GIS空间分析方法解决单个交通线路上站点规划问题。
该方法依据乘客出行时间最短确定单个线路上的站点个数,结合GIS缓冲区分析和叠合分析,在路线上做站点设置的适宜性讨论,提出基于最优化理论和GIS空间分析技术的站点规划方法,确定站点的位置,从而提供一种可行的行驶方案。
问题二中,考虑固定停车和招手即停相结合的方案,我们首先将最佳行驶路线定义为车辆运行时间最短的路线,将图论中经典的Dijkstra算法(单源最短路径)进行改进,结合哈密尔顿图,以结点之间的时间作为权数,利用C++编程得到最佳推销员回路,也就是通行车行驶的最佳路径。
考虑到招手即停模式具有极大的随机性,为了便于调度,我们首先对乘车人次密度分布进行了调查和分析,并通过随机模拟出概率分布值较大的区域,将其抽象为一假想固定停车点,这样就将模型简化为固定停车点最佳行驶路径的问题。
根据已得到的乘车时段分布规律和学校实际的作息时间表,按照模糊聚类分析法将一工作日数单位时间段划分为更概括的高峰期、低潮期和一般期,并应用Matlab中的fgoalattain进行非线性规划求出实际发车数,以及应用时间步长法估计发车间隔,从而给出两种模式结合下通行车每周运行的车辆数、路线和时刻表。
问题三中,我们首先对校区师生乘车需求人数进行了描述性统计,从乘车人数的均值、方差、峰度以及正态性四个角度对样本进行检测,找到相关的分布规律与结论,即每日在各时段中的乘车人数分布相似。
公共自行车调度问题-数学建模论文

目录一、问题引入..................................................................................................................................... - 3 -二、问题分析..................................................................................................................................... - 3 -2.1第一问分析................................................................................................................... - 4 -2.2第二问分析................................................................................................................... - 4 -2.3第三问分析................................................................................................................... - 4 -三、模型假设和符号说明................................................................................................................. - 5 -3.1模型假设....................................................................................................................... - 5 -3.2符号系统....................................................................................................................... - 6 -四、模型建立..................................................................................................................................... - 6 -4.1模型分类....................................................................................................................... - 6 -4.2 租赁点分配方案建模.................................................................................................. - 7 -4.3 调度车调度方案建模.................................................................................................. - 8 -4.3.1一辆调度车调度方案....................................................................................... - 8 -4.3.2多辆调度车调度方案....................................................................................... - 9 -4.4租赁点数目和位置的确定......................................................................................... - 11 -4.5 调度时间的模型........................................................................................................ - 12 -五、模型的求解............................................................................................................................. - 13 -5.0经纬度转换为横纵坐标............................................................................................. - 13 -5.1 求解最短路径............................................................................................................ - 13 -5.2 模型一次运行后的单车重分配求解........................................................................ - 14 -5.3 求解分配方案的预估—校正算法............................................................................ - 16 -5.4 求解调度方案的启发式算法.................................................................................... - 16 -5.4.1算法简介......................................................................................................... - 16 -5.4.2算法内容......................................................................................................... - 17 -5.4.3约束条件......................................................................................................... - 18 -5.4.4算法流程图..................................................................................................... - 19 -5.5租赁点位置................................................................................................................. - 20 -5.6计算结果..................................................................................................................... - 20 -5.6.1第一问结果..................................................................................................... - 20 -5.6.2第二问结果..................................................................................................... - 21 -5.6.3第三问结果..................................................................................................... - 23 -六、模型检验................................................................................................................................... - 26 -七、模型优缺点以及改进............................................................................................................... - 26 -7.1分配方案的优点......................................................................................................... - 27 -7.2调度方案的缺优点..................................................................................................... - 27 -7.3新增节点模型的优缺点............................................................................................. - 27 -7.4模型和算法的改进..................................................................................................... - 28 -7.4.1算法的改进..................................................................................................... - 28 -7.4.2模型的改进..................................................................................................... - 28 -八、参考文献................................................................................................................................... - 30 -附录................................................................................................................................................... - 30 -一、问题引入近年来,随着经济的发展,我国各级城市的机动车保有量都进入了持续高速增长时期,但由此所引发的道路拥堵、空气污染也引起了政府以及百姓的极大关注。
论文

公交车调度问题的数学模型摘要:本文利用整数规划方法建立了公交车调度的数学模型。
首先通过数据分析,得出早高峰、平峰、晚高峰。
然后为了方便计算和公交车的实际运行情况,将1小时为一时段间隔的统计数据转化成以45分钟为一时段间隔,利用整数规划,以公交公司运营的公交车数最少为目标,以公交车运行时各项需求为约束条件建立了数学模型,利用lingo 求解,得出最少需要55辆公交车,其中上行方向49辆车,下行方向安排6辆车,并计算出发车间隔。
最后考虑公交公司和乘客的利益对发车间隔做出调整并计算出公交车的平均满载率,其中上行方向为:=β93.3%,下行方向为:=β92.5%。
关键词:公交车调度;数学规划;lingoA Mathematical Model of Bus SchedulingAbstract :Key word :bus scheduling;1、引言:随着改革开放和经济的发展,人民的生活水平越来越好,人们的环保和低碳意识也更加强烈,因此作为人们出行工具之一的公共交通也倍受人们青睐。
发展公交是城市交通发展的方向,如果公交方便、准点、舒适、安全,市民就更愿意坐公交,公交才能真正成为城市的主要交通工具。
这样,城市的交通才能得到改善。
2012年5月1日,温家宝与北京环卫公交职工共度"五一"国际劳动节说,城市发展就是要坚持公交优先的原则,进一步发展和完善公交系统。
怎样做好一个城市公交车的调度对完善城市交通环境、改善市民的出行状况、提高公交公司的经济效益和社会效益都有重要意义。
城市公交车调度受到各种因素的影响, 其中包括公交车本身、乘客、交通事故、交通阻塞、自然气候因素以及其他交通方式等。
这些影响因素就会造成乘客和公交公司双方利益的矛盾冲突。
乘客希望出行时等车时间尽可能短,即公交公司调用更多的公交车;公交公司希望尽可能的降低成本来提高收益,即减少公交车数量。
由于上述矛盾的复杂性和重要性,在1985年Peter G Furth针对公交上下行方向客流不均的问题,讨论了起始站空车发车,在中途载客问题,并提出了相关模型[1]。
三篇公交车合理调度的优化模型论文节选

下面论文非优秀文章,只作参考。
公交车合理调度的优化模型温育权、梁海花、侯飞燕摘要:公共交通是城市交通的中央组成部分,公交车的调度具有重要的现实意义.本模型利用统计资料的特点,运行统计,最优化等数学方法以及Maple 软件,考虑到公交公司和乘客双方的利益相矛盾,给出了一个最优的调度时刻表,计算出了所需车辆至少要53辆.进而劳力到调度方案的可行性,通过计算机模拟搜索,给出了一个便于操作的优化方案,计算出所需车辆至少为44辆.校验该方案,公交公司的利益很大程度满足,原来每天每车次的平均载客量只降低了39人/车次,而乘客满意度也不会有很大降低.关键词:公交车调度;载客率;发车时刻表;最优模型;优化方案一、问题的提出公共交通是城市交通的重要组成部分,作为公交车的调度具有重要的现实意义.某城市的公交公司统计了上行下行两个方向的某条公交线路上的客观情况.给出了一个典型工作日各时组两个运行方向每站上下车人数.该条公交线路上行方向共14站,总长14.58公里;下行方向共13站,总长14.61公里.公交公司配给该线路标准载客100人的同一型号的大客车,客车在该线路上运行的平均速度为20公里/小时.现在要根据这些资料,为该线路设计一个便于操作的全天(工作日)的公交调度方案,包括:1.两个起点站的发车时间;2.一共需要多少辆车;3.该方案以这样的程度照顾到了乘客和公交公司双方的利益.其中,营运调度要求: (1).每一辆客车的满载率50%~120%.(2).乘客候车时间一般不超过10分钟,早高峰期不超过5分钟. 二、模型的假设1、交通顺畅,公交车运行秩序良好,路上无阻塞情况,汽车也不会出现突然坏掉或燃料不足等情况.2、每辆客车始终以20公里/小时的平均速度行驶,到各站的停留载客时间也涵盖在这个车速里,即不考虑每个乘客的上下时间.3、汽车一到总站,乘客全部下车,从而保证了总站发车时空车.4、不论乘车距离长短,上车票价都相同.(如:1元/人)5、公交公司的利益只考虑汽车在路面上行驶的车辆次数与载客率.6、全天(工作日)的公交车调度从5:00开始到23:00结束,分为18个单位时组,每个时组为1小时,表示为i T ()18,,2,1 =i7、乘客到各站点的人数,在各时组里均匀分布. 8、乘客利益只考虑等车时间的长短.三、符号的约定1i N 、2i N 分别表示上下行线第i T 时组内需要开出的乘客总次数,i=18,,2,1 1i n 、2i n 分别表示在上下行线第i T 时组内正在路上行驶的车辆数,i=18,,2,1 上T 、下T 分别表示在上下行线客车从始点到终点所需行驶时间.i d 、 'i d 分别表示在上下行线个站点间距离()1413,,2,1或 =i v 表示汽车行驶的平均速度v=20公里/小时.i t ∆ 表示从第i+1个车次的发车间隔时间() ,1,0=ii t 表示从起点到i A 站所需时间()1413,,2,1或 =iM 表示每次车的平均载客量.四、问题的分析本案例给出了上下行两方向个时组i T 上行下效每站点上下车总人数的统计数,由这些资料来确定一个便于操作的全天(工作日)的公交车合理调度的方案,它要求某程度照顾到乘客与公交公司双方利益衡量.乘客利益是与等待时间有关,等待时间越少,满意度越高;汽车公司利益与满载率和两站发出次数有关.显然减少乘客等待是与增加公司利益是两个相互矛盾的问题.我们可求出一个在每一组内各相邻站点见的公交车上乘坐的总人数,以满载率为约束条件,求得每一个时组i T 内上下行线两方向所需车次数,在此基础上寻找最高峰时段所需的最少车辆数.考虑到上下全线车行驶时间分别为43.78分和43.83分,都不足一个小时,在余下近16分钟内车辆可循环利用,同时可以补充车辆,从而得出所需最少车辆数.在此基础上,我们用计算机搜索法搜索出一个同时照顾汽车公司与乘客利益的最优模型,从现实考虑,却不可能合理调度,因此再在此基础上模拟搜索,得出一个合理的调车时刻表.五、模型的过程与求解在上下行线的每一个站点,乘客都是随机的到达,按到达时间先后次序排队等车,然后乘客到各自的目的地.影响公交车调度的因素主要有三方面:公交车的数量,乘车的人数以及发车时间间隔.在调度中以汽车的活动为主,同时照顾到乘客与公交公司的双方利益.乘客的利益主要与等待时间有关,等待时间越少,满意度越高,公交公司利益与车辆的满载率以及两个总站车数有关.从表中可求1S =14.58公里, 2S =14.61公里, 3S =43.74分钟, 4S =43.83分钟. (1) 根据资料显示的每一个时间段内上车的人数,以及运营调度要求,求所需车辆数.通过表中资料分析i T (i=18,,2,1 )时组发出的车次不可能进入时组2+i T 来载客,但可能进入1+i T 时组.首先考虑沿下行线:在某一时组i T (i=18,,2,1 )内,需要i n 车次来完全载客运输任务.在i T 时组前j 个站点上车总人数:∑-=⎪⎭⎫⎝⎛+++=1221110160j k j i j k j x t x X X X 13,,3,2 =j)60(12211101∑-=+++=j k j i j k j y t y Y Y Y j=2,3, (13)分别在2T --18T 时组内,前j 个站点上车总人数:⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-++=+-=∑j i jjij j m im i ij x t t x X X X ,112060601 ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-++=+-=∑j i jjij j m imi ij y t t y YY Y ,112060601, ,3,2=i …,18, j=0,2,3,…,13 这样,在i T (=i 1,2,…,18)时组,装载前j 个站点上车的总人数所需车次应满足:120)(max 50≤-≤iij ij jn Y X13,2,018,2,1 ==j i应用Maple 软件,可求出下行线各时组内需发出的车次数.同样方法,可处理上行线, 各时组内需发出的车次数,请参见表1根据资料显示的资料和调度要求,以及我们所得表1可看出,早高峰期为7:00~8:00,这段时间内所需的车次数上下行线各需41次和24次.每一个时期内,到各站点来候车的人数在该时组内均匀分布.由表1选择最高时期3T ,在3T 时组内,从上行线至少需要41辆车次,下行线至少需要24辆车次,然后考虑该时组内车辆的具体运作情况,我们假设N i1>n i2时,上行线路上正在路上所需的车辆数分别为6060222111T N n T N n i i i i ⨯=⨯=易知,21i i n n >.所以下行车辆数可由上行车辆来补充,而下行车辆数有(21i i N N -)由下行线车和公司另外补充:下行车可提供:22i i n N - (辆)公司另外补充: )()(2211i i i i n N n N k ---= (辆) 共需车辆=行线路行走车辆+下行路上行走车辆+补充 即:212212i i i i i N N n k n n -+⨯=++ ,具体分析见附录.根据上述方法.可以求得 7:00 — — 8:00 至少需要53辆车,也是公交公司至少需要的车辆数.(2)求发车时刻表设第个时组内发车间隔相等,要得到时刻表,关键在于要得出在第1T 时组首发车的发车时刻.在1T 时组,我们主要照顾公交公司的利益.设在5点t 分时刻(可以大于零或小于零),我们有下面的方程(上行线) ()()()()120606060606012121211111122211100=+⎪⎭⎫⎝⎛-++⎪⎭⎫⎝⎛-+++⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-t t y x t t y x t t y x t t y x t y x解得03856.7=t (分钟).所以在1T 内第一辆发车时间在5:07时刻.将在1T 时组内上行线的首发车到终点站0A 的时刻作为下行线的首发车时间.在1T 时组内,上下行线的首发车时间确定,主要是考虑到公交公司的利益,这个时间时组内乘车人数极少.另外,公交公司首发车时刻是稳定的,乘客可按规律(时间)来等车.因为我们总是假定在每个时组内发车时间间隔相等,则在确定了首发车以后容易确定该时组各辆车的发车时刻,在1T 时组内最后一趟车发车时间在5:58时刻,2T 时组内发车时间间隔是4.2分钟,这两个时间相加取整,就得到2T 时组内首发车的时间.将上述方法依次做下去,首先就可以得到上行线时刻表.同样考虑到公司利益和乘客对发车时间的理解,上行线的首发车到0A 站后(即5:51时)0A 站发出下行线的第一趟车,然后再利用上述同样方法,可得到下行线时刻表.从而得到时刻表(表2):分析上表可知,在不同时组内的发车间隔不相等,并且不是整数分钟数.至少我们的结果是最优的,但在现实操作中不方便,因此在表2的基础上,用计算机模拟搜索得出一个可行性强的发车时刻表(表3):(3)、下面讨论表3所反映的公交公司和乘客双方的利益公司利益用每次车的平均载客量M 来反映.(I )1M =一天内上车人数的总和(包括上行下行线)/一天内总的发车次数(包括上行下行线).由表2的调度方案通过简单计算,M =234.12(人/车次).这最大限度照顾了公司的利益.关于乘客的抱怨,主要发生在5:00--6:00和22:00--23:00两个时组内.而在其它时组内,由表2可知不会产生.(II )通过表3中的调度方案,可计算出2M=194.25(人/车次).234.12-194.25=39(人/车次),也就是说每次车的平均载客量全天只降低了39(人/车次),但满意度不会有很大降低.方案二已对方案一进行了调整,使得公交公司的利益仍然得到很大程度满足.另外,方案二的顾客抱怨还会在高峰时期发生,但从现实中来考虑,方案二至少需44辆车,公交公司的利益也算挺高,说明方案二是便于操作、且可行的.六、模型的评价和改进:1、本模型分别从理论和实际操作两个角度,利用计算机模拟搜索,得到公交车调度的最优时刻表和便于操作的时刻表.2、在安排理想时刻表(理论上的最优时刻表)的首发车时间上,我们较多地考虑到了汽车公司的利益,并末很好地兼顾到顾客方面的利益.而在通常情况下,该求解方案是合理的.因为考虑到公司的信誉以及行车的规律,乘坐首班车的乘客不会太早到达车站,从而其等待时间不会太长,那么他们的抱怨程度将降低.3、 第二个时刻表是在理论的基础上,结合实际情况而提出来的,具有易操作性的特点.4、由于乘客与公交公司双方的利益是相互矛盾,所以求出的解并不是唯一的,而只能是一个优化解.参考文献:[1] 周义仓 赫孝良 数学建模实验 西安交通大学出版社 1999.10 [2] 魏宗舒 概率论与数理统计教程 高等教育出版社 1997.6 [3] 李世李 杜慧琴 Maple 计算机代数系统应用及程序设计 1999.5 附录1:求解最大车辆数的方法:假设每一时间段各站点所增加人数是均匀分布的,在第i 时间段内,上、下车行线路需要开出的车辆班数总数分别为1i N ,2i N .需要多少辆公交车,就可以保证高峰期正常运转,不会出现一边车站有车滞留而另一边又不够用的情况,对此,我们用下面方法解决.考虑出现在全日最高峰时,两边车辆都已出发,在43.78分钟后,两边首发车辆已达对方总站,均可补充给对方.由于西总站发车时间间隔不同,会出现一边补充不上,而另一边会出现滞留情况.当补充不上时,就要增加车辆来补充上去.--------(略)关于公交车调度的数学模型摘要:本文根据典型的一个工作日两个运行方向各站上下车的乘客数量统计,首先探讨了如何利用平滑法来确定一个有价值并且效率高的车辆运行时刻表,使其满足乘客的舒适性和公交公司低成本的服务;接着,又利用最优化的基本思想,对此问题进行了进一步的讨论,得到了最小配车辆的数量,然后针对满意度的评价水平问题,建立了几个良好刻画公司以及乘客满意度的满意度函数并求出了乘客与公交公司双方的满意度。
公交车的调度问题

公交车调度的最优方案摘要公共交通系统是城市交通的重要组成部分,做好公交车的调度对于改进市民出行状况、提高公交公司的经济和社会效益,都具有十分重要的意义。
发车时刻表是公共交通管理系统中的一个重要组成部分。
一个好的发车时刻表应体现乘客和公交公司双方利益的均衡,而编制发车时刻表的关键是确定发车的时间间隔。
对于乘客来说,发车时间间隔越短,乘客的等车时间越少,而且不显拥挤;另一方面,公交公司希望发车间隔长些,这样满载率就会提高,投入运营的车子总数和发车总次数就会减少,有利于降低成本。
根据本文兼顾公司与乘客的利益,建立了公交车辆行车时刻表优化模型。
本文采用线性规划的方法,根据首站的人数和在该时间段车上的人数的峰值确定所必须的总车数,然后根据乘客的候车时间和公交公司的利润综合比较确定每一时间段派出的车辆数,最后根据首尾两站的公交总数进行合理的调配,算出一天需要派出79辆公交车。
关键词:车辆调度线性规划行车时刻表候车时间1、问题重述以考虑一条公交线路上公交车的调度问题为例,本方案设计数据如下表1、表2是来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,表1、表2给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
现知公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
且运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过 120%,一般也不要低于50%。
现根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,即用尽可能少的车来运送乘客,同时不能让乘客等待时间过长,也不能超载;包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益。
我们的目标就是根据所提供的这些统计资料,对该调度问题建立起一个明确、完整的数学模型之后,再根据实际问题的要求,提出一个数据采集方案,以设计出一个更好的公交调度方案。
数学建模论文

公交车调度方案的模型摘要:关键词:.1 问题的重述公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过 120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
某路公交汽车各时组每站上下车人数统计表如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
.2 符号约定n1,n2:发车的辆数N1,N2每小时发车的辆数.3 问题分析本问题分三部分内容,一是求解两个起点站的发车时刻表,二是求解一共需要多少辆车,三是照顾到了乘客和公交公司双方的利益如何安排发车时间和车辆。
对于问题一,起点发车时间由等车人数决定,比如5:00—6:00等车人数是371人,6:00—7:00等车人数是1990人,那么在六点左右等车的人数就相对于五点左右等车的人数多,那么让车在快六点发车的车辆数就应该比在五点左右发车的车辆数多。
对顾客来说,车越多越好,等的时间越少越好,但对公交公司来说,满载最好,车辆越少越好,显然,这两个利益相互冲突!.4 基本假设.4.1 路况,天气等良好,没有堵车情况,终起点站公交车的掉头时间为0;.4.2 市民素质良好,遵循先上后下,先到先服务等规则;.4.3 每个公交车的往返时间相等,中途到站时停车时间为0;.5 模型建立与求解1.51 模型一{min=n;50n<总人数<120n;60/n<10;}表1.51 从A13开往A0 从A0开往A13时间总人数1车辆数时间总人数车辆数2车辆数1的中位数N1车辆数2的中位数N25-6103595-65012117 6-76444546-72018177-810713897-85489468-95874498-96083519-103471299-1034672910-1125992210-1122151811-1229532511-1218761512-1325692112-1315901313-1422591913-1416821414-1519351614-1519371615-1619251515-1625072116-1746333916-1742923617-1860075017-1871366018-1920961718-1949784119-201051919-2021821820-21863720-2115821321-22617521-2215401322-2357122-236716说明:总人数是每个时间段各站人数的和。
数学建模-公交车调度问题
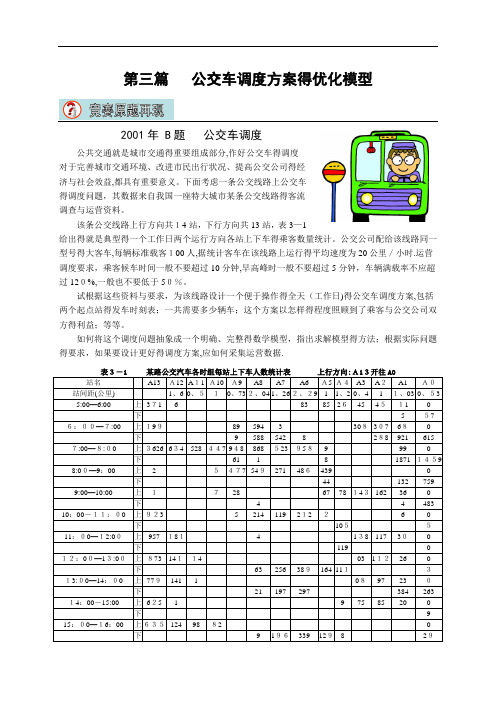
第三篇公交车调度方案得优化模型2001年 B题公交车调度Array公共交通就是城市交通得重要组成部分,作好公交车得调度对于完善城市交通环境、改进市民出行状况、提高公交公司得经济与社会效益,都具有重要意义。
下面考虑一条公交线路上公交车得调度问题,其数据来自我国一座特大城市某条公交线路得客流调查与运营资料。
该条公交线路上行方向共14站,下行方向共13站,表3—1给出得就是典型得一个工作日两个运行方向各站上下车得乘客数量统计。
公交公司配给该线路同一型号得大客车,每辆标准载客100人,据统计客车在该线路上运行得平均速度为20公里/小时.运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料与要求,为该线路设计一个便于操作得全天(工作日)得公交车调度方案,包括两个起点站得发车时刻表;一共需要多少辆车;这个方案以怎样得程度照顾到了乘客与公交公司双方得利益;等等。
如何将这个调度问题抽象成一个明确、完整得数学模型,指出求解模型得方法;根据实际问题得要求,如果要设计更好得调度方案,应如何采集运营数据.公交车调度方案得优化模型*摘要:本文建立了公交车调度方案得优化模型,使公交公司在满足一定得社会效益与获得最大经济效益得前提下,给出了理想发车时刻表与最少车辆数。
并提供了关于采集运营数据得较好建议。
在模型Ⅰ中,对问题1建立了求最大客容量、车次数、发车时间间隔等模型,运用决策方法给出了各时段最大客容量数,再与车辆最大载客量比较,得出载完该时组乘客得最少车次数462次,从便于操作与发车密度考虑,给出了整分发车时刻表与需要得最少车辆数61辆。
模型Ⅱ建立模糊分析模型,结合层次分析求得模型Ⅰ带给公司与乘客双方日满意度为(0、941,0、811)根据双方满意度范围与程度,找出同时达到双方最优日满意度(0、8807,0、8807),且此时结果为474次50辆;从日共需车辆最少考虑,结果为484次45辆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年数学建模论文
——对公交车调度问题的研究
摘要:本文根据所给的客流量及运营情况排出公交车调度时刻表,以及反映客运公司和乘客的利益有多个指标,建立了乘客的利益及公司利益两个目标函数的多目标规划数学模型。
基于多目标规划分析法,进行数值计算,从而得到原问题的一个明确、完整的数学模型,并在模型扩展中运用已建的计算机模拟系统对所得的结果和我们对于调度方案的想法进行分析和评价。
首先通过数据的分析,并考虑到方案的可操作性,将一天划为;引入乘客的利益、公司利益作为两个目标函数,建立了两目标优化模型。
通过运客能力与运输需求(实际客运量) 达到最优匹配、满载率高低体现乘客利益;通过总车辆数较少、发车次数最少表示公司利益建立两个目标函数。
应用matlab中的fgoalattain进行多目标规划求出发车数,以及时间步长法估计发车间隔和车辆数。
关键字:公交车调度;多目标规划;数据分析;数学模型;时间步长法,matlab
一问题的重述:
1、路公交线路上下行方向各24站,总共有L 辆汽车在运行,开始时段线路两端的停车场中各停放汽车m辆,每两车可乘坐S人。
这些汽车将按照发车时刻表及到达次序次发车,循环往返地运行来完成运送乘客的任务。
建立数学模型,根据乘客人数大小,配多少辆车、多长时间发一班车使得公交公司的盈利最高,乘客的抱怨程度最小。
假设公交车在运行过程中是匀速的速度为v。
1路公交车站点客流量见下表。
