操作篇 09_等级相关系数的计算与检验
相关系数确定方法实验

相关系数确定方法实验1、下表是平时两次考试的成绩分数,假设其分布为正态,分别用积差相关与等级相关方法计算相关系数,并回答,就这份资料用哪种相关法更恰当?被试12345678910A86587964914855823275B83528978856847762556解:①求积差相关系数解法一:用原始分数计算被试A B X2Y2XY 1868373966889713825852336427043016 37989624179217031 46478409660844992 59185828172257735 64868230446243264 75547302522092585 88276672457766232 932251024625800 107556562531364200∑670659480804719346993解法二:用离均差、标准差计算被试A B x y xy 186831917.1324.9 25852-9-13.9125.1 379891223.1277.2 46478-312.1-36.3 591852419.1458.4 64868-19 2.1-39.97 55 47 -12 -18.9 226.88 82 76 15 10.1 151.59 32 25 -35 -40.9 1431.510 75 56 8 -9.9 -79.2∑ 670 6592840根据表中数据求得:40.19s 86.17s 9.65 67Y ====,,,X Y X把∑xy 、N 、s X 、s Y 代入公式得:82.040.1986.17102840=⨯⨯==∑YX s Ns xy r②求等级相关系数被试 A BR XR YDD 2R X R Y1 86 8323 -1 1 62 58 52 7 8 -1 1 563798941394 46478642424 5918512-112 64868963954 7554789-1172 8827635-2415 93225101000100 10755657-2435∑555534368解法一:根据表中的计算,已知N=10,∑D2=34,把N、∑D2代入公式,得:()()79.0110103461161222=-⨯-=--=∑N N D r R解法二:根据表中的计算,已知N=10,∑R X R Y =368,把N 、∑R X R Y 代入公式,得:()()()()79.0110110103684110311413=⎥⎦⎤⎢⎣⎡+-+⨯⨯-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⋅-=∑N N N R R N r YX R③这份资料用积差相关法更恰当,如用等级相关法,其精度要差于积差相关,因此,凡符合计算积差相关的资料,不要用等级相关计算。
相关系数检验法步骤

相关系数检验法步骤一、相关系数检验法步骤相关系数检验法是一种用于检验两个变量之间关系强度的统计方法。
它可以衡量两个变量之间的相关性,并判断这种相关性是否显著。
以下是相关系数检验法的步骤:1. 收集数据:首先,需要收集相关的数据,包括两个变量的观测值。
这些数据可以通过实地调查、实验或其他可靠的数据源获得。
2. 计算相关系数:接下来,需要计算两个变量之间的相关系数。
常用的相关系数包括皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于连续变量,而斯皮尔曼相关系数适用于等级变量或非线性关系。
3. 假设检验:在进行相关系数检验前,需要先建立假设。
通常,零假设为两个变量之间不存在相关关系,备择假设为两个变量之间存在相关关系。
4. 计算检验统计量:根据所选的相关系数和样本大小,计算相关系数的检验统计量。
检验统计量的计算方式与所选的相关系数有关。
5. 确定显著性水平:确定显著性水平,通常将其设定为0.05或0.01。
显著性水平表示拒绝零假设的临界值。
6. 判断是否拒绝零假设:将计算得到的检验统计量与显著性水平进行比较。
如果检验统计量的值小于显著性水平对应的临界值,则拒绝零假设,认为两个变量之间存在相关关系;如果检验统计量的值大于临界值,则接受零假设,认为两个变量之间不存在相关关系。
7. 解释结果:最后,根据检验结果对两个变量之间的相关性进行解释。
如果拒绝了零假设,可以说明两个变量之间存在相关关系,并根据相关系数的值来判断相关关系的强度和方向。
二、相关系数检验法的应用相关系数检验法广泛应用于各个领域的研究中。
以下是一些常见的应用场景:1. 经济学研究:在经济学中,相关系数检验法常用于分析不同变量之间的关系,如GDP与失业率、通货膨胀与利率等。
通过相关系数检验,可以了解变量之间的关系强度,为经济政策的制定提供依据。
2. 市场营销研究:在市场营销领域,相关系数检验法可以用来分析产品销售与广告投入、价格变动等因素之间的关系。
等级相关系数计算公式及其

Semn pa a 等级相关系数计算公式及其 r
相互关系的探讨
何 艳频 孙爱峰
在对两个变盆c Y) X, 进行相关分析 时, 资料不呈正态 若 分 布、 总体分布类型未知或 为有序分类 资料时, 应用 基于秩 次 的非参数 统计方法-pam n 级相关。但是 , 大部分 Sera 等 绝 统 计学书籍介绍的等级相关系数( 的一般计算公式为 : r) ,
的作用。 今考文献
陈启光, 沈其君. 医学统计学. 苏科 学技术出版社,9 江 1”:
1 ·2 . 7 2 18
写“ 等级相关” 一节时, 采用对双变盆( , 编写的 xY ) 秩次R、 : R 直接作 P n 积差相关系数公式计算等级相关系数。 : e 拼o
这样, 教师讲授其计 算公式时只需 简单 回顾一下 P明 。 e 。积 差相关 系数的计算公式即可 计算时只需将两变且 的对应秩
学) ] ) 采用对每对变盘 XY 编写的 p 值( ,) 秩次 R,, e- xR 作Ps r
sn o 积差相关的公式计算 r值 : , #R 一 R )R 一 , (: R r ( , R ) ( R ) ,/ % .( R )n 艺
r, (-)Y.r . 厂RR (-) 二[ r,[RR] I 〕 ]
0 ( 时 前r 0 得 r 钾、 〕 。、 < 时 此 校正 .< ,到} 1 }1 , .孙 。 :) 。 , [ 即t
综上所 在 x与Y中无相同秩次的情况下,: r , 述. . r 二。 、; x Y 在 与 中有较多相同秩次的情况下, > 二 即 ‘ 、 与; 正 ,
相关校正后 可使相 关系数绝 对值减 小, 尸值 增大 ; 相关校 负 正后可使相关系 数绝对值 增大 , 尸值减 小。因此 , 建议 在编 次摘人计算器或 0 吧系列组件 E e即能求 得等级相关系 伍c c xl 数, 学生更容易理 解, 更容易掌握 , 起到触类旁 通和融会贯通
斯皮尔曼二列等级相关系数的检验

df n 3
斯皮尔曼二列等级相关系数的 检验
样本与总体的斯皮尔曼等级相关系数之 差异的检验
1.直接查表法 当n=1~1000时,查“积差相关系数临界值”表
df n 2
2.直接查表法 当n=4~50时,查“等级相关系数临界值”表
3.显著性检验法 (1)ρ=0,n>20 时,等级相关系数抽样分布接近于 正态,用Z检验(张)
Z zrR zR SEzrR
1 SEzrR n 3
例:
两样本斯皮尔等级相关系数之差的 检验
(4)两独立样本相关系 数差异抽样分布为偏 态,将r转换为费舍Z分 数,用Z检验
例:
Z zrR1 zrR2 SEDzrR
1
1
SEDzrR
n1 3 n 2 3
(5)两相关样本相关系 数差异抽样分布为偏 态,用t检验
Z rR
SErR
SErR
1 rR2 n2
(2)ρ=0,n=9~20 时, 相关系数抽样分布为 偏态,用t检验
r-
t SEr
1 r2 SEr = n-2
df=n-2
例 : 10 个 学 生 学 习 潜 在能力与自学能力测 验成绩相关系数为 0.891,问从总体上说, 两者是否存在相关?
(3)ρ≠0, 时,相关系数 抽样分布为偏态,将r转 换为费舍Z分数,用Z 检验
相关系数确定方法实验
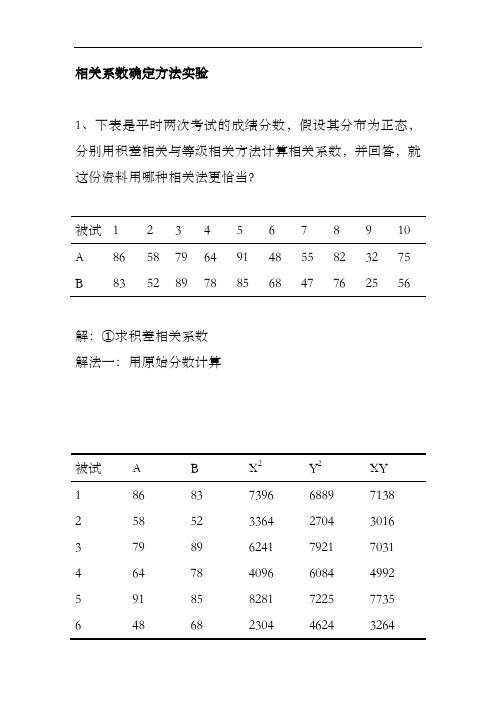
相关系数确定方法实验1、下表是平时两次考试的成绩分数,假设其分布为正态,分别用积差相关与等级相关方法计算相关系数,并回答,就这份资料用哪种相关法更恰当?被试 1 2 3 4 5 6 7 8 9 10A 86 58 79 64 91 48 55 82 32 75B 83 52 89 78 85 68 47 76 25 56解:①求积差相关系数解法一:用原始分数计算被试 A B X2 Y2 XY1 86 83 7396 6889 71382 58 52 3364 2704 30163 79 89 6241 7921 70314 64 78 4096 6084 49925 91 85 8281 7225 77356 48 68 2304 4624 32647 55 47 3025 2209 25858 82 76 6724 5776 62329 32 25 1024 625 80010 75 56 5625 3136 4200 ∑670 659 48080 47193 46993解法二:用离均差、标准差计算被试 A B x y xy1 86 83 19 17.1 324.92 58 52 -9 -13.9 125.13 79 89 12 23.1 277.24 64 78 -3 12.1 -36.35 91 85 24 19.1 458.46 48 68 -19 2.1 -39.97 55 47 -12 -18.9 226.88 82 76 15 10.1 151.5 9 32 25 -35 -40.9 1431.5 10 75 56 8 -9.9 -79.2 ∑6706592840根据表中数据求得:40.19s 86.17s 9.65 67Y ====,,,X Y X 把∑xy 、N 、s X 、s Y 代入公式得:82.040.1986.17102840=⨯⨯==∑YX s Ns xy r②求等级相关系数 被试 A B R X R Y D D 2 R X R Y 1 86 83 2 3 -1 1 6 2 58 52 7 8 -1 1 56 3 79 89 4 1 3 9 4 4 64 78 6 4 2 4 24 5 91 85 1 2 -1 1 2 6 48 68 9 6 3 9 54 7 55 47 8 9 -1 1 72 8 82 76 3 5 -2 4 15 9 32 25 10 10 0 0 100 10 75 56 5 7 -2 4 35 ∑555534368解法一:根据表中的计算,已知N=10,∑D 2=34,把N 、∑D 2代入公式,得:()()79.0110103461161222=-⨯-=--=∑N N D r R解法二:根据表中的计算,已知N=10,∑R X R Y =368,把N 、∑R X R Y 代入公式,得:()()()()79.0110110103684110311413=⎥⎦⎤⎢⎣⎡+-+⨯⨯-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⋅-=∑N N N R R N r YX R③这份资料用积差相关法更恰当,如用等级相关法,其精度要差于积差相关,因此,凡符合计算积差相关的资料,不要用等级相关计算。
怎么算等级相关系数的方法

怎么算等级相关系数的方法
等级相关系数(Spearman's Rank Correlation Coefficient)是一种用于衡量两个变量之间等级顺序相关性的统计方法。
它不要求变量服从正态分布,适用于有序变量或等级数据。
以下是计算等级相关系数的步骤:
1. 首先,对两个变量的数据进行排序,将其转换为等级数据。
如果有相同的数值,则使用平均排名。
2. 计算每个变量的等级之差(D)。
对于每一对等级(X和Y),计算Y的等级减去X的等级,得到差值D。
3. 计算每个D的平方值(D^2)。
4. 计算等级差值的和(SigmaD)。
5. 使用以下公式计算等级相关系数:
等级相关系数= 1 - [6 * SigmaD^2 / (n^3 - n)]
其中,n表示样本的数量。
等级相关系数的取值范围为-1到1。
当相关系数接近1时,表示变量的等级顺序高度一致;当相关系数接近-1时,表示变量的等级顺序完全相反;当相关系数接近于0时,表示变量的等级顺序无关。
请注意,以上是计算等级相关系数的传统方法。
在某些统计软件中,也可以直接使用相应的函数来计算等级相关系数。
2019心理学考研统计知识:斯皮尔曼等级相关计算_毙考题

下载毙考题APP
免费领取考试干货资料,还有资料商城等你入驻
邀请码:8806 可获得更多福利
2019心理学考研统计知识:斯皮尔曼等级相关计算
斯皮尔曼等级相关(Spearman s correlation coefficient for ranked data)主要用于解决称名数据和顺序数据相关的问题。
适用于两列变量,而且具有等级变量性质具有线性关系的资料。
由英国心理学家、统计学家斯皮尔曼根据积差相关的概念推到而来,一些人把斯皮尔曼等级相关看做积差相关的特殊形式。
等级相关系数的计算步骤:
1、把数量标志和品质标志的具体表现按等级次序编号。
2、按顺序求出两个标志的每对等级编号的差。
3、按下式计算相关系数:
考试使用毙考题,不用再报培训班。
相关系数的检验可用

相关系数的检验可用
相关系数的检验可以使用自由度自适应(F-testing)和T检验来检验其统计显著性。
自由度自适应F检验方法是检验相关系数统计显著性的一种重要方法。
它通过比较F值(即样本相关系数除以样本相关系数的标准误差所得的比值)和临界F值的值来确定相关系数的统计显著性,其统计检验的样本量没有硬性要求。
F检验的过程如下:
(1)计算样本的相关系数;
(2)根据自由度自适应F分布表,根据样本的规模计算临界F 值(越大,统计显著性越强);
(3)比较两个值的大小,如果临界F值大于样本的F值,则可以推断相关系数的统计显著性.
此外,T检验也可以用来检验相关系数的统计显著性。
它的过程如下:
(1)计算样本的相关系数;
(2)计算样本的自由度;
(3)根据T分布表,根据样本的自由度计算临界值;
(4)比较两个值,如果临界值大于样本的相关系数,则可以推断相关系数的统计显著性。
- 1 -。
相关系数确定方法实验

相关系数确定方法实验 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#相关系数确定方法实验1、下表是平时两次考试的成绩分数,假设其分布为正态,分别用积差相关与等级相关方法计算相关系数,并回答,就这份资料用哪种相关法更恰当被试12345678910 A86587964914855823275 B83528978856847762556解:①求积差相关系数解法一:用原始分数计算被试A B X2Y2XY 18683739668897138 25852336427043016 37989624179217031 46478409660844992 59185828172257735 64868230446243264 75547302522092585 88276672457766232107556562531364200∑670659480804719346993解法二:用离均差、标准差计算被试A B x y xy 186831925852-9-379891246478-3-591852464868-19-75547-12-882761593225-35-1075568--∑6706592840根据表中数据求得:==,=67Y=Y65X,X,40s19.9.86s17.把∑xy、N、s X、s Y代入公式得:82.040.1986.17102840=⨯⨯==∑YX s Ns xy r②求等级相关系数 被试 A B R X R Y D D 2R X R Y 1 86 83 2 3 -1 1 6 2 58 52 7 8 -1 1 56 3 79 89 4 1 3 9 4 4 64 78 6 4 2 4 24 5 91 85 1 2 -1 1 2 6 48 68 9 6 3 9 54 7 55 47 8 9 -1 1 72 8 82 76 3 5 -2 4 15 9 32 25 10 10 0 0 100 10 75 56 5 7 -2 4 35 ∑555534368解法一:根据表中的计算,已知N=10,∑D 2=34,把N 、∑D 2代入公式,得:()()79.0110103461161222=-⨯-=--=∑N N D r R解法二:根据表中的计算,已知N=10,∑R X R Y =368,把N 、∑R X R Y 代入公式,得:()()()()79.0110110103684110311413=⎥⎦⎤⎢⎣⎡+-+⨯⨯-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⋅-=∑N N N R R N r YX R③这份资料用积差相关法更恰当,如用等级相关法,其精度要差于积差相关,因此,凡符合计算积差相关的资料,不要用等级相关计算。
相关分析及检验、相关系数

6.继续-确定
结果分析 描述性统计量表 参与相关分析的两个变量的样本数都是 12,平均气温的均值都是 18.250, 标准差是 8.8149,日照时数的均值是 118.567,标准差是 48.3840. 相关性分析结果表 平均气温和日照时数的 person 相关系数为 0.758,显著性水平为 0.004,小 于 0.01(在.01 水平(双侧)上显著相关) 。所以平均气温和日照对数的相 关关系为正向,且相关性很强。
描述性统计量表 参与相关分析的两个变量的样本数都是 12,平均气温的均值都是 18.250, 标准差是 8.8149,日照时数的均值是 118.567,标准差是 48.3840. 相关性分析结果表 平均气温和日照时数的 person 相关系数为 0.758,显著性水平为 0.004,小 于 0.01(在.01 水平(双侧)上显著相关) 。所以平均气温和日照对数的相 关关系为正向,且相关性很强。 结果分析 描述性统计量表 参与相关分析的两个变量的样本数都是 12,平均气温的均值都是 18.250, 标准差是 8.8149,日照时数的均值是 118.567,标准差是 48.3840. 相关性分析结果表 平均气温和日照时数的 person 相关系数为 0.758,显著性水平为 0.004,小 于 0.01(在.01 水平(双侧)上显著相关) 。所以平均气温和日照对数的相 关关系为正向,且相关性很强。
零阶相关系数:输出所有变量的相关系数阵 结果分析 描述性统计量表 参与相关分析的两个变量的样本数都是 12,平均气温的均值都是 18.250, 标准差是 8.8149,日照时数的均值是 118.567,标准差是 48.3840. 相关性分析结果表 平均气温和日照时数的 person 相关系数为 0.758,显著性水平为 0.004,小 于 0.01(在.01 水平(双侧)上显著相关) 。所以平均气温和日照对数的相 关关系为正向,且相关性很强。 结果分析
标准曲线的相关系数

标准曲线的相关系数标准曲线是科学研究中常用的一种方法,可以用来确定某种物质的浓度或活性。
在进行标准曲线实验时,我们经常需要计算相关系数来评估数据之间的相关性。
相关系数是一个重要的指标,可以帮助我们确定实验结果的正确性和可靠性。
在本文中,将详细介绍如何计算标准曲线的相关系数。
第一步:准备标准曲线首先我们需要准备一条标准曲线。
标准曲线通常是通过制备不同浓度的标准品并进行测试来获得的。
一般来说,我们需要至少五种不同的标准浓度值(按升序排序),用来确定浓度和响应之间的线性关系。
这样我们就可以得到一条标准曲线。
标准曲线要求线性程度高且与标准品的浓度范围相匹配,这样才能使我们的分析结果准确。
第二步:准备样品接下来我们需要准备待测试的样品。
一般来说,我们需要按已知标准曲线的方法来制备样品。
如果我们要测定的物质与标准品具有相同的性质,我们可以使用标准品来制备样品。
如果我们要测定的物质与标准品性质不同,则需要使用不同的方法来制备样品。
第三步:测试样品一旦我们准备好了样品,我们就需要对样品进行测试并记录所获得的数据。
通常,我们需要记录响应值和标准品的浓度值,使得可以通过响应值确定样品中物质的浓度。
第四步:计算相关系数计算相关系数是确定标准曲线的线性度和测量数据的可靠性的关键步骤。
我们可以使用pearson相关系数公式来计算相关性。
pearson相关系数公式如下:r = (nΣxy - ΣxΣy) / sqrt{(nΣx^2 - (Σx)^2)(nΣy^2 - (Σy)^2)}其中,n是样本数量,x和y是样本的响应值和浓度值,Σ表示求和符号。
相关系数的值可以介于-1到+1之间。
如果相关系数接近1,说明两个数据之间存在强正相关性;如果相关系数接近-1,则说明两个数据之间存在强负相关性;如果相关系数接近于0,则说明两个数据之间不存在明显的相关性。
综上所述,计算标准曲线的相关系数是非常重要的,可以帮助我们评估数据之间的相关性。
相关系数检验

相关系数检验一、相关系数简介相关系数是用以衡量两个变量之间的关联程度的统计学指标。
在实际数据分析中,相关系数检验是一种常用方法,用来验证变量之间的相关性是否显著。
二、Pearson相关系数Pearson相关系数是衡量两个连续变量之间线性关联程度的指标,范围在-1到1之间。
当相关系数接近1时,表示两个变量呈正相关;当相关系数接近-1时,表示两个变量呈负相关;相关系数接近0时,表示两个变量之间没有线性关系。
三、相关系数检验步骤1.提出假设:零假设为“两个变量之间不存在相关性”,备择假设为“两个变量之间存在相关性”。
2.计算相关系数:使用统计软件计算得到两个变量的Pearson相关系数。
3.确定显著性水平:选择适当的显著性水平α,一般取0.05。
4.计算临界值:根据显著性水平和样本容量自由度,查找相关系数的临界值。
5.判断显著性:比较计算得到的相关系数和临界值,若计算得到的相关系数显著大于临界值,则拒绝零假设,否则接受零假设。
四、案例分析以两种肥胖度评价方法为例,比较其与BMI指数之间的相关系数。
假设零假设为两种肥胖度评价方法与BMI指数之间不存在相关性,备择假设为存在相关性。
通过数据收集和计算得到相关系数后,进行相关系数检验,判断两种评价方法与BMI指数之间的关联程度是否显著。
五、结论相关系数检验是一种常用的统计方法,用来验证两个变量之间的相关性是否显著。
在实际数据分析中,通过计算相关系数并进行显著性检验,可以帮助我们理解变量之间的关联程度,从而做出合理的推断和决策。
以上是关于相关系数检验的简要介绍和步骤说明,希望能对您有所帮助。
相关系数的检验方法

分析实例
【统计量】
残差:用于选择输出残差诊断的信息,可选的有 Durbin-Watson残差序列相关性检验、超出规定的n 倍标准误的残差列表。 共线性诊断:给出一些用于共线性诊断的统计量, 如特征根(Eigenvalues)、方差膨胀因子(VIF)等。
分析实例
【统计量】
模型拟合度:显示模型拟合过程中进入、退出的变量的 列表,以及一些有关拟合优度的检验:R,R2和调整的 R2, 标准误及方差分析表。 R方变化:显示模型拟合过程中R2 、F值和p值的改变 情况。 描述性:提供一些变量描述,如有效例数、均数、标准 差等,同时还给出一个自变量间的相关矩阵。 部分相关和偏相关性:显示自变量间的相关、部分相关 和偏相关系数。
Mileage (mpg) Weight 1 -.469 ** .000 74 74 -.469 ** 1 .000 74 74 .539 ** -.807 ** .000 .000 74 74
பைடு நூலகம்
(lbs.) .539 ** .000 74 -.807 ** .000 74 1
74
分析实例
SPSS分析过程
如何求解a、b?
1 n 2 l xx ( x x ) i n 1 i 1 1 n l xy ( xi x )( yi y ) n 1 i 1 b l xy / l xx a y bx
分析实例
例:上海医科大学儿科医院研究某种代乳粉的 营养价值,大白鼠的进食量和体重增量间的关 系,试求进食量对体重的线性回归方程。数据 文件Corr.sav
【个案标签】
初中数学知识归纳统计相关系数的计算与分析

初中数学知识归纳统计相关系数的计算与分析统计学是一门研究收集、整理、分析和解释数据的学科。
在数学中,统计学起着至关重要的作用,可以帮助我们理解数据的分布和关系。
相关系数是统计学中用来衡量两个变量之间相关程度的指标。
在本文中,我们将介绍相关系数的计算方法以及如何分析相关系数的含义和解释结果。
1. 相关系数的计算方法相关系数是用来度量两个变量之间线性关系的强度和方向的。
相关系数的取值范围在-1到1之间,其具体计算方法有多种。
我们这里介绍常用的皮尔逊相关系数的计算方法。
假设我们有两个变量X和Y,它们的取值分别为x1, x2, ..., xn和y1, y2, ..., yn。
首先,计算X和Y的均值分别为x和ȳ。
然后,计算X和Y的差值分别为xi - x和yi - ȳ。
接下来,计算差值的平方和分别为Σ(xi - x)^2和Σ(yi - ȳ)^2。
最后,计算X和Y差值的乘积的累加和Σ(xi -x)(yi - ȳ)。
皮尔逊相关系数的计算公式如下:r = Σ(xi - x)(yi - ȳ) / √(Σ(xi - x)^2 * Σ(yi - ȳ)^2)计算得到的相关系数r的取值范围在-1到1之间,r越接近1表示两个变量之间正相关性越强,r越接近-1表示两个变量之间负相关性越强,r接近0表示两个变量之间无线性相关性。
2. 相关系数的分析与解释在计算得到相关系数之后,我们需要对其进行分析和解释。
相关系数为我们提供了两个变量之间关系的信息,但并不意味着因果关系。
以下是对相关系数进行分析和解释的一些例子:- 如果相关系数r接近1,表示两个变量之间存在强正相关关系。
例如,如果相关系数r约等于0.9,那么可以认为这两个变量之间存在着很强的正相关性。
- 如果相关系数r接近-1,表示两个变量之间存在强负相关关系。
例如,如果相关系数r约等于-0.8,那么可以认为这两个变量之间存在着很强的负相关性。
- 如果相关系数r接近0,表示两个变量之间不存在线性相关关系。
等级相关系数计算公式及其

陈启光, 沈其君. 医学统计学. 苏科 学技术出版社,9 江 1”:
1 ·2 . 7 2 18
写“ 等级相关” 一节时, 采用对双变盆( , 编写的 xY ) 秩次R、 : R 直接作 P n 积差相关系数公式计算等级相关系数。 : e 拼o
这样, 教师讲授其计 算公式时只需 简单 回顾一下 P明 。 e 。积 差相关 系数的计算公式即可 计算时只需将两变且 的对应秩
73
由表 2可得 :二 ,, ; T 0T 二1同时将表 2 行数据代人公 下
式得 :
几 二
由此可见, 当 x与 Y中相 同秩次较多时 , 二r。 、 。
[1 1) 一0 1 一 ( 护一0历] (+) 刃 二住 8 7 1 1 了[1 1) 一 x 了[1 1巧〕 Z f ( 护一0历〕 Z o ( 护一0 一 x )
0 ( 时 前r 0 得 r 钾、 〕 。、 < 时 此 校正 .< ,到} 1 }1 , .孙 。 :) 。 , [ 即t
综上所 在 x与Y中无相同秩次的情况下,: r , 述. . r 二。 、; x Y 在 与 中有较多相同秩次的情况下, > 二 即 ‘ 、 与; 正 ,
相关校正后 可使相 关系数绝 对值减 小, 尸值 增大 ; 相关校 负 正后可使相关系 数绝对值 增大 , 尸值减 小。因此 , 建议 在编 次摘人计算器或 0 吧系列组件 E e即能求 得等级相关系 伍c c xl 数, 学生更容易理 解, 更容易掌握 , 起到触类旁 通和融会贯通
YR_ R,
l . r ” 恶
乡 约号
. 且 内 ‘ , } 4 . 曰 6 7 已 6 ,
么, 上述 3个
当 X与 Y中相同秩次较多时, 应计算 r的校正值 : ,
相关系数判断标准

相关系数判断标准相关系数是衡量两个变量之间联系强度的一种统计方法。
相关系数的范围在-1和1之间,其中-1表示完全反相关,0表示不存在相关关系,1表示完全正相关。
在实际中,相关系数往往被用于分析两个变量之间的相关性,以便于得出更准确的结论和做出更有效的决策。
一般地,根据相关系数的值,可以将相关关系分为以下几种情况:1. 完全正相关当相关系数为1时,表示两个变量完全正相关,它们的值总是同时变化。
这种情况下,两者之间的线性关系非常强,当一个变量的值变大时,另一个变量的值也会相应地变大。
例如,身高和体重之间的相关系数通常是正相关的,因为体重在一定程度上取决于身高。
当相关系数在0.7到1之间时,表示两个变量高度正相关。
这意味着两个变量之间有着很强的线性关系,但并不是完全正相关。
例如,人的年龄和学历之间的相关性可能是高度正相关,因为通常来说,年龄越大,所获得的学历水平也会相对较高。
4. 无相关性当相关系数接近于0时,表示两个变量之间不存在线性关系。
这种情况下,两个变量的值之间没有显著的关联。
例如,一个人的学历和身高之间可能就不存在明显的相关性。
5. 中度负相关当相关系数在-0.3到-0.7之间时,表示两个变量之间中度负相关。
这意味着当一个变量的值增加时,另一个变量的值可能会减少。
例如,地区的犯罪率和政府的支出之间的相关系数可能是中度负相关的,因为加强政府支出可能会降低地区的犯罪率。
综上所述,通过判断相关系数的值,我们可以得出两个变量之间关系的强度和趋势性。
因此,在实际中,通过对相关系数的分析,我们可以更好地理解两个变量之间的关系。
然而,值得注意的是,虽然相关系数可以用于衡量两个变量之间的联系强度,但它并不代表因果关系,仅仅是表达两者之间的相关性。
常用相关分析方法及其计算

二、常用相关分析方法及其计算在教育与心理研究实践中,常用的相关分析方法有积差相关法、等级相关法、质量相关法,分述如下。
(一)积差相关系数1. 积差相关系数又称积矩相关系数,是英国统计学家皮尔逊(Pearson )提出的一种计算相关系数的方法,故也称皮尔逊相关。
这是一种求直线相关的基本方法。
积差相关系数记作XY r ,其计算公式为∑∑∑===----=ni in i ini iiXY Y y X x Y y X x r 12121)()())(( (2-20)式中i x 、i y 、X 、Y 、n 的意义均同前所述。
若记X x x i -=,Y y y i -=,则(2-20)式成为YX XY S nS xyr ∑= (2-21)式中nxy ∑称为协方差,nxy ∑的绝对值大小直观地反映了两列变量的一致性程度。
然而,由于X 变量与Y 变量具有不同测量单位,不能直接用它们的协方差nxy ∑来表示两列变量的一致性,所以将各变量的离均差分别用各自的标准差除,使之成为没有实际单位的标准分数,然后再求其协方差。
即:∑∑⋅==)()(1YX YX XY S yS x n S nS xyr Y X Z Z n∑⋅=1(2-22) 这样,两列具有不同测两单位的变量的一致性就可以测量计算。
计算积差相关系数要求变量符合以下条件:(1)两列变量都是等距的或等比的测量数据;(2)两列变量所来自的总体必须是正态的或近似正态的对称单峰分布;(3)两列变量必须具备一一对应关系。
2. 积差相关系数的计算利用公式 (2-20)计算相关系数,应先求两列变量各自的平均数与标准差,再求离中差的乘积之和。
在统计实践中,为方便使用数据库的数据格式,并利于计算机计算,一般会将(2-20)式改写为利用原始数据直接计算XY r 的公式。
即: ∑∑∑∑∑∑∑---=2222)()(i ii iii i i XY y y n x x n y x y x n r (2-23)(二)等级相关在教育与心理研究实践中,只要条件许可,人们都乐于使用积差相关系数来度量两列变量之间的相关程度,但有时我们得到的数据不能满足积差相关系数的计算条件,此时就应使用其他相关系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机辅助英语教学与研究(操作篇)浙江师范大学外语学院夏建新第9讲用Excel计算等级相关系数目次9.1 等级相关的概念 (1)9.2 适用条件与计算公式 (1)9.3 操作练习 (1)9.4 课堂练习 (3)9.5 积差相关与等级相关比较 (4)9.6 肯德尔和谐系数的计算 (5)9.7 Task 9 (6)9.1 等级相关的概念等级相关是指以等级次序排列或以等级次序表示的变量之间的相关。
主要包括斯皮尔曼(Spearman)二列等级相关及肯德尔和谐系数(the Kandall Coefficient of Concordance)多列等级相关。
9.2 适用条件与计算公式z当测量到的数据不是等距或等比数据,而是具有等级顺序的测量数据;z(或)得到的数据是等距或等比的测量数据,但其所来自的总体分布不是正态的;z(或)样本容量不一定大于50(或30)在无法满足积差相关系数的适用条件时,只要满足上述三个条件中的任何一个,都可以计算其等级相关系数。
由于该系数并不要求总体是否呈正态分布,也不要求N>50(或N>30),所以应用范围较广。
斯皮尔曼等级相关系数r R的计算公式为:在该式中,D = (Rx – Ry),它表示对偶等级之差。
9.3 操作练习计算下表的相关系数。
学号学习潜能自学能力199901 71 7199902 68 7199903 84 2199904 64 9199905 76 5199906 69 8199907 90 3199908 71 8199909 66 10199910 71 6(注:自学能力是按能力高低从小往大的数字打的,即数值越小,说明自学能力越强)步骤一:先用Excel中的“排序”工具对“学习潜能”进行等级赋值,操作步骤如下所示:数据→ 排序 → 主要关键字 → 学习潜能 → 递减 → 有标题行→ 确定结果如下:学号 学习潜能自学能力19990790 319990384 219990576 519990171 719990871 819991071 619990669 819990268 719990966 1019990464 9然后对“学习潜能”进行赋值,结果如下:序号学号学习潜能等级1 自学能力1 19990790 1 32 19990384 2 23 19990576 3 55 19990171 5 74 199908715 86 19991071 5 67 19990669 7 88 19990268 8 79 19990966 9 1010 19990464 10 9说明:因4、5、6号三位学生的“学习潜能”分相等,其赋值取三者的平均等级5(计算方法为名次的总和除以同名次人数,即(4+5+6)/3=5)。
步骤二:按步骤一中所述方法对“自学能力”进行排序和赋值(考虑到“自学能力”的数值越小,等级越高,排序时应该选“递增”)。
结果如下:序号学号学习潜能等级1自学能力等级22 199903 84 2 2 11 199907 90 1 3 23 199905 76 3 5 36 199910 71 5 6 45 199901 71 5 7 5.58 199902 68 8 7 5.54 199908 715 8 7.57 199906 69 7 8 7.510 199904 64 10 9 9199909 66 9 10 109步骤三:算出等级差数与差数平方。
在Excel表中的G2单元格中输入:=D2-F2,得数为-1。
用填充柄工具完成等级差数的计算;在H2单元格中输入:=G2*G2,得数为1,用填充柄工具完成差数平方的计算。
结果如下:等级差数 差数平方-1 11 10 0-2.5 6.25-0.5 0.251 1-0.5 0.252.5 6.25-1 11 1步骤四:算出差数平方之和。
用Σ工具或在某单元格输入=sum(H2:H11),得数为18。
步骤五:把差数平方和代入公式中进行计算。
在Excel中可输入=1-(6*18)/(10*(10*10-1)),得数为0.890909。
步骤六:进行显著性检验。
由于样本数n=10,用t检验。
在Excel中输入:=0.890909*SQRT(10-2)/SQRT(1-0.890909*0.890909),得数为5.548155。
注意:为简便起见,上述有些数值可以直接用单元格代号代入计算公式。
步骤七:统计决断。
查t值表,得t(8)0.01=3.355。
我们算出的数值大于该t值,可以判定学生的学习潜能与自学能力的相关系数有显著差异,即这两者有高度的正相关。
9.4 课堂练习以下是10个学生的数学和物理分数,请计算数学与物理的相关系数。
学号数学成绩物理成绩20020186 7020020268 6520020372 8220020490 9220020564 6820020661 6020020794 9320020886 9220020966 7620021070 769.5 积差相关与等级相关比较例:两位英语教师(x, y)分别给20个学生的英语作文打分,用相关系数原理说明两者打分的一致性程度。
作文编号教师X 教师Y1 17 172 13 143 8 124 15 175 15 166 7 77 10 148 12 109 11 1510 14 1311 15 1512 12 1513 10 714 18 1615 15 1216 16 1617 10 1618 10 1019 19 1520 9 8用积差相关系数原理计算,r=0.67注:除了“操作篇 08”所示的显著性检验方法,还可查积差相关系数检验表来进行检验。
这里所查的α=0.05双尾临界值为0.444,单尾临界为0.378(自由度不用减)。
结论:相关显著。
用等级相关系数原理计算,r=0.69查等级相关系数表,α=0.05双尾临界值为0.447,单尾临界为0.380(自由度不用减)。
相关显著。
之所以等级相关系数高于积差相关系数,是因为等级赋值时会出现一些并列等级,这样计算出来的相关系数会略高于积差相关系数。
所以,如果能用积差相关原理计算的,尽量用积差相关公式,这样可以精确些。
9.6 肯德尔和谐系数的计算适用情况:用于描述或检验几个评估者对一组被评者的等级评定的一致性程度,或同一评估者对同一组被评者前后几次评定结果的一致性程度。
当多个(两个以上)变量以等级次序排列或以等级次序表示,描述这几个变量之间的一致性程度(即相关)的量,称为肯德尔和谐系数。
它常用来表示几个评定者对同一组学生学习成绩等级评定的一致性程度,或同一个评定者对同一组学生的学习成绩用等级先后评定多次之间的一致性程度。
公式如下:)(121/)(3222n n K nR R w r −−∑∑=其中R 为某一学生得到的4个等级分之和;K 为评定者的人数。
例:4位教师对6个学生作文竞赛的名次排列次序如下表。
问评定的一致性程度如何(α=0.01)?评定者(2)R (3) R 2 (4) 学生 n=6 (1) 1 2 3 413 4 2 1 10 100 24 3 1 3 11 121 32 134 10 100 46 5 6 5 22 484 51 2 4 2 9 81 65 6 5 6 22 484 总和84 1370在Excel 中,输入=(G10-POWER(F10,2)/6)/(1/12*POWER(4,2)*(POWER(6,3)-6))得数:0.692857检验方式为卡方检验,公式:w r m n )1(2−=χ则:x 2 = 4×(6-1) ×0.692857=13.85714查卡方分布表,df=6-1=5的卡方临界值是15.09,结论是没有显著相关。
(这类检验用SPSS做更方便)9.7 Task 9a. 两位教师以评定等级的形式对某班级15名学生的英语口语能力进行独立打分,结果如下:学生序号教师A教师B1 11 152 2 13 5 74 15 125 9 66 10 107 1 38 4 59 13 1310 3 211 8 912 7 813 6 414 12 1415 14 11请计算两组等级之间的等级相关系数,并对之进行假设检验(α=0.01,双尾)b. 自建一学生成绩或某两个项目(如德育与英语、学习动机与英语成绩、家庭条件与学习成绩、父母关心程度与学习动机,等等)的评比等级数据库,对其进行等级相关系数的计算和显著性检验,并简要说明之。
(a、b任选其一)。
