第三章 力法( 4)2014(2学时)集美大学船舶结构力学(48学时)
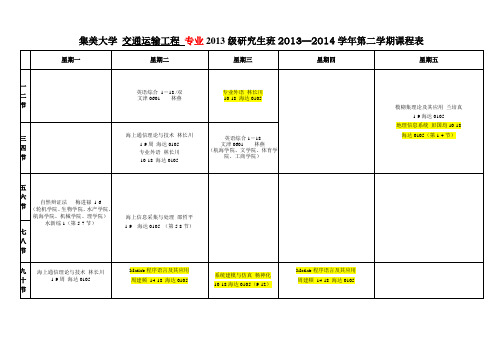
2014集美大学交通运输工程课表
星期一
星期二
星期三
星期四
星期五
一二节
英语综合1-18 /双
文津0601林燕
专业外语林长川
10-18海达0105
模糊集理论及其应用兰培真
1-9海达0105
地理信息系统彭国均10-18
海达0105(第1-4节)
三四节
海上通信理论与技术林长川
1-9周海达0105
专业外语林长川
10-18海达0105
英语综合1-18
文津0601林燕
(航海学院、文学院、体育学院、工商学院)
五六节
自然辩证法梅进禄1-6
(轮机学院、生物学院、水产学院、航海学院、机械学院、理学院)
水新综1(第5-7节)
海上信息采集与处理邵哲平
1-9海达0105(第5-8节林长川
1-9周海达0105
Matlab程序语言及其应用
周建频14-18海达0105
系统建模与仿真杨神化
10-18海达0105(9-12)
Matlab程序语言及其应用
周建频14-18海达0105
船舶结构力学课程教学大纲

的实际概念;五弯矩方程;一根交叉构件板架计算。
位移法原理;位移法在杆系结构中的应用。应变能与余能;杆
5
件的应变能计算;虚功原理;虚位移原理的应用;位能驻值原 6 课时
理的近似解法。
6
矩阵位移法的基本思想;杆元的基本类型;杆件刚度矩阵;结 6 课时
(二)英文简介 Ship Structural Mechanics describes the components and subsystems deformation
and instability, like bending theory of single span beam, torsion theory of shaft parts, torsion theory for rectangle plate and Stability of shaft or board, and so on. Several methods are also presents for stress and deformation analysis. It contains not only the force method, displacement method and energy method in the classical structure mechanics, but also the finite element method and its application in ship structures. Finally the basic principles and methods for structure design of ships will be introduced together with the design standards of ships. 二、教学目标
集美大学 船舶结构力学(48学时)第二章 单跨梁(3)2014年 4学时

3)单跨梁弯曲要素表类同 《材力》的对应表,但要 注意船舶结构力学符号法 则。 4)注意弯矩图的叠加;剪力 图的叠加(正负抵消)。
五、弯矩图与剪力图 1) 定义:载荷作用下梁 截面的弯矩和剪力沿梁轴 线的分布图形。 2)绘制目的:
a. 最为直观地描述弯曲梁的 内力分布; b. 帮助工程师预测和分析载 荷作用下结构的基本变形情 况。
3
求梁右端转角
梁右端的转角,用叠加法求 得如下:
Ml Ql Pl l 6 EI 24EI 16EI 2 Ql 32EI
2
2
画梁的弯矩图也采用
叠加法:先分别画出M、Q、 P单独作用下简支梁的弯矩、 剪力图,
P
M图
中点挠度
端点转角大小
0.25 Pl
Pl3 48EI
m l2 16EI
六、单跨梁的弯曲要素 表及叠加原理应用
1.(普通)叠加法: 仅应用弯曲要素表及 叠加原理求静定或超静定 单跨梁特殊点的弯曲要素 并画内力图的方法。
2.单跨梁力法: 应用简支梁弯曲要素 表、叠加原理及变形协调 条件或静力平衡条件求超 静定单跨梁特殊点的弯曲 要素并画内力图的方法。
3、在应用弯曲要素表及 叠加原理解题时,应充 分了解已有的弯曲要素 表的种类、应用范围、 坐标及符号法则。
EI , l
P ql
q
EI , l
P ql
解:据叠加原理有
q
q
vq
EI , l
P
vP
P
EI , l
P
EI ,ቤተ መጻሕፍቲ ባይዱl
M图
中点挠度
端点转角大小
0.25 Pl
Pl3 48EI
m l2 中点挠度 16EI
集美大学 船舶结构力学(48学时)第一章 绪论(2014年)

8、船体扭转强度:当船舶在 斜浪上航行,整个船体将发生 扭转,船舶抵抗发生过大扭转 变形或受到破坏的能力。
9、应力集中:在船体结构不 连续的地方,发生应力汇集或 突然增大的现象,将引起构件 裂缝形成或蔓延。(参见图16及图片)
注: (1) 船舶强度(或船体强度) 是泛指研究船体结构强度的科 学,它包括外力、结构在外力 作用下的反应即内力研究和许 用应力的确定等一系列的问题。
3、工艺力学; 4、船体结构强度分析的一些特 殊力学问题。
(船舶进坞及下水强度、温度对船体结构的作 用及船舶抗冰强度)
教学目的:
1、通过本课程的学习,使学生掌 握船舶结构力学的基本理论与方 法; 2、 力求培养学生船舶结构分析 与计算等方面的能力;
3、 培养学生自学和独立思考 能力,以便在走上工作岗位后, 能通过自学不断地吸收新知识, 开拓新领域,研究新问题,探 求新的机理,充分发挥自己的 才能。
2、骨架的计算模型(连续梁、 板架、刚架)
就整个船体来说,船体的骨架 系统是一个复杂的空间杆系结构。 在实际计算时,尤其是采用经典方 法计算时,常常把杆系简化成一些 形状比较规则的简单的计算图形。
1) 杆件(杆):细长的型钢 或组合型材如横梁、肋骨、肋 板、纵骨、纵桁等船体骨架。
2) 杆件系统(杆系):相互 连接的船体骨架系统。船体的 杆系是一个复杂的空间系统。 简化后的典型杆系:连续梁; 板架;刚架。
3)连续梁(刚性支座上的连续 梁):两端以一定的形式固定, 中间具有多个刚性支座,且在 横向荷重作用下的直杆。(注: 属多次静不定结构。)
以远洋干货船船体结构甲 板部分(图1-7)为例介绍连 续梁模型的建立: (参见图1-8)
甲板纵骨
当计算甲板纵骨在垂直于甲板 的载荷作用下的弯曲应力与变形时, 可将其取为图1-6 a所示的计算图 形——两端刚性固定、中间自由支 持在刚性支座上的连续梁。
船体结构 第四A章(下) (集美大学船体结构与制图(48学时)课件2015年)

大型船舶采 用的球鼻艏, 可以减少航 行阻力,但 对抛锚、起 锚、船舶停 靠码头有妨 碍,且工艺 复杂,强度 要求高。
艉端:艉尖舱壁以后、上
甲板以下的船体部分。包括 艉尖舱和艉部悬伸端,结构 比较复杂。受舵、螺旋桨、 机舱的影响较大,艉端多采用 横骨架式,呈U形。
球尾 方尾
尾部的受力特点
船尾除受静水压力外,还承受 舵和螺旋桨的自身重量和螺旋 桨运转时的水动压力、激振力。
为抵抗抨击和浮冰撞击,可在 两档肋位之间加中间肋骨。或 在两舷之间加强胸横梁(或撑杆)。 大型船舶还会设计一至数道舷侧 纵桁或开孔平台。
横梁
制荡舱壁:设置在 首尖舱中线面上的 开孔的舱壁,它的 作用是防止首尖舱 内的压载水左右摇 荡和缓和冲击的作 用。
首尖舱外舷侧的加强:
从距首垂线0.15L至防撞舱壁 区域内设置间断的舷侧纵桁 或加厚舷侧外板。
1.钢板焊接首柱
钢板焊接的首柱具有弧形变化的截面,它比铸钢的首柱为 “软”,当发生碰撞时,钢板首柱只在局部变形或损坏,可以 避免造成较大范围的损坏。局部损坏的地方修理和更换钢板也 比较方便。钢板首柱主要的优点是制造方便,重量轻,容易修 理。
钢板焊接首柱
2.铸钢和钢板混合首柱
铸钢首柱刚性好但重量较大,适用于截面形状比较复杂,刚 性要求较大的地方,如破冰船的首柱。现在大型的运输船上仍有 这种首柱,但通常只在水线附近及首柱下部采用铸钢件,而水线 以上部分采用钢板焊接,然后将这两部分焊接起来,这种首柱称 为混合首柱,见右图。图中铸钢的一段,铸有横向和纵向的加强 筋,加强筋可与船体的其它构件相焊接。铸钢首柱的边缘有凹槽, 便于外板嵌入焊接。
升高肋板
当h 100m m时,l 2h 当h 100m m时,l 1.5h, 且l 200m m
集美大学船舶结构力学(48学时)第三章 力法(1)2014(2学时)

静定基
这时原来仅受均布荷重q作用的静 不定的双跨梁变为受均布荷重q与集中 力R共同作用的静定的单跨梁;
2)比较前后两种梁的变 形情况,根据变形一致 (协调、连续)条件建 立方程式;
原超静定结构
v1 0
静定基
变形一致条件:
v1 0
静定基
变形一致条件:
v1 0
vq1 vR1 0
4
3
Rl 5ql 0 5 6 EI 24 EI R ql 4
P
M图
中点挠度大小
3
端点转角大小
2
m
Pl Pl EI , l 48EI 16EI Pl / 4 2 m ml ml ml 左 右 查单跨梁的弯曲要素表(附录A表A-2),得到: 3EI 6EI 16EI
Q
EI , l
Ql / 8
(力法基本未知数数目与结构的 静不定次数相同。)
2、在去掉约束或截断处, 列出变形一致(连续) 方程式以保证基本结构 的变形与原结构的变形 相同。
(方程数目与基本未知数数目相同。)
3、从变形一致(或连续、 协调)方程式中求出未 知“力”,进一步可求 出结构的其他弯曲要素。
五、三弯矩方程法 1、三弯矩方程式:一般来 说,在用力法的第二种方法 (截面法)解静不定杆系问 题时,列出的变形连续方程 式(或称节点转角连续方程) 是以各断面弯矩为未知数的 方程组,
1 2 M 1 ql 14
3 2 M2 ql 28
7)画弯矩图
求出了 M 1 、M 2 后, 就可以分别对两个单跨 梁1-2、2-3画弯矩图。
其中每一个单跨梁 的弯矩图都可以用叠加 法来画。最后组合起来 得到双跨梁的弯矩图, 图3-7(a)。
船舶结构力学课后题答案上海交大版

s目录第1章绪论1第2章单跨梁的弯曲理论2第3章杆件的扭转理论6第4章力法8第5章位移法10第6章能量法20第7章矩阵法28第9章矩形板的弯曲理论32第10章杆和板的稳定性35第1章绪论1.1题1〕承受总纵弯曲构件:连续上甲板,船底板,甲板及船底纵骨,连续纵桁,龙骨等远离中和轴的纵向连续构件〔舷侧列板等〕2〕承受横弯曲构件:甲板强横梁,船底肋板,肋骨3〕承受局部弯曲构件:甲板板,平台甲板,船底板,纵骨等4〕承受局部弯曲和总纵弯曲构件:甲板,船底板,纵骨,递纵桁,龙骨等1.2题甲板板:纵横力〔总纵弯曲应力沿纵向,横向货物或上浪水压力,横向作用〕舷侧外板:横向水压力等骨架限制力沿中面内底板:主要承受横向力货物重量,骨架限制力沿中面为纵向力舱壁板:主要为横向力如水,货压力也有中面力第2章单跨梁的弯曲理论2.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x)1〕图2.1333 2334243()()()424 ()26666l l ll l lp x p x p x M x N xv xEI EI EI EI EI---=++++原点在跨中:3230111104()4()266llp xM x N xv x vEI EI EI-=+++,'11'11()0()022(0)0(0)2l lv vpv N⎧==⎪⎨⎪==⎩2〕3323()3 2.2()266llp xN xMxv x xEI EI EIθ-=+++图3〕333002()2 2.3()666xx x llp xN x qx dxv x xEI EI EIθ-=++-⎰图2.2题a)33111311131(3)(2)616444641624 pp ppl plv v vEI EI⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦=3512plEIb)2'292(0)(1)3366Ml Ml PlvEI EI EI-=+++=2220.157316206327Pl Pl PlEIEI EI-+=⨯=2220.1410716206327Pl Pl PlEIEI EI---=⨯=2372430plEIc) ()44475321927682304qlql qllvEI EI EI=-=d)2.1图、2.2图和2.3图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1图2.2图2.32.3题1〕2〕32101732418026q l Ml l l Ml lq EI EI EIEI θ⎡⎤=-++-⎢⎥⎣⎦=3311117131824360612080q l q l EI EI⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5图3000()6N x v x v x EIθ=++,()00v A p N =-如图2.4, ()()0v l v l '==由得3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭ 图2.42.5题2.5图:〔剪力弯矩图如2.5〕()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-= ⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦, 图2.5 111,0,6632A l a l b A K ====+=将代入得:()16312pl pl M ==2.7图:〔剪力弯矩图如2.6〕图2.62.8图〔剪力弯矩图如2.7〕图2.72.6题.[]1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx GGA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s s sd b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EI qx qlx qx qx qlv x x EI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++⎪⎝⎭∴=+可得出由得方程组:解出:a=2.7.题先推广到两端有位移,,,i i j j θθ∆∆情形:212,i j s EI GA l β⎛⎫∆=∆-∆= ⎪⎝⎭令 2.8题 :20375225,1.8,751050kgl cm t cm s cm cm σ=⨯====面积2cm 距参考轴cm面积距 3cm惯性矩 4cm自惯性矩4cm外板1.845⨯ 81 0 0 0 (21.87)略 球扁钢O N 24a38.75 9430.2 2232 ∑119.8 15.6 604.5 9430.22253.9ABC=11662224604.55.04116628610119.8BBe cm I C cm AA===-=-=275 1.838.75174min ,4555A cm l lI be s cm=⨯+=⎧⎫===⎨⎬⎩⎭计算外力时面积计算时,带板1〕.计算组合剖面要素:形心至球心外表1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维假设不计轴向力影响,那么令u=0重复上述计算: 2.9.题 解得: 2.10题 2.11题 图2.120 2.12题1〕先计算剖面参数:图2.8a2422u u P P l δδδ⎛⎫⋅⎛⎫ ⎪⋅+= ⎪⎝⎭ ⎪⎝⎭p M图2.8b2.13补充题剪切对弯曲影响补充题,求图示构造剪切影响下的v(x)解:可直接利用 2.14. 补充题试用静力法及破坏机构法求右图示机构的极限载荷p ,梁的极限弯矩为p M 〔20分〕 〔1983年华中研究生入学试题〕 解: 1〕用静力法:〔如图2.9〕由对称性知首先固端和中间支座到达塑性铰,再加力u p p →,当p 作用点处也形成塑性铰时构造到达极限状态。
集美大学船舶结构力学(48学时)第三章 力法(3)2014(2学时)

216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图3-16(a)
q
l
z
l1
直观上就能发现无荷重杆1-3 对有荷重杆4-5的作用 相当于一个弹性支座。
x
y
1、首先用力法节点力替代法 来解这个板架: 1)将两杆在相交的节点处分 开并代以节点力,所得计算 图形如图3-16(b) 所示;
q
2
v主2
计算图形
2
EI , l
m
A
3
E ,2 I , l
q
2
1
m
EI , l
3
E ,2 I , l
A
l1 公式 4 EI1
题3
0
1
P
EI , l
2
EI , l
l 4 EI
A P
2
1
EI , l
2
A
题4
l1 公式 4 EI1
0
P P
EI , l
l 4 EI
EI , l
2
EI , l
题5
1
2)是否可以说受载杆与不 受载杆相连时,不受载杆 就相当于受载杆的弹性固 定端?
3)怎样计算弹性固定端的 柔性系数?
只需把受载杆与不受载杆 在相交处切开并加上相互作用 的弯矩M,计算无载杆在该弯 /M 即 矩作用下的转角 , 得柔性系数 。
3
3
2
2
1
关键是线性表达 21
21
1
x
1
EI , l 3
1
P
1
EI , l
两端刚固无载杆:
2
A
l3 192EI
l A 192 EI 1 公式
v/R
3 1
P
1
EI , l 3
4 2 EI , l EI , l
1
1
R
4 2 EI , l 3 EI , l
1
1
l R v2 AR 192EI
3
例3:
将下图所示的杆系 简化为具有弹性支座的 单跨梁。
M2
M1
2
1 得M 1 M 2代入 21中有 2 EI1 , l1 l1 21 M2 4 EI1
1
l1 4EI1
公式
P
m
P
m
0
l1 4 EI 1 例2 公式
0
E, I1 , l1
q P
1
m
2
EI , l
事实上本例中甲板间 肋骨的下端是介于简支、 刚固之间的情况,因此实 际上柔性系数的数值介于 l1 l1 与 之间。
q
z
0
y
3
x
0
EI , l
EI , l
1
EI , l
E , I 1 I , l 1 2l
2
q
0
1
EI , l
l A 6 EI
q
0
EI , l
EI , l
3
两端简支无载杆: 3 公式
3
EI , l
l1 A 48EI1
3
1
R
2
1 EI ,2l
EI 1, l 1
3
v1 AR ( 2l ) R 48EI 3 l R 6 EI
2
A
7l 3 768EI
一端刚固一端简 支的无载杆: 公式 3
P
1
EI , l
R
4 2 EI , l EI , l
1
7l1 A 768EI1
v/R
4
3
1
3
2 EI , l EI , l
1
1
7l R v2 AR 768EI
3
例2:
将下图所示的板架 简化为具有弹性支座的 单跨梁。
P
z
0
y
4 2 EI , l EI , l
其计算模型如该图所示, 图中甲板间肋骨的下端 暂时假定是自由支持的。
1
3-18
1、 先用力法来解这个刚架:
2 3
3-18 1
1)静定的基本结构的图形如 图3-18(b)所示;
2
3
2
l ll EI
静定基
l1 1l 1 EI
1
变协方: 21 23
3-18
2)建立支座2处的转角连续 方程式为 21 23
m
均I , l
3
2
, l
4
l3 A 12EI
2
单跨梁!
复杂刚架! 原模型几个基本未知数?
l3 A 12EI
力法解该单跨梁:
ql2 m 2
q
EI , l
3 l 4 A 12EI
l 8 EI
ql2 m 2
2
q
静定基:
4
2 7 2 M 2 ql M 2 EI , l 13 4 6 ql R4 ql v4 13 26EI
3
比较:
(1)
3
Ml l1 ql M 3EI1 3EI 24EI
(2)
ql M 3EI 24EI
Ml
3
可得出以下结论:
3.结论: 1)不受载的甲板间肋骨对横梁的
影响相当于横梁的弹性固定端。
3 2
3 2
1
3 2
3
21
线性表达
2
1
l1 M 3EI1
l1 或令M等于1 21 3EI1
l1 M 3EI1
M
2
EI1 , l1
1
可作为公式记忆, 以提高解题效率
l1 3 EI 1 公式
关键: 用无载杆的参数,线性
表达出无载杆与有载杆连接 点的转角 , 除M 即得 。
模型简化时有些情 况可由“公式”直 举例如 接写出
P
m
P
m
例1
l1 3 EI 1 公式
0
1
q
ql Rl AR 384EI 192EI ( B)
4
3
因此可以认为无载杆 1-3 就是有载杆一个柔性 系数为 A 的弹性支座。
若无载杆两端简支:
q
l
I 1 l1
z
x
y
l A 48 EI 公式 1
3 1
本例计算弹性支座的柔 性系数 A 方法: 据弯曲要素表写出无 载杆1-3在R节点力作用下 的挠度 v ,A = v /R 。
Ml l1 ql M 3EI1 3EI1 24EI
3
(1)
2、 再考虑同样荷重作用 下的横梁,左端为弹性固 定时的情况:
横梁在左端弹性固定时(如图3-18(c))
3 2
3-18( c)
静定基
3-18(c)
M
3
2
变协方: M 23
(2)
EI
Ml ql M 3EI 24EI
3EI1
4 EI1
5)怎样计算杆系结构中有 多根不受载杆件直接与受 载杆件相连时,其弹性固 定端的柔性系数?
教材43页例题用力法证明了一 个结论(“弹性固定端刚性系数的叠加
原理”):
几个无载杆共同作用于 某受载杆同一端的刚性系数 等于各杆单独作用于该端刚 性系数之和。
P
1
l
2
l l
3
静定基
M 21 M 23
Q
2
EI , l
单跨梁!
4
3
l 8 EI
l 4 EI 21 ; K 21 4 EI l
l 4 EI 2 3 ; K 2 3 4 EI l
8EI K K 21 K 23 ; l 1 l K 8 EI
例7
模型简化:
1 复杂刚架! 3 2
教学要求: 1、理解本节基本概念; 2、掌握结构简化成弹性固定 与弹性支座的方法及柔性系 数计算方法。
下面通过力法对杆系 的分析,介绍实际结构中 弹性固定与弹性支座是如 何形成的。
一、弹性固定的实际概念 某双甲板船的上甲板 强横梁、甲板间肋骨及连 接肘板组成的肋骨刚架如 下图片所示,
q
3 2
第三章 力法
§3.5 弹性固定端与 弹性支座的实际概念
教学目的: 1、在实际的船体结构中 弹性固定与弹性支座是如 何形成的?它们的柔性系 数如何计算?
这些问题可以在本节 中通过力法对杆系的分析 得到合理解释。
2、 理解弹性固定与弹性 支座的实际概念,对于正 确建立船体结构(特别是 空间杆系结构)的简化力 学模型非常重要。
l 6 EI
l 3EI 2 3 ; K 2 3 3EI l
K K 2 3 K 2 4 1 l K 6 EI
6 EI ; l
l 3EI 2 4 ; K 24 3EI l
例6
均I , l
原模型几个基本未知数?
1
模型简化:
Q
2
4
复杂刚架!
图3-16(b)
ql Rl 384EI 192EI
v交 2 Rl 48EI1
3 1
4
3
2
变协方
v主2 v交2
2)根据变形一致条件(节点2 处挠度相等),有变形连续方 程式为 v主2 v交2 即
ql Rl Rl 384EI 192EI 48EI1
(A)
4
3
3 1
2、 再考虑撤去无荷重杆 1-3,在节点2(梁4-5的中 点)处加一弹性支座的情 况:如图3-16(c)所示,
6 EI ; l
l 3EI 21 ; K 21 3EI l
