最新精选《有理数的乘法运算律》同步提升训练
人教版七年级数学上册《有理数的乘法运算律》 同步训练卷

人教版七年级数学上册 1.4.1.3有理数的乘法运算律同步训练卷一、选择题(共10小题,3*10=30) 1.计算(-4)×(-7)×(-14)的结果是( ) A .-1 B .-7 C .1 D .72.式子(12-310+25)×4×25=(12-310+25)×100=50-30+40中运用的运算律有( )A .乘法交换律和乘法结合律B .乘法交换律和分配律C .加法结合律和分配律D .乘法结合律和分配律3.n 个不等于零的有理数相乘,积的符号( ) A .由因数的个数决定 B .由正因数的个数决定 C .由负因数的个数决定 D .由负因数的大小决定4.下列乘积的结果,符号为正的是( ) A .0×(-3)×(-4)×(-5) B .(-6)×(-15)×(-0.5)× 3 C .-2×(-12)×(+2) D .-1×(-5)×(-3)5.下列运用简便方法计算57×99+44×99-99,正确的是( ) A .99×(57+44)=99×101=9 999 B .99×(57+44-1)=99×100=9 900 C .99×(57+44+1)=99×102=10 098 D .99×(57+44-99)=99×2=198 6. 计算1457×715,最简便的方法是( )B .(14+57)×715C .(15-27)×715D .(10+457)×7157. 若a ,b ,c 在数轴上对应点的位置如图所示,则必有( )A .abc >0B .a(b -c)>0C .(a +b)c >0D .(a -c)b >08.在计算(-0.125)×15×(-8)×⎝⎛⎭⎫-45=[(-0.125)×(-8)]×⎣⎡⎦⎤15×⎝⎛⎭⎫-45的过程中,没有运用的运算律是( )A .乘法交换律B .乘法结合律C .分配律D .乘法交换律和乘法结合律9.计算⎝⎛⎭⎫-17×15+⎝⎛⎭⎫-17×45的最简便的方法是( ) A .利用加法交换律与加法结合律 B .利用乘法交换律 C .利用乘法结合律 D .逆用分配律10.用简便方法计算:-6×(-12)×(-0.5)×(-4),结果为( )A .6B .-6C .3D .2 二.填空题(共8小题,3*8=24)11.式子5×(-2)=(-2)×5变形的依据是_______________. 12. 计算(12-13+16)×6的结果是_______.13. 三个有理数相乘,积为负数,则其中负因数有___________个. 14.计算:(-8)×(-2)+(-1)×(-8)-(-3)×(-8)=_______. ⎛⎫-11⎛⎫-312的结果为__________.16.在计算⎝⎛⎭⎫512-79+23×(-36)时,可以避免通分的运算律是__________. 17.计算:(-691516)×(-8)= __________.18.计算:⎝⎛⎭⎫1+12×⎝⎛⎭⎫1+14×⎝⎛⎭⎫1+16×…×⎝⎛⎭⎫1+120×⎝⎛⎭⎫1-13×⎝⎛⎭⎫1-15×⎝⎛⎭⎫1-17×…×⎝⎛⎭⎫1-121=__________. 三.解答题(共6小题, 46分) 19.(7分) 计算: (1)-2×3×(-4); (2)-6×(-5)×(-7).20.(8分) 计算: (1)(-85)×(-25)×(-4); (2)⎝⎛⎭⎫-78×15×⎝⎛⎭⎫-117.21.(7分) 计算:(1)⎝⎛⎭⎫910-115×30. (2)⎝⎛⎭⎫-14-12-18×16.22.(8分) 用简便方法计算: (1)(-8)×(-7)×(-0.125); (2)(-13+25-56)×(-30).23.(8分) 运用运算律进行简便运算: (1)(-4)×(-0.99)×(-25); (2)(-76)×(-15)×(-67)×15;(3)(14-16+12)×(-24).24.(9分) 观察下列各式:第1个等式:a 1=11×3=12×(1-13);第2个等式:a 2=13×5=12×(13-15);第3个等式:a 3=15×7=12×(15-17);第4个等式:a 4=17×9=12×(17-19);… 请解答下列问题:(1)按以上规律列出第5个等式; (2)求a 1+a 2+a 3+a 4+…+a 100的值.参考答案 1-5 6-10 11. 乘法交换律 12. 2 13. 1或3 14. 0 15.13416. 分配律 17. 55912.18. 119. 解:(1)原式=2×3×4=24. (2)原式=-6×5×7=-210.20. 解:(1)原式=(-85)×[(-25)×(-4)]=(-85)×100=-8 500. (2)原式=⎝⎛⎭⎫-78×15×⎝⎛⎭⎫-87=78×87×15=15. 21. 解:(1)原式=910×30-115×30=27-2=25.(2)原式=⎝⎛⎭⎫-14×16-12×16-18×16=-4-8-2=-14. 22. 解:(1)原式=(-8)×(-0.125)×(-7)=1×(-7)=-7 (2)原式=-13×(-30)+25×(-30)-56×(-30)=10+(-12)+25=2323. 解:(1)原式=-4×0.99×25=-(4×25)×0.99=-100×0.99=-99 (2)原式=-(76×15×67×15)=-[(76×67)×(15×15)]=-(1×3)=-3(3)原式=14×(-24)-16×(-24)+12×(-24)=-6+4+(-12)=-1424. 解:(1)a 5=19×11=12×(19-111);(2)a 1+a 2+a 3+a 4+…+a 100=12×(1-13)+12×(13-15)+…+12×(1199-1201) =12×(1-13+13-15+…+1199-1201) =12×(1-1201)1、在最软入的时候,你会想起谁。
苏科版数学七年级上册第二章有理数有理数乘法运算法则(习题)

1.4.1 有理数乘法运算法则【夯实基础】1.一个有理数与其相反数的积( )A 、符号必定为正B 、符号必定为负C 、一定不大于零D 、一定不小于零2.若a 与−3的积是一个负数,则a 的值可以是( )A. −15B. −2C. 0D.153.下列说法错误的是( )A 、任何有理数都有倒数B 、互为倒数的两个数的积为1C 、互为倒数的两个数同号D 、1和-1互为负倒数4.如果水位上升为正,水位下降为负,某水库的水位每天下降5cm ,4天后,该水库水位总的变化量是( )A.9 cmB. −9 cmC.20 cmD. −20 cm4.−114的倒数乘14的相反数,其值为( )A.5B.−5C.15D.−155.下列说法,正确的有( )①一个数同1相乘,仍得这个数;②一个数同−1相乘,得这个数的相反数;③一个数同0相乘,仍得0;④互为倒数的两个数的积为1.A.1个B.2个C.3个D.4个6.已知两个有理数a ,b ,如果ab <0且a +b >0,那么( )A.a >0,b >0B.a <0,b >0D.a,b 同号 C. a,b 异号,且正数的绝对值较大7.的倒数的相反数是___。
8.|−12|的倒数是______.9.小明有5张写着不同数字的卡片:−5,+1,0,−2,+6,他从中任取三张卡片,−23计算卡片上数字的乘积,其中最小的乘积是______.10.已知|x +2|+|y −3|=0,则4xy =______.11.计算:(1)15×(−6) (2)(−0.24)×0 (3)(−8)×(−14)(4)(−0.8)×(−134) (5)135×(−334) (6)(−3.48)×(−0.7)12.甲水库的水位每天升高3cm ,乙水库的水位每天下降5cm ,4天后,甲、乙水库水位总的变量各是多少?13.今抽查10袋盐,每袋盐的标准质量是500克,超出部分记为正,统计成下表: 问:这10袋盐一共有多重?14.已知a ,b 互为相反数, c ,d 互为倒数,x 的绝对值为5,求a +b +cd −2x 的值.【能力提升】15.正整数x,y满足(2x−5)(2y−5)=25,则x+y等于()A.18或10B.18C.10D.2616.下列说法正确的是()①两个正数中倒数大的反而小;②两个负数中倒数大的反而小;③两个有理数中倒数大的反而小;④两个符号相同的有理数中倒数大的反而小.A.①②④B.①C.①②③D.①④17.在数轴上的三点A,B,C所表示的数分别为a,b,c,根据图中各点的位置,判断下列各式正确的是()A.(a−1)(b−1)>0B.(b−1)(c−1)>0C.(a+1)(b+1)<0D.(b+1)(c+1)<018.已知|x|=2,|y|=3,且xy<0,求4x−2y的值.【思维挑战】19.若x是不等于1的数,我们把11−x 称为x的差倒数,如2的差倒数是11−2=−1,−1的差倒数是11−(−1)=12,现已知x1=13,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差。
北师大版(2024)七年级上册《2.3_有理数的乘除运算1》2024年同步练习卷+答案解析

北师大版(2024)七年级上册《2.3有理数的乘除运算1》2024年同步练习卷一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.用简便方法计算:,其结果是()A.2B.1C.0D.2.下列算式中,积为负数的是()A. B.C.D.3.下列选项错误的是()A. B.C.D.4.下面计算的过程正确的是()A. B.C.D.5.下列各式中,m 和n 互为倒数的是()A.B.C.D.6.一个数的相反数的倒数是,则这个数为()A. B.C.D.7.式子中用的运算律是()A.乘法交换律及乘法结合律B.乘法交换律及乘法对加法的分配律C.乘法结合律及乘法对加法的分配律D.乘法对加法的分配律及加法结合律8.的倒数是()A.B.C. D.9.下列计算正确的是()A.原式B.原式C.原式D.原式10.运用了()A.加法交换律B.乘法结合律C.乘法分配律D.乘法交换律和结合律11.如图所示,数轴上点A,B,C分别表示有理数a,b,c,若a,b,c三个数的乘积为正数,这三个数的和与其中一个数相等,则下列正确的是()A. B. C. D.12.如果两个有理数的积是正数,那么这两个有理数()A.同号,且均为负数B.异号C.同号,且均为正数D.同号二、填空题:本题共6小题,每小题3分,共18分。
13.写出下列各数的倒数.的倒数是______;的倒数是______;的倒数是______;的倒数是______;的倒数是______.14.两数相乘,同号______异号______,并把______相乘;任何数与0相乘都得______.15.填空题.______;______;______;______;______;______.16.若a、b互为倒数,则______.17.一个有理数的倒数等于它本身,则这个数只能是______判断对错18.已知有理数,我们把为a的差倒数,如:2的差倒数是,的差倒数是如果,是的差倒数,是的差倒数,是的差倒数……依此类推,那么…的值是______三、计算题:本大题共1小题,共6分。
人教版七年级数学上册第一章 1.4.1.3有理数的乘法运算律 同步测试题

人教版七年级数学上册第一章 1.4.1.3有理数的乘法运算律 同步测试题一、选择题1.在2×(-7)×5=-7×(2×5)中,运用了( )A .乘法交换律B .乘法结合C .分配律D .乘法交换律和乘法结合律2.计算(1-12+13+14)×(-12),运用哪种运算律可避免通分( ) A .加法交换律 B .加法结合律 C .乘法交换律 D .分配律3.算式(-32)×(-314)×23的值为( ) A .14 B .1112 C .114 D .1344.在运用分配律计算3.96×(-99)时,下列变形较合理的是( )A .(3+0.96)×(-99)B .(4-0.04)×(-99)C .3.96×(-100+1)D .3.96×(-90-9)5.计算1357×316,最简便的方法是( ) A .(13+57)×316 B .(14-27)×316 C .(16-227)×316 D .(10+357)×3166.计算(-55)×99+(-44)×99-99正确的是( )A .原式=99×(-55-44)=-9 801B .原式=99×(-55-44+1)=-9 702C .原式=99×(-55-44-1)=-9 900D .原式=99×(-55-44-99)=-19 602二、填空题7.在算式每一步后面填上这一步应用的运算律:[(8×4)×125-5]×25=[(4×8)×125-5]×25(________)=[4×(8×125)-5]×25(________)=4 000×25-5×25(________)=99875.8.计算:(-8)×(-2)+(-1)×(-8)-(-3)×(-8)=-8×[(________)+(________)-(________)]=-8×________=________.9.计算:25×(-0.125)×(-4)×(-45)×(-8)×54=[25×(________)]×[(-0.125)×(________)]×[(________)×________]=________×1×(________)=________.三 、解答题10.运用运算律进行简便运算:(1)(-10)×13×(-110)×6;(2)36×(-34-59+712);(3)(-5)×(+223)+7×(-223)-(+12)×(-223).11.某场馆建设需烧制半径为0.24 m ,0.37 m ,0.39 m 的三个圆形钢筋环,问:需要钢筋多少米?(π取3.14)12.计算:-48×(12-3-58+56-112).13.用简便方法计算:(1)(-8)×(-43)×(-1.25)×54;(2)(-112-136+16)×(-36);(3)0.7×149+234×(-15)+0.7×59+14×(-15);(4)9978×(-4)-(12-13-56)×24.14.请你参照黑板上老师的讲解,用运算律简便计算:(1)999×(-15);(2)999×11845+999×(-15)-999×1835.15.在学习有理数乘法时,李老师和同学们做了这样的游戏,将2 020这个数说给第一位同学,第一位同学将它减去它的12的结果告诉第二位同学,第二位同学再将听到的结果减去它的13的结果告诉第三位同学,第三位同学再将听到的结果减去它的14的结果告诉第四位同学……照这样的方法直到全班40人全部传完,最后一位同学将听到的结果告诉李老师,你知道最后的结果吗?参考答案一、选择题1.在2×(-7)×5=-7×(2×5)中,运用了(D )A .乘法交换律B .乘法结合C .分配律D .乘法交换律和乘法结合律2.计算(1-12+13+14)×(-12),运用哪种运算律可避免通分(D) A .加法交换律 B .加法结合律 C .乘法交换律 D .分配律3.算式(-32)×(-314)×23的值为(D ) A .14 B .1112 C .114 D .1344.在运用分配律计算3.96×(-99)时,下列变形较合理的是(C)A .(3+0.96)×(-99)B .(4-0.04)×(-99)C .3.96×(-100+1)D .3.96×(-90-9)5.计算1357×316,最简便的方法是(C )A .(13+57)×316B .(14-27)×316C .(16-227)×316D .(10+357)×3166.计算(-55)×99+(-44)×99-99正确的是(C )A .原式=99×(-55-44)=-9 801B .原式=99×(-55-44+1)=-9 702C .原式=99×(-55-44-1)=-9 900D .原式=99×(-55-44-99)=-19 602二、填空题7.在算式每一步后面填上这一步应用的运算律:[(8×4)×125-5]×25=[(4×8)×125-5]×25(乘法交换律)=[4×(8×125)-5]×25(乘法结合律)=4 000×25-5×25(分配律)=99875.三 、解答题8.计算:(-8)×(-2)+(-1)×(-8)-(-3)×(-8)=-8×[(-2)+(-1)-(-3)]=-8×0=0.9.计算:25×(-0.125)×(-4)×(-45)×(-8)×54=[25×(-4)]×[(-0.125)×(-8)]×[(-45)×54] =-100×1×(-1)=100.10.运用运算律进行简便运算:(1)(-10)×13×(-110)×6; 解:原式=(10×110)×(13×6) =2.(2)36×(-34-59+712); 解:原式=36×(-34)-36×59+36×712=-27-20+21=-26.(3)(-5)×(+223)+7×(-223)-(+12)×(-223). 解:原式=(-5)×223-7×223+12×223=(-5-7+12)×223=0×223=0.11.某场馆建设需烧制半径为0.24 m ,0.37 m ,0.39 m 的三个圆形钢筋环,问:需要钢筋多少米?(π取3.14)解:2π×0.24+2π×0.37+2π×0.39=2π×(0.24+0.37+0.39)=2π×1=2π≈6.28(m).答:需要钢筋约6.28 m.12.计算:-48×(12-3-58+56-112). 解:原式=-48×12-3×(-48)-58×(-48)+56×(-48)-112×(-48) =-24+144+30-40+4=114.13.用简便方法计算:(1)(-8)×(-43)×(-1.25)×54; 解:原式=-(8×1.25)×(43×54) =-10×53=-503.(2)(-112-136+16)×(-36);解:原式=(-112)×(-36)+(-136)×(-36)+16×(-36) =3+1-6=-2.(3)0.7×149+234×(-15)+0.7×59+14×(-15); 解:原式=(0.7×149+0.7×59)+[234×(-15)+14×(-15)] =0.7×(149+59)+(-15)×(234+14) =0.7×2+(-15)×3=1.4+(-45)=-43.6.(4)9978×(-4)-(12-13-56)×24. 解:原式=(100-18)×(-4)-(12-8-20) =-400+12+16 =-38312.14.请你参照黑板上老师的讲解,用运算律简便计算:(1)999×(-15);(2)999×11845+999×(-15)-999×1835. 解:(1)原式=(1 000-1)×(-15)=-15 000+15=-14 985.(2)原式=999×[11845+(-15)-1835] =999×100=99 900.15.在学习有理数乘法时,李老师和同学们做了这样的游戏,将2 020这个数说给第一位同学,第一位同学将它减去它的12的结果告诉第二位同学,第二位同学再将听到的结果减去它的13的结果告诉第三位同学,第三位同学再将听到的结果减去它的14的结果告诉第四位同学……照这样的方法直到全班40人全部传完,最后一位同学将听到的结果告诉李老师,你知道最后的结果吗?解:2 020×(1-12)×(1-13)×(1-14)×…×(1-140) =2 020×12×23×34×…×3940=2 020×140101=2.。
专题 有理数的乘除法计算题(八大题型共50题)(解析版) -2024-2025学年七年级数学上册同步
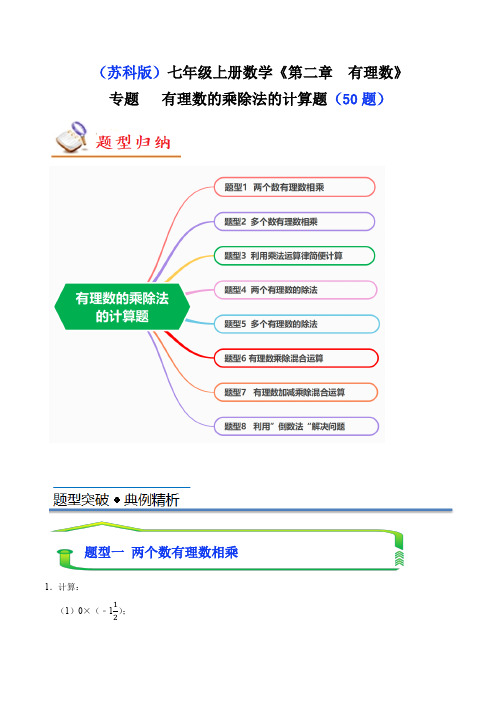
(苏科版)七年级上册数学《第二章 有理数》 专题 有理数的乘除法的计算题(50题)1.计算:(1)0×(﹣112);题型一 两个数有理数相乘(2)(﹣0.25)×(−45); (3)85×(−154); (4)(﹣416)×0.2.【分析】根据有理数的乘法运算法则进行计算即可得解. 【解答】解:(1)0×(﹣112)=0;(2)(﹣0.25)×(−45) =14×45 =15;(3)85×(−154)=−85×154 =﹣6;(4)(﹣416)×0.2=−256×15 =−56.【点评】本题考查了有理数的乘法运算,熟记运算法则是解题的关键. 2.计算:(1)(﹣3)×(﹣4); (2)(﹣3.2)×1.5; (3)49×(−32);(4)134×(﹣8).【分析】(1)两数相乘,同号得正,再把绝对值相乘即可求解; (2)两数相乘,异号得负,再把绝对值相乘即可求解; (3)两数相乘,异号得负,再把绝对值相乘即可求解; (4)两数相乘,异号得负,再把绝对值相乘即可求解.【解答】解:(1)原式=3×4=12; (2)原式=﹣(3.2×1.5)=﹣4.8; (3)原式=﹣(49×32)=−23;(4)原式=﹣(74×8)=﹣14.【点评】本题主要考查有理数的乘法,掌握有理数的乘法法则是解题的关键.3.计算:(1)(﹣3)×(﹣4); (2)(+45)×(﹣114);(3)(﹣2022)×0; (4)(﹣0.125)×8; (5)25×(﹣1); (6)(−13)×(﹣3).【分析】(1)根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘即可求解; (2)根据有理数乘法法则:两数相乘,异号得负,并把绝对值相乘即可求解; (3)根据有理数乘法法则:任何数与0相乘,都得0即可求解;(4)根据有理数乘法法则:两数相乘,异号得负,并把绝对值相乘即可求解; (5)根据有理数乘法法则:两数相乘,异号得负,并把绝对值相乘即可求解; (6)根据有理数乘法法则:两数相乘,同号得正,并把绝对值相乘即可求解. 【解答】解:(1)原式=3×4=12; (2)原式=﹣(45×54)=﹣1;(3)原式=0;(4)原式=﹣(0.125×8)=﹣1; (5)原式=﹣(25×1)=﹣25; (6)原式=13×3=1.【点评】本题主要考查了有理数的乘法,掌握有理数的乘法法则是解题的关键. 4.计算:(1)0×(−5 6);(2)3×(−1 3);(3)(﹣7)×(﹣1);(4)(−16)×(−67).【分析】根据有理理数的乘法法则进行计算即可.【解答】解:(1)原式=0;(2)原式=﹣3×13=−1;(3)原式=7×1=7;(4)原式=16×67=17.【点评】本题考查了有理数的乘法.解题的关键是掌握有理数的乘法法则,特别要注意积的符号.5.(−47)×23×(−114)×12.【分析】根据有理数的乘法法则有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同零相乘,都得0,进行计算即可得出答案.【解答】解:原式=[(−47)×(−54)]×(23×12)=57×13=521.【点评】本题主要考查了有理数的乘法,熟练掌握有理数的乘法法则进行计算是解决本题的关键.6.计算:(1)(﹣2)×(−12)×(﹣3);(2)(﹣0.1)×1000×(﹣0.01).【分析】根据有理数的乘法法则进行计算便可.【解答】解:(1)(﹣2)×(−12)×(﹣3)=﹣2×12×3=﹣3;题型二多个有理数相乘(2)(﹣0.1)×1000×(﹣0.01) =+0.1×1000×0.01 =1.【点评】本题主要考查了有理数的乘法,关键是熟记有理数乘法法则. 7.(2022秋•宁远县校级月考)求值:(1)14×(﹣16)×(−45)×(﹣114);(2)(−511)×(−813)×(﹣215)×(−34).【分析】根据有理数乘法法则进行计算便可. 【解答】解:(1)14×(﹣16)×(−45)×(﹣114)=−14×16×45×54 =﹣4;(2)(−511)×(−813)×(﹣215)×(−34)=511×813×115×34 =613. 【点评】本题考查了有理数乘法,关键是熟记和应用有理数法则:两数相乘,同号得正,异号得负,并把绝对值相乘,任何数与零相乘积为零;几个不为零的数相乘,积的符号由负因数个数决定,负因数的个数为奇数时,积为负,负因数的个数为偶数时,积为正.8.计算: (1)(﹣8)×154×(−13); (2)(−37)×(−89)×(﹣6); (3)23×(−12)×(−45)×(﹣5).【分析】应用有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘,进行计算即可得出答案.【解答】解:(1)原式=(﹣30)×(−13)=10;(2)(−37)×(−89)×(﹣6) 原式=821×(﹣6) =−4821; (3)23×(−12)×(−45)×(﹣5) 原式=(−13)×[(−45)×(﹣5)] =(−13)×4 =−43.【点评】本题主要考查了有理数的乘法,熟练掌握有理数的乘法法则进行求解是解决本题的关键. 9.计算下列各题:(1)6)2.0()61()30(⨯-⨯-⨯- (2))98()321(87)53(-⨯-⨯⨯- (3)411)54()16(41-⨯-⨯-⨯ (4))]751([)91()2.1(45--⨯-⨯-⨯- 【分析】根据有理数的乘法计算即可得出答案.【解答】解:(1)原式=6)62.06130(-=⨯⨯⨯- (2)原式=97)98358753(-=⨯⨯⨯-(3)原式=45)54()16(41⨯-⨯-⨯=4)45541641(=⨯⨯⨯+ (4)原式=72)712915645(751)91()2.1(45-=⨯⨯⨯-=⨯-⨯-⨯-【点评】本题考查多个有理数的乘法,正确掌握运算法则是解题的关键.10.计算:(1)3×(﹣1)×(−13). (2)﹣1.2×5×(﹣3)×(﹣4). (3)(−512)×415×(−32)×(﹣6).(4)54×(﹣1.2)×(−19).【分析】根据有理数的乘法法则进行计算便可. 【解答】解:(1)3×(﹣1)×(−13) =+3×1×13=1;(2)﹣1.2×5×(﹣3)×(﹣4) =﹣1.2×5×3×4 =﹣72; (3)(−512)×415×(−32)×(﹣6) =−512×415×32×6 =﹣1;(4)54×(﹣1.2)×(−19)=+54×1210×19 =16.【点评】本题主要考查了有理数的乘法,熟记运算法则与是解题的关键.11.计算:(﹣8)×9×(﹣1.25)×(−19)【分析】根据有理数的乘法法则和乘法的交换律进行计算即可. 【解答】解:(﹣8)×9×(﹣1.25)×(−19) =[(﹣8)×(﹣1.25)]×9[×(−19)] =10×(﹣1) =﹣10.【点评】此题考查了有理数的乘法,掌握有理数的乘法法则是解题的关键,是一道基础题.题型三 利用乘法运算律简便计算12.用简便方法计算:(﹣8)×(−43)×(﹣1.25)×54.【分析】根据有理数的乘法法则,运用乘法交换律和结合律进行简便计算. 【解答】解:原式=[(﹣8)×(﹣1.25)]×[(−43)×54] =10×(−53) =−503.【点评】本题主要考查有理数的乘法,掌握乘法法则,运用乘法交换律和结合律进行简便计算是解题的关键.13.(2022秋•惠城区月考)计算:45×(−25)×78×(−1115)÷14×(−117).【分析】先确定符号.把除法化为化为乘法,带分数化为假分数,最后计算出结果. 【解答】解:45×(﹣25)×78×(−1115)÷14×(﹣117) =﹣(45×25×78×1115×4×87) =﹣(78×87×45×1115×25×4)=﹣3300.【点评】本题考查有理数的混合运算,掌握乘法的交换律和结合律的熟练应用,把除法化为乘法是解题关键.14.计算:(﹣36)×997172【分析】直接利用有理数的乘法运算法则进而得出答案. 【解答】解:原式=(﹣36)×(100−172) =(﹣36)×100﹣(﹣36)×172 =﹣3600+12 =﹣359912.【点评】此题主要考查了有理数的乘法运算,正确掌握相关运算法则是解题关键.15.计算:−(−595960)×60; 【分析】根据有理数的乘法法则以及乘法运算律则计算即可. 【解答】解:原式=595960×60 =(60−160)×60 =60×60−160×60 =3600﹣1 =3599.【点评】本题主要考查了有理数的乘法,熟练掌握乘法运算律是解答本题的关键.16.用简便方法计算 (1)﹣392324×(﹣12) (2)(23−112−115)×(﹣60)【分析】根据乘法分配律,可得答案. 【解答】解:(1)原式=(﹣40+124)×(﹣12)=﹣40×(﹣12)−124×12=480−12=47912; (2)原式=23×(﹣60)+112×60+115×60=﹣40+5+4=﹣31. 【点评】本题考查了有理数的乘法,利用拆项法得出乘法分配律是解题关键. 17.用简便方法计算:(1)﹣13×23−0.34×27+13×(﹣13)−57×0.34 (2)(−13−14+15−715)×(﹣60)【分析】(1)首先应用乘法交换律,把﹣13×23−0.34×27+13×(﹣13)−57×0.34化成 ﹣13×23−13×13−57×0.34﹣0.34×27,然后应用乘法分配律,求出算式的值是多少即可. (2)应用乘法分配律,求出算式(−13−14+15−715)×(﹣60)的值是多少即可. 【解答】解:(1)﹣13×23−0.34×27+13×(﹣13)−57×0.34 =﹣13×23−13×13−57×0.34﹣0.34×27=﹣13×(23+13)﹣(57+27)×0.34=﹣13×1﹣1×0.34 =﹣13﹣0.34 =﹣13.34(2)(−13−14+15−715)×(﹣60)=(−13)×(﹣60)−14×(﹣60)+15×(﹣60)−715×(﹣60) =20+15﹣12+28 =51【点评】(1)此题主要考查了有理数的乘法,要熟练掌握,解答此题的关键是要明确有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘. (2)此题还考查了乘法运算定律的应用,要熟练掌握.18.用乘法运算律,将下列各式进行简便计算:(1)(﹣112)×(﹣7)×23; (2))25.1()541(8)5(-⨯-⨯⨯-(3)(﹣48)×(−34+56−712); (4)0.7×311−6.6×37−1.1×37+0.7×811. (5)﹣392324×(﹣12) (6)4.61×37−5.39×(−37)+3×(−37).【分析】(1)利用乘法的交换律与结合律计算; (2)利用乘法的交换律与结合律计算; (3)利用乘法的分配律计算即可; (4)逆用乘法的分配律,以简化运算即可. (5)利用乘法的分配律计算即可; (6)逆用乘法的分配律,以简化运算即可. 【解答】解:(1)(﹣112)×(﹣7)×23=(−32)×23×(−7) =7;(2))25.1()541(8)5(-⨯-⨯⨯- =)]25.1(8[)]59()5[(-⨯⨯-⨯-=)10(9-⨯=90(3)(﹣48)×(−34+56−712)=−48×(−34)−48×56−48×(−712)=36﹣40+28=24;(4)0.7×311−6.6×37−1.1×37+0.7×811=0.7×(311+811)+37×(−6.6−1.1)=0.7﹣3.3=﹣2.6.(5)原式=(﹣40+124)×(﹣12)=﹣40×(﹣12)−124×12 =480−12=47912; (6)原式=4.61×37+5.39×37−3×37=37×(4.61+5.39﹣3)=37×7=3.【点评】本题主要考查有理数的运算,关键是使用运算律可使运算简便.19.计算:(1)(﹣6.5)÷(﹣0.5);(2)4÷(﹣2);(3)0÷(﹣1 000);(4)(﹣2.5)÷5 8.【分析】(1)先判断出符号,再绝对值相除即可;(2)先判断出符号,再绝对值相除即可;(3)零除以任何一个不为零的数,商为零,(4)先判断出符号,再绝对值相除,既有分数,又有小数,一般把小数化为分数直接约分即可;【解答】解:(1)(﹣6.5)÷(﹣0.5)=6.5÷0.5=13;(2)4÷(﹣2)=﹣4÷2=﹣2(3)0÷(﹣1 000)=0;(4)(﹣2.5)÷58=−2.5÷58=−52×85=−4;【点评】此题是有理数的除法,主要考查了有理数除法的法则,进行计算时,先判断符号,再绝对值相除.20.计算:(1)0÷(﹣2022);(2)(﹣27)÷9;(3)(−43)÷43;(4)−32÷1.5【分析】(1)0除以任何数都为0;(2)根据九九乘法表计算;(3)根据有理数的除法运算进行计算;(4)换算成小数进行计算;题型四两个有理数的除法【解答】解:(1)0÷(﹣2022)=0;(2)(﹣27)÷9=﹣3;(3)(−43)÷43=﹣1;(4)−32÷1.5=﹣1;【点评】本题考查了有理数的除法运算,解题关键在于熟知除以一个数等于乘以它的倒数.21.计算:(1)(﹣68)÷(﹣17);(2)(﹣0.75)÷0.25;(3)(−78)÷(﹣1.75);(4)312÷(﹣7) 【分析】(1)直接利用有理数的除法运算法则计算得出答案;(2)直接利用有理数的除法运算法则计算得出答案;(3)直接利用有理数的除法运算法则计算得出答案;(4)直接利用有理数的除法运算法则计算得出答案.【解答】解:(1)(﹣68)÷(﹣17)=4;(2)(﹣0.75)÷0.25=﹣0.75×4=﹣3;(3)(−78)÷(﹣1.75)=78×47=12;(4)312÷(﹣7) =72×(−17)=−12.【点评】此题主要考查了有理数的乘除运算,正确掌握相关运算法则是解题关键.(1)(+48)÷(+6);(2)(−323)÷(512);(3)4÷(﹣2);(4)0÷(﹣1000).【分析】原式各项利用除法法则计算即可得到结果.【解答】解:(1)原式=8;(2)原式=−113×211=−23;(3)原式=﹣2;(4)原式=0.【点评】此题考查了有理数的除法,熟练掌握运算法则是解本题的关键.23.计算:(1)(−47)÷(−314)÷(−23);(2)(﹣0.65)÷(−57)÷(﹣213)÷(+310).【分析】根据有理数的乘除法则和混合运算顺序进行计算便可.【解答】解:(1)(−47)×(−143)÷(−23)=−47×143×32=﹣4;(2)(﹣0.65)÷(−57)÷(﹣213)÷(+310).=−65100×75×37×103=﹣1.3.【点评】本题主要考查了有理数乘除法,关键是熟记有理数乘除法法则和混合运算顺序.题型五多个有理数的除法(1)(﹣24)÷(﹣2)÷(﹣115); (2)﹣27÷214÷94÷(﹣24).【分析】(1)先确定符号再把绝对值相除;(2)先确定符号再把绝对值相除或相乘,最后把除法化为乘法计算.【解答】解:(1)(﹣24)÷(﹣2)÷(﹣115) =12÷(﹣115) =﹣10;(2)﹣27÷214÷94÷(﹣24)=27÷94×49÷24=27×49×49×124=29.【点评】本题主要考查了有理数除法、乘法,掌握有理数的除法、乘法法则,符号的确定是解题关键.25.计算:(1)(−35)÷(﹣27)÷(﹣114)÷3; (2)(﹣8)÷23÷(﹣23)÷(﹣9). 【分析】各式利用除法法则把除法转化成乘法运算,通过约分即可得到结果.【解答】解:(1)(−35)÷(﹣27)÷(﹣114)÷3=−35×72×45×13=−1425; (2)(﹣8)÷23÷(﹣23)÷(﹣9)=﹣8×32×32×19=−2. 【点评】此题考查了有理数的乘除法,熟练掌握乘除法则是解本题的关键.26.计算:(1)﹣3÷(−34)÷(−34);(2)(﹣12)÷(﹣4)÷(﹣115); (3)(−23)÷(−87)÷0.25;(4)(﹣212)÷(﹣5)÷(﹣310).【分析】(1)直接利用有理数的除法运算法则除法变乘法,再利用有理数的乘法运算法则计算得出答案;(2)直接利用有理数的除法运算法则除法变乘法,再利用有理数的乘法运算法则计算得出答案;(3)直接利用有理数的除法运算法则除法变乘法,再利用有理数的乘法运算法则计算得出答案;(4)直接利用有理数的除法运算法则除法变乘法,再利用有理数的乘法运算法则计算得出答案.【解答】解:(1)原式=﹣3×(−43)×(−43)=−163;(2)原式=(﹣12)×(−14)×(−56)=−52;(3)原式=(−23)×(−78)×4=73;(4)原式=(−52)×(−15)×(−103)=−53.【点评】此题主要考查了有理数的除法运算,正确掌握相关运算法则是解题关键.27.计算:(1)(−23)÷(−85)÷(﹣0.25);(2)(﹣81)÷94÷94÷(﹣16);(3)(﹣6.5)÷(−12)÷(−25)÷(﹣5).【分析】应用有理数除法法则:有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数,即:a ÷b =a •1b (b ≠0),有理数乘法法则:(1)有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘. (2)任何数同零相乘,都得0,(3)多个有理数相乘的法则:①几个不等于0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.②几个数相乘,有一个因数为0,积就为0.进行计算即可得出答案.【解答】解:(1)原式=(−23)×(−58)×(﹣4) =﹣(23×58×4)=−53;(2)原式=(﹣81)×49×49×(−116)=(﹣16)×(−116) =1;(3)(﹣6.5)×(﹣2)÷(−25)÷(﹣5).原式=13×(−52)×(−15)=13×(52×15) =13×12=132.【点评】本题主要考查了有理数乘法及有理数除法,熟练掌握有理数乘法及有理数除法法则进行求解是解决本题的关键.28.计算:59÷20×185.【分析】根据有理数的除法运算以及乘法运算即可求出答案.【解答】解:原式=59×120×185=110.【点评】本题考查有理数的乘除运算,解题的关键是熟练运用有理数的乘除运算法则,本题属于基础题型.题型六 有理数乘除混合运算29.(2022秋•榆树市期中)计算:(﹣54)÷34×43÷(﹣32).【分析】先确定符号,再把除法化为乘法,根据有理数乘法法则计算.【解答】解:原式=54×43×43×132=3.【点评】本题主要考查了有理数的乘法、除法,掌握有理数乘法、除法法则,符号的确定是解题关键.30.(2022秋•丰台区校级期中)计算:(−35)×(−27)÷37.【分析】根据有理数除法法则把有理数除法转化为乘法,再按照有理数乘法法则进行计算便可.【解答】解:(−35)×(−27)÷37=35×27×73=25.【点评】本题考查的是乘除混合运算,掌握“同级运算按照从左往右的顺序进行运算”是解本题的关键.31.计算:(﹣223)×1516÷(﹣1.5) 【分析】化有理数除法为乘法,然后计算有理数乘法.【解答】解:(﹣223)×1516÷(﹣1.5), =(−83)×1516÷(−32),=(−83)×1516×(−23),=8×15×23×16×3, =53.【点评】本题考查了有理数的乘除法,熟记计算法则即可解题,属于基础题.32.计算:(﹣81)÷214×49÷(﹣16)【分析】原式从左到右依次计算即可得到结果.【解答】解:原式=81×49×49×116=1.【点评】此题考查了有理数的乘除法,熟练掌握有理数乘除法则是解本题的关键.33.(2022秋•香洲区校级月考)计算:(1)(−5)×6×(−45)×14;(2)−9÷(−0.1)÷(−335 ).【分析】(1)利用有理数的乘法法则原式即可;(2)将有理数的除法转化成乘法后,利用有理数的乘法法则原式即可.【解答】解:(1)原式=5×6×45×14=6;(2)原式=﹣9×(﹣10)×(−5 18)=﹣9×10×5 18=﹣25.【点评】本题主要考查了有理数的乘、除法,正确利用有理数的乘除法则运算是解题的关键.34.计算:(1)(﹣32)÷4×(−1 16);(2)(−23)×(−85)÷(﹣178).【分析】根据有理数的乘除法则进行计算便可.【解答】解:(1)(﹣32)÷4×(−1 16)=+32×14×116=12;(2)(−23)×(−85)÷(﹣178)=−23×85×815=−128225.【点评】本题考查了有理数乘除法,熟记有理数乘除法则是解题的关键.35.计算:(1)(﹣134)×(﹣112)÷(﹣118). (2)(﹣1.25)×54×(﹣8)÷(−34).【分析】(1)先确定结果的符号,再计算乘除法;(2)先确定结果的符号,再计算乘除法.【解答】解:(1)原式=﹣134×112÷118 =−74×32×89=−73;(2)原式=﹣1.25×54×8÷34=−54×54×8×43=−503. 【点评】本题考查了有理数乘除法,有理数的除法要分情况灵活选择法则,若是整数与整数相除一般采用“同号得正,异号得负,并把绝对值相除”.如果有了分数,则采用“除以一个不等于0的数,等于乘这个数的倒数”,再约分.乘除混合运算时一定注意两个原则:①变除为乘,②从左到右.36.计算:(1)(−35)×(﹣312)÷(﹣114)÷3; (2)(﹣8)÷23×(﹣112)÷(﹣9). 【分析】各式利用除法法则把除法转化成乘法运算,通过约分即可得到结果.【解答】解:(1)(−35)×(﹣312)÷(﹣114)÷3=−35×72×45×13=−1425; (2)(﹣8)÷23×(﹣112)÷(﹣9)=﹣8×32×32×19=−2. 【点评】此题考查了有理数的乘除法,熟练掌握乘除法则是解本题的关键.37.计算:(1)(−517)×(−34)÷9×(﹣325); (2)(−72)÷(﹣114)÷3×(−35);(3)(−320)×246÷910×(−341). 【分析】(1)先将带分数化成假分数,再根据有理数的乘法法则和除法法则求解即可;(2)先将带分数化成假分数,再根据有理数的乘法法则和除法法则求解即可;(3)根据有理数的乘法法则和除法法则求解即可.【解答】解:(1)原式=−517×(−34)×19×(−175)=[(−517)×(−175)]×[(−34)×19]=1×(−112)=−112; (2)原式=(−72)×(−45)×13×(−35)=﹣(72×45×13×35) =−1425; (3)原式=(−320)×246×109×(−341) =320×109×341×246=16×341×246=3246×246 =3.【点评】本题主要考查了有理数的乘除混合运算,掌握有理数的乘法和除法法则是解题的关键,注意运算顺序.38.(−73)÷(−79)+54×(−85).【分析】根据除以一个数等于乘以这个数的倒数,可把除法转化成乘法,根据有理数的乘法,可得答案.【解答】解:原式=(−73)×(−97)+54×(−85)=3+(﹣2)=1.【点评】本题考查了有理数的除法,先转化成乘法,再进行乘法运算,注意两数相乘同号得正,异号得负,再把绝对值相乘.39.计算:113×(−212+34)÷(−213).【分析】直接利用二次根式的乘除运算法则进行计算得出答案.【解答】解:原式=43×(−52+34)÷(−73)=43×(−104+34)×(−37) =43×(−74)×(−37)=1.40.计算:1.25×(25−215)+125÷6.【分析】把小数化为分数,利用乘法分配律计算,把除法转化为乘法,利用有理数的乘法法则计算,最后算加减即可.【解答】解:原式=54×25−54×215+125×16=12−16+25=1115.【点评】本题考查了有理数的混合运算,掌握乘法分配律a(b+c)=ab+ac是解题的关键,注意运算顺序.41.计算:(−73)÷(−76)+34×(−83).题型七有理数加减乘除混合运算【分析】首先将除法转化为乘法,然后按照有理数的乘法法则计算即可.【解答】解;原式=(−73)×(−67)+34×(−83)=2+(﹣2)=0.【点评】本题主要考查的是有理数的乘除运算,掌握有理数的乘法和除法法则是解题的关键.42.计算:(−72)×(16−12)×314÷(−12) 【分析】根据除以一个数等于乘以这个数的倒数,可转化成乘法运算,再根据乘法运算法则,可得答案.【解答】解:原式=(−72)×(−13)×314×(−2) =−12.【点评】本题考查了有理数的除法运算,除以一个数等于乘以这个数的倒数是解题关键.43.计算:(1)[1124−(38+16−34)×24]×(−15)(2)−5×(−115)+11×(−115)−3×(−225).【分析】(1)先把括号里面的利用乘法分配律进行计算,然后再次利用乘法分配律进行计算即可得解;(2)先把第三项整理,然后逆运用乘法分配律进行计算即可得解.【解答】解:(1)[1124−(38+16−34)×24]×(−15), =[1124−(38×24+16×24−34×24)]×(−15), =[2524−(9+4﹣18)]×(−15),=(2524+5)×(−15), =2524×(−15)+5×(−15), =−524−1,=−2924;(2)﹣5×(−115)+11×(−115)﹣3×(−225),=﹣5×(−115)+11×(−115)﹣6×(−115),=(﹣5+11﹣6)×(−11 5),=0.【点评】本题考查了有理数的乘法,利用运算定律可以使计算更加简便,难点在于(2)的整理.44.计算:(1)−1÷(−18)−3÷(−12);(2)−81÷13−13÷(−19).(3)−1+5÷(−16)×(−6);(4)(13−12)÷114÷110.【分析】(1)(2)(3)根据除以一个数等于乘以这数的倒数把除法转化为乘法运算,然后根据有理数的乘法运算法则和加法运算法则进行计算即可得解;(4)先算小括号里面的,再根据除以一个数等于乘以这数的倒数把除法转化为乘法运算并把带分数化为假分数,然后根据有理数的乘法运算法则进行计算即可得解.【解答】解:(1)﹣1÷(−18)﹣3÷(−12)=﹣1×(﹣8)﹣3×(﹣2)=8+6=14;(2)﹣81÷13−13÷(−19)=﹣81×3−13×(﹣9)=﹣243+3=﹣240;(3)﹣1+5÷(−16)×(﹣6)=﹣1+5×(﹣6)×(﹣6)=﹣1+180=179;(4)(13−12)÷114÷110=−16×45×10=−43.【点评】本题考查了有理数的除法,有理数的乘法,有理数的加减法运算,熟记运算法则和运算顺序是解题的关键,计算时要注意运算符号的处理.45.计算.(1)1.25÷(−0.5)÷(−212);(2)(−45)÷[(−13)÷(−25)];(3)(13−56+79)÷(−118);(4)−32324÷(−112). 【分析】(1)先把小数化为分数,再把除法运算化为乘法运算,然后约分即可;(2)要算中括号内的除法运算;(3)先把除法运算化为乘法运算,然后利用乘法的分配律计算;(4)先确定符合,再把带分数写成整数与真分数的和,然后利用乘法的分配律计算.【解答】解:(1)原式=54×(﹣2)×(−25)=1;(2)原式=﹣45÷(13×52) =﹣45÷56=﹣45×65=﹣54;(3)原式=(13−56+79)×(﹣18) =13×(﹣18)−56×(﹣18)+79×(﹣18)=﹣6+15﹣14=﹣5;(4)原式=(3+2324)×12 =3×12+2324×12 =36+232 =36+1112 =4712. 【点评】本题考查了有理数除法:除以一个不等于0的数,等于乘这个数的倒数.46.计算:(1)75×(13−12)×37÷54; (2)(56−37+13−914)÷(−142).【分析】(1)先计算括号中的运算,以及除法化为乘法运算,约分即可得到结果;(2)原式先将除法运算化为乘法运算,再利用乘法分配律计算即可得到结果.【解答】解:(1)原式=75×(−16)×37×45=−225; (2)原式=(56−37+13−914)×(﹣42)=﹣35+18﹣14+27=﹣4. 【点评】此题考查了有理数的乘法与除法,熟练掌握运算法则是解本题的关键.题型八 利用“倒数法”解决问题47.数学老师布置了一道思考题“计算:(−112)÷(13−56)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题. 小明的解法:原式的倒数为(13−56)÷(−112)=(13−56)×(﹣12)=﹣4+10=6, 所以(−112)÷(13−56)=16. (1)请你判断小明的解答是否正确,并说明理由.(2)请你运用小明的解法解答下面的问题.计算:(−124)÷(13−16+38). 【分析】(1)正确,利用倒数的定义判断即可;(2)求出原式的倒数,即可确定出原式的值.【解答】解:(1)正确,理由为:一个数的倒数的倒数等于原数;(2)原式的倒数为(13−16+38)÷(−124)=(13−16+38)×(﹣24)=﹣8+4﹣9=﹣13, 则(−124)÷(13−16+38)=−113. 【点评】此题考查了有理数的除法,熟练掌握运算法则是解本题的关键.48.请你认真阅读下列材料计算:(−130)÷(23−110+16−25) 解法1:原式=(−130)÷[23+16−(110+25)]=(−130)÷(56−12)=(−130)×3=−110 解法2:将原式的除数与被除数互换(23−110+16−25)÷(−130)=(23−110+16−25)×(﹣30)=﹣20+3﹣5+12=﹣10 故原式=−110根据你对所提供的材料的理解,选择适当的方法计算下面的算式:(−142)÷(−16−314+23−47)【分析】法1:原式先计算括号中的加减运算,再计算除法运算即可得到结果;法2:将原式除数与被除数互换求出值,即可确定出原式的值.【解答】解:法1:原式=(−142)÷[23−16−(314+47)]=(−142)÷(12−1114)=(−142)÷(−27) =(−142)×(−72)=112; 法2:将原式的除数与被除数互换,(−16−314+23−47)÷(−142) =(−16−314+23−47)×(﹣42) =7+9﹣28+24=12,则原式=112.【点评】此题考查了有理数的除法,熟练掌握运算法则是解本题的关键.49.(2022秋•徐州月考)认真阅读材料后,解决问题:计算:130÷(23−110+16−25). 分析:利用通分计算23−110+16−25的结果很麻烦,可以采用以下方法进行计算. 解:原式的倒数是(23−110+16−25)÷130 =(23−110+16−25)×30 =(23×30−110×30+16×30−25×30=20﹣3+5﹣12=10,故原式=110. 仿照阅读材料计算:(−120)÷(−14−25+910−32).【分析】仿照所给的求解方式进行运算即可.【解答】解:原式的倒数是:(−14−25+910−32)÷(−120)=(−14−25+910−32)×(﹣20)=14×20+25×20−910×20+32×20 =5+8﹣18+30=25,故原式=125. 【点评】本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.50.阅读材料:计算130÷(23−110+16−25) 分析:利用通分计算23−110+16−25的结果很麻烦,可以采用以下方法进行计算 解:原式的倒数是:=(23−110+16−25)×30 =(23−110+16−25)×30 =23×30−110×30+16×30−25×30=10故原式=110请你根据对所提供材料的理解,选择合适的方法计算:148÷(112−316+524+23) 【分析】仿照阅读材料中的方法求出原式的值即可.【解答】解:原式的倒数是:(112−316+524+23)÷148 =(112−316+524+23)×48=4﹣9+10+32=37,故原式=137. 【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.。
七年级数学上册2.9有理数的乘法2.9.2有理数乘法的运算律课时提升作业(含解析)(新版)华东师大版

2.9.2有理数乘法的运算律一、选择题(每小题4分,共12分)1.计算(-6)×0.75×51()()613⨯--的结果是( ) A.-7 B.-5 C.5 D.6【解题指南】【解析】选B.原式= ()()[6()][0.75(1)]51 5.63-⨯⨯⨯-=⨯-=--2.绝对值小于4的所有整数的积是( ) A.6 B.-36 C.0 D.36 【解析】选C.绝对值小于4的整数有±3,±2,±1,0.因为0是其中的一个因数,所以它们的积是0.【变式训练】绝对值大于3且小于6的所有整数的积是_________.【解析】绝对值大于3且小于6的所有整数有±4,±5,故它们的积:(-5)×(-4)×4×5=[(-5)×(-4)]×(4×5)=20×20=400. 答案:4003.计算:15113()(24)12()812232+⨯+⨯⨯--的正确结果是( ) A.-16 B.-10 C.6 D.12【解析】选B.15113()(24)12()812232+⨯+⨯⨯--=18×(-24)+512×(-24)+18×11()23- =-3+(-10)+18×16=-13+3=-10.二、填空题(每小题4分,共12分)4.计算:(-4)×2×(-0.25)×(-5)=______.【解析】原式=(-4×2×14×5)=-10. 答案:-105.从-3,-2,-1,4,5中,任取三个不同的数做乘法运算,则所得到的积的最大值是_____.【解析】绝对值最大的三个数是5,4,-3,积为-60,不符.之后是5,-3,-2,积为30,即最大值.答案:30【互动探究】上题中任取三个不同数相乘,积的最小值是多少?提示:首先积的符号是负的,其次积的绝对值最大.所以选择绝对值最大的且相乘积的符号是负数的三个数进行计算,上题中积的最小值为-3×4×5=-60.【方法技巧】求给定几个数的积的最大值的方法求积的最大值,要求符号必须为正,为了保证积为正,需要找到两负一正或者三正.然后找到绝对值最大的三个数,判别积的符号是否为正,如果不符,依次往下寻找,直到符合为止.6.计算:1175()12918--×36-6×1.43+3.93×6=______.【解析】1175()12918--×36-6×1.43+3.93×6=1112×36-79×36-518×36+6×(3.93-1.43)=33-28-10+6×2.5=-5+15=10.答案:10三、解答题(共26分)7.(8分)计算:(1)(-8)×(-5)×(-0.125).(2)155()296--+×(-36).【解析】(1)原式=-8×0.125×5=-5.(2)原式=-12×(-36)-59×(-36)+56×(-36)=18+20-30=8.8.(8分)某校体育器材室共有60个篮球.一天课外活动,有3个班级分别计划借篮球总数的12,13和14.请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?【解析】60×(1-12-13-14)=60×1-60×12-60×13-60×14=60-30-20-15=-5.所以这60个篮球不够借,还缺5个.【培优训练】9.(10分)对于任意的有理数a,b,定义新运算※:a※b=2ab+1,如(-3)※4=2×(-3)×4+1=-23.试计算:(1) 3※(-5).(2)[8※(-2)]※(-6).【解析】(1)3※(-5)=2×3×(-5)+1=-30+1=-29.(2)[8※(-2)]※(-6)=[2×8×(-2)+1]※(-6)=(-31)※(-6)=2×(-31)×(-6)+1=373.。
人教版初中七年级上册数学《有理数乘法的运算律及运用》练习题

1.4 有理数的乘除法1.4.1 有理数的乘法第2课时 有理数乘法的运算律及运用1、已知两个有理数a,b ,如果ab <0,且a+b <0,那么( )A 、a >0,b >0B 、a <0,b >0C 、a,b 异号D 、a,b 异号,且负数的绝对值较大2、计算:(1))32()109(45)2(-⨯-⨯⨯-; (2)(-6)×5×72)67(⨯-;(3)(-4)×7×(-1)×(-0.25);(4)41)23(158)245(⨯-⨯⨯-3、计算:(1))5(252449-⨯; (2)125)5.2()2.7()8(⨯-⨯-⨯-;(3)6.190)1.8(8.7-⨯⨯-⨯-; (4))251(4)5(25.0-⨯⨯-⨯--。
4、已知,032=-++y x 求xy y x 435212+--的值。
5、若a,b 互为相反数,c,d 互为倒数,m 的绝对值是1,求m cd b a 2009)(-+的值。
参考答案1、D .ab <0,说明a,b 异号;又a+b <0,说明负数的绝对值较大2、(1)23)32109452()32()109(45)2(-=⨯⨯⨯-=-⨯-⨯⨯-;(2)(-6)×5×1072675672)67(=⨯⨯⨯=⨯-;(3)(-4)×7×(-1)×(-0.25)=7)41174(-=⨯⨯⨯-;(4)241412315824541)23(158)245(=⨯⨯⨯=⨯-⨯⨯-3、(1)54249)5(251)5(50)5()25150()5(252449-=-⨯--⨯=-⨯-=-⨯;(2)60)125255368(125)5.2()2.7()8(-=⨯⨯⨯-=⨯-⨯-⨯-;(3)06.190)1.8(8.7=-⨯⨯-⨯-;(4)51)251(4)5(25.0)251(4)5(25.0-=-⨯⨯-⨯-=-⨯⨯-⨯--。
华东师大版七年级数学上册 2.9.2 有理数乘法的运算律 同步测试题

6 / 10
9
5
10.计算:0.125×(-2)×(-8)×(-19)=-7.
11.计算:2 020×(12-1)×(13-1)×(14-1)×…×(2 1020-1)的结果为-1.
D.(-2)×(-3)×(-4)×(-5)
3.若 4 个有理数相乘,积的符号是负号,则这 4 个有理数中,负数有( )
A.1 个或 3 个
B.1 个或 2 个 C.2 个或 4 个
D.3 个或 4 个
4.若有 2 020 个有理数相乘所得的积为零,则这 2 020 个数中( )
A.最多有一个数为 0
(2)还有更好的解法如下: 492245×(-5)
=(50-215)×(-5)
9 / 10
1 =50×(-5)-25×(-5) =-250+15
4 =-2495. (3)191156×(-8) =(20-116)×(-8) =20×(-8)-116×(-8) =-160+12
1 =-1592.
10 / 10
5 / 10
A.1
B.2
C.3
D.4
6.有理数 a,b,c 满足 a+b+c>0,且 abc<0,则 a,b,c 中正数有(C)
A.0 个
B.1 个
C.2 个
D.3 个
7.若 967×85=p,则 967×84 的值可表示为(A)
A.p-967
B.p-85
C.p-1
二、填空题
D.8854p
8.写出下列运算中每一步所依据的运算律或法则:
1 249
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有理数的乘法运算律》提升训练1.计算(55)99(44)9999
-⨯+-⨯-正确的是()
A.原式99(5544)9801
=⨯--=-
B.原式99(55441)9702
=⨯--+=-
C.原式99(55441)9900
=⨯---=-
D.原式99(554499)19602
=⨯---=-
2.用简便方法计算:
(1)
45 (8)( 1.25)
34
⎛⎫
-⨯-⨯-⨯
⎪
⎝⎭
;
(2)
111
(36)
12366
⎛⎫
--+⨯-
⎪
⎝⎭
;
(3)
4351
0.712(15)0.7(15)
9494
⨯+⨯-+⨯+⨯-;
(4)
7115
99(4)24 8236
⎛⎫
⨯----⨯
⎪
⎝⎭
.
3.(河北中考)
请你参考黑板中老师的讲解,用运算律简便计算:(1)999(15)
⨯-;
(2)
413 99911899999918
555
⎛⎫
⨯+⨯--⨯
⎪
⎝⎭
.
4.在学习有理数乘法时,李老师和同学们做了这样的游戏,将2020这个数说给第一
位同学,第一位同学将它减去它的1
2
的结果告诉第二位同学,第二位同学再将听到
的结果减去它的1
3
的结果告诉第三位同学,第三位同学再将听到的结果减去它的
1
4
的结果告诉第四位同学照这样的方法直到全班40人全部传完,最后一位同学将听到的结果告诉李老师,你知道最后的结果吗?
参考答案
1.C
2.解:(1)原式=
50
3
-.(2)原式=2-.(3)原式=43.6.
-(4)原式=
1
383
2
-.
3.解:(1)原式=14985
-.(2)原式=99900.
4.解:
1111 20201111
23440⎛⎫⎛⎫⎛⎫⎛⎫
⨯-⨯-⨯-⨯⨯-=
⎪ ⎪ ⎪ ⎪
⎝⎭⎝⎭⎝⎭⎝⎭123391101
20202020
23440402
⨯⨯⨯⨯⨯=⨯=.。
