广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (17) Word版含答案
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(10)

高考数学三轮复习冲刺模拟试题10立体几何01一、选择题1 .已知正四棱柱ABCD —A 1B 1C l D 1中,AA 1=2AB ,E 是AA 1的中点,则异面直线DC 1与BE 所成角的余弦值为 ( )A .15B C D .352 .某几何体的三视图如图所示,则它的体积是( )A .283π-B .83π-C .82π-D .23π3 .几何体的三视图如图所示,则该几何体的体积为( )A .223π+B .423π+C .2πD .4π+4 .已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC为球O 的直径,且2SC =,则此棱锥的体积为 ( )A .6B .6C .3D .25 .设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是( )A .βαβα⊥⊥,//,b aB .βαβα//,,⊥⊥b aC .βαβα//,,⊥⊂b aD .βαβα⊥⊂,//,b a6 .如图,E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点,PC=10,AB=6,EF=7,则异面直线AB 与PC 所成的角为( ) ( ) A .90° B .60° C .45° D .30°二、填空题7 .某几何体的三视图如图所示,则该几何体的体积为__________.8.一个几何体的三视图如上图所示,且其侧视图为正三角形,则这个几何体的体积为 .9 .一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为________.10.一个几何体的三视图如图所示,则该几何体的表面积与体积分别为___________11.如图为一个几何体的三视图,其中俯视为正三角形,A1B1=2,AA1=4,则该几何体的表面积为_______。
12.右图是一个空间几何体的三视图,则该几何体的体积大小为___________________.13.已知直线m,n 与平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n; ②若m∥α,n⊥α,则n⊥m; ③若m⊥α,m∥β,则α⊥β. 其中真命题的个数是______个14.已知某几何体的三视图如图所示,则该几何体的体积为___________.15.已知一个几何体的三视图如下图所示(单位:cm),其中正视图是直角梯形,侧视图和俯视图都是矩形,则这个几何体的体积是________cm 3.16.一个几何体的三视图如图所示,则该几何体的体积为____________;参考答案 一、选择题 1. B 2. A3. 【答案】C解:由三视图可知,该几何体下面是半径为1,高为2的圆柱.上面是正四棱锥.真四棱锥的=,所以四棱锥的体积为213⨯=,圆柱的体积为2π,所以该几何体的体积为23π+,选C. 4. 【答案】A【解析】因为ABC ∆为边长为1的正三角形,且球半径为1,所以四面体O ABC -为正四面体,所以ABC ∆的外接圆的半径为,所以点O 到面ABC 的距离3d ==,所以三棱锥的高23SF OE ==,所以三棱锥的体积为1132236⨯⨯=,选A.5. 【答案】C【解析】若b β⊥,//αβ,所以b α⊥,又a α⊂,所以b a ⊥,即a b ⊥,所以选C. 6. 【答案】B【解析】,取AC 的中点M,连结EM,MF ,因为E,F 是中点,所以16//,322MF AB MF AB ===,110//,522ME PC ME PC ===,所以MF 与ME 所成的角即为AB 与PC 所成的角。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (2)
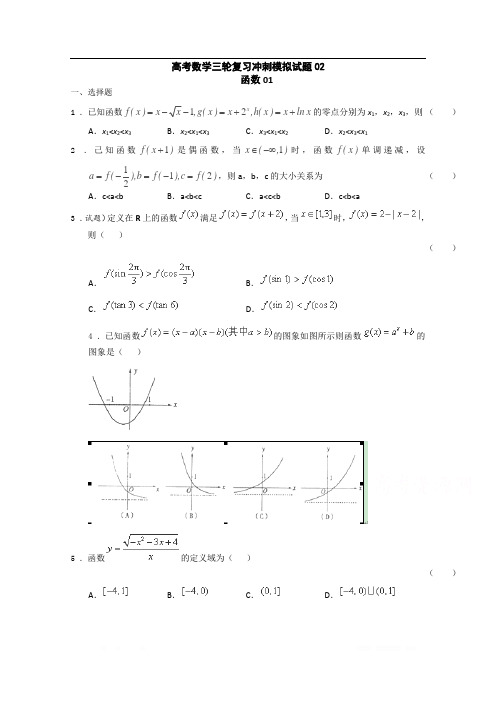
高考数学三轮复习冲刺模拟试题02函数01一、选择题1 .已知函数12x f (x )x ,g(x )x ,h(x )x ln x =-=+=+的零点分别为x 1,x 2,x 3,则 ( )A .x 1<x 2<x 3B .x 2<x 1<x 3C .x 3<x 1<x 2D .x 2<x 3<x 12 .己知函数1f (x )+是偶函数,当1x (,)∈-∞时,函数f (x )单调递减,设1122a f (),b f (),c f ()=-=-=,则a ,b ,c 的大小关系为( )A .c<a<bB .a<b<cC .a<c<bD .c<b<a3 .试题)定义在R 上的函数满足,当时,,则( )( )A .B .C .D .4 .已知函数的图象如图所示则函数的图象是( )5 .函数的定义域为( )( )A .B .C .D .6 .设函数1()ln (0)3f x x x x =->,则函数()f x( )A .在区间(0,1)(1,)+∞, 内均有零点B .在区间(0,1)(1,)+∞, 内均无零点C .在区间(0,1)内有零点,在区间(1,)+∞内无零点D .在区间(0,1)内无零点,在区间(1,)+∞内有零点7 .定义在R 上的奇函数f(x),当x≥0时,f(x)=⎪⎩⎪⎨⎧+∞∈∈+),1[3-x -1)1,0[x ),1x (log 21x ,则关于x 的函数F(x)=f(x)-a(0<a<1)的所有零点之和为 ( )A .2a -1B .1-2aC .2-a -1D .1-2-a8 .设)(x f 是定义在R 上的周期函数,周期为4=T ,对R x ∈都有)()(x f x f =-,且当]0,2[-∈x 时,121)(-⎪⎭⎫⎝⎛=xx f ,若在区间]6,2(-内关于x 的方程)2(log )(+-x x f a =0)1(>a 恰有3个不同的实根,则a 的取值范围是 ( )A .(1,2)B .),2(+∞C .()4,1D .()32,49 .已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)10.定义域为R 的函数()f x 满足(+2)=2()f x f x ,当x ∈[0,2)时,2|x-1.5|-,[0,1)()=-(0.5),[1,2)x x x f x x ⎧∈⎨∈⎩若[-4,-2]x ∈时,1()-42t f x t ≥恒成立,则实数t 的取值范围是( )A .[-2,0)(0,l)B .[-2,0)[l ,+∞)C .[-2,l]D .(-∞,-2](0,l]11.在下列区间中,函数()=+43xf x e x -的零点所在的区间为( )A .(1-4,0) B .(0,14) C .(14,12) D .(12,34) 12.定义在R 上的偶函数f(x),当x ∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( ) A .f(π)>f(-3)>f(-2) B .f(π)>f(-2)>f(-3)C .f(π)<f(-3)<f(-2)D .f(π)<f(-2)<f(-3)13.偶函数f (x )满足(1)(1)f x f x +=-,且在x ∈[0,1]时,f (x )=x 2,则关于x 的方程f (x )=x⎪⎭⎫⎝⎛101在10[0,]3上根的个数是( )A .1个B .2个C .3个D .5个14.设5log 4a =, 25(log 3)b =,4log 5c =,则( )A .a<c<bB .b<c<aC .a<b<cD .b a c <<15.设函数1(1)|-1|)=1(=1)x x f x x ⎧≠⎪⎨⎪⎩(,若关于x 的方程2[()]+()+c=0f x bf x 有三个不同的实数根123,,x x x ,则222123++x x x 等于( )A .13B .5C .223c +2cD .222b +2b16.函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则( )A .()f x 是偶函数B .()f x 是奇函数C .()(2)f x f x =+D .(3)f x +是奇函数17.给定函数①12=y x-,②23+3=2xx y -,③12=log |1-|y x ,④=sin2xy π,其中在(0,1)上单调递减的个数为 ( ) A .0B .1 个C .2个 D .3个18.已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为19.已知函数()()2531m f x m m x --=--是幂函数且是()0,+∞上的增函数,则m 的值为( )A .2B .-1C .-1或2D .020.已知函数2342013()12342013xx x x f x x =+-+-++,2342013()12342013x x x x g x x =-+-+--,设函数()(3)(4)F x f x g x =+⋅-,且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内,则-b a 的最小值为 ( )A .8B .9C .10D .1121.函数21(0)()(1)(0)x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不等的实数根,则实数a 的取值范围为 ( )A .(-∞,0)B .[0,1)C .(-∞,1)D .[0,+∞)22.函数x x x f 2log 12)(+-=的零点所在的一个区间是( )A .⎪⎭⎫⎝⎛41,81 B .⎪⎭⎫⎝⎛21,41 C .⎪⎭⎫⎝⎛1,21 D .)2,1(23.若直角坐标平面内的两点P 、Q 满足条件:①P 、Q 都在函数)(x f y =的图像上;②P 、Q关于原点对称,则称点对[P ,Q]是函数)(x f y =的一对“友好点对”(注:点对[P ,Q]与[Q,P]看作同一对“友好点对”).已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ,则此函数的“友好点对”有( )A .0对B .1对C .2对D .3对参考答案一、选择题 1. D 2. A3. 【答案】D【解析】由题意可知,函数的图象关于y 轴对称,且周期为2,故可画出它的大致图象,如图所示:∵且,而函数在是减函数, ∴,选D.4. 【答案】A【解析】由函数的两个根为.x a x b ==,图象可知01,1a b <<<-。
广东省普通高中2018届高考数学三轮复习冲刺模拟试题(29)201805300323

广东省中山市普通高中2017-2018学年高一数学1月月考试题共150分。
时间120分钟。
第Ⅰ卷 (60分)一、选择题(本大题共12个小题,每题5分,共60分;在每个小题给出的四个选项中,只有一项符合要求。
) 1.设{}021>-=x x S {}053>+=x x T 则=⋂T S ( )A.φB. ⎭⎬⎫⎩⎨⎧>21x x C. ⎭⎬⎫⎩⎨⎧<<-2135x x D. ⎭⎬⎫⎩⎨⎧<<-3521x x 2.若集合{}3,2,1=A ,则满足A B A =⋃的集合B 的个数是( )A.1B.2C.7D.83. 下列四组中,)(x f 与)(x g 表示同一函数的是( )Ax x f =)(, 2)(x x g =Bx x f =)(, 2)()(x x g =C2)(x x f =,xx x g 3)(=Dx x f =)(, =)(x g ⎩⎨⎧<-≥)0(,)0(,x x x x4.函数)(x f =2x11+的值域是( ) A.)1,0(B.]1,0(C.)1,0[D.[0,1]5.设)(x f =⎪⎩⎪⎨⎧≥-2)1(log 2e2231-x x x x <,则))2((f f =( )A.0B.1C.2D.36.下列结论正确的是( )A.kx y = (0<k )是增函数B.2x y =是R 上的增函数C. 11-=x y 是减函数 D. 22x y =(x =1,2,3,4,5)是增函数7.若b ax x f +=)(只有一个零点2,则ax bx x g -=2)(的零点是( )A.0,2B.0,21 C.0,21-D.2,21-8.若12822+++=kx kx kx y 定义域为R ,则k 取值范围是( ) A.)1,0[ B. ]1,0[C.]1,0(D. )1,0(9.已知14)(-+=x ax f 图象经过定点P ,则点P 的坐标是( )A.(1,5)B.(1,4)C.(0,4)D.(4,0)10.已知5)2(22+-+=x a x y 在(4,+∞)上是增函数,则a 取值范围是( )A.2-≤aB. 2-≥aC. 6-≤aD. 6-≥a11.已知3log 2=x ,则=-21x( )A.31 B.321C.331 D.42 12. )(x f 满足对任意的实数b a ,都有),()()(b f a f b a f ⋅=+且2)1(=f ,则=++++)2009()2010()5()6()3()4(f(1)f(2)f f f f f f ( ) A.1003B. 2010C.2008D. 1004第Ⅱ卷 (90分)二、填空题(本大题共4小题,每题4分,共16分)13.已知{}2,3,1+=m A ,{}2,3m B =,若B ⊆A ,则m =。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (4) 含答案

个长度单位 12 D.向右平移 个长度单位 6
B.向右平移
8 .在 ABC 中,角 A, B, C 所对边长分别为 a, b, c ,若 a
2
b2 2c 2 ,则 cos C 的最小值为(
D.
)
A.
3 2
B.
2 2
C.
1 2
1 2
9 .在△ABC 中,a,b,c 分别是角 A,B,C 的对边,a=
( A. B. C. D. (
)
3 .在钝角△ABC 中,已知 AB=
3 , AC=1,∠B=30°,则△ABC 的面积是
C.
)
A.
3 2
B.
3 4
3 2
D.
3 4
4 .设函数 f(x)=Asin( x
)(A>0, >0,-
2 < < )的图象关于直线 x= 对称,且周期 2 2 3
高考数学三轮复习冲刺模拟试题 04 三角函数 01
一、选择题 1 .若 f ( x ) a sin x b (a,b 为常数)的最大值是 5,最小值是-1,则
A. 、
2 .边长为
2 3
B. 、
2 2 或 3 3
C. 、
3 2
)
a 的值为 b 3 D. 、 2
(
)
的三角形的最大角与最小角的和是(
值是(
)
A.
2 3
4 B. 3
6 .已知 tan(
4
) 3 5
sin 2 cos 2 1 ,则 的值为( 1 cos 2 2
B.
)
A.
5 6
C. 1
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题201805300328

高考数学三轮复习冲刺模拟试题05三角函数02三、解答题 1. 已知函数.(1)求函数图象的对称轴方程; (2)求的单调增区间.(3)当时,求函数的最大值,最小值.2. 如图,在平面直角坐标系中,以轴为始边作两个锐角,它们的终边分别与单位圆交于两点.已知的横坐标分别为.(1)求的值; (2)求的值.3.设函数22()(sin cos )2cos (0)f x x x x ωωωω=++>的最小正周期为23π. (Ⅰ)求ω的值; (Ⅱ)求()f x 在区间-63ππ⎡⎤⎢⎥⎣⎦,上的值域; (Ⅲ)若函数()y g x =的图像是由()y f x =的图像向右平移2π个单位长度得到,求()y g x =的单调增区间.4.在△ABC 中,a,b,c 分别为角A,B,C 的对边,A 为锐角,已知向量→p =(1,3cos 2A ),→q =(2sin 2A,1-cos2A),且→p ∥→q .(1)若a 2-c 2=b 2-mbc,求实数m 的值;(2)若a=3,求△ABC 面积的最大值,以及面积最大是边b,c 的大小.5.设函数22()cos()2cos ,32xf x x x R π=++∈.(Ⅰ) 求()f x 的值域;(Ⅱ) 记△ABC 的内角A 、B 、C 的对边长分别为a 、b 、c,若()1f B =,1b =,3c =求a 的值.6.已知向量⎪⎭⎫⎝⎛-=-=21,cos 3),1,(sin x b x a ,函数()x f +=)(·2-a (1)求函数)(x f 的最小正周期T 及单调减区间(2)已知c b a ,,分别是△ABC 内角A,B,C 的对边,其中A 为锐角,4,32==c a 且1)(=A f ,求A,b 和△ABC 的面积S7.已知函数1sin cos )2sin sin 32()(2+⋅-=xx x x x f .(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 在区间[,]42ππ上的最值.8. (本小题满分13分)在△ABC 中,A ,C 为锐角,角A ,B ,C 所对应的边分别为a ,b ,c ,且3102=,5cos A sinC 。
2018届广东省中山市高考数学三轮复习冲刺模拟试题(4)含答案

2018届广东省中山市高考数学三轮复习冲刺模拟试题(4)含答案高考数学三轮复习冲刺模拟试题04三角函数01一、选择题1 .若f (x )a sin x b =+(a ,b 为常数)的最大值是5,最小值是-1,则ab 的值为 ( )A .、23-B .、23或23- C .、 32-D .、322 .边长为的三角形的最大角与最小角的和是( )( )A .B .C .D .3 .在钝角△ABC 中,已知AB=3, AC=1,∠B=30°,则△ABC 的面积是( )A .23 B .43 C .23 D .43 4 .设函数f(x)=Asin(ϕω+x )(A>0,ω>0,-2π<ϕ<2π)的图象关于直线x=32π对称,且周期为π,则f(x) ( )A .图象过点(0,21) B .最大值为-AC .图象关于(π,0)对称D .在[125π,32π]上是减函数 5 .设ω>0,函数y=sin(ωx+3π)+2的图像向右平移34π个单位后与原图像重合,则ω的最小值是( )A .23B .43C .32D .36 .已知21)4tan(=+απ,则ααα2cos 1cos 2sin 2+-的值为( )7 .为了得到函数x x x y 2cos 21cos sin 3+=的图象,只需将函数x y 2sin =的图象 ( )A .向左平移12π个长度单位 B .向右平移12π个长度单位 C .向左平移6π个长度单位D .向右平移6π个长度单位8 .在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为 ( )A .35-B .56-C .-1D .2A .2B .2C .12D .12-9 .在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,1+2cos(B+C)=0,则BC 边上的高等于 ( )A B C .D 10.把函数=()y sin x x R ∈的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是 ( )A .=(2-),R 3y sin x x π∈B .=(+),R 26x y sin x π∈C .=(2+),R 3y sin x x π∈D . 2=(2+),R 3y sin x x π∈ 11.在∆ABC 中,A,B,C 为内角,且sin cos sin cos A A B B =,则∆ABC 是( ) A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形12.设函数sin()3yx π=+(x ∈R),则f(x)( )A .在区间[-π,2π-]上是减函数B .在区间27[,]36ππ上是增函数 C .在区间[8π,4π]上是增函数 D .在区间5[,]36ππ上是减函数 13.函数f(x)=sin2x-4sin 3xcosx(x ∈R)的最小正周期为( )A .8π B .4π C .2π D .π14.把函数sin(2)4y x π=+的图象向右平移8π个单位,再把所得图象上各点的横坐标缩短到原来的一半,则所得图象对应的函数解析式是 ( )A .y=sin (4x+83π)B .y=sin (4x+8π) C . y=sin4x D .y=sinx15.函数ln cos y x=⎪⎭⎫ ⎝⎛<<-22ππx 的图象是16.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,其中120,1A b ==,且ABC ∆面积为则sin sin a bA B+=+( )A B C . D .17.函数2()22sin f x x x -,(02x π≤≤)则函数f(x)的最小值为( )A .1B .-2C .√3D .-√318.在∆ABC 中,tanA 是以-4为第三项,4为第七项的等差数列的公差,tanB 是以13为第三项,9为第六项的等比数列的公比,则这个三角形是 ( )A .钝角三角形B .锐角三角形C .等腰直角三角形D .以上都不对19.△ABC 的三个内角C B A ,,所对的边分别为c b a ,,,a A b B A a 2cossin sin 2=+,则=ab( )A .32B .22C .3D .220.将函数⎪⎭⎫⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位,再将图像上每一点横坐标缩短到原来的21倍,所得图像关于直线4π=x 对称,则ϕ的最小正值为 ( )A .8πB .83πC .43πD .2π二、填空题 21.已知函数,给出下列四个说法: ①若,则; ②的最小正周期是;③在区间上是增函数; ④的图象关于直线对称.其中正确说法的序号是______.22.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若222+=2012a b c ,则(+)t a nAt a nBt a n C t a nA t a nB 的值为 ;23.函数()=(+)(,,f x Asin x A ωϕωϕ为常数,A>0, ω>0)的部分图象如图所示,则f (0)的值是 ;24.函数()sin(2)3f x x π=-(x ∈R)的图象为C,以下结论中:①图象C 关于直线1112x π=对称;②图象C 关于点2(,0)3π对称; ③函数f(x)在区间5(,)1212ππ-内是增函数; ④由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C. 则正确的是 .(写出所有正确结论的编号)25.已知3sin cos 8x x =,且(,)42x ππ∈,则cos sin x x -=_________. 26.在△ABC 中,若sinA=2sinBcosC 则△ABC 的形状为________。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题201805300317

高考数学三轮复习冲刺模拟试题13解析几何02三、解答题1.已知中心在坐标原点,焦点在x 轴上的椭圆过点3)P ,且它的离心率21=e . (Ⅰ)求椭圆的标准方程;(Ⅱ)与圆22(1)1x y -+=相切的直线t kx y l +=:交椭圆于N M ,两点,若椭圆上一点C 满足OC ON OM λ=+,求实数λ的取值范围.2.椭圆E:22a x +22by =1(a>b>0)离心率为23,且过P(6,22).(1)求椭圆E 的方程; (2)已知直线l 过点M(-21,0),且与开口朝上,顶点在原点的抛物线C 切于第二象限的一点N,直线l 与椭圆E 交于A,B 两点,与y 轴交与D 点,若→AD =λ→AN ,→BD =μ→BN ,且λ+μ=25,求抛物线C 的标准方程.OxyMN3.已知一条曲线C 在y 轴右边,C 上每一点到点F(1,0)的距离减去它到y 轴的距离的差都是1.(Ⅰ)求曲线C 的方程;(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C 有两个交点A,B 的任一直线,都有FA FB ⋅﹤0?若存在,求出m 的取值范围;若不存在,请说明理由.4.设点P 是曲线C:)0(22>=p py x 上的动点,点P 到点(0,1)的距离和它到焦点F 的距离之和的最小值为45 (1)求曲线C 的方程(2)若点P 的横坐标为1,过P 作斜率为)0(≠k k 的直线交C 与另一点Q,交x 轴于点M,过点Q 且与PQ 垂直的直线与C 交于另一点N,问是否存在实数k,使得直线MN 与曲线C 相切?若存在,求出k 的值,若不存在,说明理由.5.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,直线l 过点(4,0)A ,(0,2)B ,且与椭圆C 相切于点P .(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点(4,0)A 的直线m 与椭圆C 相交于不同的两点M 、N ,使得23635AP AM AN =⋅?若存在,试求出直线m 的方程;若不存在,请说明理由.6.设椭圆)0(1:2222>>=+b a by a x C 的左、右焦点分别为12,F F ,上顶点为A ,在x 轴负半轴上有一点B ,满足112BF F F =,且2AF AB ⊥. (Ⅰ)求椭圆C 的离心率;(Ⅱ)D 是过2F B A 、、三点的圆上的点,D 到直线033:=--y x l 的最大距离等于 椭圆长轴的长,求椭圆C 的方程;(Ⅲ)在(Ⅱ)的条件下,过右焦点2F 作斜率为k 的直线l 与椭圆C 交于N M 、两点,线段MN 的中垂线 与x 轴相交于点)0,(m P ,求实数m 的取值范围.1F 2F xy AOB7.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为x y 34=,右焦点)0,5(F ,双曲线的实轴为21A A ,P 为双曲线上一点(不同于21,A A ),直线P A 1,P A 2分别与直线59:=x l 交于N M ,两点 (1)求双曲线的方程;(2)FN FM ⋅是否为定值,若为定值,求出该值;若不为定值,说明理由.8.(本小题满分13分)如图F 1、F 2为椭圆1:2222=+by a x C 的左、右焦点,D 、E 是椭圆的两个顶点,椭圆的离心率23=e ,2312-=∆DEF S .若点),(00y x M 在椭圆C 上,则点),(0by a x N 称为点M 的一个“椭点”,直线l 与椭圆交于A 、B 两点,A 、B 两点的“椭点”分别为P 、Q.(1)求椭圆C 的标准方程;(2)问是否存在过左焦点F 1的直线l ,使得以PQ 为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.参考答案三、解答题1.解:(Ⅰ) 设椭圆的标准方程为)0(12222>>=+b a by a x由已知得:2222243112a b c a c a b ⎧+=⎪⎪⎪=⎨⎪⎪=-⎪⎩解得 2286a b ⎧=⎪⎨=⎪⎩所以椭圆的标准方程为: 22186x y += (Ⅱ) 因为直线l :y kx t =+与圆22(1)1x y -+=相切所以22112(0)1t kt k t t k+-=⇒=≠+把t kx y +=代入22186x y +=并整理得: 222(34)8(424)0k x ktx t +++-=┈7分 设),(,),(2211y x N y x M ,则有 221438k ktx x +-=+ 22121214362)(k tt x x k t kx t kx y y +=++=+++=+ 因为,),(2121y y x x OC ++=λ, 所以,⎪⎪⎭⎫⎝⎛++-λλ)43(6,)43(822k t k ktC 又因为点C 在椭圆上, 所以,222222222861(34)(34)k t t k k λλ+=++ 222222221134()()1t kt tλ⇒==+++ 因为 02>t 所以 11)1()1(222>++tt 所以 202λ<<,所以 λ的取值范围为 (20)(0,2)2. 【解析】解. (1)2311-222b e e a b a ===∴=,,,222214x y b b+=代入椭圆方程得:,222440x y b +-=化为 点P(6,22)在椭圆E 上222624028b b a +-=∴==,,22182x y ∴+=椭圆E 方程为,(2)设抛物线C 的方程为20y ax a =>(),直线与抛物线C 切点为 200(,)x ax ,200002,2,2()y ax l ax l ax ax x x '=∴=-直线的斜率为的方程为y- 0000002211(,0),2(),(,)022l ax ax x N x ax x -∴-=--∴<直线过在第二象限,解得01x =-,(1,)N a ∴-,l 直线的方程为:2y ax a =--代入椭圆方程并整理得:2222(116)16480(1)a x a x a +++-=1122(,)(,)A x y B x y 设、则12x x 、是方程(1)的两个根,221212224816116116a a x x x x a a --=+=++则,由λ=,μ=,111x x +=λ,221x x +=μ 21212122121212281611174x x x x x x a x x x x x x a λμ++++===+++++-+ 52λμ+=∴,228165742a a +=-,解得330,66a a a =±>∴=,223,236y x x y ∴==抛物线C 的方程为其标准方程为3.本题主要考查直线与抛物线的位置关系,抛物线的性质等基础知识,同时考查推理运算的能力.解:(I)设P ),(y x 是直线C 上任意一点,那么点P(y x ,)满足:)0(1)1(22>=-+-x x y x化简得)0(42>=x x y(II)设过点M(m,0))0(>m 的直线l 与曲线C 的交点为A(11,y x ),B(22,y x ) 设l 的方程为m ty x +=,由⎩⎨⎧=+=x42y mty x 得0442=--m ty y ,0)(162>+=∆m t .于是⎩⎨⎧-==+m y y t y y 442121 ①又),1(),,1(2211y x y x -=-=01)()1)(1(021********<+++-=+--⇔<⋅y y x x x x y y x x②又42y x =,于是不等式②等价于⋅421y 01)44(422212122<++-+y y y y y 01]2)[(4116)(2122121221<+-+-+⇔y y y y y y y y ③由①式,不等式③等价于22416t m m <+- ④对任意实数t,24t 的最小值为0,所以不等式④对于一切t 成立等价于0162<+-m m ,即223223+<<-m由此可知,存在正数m,对于过点M(m ,0)且与曲线C 有A,B 两个交点的任一直线,都有0<⋅FB FA ,且m 的取值范围是)223,223(+-4.解:(1)依题意知4521=+p ,解得21=p ,所以曲线C 的方程为2x y = (2)由题意设直线PQ 的方程为:1)1(+-=x k y ,则点⎪⎭⎫ ⎝⎛-0,11k M 由⎩⎨⎧=+-=21)1(xy x k y ,012=-+-k kx x ,得()2)1(,1--k k Q , 所以直线QN 的方程为)1(1)1(2+--=--k x kk y 由⎪⎩⎪⎨⎧=+--=--22)1(1)1(x y k x kk y ,0)1(11122=--+-+k k x k x得⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛----211,11k k k k N所以直线MN 的斜率为k k k k k k k k k MN2211111111⎪⎭⎫ ⎝⎛---=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--= 过点N 的切线的斜率为⎪⎭⎫ ⎝⎛--k k 112 所以⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--k k k k k 112112,解得251±-=k 故存在实数k=251±-使命题成立. 5. (Ⅰ)由题得过两点(4,0)A ,(0,2)B 直线l 的方程为240x y +-=.因为12c a =,所以2a c =,3b c =. 设椭圆方程为2222143x y c c +=,………2分由2222240,1,43x y x y c c+-=⎧⎪⎨+=⎪⎩消去x 得,224121230y y c -+-=.又因为直线l 与椭圆C 相切,所以 ………4分………6分………8分又直线:240l x y +-=与椭圆22:143x y C +=相切,由22240,1,43x y x y +-=⎧⎪⎨+=⎪⎩解得31,2x y ==,所以3(1,)2P …………10分则2454AP =. 所以3645813547AM AN ⋅=⨯=. 又22221122(4)(4)AM AN x y x y ⋅=-+-+2222221122(4)(4)(4)(4)x k x x k x =-+--+-212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++2236(1).34k k =++ 所以223681(1)347k k +=+,解得24k =±.经检验成立. 所以直线m 的方程为24)4y x =±-.………14分 6. 【解】(Ⅰ)连接1AF ,因为2AF AB ⊥,211F F BF =,所以112AF F F =,即2a c =,故椭圆的离心率21=e (其他方法参考给分) (Ⅱ)由(1)知,21=a c 得a c 21=于是21(,0)2F a , 3(,0)2a B -,Rt ABC ∆的外接圆圆心为11(,0)2F a -),半径21||2r F B a ==D 到直线033:=--y x l 的最大距离等于2a ,所以圆心到直线的距离为a ,所以a a =--2|321|,解得2,1,3a c b =∴==所求椭圆方程为13422=+y x . (Ⅲ)由(Ⅱ)知)0,1(2F , l :)1(-=x k y⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 代入消y 得 01248)43(2222=-+-+k x k x k 因为l 过点2F ,所以0∆>恒成立设),(11y x M ,),(22y x N 则2221438k k x x +=+,121226(2)34ky y k x x k-+=+-=+ MN 中点22243(,)3434k kk k -++ 当0k =时,MN 为长轴,中点为原点,则0m =当0k ≠时MN 中垂线方程222314()3434k k y x k k k +=--++. 令0y =,43143222+=+=∴k k k m 230k >,2144k +>, 可得410<<∴m 综上可知实数m 的取值范围是1[0,)47. (1)221916x y -= (2)1209(3,0),(3,0),(5,0)(,),(,)5A A F P x y M y -设11024(3,),(,)5A P x y A M y ∴=+ 因为1,,A P M 三点共线002424(3)05515yx y y y x ∴+-=∴=+ 924(,)5515y M x ∴+,同理96(,)5515yN x --1624166(,),(,)55155515y yFM FN x x ∴=-=--+-2225614425259y FM FN x ⋅=-⋅-221699y x =- 0FM FN ∴⋅=8.解:(1)由题意得23==a c e ,故ab ac 21,23==,231)231(412)23(21)(2122-=-⨯=⨯-=⨯-⨯=∆a a a a b c a S DEF , 故42=a ,即a=2,所以b=1,c=3,故椭圆C 的标准方程为1422=+y x .百度文库 - 让每个人平等地提升自我- 11 - (2)①当直线l 的斜率不存在时,直线l 的方程为3-=x联立⎪⎩⎪⎨⎧=+-=14322y x x 解得⎪⎩⎪⎨⎧=-=213y x 或⎪⎩⎪⎨⎧-=-=213y x ,不妨令)21,3(),21,3(---B A , 所以对应的“椭点”坐标)21,23(),21,23(---Q P .而021≠=⋅OQ OP . 所以此时以PQ 为直径的圆不过坐标原点. ②当直线l 的斜率存在时,设直线l 的方程为)3(+=x k y联立⎪⎩⎪⎨⎧=++=14)3(22y x x k y ,消去y 得:041238)14(2222=-+++k x k x k 设),(),,(2211y x B y x A ,则这两点的“椭点”坐标分别为),2(),,2(2211y x Q y x P ,由根与系数的关系可得:14382221+-=+k k x x ,144122221+-=k k x x 若使得以PQ 为直径的圆经过坐标原点,则OP ⊥OQ ,而),2(),,2(2211y x y x ==,因此0=⋅, 即042221212121=+=+⨯y y x x y y x x 即141222+-k k =0,解得22±=k 所以直线方程为2622+=x y 或2622--=x y。
广东省普通高中2018届高考数学三轮复习冲刺模拟试题(35)201805300323

广东省中山市普通高中2017-2018学年高一数学1月月考试题一选择题(本大题共12个小题,每题5分共60分)1.设集合A={x|1<x <4},集合B ={x|2x -2x-3≤0}, 则A ∩(C R B )=( )A .(1,4)B .(3,4) C.(1,3) D .(1,2)∪(3,4) 2.设a =π0.3,b =log π3,c =30,则a ,b ,c 的大小关系是( )A .a >b >cB .b >c >aC .b >a >cD .a >c >b3.下列函数中,既是奇函数又是增函数的为( ) A. 1y x =+ B. 2y x =- C. 1y x=D. ||y x x = 4. 若f (x )=x 2-x +a ,f (-m )<0,则f (m +1)的值为( )A .正数B .负数C .非负数D .与m 有关5.若函数⎩⎨⎧>≤+=1,lg 1,1)(2x x x x x f ,则f(f(10)= ( )A.lg101B.1C.2D.06 设)(x f 是定义在R 上的一个函数,则函数)()()(x f x f x F --=在R 上一定是( )A 奇函数B 偶函数C 既是奇函数又是偶函数D 非奇非偶函数7 已知22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪=-<<⎨⎪≥⎩,若()3f x =,则x 的值是( )A 1B 1或32 C 1,32或 D8.若函数f (x )=(a 2-2a -3)x 2+(a -3)x +1的定义域和值域都为R ,则a 的取值范围是( )A .a =-1或a =3B .a =-1C .a =3D .a 不存在9 下列函数与x y =A 2x y = B xx y 2=x a a y log =10、偶函数)(x f y =在区间[0,4]上单调递减,则有( )A 、)()3()1(ππ->>-f f fB 、)()1()3(ππ->->f f fC 、)3()1()(ππf f f >->-D 、)3()()1(ππf f f >->-11、若函数)(x f 满足)()()(b f a f ab f +=,且n f m f ==)3(,)2.(,则)72(f 的值为( ) A 、n m +B 、n m 23+C 、n m 32+D 、23n m +12.当0<a <1时,函数①y =a |x |与函数②y =log a |x |在区间(-∞,0)上的单调性为( )A .都是增函数B .都是减函数C .①是增函数,②是减函数D .①是减函数,②是增函数二填空题(本大题共4小题,每题4分共16分)13.函数y =(13)x -3x在区间[-1,1]上的最大值为________.14.化简11410104848++的值等于_________15.已知函数f (x )=x 2-2x +2的定义域和值域均为[1,b ],则b =________.16.函数y =lg x +1x -1的定义域为________.三、解答题(本大题共6个题,17-21题每题12分,22题14分共74分,要求写出必要的过程) 17(本小题12分)设A={x }01)1(2{,04222=-+++==+a x a x x B x x ,其中x ∈R,如果A ⋂B=B ,求实数a 的取值范围。
中山市普通高中2018届高考数学三轮复习冲刺模拟试题7

高考数学三轮复习冲刺模拟试题07数列01一、选择题1 .已知函数5(4)4(6),()2(6).x a x x f x a x -⎧-+≤⎪=⎨⎪>⎩()0,1a a >≠ 数列{}n a 满足*()()n a f n n N =∈,且{}n a 是单调递增数列,则实数a 的取值范围是( )A .[)7,8B .()1,8C .()4,8D .()4,72 .已知等差数列{}n a 中,a 7+a 9=16,S 11=299,则a 12的值是 ( )A .15B .30C .31D .643 .数列}{n a 的前n 项和为)()1(,1*2N n a b n n S n n n n ∈-=++=,则数列}{n b 的前50项的和为( )A .49B .50C .99D .1004 .已知正项等比数列{a n }满足:765=2a a a +,若存在两项,n m a a使得14a =,则nm 41+的最小值为 ( )A .23 B .35 C .625D .不存在5 .等差数列{a n }中,如果147=39a a a ++,369=27a a a ++,数列{a n }前9项的和为 ( )A .297B .144C .99D .66 6 .若∆ABC 的三个内角成等差数列,三边成等比数列,则∆ABC 是( )A .直角三角形B .等腰直角三角形C .等边三角形D .钝角三角形7 .已知正项等比数列{}n a 满足:7652a a a =+,若存在两项,m n a a14a =,则14m n+的最小值为 ( )A .32B .53C .256D .不存在8 .设n S 是等差数列{a n }的前n 项和,5283()S a a =+,则53a a 的值为 ( )A .16B .13C .35D .569 .已知等比数列{a n }的首项为1,若1234,2,a a a 成等差数列,则数列⎭⎬⎫⎩⎨⎧n a 1的前5项和为 ( ) A .1631 B .2 C .1633 D .3316二、填空题 10.正项等比数列中,若,则等于______.11.某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层均堆成正六边形,且逐层每边增加一个花盆(如图).设第n 层共有花盆的个数为)(n f ,则)(n f 的表达式为_____________________. 12.数列{a n }中,若a 1=1,123n n a a +=+(n ≥1),则该数列的通项a n =________。
2018届广东省中山市高考数学三轮复习冲刺专题(1-5)含答案

高考数学三轮复习冲刺模拟试题01集合一、选择题1 .已知集合,,则( ) A .B .C .D .2 .设集合{1}A x x a x R =-<∈,,B={x|1<x<5,x ∈R},若A ⋂B=φ,则实数a 的取值范围是 ( )A .{a|0≤a ≤6}B .{a|a ≤2,或a ≥4}C .{a|a ≤0,或a ≥6}D .{a|2≤a ≤4}3 .已知集合2A={|log <1},B={x|0<<c}x x x ,若=AB B ,则c 的取值范围是( )A .(0,1]B .[1,+)∞C .(0,2]D .[2,+)∞二、填空题4 .若不等式4+-2+1x m x≥对一切非零实数x 均成立,记实数m 的取值范围为M .已知集合{}=A x x M ∈,集合{}2=--6<0B x R x x ∈,则集合=A B ___________.5 .设集合是A={32|()=83+6a f x xax x -是(0,+∞)上的增函数},5={|=,[-1,3]}+2B y y x x ∈,则()R AB ð= ;6 .试题)己知集合222{|28},{|240}xxA xB x x mx -=<=+-<, 若{|11},{|43}A B x x A B x x =-<<=-<<,则实数m 等于__________ .7 .设集合{}1,R A x x a x =-<∈,{}15,R B x x x =<<∈,若∅=B A ,则实数a 取值范围是___________.三、解答题8 .已知={()|1},B={()|3,0x 3}2A x,y y =-x+mx -x,y x+y =≤≤,若A B ⋂是单元素集,求实数m 的取值范围.参考答案一、选择题 1. 【答案】B【解析】{(3)0}{03}P x x x x x =-<=<<,={2}{22}Q x x x x <=-<<,所以{02}(0,2)P Q x x =<<=, 选B.2. 【答案】C【解析】{1}{11}A x x a x R x a x a =-<∈==-<<+,,因为=A B φ,所以有15a -≥或11a +≤,即6a ≥或0a ≤,选C.3. 【答案】D【解析】2{log 1}{01}A x x x x =<=<<.因为AB B =,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.二、填空题4. {}-1<3x x ≤; 5. 【答案】(,1)(4,)-∞+∞【解析】2()=2466f 'x x a x -+,要使函数在(0,)+∞上是增函数,则2()=24660f 'x x ax -+>恒成立,即14a x x <+,因为144x x +≥=,所以4a ≤,即集合{4}A a a =≤.集合5={|=,[-1,3]}+2B y y x x ∈{15}y x =≤≤,所以{14}A B x x ⋂=≤≤,所以()=R A B ð(,1)(4,)-∞+∞.6. 【答案】32222{|28}{|230}{13}x xA x x x x x x -=<=--<=-<<,因为{|11},{|43}AB x x A B x x =-<<=-<<,所以由数轴可知{|41}B x x =-<<,即4,1-是方程2240x mx +-=的两个根,所以4123m -+=-=-,解得32m =。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(8)

高考数学三轮复习冲刺模拟试题08数列02三、解答题1.已知A(,),B(,)是函数的图象上的任意两点(可以重合),点M 在 直线上,且. (1)求+的值及+的值 (2)已知,当时,+++,求;(3)在(2)的条件下,设=,为数列{}的前项和,若存在正整数、,使得不等式成立,求和的值.2.设等差数列的首项及公差d 都为整数,前n 项和为S n . (1)若,求数列的通项公式;(2)若求所有可能的数列的通项公式.3.设等比数列{}n a 的前n 项和为n S ,已知122()n n a S n N *+=+∈.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)在n a 与1n a +之间插入n 个数,使这2n +个数组成公差为n d 的等差数列, 设数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T ,证明:1516nT <.4.已知数列{a n }中,a 1=1,若2a n+1-a n =)2n )(1n (n 2-n ++,b n =a n -)1n (n 1+(1)求证:{ b n }为等比数列,并求出{a n }的通项公式; (2)若C n =nb n +)1n (n 1+,且其前n 项和为T n ,求证:T n <3.5.已知数列{}n a 的前n 项和11()22n n n S a -=--+(n 为正整数)(Ⅰ)令2nn n b a =,求证:数列{}n b 是等差数列,并求数列{}n a 的通项公式;(Ⅱ)令121,n n n n n C a T C C C n+==+++,试比较n T 与521nn +的大小,并予以证明6.已知数列}{n a 满足()2,34,3,1*1121≥∈-===-+n N n a a a a a n n n ,(1)证明:数列}{1n n a a -+是等比数列,并求出}{n a 的通项公式 (2)设数列}{n b 的前n 项和为n S ,且对任意*N n ∈,有1222211+=+++n na b a ba b nn 成立,求n S 7.设数列{}na的前n 项和为n S .已知11a =,131n n a S +=+,n *∈N .(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)记n T 为数列{}n na 的前n 项和,求n T .8.设数列{a n }的前n 项和为S n ,且满足S n =2-a n ,n=1,2,3,…(1)求数列{a n }的通项公式;(4分)(2)若数列{b n }满足b 1=1,且b 1+n =b n +a n ,求数列{b n }的通项公式;(6分) (3)设C n =n (3- b n ),求数列{ C n }的前n 项和T n 。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(17)

高考数学三轮复习冲刺模拟试题17常用逻辑用语一、选择题1 .已知命题p :关于x 的函数221f (x )x ax =+-在[3,+∞)上是增函数;命题q :关于x的方程x 2-a x +4=0有实数根。
若p ∨q 为真命题,p ∧q 为假命题,则实数a 的取值范围是 ( ) A .(-12,4)(4,+∞) B .(-12,4][4,+∞) C .(-∞,-12)(-4,4) D .[-12,+∞)2 .下列命题中是假命题的是( )A .都不是偶函数B .有零点C .D .上递减3 . “lg ,lg ,lg x y z 成等差数列”是“2y xz =”成立的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不充分也不必要条件 4 .如果命题“p 且q”是假命题,“¬p”也是假命题,则 ( )A .命题“¬p 或q”是假命题B .命题“p 或q”是假命题C .命题“¬p 且q”是真命题D .命题“p 且¬q”是真命题 5 .已知条件2|1:|>+x p ,条件a x q >|:|,且p ⌝是q ⌝的必要不充分条件,则实数a 的取值范围是( )A .10≤≤aB .31≤≤aC .1≤aD .3≥a6 . “0ϕ”是“函数()sin()f x x ϕ为奇函数”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7 .设a ,b ∈R ,那么“>1ab”是“>>0a b ”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8 .下列命题中是假命题的是( )A .(0,),>2x x sin x π∀∈B .000,+=2x R sin x cos x ∃∈C . ,3>0xx R ∀∈ D .00,=0x R lg x ∃∈9 .有关下列命题的说法正确的是( )A .命题“若x 2=1,则x=1”的否命题为:若“x 2=1则x ≠1”B .“1x =-”是“2560x x --=”的必要不充分条件C .命题“∃x ∈R,使得x 2+x+1<0”的否定是:“∀x ∈R,均有x 2+x+1<0” D .命题“若x=y,则sinx=siny ”的逆否命题为真命题 10.下列有关命题的叙述,错误的个数为①若p ∨q 为真命题,则p ∧q 为真命题。
2018届广东省中山市高考数学三轮复习冲刺模拟试题(3)有答案

高考数学三轮复习冲刺模拟试题03函数02二、填空题1.定义一种运算,令,且,则函数的最大值是______.2.设函数______.3.函数f(x)的定义域为D,若对于任意的x 1,x 2∈D,当x 1<x 2时都有f(x 1)≤f(x 2),则称函数f(x)为D 上的非减函数.设f(x)为定义在[0,1]上的非减函数,且满足一下三个条件: (1)f(0)=0; (2)f(1-x)+f(x)=1 x ∈[0,1]; (3)当x ∈[0,31]时,f(x)≥23x 恒成立,则f(73)+f(95)= . 4.设f (x )=⎩⎪⎨⎪⎧lg x ,x >0,10x,x ≤0,则f (f (-2))=________.5.已知函数y mx =的图像与函数11x y x -=-的图像没有公共点,则实数m 的取值范围是 6.已知a>0,且a ≠1,若函数2(-2+3)()=lg xx f x a 有最大值,则不筹式2(-5+7)>0a log x x 的解集为 ;7.函数f(x)=a x+2+x a 的值域为_________.8.已知函数f (x )=⎩⎨⎧>≤--.1,log 1,1)2(x x ,x x a a若f (x )在(-∞,+∞)上单调递增,则实数a 的取值范围为________。
9.定义:如果函数)(x f y =在定义域内给定区间b][,a 上存在)(00b x a x <<,满足ab a f b f x f --=)()()(0,则称函数)(x f y =是b][,a 上的“平均值函数”,0x 是它的一个均值点,如4x y =是]1,1[-上的平均值函数,0就是它的均值点.现有函数1)(2++-=mx x x f 是]1,1[-上的平均值函数,则实数m 的取值范围是 .10.已知x R ∀∈,(1+)=(1-)f x f x ,当1x ≥时,()=(1)f x ln x+,则当<1x 时,()=f x .11.已知函数2=+-1+2y x ax a [0,+)∞,则a 的取值范围是 .12.函数212()=log (-2-3)f x x x 的单调递减区间为 .13.已知1f x -,则()=f x (x ∈ ). 14.若(f x ,则()f x 的定义域为 .15.已知函数3111,0,362()21,,112x x f x x x x ⎧⎡⎤-+∈⎪⎢⎥⎣⎦⎪=⎨⎛⎤⎪∈ ⎥⎪+⎝⎦⎩ ,函数π()sin()22,(0)6=-+>g x a x a a ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是____________.16.定义在)1,1(-上的函数⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1)()(,当)0,1(-∈x 时0)(>x f .若)0(,21,11151f R f Q f f P =⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=,则P ,Q,R 的大小关系为_____________.三、解答题17.对于函数()f x 若存在0x R ∈,00()=f x x 成立,则称0x 为()f x 的不动点.已知2()=(1)-1(0)f x ax b x b a +++≠ (1)当=1,=-2a b 时,求函数(f x )的不动点;(2)若对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围;(3)在(2)的条件下,若=()y f x 图象上A 、B 两点的横坐标是函数()f x 的不动点,且A 、B 两点关于直线2121y kx a =++对称,求b 的最小值.18.已知函数()f x 对任意实数,x y 恒有()()()f x y f x f y +=+,且当x >0时,()0f x <又(1)2f =-.(1)判断()f x 的奇偶性;(2)求证:()f x 是R 上的减函数; (3)求()f x 在区间[-3,3]上的值域;(4)若x R ∀∈,不等式2()2()()4f ax f x f x -<+恒成立,求a 的取值范围.参考答案二、填空题 1. 【答案】54【解析】令,则∴由运算定义可知,∴当1sin 2x =,即6x π=时,该函数取得最大值54. 由图象变换可知,所求函数的最大值与函数在区间上的最大值相同.2. 【答案】52【解析】令1x =-得(1)(1)(2)f f f =-+,即1(2)(1)(1)2(1)212f f f f =--==⨯=。
广东省普通高中2018届高考数学三轮复习冲刺模拟试题(56)201805300323

高考数学三轮复习冲刺模拟试题18导数01一、选择题1 .函数的图象与x 轴所围成的封闭图形的面积为( )( )A .B .1C .2D .2 .已知函数2()=f x x cos x -,则(0.6),(0),(-0.5)f f f 的大小关系是 ( )A .(0)<(0.6)<(-0.5)f f fB .(0)<(-0.5)<(0.6)f f fC .(0.6)<(-0.5)<(0)f f fD .(-0.5)<(0)<(0.6)f f f3 .定义在R 上的可导函数f(x),且f(x)图像连续,当x ≠0时, 1'()()0f x x f x -+>,则函数1()()g x f x x -=+的零点的个数为( )A .1B .2C .0D .0或24 .已知函数))((R x x f ∈满足1)1(=f ,且)(x f 的导函数21)('<x f ,则212)(+<x x f 的解集为( ) A .{}11<<-x x B .{}1-<x x C .{}11>-<x x x 或D .{}1>x x二、填空题5 .若f(x)在R 上可导,f(x)=x 2+2f’(2)+3,则⎰=3dx)x (f .6 .若不等式1|ln |3≥-x ax 对任意]1,0(∈x 都成立,则实数a 取值范围是________. 7 .计算1-1(2+)x x e dx ⎰= ;8 .曲线1xy =与直线y=x 和y=3所围成的平面图形的面积为_________.9 .设10x m e dx =⎰,11en x dx -=⎰,则m 与n 的大小关系为______.10.已知函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数,那么b c +的最大值为________________; 参考答案 一、选择题 1. 【答案】A【解析】根据积分的应用可求面积为02211()(1)cos S f x dx x dx xdx ππ--==++⎰⎰⎰2021113()sin 1222x x xπ-=++=+=,选A.2. 【答案】B【解析】因为函数2()=f x x cos x -为偶函数,所以(0.5)(0.5)f f -=,()=2f 'x x sin x +,当02x π<<时,()=20f 'x xs i n x +>,所以函数在02x π<<递增,所以有(0)<(0.5)<(0.6)f f f ,即(0)<(0.5)<(f f f -,选B.3. 【答案】C【解析】由1'()()0f x x f x -+>,得'()()0x f x f x x+>,当0x >时,'()()0xf x f x +>,即(()'0x f x >,函数()xf x 此时单调递增。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(7)201805300330

高考数学三轮复习冲刺模拟试题 07数列 01一、选择题1. .已知函数a(4 )x 4 (x 6),f (x )2axx 5(6).a 0,a 1数列a 满足 af (n )(nN * ) ,且nna 是 单 调 递 增 数 列 ,则 实 数 a 的 取 值 范 围 是n( ) A .7,8B .1,8C .4,8D .4,72..已 知 等 差 数 列a 中 ,a 7+a 9=16,S 11=n99 2 ,则 a 12的 值 是( )A .15B .30C .31D .643..数列{ }n,则数列{ } a 的前 n 项和为 Sn 2n 1,b( 1) a (n N * ) b 的前 50项的nnnnn和 为( ) A .49B .50C .99D .1004. .已知正项等比数列{a n }满足: a 7 =a 6 2a 5 ,若存在两项 a ,a 使得 nma a4a ,则m n11 4 的最 小 值 为m n( )3 2B .5 325 C . 6A .D .不存在5. .等差数列{a n}中,如果a1a4a7=39,a a a,数列{a369=27n}前9项的和为()A.297 B.144 C.99 D.666. .若∆ABC的三个内角成等差数列,三边成等比数列,则∆ABC是()- 1 -A .直角三角形B .等腰直角三角形C .等边三角形D .钝角三角形7. .已知正项等比数列a 满足:na 7 a 62a 5 ,若存在两项 , a a 使得 m na a4a ,则m n11 4的 最 小 值 为m n( )A .3 25 3B .C .256D .不存在8. . 设S 是 等 差 数 列 {a n }的 前 n 项 和 ,na Sa a , 则5 53(28)a3的 值 为( )A .1 61 3B .C .35D .5 619. .已知等比数列{a n }的首项为 1,若 4a 1,2a 2 ,a 3 成等差数列,则数列an的前 5项和为( )31 16A .33 16B .2C .16 33D .二、填空题 10..正项等比数列中,若,则等于______.11..某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层均堆成正六边形,且逐层每边增加一个花盆(如图).设第 n 层共有花盆的个数为 f (n ) ,则 f (n ) 的表达式为_____________________. 12..数列{a n }中,若 a=1,n=________。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (1)

高考数学三轮复习冲刺模拟试题01集合一、选择题1. .已知集合,,则( )A .B .C .D .2. .设集合{1}A x x a x R =-<∈,,B={x|1<x<5,x∈R},若A ⋂B=φ,则实数a 的取值范围是( )A .{a|0≤a≤6}B .{a|a≤2,或a≥4}C .{a|a≤0,或a≥6}D .{a|2≤a≤4}3. .已知集合2A={|log <1},B={x|0<<c}x x x ,若=A B B ,则c 的取值范围是( )A .(0,1]B .[1,+)∞C .(0,2]D .[2,+)∞二、填空题4. .若不等式4+-2+1x m x≥对一切非零实数x 均成立,记实数m 的取值范围为M .已知集合{}=A x x M ∈,集合{}2=--6<0B x R x x ∈,则集合=A B ___________.5. .设集合是A={32|()=83+6a f x x ax x -是(0,+∞)上的增函数},5={|=,[-1,3]}+2B y y x x ∈,则()R A B ð= ; 6. .试题)己知集合222{|28},{|240}x x A x B x x mx -=<=+-<, 若{|11},{|43}A B x x A B x x =-<<=-<< ,则实数m 等于__________ .7. .设集合{}1,R A x x a x =-<∈,{}15,R B x x x =<<∈,若∅=B A ,则实数a 取值范围是___________.三、解答题8. .已知={()|1},B={()|3,0x 3}2A x,y y =-x +mx -x,y x+y =≤≤,若A B ⋂是单元素集,求实数m 的取值范围.参考答案一、选择题1. 【答案】B 【解析】{(3)0}{03}P x x x x x =-<=<<,={2}{22}Q x x x x <=-<<,所以{02}(0,2)P Q x x =<<= ,选B.2. 【答案】C 【解析】{1}{11}A x x a x R x a x a =-<∈==-<<+,,因为=A B φ ,所以有15a -≥或11a +≤,即6a ≥或0a ≤,选C.3. 【答案】D 【解析】2{log 1}{01}A x x x x =<=<<.因为A B B = ,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.二、填空题4. {}-1<3x x ≤;5. 【答案】(,1)(4,)-∞+∞ 【解析】2()=2466f 'x x ax -+,要使函数在(0,)+∞上是增函数,则2()=24660f 'x x ax -+>恒成立,即14a x x <+,因为11444x x x x +≥⨯=,所以4a ≤,即集合{4}A a a =≤.集合5={|=,[-1,3]}+2B y y x x ∈{15}y x =≤≤,所以{14}A B x x ⋂=≤≤,所以()=R A B ð(,1)(4,)-∞+∞ .6. 【答案】,因为32222{|28}{|230}{13}x x A x x x x x x -=<=--<=-<<,所以由数轴可知,{|11},{|43}A B x x A B x x =-<<=-<< {|41}B x x =-<<即是方程的两个根,所以,解得。
广东省中山市普通高中高考数学三轮复习冲刺模拟试题(6)(2021年整理)

广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(6) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(6))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题(6)的全部内容。
高考数学三轮复习冲刺模拟试题06平面向量一、选择题1 .△ABC 的外接圆的圆心为O,半径为1,2→AO =→AB +→AC 且→AO =→AB ,则向量→AB 在→BC 方向上的投影为 ( )A .21B .23 C .—23 D .—212 .平面向量a 与b 的夹角为)0,3(,32=a π,2||=b ,则b a 2+= ( )A .13B .37C .7D .33 .如图,边长为1的正方形ABCD 的顶点A ,D 分别在x 轴、y 轴正半轴上移动,则OC OB ⋅的最大值是 ( )A .2B .12+C .πD .44 .已知向量,,a b c 中任意两个都不共线,且a b +与c 共线, b c +与a 共线,则向量a b c++ ( )A .aB .bC .cD .05 .已知a =(-3,2),b =(—1,0),向量a λ+b 与a —2b 垂直,则实数λ的值为 ( )A .-71B .71C .-61D .616 .在平行四边形ABCD 中,2,AE EB CF FB ==,连接CE 、DF 相交于点M ,若AM AB AD λμ=+,则实数λ与μ的乘积为( )A .14B .38C .34D .437 .在平面内,已知1,3OA OB ==,0=⋅OB OA , 30=∠AOC ,设OB n OA m OC +=,(,R m n ∈),则nm等于 ( )A .3±B .3±C .13±D .33±二、填空题8 .已知点M 为等边三角形ABC 的中心,=2AB ,直线L 过点M 交线段AB 于点P ,交线段AC 于点Q ,则BQ CP ⋅的最大值为______________.9 .已知OA =1,OB =3,OA ·OB =0,点C 在∠AOB 内,且∠AOC=30°,设OC =m OA +n OB(m ,n ∈R),则nm=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学三轮复习冲刺模拟试题17常用逻辑用语一、选择题1 .已知命题p :关于x 的函数221f (x )x ax =+-在[3,+∞)上是增函数;命题q :关于x的方程x 2-a x +4=0有实数根。
若p ∨q 为真命题,p ∧q 为假命题,则实数a 的取值范围是 ( ) A .(-12,4)(4,+∞) B .(-12,4][4,+∞) C .(-∞,-12)(-4,4) D .[-12,+∞)2 .下列命题中是假命题的是( )A .都不是偶函数B .有零点C .D .上递减3 . “lg ,lg ,lg x y z 成等差数列”是“2y xz =”成立的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不充分也不必要条件 4 .如果命题“p 且q”是假命题,“¬p”也是假命题,则 ( )A .命题“¬p 或q”是假命题B .命题“p 或q”是假命题C .命题“¬p 且q”是真命题D .命题“p 且¬q”是真命题5 .已知条件2|1:|>+x p ,条件a x q >|:|,且p ⌝是q ⌝的必要不充分条件,则实数a 的取值范围是( )A .10≤≤aB .31≤≤aC .1≤aD .3≥a6 . “0ϕ=”是“函数()sin()f x x ϕ=+为奇函数”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7 .设a ,b ∈R ,那么“>1ab”是“>>0a b ”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8 .下列命题中是假命题的是( )A .(0,),>2x x sin x π∀∈B .000,+=2x R sin x cos x ∃∈C . ,3>0xx R ∀∈D .00,=0x R lg x ∃∈9 .有关下列命题的说法正确的是( )A .命题“若x 2=1,则x=1”的否命题为:若“x 2=1则x ≠1” B .“1x =-”是“2560x x --=”的必要不充分条件C .命题“∃x ∈R,使得x 2+x+1<0”的否定是:“∀x ∈R,均有x 2+x+1<0” D .命题“若x=y,则sinx=siny ”的逆否命题为真命题10.下列有关命题的叙述,错误的个数为①若p ∨q 为真命题,则p ∧q 为真命题。
②“5x >”是“2450x x -->”的充分不必要条件。
③命题P :∃x ∈R,使得x 2+x-1<0,则⌝p :∀x ∈R,使得x 2+x-1≥0。
④命题“若2320x x -+=,则x=1或x=2”的逆否命题为“若x ≠1或x ≠2,则2320x x -+≠”。
( )A .1B .2C .3D .411.已知命题:"[1,2],-0"2p x x a ∀∈≥,命题:"R,+2+2=0"2q x x ax -a ∃∈使,若命题“p q 且”是真命题,则实数a 的取值范围是 ( )A .{|-2=1}a a a ≤或B .{|-2}a a ≤C .{|-22}a a a ≤≤≤或1D .{|-21}a a ≤≤12.:||2p x >是:2q x <-的( )A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件13.α,β为平面,m 为直线,如果//αβ,那么“//m α”是“m β⊆”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件.14. “1m =-”是“直线(21)10mx m y +-+=和直线330x my ++=垂直”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件15.条件甲:⎩⎨⎧<<<+<3042xy y x ;条件乙:⎩⎨⎧<<<<3210y x ,则甲是乙的( )A .充要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件二、解答题16.设命题p:函数f(x)=lg(ax 2-4x+a)的定义域为R;命题q:不等式2x 2+x>2+ax,对∀x ∈(-∞,-1)上恒成立,如果命题“p ∨q ”为真命题,命题“p ∧q ”为假命题,求实数a 的取值范围.17.已知(+1)(2-)0x x ≥的解为条件p ,关于x 的不等式222+-2-3-1<0(>-)3x mx m m m 的解为条件q .(1)若p 是q 的充分不必要条件时,求实数m 的取值范围. (2)若p ⌝是q ⌝的充分不必要条件时,求实数m 的取值范围.参考答案一、选择题 1. C2. 【答案】A【解析】当=2πϕ时,()=sin(2)=cos 22f x x x π+为偶函数,所以A 错误,选A.3. A4. C5. C6. A7. 【答案】B【解析】由>1a b 得,10a a bb b --=>,即()0ba b ->,得0b a b >⎧⎨>⎩或0b a b <⎧⎨<⎩,即0a b >>或0a b <<,所以“>1ab ”是“>>0a b ”的必要不充分条件,选B.8. 【答案】B【解析】因为000+4sin x cos x x π+≤()B 错误,选B.9. 【答案】D【解析】若x 2=1,则x=1”的否命题为21x ≠,则1x ≠,即A 错误。
若2560x x --=,则6x =或1x =-,所以“1x =-”是“2560x x --=”的充分不必要条件,所以B 错误。
∃x ∈R,使得x 2+x+1<0的否定是∀x ∈R,均有210x x ++≥,所以C 错误。
命题若x=y,则sinx=siny 正确,所以若x=y,则sinx=siny 的逆否命题也正确,所以选D.10. 【答案】B【解析】若p ∨q 为真命题,则,p q 至少有有一个为真,所以p q ∧不一定为真,所以①错误。
2450x x -->得5x >或1x <-,所以“5x >”是“2450x x -->”的充分不必要条件,②正确。
根据特称命题的否定式全称命题知③正确。
“若2320x x -+=,则x=1或x=2”的逆否命题为“若x ≠1且x ≠2,则2320x x -+≠”,所以④错误,所以错误命题的个数为2个,选B.11. 【答案】A【解析】由20x a -≥,得2,[1,2]a x x ≤∈,所以1a ≤.要使q 成立,则有244(2)0a a ∆=--≥,即220a a +-≥,解得1a ≥或2a ≤-.因为命题“p q 且”是真命题,则,p q 同时为真,即112a a a ≤⎧⎨≥≤-⎩或,即2a ≤-或1a =,选A.12. 【答案】C 由2x >得2x >或2x <-,所以:||2p x >是:2q x <-的必要不充分条件,选C.13. 【答案】B解:若//αβ,当//m α时,m β⊆或m β⊄.当m β⊆时,若//αβ,则一定有//m α,所以//m α是m β⊆的必要不充分条件,选B.14. 【答案】A解:若0m =,两直线方程为1y =和1x =-,此时两直线垂直.若12m =,两直线方程为2x =-和13302x y ++=,此时两直线相交.当0m ≠且12m ≠时,两直线方程为11212m y x m m =+--和33y x m m =--,两直线的斜率为12m m -和3m-.若两直线垂直,则有3()112m m m ⨯-=--,解得1m =-,所以直线(21)10mx m y +-+=和直线330x my ++=垂直时的条件为1m =-或0m =.所以1m =-是直线(21)1m x m y +-+=和直线330x my ++=垂直的充分不必要条件,选A. 15. 【答案】C解:当⎩⎨⎧<<<<3210y x 能得到⎩⎨⎧<<<+<3042xy y x ,但当⎩⎨⎧<<<+<3042xy y x 时,不妨取21x y ==,满足⎩⎨⎧<<<+<3042xy y x ,但⎩⎨⎧<<<<3210y x 不满足,所以甲是乙的必要而不充分条件 选C.二、解答题16.解:p:∆<0且a>0,故a>2;q:a>2x-2/x+1,对∀x ∈(-∞,-1),上恒成立,增函数(2x-2/x+1)<1此时x=-1,故a≥1 “p∨q ”为真命题,命题“p∧q ”为假命题,等价于p,q 一真一假.故1≤a≤217.解:(1)设条件p 的解集为集合A,则2}x -1|{x ≤≤=A设条件q 的解集为集合B,则1}m x 1--2m |{x +<<=B 若p 是q 的充分不必要条件,则A 是B 的真子集13211221>⇒⎪⎪⎩⎪⎪⎨⎧->-<-->+m m m m (2)若p ⌝是q ⌝的充分不必要条件, 则B 是A 的真子集0323211221≤<-⇒⎪⎪⎩⎪⎪⎨⎧->-≥--≤+m m m m。
