高一数学 培优教材(3) 新人教版
高一年级2020寒假培优数学教材

三、函数思想方法的应用【要点】1.函数的思想,是指运用运动变化的观点,分析和研究数量关系,通过建立或构造函数关系式,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决的思想方法.2.方程的思想,是指根据数学问题中变量间的特殊关系,有意识地构造方程或方程组,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决的思想方法.3.函数和方程是密切相关的,可以互相转化。
比如研究函数y=f(x)与y=g(x)的图象的交点问题,就是研究方程f(x)=g(x)的实数解的问题;解方程f(x)=0,就是求函数y=f(x)的零点.4.函数应用题的解题步骤简述如下:(1)审题:阅读理解文字表达的题意,分清条件和结论;(2)建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型,; (3)求模:求解数学模型,得到数学结论;(4)作答:对结果进行验证或评估,作出解释或回答。
解应用题可归结为“过三关”:一是事理关,即读懂题意,需要一定的阅读理解能力;二是文理关,即把文字语言转化为数学的符号语言;三是数理关,即构建相应的数学模型,构建之后还需要扎实的基础知识和较强的数理能力。
【例题】1.方程x 2=2x 的解的个数为( )A .0B .1C .2D .32.已知155=-a cb ,(a 、b 、c ∈R ),则有( )A .ac b 42>B .ac b 42≥C .ac b 42<D .ac b 42≤3.已知关于x 的方程 2x -(2 m -8)x +2m -16 = 0的两个实根 1x 、2x 满足 1x <23<2x ,则实数m 的取值范围_______________.4.关于x 的方程|x 2-4x +3|-a =0有三个不相等的实数根,则实数a 的值是______. 5.若不等式x 4x 2--≥34x+11-a 的解集为{x|-4≤x≤-2},求实数a 的值.6.已知直线y=3-x 和坐标轴交于A 、B 两点,若抛物线y=-x 2+mx-1和线段AB 有两个不同的交点,求实数m 的范围.7.设不等式2x -1>m (x 2-1)对满足|m|≤2的一切实数m 的取值都成立.求x 的取值范围.8.设f (x )=lg 3421ax x ++,如果当x ∈(-∞,1]时f (x )有意义,求实数a 的取值范围.9.若方程lg (-x 2+3x -m )=lg (3-x )在x ∈(0,3)内有唯一解,求实数m 的取值范围.10.已知函数f (x )=log m33+-x x (1)若f (x )的定义域为[α,β],(β>α>0),判断f (x )在定义域上的增减性,并加以说明; (2)当0<m <1时,使f (x )的值域为[log m [m (β–1)],log m [m (α–1)]]的定义域区间为[α,β](β>α>0)是否存在?请说明理由.11.(xx 年全国高考题)甲、乙两地相距S 千米,汽车从甲地匀速行驶到乙地,速度不得超过c 千米/时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 v (千米/时)的平方成正比,比例系数为b ;固定部分为a 元.(1)把全程运输成本y (元)表示为速度v (千米/时)的函数,并指出函数的定义域; (2)为了使全程运输成本最小,汽车应以多大速度行驶?12.某海滨浴场的岸边可以近似的看成直线,位于岸边A 处的救生员发现海中B 处有人求救,救生员没有直接从A 处游向B 处,而是沿岸边自A 跑到距离B 最近的D 处,然后游向B 处,若救生员在岸边的行进速度为6米/秒,在海中的行进速度2米/秒(1)分析救生员的选择是否正确;(2)在AD 上找一落点C ,使救生员从A 到B 的时间最短,并求出最短时间。
高一数学培优教材

1 = 0 的实根. 2
例 2.设集合 A = −4,3a, a 2 ,且 9 ∈ A ,求实数 a 的值.
{
}
例 3.集合的表示方法 (1)用列举法表示集合 A = x x 2 + 3 x = 4 ; (2)用列举法表示集合 B = y y = 4 − x , x、y ∈ N ;
2
{
}
{
}
(3)用列举法表示集合 C = ( x, y ) y = 4 − x , x、y ∈ N ;
1 不一定属于集合 G . x
3
【课堂练习】
1.下列各组对象不能形成集合的是( A.高一全体女生 C.高中所有课程 2.下列表述中正确的是( A. {0} = ∅ ) C. {∅} = ∅ D. 0 ∉ N ) B.高三(1)班家长全体 D.高一(1)班中个子较高的学生
B. {1,3} = {3,1}
2
{
}
(4)用列举法表示集合 D = x
6 ∈ Z, x ∈ N ; 3− x
(5)用描述法表示 100 内被 3 除余 2 的正整数所组成的集合 P ; (6)平面直角坐标系内在 x 轴上方的点组成的集合.
1
例 4. 已知集合 A = x ax + 2 x + 1 = 0, a ∈ R, x ∈ R .
Q = {1,2,6} ,则 P + Q 中元素的个数是
8.化简: x x =
.
m , m ∈ Z , m < 2, n ∈ N * , n ≤ 3 = n
a , b , Q = 0, a + b, b 2 ,且 P = Q ,则 a 2011 + b 2011 = b
高中数学 培优复习专用教材 第3章 数列 数列综合应用 改好309页 最新版

高考第一轮复习用书·数学(理科)
第三章
3.(2014 年北京联考)已知 f(x)=log2x-logx2(0<x<1),数列{an}满足 f(2������ ������ )=2n(n∈N*),则数列{an}( ). A.有最大项无最小项 B.有最小项无最大项 C.既有最大项又有最小项 D.无最大项也无最小项
高考第一轮复习用书·数学(理科)
第三章
1.(2015 年南昌一中)若数列{an}的通项公式为 an=-2n2+13n,关 于该数列有下列四种说法:①该数列有无穷多个正数项;②该数列有 2 无穷多个负数项;③该数列的最大项就是函数 f(x)=-2x +13x 的最大 值;④-70 是该数列中的一项;其中正确命题的序号为( ). A.①② B.②④ C.①③ D.③④
高考第一轮复习用书·数学(理科)
第三章
பைடு நூலகம்
2.(2015 年高安中学第二次月考)数列{an}满足 an+1+an-1=an,且
a1=1,a2=5,那么 a1-a2+a3-…+a15-a16+a17 的值为
.
高考第一轮复习用书·数学(理科)
第三章
【解析】由 an+1+an-1=an,得 an-1-an+an+1=0,那么 a3-a4+a5=0,a6-a7+a8=0,…,a15-a16+a17=0,于是 a1-a2+a3-… +a15-a16+a17=a1-a2=-4. 【答案】-4
2������ +1
列{an}有最小项 a1,无最大项. 【答案】B
an+1-an=(n+1- (������ + 1) + 1)-(n- ������2 + 1)=1-( (������ + 1) + 1������2 + 1)=12������ +1
高中数学同步课堂培优联系必修一教师用书 第1~3章含答案 有详解 教师专用版

第1讲集合知识梳理1.元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.(3)集合的三种表示方法:列举法、描述法、图示法.2.集合间的基本关系(1)子集:若对任意x∈A,都有x∈B,则A⊆B或B⊇A.(2)真子集:若A⊆B,且集合B中至少有一个元素不属于集合A,则A B或B A.(3)相等:若A⊆B,且B⊆A,则A=B.(4)空集的性质:∅是任何集合的子集,是任何非空集合的真子集.3.集合的基本运算(1)若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个.(2)子集的传递性:A⊆B,B⊆C⇒A⊆C.(3)A⊆B⇔A∩B=A⇔A∪B=B.(4)∁U(A∩B)=(∁U A)∪(∁U B),∁U(A∪B)=(∁U A)∩(∁U B).诊断自测1.判断正误(在括号内打“√”或“³”)精彩PPT展示(1)任何集合都有两个子集.( )(2)已知集合A ={x |y =x 2},B ={y |y =x 2},C ={(x ,y )|y =x 2},则A =B =C .( ) (3)若{x 2,1}={0,1},则x =0,1.( ) (4)若A ∩B =A ∩C ,则B =C .( )解析 (1)错误.空集只有一个子集,就是它本身,故该说法是错误的.(2)错误.集合A 是函数y =x 2的定义域,即A =(-∞,+∞);集合B 是函数y =x 2的值域,即B =[0,+∞);集合C 是抛物线y =x 2上的点集.因此A ,B ,C 不相等. (3)错误.当x =1,不满足互异性. (4)错误.当A =∅时,B ,C 可为任意集合. 答案 (1)³ (2)³ (3)³ (4)³2.(必修1P7练习2改编)若集合A ={x ∈N |x ≤10},a =22,则下列结论正确的是( ) A.{a }⊆AB.a ⊆AC.{a }∈AD.a ∉A解析 由题意知A ={0,1,2,3},由a =22,知a ∉ A . 答案 D3.(2016·全国Ⅰ卷)设集合A ={x |x 2-4x +3<0},B ={x |2x -3>0},则A ∩B =________. A.⎝ ⎛⎭⎪⎫-3,-32 B.⎝ ⎛⎭⎪⎫-3,32 C.⎝ ⎛⎭⎪⎫1,32D.⎝ ⎛⎭⎪⎫32,3 解析 易知A =(1,3),B =⎝ ⎛⎭⎪⎫32,+∞,所以A ∩B =⎝ ⎛⎭⎪⎫32,3.答案 D4.(2017·石家庄模拟)设全集U ={x |x ∈N *,x <6},集合A ={1,3},B ={3,5},则∁U (A ∪B )等于( ) A.{1,4} B.{1,5} C.{2,5}D.{2,4}解析 由题意得A ∪B ={1,3}∪{3,5}={1,3,5}.又U ={1,2,3,4,5},∴∁U (A ∪B )={2,4}. 答案 D5.已知集合A ={(x ,y )|x ,y ∈R ,且x 2+y 2=1},B ={(x ,y )|x ,y ∈R ,且y =x },则A ∩B 的元素个数为________.解析 集合A 表示圆心在原点的单位圆,集合B 表示直线y =x ,易知直线y =x 和圆x 2+y 2=1相交,且有2个交点,故A ∩B 中有2个元素. 答案 2考点一 集合的基本概念【例1】 (1)已知集合A ={0,1,2},则集合B ={x -y |x ∈A ,y ∈A }中元素的个数是( ) A.1B.3C.5D.9(2)若集合A ={x ∈R |ax 2-3x +2=0}中只有一个元素,则a =( ) A.92B.98C.0D.0或98解析 (1)当x =0,y =0,1,2时,x -y =0,-1,-2; 当x =1,y =0,1,2时,x -y =1,0,-1; 当x =2,y =0,1,2时,x -y =2,1,0.根据集合中元素的互异性可知,B 的元素为-2,-1,0,1,2,共5个. (2)若集合A 中只有一个元素,则方程ax 2-3x +2=0只有一个实根或有两个相等实根.当a =0时,x =23,符合题意;当a ≠0时,由Δ=(-3)2-8a =0,得a =98, 所以a 的取值为0或98. 答案 (1)C (2)D规律方法 (1)第(1)题易忽视集合中元素的互异性误选D.第(2)题集合A 中只有一个元素,要分a =0与a ≠0两种情况进行讨论,此题易忽视a =0的情形. (2)用描述法表示集合,先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.【训练1】 (1)设a ,b ∈R ,集合{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,ba ,b ,则b -a =________.(2)已知集合A ={x ∈R |ax 2+3x -2=0},若A =∅,则实数a 的取值范围为________.解析 (1)因为{1,a +b ,a }=⎩⎨⎧⎭⎬⎫0,ba ,b ,a ≠0,所以a +b =0,且b =1,所以a =-1,b =1,所以b -a =2. (2)由A =∅知方程ax 2+3x -2=0无实根, 当a =0时,x =23不合题意,舍去; 当a ≠0时,Δ=9+8a <0,∴a <-98. 答案 (1)2 (2)⎝ ⎛⎭⎪⎫-∞,-98考点二 集合间的基本关系【例2】 (1)已知集合A ={x |y =1-x 2,x ∈R },B ={x |x =m 2,m ∈A },则( ) A.A B B.B A C.A ⊆B D.B =A(2)已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围是________.解析 (1)易知A ={x |-1≤x ≤1}, 所以B ={x |x =m 2,m ∈A }={x |0≤x ≤1}. 因此B A .(2)当B =∅时,有m +1≥2m -1,则m ≤2. 当B ≠∅时,若B ⊆A ,如图.则⎩⎨⎧m +1≥-2,2m -1≤7,m +1<2m -1,解得2<m ≤4.综上,m 的取值范围为(-∞,4]. 答案 (1)B (2)(-∞,4]规律方法 (1)若B ⊆A ,应分B =∅和B ≠∅两种情况讨论.(2)已知两个集合间的关系求参数时,关键是将两个集合间的关系转化为元素或区间端点间的关系,进而转化为参数满足的关系.解决这类问题常常要合理利用数轴、Venn图,化抽象为直观进行求解.【训练2】(1)(2017·长郡中学质检)若集合A={x|x>0},且B⊆A,则集合B可能是()A.{1,2}B.{x|x≤1}C.{-1,0,1}D.R(2)(2016·郑州调研)已知集合A={x|x=x2-2,x∈R},B={1,m},若A⊆B,则m的值为()A.2B.-1C.-1或2D.2或2解析(1)因为A={x|x>0},且B⊆A,再根据选项A,B,C,D可知选项A正确.(2)由x=x2-2,得x=2,则A={2}.因为B={1,m}且A⊆B,所以m=2.答案(1)A(2)A考点三集合的基本运算【例3】(1)(2015·全国Ⅰ卷)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中元素的个数为()A.5B.4C.3D.2(2)(2016·浙江卷)设集合P={x∈R|1≤x≤3},Q={x∈R|x2≥4},则P∪(∁R Q)=()A.[2,3]B.(-2,3]C.[1,2)D.(-∞,-2)∪[1,+∞)解析(1)集合A中元素满足x=3n+2,n∈N,即被3除余2,而集合B中满足这一要求的元素只有8和14.共2个元素.(2)易知Q={x|x≥2或x≤-2}.∴∁R Q={x|-2<x<2},又P={x|1≤x≤3},故P∪(∁R Q)={x|-2<x≤3}.答案(1)D(2)B规律方法(1)在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直(2)一般地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍.【训练3】(1)(2017·石家庄模拟)设集合M={-1,1},N={x|x2-x<6},则下列结论正确的是()A.N⊆MB.N∩M=∅C.M⊆ND.M∩N=R(2)(2016·山东卷)设集合U={1,2,3,4,5,6},A={1,3,5},B={3,4,5},则∁U(A∪B)=()A.{2,6}B.{3,6}C.{1,3,4,5}D.{1,2,4,6}解析(1)易知N=(-2,3),且M={-1,1},∴M⊆N.(2)∵A={1,3,5},B={3,4,5},∴A∪B={1,3,4,5},又全集U={1,2,3,4,5,6},因此∁U(A∪B)={2,6}.答案(1)C(2)A[思想方法]1.集合中的元素的三个特征,特别是无序性和互异性在解题时经常用到.解题后要进行检验,要重视符号语言与文字语言之间的相互转化.2.对连续数集间的运算,借助数轴的直观性,进行合理转化;对已知连续数集间的关系,求其中参数的取值范围时,要注意单独考察等号能否取到.3.对离散的数集间的运算,或抽象集合间的运算,可借助Venn图.这是数形结合思想的又一体现.[易错防范]1.集合问题解题中要认清集合中元素的属性(是数集、点集还是其他类型集合),要对集合进行化简.2.空集是任何集合的子集,是任何非空集合的真子集,时刻关注对空集的讨论,防止漏解.3.解题时注意区分两大关系:一是元素与集合的从属关系;二是集合与集合的包4.Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用数轴图示法时要特别注意端点是实心还是空心.基础巩固题组(建议用时:25分钟)一、选择题1.(2015·全国Ⅱ卷)已知集合A={1,2,3},B={2,3},则()A.A=BB.A∩B=∅C.A BD.B A解析∵A={1,2,3},B={2,3},∴2,3∈A且2,3∈B,1∈A但1∉B,∴B A.答案 D2.(2016·全国Ⅱ卷)已知集合A={1,2,3},B={x|(x+1)·(x-2)<0,x∈Z},则A∪B=()A.{1}B.{1,2}C.{0,1,2,3}D.{-1,0,1,2,3}解析由(x+1)(x-2)<0,得-1<x<2,又x∈Z,所以B={0,1},因此A∪B={0,1,2,3}.答案 C3.(2017·肇庆模拟)已知集合A={x|lg x>0},B={x|x≤1},则()A.A∩B≠∅B.A∪B=RC.B⊆AD.A⊆B解析由B={x|x≤1},且A={x|lg x>0}=(1,+∞),∴A∪B=R.答案 B4.已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(-∞,-1]B.[1,+∞)C.[-1,1]D.(-∞,-1]∪[1,+∞)解析因为P∪M=P,所以M⊆P,即a∈P,得a2≤1,解得-1≤a≤1,所以a的取值范围是[-1,1].答案 C5.(2016·山东卷)设集合A ={y |y =2x ,x ∈R },B ={x |x 2-1<0},则A ∪B =( ) A.(-1,1) B.(0,1) C.(-1,+∞)D.(0,+∞)解析 由y =2x ,x ∈R ,知y >0,则A =(0,+∞). 又B ={x |x 2-1<0}=(-1,1). 因此A ∪B =(-1,+∞). 答案 C6.(2016·浙江卷)已知全集U ={1,2,3,4,5,6},集合P ={1,3,5},Q ={1,2,4},则(∁U P )∪Q =( ) A.{1}B.{3,5}C.{1,2,4,6}D.{1,2,3,4,5}解析 ∵U ={1,2,3,4,5,6},P ={1,3,5},∴∁U P ={2,4,6},∵Q ={1,2,4},∴(∁U P )∪Q ={1,2,4,6}. 答案 C7.若x ∈A ,则1x ∈A ,就称A 是伙伴关系集合,集合M =⎩⎨⎧⎭⎬⎫-1,0,12,2,3的所有非空子集中具有伙伴关系的集合的个数是( ) A.1 B.3 C.7D.31解析 具有伙伴关系的元素组是-1,12,2,所以具有伙伴关系的集合有3个:{-1},⎩⎨⎧⎭⎬⎫12,2,⎩⎨⎧⎭⎬⎫-1,12,2. 答案 B8.已知全集U =R ,A ={x |x ≤0},B ={x |x ≥1},则集合∁U (A ∪B )=( ) A.{x |x ≥0} B.{x |x ≤1} C.{x |0≤x ≤1}D.{x |0<x <1}解析 ∵A ={x |x ≤0},B ={x |x ≥1},∴A ∪B ={x |x ≤0或x ≥1},在数轴上表示如图. ∴∁U (A ∪B )={x |0<x <1}. 答案 D二、填空题9.已知集合A={x|x2-2x+a>0},且1∉A,则实数a的取值范围是________.解析∵1∉{x|x2-2x+a>0},∴1∈{x|x2-2x+a≤0},即1-2+a≤0,∴a≤1.答案(-∞,1]10.(2016·天津卷)已知集合A={1,2,3},B={y|y=2x-1,x∈A},则A∩B=________.解析由A={1,2,3},B={y|y=2x-1,x∈A},∴B={1,3,5},因此A∩B ={1,3}.答案{1,3}11.集合A={x|x<0},B={x|y=lg[x(x+1)]},若A-B={x|x∈A,且x∉B},则A-B=________.解析由x(x+1)>0,得x<-1或x>0,∴B=(-∞,-1)∪(0,+∞),∴A-B=[-1,0).答案[-1,0)12.(2017·石家庄质检)已知集合A={x|x2-2 016x-2 017≤0},B={x|x<m+1},若A⊆B,则实数m的取值范围是________.解析由x2-2 016x-2 017≤0,得A=[-1,2 017],又B={x|x<m+1},且A⊆B,所以m+1>2 017,则m>2 016.答案(2 016,+∞)能力提升题组(建议用时:10分钟)13.(2016·全国Ⅲ卷改编)设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则(∁R S)∩T =()A.[2,3]B.(-∞,-2)∪[3,+∞)C.(2,3)D.(0,+∞)解析易知S=(-∞,2]∪[3,+∞),∴∁R S=(2,3),因此(∁R S )∩T =(2,3). 答案 C14.(2016·黄山模拟)集合U =R ,A ={x |x 2-x -2<0},B ={x |y =ln(1-x )},则图中阴影部分所表示的集合是( ) A.{x |x ≥1} B.{x |1≤x <2} C.{x |0<x ≤1}D.{x |x ≤1}解析 易知A =(-1,2),B =(-∞,1),∴∁U B =[1,+∞),A ∩(∁U B )=[1,2).因此阴影部分表示的集合为A ∩(∁U B )={x |1≤x <2}. 答案 B15.(2017·南昌十所省重点中学模拟)设集合A =⎩⎨⎧⎭⎬⎫x ∈N |14≤2x≤16,B ={x |y =ln(x 2-3x )},则A ∩B 中元素的个数是________. 解析 由14≤2x ≤16,x ∈N ,∴x =0,1,2,3,4,即A ={0,1,2,3,4}. 又x 2-3x >0,知B ={x |x >3或x <0}, ∴A ∩B ={4},即A ∩B 中只有一个元素. 答案 116.已知集合A ={x ∈R ||x +2|<3},集合B ={x ∈R |(x -m )(x -2)<0},且A ∩B =(-1,n ),则m +n =________.解析 A ={x ∈R ||x +2|<3}={x ∈R |-5<x <1}, 由A ∩B =(-1,n )可知m <1,则B ={x |m <x <2},画出数轴,可得m =-1,n =1.所以m +n =0. 答案 0第2讲 命题及其关系、充分条件与必要条件最新考纲 1.理解命题的概念,了解“若p ,则q ”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;2.理解必要条件、充分条件与充要条件的含义.知识梳理1.命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其相互关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题,它们具有相同的真假性.②两个命题为互逆命题或互否命题时,它们的真假性没有关系.3.充分条件、必要条件与充要条件的概念p⇒ppq诊断自测1.判断正误(在括号内打“√”或“³”)精彩PPT展示(1)“x2+2x-3<0”是命题.()(2)命题“若p,则q”的否命题是“若p,则綈q”.()(3)当q是p的必要条件时,p是q的充分条件.()(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”.()解析(1)错误.该语句不能判断真假,故该说法是错误的.(2)错误.否命题既否定条件,又否定结论.答案(1)³(2)³(3)√(4)√2.(教材练习改编)命题“若α=π4,则tan α=1”的逆否命题是()A.若α≠π4,则tan α≠1 B.若α=π4,则tan α≠1C.若tan α≠1,则α≠π4 D.若tan α≠1,则α=π4解析命题“若p,则q”的逆否命题是“若綈q,则綈p”,显然綈q:tan α≠1,綈p:α≠π4,所以该命题的逆否命题是“若tanα≠1,则α≠π4”.答案 C3.(2016·天津卷)设x>0,y∈R,则“x>y”是“x>|y|”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析x>y x>|y|(如x=1,y=-2).但x>|y|时,能有x>y.∴“x>y”是“x>|y|”的必要不充分条件.答案 C4.命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中假命题的个数为()A.1B.2C.3D.4解析原命题正确,从而其逆否命题也正确;其逆命题为“若a>-6,则a>-3”是假命题,从而其否命题也是假命题.因此四个命题中有2个假命题.答案 B5.(2017·大连双基检测)已知函数f(x)的定义域为R,则命题p:“函数f(x)为偶函数”是命题q:“∃x0∈R,f(x0)=f(-x0)”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析若f(x)为偶函数,则有f(x)=f(-x),所以p⇒q;若f(x)=x,当x=0时,f(0)=f(-0),而f(x)=x为奇函数,所以q p.∴“命题p”是“命题q”的充分不必要条件.答案 A考点一四种命题的关系及其真假判断【例1】(1)命题“若x2-3x-4=0,则x=4”的逆否命题及其真假性为()A.“若x=4,则x2-3x-4=0”为真命题B.“若x≠4,则x2-3x-4≠0”为真命题C.“若x≠4,则x2-3x-4≠0”为假命题D.“若x=4,则x2-3x-4=0”为假命题(2)原命题为“若z1,z2互为共轭复数,则|z1|=|z2|”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是()A.真、假、真B.假、假、真C.真、真、假D.假、假、假解析(1)根据逆否命题的定义可以排除A,D;由x2-3x-4=0,得x=4或-1,所以原命题为假命题,所以其逆否命题也是假命题.(2)由共轭复数的性质,|z1|=|z2|,∴原命题为真,因此其逆否命题为真;取z1=1,z2=i,满足|z1|=|z2|,但是z1,z2不互为共轭复数,∴其逆命题为假,故其否命题也为假.答案(1)C(2)B规律方法(1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,如果命题不是“若p,则q”的形式,应先改写成“若p,则q”的形式;如果命题有大前提,写其他三种命题时需保留大前提不变.(2)判断一个命题为真命题,要给出推理证明;判断一个命题为假命题,只需举出反例.(3)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.【训练1】已知:命题“若函数f(x)=e x-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是()A.否命题是“若函数f(x)=e x-mx在(0,+∞)上是减函数,则m>1”,是真命题B.逆命题是“若m≤1,则函数f(x)=e x-mx在(0,+∞)上是增函数”,是假命题C.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上是减函数”,是真命题D.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上不是增函数”,是真命题解析由f(x)=e x-mx在(0,+∞)上是增函数,则f′(x)=e x-m≥0恒成立,∴m≤1.因此原命题是真命题,所以其逆否命题“若m>1,则函数f(x)=e x-mx在(0,+∞)上不是增函数”是真命题.答案 D考点二充分条件与必要条件的判定【例2】(1)函数f(x)在x=x0处导数存在.若p:f′(x0)=0;q:x=x0是f(x)的极值点,则()A.p是q的充分必要条件B.p是q的充分条件,但不是q的必要条件C.p是q的必要条件,但不是q的充分条件D.p既不是q的充分要件,也不是q的必要条件(2)(2017·衡阳一模)“a=1”是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析(1)由极值的定义,q⇒p,但p q.例如f(x)=x3,在x=0处f′(0)=0,f(x)=x3是增函数,x=0不是函数f(x)=x3的极值点.因此p是q的必要不充分条件.(2)直线ax+y+1=0与直线(a+2)x-3y-2=0垂直的充要条件为a(a+2)+1³(-3)=0,解得a=1或-3,故“a=1”是“直线ax+y+1=0与直线(a+2)x -3y-2=0垂直”的充分不必要条件.答案(1)C(2)B规律方法充要条件的三种判断方法(1)定义法:根据p⇒q,q⇒p进行判断.(2)集合法:根据使p,q成立的对象的集合之间的包含关系进行判断.(3)等价转化法:根据一个命题与其逆否命题的等价性,把判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题,如“xy ≠1”是“x ≠1或y ≠1”的何种条件,即可转化为判断“x =1且y =1”是“xy =1”的何种条件.【训练2】 (2016·山东卷)已知直线a ,b 分别在两个不同的平面α ,β内,则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析 由题意知a ⊂α,b ⊂β,若a ,b 相交,则a ,b 有公共点,从而α,β有公共点,可得出α,β相交;反之,若α,β相交,则a ,b 的位臵关系可能为平行、相交或异面.因此“直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件. 答案 A考点三 充分条件、必要条件的应用(典例迁移)【例3】 (经典母题)已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若x ∈P 是x ∈S 的必要条件,求m 的取值范围.解 由x 2-8x -20≤0,得-2≤x ≤10,∴P ={x |-2≤x ≤10}.∵x ∈P 是x ∈S 的必要条件,则S ⊆P .∴⎩⎨⎧1-m ≥-2,1+m ≤10,解得m ≤3. 又∵S 为非空集合,∴1-m ≤1+m ,解得m ≥0.综上,可知m ≥0≤3时,x ∈P 是x ∈S 的必要条件.【迁移探究1】 本例条件不变,问是否存在实数m ,使x ∈P 是x ∈S 的充要条件? 解 由例题知P ={x |-2≤x ≤10}.若x ∈P 是x ∈S 的充要条件,则P =S ,∴⎩⎨⎧1-m =-2,1+m =10,∴⎩⎨⎧m =3,m =9,这样的m 不存在. 【迁移探究2】 本例条件不变,若綈P 是綈S 的必要不充分条件,求实数m 的取值范围.解 由例题知P ={x |-2≤x ≤10}.∵綈P 是綈S 的必要不充分条件,∴P 是S 的充分不必要条件,∴P ⇒S 且S P .∴[-2,10] [1-m ,1+m ].∴⎩⎨⎧1-m ≤-2,1+m >10或⎩⎨⎧1-m <-2,1+m ≥10, ∴m ≥9,则m 的取值范围是[9,+∞).规律方法 充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解;(2)要注意区间端点值的检验.【训练3】 ax 2+2x +1=0只有负实根的充要条件是________.解析 当a =0时,原方程为一元一次方程2x +1=0,有一个负实根x =-12.当a ≠0时,原方程为一元二次方程,又ax 2+2x +1=0只有负实根,所以有⎩⎪⎨⎪⎧Δ=4-4a ≥0,-2a<0,1a >0,即0<a ≤1. 综上,方程只有负根的充要条件是0≤a ≤1.答案 0≤a ≤1[思想方法]1.写出一个命题的逆命题、否命题及逆否命题的关键是分清原命题的条件和结论,然后按定义来写;在判断原命题、逆命题、否命题以及逆否命题的真假时,要借助原命题与其逆否命题同真或同假,逆命题与否命题同真或同假来判定.2.充要条件的几种判断方法(1)定义法:直接判断若p 则q 、若q 则p 的真假.(2)等价法:即利用A⇒B与綈B⇒綈A;B⇒A与綈A⇒綈B;A⇔B与綈B⇔綈A 的等价关系,对于条件或结论是否定形式的命题,一般运用等价法.(3)利用集合间的包含关系判断:设A={x|p(x)},B={x|q(x)};若A⊆B,则p是q 的充分条件或q是p的必要条件;若A B,则p是q的充分不必要条件,若A =B,则p是q的充要条件.[易错防范]1.当一个命题有大前提而要写出其他三种命题时,必须保留大前提.2.判断命题的真假及写四种命题时,一定要明确命题的结构,可以先把命题改写成“若p,则q”的形式.3.判断条件之间的关系要注意条件之间关系的方向,正确理解“p的一个充分而不必要条件是q”等语言.基础巩固题组(建议用时:25分钟)一、选择题1.(2015·山东卷)设m∈R, 命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是()A.若方程x2+x-m=0有实根,则m>0B.若方程x2+x-m=0有实根,则m≤0C.若方程x2+x-m=0没有实根,则m>0D.若方程x2+x-m=0没有实根,则m≤0解析根据逆否命题的定义,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是“若方程x2+x-m=0没有实根,则m≤0”.答案 D2.“x=1”是“x2-2x+1=0”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析因为x2-2x+1=0有两个相等的实数根为x=1,所以“x=1”是“x2-2x +1=0”的充要条件.答案 A3.设α,β是两个不同的平面,m是直线且m⊂α,则“m∥β”是“α∥β”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件解析m⊂α,m∥βα∥β,但m⊂α,α∥β⇒m∥β,∴“m∥β”是“α∥β”的必要不充分条件.答案 B4.(2017·安徽江南十校联考)“a=0”是“函数f(x)=sin x-1x+a为奇函数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析显然a=0时,f(x)=sin x-1x为奇函数;当f(x)为奇函数时,f(-x)+f(x)=0.又f(-x)+f(x)=sin(-x)-1-x+a+sin x-1x+a=0.因此2a=0,故a=0.所以“a=0”是“函数f(x)为奇函数”的充要条件.答案 C5.下列结论错误的是()A.命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”B.“x=4”是“x2-3x-4=0”的充分条件C.命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题D.命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”解析C项命题的逆命题为“若方程x2+x-m=0有实根,则m>0”.若方程有实根,则Δ=1+4m≥0,即m≥-14,不能推出m>0.所以不是真命题.答案 C6.设x∈R,则“1<x<2”是“|x-2|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析由|x-2|<1,得1<x<3,所以1<x<2⇒1<x<3;但1<x<31<x<2.所以“1<x<2”是“|x-2|<1”的充分不必要条件.答案 A7.已知命题p:x2+2x-3>0;命题q:x>a,且綈q的一个充分不必要条件是綈p,则a的取值范围是()A.[1,+∞)B.(-∞,1]C.[-1,+∞)D.(-∞,-3]解析由x2+2x-3>0,得x<-3或x>1,由綈q的一个充分不必要条件是綈p,可知綈p是綈q的充分不必要条件,等价于q是p的充分不必要条件.故a≥1.答案 A8.(2017·佛山模拟)已知a,b都是实数,那么“a>b”是“ln a>ln b”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析由ln a>ln b⇒a>b>0⇒a>b,故必要性成立.当a=1,b=0时,满足a>b,但ln b无意义,所以ln a>ln b不成立,故充分性不成立.答案 B二、填空题9.“若a≤b,则ac2≤bc2”,则命题的原命题、逆命题、否命题和逆否命题中真命题的个数是________.解析其中原命题和逆否命题为真命题,逆命题和否命题为假命题.答案 210.“sin α=cos α”是“cos 2α=0”的________条件.解析cos 2α=0等价于cos2α-sin2α=0,即cos α=±sin α.由cos α=sin α得到cos 2α=0;反之不成立.∴“sin α=cos α”是“cos 2α=0”的充分不必要条件.答案充分不必要11.已知命题p:a≤x≤a+1,命题q:x2-4x<0,若p是q的充分不必要条件,则a的取值范围是________.解析 令M ={x |a ≤x ≤a +1},N ={x |x 2-4x <0}={x |0<x <4}.∵p 是q 的充分不必要条件,∴M N ,∴⎩⎨⎧a >0,a +1<4,解得0<a <3. 答案 (0,3)12.有下列几个命题:①“若a >b ,则a 2>b 2”的否命题;②“若x +y =0,则x ,y 互为相反数”的逆命题;③“若x 2<4,则-2<x <2”的逆否命题.其中真命题的序号是________.解析 ①原命题的否命题为“若a ≤b ,则a 2≤b 2”错误.②原命题的逆命题为:“若x ,y 互为相反数,则x +y =0”正确.③原命题的逆否命题为“若x ≥2或x ≤-2,则x 2≥4”正确.答案 ②③能力提升题组(建议用时:10分钟)13.(2016·四川卷)设p :实数x ,y 满足(x -1)2+(y -1)2≤2,q :实数x ,y 满足⎩⎨⎧y ≥x -1,y ≥1-x ,y ≤1,则p 是q 的() A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件解析 如图作出p ,q 表示的区域,其中⊙M 及其内部为p 表示的区域,△ABC 及其内部(阴影部分)为q 表示的区域.故p 是q 的必要不充分条件.答案 A14.(2017·南昌十所省重点中学联考)已知m ∈R ,“函数y =2x +m -1有零点”是“函数y =log m x 在(0,+∞)上为减函数”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析 由y =2x +m -1=0,得m =1-2x ,则m <1. 由于函数y =log m x 在(0,+∞)上是减函数, 所以0<m <1.因此“函数y =2x +m -1有零点”是“函数y =log m x 在(0,+∞)上为减函数”的必要不充分条件. 答案 B 15.已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12<2x <8,x ∈R ,B ={x |-1<x <m +1,x ∈R },若x ∈B 成立的一个充分不必要的条件是x ∈A ,则实数m 的取值范围是________. 解析A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12<2x<8,x ∈R ={x |-1<x <3}, ∵x ∈B 成立的一个充分不必要条件是x ∈A , ∴A B ,∴m +1>3,即m >2. 答案 (2,+∞)16.(2017·临沂模拟)下列四个结论中正确的是________(填序号).①“x 2+x -2>0”是“x >1”的充分不必要条件;②命题:“∀x ∈R ,sin x ≤1”的否定是“∃x 0∈R ,sin x 0>1”;③“若x =π4,则tan x =1”的逆命题为真命题;④若f (x )是R 上的奇函数,则f (log 32)+f (log 23)=0.解析 ①中“x 2+x -2>0”是“x >1”的必要不充分条件,故①错误.对于②,命题:“∀x ∈R ,sin x ≤1”的否定是“∃x 0∈R ,sin x 0>1”,故②正确. 对于③,“若x =π4,则tan x =1”的逆命题为“若tan x =1,则x =π4”,其为假命题,故③错误.对于④,若f (x )是R 上的奇函数,则f (-x )+f (x )=0,∵log 32=1log 23≠-log 32,∴log 32与log 23不互为相反数,故④错误. 答案 ②第3讲 简单的逻辑联结词、全称量词与存在量词最新考纲 1.了解逻辑联结词“或”、“且”、“非”的含义;2.理解全称量词与存在量词的意义;3.能正确地对含有一个量词的命题进行否定.知识梳理1.简单的逻辑联结词(1)命题中的且、或、非叫做逻辑联结词.(2)命题p且q、p或q、非p的真假判断2.(1)全称量词:短语“所有的”、“任意一个”等在逻辑中通常叫做全称量词,用符号“∀”表示.(2)全称命题:含有全称量词的命题.全称命题“对M中任意一个x,有p(x)成立”简记为∀x∈M,p(x).(3)存在量词:短语“存在一个”、“至少有一个”等在逻辑中通常叫做存在量词,用符号“∃”表示.(4)特称命题:含有存在量词的命题.特称命题“存在M中的一个元素x0,使p(x0)成立”,简记为∃x0∈M,p(x0). 3.含有一个量词的命题的否定1.判断正误(在括号内打“√”或“³”)精彩PPT展示(1)命题“5>6或5>2”是假命题.()(2)命题綈(p∧q)是假命题,则命题p,q中至少有一个是真命题.()(3)“长方形的对角线相等”是特称命题.()(4)∃x 0∈M ,p (x 0)与∀x ∈M ,綈p (x )的真假性相反.( ) 解析 (1)错误.命题p ∨q 中,p ,q 有一真则真. (2)错误.p ∧q 是真命题,则p ,q 都是真命题. (3)错误.命题“长方形的对角线相等”是全称命题. 答案 (1)³ (2)³ (3)³ (4)√2.(选修2-1P18B 组改编)已知p :2是偶数,q :2是质数,则命题綈p ,綈q ,p ∨q ,p ∧q 中真命题的个数为( ) A.1 B.2 C.3 D.4 解析 p 和q 显然都是真命题,所以綈p ,綈q 都是假命题,p ∨q ,p ∧q 都是真命题. 答案 B3.(2015·全国Ⅰ卷)设命题p :∃n ∈N ,n 2>2n ,则綈p 为( ) A.∀n ∈N ,n 2>2n B.∃n ∈N ,n 2≤2n C.∀n ∈N ,n 2≤2n D.∃n ∈N ,n 2=2n解析 命题p 的量词“∃”改为“∀”,“n 2>2n ”改为“n 2≤2n ”,∴綈p :∀n ∈N ,n 2≤2n . 答案 C4.(2017·贵阳调研)下列命题中的假命题是( ) A.∃x 0∈R ,lg x 0=1 B.∃x 0∈R ,sin x 0=0 C.∀x ∈R ,x 3>0D.∀x ∈R ,2x >0解析 当x =10时,lg 10=1,则A 为真命题;当x =0时,sin 0=0,则B 为真命题;当x <0时,x 3<0,则C 为假命题;由指数函数的性质知,∀x ∈R ,2x >0,则D 为真命题.故选C. 答案 C5.(2015·山东卷)若“∀x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________.解析 ∵函数y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上是增函数,∴y max =tan π4=1,依题意,m ≥y max ,即m ≥1. ∴m 的最小值为1. 答案 1考点一含有逻辑联结词的命题的真假判断【例1】设a,b,c是非零向量.已知命题p: 若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是()A.p∨qB.p∧qC.(綈p)∧(綈q)D.p∧(綈q)解析取a=c=(1,0),b=(0,1),显然a·b=0,b·c=0,但a·c=1≠0,∴p是假命题.又a,b,c是非零向量,由a∥b知a=x b,由b∥c知b=y c,∴a=xy c,∴a∥c,∴q是真命题.综上知p∨q是真命题,p∧q是假命题.又∵綈p为真命题,綈q为假命题.∴(綈p)∧(綈q),p∧(綈q)都是假命题.答案 A规律方法(1)“p∨q”、“p∧q”、“綈p”形式命题真假的判断关键是对逻辑联结词“或”“且”“非”含义的理解,其操作步骤是:①明确其构成形式;②判断其中命题p,q的真假;③确定“p∨q”“p∧q”“綈p”形式命题的真假.(2)p且q形式是“一假必假,全真才真”,p或q形式是“一真必真,全假才假”,非p则是“与p的真假相反”.【训练1】(2017·郑州调研)命题p:函数y=log2(x-2)的单调增区间是[1,+∞),命题q:函数y=13x+1的值域为(0,1).下列命题是真命题的为()A.p∧qB.p∨qC.p∧(綈q)D.綈q解析由于y=log2(x-2)在(2,+∞)上是增函数,∴命题p是假命题.由3x>0,得3x+1>1,所以0<13x+1<1,所以函数y =13x+1的值域为(0,1),故命题q 为真命题. 所以p ∧q 为假命题,p ∨q 为真命题,p ∧(綈q )为假命题,綈q 为假命题. 答案 B考点二 含有一个量词命题的否定及真假判定【例2】 (1)(2016·东北师大附中质检)已知命题p :∀x ∈R ,e x -x -1>0,则綈p 是( )A.∀x ∈R ,e x -x -1<0B.∃x 0∈R ,e x 0-x 0-1≤0C.∃x 0∈R ,e x 0-x 0-1<0D.∀x ∈R ,e x -x -1≤0(2)(2014·全国Ⅰ卷)不等式组⎩⎨⎧x +y ≥1,x -2y ≤4的解集为D ,有下面四个命题:p 1:∀(x ,y )∈D ,x +2y ≥-2, p 2:∃(x 0,y 0)∈D ,x 0+2y 0≥2, p 3:∀(x ,y )∈D ,x +2y ≤3, p 4:∃(x 0,y 0)∈D ,x 0+2y 0≤-1. 其中的真命题是( ) A.p 2,p 3 B.p 1,p 2 C.p 1,p 4D.p 1,p 3解析 (1)因为全称命题的否定是特称命题,命题p :∀x ∈R ,e x -x -1>0的否定为綈p :∃x 0∈R ,e x 0-x 0-1≤0. (2)画出可行域如图中阴影部分所示,由图可知,当目标函数z =x +2y ,经过可行域的点A (2,-1)时,取得最小值0,故x +2y ≥0. 因此p 1,p 2是真命题. 答案 (1)B (2)B规律方法 (1)全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论. (2)判定全称命题“∀x ∈M ,p (x )”是真命题,需要对集合M 中的每一个元素x ,证明p (x )成立;要判断特称命题是真命题,只要在限定集合内至少找到一个x =x 0,使p (x 0)成立.【训练2】 (2017·安徽皖江名校联考)命题p :存在x ∈⎣⎢⎡⎦⎥⎤0,π2,使sin x +cosx >2;命题q :“∃x 0∈(0,+∞),ln x 0=x 0-1”的否定是“∀x ∈(0,+∞),ln x ≠x -1”,则四个命题:(綈p )∨(綈q ),p ∧q ,(綈p )∧q ,p ∨(綈q )中,正确命题的个数为( ) A.1B.2C.3D.4解析 因为sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4≤2,所以命题p 是假命题;又特称命题的否定是全称命题,因此命题q 为真命题.则(綈p )∨(綈q )为真命题,p ∧q 为假命题,(綈p )∧q 为真命题,p ∨(綈q )为假命题. ∴四个命题中正确的有2个命题. 答案 B考点三 由命题的真假求参数的取值范围【例3】 (1)已知命题“∃x 0∈R ,使2x 20+(a -1)x 0+12≤0”是假命题,则实数a 的取值范围是( ) A.(-∞,-1) B.(-1,3) C.(-3,+∞)D.(-3,1)(2)已知p :∃x 0∈R ,mx 20+1≤0,q :∀x ∈R ,x 2+mx +1>0,若p ∨q 为假命题,则实数m 的取值范围是( ) A.[2,+∞)B.(-∞,-2]C.(-∞,-2]∪[2,+∞)D.[-2,2]解析 (1)原命题的否定为∀x ∈R ,2x 2+(a -1)x +12>0,由题意知,其为真命题,即Δ=(a -1)2-4³2³12<0, 则-2<a -1<2,则-1<a <3.(2)依题意知,p ,q 均为假命题.当p 是假命题时,mx 2+1>0恒成立,则有m ≥0;当q 是假命题时,则有Δ=m 2-4≥0,m ≤-2或m ≥2. 因此由p ,q 均为假命题得⎩⎨⎧m ≥0,m ≤-2或m ≥2,即m ≥2.答案 (1)B (2)A规律方法 (1)根据含逻辑联结词的命题真假求参数的方法步骤: ①根据题目条件,推出每一个命题的真假(有时不一定只有一种情况); ②求出每个命题是真命题时参数的取值范围; ③根据每个命题的真假情况,求出参数的取值范围. (2)全称命题可转化为恒成立问题.【训练3】 (2017·衡水中学月考)设p :实数x 满足x 2-5ax +4a 2<0(其中a >0),q :实数x 满足2<x ≤5.(1)若a =1,且p ∧q 为真,求实数x 的取值范围.(2)若綈q 是綈p 的必要不充分条件,求实数a 的取值范围.解 (1)当a =1时,x 2-5ax +4a 2<0即为x 2-5x +4<0,解得1<x <4, 当p 为真时,实数x 的取值范围是1<x <4. 若p ∧q 为真,则p 真且q 真, 所以实数x 的取值范围是(2,4).(2)綈q 是綈p 的必要不充分条件,即p 是q 的必要不充分条件. 设A ={x |p (x )},B ={x |q (x )},则B A . 由x 2-5ax +4a 2<0得(x -4a )(x -a )<0, ∵a >0,∴A ={x |a <x <4a },又B ={x |2<x ≤5},则a ≤2且4a >5,解得54<a ≤2. ∴实数a 的取值范围是⎝ ⎛⎦⎥⎤54,2.[思想方法]1.把握含逻辑联结词的命题的形式,特别是字面上未出现“或”“且”“非”字眼,要结合语句的含义理解.2.含有逻辑联结词的命题真假判断口诀:p ∨q →见真即真,p ∧q →见假即假,p。
福建省福鼎一中高一数学 培优教材(3)素材 新人教版

福鼎一中高一年段数学培优教材第三讲 三角恒等变换一、基础知识:1. 三角的恒等变化:要注意公式间的内在联系和特点,审题时要善于观察差异,寻找联系,实现转化;要熟悉公式的正用和、逆用和变形应用。
化简三角函数式可以采用“切化弦”来减少函数种类,采用“配方法”和“降次公式”来逐步降低各项次数,并设法去分母、去根号、利用特殊值来向目标靠拢。
2. 常见的变形公式:1sin cos sin 22ααα= 221cos 2cos 1cos 2sin 22αααα+=-=22221sin (sincos )2sin ()1sin (sincos )2sin ()22242224αααπαααπαα+=+=+-=-=-tan tan tan()[1tan tan ]αβαβαβ±=±sin cos )a x b x x ωωωϕ+=+3. 通过对角的变换推出万能公式和半角公式以及和差与积的互化公式。
如常见的角的拆并有2()(),(),,(),)2266424αβαβπππππααβαβααββααααα+-=++-=+-=+=+--=-+(等二、综合应用:例1:已知角α的终边上一点(2sin3,2cos3)P -,则α的弧度数为_____________已知32,cot 2παπα<<=3cot cot 22αα-=_________________函数2sin cos ()y x x x x R =∈的最大值是____________________ 化简42212cos 2cos 22tan()sin ()44x x x x ππ-+=-+____________________________ 例2:已知1sin cos 4αβ=,求cos sin αβ的取值范围。
例3:求22sin 20cos 50sin 20cos50++的值。
例4:已知222()sin sin ()sin (),f θθθαθβ=++++其中,αβ是适合0αβπ≤<≤的常数,试问,αβ取何值时,()f θ的值恒为定值?例5:求值:cot15cot 25cot35cot85例6:已知,(0,),sin csc cos()2παββααβ∈⋅=+;(1)求证:2sin cos tan 1sin ααβα=+;(2)求tan β的最大值,并求当tan β取得最大值时tan()αβ+的值。
人教版高中数学高一培优讲义第三章3三角恒等变换复习

第三章 三角恒等变换复习【知识结构】()αααβαβαβαβαcos sin 22sin sin cos cos sin sin =−−−→−=±=±令()cos cos cos sin sin cos cos sin αβαβαβαβααα±==−→−−−=- 令222()t a n t a n t a n t a n t a n αβαβαβ±=±1 ·=-=-⇒211222c o s s i n ααt a n t a n t a n 2212ααα=-c o s c o s s i n c o s 22122122αααα=+=-)sin(cos sin 22ϕ++=+x b a x b x a ,其中2222cos ,sin ba a ba b +=+=ϕϕ。
⎪⎪⎭⎫ ⎝⎛+=+4sin 2cos sin πααα; ⎪⎭⎫ ⎝⎛+=+3sin 2cos 3sin πααα【知识要点】1、化简要求:项数最少、函数种类最少,分母中不含三角函数,能求值,尽可能求值。
2、具体方法:()……222,)角的变换:如1(⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=+-+=βαβαβααβαβ (2)名的变换:化弦或化切 (3)次数的变换:升、降幂公式(4)形的变换:统一函数形式,注意运用代数运算。
()()的值。
,求,如:已知αββαααα2tan 32tan 12cos 1cos sin --=-=- 【章节测试】一、选择题(本大题共10小题,共50.0分) 1、已知,则 A.B. C. D .2、已知,,则的值为A. B. C. D.3、若,则 A. B. C. D.4、若,则 A. B. C. 1 D.5、函数的最大值为A. 4B. 5C. 6D. 76、已知是锐角,,且,则为A. 15B. 30C. 30或60D. 15或757、已知向量,,设函数,则下列关于函数的性质的描述正确的是A. 关于直线对称B. 关于点对称C. 周期为D. 在上是增函数8、如图,扇形的半径为1,圆心角,点P在弧BC上运动,,则的最大值是 A. 1 B. C. 2 D.9、已知,则的值为A. B. C. D.10、若,的值为A. B. C. D.二、填空题(本大题共4小题,共20.0分)11、______.12、函数的图象可由函数的图象至少向右平移______个单位长度得到.13、化简的结果是______.14、设常数a使方程在闭区间上恰有三个解,,,则______.三、解答题(本大题共2小题,共30.0分) 15、已知,且.求 的值;若,,求 的值.16、已知函数R x x x x x f ∈-+=,sin 2cos sin 321)(2求函数 的单调区间;若把 向右平移个单位得到函数 ,求 在区间上的最小值和最大值.答案和解析1.【答案】A【分析】本题考查了二倍角公式,属于基础题.由条件,两边平方,根据二倍角公式和平方关系即可求出.【解答】解:,,,故选A.2.【答案】C【分析】本题考查两角差的正切函数公式在三角函数化简求值中的应用,属于基础题.由已知利用两角差的正切函数公式,即可化简求值得解.【解答】解:,,.故选C.3.【答案】D【分析】本题考查了同角三角函数的基本关系和二倍角的余弦函数公式,解题的关键是利用同角三角函数中的平方关系,完成弦切的互化,属于基础题.利用余弦函数的二倍角公式可求得,进而利用同角三角函数的基本关系式完成弦切的互化,然后把的值代入即可.【解答】解:由,得,故选D.4.【答案】A【分析】本题主要考查三角函数的化简求值,同角三角函数的关系式,二倍角公式的应用,“弦”化“切”是关键,属于基础题.将所求的关系式的分母“1”化为,再将“弦”化“切”即可得到答案.【解答】解:,.故选A.5.【答案】B【分析】本题考查三角函数的最值的求法,注意运用二倍角公式和诱导公式,同时考查可化为二次函数的最值的求法,属于中档题.运用二倍角的余弦公式和诱导公式,可得 ,令 ,可得函数 ,配方,结合二次函数的最值的求法,以及正弦函数的值域即可得到所求最大值.【解答】解:函数, 令 ,可得函数,函数 在 上单调递增,即当 ,,时,函数取得最大值5.故选B . 6.【答案】C【分析】本题主要考查平面向量平行的坐标表示,二倍角的正弦公式,属于一般题.根据题意,由 ,结合向量平行的坐标表示公式可得,由二倍角的正弦公式可得,又由 的范围可得 或 ,即可得答案.【解答】解:根据题意,)31,(cos ),sin ,43(αα==b a , 若 ,则有,即有, 又由 是锐角,则有 ,得 或 ,则 或 ,故选C . 7.【答案】D【分析】本题考查了三角恒等变换,正弦函数的图象与性质,考查向量的数量积,属于中档题.利用三角恒等变换化简 的解析式,根据正弦函数的性质判断. 【解答】解:,当 时, , 不关于直线对称,选项A 错误; 当时, , 关于点 对称,不关于点对称,选项B错误;得周期,选项C错误;当时,,在在上是增函数,选项D正确.故选D.8.【答案】C【分析】本题考查了向量的坐标运算,向量的几何运用,三角函数的性质,辅助角公式.建立坐标系,求出向量坐标,设,,根据向量坐标的运算得到,,则,根据三角函数的性质即可求出最值.【解答】解:以AB为x轴,以A为原点,建立坐标系,如图,设,,则,,,,,,,,,,,,当时,的最大值为2.故选C.9.【答案】A【分析】本题主要考查同角三角函数的基本关系、二倍角的余弦公式的应用,属于基础题.由题意利用同角三角函数的基本关系求得的值,再利用二倍角的余弦公式求得的值.【解答】解:已知,,则,故选A.10.【答案】A【解析】解:,.故选:A.本题主要考查了诱导公式和二倍角的余弦公式的应用,属于基本知识的考查.由已知利用诱导公式及二倍角的余弦求得的值.11.【答案】1【分析】本题考查了两角和与差的三角函数公式,属于基础题.根据 ,利用两角和的正切公式,化简整理得到 ,再代入原式即可算出所求的值.【解答】解: , ,,去分母整理,得 , 原式 .故答案为1. 12.【答案】【分析】本题考查辅助角公式的应用和函数 的图象变换得到 的图象,属于中档题.令,则,依题意可得,由)(323Z k k ∈-=-ππϕπ,可得答案.【解答】解:,,,令,则)(323Z k k ∈-=-ππϕπ,即)(322-Z k k ∈+=ππϕ,当 时,正数 ,故答案为. 13.【答案】1【分析】本题主要考查了三角函数的切化弦及辅助角公式、诱导公式,二倍角公式,在化简求值中的应用 利用三角函数的切化弦及辅助角公式、诱导公式等对函数式化简即可求解,属于中档题.【解答】解:110cos )1030sin(50sin 20000=+= ,故答案为1.14.【答案】【分析】本题主要考查了三角函数图象与性质.运用了数形结合的思想,较为直观的解决问题,属于中档题.先利用两角和公式对函数解析式化简,画出函数的图象,方程的解即为直线与三角函数图象的交点,在上,当时,直线与三角函数图象恰有三个交点,进而求得此时,,最后相加即可.【解答】解:,方程的解即为在上直线与三角函数图象的交点,当时,直线与三角函数图象恰有三个交点,不妨令,,即,或,即,此时,,,.故答案为.15.【答案】解:,且,,.,,,,,.【解析】本题主要考查同角三角函数的基本关系,三角函数在各个象限中的符号,二倍角的正弦公式,以及两角和差的正弦公式的应用,属于中档题.利用同角三角函数的基本关系,三角函数在各个象限中的符号,求得的值,再利用二倍角的正弦公式求得的值.先确定,可得的值,再根据,利用两角差的正弦公式求得结果.16.【答案】解:,,令,,得,,可得函数的单调增区间为,;令,,得,,可得函数 的单调减区间为, ;若把函数 的图像向右平移个单位, 得到函数)62sin(2]6)6(2sin[2)(πππ-=+-=x x x g 的图像,,,]1,2[)62sin(2)(-∈-=∴πx x g .故 在区间上的最小值为 ,最大值为1.【解析】本题主要考查三角函数的化简及函数 的图象性质和最值,考查了学生的计算能力,培养了学生分析问题与解决问题的能力,属于中档题.利用二倍角公式和辅助角公式,化简函数 的解析式,再利用正弦函数的单调性,求得函数 的单调区间;利用函数 的图象变换规律求得 的解析式,由x 的范围求出 的范围,即可利用正弦函数的性质求出 的范围.。
2018-2019版培优导学计划数学必修3人教A版课件:第一

(3)将解决问题的过程划分为若干步骤.
(4)用简练的语言将这个步骤表示出来.
跟踪训练4 判断一个大于2的整数是否为质数的算法步骤如何设计? 解 第一步,给定大于2的整数n. 第二步,令i=2. 第三步,用i除n,得到余数r. 第四步,判断“r=0”是否成立. 若是,则n不是质数,结束算法; 否则,将i的值增加1,仍用i表示. 第五步,判断“i>(n-1)”是否成立. 若是,则n是质数,结束算法; 否则,返回第三步.
跟踪训练3
已知一个等边三角形的周长为 a,求这个三角形的面积.
设计一个算法解决这个问题. 解 第一步,输入a的值.
a 第二步,计算 l=3的值.
3 2 第三步,计算 S= 4 ×l 的值.
第四步,输出S的值.
解答
命题角度2 非数值性问题的算法
例4
所谓正整数 p 为素数是指: p 的所有约数只有 1 和p.例如,35 不是
来完成.设计算法的关键是把过程分解成若干个明确的步骤,然后用计算
机能够接受的“语言”准确地描述出来,从而达到让计算机执行的目的.
(2)设计算法的要求
①写出的算法必须能解决一类问题.
②要使算法尽量简单、步骤尽量少.
③要保证算法步骤有效,且计算机能够执行.
[思考辨析 判断正误]
1.算法是解决一个问题的方法.( × )
第一章 §1.1
算法与程序框图
1.1.1 算法的概念
学习目标
1.了解算法的含义和特征.
2.会用自然语言描述简单的具体问题的算法.
内容索引
问题导学
题型探究
达标检测
问题导学
知识点一
算法的概念
思考 解决一个问题的算法是唯一的吗? 答案 不唯一.如解二元一次方程组的算法有加减消元法和代入消元
新高考高三数学培优教辅

新高考高三数学培优教辅
以下是几款常见的新高考高三数学培优教辅书籍:
1. 《高考数学新高度》:该教辅主要是根据新高考考纲编写的,重点讲解了高考数学的基础知识和应用题的解题技巧。
书中还包含大量的例题和习题,以帮助学生巩固所学内容。
2. 《高中数学必修一二三新教程》:这是一套完整的高中数学教辅书,涵盖了高一、高二、高三的数学内容。
书中结构清晰,讲解详细,题型齐全,对于希望系统复习数学知识的学生来说非常适用。
3. 《新高考数学理综同步备考辅导教材》:该教辅是专门针对新高考数学理综科目编写的,包括了数学和理科其他学科的内容。
书中的知识点讲解深入浅出,题目类型丰富多样,适合高三学生备考复习。
4. 《高中数学考点全解析》:这本教辅针对高中数学的重点、难点进行了详细讲解,并附有大量例题和习题,帮助学生加深对知识点的理解和掌握。
5. 《新高考数学冲刺复习指南》:这是一本针对高三学生的冲刺复习教辅,主要涵盖了各个章节的核心知识点和重要题型的解题方法。
书中还包括模拟试题和真题训练,帮助学生熟悉考试形式和提高应试能力。
以上仅为一些建议,具体选择教辅书还需根据个人学习情况和需求进行选择。
新教材高中数学培优课__排列与组合的综合应用新人教A版选择性必修第三册

C24 ×C36
第 2 类,两组都是 3 男 2 女,考虑两组没有顺序,因此有
因此不同的分派种数为C41 × C64 +
C24 ×C36
A22
A22
种不同的选法.
=120.
分派到两地有A22 种方法,每个小组选出正、副组长各有A25 种选法,故一共有
N=120A22 × A25 × A25 =96 000 种方法.
法;第 3 步,将 3 名副局长分到 3 地有A33 种不同的方法.根据分步乘法计数原
C35 ×C12 ×C11
理,不同的安排方法共有(
A22
+
C15 ×C24 ×C22
A22
)×A33 × A33 =900 种,故选 B.
探究点四
排列、组合的综合应用
【例4】 从1到6这6个数字中,取2个偶数和2个奇数组成没有重复数字的四
36 种.
邻,则不同的摆法有
解析 记其余两种产品为 D,E,由于 A,B 相邻,则视为一个元素,先与 D,E 排列,
有A22 × A33 种方法.
再将 C 插入,仅有 3 个空位可选,故共有A22 × A33 × C31 =2×6×3=36 种不同的摆
法.
规律方法
求解排列问题的六种主要方法
直接法
把符合条件的排列数直接列式计算
均分 后一定要除以 A (n为均分的组数),避免重复计数
部分 解题时注意重复的次数是均匀分组的阶乘数,即若有m组元素个数相
均分 等,则分组时应除以m!
不等 只需先分组,后排列,注意分组时任何组中元素的个数都不相等,所以
分组 不需要除以全排列数
变式训练3某局安排3名副局长带5名职工去3地调研,每地至少去1名副局
人教版高中数学高一培优讲义第二章复习
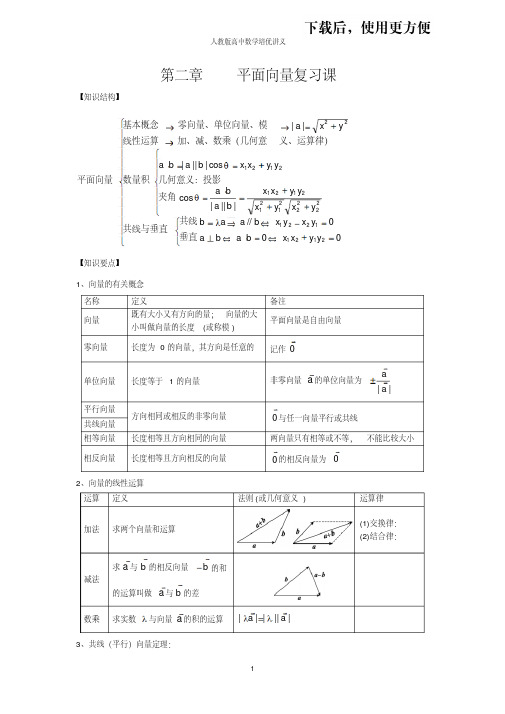
则
,
,
,设
,则
,
,则
,当
,
时,
, 取得最小值,
其最小值为
,故选 B .
4.【答案】 A
【分析】本题考查了平面向量的线性表示与数量积运算问题,属于基础题.
根据平面向量的线性表示与数量积运算,结合题意可得出
是等腰三角形.
【解答】解:因为
,即
, 又因 为
,所以
,
所以
,即
,所以
是等腰三角形.故选 A .
5.【答案】 D
答案和解析
1.【答案】 A
【分析】本题考查向量的加法、减法、数乘运算,平面向量的基本定理及其应用,考查了推 理能力与计算能力, 属于基础题.通过利用向量的三角形法则,以及向量共线,代入化简即 可得出.
【解答】解:
,
.故选 A .
2.【答案】 A
【分析】本题考查两个向量的关系的判断,属于基础题.由已知得
(4)、向量的数量积的几何意义:等于 a 的长度与 b 在 a 方向上投影 | b | cos 的乘积 .
7、两个向量的数量积的性质:
设 a 、 b 为两个非零向量
(1) a b a b 0
(2)当 a 与 b 同向时, a b | a || b |;当 a 与 b 反向时, a b | a ||b | .
【分析】本题考查了向量坐标运算性质、同角三角函数的关系,两角和差的三角函数公式,
属于中档题. 建立适当坐标系, 利用同角三角函数的关系和两角和差的三角函数的公式求得
各点的坐标,进而利用平面向量的坐标运算得到关于
m, n 的方程组,求得 m, n 的值,即
得.
【解答】解:如图所示,建立直角坐标系.
2019-2020学年新培优同步人教B版高中数学必修一课件:第3章 基本初等函数 3.2.2

题型一 题型二 题型三 题型四 题型五
【变式训练2】 求下列函数的值域: (1)f(x)=log3(2x-1),x∈[2,14];
解:(1)当2≤x≤14时,3≤2x-1≤27, 故1≤log3(2x-1)≤3, 即函数的值域为[1,3]. (2)因为3+2x-x2=-x2+2x-1+4=-(x-1)2+4≤4,
题型一 题型二 题型三 题型四 题型五
分析:按照求函数定义域的基本要求以及对数式中“真数大于0” 这一限制条件,列不等式组求解.
题型一 题型二 题型三 题型四 题型五
题型一 题型二 题型三 题型四 题型五
反思根据解析式,求与对数有关的函数的定义域,除了我们以前知 道的限制条件外,还要注意对数的底数大于0不等于1,真数大于0.
题型一 题型二 题型三 题型四 题型五
题型一 题型二 题型三 题型四 题型五
【例5】 画出函数y=|log2(x+1)|+2的图象. 分析:可先画出它的基本函数的图象,再做适当的变换,然后分步 骤完成.
解:第一步:作y=log2x的图象,如图①所示.
第二步:将y=log2x的图象沿x轴向左平移1个单位,得y=log2(x+1)
题型一 题型二 题型三 题型四 题型五
题型一 题型二 题型三 题型四 题型五
【例4】 画出函数y=log2x2的图象,并根据图象指出它的单调区 间.
分析:先对函数的定义域及奇偶性进行探索,再画图象研究函数 的单调区间.
题型一 题型二 题型三 题型四 题型五
解:由题意知,函数的定义域为(-∞,0)∪(0,+∞),关于原点对称. 因为f(-x)=log2(-x)2=log2x2=f(x), 所以y=log2x2是偶函数,它的图象关于y轴对称. 当x>0时,y=log2x2=2log2x,因此先画出 y=2log2x(x>0)的图象为C1,再作出C1关于y轴对 称的图象C2,C1与C2构成函数y=log2x2的图象,如图所示. 由图象可以知道函数y=log2x2的单调递减区间是(-∞,0),单调递增 区间是(0,+∞). 反思作图象时一定要考虑函数的定义域,否则会求出错误的单调 区间.同时在确定单调区间时,要注意单调区间的分界点,特别要注 意区间的开与闭.
2019-2020学年人教A版数学必修第一册培优教程课件:第3章 函数的概念与性质 3.2 3.2.

=f(x)的单调区间.
第五页,编辑于星期六:二十三点 十五分。
【新知拓展】 1.单调性是函数的局部性质,但在其单调区间上是整体性质,因此对 x1,x2 有下列要求: (1)属于同一个区间 D; (2)任意性,即 x1,x2 是定义域中某一区间 D 上的任意两个值,不能用特 殊值代替; (3)有大小,即确定的任意两值 x1,x2 必须区分大小,一般令 x1<x2. 2.并非所有的函数都具有单调性.如 f(x)=01,,xx是是奇偶数数,, 它的定义域为 N,但不具有单调性.
由图象知函数的单调区间为(-∞,-3],[3,+∞). 其中,单调递减区间为(-∞,-3],单调递增区间为[3,+∞).
答案
第二十一页,编辑于星期六:二十三点 十五分。
金版点睛 常用画图象求单调区间
(1) 对 于函数 y=kx+bk≠0,y=ax2+bx+ca≠0,y=kxk≠0 单 调区 间的确定,常借助于函数图象直接写出.
第二页,编辑于星期六:二十三点 十五分。
核心概念掌握
第三页,编辑于星期六:二十三点 十五分。
【知识导学】
知识点一
函数的单调性及其符号表达
(1)函数单调性的概念
_□0_1_函__数__值__随__自__变_量__的__增__大__而_增__大__(_或_减 __小__)_的__性_质______叫做函数的单调性.
第1课时 函数的单调性
第一页,编辑于星期六:二十三点 十五分。
(教师独具内容) 课程标准:1.理解函数的单调性和单调区间的概念.2.会划分函数的单调 区间,判断函数的单调性,会用符号语言表达函数的单调性.3.会用定义证明 函数的单调性. 教学重点:1.函数单调性的定义及其几何特征.2.用定义证明函数的单调 性. 教学难点:用定义证明函数的单调性.
2019-2020学年人教A版数学必修第一册培优教程课件:第3章 函数的概念与性质 3.2 3.2.

4.已知f(x)为R上的奇函数,且当x>0时,f(x)=x2+1x,则f(-1)=(
)
A.1 B.2 C.-1 D.-2
答案 D
解析 因为函数f(x)为R上的奇函数,且当x>0时,f(x)=x2+1x,所以f(- 1)=-f(1)=-(1+1)=-2.故选D.
答案
解析
第五页,编辑于星期六:二十三点 十五分。
∴f(-x)=-f(x). ∴f(x)=-f
x2-2x,x≥0, -x2-2x,x<0.
答案
解析
第八页,编辑于星期六:二十三点 十五分。
8.已知奇函数f(x)在R上单调递增,∀m∈[-2,2],f(mx-2)+f(x)<0恒成 立,则x的取值范围是________.
答案
第十一页,编辑于星期六:二十三点 十五分。
B级:“四能”提升训练 1.定义在R上的函数f(x)满足f(x)=f(4-x),且f(2-x)+f(x-2)=0,求 f(2020)的值.
解 ∵f(2-x)+f(x-2)=0, 令t=x-2,得x=t+2,代入有f(-t)+f(t)=0, ∴f(x)为奇函数,则有f(0)=0. 又∵f(x+4)=f[4-(x+4)]=f(-x)=-f(x), ∴f(x+8)=-f(x+4)=f(x),f(4)=f(0)=0, ∴f(2020)=f(2012+8)=f(2012)=f(2004+8)=f(2004)=…=f(4)=f(0)= 0.
是偶函数.
答案
解析
第二页,编辑于星期六:二十三点 十五分。
2.函数f(x)=1x-x的图象( A.关于y轴对称 C.关于坐标原点对称
)
B.关于直线y=x对称 D.关于直线y=-x对称
答案 C
2019-2020学年人教A版高中数学必修三培优新方案同步课件:1.1 第2课时 程序框图、顺序结构

D.4 个
第九页,编辑于星期六:二十三点 三十六分。
[解析] 任何一个程序必须有开始和结束,从而流程 图必须有起止框,①正确.输入、输出框可以用在算法中 任何需要输入、输出的位置,②错误.③正确.判断框内 的条件不是唯一的,④错误.故选 B.
[答案] B
第十页,编辑于星期六:二十三点 三十六分。
[类题通法]
第八页,编辑于星期六:二十三点 三十六分。
[典例精析]
下列关于程序框图中图形符号的理解正确的有( )
①任何一个流程图必须有起止框;②输入框只能放在开
始框后,输出框只能放在结束框前;③判断框是唯一的具有
超过一个退出点的图形符号;④对于一个程序框图来说,判
断框内的条件是唯一的.
A.1 个
B.2 个
C.3 个
第十二页,编辑于星期六:二十三点 三十六分。
解析:选 D 由程序框图的定义知,①②③④均正 确,故选 D.
第十三页,编辑于星期六:二十三点 三十六分。
探究点二 顺序结构 [思考探究] 观察如图所示的内容:
第十四页,编辑于星期六:二十三点 三十六分。
(1)顺序结构有哪些结构特征? 名师指津:顺序结构的结构特征: ①顺序结构的语句与语句之间、框与框之间按从上 到下的顺序执行,不会引起程序步骤的跳转. ②顺序结构是最简单的算法结构. ③顺序结构只能解决一些简单的问题.
第五页,编辑于星期六:二十三点 三十六分。
三、综合迁移·深化思维
(1)一个完整的程序框图一定是以起止框开始,同时又 以起止框表示结束吗?
提示:由程序框图的概念可知一个完整的程序框图一定 是以起止框开始,同时又以起止框表示结束.
(2)顺序结构是任何算法都离不开的基本结构吗? 提示:根据算法基本逻辑结构可知顺序结构是任何算法 都离不开的基本结构.
2019-2020学年新培优同步人教B版高中数学必修一课件:第3章 基本初等函数 3.1.2

题型一 题型二 题型三 题型四 题型五
题型一 题型二 题型三 题型四 题型五
反思1.在进行幂值的大小比较时,若底数相同,则可根据指数函数 的单调性得出结果;若底数不相同,则首先考虑能否化为同底数,然 后根据指数函数的单调性得出结果;不能化成同底数的,要考虑引 进第三个数(如0,1等)分别与之比较,从而得出结果.总之,比较时要 尽量转化成同底的形式,根据指数函数的单调性进行判断.
3增加到27,说明当x>0时,函数y=3x的函数值比y=2x的函数值增长得 快.
对于指数函数y=ax(a>0,且a≠1),将底数a由2变为3,发现它们的图 象发生了显著变化,在第一象限内,底数a越小,函数的图象越接近x 轴.
归纳总结指数幂ax和1的比较: 当x<0,a<1或x>0,a>1时,ax>1,即指数x和0比较,底数a和1比较,当 不等号的方向相同时,ax大于1,简称为“同大”; 当x<0,a>1或x>0,a<1时,ax<1,即指数x和0比较,底数a和1比较,当 不等号的方向相反(异)时,ax小于1,简称为“异小”. 因此简称为“同大异小”.
解:如图所示,由图象经过第一、三、四象限,可知a>1.当x=0时,y<0, 即a0+b<0,故b<-1. 故a,b的取值范围分别是(1,+∞),(-∞,-1).
知识拓展1.当底数a的大小不确定时,必须分“a>1”和“0<a<1”两 种情形讨论.
2022人教A版高中数学选择性必修第三册同步培优第六章计数原理第2节排列与组合 习题课 排列数的应用

第六章 习题课A 组·素养自测一、选择题1.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( D ) A .24 B .48 C .60D .72[解析] 由题意,可知个位可以从1,3,5中任选一个,有A 13种方法,其他数位上的数可以从剩下的4个数字中任选,进行全排列,有A 44种方法,所以奇数的个数为A 13A 44=3×4×3×2×1=72.2.(2021·嘉兴一中月考)从2,3,4,5,6,7,8,9这8个数字中任取2个不同的数字分别作为一个对数的底数和真数,则可以组成不同对数值的个数为( D )A .56B .54C .53D .52[解析] 在8个数中任取2个不同的数可以组成A 28=56(个)对数值.但在这56个对数值中,log 24=log 39,log 42=log 93,log 23=log 49,log 32=log 94,即满足条件的对数值共有56-4=52(个).3.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,那么不同的排法有( C )A .48种B .24种C .60种D .120种[解析] 五门课程随意安排有A 55种排法,数学课在历史课前和历史课在数学课前各占总排法数的一半,所以数学课排在历史课前的排法有12A 55=60(种).4.(多选)停车站划出一排12个停车位置,今有8辆不同的车需要停放,若要求剩余的4个空车位连在一起,则不同的停车方法有( AD )A .A 99种B .A 99A 44种 C .8A 88种D .9A 88种 [解析] 将4个空车位视为一个元素,与8辆车共9个元素进行全排列,共有A 99=9A 88种.5.三位女生坐到二排四列的8个位置中,要求同列中最多只有一个女生,同排中任两个女生不相邻,则不同的排法数为(A)A.72 B.36C.48 D.96[解析]根据题意,完成这件事可分两步:第一步,先在8个位置中选取符合条件的3个位置,有2×2+2×4=12种情况;第二步,将三位女生全排列,安排到选出的3个位置,有A33=6种情况.根据分步乘法计数原理,共有12×6=72种排法.二、填空题6.用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1,2相邻,这样的六位数的个数是__40__.[解析]可分为三步来完成这件事:第一步:先将3,5进行排列,共有A22种排法;第二步:再将4,6插空排列,共有2A22种排法;第三步:将1,2放入3,5,4,6形成的空中,共有A15种排法;由分步乘法计数原理得,共有2A22A22A15=40种不同的排法.7.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是__96__.[解析]先分组后用分配法求解,5张参观券分为4组,其中2个连号的有4种分法,每一种分法中的排列方法有A44种,因此共有不同的分法4A44=4×24=96(种).8.2020年某地举行博物展,某单位将展出5件艺术作品,其中不同书法作品2件、不同绘画作品2件、标志性建筑设计1件,在展台上将这5件作品排成一排,要求2件书法作品必须相邻,2件绘画作品不能相邻,则该单位展出这5件作品不同的方案有__24__种.(用数字作答)[解析]将2件书法作品排列,方法数为2种,然后将其作为1件作品与标志性建筑设计作品共同排列有2种排法,对于其每一种排法,在其形成的3个空位中选2个插入2件绘画作品,故共有不同展出方案:2×2×A23=24种.三、解答题9.一场晚会有5个演唱节目和3个舞蹈节目,要求排出一个节目单.(1)3个舞蹈节目不排在开始和结尾,有多少种排法?(2)前四个节目要有舞蹈节目,有多少种排法?[解析](1)先从5个演唱节目中选两个排在首尾两个位置有A25种排法,再将剩余的3个演唱节目,3个舞蹈节目排在中间6个位置上有A 66种排法,故共有不同排法A 25A 66=14 400种.(2)先不考虑排列要求,有A 88种排列,其中前四个节目没有舞蹈节目的情况,可先从5个演唱节目中选4个节目排在前四个位置,然后将剩余四个节目排列在后四个位置,有A 45A 44种排法,所以前四个节目要有舞蹈节目的排法有A 88-A 45A 44=37 440种.10.从-3,-2,-1,0,1,2,3,4八个数字中任取3个不同的数字作为二次函数y =ax 2+bx +c 的系数a ,b ,c ,问:(1)共能组成多少个不同的二次函数?(2)在这些二次函数中,图象关于y 轴对称的有多少个? [解析] (1)方法一(直接法——优先考虑特殊位置)因为a ≠0,所以确定二次项系数有7种,确定一次项和常数项有A 27种,所以共有7A 27=294个不同的二次函数.方法二(直接法——优先考虑特殊元素)当a ,b ,c 中不含0时,有A 37个;当a ,b ,c 中含有0时,有2A 27个,故共有A 37+2A 27=294(个)不同的二次函数.方法三(间接法)共可构成A 38个函数,其中当a =0时,有A 27个均不符合要求,从而共有A 38-A 27=294(个)不同的二次函数.(2)依题意b =0,所以共有A 27=42(个)符合条件的二次函数.B 组·素养提升一、选择题1.(多选)用0,1,2,3,4,5组成没有重复数字的6位数,其中个位数字小于十位数字的六位数共有( AB )A .A 15A 35个 B .12A 15A 55个C .A 15A 55个D .2A 15A 44个 [解析] 解法一:确定最高位有A 15种不同方法.确定万位、千位、百位,从剩下的5个数字中取3个排列,共有A 35种不同的方法,剩下两个数字,把大的排在十位上即可,由分步乘法计数原理知,共有A 15·A 35=300(个).解法二:由于个位数字大于十位数字与个位数字小于十位数字的应各占一半,故有12 A15·A55=300(个).2.某地为了迎接运动会,在某大楼安装了5个彩灯,它们闪亮的顺序不固定.每个彩灯只能闪亮红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯所闪亮的颜色各不相同,记这5个彩灯有序地各闪亮一次为一个闪烁.在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒.如果要实现所有不同的闪烁,那么需要的时间至少是(C)A.1 205秒B.1 200秒C.1 195秒D.1 190秒[解析]由题意每次闪烁共5秒,所有不同的闪烁为A55个,相邻两个闪烁的时间间隔为5秒,因此需要的时间至少是5A55+(A55-1)×5=1 195(秒).3.有4本不同的书A,B,C,D,要分给三个同学,每个同学至少分一本,书A,B 不能分给同一人,则这样的分法共有(C)A.18种B.24种C.30种D.36种[解析]4本不同的书分给三个同学,共有6A33=36,书A,B分给同一人有A33=6,所以共有36-6=30种,故选C.4.(北京高考题)把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有(B)A.48 B.36C.30 D.24[解析]将A,B捆绑在一起,有A22种摆法,再将它们与其他3件产品全排列,有A44种摆法,共有A22A44种摆法,而A,B,C 3件产品在一起,且A,B相邻,A,C相邻时有2种情况,将这3件产品与剩下2件产品全排列,有2A33种摆法.故A,B相邻,A,C不相邻的摆法有A22A44-2A33=36(种).二、填空题5.6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为__576__.[解析]“不能都站在一起”与“都站在一起”是对立事件,由间接法可得A66-A33A44=576.6.如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形后,按虚线折成正方体,则所得到的正方体相对面上的两个数的和都相等的概率是__115__.[解析] 6个数任意填入6个小正方形中有A 66=720种方法;将6个数分三组(1,6),(2,5),(3,4),每组中的两个数填入一对面中,共有不同填法A 33×2×2×2=48种,故所求概率P =48720=115. 三、解答题7.用0,1,2,3,4五个数字:(1)可组成多少个五位数;(2)可组成多少个无重复数字的五位数;(3)可组成多少个无重复数字的且是3的倍数的三位数;(4)可组成多少个无重复数字的五位奇数.[解析] (1)各个数位上的数字允许重复,故由分步乘法计数原理知,共有4×5×5×5×5=2 500(个).(2)解法一:先排万位,从1,2,3,4中任取一个有A 14种填法,其余四个位置四个数字共有A 44种,故共有A 14·A 44=96(个).解法二:先排0,从个、十、百、千位中任选一个位置将0填入有A 14种方法,其余四个数字全排有A 44种方法,故共有A 14·A 44=96(个).(3)构成3的倍数的三位数,各个位上数字之和是3的倍数,按取0和不取0分类:①取0,从1和4中取一个数,再取2进行排,先填百位A 12,其余任排有A 22,故有2A 12·A 22种.②不取0,则只能取3,从1或4中再任取一个,再取2然后进行全排为2A 33,所以共有2A 12A 22+2A 33=8+12=20(个).(4)考虑特殊位置个位和万位,先填个位,从1,3中选一个填入个位有A 12种填法,然后从剩余3个非0数中选一个填入万位,有A 13种填法,包含0在内还有3个数在中间三位置上全排列,排列数为A 33,故共有A 12·A 13·A 33=36(个).8.4名男同学和3名女同学站成一排.(1)7名同学中,甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种不同的排法?(2)7名同学中,甲乙两名同学之间必须恰有3名同学,有多少种不同的排法?(3)7名同学中,甲、乙两名同学相邻,但都不与丙相邻,有多少种不同的排法?(4)女同学从左到右按从高到矮的顺序排,有多少种不同的排法?(3名女生身高互不相等)[解析](1)7名同学的所有排法有A77种,其中甲、乙、丙的排序有A33种,所以甲、乙、=840(种).丙排序一定的排法有A77A33(2)先排甲、乙两名同学,有A22种排法,再从余下5名同学中选3名同学排在甲、乙两名同学中间,有A35种排法,这时把已排好的5名同学视为一个整体,与最后剩下的2名同学进行全排列,有A33种排法,故不同的排法共有A22A35A33=720(种).(3)先排除甲、乙、丙3名同学以外的其他4名同学,有A44种排法,由于甲、乙要相邻,故再把甲、乙排好,有A22种排法,最后把排好的甲、乙看作一个整体与丙分别插入原先排好的4名同学形成的5个空位中,有A25种排法,故不同的排法共有A44A22A25=960(种).(4)从7个位置中选出4个位置把男生排好,有A47种排法,然后在余下的3个位置中排女生,由于要求女生从左到右按从高到矮的顺序排,故女生的排法只有1种,故不同的排法共有A47×1=840(种).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一年段数学培优教材第三讲 三角恒等变换
一、基础知识:
1. 三角的恒等变化:要注意公式间的内在联系和特点,审题时要善于观察差异,寻找联系,实现转化;
要熟悉公式的正用和、逆用和变形应用。
化简三角函数式可以采用“切化弦”来减少函数种类,采用“配方法”和“降次公式”来逐步降低各项次数,并设法去分母、去根号、利用特殊值来向目标靠拢。
2. 常见的变形公式:1sin cos sin 22ααα= 22
1cos 2cos 1cos 2sin 2
2
α
α
αα+=-=
22221sin (sin
cos )2sin ()
1sin (sin
cos )2sin ()2224
2224
α
ααπ
α
ααπ
αα+=+=+-=-=-
tan tan tan()[1tan tan ]αβαβαβ±=±
sin cos )a x b x x ωωωϕ++
3. 通过对角的变换推出万能公式和半角公式以及和差与积的互化公式。
如常见的角的拆并有
2()(),(),,(),)
2
2
66424
αβ
αβ
πππππ
ααβαβααββααααα+-=++-=+-=
+
=+--=-+(等
二、综合应用:
例1:已知角α的终边上一点(2sin 3,2cos3)P -,则α的弧度数为_____________
已知
32,cot 2παπα<<=3cot cot 22αα-=_________________
函数2
sin cos ()y x x x x R =∈的最大值是____________________ 化简
4221
2cos 2cos 22tan()sin ()
44
x x x x ππ-+
=-+____________________________ 例2:已知1
sin cos 4
αβ=,求cos sin αβ的取值范围。
例3:求22
sin 20cos 50sin 20cos50++的值。
例4:已知222
()sin sin ()sin (),f θθθαθβ=++++其中,αβ是适合0αβπ≤<≤的常数,试问,αβ取
何值时,()f θ的值恒为定值?
例5:求值:cot15cot 25cot 35cot 85
例6:已知,(0,
),sin csc cos()2
π
αββααβ∈⋅=+;
(1)求证:2sin cos tan 1sin αα
βα
=+;
(2)求tan β的最大值,并求当tan β取得最大值时tan()αβ+的值。
例7:已知0,2
π
αβ<<
,且sin()2sin αβα+=,求证:αβ<
例8:已知当[0,1]x ∈时,不等式22cos (1)(1)sin 0x x x x θθ--+->恒成立,求θ的取值范围。
三、强化练习:
1.若角α满足条件sin20α<,cos sin 0αα-<,则α在( )
A 第一象限
B 第二象限
C 第三象限
D 第四象限 2.以下命题正确的是( )
(A )βα,都是第一象限角,若βαcos cos >,则βαsin sin > (B )βα,都是第二象限角,若βαsin sin >,则βαtan tan > (C )βα,都是第三象限角,若βαcos cos >,则βαsin sin > (D )βα,都是第四象限角,若βαsin sin >,则βαtan tan > 3.若ππ43<<x ,则
2
cos 12cos 1x
x -+
+等于 (A ))24cos(2x -π (B ))24cos(2x --π (C ))24sin(2x -π (D ))2
4sin(2x
--π
4.在(0,π2)内,使x x x tan sin cos >>成立的x 的取值范围是 (A )(
4π,43π) (B )(45π,23π) (C )(23π,π2) (D )(23π,4
7π) 5.设βα,是一个钝角三角形的两个锐角,则下列四个不等式中不正确的是
(A )1tan tan <βα (B )2sin sin <+βα (C )1cos cos >+βα (D )2
tan )tan(21β
αβα+<+
6.已知22
cos()cos sin αβθθ++=-,则sin(2)sin αββ++的值为( )
A .0
B .1 C.2sin β D .以上都不对
7.在△ABC 中,已知A 、B 、C 成等差数列,则tan
tan
tan
2
2
2
2
A C A C +=__________
8.已知点P(sin cos αα-,tan α)在第一象限,则在[0,2π)内α的取值范围是____________ 9.cot104cos10-的值为
10.已知2sin 2sin 2cos cos21,(0,)2
π
ααααα+-=∈,求sin ,tan αα的值。
11.已知cos(α-2
β
)=19
-
,sin(
2
α
-β)=
23
,
2
π
<α<π,0<β<
2
π
,求cos(α+β)之值.
12.求值:2345cos
cos
cos cos cos
11
11111111
π
ππππ
13.是否存在锐角,αβ,使得①223
π
αβ+=;②tan tan 22αβ=,αβ的
值;若不存在,说明理由。
参考答案:
例1:32,2
k k π
αππ=-
+∈
1)
1
cos 22
x 例2:法1:11cos sin 13341sin()1,1sin()1cos sin 1441cos sin 1
4
αβαβαβαβαβ⎧-≤+≤⎪⎪-≤+≤-≤-≤⇒⇒-≤≤⎨⎪-≤-≤⎪⎩
法2:
2222222117
cos sin (1sin )(1cos )1(sin cos )[(sin cos )2sin cos ]1616
αβαβαβαβαβ=--=+-+=--+29933
(sin cos ),sin cos 161644
αβαβ=
--≤∴-≤≤ 例3:多种方法。
(构造对偶式)设2222
sin 20cos 50sin 20cos50
2sin 70cos 20sin 50cos 20sin 50a a b b ⎧=++∴+=+⎨=++⎩
1113
cos40cos100sin(30)2sin 70sin30sin 70,222224
a b a a -=-++-=--
=--∴=-∴= 例4:31
()[12cos()cos()]cos2[sin()sin()]sin 222
f θαβαβθαβαβθ=
-++--+- ()f θ恒为定值,12cos()cos()0
sin()0sin()cos()αβαβαβαβαβ++-=⎧∴⇒+=⎨
+-⎩
,考虑到0αβπ≤<≤ 1
22cos(),0,,2
3
3
3
π
π
παβπαβπαβαβαβ∴+=∴-=
-<-<∴-=-
∴=
=
(提示:本题也可以用赋值法:令0,
,,,(0)()()()22
f f f f π
π
θαβαβ=--∴==-=-) 例5:1 (本题要总结公式sin34sin sin(60)sin(60)θθθθ=-+
cos34cos cos(60)cos(60)θθθθ=-+ tan3tan tan(60)tan(60)θθθθ=-+
例6:(2
)2tan 1
tan (tan 12tan 12tan tan αβαααα
=
=
≤
=
++
例7:2sin sin cos cos sin sin sin sin sin ααβαβαββα=+<+⇒>
例8:令0x =则sin 0θ>,令1x =则cos 0θ> 故原不等式化为
2
sin 0
2sin 1(1sin cos )(2sin 1)sin 0,
(0,1),cos 01sin cos 0
x x θθθθθθθθθ>⎧+⎪
++-++>∈∴>⇒⎨++⎪∆<⎩
sin 05cos 0(2,2),12121
sin 22
k k k Z θππ
θθππθ⎧
⎪>⎪>⇒∈++∈⎨⎪⎪>⎩
强化练习: 1. B 2. D 3. C 4. C 5. D 6. A
8. 5(,
)(,
)424
ππ
π
π1sin ,tan 2αα==
11. +
239
cos cos()2
729
αβαβ=
+=- 12.
1
32
13. 存在,6
4
π
π
αβ=
=。
