初中数学竞赛辅导资料(62)
初中数学竞赛辅导资料.doc

初中数学竞赛辅导资料初中数学竞赛辅导资料初一上目录1数的整除(一) 2倍数约数 3质数合数4 零的特性5a n的个位数6数学符号 7用字母表示数 8 抽屉原则初一下目录9一元一次方程解的讨论10二元一次方程的整数解11二元一次方程组解的讨论12用交集解题13用枚举法解题14经验归纳法15乘法公式16整数的一种分类初二上目录17 奇数偶数18 式的整除19因式分解20 恒等式证明21 比较大小22 分式23递推公式24 连续正整数25 十进制的记数法26 选择题解法(一)27识图28三角形边角性质初中数学竞赛辅导资料初二下目录29概念的定义30概念的分类31勾股定理32中位线33同一法34 反证法35两种对称36三点共线37不等关系38、垂直平行39线段、角相等40线段、角和差倍分41线段的比、积、幂42形如1/a+1/b=1/c问题的证明43面积法44数的整除(二)初三上目录45一元二次方程46完全平方式(数)47配方法48非负数49对称式50 基本对称式51待定系数52换元法53 条件等式54整数解55未知数多于方程的个数56列表法57逆推法58观察法59“或者”“并且”60解三角形初三下目录61函数的图象62绝对值63动态几何的定值64最大最小值65图象法66辅助圆67参数法证平几68选择题(二)69数的整除(三) 70正整数简单性质的复习美文欣赏1、走过春的田野,趟过夏的激流,来到秋天就是安静祥和的世界。
秋天,虽没有玫瑰的芳香,却有秋菊的淡雅,没有繁花似锦,却有硕果累累。
秋天,没有夏日的激情,却有浪漫的温情,没有春的奔放,却有收获的喜悦。
清风落叶舞秋韵,枝头硕果醉秋容。
秋天是甘美的酒,秋天是壮丽的诗,秋天是动人的歌。
2、人的一生就是一个储蓄的过程,在奋斗的时候储存了希望;在耕耘的时候储存了一粒种子;在旅行的时候储存了风景;在微笑的时候储存了快乐。
聪明的人善于储蓄,在漫长而短暂的人生旅途中,学会储蓄每一个闪光的瞬间,然后用它们酿成一杯美好的回忆,在四季的变幻与交替之间,散发浓香,珍藏一生!3、春天来了,我要把心灵放回萦绕柔肠的远方。
初中数学竞赛辅导资料
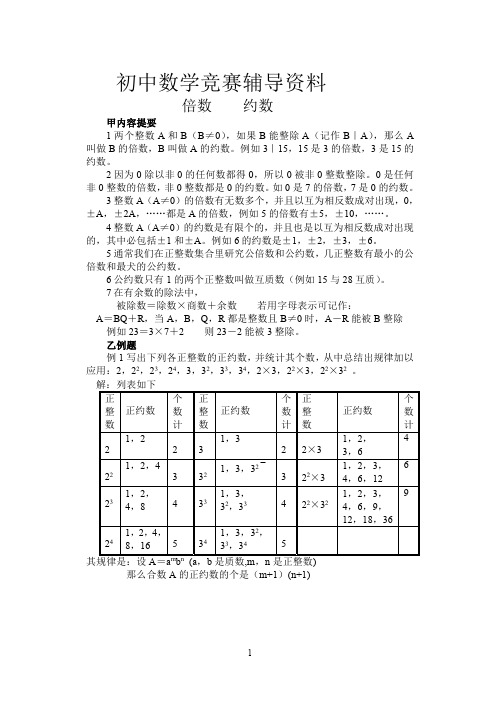
初中数学竞赛辅导资料倍数约数甲内容提要1两个整数A和B(B≠0),如果B能整除A(记作B|A),那么A 叫做B的倍数,B叫做A的约数。
例如3|15,15是3的倍数,3是15的约数。
2因为0除以非0的任何数都得0,所以0被非0整数整除。
0是任何非0整数的倍数,非0整数都是0的约数。
如0是7的倍数,7是0的约数。
3整数A(A≠0)的倍数有无数多个,并且以互为相反数成对出现,0,±A,±2A,……都是A的倍数,例如5的倍数有±5,±10,……。
4整数A(A≠0)的约数是有限个的,并且也是以互为相反数成对出现的,其中必包括±1和±A。
例如6的约数是±1,±2,±3,±6。
5通常我们在正整数集合里研究公倍数和公约数,几正整数有最小的公倍数和最犬的公约数。
6公约数只有1的两个正整数叫做互质数(例如15与28互质)。
7在有余数的除法中,被除数=除数×商数+余数若用字母表示可记作:A=BQ+R,当A,B,Q,R都是整数且B≠0时,A-R能被B整除例如23=3×7+2则23-2能被3整除。
乙例题例1写出下列各正整数的正约数,并统计其个数,从中总结出规律加以应用:2,22,23,24,3,32,33,34,2×3,22×3,22×32。
解:列表如下正整数正约数个数计正整数正约数个数计正整数正约数个数计21,2231,322×31,2,3,64221,2,43321,3,32322×31,2,3,4,6,126231,2,4,84331,3,32,33422×321,2,3,4,6,9,12,18,369241,2,4,8,165341,3,32,33,345其规律是:设A=a m b n(a,b是质数,m,n是正整数)那么合数A的正约数的个是(m+1)(n+1)例如求360的正约数的个数解:分解质因数:360=23×32×5,360的正约数的个数是(3+1)×(2+1)×(1+1)=24(个)例2用分解质因数的方法求24,90最大公约数和最小公倍数解:∵24=23×3,90=2×32×5∴最大公约数是2×3,记作(24,90)=6最小公倍数是23×32×5=360,记作[24,90]=360例3己知32,44除以正整数N有相同的余数2,求N解:∵32-2,44-2都能被N整除,∴N是30,42的公约数∵(30,42)=6,而6的正约数有1,2,3,6经检验1和2不合题意,∴N=6,3例4一个数被10余9,被9除余8,被8除余7,求适合条件的最小正整数分析:依题意如果所求的数加上1,则能同时被10,9,8整除,所以所求的数是10,9,8的最小公倍数减去1。
初中数学竞赛辅导资料(七年级用)

初中数学竞赛辅导资料第一讲 数的整除一、内容提要:如果整数A 除以整数B(B ≠0)所得的商A/B 是整数,那么叫做A 被B 整除. 0能被所有非零的整数整除.能被7整除的数的特征:①抹去个位数 ②减去原个位数的2倍 ③其差能被7整除。
如 1001 100-2=98(能被7整除)又如7007 700-14=686, 68-12=56(能被7整除) 能被11整除的数的特征:①抹去个位数 ②减去原个位数 ③其差能被11整除 如 1001 100-1=99(能11整除)又如10285 1028-5=1023 102-3=99(能11整除) 二、例题例1已知两个三位数328和92x 的和仍是三位数75y 且能被9整除。
求x,y解:x,y 都是0到9的整数,∵75y 能被9整除,∴y=6. ∵328+92x =567,∴x=3 例2已知五位数x 1234能被12整除,求x解:∵五位数能被12整除,必然同时能被3和4整除, 当1+2+3+4+x 能被3整除时,x=2,5,8 当末两位4x 能被4整除时,x =0,4,8∴x=8例3求能被11整除且各位字都不相同的最小五位数解:五位数字都不相同的最小五位数是10234,但(1+2+4)-(0+3)=4,不能被11整除,只调整末位数仍不行调整末两位数为30,41,52,63,均可,∴五位数字都不相同的最小五位数是10263。
练习一1、分解质因数:(写成质因数为底的幂的连乘积)①756②1859③1287④3276⑤10101⑥10296987能被3整除,那么a=_______________2、若四位数ax能被11整除,那么x=__________3、若五位数123435m能被25整除4、当m=_________时,59610能被7整除5、当n=__________时,n6、能被11整除的最小五位数是________,最大五位数是_________7、能被4整除的最大四位数是____________,能被8整除的最大四位数是_________。
南开中学初中数学竞赛辅导资料

初中数学竞赛辅导资料第一讲 数的整除一、内容提要:如果整数A 除以整数B(B ≠0)所得的商A/B 是整数,那么叫做A 被B 整除. 0能被所有非零的整数整除.①抹去个位数 ②减去原个位数的2倍 ③其差能被7整除。
如 1001 100-2=98(能被7整除)又如7007 700-14=686, 68-12=56(能被7整除) 能被11整除的数的特征:①抹去个位数 ②减去原个位数 ③其差能被11整除 如 1001 100-1=99(能11整除)又如10285 1028-5=1023 102-3=99(能11整除) 二、例题例1已知两个三位数328和92x 的和仍是三位数75y 且能被9整除。
求x,y解:x,y 都是0到9的整数,∵75y 能被9整除,∴y=6. ∵328+92x =567,∴x=3 例2已知五位数x 1234能被12整除,求x解:∵五位数能被12整除,必然同时能被3和4整除, 当1+2+3+4+x 能被3整除时,x=2,5,8 当末两位4x 能被4整除时,x =0,4,8∴x=8例3求能被11整除且各位字都不相同的最小五位数解:五位数字都不相同的最小五位数是10234,但(1+2+4)-(0+3)=4,不能被11整除,只调整末位数仍不行调整末两位数为30,41,52,63,均可,∴五位数字都不相同的最小五位数是10263。
练习一1、分解质因数:(写成质因数为底的幂的连乘积)①756 ②1859 ③1287 ④3276 ⑤10101 ⑥10296987能被3整除,那么a=_______________2、若四位数ax能被11整除,那么x=__________3、若五位数123435m能被25整除4、当m=_________时,59610能被7整除5、当n=__________时,n6、能被11整除的最小五位数是________,最大五位数是_________7、能被4整除的最大四位数是____________,能被8整除的最大四位数是_________。
(完整版)初中数学竞赛专题选讲-配方法(含答案)

初中数学竞赛专题[配方法]一、内容提要1. 配方:这里指的是在代数式恒等变形中,把二次三项式a2土2ab+b2写成完全平方式(a土b) 2.有时需要在代数式中添项、折项、分组才能写成完全平方式.常用的有以下三种:①由a +b配上2ab, ②由 2 ab 配上a +b ,③由a2土2ab配上b2.2. 运用配方法解题,初中阶段主要有:①用完全平方式来因式分解例如:把x4+4因式分解.2 2 2 2 2母乱=x +4 + 4x — 4x =(x +2) — 4x = ...........这是由a2+b2配上2ab.②二次根式化简常用公式:福|a ,这就需要把被开方数写成完全平方式.例如:化简、一5一2 6.我们把5-2*写成2 - 2逐+ 3=(克V - ^ 2^3 + (V3)2=(V2 —V3 ).这是由2 ab配上a2+b2.③求代数式的最大或最小值,方法之一是运用实数的平方是非负数,零就是最小值.即a >0, .,•当a=0时, a2的值为0是最小值.例如:求代数式a2+2a — 2的最值... a2+2a— 2= a2+2a+1 - 3=(a+1) 2- 3当a=— 1时,a +2a— 2有最小值—3.这是由a2土2ab配上b2④有一类方程的解是运用几个非负数的和等于零,则每一个非负数都是零,有时就需要配方.例如::求方程x2+y2+2x-4y+5=0的解x, y.解:方程x2+y2+2x-4y+1 + 4= 0.配方的可化为(x+1) 2+(y - 2) 2=0.要使等式成立,必须且只需x 1 0y 2 0x 1 y2解得此外在解二次方程中应用根的判别式,或在证明等式、不等式时,也常要有配方的知识和技巧.二、例题2 2 2 2例 1.因式分解:a b —a +4ab— b +1.解:a b — a +4ab — b +1 = a b +2ab+1+( — a +2ab — b ) (折项,分组)=(ab+1 ) 2 - (a - b):(配方)= (ab+1+a-b ) (ab+1-a+b) (用平方差公式分解)本题的关键是用折项,分组,树立配方的思想^例2.化简下列二次根式:①J7 5 ;②*2焰;③了10时3 2豆. 解:化简的关键是把被开方数配方①(7 4>/3 = J4 2 2/3 3 = J(2 V3)2=2 < 3 = 2 + 43.②户=居=疗=\吁<2(73 1)=无V2 2 . 2③\;10 4^3 2龙=寸10 4》(。
初中数学竞赛辅导资料(62)

初中数学竞赛辅导资料(62)绝对值甲内容提要1. 绝对值的定义:正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值是零.用式子表示如下:⎪⎩⎪⎨⎧=<->=)0(0)0()0(a a a a a a2. 初中阶段学习含绝对值符号的代数式化简,方程、不等式的解法,以及函数作图等.解答时,一般是根据定义先化去绝对值符号,这时关健是按已知条件判断绝对值符号内的式子的值是正或是负,若含有变量的代数式,不能确定其正、负时,则采取零点分区讨论法. 例如:(1)化简 )2(-x x解:当x=0, x=2时, )2(-x x =0;当x<0或x>2时, )2(-x x =x(x -2)=x 2-2x ;当0<x<2时,)2(-x x =-x(x -2)=-x 2+x.(2)解方程2-+x x =6.解:当x<0时,x=-2;当0≤x ≤2时,方程无解;当x>2时,x=4.∴原方程的解是:x=-2, x=4..(3)作函数y=2-+x x 的图象.解:化去绝对值符号,得y=-2x+2 (x<0);y=2 (0≤x ≤2) ;y=2x -2 (x>2).分别作出上述三个函数的图象(如图),就是函数y=2-+x x 的图象.3. 绝对值的几何意义是:在数轴上一个数的绝对值,就是表示这个数的点离开原点的距离. 用这一定义,在解含绝对值符号的方程、不等式时,常可用观察法. 例如: ①解方程3=x ; ②解不等式3<x ; ③解不等式32>+x .解:①∵3=x 的几何意义是:x 是数轴上到原点的距离等于3个单位的点所表示的数,即3和-3,∴方程3=x 的解是x=3, x=-3. ②∵3<x 的几何意义是:x 是数轴上到原点的距离小于3个单位的点所表示的数,∴不等式3<x 的解集是 -3<x <3. ③∵2+x 的零点是x=-2, ∴32>+x 的几何意义是:x 是数轴上到点(-2)的距离大于3个单位的点所表示的数, ∴32>+x 的解集是x<-5或x>1.(如下图)4.①绝对值是非负数; ②两个互为相反数,它们的绝对值相等.根据这些性质,可简化函数的作图步骤. 例如:(1)对整个函数都在绝对值符号内时,可先作出不含绝对值符号的图象,再把横轴下方的部份,绕x 轴向上翻折作函数图象:①y=1-x ②y=22--x x(2) 当f (-x )=f(x),图象关于纵轴对称,这时可先作当x<0时函数图象,再画出关于纵轴对称的图象.例如:y=x 2-2x -3的图象,可先作y=x 2+2x -3自变量x<0时的图象(左半图)再画右半图(与左半图关于纵轴对称).(3) 把y=x 的图象向上平移a 个单位,所得图象解析式是y=a x +; 把y=x 的图象向右平移3个单位,所得图象解析式是y=3-x .(4) 利用图象求函数最大值或最小值,判断方程解的个数都比较方便.乙例题例1. 已知方程x =ax+1有一个负根并且没有正根,求a 的值.(1987年全国初中数学联赛题)解:当x<0时,原方程为-x=ax+1, x=011<+a -, ∴ a+1>0. ∴a>-1;当x>0时,原方程为x=ax+1, x=011>a-, ∴1-a>0. ∴a<1.∵方程有一个负根并且没有正根,∴a>-1且a ≦1,∴a 的取值范围是a ≥1.例2. 求函数y=2x x -3-的最小、最大值. 解:当x<0时, y=-x+6;当0≤x<3时,y=-3x+6;当x ≥3时, y=x -6 .根据图象有最低点而没有最高点∴函数没有最大值只有最小值-3(当x=3时).例3. 解方程:①x x -=+42; ②421=-++x x .解:①∵点(x )到点A (-2)和点B (4)的距离相等(如下图),∴x=1.②∵点(x )到点A (-1)与到点B (2)的距离的和等于4,AB =3∴x=2.5, x=-1.5.例4. 解不等式: ①1≤2+x ≤3; ②121>--+x x .解:①点(x )到点A (-2)的距离大于或等于1而小于或等于3在数轴上表示如图,∴不等式的解集是: -5≤x ≤-3 或-1≤x ≤1②点(x) 到点(-1)的距离,比到点(2)的距离大1个单位以上.在数轴上表示,如图:∴不等式的解集是x>1.例5. a 取什么值时,方程a x =--12 有三个整数解?(1986年全国初中数学联赛题) 解:化去绝对值符号,得12--x =±a, 2-x =1±a , x -2=±(1±a),∴x=2±(1±a) .当a=1时,x 恰好是三个解4,2,0.用图象解答更直观;(1)先作函数 y=12--x 图象,(2)再作y=a(平行于横轴的直线 )与y=12--x 图象相交,恰好是三个交点时,y=1,即a=1.本题若改为:有四个解,则0<a<1;两个解,则 a=0 或a>1;一个解,则a 不存在;无解,则a<0.丙练习621. 方程3+x =4的解是_______.2. 方程6-2-+x x =0的解是________.3. 方程21-++x x =3的解是________.4. 方程x x +-3=5的解是_______.5. 不等式2≤3 -x ≤5的解集是___________________.6. 不等式21-++x x <5的解集是_______________________.7. 不等式21-++x x <3的解集是_______________________.8. 不等式11-2-<x x 的解集是_______________________.9. 已知=-2)3(x 3-x, 那么 =+-x x 1_______________.10. 关于x 的方程x =ax+2有根且只有负根,求a 取值范围.11. a 取什么值时,方程a x =--12无解?有解?有最多解?12. 作函数y=312-+-++x x x 的图象;并求在-3≤x ≤3中函数的最大、最小值.13. 解方程451=-+-x x .14. 作函数y=12+-x x 的图象.15. 选择题:(1972、1973年美国中学数学竞赛试题)①.对于实数x ,不等式1≤|x -2|≤7等价于( )(A ) x ≤1或x ≥3 (B )1≤x ≤3 (C )-5≤x ≤0(D )-5≤x ≤1或3≤x ≤9 (E )-6≤x ≤1或3≤x ≤10②不等式|x -1|+|x+2|<5的所有的实数解的集合是( )(A ){}23<<-x x :(B) {}21<<-x x : (C) {}12<<-x x : (D) {}5.35.1<<-x x :(E) φ(空集)返回目录 参考答案。
初中数学竞赛《容斥原理》练习题及答案 (62)

初中数学竞赛《容斥原理》练习题
1.求1到100的自然数中,所有既不是2的倍数又不是3的倍数的整数之和S.
【分析】先分别计算出所有自然数的和、所有2的倍数的自然数和、所有3的倍数的自然数和、所有6的倍数的自然数和,然后根据容斥定理即可得出答案.
【解答】解:1到100的自然数中,所有自然数的和是:1+2+3+…+100=5050,
1到100的自然数中,所有2的倍数的自然数和是:
2×1+22+…+2×50=2×(1+2+3+…+50)=2×1275=2550,
1到100的自然数中,所有3的倍数的自然数和是:
3×1+3×2+…+3×33=3×(1+2+3+…+33)=3×561=1683,
1到100的自然数中,所有既是2的倍数又是3的倍数,即是所有6的倍数的自然数和是:6×1+6×2+…+6×16=6×(1+2+3+…+16)=6×136=816,
∴1到100的自然数中,所有既不是2的倍数又不是3的倍数的整数之和
S=5050﹣2550﹣1683+816=1633.
【点评】本题考查了数的整除性的知识,难度不算太大,注意分别求出各类数之和,运用容斥定理进行解答.。
初中数学竞赛辅导资料及参考答案(初二上部分,共12份)-8

初中数学竞赛辅导资料(27)识图甲内容提要1.几何学是研究物体形状、大小、位置的学科。
2.几何图形就是点,线,面,体的集合。
点是组成几何图形的基本元素。
《平面几何学》只研究在同一平面内的图形的形状、大小和相互位置。
3.几何里的点、线、面、体实际上是不能脱离物体而单独存在的。
因此单独研究点、线、面、体,要靠正确的想像点:只表示位置,没有大小,不可再分。
线:只有长短,没有粗细。
线是由无数多点组成的,即“点动成线”。
面:只有长、宽,没有厚薄。
面是由无数多线组成的,“线动成面”。
4.因为任何复杂的图形,都是由若干基本图形组合而成的,所以识别图形的组合关系是学好几何的重要基础。
识别图形包括静止状态的数一数,量一量,比一比,算一算;运动状态中的位置、数量的变化,图形的旋转,摺叠,割补,并合,比较等。
还要注意一般图形和特殊图形的差别。
乙例题例1.数一数甲图中有几个角(小于平角)?乙图中有几个等腰三角形?丙图中有几全等三角形?丁图中有几对等边三角形?E解:甲图中有10个角:∠AOB, ∠AOC,∠BOC,∠BOD,∠COD,∠COE,∠DOE,∠DOA,∠EOA,∠EOB.如果OA和OC成一直线,则少一个∠AOC,余类推。
乙图中有5个等腰三角形:△ABC,△ABD,△BDC,△BDE,△DEC 丙图中有全等三角形4对:(设AC和DB相交于O)△AOB≌△COD,△AOD≌△BOC,△ABC≌△CDA,△BCD≌△DAB。
丁图中共有等边三角形48个:边长1个单位:顶点在上▲的个数有 1+2+3+4+5=15顶点在下▼的个数有 1+2+3+4=10边长2个单位:顶点在上▲的个数有 1+2+3+4=10顶点在下▼的个数有 1+2=3边长3个单位:顶点在上▲的个数有 1+2+3=6边长4个单位:顶点在上▲的个数有 1+2=3边长5个单位:顶点在上▲的个数有 1以上要注意数一数的规律例2.设平面内有6个点A 1,A 2,A 3,A 4,A 5,A 6,其中任意3个点都不在同一直线上,如果每两点都连成一条线,那么共有线段几条?如果要使图形不出现有4个点的两两连线,那么最多可连成几条线段?试画出图形。
初中数学竞赛辅导材料目录

初中数学竞赛辅导材料目录一、初中数学竞赛基础知识1.数集及其运算-自然数、整数、有理数、实数、复数的概念及运算性质-数集的表示方法与运算法则2.代数式与方程-一元一次方程与一元一次不等式的解法及应用-一次函数的定义、性质与图像-一元二次方程的解法及应用3.几何基本概念-点、线、面、角的定义与性质-直线、射线、线段、平行线、垂直线的概念与判定-多边形、三角形、四边形的性质4.图形的相似与投影-图形的相似判定条件及相似比的计算-平面图形在对称、旋转、平移、投影中的性质与运用5.数据的整理与表示-数据的收集、整理、描述和分析方法-列联表的制作与应用-分组频数统计图的制作与读图6.立体几何-空间图形的基本概念及性质-空间图形的展开与剖析-空间图形的体积与表面积计算方法二、初中数学竞赛解题技巧与方法1.快速计算技巧-快速计算小技巧的应用(如乘法口诀、整数加减乘除的计算等)-快速计算较大数的方法(如分解因数、整理计算顺序等)2.思维训练与问题解决-近似计算与估算的方法与应用-分析解题条件与利用信息求解问题-数学问题的逻辑和推理方法3.策略与技巧-消元法与代入法的使用-枚举与特例法的应用-逆向思维与反证法的运用4.考试技巧与应试心理-数学竞赛常见题型的解题思路-如何正确阅读题目与审题技巧-考试时间分配与答题顺序规划-心理调适与压力应对方法三、数学竞赛真题及解析1.真题分析与解题方法讲解-分析数学竞赛真题的特点与难点-理解题目要求、辅助线的作法、巧用条件等解题技巧-真题解析与解题思路讲解2.解题思路总结与题型归纳-简述各种常见数学竞赛题型的解题思路-总结解题中常用的技巧与方法-提供大量的练习题目,以加强学生对各类题型的掌握以上为初中数学竞赛辅导材料的目录,通过系统的学习与实践,相信学生们可以提升数学竞赛的能力,取得更好的成绩。
祝学习愉快!。
初中数学竞赛辅导资料课件.doc

初中数学竞赛辅导资料一元一次方程解的讨论甲内容提要1, 方程的解的定义:能使方程左右两边的值相等的未知数的值叫做方程的解。
一元方程的解也叫做根。
例如:方程 2x +6=0, x (x-1)=0, |x|=6, 0x=0, 0x=2的解分别是: x=-3, x=0或x=1, x=±6, 所有的数,无解。
2, 关于x 的一元一次方程的解(根)的情况:化为最简方程ax=b 后,讨论它的解:当a ≠0时,有唯一的解 x=ab ; 当a=0且b ≠0时,无解;当a=0且b =0时,有无数多解。
(∵不论x 取什么值,0x =0都成立)3, 求方程ax=b(a ≠0)的整数解、正整数解、正数解当a |b 时,方程有整数解;当a |b ,且a 、b 同号时,方程有正整数解;当a 、b 同号时,方程的解是正数。
综上所述,讨论一元一次方程的解,一般应先化为最简方程ax=b乙例题例1 a 取什么值时,方程a(a -2)x=4(a -2) ①有唯一的解?②无解?③有无数多解?④是正数解?解:①当a ≠0且a ≠2 时,方程有唯一的解,x=a 4 ②当a=0时,原方程就是0x= -8,无解;③当a=2时,原方程就是0x=0有无数多解④由①可知当a ≠0且a ≠2时,方程的解是x=a4,∴只要a 与4同号, 即当a>0且a ≠2时,方程的解是正数。
例2 k 取什么整数值时,方程①k(x+1)=k -2(x -2)的解是整数?②(1-x )k=6的解是负整数?解:①化为最简方程(k +2)x=4当k+2能整除4,即k+2=±1,±2,±4时,方程的解是整数∴k=-1,-3,0,-4,2,-6时方程的解是整数。
②化为最简方程kx=k -6,当k ≠0时x=k k 6 =1-k6, 只要k 能整除6, 即 k=±1,±2,±3,±6时,x 就是整数当 k=1,2,3时,方程的解是负整数-5,-2,-1。
初中数学竞赛辅导资料
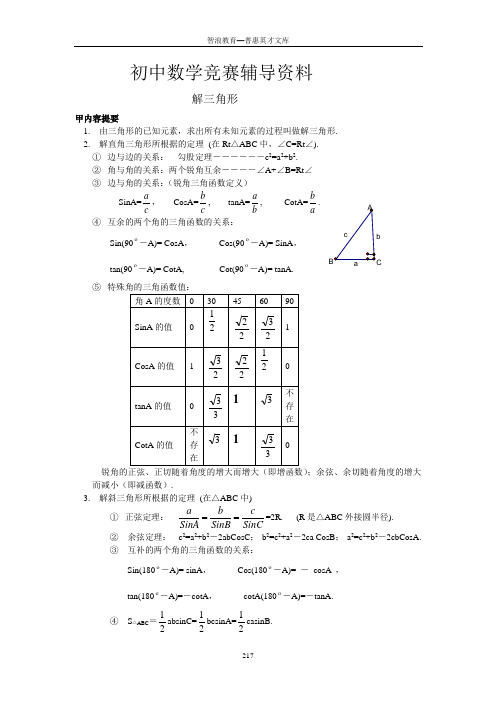
初中数学竞赛辅导资料解三角形甲内容提要1. 由三角形的已知元素,求出所有未知元素的过程叫做解三角形.2. 解直角三角形所根据的定理 (在Rt △ABC 中,∠C=Rt ∠). ① 边与边的关系: 勾股定理----――c 2=a 2+b 2. ② 角与角的关系:两个锐角互余----∠A+∠B=Rt ∠ ③ 边与角的关系:(锐角三角函数定义)SinA=c a , CosA=c b , tanA=b a , CotA=ab. ④ 互余的两个角的三角函数的关系:Sin(90-A)= CosA , Cos(90-A)= SinA , tan(90-A)= CotA, Cot(90-A)= tanA. ⑤;余弦、余切随着角度的增大而减小(即减函数).3. 解斜三角形所根据的定理 (在△ABC 中)① 正弦定理:SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径). ② 余弦定理: c 2=a 2+b 2-2abCosC ; b 2=c 2+a 2-2ca CosB ; a 2=c 2+b 2-2cbCosA. ③ 互补的两个角的三角函数的关系:Sin(180-A)= sinA , Cos(180-A)= - cosA , tan(180-A)=-cotA , cotA(180-A)=-tanA. ④ S △ABC =21absinC=21bcsinA=21casinB.4. 与解三角形相关的概念:水平距离,垂直距离,仰角,俯角,坡角,坡度,象限角,方位角等. 乙例题例1. 已知:四边形ABCD 中,∠A =60,CB ⊥AB ,CD ⊥AD ,CB =2,CD =1.求:AC 的长.解:延长AD 和BC 相交于E ,则∠E =30.在Rt △ECD 中,∵sinE=CECD, ∴CE=30sin 1=1÷21=2. EB =4. 在Rt △EAB 中, ∵tanE=EBAB,∴AB=EBtan30。
(共30套)初中数学竞赛辅导讲义及习题解答大全 (含竞赛答题技巧)

(共30套)初中数学竞赛辅导讲义及习题解答大全适合中学教师作为辅导教材使用第一讲 走进追问求根公式形如02=++c bx ax (0≠a )的方程叫一元二次方程,配方法、公式法、因式分解法是解一元二次方程的基本方法。
而公式法是解一元二次方程的最普遍、最具有一般性的方法。
求根公式aacb b x 2422,1-±-=内涵丰富:它包含了初中阶段已学过的全部代数运算;它回答了一元二次方程的诸如怎样求实根、实根的个数、何时有实根等基本问题;它展示了数学的简洁美。
降次转化是解方程的基本思想,有些条件中含有(或可转化为)一元二次方程相关的问题,直接求解可能给解题带来许多不便,往往不是去解这个二次方程,而是对方程进行适当的变形来代换,从而使问题易于解决。
解题时常用到变形降次、整体代入、构造零值多项式等技巧与方法。
【例题求解】【例1】满足1)1(22=--+n n n 的整数n 有 个。
思路点拨:从指数运算律、±1的特征人手,将问题转化为解方程。
【例2】设1x 、2x 是二次方程032=-+x x 的两个根,那么1942231+-x x 的值等于( )A 、一4B 、8C 、6D 、0思路点拨:求出1x 、2x 的值再代入计算,则计算繁难,解题的关键是利用根的定义及变形,使多项式降次,如1213x x -=,2223x x -=。
【例3】 解关于x 的方程02)1(2=+--a ax x a 。
思路点拨:因不知晓原方程的类型,故需分01=-a 及01≠-a 两种情况讨论。
【例4】设方程04122=---x x ,求满足该方程的所有根之和。
思路点拨:通过讨论,脱去绝对值符号,把绝对值方程转化为一般的一元二次方程求解。
【例5】 已知实数a 、b 、c 、d 互不相等,且x ad d c c b b a =+=+=+=+1111, 试求x 的值。
思路点拨:运用连等式,通过迭代把b 、c 、d 用a 的代数式表示,由解方程求得x 的值。
初中数学竞赛辅导资料(六)

初中数学竞赛辅导资料(六)(含答案) 分式甲内容提要1. 除式含有字母的代数式叫做分式。
分式的值是由分子、分母中的字母的取值确定的。
(1)分式BA 中,当B ≠0时有意义;当A 、B 同号时值为正,异号时值为负,反过来也成立。
分子、分母都化为积的形式时,分式的符号由它们中的负因数的个数来确定。
(2)若A 、B 及BA 都是整数,那么A 是B 的倍数,B是A 的约数。
(3)一切有理数可用BA 来表示,其中A 是整数,B是正整数,且A 、B 互质。
2. 分式的运算及恒等变形有一些特殊题型,要用特殊方法解答方便。
乙例题 例1.x取什么值时,分式xx x x 23222+--的值是零?是正数?是负数?解: xx x x 23222+--=)2()3)(1+-+x x x x (以零点-2,-1,0,3把全体实数分为五个区间,标在数轴上(如上图)当x=-1,x=3时分子是0,分母不等于0,这时分式的值是零;当x<-2, -1<x<0, x>3时,分式的值是正数(∵负因数的个数是偶数)当-2<x<-1, 0<x<3时,分式的值是负数(∵负因数的个数是奇数)例2.m 取什么值时,分式172-+m m 的值是正整数?解:172-+m m =1922-+-m m =2+19-m当例3.计算14++x x +32--x x -12-+x x -34++x x19-m >-2且m -1是9的约数时,分式的值是正整数即m -1=1,3,9,-9 解得m=2,4,10,-8。
3答:(略)解:用带余除法得,原式=1+13+x +1+31-x -1-13-x -1-31+x =)1)(1()1(3)1(3-++--x x x x +)3)(3()3()3(+---+x x x x=162-x -+962-x =)9)(1(4822--x x 4.已知(a+b )∶(b+c)∶(c+a)=3∶4∶5 求①a ∶b ∶c ②bcc aba +-22解:设a+b=3k,则b+c=4k,c+a=5k,全部相加 得2(a+b+c )=12k, 即a+b+c=6k, 分别减上列各式得a=2k, b=k, c=3k∴①a ∶b ∶c =2∶1∶3 ②bc c ab a +-22=k k k kk k 3)3(2)2(22⨯⨯-+=61例5.一个两位数除以它的两个数位上的数字和,要使商为最小值,求这个两位数;如果要使商为最大值呢?解:设这个两位数为10x+y ,那么0<x ≤9, 0≤y ≤9y x yx ++10=1+yx x +9 当x 取最小值1,y 取最大值9时,分式yx x+9的值最小;当x 取最大值9,y 取最小值0时,分式yx x +9的值最大。
初中数学竞赛辅导资料

第一篇 一元一次方程的讨论第一部分 基本方法1。
方程的解的定义:能使方程左右两边的值相等的未知数的值叫做方程的解。
一元方程的解也叫做根。
例如:方程 2x +6=0, x (x -1)=0, |x |=6, 0x =0, 0x =2的解 分别是: x =-3, x =0或x =1, x =±6, 所有的数,无解. 2. 关于x 的一元一次方程的解(根)的情况:化为最简方程ax =b 后, 讨论它的解:当a ≠0时,有唯一的解 x =ab; 当a =0且b ≠0时,无解;当a =0且b =0时,有无数多解。
(∵不论x 取什么值,0x =0都成立) 3. 求方程ax =b (a ≠0)的整数解、正整数解、正数解 当a |b 时,方程有整数解;当a |b ,且a 、b 同号时,方程有正整数解; 当a 、b 同号时,方程的解是正数。
综上所述,讨论一元一次方程的解,一般应先化为最简方程ax =b 第二部分 典例精析例1 a 取什么值时,方程a (a -2)x =4(a -2) ①有唯一的解?②无解? ③有无数多解?④是正数解?例2 k取什么整数值时,方程①k(x+1)=k-2(x-2)的解是整数?②(1-x)k=6的解是负整数?例3己知方程a(x-2)=b(x+1)-2a无解.问a和b应满足什么关系?例4a、b取什么值时,方程(3x-2)a+(2x-3)b=8x-7有无数多解?第三部分典题精练1. 根据方程的解的定义,写出下列方程的解:① (x +1)=0, ②x 2=9, ③|x |=9, ④|x |=-3, ⑤3x +1=3x -1, ⑥x +2=2+x2。
关于x 的方程ax =x +2无解,那么a __________ 3。
在方程a (a -3)x =a 中,当a 取值为____时,有唯一的解; 当a ___时无解; 当a _____时,有无数多解; 当a ____时,解是负数. 4。
初中八年级数学培优竞赛辅导讲义全册(213页)

初中八年级数学培优竞赛辅导讲义(共213页,按住ctrl键点击目录直接跳转到对应章节)第1讲全等三角形的性质与判定 (2)第2讲角平分线的性质与判定 (12)第3讲轴对称及轴对称变换 (17)第4讲等腰三角形 (25)第5讲等边三角形 (37)第06讲实数 (43)第7讲变量与函数 (50)第8讲一次函数的图象与性质 (55)第9讲一次函数与方程、不等式 (64)第10讲一次函数的应用 (69)第11讲幂的运算 (81)第12讲整式的乘除 (87)第13讲因式分解及其应用 (94)第14讲分式的概念•性质与运算 (101)第15讲分式的化简求值与证明 (109)第16讲分式方程及其应用 (118)第17讲反比例函数的图象与性质 (126)第18讲反比例函数的应用 (139)第19讲勾股定理 (146)第20讲平行四边形 (158)第21讲菱形与矩形 (167)第22讲正方形 (175)第23讲梯形 (185)第24讲数据的分析 (194)B AC D EF 第1讲 全等三角形的性质与判定考点·方法·破译1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同; 2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;3.全等三角形判定方法有:SAS ,ASA ,AAS ,SSS ,对于两个直角三角形全等的判定方法,除上述方法外,还有HL 法;4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.经典·考题·赏析【例1】如图,AB ∥EF ∥DC ,∠ABC =90°,AB =CD ,那么图中有全等三角形( ) A .5对 B .4对 C .3对 D .2对【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.解:⑴∵AB ∥EF ∥DC ,∠ABC =90. ∴∠DCB =90. 在△ABC 和△DCB 中AB DC ABC DCB BC CB =⎧⎪=⎨⎪=⎩∠∠ ∴△ABC ≌∴△DCB (SAS ) ∴∠A =∠D ⑵在△ABE 和△DCE 中A DAED DEC AB DC =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ABE ≌∴△DCE ∴BE =CE ⑶在Rt △EFB 和Rt △EFC 中BE CEEF EF=⎧⎨=⎩ ∴Rt △EFB ≌Rt △EFC (HL )故选C . 【变式题组】 01.(天津)下列判断中错误的是( )A .有两角和一边对应相等的两个三角形全等B .有两边和一角对应相等的两个三角形全等C .有两边和其中一边上的中线对应相等的两个三角形全等A F C E DB D .有一边对应相等的两个等边三角形全等 02.(丽水)已知命题:如图,点A 、D 、B 、E 在同一条直线上,且AD =BE ,∠A =∠FDE ,则△ABC ≌△DEF .判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.03.(上海)已知线段AC 与BD 相交于点O , 连接AB 、DC ,E 为OB 的中点,F 为OC 的中点,连接EF (如图所示).⑴添加条件∠A =∠D ,∠OEF =∠OFE ,求证:AB =DC ; ⑵分别将“∠A =∠D ”记为①,“∠OEF =∠OFE ”记为②,“AB =DC ”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).【例2】已知AB =DC ,AE =DF ,CF =FB . 求证:AF =DE .【解法指导】想证AF =DE ,首先要找出AF 和DE 所在的三角形.AF 在△AFB 和△AEF 中,而DE 在△CDE 和△DEF 中,因而只需证明△ABF ≌△DCE 或△AEF ≌△DFE 即可.然后再根据已知条件找出证明它们全等的条件.证明:∵FB =CE ∴FB +EF =CE +EF ,即BE =CF 在△ABE 和△DCF 中, AB DCAE DF BE CF =⎧⎪=⎨⎪=⎩∴△ABE ≌△DCF (SSS ) ∴∠B =∠C在△ABF 和△DCE 中, AB DC B C BF CE =⎧⎪=⎨⎪=⎩∠∠ ∴△ABF ≌△DCE ∴AF =DE【变式题组】01.如图,AD 、BE 是锐角△ABC 的高,相交于点O ,若BO =AC ,BC =7,CD =2,则AO 的长为( ) A .2 B .3 C .4 D .5A B C D O FE A CEFBD02.如图,在△ABC 中,AB =AC ,∠BAC =90°,AE 是过A 点的一条直线,AE ⊥CE 于E ,BD⊥AE 于D ,DE =4cm ,CE =2cm ,则BD =__________. \ 03.(北京)已知:如图,在△ABC 中,∠ ACB =90°,CD ⊥AB 于点D ,点E 在AC 上,CE =BC ,过点E 作AC 的垂线,交CD 的延长线于点F . 求证:AB =FC .【例3】如图①,△ABC ≌△DEF ,将△ABC 和△DEF 的顶点B 和顶点E 重合,把△DEF 绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .⑴当△DEF 旋转至如图②位置,点B (E )、C 、D 在同一直线上时,∠AFD 与∠DCA 的数量关系是________________;⑵当△DEF 继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.【解法指导】⑴∠AFD =∠DCA⑵∠AFD =∠DCA 理由如下:由△ABC ≌△DEF ,∴AB =DE ,BC =EF , ∠ABC =∠DEF , ∠BAC =∠EDF ∴∠ABC -∠FBC =∠DEF -∠CBF , ∴∠ABF =∠DEC在△ABF 和△DEC 中, AB DE ABF DEC BF EC =⎧⎪=⎨⎪=⎩∠∠∴△ABF ≌△DEC ∠BAF =∠DEC ∴∠BAC -∠BAF =∠EDF -∠EDC , ∴∠FAC =∠CDF∵∠AOD =∠FAC +∠AFD =∠CDF +∠DCA∴∠AFD =∠DCAAFECB DAE第1题图A BCDEBCDO第2题图B (E )OC F 图③DA【变式题组】01.(绍兴)如图,D、E分别为△ABC的AC、BC边的中点,将此三角形沿DE折叠,使点C 落在AB边上的点P处.若∠CDE=48°,则∠APD等于()A.42°B.48°C.52°D.58°02.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是()A.△ABC≌△DEF B.∠DEF=90°C.AC=DF D.EC=CF03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B、F、C、D在同一条直线上.⑴求证:AB⊥ED;⑵若PB=BC,找出图中与此条件有关的一对全等三角形,并证明.【例4】(第21届江苏竞赛试题)已知,如图,BD、CE分别是△ABC的边A C和AB边上的高,点P在BD的延长线,BP=AC,点Q在CE上,CQ=AB.求证:⑴AP=AQ;⑵AP⊥AQ【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP=AQ,也就是证△APD和△AQE,或△APB和△QAC全等,由已知条件BP=AC,CQ=AB,应该证△APB≌△QAC,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP⊥AQ,即证∠PAQ=90°,∠PAD+∠QAC=90°就可以.证明:⑴∵BD、CE分别是△ABC的两边上的高,∴∠BDA=∠CEA=90°,∴∠1+∠BAD=90°,∠2+∠BAD=90°,∴∠1=∠2.在△APB和△QAC中, 2AB QCBP CA=⎧⎪=⎨⎪=⎩∠1∠∴△APB≌△QAC,∴AP=AQE FBACDG第2题图21ABCPQEFD⑵∵△APB ≌△QAC ,∴∠P =∠CAQ , ∴∠P +∠PAD =90° ∵∠CAQ +∠PAD =90°,∴AP ⊥AQ 【变式题组】01.如图,已知AB =AE ,∠B =∠E ,BA =ED ,点F 是CD 的中点,求证:02.直距离MA 为am ,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB 为bm ,梯子倾斜角为45°,这间房子的宽度是( )A .2a bm + B .2a bm - C .bm D .am03.如图,已知五边形ABCDE 中,∠ ABC =∠AED =90°,AB =CD =AE =BC +DE =2,则五边形ABCDE 的面积为__________演练巩固·反馈提高01.(海南)已知图中的两个三角形全等,则∠α度数是( )A .72°B .60°C .58°D .50°02.如图,△ACB ≌△A /C /B /,∠ BCB /=30°,则∠ACA /的度数是( )A .20°B .30°C .35°D .40° 03.(牡丹江)尺规作图作∠AOB 的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得△OCP ≌△ODP 的根据是( )AECBA 75° C45° BNM第2题图第3题图D第1题图a αcca50° b72° 58°A .SASB .ASAC .AASD .SSS 04.(江西)如图,已知AB =AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是( )A . CB =CD B .∠BAC =∠DAC C . ∠BCA =∠DCAD .∠B =∠D =90°05.有两块不同大小的等腰直角三角板△ABC 和△BDE ,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A 、B 、D 不在一条直线上时,下面的结论不正确的是( )A . △ABE ≌△CBDB . ∠ABE =∠CBDC . ∠ABC =∠EBD =45° D . AC ∥BE06.如图,△ABC 和共顶点A ,AB =AE ,∠1=∠2,∠B =∠E . BC 交AD 于M ,DE 交AC 于N ,小华说:“一定有△ABC ≌△AED .”小明说:“△ABM ≌△AEN .”那么( ) A . 小华、小明都对 B . 小华、小明都不对 C . 小华对、小明不对 D .小华不对、小明对07.如图,已知AC =EC , BC =CD , AB =ED ,如果∠BCA =119°,∠ACD =98°,那么∠ECA 的度数是___________.08.如图,△ABC ≌△ADE ,BC 延长线交DE 于F ,∠B =25°,∠ACB =105°,∠DAC =10°,则∠DFB 的度数为_______.09.如图,在Rt △ABC 中,∠C =90°, DE ⊥AB 于D , BC =BD . AC =3,那么AE +DE =______10.如图,BA ⊥AC , CD ∥AB . BC =DE ,且BC ⊥DE ,若AB =2, CD =6,则AE =_____. 11.如图, AB =CD , AB ∥CD . BC =12cm ,同时有P 、Q 两只蚂蚁从点C 出发,沿CB 方向爬行,P 的速度是0.1cm /s , Q 的速度是0.2cm /s . 求爬行时间t 为多少时,△APB ≌△QDC .DA C .Q P.BA E FB DC 12.如图, △ABC 中,∠BCA =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D . ⑴求证:AE =CD ;⑵若AC =12cm , 求BD 的长.13.(吉林)如图,AB =AC ,AD ⊥BC 于点D ,AD 等于AE ,AB 平分∠DAE 交DE 于点F , 请你写出图中三对全等三角形,并选取其中一对加以证明.14.如图,将等腰直角三角板ABC的直角顶点C 放在直线l 上,从另两个顶点A 、B 分别作l 的垂线,垂足分别为D 、E .⑴找出图中的全等三角形,并加以证明; ⑵若DE =a ,求梯形DABE 的面积.(温馨提示:补形法)15.如图,AC ⊥BC , AD ⊥BD , AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F .求证:CE =DF .16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等? ⑴阅读与证明:对于这两个三角形均为直角三角形,显然它们全等;对于这两个三角形均为钝角三角形,可证明它们全等(证明略); 对于这两个三角形均为锐角三角形,它们也全等,可证明如下;已知△ABC 、△A 1B 1C 1均为锐角三角形,AB =A 1B 1,BC =B 1C 1,∠C =∠C 1.求证:△ABC ≌△A 1B 1C 1.(请你将下列证明过程补充完整)⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.ABCDA 1B 1C 1D 1D B A C EF A E B F D CAEF C DB 培优升级·奥赛检测01.如图,在△ABC 中,AB =AC ,E 、F 分别是AB 、AC 上的点,且AE =AF ,BF 、CE 相交于点O ,连接AO 并延长交BC 于点D ,则图中全等三角形有( ) A .4对 B .5对 C .6对 D .7对02.如图,在△ABC 中,AB =AC ,OC =OD ,下列结论中:①∠A =∠B ②DE =CE ,③连接DE , 则OE 平分∠AOB ,正确的是( ) A .①② B .②③ C .①③ D .①②③03.如图,A 在DE 上,F 在AB 上,且AC =CE , ∠1=∠2=∠3, 则DE 的长等于()A .DCB . BC C . ABD .AE +AC04.下面有四个命题,其中真命题是( )A .两个三角形有两边及一角对应相等,这两个三角形全等B .两边和第三边上的高对应相等的两个三角形全等C . 有一角和一边对应相等的两个直角三角形全等D . 两边和第三边上的中线对应相等的两个三角形全等05.在△ABC 中,高AD 和BE 所在直线相交于H 点,且BH =AC ,则∠ABC =_______.06.如图,EB 交AC 于点M , 交FC 于点D , AB 交FC 于点N ,∠E =∠F =90°,∠B =∠C , AE=AF . 给出下列结论:①∠1=∠2;②BE =CF ; ③△ACN ≌△ABM ; ④CD =DB ,其中正确的结论有___________.(填序号)07.如图,AD 为在△ABC 的高,E 为AC 上一点,BE 交AD 于点F ,且有BF =AC ,FD =CD .⑴求证:BE ⊥AC ;⑵若把条件“BF =AC ”和结论“BE ⊥AC ”互换,这个命题成立吗?证明你的判定.08.如图,D 为在△ABC 的边BC 上一点,且CD =AB ,∠BDA =∠BAD ,AE 是△ABD 的中线.求证:AC =2AE .09.如图,在凸四边形ABCD 中,E 为△ACD 内一点,满足AC =AD ,AB =AE , ∠BAE +∠BCEABE D CF第6题图2 1AB CE N M3 21ADEBC FADECOA E O BFCD 第1题图B第2题图第3题图AB C DEAEBDC=90°, ∠BAC =∠EAD .求证:∠CED =90°.10.(沈阳)将两个全等的直角三角形ABC 和DBE 按图①方式摆放,其中∠ACB =∠DEB =90°,∠A =∠D =30°,点E 落在AB 上,DE 所在直线交AC 所在直线于点F .⑴求证:AF +EF =DE ;⑵若将图①中△DBE 绕点B 顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;⑶若将图①中△DBE 绕点B 按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF 、EF 与DE 之间的关系,并说明理由。
初中数学竞赛辅导讲义(总77页)

初中数学竞赛辅导讲义-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除初中数学竞赛辅导讲义(初三)第一讲 分式的运算[知识点击]1、分部分式:真分式化为另几个真分式的和,一般先将分母分解因式,后用待定系数法进行。
2、综合除法:多项式除以多项式可类似于是有理数的除法运算,可列竖式来进行。
3、分式运算:实质就是分式的通分与约分。
[例题选讲]例1.化简2312++x x + 6512++x x + 12712++x x 解:原式= )2)(1(1++x x + )3)(2(1++x x + )4)(3(1++x x = 11+x - 21+x + 21+x - 31+x + 31+x - 41+x =)4)(1(3++x x例2. 已知z z y x -+ = y z y x +- = x z y x ++- ,且xyz ≠0,求分式xyz x z z y y x ))()((+-+的值。
解:易知:z y x + = y z x + = x z y + =k 则⎪⎩⎪⎨⎧=+=+=+)3()2()1(kx z y ky z x kz y x (1)+(2)+(3)得:(k-2)(x+y+z)=0 k=2 或 x+y+z=0 若k=2则原式= k 3 = 8 若 x+y+z=0,则原式= k 3 =-1例3.设 12+-mx x x =1,求 12242+-x m x x 的值。
解:显然X 0≠,由已知x mx x 12+- =1 ,则 x +x1 = m + 1 ∴ 22241x x m x +- = x2 + 21x - m2= (x +x1)2-2 –m2 =( m +1)2-2- m2= 2m -1 ∴原式=121-m例4.已知多项式3x 3 +ax 2 +3x +1 能被x 2+1整除,求a的值。
解:1- a=0 ∴ a=1例5:设n为正整数,求证311⨯ + 511⨯ + …… +)12)(12(1+-n n < 21证:左边=21(1 - 31 + 31 - 51+ …… +121-n - 121+n ) =21(1- 121+n )∵n 为正整数,∴121+n < 1 ∴1- 121+n < 1 故左边< 21 [小结归纳]1、部分分式的通用公式:)(1k x x + = k 1 (x 1 - kx +1) 2、参数法是解决比例问题特别是连比问题时非常有效的方法,其优点在于设连比值为K ,将连等式化为若干个等式,把各字母用同一字母的解析式表示,从而给解题带来方便。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛辅导资料(62)
绝对值
甲内容提要
1. 绝对值的定义:正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值是零.用式子表示如下:⎪⎩
⎪⎨⎧=<->=)0(0)0()0(a a a a a a
2. 初中阶段学习含绝对值符号的代数式化简,方程、不等式的解法,以及函数作图等.解答时,一般是根据定义先化去绝对值符号,这时关健是按已知条件判断绝对值符号内的式子的值是正或是负,若含有变量的代数式,不能确定其正、负时,则采取零点分区讨论法. 例如:
(1)化简 )2(-x x
解:当x=0, x=2时, )2(-x x =0;
当x<0或x>2时, )2(-x x =x(x -2)=x 2-2x ;
当0<x<2时,)2(-x x =-x(x -2)=-x 2+x.
(2)解方程2-+x x =6.
解:当x<0时,x=-2;
当0≤x ≤2时,方程无解;
当x>2时,x=4.
∴原方程的解是:x=-2, x=4..
(3)作函数y=2-+x x 的图象.
解:化去绝对值符号,得y=-2x+2 (x<0);
y=2 (0≤x ≤2) ;
y=2x -2 (x>2).
分别作出上述三个函数的图象(如图),就是函数y=2-+x x 的图象.
3. 绝对值的几何意义是:在数轴上一个数的绝对值,就是表示这个数的点离开原点的距离. 用这一定义,在解含绝对值符号的方程、不等式时,常可用观察法. 例如: ①解方程3=x ; ②解不等式3<x ; ③解不等式32>+x .
解:①∵3=x 的几何意义是:x 是数轴上到原点的距离等于3个单位的点所表示的数,即3和-3,
∴方程3=x 的解是x=3, x=-3. ②∵3<x 的几何意义是:x 是数轴上到原点的距离小于3个单位的点所表示的数,∴不等式3<x 的解集是 -3<x <3. ③∵2+x 的零点是x=-2, ∴32>+x 的几何意义是:x 是数轴上到点(-2)的距离大于3个单位的点所表示的数, ∴32>+x 的解集是x<-5或x>1.(如下图)
4.
①绝对值是非负数; ②两个互为相反数,它们的绝对值相等.
根据这些性质,可简化函数的作图步骤. 例如:
(1)对整个函数都在绝对值符号内时,可先作出不含绝对值符号的图象,再把横轴下方的
部份,绕x 轴向上翻折
作函数图象:①y=1-x ②y=22--x x
(2) 当f (-x )=f(x),图象关于纵轴对称,这时可先作当x<0时函数图象,再画出关于纵
轴对称的图象.
例如:y=x 2-2x -3的图象,
可先作y=x 2+2x -3自变量x<0时的图象(左半图)
再画右半图(与左半图关于纵轴对称).
(3) 把y=x 的图象向上平移a 个单位,所得图象解析式是y=a x +; 把y=x 的图象向右平移3个单位,所得图象解析式是y=3-x .
(4) 利用图象求函数最大值或最小值,判断方程解的个数都比较方便.
乙例题
例1. 已知方程x =ax+1有一个负根并且没有正根,求a 的值.
(1987年全国初中数学联赛题)
解:当x<0时,原方程为-x=ax+1, x=
011<+a -, ∴ a+1>0. ∴a>-1;
当x>0时,原方程为x=ax+1, x=
011>a
-, ∴1-a>0. ∴a<1.
∵方程有一个负根并且没有正根,
∴a>-1且a ≮1,
∴a 的取值范围是a ≥1.
例2. 求函数y=2x x -3-的最小、最大值. 解:当x<0时, y=-x+6;
当0≤x<3时,y=-3x+6;
当x ≥3时, y=x -6 .
根据图象有最低点而没有最高点
∴函数没有最大值只有最小值-3(当x=3时).
例3. 解方程:①x x -=+42; ②421=-++x x .
解:①∵点(x )到点A (-2)和点B (4)的距离相等(如下图),
∴x=1.
②∵点(x )到点A (-1)与到点B (2)的距离的和等于4,AB =3
∴x=2.5, x=-1.5.
例4. 解不等式: ①1≤2+x ≤3; ②121>--+x x .
解:①点(x )到点A (-2)的距离大于或等于1而小于或等于3
在数轴上表示如图,
∴不等式的解集是: -5≤x ≤-3 或-1≤x ≤1
②点(x) 到点(-1)的距离,比到点(2)的距离大1个单位以上.
在数轴上表示,如图:
∴不等式的解集是x>1.
例5. a 取什么值时,方程a x =--12 有三个整数解?
(1986年全国初中数学联赛题) 解:化去绝对值符号,得12--x =±a, 2-x =1±a , x -2=±(1±a),
∴x=2±(1±a) .
当a=1时,x 恰好是三个解4,2,0.
用图象解答更直观;
(1)先作函数 y=12--x 图象,
(2)再作y=a(平行于横轴的直线 )与y=12--x 图象相交,
恰好是三个交点时,y=1,
即a=1.
本题若改为:
有四个解,则0<a<1;
两个解,则 a=0 或a>1;
一个解,则a 不存在;
无解,则a<0.
丙练习62
1. 方程3+x =4的解是_______.
2. 方程6-2-+x x =0的解是________.
3. 方程21-++x x =3的解是________.
4. 方程x x +-3=5的解是_______.
5. 不等式2≤3 -x ≤5的解集是___________________.
6. 不等式21-++x x <5的解集是_______________________.
7. 不等式21-++x x <3的解集是_______________________.
8. 不等式11-2-<x x 的解集是_______________________.
9. 已知=-2)3(x 3-x, 那么 =+-x x 1_______________.
10. 关于x 的方程x =ax+2有根且只有负根,求a 取值范围.
11. a 取什么值时,方程a x =--12无解?有解?有最多解?
12. 作函数y=312-+-++x x x 的图象;并求在-3≤x ≤3中函数的最大、最小值.
13. 解方程451=-+-x x .
14. 作函数y=12
+-x x 的图象.
15. 选择题:(1972、1973年美国中学数学竞赛试题)
①.对于实数x ,不等式1≤|x -2|≤7等价于( )
(A ) x ≤1或x ≥3 (B )1≤x ≤3 (C )-5≤x ≤0
(D )-5≤x ≤1或3≤x ≤9 (E )-6≤x ≤1或3≤x ≤10
②不等式|x -1|+|x+2|<5的所有的实数解的集合是( ) (A ){}23<<-x x :
(B) {}21<<-x x : (C) {}12<<-x x : (D) {}5.35.1<<-x x :
(E) φ(空集)。
