多种回归行为在受迫摆系统状态空间内共存现象的分析
多元回归分析的原理和应用

多元回归分析的原理和应用1. 引言多元回归分析是统计学中一种常用的分析方法,用于研究多个自变量和一个因变量之间的关系。
它可以帮助我们理解多个变量对一个变量的影响程度,并通过建立数学模型来预测因变量的值。
2. 基本原理多元回归分析基于线性回归模型进行建模,其中一个因变量可以通过多个自变量的线性组合来描述。
该模型的数学表示为:Y = β0 + β1*X1 + β2*X2 + ... + βn*Xn + ε其中,Y是因变量的值,X1、X2、…、Xn是自变量的值,β0、β1、β2、…、βn是回归系数,ε是误差项。
3. 模型建立与评估在进行多元回归分析时,首先需要选择合适的自变量来建立模型。
可以通过观察变量之间的相关性、领域知识和实际经验来选择自变量。
然后,通过最小二乘法估计回归系数,使得模型在样本中的拟合误差最小化。
模型的拟合优度可以通过判定系数R2来评估。
R2越接近1,说明模型能够较好地解释因变量的变异;R^2越接近0,说明模型解释能力较差。
4. 样本数据分析多元回归分析通常需要一定量的样本数据来建立和验证模型。
样本数据应该具有代表性,并且满足一些基本假设,例如线性关系和误差项的独立性。
在分析样本数据时,可以使用统计软件如SPSS、R或Python等来实现多元回归分析。
这些软件提供了丰富的功能和工具,帮助研究者快速、准确地进行分析。
5. 应用领域多元回归分析在许多领域有着广泛的应用。
以下是一些常见的应用领域:5.1 经济学多元回归分析在经济学中用于研究经济变量之间的关系,如GDP、通货膨胀率、失业率等,帮助经济学家预测经济发展趋势、评估政策效果等。
5.2 社会科学在社会科学领域,多元回归分析被广泛应用于研究人类行为、社会问题等。
通过分析不同因素对社会现象的影响,可以帮助社会科学家理解社会现象的成因和解决途径。
5.3 健康科学多元回归分析在健康科学中用于研究健康影响因素,如疾病发生率、死亡率等。
通过分析各种生活方式、环境因素对健康的影响,可以帮助医生和公共卫生工作者制定合理的防控措施。
多重回归分析方法

多重回归分析方法多重回归分析是一种统计分析方法,用于探究多个自变量与一个因变量之间的关系。
通过回归方程,我们能够预测和解释因变量的变化程度。
本文将介绍多重回归分析的基本原理、应用场景和步骤,并详细讨论模型建立、参数估计和结果解释的相关内容。
一、多重回归分析的基本原理多重回归分析是在简单回归分析的基础上进行拓展,考虑了多个自变量对因变量的影响。
简单回归分析中,我们通过一条直线来建立自变量和因变量之间的关系;而多重回归分析中,我们考虑了多个自变量,通过一个多维的平面或超平面来建立模型。
多重回归分析基于以下假设:1. 自变量与因变量之间存在线性关系;2. 自变量彼此之间不存在多重共线性;3. 残差项满足独立同分布的假设。
二、多重回归分析的应用场景多重回归分析广泛应用于社会科学、经济学以及其他研究领域。
例如,在市场营销研究中,我们可以利用多重回归分析探究不同市场因素对产品销量的影响;在医学研究中,我们可以利用多重回归分析研究不同药物剂量对患者病情的改善程度。
三、多重回归分析的步骤多重回归分析一般包括以下步骤:1. 数据收集:收集相关的自变量和因变量的数据;2. 变量选择:根据研究目的和领域知识,选择适当的自变量进行分析;3. 模型建立:建立多重回归模型,构建回归方程;4. 参数估计:利用最小二乘法或其他方法,估计回归方程中的参数;5. 模型拟合:评估回归模型的拟合效果,如调整决定系数、F检验等;6. 结果解释:解释回归系数的含义和统计显著性,分析自变量对因变量的影响程度。
四、模型建立和参数估计在多重回归分析中,我们需要选择适当的自变量,并建立回归方程。
回归方程的形式为:Y = β0 + β1X1 + β2X2 + … + βnXn + ε,其中Y表示因变量,X1至Xn表示自变量,β0至βn表示回归系数,ε表示误差项。
参数估计可以通过最小二乘法来进行,即寻找一组参数估计值,使得观测值与模型预测值之间的残差平方和最小化。
多元线性回归的原理和应用

多元线性回归的原理和应用1. 原理介绍多元线性回归是一种统计分析方法,用于研究多个自变量与一个因变量之间的关系。
它是线性回归分析的一种拓展,可以同时考虑多个自变量对因变量的影响。
多元线性回归的基本原理可以通过以下公式表示:**Y = β0 + β1X1 + β2X2 + … + βn*Xn + ε**其中,Y表示因变量,X1、X2、…、Xn表示自变量,β0、β1、β2、…、βn表示自变量的系数,ε表示误差项。
多元线性回归通过最小二乘法来估计自变量的系数,使得预测值与实际观测值之间的平方误差最小化。
通过最小二乘法的计算,可以得到自变量的系数估计值,进而可以进行预测和解释因变量的变化。
2. 应用领域多元线性回归在各个领域都有广泛的应用,以下列举了一些常见的应用领域:2.1 经济学多元线性回归在经济学中是一个重要的工具,可以用于研究不同变量对经济发展的影响。
例如,可以通过多元线性回归来分析GDP增长率与投资、消费、出口等变量之间的关系,并进一步预测未来的经济发展趋势。
2.2 市场营销在市场营销领域,多元线性回归可以用于研究市场需求的影响因素。
通过分析不同的市场变量(如产品价格、广告投入、竞争对手的行为等),可以预测市场需求的变化,并制定相应的营销策略。
2.3 医学研究多元线性回归在医学研究中也有广泛的应用。
例如,可以使用多元线性回归来研究不同的遗传、环境和生活方式因素对人体健康的影响。
通过分析这些因素,可以预测患病风险并制定相应的预防措施。
2.4 社会科学多元线性回归在社会科学领域中被广泛应用,用于研究各种社会现象。
例如,可以使用多元线性回归来研究教育、收入、职业等因素对犯罪率的影响,并进一步分析这些因素的相互关系。
2.5 工程与科学研究多元线性回归在工程和科学研究中也有一定的应用。
例如,在工程领域中可以使用多元线性回归来研究不同因素对产品质量的影响,并优化生产过程。
在科学研究中,多元线性回归可以用于分析实验数据,探索不同变量之间的关系。
多重系统动力学的原理及其在复杂系统中的应用

多重系统动力学的原理及其在复杂系统中的应用随着科学技术的发展,人们对于复杂系统的研究也越来越重视。
在这个过程中,多重系统动力学的理论应用越来越广泛。
多重系统动力学主要是对于由多个单独的系统相互作用而形成的复合系统进行研究的科学方法。
这个理论的出现,使得我们可以更好地了解不同系统之间的关联性以及相互作用的规律。
多重系统动力学的原理多重系统动力学是一种多学科交叉的研究方法,涉及到数学、物理学、化学、生物学等多个领域。
它主要是基于系统动力学的理论分析,并将其应用到相互作用的复合系统中。
这个理论的基本原理是从微观和宏观两个不同的角度来研究复合系统。
微观角度主要是分析单个系统的特性和影响;而宏观角度则关注复合系统的整体行为以及包含子系统间相互作用的动态过程。
另外,多重系统动力学也强调系统中各个子系统之间的相互反馈。
系统中的任何一个变化都会影响其他子系统以及整个系统的状态,从而导致整个系统的变化。
换言之,多重系统动力学认为系统中的变化都是一个反馈过程,子系统间的相互作用是系统动态变化的一个重要因素。
多重系统动力学的应用多重系统动力学应用非常广泛,尤其是在复杂系统领域。
下面将以城市规划、环境保护和社会经济发展等方面的应用为例进行介绍:1. 城市规划:城市规划是一个非常复杂的系统,涉及到很多因素。
多重系统动力学可以将城市规划分为不同子系统,例如建筑、交通、人口分布等。
然后通过对子系统间的相互作用进行分析,以得出一个最佳的城市规划方案。
2. 环境保护:环境保护是面临的一个重要挑战。
通过对多个子系统的分析,多重系统动力学可以帮助人们了解与环境相关的各种因素,例如空气污染、水污染等。
通过对这些因素的相互作用进行分析,可以得出如何保护环境的最佳方案。
3. 社会经济发展:社会经济发展也是一个复杂的系统。
通过对多个子系统的分析,例如经济、教育、人口、政治等不同系统的影响,多重系统动力学可以帮助人们了解不同因素的相互作用,以制定最适合的社会经济发展计划。
多元回归分析法介绍和具体应用

多元回归分析法介绍和具体应用Y=β0+β1X1+β2X2+...+βpXp+ε其中,Y是依变量,X1,X2,...,Xp是自变量,β0,β1,β2,...,βp 是回归系数,ε是误差项。
1.收集数据:收集与研究对象相关的自变量和依变量数据。
2.建立模型:根据理论分析或经验,选择合适的自变量,并构建线性回归模型。
3.估计回归系数:利用最小二乘法等方法,估计模型中的回归系数。
4.检验回归模型的显著性:通过计算F统计量或t统计量,判断回归模型是否显著。
5.判断自变量的重要性:利用回归系数的显著性检验或变量的贡献度等指标,判断自变量对依变量的重要性。
6.检查模型的拟合度:通过分析残差、检验回归模型的假设条件等方法,检查模型的拟合度。
7.利用模型进行预测和推断:利用已建立的回归模型,进行依变量的预测和自变量的推断。
1.经济学:多元回归分析可用于研究宏观经济指标与影响因素之间的关系,如利率与货币供应量、GDP与投资、通胀率与产出等。
2.金融学:多元回归分析可用于分析影响股价、汇率、利率等金融变量的因素,帮助投资者制定合理的投资策略。
3.市场营销:多元回归分析可用于研究产品销售量与产品特征、价格、广告投入等之间的关系,为市场营销决策提供依据。
4.生物学:多元回归分析可用于研究生物学变量与环境因素之间的关系,如物种多样性与温度、植物生长与土壤养分等。
5.医学:多元回归分析可用于研究疾病发生与影响因素之间的关系,如心脏病与高血压、肥胖与糖尿病等。
6.社会科学:多元回归分析可用于研究社会科学变量与社会因素之间的关系,如教育水平与收入、犯罪率与失业率等。
总之,多元回归分析是一种重要的统计分析方法,可用于研究多个自变量对一个依变量的影响,并在各个领域中发挥重要作用,为决策提供科学依据。
在实际应用中,需要注意合理选择自变量、遵守回归模型的假设条件,并进行适当的模型检验和解释。
多元回归分析原理及例子

多元回归分析原理回归分析是一种处理变量的统计相关关系的一种数理统计方法。
回归分析的基本思想是: 虽然自变量和因变量之间没有严格的、确定性的函数关系, 但可以设法找出最能代表它们之间关系的数学表达形式。
回归分析主要解决以下几个方面的问题:(1) 确定几个特定的变量之间是否存在相关关系, 如果存在的话, 找出它们之间合适的数学表达式;(2) 根据一个或几个变量的值, 预测或控制另一个变量的取值, 并且可以知道这种预测或控制能达到什么样的精确度;(3) 进行因素分析。
例如在对于共同影响一个变量的许多变量(因素)之间, 找出哪些是重要因素,哪些是次要因素, 这些因素之间又有什么关系等等。
回归分析有很广泛的应用, 例如实验数据的一般处理, 经验公式的求得, 因素分析, 产品质量的控制, 气象及地震预报, 自动控制中数学模型的制定等等。
多元回归分析是研究多个变量之间关系的回归分析方法, 按因变量和自变量的数量对应关系可划分为一个因变量对多个自变量的回归分析(简称为“一对多”回归分析)及多个因变量对多个自变量的回归分析(简称为“多对多”回归分析), 按回归模型类型可划分为线性回归分析和非线性回归分析。
本“多元回归分析原理”是针对均匀设计3.00软件的使用而编制的, 它不是多元回归分析的全面内容, 欲了解多元回归分析的其他内容请参阅回归分析方面的书籍。
本部分内容分七个部分, §1~§4介绍“一对多”线性回归分析, 包括数学模型、回归系数估计、回归方程及回归系数的显著性检验、逐步回归分析方法。
“一对多”线性回归分析是多元回归分析的基础, “多对多”回归分析的内容与“一对多”的相应内容类似, §5介绍“多对多”线性回归的数学模型, §6介绍“多对多”回归的双重筛选逐步回归法。
§7简要介绍非线性回归分析。
§1 一对多线性回归分析的数学模型§2 回归系数的最小二乘估计§3 回归方程及回归系数的显著性检验§4 逐步回归分析§5 多对多线性回归数学模型§6 双重筛选逐步回归§7 非线性回归模型1 一对多线性回归分析的数学模型§个自变量存在线性关系设随机变量与:, (1.1)式中为回归系数, 为随机误差。
多元回归分析的原理与应用

Yˆ 0 1X
总体未知参数
14
体重(Y)
10名学生的身高与体重散点图
最75 小二乘法(Least squares method):
以70 极小化 ( y yˆ)2 为目标,求估yˆ 计a bx
方65 程的过程。
yˆ a bx
60
55
50
残差(Residual):e
45
40
158
163
9
1.2 回归分析的分类
回归分析
按自变量 个数分类
一元回归 简单回归
多元回归 复回归
按方程式 特征分类
线性回归 非线性回归
10
只有一个自变量的线性回归叫一元线 性回归,也叫简单回归。
与方差分析不同,在回归分析中,“ 元”是指自变量,而不是指因变量。
11
总体的一元线性回归模型:
Yˆ 0 1X
8
对于自变量x1,x2,x3,…,xi的每一组确定的值, f(x1,x2,x3,…,xi)的值也是确定的;但由于是不确定 的,所以,y也是不确定的,但在每一组确定的自 变量之下,所有的服从均数为零的正态分布,因 此,对于自变量的每一组确定的值,因变量也服从 正态分布,其平均数就是f(x1,x2,x3,…,xi),该公式即 为回归方程,记为:
方差齐性:就X1,X2,X3,……XK任何一个组合而言, 因变量Y的变异数均相同。
正态性:就任何X1,X2,X3,……XK的线性组合而言, 因变量Y的分配是正态的。
全的拟合。
差的拟合。
17
r
2
(n
x2
(n xy x y)2 ( x)2) (n y2 (
y)2
)
r
n xy x y
受迫振动下多自由度隔振系统的动态特性研究

输 入通 道 偏 心 质量 在 激 振 力 卜的受 迫 振 动 ,输
f}I通 道 为被 一V.-挂 体 质 心 ' (竖 丘)、 (水 平 )
方 向上 的 化 移 幅值 以及 弹 簧悬 挂 点 、阻 安装
点 的受 力幅 值 由 丁驱 动 电 机 的极 限 [作转 述 为
l 200 r/mi., 此 定 义激 振 顿 率 t I(单 化 Hz)的
l[ …【 【 』
I
!
f
—
j J .
JI
、
.
I"requencvltlz
a) '力 向 f 移 !顷 响 应
研 究 与
DOI:10.3969/j.issn.1009-9492.2018.03.008
受迫振动下 多 自由度隔振 系统 的动态特性研 究
孙维丽 ,马 玉华 ,宋爱利 ,葛伟伟
(青 岛黄 海学院 , 山东青 岛 266427)
摘要 :多 自由度隔振系统在受迫振 动下的动力学特性是 目前工程 机械振动控制研究 的热点 。基 于广 义拉格 朗 日方程和矢量环方
s J,在 这 种 条 件 得 到 的 功 力学 特 性 埘 比 分 析结
果 如 f割3所 爪 fH- 3巾可 以看 fl{:阻 尼 系数 对振 动
特 性 的 影 响 与弹 簧 刚 度 小 质 的 别 ; 个 隔振
系统 的 仃 率 阻 尼 系数 的 变 化无 关 ,仉 足 对 于』t.7振 振 幅 变 化 的 敏 度 非 常 高 ;对 丁 I5f【尼 ,
文献标识码 :A
文章编号 :1009—9492(2018)03—0029—03
Study on Dynam ic Characteristics 0f M ulti Degree Freedom Isolation System under Forced Vibration
回归分析中的共和异方差性问题处理方法(十)

回归分析是统计学中常用的一种方法,用来研究自变量和因变量之间的关系。
在进行回归分析时,我们经常会遇到共和异方差性问题,也就是误差项的方差不恒定。
这会影响到回归系数的估计准确性,因此需要采取相应的处理方法。
本文将介绍一些处理共和异方差性问题的方法。
首先,我们来了解一下什么是共和异方差性。
共方差性指的是误差项的方差在所有观测值上是恒定的,即方差不随自变量的取值而变化。
而异方差性则是指误差项的方差与自变量的取值有关,呈现出不恒定的特点。
共和异方差性问题在回归分析中是比较常见的,尤其是在实际数据中,很多情况下误差项的方差并不是恒定的。
针对共和异方差性问题,我们可以采取不同的处理方法。
一种常见的方法是进行加权最小二乘法(Weighted Least Squares, WLS)估计。
这种方法通过对方程进行加权处理,使得方差不恒定的问题得到一定程度的缓解。
在进行WLS估计时,需要首先对误差项的方差进行估计,然后将估计的方差作为权重引入到最小二乘法中,从而得到修正后的回归系数估计值。
通过WLS估计,我们可以有效地处理共和异方差性问题,提高回归模型的拟合度和预测准确性。
除了WLS估计外,我们还可以使用异方差稳健标准误(Heteroscedasticity-robust standard errors)来处理共和异方差性问题。
这种方法通过对标准误进行修正,使得回归系数的显著性检验和置信区间的估计不再依赖于误差项方差的恒定性。
异方差稳健标准误的计算方法相对简单,通常可以在常见的统计软件中直接得到。
使用异方差稳健标准误可以有效地应对共和异方差性问题,提高回归分析的准确性和稳健性。
除了上述方法外,我们还可以采用变量转换的方式来处理共和异方差性问题。
对于存在异方差性的数据,我们可以对自变量或因变量进行对数变换、幂变换或其他形式的变换,从而使得数据的方差变得更加均匀,降低异方差性对回归分析结果的影响。
变量转换是一种简单而有效的处理共和异方差性问题的方法,通常可以在数据预处理阶段进行,有助于提高回归模型的拟合度和预测准确性。
第三章受约束回归问题讲述

可用二者的差 :RSSR - RSSU的大小来检验约 束的真实性
根据数理统计学的知识:
RSSU / 2 ~ 2 (n kU 1)
RSSR / 2 ~ 2 (n k R 1)
(RSSR RSSU ) / 2 ~ 2 (kU k R )
其中k 为无约束模型解释变量个数, kR为受约束模 型解释变量个数,于是:
1/9/2019
受约束样本回归模型的残差平方和:RSSR
ˆ ˆ ˆ ˆ e e e e ( β β ) X X( β β ) * * * *
于是
e *e* e e
(3)
e′e为无约束样本回归模型的残差平方和:RSSU 受约束与无约束模型都有相同的总离差平方 和TSS(因为受约束与无约束模型都有相同 的被解释变量和样本)
然而,对所研究的具体问题能否施加约束?需 进一步进行相应的检验。 常用的检验有:F检验、x2检验与t检验。
1/9/2019
F检验
在同一样本下,记无约束样本回归模型为:
ˆ e Y Xβ
受约束样本回归模型为: ˆ * e* Y Xβ 于是:
ˆ * Xβ ˆ e Xβ ˆ * e X(β ˆ * β ˆ) e* Y Xβ
1/9/2019
建立1981~1994年中国城镇居民对食品的消费 需求模型:
ˆ ) 3.63 1.05 ln( X ) 0.08 ln( P1 ) 0.92 ln( P0 ) ln(Q
(9.03) (25.35) (-2.28) (-7.34)
各变量的弹性之和 1 2 3 0.05 ,比较接 近于零,但不为零。
多自由度有阻尼体系的受迫振动

4.3.1坐标的耦联与正则坐标
通过前面给出的两质点运动方程知:由于方程组的未知数(坐标)
u 和u 是耦联的,也就是说必须联立求解才能得到u 和u 的解,这种方程
1
2
1
2
称为坐标耦联。坐标耦联又可以分为刚度(静力)耦联,以及惯性(加速
度或质量)耦联。因此,微分方程组耦联的数目越少,方程的解法就越
简单。为此,引入广义坐标(独立坐标)的概念对微分方程组进行耦联。
1
2
-
1
12
1
2
-
1
22
1
2
-
1
32
=0
展开后,有
(4.81)
1
2
3
-
1
12
+
1
22
+
1
32
1
2
2
0
(4.82)
比较式(4.82)和式(4.80),有
1
12
+
1
22
+
1
32
=11m1+22m2 +33m3
(4.83)
由于工程实际中的高频部分较基频高的多,所以,忽略上式左端的 高阶频 1 、1 后,可以得到关于体系第一频率的近似公式。
MX
i
qi这一项不为0.其他
项均为0,故得:
X
T i
Mu
X
T i
MX
i
qi
(4.59)
q(i t)=
X
T i
Mu
X
T i
MX
i
X
T i
Mu
Mi
(4.60)
多元线性回归实例分析报告

SPSS--回归-多元线性回归模型案例解析!(一)多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:毫无疑问,多元线性回归方程应该为:上图中的 x1, x2, xp分别代表“自变量”Xp截止,代表有P个自变量,如果有“N组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:那么,多元线性回归方程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:无偏性假设,即指:期望值为03:同共方差性假设,即指,所有的随机误差变量方差都相等4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释。
今天跟大家一起讨论一下,SPSS---多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型。
数据如下图所示:点击“分析”——回归——线性——进入如下图所示的界面:将“销售量”作为“因变量”拖入因变量框内,将“车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在“方法”旁边,选择“逐步”,当然,你也可以选择其它的方式,如果你选择“进入”默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入)如果你选择“逐步”这个方法,将会得到如下图所示的结果:(将会根据预先设定的“F统计量的概率值进行筛选,最先进入回归方程的“自变量”应该是跟“因变量”关系最为密切,贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05,当概率值大于等于0.1时将会被剔除)“选择变量(E)" 框内,我并没有输入数据,如果你需要对某个“自变量”进行条件筛选,可以将那个自变量,移入“选择变量框”内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所示:点击“统计量”弹出如下所示的框,如下所示:在“回归系数”下面勾选“估计,在右侧勾选”模型拟合度“和”共线性诊断“两个选项,再勾选“个案诊断”再点击“离群值”一般默认值为“3”,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
第三章多变量回归分析计量经济学,南开大学

方差分析表( ANOVA) 平方和 ESS
ˆ Y ˆ ) Y' Y β ˆ ' X' Y (Y i
2
df k-1
均方差
ˆ ' X' Y) /(k 1) (Y' Y β
RSS
TSS
ˆ ' X' Y nY ˆ β u (Y Y ) Y' Y nY
2 2
i
n-k
2
ˆ ' X' Y nY 2 ) /(n k ) (β
2
(4)判断: t t (n k ), 则接受H 0 , 参数 i显著异于0 2 若 t t (n k ), 则拒绝H 0 , 接受H1 , 参数 i不显著异于 0
i 非负,则可做单侧检验,比较 t 与tα。 如果根据理论或常识,
若 t t (n k ), 则接受H 0 , 参数 i不显著异于 0 t t (n k ), 则拒绝H 0 , 接受H1 , 参数 i显著异于0
R 2 /(k 1) 可得到F (1 R 2 ) /(n k )
显然,R2 越大,F越大,当R2 =1时,F 无限大。
选择显著水平α ,计算F统计量的值,与F分布表中的临界值进行比 较: F F (k 1, n k ), 则接受H 0 , 不显著 若 F F (k 1, n k ), 则拒绝H 0 , 接受H1 , 显著
Y为因变量观测值列向量
在 Y Xβ u
X为数据矩阵。 中, β 为待估计参数列向量 u为随机扰动项列向量
二、多 变量线性回归模型的基本假定
1 、 E u 0
随机干扰项的期望值为0。
u1 u2 2、 E u u ' u1 u n 2 0 0 0 0 0 0
(整理)多元线性回归分析.
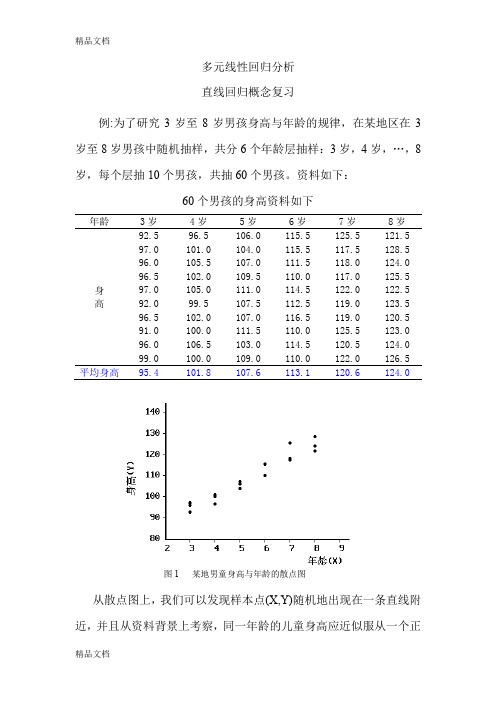
多元线性回归分析 直线回归概念复习例:为了研究3岁至8岁男孩身高与年龄的规律,在某地区在3岁至8岁男孩中随机抽样,共分6个年龄层抽样:3岁,4岁,…,8岁,每个层抽10个男孩,共抽60个男孩。
资料如下:60个男孩的身高资料如下年龄3岁 4岁 5岁 6岁 7岁 8岁 身 高92.5 96.5 106.0 115.5 125.5 121.5 97.0 101.0 104.0 115.5 117.5 128.5 96.0 105.5 107.0 111.5 118.0 124.0 96.5 102.0 109.5 110.0 117.0 125.5 97.0 105.0 111.0 114.5 122.0 122.5 92.0 99.5 107.5 112.5 119.0 123.5 96.5 102.0 107.0 116.5 119.0 120.5 91.0 100.0 111.5 110.0 125.5 123.0 96.0 106.5 103.0 114.5 120.5 124.0 99.0 100.0 109.0 110.0 122.0 126.5 平均身高95.4101.8107.6113.1120.6124.0从散点图上,我们可以发现样本点(X,Y)随机地出现在一条直线附近,并且从资料背景上考察,同一年龄的儿童身高应近似服从一个正图1 某地男童身高与年龄的散点图态分布,而儿童身高的总体均数应随着年龄增长而增大,并由每个年龄的身高样本均数与儿童年龄的散点图可以发现:这些点非常接近一条直线以及样本均数存在抽样误差,因此推测儿童身高的总体均数与年龄可能呈直线关系。
故假定身高Y 在年龄X 点上的总体均数X Y |μ与X 呈直线关系。
x μαβ=+y其中y 表示身高,x 表示年龄。
由于身高的总体均数与年龄有关,所以更准确地标记应为x μαβ=+y|x表示在固定年龄情况下的身高总体均数。
身高的样本均数与年龄的散点图故有理由认为身高的总体均数与年龄的关系可能是一条直线关系 上述公式称为直线回归方程。
一类拟 Hamilton 碰振系统的全局分岔及多解共存现象分析

一类拟 Hamilton 碰振系统的全局分岔及多解共存现象分析张思进;尹磊磊;桂林【摘要】研究了一类拟 Hamilton碰振系统的全局动力学特性,参照同宿轨道的Melni-kov函数形式,构造了周期轨道次谐Melnikov函数。
并用一类拟Hamilton碰振系统详细介绍了其计算方法和运用,数值结果验证了构造的次谐Melnikov 函数的有效性。
另外用改进的胞映射方法对这类系统的全局分岔和多解共存现象进行了分析,发现随着外激励力的变动吸引子数量发生变化,各个吸引域形态复杂且相互缠绕。
%This paper studied the global dynamic properties of a quasi-Hamiltonian vibro-impact sys-tem.By referring to Melnikov function for homoclinic orbit in the quasi-Hamiltonian system,the subhar-monic Melnikov function for periodic orbit was constructed.A quasi-Hamiltonian vibro-impact system was given to illustrate the application of the procedures,and the validity of the function was verified with nu-merical results.At the same time,the global bifurcations and coexistence of multiple solutions for this vi-bro-impact system were analyzed in the improved cell mapping method.The number of coexistent attractor changes with the change of external excitation force,and domains of attraction with complicated fractal boundaries are intertwined.【期刊名称】《湖南大学学报(自然科学版)》【年(卷),期】2014(000)010【总页数】7页(P55-61)【关键词】拟Hamilton系统;Melnikov方法;同宿轨道;分岔;多解共存;胞映射【作者】张思进;尹磊磊;桂林【作者单位】湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙410082;湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙 410082;湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙 410082【正文语种】中文【中图分类】O322非光滑动力系统广泛地存在于工程力学、工程机械、电子电路、生态种群等多个科学领域,主要形式包括碰撞、冲击和干摩擦等.由于非光滑系统的相空间中的流不连续,这类系统常常有非常复杂的动力学行为,包括传统上的倍周期分岔、鞍结点分岔,也会产生新的分岔形式,如擦边分岔、黏滞-滑移分岔等[1-4].在光滑非线性动力学系统中,通过计算稳定流形和不稳定流形之间的距离,Melnikov 方法广泛运用于计算拟Hamilton系统产生混沌运动的参数阈值[5-7];郑吉兵等[5]计算了拟Hamilton系统的Melnikov函数,并得出了系统的Hopf分岔条件.赵跃宇等[7]研究了杜芬方程同宿轨道所对应的Melnikov函数,并且得到了产生混沌时的系统参数阈值.由于非光滑拟Hamilton系统相空间中的流在切换面附近的可微性被破坏,直接采用Melnikov方法变得不可行.针对非光滑动力学系统必须构建新的Melnikov函数来分析系统的全局特性,目前国内外研究的还比较少[8-10].Xu等[9]构建了非光滑碰振系统同宿轨道的Melnikov函数,能很好地预测在碰撞面和外激励共同作用下同宿轨道发生破裂产生混沌的参数范围.Liang等[10]研究了分段形式的拟Hamilton系统,给出了有关极限环分岔以及Melnikov函数展开形式的结果.但是这些少量关于非光滑系统的Melnikov函数计算方法的文章也只是针对同宿轨道而言的,并没有考虑同时存在的同宿轨道内部周期轨道族在碰撞面和激励力共同作用下的多种非线性动力学现象.本文首先介绍了拟Hamilton碰振系统同宿轨道的Melnikov函数的计算方法,得到同宿轨破裂产生混沌的参数范围;然后参照同宿轨道的Melnikov函数形式,类似给出了周期轨道次谐Melnikov函数形式,并用一类拟Hamilton碰振系统作为算例,详细介绍了其计算方法和运用,数值结果验证了我们构造的Melnikov函数的有效性.另外根据同宿轨道的Melnikov函数和次谐轨道Melnikov函数确定的区域将整个参数范围分为3个区域,并对其中运动形式较复杂的重叠区域绘制了全局分岔图,运用改进的胞映射方法进行全局动力学分析,发现系统存在多种吸引子共存现象,随着激励力变化吸引子数目形态发生变动,且各个吸引域形态复杂、相互缠绕.1 同宿轨道的Melnikov方法考虑以下双边刚性的约束广义碰振系统,系统的模型方程如下:(1)式中:ε为一小量;h表示位移间隙,R=1-εr表示碰撞恢复系数,若是完全弹性碰撞,R=1;左右碰撞边界分别被定义为用来描述系统碰撞位置;下标“-”和“+”分别表示碰撞前后的时刻.方程可以化为:(2)式中:假设当ε=0时,未扰系统是一个Hamilton系统,存在一个双曲鞍点和一条连接鞍点的同宿轨道,由参考文献[8-9]可得到拟Hamilton碰振系统同宿轨道的Melnikov函数为:F(Xh(τ))∧G(Xh(τ),t0+τ)dt-2rf(x)dx.(3)其公式分为两个部分:前两项为类似光滑非线性动力学系统部分,“∧”表示楔积运算;最后一项是由于系统的非光滑性(碰撞面)产生的.2 周期轨道次谐Melnikov函数及混沌分析虽然针对非光滑碰振系统同宿轨道的Melnikov函数已给出,能很好地预测同宿轨道破裂产生混沌的参数范围,但是并不能解释(在非混沌区域)同宿轨道内部存在的一簇簇周期轨道在激励力和碰撞面的共同作用下产生的各种非线性运动现象.本文尝试给出非光滑碰振系统共振周期轨道次谐Melnikov函数,用以确定系统可能出现的次谐周期解参数范围.考虑双边刚性的约束广义碰振系统,系统的模型方程同上,具体表达式见(1).在同宿轨道内部围绕中心有以参数为α的周期轨道族(如图1所示),左右对称,本文分析x>0部分.参照同宿轨形式,类似给出周期轨道次谐Melnikov函数的形式,也是分为两个部分:类似光滑非线性动力系统部分和碰撞面部分,分别为第一部分和第二部分(如公式(3)).则次谐轨道Melnikov函数可以假定定义为:图1 未扰系统周期轨道图Fig.1 The periodic orbit of the unperturbed systemt+t0)dt-2rf(x)dx.(4)式中:α为同宿轨内部周期轨道参数;周期闭轨的周期为Tα;T为外激励周期.因为周期轨道起始点位于碰撞面以外,我们对周期轨道方程作坐标变换.故用t-Tα/2代替t;积分区域为(-mT/2,mT/2)是考虑积分区域应位于碰撞面以内(位于x=h碰撞面的左侧)作的变换,且T为外激励周期;x1min 指的是未扰周期轨离碰撞面最远处x1的坐标值(周期轨道左右对称以右边为参考,见图1),这里和同宿轨道的Melnikov函数不同,是由于同宿轨轨线连接鞍点(原点),而周期轨轨线只是围绕系统中心处.定义坐标变换后未扰系统周期轨线离开和到达碰撞面分别为τ+和为未进行坐标变换前未扰周期轨道由零时刻运动到碰撞面的时间(且不考虑碰撞面作用),则(5)考虑对称性有:(6)根据系统产生共振的参数条件,有:n(Tα-(τ+-τ-))=mT,(7)且m,n为互质的正整数.考虑共振的参数条件由式(5)和(7)可确定周期轨道参数α,从而得到共振周期轨道方程,代入式(4)可确定周期轨道次谐Melnikov函数,由Melnikov函数出现零点的条件,从而得到系统可能出现次谐周期解参数范围.下面介绍一个运用周期轨道次谐Melnikov函数的算例.2.1 周期轨道次谐Melnikov函数运用算例考虑谐和激励下的 Duffing 双边刚性碰撞系统,系统的模型方程如下:(8)式中:常量εb和εf分别表示系统的阻尼系数和谐和激励的强度;h表示位移间隙,描述系统状态的碰撞位置;R=1-r0,r0=εr表示碰撞恢复系数,若是完全弹性碰撞,则R=1;下标“-”和“+”分别表示碰撞前后的时刻.令系统(1)可化为一阶方程:(9)未扰系统有3个奇点:(0,0),(±1,0).其中(0,0)点为鞍点,(±1,0)点为中心,存在过鞍点P(0,0)的同宿轨道Γ.未扰同宿轨道表达式为:(10)这里Th,±表示到达轨线到达碰撞面的时间.计算得未扰系统周期轨道参数方程为:(11)闭轨的周期为:式中:sn,cn,dn均为Jacobi椭圆函数;K(α)为第一类完全椭圆积分.取h=1,ω=1未扰系统相空间如图2所示.图2中粗线表示同宿轨,同宿轨线内部有一簇簇周期轨线.由式(3)系统同宿轨道的 Melnikov 函数为:M(t0)=-bI1+fZ(t0)-rI2.式中:I2=2(x-x3)dx;x1图2 未扰系统的相轨迹图Fig.2 Phase portrait of the unperturbed system通过数值积分算得(12)依据 Melnikov 函数理论系统产生混沌的参数必要条件为:f>5.290 088 281+0.991 891 552 5r.(13)由式(13)得到分界线为直线A(如图3所示),分界线上一点(如点1)系统同宿轨发生横截相交,出现马蹄混沌.当位于分界线以下(如点2)时,系统是周期运动[9].r图3 系统可能出现次谐周期解的参数范围Fig.3 The parameter range where subharmonic periodic solutions may emerge下面计算系统共振周期轨次谐Melnikov函数.考虑主共振:m=1,n=1将周期轨道参数方程代入式(5)和(7),可以确定轨道参数α值,α=0.994 607 173 456 642 2.代入式(4)数值计算得:(14)由Melnikov函数出现零点的条件,系统可能出现次谐周期解的分界线为:f=1.542 338 170 38+3.316 808 335 68r.(15)由式(15)得到分界线为直线B(如图3所示).当参数范围位于分界线以下时Melnikov函数没有简单零点,则系统为次谐轨道混沌的区域.当位于分界线以上时,系统有可能出现次谐周期解.验证上面的结果参考点2,继续降低激励力.位于B分界线以上(如点3)f=2.6,r=2,ε=0.1.计算相图如图4(a),左右对称, 这里只画出右碰撞面相图;取分界线下区域(如点4)f=2.2,r=2,计算相图如图4(b);然后增大回弹系数r0(即降低r),位于分界线以上(如点5)f=2.2,r=1,计算相图如图4(c).然后再降低外激励,位于分界线以下(如点6) f=1.9,r=1,计算相图如图4(d).由相图可知:分界线以上参数范围系统出现次谐周期解,而分界线下是混沌解.验证了我们构造的周期轨道次谐Melnikov函数的有效性.2.2 系统全局分岔及胞映射计算通过我们的分析,如图3所示,系统的参数范围被同宿轨道的Melnikov函数(直线A)和次谐Melnikov函数(直线B)划分为3个区域,由上到下分别用Ⅰ,Ⅱ,Ⅲ表示,则Ⅰ区域表示系统同宿轨发生横截相交可能出现混沌的区域;Ⅲ区域表示系统次谐轨道混沌的区域;Ⅱ区域为一重叠区域,分别为同宿轨道未发生破裂的(双边碰撞)周期运动区域和共振周期轨道可能出现次谐周期解(单边碰撞)的区域.由于重叠区域Ⅱ既有同宿轨道的周期运动又可能存在次谐周期运动,存在多种吸引子共存现象,运动形式复杂,故我们对区域Ⅱ进行全局分岔分析及用改进胞映射法计算吸引域.通过分析,固定r=2,我们发现,当激励力太小,振子没有足够的能量时,同时与两个碰撞面发生作用,只会出现单边碰撞的情况,f<3.63;反之激励力太大,表示外输入能量值越大,系统越容易脱离一个中心的吸引,与两个碰撞面作用,故单边碰撞现象消失,f>4.5,只有同宿轨道的双碰周期极限环运动.我们感兴趣的范围为激励力适中,此时同宿轨道双碰周期运动和周期轨产生的各种单碰运动形式都存在.故我们选定激励力范围为f∈(3.6,4.6).依据多初值打靶法,我们建立f∈(3.6,4.6)的系统全局分岔图,如图5所示.图4 次谐轨道相图Fig.4 Phase portraits of subharmonic orbitf图5 系统的全局分岔图Fig.5 The global bifurcation diagram of the system图5中,中间一条线表示同宿轨道产生的双碰极限环运动;上下各两支表示周期轨道在碰撞面和外激励的作用下产生的各种运动形式,上下各代表与左和右两个碰撞面作用.通过分岔图我们可选几个具代表意义的f值画出其相图如图6所示,并进行分析.当f=3.7时系统有5种不同的运动形式共存,如图6(a)分别为同宿轨产生的双碰极限环运动,周期轨产生的幅值大小不同的单碰极限环运动(左右对称),当f>4.5时,系统只剩下双碰极限环运动.对应分岔图分别绘制f为3.7,3.92,4.0,4.4的相图,对应图6的(a)(b)(c)(d).大部分混沌的产生都是倍周期分岔产生的.在特定的参数区域,周期轨道极限环运动也是通过倍周期分岔通往混沌的,通过分岔图5可以看出,当3.75<f<3.95时周期轨产生的单边碰撞大幅值极限环运动(左右对称)通过倍周期分岔通往混沌.由于非光滑动力学系统在切换面处需要较高的积分精度,而一味地降低步长,计算量很大,因此我们采用连续拉回积分[11],只是用小步长积分跨越碰撞面,大大缩短了计算时间,计算精度也没有损失.用改进的胞映射方法,对同宿轨道产生周期解和周期轨道产生的多种单碰运动形式各自的吸引域进行了区分,分析系统的全局动力学行为.首先对双碰极限环和周期轨产生的单边碰撞混沌的各自吸引子进行了计算.此时外激励f=4.4,共存相图如图6(d)所示.我们研究区间{x,y|-1<x<1,-1.2<y<1.2,x,y∈R},将区间细化为200×240个胞空间.计算出双碰极限环的吸引域(黑色区域)如图7所示.从图7吸引域可以看出,双碰极限环的区域主要位于鞍点(0,0)的上方区域,左右两边的单碰混沌吸引域的区域主要位于中心点(±1,0)的周围,这与未扰 Hamilton系统同宿轨道和周期轨道的产生区域大体是吻合的.同时我们计算了f=3.7时5个周期吸引子共存时各自的吸引域,如图8所示,将区间细化为400×480个胞空间,由于周期轨道产生的周期吸引子具有左右对称性,分别与左碰撞面和右碰撞面作用,故我们将其吸引域合在一起.灰色和黑色区域分别为单碰大小幅值极限环运动吸引域;空白区域为双碰极限环的吸引域.图6 多吸引子共存相图Fig.6 Coexistence of attractors in the phase portraitsx1图7 双碰极限环的吸引域Fig.7 The attraction basin of limit cycles with 2-impact(f=4.4)各个周期吸引子的吸引域相互交错在一起,特别是鞍点附近.小的扰动可能使鞍点附近出发的轨线具有不同的运动形式.对比图7和图8,同宿轨产生的双碰极限环的吸引域随着激励力的减小是不断缩小的,这和分岔图结果是吻合的.另外从图8也可以看出,周期轨产生的大幅值单碰极限环运动的吸引域(灰色区域)远小于小幅值单碰极限环运动的吸引域(黑色区域).另外我们计算了f=4.0时各自的吸引域,如图9所示,可以看出双碰极限环运动的吸引域(黑色区域)基本不变化,消失的单碰大幅值运动的吸引域合并为单碰小幅值运动的吸引域(空白区域),只有双碰极限环和单碰小幅值极限环共存.x1图8 各吸引子的吸引域Fig.8 The attraction basin of each attractor(f=3.7)x1图9 双碰极限环的吸引域Fig.9 The attraction basin of limit cycles with 2-impact(f=4.0)通过以上胞映射的分析,我们发现:鞍点附近初值区域是比较敏感的区域,在此区域内,稍微变动的初值可能具有不同的运动形式,在设计这类碰振系统时,应远离鞍点附近初值区域,增强系统的抗扰动能力;另外各吸引子的吸引域区域与未扰Hamilton系统同宿轨道和周期轨道的产生区域大体是吻合的,并且具有相似的拓扑结构;同时各吸引子吸引域随激励力变动而不断变动,特别是周期轨在碰撞面和外激励作用下同时能产生多个吸引子,吸引域相互缠绕.并且随着激励力变动,吸引子减少或者形态可以发生变动.3 结论参照拟Hamilton碰振系统同宿轨道的Melnikov函数形式,构造了周期轨道次谐Melnikov函数.并给出计算算例,验证了构造的Melnikov函数的正确性.构造的次谐Melnikov函数能得到系统可能出现次谐周期解的参数区域.根据同宿轨道Melnikov函数和周期轨道次谐Melnikov函数确定的区域将整个参数范围划分为3个区域,这样我们就可以根据参数值所在区域,预测这类系统运动形式,包括混沌区,对工程运用具有参考价值.另外我们取系统运动形态比较复杂的重叠区域Ⅱ绘制了全局分岔图,并用胞映射方法做全局动力学分析.发现随着激励力的变动吸引子数量发生变化,各个吸引域形态复杂且相互缠绕,使系统初值远离混沌吸引域和鞍点附近初值敏感地带,可以为拟Hamilton碰振系统的混沌控制提供参考的初值范围以及增强系统抗扰动能力. 参考文献[1] CHILLINGWORTH D. Dynamics of an impact oscillator near a degenerate graze [J]. Nonlinearity, 2010, 23:2723-2748.[2] 胡海岩. 分段线性系统动力学的非光滑分析[J]. 力学学报,1996, 28(4):483-488.HU Hai-yan. Nonsmooth analysis of dynamics of a piecewise linear system [J]. Acta Mechanica Sinica, 1996, 28(4):483-488.(In Chinese)[3] 张思进,傅衣铭,陆启韶. 一类转子碰摩映射的分岔分析[J]. 振动工程学报,2005, 18(4):389-394.ZHANG Si-jin, FU Yi-ming, LU Qi-shao. Analysis of the rub-impacting map of rotor systems [J]. Journal of Vibration Engineering, 2005, 18(4): 389-394.(In Chinese)[4] WEN G L, XU H D, XIE J H. Controlling Hopf-Hopf interaction bifurcations of a two-degree-of-freedom self-excited system with dry friction [J]. Nonlinear Dynamics, 2011, 64: 49-57.[5] 郑吉兵,谢建华,孟光. 近哈密顿系统的Hopf分岔[J]. 力学学报,2001,33(1):134-141.ZHENG Ji-bing, XIE Jian-hua, MENG Guang. Hopf bifurcation of a perturbed hamiltonian system [J]. Acta Mechanica Sinica, 2001, 33(1):134-141. (In Chinese)[6] 甘春标,王振林. 一类非线性振子中有界噪声诱发的混沌运动[J]. 振动工程学报,2004, 17(3):321-325.GAN Chun-biao, WANG Zhen-lin. Chaotic motions induced by bounded noise in a nonlinear oscillator [J]. Journal of Vibration Engineering,2004,17(3):321-325. (In Chinese)[7] 赵跃宇,蒋丽忠. 非惯性系中弹性薄板的全局分叉和混沌性质[J]. 湖南大学学报:自然科学版,1997, 24(3): 28-33.ZHAO Yue-yu,JIANG Li-zhong. The global bifurcation and chaotic behavior of the thin elastic plates in noninertia system [J]. Journal of Hunan University: Natural Sciences, 1997, 24(3):28-33. (In Chinese)[8] DU Z D, ZHANG W N. Melnikov method for homoclinic bifurcation in nonlinear impact oscillators [J]. Comput Math Appl, 2005, 50: 445-458. [9] XU W, FENG J Q, RONG H W. Melnikov’s method for a general nonlinear vibro-impact oscillato [J]. Nonlinear Anal, 2009, 71: 418-426. [10]LIANG F, HAN M. Limit cycles near generalized homoclinic and doublehomoclinic loops in discontinuous systems [J]. Chaos, Solitons & Fractals, 2012, 45: 454-464.[11]李健,张思进. 非光滑动力系统胞映射计算方法[J]. 固体力学学报,2007, 28(1):93-96.LI Jian, ZHANG Si-jin. Cell-mapping computation method for non-smooth dynamical systems [J]. Chinese Journal of Solid Mechanics,2007,28(1):93-96.(In Chinese)。
多重回归方程介绍

多重回归方程介绍1. 引言多重回归方程是一种经济学和统计学中常用的分析方法,用于研究一个或多个自变量对因变量的影响关系。
它可以帮助我们理解自变量与因变量之间的关系,并预测因变量的取值。
本文将介绍多重回归方程的概念、建立方法和应用场景。
2. 多重回归方程的概念多重回归方程是通过使用多个自变量来解释因变量变化的统计模型。
它可以用数学方程的形式表示为:Y = β0+ β1X1 + β2X2 + ... + βnXn + ε其中,Y是因变量,X1、X2、…、Xn是自变量,β0、β1、β2、…、βn是各个自变量的系数,ε是误差项。
多重回归方程的目标是找到最佳的系数估计值,使得方程中的预测值与实际观测值之间的差异最小化。
3. 多重回归方程的建立方法3.1 数据收集和准备在建立多重回归方程之前,需要收集自变量和因变量的相关数据。
这些数据可以来自实验、调查或观测。
在收集数据时,需要注意数据的准确性和完整性。
在选择模型时,需要确定哪些自变量应该包括在多重回归方程中。
这可以通过领域知识、统计测试和特征选择算法等方法进行。
3.3 模型拟合模型拟合是通过最小化预测值与实际观测值之间的差异来确定系数估计值。
常用的方法是最小二乘法,它通过最小化残差平方和来寻找最佳的系数估计值。
在建立多重回归方程后,需要对模型进行评估以确定其拟合程度和预测能力。
常用的评估指标包括决定系数(R^2)、调整决定系数、均方根误差等。
4. 多重回归方程的应用场景多重回归方程在实际应用中具有广泛的用途。
以下是一些常见的应用场景:4.1 金融分析多重回归方程可以用于分析影响股票价格、汇率波动等金融指标的自变量,并预测未来的变化趋势。
4.2 市场营销多重回归方程可以帮助企业确定影响销售额的因素,并优化营销策略。
4.3 医学研究多重回归方程可以用于研究疾病发生的危险因素,并预测患病的可能性。
4.4 社会科学研究多重回归方程可以用于研究社会现象的影响因素,并提供政策建议。
回归的原理

回归的原理回归分析是一种基本的统计方法,用于研究变量之间的关系。
它的目标是建立一个数学模型,以预测一个或多个自变量(解释变量)对应因变量(被解释变量)的影响程度。
回归分析可以用于解释变量与因变量之间的线性关系,也可以拓展到非线性关系。
回归分析基于最小二乘法原理,即通过最小化残差平方和来确定最佳拟合曲线或平面。
在简单线性回归中,只有一个自变量和一个因变量,回归模型可以表示为y = β0 + β1x + ε,其中 y 是因变量,x 是自变量,β0 和β1 是回归系数,ε 是随机误差项。
多元回归分析可以处理多个自变量和一个因变量的情况。
多元回归模型可以表示为y = β0 + β1x1 + β2x2 + ... + βnxn + ε,其中 x1、x2、...、xn 是自变量,β1、β2、...、βn 是回归系数。
多元回归分析可以解决多个自变量对因变量的影响效果,并控制其他自变量的影响。
回归分析的应用广泛,可以用于预测和预测建模。
它可以帮助研究者理解和预测变量之间的关系,并用于市场预测、经济分析、风险评估等方面。
此外,回归分析还可以用于发现变量之间的潜在关系,进行因果推断,评估政策和干预措施的效果等。
在进行回归分析时,需要注意几个方面。
首先,回归模型的可解释性要合理,不能过度解释或过度简化。
其次,需要考虑自变量之间的多重共线性问题,以避免结果的不准确性。
此外,还要注意样本的选择和数据的质量,以及选取合适的回归方法和检验方法。
总而言之,回归分析是一种重要的统计分析方法,可以用于分析和解释变量之间的关系。
它提供了一种量化的方式来理解因果关系,并预测未来的变化趋势。
在实际应用中,需要综合考虑多个因素,以得出准确的结论和可行的建议。
R语言回归及混合效应(多水平层次嵌套)模型应用及贝叶斯实现

R语言回归及混合效应(多水平层次嵌套)模型应用及贝叶斯实现回归及混合效应模型是统计学中常用的分析方法,可以用来研究变量之间的关系。
R语言是一种常用的统计软件,可以实现回归及混合效应模型的应用。
此外,还可以使用贝叶斯统计学方法对这些模型进行实现。
回归模型是研究自变量与因变量之间关系的一种统计模型。
通常使用最小二乘法来估计回归系数,可以通过R语言中的lm(函数来实现。
例如,可以用回归模型来研究身高与体重之间的关系:```Rdata <- read.csv("data.csv")model <- lm(weight ~ height, data = data)summary(model)```这个简单的回归模型可以通过计算回归系数和拟合优度来评估身高对体重的影响。
混合效应模型是一种考虑随机因素的回归模型。
它可以用来分析多个层次嵌套的数据,例如,在研究学生成绩时,可以考虑学生之间的差异以及学校之间的差异。
R语言中的lme4包可以实现混合效应模型的拟合。
考虑到学生成绩受学生和学校的影响,可以建立如下的混合效应模型:```Rlibrary(lme4)model <- lmer(grade ~ (1 , student) + (1 , school), data = data)summary(model)```这个混合效应模型可以通过计算学生和学校的随机因子的方差来评估学生和学校对学生成绩的影响。
贝叶斯实现是一种不同于传统统计方法的统计学方法,它基于贝叶斯定理,通过引入先验分布和后验分布来进行推断。
在R语言中,可以使用Stan语言和rstan包来实现贝叶斯回归和混合效应模型。
贝叶斯回归模型可以使用Stan语言编写,并通过rstan包在R中进行调用和拟合。
例如,可以使用贝叶斯方法来估计身高对体重的影响:```Rlibrary(rstan)data <- read.csv("data.csv")stan_code <- "dataint<lower=0> N;vector[N] height;vector[N] weight;parametersreal a;real b;real<lower=0> sigma;modelheight ~ normal(a + b * weight, sigma);model <- stan_model(model_code = stan_code)fit <- sampling(model, data = list(N = nrow(data), height = data$height, weight = data$weight))```这个贝叶斯回归模型使用了正态分布的先验分布来推断身高对体重的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2 2卷第 4期 20 0 8年 8月
江 苏 科 技 大 学 学 报( 自然科学 版) Junl f i guU i r t o c n eadTc nl y N tr| c neE io ) ora o a s nV Sy f i c n eh o g ( aua Si c dtn Jn e i S e o e i
摘
要 : 混沌行 为和常规行为在受迫摆系统 的状态空 间上共存 的动力学现象进行 了分析 , 对 并在其 P icr 映射 的状态 onae
空 间上 , 使用分岔 图、yp nv指数 谱 、 图分析 等手段 , L au o 相 对常规行为 向混沌行 为的过渡 过程进 行 了数 值分析 , 对混 沌行 为 区和 常规行为 区的分布进行 了划分. 关键词 : 受迫摆 ;Picr 映射 ;状态空间 onae
( .Cl g f uo t n N migU iesyo ot adTlcm nctn ,N migJagu20 0 C ia 2 ol eo tmao , a n nvri f s n ee0 mu i i s a n i s 10 3,hn ) e A i t P s ao n
Ab t a t Th y a c h n me o ha o ma h vo nd c a tc b h v o o x s n t tt p c f sr c : e d n mi sp e o n n t tn r lbe a i ra h oi e a ir c e ito he sae s a e o a f r e nd u wa ic s e oc d pe ul m s ds u s d. Nume ia n lsswa s d t i lt he ta sto o e sfo n r l rc la ay i s u e o smu ae t r n i n pr c s r m o ma i be a i rt h o i e a irt r ug iu c to ig a , y p o x o e i ls e tu a a e ma h vo o c a tc b h v o h o h b f r ai n d a r m c a un v e p n nt p cr m nd ph s p.Th a e noma e a irr g o n h h oi e a ir r go n t e sa e s a e o o n ae ma p n r o ae . r lb h v o e in a d t e c a tc b h v o e i n o h t t p c fP i c r p i g a e lc t d
Ke r s o c d p n u u ;P i c r p i g t t p c y wo d :f r e e d l m o n a e ma p n ;s e s a e a
0 引 言
18 93年 , 献 [ ] 出了枢 轴作 周期 性上 下振 动 的受 迫摆 模 型 模 型形 式 很 简单 , 文 1提 该 但动 力 学 行 为 却 被证 明是 极复 杂 的 j已经发 现它有 很 多 独 特 的特 征 . 献 [ : , 文 6 在研 究 随着 外 力 的变 化 , 最 低 点 摆 的稳定性 向混沌分 岔 过渡 的过 程时 , 发现 并 实验 验 证 了 随着 作会 不 稳定交 替 的序列 , 而 出现使 系统 走 向混沌 的倍 周期 分岔 过程 的无 限重 复. 从 文献 [ ] 该模 型进 行 了 3对
够的知识 以对受迫摆系统进行控制是做不 到的.07年 , 20 文献 [ ] 7 通过对受 迫摆系统 的两种典型响应
WA G M o H N X ah i N aj ,C E i u i o
( .S ho o lc oisadIf mao , ins nvrt f c nea dT cnlg Z e agJ n s 1 03, hn ) 1 c ol fEet nc n o t n JaguU i syo Si c eh ooy, h in i gu2 20 C ia r nr i ei e n a
中图分类号 : P3 T 1 文献标识码 : A 文 章 编 号 : 6 3— 87 2 0 )3— 0 8— 6 17 4 0 (0 8 O 0 6 0
A n l ss o u tp e r g e so e v o o x si a y i f m li l e r s i n b ha i r c e itng o t t p c ff r e n l n sa e s a e o o c d pe du um
分析 , 发现该系统在外界扰动不太大的情况下 , 任意规定摆锤顺时针 、 逆时针穿越最高点或最低点的序 列, 总可 以选 出无数多的初始条件 , 使受迫摆 的运动符合给定的要求. 文献 [ ] 4 使用 Lr z o n 系统作为受 e 追 摆 的一个 近似 , 对其 进行 了控 制 .
文献 [ ] 5 给出了受迫摆混沌控制 的一个失败案例 , 说明了试 图通过分析试验的时间序列来获得足
V 12 N ・ o .2 o4 A g 2 0 u・ 08
多种回归行为在 受迫摆 系统状 态 空 问内共存现 象的分析
王茂基 ,陈小 惠。
(. 1 江苏科 技大学 电子信息学院 , 江苏 镇江 22 0 ) 10 3 ( . 京邮电大学 自动化学院 , 2南 江苏 南京 2 0 0 ) 10 3
