复杂阻尼结构阻尼模型研究
阻尼综述——阻尼模型、阻尼机理、阻尼分类和结构阻尼建模方法

阻尼1 引言静止的结构,一旦从外界获得足够的能量(主要是动能),就要产生振动。
在振动过程中,若再无外界能量输入,结构的能量将不断消失,形成振动衰减现象。
振动时,使结构的能量散失的因素的因素称为结构的阻尼因素。
索罗金在其论著中将结构振动时的阻尼因素概括为几种类型,即界介质的阻尼力;材料介质变形而产生的内摩擦力;各构件连接处的摩擦及通过地基散失的能量。
百多年来,不同领域的专家,均根据自身研究的需要,着重研究某种阻尼因素,如外阻尼、摩擦阻尼、材料阻尼及辐射阻尼等。
对于材料阻尼的物理机制,文献[82]、[126]、[127]等分别做了简要描述。
材料阻尼是一个机制比较复杂的物理量,由多种基本的物理机制组合而成。
如金属材料中的热弹性、晶体的粘弹性、松弛效应、旋转流效应、电子效应等对阻尼均有贡献。
对一般的非金属材料(如玻璃、各种聚合物等),电子效应对能量的损失影响较小。
温度、绝热系数等也是影响阻尼的重要因素。
一般来说,非金属材料的能量损失比金属大。
此外地质岩石由不同种固体微粒组成,且有空隙体积,因此,其阻尼特性与一般材料不同。
岩石中能量损失主要由三个物理机制构成:岩石内部微粒间的粘性=岩石的内摩擦及较大的塑性变形,而岩石的内摩擦与岩石内部微粒间接触处的位错及塑性变形有关。
如献[82]所述,为了计算、分析结构在外界载荷作用下产生的反应,人们建立了描述固体材料应力应变关系的物理模型。
最简单的物理模型是单参数模型,即材料只产生弹性应力或只产生粘滞应力,但这两种模型不能代表材料中真实存在的粘弹性。
人们又建立了双参数线性模型,即Maxwell及Kelvin模型。
其中Maxwell模型由线性粘滞体和线弹性体串联而成,Kelvin模型是此二者并联而成的。
若设线粘滞体的应变为一般情况下,在结构振动分析设计中,与弹性力和惯性力相比,阻尼力在数值上较小。
然而,在一定条件下,阻尼因素将起很重要的作用。
如果没有阻尼力存在,振动体系在共振时将达到非常大的幅值。
浅谈阻尼器的类型和原理分析

广州大学研究生文献综述论文题目浅谈阻尼器的类型学院土木工程学院班级名称2016级专硕一班学号2111616149 学生姓名陆富龙2016 年12 月18 日关于阻尼器的类型总结摘要:随着抗震在结构中的重要性越来越重要,高强轻质材料的采用,高层、超高层等高柔结构及特大跨度桥梁不断涌现,相关的研究也越来越多,从结构抗震到结构的减震再到结构的隔振,各种的理念层出不穷,然在抗震中,现在比较方便和比较常用的就是在建筑结构上加入阻尼器,用以吸收地震或风震产生的能量,以提高结构的抗震性能,随着科技的发展,各种阻尼器不断的更新创新,运用各种的原理来优化阻尼器,对于形式多样、要求各异的工程结构,如何在推广应用消能技术时,选择适合的阻尼器类型并进行阻尼器的合理优化设计将关系到这一技术的发展前景,具有重要的现实意义,值得进一步探讨研究。
关键词:阻尼器,类型,适用Abstract: withthe earthquakeis becoming more and more important inthe importance ofthe structure,high-strength lightweight material used, high-risestructure and extra long—span Bridgesand super—tall soft, related research also more and more, from the structure seismic to structureofshock absorption and vibration isolation of the structure,variousLiNianCeng outone after another, butin the earthquake, is nowmore convenientand more commonly usedin building structureswith dampers,earthquakeor windtoabsorbenergy,to improve theseismic performance of structure, with the development of science and t echnology, theupdatingand innovation of variousdampers, use all kinds oftheprinciple to optimize damper, foravarietyof formsandrequirements of different engineering structure,howto promoteapplication ofenergydissipation technology,select the appropriatetype ofdamper andthe optimization of damper design will be related to the developmentprospects of thistechnology,hasimportant practicalsignificance and worthy of further research arediscussed。
建筑结构计算模型中的阻尼比讨论
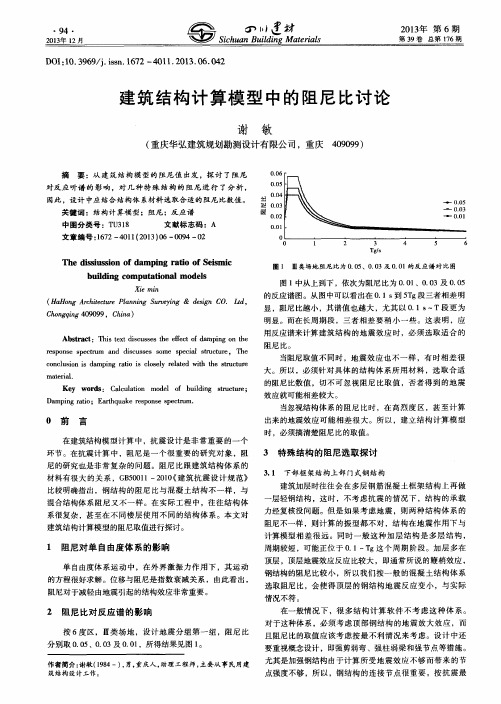
一
3 特殊结构 的阻尼选 取探讨
3 . 1 下 部 框 架结 构 上 部 门式 钢 结 构
建筑加层时往往会在 多层钢 筋混凝 土框架 结构 上再做
中 图 分 类 号 :T U 3 1 8 文 献标 志码 :A
蓝
文章编号 : 1 6 7 2— 4 0 1 1 ( 2 0 1 3 ) 0 6— 0 0 9 4— 0 2
Th e d i s s i u s s i o n o f d a mp i n g r a t i o o f S e i s mi c
的阻尼 比数值 ,切不可 忽视 阻尼 比取 值 ,否者得 到 的地 震 效应就 可能相差较大 。
当忽视结构 体系 的阻尼 比时 ,在高烈 度 区 ,甚至计 算
0 前
言
出来的地震 效应 可能相差 很大 。所 以 ,建 立结 构计算 模型
时 ,必须搞 清楚 阻尼 比的取值 。 在建 筑结 构模 型计算 中,抗震设 计是非 常重要 的一 个 环节 。在抗震 计算 中 ,阻尼是一 个很重 要 的研 究对 象 ,阻 尼的研究也是 非常复 杂的 问题 。阻尼 比跟建筑 结构体 系 的
Da mpi n g r a t i o; Ea r t hq u a ke r e s p o n s e s p e c t r um.
用反应谱来计算建 筑结构 的地震 效应 时 ,必须选 取适 合的
阻尼比。
当阻尼取值不 同时 ,地震 效应也 不一 样 ,有 时相差 很
大 。所 以,必须针对 具体 的结构体 系所用 材料 ,选 取合 适
阻尼性能及阻尼机理综述

阻尼性能及阻尼机理前言机械构件受到外界激励后将产生振动和噪声;宽频带随机激振引起结构的多共振峰响应,可以使电子器件失效,仪器仪表失灵,严重时甚至造成灾难性后果。
目前,武器装备和飞行器的发展趋向高速化和大功率化,因而振动和噪声带来的问题尤为突出[1]。
振动也会影响机床的加工精度和表面粗糙度,加速结构的疲劳损坏和失效,缩短机器寿命;另外振动还可以造成桥梁共振断裂,产生噪声,造成环境污染[2]。
由此可见,减振降噪在工程结构、机械、建筑、汽车,特别是在航空航天和其他军事领域具有及其重要的意义。
阻尼技术是阻尼减振降噪技术的简称。
通常把系统耗损振动能或声能的能力称为阻尼,阻尼越大,输入系统的能量则能在较短时间内耗损完毕。
因而系统从受激振动到重新静止所经历的时间过程就越短,所以阻尼能力还可理解为系统受激后迅速恢复到受激前状态的一种能力。
由于阻尼表现为能量的内耗吸收,因此阻尼材料与技术是控制结构共振和噪声的最有效的方法[1]。
研究阻尼的基本方法有三大类[1~3]:(1)系统阻尼。
就是在系统中设置专用阻尼减振器,如减振弹簧,冲击阻尼器,磁电涡流装置,可控晶体阻尼等。
(2)结构阻尼。
在系统的某一振动结构上附加材料或形成附加结构,增大系统自身的阻尼能力,这类方法包括接合面、库伦摩擦阻尼、泵动阻尼和复合结构阻尼。
(3)材料阻尼。
是依靠材料本身所具有的高阻尼特性达到减振降噪的目的。
它包括粘弹性材料阻尼、阻尼合金和复合材料阻尼。
本文主要论述阻尼材料的表征方法,阻尼分类,阻尼测试方法,各种阻尼机理,高阻尼合金及其复合材料,高阻尼金属材料最新研究进展,高阻尼金属材料发展中存在的问题及发展方向,高阻尼金属的应用等内容。
第一章内耗(阻尼)机理1.1、内耗(阻尼)的定义振动着的物体,即使与外界完全隔绝,其机械振动也会逐渐衰减下来。
这种使机械能量耗散变为热能的现象,叫做内耗,即固体在振动当中由于内部的原因而引起的能量消耗。
在英文文献中通用“internal friction”表示内耗。
阻尼基本理论及阻尼模型评价方法综述

阻尼基本理论及阻尼模型评价方法综述摘要:阻尼是结构动力分析的基本参数,对结构动力分析结果的准确性有很大的影响。
因此,从基本概念着手,分析阻尼产生原因以及从不同角度分类,得出建筑结构中动力分析常用的阻尼为瑞利阻尼;经过很多专家学者多年的研究,提出了多种阻尼模型,它们各有优缺点,文中介绍了一种统一的阻尼模型的定量评价方法,对于具体问题应采用合理的模型。
关键词:阻尼;阻尼模型;瑞利阻尼;阻尼模型的评价方法Abstract: the damping is structure dynamic analysis of the basic parameters, the structure of the dynamic analysis of the results of the accuracy has very big effect. Therefore, from the basic concept, the thesis analyzes damping causes and classification from different angles, and concludes that the building structure dynamic analysis of the commonly used for damping Rayleigh damping; After many years of research experts and scholars, and puts forward a variety of damping model, and they all have the advantages and disadvantages, this paper introduces a unified damping model of quantitative evaluation method, for a specific problem should be the use of reasonable model.Keywords: damping; Damping model; Rayleigh damping; Damping model evaluation method1 阻尼的基本概念我们知道,若无外部能源,则任何原来振动的物理系统都会随着时间的增长趋于静止。
土木结构的阻尼类型及常用阻尼模型综述

土木结构的阻尼类型及常用阻尼模型综述
土木建筑结构阻尼(Structural Damping)主要是指土木结构抗震受力时,因材料本身放电、变形超限、声发射及流体部件和元件散发等机制产生的力,从而使受力对象在一定时间内衰减受力的作用。
它与振动控制有着密切的联系。
阻尼类型一般可分为静态阻尼和动态阻尼,其中前者一般通过材料的潜能及抗等效刚度等基本物理理论进行研究,后者则是针对土木结构动力特性的特殊性进行相关原理的研究。
目前常见的阻尼模型包括时变弹簧、瞬时弹性、模拟非线性、惯性质量、变弹簧、环境湿度及温度影响等等。
其中时变弹簧模型是目前最常用的阻尼模型,它基于橡胶材料在拉伸、压块及挠应变中的时变刚度来模拟材料的非线性特性。
时变弹簧模型由一个瞬时弹性系数和一个非线性拟合弹性系数及时变模型组成,并利用位平衡理论得出其动定常方程以进行数值模拟。
此外,瞬时弹性模型和环境湿度等温度影响的模型也被广泛应用于具体结构的阻尼模拟仿真。
在分析土木结构动力特性的衰减过程中,选择合适的阻尼模型来反映材料的非线性特性对研究效果极为重要。
采用不同的阻尼模型反映材料不同的特性,可以更准确地模拟实际结构的变形及力学参数。
因此,通过正确使用合适阻尼模型随之而来的模拟结果,能使结构的抗震性能大大提高,提供给地震防护工作者足够的依据,从而对地震灾害的防治作出有效的贡献。
时程分析阻尼模型及数值计算方法

时程分析阻尼模型及数值计算方法1、阻尼模型阻尼是用以描述结构在振动过程中能量的耗散方式,是结构的动力特性,是影响结构动力反应的重要因素之一。
结构振动时,由于结构材料的内摩擦、材料的滞回效应等机制导致能量消耗,使结构振动幅值逐渐减少,最后直至完全静止。
结构的耗能机制非常复杂,它与介质的特征、结构粘性等诸多因素有关。
常用的是粘滞阻尼理论,它认为,阻尼力与速度成正比。
试验也证明,对于许多材料,这种阻尼理论是可行的,并且物理关系简单,便于应用和计算。
根据实测去确定阻尼大小是相当困难的,但由于阻尼的影响通常比惯性力和刚度的影响小,所以一般都采用简化的方法考虑阻尼。
本文采用最为广泛应用的瑞雷阻尼。
瑞雷阻尼假设阻尼矩阵是质量矩阵和刚度矩阵的线性组合,即[][][]C M K αβ=+ (4.15)式中,α、β为常数,可以直接给定,或由给定的任意二阶振型的阻尼比i ξ、j ξ反算求得。
根据振型正交条件,待定常数α和β与振型阻尼比之间的关系应满足:22k k k βωαξω=+(k =1,2,3,…,n ) (4.16a) 任意给定两个振型阻尼比i ξ和j ξ后,可按下式确定比例常数222j i i ji ji jξωξωαωωωω-=- 222j i i ji jξωξωβωω-=- (4.16b)i ω、j ω分别为第i 、j 振型的原频率。
本文取前两阶振型频率求得α、β值。
2、数值积分方法多自由度结构体系动力微分方程为:[]{}[]{}[]{}[]{}()gM x C x K x M x t I ++=-(4.17) 其中,[]M -质量矩阵;[]C -阻尼矩阵;[]K -刚度矩阵;{}I -单位对角阵;()g x t -地面运动加速度;{}x 、{}x 、{}x-结构楼层相对于地面的位移、速度和加速度反应。
在结构动力计算中,常用的直接积分法有中心差分法、线性加速度法、Wilson-θ法和Newmark-β法等。
浅谈阻尼器的类型和原理分析

广州大学研究生文献综述论文题目浅谈阻尼器的类型学院土木工程学院班级名称2016级专硕一班学号**********学生姓名陆富龙2016 年12 月18 日关于阻尼器的类型总结摘要:随着抗震在结构中的重要性越来越重要,高强轻质材料的采用,高层、超高层等高柔结构及特大跨度桥梁不断涌现,相关的研究也越来越多,从结构抗震到结构的减震再到结构的隔振,各种的理念层出不穷,然在抗震中,现在比较方便和比较常用的就是在建筑结构上加入阻尼器,用以吸收地震或风震产生的能量,以提高结构的抗震性能,随着科技的发展,各种阻尼器不断的更新创新,运用各种的原理来优化阻尼器,对于形式多样、要求各异的工程结构,如何在推广应用消能技术时,选择适合的阻尼器类型并进行阻尼器的合理优化设计将关系到这一技术的发展前景,具有重要的现实意义,值得进一步探讨研究。
关键词:阻尼器,类型,适用Abstract: with the earthquake is becoming more and more important in the importance of the structure, high-strength lightweight material used, high-rise structure and extra long-span Bridges and super-tall soft, related research also more and more, from the structure seismic to structure of shock absorption and vibration isolation of the structure, various LiNianCeng out one after another, but in the earthquake, is now more convenient and more commonly used in building structures with dampers, earthquake or wind to absorb energy, to improve the seismic performance of structure, with the development of science and technology, the updating and innovation of various dampers, use all kinds of the principle to optimize damper, for a variety of forms and requirements of different engineering structure, how to promote application of energy dissipation technology, select the appropriate type of damper and the optimization of damper design will be related to the development prospects of this technology, has important practical significance and worthy of further research are discussed.Keywords: damper,type,apply前言近年来,国内外在工程结构的隔震、减振与振动控制方面进行了大量的研究工作,取得了丰硕的成果。
基于复阻尼理论的混合结构Rayleigh阻尼模型

基于复阻尼理论的混合结构Rayleigh阻尼模型刘庆林;孙攀旭;杨红【摘要】混合结构的阻尼矩阵不满足经典阻尼条件,导致传统的模态叠加法无法适用.复阻尼理论无法适用于时域计算,其自由振动响应中存在发散现象.针对混合结构的阻尼矩阵非比例性和复阻尼理论的时域发散性,基于频域等效原则构建了求解Rayleigh阻尼系数的数学优化模型,进而得到与复阻尼理论等效的Rayleigh阻尼运动方程.算例分析表明:依据位移时程响应和结构等效阻尼比可证明Rayleigh阻尼运动方程的正确性.基于本文研究成果,等效复阻尼理论的混合结构Rayleigh阻尼运动方程可直接采用模态叠加法,结合其确定的结构等效阻尼比,为混合结构的振型分解反应谱法提供理论依据.【期刊名称】《地震工程学报》【年(卷),期】2018(040)005【总页数】5页(P983-987)【关键词】混合结构;复阻尼;频域等效原则;Rayleigh阻尼;等效阻尼比【作者】刘庆林;孙攀旭;杨红【作者单位】深圳信息职业技术学院交通与环境学院,广东深圳 518172;重庆大学土木工程学院,重庆 400045;重庆大学土木工程学院,重庆 400045;重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045【正文语种】中文【中图分类】TU311.30 引言复阻尼理论具有使结构能量耗散与激励频率无关从而与实际相符的优点[1],但存在计算结果可能发散的缺陷[2]。
Rayleigh阻尼矩阵为结构质量矩阵和刚度矩阵的线性组合,满足经典阻尼条件,易于求解且不存在计算结果发散现象,因而得到广泛应用[3]。
Rayleigh阻尼矩阵依赖于质量矩阵和刚度矩阵的合理组合,系数的选取对计算结果的合理性影响显著[4-5],因此许多学者针对Rayleigh阻尼矩阵系数提出了不同的计算方法:Yoshida等[6]提出了在结构频率敏感范围内构建Rayleigh阻尼矩阵的方法;董云等[7]建议基于结构基频、地震波反应谱和结构模态分析结果确定Rayleigh阻尼矩阵系数;邹德高等[8]依据结构的频率特性和地震动的频谱特性计算Rayleigh阻尼矩阵系数;陈旭等[9]选取控制结构反应的子结构周期来计算Rayleigh阻尼矩阵系数;潘旦光[10]以结构位移反应峰值的误差为目标函数,建立求解Rayleigh阻尼系数的优化方程;黄维等[11]基于随机地震动激励下位移响应误差最小,得到相应的混合结构Rayleigh阻尼模型。
阻尼基本理论及阻尼模型评价方法综述

阻尼基本理论及阻尼模型评价方法综述摘要:阻尼是结构动力分析的基本参数,对结构动力分析结果的准确性有很大的影响。
因此,从基本概念着手,分析阻尼产生原因以及从不同角度分类,得出建筑结构中动力分析常用的阻尼为瑞利阻尼;经过很多专家学者多年的研究,提出了多种阻尼模型,它们各有优缺点,文中介绍了一种统一的阻尼模型的定量评价方法,对于具体问题应采用合理的模型。
关键词:阻尼;阻尼模型;瑞利阻尼;阻尼模型的评价方法abstract: the damping is structure dynamic analysis of the basic parameters, the structure of the dynamic analysis of the results of the accuracy has very big effect. therefore, from the basic concept, the thesis analyzes damping causes and classification from different angles, and concludes that the building structure dynamic analysis of the commonly used for damping rayleigh damping; after many years of research experts and scholars, and puts forward a variety of damping model, and they all have the advantages and disadvantages, this paper introduces a unified damping model of quantitative evaluation method, for a specific problem should be the use of reasonable model.keywords: damping; damping model; rayleigh damping;damping model evaluation method中图分类号:p754.1 文献标识码:a 文章编号1 阻尼的基本概念我们知道,若无外部能源,则任何原来振动的物理系统都会随着时间的增长趋于静止。
几种阻尼模型的建模方法及评价

c pr . tn adpo lm ein d t ie a h d l a mp ra etNu r a ts n tesa dr ete f t m a ̄ A s dr rbe i d s e o g ltemo esn i atlts. mei l et o tn ad ts le,i a s g v l i c s h t l so sta iee t a to sh v os iu u f t npe io f ed n is nt me t d l ftesrcue T i hw h t f rn mpmehd aec npc o se e so rcs no t y a c i ede n e h t tr. hs d d c i h m i f mo o u
虑; 单元阻尼法 , 对实际的工程结构来说更 有意义。 。 关键词 : 阻尼模型 ; 阻尼特性 ; 单元 阻尼 比; 体阻尼比 整
中圈分类号: l r 1 I P
文献标识码: A
文章编号: 7 9420)2 02 4 1 2 8( 6o— 6— 6 4 o 0 0
M o eig meh d n p r i n fd mp mo es d l t o sa d a p as g o a d l n i维普资讯 第3 2卷第 2 期
20 年 3月 O6
中国测试 技术
C N HI A MEA I M研 E HN0 DGY sI RE rIC 【
V 13 N . o .2 o2 Ma , O 6 r2 0
几 种 阻尼模 型 的 建模 方 法 及 评 价
Ab ta tA nfr eau t nmeh d n v u t nid xfr o a sr c : u i m v]ao o i to sa dea ai n e o medmpmo esaeq oe yti p p r tn adlS os ] o s d l r u tdb ls a e ,A sad r E t_ e l , a
机械设计中的阻尼分析与优化方法研究

机械设计中的阻尼分析与优化方法研究引言:在机械设计中,阻尼是一个重要的设计参数。
准确分析和优化阻尼对于确保机械系统的稳定性、可靠性和性能至关重要。
本文将探讨机械设计中的阻尼分析方法以及优化策略。
一、阻尼的定义和作用阻尼是指由于摩擦、粘滞、流体阻力等因素导致的能量损耗,从而减缓或抑制机械系统的振动。
阻尼的作用主要有两个方面:一是减小机械系统的振动幅值,降低共振峰值;二是消耗振动能量,提高系统的稳定性和控制性能。
二、阻尼的分类根据不同的物理特性和结构形式,可以将阻尼分为四类:干摩擦阻尼、液体摩擦阻尼、固体材料内耗阻尼和结构材料内部不完全接触产生的相对运动形成的阻尼。
不同类型的阻尼对机械系统的振动特性和稳定性具有不同的影响。
三、阻尼分析的方法1. 实验测试法:通过实际测量机械系统振动的相关参数,比如振动幅值、频率等,来分析阻尼效果。
2. 数值模拟法:利用计算机建立机械系统的数学模型,并基于物理原理和数学方法进行计算和仿真,从而评估阻尼对系统振动的作用。
3. 模态分析法:通过分析机械系统的固有频率、阻尼比等模态参数,结合振动实验数据,可以间接推测阻尼对振动的抑制效果。
四、阻尼优化的策略1. 材料选择:选择具有良好阻尼性能的材料,如聚合物材料、复合材料等。
这些材料具有较高的内耗能力,可以有效地消耗振动能量。
2. 结构设计:通过合理的结构设计,可增加机械系统的阻尼。
例如,在关键位置添加阻尼弹簧、阻尼器等装置,增加机械系统的能量耗散路径,从而抑制振动。
3. 控制策略:采用主动或被动控制策略来实现阻尼优化。
主动控制采用传感器、执行器等主动控制器来实时调节系统阻尼;被动控制则通过调节材料、结构参数等来实现阻尼的优化。
五、阻尼优化实例分析以汽车悬挂系统为例,通过分析阻尼对悬挂系统的影响,可以对系统的设计和优化提供参考。
通过调节悬挂系统的阻尼参数,可以改变汽车行驶时的悬挂刚度和振动特性,提高乘坐舒适性和行驶稳定性。
六、结论机械设计中的阻尼分析和优化是确保系统振动稳定性和性能的重要环节。
1工程结构中的阻尼及其力学模型

y1 2 ln y 2 1 2
一、工程结构中的阻尼及其力学模型
例题:研究一座桥梁的竖向振动,对于基频,结 构可以看成是单自由度体系。让桥梁在跨中产生 挠度(用绞车把桥梁向下拉),然后突然释放。
在初始扰动之后,求得振动按指数衰减,即在频
率为1.62Hz的三个周期内,振幅从10mm衰减为 5.8mm。在跨中停放质量为40000kg的车辆重复进
宏观尺度的滑动被降低而微观滑动开始这种微观滑动包括接触面间的相互凹凸的微小位移相对于滑动面的对面3连接处嵌固压力的进一步增加将使粗糙面的贯入度变得更大
结构动力学
——单自由度系统的振动 湖南大学土木工程学院
尹华伟
2013年7月
一、工程结构中的阻尼及其力学模型
粘滞阻尼
k c m
cy ky 0 m y
对库仑阻尼,可导出等效粘滞阻尼系数:
cd
4 Fd
一、工程结构中的阻尼及其力学模型
阻尼引起的能量耗散
滞变阻尼: 对简谐激励: 得:
y sin t
Fdy k (1 j )ydy
y , cost y /
2 2
2 2
F k sin t jk sin t k sin t k cost
行试验,并测得其自振频率为1.54HZ。
求有效质量,有效刚度系数和结构阻尼。
设m为有效质量,k为有效刚度系数。
一、工程结构中的阻尼及其力学模型
因为:
1 f1 1.62 2 1 f 2 1.54 2
k m k 3 m 4010
3
故得:
1.62 m 4010 m 1.54 因此有效质量: m 375103 kg 2 有效刚度: k (2f1 ) m 38850 kN/m
阻尼及阻尼在结构中的作用分析

阻尼及阻尼在结构中的作用分析摘要:阻尼对结构的振动反应有重要的影响,阻尼比是阻尼作用在结构体系振动过程中耗能减震能力的参数。
目前结构设计通常对某一类结构的阻尼比取为常数中的定值,这不能完全真实反映建筑物的阻尼,且未能反映同一类结构阻尼比的变化规律。
本文通过对阻尼的机理、阻尼的影响因素,阻尼的作用,阻尼比的计算,阻尼比在结构设计中的取值,阻尼在结构中的应用等进行具体分析,以便结构设计者对阻尼有更好的了解及,对结构进行更好的、适当的调整。
关键词:阻尼,阻尼比引言阻尼(英语:damping)是指物体或系统在振动中,由于外界作用或系统本身固有的原因引起的振动幅度逐渐下降的特性,以及此一特性的量化表征,使振动衰减的各种摩擦和其他阻碍作用。
阻尼技术在航天、航空、军工、机械等行业中广泛应用,二十世纪七十年代,人们开始逐步地把这些阻尼技术应用到建筑、桥梁、铁路等结构工程中,阻尼技术能在结构中振动中耗能减震,并被广泛应用[1]。
一.阻尼的机理阻尼的机理有两种形式:一种是因摩擦阻力生热,使系统的机械能减小,转化为内能,这种阻尼叫摩擦阻尼;另一种是系统引起周围质点的震动,使系统的能量逐渐向四周辐射出去,变为波的能量,这种阻尼叫辐射阻尼。
阻尼比(ζ)指阻尼系数与临界阻尼系数之比,表达结构体标准化的阻尼大小,是无单位量纲。
阻尼比(ζ)一般可分为:ζ=0;01共4种情况。
阻尼比ζ=0即不考虑阻尼系统;结构常见的阻尼比都在ζ在0~1之间。
二.阻尼的作用主要有以下五个方面[3]:(1)有助于减少结构的共振振幅,从而避免结构因震动应力达到极限造成机构破坏;(2)有助于结构系统受到瞬时冲击后,很快恢复到稳定状态;(3)有助于减少因结构振动产生的声辐射,降低机械性噪声及损害。
许多结构构件主要是由振动引起的,采用阻尼能有效的抑制共振,从而降低损害;(4)有助于提高其动态性能,较高的抗震性和动态稳定性;(5)有助于降低结构传递振动的能力。
浅谈阻尼的分类

浅谈阻尼的分类
'
阻尼 (damping) 是指任何振动系统在振动中,由于外界作用或系统本身固有的原因引起的振动幅度逐渐下降的特性,以及此一特性的量化表征。
阻尼阻碍物体的相对运动、并把运动能量转化为热能或其他可以耗散能量。
常见的阻尼主要包括材料阻尼(内部阻尼)、结构阻尼、流体阻尼三大类。
1. 材料阻尼(内部阻尼):包括粘性阻尼和滞后阻尼
材料内部颗粒摩擦、缺陷变化,机械能转化为热能,能量在内部就被部分消耗。
应力-应变曲线存在一个迟滞回线,回线的面积等于克服阻尼力所做的功也是每周期振动耗散的能量。
粘性阻尼:在稳态振动的一个周期内,耗能与激励频率显著相关。
滞后阻尼:耗能并不显著地取决于激励频率,但与应变大小有显著关系:大小与位移成正比,方向与速度方向相反。
2. 结构阻尼
结构存在支撑、连接或声辐射都会在振动过程中消耗能量典型的有,由于干摩擦产生的耗能,称为库伦阻尼,阻尼力模型:
3. 流体阻尼
结构在流体中运动,包含振动,受到的阻力。
与流体介质的密度、黏性等都有关,一般与速度的平方成比例。
在低密度介质(空气)中低速运动,一般采用线性模型。
4. 等效阻尼
由于其它阻尼模型相对复杂,因此常将其它模型等效为黏性阻尼进行计算。
等效阻尼通过能量相等进行参数代换。
在简谐振动稳态响应的一个周期内,黏性阻尼耗能πcωA²=其他阻尼耗能WD。
阻尼主要在共振区内起作用
对应的等效黏性阻尼比
'。
结构不同阶频率 阻尼关系曲线

结构不同阶频率阻尼关系曲线一、引言结构工程中,频率和阻尼是一个结构动态特性的重要指标,对结构的安全性、舒适性以及耐久性都有着重要的影响。
而不同结构的频率和阻尼的关系曲线又是一个比较复杂的问题。
本文将深入探讨结构不同阶频率和阻尼的关系曲线的理论基础、计算方法和实际应用等内容。
二、结构频率和阻尼的理论基础1. 结构的频率结构的频率是指结构在受到外部激励时,产生共振现象的频率。
在自由振动的情况下,结构的振动频率与结构体系的刚度和质量有关,可以通过有限元分析等方法进行计算和预测。
2. 结构的阻尼结构的阻尼是指结构在振动时受到的阻碍和耗散作用。
阻尼可以分为固有阻尼和非固有阻尼,固有阻尼是由结构本身的材料和结构形式所决定的,而非固有阻尼则是由结构与周围环境的相互作用所产生的。
3. 结构频率和阻尼的关系结构的频率和阻尼之间有着密切的关系,频率与阻尼的大小和分布都会对结构的动态特性产生重要的影响。
不同阶频率和阻尼之间存在着复杂的关系,对于结构的设计和分析来说,需要对这种关系进行深入的研究。
三、结构不同阶频率和阻尼的计算方法1. 频率的计算方法结构的频率可以通过有限元分析或者是分析解法进行计算。
在有限元分析中,可以通过建立结构的模型,进行模态分析来获得结构的频率。
而在分析解法中,则需要对结构的特征方程进行求解,在求解得到的特征值中,频率就是这些特征值的平方根。
2. 阻尼的计算方法对于结构的阻尼,其计算方法通常包括实验法和理论计算法。
实验法主要通过现场测试或者试验进行测定;理论计算法则包括了振动材料的阻尼、结构与基础的耦合阻尼、结构内部的阻尼等多个方面。
3. 不同阶频率和阻尼的关系曲线的计算方法不同阶频率和阻尼的关系曲线可以通过结构的模态分析来求解。
结构的模态分析可以得到结构的模态振型和频率,然后可以根据公式计算不同阶频率和阻尼的关系曲线。
四、结构不同阶频率和阻尼的实际应用1. 结构设计在结构设计中,频率和阻尼是一个重要的设计指标。
《2024年阻尼Euler方程以及相关模型真空自由边界问题研究》范文

《阻尼Euler方程以及相关模型真空自由边界问题研究》篇一阻尼Euler方程及其相关模型在真空自由边界问题研究中的探讨一、引言阻尼Euler方程是一种用于描述动力学系统中振动的物理模型。
这个方程主要研究阻尼作用下质点的加速度与所受的阻尼力和外界施加的力的关系。
在实际应用中,阻尼Euler方程经常被用于研究各种复杂系统中的振动问题,特别是在涉及真空自由边界问题的研究中。
本文将深入探讨阻尼Euler方程及其相关模型在真空自由边界问题中的应用。
二、阻尼Euler方程概述阻尼Euler方程是一种描述流体动力学行为的偏微分方程。
在流体中引入阻尼因子,我们便可以应用此方程来分析带有能量耗散效应的动力学行为。
方程的具体形式根据具体的物理系统和研究目标有所不同,但核心思想在于表达了在给定力作用下,系统中各元素加速度、速度、位置及阻尼的相互关系。
三、相关模型研究为了更全面地理解和分析真空自由边界问题,需要构建与阻尼Euler方程相关的数学模型。
这些模型通常包括流体动力学模型、振动模型等。
这些模型通过引入不同的边界条件和初始条件,来描述系统在不同条件下的动态行为。
四、真空自由边界问题研究真空自由边界问题是一个涉及流体动力学和振动特性的复杂问题。
在这个问题中,我们关注的是在真空环境中,如何通过阻尼Euler方程及相关模型来描述和预测系统的动态行为。
这一问题的研究涉及到许多复杂的物理过程,如流体的传播、反射、散射等。
五、阻尼Euler方程在真空自由边界问题中的应用在真空自由边界问题中,阻尼Euler方程的应用主要体现在以下几个方面:首先,通过引入阻尼因子,可以更好地描述流体在传播过程中由于内部摩擦等因素而产生的能量损失;其次,利用阻尼Euler方程,我们可以分析流体在遇到边界时的反射和散射现象;最后,通过构建相应的数学模型,我们可以对系统的动态行为进行预测和优化。
六、实验与仿真验证为了验证阻尼Euler方程在真空自由边界问题中的有效性,我们进行了大量的实验和仿真研究。
阻尼阻尼系数阻尼比

阻尼阻尼系数阻尼比阻尼(英语:damping)是指任何振动系统在振动中,由于外界作用和/或系统本身固有的原因引起的振动幅度逐渐下降的特性,以及此一特性的量化表征。
概述在物理学和工程学上,阻尼的力学模型一般是一个与振动速度大小成正比,与振动速度方向相反的力,该模型称为粘性(或粘性)阻尼模型,是工程中应用最广泛的阻尼模型。
粘性阻尼模型能较好地模拟空气、水等流体对振动的阻碍作用.本条目以下也主要讨论粘性阻尼模型.然而必须指出的是,自然界中还存在很多完全不满足上述模型的阻尼机制,譬如在具有恒定摩擦系数的桌面上振动的弹簧振子,其受到的阻尼力就仅与自身重量和摩擦系数有关,而与速度无关。
除简单的力学振动阻尼外,阻尼的具体形式还包括电磁阻尼、介质阻尼、结构阻尼,等等。
尽管科学界目前已经提出了许多种阻尼的数学模型,但实际系统中阻尼的物理本质仍极难确定.下面仅以力学上的粘性阻尼模型为例,作一简单的说明.粘性阻尼可表示为以下式子:其中F表示阻尼力,v表示振子的运动速度(矢量),c是表征阻尼大小的常数,称为阻尼系数,国际单位制单位为牛顿·秒/米.上述关系类比于电学中定义电阻的欧姆定律。
在日常生活中阻尼的例子随处可见,一阵大风过后摇晃的树会慢慢停下,用手拨一下吉他的弦后声音会越来越小,等等。
阻尼现象是自然界中最为普遍的现象之一。
理想的弹簧阻尼器振子系统如右图所示。
分析其受力分别有:弹性力(k为弹簧的劲度系数,x为振子偏离平衡位置的位移):F s = −kx阻尼力(c为阻尼系数,v为振子速度):假设振子不再受到其他外力的作用,于是可利用牛顿第二定律写出系统的振动方程:其中a为加速度。
[编辑]运动微分方程上面得到的系统振动方程可写成如下形式,问题归结为求解位移x关于时间t函数的二阶常微分方程:将方程改写成下面的形式:然后为求解以上的方程,定义两个新参量:上面定义的第一个参量,ω,称为系统的(无阻尼状态下的)固有频率. 第二个参量,ζ,称为n阻尼比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 eat n o Cv n ier g H nnU i rt,C a gh 10 2 C ia .D pr t f iiE g ei , u a nv sy hn sa4 0 8 , hn ) me l n n ei
Ab t a t Da i g r t s c i c lt y a c a ay i o o lx sr c u e .Ho v r u o t e s e i ct f sr c : mp n a i i rt a o d n mi n l s fc mp e t t r s o i s u we e ,d e t h p cf i o i y d mp n d lo o l x s cu e ,t e e a e n e fc h o y a d meh d t ee mi e d mp n ai n O o .A a i g mo e f c mp e t t r s h r r o p re tt e r n t o o d t r n a i g r t a d S n u r o d mp n d l a e n c n e e d l a i g r t swa r p s d f rc mp e t c u e o sr ce i t r l f a i g mo e b s d o o v n d mo a mp n a i sp o o e o lx sr t r sc n t td w t mae i s o d o o u u h a d f r n a i g p o e t s W i t i mo e , t e c n e e mo a a i g r t s we e e v d b s g o lx i e e td mp n rp ri . f e t hs h d l h o vr d t d l d mp n ai r d r e y u i c mp e o i n d mp n h o n d ls an e e g t o a i g t e r a d mo a t i n r y meh d,a d t e r l t n h p b t e h o v r d mo a a i g r t sa d te y r n h eai s i ewe n t e c n e e d ld mp n a i n o t o h
d mp n ai s f a i g r to o ma e il wa o ti e t ra s s b an d. Th vb ain e po s s f n n i e n sr cu e n e tg td e i r to r s n e o a e gne r g tu t r i v sia e wi t e i t h h
,
( .C l g f i l nier ga dM c ai ,C n a SuhU i ri f oet n eh o g ,C a gh 104, hn ; 1 o eeo v g ei n eh n s et l o t n esyo F rsyadT c nl y hnsa40 0 C ia l C iE n n c r v t r o
中图分类号 :T 3 2 1 ;U 1 . U 5 . +1T 3 13 文献标识码 :A
Da pi o e fa c m p e t u t e m ng m d lo o l x s r c ur DU AN h o we ,XI S a— i ANG a g—i 。 S Xi n ln HEN —h n 。 Pu s e g
振
第3 O卷第 2期
动
与
冲 击
Vo. O 13 No 2 0 1 . 2 1
J OURNAL OF VI BRAT ON I AND S HOCK
复 杂 阻 尼 结 构 阻 ห้องสมุดไป่ตู้ 模 型 研 究
段 绍伟 向湘林 , ,沈蒲生
(. 1 中南林业科技 大学 土木工程 与力学学院 , 长沙 400 ; 10 4 2 湖南科技大学 土木工程学 院 , . 湘潭 4 10 ;.湖南大学 土木工程 学院 , 沙 40 8 ) 12 1 3 长 10 2 摘 要 :复杂结构动力分 析过程 中, 阻尼 比的计算显得非 常重要 。由于复杂结构 的阻尼模 型具有特 殊性 , 对如何 确定 阻尼 比等参数 , 至今没有较好 的理论 和方法。针对 由多种不 同阻尼 特性材料建 造的复杂 结构 , 提出 了一种基 于换算 模 态阻尼 比的阻尼模型 。通 过复阻尼理论和模态应 变能法 , 导了换算模 态阻尼 比 , 推 并得 到了换算模 态阻尼 比与各种材 料 阻尼 比之间 的关系 。将所提 出的方法应用于工程结构 , 该方法计算 的动力 响应 与子结构瑞雷阻尼法相 比, 其精度更 高 , 接近 于单元 阻尼 比法的结果 。由于其 方法 简单 、 物理 意义 明确 , 复杂 结构动力分析 中具有广泛 的应用前景 。 在 关键词 :复阻尼理论 ; 模态 应变能法 : 换算 模态阻尼 比; 结构瑞雷阻尼法 ; 子 单元阻尼 比法
