二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(提高)
《二次函数y=a(x-h)^2+k的图象与性质》提升训练

课时3二次函数,y=a(x-h)2+k的图象与性质过能力1.[2018天津市实验中学课时作业]在平面直角坐标系中,如果抛物线y=3x2不动,而把x 轴、y轴分别向上、向右平移2个单位长度,那么在新坐标系中抛物线的函数表达式是( )A.y=3(x-2)2-2B.y=3(x+2)2-2C.y=3(x-2)2+2D.y=3(x+2)2+22.[2018江西上饶二中月考]已知二次函数y=3(x+1)2-4的图象上有三点A(-2,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系为( )Ay1>y2>y3B.y2>y1>y3C.y3>y2>ylD.y3>y1>y23.[2018河北邯郸二十五中课时作业]为了美观,在加工太阳镜时将下半部分轮廓制作成拋物线的形状(如图),对应的两条拋物线关于y轴对称,AE∥x轴,AB=4cm,最低点C 在x轴上,CH=1cm,BD=2cm.则右轮廓线DFE所在拋物线对应的函数表达式为( )A.y=14(x+3)2 B.y=-14(x-3)2 C.-14(x+3)2 B.y=14(x-3)24.[2018山西大学附中课时作业]把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的函数表达式为____.5.[2018安徽合肥四十五中课时作业]已知二次函数y=-(x-m)2+1,当x>3时,y随x 的增大而减小,则m的取值范围是____.6.[2018河南鹤壁市外国语中学课时作业]如图,在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为____.7.[2018陕西宝鸡一中课时作业]已知直线y=x+1与x轴交于点A,令抛物线y=-2x2平移后得到拋物线l,且抛物线l的顶点与点A重合.(1)求抛物线l对应的函数表达式;(2)若点B(x1,y1),C(x2,y2)在拋物线l上,且-12<x1<x2,试比较y1,y2的大小.8.[2018安徽淮南实验中学课时作业]已知抛物线y=a(x+m)2的顶点坐标为(-1,0),且经过点A(-2,-12 ).(1)求该拋物线对应的函数表达式;(2)该抛物线是否经过点B(2,-2)?若不经过,怎样沿x轴方向平移,才能使它经过点B?并写出平移后的抛物线对应的函数表达式.9.[2018江苏南京市中华中学课时作业]如图,在平面直角坐标系中,已知点A(-5,0),B(2,1),抛物线y=-(x-h)2+l(h为常数)与y轴的交点为C.(1)若抛物线经过点B,求它的函数表达式,并写出此时抛物线的对称轴及顶点坐标;(2)设点C的纵坐标为yC ,求yC的最大值,此时抛物线上有两点(x1,y1),(x2,y2),其中x 1>x2>0,比较y1与y2的大小;(3)当线段0A被拋物线分为两部分,且这两部分的比是1:4时,求h的值.参考答案1.B【解析】求解本题时,可看成把抛物线y=3x2分别向下、向左平移2个单位长度.抛物线y=3x2的顶点坐标为(0,0),把点(0,0)向下、向左平移2个单位长度得到点(-2,-2),所以在新坐标系中抛物线的函数表达式为y=3(x+2)2-2.故选B.2.C【解析】由抛物线的对称性可知,点A(-2,y1)在抛物线上的对称点为A'(0,y1),对于抛物线7=3(x+1)2-4,当x>-1时,y随x的增大而增大,所以y3>y2>y1.故选C.3.D【解析】∵CH=lcm,BD=2cm,且点B,D关于y轴对称,∴点D的坐标为(1,1).∵AB∥x 轴,AB=4cm,最低点在x轴上,∴点A,B关于直线CH对称,∴右轮廓所在抛物线的顶点F的坐标为(3,0),设右轮廓所在抛物线对应的函数表达式为y=a(x-3)2,把点D(1,1)代入,得1=a(1-3)2,解得a=14,∴右轮廓所在抛物线对应的函数表达式为y=14(x-3)2.故选D.4.y=-(x+l)2-2【解析】二次函数y=(x-l)2+2图象的顶点坐标为(1,2),绕原点旋转180°后顶点坐标变为(-1,-2),所以旋转后得到的图象的函数表达式为y=a(x+l)2-2,因为旋转过程中开口大小不变,仅开口方向改变,所以a=-1,即旋转后得到的图象的函数表达式为y=-(x+1)2-2.5.m≤3【解析】对于二次函数y=-(x-m)2+1,当x>m时,y随x的增大而减小,结合题意可知m≤3.6.18【解析】∵抛物线y=a(x-3)2+k的对称轴为直线x=3,点A,B为抛物线上的点,且AB∥x轴,∴点A,B关于直线x=3对称,又∵点A在y轴上,∴AB=2×3=6,∴等边三角形ABC的周长为3×6=18.7.【解析】(1)在y=x+1中,令y=0,则x=-1,∴A(-1,0),艮P抛物线l的顶点坐标为(-1,0).∵抛物线l是由抛物线y=-2x2平移得到的,∴抛物线l对应的函数表达式为-2(x+1)2.(2)∵抛物线l的对称轴为直线X=-1,a=-2<0,∴在其对称轴右侧,y的值随x值的增大而减小,又∵-1<-12<x1<x2,∴y1>y2.8.【解析】(l)∵抛物线y=a(x+m)2的顶点坐标为(-1,0),∴m=1,∵抛物线y=a(x+l)2经过点A(-2,-12),∴a(-2+l)2=-12,解得a=-12,∴该抛物线对应的函数表达式为y=-12(x+l)2.(2)不经过当x=2时,y=-12×(2+1)2=-92≠-2,∴抛物线y=-12(x+l)2不经过B(2,-2).设平移后的抛物线对应的函数表达式为y=-12(x+1+n)2,∵它经过点B(2,-2),∴-1 2(2+1+n)2=-2,n=-l或n=-5,∴将抛物线y=-12(x+1)2向右平移1个或5个单位长度,即可使它经过点B(2,-2),平移后的抛物线对应的函数表达式y=-12x2或y=-12(x-4)29.【解析】(1)把点B(2,l)代入y=-(x-h)2+l,得h=2,∴抛物线的函数表达式为y=-(x-2)2+l,对称轴为直线x=2,顶点坐标为(2,1).(2)由题意知点C的横坐标为0,则yC =-h2+1,∵当h=0时,yC取最大值,最大值为1.此时抛物线的函数表达式为y=-x2+1,对称轴为y轴,当x>0时,y的值随x值的增大而减小,∴当x1>x2>0时,y1<y2.(3)抛物线把线段OA分为1:4两部分的点为(-1,0)或(-4,0).把点(-1,0)代入y=-(x-h)2+1,得h=0或h=-2.当h=-2时,抛物线的函数表达式为y=-(x+2)2+1,经过点(-1,0),(-3,0),将线段OA分为三部分,不符合题意,故舍去.同理,把点(-4,0)代入y=-(x-h)2+1,得h=-5或h=-3(舍去).故h的值为0或-5.。
二次函数y=a(x-h)2+k(a≠0)的图象与性质

2.课后检测设计
1.对于抛物线y=﹣(x+1)2+3,下列结论:
①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>2
时,y随x的增大而减小,
其中正确结论的个数为()
A.1 B.2 C.3 D.4
2.对于二次函数y=﹣(x+1)2+2的图象与性质,下列说法正确的是()
A.对称轴是直线x=1,最小值是2
B.对称轴是直线x=1,最大值是2
C.对称轴是直线x=﹣1,最小值是2
D.对称轴是直线x=﹣1,最大值是2
3.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长
度,平移后所得抛物线的解析式为()
A.y=2x2+1 B.y=2x2﹣3
C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣3
4.设A(﹣2,y1),B(﹣1,y2),C(2,y3)是抛物线y=﹣2(x﹣1)2+k(k为
常数)上的三点,则y1,y2,y3的大小关系为()
A.y3>y2>y1B.y1>y2>y3C.y3>y1>y2D.y2>y3>y1
5.已知二次函数y=(x﹣2a)2+(a﹣1)(a为常数),当a取不同的值时,其图象
构成一个“抛物线系”.如图分别是当a=﹣1,a=0,a=1,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是y=.。
二次函数y=a(x-h)2+k的图象和性质同步练习

二次函数y=a(x-h)2+k 的图象和性质同步练习1、抛物线21)1(22+--=x y 的顶点坐标为( ) A 、(-1,21) B 、(1,21) C 、(-1,—21) D 、(1,—21)2、对于2)3(22+-=x y 的图象,下列叙述正确的是( )A 、顶点坐标为(-3,2)B 、对称轴是直线3-=yC 、当3≥x 时,y 随x 的增大而增大D 、当3≥x 时,y 随x 的增大而减小3、将抛物线2x y =向右平移一个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为( )A 、3)1(2++=x yB 、3)1(2+-=x yC 、3)1(2-+=x yD 、3)1(2--=x y4、抛物线2)1(22-+-=x y 可由抛物线22x y -=平移得到,则下列平移过程正确的是( )A 、先向右平移1个单位,再向上平移2个单位B 、先向右平移1个单位,再向下平移2个单位C 、先向左平移1个单位,再向上平移2个单位D 、先向左平移1个单位,再向下平移2个单位5、如右上图,把抛物线y=x 2沿直线y=x 平移2个单位后,其顶点在直线上的A 处,则平移后的抛物线解析式是( )A 、y=(x+1)2-1B .y=(x+1)2+1C .y=(x-1)2+1D .y=(x-1)2-16、设A (-1,1y )、B (1,2y )、C (3,3y )是抛物线k x y +--=2)21(21上的三个点,则1y 、2y 、3y 的大小关系是( )A 、1y <2y <3yB 、2y <1y <3yC 、3y <1y <2yD 、2y <3y <1y7、若二次函数2()1y x m =--.当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是( )A .m =lB .m >lC .m ≥lD .m ≤l8、抛物线n m x a y ++=2)(的图象如右图所示,则直线n mx y +=的图象经过( )A 、第一、二、三象限B 、第一、二、四象限C 、第二、三、四象限D 、第一、三、四象限二、填空题:1、抛物线k h x a y +-=2)(的顶点为(3,-2),且与抛物线231x y -=的形状相同,则a = ,h = ,k = 。
二次函数y=a(x-h)^2+k(a≠0)的图象与性质—巩固练习(基础).doc

二次函数y=a (x-h)2+k(a ≠0)的图象与性质—巩固练习(基础)【巩固练习】一、选择题1.抛物线2(2)3y x =-+-的顶点坐标是( )A .(2,-3)B .(-2,3)C .(2,3)D .(-2,-3) 2.函数y=21x 2+2x+1写成y=a(x -h)2+k 的形式是( ) A.y=21(x -1)2+2 B.y=21(x -1)2+21 C.y=21(x -1)2-3 D.y=21(x+2)2-1 3.抛物线y=21x 2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( ) A.y=21(x+3)2-2 B.y=21(x -3)2+2 C.y=21(x -3)2-2 D.y=21(x+3)2+2 4.把二次函数122--=x x y 配方成顶点式为( )A .2)1(-=x yB . 2)1(2--=x yC .1)1(2++=x yD .2)1(2-+=x y 5.由二次函数22(3)1y x =-+,可知( )A .其图象的开口向下B .其图象的对称轴为直线3x =-C .其最小值为1D .当3x <时,y 随x 的增大而增大6.(2015•泰安)在同一坐标系中,一次函数y=﹣mx+n 2与二次函数y=x 2+m 的图象可能是( ).A. B. C. D.二、填空题7. (2015•怀化)二次函数y=x 2+2x 的顶点坐标为 ,对称轴是直线 .8.已知抛物线y=-2(x+1)2-3,如果y 随x 的增大而减小,那么x 的取值范围是_ _____.9.抛物线y=-3(2x 2-1)的开口方向是_____,对称轴是_____.10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .11.将抛物线22y x x =-向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.12.抛物线22(2)6y x =--的顶点为C ,已知3y kx =-+的图象经过点C ,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.三、解答题13.已知抛物线的顶点(-1,-2),且图象经过(1,10),求抛物线的解析式.14. 已知抛物线212y x =-向上平移2个单位长度,再向右平移1个单位长度得到 抛物线2()y a x h k =-+;(1)求出a ,h ,k 的值;(2)在同一直角坐标系中,画出2()y a x h k =-+与212y x =-的图象; (3)观察2()y a x h k =-+的图象,当x ________时,y 随x 的增大而增大;当x ________时,函数y 有最________值,最________值是y =________;(4)观察2()y a x h k =-+的图象,你能说出对于一切x 的值,函数y 的取值范围吗?15.(2015•珠海)已知抛物线y=ax 2+bx+3的对称轴是直线x=1.(1)求证:2a+b=0;(2)若关于x 的方程ax 2+bx ﹣8=0的一个根为4,求方程的另一个根.【答案与解析】一、选择题1.【答案】D ;【解析】由顶点式可求顶点,由20x +=得2x =-,此时,3y =-.2.【答案】D ;【解析】通过配方即可得到结论.3.【答案】A ;【解析】抛物线 y=21x 2向左平移3个单位得到y=21(x+3)2,再向下平移2个单位后, 所得的抛物线表达式是y=21(x+3)2-2. 4.【答案】B ;【解析】通过配方即可得到结论.5.【答案】C ;【解析】可画草图进行判断.6.【答案】D ;【解析】解:A 、由直线与y 轴的交点在y 轴的负半轴上可知,n 2<0,错误;B 、由抛物线与y 轴的交点在y 轴的正半轴上可知,m >0,由直线可知,﹣m >0,错误;C 、由抛物线y 轴的交点在y 轴的负半轴上可知,m <0,由直线可知,﹣m <0,错误;D 、由抛物线y 轴的交点在y 轴的负半轴上可知,m <0,由直线可知,﹣m >0,正确,故选D .二、填空题7.【答案】(﹣1,﹣1); x=﹣1;【解析】∵y=x 2+2x=(x+1)2﹣1,∴二次函数y=x 2+4x 的顶点坐标是:(﹣1,﹣1),对称轴是直线x=﹣1.8.【答案】x ≥-1;【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y 随x 的增大而减小,故x ≥-1.9.【答案】向下,y 轴;10.【答案】249y x x =---;【解析】设2(2)5y a x =+-过点(1,-14)得1a =-,所以22(2)549y x x x =-+-=---.11.【答案】21027y x x =-+;【解析】先化一般式为顶点式,再根据平移规律求解.12.【答案】 1;【解析】C(2,-6),可求932y x =-+与x 轴交于2(,0)3,与y 轴交于(0,3),∴ 123123S =⨯⨯=. 三、解答题13.【答案与解析】∵ 抛物线的顶点为(-1,-2),∴ 设其解析式为2(1)2y a x =+-,又图象经过点(1,10),∴ 1042a =-,∴ 3a =,∴ 解析式为23(1)2y x =+-.14.【答案与解析】(1)由212y x =-向上平移2个单位,再向右平移1个单位所得到的抛物线是21(1)22y x =--+. ∴ 12a =-,1h =,2k =. (2)函数21(1)22y x =--+与212y x =-的图象如图所示.(3)观察2()y a x h k =-+的图象,当1x <时,y 随x 的增大而增大;当1x =时,函数y 有最大值,最大值是2y =.(4)由图象知,对于一切x 的值,总有函数值2y ≤.15.【答案与解析】(1)证明:∵对称轴是直线x=1=﹣, ∴2a+b=0;(2)解:∵ax 2+bx ﹣8=0的一个根为4,∴16a+4b ﹣8=0,∵2a+b=0,∴b=﹣2a ,∴16a ﹣8a ﹣8=0,解得:a=1,则b=﹣2,∴ax 2+bx ﹣8=0为:x 2﹣2x ﹣8=0,则(x ﹣4)(x+2)=0,解得:x 1=4,x 2=﹣2,故方程的另一个根为:﹣2.。
22.1.3 二次函数y=a(x-h)2+k的图象和性质 重难点专项练习(五大题型)(解析版)

22.1.3《二次函数y=a (x-h )2+k 的图象和性质》分层练习考查题型一 二次函数y=a (x-h )2的顶点坐标1.(2021秋·福建宁德·九年级校考期中)()21y x =-的顶点坐标是( )A .()1,0B .()0,0C .()0,1D .()1,1【答案】A 【分析】直接根据二次函数的性质可得答案.【详解】解:()21y x =-的顶点坐标是()1,0.故选A .【点睛】本题考查了二次函数2()y a x h =-(a ,h 为常数,a ≠0)的性质,熟练掌握二次函数2()y a x h =-的性质是解答本题的关键.2()y a x h =-是抛物线的顶点式,a 决定抛物线的形状和开口方向,其顶点是(h ,0),对称轴是直线x =h .2.(2022秋·河南信阳·九年级校考阶段练习)抛物线()21y x =-+的顶点坐标为( )A .(-1,0)B .(1,0)C .(1,1)D .(-1,-1)【答案】A 【分析】根据抛物线的顶点式即可得出答案.【详解】解:∵抛物线y =-(x +1)2,∴该抛物线的顶点坐标为(-1,0),故选:A .【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.3.(2022秋·新疆省直辖县级单位·九年级校考阶段练习)抛物线2(3)y x =+的顶点是( ).A .(0,3)B .(0,3)-C .(3,0)D .(3,0)-【答案】D【分析】根据二次函数2()y a x h k =-+的顶点坐标是(h ,k )即可解答.【详解】解:抛物线2(3)y x =+的顶点是(﹣3,0),1.(2023·黑龙江哈尔滨·统考三模)抛物线22(1)6y x =-+-的顶点坐标为( )A .()1,6-B .()1,6-C .()1,6D .()1,6--【答案】D【分析】根据抛物线的顶点坐标公式解答即可.【详解】解:抛物线22(1)6y x =-+-的顶点坐标为()1,6--;故选:D.【点睛】本题考查了二次函数的性质,熟知抛物线()()20=-+¹y a x h k a 的顶点坐标是(),h k 是解题的关键.2.(2020秋·广东韶关·九年级校考期末)抛物线()2213y x =-+的顶点坐标是( )A .()1,3-B .()1,3-C .()3,1D .()1,3【答案】D 【分析】利用顶点式直接求解即可.【详解】解:抛物线()2213y x =-+的顶点坐标是()1,3.故选:D .【点睛】此题考查了二次函数的性质,二次函数()2y a x h k =-+的顶点坐标为(),h k ,对称轴为x h =,熟练掌握二次函数的基本性质是解题关键.3.(2023·黑龙江哈尔滨·哈尔滨市萧红中学校考二模)抛物线2(9)10y x =---的顶点坐标是( )A .(9,10)B .(9,10)-C .(9,10)-D .(9,10)--【答案】B【分析】直接根据二次函数的顶点坐标式进行解答即可.【详解】∵二次函数的解析式为2(9)10y x =---,其顶点坐标为:(9,10)-.故选B .【点睛】本题考查的是二次函数的性质,熟知二次函数的顶点式是解答此题的关键.4.(2023·黑龙江哈尔滨·统考一模)抛物线()2251y x =-++的顶点坐标是( )A .()5,1B .()5,1--C .()5,1-D .()5,1-【答案】C 【分析】根据抛物线()2y a x h k =-+的顶点坐标是(),h k ,即可求解.【详解】解:抛物线()2251y x =-++的顶点坐标是()5,1-.故选:C【点睛】本题主要考查了二次函数的性质,熟练掌握抛物线()2y a x h k =-+的顶点坐标是(),h k 是解题的关键.考查题型三 二次函数y=a (x-h )2+k 的对称轴1.(2023春·广东云浮·九年级校考期中)抛物线()232y x =-+的对称轴是( )A .3x =-B .3x =C .2x =-D .2x =【答案】B 【分析】根据题干中抛物线的顶点式,可以直接写出它的对称轴.【详解】∵抛物线()232y x =-+∴对称轴是直线3x =,故选:B【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质进行分析解答.2.(2022秋·北京西城·九年级校考期中)抛物线()212y x =++的对称轴为( )A .直线=1x -B .直线5x =C .直线3x =D .直线4x =考查题型四二次函数y=a(x-h)1.(2020秋·广东广州·九年级广州市第十三中学校考期中)在函数()213y x =-+,y 随x 增大而减小,则x 的取值范围为( )A .1x >B .0x >C .3x <D .1x <【答案】D【分析】根据抛物线的开口方向和顶点式判断即可.【详解】解:在()213y x =-+中,∵10a =>,∴函数图像开口向上,当1x <时,y 随x 的增大而减小.故选:D .【点睛】本题考查了二次函数的性质,二次函数2y ax bx c =++(a ,b ,c 为常数,0a ¹),当0a >时,在对称轴左侧y 随x 的增大而减小,在对称轴右侧y 随x 的增大而增大;当a<0时,在对称轴左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小.2.(2022秋·山东临沂·九年级统考期中)若二次函数2y x m h ++=(),当1x <时,y 随x 的增大而减小,则m 的取值范围是()A .1m =B .1m >C .1m ³-D .1m £-【答案】D 【分析】根据二次函数的表达式可知对称轴为x m =-,根据二次函数图像的性质即可求出结论.【详解】由2y x m h ++=()得二次函数的对称轴为x m =-,∵该函数图像的开口向上,∴在对称轴左侧y 随x 的增大而减小,∴1m -³解得1m £-故选:D【点睛】本题主要考查了二次函数图像的性质,根据开口方向和对称轴确定图像的增减性是解题的关键.3.(2022秋·浙江金华·九年级统考期中)已知二次函数()231y x =-+,当y 的值随x 的增大而增大时,x 的取值满足( )A .1x ³B .1x £C .3x ³D .3x £【答案】C 【分析】根据二次函数的性质解答即可.【详解】解:2=(3)+1y x -,10a =>Q ,对称轴3x =,当3x ³时,y 随x 的增大而增大,故选:C .【点睛】此题主要考查了二次函数的性质,关键是掌握二次函数的增减性.4.(2022秋·山东济宁·九年级统考期中)已知二次函数()2y x k h =--+,当3x >时,y 随x 的增大而减小,则函数中k 的取值范围是( )A .3k ³B .3k £C .3k =D .3k £-【答案】B【分析】先利用二次函数的性质求出抛物线的对称轴为直线x k =,则当x k >时,y 的值随x 值的增大而减小,由于3x >时,y 的值随x 值的增大而减小,于是得到3k £.【详解】解:抛物线的对称轴为直线x k =,因为10a =-<,所以抛物线开口向下,所以当x k >时,y 的值随x 值的增大而减小,而3x >时,y 的值随x 值的增大而减小,所以3k £.故选:B .【点睛】本题考查的是二次函数的性质,熟知二次函数的增减性是解答此题的关键.考查题型五 二次函数y=a (x-h )2+k 的最值1.(2023·浙江·一模)关于二次函数22)3(5y x =--+的最大值或最小值,下列说法正确的是( )A .有最大值2B .有最小值2C .有最大值5D .有最小值5【答案】C【分析】由抛物线解析式可求得开口方向、对称轴、顶点坐标,可求得答案.【详解】解:∵二次函数22)3(5y x =--+,∴抛物线开口向下,对称轴为x =2,顶点坐标为(2,5),∴当x =2时,y 有最大值为5;∴选项A ,B ,D 错误,C 正确,故选:C .【点睛】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y =a (x -h )2+k 中,对称轴为x =h ,顶点坐标为(h ,k ).2.(2023·黑龙江哈尔滨·统考三模)抛物线()2345y x =---的最大值为( )A .4B .4-C .5D .5-【答案】D 【分析】根据二次函数的顶点式的特点即可解答.【详解】解:∵()2345y x =---,∴抛物线开口方向向下,对应函数有最大值5-.故选D .【点睛】本题主要考查了二次函数图像与性质,二次函数()()20y a x b k a =++¹的对称轴为x b =-,顶点坐标为(),b k -,当a<0,函数有最大值k .3.(2022秋·浙江绍兴·九年级校考期中)关于二次函数()223y x =-+,下列叙述正确的是( )A .当2x =时,y 有最大值3B .当2x =-时,y 有最大值3C .当2x =时,y 有最小值3D .当2x =-时,y 有最小值3【答案】C 【分析】()2y a x h k =-+是抛物线的顶点式,a 决定抛物线的形状和开口方向,其顶点是(),h k ,对称轴是x h =.【详解】∵二次函数()223y x =-+,∵10>,∴抛物线开口向上,函数有最小值,∴当2x =时,y 有最小值3.故选:C .【点睛】本题考查了二次函数()2y a x h k =-+(a ,b ,c 为常数,0a ¹)的性质,熟练掌握二次函数()2y a x h k =-+的性质是解答本题的关键.4.(2021秋·湖南长沙·九年级湖南师大附中校考期末)二次函数()225y x =--的最小值是( )A .2-B .2C .5-D .5【答案】C 【分析】根据二次函数()2y a x h k =-+的性质,即可求解.【详解】解∶ ∵10>,∴二次函数图象开口向上,∴当2x =时,二次函数有最小值,最小值为5-,即二次函数()225y x =--的最小值是5-.故选:C【点睛】本题主要考查了二次函数的性质,熟练掌握二次函数()2y a x h k =-+的性质是解题的关键.【点睛】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是数形结合得出2.(2021秋·山东德州·九年级统考期中)已知抛物线(1)若抛物线C的顶点在第二象限,求(2)若m=﹣2,求抛物线C与坐标轴的交点围成的三角形的面积.-<【答案】(1)m的取值范围是1m【分析】(1)先根据抛物线解析式得到抛物线的顶点坐标为(行求解即可;【点睛】本题主要考查了抛物线的顶点坐标,第二象限点的坐标特征,抛物线与坐标轴的交点坐标,解题。
26.1.2二次函数y=a(x-h)2+k(a不等以0)的图象和性质(三)每课一练(人教版九年级下册)

26.1.2 二次函数y=a(x-h)2+k(a不等以0)的图象和性质(三)每课一练(人教版九年级下册)知识点:1、抛物线的对称轴为,顶点坐标为。
2、抛物线与抛物线的形状,位置,将抛物线进行平移可得到抛物线,平移规律为:当时,将抛物线得到抛物线;当时,将抛物线得到抛物线;当时,将抛物线得到抛物线;当时,将抛物线得到抛物线;3、抛物线的图象特点:时,抛物线开口向,左右,顶点最;时,抛物线开口向,左右,顶点最;一、选择题:1、抛物线的顶点坐标为()A、(-1,)B、(1,)C、(-1,—)D、(1,—)2、对于的图象,下列叙述正确的是()A、顶点坐标为(-3,2)B、对称轴是直线C、当时,随的增大而增大D、当时,随的增大而减小3、将抛物线向右平移一个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为()A、 B、 C、 D、4、抛物线可由抛物线平移得到,则下列平移过程正确的是()A、先向右平移1个单位,再向上平移2个单位B、先向右平移1个单位,再向下平移2个单位C、先向左平移1个单位,再向上平移2个单位D、先向左平移1个单位,再向下平移2个单位5、如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是()A、y=(x+1)2-1 B.y=(x+1)2+1 C.y=(x-1)2+1 D.y=(x-1)2-16、设A(-1,)、B(1,)、C(3,)是抛物线上的三个点,则、、的大小关系是()A、<<B、<<C、<<D、<<7、若二次函数.当≤l时,随的增大而减小,则的取值范围是()A.=l B.>l C.≥l D.≤l8、二次函数的图象如图所示,则一次函数的图象经过()A、第一、二、三象限B、第一、二、四象限C、第二、三、四象限D、第一、三、四象限二、填空题:1、抛物线的对称轴是,顶点坐标是;当时,随的增大而增大,当时,随的增大而减小,当时,取最值为。
二次函数y=a(x-h)^2+k(a≠0)的图象与性质—巩固练习(基础)

二次函数y=a (x-h)2+k(a ≠0)的图象与性质—巩固练习(基础)【巩固练习】一、选择题1.抛物线2(2)3y x =-+-的顶点坐标是( )A .(2,-3)B .(-2,3)C .(2,3)D .(-2,-3) 2.函数y=21x 2+2x+1写成y=a(x -h)2+k 的形式是( ) A.y=21(x -1)2+2 B.y=21(x -1)2+21 C.y=21(x -1)2-3 D.y=21(x+2)2-1 3.抛物线y=21x 2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( ) A.y=21(x+3)2-2 B.y=21(x -3)2+2 C.y=21(x -3)2-2 D.y=21(x+3)2+2 4.把二次函数122--=x x y 配方成顶点式为( )A .2)1(-=x yB . 2)1(2--=x yC .1)1(2++=x yD .2)1(2-+=x y 5.由二次函数22(3)1y x =-+,可知( )A .其图象的开口向下B .其图象的对称轴为直线3x =-C .其最小值为1D .当3x <时,y 随x 的增大而增大6.(2015•泰安)在同一坐标系中,一次函数y=﹣mx+n 2与二次函数y=x 2+m 的图象可能是( ).A. B. C. D.二、填空题7. (2015•怀化)二次函数y=x 2+2x 的顶点坐标为 ,对称轴是直线 .8.已知抛物线y=-2(x+1)2-3,如果y 随x 的增大而减小,那么x 的取值范围是_ _____.9.抛物线y=-3(2x 2-1)的开口方向是_____,对称轴是_____.10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .11.将抛物线22y x x =-向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.12.抛物线22(2)6y x =--的顶点为C ,已知3y kx =-+的图象经过点C ,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.三、解答题13.已知抛物线的顶点(-1,-2),且图象经过(1,10),求抛物线的解析式.14. 已知抛物线212y x =-向上平移2个单位长度,再向右平移1个单位长度得到 抛物线2()y a x h k =-+;(1)求出a ,h ,k 的值;(2)在同一直角坐标系中,画出2()y a x h k =-+与212y x =-的图象; (3)观察2()y a x h k =-+的图象,当x ________时,y 随x 的增大而增大;当x ________时,函数y 有最________值,最________值是y =________;(4)观察2()y a x h k =-+的图象,你能说出对于一切x 的值,函数y 的取值范围吗?15.(2015•珠海)已知抛物线y=ax 2+bx+3的对称轴是直线x=1.(1)求证:2a+b=0;(2)若关于x 的方程ax 2+bx ﹣8=0的一个根为4,求方程的另一个根.【答案与解析】一、选择题1.【答案】D ;【解析】由顶点式可求顶点,由20x +=得2x =-,此时,3y =-.2.【答案】D ;【解析】通过配方即可得到结论.3.【答案】A ;【解析】抛物线 y=21x 2向左平移3个单位得到y=21(x+3)2,再向下平移2个单位后, 所得的抛物线表达式是y=21(x+3)2-2. 4.【答案】B ;【解析】通过配方即可得到结论.5.【答案】C ;【解析】可画草图进行判断.6.【答案】D ;【解析】解:A 、由直线与y 轴的交点在y 轴的负半轴上可知,n 2<0,错误;B 、由抛物线与y 轴的交点在y 轴的正半轴上可知,m >0,由直线可知,﹣m >0,错误;C 、由抛物线y 轴的交点在y 轴的负半轴上可知,m <0,由直线可知,﹣m <0,错误;D 、由抛物线y 轴的交点在y 轴的负半轴上可知,m <0,由直线可知,﹣m >0,正确,故选D .二、填空题7.【答案】(﹣1,﹣1); x=﹣1;【解析】∵y=x 2+2x=(x+1)2﹣1,∴二次函数y=x 2+4x 的顶点坐标是:(﹣1,﹣1),对称轴是直线x=﹣1.8.【答案】x ≥-1;【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y 随x 的增大而减小,故x ≥-1.9.【答案】向下,y 轴;10.【答案】249y x x =---;【解析】设2(2)5y a x =+-过点(1,-14)得1a =-,所以22(2)549y x x x =-+-=---.11.【答案】21027y x x =-+;【解析】先化一般式为顶点式,再根据平移规律求解.12.【答案】 1;【解析】C(2,-6),可求932y x =-+与x 轴交于2(,0)3,与y 轴交于(0,3),∴ 123123S =⨯⨯=. 三、解答题13.【答案与解析】∵ 抛物线的顶点为(-1,-2),∴ 设其解析式为2(1)2y a x =+-,又图象经过点(1,10),∴ 1042a =-,∴ 3a =,∴ 解析式为23(1)2y x =+-.14.【答案与解析】(1)由212y x =-向上平移2个单位,再向右平移1个单位所得到的抛物线是21(1)22y x =--+. ∴ 12a =-,1h =,2k =. (2)函数21(1)22y x =--+与212y x =-的图象如图所示.(3)观察2()y a x h k =-+的图象,当1x <时,y 随x 的增大而增大;当1x =时,函数y 有最大值,最大值是2y =.(4)由图象知,对于一切x 的值,总有函数值2y ≤.15.【答案与解析】(1)证明:∵对称轴是直线x=1=﹣,∴2a+b=0;(2)解:∵ax 2+bx ﹣8=0的一个根为4,∴16a+4b ﹣8=0,∵2a+b=0,∴b=﹣2a ,∴16a ﹣8a ﹣8=0,解得:a=1,则b=﹣2,∴ax 2+bx ﹣8=0为:x 2﹣2x ﹣8=0,则(x ﹣4)(x+2)=0,解得:x 1=4,x 2=﹣2,故方程的另一个根为:﹣2.。
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(提高)

二次函数y=a (x-h)2+k(a ≠0)的图象与性质—巩固练习(提高)【巩固练习】 一、选择题1. 不论m 取任何实数,抛物线y=a(x+m)2+m(a ≠0)的顶点都( )A.在y=x 直线上B.在直线y=-x 上C.在x 轴上D.在y 轴上 2.二次函数2(1)2y x =-+的最小值是( ).A .-2B .2C .-lD .13.如图所示,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( ). A .h m = B .k n = C .k n > D .0k >,0n <第3题 第5题4.把抛物线2y x =-向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( ).A .2(1)3y x =---B .2(1)3y x =-+-C .2(1)3y x =--+ D .2(1)3y x =-++5.如图所示,抛物线的顶点坐标是P(1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( ). A .3x > B .3x < C .1x > D .1x <6.若二次函数2()1y x m =--.当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是( )A .m =lB .m >lC .m ≥lD .m ≤l二、填空题7.若抛物线y=a (x+m )2的对称轴为x=-3,且它与抛物线y=-2x 2的形状相同,开口方向相同, 则点(a ,m )关于原点的对称点为________.8.若点A (3,-4)在函数2)(m x y --=的图象上,则=m _ _.这个抛物线的对称轴是 ;点A关于抛物线对称轴的对称点是 .9.如果把抛物线2)(b x a y +=向上平移-3个单位,再向右平移3个单位长度后得到抛物线3)2(212-+=x y ,则求a 的值为 ;b 的值为 . 10.请写出一个二次函数,图象顶点为(-1,2),且不论x 取何值,函数值y 恒为正数.则此二次函数为______ __. 11.若二次函数23(1)2y x =-+中的x 取值为2≤x ≤5,则该函数的最大值为 ;最小值为 .12.已知抛物线y=x 2+x+b 2经过点,则y 1的值是_____.三、解答题13.抛物线y=3(x -2)2与x 轴交于点A ,与y 轴交于点B ,求△AOB 的面积和周长.14. 如图,抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B . (1)求抛物线的解析式; (2)求△AOB 的面积;(3)若点P (m ,-m )(m ≠0)为抛物线上一点,求与P 关于抛物线对称轴对称的点Q 的坐标.(注:抛物线y=ax 2+bx+c 的对称轴是x=-2ba).15.如图,在正方形ABCD 中,AB=2,E 是AD 边上一点(点E 与点A ,D 不重合).BE•的垂直平分线交AB 于M ,交DC 于N .(1)设AE=x ,四边形ADNM 的面积为S ,写出S 关于x 的函数关系式;(2)当AE 为何值时,四边形ADNM 的面积最大?最大值是多少?【答案与解析】 一、选择题 1.【答案】B ;【解析】抛物线y=a(x+m)2+m(a ≠0)的顶点为(-m,m ),所以顶点在直线y=-x 上. 2.【答案】B ;【解析】当1x =时,二次函数2(1)2y x =-+有最小值为2.3.【答案】B ;【解析】由两抛物线对称轴相同可知h m =,且由图象知k n >,0k >,0n <. 4.【答案】D ;【解析】由抛物线2()(0,0)y a x h k h k =++>>与抛物线2y ax =之间的关系知,将抛物线2y ax =向左平移|h|个单位后得到抛物线解析式为2()y a x h =+, 再向上平移|k|个单位即得到抛物线的解析式为2()y a x h k =++. 根据这一规律不难得平移后的抛物线的解析式.也可画草图帮助分析, 即把2y x =-的图象平移到使(-1,3)为其顶点,则解析式为2(1)3y x =-++.5.【答案】C ;【解析】由顶点坐标P(1,3)知抛物线的对称轴为直线1x =,因此当1x >时,y 随x 的增大而减小. 6.【答案】C ;【解析】画出草图进行分析得出结论.二、填空题 7.【答案】(2,-3);【解析】因为抛物线y=a (x+m )2的对称轴为x=-3,且它与抛物线y=-2x 2的形状相同,开口方向相同, 所以a=-2,m=3, 故点(a ,m )关于原点的对称点为(2,-3). 8.【答案】5或1; 5x =或1x =; (7,4)-或(-1,-4);【解析】因为点A (3,-4)在函数2)(m x y --=的图象上,所以把点A (3,-4)代入函数2)(m x y --=得5m =或1m =;对称轴是5x =或1x =;点A关于抛物线对称轴的对称点是(7,4)-或(-1,-4).9.【答案】 12a =,5b =; 【解析】抛物线2)(b x a y +=向上平移-3个单位得到2()3y a x b =+-,再向右平移3个单位长度得到2(3)3y a x b =+--,即2(3)3y ax b=+--与3)2(212-+=x y 相同,故12a =,5b =.10.【答案】2(1)2y x =++ 等;【解析】答案不唯一,只要抛物线开口向上即可,即0a >,所以2(1)2y x =++或22(1)2y x =++等均可.11.【答案】50;5.【解析】由于函数23(1)2y x =-+的顶点坐标为(1,2),30a =>,当1x >时,y 随x 的增大而增大,当x =5时,函数在2≤x ≤5范围内的最大值为50; 当x =2时,函数的最小值为23(21)25y =⨯-+=最小.12.【答案】;【解析】把1(,)4a -代入y=x 2+x+b 2得22104a a b +++=,221()02a b ++=,,代入即可求得.三、解答题13.【答案与解析】∵ 抛物线y=3(x -2)2与x 轴交于点A ,与y 轴交于点B , ∴ A(2,0),B(0,12),∴ S △AOB =12,△AOB 的周长为14十237.14.【答案与解析】解:(1)设二次函数的解析式为y=a (x-2)2+1,将点O (0,0)的坐标代入得:4a+1=0,解得a=-14. 所以二次函数的解析式为y=-14(x-2)2+1; (2)∵抛物线y=-14(x-2)2+1的对称轴为直线x=2,且经过原点O (0,0), ∴与x 轴的另一个交点B 的坐标为(4,0), ∴△AOB 的面积=12×4×1=2;(3)∵点P (m ,-m )(m ≠0)为抛物线y=-14(x-2)2+1上一点, ∴-m=-14(m-2)2+1, 解得m 1=0(舍去),m 2=8, ∴P 点坐标为(8,-8), ∵抛物线对称轴为直线x=2,∴P 关于抛物线对称轴对称的点Q 的坐标为(-4,-8).15.【答案与解析】(1)连接ME ,设MN 交BE 交于P , 根据题意得MB=ME ,MN ⊥BE .过N 作NF ⊥AB 于F ,在Rt △MBP 和Rt △MNF 中,∠MBP+∠BMN=90°, ∠FNM+∠BMN=90°,∠MBP=∠MNF ,又AB=FN ,Rt △EBA ≌Rt △MNF ,MF=AE=x . 在Rt△AME 中,由勾股定理得 ME 2=AE 2+AM 2,所以MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,解得AM=1-14x 2. 所以四边形ADNM 的面积S=22AM DN AM AF AD ++⨯=×2=AM+AM+MF=2AM+AE=2(1-14x 2)+x=-12x 2+x+2. 即所求关系式为S=-12x 2+x+2.(2)S=-12x 2+x+2=-12(x 2-2x+1)+52=-12(x-1)2+52. 当AE=x=1时,四边形ADNM 的面积S 的值最大,此时最大值是52.。
二次函数y=a(x-h)2k的图像及其性质练习

二次函数y=a(x-h)2+k一选择题:1.抛物线y = x2-1的顶点坐标为( )A.(1,0) B.(-1,0) C.(0,-1) D.(2,3)2.抛物线y = -3(x-2)2+4的开口方向、对称轴、顶点坐标分别为( ) A.开口向下,对称轴为x = -2,顶点坐标为(-2,4)B.开口向上,对称轴为x = 2,顶点坐标为(2,4)C.开口向上,对称轴为x = 2,顶点坐标为(2,-4)D.开口向下,对称轴为x = 2,顶点坐标为(2,4)3.抛物线y = 2+(m-5)的顶点在x轴下方,则( )A.m = 5 B.m = - 1 C.m = 5或m = -1 D.m = -5或m = 14.把抛物线y =x2向左平移1个单位长度,再向下平移1个单位,得抛物线为( )A.y =(x2+2x+2) B.y =(x2+2x-1) C.y =(x2-2x-1) D.y =(x2-2x+1)5.二次函数y = 2(x-1)2+2的图象可由y = 2x2的图象( )得到A.向左平移1个单位长度,再向下平移2个单位长度B.向左平移1个单位长度,再向上平移2个单位长度C.向右平移1个单位长度,再向下平移2个单位长度D.向右平移1个单位长度,再向上平移2个单位长度6.将抛物线y= -x2-1向上平移两个单位得到抛物线的表达式()A.y= -x2B.y= -x2-2 C.y= -x2+1 D.y= x2+17.抛物线y = x2+b与抛物线y = ax2-2的形状相同,只是位置不同,则a、b值分别是()A.a=1,b≠-2 B.a= -2,b≠2 C.a=1,b≠2 D.a=2,b≠28. 函数y = - x2与y = x - 1的函数在同一坐标系中图象大致是_____。
9. 函数y = ax2与y = a(x - 2)(a〈0 ) 函数在同一坐标系里的图象大致是____。
人教初中数学 二次函数y=a(x-h)2(a≠0)与y=a(x-h)2+k(a≠0)的图象与性质
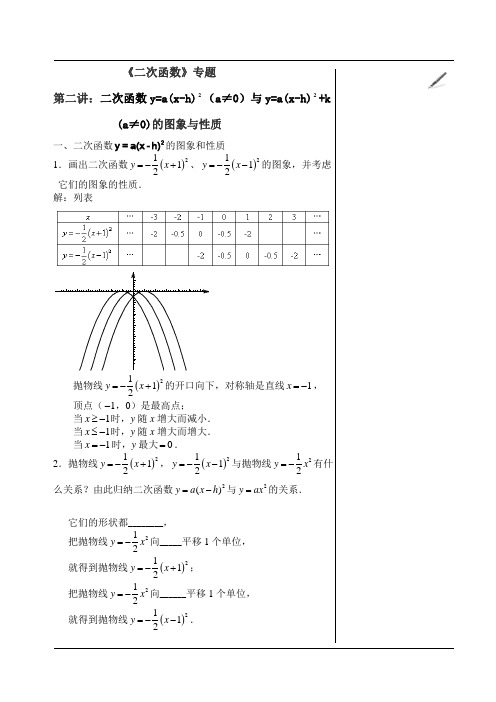
《二次函数》专题 第二讲:二次函数y=a(x-h)2(a ≠0)与y=a(x-h)2+k(a ≠0)的图象与性质一、二次函数2y =a(x -h)的图象和性质1.画出二次函数()2112y x =-+、()2112y x =--的图象,并考虑 它们的图象的性质.解:列表抛物线()2112y x =-+的开口向下,对称轴是直线1x =-, 顶点(1-,0)是最高点;当1x ≥-时,y 随x 增大而减小.当1x ≤-时,y 随x 增大而增大.当1x =-时,y 最大0=.2.抛物线()2112y x =-+,()2112y x =--与抛物线212y x =-有什 么关系?由此归纳二次函数2()y a x h =-与2y ax =的关系.它们的形状都________,把抛物线212y x =-向_____平移1个单位, 就得到抛物线()2112y x =-+; 把抛物线212y x =-向______平移1个单位, 就得到抛物线()2112y x =--.3.归纳:二次函数2()y a x h =-的图象及其性质(1)二次函数2()y a x h =-与2y ax =的最值相同,都是______;(2)抛物线2()y a x h =-与抛物线2y ax =形状相同,开口方向相 同,最高点(或最低点)的______坐标相同;抛物线2()y a x h =-的顶点(h ,0)可以由抛物线2y ax =的顶 点(0,0)向左(或向右)平移______个单位得到,抛物线和 对称轴也随之改变.(3)开口看a ;平移看顶点,_____加_____减.二、猜想并验证二次函数2y =a(x -h)+k 的图象和性质1.画出函数21(1)22y x =-+-的图象,指出它的开口方向、对称 轴和顶点坐标. 解:用平移的方法画出图象,把抛物线212y x =-向左平移1个单 位,得到抛物线21(1)2y x =-+, 再向下平移2个单位, 得到抛物线21(1)22y x =-+-. 开口向下,对称轴是直线1x =-,顶点是(1-,2-).2.归纳:(1)抛物线2()y a x h k =-+和2y ax =形状相同,把抛物线 2y ax =向上(下)平移_____个单位向左(右)平移______个单位, 得到抛物线2()y a x h k =-+.____加___减,___加___减.(2)当0a >时,开口向_____;顶点坐标是__________; 123456-1-2-3-4-5-1-2-3-4-5-6-7-8-91x y O对称轴是直线_________;当x h =时,y 有最小值_____;当x h ≤时,y 随x 的增大而________;当x h ≥时,y 随x 的增大而________.(3)当0a <时,开口向_____;顶点坐标是________;对称轴是直线________;当x h =时,y 有最大值______;当x h ≤时,y 随x 的增大而________;当x h ≥时,y 随x 的增大而________.【小结】之前三种二次函数的解析式形式实质都是顶点式.练习:1、填写下表2.(1)将抛物线23y x =-向右平移2个单位,再向上平移5个 单位,得到的抛物线解析式为 .(2)二次函数21(3)42y x =-+的图象可以看作是二次函数212y x = 的图象向 平移4个单位,再向 平移3个单位得到的.3.把二次函数2()y a x h k =-+的图象先向左平移2个单位,再向上平移4个单位,得到二次函数21(1)12y x =-+-的图象. ①试确定a 、h 、k 的值;②画出抛物线2()y a x h k =-+的示意图,指出二次函数 2()y a x h k =-+的开口方向,对称轴和顶点坐标,分析函数的增 减性.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数y=a (x-h)2+k(a ≠0)的图象与性质—巩固练习(提高)
【巩固练习】 一、选择题
1. 不论m 取任何实数,抛物线y=a(x+m)2
+m(a ≠0)的顶点都( )
A.在y=x 直线上
B.在直线y=-x 上
C.在x 轴上
D.在y 轴上 2.二次函数2(1)2y x =-+的最小值是( ).
A .-2
B .2
C .-l
D .1
3.如图所示,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( ). A .h m = B .k n = C .k n > D .0k >,0n <
第3题 第5题
4.把抛物线2
y x =-向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( ).
A .2
(1)3y x =--- B .2
(1)3y x =-+- C .2
(1)3y x =--+ D .2
(1)3y x =-++ 5.如图所示,抛物线的顶点坐标是P(1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( ). A .3x > B .3x < C .1x > D .1x <
6.若二次函数2()1y x m =--.当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是( )
A .m =l
B .m >l
C .m ≥l
D .m ≤l
二、填空题
7.若抛物线y=a (x+m )2的对称轴为x=-3,且它与抛物线y=-2x 2
的形状相同,开口方向相同, 则点(a ,m )关于原点的对称点为________.
8.若点A (3,-4)在函数2
)(m x y --=的图象上,则=m _ _.这个抛物线的对称轴是 ; 点A关于抛物线对称轴的对称点是 .
9.如果把抛物线2
)(b x a y +=向上平移-3个单位,再向右平移3个单位长度后得到抛物线
3)2(2
1
2-+=
x y ,则求a 的值为 ;b 的值为 . 10.请写出一个二次函数,图象顶点为(-1,2),且不论x 取何值,函数值y 恒为正数.则此二次函数为
______ __. 11.若二次函数2
3(1)2y x =-+中的x 取值为2≤x ≤5,则该函数的最大值为 ;最小值为 .
12.已知抛物线y=x 2+x+b 2
经过点,则y 1的值是_____.
三、解答题
13.抛物线y=3(x -2)2
与x 轴交于点A ,与y 轴交于点B ,求△AOB 的面积和周长.
14. 如图,抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B . (1)求抛物线的解析式; (2)求△AOB 的面积;
(3)若点P (m ,-m )(m ≠0)为抛物线上一点,求与P 关于抛物线对称轴对称的点Q 的坐标.
(注:抛物线y=ax 2
+bx+c 的对称轴是x=-2b
a
).
15.如图,在正方形ABCD 中,AB=2,E 是AD 边上一点(点E 与点A ,D 不重合).BE•的垂直平分线交AB 于M ,交DC 于N .
(1)设AE=x ,四边形ADNM 的面积为S ,写出S 关于x 的函数关系式; (2)当AE 为何值时,四边形ADNM 的面积最大?最大值是多少?
【答案与解析】 一、选择题 1.【答案】B ;
【解析】抛物线y=a(x+m)2
+m(a ≠0)的顶点为(-m,m ),所以顶点在直线y=-x 上. 2.【答案】B ;
【解析】当1x =时,二次函数2
(1)2y x =-+有最小值为2.
3.【答案】B ;
【解析】由两抛物线对称轴相同可知h m =,且由图象知k n >,0k >,0n <. 4.【答案】D ;
【解析】由抛物线2
()(0,0)y a x h k h k =++>>与抛物线2
y ax =之间的关系知,
将抛物线2
y ax =向左平移|h|个单位后得到抛物线解析式为2
()y a x h =+, 再向上平移|k|个单位即得到抛物线的解析式为2
()y a x h k =++. 根据这一规律不难得平移后的抛物线的解析式.也可画草图帮助分析, 即把2
y x =-的图象平移到使(-1,3)为其顶点,则解析式为2
(1)3y x =-++.
5.【答案】C ;
【解析】由顶点坐标P(1,3)知抛物线的对称轴为直线1x =,因此当1x >时,y 随x 的增大而减小. 6.【答案】C ;
【解析】画出草图进行分析得出结论.
二、填空题
7.【答案】(2,-3);
【解析】因为抛物线y=a (x+m )2的对称轴为x=-3,且它与抛物线y=-2x 2
的形状相同,开口方向相同, 所以a=-2,m=3, 故点(a ,m )关于原点的对称点为(2,-3). 8.【答案】5或1; 5x =或1x =; (7,4)-或(-1,-4);
【解析】因为点A (3,-4)在函数2
)(m x y --=的图象上,所以把点A (3,-4)代入
函数2
)(m x y --=得5m =或1m =;对称轴是5x =或1x =;点A关于抛物线对称轴的对称点是(7,4)-或(-1,-4).
9.【答案】 1
2
a =
,5b =; 【解析】抛物线2)(b x a y +=向上平移-3个单位得到2()3y a x b =+-,再向右平移3个单位长度得
到2
(3)3y a x b =+--,即2
(3)3y a x b =+--与3)2(212-+=
x y 相同,
故1
2
a =,5
b =. 10.【答案】2(1)2y x =++ 等;
【解析】答案不唯一,只要抛物线开口向上即可,即0a >,所以2(1)2y x =++或22(1)2y x =++等均可.
11.【答案】50;5.
【解析】由于函数23(1)2y x =-+的顶点坐标为(1,2),30a =>,
当1x >时,y 随x 的增大而增大,
当x =5时,函数在2≤x ≤5范围内的最大值为50; 当x =2时,函数的最小值为2
3(21)25y =⨯-+=最小.
12.【答案】;
【解析】把1
(,)4
a -代入y=x 2
+x+b 2
得22
104a a b +++
=,221
()02
a b ++=, ,代入即可求得.
三、解答题
13.【答案与解析】
∵ 抛物线y=3(x -2)2
与x 轴交于点A ,与y 轴交于点B , ∴ A(2,0),B(0,12),
∴ S △AOB =12,△AOB 的周长为14十237.
14.【答案与解析】
解:(1)设二次函数的解析式为y=a (x-2)2
+1,
将点O (0,0)的坐标代入得:4a+1=0,
解得a=-14
. 所以二次函数的解析式为y=-14
(x-2)2
+1; (2)∵抛物线y=-14
(x-2)2
+1的对称轴为直线x=2,且经过原点O (0,0), ∴与x 轴的另一个交点B 的坐标为(4,0),
∴△AOB 的面积=
1
2
×4×1=2; (3)∵点P (m ,-m )(m ≠0)为抛物线y=-14
(x-2)2
+1上一点, ∴-m=-
14
(m-2)2
+1, 解得m 1=0(舍去),m 2=8, ∴P 点坐标为(8,-8), ∵抛物线对称轴为直线x=2,
∴P 关于抛物线对称轴对称的点Q 的坐标为(-4,-8).
15.【答案与解析】
(1)连接ME ,设MN 交BE 交于P , 根据题意得MB=ME ,MN ⊥BE .
过N 作NF ⊥AB 于F ,在Rt △MBP 和Rt △MNF 中,∠MBP+∠BMN=90°, ∠FNM+∠BMN=90°,∠MBP=∠MNF ,又AB=FN ,Rt △EBA ≌Rt △MNF ,MF=AE=x . 在Rt △AME 中,由勾股定理得 ME 2
=AE 2
+AM 2
,
所以MB 2
=x 2
+AM 2
,即(2-AM )2
=x 2
+AM 2
,解得AM=1-14
x 2
. 所以四边形ADNM 的面积
S=
22AM DN AM AF AD ++⨯=×2=AM+AM+MF=2AM+AE=2(1-14x 2)+x=-12
x 2
+x+2. 即所求关系式为S=-12
x 2
+x+2.
(2)S=-12x 2+x+2=-12(x 2-2x+1)+52=-12(x-1)2+52
. 当AE=x=1时,四边形ADNM 的面积S 的值最大,此时最大值是5
2
.。
