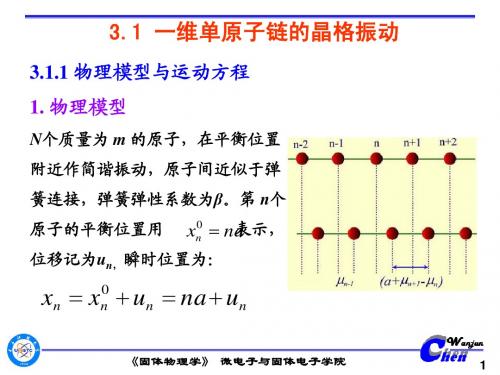
固体物理31一维晶格振动
固体物理学中的晶格振动和声子

固体物理学中的晶格振动和声子晶体是由原子、离子或分子组成的三维周期性结构,在固体物理学中起着重要的作用。
而晶体中的晶格振动是指晶体中原子的振动行为,它是固体物理学中的一个重要研究领域。
在这个领域中,声子是一种非常重要的概念,它可以用来描述晶体中各个原子的振动状态。
晶格振动是由于晶格结构的周期性而出现的。
当我们把晶体简化成最简单的一维线性链结构来研究,就可以更好地理解晶格振动的性质。
假设晶体中的原子按照一定的规则排列,形成一个周期性的结构。
当晶体中的原子发生微小的振动时,它会传递给相邻的原子,从而引起整个晶体的振动。
声子是晶体中的一种元激发,它描述了晶体中各个原子的振动状态,并且可以传递能量和动量。
在一维线性链结构中,我们可以通过人为设定边界条件来研究声子的行为。
假设链的两端被固定住,这意味着链中的第一个和最后一个原子不能移动。
在这种情况下,我们称之为固定边界条件。
根据固定边界条件,声子的振动模式可以分为两种类型,即长波动和短波动。
在长波动中,链中的每个原子振动的幅度大致相同,而在短波动中,链中的原子振动的幅度逐渐减小,直到最后一个原子完全不振动。
在晶体中,声子的振动模式可以更加复杂。
由于晶体的周期性结构,声子的能量和动量也有一定的限制。
根据晶体的对称性和周期性,声子的振动模式可以分为不同的类型,称之为晶格振动模式。
在固体物理学中,研究晶体中声子的行为是非常重要的,因为声子的能量影响了晶体的热传导性能,而声子的动量则影响了晶体的电导性能。
在研究晶体中的声子时,科学家们发现了一些有趣的现象。
例如,在一些特殊的晶体结构中,声子的能带结构会出现禁带。
这意味着在某些能量范围内,声子是无法存在的。
这种现象与电子在固体中的行为非常相似,因为晶体中的声子和电子都具有波粒二象性。
这种禁带结构对于理解固体的热传导性和光学性质都是非常重要的。
此外,声子还可以与其他凝聚态物理中的激发类似,例如声子与电子之间的相互作用。
一维单原子链晶格振动解析步骤

一维单原子链晶格振动解析步骤一维单原子链模型是固体物理中的经典模型之一,用于描述晶体中原子的振动行为。
在这个模型中,原子由质量为m的核和劲度系数为K的弹性相互作用构成。
通过对一维单原子链的晶格振动进行分析,可以更好地理解固体中的声子模式和声子色散关系。
下面将介绍一维单原子链晶格振动解析步骤:第一步:建立模型首先,我们要建立一维单原子链的模型。
假设晶格常数为a,原子间距为a/2,一维晶格中的每个原子都沿着x轴定位。
原子间的相互作用由弹簧模型描述,即相邻原子间的相互作用劲度系数为K。
这个模型是一个简单的原子链模型,可以通过它来研究晶格振动的基本性质。
第二步:求解运动方程接下来,我们需要求解原子在这个一维单原子链中的运动方程。
假设第n个原子的位移为Un(t),那么根据牛顿第二定律,可以得出该原子的运动方程为:m*Un’’(t) = -K*(Un(t+0) - 2*Un(t) + Un(t-0))上式中,Un’’(t)表示Un对时间的二阶导数,-K*(Un(t+0) -2*Un(t) + Un(t-0))表示受到的弹性相互作用力。
第三步:假设解的形式由于原子在一维单原子链中的振动属于谐振动问题,我们可以假设原子的位移满足解的形式为:Un(t) = An*exp(i*(k*n*a - ω*t))其中,An是振幅,k是波数,ω是角频率,n是原子的编号。
将这个解代入到运动方程中,可以得到关于角频率ω和波数k的关系式,即声子色散关系。
声子色散关系描述了声子的能量随波数变化的关系,是描述晶体中声子性质的重要工具。
第四步:得到声子色散关系将解的形式代入运动方程,我们可以得到关于角频率ω和波数k的关系式。
具体地,我们可以得到一维单原子链中的声子色散关系为:ω(k) = 2*sqrt(K/m)*|sin(ka/2)|声子色散关系描述了一维单原子链中的声子能量随波数变化的规律。
从这个关系式可以看出,一维单原子链中的声子有声学支和光学支两种振动模式,它们的能量随波数的变化方式不同。
《固体物理基础》晶格振动与晶体的热学性质

一、三维简单格子
二、三维复式格子
三、第一布里渊区
四、周期性边界条件
◇一个原胞内有P
个不同原子,则
有3P个不同的振
动模式,其中3支 声学波。
◇具有N个原胞的 晶体中共有3PN个
振动模式,其中
3N个声学波, 3N(P-1)个光学波。
四、周期性边界条件 总结
§ 3.4 声子
声子:晶格振动中格波的能量量子
二、一维单原子链的振动
格波
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
周期性边界条件
玻恩—卡曼边界条件
二、一维单原子链的振动
周期性边界条件
即q有N个独立的取值—晶格中的原胞数第一布
◇非弹性X射线散射、非弹性中子散射、可见光 的非弹性散射。
§ 3.4 声子
§ 3.4 声子
90K下钠晶体沿三个方向的色散关系
§ 3.5 晶格热容
一、晶格振动的平均能量
热力学中,固体定容热容:
根据经典理论,每一个自由度的平均能量是kBT, kBT/2为平均动能,kBT/2为平均势能,若固体有
N个原子,总平均能量: 取N=1摩尔原子数,摩尔热容是:
二、一维单原子链的振动
一维单原子链的振动
二、一维单原子链的振动
简谐近似下的运动方程
二、一维单Hale Waihona Puke 子链的振动简谐近似下的运动方程
在简谐近似下,原子的相互作用像一个弹 簧振子。一维原子链是一个耦合谐振子,各原 子的振动相互关联传播,形成格波。
第3章 晶格振动
《固体物理学》 微电子与固体电子学院
12
3.1 一维单原子链的晶格振动
3. 格波的意义
连续介质波:
x i 2 t
Ae
Ae
i qxt
波矢:q
2
格波: u
n
Ae
i qnat
《固体物理学》 微电子与固体电子学院
13
3.1 一维单原子链的晶格振动
25
3.1 一维单原子链的晶格振动
相邻原子之间的作用力:
f ,
f a
a
K=βa是原子链的伸长模量。 格波传播速度:
c a ,c a a K m m/a
连续介质弹性波的相速度:VElastic K
可见两者相速度相同。因此在长波极限下,对以一维单原
《固体物理学》 微电子与固体电子学院 24
3.1 一维单原子链的晶格振动
2. 长波极限
当q趋近0,即波长很长时:
sin(qa ) qa 2 2
aq m
在长波极限下一维单原子晶格
格波的色散关系和连续介质中 弹性波的色散关系 VElasticq 一致。
《固体物理学》 微电子与固体电子学院
晶体中格波和连续介质波具有完 全类似的形式。一个格波表示的 是所有原子同时做频率为ω的振 动。在简谐近似下,格波是简谐
平面波。
图中的向上箭头代表原子沿X轴 向右振动,向下箭头代表原子沿 X轴向左振动。箭头的长度代表 原子离开平衡位臵位移的大小。
《固体物理学》 微电子与固体电子学院 14
3.1 一维单原子链的晶格振动
格波的波长:
2 q
格波的波矢:q 2 n n 代表沿格波传播方向的单位
固体物理基础第3章 晶格振动理论

第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx,t)和μ(x+Δx,t)在x处泰勒展开,并且只保留到二 阶项,这种假设称为简谐近似,于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到:
率。
根据这种长波近似的极限情形,就可以设想,当长波近
似的条件λ>>a不成立时,方程(3.1)的解仍应具有类似的形式,
即只需在式(3.4)的简谐波的解中用na替代x即可,也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点,可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1),得:
10
第3章 晶格振动理论
-π<qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
,π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点,可以用图3.2来说明。为了便于图示,图中把
固体物理 第三章 晶格振动
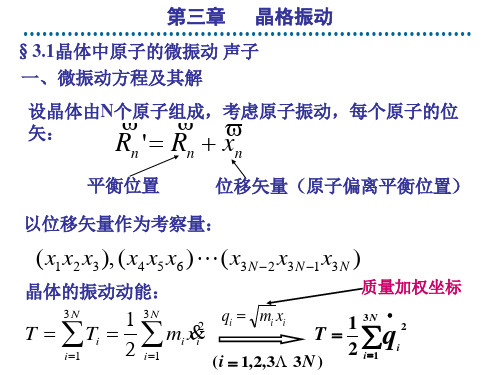
1 2 T = ∑q 2 i =1 i
3N •
3.1晶体中原子的微振动 3.1晶体中原子的微振动 声子 晶体振动势能U (qi ) 按 qi 的幂将势能在平衡位置附近展开为泰勒级数 ∂U 1 ∂ 2U U = U0 + ∑ ( ) 0 qi + ∑ ( ) 0 qi q j + 高阶项 ∂q i 2 ij ∂qi ∂q j i 其中 U 0 = 0 平衡位置处的势能为零势能点
xn = x N + n
又 : xn = Ae
i ( kna − ωt )
又 − π < k ≤ π s = − N + 1,− N + 2⋯⋯ N 共有N个取值 : a a 2 2 2
=1 e ⇒ 2π ⋅ s, = N+ 2π ,− π + 2 2π ,..., π 有N种均匀分布的分立取值 种均匀分布的分立取值 a L a L a 2π L 间隔∆k = ,密度 ,第一布里渊区倒格点数N。 L 2π
, ( l =1, 2, ⋯ 3N )
Ql = Ql0 sin(ωl t + α 1 )
1 ε l = (Q l + ωl2Ql2 ) 2
• 2
能量量子化
1 εl = (nl + )hυl 2
3.2 一维布拉菲格子的晶格振动 一、简谐近似
du 1 d 2u u( x) ≈ u( x0 ) + ∆x + (∆x)2 2 dx r0 2 dx x
3.1晶体中原子的微振动 声子 3.1晶体中原子的微振动 晶格振动模式
质量加权坐标下: 质量加权坐标下:
•• 3N
↔
独立的谐振子
↔
声子
固体物理学中的晶格振动与声子理论

固体物理学中的晶格振动与声子理论晶体是由原子或分子按照一定的规则排列形成的三维空间周期性结构。
在晶体中,原子或分子不是静止不动的,而是以不同的方式振动。
这种振动称为晶格振动,它是固体物理学中的一个重要研究课题,与晶体的性质和行为密切相关。
晶格振动是晶体中原子或分子的协同振动。
晶格振动可以分为长波和短波两种类型。
长波振动是指原子或分子在晶格中以相对偏移的方式振动,而短波振动则是指原子或分子在晶格中以体积变化的方式进行振动。
晶格振动是通过声波传播的,因为声波是介质中粒子振动的传递方式。
声子理论是描述固体中晶格振动的重要理论框架。
根据声子理论,晶体中的振动可以看做是自由度离散的量子力学系统。
它引入了一个新的物理量,即声子,它代表了晶格中的元激发,类似于固体中的粒子。
声子具有能量和动量,并且可以在固体中传播和相互作用。
声子的能量与振动模式相关。
在晶体中,存在不同的振动模式,每种振动模式对应一个特定的波矢和频率。
通过声子理论,可以计算出不同振动模式的能量,进而获得晶体中的频谱信息。
频谱信息反映了晶体中的振动性质,可以用来解释和预测材料的热力学性质、电子结构等。
声子理论还可以解释和预测晶体的热传导性能。
晶体的热传导是通过声子的散射传递热量的,因此理解声子的传播性质对于研究和优化热传导材料至关重要。
通过声子理论,可以计算声子的群速度和散射率,进而预测材料的热导率。
这对于设计新的热障涂层、热电材料等具有重要意义。
声子理论也在纳米材料和低维材料中发挥着重要作用。
在这些材料中,表面效应和尺寸效应导致晶格振动的变化,进而影响材料的性质。
声子理论可以用来研究这种尺寸效应,并解释纳米材料的热力学性质、凝聚态物理行为等。
总之,固体物理学中的晶格振动与声子理论是研究晶体性质和行为的重要工具。
通过声子理论,可以揭示晶体中振动模式的能量、频率和传播性质,进而解释和预测材料的热力学性质、热传导性能等。
声子理论在材料科学和凝聚态物理研究中具有广泛的应用前景。
固体物理:3_3 一维双原子链 声学波和光学波

m2 2 2 cos aq
在长波极限下, q 0
2 max
2
(M Mm
m)
2
B ( A)
m
2
2
2 cosqa
m M
表明:长波光学模中原胞内两原子作相对振动,而且原胞
质心保持不动。这一点很重要,例如离子晶体中,原胞内正、 负离子振动方向相反,产生迅速变化的电偶极矩,与光波耦 合必然影响其光学性质,这就是为什么称为光学模的原因。
2 min
m 2
m
2
(
B A)
m2 2 2 cos aq
B ( A)
m2 2 2 cosqa
0
表明基元中相邻原子作相对振动,这是光 学模的振动特点。
东北师范大学物理学院
3 – 3 一维双原子链
第三章 晶格振动与晶体的热学性质
相邻原子的运动情况
(声学支Acoustic branches)
24516710gmk???maxoeminoemaxaemino?15nm??maxo?4mm?maxa?41510dyncm?第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院1声学波的最大频率14max310arads???光学波的最大频率光学波的最小频率14610rads??max2am???4mm?15nm??max2o????02mmmmm????14max256710oradsm?????min2om???cmgs2m???radsgdyncm第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院max0442oeev?min0396oeev?max0198aeev?2相应声子的能量minminooe??min2om???maxmaxooe??max2o????max2am???maxmaxaae??第三章晶格振动与晶体的热学性质33一维双原子链东北师范大学物理学院6周期性边界条件periodicboundarycondition表明
固体物理基础第3章 晶格振动理论

第3章 晶格振动理论
基于如下的物理考虑:首先,晶体的宏观热性质取决于 组成晶体的绝大多数原子的运动状态;其次,晶体边界(表 面)原子的数目远小于晶体内部原子数目,因此对晶体热性 质的影响很小;第三,按照近邻作用近似,边界原子对内部 原子运动状态的影响很小。于是,玻恩-卡曼提出了这样的 周期性边界条件:假定由数目巨大的N个原子组成的一维单 原子链首尾衔接(间距也为a),构成一个如图3.3所示的半径 很大的圆环,局部范围内原子沿环方向的振动仍然可以看做
2
第3章 晶格振动理论 μn+2,…表示,第n个原子的实际位移为Xn=na+μn,如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用,但是这种作用会随着原子间距的增加而快速减小, 这是比较容易理解的,因此,为了使问题进一步简化,可以 进行近邻作用近似,即假定晶格中任一原子只受到其最近邻 原子的作用。这样的话,由于晶格中相邻原子间的相互作用 (化学键)都相同,就可以把一维单原子链想象成N个原子由 完全相同的弹簧连接的情况,如图3.1(c)所示,于是对于第n 个原子,只受到前后两个原子的作用fn-1,fn+1,它们与原子 的相对位移成正比,并且具有相同的弹性系数(或者叫回复 力系数)β。
把这些连续量带入方程(3.1)整理后即可得到:
m 2 ( t2 x ,t) 2 x (x 2 ,t)a 2 2 ( t2 x ,t)0 2 2 x (x 2 ,t)
(3.3)
7
第3章 晶格振动理论
这是数理方程中的波动方程,其中
2 0
程的特解为
a2 m
为波速度,该方
(x,t)Aei(tqx)
这是由2N个方程组成的联立方程组。同样,该方程组 应该具有下列形式的格波解,只是由于P原子和Q原子质量 的不同,其格波解的振幅不同:
固体物理:3-1 一维晶格的振动

4
第n个原子受到近邻原子的 作用力(最近邻近似)为: 第n个原子的运动方程:
5
通式 Born-Karman周期性边界条件
简谐振动
第n’个原子的位移: 若 若 格波,其中q为波矢
两个原子 位移相同
两个原子 位移相反
6
说明:原子的运动不是孤立的,而是以行波形式在晶体中 传播,不同原子通过相位qna相关联。对于每一波矢q,每 个原子的运动情况均由通解所描述,所以由波矢q所确定 的行波是晶体中原子的一种集体运动,这种波称为格波。
晶格振动的 普遍规律
24
a1,a2,a3为晶体原胞的基矢,沿基矢方向晶体各有N1,N2,N3 个原胞。共有N= N1N2N3个原胞;晶体由n种不同原子构成, 原子的质量分别为m1,m2…mn ,每个原胞中n个不同原子平 衡位置的相对坐标为r1,r2…rn.设顶点的位置矢量为
Rl l1a1 l2a2 l3a3
晶格振动的模式数目等 于原子的自由度数之和。
2、声学波与光学波
q0
sin2(qa/2)
(qa/2)2
18
当q0时,波速中无q,即传播速度 与波矢无关,弹性波,类似于声波 A格波为声学波,频率可以到0(实际到无限低)。整体运动。
omin> Amax
o格波为光学波,频率大概在远红外波段。 原子间相对运动,与电磁波耦合。
19
20
声学波: q0
A0
B/A1
对于长声学波,相邻原子的 位移相同,描述的是刚性的 运动,代表原胞质心的运动。
21
光学波:
长光学波, q0
Mu2n mu2n1 0 M m
22
光学波:产生交变的偶极矩, 可以和外界电磁波发生耦合
固体物理学中的晶格振动

固体物理学中的晶格振动晶格振动是固体物理学中一个重要的研究课题,涉及到材料的结构、热力学性质以及电子传输等多个方面。
晶格振动指的是晶体中原子的振动行为,这种振动是由原子间的相互作用引起的,形成了固体的稳定结构。
晶格振动的研究与材料的热传导性能密切相关。
晶格结构中的原子通过弹性束缚力相互作用,形成了周期性的振动。
这些振动可以看作是一连串的微小位移,沿着晶格的方向传播。
振动的传播速度和强度影响了材料的导热性能。
热导率是材料导热性能的一个重要指标,与晶格振动密切相关。
因此,研究晶格振动对于理解热传导机制以及开发高效热电材料具有重要意义。
晶格振动还涉及到材料的光学性质。
尤其是在光电子学和半导体器件中,晶格振动的研究对于理解材料的光学响应和能带结构具有重要意义。
晶格振动可以通过散射实验来研究,如X射线散射和中子散射等技术。
借助于这些实验手段,研究人员可以探测晶格振动的频率、强度以及耦合效应。
晶格振动的理论基础是固体物理学中的晶格动力学理论。
根据这个理论,晶格振动可以视为离散的荷质点在周期势场中的运动。
通过数学方法可以得到晶格振动的频率和振动模式等信息。
晶格动力学理论也可以用来解释晶格振动的热力学性质,如热容和热膨胀等。
从实际研究的角度来看,现代固体物理学中涌现了许多晶格振动的相关研究领域。
一个重要的研究方向是声子学,它研究的是固体中的声子,即晶格振动的量子态。
声子学的实验技术既包括晶格振动的散射实验,也包括通过激光和超导器件等手段产生和探测声子的方法。
另一个研究领域是热声学,它研究的是晶格振动和热传导之间的相互作用。
热声学研究的对象是晶体中热激励所引起的声学振动,从而揭示了热力学和声学性质之间的联系。
此外,也有一些新颖的研究方向在固体的晶格振动领域获得了突破性的进展。
例如,超导态材料中的相场调控、拓扑绝缘体中的表面声子等。
这些研究不仅提供了新的理论认识,也为应用领域的发展提供了基础。
总的来说,固体物理学中的晶格振动是一个广泛而具有深度的研究领域。
固体物理学中的晶格振动

固体物理学中的晶格振动在固体物理学中,晶格振动是一个重要而有趣的研究领域。
晶格振动指的是晶体中原子或离子在其平衡位置附近发生的微小振动。
这种振动是由于原子或离子之间的相互作用而产生的。
晶格振动广泛应用于各种领域,如材料科学、固体力学和纳米技术等。
本文将介绍晶格振动的基本原理和应用。
晶格振动的基本原理是基于区域平衡理论。
根据这个理论,晶体中的每个原子或离子都处于一个平衡位置,附近的原子或离子对其施加一个平衡力。
当原子或离子受到微小扰动时,平衡力会使其回到平衡位置,并且会引起周围原子或离子的扰动。
这种扰动会在整个晶体中传播,形成晶格振动。
晶格振动有两种基本类型:声子振动和光子振动。
声子振动是通过晶体中的弹性介质传播的机械波。
它的频率和波矢由晶体的结构确定。
光子振动是通过晶体中的电磁介质传播的电磁波。
它的频率和波矢由晶体的电子结构和禁带结构决定。
晶格振动在材料科学中有广泛的应用。
例如,在合金的研究中,了解晶格振动对合金的力学性能和热学性能的影响非常重要。
通过研究晶格振动,可以预测合金的热膨胀性质、热导率和声速等。
这对于材料的设计和制备具有重要意义。
此外,晶格振动还在固体力学中起着重要作用。
晶格振动对晶体的弹性性能和声学性能有直接影响。
通过研究晶格振动,可以预测晶体的弹性恢复和声学传播特性,这对于材料的强度和稳定性分析非常重要。
晶格振动在纳米技术中也发挥了关键作用。
由于纳米材料的尺寸非常小,其表面与体积之比很大,晶格振动对它们的性质有显著影响。
例如,纳米材料的热导率会因为晶格振动的限制而降低。
这一特性被广泛应用于热电材料和热障涂层等领域。
尽管晶格振动在许多领域中都起着关键作用,但要准确地描述和理解它仍然具有挑战性。
由于晶格振动是一个多粒子系统,需要考虑到多个原子或离子之间的相互作用和非线性效应。
因此,研究晶格振动需要使用复杂的数学模型和计算方法。
总之,晶格振动在固体物理学中是一个重要的研究领域。
通过研究晶格振动,我们可以更好地理解晶体的性质和行为,并在材料科学、固体力学和纳米技术等领域中应用这一知识。
固体物理--第三章 晶格振动
三、周期性边界条件 周期性边界条件:
N n n
e
iNaq
1
2 q h Na
q的分布密度:
h =整数, N:晶体链的原胞数
Na L q const. 2 2
{
简约区中q的取值总数 = q
2 N =晶体的原胞数 a 晶格振动的格波总数=2N=晶体的自由度数
2 1
两个色散关系即有两支格波:(+:光学波; -:声学波)
简约区:
a
q
a
π a
π a
对于不在简约区中的波数q’ ,一定可在简约区中 找到唯一一个q,使之满足:
2 q q G a
G 为倒格矢
二、光学波和声学波的物理图象 第n个原胞中P、Q两种原子的位移之比
n m M n q0
离子晶体在某种光波的照射下,光波的电场可以激发这 种晶格振动,因此,我们称这种振动为光学波或光学支。
对于单声子过程(一级近 似),电磁波只与波数相同的格
(q)
=c0q +
+(0)
波相互作用。如果它们具有相同
的形式在整个晶体中传播,称为格波。
q取不同的值,相邻两原子间的振动位相差不同,则 晶格振动状态不同。 2 则 q 与 q描述同一晶格振动状态 若 q q a
1 4a
例:
q1
q2
2
1
2 a
5
4
2
2a 5
2a
2
2 q2 q1 a
三、周期性边界条件(Born-Karman边界条件)
N+1
晶格振动-31简谐震动简正坐标

通过该模型,我们能够解释晶体 中原子或分子的振动频率、耦合 机制以及与热力学性质的关系。
该模型在材料科学、化学和物理 学等领域具有广泛的应用前景, 有助于深入理解材料的物理和化
学性质。
研究展望
01
02
03
04
进一步研究晶格振动-31简谐 震动简正坐的适用范围和局限
性,以拓展其应用领域。
结合实验手段,验证该模型的 预测结果,提高模型的可靠性
在化学物理中的应用
分子振动光谱分析
简正坐标在化学物理中常用于分析分子振动光谱,从而了解分子 的结构和化学键信息。
计算分子热容
通过简正坐标,可以计算分子热容,从而了解分子在温度变化时 的热学性质。
分子动力学模拟
简正坐标可以用于分子动力学模拟,通过模拟分子的振动行为, 进一步理解化学反应的动力学过程。
质。
03 简谐振动的数学模型
简谐振动的定义
简谐振动
在物理学中,简谐振动是指物体 在平衡位置附近做周期性往复运 动的振动。
描述参数
简谐振动可以用振幅、频率、相 位等参数来描述。
简谐振动的数学表达式
01
简谐振动的数学表达式通常为: x=A*sin(ωt+φ),其中x表示位移, A表示振幅,ω表示角频率,t表示 时间,φ表示初相角。
05 简正坐标的应用
在固体物理中的应用
1 2
描述晶体中原子或分子的振动
简正坐标是用来描述晶体中原子或分子的振动状 态的,可以用来研究晶体的热容、热膨胀等现象。
计算晶格热容
通过简正坐标,可以计算晶格热容,从而了解晶 体在温度变化时的热学性质。
3
研究声子谱
简正坐标可以用来研究晶格的声子谱,了解晶体 的振动频率和模式,进一步理解晶体的物理性质。
固体物理学3晶格振动

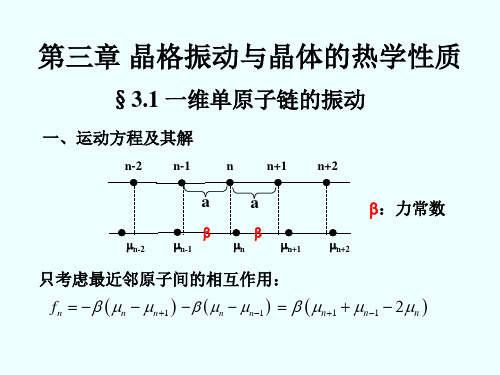
第三章 晶格振动与晶体热力学性质3-1 一维晶格的振动一、 一维单原子链(简单格子)的振动 1. 振动方程及其解(1)模型:一维无限长的单原子链,原子间距(晶格常量)为a ,原子质量为m 。
用xn 和xk 分别表示序号为n 和k 的原子在t 时刻偏离平衡位置的位移,用x nk = x n -x k 表示在t 时刻第n 个和第k 个原子的相对位移。
(2)振动方程和解平衡时,第k 个原子与第n 个原子相距0r a k n =-)(r u 为两个原子间的互作用势能,平衡时为)(0r u ,t 时刻为)()(0r r u r u δ+=)()(0r r u r u δ+=⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=3332220)(d d 61)(d d 21d d )(000r r u r r u r r u r u r r r δδδ ⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=3332220000d d 61d d 21d d )()(nk r nk r nk r x r u x r u x r u r u r u 第 n 个与第 k 个原子间的相互作用力:⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-=2332200d d 21d d d d nk r nk r nkx r u x r u r u f 振动很微弱时,势能展开式中忽略掉(δr )二次方以上的高次项---简谐近似。
(忽略掉作用力中非线性项的近似---简谐近似。
) 得: nk nk r nkx x r u f β-=⎪⎪⎭⎫ ⎝⎛-=022d d 022d d r r u ⎪⎪⎭⎫⎝⎛=β()k n kn x x f --=∑β原子的振动方程: ()k n knx x mx--=∑β..只考虑最近邻原子间的相互作用,且恢复力系数相等:()()11..+-----=n n n n x x x x n m x ββ ()11..2+----=n n n x x x nm x β给出试探解:()naq t i n A x --=ωe ])1([1e aq n t i n A x +--+=ω原子都以同一频率ω,同一振幅A 振动,其中naq 表示第n 个原子在t=0时刻的振动相位,相邻原子间的位相差为aq 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动很微弱时,势能展开式中忽略掉(r)二次方以上的
高次项,只保留到(r)2项---简谐近似。
(忽略掉作用力中非线性项的近似---简谐近似。)
得:
f nk
d2u dr 2
r0
xnk
nk xnk
fn nk xn xk
nk
d2u dr 2
r0
弹性恢复力系数
k
原子的振动方程:
m
..
xn
nk xn
第一节 一维晶格的振动
本节主要内容: 3.1.1 一维单原子链的振动 3.1.2 一维双原子链(复式格子)的振动
§3.1 一维晶格的振动
3.1.1 一维单原子链的振动
1. 振动方程及其解 (1)模型:一维无限长的单原子链,原子间距(晶格常量)为 a,原子质量为m。
第n-2个原子
第n-1个原子 第n个原子
2 sin aq
m2
1 2
m
sin
2π 5
, 21
2
sin
m
π 5
, 3
0,4
2
,5
1
模型 运动方程
试探解
色散关系
波矢q范围 B--K条件
波矢q取值
一维无限长原子链,m,a,
n-2 n-1 n mm
n+1 n+2
a
..
xn Aeitnaq
将试探解代入振动方程得色散关系:
2 sin aq
m2
由玻恩---卡门周期性边界条件:
x1 x1 N
eiNaq 1
S为整数
Naq 2π s
q 2π s 5a
π q π
a
a
5<s 5
2
2
5<s 5
2
2
s 2, 1, 0, 1, 2
q 4π , 2π ,0, 2π , 4π 5a 5a 5a 5a
的传播速度: v p 介质密度
q 2π a
vp a m
在长波近似的情况下,晶体可视为连续介质,格波可视 为弹性波。
例1.求由5个原子组成的一维单原子晶格的振动频率。设原
子质量为m,恢复力常数为(只考虑近邻原子间的相互作用)。
解:设最近邻原子间的恢复力系数为,则:
..
m xn xn xn1 xn xn1
为aq。晶格中各个原子间的振动相互间都存在着固定的位相关
系,即原子的振动形成了波,这种波称为格波。
将试探解代入振 动方程得振动频率:
2 sin aq
m2
色散关系 (晶格振动谱) 推导略
..
m xn 2xn xn1 xn1
给出试探解: xn Aei t naq
.xnຫໍສະໝຸດ iAei t naq 2
2
2
2
波矢 q
2π Na
s
也只能取N个不同的值。
晶格振动波矢只能取分立的值
波矢的数目(个数)=晶体原胞的数目
4. 长波极限: q 2π 0
2 sin aq 2 aq a q
m2
m2
m
Vp q
vp a m
弹性波
m
2π a
π a
o
πa
Vp q
vp a m
由连续介质波
弹性模量
(q) (q)
m
故取 π q π
a
a
π a
o
πa
简约布里渊区
3. 玻恩---卡门周期性边界条件及波矢q的取值
(1)玻恩---卡门周期性边界条件
设在实际晶体外,仍然有无限多个完全相同的晶体相连接, 各晶体中相对应的原子的运动情况都一样。
晶体中任一个原子,当其原胞标数增加N(N为晶体中 原胞的个数 )后,其振动情况复原。由N个原胞组成的单原
第n+1个原子 第n+2个原子
a
Xn-2
Xn-1
Xn
Xn+1
Xn+2
第n-2个原子
第n-1个原子 第n个原子
第n+1个原子 第n+2个原子
a
Xn-2
Xn-1
Xn
Xn+1
Xn+2
用xn和xk分别表示序号为n和k的原子在t时刻偏离平衡位置的
位移,用xnk= xn-xk表示在t时刻第n个和第k个原子的相对位移。
子链,由玻恩---卡门周期性边界条件: xn xn N
(2)波矢q的取值 对于一维布拉维晶格(原胞标数与原子标数相同):
xn xnN
Aei t naq Aei[t ( n N )aq]
eiNaq 1
π q π
a
a
Naq 2π s
N s N
2
2
整数
q 2π s Na
s ( N 1),( N 2),( N 3), ,1, 0,1, 2, , N (共N个值)
x nk
u(r )
u(r0 )
1 2
d2u dr 2
r0
xn2k
1 6
d3u dr 3
r0
xn3k
第 n个与第 k个原子间的相互作用力:
f nk
du dr
d2u dr 2
r0
xnk
1 2
d3u dr 3
r0
xn2k
f nk
du dr
d2u dr 2
r0
xnk
1 2
d3u dr 3
r0
xn2k
..
xn
( i
)2
Aei t naq
2 Aeit naq
m A 2eit naq
2 Aeiwt naq Aeit n1aq Aeit n1aq
m 2 ( 2 eiaq eiaq )
m 2 [2 (cos aq i sinaq) (cos aq i sinaq)]
m
2
2π a
π a
o
πa
2π a
当 q , q 2π s ( s为 整 数), a
(q) (q)
且
i t na ( q 2π s )
xn (q) Ae
a xn ( q )
a
4a
a
4a 5
x
当 q , q 2π s ( s为 整 数), a
且 xn( q ) xn( q )
xk
k
n k a r0
只考虑最近邻原子间的相互作用,且恢复力系数相等:
..
m xn xn xn1 xn xn1
..
m xn 2xn xn1 xn1
给出试探解: xn Aeitnaq
x Aei[t( n1 )aq] n1
原子都以同一频率,同一振幅A振动,相邻原子间的位相差
(2 2cos aq) 4 sin2 aq
2
2
aq
sin
m
2
2.色散关系
当
q
a
,
max
2
;
m
当 q 0, min 0
由色散关系式可画图如下:
m
2 sin aq
m
2
2π / a π / a
0
π/ a
2π / a
是波矢q的周期性函数,且(-q)= (q)。
m
2 sin aq
(2)振动方程和解
平衡时,第k个原子与第n个原子相距 n k a r0
u(r)为两个原子间的互作用势能,平衡时为 u(r0 ) ,
t时刻为 u(r) u(r0 r)
u(r) u(r0 r)
u(r0
)
du dr
r0
r
1 2
d2u dr 2
r0
(
r
)2
1 6
d3u dr 3
r0
(
r
)3
