线性系统理论Matlab实践仿真报告

合集下载

线性系统理论Matlab实践仿真报告

线性系统理论Matlab实验报告1、本题目是在已知状态空间描述的情况下要求设计一个状态反馈控制器，从而使得系统具有实数特征根，并要求要有一个根的模值要大于5，而特征根是正数是系统不稳定，这样的设计是无意义的，故而不妨设采用状态反馈后的两个期望特征根为-7，-9，这样满足题目中所需的要求。

（1）要对系统进行状态反馈的设计首先要判断其是否能控，即求出该系统的能控性判别矩阵，然后判断其秩，从而得出其是否可控；判断能控程序设计如下：>> A=[-0.8 0.02;-0.02 0];B=[0.05 1;0.001 0];Qc=ctrb(A,B)Qc =0.0500 1.0000 -0.0400 -0.80000.0010 0 -0.0010 -0.0200Rc=rank(Qc)Rc =2Qc =0.0500 1.0000 -0.0400 -0.80000.0010 0 -0.0010 -0.0200得出结果能控型判别矩阵的秩为2，故而该系统是完全可控的，故可以对其进行状态反馈设计。

（2）求取状态反馈器中的K，设的期望特征根为-7，-9；其设计程序如下：>> A=[-0.8 0.02;-0.02 0];B=[0.05 1;0.001 0];P=[-7 -9];k=place(A,B,P)k =1.0e+003 *-0.0200 9.00000.0072 -0.4500程序中所求出的k即为所求状态反馈控制器的状态反馈矩阵，即由该状态反馈矩阵所构成的状态反馈控制器能够满足题目要求。

2、（a）要求求该系统的能控型矩阵，并验证该系统是不能控的。

设计程序：>> A=[0 1 0 0 0;-0.1 -0.5 0 0 0;0.5 0 0 0 0;0 0 10 0 0;0.5 1 0 0 0];>> B=[0;1;0;0;0];>> C=[0 0 0 1 0];>> Qc=ctrb(A,B)Qc =0 1.0000 -0.5000 0.1500 -0.02501.0000 -0.5000 0.1500 -0.0250 -0.00250 0 0.5000 -0.2500 0.07500 0 0 5.0000 -2.50000 1.0000 0 -0.1000 0.0500>> Rc=rank(Qc)Rc =4从程序运行的结果可得，系统能控型判别矩阵的秩为4，而系统为5阶系统，故而就验证了该系统为不可控的。

成都理工大学信号与线性系统MATLAB实验报告

成都理工大学信号与线性系统MATLAB实验报告本科生实验报告实验课程信号与系统分析学院名称信息科学与技术学院专业名称电子信息科学与技术学生姓名邓泉铃学生学号201313020220指导教师杨斯涵实验地点6A502实验成绩二〇一四年十一月十八日二〇一四年十二月二日《信号与系统分析》实验报告实验一MATLAB编程初步应用及产生常用典型信号一、实验目的及要求：1，掌握MATLAB的使用的使用方法；2，熟悉Matlab常用命令的使用；3，试用Matlab语言产生典型信号。

二、实验内容：1，熟悉MATLAB平台的使用；2，产生常用的典型信号单位阶跃信号，指数信号，抽样函数信号；3，画出以上典型信号的波形图。

三、实验原理：在MATLAB中，使用连续信号在等时间间隔点的样值来近似地表示连续信号的，当取样时间间隔足够小时，这些离散的样值就能较好的表示连续信号，在MATLAB中连续信号可用向量或符号运算功能来表示。

四、程序清单：1，单位阶跃信号定义：在MATLAB中调用单位阶跃函数heaviside来实现。

Heaviside.m文件代码如下：function Y = heaviside(X)%HEA VISIDE Step function% HEA VISIDE(X)is 0 for X<0,1 for X>0,and NaN for X==0.% HEA VISIDE(X)is not a function in the strict sense.% See also DIRAC>% Copyright 1993-2003 The MathWorks,lnc.% $Revision:1.1.6.2$ $Date; 2004/04/16 22:23:24$Y=zeros(size(X));Y(X>0)=1;Y(X==0)=NAN;利用heaviside绘制阶跃图形：t=-2:0.05:2f=heaviside(t)plot(t,f)axis([-1,3,-0.2,1.2])图形如图图1所示：图 12，指数函数信号用MATLAB命令绘制单边指数信号在时间0≤t≤3区间的波形。

线性系统的频域分析报告MATLAB实验

1γ=50 20-=sK0原系统的伯德图：num/den =1.2347 s + 1 ------------- 0.20154 s + 1校正之后的系统开环传递函数为:num/den =6.1734 s + 5 ------------------------------------------- 0.20154 s^4 + 1.6046 s^3 + 3.4031 s^2 + 2 sP h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , P m = 9.04 deg (at 3.14 rad/sec)-20020406080M a g n i t u d e (d B )alpha =6.1261;[il,ii]=min(abs(mag1-1/sqrt(alpha))); wc=w( ii); T=1/(wc*sqrt(alpha)); numc=[alpha*T,1]; denc=[T,1];[num,den]=series(num0,den0,numc,denc);[gm,pm,wcg,wcp]=margin(num,den); printsys(numc,denc)disp('Ð£ÕýÖ®ºóµÄÏµÍ³¿ª»·´«µÝº¯ÊýÎª:');printsys(num,den) [mag2,phase2]=bode(numc,denc,w); [mag,phase]=bode(num,den,w); subplot(2,1,1);semilogx(w,20*log10(mag),w,20*log10(mag1),'--',w,20*log10(mag2),'-.');grid; ylabel('·ùÖµ(db)'); title('--Go,-Gc,GoGc'); subplot(2,1,2);semilogx(w,phase,w,phase1,'--',w,phase2,'-',w,(w-180-w),':'); grid; ylabel('ÏàÎ»(0)'); xlabel('ÆµÂÊ(rad/sec)');title(['Ð£ÕýÇ°£º·ùÖµÔ£Á¿=',num2str(20*log10(gm1)),'db','ÏàÎ»Ô£Á¿=',num2str(pm1),'0';'Ð£Õýºó£º·ùÖµÔ£Á¿=',num2str(20*log10(gm)),'db','ÏàÎ»Ô£Á¿=',num2s tr(pm),'0']);10-110101102-60-40-2002040幅值(d b )--Go,-Gc,GoGc10-110101102-300-200-1000100相位(0)频率(rad/sec)矫正后系统的伯德图矫正之前系统单位阶跃响应矫正之后系统的单位阶跃响应：比较矫正前后系统的响应情况：可以看出超前矫正使系统的调节时间变短，响应更加迅速，但是超调量偏大，对改善系统的动态性能起到了巨大的作用。

仿真实验线性系统稳定性分析报告

实验四 Stability analysis of linear systems线性系统稳定性分析一、实验目的1．通过响应曲线观测特征参量ζ和n ω对二阶系统性能的影响。

2．熟练掌握系统的稳定性的判断方法。

二、基础知识及MATLAB 函数注意：routh （）和hurwitz （）不是MATLAB 中自带的功能函数，(在共享文件夹里有劳斯判据和赫尔维茨判据的m 文件，把其中的routh.m 和hurwitz .m 放到MATLAB 文件夹下的work 文件夹中才能运行)。

1）直接求根判稳roots()控制系统稳定的充要条件是其特征方程的根均具有负实部。

因此，为了判别系统的稳定性，就要求出系统特征方程的根，并检验它们是否都具有负实部。

MATLAB 中对多项式求根的函数为roots()函数。

若求以下多项式的根24503510234++++s s s s ，则所用的MATLAB 指令为： >> roots([1,10,35,50,24])ans =-4.0000 -3.0000 -2.0000 -1.0000特征方程的根都具有负实部，因而系统为稳定的。

2）劳斯稳定判据routh （）劳斯判据的调用格式为：[r, info]=routh(den)该函数的功能是构造系统的劳斯表。

其中，den 为系统的分母多项式系数向量，r 为返回的routh 表矩阵，info 为返回的routh 表的附加信息。

以上述多项式为例，由routh 判据判定系统的稳定性。

>> syms EPS den=[1,10,35,50,24]; ra=routh(den,EPS) r=1 35 24 10 50 0 30 24 0 42 0 0 24 0 0 info=[ ]由系统返回的routh 表可以看出，其第一列没有符号的变化，系统是稳定的。

3）赫尔维茨判据hurwitz （）赫尔维茨的调用格式为：H=hurwitz （den ）。

线性代数MATLAB仿真实验报告

合肥学院2018—2019学年第2学期线性代数及应用 (模块)实验报告实验名称：线性代数MATLAB实验实验类别：综合性设计性□验证性专业班级： 17通信工程（2）班实验时间： 9-12周组别：第组人数 3人指导教师：牛欣成绩：完成时间： 2019年 5 月9日一. 小组成员姓名学号具体分工汪蔚蔚(组长) 1705022025 A报告最后的整合，编写，案例四的计算与应用以及案例一的计算与证明陶乐 1 1705022009 C案例二，化学方程式配平问题程赢妹1505022036 A案例三，应用题灰度值的计算问题二. 实验目的1、案例一利用MATLAB进行线性代数计算，求出矩阵B2、案例二利用MATLAB计算出每一个网格数据的值，然后每一个网格数据的值乘以256以后进行归一化处理，根据每个网格中的灰度值，绘制出灰度图像。

3、案例三利用MATLAB完成对化学方程式进行配平的应用4、案例四利用MATLAB求极大线性无关组，并表示出其余向量三. 实验内容1、案例一：0,1,0,=1,0,0,0,0,0A B AB BA A B⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦已知矩阵和矩阵满足乘法交换律，即且求矩阵。

2、案例二配平下列化学方程式：3、案例三：3*320.81.21.70.20.30.6021.61.20.6.1MATLAB2256MATLAB给定一个图像的个方向上的灰度叠加值：沿左上方到右下方的灰度叠加值依次为，，，，；沿右上方到左下方的灰度叠加值依次为，。

，，，）建立可以确定网络数据的线性方程组，并用求解）将网络数据乘以，再取整，用绘制该灰度图像>> X1=B\C1X1 =3.00001.0000-0.0000>> X2=B\C2X2 =-0.50001.00002.5000六．实验结果1、实验一结果我们本来设,,=,,,,a b cB d e fg h i⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦最终得到d=b, e=a, f=c=h=g=0,i=i,即矩阵,,0=,,00,0,a bB d ei⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，其中a=e,b=d.因此B是一个对称矩阵。

MATLAB实训报告_2

M AT L A B语言编程实训报告题目MATLAB在信号与系统中的应用年级2008 专业电子信息工程目录第一章绪论 (2)1.1 本设计课题目的及意义, 重点解决的问题 (2)1.1.1 MATLAB在信号与系统中应用的目的及意义 (2)1.1.2 重点解决的问题 (2)1.2 课题的社会和技术背景 (2)1.3 实现的具体功能 (3)第二章课题的基本概念和原理 (4)2.1 MATLAB的概念 (4)2.2 信号与系统的概念 (4)2.3 信号与系统分析的基本内容与方法 (5)2.4 离散系统的基本概念 (6)2.5连续系统模型及表示 (6)第三章系统设计和实现 (7)3.1采用的软件及开发平台 (7)3.1.1系统设计软件 (7)3.1.2开发平台和编程环境 (7)3.2系统的详细设计 (8)3.2.1建模 (8)3.2.2解决方法 (9)3.3系统设计的亮点 (9)第四章结束语 (10)参考文献 (10)第一章绪论1.1 本设计课题目的及意义, 重点解决的问题1.1.1 MATLAB在信号与系统中应用的目的及意义MATLAB在信号与系统中应用能够让学生熟悉MATLAB软件平台、工具箱、高效的数值计算及符号计算功能。

熟悉MATLAB软件的信号处理编程方法和结果的可视化。

了解数字信号处理的计算机仿真方法。

进一步加深对信号与系统的基本原理、方法及应用的理解。

MATLAB软件具有强大的数值分析和计算结果可视化的功能.运用MATLAB软件,通过一个应用实例,将信号与系统课程的理论与实践教学有机地结合,有效地解决了教学中的难点问题,说明了MATLAB软件在信号与系统课程的实践教学中具有重要的实际意义1.1.2 重点解决的问题matlab的基本使用方法, matlab的预定义函数, 如何用matlab绘图, 如何在matlab中编程, 基于matlab的矩阵运算、符号运算、数值分析等。

1.2 课题的社会和技术背景长期以来, “信号与系统”课程一直采用黑板式的单一的教学方式, 学生仅依靠做习题来巩固和理解教学内容, 对课程中大量的应用性较强的内容不能实际动手设计、调试、分析, 严重影响和制约了教学效果。

matlab实验心得总结（5篇范例）

matlab实验心得总结（5篇范例）第一篇：matlab实验心得总结通过《matlab仿真》实验使我学习掌握了许多知识。

首先是对matlab有了一个全新的认识，其次是对matlab的更多操作和命令的使用有了更高的掌握，最重要的事对matlab的处理能力有了一个更高的飞跃尤其是对相关函数的使用及相关问题的处理。

就对matlab相关的命令操作而言，通过这次实验的亲身操作和实践，学习掌握了许多原本不知道的或者不太熟悉的命令。

比如说相关m文件的建立，画图用到的标注，配色，坐标控制，同一张图里画几幅不同的图像，相关参数的设置以及相关函数的调用格式等等。

就拿建立一个数学方程而言，通过设置不同的参数达到所需要的要求和结果，而且还可以在不同的窗口建立不同的函数而达到相同的效果，比如说可以再命令窗口和m文件中通过不同的命令设置的到相同的所需的效果图。

而自己对于矩阵及闭环传递函数的建立原本所掌握的知识几乎为零，而通过这次实验使我彻底的掌握了相关的命令操作和处理的方法，在这里我们不仅可以通过建立函数和参数来达到目标效果，而且还可以通过可视化的编程达到更快更方便，更简洁的效果。

就拿可视化编程而言原本根本就只是听说而已罢了，从来就没有亲身去尝试过，然而现在自己却可以和容易的通过搭建不同功能木块来实现相关的函数及功能。

这些在原本根本就不敢相信，然而通过《matlab仿真》的学习和实验亲身操作这些原本看似不可能的操作在此就变的轻而易举的事了。

再此我不得不题到的事指导老师教我们怎么去搭建构造相关闭环传递函数的实验，这个实验几乎在我们的这次实验中占据了非常大的比重，在后面的几个大一点的实验中几乎都是涉及这个方面的内容，我现在想说的事怎么去搭建相关的函数和功能模块对我们来说几乎已经不是什么难事了，就拿怎么去对模块功能的实现以及分析确实是个重点和难点。

通过对同一个模块分析其对应的不同的参数分析图的建立去分析和解释其对应的相关功能和技术指标和性能分析是非常重要的，我们不可能只需要建立相关的模块和功能就说自己掌握了所有的相关知识和技术，真正的技术和知识是怎么去分析和解释相关的技术指标和功能参数才是重中之重。

MATLAB实验报告——运用MATLAB求解和分析线性时不变系统1

MATLAB实验报告课程名称 MATLAB程序设计实验日期 2015 年 05 月 11 日数据记录及分析1.例12.4-1（1）用MATLAB在时域中求解)()(12)(16)(7)(2233t et rdttdrdtt r ddtt r d=+++的齐次解。

程序截图：（2）程序截图：运行图像截图：2.例12.4-2求连续时间系统)()()(3)t(2)(22t edttdet rdtdrdtt rd+=++，当2)(tt e=时的特解。

程序截图：运行图像截图：3. 例12.4-3用户MATLAB在时域中求解)()()(t et rdttdr=+，)()1()(3tuete t-+=的零响入相应。

解法一：程序截图：运行图像截图：解法二：用MATLAB的dsolve函数直接获得零状态响应的表达式程序截图：运行图像截图：解法三：程序截图：运行图像截图：4.例12.4-5用MATLAB求解方程零状态响应分量，已知系统差分方程为nxyx-+nnnnunx=。

(n) y系统的激励序列)( y+7)+()2)1(21.0()1+=(+-)2(7.0程序截图：运行图像截图：。

matlab 仿真实验报告

matlab 仿真实验报告Matlab 仿真实验报告引言：在科学研究和工程应用中，仿真实验是一种非常重要的手段。

通过在计算机上建立数学模型和进行仿真实验，我们可以更好地理解和预测现实世界中的各种现象和问题。

Matlab作为一种强大的科学计算软件，被广泛应用于各个领域的仿真实验中。

本文将介绍我进行的一次基于Matlab的仿真实验，并对实验结果进行分析和讨论。

实验背景：在电子通信领域中，信号的传输和接收是一个重要的研究方向。

而在进行信号传输时，会受到各种信道的影响，如噪声、衰落等。

为了更好地理解信道的特性和优化信号传输方案，我进行了一次关于信道传输的仿真实验。

实验目的：本次实验的目的是通过Matlab仿真，研究不同信道条件下信号传输的性能，并对比分析不同传输方案的优劣。

实验步骤：1. 信道建模：首先，我需要建立信道的数学模型。

根据实际情况，我选择了常见的高斯信道模型作为仿真对象。

通过Matlab提供的函数，我可以很方便地生成高斯噪声，并将其加入到信号中。

2. 信号传输方案设计：接下来，我需要设计不同的信号传输方案。

在实验中，我选择了两种常见的调制方式：频移键控（FSK）和相移键控（PSK）。

通过调整不同的调制参数，我可以模拟不同的传输效果。

3. 信号传输仿真：在信道模型和传输方案设计完成后，我开始进行信号传输的仿真实验。

通过Matlab提供的信号处理函数，我可以很方便地生成调制后的信号，并将其传输到信道中。

4. 信号接收和解调：在信号传输完成后，我需要进行信号接收和解调。

通过Matlab提供的信号处理函数，我可以很方便地对接收到的信号进行解调，并还原出原始的信息信号。

5. 仿真结果分析：最后，我对仿真结果进行分析和讨论。

通过对比不同信道条件下的传输性能，我可以评估不同传输方案的优劣，并得出一些有价值的结论。

实验结果与讨论：通过对不同信道条件下的信号传输仿真实验，我得到了一些有价值的结果。

首先，我观察到在高斯噪声较大的信道条件下，PSK调制比FSK调制具有更好的抗干扰性能。

南昌大学MATLAB实验报告5

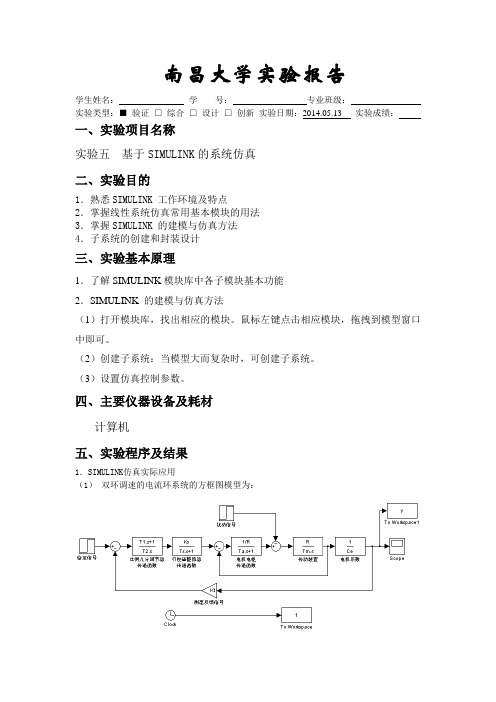
南昌大学实验报告学生姓名：学号：专业班级：实验类型：■验证□综合□设计□创新实验日期：2014.05.13 实验成绩：一、实验项目名称实验五基于SIMULINK的系统仿真二、实验目的1．熟悉SIMULINK 工作环境及特点2．掌握线性系统仿真常用基本模块的用法3．掌握SIMULINK 的建模与仿真方法4．子系统的创建和封装设计三、实验基本原理1．了解SIMULINK模块库中各子模块基本功能2．SIMULINK 的建模与仿真方法（1）打开模块库，找出相应的模块。

鼠标左键点击相应模块，拖拽到模型窗口中即可。

（2）创建子系统：当模型大而复杂时，可创建子系统。

（3）设置仿真控制参数。

四、主要仪器设备及耗材计算机五、实验程序及结果1．SIMULINK仿真实际应用（1）双环调速的电流环系统的方框图模型为：图中参数设为Ks=44；Ts=0.00167；Ta=0.017；R=1；Tm=0.075；Ce=0.1925；Kt=0.01178；T1=0.049；T2=0.088(1)在Simulink集成环境下建立模型，在给定信号作用点处输入单位给定阶跃响应信号，0.3秒后在扰动信号点输入单位阶跃响应信号。

并绘制相应的响应曲线(2)计算仿真结果的超调量、上升时间、调节时间、稳态误差。

(3)设计PID调节器替代图中的比例积分调节器，调节Kp,Ti,Td，用使系统满足超调量15%，上升时间0.3s，调节时间0.4s的要求。

(4)要求对加入的PID控制器封装成一个模块使用。

加入PID调节封装成一个模块新系统2．用Simulink对以下系统进行仿真其中u(t)为系统输入，y(t)为系统输出，仿真当输入为正弦信号时，输出的信号的波形，仿真时间0<t<100。

3．在滑艇的运行过程中，滑艇主要受到如下作用力的控制：滑艇自身的牵引力F，滑艇受到的水的阻力f。

其中水的阻力 f = u^2 -u，u为滑艇的运动速度。

由运动学的相关定理可知，整个滑艇系统的动力学方程为：其中，m为滑艇的质量。

matlab实习报告二5篇

matlab实习报告二5篇第一篇：matlab实习报告二MATLAB实习报告(2)实验二 MATLAB矩阵分析与处理王夏一、实验目的1、掌握生成特殊矩阵的方法。

2、掌握矩阵分析的方法。

3、用矩阵求逆发解线性方程组。

二、实验内容1、设有分块矩阵A=[E3×3 R3×2;O2×3 S2×2],其中E、R、O、S分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证A²=[E R+RS;O S²]。

程序清单：E=eye(3);R=rand(3,2);O=zeros(2,3);S=diag([4,5]);A=[E R;O S] ;A2=A^2;C=[E R+R*S;O S^2];length(find(A2==C))==25 运行结果：ans =12、产生5阶希尔伯特矩阵H和5阶帕斯卡矩阵P，且求其行列式的值Hh和Hp以及他们的条件数Th和Tp，判断哪个矩阵的性能更好，为什么？程序清单：format rat H=hilb(5);format short P=pascal(5);Hh=det(H);Hp=det(P);Th=cond(A);Tp=cond(P);运行结果：Hh =3.7493e-012 Hp =1 Th =5.5228 Tp =8.5175e+003 实验收获：会建立希尔伯特矩阵和帕斯卡矩阵，知道怎么求矩阵行列式的值以及条件数。

希尔伯特矩阵的性能更好，条件数越接近1的矩阵性能越好。

3、建立一个5×5矩阵，求它的行列式值、迹、秩和范数。

程序清单：A=[1:5;1:0.1:1.5;2 5 7 3 9;2:6;3:0.4:4.6]Ha=det(A);Ra=rank(A);Ta=trace(A);Na=norm(A);运行结果：Ha =1.4421e-031 Ra = 3 Ta =18.7000 Na =19.49664、已知向量A，求A的特征值及特征向量，并分析其数学意义。

MATLAB系统仿真实验报告一

MATLAB系统仿真实验报告（一实验一、MATLAB语言环境与基本运算一、实验目的及要求1．学习了解MATLAB语言环境2．练习MATLAB命令的基本操作3．练习MATLAB数值运算相关内容4．练习MATLAB符号运算相关内容5．撰写实验报告二、实验内容1．熟悉Matlab语言环境1)．学习了解MATLAB语言环境MATLAB语言操作界面(主界面的各个窗口)主界面：工具栏：状态栏：命令窗口：文件窗口：工作空间窗口：历史命令窗口：变量查询命令who, whosWho：列出当前存储器中的所有变量Whos：列出当前工作空间中的所有变量，包括与他们的维数、字节、类型有关的变量目录与目录结构目录，文件夹，文件搜索路径联机帮助2)．MATLAB基本操作命令demos，clc，clf，clear，contro-c(^c)，diary Demos：Clc：命令窗口清屏。

Clf：清楚当前图形。

清楚工作空间。

Control+c：复制选定区域到粘贴板。

Diary:用于记录MATLAB窗口的输入的命令和响应输出,diary off关闭记录，diary on打开记录。

2．Matlab数值运算与符号运算1)．MATLAB数值运算相关内容MATLAB变量及变量赋值变量名以字母开头，后接字母、数字或下划线的字符序列，最多63个字符。

变量名区分大小写，不可使用保留字。

变量赋值：变量名=表达式。

初等矩阵函数ones, zeros, eye, rand, randn, sizeOnes:生成常熟1构成的数组。

Zeros：零数组。

Eye：生成单位矩阵。

Rand：生成随机数和矩阵。

产生标准正态分布的随机数或矩阵的函数。

Size：求矩阵的维数。

矩阵的基本运算+ 加- 减* 乘^ 乘方‘共轭转置/或\ 矩阵相除./或.\ 数组相除矩阵的特征运算det, eig, rank, svdDet：求行列式。

Eig：求特征值和特征向量。

Rank：计算矩阵的秩。

matlab实习报告7

matlab实习报告7《matlab 实习报告 7》在大学的学习生涯中，我有幸参与了一次 MATLAB 的实习，这次实习让我对这一强大的数学计算和可视化工具，有了更深入的理解和掌握。

实习伊始，我对 MATLAB 的认知还停留在书本上的理论知识和简单的示例代码。

然而，随着实习的推进，我逐渐发现 MATLAB 的强大功能远远超出了我的想象。

首先，我学习了MATLAB 的基本语法和数据类型。

整数、浮点数、字符串、数组等各种数据类型在 MATLAB 中都有独特的表示和操作方式。

通过不断地练习和实践，我逐渐熟悉了如何定义变量、进行数据运算以及处理不同类型的数据。

在掌握了基本的数据操作后，我开始深入学习 MATLAB 的函数编写。

函数是 MATLAB 中实现复杂功能的重要手段。

通过自定义函数，我能够将重复使用的代码段封装起来，提高代码的可读性和可维护性。

例如，我编写了一个用于计算两个矩阵乘积的函数，通过输入两个矩阵，函数能够返回它们的乘积结果。

这个过程不仅锻炼了我的编程思维，还让我更加熟悉了矩阵运算的原理和方法。

接下来，我接触到了 MATLAB 的绘图功能。

绘图是直观展示数据和结果的重要方式。

我学会了使用 plot 函数绘制简单的折线图、使用bar 函数绘制柱状图、使用 hist 函数绘制直方图等等。

通过对数据进行可视化，我能够更清晰地理解数据的分布和趋势，从而为进一步的分析和处理提供了有力的支持。

在实习过程中，我还参与了一个实际的项目——图像去噪。

图像在采集和传输过程中往往会受到噪声的干扰，影响图像的质量和后续的处理。

利用 MATLAB 提供的图像处理工具和函数，我尝试了多种去噪算法，如均值滤波、中值滤波和高斯滤波等。

通过对不同算法的效果进行比较和分析，我最终找到了一种最适合当前图像的去噪方法。

这个过程让我深刻体会到了 MATLAB 在实际应用中的强大能力，也让我明白了理论知识与实际应用之间的紧密联系。

另外，MATLAB 的矩阵运算功能给我留下了深刻的印象。

线性代数的MATLAB软件实验报告

线性代数的MATLAB 软件实验一、实验目的1.熟悉矩阵代数主要MATLAB 指令。

2.掌握矩阵的转置、加、减、乘、除、乘方、除法等MATLAB 运算。

3.掌握特殊矩阵的MATLAB 生成。

4.掌握MATLAB 的矩阵处理方法。

5.掌握MATLAB 的矩阵分析方法。

6.掌握矩阵的特征值与标准形的MATLAB 验算。

7.掌握线性方程组的MATLAB 求解算法。

二、实验原理1.线性方程组【基本观点】自然科学和工程实践很多问题的解决都涉及线性代数方程组的求解和矩阵运算.一方面，许多问题的数学模型本身就是一个线性方程组，例如结构应力分析问题、电子传输网分析问题和投入产出分析问题；另一方面，有些数值计算方法导致线性方程组求解，如数据拟合，非线性方程组求解和偏微分方程组数值解等.n 个未知量m 个方程的线性方程组一般形式为⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.,,22112222212111212111m n mn m m n n n n b x a x a x a b x a x a x a b x a x a x a (3.1) 令,,,2121212222111211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=m n mn m m n n b b b b x x x x a a a a a aa a a A则得矩阵形式Ax=b. (3.2)若右端b=0,即Ax=0, (3.3)则称方程组为齐次的.方程组（3.1）可能有唯一解，可能有无穷多解，也可能无解，主要取决于系数矩阵A 及增广矩阵（A,b ）的秩.若秩（A ）=秩（A,b ）=n,存在唯一解，其解理论上用Cramer 法则求出，但由于这种方法要计算n+1个n 阶行列式，计算量太大通常并不采用；若秩（A ）=秩（A,b ）<n,存在无穷多解，其通解可表示为对应齐次方程组（3.3）的一个基础解系与（3.2）的一个特解的叠加；若秩（A ）≠秩（A,b ），则无解，这时一般寻求最小二乘近似解，即求x 使向量Ax-b 模最小.P50矩阵左除的数学思维:恒等变形Ax=b 方程两边的左边同时除以A ，得：b AAx A11=，即：b A b Ax 11-==MATLAB 的实现（左除）：x=A\b 2.逆矩阵【基本观点】方阵A 称为可逆的，如果存在方阵B ，使 AB=BA=E,这里E 表示单位阵.并称B 为A 的逆矩阵，记B=1-A .方阵A 可逆的充分必要条件是A 的行列式det A ≠0.求逆矩阵理论上的公式为*1det 1A AA =-， (3.4)这里*A 为A 的伴随矩阵.利用逆矩阵，当A 可逆时，（3.2）的解可表示为b A x 1-=.由于公式（3.4）涉及大量行列式计算，数值计算不采用.求逆矩阵的数值算法一般是基于矩阵分解的方法.3.特征值与特征向量【基本观点】对于方阵A ，若存在数λ和非零向量x ，使,x Ax λ= (3.5) 则称λ为A 的一个特征值，x 为A 的一个对应于特征值λ的特征向量.特征值计算归结为特征多项式的求根.对于n 阶实数方阵，特征多项式在复数范围内总有n 个根。

matlab 模拟实验报告

matlab 模拟实验报告《利用Matlab模拟的实验报告》摘要：本实验利用Matlab软件对某一特定系统进行了模拟实验。

通过对系统的建模和仿真，我们得出了一些有价值的结论，并对系统的性能进行了评估。

本文将详细介绍实验的目的、方法、结果和分析，以及对实验结果的讨论和总结。

1. 引言Matlab是一种强大的数学建模和仿真工具，广泛应用于工程、科学和技术领域。

利用Matlab进行系统仿真可以帮助我们更好地理解系统的行为和性能，优化系统设计，并预测系统在不同条件下的表现。

本实验旨在利用Matlab对某一特定系统进行仿真，以验证系统的性能和稳定性。

2. 实验目的本实验的主要目的是利用Matlab对某一特定系统进行建模和仿真，分析系统的动态响应和稳定性，并评估系统的性能。

具体来说，我们将通过仿真实验探讨系统的频率响应、阶跃响应和脉冲响应，以及系统的稳定性和鲁棒性。

3. 实验方法首先，我们对系统进行了建模，包括系统的传递函数、状态空间模型等。

然后，利用Matlab软件进行仿真实验，分别对系统的频率响应、阶跃响应和脉冲响应进行了分析。

最后，我们对仿真结果进行了统计和评估，得出了一些有价值的结论。

4. 实验结果与分析通过Matlab的仿真实验，我们得到了系统的频率响应曲线、阶跃响应曲线和脉冲响应曲线。

通过对这些曲线的分析，我们可以得出系统的动态特性和稳定性。

同时，我们还对系统的性能进行了评估，包括系统的超调量、调节时间等指标。

5. 结果讨论与总结通过对实验结果的讨论和总结，我们得出了一些结论和建议。

我们对系统的性能和稳定性进行了评估，发现系统在某些条件下存在一些问题，提出了一些建议和改进措施。

同时，我们也对Matlab软件在系统仿真中的应用进行了总结和展望。

结论本实验利用Matlab对某一特定系统进行了建模和仿真，得出了一些有价值的结论。

通过对系统的动态响应和稳定性进行分析，我们发现了系统存在的一些问题，并提出了一些建议和改进措施。

matlab实验(线性系统的数学模型)

实验一线性系统的数学模型一、MATLAB基础1、提示符命令窗口：是使用者和MA TLAB交互的地方，使用者输入命令、程序，点击菜单项命令或工具栏按钮，指挥MA TLAB计算、仿真，其结果也都在命令窗口显示。

在提示符后面输入MA TLAB程序，按Enter键，MA TLAB将给出运行结果。

历史窗口：显示所有命令的历史记录，并且标明使用时间。

用鼠标双击其中一条命令行，就可以在命令窗口中执行该命令，MA TLAB将给出运行结果。

用鼠标单击其中的一条命令行，再按Enter键，MA TLAB也将给出运行结果。

工作空间窗口：显示目前内存中所有的MA TLAB变量名、数据结构、字节数以及类型。

发布窗口：点击主窗口的“view”“Launch Pad”，即可打开和关闭发布窗口。

其中显示Mathworks公司的工具箱（Toolbox）、Simulink和功能块（Blockset）等产品信息，点击显示的相应的图标，即可获得演示、帮助信息等信息。

程序编辑器：点击主窗口的“File”“New”“M--file”，即可打开MA TLAB的程序编辑器。

MA TLAB的程序编辑器2、MATLAB在建模仿真中的应用Simulink提供了大量的功能模块以方便用户快速地建立动态系统模型。

建模时只需使用鼠标拖动库中的功能模块并将他们连接起来。

使用者可以通过将他们连接起来。

使用者可以通过将模块组成子系统来建立多级模型。

Simulink对模块和连接的数目没有限制。

通过Simulink 提供的丰富的功能模块，可以迅速地创建系统的模型，不需要书写一行代码。

启动Simulink的方法有三种：1．在MA TLAB COMMAND窗口下，直接键入“Simulink”回车即可；2．单击MA TLAB COMMAND窗口工具条上的Simulink图标；3．在MA TLAB COMMAND窗口菜单上选择file---new-----model运行。

二、常用的函数：1、建立数学模型用到的MA TLAB 函数 (1)、多项式乘法处理函数conv()C=conv(A,B)，其中A 、B 为进行相乘的多项式的系数；返回值C为两个多项式相乘后的多项式系数。

MATLAB实验报告(信号与线性系统分析)

实验一 MATLAB 的基本使用【一】实验目的1.了解MA TALB 程序设计语言的基本特点，熟悉MATLAB 软件的运行环境；2.掌握变量、函数等有关概念，掌握M 文件的创建、保存、打开的方法，初步具备将一般数学问题转化为对应计算机模型处理的能力；3.掌握二维图形绘制的方法，并能用这些方法实现计算结果的可视化。

【二】 MATLAB 的基础知识通过本课程的学习，应基本掌握以下的基础知识：一. MATLAB 简介二. MATLAB 的启动和退出三. MATLAB 使用界面简介四. 帮助信息的获取五. MATLAB 的数值计算功能六. 程序流程控制七. M 文件八. 函数文件九. MATLAB 的可视化【三】上机练习1. 仔细预习第二部分内容，关于MATLAB 的基础知识。

2. 熟悉MATLAB 环境，将第二部分所有的例子在计算机上练习一遍3.已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=123456789,987654321B A 。

求A*B ，A .* B ，比较二者结果是否相同。

并利用MATLAB 的内部函数求矩阵A 的大小、元素和、长度以及最大值。

解：代码：A=[1,2,3;4,5,6;7,8,9];B=[9,8,7;6,5,4;3,2,1]; A*B A.*B两者结果不相同A*B=30 24 18 84 69 54 138 114 90 A.*B= 9 16 21 24 25 24 21 16 9求A 矩阵的行和列： [M,N]=size(A)M =3N =3 求A 矩阵的长度：x=length(A)x =3 元素和：sum(sum(A))ans =45最大值：max(max(A))ans =94. Fibonacci 数组的元素满足Fibonacci 规则：),2,1(,12=+=++k a a a k k k ；且121==a a 。

现要求该数组中第一个大于10000的元素。

matlab实习报告总结

MATLAB实习报告总结介绍本文是对我在MATLAB实习过程中的总结与反思。

通过这次实习，我对MATLAB的使用有了更深入的了解，并且对实际问题的解决能力也有了提升。

实习目标在实习开始之前，我设定了以下几个目标： 1. 熟悉MATLAB的基本语法和常用函数； 2. 学习如何使用MATLAB解决实际问题； 3. 提升自己的编程能力和解决问题的思维能力。

实习过程第一阶段：熟悉MATLAB基本语法在实习开始之初，我花了一段时间来学习MATLAB的基本语法。

通过阅读官方文档和参考书籍，我了解了MATLAB的变量定义、矩阵运算、函数定义等基本概念和用法。

我利用空闲时间编写了一些简单的代码来巩固这些知识。

第二阶段：学习MATLAB的常用函数在熟悉基本语法之后，我开始学习MATLAB的常用函数。

我学习了MATLAB 中的统计分析函数、数据可视化函数、图像处理函数等。

通过学习这些函数，我可以更高效地处理和分析数据，同时也能够更好地展示我的结果。

第三阶段：实际问题的解决在掌握了MATLAB的基本语法和常用函数后，我开始尝试使用MATLAB解决一些实际问题。

我选择了一个与我的专业相关的问题，通过MATLAB对数据进行分析和建模。

在这个过程中，我遇到了一些困难和挑战，但通过查阅资料和请教同学，我最终成功解决了这些问题。

第四阶段：编程能力和思维能力的提升通过这次实习，我的编程能力和解决问题的思维能力得到了提升。

在实际问题的解决过程中，我学会了如何分析问题、设计算法、编写代码并调试。

通过与同学的讨论和交流，我也学会了如何思考和解决问题的不同角度。

总结与反思这次MATLAB实习让我受益匪浅。

通过实际操作，我深入了解了MATLAB的使用方法和技巧。

我学会了如何使用MATLAB解决实际问题，并且在这个过程中提升了自己的编程能力和解决问题的思维能力。

然而，我也发现了自己的不足之处。

在实习过程中，我有时会陷入“死记硬背”的状态，只注重语法和函数的使用，而不去思考问题背后的本质，这导致我在解决一些复杂问题时遇到了困难。

仿真实验线性系统稳定性分析报告文案

实验四Stability analysis of linear systems线性系统稳定性分析一、实验目的1．通过响应曲线观测特征参量ζ和ω对二阶系统性能的影响。

n2．熟练掌握系统的稳定性的判断方法。

二、基础知识及MATLAB函数注意：routh（）和hurwitz（）不是MATLAB中自带的功能函数，(在共享文件夹里有劳斯判据和赫尔维茨判据的m文件，把其中的routh.m和hurwitz .m 放到MATLAB文件夹下的work文件夹中才能运行)。

1）直接求根判稳roots()控制系统稳定的充要条件是其特征方程的根均具有负实部。

因此，为了判别系统的稳定性，就要求出系统特征方程的根，并检验它们是否都具有负实部。

MATLAB中对多项式求根的函数为roots()函数。

若求以下多项式的根2410235504+3+s，则所用的MATLAB指令ss++s为：>> roots([1,10,35,50,24])ans =-4.0000-3.0000-2.0000-1.0000特征方程的根都具有负实部，因而系统为稳定的。

2）劳斯稳定判据routh（）劳斯判据的调用格式为：[r, info]=routh(den)该函数的功能是构造系统的劳斯表。

其中，den为系统的分母多项式系数向量，r为返回的routh表矩阵，info为返回的routh表的附加信息。

以上述多项式为例，由routh判据判定系统的稳定性。

>> syms EPSden=[1,10,35,50,24];ra=routh(den,EPS)r=1 35 2410 50 030 24 042 0 024 0 0info=[ ]由系统返回的routh表可以看出，其第一列没有符号的变化，系统是稳定的。

3）赫尔维茨判据hurwitz（）赫尔维茨的调用格式为：H=hurwitz（den）。

该函数的功能是构造hurwitz矩阵。

其中，den为系统的分母多项式系数向量。

线性系统理论Matlab实践仿真报告