复合型裂纹的断裂准则
第五章 裂纹断裂判据

第五章 裂纹断裂判据
河 北 工 业 大 学 土 木 工 程 学 院
5.1 单一型裂纹的判据
E-399规范规定,按Δ a/a=2%
的相对等效扩展量来确定临界点。 在同时满足裂纹尺寸 件下,临界点处的扩展量应为:
K1c a 0.02 a 0.02 2.5 s
K1c a 0 . 05 由图看出, s
2
K1c a 2.5 s
2
2
条
图5.2
2
K1c 0.05 s
定义的临界点和阻力曲线上的饱和点(即R曲线切点)是 基本一致的。
K1c a 0 . 05 时,R曲线已近饱和,即由 s
河 北 工 业 大 学 土 木 工 程 学 院
5.3 最大周向正应力理论 ( ) max 判据 实验表明,对于图5.7所 示的剪应力方向,开裂角 为 θ0=-70.5°。 当剪应力改变方向时, 将得到: θ0=70.5°。
第五章 裂纹断裂判据
河 北 工 业 大 学 土 木 工 程 学 院
5.1 单一型裂纹的判据 3. 平面应力下的临界条件 由图看出,动力曲线和阻力曲线 相交的A0、A1、A2三点中, A0、 A1都不会使裂纹失稳扩展,只有 A2才是失稳扩展的条件。 这就是:为了使裂纹失稳扩展,必须保证推动力增长率大 于或等于阻力增长率G≥R。所以:裂纹失稳扩展的临界条 件就是推动力曲线和阻力曲线相切。即G=R
2
第五章 裂纹断裂判据
河 北 工 业 大 学 土 木 工 程 学 院
5.1 单一型裂纹的判据
二、能量判据
裂纹失稳扩展,必须使动力G1大于临界点的阻力 Rc=G1c,即
08--复合型断裂准则a@@@

得到:
求导
0 2arctg
KI K II
G 0 1 K K K I0 I0 K II0 II0 0 0 4 0 0
由裂纹尖端的K场分布得:
最大能量释放率准则
该准则的基本思想与原始的Griffith断裂 理论是相通的,即裂纹的扩展,将引起 总体势能的释放,与此同时,新裂纹表 面的形成需要能量,当这两部分能量相 等时,裂纹即可以扩展。 复合型的最大能量释放率准则是Griffith 理论的发展,它不再假设裂纹沿原始的 裂纹面方向扩展,而是认为裂纹沿能量 释放率最大的方向0 扩展。
令 c0 为 2 时的临界应力,由 0 0 0 得 C K IC ,则上式变为:
πa
K II a sin cos
C 2 0 C cos 0 sin 1 cos sin 3sin cos 0 0
最大环向应力准则
1963年,Erdogan和 G.C.Sih(薛昌明)根据 中心斜裂纹承受均匀 拉伸的树脂玻璃板的 实验,提出以裂纹尖 端的最大环向应力作 为复合型裂纹扩展的 控制参数。 最大环向应力准则假 设: – 裂纹沿环向应力 取最大值的方向0 扩展; – 当此方向上的环向 应力 达到临界值 时,裂纹启裂。
第六讲· 复合型断裂准则
复合型裂纹ቤተ መጻሕፍቲ ባይዱ扩展
Griffith理论和Irwin理论主要是分析 I 型裂纹的 断裂问题,裂纹扩展沿原裂纹面方向进行,而 在工程实际中,裂纹大多处于复合型变形状态, 裂纹的扩展方向也往往会偏离原来的裂纹面方 向。因此,对于最一般的裂纹情况,就需要解 决以下两个问题: 复合型裂纹在什么条件下发生扩展? 裂纹的扩展方向如何确定?
第十三章复合型裂纹的脆性断裂理论

第六章 二维脆性断裂§6.1 引 言破裂判据是断裂力学的核心问题, 这需要从微观、亚微观、宏观三个层次进行研究。
所谓微观就是涉及物体的终极结构单元发生相对运动时其间内聚力的破坏。
亚微观涉及颗粒及粒间界面这一水平上的破坏。
宏观涉及肉眼可以看得见的破坏。
破裂判据是针对某一特定尺度、特定层次提出的, 做为一个完整的破裂判据,至少应该能够回答两个问题: ① 破裂在什么可测条件下起始或继续? ② 破裂向什么方向扩展? 岩石微观、亚微观破裂机制与宏观不同, 因而破裂判据也不同。
实际上, 迄今为止并不存在一种万能判据, 能够同时包括这三个层次。
为有所区分, 本文仍沿袭惯例, 对于微观、亚微观的 Griffth 裂纹, 按照Ⅰ型、Ⅱ型、Ⅲ型命名, 对于宏观断层模型化的裂纹,按照张破裂、平面内剪切裂纹、反平面剪切裂纹命名。
一些共用名词, 例如内聚力, 内聚区等, 在宏观中的含义也与微观不同。
对于岩石中的断裂机理的研究, 最早可以追溯到Griffith(1921)提出的脆性破坏理论, 该理论认为, 当裂纹端部扩展一小段长度时, 弹性势能的释放率如果大于或等于表面能的增加率时, 裂纹才能持续扩展。
在这之后, 发展了两种受压闭合裂纹模式, 即扁椭圆裂纹模式和Griffith 裂纹模式(Jaeger 和Cook, 1979)。
扁椭圆裂纹模式在第四章中已经介绍。
这里讨论的是Griffith 裂纹模式(也叫做数学裂缝), 是在Irwin(1957)引入应力强度因子的概念之后发展起来的, 它以断裂韧性作为材料抗脆断能力的指标, 也叫做K 判据。
断裂力学的其它模式和判据都是在这个模式的基础上加以修正或发展起来的, 也是断裂动力学的基础模式。
K 判据不能回答破裂方向问题, 特别是复合型裂纹问题, 因此产生了一系列脆性断裂理论。
线弹性断裂力学中关于脆性断裂的理论可分为两类:一类是应力场参数法,以应力场的某一特征量为参数。
裂纹断裂准则

开裂条件: ()m a x 22 1r 0c o s2 0 [K Ⅰ ( 1 c o s0 ) 3 K Ⅱ s in0 ]c
c :由Ⅰ型裂纹的断裂韧性来确定.
00 ,K Ⅰ K Ⅰ c,K Ⅱ 0
临界失稳条件 1 2 c o s2 0[K Ⅰ (1 c o s0 ) 3 K Ⅱ s in0 ] K Ⅰ c
编辑本段加工余量
加工余量概述
为了加工出合格的零件,必须从毛坯上 切去的 那层金 属的厚 度,称 为加工 余量。 加工余 量又可 分为工 序余量 和总余 量。某 工序中 需要切 除的那 层金属 厚度, 称为该 工序的 加工余 量。从 毛坯到 成品总 共需要 切除的 余量, 称为总 余量, 等于相 应表面 各工序 余量之 和。 机床
二.最大周向正应力判据
1.假定: 裂纹初始扩展沿着周向正应力 为最大的方向. 当这个方向上的周向正应力的最大值( )max 达到临界
时,裂纹开始扩展.
5
2.举例:Ⅰ、Ⅱ型复合裂纹
21 2 rc o s 2 [K Ⅰ (1 c o s) 3 K Ⅱ sin ]
r 21 2r[K Ⅰ ( 3 c o s)c o s2 K Ⅱ ( 3 c o s 1 )s in 2 ]
4、光整加工
光整加工后的工件独特作用也证实了二 者的有 机结合 ,具有 肯定的 临床疗 效。
编辑本段东西方医学交融(df高血压958心脏 病983u6糖尿 病87fr)
不管是中医学还是西医学,从二者现有 的思维 方式的 发展趋 势来看 ,均是 走向现 代系统 论思维 ,中医 药学理 论与现 代科学 体系(45传染 病q566丙肝964jo乙肝 28jgsx甲肝gh)之间 具有系 统同型 性,属 于本质 相同而 描述表 达方式 不同的 两种科 学形式 。可望 在现代 系统论 思维上 实现交 融或统 一,成 为中西 医在新 的发展 水平上 实现交 融或统 一的支 撑点, 希冀籍 此能给 (df高 血压958心脏病 983u6糖尿病87fr)中 医学以 至生命 科学带 来良好 的发展 机遇, 进而对 医学
断裂力学讲义ch6-复合型断裂判据_21750861

K II 3 3 3 sin sin 2 4 2 2r 4 K II 1 3 3 cos cos 2 4 2 2r 4
最大环向拉应力要求
r
2 0 并且 2
0
r
同时有 r 0 , 【习题 6-1】 是巧合还是有别的原因?
最小应变能密度强度因子理论??? 应变能密度: w ij ij / 2 ,对于线弹性易知 w 1 / r
1 I II K II , 3 K III 3 K I 2r 2r
定义应变能密度强度因子: S wr 可以表示为应力强度因子及角度 的函数 2 2 S a11K I2 2a12 K I K II a22 K II a33 K III (为什么没有别的耦合项?) 其中 a11 , a12 , a22 , a33 是角度 及材料常数的函数 (引自沈成康书)如果裂纹体只受牵引力作用,则体系的势能 与 应变能 U 之和为零,因此 U 。以 表示体积,则势能密度为
3 3 3 sin sin 4 2 4 2
1 3 3 纯I型: cos cos 2 4 2 4
3 3 3 纯II型: sin sin 2 4 2 4
K IIc
3 K Ic 2
【题 6-2】 推导 I 型和 II 型混合裂纹的断裂准则 K KI , KII Kc KIc
纯 II 型裂纹在 70.5 产生最大环向应力, 如何理解记忆?
最大环向拉应力强度因子理论——开裂角的确定
0 纯 I 型问题 max
70 . 5 纯 II 型问题 max
混凝土复合型裂缝最大拉应变断裂准则

图 3 给出了用拉应变理论、拉应力理论和应变能密度因子
理论求得的无限大板中心斜裂纹单向受拉时, 裂纹倾斜角 Β(Β
= a rctg (K K ) ) 与开裂角 Η0 的相关曲线, 同时标出了由试验
测得的开裂角
Η [ 2~ 0
5 ].
由图 3 可以看出, 当 K
K ≥0. 83 (Β≥
39. 6°) 时, 拉应力理论与应变能密度因子理论曲线十分接近, 与
项目
Η0 (°) K cK c
拉应力 应变能密度 拉应变 理论 因子理论 理论
- 70. 5 - 78. 46 - 65. 03
0. 87
1. 074
0. 644
文献[ 2 ] - 57. 9
0. 69
文献[ 3 ] - 62 0. 65
实测值 文献[ 4 ]
- 62 0. 78
文献[ 5 ] - 58 0. 68
第 27 卷 第 1 期 1999 年 2 月
西北农业大学学报 A cta U n iv. A g ric. Bo rea li2occiden ta lis
V o l. 27 N o. 1 Feb. 1999
混凝土复合型裂缝最大拉应变断裂准则
邓宗才1 卢云斌2 李宗利3 娄宗科3
(1 山东建筑材料工业学院, 济南 250022) (2 济南市公路局, 济南 250000) (3 西北农业大学水利与建筑工程学院, 陕西杨凌 712100)
最大拉应变理论值有一定差距。当 K K ≤1 (Β≤45°) 时, 拉应
变理论曲线较为平缓。
从实测结果的分布看, 当 Β≤70°时, 实测值与拉应变曲线吻
合较好, 线型也比较一致, 尤其是当 K K 较小时, 吻合更好。 但当 Β> 70°时, 实测值与其他两个理论曲线吻合较好, 造成这种 差异的原因, 还有待于进一步研究。
复合材料失效准则

复合材料失效准则复合材料是由两种或多种不同材料的复合结合而成的材料,具有较好的强度、刚度和重量比等优点。
然而,复合材料在使用过程中也会出现失效现象,为了保证复合材料的可靠性和安全性,需要建立相应的失效准则来预测和评估其失效情况。
复合材料的失效准则主要有以下几种:强度失效准则、疲劳失效准则和断裂失效准则。
强度失效准则是指在复合材料承受外载荷作用下,由于应力达到或超过了材料本身的强度极限而导致失效。
强度失效准则主要分为静力失效准则和动力失效准则两种。
静力失效准则是指在静态载荷作用下,当复合材料中的应力达到或超过其本身的强度极限时,会引发失效现象。
常见的静力失效准则有最大应力准则、最大应变准则和von Mises准则等。
最大应力准则是利用材料本身的强度敏感参数(如材料的最大拉伸强度、最大压缩强度等)来判断材料的失效情况,当应力超过这些强度参数时,材料发生失效。
最大应变准则是通过根据材料的最大应变来判断失效情况,当应变超过材料的最大应变极限时,材料发生失效。
von Mises准则是利用材料的等效应力与材料的强度参数进行比较,当等效应力超过强度参数时,材料发生失效。
动力失效准则是指在动态载荷作用下,由于应力的急剧变化或加载速率的变化而导致的失效。
动力失效准则主要有Johnson-Cook准则、Cockcroft-Latham准则和Chaboche准则等。
这些准则是根据材料的动态力学性能参数来判断材料的失效情况,如动态增强系数、应变硬化指数等。
这些参数是在试验或数值模拟中得到的,通过与材料的动态力学性能进行比较,可以判断材料的失效情况。
疲劳失效准则是指在复合材料中,由于长时间作用的循环载荷引起的失效现象。
疲劳失效准则主要有S-N曲线准则和e-N曲线准则等。
S-N曲线准则是指在不同应力水平下,循环载荷下发生失效的循环次数与应力的关系,通过试验得到的S-N曲线可以用来预测材料的疲劳寿命。
e-N曲线准则是指在不同应变水平下,循环载荷下发生失效的循环次数与应变的关系。
复合型断裂准则a

由于该准则形式简单,应用比较方便, 误差不大,因而得到广泛的应用。
最大能量释放率准则
该准则的基本思想与原始的Griffith断裂 理论是相通的,即裂纹的扩展,将引起 总体势能的释放,与此同时,新裂纹表 面的形成需要能量,当这两部分能量相 等时,裂纹即可以扩展。
对于Ⅰ-Ⅱ复合型裂纹,裂
纹尖端的K场在极坐标系中表 示为:
r 2
1 2 r
K
I
3 cos
cos
2
KII
3 cos
1 sin
2
2
1 2 r
K I
1
cos
3KII
sin
cos
2
r 2
1 2 r
K I
sin
KII
3 cos
1
cos
2
为了求得 0,将上式中的第
3sin0
cos
令
0 c
得
0 C
为 π 时的临界应力,由 KIC ,2 则上式变为:
πa
0
0
C
0 C
cos 0 2
sin
2
1 cos0 sin
3sin0
cos
得到在裂纹临界扩展时的应 力强度因子为:
KI
C
cos 0 2ห้องสมุดไป่ตู้
1
2KIC sin
cos0 sin 3sin0
cos
最大环向应力准则
1963年,Erdogan和 G.C.Sih(薛昌明)根据 中心斜裂纹承受均匀 拉伸的树脂玻璃板的 实验,提出以裂纹尖 端的最大环向应力作 为复合型裂纹扩展的 控制参数。
基于统一强度理论的复合型裂纹断裂准则_龚俊

机械强度
2003, 25(3):347~ 351
○研究简报 ○
基于统一强度理论的复合型裂纹断裂准则
MIXED MODE FRACTURE CRITERIA BASED ON UNIFIED STRENGTH THEORY
龚 俊 1 郎福元 1 王 珉 2 李建华 3 刘 展 4 (1 .甘肃工业大学 机电工程学院 , 兰州 730050)(2 .西北工业大学 机电学院 , 西安 710072)
20010110 收到初稿 , 20010518 收到修改稿 。 甘肃省劳动厅基金资助项目(199923)。 龚 俊 , 男, 1963 年 2 月生 , 四川省中江县人 , 汉族 。 副研究员, 主要从事断裂力学 、疲劳 、裂纹技术 、机电一体化的研究 。
机 械 强 度
2003 年
2 统一强度理论[ 1 , 2]
F
=σ1
-1
α +b
(bσ2
+σ3 )=σt ,
当 σ2 ≤σ11++αασ3 时
F
=1
1 +b
(σ1
+bσ2)-ασ3
=σt
,
当
σ2 ≥σ11++αασ3 时
其中 α=σt σc 是材料的强度特性参数(拉压强度极限
比)
b
=(1
+α)τb -σt σt -τb
中间应力参数(α<1
龚 俊等 :基于统一强度理论的复合型裂纹 断裂准则
表 2 理论计算与试验结果的比较 Tab.2 Comparison of calculation and experiment
复合型裂纹准则

复合型裂纹准则实际的裂纹往往是张开型和滑移型(I、II)并存或张开型和撕开型(I、III)并存。
Irwin断裂准则不能简单地用于复合型裂纹问题(Irwin的K准则理论假定裂纹按原方向开裂)1)I、III型裂纹一般按原方向开裂2)II型裂纹一般不按原方向开裂3)复合型裂纹一般不按原方向开裂复合型裂纹要解决的问题1)裂纹沿什么方向开裂2)裂纹在什么条件下开裂1.最大切向应力准则(Erdogan and Sih, 1963)I、II复合型裂纹尖端应力场o - 3 cos^ . sm 幺in 为X、而2〔 2 2 )ttuwxwu 一』 sin 与 + cos i cos当回 21 2 2 )o 二上cos i[1 + sin幺in当y ?冗r2( 2 2 )K .00 30+ 开 sin — cos — cos —J2兀r222rrrrmTmnK 0 . 0 30T = i cos — sin - cos 一冲,:2 兀 r 2 2 2K + iiA ro r cos— 1 . sm 0sin30)转化为极坐标形式o = o cos 20 +a sin 20 + 2T sin0cos0。
0 =。
sin 20+o cos 20 -2T sin0 cos0T 0 = -(o -o )sin0 cos0 +T (cos 2 0 -sin 2 0)u = u cos 0 + v sin 0u 0 = - u sin 0 + v cos 01 0 1 得: o = ------ ----- K (3 — cos 0) cos + ----- ---- K 22r i2 2V2兀rii(3cos 0 - 1)sin : 1 八 0 o = ------- ----- [K (1 + cos 0) — 3K sin 0 ]cos - 0 2“ 2兀 r i ii 2 T r 0 12V 2K 7 [K sin 0+ K (3cos 0 - 1)]cosii最大切向应力准则的基本假设1)裂纹沿最大切向应力。
4.第三章 断裂准则

K IC 只适用于线弹性,材料必须在小范围屈服下失稳.
21
二.试验
E39970 标准:金属材料平面应变断裂韧度标准测试方法 72
(美国材料试验协会)
GB 416`84 :中国标准
1.试件 a.三点弯曲试件
KI pQ S BW
3 2
f1 (
a ) W
a a 1 a 3 a 5 a 7 a 9 2 2 2 2 f1 ( ) 2.9( ) 4.6( ) 21.8( ) 37.6( ) 38.7( ) 2 W W W W W W
3KⅡ2 KⅠ4 8KⅠ2 KⅡ2 KⅠ2 9 KⅡ2
1 ( )max cos 0 [ KⅠ(1 cos 0 ) 3KⅡ sin 0 ] c 开裂条件: 2 2 2 r0
c :由Ⅰ型裂纹的断裂韧性来确定.
0 0, KⅠ KⅠc , KⅡ 0
拱形三点弯曲试件 单边切口拉伸试件 中心切口拉伸试件 圆周切口杆状拉伸
23
2.测试原理
载荷
裂纹张开位移
3.测试方法步骤 加工并预制裂纹 在试件切开张开端安装位移传感器 将试件放于试验机上 连接 x y 记录仪 加载试验,记录 P V 曲线 当试件不能承受更大载荷为止,记录最大 Pmax
y
KⅠ
K 3 3 cos (1 sin sin ) Ⅱ sin cos cos 2 2 2 2 2 2 2 r 2 r
15
xy
KⅠ
K 3 3 sin cos cos Ⅱ cos (1 sin sin ) 2 2 2 2 2 2 2 r 2 r
2.裂纹扩展阻力 裂纹扩展单位长度所需要消耗的能量. 裂纹扩展 测定ai i 计算 R R a 阻力曲线 3.临界条件 只有 A3 点是失稳的扩展条件
复合材料断裂公式

复合材料断裂公式复合材料断裂公式是在研究复合材料断裂行为时常用的数学表达式。
复合材料由两种或更多种材料的组合而成,具有良好的力学性能和轻质化特征,因此在各个领域得到广泛应用。
断裂是指当复合材料在承受外部载荷时,出现破裂或破坏的现象。
为了研究材料的断裂行为并预测其性能,科学家们提出了许多断裂公式。
其中最常用的是最大应力理论和线性弹性断裂力学。
最大应力理论是一种基于断裂强度的断裂准则,也称为Tresca准则。
它认为当复合材料中最大主应力达到材料的屈服强度时,材料会发生破裂。
根据最大应力理论,可以使用以下公式来计算复合材料的断裂强度:σ_max = σ_yield / n其中,σ_max 是最大主应力,σ_yield 是材料的屈服强度,n 是安全系数。
线性弹性断裂力学是一种基于线性弹性力学和应力集中理论的断裂准则,也称为Von Mises准则。
它认为当复合材料中的等效应力较大时,材料会发生破裂。
根据线性弹性断裂力学,可以使用以下公式来计算复合材料的断裂强度:σ_eq = k * (σ_1 - σ_3) / √(2)其中,σ_eq 是等效应力,k 是材料的辅助系数,σ_1 和σ_3 是主应力。
除了最大应力理论和线性弹性断裂力学,还有其他一些断裂公式可以用来研究复合材料的断裂行为,如能量释放率法、断裂韧度等。
选择适当的断裂公式取决于实际应用中所需考虑的因素和材料的性质。
综上所述,复合材料断裂公式是研究复合材料断裂行为的数学表达式。
最大应力理论和线性弹性断裂力学是两种常用的断裂准则,可用于计算复合材料的断裂强度。
在实际应用中,根据具体需求和材料性质选择适合的断裂公式是十分重要的。
第2章 复合型裂纹

Mechanic Department
Ⅰ-Ⅱ复合型裂纹区域应力场
然后代人坐标变换式,即可得Ⅰ-Ⅱ复合型裂纹 尖端附近的极坐标应力分量表达式:
我们关心周向应力:
School of Appllied Science in TYUST
Mechanic Department
求解开裂角
开裂角的求解公式
School of Appllied Science in TYUST
断裂判据的统一公式
School of Appllied Science in TYUST
38 Mechanic Department
第二章 总结
最大周向应力准则有两个基本假设: 最大周向应力准则有两个基本假设: 周向应力准则有两个基本假设 (1)裂纹沿最大周向应力σθmax的方向开裂; (1)裂纹沿最大周向应力σθmax的方向开裂; 裂纹沿最大周向应力σθmax的方向开裂 (2)当此方向的周向应力达到临界值时,裂纹失稳扩展。 (2)当此方向的周向应力达到临界值时,裂纹失稳扩展。 当此方向的周向应力达到临界值时
求解(2)
还可知: 由(2-1)还可知: 还可知
结论: 结论:能量释放率开裂方向与最大周 向应力准则的断裂判据表达式相同。 向应力准则的断裂判据表达式相同。
思考:如何确定开裂方向? 思考:如何确定开裂方向?
School of Appllied Science in TYUST
Mechanic Department
Mechanic Department
例
开裂角:
题(续)
开裂判据:
开裂临界应力:
School of Appllied Science in TYUST
Mechanic Department
断裂力学复合应力状态下的断裂判据

∂ 2 S ν KΙ2 (1 − 2ν )σ 2 a (1) θ 0 = 0, 2 = > 0, S = Smin = ∂θ 4π G 4G
KΙ 2 ∂2S (1 −ν ) 2 2 2 σ a (2) cos θ 0 = 1 − 2ν , 2 = − sin θ < 0, S = Smax = ∂θ 8π G 4G
当0 < β <
断裂角 θ 0与材料常数无关
π
2 特别地,当 β = 0时,有 − θ 0 = 70 o 32′ ( 70.5 o ).
时, θ 0 < 0
将 K I , K II 代入开裂条件 K * = K IC中可得临界应力
σC =
π a cos
θ0
2
2 K IC [(1 + cos θ 0 ) sin 2 β − 3sin θ 0 sin β cos β ]
第四章 复合应力状态下的断裂判据
穿透性裂纹(平面问题) 裂纹 埋藏裂纹和表面裂纹(空间问题) 裂纹与主应力方向垂直 若裂纹与主应力方向不垂直,倾斜一个角度,则裂纹受到拉伸 和剪切的复合应力的影响,导致两个问题 (1)在复合应力状态下裂纹将沿什么方向扩展? (2)在复合应力状态下裂纹开裂的条件是什么?
KI θ θ 3θ K II θ θ 3θ cos (1 + sin sin ) + sin cos cos 2 2 2 2 2 2 2π r 2π r KΙ K II θ θ θ θ 3θ 3θ = sin cos cos + cos (1 − sin sin ) 2 2 2 2 2 2 2π r 2π r
复合型裂纹准则
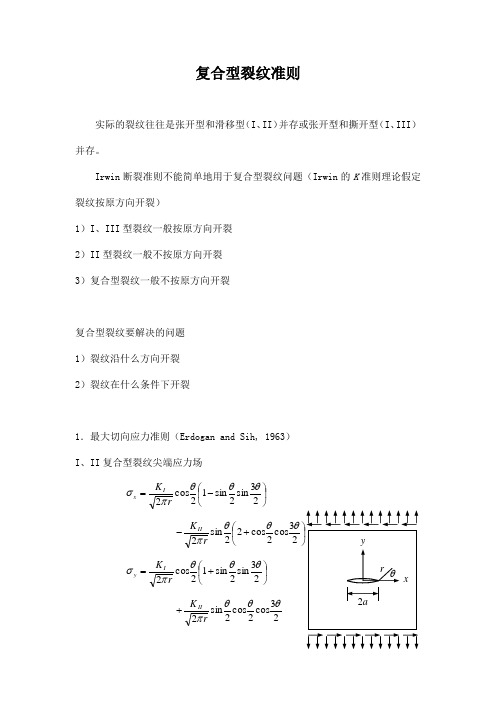
复合型裂纹准则实际的裂纹往往是张开型和滑移型(I 、II )并存或张开型和撕开型(I 、III )并存。
Irwin 断裂准则不能简单地用于复合型裂纹问题(Irwin 的K 准则理论假定裂纹按原方向开裂)1)I 、III 型裂纹一般按原方向开裂 2)II 型裂纹一般不按原方向开裂 3)复合型裂纹一般不按原方向开裂复合型裂纹要解决的问题 1)裂纹沿什么方向开裂 2)裂纹在什么条件下开裂1.最大切向应力准则(Erdogan and Sih, 1963) I 、II 复合型裂纹尖端应力场⎪⎭⎫⎝⎛-=23sin 2sin 12cos 2θθθπσrK Ix⎪⎭⎫⎝⎛+-23cos 2cos 22sin 2θθθπrK II⎪⎭⎫ ⎝⎛+=23sin 2sin 12cos 2θθθπσrK Iy23cos 2cos 2sin 2θθθπrK II+23cos 2sin 2cos 2θθθπτrK Ixy =⎪⎭⎫⎝⎛-+23sin 2sin 12cos 2θθθπrK II转化为极坐标形式θθτθσθσσcos sin 2sin cos 22xy y x r ++= θθτθσθσσθcos sin 2cos sin 22xy y x -+=)sin (cos cos sin )(22θθτθθσστθ-+--=xy y x rθθsin cos v u u r += θθθcos sin v u u +-= 得: 2sin )1cos 3(2212cos )cos 3(221θθπθθπσ-+-=II I r K r K r2cos ]sin 3)cos 1([221θθθπσθII I K K r-+=2cos )]1cos 3(sin [221θθθπτθ-+=II I r K K r 最大切向应力准则的基本假设 1)裂纹沿最大切向应力σθmax的方向开裂2)此方向的切向应力达到临界值时裂纹 扩展假设1要求开裂角σθ满足0=∂∂θσθ, 022<∂∂θσθ0)1cos 3(sin =-+θθII I K Kxy2222420983cos III III I II KK K K K K +++=θ该方向上的切向应力rK K K rII I πθθθπσθθ22cos ]sin 232cos [210002=-=K θ:等效应力强度因子假设2认为切向应力达到临界值σθC时裂纹失稳,而临界值σθC由I 型条件给出IC II I K K K K =-=2cos ]sin 232cos [0002θθθθ 将复合型裂纹转化为当量I 型裂纹问题 讨论1)纯I 型,K II = 0,简化为K I = K IC2)纯II 型,K I = 0,开裂角θ0 = -70.50,起裂条件IC IC II K K K 866.023≈≥与实验结果基本相符最大切向应力准则在K II 较小时与实验结果较为一致2.无限板中斜裂纹图示含穿透斜裂纹无限大板,沿裂纹面βσσ2sin =y , ββστcos sin =xy相应的应力强度因子σβπσπσ2sin a a K y I == ββπσπτcos sin a a K xy II == 开裂角θ0ββββθ22220cos 81cos 8sin cos cos +++= 断裂发生的临界条件为IC K a K =⎪⎭⎫⎝⎛-=0020sin cos 232cos sin sin 2cos θβθββθπσθ3.应变能密度因子准则(Sih, 1972)应变能密度因子准则(S 准则)综合考虑了裂纹尖端六个应力分量(σx ,σy ,σz ,τxy,τxz,τyz)的作用而提出的裂纹失稳判据。
第三章 断裂准则
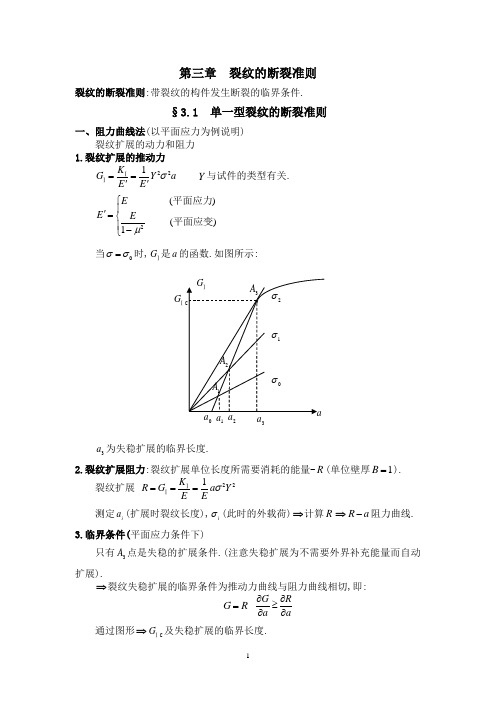
第三章 裂纹的断裂准则裂纹的断裂准则:带裂纹的构件发生断裂的临界条件.§3.1 单一型裂纹的断裂准则一、阻力曲线法(以平面应力为例说明)裂纹扩展的动力和阻力 1.裂纹扩展的推动力221K G Y a E E σ==''ⅠⅠ Y与试件的类型有关.2()()1E E Eμ⎧⎪'=⎨⎪-⎩平面应力平面应变当0σσ=时,G Ⅰ是a 的函数.如图所示:3a 为失稳扩展的临界长度.2.裂纹扩展阻力:裂纹扩展单位长度所需要消耗的能量-R (单位壁厚1B =).裂纹扩展 221K R G a YE E σ===ⅠⅠ测定i a (扩展时裂纹长度),i σ(此时的外载荷)⇒计算R ⇒R a -阻力曲线. 3.临界条件(平面应力条件下)只有3A 点是失稳的扩展条件.(注意失稳扩展为不需要外界补充能量而自动扩展).⇒裂纹失稳扩展的临界条件为推动力曲线与阻力曲线相切,即:G R=G R aa∂∂≥∂∂通过图形⇒G ⅠC 及失稳扩展的临界长度.0123aG Ⅰ二、能量判据=G GⅠⅠC 三、应力强度因子判据=K KⅠⅠC:材料的力学性能,由实验测定。
其中KⅠC§3.2 最大周向正应力理论m ax ()θσ判据.一.复合型裂纹断裂判据需要解决的问题1.裂纹沿什么方向扩展⇒确定开裂角;2.裂纹在什么条件下开始扩展⇒确定临界条件 二、 m ax ()θσ判据1.假定:裂纹初始扩展沿着周向正应力θσ为最大的方向.当这个方向上的周向正应力的最大值m ax ()θσ达到临界时,裂纹开始扩展. 2.举例:Ⅰ、Ⅱ型复合裂纹.[(1cos )3sin ]2K K θθσθθ=+-ⅠⅡ(3cos )cos(3cos 1)sin]22r K K θθσθθ=++-ⅠⅡ[sin (3cos 1)]2r K K θθτθθ=+-ⅠⅡ因0r =,各项均趋于无穷大. 取0r r =(微小值)圆周上个点的θσ0r r θθσθ=∂⎛⎫= ⎪∂⎝⎭ 220θσθ∂<∂ 000cos[sin (3cos 1)]02K K θθθ⇒+-=ⅠⅡθπ=±无实际意义00sin (3cos 1)0K K θθ⇒+-=ⅠⅡ0arccos9KK θ⇒=+ⅠⅡ开裂条件: 0m ax 001()[(1cos )3sin ]2cK K θθθσθθσ=+-=ⅠⅡc θσ:由Ⅰ型裂纹的断裂韧性来确定.即00,,0K K K θ===ⅠⅠc Ⅱ.(Ⅰ型裂纹由原裂纹面扩展)⇒临界失稳条件: 0001cos[(1cos )3sin ]22K K K θθθ+-=ⅠⅡⅠc3.几种特殊情况a.Ⅰ型, 00,0,K K K θ===ⅡⅠⅠcb.Ⅱ型, 000,(3cos 1)070.5K K K τθθ==-=⇒=± ⅠⅡⅡ 实验证明:如图所示剪应力方向,070.5θ=- 如图所示剪应力方向相反, 070.5θ= 0.87K K =ⅡⅠcc.中心斜裂纹的单向拉伸.分解σ:沿裂纹面:1cos sin τσββ=⋅τ垂直裂纹面:21sin σσβ=2,cos K K σβσββ⇒==ⅠⅡ13cos tan sin θβθ-⇒=给定0βθ⇒ 由0001cos[(1cos )3sin ]22K K K θθθ+-=ⅠⅡⅠc ,确定临界应力cσ.§3.3 能量释放率理论G判据,由帕立.尼斯威米(K.Palaniswamy)提出. 假设:(1).裂纹沿产生最大能量释放率的方向扩展.(2).当在上述确定的方向上,能量释放率达到临界值时,裂纹开始扩展.纽斯曼(Nuismer)利用连续性假设研究了能量释放率与最大周向正应力之间的关系.假设:沿0θθ=方向产生支裂纹,长度为a .平面应变下,裂纹沿本身平面扩展时的能量释放率为:22201()G K K Eμ-=+ⅠⅡ (沿裂纹方向扩展)支裂纹的能量释放率为:22201()G K K Eμ-=+ⅠⅡ谈论的问题:令0a →.假设支裂纹尖端的应力场趋近于扩展开始的原有裂纹尖端应力场.00lim |y a θθθσσ=→=00lim |xy a θθθττ=→=limr K →=Ⅰlim r K →=Ⅱ[(1cos )3sin ]2K K θθσθθ=+-ⅠⅡ--(1)[sin (3cos 1)]2r K K θθτθθ=+-ⅠⅡ --(2)⇒00001lim cos [(1cos )3sin ]22a K K K K θθσθθ→===+-Ⅰ0ⅠⅠⅡ--(3) 00001lim cos[sin (3cos 1)]22r r K K K K θθτθθ→===+-Ⅱ0ⅡⅠⅡ--(4)⇒支裂纹沿0θθ=方向开始从原有裂纹扩展时的能量释放率:22201()G K K Eθμ-=+Ⅰ0Ⅱ0 --(5)⇒决定因素⎧⎨⎩裂纹开始前的应力状态支裂纹所走的路径⇒2000021()0K G K K K E θμθθθ∂∂∂-=+=∂∂∂Ⅰ0Ⅱ0Ⅰ0Ⅱ0()结合(1),(2),(3),(4)⇒ 0()|0r r θθθθθθστστθθ=∂∂+=∂∂又由(1)式,32r θθστθ∂=-∂⇒03[()]02r r θθθθθττσθ=∂-=∂0r θτ⇒=和302r θθτσθ∂-=∂分析:03(|0cossin0arctan)2222r K K K K θθθθτθθθσθ=∂-=⇒-=⇒=∂ⅠⅠⅡⅡ⇒代入(3),(4),(5)042221()K G EKK θμ-=+ⅡⅠⅡ又22201()G K K Eμ-=+ⅠⅡ (0G 表示沿原始方向扩展)⇒00G G θ>⇒根不是解.⇒起始裂纹方向取于:002||03θθθθθθστθ==∂-==∂⇒周向应力取平稳值的方向与能量释放率取平稳值的方向又当0001|0cos[sin (3cos 1)]022r K K K θθθθτθθ==⇒=+-=Ⅱ0ⅠⅡ00122222011lim[(2)]r G K r EEθθμμπσ→--⇒==Ⅰ0⇒周向应力绝对值最大的方向是能量释放率最大的方向。
第6章复合型裂纹

θ θ 3θ sin (2 + cos cos ) 2 2 2 σ xx K θ 3θ θ II型裂尖场 型裂尖场: II型裂尖场: σ yy = II sin cos cos 2 2 2 2π r τ xy 3θ θ θ cos (1 sin sin ) 2 2 2
σ zz
θ θ 2ν ( K I cos + K II sin ) 2 2 = 2πr 0
θo
2
[ K I (1 + cos θ o ) 3K II sin θ o ]
按照最大周向应力理论建立的脆断判据是: 按照最大周向应力理论建立的脆断判据是:
(σ θθ ) max = (σ θθ ) cr
这儿 (σ θθ ) cr 是一个只与材料性质有关而与复合裂纹 状态无关的常数。因为纯 型问题是 型问题是I+II复合型问题的特 状态无关的常数。因为纯I型问题是 复合型问题的特 例,而其脆断条件是 I = K IC K 复合型裂纹的关系中找到 ) cr (σ θθ 。所以可以从 I 型裂纹与 所以可以从 。
Ι
平行于裂纹的分力产生 K ,这就是一个复合型问题。 这就是一个复合型问题。 ΙΙ 在复合型情况时, 在复合型情况时,仅用 I 型的准则 就不能预示实际裂纹的扩展情况, 就不能预示实际裂纹的扩展情况,因此 必须研究复合型脆性断裂准则。 必须研究复合型脆性断裂准则。
断裂力学电子教案
研究复合型断裂准则,就是要解决两个关键问题: 研究复合型断裂准则,就是要解决两个关键问题: 两个关键问题 裂纹在复合应力状态下将向什么方向扩展? 裂纹在复合应力状态下将向什么方向扩展? 裂纹在复合应力状态下什么时候开始扩展? 裂纹在复合应力状态下什么时候开始扩展? II、 我们已找到 I、II、III 型裂纹裂尖附近全部应力分 量,怎样来判断既有 K ΙΙ KΙ 、 知名的有以下两种。 知名的有以下两种。 又有ΙΙΙ K 时裂纹怎样脆断呢? 时裂纹怎样脆断呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter Five Fracture criterion for mixed mode crackIn the material mechanics, for the multiaxial stress state, four strength theories have been developed. In the fracture mechanics for the mixed mode crack problem, we need to develop the fracture theory accordingly. Many fracture theories have been developed. Two key questions must be answered.(1) What direction does a crack propagate along?(2) What is the critical case?In what follows, five theories will be introduced.§5-1 Maximum normal stress criterionMaximum stress criterion can be applied to the mixed mode crack of mode I and mode II.The asymptotic stress solution is)23cos 2cos 2(2sin 2)23sin 2sin 1(2cos 2θθ+θπ-θθ-θπ=σrK r K II I xx 23cos 2cos 2sin 2)23sin 2sin 1(2cos 2θθθπ+θθ+θπ=σr K r K II Iyy )23sin 2sin 1(2cos 223cos 2sin 2cos 2θθ-θπ+θθθπ=σrK r K II I xy By application of the coordinate transformation formulas, we can obtain the expressions of three stress components in the polar coordinates (r , θ). The circumferential normal stress is]sin 3)cos 1([2cos 2121θ-θ+θπ=σθθII I K K r The circumferential normal stress intensity factor θθK is defined as]sin 3)cos 1([2cos 212lim 0θ-θ+θ=σπ=θϑ→θθII I r K K r KHence, θθσ can be written asr K π=σθθθθ2Assumptions:(1) Crack initiation direction is the direction of the maximum θθK ;(2) When θθK reaches its critical value c K θθ, break occurs. c K θθ is a material constant.The crack initiation angle 0θ can be determined from0=θ∂∂θθK , 022<θ∂∂θθK The result is0)1cos 3(sin 00=-θ+θII I K K0)5cos 9(2sin )cos 31(2cos 0000<+θθ+θ-θII I K K The critical condition is c II I K K K K θθθ=θ-θθ=)sin 232cos (2cos0020maxDetermination of c K θθ:For mode I crack, 0≠I K , 0=II K , 00=θ, the critical condition reduces to c Ic K K K θθθ==maxNote that c K θθ is a material constant. When, 0≠I K and 0≠II K , there still prevails Ic c K K =θθ. The maximum stress criterion is expressed asIc II I K K K ≤θ-θθ)sin 232cos (2cos 0020Application to mode II crack:For a mode II crack, 0=I K and 0≠II K . The crack initiation angle can be solved,o 5.700-=θ. FromIc c II I K K K K K ==θ-θθ=θθθ)sin 232cos (2cos 0020max one can obtain thatIc IIc K K =149.1, Ic IIc K K 87.0=,The fracture criterion for Mode II crack can be derived from the maximum stress criterion thatIIc II K K ≤It is convenient for the engineering application. However, there is no difference between the plane stress and plane strain.§5-2 Maximum normal strain criterionNear the crack tip, the circumferential normal strain is]}2sin )1cos 3(2cos sin 3[2cos )]cos 3()cos 1[({2121)(111111θ-θν+θθ-θθ-ν-θ+π=σν-σ=εθθθθII I rr K K E r E E E =1, νν=1, for plane stress; 211ν-=E E , ννν-=11, for plane strain. The circumferential normal strain intensity factor *θθK is defined as]}2sin )1cos 3(2cos sin 3[2cos )]cos 3()cos 1[({212lim 1110*θ-θν+θθ-θθ-ν-θ+=επ=θθ→θθII I r K K E r K Then,r K π=εθθθθ2*Assumptions:(1) Crack initiation direction is the direction of the maximum *θθK ;(2) When *θθK reaches its critical value *c K θθ, break occurs. *c K θθ is a materialconstant.The cracking angle 0θ satisfies0*=θ∂∂θθK , 02*2<θ∂∂θθK The critical value *c K θθ can be determined by Ic K . For Mode I, 0=II K , 00=θ. It can be obtained thatIc c K E K 11*1ν-=θθ The maximum normal strain criterion isIc II I K K K ≤θ-θν+θθ-θθ-ν-θ+ν-}2sin )]1cos 3(2cos sin 3[2cos )]cos 3()cos 1[({)1(210010000101Now the plane stress and plane strain can be distinguished.§5-3 Strain energy density factor theoryStrain energy density factor theory was proposed by Prof. G . C. Sih that can be applied to the three dimensional problem.When, 0≠I K , 0≠II K , 0≠III K , the asymptotic stress solution is)23cos 2cos 2(2sin 2)23sin 2sin 1(2cos 2θθ+θπ-θθ-θπ=σrK r K II I xx 23cos 2cos 2sin 2)23sin 2sin 1(2cos 2θθθπ+θθ+θπ=σr K r K II Iyy )23sin 2sin 1(2cos 223cos 2sin 2cos 2θθ-θπ+θθθπ=σrK r K II I xy 2sin 222cos 22θπν-θπν=σr K r K II I zz 2cos 2θπ=σrK III yz , 2sin 2θπ-=σr K III zx The strain energy density w is)(21)()(21222222zx yz xy xx zz zz yy yy xx zz yy xx E E w σ+σ+σμ+σσ+σσ+σσν-σ+σ+σ= The strain energy density w can be expressed in the form ofrS w = where233222122112IIIII II I I K a K a K K a K a S +++=, strain energy density factor )cos )(cos 1(16111θ-κθ+πμ=a )1cos 2(sin 16112+κ-θθπμ=a )]1cos 3)(cos 1()cos 1)(1[(16122-θθ++θ-+κπμ=a πμ=4133a Assumptions: it is physics, not mathematics.(1) Crack initiation direction is the direction of the minimum S ;(2) When S reaches its critical value c S , break occurs. c S is a material constant.The cracking angle 0θ can be solved from0=θ∂∂S , 022>θ∂∂S The critical condition isc S S S =θ=)(0minDetermination of S c :For mode I, it can be derived that2421Ic c K S πμν-= The minimum strain energy density factor criterion can be expressed asS ≤S c , i.e.,223322212211]2[214Ic III II II I I K K a K a K K a K a ≤+++ν-πμ.Mode II crack: 0==III I K K , )321arccos(0ν-=θ, Ic IIc K K 2)1(2)21(3ν-ν-ν-= Take 31=ν. There is 7383o 0'-=θ, Ic IIc K K 9.0=Recall that for the maximum normal stress criterion, there iso 05.70-=θ, Ic IIc K K 87.0=Two results have little difference.§5-4 Modified maximum normal stress criterionSometime the maximum normal stress criterion is not so good. A modified maximum normal stress criterion has been proposed.It has been known that in view ofrS w = a strain energy density factor S is defined. For the mixed mode of mode I and II, S canbe written as222122112IIII I I K a K K a K a S ++= Let constant ==C w .)(]2[122212211θ=++===F K a K K a K a CC S w S r II II I I For different values of C , we can obtain a group of curves called as isolines of strain energy density.The circumferential normal stress is]sin 3)cos 1([2cos 2121θ-θ+θπ=σθθII I K K r Let )cos 1(2cos 21)(θ+θ=θI f , θθ-=θsin 2cos 23)(II f . )]()([21θ+θπ=σθθII II I I f K f K rLet )]()([21)(θ+θπ=θII II I I f K f K S f . This gives )(θ=σθθf rS On the isolines of the strain energy density, C S r =, the circumferential normal stress is)(θ=σθθf CThe circumferential normal stress intensity factor θθK is identical with §5-1. )()(2lim 0θ+θ=σπ=θθ→θθII II I I r f K f K r K Assumptions:(1) Crack initiation direction is the direction of the maximum θθK on the isoline of the strain energy density. The crack initiation angle 0θ can be determined from0=θ∂∂θθK , 022<θ∂∂θθK(2) When θθK reaches its critical value c K θθ, break occurs.c II II I I K f K f K K θθθθ=θ+θ=)()(00maxIt can be derived from Mode I problem thatIc c K K =θθThe fracture criterion isIc II II I I K f K f K ≤θ+θ)()(00§5-5 Energy release rate theoryNear the crack tip, the stresses in the polar coordinates are]sin 3)cos 1([2cos 2121θ-θ+θπ=σθθII I K K r )]1cos 3(sin [2cos 2121-θ+θθπ=σθII I r K K r Let]sin 3)cos 1([2cos 21θ-θ+θ=θII I I K K K )]1cos 3(sin [2cos 21-θ+θθ=θII I II K K K There resultsr K I π=σθθθ2, r K II r π=σθθ2Energy release rate θG along the angle θ:G denotes the energy release rate along the direction θ=0. Now we need to know the energy release rate θG along the direction θ.It is known that002lim =θ→σπ=yy r I r K , 002lim =θ→σπ=yx r II r K , )(8122II I K K G ++=μκRecall the definitions of θI K and θII K . It is known thatθθ→θσπ=r K r I 2lim 0, θ→θσπ=r r II r K 2lim 0Comparing two cases, we know that θI K and θII K are the stress intensity factors of the virtual crack. The stress fields for two cracks are completely same. The conclusion is that the energy release rate θG along angle θ for the real crack is equal to the energy release rate G along its own direction for the virtual crack. Hence, we have )(8122θθθ+μ+κ=II I K K GAssumptions:(1) Crack initiation direction is the direction of the maximum θG . The crack initiation angle 0θ can be determined from0=θ∂∂θG , 022<θ∂∂θG (2) When θG reaches its critical value c G θ, the break occurs.In a same way, it is obtained that281Ic c K G μ+κ=θ The cracking angle 0θ satisfies the equation0)cos 31(sin )cos cos (sin 2)cos 1(sin 00200202002=θ-θ+θ-θ-θ-θ+θII II I I K K K K The fracture criterion is2020020)]cos 35(sin 4)cos 1()[cos 1(41Ic II II I I K K K K K ≤θ-+θ-θ+θ+§5-6 Fatigue crack propagation problemFatigue process:(1) Fatigue crack initiation period: empirical formula (Miner ’s liner damage accumulation theory) or damage mechanics;(2) Fatigue crack propagation period: fracture mechanics.max σ, maximum stress; min σ, minimum stress; )(21min max σ+σ=σm , mean stress; min max σ-σ=σ∆, stress amplitude; maxmin σσ=R , cyclic stress ratio. In a fatigue process, the stress intensity factor )(t K I also varies with time t. a K K K I I I πσ∆=-=∆min maxThe fatigue crack propagation rate dN da / depends on the amplitude of SIF. )(I K f dNda ∆=Experimental result:Fracture and Damage Mechanics Chapter Five Fracture criterion for mixed mode crack 77Region I: small crack, microscopic effect is important.Region II: crack stable propagation.Region III: crack instable propagation to failure.Paris equation: 1960s, Lehigh University, USA For the region II, the relation can be given byn I K C dNda )(∆= )log(log )log(I K n C dNda ∆+=, straight line Parameters C and n can be determined by the experimental data, which depend on the stress ratio R , material property, temperature and so on.The fatigue crack growth life can be calculated by using the Paris equation. There are many improvements for Paris equation.第五章完。
