全国各地2013届高考数学 押题精选试题分类汇编7 立体几何 理
2013年全国高考理科数学试题分类汇编7:立体几何-推荐下载

的坐标分别是 (1,0,1),(1,1,0),(0,1,1),(0,0,0) ,画该四面体三视图中的正视图时,以 zOx 平面为投影面,则得到
正视图可以为
A.
B.
【答案】A 15..(2013 年普通高等学校招生统一考试安徽数学(理))在下列命题中,不是公理的是
C.
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2013年高考理科数学试题分类汇编:立体几何

2013年全国各省市高考理科数学试题分类汇编:立体几何一、选择题错误!未指定书签。
1.(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm πB .38663cm πC .313723cm πD .320483cm π【答案】A错误!未指定书签。
2.(2013年普通高等学校招生统一考试广东省数学(理)卷)设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D错误!未指定书签。
3.(2013年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C错误!未指定书签。
4.(2013年普通高等学校招生统一考试大纲版数学(理))已知正四棱柱1111ABCD A BC D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B C D .13【答案】A错误!未指定书签。
5.(2013年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A错误!未指定书签。
6.(2013年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( ) A .1243V V V V <<< B .1324V V V V <<< C .2134V V V V <<<D .2314V V V V <<<【答案】C错误!未指定书签。
2013年全国各地高考文科数学试题分类汇编7:立体几何含答案

2013年全国各地高考文科数学试题分类汇编7:立体几何一、选择题1 .(2013年高考重庆卷(文))某几何体的三视图如题(8)所示,则该几何体的表面积为()A.180B.200C.220D.240【答案】D2 .(2013年高考课标Ⅱ卷(文))一个四面体的顶点在空间直角坐标系O xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为( ) A.B.C.D.【答案】A3 .(2013年高考课标Ⅰ卷(文))某几何函数的三视图如图所示,则该几何的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 .(2013年高考大纲卷(文))已知正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于 ()A .23B .33C .23D .13【答案】A5 .(2013年高考四川卷(文))一个几何体的三视图如图所示,则该几何体可以是 ( )A .棱柱B .棱台C .圆柱D .圆台【答案】D6 .(2013年高考浙江卷(文))已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .108cm 3B .100 cm 3C .92cm 3D .84cm 3 【答案】B7 .(2013年高考北京卷(文))如图,在正方体1111ABCD A B C D 中,P 为对角线1BD 的三等分点,则P 到各顶点的距离的不同取值有( )A .3个B .4个C .5个D .6个第二部分(非选择题 共110分) 【答案】B8 .(2013年高考广东卷(文))某三棱锥的三视图如图2所示,则该三棱锥的体积是1D1BPD 1CCBA1A图 2俯视图侧视图正视图 ( )A .16B .13C .23D .1【答案】B9 .(2013年高考湖南(文))已知正方体的棱长为1,其俯视图是一个面积为1的正方形,的矩形,则该正方体的正视图的面积等于______ ( )AB .1 CD 【答案】D10.(2013年高考浙江卷(文))设m 。
2013年高考试题分类汇编(立体几何)

2013年高考试题分类汇编(立体几何)考点1 公理体系1.(2013·新课标卷Ⅱ·理科)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,l α⊄,l β⊄,则 A.α∥β且l ∥α B.α⊥β且l ⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l 2.(2013·广东卷·理科)设,m n 是两条不同的直线,αβ,是两个不同的平面,下列命题中正确的是A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若αβ∥,m α⊂,n β⊂,则m n ∥C .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊂,m n ∥,n β∥,则αβ⊥ 3.(2013·安徽卷·理科)在下列命题中,不是公理..的是 A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线4.(2013·江西卷·理科)如图,正方体的底面与正四面体的底面 在同一平面α上,且AB ∥CD ,正方体的六 个面所在的平面与直线CE ,EF 相交的平面 个数分别记为,m n ,那么m n += A.8 B.9 C.10 D.11考点2多面体1.(2013·江苏卷)如图,在三棱柱ABC C B A -111中, F E D ,,分别是AB ,AC ,1AA 的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .ABC1ADEF1B1CABCDEFα2.(2013·江苏卷)如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点. 求证:(Ⅰ)平面EFG ∥平面ABC ;(Ⅱ)SA BC ⊥.3.(2013·北京卷·理科)如图,在棱长为2的正方体1111ABCD A BC D -中,E 为BC 的中点,点P 在线段1D E 上,点P 到直线1CC 的 距离的最小值为 .4.(2013·北京卷·文科)如图,在正方体1111ABCD A BC D-中,P 为对角线1BD 的三等分点,P 到各顶点的距离的不同取值有 A.3个 B.4个 C.5个 D.6个5.(2013·辽宁卷·文科)如图,如图,AB 是圆的直径,PA 垂直圆O 所在的平面,C 是圆上的点.(Ⅰ)求证:BC ⊥平面PAC ;(Ⅱ)设Q 为的中点,G 为的AOC ∆重心, 求证:平面∥平面PCB .考点3 旋转体1.(2013·新课标卷Ⅰ·文科)已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为____. 2.(2013·全国大纲卷·理科)已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =且圆O 与圆K 所在的平面所成的角为60,则球O 的表面积等于 .A BCSG FE AB 1 BC DA 1C 1D 1P A BCDA 1B 1C 1D 1P B考点4 组合体1.(2013·新课标卷Ⅰ·理科)如图,容器高8cm 面恰好接触水面时测得水深为6cm 则球的体积为 A.35003cm π B.38663cm πC.313723cm πD.320483cm π2.(2013·新课标卷Ⅱ·文科)已知正四棱锥O ABCD -的体积为2,底面边O 为球心,OA 为半径的球的表面积为________.3.(2013·天津卷·文科)已知一个正方体的所有顶点在一个球面上,若球的体积为92π,则正方体的棱长为 .4.(2013·辽宁卷·理科)已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球O 的半径为A B . C .132 D .考点5解答题考法1 线线所成的角 考法2 线面所成的角1.(2013·全国大纲卷·文理科)已知正四棱柱1111ABCD A BC D -中,12AA AB =,CD 与平面1BDC 所成角的正弦值等于A.23 C.3D.13 2.(2013·山东卷·理科)已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,,若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为A.512π B.3π C.4π D.6π 3.(2013·新课标卷Ⅰ·理科)如图,三棱柱111ABC A B C -中,CA CB =,4.(2013·浙江卷·文科)如图,在在四棱锥P ABCD -中,PA ⊥面ABCD ,2AB BC ==,AD CD ==PA =120ABC ∠=,G 为线段PC 上的点.(Ⅰ)证明:BD ⊥面PAC ;(Ⅱ)若G 是PC 的中点,求DG 与PAC 所成的角的正切值;(Ⅲ)若G 满足PC ⊥面BGD ,求PGGC 的值.5.(2013·天津卷·理科)如图,四棱柱1111ABCD A BC D -中,侧棱1AA ⊥底面ABCD ,AB ∥DC ,AB AD ⊥,1AD CD ==,12AA AB ==,E 为棱1AA 的中点.(Ⅰ)证明11B C CE ⊥(Ⅱ)求二面角11B CE C --的正弦值.(Ⅲ)设点M 在线段1C E 上,且直线AM 与平面11ADD A ,求线段AM 的长.6.(2013·天津卷·文科)如图,三棱柱111ABC A B C -中,侧棱1AA ⊥底面ABC ,且各棱长均相等.,,D E F 分别为棱AB ,BC ,11AC 的中点. (Ⅰ)证明EF ∥平面1ACD ; (Ⅱ)证明平面1ACD ⊥平面11A ABB ; (Ⅲ)求直线BC 与平面1ACD 所成角的正弦值 AC BDPG AB CDEA 1B 1C 1D 1BAC D EF A 1B 1C 17.(2013·福建卷·理科)如图,在四棱柱1111ABCD A BC D -中,侧棱⊥1AA底面ABCD ,)0(,6,5,4,3,1,//1>=====k k DC kBC k AD k AB AA DC AB (Ⅰ)求证:⊥CD 平面11A ADD(Ⅱ)若直线1AA 与平面C AB 1所成角的正弦值为76, 求k 的值8.(2013·湖南卷·理科)如图,在直棱柱1111ABCD A BC D -中,AD ∥BC , 90BAD ∠=,AC BD ⊥,1BC =,13AD AA ==.(Ⅰ)证明:1AC B D ⊥;(Ⅱ)求直线11B C 与平面1ACD 所成角的正弦值.考法3 二面角1.(2013·辽宁卷·理科)如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是3.(2013·全国大纲卷·理科)如图,四棱锥P ABCD -中,90ABC BAD ∠=∠=,2BC AD =,PAB ∆与PAD ∆都是等边三角形.(Ⅰ)证明:PB CD ⊥;ADPABCDA 1B 1C 1D 1B 1 BCDA 1C 1D 1A(Ⅱ)求二面角A PD C --的大小.4.(2013·山东卷·理科)如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,D ,C ,E ,F 分别是AQ ,BQ , AP ,BP 的中点,2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB ∥GH ;(Ⅱ)求二面角D GH E --的余弦值.5.(2013·北京卷·理科)如图,在三棱柱111ABC A B C -中,11AAC C 是边长为4的正方形.平面ABC ⊥平面11AAC C ,3AB =,5BC =. (Ⅰ)求证:1AA ⊥平面ABC ; (Ⅱ)求二面角111A BC B --的余弦值;(Ⅲ)证明:在线段1BC 存在点D ,使得1AD A B ⊥,并求1BDBC 的值. 6.(2013·陕西卷·理科)如图,四棱柱1111ABCD A B C D -的底面ABCD 是正方形,O 为底面中心,1AO ⊥平面ABCD ,1AB AA =(Ⅰ)证明:1AC ⊥平面11BB D D ; (Ⅱ)求平面11OC B 与平面11BB D D 的夹角θ的大小. 考法4 距离或体积1. (2013·新课标卷Ⅰ·文科)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=.ABCDEFGH PQA BCA 1B 1C 12.(2013·新课标卷Ⅱ·文科)如图,直三棱柱111ABC A B C -中,,D E 分别是AB ,1BB 的中点.(Ⅰ)证明:1BC ∥平面1ACD ; (Ⅱ)设12AA AC CB ===,AB =求三棱锥1C ADE -的体积. 3.(2013·全国大纲卷·文科)如图,四棱锥P ABCD -中,90ABC BAD ∠=∠=,2BC AD =,PAB ∆与PAD ∆都是边长为2的等边三角形.(Ⅰ)证明:PB CD ⊥; (Ⅱ)求点A 到PCD 平面的距离.4.(2013·安徽卷·文科)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=,已知2PB PD ==,PA =(Ⅰ)证明:PC BD ⊥; (Ⅱ)若E 为PA 的中点, 求三菱锥P BCE -的体积.5.(2013·福建卷·文科)如图,在四棱柱P ABCD -中,PD ⊥平面ABCD ,AB ∥DC ,AB AD ⊥,5BC =,3DC =,4AD =,60PAD ∠=.(Ⅰ)当正视方向与向量AD 的方向相同时,画出四棱锥P ABCD -的正视图(要求标出尺寸,并写出演算过程);(Ⅱ)若M 为PA 的中点,求证:求二面角DM ∥平面PBC . (Ⅲ)求三棱锥D PBC -的体积.6.(2013·陕西卷·文科)如图,四棱柱1111ABCD A B C D -的底面ABCD 是正方形,O 为底面中心,ABCDA 1B 1C 1 EABCDPCABCDP1AO ⊥平面ABCD,1AB AA =(Ⅰ)证明:1A BD ∥平面11CD B ; (Ⅱ)求三棱柱111ABD A B D -的体积.7.(2013·湖南卷·文科)如图,在直菱柱111ABC A B C -中,90ABC ∠=,AB AC ==13AA =,D 是BC 的中点,点E 在菱1BB 上运动.(Ⅰ)证明:1AD C E ⊥;(Ⅱ)当异面直线AC ,1C E 所成的角 为60时,求三菱锥111C AB E -的体积.8.(2013·江西卷·文科)如图,直四棱柱1111ABCD A BC D -中,AB ∥CD ,AD AB ⊥,2AB =,AD =,13AA =,E 为CD 上一点,1DE =,3CE =(Ⅰ)证明:BE ⊥平面11BB C C ; (Ⅱ)求点1B 到平面11EAC 的距离.ABCD A 1B 1C 1D 1OAB CDEA 1B 1C 1ACDA 1B 1C 1D 1E。
2013年高考真题理科数学解析分类汇编7-立体几何
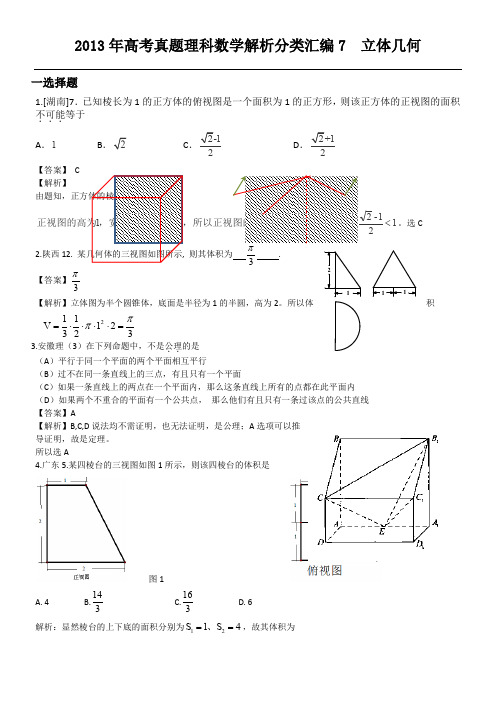
2013年高考真题理科数学解析分类汇编7 立体几何一选择题1.[湖南]7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 A .1 BCD【答案】 C 【解析】1<。
选C 2.陕西12. 则其体积为3. 【答案】3π【解析】立体图为半个圆锥体,底面是半径为1的半圆,高为2。
所以体积32121312ππ=⋅⋅⋅⋅=V3.安徽理(3)在下列命题中,不是公理..的是 (A )平行于同一个平面的两个平面相互平行(B )过不在同一条直线上的三点,有且只有一个平面(C )如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 (D )如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A【解析】B,C,D 说法均不需证明,也无法证明,是公理;A 选项可以推导证明,故是定理。
所以选A4.广东5.某四棱台的三视图如图1所示,则该四棱台的体积是图1A. 4B.143 C.163D. 6 解析:显然棱台的上下底的面积分别为1214S S ==、,故其体积为121114V=()(124)2333S S h +=++⨯= 选B5.广东6.设m ,n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 A.若,,m n αβαβ⊥⊂⊂,则m ⊥n ; B. 若//,,m n αβαβ⊂⊂,则//m n C. 若,,m n m n αβ⊥⊂⊂,则αβ⊥; D. 若,//,//m m n n αβ⊥,则αβ⊥ 解析:选D ∵,//,//m m n n αβ⊥,∴平面β内存在直线α⊥,故αβ⊥ 其它选项均错。
6.新课标I ,6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为 ( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 3【解析】设球的半径为R ,则由题知球被正方体上面截得圆的半径为4,球心到截面圆的距离为R-2,则222(2)4R R =-+,解得R=5,∴球的体积为3453π⨯=500π33cm ,故选A.7.新课标I ,8、某几何体的三视图如图所示,则该几何体的体积为A .168π+B .88π+C .1616π+D .816π+【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式,是中档题.【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2高为4,上边放一个长为4宽为2高为2长方体,故其体积为21244222π⨯⨯+⨯⨯ =168π+,故选A .8.新课标II 4、已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,l ⊄α,l ⊄β,则( )(A ) α∥β且l ∥α (B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l【答案】D设m ∥γ n ∥γ 因为 m ⊥β⟹m ⊥a n ⊥α⟹n ⊥a 所以a ⊥γ又l ⊥m ,l ⊥n 所以l ⊥γ 因此l ∥a新课标II 7、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )(A)(B)(C)(D)【答案】A【解析】在空间直角坐标系中,先画出四面体O ABC -的直观图,以zOx 平面为投影面,则得到正视图(坐标系中红色部分),所以选A.AB CD ,正方9.江西8.如图,正方体的底面与正四面体的底面在同一平面α上,且体的六个面所在的平面与直线CE ,EF 相交的平面个数分别记为,m n ,那么m n += A.8 B.9 C.10 D.1110.辽宁(10)已知三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若,,A .2 B . C .132D .[答案]C【解析】如图:因为,AB AC ⊥所以BC 是小圆的直径,是小圆的直径,所以球心在的中点R==11.全国(10)已知正四棱柱1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于(A )23 (B (C )3 (D )13【答案】A【解析】如下图,连接AC 交BD 于点O ,连接1C O ,过C 作1CH C O ⊥于H 为垂足, ⟹⟹CH ⊥平面CD 与平面所成的角为∠CDH设AB=a 则OC=,CH==,sin ∠CDH=12.山东4、已知三棱柱111-ABC A B C 的侧棱与底面垂直,体积为94,若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为(A)512π (B) 3π (C) 4π (D) 6π13.四川3、一个几何体的三视图如图所示,则该几何体的直观图可以是( )14.重庆5、某几何体的三视图如题()5图所示,则该几何体的体积为( )A 、5603 B 、5803C 、200D 、240【答案】:C 15.湖北16.浙江二填空题 17.上海13.在x O y 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y =和1y =-围成的封闭图形记为D ,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________ 答案2216ππ+[解析]:构造如图所示的圆柱和长方体长方体的长与圆柱的高是2π,圆柱的底面园的直径为2与长方体的侧面长方形的长为4,高为2则水平截面,所得截面面积为48π 由祖暅原理得Ω的体积值==2π×4×2+π×2216ππ+18.浙江19. [江苏] 8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V . 【答案】1:24【解析】三棱锥ADE F -与三棱锥ABC A -1的相似比为1:2,故体积之比为1:8.又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比为1:3.所以,三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1:24.20.[全国] (16)已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,3602OK O K =,且圆与圆所在的平面所成角为,则球O 的表面积等于 . 答案16π 解析:如图:过两圆相交弦AB 的中点E 分别与两圆圆心O,K 连线 ,得到两圆直径 CD,和GH 则CD ⊥AB ,和GH ⊥AB ,∠GEC 为两圆的二面角的平面角∠GEC =,O 是大圆圆心即为球心所以OK ⊥圆K 所在平面,AB=OA=OB=OC=R在正三角形AOB 中 高OE=R ,在直角三角形OKE 中OK=OE ⟹ R = ⟹ R= 2⟹ S =16π21.辽宁(13)某几何体的三视图如图所示,则该几何体的体积是 .【答案】1616π-【解析】直观图是圆柱中去除正四棱柱。
2013年全国高考理科数学考试试题分类汇编7:立体几何

2013年全国高考理科数学试题分类汇编7:立体几何一、选择题1 .(2013年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm π B .38663cm π C .313723cm πD .320483cm π【答案】A2 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 .(2013年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B .3C .3D .13【答案】A5 .(2013年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2013年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A .1243V V V V <<< B.1324V V V V <<<C .2134V V V V <<<D .2314V V V V <<<【答案】C7 .(2013年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1BC .2D .2【答案】C8 .(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143C .163D .6【答案】B9 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l【答案】D10.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,的正三角形.若P 为底面111A B C的中心,则PA 与平面ABC所成角的大小为( )A .512πB .3πC .4πD .6π【答案】B11.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为 ( )A .5603B .5803C .200D .240正视图俯视图侧视图第5题图【答案】C12.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为 ( )A B .C .132D .【答案】C13.(2013年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且ABCD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=( )A .8B .9C .10D .11【答案】A14.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )A .B .C .D .【答案】A15.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))在下列命题中,不是公理..的是( )A .平行于同一个平面的两个平面相互平行B .过不在同一条直线上的三点,有且只有一个平面C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A16.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A17.(2013年高考四川卷(理))一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D 二、填空题18.(2013年高考上海卷(理))在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19.(2013年高考陕西卷(理))某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60,则球O 的表面积等于______.【答案】16π21.(2013年高考北京卷(理))如图,在棱长为2的正方体ABCD -A1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E上,点P 到直线CC 1的距离的最小值为__________.【答案】51B22.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,SA BCADEF BC【答案】①②③⑤25.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-26.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27.(2013年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3π三、解答题28.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;D 1 C 1 B 1A 1D C AB(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值【答案】29.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】1.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))如图,圆锥顶点为p.底面圆心为o,其母线与底面所成的角为22.5°.AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠.【答案】解: (Ⅰ) PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒设面面直线且面面//AB m ⇒直线 ABCD m ABCD AB 面直线面//⇒⊂ . 所以,ABCD D P PAB 的公共交线平行底面与面面C . (Ⅱ) rPOOPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为. ︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF . )223(3)],1-2(3[21cos ,1-25.22tan 12cos 2cos 22-==+∠=︒⇒-∠=∠COD COD COD 212-17cos .212-17cos =∠=∠COD COD 所以.法二:1.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,在四面体BCDA -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD =.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以//PQ 面BDC ;ABCDPQM(第20题图)方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P OQ H P Q O H ∴,且OH BCD ⊂,所以//PQ 面BDC ;(Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD ⊥,过G 作GH BM ⊥于H ,连接CH ,所以C H G ∠就是C B M D--的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===, 在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在R T B H G ∆中,2133HG α=∴=,所以在RT CHG ∆中tan tan 6033CGCHG HG ∠==== tan (0,90)6060BDC ααα∴=∈∴=∴∠=;2.(2013年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,11tan 6BC CC BC C =⋅∠==,从而2ABC S ∆==因此该三棱柱的体积为16ABC V S AA ∆=⋅==3.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SAABCSGFEB 1A 1C 1ACB4.(2013年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯= 而1AD C ∆中,11AC DC AD ===,故132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.5.(2013年高考湖北卷(理))如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(I)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(II)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.【答案】解:(I)EF AC ,AC ABC ⊆平面,EF ABC ⊆平面EF ABC ∴平面第19题图⊆平面又EF BEF∴EF l∴平面l PAC(II)连接DF,用几何方法很快就可以得到求证.(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦.个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)6.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=.(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.CO BDEA CDOBE'A图1图2连结,OD OE ,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故2OH =,从而2AH '== 所以cos OH A HO A H '∠=='所以二面角A CD '--.向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-+=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,53n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦值为5.7.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD -A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB //DC , AB ⊥AD , AD = CD = 1, AA 1 = AB = 2,E 为棱AA 1的中点.(Ⅰ) 证明B 1C 1⊥CE ;C D OBE'AH(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1, 求线段AM的长.【答案】8.(2013年高考新课标1(理))如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA ,∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA |为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A(0,,0),C(0,0,),B(-1,0,0),则BC1BB =1AA),1A C设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧+=⎪⎨+=⎪⎩,可取n,1,-1), ∴1cos ,A C n =11|A C A C ∙n |n ||∴直线A 1C 与平面BB1C 1C9.(2013年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形AB CD中,BD C A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且. 在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设. [来源:学_科_网],所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OB A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅n OB n n ).1-,1,0(法向量2=n 为解得其中一个21221|||,cos |cos 212111=⋅=⋅=><=n n n n θ. 所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π1A10.(2013年高考江西卷(理))如图,四棱锥P A B-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG .(3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(2A B C D ,(4)3(0,0,)2P ,故133333(0),(,),(2222BC CP CD ==--=-,,,设平面BCP 的法向量111(1,,)n y z =,则11110233022y y z ⎧=⎪⎪⎨⎪-+=⎪⎩ ,解得1123y z ⎧=⎪⎪⎨⎪=⎪⎩,即12(1,)3n =. 设平面DCP 的法向量222(1,,)n y z =,则2223233022y y z ⎧-=⎪⎪⎨⎪-+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩,即2n =.从而平面BCP 与平面DCP 的夹角的余弦值为12124cos 416n n n n θ⋅===. 11.(2013年高考四川卷(理))如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠=,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.[来源:学,科,网](Ⅰ)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值.1C【答案】解:()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行的判定定理可知, l //平面1A BC .由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1A M AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --的平面角(设为θ).设11AA =,则由12AB AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==. 又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==, 在1Rt AA P 中, 12A P =;在1Rt A AM中, 1AM =从而,11AA AP AE A P ∙==11AA AM AF A M ∙==,所以sin AE AF θ==.所以cos θ===. 故二面角1A A M N --解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,A E A D ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,12222M N ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,所以131,12A M ⎛⎫= ⎪⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有 ()()()1111111,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫∙=⎪⎪ ⎪⎨⎝⎭⎪∙=⎩ 从而111110,20.y z z ++=⎪=⎩取11x =,则1y =所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,2,,0,x y z x y z ⎧⎫∙=⎪⎪⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,220.x y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A A M N --的平面角为θ,又θ为锐角,则1212cos 5n n n n θ∙===∙.故二面角1A A M N -- 12.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分.如图,在直三棱柱111A B C ABC -中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点 (1)求异面直线B A 1与D C1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=B A ,)4,1,1(1--=B A∴10103182018,cos 11==>=<C A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(=AC 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x m =,∵)0,1,1(=AD ,)4,2,0(1=AC 由1,AC ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=m AC θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))如图,四棱锥P ABCD-中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形. (I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】14.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,AQ BQ AP BP 的中点,2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB GH ; (Ⅱ)求二面角D GH E --的余弦值. 【答案】解:(Ⅰ)证明:因为,,,D C E F 分别是,,,AQ BQ AP BP 的中点,所以EF ∥AB ,DC ∥AB ,所以EF ∥DC ,又EF ⊂平面PCD ,DC ⊂平面PCD ,所以EF ∥平面PCD ,又EF ⊂平面EFQ ,平面EFQ平面PCD GH =,所以EF ∥GH ,又EF ∥AB ,所以AB ∥GH . (Ⅱ)解法一:在△ABQ 中, 2AQ BD =,AD DQ =,所以=90ABQ ∠,即AB BQ ⊥,因为PB ⊥平面ABQ ,所以AB PB ⊥,又BP BQ B =,所以AB ⊥平面PBQ ,由(Ⅰ)知AB ∥GH ,所以GH ⊥平面PBQ ,又FH ⊂平面PBQ ,所以GH FH ⊥,同理可得GH HC ⊥,所以FHC ∠为二面角D GH E --的平面角,设2BA BQ BP ===,连接PC ,在t R △FBC 中,由勾股定理得,FC =在t R △PBC 中,由勾股定理得,PC =又H 为△PBQ 的重心,所以133HC PC == 同理3FH =,在△FHC 中,由余弦定理得552499cos 5529FHC +-∠==-⨯,即二面角D GH E --的余弦值为45-. 解法二:在△ABQ 中,2AQ BD =,AD DQ =,所以90ABQ ∠=,又PB ⊥平面ABQ ,所以,,BA BQ BP 两两垂直,以B 为坐标原点,分别以,,BA BQ BP 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,设2BA BQ BP ===,则(1,0,1)E ,(0,0,1)F ,(0,2,0)Q ,(1,1,0)D ,(0,1,0)C (0,0,2)P ,,所以(1,2,1)EQ =--,(0,2,1)FQ =-,(1,1,2)DP =--,(0,1,2)CP =-,设平面EFQ 的一个法向量为111(,,)m x y z =,由0m EQ ⋅=,0m FQ ⋅=,得111112020x y z y z -+-=⎧⎨-=⎩取11y =,得(0,1,2)m =.设平面PDC 的一个法向量为222(,,)n x y z =由0n DP ⋅=,0n CP ⋅=,得222222020x y z y z --+=⎧⎨-+=⎩取21z =,得(0,2,1)n =.所以4cos ,5m n m n m n ⋅==因为二面角D GH E --为钝角,所以二面角D GH E --的余弦值为45-.15.(2013年高考湖南卷(理))如图5,在直棱柱1111//ABCD A B C D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解:(Ⅰ) AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
【免费下载】13年高考真题理科数学7立体几何

2013高考真题分类汇编:立体几何1.【2013新课标】如图,有一个水平放置的透明无盖的正方体容器,容器高8,将一个球放在容器口,再向容器内注水,当球cm 面恰好接触水面时测得水深为6,如果不计容器的厚度,则球的cm 体积为( )(A )(B ) (C ) (D )35003cm π38663cm π313723cm π320483cm π2.【2013广东】设是两条不同的直线,是两个不同的,m n ,αβ平面,下列命题中正确的是( )(A )若,,,则αβ⊥m α⊂n β⊂m n⊥(B )若,,,则//αβm α⊂n β⊂//m n(C )若,,,则m n ⊥m α⊂n β⊂αβ⊥(D )若,,,则m α⊥//m n //n βαβ⊥3.【2013湖北8】一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为,,,,上面两个简单几何体均为1V 2V 3V 4V 旋转体,下面两个简单几何体均为多面体,则有( )(A ) (B )1243V V V V <<<1324V V V V <<<(C ) (D )2134V V V V <<<2314V V V V <<<4.【2013大纲版】已知正四棱柱中1111ABCD A B C D -,则与平面所成角的正弦值等于( )12AA AB =CD 1BDC(A ) (B (C (D )2315.【2013新课标】某几何体的三视图如图所示,则该几何体的体积为( ) (A ) (B ) (C ) (D )168π+88π+1616π+816π+6.【2013湖南】已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于() (A )1(B(C )(D ))12)12+7.【2013新课标】已知n m ,为异面直线,⊥m 平面α,⊥n 平面β。
2013年高考真题理科数学解析分类汇编7-立体几何 2范文

2013年高考真题理科数学解析分类汇编7 立体几何一选择题1.[湖南]7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于A .1 B.C.D2.陕西12. 某几何体的三视图如图所示, 则其体积3π. 3.安徽理(3)在下列命题中,不是公理..的是 (A )平行于同一个平面的两个平面相互平行(B )过不在同一条直线上的三点,有且只有一个平面(C )如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 (D )如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 4.广东5.某四棱台的三视图如图1所示,则该四棱台的体积是图1A. 4B.143 C.163D. 6 5.广东6.设m ,n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 A.若,,m n αβαβ⊥⊂⊂,则m ⊥n ; B. 若//,,m n αβαβ⊂⊂,则//m nC. 若,,m n m n αβ⊥⊂⊂,则αβ⊥;D. 若,//,//m m n n αβ⊥,则αβ⊥6.新课标I ,6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为 ( ) A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 37.新课标II 4、已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,l ⊄α, l ⊄β,则( )(A ) α∥β且l ∥α (B )α⊥β且l ⊥β (C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l8、新课标II 7、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )(A)(B)(C)(D)9.江西8.如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE ,EF 相交的平面个数分别记为,m n ,那么m n +=A.8B.9C.10D.11 10.辽宁(10)已知三棱柱1116.34ABC A BC O AB AC -==的个顶点都在球的球面上若,, ,AB AC ⊥112AA O =,则球的半径为A B .C .132D .11.全国(10)已知正四棱柱1111112,ABCD A BC D AA AB CD BDC -=中,则与平面所成角的正弦值等于(A )23(B )3 (C )3(D )1312.山东4、已知三棱柱111-ABC A B C 的侧棱与底面垂直,体积为94若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为(A)512π (B)3π (C) 4π (D) 6π 13.四川3、一个几何体的三视图如图所示,则该几何体的直观图可以是( )14.重庆5、某几何体的三视图如题()5图所示,则该几何体的体积为( )A 、5603B 、5803C 、200D 、240二填空题15.[江苏] 8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F-的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .【答案】1:2416.[全国] (16)已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,3602OK O K =,且圆与圆所在的平面所成角为,则球O 的表面积等于 . 答案16π17.辽宁(13)某几何体的三视图如图所示,则该几何体的体积是1616π-.三解答题18.广东18.如图5,在等腰直角三角形ABC 中,∠A=90°,BC=6,D 、E 分别是AC ,AB 上的点,O 是BC 的中点,将△ADE 折起得到如图6所示的四棱锥'ABCDE -,其中'A O =(1)证明'A O ⊥平面BCDE ;(2)求二面角'A CD B --的平面角的余弦值。
2013年高考真题解析分类汇编(文科数学)7:立体几何

2013年高考解析分类汇编7:立体几何一、选择题1 .(2013年高考重庆卷(文8))某几何体的三视图如题(8)所示,则该几何体的表面积为( )A .180B .200C .220D .240【答案】D【解析】本题考查三视图以及空间几何体的表面积公式。
由三视图可知该几何体是个四棱柱。
棱柱的底面为等腰梯形,高为10.等腰梯形的上底为2,下底为8,高为4,腰长为5。
所以梯形的面积为284202+⨯=,梯形的周长为282520++⨯=。
所以四棱柱的表面积为2022010240⨯+⨯=,选D.2 .(2013年高考课标Ⅱ卷(文9))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )(A)(B)(C)(D)【答案】A【解析】在空间直角坐标系中,先画出四面体O ABC -的直观图,以zOx 平面为投影面,则得到正视图(坐标系中红色部分),所以选A.3 .(2013年高考课标Ⅰ卷(文11))某几何函数的三视图如图所示,则该几何的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A【解析】由三视图可知,该几何体的下部分是平放的半个圆柱,圆柱的底面半径为2,圆柱的高为4。
上部分是个长方体,长方体的棱长分别为2,2,4.所以半圆柱的体积为212482ππ⨯⨯⨯=,正方体的体积为22416⨯⨯=,所以该几何体的体积为168π+,选A.4.(2013年高考大纲卷(文11))已知正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于( )A .23BCD .13【答案】A【解析】如图,因为BD ⊥平面ACC 1A 1,所以平面ACC 1A 1⊥平面BDC 1,在Rt △CC 1O 中,过C 作CH ⊥C 1O 于H ,连结DH ,则∠CDH 即为所求,令a AB =,显然2223aCH a ⨯===,所以223sin3aCDHa∠==,故选A.5 .(2013年高考四川卷(文2))一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由三视图可知,该几何体为圆台.6 .(2013年高考浙江卷(文5))已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100 cm3C.92cm3D.84cm3【答案】B【解析】此图的直观图是一个底面边长为6和3,高为6的长方体截去一个角,对应三棱锥的的三条侧棱上分别为3,4,4.如图。
高考真题理科数学解析分类汇编7立体几何
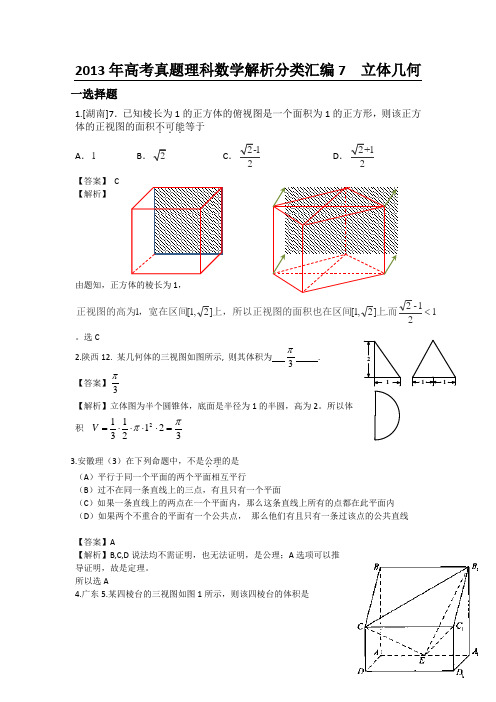
2013年高考真题理科数学解析分类汇编7 立体几何一选择题1.[湖南]7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 A .1 BCD【答案】 C 【解析】由题知,正方体的棱长为1,1]2,1[1<,宽在区间正视图的高为。
选C2.陕西12. 某几何体的三视图如图所示, 则其体积为 3π. 【答案】3π 【解析】立体图为半个圆锥体,底面是半径为1的半圆,高为2。
所以体积32121312ππ=⋅⋅⋅⋅=V3.安徽理(3)在下列命题中,不是公理..的是 (A )平行于同一个平面的两个平面相互平行(B )过不在同一条直线上的三点,有且只有一个平面(C )如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 (D )如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线【答案】A【解析】B,C,D 说法均不需证明,也无法证明,是公理;A 选项可以推导证明,故是定理。
所以选A4.广东5.某四棱台的三视图如图1所示,则该四棱台的体积是图1A. 4B.143C.163D. 6解析:显然棱台的上下底的面积分别为1214S S==、,故其体积为121114V=()(124)2333S S h+=++⨯=选B5.广东6.设m,n是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是A.若,,m nαβαβ⊥⊂⊂,则m⊥n; B. 若//,,m nαβαβ⊂⊂,则//m nC. 若,,m n m nαβ⊥⊂⊂,则αβ⊥; D. 若,//,//m m n nαβ⊥,则αβ⊥解析:选D ∵,//,//m m n nαβ⊥,∴平面β内存在直线α⊥,故αβ⊥其它选项均错。
6.新课标I,6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为 ( )A、500π3cm3B、866π3cm3C、1372π3cm3 D、2048π3cm3【解析】设球的半径为R,则由题知球被正方体上面截得圆的半径为4,球心到截面圆的距离为R-2,则222(2)4R R=-+,解得R=5,∴球的体积为3453π⨯=500π3 3cm,故选A.7.新课标I,8、某几何体的三视图如图所示,则该几何体的体积为A.168π+B.88π+C.1616π+D.816π+【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式,是中档题.【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2高为4,上边放一个长为4宽为2高为2长方体,故其体积为21244222π⨯⨯+⨯⨯ =168π+,故选A .8.新课标II 4、已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,l ⊄α, l ⊄β,则( )(A ) α∥β且l ∥α (B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l【答案】D设m ∥γ n ∥γ 因为 m ⊥β⟹m ⊥a n ⊥α⟹n ⊥a 所以a ⊥γ又l ⊥m ,l ⊥n 所以l ⊥γ 因此l ∥a新课标II 7、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )(A)(B)(C)(D)【答案】A【解析】在空间直角坐标系中,先画出四面体O ABC -的直观图,以zOx 平面为投影面,则得到正视图(坐标系中红色部分),所以选A.9.江西8.如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE ,EF 相交的平面个数分别记为,m n ,那么m n +=A.8B.9C.10D.1110.辽宁(10)已知三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若,,,AB AC ⊥112AA O =,则球的半径为A B ..132D .[答案]C【解析】如图:因为,AB AC ⊥所以BC 是小圆的直径,是小圆的直径,所以球心在的中点R==11.全国(10)已知正四棱柱1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于(A )23 (B )3 (C )3 (D )13【答案】A【解析】如下图,连接AC 交BD 于点O ,连接1C O ,过C 作1CH C O ⊥于H 为垂足, ⟹⟹CH ⊥平面CD 与平面所成的角为∠CDH设AB=a 则OC=,CH==,sin ∠CDH=12.山东4、已知三棱柱111-ABC A B C 的侧棱与底面垂直,体积为94,的正三角形,若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为(A)512π (B) 3π (C) 4π (D) 6π13.四川3、一个几何体的三视图如图所示,则该几何体的直观图可以是()14.重庆5、某几何体的三视图如题()5图所示,则该几何体的体积为()A、5603B、5803C、200D、240【答案】:C15.湖北16.浙江二填空题17.上海13.在x O y平面上,将两个半圆弧22x y x(3)1(3)-+=≥、两条直线x y x(1)1(1)-+=≥和221y =和1y =-围成的封闭图形记为D ,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________ 答案2216ππ+[解析]:构造如图所示的圆柱和长方体长方体的长与圆柱的高是2π,圆柱的底面园的直径为2与长方体的侧面长方形的长为4,高为2则水平截面,所得截面面积为48π由祖暅原理得Ω的体积值==2π×4×2+π×2216ππ+18.浙江19. [江苏] 8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .【答案】1:24【解析】三棱锥ADE F -与三棱锥ABC A -1的相似比为1:2,故体积之比为1:8.又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比为1:3.所以,三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1:24.20.[全国] (16)已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,3602OK O K =,且圆与圆所在的平面所成角为,则球O 的表面积等于 .答案16π 解析:如图:过两圆相交弦AB 的中点E 分别与两圆圆心O,K 连线 ,得到两圆直径 CD,和GH 则CD ⊥AB ,和GH ⊥AB ,∠GEC 为两圆的二面角的平面角∠GEC =,O 是大圆圆心即为球心所以OK ⊥圆K 所在平面,AB=OA=OB=OC=R在正三角形AOB 中 高OE=R ,在直角三角形OKE 中OK =OE ⟹R=⟹ R= 2⟹ S =16π21.辽宁(13)某几何体的三视图如图所示,则该几何体的体积是 .ABC1A DE F1B1C【答案】1616π-【解析】直观图是圆柱中去除正四棱柱。
2013高考数学各省题目分类整理:立体几何基础
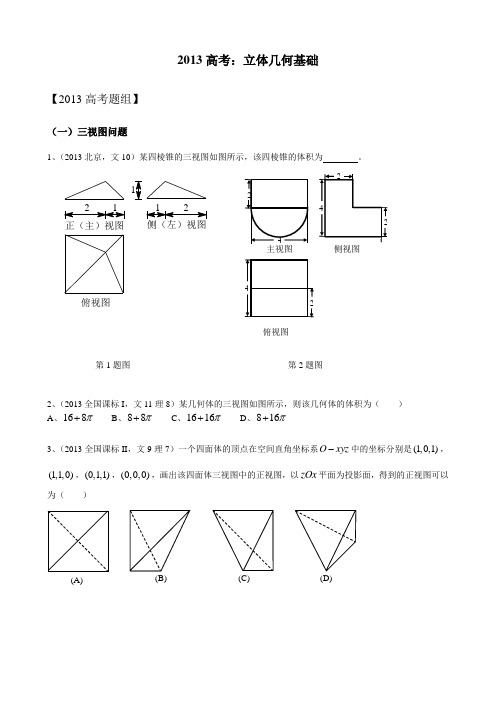
2013高考:立体几何基础【2013高考题组】(一)三视图问题1、(2013北京,文10)某四棱锥的三视图如图所示,该四棱锥的体积为 。
第1题图 第2题图2、(2013全国课标I ,文11理8)某几何体的三视图如图所示,则该几何体的体积为( ) A 、168π+ B 、88π+ C 、1616π+ D 、816π+3、(2013全国课标II ,文9理7)一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画出该四面体三视图中的正视图,以zOx 平面为投影面,得到的正视图可以为( )(A) (B) (C)(D)俯视图正(主)视图侧视图俯视图4、(2013山东,文4)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积和体积分别是( )A 、8B 、83C 、1),83D 、8,8第4题图 第5题图 第6题图 第7题图5、(2013浙江,文5)已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( ) A 、108cm 3 B 、100cm 3 C 、92cm 3 D 、84cm 36、(2013浙江,理12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于 cm 3。
7、(2013福建,理12)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是 。
8、(2013辽宁,文理13)某几何体的三视图如图所示,则该几何体的体积是 。
第8题图 第9题图 第10题图9、(2013陕西,文12)某几何体的三视图如图所示,则其表面积为 。
10、(2013陕西,理12)某几何体的三视图如图所示,则其体积为 。
11、(2013湖南,文7)已知正方体棱长为1,其俯视图是一个面积为1的正方形,的矩形,则该正方体的正视图的面积为( )A B 、1 C D12、(2013湖南,理7)已知棱长为1的的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于( )A 、1BC D13、(2013江西,文8)一几何体的三视图如图所示,则该几何体的体积是( ) A 、2009π+ B 、20018π+ C 、1409π+ D 、14018π+第13题图 第14题图 14、(2013湖北,理8)一个简单几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则由( )A 、1243V V V V <<<B 、1324V V V V <<<C 、2134V V V V <<<D 、2314V V V V <<< 15、(2013湖北,文16)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水。
全国各地2013届高考数学 押题精选试题分类汇编7 立体几何 文

2013届全国各地高考押题数学(文科)精选试题分类汇编7:立体几何一、选择题1 .(2013届广东省高考压轴卷数学文试题)如图3所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体体积为( )A .53 BC .73D .103【答案】A 该几何体的直观图如图所示,由题意知该几何体可分割为两个等体积的四棱锥和一个直三棱柱.四棱锥的体积为111133V =⨯=,直三棱柱的体积为2111212V =⨯⨯⨯=,∴该几何体的体积为12523V V +=.2 .(2013新课标高考压轴卷(一)文科数学)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )正视图俯视图侧视图图3A .π12B .π24C .π32D .π48 【答案】D 【解析】由三视图可知该几何体是有一条侧棱垂直于底面的四棱锥.其中底面ABCD 是边长为4的正方形,高为4,该几何体的所有顶点在同一球面上,则球的直径为4=,即球的半径为,所以该球的表面积是2448ππ=.选D .3 .(2013届福建省高考压轴卷数学文试题)一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )A B C D【答案】D 4 .(2013届海南省高考压轴卷文科数学)如图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如下图; ②存在四棱柱,其正(主)视图、俯视图如下图; ③存在圆柱,其正(主)视图、俯视图如下图. 其中真命题的个数是( )A .3B .2C .1D .0 【答案】答案:A考点:简单空间图形的三视图.分析:由三棱柱的三视图中,两个矩形,一个三角形可判断①的对错,由四棱柱的三视图中,三个均矩形,可判断②的对错,由圆柱的三视图中,两个矩形,一个圆可以判断③的真假.本题考查的知识点是简单空间图形的三视图,其中熟练掌握各种几何体的几何特征进而判断出各种几何体中三视图对应的平面图形的形状是解答本题的关键.解答:解:存在正三棱柱,其三视图中有两个为矩形,一个为正三角形满足条件,故①为真命题;存在正四棱柱,其三视图均为矩形,满足条件,故②为真命题;对于任意的圆柱,其三视图中有两个为矩形,一个是以底面半径为半径的圆,也满足条件,故③为真命题; 5 .(2013届湖南省高考压轴卷数学(文)试题)在空间中,a 、b 是两条不同的直线,α、β是两个不同的平面,下列命题正确的是 ( ) A .若a ∥α,b ∥a ,则b ∥αB .若a ∥α,b ∥α,a ⊂β,b ⊂β,则β∥αC .若α∥β,b ∥α,则b ∥βD .若α∥β,aα,则a ∥β【答案】D 6 .(2013届江西省高考压轴卷数学文试题)在空间,下列命题正确的是 ( )A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行【答案】D 【解析】由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案. 7 .(2013届全国大纲版高考压轴卷数学文试题(二))正三棱锥底面边长为3,侧棱与底面成60 角,则正三棱锥外接球面积为 ( )A .4πB .C .16πD .【答案】C 8 .(2013届山东省高考压轴卷文科数学)(2013青岛市一模)已知m 、n 、l 是三条不同的直线,α、β、γ是三个不同的平面,给出以下命题:①若,//m n αα⊂,则//m n ; ②若l m l n m ⊥=⋂⊥⊂⊂,,,,βαβαβα,则n m ⊥;③若//n m ,m α⊂,则//n α;④若//αγ,//βγ,则//αβ.其中正确命题的序号是( ) ( ) A .②④ B .②③ C .③④ D .①③ 【答案】 ( ) A .【解析】①中直线还可能异面;③中需指明直线n 不在平面内. 9 .(2013届北京市高考压轴卷文科数学)如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边均为1,则该几何体的体积为( )326【答案】A 【解析】由三视图可知,该几何体是四棱锥,底面为边长为1的正方形,高为1的四棱锥,所以体积为1111133⨯⨯⨯=,选 ( )A . 10.(2013届陕西省高考压轴卷数学(文)试题)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 ( )A .9B .10C .11D .232【答案】C 【解析】由三视图可知该几何体是在底面为边长是2的正方形高是3的直四棱柱的基础上截去一个底面积为12112⨯⨯=高为3的三棱锥形成的,所以43111.V =⨯-=11.(2013届重庆省高考压轴卷数学文试题)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为 ( )A .2a πB .273a πC .2113a πD .25a π 【答案】解析:根据题意条件可知三棱柱是棱长都为a 的正三棱柱,则其外接球的半径为R ==,球的表面积为222774123a R a ππ=⋅=,应选 B .命题意图:本题主要考查空间几何体中位置关系、球和正棱柱的性质以及相应的运算能力和空间形象能力. 12.(2013届浙江省高考压轴卷数学文试题)已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )333【答案】C【解析】几何体是正方体截去一个三棱台, 311172(22323V =-⋅++⨯=13.(2013届全国大纲版高考压轴卷数学文试题(一))如图,已知球O 是棱长为1的正方体ABCD —A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为( )A .6πB .3πC D 【答案】A 14.(2013届新课标高考压轴卷(二)文科数学)某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为5的等腰三角形.则该儿何体的体积为( )A .24B .80C .64D .240【答案】B15.(2013届全国大纲版高考压轴卷数学文试题(二))设αβγ、、为平面,a b 、为直线,给出下列条件:①,,//,//a b a b αββα⊂⊂ ②//,//αγβγ③,αγβγ⊥⊥ ④,,//b a b ααβ⊥⊥基中能//αβ能的条件是 ( )A .①②B .②③C .②④D .③④【答案】C16.(2013届浙江省高考压轴卷数学文试题)已知直线l m 、,平面βα、,且βα⊂⊥l m ,,给出下列命题:①若α∥β,则m⊥l ; ②若α⊥β,则m∥l ; ③若m⊥l ,则α∥β; ④若m∥l ,则α⊥β 其中正确命题的个数是 ( )A .1B .2C .3D .4【答案】B【解析】①④对,②③错17.(2013届北京市高考压轴卷文科数学)已知m ,n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是( )A .若l m ⊥,l n ⊥,且,m n α⊂,则l α⊥B .若平面α内有不共线的三点到平面β的距离相等,则βα//C .若n m m ⊥⊥,α,则α//nD .若α⊥n n m ,//,则α⊥m【答案】D 【解析】根据线面垂直的性质可知,选项D 正确. 18.(2013届山东省高考压轴卷文科数学)(2013日照市一模)右图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为.则该几何体的表面积是( )A.20+B.24+C .8D .16【答案】 ( )A .【解析】由已知俯视图是矩形,则该几何体为一个三棱柱,根据三视图的性质,俯视图的矩形宽为,由面积得长为4,则1+2=24+2S S S =⨯⨯⨯⨯侧底()2 =2820+.19.(2013届四川省高考压轴卷数学文试题)已知三棱锥底面是边长为1的正三角形,侧棱长均为2,则侧棱与底面所成角的余弦值为 ( )AB.12CD【答案】D二、填空题20.(2013届全国大纲版高考压轴卷数学文试题(一))已知直二面角βα--l ,点C l AC A ,,⊥∈α为垂足,点D l BD B ,,⊥∈β为垂足,点AC=BD=1,CD=2,异面直线AB与CD 所成的角等于________(用反余弦表示) 【答案】36arccos21.(2013届湖北省高考压轴卷 数学(文)试题)如图为某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是_______________.【答案】2π+ 词【解析】:由三视图知,该几何体由两个共底面的半圆锥构成(如图所示),两个半圆锥侧面积的和为2π,四边形ABCD 由两个等边三角形构成,其面积为24=,故该几何体的表面积为2π+.22.(2013届重庆省高考压轴卷数学文试题)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,AB BC ==,则棱锥O ABCD -的体积为_____.【答案】解析:设ABCD 所在的截面圆的圆心为M,则=,22=,1623O ABCD V -=⨯⨯=. 23.(2013届天津市高考压轴卷文科数学)一个几何体的三视图如图所示,则该几何体的体积为_____________【答案】54【解析】由三视图可知,该几何体是底面是直角梯形的四棱柱.棱柱的高为4,,底面梯形的上底为4,下底为5,腰CD ==所以梯形的面积为(45)32722S +⨯==,所以该几何体的体积为274542⨯=.24.(2013届江西省高考压轴卷数学文试题)如图,若一个几何体的正视图、侧视图、俯视图相同,且均为面积等于2的等腰直角三角形,则该几何体的体积为______.【答案】π25.(2013届安徽省高考压轴卷数学文试题)某几何体的三视图如图所示,根据图中的数据,可得该几何体的体积是______.【答案】323【解析】本题考查三视图还原成立体图和棱锥的体积公式.由题知立体图如图所示4,4,3,1,,AE BD BE CE AE BC BD ABC ====⊥⊥面,所以14482ABC S ∆=⨯⨯=, 132433ABC V S ∆=⨯⨯=. 26.(2013届辽宁省高考压轴卷数学文试题)某几何体的三视图如图1所示,它的全面积为_____.【答案】 π54三、解答题27.(2013届江西省高考压轴卷数学文试题)如图,在三棱锥A BCD-中,90ABC BCD CDA ︒∠=∠=∠=,6AC BC CD ===,设顶点A 在底面BCD 上的射影为E . (Ⅰ)求证:CE BD ⊥;(Ⅱ)设点G 在棱AC 上,且2CG GA =,试求二面角C EG D --的余弦值.【答案】证明:(I)方法一:由AE ⊥平面BCD 得AE ⊥CD , 又AD ⊥CD ,则CD ⊥平面AED , 故CD DE ⊥,同理可得CB BE ⊥,则BCDE 为矩形,又BC CD =, 则BCDE 为正方形,故CE BD ⊥方法二:由已知可得AB BD AD ===,设O 为BD 的中点,则,AO BD CO BD ⊥⊥,则BD ⊥平面AOC ,故平面BCD ⊥平面AOC ,则顶点A 在底面BCD 上的射影E 必在OC ,故CE BD ⊥.(II)方法一:由(I)的证明过程知OD ⊥平面AEC ,过O 作OF EG ⊥,垂足为F ,则易证得DF EG ⊥,故OFD ∠即为二面角C EG D --的平面角,由已知可得6AE =,则2AE AG AC =⋅,故EG AC ⊥,则2CGOF ==,又OD =则DF =故cos OFD ∠=,即二面角C EG D --方法二: 由(I)的证明过程知BCDE 为正方形,如图建立坐标系,则(0,0,0),(0,6,0),(0,0,6),(6,0,0),(6,6,0)E D A B C ,AGEDCB可得(2,2,4)G ,则)4,2,2(),0,6,0(==→→EG ED ,易知平面CEG的一个法向量为)0,6,6(-=→BD ,设平面DEG 的一个法向量为)1,,(y x n =→,则由⎪⎩⎪⎨⎧=⋅=⋅→→→→00EG n ED n 得)1,0,2(-=→n ,则510cos =⋅=〉⋅〈→→→→→→nBD n BD n BD ,即二面角C EG D --28.(2013届湖北省高考压轴卷 数学(文)试题)如图,1AA 、1BB 为圆柱1OO 的母线,BC是底面圆O 的直径,D 、E 分别是1AA 、1CB 的中点,1DE CBB ⊥平面.(1) 证明://DE ABC 平面; (2)求四棱锥11C ABB A -与圆柱1OO 的体积比;(3)若1BB BC =,求直线1CA 与平面1BB C所成角的正弦值.【答案】(1)如图,连接.E OA O O E 、、分别为1CB BC 、的中点,EO ∴是1BB C ∆的中位线,1//EO BB ∴且112EO BB =.又111//,DA BB AA BB =,故11,2DA BB EO DA ==∴//EO 且DA EO =, ∴四边形AOED 是平行四边形,即//DE OA ,又,,//DE ABC OA ABC DE ABC ⊄⊂∴平面平面平面. (2)如图,连接CA .由题知1DE CBB ⊥平面,且由(1)知//DE OA ,1,AO CBB AO BC ∴⊥∴⊥平面,AC AB ∴==.BC 是底面圆O 的直径,CA AB ∴⊥.又1AA 是圆柱的母线,1AA ABC ∴⊥平面,11,AA CA AA AB A ∴⊥= 又,11CA AA B B ∴⊥平面, 即CA 为四棱锥11C ABB A -的高. 设圆柱高为h ,底面半径为r ,则))112212=,33C ABB A V r h V h hr π-=⋅=圆柱, 1122223:3C ABB A hrV V r h ππ-∴==圆柱. (3)如图,作过C 的母线1CC ,连接11B C ,则11B C 是上底面圆1O 的直径,连接11A O ,则11//AO AO ,又111111,AO CBB C AO CBB C ⊥∴⊥平面平面,连接1CO ,则11ACO ∠为直线1CA 与平面1BB C 所成的角.111,AC AO r ==== ,∴在11Rt AO C ∆中,11111sin A O A CO A C ∠==∴直线1CA 与平面1BB C 29.(2013届山东省高考压轴卷文科数学)在如图所示的几何体中,AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,AD =DE =2AB ,F 为CD 的中点. (Ⅰ)求证:AF ∥平面BCE ;(Ⅱ)求证:平面BCE ⊥平面CDE.【答案】证明:(1)如图,取CE 的中点G ,连接FG ,BG . ∵F 为CD 的中点,∴GF ∥DE ,且GF =12DE .∵AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB ∥DE .∴GF ∥AB . 又AB =12DE ,∴GF =AB .∴四边形GFAB 为平行四边形,则AF ∥BG .∵AF ⊄平面BCE ,BG ⊂平面BCE ,∴AF ∥平面BCE.(2)∵△ACD 为等边三角形,F 为CD 的中点,∴AF ⊥CD .∵DE ⊥平面ACD ,AF ⊂平面ACD ,∴DE ⊥AF .又CD ∩DE =D ,∴AF ⊥平面CDE . ∵BG ∥AF ,∴BG ⊥平面CDE .∵BG ⊂平面BCE ,∴平面BCE ⊥平面CDE . 30.(2013届福建省高考压轴卷数学文试题)如图(1),在等腰梯形CDEF 中,CB.DA 是梯形的高,2AE BF ==,AB =现将梯形沿CB.DA 折起,使EF//AB 且2EF AB =,得一简单组合体ABCDEF 如图(2)所示,已知,,M N P 分别为,,AF BD EF 的中点. (Ⅰ)求证://MN 平面BCF ;(Ⅱ)求证:AP ⊥平面DAE .DCBAEFMNPFEABCD【答案】解:(Ⅰ)证明:连结AC ,∵四边形ABCD 是矩形,N 为BD 中点,MNPFEABCD∴N 为AC 中点,在ACF ∆中,M 为AF 中点 ∴//MN CF∵CF ⊂平面BCF ,MN ⊄平面BCF //MN ∴平面BCF(Ⅱ)证明:依题意知,DA AB DA AE ⊥⊥ 且AB AE A =I ∴AD ⊥平面ABFE ∵AP ⊂平面ABFE ∴AP AD ⊥∵P 为EF中点,∴FP AB ==结合//AB EF ,知四边形ABFP 是平行四边形 ∴//AP BF ,2AP BF ==而2,AE PE ==∴222AP AE PE += ∴90EAP ∠= ,即AP AE ⊥ 又AD AE A =I ∴AP ⊥平面ADE31.(2013届天津市高考压轴卷文科数学)如图,在四棱锥ABCD -PGFE 中,底面ABCD 是直角梯形,侧棱垂直于底面,AB //DC ,∠ABC =45o,DC =1,AB =2,PA =1. (Ⅰ)求PD 与BC 所成角的大小; (Ⅱ)求证:BC ⊥平面PAC ; (Ⅲ)求二面角A -PC -D 的大小.【答案】(Ⅰ)取的AB 中点H ,连接DH ,易证BH//CD ,且BD =CD所以四边形BHDC 为平行四边形,所以BC//DH 所以∠PDH 为PD 与BC 所成角因为四边形,ABCD 为直角梯形,且∠ABC =45o, 所以DA ⊥AB 又因为AB =2DC =2,所以AD =1, 因为Rt△PAD 、Rt△DAH 、Rt△PAH 都为等腰直角三角形,所以PD =DH =PH故∠PDH =60o(Ⅰ)连接CH ,则四边形ADCH 为矩形, ∴AH =DC 又AB =2,∴BH =1 在Rt△BHC 中,∠ABC =45o, ∴CH =BH =1,CB∴AD =CH =1,AC∴AC 2+BC 2=AB 2∴BC ⊥AC 又PA 平面ABCD ∴PA ⊥BC ∵PA ∩AC =A ∴BC ⊥平面PAC(Ⅲ)如图,分别以AD 、AB 、AP 为x 轴,y 轴,z 轴 建立空间直角坐标系,则由题设可知: A (0,0,0),P (0,0,1),C (1,1,0),D (1,0,0), ∴AP =(0,0,1),PC=(1,1,-1)设m =(a ,b ,c )为平面PAC 的一个法向量, 则00AP PC ⎧=⎪⎨=⎪⎩m m ,即00c a b c =⎧⎨+-=⎩ 设1a =,则1b =-,∴m =(1,-1,0)同理设n =(x ,y ,z ) 为平面PCD 的一个法向量,求得n =(1,1,1)∴1cos ,2=== m n m n m n 所以二面角A -PC -D 为60o32.(2013新课标高考压轴卷(一)文科数学)如图,四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB . (1) 求证:CE ⊥平面PAD ;(11)若PA =AB =1,AD =3,CD,∠CDA =45°,求四棱锥P-ABCD 的体积.【答案】(1)证明:因为PA ⊥平面ABCD,CE ⊂平面ABCD,所以PA⊥CE,因为AB⊥AD,CE∥AB,所以CE⊥AD,又PA ⋂AD=A,所以CE ⊥平面PAD(2)解:由(1)可知CE⊥AD,在直角三角形ECD 中,DE=CD cos 451⋅= ,CE=CD sin 451⋅= .又因为AB=CE=1,AB∥CE,所以四边形ABCE 为矩形,所以ABCD ABCE BCD S S S ∆=+=12AB AE CE DE ⋅+⋅=15121122⨯+⨯⨯=,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD 的体积等于115513326ABCD S PA ⋅=⨯⨯=33.(2013届辽宁省高考压轴卷数学文试题)如图所示,已知圆O 的直径AB 长度为4,点D为线段AB 上一点,且13AD DB =,点C 为圆O 上一点,且BC =.点P 在圆O 所在平面上的正投影为点D ,PD BD =. (Ⅰ)求证:CD ⊥平面PAB ;(Ⅱ)求PD 与平面PBC 所成的角的正弦值.【答案】解答:(Ⅰ)连接CO ,由3AD DB =知,点D 为AO 的中点,又∵AB 为圆O 的直径,∴AC CB ⊥, BC =知,60CAB ∠= , ∴ACO ∆为等边三角形,从而CD AO ⊥ ∵点P 在圆O 所在平面上的正投影为点D , ∴PD ⊥平面ABC ,又CD ⊂平面ABC , ∴PD CD ⊥,由PD AO D = 得,CD ⊥平面PAB(注:证明CD ⊥平面PAB 时,也可以由平面PAB ⊥平面ACB 得到,酌情给分.) (Ⅱ)法1:过D 作⊥DH 平面PBC 交平面于点H ,连接PH ,则DPH ∠即为所求的线面角由(Ⅰ)可知CD =,3PD DB ==,∴111113333232P BDC BDC V S PD DB DC PD -∆=⋅=⋅⋅⋅=⨯⨯=又PB ==,PC ==,BC ==,∴PBC ∆为等腰三角形,则12PBC S ∆=⨯=. 由P BDC D PBC V V --=得,553=DH ∴55sin ==∠PD DH DPH法2:由(Ⅰ)可知CD =,3PD DB ==,过点D 作DE CB ⊥,垂足为E ,连接PE ,再过点D 作DF PE ⊥,垂足为F∵PD ⊥平面ABC ,又CB ⊂平面ABC , ∴PD CB ⊥,又PD DE D = , ∴CB ⊥平面PDE ,又DF ⊂平面PDE , ∴CB DF ⊥,又CB PE E = ,∴DF ⊥平面PBC ,故DPF ∠为所求的线面角在Rt DEB ∆中,3sin 302DE DB =⋅=,PE ==55sin sin ==∠=∠PE DE DPE DPF 34.(2013届陕西省高考压轴卷数学(文)试题)已知直角梯形ABCD中,//AD BC ,122AD AB BC ===,90ABC ∠=︒,PAB ∆是等边三角形,平面PAB ⊥平面ABCD . (Ⅰ)求证:BD DC ⊥;(Ⅱ)求三棱锥P BCD -的体积.【答案】【解析】(Ⅰ)∵2AD =,2AB =,45AD AB ADB DBC ⊥⇒∠=∠=︒ 过D 作DM BC ⊥,垂足为M ,则2DM AB MC === ∴45DCM ∠=︒,∴90BDC ∠=o ,∴BD DC ⊥.(Ⅱ)21132P BCD V -===. 35.(2013届湖南省高考压轴卷数学(文)试题)如图,已知在四棱锥PABCD 中,底面ABCD是矩形,且AD=2,AB=1,PA ⊥平面ABCD,E,F 分别是线段AB,BC 的中点.(1)证明:PF ⊥FD ;(2)判断并说明PA 上是否存在点G ,使得EG ∥平面PFD ;(3)若PB 与平面ABCD 所成的角为45°,求二面角A PD F 的余弦值.【答案】(1)证明:∵PA ⊥平面ABCD ,∠BAD =90°,AB =1,AD =2,建立如图所示的空间直角坐标系A xyz ,则A (0,0,0),B (1,0,0),F (1,1,0),D (0,2,0).不妨令P (0,0,t ),∵PF =(1,1,-t ),DF=(1,-1,0), ∴PF DF ⋅=1×1+1×(-1)+(-t )×0=0,即PF ⊥FD(2)解:设平面PFD 的法向量为n =(x ,y ,z ),由0,0,n PF n DF ⎧⋅=⎪⎨⋅=⎪⎩ 得⎩⎪⎨⎪⎧x +y -tz =0,x -y =0,令z =1,解得:x =y =t2. ∴n =⎝ ⎛⎭⎪⎫t 2,t2,1. 设G 点坐标为(0,0,m ),E ⎝ ⎛⎭⎪⎫12,0,0,则EG =⎝ ⎛⎭⎪⎫-12,0,m ,要使EG ∥平面PFD ,只需EG ·n =0,即⎝ ⎛⎭⎪⎫-12×t2+0×t 2+1×m =m -t 4=0,得m =14t ,从而满足AG =14AP 的点G 即为所求(3)解:∵AB ⊥平面PAD ,∴AB 是平面PAD 的法向量,易得AB=(1,0,0),又∵PA ⊥平面ABCD ,∴∠PBA 是PB 与平面ABCD 所成的角,得∠PBA =45°,PA =1,平面PFD 的法向量为n =⎝ ⎛⎭⎪⎫12,12,1.∴cos<AB ,n >=AB n AB n⋅=1214+14+1=66. 故所求二面角A PD F 的余弦值为6636.(2013届重庆省高考压轴卷数学文试题)在直角梯形ABCD 中90ABC DAB ∠=∠= ,30CAB ∠= ,BC=1,AD=CD,把△DAC 沿对角线AC 折起后如图所示(点D 记为点P),点P 在平面ABC 上的正投影E 落在线段AB 上,连接PB.若F 是AC 的中点,连接PF,EF. (1) 求证:平面PEF⊥AC. (2) 求直线PC 与平面PAB 所成的角的大小.AC【答案】解:1.AC90,30,1ABC DAB CAB BC ∠=∠=∠== 2,60.2tan 30BC AB AC DAC AD CD AC ∴===∠=∴===,.PA PC PF AC =∴⊥E P ABC PE ABC PE AC ∴⊥∴⊥ 点为点在平面上的正投影,平面.,,PF PE P PF PEF PE PEF AC PEF =⊂⊂∴⊥ 平面平面平面【D 】2. PE ABC PE BC ⊥∴⊥ 平面,,,BC AB PE AB E PE PAB BC PAB ⊥=⊂∴⊥ 平面平面CPB PC PAB ∴∠为直线与平面所成的角.1t sin =.2BC PC ∴∠ 在R CBP 中,BC=1,PC=DC=2,CPB=00,30.<∠∴∠=CPB<9CPB ∴直线PC 与平面PAB 所成的角为 30 37.(2013届浙江省高考压轴卷数学文试题)如图,在斜三棱柱111ABC A B C -中,侧面11AA B B ⊥底面ABC ,侧棱1AA 与底面ABC 成60°的角,12AA =.底面ABC 是边长为2的正三角形,其重心为G 点, E 是线段1BC 上一点,且113BE BC =.(1)求证:GE //侧面11AA B B ;(2)求平面1B GE 与底面ABC 所成锐二面角的正切值;(3)在直线..AG 上是否存在点T,使得AG T B ⊥1?若存在,指出点T 的位置;若不存在,说明理由.【答案】【解析】解法1:(1)延长B 1E 交BC 于点F,11B EC ∆ ∽△FEB,BE=21EC 1,∴BF=21B 1C 1=21BC, 从而点F 为BC 的中点.∵G 为△ABC 的重心,∴A、G 、F 三点共线.且11//,31AB GE FB FE FA FG ∴==, 又GE ⊄侧面AA 1B 1B,∴GE//侧面AA 1B 1B.(2)在侧面AA 1B 1B 内,过B 1作B 1H⊥AB,垂足为H,∵侧面AA 1B 1B⊥底面ABC, ∴B 1H⊥底面ABC.又侧棱AA 1与底面ABC 成60°的角,AA 1=2,∴∠B 1BH=60°,BH=1,B 1H=.3在底面ABC 内,过H 作HT⊥AF,垂足为T,连B 1T,由三垂线定理有B 1T⊥AF, 又平面B 1CE 与底面ABC 的交线为AF,∴∠B 1TH 为所求二面角的平面角. ∴AH=AB+BH=3,∠HAT=30°,∴HT=AH 2330sin =︒.在Rt△B 1HT中,332tan 11==∠HT H B TH B ,从而平面B 1GE 与底面ABC (3)(2)问中的T 点即为所求,T 在AG 的延长线上,距离A 点233处. 38.(2013届北京市高考压轴卷文科数学)如图所示,在正方体1111ABCD A B C D -中,E 、F分别为DD 1、DB 的中点.(I)求证:EF//平面ABC 1D 1; (II)求证:1EF B C ⊥..【答案】(Ⅰ)连结1BD ,在B DD 1∆中,E 、F 分别为1D D ,DB 的中点,则11111111////EF D BD B ABC D EF ABC D EF ABC D ⎫⎪⊂⇒⎬⎪⊄⎭平面平面平面(Ⅱ)⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂⊥⊥B BC AB D ABC C B D ABC AB BC C B ABC B 111111111 面面⇒111111B C ABC D BD ABC D ⊥⎫⇒⎬⊂⎭平面平面111//B C BD EF BD ⊥⎫⎬⎭1EF B C ⇒⊥39.(2013届全国大纲版高考压轴卷数学文试题(二))已知矩形ABCD中,1AB AD ==,将ABD ∆沿BD 折起,使点A 在平面BCD 内的射影落在DC上.(Ⅰ)求证:平面ADC ⊥平面BCD ; (Ⅱ)求点C 到平面ABD 的距离;(Ⅲ)若E 为BD 中点,求二面角B AC E --的大小.【答案】证明:(Ⅰ)∵点A 在平面BCD 上的投影落在DC 上,即平面ACD 经过平面BCD 的垂线,∴平面ACD ⊥平面BCD (Ⅱ)如图所示建立空间直角坐标系,则(0,0,0),(1,0,0)(0,C B D∵A 的投影在DC 上,令00(0,,)A y z 由 0||1DA AB DA ⋅==即2200022000010y z y z ++=+++= (0,A ∴,由(0,AB AD == ,求得平面ABD 的一个法向量为(1)n =-,而AC = ,∴C 到平面BCD 的距离为||||AC n d n ⋅==(Ⅲ)由(1,(1,0,0)BA CB =-=,求得平面BAC 的一个法向量1(0,1,1)n =FC DBAE1A 1B 1C 1D1(,0,2AC AE == ,求得平面AEC 的一个法向量2n =由图可见B AC E --为锐二面角,设此平面角为θ,则1212||cos ||||n n n n θ⋅==⋅45θ∴=︒40.(2013届上海市高考压轴卷数学(文)试题)本题共2小题,第(Ⅰ)小题6分,第(Ⅱ)小题8分.如图,在长方体1111ABCD A B C D -中, 111,2AD A A AB ===,点E 在棱AB 上.(Ⅰ)求异面直线1D E 与1A D 所成的角;(Ⅱ)若二面角1D EC D --的大小为45︒,求点B 到平面1D EC 的距离.【答案】解法一:(1)连结1AD .由11AA D D 是正方形知11AD A D ⊥. ∵AB ⊥平面11AA D D ,∴1AD 是1D E 在平面11AA D D 内的射影. 根据三垂线定理得11AD D E ⊥,则异面直线1D E 与1A D 所成的角为90︒.(Ⅱ)作DF CE ⊥,垂足为F ,连结1D F ,则1CE D F ⊥.所以1DFD ∠为二面角1D EC D --的平面角,145DFD ∠=︒.于是111,DF DD D F ===,易得Rt Rt BCE CDF ∆≅∆,所以2CE CD ==,又1BC =,所以BE =. 设点B 到平面1D EC 的距离为h ,则由于1,B CED D BCE V V --=即1111113232CE D F h BE BC DD ⋅⋅⋅=⋅⋅⋅, 因此有11CE D F h BE BC DD ⋅⋅=⋅⋅,即=,∴h =.解法二:分别以1,,DD DC DA 为x 轴,y 轴,z 轴,建立空间直角坐标系.(Ⅰ)由1(1,0,1)A ,得1(1,0,1)DA =,设(1,,0)E a ,又1(0,0,1)D ,则1(1,,1)D E a =-.∵111010DA D E ⋅=+-= ∴11DA D E ⊥,则异面直线1D E 与1A D 所成的角为90︒.(Ⅱ)(0,0,1)=m 为面DEC 的法向量,设(,,)x y z =n 为面1CED 的法向量,则(,,)x y z =n|||cos ,|cos 45||||⋅<>===︒=m n m n m n ,∴222z x y =+. ①由(0,2,0)C ,得1(0,2,1)D C =- ,则1D C ⊥ n ,即10D C ⋅=n ,∴20y z -=②由①、②,可取2)=n ,又(1,0,0)CB =,所以点B 到平面1D EC 的距离||CB d ⋅===n |n |. 41.(2013届四川省高考压轴卷数学文试题)如图,在三棱柱ABC —111A B C 中,侧棱垂直底面,90ACB ∠=︒,12AC BC CC ===. (1)求证:11AB BC ⊥;(2)求二面角1C —1AB —1A 的大小.【答案】方法一(1)BC AC ⊥,1CC AC ⊥且C CC BC =1 ,∴⊥AC 平面11CBB C , 又⊂1BC 平面11CBB C , ∴1BC AC ⊥,11BC C B ⊥且C C B AC =1∴⊥1BC 平面C AB 1,又⊂1AB 平面C AB 1∴ 11BC AB ⊥(2)取11B A 的中点为H ,在平面11ABB A 内过H 作1AB HQ ⊥于Q ,连接Q C 1 则⊥H C 1平面11ABB A ,所以11AB H C ⊥ , 而且H HQ H C = 1所以⊥1AB 平面HQ C 1,所以⊥1AB Q C 1 所以QH C 1∠是二面角111A AB C --的平面角 , 又21=H C在AB A 1∆内,解得36=HQ , 所以 3tan 11==∠HQHC QH C 所以二面角111A AB C --的平面角为060方法2: 建立空间直角坐标系(以C 为原点,CA 为x 轴正半轴,CB 为y 轴正半轴,1CC 为z 轴正半轴)则)2,0,2(),2,0,0(),2,2,0(),0,2,0(),0,0,2(111A C B B A (1)),2,2,2(1-=AB)2,2,0(1-=BC022)2(20211=⨯+-⨯+⨯-=⋅∴BC AB11BC AB ⊥∴(2)取11B A 的中点为H ,则)2,1,1(H .平面11A AB 的法向量)0,1,1(1=C 设平面11AB C 的法向量),,(z y x n =)0,2,0(),2,0,2(111=-=B C C⎩⎨⎧==-∴02022y z x z x y ==∴,0,令1=z∴得平面11AB C 的一个法向量)1,0,1(=n2122|011011|cos =⨯⨯+⨯+⨯=∴θ 又所求二面角111A AB C --的平面角为锐角, 所以二面角111A AB C --的平面角为06042.(2013届海南省高考压轴卷文科数学)如图,在四棱台ABCD ﹣A 1B 1C 1D 1中,D 1D⊥平面ABCD,底面ABCD 是平行四边形,AB=2AD,AD=A 1B 1,∠BAD=60°. (Ⅰ)证明:AA 1⊥BD;(Ⅱ)证明:CC 1∥平面A 1BD.【答案】分析:(Ⅰ) 由D 1D⊥平面ABCD,可证 D 1D⊥BD.△ABD 中,由余弦定理得 BD 2,勾股定理可得 AD⊥BD,由线面垂直的判定定理可证 BD⊥面ADD 1A 1,再由线面垂直的性质定理可证 BD⊥AA 1.(Ⅱ)连接AC 和A 1C 1,设AC∩BD=E,先证明四边形ECC 1A 1为平行四边形,可得CC 1∥A 1E,再由线面平行的判定定理可证CC 1∥平面A 1BD.解答:证明:(Ⅰ)∵D 1D⊥平面A BCD,∴D 1D⊥BD. 又AB=2AD,AD=A 1B 1,∠BAD=60°,△ABD 中,由余弦定理得 BD 2=AD 2+AB 2﹣2AB•ADcos60°=3AD 2,∴AD 2+BD 2=AB 2, ∴AD⊥BD,又 AD∩DD 1=D,∴BD⊥面ADD 1A 1.由 AA 1⊂面ADD 1A 1,∴BD⊥AA 1.(Ⅱ)证明:连接AC 和A 1C 1,设 AC∩BD=E,由于底面ABCD 是平行四边形,故E 为平行四边形ABCD 的中心,由棱台的定义及AB=2AD=2A 1B 1,可得 EC∥A 1C 1,且 EC=A 1C 1,故ECC 1A 1为平行四边形,∴CC 1∥A 1E,而A 1E ⊂平面A 1BD,∴CC 1∥平面A 1BD 43.(2013届全国大纲版高考压轴卷数学文试题(一))如图,已知四棱锥E- ABCD 的底面为菱形,且∠ABC =600,AB =EC =2,AE =BE =2.(I)求证:平面EAB ⊥平面ABCD ;(II)求二面角A- EC- D 的余弦值.【答案】解法1:(1)证明:取AB 的中点O,连接EO ,CO∵2==EB AE ,AB =2 ∴△ABC 为等腰三角形∴AB EO ⊥,EO =1 又∵AB =BC ,∠ABC =600∴△ABC 为等边三角形 ∴3=CO ,又EC =2∴222CO EO EC += 即CO EO ⊥,⊥EO 平面ABCD ,且⊂EO 平面EAB∴ 平面EAB⊥平面ABCD,(2)过A 作AH⊥CE 于H 点,过H 作HM//CD,OHM又Rt△EDO 解得DE=22, 所以222DE EC DC =+即EC DC ⊥,所以MH⊥CE,因此∠AHM 为二面角A EC D --的平面角,通过计算知27=AH ,21=MH ,1=AM ,所以7722127214147cos =⨯⨯-+=∠AHM 所以二面角D EC A --的余弦值为772 解法2.(1)设A C∩BD=O,如图,以O 为原点, OC,OB 为x,y 轴建立空间直角坐标系O-xyz 设E(m,n,t ),则A(-1,0,0),C(1,0,0), B(0,3,0), D(0,-3,0),∴),,1(t n m AE +=, ),3,(t n m BE -=,),,1(t n m CE -=所以⎪⎪⎩⎪⎪⎨⎧=++-==+-+==+++=4)1(23(2)1(222222222222t n m CE t n m BE t n m AE 解得:1,23,21==-=t n m所以)1,23,21(-E ,因为AB 的中点)0,33,21(-M ,所以)1,0,0(=ME 即ME⊥平面ABCD,又⊂ME 平面EAB,所以平面EAB⊥平面ABCD, (2))1,23,23(-=CE ,)0,0,2(=AC ,)0,3,1(=DC ,分别设平面AEC,平面ECD 的法向量为),,(),,,(z y x m z y x n '''==则⎪⎩⎪⎨⎧==⋅=+⋅+⋅-=⋅0202323x n AC z y x n CE 令y= -2,得)3,2,0(-=n OMxyz⎪⎩⎪⎨⎧='+'=⋅='+'⋅+'⋅-=⋅0302323y x n DC z y x n CE令1-='y ,)32,1,3(-=m 7724762||||,cos =⨯+=⋅⋅>=<m n m n m n所以二面角D EC A --的余弦值为772 解法3:(1)(同解法1);(2)以AB 中点O 为坐标原点,以OB 所在直线y 轴,OE 所在直线为z 轴, 建立空间直角坐标系如图所示,则)0,1,0(-A ,)0,0,3(C ,)0,2,3(-D ,)1,0,0(E)0,1,3(=AC ,)1,0,3(-=EC .)0,2,0(=DC设平面DEC 的法向量),,(z y x n =⎪⎩⎪⎨⎧==⋅=-=⋅0203y n DC z x n CE ,令1=z ,得)1,0,33(=n 设平面EAC 的法向量),,(z y x m '''=⎪⎩⎪⎨⎧='+'=⋅='-'=⋅0303y x n AC z x n CE ,令1='z ,得)1,1,33(-=m 7723237131||||,cos =⨯+=⋅⋅>=<m n m n m n∴二面角D EC A --的余弦值为772 44.(2013届安徽省高考压轴卷数学文试题)( )如图所示,在棱长为2的正方体1111ABCD A B C D -中,E F 、分别为1DD 、DB 的中点.(1)求证:1EF B C ⊥;(2)求三棱锥1B EFC V -的体积.FE D 1C 1B 1A 1DCB A【答案】【解析】(1)证明:FE D 1C 1B 1A 1DCB A1111111B C ABB C BC AB BC ABC D AB BC B ⊥⎫⎪⊥⎪⇒⎬⊂⎪⎪=⎭、面111111B C ABC D BD ABC D ⊥⎫⇒⎬⊂⎭面面1111//B C BD EF B C EF BD ⊥⎫⇒⊥⎬⎭(2)11CF BDD B ⊥ 面1CF EFB ∴⊥面,且CF BF ==1112EF BD B F =====13B E === 22211EF B F B E ∴+=即190EFB ︒∠=9分111111111133232B EFC C B EF B EF V V S CF EF B F CF --∆∴==⨯⨯=⨯⨯⨯⨯=⨯=45.(2013届新课标高考压轴卷(二)文科数学)如图所示,在正三棱柱ABC -A 1B 1C 1中,底面边长和侧棱长都是2,D 是侧棱CC 1上任意一点,E 是A 1B 1的中点. (I)求证:A 1B 1//平面ABD; (II)求证:AB⊥CE;(III)求三棱锥C-ABE 的体积.【答案】解(Ⅰ)证明:由正三木棱住的性质知11B A ∥AB,因为ABD B A ABD AB 平面,平面⊄⊂11, 所以11B A ∥平面ABD.(Ⅱ)设AB 中点为G,连结GE,GC.GC AB G ABC ⊥∴∆为中心,为正三角形,且又EG∥1AA ,GE AB AB AA ⊥∴⊥,1 又GEC AB G GE CG 平面所以⊥=⋂, 而CE AB GEC CE ⊥⊂,所以平面(Ⅲ)由题意可知:ABCABC E ABE c S EG V V ∆--⨯⨯==3146.(2013届广东省高考压轴卷数学文试题)将棱长为a 正方体截去一半(如图7所示)得到如图8所示的几何体,点E ,F 分别是BC ,DC 的中点. (1)证明:1AF ED ⊥;(2)求三棱锥1E AFD -的体积.【答案】(1)证:连接DE ,交AF 于点O ∵1D D ⊥平面ABCD ,AF ⊂平面ABCD ∴1D D AF ⊥∵点E ,F 分别是BC ,1D C 的中点,∴DF CE =又∵AD DC =,90ADF DCE ∠=∠=∴ADF ∆≌DCE ∆,∴AFD DEC ∠=∠ 又∵90CDE DEC ∠+∠=∴90CDE AFD ∠+∠=∴()18090DOF CDE AFD ∠=-∠+∠=,即AF DE ⊥又∵1D D DE D=∴AF ⊥平面1D DE又∵1ED ⊂平面1D DE∴1AF ED ⊥(2)解:∵1D D ⊥平面ABCD ,∴1D D是三棱锥1D AEF-的高,且1D D a=D 1D C BA 1AE F OA 1B 1C 1D 1 ABCD 图7D 1DCBA 1AE F图8∵点E ,F 分别是BC ,1D C 的中点,∴2a DF CF CE BE ====∴AEF ADF FCE ABE ABCD S S S S S ∆∆∆∆=---正方形2111222a AD DF CF CE AB BE=-⋅⋅-⋅⋅-⋅⋅2222234848a a a a a =---=∴11E AFD D AEFV V --=113AEF S D D ∆=⋅⋅2313388a a a =⋅⋅=。
2013年高考押题精粹数学(理)试题 Word版含答案

一.选择题(30道)1.设集合{}2,ln A x =,{},B x y =,若{}0A B ⋂=,则y 的值为( ) A .0 B .1 C .e D .1e2. 已知R 是实数集,集合3|1M x x ⎧⎫=<⎨⎬⎩⎭,{}|3N y y t t ==-≥,则R N C M ⋂=( )A. []0,2B. [2,)+∞C.(,2]-∞D. []2,33.已知i 为虚数单位,则复数321ii+等于( )A .-1-iB .-1+iC .1+iD .1—i4.复数41(,)22m m i m R i -+-⋅∈其中为虚数单位在复平面上对应的点不可能位于A .第一象限B .第二象限C .第三象限D .第四象限5. “0m n >>”是“方程221m x ny +=表示焦点在y 轴上的椭圆”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件6.若命题“x ∃∈0R ,使得x m x m ++-<200230”为假命题,则实数m 的取值范围是( )(A )[,]26(B )[,]--62(C )(,)26(D )(,)--627.一个算法的程序框图如右,则其输出结果是( )A.0B.2C.12+18.下面的程序框图中,若输出S 的值为126,则图中应填上的条件为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤9.右图是函数sin()()y A x x R ωϕ=+∈在区间5[,]66ππ-上的图象.为了得到这个函数的图象,只需将sin ()y x x R =∈的图象上所有的点( )A .向左平移3π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变B .向左平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D .向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变10.已知,40,tan 12sin sin22πθθθθ<<=++k 则)4sin(πθ-的值( )A .随着k 的增大而增大B .有时随着k 的增大而增大,有时随着k 的增大而减小C .随着k 的增大而减小D .是一个与k 无关的常数11.关于函数x x x x f cos )cos (sin 2)(-=的四个结论:P 1:最大值为2; P 2:最小正周期为π; P 3:单调递增区间为∈⎥⎦⎤⎢⎣⎡+-k k k ,83,8ππππZ ;P 4:图象的对称中心为∈-+k k ),1,82(ππZ .其中正确的有( )A .1 个B .2个C .3个D .4个12.,a b 是两个向量,||a =1 ,||b =2 ,且()a b a +⊥,则a 与b 的夹角为( )(A )︒30 (B )︒60 (C )︒120 (D )︒15013.已知a ,b 是两个互相垂直的单位向量,且c ·a =c ·b =1,,则对任意正实数t ,1c ta b t++的最小值是( )A .2B .C .4D .14.一个几何体的三视图如右图所示,则它的体积为( )A .203B .403C .20D .4015.正方形A B C D 的边长为4,中心为M ,球O 与正方形A B C D 所在平面相切于M 点,过点M 的球的直径的另一端点为N ,线段N A 与球O 的球面的交点为E ,且E 恰为线段N A 的中点,则球O 的体积为( )A .83πB.3C .43πD.316.不等式组1,40,0x x y kx y ≥⎧⎪+-≤⎨⎪-≤⎩表示面积为1的直角三角形区域,则k 的值为( )A.2- B. 1- C. 0 D.1 17.设函数3()f x x x =+,x R ∈. 若当02πθ<<时,不等式0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是 ( ). A.(,1]-∞ B.[1,)+∞ C.1(,1)2D.1(,1]218、一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有( ) A.12种 B. 15种 C. 17种 D.19种 19、二项式8(2x-的展开式中常数项是( )A .28B .-7C .7D .-2820、高三毕业时,甲,乙,丙等五位同学站成一排合影留念,已知甲,乙相邻,则甲丙相邻的概率为( )A.110B.14C.310D.25某苗圃基地为了解基地内甲、乙两块地种植的同一种 树苗的长势情况,从两块地各随机抽取了10株树苗测 量它们的高度,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数x x 甲乙、和中位数y y 甲乙、进行比 较,下面结论正确的是( )A .x x y y >>甲乙甲乙,B .x x y y <<甲乙甲乙,C .x x y y <>甲乙甲乙,D .x x y y ><甲乙甲乙,22、公差不为0的等差数列{n a }的前21项的和等于前8项的和.若80k a a +=,则k =( ) A .20 B .21 C .22 D .2323、已知数列}{n a 为等比数列,274=+a a ,865-=⋅a a ,则101a a +的值为( )A .7B .5-C .5D .7-24. 已知21,F F 分别是双曲线12222=-by ax 的左、右焦点,过1F 且垂直于x 轴的直线与双曲线交于B A ,两点,若2ABF ∆是锐角三角形,则该双曲线离心率的取值范围是( )A .⎪⎪⎭⎫⎝⎛+221,1 B .⎪⎪⎭⎫ ⎝⎛+∞+,221 C .()21,1+D .()+∞+,2125.圆2x 2+y -2x +my -2=0关于抛物线2x =4y 的准线对称,则m 的值为( )A.1B. 2C. 3D. 4 26.已知抛物线)0(:2>=a ax y C 的焦点到准线的距离为41, 且C 上的两点()()2211,,,y x B y x A 关于直线m x y +=对称, 并且2121-=x x , 那么m =( )A .23 B .25 C .2 D .327.如果函数()y f x =图像上任意一点的坐标(,)x y 都满足方程 lg()lg lg x y x y +=+,那么正确的选项是( )(A)()y f x =是区间(0,+∞)上的减函数,且4x y +≤ (B)()y f x =是区间(1,+∞)上的增函数,且4x y +≥(C)()y f x =是区间(1,+∞)上的减函数,且4x y +≥ (D)()y f x =是区间(1,+∞)上的减函数,且4x y +≤28.定义在R 上的奇函数()f x ,当x ≥0时, ))12lo g (1),0,1,()1|3|,1,,x x f x x x ⎧+∈⎡⎣⎪=⎨⎪--∈+∞⎡⎣⎩则关于x 的函数()()F x f x a =-(0<a <1)的所有零点之和为( )(A )1-2a(B )21a-(C )12a-- (D )21a--29.5(2)x a +的展开式中,2x 的系数等于40,则0(2)axe x dx +⎰等于( )A .eB .1e -C .1D .1e +30.已知函数2342013()12342013xxxxf x x =+-+-++,2342013()12342013xxxxg x x =-+-+--,设函数()(3)(4)F x f x g x =+⋅-,且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内,则-b a 的最小值为( ) A .8 B .9 C . 10 D . 11二.填空题(8道)31.已知A 0),B(0,1)),坐标原点O 在直线AB 上的射影为点C,则OCOA ⋅= .32.在6)11(x+的展开式中,含1x项的系数是________.(用数字作答)33.若实数x 、y 满足⎪⎩⎪⎨⎧+-≥≥≥-b x y x y y x 02,且2z x y =+的最小值为3,则实数b 的值为__34.已知四面体ABC P -的外接球的球心O 在AB 上,且⊥PO 平面ABC , AB AC 32=,若四面体ABC P -的体积为23,则该球的体积为_____________35.已知{,)|||1,||1}x y x y A Ω=≤≤(,是曲线2y x =与12y x =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为 .36.公比为4的等比数列{}n b 中,若n T 是数列{}n b 的前n 项积,则有304020301020,,T T T T TT 也成等比数列,且公比为1004;类比上述结论,相应的在公差为3的等差数列{}n a 中,若n S 是{}n a 的前n 项和,则有一相应的等差数列,该等差数列的公差为_____________. 37.在ABC ∆中,角C B A 、、所对的边分别为c b a 、、,且c A b B a 21cos cos =-,当)tan(B A -取最大值时,角C 的值为_______________38.已知抛物线)0(2:2>=p px y C 的准线为l ,过点)0,1(M 且斜率为3的直线与l 相交于点A ,与C 的一个交点为B ,若MB AM =,则p 等于____________三.解答题(12道)39、ABC ∆中,a ,b ,c 分别是角,,A B C 的对边,向量m (2sin ,2cos 2)B B =-,2(2sin (),1)42B n π=+- ,n m ⊥.(1)求角B 的大小; (2)若a =1b =,求c 的值.40、已知等差数列{}n a 的首项11a =,公差0d >.且1452a a a ,,分别是等比数列}{n b 的432b b b ,,.(Ⅰ)求数列}{n a 与}{n b 的通项公式; (Ⅱ)设数列{}n c 对任意自然数n 均有1212c c b b ++ (1)n n nc a b ++=成立,求12c c ++ (2013)c +的值.41、一次考试中,五名同学的数学、物理成绩如下表所示:(1)请在直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程; (2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X 表示选中的同学的物理成绩高于90分的人数,求随机变量X 的分布列及数学期望)(X E 的值. 42、十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:性别与对景区的服务是否满意 单位:名(1)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关 附:()()()()()22n a d b c K a b c d a c b d -=++++43、如图在四棱锥P A B C D -中,底面A B C D 是边长为a 的正方形,侧面P A D ⊥底面A B C D ,且2P A P D A D ==,设E 、F 分别为P C 、B D 的中点.(Ⅰ) 求证:E F //平面P A D ;(Ⅱ) 求证:面P A B ⊥平面P D C ; (Ⅲ) 求二面角B P D C --的正切值.44、已知椭圆C :22221(0)x y a b ab+=>>的焦距为离心率为2,其右焦点为F ,过点(0,)B b 作直线交椭圆于另一点A .(Ⅰ)若6A B B F ⋅=-,求A B F ∆外接圆的方程;(Ⅱ)若过点(2,0)M 的直线与椭圆:N 222213x y ab+=相交于两点G 、H ,设P 为N 上一点,且满足O G O H t O P += (O 为坐标原点),当3P G P H -< 时,求实数t 的取值范围.45. 已知定点A(1,0), B 为x 轴负半轴上的动点,以AB 为边作菱形ABCD,使其两对 角线的交点恰好落在y 轴上. (1) 求动点D 的轨迹五的方程.(2) 若四边形MPNQ 的四个顶点都在曲线E 上,M ,N 关于x 轴对称,曲线E 在M 点处的切线为l ,且PQ//l①证明直线PN 与QN 的斜率之和为定值;②当M 的横坐标为43,纵坐标大于O,PQN ∠=60°时,求四边形MPNQ 的面积46. 对于函数f (x )(x ∈D ),若x ∈D 时,恒有()f x '>()f x 成立,则称函数()f x 是D 上的J 函数.(Ⅰ)当函数f (x )=m xe lnx 是J 函数时,求m 的取值范围; (Ⅱ)若函数g (x )为(0,+∞)上的J 函数, ①试比较g (a )与1a e-g (1)的大小;②求证:对于任意大于1的实数x 1,x 2,x 3,…,x n ,均有 g (ln (x 1+x 2+…+x n ))>g (lnx 1)+g (lnx 2)+…+g (lnx n ).47. 设函数()ln a f x x x x=+, 32()3g x x x =--.(Ⅰ)讨论函数()()f x h x x=的单调性;(Ⅱ)如果存在12,[0,2]x x ∈,使得12()()g x g x M -≥成立,求满足上述条件的最大整数M ; (Ⅲ)如果对任意的1,[,2]2s t ∈,都有()()f s g t ≥成立,求实数a 的取值范围.48.选修4-1:几何证明选讲.如图,过圆E 外一点A 作一条直线与圆E 交B,C 两点,且AB=31AC,作直线AF 与圆E 相切于点F ,连接EF 交BC 于点D,己知圆E 的半径为2,EBC ∠ =30. (1)求AF 的长. (2)求证:AD=3ED.49. 在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建坐标系.已知曲线θθρc o s 2s i n :2a C =)0(>a ,已知过点)4,2(--P 的直线l的参数方程为:⎪⎪⎩⎪⎪⎨⎧+-=+-=t y t x 224222,直线l 与曲线C 分别交于N M ,两点. (1)写出曲线C 和直线l 的普通方程; (2)若|||,||,|PN MN PM 成等比数列,求a的值.50. 选修4-5:不等式选讲设.,)(R a a x x f ∈-=(1)当13,()3x f x -≤≤≤时,求a 的取值范围;(2)若对任意x ∈R ,()()12f x a f x a a -++≥-恒成立,求实数a 的最小值.11.【答案】C【点评】根据三角函数的图像确定三角函数的解析式是综合考察三角函数知识的掌握程度的重要手段,再结合三角函数图象的平移问题,使得这种题型常考常新,作为中档题是历年高考考察的重点,如9题;三角函数求值是历年高考的常考点,应用三角函数恒等变换化简式子并引入参数是一种创新题型,知识的综合程度较高,或许这种题型在未来几年的高考中会出现,如10题;结合三角函数的恒等变换,综合分析函数的性质,是对三角函数知识点的综合考察,要求知识的掌握程度为中等,历年高考对三角函数知识点的考察亦以中档容易为主,如11题。
2013年全国高考理科数学试题分类汇编7:立体几何

2013年全国高考理科数学试题分类汇编7:立体几何2013年国理科数学试题分类汇编7立体几何一、选择题1 .(2013年新课标1(理))如图有一个水平放置的透明无盖的正方体容器容器8cm 将一个球放在容器口再向容器内注水当球面恰好接触水面时测得水深为6cm 如果不计容器的厚度则球的体积为( )A .35003cm πB .38663cm πC .313723cm πD .320483cm π【答案】A2 .(2013年普通等学校招生统一试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,αβ是两个不同的平面下列命题正确的是( )[]A .若αβ⊥m α⊂n β⊂则m n ⊥B .若//αβm α⊂n β⊂则//m nC .若m n ⊥m α⊂n β⊂则αβ⊥D .若m α⊥//m n //n β则αβ⊥ 【答案】D3 .(2013年上海市春季数学试卷(含答案))若两个球的表面积之比为1:4则这两个球的体积之比为( ) A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2013年普通等学校招生统一试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A B C D-12AA AB=则CD 与平面1BDC 所成角的正弦值等于( ) A .23B .33C .23D .13【答案】A []5 .(2013年新课标1(理))某几何体的三视图如图所示则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2013年湖北卷(理))一个几何体的三视图如图所示该几何体从上到下由四个简单几何体组成其体积分别记为1V 2V 3V 4V 上面两个简单几何体均为旋转体下面两个简单几何体均为多面体则有( ) A .1243V VV V <<<B .1324V VV V <<<C .2134VV V V <<<D .2314V V V V <<<【答案】C7 .(2013年湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形则该正方体的正视图的面积不可能...等于( ) A .1 B .2C .2-12D .2+12【答案】C8 .(2013年普通等学校招生统一试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示则该四棱台的体积是( )A .4B .143C .163D .6【答案】B9 .(2013年普通等学校招生统一试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知nm ,为异面直线⊥m 平面α⊥n 平面β直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄则( )A .βα//且α//lB .βα⊥且β⊥lC .α与β相交且交线垂直于lD .α与β相交且交线平行于l【答案】D10.(2013年普通等学校招生统一试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -94长为3的正三角形若P 为底面111A B C 的心则PA 与平面ABC 所成角的大小为( ) A .512πB .3πC .4πD .6π1 2211正视图俯视图侧视图第5题图【答案】B11.(2013年普通等学校招生统一试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示则该几何体的体积为( )A .5603B .5803C .200D .240【答案】C12.(2013年普通等学校招生统一试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上若34AB AC ==,AB AC ⊥112AA =则球O 的半径为( )A .3172B .210C .132D .310【答案】C13.(2013年江西卷(理))如图正方体的底面与正四面体的底面在同一平面α上且AB CD P 正方体的六个面所在的平面与直线CEEF 相交的平面个数分别记为,m n 那么m n +=()A.8B.9C.10D.11【答案】A14.(2013年普通等学校招生统一试新课标Ⅱ卷数学(理)(纯WORD版含答案))一个四面体的顶点在空间直角坐标系O xyz 的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0)画该四面体三视图的正视图时以zOx平面为投影面则得到正视图可以为()A.B.C.D.【答案】A15.(2013年普通等学校招生统一试安徽数学(理)试题(纯WORD版))在下列命题不是公理..的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点有且只有一个平面C .如果一条直线上的两点在一个平面内那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点 那么他们有且只有一条过该点的公共直线【答案】A16.(2013年普通等学校招生统一试浙江数学(理)试题(纯WORD 版))在空间过点A 作平面π的垂线垂足为B 记)(A fB π=设βα,是两个不同的平面对空间任意一点P )]([)],([21P f f Q P f f Q βααβ==恒有21PQ PQ =则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A17.(2013年四川卷(理))一个几何体的三视图如图所示则该几何体的直观图可以是【答案】D二、填空题18.(2013年上海卷(理))在xOy 平面上将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D 如图阴影部分记D绕y 轴旋转一周而成的几何体为Ω过(0,)(||1)y y ≤作Ω的水平截面所得截面面积为2418y ππ-+试利用祖暅原理、一个平放的圆柱和一个长方体得出Ω的体积值为__________【答案】2216ππ+19.(2013年陕西卷(理))某几何体的三视图如图所示 则其体积为___3π_____1121【答案】3π20.(2013年普通等学校招生统一试大纲版数学(理)WORD 版含答案(已校对))已知圆O 和圆K 是球O 的大圆和小圆其公共弦长等于球O 的半径32OK =O 与圆K 所在的平面所成的一个二面角为60o则球O 的表面积等于______【答案】16π21.(2013年北京卷(理))如图在棱长为2的正方体ABCD -A 1B 1C 1D 1E 为BC 的点点P 在线段D 1E 上点P 到直线CC 1的距离的最小值为__________【答案】 25522.(2013年普通等学校招生国统一招生试江苏卷(数学)(已校对纯WORD 版含附加题))1D1BP gD1CC EB A 1A如图在三棱柱ABC C B A -111FE D ,,分别是1AAAC AB ,,的点设三棱锥ADEF -的体积为1V 三棱柱ABCC B A -111的体积为2V 则=21:V V____________【答案】1:2423.(2013年普通等学校招生统一试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示则此几何体的体积等于________2cm【答案】2424.(2013年普通等学校招生统一试安徽数学(理)试题(纯WORD 版))如图正方体1111ABCD A B C D -的棱长为1P 为BC 的点Q 为线段1CC 上的动点过点APQ 的平面截该正方体所得的截面记为S 则下列命题正确的是__①②③⑤___(写出所有正确命题的编号)[]43 233正视图侧视图俯视图(第12题图)ABC1A DEF 1B 1C①当102CQ <<时S 为四边形;②当12CQ =时S 为等腰梯形;③当34CQ =时S 与11C D 的交点R 满足1113C R =;④当314CQ <<时S 为六边形;⑤当1CQ =时S 的面积为62【答案】①②③⑤25.(2013年普通等学校招生统一试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示则该几何体的体积是____________【答案】1616π-26.(2013年普通等学校招生统一试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体如果该组合体的正视图测试图俯视图均如图所示且图的四边形是边长为2的正方形则该球的表面积是_______________【答案】12π27.(2013年上海市春季数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -异面直线1A B 与1B C 所成角的大小为_______D C B A D C ABπ【答案】3三、解答题28.(2013年普通等学校招生统一试辽宁数学(理)试题(WORD版))如图AB是圆的直径PA垂直圆所在的平面C是圆上的点(I)求证:PAC PBC平面平面;⊥(II)2.若,1,1,求证:二面角的余弦值===--AB AC PA C PB A【答案】[]29.(2013年普通等学校招生统一试重庆数学(理)试题(含答案))如图四棱锥P ABCD -PA ABCD ⊥底面2,4,3BC CD AC ACB ACD π===∠=∠=F为PC的点AF PB ⊥(1)求PA 的长; (2)求二面角B AF D --的正弦值【答案】1.(2013年普通等学校招生统一试安徽数学(理)试题(纯WORD版))如图圆锥顶点为p底面圆心为o其母线与底面所成的角为225°AB和CD是底面圆O上的两条平行的弦轴OP与平面PCD所成的角为60°(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠【答案】解:(Ⅰ)PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒Q 设面面直线且面面//AB m⇒直线 ABCD m ABCD AB 面直线面//⇒⊂Θ所以ABCD D P PAB 的公共交线平行底面与面面C (Ⅱ)rPO OPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF法二:1.(2013年普通等学校招生统一试浙江数学(理)试题(纯WORD 版))如图在四面体BCD A -⊥AD 平面BCD 22,2,==⊥BD AD CD BC M是AD的点P 是BM 的点点Q 在线段AC 上且QC AQ 3= (1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060求BDC ∠的大小【答案】解:证明(Ⅰ)方法一:如图6取MD的点F 且M是AD点所以3AF FD=因为P是BM点所以//PF BD;又因为(Ⅰ)3AQ QC=且3AF FD=所以//QF BD所以面//PQF面BDC且PQ⊂面BDC所以//PQ面BDC;方法二:如图7所示取BD点O且P是BM点所以1//2PO MD;取CD的三等分点H使3DH CH=且3AQ QC=11////42QH AD MD////PO QH PQ OH∴OH BCD⊂所以//PQ面BDC;(Ⅱ)如图8所示由已知得到面ADB⊥面BDC过C作CG BD⊥于G所以CG BMD⊥过G作GH BM⊥于HABCDPQM(第20题图)连接CH所以CHG∠就是CBM D--的二面角;由已知得到813BM=+=设BDCα∠=所以cos,sin22cos,22cos sin,22sin, CD CG CBCD CG BC BD CD BDαααααα===⇒===在RT BCG∆2sin22sinBGBCG BGBCααα∠=∴=∴=所以在RT BHG∆22122sin3322sinHGHGαα=∴=所以在RT CHG∆222cos sintan tan60322sin3CGCHGHGααα∠====otan3(0,90)6060BDCααα∴=∴∈∴=∴∠=o o o;2.(2013年上海市春季数学试卷(含答案))如图在正三棱锥111ABC A B C-16AA=异面直线1BC与1AA所成角的大小为6π求该三棱柱的体积【答案】[解]因为1CC 1AA所以1BC C ∠为异面直线1BC 与1AA 所成的角即1BC C∠=6π 在Rt 1BC C ∆113tan 6233BC CC BC C =⋅∠=⨯=从而23334ABCSBC ∆==因此该三棱柱的体积为1336183ABCV S AA ∆=⋅=⋅=3.(2013年普通等学校招生国统一招生试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分 如图在三棱锥ABCS -平面⊥SAB 平面SBC BC AB ⊥ABAS =过A 作SB AF ⊥垂足为F 点G E ,分别是棱SC SA ,的点求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥ABC SG FE B A C ACB【答案】证明:(1)∵AB AS =SB AF ⊥∴F 分别是SB 的点∵EF 分别是SASB 的点 ∴EF∥AB 又∵EF ⊄平面ABC AB ⊆平面ABC ∴EF∥平面ABC同理:FG∥平面ABC又∵EF I FG=F EFFG ⊆平面ABC∴平面//EFG 平面ABC(2)∵平面⊥SAB 平面SBC 平面SAB I 平面SBC =BC AF ⊆平面SAB AF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC 又∵BCAB ⊥ ABIAF=A ABAF⊆平面SAB∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA4.(2013年上海卷(理))如图在长方体ABCD-A 1B 1C 1D 1AB=2AD=1A 1A=1证明直线BC 1平行于平面DA 1C 并求直线BC 1到平面D 1AC 的距离D 1C 1B 1A 1D C BA【答案】因为ABCD-A 1B 1C 1D 1为长方体故1111//,AB C D AB C D =故ABC 1D 1为平行四边形故11//BC AD 显然B 不在平面D 1AC 上于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h虑三棱锥ABCD 1的体积以ABC 为底面可得111(12)1323V =⨯⨯⨯⨯= 而1AD C ∆115,2AC D C AD ===故132AD CS∆=所以13123233V h h =⨯⨯=⇒=即直线BC 1到平面D 1AC 的距离为235.(2013年湖北卷(理))如图AB 是圆O 的直径点C 是圆O 上异于,A B 的点直线PC ⊥平面ABC E F 分别是PA PC 的点 (I)记平面BEF 与平面ABC 的交线为l 试判断直线l 与平面PAC 的位置关系并加以证明; (II)设(I)的直线l 与圆O 的另一个交点为D且点Q 满足12DQ CP=u u u ru u u r 记直线PQ 与平面ABC 所成的角为θ异面直线PQ 与EF 所成的角为α二面角E l C --的大小为β求证:sin sin sin θαβ=【答案】解:(I)EF AC Q P AC ABC ⊆平面EF ABC ⊆平面 EF ABC ∴P 平面又EF BEF ⊆平面 EF l ∴P l PAC ∴P 平面(II)连接DF 用几何方法很快就可以得到求证(这一题用几何方法较快向量的方法很麻烦特别是用向量不能方便的表示角的正弦个人认为此题与新课程对立体几何的处理方向有很大的偏差)第19题6.(2013年普通等学校招生统一试广东省数学(理)卷(纯WORD版))如图1在等腰直角三角形ABC90BC=,D E分别是,AC ABA∠=︒6上的点2==O为BC的点将ADECD BE∆沿DE折起得到如图2所示的四棱锥A BCDE'-其3A O'=(Ⅰ) 证明:A O'⊥平面BCDE; (Ⅱ) 求二面角A CD B'--的平面角的余弦值【答案】(Ⅰ) 在图1易得3,32,22OC AC AD ===连结,OD OE 在OCD ∆由余弦定理可得222cos 455OD OC CD OC CD =+-⋅︒=由翻折不变性可知22A D '= 所以222A OOD A D ''+=所以A O OD '⊥理可证A O OE '⊥ 又OD OE O =I 所以A O '⊥平面BCDE (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H连结A H '因为A O '⊥平面BCDE 所以A H CD '⊥ 所以A HO '∠为二面角A CD B '--的平面角 结合图1可知H为AC点故322OH =从而22302A H OH OA ''=+=C D OBE'AHC OB DEACDOBE'A图图C D O x E 'A 向量法图y zB 所以15cos 5OH A HO A H '∠=='所以二面角A CD B '--的平面角的余弦值为155向量法:以O 点为原点建立空间直角坐标系O xyz -如图所示 则()0,0,3A '()0,3,0C -()1,2,0D -所以()0,3,3CA '=u u u r ()1,2,3DA '=-u u u u r设(),,n x y z =r为平面A CD '的法向量则0n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩r u u u r r u u u u r 即330230y z x y z ⎧+=⎪⎨-++=⎪⎩解得3y xz x=-⎧⎪⎨=⎪⎩令1x =得()1,1,3n =-r()0,0,3OA '=u u u rCDB 的一个法向量 所以315cos ,535n OA n OA n OA '⋅'===⋅'r u u u rr u u u r r u u u r A CD B'--的平面角的余弦值为1557.(2013年普通等学校招生统一试天津数学(理)试题(含答案))如图 四棱柱ABCD -A 1B 1C 1D 1 侧棱A 1A ⊥底面ABCD AB //DC AB ⊥AD AD = CD = 1 AA 1 = AB = 2 E 为棱AA 1的点(Ⅰ) 证明B 1C 1⊥CE ;(Ⅱ) 求二面角B 1-CE -C 1的正弦值(Ⅲ) 设点M在线段C1E上且直线AM与平面ADD1A1所成角的正弦值为2求线段AM的6长【答案】8.(2013年新课标1(理))如图三棱柱ABC-A 1B 1C 1CA=CBAB=A A 1∠BA A 1=60° (Ⅰ)证明AB ⊥A 1C;(Ⅱ)若平面ABC⊥平面AA 1B 1BAB=CB=2求直线A 1C 与平面BB 1C 1C 所成角的正弦值【答案】(Ⅰ)取AB 点E 连结CE 1A B 1A E∵AB=1AA 1BAA ∠=060∴1BAA ∆是正三角形∴1A E⊥AB ∵CA=CB ∴CE⊥AB∵1CE A E ⋂=E∴AB⊥面1CEA∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB 1EA ⊥AB又∵面ABC⊥面11ABB A 面ABC∩面11ABB A =AB∴EC⊥面11ABB A ∴EC⊥1EA∴EAEC 1EA 两两相互垂直以E 为坐标原点EAu u u r 的方向为x 轴正方向|EAu u u r |为单位长度建立如图所示空间直角坐标系O xyz -有题设知A(100)1A (030)C(003)B(-100)则BCu u u r =(103)1BB u u u r=1AA u u u r =(-103)1AC u u u r =(0-33)设n =(,,)x y z 是平面11CBB C 的法向量 则100BC BB ⎧•=⎪⎨•=⎪⎩u u u r u u u r n n 即3030x z x y ⎧+=⎪⎨+=⎪⎩可取n =(31-1)∴1cos ,AC u u u rn =11|AC AC •u u u r u u u rn |n ||105∴直线A 1C 与平面BB 1C 1C 所成角的正弦值为1059.(2013年陕西卷(理))如图 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形 O 为底面心 A 1O ⊥平面ABCD12AB AA ==(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小OD 1B 1C 1D ACBA 1【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面Θ;又因为在正方形ABCDBDC A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且在正方形AB CDAO = 1 .111=∆O A OA A RT 中,在OE C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设 [],所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,DD BB C A 111面⊥(证毕)(Ⅱ) 建立直角坐标系统使用向量解题 以O 为原点以OC 为X 轴正方向以OB 为Y 轴正方向则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒C A B A C B ,,,,)(由(Ⅰ)知 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OC OB C A n设平面OCB 1的法向量为D 1B 1C 1A 1,则0,0,2122=⋅=⋅OC n OB n n).1-,1,0(法向量2=n 为解得其中一个21221|||||||,cos |cos 212111=⋅=⋅⋅=><=n n n n n n θ所以平面OCB 1与平面BB 1D 1D 的夹角θ为3π 10.(2013年江西卷(理))如图四棱锥P ABCD -PA ,ABCD E BD ⊥平面为的中点G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,连接CE 并延长交AD于F(1)求证:AD CFG ⊥平面;(2)求平面BCP 与平面DCP 的夹角的余弦值【答案】解:(1)在ABD ∆因为E 是BD 的点所以1EA EB ED AB ====故,23BAD ABE AEB ππ∠=∠=∠=因为DAB DCB ∆≅∆所以EAB ECB ∆≅∆ 从而有FED FEA ∠=∠故,EF AD AF FD ⊥=又因为,PG GD =所以FG ∥PA 又PA ⊥平面ABCD所以,GF AD ⊥故AD ⊥平面CFG(3)以点A 为坐标原点建立如图所示的坐标系则33(0,0,0),(1,0,0),(,,0),(0,3,0)22A B C D(4)3(0,0,)2P 故1333333(0),(,),(,,0)2222222BC CP CD ==--=-u u u r u u u r u u u r ,,, 设平面BCP 的法向量111(1,,)n y z =u r则111130223330222y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩解得113323y z ⎧=-⎪⎪⎨⎪=⎪⎩即132(1,,)33n =-u r设平面DCP 的法向量222(1,,)n y z =u u r则222330223330222y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩解得2232yz ⎧=⎪⎨=⎪⎩即2(1,3,2)n =u u r从而平面BCP 与平面DCP 的夹角的余弦值为1212423cos 41689n n n n θ⋅===⋅u r u u r u r u u r11.(2013年四川卷(理))如图在三棱柱11ABC A B C -侧棱1AA ⊥底面ABC 12AB AC AA ==120BAC ∠=o1,D D 分别是线段11,BC B C 的点P 是线段AD 的点[](Ⅰ)在平面ABC 内试作出过点P 与平面1A BC 平行的直线l 说明理由并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)的直线l 交AB 于点M 交AC 于点N 求二面角1A A M N --的余弦值D 1DCBA 1B 1C 1A P【答案】解:()I 如图在平面ABC 内过点P 做直线l//BC 因为l 在平面1A BC 外BC 在平面1A BC 内由直线与平面平行的判定定理可知 l //平面1A BC由已知AB AC =D 是BC 的点所以BC AD ⊥则直线l AD ⊥因为1AA ⊥平面ABC 所以1AA ⊥直线l 又因为1,AD AA在平面11ADD A 内且AD 与1AA 相交所以直线平面11ADD A()II 解法一:连接1A P 过A 作1AE A P ⊥于E 过E 作1EF A M ⊥于F 连接AF由()I 知MN ⊥平面1AEA 所以平面1AEA ⊥平面1A MN所以AE ⊥平面1A MN 则1A M AE ⊥所以1A M ⊥平面AEF 则1A M ⊥AF故AFE ∠为二面角1A A M N --的平面角(设为θ)设11AA =则由12AB AC AA ==120BAC ∠=o有60BAD ∠=o2,1AB AD ==又P 为AD 的点所以M 为AB 的点且1,12AP AM == 在1Rt AA P V 152A P =;在1Rt A AM V 12A M =从而1115AA AP AE A P •==1112AA AM AF A M •==[]所以2sin 5AEAF θ==所以22215cos 1sin 155θθ⎛⎫=-=-= ⎪ ⎪⎝⎭故二面角1A A M N --的余弦值为155解法二:设11AA =如图过1A 作1A E 平行于11B C 以1A 为坐标原点分别以111,A E A D u u u r u u u u r 1AA u u u r 的方向为x 轴y 轴z 轴的正方向建立空间直角坐标系Oxyz (点O 与点1A 重合)则()10,0,0A ()0,0,1A因为P 为AD 的点所以,M N 分别为,AB AC 的点 故3131,,1,,,12222M N ⎛⎫⎛⎫- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭所以131,,122A M ⎛⎫= ⎪ ⎪⎝⎭u u u u r ()10,0,1A A =u u ur ()3,0,0NM =u u u u r设平面1AA M 的一个法向量为()1111,,n x y z =则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩u u u u u ru u u u r 即11110,0,n A M n A A ⎧•=⎪⎨•=⎪⎩u u u u ru u u r 故有()()()11111131,,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫•=⎪ ⎪ ⎪⎨⎝⎭⎪•=⎩ 从而1111310,220.x y z z ⎧++=⎪⎨⎪=⎩取11x =则13y=-所以()11,3,0n =-设平面1A MN 的一个法向量为()2222,,nx y z =则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩u u u u u ru u u u u r 即2120,0,n A M n NM ⎧•=⎪⎨•=⎪⎩u u u u r u u u u r 故有()()()22222231,,,,10,22,,3,0,00,x y z x y z ⎧⎛⎫•=⎪⎪ ⎪⎪⎝⎭⎨⎪•=⎪⎩从而2222310,2230.x y z x ⎧++=⎪⎨⎪=⎩取22y=则21z=-所以()20,2,1n=-设二面角1A A M N --的平面角为θ又θ为锐角则()()12121,3,00,2,115cos 525n n n n θ-•-•===••故二面角1A A M N --的余弦值为15512.(2013年普通等学校招生国统一招生试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分如图在直三棱柱111A B C ABC -AC AB ⊥2==AC AB 41=AA点D 是BC 的点(1)求异面直线B A 1与D C 1所成角的余弦值(2)求平面1ADC 与1ABA 所成二面角的正弦值【答案】本题主要察异面直线二面角空间向量等基础知识以及基本运算察运用空间向量解决问题的能力解:(1)以{}1,,AA AC AB 为为单位正交基底建立空间直角坐标系xyz A -则)0,0,0(A )0,0,2(B )0,2,0(C )4,0,0(1A )0,1,1(D )4,2,0(1C∴)4,0,2(1-=B A )4,1,1(1--=B A []∴10103182018,cos 111111==•>=<DC B AD C B A D C B A∴异面直线B A 1与D C 1所成角的余弦值为10103(2))0,2,0(=AC 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x m =∵)0,1,1(=AD )4,2,0(1=AC由1,AC m AD m ⊥⊥∴⎩⎨⎧=+=+0420z y y x 取1=z 得2,2=-=x y ∴平面1ADC 的法向量为)1,2,2(-=m设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-=•=><=mAC m AC m AC θ得35sin =θ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2013年普通等学校招生统一试大纲版数学(理)WORD 版含答案(已校对))如图四棱锥P ABCD -902,ABC BAD BC AD PAB ∠=∠==∆o,与PAD ∆都是等边三角形(I)证明:;PB CD ⊥ (II)求二面角A PD C--的大小【答案】14.(2013年普通等学校招生统一试山东数学(理)试题(含答案))如图所示在三棱锥P ABQ-PB⊥平面ABQ BA BP BQ==,,,D CE F分别是,,,AQ BQ AP BP的点2AQ BD=PD与EQ交于点G PC与FQ交于点H连接GH(Ⅰ)求证:AB GHP; (Ⅱ)求二面角D GH E--的余弦值【答案】解:(Ⅰ)证明:因为,,,D CE F分别是,,,AQ BQ AP BP的点所以EF∥AB DC∥AB所以EF∥DC又EF⊂平面PCD DC⊂平面PCD所以EF∥平面PCD又EF⊂平面EFQ平面EFQ I平面PCD GH=所以EF∥GH又EF∥AB所以AB∥GH(Ⅱ)解法一:在△ABQ2AQ BD=AD DQ=所以=90ABQ∠o即AB BQ⊥因为PB⊥平面ABQ所以AB PB⊥又BP BQ B=I所以AB⊥平面PBQ由(Ⅰ)知AB∥GH 所以GH⊥平面PBQ又FH⊂平面PBQ所以GH FH⊥同理可得GH HC⊥所以FHC∠为二面角D GH E--的平面角设2BA BQ BP===连接PC在t R△FBC由勾股定理得2FC=在t R△PBC由勾股定理得5PC=又H为△PBQ的重心所以1533 HC PC==同理53 FH=在△FHC由余弦定理得552499cos5529FHC+-∠==-⨯即二面角D GH E--的余弦值为4 5 -解法二:在△ABQ2AQ BD=AD DQ=所以90ABQ∠=又PB⊥平面ABQ所以,,BA BQ BP两两垂直以B为坐标原点分别以,,BA BQ BP所在直线为x轴y 轴z 轴建立如图所示的空间直角坐标系设2BA BQ BP ===则(1,0,1)E (0,0,1)F (0,2,0)Q (1,1,0)D (0,1,0)C (0,0,2)P 所以(1,2,1)EQ =--u u u r (0,2,1)FQ =-u u u r (1,1,2)DP =--u u u r (0,1,2)CP =-u u u r设平面EFQ的一个法向量为111(,,)m x y z =u r由0m EQ ⋅=u r u u u r 0m FQ ⋅=u r u u u r得111112020x y z y z -+-=⎧⎨-=⎩ 取11y =得(0,1,2)m =u r设平面PDC 的一个法向量为222(,,)n x y z =r由0n DP ⋅=r u u u r 0n CP ⋅=r u u u r得222222020x y z y z --+=⎧⎨-+=⎩ 取21z=得(0,2,1)n =r所以4cos ,5m n m n m n ⋅==u r ru r r u r r因为二面角D GH E--为钝角所以二面角D GH E--的余弦值为45-15.(2013年湖南卷(理))如图5在直棱柱1111//ABCD A B C D AD BC -中,90,,1BAD AC BD BC ∠=⊥=o 13AD AA ==(I)证明:1AC B D ⊥; (II)求直线111B C ACD与平面所成角的正弦值【答案】解: (Ⅰ)ACBB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱ΘDB AC BDBD B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
2013年全国各地高考文科数学试题分类汇编:立体几何(解析版

2013年全国各地高考文科数学试题分类汇编:立体几何一、选择题1 . (2013年高考重庆卷(文某几何体的三视图如图所示 , 则该几何体的表面积为 (A. 180 B . 200C . 220D . 240【答案】 D2 . (2013年高考课标Ⅱ卷 (文一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1,(1,1,0,(0,1,1,(0,0,0, 画该四面体三视图中的正视图时 , 以 zOx 平面为投影面 , 则得到正视图可以为(A.B.C.D.【答案】 A3 . (2013年高考课标Ⅰ卷(文某几何函数的三视图如图所示 , 则该几何的体积为 (A. 168π+B. 88π+C. 1616π+D. 816π+ 【答案】 A4 . (2013年高考大纲卷(文已知正四棱锥 1111112, ABCD A B C D AA AB CD BDC -=中, 则与平面所成角的正弦值等于 ( A.23 D. 13 【答案】 A5 . (2013年高考四川卷(文一个几何体的三视图如图所示 , 则该几何体可以是A. 棱柱B. 棱台C. 圆柱D. 圆台【答案】 D6 . (2013年高考浙江卷(文已知某几何体的三视图 (单位 :cm如图所示 , 则该几何体的体积是(A.108cm 3B.100 cm3C.92cm 3D.84cm 3 【答案】 B图 2俯视图侧视图正视图7 . (2013年高考北京卷(文如图 , 在正方体 1111ABCD A B C D -中 , P 为对角线1BD 的三等分点 , 则 P 到各顶点的距离的不同取值有A.3个B.4个C.5个D.6个【答案】 B8 . (2013年高考广东卷(文某三棱锥的三视图如图 2所示 , 则该三棱锥的体积是( A.16 B.13C.23D. 1【答案】 B9 . (2013年高考湖南(文已知正方体的棱长为 1, 其俯视图是一个面积为 1的正方形 , 的矩形 , 则该正方体的正视图的面积等于 ______B.1【答案】 D10. (2013年高考浙江卷(文设 m.n 是两条不同的直线,α.β是两个不同的平面 , 则(A. 若 m ∥ α,n∥ α,则 m ∥ nB. 若 m ∥ α,m∥ β,则α∥ βC. 若 m ∥ n,m ⊥ α,则n ⊥ αD. 若 m ∥ α,α⊥ β,则 m ⊥ β 【答案】 C11. (2013年高考辽宁卷 (文已知三棱柱 111A B C A B C-的 6个顶点都在球 O 的球面上 , 若 34AB AC ==, , AB AC ⊥, 112AA =, 则球 O 的半径为 (A.2B.C.132D.【答案】 C12. (2013年高考广东卷(文设 l 为直线, , αβ是两个不同的平面 , 下列命题中正确的是 (A. 若//l α, //l β, 则//αβB. 若l α⊥, l β⊥, 则//αβC. 若l α⊥, //l β, 则//αβD. 若αβ⊥, //l α, 则l β⊥【答案】 B13. (2013年高考山东卷(文一个四棱锥的侧棱长都相等 , 底面是正方形 , 其正(主视图如右图所示该四棱锥侧面积和体积分别是(A. B. 83 C. 81, 3+ D.8,8【答案】 B14. (2013年高考江西卷(文一几何体的三视图如右所示 , 则该几何体的体积为( A. 200+9π B. 200+18π C. 140+9π D. 140+18π 【答案】 A 二、填空题15. (2013年高考课标Ⅱ卷 (文已知正四棱锥 O-ABCD 的体积为, 底面边长为 , 则以 O 为球心 ,OA 为半径的球的表面积为 ________.【答案】24π16. (2013年高考湖北卷(文我国古代数学名著《数书九章》中有“ 天池盆测雨” 题 :在下雨时 , 用一个圆台形的天池盆接雨水 . 天池盆盆口直径为二尺八寸 , 盆底直径为一尺二寸 , 盆深一尺八寸 . 若盆中积水深九寸 , 则平地降雨量是__________寸 . (注 :①平地降雨量等于盆中积水体积除以盆口面积 ; ②一尺等于十寸【答案】 317. (2013年高考课标Ⅰ卷(文已知 H 是球 O 的直径 AB 上一点 , :1:2AH HB =, AB ⊥平面α, H 为垂足, α截球 O 所得截面的面积为π, 则球 O 的表面积为 _______. 【答案】92π; 18. (2013年高考北京卷(文某四棱锥的三视图如图所示 , 该四棱锥的体积为__________.【答案】 319. (2013年高考陕西卷(文某几何体的三视图如图所示 , 则其表面积为________. 【答案】π320. (2013年高考大纲卷 (文已知圆 O 和圆 K 是球 O 的大圆和小圆 , 其公共弦长等于球 O 的半径 , 3602OK O K =,且圆与圆所在的平面所成角为 , 则球 O 的表面积等于 ______. 【答案】16π21. (2013年上海高考数学试题(文科已知圆柱Ω的母线长为 l , 底面半径为 r , O 是上地面圆心 , A 、 B 是下底面圆周上两个不同的点 , BC 是母线 , 如图 . 若直线 OA 与 BC 所成角的大小为π6, 则 1r=________.22. (2013年高考天津卷 (文已知一个正方体的所有顶点在一个球面上 . 若球的体积为 92π, 则正方体的棱长为23. (2013年高考辽宁卷(文某几何体的三视图如图所示 , 则该几何体的体积是____________.【答案】1616π-24. (2013年高考江西卷(文如图 , 正方体的底面与正四面体的底面在同一平面α上 , 且 AB//CD,则直线 EF 与正方体的六个面所在的平面相交的平面个数为_____________.【答案】 425. (2013年高考安徽(文如图 , 正方体 1111ABCD A B C D -的棱长为 1, P 为BC 的中点 , Q 为线段 1CC 上的动点 , 过点 , , A P Q 的平面截该正方体所得的截面记为 S , 则下列命题正确的是 __________(写出所有正确命题的编号.①当 102CQ <<时 , S 为四边形 ; ②当 12CQ =时 , S 为等腰梯形 ; ③当 34CQ =时 , S 与 11C D 的交点 R 满足113C R =; ④当 314CQ <<时 , S 为六边形 ; ⑤当 1CQ =时 , S【答案】①②③⑤三、解答题26. (2013年高考辽宁卷(文如图 , . AB O PA O C O 是圆的直径, 垂直圆所在的平面, 是圆上的点 (I求证 :BC PAC ⊥平面 ;(II设//. Q PA G AOC QG PBC ∆为的中点, 为的重心,求证:平面【答案】27. (2013年高考浙江卷 (文如图 , 在在四棱锥 P-ABCD 中 ,PA ⊥面ABCD,AB=BC=2,AD=CD=7,PA=3, ∠ ABC=120°,G 为线段 PC 上的点 . (Ⅰ证明 :BD⊥面 PAC ;(Ⅱ若 G 是 PC 的中点 , 求 DG 与 APC 所成的角的正切值 ; (Ⅲ若 G 满足 PC ⊥面 BGD, 求 PGGC的值 .【答案】解 :证明 :(Ⅰ由已知得三角形ABC是等腰三角形 , 且底角等于 30°, 且6030AB CB AD CD ABD CBD ABD CBD BAC BD DB =⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭且 , 所以 ; 、 BD AC ⊥, 又因为 PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭;(Ⅱ设 AC BD O =, 由 (1知 DO PAC ⊥, 连接 GO , 所以 DG 与面 APC 所成的角是 DGO ∠, 由已知及(1知:1, 2BO AO CO DO =====,12tan 2OD GO PA DGO GO ==⇒∠===, 所以 DG 与面 APC 所成的角的正切值是; (Ⅲ由已知得到 :PC===, 因为 PC BGD PC GD ⊥∴⊥, 在 PDC∆中, PD CD PC====, 设223 1072 PGPG x CG x x x PG x GCGC=∴=-∴-=--∴==== 28. (2013年高考陕西卷(文如图 , 四棱柱 ABCD -A 1B 1C 1D 1的底面 ABCD 是正方形 , O 为底面中心 , A 1O ⊥平面ABCD,1 AB AA =1A(Ⅰ证明 : A 1BD // 平面 CD 1B 1;(Ⅱ求三棱柱 ABD -A 1B 1D 1的体积 .【答案】解 : (Ⅰ设111ODB 线段的中点为 . 11111111//DBBDDCBAABCDDBBD ∴-的对应棱是和. 的对应线段是棱柱和同理,111111DCBAABCDOAAO -为平行四边形四边形且且11111111//////OCO AOCOAOCOAOC AOOAAO ⇒=⇒∴111 1 1 1 1 1 1 1 // , . //B CD BD A O D B COOBDOACOOA 面面且⇒==⇒.(证毕(Ⅱ的高是三棱柱面 ABD DBAOAABCDOA -∴⊥11111.在正方形 AB CD中 ,AO = 1 . . 1 11=∆OAOAART 中, 在112 (2121111111=⋅⋅=⋅=-∆-OASV ABD DBA ABD ABDDBA的体积三棱柱 . 所以 , 1 111111=--ABD DBAVABDDBA 的体积三棱柱 .29. (2013年高考福建卷 (文如图 , 在四棱锥 P ABCD -中 , PD ABCD⊥面 , //AB DC , AB AD⊥, 5BC =, 3DC =, 4AD =, 60PAD∠=.(1当正视图方向与向量 AD 的方向相同时 , 画出四棱锥 P ABCD-的正视图 .(要求标出尺寸 , 并画出演算过程 ; (2若 M 为 PA 的中点 , 求证 :// DM PBC面 ;(3求三棱锥 D PBC-的体积 .【答案】解法一 :(Ⅰ在梯形 ABCD 中 , 过点 C 作 CE AB ⊥, 垂足为 E , 由已知得 , 四边形 ADCE 为矩形 , 3AE CD == 在Rt BEC ∆中 , 由 5BC =, 4CE =, 依勾股定理得 :3BE =, 从而 6AB =又由 PD ⊥平面 ABCD 得 , PD AD ⊥从而在Rt PDA ∆中 , 由 4AD =, 60PAD ∠=︒,得 PD = 正视图如右图所示 :(Ⅱ取 PB 中点 N , 连结 MN , CN 在PAB ∆中 , M 是 PA 中点 ,∴ MN AB , 132MN AB ==, 又 CD AB , 3CD = ∴ MN CD , MN CD =∴四边形 MNCD 为平行四边形 , ∴ DM CN 又 DM ⊄平面 PBC , CN ⊂平面PBC ∴ DM 平面 PBC(Ⅲ 13D PBC P DBC DBC V V S PD --∆==⋅又6PBC s ∆=, PD =,所以 D PBC V -= 解法二 : (Ⅰ同解法一(Ⅱ取 AB 的中点 E , 连结 ME , DE 在梯形 ABCD 中 , BE CD , 且 BE CD = ∴四边形 BCDE 为平行四边形∴ DE BC , 又 DE ⊄平面 PBC , BC ⊂平面 PBC ∴ DE 平面 PBC , 又在PAB ∆中 , ME PBME ⊄平面 PBC , PB ⊂平面 PBC∴ ME 平面 PBC . 又 DEME E =,∴平面 DME 平面 PBC , 又 DM ⊂平面 DME ∴ DM 平面 PBC (Ⅲ同解法一30. (2013年高考广东卷(文如图 4, 在边长为 1的等边三角形 ABC 中 , , D E 分别是 , AB AC边上的点 , AD AE =, F 是 BC 的中点 , AF 与 DE 交于点 G , 将ABF ∆沿 AF 折起 , 得到如图 5所示的三棱锥 A BCF -,其中 BC =. (1 证明 :DE //平面 BCF ; (2 证明 :CF ⊥平面 ABF ; (3 当 23AD =时 , 求三棱锥 F DEG -的体积 F DEG V -. 图 4 【答案】 (1在等边三角形 ABC 中 , AD AE = AD AEDB EC ∴=, 在折叠后的三棱锥 A BCF -中也成立 , //DE BC ∴ ,DE ⊄平面 BCF ,BC ⊂平面 BCF , //DE ∴平面 BCF ;(2在等边三角形 ABC 中 , F 是 BC 的中点 , 所以 AF BC ⊥① ,12BF CF ==.在三棱锥 A BCF -中 ,2BC =, 222BC BF CF CF BF ∴=+∴⊥②BF CF F CF ABF ⋂=∴⊥平面 ;(3由 (1可知 //GE CF , 结合 (2可得 GEDFG ⊥平面 .111111132323323324F DEG E DFG V V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎝⎭31. (2013年高考湖南(文如图 2. 在直菱柱 ABC-A 1B 1C 1中 , ∠BAC=90°,AB=AC=,AA 1=3,D是 BC 的中点 , 点E 在菱 BB 1上运动 .(I 证明 :AD⊥ C 1E;(II 当异面直线 AC,C 1E 所成的角为 60°时 , 求三菱子 C 1-A 2B 1E 的体积.【答案】解 : (Ⅰ 11C CBB AD E 面为动点,所以需证因为⊥.AD BB ABC AD ABC BB C B A ABC ⊥⇒⊂⊥∴-11111, 面且面是直棱柱AD BC BC D ABC RT ⊥∴∆的中点, 为是等腰直角且又 .. 1111111E C AD C CBB E C C CBB AD B BB BC ⊥⇒⊂⊥⇒=⋂面且面由上两点,且 (证毕(Ⅱ 660, //111111=∆⇒︒=∠∴AE E C A RT E C A A C CA 中, 在 .的高是三棱锥是直棱柱中, 在 1111111111. 2C B A E EB C B A ABC EB E B A RT -∴-=∆⇒ .. 3232213131111111111111的体积为所以三棱锥 E B A C EB S V V C B A C B A E E B A C -⋅=⋅⋅=⋅⋅==∆-- 32. (2013年高考北京卷(文如图 , 在四棱锥 P ABCD -中 , //AB CD , AB AD ⊥, 2CD AB =, 平面 PAD ⊥底面 ABCD , PA AD ⊥, E 和 F 分别是 CD 和 PC 的中点 , 求证 : (1PA ⊥底面ABCD ;(2//BE 平面 PAD ;(3平面 BEF ⊥平面 PCD【答案】 (I因为平面 PAD ⊥平面 ABCD, 且 PA 垂直于这个平面的交线 AD 所以 PA 垂直底面 ABCD.(II因为 AB ∥ CD,CD=2AB,E为 CD 的中点所以 AB ∥ DE, 且 AB=DE 所以ABED 为平行四边形 ,所以 BE ∥ AD, 又因为 BE ⊄平面 PAD,AD ⊂平面 PAD 所以 BE ∥平面 PAD.(III因为 AB ⊥ AD, 而且 ABED 为平行四边形所以 BE ⊥ CD,AD ⊥ CD, 由 (I 知 PA ⊥底面 ABCD,所以 PA ⊥ CD, 所以 CD ⊥平面 PAD所以 CD ⊥ PD, 因为 E 和 F 分别是 CD 和 PC 的中点所以 PD ∥ EF, 所以 CD ⊥ EF, 所以 CD ⊥平面 BEF, 所以平面 BEF ⊥平面PCD.33. (2013年高考课标Ⅰ卷(文如图 , 三棱柱 111ABC A B C -中 , CA CB =, 1AB AA =, 160BAA ∠=. (Ⅰ证明 :1AB AC ⊥; (Ⅱ若 2AB CB ==, 1AC =, 求三棱柱 111ABC A B C -的体积 .11A1【答案】【答案】 (I取 AB 的中点 O, 连接 OC O 、 1OA O 、 1A B , 因为CA=CB,所以 OC AB ⊥, 由于 AB=A A1, ∠ BA A 1=600, 故, AA B ∆为等边三角形 , 所以 OA 1⊥ AB.因为 OC ⨅ OA 1=O,所以 AB ⊥平面 OA 1C. 又 A 1CC 平面 OA 1C, 故 AB ⊥AC. (II由题设知12ABC AA B ∆∆与都是边长为的等边三角形,12AAB 都是边长为的等边三角形,所以2211111. OC OA AC AC OA OA OC =+⊥又 ,故111111111, --=3.ABC ABCOC AB O OA ABC OA ABC A B CABC S A B C V S OA=⊥∆=⨯=因为所以平面 , 为棱柱的高,又的面积 ABC 的体积34. (2013年高考山东卷 (文如图 , 四棱锥 P ABCD -中 , , AB AC AB PA⊥⊥, , 2AB CD AB CD=∥ , , , , ,E F G M N 分别为,, , ,PBAB BC PDPC 的中点(Ⅰ求证 :CE PAD∥平面 ; (Ⅱ求证 :EFG EMN ⊥平面平面【答案】35. (2013年高考四川卷(文如图 , 在三棱柱 11ABC A B C -中 , 侧棱 1AA ⊥底面 ABC , 122AB AC AA ===, 120BAC ∠=, 1, D D 分别是线段 11, BC B C 的中点 , P 是线段 AD 上异于端点的点 .(Ⅰ在平面 ABC 内 , 试作出过点 P 与平面 1A BC 平行的直线 l , 说明理由 , 并证明直线 l ⊥平面 11ADD A ; (Ⅱ设 (Ⅰ中的直线 l 交 AC 于点 Q , 求三棱锥 11A QC D -的体积 .(锥体体积公式 :13V Sh =, 其中 S 为底面面积 , h 为高【答案】解 :(Ⅰ如图 , 在平面 ABC 内 , 过点 P 作直线 BC l //, 因为 l 在平面BC A 1外 , BC 在平面 BC A 1内 , 由直线与平面平行的判定定理可知 , //l 平面 1A BC .由已知 , AC AB =, D 是 BC 中点 , 所以 BC ⊥ AD , 则直线 AD l ⊥, 又因为1AA ⊥底面 ABC , 所以 l AA ⊥1,又因为 AD , 1AA 在平面 11A ADD 内 , 且 AD 与 1AA 相交 , 所以直线⊥l 平面11A ADD(Ⅱ过 D 作 AC DE ⊥于 E , 因为 1AA ⊥平面 ABC , 所以 DE AA ⊥1,又因为 AC , 1AA 在平面 C C AA 11内 , 且 AC 与 1AA 相交 , 所以⊥DE 平面C C AA 11, 由 2==AC AB , ∠ BAC ︒=120, 有 1=AD , ∠ DAC ︒=60, 所以在△ACD 中 , 232==AD DE , 又 1211111=⋅=∆AA C A S AQC , 所以 6123131111111=⋅⋅=⋅==--QC A QC A D D QC A S DE V V 因此三棱锥 11A QC D -的体积为 6336. (2013年高考湖北卷(文如图 , 某地质队自水平地面 A , B , C 三处垂直向地下钻探 , 自 A 点向下钻到 A 1处发现矿藏 , 再继续下钻到 A 2处后下面已无矿 , 从而得到在 A 处正下方的矿层厚度为 121A A d =. 同样可得在 B , C 处正下方的矿层厚度分别为 122B B d =, 123C C d =, 且 123d d d <<. 过 AB , AC 的中点 M , N 且与直线 2AA 平行的平面截多面体 111222A B C A B C -所得的截面 DEFG 为该多面体的一个中截面 , 其面积记为 S 中 .(Ⅰ证明 :中截面 DEFG 是梯形 ;(Ⅱ在△ ABC 中 , 记 BC a =, BC 边上的高为 h , 面积为 S . 在估测三角形 ABC 区域内正下方的矿藏储量 (即多面体111222A B C A B C -的体积 V 时 , 可用近似公式 V S h =⋅估中来估算 . 已知1231( 3V d d d S =++, 试判断 V 估与 V 的大小关系 , 并加以证明 .C 11BCB 1【答案】 (Ⅰ依题意 12A A ⊥平面 ABC , 12B B ⊥平面 ABC , 12C C ⊥平面ABC , 所以 A 1A 2∥ B 1B 2∥ C 1C 2. 又 121A A d =, 122B B d =, 123C C d =, 且123d d d << . 因此四边形 1221A A B B 、 1221A A C C 均是梯形 .由 2AA ∥平面 MEFN , 2AA ⊂平面 22AA B B , 且平面 22AA BB平面 MEFN ME =,可得 AA 2∥ ME , 即 A 1A 2∥ DE . 同理可证 A 1A 2∥ FG , 所以 DE ∥ FG . 又 M 、 N 分别为 AB 、 AC 的中点 ,则 D 、 E 、 F 、 G 分别为 11A B 、 22A B 、 22A C 、 11AC 的中点 , 即DE 、 FG 分别为梯形 1221A A B B 、 1221A A C C 的中位线 .因此 12121211( ( 22DE A A B B d d =+=+, 12121311( ( 22FG A A C C d d =+=+,而 123d d d <<, 故 DE FG <, 所以中截面 DEFG 是梯形 . (Ⅱ V V <估 . 证明如下 :由 12A A ⊥平面 ABC , MN ⊂平面 ABC , 可得 12A A MN ⊥. 而 EM ∥ A 1A 2, 所以 EM MN ⊥, 同理可得 FN MN ⊥. 由 MN 是△ ABC 的中位线 , 可得 1122MN BC a ==即为梯形 DEFG 的高 , 因此 13121231( (2 22228DEFG d d d d a aS S d d d ++==+⋅=++中梯形 ,即 123(2 8ahV S h d d d =⋅=++估中 . 又 12S ah =, 所以 1231231( ( 36ahV d d d S d d d =++=++.于是 1231232131( (2 [( (]6824ah ah ahV V d d d d d d d d d d -=++-++=-+-估 . 由 123d d d <<, 得 210d d ->, 310d d ->, 故 V V <估 .37. (2013年高考课标Ⅱ卷(文如图 , 直三棱柱 ABC-A 1B 1C 1中 ,D,E 分别是AB,BB 1的中点 .第 20题图(1 证明 : BC1//平面 A 1CD;(2 设 AA 1= AC=CB=2,AB=2, 求三棱锥 C 一 A 1DE 的体积.【答案】38. (2013年高考大纲卷(文如图 , 四棱锥902, P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中, , 与都是边长为 2的等边三角形 .(I证明 :; PB CD ⊥ (II求点 . A PCD 到平面的距离【答案】 (Ⅰ证明 :取 BC 的中点 E, 连结 DE, 则 ABED 为正方形 .过 P 作 PO ⊥平面 ABCD, 垂足为 O.连结 OA,OB,OD,OE.由PAB ∆和PAD ∆都是等边三角形知 PA=PB=PD,所以 OA=OB=OD,即点 O 为正方形 ABED 对角线的交点 ,故 OE BD ⊥, 从而 PB OE ⊥.因为 O 是 BD 的中点 ,E 是 BC 的中点 ,所以 OE//CD.因此 , PB CD ⊥.(Ⅱ解 :取 PD 的中点 F, 连结 OF, 则 OF//PB.由 (Ⅰ知 , PB CD ⊥, 故 OF CD ⊥.又 12OD BD ==OP = 故POD ∆为等腰三角形 , 因此 , OF PD ⊥. 又 PD CD D =, 所以 OF ⊥平面PCD.因为 AE//CD,CD ⊂平面 PCD, AE ⊄平面 PCD, 所以 AE//平面 PCD.因此 ,O 到平面 PCD 的距离 OF 就是 A 到平面 PCD 的距离 , 而 112OF PB = =, 所以 A 至平面 PCD 的距离为 1.39. (2013年高考安徽(文如图 , 四棱锥 P ABCD -的底面 ABCD 是边长为 2的菱形 , 60BAD ∠=.已知 2, PB PD PA === .(Ⅰ证明 :PC BD ⊥(Ⅱ若 E 为 PA 的中点 , 求三菱锥 P BCE -的体积.【答案】解 :(1证明 :连接 , BD AC 交于 O 点PB PD = PO BD ∴⊥又 ABCD 是菱形 BD AC ∴⊥而 AC PO O ⋂= BD ∴⊥面 PAC ∴BD ⊥ PC(2 由 (1BD ⊥面 PAC︒⨯⨯⨯==45sin 3262121PAC PEC S S △△ =32236=⨯⨯ 111132322P BEC B PEC PEC V V S BO --∆==⋅⋅=⨯⨯= 40. (2013年上海高考数学试题(文科如图 , 正三棱锥 O ABC -底面边长为 2, 高为 1, 求该三棱锥的体积及表面积 .第19题图B【答案】41. (2013年高考天津卷(文如图 , 三棱柱 ABC -A 1B 1C 1中 , 侧棱 A 1A ⊥底面 ABC , 且各棱长均相等 . D , E , F 分别为棱 AB , BC , A 1C 1的中点 .(Ⅰ证明 EF //平面 A 1CD ;(Ⅱ证明平面 A 1CD ⊥平面 A 1ABB 1;(Ⅲ求直线 BC 与平面 A 1CD 所成角的正弦值 .【答案】42. (2013年高考重庆卷(文 (本小题满分 12分 ,(Ⅰ小问 5分 ,(Ⅱ小问 7分如题 (19图 , 四棱锥 P ABCD -中 , PA ⊥底面 A B C D, PA =, 2BC CD ==, 3ACB ACD π∠=∠=. (Ⅰ求证 :BD ⊥平面 PAC ;(Ⅱ若侧棱 PC 上的点 F 满足 PF 7 FC ,求三棱锥 P BDF 的体积. 【答案】43.(2013 年高考江西卷(文如图,直四棱柱 ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD= ,AA1=3,E 为CD 上一点,DE=1,EC=3 (1 证明:BE⊥平面 BB1C1C; (2 求点 B1 到平面 EA1C1 的距离【答案】解.(1证明:过 B 作 CD 的垂线交 CD 于 F,则 BF AD 2, EF AB DE 1, FC 2 在 Rt BFE中,BE= 3 ,Rt BFC中,BC= 6 . 2 2 2 在 BCE中,因为BE BC =9=EC ,故 BE BC 由 BB1 平面ABCD,得BEBB1,所以BE 平面BB1C1C (2 三棱锥E A1 B1C1的体积V= AA1 S A1B1C1= 2 1 3 在Rt A1 D1C1中,A1C1= A1 D12 D1C12 =3 2 , EA1=AD ED AA1 =2 3 同理, EC1= EC CC1 =3 2 , 2 2 2 2 2 因此 S A C E 3 5 .设点 B1 到平面 EAC 的体积 1 EAC 1 1 1 1 的距离为 d,则三棱锥B 1 1 1 10 V= d S A1EC1= 5d ,从而 5d 2, d 3 5。
2013届全国各地高考押题数学(文科)精选试题分类汇编7立体几何(2)

2013届全国各地高考押题数学(文科)精选试题分类汇编7:立体几何(2)1.(2013届江西省高考压轴卷数学文试题)如图,在三棱锥A BCD-中,90ABC BCD CDA ︒∠=∠=∠=,6AC BC CD ===,设顶点A 在底面BCD 上的射影为E . (Ⅰ)求证:CE BD ⊥;(Ⅱ)设点G 在棱AC 上,且2CG GA =,试求二面角C EG D --的余弦值.【答案】证明:(I)方法一:由AE ⊥平面BCD 得AE ⊥CD ,又AD ⊥CD ,则CD ⊥平面AED , 故CD DE ⊥,同理可得CB BE ⊥,则BCDE 为矩形,又BC CD =, 则BCDE 为正方形,故CE BD ⊥方法二:由已知可得AB BD AD ===,设O 为BD 的中点,则,AO BD CO BD ⊥⊥,则BD ⊥平面AOC ,故平面BCD ⊥平面AOC ,则顶点A 在底面BCD 上的射影E 必在OC ,故CE BD ⊥. (II)方法一:由(I)的证明过程知OD ⊥平面AEC ,过O 作OF EG ⊥,垂足为F ,则易证得DF EG ⊥,故OFD ∠即为二面角C EG D --的平面角,由已知可得6AE =,则2AE AG AC =⋅,故EG AC ⊥,则2CGOF ==,又OD =则DF =,故cos OFD ∠=,即二面角C EG D --AGEDB方法二: 由(I)的证明过程知BCDE 为正方形,如图建立坐标系,则(0,0,0),(0,6,0),(0,0,6),(6,0,0),(6,6,0)E D A B C,可得(2,2,4)G ,则)4,2,2(),0,6,0(==→→EG ED ,易知平面CEG的一个法向量为)0,6,6(-=→BD ,设平面DEG 的一个法向量为)1,,(y x n =→,则由⎪⎩⎪⎨⎧=⋅=⋅→→→→00EG n ED n 得)1,0,2(-=→n ,则510cos =⋅=〉⋅〈→→→→→→nBD n BD n BD ,即二面角C EG D --2.(2013届湖北省高考压轴卷 数学(文)试题)如图,1AA 、1BB 为圆柱1OO 的母线,BC 是底面圆O 的直径,D 、E 分别是1AA 、1CB 的中点,1DE CBB ⊥平面.(1) 证明://DE ABC 平面; (2)求四棱锥11C ABB A -与圆柱1OO 的体积比;(3)若1BB BC =,求直线1CA 与平面1BB C 所成角的正弦值.【答案】(1)如图,连接.E OA O O E 、、分别为1CB BC 、的中点,EO ∴是1BB C ∆的中位线,1//EO BB ∴且112EO BB =.又111//,DA BB AA BB =,故11,2DA BB EO DA ==∴//EO 且DA EO =, ∴四边形AOED 是平行四边形,即//DE OA ,又,,//DE ABC OA ABC DE ABC ⊄⊂∴平面平面平面. (2)如图,连接CA .由题知1DE CBB ⊥平面,且由(1)知//DE OA ,1,AO CBB AO BC ∴⊥∴⊥平面,AC AB ∴==.BC是底面圆O的直径,CA AB∴⊥.又1AA 是圆柱的母线,1AA ABC ∴⊥平面,11,AA CA AA AB A ∴⊥=又,11CA AA B B ∴⊥平面,即CA 为四棱锥11C ABB A -的高. 设圆柱高为h ,底面半径为r ,则))112212=,33C ABB A V r h V h hr π-=⋅=圆柱, 1122223:3C ABB A hrV V r h ππ-∴==圆柱. (3)如图,作过C 的母线1CC ,连接11B C ,则11B C 是上底面圆1O 的直径,连接11A O ,则11//AO AO ,又111111,AO CBB C AO CBB C ⊥∴⊥平面平面,连接1CO ,则11ACO ∠为直线1CA 与平面1BB C 所成的角.111,AC AO r ====,∴在11Rt AO C ∆中,11111sin A O ACO A C ∠==.∴直线1CA 与平面1BB C 3.(2013届山东省高考压轴卷文科数学)在如图所示的几何体中,AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,AD =DE =2AB ,F 为CD 的中点.(Ⅰ)求证:AF ∥平面BCE ;(Ⅱ)求证:平面BCE ⊥平面CDE.【答案】证明:(1)如图,取CE 的中点G ,连接FG ,BG . ∵F 为CD 的中点,∴GF ∥DE ,且GF =12DE .∵AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB ∥DE .∴GF ∥AB . 又AB =12DE ,∴GF =AB .∴四边形GF AB 为平行四边形,则AF ∥BG .∵AF ⊄平面BCE ,BG ⊂平面BCE ,∴AF ∥平面BCE .(2)∵△ACD 为等边三角形,F 为CD 的中点,∴AF ⊥CD .∵DE ⊥平面ACD ,AF ⊂平面ACD ,∴DE ⊥AF .又CD ∩DE =D ,∴AF ⊥平面CDE . ∵BG ∥AF ,∴BG ⊥平面CDE .∵BG ⊂平面BCE ,∴平面BCE ⊥平面CDE .4.(2013届福建省高考压轴卷数学文试题)如图(1),在等腰梯形CDEF 中,CB.DA 是梯形的高,2AE BF ==,AB =,现将梯形沿CB.DA 折起,使EF//AB 且2EF AB =,得一简单组合体ABCDEF 如图(2)所示,已知,,M N P 分别为,,AF BD EF 的中点.(Ⅰ)求证://MN 平面BCF ; (Ⅱ)求证:AP ⊥平面DAE .DCBAEFMNPFEABCD【答案】解:(Ⅰ)证明:连结AC ,∵四边形ABCD 是矩形,N 为BD 中点,MNPFEABCD∴N 为AC 中点,在ACF ∆中,M 为AF 中点 ∴//MN CF∵CF ⊂平面BCF ,MN ⊄平面BCF //MN ∴平面BCF(Ⅱ)证明:依题意知,DA AB DA AE ⊥⊥ 且AB AE A =I ∴AD ⊥平面ABFE ∵AP ⊂平面ABFE ∴AP AD ⊥∵P 为EF中点,∴FP AB ==结合//AB EF ,知四边形ABFP 是平行四边形 ∴//AP BF ,2AP BF ==而2,AE PE ==∴222AP AE PE += ∴90EAP ∠=,即AP AE ⊥ 又AD AE A =I ∴AP ⊥平面ADE5.(2013届天津市高考压轴卷文科数学)如图,在四棱锥ABCD -PGFE 中,底面ABCD 是直角梯形,侧棱垂直于底面,AB //DC ,∠ABC =45o,DC =1,AB =2,PA =1. (Ⅰ)求PD 与BC 所成角的大小; (Ⅱ)求证:BC ⊥平面PAC ; (Ⅲ)求二面角A -PC -D 的大小.【答案】(Ⅰ)取的AB 中点H ,连接DH ,易证BH//CD ,且BD =CD所以四边形BHDC 为平行四边形,所以BC//DH所以∠PDH 为PD 与BC 所成角因为四边形,ABCD 为直角梯形,且∠ABC =45o, 所以DA ⊥AB又因为AB =2DC =2,所以AD =1, 因为Rt△PAD 、Rt△DAH 、Rt△PAH 都为等腰直角三角形,所以PD =DH =PH,故∠PDH =60o(Ⅰ)连接CH ,则四边形ADCH 为矩形, ∴AH =DC 又AB =2,∴BH =1 在Rt△BHC 中,∠ABC =45o, ∴CH =BH =1,CB∴AD =CH =1,AC∴AC 2+BC 2=AB 2∴BC ⊥AC 又PA 平面ABCD ∴PA ⊥BC ∵PA ∩AC =A ∴BC ⊥平面PAC(Ⅲ)如图,分别以AD 、AB 、AP 为x 轴,y 轴,z 轴 建立空间直角坐标系,则由题设可知: A (0,0,0),P (0,0,1),C (1,1,0),D (1,0,0), ∴AP =(0,0,1),PC =(1,1,-1)设m =(a ,b ,c )为平面PAC 的一个法向量, 则0AP PC ⎧=⎪⎨=⎪⎩m m ,即00c a b c =⎧⎨+-=⎩设1a =,则1b =-,∴m =(1,-1,0)同理设n =(x ,y ,z ) 为平面PCD 的一个法向量,求得n =(1,1,1)∴1cos ,2===m n m n m n 所以二面角A -PC -D 为60o6.(2013新课标高考压轴卷(一)文科数学)如图,四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1) 求证:CE ⊥平面PAD;(11)若PA =AB =1,AD =3,CD ,∠CDA =45°,求四棱锥P-ABCD 的体积.【答案】(1)证明:因为PA⊥平面ABCD,CE ⊂平面ABCD,所以PA⊥CE,因为AB⊥AD,CE∥AB,所以CE⊥AD,又PA ⋂AD=A,所以CE ⊥平面PAD(2)解:由(1)可知CE⊥AD,在直角三角形ECD 中,DE=CD cos 451⋅=,CE=CD sin 451⋅=. 又因为AB=CE=1,AB∥CE,所以四边形ABCE 为矩形,所以ABCD ABCE BCD S S S ∆=+=12AB AE CE DE ⋅+⋅=15121122⨯+⨯⨯=,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD 的体积等于115513326ABCD S PA ⋅=⨯⨯= 7.(2013届辽宁省高考压轴卷数学文试题)如图所示,已知圆O 的直径AB 长度为4,点D 为线段AB 上一点,且13AD DB =,点C 为圆O 上一点,且BC =.点P 在圆O 所在平面上的正投影为点D ,PD BD =.(Ⅰ)求证:CD ⊥平面PAB ;(Ⅱ)求PD 与平面PBC 所成的角的正弦值.【答案】解答:(Ⅰ)连接CO ,由3AD DB =知,点D 为AO 的中点,又∵AB 为圆O 的直径,∴AC CB ⊥,由BC =知,60CAB ∠=, ∴ACO ∆为等边三角形,从而CD AO ⊥ ∵点P 在圆O 所在平面上的正投影为点D , ∴PD ⊥平面ABC ,又CD ⊂平面ABC , ∴PD CD ⊥,由PD AO D =得,CD ⊥平面PAB(注:证明CD ⊥平面PAB 时,也可以由平面PAB ⊥平面ACB 得到,酌情给分.) (Ⅱ)法1:过D 作⊥DH 平面PBC 交平面于点H ,连接PH ,则DPH ∠即为所求的线面角由(Ⅰ)可知CD =,3PD DB ==,∴111113333232P BDC BDC V S PD DB DC PD -∆=⋅=⋅⋅⋅=⨯⨯=又PB ==,PC ==,BC ==∴PBC ∆为等腰三角形,则12PBC S ∆=⨯=. 由P BDC D PBC V V --=得,553=DH ∴55sin ==∠PD DH DPH法2:由(Ⅰ)可知CD =,3PD DB ==,过点D 作DE CB ⊥,垂足为E ,连接PE ,再过点D 作DF PE ⊥,垂足为F∵PD ⊥平面ABC ,又CB ⊂平面ABC , ∴PD CB ⊥,又PD DE D =, ∴CB ⊥平面PDE ,又DF ⊂平面PDE , ∴CB DF ⊥,又CB PE E =,∴DF ⊥平面PBC ,故DPF ∠为所求的线面角在Rt DEB ∆中,3sin 302DE DB =⋅=,PE ==,55sin sin ==∠=∠PE DE DPE DPF 8.(2013届陕西省高考压轴卷数学(文)试题)已知直角梯形ABCD中,//AD BC ,122AD AB BC ===,90ABC ∠=︒,PAB ∆是等边三角形,平面PAB ⊥平面ABCD .(Ⅰ)求证:BD DC ⊥;(Ⅱ)求三棱锥P BCD -的体积.【答案】【解析】(Ⅰ)∵2AD =,2AB =,45AD AB ADB DBC ⊥⇒∠=∠=︒ 过D 作DM BC ⊥,垂足为M ,则2DM AB MC ===∴45DCM ∠=︒,∴90BDC ∠=o ,∴BD DC ⊥.(Ⅱ)21132P BCD V -===. 9.(2013届湖南省高考压轴卷数学(文)试题)如图,已知在四棱锥PABCD 中,底面ABCD 是矩形,且AD=2,AB=1,PA ⊥平面ABCD,E,F 分别是线段AB,BC 的中点.(1)证明:PF ⊥FD ;(2)判断并说明PA 上是否存在点G ,使得EG ∥平面PFD ;(3)若PB 与平面ABCD 所成的角为45°,求二面角A PD F 的余弦值.【答案】(1)证明:∵P A ⊥平面ABCD ,∠BAD =90°,AB =1,AD =2,建立如图所示的空间直角坐标系A xyz ,则A (0,0,0),B (1,0,0),F (1,1,0),D (0,2,0).不妨令P (0,0,t ),∵PF =(1,1,-t ),DF =(1,-1,0), ∴PF DF ⋅=1×1+1×(-1)+(-t )×0=0,即PF ⊥FD (2)解:设平面PFD 的法向量为n =(x ,y ,z ), 由0,0,n PF n DF ⎧⋅=⎪⎨⋅=⎪⎩得⎩⎪⎨⎪⎧x +y -tz =0,x -y =0,令z =1,解得:x =y =t2.∴n =⎝ ⎛⎭⎪⎫t 2,t2,1. 设G 点坐标为(0,0,m ),E ⎝ ⎛⎭⎪⎫12,0,0,则EG =⎝ ⎛⎭⎪⎫-12,0,m , 要使EG ∥平面PFD ,只需EG ·n =0,即⎝ ⎛⎭⎪⎫-12×t2+0×t 2+1×m =m -t 4=0,得m =14t ,从而满足AG =14AP 的点G即为所求(3)解:∵AB ⊥平面P AD ,∴AB 是平面P AD 的法向量,易得AB =(1,0,0),又∵P A ⊥平面ABCD ,∴∠PBA 是PB 与平面ABCD 所成的角,得∠PBA =45°,P A =1,平面PFD 的法向量为n =⎝ ⎛⎭⎪⎫12,12,1.∴cos<AB ,n >=AB n AB n⋅=1214+14+1=66.故所求二面角A PD F 的余弦值为6610.(2013届重庆省高考压轴卷数学文试题)在直角梯形ABCD 中90ABC DAB ∠=∠=,30CAB ∠=,BC=1,AD=CD,把△DAC 沿对角线AC 折起后如图所示(点D 记为点P),点P 在平面ABC 上的正投影E 落在线段AB 上,连接PB.若F 是AC 的中点,连接PF,EF. (1) 求证:平面PEF⊥AC. (2) 求直线PC 与平面PAB 所成的角的大小.AC【答案】解:1.AC90,30,1ABC DAB CAB BC ∠=∠=∠==3,2,60.2tan 30BCAB AC DAC AD CD AC ∴===∠=∴===,.PA PC PF AC =∴⊥E P ABC PE ABC PE AC ∴⊥∴⊥点为点在平面上的正投影,平面.,,PF PE P PF PEF PE PEF AC PEF =⊂⊂∴⊥平面平面平面【D 】2. PE ABC PE BC ⊥∴⊥平面,,,BC AB PE AB E PE PAB BC PAB ⊥=⊂∴⊥平面平面CPB PC PAB ∴∠为直线与平面所成的角.1t sin =.2BC PC ∴∠在R CBP 中,BC=1,PC=DC=2,CPB=00,30.<∠∴∠=CPB<9CPB ∴直线PC 与平面PAB 所成的角为 3011.(2013届浙江省高考压轴卷数学文试题)如图,在斜三棱柱111ABC A B C -中,侧面11AA B B ⊥底面ABC ,侧棱1AA 与底面ABC 成60°的角,12AA =.底面ABC 是边长为2的正三角形,其重心为G 点, E 是线段1BC 上一点,且113BE BC =. (1)求证:GE //侧面11AA B B ;(2)求平面1B GE 与底面ABC 所成锐二面角的正切值;(3)在直线..AG 上是否存在点T,使得AG T B ⊥1?若存在,指出点T 的位置;若不存在,说明理由.【答案】【解析】解法1:(1)延长B 1E 交BC 于点F,11B EC ∆∽△FEB,BE=21EC 1,∴BF=21B 1C 1=21BC,从而点F 为BC 的中点.∵G 为△ABC 的重心,∴A、G 、F 三点共线.且11//,31AB GE FB FE FA FG ∴==, 又GE ⊄侧面AA 1B 1B,∴GE//侧面AA 1B 1B.(2)在侧面AA 1B 1B 内,过B 1作B 1H⊥AB,垂足为H,∵侧面AA 1B 1B⊥底面ABC,∴B 1H⊥底面ABC.又侧棱AA 1与底面ABC 成60°的角,AA 1=2,∴∠B 1BH=60°,BH=1,B 1H=.3 在底面ABC 内,过H 作HT⊥AF,垂足为T,连B 1T,由三垂线定理有B 1T⊥AF,又平面B 1CE 与底面ABC 的交线为AF,∴∠B 1TH 为所求二面角的平面角. ∴AH=AB+BH=3,∠HAT=30°,∴HT=AH 2330sin =︒.在Rt△B 1HT 中,332tan 11==∠HT HB TH B ,从而平面B 1GE 与底面ABC (3)(2)问中的T 点即为所求,T 在AG 的延长线上,距离A 点233处. 12.(2013届北京市高考压轴卷文科数学)如图所示,在正方体1111ABCD A B C D -中,E 、F 分别为DD 1、DB的中点.(I)求证:EF//平面ABC 1D 1; (II)求证:1EF B C ⊥..【答案】(Ⅰ)连结1BD ,在B DD 1∆中,E 、F 分别为1D D ,DB 的中点,则11111111////EF D BD B ABC D EF ABC D EF ABC D ⎫⎪⊂⇒⎬⎪⊄⎭平面平面平面(Ⅱ)⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂⊥⊥B BC AB D ABC C B D ABC AB BC C B ABC B 111111111 面面⇒111111B C ABC D BD ABC D ⊥⎫⇒⎬⊂⎭平面平面111//B C BD EF BD ⊥⎫⎬⎭1EF B C ⇒⊥13.(2013届全国大纲版高考压轴卷数学文试题(二))已知矩形ABCD 中,1AB AD ==,将ABD ∆沿BD 折起,使点A 在平面BCD 内的射影落在DC 上.(Ⅰ)求证:平面ADC ⊥平面BCD ; (Ⅱ)求点C 到平面ABD 的距离;(Ⅲ)若E 为BD 中点,求二面角B AC E --的大小.【答案】证明:(Ⅰ)∵点A 在平面BCD 上的投影落在DC 上,即平面ACD 经过平面BCD 的垂线,∴平面ACD ⊥平面BCD (Ⅱ)如图所示建立空间直角坐标系,则(0,0,0),(1,0,0)(0,C B D ∵A 的投影在DC 上,令00(0,,)A y z 由0||1DA AB DA ⋅== 即2200022000010y z y z ++=+++=FC DBAE1A 1B 1C 1D(0,A ∴,由22(1,,),(0,AB AD =-=-, 求得平面ABD的一个法向量为(2,1,1)n =--, 而(0,AC =,∴C 到平面BCD 的距离为||2||AC n d n ⋅==(Ⅲ)由22(1,,),(1,0,0)BA CB =--=,求得平面BAC 的一个法向量1(0,1,1)n= 221(0,,),(,0,2AC AE=-=,求得平面AEC 的一个法向量2n = 由图可见B AC E --为锐二面角,设此平面角为θ,则1212||2cos ||||n n n n θ⋅==⋅45θ∴=︒14.(2013届上海市高考压轴卷数学(文)试题)本题共2小题,第(Ⅰ)小题6分,第(Ⅱ)小题8分.如图,在长方体1111ABCD A B C D -中, 111,2AD A A AB ===,点E 在棱AB 上. (Ⅰ)求异面直线1D E 与1A D 所成的角;(Ⅱ)若二面角1D EC D --的大小为45︒,求点B 到平面1D EC 的距离.【答案】解法一:(1)连结1AD .由11AA D D 是正方形知11AD A D ⊥.∵AB ⊥平面11AA D D ,∴1AD 是1D E 在平面11AA D D 内的射影. 根据三垂线定理得11AD D E ⊥,则异面直线1D E 与1A D 所成的角为90︒.(Ⅱ)作DF CE ⊥,垂足为F ,连结1D F ,则1CE D F ⊥.所以1DFD ∠为二面角1D EC D --的平面角,145DFD ∠=︒.于是111,DF DD D F ===,易得RtRt BCE CDF ∆≅∆,所以2CE CD ==,又1BC =,所以BE =. 设点B 到平面1D EC 的距离为h ,则由于1,B CED D BCE V V --=即1111113232CE D F h BE BC DD ⋅⋅⋅=⋅⋅⋅,因此有11CE D F h BE BC DD ⋅⋅=⋅⋅,即=,∴h =. 解法二:分别以1,,DD DC DA 为x 轴,y 轴,z 轴,建立空间直角坐标系. (Ⅰ)由1(1,0,1)A ,得1(1,0,1)DA =,设(1,,0)E a ,又1(0,0,1)D ,则1(1,,1)D E a =-.∵111010DA D E ⋅=+-=∴11DA D E ⊥,则异面直线1D E 与1A D 所成的角为90︒. (Ⅱ)(0,0,1)=m 为面DEC 的法向量,设(,,)x y z =n 为面1CED 的法向量,则(,,)x y z =n|||cos ,|cos 45||||⋅<>===︒=m n m n m n ,∴222z x y =+. ①由(0,2,0)C ,得1(0,2,1)D C =-,则1D C ⊥n ,即10D C ⋅=n ,∴20y z -= ②由①、②,可取2)=n ,又(1,0,0)CB =,所以点B 到平面1D EC 的距离||CB d ⋅===n |n |. 15.(2013届四川省高考压轴卷数学文试题)如图,在三棱柱ABC —111A B C 中,侧棱垂直底面,90ACB ∠=︒,12AC BC CC ===. (1)求证:11AB BC ⊥;(2)求二面角1C —1AB —1A 的大小.【答案】方法一(1)BC AC ⊥,1CC AC ⊥且C CC BC =1 ,∴⊥AC 平面11CBB C , 又⊂1BC 平面11CBB C ,∴1BC AC ⊥,11BC C B ⊥且C C B AC =1∴⊥1BC 平面C AB 1,又⊂1AB 平面C AB 1∴ 11BC AB ⊥(2)取11B A 的中点为H ,在平面11ABB A 内过H 作1AB HQ ⊥于Q ,连接Q C 1 则⊥H C 1平面11ABB A ,所以11AB H C ⊥ , 而且H HQ H C = 1所以⊥1AB 平面HQ C 1,所以⊥1AB Q C 1 所以QH C 1∠是二面角111A AB C --的平面角 , 又21=H C在AB A 1∆内,解得36=HQ , 所以 3tan 11==∠HQHC QH C 所以二面角111A AB C --的平面角为060方法2: 建立空间直角坐标系(以C 为原点,CA 为x 轴正半轴,CB 为y 轴正半轴,1CC 为z 轴正半轴) 则)2,0,2(),2,0,0(),2,2,0(),0,2,0(),0,0,2(111A C B B A (1)),2,2,2(1-=AB)2,2,0(1-=BC022)2(20211=⨯+-⨯+⨯-=⋅∴BC AB11BC AB ⊥∴(2)取11B A 的中点为H ,则)2,1,1(H .平面11A AB 的法向量)0,1,1(1=C 设平面11AB C 的法向量),,(z y x =)0,2,0(),2,0,2(111=-=B C A C⎩⎨⎧==-∴02022y z x z x y ==∴,0,令1=z∴得平面11AB C 的一个法向量)1,0,1(=2122|011011|cos =⨯⨯+⨯+⨯=∴θ 又所求二面角111A AB C --的平面角为锐角, 所以二面角111A AB C --的平面角为06016.(2013届海南省高考压轴卷文科数学)如图,在四棱台ABCD ﹣A 1B 1C 1D 1中,D 1D⊥平面ABCD,底面ABCD 是平行四边形,AB=2AD,AD=A 1B 1,∠BAD=60°.(Ⅰ)证明:AA 1⊥BD;(Ⅱ)证明:CC 1∥平面A 1BD.【答案】分析:(Ⅰ) 由D 1D⊥平面ABCD,可证 D 1D⊥BD.△ABD 中,由余弦定理得 BD 2,勾股定理可得 AD⊥BD,由线面垂直的判定定理可证 BD⊥面ADD 1A 1,再由线面垂直的性质定理可证 BD⊥AA 1.(Ⅱ)连接AC 和A 1C 1,设AC∩BD=E,先证明四边形ECC 1A 1为平行四边形,可得CC 1∥A 1E,再由线面平行的判定定理可证CC 1∥平面A 1BD.解答:证明:(Ⅰ)∵D 1D⊥平面ABCD,∴D 1D⊥BD. 又AB=2AD,AD=A 1B 1,∠BAD=60°,△ABD 中,由余弦定理得 BD 2=AD 2+AB 2﹣2AB•ADcos60°=3AD 2,∴AD 2+BD 2=AB 2, ∴AD⊥BD,又 AD∩DD 1=D,∴BD⊥面ADD 1A 1.由 AA 1⊂面ADD 1A 1,∴BD⊥AA 1.(Ⅱ)证明:连接AC 和A 1C 1,设 AC∩BD=E,由于底面ABCD 是平行四边形,故E 为平行四边形ABCD 的 中心,由棱台的定义及AB=2AD=2A 1B 1,可得 EC∥A 1C 1,且 EC=A 1C 1,故ECC 1A 1为平行四边形,∴CC 1∥A 1E,而A 1E ⊂平面A 1BD,∴CC 1∥平面A 1BD17.(2013届全国大纲版高考压轴卷数学文试题(一))如图,已知四棱锥E- ABCD 的底面为菱形,且∠ABC=600,AB =EC =2,AE =BE =2.(I)求证:平面EAB ⊥平面ABCD ;(II)求二面角A- EC- D 的余弦值.【答案】解法1:(1)证明:取AB 的中点O,连接EO ,CO∵2==EB AE ,AB =2 ∴△ABC 为等腰三角形∴AB EO ⊥,EO =1 又∵AB =BC ,∠ABC =600∴△ABC 为等边三角形 ∴3=CO ,又EC =2∴222CO EO EC += 即CO EO ⊥,⊥EO 平面ABCD ,且⊂EO 平面EAB∴ 平面E AB⊥平面ABCD,(2)过A 作AH⊥CE 于H 点,过H 作HM//CD,又Rt△EDO 解得DE=22, 所以222DE EC DC =+即EC DC ⊥,所以MH⊥CE,因此∠AHM 为二面角A EC D --的平面角,通过计算知27=AH ,21=MH ,1=AM ,所以7722127214147cos =⨯⨯-+=∠AHM所以二面角D EC A --的余弦值为772 解法2.(1)设AC∩BD=O,如图,以O 为原点,OHMOMyzOC,OB 为x,y 轴建立空间直角坐标系O-xyz 设E(m,n,t ),则A(-1,0,0),C(1,0,0), B(0,3,0), D(0,-3,0),∴),,1(t n m AE +=, ),3,(t n m BE -=,),,1(t n m CE -=所以⎪⎪⎩⎪⎪⎨⎧=++-==+-+==+++=4)1(23(2)1(222222222222t n m CE t n m BE t n m AE 解得:1,23,21==-=t n m所以)1,23,21(-E ,因为AB 的中点)0,33,21(-M ,所以)1,0,0(=ME 即ME⊥平面ABCD,又⊂ME 平面EAB,所以平面EAB⊥平面ABCD, (2))1,23,23(-=CE ,)0,0,2(=AC ,)0,3,1(=DC,分别设平面AEC,平面ECD 的法向量为),,(),,,(z y x m z y x n '''==则⎪⎩⎪⎨⎧==⋅=+⋅+⋅-=⋅0202323x n AC z y x n CE 令y= -2,得)3,2,0(-=n ⎪⎩⎪⎨⎧='+'=⋅='+'⋅+'⋅-=⋅0302323y x n DC z y x n CE令1-='y ,)32,1,3(-=m 7724762||||,cos =⨯+=⋅⋅>=<m n m n m n所以二面角D EC A --的余弦值为772 解法3:(1)(同解法1);(2)以AB 中点O 为坐标原点,以OB 所在直线y 轴,OE 所在直线为z 轴, 建立空间直角坐标系如图所示,则)0,1,0(-A ,)0,0,3(C ,)0,2,3(-D ,)1,0,0(E)0,1,3(=AC ,)1,0,3(-=EC .)0,2,0(=DC设平面DEC 的法向量),,(z y x n =⎪⎩⎪⎨⎧==⋅=-=⋅0203y n DC z x n CE ,令1=z ,得)1,0,33(=n 设平面EAC 的法向量),,(z y x m '''=⎪⎩⎪⎨⎧='+'=⋅='-'=⋅0303y x n AC z x n CE ,令1='z ,得)1,1,33(-=m 7723237131||||,cos =⨯+=⋅⋅>=<m n m n m n∴二面角D EC A --的余弦值为772 18.(2013届安徽省高考压轴卷数学文试题)( )如图所示,在棱长为2的正方体1111ABCD A B C D -中,E F、分别为1DD 、DB 的中点.(1)求证:1EF B C ⊥;(2)求三棱锥1B EFC V -的体积.FE D 1C 1B 1A 1DCBA【答案】【解析】(1)证明:FE D 1C 1B 1A 1DCB A1111111B C ABB C BC AB BC ABC D AB BC B ⊥⎫⎪⊥⎪⇒⎬⊂⎪⎪=⎭、面111111B C ABC D BD ABC D ⊥⎫⇒⎬⊂⎭面面1111//B C BD EF B C EF BD ⊥⎫⇒⊥⎬⎭(2)11CF BDD B ⊥面1CF EFB ∴⊥面,且CF BF ==1112EF BD B F =====13B E ===22211EF B F B E ∴+=即190EFB ︒∠=9分111111111133232B EFC C B EF B EF V V S CF EF B F CF --∆∴==⨯⨯=⨯⨯⨯⨯=⨯=19.(2013届新课标高考压轴卷(二)文科数学)如图所示,在正三棱柱ABC -A 1B 1C 1中,底面边长和侧棱长都是2,D 是侧棱CC 1上任意一点,E 是A 1B 1的中点. (I)求证:A 1B 1//平面ABD; (II)求证:AB⊥CE;(III)求三棱锥C-ABE 的体积.【答案】解(Ⅰ)证明:由正三木棱住的性质知11B A ∥AB,因为ABD B A ABD AB 平面,平面⊄⊂11, 所以11B A ∥平面ABD.(Ⅱ)设AB 中点为G,连结GE,GC.GC AB G ABC ⊥∴∆为中心,为正三角形,且 又EG∥1AA ,GE AB AB AA ⊥∴⊥,1又GEC AB G GE CG 平面所以⊥=⋂,而CE AB GEC CE ⊥⊂,所以平面(Ⅲ)由题意可知:ABC ABC E ABE c S EG V V ∆--⨯⨯==3120.(2013届广东省高考压轴卷数学文试题)将棱长为a 正方体截去一半(如图7所示)得到如图8所示的几何体,点E ,F 分别是BC ,DC 的中点.(1)证明:1AF ED ⊥;(2)求三棱锥1E AFD -的体积.【答案】(1)证:连接DE ,交AF 于点O ∵1D D ⊥平面ABCD ,AF ⊂平面ABCD ∴1D D AF ⊥∵点E ,F 分别是BC ,1D C 的中点,∴DF CE =又∵AD DC =,90ADF DCE ∠=∠=D 1DC BA 1A EF O A 1 B 1C 1D 1AB C D图7D 1 D C B A 1 AEF 图8∴ADF ∆≌DCE ∆,∴AFD DEC ∠=∠又∵90CDE DEC ∠+∠=∴90CDE AFD ∠+∠=∴()18090DOF CDE AFD ∠=-∠+∠=,即AF DE ⊥ 又∵1D D DE D = ∴AF ⊥平面1D DE 又∵1ED ⊂平面1D DE ∴1AF ED ⊥(2)解:∵1D D ⊥平面ABCD ,∴1D D 是三棱锥1D AEF -的高,且1D D a =∵点E ,F 分别是BC ,1D C 的中点,∴2a DF CF CE BE ==== ∴AEF ADF FCE ABE ABCD S S S S S ∆∆∆∆=---正方形2111222a AD DF CF CE AB BE =-⋅⋅-⋅⋅-⋅⋅2222234848a a a a a =---= ∴11E AFD D AEF V V --=113AEF S D D ∆=⋅⋅2313388a a a =⋅⋅=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m , m / / ,则 ;④若 m / / , n / / ,且 m / / n ,则 / / .其中正确命题的
序号是 A.①④ 【答案】B ( B.②③ C.②④ D.①③ )
【 解 析 】 ① 当 , m / / 时 , 不 一 定 成 立 , 所 以 错 误 .② 成 立 .③ 成 立.④ m / / , n / / ,且 m / / n , , 也可能相交,所以错误.所以选 B.
பைடு நூலகம்
B.
( A.8 B.
)
20 3
C.
17 3
D.
14 3
【 答 案 】 C 【 解 析 】 几 何 体 是 正 方 体 截 去 一 个 三 棱 台 ,
1 1 1 17 V 23 ( 2 2 ) 2 3 2 2 3
15. (2013 届北京市高考压轴卷理科数学)一个几何体的三视图如图 l 所示,其中正视图是
r ( 6 2) R
4 . (2013 届山东省高考压轴卷理科数学)(2013 青岛市一模)已知 m 、 n 、 l 是三条不同的 直线, 、 、 是三个不同的平面,给出以下命题: ①若 m , n / / ,则 m / / n ; ②若 m , n , , l , m l ,则
2 2
)
,
由
面
积
8 2
得
长
为
4,
则
S S侧 +2S底 =(8 2+2 2 4) +2 1 2 2 2 20 8 2 = . 2
11. (2013 届江西省高考压轴卷数学理试题)在空间,下列命题正确的是 ( A.平行直线的平行投影重合 B.平行于同一直线的两个平面平行 C.垂直于同一平面的两个平面平行 D.垂直于同一平面的两条直线平行 【答案】D【解析】由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理 可以得出答案. 12. (2013 届新课标高考压轴卷(二)理科数学)某几何体的俯视图是如右图所示的矩形, 正视图(或称主视图)是一个底边长为 8、高为 5 的等腰三角形,侧视图(或称左视图)是 一个底边长为 6、高为 5 的等腰三角形.则该儿何体的体积为
一个正三角形,则该几何体的体积为
( C. 3
)
A.1
B.
3 3
D.
2 3 3
5
【答案】B 【解析】由三视图可知,此几何体为三棱锥,如图 1,其中正视图为 △PAC ,是边长为 2 的 正 三 角 形 , PD 平面ABC , 且 PD 3 , 底 面 △ABC 为 等 腰 直 角 三 角
1 1 3 V 3 2 2 3 2 3 ,故选
2 . ( 2013 届湖北省高考压轴卷 数学(理)试题)已知直角三角形 ABC, 其三边分为 a,b,c,(a>b>c).分别以三角形的 a 边,b 边,c 边所在直线为轴,其余各边旋转一周形成的 曲面围成三个几何体,其表面积和体积分别为 S1,S2,S3 和 V1,V2,V3.则它们的关系为 ( A.S 1 >S 2 >S 3 , C.S 1 >S 2 >S 3 , V 1 >V 2 >V 3 V 1 =V 2 =V 3 B.S 1 <S 2 <S 3 , V 1 <V 2 <V 3
1
r
四个小球的球心分别为 A,B,C,D,大球半径为
R
.则四面体 A-BCD 是棱长为
2r
的正四面
体,将正四面体 A-BCD 补形成正方体,则正方体棱长为
2r
,大球球心 O 为体对角线中点,
易求
OA
1 6 6 ( 2r ) 2 ( 2r ) 2 ( 2 r ) 2 r R r OA r 2 2 ,所以 2 ,解得
)
3 2
B
1 .2
C
3 . 3
D
3 . 6
【答案】D 10. (2013 届山东省高考压轴卷理科数学)右图是一个几何体的正(主)视图和侧(左)视图, 其俯视图是面积为 8 2 的矩形.则该几何体的表面积是
( A. 20 8 2 B. 24 8 2 C.8 D.16
)
【答案】 ( A. 【解析】由已知俯视图是矩形,则该几何体为一个三棱柱,根据三视图的性质,俯视图 的 矩 形 宽 为
3 . (2013 届全国大纲版高考压轴卷数学理试题) 在半径为 R 的球内放入大小相等的 4 个小 球,则小球半径 r 的最大值为 ( A. )
62 R
B.
2 1 R
C.
1 R 4
D.
1 R 3
( )
【答案】
A.当三个小球在下、第四个小球在上相切时,小球的半径最大.设小球的最大半径为 ,
)
D.S 1 <S 2 <S 3 , V 1 =V 2 =V 3
【
答
案
】
B
【
解
析
】
:
1 bc bc S1 b c ,V1 a 3 a a
2
1 S 2 a c c 2 ,V2 b c 2 3 1 S3 a b b 2 ,V3 b 2 c 3 则选 B
)
4
( A.24 B.80 C.64 D.240 【答案】B 13. (2013 届重庆省高考压轴卷数学理试题)设三棱柱的侧棱垂直于底面,所有棱长都为 a , 顶点都在一个球面上,则该球的表面积为 (
)
)
11 2 D. 5 a 2 a 3 【答案】 解析:根据题意条件可知三棱柱是棱长都为 a 的正三棱柱,则其外接球的半径为
( A.3 B.2 C.1 D.0 【答案】答案:A 考点:简单空间图形的三视图. 分析:由三棱柱的三视图中,两个矩形,一个三角形可判断①的对错,由四棱柱的三视图 中,三个均矩形,可判断②的对错,由圆柱的三视图中,两个矩形,一个圆可以判断③的真 假.本题考查的知识点是简单空间图形的三视图 ,其中熟练掌握各种几何体的几何特征 进而判断出各种几何体中三视图对应的平面图形的形状是解答本题的关键. 解答:解:存在正三棱柱,其三视图中有两个为矩形,一个为正三角形满足条件,故①为真 命题; 存在正四棱柱,其三视图均为矩形,满足条件,故②为真命题; 对于任意的圆柱,其三视图中有两个为矩形,一个是以底面半径为半径的圆,也满足条件, 故③为真命题; 7 . (2013 届浙江省高考压轴卷数学理试题)已知直线 m、l ,平面 、 ,且 m , l , 给出下列命题: ①若 ∥ ,则 m⊥ l ; ③若 m⊥ l ,则 ∥ ; ②若 ⊥ ,则 m∥ l ; ④若 m∥ l ,则 ⊥
2013 届全国各地高考押题数学(理科)精选试题分类汇编 7:立 体几何
一、选择题 1 . (2013 届北京市高考压轴卷理科数学)已知 m 、 n 是两条不同的直线, 、 是两个不 同的平面,给出下列命题: ① 若 , m / / , 则 ;② 若 m , n , 且 m n, 则 ;③ 若
cos B
AB 2 BC 2 AC 2 1 , 所 以 B , 当 D 点 和 C 点 重 合 2 AB BC 2 3
时, BM AB cos
)
其中正确命题的个数是 ( A.1 B.2 C.3 D.4 【答案】B 【解析】①④对,②③错 8 . (2013 届湖南省高考压轴卷数学(理)试题)某几何体的三视图如图所示,则该几何体 的表面积为 ( A.2 2 B. 2 C.(2 2 +1)π D.(2 2 +2)π
)
)
3
【答案】A 9 . (2013 届四川省高考压轴卷数学理试题)已知三棱锥底面是边长为 1 的正三角形,侧棱 长均为 2,则侧棱与底面所成角的余弦值为 ( A.
锥 A BCD ,若该三棱锥的顶点 A 在底面 BCD 的射影 M 在线段 BC 上,设 BM x , 则 x 的取值范围是 ( A. 0, 2 7 )
B. 0, 7
C.
7, 2 7
D. 2 7,3 7
【答案】C 【解析】本题考查立体几何中的折叠问题和解三角形问题,直接计算比较复 杂 , 可以采用极限思想特殊化法 , 在 ABC 中 AB 2 7, BC 3 7, AC 7 , 由余弦 定理得
m n ;③若 n / / m , m ,则 n / / ;④若 / / , / / ,则 / / .
其中正确命题的序号是( ) A.②④ B.②③ C.③④ D.①③ 【答案】 A. 【解析】①中直线还可能异面;③中需指明直线 n 不在平面内. 5 . (2013 届全国大纲版高考压轴卷数学理试题)在正方形 ABCD 中, AB 4, 沿对角线 ( ( ) )
A
c
B
E 是 CD 的中点, 又 在
BO 平面ACD BE CD
,
,BE 是点 B 到直线 CD 的距离.
Rt BOE
中,求
BE 2 3
.
6 . (2013 届海南省高考压轴卷理科数学)如图是长和宽分别相等的两个矩形.给定下列三
2
个命题: ①存在三棱柱,其正(主)视图、俯视图如下图; ②存在四棱柱,其正(主)视图、俯视图如下图; ③存在圆柱,其正(主)视图、俯视图如下图. 其中真命题的个数是
形, AB BC 2 ,所以体积为
B.
图1
16. (2013 新课标高考压轴卷(一)理科数学)一个几何体的三视图如图所示,其中俯视图 与左视图均为半径是 2 的圆,则这个几何体的表面积是
