第10章 联立方程计量经济学模型
计量经济学之联立方程模型

计量经济学之联立方程模型引言联立方程模型(Simultaneous Equation Model,简称SEM)是计量经济学中的一个重要分析工具,用于研究多个经济变量之间的相互关系。
通过建立一组方程,可以理解变量之间的联动效应,并进行预测和政策分析。
本文将介绍联立方程模型的基本概念、建模步骤和常见的估计方法等内容。
基本概念联立方程模型的定义联立方程模型是指由多个方程组成的一种数学模型,用于描述多个经济变量之间的关系。
每个方程都包含一个因变量和若干个解释变量,以及一个误差项。
联立方程模型的核心思想是通过解方程组,得到各个变量的估计值,进而分析它们之间的关系。
基本假设在建立联立方程模型时,需要对变量之间的关系进行假设。
常见的基本假设有:1.线性关系假设:方程中的变量之间的关系是线性的。
2.独立性假设:各个方程中的误差项是独立的,即它们之间不存在相关性。
3.零条件均值假设:解释变量的条件均值为零,即解释变量的期望与误差项无关。
4.同方差假设:各个方程中的误差项方差相等。
建模步骤建立联立方程模型的步骤如下:步骤一:确定变量根据研究主题和数据可获得的变量,确定需要建立模型的变量集合。
步骤二:构建方程根据经济理论和实际问题,构建联立方程模型的方程形式。
每个方程包含一个因变量和若干个解释变量。
步骤三:参数估计通过收集数据,对联立方程模型进行参数估计。
常用的估计方法有最小二乘估计(Ordinary Least Squares,简称OLS)和广义矩估计(Generalized Method of Moments,简称GMM)等。
步骤四:模型诊断对估计得到的模型进行诊断,检验模型的拟合优度、参数显著性和误差项的假设等。
常见的诊断方法有虚拟变量检验、异方差性检验和序列相关性检验等。
步骤五:模型解释与政策分析根据估计得到的模型结果,解释各个变量之间的关系,并进行政策分析。
可以利用模型进行预测和模拟,评估不同政策对经济变量的影响。
计量经济学第十章联立方程组模型

第十章 联立方程组模型第一节 联立方程组模型概述一、问题的提出1、单一方程模型存在的条件是单向因果关系。
2、对于变量之间存在的双向因果关系,则需要建立联立方程组模型。
3、经济现象的表现多以系统或体系的形式进行,仅用单一方程来反映存在局限性。
二、联立方程组的概念1、联立方程组模型的定义。
由一个以上的相互联系的单一方程组成的系统(模型),每一个单一方程中包含了一个过多个相互联系(相互依存)的内生变量。
联立方程组表现的是多个变量间互为因果的联立关系。
联立方程组与单一方程的区别是估计联立方程组模型的参数必须考虑联立方程组所能提供的信息(包括联立方程组里方程之间的关联信息),而单一方程模型的参数估计仅考虑被估计方程自身所能提供的信息。
2、联立方程组模型的例子。
(1)一个均衡条件下市场供给与需求的关系。
)3()2(0)1(012101110s i d i ii s i ii d i Q Q u P Q u P Q =>++=<++=βββααα 称(1)式为需求方程,(2)式为供给方程,(3)式为供需均衡式;d i Q 表示需求量,s i Q 表示供给量,i P 表示价格,i i u u 21,分别为(1)式和(2)式的随机误差项。
按照经济学基本原理,商品的供给与商品的需求共同作用于价格,反过来,价格也要分别决定商品的供给与需求。
这就是方程(1)与方程(2)的作用机制,如果考虑了均衡条件,这又是方程(3)的作用。
因此,通过这一联立方程组将上述商品的供需与价格的相互作用过程得到了反映。
(2)一个凯恩斯宏观经济模型。
011012(4)(5)(6)t t tt t tt t t t C Y u I Y u T C I G ββαα=++=++=++ 式中,C 表示消费,Y 表示国民总收入(又GDP ,实际上它们是有区别的),I 表示私人投资,G 表示政府支出,u1、u2分别为消费函数和投资函数中的随机误差项。
联立方程计量经济学模型的识别(计量经济学武汉大

都用国内生产总值解释,在经济学上也是可以接受的。所以,
如果该模型可以估计,不失为一个描述消费总额、投资总额
和国内生产总值关系的总量宏观经济模型。
但是,分析发现 : • 消费方程是包含C、Y和常数项的直接线性方程;
• 投资方程和国内生产总值方程的某种线性组合 (消去I)所构成的新方程也是包含C、Y和常数项 的直接线性方程。
3 31 13 1 1 1
20
0
10 01 1 1 1
21
2 12 1 1 1
2 1 22 1 1 1
3 1 23 1 1 1
30
0 0 1 1 1
31
2 1 1
1
32
2 1 1 1
33
3 1 1 1
• 上述参数关系体系由12个方程组成,其中包含4个矛 盾方程。
而且,投资方程也是可以识别的,因为任何方程的线性组 合都不能构成与它相同的统计形式。
于是,该模型系统是可以识别的。
• 注意:与模型2相比,在模型3的消费方 程中增加了1个变量,投资方程也变成可 以识别的了。
例:判断下列模型4的可识别性。
模型4
C Y C P
t 0 1 t 2 t 1 3 t 1 1t
例1 用结构式条件判断下列联立方程模型的可识别性。
C Y C P t 0 1 t 2 t 1 3 t 1 1t
It
0
Y
1t
Y
2 t 1
2t
Yt
C
t
I
t
t=1,2,…,n
解:该模型包含 g=3个内生变量:Ct、It、Yt ;
k=4个先决变量:X0(常数项)、Yt-1、Ct-1、Pt-1 。
如果其中的第i个结构方程包含gi个内生变量和ki个先决变量 (含常数项),第i个方程中未包含的变量(包括内生变量和 先决变量)在其它g-1个方程中对应勇功系于的数开路始所,组才成能找的到矩成阵为(B00), 那么,判断第i个结构方程识别状态的结构式条件为:
计量经济学第十章联立方程模型

计量经济学第十章联立方程模型(simultaneous-equations model )10.1 联立方程模型的概念 10.1.1联立方程模型及其特点有时由于两个变量之间存在双向因果关系,用单一方程模型就不能完整的描述这两个变量之间的关系。
有时为全面描述一项经济活动只用单一方程模型是不够的。
这时应该用多个方程的组合来描述整个经济活动。
从而引出联立方程模型的概念。
联立方程模型:关于实际经济问题,描述变量间联立依存性的方程体系。
联立方程模型的最大问题是E(X 'u ) ≠ 0,当用OLS 法估量模型中的方程参数时会产生联立方程偏倚,即所得参数的OLS 估量量βˆ是有偏的、不一致的。
比如需求供给模型:011012d t t t s t t t d st t Q a a P u Q b b P u Q Q =++=++= 从需求方程看,u 1t 代表了除商品价格以外的其他阻碍因素,如消费者收入水平、替代商品价格、消费者爱好和消费政策等。
当这些回素变化时,u 1t 将发生变化,进而引起需求典线的移动,这将改变均衡价格P 和均衡交易量Q 。
同理u 2t 的变化(由于生产技术水平,产品成本、气候变化及产业政策等因素),将会使供给曲线发生移动,从而改变均衡价格和均衡交易量。
这种现象被称为相互依存性。
正是这种相互依存性,使得u 1t 、u 2t 与P 将严峻违抗说明变量与随机误差项不相关的假设,产生联立方程偏误。
凯恩斯的收入决定模型:01t t t t t tC a a Y u Y C I =++=+其中,C 为消费支出,Y 为收入,I 为投资(假设为外生变量),当u t 发生位移时,消费函数将随之发生位移,进而阻碍Y ,即Y 与u t 不相互独立。
假如考虑政府支出G ,投资为内生变量,模型可变为:01101212t t tt t t t t t t tC a a Y u I b bY b Y u Y C I G -=++=+++=++这是一个简单的宏观经济模型,反映了国内生产总值中各项指标之间的关系。
《计量经济学》-联立方程模型

γ 2k
X
kt
u2t
L L L L L L
bg1Y1t b Y g2 2t L b Y gg gt γ X g1 1t γ X g2 2t L γ X gk kt ugt
结构方程的个数等于内生变量的个数,称为完备模型
10
结构型的矩阵表示(一)
b11 b12 L
b21
b22
L
L L L
c5
a2b1 a b
,
c6
a3b1 a b
17
1.结构方程的识别
恰好识别:通过简化模型的参数估计值和参数关系式可以得到 结构方程的参数估计值的惟一解,该结构方程恰好识别
过度识别:通过简化模型的参数估计值和参数关系式可以得到 结构方程的参数估计值的多个解,该结构方程过度识别
不可识别:通过简化模型的参数估计值和参数关系式可以得不 到结构方程的参数估计值,该结构方程不可识别
u1t
u2
t
Ut
u
BYt ΓXt Ut
或
B
Γ
Yt Xt
Ut
12
2. 简化型
Ct
a1b2 1 a1
b1
Yt 1
a1 1 a1
b1
Gt
u1t
a1u2t b1u1t 1 a1 b1
It
b2 ( 1
1 a1 ) a1 b1
Yt
1
b1 1 a1 b1
Gt
u2 t
第九章
联立方程模型
主要内容
联立方程模型的概念 联立方程模型的形式 模型的识别 联立方程模型的参数估计
2
一. 联立方程模型的概念
由若干个单一线性经济计量方程构成联立方程组,描述整个经 济系统的模型称为联立方程经济计量模型,简称联立方程模型
第10章计量经济预测方法

(二)确定模型中的待定参数 选择适当的预测方法并确定模型中的待定
参数。在此阶段,通过搜集和整理用于估算 参数所需使用的各类数据资料(时间序列资料、 静态资料和虚拟变量)。其中虚拟变量是由研 究者根据待定参数的需要而构造的,一般取0 或1
第10章计量经济预测方法
当在模型中要考虑某些因素的影响时(如 自然灾害、战争、政治运动等),就需要引 入虚拟变量。
计量经济模型广泛应用于宏观经济和微观 经济分析和预测中。在实际应用中,可以用 单一方程式的计量经济模型,描述企业产品 需求函数,在已知消费者收入、竞争价格、 广告费用和企业拟定的产品售价等各种估计 量的条件下,预测产品未来销售额;也可以 用多个方程式经济模型,描述产业部门或整 个国民经济运行过程中复杂经济关系的大型 计量经济模型。
第10章计量经济预测方法
第10章计量经济预测方法
(3)生命周期假定消费模型 该假定消费模型由莫迪格里安尼提出。该
假定认为,人们的现期以及将来计划消费是 现期收入加上预期收入和将来的财产的函数, 消费者按其一生中可动用的总资源,在各个 时期进行大体均匀的消费支出。用计量经济 模型表示为:
第10章计量经济预测方法
第10章计量经济预测方法
(二)投入产出表的结构
它是产品部门×产品部门的对称型表式,为 便于分析研究和应用,以字母形式表示的基本 表式,见表2 投入-产出表是由经济总量和 三个象限组成,参见表1。(1)经济总量即表1的 最下面一行或最右边一列,这是投-入产出表的 总控矩阵(向量); (2)左上、右上、左下角的矩阵分别叫第Ⅰ象限、 第Ⅱ象限和第Ⅲ象限; (3)第Ⅰ象限,是由名称相同、排列次序相同、数 目一致的产品部门纵横交叉而成的,主栏(行标 题)为中间投入,宾栏(列标题)为中间使用;这一 部分侧重分析国民经济各部门之间相互依存、 相互制约的技术、经济联系;
《计量经济学》第10章数据
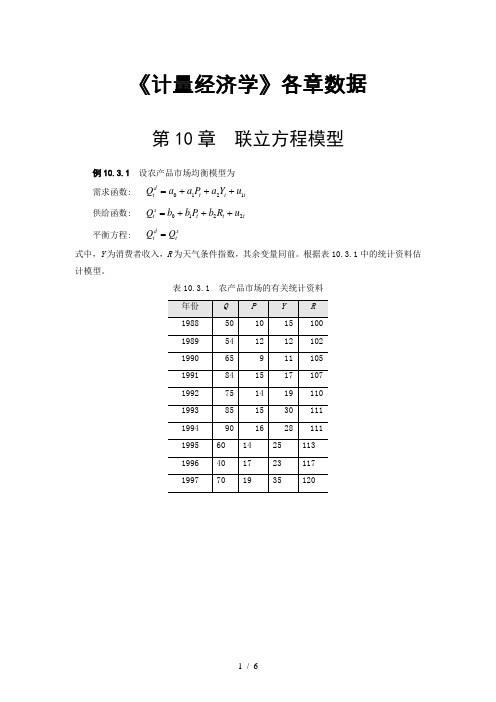
《计量经济学》各章数据第10章 联立方程模型例10.3.1 设农产品市场均衡模型为需求函数: t t t dt u Y a P a a Q 1210+++= 供给函数: t t t st u R b P b b Q 2210+++= 平衡方程: st d t Q Q =式中,Y 为消费者收入,R 为天气条件指数,其余变量同前。
根据表10.3.1中的统计资料估计模型。
表10.3.1 农产品市场的有关统计资料10.5 案例分析10.5.1 中国宏观经济模型中国1978-2003年居民宏观消费CONS、国内生产总值GDP、国内投资总额INV、政府支出GOV、净出口NEX(单位:亿元)统计数据,如表10.5.1所示:表10.5.1 中国宏观经济统计数据10.5.2 克莱因战争间模型根据美国1920~1941年的统计资料,如表10.5.6所示。
用2SLS和系统估计法等方法对模型参数进行估计。
表10.5.6 美国1920~1941年的统计数据思考与练习17.设我国的价格、消费、工资模型设定为t t t u I a a W 110++= t t t Pt u W b I b b C 2210+++= t pt t t t u C W I P 33210++++=γγγγ其中:I =固定资产投资(亿元);W =国营企业职工年平均工资(元);C =居民消费水平指数(%);P =价格指数(%)。
C 、P 均以上年为100%。
样本观察值如表2所示:表2 固定资产投资、职工平均工资与居民消费指数等统计资料(1)用递归模型参数估计法求出该模型的估计式;(2)用普通最小二乘法逐一估计每个方程;(3)比较以上两种做法的结果。
18.表3是我国1978-2003年国内生产总值(GDP )、货币供给量(2M )、政府支出(G )和投资支出(I )的统计资料,试用表中数据建立我国的收入——货币供给模型:t t t t t u G a I a M a a GDP 132210++++= t t t t u M b GDP b b M 2122102+++=-(1)判别模型的识别性。
计量经济学第10章 联立方程模型

第三,由于内生变量是由模型系统决定的变量,所以,大多数情况下, 内生变量是出现在各个方程的等号左边的变量;
第四,在完备的联立方程模型(完整描述了经济系统中变量之间的依存关 系的联立方程模型)中,内生变量的个数等于方程的个数。
3t
1t 2t 11 1
引人矩阵
C1 C2 L Cn
Y
I1
I2 L
In
Y1 Y2 L Yn
1 1 L X Y0 Y1 L
G1 G2 L
1
Yn1
Gn
10 11 12
20
21
22
30 31 32
11 12 L 1n
21
22
L
2
n
31 32 L 3n
可表示为
Dt 0 1Pt 2Yt 1t
St
0
1Pt
2 Pt1
2t
Dt St
联立方程模型定义:
由多个方程构成的,用于描述经济系统中变量之间的相互依存关系的, 联立方程组形式的计量经济学模型。
提出原因:
1)为了完整、准确地描述经济系统中的变量之间的复杂关系, 2)为了进一步分析经济系统中的这种变量之间的复杂关系。
Ct 0 1Yt 1t
It
0
1Yt
2Yt 1
2t
Yt Ct It Gt
(10-1)
析:
解方程组可得简化式模型
Ct
0 01 10 11 1
12 11 1
Yt 1
1 11
1
Gt
1t
11t 12t 11 1
计量经济学联立方程组模型课件

单一方程因果关系简单; 联立方程组模型中,因果关系复杂,某一变量在一个方程中作为 被解释变量,在另一方程中又可能作为解释变量,故需要进行分类。 * 按方程是否含有随机项分为:随机方程;确定性方程 * 按模型对象的行为方式和性质分为: 行为方程、技术方程、制度方程和恒等式(P11-12) ** 以变量间的联系形式作为标准,分为:
第一节 联立方程组模型概述
一、联立方程组模型的例子 联立方程模型:由多个相互联系的单一方程组成的方程组
(每个单一方程中包含一个或多个相互关联的内生变量(模型求解的结果))。
例1 一个小型的宏观计量经济模型。
Ct 0 1Yt u1t I t 0 1Yt 2Yt 1 u 2 t Y C I G t t t t
3)结构参数表示解释变量对被解释变量的直接影响。 (它们之间的间接关系(影响)只能通过解方程才能取得)
消费支出Ct改变1个单位。
前述例 1中的方程( 1 )中的1表示:GDP(Y)每变动一个单位引起
注:结构型模型中:方程个数与内生变量变量个数相同,则称 结构型模型为“完备方程组(模型)” (完备式方程组(模型)是 存在唯一解的必要条件) 。
例3 凯恩斯的收入决定模型
消费函数: Ct 0 1Yt ut 收入衡等式: Yt Ct I t ( St )
其中: Ct = 消费支出; Yt = 收入; It =投资(假设是外生变量); St =储蓄
0 1 1
参数1为边际消费倾向
ut的位移 会引起消费函数 Ct 位移 进而影响Yt。
It是一个内生变量( It受 Yt 、Yt-1的影响,同时又影响着Yt)
Yt是一个内生变量( Yt受It、G t的影响,同时又影响着It) 滞后内生变量Yt-1、外生变量G t (统称前定变量)
经济计量学第十讲 联立方程模型

东北财经大学数量经济系
二、模型识别问题分类
(一)方程识别问题的含义
它是指能否估计出某一方程的参数。如果能唯 一估计出方程的参数,称该方程恰度可识别;如 果方程的一个或几个参数有若干个估计值,称该 方程过度识别;如果方程的一个或几个参数不能 得到其估计值,称该方程不可识别。
东北财经大学数量经济系
(二)方程识别状态
(10.5)
可见在(12.4) 中,则Yt与随机干扰项是相关的。
东北财经大学数量经济系
(三)工资价格模型
Wt= α0 +α1UNt+α2Pt +u1t Pt=β0+β1Wt +β2Rt +β3Mt + u2t
(10.6) (10.7)
东北财经大学数量经济系
(四)宏观经济学中的IS模型
消费函数:Ct= β0 + β1Y dt
东北财经大学数量经济系
三、联立方程偏误:OLS估计量的非一致性(2)
Yt-E(Yt ) = ut/(1- β1) cov(Yt,ut )=E[Yt-E(Yt ) ][ut-E(ut)] =E( ut2)/(1- β1) =s 2/(1- β1) 因此,Yt和 ut是相关的。这就违背了OLS假定之一。
(二)模型的简化型
将结构模型中的全部内生变量表示成前定变量和 随机干扰项的函数而形成的模型形式。 消费函数:Ct= β0 + β1Yt+ut 收入恒等式:Yt=Ct+It Yt=β0 /(1- β1) +1 /(1- β1) It + ut /(1- β1) Ct= β0 /(1- β1) + β1 /(1- β1) It + ut /(1- β1) Yt=P0 +P1 It +wt Ct=P2 +P3 It +wt 东北财经大学数量经济系 (10.4) (10.5)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论:对联立方程模型,一是必须讨论如
何解决上述3个问题;二是必须发展新的联立 方程模型估计方法 。 我们关于联立方程模型的讨论就是围绕 研究解决以上问题展开的。
三、变量分类
1.内生变量:由联立方程模型系统内部决定 的变量。一般是随机的,既由模型系统决定, 又影响模型系统。 例如: Yt 、Ct 、It、 S、P、D 在联立方程模型中,内生变量一般与随机项 相关。用Yi表示内生变量,则一般下式成立:
3.前定变量(预定变量、先决变量):外生 变量和滞后变量的统称 。例如 Y t-1和Gt 在联立方程模型中,前定变量一般与随 机项无关。用Xi 、Yi-s表示前定变量,则一 般下式成立:
Cov(Xi,ui)=E(Xiui)=0 (满足 假定6) Cov( Yi-s ,ui)=E( Yi-s ui)=0
四、识别的条件(以完备的结构型模型为例)
.
识别的阶条件 [待识别方程被斥变量数目]≥[联立方程中方程数 目-1] K:联立方程模型中变量总数 M:待识别方程中变量数目 G:联立方程中方程数目 则:阶条件为 K-M ≥ G-1 阶条件为必要条件
.秩条件
在含有G个方程的联立方程模型结构型中, 第I 个方程可识别的充分必要条件是:第I 个 方程被斥变量在其他方程中所对应的系数矩 阵(简称被斥变量系数矩阵)的秩等于方程 数目减一。 秩条件为充分必要条件 考察秩条件的步骤:(1)写出结构型的一般 形式,求出结构参数矩阵;(2)求出被斥变 量系数矩阵;(3)验证秩条件
Yt =Ct +It +Gt
Ct =11 Y t-1 +12 Gt + v1t It = 21 Y t-1 +22 Gt +v2t Yt = 31 Y t-1 +32 Gt +v3t
a、b为结构型系数
简化型
为简化型系数,其中,
ab 1 a b (1 a )b 1 a b b 1 a b
关系。例如,用进出口总额来解释关税等。
(4)统计方程:描述由数据之间的相关性决定 的变量之间的关系。例如,描述城市居民收入与农 村居民收入关系的方程。 2.恒等方程: (1)定义方程 GDP=消费+投资+出口 (2)平衡方程 总人口=城市人口+农村人口 (3)经验方程 城镇居民平均收入=3.2农村 居民平均收入
11
1 2 1 1 1 21 1 2 31 1 1
2
1
a 1 a b b 1 a b
12
1
1
1
1
11
1
1
32
1 1 a1 b1
上面结构型系数与简化型系数之间的关系 式叫“参数关系体系”
2.求简化型的两种方法: (1)无约束最小二乘法:直接表示
Ct =11 Y t-1 +12 Gt + v1t It = 21 Y t-1 +22 Gt +v2t Yt = 31 Y t-1 +32 Gt +v3t 然后估计
S=Q
S供给、D需求、P价格
例题2:简单的Keynesian宏观模型
Ct =a0 +a1Yt+ut
It =b0 +b1Yt+b2Y t-1+vt Yt =Ct +It +Gt
Ct 居民消费,Yt 国民收入, Y t-1 前期国民 收入,It 投资,Gt 政府消费。
D=b0+b1P+u
S=a0+a1P+v
是方法复杂(不介绍)
一、OLS估计
1. 适用范围: 递归模型 2. 参数估计值统计性质:具有BLUE 性质
二、间接最小二乘法(ILS)
1.适用范围: 恰好识别的方程 2. 参数估计值统计性质: 对小样本是有偏 的,对大样本是渐进无偏的。 3.基本思想:P166页 4.具体步骤 5.例题
三、工具变量法(IV)
例题 Ct =a1Yt+ut
It =b1Yt+b2Y t-1+vt
Yt =Ct +It +Gt
判断投资函数的识别状态
1.写出结构型的一般形式,求出结构参数矩阵
Ct +0* It - a1Yt+0* Y t-1 +0* Gt =ut
0*Ct + It -b1Yt -b2Y t-1 +0* Gt =vt -Ct - It +Yt +0* Y t-1 - Gt =0
第十章 联立方计量经济学模型
目的与要求: 1.掌握联立方程模型的概念 2.理解联立方程模型估计时会出现什么问题
3.掌握关于联立方程模型的若干基本概念
4.理解联立方程模型的识别问题
5.掌握联立方程模型结构型的识别判断条件
6.掌握联立方程模型的部分估计方法
第一节 联立方程模型
一、联立方程模型的概念
1.单方程计量经济学模型: 用一个方程来描述某一经济变量与影响该变 量的诸因素之间的数量关系。
Y b0 b1 X 1 b2 X 2 ... bk X k u
2.联立方程计量经济学模型:
用一组方程来描述某一经济系统变量之间相 互依赖、互为因果的数量关系。这组单方程计量
例题1:市场局部均衡模型
经济学模型组成的方程组称为联立方程模型。
D=b0+b1P+u
S=a0+a1P+v
S=a0+a1P+v……. (2) S=D …… (3) (1)式代入(3)式得 S= b0+b1P+u
这时,如果用S、P的数据进行参数估计,可能会出现 歧义。
有人可能说估计的是需求方程参数b0、b1的估 计值,有人可能说估计的是供给方程参数a0、a1的 估计值—— 这就是估计出现歧义。
2.随机解释变量和解释变量与随机项相关问题 例如:简单的Keynesian宏观模型
S=D
既然联立方程模型是单方程计 量经济学模型联立组成的方程 组,我们能否简单利用所学的 单方程模型理论和方法去估计 和检验联立方程模型呢?
哈哈!那是不 可能的!
二、联立方程模型估计时可能出现的新问 题
1.识别问题:
即联立方程模型中某一单方程模型统计形式 是否唯一的问题。
例如:市场局部均衡模型
D=b0+b1P+u ……(1)
3.结构型的一般形式 :Y 表示内生变量(g 个),
X表示前定变量(k个), U表示随机变量 结构参数矩阵用B和表示,则:结构型的一般形式 为:BY+X=U 其中 : u1 X 1 Y 1 U u 2 Y X X 2 Y 2 u n Y g X k
结构参数矩阵为: Ct
1
It 0
Yt - a1
Y t-1 0
Gt 0
0
1
-b1 -b2
0
-1
-1
-1
1
0
(二)模型的简化式
1.概念:把内生变量表示成前定变量和随机 项的函数。内生变量=F(前定变量、随机项) 例:将Keynesian宏观模型,通过求解表示成 简化型。
Ct =a1Yt+ut
结构型
It =b1Yt+b2Y t-1+vt
Cov(Yi,ui)=E(Yiui)0 (违背假定6)
2.外生变量:由联立方程模型系统以外的因素决 定的变量。一般影响模型系统但不受模型系统的 影响。 例如: Gt 在联立方程模型中,外生变量一般与随机项 不相关。用Xi表示外生变量,则一般下式成立: Cov(Xi,ui)=E(Xiui)=0 (满足假定6)
2
b b (提问) 1 a b
1 2 1 1
t-1对It的总影响
(三)模型递归型
1、定义式 如果一个模型的结构方程可以表示为: Y1=f(X1,X2,…,Xk,u1) Y2=f(X1,X2,…,Xk,Y1,u2) Y3=f(X1,X2,…,Xk,Y1,Y2,u3) …….. Yg=f(X1,X2,…,Xk,Y1,Y2,…Yg-1,ug) 称为递归模型
(2)间接估计法:通过变量代换,求得 结构型参数与简化型参数之间的关系式(参 数关系体系)。然后,通过结构型参数求出 简化型参数。
3.简化型模型系数的含义:表示前定 变量对内生变量的总影响
总影响=直接影响+间接影响
例如 表示Y
b (1 a ) 1 b a b
2 1 21 1 1
例题 :
五、联立方程模型的分类 (一)模型结构型
1.概念: 根据经济理论和变量的行为规律直 接建立的计量经济学方程体系。 结构模型中的方程称为结构方程,其中的 参数称为 结构系数 Ct =a0 +a1Yt+ut It =b0 +b1Yt+b2Y t-1+vt Yt =Ct +It +Gt
2.模型结构型的正规形式:将一个内生 变量表示为其它内生变量和前定变量及 随 机项的函数; 完备形式:内生变量的个数与结构方程的 个数相等 内生变量=F(其它内生变量、前定变量、 随机项)------正规形式 结构方程个数=内生变量个数 --------完备形 式
2、 模型递归型的估计
• 一般可以用OLS估计
第二节 联立方程模型的识别
一、识别概念 例:市场局均衡模型 D=b0+b1P+u S=a0+a1P+v D=S 该模型中需求函数D与供给函数S统计形式不唯 一,估计会出现歧义 1、识别的定义 第一种:结构型参数可以从参数关系体系中求 出 第二种:被识别方程统计形式是唯一的
四、方程分类
1.随机方程
