美国数学竞赛AMCA新编B试题及答案
M美国数学竞赛 AMC B 试题及答案解析

2003 AMC 10B1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pillscost a total of for the two weeks. How much does one green pill cost?Solution3、The sum of 5 consecutive even integers is less than the sum of the ?rstconsecutive odd counting numbers. What is the smallest of the even integers?Solution4、Rose fills each of the rectangular regions of her rectangular flower bed witha different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias 1.50 each, cannas 2 each, dahlias2.50 each, and Easter lilies 3 each. What is the least possible cost, in dollars,for her garden?Solution5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swathhe cuts is inches wide, but he overlaps each cut by inches to make sure thatno grass is missed. He walks at the rate of feet per hour while pushing themower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?Solution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen isclosest, in inches, to which of the following?Solution7、The symbolism denotes the largest integer not exceeding . For example., and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and . Which ofthe following is a possible first term?Solution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?Solution11、A line with slope intersects a line with slope at the point . What isthe distance between the -intercepts of these two lines?Solution12、Al, Betty, and Clare split among them to be invested in different ways.Each begins with a different amount. At the end of one year they have a total of. Betty and Clare have both doubled their money, whereas Al has managedto lose . What was Al’s original portion?Solution.13、Let denote the sum of the digits of the positive integer . For example,and . For how many two-digit values of is?Solution14、Given that , where both and are positive integers, find thesmallest possible value for .Solution15、There are players in a singles tennis tournament. The tournament issingle elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remainingplayers are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?Solution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of thevolume of the frozen ice cream. What is the ratio of the cone’s height to its radius?Solution18、What is the largest integer that is a divisor offor all positive even integers ?Solution19、Three semicircles of radius are constructed on diameter of a semicircleof radius . The centers of the small semicircles divide into four linesegments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?Solution20、In rectangle , and . Points and are on so thatand . Lines and intersect at . Find the area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?Solution22、A clock chimes once at minutes past each hour and chimes on the houraccording to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , ,on what date will the chime occur?Solution23、A regular octagon has an area of one square unit. What is thearea of the rectangle ?Solution24、The ?rst four terms in an arithmetic sequence are , , , and ,in that order. What is the ?fth term?Solution25、How many distinct four-digit numbers are divisible by and have as theirlast two digits?Solution。
AMC/AIME美国数学竞赛 试题真题

AMC/AIME美国数学竞赛试题真题考试信息AMC最新考试时间:●2010年第26届AMC8于11月16日,星期二●2011第12届AMC10A,第62届AMC12A 于2月8日,星期二●2011第12届AMC10B,第62届AMC12B 于2月23日,星期三●2011第29届AIME-1于3月17日,星期四2011第29届AIME-2于3月30日,星期三●2009年AMC8考试情况●2008年考试情况AMC/AIME中国历程:1983第1届AIME上海有76名同学获得参赛资格1984年第2届AIME有110人获得参赛资格1985年第3届AIME北京有118名同学获得参赛资格1986年第4届AIME上海有154名同学获得参赛资格,我国首次参加IMO的上海向明中学吴思皓就是在第四届AIME中获得满分1992年第10届AIME上海有一千多名同学获得参赛资格,其中格致中学潘毅明,交大附中张觉,上海中学葛建庆均获满分1993年第11届AIME上海有一千多名同学获得参赛资格,其中华东师大二附中高一王海栋,格致中学高二(女)黄静,市西中学高二张亮,复旦附中高三韩志刚四人获得满分,前三名总分排名复旦附中41分,华东师大二附中41分,上海中学40分。
北京地区参加2006年AMC的共有7所市重点学校的842名学生,有515名学生获得参加AIME资格,其中,清华附中有61名学生参加AMC,45名学生获得AIME资格,20名学生获得荣誉奖章据悉中国大陆以下地区可以报名参加考试:北京地区:中国数学会奥林匹克委员会负责组织实施长春地区、哈尔滨地区也有参加考试在华举办的美国人子弟学校也有参加考试广州地区:《数学奥林匹克报》负责组织实施。
在中国大陆报名者就在中国大陆考试。
考题采用英文版。
2009年AMC中国地区参赛学校一览表more info。
AMC/AIME美国数学竞赛试题真题

AMC/AIME美国数学竞赛试题真题AMC/AIME美国数学竞赛试题真题考试信息AMC最新考试时间:●2010年第26届AMC8于11月16日,星期二●2011第12届AMC10A,第62届AMC12A 于2月8日,星期二●2011第12届AMC10B,第62届AMC12B 于2月23日,星期三●2011第29届AIME-1于3月17日,星期四2011第29届AIME-2于3月30日,星期三●2009年AMC8考试情况●2008年考试情况AMC/AIME中国历程:1983第1届AIME上海有76名同学获得参赛资格1984年第2届AIME有110人获得参赛资格1985年第3届AIME北京有118名同学获得参赛资格1986年第4届AIME上海有154名同学获得参赛资格,我国首次参加IMO的上海向明中学吴思皓就是在第四届AIME中获得满分1992年第10届AIME上海有一千多名同学获得参赛资格,其中格致中学潘毅明,交大附中张觉,上海中学葛建庆均获满分1993年第11届AIME上海有一千多名同学获得参赛资格,其中华东师大二附中高一王海栋,格致中学高二(女)黄静,市西中学高二张亮,复旦附中高三韩志刚四人获得满分,前三名总分排名复旦附中41分,华东师大二附中41分,上海中学40分。
北京地区参加2006年AMC的共有7所市重点学校的842名学生,有515名学生获得参加AIME资格,其中,清华附中有61名学生参加AMC,45名学生获得AIME资格,20名学生获得荣誉奖章据悉中国大陆以下地区可以报名参加考试:北京地区:中国数学会奥林匹克委员会负责组织实施长春地区、哈尔滨地区也有参加考试在华举办的美国人子弟学校也有参加考试广州地区:《数学奥林匹克报》负责组织实施。
在中国大陆报名者就在中国大陆考试。
考题采用英文版。
2009年AMC中国地区参赛学校一览表more info。
2010_2015年AMC10A和B竞赛真题与答案(英文版)

201052015年aamc10a和bb竞赛真题及答案英文版你好目前只分享了20102013年amc10a和b竞赛真题及答案英文版20142015年的暂时还没有上传等采纳后再私信我吧
2010-2015年AMC 10A和B竞赛真题及答案(英文版)
你好,目前,只分享了2010-2013年AMC 10A和B竞赛真题及答案(英文版),2014-2015年的暂时还没有上传,等采纳后再私信我吧!需要的话,我可以将Word文档中的原图文件一同发给你,求采纳,毕竟我花了差不多一个下午才整理完,谢谢!(@_@)
2010年AMC 10A竞赛真题及答案(英文版)
2010年AMC 10B竞赛真题及答赛真题及答案(英文版)
2011年AMC 10B竞赛真题及答案(英文版)
Problem 4
2012年AMC 10A竞赛真题及答案(英文版)
2012年AMC 10B竞赛真题及答案(英文版)
-年amc 10a和b竞赛真题及答案(英文版)

2010-2015年AMC 10A和B竞赛真题及答案(英文版)
你好,目前,只分享了2010-2013年AMC 10A和B竞赛真题及答案(英文版),2014-2015年的暂时还没有上传,等采纳后再私信我吧!需要的话,我可以将Word文档中的原图文件一同发给你,求采纳,毕竟我花了差不多一个下午才整理完,谢谢!(@_@)
2010年AMC 10Aห้องสมุดไป่ตู้赛真题及答案(英文版)
2010年AMC 10B竞赛真题及答案(英文版)
2011年AMC 10A竞赛真题及答案(英文版)
2011年AMC 10B竞赛真题及答案(英文版)
Problem 4
2012年AMC 10A竞赛真题及答案(英文版)
go去wentgone
2012年AMC 10B竞赛真题及答案(英文版)
get得到gotgot
sink下沉sank / sunksunk / sunken
give给gavegiven
hit打hithit
不规则动词表
2013年AMC 10A竞赛真题及答案(英文版)
mistake误认mistookmistaken
grow成长grewgrown
think思考thoughtthought
美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说:人有两种,一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大,首先是因为他有超于常人的心。
-年amc 10a和b竞赛真题及答案(英文版)演示教学

sink下沉sank / sunksunk / sunken
give给gavegiven
hit打hithit
weave编织wovewoven不规则动词表
2013年AMCபைடு நூலகம்10A竞赛真题及答案(英文版)
2.以d结尾的词,把d变成t。如:build—built, lend—lent, send—sent, spend—spent
2010年AMC 10A竞赛真题及答案(英文版)
2010年AMC 10B竞赛真题及答案(英文版)
2011年AMC 10A竞赛真题及答案(英文版)
2011年AMC 10B竞赛真题及答案(英文版)
Problem 4
2012年AMC 10A竞赛真题及答案(英文版)
go去wentgone
2012年AMC 10B竞赛真题及答案(英文版)
think思考thoughtthought
hit打hithit
hold拿住heldheldlay放置laidlaid
find找出foundfoundmistake误认mistookmistaken
read读readread
misunderstand误会misunderstoodmisunderstood
take拿tooktakengrow成长grewgrown
动词原形中文意思过去式过去分词
spell拼写spelt / spelledspelt / spelled
2010-2015年AMC 10A和B竞赛真题及答案(英文版)
你好,目前,只分享了2010-2013年AMC 10A和B竞赛真题及答案(英文版),2014-2015年的暂时还没有上传,等采纳后再私信我吧!需要的话,我可以将Word文档中的原图文件一同发给你,求采纳,毕竟我花了差不多一个下午才整理完,谢谢!(@_@)
AMC美国数学竞赛AMC.B 试题及答案解析
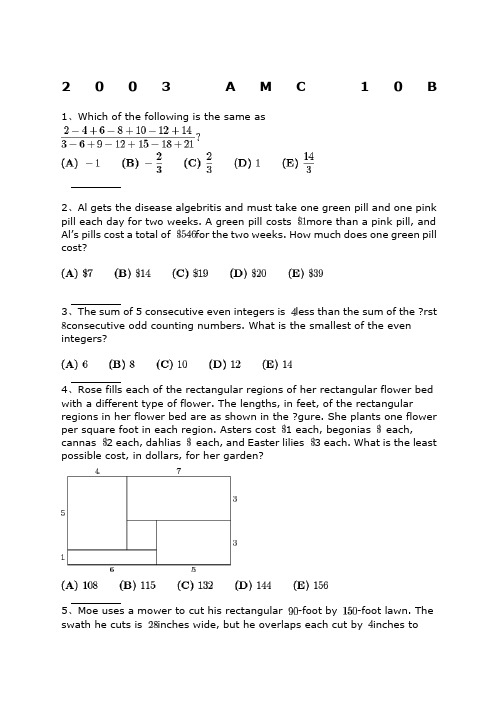
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。
amc2023试题

amc2023试题
2023年AMC8的试卷整体情况为知识难度中上,且较为平均地分配全卷,题型新颖灵活。
其难点主要体现在应用题题干较为繁琐,条件处理步骤多,总读题量较大;图形结合表示的题目过多,观察压力大;出现需要搭配手工求解的题目,同学们准备不充分等。
2023年AMC10A卷的难度相对较低,中档题和高档题难度大幅下降,几何题型大量增加,解析几何,真正的高难题目集中在代数变形和组合计数上。
1. 请解释AMC(美国数学竞赛)的历史和目的。
2. 在AMC2023中,有哪些题型?请简要描述每种题型的特点。
3. 请列举5个AMC2023的代数题目,并给出解题思路。
4. 请列举5个AMC2023的几何题目,并给出解题思路。
5. 请列举5个AMC2023的组合题目,并给出解题思路。
6. 请列举5个AMC2023的数论题目,并给出解题思路。
7. 在AMC2023中,有哪些策略可以帮助学生提高解题速度和正确率?
8. 请分析AMC2023对于学生数学能力的考察重点,以及如何针对性地进行复习和准备。
9. 请分享一些成功应对AMC2023的经验和方法。
10. AMC2023对于学生的未来发展有哪些积极影响?。
2019AMCAB卷详解及AIME班课

2019AMCAB卷详解及AIME班课2019年AMC10B及12B本⽇完赛, 应官⽅要求,B卷题不得当⽇内公开讨论,翰林学院将同步公开2019AMC10B和12B卷答案及详解。
预览链接获取⽅式公众号后台回复2019AMC10B或2019AMC12B可获取2019AMC B卷答案,解析及结果发布链接,我们同步跟新2019amc 晋级2019 AIME cutoff 分数线。
2019年美国数学竞赛AMC10/12A第⼀轮考试于2019年2⽉7⽇结束!翰林学院整理了2019AMC10A/12A 真题及答案还有翰林导师的独家解析,供⼤家参考传阅。
2019 AMC 10A 真题及答案详解2019 AMC 10A 真题⾸发⽂字版点击此处下载参考答案和解析(仅供参考)2019 AMC 12A 真题及答案详解2019AMC12A 真题⾸发⽂字版点击此处下载参考答案和解析(仅供参考)AIME II卷中国时间 3⽉22⽇开赛错过寒假AIME考前冲刺班的学员不⽤着急应备考学员和家长的强烈要求翰林已再度增开了新冲刺班!时间不等⼈,赶紧上车!AIME春季考前冲刺班春季⾸班暂定2019年2⽉17⽇开课点击此处快速报名备注:3⼩时/次课,中途会加课⼀次,全班学员时间⼀致可以按照学员要求调整课时;早班时段同样适⽤海外学员。
如需1对1辅导可咨询⼩助⼿微信:linstitute1课程适⽤对象2019AMC12分数或预测分数在90*分及以上的学⽣2019AMC10分数或预测分数在110*分及以上的学⽣*翰林学院预估分数,实际分数以稍后MAA官⽅数据为准点击查看往年参赛标准课程⼤纲授课内容如下,具体以⽼师授课情况为准。
代数部分多项式,代数⼿法进阶,数列,⼆次数列进阶不等式进阶Rearrngement Inequality, Cauchy-Schwarz, Jensonʼs Inequlity and more⼏何欧⽒⼏何的处理⼿法,共点和共线,多边形和圆,radical axis, 射影⼏何⼊门三⾓函数进阶,解析⼏何solving geometric problems using vectors, solving geometric problems in complex plane.⽴体⼏何进阶数论类费布拉奇数列和质数分解的⼏个有趣结论模运算进阶Eulerʼs Toteint Function, Fermatʼs Christmas Theorem, Fermatʼs little Theroem快速筛数Quadatic Residue, Lifting the Exponent Lemma排列组合⼆项式系数的运算 Vandermondeʼs identity⼏种常见的排列组合思维⽅法,图论⼊门Probability and Expectation随机过程 Markov ChainRoots of Unity Filter知识综合运⽤数形结合,构造函数,竞赛技巧和总复习课程导师介绍苟岩北京师范⼤学材料物理本科,布⾥斯托⼤学应⽤数学硕博,国内数学物理竞赛背景,⾼考数学148分,曾负责国内⼀线机构AMC项⽬研发和教师培训,担任国内知名⾼中国际部数学⽼师/竞赛教练。
amc数学竞赛题目

amc数学竞赛题目国际数学竞赛amc改时间后,今年11月会考amc10和12,明年1月会考amc8。
如果想在比赛中拿奖的话,现在开始 amc数学竞赛培训已经不算晚了。
本文就带大家了解一下amc培训哪里比较好、不同水平的学生怎么进行训练等备考建议。
amc数学竞赛简介amc竞赛涵盖amc8,amc10,amc12,aime,usjmo,usamo(最后两个级别仅针对美国学生),amc比赛在全球范围内都能够获得广为的普遍认可,含金量较低,应该出席。
其中amc8就是小初阶段学生适宜出席的竞赛,适宜8年级及以下的学生参予,主要针对七八年级的学生,4-6年级的优秀学生也可以出席。
amc10和12适宜高中年级的学生出席。
不同水平学生的amc备考建议l 初次出席amc竞赛,或没竞赛经验的同学这次amc数学竞赛培训可以掌握竞赛知识点,拓展数学兴趣为主,目标分数可定在分(分是历年amc晋级aime的平均分数线),争取完美回答aime竞赛前五题。
l 存有过竞赛经验,曾晋级aime的同学这次以准备竞赛技巧为主,尽量提高aime分数,同时尽量将amc10/12的分数保持在分左右,对总分有利。
l 吻合amc晋级线的学生如果我们的分数在aime分数线左右,那就更要加把劲了。
因为每年的试题难度在增加,如果考试的时候只差了1-2题没有进,还是有点可惜的。
达至这个水平的同学,基本的科学知识储备就是有的,可能将就是某一板块比较脆弱,那么可以存有针对性地展开强化训练。
刷题时著重15-20题的练,21-25题如果存有时间也必须谋求,即使搞不出也必须看一看答案,强化一下解题技巧与方法也就是不好的。
