离散数学04

合集下载

年秋国家开放大学《离散数学》形考4试题及答案(答案全部正确)

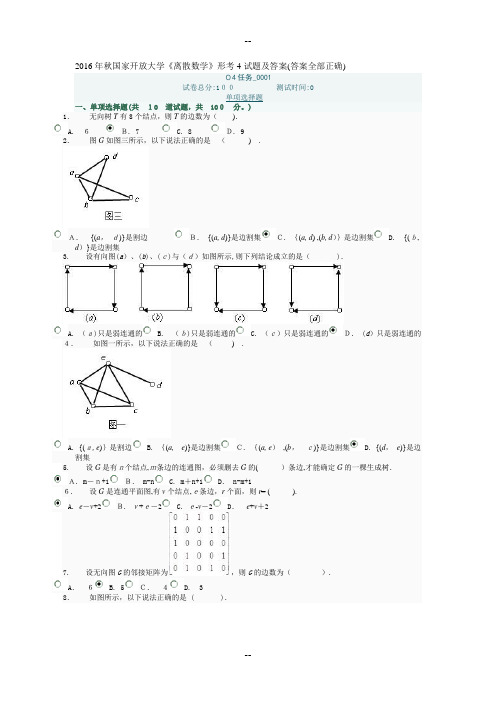
2016年秋国家开放大学《离散数学》形考4试题及答案(答案全部正确)０4任务_0001试卷总分:1００测试时间:0单项选择题一、单项选择题(共１0 道试题，共10０分。

)1．无向树T有8个结点，则T的边数为（)．A. ６Ｂ. 7 C. 8 Ｄ. 92．图G如图三所示，以下说法正确的是（).Ａ．{(a，ｄ)}是割边Ｂ．{(a, d)}是边割集Ｃ. ｛(a, d) ,(b, d）｝是边割集 D. {(ｂ, d）}是边割集3. 设有向图(a）、(b)、(ｃ)与（ｄ）如图所示,则下列结论成立的是（ )．A. （ａ)只是弱连通的B. （ｂ)只是弱连通的C. （ｃ）只是弱连通的Ｄ． (d）只是弱连通的４．如图一所示，以下说法正确的是（).A. {(ａ, e)｝是割边B. ｛(a,e)}是边割集Ｃ. ｛(a, e）,(b，ｃ)}是边割集 D. {(d，e)}是边割集5. 设G是有ｎ个结点,ｍ条边的连通图，必须删去G的(）条边,才能确定G的一棵生成树．Ａ. m－ｎ+1Ｂ． m-n C. m＋n+1D． n-m+1６. 设G是连通平面图,有v个结点,ｅ条边，r个面，则r= ().A. e－v+2Ｂ. ｖ+ｅ－2 C. ｅ-v－2D．e+v＋27. 设无向图G的邻接矩阵为，则G的边数为（）.A．６ B. 5Ｃ．４ D. 38．如图所示，以下说法正确的是 ( )．A. ｅ是割点B. {a，ｅ}是点割集C．｛ｂ, e}是点割集D．｛d}是点割集9. 无向简单图Ｇ是棵树，当且仅当（).A. Ｇ连通且边数比结点数少１B. G连通且结点数比边数少1C. G的边数比结点数少１D. Ｇ中没有回路．10．以下结论正确的是( ).Ａ. 无向完全图都是欧拉图 B. 有n个结点n-1条边的无向图都是树C. 无向完全图都是平面图D. 树的每条边都是割边0４任务＿０002试卷总分:１00 测试时间：0单项选择题一、单项选择题（共10 道试题，共1０0 分。

离散数学第四版课后答案(第4章)

第4章习题解答4．1 A ：⑤； B ：③； C ：①； D ：⑧； E ：⑩4．2 A ：②； B ：③； C ：⑤； D ：⑩； E ：⑦4．3 A ：②； B ：⑦； C ：⑤； D ：⑧； E ：④分析题4.1-4.3 都涉及到关系的表示。

先根据题意将关系表示成集合表达式，然后再进行相应的计算或解答，例如，题4.1中的}2,2,1,2,2,1,1,1{},2,2,1,1{><><><><=><><=s s E I};2,2,2,1,1,1{><><><=s I而题4.2中的}.1,4,4,3,1,2,4,1,1,1{><><><><><=R为得到题4.3中的R 须求解方程123=+y x ，最终得到}.1,9,2,6,3,3{><><><=R求R R 有三种方法，即集合表达式、关系矩阵和关系图的主法。

下面由题4.2的关系分别加以说明。

1°集合表达式法将ranR ran domR domR,, 的元素列出来，如图4.3所示。

然后检查R 的每个有序对，若R y x >∈<,，则从domR 中的x 到ranR 中的y 画一个箭头。

若danR 中的x 经过2步有向路径到达ranR 中的y ，则R R y x >∈<,。

由图4.3可知}.1,3,4,2,1,2,4,4,1,44,1,1,1{><><><><>><<><=R R如果求G F ，则将对应于G 中的有序对的箭头画在左边，而将对应于F 中的有序对的箭头画在右边。

对应的三个集合分别为ranF domF ran domG ,, ，然后，同样地寻找domG 到ranF 的2步长的有向路径即可。

离散数学(微课版) 第4章

离散数学（微课版）第4章1. 引言在离散数学的第4章中，我们将讨论图论的基本概念和应用。

图论是研究图及其在现实生活中的应用的数学分支，它在计算机科学、网络设计、运筹学等领域中具有重要的应用价值。

本章将介绍图的定义、图的表示方法、图的遍历算法等内容。

2. 图的定义图由一组节点和一组节点之间的边构成。

节点通常表示现实世界中的对象，而边则表示对象之间的关系。

图可以用于描述各种问题，如社交网络中的用户关系、城市之间的交通网络等。

2.1 有向图和无向图图可以分为有向图和无向图两种类型。

在有向图中，边具有方向，表示节点之间的单向关系。

而在无向图中，边没有方向，表示节点之间的双向关系。

2.2 顶点和边图由顶点和边组成。

顶点是图的节点，用来表示对象。

边连接两个顶点，表示两个对象之间的关系。

2.3 路径和环路径是指在图中从一个顶点到另一个顶点的连接序列。

环是一条路径，其起点和终点相同。

3. 图的表示方法在计算机中，图可以用不同的数据结构来表示。

常见的表示方法包括：3.1 邻接矩阵邻接矩阵是用二维数组表示图的连接关系。

对于无向图，邻接矩阵是对称的，而对于有向图，则不对称。

A B CA010B101C010上述邻接矩阵表示了一个无向图，其中顶点A与顶点B相连，顶点B与顶点C相连。

3.2 邻接表邻接表是用链表表示图的连接关系。

对于每个顶点，邻接表保存了与其相连的其他顶点的信息。

A ->B -> NULLB -> A ->C -> NULLC -> B -> NULL上述邻接表表示了一个无向图，顶点A与顶点B相连，顶点B与顶点A、C相连，顶点C与顶点B相连。

4. 图的遍历算法图的遍历算法是指按照一定的方式访问图中的所有节点。

常见的图的遍历算法有深度优先搜索和广度优先搜索。

4.1 深度优先搜索深度优先搜索从起点开始，尽可能深地访问尚未访问的节点，直到无法继续深入为止，然后回溯到上一个节点，继续深入其他未访问的节点。

离散数学第四章(第1讲)

xy??a??bc?xy??xyx??a??y??bc?xy??xyx??a??y??b??y??c?xy??xyx??a??y??b??x??a??y??c?xy??a??ba??c即a??bca??ba??c例
第四章二元关系
§1 序偶与笛卡尔积 §2 关系及其表示 §3 关系的性质 §4 关系的运算 §5 等价关系与划分 §6 相容关系与覆盖 §7 偏序关系
§1 序偶与笛卡尔乘积
1 序偶《定义》由二个具有给定次序的客体所组成的序列
称为序偶。记作〈x，y〉例：X—Y二维平面上的一个点的坐标〈x，y〉就
是一个序偶。
说明： (1)在序偶中二个元素要有确定的排列次序。若ab时，则〈a，b〉〈b，a〉若〈x，y〉=〈a，b〉（x=a y=b） (2) 多重序元：三元组：〈〈x，y〉，z〉 =〈x，y，z〉 n元组：〈〈〈〈x1，x2〉，x3〉…〉，xn〉= 〈x1,…,xn〉
ran R={a,b,c,d}
FLD R={1,2,3,4,a,b,c,d}
４．关系和笛卡尔乘积笛卡尔乘积的任何子集都可以定义一种二元关系。例：X={1,2,3,4}，Y={1,2}
X Y {1,1 ,1,2 , 2,1 , 2,2 , 3,1 , 3,2 , 4,1 , 4,2 }
S1={<x,y>|x X yYx ≤ y}={<1,1><1,2><2,2>}
2 笛卡尔乘积《定义》设A，B为二个任意集合，若序偶的第一个成员（左元素）是A的一个元素，序偶的第二个成员（右元素）是B的一个元素，则所有这样的序偶构成的集合称为A和B的笛卡尔乘积。
记作：A B={〈x，y〉|（xA）（yB）}

离散数学ch04图论根树(课件)

04
根树的性质与算法
根树的性质
根树的定义
根树的性质1
根树的性质2
根树的性质3
根树是一种有向无环图，其中有一个节点被指定为根节点，其他节点按层次结构排列，从根节点出发，每个节点恰好有一条有向边指向其子节点。
根树的节点数等于其子树的节点数之和加一。
根树的深度等于其最深叶子节点的深度加一。
路径与回路
总结词
路径与回路是图论中重要的概念，路径是指一系列连续的边和顶点，回路是指起点和终点相同的路径。
详细描述
在图论中，路径是指从起始顶点到终止顶点的一系列连续的边和顶点。每个顶点和边在路径中只出现一次，且顺序必须一致。回路则是指起点和终点相同的路径，即路径中存在一个顶点，通过一系列的边回到该顶点。回路在图论中具有重要意义，如在欧拉路径。
图论的重要性
图论在计算机科学、电子工程、交通运输、生物信息学等领域有
广泛应用。
图论为复杂系统提供了统一的数学框架，使得可以运用数学方法和计算机技术来分析和优化这些
系统。
图论在解决实际问题中发挥了关键作用，如路由优化、社交网络分析、蛋白质相互作用网络等。
算法效率和复杂性的优化
在解决实际问题时，算法的效率和复杂性是关键因素。如何优化图论和根树的算法，提高其计算效率和降低其计算复杂性，是一个具有挑战性的问题。
THANKS
感谢观看
低运输成本。
交通控制
03
根树可以用于构建交通信号灯的控制逻辑，提高道路的通行效
率。
06
总结与展望
图论与根树的重要性和发展前景
重要应用领域
图论和根树在计算机科学、电子工程、交通运输、生物信息学等领域有广泛的应用，对解决实际问题具有重要意义。

离散数学CH04_图论_根树

4.6 树
4.6 树
图中的三棵树T1，T2和T3都是带权2，2，3，3，5
的二叉树，它们的权分别是：
W(T1)=2×2＋2×2＋3×3＋5×3＋3×2=38 W(T2)=3×4＋5×4＋3×3＋2×2＋2×1=47 W(T3)=3×3＋3×3＋5×2＋2×2＋2×2=36 以上三棵树都是带权2,2,3,3,5的赋权二叉树，但不是最优树。
【例】求图所示的二叉树产生的前缀码。解：在图(a)中，每一个分枝点引出的左侧边标记0，右侧边标记1。由根结点到树叶的路经上各边的标记组成的0、1序列作为对应树叶的标记，如图 (b)所示。产生的前缀码为： 01,11,000,0010,0011
4.6 树
定理任意一个前缀码，都对应一个二叉树。证明：
4.6 树
给定了一个前缀码，设h是其中最长序列的长度。画出一个高为 h的正则二叉树。按定理9.6.7中描述的办法给各边标记0或1。每一个结点对应一个0、1序列，它是由根结点到该结点的路经上各边的标记组成的。如果某个0、1序列是前缀码的元素，则标记该结点。将已标记结点的所有后代和该结点的射出边全部删除，得到了一个二叉树，再删除未加标记的树叶，就得到要求的二叉树。
在通信中常用0、1字符串表示英文字母，即用二进制数表示英文字母。最少用多少位二进制数就能表示26
个英文字母呢？1位二进数可以表示2=21个英文字母
，两位二进制数可以表示4=22个英文字母，……，n 位二进制数可以表示2n个英文字母。如果规定，可以用1位二进制数表示英文字母，也可以用两位二进制数表示英文字母。
4.6 树
定理在完全m叉树中，其树叶数为t，分枝点数为i，则 (m1)*i=t-1。证明：

[离散数学]第四章

第四章代数代数又称为代数结构或代数系统，是用代数方法构造的数学模型。

代数系统对于研究各种数学问题和许多实际问题是很有用的，对计算机科学研究也有很大的实用意义，例如，在程序设计语言的语义研究中，数据结构的研究中，编码理论的研究中，系统生成与结构，语言代数，计算理论以及逻辑电路设计中均有重要的理论和实际意义。

§4.1 一般代数结构这一节开始讨论系统及系统的结构。

第一章与第二章着重讨论了一些集合，一般来讲，不论是什么系统，都是若干个集合按一定的条件构成。

构成的条件可以用列举法给出，更多的是由命题法和归纳法给出。

如果结出的若干个集合不是一些具体的集合，这些不具体的集合概念完全由命题来决定通用的概念，则这种构成系统的方法称为公理的方法。

所以这一节还有一个任务是向公理方法过渡。

4.1.1 代数运算关系是集合，函数是关系，函数是“单值”的关系也是集合。

下面定义的代数运算是一个特殊的函数。

定义4.1.1设X为非空集合，n∈I+，n→称为X上的n元运算，其中n为运算ω的阶(类型)，记为n ω。

①函数ω：X X②X中的每一个元素称为X上的0元运算。

当n ω＝1时，称ω为一元运算，例如实数集合R上的“负”运算；当n ω＝2时，称ω为二元运算，例如R上的“＋”和“*”运算。

二元运算在许多方面的研究中有着重要的意义，在后面二元运算用一个字母θ来表示。

实际上用的0元运算只是集合X中的某些特定的元素，例如R中的0和1。

在上一节中所定义的运算是一元运算。

由定义可以看出，所谓集合X上的n元运算，乃是指某种规则，对于X上的每一个n元序偶，规定了X中唯一的元素与之对应。

,,...,∈S，都有ω定义4.1.2设ω为X上的n元运算，S∈X，如果对于任意a a a n12,,...,‡)∈S，则称S关于ω封闭的。

(†a a a n12例如，考察自然数集合N上的加法运算“＋”，显然非负偶数集合关于“＋”是封闭的，但非负奇数关于“＋”是不封闭的。

离散数学-04-关系的性质

7
4.3.1 关系性质的定义和判别
对称性与反对称性（续）
例2 设A＝{a,b,c}, R1, R2, R3和R4都是A上的关系, 其中 R1＝{<a,a>,<b,b>}， R2＝{<a,a>,<a,b>,<b,a>} R3＝{<a,b>,<a,c>}， R4＝{<a,b>,<b,a>,<a,c>} R1 对称 R2 对称 R3 对称？？？反对称反对称反对称？？？
12
4.3.1 关系性质的定义和判别
传递性（续）
例3 设A＝{a, b, c}, R1, R2, R3是A上的关系, 其中 R1＝{<a,a>,<b,b>} R2＝{<a,b>,<b,c>} R3＝{<a,c>}
R1 和 R3 是A上的传递关系, R2 不是A上的传递关系.
13
4.3.1 关系性质的定义和判别
R∘RR 对MR2中1所在位置, MR中相位置都是1
如果顶点xi到 xj有边, xj到xk 有边,则从xi到 xk也有边
20
主对角主对角线元素线元素全是1 全是0
每个顶点都有环
每个顶点都没有环
注意：IA是对称关系也是反对称关系
4.3.1 关系性质的定义和判别
实例
例8 判断下图中关系的性质, 并说明理由
18
4.3.1 关系性质的定义和判别
传递性证明
证明模式证明 R 在 A上传递任取<x, y>，<y, z> <x, y>R<y, z>R …..………. <x, z>R 前提推理过程结论

离散数学__函数

f3={<x1, y1>,<x3, y2>,<x4, y3>}
解答
f1={<x1, y1>,<x2, y2>,<x2, y3>,<x3, y1>,<x4, y3>}
不是函数。 ∵ x2对应两个不同的像点y2和y3 ∴不满足唯一性。
解答
f2={<x1, y1>,<x2, y1>,<x3, y1>,<x4, y2>}
缩小的举例
X={a1,a2,a3,x4,x5} Y={y1,y2,y3,y4,y5} A={a1,a2,a3} f={<a1,y1>,<a2,y2>,<a3,y5>,
<x4,y4>,<x5,y3>} 求：f/A
解答
f/A={<a1,y1>,<a2,y2>,<a3,y5>}
1、满射函数 2、内射函数 3、单射函数 4、双射函数 5、恒等函数
从左到右从右到左
定理
函数f: X→Y 函数g: Y→Z g◦f: X→Z是函数 xX (g◦f)(x)=g(f(x))
证明
显然g◦f是从X到Z的关系 (1)任意性： f是函数:对任意的xX 存在yY，使得<x,y>f g是函数:对任意的yY 存在zZ，使得<y,z>g
<x,y>f 由复合关系的定义：
<<0,-1> ,1>,<<0,0> ,0>,<<0,1> ,-1>, <<1,-1> ,2>,<<1,0> ,1>,<<1,1> ,0>}

离散数学_第_4_章习题解答讲解

第四章归结法原理习题与解答1. 用归结法证明：(1)(2)(3)(4)(5)(6)解(1) 首先将p→q,p→r，¬(p→q∧r)化为合取范式。

p→q⇔¬p∨qp→r⇔¬p∨r¬(p→q∧r)⇔¬(¬p∨(q∧r))⇔p∧(¬q∨¬r) 给出子句集{¬p∨q,¬p∨r,p,¬q∨¬r}的反驳如下。

⑴ ¬p∨q⑵ ¬p∨r⑶ p⑷ ¬q∨¬r⑸ q 由⑴和⑶由⑵和⑶⑹ r⑺ ¬r 由⑷和⑸⑻ □ 由⑹和⑺因此，p→q,p→r|=p→q∧r(2) 首先将p→r，q→r，¬(p∨q→r)化为合取范式。

p→r⇔¬p∨rq→r⇔¬q∨r¬(p∨q→r)⇔(p∨q)∧¬r给出子句集{¬p∨r,¬q∨r,p∨q,¬r}的反驳如下。

p→q∨r⇔¬p∨q∨r¬((p→q)∨(p→r))⇔¬((¬p∨q)∨(¬p∨r))⇔p∧¬q∧¬r 给出子句集{¬p∨q∨r,p,¬q,¬r}的反驳如下。

⑴ ¬p∨q∨r⑵ p⑶ ¬q⑷ ¬r⑸ q∨r 由⑴和⑵⑹ r 由⑶和⑸⑺ □ 由⑷和⑹因此，p→q∨r|=(p→q)∨(p→r)(4) 首先将p∧q→r,¬((p→r)∨(q→r))化为合取范式。

离散数学习题及答案04

SOLUTIONS OF HOMEWORK 4CIS 607: Mathematical Basis for ComputingHomework 4Due Date: April 27, 2017In this homework, you will answer the following questions. Prepare a pdf file for your solutions and upload that pdf file into the blackboard system.Q1)∙Show that 3x4 + 1 is O(x4/2) and x4/2 is O(3x4 + 1).3x4+1 <= cx4/2 whenever x>x06+1/ x4 <= c → c=7 x0=2x4/2 <= c(3x4 + 1) whenever x>x0x4/2 - c <= c3x41/6 –c/3x4 <= c → c=1 x0=1∙Suppose that f (x), g(x), and h(x) are functions such that f (x) is O(g(x)) and g(x) is O(h(x)). Show that f (x) is O(h(x)).f(x) <= c1*g(x) whenever x>x1g(x) <= c2*h(x) whenever x>x2f(x) <= c1*c2*h(x) whenever x > max(x1,x2)f(x) <= c*h(x) where c=c1*c2 whenever x > max(x1,x2)f(x) is O(h(x))Q2) Using mathematical induction,∙Prove that 12 + 32 + 52 +· · ·+(2n + 1)2 = (n + 1)(2n + 1)(2n + 3)/3 whenever n is a nonnegative integer.Basis Step:n=0 12 = 1 (0+1)(2*0+1)(2*0+3)/3 =1Inductive Hypothesis:12 + 32 + 52 +· · ·+(2n + 1)2 = (n + 1)(2n + 1)(2n + 3)/3Inductive Step:12 + 32 + 52 +· · ·+(2n + 1)2+(2(n+1) + 1)2= (n + 1)(2n + 1)(2n + 3)/3+(2(n+1) + 1)2by IH= (n + 1)(2n + 1)(2n + 3)/3+(2n+3)2= (2n+3) ((n + 1)(2n + 1)+3(2n+3))/3= (2n+3)(n+2)(2n+5)/3 = ((n+1)+1)+(2(n+1)+1)(2(n+1)+3)/3∙Prove that for every positive integer n, 1 · 2 + 2 · 3+· · ·+n(n + 1) = n(n + 1)(n + 2)/3.Basis Step:n=1 1.2=2 1(1+1)(1+2)/3=2Inductive Hypothesis:1 ·2 + 2 · 3+· · ·+n(n + 1) = n(n + 1)(n + 2)/3Inductive Step:1 ·2 + 2 · 3+· · ·+n(n + 1)+(n+1)(n+2)= n(n+1)(n+2)/3+(n+1)(n+2) by IH= (n+1)(n+2)(n+3)/3∙Prove that for every positive integer n,Q3) Let P(n) be the statement that a postage of n cents can be formed using just 3-cent stamps and 5-cent stamps. The parts of this exercise outline a strong induction proof that P(n) is true for n ≥ 8.a) Show that the statements P(8), P(9), and P(10) are true, completing the basis step of the proof.b) What is the inductive hypothesis of the proof?c) What do you need to prove in the inductive step?d) Complete the inductive step for k ≥ 10.e) Explain why these steps show that this statement is true whenever n ≥ 8.a)Basis Step:P(8) is true 3+5=8P(9) is true 3+3+3=9P(10) is true 5+5=10b)Inductive Hypothesis:The inductive hypothesis is the statement that using just 3-cent and 5-cent stamps we can form j cents postage for all j with 8<= j <= k , where we assume that k >= 10.c)In the inductive step we must show, assuming the inductive hypothesis, that we can form k + 1 centspostage using just 3-cent and 5-cent stamps.d)We want to form k + 1 cents of postage. Since k >= 10, we know that P(k−2) is true, that is, that wecan form k−2 cents of postage. Put one more 3-cent stamp on the envelope, and we have formed k+1 cents of postage, as desired.e)We have completed both the basis step and the inductive step, so by the principle of strong induction,the statement is true for every integer n greater than or equal to 10.a) How many strings of three decimal digits∙do not contain the same digit three times?= 900 – 9∙begin with an odd digit?= 5*100∙have exactly two digits that are 4s?o There are 3 ways to choose the position that is to be different from 4, and 9 ways to choose the digit to go there. Therefore there are 3 · 9 = 27 strings.b) How many functions are there from the set {1, 2, . . . , n}, where n is a positive integer, to the set {0, 1}∙that are one-to-one?= 0 when n>2= 2 when n=1 or n=2∙that assign 0 to both 1 and n?= 2(n-2)∙that assign 1 to exactly one of the positive integers less than n?= (n-1)*1 (n-1) ways to select the number and 1 way (all other goes to 0)Q5)a) How many bit strings of length 10 contain∙exactly four 1s?= C(10,4) =10*9*8*7/4*3*2 = 210∙at most four 1s?= C(10,4)+C(10,3)+C(10,2)+C(10,1)+C(10,0)∙an equal number of 0s and 1s?= C(10,5)b) How many permutations of the letters ABCDEFG contain∙the string BCD?= P(5,5) = 5! Strings with A,BCD,E,F,G (5 tokens)∙the strings BA and GF?= P(4,4) = 4! Strings with BA,C,D,E,GFa) Show that ≤ 2n for all positive integers n and all integers k with 0 ≤ k ≤ n.Since (nk ) is equal to (nn−k)we look at cases 0 ≤ k ≤ ⎿n/2⏌Proof by Induction: Basis Step:n=1 (10)= 1 ≤ 21Inductive Hypothesis:(n k )≤ 2n for all positive integers n and all integers k with 0 ≤ k ≤ ⎿n/2⏌Inductive Step:(n+1k )= (n+1)! / (n+1-k)!k!= ((n+1)/(n+1-k)) * (n!/(n-k)!k!)≤ ((n+1)/(n+1-k)) * 2n for all integers k with 0 ≤ k ≤ ⎿(n+1)/2⏌by IH Since possible values for ((n+1)/(n+1-k)) are between 1 and 2≤ 2 * 2n≤ 2n+1b) Prove that if n and k are integers with 1 ≤k ≤n, thenk(nk)= k*( n! / (n-k)!k!) = n! / (n-k)!(k-1)!n(n−1k−1)= n * ((n-1)! / (n-1-k+1)!(k-1)!) = n! / (n-k!)(k-1)!a) How many solutions are there to the equationx1 + x2 + x3 + x4 + x5 = 21,where xi , i = 1, 2, 3, 4, 5, is a nonnegative integer such that∙x1 ≥ 1?We require x1 >= 1. This uses up 1 of the 21 total required, so the problem is the same as finding the number of solutions to x1+x2 +x3 +x4 +x5 = 20 with each xi a nonnegative integer. The number of solutions is therefore C(5 + 20 − 1, 20) = C(24, 20)∙xi ≥ 2 for i = 1, 2, 3, 4, 5?the problem is the same as finding the number of solutions to x1+x2 +x3 +x4 +x5 = 11 with each xi a nonnegative integer. The number of solutions is therefore C(5 + 11 − 1, 11) = C(15, 4)∙0 ≤x1 ≤ 10?Total solutions = C(21+5-1,21) = C(25,4)Violating Solutions = C(10+5-1,10) = C(14,4)Non-Violating Solutions = C(25,4)-C(14,4)b) How many strings of 10 ternary digits (0, 1, or 2) are there that contain exactly two 0s, three 1s, and five 2s?= 10! / 2!3!5! = 10*9*4*7 = 1890a) What is the probability that the sum of the numbers on two dice is even when they are rolled?=1/2*1/2 + 1/2*1/2 = 1/2b) What is the probability that a card selected at random from a standard deck of 52 cards is an ace ora heart?=1/13+1/4-1/52c) Which is more likely: rolling a total of 9 when two dice are rolled or rolling a total of 9 when threedice are rolled?= 4/36 for two dice= 13/216 for three diceQ9)What is the probability of these events when we randomly select a permutation of the 26 lowercase letters of the English alphabet?a) The first 13 letters of the permutation are in alphabetical order.= 13!b) a is the first letter of the permutation and z is the last letter.= 24!/26!c) a and z are next to each other in the permutation.= 2*25! / 26!d) z precedes both a and b in the permutation.= 1/3Looking at the relative placements of z , a, and b, we see that one third of the time, z will come first.Therefore the answer is 1/3.Q10) Suppose that 8% of all bicycle racers use steroids, that a bicyclist who uses steroids tests positive for steroids 96% of the time, and that a bicyclist who does not use steroids tests positive for steroids 9% of the time. What is the probability that a randomly selected bicyclist who tests positive forsteroids actually uses steroids?P(S) = 0.08 P(NS) = 0.92P(Pos/S) = 0.96 P(Pos/NS) = 0.09P(S/Pos) = P(Pos/S)*P(S) / (P(Pos/S)*P(S)+P(Pos/NS)*P(NS))= 0.96*0.08 / (0.96*0.08+0.09*0.92) = 0.0768 / (0.0768+0.0828) = 0.0768 / 0.1596= 0.48。

离散数学第四章课件ppt

例1 设R＝{<x，y>|x、y∈N∧y＝x2}和S＝{<x，y>|x、 y∈N∧y＝x＋1}是N上的关系，求R-1、R*S、S*R。
解 R-1＝{<y，x>|x、y∈N∧y＝x2}
R*S＝{<x，y>|x、y∈N∧y＝x2＋1}
S*R＝{<x，y>|x、y∈N∧y＝(x＋1)2}
定理4.9 设R和S为任意两个二元关系，则： (1)(R-1)-1＝R。 (2)(R∪S)-1＝R-1∪S-1。 (3)(R∩S)-1＝R-1∩S-1。 (4)(R－S)-1＝R-1－S-1。 (5)(A×B)-1＝B×A。证 (2)因为<x，y>∈(R∪S)-1<y，x>∈(R∪S) 明 <y，x>∈R∨<y，x>∈S
注： (1)当x≠y时，<x，y>≠<y，x>； (2)<x，y>＝ <u，v>当且仅当x＝u∧y＝v； (3)序偶<x，y>与集合 {x，y}不同。
定义4.2 n个元素x1、x2、…、xn按一定的次序排列组成的有序序列称为有序n元组，记作<x1，x2，…，xn>。
例如，表示时间的年月日组成一个三元组。
证明
(2)因为y∈R[A∩B] x(x∈A∩B∧xRy) c∈A∧c∈B∧cRy
(c∈A∧cRy)∧(c∈B∧cRy)
y∈R[A]∧y∈R[B] y∈R[A]∩R[B]，所以R[A∩B] R[A]∩R[B]。
4.2.2关系矩阵与关系图
定义4.11 设A＝{x1，x2，…，xn}，B＝{y1，

定理4.10 设R、S和T为任意三个二元关系，则： (1)DR*SDR，RR*SRS。 (2)RS∧TWR*TS*W。 (3)R*(S∪T)＝(R*S)∪(R*T)。 (4)R*(S∩T)(R*S)∩(R*T)。 (5)R*S－R*TR*(S－T)。 (6)(R*S)-1＝S-1*R-1。 (7)(R*S)*T＝R*(S*T)。

离散数学第04章习题 (1)

P156 (6)一个函数：S→T是称作函数：T→S的左逆，若一个函数g：是称作函数f：的左逆，一个函数是称作函数的左逆的左逆，是的右逆 ∀t∈T，g(f(t))=t，若g是f的左逆，则f是g的右逆 ∈ ，，是的左逆证明：有一个右逆，证明：(b)f：T→S有一个右逆，当且仅当它是满射的：有一个右逆的一个右逆，证：1）若g：S →T是f的一个右逆，则跟据定义）：是的一个右逆是一个函数，为其定义域为其定义域， ∀s∈S，g是一个函数，S为其定义域， ∈ ，是一个函数所以∃ ∈ ，使得g(s)=t，所以∃t∈T，使得，也即f(t)= f(g(s))=s，因此是满射的。是满射的。也即，因此f是满射的 2）若f是满射的，则∀s∈S满足是满射的，满足f(t)=s的t为多个，设为为多个，）是满射的 ∈ 满足的为多个 t1，t2，…，tn，则构造函数：S→T使得则构造函数g：，使得 g(s)=ti s∈S，且ti为满足 i)=s中的某一个，为满足f(t 中的某一个中的某一个， ∈ ，上述构造的函数g显然满足显然满足f(g(s))=s，因此是f的一个上述构造的函数显然满足，因此g是的一个右逆，右逆，综上1））所述…… 综上）2）所述
P156 (6)一个函数：S→T是称作函数：T→S的左逆，若一个函数g：是称作函数f：的左逆，一个函数是称作函数的左逆的左逆，是的右逆的右逆。 ∀t∈T，g(f(t))=t，若g是f的左逆，则f是g的右逆。 ∈ ，，是的左逆证明：有一个左逆，证明：(a)f：T→S有一个左逆，当且仅当它是入射的。：有一个左逆当且仅当它是入射的。的一个左逆，证：1）若g：S→T是f的一个左逆，则根据定义，）：是的一个左逆则根据定义，若∀t1，t2∈T，且t1≠t2，，也是一个函数，则g(f(t1))≠g(f(t2)) ，又g也是一个函数，也是一个函数所以f(t 所以 1)≠f(t2) ，故f是入射的是入射的 2）若f是入射的，则构造函数：S→T使得是入射的，）是入射的则构造函数g：使得 g(s)=t s∈f(T)，且f(t)=s ∈ ， g(s)=c s∈S-f(T)，且c为T的某一个元素 ∈ ，为的某一个元素上述构造的函数g：上述构造的函数：S→T，满足，满足g(f(t))=t，，因此g是的一个左逆因此是f的一个左逆综上1））所述…… 综上）2）所述

自考离散数学第4章

例：V1=<R,+,·,-,0,1>,V2=<p(s),U,∩,~,ᴓ,S>,称V1和V2是同类型的代数系统。
4.1 代数系统
定义4.1.8 设V=<S,f1,f2,...,fk>是代数系统，B S，且B对f1,f2,...,fk都是封闭的， B和S还含有相同的代数常数，则称<B,f1,f2,...,fk>是V的子代数系统，简称子代数。
因为b=b,d=b2,a=b3.c=b4,e=b5，生成元为b；
因为c=c,a=c2,d=c3.b=c4,e=c5，生成元为c；
例：设A={a,b,c,d}，*为A上的二元运算，
*
a
b
c
d
a
a
b
c
d
b
b
d
a
c
c
c
a
b
b
d
d
a
c
d
可以看出a为单位元。由a*a=a,b*c=a,c*b=a,d*b=a,
故a有逆元a；b有左逆元c，d；c有左逆元b；b有右逆元c；c有右逆元b；d有右逆元b。其中b是c的逆元，c是b的逆元。
一个元素的左逆元不一定等于它的右逆元，而且一个元素可以有左（右）逆元而没有右（左）逆元。一个元素的左右逆元也不一定是唯一的。
*
e
a
b
c
e
e
a
b
c
a
a
e
c
b
b
b
c
e
a
c
c
b
a
e
验证<G,*>是一个群。
解：*运算容易验证是可结合的，e是G中的单位元，对任意x G，x-1=x。G 关于*运算，构成一个群，这个群称作Klein四元群。

离散数学04

19
例题 n元谓词的符号化
例4.5 将下列命题符号化（1）兔子比乌龟跑得快。（2）有的兔子比所有的乌龟跑得快。（3）并不是所有的兔子都比乌龟跑得快。（4）不存在跑得同样快的两只兔子。
解：令 F(x):x是兔子， G(y):y是乌龟， H(x,y):x比y跑得快， L(x,y):x与y跑得同样快。
(1) “凡人都呼吸”应符号化为 x(M(x)→F(x))
(2) “有的人用左手写字”符号化为 x(M(x)∧G(x))
在使用全总个体域时，要将人从其他事物中区别出来，为此结引进了谓词M(x)，称为特性谓词。论同一命题在不同的个体域中符号化的形式可能不同。
思考：在全总个体域中，能否将(1)符号化为 x(M(x)∧F(x))？能否将15(2)符号化为x(M(x)→G(x))？
定义4.4 一阶语言F的合式公式定义如下:
(1) 原子公式是合式公式。
(2) 若A是合式公式，则(┐A)也是合式公式。
(3) 若A，B是合式公式，则(A∧B)，(A∨B)，(A→B)，(AB) 也是合式公式。
(4) 若A是合式公式，则xA，xA也是合式公式。
(5) 只有有限次的应用(1)～(4)构成的符号串才是合式公式。
11
量词及相关概念
量词（quantifiers）是表示个体常项或个体变项之间数量关系的词。
1. 全称量词：符号化为“”
日常生活和数学中所用的“一切的”、“所有的”、“每一个”、“任意的”、“凡”、“都”等词可统称为全称量词。
x表示个体域里的所有个体，xF(x)表示个体域里所有个体都有性质F。
命题真值为假。（2）有的人登上过月球。
令G(x):x登上过月球， M(x):x是人。命题符号化为 x(M(x)∧G(x))。

离散数学CH04图论基本概念

4.1 图的基本概念
定义9 给每条边或弧都赋予权的图G=<V，E>，称为加权图，记为G=<V，E，W>，其中W表示各边之权的集合。
加权图在实际中有许多应用，如在输油管系统图中权表示单位时间流经管中的石油数量；在城市街道中，权表示表示通行车辆密度；在航空交通图中，权表示两城市的距离等等。
有趣的图论问题
解这是通路问题的一个典型实例。用f表示人，w表示狼，s表示羊，h表示草。
集合{f，w，s，h}中能平安在一起的子集有：{f，w，s ，h}，{f，w，s}，{f，s，h}，{f，w，h}，{f，w}，{f，s}， {f，h}，{w，h}，{f}，{w}，{s}，{h}。用顶点表示渡河过程中的状态，状态是二元组：第一元素是集合{f，w，s，h} 在渡河过程中留在原岸的子集，第二元素是在彼岸的子集，将一次渡河后代表状态变化的顶点间连边，得图。容易看出，一条路径就是一种渡河方案。
4.1 图的基本概念
由定义可知，图G中的每条边都与图中的无序或有序结点对相联系的。若边e∈E与无序结点对（vi，vj）相联系，则φ(e)=（vi，vj），这时边e称为无向边，有时简称为边；若边e∈E与有序结点对<vi，vj>相联系，则φ(e)=<vi ，vj>，此时边e称为有向边或弧，vi称为弧e的始结点，vj 称为弧e的终结点。
4.1 图的基本概念
例如，在图 (a)中结点a和b之间有两条平行边，结点b和c之间有三条平行边，结点b上有两条平行边，这两条平行边都是环。图 (a)不是简单图。
在图 (b)中结点v1和v2之间有两条平行边。v2和v3之间的两条边，因为方向不同，所以不是平行边。图 (b)不是简单图。

年秋国家开放大学《离散数学》形考4试题及答案(答案全部正确)

离散数学第4章关系

第一个关系中的顺序排列。
关系的复合运算
总结词
复合运算是一种二元运算，它返回两个关系中满足一定条件的元素组成的新关系。
VS
详细描述
关系的复合运算是指将两个关系中的元素按照一定的顺序组合在一起，形成一个新的关系。这个新的关系只包含满足一定条件的元素，这些元素按照它们在各自关系中的顺序排列。
关系的表示
总结词
关系的表示方法有多种，包括表格、图形和符号等。
详细描述
关系的表示方法可以根据具体情况选择。表格表示法是一种常用的方法，通过二维表格的形式列出所有可能的元素对及其关系状态。图形表示法则更加直观，通过节点和边的形式展示关系。符号表示法则使用特定的符号或字母来表示关系，如集合论中的笛卡尔积等。
04
关系闭包
闭包的定义
闭包
对于给定的关系R，其闭包记作R+，是指在R的基础上通过添加某些有序对后得到的新的关系。
定义方式
如果存在一个集合A，对于A中的任意元素x和y，如果(x,y)在R+中，那么(x,y) 在R中也一定存在。
闭包的性质
02
01
03
自反性
如果一个关系是自反的，那么其闭包也是自反的。
详细描述
如果集合中的任何一个元素x，都不满足关系 R，使得x与自己有R关系，则称关系R具有反自反性。例如，在一个班级中，“是自己的老师”这个关系不具有自反性，因为没有人
是自己的老师。
对称性
总结词
对称性是指如果元素x和元素y之间有关系R，并且元素y 和元素x之间也有关系R，则称关系R是对称的。
详细描述
02
关系的运算
关系的并运算
总结词
并运算是一种二元运算，它将两个关系合并成一个新的关系。

离散数学(第4讲PPT课件

•
（～Ｐ∧Ｐ）∨Q=Q
• 将命题变元P补进去，并利用分配律展开，然后合并相同的子句，此时得到的子句将是标准的极大项。
• （8）利用幂等律将相同的极小项和极大项合并，
同时利用交换律进行顺序调整，由此可转换成标准
的主析取范式和主合取范式。
28
第28页/共33页
例1-5.4
利用公式的等价求G＝(P→Q)∧R的主合取范式和主析取范式。
解：G＝(P→Q)∧R＝(～P∨Q)∧R（蕴涵）
＝(～P∨Q∨(R∧～R))∧
((～P∧P)∨(～Q∧Q)∨R)（添加R、P、Q）
＝(～P∨Q∨R)∧(～P∨Q∨～R)∧ (～P∨～Q∨R)∧(～P∨Q∨R)∧
(P∨～Q∨R)∧(P∨Q∨R) （分配律）
＝(P∨Q∨R)∧(P∨～Q∨R)∧(～P∨Q∨R)∧
第24页/共33页
例1-5.3（续）
• 2)、求公式的主合取范式
P Q R (P→Q)
R
000 0 001 1 010 0 011 1 100 1 101 0 110 0 111 1
极大项
P∨Ｑ∨Ｒ
极大项
P∨～Ｑ∨Ｒ
极大项极大项
～P∨Ｑ∨～Ｒ～P∨～Ｑ∨Ｒ
2021/4/22
25
第25页/共33页
4种不同的组合极大项对于n个命题变元共有2个不同的极大项记为2020310计算机学院16极大项公式成假赋值名称2020310计算机学院17没有两个不同的极小项是等价的且每个极小项只有一组真值指派使该极小项的真值没有两个不同的极大项是等价的且每个极大项只有一组真值指派使该极大项的真值2020310计算机学院182020310计算机学院19极大项取值0当且仅当
要解决这个问题，我们引入范式(公式的标准型)的概念。