二阶系统的性能指标
机械工程控制基础29_二阶系统的性能指标

机械工程控制基础29_二阶系统的性能指标二阶系统是指具有两个自由度的机械工程控制系统。
在控制系统理论中,衡量系统性能的指标有许多,比如超调量、调节时间、稳态误差等。
下面将详细介绍二阶系统的性能指标。
一、超调量:超调量是指过渡过程中输出量超过稳态值的最大偏离量。
对于二阶系统而言,其超调量可以通过过冲幅值与稳态值的差进行计算。
具体公式如下:超调量(%)=(过冲幅值-稳态值)/稳态值×100超调量主要反映了系统在过渡过程中的动态性能,是指标中最容易获取的。
二、调节时间:调节时间是指系统输出量从初始稳态值到达稳态值所需要的时间。
对于二阶系统而言,其调节时间通常从过渡过程的时间t1开始计算。
具体公式如下:调节时间=t2-t1其中,t2表示系统输出量进入超定态的时刻。
三、上升时间:上升时间是指系统输出量从初始稳态值到达稳态值所需要的时间,也即是调节时间的一部分。
对于二阶系统而言,上升时间是系统输出量从过渡过程的时间t1到达过冲幅值和稳态值之间的时间间隔。
四、峰值时间:峰值时间是指系统输出量达到过冲幅值或者偏离过冲幅值最远的时刻。
对于二阶系统而言,峰值时间是系统从过渡过程的时间t1到达过冲幅值的时间间隔。
五、稳态误差:稳态误差是指系统输出量在稳态下与期望输入量之间的偏差。
对于二阶系统而言,稳态误差可以通过比较系统稳态值与期望输入量来计算。
稳态误差主要反映系统的静态性能,也即系统对于不同输入的输出表现。
综上所述,二阶系统的性能指标主要包括超调量、调节时间、上升时间、峰值时间和稳态误差。
这些指标可以通过理论计算、仿真分析和实验测试等方法来获取,用于评估和比较不同二阶系统的控制性能。
在实际应用中,根据具体需求和控制要求,可以通过调整系统参数和控制策略等来改善系统的性能指标,并使系统能够更好地满足要求。
二阶系统的性能指标

一、二阶系统传递函数的标准形式二阶系统的闭环传递函数写成标准形式为:2222)()(nn ns s s R s C ωξωω++=式中,ξ为阻尼比;n ω为无阻尼自振频率。
所以,二阶系统的特征方程为:022=++n n s s ωξω由上式解得二阶系统的二个特征根(即闭环极点)为:22.11ξωξω-±-=n n j s 随着阻尼比ξ取值的不同,二阶系统的特征根(即闭环极点)也不相同。
二、单位阶跃函数作用下二阶系统的过渡过程(针对欠阻尼状态,10<<ξ )令)(1)(t t r =,则有s s R 1)(=,二阶系统在单位阶跃函数作用下输出信号的拉氏变换为:2222222)()(1))((2112)(d n d d n d n n d n d n n n n n s s s s j s j s s s ss s s C ωξωωωξωωξωξωωξωωξωξωωξωω++⋅-+++-=-++++-=⋅++=式中,21ξωω-=n d 为有阻尼自振频率对上式进行反拉氏变换,得:)sin(11)sin 1(cos 1sin cos 1)(22ϕωξωξξωωωξωωξωξωξωξω+--=-+-=⋅--=----t e t t e t e t e t c d t d d t d td n d t n nnn式中,ξξϕ21-=arctg由上式看出,对应10<<ξ时的过渡过程,)(t c 为衰减的正弦振荡曲线.其衰减速度取决于ϕ角的定义n ξω值的大小,其衰减振荡的频率便是有阻尼自振频率d ω,即衰减振荡的周期为:2122ξωπωπ-==n dd T三、二阶系统的性能指标1.上升时间tr:上升时间是响应曲线由零上升到稳态值所需要的时间。
根据定义,当r t t =时,1)(=r t c 。
即 0sin 1cos 2=-+r d r d t t ωξξω或 nn r d t tg ξωξωω21-=,)(ϕπω-=tg t tg r d所以,上升时间为:21ξωϕπ--=n r t2.峰值时间tp:过渡过程曲线达到第一个峰值所需的时间。
自动控制理论时域分析2--二阶系统

4.调整时间 t s(又称过渡过程时间) :响应曲线达到并 保持与稳态值之差在预定的差值△内(又叫误差带 )所 需要的时间。一般△取±2%或±5%。
二、二阶系统的动态响应性能指标 (1)峰值时间 t P
因为
c (t ) 1 e nt 1
2
sin( d t )
t n p d
dc ( t ) dt
d p
0
ttp
e sin( t ) e cos( t ) 0
t n p n d p
整理得:
tg ( ) dtp
12
p t p 0, ,2 ,3
n
0 Re
s1
s2
0
Re
s2
s1
0
Re
0
Re
s2
(a) 0 1 (b) 1 (c) 1 (d) 0
特征根为:共扼复数 特征根为:
相等实数
不等实数
共扼虚数
1.欠阻尼情况 :
( 0 1 )
2
s n 1 1 , 2 n
s j 1 , 2 n d
c ( t) 1 cos t n
c (t )
( 0)
(t 0)
2
1
0
t
这是一条等幅振荡曲线。
( 0)
c (t )
1
c (t ) r (t )
2
1
1
c (t )
0
t
0
t
( 0 1 )
1
r (t )
二阶系统的性能指标

●二阶系统的性能指标控制系统的时域性能指标控制系统的性能指标是评价系统动态品质的定量指标,是定量分析的基础。
系统的时域性能指标通常通过系统的单位阶跃响应进行定义。
常见的性能指标有:上升时间tr、峰值时间tp、调整时间ts、最大超调量Mp、振荡次数N、稳态误差e ss。
✓上升时间tr (rise time)响应曲线从零时刻出发首次到达稳态值所需时间。
对无超调(过阻尼)系统,上升时间一般定义为响应曲线从稳态值的10%上升到90%所需的时间。
✓峰值时间tp (peak time)响应曲线从零上升到第一个峰值所需时间。
调整时间ts (settling time)响应曲线到达并保持在允许误差范围(稳态值的2%或5%)内所需的时间。
❑评价系统稳定性的性能指标❑最大超调量Mp (maximum overshoot)响应曲线的最大峰值与稳态值之差。
通常用百分数表示:✓振荡次数N在调整时间ts内系统响应曲线的振荡次数实测时,可按响应曲线穿越稳态值次数的一半计数。
评价系统准确性的性能指标✓稳态误差e ss系统进入稳态后期望值与实际值之差。
▪二阶系统的动态性能由ωn和ξ决定。
增加ξ可以降低振荡,减小超调量Mp 和振荡次数N ,但系统快速性降低,tr、tp增加;ξ一定,ωn越大,系统响应快速性越好,tr、tp、ts越小。
▪通常根据允许的最大超调量来确定ξ。
ξ一般选择在0.4~0.8之间,然后再调整ωn以获得合适的瞬态响应时间。
系统的误差分析和计算误差定义:理想输出与实际输出的差。
误差组成与分析在过渡过程中,瞬态误差是误差的主要部分,但它随时间逐渐衰减,稳态误差逐渐成为误差的主要部分。
误差产生的原因:内因:系统本身的结构。
外因:系统输入量及其导数的连续变化。
3.3二阶系统的动态性能(上)解析

s 2n 1 s [( s n ) jd )][( s n ) jd ]
s 2n 1 s 2n 1 s ( s n )2 ( jd )2 s ( s n )2 d 2
at
s n n 1 s (s n )2 d 2 (s n )2 d 2 n 1 2 1 s n 1 2 2 s ( s n ) d ( s n )2 d 2
5.84 n ts 4.75 n
4、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误差, 系统为无静差系统。
4.过阻尼(ζ>1)状态
闭环特征方程
特征根
2 s 2 2n s n 0
s1 n n 2 1
s2 n n 2 1
nt
d
L[e at cos t ]
上式取拉氏反变换,得
y(t ) 1 e
1 1
cos d t
1
2
sa ( s a)2 2 L[e at sin t ] ( s a)2 2
ent sin d t
e nt 1 2 e
Δ 2 Δ 5
4T1 1.25 ts 3T 1
Δ 2 Δ 5
1.34
3、稳态误差为0,说明典型二阶系统跟踪阶跃输入信号时,无稳态误 Y(t) 差,系统为无静差系统。
2
4、需要说明的是,对于临界阻尼和过阻 尼的二阶系统,其单位阶跃响应都没有 振荡和超调,系统的调节时间随ζ的增加 而变大,在所有无超调的二阶系统中, 临界阻尼时,响应速度最快。
2 n 1 1 s Y ( s ) ( s ) R( s ) 2 2 2 s n s s s 2 n
自动控制原理第三章二阶系统

1. ζ >1 过阻尼
1 T
e-t/T
c(t)=1-e-t/T
r(t)=t
c(t)=t-T+Te-t/T
可知: 系统输入信号导数的输出响应,等 于该输入信号输出响应的导数;根据一种 典型信号的响应,就可推知于其它。
自动控制原理第三章二阶系统
第二节 一阶系统性能分析
设例ФKk(若=s一 调 t)=s1要=阶 节000CR求系 时.1((ss:sK统 间)),=H的t=求1s+0结(反t1.11s0构0±=馈000•如/5K.系S1%HR图/s(数Ss)),。;=试(_E如0(求.则s0果)11系://K要KKS统HkH求)的S+C1(s) 解Ф:(系s)统=t s=闭CR3((T环ss=))传=3×1递+K01H1函.000=010数0•/./0K3S.1H/=SK0k .=K1HT0.s=11S00K+.0H11/KH
有性任何着 能=二对 指S2阶应 标+GR系(的 与sS1)/=统/L关 其L+CUU的1系 参rc(/(ssL动))C数。=态L间求C=性S的出2能S+2关标R+1指C2系准Sζω标+ω形,1n。2n 式S便+ω的可n动求2
ቤተ መጻሕፍቲ ባይዱ
态 得
2ζ ω n=R/L
得:
ω
2 n
=
1/LC
ω n=1/ LC
ζ=
RC 2L
一阶系统ts =单3位T 阶跃响应:
(±R5%(s))=
1 S
C(s)= tФs =(s4)•TS1
=
1 TS+1
•
1S(=±1S2%- S)+11/T
二阶系统性能指标.
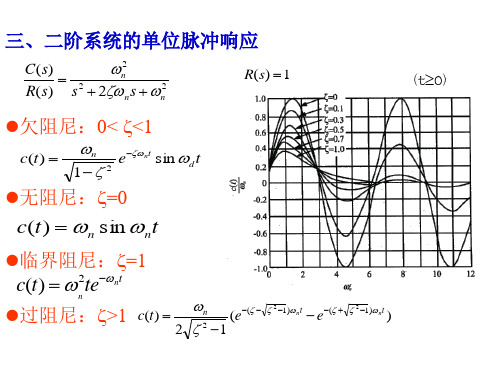
c(t )
n
2 1
2
(e
( 2 1 ) nt
e
( 2 1 ) nt
)
二、二阶系统阶跃响应的特征量
第一次进入误差带 不再出来的时间 c(t) r(t) 1.0
最大超调量Mp,常用相对量描述 第一次达到稳态值时间 Mp%= [c(tp)-c(∞)]/c(∞)*100% ±Δ 带 误差
ts
因1、符合上式答案有多个;2、ts不连续 用包络线近似来简化计算
e 1 1
n tsnts e 1 21
1 Sin ( d t s ) 2
1
nts e 1 2
Sin(dts ) 1
取得包络线方程
1
1
上升时间tr
峰值时间tp
0
5% c() or 2% c()
调节时间ts
t
tr t p
ts
当(>=1)时阶跃响应没有超调,此时, 上升时间的定义修改如下:
1.0 0.9 0.5 0.1 0
C(t)
t ( 0.10.9 ) t ( 0 0. 9 )
tr tr
t
2) 欠阻尼二阶系统阶跃响应的特征量的计算: 上升时间
2
Sin (dtp ) Sin ( ) Sin 1
np
t e MP % Sin(dtp ) 100%
1 2
e
1 2
Sin(dtp ) 100%
1 2
Mp e
100%
最大超调量
仅与阻尼比ξ有关, 故可以通过实验 求取最大超调量 然后可求系统阻 尼比。 ξ越大,Mp 越小, 系统的平稳性越好 ξ = .4~0.8 Mp = 25.4%~1.5%。
(整理)二阶系统的性能分析1.
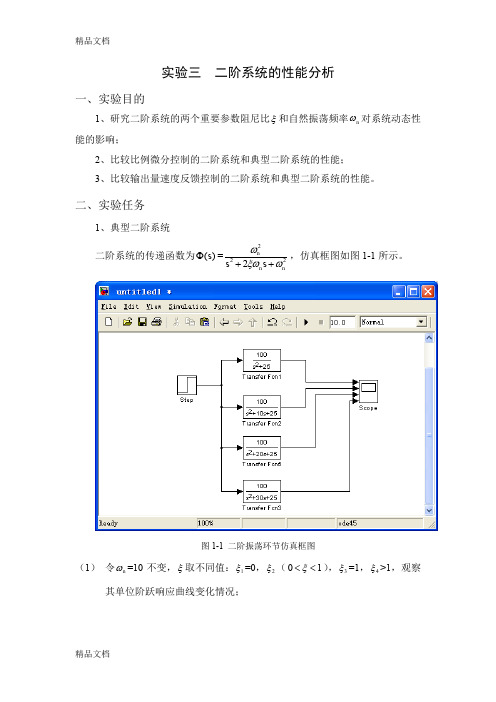
实验三 二阶系统的性能分析一、实验目的1、研究二阶系统的两个重要参数阻尼比ξ和自然振荡频率n ω对系统动态性能的影响;2、比较比例微分控制的二阶系统和典型二阶系统的性能;3、比较输出量速度反馈控制的二阶系统和典型二阶系统的性能。
二、实验任务1、典型二阶系统二阶系统的传递函数为()s Φ=2222nn ns s ωξωω++,仿真框图如图1-1所示。
图1-1 二阶振荡环节仿真框图(1) 令n ω=10不变,ξ取不同值:1ξ=0,2ξ(01ξ<<),3ξ=1,4ξ>1,观察其单位阶跃响应曲线变化情况;ω取不同值,观察其单位阶跃响应曲线变化情况;(2)令ξ=0不变,n(3) 令ξ=0.2不变,n ω取不同值,观察其单位阶跃响应曲线变化情况,并计算超调量%σ和s t ;n ω=5 和n ω=10时单位阶跃响应曲线:n ω=5超调量%σ和s tn ω=10时超调量%σ和s t :求超调量%σ和s t 的方法:以25425)(2++=Φs s s 为例说明。
方法一:num=[0,0,25];den=[1,4,25]; step(num,den)grid % 绘制网格线。
title('Unit-Step Response of G(s)=25/(s^2+4s+25) ') % 图像标题说明:游动鼠标法:用鼠标左键点击时域响应图线任意一点,系统会自动跳出一个小方框,小方框显示了这一点的横坐标(时间)和纵坐标(幅值)。
按住鼠标左键在曲线上移动,可以找到曲线幅值最大的一点――即曲线最大峰值,此时小方框中显示的时间就是此二阶系统的峰值时间,根据观察到的稳态值和峰值可以计算出系统的超调量。
系统的上升时间和稳态响应时间可以依此类推。
这种方法简单易用,但同时应注意它不适用于用plot()命令画出的图形。
方法二:(不显示阶跃响应曲线,若要显示可在“[y,t]=step(G);”后加plot(t,y))G=tf([0,0,25],[1,4,25]);C=dcgain(G)[y,t]=step(G);[Y,k]=max(y);percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C)i=i-1;endsetllingtime=t(i) 方法三: G=tf([25],[1,4,25]);% 计算最大峰值时间和它对应的超调量。
二阶系统的性能指标分析.

邢台学院物理系《自动控制理论》课程设计报告书设计题目:二阶系统的性能指标分析专业:自动化班级:学生姓名:学号:指导教师:2013年3 月24 日邢台学院物理系课程设计任务书专业:自动化班级:2013年3 月24 日摘要二阶系统是指由二阶微分方程描述的自动控制系统。
例如,他励直流电动机﹑RLC电路等都是二阶系统的实例。
二阶系统的性能指标分析在自动控制原理中具有普遍的意义。
控制系统的性能指标分为动态性能指标和稳态性能指标,动态性能指标又可分为随动性能指标和抗扰性能指标。
稳态过程性能稳态误差是系统稳定后实际输出与期望输出之间的差值本次课程设计以二阶系统为例,研究控制系统的性能指标。
关键词:二阶系统性能指标稳态性能指标动态性能指标稳态误差调节时间目录1.二阶系统性能指标概述 (1)2. 应用模拟电路来模拟典型二阶系统。
(1)3.二阶系统的时间响应及动态性能 (4)3.3.1 二阶系统传递函数标准形式及分类 (4)3.3.2 过阻尼二阶系统动态性能指标计算 (5)3.3.3 欠阻尼二阶系统动态性能指标计算 (7)3.3.4 改善二阶系统动态性能的措施 (14)4. 二阶系统性能的MATLAB 仿真 (18)5 总结及体会 (19)参考文献 (19)1.二阶系统性能指标概述二阶系统是指由二阶微分方程描述的自动控制系统。
例如,他励直流电动机﹑RLC 电路等都是二阶系统的实例。
二阶系统的性能指标分析在自动控制原理中具有普遍的意义。
控制系统的性能指标分为动态性能指标和稳态性能指标,动态性能指标又可分为随动性能指标和抗扰性能指标。
稳态过程性能稳态误差是系统稳定后实际输出与期望输出之间的差值2. 应用模拟电路来模拟典型二阶系统。
1.2—l 是典型二阶系统原理方块图,其中T0=1秒;T1=0.1秒;K1分别为10;5;2.5;1。
开环传递函数为:)1()1()(11101+=+=S T S K S T S T K S G (2-1)其中,==1T K K 开环增益。
二阶系统的性能指标

二阶系统的性能指标1. 超调量(Overshoot):超调量是指系统实际输出值达到或超过设定值后的最大偏离程度。
超调量大小与系统阻尼比有关,阻尼比越小,超调量越大。
超调量的大小是评价系统抗干扰性的重要指标之一、超调量较小的系统具有更好的稳定性和抗扰性能。
2. 调节时间(Settling Time):调节时间是指系统从初始状态到稳定状态的时间。
也就是系统输出值从设定值到接近设定值所需要的时间。
系统的调节时间越短,说明系统响应快速,性能越好。
3. 稳态误差(Steady-state Error):稳态误差是指系统输出与期望输出之间的差异,它表示系统在稳态下的输出误差大小。
稳态误差大小可以反映系统的静态稳定性能。
稳态误差越小,说明系统的精度越高。
4. 峰值时间(Peak Time):峰值时间是指从初始状态到系统输出值首次达到超调值的时间。
峰值时间越短,说明系统响应速度越快。
峰值时间较短的系统对输入信号的快速变化能够更快地响应,并快速趋于稳定。
除了上述常见指标外,还有一些常用的性能指标包括上升时间(Rise Time),峰值偏差(Peak Overshoot),调节时间百分比(Percent Overshoot)等,这些指标可根据需要进行评价。
上升时间是指系统响应从0%到100%的时间,或者从10%到90%的时间。
上升时间越短,说明系统的响应速度越快。
峰值偏差是指系统在超调过程中达到的最大偏差值。
系统的峰值偏差越小,说明系统对输入信号的超调响应越小。
调节时间百分比是指系统从初始状态到输出值在一定范围内的时间。
调节时间百分比的指标可以根据具体要求进行设置,一般常见的有2%,5%或10%等。
评价二阶系统性能的指标取决于具体的应用和要求,需要根据实际情况进行选择。
对于不同的应用领域,对于性能指标的要求可能会有所不同。
因此,在实际应用中,需要根据系统的具体要求和特点,选择和优化适合的性能指标,以便更好地评估和改进系统的性能。
二阶系统过冲量

二阶系统过冲量
二阶系统的过冲量是指系统在受到输入信号时,输出信号超过稳态值的最大幅度。
在控制系统中,过冲量是一个重要的性能指标,它影响到系统的稳定性和响应速度。
过冲量的计算公式为:
I_overshoot = 1/G(s) * (1/2 * a(s) * s^2 + b(s) * s + c(s))
其中,G(s)是系统的传递函数,a(s)、b(s)和c(s)分别是系统的一阶、二阶和零阶传递函数。
需要注意的是,过冲量并非针对所有控制系统都具有相同的意义,它与系统的具体设计和需求有关。
在某些情况下,过冲量可能需要优化以提高系统性能,而在其他情况下,过冲量可能并不是一个关键因素!。
二阶系统的幅值裕度

二阶系统的幅值裕度二阶系统的幅值裕度是衡量系统稳定性和抗干扰性能的重要指标之一。
它描述了系统输出与输入之间的增益差异,在频率响应曲线上体现为系统的切线与单位增益线之间的垂直距离。
幅值裕度越大,系统的稳定性和抗干扰性能就越好。
在频域中,二阶系统的传递函数通常可以表示为:H(s) = K / (s^2 + 2ξω_ns + ω_n^2)其中,K为开环增益,ξ为阻尼比,ω_n为无阻尼自然频率。
根据这个传递函数,可以得到幅值裕度的计算公式。
首先,需要找到系统的增益边界频率,即系统在该频率处的幅值与单位增益线之间的距离最小。
然后,根据系统的传递函数,计算增益边界频率处的幅值。
通过将s替换为jω,其中j为虚数单位,ω为频率,可以得到系统的频率响应函数H(jω),并将其转化为幅值谱:|H(jω)| = |K / (jω^2 + 2ξω_njω + ω_n^2)|计算幅值谱的大小,即可得到增益边界频率处的幅值。
接下来,计算单位增益线的幅值。
单位增益线在dB域中表示为0dB。
最后,根据以上计算结果,可以得到系统的幅值裕度,即增益边界频率处的幅值与单位增益线之间的差值。
幅值裕度的计算公式为:幅值裕度 = 20log10(幅值)幅值裕度通常以dB为单位,也可以用倍数表示。
一般来说,幅值裕度大于3dB(或幅值大于1.414倍)被认为是系统稳定的要求。
如果幅值裕度过大,系统可能会出现过大的震荡或不稳定现象;如果幅值裕度过小,则系统可能对干扰信号过于敏感或无法抑制干扰。
因此,适当选择幅值裕度是设计稳定可靠的控制系统的关键。
在实际应用中,可以通过改变系统的控制参数,如增益、阻尼比和自然频率,来调节系统的幅值裕度。
此外,还可以通过增加合适的补偿元件,如比例控制器、积分控制器和微分控制器等来增加幅值裕度。
总之,对于二阶系统而言,幅值裕度是描述系统稳定性和抗干扰性能的重要指标,可以通过计算增益边界频率处的幅值与单位增益线之间的差值来求得。
二阶系统性能指标解读
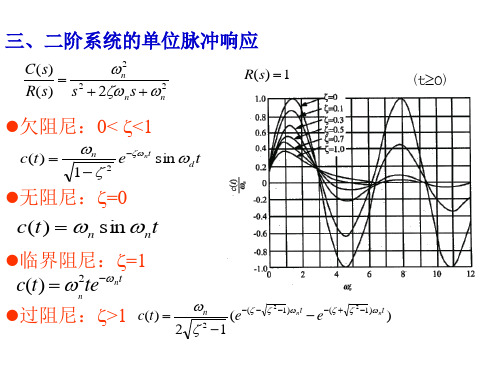
0.5, n 4(弧 度/秒) 当 输
入信号为单位阶跃 信号时 , 试求系统的动态 性能指标 . 解:
ln 1 1-
2
2
n
代 入,并 取 整 数 得 1- 2
1- 2 1 N N( ln 2 2 1- N (.)表 示 取 整 数 ts N Td
arctg荡周期
三.计 算 举 例
例1.二 阶 系 统 如 图 所 示 ,其 中
nentp Sin(dtp ) dentpCos(dtp ) 0
Sin(dtp ) 1 2 Cos(dtp ) 0
1 2 tg (dtp ) 2 1 d tan d t tan n
1.5(s) 这里取Δ=0.05。
或者按近似算法:
ts
3
n
3T
3 0.125 1.5( s) 0.25
(2)要使σ%=10%,求ζ。 由
% exp(
解得
1 2 ) 100 % 10%
0.6
2
K0
ts T
1 4 T0
ln 1
上升时间tr
峰值时间tp
0
5% c() or 2% c()
调节时间ts
t
tr t p
ts
当(>=1)时阶跃响应没有超调,此时, 上升时间的定义修改如下:
1.0 0.9 0.5 0.1 0
C(t)
t ( 0.10.9 ) t ( 0 0. 9 )
tr tr
t
2) 欠阻尼二阶系统阶跃响应的特征量的计算: 上升时间
二阶系统的性能分析
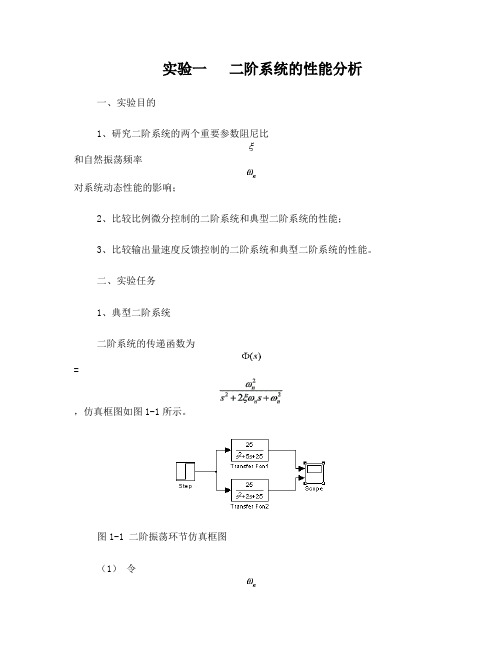
实验一二阶系统的性能分析一、实验目的1、研究二阶系统的两个重要参数阻尼比和自然振荡频率对系统动态性能的影响;2、比较比例微分控制的二阶系统和典型二阶系统的性能;3、比较输出量速度反馈控制的二阶系统和典型二阶系统的性能。
二、实验任务1、典型二阶系统二阶系统的传递函数为=,仿真框图如图1-1所示。
图1-1 二阶振荡环节仿真框图(1)令取不同值:=0,=0.2、=0.4(),=1,=2>1,观察其单位阶跃响应曲线变化情况;(2)令取不同值,=0.2,=1,=1.2,=3,=5观察其单位阶跃响应曲线变化情况;(3)令=0.2不变,=0.25,=1,=5,=8,=30,观察其单位阶跃响应曲线变化情况,并计算超调量和;计算超调量和程序:G=tf([100 ],[1,0.1,100]);C=dcgain(G)[y,t]=step(G);[Y,k]=max(y);percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C)i=i-1;endsetllingtime=t(i)结果:Percentovershoot =98.4415 setllingtime = 78.2257 percentovershoot = 96.9071 setllingtime =38.9557 percentovershoot =72.9156 setllingtime = 3.8327 percentovershoot = 60.046 setllingtime = 2.2934 percentovershoot = 9.4778 setllingtime = 0.5858仿真图(4)令=10不变,取不同值(),=0.1,=0.3=0.6=0.8=0.9观察其单位阶跃响应曲线变化情况,并计算超调量和。
计算超调量和程序:G= tf([100 ],[1,2,100]);C=dcgain(G)[y,t]=step(G);[Y,k]=max(y);percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C)i=i-1;endsetllingtime=t(i)结果:percentovershoot =72.9156 setllingtime = 3.8327 percentovershoot = 25.3786 setllingtime = 0.8393 percentovershoot = 9.4778 setllingtime = 0.5858 percentovershoot =1.5164 setllingtim e = 0.3738 percentovershoot =-0.2528 setllingtime = 2.1447e-004(5)已知传递函数为:利用MATLAB命令绘制阶跃响应曲线。
自动控制 二阶系统性能分析

c(t1p)-1100% = e-ζπ
1-ζ
2
100%
整理ppt
第三节 二阶系统性能分析
4. 调节时间ts
c(t)=1-
e-ζ
ωnt
2
sin(ω
d
t+β
)
1-ζ
c(t)
1
误差带
可用近似公式: 0
ts =3T=ζω3n
ts
=4T=ζ
4 ωn
ζ<0.68 ζ<0.76
ts t
±5%误差带 ±2%误差带
整理ppt
第三节 二阶系统性能分析
四、带零点二阶系统单位阶跃响应
c(cФ=t=1τ)d(c=(1tsdc(s)系1(t21)=t)s+-(==2Lt统ω2ζe+)1cRC-ω=ω-ζ-12ζ1ζn结2(ω(([e1s(nsωtnns22s)t-ζ))-ζ(构s++=ωnsz+τ1n2ωsz2t11s为+[+(ζ[2ωd2nz)ω+ζ2ωω-ζdcω2nζ+ω21tn2nn(2ω)sz(τntni)=(sn)nsRs+zs2sω(+ω((i++sns1ωn)τ222ωdζ设(ω)+s)ωstωn++]2n2ζ2dβ=1n2n(ωt1+ssR)β+-+n-ωω(zse1)s+-)-ζ+n-)ω2ζdωω=c)时nnso22tds(1)sss间c+ωi(ωon闭2ζns20常(ωωd(ω<环nt数ζ+d)dβ<tC零t++1(β)βs]点)))] 设=C11-(se1)-ζ-ζ=ωn2ts2z+lω2[ζ2nzωR-ζlωn(ssn)+ωsinn2(ω则d t+βC()s+)ω=lCd c1o(ss)(ω+ dzstC+β1(s))]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、二阶系统传递函数的标准形式
二阶系统的闭环传递函数写成标准形式为:22
2
2)()(n
n n s s s R s C ωξωω++=
式中,ξ为阻尼比;n ω为无阻尼自振频率。
所以,二阶系统的特征方程为:022=++n n s s ωξω
由上式解得二阶系统的二个特征根(即闭环极点)为:2
2.11ξωξω-±-=n n j s
随着阻尼比ξ取值的不同,二阶系统的特征根(即闭环极点)也不相同。
二、单位阶跃函数作用下二阶系统的过渡过程(针对欠阻尼状态,10<<ξ )
令)(1)(t t r =,则有s
s R 1
)(=
,二阶系统在单位阶跃函数作用下输出信号的拉氏变换为:2
2222
22)()(1
)
)((211
2)(d n d d n d n n d n d n n n n n s s s s j s j s s s s
s s s C ωξωωωξωωξωξωωξωωξωξωωξωω++⋅
-+++-=-++++-
=⋅++=
式中,2
1ξωω-=n d 为有阻尼自振频率
对上式进行反拉氏变换,得:
)
sin(11)
sin 1(cos 1sin cos 1)(2
2
ϕωξ
ωξ
ξ
ωωωξωωξωξωξωξω+--
=-+-=⋅-
-=----t e t t e t e t e t c d t d d t d t
d n d t n n
n
n
式中,ξ
ξϕ2
1-=arctg
由上式看出,对应10<<ξ时的过渡过程,)(t c 为衰减的正弦振荡曲线。
其衰减速度取决
ϕ角的定义
于n ξω值的大小,其衰减振荡的频率便是有阻尼自振频率d ω,即衰减振荡的周期为:
2
122ξ
ωπ
ωπ
-=
=
n d
d T
三、二阶系统的性能指标
1.上升时间tr :上升时间是响应曲线由零上升到稳态值所需要的时间。
根据定义,当r t t =时,1)(=r t c 。
即 0sin 1cos 2
=-+
r d r d t t ωξ
ξ
ω
或 n
n r d t tg ξωξωω2
1-=,)(ϕπω-=tg t tg r d
所以,上升时间为:2
1ξ
ωϕπ--=
n r t
2.峰值时间tp :过渡过程曲线达到第一个峰值所需的时间。
ϕϕωtg t tg dt t dc p d t t p
=+⇒==)(0)
( ( ,3,2,,0πππω=p d t )
由于峰值时间tp 是过渡过程曲线达到第一个峰值所需的时间,故取πω=p d t
即 21ξ
ωπωπ-=
=
n d p t 3.最大超调量p σ
最大超调量为:%100)
()()(∙∞∞-=
c c t c p p σ
%
100%
100)sin 1(cos %
100)sin 1(cos 2
12
2
⋅=⇒∙-+
-=∙-+-=--
--ξξπ
ξωξωσπξξ
πωξ
ξ
ωe
e
t t e p t p d p d t p
n p
n
式中,)(p t c 为过渡过程曲线第一次达到的最大输出值;)(∞c 为过渡过程的稳态值()(∞c =1)。
4.过渡过程时间ts :在过渡过程的稳态线上,用稳态值的百分数∆(通常取∆=5%或∆=2%)作一个允许误差范围,进入允许误差范围所对应的时间叫~。
)
1sin(11)(22
ξ
ξωξξω-+--
=-arctg t e t c d t n
从上式看出,2
11ξ
ξω-±
-t n e 是此时系统
过渡过程)(t c 的包络线方程。
即过渡过程
)(t c 总是包含在一对包络线内,包络线的
时间常数为
n
ξω1。
根据过渡过程时间的定义,可近似认
为就是包络线衰减到∆区域所需的时间,则有:
)
11ln 1(ln
1
122
ξ
ξωξξω-+∆=
⇒∆=--n
s t t e n
若取%5=∆,并忽略2
11ln
ξ-,则得:n
s t ξω3
≈
若取%2=∆,并忽略2
11ln ξ-,则得:n
s t ξω4
≈
二阶系统单位阶跃响应的一对包络线。
