新课标数学中考专题复习5：探索性问题

合集下载

中考数学探索性问题的解法.doc

L_J 中考数学探索性问题的解法随着应试教育向素质教育的转轨，加强对学生各方面能力考察的题目成了近年来各省市中考试题中的热门问题，探索性问题便是其中一类应运血生的新题型, 这•类问题对培养学生的创造性思维、想象能力和探索能力有很大帮助。

探索性问题又可分为结论探索型和存在探索型两种。

一、结论探索型问题此类题型一般是在给定题设条件下探求结论，它要求学生在对题设条件或图形认真分析的基础上，进行归纳，大胆猜想，然后通过推理、计算获得结论。

例1、长方形的周长为24cm,面积为64cm2,则这样的长方体（）（A）有一个（B）有二个（C）有无数个（D）不存在a +b = 12解：设长方体的长为d,宽为b,贝U、址' = 64a> b可视为X2—12x+64=0的两个根•/ △二（一12） 2-4 X 64 = 144-256V0・.・该方程无实根即a、b不存在，因此选（D）a例2、在宽为a的纸带中剪出直径为a的圆5个，直径为5的圆10个，排列方法如图1,计算所用纸带长度，请考虑能否再设计一种排列方法，使所用纸带的长度比原排列方法节省原材料？ffll图2买•恩•收瓦潟暴圈3分析：通过图1观察易发现图中虚线部分具有典型性，为计算方便，取具有典型的部分（图2）进行分析，计算出结果。

易知，在等腰三角形ABC中，BC边上的高为AD,..a V2 a 今27+ 2 龙4 = 4a + — + — a 十一+ 2a = - a..•原排列方法使用纸带长为 2 2 4 4通过计算启发我们，如果把小圆分别插到大圆中，采用如下的排列方法，（如图3）这时纸带长为,a , 72 ° a ,3 ,9」、 3+18>/23 2 24 4 244- A = （6-4很）a a 0.344a可见改进后的排列方法比较合理例3、如图6、有四个动点P、Q、E、F分别从正方形ABCD的顶点A、B、C、D同时出发，沿着AB、BC、CD、DA以同样的速度向点B、C、D、A移动。

中考数学专题复习5：探索性问题

中考数学专题复习5：探索性问题Ⅰ、综合问题精讲：探索性问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的题型．探索性问题一般有三种类型：（1）条件探索型问题；（2）结论探索型问题；（3）探索存在型问题．条件探索型问题是指所给问题中结论明确，需要完备条件的题目；结论探索型问题是指题目中结论不确定，不唯一，或题目结论需要类比，引申推广，或题目给出特例，要通过归纳总结出一般结论；探索存在型问题是指在一定的前提下，需探索发现某种数学关系是否存在的题目．探索型问题具有较强的综合性，因而解决此类问题用到了所学过的整个初中数学知识．经常用到的知识是：一元一次方程、平面直角坐标系、一次函数与二次函数解析式的求法（图象及其性质）、直角三角形的性质、四边形（特殊）的性质、相似三角形、解直角三角形等．其中用几何图形的某些特殊性质：勾股定理、相似三角形对应线段成比例等来构造方程是解决问题的主要手段和途径．因此复习中既要重视基础知识的复习，又要加强变式训练和数学思想方法的研究，切实提高分析问题、解决问题的能力． Ⅱ、典型例题剖析【例1】（2005，临沂）如图2－6－1，已知抛物线的顶点为A(O ，1)，矩形CDEF 的顶点C 、F 在抛物线上，D 、E 在x 轴上，CF 交y 轴于点B(0，2)，且其面积为8．(1)求此抛物线的解析式；(2)如图2－6－2，若P 点为抛物线上不同于A 的一点，连结PB 并延长交抛物线于点Q ，过点P 、Q 分别作x 轴的垂线，垂足分别为S 、R ．①求证：PB ＝PS ； ②判断△SBR 的形状；③试探索在线段SR 上是否存在点M ，使得以点P 、S 、M 为顶点的三角形和以点Q 、R 、M 为顶点的三角形相似，若存在，请找出M 点的位置；若不存在，请说明理由． ⑴解：方法一：∵B 点坐标为(0，2)，∴OB＝2， ∵矩形CDEF 面积为8，∴CF=4.∴C 点坐标为(一2，2)．F 点坐标为(2，2)。

中考数学专题--探索性问题

AB 此时 A B > B C , k= BC > 1;
当△B G F 为直角三角形时, ∠B G F = 90°, ∴∠B A C = 45°. 此时 A B
AB = BC , k= BC = 1;
当△B G F 为钝角三角形时, ∠B G F > 90°, ∴∠B A C > 45°,
AB 此时 A B < B C , k= BC < 1,
1.(随州)如图,点 F,B,E,C 在同一直线上,并且 BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明. 提供的三个条件是①AB=DE;②AC=DF;③AC∥DF.
专题考点 01 条件探索问题
条件探索型是指所给问题中的结论明确,需要完备条件的题目类型.其解题基本思路类似于分析法,假设结论成立,逐步探索其成立的条件;或把可能产生的条件一一列出,逐个分析考查,多采用逆向思维方式.
例
(新疆)如图,▱ABCD 中,点 O 是 AC 与 BD 的交点,过点 O 的直线与 BA,DC
∴0< k< 1.
2.(福州中考)我们知道,经过原点的抛物线的解析式可以是 y=ax2+bx(a≠0). (1)对于这样的抛物线: 当顶点坐标为(1,1)时,a= ; ;
当顶点坐标为(m,m),m≠0 时,a 与 m 之间的关系式是
(2)继续探究,如果 b≠0,且过原点的抛物线顶点在直线 y=kx(k≠0)上,请用含 k 的代数式表示 b;
( 2) 连接 E C , AF, 则 E F 与 A C 满足 E F = A C 时, 四边形 A E C F 是矩形, 理由如下: 由( 1) 可知△A O E ≌△C O F , ∴O E = O F . ∵A O = C O , ∴四边形 A E C F 是平行四边形, ∵E F = A C , ∴四边形 A E C F 是矩形.

中考数学探索性问题简析

中考数学探索性问题简析锦州市第八中学陈树海一、规律探索问题【简要分析】规律探索问题是根据已知条件或所提供的若干个特例，通过观察、类比、归纳、揭示和发现题目所蕴含的本质规律与特征的一类探索性问题．【典型考题例析】例1 观察下列各式：1×3=12＋2×1；2×4=22＋2×2；3×5=32＋2×3；……请你将猜想到的规律用自然数年n(n≥1)表示出来：.（2005年陕西省中考题）分析与解答观察比较以上各等式知，等式左端是两个因数的乘积，前一个因数依次是1、2、3、……，后一个因数依次是3、4、5、……，它们都是连续的，且后一个因数比前一个因数均大2；等式右端是两项的和，前一个加数依次为12、22、32、……，后一个加数依次是连续自然数的2倍，因而猜想到的规律用自然n(n≥1)表示为n(n+2)=n2+2n．例2 观察下列数表：1 2 3 4 (1)2 3 4 5 (2)3 4 5 6 (3)4 5 6 7 (4)┇ ┇ ┇┇第第第第1 2 3 4列列列列根据数表所反映的规律，猜想第6行与第6列交叉点上的数应为．第n行（n为正整数）与第n列交叉点上的数应为．（2005年北京市丰台区中考题）分析与解答本例属于数字规律的探索问题．经观察，本数表是一个n×n型表，每一行的第1个数字就是该行的序数，后面的第2、3、……、n个数为自然数递增的顺序排列．第n行与第n列的交叉点上的数就是第n行的第n个数．据此，第6行与第6列的交叉点上的数就是第6行的第6个数，即6＋5=11．第n行的第n个数为n ＋(n-1)=2n-1.例3 用同样大小的黑、白两种颜色的棋子摆设如图2-2-1所示的正方形图案．则第n个图案需要用白色棋子枚．（用含有n的代数式表示）（2005年广东省茂名市中考题）分析与解答根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题.解决这尖问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．很显然，第1个正方形图案有棋子共32=9枚，其中黑色棋子有12=1枚，白色棋子有（32－12）枚；第2个正方形图案有棋子共42=16枚，其中黑色棋子有22=4枚，白色棋子有（42－22）枚；…由此可猜出想第n个图案的白色棋子数为（n＋2）2－n2=4(n＋1).【提高训练】1.观察下列各式，探索发现规律：1×3=3=22－1；3×5=15=42－1；5×7=35=62－1；7×9=63=82－1；9×11=99=102－1；…用含正整数n的等式表示你所发现的规律为．（2005年山东菏泽市中考题）2．图2-2-2是用积木摆放的一组图案，观察图形并探索：第5个图案中共有块积木．第n个图形共有块积木．（2005年内蒙古呼和浩特市中考题）3．观察下列各式：,…请你将猜想到的规律用含自然数n （n≥1）的代数式表示出来是．（2004年山西省中考题）4．观察下列图形（每个正方形的边长均为1）和相应等式，探索其中的规律：①←→②←→③←→④←→……………………（1）写出第五个等式，并在下面给出的五个正方形上画出与之对应的图示：（2）猜想并写第n个图形相对应的等式．（2005年河北省中考题）【提高训练答案】1．2．n23．4．（1），图示略；（2）二、结论探索问题【简要分析】结论探索问题是指仅给出某种情境而没有明确指出结论，需要解题者去探索符合条件的一类试题．这类探索问题的设问常以适合某种条件的结论“成立”、“不成立”、“是否成立”等语句加以表述，或直接问“有何结论”等．它与传统题的区别在于：探索问题的结论往往也是解题过程．【典型考题例析】例1 如图①，已知AB是⊙O的直径，AC是弦，直线CD切⊙O于点C，AD⊥CD，垂足为D．(1)求证：AC2=AB·AD；(2)若将直线CD向上平移，交⊙O于C1、C2两点，其他条件不变，可得到图②所示的图形，试探索AC1、AC2、AB、AD之间的关系，并说明理由；(3)把直线C1D继续向上平移，使弦C1C2与直径AB相交（交点不与A、B重合），其他条件不变，请你在图③中画出变化后的图形，标好字母，并试着写与（2）相应的结论，判断你的结论是否成立？若不成立，请说明理由；若成立，请给出证明．（2005年内蒙古呼和浩特市中考题）分析与解答第（1）题，连结BC，证明△ACD∽△ABC；第（2）题，探索AC1、AC2、AB、AD所在的两个三角形是否与（1）中有类似的相似；第（3）题的关键是在图③中正确画出图形．（1）连结BC．∵AB是⊙O的直径，∴∠ACB=900．∵AD⊥CD，∴∠ADC=900．∴∠ACB=∠ADC.∵CD切⊙O于C，可证∠ACD＝∠ABC.∴△ACD∽△ABC．∴．∴AC2＝AB·AD．（2）关系式：AC1·AC2＝AB·AD．理由：连结BC1、AC2．∵四边形ABC1C2是圆内接四边形，∴可证∠AC2D∠B．同（1）有∠ADC2=∠AC1B，∴△ADC2∽△AC1B.∴，即AC1·AC2＝AB·AD．（3）如图③，结论：AC1·AC2＝AB·AD．．理由：连结BC1、AC2．同（1）有∠ADC2=∠AC1B．又∵∠AC2D=∠B，∴△ADC2∽△AC1B．∴，即AC1·AC2＝AB·AD．说明：本题是一道典型的结论探索题，题中设计的三个问题从特殊到一般，客观地反映了思维的渐进过程．解题的关键是先用常规方法证明第（1）小题的结论，然后第（2）、（3）小题仿照第（1）小题的方法连结及AC2去探索结论并给出证明．例2 如图①，已知E、F为平行四边形ABCD对角线DB的三等分点，连结AE并延长交DC于P，连结PF并延长交AB于Q．（1）在图②的备用图中，画出满足上述条件的图形，试用刻度尺在图①、图②中量得AQ、BQ的长度，估计AQ、BQ间的关系，并填入下表：由上表可猜测AQ、BQ间的关系是．（2）上述（1）中的猜测AQ、BQ间的关系成立吗？为什么？（3）若将平行四边形ABCD改为梯形（AB∥CD），其他条件不变，此时（1）中猜测AQ、BQ间的关系是否成立？（不必说明理由）（2005年浙江省绍兴市中考题）分析与解答本题是一道集操作、测量、猜想、证明于一体的结论开放性试题．解答本题的关键是准确进行测量，然后根据测量的结果合理、正确地猜想．(1)填表格略．猜测：AQ=3BQ．(2)成立．∵四边形ABCD是平行四边形，∴DC∥AB．∴△PDF∽△QBF．∴．∵E、F为BD的三等分点，∴DP：BQ=2．同理AB：PD=2．∴AB：BQ=4．∴AQ：BQ=3，即AQ=3BQ．(3)成立.【提高训练】1．如图①，已知AC、AB是⊙O的弦，AB>AC．（1）在图①中，能否在AB上确定一点E，使得AC2=AE·AB？为什么？（2）在图②中在条件（1）的结论下延长EC到P，连结PB，如果PB=PE，试判断PB和⊙O的位置关系，并说明理由．（2005年甘肃省中考题）2.已知矩形ABCD和点P，当点P在图①中的位置时，则有结论：S△PBC＝S△PAC＋S△PCD.理由：过点P作EF⊥BC，分别交AD、BC于E、F两点.∵，又∵，∴S△PBC+S△PAD=S△PAC+S△PCD+S PAD.∴S△PBC=S△PAC+S△PCD.请你参照上述信息，当点P分别在图②、图③中的位置时，S△PBC、S△PAC、S△PCD又有怎样的数量关系？请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明.（2005年黑龙江省中考题）3．已知A为⊙O上一点，B为⊙A与OA的交点，⊙A与⊙O的半径分别为r、R，且r＜R．（1）如图①，过点B作⊙A的切线与⊙O交于M、N两点.求证：AM·AN＝2Rr；（2）如图②，若⊙A与⊙O的交点为E、F，C是上任意一点，过点C作⊙A的切线与⊙O交于P、Q两点，试问AP·AQ=2Rr是否成立？并证明你的结论．（2004年天津市中考题）【提高训练答案】1．（1）作法有多种，如在⊙O上取点D，使，连结CD交AB于点E，则有AC2=AE·AB，证明略（2）PB是⊙O的切线，连BO并延长交⊙O于F，证∠AFB=∠BEP=∠ABP，故∠PBO=9002．猜想结果：图②结论S△PBC＝S△PAC+S△PCD，图③结论S△PBC=S△PAC-S△PCD3．（1）延长AO与⊙O交于点D，连结DM.证明Rt△ABM∽Rt△AMD，由垂径定理得AM=AN，又AB=r，AD=2R，∴AM·AN＝2Rr（2）提示：延长AO与⊙O交于点D，连结DQ、AC.证Rt△ADQ∽Rt△APC.∵AD=2R，AC=r,，∴AP·AQ=2Rr（三）方案设计探索问题【简要分析】方案设计探索问题，指的是提出一个数学问题情况如几何图形或图案的设计，物长物高的测量等，要求考生按要求设计某种方案来解决问题的一类探索题．【典型考题例析】例1 请用几何图形“△”、“││”、“⌒”（一个三角形，两条平行线，一个半圆，如图2-2-14）作为构件，尽可能构思独特且有意义的图形，并写一两句帖切、诙谐的解说词．（至少两幅）．（2005年青海省湟中县中考题）分析与解答这是几何构件类方案设计题．解答这类问题无固定的模式可套，需要考生去探索、创新．现给出两个参考作案（如图2-2-15），请大家开动脑筋，再设计几幅出来．例2 在某居民小区的中心地带，留有一块长16m，宽12m的矩形空地，计划用于建造一个花圆，设计要求：花圆面积为空地面积的一半，且整体图案成轴对称图形．（1）小明的设计方案如图①所示，其中花园四周是人行道，且人行道的宽度都相等，你知道人行道的宽度是多少吗?，请通过计算，给予解答．（2）其实，设计的方案可以是多种多样的，请你按设计要求，另设计一种方案．（2005年广西钦州市中考题）分析与解答本例集计算、设计于一体，综合考查了学生运用数学知识解决实际问题的能力．(1)设人行道宽为xm，根据题意，得.解之，得．人行道的宽度为2m.（2）符合要求的答案很多，如图②～⑤均可．其中图②中的花园是底边长为16M 的等腰三角形,图③中的花园是两边底长为8M的等腰三角形.图④中的花园是顶点分别是矩形中点的菱形,图⑤中的花园是上底与下底之和为16的等腰梯形．v例3已知：如图①，现有边长为a、边长为b的正方形纸片和宽为a、长为b 的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图痕迹），使拼出的图形面积为2a2+5ab+2b2，并标出此矩形的长和宽．（2005年江苏省盐城市中考题）分析与解答本题是一道实践操作的拼图设计题．解决这类问题我们应从图形的面积着手进行考虑，看看要拼成的矩形与已知正方形、矩形的面积有何倍数关系，然后尝试着进行拼图，下面给出两种拼法（如图②）供参考．例4 高为12.6米的教学楼ED前有一棵大树AB（如图①）．（1）某一时刻测得大树AB，教学楼ED在阳光下的投影长分别是BC=2．4米，DF=7．2米．求大树AB的高度；（2）用刻度尺、高为h米的测角仪，请你设计另一种测量大树AB高度的方案．要求：①在图②上，画出你设计的测量方案示意图，并将应测数据标记在图上（长度用字母m、n……表示，角度用希腊字母α、β……表示）；②根据你所画的示意图和标注的数据．计算大树AB的高度．（用字母表示）（2005年江苏省泰州市中考题）分析与解答本例属于相似三角形和解直角三角形应用类的方案设计问题．（1）连结AC、EF，则有AC∥EF，易得△ABC～△EDF，∴.∴.∴AB=4.2．故大树AB的高度为4．2米．（2）方案很多，下面提供两种设计方案供参考．方案1：如图③，MG＝BN＝m，AG＝m·tanα，∴AB＝（m·tanα＋h）米．方案2：如图④，MF＝NE＝m，AG＝,∴AB=(+h)米．【提高训练】1．在图的方格纸中设计一个轴对称图案．在这个图案中必须用到等腰三角形、正方形、圆三种基本图形．（2005年宁夏灵武市中考题）2．在一次数学探索活动中，小强用两条直线把平行四边形ABCD分别割成四部分，使含有一组对项角的两个图形全等．（1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有组．（2）请在如图的三个平行四边形中画出满足小强分割方法的直线．（3）由上述实验操作过程，你发现所画的直线有什么规律？（2005年贵州省贵阳市中考题）3．如图①，A、B两点被池塘隔开，为测量AB两点的距离，在AB外选一点C，连结AC和BC，并分别找出AB和BC的中点M、N，如果测行MN=20m，那么AB=2×20m=40m．（1）测AB距离也可由图②所示用三角形相似的知识来解决，请根据题意填空：延长AC到N，使，延长BC到M，使CM= ．则由相似三角形得AB= ．（2）测AB距离还可由三角形全等的知识来设计测量的方案，求出AB的长，请用上面类似的方法，在图③中画出图形，并叙述你的测量方案．（2005年辽宁省大连市中考题）4．阳光小区有一块正方形空地,设计用作休闲场地和绿化场地.如图①是小聪根据正方形空地完成的设计方案示意图(阴影部分为绿化场地),请你用圆规和直尺在同样的正方形内(图②、图③)，画出二种不同于小聪的设计方案示意图，使它们的绿化面积（用阴影表示）与图①中的绿化面相同（不要求写画法）（2005年湖北省孝感市中考题）．【提高训练答案】1．略2．(1)无数 (2)只要两条直线都过对角线的交点就行 (3)这两条直线过平行四边形的对称中心(或对角线的交点)3．(1) ，2MN (2)延长AC到D，使CD=AC，延长BC到E，使CE=BC，连结DE，则AB=DE4．设计方案图略．（四）存在性探索问题【简要分析】存在性探索问题是指在某种题设条件下，判断具有某种性质的数学对象是否存在的一类问题．解题的策略与方法是：先假设数学对象存在．以此为条件进行运算或推理，若无矛盾，说明假设正确．由此得出符合条件的数学对象存在；否则说明不存在．【典型考题例析】例1 已知：抛物线y=-(x-m)2+1与x轴相交于A、B（B在A的右边），与y轴的交点为C．当点B原点的右边，点C在原点的下方时，是否存在△BOC为等腰三角形的情形？若存在，求出m的值，若不存在，请说明理由．分析与解答当y=0时，-(x-m)2+1=0，即有(x-m)2=1∴x1=m-1，x2=m+1.∴A(m-1,0),B(m+1,0)．∵点B在原点右边，∴OB=m+1.当x=0时，y=-m2+1，点C在原点下方，∴OC=m2-1．假如△BOC是等腰直角三角形,则有OB=OC．即m+1=m2-1．解之，得m1=2,m2=-1．当m=-1时，OC=m2-1，不符合题意，∴m=-1舍去．∴存在△BOC为等腰直角三角形，此时m=2．例2 如图2-2-33，已知O为坐标原点，∠AOB=300，∠AB O=900，且点A的坐标为（2，0）．（1）求点B的坐标；（2）若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；（3）在（2）中的二次函数图象的OB段（不包括点O、B）上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标，若不存在，请说明理由．（2005年四川省资阳市中考题）分析与解答（1）在Rt△OAB中，∵∠AOB=300，∴．过点B作BD垂直于x轴，垂足为D，则，∴点B的坐标为．（2）将A（2，0）、B、O（0，0）三点的坐标代入y=ax2+bx+c，得，解得．∴二次函数解板式为．（3）设存在点，使四边形ABCD面积最大．∵△OAB面积为定值，∴只要△OBC面积最大，四边形ABCO就有最大面积．过点C作轴的垂线CE，垂足为E，交OB于点F，则.而.∴．∴当时，△OBC面积最大，最大面积为．此时，点C坐标为，四边形ABCD的面积为．【提高训练】1．如图，平面直角坐标系中，Rt△ABC的斜边AB在x轴上，项点C在y轴的负半轴上，，点P在线段OC上，且PO、PC的长（PO<PC）是方程x2-12x+27=0的两根．（1）求P点的坐标；（2）求AP的长；（3）在轴上是否存在点Q，使得以A、C、P、Q为项点的四边形是梯形？若存在，请直接写出直线PQ的解析式；若不存在，请说明理由．（2005年黑龙江省中考题）2．如图，已知两点A（-1，0）、B（4，0）在x轴上，以AB为直径的半圆P交y轴于点C．（1）求经过A、B、C三点的抛物线的解析式；（2）设AC的垂直平分线交OC于D，连结AD并延长AD交半圆P于点E，相等吗？请证明你的结论；（3）设点M为x轴负半轴上一点，，是否存在过点M的直线，使该直线与（1）中所得抛物线的两个交点到y轴的距离相等？若存在，求出这条直线对应函数的解析式；若不存在，请说明理由．（2005年甘肃省中考题）3．如图，已知二次函数y=ax2+2x+3的图象与轴交于点A、点B（点B在x轴的正半轴上），与y轴交于点C，其项点为D，直线DC的函数关系式为y=kx+3，又tan∠OBC=1．（1）求a,k的值；（2）探究：在该二次函数的图象上是否存在点P（点P与B、C不重合），使得△PBC是以BC为一条直角边的直角三角形？若存在，求出P的坐标；若不存在，请说明理由．（2005年广东省茂名中考题）【提高训练答案】1．（1）P（0，-3）（2）（3）存在，直线PQ的解析式为或2．（1）（2），证明略（3）不存在符合要求的直线.连BE，在Rt△AOD中，可得，由△AOD∽△AEB得AE=4．故点M的坐标为（-2，0）．设过点M的直线的解析式为y=kx+b，将点M的坐标代入得y=kx+2k，再代入抛物线方程得．由题意知此方程的两根互为相反数，故，这时方程无实数根.3．（1）a=-1,k=1 （2）二次函数y=-x2+2x+3的图象上存在点P（1，4）或P（-2，-5），使得△PBC是以BC为一条直角边的直角三角形．关闭窗口。

中考数学题型解法：规律探索性问题

中考数学题型解法：规律探索性问题第一部分讲解部分一．专题诠释规律探索型题是根据已知条件或题干所提供的若干特例，通过观察、类比、归纳，发现题目所蕴含的数字或图形的本质规律与特征的一类探索性问题。

这类问题在素材的选取、文字的表述、题型的设计等方面都比较新颖新。

其目的是考查学生收集、分析数据，处理信息的能力。

所以规律探索型问题备受命题专家的青睐，逐渐成为中考数学的热门考题。

二．解题策略和解法精讲规律探索型问题是指在一定条件下，探索发现有关数学对象所具有的规律性或不变性的问题，它往往给出了一组变化了的数、式子、图形或条件，要求学生通过阅读、观察、分析、猜想来探索规律．它体现了“特殊到一般”的数学思想方法，考察了学生的分析、解决问题能力，观察、联想、归纳能力，以及探究能力和创新能力．题型可涉及填空、选择或解答．。

三．考点精讲考点一：数与式变化规律通常根据给定一列数字、代数式、等式或者不等式，然后写出其中蕴含的一般规律，一般解法是先写出数式的基本结构，然后通过比较各式子中相同的部分和不同的部分，找出各部分的特征，改写成要求的规律的形式。

例1. 有一组数：13,25579,,101726，请观察它们的构成规律，用你发现的规律写出第n（n 为正整数）个数为．分析：观察式子发现分子变化是奇数，分母是数的平方加1．根据规律求解即可．解答：解：21211211⨯-=+； 23221521⨯-=+； 252311031⨯-=+； 272411741⨯-=+； 219251265+⨯-=；…； ∴第n （n 为正整数）个数为2211n n -+．点评：对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．此题的规律为：分子变化是奇数，分母是数的平方加1．例2 阅读下列材料：1×2 ＝31(1×2×3－0×1×2)， 2×3 ＝ 31(2×3×4－1×2×3)， 3×4 ＝ 31(3×4×5－2×3×4)，由以上三个等式相加，可得1×2＋2×3＋3×4＝31×3×4×5 ＝ 20．读完以上材料，请你计算下列各题：(1) 1×2＋2×3＋3×4＋···＋10×11（写出过程）；(2) 1×2＋2×3＋3×4＋···＋n ×(n ＋1) ＝ ______________；(3) 1×2×3＋2×3×4＋3×4×5＋···＋7×8×9 ＝ ______________．分析：仔细阅读提供的材料，可以发现求连续两个正整数积的和可以转化为裂项相消法进行简化计算，从而得到公式)1(433221+⨯++⨯+⨯+⨯n n [])1()1()2)(1()321432()210321(31+--++++⨯⨯-⨯⨯+⨯⨯-⨯⨯⨯=n n n n n n )2)(1(31++=n n n ；照此方法，同样有公式： )2()1(543432321+⨯+⨯++⨯⨯+⨯⨯+⨯⨯n n n[])2()1()1()3()2()1()43215432()32104321(41+⨯+⨯⨯--+⨯+⨯+⨯++⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯=n n n n n n n n )3)(2)(1(41+++=n n n n ．解：（1）∵1×2 ＝31(1×2×3－0×1×2)， 2×3 ＝ 31(2×3×4－1×2×3)， 3×4 ＝ 31(3×4×5－2×3×4)，… 10×11 ＝ 31(10×11×12－9×10×11)， ∴1×2＋2×3＋3×4＋···＋10×11＝31×10×11×12＝440．（2）)2)(1(31++n n n ．（3）1260．点评：本题通过材料来探索有规律的数列求和公式，并应用此公式进行相关计算．本题系初、高中知识衔接的过渡题，对考查学生的探究学习、创新能力及综合运用知识的能力都有较高的要求．如果学生不掌握这些数列求和的公式，直接硬做，既耽误了考试时间，又容易出错．而这些数列的求和公式的探索，需要认真阅读材料，寻找材料中提供的解题方法与技巧，从而较为轻松地解决问题．例3 我们知道不等式的两边加（或减）同一个数（或式子）不等号的方向不变．不等式组是否也具有类似的性质？完成下列填空：一般地，如果⎩⎨⎧>>d c b a , 那么a +c b +d ．（用“>”或“<”填空）你能应用不等式的性质证明上述关系式吗？分析：可以用不等式的基本性质和不等式的传递性进行证明。

初中探索性问题教案

初中探索性问题教案教案概述：本教案旨在通过探索性问题，激发学生的思维潜能，培养学生的创新能力和解决问题的能力。

教学过程中，教师需要引导学生主动探究，积极思考，通过小组合作、讨论交流等方式，找到问题的答案。

教学目标：1. 培养学生提出问题、分析问题、解决问题的能力。

2. 培养学生团队合作、沟通交流的能力。

3. 培养学生创新思维、批判性思维的能力。

教学内容：1. 探索性问题：如何提高学生的学习效率？2. 教学方法：小组合作、讨论交流、PPT展示等。

教学步骤：1. 导入：教师通过一个有趣的例子，引出探索性问题：“如何提高学生的学习效率？”2. 小组讨论：学生分组，每组选择一个角度，进行讨论交流，寻找提高学习效率的方法。

3. 分享交流：每个小组选择代表，向全班同学分享他们的讨论成果。

其他同学可以对分享的内容进行评价、补充。

4. PPT展示：每个小组制作一份PPT，展示他们的探索过程和最终成果。

5. 总结：教师引导学生对各个小组的探索成果进行总结，筛选出提高学习效率的有效方法。

6. 课后作业：让学生根据自己的探索成果，制定一个提高学习效率的计划，并在课后进行实施。

教学评价：1. 学生参与度：观察学生在课堂上的参与情况，包括发言、讨论、展示等。

2. 学生创新能力：评价学生在探索过程中提出的新观点、新方法。

3. 学生团队合作能力：评价学生在小组合作中的表现，包括沟通交流、分工合作等。

4. 学生解决问题能力：评价学生对探索性问题的回答是否具有深度、广度。

教学反思：教师需要在教学过程中关注学生的反馈，根据学生的实际情况调整教学策略。

同时，教师也需要不断学习，提高自己的专业素养，以便更好地引导学生进行探索性学习。

通过本教案，学生能够培养探索问题的习惯，提高自己的学习效率，为未来的学习和生活打下坚实的基础。

中考数学复习中探索性问题教学初探

顺次结四形连边 ABCD各边中得到四形点，边 A,B,C,D,，再
顺连四形尽 ,D 边中，到边入 Z Z 次结边 A C ,各点得四形尹 . C尹
……如此下去得到四边形A B.C.D .
( 1)证明:四形边 A,B,C,D,是矩形。
(2)写出边 A,B,C,D，边 A BCD 面四形和四形 Z 2 2 2的积。
厂 F_ A宜 B C 夕
D
并且考查的是同学们非常熟悉的垂径定理的推论，通
过此问题探索，可使学生对垂径定理更深刻的掌握。例2加图， P是0 0 外一点 ,OP垂直弦AB于点C，交
丽于点D，连结OA,OB,AP,BP ，以上条件，根据写出三
个正确结论， OA=OB除外:
( 1) (2 )
} B mmmN O R " N a me n Pw *mq
昌宁县第二中学唐泽梅
数学探索性问题已成为近年来中考数学热点之一，也是摆在我们每位数学老师面前的一个重要课题，所以研究数学探索性问题的类型和解题策略，教会学生去分析、解决此类问题，有助于大面积提高中考数学
教学质量。下面，自己复习心得和同行探讨。就一、在分块复习中逐渐渗透数学探索性问题，消除学生的恐惧心理和畏难情绪分块复习是将整个初中数学知识按知识的结构分单元复习，这一阶段的主要任务是夯实基础，即使学生对单元的基本概念、公式、性质、定理和所涉及的基本
(3)写出四边形A B} D}的面积。 C 评析:这是一个规律探索题，此题着重考查用三角形中位线定理证明中点四边形是矩形及四边形面积求法，它体现了特殊到一般，有限到无限的化归，既考查学生逻辑推理能力，又培养了学生想象、猜想和验证直觉思维和抽象思维能力。以上三个例题均源于课本，又高于课本，并且都从学生所熟悉的问题出发，只要稍微点拨，学生可自己探究并尝试和体验成功。二、在综合复习中激发学生探索的激情和创新思维火花，稳定巩固探究的兴趣综合复习就是学生在熟悉掌握初中数学基础知识、基本方法和基本技能的基础上，能够综合运用所学知识去分析、解决问综合题涉及的知识广，题，思维、方法多，无固定的解题模式，这一阶段穿插的探索性问题要有一定的思维价值，选题注意围绕中考命题的总思路“ 稳中求新，注重能力考查”立足课本，，源于生活，让学生体现到生活中数学无处不在，数学即生活，生活即数学。例1.如图， ABC是某城市的一个新区， A AD是BC边上的高， BC=8千米， AD=4千米，现在规划新区内有两条主干道PE, PF,P, E, F分别在 △ABC的三条边上，且

新课标九年级数学中考复习强效提升分数精华版探索性问题教案

（1）图①中∠APD的度数为________；
（2）图②中∠APD的度数为________，
图③∠APD的度数为_______；
（3）根据前面的探索，你能否将本题推
广到一般的正n变形情况？若能，写出推广的题目和结论：若不能，请说明理由。
4.一只青蛙在如图8×8的正方形（每个小正方形的边长为1）网格的
2
3
4
5
6
...
分成的最多平面数
2
4
7
11
...
(1)填表：
(2)设n条直线把平面最多
分成的块数是，请学出
S关于n的表达式，（不需要解题过程）。
9.将正六边形纸片按下列要求分别分割（每次分割，纸片均不得有剩余）：
第一次分割：将正六边形纸片分割成三个全等的菱形，然后选取其中的
一个菱形再分割成一个正六边型和两个全等的正三角形；第二次分割：将第一次分割后所得的正六边形纸片分割成三个全等的菱形，然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形；按上述分割方法进行下去……
第周星期第课时总课时初三备课组
章节
专题
课题
探索性问题
课型
复习课
教法
讲练结合
教学目标（知识、能力、教育）
1.掌握探索性问题的特点及类型，熟练运用探索性问题的解题解题策略解决有关问题。
2.通过对各种类型的探索性问题的探索，培养学生分析问题的能力和解决问题能力。
3.通过富有情趣的问题，激发学生进一步探索知识的激情。感受到数学来源于生活。
教学重点
熟练运用探索性问题的解题解题策略解决有关问题。
教学难点
分析问题以及解决问题能力的培养.
教学媒体
学案

九年级数学中考综合复习：开放与探索性问题复习讲义

综合复习.开放与探索性问题＆.综合评述：开放与探索性问题改变了过去试题形式单一，知识点考查僵硬，不能充分调动学生的创新意识和探究兴趣的缺点，为学生提供了更广阔的思维空间，正因为如此，开放与探究性题成为近几年中考的热点题型之一。

一、开放性问题这类题一般没有具体的标准答案，解题时要灵活运用所学基础知识，多层次、多角度地思考问题，解决问题，一般答案只要符合题意即可。

二、探究性问题探究性问题是指命题中缺少一定的条件或无明确的结论，需要经过推断、补充并加以证明的题型，探究性问题一般分为三类：1、条件探索型题；2、结论探究型题；3、探究存在型题。

条件型题是指所给问题中结论明确，需要完备条件的题目；结论探究型题是指题目中的结论不确定，不唯一，或题目结论需要类比，引申推广，或题目给出特例，要通过归纳总结出一般结论。

探究存在型题是指在一定的基础上，需探究发现某种数学关系是否存在的题目。

这类问题具有较强的综合性，涉及的数学基础知识非常广泛。

这种题型既能考查学生对基础知识掌握的熟练程度，又能较好的考查学生的观察、分析、概括能力，因此复习时，既要重视基础知识，又要强化数学思想方法训练，切实提高自己分析问题、解决问题的能力。

＆.典型例题剖析：§.例1、多项式192+x 加上一个单项式后，使它成为一个整式的完全平方，那么加上的单项式可以是 .（填上一个你认为正确的即可）思路点拨：本题主要考查了完全平方式。

解：按完全平方公式得()2213619+=++x x x ，()2213619-=-+x x x ，另外22919x x -+21=，()22239119x x x ==-+，224212948119⎪⎭⎫⎝⎛+=++x x x ，故其答案是x 6±或29x -或1-或4481x .规律总结：本题属于条件探索题，可以从完全平方式入手，多层次、多角度思考问题，可繁可简，可难可易，一般答案只要符合题意即可。

中考数学复习指导：相似三角形的探索性问题

相似三角形的探索性问题探索性问题一般没有明确的结论，没有固定的形式和方法，要求学生通过自己的观察、分析、比较、概括，得出结论，形成方法和思路的数学问题，这类题是考查学生分析问题和解决问题的重要题型，它可以分为三类：一、条件探索性问题条件探索性问题是指所给问题中结论明确，而需要完备使结论成立的条件的题目，这类问题大致分为两种类型：一是问题中的条件未知或不足需要探求，二是条件多余或有错，要求排除或修正.例1:如图1,已知△ABC ,P 是AB 边上的一点,连结CP .要使△APC ∽△ACB ,则应添加一个条件是_______.分析:⑴∠ACP =∠B (或∠APC =∠ACB )时,可得到△APC ∽△ACB ;⑵即△APC ∽△ACB方法探究:在△APC 和△ACB 中,已有一角对应相等,因此添加的条件应从“有两个角对应相等，两个三角形相似”和“两边对应成比例，且夹角相等的两个三角形形似”两个途径进行思考，本题是一个条件探究题，这类问题一般解法是把结论当作已知反溯条件.二、结论探索性问题它是指题目结论不确定,不唯一,或题目结论需要通过类比引申推广,或题目给出特例,要通过归纳总结出一般结论.例2:已知:如图2, △ABC 中,点D.E 分别在边AB.AC 上,连结DE 并延长交BC 的延长线于点F ,连结DC.BE .若∠BDE +∠BCE =180°.(1)写出图中三对相似三角形(注意:不得加字母和线);(2)请在你所找出的相似三角形中选取一对,说明他们相似的理由.分析: 先由角的关系入手,由∠BDE +∠BCE =180°和图形中∠BDE +∠ADE =∠BCE +∠ECF =180°, 可得∠BDE =∠ECF , ∠ADE =∠BCE , 易得△ADE ∽△ACB (∠A 为公共角)、 △ECF ∽△BDF (∠F 为公共角), 其次，由△ECF ∽△BDF 得可得△FDC ∽△FBE (∠F 为公共角).图2A图1PCB解：⑴△ADE ∽△ACB ，△ECF ∽△BDF ，△FDC ∽△FBE .⑵①△ADE ∽△ACB . 证明如下：∵∠BDE +∠BCE =180°.又∵∠BDE +∠ADE =180°，∴∠ADE =∠BCE . ∵∠A =∠A ，∴△ADE ∽△ACB 。

中考数学探索性问题知识点

中考数学探索性问题知识点中考数学探索性问题知识点一、探索性问题是指命题中缺少一定的题设或没有明确的结论，需要经过推断、补充、并加以证明的问题。

其典型特点是不确定性。

主要包括（1）条件探索型，（2）结论探索型，（3）存在性探索型等。

条件探索型是指结论已明确，需要探索发现使结论成立的条件的题目；结论探索型是指在一定的条件下无结论或结论不明确，需要探索发现与之相应的结论的题目；而存在型探索题是指在一定的前提下，需探索发现某种数学关系是否存在的题目。

探索性问题由于它的题型新颖、涉及面广、综合性强、难度较大，不仅能考查学生的数学基础知识，而且能考查学生的创新意识以及发现问题、提出问题、分析问题并解决问题的能力，因而倍受关注。

探索性问题解法，根据已知条件，从基础知识和基本数学思想方法出发，结合基本图形，抓住本质联系进行探究，常用观察、试验、联想、归纳、类比等方法，进行分析、归纳、猜想、比较、推理等，直到得出答案。

题目的答案也是多种多样的，有的题目有唯一解，有的题无解，也有的题要分几种情况讨论。

解结论探索型题的方法是由因导果；解条件探索型的方法是执果索因；解存在性探索题先假设要探索的问题存在，继而进行推导与计算，若得出矛盾或错误的结论，则不存在，反之即为所求的结论。

解题时应注意知识的综合运用。

二、理解掌握例一、已知：（如图）要使ΔABC∽ΔAPB，需要添加的条件是_____（只填一个）。

（答案：∠ABP=∠C，或∠ABC=∠APC，或AB2=APAC）说明：该图是初二几何的基本图形，是解决其他问题的基础，应牢记。

例二、如图，☉O与☉O1外切于点T，AB为其外公切线，PT为内公切线，AB与PT相交于点P，根据图中所给出的已知条件及线段，请写出一个正确结论，并加以证明。

（本题将按正确答案的难易程度评分）结论1： PA=PB=PT 结论2：AT⊥BT。

（或AT2+BT2=AB2）结论3：∠BAT=∠TBO1 结论4：∠OTA=∠PTB结论5：∠APT=∠BO1T 结论6：∠BPT=∠AOT结论7：ΔOAT∽ΔPBT 结论8：ΔAPT∽ΔBO1T设OT=R， O1T=r，结论9：PT2=Rr结论10：AB=2√Rr 结论11：S梯形AOO1B=（R+r）√Rr结论12：以AB为直径的☉P必定与直线OO1相切于T点。

中考专题复习——探索性问题归类

中考备考——探索性问题归类一、找规律问题 1.（07年11．）在五环图案内，分别填写五个数a ，b ，c ，d ，e ，如图：，其中a ，b ，c 是三个连续偶数（a < b ），d ，e 是两个连续奇数(d < e )，且满足a b c d e ++=+，例如：．请你在0到20之间选择另一组符合条件的数填入右图：2. （08年12．）一组按规律排列的式子：a b 2-，25a b ，38a b -，411ab ，…(ab ≠0)．其中第7个式子是________，第n 个式子是________(n 为正整数)．3.（09年12．）如图，正方形纸片ABCD 的边长为1，M 、N 分别是AD 、BC 边上的点，将纸片的一角沿过点B 的直线折叠，使点A 落在MN 上，落点记为A ′，折痕交AD 于点E ．若 M 、N 分别是AD 、BC 边的中点，则A ′N ＝________；若M 、N 分别是AD 、BC 边上距DC 最近的n 等分点(n ≥2，且n 为整数)，则A ′N ＝________(用含有n 的式子表示)．4.（09.东城一模12）.按一定规律排列的一列数依次为：1111112310152635，，，，，……，按此规律排列下去，这列数中的第９个数是．Ａ．861Ｂ．865 Ｃ．867 Ｄ．8696.已知：2222233+=⨯，2333388+=⨯，244441515+=⨯，…，若299a ab b+=⨯（a b ，为正整数），则ab =．7.观察下列顺序排列的等式：1234111111113243546a a a a =-=-=-=-，，，，…．试猜想第n个等式（n 为正整数）：n a = ．8.观察图给出的四个点阵，s 表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n 个点阵中的点的个数s 为 .9.用火柴棒按下图中的方式搭图形，按照第1个 1s =第2个 5s = 第3个 9s = 第4个13s = ……这种方式搭下去，搭第n 个图形需____________根火柴棒．10.（2009年泸州）如图1，已知Rt △ABC 中，AC=3，BC= 4，过直角顶点C 作CA 1⊥AB ，垂足为A 1，再过A 1作A 1C 1⊥BC ，垂足为C 1，过C 1作C 1A 2⊥AB ，垂足为A 2，再过A 2作A 2C 2⊥BC ，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，12C A ，…，则CA 1= ，=5554C A A C 图211（08昌平一模）如图2，在Rt ABC △中，90C = ∠，12BC AC ==，，把边长分别为123n x x x x ，，，，的n 个正方形依次放入ABC △中：第一个正方形CM 1P 1N 1的顶点分别放在Rt ABC △的各边上；第二个正方形M 1M 2P 2N 2的顶点分别放在11Rt APM △的各边上,……,其他正方形依次放入。

[整理]中考数学探索性问题的解法

中考数学探索性问题的解法随着应试教育向素质教育的转轨，加强对学生各方面能力考察的题目成了近年来各省市中考试题中的热门问题，探索性问题便是其中一类应运而生的新题型，这一类问题对培养学生的创造性思维、想象能力和探索能力有很大帮助。

探索性问题又可分为结论探索型和存在探索型两种。

例1、长方形的周长为24cm，面积为64cm2，则这样的长方体（）（A）有一个（B）有二个（C）有无数个（D）不存在解：设长方体的长为a，宽为b,则a、b可视为x2－12x+64=0的两个根∵△=(－12)2－4×64=144－256<0∴该方程无实根即a、b不存在,因此选（D）例2、在宽为a的纸带中剪出直径为a的圆5个，直径为的圆10个，排列方法如图1，计算所用纸带长度，请考虑能否再设计一种排列方法，使所用纸带的长度比原排列方法节省原材料？分析:通过图1观察易发现图中虚线部分具有典型性，为计算方便，取具有典型的部分（图2）进行分析，计算出结果。

易知，在等腰三角形ABC中，BC边上的高为AD，∴原排列方法使用纸带长为通过计算启发我们，如果把小圆分别插到大圆中，采用如下的排列方法，（如图3）这时纸带长为可见改进后的排列方法比较合理例3、如图6、有四个动点P、Q、E、F分别从正方形ABCD的顶点A、B、C、D同时出发，沿着AB、BC、CD、DA以同样的速度向点B、C、D、A移动。

（1）证明四边形PQEF是正方形；（2）PE是否总过某一定点，并说明理由；（3）四边形PQEF的顶点位于何处时其面积有最大值、最小值，各是多少？解:（1）证明由已知易得△AFP≌△BPQ≌△CQE≌△DEF，∴FP=PQ=QE=EF；又由∠BPQ=∠AFP，得∠BPQ+∠APF=∠AFP+∠APF=90°，∴∠FPQ=90°，∴四边形PQEF 是正方形。

专题五中考数学探索性问题(含答案)

第5讲探索性问题概述：探索性题目一般作为压轴题或次压轴题出现，题目较难，难在结论不肯定，要通过探索证明或计算，得出结论，并给予肯定或否定回答：这种题目的结论有多样性，需要解题的周密考虑，解这种题目有两种方法：一种是假定结论成立，去证明它的可能性或存在性；另一种是从条件出发直接证明或计算回答存在或不存在．典型例题精析例．（2005，绵阳）如图1，分别以直角三角形ABC三边为直径向外作三个半圆，•其面积分别用S1、S2、S3表示，则不难证明S1=S2+S3．（1）如图2所示，分别以直角三角形ABC三边为边向外作三个正方形，•其面积分别用S1、S2、S3表示，那么S1、S2、S3之间有什么关系？（不必证明）（2）如图3所示，分别以直角三角形ABC三边为边向外作三个正三角形，•其面积分别用S1、S2、S3表示，请你确定S1、S2、S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别为S1、S2、S3表示，使S1、S2、S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件？并证明你的结论；（4）类比（1）、（2）、（3）的结论，请你总结出一个更具一般意义的结论．S3S2S1图1BCABCAS3S2S1图2BCAS3S2S1图3解：设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c，则c2=a2+b2．（1）S1=S2+S3；（2）S1=S2+S3，证明如下：显然：S12，S22，S32，∴S2+S3a2+b2）2=S1．（也可用三角形相似证明）（3）当所作的三个三角形相似时，S 1=S 2+S 3．证明如下：∵所作三个三角形相似，∴2221S a S c =，2321S b S c =，∴222321S S a b S c++==1， ∴S 1=S 2+S 3．（4）分别以直角三角形ABC 的三边为一边向外作相似图形，其面积分别用S 1、S 2、•S 3表示，则S 1=S 2+S 3．中考样题训练1．（2005，黄冈）如图，在直角坐标系中，O 是原点，A 、B 、•C•三点的坐标分别为A （18，0），B （18，6），C （8，6），四边形OABC 是梯形，点P 、Q 同时从原点出发，分别作饼速运动，其中点P 沿OA 向终点A 运动，速度为每秒1个单位，点Q 沿OC 、CB 向终点B 运动，当这两点有一点到达自己的终点时，另一点也停止运动．（1）求出直线OC 的解析式及经过O 、A 、C 三点的抛物线的解析式．（2）试在（1）中的抛物线上找一点D ，使得以O 、A 、D 为顶点的三角形与△AOC 全等，请直接写出点D 的坐标．（3）设从出发起运动了t 秒，如果点Q 的速度为每秒2个单位，试写出点Q 的坐标，并写出此时t 的取值范围．（4）设从出发起，运动了t 秒钟，当P 、Q 两点运动的路程之和恰好等于梯形OABC 周长的一半，这时，直线PQ 能否把梯形的面积也分成相等的两部分，如有可能，•请求出t 的值；如不可能，请说明理由．C(8,6)B(18,6)A(18,0)xOyQ P3．（2003，浙江）如图，⊙A 和⊙B 是外离两圆，⊙A 半径长为2，⊙B 的半径长为1，•AB=4，P 为连结两圆圆心的线段AB 上的一点，PC 切⊙A 于点C ，PD 切⊙B 于点D ．（1）若PC=PD，求PB的长；（2）试问线段AB上是否存在一点P，使PC+PD=4？如果存在，问这样的P点有几个；并求出PB的值；如果不存在，说明理由；（3）当点P在线段AB上运动到某处，使PC⊥PD时，就有△APC∽△PBD，请问：除上述情况外，当点P在线段AB上运动到何处（说明PB的长为多少；或PC、PD具有何种关系）•时，这两个三角形仍相似；并判断此时直线CP与⊙B的位置关系，证明你的结论．考前热身训练1．填空题（1）观察下列等式，你会发现什么规律？3×5=15，而15=42-1，5×7=35，而35=62-1，…11×13=143，而143=122-1，…将你猜想到的规律用只含一个字母的式子表示出来________．（2）（2002，武汉）如图，以△ABC的边AB为直径作⊙O交BC于D，过D作⊙O•的切线交AC于E，使得DE⊥AC，则△ABC的边必须满足的条件是________．B2．已知反比例函数y=kx（k≠0）和一次函数y=-x+8．（1）若一次函数和反比例函数的图象交于点（4，m），求m和k；（2）k满足什么条件时，这两个函数图象有两个不同的交点？（3）设（2）中的两个交点为A、B，试判定∠AOB是锐角还是钝角？中考样题看台1．（1）y=34x．∴y=-340x2+2720x（2）D（10，6）（3）当Q在OC上运动时，可设Q（m，34m），依题意有：m2+（34m2）=（2t）2．∴m=85t，∴Q（85t，65t），（0≤t≤5）当Q在BC上时，Q点所走过的路程为2t．∵OC=10，∴CQ=2t-10，∴Q点在横坐标为2t-10+8=2t-2，∴Q（2t-2，6）（5<t≤10）．（4）∵梯形OABC的周长为44，当Q点在OC上，P运动的路程为t，则Q•运动的路程为（22-t）△OPQ中，OP边上的高为：（22-t）×35，∴S△OPQ=12t（22-t）×35，S梯形OABC=12（180+10）×6=84．依题意有：12t（22-t）×35=84×12，整理得：t2-22t+140=0．∴△=222-4×140<0，∴这样的t不存在．当Q在BC上时，Q走过的路程为22-t，∴CQ的长为：22-t-10=12-t，∴S梯形OCQP=12×6（22-t-10+t）=36≠84×12，∴这样的t值也不存在．综上所述，不存在这样的t值，使得直线PQ同时平分梯形的周长和面积．3．（1）∵PC切⊙A于点C，∴PC⊥AC，P C2=PA2-AC2，同理PD2=PB2-BD2，∵PC=PD，∴PC2-•A C2=PB2-B D2，设PB=x，PA=4-x代入得x2-1=（4-x）2-22，解得x=138，1<138<2，即PB的长为138（PA长为198>2）．（2）假定有在一点P使PC2+PD2=4，设PB=x，则PD2=x2-1，PC2=（4-x）2-22，代入条件得（4-x）2-22+x2-1=4，解得x=2±2，∵P在两圆间的圆外部分，∴1<PB<2，即1<x<2，满足条件的P点只有一个，这时PB=2-2．（3）当PC：PD=2：1或PB=43时，也有△PCA∽△PDB，这时，在△PCA与△PDB中21AC PCBD PD==（或APBP），∠C=∠D=Rt∠，∴△PCA∽△PDB，∴∠BPD=∠APC=∠BPE（E在CP的延长线上），∴B点在∠DPE的角平分线上，B到PD与PE的距离相等，∵⊙B与PD相切，∴⊙B也与CP•的延长线PE相切．考前热身训练1．（1）（2n-1）（2n+1）=（2n）2-1 （n≥2）（2）等腰三角形（AB=AC）2．（1）m=4，k=16，（2）k<16且k≠0（3）当0<k<16时，∠AOB为锐角，当k<0时，∠AOB为钝角3．（1）直线DP的解析式为：y=-43x+2（2）DE=DP，Rt△APD≌Rt△AOB，∴BO=DP=4，∴点B（4，0），可以看出，四边形OBED是矩形，或切线DP的长等于B的横坐标．。

备战中考数学分类复习专题(探索性问题专题)

备战2008中考分类复习专题（探索性问题专题）1知识网络梳理探索是人类认识客观世界过程中最生动、最活跃的思维活动，探索性问题存在于一切学科领域之中，在数学中则更为普遍．初中数学中的“探索发现”型试题是指命题中缺少一定的题设或未给出明确的结论，需要经过推断、补充并加以证明的命题，它不像传统的解答题或证明题，在条件和结论给出的情景中只需进行由因导果或由果导因的工作，从而定格于“条件——演绎——结论”这样一个封闭的模式之中，而是必须利用题设大胆猜想、分析、比较、归纳、推理，或由条件去探索不明确的结论；或由结论去探索未给予的条件；或去探索存在的各种可能性以及发现所形成的客观规律．通常情景中的“探索发现”型问题可以分为如下类型：2条件探索型——结论明确，而需探索发现使结论成立的条件的题目．3结论探索型——给定条件但无明确结论或结论不惟一，而需探索发现与之相应的结论的题目．4存在探索型——在一定的条件下，需探索发现某种数学关系是否存在的题目．5规律探索型——在一定的条件状态下，需探索发现有关数学对象所具有的规律性或不变性的题目．由于题型新颖、综合性强、结构独特等，此类问题的一般解题思路并无固定模式或套路，但是可以从以下几个角度考虑：1.利用特殊值（特殊点、特殊数量、特殊线段、特殊位置等）进行归纳、概括，从特殊到一般，从而得出规律．2.反演推理法(反证法)，即假设结论成立，根据假设进行推理，看是推导出矛盾还是能与已知条件一致．3．分类讨论法．当命题的题设和结论不惟一确定，难以统一解答时，则需要按可能出现的情况做到既不重复也不遗漏，分门别类加以讨论求解，将不同结论综合归纳得出正确结果．4．类比猜想法．即由一个问题的结论或解决方法类比猜想出另一个类似问题的结论或解决方法，并加以严密的论证．以上所述并不能全面概括此类命题的解题策略，因而具体操作时，应更注重数学思想方法的综合运用．2知识运用举例（一）、条件探索型，，，，构成一例1．（2007呼和浩特市）在四边形ABCD中，顺次连接四边中点E F G H个新的四边形，请你对四边形ABCD填加一个条件，使四边形EFGH成为一个菱形．这个条件是__ ．或四边形ABCD是等腰梯形（符合要求的其它答案也可以）解：AC BD例2．（2007荆门市）将两块全等的含30°角的三角尺如图1摆放在一起，设较短直角边为1．30︒30︒BD ACD 1C 1B 1C AD BC AD BC AD B（1）四边形ABCD 是平行四边形吗？说出你的结论和理由：________________________．（2）如图2，将Rt △BCD 沿射线BD 方向平移到Rt △B 1C 1D 1的位置，四边形ABC 1D 1是平行四边形吗？说出你的结论和理由：_________________________________________．（3）在Rt △BCD 沿射线BD 方向平移的过程中，当点B 的移动距离为______时，四边形ABC 1D 1为矩形，其理由是_____________________________________；当点B 的移动距离为______时，四边形ABC 1D 1为菱形，其理由是_______________________________．(图3、图4用于探究)解：（1）是，此时AD BC ，一组对边平行且相等的四边形是平行四边形．（2）是，在平移过程中，始终保持AB C 1D 1，一组对边平行且相等的四边形是平行四边形．（3，此时∠ABC 1＝90°，有一个角是直角的平行四边形是矩形．，此时点D 与点B 1重合，AC 1⊥BD 1，对角线互相垂直的平行四边形是菱形．例3．（2006广东）如图所示，在平面直角坐标中，四边形OABC 是等腰梯形，BC ∥OA ，OA ＝7，AB ＝4，∠ COA ＝60°，点P 为x 轴上的—个动点，点P 不与点0、点A 重合．连结CP ，过点P 作PD 交AB 于点D ．（1）求点B 的坐标；（2）当点P 运动什么位置时，△OCP 为等腰三角形，求这时点P 的坐标；（3）当点P 运动什么位置时，使得∠CPD ＝∠OAB ，且AB BD ＝85，求这时点P 的坐标．[解析]（1）；过C 作CD ⊥OA 于A ，BE ⊥OA 于E则△OCD ≌△ABE ，四边形CDEB 为矩形∴OD ＝AE ，CD ＝BE∵OC ＝AB ＝4，∠COA ＝60°∴CD ＝，OD ＝2∴CB ＝DE ＝3∴OE ＝OD ＋DE ＝5∵BE ＝CD ＝∴B （5，）（2）∵∠COA ＝60°，△OCP 为等腰三角形∴△OCP 是等边三角形∴OP ＝OC ＝4∴P （4，0）即P 运动到（4，0）时，△OCP 为等腰三角形（3）∵∠CPD ＝∠OAB ＝∠COP ＝60°∴∠OPC ＋∠DPA ＝120°又∵∠PDA ＋∠DPA ＝120°∴∠OPC ＝∠PDA∵∠OCP ＝∠A ＝60°∴△COP ∽△PAD ∴OP OC AD AP = ∵58BD AB =，AB ＝4∴BD ＝52∴AD ＝32即 4372OP OP=-∴276OP OP -=得OP ＝1或6∴P 点坐标为（1，0）或（6，0）（二）、结论探索型例4．（2007云南省）已知：如图，四边形ABCD 是矩形（AD ＞AB ），点E 在BC 上，且AE ＝AD ，DF ⊥AE ，垂足为F ．请探求DF 与AB 有何数量关系？写出你所得到的结论并给予证明．解：经探求，结论是：DF ＝ AB ．证明如下：∵四边形ABCD 是矩形，∴ ∠B ＝ 90 ， AD ∥BC ，∴ ∠DAF ＝ ∠AEB ．∵ DF ⊥AE ， ∴ ∠AFD ＝ 90，∵ AE ＝ AD ，∴ △ABE ≌△DFA ．∴ AB ＝ DF ．例5．（2007北京市）我们知道：有两条边相等的三角形叫做等腰三角形．类似地，我们定义：至少有一组对边相等的四边形叫做等对边四边形．（1）请写出一个你学过的特殊四边形中是等对边四边形的图形的名称；（2）如图，在ABC △中，点D E ，分别在AB AC ，上，设CD BE ，相交于点O ，若60A ∠=°，12DCB EBC A ∠=∠=∠．请你写出图中一个与A ∠相等的角，并猜想图中哪个四边形是等对边四边形；（3）在ABC △中，如果A ∠是不等于60°的锐角，点D E ，分别在AB AC ，上，且12DCB EBC A ∠=∠=∠．探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论．解：（1）回答正确的给1分（如平行四边形、等腰梯形等）．（2）答：与A ∠相等的角是BOD ∠（或COE ∠）．四边形DBCE 是等对边四边形．（3）答：此时存在等对边四边形，是四边形DBCE ．证法一：如图1，作CG BE ⊥于G 点，作BF CD ⊥交CD 延长线于F 点．因为12DCB EBC A ∠=∠=∠，BC 为公共边，所以BCF CBG △≌△．所以BF CG =．因为BDF ABE EBC DCB ∠=∠+∠+∠，BEC ABE A ∠=∠+∠，所以BDF BEC ∠=∠．可证BDF CEG △≌△．所以BD CE =．所以四边形DBCE 是等边四边形．证法二：如图2，以C 为顶点作FCB DBC ∠=∠，CF 交BE 于F 点．因为12DCB EBC A ∠=∠=∠，BC 为公共边，所以BDC CFB △≌△．所以BD CF =，BDC CFB ∠=∠．所以ADC CFE ∠=∠．因为ADC DCB EBC ABE ∠=∠+∠+∠，FEC A ABE ∠=∠+∠，所以ADC FEC ∠=∠．所以FEC CFE ∠=∠．所以CF CE =．所以BD CE =．所以四边形DBCE 是等边四边形．说明：当AB AC =时，BD CE =仍成立．只有此证法，只给1分．例6．（07山东滨州）如图1所示，在ABC △中，2AB AC ==，90A =∠，O 为BC 的中点，动点E 在BA 边上自由移动，动点F 在AC 边上自由移动．（1）点E F ，的移动过程中，OEF △是否能成为45EOF =∠的等腰三角形？若能，请指出OEF △为等腰三角形时动点E F ，的位置．若不能，请说明理由．（2）当45EOF =∠时，设BE x =，CF y =，求y 与x 之间的函数解析式，写出x 的取值范围．（3）在满足（2）中的条件时，若以O 为圆心的圆与AB 相切（如图2），试探究直线EF 与O 的位置关系，并证明你的结论．解：如图，（1）点E F ，移动的过程中，OEF △能成为45EOF ∠=°的等腰三角形．此时点E F ，的位置分别是：①E 是BA 的中点，F 与A 重合．②BE CF ==．③E 与A 重合，F 是AC 的中点．（2）在OEB △和FOC △中，135EOB FOC ∠+∠=°，135EOB OEB ∠+∠=°，FOC OEB ∠=∠∴．又B C ∠=∠∵，OEB FOC ∴△∽△．BE BO CO CF =∴．BE x =∵，CF y =，OB OC === 2(12)y x x =∴≤≤．（3）EF 与O 相切．OEB FOC ∵△∽△，BE OE CO OF =∴．BE OE BO OF =∴．即BE BO OE OF =．又45B EOF ∠=∠=∵°，BEO OEF ∴△∽△．BEO OEF ∠=∠∴．∴点O 到AB 和EF 的距离相等．AB ∵与O 相切，∴点O 到EF 的距离等于O 的半径．EF ∴与O 相切．（三）、存在探索型存在性探索问题是指在某种题设条件下，判断具有某种性质的数学对象是否存在的一类问题.解题的策略与方法是：先假设数学对象存在，以此为条件进行运算或推理.若无矛盾，说明假设正确，由此得出符合条件的数学对象存在；否则，说明不存在．例7．(2006山东省威海市)抛物线y ＝ ax 2＋bx ＋c (a ≠0)过点A （1，－3），B （3，－3），C （－1，5），顶点为M 点．⑴求该抛物线的解析式．⑵试判断抛物线上是否存在一点P ，使∠POM ＝90.若不存在，说明理由；若存在，求出P 点的坐标．解：⑴ y ＝ x 2 4x⑵ 易求得顶点M 的坐标为(2，4)．设抛物线上存在一点P ，使OP ⊥OM ，其坐标为(a ，a 2 4a )．过P 作PE ⊥y 轴，垂足为E ；过M 点作MF ⊥y 轴，垂足为F ，则∠POE ＋∠MOF ＝90，∠POE ＋∠EPO ＝90.∴∠EPO ＝∠FOM ．∵∠OEP ＝∠MFO ＝90，∴Rt △OEP ∽Rt △MFO ．∴OE ∶MF ＝EP ∶OF .即(a 2 4a )∶2＝a ∶4.解得a 1 ＝0(舍去)，a 2 ＝29．故抛物线上存在一点P ，使∠POM ＝90，P 点的坐标为(29，49) 例8．(2006武汉市)已知：二次函数y ＝x 2(m ＋1)x ＋m 的图象交x 轴于A (x 1，0)、B (x 2，0)两点，交y 轴正半轴于点C ，且x 12 ＋x 22 ＝10．⑴求此二次函数的解析式；⑵是否存在过点D (0，25)的直线与抛物线交于点M 、N ，与x 轴交于点E ，使得点M 、N 关于点E 对称？若存在，求直线MN 的解析式；若不存在，请说明理由．分析与解答 ⑴依题意，得x 1x 2＝m ，x 12 ＋x 22＝10，∵x 1 ＋x 2 ＝ m ＋1，∴(x 1 ＋x 2)2 2x 1x 2 ＝10，∴(m ＋1)2 2m ＝10，m ＝3或m ＝ 3，又∵点C 在y 轴的正半轴上，∴m ＝3．∴所求抛物线的解析式为y ＝x 2 4x ＋3．⑵假设存在过点D (0，25)的直线与抛物线交于M (x M ，y M )、N (x N ，y N )两点，与x 轴交于点E ，使得M 、N 两点关于点E 对称．∵M 、N 两点关于点E 对称，∴y M ＋y N ＝0. 设直线MN 的解析式为：y ＝kx25．由⎪⎩⎪⎨⎧=+-=.25-kx y 3x 4x y 2，得x 2 (k ＋4)x ＋211＝0，∴x M ＋x N ＝4＋k ，∴y M ＋y N ＝k (x M ＋x N )5＝0．∴k (k ＋4)5＝0，∴k ＝1或k ＝ 5．当k ＝5时，方程x 2 (k ＋4)x ＋211＝0的判别式⊿＜0，∴k ＝1，∴直线MN 的解析式为y ＝x25． ∴存在过点D (0，25)的直线与抛物线交于M 、N 两点，与x 轴交于点E ，使得M 、N 两点关于点E 对称．例9．（2007乐山）如图（13），在矩形ABCD 中，4AB =，10AD =．直角尺的直角顶点P 在AD 上滑动时（点P 与A D ，不重合），一直角边经过点C ，另一直角边AB 交于点E ．我们知道，结论“Rt Rt AEP DPC △∽△”成立．（1）当30CPD =∠时，求AE 的长；（2）是否存在这样的点P ，使DPC △的周长等于AEP △周长的2倍？若存在，求出DP 的长；若不存在，请说明理由．解（1）在Rt PCD △中，由tan CD CPD PD =∠，得44tan tan 30CD PD CPD===∠10AP AD PD ∴=-=-由AEP DPC △∽△知AE APPD CD =，12AP PD AE CD ∴==-．（2）假设存在满足条件的点P ，设DP x =，则10AP x =-由AEP DPC △∽△知2CD AP =，4210x ∴=-，解得8x =，此时2AP =，4AE =符合题意．（四）、规律探索型规律探索问题是根据已知条件或所提供的若干个特例，通过观察、类比、归纳，提示和发现题目所蕴含的本质规律与特征的一类探索性问题．例10．(2006湖南衡阳)观察算式：1＝12；1＋3＝4＝22；1＋3＋5＝9＝32；1＋3＋5＋7＝16＝42；1＋3＋5＋7＋9＝25＝52 ；……用代数式表示这个规律(n 为正整数)：1＋3＋5＋7＋9＋＋(2n 1)＝______________________．分析与解答由以上各等式知，等式左端是从1开始的连续若干个奇数之和，右端是左端奇数个数的平方，由此易得1＋3＋5＋7＋…＋(2n 1)＝n 2.填n 2．例11 （2006吉林省）如图2－2－1，用灰白两色正方形瓷砖铺设地面，第n 个图案中白色瓷砖数为___________．分析与解答根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题.解决这类问题，首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加(或倍数)情况的变化，找出数量上的变化规律，从而推出一般性的结论．第1个图案有白色瓷砖5(即2＋31)块；第2个图案有白色瓷砖8(即2＋32)块；第3个图案有白色瓷砖11(即2＋33)块. 由此可得，第n 个图案有白色瓷砖(2＋3n )块. 填3n ＋2．例12．（2007资阳）设a 1＝32－12，a 2＝52－32，…，a n ＝(2n ＋1)2－(2n －1)2(n 为大于0的自然数)．（1）探究a n 是否为8的倍数，并用文字语言表述你所获得的结论；（2）若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”. 试找出a 1，a 2，…，a n ，…这一列数中从小到大排列的前4个完全平方数，并指出当n 满足什么条件时，a n 为完全平方数(不必说明理由) ．解：（1） ∵ a n ＝(2n ＋1)2－(2n －1)2＝224414418n n n n n ++-+-=，又 n 为非零的自然数，∴ a n 是8的倍数．这个结论用文字语言表述为：两个连续奇数的平方差是8的倍数．说明：第一步用完全平方公式展开各1分，正确化简1分．（2）这一列数中从小到大排列的前4个完全平方数为16，64，144，256． n 为一个完全平方数的2倍时，a n 为完全平方数． 3 知识巩固训练（题组训练）1．（2006年山东省）如图，△ABC 中，D 、E 分别是AC 、AB 上的点，BD 与CE 交于点O ．给出下列三个条件：①∠EBO ＝∠DCO ；②∠BEO ＝∠CDO ；③BE ＝CD ．（1）上述三个条件中，哪两个条件可判定△ABC 是等腰三角形（用序号写出所有情形）；（2）选择第（1）小题中的一种情形，证明△ABC 是等腰三角形．2．（2006年随州市）如图，矩形ABCD 中，M 是AD 的中点．（1）求证：△ABM ≌△DCM ；（2）请你探索，当矩形ABCD 中的一组邻边满足何种数量关系时，有BM ⊥CM 成立，说明你的理由．3．如图，在△ABC 中，D 为BC 上一个动点（D 点与B 、C 不重合），且DE ∥AC 交AB •于点E ，DF∥AB交AC于点F．（1）试探究，当AD满足什么条件时，四边形AEDF是菱形？并说明理由．（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF是正方形？请说明理由．4．如图，AB是⊙O的直径，EF是⊙O的切线，切点是C．点D是EF上一个动点，连接AD．试探索点D运动到什么位置时，AC是∠BAD的平分线，请说明理由．5．（2006年成都市）已知：如图，在△ABC中，D是AC的中点，E是线段BC•延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF．（1）求证：AF＝CE；（2）若AC＝EF，试判断四边形AFCE是什么样的四边形，并证明你的结论．6．（2006年常德市）如图，P是等边三角形ABC内的一点，连结PA、PB、PC，以BP•为边作∠PBQ＝60°，且BQ＝BP，连结CQ．（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论．（2）若PA：PB：PC＝3：4：5，连结PQ，试判断△PQC的形状，并说明理由．7．如图，AB是⊙O的直径，AD、BC、DC都是⊙O的切点，A、B、E分别是切点．（1）判定△COD的形状，并说明理由．（2）设AD＝a，BC＝b，⊙O的半径为r，试探究r与a，b之间满足的关系式，并说明理由．8．（2006年绵阳市）在正方形ABCD 中，点P 是CD 上一动点，连结PA ，分别过点B 、D 作BE ⊥PA 、DF ⊥PA ，垂足分别为E 、F ，如图①．（1）请探索BE 、DF 、EF 这三条线段长度具有怎样的数量关系．若点P 在DC •的延长线上（如图②），那么这三条线段的长度之间又具有怎样的数量关系？若点P 在CD •的延长线上呢（如图③）？请分别直接写出结论；（2）请在（1）中的三个结论中选择一个加以证明．9．（2007云南省）已知：如图，抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点．（1）求抛物线的函数关系式；（2）若过点C 的直线y kx b =+与抛物线相交于点E （4，m ），请求出△CBE 的面积S 的值；（3）在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标；（4）除（3）中所求的0P 点外，在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形？若存在，请求出一共有几个满足条件的点P （要求简要说明理由，但不证明）；若不存在这样的点P ，请说明理由．10．（2007呼和浩特市）如图，在矩形ABCD 中，AB =1AD =．点P 在AC 上，PQ BP ⊥，交CD 于Q ，PE CD ⊥，交于CD 于E ．点P 从A 点（不含A ）沿AC 方向移动，直到使点Q 与点C 重合为止．（1）设AP x =，PQE △的面积为S ．请写出S 关于x 的函数解析式，并确定x 的取值范围．（2）点P 在运动过程中，PQE △的面积是否有最大值，若有，请求出最大值及此时AP 的取值；若无，请说明理由．11．（2007成都市）在平面直角坐标系xOy 中，已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A B ，两点（点A 在点B 的左边），与y 轴交于点C ，其顶点的横坐标为1，且过点(23)，和(312)--，．（1）求此二次函数的表达式；（2）若直线:(0)l y kx k =≠与线段BC 交于点D （不与点B C ，重合），则是否存在这样的直线l ，使得以B O D ，，为顶点的三角形与BAC △相似？若存在，求出该直线的函数表达式及点D 的坐标；若不存在，请说明理由；（3）若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角PCO ∠与ACO ∠的大小（不必证明），并写出此时点P 的横坐标p x 的取值范围．12（2007绵阳市）如图，已知抛物线y ＝ ax 2＋ bx －3与x 轴交于A 、B 两点，与y 轴交于C 点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为5．设⊙M与y轴交于D，抛物线的顶点为E．（1）求m的值及抛物线的解析式；（2）设∠DBC＝，∠CBE＝，求sin（－）的值；（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．13（07日照）如图，直线EF将矩形纸片ABCD分成面积相等的两部分，E、F分别与BC交于点E，与AD交于点F（E，F不与顶点重合），设AB＝a，AD＝b，BE＝x．(Ⅰ)求证：AF＝EC；(Ⅱ)用剪刀将纸片沿直线EF剪开后，再将纸片ABEF沿AB对称翻折，然后平移拼接在梯形ECDF的下方，使一底边重合，直腰落在边DC的延长线上，拼接后，下方的梯形记作EE′B′C．（1）求出直线EE′分别经过原矩形的顶点A和顶点D时，所对应的 x︰b的值；（2）在直线EE′经过原矩形的一个顶点的情形下，连接BE′，直线BE′与EF是否平行？你若认为平行，请给予证明；你若认为不平行，请你说明当a与b满足什么关系时，它们垂直？14．(2006江西省）如图2－2－2，用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：⑴ 第4个图案中有白色纸片___________张； ⑵ 第n 个图案台有白色纸片___________张．15．(2006广西贺州市)观察图2－2－3中一列有规律的数，然后在“？”处填上一个合适的数，这个数是______________．16．(2006广西百色市)如图2－2－4，A 1A 2B 是直角三角形，且A 1A 2＝A 2B ＝a ，A 2A 3⊥A 1B ，垂足为A 3，A 3A 4⊥A 2B ，垂足为A 4，A 4A 5⊥A 3B ，垂足为A 5，……，A n ＋1A n ＋2⊥A n B ，垂足为A n ＋2，则线段A n ＋1A n ＋2(n 为自然数)的长为（）．（A ） n)2(a（B（C ） 2a（D ） 2na17．(2006江苏泰州市)如图2－2－5，每个正方形点阵均被一直线分成两个三角形点阵，根据图中提供的信息，用含n 的等式表示第n 个正方形点阵中的规律_______．18．(2006浙江绍兴市)如图2－2－6，将边长为1的正方形OAPB 沿x 轴正方向连续翻转2 006次，点P 依次落在点P 1，P 2，P 3，P 4，…，P 2006的位置，则P 2006的横坐标x 2006＝_______________．19．（2007内江）如图（11），某小区有东西方向的街道3条，南北方向的街道4条，从位置A 出发沿街道行进到达位置B ，要求路程最短，研究共有多少种不同的走法．小东是这样想的：要使路程最短，就不能走“回头路”，只能分五步来完成，其中三步向右行进，两步向上行进，如果用用数字“1”表示向右行进，数字“2”表示向上行进，那么“11221”与“11212”就表示两种符合要求的不同走法，请你思考后回答：符合要求的不同走法共有________种．20．（2007内江）探索研究（1）观察一列数2，4，8，16，32，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是________；根据此规律，如果n a （n 为正整数）表示这个数列的第n 项，那么18a =________，n a =________；（2）如果欲求232013333+++++的值，可令232013333S =+++++……………………………………………………①将①式两边同乘以3，得_______________________………………………………………………………② 由②减去①式，得S =____________________．（3）用由特殊到一般的方法知：若数列123n a a a a ，，，，，从第二项开始每一项与前一项之比的常数为q ，则n a =________（用含1a q n ，，的代数式表示），如果这个常数1q ≠，那么123n a a a a ++++=________（用含1a q n ，，的代数式表示）．21．（07自贡）一个叫巴尔末的中学教师成功地从光谱数据59，1216，2125，3236，…中得到巴尔末公式，从而打开了光谱奥秘的大门，请你按照这种规律，写出第n （n ≥1）个数据是___________．22．（2007德阳）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）根据这个规律探索可得，第100个点的坐标为____________．23．（2007河南省）将图①所示的正六边形进行进行分割得到图②，再将图②中最小的某一个正六边形按同样的方式进行分割得到图③，再将图③中最小的某一个正六边形按同样的方式进行分割…，则第n个图形中，共有________个正六边形．24．（2007安徽省）探索n×n的正方形钉子板上(n是钉子板每边上的钉子数)，连接任意两个钉子所得到的不同长度值的线段种数：当n＝2时，钉子板上所连不同线段的长度值只有1，所以不同长度值的线段只有2种，若用S表示不同长度值的线段种数，则S＝2；当n＝3时，钉子板上所连不同线段的长度值只有1，2五种，比n＝2时增加了3种，即S ＝2＋3＝5．(2) 观察图形，填写下表：(7) 写出(n －1)×(n －1)和n ×n 的两个钉子板上，不同长度值的线段种数之间的关系；(用式子或语言表述均可) 【解】（3）对n ×n 的钉子板，写出用n 表示S 的代数式．【解】25．（07贵阳市）如图12，平面内有公共端点的六条射线OA ，OB ，OC ，OD ，OE ，OF ，从射线OA 开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，…．（1）“17”在射线________上．（2）请任意写出三条射线上数字的排列规律．（3）“2007”在哪条射线上？26．（07无锡）图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n 层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为(1)1232n n n +++++=．图1 图2 图3 图4如果图1中的圆圈共有12层，（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1234，，，，，则最底层最左边这个圆圈中的数是；（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数23-，22-，21-，，求图4中所有圆圈中各数的绝对值之和．27．（07乐山）如图（15），在直角坐标系中，已知点0P 的坐标为(10)，，将线段0OP 按逆时针方向旋转45，再将其长度伸长为0OP 的2倍，得到线段1OP ；又将线段1OP 按逆时针方向旋转45，长度伸长为1OP 的2倍，得到线段2OP ；如此下去，得到线段3OP ，4OP ，，n OP （n 为正整数）（1）求点6P 的坐标；（2）求56P OP △的面积；（3）我们规定：把点()n n n P x y ，（0123n =，，，，）的横坐标n x 、纵坐标n y 都取绝对值后得到的新坐标()nnxy ，称之为点nP 的“绝对坐标”．根据图中点n P 的分布规律，请你猜想点n P 的“绝对坐标”，并写出来．28．（07山东东营）根据以下10个乘积，回答问题：11×29； 12×28； 13×27； 14×26； 15×25； 16×24； 17×23； 18×22； 19×21； 20×20．（1）试将以上各乘积分别写成一个“□2－○2”（两数平方差）的形式，并写出其中一个的思考过程；（2）将以上10个乘积按照从小到大的顺序排列起来；（3）试由⑴、⑵猜测一个一般性的结论．（不要求证明）答案：1．答案不惟一，符合题意即可．2．（1）略（2）当AD ＝2AB 时，有BM •⊥CM 成立．说明理由（略）3．（1）当AD 平分∠BAC 时，四边形AEDF 是菱形．理由（略）（2）在（1）的条件下，当∠BAC ＝90°时，四边形AEDF 是正方形．说明理由（略）4．当点D •运动到满足条件AD ⊥EF 时，AC 平分∠BAD ．证明（略）5．（1）证明△ADF ≌△CDE 即可（2）四边形AFCE 是矩形．（证明略）6．（1）证明△BPA ≌△BQC ，AP ＝CQ（2）△PQC 是直角三角形，∵PA ：PB ：PC ＝3：4：5，设PA ＝3k ，PB ＝4k ，PC ＝5k ，∵∠PBQ ＝60°，BP ＝BQ ，∴△PBQ 是等边三角形，∴PQ ＝PB ＝4k ，在△PQC 中，∵PQ 2＋QC 2＝（4k ）2＋（3k ）2＝25k 2，PC 2＝（5k ）2＝25k 2，∴PQ 2＋QC 2＝PC 2，∴△PQC 是Rt △．7．（1）△COD 是直角三角形，连OE ，由圆的切线的性质可证得：•△OAD ≌△OED ，△OEC ≌△OBC ，∴∠AOD ＝∠EOD ，∠EOC ＝∠BOC ，可证得∠DOC ＝90°，•所以△COD 是直角三角形．（2）r 与a 、b 之间满足的关系是r 2＝ab ．证明△OAD ∽△CBO ，得OA AD BC OB =，OA ·OB ＝AD ·BC 即r 2＝ab ．8．解：（1）①BE ＝DF ＋EF ，②BE ＝DF －EF ，③EF ＝BE ＋DF ．（2）•证明略．9．解：（1）∵抛物线经过点(1,0)A 、(5,0)B ，∴(1)(5)y a x x =--．又∵抛物线经过点(0,5)C ，∴55a =，1a =．∴抛物线的解析式为2(1)(5)65y x x x x =--=-+．（2）∵E 点在抛物线上，∴m ＝ 42–4×6＋5 ＝－3．∵直线y ＝ kx ＋b 过点C （0， 5）、E （4， –3），∴5,4 3.b k b =⎧⎨+=-⎩ 解得k ＝－2，b ＝ 5．设直线y ＝－2x ＋5与x 轴的交点为D ，当y ＝0时，－2x ＋5＝0，解得x ＝52．∴D 点的坐标为（52，0）．∴S ＝S △BDC ＋ S △BDE ＝1515(5)5+(5)32222⨯-⨯⨯-⨯＝10．（3）∵抛物线的顶点0(3,4)P -既在抛物线的对称轴上又在抛物线上， ∴点0(3,4)P -为所求满足条件的点．（4）除0P 点外，在抛物线上还存在其它的点P 使得△ABP 为等腰三角形．理由如下：∵004AP BP ===>， ∴分别以A 、B 为圆心半径长为4画圆，分别与抛物线交于点B 、1P 、2P 、3P 、A 、4P 、5P 、6P ，除去B 、A 两个点外，其余6个点为满足条件的点．（说明：只说出P 点个数但未简要说明理由的不给分）10．解：（1）解：过点P 作PF BC ⊥，垂足为F ．在矩形ABCD 中，PF AB ∥PFC ABC ∴△∽△FC PC PF BC AC AB ==∴又AP x =∵，1BC AD ==，AB =又∵在Rt ABC △中，3AC ===3PC x =-313FC x -=∴ 33xFC -=∴3133x x BF BC FC -=-=-=∴ 又PE CD ⊥∵ 90PEC ∠=∴°又在四边形PFCE 中，90PFC BCD PEC ∠=∠=∠=°∴四边形PFCE 为矩形90FPE ∠=∴° 又PQ BP ⊥∵ 90BPQ ∠=∴°FPE BPQ ∠=∠∴ EPQ QPF BPF FPQ ∠+∠=∠+∠∴EPQ BPF ∠=∠∴ 又90PEQ BFP ∠=∠=°PEQ PFB ∴△∽△EQ PE BF PF =∴ 又PE FC =EQ FC BF PF =∴又FC PF BC AB =FC BC PF AB =∴ EQ BC BF AB =∴ BC BF EQ AB =·∴3x EQ ==∴113223x S EQ PE -==∴··2S =+∴或23)S x x =-+ 过点B 作BK AC ⊥，垂足为K ．在Rt ABC △中，由等积法可得1122AC BK AB BC =··AC BK AB BC =∴··31BK ⨯=BK =∴由题意可得当Q 与C 重合时，P 与K 重合即AP AK =，由ABK ABC △∽△得AK AB BK BC ==83x =∴ x ∴的取值范围是803x <≤ （2）PQE △面积有最大值由（1）可得2S x =+232x ⎫=-+⎪⎭∴当32x =即32AP =时，S面积最大，即S =最大11．解：（1）二次函数图象顶点的横坐标为1，且过点(23)，和(312)--，， ∴由1242393212.b a a b c a b ⎧-=⎪⎪++=⎨⎪-+=-⎪⎩，，解得123.a b c =-⎧⎪=⎨⎪=⎩，，∴此二次函数的表达式为 223y x x =-++．（2）假设存在直线:(0)l y kx k =≠与线段BC 交于点D （不与点B C ，重合），使得以B O D ，，为顶点的三角形与BAC △相似．在223y x x =-++中，令0y =，则由2230x x -++=，解得1213x x =-=， (10)(30)A B ∴-，，，．令0x =，得3y =．(03)C ∴，．设过点O 的直线l 交BC 于点D ，过点D 作DE x ⊥轴于点E ．点B 的坐标为(30)，，点C 的坐标为(03)，，点A 的坐标为(10)-，． 4345.AB OB OC OBC ∴===∠=，，BC ∴==．要使BOD BAC △∽△或BDO BAC △∽△，已有B B ∠=∠，则只需BD BO BC BA =， ① 或.BO BD BC BA = ②成立．若是①，则有BO BC BD BA ===．而45OBC BE DE ∠=∴=，． ∴在Rt BDE △中，由勾股定理，得222222BE DE BE BD +===．解得 94BE DE ==（负值舍去）．93344OE OB BE ∴=-=-=． ∴点D 的坐标为3944⎛⎫ ⎪⎝⎭，．将点D 的坐标代入(0)y kx k =≠中，求得3k =．∴满足条件的直线l 的函数表达式为3y x =．［或求出直线AC 的函数表达式为33y x =+，则与直线AC 平行的直线l 的函数表达式为3y x =．此时易知BOD BAC △∽△，再求出直线BC 的函数表达式为3y x =-+．联立33y x y x ==-+，求得点D 的坐标为3944⎛⎫ ⎪⎝⎭，．］若是②，则有BO BA BD BC ===．而45OBC BE DE ∠=∴=，． ∴在Rt BDE △中，由勾股定理，得222222BE DE BE BD +===．解得 2BE DE ==（负值舍去）．321OE OB BE ∴=-=-=． ∴点D 的坐标为(12)，．将点D 的坐标代入(0)y kx k =≠中，求得2k =．∴满足条件的直线l 的函数表达式为2y x =．∴存在直线:3l y x =或2y x =与线段BC 交于点D （不与点B C ，重合），使得以B O D ，，为顶点的三角形与BAC △相似，且点D 的坐标分别为3944⎛⎫ ⎪⎝⎭，或(12)，．（3）设过点(03)(10)C E ，，，的直线3(0)y kx k =+≠与该二次函数的图象交于点P ．将点(10)E ，的坐标代入3y kx =+中，求得3k =-． ∴此直线的函数表达式为33y x =-+．设点P 的坐标为(33)x x -+，，并代入223y x x =-++，得250x x -=．解得1250x x ==，（不合题意，舍去）．512x y ∴==-，．∴点P 的坐标为(512)-，．此时，锐角PCO ACO ∠=∠．又二次函数的对称轴为1x =，∴点C 关于对称轴对称的点C '的坐标为(23)，． ∴当5p x >时，锐角PCO ACO ∠<∠；当5p x =时，锐角PCO ACO ∠=∠；当25p x <<时，锐角PCO ACO ∠>∠． 12．解：（1）由题意可知C （0，－3），12=-a b ， ∴ 抛物线的解析式为y ＝ ax 2－2ax －3（a ＞0），过M 作MN ⊥y 轴于N ，连结CM ，则MN ＝ 1，5=CM ， ∴ CN ＝ 2，于是m ＝－1．同理可求得B （3，0），∴ a ×32－2－2a ×3－3 ＝ 0，得 a ＝ 1，∴ 抛物线的解析式为y ＝ x 2－2x －3．（2）由（1）得 A （－1，0），E （1，－4），D （0，1）．∴ 在Rt △BCE 中，23=BC ，2=CE ，∴ 313==OD OB ，3223==CE BC ，∴ CE BC OD OB =，即CE OD BC OB =， ∴ Rt △BOD ∽Rt △BCE ，得 ∠CBE ＝∠OBD ＝，因此 sin （－）＝ sin （∠DBC －∠OBD ）＝ sin ∠OBC ＝22=BCCO ．（3）显然 Rt △COA ∽Rt △BCE ，此时点P 1（0，0）．过A 作AP 2⊥AC 交y 正半轴于P 2，由Rt △CAP 2 ∽Rt △BCE ，得)31,0(2P ．过C 作CP 3⊥AC 交x 正半轴于P 3，由Rt △P 3CA ∽Rt △BCE ，得P 3（9，0）．故在坐标轴上存在三个点P 1（0，0），P 2（0，1∕3），P 3（9，0），使得以P 、A 、C 为顶点的三角形与BCE 相似．13．解：(Ⅰ)证明：∵AB ＝a ，AD ＝b ，BE ＝x ，S 梯形ABEF ＝ S 梯形CDFE ． ∴21a (x ＋AF )＝21a (EC ＋b －AF )，∴2AF ＝EC ＋(b －x )．又∵EC ＝b －x ，∴2AF ＝2EC ，即AF ＝EC ；(Ⅱ)（1）当直线EE ′经过原矩形的顶点D 时，如图（一），∵EC ∥E ′B ′， ∴B E EC ''＝B D DC'．由EC ＝b －x ，E ′B ′＝EB ＝x ， DB ′＝DC ＋CB ′＝2a ，得a a xx b 2=-， ∴x ︰b ＝32；当直线E ′E 经过原矩形的顶点A 时，如图（二），在梯形AE ′B ′D 中，∵EC ∥E ′B ′，点C 是DB ′的中点，∴CE ＝21(AD ＋ E ′B ′)，即b －x ＝21（b ＋x ），∴x ︰b ＝31．（2）如图（一），当直线EE ′ 经过原矩形的顶点D 时，BE ′∥EF ．证明：连接BF ．∵FD ∥BE ， FD ＝BE ，∴四边形FBED 是平行四边形，∴FB ∥DE ， FB ＝DE ，又∵EC ∥E ′B ′，点C 是DB ′的中点，∴DE ＝EE ′，∴FB ∥EE ′， FB ＝ EE ′，∴四边形BE ′EF 是平行四边形∴BE ′∥EF ．如图（二），当直线EE ′ 经过原矩形的顶点A 时，显然BE ′与EF 不平行，设直线EF 与BE ′交于点G .过点E ′作E ′M ⊥BC 于M ，则E ′M ＝a .．∵x ︰b ＝31，∴EM ＝31BC ＝31b ．若BE ′与EF 垂直，则有∠GBE ＋∠BEG ＝90°，又∵∠BEG ＝∠FEC ＝∠MEE ′， ∠MEE ′＋∠ME ′E ＝90°，。

中考数学中探索性问题的分析

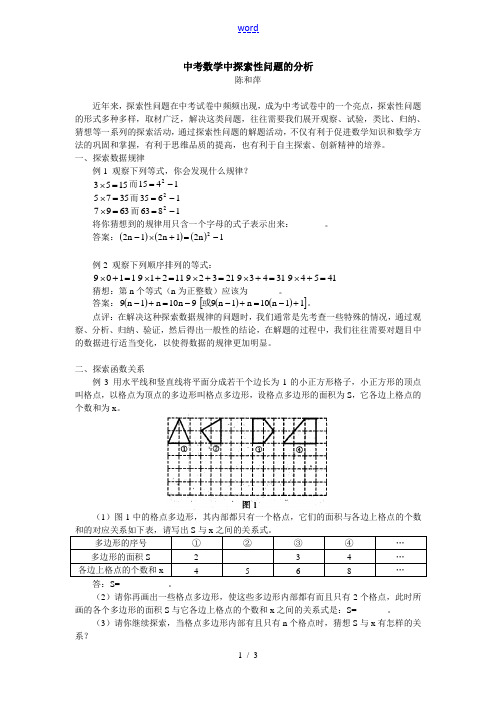
中考数学中探索性问题的分析陈和萍近年来，探索性问题在中考试卷中频频出现，成为中考试卷中的一个亮点，探索性问题的形式多种多样，取材广泛，解决这类问题，往往需要我们展开观察、试验，类比、归纳、猜想等一系列的探索活动，通过探索性问题的解题活动，不仅有利于促进数学知识和数学方法的巩固和掌握，有利于思维品质的提高，也有利于自主探索、创新精神的培养。

一、探索数据规律例1 观察下列等式，你会发现什么规律？1553=⨯而14152-=3575=⨯而16352-=6397=⨯而18632-=将你猜想到的规律用只含一个字母的式子表示出来：_______。

答案：()()()1n 21n 21n 22-=+⨯-例2 观察下列顺序排列的等式：1109=+⨯11219=+⨯21329=+⨯31439=+⨯41549=+⨯猜想：第n 个等式（n 为正整数）应该为_______。

答案：()9n 10n 1n 9-=+-()()[]11n 10n 1n 9+-=+-或。

点评：在解决这种探索数据规律的问题时，我们通常是先考查一些特殊的情况，通过观察、分析、归纳、验证，然后得出一般性的结论，在解题的过程中，我们往往需要对题目中的数据进行适当变化，以使得数据的规律更加明显。

二、探索函数关系例3 用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形，设格点多边形的面积为S ，它各边上格点的个数和为x 。

（1）图1中的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数多边形的序号① ② ③ ④ … 多边形的面积S2 3 4 … 各边上格点的个数和x 4 5 6 8 … 答：S=___________。

（2）请你再画出一些格点多边形，使这些多边形内部都有而且只有2个格点，此时所画的各个多边形的面积S 与它各边上格点的个数和x 之间的关系式是：S=_______。

（3）请你继续探索，当格点多边形内部有且只有n 个格点时，猜想S 与x 有怎样的关系？答：S=_______。

中考数学复习专题探索性问题

[中考数学复习专题] 探索性问题:就是问题的条件或结论不直接给出，需要经过观察、分析、分类、推理、化归、特殊化、一般化、数形结合及猜想等一系列的探索活动，逐步确定要求的结论或条件．其命题方式主要有填空题、选择题和综合题，其中以综合题为主．下面结合具体题目进行分析.1、条件探索型：总体思路是采用分析法，把结论看作已知进行逆推，探索结论成立需要的条件．【例1】点D E ，分别在线段A B A C ，上，B E C D ，相交于点O AE AD=，，要使A B E A C D△≌△，需添加一个条件是（只要写一个条件）．【例2】求出一个二次函数，使得当时，当时，当时.【练习】1。

()P x y ，位于第二象限，并且4y x +≤(x y ，为整数)写出符合上述条件的点P的坐标______：．2. M,N,P,Q 分别是四边形ABCD 各边AB 、BC 、CD 、DA 的中点，当四边形ABCD 满足条件时，四边形MNPQ 为矩形；3.关于的方程，是否存在负数，使方程的两个实数根的倒数和为？若存在，求出满足条件的负数值，若不存在，请说明理由？2、结论探索型：解这类探索题的总体思路是先假定结论存在，并以此进行推理．【例1】如图①，已知AB 是⊙O 的直径，AC 是弦，直线CD 切⊙O 于点C ，AD⊥CD，垂足为D ．(1)求证：AC 2=AB·AD； (2)若将直线CD 向上平移，交⊙O 于C 1、C 2两点，其他条件不变，可得到图②所示的图形，试探索AC 1、AC 2、AB 、AD 之间的关系，并说明理由；(3)把直线C 1D 继续向上平移，使弦C 1C 2与直径AB 相交（交点不与A 、B 重合），其他条件不变，请你在图③中画出变化后的图形，标好字母，并试着写与（2）相应的结论，判断你的结论是否成立？若不成立，请说明理由；若成立，请给出证明。

【例2】如图2－6－4所示，已知：直线m∥n，A 、B 为直线n 上两点，C 、P 为直线m 上两点．（1）请写出图2－6－4中，面积相等的各对三角形______________；理由是：__________.（2）如图 2－6－5所示，五边形 ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图2－6－6所示的形状，但承包土地与开垦荒地的分界小路（2－6－6中折线CDE）还保留着；张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案（不计分界小路与直路的占地面积）．（1）写出设计方案．并画出相应的图形；（2）说明方案设计理由．【练习】（1）写出一个两实数根符号相反的一元二次方程：__________________．（2）请你写一个先提公因式、再运用公式来分解因式的三项式，并写出分解的结果．（3）已知E、F为平行四边形ABCD对角线DB的三等分点，连结AE并延长交CD于P，连结PF并延长交AB于Q．猜测AQ、BQ间的关系是．猜测AQ、BQ间的关系成立吗？为什么？3、存在性探索型【例1】如图，四边形O A B C是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边B C折叠，使点B落在边O A的点D处．已知折痕C E=，且3tan4E D A∠=．（1）判断O C D△与AD E△是否相似？请说明理由；（2）求直线C E与x轴交点P的坐标；（3）是否存在过点D的直线l，使直线l、直线C E与x轴所围成的三角形和直线l、直线C E与y轴所围成的三角形相似？如果存在，请直接写出其解析式并画出相应的直线；如果不存在，请说明理由．例2 如图，已知O为坐标原点，∠AOB=300，∠ABO=900，且点A的坐标为（2，0）．（1）求点B的坐标；（2）若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；（3）在（2）中的二次函数图象的OB段（不包括点O、B）上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标，若不存在，请说明理由．【练习】1。