最新苏科版初中数学八年级上册轴对称图形复习重点习题

合集下载

苏科版八年级数学上册第二章轴对称复习题基础题含答案

苏科版八年级上册第二章轴对称复习题基础题一、选择题1．下列命题中：①两个全等三角形合在一起是一个轴对称图形；②等腰三角形的对称轴是底边上的中线；③等边三角形一边上的高就是这边的垂直平分线；④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有（）个 A ．1个 B ．2个 C ．3个 D ．4个2．下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（）个 A ．1个 B ．2个 C ．3个 D ．4个 3．已知∠AOB ＝30°，点P 在∠AOB 的内部，P 1与P 关于OA 对称，P 2与P 关于OB 对称，则△P 1OP 2是 ( ) A ．含30°角的直角三角形； B ．顶角是30的等腰三角形； C ．等边三角形 D ．等腰直角三角形.4．如图：等边三角形ABC 中，BD ＝CE ，AD 与BE 相交于点P ，则∠APE 的度数（） A ．45° B ．55° C ．60° D ．75°(4题) (8题) (15题) (16题)5. 下列关于等腰三角形的性质叙述错误的是（） A ．等腰三角形两底角相等B ．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合C ．等腰三角形是中心对称图形D ．等腰三角形是轴对称图形6．已知点P 在线段AB 的垂直平分线上，点Q 在线段AB 的中垂线外，则（） A ．PA+PB ＞QA+QB B ．PA+PB ＜QA+QB D ．PA+PB ＝QA+QB D ．不能确定7．已知△ABC 与△A 1B 1C 1关于直线MN 对称，且BC 与B 1C 1交与直线MN 上一点O ，则（）A ．点O 是BC 的中点B ．点O 是B 1C 1的中点 C ．线段OA 与OA 1关于直线MN 对称D ．以上都不对8．如图：已知∠AOP=∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=4，则PD= （） A ．4 B ．3 C ．2 D ．19．∠AOB 的平分线上一点P 到OA 的距离为5，Q 是OB 上任一点，则（） A ．PQ ＞5 B ．PQ≥5 C．PQ ＜5 D ．PQ≤510．等腰三角形的周长为15cm ，其中一边长为3cm ．则该等腰三角形的底长为B ADP O CPAE CB D（）A ．3cm 或5cmB ．3cm 或7cmC ．3cmD ．5cm二．填空题11．线段轴是对称图形，它有_______条对称轴．12．等腰△ABC 中，若∠A=30°，则∠B=________．13．在Rt △ABC 中，∠C=90°，AD 平分∠BAC 交BC 于D ，若CD=4，则点D 到AB 的距离是__________． 14．等腰△ABC 中，AB=AC=10，∠A=30°，则腰AB 上的高等于___________． 15．如图，在△ABC 中，∠ABC=∠ACB=72°，BD 、CE 分别是∠ABC 和∠A CB 的平分线，它们的交点为F ，则图中等腰三角形有___________个． 16．（2012•梧州）如图，在△ABC 中，AB=AD=DC ，∠BAD=32°，则∠BAC= ___________°．17．若D 为△ABC 的边BC 上一点，且AD=BD ，AB=AC=CD ，则∠BAC=____________．18．△ABC 中，AB 、AC 的垂直平分线分别交BC 于点E 、F ，若∠BAC=115°，则∠EAF=___________．三．解答题19．如图：已知∠AOB 和C 、D 两点，求作一点P ，使PC=PD ，且P 到∠AOB 两边的距离相等．20.如图在ABC △中，AB=AC=10，点H 在BC 上，AH=8，BH=6。

苏科版八年级上册数学第二章轴对称图形含答案(黄金题型)

苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE ∥BC，则结论：①△BDF是等腰三角形；②DE= BC；③四边形ADFE是菱形；④∠BDF+∠FEC=2∠A。

其中正确结论的序号是( )A.①②③B.①②④C.①③④D.②③④2、如图，直线y=-x+2分别交x轴、y轴于点A，B，点D在BA的延长线上，OD 的垂直平分线交线段AB于点C．若△OBC和△OAD的周长相等，则OD的长是( )A.2B.2C.D.43、彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样，穿越时空，向人们呈现出古代中国丰富多彩的物质与精神世界，各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起，形成复杂而精美的图案.以下图案纹样中，从整体观察（个别细微之处的细节忽略不计），大致运用了旋转进行构图的是（）A. B. C.D.4、下列图形中既是中心对称图形又是轴对称图形的是（）A. B. C. D.5、如图，在△ABC中，∠B＝50°，∠C＝30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD，则∠BAD的度数为（）A.50°B.60°C.70°D.80°6、如图，在△ABC中，∠ABC=90°，DE垂直平分AC，垂足为O，AD∥BC，且AB=3，BC=4，则AD的长为（）A. B. C. D.7、如图，在四边形中，点是对角线的中点，点、分别是、的中点，，，则的度数是（）A. B. C. D.8、如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE。

若AC=7，BC=4，则BD的长为（）A.2.5B.1.5C.2D.19、如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC 上），折叠后顶点D恰好落在边OC上的点F处，若点D的坐标为（−10，8），则△AEF的面积为（）A.15B.20C.25D.3010、设等腰三角形的顶角度数为y，底角度数为x，则( )A.y＝180°－2x(x可为全体实数)B.y＝180°－2x(0°≤x≤90°) C.y＝180°－2x(0°＜x＜90°) D.y＝180°－x(0°＜x＜90°)11、如图：将一个矩形纸片ABCD，沿着BE折叠，使C、D点分别落在点C1，D 1处．若∠C1BA=50°，则∠ABE的度数为（）A.15°B.20°C.25°D.30°12、长城是我国古代劳动人民创造的伟大奇迹，是中国悠久历史的见证，是中华民族的象征，被列为世界文化遗产．下列以长城为背景的标志设计中，不是轴对称图形的是（）A. B. C. D.13、正方形ABCD中，点P是对角线AC上的任意一点（不包括端点），以P为圆心的圆与AB相切，则AD与⊙P的位置关系是（）A.相离B.相切C.相交D.不确定14、如图，是一张直角三角形的纸片，两直角边，现将折叠，使点B点A重合，折痕为DE，则BD的长为（）A.7B.C.6D.15、已知AB=8cm，小红在作线段AB的垂直平分线时操作如下：分别以A和B 为圆心，5cm的长为半径画弧，两弧相交于C、D，则直线CD即为所求，根据此种作图方法所得到的四边形ADBC的面积是（）A.12cm 2B.24cm 2C.36cm 2D.48cm 2二、填空题(共10题，共计30分)16、在①线段、②角、③圆、④长方形、⑤梯形、⑥三角形、⑦等边三角形中，是轴对称图形的有________（只填序号）．17、如图，一个宽度相等的纸条按如图所示方法折叠压平，则∠1的度数等于________°.18、将一张长方形纸片按如图方式折叠，使A点落在BI上，与BI上的E点重合，BC、BD为折痕，则∠CBD=________.19、某公路急转弯处设立了一面圆型大镜子，从镜子中看到汽车车的部分号码如图所示，则该车牌照的部分号码为________.20、如图，矩形中，，，点E在边上，，点是边上的动点，将矩形沿直线折叠，点，的对应点分别为，，当，，三点恰好在同一直线上时，的长为________．21、如图，在正方形中，，E为的中点，将沿折叠，使点B落在正方形内点F处，连接，则的长为________．22、阅读后填空：已知：如图，∠A＝∠D＝90°，AC＝DB，AC、DB相交于点O.求证：OA＝OD.分析：要证OA＝OD，可证ABO≌DCO；要证ABO≌DCO，可先证ABC≌DCB得出AB＝DC这个结论；而用________可证ABC≌DCB（填SAS或AAS或HL）.23、如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C．若P是BC边上一动点，则DP长的最小值为________．24、如图，已知，平分，，若，，则=________．25、如图，B，C，D在同一直线上，∠B＝∠D＝90°，AB＝CD，BC＝DE，则△ACE的形状为________.三、解答题(共5题，共计25分)26、已知：如图，在△ABC中，AB=AC，点D，E在边BC上，且BD=CE．求证：AD=AE．27、如图所示，已知△ABC的角平分线BM，CN相交于点P，求证点P到AB，BC，CA的距离相等．28、如图，在四边形ABCD中，∠BAC＝∠ACD＝90°，∠B＝∠D．若AB＝3cm，BC＝5cm，点P从B点出发，以1cm/s的速度沿BC→CD→DA运动至A点停止，则从运动开始经过多少时间，△ABP为等腰三角形？29、如图①，将△ABC纸片沿DE折叠，使点A落F的位置，DF与BC交于点G，EF与BC交于点M，∠A=80°，求∠1+∠2的度数；30、阅读材料：已知△ABC中，AD平分∠BAC，AD是△ABC的中线，求证：AB=AC.小明根据已知条件发现若AD平分∠BAC可得∠BAD=∠CAD，又AD是△ABC的中线，可得BD=CD，加上公共边的条件AD=AD，有两条边和一个角对应相等，就下结论得到△ABD和△ACD是全等的，从而得到结论∠B=∠C，可证出AB=AC成立；小芳的方法是用角平分线的性质得到DE=DF，再用中线分三角形的面积为相等两部分，再用等面积的方法可以得到结论.请你回答小明和小芳的证明思路谁正确的？请任选择一个方法进行完整的证明（可以与小明和小芳的方法不同）参考答案一、单选题(共15题，共计45分)1、B2、B3、B4、B5、C6、B7、C8、B9、C10、C11、B12、A13、B14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、30、。

【精选】苏科版数学八年级上册轴对称解答题单元复习练习(Word版含答案)

【精选】苏科版数学八年级上册轴对称解答题单元复习练习(Word版含答案)一、八年级数学轴对称解答题压轴题（难）1．教材呈现：如图是华师版八年级上册数学教材第94页的部分内容.2．线段垂直平分线.我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图，直线MN是线段AB的垂直平分线，P是MN上任一点，连结PA、PB，将线段AB沿直线MN对称，我们发现PA与PB完全重合，由此即有：线段垂直平分线的性质定理线段垂直平分线上的点到线段的距离相等．已知：如图，MN⊥AB，垂足为点C，AC＝BC，点P是直线MN上的任意一点．求证：PA＝PB．分析：图中有两个直角三角形APC和BPC，只要证明这两个三角形全等，便可证明PA＝PB．定理证明：请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．定理应用：（1）如图②，在△ABC中，直线m、n分别是边BC、AC的垂直平分线，直线m、n的交点为O．过点O作OH⊥AB于点H．求证：AH＝BH．（2）如图③，在△ABC中，AB＝BC，边AB的垂直平分线l交AC于点D，边BC的垂直平分线k交AC于点E．若∠ABC＝120°，AC＝15，则DE的长为．【答案】（1）见解析；（2）5【解析】【分析】定理证明：先证明△PAC≌△PBC，然后再运用三角形全等的性质进行解答即可；（1）连结AO、BO、CO利用线段的垂直平分线的判定和性质即可解答；（2）连接BD，BE，证明△BDE是等边三角形即可解答.【详解】解：定理证明：∵MN⊥AB，∴∠PCA＝∠PCB＝90°．又∵AC＝BC，PC＝PC，∴△PAC≌△PBC（SAS），∴PA＝PB．定理应用：（1）如图2，连结OA、OB、OC．∵直线m 是边BC 的垂直平分线，∴OB ＝OC ，∵直线n 是边AC 的垂直平分线，∴OA ＝OC ，∴OA ＝OB∵OH ⊥AB ，∴AH ＝BH ；（2）如图③中，连接BD ，BE ．∵BA ＝BC ，∠ABC ＝120°，∴∠A ＝∠C ＝30°，∵边AB 的垂直平分线交AC 于点D ，边BC 的垂直平分线交AC 于点E ，∴DA ＝DB ，EB ＝EC ，∴∠A ＝∠DBA ＝30°，∠C ＝∠EBC ＝30°，∴∠BDE ＝∠A +∠DBA ＝60°，∠BED ＝∠C +∠EBC ＝60°，∴△BDE 是等边三角形，∴AD ＝BD ＝DE ＝BE ＝EC ，∵AC ＝15＝AD +DE +EC ＝3DE ，∴DE ＝5，故答案为：5．【点睛】本题考查了线段的垂直平分线的性质、全等三角形的判定和性质、等边三角形的判定和性质等知识，掌握并灵活运用数学基本知识是解答本题的关键.2．如图1，在ABC 中，90BAC ∠=︒，点D 为AC 边上一点，连接BD ，点E 为BD 上一点，连接CE ，CED ABD ∠=∠，过点A 作AG CE ⊥，垂足为G ，交ED 于点F ．(1)求证：2FAD ABD ∠=∠；(2)如图2，若AC CE =，点D 为AC 的中点，求证：AB AC =；(3)在(2)的条件下，如图3，若3EF =，求线段DF 的长．【答案】（1）详见解析；（2）详见解析；（3）6【解析】【分析】（1）根据直角三角形的性质可得90ADB ABD ∠=︒-∠，90EFG CED ∠=︒-∠，然后根据三角形的内角和和已知条件即可推出结论；（2）根据直角三角形的性质和已知条件可得AFD ADF ∠=∠，进而可得AF AD =，BFA CDE ∠=∠，然后即可根据AAS 证明ABF ∆≌CED ∆，可得AB CE =，进一步即可证得结论；（3）连接AE ，过点A 作AH AE ⊥交BD 延长线于点H ，连接CH ，如图4．先根据已知条件、三角形的内角和定理和三角形的外角性质推出45AED ∠=︒，进而可得AE AH =，然后即可根据SAS 证明△ABE ≌△ACH ，进一步即可推出90CHD ∠=︒，过点A 作AK ED ⊥于K ，易证△AKD ≌△CHD ，可得DK DH =，然后即可根据等腰三角形的性质推得DF =2EF ，问题即得解决．【详解】（1）证明：如图1，90BAC ∠=︒，90ADB ABD ∴∠=︒-∠， AG CE ⊥，90FGE ∴∠=︒，90EFG AFD CED ∴∠=∠=︒-∠，180FAD AFD ADF CED ABD ∴∠=︒-∠-∠=∠+∠，CED ABD ∠=∠，2FAD ABD ∴∠=∠；（2）证明：如图2，90AFD CED ∠=︒-∠，90ADB ABD ∠=︒-∠，CED ABD ∠=∠，AFD ADF ∴∠=∠，AF AD ∴=，BFA CDE ∠=∠，∵点D 为AC 的中点，∴AD=CD ，AF CD ∴=，ABF ∴∆≌CED ∆（AAS ），AB CE ∴=， CE AC =，AB AC ∴=；（3）解：连接AE ，过点A 作AH AE ⊥交BD 延长线于点H ，连接CH ，如图4． 90BAC ∠=︒，BAE CAH ∴∠=∠，设ABD CED α∠=∠=，则2,902FAD ACG αα∠=∠=︒-，CA CE =，45AEC EAC α∴∠=∠=︒+，45AED ∴∠=︒，45AHE ∴∠=︒，AE AH ∴=，AB AC =，∴△ABE ≌△ACH （SAS ），135AEB AHC ∴∠=∠=︒，90CHD ∴∠=︒，过点A 作AK ED ⊥于K ，90AKD CHD ∴∠=∠=︒，AD CD =，ADK CDH ∠=∠，∴△AKD ≌△CHD （AAS ），DK DH ∴=，∵,,AK DF AF AD AE AH ⊥==，,FK DK EK HK ∴==，3DH EF ∴==，6DF ∴=．【点睛】本题考查了直角三角形的性质、三角形的内角和定理、三角形的外角性质、等腰直角三角形的判定和性质、全等三角形的判定和性质以及等腰三角形的性质等知识，考查的知识点多、综合性强、难度较大，正确添加辅助线、构造等腰直角三角形和全等三角形的模型、灵活应用上述知识是解题的关键．3．已知在△ABC 中，AB ＝AC ，射线BM 、BN 在∠ABC 内部，分别交线段AC 于点G 、H ．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求ABFACFSS的值．【答案】（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF＝∠1+∠BAF＝60°即可解决问题；②只要证明△BFC≌△ADB，即可推出∠BFC＝∠ADB＝90°；（2）在BF上截取BK＝AF，连接AK．只要证明△ABK≌CAF，可得S△ABK＝S△AFC，再证明AF＝FK＝BK，可得S△ABK＝S△AFK，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt △BFD 中，∵∠FBD ＝30°，∴BF ＝2DF ，∵BF ＝2AF ，∴BF ＝AD ，∵∠BAE ＝∠FBC ，AB ＝BC ，∴△BFC ≌△ADB ，∴∠BFC ＝∠ADB ＝90°，∴BF ⊥CF（2）在BF 上截取BK ＝AF ，连接AK．∵∠BFE ＝∠2+∠BAF ，∠CFE ＝∠4+∠1，∴∠CFB ＝∠2+∠4+∠BAC ，∵∠BFE ＝∠BAC ＝2∠EFC ，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB ＝AC ，∴△ABK ≌CAF ，∴∠3＝∠4，S △ABK ＝S △AFC ，∵∠1+∠3＝∠2+∠3＝∠CFE ＝∠AKB ，∠BAC ＝2∠CEF ，∴∠KAF ＝∠1+∠3＝∠AKF ，∴AF ＝FK ＝BK ，∴S △ABK ＝S △AFK ，∴ABF AFCS 2S ∆∆=．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．4．如图，在ABC ∆中，CE 为三角形的角平分线，AD CE ⊥于点F 交BC 于点D （1）若9628BAC B ︒︒∠=∠=，，直接写出BAD ∠= 度（2）若2ACB B ∠=∠，①求证：2AB CF =②若 ,CF a EF b ==，直接写出BD CD= （用含 ,a b 的式子表示）【答案】（1）34；（2）①见详解；②2b a b- 【解析】【分析】（1）由三角形内角和定理和角平分线定义即可得出答案；（2）①证明B BCE ∠=∠，得出BE=CE ，过点A 作//AH BC 交CE 与点H ，则,H BCE ACE EAH B ∠=∠=∠∠=∠，得出AH=AC ，H EAH ∠=∠，得出AE=HE ，由等腰三角形的性质可得出HF=CF ，即可得出结论；②证明AHF DCF ≅，得出AH=DC ，求出HF=CF=a ，HE=HF-EF=a-b ，CE=a+b ，由 //AH BC 得出AH AE a b BC BE a b-==+，进而得出结论．【详解】解：（1）∵9628BAC B ︒︒∠=∠=，，∴180962856ACB ∠=︒-︒-︒=︒，∵CE 为三角形的角平分线，∴1282ACE ACB ∠=∠=︒， ∵AD CE ⊥，∴902862CAF ∠=︒-︒=︒，∴966234BAD ∠=︒-︒=︒．故答案为：34；（2）①证明：∵22ACB B BCE ∠=∠=∠∴B BCE ∠=∠∴BE CE =过点A 作//AH BC 交CE 与点H ，如图所示：则,H BCE ACE EAH B ∠=∠=∠∠=∠∴AH=AC ，H EAH ∠=∠∴AE=HE∵AD CE ⊥∴HF=CF∴AB=HC=2CF ；②在AHF △和DCF 中，H DCF HF CFAFH DFC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AHF DCF ≅∴AH=DC∵,CF a EF b == ∴ HF CF a ==，由①得 AE HE HF EF a b ==-=-， BE CE a b ==+∵ //AH BC ∴AH AE a b BC BE a b -==+ ∴CD a b BC a b -=+ ∴2BD b CD a b=-．故答案为：2b a b -．【点睛】本题考查的知识点是全等三角形的判定及其性质、等腰三角形的判定及其性质、三角形的内角和定理、三角形的角平分线定理等，掌握以上知识点是解此题的关键．5．问题探究：如图1，△ACB 和△DCE 均为等边三角形，点A 、D 、E 在同一直线上，连接BE ．（1）证明：AD=BE；（2）求∠AEB的度数．问题变式：（3）如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．（Ⅰ）请求出∠AEB的度数；（Ⅱ）判断线段CM、AE、BE之间的数量关系，并说明理由．【答案】（1）见详解；（2）60°；（3）（Ⅰ）90°；（Ⅱ）AE=BE+2CM，理由见详解.【解析】【分析】（1）由条件△ACB和△DCE均为等边三角形，易证△ACD≌△BCE，从而得到对应边相等，即AD=BE；（2）根据△ACD≌△BCE，可得∠ADC=∠BEC，由点A，D，E在同一直线上，可求出∠ADC=120°，从而可以求出∠AEB的度数；（3）（Ⅰ）首先根据△ACB和△DCE均为等腰直角三角形，可得AC=BC，CD=CE，∠ACB=∠DCE=90°，据此判断出∠ACD=∠BCE；然后根据全等三角形的判定方法，判断出△ACD≌△BCE，即可判断出BE=AD，∠BEC=∠ADC，进而判断出∠AEB的度数为90°；（Ⅱ）根据DCE=90°，CD=CE，CM⊥DE，可得CM=DM=EM，所以DE=DM+EM=2CM，据此判断出AE=BE+2CM．【详解】解：（1）如图1，∵△ACB和△DCE均为等边三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°，∴∠ACD=∠BCE．在△ACD和△BCE中，AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE（SAS），∴AD=BE；（2）如图1，∵△ACD≌△BCE，∴∠ADC=∠BEC，∵△DCE为等边三角形，∴∠CDE=∠CED=60°，∵点A，D，E在同一直线上，∴∠ADC=120°，∴∠BEC=120°，∴∠AEB=∠BEC-∠CED=60°；（3）（Ⅰ）如图2，∵△ACB和△DCE均为等腰直角三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=90°，∠CDE=∠CED=45°，∴∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE，在△ACD和△BCE中，AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△BCE（SAS），∴BE=AD，∠BEC=∠ADC，∵点A，D，E在同一直线上，∴∠ADC=180-45=135°，∴∠BEC=135°，∴∠AEB=∠BEC-∠CED=135°-45°=90°，故答案为：90°；（Ⅱ）如图2，∵∠DCE=90°，CD=CE，CM⊥DE，∴CM=DM=EM，∴DE=DM+EM=2CM，∵△ACD≌△BCE（已证），∴AE=AD+DE=BE+2CM ，故答案为：AE=BE+2CM ．【点睛】本题属于三角形综合题，主要考查了全等三角形的判定方法和性质，等边三角形的性质以及等腰直角三角形的性质的综合应用．在判定三角形全等时，关键是选择恰当的判定条件，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．6．某数学兴趣小组开展了一次活动，过程如下：设(090BAC θθ∠=︒<<︒).现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB 、AC 上．活动一、如图甲所示，从点1A 开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直（12A A 为第1根小棒）数学思考：（1）小棒能无限摆下去吗？答：（填“能”或“不能”）（2）设11223AA A A A A ==，求θ的度数；活动二：如图乙所示，从点1A 开始，用等长的小棒依次向右摆放，其中12A A 为第一根小棒，且121A A AA =．数学思考：（3）若已经摆放了3根小棒，则213A A A ∠= ，423A A A ∠= ，43 A A C ∠= ；（用含θ的式子表示）（4）若只能摆放5根小棒，则θ的取值范围是．【答案】（1）能；（2）θ＝22.5°；（3）2θ，3θ，4θ；（4）15°≤θ＜18°．【解析】【分析】（1）由小棒与小棒在端点处互相垂直，即可得到答案；（2）根据等腰直角三角形的性质和三角形外角的性质，即可得到答案；（3）由121A A AA =，得∠AA 2A 1=∠A 2AA 1=θ，从而得213A A A ∠=∠AA 2A 1+∠A 2AA 1=2θ，同理得423 A A A ∠=∠A 2AA 1+231A A A ∠=θ+2θ=3θ，43 A A C ∠=∠A 2AA 1+243 A A A ∠=θ+3θ=4θ；（4）根据题意得：5θ＜90°且6θ≥90°，进而即可得到答案．（1）∵小棒与小棒在端点处互相垂直即可，∴小棒能无限摆下去，故答案是：能；（2）∵A 1A 2＝A 2A 3，A 1A 2⊥A 2A 3，∴∠A 2A 1A 3＝45°，∴∠AA 2A 1+θ＝45°，∵AA 1＝A 1A 2∴∠AA 2A 1＝∠BAC=θ，∴θ＝22.5°；（3）∵121A A AA =，∴∠AA 2A 1=∠A 2AA 1=θ，∴213A A A ∠=∠AA 2A 1+∠A 2AA 1=2θ，∵3122A A A A =，∴213A A A ∠=231A A A ∠=2θ，∴423A A A ∠=∠A 2AA 1+231A A A ∠=θ+2θ=3θ， ∵3342A A A A =，∴423A A A ∠=243 A A A ∠=3θ， ∴43A A C ∠=∠A 2AA 1+243 A A A ∠=θ+3θ=4θ，故答案是：2θ，3θ，4θ；（4）由第（3）题可得：645A A A ∠=5θ，65 A A C ∠=6θ， ∵只能摆放5根小棒，∴5θ＜90°且6θ≥90°，∴15°≤θ＜18°．故答案是：15°≤θ＜18°．【点睛】本题主要考查等腰三角形的性质以及三角形外角的性质，掌握等腰三角形的底角相等且小于90°，是解题的关键．7．如图所示，已知ABC ∆中，10AB AC BC ===厘米，M 、N 分别从点A 、点B 同时出发，沿三角形的边运动，已知点M 的速度是1厘米/秒的速度，点N 的速度是2厘米/秒，当点N 第一次到达B 点时，M 、N 同时停止运动.（1）M 、N 同时运动几秒后，M 、N 两点重合？（2）M 、N 同时运动几秒后，可得等边三角形AMN ∆？（3）M 、N 在BC 边上运动时，能否得到以MN 为底边的等腰AMN ∆，如果存在，请求出此时M 、N 运动的时间？【答案】（1）10；（2）点M 、N 运动103秒后，可得到等边三角形AMN ∆；（3）当点M 、N 在BC 边上运动时，能得到以MN 为底边的等腰AMN ∆，此时M 、N 运动的时间为403秒．【解析】【分析】（1）设点M 、N 运动x 秒后，M 、N 两点重合,1102x x ⨯+=；（2）设点M 、N 运动t 秒后，可得到等边三角形AMN ∆，如图①，1AM t t =⨯=,102AN AB BN t =-=-根据等边三角形性质得102t t =-；（3）如图②，假设AMN ∆是等腰三角形，根据等腰三角形性质证ACB ∆是等边三角形，再证ACM ∆≌ABN ∆（AAS ），得CM BN =，设当点M 、N 在BC 边上运动时，M 、N 运动的时间y 秒时，AMN ∆是等腰三角形，故10CM y =-，302NB y =-，由CM NB =，得10302y y -=-；【详解】解：（1）设点M 、N 运动x 秒后，M 、N 两点重合,1102x x ⨯+=解得：10x =（2）设点M 、N 运动t 秒后，可得到等边三角形AMN ∆，如图①1AM t t =⨯=,102AN AB BN t =-=-∵三角形AMN ∆是等边三角形∴102t t =-解得103t =∴点M 、N 运动103秒后，可得到等边三角形AMN ∆. （3）当点M 、N 在BC 边上运动时，可以得到以MN 为底边的等腰三角形，由（1）知10秒时M 、N 两点重合，恰好在C 处，如图②，假设AMN ∆是等腰三角形，∴AN AM =，∴AMN ANM ∠=∠，∴AMC ANB ∠=∠，∵AB BC AC ==，∴ACB ∆是等边三角形，∴C B ∠=∠，在ACM ∆和ABN ∆中，∵AC AB C B AMC ANB =⎧⎪∠=∠⎨⎪∠=∠⎩，∴ACM ∆≌ABN ∆（AAS ），∴CM BN =，设当点M 、N 在BC 边上运动时，M 、N 运动的时间y 秒时，AMN ∆是等腰三角形， ∴10CM y =-，302NB y =-，CM NB =，10302y y -=-解得：403y =，故假设成立. ∴当点M 、N 在BC 边上运动时，能得到以MN 为底边的等腰AMN ∆，此时M 、N 运动的时间为403秒．【点睛】考核知识点：等边三角形判定和性质，全等三角形判定和性质.理解等腰三角形的判定和性质,把问题转化为方程问题是关键.8．定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段．．．．叫做这个三角形的三分线.（1）图①是顶角为36︒的等腰三角形，这个三角形的三分线已经画出，请你在图②中用不同于图①的方法画出顶角为36︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数（若两种方法分得的三角形成3对全等三角形，则视为同一种）；（2）图③是顶角为45︒的等腰三角形，请你在图③中画出顶角为45︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数.（3）ABC 中，30B ∠=︒，AD 和DE 是ABC 的三分线，点D 在BC 边上，点E 在AC 边上，且AD BD =，DE CE =，设c x ∠=︒，则x 所有可能的值为_________.【答案】（1）见详解；（2）见详解；（3）20或40.【解析】【分析】(1)作底角的平分线，再作底边的平行线，即可得到三分线；(2)过底角定点作对边的高，形成一个等腰直角三角形和一个直角三角形，然后再构造一个等腰直角三角形，即可.(3)根据题意，先确定30°角然后确定一边为BA ，一边为BC ，再固定BA 的长，进而确定D 点，分别考虑AD 为等腰三角形的腰和底边，画出示意图，列出关于x 的方程，即可得到答案.【详解】（1）如图所示：（2）如图所示：（3）①当AD=AE 时，如图4，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠ADE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30=2x+x ，解得：x=20；②当AD=DE 时，如图5，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠DAE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30+2x+x=180，解得：x=40.③当AE=DE 时，则∠EAD=∠EDA=1802(90)2x x -=-， ∴∠ADC=∠EDA+∠EDC=(90-x)+x=90°又∵∠ADC=30+30=60°，∴这种情况不存在.∴x 所有可能的值为20或40.故答案是：20或40图4 图5【点睛】本题主要考查等腰三角形的判定和性质定理的综合应用，分类讨论，画出图形，是解题的关键.9．如图，在△ABC 中，AB =AC =2，∠B =40°，点D 在线段BC 上运动（D 不与B 、C 重合），连接AD ，作∠ADE =40°，DE 交线段AC 于E 点．（1）当∠BDA =115°时，∠BAD =___°，∠DEC =___°；（2）当DC 等于多少时，△ABD 与△DCE 全等？请说明理由；（3）在点D 的运动过程中，△ADE 的形状可以是等腰三角形吗？若可以，请直接写出∠BDA 的度数；若不可以，请说明理由．【答案】（1） 25，115；（2）当DC =2时，△ABD ≌△DCE ，理由见解析；（3）可以；当∠BDA 的度数为110°或80°时，△ADE 的形状是等腰三角形．【解析】【分析】（1）根据三角形内角和定理，将已知数值代入即可求出BAD ∠，根据平角的定义，可求出EDC ∠的度数，根据三角形内和定理，即可求出DEC ∠．（2）当AB DC =时，利用AAS 可证明ABD DCE ∆≅∆，即可得出2AB DC ==．（3）假设ADE ∆是等腰三角形，分为三种情况讨论：①当AD AE =时，40ADE AED ∠=∠=︒，根据AED C ∠>∠，得出此时不符合；②当DA DE =时，求出70DAE DEA ∠=∠=︒，求出BAC ∠，根据三角形的内角和定理求出BAD ∠，根据三角形的内角和定理求出BDA ∠即可；③当EA ED =时，求出DAC ∠，求出BAD ∠，根据三角形的内角和定理求出ADB ∠．【详解】（1）在BAD 中，40B ∠= ，115BDA ∠=，1801804011525BAD ABD BDA ∴∠=︒-∠-∠=︒-︒-︒=︒，1801801154025EDC ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒．AB AC =，40B ∠=，40B C ∴∠=∠=，1801804025115C E DC D E C ︒-∠-∠=︒-︒-︒=∠=︒．故答案为：25，115；（2）当2DC =时，ABD DCE ∆≅∆．理由如下：40C ∠=，140EDC DEC ∴∠+∠=︒，又40ADE ∠=，140ADB EDC ∴∠+∠=︒，ADB DEC ∴∠=∠．在ABD △和DCE ∆中，B C ∠=∠，ADB DEC ∠=∠，当AB DC =时，()ABD DCE AAS ∆≅∆，2AB DC ∴==；（3）AB AC =，40B C ∴∠=∠=︒，分三种情况讨论：①当AD AE =时，40ADE AED ∠=∠=︒，AED C ∠>∠，∴此时不符合； ②当DA DE =时，即1(18040)702DAE DEA ∠=∠=︒-︒=︒，1804040100BAC ∠=︒-︒-︒=︒，1007030BAD ∴∠=︒-︒=︒；1803040110BDA ∴∠=︒-︒-︒=︒；③当EA ED =时，40ADE DAE ∠=∠=︒，1004060BAD ∴∠=︒-︒=︒，180604080BDA ∴∠=︒-︒-︒=︒；∴当110ADB ∠=︒或80︒时，ADE ∆是等腰三角形．【点睛】本题考查了学生对等腰三角形的判定与性质，全等三角形的判定与性质，三角形内角和定理等知识点的理解和掌握，此题涉及到的知识点较多，综合性较强．10．小明在学习了“等边三角形”后，激发了他的学习和探究的兴趣，就想考考他的朋友小崔，小明作了一个等边ABC ∆，如图1，并在边AC 上任意取了一点F （点F 不与点A 、点C 重合），过点F 作FH AB ⊥交AB 于点H ，延长CB 到G ，使得BG AF =，连接FG 交AB 于点l .（1）若10AC =，求HI 的长度；（2）如图2，延长BC 到D ，再延长BA 到E ，使得AE BD =，连接ED ，EC ，求证：ECD EDC ∠=∠.【答案】（1）HI =5；(2)见解析.【解析】【分析】（1）作FP ∥BC 交AB 于点P ，证明APF ∆是等边三角形得到AH=PH ，再证明PFI BGI ∆≅∆得到PI=BI ，于是可得HI =12AB ，即可求解；（2）延长BD 至Q ，使DQ=AB ，连结EQ ，就可以得出BE=BQ ，得出△BEQ 是等边三角形，就可以得出BE=QE ，得出△BCE ≌△QDE 就可以得出结论．【详解】解：如图1，作FP ∥BC 交AB 于点P ，∵ABC ∆是等边三角形,∴∠ABC=∠A=60°,∵FP ∥BC,∴∠APF=∠ABC=60°, ∠PFI=∠BGI,∴∠APF=∠A=60°,∴APF ∆是等边三角形,∴PF=AF,∵FH AB ⊥，∴AH=PH,∵AF=BG,∴PF=BG,∴在PFI ∆和BGI ∆中，PIF BIGPFI BGIPF BG∠=∠⎧⎪∠=∠⎨⎪=⎩,∴PFI BGI∆≅∆,∴PI=BI,∴PI+PH=BI+AH=12AB,∴HI=PI+PH =12AB=1102⨯=5；(2)如图2，延长BD至Q，使DQ=AB，连结EQ，∵△ABC是等边三角形，∴AB=BC=AC，∠B=60°．∵AE=BD，DQ=AB，∴AE+AB=BD+DQ，∴BE=BQ．∵∠B=60°，∴△BEQ为等边三角形，∴∠B=∠Q=60°，BE=QE．∵DQ=AB，∴BC=DQ．∴在△BCE和△QDE中，BC DQB QBE QE=⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△QDE（SAS），∴EC=ED．∴∠ECD=∠EDC.【点睛】本题考查了等边三角形的判定及性质的运用，全等三角形的判定及性质的运用，解答时作出相应辅助线构造全等三角形是关键．本题难度较大，需要有较强的综合能力.。

(精练)(汇总)苏科版八年级上册数学第二章轴对称图形含答案

苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、如图，在钝角三角形中，为钝角，以点为圆心，长为半径画弧；再以点为圆心，长为半径画弧；两弧交于点连结的延长线交于点.下列结论：垂直平分；平分；是等腰三角形；是等边三角形.其中正确的有（）A. 个B. 个C. 个D. 个2、下列各图中，∠1＝∠2的图形的个数有（）A.3B.4C.5D.63、下列交通警示标志中，是轴对称图形的是（）A. B. C. D.4、如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A恰好落在∠BCD的平分线上时,则AE的长为1( )A.2或3B. 或C. 或D.3或45、如图，平面直角坐标系中存在点A（3，2），点B（1,0），以线段AB为边作等腰三角形ABP，使得点P在坐标轴上.则这样的P点有（）A.4个B.5个C.6个D.7个6、等腰三角形的两边长是6cm和3cm，那么它的周长是（）A.9cmB.12 cmC.12 cm或15 cmD.15 cm7、下列图形中既是中心对称图形又是轴对称图形的是（）A. B. C. D.8、如图，网格中的每个小正方形的边长为1，A，B是格点，则以A，B，C为等腰三角形顶点的所有格点C的位置有（）A.2个B.3个C.4个D.5个9、以下由两个全等的30°直角三角板拼成的图形中，属于中心对称图形的是（）A. B. C. D.10、如图，在等腰中，，点为反比例函数（其中）图象上的一点，点在轴正半轴上，过点作，交反比例函数的图象于点，连接交于点，若的面积为2，则的值为（）A.20B.C.16D.11、如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE；上述结论一定正确的是（）A.①②③B.②③④C.①③⑤D.①③④12、如图，△ABC中，AB=AC，AD平分∠CAB，则下列结论中：①AD⊥BC；②AD=BC；③∠B=∠C；④BD=CD。

苏科版八年级数学上册期末复习轴对称图形解答题(难题)训练.docx

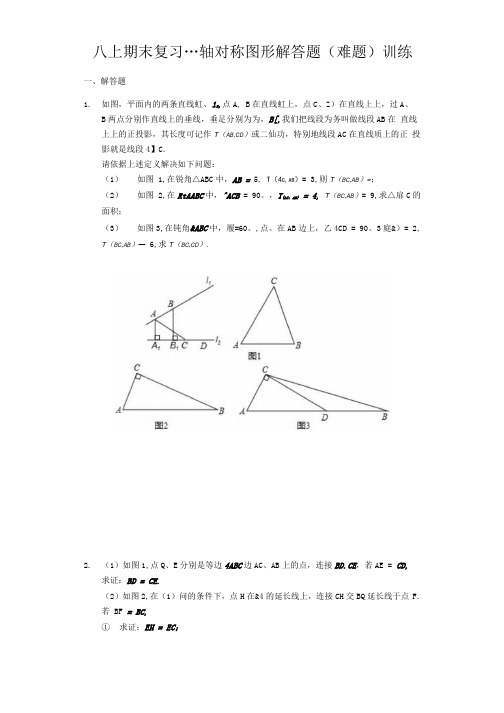
八上期末复习…轴对称图形解答题（难题）训练一、解答题1.如图，平面内的两条直线虹、12,点A, B在直线虹上，点C、Z）在直线上上，过A、B两点分别作直线上的垂线，垂足分别为为，B[,我们把线段为务叫做线段AB在直线上上的正投影，其长度可记作T（AB,CD）或二仙功，特别地线段AC在直线质上的正投影就是线段4】C.请依据上述定义解决如下问题：（1）如图 1,在锐角△ABC中，AB = 5, T（4C,AB）= 3,则T（BC,AB）=；（2）如图 2,在RtAABC中，^ACB = 90。

，T{AC：AB} = 4, T（BC,AB）= 9,求△扉C的面积；（3）如图3,在钝角&ABC中，履=60。

,点。

在AB边上，乙4CD = 90。

3庭&）= 2, T（BC,AB）— 6,求T（BC,CD）.2.（1）如图1,点Q、E分别是等边4ABC边AC、AB上的点，连接BD.CE，若AE = CD,求证：BD = CE.（2）如图2,在（1）问的条件下，点H在&4的延长线上，连接CH交BQ延长线于点 F.若 BF = BC,①求证：EH = EC；②请你找出线段AH、AD, QF之间的数量关系，并说明理由.3,在平面直角坐标系xOy中，对于任意两点PiOi，%)与「2(>2，无)的"识别距离”，给出如下定义：若ki -x2l > |yi -y21>则点Pi(xi,yD与点「2(*2,光)的"识别距离”为次1 一电；若ki -%2| <也1 一光1，贝。

点031况)与点「2(>2，光)的"识别距离"为1% -光1.(1)已知点4(—1,0), B为y轴上的动点，①若点A与点B的“识别距离”为2,写出满足条件的点B的坐标②点A与点3的"识别距离"的最小值为.(2)已知点C坐标为(m,|m + 3), D(0,l),求点C与点。

苏科版数学八年级上册轴对称解答题单元复习练习(Word版含答案)

苏科版数学八年级上册轴对称解答题单元复习练习(Word 版含答案)一、八年级数学轴对称解答题压轴题（难）1．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．【答案】（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS∴∆≅∆，CBE CAD∴∠=∠，同理可得：30CAM∠=︒150CBE CAD∴∠=∠=︒30CBO∴∠=︒，∵30BAM∠=︒，903060BOA∴∠=︒-︒=︒．综上，当动点D在直线AM上时，AOB∠是定值，60AOB∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.2．再读教材:宽与长的比是5-1(约为0.618)的矩形叫做黄金矩形，黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步，如图②.把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处，第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形，问题解决:（1）图③中AB=________(保留根号);（2）如图③,判断四边形 BADQ的形状,并说明理由;（3）请写出图④中所有的黄金矩形,并选择其中一个说明理由.（4）结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.【答案】（1）5；(2)见解析;(3)见解析; (4) 见解析.【解析】分析：（1）由勾股定理计算即可；（2）根据菱形的判定方法即可判断；（3）根据黄金矩形的定义即可判断；（4）如图④﹣1中，在矩形BCDE上添加线段GH，使得四边形GCDH为正方形，此时四边形BGHE为所求是黄金矩形．详解：（1）如图3中．在Rt△ABC中，AB=22+=22AC BC+=5．12故答案为5．（2）结论：四边形BADQ是菱形．理由如下：如图③中，∵四边形ACBF是矩形，∴BQ∥AD．∵AB∥DQ，∴四边形ABQD是平行四边形，由翻折可知：AB=AD，∴四边形ABQD是菱形．（3）如图④中，黄金矩形有矩形BCDE，矩形MNDE．∵AD =5．AN =AC =1，CD =AD ﹣AC =5﹣1．∵BC =2，∴CD BC =512-，∴矩形BCDE 是黄金矩形． ∵MN DN =215+=512-，∴矩形MNDE 是黄金矩形．（4）如图④﹣1中，在矩形BCDE 上添加线段GH ，使得四边形GCDH 为正方形，此时四边形BGHE 为所求是黄金矩形．长GH =5﹣1，宽HE =3﹣5．点睛：本题考查了几何变换综合题、黄金矩形的定义、勾股定理、翻折变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考创新题目．3．已知在△ABC 中，AB ＝AC ，射线BM 、BN 在∠ABC 内部，分别交线段AC 于点G 、H ．（1）如图1，若∠ABC ＝60°，∠MBN ＝30°，作AE ⊥BN 于点D ，分别交BC 、BM 于点E 、F ．①求证：∠1＝∠2；②如图2，若BF ＝2AF ，连接CF ，求证：BF ⊥CF ；（2）如图3，点E 为BC 上一点，AE 交BM 于点F ，连接CF ，若∠BFE ＝∠BAC ＝2∠CFE ，求ABFACF S S 的值．【答案】（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF ＝∠1+∠BAF ＝60°即可解决问题；②只要证明△BFC ≌△ADB ，即可推出∠BFC ＝∠ADB ＝90°；（2）在BF 上截取BK ＝AF ，连接AK ．只要证明△ABK ≌CAF ，可得S △ABK ＝S △AFC ，再证明AF ＝FK ＝BK ，可得S △ABK ＝S △AFK ，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴ABFAFCS2S∆∆=．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．4．如图，在ABC∆中，CE为三角形的角平分线，AD CE⊥于点F交BC于点D （1）若9628BAC B︒︒∠=∠=，，直接写出BAD∠=度（2）若2ACB B∠=∠，①求证：2AB CF=②若,CF a EF b==，直接写出BDCD=（用含,a b的式子表示）【答案】（1）34；（2）①见详解；②2ba b-【解析】【分析】（1）由三角形内角和定理和角平分线定义即可得出答案；（2）①证明B BCE ∠=∠，得出BE=CE ，过点A 作//AH BC 交CE 与点H ，则,H BCE ACE EAH B ∠=∠=∠∠=∠，得出AH=AC ，H EAH ∠=∠，得出AE=HE ，由等腰三角形的性质可得出HF=CF ，即可得出结论；②证明AHF DCF ≅，得出AH=DC ，求出HF=CF=a ，HE=HF-EF=a-b ，CE=a+b ，由 //AH BC 得出AH AE a b BC BE a b-==+，进而得出结论．【详解】解：（1）∵9628BAC B ︒︒∠=∠=，，∴180962856ACB ∠=︒-︒-︒=︒，∵CE 为三角形的角平分线，∴1282ACE ACB ∠=∠=︒， ∵AD CE ⊥，∴902862CAF ∠=︒-︒=︒，∴966234BAD ∠=︒-︒=︒．故答案为：34；（2）①证明：∵22ACB B BCE ∠=∠=∠∴B BCE ∠=∠∴BE CE =过点A 作//AH BC 交CE 与点H ，如图所示：则,H BCE ACE EAH B ∠=∠=∠∠=∠∴AH=AC ，H EAH ∠=∠∴AE=HE∵AD CE ⊥∴HF=CF∴AB=HC=2CF ；②在AHF △和DCF 中，H DCF HF CF AFH DFC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AHF DCF ≅∴AH=DC∵ ,CF a EF b == ∴ HF CF a ==，由①得 AE HE HF EF a b ==-=-， BE CE a b ==+∵ //AH BC∴AH AE a b BC BE a b -==+ ∴CD a b BC a b -=+ ∴2BD b CD a b=-．故答案为：2b a b -．【点睛】本题考查的知识点是全等三角形的判定及其性质、等腰三角形的判定及其性质、三角形的内角和定理、三角形的角平分线定理等，掌握以上知识点是解此题的关键．5．某数学兴趣小组开展了一次活动，过程如下：设(090BAC θθ∠=︒<<︒).现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB 、AC 上．活动一、如图甲所示，从点1A 开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直（12A A 为第1根小棒）数学思考：（1）小棒能无限摆下去吗？答：（填“能”或“不能”）（2）设11223AA A A A A ==，求θ的度数；活动二：如图乙所示，从点1A 开始，用等长的小棒依次向右摆放，其中12A A 为第一根小棒，且121A A AA =．数学思考：（3）若已经摆放了3根小棒，则213A A A ∠= ，423A A A ∠= ，43 A A C ∠= ；（用含θ的式子表示）（4）若只能摆放5根小棒，则θ的取值范围是．【答案】（1）能；（2）θ＝22.5°；（3）2θ，3θ，4θ；（4）15°≤θ＜18°．【解析】【分析】（1）由小棒与小棒在端点处互相垂直，即可得到答案；（2）根据等腰直角三角形的性质和三角形外角的性质，即可得到答案；（3）由121A A AA =，得∠AA 2A 1=∠A 2AA 1=θ，从而得213A A A ∠=∠AA 2A 1+∠A 2AA 1=2θ，同理得423 A A A ∠=∠A 2AA 1+231A A A ∠=θ+2θ=3θ，43 A A C ∠=∠A 2AA 1+243 A A A ∠=θ+3θ=4θ；（4）根据题意得：5θ＜90°且6θ≥90°，进而即可得到答案．【详解】（1）∵小棒与小棒在端点处互相垂直即可，∴小棒能无限摆下去，故答案是：能；（2）∵A 1A 2＝A 2A 3，A 1A 2⊥A 2A 3，∴∠A 2A 1A 3＝45°，∴∠AA 2A 1+θ＝45°，∵AA 1＝A 1A 2∴∠AA 2A 1＝∠BAC=θ，∴θ＝22.5°；（3）∵121A A AA =，∴∠AA 2A 1=∠A 2AA 1=θ，∴213A A A ∠=∠AA 2A 1+∠A 2AA 1=2θ，∵3122A A A A =，∴213A A A ∠=231A A A ∠=2θ，∴423A A A ∠=∠A 2AA 1+231A A A ∠=θ+2θ=3θ， ∵3342A A A A =，∴423A A A ∠=243 A A A ∠=3θ， ∴43A A C ∠=∠A 2AA 1+243 A A A ∠=θ+3θ=4θ，故答案是：2θ，3θ，4θ；（4）由第（3）题可得：645A A A ∠=5θ，65 A A C ∠=6θ， ∵只能摆放5根小棒，∴5θ＜90°且6θ≥90°，∴15°≤θ＜18°．故答案是：15°≤θ＜18°．【点睛】本题主要考查等腰三角形的性质以及三角形外角的性质，掌握等腰三角形的底角相等且小于90°，是解题的关键．6．知识背景：我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边，进而解决问题.问题：如图1，ABC 是等腰三角形，90BAC ∠=︒，D 是BC 的中点，以AD 为腰作等腰ADE ，且满足90DAE ∠=︒，连接CE 并延长交BA 的延长线于点F ，试探究BC 与CF 之间的数量关系.图1发现：（1）BC 与CF 之间的数量关系为 .探究：（2）如图2，当点D 是线段BC 上任意一点（除B 、C 外）时，其他条件不变，试猜想BC 与CF 之间的数量关系，并证明你的结论.图2拓展：（3）当点D 在线段BC 的延长线上时，在备用图中补全图形，并直接写出BCF 的形状.备用图【答案】（1）BC CF =；（2）BC CF =，证明见解析；（3）画图见解析，等腰直角三角形.【解析】【分析】（1）根据等腰三角形的性质即可得BC CF =；（2）由等腰直角三角形的性质可得()ABD ACE SAS ∴≌，再根据全等三角形的性质及等角对等边即可证明；（3）作出图形，根据等腰三角形性质易证()ABD ACE SAS ∴≌，进而根据角度的代换，得出结论．【详解】解：（1）BC CF =.∵△ABC 是等腰三角形，且90BAC ∠=︒，AB AC ∴=，45B ACB ∠=∠=︒.90DAE ∠=︒，DAE BAC ∴=∠∠，DAE DAC BAC DAC ∴∠-∠=∠-∠，BAD CAE ∴∠=∠. ADE 是以AD 为腰的等腰三角形，AD AE ∴=.在ABD △与ACE △中，AB AC =，BAD CAE ∠=∠，AD AE =，()ABD ACE SAS ∴≌，45ACE B ∴∠=∠=︒.45ACB =︒∠，90BCF ACB ACE ∴∠=∠+∠=︒，90B F ∴∠+∠=︒，45F ∴∠=︒，B F ∴∠=∠，BC CF ∴=.（2）BC CF =.证明：ABC 是等腰三角形，且90BAC ∠=︒，AB AC ∴=，45B ACB ∠=∠=︒.90DAE ∠=︒，DAE BAC ∴=∠∠，DAE DAC BAC DAC ∴∠-∠=∠-∠，BAD CAE ∴∠=∠. ADE 是以AD 为腰的等腰三角形，AD AE ∴=.在ABD △与ACE △中，AB AC =，BAD CAE ∠=∠，AD AE =，()ABD ACE SAS ∴≌，45ACE B ∴∠=∠=︒.45ACB =︒∠，90BCF ACB ACE ∴∠=∠+∠=︒，90B F ∴∠+∠=︒，45F ∴∠=︒，B F ∴∠=∠，BC CF ∴=.（3）BCF 是等腰直角三角形. 提示：如图，ABC 是等腰三角形，90BAC ∠=︒，AB AC ∴=，45B ACB ∠=∠=︒.90DAE ∠=︒，DAE BAC ∴=∠∠，DAE DAC BAC DAC ∴∠+∠=∠+∠，BAD CAE ∴∠=∠.ADE 是以AD 为腰的等腰三角形，AD AE ∴=.在ABD △与ACE △中，AB AC =，BAD CAE ∠=∠，AD AE =，()ABD ACE SAS ∴≌，45ACE B ∴∠=∠=︒.45ACB =︒∠，90BCF ACB ACE ∴∠=∠+∠=︒，90B BFC ∴∠+∠=︒，45BFC ∴∠=︒，B BFC ∴∠=∠，BCF ∴是等腰三角形，90BCF ∠=︒，BCF ∴是等腰直角三角形.【点睛】本题考查等腰三角形及全等三角形的性质，熟练运用角度等量代换及等腰三角形的性质是解题的关键．7．如图，已知DCE ∠与AOB ∠，OC 平分AOB ∠．(1)如图1，DCE ∠与AOB ∠的两边分别相交于点 D 、E ，90AOB DCE ∠=∠=︒，试判断线段CD 与CE 的数量关系，并说明理由.以下是小宇同学给出如下正确的解法：解：CD CE =．理由如下：如图1，过点 C 作 C F OC ⊥，交 O B 于点 F ，则90OCF ∠=︒，…请根据小宇同学的证明思路，写出该证明的剩余部分．(2)你有与小宇不同的思考方法吗？请写出你的证明过程．(3)若120AOB ∠=︒，60DCE ∠=︒．①如图3，DCE ∠与AOB ∠的两边分别相交于点 D 、E 时，(1)中的结论成立吗？为什么？线段 O D 、OE 、OC 有什么数量关系？说明理由．②如图4，DCE ∠的一边与 AO 的延长线相交时，请回答(1)中的结论是否成立，并请直接写出线段 O D 、OE 、OC 有什么数量关系；如图5，DCE ∠的一边与 BO 的延长线相交时，请回答(1)中的结论是否成立，并请直接写出线段 O D 、OE 、OC 有什么数量关系．【答案】(1)见解析；(2)证明见解析；(3)①成立，理由见解析；②在图4中，(1)中的结论成立，OE OD OC -=.在图5中，(1)中的结论成立，OD OE OC -=【解析】【分析】（1）通过ASA 证明CDO CEF ∆∆≌即可得到CD=CE ；（2）过点 C 作CM OA ⊥，CN OB ⊥，垂足分别为 M ，N ，通过AAS 证明CMD CNE ∆∆≌同样可得到CD=CE ；（3）①方法一：过点 C 作 C M OA ⊥，CN OB ⊥垂足分别为 M ，N ，通过AAS 得到CMD CNE ∆∆≌，进而得到,CD CE DM EN ==，利用等量代换得到=OE OD ON OM++，在Rt CMO∆中，利用30°角所对的边是斜边的一半得12OM OC=，同理得到12ON OC=，所以OE OD OC+=；方法二：以CO为一边作60FCO∠=︒，交O B于点F，通过ASA证明CDO CEF∆∆≌，得到,CD CE OD EF==，所以OE OD OE EF OF OC+=+==；②图4：以OC为一边，作∠OCF=60°与OB交于F点，利用ASA证得△COD≌△CFE，即有CD=CE，OD=EF得到OE=OF+EF=OC+OD；图5:以OC为一边，作∠OCG=60°与OA交于G点，利用ASA证得△CGD≌△COE，即有CD=CE，OD=EF，得到OE=OF+EF=OC+OD.【详解】解：(1)OC平分AOB∠，145∠=∠2=︒∴，390245,123︒︒∴∠=-∠=∴∠=∠=∠OC FC∴=又456590︒∠+∠=∠+∠=在CDO∆与CEF∆中，1346OC FC∠=∠⎧⎪=⎨⎪∠=∠⎩()CDO CEF ASA∴∆∆≌CD CE∴=(2)如图2，过点C作CM OA⊥，CN OB⊥，垂足分别为M，N，∴90CMD CNE∠=∠=︒，又∵OC平分AOB∠，∴CM CN=，在四边形O DCE中，12360AOB DCE∠+∠+∠+∠=︒，又∵90AOB DCE∠=∠=︒，∴12180∠+∠=︒，又∵13180∠+∠=︒，∴32∠=∠，在CMD∆与CNE∆中，32CMD CNECM CN∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMD CNE AAS∆∆≌，∴CDCE=.(3)①(1)中的结论仍成立.OE OD OC+=.理由如下：方法一：如图3(1)，过点C作C M OA⊥，CN OB⊥，垂足分别为M，N，∴90CMD CNE∠=∠=︒，又∵OC平分AOB∠，∴CM CN=，在四边形ODCE中，12360AOB DCE∠+∠+∠+∠=︒，又∵60120180AOB DCE∠+∠=︒+︒=︒，∴12180∠+∠=︒，又∵23180∠+∠=︒，∴13∠=∠，在CMD∆与CNE∆中，13CMD CNECM CN∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()CMD CNE AAS∆∆≌，∴,CD CEDM EN ==.∴OE OD OE OM DM OE OM EN ON OM +=++=++=+.在 Rt CMO ∆中，1490590302AOB ∠=︒-∠=︒-∠=︒， ∴12OM OC =，同理1 2ON OC =， ∴1122OE OD OC OC OC +=+=. 方法二：如图3（2），以CO 为一边作60FCO ∠=︒，交 O B 于点 F ，∵OC 平分AOB ∠，∴1260∠=∠=︒，∴3180260FCO ∠=︒-∠-∠=︒，∴13∠=∠，32FCO ∠=∠=∠，∴COF ∆是等边三角形，∴CO CF =，∵4560DCE ∠=∠+∠=︒，6560FCO ∠=∠+∠=︒，∴46∠=∠，在CDO ∆与CEF ∆中，1346CO CF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()CDO CEF ASA ∆∆≌，∴,CD CE OD EF ==.∴OE OD OE EF OF OC +=+==.②在图4中，(1)中的结论成立，OE OD OC -=.如图，以OC 为一边，作∠OCF=60°与OB 交于F 点∵∠AOB=120°，OC 为∠AOB 的角平分线∴∠COB=∠COA=60°又∵∠OCF=60°∴△COF为等边三角形∴OC=OF∵∠COF=∠OCD+∠DCF=60°，∠DCE=∠DCF+∠FCB=60°∴∠OCD=∠FCB又∵∠COD=180°-∠COA=180°-60°=120°∠CFE=180°-∠CFO=180°-60°=120°∴∠COD=∠CFE∴△COD≌△CFE（ASA）∴CD=CE，OD=EF∴OE=OF+EF=OC+OD即OE-OD=OC-=.在图5中，(1)中的结论成立，OD OE OC如图，以OC为一边，作∠OCG=60°与OA交于G点∵∠AOB=120°，OC为∠AOB的角平分线∴∠COB=∠COA=60°又∵∠OCG=60°∴△COG为等边三角形∴OC=OG∵∠COG=∠OCE+∠ECG=60°，∠DCE=∠DCG+∠GCE=60°∴∠DCG=∠OCE又∵∠COE=180°-∠COB=180°-60°=120°∠CGD=180°-∠CGO=180°-60°=120°∴∠CGD=∠COE∴△CGD≌△COE（ASA）∴CD=CE，OE=DG∴OD=OG+DG=OC+OE即OD-OE=OC【点睛】本题主要考查全等三角形的综合应用，有一定难度，解题关键在于能够做出辅助线证全等.8．定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段．．．．叫做这个三角形的三分线.（1）图①是顶角为36︒的等腰三角形，这个三角形的三分线已经画出，请你在图②中用不同于图①的方法画出顶角为36︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数（若两种方法分得的三角形成3对全等三角形，则视为同一种）；（2）图③是顶角为45︒的等腰三角形，请你在图③中画出顶角为45︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数.（3）ABC 中，30B ∠=︒，AD 和DE 是ABC 的三分线，点D 在BC 边上，点E 在AC 边上，且AD BD =，DE CE =，设c x ∠=︒，则x 所有可能的值为_________.【答案】（1）见详解；（2）见详解；（3）20或40.【解析】【分析】(1)作底角的平分线，再作底边的平行线，即可得到三分线；(2)过底角定点作对边的高，形成一个等腰直角三角形和一个直角三角形，然后再构造一个等腰直角三角形，即可.(3)根据题意，先确定30°角然后确定一边为BA ，一边为BC ，再固定BA 的长，进而确定D 点，分别考虑AD 为等腰三角形的腰和底边，画出示意图，列出关于x 的方程，即可得到答案.【详解】（1）如图所示：（2）如图所示：（3）①当AD=AE 时，如图4，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠ADE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30=2x+x ，解得：x=20；②当AD=DE 时，如图5，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠DAE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30+2x+x=180，解得：x=40.③当AE=DE 时，则∠EAD=∠EDA=1802(90)2x x -=-， ∴∠ADC=∠EDA+∠EDC=(90-x)+x=90°又∵∠ADC=30+30=60°，∴这种情况不存在.∴x所有可能的值为20或40.故答案是：20或40图4 图5【点睛】本题主要考查等腰三角形的判定和性质定理的综合应用，分类讨论，画出图形，是解题的关键.9．如图，在等边△ABC中，线段AM为BC边上的高，D是AM上的点，以CD为一边，在CD的下方作等边△CDE，连结BE．（1）填空：∠ACB=____；∠CAM=____；（2）求证：△AOC≌△BEC；（3）延长BE交射线AM于点F，请把图形补充完整，并求∠BFM的度数；（4）当动点D在射线AM上，且在BC下方时，设直线BE与直线AM的交点为F．∠BFM 的大小是否发生变化？若不变，请在备用图中面出图形，井直接写出∠BFM的度数；若变化，请写出变化规律．【答案】（1）60°，30°；（2）答案见解析；（3）60°；（4）∠BFM＝60°．【解析】【分析】（1）根据等边三角形的性质即可进行解答；（2）根据等边三角形的性质就可以得出AC=AC，DC=EC，∠ACB=∠DCE=60°，由等式的性质就可以∠BCE=∠ACD，根据SAS就可以得出△ADC≌△BEC；（3）补全图形，由△ADC≌△BEC得∠CAM=∠CBE=30°,由三角形内角和定理即可求得∠BFM 的度数；（4）画出相应图形，可知当点D 在线段AM 的延长线上且在BC 下方时，如图，可以得出△ACD ≌△BCE ，进而得到∠CBE=∠CAD=30°，据此得出结论．【详解】(1)∵△ABC 是等边三角形，∴∠ACB=60°；∴线段AM 为BC 边上的高，∴∠CAM=12∠BAC=30°，故答案为60，30°；（2）∵△ABC 与△DEC 都是等边三角形，∴AC=BC,CD=CE,∠ACB=∠DCE=60°，∴∠ACD+∠DCB=∠DCB+∠BCE ，∴∠ACD=∠BCE.在△ADC 和△BEC 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BCE(SAS)；（3）补全图形如下：由（1）（2）得∠CAM=30°，△ADC ≌△BEC ，∴∠CBE=∠CAM=30°，∵∠BMF=90°，∴∠BFM=60°；（4）当动点D 在射线AM 上，且在BC 下方时，画出图形如下：∵△ABC 与△DEC 都是等边三角形，∴AC=BC,CD=CE,∠ACB=∠DCE=60°，∴∠ACB+∠DCB=∠DCB+∠DCE ，∴∠ACD=∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BCE(SAS)，∴∠CBE=∠CAD=30°，又∵∠AMC=∠BMO ，∴∠AOB=∠ACB=60°.即动点D 在射线AM 上时,∠AOB 为定值60°.【点睛】本题考查了等边三角形的性质的运用，直角三角形的性质的运用，等式的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键.解题时注意：全等三角形的对应角相等，等边三角形的三个内角都相等，等边三角形的三个内角相等，且都等于60°.10．（1）操作：如图，在已知内角度数的三个三角形中，请用直尺从某一顶点画一条线段，把原三角形分割成两个等腰三角形，并在图中标注相应的角的度数（2）拓展，△ABC 中，AB=AC ，∠A=45°，请把△ABC 分割成三个等腰三角形，并在图中标注相应的角的度数.（3）思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP，△BPQ，△PQC若分割成的这三个三角形都是等腰三角形，求∠C的度数所有可能值直接写出答案即可.【答案】（1）见解析；（2）见解析；（3）∠C所有可能的值为10°、20°、25°，35°、40°、50°、80°、100°.【解析】【分析】（1）在图1、图2、图3中，分别作AB、AB、BC的垂直平分线，根据垂直平分线的性质及外角的性质求出各角度数即可；（2）分别作AB、BC的垂直平分线，交于点O，连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形，根据等腰三角形的性质及外角性质求出各角度数即可；（3）分PB=PA、AB=AP、BA=BP时，PB=PQ、BP=BQ、QB=QP，PQ=QC、PC=QC、PQ=PC等10种情况，根据等腰三角形的性质分别求出∠C的度数即可.【详解】（1）在图1、图2、图3中，分别作AB、AB、BC的垂直平分线，如图1，∵∠ABC=23°，∠BAC=90°，∴∠C=90°-23°=67°，∵MN垂直平分AB，∴BD=AD，∴△ABD是等腰三角形，∴∠BAD=∠ABC=23°，∴∠ADC=2∠ABC=46°，∵∠BAC=90°，∴∠DAC=∠BAC-∠BAD=67°，∴∠DAC=∠C，∴△DAC是等腰三角形，同理：图2中，∠ADC=46°，∠DAC=88°，∠C=46°，△ABD和△ACD是等腰三角形，图3中，∠BCD=23°，∠ADC=46°，∠ACD=46°，△BCD和△ACD是等腰三角形.（2）作AB、BC的垂直平分线，交于点O，连接OA、OB、OC，∵点O是三角形垂直平分线的交点，∴OA=OB=OC，∴△OAB、△OAC、△OBC是等腰三角形，∵AB=AC，∠BAC=45°，∴∠ABC=∠ACB=67.5°，∴AD是BC的垂直平分线，∴∠BAD=∠CAD=22.5°，∴∠OBA=∠OAB=22.5°，∠OCA=∠OAC=22.5°，∴∠OBC=∠OCB=45°.（3）①如图，当PB=PA，PB=PQ，PQ=CQ时，∵∠A=30°，PB=PQ，∴∠ABP=∠A=30°，∴∠APB=120°，∵PB=PQ，PQ=CQ，∴∠PQB=∠PBQ，∠C=∠CPQ，∴∠PBQ=2∠C，∴∠APB=∠PBQ+∠C=3∠C=120°，解得：∠C=40°.②如图，当PB=PA，PB=BQ，PQ=CQ时，∴∠PQB=2∠C，∠PQB=∠BPQ，∴∠PBQ=180°-2∠PQB=180°-4∠C，∴180°-4∠C+∠C=120°，解得：∠C=20°，③如图，当PA=PB，BQ=PQ，CQ=CP时，∵∠PQC=2∠PBQ，∠PQC=12（180°-∠C），∴∠PBQ=14（180°-∠C），∴14（180°-∠C）+∠C=120°，解得：∠C=100°.④如图，当PA=PB，BQ=PQ，PQ=CP时，∵∠PQC=∠C=2∠PBQ,又∵∠C+∠PBQ=120°，∴∠C=80°；⑤如图，当AB=AP，BP=BQ，PQ=QC时，∵∠A=30°，∴∠APB=12（180°-30°）=75°，∵BP=BQ，PQ=CQ，∴∠BPQ=∠BQP，∠QPC=∠QCP，∴∠BQP=2∠C，∴∠PBQ=180°-4∠C，∴∠C+180°-4∠C=75°，解得：∠C=35°.⑥如图，当AB=AP，BQ=PQ，PC=QC时，∴∠PQC=2∠PBC，∠PQC=12（180°-∠C），∴∠PBC=14（180°-∠C），∴14（180°-∠C）+∠C=75°，解得：∠C=40°.⑦如图，当AB=AP，BQ=PQ，PC=QP时，∵∠C=∠PQC=2∠PBC，∠C+∠PQC=75°，∴∠C=50°；⑧当AB=AP，BP=PQ，PQ=CQ时，∵AB=BP，∠A=30°，∴∠ABP=∠APB=75°，又∵∠PBQ=∠PQB=2∠C，且有∠PBQ+∠C=180°-30°-75°=75°，∴3∠C=75°，∴∠C=25°；⑨当AB=BP，BP=PQ，PQ=CQ时，∵AB=BP，∴∠BPA=∠A=30°，∵∠PBQ=∠PQB=2∠C，∴2∠C+∠C=30°，解得：∠C=10°.⑩当AB=BP，BQ=PQ，PQ=CQ时，∴∠PQC=∠C=2∠PBQ，∴12∠C+∠C=30°，解得：∠C=20°.综上所述：∠C所有可能的值为10°、20°、25°，35°、40°、50°、80°、100°.【点睛】本题考查复杂作图及等腰三角形的性质，熟练掌握等腰三角形的性质是解题关键.。

苏科版本初中八年级的上第二章轴对称图形提优练习包括答案.docx

苏科版八年级上第二章《轴对称图形》提优练习（含答案）第2 章轴对称图形第1 课时轴对称与轴对称图形1.下列图形中，对称轴的数量小于 3 的是 ()2.已知各边相等，各角也相等的多边形叫做正多边形，也称为正数 ).如图，请你探究下列正多边形的对称轴的条数，并填在表格中正多边形的边教345678n 边形(这里.n 3 且n为整对称轴的条数(1) 猜想 :正n边形有条对称轴;(2) 当n越来越大时，正多边形接近于，该图形有条对称轴.3.小明学习了轴对称知识后，忽然想起了参加数学兴趣小组时老师布置的一道题，当时小明没做出来，题目是这样的:有一组数据排列成方阵，如图.试用简便方法计算这组数据的和.小明想 :不考虑每个数据的大小，只考虑每个数据的位置，这个图形是个轴对称图形，能不能用轴对称思想来解决这个问题呢 ?小明顺着这个思路很快解决了这个题目，请你写出他的解题过程 .第 2 课时轴对称的性质(1)1.如图，把一张长方形纸片点 B 处，若 2 40ABCD 沿 EF，则 1 的度数为折叠后，点()A 落在 CD边上的点A处，点B 落在A. 115 °B. 120 °C. 130°D. 140 °2.如图，点P 关于 OA, OB 的对称点分别是P1, P2， PP12分别交OA,OB于点D, C, PP12=16cm，则PCD 的周长为cm.如图， O 为 ABC 内部一点13., OB 3 .2(1)分别画出点 O 关于直线 AB, BC 的对称点 P, Q ;(2) 请指出当ABC 的度数为多少时，PQ =7，并说明理由;(3) 请判断当ABC 的度数不是(2)中的度数时，PQ 的长度是小于7 还是大于7，并说明你的判断的理由.第 3 课时轴对称的性质(2)1.如图，点A, B 在方格纸的格点位置上，若要再找一个格点 C ，使它们所构成的三角形为轴对称图形，则这样的格点 C 在图中共有()A. 4 个B. 6 个C. 8 个D. 10 个2.如图，在 2× 2 的正方形网格纸中，有一个以格点为顶点的ABC .请你找出网格纸中所有与ABC 成轴对称且也以格点为顶点的三角形，这样的不角形共有个.3.如图，在由边长为 1 的正方形组成的6× 5 方格中，点A, B 都在格点上.(1) 在给定的方格中将线段AB 平移到 CD ，使得四边形ABDC 是长方形，且点 C , D 都落在格点上 .画出四边形ABDC ,并叙述线段AB 的平移过程.(2) 在方格中画出ACD 关于直线 AD 对称的AED .(3)求五边形 AEBDC 的面积.第 4 课时轴对称的性质—习题课7.如图，线段AB在直线l的一侧，请在直线l上找一点P，使PAB 的周长最短.画出图形，保留画图痕迹，不写画法.2.如图，在直线l 上找一点 Q ，使得 QA,QB 与直线 l 的夹角相等.画出图形，保留画图痕迹，不写画法 .3. (1) 如图① ,P 是 AOB 内一点，在 OA, OB 上分别找点 C , D ，使得PCD 的周长最短.画出图形，保留画图痕迹，不写画法.(2) 如图② ,P, Q 是AOB 内的两点，在 OA, OB 上分别找点 C , D ，使得以 P,Q, C , D 为顶点的四边形的周长最短.画出图形，保留画图痕迹，不写画法.第 5 课时设计轴对称图案1.在一次数学活动课上，小颖将一个四边形纸片依次按如图①②所示的方式对折，然后按图③中的虚线裁剪成图④样式，将纸片展开铺平，所得到的图形是()2.在 4× 4 的方格中，有五个同样大小的正方形按如图所示的方式摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种.3.在 3× 3 的正方形网格图中，有格点三角形ABC 和格点三角形DEF关于某条直线成轴对称，请在如图①~⑥所示的网格中画出六个这样的均不相同 )，且ABCDEF和DEF.( 每种方案第 6 课时线段、角的轴对称性(1)1.ABC 中， AC 的垂直平分线分别交AC , BC于点E, D , EC = 4 ,ABC 的周长如图，在为 23，则ABD 的周长为()A. 13B. 15C. 17D. 192.如图，在ABC 中， AB 的垂直平分线分别交AB, BC 于点 D , E, AC 的垂直平分线分别交 AC , BC 于点 F ,G .若 AEG 的周长为2018，则线段 BC 的长为.如图，在ABC 中， AB 的垂直平分线EF 交 BC 于点 E ，交 AB 于点F , D 为线段 CE的3.中点，且CAD 18 , ACB 72.求证 :BE AC .第 7 课时线段、角的轴对称性(2)1.设P是ABC 内一点，满足PA PB PC ，则 P 是ABC()A.三条内角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点2.如图，在EDC ABC 的周长为中， BC24,边上的垂直平分线ABC 与四边形DEAEDC交边 BC 于点的周长之差为D，交边 AB12 ，则线段于点DEE .若的长为.3.在ABC 中， AB AC, O 为平面上一点，且OB OC .点 A 到 BC 的距离为8，点O到BC 的距离为 3.求 AO 的长.第 8 课时线段、角的轴对称性(3)1.如图，上的点ABC 的面积为6, ACC 处， P 为直线 AD=3，现将ABC上的一点，则线段沿AB 所在直线翻折，使点BP 的长不可能是()C 落在直线ADA. 3B. 4C. 5. 5D. 102.AB // CD , BP, CP分别平分ABC , DCB , AD.=8，如图，过点 P ，且与 AB 垂直若 AD 则点 P 到 BC 的距离为.3.ABC 的边 AC 的垂直平分线，过点 M 作ABC 另外两边AB, BC所在直如图， MN 为线的垂线，垂足分别为 D , E ,且 AD CE ，作射线 BM.求证 : BM平分ABC .第 9 课时线段、角的轴对称性(4)1.ABC , EAC的平分线BP, AP交于点 P ，过点 P作PM BE , PN BF，垂如图，足分别为 M , N .下列结论:① CP 平分 A C F;②ABC APC180 ;③AM CN AC ;④BAC 2 BPC .其中正确的是()A. ①②③B.①③④C. ②③④D.①③如图， AD 是ABC 的角平分线，DE , DF 分别是ABD 和 ACD 的高，连接 EF 交 AD2.,于点 O .下列结论:① DE DF ;② OA OD ;③ AD EF ;④ AE DF AF DE ;⑤AD垂直平分EF.其中一定正确的是.(填序号 )3.如图 .在 ABC 中，ABAC，边BC 的垂直平分线DE交ABC 的外角BAM的平分线于点D ,垂足为 E, DFAB ，垂足为F.求证 :BFACAF .第 10 课时等腰三角形的轴对称性 (1)如图，在ABC 中，B55 , C 30，分别以点 A 和点 C 为圆心，大于 1的长1.AC2为半径画弧，两弧相交于点 M , N ，作直线 MN ，交 BC 于点 D ，连接 AD ，则 BAD的度数为 ()A. 65 °B. 60°C. 55°D. 45 °2. 如图，在ABC 中， D 为AB 上一点， E 为 BC 上一点，且A C C D，则CDE 的度数为.B D, B E5 0 A3.如图，在 ACB 中，ACB90 , D , E 为斜边 AB 上的两点，且 BD BC, AE AC ，求DCE 的度数 .第 11 课时等腰三角形的轴对称性(1)—习题课1.已知等腰三角形一腰上的高与另一腰的夹角为 60°，则这个等腰三角形的底角的度数为()A. 30 °B. 75 °C. 15°或 30°D. 75 °或15°2.如图，在ABC 中， ACBABP 是等腰三角形，此时90 , ABCAPB 的度数为60，在边AC .所在的直线上找一点P ，使3.在ABC 中， ABAC, AB 的垂直平分线DE 与 AC 所在的直线相交所成的锐角为40°，求B 的度数 .第12 课时等腰三角形的轴对称性(2)1.如图，在ABC 中， ABAC ,A 36 , BD , CE分别是ABC , ACB的平分线，且相交于点A. 5 个F ，则图中的等腰三角形有B. 6 个()C. 7个D. 8 个2.在 ABC 中， A 50 ，当 B 的度数为时， ABC 为等腰三角形 .如图①，在 ABC 中， AB AC, ABC , ACB 的平分线交于点 O ，过点 O 作 EF // BC3.交 AB , AC 于点 E, F .(1)图中有几个等腰三角形 ?EF 与 BE, CF 之间有怎样的数量关系，并说明理由 .猜想(2) 如图②，若 AB AC ，其他条件不变，则图中还有等腰三角形吗?如果有，分别写出来 ;另外在 (1)中 EF 与 BE, CF 之间的数量关系还存在吗 ?(3) 如图③，若在 ABC 中 ,ABC 的平分线 BO 与 ABC 的外角平分线交于点O ，过点 O 作 OE // BC 交 AB 于点 E 、交 AC 于点 F .这时图中还有等腰三角形吗 ? EF 与BE, CF 之间的数量关系又如何?并说明你的理由 .第 13 课时等腰三角形的轴对称性(2)—习题课1.如图，AOB120 , OP平分AOB ，且OP=2.若点M , N分别在OA,OB上，且PMN A. 1 个为等边三角形，则满足上述条件的B. 2 个PMNC. 3有 (个)D. 3个以上2.ABC 中，AE CD , AD, BE相交于点P, BQ AD于点Q ,如图，在等边三角形则线段BP, PQ 的数量关系为.3. 如图，C为线段AB上一点， ACM , CBN 是等边三角形. AN , BM 相交于点O, AN ,CM 交于点 P ,BM ,CN 交于点 Q ，连接 PQ .(1)求证 : AN MB ;(2)求 AOB 的度数;(3)求证 : PQ // AB .第 14 课时等腰三角形的轴对称性(3)1.如图，在ABC 中，BE AC ,CF AB ,垂足分别为E, F .若 M 是 BC 的中点，则图中等腰三角形有 ()A. 1 个B. 3 个C. 4 个D. 5 个2.如图，在四边形ABCD 中，BCD BAD 90 , AC , BD 相交于点 E,G , H 分别是AC, BD 的中点如果 BEC80，那么GHE 的度数为..如图，在 Rt ABC 中， ACB 90 ，点 D 在边 AC 上不与点A,C 重合),DE AB 于3.(点 E ，连接BD, F 为 BD 的中点.试猜想 A 与CEF 的关系并证明.第 2 章轴对称图形第 1 课时轴对称与轴对称图形1.D2. 3 4 5 6 7 8(1)n(2) 圆无数3. 从方阵的数据看出，正方形的一条对角线上的数据都是10.若把这条对角线所在的直线作为对称轴，把这个方阵对折，对称轴两侧重合的小正方形内的数据之和都是 10，相加后如图所示，这样方阵中的所有数据之和为10 10 100第 2 课时轴对称的性质 (1)1.A2. 163. (1) 如图，过点 O 画 OH AB ，垂足为 H ，在垂线段 OH 的延长线上取一点P ，使得PHOH P ，此时点 P 就是点 O 关于直线 AB 的对称点，同理画出点Q .(2) 当 ABC90 时， PQ 7理由：如图，连接 BP 、 BQ ∵点 O 、 P 关于直线 AB 对称 ∴直线 AB 垂直平分 OP∴ BHO BHP 90 ， PH OH∵ BH BH∴ BHO BHP∴ OBPB 3 1， OBHPBH2同理 OBQB 3 1， OBCQBC2 ∴ PBQB 313172 2若 PQ 7 ，则 PB QB PQ ，此时 P 、 B 、 Q 三点共线∴ PBQ 180∴ABCOBH OBC1PBQ 902(3) 当 ABC90 时， PQ 7理由：∵ABC90∴ P 、 B 、 Q 三点不在同一直线上，此时构成PBQ ∴ PB BQ PQ .由 (2) ，得 PB BQ 7∴ PQ7第 3 课时轴对称的性质 (2)1.D2. 53.(1) 如图，将线段AB 先向右平移 1 个单位长，再向上平移2 个单位长度，得线段CD (平移过程不唯一 ).(2) 如图，画点 C 关于直线 AD 的对称点 E ，连接 AE 、 DE ，则 AED 即为所求 .( 3) S 五边形 AEBDC S ACD S 梯形 AEBD1 52 1(3 5)2 1322第 4 课时轴对称的性质—习题课1. 由干线段 AB 的长度是固定的，要使PAB 的周长最短，只要 PA PB 最短即可 .如图，过点 A 作它关于直线 l 的对称点 A ' ，连接 A' B 交直线 l 于点 P ，连接 PA 、 PB ，此时PAB 就是周长最短的三角形，∴点P 即为所求 .2.如图，过点A 作它关干直线 l 的对称点 A' ，连接 A 'B 交直线 l 于点 Q .连接 QA 、 QB ，此时AQHBQD ，∴点 Q 即为所求 .3. (1) 如图①，过点P分别作关于射线OA 、 OB的对称点 P1、 P2，连接 PP12，分别交OA、OB 于点 C 、D ，连接 PC 、 PD 、CD ，此时PCD 的周长最短，∴点 C 、 D 和 PCD即为所求 .(2) 如图② .过点P、Q分别作射线OA、OB的对称点P、Q，连接PQ，分别交OA、11 1 1OB 于点 C 、D ，连接 PC 、PQ 、QD 、CD ，此时四边形PCDQ 的周长最短，∴点 C 、D 和四边形 PCDQ 即为所求.第 5 课时设计轴对称图案1.A2. 133.要使DEF 和ABC 于某条直线成轴对称，关键是确定适当的对称轴.再根据轴对称的性质画出符合条件的图案，可以以 3 3 的正方形网格图的对称轴为对称轴画出所求的DEF，有四个不同位置的三角形;也可以以ABC的边AC、 BC的中点连线所在的直线为对称轴画出所求的DEF 的直线作为对称轴画出所求的，有一个三角形 ; 还可以把过ABC 的顶点DEF ，也有一个三角形.如图① ~⑥中的C 与边DEFAB 平行即为所求第 6 课时线段、角的轴对称性(1)1.B2. 20183.连接 AE ，∵EF 是 AB 的垂直平分线∴ AE BE∵在ADC 中.，CAD ∴ADC 180CAD 18 ，ACBACB9072即AD EC∵D 为线段 CE 的中点∴ ED CD∴AD 垂直平分 EC∴AE AC∴BE AC第 7 课时线段、角的轴对称性(2)1.D2. 63.∵AB AC∴点 A 在线段 BC 的垂直平分线上∵OB OC∴点 O 也在线段 BC 的垂直平分线上∴ AO 所在的直线即为线段BC 的垂直平分线.设直线 AO 与 BC 交于点 M .由题意，得 AM8, OM3如图① .当点A、O在BC的同侧时，AO AM OM83 5 ;如图②，当点 A 、 O 在 BC 的异侧时， AO AM OM8311第 8 课时线段、角的轴对称性(3)1.A2. 43.连接MA、MC∵点 M 在 AC 的垂直平分线上∴MA MC∵MD AB , ME BC∴ADM CEM 90在Rt MAD 和 Rt MCE 中MA MCAD CE∴Rt MAD Rt MCE∴点 M 在ABC的平分线上，即第 9 课时BM 平分ABC .线段、角的轴对称性(4)1.B2. ①③④⑤3.如图 .在ABC 中，AB AC，边的垂直平分线DE交ABC 的外角BAM的平分线于点 D ,垂足为 E, DF AB ，垂足为F.求证 :BF AC AF.3.过点D 作 DN MC ，垂足为N，连接DB 、 DC.∵ DN MC , DF AB∴AND AFD 90∵AD 平分 BAM∴NAD FAD在DNA 和 DNA 中，AND AFDNAD FADAD AD∴DNA DFA∴AN AF , DN DF∵ DE 是边 BC 的垂直平分线∴ DB DC∵ DN MC , DF AB∴DNC DFB90在 Rt DFB和 Rt DNC 中DB DCDF DN∴Rt DFB Rt DNC∴BF CN∵ CN ∴ BF ACACANAFAC AF第 10 课时等腰三角形的轴对称性(1)1.A2. 52.5°3.设BDC x,AEC y∵BD BC∴BDC BCD x∵BDC 的内角和为180°∴ B 180 2x同理可求 A180 2 y∵在ACB 中，ACB90∴A B90即1802x180 2 y90整理，得 x y135∵DEC 的内角和为180°第 11 课时等腰三角形的轴对称性(1) —习题课1.D 2. 15°或 30°或 75°或 120°3.分三种情况讨论:①当顶角BAC 为锐角时，如图①.∵DE 垂直平分 AB∴ADE 90∵AED 40∴在 Rt ADE 中， A 90 4050∵AB AC ∴ B C 1(180 50 )65 2②当顶角BAC 为直角时， BA AC ，此时 DE // AC ，不合题意，舍去.③当顶角BAC 为钝角时，如图②.∵DE 垂直平分 AB∴ ADE 90∵AED 40∴在 Rt ADE 中，BAE50∵BAE B C∴B C50∵ AB AC∴B C 150 25 2综上所述， B 的度数为 65或 25第 12 课时等腰三角形的轴对称性(2)1.D2. 50 °或 80°或 65°2.在ABC 中， A 50 ，当 B 的度数为时，ABC 为等腰三角形.3. (1) 图中有 5 个等腰三角形：ABC 、AEF 、OBC 、EBO 、 FOCEF 与 BE 、 CF 之间的数量关系是EF BE CF理由：∵ BO 平分 ABC∴ EBO OBC∵EF // BC∴EOB ∴EBO OBC EOB∴BE OE同理可证 CF OF∴EF OE OF BE CF(2) 若AB AC ，则图中仍旧存在 2 个等腰三角形：EBO 和FOC ， EF 与 BE 、CF之间的数量关系是EF BE (3) 图中存在等腰三角形CFEBO仍旧存在 .和FOC， EF与 BE、 CF之间的数量关系是E F B E C F理由：∵ BO 平分ABC ∴EBO OBC∵EF // BC∴EOB ∴EBO OBC EOB∴BE OE同理可证 CF ∴ EF OEOFOF BE CF第 13 课时等腰三角形的轴对称性(2)—习题课1.D2. BP2PQ3.(1) 如图，∵ACM , CBN都是等边三角形∴6 1 60 , AC CM ,CN BC∵ACB 180∴ 3 60 , ACN MCB 120在ACN 和 MCB 中AC MCACN MCBCN CB∴ACN MCB∴AN MB(2) 如图，由 (1) ，知ACN MCB∴54∵OQN与CQB 的内角和均为180°，且 OQNCQB ∴NOQ 1 60∵AOB NOQ180∴AOB 120(3) 如图，∵ 1 60 ， 3 60∴31在PCN 和 QCB 中3 1CN CB5 4∴ PCNQCB∴ PC QC又 3 60∴ PCQ 为等边三角形∴ 2 60 ∴21∴ PQ // AB第 14 课时等腰三角形的轴对称性 (3)1.D2. 10°3. ACEF证明：EBF x, CBF y∵在 Rt ABC 中， ACB 90∴ A 180 90 x y 90 x y∵ACB 90 ， F 为 BD 的中点∴ CF1BDBF2∴FCB FBC y∴DFCFCBFBC2 y∵ DE AB ， F 为 BD 的中点∴ EF1BD BF2∴ FEB FBE x∴ DFE FEB FBE 2x ∴EFCDFEDFC2x 2 y又∵ CF1BD ， EF1BD22∴ CF EF∴ CEFECF∵ CEF 的内角和为 180° ∴CEF 1(180EFC )1(180 2x 2y) 90 x y2 2∴ACEF。

苏科版八年级上册数学第二章轴对称图形含答案(完整版)

苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、下列图形中，是轴对称图形的是（）A. B. C. D.2、如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，若∠B=70°，则∠EDC的大小为（）A.10°B.15°C.20°D.30°3、如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（）A. cm 2B. cm 2C. cm 2D. cm 24、如图，矩形纸片中，，．点E、G分别在，上，将、分别沿、翻折，点A的对称点为点F，点D的对称点为点H，当E、F、H、C四点在同一直线上时，连接，则线段长为（）A. B. C. D.5、下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.6、如图，在△ABC中，BA＝BC，∠ABC＝120°，AB的垂直平分线交AC于点M，交AB于点E，BC的垂直平分线交AC于点N，交BC于点F，连接BM，BN，若AC＝24，则△BMN的周长是（）A.36B.24C.18D.167、如图，在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，若BC=18，DE=8，则△BCE的面积等于（）A.36B.54C.63D.728、如图，在△ABC中，∠B=45°，∠D=64°，AC=BC，则∠E的度数是（）A.45°B.26°C.36°D.64°9、下列四个图形中，既是轴对称图形，又是中心对称图形的是 ( )A.①②B.①③C.②③D.①②③10、如图，在△ABC中，点D、E、F分别在边BC、AB、AC上，且BD=BE，CD=CF，∠A=70°，那么∠FDE等于（）A.40°B.45°C.5 5°D.3 5°11、如图，MN是线段AB的垂直平分线，C在MN外，且与A点在MN的同一侧，BC交MN于P点，则( )A. BC> PC+ APB. BC< PC+ APC. BC= PC+ APD. BC≥ PC+ AP12、如图，正方形ABCD中，AB=12，点E在边CD上，且BG=CG，将△ADE沿AE 对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：①△ABG≌△AFG；②∠EAG=45°；③CE=2DE；④AG∥CF；⑤S= .其中正△FGC确结论的个数是（）A.2个B.3个C.4个D.5个13、下列手机软件图标中，是轴对称图形的是（）A. B. C. D.14、下列食品标识中，既是轴对称图形又是中心对称图形的是（）A. 绿色饮品B. 绿色食品C. 有机食品D. 速冻食品15、如图，将矩形纸片ABCD折叠，使点A落在BC上的点F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是（）A.邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.两个全等的直角三角形构成正方形D.轴对称图形是正方形二、填空题(共10题，共计30分)16、如图，在边长为4的正方形中，是边的中点，将沿对折至，延长交于点，连接，则的长为________．17、如图，在矩形中，，，点为的中点，将沿折叠，使点落在矩形内点处，连接，则的长为________．18、如图，已知点A（0，1），B（0，﹣1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于________度．19、如图，在四边形中，，，，，点和点分别是和的中点，连接，，，若，则的面积是________.20、如图是某商场营业大厅自动扶梯示意图．自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为4m．则自动扶梯的垂直高度BD＝________m．（结果保留根号）21、已知等边三角形ABC的边长为8，P是BC边上一点，连接AP，若AP=7，则BP的长为________．22、如图所示，在等边三角形ABC中，剪去∠A，∠C后，∠1+∠2+∠3+∠4=________．23、小明在镜子中看到的时钟的指针如图所示,那么此时时间为________．24、如图，在Rt△ABC中，∠ACB=90°，DE是AB的中垂线，分别交AB，AC于点D，E．已知AB=10，AC=8，则△BCE的周长是________．25、如图，己知是的垂直平分线，的周长为，，则的周长为________.三、解答题(共5题，共计25分)26、已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F，AEF 的周长为10㎝,求BC的长度和∠EAF的度数.27、如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF.求证：AB=AC28、判断下列图形是否为轴对称图形？如果是，说出它有几条对称轴．29、请你写出命题“等腰三角形的两个底角相等”的逆命题，并判断逆命题的真假；若是真命题，请写出已知、求证、证明；若是假命题，则请举反例证明．30、如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE.求证：△ABC是等腰三角形.（过D作DG∥AC交BC于G）参考答案一、单选题(共15题，共计45分)1、B2、B3、C5、D6、B7、D8、B9、B10、C11、C12、D13、C14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、27、28、。

苏科版八年级上册数学第二章轴对称图形含答案(考点梳理)

苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题，共计45分)1、下列是轴对称的图形的是（）A. B.C. D.2、如图，将边长为2的等边△OAB放置于平面直角坐标系xOy中，C是AB边上的一个点（不与端点A、B重合），作CD⊥OB于点D，若点C、D都在双曲线y= 上（k＞0，x＞0），则k的值为（）A. B. C. D.3、等腰三角形的两边长分别为，，则该三角形的周长为（）A. B. C. 或 D.以上都不对4、如果等腰三角形的底角为50°，那么它的顶角为（）A.50°B.60°C.70°D.80°5、若△ABC的三边长是a，b，c，且满足（a-b）（a-c）=0，则△ABC是（）A.钝角三角形B.直角三角形C.等腰直角三角形D.等腰三角形6、如图，已知矩形ABCD中，BC＝2AB，点E在BC边上，连接DE、AE，若EA 平分∠BED，则的值为（）A. B. C. D.7、在△ABC和△DEF中，∠A=∠D=90°，则下列条件中不能判定△ABC和△DEF 全等的是（）A.AB=DE，AC=DFB.AC=EF，BC=DFC.AB=DE，BC=EFD.∠C=∠F，BC=EF8、有下列说法：其中正确的个数是（）(1)有一个角为60°的等腰三角形是等边三角形；(2)三角之比为3：4：5的三角形为直角三角形；(3)等腰三角形的两条边长为2，4，则等腰三角形的周长为10；(4)一边上的中线等于这边长的一半的三角形是直角三角形；A.2个B.3个C.4个D.1个[9、如图，把一长方形纸片沿折盈后，点、分别落在、的位置，若，则等于（）A.65ºB.62ºC.56ºD.64º10、下列说法中：①线段是轴对称图形，②已知两腰就能确定等腰三角形的形状和大小，③等腰三角形的角平分线就是底边的垂直平分线，正确的有( )A.0个B.1个C.2个D.3个11、下列说法正确的是（）A.等腰三角形的两条高相等B.等腰三角形的两条角平分线相等C.等腰三角形的两条中线相等D.等腰三角形两腰上的中线相等12、如图，将等腰三角板向右翻滚，依次得到b、c、d，下列说法中，不正确的是（）A.a到b时旋转B.a到c是平移C.a到d是平移D.b到c是旋转13、下面的图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.14、如图，在中，E为边上一点，将沿折叠至处，与交于点F，若，，则的大小为（）A. B. C. D.15、如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（）A.13B.16C.8D.10二、填空题(共10题，共计30分)16、如图，在△ABC中，∠C=90°，AC=3，BC=2，边AB的垂直平分线交AC边于点D，交AB边于点E，联结DB，那么tan∠DBC的值是________．17、如图，在中，，D是AB的中点，若，则的度数为________。

苏科版八年级上册数学轴对称复习题

2021 年八年级上学期周复习资料〔4〕——轴对称『根底练习』1．“羊〞字象征桔祥和美好，以下图的图案与羊有关，其中是轴对称图形的个数是〔〕A ． 1B ． 2C． 3D． 42．如图，∠ AOB=40°， OM 平分∠ AOB ， MA ⊥ OA ，MB ⊥OB，垂足分别为 A、 B 两点，那么∠ MOB 和∠ MAB 等于〔〕A ． 50°和 30°B． 40°和 70°C．30°和 20°D． 20°和 70°3．如图，DE 是△ ABC 中边 AC 的垂直平分线，假设 BC=18 cm ，AB=10 cm ，那么△ ABD 的周长为〔〕A ． 16 cm B ．28 cm C． 26 cm D ． 18 cm4．如图，ABC≌DEF，点A与 D ，B 与 E 分别是对应顶点，且测得BC 5cm，BF7cm ，那么 EC 长为〔〕新 |课| 标 |第|一 | 网A ．1cmB ．2cm C．3cm D ．4cmA DGB EC F第 2 题第3题第4题5．如图，AB AD，那么添加以下一个条件后，仍无法判定△ ABC≌△ ADC的是〔〕A ．CB CD B．∠BAC∠ DAC C．∠BCA∠ DCA D．∠B∠ D90 6．∠ AOB 的平分线上一点P 到 OA 的距离为5， Q 是 OB 上任一点，那么〔〕A ． PQ＞ 5B．PQ≥ 5C． PQ＜ 5D． PQ≤57．如图 , AC 和 BD 相交于 O,且 BO＝ DO,AO ＝CO,以下判断正确的选项是〔〕A ．只能证明△ AOB ≌△ COD B ．只能证明△ AOD ≌△ COBC．只能证明△AOB ≌△ COB D ．能证明△ AOB ≌△ COD 和△ AOD ≌△ COB8．如图， OP 平分AOB ， PA OA ， PB OB ，垂足分别为A， B．以下结论中不一定成立的是〔〕 X|k | B| 1 . c|O|mA ．PA PB B．PO平分APB C．OA OB D．AB垂直平分OPDA CB第 4 题第4题第4题『重点讲解』1．如图，点 A 、B、C 在同一直线上，△ ABD ，△ BCE 都是等边三角形．〔 1〕求证： AE=CD ；〔2〕假设 M ，N 分别是 AE ，CD 的中点，试判断△ BMN 的形状，并证明你的结论．DN EMA B C2．如图， E 是正方形ABCD 的边 CD 的中点，点 F 在 BC 上，且∠ DAE= ∠ FAE ，求证：AF=AD — CF．新课标第一网ADEB F C3．如图，BD 是∠ ABC 的内角平分线，CD 是∠ ACB 的外角平分线，由 D 出发，作点 D 到BC 、AC 是和AB的垂线。

最新苏科版初中数学八年级上册轴对称图形复习重点习题

苏科版八年级数学上册第二章轴对称复习题基础题含答案

苏科版八年级上册数学第二章 轴对称图形 含答案(黄金题型)

【精选】苏科版数学八年级上册 轴对称解答题单元复习练习(Word版 含答案)

(精练)(汇总)苏科版八年级上册数学第二章 轴对称图形含答案

苏科版八年级数学上册期末复习轴对称图形解答题(难题)训练.docx

苏科版数学八年级上册 轴对称解答题单元复习练习(Word版 含答案)

苏科版本初中八年级的上第二章轴对称图形提优练习包括答案.docx

苏科版八年级上册数学第二章 轴对称图形含答案(完整版)

最新苏科版八年级数学上册 轴对称与轴对称图形(含解析)

苏科版八年级上册数学第二章 轴对称图形 含答案(考点梳理)