流体流动阻力测定实验报告数据处理
流体阻力测定实验报告

流体阻力测定实验报告流体阻力测定实验报告引言:流体力学是研究流体在运动中的力学性质和规律的学科。
流体阻力是流体运动中的一个重要现象,对于理解流体运动及其应用具有重要意义。
本实验旨在通过测定不同物体在流体中的运动速度和受到的阻力,探究流体阻力的特性和影响因素。
实验器材和方法:实验器材包括流体阻力测定装置、不同形状的物体、计时器等。
首先,将流体阻力测定装置放置在水槽中,调整好水流速度。
然后,选取不同形状的物体,如圆柱体、平板等,分别放入流体中,记录物体在流体中的运动速度和受到的阻力。
实验过程中,注意保持实验环境的稳定和准确测量。
实验结果:通过实验测量,得到了不同形状物体在流体中的运动速度和受到的阻力数据。
根据数据分析,发现不同形状的物体受到的阻力大小存在差异。
圆柱体在流体中受到的阻力相对较小,而平板受到的阻力较大。
这是因为圆柱体的形状对流体的流动产生较小的阻力,而平板的形状则会导致流体流动时产生较大的阻力。
讨论:流体阻力的大小与物体的形状密切相关。
在流体中运动的物体,其形状越流线型,阻力越小。
这是因为流体在物体表面形成的流动层越光滑,阻力就越小。
而对于平板形状的物体,由于其边缘会产生较大的涡流,导致阻力增大。
因此,在设计流体运动的装置时,应尽量减小物体的阻力,提高流体的运动效率。
此外,流体阻力还与流体的黏性、流速和物体表面粗糙度等因素有关。
当流体黏性较大时,阻力也会增大。
流速越大,流体对物体的冲击力也越大,从而增加阻力。
物体表面越粗糙,流体对其的阻力也会增加。
因此,在实际应用中,需要考虑这些因素对流体阻力的影响,以便准确预测和控制流体运动的阻力。
结论:通过流体阻力测定实验,我们深入了解了流体阻力的特性和影响因素。
实验结果表明,物体的形状、流体的黏性、流速和物体表面粗糙度等因素都会对流体阻力产生影响。
在实际应用中,我们应根据具体情况选择合适的物体形状和流体条件,以减小阻力,提高流体运动的效率。
参考文献:[1] 王某某. 流体力学实验[M]. 北京:科学出版社,2010.[2] 张某某. 流体阻力的研究进展[J]. 流体力学杂志,2015,28(2): 34-45.。
化工原理实验报告-流体流动阻力的测定
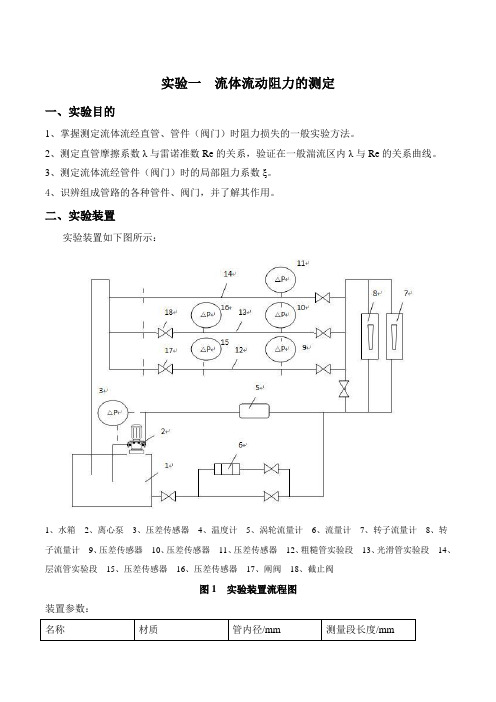
实验一流体流动阻力的测定一、实验目的1、掌握测定流体流经直管、管件(阀门)时阻力损失的一般实验方法。
2、测定直管摩擦系数λ与雷诺准数Re的关系,验证在一般湍流区内λ与Re的关系曲线。
3、测定流体流经管件(阀门)时的局部阻力系数ξ。
4、识辨组成管路的各种管件、阀门,并了解其作用。
二、实验装置实验装置如下图所示:1、水箱2、离心泵3、压差传感器4、温度计5、涡轮流量计6、流量计7、转子流量计8、转子流量计9、压差传感器10、压差传感器11、压差传感器12、粗糙管实验段13、光滑管实验段14、层流管实验段15、压差传感器16、压差传感器17、阐阀18、截止阀图1 实验装置流程图装置参数:名称材质管内径/mm 测量段长度/mm三、实验原理1、直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时,阻力损失为:2122ff p p p l u h d λρρ∆-=== ⑴即 22fd p luλρ∆=⑵Re du ρμ=⑶采用涡轮流量计测流量V2900Vu dπ=⑷ 用压差传感器测量流体流经直管的压力降f p ∆。
根据实验装置结构参数l 、d ,流体温度T (查流体物性ρ、μ),及实验时测定的流量V 、压力降ΔPf ,求取Re 和λ,再将Re 和λ标绘在双对数坐标图上。
2、局部阻力系数ζ的测定流体通过某一管件或阀门时的机械能损失表示为流体在小管径内流动时平均动能的某一倍数,这种方法称为阻力倍数法。
即:'2'2ffp u h g gζρ∆== ⑸ 故 '22fp u ζρ∆=⑹根据连接管件或阀门两端管径中小管的直径d ,流体温度T (查流体物性ρ、μ),及实验时测定的流量V 、压力降ΔPf ’,通过式⑸或⑹,求取管件(阀门)的局部阻力系数ζ。
四、实验步骤1、开启仪表柜上的总电源、仪表电源开关。
2、首先对水泵进行灌水,然后关闭出口阀,启动水泵,待电机转动平稳后,把出口阀缓缓开到最大。
3、实验从做大流量开始做起,最小流量应控制在1.5m3/h。
流体流动阻力的测定实验报告2

1.93 0.00054 1.31 1.477 32322 0.0172
2.24 0.00062 1.61 1.715 37513 0.0157
2.61 0.00073 2.01 1.998 43710 0.0145
3.00 0.00083 2.51 2.297 50241 0.0137
查表得:21.3℃下水的密度 998.2kg/m³,粘度为 0.981mpa*s 以第三组数据为例: 流量:q=0.93m³/h=0.00026m³/s 流速:u=q/A= 雷诺数:Re= 由 hf
突然扩大管的局部阻力系数数据表 水流量(m ³ / h ) 1.99 3 4.04 压降(k P a ) 1.04 2.35 4.44 流速u 2 (m / s ) 0.3992 0.6018 0.8104 流速u 1 (m / s ) 2.7507 4.1468 5.5843 局部阻力系数ζ 1.2544 1.2528 1.2643
局部阻力数据记录表
扩 大 管 水流量/ m .h 压降/kPa
3 -1
1.99 1.06
3.00 2.37
4.04 4.46
管径:由 Φ(22×3) mm 扩大到 Φ(48×3) mm(23.2℃,初始压降 0.02kpa)
层流管数据记录表 时间/s 体积/ml 压降 /kpa 温度/℃ 180 118 0.44 24.5 120 162 0.94 24.3 120 208 1.34 24.6 90 202 1.48 24.9 60 163 1.84 25.1 60 200 2.46 25.6 层流管 径 Φ(6×1.5) 长 1.5m,
0.87 1.05 2.42E-04 2.92E-04 0.698 0.843 0.58 0.77 15379 18561 0.0334 0.0304
流体流动阻力的测定(化工原理实验报告)

北 京 化 工 大 学实 验 报 告课程名称: 化工原理实验 实验日期: 2008.10.29 班 级: 化工0602 姓 名:许兵兵学 号: 200611048 同 组 人 :汤全鑫 阮大江 阳笑天流体流动阻力的测定摘要● 测定层流状态下直管段的摩擦阻力系数(光滑管、粗糙管和层流管)。
● 测定湍流状态不同(ε/d)条件下直管段的摩擦阻力系数(突然扩大管)。
● 测定湍流状态下管道局部的阻力系数的局部阻力损失。
● 本次实验数据的处理与图形的拟合利用Matlab 完成。
关键词流体流动阻力 雷诺数 阻力系数 实验数据 Matlab一、实验目的1、掌握直管摩擦阻力系数的测量的一般方法;2、测定直管的摩擦阻力系数λ以及突扩管的局部阻力系数ζ;3、测定层流管的摩擦阻力4、验证湍流区内λ、Re 和相对粗糙度的函数关系5、将所得光滑管的Re -λ方程与Blasius 方程相比较。
二、实验原理不可压缩流体(如水),在圆形直管中作稳定流动时,由于粘性和涡流的作用产生摩擦阻力;流体在流过突然扩大和弯头等管件时,由于流体运动的速度和方向突然发生变化,产生局部阻力。
影响流体流动阻力的因素较多,在工程研究中,利用因次分析法简化实验,引入无因此数群雷 诺 数:μρdu =Re相对粗糙度: d ε管路长径比: d l可导出:2)(Re,2u d d l p⋅⋅=∆εφρ这样,可通过实验方法直接测定直管摩擦阻力系数与压头损失之间的关系:22u d l pH f ⋅⋅=∆=λρ因此,通过改变流体的流速可测定出不同Re 下的摩擦阻力系数,即可得出一定相对粗糙度的管子的λ—Re 关系。
在湍流区内,λ = f(Re ,ε/ d ),对于光滑管大量实验证明,当Re 在3×103至105的范围内,λ与Re 的关系遵循Blasius 关系式,即:25.0Re 3163.0=λ对于层流时的摩擦阻力系数,由哈根—泊谡叶公式和范宁公式,对比可得:Re 64=λ局部阻力:f H =22u ⋅ξ [J/kg]三、装置和流程四、操作步骤1、启动水泵,打开光滑管路的开关阀及压降的切换阀,关闭其它管路的开关阀和切换阀;2、排尽体系空气,使流体在管中连续流动。
化工原理实验-流体流动阻力系数的测定实验报告

流体流动阻力系数的测定实验报告一、实验目的:1、掌握测定流体流动阻力实验的一般实验方法。
2、测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。
3、验证湍流区内摩擦阻力系数λ为雷诺系数Re和相对粗糙度的函数。
4、将所得光滑管的λ—Re方程与Blasius方程相比较。
二、实验器材:流体阻力实验装置一套三、实验原理:1、直管摩擦阻力不可压缩流体(如水),在圆形直管中做稳定流动时,由于黏性和涡流的作用产生摩擦阻力;流体在流过突然扩大、弯头等管件时,由于流体运动的速度和方向突然变化,产生局部阻力。
影响流体阻力的因素较多,在工程上通常采用量纲分析方法简化实验,得到在一定条件下具有普遍意义的结果,其方法如下。
流体流动阻力与流体的性质,流体流经处的几何尺寸以及流动状态有关,可表示为△P=f (d, l, u,ρ,μ,ε)引入下列无量纲数群。
雷诺数Re=duρ/μ相对粗糙度ε/ d管子长径比l / d从而得到△P/(ρu2)=ψ(duρ/μ,ε/ d,l / d)令λ=φ(Re,ε/ d)△P/ρ=(l / d)φ(Re,ε/ d)u2/2可得摩擦阻力系数与压头损失之间的关系,这种关系可用试验方法直接测定。
h f=△P/ρ=λ(l / d)u2/2——直管阻力,J/kg式中,hfl——被测管长,md——被测管内径,mu——平均流速,m/sλ——摩擦阻力系数。
当流体在一管径为d的圆形管中流动时,选取两个截面,用U形压差计测出这两个截面间的静压强差,即为流体流过两截面间的流动阻力。
根据伯努利方程找出静压强差和摩擦阻力系数的关系式,即可求出摩擦阻力系数。
改变流速可测出不同Re下的摩擦阻力系数,这样就可得出某一相对粗糙度下管子的λ—Re关系。
(1)、湍流区的摩擦阻力系数在湍流区内λ=f(Re,ε/ d)。
对于光滑管,大量实验证明,当Re在3×10~10 范围内,λ和Re的关系遵循Blasius关系式,即λ= / Re对于粗糙管,λ和Re的关系均以图来表示。
流体流动阻力的测定实验报告

4.00 3.71 3.45 3.13 2.90 2.57 2.33 2.09 1.84 1.62 1.30 0.98
Re
83472 77283 71930 65239 60555 53696 48678 43660 38474 33790 27099 20408
0.025 0.025 0.025 0.025 0.025 0.025 0.025 0.025 0.025 0.026 0.026 0.027
因此 式中:—局部阻力系数,无因次; -局部阻力压强降,;(本装置中,所测得的压降应扣除两测压口间直管 段的压降,直管段的压降由直管阻力实验结果求取。) —流体密度,; —流体在管内流动的平均流速,。 根据连接阀门两端管径,流体密度,流体温度 (查流体物性、),及实 验时测定的流量、压差计读数,求取阀门的局部阻力系数。 三、实验内容 1. 根据粗糙管实验结果,在双对数坐标纸上标绘出曲线,对照化工原 理教材上有关曲线图,即可估算出该管的相对粗糙度和绝对粗糙度。 2. 根据光滑管实验结果,对照柏拉修斯方程,计算其误差。
2. 实验流程 实验对象部分是由贮水箱,离心泵,不同管径、材质的水管,各种阀
门、管件,涡轮流量计和倒 U 型压差计等所组成的。管路部分有三段并联 的长直管,分别为用于测定局部阻力系数,光滑管直管阻力系数和粗糙管 直管阻力系数。测定局部阻力部分使用不锈钢管,其上装有待测管件(闸阀);
-3-
化工原理实验
-9-
化工原理实验
对数据进行与粗糙管相同方法的计算,并根据 Blasius 方程计算在 Re 条件下的理论值,计算实验值与理论值的相对误差(相对误差公式为 )。计算结果如下表所示:
序号
1
2
3
4
5
化工原理实验二_流体流动阻力测定实验

实验三 流体流动阻力测定实验一.实验目的(1) 辨别组成管路的各种管件、阀门,并了解其作用。
(2)测定流体在圆形直管内流动时摩擦系数λ与雷诺数Re 的关系。
(3)测定流体流经闸阀时的局部阻力系数ξ。
二.基本原理直管的摩擦阻力系数是雷诺数和相对粗糙度的函数,即)/(Re,d f ελ=,对一定的相对粗糙度而言,(Re)f =λ。
流体在一定长度等直径的水平圆管内流动时,其管路阻力引起的能量损失为:ρρff P P P h ∆=-=21 (1)又因为摩擦阻力系数与阻力损失之间有如下关系(范宁公式)22u d l h fP f λρ==∆ (2)整理(1)(2)两式得22u P l d f∆⋅⋅=ρλ (3) μρ⋅⋅=u d Re (4)式中:-d 管径,m ;-∆f P直管阻力引起的压强降,Pa;l管长,m;-u流速,m / s;-ρ流体的密度,kg / m3;-μ流体的粘度,N·s / m2。
-在实验装置中,直管段管长l和管径d都已固定。
若水温一定,则水的密度ρ和粘度μ也是定值。
所以本实验实质上是测定直管段流体阻力引起的压强降△P f与流速u(流量V)之间的关系。
根据实验数据和式(3)可计算出不同流速下的直管摩擦系数λ,用式(4)计算对应的Re,从而整理出直管摩擦系数和雷诺数的关系,绘出λ与Re 的关系曲线。
三.实验装置与参数1、实验装置实验流程示意图见图1。
实验装置由贮水槽、离心泵、变频器、电动调节阀、涡轮流量计、压力表、差压变送器、不同材质的水管、倒U型压差计(图中未画出)等组成。
装置上有三段并联的水平直管,自上而下分别用于测定局部阻力、光滑管直管阻力和粗糙管直管阻力。
测定局部阻力时使用不锈钢管,中间装有待测管件(闸阀);测定光滑管直管阻力时,同样使用内壁光滑的不锈钢管,而测定粗糙管直管阻力时,采用管道内壁较粗糙的镀锌管。
水泵2将储水槽1中的水抽出,送入实验系统,首先经玻璃转子流量计15、16测量流量,然后送入被测直管段测量流体在光滑管或粗糙管的流动阻力,或经10测量局部阻力后回到储水槽,水循环使用。
化工原理实验~流体流动阻力系数的测定实验报告

流体流动阻力系数的测定实验报告一、实验目的:1、掌握测定流体流动阻力实验的一般实验方法。
2、测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。
3、验证湍流区内摩擦阻力系数λ为雷诺系数Re和相对粗糙度的函数。
4、将所得光滑管的λ—Re方程与Blasius方程相比较。
二、实验器材:流体阻力实验装置一套三、实验原理:1、直管摩擦阻力不可压缩流体(如水),在圆形直管中做稳定流动时,由于黏性和涡流的作用产生摩擦阻力;流体在流过突然扩大、弯头等管件时,由于流体运动的速度和方向突然变化,产生局部阻力。
影响流体阻力的因素较多,在工程上通常采用量纲分析方法简化实验,得到在一定条件下具有普遍意义的结果,其方法如下。
流体流动阻力与流体的性质,流体流经处的几何尺寸以及流动状态有关,可表示为△P=f (d, l, u,ρ,μ,ε)引入下列无量纲数群。
雷诺数Re=duρ/μ相对粗糙度ε/ d管子长径比l / d从而得到△P/(ρu2)=ψ(duρ/μ,ε/ d, l / d)令λ=φ(Re,ε/ d)△P/ρ=(l / d)φ(Re,ε/ d)u2/2可得摩擦阻力系数与压头损失之间的关系,这种关系可=△P/ρ=λ(l / d)u2/2用试验方法直接测定。
hf——直管阻力,J/kg式中,hfl——被测管长,md——被测管内径,mu——平均流速,m/sλ——摩擦阻力系数。
当流体在一管径为d的圆形管中流动时,选取两个截面,用U形压差计测出这两个截面间的静压强差,即为流体流过两截面间的流动阻力。
根据伯努利方程找出静压强差和摩擦阻力系数的关系式,即可求出摩擦阻力系数。
改变流速可测出不同Re下的摩擦阻力系数,这样就可得出某一相对粗糙度下管子的λ—Re关系。
(1)、湍流区的摩擦阻力系数在湍流区内λ=f(Re,ε/ d)。
对于光滑管,大量实验证明,当Re在3×103~105范围内,λ和Re的关系遵循Blasius关系式,即λ= /对于粗糙管,λ和Re的关系均以图来表示。
流动阻力测定实验报告

一、实验目的1. 理解流动阻力的概念及其在流体力学中的重要性。
2. 掌握流动阻力测定的实验方法与步骤。
3. 通过实验数据,分析流动阻力与流体性质、管道结构等因素之间的关系。
4. 验证理论公式在工程实践中的应用。
二、实验原理流动阻力是指在流体流动过程中,流体与管道壁面之间产生的摩擦力。
流动阻力的大小与流体的性质、管道结构、流速等因素有关。
根据流动状态的不同,流动阻力可分为层流阻力与湍流阻力。
层流阻力:当流体以较低的流速在圆形管道中流动时,流动状态为层流。
此时,流动阻力主要由分子粘性力引起,可用牛顿粘性定律计算。
湍流阻力:当流体以较高的流速在圆形管道中流动时,流动状态为湍流。
此时,流动阻力主要由湍流涡流和粘性力共同作用引起,可用达西-魏斯巴赫公式计算。
三、实验装置与仪器1. 实验装置:圆形管道、阀门、流量计、压力表、计时器等。
2. 仪器:电子天平、秒表、游标卡尺、温度计、粘度计等。
四、实验步骤1. 准备实验装置,确保管道连接牢固,无泄漏。
2. 根据实验要求,调整管道结构参数,如管道直径、长度、阀门开度等。
3. 在管道两端安装压力表,测量流体流动过程中的压力差。
4. 使用流量计测量流体流量,记录数据。
5. 记录实验温度和流体粘度。
6. 改变流体流速,重复步骤3、4、5,记录不同流速下的压力差、流量和温度。
7. 根据实验数据,计算流动阻力、摩擦系数、雷诺数等参数。
五、实验数据与分析1. 根据实验数据,绘制流动阻力与流速的关系曲线,分析流动阻力随流速变化的规律。
2. 根据实验数据,计算摩擦系数、雷诺数等参数,分析流动状态的变化。
3. 将实验结果与理论公式进行对比,验证理论公式的适用性。
六、实验结果与讨论1. 实验结果表明,随着流速的增加,流动阻力逐渐增大,符合理论公式预测。
2. 实验结果表明,在相同流速下,摩擦系数与雷诺数呈正相关关系,符合理论公式预测。
3. 实验结果表明,在相同流速下,管道直径、长度、阀门开度等因素对流动阻力有显著影响。
化工原理实验—流体流动阻力测定实验

化工原理实验报告—流体流动阻力测定实验班级: 031112班小组:第六组指导老师:刘慧仙组长:陈名组员:魏建武曹然实验时间: 2013年10月18日目录一、实验内容 (1)二、实验目的 (1)三、实验基本原理 (1)1.直管阻力 (1)2.局部阻力 (3)四、实验设计 (3)1.实验方案 (3)2.测试点及测试方法 (3)原始数据 (3)测试点 (4)测试方法 (4)3.控制点及调节方法 (4)4.实验装置和流程设计 (4)主要设备和部件 (4)实验装置流程图 (4)五、实验操作要点 (5)六、实验数据处理和结果讨论分析 (6)实验数据处理 (6)1.实验数据记录表 (6)2.流体直管阻力测定实验数据整理表 (7)3.流体局部阻力测定实验数据整理表 (8)4.计算示例。
(9)结果讨论分析 (10)七、思考题 (11)实验一流体流动阻力的测定实验一、实验内容1.测定流体在特定材质和的直管中流动时的阻力摩擦系数,并确定和之间的关系。
2.测定流体通过阀门时的局部阻力系数。
二、实验目的1.了解测定流体流动阻力摩擦系数的工程定义,掌握测定流体阻力的实验方法。
2.测定流体流径直管的摩擦阻力和流经管件或局部阻力,确定直管阻力摩擦系数与雷诺数之间的关系。
3.熟悉压差计和流量计的使用方法。
4.认识组成管路系统的各部件、阀门并了解其作用。
三、实验基本原理流体管路是由直管、管件(如三通、肘管、弯头)、阀门等部件组成。
流体在管路中流动时,由于黏性剪应力和涡流的作用,不可避免地要消耗一定的机械能,流体在直管中流动的机械能损失为直管阻力;而流体通过阀门、管件等部件时,因流动方向或流动截面的突然改变导致的机械能损失称为局部阻力。
在化工过程设计中,流体流动阻力的测定或计算,对于确定流体输送所需推动力的大小,例如泵的功率、液位或压差,选择适当的输送条件都有不可或缺的作用。
1.直管阻力流体在水平的均匀管道中稳定流动时,由截面1流动至截面2的阻力损失表现为压力的降低,即①由于流体分子在流动过程中的运动机理十分复杂,影响阻力损失的因素众多,目前尚不能完全用理论方法来解决流体阻力的计算问题,必须通过实验研究掌握其规律。
流体流动阻力的测定 实验报告

实验一 流体流动阻力的测定摘要: 通过实验测定流体在光滑管、粗糙管、层流管中流动时, 借助于伯努利方程计算摩擦阻力系数和雷诺数之间的关系, 并与理论值相比较。
同时以实验手段计算突然扩大处的局部阻力, 并对以上数据加以分析, 得出结论。
一、目的及任务1.掌握测定流体流动阻力的实验的一般实验方法。
2.测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。
3.测定层流管的摩擦阻力。
4.验证湍流区内摩擦阻力系数λ与雷诺数Re 和相对粗糙度的函数。
5.将所得的光滑管的λ-Re 方程与Blasius 方程相比较。
二、基本原理1.直管摩擦阻力 不可压缩流体(如水), 在圆形直管中做稳定流动时, 由于黏性和涡流的作用产生摩擦阻力;流体在突然扩大、弯头等管件时, 由于流体运动速度和方向的突然变化, 产生局部阻力。
影响流体阻力的因素较多, 在工程上采用量纲分析方法简化实验, 得到在一定条件下具有普遍意义的结果, 其方法如下。
流体流动阻力与流体的性质, 流体流经处几何尺寸以及流动状态有光, 可表示为 p=f (d, l, u, , , ) 引入下列无量纲数群雷诺数Re=μρdu相对粗糙度d ε 管子的长径比dl从而得到),,du (p 2d ld u εμρρψ=∆令 = (Re, )2)(Re,2u d d l pερΦ=∆ 可得摩擦阻力系数与压头损失之间的关系, 这种关系可用实验方法直接测定。
22u d l ph f ⨯=∆=λρ式中 ——直管阻力, J/Kg ; l ——被测管长, m ; d ——被测管内径, m ; u ——平均流速, m/s ; λ——摩擦阻力系数。
当流体在一管径为d 的圆形管中流动时, 选取两个截面, 用U 形压差计测出这两个截面间的静压强差, 即为流体流过两截面间的流动阻力。
根据伯努利方程找出静压强差和摩擦阻力系数的关系式, 即可求出摩擦阻力系数。
改变流速可测出不同Re 下的摩擦阻力系数, 这样就可得出某一相对粗糙度下管子的 -Re 关系。
流体流动阻力的测定实验

实验5 流体流动阻力的测定实验一、实验目的1. 掌握流体流经直管和阀件时阻力损失的测定方法,通过实验了解流体流动中能量损失的变化规律和流体流动阻力对工程的实际意义。
2. 测定直管摩擦系数λ与雷诺准数Re 的关系,将所得的λ~Re 方程与经验公式比较。
3. 测定流体流经阀件时的局部阻力系数ζ。
4. 学会差压计和流量计的使用方法。
5. 观察组成管路的各种管件、阀件并了解其作用。
二、实验原理流体输送管路是由直管、管件和阀件组成。
流体在管路中流动时,由于粘性剪应力和涡流的存在,不可避免地要消耗一定的机械能。
这种机械能的消耗包括流体流经直管的沿程阻力,流体运动方向改变或因管子大小形状改变所引起的局部阻力。
(一)沿程阻力(直管阻力)流体在水平等径圆管中稳定流动时,在截面1和截面2间的阻力损失表现为压力降低。
即ρρpp p h f ∆=-=21 (6-1)影响阻力损失的因素很多,尤其对湍流流体,目前尚不能完全用理论方法求解,必须通过实验研究其规律。
为了减少实验工作量,简化实验工作难度,使实验结果具有普遍意义,可采用量纲分析方法将各变量组合成准数关联式。
根据实验结果分析,影响阻力损失的因素有三类变量。
1. 流体性质:密度ρ、粘度μ;2. 管路的几何尺寸:管径d 、管长l 、管壁粗糙度ε;3. 流动条件:流速u ;可将阻力损失与各变量之间表示为如下的函数形式),,,,,(ερμu l d f p =∆ (6-2)根据量纲分析法,可将上述各变量间的关系转变为无因次准数之间的关系),,(2d d l du up εμρρΦ=∆ (6-3)2),(2u d l d du p⋅⋅=∆εμρϕρ (6-4) 令 ),(ddu εμρϕλ= (6-5) 则 22u d l ph f ⋅=∆=λρ (6-6) 式中 Δp ——压力降,Pa ;h f ——直管阻力损失,J/kg ; ρ——流体密度,kg/m 3;λ——直管摩擦系数,无因次;层流 (滞流)时,λ=64/Re ;湍流时λ是雷诺准数Re 和相对粗糙度ε/d 的函数,需由实验确定;l ——直管长度,m ; d ——直管内径,m ; ε——管壁绝对粗糙度,m ; u ——流体流速,m/s ,由实验测定。
流体流动阻力的测定实验数据处理
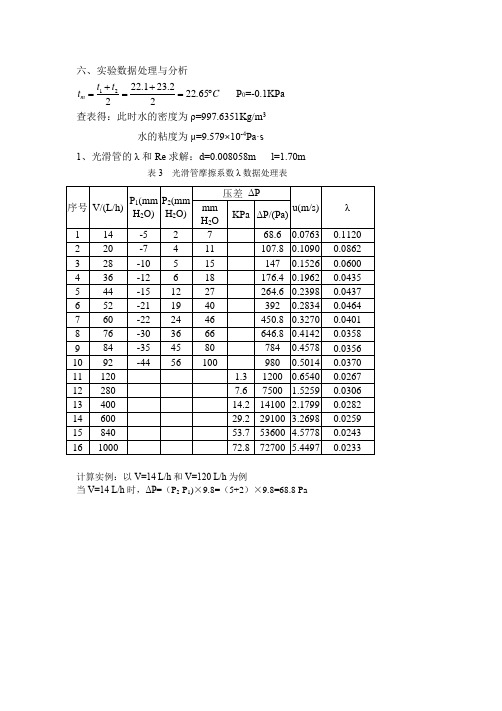
六、实验数据处理与分析C t t t m ︒=+=+=65.2222.231.22221 P 0=-0.1KPa 查表得:此时水的密度为ρ=997.6351Kg/m 3水的粘度为μ=9.579×10-4Pa·s1、光滑管的λ和Re 求解:d=0.008058m l=1.70m表3 光滑管摩擦系数λ数据处理表计算实例:以V=14 L/h 和V=120 L/h 为例当V=14 L/h 时,ΔP =(P 2-P 1)×9.8=(5+2)×9.8=68.8 Pasm d V d VA V u /0763.0)008058.0(14.336001000144360010004)21(36001000222=⨯⨯⨯⨯=⨯∏⨯⨯=⨯∏⨯==1120.00763.070.16351.997008058.06.68222222=⨯⨯⨯⨯=∆=∴=∆=lu Pd u d l Ph f ρλλρ当V=120 L/h 时,ΔP =(1.3-0.1)×1000=1200 Pasm d V A V u /6540.0)008058.0(14.336001000120436001000422=⨯⨯⨯⨯=⨯∏⨯⨯===0267.06540.070.16351.997008058.012002222=⨯⨯⨯⨯=∆=lu Pd ρλ 表4 光滑管λ与Re 数据处理表计算实例:以λ=0.1120和λ=0.0267为例 当λ=0.1120时,u=0.0763 m/s2851.64010579.96351.9970763.0008508.0e 4=⨯⨯⨯==-μρdu R0.1000640.295164e 64 6.4619640.2951ln e ln -2.18940.1120ln ln =======R R λλ理论)()(当λ=0.0267时,u=0.6540 m/s5488.243510579.96351.9976540.0008508.0e 4=⨯⨯⨯==-μρdu R0.03685488.24350.3164e 0.31648.61045488.2435ln e ln -3.62450.0267ln ln 0.250.25=======R R λλ理论)()(图1 光滑管层流区λ—Re 双对数关系l n λln Re图2 光滑管过渡区λ—Re 双对数关系图3 光滑管湍流区λ—Re 双对数关系l n λln Reln Rel n λRe图4 光滑管λ实际值与理论值对比关系曲线2、粗糙管的λ和Re求解:d=0.010m l=1.70m表5 粗糙管摩擦系数λ数据处理表计算实例:以V=16 L/h和V=84 L/h为例当V=16 L/h 时,ΔP =(P 2-P 1)×9.8=(8+11)×9.8=186.2 Pasm d V d VA V u /5660.0)100.0(14.336001000614360010004)21(36001000222=⨯⨯⨯⨯=⨯∏⨯⨯=⨯∏⨯==6850.05660.070.16351.997100.0186.2222222=⨯⨯⨯⨯=∆=∴=∆=lu Pd u d l Ph f ρλλρ当V=84 L/h 时,ΔP =(2.8-0.1)×1000=2700 Pasm d V A V u /2972.0)100.0(14.33600100084436001000422=⨯⨯⨯⨯=⨯∏⨯⨯===3604.02972.070.16351.997100.027002222=⨯⨯⨯⨯=∆=lu Pd ρλ 表6 粗糙管λ与Re 数据处理表计算实例:以λ=0.6850和λ=0.3604为例 当λ=0.6850时,u=0.0566 m/s589.656910579.96351.9975660.0100.0e 4=⨯⨯⨯==-μρdu R 6.3795589.6569ln e ln -0.37830.6850ln ln ====)()(R λ当λ=0.3604时,u=0.2976 m/s3095.698610579.96351.9972976.0100.0e 4=⨯⨯⨯==-μρdu R8.03783095.6986ln e ln -1.02060.3604ln ln ====)()(R λ图5 光滑管层流区λ—Re 双对数ln Rel n λ图6 光滑管过渡区λ—Re 双对数关系图7 光滑管湍流区λ—Re 双对数关系l n λln Reln Rel n λ图8 光滑管与粗糙管λ—Re 双对数关系对比ln Rel n λ。
雷诺实验报告数据处理

雷诺实验报告数据处理本报告旨在对雷诺实验所得数据进行处理和分析,以得出结论并提出相应建议。
雷诺实验是一项重要的流体力学实验,通过测量流体在管道中的流速分布,可以得出管道流体的阻力特性和流动规律。
数据处理是实验过程中不可或缺的一环,其结果直接影响对实验结论的准确性和可靠性。
首先,我们对实验中得到的原始数据进行了整理和筛选,去除了可能存在的异常值和误差数据。
然后,我们对筛选后的数据进行了统计分析,包括平均值、标准差、偏度、峰度等统计量的计算。
通过统计分析,我们可以对数据的分布情况有一个直观的了解,为后续的数据处理和分析提供基础。
接下来,我们对数据进行了图表展示,包括直方图、箱线图、散点图等。
通过图表展示,我们可以更直观地观察数据的分布情况和异常点的存在情况,为后续的数据处理和分析提供参考。
在图表展示的基础上,我们对数据进行了进一步的处理,包括数据平滑、插值、拟合等操作,以便更好地观察数据的规律和趋势。
在数据处理的基础上,我们对数据进行了相关性分析和回归分析。
通过相关性分析,我们可以了解各个变量之间的相关程度,为后续的因果分析和结论推断提供依据。
而通过回归分析,我们可以建立起数据之间的数学模型,从而预测未来的数据变化趋势和规律,为实验结论的推断和应用提供支持。
最后,我们对实验数据进行了结论和建议的提出。
在结论部分,我们对实验数据进行了总结和归纳,得出了对实验问题的解答和对实验结论的说明。
在建议部分,我们针对实验中存在的问题和不足,提出了相应的改进和完善措施,以期提高实验的准确性和可靠性。
综上所述,本报告对雷诺实验报告数据处理的过程进行了详细的描述和分析,通过数据处理和分析,我们得出了对实验结论的准确性和可靠性的评价,为实验结果的推断和应用提供了支持。
同时,我们也提出了对实验的改进和完善建议,以期提高实验的质量和效果。
希望本报告能为雷诺实验的数据处理和分析提供参考和借鉴,为相关研究和实践工作提供支持和帮助。
流体力学综合实验装置——流体流动阻力测定实验---实验报告

流体流动阻力测定实验一、实验目的1.掌握测定流体流经直管、管件和阀门时阻力损失的一般实验方法。
2.测定直管摩擦系数λ与雷诺准数Re的关系,验证在一般湍流区内λ与Re 的关系曲线。
3.测定流体流经管件、阀门时的局部阻力系数ξ。
4.学会倒U形压差计和涡轮流量计的使用方法。
5.识辨组成管路的各种管件、阀门,并了解其作用。
二、基本原理流体通过由直管、管件(如三通和弯头等)和阀门等组成的管路系统时,由于粘性剪应力和涡流应力的存在,要损失一定的机械能。
流体流经直管时所造成机械能损失称为直管阻力损失。
流体通过管件、阀门时因流体运动方向和速度大小改变所引起的机械能损失称为局部阻力损失。
1.直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时,阻力损失为:即,式中:λ—直管阻力摩擦系数,无因次;d —直管内径,m;—流体流经l米直管的压力降,Pa;hf—单位质量流体流经l米直管的机械能损失,J/kg;ρ—流体密度,kg/m3;l —直管长度,m;u —流体在管内流动的平均流速,m/s。
滞流(层流)时,式中:Re —雷诺准数,无因次;μ—流体粘度,kg/(m·s)。
湍流时λ是雷诺准数Re和相对粗糙度(ε/d)的函数,须由实验确定。
由式(2)可知,欲测定λ,需确定l、d,测定、u、ρ、μ等参数。
l、d 为装置参数(装置参数表格中给出),ρ、μ通过测定流体温度,再查有关手册而得, u通过测定流体流量,再由管径计算得到。
例如本装置采用涡轮流量计测流量V(m3/h)。
可用U型管、倒置U型管、测压直管等液柱压差计测定,或采用差压变送器和二次仪表显示。
根据实验装置结构参数l、d,指示液密度,流体温度 (查流体物性ρ、μ),及实验时测定的流量V、压差,通过式(5)、(6)或(7)、(4) 和式(2)求取Re和λ,再将Re和λ标绘在双对数坐标图上。
2.局部阻力系数ξ的测定局部阻力损失通常有两种表示方法,即当量长度法和阻力系数法。
化工原理实验~流体流动阻力系数的测定实验报告

流体流动阻力系数的测定实验报告一、实验目的:1、掌握测定流体流动阻力实验的一般实验方法。
2、测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。
3、验证湍流区内摩擦阻力系数λ为雷诺系数Re和相对粗糙度的函数。
4、将所得光滑管的λ—Re方程与Blasius方程相比较。
二、实验器材:流体阻力实验装置一套三、实验原理:1、直管摩擦阻力不可压缩流体(如水),在圆形直管中做稳定流动时,由于黏性和涡流的作用产生摩擦阻力;流体在流过突然扩大、弯头等管件时,由于流体运动的速度和方向突然变化,产生局部阻力。
影响流体阻力的因素较多,在工程上通常采用量纲分析方法简化实验,得到在一定条件下具有普遍意义的结果,其方法如下。
流体流动阻力与流体的性质,流体流经处的几何尺寸以及流动状态有关,可表示为△P=f (d, l, u,ρ,μ,ε)引入下列无量纲数群。
雷诺数Re=duρ/μ相对粗糙度ε/ d管子长径比l / d从而得到△P/(ρu2)=ψ(duρ/μ,ε/ d, l / d)令λ=φ(Re,ε/ d)△P/ρ=(l / d)φ(Re,ε/ d)u2/2可得摩擦阻力系数与压头损失之间的关系,这种关系可=△P/ρ=λ(l / d)u2/2用试验方法直接测定。
hf——直管阻力,J/kg式中,hfl——被测管长,md——被测管内径,mu——平均流速,m/sλ——摩擦阻力系数。
当流体在一管径为d的圆形管中流动时,选取两个截面,用U形压差计测出这两个截面间的静压强差,即为流体流过两截面间的流动阻力。
根据伯努利方程找出静压强差和摩擦阻力系数的关系式,即可求出摩擦阻力系数。
改变流速可测出不同Re下的摩擦阻力系数,这样就可得出某一相对粗糙度下管子的λ—Re关系。
(1)、湍流区的摩擦阻力系数在湍流区内λ=f(Re,ε/ d)。
对于光滑管,大量实验证明,当Re在3×103~105范围内,λ和Re的关系遵循Blasius关系式,即λ=0.3163 / Re0.25对于粗糙管,λ和Re的关系均以图来表示。
